Convolution-Transformer for Image Feature Extraction

Highlight:

1.    Inductive biases were introduced to Transformer framework to reduce the computational cost.

2.    The efficient Transformer model CEFormer was proposed.

3.    E-Attention, depthwise separable convolution, and dilated convolution are incorporated into Transformer.

4.    A light convolution module is added to the Transformer to accelerate convergence and enhance stability.

1  Introduction

Computer vision, a highly successful application in deep learning, encompasses various tasks such as face recognition [1–3], object tracking [4–6], pedestrian detection [7–9], and license plate recognition [10,11]. The advent of big data has accelerated the development of internet information and intelligent technologies, leading to a surge in image data [12]. Concurrently, advancements in computer performance enhance the significance of computer vision for industrial progress. Computer vision also ranks first in the artificial intelligence market.

The current deep learning algorithms perform well in many visual subtasks, including object detection, object tracking, semantic segmentation, image classification, etc. However, in any practical application scenario, achieving good results in these visual tasks largely depends on feature extraction. The full extraction of image feature information can improve the accuracy (acc) and efficiency of various visual tasks, so the research on image feature extraction methods is extremely necessary and of great significance.

In deep learning, convolutional neural networks (CNNs) are primarily used to extract features from images [8]. However, CNNs may not capture the full context of an image or model inter-feature dependencies effectively, and their fixed weights do not adapt dynamically to input changes. To address these issues, researchers have recently adopted Transformers [13] from natural language processing for computer vision [14,15]. Transformers excel at modeling long-range dependencies and enable parallel processing, leading to promising results in visual tasks.

The self-attention mechanism in Transformers offers a novel approach to image processing. Each pixel generates a query, and other pixels provide corresponding keys, allowing the entire image to be considered during the computation. This contrasts with CNNs, where each pixel’s analysis is limited to its local receptive field without considering the broader context of the image. Thus, the self-attention mechanism can be viewed as an advancement over the traditional CNN, capable of integrating global context into its feature extraction process.

However, there are still some deficiencies in this emerging field that need to be addressed. Firstly, any Transformer-based image feature extraction model has inherent bottlenecks. That is, given the Token sequence obtained by segmenting and transforming the input image, the self-attention mechanism associates any Token in the sequence with other Tokens to iteratively learn feature representation. This mode leads to a quadratic correlation between the time and space complexity and the quantity of input tokens. This quadratic complexity prevents Transformer from modeling high-resolution images, thus hindering its practical implementation on edge devices due to the high computational costs involved. In addition, Transformer needs to use a large data set for pre-training in order to be comparable to CNN in terms of experimental effect. In addition, compared with CNN, Transformer is less stable. For the optimizer, the selection of hyperparameters is more sensitive, and the convergence speed is slower.

Compared with a CNN of the equivalent size, the Transformer model not only generally exhibits marginally inferior performance, but also requires a much larger amount of training data. In addressing this issue, the academic community has conducted extensive research. It is widely acknowledged that the Transformer model lacks some desirable properties inherent in CNN architectures, often referred to as inductive bias [16–19].

This research addresses the challenges faced by Transformers in computer vision by introducing a novel architecture, designated as the Convolution-based Efficient Transformer Image Feature Extraction Network (CEFormer). The CEFormer adeptly integrates convolutional strategies to enhance properties such as translation invariance, spatial locality, and scale invariance. It also incorporates a lightweight convolutional module into the standard Transformer framework for image processing, which not only improves the convergence rate but also strengthens the model’s stability. Transformer approach for image processing. This integration not only accelerates convergence speed but also enhances the overall stability of the model.

2  Method

2.1 Overall Structure

The overall architecture of CEFormer is shown in Fig. 1. This network enhances a traditional Transformer by integrating convolutional layers to achieve translation invariance, scale invariance, and locality, and employs a lightweight convolution module. In the following sections, specific explanations of these aspects are provided.

Figure 1: Overall architecture of CEFormer

2.2 Convolution-Based Inductive Bias

In CNNs, only the information in the receptive field is considered, and the range and size are given in advance. In contrast, the self-attention mechanism in Transformers dynamically learns to consider various ranges and sizes based on the input data. Therefore, it can be argued that CNNs represent a specific instance of the self-attention mechanism, where the scope of consideration is fixed rather than learned.

Adjacent pixels in an image are usually highly correlated and have obvious two-dimensional local structures. CNN utilizes local receptive fields, spatial downsampling, and other operations to effectively capture the local structure within images. Furthermore, the hierarchical structure of convolutional kernels enables the learning of local spatial context from different levels and perspectives, from the simplest low-level edge and texture features to relatively high-level semantic information. These are properties that CNNs possess that are suitable for vision tasks. Therefore, convolution and Transformer can be combined to introduce inductive bias. This section introduces depthwise separable convolution and dilated convolution.

2.2.1 Depthwise Separable Convolution

Depthwise separable convolution [20] was proposed because CNN has a large amount of computation. In order to reduce overhead, it is convenient to deploy on the mobile end. Building upon the foundation of convolutional operations, researchers have introduced the concept of depthwise separable convolution, which involves the spatial dimension as well as the depth dimension (i.e., channel dimension). Usually, the input image will have 3 channels. After a series of convolution operations, the input feature map becomes multiple channels. For each channel, it can be seen as an explanation of a certain feature of the input image. Depthwise separable includes two separate small convolution kernels: depthwise convolution and pointwise convolution. The computational method of depthwise convolution is illustrated in Fig. 2. In this process, three separate 5 × 5 × 1 convolution kernels are utilized to extract features from each of the three channels of the input image. Upon completing the calculations with each convolution kernel, the result is three distinct 8 × 8 × 1 output feature maps. These feature maps are then stacked, resulting in a final composite output with dimensions of 8 × 8 × 3.

Figure 2: Schematic diagram of depthwise convolution

However, the depthwise convolution operation has limitations. For the input feature map, it will only calculate one channel alone, while ignoring the information interaction between each channel, resulting in a lack of information between channels in the subsequent flow of information. Therefore, a pointwise convolution needs to be connected to make up for its shortcomings.

Pointwise convolution is 1 × 1 convolution because it traverses every position of the input feature map. Different from the depthwise convolution that ignores the information interaction of each channel, the pointwise convolution can further fuse the information between channels and scale the dimension of the input feature map.

As shown in Fig. 3, a 3-channel 1 × 1 convolution can be used for the 8 × 8 × 3 feature map obtained in Fig. 2. Thus, an 8 × 8 × 1 output feature map can be obtained. At this time, pointwise convolution is used to realize the function of fusing the features between the three channels, which plays the role of information interaction.

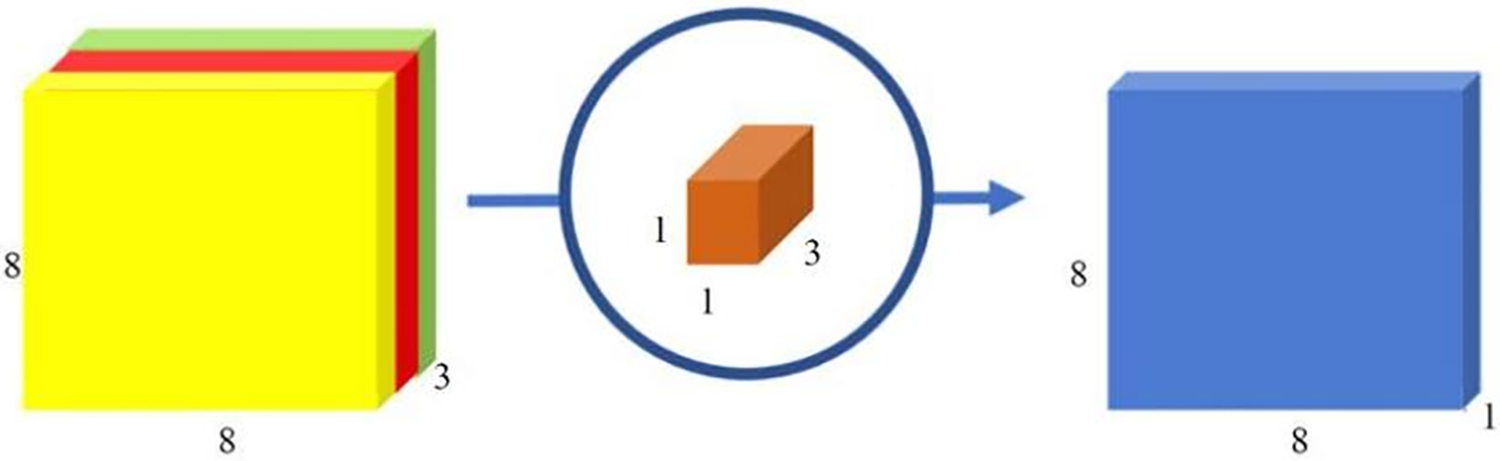
Figure 3: Pointwise convolution with an output channel of 1

2.2.2 Dilated Convolution

The dilated convolution [21] was first proposed to better solve the problems of image resolution reduction and information loss faced by image segmentation. Most image segmentation algorithms usually use convolution or pooling to increase the local receptive field, which narrows the size of the feature map and finally uses the upsampling method to restore the size of the image. However, the operation of reducing the feature map’s size first and then zooming in will cause an inevitable decrease in accuracy, thus losing the detailed information of the input image. Therefore, there is a need for an operation that can replace upsampling and downsampling, so that the feature map’s size remains unchanged while increasing the receptive field. Dilated convolution is a convolution method designed to meet this requirement.

The core idea of dilated convolution is to expand the receptive field by adding 0 s. Thus, the convolution kernel with an initial size of 3 × 3 can have a 5 × 5 (the corresponding expansion rate is set to 2) or even larger receptive field while maintaining the same amount of parameters and calculations. This avoids the use of downsampling methods that can cause a loss of accuracy.

As shown in Fig. 4a, when the hyperparameter expansion rate is set to 1, the dilated convolution is calculated in the same way as the standard convolution. However, when the hyperparameter expansion rate is greater than 1, then based on the standard convolution, holes will be injected, and the values in the holes are all filled with 0. Figs. 4b and 4ccorrespond to the cases where the expansion rate is 2 and the expansion rate is 4, respectively.

Figure 4: 3 × 3 dilated convolution with dilation rates 1, 2, 4

Dilated convolution mainly introduces the following benefits to our CEFormer:

(1) Expand the receptive field. The pooling operation can also expand the receptive field, but it will cause a decrease in spatial resolution. In contrast, dilated convolutions can maintain the relative spatial positions of pixels while increasing the receptive field size without loss of resolution.

(2) Obtain multi-scale context information. The superimposition of dilated convolution kernels with varying expansion rates results in the incorporation of diverse receptive fields, thus enabling the extraction of multi-scale information.

(3) Reduce the amount of calculation. No additional parameters need to be introduced.

2.3 Translation Invariance

The reason for choosing to combine depthwise convolution with efficient attention is that both depthwise convolution and efficient attention can be expressed as a weighted sum of values in a pre-defined receptive field. Depthwise convolution relies on a fixed-size single-layer convolution kernel to collect information from local receptive fields, as shown in Eq. (1):

yi=∑j∈L(i)wijxj(1)

where xi and yi are the input and output of position i, respectively, and L(i) represents the local receptive field of position i. An efficient attention mechanism can be written in a form similar to Eq. (1), as shown in Eq. (2):

yi=∑j∈Gf(xi)Tf(xj)sin⁡(π(i+n−j)2n)xj(2)

f(⋅) is shown in Eq. (3), G represents the global space, i, j=1,…,n.

f(x)={x+1x≥0exx<0(3)

Before exploring optimal strategies to integrate depthwise convolution and efficient attention mechanisms, let’s first analyze their respective strengths and weaknesses.

The weight of the depthwise convolutional kernel is a fixed parameter independent of the input. The weight of efficient attention is the opposite. It is a dynamic input-dependent parameter that changes with the input value. Therefore, it is easier for efficient attention mechanisms to model complex relationships at different spatial locations. However, this approach also has a higher risk of overfitting and necessitates a larger dataset for effective training. For a given arbitrary position pair (i, j), the depthwise convolution kernel weight is only related to the relative displacement of these two positions and has nothing to do with their respective absolute values. This property comes from the weight-sharing feature of convolution, which is also called translation invariance. This property is very helpful in improving the generalization ability in the case of limited data sets [22]. The efficient attention mechanism, and even the most primitive Softmax attention mechanism does not have this property. Therefore, when the data set is small, the effect of CNN is usually better than the Transformer model.

The receptive field sizes of depthwise convolution and efficient attention mechanisms are different. Generally speaking, the expansion of the receptive field size allows for a greater amount of contextual information to be captured. Consequently, the model’s capacity also increases correspondingly. Accordingly, more calculations are required. For the original Softmax attention mechanism, the computational complexity is quadratic.

In summary, the three key characteristics discussed can be categorized as follows: translation invariance (specific to depthwise convolution), weights for global receptive fields and adaptive inputs (both specific to efficient self-attention mechanisms). Therefore, the integration strategy should aim to combine these three distinct features. Specifically, while retaining the two characteristics of the efficient self-attention mechanism, it introduces the unique translation invariance of deep convolution.

A simple approach is to add the weights of depthwise convolutions to an efficient attention mechanism, as shown in Eq. (4):

yi=∑j∈G(xi′T+wij)(xj′+wij)sin⁡(π(i+n−j)2n)xj(4)

2.4 Locality

This section introduces locality by incorporating deep convolutions in feedforward neural networks. First, the feedforward neural network contains two fully connected layers. Between these two fully connected layers, the hidden dimension will be expanded to extract a richer set of features. From the perspective of convolution, this operation is equivalent to the 1 × 1 pointwise convolution used to increase or decrease the dimension of the feature map. This is similar to the inverted residual structure [23,24] in the lightweight model MobileNet family. In the reverse residual block, two 1 × 1 pointwise convolutions are also expanded.

Compared with the feedforward neural network in the Transformer model, the reverse residual structure only has one more deep convolution that can aggregate local information. Inspired by this, we introduce deep convolution into the feedforward neural network of the Transformer model encoder module and directly replace the two fully connected layers with two 1 × 1 pointwise convolutions.

In the Transformer model, the input and output between each block are Token sequences. Therefore, before the whole operation process, the Token sequence needs to be rearranged into a feature map, and after the convolution operation, the feature map needs to be flattened into the original Token sequence. It should be noted that the Token sequence involved in the whole process starts from the second Token. Because the first Token has nothing to do with the input image, it is additionally introduced to judge the image category in the final stage. The overall calculation flow chart of the feedforward network after the locality is introduced is shown in Fig. 5.

Figure 5: Flow chart of feedforward network calculation with locality introduced

2.5 Scale Invariance

In the era dominated by CNNs, multi-resolution, and multi-scale features have been pivotal for various downstream tasks, such as object detection and semantic segmentation. These approaches enable the extraction of features from objects of different scales, catering to the diverse requirements of these tasks. However, the Vision Transformer (ViT), originally designed for image classification, presents a limitation in this context. Its inherent architecture, characterized by a linear output structure, restricts its direct applicability to downstream tasks that require dense predictions, such as pixel-level segmentation or object detection. Therefore, the acquisition of multi-scale information is particularly important.

To introduce scale invariance to the Transformer-based image feature extraction network, we employ dilated convolution to the feedforward network. The feature map converted from the Token sequence is introduced into locality after a 3 × 3 depthwise convolution operation. After dilated convolution operations with different expansion rates, scale invariance is additionally introduced to obtain multi-scale information. The updated feedforward network calculation is shown in Fig. 6.

Figure 6: Architecture of feedforward network with locality and scale invariance

2.6 Stability Improvement Based on Convolution

Training a Transformer model, particularly for vision tasks, can be challenging. It requires precise tuning of hyperparameters like learning rate and weight decay. Additionally, the convergence speed is very slow, requiring an AdamW optimization. MoCov3 [25] mentioned that the ViT architecture can lead to regression during the training process. This regression is speculated to be linked to the process of patch, where the input image is initially segmented into a series of non-overlapping patches. Therefore, by fixing the parameters of the patch mapping, the recession phenomenon is alleviated. This issue may stem from the initial coarse segmentation of the input image into patches, which are then fed into the model.

Viewing this practice from a convolutional perspective, the original Transformer model divides the input image into non-overlapping p × p patches, mapping each patch into a d-dimensional feature vector. Suppose the size of the input image is 224 × 224, and the side length of a single patch is 16. Then the number of patches is 14 × 14, and the patch map is equivalent to a large convolution kernel with a size of 16 × 16 and a step size of 16. However, when designing a convolutional neural network, the preference is generally smaller, deeper convolution kernels. A large convolution kernel with a size of 16 × 16 and a step size of 16 corresponds to a large number of parameters and high randomness. Therefore, processing the input image in this way will cause greater instability.

To tackle the instability associated with large convolution kernels in Transformer models, we are inspired by the design principles of the Visual Geometry Group (VGG) network. The VGG network demonstrates that the regularization of one 7 × 7 convolutional layer is equivalent to the superposition of three 3 × 3 convolutional layers. This layered approach significantly reduces the number of parameters and helps in mitigating overfitting. Following this insight, we propose to replace the large convolution kernel in the Transformer model with a lightweight convolution module. This module is designed to achieve similar functionality while reducing complexity and enhancing stability. The proposed lightweight module comprises a convolution operation followed by Batch Normalization and then a Max Pooling operation. By adopting this strategy, the model is expected to maintain effective feature extraction capabilities while enhancing stability and reducing the likelihood of overfitting.

3  Experiment Settings and Dataset

3.1 Dataset

The datasets used in this experiment are the ImageNet1k dataset and the COCO dataset.

The ImageNet dataset is a dataset extensively employed in the field of artificial intelligence images [26]. Most of the work on image positioning, classification, and detection is based on this dataset. It is extensively employed in computer vision, maintained by the team at Stanford University, and easy to use. ImageNet contains more than 14 million images with more than 20,000 classification categories.

The COCO dataset, maintained by Microsoft, is a large-scale detection and segmentation dataset sourced from complex daily scenes [27]. It addresses three key challenges: the contextual relationship between targets, target detection, and precise two-dimensional positioning. Although the number of categories is much smaller than that of the ImageNet dataset, each category contains a very large number of pictures, and more specific scenes in each category can be obtained. At the last update, the COCO dataset encompasses around 328,000 images and 250,000 labels within 91 categories, including common objects such as humans, animals, vehicles, furniture, etc., making it arguably the most extensive public object detection dataset. COCO contains 20 G pictures and 500 M labels, and the ratio of the training set, test set, and validation set is 2:1:1.

3.2 Experimental Environment and Hyperparameter Settings

The software and hardware are shown in Table 1.

The model settings of different sizes are shown in Table 2.

The hyperparameters are set as follows: Epochs is 300, Batch size is set to 1024, and the basic learning rate is 0.0005. The optimizer chooses AdamW, and the learning rate decay strategy uses Cosine. Weight decay is 0.05, Dropout is 0.1, and Warmup epochs is 5. Both depthwise and dilated convolutions are 3 × 3, and the convolutions in the lightweight convolution module are 7 × 7.

3.3 Evaluation Metrics

Evaluating the performance of models in image classification and object detection requires a diverse set of metrics, each focusing on different aspects of model effectiveness and efficiency. The methods proposed in this study prioritize enhancing the computational efficiency of the model while balancing complexity and processing speed. Therefore, Params, Floating Point Operations Per Second (FLOPs), and Frames Per Second (FPS) are selected. On the other hand, to assess the performance of the model itself, Top-1 Acc and mean Average Precision (mAP) are selected.

In the image classification task, evaluating the quality of a classification model is mainly judged by the accuracy and error rate identified by the classification model. The error rate includes Top-5 error and Top-1 error, and the accuracy rate includes Top-5 accuracy and Top-1 accuracy. This study selects the Top-1 accuracy metric to test the accuracy of model classification after introducing the two methods of linear attention mechanism and Token pruning. On the other hand, this study selects the FLOPs index to describe the calculation amount of the model.

In the target detection task, to evaluate the quality of a detection model is mainly through the detection model mAP value. On the other hand, when using various methods to speed up the detection model and reduce its complexity, the corresponding performance metrics generally use FPS and Params.

3.4 Baselines

To thoroughly evaluate the performance of the proposed CEFormer, we conduct a comprehensive set of comparative analyses. A diverse array of image feature extraction networks in three categories are selected to perform image classification and target detection experiments on ImageNet1k and COCO datasets for comparison, encompassing convolution-based models, Transformer-based models, and hybrid models that combine convolutional and Transformer features.

1. Covolution-based model: ResNet [28] and RegNet [29].

2. Transformer-based model: DeepVit [30], AutoFormer [31], NesT [32], Focal Transformer [33], CrossFormer++ [34], ViT [35], DeiT [36], PVT [37], Swin [38], TNT [39], T2T-ViT [17], CaiT [40], Shuffle Transformer [41] and CSWin [42].

3. Hybrid model: ConViT [43], PiT [44], CvT [45], LV-ViT [46], GG-Transformer [47], CMT [48], GLiT [49] and ConTNet [50].

4  Results

4.1 Experiment on Image Classification

For the task of image classification, experiments are conducted on the ImageNet1k dataset. The results shown are averaged across 5 repeated experiments.

(1)   Comparison with Convolution-Based Models

The experimental results for the fully convolution-based model and CEFormer are presented in Table 3, assessed under two metrics: Top-1 Acc and FLOPs. The models are categorized into three sizes—small, medium, and large—based on their parameter count to facilitate a comparative analysis. Within each size category, the best-performing data is highlighted in bold.

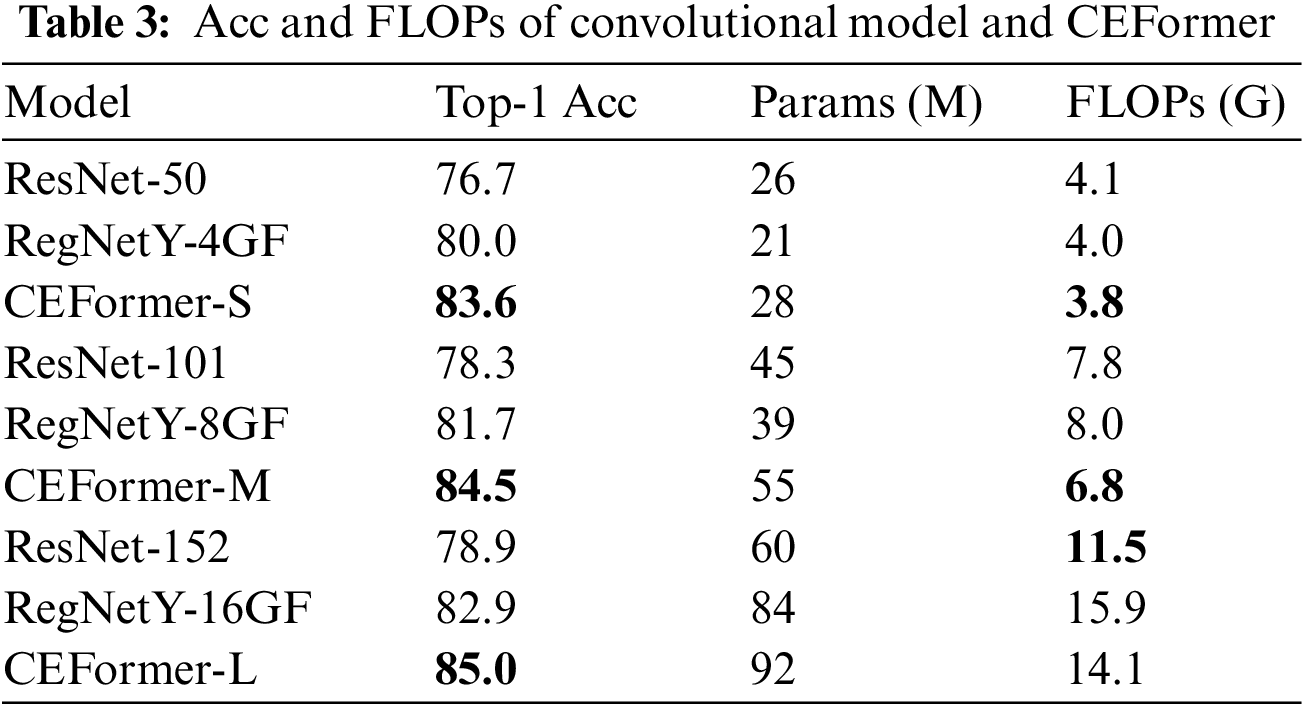
Table 3 shows that compared with the two convolution-based models ResNet and RegNetY, the Top-1 Acc of the CEFormer series has achieved the best. CEFormer-S outperforms the next-best model, RegNetY-4GF, by 4.5%. CEFormer-M outperforms the next-best model, RegNetY-8GF, by 3.4%. CEFormer-L outperforms the next-best model, RegNetY-16GF, by 2.5%.

Next, from the perspective of FLOPs, in addition to CEFormer-L, CEFormer-S, and CEFormer-M have achieved the best results, leading the suboptimal models by 5% and 13%, respectively. Then CEFormer-L is 23% behind the best model ResNet-152. This is because the parameters of CEFormer are from both Transformer and CNN. With the large size of the depth of networks and high feature dimensions, CEFormer-L requires a little larger number of computations than ResNet-152 while achieving much higher accuracy.

From the comparison of these two metrics, it can be seen that compared with the fully convolution-based model, the model CEFormer proposed in this study is more advanced in the metric Top-1 Acc, indicating that the model has better performance.

(2)   Comparison with Transformer-Based Model

The results of the Transformer-based model and CEFormer under the two metrics of Acc and FLOPs are shown in Table 4. It shows that compared with Transformer-based models, CEFormer also achieved higher results in terms of the metric Top-1 Acc. CEFormer-S, CEFormer-M, and CEFormer-L outperform the sub-optimal models CSWin-T, CSWin-S, and CEFormer-B by 1%, which is ahead of the fully Transformer-based model.

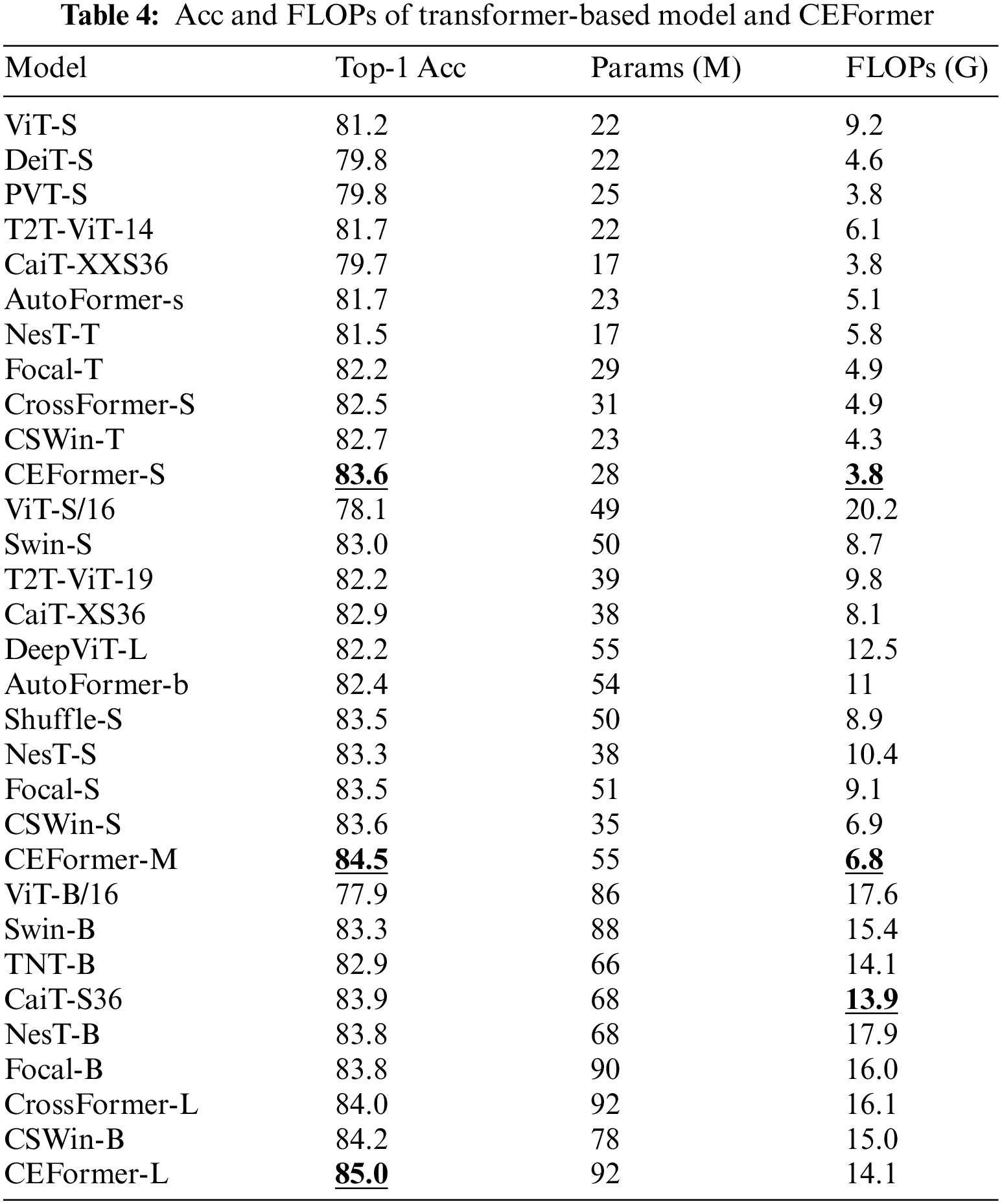
In terms of FLOPs, CEFormer-S, and CEFormer-M achieve the best results. CEFormer-L achieves suboptimal results, and PVT-S has the same FLOPs as CaiT-XXS36 for model CEFormer-S.

(3)   Comparison with Hybrid Models

The experimental results of hybrid models and CEFormer under the two metrics of Acc and FLOPs are shown in Table 5. As can be seen from Table 5, compared with hybrid models, CEFormer-S and CEFormer-M have achieved the best results in terms of the index Top-1 Acc, and CEFormer-L has achieved suboptimal results. Among them, CEFormer-S has improved by 0.1% compared with the sub-optimal model CMT-S. CEFormer-M is the same as CMT-B, and both are the best in the same series. CEFormer-L lags behind the best model LV-ViT-L by 0.3%. For this metric, CEFormer has achieved better results, which is comparable to the current optimal model.

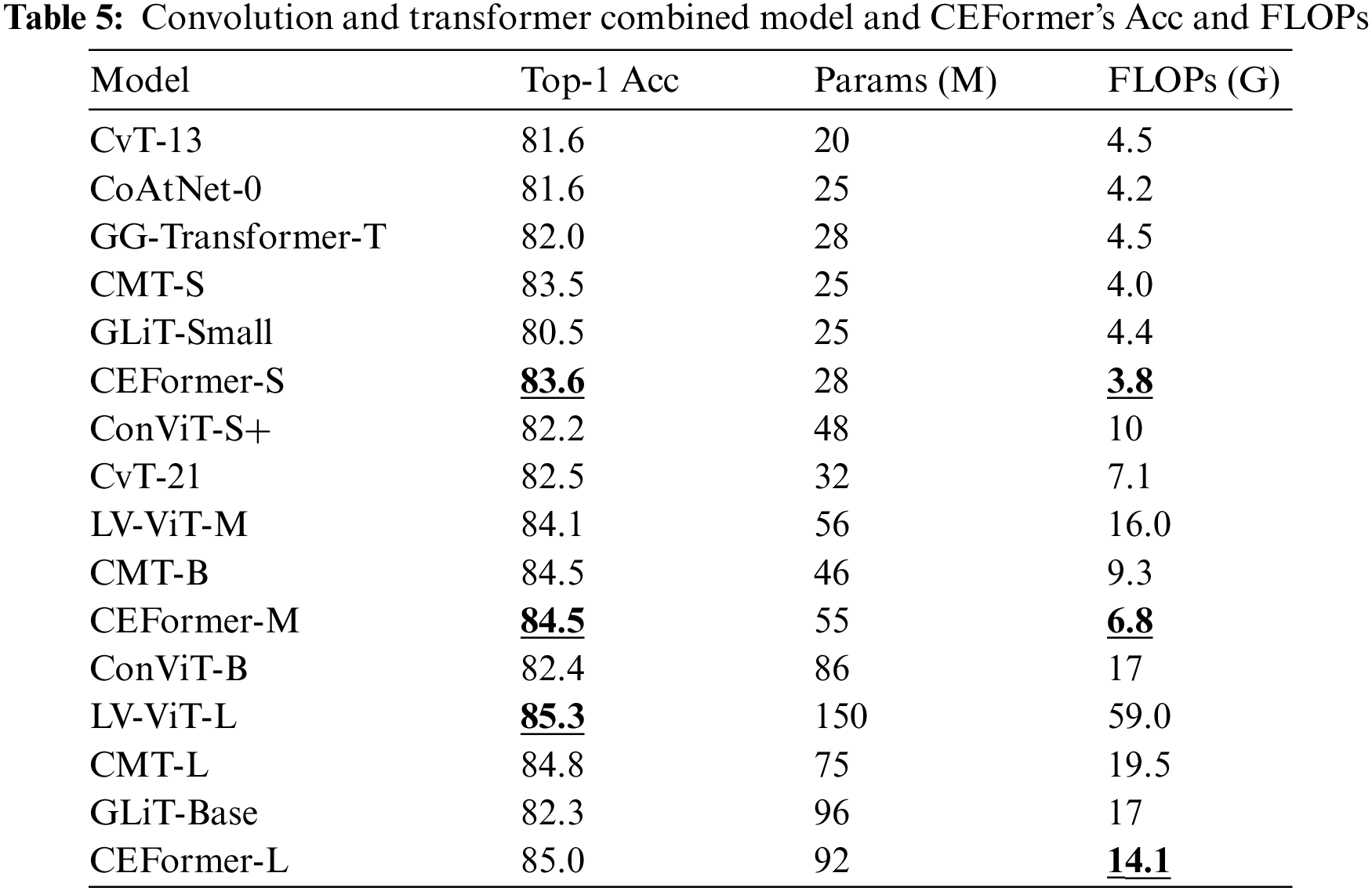
In terms of index FLOPs, CEFormer-S, CEFormer-M, and CEFormer-L all achieved the best results, and their respective improvements were 5%, 4%, and 17% compared to the suboptimal model. Compared with the visual Transformer model that also introduces convolution, the advantages of the improved attention mechanism are reflected. In this regard, CEFormer is significantly ahead of similar models.

4.2 Experiments on Target Detection

In this experiment, we employed the Mask Region-Convolutional Neural Network (R-CNN) object detector, initially trained on the COCO dataset, and modified it by substituting its backbone network with an alternative model. Subsequently, we conducted a comparative analysis of the modified Mask R-CNN against the CEFormer model, focusing on the metrics of mAP and FPS. The results of this comparison are detailed in Table 6.

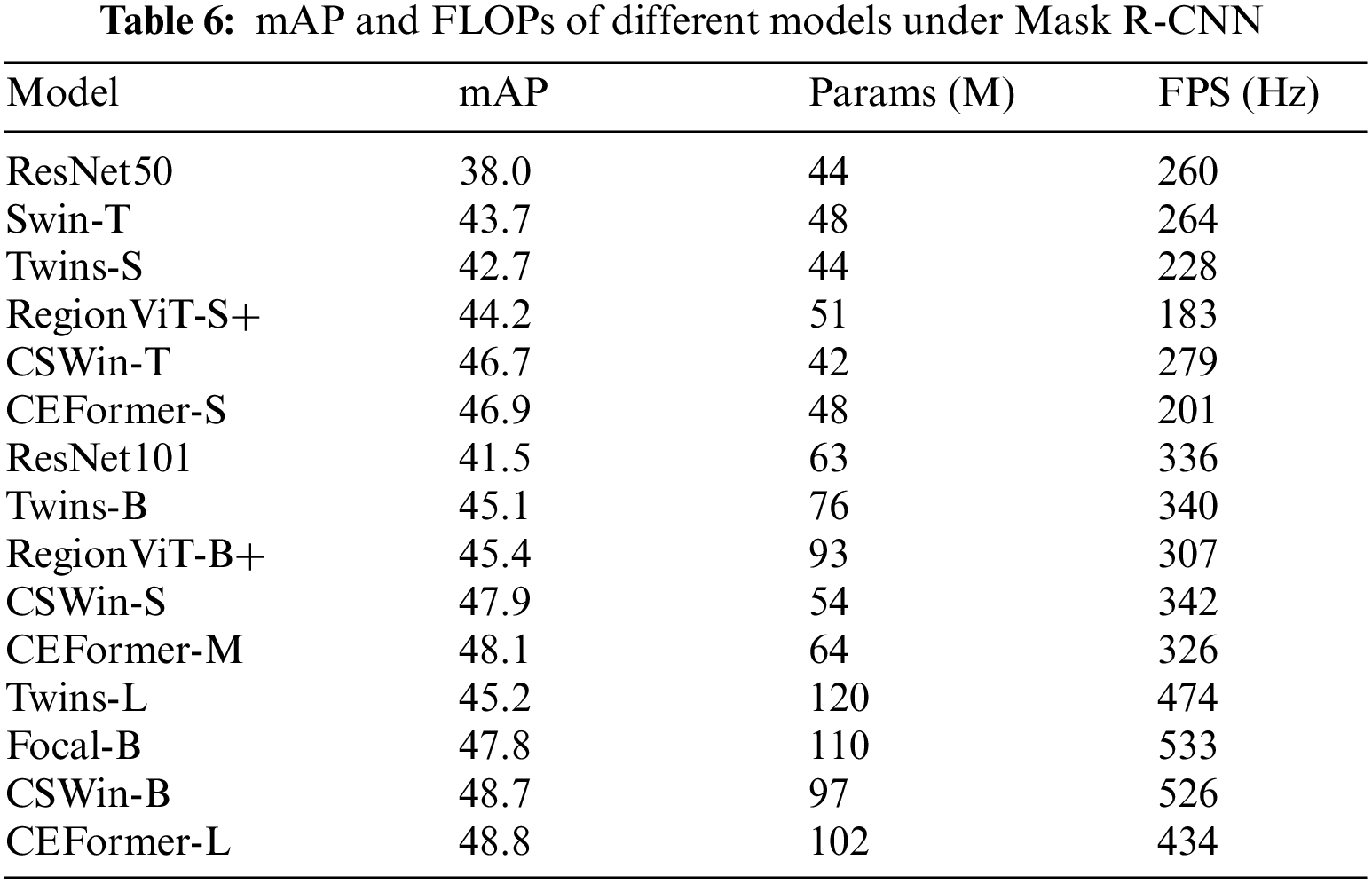
It can be learned from Table 6 that, CEFormer-S, CEFormer-M, and CEFormer-L have achieved the best results in terms of mAP, and each of them has improved by 0.4% compared with the suboptimal model. After introducing different features, the model CEFormer has indeed been greatly improved.

From the perspective of FLOPs, CEFormer-L achieves the best results, which is 8.4% higher than the sub-optimal model Twins-L. CEFormer-S achieves the second-best result, slower than the best model RegionViT-S+ by 10% and leading the third-best model Twins-S by 12%. CEFormer-M achieves the second-best result, 6% behind the best model RegionViT-B+, and 3% ahead of the third-best model, ResNet101. The calculation amount FLOPs of the forward reasoning of the model CEFormer proposed in this study has achieved good results.

4.3 Ablation Study

The model proposed in this experiment combines various convolutions to incorporate the corresponding inductive bias, which improves the translation invariance, locality, scale invariance, and stability of the model from different perspectives. In this section, these four characteristics are used as the object of the ablation experiment, and the influence of each characteristic on the performance of the final model is explored.

These four properties translation invariance, locality, scale invariance, and stability are named C1, C2, C3, and C4. Subsequently, each of the four characteristics is ablated individually, and the performance metrics of the resulting ablated models are recorded as w/o. The ‘Full’ model implies all characteristics are retained, while other experimental settings remain unaltered. The experimental results are shown in Table 7.

It can be learned from Table 7 that the accuracy rate will decrease to a certain extent if any feature is ablated. Among them, ablation C4, that is, after the stability is removed, the accuracy rate drops the most. It shows that this feature has the largest increase in the model. Secondly, after ablation locality or scale invariance, the accuracy rate drops the same, indicating that the two features have the same increase in the model. Finally, ablation C1, that is, after removing the translation invariance, the accuracy rate drops the least. It shows that among the four characteristics, the relatively least gain is the translation invariance.

4.4 Stability Experiment

In this subsection, experiments are conducted to verify whether the stability convolution design introduced in this study is effective. Specifically, the models that discard stability and those that do not discard stability are compared from different angles. The experimental data is based on the dataset ImageNet1k.

(1)   Convergence speed analysis

As shown in Fig. 7, the model that retains stability exhibits a slower convergence speed. The accuracy of the model without discarding stability at 200 epochs is closer to the accuracy of 300 epochs. However, the accuracy of the model without stability at 200 epochs is far from the accuracy of 300 epochs. It shows that the stability design of this model can indeed accelerate the convergence of the model.

Figure 7: Convergence speed experiment results

(2)   Optimizer analysis

Transformer generally uses AdamW as the optimizer, because the Stochastic Gradient Descent (SGD) optimizer will reduce the accuracy by about 7 points on the ImageNet dataset. However, this is not the case with convolutional neural networks. The SGD optimizer can also optimize convolutional neural networks very well. Compared with the AdamW optimizer, the SGD optimizer has fewer parameters and occupies only about half of the video memory of the AdamW optimizer. Therefore, the experiments in this section verify the use of the SGD optimizer or the AdamW optimizer for the models that discard stability and do not discard stability. Based on the above situation, analyze whether the stability design in this chapter can alleviate the Transformer’s sensitivity to the optimizer. The experimental results are shown in Fig. 8.

Figure 8: Experimental results of optimizer changes

It can be told from Fig. 8 that the accuracy of the model that retains the stability design does not change much no matter whether the SGD optimizer or the AdamW optimizer is used. However, the accuracy of the model that abandons the stability design is greatly reduced when the SGD optimizer is used. And after 200 Epochs, the improvement in accuracy is very slight. It shows that the stability design of this study can indeed alleviate the sensitivity of the Transformer to the optimizer.

5  Discussions

The proposed CEFormer model leverages the strengths of both convolutional neural networks and Transformer architectures, effectively addressing the need for inductive biases such as translation invariance, locality, and scale invariance. Through extensive experiments, CEFormer shows significant performance improvement against either convolution-based or Transformer-based models and achieves competitive accuracy against other state-of-the-art methods combining these two while requiring smaller FLOPs. However, there are some remaining directions for future exploration:

Scalability. Investigating the scalability of the CEFormer model to larger datasets and more complex image classification tasks will be essential. This includes examining the model’s performance on high-resolution imagery and its adaptability to different domains such as medical imaging or satellite image analysis.

Inductive Bias Tuning. Given the varying impacts of different inductive biases on the model’s performance, a more nuanced approach to tuning these biases could be explored. This might involve adaptive mechanisms that can adjust the strength of each bias based on the specific requirements of the task or data.

Ablation Study Extensions. Further ablation studies could provide deeper insights into the interactions between the various inductive biases and components of the CEFormer model. Understanding these interactions may lead to more informed decisions when designing models for specific applications.

6  Conclusions

This paper introduces and evaluates the CEFormer, an innovative model that enhances Transformer-based image feature extraction by addressing its inherent limitations such as the lack of inductive bias and difficulties of hyperparameter fine-tuning. The CEFormer model integrates elements of CNNs and Transformers, employing a unique blend of E-Attention, depthwise separable convolution, and dilated convolution. This integration introduces crucial inductive biases like translation invariance, locality, and scale invariance, which are typically absent in standard Transformer models.

Extensive experimental analysis is conducted on tasks of image classification and target detection. By comparing our CEFormer against convolution-based models, pure Transformer models, and models that combine convolution and Transformer features, we show that CEFormer consistently outperforms its counterparts in terms of Top-1 Accuracy while maintaining computational efficiency. Specifically, for the image classification task, CEFormer outperforms convolution-based models like ResNet and RegNetY with an accuracy of up to 4.5% and achieves competitive accuracy while requiring much smaller FLOPs than the state-of-the-art vision Transformers.

We also conduct the ablation study on the CEFormer model revealing significant insights into the contributions of four key characteristics: translation invariance (C1), locality (C2), scale invariance (C3), and stability (C4). We find that although all four components contribute to the model’s performance, they play different roles. Specifically, the removal of stability had the most pronounced negative impact on accuracy. This highlights stability as a crucial factor in the model’s performance. On the other hand, translation invariance appears to be less critical compared to the other characteristics.

The incorporation of multiple convolutional modules in this study, aimed at enhancing the model’s performance across various dimensions, leads to an expansion in the model’s parameter count and an increase in time complexity. As a result, during comparative experiments, the FLOPs metric does not attain its most efficient state. For future research, it is advisable to explore advanced techniques such as pruning and knowledge distillation to achieve a more streamlined model without compromising its performance.

Acknowledgement: Distinguished Scientist Fellowship Program (DSPF), King Saud University, Riyadh, Saudi Arabi.

Funding Statement: Support by Sichuan Science and Technology Program (2021YFQ0003, 2023YFSY0026, 2023YFH0004).

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization: Wenfeng Zheng; methodology: Youshuai Yang, Bo Yang, Shan Liu; software: Youshuai Yang; formal analysis: Ahmed AlSanad, and Salman A. AlQahtani; data curation: Youshuai Yang, Zhengtong Yin, Xiaobing Chen, Xiaolu Li, Lei Wang; writing—original draft preparation: Lirong Yin, Siyu Lu, and Wenfeng Zheng; writing—review and editing: Lirong Yin, Siyu Lu, Ruiyang Wang, and Wenfeng Zheng; funding acquisition: Wenfeng Zheng. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: ImageNet1k: https://www.image-net.org/download.php. COCO: https://cocodataset.org/#download.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Kim M, Jain AK, Liu X. AdaFace: quality adaptive margin for face recognition. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2022; New Orleans, LA, USA; p. 18750–9. [Google Scholar]

2. Boutros F, Damer N, Kirchbuchner F, Kuijper A. ElasticFace: elastic margin loss for deep face recognition. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2022; New Orleans, LA, USA. p. 1578–87. [Google Scholar]

3. Bae G, de La Gorce M, Baltrušaitis T, Hewitt C, Chen D, Valentin J, et al. DigiFace-1M: 1 million digital face images for face recognition. In: Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision; 2023; Waikoloa, HI, USA. p. 3526–35. [Google Scholar]

4. Ma F, Shou MZ, Zhu L, Fan H, Xu Y, Yang Y, et al. Unified transformer tracker for object tracking. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2022; New Orleans, LA, USA. p. 8781–90. [Google Scholar]

5. Zhang Y, Sun P, Jiang Y, Yu D, Weng F, Yuan Z, et al. ByteTrack: multi-object tracking by associating every detection box. In: Avidan S, Brostow G, Cissé M, Farinella GM, Hassner T, editors. Lecture notes in computer science. Cham: Springer; 2022. vol. 13682. doi:10.1007/978-3-031-20047-2_1. [Google Scholar] [CrossRef]

6. Zhou C, Luo Z, Luo Y, Liu T, Pan L, Cai Z, et al. PTTR: relational 3D point cloud object tracking with transformer. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2022; New Orleans, LA, USA. p. 8531–40. [Google Scholar]

7. Song X, Chen B, Li P, Wang B, Zhang H. PRNet++: learning towards generalized occluded pedestrian detection via progressive refinement network. Neurocomputing. 2022;482:98–115. doi:10.1016/j.neucom.2022.01.056. [Google Scholar] [CrossRef]

8. Tan F, Xia Z, Ma Y, Feng X. 3D sensor based pedestrian detection by integrating improved HHA encoding and two-branch feature fusion. Remote Sens. 2022;14(3):645. doi:10.3390/rs14030645. [Google Scholar] [CrossRef]

9. Wang J, Zhao C, Huo Z, Qiao Y, Sima H. High quality proposal feature generation for crowded pedestrian detection. Pattern Recognit. 2022;128:108605. doi:10.1016/j.patcog.2022.108605. [Google Scholar] [CrossRef]

10. Xiao Y, He X, Yang C, Liu H, Liu Y. Dynamic graph computing: a method of finding companion vehicles from traffic streaming data. Inf Sci. 2022;591:128–41. doi:10.1016/j.ins.2022.01.022. [Google Scholar] [CrossRef]

11. Bian L, Wang H, Zhu C, Zhang J. Image-free multi-character recognition. Opt Lett. 2022;47(6):1343–6. doi:10.1364/OL.451777. [Google Scholar] [PubMed] [CrossRef]

12. Ikotun AM, Ezugwu AE, Abualigah L, Abuhaija B, Heming J. K-means clustering algorithms: a comprehensive review, variants analysis, and advances in the era of big data. Inf Sci. 2023;622:178–210. doi:10.1016/j.ins.2022.11.139. [Google Scholar] [CrossRef]

13. Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, et al. Attention is all you need. In: Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17); 2017; Red Hook, NY, Curran Associates Inc. p. 6000–10. [Google Scholar]

14. Liang P, Yu Z, Wang B, Xu X, Tian J. Fault transfer diagnosis of rolling bearings across multiple working conditions via subdomain adaptation and improved vision transformer network. Adv Eng Inform. 2023;57:102075. doi:10.1016/j.aei.2023.102075. [Google Scholar] [CrossRef]

15. Wang S, Tian J, Liang P, Yang Z, Zhu J, Zhang Z. Single and simultaneous fault diagnosis of gearbox via deep learning-based feature learning. Eng Appl Artif Intell. 2024;133:108146. doi:10.1016/j.engappai.2024.108146. [Google Scholar] [CrossRef]

16. Chen T, Cheng Y, Gan Z, Yuan L, Zhang L, Wang Z. Chasing sparsity in vision transformers: an end-to-end exploration. In: Advances in neural information processing systems; 2021; California, Neural Information Processing Systems (Nips). vol. 34. [Google Scholar]

17. Yuan L, Chen Y, Wang T, Yu W, Shi Y, Jiang Z, et al. Tokens-to-token ViT: training vision transformers from scratch on imagenet. In: Proceedings of the IEEE/CVF International Conference on Computer Vision; 2021; Montreal, QC, Canada. p. 558–67. [Google Scholar]

18. Zhang H, Duan J, Xue M, Song J, Sun L, Song M. Bootstrapping ViTs: towards liberating vision transformers from pre-training. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2022; New Orleans, LA, USA. p. 8944–53. [Google Scholar]

19. Chen Z, Xie L, Niu J, Liu X, Wei L, Tian Q. Visformer: the vision-friendly transformer. In: Proceedings of the IEEE/CVF International Conference on Computer Vision; 2021; Montreal, QC, Canada. p. 589–98. [Google Scholar]

20. He J, Wang X, Song Y, Xiang Q. A multiscale intrusion detection system based on pyramid depthwise separable convolution neural network. Neurocomputing. 2023;530:48–59. doi:10.1016/j.neucom.2023.01.072. [Google Scholar] [CrossRef]

21. Chalavadi V, Jeripothula P, Datla R, Ch SB, Krishna Mohan C. mSODANet: a network for multi-scale object detection in aerial images using hierarchical dilated convolutions. Pattern Recognit. 2022;126:108548. doi:10.1016/j.patcog.2022.108548. [Google Scholar] [CrossRef]

22. Mansuroglu R, Eckstein T, Nützel L, Wilkinson SA, Hartmann MJ. Variational Hamiltonian simulation for translational invariant systems via classical pre-processing. Quantum Sci Technol. 2023;8(2):25006. doi:10.1088/2058-9565/acb1d0. [Google Scholar] [CrossRef]

23. Qiu Y, Wu F, Yin J, Liu C, Gong X, Wang A. MSL-Net: an efficient network for building extraction from aerial imagery. Remote Sens. 2022;14(16):3914. doi:10.3390/rs14030645. [Google Scholar] [CrossRef]

24. Guo G, Zhang Z. Road damage detection algorithm for improved YOLOv5. Sci Rep. 2022;12(1):15523. doi:10.1038/s41598-022-19674-8. [Google Scholar] [PubMed] [CrossRef]

25. Ci Y, Lin C, Bai L, Ouyang W. Fast-MoCo: boost momentum-based contrastive learning with combinatorial patches. In: Avidan S, Brostow G, Cissé M, Farinella GM, Hassner T, editors. Computer vision–ECCV 2022. Cham: Springer Nature Switzerland; 2022. p. 290–306. [Google Scholar]

26. Li D, Ling H, Kim SW, Kreis K, Fidler S, Torralba A. BigDatasetGAN: synthesizing ImageNet with pixel-wise annotations. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2022; New Orleans, LA, USA. p. 21330–40. [Google Scholar]

27. Alinezhad Noghre G, Danesh Pazho A, Sanchez J, Hewitt N, Neff C, Tabkhi H. ADG-pose: automated dataset generation for real-world human pose estimation. In: El Yacoubi M, Granger E, Yuen PC, Pal U, Vincent N, editors. Pattern recognition and artificial intelligence. Cham: Springer International Publishing; 2022. p. 258–70. [Google Scholar]

28. Sun T, Ding S, Guo L. Low-degree term first in ResNet, its variants and the whole neural network family. Neural Netw. 2022;148:155–65. doi:10.1016/j.neunet.2022.01.012. [Google Scholar] [PubMed] [CrossRef]

29. Radosavovic I, Kosaraju RP, Girshick R, He K, Dollár P. Designing network design spaces. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2020; Seattle, WA, USA. p. 10428–36. [Google Scholar]

30. Zhou D, Kang B, Jin X, Yang L, Lian X, Jiang Z, et al. DeepViT: towards deeper vision transformer. 2021. doi:10.48550/arXiv.2103.11886. [Google Scholar] [CrossRef]

31. Chen M, Peng H, Fu J, Ling H. Autoformer: searching transformers for visual recognition. In: Proceedings of the IEEE/CVF International Conference on Computer Vision; 2021; Montreal, QC, Canada. p. 12270–80. [Google Scholar]

32. Zhang Z, Zhang H, Zhao L, Chen T, Arik S Ö., Pfister T. Nested hierarchical transformer: towards accurate, data-efficient and interpretable visual understanding. Proc AAAI Conf Artif Intell. 2022;36(3):3417–25. doi:10.1609/aaai.v36i3.20252. [Google Scholar] [CrossRef]

33. Huang X, Bi N, Tan J. Visual transformer-based models: a survey. In: El Yacoubi M, Granger E, Yuen PC, Pal U, Vincent N, editors. Pattern recognition and artificial intelligence. Cham: Springer International Publishing; 2022. p. 295–305. [Google Scholar]

34. Wang W, Chen W, Qiu Q, Chen L, Wu B, Lin B, et al. CrossFormer++: a versatile vision transformer hinging on cross-scale attention. 2023. doi:10.48550/arXiv.2303.06908. [Google Scholar] [CrossRef]

35. Dosovitskiy A, Beyer L, Kolesnikov A, Weissenborn D, Zhai X, Unterthiner T, et al. An image is worth 16 × 16 words: transformers for image recognition at scale. In: Proceedings of the International Conference on Learning Representations; 2021. doi:10.48550/arXiv.2010.11929. [Google Scholar] [CrossRef]

36. Bunk T, Varshneya D, Vlasov V, Nichol A. DIET: lightweight language understanding for dialogue systems. arXiv preprint arXiv:2004.09936. 2020. [Google Scholar]

37. Wang W, Xie E, Li X, Fan DP, Song K, Liang D, et al. Pyramid vision transformer: a versatile backbone for dense prediction without convolutions. In: Proceedings of the IEEE/CVF International Conference on Computer Vision; 2021; Montreal, QC, Canada. p. 568–78. [Google Scholar]

38. Liu Z, Lin Y, Cao Y, Hu H, Wei Y, Zhang Z, et al. Swin transformer: hierarchical vision transformer using shifted windows. In: Proceedings of the IEEE/CVF International Conference on Computer Vision; 2021; Montreal, QC, Canada. p. 10012–22. [Google Scholar]

39. Han K, Xiao A, Wu E, Guo J, Xu C, Wang Y. Transformer in transformer. In: Advances in neural information processing systems; 2021; California, USA. vol. 34. [Google Scholar]

40. Touvron H, Cord M, Sablayrolles A, Synnaeve G, Jégou H. Going deeper with image transformers. In: Proceedings of the IEEE/CVF International Conference on Computer Vision; 2021; Montreal, QC, Canada. p. 32–42. [Google Scholar]

41. Huang Z, Ben Y, Luo G, Cheng P, Yu G, Fu B. Shuffle transformer: rethinking spatial shuffle for vision transformer. 2021. doi:10.48550/arXiv.2106.03650. [Google Scholar] [CrossRef]

42. Dong X, Bao J, Chen D, Zhang W, Yu N, Yuan L, et al. CSWin transformer: a general vision transformer backbone with cross-shaped windows. 2021. doi:10.48550/arXiv.2107.00652. [Google Scholar] [CrossRef]

43. Ascoli S, Touvron H, Leavitt ML, Morcos AS, Biroli G, Sagun L. ConViT: improving vision transformers with soft convolutional inductive biases. In: Proceedings of the International Conference on Machine Learning; 2021. p. 2286–96. [Google Scholar]

44. Heo B, Yun S, Han D, Chun S, Choe J, Oh SJ. Rethinking spatial dimensions of vision transformers. In: Proceedings of the IEEE/CVF International Conference on Computer Vision; 2021; Montreal, QC, Canada. p. 11936–45. [Google Scholar]

45. Wu H, Xiao B, Codella N, Liu M, Dai X, Yuan L, et al. CVT: introducing convolutions to vision transformers. In: Proceedings of the IEEE/CVF International Conference on Computer Vision; 2021; Montreal, QC, Canada. p. 22–31. [Google Scholar]

46. Jiang ZH, Hou Q, Yuan L, Zhou D, Shi Y, Jin X, et al. All tokens matter: token labeling for training better vision transformers. In: Advances in neural information processing systems; 2021; California, USA. vol. 34. [Google Scholar]

47. Yu Q, Xia Y, Bai Y, Lu Y, Yuille A, Shen W, et al. Glance-and-gaze vision transformer. In: Neural information processing systems; 2021; California, USA. vol. 34. [Google Scholar]

48. Guo J, Han K, Wu H, Tang Y, Chen X, Wang Y, et al. CMT: convolutional neural networks meet vision transformers. In: 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2022; New Orleans, LA, USA. p. 12165–75. doi:10.1109/CVPR52688.2022.01186. [Google Scholar] [CrossRef]

49. Chen B, Li P, Li C, Li B, Bai L, Lin C, et al. GLiT: neural architecture search for global and local image transformer. In: Proceedings of the IEEE/CVF International Conference on Computer Vision; 2021; Montreal, QC, Canada. p. 12–21. [Google Scholar]

50. Yan H, Li Z, Li W, Wang C, Wu M, Zhang C. ConTNet: why not use convolution and transformer at the same time? 2021. doi:10.48550/arXiv.2104.13497. [Google Scholar] [CrossRef]