Image Steganography by Pixel-Value Differencing Using General Quantization Ranges

1  Introduction

The pixel-value differencing (PVD) method, proposed by Wu et al. [1], is well-known in the field of steganography [2–5] for embedding messages into the spatial domain of images. Images are partitioned by the method into non-overlapping two-pixel blocks, and human vision’s sensitivity to variations in gray values is employed to embed less bit information in smooth image blocks and more in edge blocks to maximize the data-hiding effect. The method usually yields a better image quality than the least-significant-bit (LSB) replacement method [6]. However, many methods have been proposed to improve Wu and Tsai’s original PVD method [1]. Some of these methods are surveyed in this study in a classified manner as follows:

(1)   PVD involving the use of LSB replacement

Wu et al. [7] proposed a method that enhances the embedding capacity of secret messages by combining the PVD and LSB replacement methods. The LSB replacement technique is used in the smooth image area, while the PVD method is applied to the contrast area. Chang et al. [8] employed the concept of overlapping pixel-pair to produce more difference values from the cover image, which can improve the hiding capacity of the PVD method [1]. The secret bits are hidden in the second pixel of a pixel pair using LSB replacement. Khodaei et al. [9] partitioned the cover image into image blocks with three consecutive pixels. Two pixel-pairs are formed in each image block, overlapping at the central pixel in the block. Secret bits are embedded into the central pixel using LSB replacement, and the PVD technique is applied to the two pixel-pairs. Swain [10] extended the method proposed by Khodaei et al. [9] by modifying the PVD and LSB replacement techniques used in [9]. Shukla et al. [11] proposed a data-hiding method that incorporates a modified version of [9] and arithmetic coding to increase the embedding capacity. Hameed et al. [12] proposed a steganographic method for images in which the pixel pair on the dominant gradient in each 2 × 2 image block is used for data embedding by the PVD technique, and the other two pixels in the block are utilized for embedding message bits by the LSB replacement technique.

(2)   Multi-directional PVD

The pixel value difference proposed by Wu et al. [1] originally is a single edge in a pixel pair. This concept was generalized afterward to the directional edges in larger blocks such as 1 × 3 blocks in [9,13], 2 × 2 blocks in [11,13–15], 2 × 3 blocks in [10,13,16], and 3 × 3 blocks in [10–11,13,16]. More specifically, the PVD method proposed by Khodaei et al. [9], mentioned previously, used the bi-directional edges in each 1 × 3 image block to embed secret data. Chang et al. [14] used the three directional edges in each 2 × 2 image block to design a tri-way PVD scheme to increase the hiding capacity. Sahu et al. [15] also used 2 × 2 blocks, each with two directional edges for data embedding, which are selected as horizontal, vertical, or diagonal. Also, the previously-mentioned Swain [10] and Shukla et al. [11] extended Khodaei et al. [9] to generate more directional edges and so increase the embedding capacity, with the former using 2 × 3 and 3 × 3 blocks and the latter using 3 × 3 and 2 × 2 ones. Recently, Wu et al. [13] partitioned a cover image into 1 × 3, 2 × 2, 2 × 3, or 3 × 3 blocks, which can be employed to embed message bits, regardless of whether they are complete or partial. Partial blocks are handled by assigning the missing pixels the values of the existing neighboring pixels. Sahu et al. [16] also utilized 3 × 3 blocks and exploited the use of all the edges in the horizontal, vertical, and diagonal directions by the multi-directional PVD technique.

(3)   Staganalysis resistant PVD

It is well known that the RS (Regular and Singular) analysis proposed by Fridrich et al. [17] can be employed to attack many data-hiding methods, particularly those based on LSB replacement. However, Wu et al. [1] demonstrated that the original PVD method can resist the RS analysis. Subsequently-proposed PVD-based methods [9,11,13–14] have also shown experimentally their abilities to resist the RS analysis. However, Zhang et al. [18] detected the presence of secret data embedded by the PVD method [1] by finding obvious unusual steps in the shape of the pixel difference histogram (PDH). In order to eliminate this phenomenon, Zhang et al. [18] randomly adjusted the bounds of each range in the quantization range table for different blocks, preventing the creation of irregularities in the resulting PDH. In addition, as mentioned previously, the method proposed by Swain [10] combined the use of the PVD and LSB replacement techniques to give higher capacity, which can resist both the PDH and RS analyses. The resistance to the PDH and RS analyses was also demonstrated in Hameed et al. [12], Sahu et al. [15], and Sahu et al. [16]. The steganalysis-resisting capability found in the four methods of [10,12,15,16] is due to the utilization of the multi-directional edges in image blocks.

(4)   PVD techniques solving the fall-off-boundary problem

The fall-off-boundary problem in the original PVD method [1] occurs when the new values of the stego-image pixels, which are computed from the pixel-value difference values, fall off the normal range of 0–255, as mentioned and solved by Wu et al. [1] utilizing a checking process to skip pixel pairs that can yield this problem to maintain the resulting image quality. Swain [10] solved the falling-off-boundary problem to obtain more data embedding space by providing two candidate values for each new pixel value in the stego-image and selecting the one causing less distortion without falling off the range boundary. Alternatively, Sahu et al. [19] solved the problem by shifting the values of the falling-off-boundary pixel pair into the normal range, where the shifting value was 2n, with n being the number of embeddable bits in the pixel pair. This solution was followed by Sahu et al. [15] mentioned above. Finally, Sahu et al. [16] and Sahu et al. [20] solved the problem similarly by simply shifting the falling-off-boundary pixel pair values to the closer boundary at 0 or 255.

Regarding the message data to be embedded into the cover image, three approaches have been taken to deal with the form of the message data before they are embedded: data encryption, data encoding, and data transformation. These approaches are detailed with examples of existing methods introduced in the following, emphasizing the third approach, which is the primary concern in this study.

(1)   Encryption of the message data

It is common for a message to be encrypted before being embedded into the cover image to enhance the security of the embedded message. Examples of PVD-based methods that took this approach include Roselinkiruba et al. [21], Shukla et al. [11], Phad et al. [22], and others.

(2)   Encoding of the message data

Encoding the message data is also a feasible approach to increase the security of the messages after they are embedded. Examples adopting this approach include Filler et al. [23] and Li et al. [24]. Specifically, the method [23] deals with the message data using syndrome-trellis coding (STC) based on convolution codes before data embedding. The method can minimize additive distortion for a given payload, enable the transmission of the largest payloads for a given embedding distortion rate, and enhance security by minimizing statistical detectability. Li et al. [24] proposed a near-optimal steganographic coding method based on steganographic polar codes (SPC) to minimize arbitrary additive distortion with low embedding complexity, which outperforms traditional STC methods. The method by Shukla et al. [11] also belongs to this class.

(3)   Transformation of message data

Message data forms can be changed before being embedded to enhance the flexibility of data usage or/and the rate of data embedding. Wu et al. [25] proposed a multiple-based number system that converts the bitstream of a secret message into a set of digits in a multiple-based number and embeds the digits in a group of pixels. Wu et al. [26] also combined the multiple-based number conversion mechanism proposed in [25] with a human visual model to imperceptibly embed secret messages in the central pixels of 3 × 3 image blocks. Zhang et al. [27] proposed a scheme that uses a multiple-based notational system and employs human vision sensitivity, where the amount of information that can be embedded in a pixel is determined by the degree of local gray-value variation of the pixel. Geetha et al. [28] proposed an adaptive steganographic scheme for embedding messages in pixels; the scheme utilizes a varying radix numeral system and the variance of the eight pixels surrounding the data-embedded pixel. Tang et al. [29] proposed a hiding method for improving that was proposed by [28], achieving enhanced image quality and embedding capacity performance. Chen et al. [30] proposed a general multiple-based data embedding scheme in which an optimal base vector is adopted for embedding secret messages in images with minimal distortion. Wu et al. [13] combined the concepts of general quantization ranges and multiple-based number conversion [31], which is the basic idea of the proposed method in this study, with a modified multiway PVD mechanism to improve the data embedding rates yielded by [9,10].

Recently, more steganographic techniques were proposed, with some novel and worth mentioning in this study, as described in the following:

With the advancement of deep learning, the convolutional neural network (CNN) can be used to enhance steganalysis or misleading steganalyzers. Boroumand et al. [4] proposed a deep residual network architecture called SRNet (Steganalysis Residual Network) for steganalysis of digital images, which can minimize the use of externally enforced constraints or heuristics and provide detection accuracy for both spatial-domain and JPEG (Joint Photographic Experts Group) steganography with very low false-alarm rates. Ma et al. [32] proposed a method based on the use of multiple adversarial networks and channel attention modules, which yields high-quality adversarial images with an anti-steganalysis capability to enhance steganography security, i.e., the method can be employed to create images that mislead steganalyzers.

Furthermore, Sahu et al. [33] proposed a data-hiding method based on a modified LSB matching scheme and uses multiple stego-images to increase data embedding rates. Each pixel in a cover image generates four new ones for data embedding, resulting in four distinct stego-images with reasonable PSNRs. The method was shown to resist RS attacks.

In the method proposed in this study, quantization ranges with non-power-of-two widths are employed to derive the base value for use in the multiple-based number conversion procedure. This concept of using non-power-of-two range widths in the quantization table was also adopted by Tseng et al. [34], but some range widths used by them are still limited to power-of-two. Specifically, their method divides non-power-of-two ranges into subranges for embedding more secret bits, but with specific subrange widths being power-of-two. This phenomenon is owing to their use of a perfect-square number to design the quantization range table. In addition, the non-power-of-two range widths they used were not utilized to derive the base value as in the proposed method of this study. In contrast, the proposed method is applicable for selecting arbitrarily more general non-power-of-two range tables for more flexible applications, showing the novelty of the proposed method.

The novelties of the proposed method in the aspect of determining the bases for converting binary numbers into multiple-based numbers, which differ from those in the references, are elaboratively explained in the following discussions:

1. In Wu et al. [25], the method is used as the base for “the difference between the gray values of a pair of corresponding pixels in two images.”

2. In Wu et al. [26], the method is used as the base, “the range of the gray value changes at the central pixel of an image block, each of which does not alter the contrast of the block.”

3. In Zhang et al. [27], the method is used as the base for “the degree of local variation computed based on the gray values of a pixel’s three neighbors.”

4. In Geetha et al. [28] and Tanga et al. [29], the methods are used as the base for “the variance of the gray values of the eight neighboring pixels around a pixel.”

5. In Chen et al. [30], the method uses the bases in the “optimal base vector” selected for every set of pixels in the sense of minimizing the resulting image distortion.

6. In Wu [31], the basic concept of the proposed method is roughly applied, as seen in the Acknowledgments section, to check the detailed differences from what has been done in this study.

Note also that the proposed method in this study uses as the base “the width of the quantization range to which a pixel pair’s difference value belongs,” which is different from those mentioned above.

Finally, as a brief introduction to the original PVD method proposed by Wu et al. [1], given a grayscale image, it is partitioned by the method into 1 × 2 non-overlapping blocks, with each containing a pair of neighboring pixels. A difference value is computed from the grayscale values of the two pixels. All possible absolute difference values in the block are in the range of [0, 255], divided into multiple quantization ranges in advance. w is defined as the width of a quantization range R=[l, u] with l and u being the lower and upper bound values of R, respectively, so that w=u−l+1. If a pixel pair’s difference value belongs to R, then ⌊log2⁡w⌋ message bits are embedded in the pixel pair, where ⌊⋅⌋ is the floor function. In conventional PVD methods [1,7–10], w is set to be a power of two. Therefore, log2⁡w is already a whole number with its value identical to that of ⌊log2⁡w⌋. The use of power-of-two ranges results in high embedding rates and full utilization of all the integer numbers in the range R (i.e., no integer number in R is wasted) for message embedding. In contrast, if w is not a power of two, log2⁡w will not be a whole number, and the number of bits that can be embedded in a pixel pair is only ⌊log2⁡w⌋ because only 2⌊log2⁡w⌋ integer numbers in the range are used for embedding messages, meaning that w−2⌊log2⁡w⌋ integer numbers in the range are wasted.

Also, a new PVD method is proposed in this study, which uses non-power-of-two quantization range widths to yield a higher embedding rate than those yielded by conventional PVD methods using power-of-two range widths. The bitstream of a secret message is embedded into a group of pixel pairs in the cover image through a multiple-based number conversion scheme. This scheme allows the number of bits that can be embedded in a pixel pair to be more flexible, achieving the maximum of log2⁡w when using a non-power-of-two range width of w. That is, all the w integer numbers in the range are used for embedding messages, and nothing is wasted. This achievement is not reachable by other conventional PVD methods. Fig. 1 provides a more detailed comparison of the numbers of embedded bits achievable through conventional PVD methods and the proposed method for different quantization range widths. In addition, the embedding process of the proposed method achieves message secrecy by traversing the cover image in a random order provided by a pseudo-random mechanism.

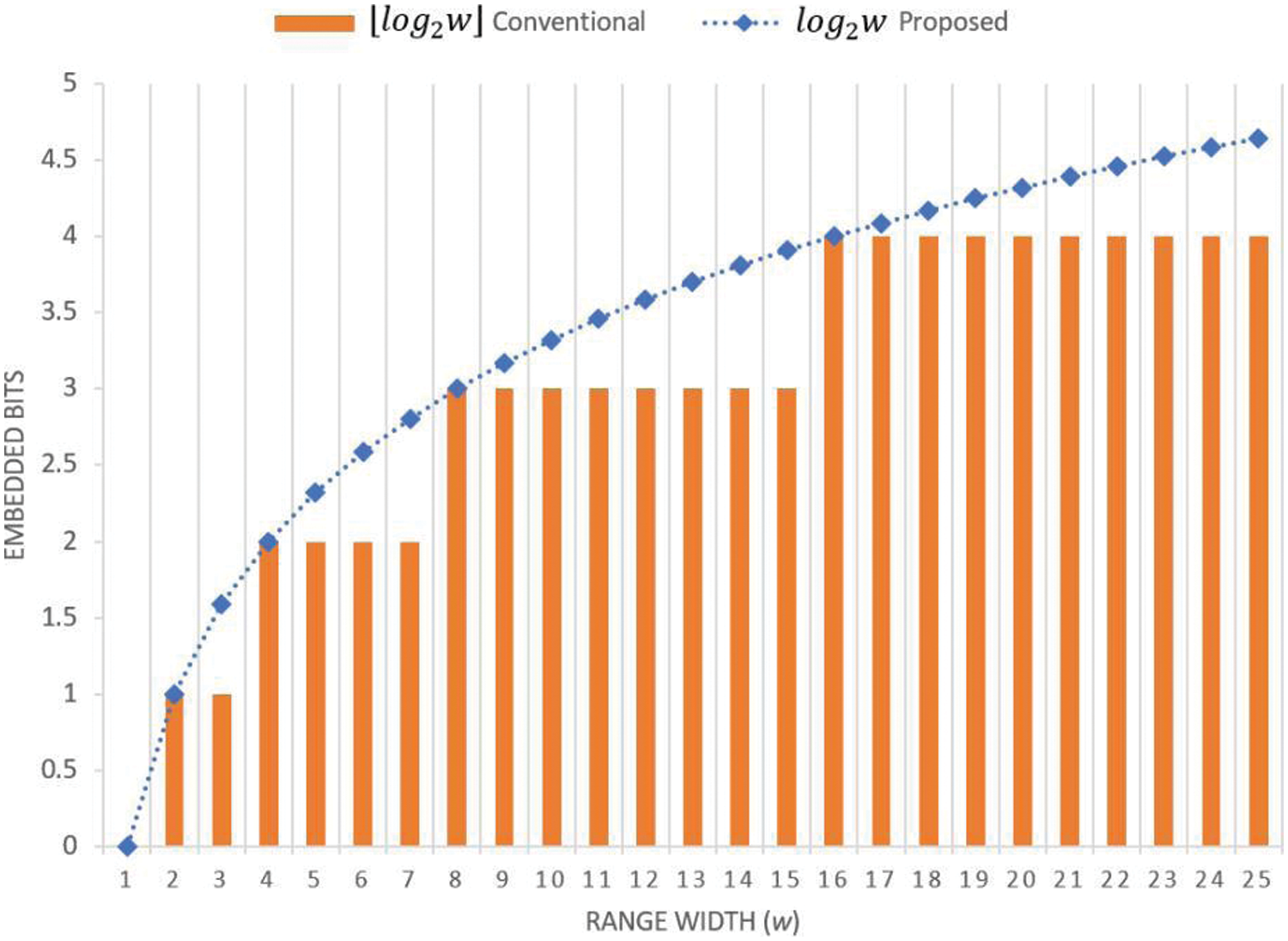
Figure 1: An illustration comparing the number of embedded bits where conventional PVD methods yield ⌊log2w⌋ bits and the proposed method yields log2w bits for various quantization range widths

With the advantages above, the proposed method can enhance the applicability of PVD-based methods across a broader range of domains. Employing more general non-power-of-two range widths and implementing the multiple-based number conversion scheme, the proposed method enhances application flexibility and increases data embedding rates. Hence, the proposed method can be utilized to extend the capabilities of other PVD methods. Examples of such capability extensions of existing PVD methods will be presented in the later sections of this paper.

The content of the subsequent sections of this paper is organized as follows. The relevant PVD techniques are reviewed in more detail in Section 2. Section 3 presents the proposed method and the algorithms designed for implementing the data embedding and extraction processes of the proposed data-hiding model. An application of general quantization ranges is demonstrated in Section 4. Experimental results are covered in Section 5. Concluding remarks and suggestions for future works are included in Section 6.

2  Review of Related Techniques

This section conducts a detailed review of the original PVD method and the multiple-based number conversion scheme.

2.1 PVD Data-Hiding Method

Wu et al. [1] proposed the PVD data-hiding method in 2003. By the method, an image is partitioned into 1 × 2 non-overlapping image blocks, each containing a pair of neighboring pixels. Let (g1, g2) be the two-pixel values of a pixel pair in an image block. The difference value of the two pixels in the image block is denoted as d, which can be expressed as follows:

d=g2−g1.(1)

A block with a small absolute difference value |d| is regarded as a smooth block, whereas a block with a large value of |d| is regarded as an edged block. The possible values of |d| (0 to 255) are classified into several contiguous ranges for Rk, where k=1,2, ⋯, r, with r being the number of ranges. Table 1 shows the quantization ranges used in [1]. The width of Rk is uk−lk+1, where lk and uk are the lower and upper bound values of Rk, respectively. To facilitate the direct embedding of bit information, the width of each range is taken to be a power of two in [1]. Small widths are selected for ranges close to 0, representing the gray value differences of smooth blocks; in contrast, large widths are chosen for ranges close to 255, illustrating the gray value differences of edged blocks. The strategies for selecting widths are developed based on the human eye’s sensitivity to gray value variations from smoothness to contrast. These strategies allow for embedding more and fewer bits of secret messages in edged and smooth blocks, respectively. Let nk be the number of bits that can be embedded in the image block B with an absolute difference value |d|, which belongs to Rk; nk is defined by the following equation:

nk=log2⁡ (uk−lk+1),(2)

where lk and uk are the lower and upper bound values of Rk, respectively. The value of uk−lk+1 is selected to be a power of two in [1], and nk is thus a whole number. If nk bits of a secret message with value b are embedded into the image block B with an absolute difference value |d| that belongs to Rk, the new difference value d′ of the two pixels in the image block, following the embedding of the secret message, is defined to be as defined by the following equation:

d′={lk+bif d≥0;−(lk+b)if d<0.(3)

The two-pixel values g1 and g2 in the image block are evenly adjusted to embed the nk-bit secret message, and the two new pixel values (g′1, g′2)after the adjustment can be expressed by the following equation:

(g′1,g′2)={(g1−⌈d′−d2⌉,g2+⌊d′−d2⌋)if d mod 2≠0;(g1−⌊d′−d2⌋,g2+⌈d′−d2⌉)if d mod 2=0,(4)

where ⌊⋅⌋ is the floor function, ⌈⋅⌉ is the ceiling function, and the mod operation yields the remainder of the integer division.

The values of g′1 or g′2 can be larger than 255 or smaller than 0, which can lead to the production of abnormal spots that create salt-and-pepper noise in an image. Hence, to determine whether a pixel pair has the possibility of creating an undesired noisy spot, the PVD method proposed by Wu et al. [1] adopts a falling-off-boundary checking process to the two-pixel values of g1 and g2 of the pixel pair prior to embedding message bits in the image block. The falling-off-boundary checking process uses the maximum value (the upper bound value uk) in Rk as the new differencing value for the subsequent steps of the checking process. The new difference value d′ in the falling-off-boundary checking process is defined according to the following equation:

d′={ukif d≥0;−ukif d<0.(5)

Then, the values of (g′1, g′2) are computed by applying Eqs. (5) and (4). If either g′1 or g′2 falls outside the boundary of 0 or 255, the image block is regarded as having the possibility of falling off, and it is abandoned to embed message bits. If both g′1 and g′2 fall inside the boundary of 0 or 255, then any substream of the secret message can be embedded in the image block without causing abnormal spots. In other words, the image block is regarded as being embeddable.

The embedded message is extracted from a stego-image by visiting two-pixel blocks in the order as determined in the embedding process. Assume that g∗1 and g∗2 are the two gray values of a visited image block in a stego-image, and that the difference value d∗ of the two gray values corresponds to the range indexed k∗ in the range table. The value d∗ can be expressed as follows:

d∗=g∗2−g∗1.(6)

At first, the falling-off-boundary checking process is also performed in the data extraction process by using the maximum value (the upper bound value uk∗) in Rk∗ as the new differencing value for the subsequent steps of the checking process. The new difference value d′∗ is defined according to the following equation:

d′∗={uk∗if d∗≥0;−uk∗if d∗<0.(7)

Then, the values (g′∗1, g′∗2) are computed according to the following equation:

(g′∗1,g′∗2)={(g∗1−⌈d′∗−d∗2⌉,g∗2+⌊d′∗−d∗2⌋)if d∗ mod 2≠0;(g∗1−⌊d′∗−d∗2⌋,g∗2+⌈d′∗−d∗2⌉)if d∗ mod 2=0.(8)

If neither g′∗1 nor g′∗2 falls outside the boundary of 0 or 255, it indicates that message bits were embedded into the image block previously. Assume that b∗ is the value of the embedded message bits. Then, b∗ can be extracted according to the following equation:

b∗=|d∗|−lk∗(9)

where lk∗ is the lower bound value of Rk∗.

2.2 Multiple-Based Number System and Multiple-Based Number Conversion

Wu et al. [25] proposed a multiple-based number system for hiding a secret message in a given image according to the following two steps: (1) transform the bits of the secret message into several multiple bases; (2) embed the digits of the number into a group of pixel pairs in a cover image.

Specifically, assume that the multiple-based number obtained in Step (2) above has the form of n digits as shown in the following:

dn−1(bn−1) dn−2(bn−2)⋯d1(b1) d0(b0),(10)

where the digit di has the base bi>1 and 0≤di<bi for i=0,1,⋯,n−1. The decimal value M of the n-digit multiple-based number can be computed by applying the following equation:

M=dn−1(bn−1)dn−2(bn−2)⋯d1(b1)d0(b0)

=dn−1×(bn−2×bn−3×⋯×b0)+dn−2×(bn−3×bn−4×⋯×b0)+⋯+d1×b0+d0

=(⋯((dn−1×bn−2+dn−2)×bn−3+dn−3)×⋯+d1)×b0+d0.(11)

M can be expressed succinctly through the function g(n), which is expressed as follows:

M=g(n)={d0ifn=1;dn−1×∏i=0n−2bi+g(n−1)ifn>1.(12)

With a decimal value of M and the bases of bi, where i=0,1, ⋯, n−1, if the condition M<∏i=0n−1bi is met, then M can be converted into an n-digit multiple-based number with the digit di, where i=0,1, ⋯, n−1. The value of di can be computed using the following equation:

di=mi mod bi(13)

and

mi={Mifi=0;mi−1 div bi−1ifi>0,(14)

where the operation of mod yields the remainder of integer division, and the operation of div yields the quotient of integer division.

3  Proposed Data-Hiding Technique

In the proposed method, the data-hiding process, including data embedding and extraction, can be illustrated by Figs. 2 and 3, respectively, which can be regarded as a model of the proposed data-hiding system.

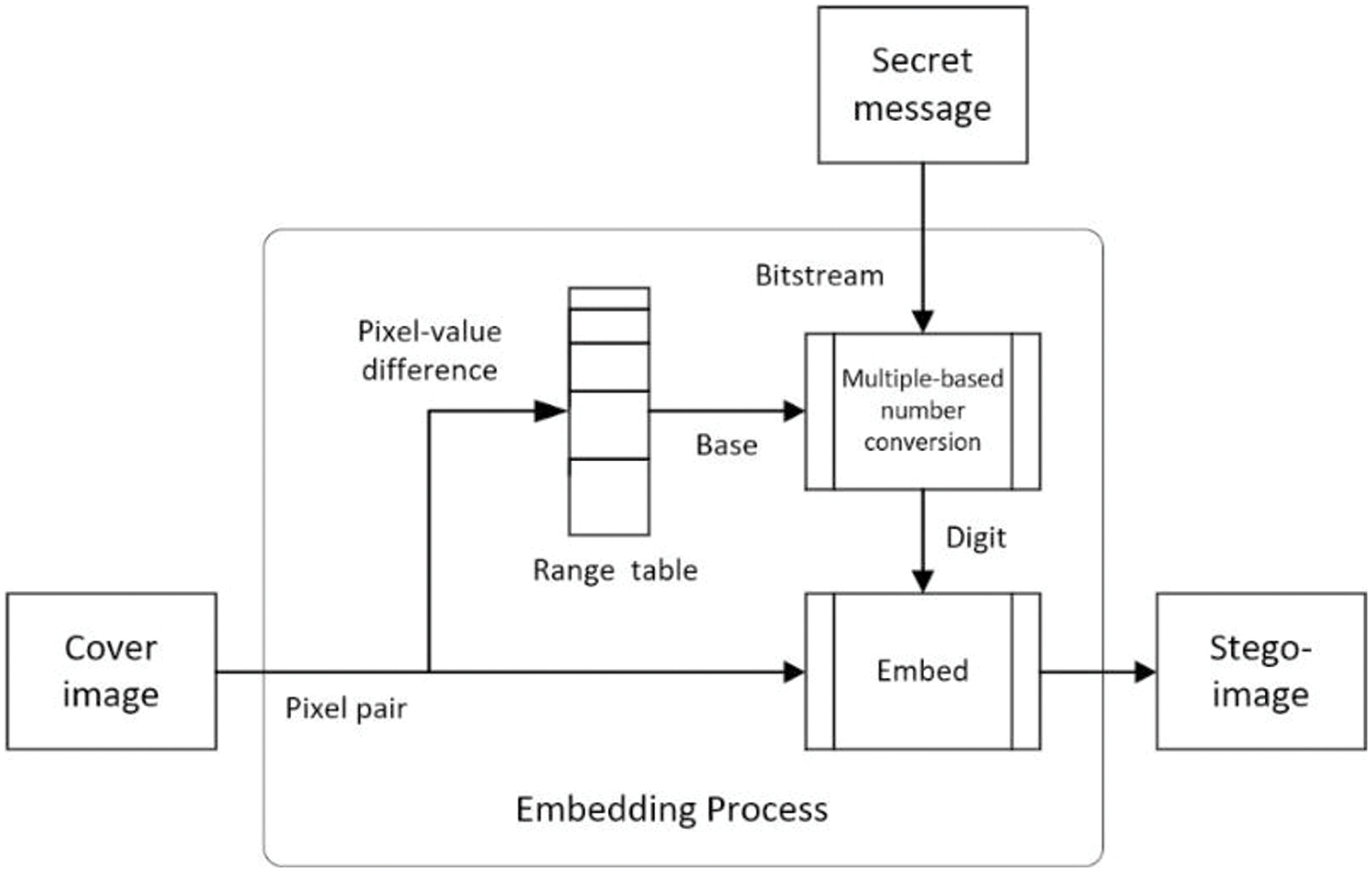
Figure 2: Illustration of the data embedding process of the proposed data-hiding model

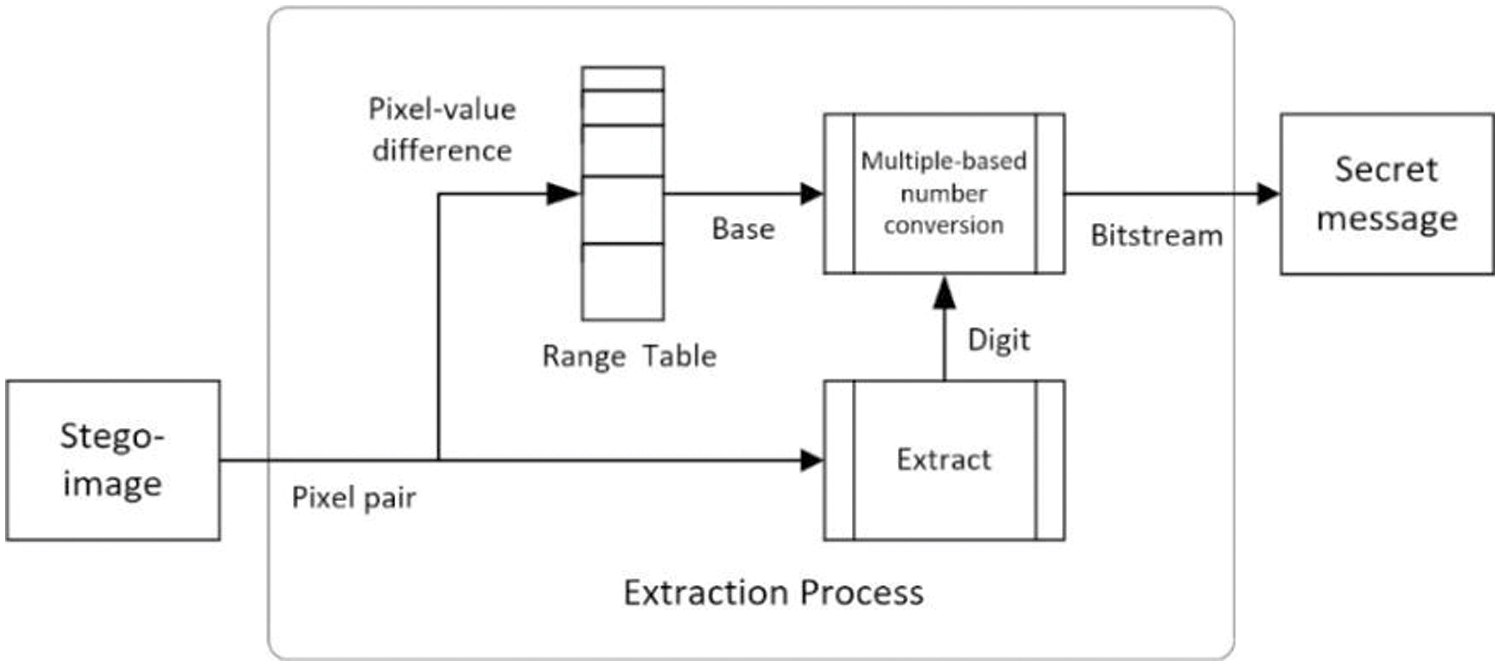
Figure 3: Illustration of the data extraction process of the proposed data-hiding model

Specifically, in the data embedding process, as depicted in Fig. 2, the difference value of each pixel pair P in the cover image is computed, and the result is employed to decide a range R in a pre-defined range table by table lookup. The width of range R is next to be a base-b according to which the value n representing the input message M is used to compute a base-b digit db (see the detail of this step in Algorithm 1 described subsequently). The digit db is then embedded into the pixel pair P. This one-digit embedding method is repeated until the value n of message M is totally processed to obtain a desired stego-image. The base-b yielded, as mentioned above, is not fixed but variable for different pixel pairs; i.e., multiple bases are generated for use in the proposed method.

In the data extraction process, as depicted in Fig. 3, each pixel pair in the stego-image is first taken to extract a pixel value difference d, from which a base-b is decided in a way identical to that taken in the data embedding process. In addition, d is also regarded as a base-b digit db. Then, db is converted into a partial value of n representing the secret message M (the detail of this conversion step in Algorithm 2). This process is repeated until all partial values of n are collected, summed up, and converted into the original bitstream of the message M.

Secret messages are embedded by the proposed method into images by use of general quantization ranges, which can be expressed using [lk, uk], where k=1,2, ⋯, r, with r being the number of ranges. l1 is 0, ur is 255, and the value of uk+1 is identical to that of lk+1, where k=1,2,⋯,r−1. Table 2A,B show the two sets of quantization ranges for the experiments conducted in this study. In Table 2A,B, the width of each quantization range is not limited to a power of two, unlike the case for the original PVD method [1].

3.1 The Data Embedding Process

To apply the data embedding process of the proposed method, the cover image C is partitioned into n 1 × 2 image blocks. Then, the cover image is traversed in an order determined by a pseudo-random mechanism, visiting each pixel pair in the image only once to achieve secrecy. Let (gi1, gi2) be the two-pixel values in the i-th visited image block. The difference value of the two-pixel values in the block is denoted as di, which can be expressed using the following equation:

di=gi2−gi1.(15)

The value of |di| is assumed to be in the range Rki, that is, lki≤|di|≤uki, where lki and uki are the lower and upper bound values of Rki, respectively. The range width of Rki is uki−lki+1. If message bits are independently embedded in each block by applying conventional PVD methods [1,7–10,14,16,18], the number of message bits that can be embedded in the block formed by the two-pixel values (gi1, gi2) is only ⌊log2⁡(uki−lki+1)⌋. The proposed method applies the concept of multiple-based number conversion [25] to combine a group of pixel pairs in the cover image for converting a secret message into a multiple-based number, i.e., the bases of the digits of the multiple-based number are determined by the pixel pairs in the group. Each digit value in the multiple-based number is then embedded in the corresponding pixel pair of the group. The number conversion scheme allows for the number of embedded bits in the block with the two values (gi1, gi2) to increase to log2⁡(uki−lki+1) bits.

Similar to the PVD method [1], the proposed method performs falling-off-boundary checking on a block (gi1, gi2) prior to the embedding of message bits in the block. If the checking process indicates that neither of the resulting pixel values falls outside the boundary of 255 or 0, then the block is used to embed data in the proposed method. During message embedding, the pixel pair in the block is employed to represent a digit of the multiple-based number, and the base of the digit is regarded as uki−lki+1. This indicates that the digit value is between 0 and uki−lki. This method uses a group of embeddable pixel pairs in image C to form a large multiple-based number and converts the bitstream of the secret message into the multiple-based number. Each digit value in the multiple-based number is then embedded into the corresponding pixel pair. Relative to conventional techniques, this mechanism allows for more message bits to be embedded in C when the quantization width of each range is not limited to a power of two. Let L be the maximum number of bits that can be embedded in C using the mechanism. Then, L can be computed according to the following equation:

L=⌊∑i=1nlog2⁡w(gi1, gi2)⌋=⌊log2⁡∏i=1nw(gi1, gi2)⌋(16)

where n denotes the number of pixel pairs in C, and w(gi1, gi2) can be defined according to the following equation:

w(gi1, gi2)={uki−lki+1if fall_off (gi1, gi2)=Fasle;1else,(17)

where fall_off(⋅) indicates whether the gray values of two-pixel values of the pixel pair have the possibility of falling out of the boundary of 0 or 255 after embedding message bits.

To embed a secret message M with a length of B bits into image C, C must have a sufficient number of pixel pairs that meet the condition

∏i=1nw(gi1, gi2)≥2B.(18)

If the condition is met, the proposed method converts M into the multiple-based number corresponding to the pixel pairs in C. The value of each digit in the multiple-based number is then embedded in the corresponding pixel pair. If images of the common size 512 × 512 are used, then the product in Eq. (16) can exceed 10100,000, and the integer data type of general programming language cannot handle this operation. Hence, specially developed modules or programming languages with big-integer types must be utilized to manage such big-integer operations. An overview of the embedding system is illustrated in Fig. 4. The data embedding algorithm designed for use in this study is as follows:

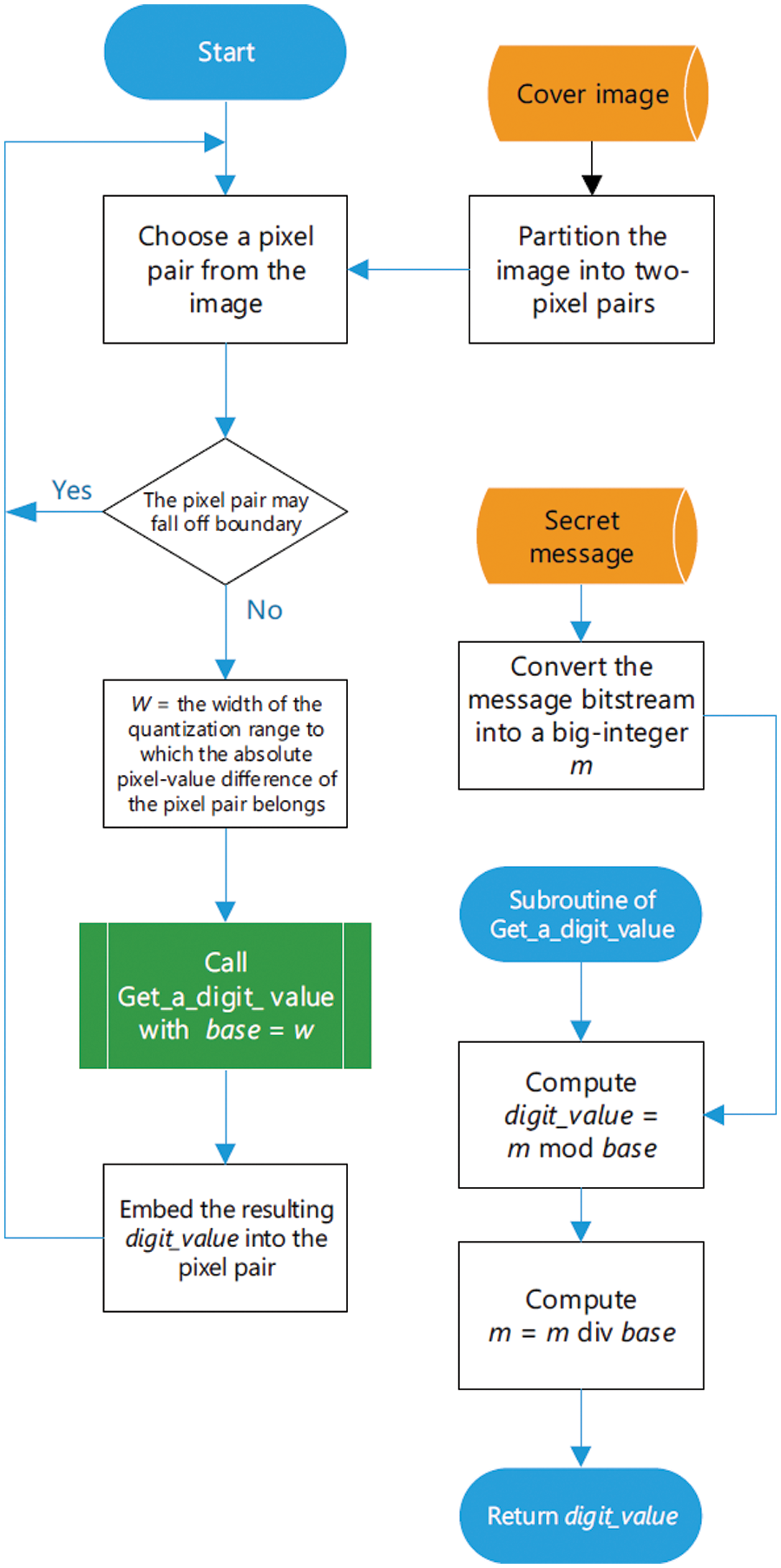
Figure 4: Overview of the proposed embedding system

Fig. 5 illustrates the embedding of a 10-bit secret bitstream 11001110012 = 82510 into four-pixel pairs with gray values of (56, 58), (110, 242), (65, 52), and (68, 90). The differences in the gray values of the four pixel-pairs are 2, 132, −13, and 22, respectively. If the quantization ranges in Table 2B are applied, the corresponding range intervals of the differences are [0, 8], [131, 255], [9, 19], and [20, 34], respectively. After falling-off-boundary checking is performed for the four pixel-pairs, only (110, 242) is checked to have a possibility of falling outside (falling-off) 0 or 255, as shown by the following computations:

(1)    pixel value difference d = 242 − 110 = 132 by Eq. (1);

(2)    d ∈ [l6, u6] = [131, 255] according to Table 2B;

(3)    d′ = u6 = 255 (⸪ d > 0) by Eq. (5);

(4)    (110 − ⌊(d′ − d)/2⌋, 250 + ⌈(d′ − d)/2⌉) = (49, 312)(∵ d mod 2 = 0) by Eq. (4);

(5)    therefore, the resulting pixel value 312 falls outside the boundary of 255 (∵312>255).

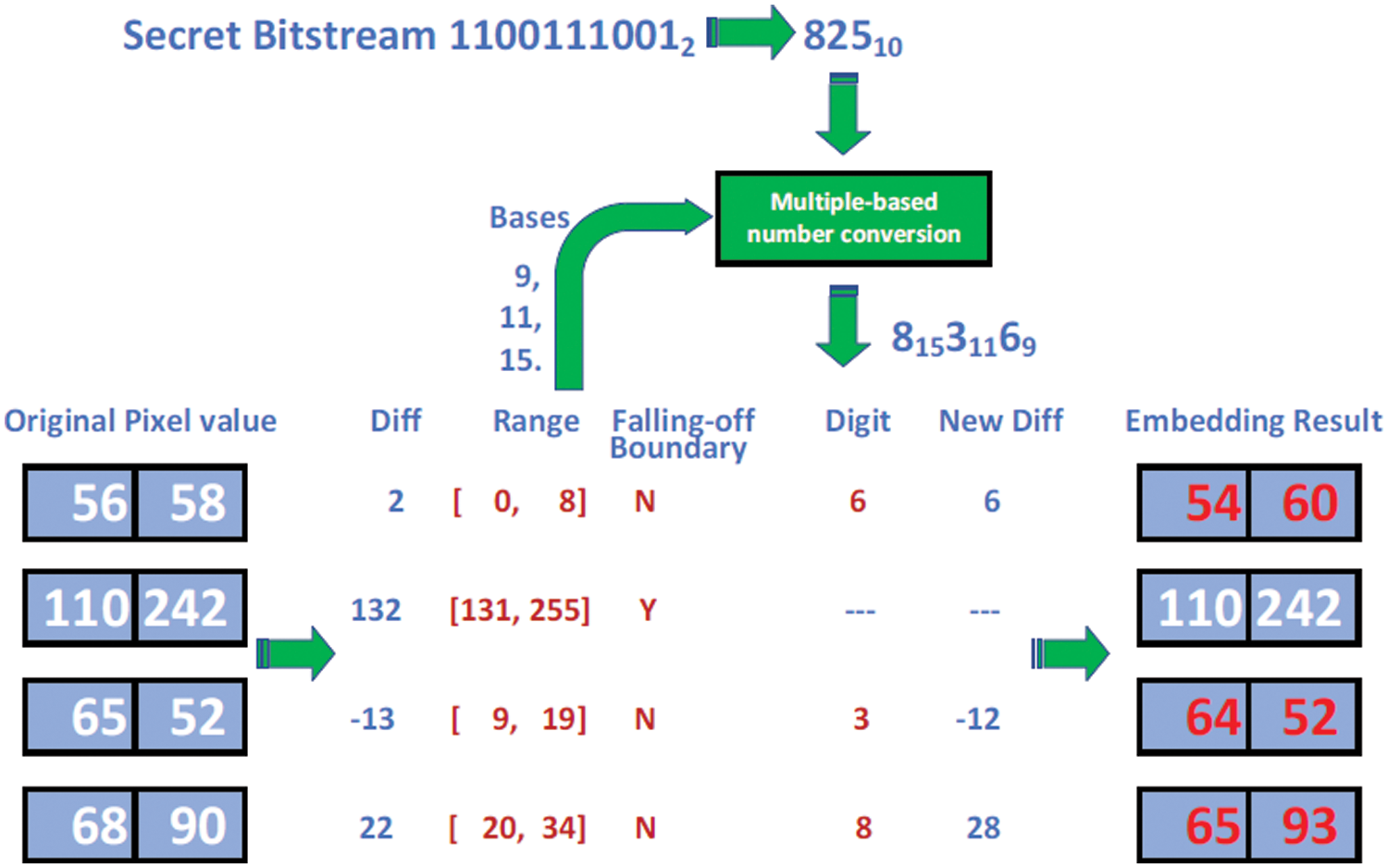
Figure 5: Embedding of a 10-bit bitstream into four pixel-pairs through multiple-based number conversion

This pixel pair is skipped and not subjected to embedding. The widths of the range intervals of the other three pixel-pairs are 9, 11, and 15. Next, the secret bitstream is converted to a multiple-based number with 9, 11, and 15 bases. The corresponding digit values in the multiple-based number can be computed to be 6, 3, and 8 respectively as shown in the following:

(1)    825 mod 9 = 6 with quotient Q1 = 91;

(2)    91 mod 11 = 3 with quotient Q2 = 8;

(3)    8 mod 15 = 8 with quotient Q3 = 0.

The conversion result is 81531169. The values 6, 3, and 8 of the digits in the multiple-based number are then embedded into (56, 58), (65, 52), and (68, 90), respectively. The new differences obtained by Eq. (3) are 6, −12, and 28, and therefore the new gray values computed by Eq. (4) are (54, 60), (64, 52), and (65, 93), respectively.

3.2 The Data Extraction Process

To extract the B-bit secret message M from the stego-image S, S is partitioned into 1 × 2 image blocks in the same way applied during the embedding process. The extraction process traverses the stego-image using the identical pseudo-random mechanism to produce the same traversing order applied during the embedding process. Then, each digit value in a multiple-based number is computed using the corresponding pixel pair. The multiple-based number is converted to a B-bit bitstream to yield the resulting secret message. The data extraction algorithm used in this study is as follows:

Fig. 6 illustrates the extraction of a 10-bit secret message from the four pixel-pairs above with gray values of (54, 60), (110, 242), (64, 52), and (65, 93), which were yielded in the previous example, with the differences of the gray values of the four pixel-pairs being 6, 132, −12, and 28, respectively. The quantization ranges in Table 2B are applied, and the corresponding range intervals of the differences are [0, 8], [131, 255], [9, 19], and [20, 34]. After falling-off-boundary checking is performed for the four pixel-pairs, only (110, 242) is revealed to have the possibility of falling outside 0 or 255; thus, it is skipped and not subjected to data extraction. The values 6, 3, and 8 of the digits in the multiple-based number are extracted by Eq. (9) from (54, 60), (64, 52), and (65, 93), respectively. The widths of the range interval of the three pixel-pairs are 9, 11, and 15. Hence, a multiple-based number with bases of 9, 11, and 15 can be formed, which is 81531169. The equivalent decimal number is 82510, which is then converted to a 10-bit bitstream 11001110012 and taken finally to be the extracted secret message bitstream.

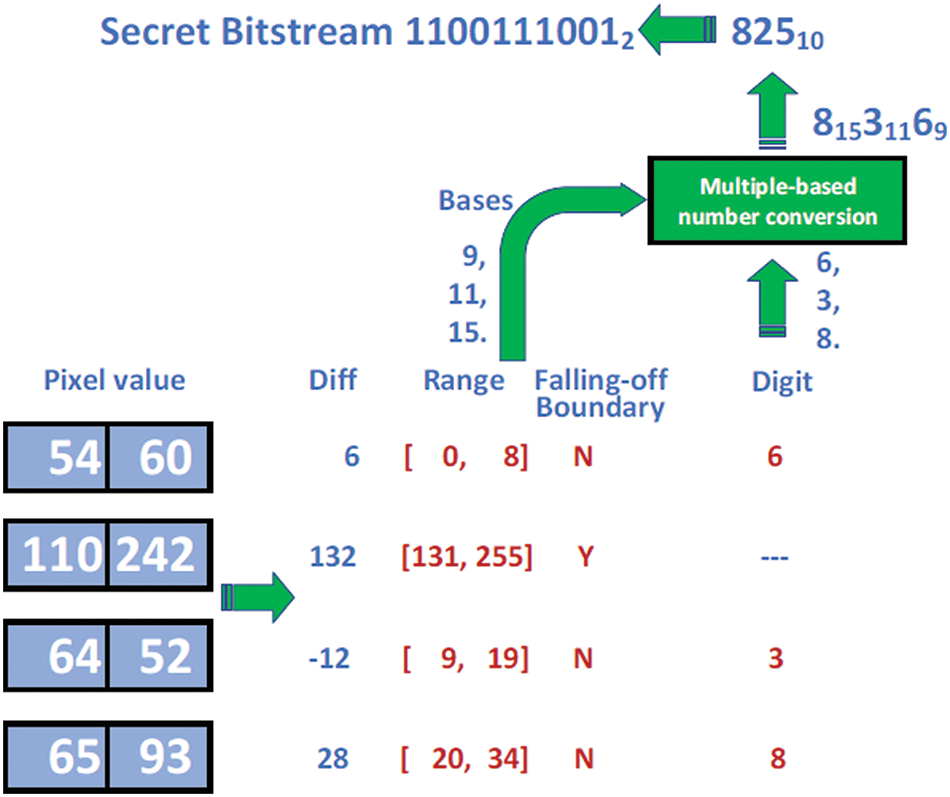
Figure 6: Extraction of 10-bit bitstream from four pixel-pairs through multiple-based number conversion

4  Application Example Using General Quantization Ranges

This section demonstrates an application example in which general quantization ranges are used. A quantization range table is required when the PVD method embeds a secret message. Small widths are selected for ranges close to 0; in contrast, large widths are chosen for ranges close to 255. Although the number of message bits that can be embedded in the large-width quantization range to which a pixel pair’s difference value belongs is larger than that achieved in the small-width quantization range, image distortion caused by the embedding of messages in the large-width quantization range is larger than that caused in the small-width quantization range. When the number of message bits to be embedded in a cover image does not exceed the maximum embedding capacity of the image, some pixel pairs in the image might not be used for data embedding. At this point, if the ranges of the quantization table can be dynamically adjusted so as not to compose the entire grayscale difference range of [0, 255], i.e., if they can be appropriately reduced to compose a smaller range from 0 to G instead of from 0 to 255, then the use of pixel pairs with pixel differences from 0 to G in the image might be sufficient for the embedding of all the secret data by avoiding embedding message data in those pixel pairs in the image with grayscale differences in the range from G+1 to 255. In this way, the image distortion caused by embedding messages in the large-width quantization ranges (in the ranges close to 255) to which the pixel pairs’ difference values belong can be reduced. A method for determining the value of G is proposed as follows:

If a cover image has n pixel-pairs, let the i-th pixel pair be (gi1, gi2) with the pixel value difference di=gi2−gi1, where i = 1, 2, …, n. The smallest integer G must be identified to satisfy the condition for embedding data using the pixel pairs with pixel value differences between 0 and G in an image, which is sufficient for embedding a secret message with a length of B bits. The quantization ranges of the originally given quantization table can be expressed as Ri(li, ui) for i = 1, 2, …, r, where r is the number of quantization ranges in the given table. If the value of G belongs to Rj, the upper bound value, uj, of Rj must be reset to G, and only the new quantization ranges Rk(lk, uk), where k = 1, 2, …, j, are used in the embedding process. Because the new width of Rj cannot be a power of two, the secret message must be embedded using the proposed embedding technique for general quantization ranges. The following equation can express a value G that satisfies the conditions above:

G=arg⁡ming∈[0,255](g|⌊log2⁡∏i=1nE(i, g)⌋≥B),(19)

where

E(i, g)={uidx(|di|)−lidx(|di|)+1if |di|≤g and fall_off (gi1,gi2)=false;1else,(20)

fall_off(⋅) is employed to determine whether the gray values of the two-pixel values of the pixel pair have the possibility of falling out of the boundary of 0 or 255 after the embedding of message bits, and idx(⋅) is the index of the quantization range to which the pixel pair’s difference value belongs.

5  Experimental Results and Discussions

This section describes various experiments conducted in this study to show the superiority of the proposed method and its use to improve the existing PVD-based methods, with the experimental results presented for conducting various required comparisons.

5.1 Comparison with the Original PVD Method–Part I: Respective Results of All Ranges for a Single Cover Image

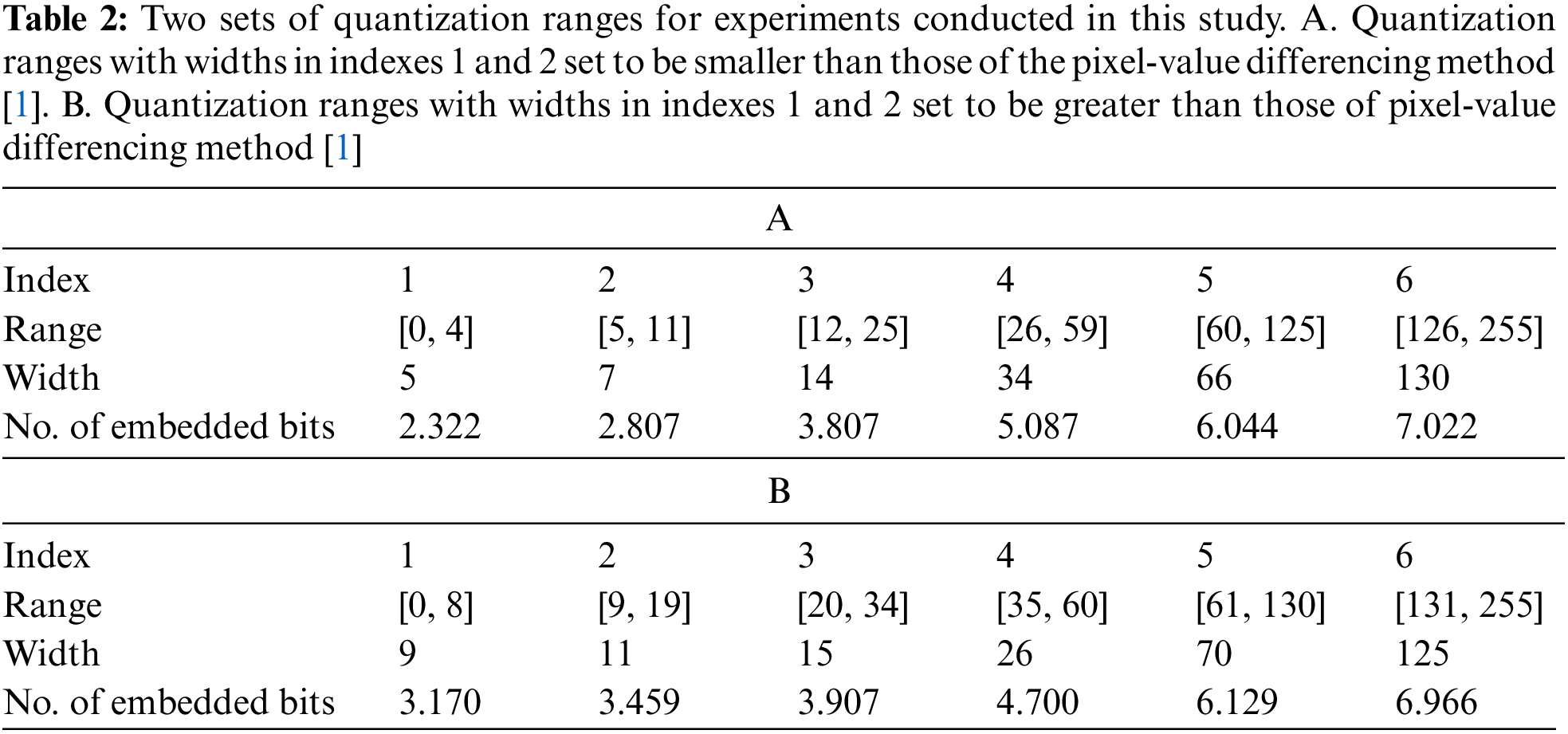
In the experiments conducted in this study to test the goodness of the proposed method, eight 512 × 512 grayscale images were used as cover images, and a random-generated bitstream was utilized as the secret message. Two of the tested cover images (i.e., named Baboon and Jet) are shown in Fig. 7. The experiments were conducted using the programming language C# with the BigInteger class being applied for big-integer processing. In the experiments, the quantization ranges in Tables 1, 2A,B were used to look up range widths based on the differences in gray values. Table 1 was used for the original PVD method [1]. The widths of the first and second quantization ranges in Table 2A were designed to be slightly smaller than those of the first and second ranges in Table 1. In contrast, the widths of the first and second quantization ranges in Table 2B were designed to be slightly larger than those in Table 1. The experimental performances from Table 2A,B were compared to those from Table 1.

Figure 7: The cover images used in the experiments. (a) Baboon. (b) Jet

Table 3 lists the results of using the Baboon image as an example of input cover images for estimating the data embedding rates, where both the conventional embedding method [1] and the proposed method with multiple-based number conversion were applied. The purpose is to conduct an initial check of the effect of the usage of non-power-of-two range widths and the multiple-based number conversion scheme. The following facts can be observed from Table 3.

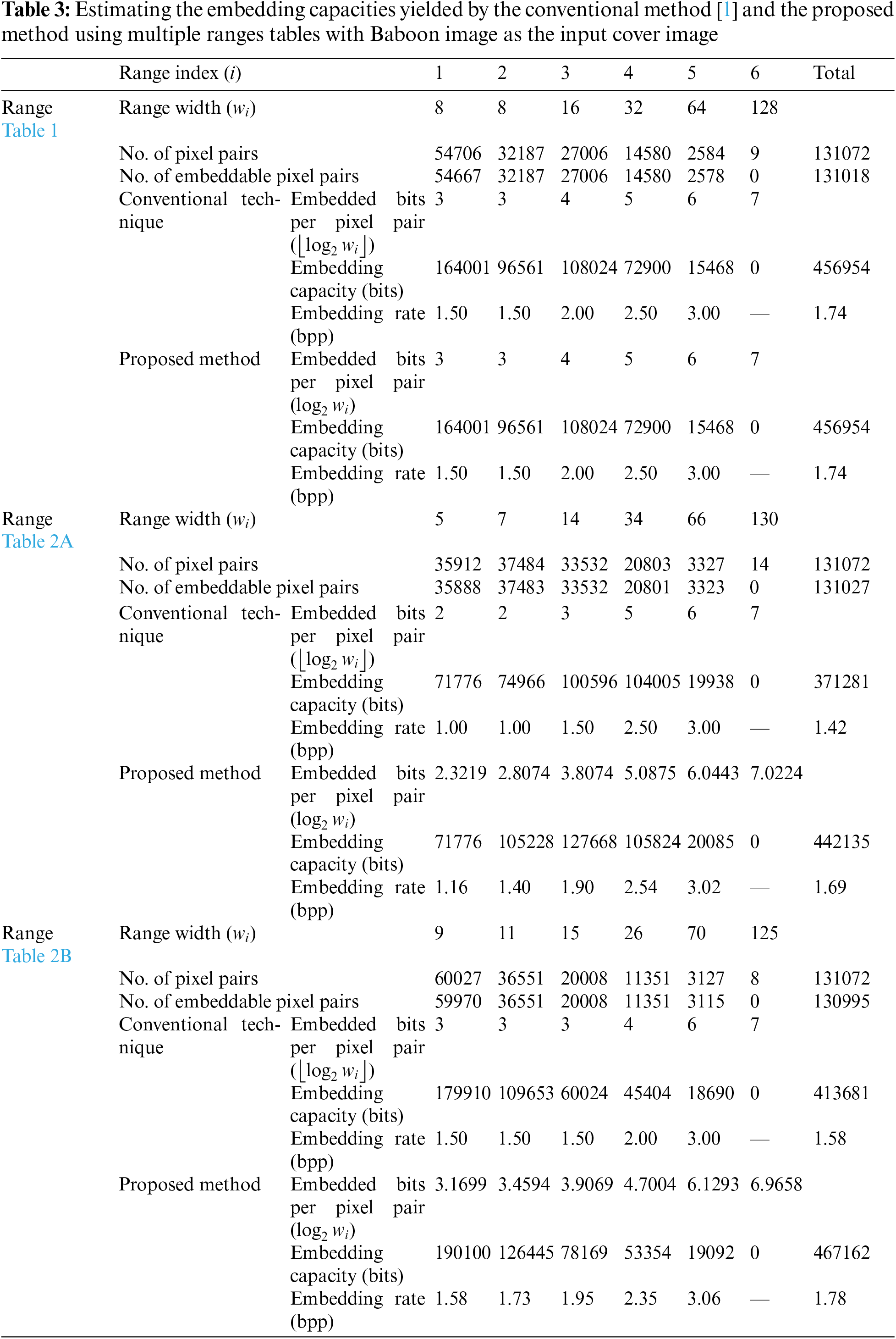
(1) In the three range tables, the value differences of the pixel pairs in the image mainly belong to the ranges with indexes 1 and 2.

(2) About the first and second ranges in the three tables, those of Table 2B are the widest, followed by those of Tables 1 and 2A; the larger the range width to which a difference value of a pixel pair belongs, the more the information that can be embedded in the pixel pair. Hence, the use of Table 2B yields the highest embedding rate, followed by the uses of Tables 1 and 2A. Here, the embedding rate of an image is defined by the following equation:

Embedding rate=Number of embedded bitsNumber of pixels in the image.(21)

(3) The width w of each range in Table 1 is a power of two that when the conventional method was applied, ⌊log2⁡w⌋ message bits can be embedded in each pixel pair individually, and when the proposed multiple-based number conversion scheme was applied, log2⁡w message bits can be embedded in each pixel pair, as mentioned in Section 1. Hence, the number of bits that can be embedded in each pixel pair is identical because with w being a power of two, ⌊log2⁡w⌋ = log2⁡w.

(4) The widths of the ranges in Table 2A,B are not powers of two, whereas those in Table 1 are. Using each range width in the two tables, the embedding rate of the stego-image yielded by the proposed method with the multiple-based number conversion scheme is always higher than that yielded by the conventional method. This is owing to the fact log2⁡w>⌊log2⁡w⌋ when w is not a power of two, as illustrated in Fig. 1.

Fig. 8 shows four resulting stego-images with the aforementioned random bitstream as the input and Table 2A,B as the quantization tables. The resulting images are not visually different from the original ones, indicating that the proposed method can embed messages in images imperceptibly.

Figure 8: The stego-images after embedding using Table 2A,B for Fig. 7a,b. (a) Using Fig. 7a and Table 2A. (b) Using Fig. 7b and Table 2A. (c) Using Fig. 7a and Table 2B. (d) Using Fig. 7b and Table 2B

5.2 Comparison with the Original PVD Method–Part 2: Results of All Ranges for a Set of Cover Images

Table 4 shows the embedding rates and the peak signal-to-noise ratios (PSNRs) yielded by the original PVD method [1] using all the ranges in Tables 1, 2A, B, for all the eight cover above images, as well as those yielded by the proposed method using the same ranges in Tables 1, 2A,B, respectively. The original PVD method uses the conventional embedding technique for message embedding, while the proposed method uses non-power-of-two range widths and multiple-based number conversion. Table 4 reveals the following facts.

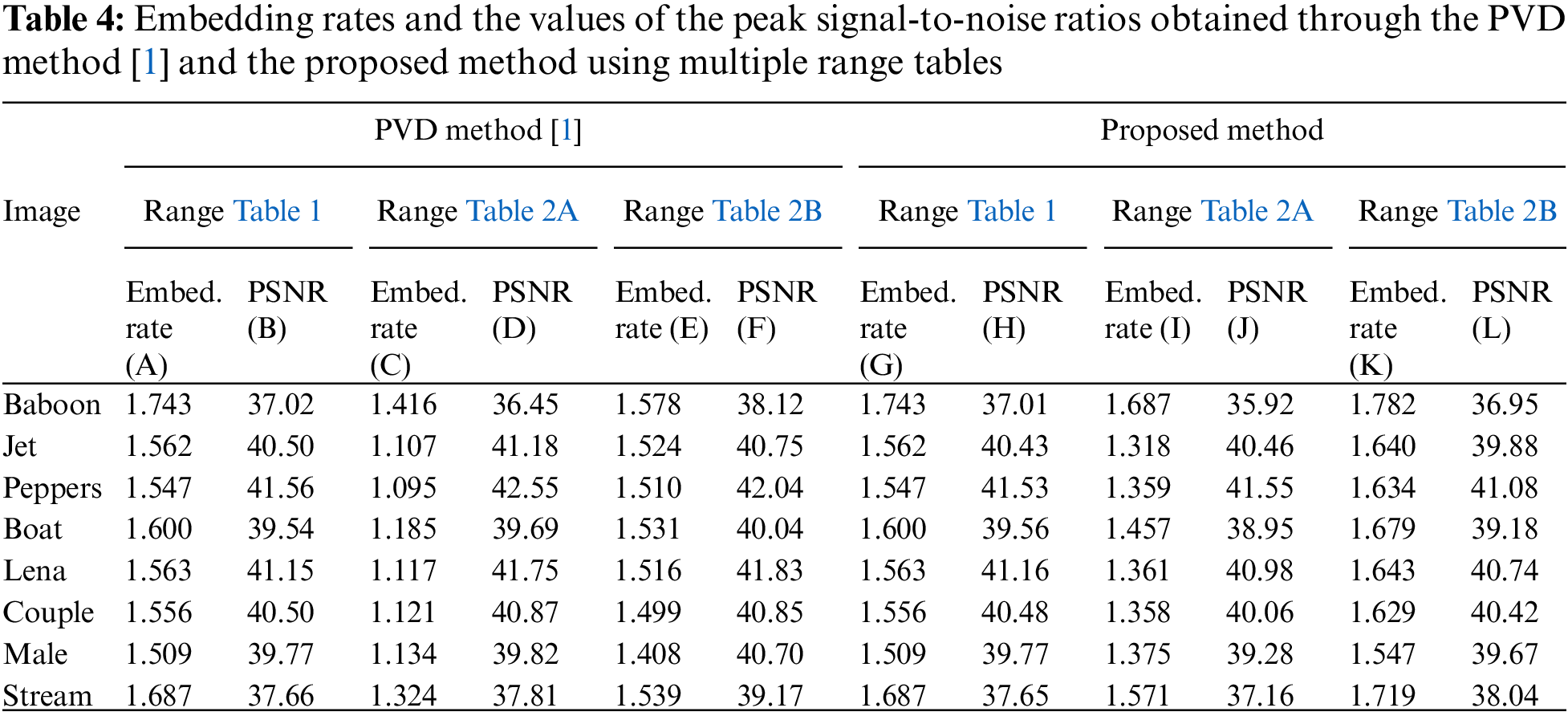
(1) The results presented in columns (A), (C), and (E) indicate that the embedding rates yielded by the original PVD method [1] using the ranges in Table 2A,B are lower than those yielded the same method using the ranges in Table 1. This is because the widths of the ranges in Table 2A,B are not powers of two, while only power-of-two range widths can be used by the original PVD method. That is, the use of the original PVD method for embedding message bits resulted in “wasting” some integer values that represent the non-power-of-two ranges in Table 2A,B, resulting in fewer embeddings of message bits and so lower embedding rates.

(2) Columns (C) and (I) show the embedding rates achieved using the ranges in Table 2A, and columns (E) and (K) show the embedding rates achieved using the ranges in Table 2B. These results indicate that the embedding rates obtained by the proposed method with multiple-based number conversion are higher than those obtained by embedding the message bits by the original PVD method [1].

(3) The results presented in columns (G), (I), and (K) indicate that the proposed method using the ranges listed in Table 2B yields the highest embedding rate, followed by those resulting from using the ranges listed in Tables 1 and 2A. This verifies that the proposed method can embed messages using non-power-of-two range widths and maintain high embedding rates.

(4) Columns (H), (J), and (L) show that the PSNR values of the resulting images are all above 35 dB, demonstrating the imperceptibility of the stego-images yielded by the proposed method.

In addition, the embedding rates achieved for image Baboon through the proposed method using the ranges in Tables 1, 2A,B are 1.743, 1.687, and 1.782, respectively, which are computed from the embedding capacities 456954, 442135, 467162, respectively. These values are identical to the estimated values listed in Table 3.

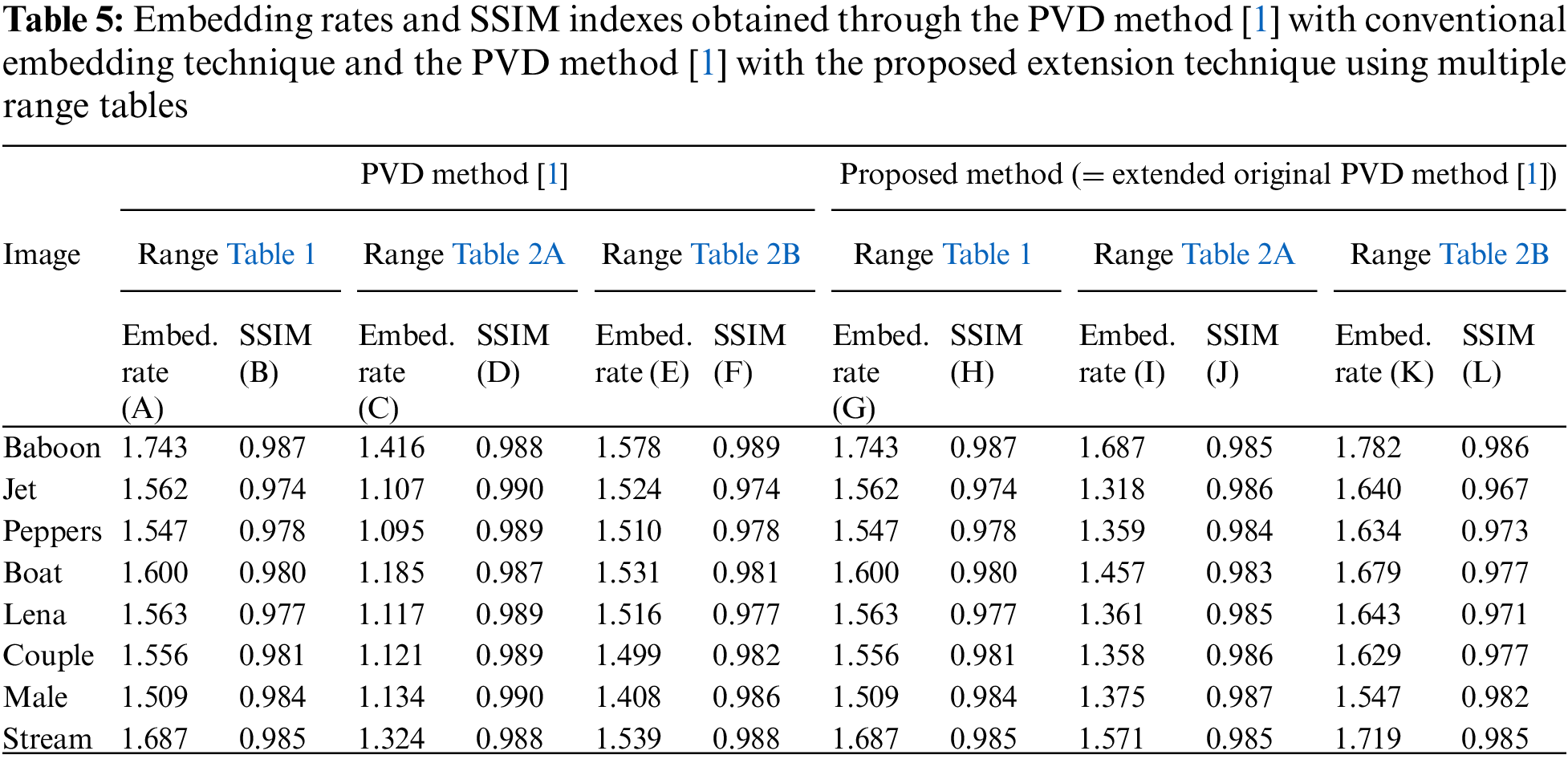
In addition, Table 5 shows the values of structure similarity (SSIM) indexes [35] yielded by the original PVD method [1] and the proposed method using the ranges in Tables 1, 2A,B, where SSIM stands for structural similarity and is another indicator used to assess image quality just like PSNR. The value of the SSIM ranges between 0 and 1, with a higher value indicating greater similarity between images. In columns (H), (J), and (L) of Table 5, the SSIM values of the resulting stego-images are all above 0.96, demonstrating the imperceptibility of the stego-image yielded by the proposed method.

5.3 Security Evaluation of the Proposed Method by RS Steganalysis

The dual statistics steganalysis method, RS steganalysis, proposed by Fridrich et al. [17], was employed to test the security of the stego-images yielded by the proposed method in this study. In Fig. 9, four RS diagrams generated from images in Fig. 8a through Fig. 8d are presented. In the diagrams, the x-axes depict the percentage of image pixels in the image in which secret messages are embedded, and the y-axes depict the percentages of regular and singular pixel groups with masks M = [0 1 1 0] and −M = [0 −1 −1 0]. In each diagram, the values of RM (i.e., regular pixel groups with mask M) are close to those of R−M (regular pixel groups with mask −M), and this association is also observed between the singular pixel groups SM and S−M. This finding verifies that the proposed steganographic method cannot be detected using the dual statistics method [17]. In other words, the proposed method is secure against steganalysis based on the dual statistics method.

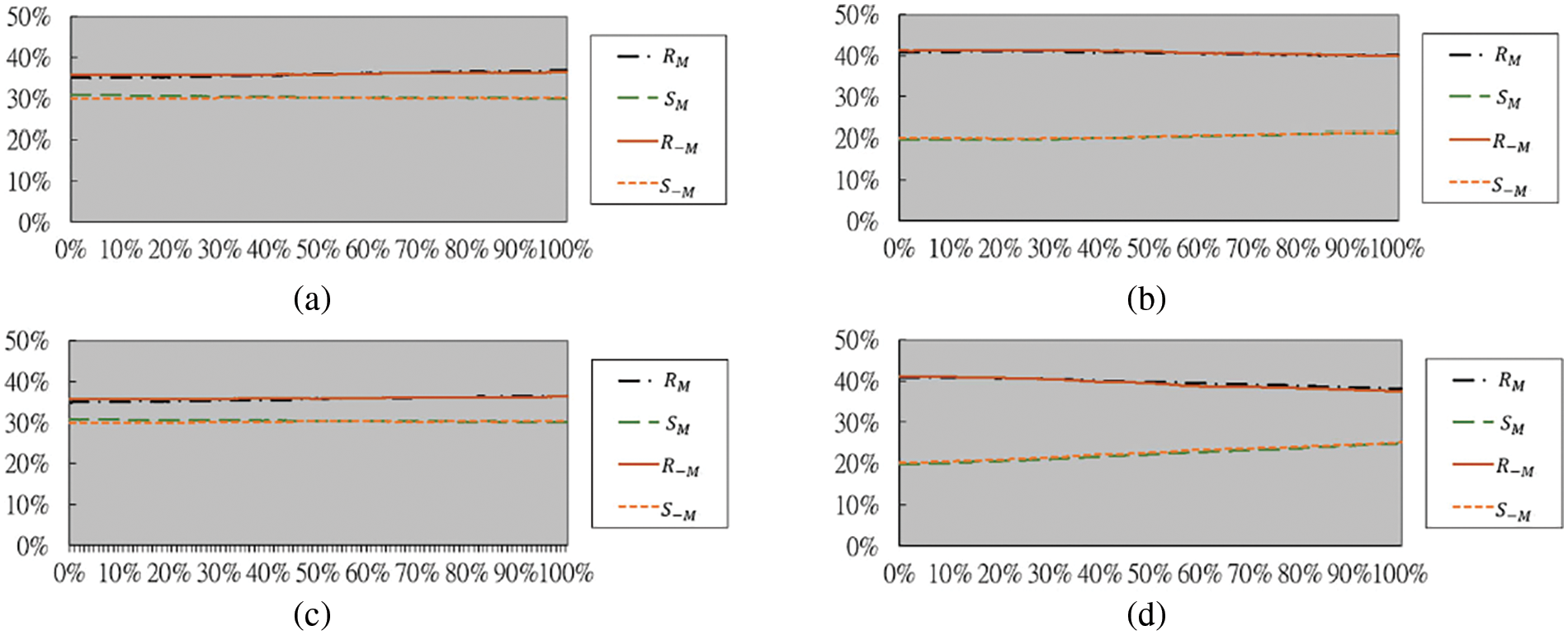
Figure 9: RS diagrams yielded by RS steganalysis for the images in Fig. 8. (a) Diagram generated from Fig. 8a. (b) Diagram generated from Fig. 8b. (c) Diagram generated from Fig. 8c. (d) Diagram generated from Fig. 8d

5.4 Demonstration of the Properties of the Swain Method [10] Extended by the Proposed Method– Part I: From Data Embedding Perspective

In the experiments above, the results obtained by the original PVD method proposed by Wu et al. [1] were compared to those obtained by the proposed method, which uses non-power-of-two range widths and carries out multiple-based number conversion. The results indicated that the proposed method can improve the data embedding rate. Theoretically, given a steganographic method that is derived from the PVD method [1] to yield higher embedding rates, if the method can be extended to use non-power-of-two range widths and multiple-based number conversion as done in the proposed method, then the high data embedding capability of the steganographic method can be maintained.

The Swain method [10], one of the methods derived from the original PVD method [1], was extended using the proposed method to demonstrate the above reasoning in this study. Then, the original Swain method and the extended version were employed to conduct experiments like those in Section 5.2, but with the image block resized to 3 × 3.

Specifically, in the experiments each 3×3 block is employed to construct eight pixel-pairs and one shared pixel (the central pixel in the block), into which message data are embedded by the PVD technique and 3-bit LSB substitution. Table 6 shows the quantization ranges used in Swain [10], in which the width of each range is taken to be a power of two, as done in the original PVD method. In addition, Table 7A,B show the two sets of quantization ranges used for the experiments with the width of each quantization range in the two tables being not limited to a power of two. In particular, the widths of the first and second quantization ranges in Table 7A were designed to be slightly smaller than those of the first and second ranges in Table 6. On the contrary, the widths of the first and second quantization ranges in Table 7B were designed to be slightly larger than those in Table 6.

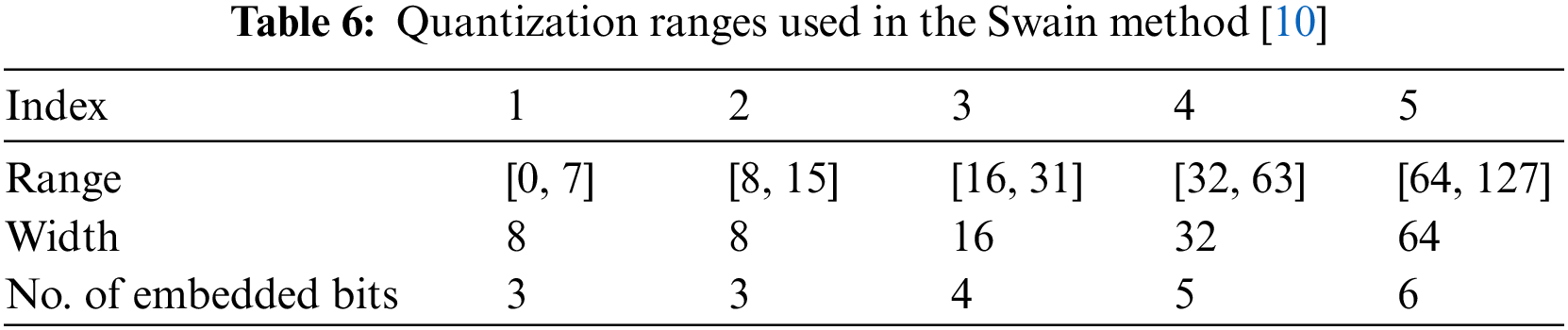
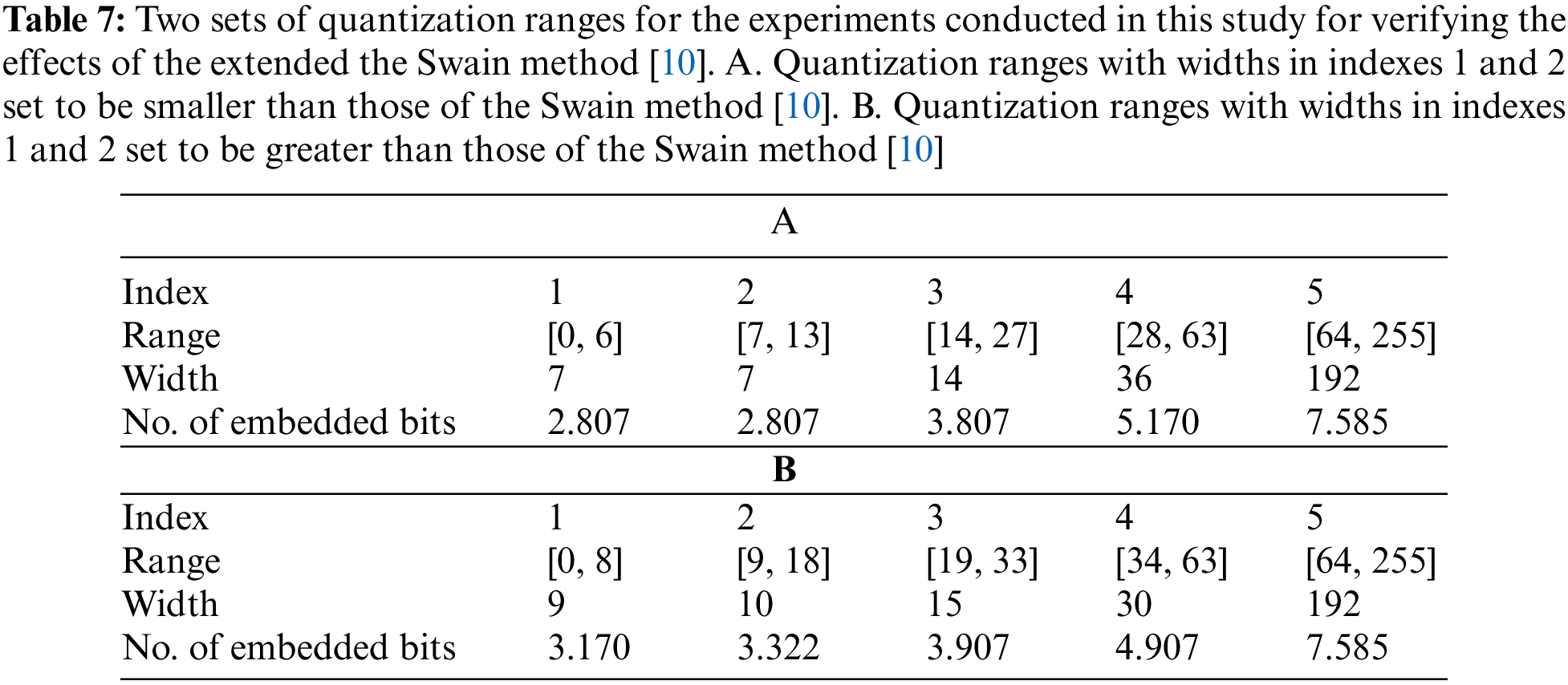
Table 8 shows the embedding rates and the values of the PSNRs yielded both by the original Swain method [10] using the ranges in Tables 6, 7A,B, respectively, as well as by the extended Swain method with multiple-based number conversion using the ranges in Tables 6, 7A,B, respectively. Accordingly, the following facts can be observed from Table 8.

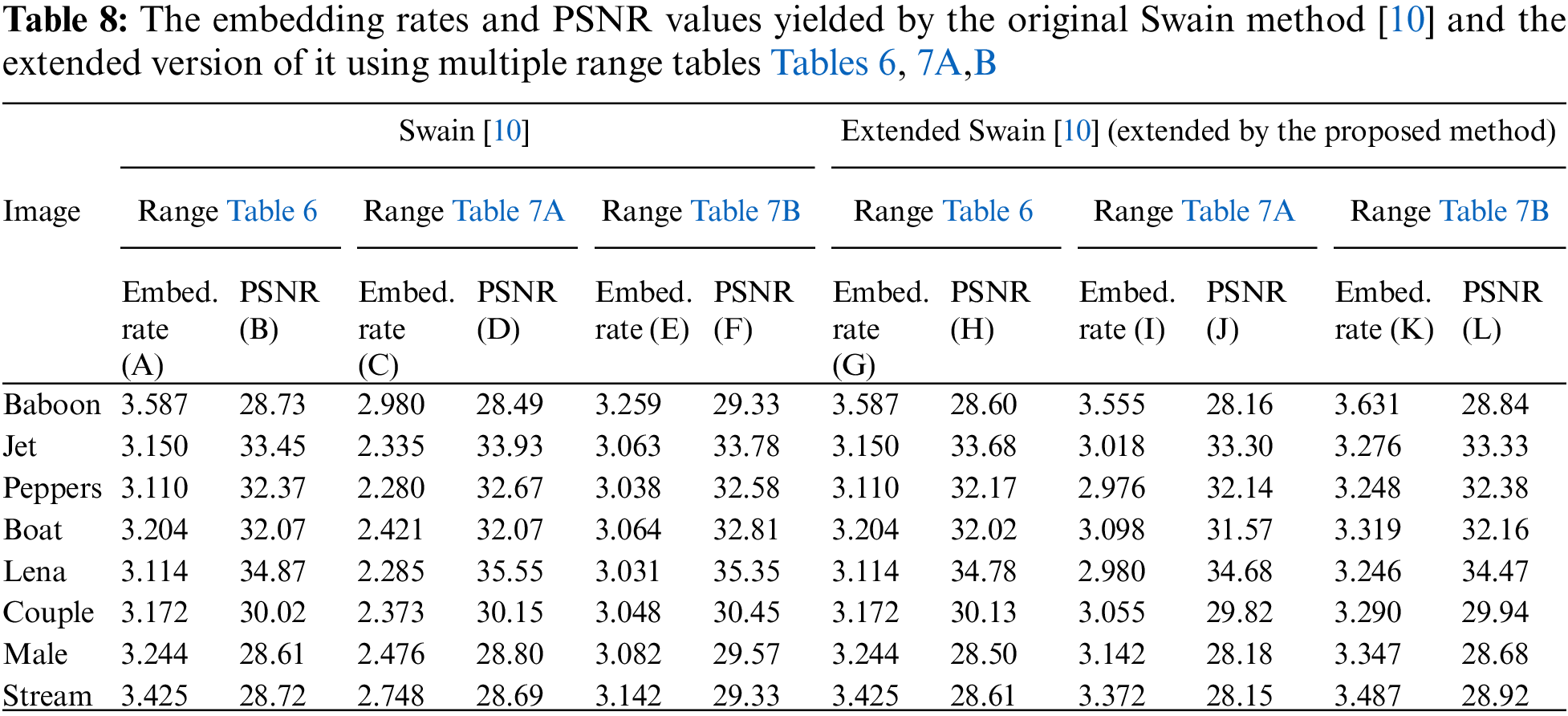
(a)   Columns (C) and (I) of Table 8 show the embedding rates yielded using the ranges in Table 7A, and columns (E) and (K) show the embedding rates yielded using the ranges in Table 7B; these results indicate that the embedding rates yielded by the extended Swain method are higher than those obtained by the original Swain method [10]. This observation proves that the proposed multiple-based number conversion scheme, together with the non-power-of-two range widths, can be utilized integrally to extend a PVD-based method, the original Swain method [10], to enhance the data-hiding capability, just like the case that the proposed method can extend the original PVD method [1] to yield higher data embedding rates, as demonstrated in Sections 5.1 and 5.2 described previously.

(b)   Columns (H), (J), and (L) in Table 8 exhibit that the resulting PSNRs of the stego-images yielded by the extended Swain method are all larger than 28, very close to those PSNRs yielded by the original Swain method as shown in Columns (B), (D), and (F) in Table 8, indicating the fact the qualities of the stego-images yielded by the original Swain method are maintained by the extended Swain method.

In order to ascertain more definitively the above fact of maintaining stego-image quality, the SSIM [35] indices were computed from the resulting stego-images yielded by the original Swain method as well as by the extended one, which is listed in Table 9 and showed the following fact. As shown in columns (H), (J), and (L) of Table 9, the values of the SSIM measures of the resulting steo-images are all above 0.90, again close to those yielded by the original Swain method, indicating again that the stego-image quality is kept by the extended Swain method.

5.5 Demonstration of the Properties of the Swain Method [10] Extended by the Proposed Method – Part II: From Security Perspectives

Additionally, efforts were made to compare the original Swain method [10] with its extended version from the steganalysis resistance perspective against the RS and PDH analyses. The results of these efforts are shown below.

Two examples of stego-images yielded by the extended Swain method and the corresponding results of RS and PDH steganalysis obtained in the experiments are depicted in Figs. 10 and 11, respectively. Fig. 11 indicates that the extended Swain method [10] with the proposed multiple-based number conversion technique using multiple range tables can also resist attacks from RS and PDH steganalysis.

Figure 10: The stego-images yielded by the extended Swain method [10] with multiple-based number conversion using multiple quantization range tables. (a) Original image. (b) Stego-image resulting from using the quantization ranges listed in Table 7A. (c) Stego-image resulting from using the quantization ranges listed in Table 7B

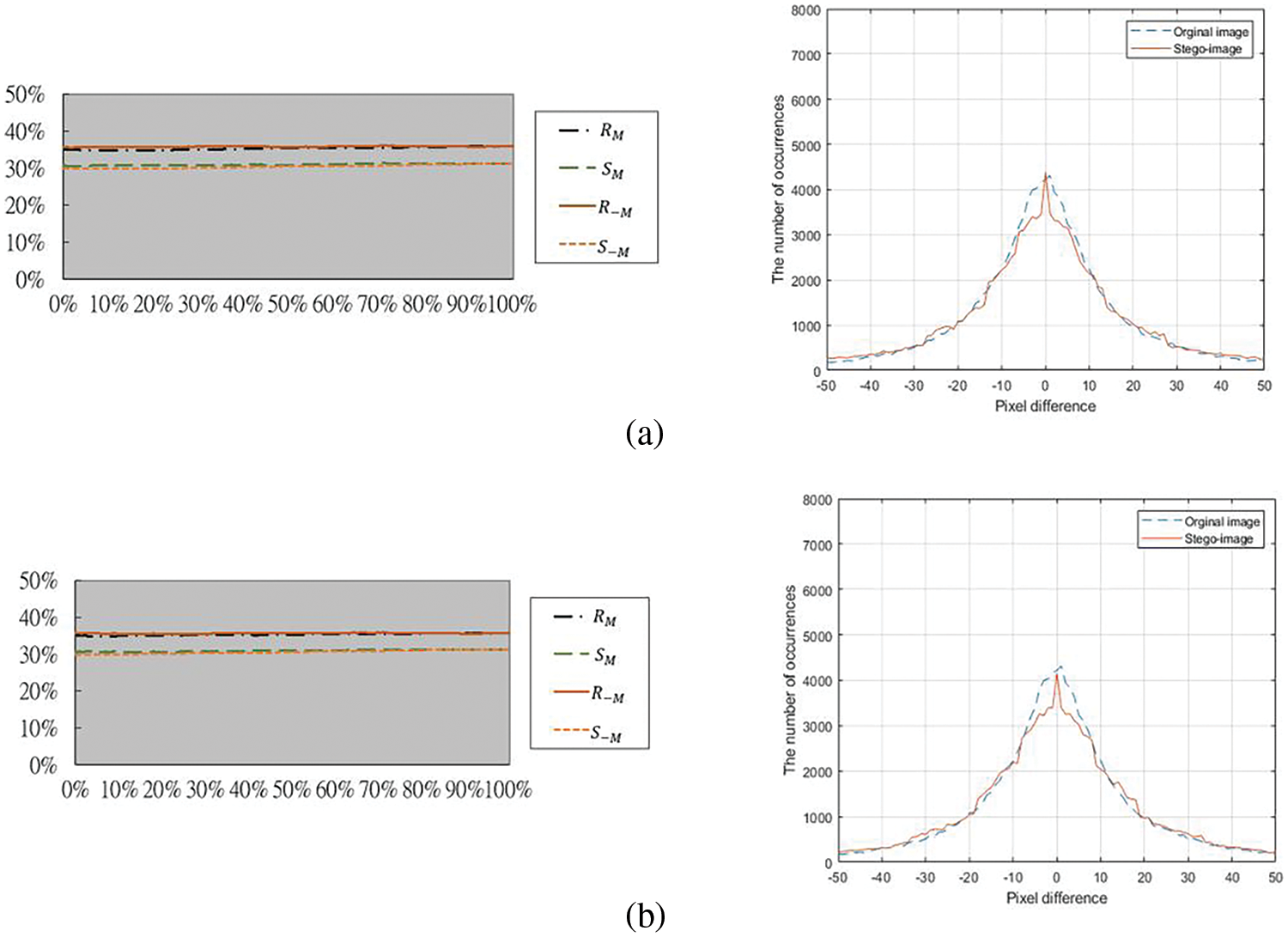
Figure 11: RS diagrams resulting from using the stego-images in Fig. 10 for the RS and PDH steganalysis. (a) Diagrams resulting from using Fig. 10b with the left diagram resulting from the RS analysis and the right for the PDH analysis. (b) Diagram resulting from using Fig. 10c for with the left diagram for resulting RS analysis and the right resulting from the PDH analysis

5.6 Experimental Results of an Application Example Using General Quantization Ranges

As an application example of the technique of using dynamically adjustable ranges mentioned in Section 4, the quantization table presented in Table 1 was used as the initially given quantization table. The cover images were employed to embed varying amounts of a random bitstream. The G values yielded using the proposed method to embed varying numbers of random bits into image Lena and the corresponding PSNR values of the resulting stego-images are presented in Fig. 12. The trend of the curves in the figure indicates that the G value becomes larger, and the PSNR values become smaller (the stego-image quality become worse) as the size of the embedded data increases.

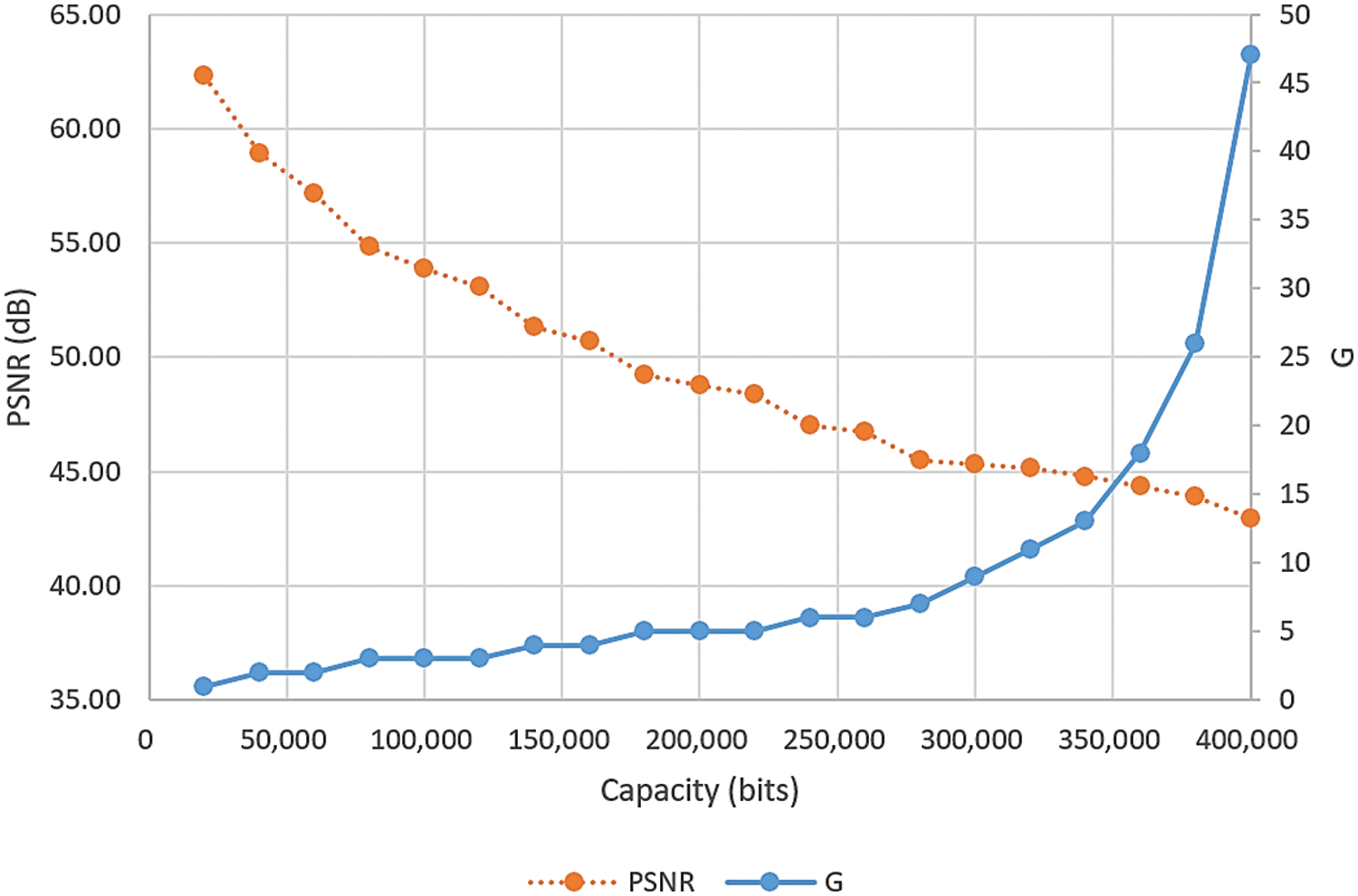
Figure 12: G values yielded when using the technique of using dynamically adjustable ranges to embed varying numbers of random bits in image Lena and the values of the PSNRs of the resulting stego-images

As a comparison, an experiment using the original PVD method [1] to embed the same sets of random bits into image Lena using the entire grayscale difference range of [0, 255] was conducted. The resulting PSNR values were computed and compared to those shown in Fig. 12. The comparison results are shown in Fig. 13, where the orange curve depicts the PSNR results already seen in Fig. 12, and the blue curve shows the PSNR values yielded by the original PVD method [1]. The former method with dynamic G values yields stego-images with better qualities.

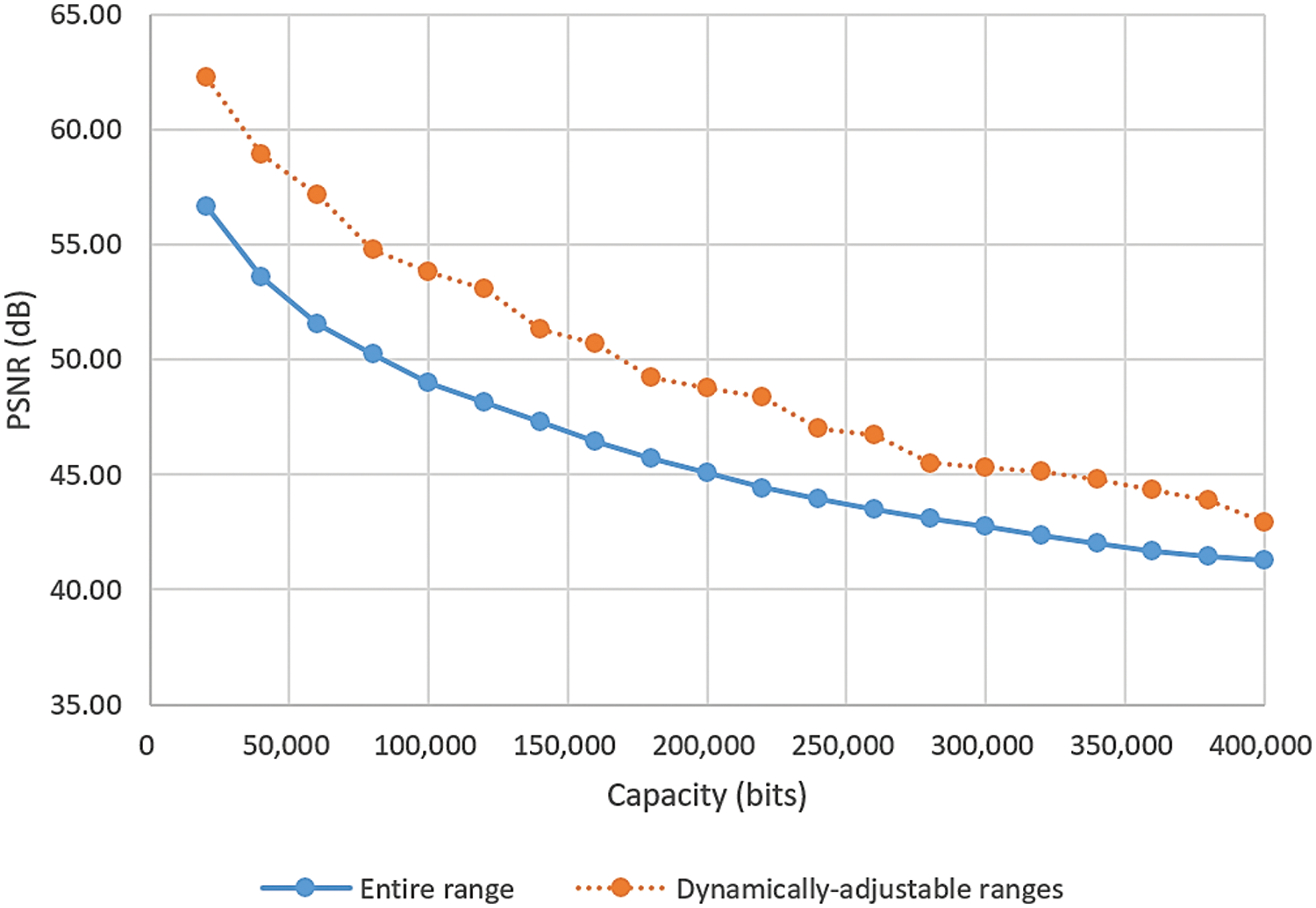
Figure 13: The values of the PSNRs yielded after embedding varying numbers of random bits in image Lena using the original PVD method [1] with the entire grayscale difference range of [0, 255] and the technique of using dynamically-adjustable ranges, respectively

6  Conclusions and Suggestions for Future Study

A new PVD data-hiding method with general quantization ranges is proposed. Under conventional PVD methods, the width of each quantization range to which a pixel pair’s difference value belongs is a power of two. The advantage of the proposed method is that it enables PVD methods to remove the restriction of power-of-two range widths and maintain high embedding rates. Firstly, the proposed method converts the bitstream of messages into digits in a multiple-based number, the bases of which are determined by the pixel pairs in the cover image. Then, the digits’ values are embedded in the pixel pairs in the image. In the process of data embedding, a pseudo-random mechanism is applied to achieve cryptography. Also, an RS steganalysis is conducted to show the security of the proposed method. In addition, the Swain method, which is derived from the PVD method, is employed to demonstrate that the proposed embedding technique can also be utilized to accomplish high embedding rates in the cases of using non-power-of-two range widths as the proposed method achieves high embedding rates in the original PVD method. Hopefully, using the proposed embedding technique, all the derived methods from the PVD method can achieve high embedding rates when using general range widths.

About future studies, at first, as demonstrated by the experimental results obtained in this study, the use of variable ranges of non-power-of-two widths seems to fix better the sensitivity of human vision to natural images, yielding better data embedding results and resulting image quality. Hence, in the future, it is suggested that non-power-of-two quantization range widths, together with the multiple-based conversion scheme, be used by all PVD-based data-hiding methods.

Next, regarding how to formulate the optimal width of each quantization range, it can be considered to minimize the resulting stego-image distortion for a secret message with a known size and to maximize the resulting data embedding capacity with reasonable image quality sensed by the human visual model. Both topics are worthwhile further explorations.

Finally, further research can also explore the application of multiple-based number conversion, and non-power-of-two quantization ranges in various aspects of digital signal processing, such as image processing, audio processing, and video processing. This can offer new opportunities for performance improvements across various technological domains.

Acknowledgement: Da-Chun Wu, the first author of this paper, wants to express his sincere thanks and appreciation to Wen-Hsiang Tsai at National Chiao Tung University, Taiwan. Tsai is the advisor who led Wu into the field of data-hiding when Wu was pursuing a doctoral degree. Also, Tsai is the corresponding author of the original PVD method [1]. Furthermore, the basic idea of the proposed method in this paper has been published previously in Wu [31] as a 5-page paper (in Chinese) with limited details and few experimental results. In this study, a great deal of improvement has been made, including (1) expanding the survey of related studies and increasing more references; (2) elaborating the presentation of the basic idea by detailed descriptions; (3) including additionally a data extraction algorithm (Algorithm 2) and describing its detailed steps; (4) giving additionally an application example using general quantization ranges; (5) using more cover images in the experiments; (6) using more quantization tables in the experimental for comparisons; (7) demonstrating additionally the proposed embedding technique by a method derived from the original PVD method for showing the generality of the proposed method; (8) providing more experimental results and analyses of them by tables, graphs or diagrams.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Da-Chun Wu, Zong-Nan Shih; data collection: Zong-Nan Shih; analysis and interpretation of results: Da-Chun Wu, Zong-Nan Shih; draft manuscript preparation: Da-Chun Wu, Zong-Nan Shih. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Wu DC, Tsai WH. A steganographic method for images by pixel-value differencing. Pattern Recognit Lett. 2003;24(10):1613–26. doi:10.1016/S0167-8655(02)00402-6. [Google Scholar] [CrossRef]

2. Cox IJ, Miller ML, Bloom JA, Fridrich J, Kalker T. Digital watermarking and steganography. 2nd ed. Burlington, MA: Morgan Kaufmann; 2008. doi:10.1016/B978-0-12-372585-1.X5001-3. [Google Scholar] [CrossRef]

3. Hussain M, Riaz Q, Saleem S, Ghafoor A, Jung KH. Enhanced adaptive data-hiding method using LSB and pixel value differencing. Multimed Tools Appl. 2021;80:20381–401. doi:10.1007/s11042-021-10652-2. [Google Scholar] [CrossRef]

4. Boroumand M, Chen M, Fridrich J. Deep residual network for steganalysis of digital images. IEEE Trans Inf Forensics Secur. 2018;14(5):1181–93. doi:10.1109/TIFS.2018.2871749. [Google Scholar] [CrossRef]

5. Sun B, Li Y, Zhang J, Xu H, Ma X, Xia P. Topic controlled steganography via graph-to-text generation. Comput Model Eng Sci. 2023;136(1):157–76. doi:10.32604/cmes.2023.025082. [Google Scholar] [CrossRef]

6. Wang RZ, Lin CF, Lin JC. Image hiding by optimal LSB substitution and genetic algorithm. Pattern Recognit. 2001;34(3):671–83. doi:10.1016/S0031-3203(00)00015-7. [Google Scholar] [CrossRef]

7. Wu HC, Wu NI, Tsai CS, Hwang MS. Image steganographic scheme based on pixel-value differencing and LSB replacement methods. IEE Proc Vis Image Signal Process. 2005;152(5):611–5. doi:10.1049/ip-vis:20059022. [Google Scholar] [CrossRef]

8. Chang CC, Chuang CJ, Hu YC. Spatial domain image hiding scheme using pixel-values differencing. Fundam Inform. 2006;70(3):171–84. doi:10.5555/2369276.2369277. [Google Scholar] [CrossRef]

9. Khodaei M, Faez K. New adaptive steganographic method using least-significant-bit substitution and pixel-value differencing. IET Image Process. 2012;6(6):677–86. doi:10.1049/iet-ipr.2011.0059. [Google Scholar] [CrossRef]

10. Swain G. High capacity image steganography using modified LSB substitution and PVD against pixel difference histogram analysis. Secur Commun Networks. 2018;1505896:1–15. doi:10.1155/2018/1505896. [Google Scholar] [CrossRef]

11. Shukla AK, Singh A, Singh B, Kumar A. A secure and high-capacity data-hiding method using compression, encryption and optimized pixel value differencing. IEEE Access. 2018;6:51130–9. doi:10.1109/ACCESS.2018.2868192. [Google Scholar] [CrossRef]

12. Hameed MA, Hassaballah M, Aly S, Awad AI. An adaptive image steganography method based on histogram of oriented gradient and PVD-LSB techniques. IEEE Access. 2019;7:185189–204. doi:10.1109/ACCESS.2019.2960254. [Google Scholar] [CrossRef]

13. Wu DC, Shih ZN, Wu JH. Modified multiway pixel-value differencing methods based on general quantization ranges for image steganography. IEEE Access. 2022;10:8824–39. doi:10.1109/ACCESS.2021.3138895. [Google Scholar] [CrossRef]

14. Chang KC, Chang CP, Huang PS, Tu TM. A novel image steganographic method using tri-way pixel-value differencing. J Multimedia. 2008;3(2):37–44. doi:10.4304/jmm.3.2.37-44. [Google Scholar] [CrossRef]

15. Sahu AK, Swain G, Sahu M, Hemalatha J. Multi-directional block based PVD and modulus function image steganography to avoid FOBP and IEP. J Inf Secur Appl. 2021;58(102808):1–16. doi:10.1016/j.jisa.2021.102808. [Google Scholar] [CrossRef]

16. Sahu M, Padhy N, Gantayat SS. Multi-directional PVD steganography avoiding PDH and boundary issue. J King Saud Univ Comput Inf Sci. 2022;34(10):8838–51. doi:10.1016/j.jksuci.2021.10.007. [Google Scholar] [CrossRef]

17. Fridrich J, Goljan M, Du R. Reliable detection of LSB steganography in color and grayscale images. In: Proceedings of the 2001 Workshop on Multimedia and Security: New Challenges; 2001; Ottawa, Ontario, Canada. p. 27–30. doi:10.1145/1232454.1232466. [Google Scholar] [CrossRef]

18. Zhang XP, Wang S. Vulnerability of pixel-value differencing steganography to histogram analysis and modification for enhanced security. Pattern Recognit Lett. 2004;25(3):331–9. doi:10.1016/j.patrec.2003.10.014. [Google Scholar] [CrossRef]

19. Sahu AK, Swain G. An optimal information hiding approach based on pixel value differencing and modulus function. Wireless Pers Commun. 2019;108:159–74. doi:10.1007/s11277-019-06393-z. [Google Scholar] [CrossRef]

20. Sahu AK, Swain G. Digital image steganography using PVD and modulo operation. Internetwork Indones J. 2018;10(2):3–13. [Google Scholar]

21. Roselinkiruba R, Sharmila TS. Performance evaluation of encryption algorithm using fruit fly optimization improved hybridized seeker and PVD algorithm. Int J Inf Technol. 2021;13:1797–803. doi:10.1007/s41870-021-00774-z. [Google Scholar] [CrossRef]

22. Phad VS, Bhosale RS, Panhalkar AR. A novel security scheme for secret data using cryptography and steganography. Int J Comput Netw Inf Secur. 2012;2:36–42. doi:10.5815/ijcnis.2012.02.06. [Google Scholar] [CrossRef]

23. Filler T, Judas J, Fridrich J. Minimizing additive distortion in steganography using syndrome-trellis codes. IEEE Trans Inf Forensics Secur. 2011;6(3):920–35. doi:10.1109/TIFS.2011.2134094. [Google Scholar] [CrossRef]

24. Li W, Zhang W, Li L, Zhou H, Yu N. Designing near-optimal steganographic codes in practice based on polar codes. IEEE Trans Commun. 2020;68(7):3948–62. doi:10.1109/TCOMM.2020.2982624. [Google Scholar] [CrossRef]

25. Wu DC, Tsai WH. Data-hiding in image via multiple-based number conversion and lossy compression. IEEE Trans Consum Electron. 1998;44(4):1406–12. doi:10.1109/30.735844. [Google Scholar] [CrossRef]

26. Wu DC, Tsai WH. Embedding of any type of data in images based on a human visual model and multiple-based number conversion. Pattern Recognit Lett. 1999;20(14):1511–17. doi:10.1016/S0167-8655(99)00118-X. [Google Scholar] [CrossRef]

27. Zhang X, Wang S. Steganography using multiple-base notational system and human vision sensitivity. IEEE Signal Process Lett. 2005;12(1):67–70. doi:10.1109/LSP.2004.838214. [Google Scholar] [CrossRef]

28. Geetha S, Kabilan V, Chockalingam SP, Kamaraj N. Varying radix numeral system based adaptive image steganography. Inf Process Lett. 2011;111(16):792–97. doi:10.1016/j.ipl.2011.05.013. [Google Scholar] [CrossRef]

29. Tanga MW, Wen SG, Chena XL, Hu J. An image information hiding using adaptation and radix. Optik. 2015;126(23):4136–41. doi:10.1016/j.ijleo.2015.07.200. [Google Scholar] [CrossRef]

30. Chen WS, Liao YK, Lin YT, Wang CM. A novel general multiple-base data embedding algorithm. Inf Sci. 2016;358:164–90. doi:10.1016/j.ins.2016.03.045. [Google Scholar] [CrossRef]

31. Wu DC. A pixel-value differencing technique for image steganography based on general quantization ranges. In: Proceedings of the 2021 Conference on Information Technology and Applications in Outlying Islands; 2021; Kinmen, Taiwan. p. 1138–42. [Google Scholar]

32. Ma B, Li K, Xu J, Wang C, Li J, Zhang L. Enhancing the security of image steganography via multiple adversarial networks and channel attention modules. Digit Signal Process. 2023;141:1–19. doi:10.1016/j.dsp.2023.104121. [Google Scholar] [CrossRef]

33. Sahu AK, Swain G. A novel multi stego-image based data-hiding method for gray scale image. Pertanika J Sci Technol. 2019;27(2):753–68. [Google Scholar]

34. Tseng WH, Leng HS. A steganographic method based on pixel-value differencing and the perfect square number. J Appl Math. 2013;2013(1):1–8. doi:10.1155/2013/189706. [Google Scholar] [CrossRef]

35. Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process. 2004;13(4):600–12. doi:10.1109/TIP.2003.819861. [Google Scholar] [PubMed] [CrossRef]