A Linked List Encryption Scheme for Image Steganography without Embedding

1  Introduction

The convergence of human life with the digital world is progressively expanding. In today’s digital landscape, communication spans not only private networks but also extends to more public platforms. The escalating demand for digital data and information transactions has, in turn, resulted in a surge in cybercrime. Therefore, there is a pressing need to develop secure methods to protect transactions and information storage from hackers. Steganography emerges as a solution, employing digital media as a cover to conceal secret data and deceive potential adversaries and hackers. Among the array of digital media options available, such as images, videos, audio texts, etc., digital images hold a prominent position. Many researchers gravitate towards digital images, making them the focal point of digital steganography research due to their widespread use, diverse formats, and rich content.

In the field of digital image steganography, Friedrich classified carriers into cover selection, cover modification, and cover synthesis according to different manipulation methods [1]. Cover selection involves selecting suitable carriers from a database by the secret message to be conveyed. The varying sizes and dimensions of the carriers can represent different meanings within the messages. The carrier modification method stands out as the most extensively researched method. Its core concept revolves around modifying the content of the carrier to embed the secret message while minimizing changes to the carrier image through a distortion function. This strategy aims to evade steganalysis checks effectively. On the other hand, cover synthesis pursues the objective of sidestepping distortion in the steganographic image by either creating an ideal cover or directly generating the steganographic image.

However, it remains undeniable that even the most advanced steganographic methods can produce distortions to the cover image. These distortions may provide steganalysis tools [2] with the means to detect the presence of the secret message itself. This challenge is pervasive across almost all image steganography techniques [3]. Therefore, from this point of view, the significance of coverless steganography (CLS), also known as Steganography without Embedding (SWE), becomes paramount. The core concept of this method revolves around capturing the unique connection between specific features in the cover image and the secret message. This approach aims to facilitate the covert transmission of the message without the need for traditional embedding, addressing the limitations posed by potential distortions in the cover image.

To solve persisting issues in existing digital image steganography methods, such as limited steganographic capacity, reliance on high-quality image datasets, and vulnerability to interference in complex transmission environments, this paper introduces a linked-list steganography scheme. This innovative approach transforms the image into multi-linked list structures, aiming to establish connections between the secret message and the image. The main contributions of this paper are as follows:

1.    A linked-list encryption scheme for SWE is proposed for the first time, which reconstructs the image into multi-linked list structures and identifies optimal lists through an addressing algorithm to facilitate message delivery. Notable, the scheme refrains from modifying the cover image, ensuring excellent security and a flawless message reduction rate. Moreover, it operates without constraints imposed by the carrier size of the dataset.

2.    The principle of linked-list steganography is analyzed in depth. The relationship between steganographic capacity and image size, the impact of addressing algorithms, and other factors on steganography are verified. The proposed linked-list construction scheme exhibits robustness by effectively resisting multiple image attacks.

3.    Evaluation results on multiple datasets confirm the feasibility as well as the effectiveness of the proposed encryption, which is robust against various attack methods, including noise attacks and filter interference while simultaneously guaranteeing steganography, security, and a high message reduction rate.

2  Related Work

Rustad et al. [4] summarized the latest research results on image steganography published since 2015, dividing image steganography into four categories based on target, domain, model, and reversibility. The goal-based steganography method mainly achieves four objectives: imperceptibility, payload, security, and robustness. The imperceptibility of targets and payloads typically relies on spatial domain-based statistical embedding models, but some methods use transformation domains, such as the earliest least significant bit (LSB) algorithm.

As the most popular content adaptation algorithms currently available, wavelet obtained weights (WOW) [5] and HIgh-pass, Low-pass, and Low-pass (HILL) [6] can automatically embed information into noisy or textured areas of an image to avoid identifying changing regions. In addition, there are also many steganographic methods on the transformation domain, among which the earlier and representative methods such as Jstem [7], F5 [8], JPEG Universal Wavelet Relative Distortion (J-UNIWARD) [9] are among them.

Recently, several new technologies have emerged in the field of spatial domain based steganography [10], such as recursive information hiding schemes, enhanced adaptive data hiding, hybrid methods, and pixel strength based embedding. Statistical models themselves are not only used in the spatial domain but also the transformation domain. In addition, in some of the latest methods, statistical-based models are considered less secure, and high-dimensional models are widely used instead. It is generally believed that steganography using high-dimensional models has better security and robustness, but its payload is relatively small. In addition, there are also some other steganographic methods classified as steganographic derivative methods, sociological steganographic methods, and special purpose steganography.

Coverless Image Steganography (CIS), also known as SWE, is a new steganography idea and concept that differs from the general image steganography discussed earlier. One idea is to realize communication by using a mapping-based approach [11–14]. Elshoush et al. devise a mapping between the message and the image and utilized the position array in which the secret message is recorded in the image [15]. Zhou et al. [16] first achieve this goal by utilizing the features in the cover image, specifically using techniques such as pixel brightness, color, texture, edges, contours, and advanced semantics to “generate” the cover. In short, the main contribution of CIS is that secret communication can be achieved without modifying the cover image, making it impossible for steganalysis tools to detect confidential information. In the development of CIS methods, the goal is generally to improve the accuracy of feature reading, to make image retrieval more appropriate, accurate, and precise. For example, research [17] uses gradient histograms, paper [18] uses partial repetition, paper [19] uses Generative Adversarial Networks (GANs), paper [20] uses Latent Dirichlet Allocation (LDA) topic classification, paper [21] uses dense network features and Discrete Wavelet Transform (DWT) sequence mapping, and paper [22] uses optical label recognition and machine learning.

Another new type of steganography method is based on GAN steganography. The increasingly powerful capabilities of steganalysis based on Convolutional Neural Networks (CNN) pose a threat to the security of steganalysis. Therefore, GAN-based methods are commonly used to improve the quality of encrypted images by combating noise, to obtain image structures consistent with the information to be embedded [23]. Among these methods, the Minimizing the Power of Optimal Detector (MiPOD) method [24] is one of the pioneers of GAN-based steganography technology. Secondly, methods such as Invisible Steganography via Generative Adversarial Network (ISGAN) [25] focus on increasing invisibility. Adversarial ENhancing (AEN) [26] and Hiding Images via GAN (HIGAN) [27] focus on minimizing distortion and improving security. Li et al. [28] propose another GAN method based on cross-feedback to improve security. Another GAN method has been proposed [29], which uses Sparse Coverage Enhancement (SPS-ENH) to increase the security of secret messages and minimize distortion. Peng et al. improve message extraction accuracy by iteratively updating noise vectors using gradient descent of the generator [30].

The cover selection method in image steganography has a long research history and was first proposed in research [31]. This method selects appropriate masks based on the image features or attributes embedded with secret information bits to maximize the message embedding rate and minimize detectability. There are not many studies on steganography like this, but this technology is constantly evolving and applied to some of the latest steganography methods, such as [32–36]. These methods use machine learning and deep learning to study features and select cover images, and even combine selection techniques and hidden generation to use GAN [37]. In a new CIS scheme based on image selection and star generated adversarial networks proposed in the article [38], image mapping is established between secret information and facial attributes. High-quality steganographic images were constructed using this mapping relationship. Paper [39] propose an intelligent search method based on deep learning for uncovered information hiding mapping relationships, but it still has not solved the dependency problem on datasets. Paper [40] establishes a mapping relationship between the target label and the binary sequence and extracts information through multi-target recognition technology. Paper [41] maps the message to the label of the image and trains the category extractor.

Among the steganography methods above, the most researched one is embedded steganography, where the overall goal is to modify parts of the carrier to embed the secret message and keep the deformation of the carrier as small as possible. This can be summarized as formula (1).

Ext(Emb(cover,m)=m ∀m∈{0,1}m(1)

And that the difference between Emb(cover,m) and m is minimized or difficult to count. However, this method inevitably causes a certain degree of image distortion because it modifies the information of the original carrier, and often becomes a key research target for steganography analysis techniques.

More current research has generative steganography methods, often using deep neural networks, combined with a variety of image generation techniques, the information is transformed into image content, and can be extracted and restored. Such as formula (2) or formula (3).

Ext(Gen(noise,m)=m ∀m∈{0,1}m(2)

Ext(Gen(m)=m ∀m∈{0,1}m(3)

But this idea currently on there are many problems, such as the quality of the image generated with a limited size of resolution, the reduction of the message is not accurate enough, the image load is limited, and other issues.

3  Method

3.1 Programme Overview

The framework proposed in this paper is based on the idea of SWE, which deconstructs the pixel points of the image into the form of nodes in a linked list, and through the predefined addressing algorithm, the steganographic transmission of the message can be accomplished without any modification of the cover picture. The secret message can be completely restored according to the extracted parameter key, such as the formula (4).

Ext(cover,key)=m  ∀m∈{0,1}m(4)

As shown in the Fig. 1, the secret message to be delivered is first encrypted as well as compressed to reduce the amount of data to be delivered. Then it is transformed into a binary bit stream and divided into multiple message segments. After that, according to the addressing algorithm, the image is transformed into the form of a linked list, combining the information fragments to find the optimal list, and returning the relevant extracted information key. The optimal linked list searching method can be categorized into two ways: fixed-length addressing and optimal-length addressing. When the receiver receives the image, the message can be extracted and recovered according to the decoding key.

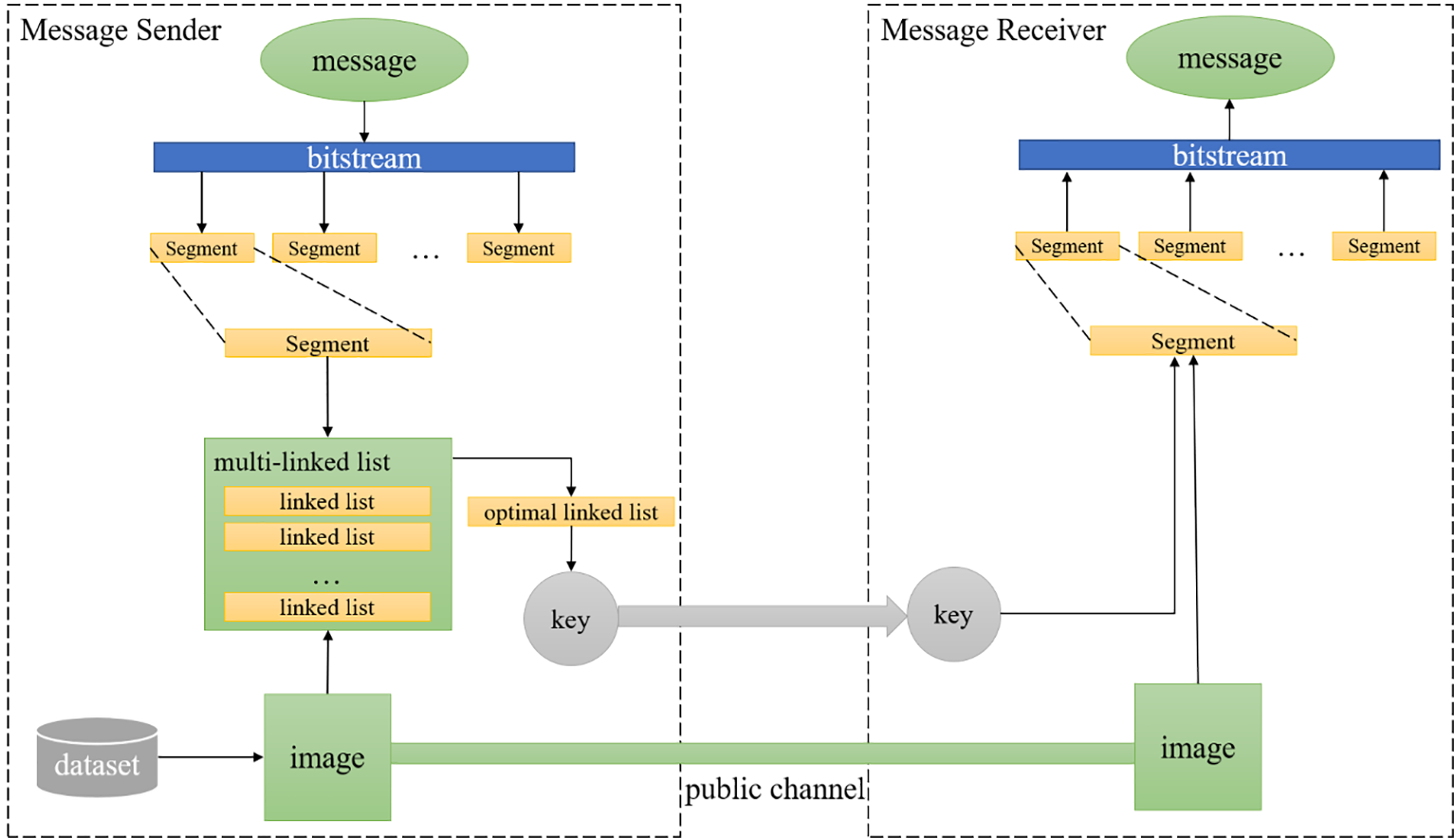
Figure 1: Process demonstration of the linked-list encryption scheme

3.2 A Theory of Linked List Method for Steganography without Embedding

Although the current commonly used digital images have many different formats, they have in common that they are composed of a very large number of pixel dots, which provides the possibility for the embedding-free steganography framework proposed in this paper. When looking at a pixel alone, it is easy to see that it is a decimal number, which tends to be in the range of 0–255, i.e., it can represent 28 numbers, and thus we can transform it into an 8-bit binary number.

Associated with the node structure of the linked lists, we can divide the 8-bit number into two parts as a simple chain table structure, for example, the first 7 bits as a node's pointer field, and the last 1 bit as the node’s data field. Then, we can find the next node according to the content of the pointer field of the node, according to the set addressing method, such as based on the length of the pointer, backward node lookup method, to find the next node. When following this method, we can get a chain table with the starting pixel as the head. Of course, if we do not stop, the chain can continue forever, as Fig. 2. A bitstream is obtained by reading the contents of the data fields in the order of the nodes in the chain table and concatenating them.

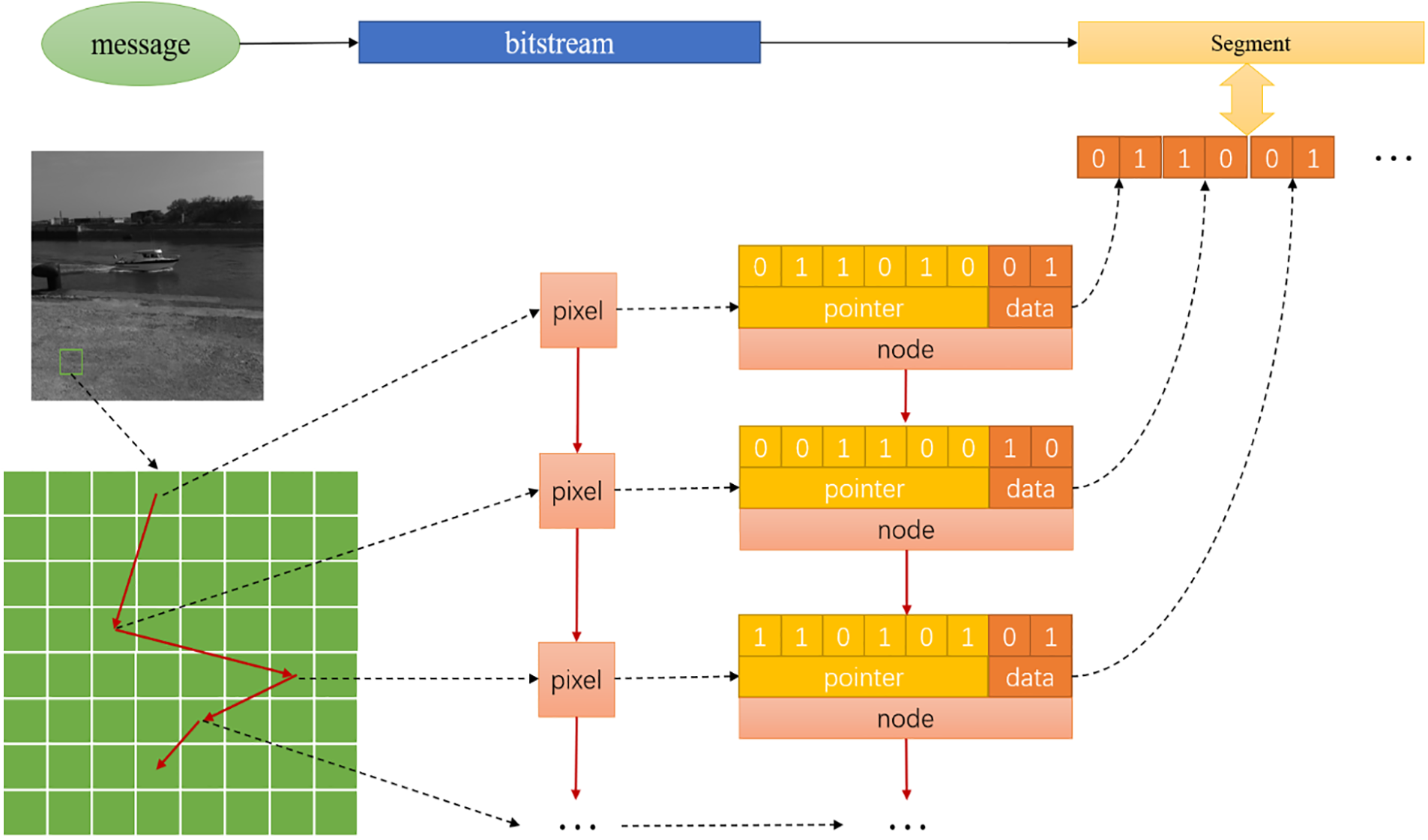
Figure 2: The construction process of linked lists

This bitstream provides the basis for the possibility of steganography, i.e., if the secret message we want to pass happens to be the same as the bitstream obtained from this chained table we constructed, then we have achieved unmodified message passing. The fact is, however, that a randomly constructed piece of our chained table will hardly fulfill the requirement. Therefore, to accomplish the goal, it is worthwhile to reverse the above order of operations: we first prepare the message bitstream to be delivered, and according to the content of this bitstream, verify the structure of the chained table starting from different pixels in the image until we find a suitable chained table whose data fields form the same bitstream as the message bitstream. If we can find this particular chained table, the covert delivery of the message is realized, which is called the optimal chained table in this paper.

In this process, we need to accomplish the following things, constructing the chained table, and creating the best way to find the chained table. Further, the part of constructing the chain table mainly has the creation of nodes (both pointer and data fields), and setting the rules for pointing to the chain table. Because the most important part of this is the best chain table finding method, which will affect the creation of the chain table and nodes, so to understand and explain more clearly, this paper will first introduce the best chain table following method in detail.

3.3 Methods for Finding the Optimal Linked List

Based on the above considered ideas, we have successfully changed our goal from hiding secret messages to how to find the special linking table, i.e., the optimal linking table, according to the secret messages. The optimal chained table search methods proposed in this paper can be categorized into two ways, fixed-length search, and variable-length search, according to the length of the secret message.

3.3.1 Fixed Length Search Method

The first way, fixed length finding, is discussed first. If we fix the length of the message to be delivered by each chain table, then we can start from the chain table composed of the first pixel point based on the message content, and compare them one by one according to the order, until we end the search process when we find the optimal chain table, or we end it after searching the whole chain table, which means that the optimal chain table is not found. Of course, at this time we can change the carrier image for another attempt. The specific algorithm is shown in the following Algorithm 1:

In this algorithm, the input is the cover image and the message fragment to be delivered and the output is the key. The specific step is to consider all the pixels in the image as independent nodes and traverse them to see if the linked list starting at that node is the best one, i.e., the same as the message fragment. If the best link is found, the function returns the position information of the starting node as a key. And in the process of comparing each link, such as the function searchNode, to check whether it is the same as the corresponding bit of the message fragment in order of the nodes, one by one. If it is the same, the function continues to check the next node until the message fragment is checked and returns the success result 1, while if the corresponding bits are not the same, the function directly returns the failure result 0.

The second function of the algorithm is to determine whether each link list is the same as the message fragment or not, so the complexity of this function should be O(i). In the first function, it is to judge all the nodes, so the complexity of this finding algorithm can be calculated should be O(i * n). Because of this the length of the message fragment indicated by i is limited, much smaller than the number of nodes, that is, the number of times n need to loop, so the time complexity of the algorithm is O(n).

3.3.2 Variable Length Search Method

Then there is the second non-fixed-length finding method, i.e., the length of the message is not fixed, and the longest possible optimal chain list is found in the image. Specifically, each pixel point in the image is matched as the beginning of the chain table, and for the secret message, the length of the message that can be carried is calculated, after which, the chain table with the largest length among them is selected as the best chain table. The specific process is shown in the following Algorithm 2:

In this algorithm, the inputs are the cover image and the message fragment to be delivered and the output is the key. The specific step is to consider all the pixel points in the image as independent nodes and traverse them to calculate the number of bits that a linked list starting at that node can match the message fragment and save it. After that all the bit lengths are compared and the largest result is selected as the message fragment length that can be delivered by the image this time and the list corresponding to that result is found. The positional information of the initial node of that list and the bit length are used as the output of the function, i.e., the key. And in the process of comparing each chain table, such as the function searchNode, to compare with the message fragment corresponding to the bit is the same or not, in the order of the nodes, one by one. If it is the same, then call itself to continue to control the next node until the message fragment control is completed, return the length of the message fragment, and if the corresponding bit is not the same, then return the current length of the same bit for the analysis of the main function.

The algorithm follows the same inference as the fixed-length search algorithm described above, where the number of loops k in the second function indicates the number of bits that can be matched with the message fragment. Because of its finite length, which is much smaller than the number of nodes, the time complexity of this algorithm is again O(n).

There are advantages and disadvantages of the above two methods, the first fixed-length search method has less computational overhead because it is likely that it does not need to compare all the linked lists, and it can compute the result faster. Moreover, the decoding key of this method only needs the position information of the starting pixel, which is characterized by simplicity and lightweight. However, this method does not ensure that the best chain table can be found for each carrier image, and this success rate is related to the length of the message that the chain table needs to carry, and the related analysis is arranged in the analysis section. The second variable length method, on the other hand, ensures that an optimal link table can be found for each specified image carrier, but at the cost of more computational overhead and additional information about the decoding key, the position of the starting pixel, and the message length.

3.4 The Construction Method of Linked Lists: Pointing Rules

In the framework proposed in this paper, after completing the optimal chain table finding method, the other work that needs to be done is to construct the chain table, which consists of two aspects, the node pointing rule and constructing the data domain and pointer domain of the nodes. This section will discuss how to construct the chain table part.

For the construction of a chained list, the following process is generally followed: use a pixel in the image as the starting node of the chained list, search the pointer field of that node to obtain the pointing length, and find a new pixel as the next node based on the pointing rule. In this process, we can deduce that the pointing rule does not affect the efficiency of steganography and the subsequent node construction method based on it only affects the robustness, so we can use any custom rule which not only improves the robustness of the algorithm but also makes it more difficult to decipher the information. In this section, the default pointing rule used is the most basic sequential pointing, which means that from the current node, the next pixel is found as a new node according to the pointing length in the order of left to right and top to bottom.

However, there is still a problem of duplicate node pointing in this process. If multiple linked lists are pointing to the same node at the same time, the subsequent nodes of these linked lists will be the same. This situation may cause some nodes in the image to not participate in the construction of the linked list, and may also result in multiple linked lists being the same. It is also easy to have cases where a pointing length of 0 causes a node to point to itself. Both of these situations will affect the number of different linked lists N that can be queried, reducing the success rate of searching for the best linked list. Therefore, to address the aforementioned issues, this section proposes a linked list construction scheme based on offset terms.

In this scheme, the first step is to construct an offset table equal to the size of the image, filled with different positive integers as offset terms. When searching the pointer field of a node, after obtaining the pointing length, it is added to the offset term corresponding to the position of the previous node and combined with the magnification factor to obtain the new pointing length, and then the next node is searched according to the pointing rule. It is worth adding that since there is no correlation between different carriers and the image size is relatively fixed, the same offset table can be used. Furthermore, in practical applications, both communication parties can use predefined and identical offset tables to search for the best linked list, which means that the offset table does not need to participate in the common channel for transmission.

The case where the subsequent nodes are the same when pointing to the same node in multiple linked lists is completely eliminated in this scheme. For example, if Node1 and Node2 in two different chains l1 and l2 point to the same next node Nodenext without an offset table, l1 and l2 will not be the same because the offset terms of Node1 and Node2 are not the same as each other, so the length of pointing to the Nodenext will be different, and therefore l1, l2 will not be the same. In addition, the case of pointing to itself due to a node pointer field of 0 is also solved.

3.5 The Construction Method of Linked Lists: Node Construction

Finally, regarding the node construction method part, based on the above chained implicit writing principle, as well as to cope with different application scenarios, this paper proposes the following different node construction schemes, which will be introduced in detail in this section. The first node construction method is based on the LSB named LSB-K, the second construction method utilizes the changing trend of the image, and the third method utilizes the image to construct a deep multi-headed linked list scheme.

The easiest to construct and at the same time the simplest solution is to follow the idea of the LSB method, and when transforming the pixels of the image into nodes of the chain table, the last valid bit of the image is used as the data field of the node. As for the pointer field, the other 7 valid bits should be designated as a pointer field as a matter of course. However, there will be the problem of insufficient robustness, i.e., the carrier image is very susceptible to changes due to external disturbances, which leads to message reduction errors.

Therefore, in this section, this paper proposes a scheme called LSB-K to avoid vulnerability by shifting the effective bits corresponding to the data domain and pointer domain of a node to higher positions. Specifically, the k-th of the eight valid bit bits is designated as the data and pointer domains of the node, and the amplification factor q is added to increase the pointing length of the node, so as to avoid the situation where valid nodes are clustered in the carrier image.

4  Comparison and Analysis

4.1 Analysis of Security and Message Restoration Rate

For the discussion and judgment of digital steganography, there are mainly the following indexes: security, message restoration rate, steganographic capacity, and robustness.

In the steganography scheme proposed in this paper, because there is no change to the carrier image, it has a very high security and can be said to be able to completely avoid any form of steganography analysis and detection. At the same time, if there is no change in the image carrier during message extraction, the message can be extracted completely and accurately. Of course, if there is an attack during transmission or due to compression and distortion, the extraction accuracy will be affected, and this part is discussed in the subsection of robustness analysis.

4.2 Analysis of Steganographic Capacity

This section mainly analyzes the steganography capacity. Based on the relevant deductions about the two best linked list search algorithms in the above chapters, we can conclude that the steganography capacity of the scheme is mainly related to image size and precision. Admittedly, the probability of matching a message fragment is very small for a single linked table. However, in the scheme proposed in this paper, the whole image is mapped into a very large number of linked lists, which in practice will be in the hundreds of thousands, so the probability of finding the best list for the whole carrier image is not very small.

Firstly, we analyze the fixed-length finding of the optimal chain table of the first method, according to the above equation, it can be seen that the relationship between the image size N and the message length m can determine the success probability of the optimal chain table of length m, as the formula (5) and the proof is placed in Appendix A.

P1(m,N)=1−(1−pm)N(5)

The parameter m is the length of a matching message segment, N is the number of linked lists used for matching, which is related to the size of the image, and p is the matching probability of a single bit, which is set to 1/2 in this article because the data of the message and the linked list nodes are uniformly distributed for 0 and 1.

The variation of this is shown in Fig. 3. From the first subfigure, it can be seen that when performing the best linked list search on each image, the search probability increases with the increase of image size N, but decreases with the increase of message fragment length. We divide the success probability of finding the acceptable best linked list into several levels: 99%, 95%, 90%, and 80%, and observe the mutual changes between message length m and image size N under the different conditions mentioned above, as shown in second subfigure. Obviously, we can segment message fragments according to actual needs in different scenarios. Based on practical operational experience, it can be seen from the figure that if the carrier image is a small-sized image, selecting 7–10 bits for the message segment is feasible. If the size of the image is approximately 250,000, which is a common 500 × 500 size, controlling the length of the message segment to 14 or 15 bits is very effective.

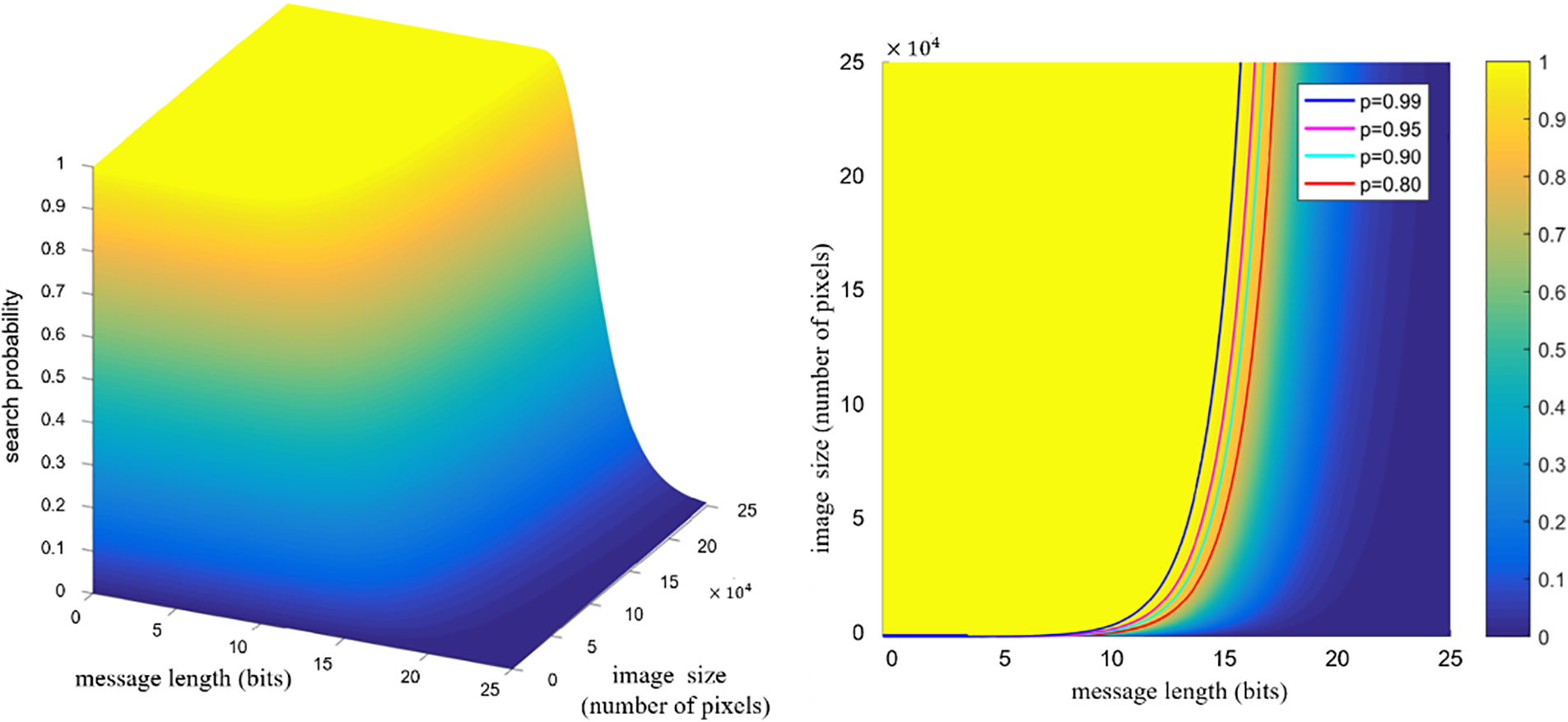
Figure 3: Analysis of factors for searching fixed length optimal linked

Next, we will continue to analyze the second method, which is the variable length search algorithm for the best linked list. The relationship between image size N, message length m, and the search rate of the best linked list can also be calculated, that is, the probability of obtaining the best linked list length when using a variable length search algorithm on an image, as shown in the formula (6) and the proof is placed in Appendix B.

P2(m,N)=(1−pm+1)N−(1−pm)N(6)

Similar to the above equation, the matching probability of p for a single bit is set to 1/2. According to the changes shown in Fig. 4, it can be seen that regardless of the size of the carrier image, there is always a high probability of finding the best linked list, and among common image sizes, the length of message fragments is basically in the range of 10–20. In addition, consistent with fixed length search methods, under certain acceptable search expectations, the larger the image, the longer the message segment, which is also in line with people’s intuition.

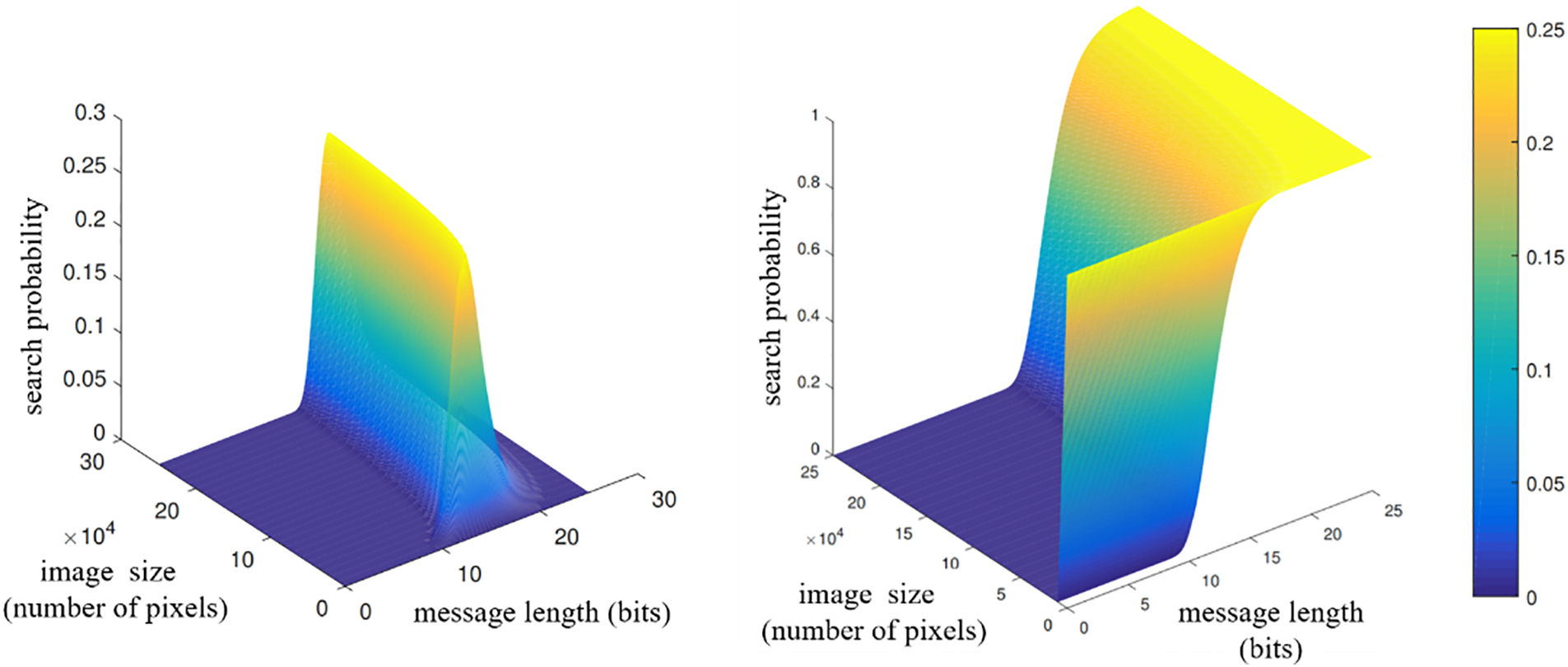
Figure 4: Analysis of factors for searching variable length optimal linked

In addition, this formula can also be understood as a probability density function of search rate under different conditions. Therefore, in order to better analyze variable fixed length search algorithms, we can obtain the probability that the length of the best linked list found on an image is not less than m, which is formula (7), and the image of this formula is shown in b of Fig. 4.

P3(m,N)=(1−pm+1)N(7)

We also divide the success probability of finding the acceptable best linked list into several levels: 99%, 95%, 90%, and 80%, and observe the mutual variation between message length m and image size N, as shown in Fig. 4. If the carrier image is a small-sized image, the length of the searched message fragment is approximately 10–13 bits. If the size of the image is approximately 250,000, which is a common 500 × 500 size, then the length of the message segment will be around 12–18, and even up to 20 bits.

From the above figure, we can see that each of the two best linked list search methods has its own advantages and disadvantages. Although there is a very small possibility that the fixed length search method cannot find the best linked list in an image, this small problem can be solved by replacing the carrier image. On the other hand, the length of message fragments that can be transmitted is relatively stable, with few changes, and generally stable between 10–15 bits. On the contrary, variable length search methods can ensure that the best linked list can be found, but the corresponding message fragment length is not stable, and the range of variation is basically between 10–20 bits. You can choose different optimal linked list search methods based on actual needs and the size of the carrier image.

4.3 Robustness Analysis

In practical application scenarios, images may undergo certain changes due to noise interference generated during encoding and transmission and often face potential attack risks. This section conducts robustness testing on the above linked list construction scheme, mainly applying different noise attack methods to images, and using common filters to mimic common noise interference and conventional processing methods to calculate the accuracy of message restoration.

The main noise attack methods selected in this experiment include Gaussian noise, salt and pepper noise, and multiplicative noise. Gaussian noise is an additive noise characterized by its probability density function following a Gaussian distribution, where the number of noise points at a certain intensity is the highest, and the further away from this intensity, the fewer noise points there are. The mean µ of the Gaussian noise added in this experiment is set to 0, and the variance σ is set to 0.001, 0.005, 0.01, and 0.05. Salt and pepper noise, also known as pulse noise, may be generated due to strong interference during signal transmission, or errors in bit transmission. In this experiment, four different noise densities were used, 0.001, 0.005, 0.01, and 0.05, which represent the ratio of noise pixels to the total number of pixels. Multiplicative noise is commonly present in real-world image applications and is related to image signals, usually caused by imperfect channels. This experiment is based on formula (8) to add multiplicative noise.

J=I+n \times I(8)

where J denotes the image after being attacked by noise and represents uniformly distributed random noise with a mean of 0, and the variance sigma is also set to four scenarios: 0.001, 0.005, 0.01, and 0.05.

Three types of filters are also chosen, mean filter, median filter and adaptive wiener filter. The mean filter is a smooth linear spatial filter that is often used to reduce noise, mainly by removing irrelevant details from an image, and is implemented by assigning the average value of the pixels in the neighborhood of the filter template to the center element. Unlike the mean filter, the median filter, as a nonlinear filter, assigns the median value of all pixels in the neighborhood window to the center element, which maintains the edge characteristics of the image without significant blurring. The wiener filter, on the other hand, better preserves the edges and other high-frequency parts of the image, adapts itself to the local variance of the image, and performs little smoothing when the variance is large and more smoothing when the variance is small. Finally, it should be mentioned that the domain operators used in this experiment uniformly use three different sizes, 3 × 3, 5 × 5, and 7 × 7.

As for the adopted datasets, there are two, BossBase and ImageNet. BossBase is a dataset often used in the field of steganography, including the field of steganalysis, which contains 10,000 grayscale images, uniformly processed into 512 × 512 size. ImageNet is a very famous dataset, which is often used in the tasks of image classification, detection, localization, recognition, etc. Its contained images have the advantages of variety and rich content, which are very suitable for the image content in the actual scenarios of the steganography algorithm. The images contained in ImageNet have the advantages of variety and richness, which are very suitable for steganography algorithms in real scenarios.

According to the steganography scheme proposed above in this article, different optimal linked list search methods will only affect the degree of message fragments that each image can carry, without affecting robustness. In addition, there are multiple other parameters that can affect its performance, such as the bit depth k of the pixel values corresponding to the node pointer field and data field, the amplification factor σ for the pointing length during node construction, used to find the optimal addressing method for the linked list, and the most important message fragment length m to be transmitted. The following experiments will gradually carry out specific testing and analysis on them.

4.3.1 Tests for Bit Depth k

Firstly, analyze the bit depth. Based on the above construction theory, the bits corresponding to the data domain and pointer domain of the node do not affect each other. Therefore, for convenience, in this experiment, the bits corresponding to the two are set to the same depth, denoted as bit depth k. It should be mentioned that the smaller k, the higher the position of the significant bit represented. That is, when k = 1, it represents the most significant bit, and when k = 8, it represents the least significant bit. In addition, the amplification factor σ is set to 1, the addressing method uses sequential addressing, and the message fragment length is set to 10, which basically ensures that the dataset image size used can find at least one optimal linked list for testing. The results of message restoration for different noise attacks are shown in Table 1, and the restoration accuracy for filters with different sizes is shown in Table 2.

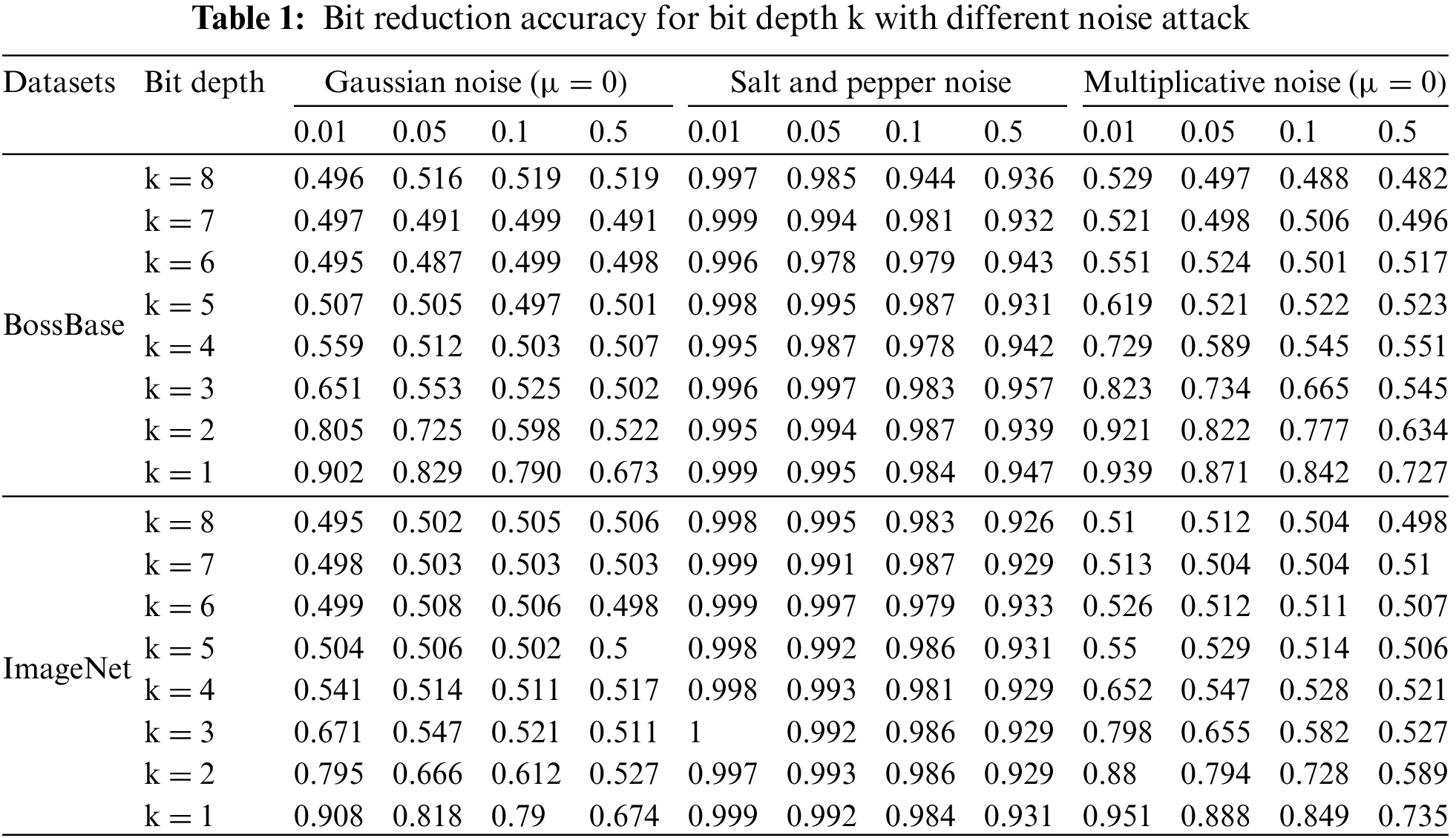
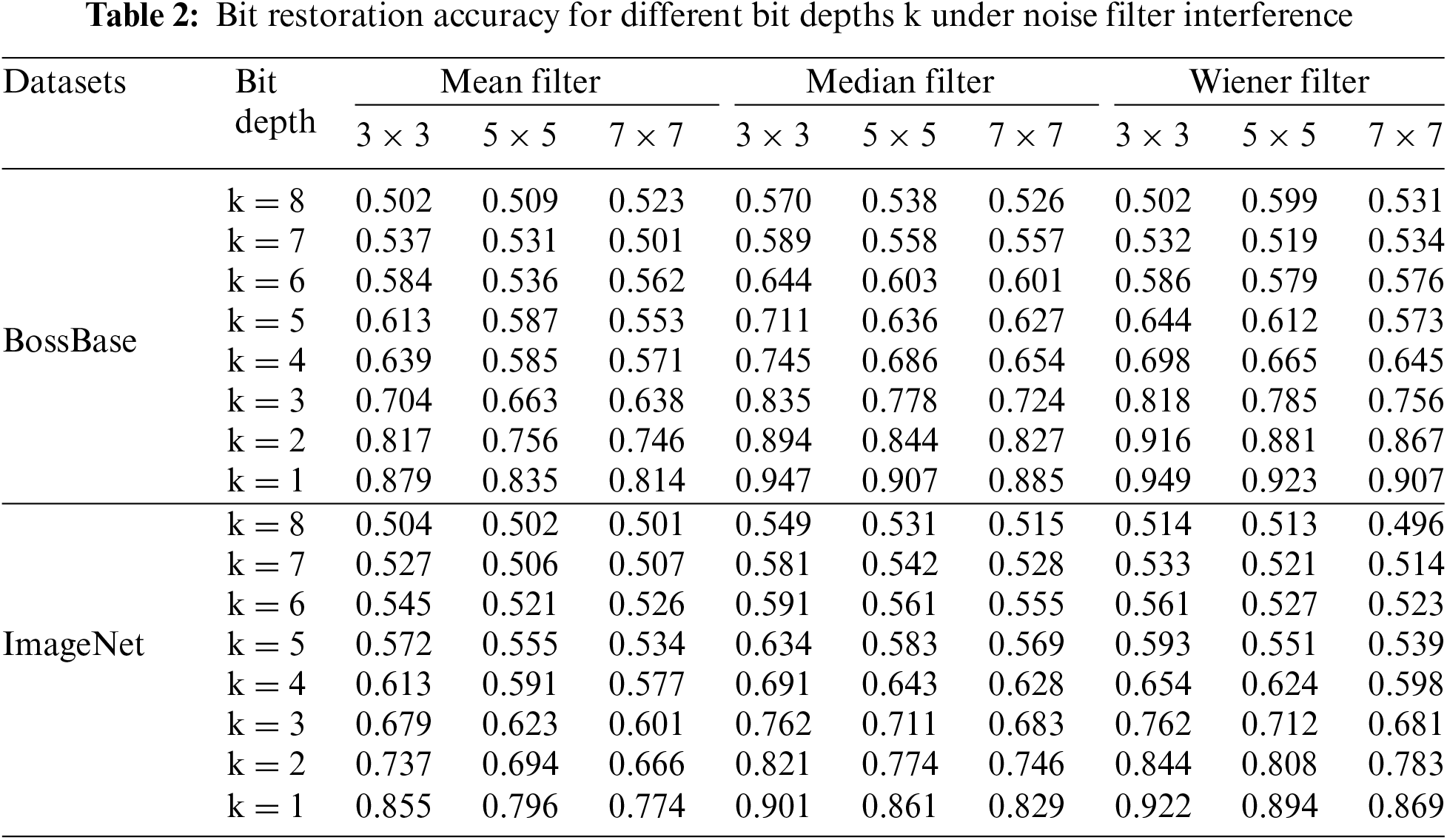
The experimental results show that in both datasets, as the bit depth increases, there will be a significant improvement in the accuracy of all noise interference restoration, especially when the bit depth is 1 (k = 1), and the accuracy is the highest. Moreover, an increase in the degree of noise interference will reduce the accuracy of message restoration to varying degrees. Secondly, the degree of message restoration may experience a certain degree of performance degradation for Gaussian noise and multiplicative noise, but it is still acceptable, while it exhibits unusual stability for salt and pepper noise, with an accuracy rate of almost 99.9%, as shown in Table 1. Similar to noise attacks, accuracy decreases to varying degrees after being processed by different filters. However, when the bit depth is 1 (k = 1), it still performs best, such as in Table 2.

Based on the analysis of the above situation, setting the bit depth to 1 can achieve the best performance in all experimental situations, which is consistent with the physical meaning corresponding to the actual situation. That is, a bit depth of 1 means that the pixel value corresponding to the node can change significantly, so it has strong resistance to numerical fluctuations caused by noise attacks or filter operations. This is exactly the opposite of the case with a bit depth of 8, which has a strong sensitivity to numerical fluctuations.

4.3.2 Tests for Addressing Methods and Amplification Factors

The next step is to test the addressing method and amplification factor σ, and based on the analysis results in the previous section, select the optimal parameter setting, that is, set the bit depth to 1. Its message restoration accuracy against different noise attacks is shown in Table 3, and its restoration accuracy against filters of different sizes is shown in Table 4.

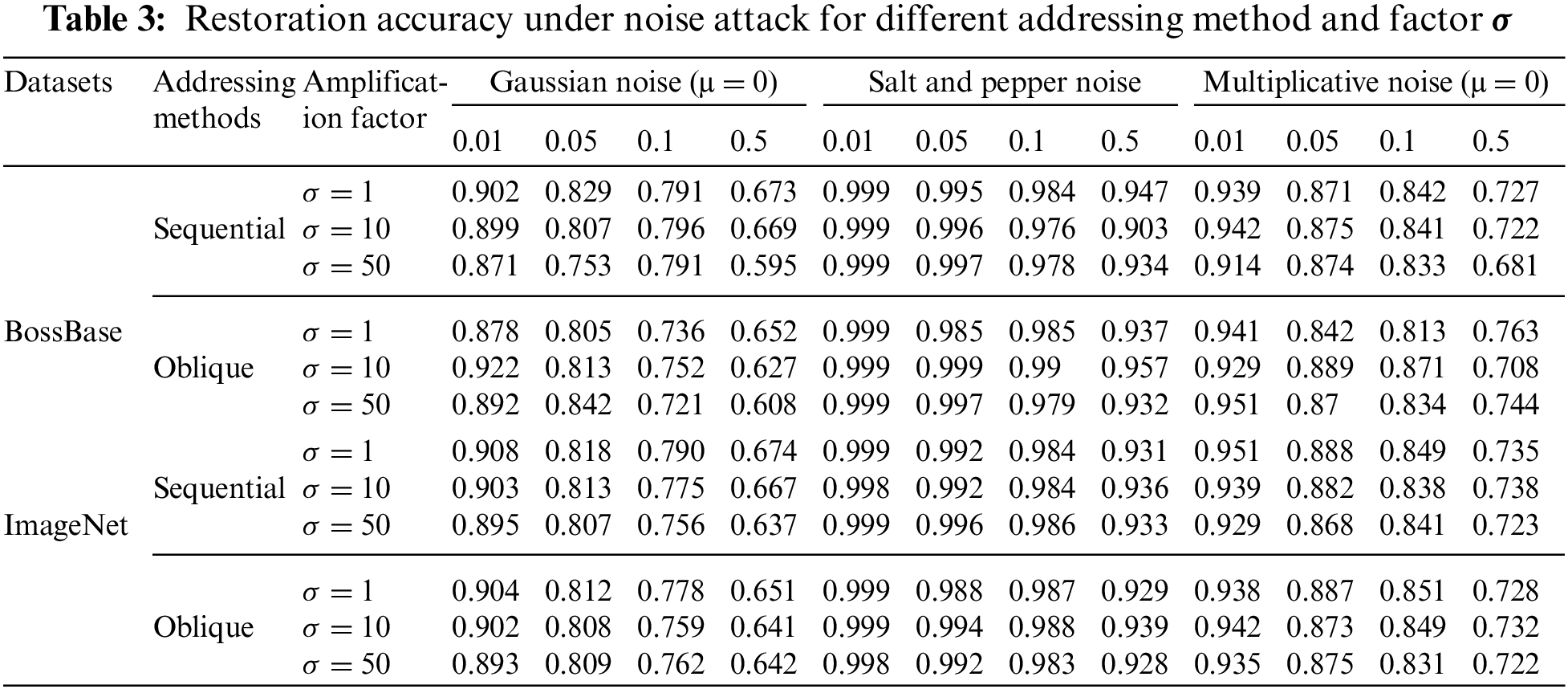
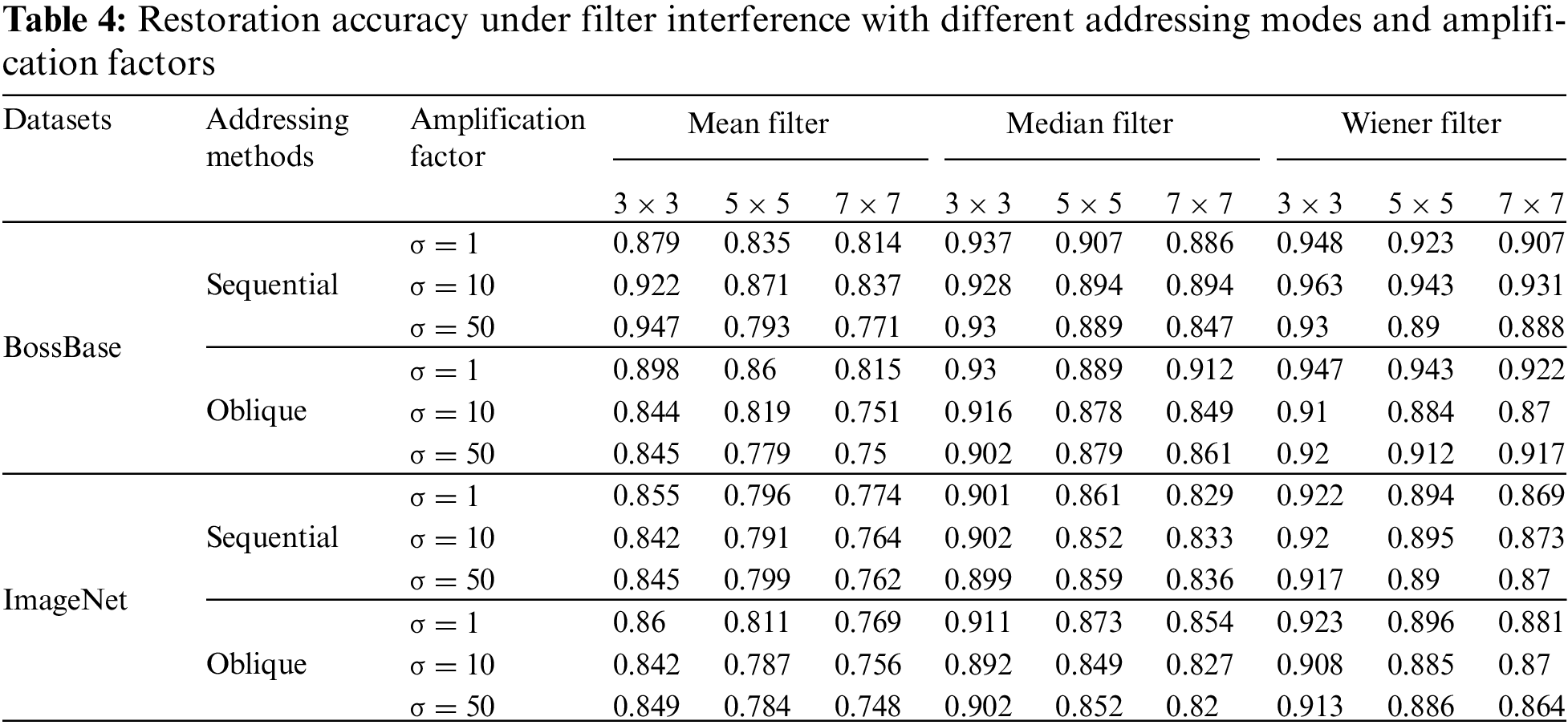
From the table, it can be seen that different datasets do not affect the performance of the scheme, as both have the same magnitude of change. Secondly, different addressing methods will not help the framework to have better resistance under different interferences, whether it is noise interference or filter operation. This experimental result is consistent with the derivation conclusion of the theoretical part above and has been further verified. Finally, the analysis of different amplification factors σ also has no impact on the performance of the scheme, and the factor that causes this situation is the addition of offset tables, which are mainly characterized by their different contents. The image sizes tested for it are all 512 × 512, so the lowest effective range for the data in the offset table is 1~512 × 512. The addition of huge offset term data has minimal impact on σ.

4.3.3 Tests for Message Segment Length

Finally, regarding the testing of message fragment length m, it can be seen from the test results in the previous section that the addressing method and amplification factor have no significant impact on robustness. Therefore, in this section of the testing experiment, oblique addressing was used and the amplification factor was set to 1. The accuracy of message restoration under various noise attacks and filter influences was also tested to analyze the robustness of the scheme. The test results are shown in Tables 5 and 6.

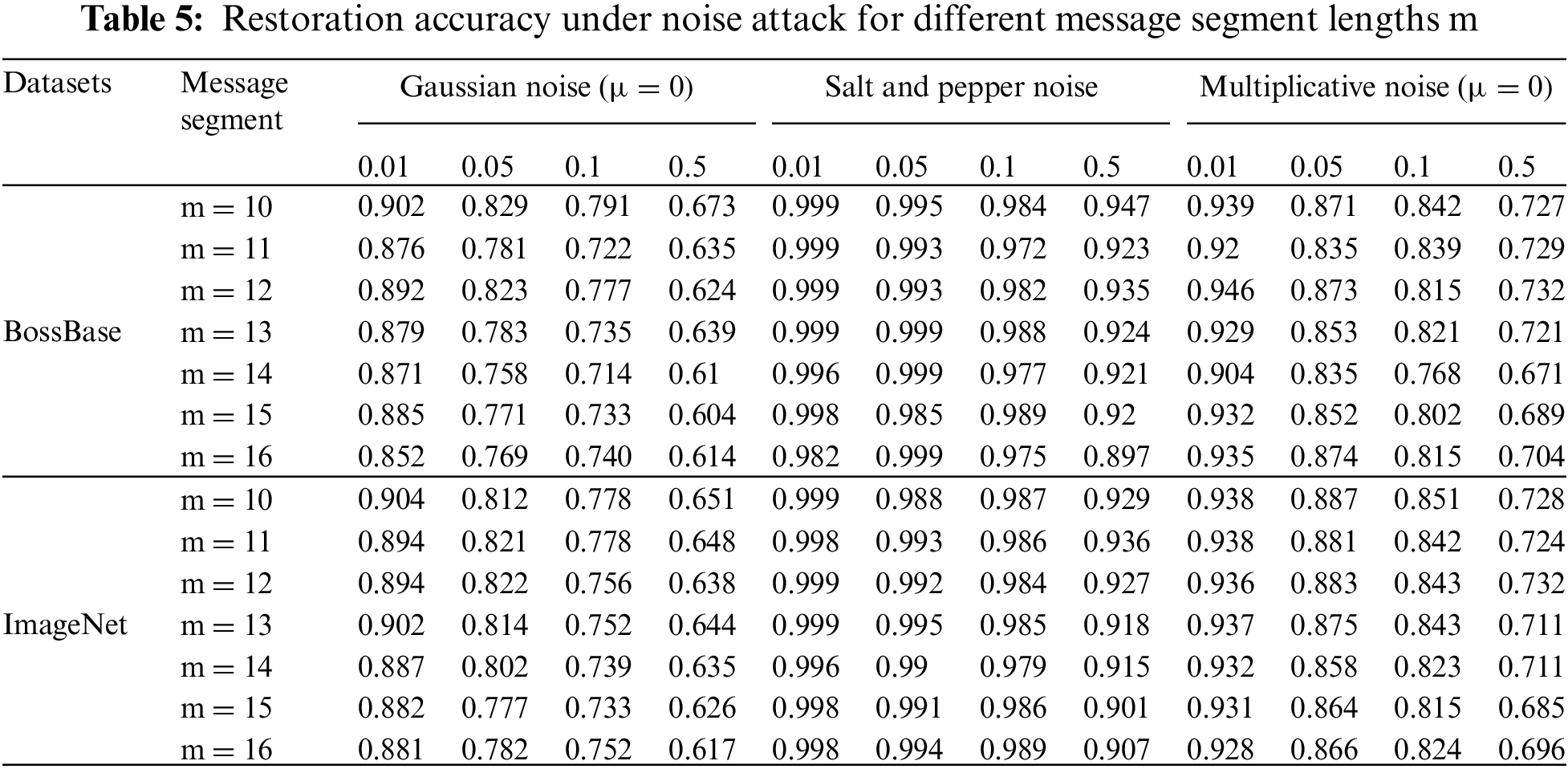
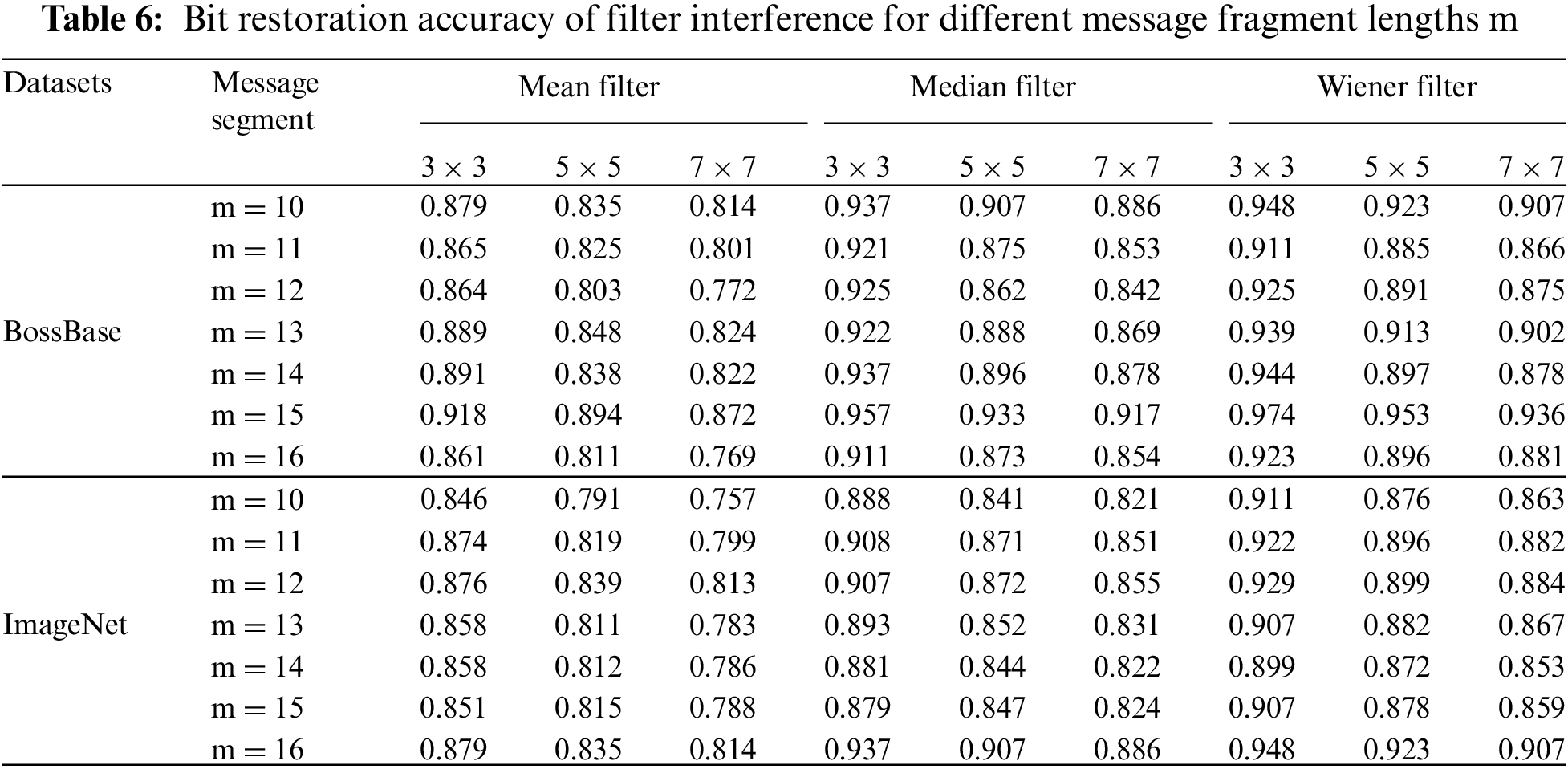
From Tables 5 and 6, it can be seen that as the fragment length increases, the scheme still has very good resistance to salt and pepper noise and is almost unaffected. For Gaussian noise and multiplicative noise, the accuracy of message restoration gradually decreases, but the amplitude of change is very small and within an acceptable range. Surprisingly, under the same filter interference, the restoration accuracy of different segment lengths is almost not affected, demonstrating a robust stability. Finally, under the same conditions, the performance calculated in the two datasets is basically the same, which indicates that the scheme has no dependency on the dataset and therefore has strong universality. It can be applied to multiple practical scenarios with more complex forms and richer content.

4.3.4 Comparison and Analysis with Other Methods

This section focuses on comparing and analyzing the performance of the steganographic framework proposed in this paper with other methods from several aspects.

Some recent works have been selected for comparison. These works, Wasserstein GAN-Gradient Penalty (WGAN-GP) [30], Deep Convolutional GAN (DCGAN) [19], Star Generative Adversarial Networks (StarGAN) [38] Attention-Guided GAN (attention-GAN) [42], all belong to coverless image steganography, mainly obtaining cover images through different neural networks, also known as generative steganography. The works Intelligent Search Method of Mapping Relation (ISMMR) [39] and Multi-Object Recognition (MOR) [40] belong to cover selection method. Synthetic Semantics Stego GAN (SSS-GAN) [41] transmits messages by combining image generation techniques and mapping rules. The main analytical analysis results are shown in Table 7.

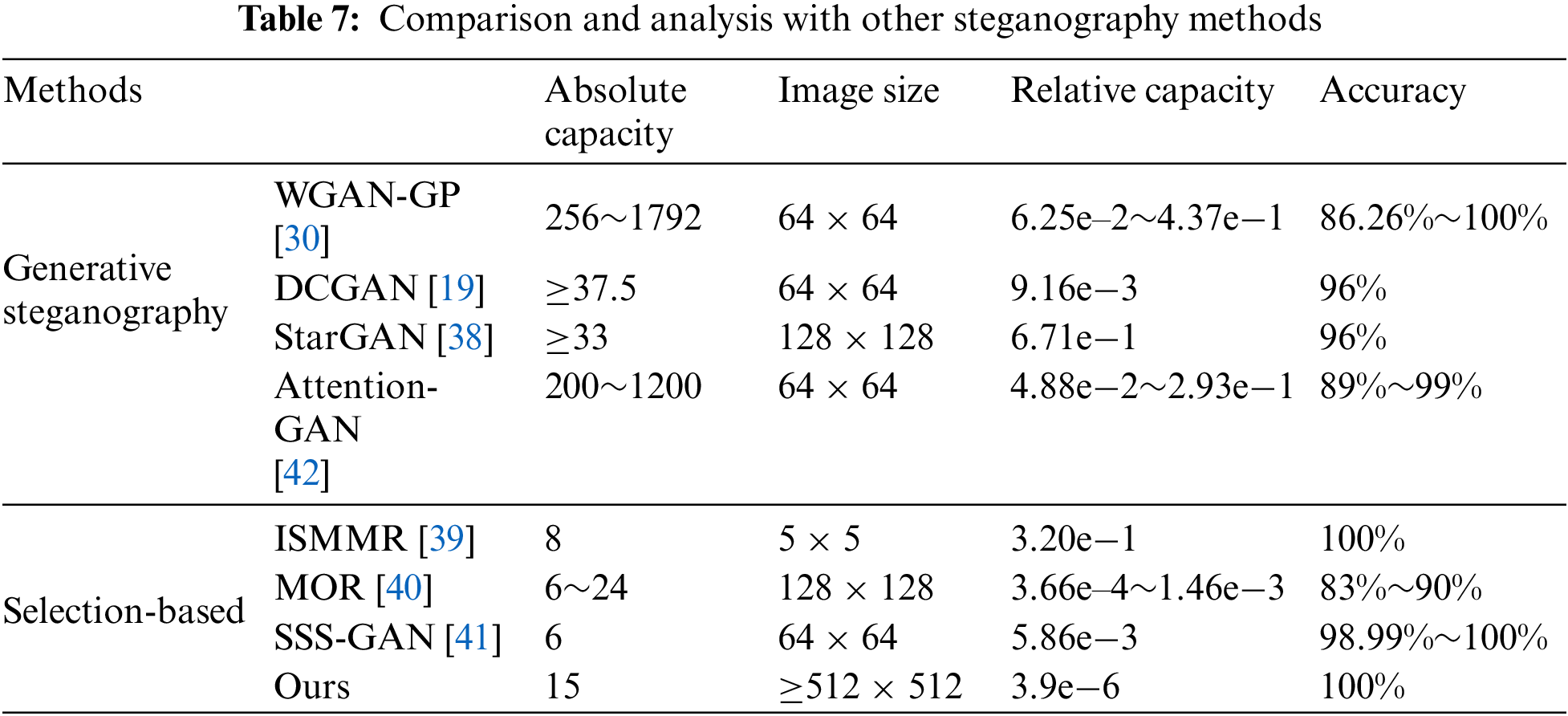
From the comparison results in Table 7, it can be seen that the proposed scheme in this article has the very distinct feature of having a very large message carrying capacity, which is different from other methods. This is because in the above process description, only a single linked list is described, and for the entire image, the number of linked lists that can be accommodated is almost the number of pixels in that image. Therefore, the payload capacity should be close to the score of the number of pixels and the length of the linked list. The recommended single linked list length is set to 15, which can better use images of size 512 and has higher efficiency.

In addition, the proposed scheme also has a very high accuracy, which is due to the same reasons as other methods in the table that also have 100% accuracy, that is, these methods all have the characteristics of accuracy, recoverability, etc.

5  Conclusion

This article proposes a new encryption communication scheme for non embedded image steganography, which generates specific decoding keys based on message fragments and encrypted images. In theory, this scheme can transmit corresponding message fragments based on the number of keys that can be transmitted and has extremely high steganography capacity and transmission efficiency. This scheme does not require any modifications to the carrier image and can completely resist steganalysis, with very high security and concealment. Finally, we have theoretically analyzed and experimented with various influencing factors to prove and verify that the method still has good robustness under various attack environments. In future work, the robustness of this communication scheme to cope with various extreme conditions will be further investigated.

Acknowledgement: The authors would like to express sincere gratitude to the DDE Lab at Binghamton University for providing code support. The resources available on their official website (http://dde.binghamton.edu/download/stego_algorithms/, accessed on 10 April 2024) were invaluable for this research. Additionally, the authors would like to thank the ImageNet team, led by Olga Russakovsky, Jia Deng, and Li Fei-Fei, for creating and maintaining the ImageNet dataset, which has become an invaluable resource for the machine learning and computer vision research community.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China (Nos. 62372083, 62072074, 62076054, 62027827, 62002047), the Sichuan Science and Technology Innovation Platform and Talent Plan (No. 2022JDJQ0039), the Sichuan Science and Technology Support Plan (Nos. 2024NSFTD0005, 2022YFQ0045, 2022YFS0220, 2023YFS0020, 2023YFS0197, 2023YFG0148), the CCF-Baidu Open Fund (No. 202312), the Medico-Engineering Cooperation Funds from University of Electronic Science and Technology of China (Nos. ZYGX2021YGLH212, ZYGX2022YGRH012).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Pengbiao Zhao, Xiaopei Wang; data collection: Pengbiao Zhao, Jingxue Chen; analysis and interpretation of results: Pengbiao Zhao, Qi Zhong, Jingxue Chen; draft manuscript preparation: Qi Zhong, Zhen Qin and Erqiang Zhou. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets used or analysed during the current study are available from the corresponding author on reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Fridrich J. Steganography in digital media: principles, algorithms, and applications. Cambridge: Cambridge University Press; 2009. [Google Scholar]

2. Li H, Dong S. Image steganalysis algorithm based on deep learning and attention mechanism for computer communication. J Electron Imaging. 2024 Jan 1;33(1):013015. [Google Scholar]

3. Qin J, Luo Y, Xiang X, Tan Y, Huang H. Coverless image steganography: a survey. IEEE Access. 2019;7:171372–94. [Google Scholar]

4. Rustad S, Andono PN, Shidik GF. Digital image steganography survey and investigation (goal, assessment, method, development, and dataset). Signal Process. 2023 May 1;206:108908. [Google Scholar]

5. Holub V, Fridrich J. Designing steganographic distortion using directional filters. In: 2012 IEEE International Workshop on Information Forensics and Security (WIFS); 2012 Dec 2; Tenerife, Spain: IEEE; 2012. p. 234–9. [Google Scholar]

6. Li B, Tan S, Wang M, Huang J. Investigation on cost assignment in spatial image steganography. IEEE Trans Inf Forensics Secur. 2014 May 29;9(8):1264–77. [Google Scholar]

7. Zhang T, Ping X. A. A fast and effective steganalytic technique against JSteg-like algorithms. In: Proceedings of the 2003 ACM Symposium on Applied Computing; 2003 Mar 9; Melbourne, Florida, USA. p. 307–11. [Google Scholar]

8. Westfeld A. F5—A steganographic algorithm. In: Moskowitz IS, editor. Information hiding. Berlin, Heidelberg: Springer; 2001. vol. 2137, p. 289–302. [Google Scholar]

9. Holub V, Fridrich J, Denemark T. Universal distortion function for steganography in an arbitrary domain. EURASIP J Inf Secur. 2014 Dec;2014:1–3. [Google Scholar]

10. Hussain M, Wahab AW, Idris YI, Ho AT, Jung KH. Image steganography in spatial domain: a survey. Signal Process: Image Commun. 2018 Jul 1;65:46–66. [Google Scholar]

11. Bilal M, Imtiaz S, Abdul W, Ghouzali S. Zero-steganography using DCT and spatial domain. In: 2013 ACS International Conference on Computer Systems and Applications (AICCSA); 2013 May 27; Ifrane, Morocco. IEEE. vol. 2013, p. 1–7. [Google Scholar]

12. Kusuma EJ, Sari CA, Rachmawanto EH, Setiadi DRI. A combination of inverted LSB, RSA, and arnold transformation to get secure and imperceptible image steganography. J ICT Res Appl. 2018;12(2):103–22. [Google Scholar]

13. Zhang X, Peng F, Lin Z, Long M. A coverless image information hiding algorithm based on fractal theory. Int J Bifurcat Chaos. 2020 Mar 30;30(4):2050062. [Google Scholar]

14. Chen J, Wang Z, Srivastava G, Alghamdi TA, Khan F, Kumari S, et al. Industrial blockchain threshold signatures in federated learning for unified space-air-ground-sea model training. J Ind Inf Integr. 2024 May 1;39:100593. [Google Scholar]

15. Elshoush HT, Mahmoud MM, Altigani A. A new high capacity and secure image realization steganography based on ASCII code matching. Multimed Tools Appl. 2022 Feb;1:1–47. [Google Scholar]

16. Zhou ZL, Cao Y, Sun XM. Coverless information hiding based on bag-of-words model of image. J Appl Sci. 2016 Sep;34(5):527–36. [Google Scholar]

17. Zhou Z, Wu QJ, Yang CN, Sun X, Pan Z. Coverless image steganography using histograms of oriented gradients-based hashing algorithm. J Internet Technol. 2017 Sep 1;18(5):1177–84. [Google Scholar]

18. Zhou Z, Mu Y, Wu QJ. Coverless image steganography using partial-duplicate image retrieval. Soft Comput. 2019 Jul 1;23(13):4927–38. doi:10.1007/s00500-018-3151-8. [Google Scholar] [CrossRef]

19. Hu D, Wang L, Jiang W, Zheng S, Li B. A novel image steganography method via deep convolutional generative adversarial networks. IEEE Access. 2018 Jul 4;6:38303–14. doi:10.1109/ACCESS.2018.2852771. [Google Scholar] [CrossRef]

20. Zhang X, Peng F, Long M. Robust coverless image steganography based on DCT and LDA topic classification. IEEE Trans Multimedia. 2018 May 21;20(12):3223–38. doi:10.1109/TMM.2018.2838334. [Google Scholar] [CrossRef]

21. Liu Q, Xiang X, Qin J, Tan Y, Tan J, Luo Y. Coverless steganography based on image retrieval of DenseNet features and DWT sequence mapping. Knowl-Based Syst. 2020;192(2):105375. doi:10.1016/j.knosys.2019.105375. [Google Scholar] [CrossRef]

22. Al Hussien SS, Mohamed MS, Hafez EH. Coverless image steganography based on optical mark recognition and machine learning. IEEE Access. 2021 Jan 11;9:16522–31. doi:10.1109/ACCESS.2021.3050737. [Google Scholar] [CrossRef]

23. Zhou L, Feng G, Shen L, Zhang X. On security enhancement of steganography via generative adversarial image. IEEE Signal Process Lett. 2019 Dec 31;27:166–70. doi:10.1109/LSP.2019.2963180. [Google Scholar] [CrossRef]

24. Sedighi V, Cogranne R, Fridrich J. Content-adaptive steganography by minimizing statistical detectability. IEEE Trans Inf Forensics Secur. 2015 Oct 5;11(2):221–34. doi:10.1109/TIFS.2015.2486744. [Google Scholar] [CrossRef]

25. Zhang R, Dong S, Liu J. Invisible steganography via generative adversarial networks. Multimed Tools Appl. 2019;78(7):8559–75. doi:10.1007/s11042-018-6951-z. [Google Scholar] [CrossRef]

26. Ma S, Zhao X, Liu Y. Adaptive spatial steganography based on adversarial examples. Multimed Tools Appl. 2019 Nov;78(22):32503–22. doi:10.1007/s11042-019-07994-3. [Google Scholar] [CrossRef]

27. Fu Z, Wang F, Cheng X. The secure steganography for hiding images via GAN. EURASIP J Image Video Process. 2020;2020(1):1–8. [Google Scholar]

28. Li F, Yu Z, Qin C. GAN-based spatial image steganography with cross feedback mechanism. Signal Process. 2022 Jan 1;190(2):108341. doi:10.1016/j.sigpro.2021.108341. [Google Scholar] [CrossRef]

29. Qin C, Zhang W, Dong X, Zha H, Yu N. Adversarial steganography based on sparse cover enhancement. J Vis Commun Image Represent. 2021 Oct 1;80(2):103325. doi:10.1016/j.jvcir.2021.103325. [Google Scholar] [CrossRef]

30. Peng F, Chen G, Long M. A robust coverless steganography based on generative adversarial networks and gradient descent approximation. IEEE Trans Circuits Syst Video Technol. 2022 Mar 22;32(9):5817–29. doi:10.1109/TCSVT.2022.3161419. [Google Scholar] [CrossRef]

31. Kharrazi M, Sencar HT, Memon N. Cover selection for steganographic embedding. In: 2006 IEEE International Conference on Image Processing; 2006 Oct 8–11; Atlanta, GA, USA: IEEE. vol. 2006, p. 117–20. [Google Scholar]

32. Wang Z, Zhang X, Yin Z. Joint cover-selection and payload-allocation by steganographic distortion optimization. IEEE Signal Process Lett. 2018 Aug 17;25(10):1530–4. doi:10.1109/LSP.2018.2865888. [Google Scholar] [CrossRef]

33. Wang Z, Zhang X. Secure cover selection for steganography. IEEE Access. 2019 May 1;7:57857–67. doi:10.1109/ACCESS.2019.2914226. [Google Scholar] [CrossRef]

34. Wang Z, Zhang X, Qian Z. Practical cover selection for steganography. IEEE Signal Process Lett. 2019 Nov 28;27:71–5. doi:10.1109/LSP.2019.2956416. [Google Scholar] [CrossRef]

35. Subhedar MS, Mankar VH. Curvelet transform and cover selection for secure steganography. Multimed Tools Appl. 2018 Apr;77(7):8115–38. doi:10.1007/s11042-017-4706-x. [Google Scholar] [CrossRef]

36. Andono PN, Setiadi DR. Quantization selection based on characteristic of cover image for PVD Steganography to optimize imperceptibility and capacity. Multimed Tools Appl. 2023 Jan;82(3):3561–80. doi:10.1007/s11042-022-13393-y. [Google Scholar] [CrossRef]

37. Liu M, Song T, Luo W, Zheng P, Huang J. Adversarial steganography embedding via stego generation and selection. IEEE Trans Dependable Secure Comput. 2022;19(5):3205–16. [Google Scholar]

38. Chen X, Zhang Z, Qiu A, Xia Z, Xiong N. Novel coverless steganography method based on image selection and StarGAN. IEEE Trans Netw Sci Eng. 2022;9(1):219–30. doi:10.1109/TNSE.2020.3041529. [Google Scholar] [CrossRef]

39. Wang Y, Wu B. An intelligent search method of mapping relation for coverless information hiding. J Cyber Secur. 2020;5:48–61. [Google Scholar]

40. Luo Y, Qin J, Xiang X, Tan Y. Coverless image steganography based on multi-object recognition. IEEE Trans Circuits Syst Video Technol. 2020 Oct 26;31(7):2779–91. doi:10.1109/TCSVT.2020.3033945. [Google Scholar] [CrossRef]

41. Zhang Z, Fu G, Ni R, Liu J, Yang X. A generative method for steganography by cover synthesis with auxiliary semantics. Tsinghua Sci Technol. 2020 Jan 13;25(4):516–27. doi:10.26599/TST.2019.9010027. [Google Scholar] [CrossRef]

42. Yu C, Hu D, Zheng S, Jiang W, Li M, Zhao ZQ. An improved steganography without embedding based on attention GAN. Peer Peer Netw Appl. 2021 May;14(3):1446–57. doi:10.1007/s12083-020-01033-x. [Google Scholar] [CrossRef]

Appendix A. Probability Calculation of the Optimal Linked List Fixed Length Search Algorithm

Appendix B. Probability Calculation of the Optimal Linked List Variable Length Search Algorithm