In-Depth Study of Potential-Based Routing and New Exploration of Its Scheduling Integration

1  Introduction

Industrial wireless mesh networks (WMNs) have been steadily gaining attention as cost-efficient backhauls for various services in industry environments, such as manufacturing process monitoring, equipment control, and sensor data collection [1]. However, they often encounter challenges related to performance degradation due to multi-hop communications. The inherent nature of multi-hop communications in industrial WMNs can lead to inefficiencies, including increased rates of packet loss in multi-hop scenarios, complexity in determining optimal routes, and difficulty in managing shared network resources. Conventional routing algorithms, such as shortest-path routing and hop-count-based routing, may struggle to improve packet delivery efficiency due to limitations in adapting to dynamic network conditions, such as varying traffic loads and link failures. Therefore, there is a pressing need for innovative routing approaches capable of addressing these challenges. One distinct attribute of industrial WMNs is that most communication originates from mesh clients and is directed toward mesh gateways, which serve as central hubs for various services. Mesh nodes act as relays for this traffic, facilitating communication between clients and gateways. Given that mesh clients must reach any one of multiple mesh gateways, the determination of routes to unspecified destinations becomes crucial for ensuring efficient and reliable communication within industrial WMNs.

In this paper, we revisit a routing algorithm suitable for WMNs, called ALFA (autonomous load-balancing field-based anycast routing) [2,3], inspired by the motion of charges in an electrostatic potential field. This algorithm represents a hybrid routing strategy that combines the strengths of back-pressure routing (BPR) [4] and geographic routing (GR) [5]. It leverages Poisson’s equation and employs numerical techniques such as the finite element method (FEM) and the local equilibrium method (LEM). Expanding on prior works [2,3], this paper provides an in-depth analysis of ALFA from various perspectives. It includes a clearer description of the analogy between an electrostatic system and a WMN system, based on a precise mapping relationship derived through detailed analysis, along with further discussions on anycast, the numerical methods (such as the FEM and the LEM) utilized in devising the ALFA scheme, as well as its characteristics, and complexity, which were not previously covered in detail. These additions enhance the depth and precision of understanding of the scheme, paving the way for meaningful future research. Additional detailed information on the differences in routing perspective from previous research is provided in the related work section to provide a comprehensive context for the paper. As a new approach, we propose a new scheduling scheme compatible with the potential-based routing scheme, utilizing the same potential-based metric as the routing metric to assign higher medium access priority to links with a steeper potential slope in scheduling. We demonstrate its ability to achieve gateway load balancing, path load balancing, and delay reduction using a single potential-based metric with low control overheads.

The main contributions and novelties of this paper can be summarized as follows: (1) an in-depth exploration of the ALFA scheme, addressing aspects that were not fully discussed in previous works [2,3]. It includes more detailed explanations of the analogy between an electrostatic system and a WMN system, based on a precise mapping relationship derived through rigorous analysis. Additionally, expanded discussions on anycast, the numerical methods utilized in designing the ALFA scheme, its characteristics, and complexity are provided; (2) the integration of the routing scheme with scheduling, representing a new addition to the existing literature for potential-based routing; and (3) extensive simulations conducted in a higher node density than that commonly found in conventional WMNs, considering the potential scenario in the industrial WMN environment.

The remainder of this paper is organized as follows. We first review related works in Section 2 to position our work. In Section 3, we present in-depth study results of the ALFA strategy, providing more comprehensive insights than previous works. This includes detailed explanations of the analogy between an electrostatic system and a WMN system, based on precise mapping relationships derived through rigorous analysis, as well as expanded discussions on anycast, the numerical methods employed in designing the ALFA scheme, its characteristics, and complexity, which serves as the foundation for our proposed scheduling model in this paper. In Section 4, we discuss potential-based routing-compatible scheduling as a new challenge and propose a scheduling scheme called potential differential scheduling. This scheme determines packet scheduling based on potential differences, which is also used in routing. Furthermore, in Section 5, we conduct a performance evaluation comparing our proposed potential-based joint routing and scheduling model with ALFA, BPR, and GR under a reference scheduling scheme, which is back-pressure scheduling. Finally, Section 6 concludes the paper.

2  Related Work

This section presents related works aligned with the primary focus of this paper, which is routing in WMNs. Routing is a fundamental aspect continuously studied in networking, resulting in various routing algorithms tailored for different network systems. This trend has also prompted the development of diverse routing schemes to address routing challenges in WMNs. BPR [4] and GR [5] are regarded as alternative approaches distinct from conventional routing schemes, such as shortest-path routing and hop-count-based routing. BPR adaptively selects paths based on traffic loads at nodes. However, it tends to overly exploit long paths, leading to performance degradation, especially in lightly-or moderately-loaded situations [6]. Despite this limitation, BPR has attracted significant attention because of its potential to achieve throughput optimality when combined with back-pressure scheduling, as theoretically proven in various studies [4,7,8]. On the other hand, GR relies on the location information of each node to make routing decisions, eliminating the need for network-wide searches by expensive control packets for routing information exchange. However, GR may face challenges in obtaining accurate location information in irregular or dynamic topologies, as well as in avoiding congested hot spots due to its simplicity in determining routes solely based on location information. Despite these challenges, GR has been extensively studied to overcome them because of its scalability, especially in wireless sensor networks and ad hoc networks [9–12].

Since then, several field-based approaches have been proposed as alternatives to address the limitations of the existing schemes, each grounded in different underlying physical principles. Nevertheless, they commonly assign scalar values to nodes to form a field used as guidance for routing, with packets traversing to destinations following the steepest gradient under the field. For example, in [13,14], mechanisms for wireless sensor networks (WSNs) consider both the distance to the sink and the energy factor, drawing inspiration from Coulomb’s law and force concept, respectively. A similar study in [15] targets WMNs in underground mines. Another routing protocol, introduced in [16], takes inspiration from hydrodynamic theory and aims to extend the network lifetime in WSNs. Additionally, reference [17] presented a real-time routing algorithm for WSNs, which considers both the node depth field for distance representation and the queue length field under the potential field methodology. A routing scheme for WSNs inspired by Ohm’s law was proposed to maximize network lifetime in [18]. Other research efforts have proposed anycast routing schemes for WMNs, with one focusing on distance and path robustness using Fourier’s equation [19], while another considers proximity to gateways and congestion levels based on Poisson’s equation [2,3,20]. As a brief comparison to closely related works [2,3,20], the former two are designed based on the FEM, while the latter is based on the finite difference method (FDM), which is limited to grid topologies. The technique designed with the FEM has fewer constraints on topology than the FDM, as the FEM can be applied to networks with both grid and non-grid topologies, making it more applicable to diverse network environments.

Among the family of field-based routing models, ALFA introduced in [2,3], serves as the foundation model of this paper. The choice of the model is twofold: first, this paper primarily targets WMNs in industrial environments, excluding models targeting WSNs previously discussed; second, ALFA exhibits high applicability as it can be employed without being constrained by network topology, as modeled using the FEM. ALFA incorporates anycast capability and load balancing for WMNs, drawing inspiration from Poisson’s equation. This approach maintains low control overheads and adapts to random network topologies. As an extension of [2,3], this paper addresses previously unexplored aspects. First, it provides in-depth explanations of the potential-based routing algorithm, focusing on areas that were not fully discussed in previous works [2,3]. This paper establishes a clearer mapping relationship between an electrostatic system and a WMN system, as shown in Table 1 in the next section, and thereby a clearer analogy, derived through intensive analysis, so that it can be immediately used for mathematical modeling. The previous works in [2,3] introduced a loose mapping relationship at the conceptual level only. This paper also introduces the anycast concept for a clearer understanding, comparing it with well-known data transmission methods such as unicast and multicast. The previous works only provided definitions or brief explanations for anycast without comparison with other transmission methods. Additionally, new equations (e.g., (3) and (4)) and a result graph demonstrating the convergence behavior by the LEM have been added, along with relevant descriptions. These additions aim to provide a more detailed explanation of the numerical methods, such as the FEM and the LEM, compared to the condensed information with a few omissions in the previous works. Lastly, this paper includes an analysis of the time and space complexities, which were not described in the previous works. Furthermore, it explores previously unconsidered aspects by integrating routing with scheduling. Here, it is important to note that we do not target the theoretical proof of the throughput optimality as in several existing works [4,7,8] to address the joint routing and scheduling problem with back-pressure algorithm. Instead, we treat the scheduling issue as an additional challenge based on the in-depth analysis of the routing model and evaluate the proposed joint routing and scheduling algorithm through extensive simulations considering realistic scenarios, different from strong assumptions applied in the theoretical proof of the throughput optimality. As another distinction, all simulations were conducted while considering scenarios with the potentially higher node density typically encountered in industrial WMNs.

3  In-Depth Study of Potential-Based Routing

This section presents in-depth research findings on potential-based routing, a key contribution of this paper that builds upon previous work. These findings encompass discussions on the suitability of utilizing anycast in industrial WMNs compared to unicast and multicast, clearer analogy with an electrostatic system through rigorous analysis, detailed exploration of numerical methods for routing metric modeling, and addressing the complexity of potential-based routing.

3.1 Scope of Discussion

Before exploring detailed explanations, we clarify the scope of our discussion in this section. The primary focus of this paper is the uplink aspect, specifically the packet delivery from mesh clients to mesh gateways. This focus is motivated by the inherent characteristics of anycast in industrial WMNs, where the majority of traffic is directed from mesh clients towards mesh gateways. While the downlink aspect from mesh gateways to mesh clients is considered out of scope, discussions regarding this topic can be found in [3].

3.2 Using Anycast in Industrial WMNs

We first explore in detail why using anycast is suitable for industrial WMNs, compared to unicast and multicast. Industrial WMNs, which serves as a backhaul for various services in industry environments, consist of mesh nodes and mesh gateways. In these networks, mesh gateways act as hubs to serve mesh clients through mesh nodes, forming a hub-and-spoke type network topology. Anycast can be utilized here for load-balancing purposes. In unicast, there is a deterministic destination for each source, whereas in multicast, there are pre-assigned multiple destinations for each source. Distinguished from them, anycast is a specialized type where each packet can be forwarded to just one of multiple destination candidates. Therefore, if mesh clients can connect to any arbitrary mesh gateway, then it is possible to receive the necessary services. According to the conventional anycast concept [21], the closest gateway is chosen as a destination. We consider that anycast can be used for scenarios where, if one gateway is overloaded, another idle or lightly loaded gateway can be selected as the destination. To achieve load balancing among mesh gateways, mechanisms for gateway handshaking and load information sharing have been proposed in previous studies [22,23]. These approaches involve route re-establishments through flooding, which consumes significant network resources. As a solution, we propose a novel load-balancing scheme that does not require gateway association or network-wide flooding.

3.3 Drawing Analogy with an Electrostatic System through Rigorous Analysis

We now establish a clearer analogy with an electrostatic system through in-depth analysis, preceding the discussion on utilizing anycast in industrial WMNs. Our work is motivated by the observation that the behavior of packet movement closely resembles the motion of charges in an electrostatic potential field. In a WMN, packets are generated by sources and traverse through mesh nodes toward the mesh gateways for uplink transmission. Similarly, in an electrostatic potential field, positive charges are created by sources, and these charges move toward potential drains with a negative potential due to the attractive forces within the potential field. Building on these analogies, we establish a terminology mapping between an electrostatic system and a WMN system, as detailed in Table 1. Specifically, (x,y) indicates a position in real space in an electrostatic system, which corresponds to the position of a mesh node or a mesh gateway. ϕ represents an electrostatic potential value in volts in an electrostatic system and a potential value as a routing metric to indicate proximity to the gateway and congestion levels in a WMN system. Additionally, ε is dielectric permittivity in the unit of Coulombs per volt-meter and it is mapped with the effect of queue lengths on the routing metric in a WMN. Conceptually, dielectric permittivity serves as a factor indicating how well a material or medium conducts electricity. Larger dielectric permittivity suggests better electrical conductivity, which refers to how easily electricity can flow through a material or medium, while smaller dielectric permittivity indicates poorer electrical conductivity. According to this principle, as dielectric permittivity decreases, the movement of charges encounters greater resistance. Consequently, lower dielectric permittivity correlates with a high probability of detouring nodes with longer queue lengths. In this context, we can understand the mapping relationship between the two systems for ε. Further, charge density ρ and sheet charge density σ refer to the amount of electric charge per unit volume and per unit surface (or area), respectively, despite there being no explicit mapping relationship to a WMN. Lastly, the amount of charge, q, in an electrostatic system is mapped with the number of packets in a queue at a node. Note that our work establishes a more detailed mapping relationship between an electrostatic system and a WMN system, enabling a clearer analogy that can be immediately applied to mathematical modeling. Unlike previous works [2,3], which introduced a loose mapping relationship at the conceptual level only, our mapping provides a more comprehensive and detailed framework for mathematical modeling.

The electrostatic behavior is governed by Poisson’s equation and it is formulated with the notations in Table 1 as follows:

∇2ϕ=−1ερ(1)

In our two-dimensional target space, Poisson’s equation [24] can be expressed as follows:

∇xy2ϕ=−1ε′′σ(2)

Based on the aforementioned analogy, consider a system model of an industrial WMN represented by a graph 𝒢=(𝒩,ℒ), where 𝒩 denotes the set of nodes and ℒ represents the set of directed links. Referring to Table 1, ϕ(n) is assigned as a potential for node n located at (xn,yn), and q(n) is considered the queue length of node n. For anycast routing, we define a set 𝒫 that consists of mesh gateways and is a subset of 𝒩. The potential of mesh gateways is assigned to a fixed minimum potential value (e.g., ϕ(p)=−1,where p∈𝒫). We refer to this condition as an internal boundary condition. On the other hand, boundary nodes ℬ⊂𝒩 located on the network boundary are assigned to a fixed potential value (e.g., ϕ(b)=0,where b∈ℬ) greater than the fixed minimum potential value determined by the internal boundary condition. The potential of the rest of the nodes is calculated using (2) in our two-dimensional network topology.

3.4 In-Depth Exploration of Numerical Methods for Routing Metric Modeling

In this subsection, we conduct an in-depth exploration of numerical methods for routing metric modeling, aiming to gain a better understanding of the detailed process of incorporating these methods to derive the routing metric based on the clearer analogy explained in the previous subsection. To construct a network potential field that corresponds to an electrostatic potential field satisfying (2), we employ numerical techniques: the FEM [24] and the LEM [25], for a distributed algorithm.

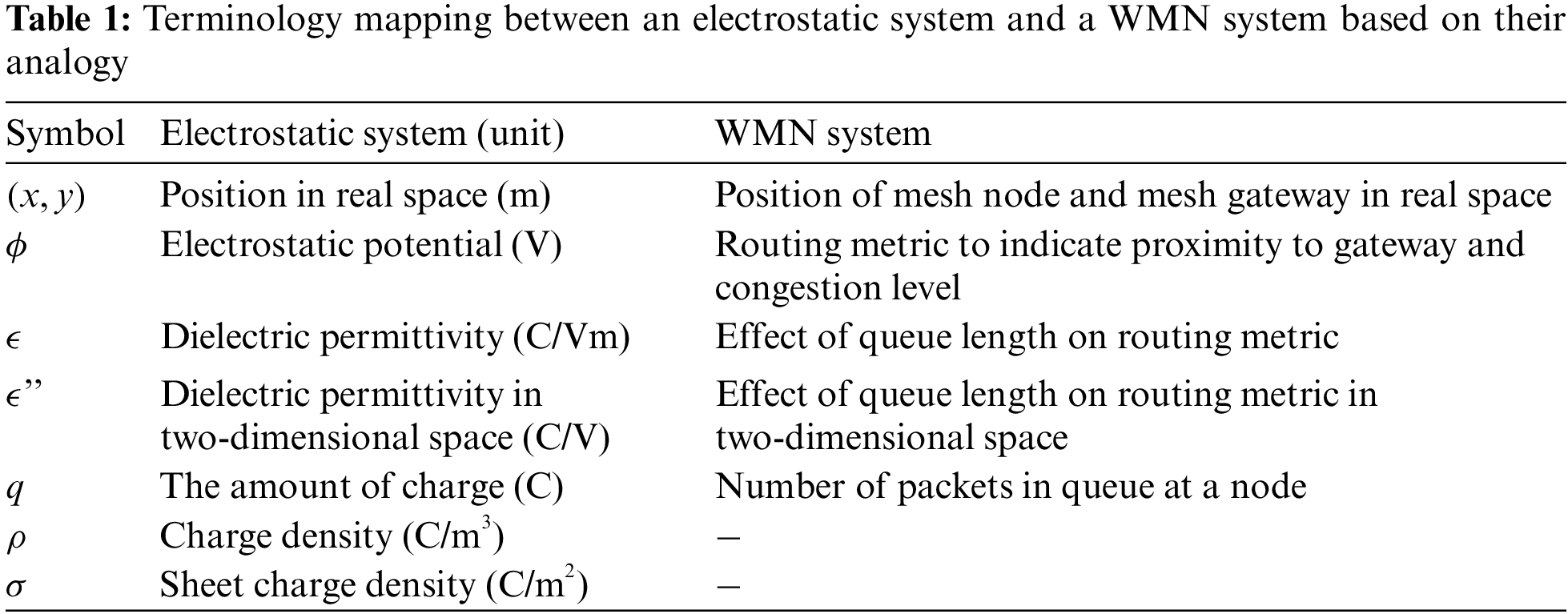
The FEM is a general numerical technique typically used to approximate solutions to partial differential equations, such as Poisson’s equation, by partitioning a large system into finite smaller elements. In our context, the FEM is utilized to determine the potential ϕ(n) for node n along with a set of its one-hop neighbors, ℛ(n), by partitioning the neighbor geometry of each node into several triangular elements, as depicted in Fig. 1. We denote the M triangle elements as E0n,⋯,EM−1n. The sheet charge density and the charge amount at node n can be represented as follows:

σn(X,Y)={σ0(n),for X2+Y2<δ20,otherwise.(3)

and

q(n)=∫X2+Y2<δ2σn(X,Y)dA(4)

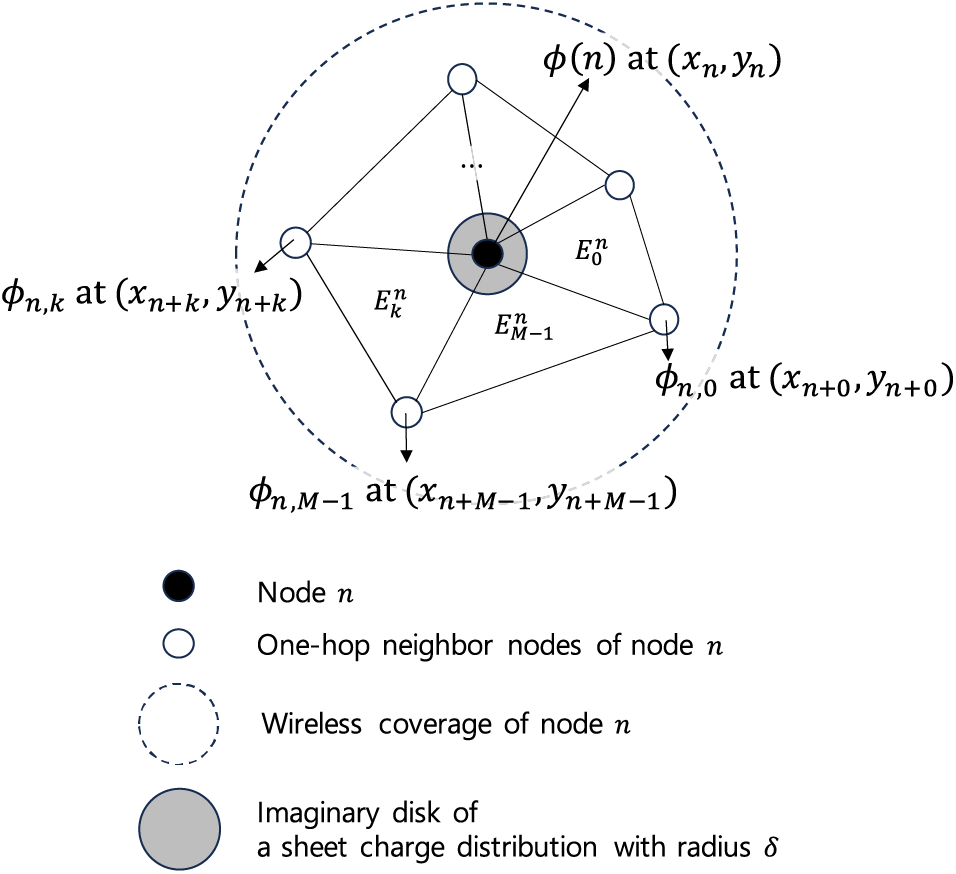
Figure 1: Illustration showing the partitioning of neighbor geometry into triangular elements for potential calculation using the FEM

In our analogy, the charge amount corresponds to the number of packets accumulated in the queue at node n. Eqs. (3) and (4) suggest that q(n) can be divided to m triangle elements such that q(n)=∑k=0M−1qn,k, where qn,k represents the fraction of q(n) in element k. Based on a typical FEM formulation of (2) and using (3) and (4), while taking the limit as δ→0, we derive a fundamental equation for a single element Ekn:

ϕ(n)‖r→n,k−r→n,k+1‖24Ak=(ϕn,k+1r→n,k−ϕn,kr→n,k+1)⋅(r→n,k−r→n,k+1)4Ak+1ε′′qn,k(5)

where the geographic distance vector r→n,k=(xn,k−xn,yn,k−yn)=(Xk,Yk) substitutes the conventional notations bi and ci in [24]. The area of element Ekn is given by Ak. Summing over all En, we obtain:

ϕ(n)=[∑k=0M−1(ϕn,k+1r→n,k−ϕn,kr→n,k+1)⋅(r→n,k−r→n,k+1)Ak+ηqn]∑k=0M−1‖r→n,k−r→n,k+1‖2Ak(6)

where Ak=|XkYk+1−Xk+1Yk|/2, η=4/ε′′, and ϕn,k+1 represents the potential value of the (k+1)-th neighboring node from node n. Remember that this result is effective only for evaluating the potential at a node using information received from its neighbors. The potential of the neighbors undergoes continuous iterative updates until a global solution is reached using the LEM, rather than solving the potential for the entire network in a centralized manner.

The LEM is a numerical technique used to asymptotically find a global solution for the potential. It guarantees that convergence towards a global solution is achieved after multiple local iterations of (6) for each element [25]. In our context, the LEM is employed to determine the potential values at equilibrium as a global solution. Each node n exchanges its potential value and location information with its one-hop neighbors for updating its potential value to satisfy (2). Neighboring nodes update their potential values in a similar iterative manner. This process propagates updated potential values to nearby neighbors, and subsequently to the neighbors of neighbors until a global solution at equilibrium is reached. In Fig. 2, we present an example of this convergence behavior in a network with 217 nodes. While similar patterns were observed across various cases, not all of them have been captured in this paper. The simulation parameters are configured in accordance with those introduced in Section 5.1. The metric is defined based on the MSE sense for the i-th iteration:

Figure 2: Convergence behavior by the LEM in terms of the number of iterations in mean square-error (MSE) sense

MSE(i)=1N∑n∈𝒩(ϕi(n)−ϕi−1(n)ϕi(n))2(7)

where N represents the total number of nodes in 𝒩 (i.e., N=|𝒩|), while ϕi(n) and ϕi−1(n) denote the potential values of node n at the i-th and (i−1)-th iterations, respectively. Fig. 2 demonstrates that convergence is achieved within 1% of the MSE after approximately 5 iterations. Once potential equilibrium is reached, potential-based routing may not require a significant recalculation of the potential value according to its operational principle, unless there is a substantial change in the traffic.

In summary, the potential field creation procedure is as follows: (1) Setting boundary conditions: An internal boundary condition to mesh gateways ϕ(p)=−1,where p∈𝒫, and an outer boundary condition to network boundary nodes ϕ(b)=0,where b∈ℬ, (2) Assigning zero as initial values for ϕ(n) of every mesh node except mesh gateways and boundary nodes, (3) Every node n, including mesh gateways and boundary nodes, periodically exchanges its potential and location information with its one-hop neighbors in ℛ(n) using a ‘hello’ message, (4) Every mesh node updates its list for ℛ(n) and determines ϕ(n) using the potential values of one-hop neighbors in ℛ(n) and its current queue length based on (6).

3.5 Gradient-Descent Hybrid Routing

In the following discussion, we explore the properties of the ALFA scheme, building upon the routing metric derived in the previous subsection. Our aim here is to provide a detailed explanation of the characteristics of the ALFA scheme, complementing previous discussions by offering a thorough examination, including the utilization of equations (e.g., (9)) not previously introduced.

The behavior of ALFA for uplink traffic is governed by a potential field. According to the ALFA policy, a packet should traverse by following the maximum attractive force, denoted as max(n,r)∈LF(n,r), where F(n,r)=−[ϕ(n)−ϕ(r)] and r∈R(n), along the steepest gradient descent direction. The behavior of ALFA is further characterized by the parameter η. When η is small, the behavior of ALFA closely resembles that of GR. In the limit where η approaches zero, (1) and (2) approximates Laplace’s equation [26]:

∇2ϕ=0(8)

The solution of (8) can be expressed as follows:

ϕ(n)=Aln⁡‖(xn,yn)−(xd,yd)‖+B(9)

where ‖(xn,yn)−(xd,yd)‖ represents the geographic distance from mesh node n at (xn,yn) to a potential drain at (xd,yd), which is mapped to a gateway. Constants A and B are determined based on boundary conditions. It is evident that ϕ(n) is directly proportional to the geographic distance. Thus, under a small value of η, the behavior of ALFA closely resembles that of GR. On the other hand, when η is sufficiently large, the behavior of ALFA closely resembles that of BPR. In this scenario, the impact of qn becomes dominant over the effect of distance in (6). ALFA exhibits autonomous load balancing among multiple mesh gateways and mesh nodes. For example, when traffic increases at a particular node, a congested hot spot may form, leading to potential increments at nearby nodes within the hot spot, thereby reflecting the congestion levels of other nodes. This potential adjustment helps divert packets away from congested regions, effectively routing them to avoid congestion.

By adjusting parameter η, ALFA can harness the strengths of both GR and BPR, effectively addressing their respective limitations. It is noteworthy that GR tends to struggle in heavily-loaded scenarios due to the formation of congested hotspots, while BPR tends to employ unnecessary long paths under lightly-and moderately-loaded scenarios. ALFA efficiently mitigates these shortcomings. In conclusion, ALFA flexibly incorporates the simplicity of GR and the adaptability of BPR.

3.6 Complexity Analysis

This subsection explores a complexity analysis similar to other algorithms, with a focus on aspects that have not been adequately addressed in prior studies [2,3]. As previously discussed, ALFA requires each mesh node to periodically exchange its potential value and location information solely with its one-hop neighbors in ℛ(n) using a ‘hello’ message. Formally, ALFA exhibits a low per-node message complexity proportional to the number of neighbors, O(|ℛ(n)|). However, computing a global potential update demands O(N) time, considering the number of information exchanges necessary for data to propagate from the farthest node in the worst-case scenario in a network comprising N nodes. Consequently, this may lead to slower convergence time. Nevertheless, achieving an identical precision in potential values to that of a global potential update might not be essential, as ALFA operates as a distributed algorithm primarily relying on neighboring congestion levels near gateways for selecting the next hop. That is, information from neighboring nodes significantly influences the selection of the next hop at each mesh node, whereas information from distant nodes holds less significance. This implies that the computational complexity of ALFA is predominantly dependent on the number of neighboring nodes, resulting in lower complexity in practice compared to the worst-case scenario complexity of O(N). In this context, ALFA emerges as a viable routing alternative in terms of scalability for industrial WMNs. Regarding storage space, each node must retain its location and the locations of its one-hop neighbors, along with maintaining its potential and that of its one-hop neighbors. Consequently, the total storage required is O(|ℛ(n)|+|ℛ(n)|)=O(N) for location and potential information. This also implies that the storage space is primarily determined by the number of neighboring nodes, resulting in lower storage requirements in practice compared to the worst-case scenario complexity of O(N).

4  Potential-Based Routing Compatible Scheduling

Here, we propose a scheduling algorithm that is compatible with ALFA, referred to as potential differential scheduling, representing a completely new challenge that has not been attempted before and is thus another key contribution of this paper. We denote the joint routing and scheduling scheme based on the potential metric by ALFA++. It utilizes the same metric as routing based on potential difference, similar to the back-pressure algorithm where a single metric based on queue backlog differential is used for both routing and scheduling. Note that the distinction between ALFA+ and ALFA++. ALFA+ refers to the integration of the ALFA scheme with a common reference scheduling method, namely back-pressure scheduling, along with its counterparts, BPR+ and GR+, which will be introduced in Section 5. In contrast, ALFA++ represents the integration of the ALFA scheme with a compatible scheduling algorithm using a potential-based metric. Through these comparisons, we can recognize the benefits of the routing and scheduling strategies, respectively. To realize this scheduling principle, we adopt an approach similar to DiffQ [27], developed for practical purposes. The model proposed in [27] introduces a scheduling scheme to enhance network performance by assigning different priority levels to each transmitted packet. It is built upon the enhanced distributed channel access (EDCA) mechanism [28] in IEEE 802.11e, extending the IEEE 802.11 standard to include quality of service (QoS) enhancements through modifications to the media access control (MAC) layer. Specifically, the IEEE 802.11e EDCA standard supports different priority levels for each packet transmission to meet various service requirements. However, the default IEEE 802.11e model only supports four priority levels. In [27], this was extended to support up to 8 different priority levels, aligning with the main objective of our proposed scheme, which aims to achieve better performance by transmitting packets with varying priority levels. Consequently, we employ the same approach, utilizing 8 different priority levels in our paper, to design the proposed potential-based scheduling scheme and conduct performance evaluations.

As detailed in [28], the IEEE 802.11e EDCA parameters, including AIFS, CWmin, CWmax, and transmission opportunity (TXOP), control medium access. AIFS determines the duration for which a node must wait before accessing the medium after it becomes idle, while TXOP defines the maximum amount of time a node can transmit data without releasing the medium. CWmin indicates the minimum interval a node must wait before initiating a data transmission, and CWmax denotes the maximum interval a node must wait before attempting to transmit data. In summary, the IEEE 802.11e EDCA mechanism controls medium access by adjusting AIFS, as well as contention windows (represented by CWmin and CWmax), and the contention-free period (represented by TXOP), based on the priority of each HOL packet. While reference [27] employed parameter adjustments based on queue differentials, in our approach, we utilized our metric, termed potential, and adjusted parameters based on potential differentials accordingly. Our proposed scheme does not involve adjustments to TXOP values, similar to the approach in [27], where TXOP values were not manipulated. Instead, we fine-tune parameters for AIFS, CWmin, and CWmax to facilitate differentiated packet scheduling based on potential differentials, as shown in Table 2.

The proposed potential differential scheduling scheme operates through the following steps in Algorithm 1. In this approach, nodes with a larger potential difference are prioritized for medium access, as indicated in line 13, aiding in congestion alleviation in hotspot areas. This potential differential scheduling scheme also aligns well with the anycast-type traffic patterns commonly observed in industrial WMNs. Given the nature of industrial WMNs, all traffic is aggregated by mesh gateways. Consequently, areas near mesh gateways can become congested due to the substantial increase in traffic. To proactively prevent congestion around mesh gateways, nodes in proximity to the mesh gateways are given higher medium access priority compared to nodes located farther away from mesh gateways.

Note that, unlike several existing works [4,7,8] that primarily approach the back-pressure algorithm from a theoretical perspective, this paper does not explore the theoretical aspects related to throughput optimality. Our main focus is on routing, with scheduling posing a novel challenge. In this context, our approach centers on conducting experimental demonstrations aimed at evaluating the proposed algorithm under realistic parameters. These parameters are set to be more relaxed, differing from the typical assumptions found in [4,7,8], such as assuming a stabilizable packet arrival rate within the network capacity region.

5  Performance Evaluation

5.1 Simulation Setup

In this section, we compare the proposed joint algorithm using the potential-based metric, ALFA++, for both routing and scheduling, with baseline joint routing and scheduling schemes, referred to as BPR+, GR+, and ALFA+. These baseline schemes integrate each distinct routing strategy with a common reference scheduling scheme of back-pressure scheduling, respectively. Specifically, BPR+ and GR+ are adjusted to include anycast capability for a fair comparison, enabling them to identify the nearest gateway and assign it as the destination. In contrast, ALFA+ and ALFA++ do not require any pre-configuration, as the routing strategy in both schemes accommodates anycast. By comparing ALFA++ with ALFA+, we can understand the advantages of the compatible scheduling scheme, while contrasting ALFA+ with BPR+ and GR+ reveals the benefits of the routing strategy. For the back-pressure scheduling integrated with BPR and GR, we adopt the queue differentials, QDn(d), as in DiffQ [27].

QDn(d)=Qn(d)−Qm(d)(10)

where QDn(d) represents the queue differential of destination d at node n and Qn(d) is the queue size for destination d at node n. These queue differentials are similar to the potential differentials in line 9 of Algorithm 1, but they are based on a different metric of queue lengths instead of potential values used in the potential differential scheduling scheme. The detailed parameters including AIFS, CWmin, and CWmax to be applied for the baseline joint algorithms, BPR+ and GR+, are the same as those applied to the potential differentials shown in Table 2, but the only difference is that the priority is determined by the queue differentials. We simply adopt the priority calculation method used in [27] where the priority is determined by the queue differential, which is calculated by evenly dividing the maximum queue size into fixed intervals corresponding to the number of supported priority levels (i.e., 8). Additionally, we compare the performance between ALFA++ utilizing the potential-based metric not only for routing but also for scheduling with ALFA+, which integrates ALFA with the common reference scheduling scheme of back-pressure scheduling. This comparison aims to demonstrate the benefits solely achieved by the ALFA-compatible scheduling scheme.

All comparisons are conducted through simulations using Network Simulator 2 (NS-2) [29]. Note that all schemes incorporate the scheduling component to differentiate the transmission of packets with different priority levels. To evaluate this differentiated packet scheduling, we implement a patch for IEEE 802.11e from [30] in NS-2. This comparative analysis helps us gain a deeper understanding and better evaluate both ALFA itself within the context of its hybrid routing strategy, and ALFA++ based on a compatible scheduling strategy within the context of a joint algorithm. We present the results using ALFA+ and ALFA++ with η=0.005 as a representative case. This value was empirically determined to exhibit the best performance through extensive simulations, following the common practice of tuning parameters in several other studies [31–33].

In our simulation, we consider a hexagonal topology with a high node density to represent an industrial WMN environment, consisting of 214 mesh nodes and 3 mesh gateways shown in Fig. 3. Mesh nodes are positioned at the vertices of hexagons under a structured deployment strategy with a distance of 200 m between neighboring nodes. This node deployment closely mimics the layout of industrial environments, where nodes are often deployed in a structured manner to optimize coverage and connectivity. To simplify our simulation setup without sacrificing realism, we select a traffic generation model where mesh nodes generate traffic on behalf of connected mesh clients, even though mesh clients typically initiate traffic in real-world scenarios, enabling us to focus on the overall network performance without modeling individual client behaviors. The physical layer model of IEEE 802.11b is applied, and the channel bandwidth is configured as 2 Mbps, which are default setting in NS-2. Packet generation follows a Poisson distribution as in other works [34,35], and the average packet generation frequency is determined by an offered load parameter, which we set as a percentage. The corresponding rate is calculated to achieve the desired channel bandwidth utilization, based on the calculation method where the channel bandwidth reaches full occupancy when a 100% offered load is specified. This calculated rate is then applied in our simulations to accurately represent the specified offered load.

Figure 3: High-density hexagonal topology consisting of 214 mesh nodes and 3 mesh gateways in industrial WMN environment

Additionally, our settings include configuring selected 12 mesh nodes in a valley region between mesh gateways to intensively generate packets as heavy traffic sources, simulating scenarios with offered loads of 80%. Background traffic is generated by randomly selecting 18 mesh nodes, each contributing a constant offered load of 10% across the network. These settings replicate situations where heavy traffic is concentrated in specific regions, similar to those often encountered in real-world industrial environments found in manufacturing plants, warehouses, or assembly lines. This setup enables us to evaluate how our algorithm maintains performance without significant degradation under c hallenging conditions, which is crucial for ensuring reliable communication in industrial settings. Each user datagram protocol (UDP) packet is set to a length of 1,000 bytes a commonly used configuration as in [36,37]. The other parameters or models, including those (e.g., transmission and interference ranges) to be mentioned below, are set to default values or options. The transmission and interference ranges are set to 250 and 550 m, respectively. We enable the default settings for the request to send (RTS)/clear to send (CTS) and hello-message-jittering parameters. RTS/CTS stands for ‘request to send’ and ‘clear to send’, and they are used for managing wireless channel access to prevent collisions caused by simultaneous packet transmissions from nearby multiple nodes. On the other hand, hello-message-jittering introduces variability in the timing of hello messages exchanged between nodes for enhanced network performance. By conducting 10 iterations of each simulation scenario and utilizing data from a 600 s period out of a 1,000 s simulation run, we ensure the reliability and stability of our results while eliminating the impact of initial transient periods.

5.2 Average Path Length

We start by exploring a lightly loaded scenario, as it provides insights into how efficiently packets are delivered, prioritizing shorter paths over detours. We primarily focus on path length, considering that in such scenarios, delivering packets through shorter routes is advantageous. However, we also consider the occurrence of route loops, which may arise when delivering packets based on congestion information. By analyzing both aspects, we aim to evaluate how effectively each algorithm utilizes short paths and whether it unnecessarily considers detour paths.

Fig. 4 shows the CDF of path lengths and the number of route loops across different algorithms in a lightly loaded scenario where λ=30% is applied. First, the CDF in Fig. 4a illustrates the proportion of packets that traverse the entire path, from source nodes generating packets to a gateway as their destination, within a specific path length. GR+ generally exhibits the shortest path lengths for packet delivery. This observation aligns naturally with the fact that GR+ performs packet routing relying on geographic information, as evident from the absence of route loops in Fig. 4b. In contrast, BPR+ demonstrates the longest path lengths for packet delivery, attributed to its routing based solely on queue lengths without direct geographical information. As a result, frequent route loops (approximately 100 times more than ALFA+ and ALFA++) occur, as observed in Fig. 4b. While GR+ and BPR+ employ the same scheduling scheme, ALFA+ as their hybrid model achieves packet delivery with path lengths comparable to GR+ in the lightly loaded case. This tendency in results suggests that path lengths and route loops are heavily dependent on routing strategies. Furthermore, ALFA++ incorporates a compatible scheduling scheme into ALFA, resulting in packet delivery with path lengths that are similar to those of GR+ at most ranges except for a specific range, approximately 1,000~1,600 m. This implies that ALFA++ tends to prefer short paths. On the other hand, ALFA++ demonstrates minimal deviation from ALFA+ in terms of path lengths, indicating that the scheduling scheme does not significantly impact path lengths. Specifically, when comparing GR+ with ALFA+, the maximum difference observed in terms of CDF is approximately 32% for a path length of around 1,200 m. However, it is important to note that while GR+ generally helps achieve shorter path lengths, this maximum difference is observed in specific segments. On average, the difference is around 3%, implying that ALFA+ inherits the advantages of GR+ as a hybrid algorithm. Additionally, when comparing BPR+ with ALFA+, the maximum difference is approximately 51% for a path length of around 1600 m, and on average, there is a difference of around 33%. This indicates that ALFA+ mitigates the weaknesses of BPR+ to the extent mentioned earlier. Moreover, as described earlier, the only difference between ALFA+ and ALFA++ is the scheduling scheme. Although this difference does not lead to significant variations in path lengths, there is still a slight difference in path lengths, indicating that they are not exactly the same. For example, the difference between ALFA+ and ALFA++ is approximately 3% for a path length of around 800 m.

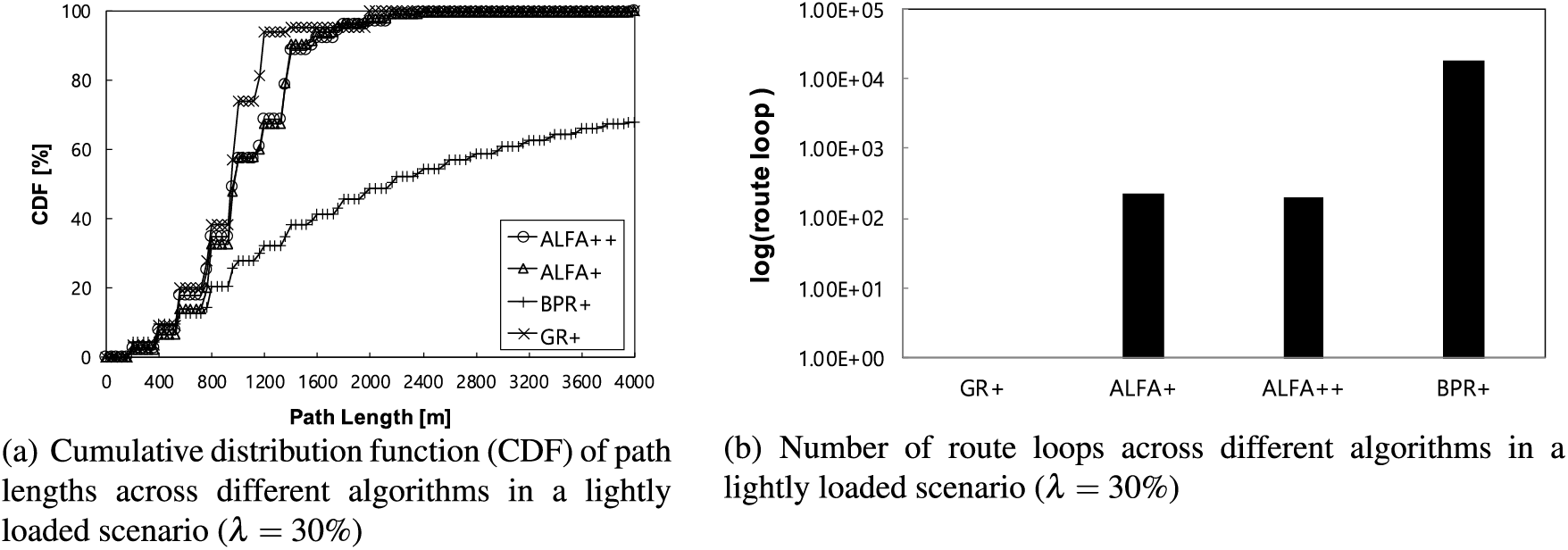
Figure 4: Comparison of algorithm performance in a lightly loaded scenario (λ=30%), demonstrating the CDF of path lengths and the number of route loops across different algorithms

Through this analysis of average path length, it is evident that the proposed scheme, ALFA++, effectively delivers packets via short paths, particularly in lightly loaded scenarios where fewer detours are required. Considering the results of end-to-end delay for lightly loaded scenarios in the following section alongside the route loop results in Fig. 4b, it can be inferred that both ALFA+ and ALFA++ do not unconditionally use solely the shortest single path as in GR+ even in lightly loaded cases. Instead, they achieve better performance by flexibly utilizing detour paths when necessary. These findings imply that ALFA+ and ALFA++ offer practical advantages in dynamically adapting to network conditions and optimizing packet delivery even in lightly loaded scenarios.

5.3 Load Balancing

In this subsection, we aim to analyze the results for a heavily loaded case, continuing from the analysis of the lightly loaded case in the previous subsection. In this scenario, congestion situations are likely to occur frequently, so prioritizing the utilization of detour paths rather than shorter paths becomes advantageous. In this context, we intend to investigate the throughput for each gateway and assess the fairness across different algorithms. For fairness evaluation, we adopt Jain’s fairness index [38] as follows:

f(x1,⋯,xn)=(∑i=1nxi)2n∑i=1nxi2(11)

where xi represents the throughput of flow i, defined for each pair consisting of a mesh node and a mesh gateway, and n is the total number of flows. A fairness index closer to 1 implies an almost equal distribution of throughput among n flows, where each flow receives a comparable share in terms of throughput. Through this analysis, we can understand how effectively each algorithm utilizes detour paths.

First, we observe from Fig. 5a that the total throughput is highest for ALFA++, followed by ALFA+, BPR+, and GR+. Specifically, upon closer examination, we note that compared to ALFA++, ALFA+ exhibits approximately 9% lower total throughput which is the summation of throughput at all the gateways, while BPR+ and GR+ show reductions of around 51% and 60%, respectively. Additionally, regarding the fairness index, it is evident from the same figure that ALFA++ achieves the highest fairness among the algorithms. Further, relative to ALFA++, ALFA+ achieves approximately 6% lower fairness, while GR+ and BPR+ achieve reductions of approximately 85% and 11%, respectively. When comparing ALFA+ with GR+ and BPR+, ALFA+ demonstrates approximately 48% better total throughput compared to GR+ and around 40% better total throughput compared to BPR+. In terms of fairness, ALFA+ is approximately 11% higher than GR+ and 4% higher than BPR+. This improvement can be attributed to the nature of ALFA+ as a hybrid algorithm, which flexibly incorporates the strengths of both GR+ and BPR+, allowing it to achieve superior throughput and fairness.

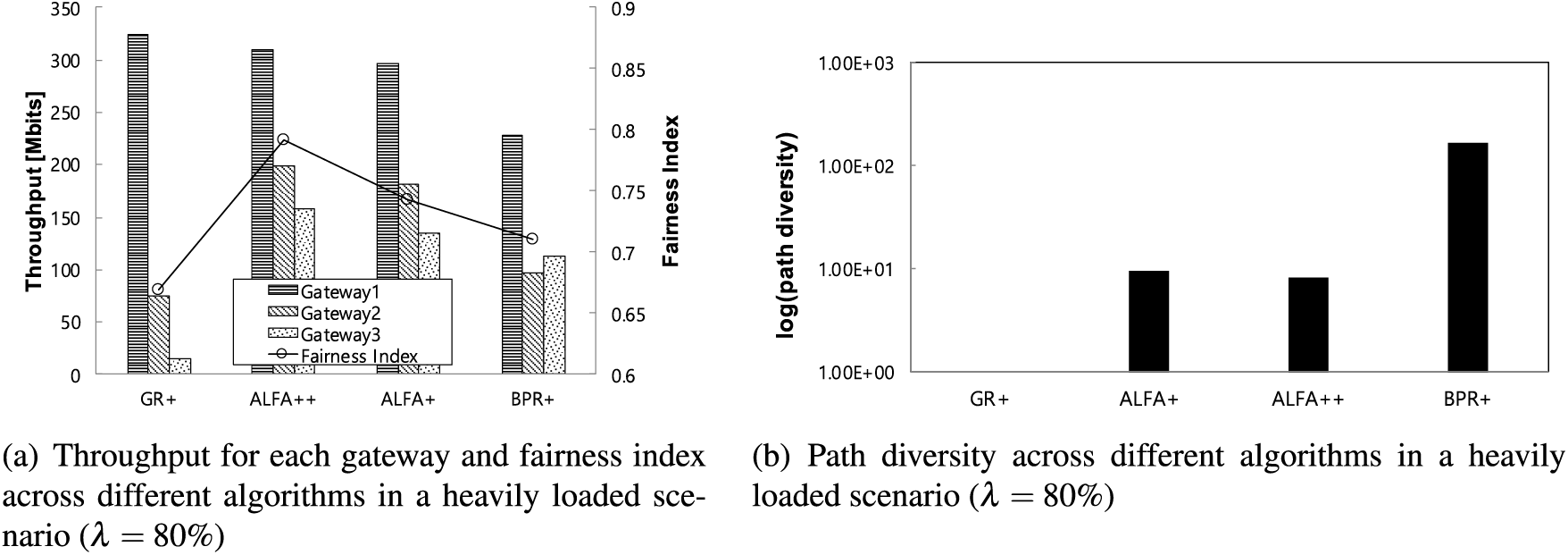
Figure 5: Comparison of algorithm performance in a heavily loaded scenario (λ=80%), demonstrating throughput for each gateway, fairness index, and path diversity across different algorithms

On the other hand, from Fig. 5b, we observe that while GR+ relies on a single path for packet delivery, resulting in no path diversity, ALFA+ demonstrates approximately 9 times greater path diversity than GR+ by dynamically utilizing alternative paths when necessary. This ability to select alternative paths dynamically mitigates the weakness of not considering detour routes, as in the case of GR+. Additionally, ALFA+ can alleviate the weakness of exploring unnecessarily long paths, as observed in BPR+, which leads to path diversity approximately 170 times higher than that of ALFA+ and ALFA++.

All the observed results in Fig. 5 can be understood as follows: ALFA+ adaptively utilizes multiple paths, traversing less congested areas toward a mesh gateway in a hop-by-hop fashion, similar to BPR+. It shows high gateway utilization, whereas GR+ exhibits degraded performance since it only considers geographical distance as a routing metric. Even though BPR+ dynamically selects paths reflecting congestion, the main reason for its lower performance compared to ALFA+ is its unnecessary long path exploration, which wastes large network resources. With the help of reasonable path diversity mitigating congestion and efficient path length selection eliminating unnecessary delays, ALFA+ efficiently and autonomously utilizes network resources in reaching the mesh gateways, as depicted in Fig. 5. Additionally, ALFA++ demonstrates superior performance compared to ALFA+, GR+, and BPR+ in terms of both throughput and fairness. This significant improvement can be attributed to the fundamental design principles of ALFA, the parent model of ALFA++, which flexibly considers short paths and detours when necessary. This design philosophy allows ALFA++ to achieve efficient packet delivery while mitigating unnecessary path lengthening. Furthermore, ALFA++ leverages the same routing metric for scheduling decisions, creating a synergistic effect between routing and scheduling that further enhances its performance. This approach ensures that ALFA++ not only delivers packets efficiently but also does so fairly, making it well-suited for real-world environments with dynamic traffic conditions and resource constraints.

5.4 Average End-to-End Delay

This subsection aims to investigate the end-to-end delay, a representative network performance metric, for both lightly loaded and heavily loaded scenarios. Through this analysis, we can gain insights into how network performance is achieved and understand why such results are obtained based on the operational characteristics of the algorithms explored earlier. Ultimately, this allows us to evaluate the practicality of each algorithm.

Regarding the end-to-end delay, ALFA+ significantly outperforms BPR+ and GR+ in terms of delivering more packets within a shorter time, as shown in Fig. 6. The overall trends in the results for BPR+ and GR+ can be explained by the inherent routing behaviors of these routing schemes. The long delays in BPR+ are caused by the longer path traversal times, regardless of traffic loads. In contrast, delays in GR+ are primarily attributed to queueing delays since it simply selects the geographically shortest paths. Despite the expectation that delay performance would be favorable in lightly loaded scenarios as long as packets are routed through short paths, the results demonstrate otherwise. The reason for the superior performance of ALFA+ can be understood by its ability to autonomously achieve load balancing and short path lengths simultaneously, as discussed earlier. Upon analyzing the remaining difference between ALFA+ and ALFA++, it becomes evident that a compatible scheduling scheme significantly influences the achievement of good performance. Specifically, in the lightly loaded case, compared to the optimal performance of ALFA++, ALFA+ exhibits a maximum difference of approximately 15% worse, GR+ approximately 36% worse, and BPR+ approximately 63% worse. ALFA+ outperformed GR+ by approximately 21% and BPR+ by approximately 48% in terms of maximum difference. On the other hand, a similar trend is also observed in heavily loaded scenarios, with the only difference being a greater degradation in delay performance. These results can be also explained using the same logic applied to lightly loaded scenarios, with the relative degradation in performance naturally stemming from the heavier traffic loads. Specifically, in the heavily loaded case, ALFA+ shows a maximum difference of approximately 13% worse compared to ALFA++, GR+ approximately 30% worse, and BPR+ approximately 60% worse. ALFA+ outperformed GR+ by approximately 17% and BPR+ by approximately 47% in terms of maximum difference.

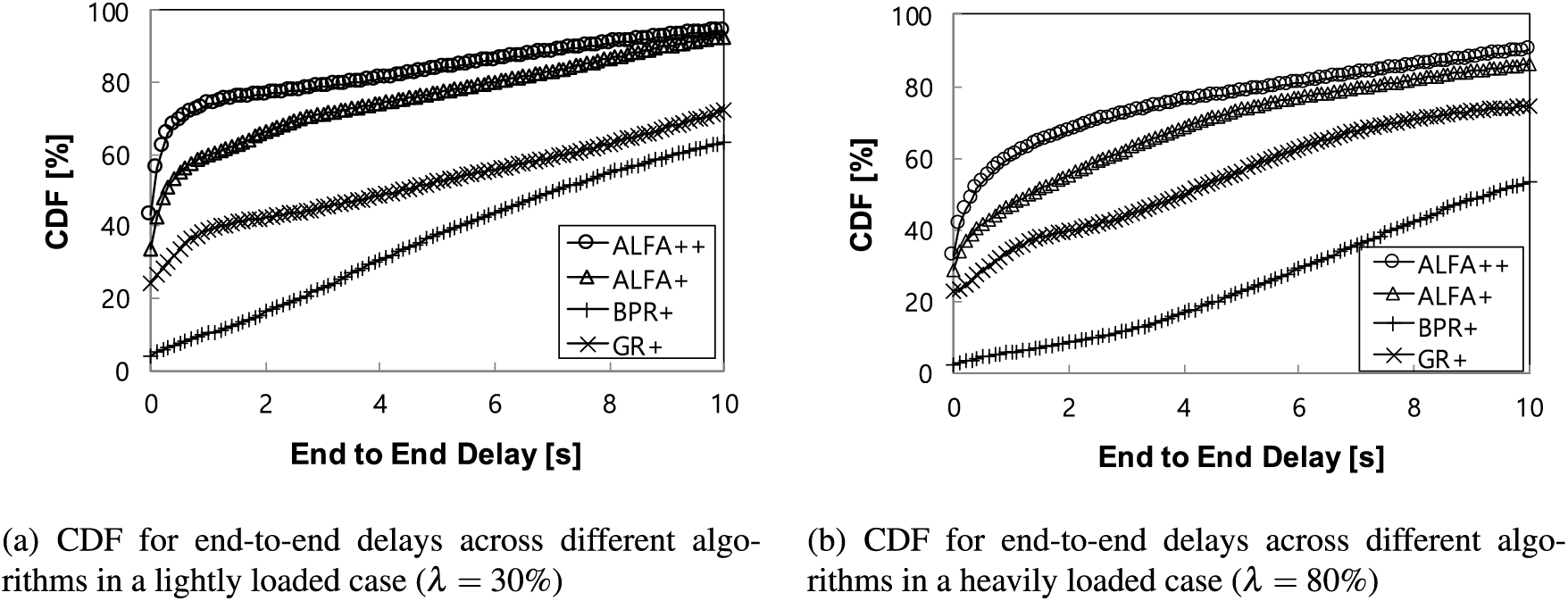
Figure 6: CDF for end-to-end delays across different algorithms in relation to offered loads

In short, ALFA++ stands out as it exhibits the best performance in both lightly and heavily loaded scenarios. As previously discussed in the complexity analysis, considering its relatively low complexity, such outstanding performance highlights the high potential of the proposed scheme in terms of practical applicability. When comparing the performance of ALFA+ with GR+ and BPR+ as a hybrid algorithm, ALFA+ demonstrates superior performance by flexibly leveraging the strengths of both GR+ and BPR+, leading to better overall performance.

5.5 Average Total Queue Length

In the previous subsection, we investigated the results of the end-to-end delay, a key metric in network performance evaluation. Here, our attention turns to observing the average total queue length, which is highly relevant to delay. Prior studies [4,39] have established a proportional relationship between delay and queue length. In this context, our first goal is to check whether such a correlation is observed as a foundational investigation. Subsequently, we aim to conduct a more thorough analysis to evaluate how queue length varies between the proposed and baseline models under various offered loads. In Fig. 7, we observe that both ALFA+ and ALFA++ maintain an acceptable queue length. However, a detailed comparison between the two algorithms reveals that ALFA+ consistently exhibits queue lengths at least 20% longer than ALFA++ across all offered loads. This difference can be attributed to the distinct factor between the two schemes, particularly the incorporation of compatible scheduling in ALFA++. This indicates that the synergy effect resulting from the combination of compatible schemes contributes to reducing queue lengths. This observation aligns with our intuition, suggesting that integrating compatible schemes leads to improved performance.

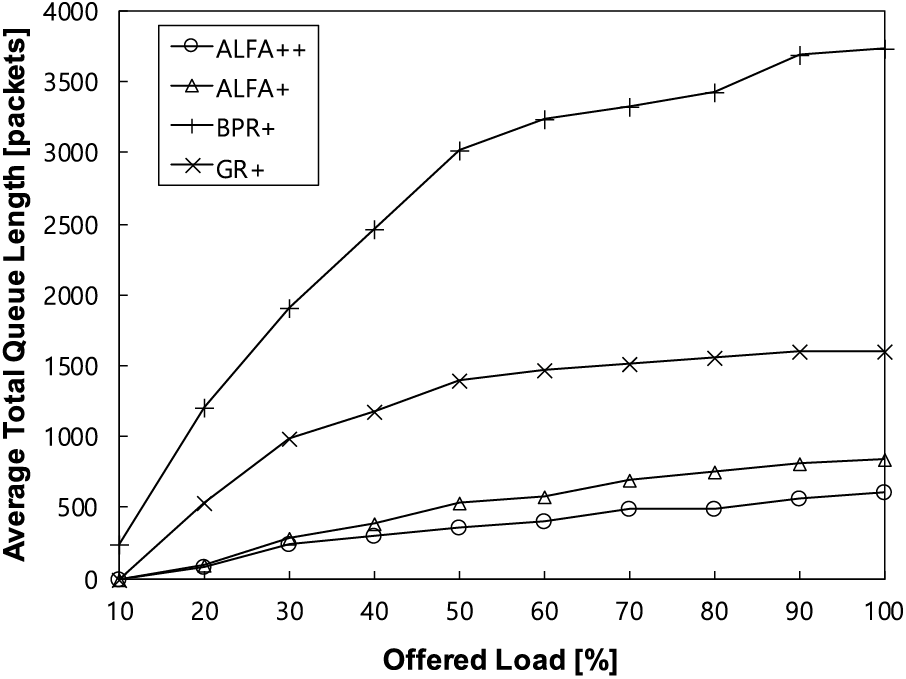
Figure 7: Average total queue length depending on offered loads across different algorithms

On the other hand, BPR+ demonstrates the longest queue length, while GR+ also exhibits a notably higher value compared to ALFA+ and ALFA++. This difference in queue length is attributed to the tendency of BPR+ to unnecessarily explore numerous paths, leading to a significant accumulation of packets within network queues. Conversely, GR+, which primarily favors shorter paths based solely on geographical information, is more prone to causing traffic concentration, resulting in congested hotspots. Specifically, ALFA++ exhibits a maximum queue length of approximately 36% shorter and an average queue length of approximately 28% shorter than ALFA+. Additionally, ALFA+ demonstrates a maximum queue length approximately 4.5 times shorter and an average queue length approximately 1.6 times shorter than GR+. Moreover, ALFA+ shows a maximum queue length approximately 1,600 times shorter and an average queue length approximately 170 times shorter than BPR+. Ultimately, the superiority of ALFA+ can be attributed to its hybrid algorithm nature, which combines the strengths of GR+ and BPR+, leading to inherent advantages. The superiority of ALFA++ is further enhanced by its highly compatible scheduling scheme, which achieves better performance compared to ALFA+.

6  Conclusion and Future Work

In this paper, we first revisit an autonomous load-balancing field-based anycast routing solution, referred to as ALFA, suitable for anycast networking in industrial WMNs. Expanding on previous work, this paper explores the routing scheme in greater depth, focusing on areas that were not previously described. These include a clearer analogy with an electrostatic system, a detailed process of incorporating numerical methods for routing metric modeling, and a clearer understanding of the characteristics and complexity of the ALFA scheme. Through this in-depth study of ALFA, we can gain a better understanding that its key capability lies in its ability to flexibly incorporate the advantages of both back-pressure routing and geographic routing, achieving load balancing and short path lengths simultaneously, based on a hybrid-type routing metric that harnesses the strengths of these routing strategies. Furthermore, as another aspect not explored in previous work, we design a scheduling strategy compatible with ALFA, utilizing the potential-based metric not only in routing but also in scheduling. This means assigning a higher medium access priority to links with a larger potential difference. Through extensive simulations, we demonstrate the superior performance of our proposed joint routing and scheduling scheme from various perspectives.

In this paper, we have pioneered the integration of ALFA with scheduling schemes, opening up new possibilities in the field. However, our current approach has a limitation in that it relies on simulation-based analysis. As future work, we need to explore theoretical aspects, such as throughput optimality. While challenging, this avenue promises to significantly contribute to stimulating new research attempts in this domain.

Acknowledgement: The authors wish to express their appreciation to the editors and reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: This work was supported by the research grant of the Kongju National University Industry-University Cooperation Foundation in 2024.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: J. Sung, Y. Kyung; data collection: J. Sung; analysis and interpretation of results: J. Sung, Y. Kyung; draft manuscript preparation: J. Sung, Y. Kyung. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Verma A, Singh H. Wireless mesh network market, key insights. 2023. Available from: https://www.researchnester.com/reports/wireless-mesh-network-market/5024. [Accessed 2023]. [Google Scholar]

2. Jung S, Kserawi M, Lee D, Rhee JK. Distributed potential field-based routing and autonomous load balancing for wireless mesh networks. IEEE Commun Lett. 2009;13(6):429–31. doi:10.1109/LCOMM.2009.090110. [Google Scholar] [CrossRef]

3. Jung S, Lee D, Kserawi M, Rhee JK. Autonomous load balancing anycast routing protocol for wireless mesh networks. In: Proceedings of the 2009 IEEE International Symposium on a World of Wireless, Mobile and Multimedia Networks & Workshops. Kos, Greece; 2009. [Google Scholar]

4. Tassiulas L, Ephremides A. Stability properties of constrained queueing systems and scheduling policies for maximum throughput in multihop radio networks. In: Proceedings of the 29th IEEE Conference on Decision and Control; 1990; Honolulu, HI, USA. [Google Scholar]

5. Karp B, Kung HT. GPSR: greedy perimeter stateless routing for wireless networks. In: Proceedings of the 6th Annual International Conference on Mobile Computing and Networking; 2000; Boston, MA, USA. [Google Scholar]

6. Ying L, Shakkottai S, Reddy A, Liu S. On combining shortest-path and back-pressure routing over multihop wireless networks. IEEE-ACM Trans Netw. 2010;19(3):841–54. [Google Scholar]

7. Deng X, Chang L, Zeng S, Cai L, Pan J. Distance-based back-pressure routing for load-balancing LEO satellite networks. IEEE Trans Veh Technol. 2022;72(1):1240–53. [Google Scholar]

8. Zhao Z, Verma G, Swami A, Segarra S. Enhanced backpressure routing with wireless link features. In: Proceedings of the IEEE 9th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP); 2023; Herradura, Costa Rica. [Google Scholar]

9. Kaur H, Singh H, Sharma A. Geographic routing protocol: a review. Int J Grid Distrib Comput. 2016;9(2):245–54. doi:10.14257/ijgdc. [Google Scholar] [CrossRef]

10. Silva A, Reza N, Oliveira A. Improvement and performance evaluation of GPSR-based routing techniques for vehicular ad hoc networks. IEEE Access. 2019;7:21722–33. doi:10.1109/ACCESS.2019.2898776. [Google Scholar] [CrossRef]

11. Zheng B, Zhuo K, Zhang H, Wu HX. A novel airborne greedy geographic routing protocol for flying Ad hoc networks. Wirel Netw. 2022;1–15. doi:10.1007/s11276-022-03030-9. [Google Scholar] [CrossRef]

12. Balaram A, Silparaj M, Nabi SA, Chandana P. A comprehensive survey of geographical routing in multi-hop wireless networks. In: Cloud Computing Enabled Big-Data Analytics in Wireless Ad-hoc Networks. USA: CRC Press; 2022. [Google Scholar]

13. Anand V, Jain A, Pattanaik K, Kumar A. Traffic aware field-based routing for wireless sensor networks. Telecommun Syst. 2019;71:475–89. doi:10.1007/s11235-018-0519-0. [Google Scholar] [CrossRef]

14. Yan J, Ding W, Guo H, Tang L. Virtual force traffic-aware routing protocol for wireless sensor networks. In: Proceedings of the 2020 International Wireless Communications and Mobile Computing (IWCMC). Limassol, Cyprus; 2020. [Google Scholar]

15. Jiang H, Lu L, Han G, Wang H, Ma S, Sun R. Routing algorithm for supporting data-differentiated service in hybrid wireless mesh networks in underground mines. Int J Distrib Sens Netw. 2018;14(11). doi:10.1177/1550147718812024. [Google Scholar] [CrossRef]

16. Zhao W, Yan XY, Shao F, Tian XH, Cheng BH. Collaborative routing protocol based on hydrodynamics for wireless sensor networks. Int J Distrib Sens Netw. 2015;11(8):276276. doi:10.1155/2015/276276. [Google Scholar] [CrossRef]

17. Xu Y, Ren F, He T, Lin C, Chen C, Das SK. Real-time routing in wireless sensor networks: a potential field approach. ACM Trans Sens Netw. 2013;9(3):1–24. doi:10.1145/2480730.2480738. [Google Scholar] [CrossRef]

18. Liu H, Zhang ZL, Srivastava J, Firoiu V. PWave: a multi-source multi-sink anycast routing framework for wireless sensor networks. In: NETWORKING 2007. Ad hoc and sensor networks, wireless networks, next generation internet. USA: Atlanta, GA; 2007. [Google Scholar]

19. Baumann R, Heimlicher S, Plattner B. Routing in large-scale wireless mesh networks using temperature fields. IEEE Netw. 2008;22(1):25–31. doi:10.1109/MNET.2008.4435899. [Google Scholar] [CrossRef]

20. Kserawi M, Jung S, Lee D, Sung J, Rhee JK. Multipath video real-time streaming by field-based anycast routing. IEEE Trans Multimedia. 2013;16(2):533–40. [Google Scholar]

21. Metz C. IP anycast point-to-(any) point communication. IEEE Internet Comput. 2002;6(2):94–8. doi:10.1109/4236.991450. [Google Scholar] [CrossRef]

22. Shin J, Lee H, Na J, Park A, Kim S. Load balancing among internet gateways in ad hoc networks. In: Proceedings of VTC-2005-Fall. 2005 IEEE 62nd Vehicular Technology Conference; 2005; Dallas, TX, USA. [Google Scholar]

23. Nandiraju D, Santhanam L, Nandiraju N, Agrawal DP. Achieving load balancing in wireless mesh networks through multiple gateways. In: Proceedings of the 2006 IEEE International Conference on Mobile Ad Hoc and Sensor Systems; 2006; Vancouver, BC, Canada. [Google Scholar]

24. Jin JM. The finite element method in electromagnetics. USA: John Wiley & Sons; 2015. [Google Scholar]

25. Li Z, Reed M. Convergence analysis for an element-by-element finite element method. Comput Meth Appl Mech Eng. 1995;123(1–4):33–42. [Google Scholar]

26. Griffiths DJ. Introduction to electrodynamics. USA: American Association of Physics Teachers; 2005. [Google Scholar]

27. Warrier A, Janakiraman S, Ha S, Rhee I. DiffQ: practical differential backlog congestion control for wireless networks. In: Proceedings of the IEEE INFOCOM 2009; 2009; Rio de Janeiro, Brazil. [Google Scholar]

28. Banchs A, Azcorra A, García C, Cuevas R. Applications and challenges of the 802.11 e EDCA mechanism: an experimental study. IEEE Netw. 2005;19(4):52–8. doi:10.1109/MNET.2005.1470683. [Google Scholar] [CrossRef]

29. Legout A, Amir E, Balakrishnan H, Bajaj S, Breslau L, Eggert L, et al. ns-2 network simulator. 2011. Available from: https://www.isi.edu/nsnam/ns. [Accessed 2023]. [Google Scholar]

30. Wiethoelter S, Emmelmann M, Hoene C, Wolisz A. TKN EDCA Model for ns-2. Technical University Berlin, Telecommunication Networks Group; 2006. [Google Scholar]

31. Shi W, Wang S, Wang Z, Wang E. An efficient channel assignment algorithm for multicast wireless mesh networks. AEU-Int J Electron Commun. 2018;89:62–9. doi:10.1016/j.aeue.2018.03.023. [Google Scholar] [CrossRef]

32. Zhang Z, Rathi R. Novel access methods in cellular networks based on the analog bloom filter. IEEE Trans Wirel Commun. 2023;22(8):5628–41. doi:10.1109/TWC.2023.3235650. [Google Scholar] [CrossRef]

33. Alzamil Z. Efficient optimal routing algorithm based on reward and penalty for mobile adhoc networks. Comput Mater Contin. 2023;75(1):1331–51. doi:10.32604/cmc.2023.033181. [Google Scholar] [CrossRef]

34. Huang C, Wang X. Distributed scheduling with centralized coordination for scalable wireless mesh networking. IEEE/ACM Trans Netw. 2022;31(1):436–51. [Google Scholar]

35. Chai Y, Zeng XJ. Load balancing routing for wireless mesh network with energy harvesting. IEEE Commun Lett. 2020;24(4):926–30. doi:10.1109/COML.4234. [Google Scholar] [CrossRef]

36. Arce P, Guerri JC, Pajares A, Lázaro O. Performance evaluation of video streaming over ad hoc networks using flat and hierarchical routing protocols. Mobile Netw Appl. 2008;13:324–36. [Google Scholar]

37. Raj RN, Nayak A, Kumar MS. NS-2 extension for interface assignment in AODV routing protocol. In: Proceedings of the 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI); 2017; Udupi, India. [Google Scholar]

38. Jain R. The art of computer systems performance analysis: techniques for experimental design, measurement, simulation, and modeling. USA: John Wiley & Sons; 2008. [Google Scholar]

39. Sung J, Lee D. Efficient design and control for network-assisted device-to-device content delivery network. IEEE Trans Multimedia. 2020;23:2442–56. [Google Scholar]