Impact Performance Research of Re-Entrant Octagonal Negative Poisson’s Ratio Honeycomb with Gradient Design

1  Introduction

As a highly representative lightweight porous material, honeycombs exhibit numerous outstanding mechanical properties and find applications in aerospace [1], vehicle engineering [2], and various other fields [3]. Over the past few decades, some novel honeycombs have been designed and explored through theoretical analysis [4], experiments [5], and numerical simulations [6]. Currently, honeycombs with various cross-sectional shapes have been developed and studied, including hexagonal [7], square [8], circular [9], and triangular [10]. However, these traditional honeycombs often fail to meet the requirements for high-performance, lightweight materials in many applications. Therefore, it is imperative to develop honeycomb materials with enhanced properties through design [11].

As commonly recognized, the topological configuration significantly impacts the performance of honeycomb materials [12]. Negative Poisson’s ratio structure has been widely investigated due to its excellent properties, such as fracture resistance, high shear modulus, and strong ductility [13]. Shen et al. [14] proposed a variable arc angle inward-corrugated honeycomb with a negative Poisson’s ratio and indicated that the arc angle significantly influences the effective elastic modulus. The effective Poisson’s ratio is more noticeably affected by the arc angle, the length of vertical wall panels, and the width between two vertical wall panels, while the impact of the length of the connecting part is less evident. Liu et al. [15] introduced an airbag-type negative Poisson’s ratio honeycomb structure, discovering that compared to the traditional inward hexagonal structure, the airbag-type honeycomb structure exhibits higher plateau stress and specific energy absorption, improving impact resistance and energy absorption capabilities. Bohara et al. [16] introduced a dual-mechanism auxetic (DMA) sandwich structure for blast protection. DMA combines auxetic compression and tension behavior, enhancing its protective capacity. Computational models in LS-DYNA were validated and employed to assess DMA’s energy absorption, stress mitigation, and deflection control. DMA outperformed an equivalent solid plate, and parametric studies revealed its optimal design for various blast environments. Liu et al. [17] proposed a novel cross-shaped negative Poisson’s ratio honeycomb structure and investigated the influence of the rod length ratio coefficient and impact velocity on its deformation modes. Focusing on star-shaped honeycomb structures, Huang et al. [18] provided a theoretical calculation model for the in-plane equivalent mechanical properties within the elastic deformation range, which has advantages over experimental methods. Liu et al. [19] introduced a novel chiral negative Poisson’s ratio structure, designed and fabricated configurations with different geometric parameters using 3D printing technology, and revealed that a stronger negative Poisson’s ratio effect within the structure corresponds to superior vibration-damping performance. Bohara et al. [20] evaluated the protective capacity of a re-entrant auxetic honeycomb-core sandwich panel (AHSP) for reinforced concrete slabs under high explosive detonations. Using numerical models validated with experimental data, AHSP outperformed a conventional honeycomb panel in energy absorption, pressure deflection, overpressure damping, and stress distribution.

In addition, gradient design is increasingly employed to enhance honeycomb performance. Numerous studies suggested that gradient honeycombs have significant potential to improve both mechanical [21] and energy absorption capacity [22]. Zhang et al. [23] proposed a variable cross-section of honeycomb materials, finding that the energy absorption performance of bidirectional negative gradient is superior to other structural configurations at medium to low speeds. Tao et al. [24] introduced a planar honeycomb with variable wall thickness, revealing that honeycombs with positive gradients exhibit significantly enhanced specific energy absorption (SEA) compared to those without gradients. Min et al. [25] investigated the in-plane impact performance of hexagonal honeycomb materials with gradient cell thickness by introducing the concept of gradient thickness, and indicated that concave hexagonal honeycomb materials with positive thickness gradients have better energy absorption and impact resistance. Wu et al. [26] introduced a novel approach by incorporating in-plane and out-of-plane thickness gradients into traditional honeycombs, resulting in a bidirectional gradient honeycomb design. They revealed that both types of gradients can augment the mechanical properties of honeycombs.

Accordingly, this study proposes a novel re-entrant octagon honeycomb (ROH) with a negative Poisson’s ratio, designed based on the traditional re-entrant honeycomb. It uses experiments and finite element methods to explore the mechanical performance and energy absorption characteristics of ROH. Hence, gradient designs along the impact and perpendicular-to-impact directions are applied to ROH while ensuring consistent relative density. Numerical simulation is then employed to investigate the mechanical performance and energy absorption capabilities of various gradients under different deformation modes and impact velocities.

2  Geometric Configurations

2.1 Geometric Description

It is known that honeycombs primarily dissipate energy through plastic deformation when subjected to impacts [24]. Hence, to improve the performance of honeycombs, a novel honeycomb with more plastic hinges is proposed in this study based on the traditional re-entrant honeycomb (TRH), as shown in Fig. 1. Since the unit cell of the novel honeycomb is created by adding two cell walls to the re-entrant octagon honeycomb, it is named the re-entrant octagon honeycomb (ROH).

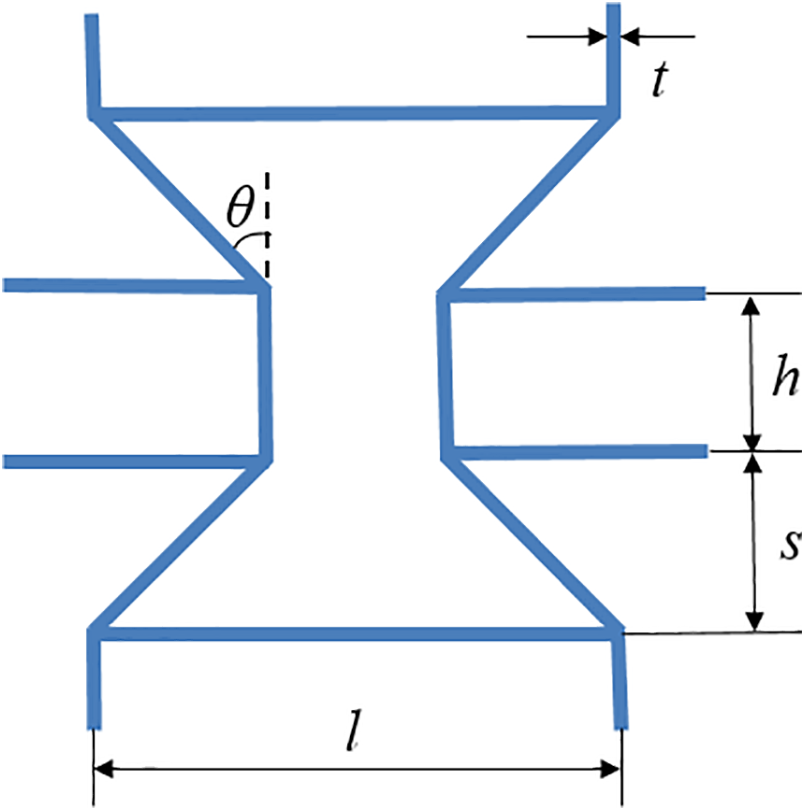
Figure 1: The geometric configurations of ROH

The deformation mode and energy absorption characteristics of the honeycomb are closely related to its relative density. The definition of relative density is as follows:

ρ¯=ρsρ0(1)

where ρs is the apparent density of the honeycomb and ρ0 is the density of the matrix material. The relative density of the ROH cell can be derived based on geometric relationships as follows:

ρ¯=(lcos⁡θ+hcos⁡θ+s)t(l−stan⁡θ)(h+s)cos⁡θ(2)

where l is the length of the horizontal cell wall, h is the length of the vertical support, θ is the concave angle, s is the height of the inclined angle, and t is the thickness.

2.2 Key Performance Index

The plateau stress (σm) and specific energy absorption (SEA) are two crucial indicators for assessing the energy absorption performance of honeycombs. The plateau stress is expressed as follows [24]:

σm=1εd∫0εdσ(ε)dε(3)

where εd is the onset strain of densification and σ(ε) denotes the stress varying with strain. Specific energy absorption is defined as the ratio of total energy absorbed to mass, calculated as follows [27]:

SEA=V∫0εdσ(ε)dεm=∫0εdσ(ε)dερ0(4)

η=∫0εdσ(ε)dεσ(ε)(5)

3  Numerical and Experimental Methods

3.1 Finite Element Model

The in-plane compression of the ROH is simulated using the explicit dynamics software ABAQUS/Explicit. Fig. 2 illustrates the finite element numerical model, where the honeycomb is sandwiched between two rigid plates. The bottom plate is subject to constraints and confinement, effectively restraining all degrees of freedom of the rigid plates. The top plate compresses the honeycomb at a constant speed. In the simulation, a rigid body is utilized to construct the steel plate model, and ROH is modeled using C4R with five integration nodes in the thickness direction. Surface-to-surface contacts are employed to mimic the interactions between the unit cell and the two plates, while general contact is utilized to simulate the self-contact within the unit cell. A friction coefficient of 0.3 is adopted in the tangential direction. In addition, the matrix material of ROH is aluminum alloy AA3003 H18 [28] with density ρ=2700 kg/m3, Young’s modulus E=69 GPa, Poisson’s ratio ν=0.3, yield stress σy=115.8 MPa, and ultimate stress σy=154.5 MPa. Because AA3003 H18 is insensitive to the strain rate, the effect of strain rate is ignored in this study [5].

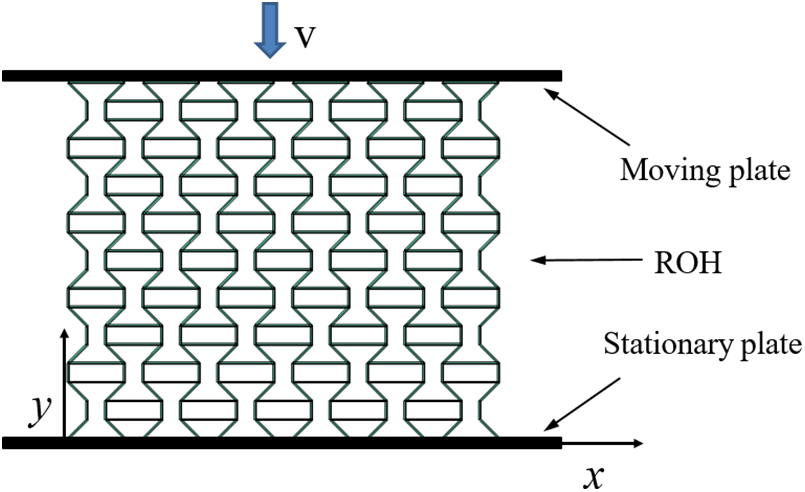
Figure 2: Finite element model of ROH under axial compression

The mesh size can specifically impact the accuracy of finite element calculations. Therefore, this section discusses five different mesh sizes of 0.25, 0.75, 1.25, 2, and 3 mm. Since the thinnest cell wall thickness of the honeycomb explored in this study is 1 mm, a mesh convergence test was conducted on ROH with t=1 mm. The results of the convergence test are shown in Fig. 3. The plateau stress of the ROH exhibits a relatively close resemblance under mesh sizes of 0.25 and 0.75 mm, with a mere 3.71% discrepancy in the results. As the mesh size enlarges, σm also rises. This analysis suggests that as the mesh size diminishes, the mesh test outcomes tend to converge. Given the minor deviation in the analysis results of the 0.75 mm mesh and the consideration of time efficiency, the 0.75 mm mesh will be utilized for subsequent research and discussions.

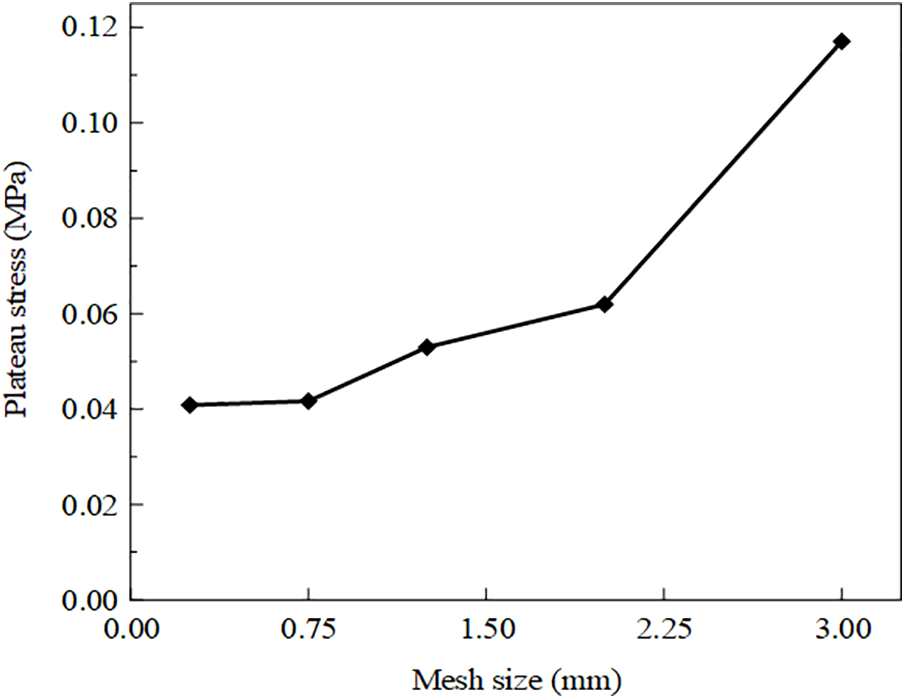
Figure 3: Plateau stress of ROH with different mesh sizes

3.2 Experimental Test

The additive manufacturing techniques was adopted in this study to fabricate the ROH. The matrix material used for 3D printing was C-UV 9400E. C-UV 9400E is a stereolithography resin with precise and durable characteristics, similar to ABS. Based on ASTM D638-22 standard [29], uniaxial tensile tests were conducted on three dog-bone shaped specimens using the SANS CMT5205 electronic universal testing machine to obtain the mechanical properties of C-UV 9400E. The loading velocity was kept at 2 mm/min. Fig. 4 shows the dog-bone shaped specimens and experimental setup. Based on the text results, the typical stress-strain curve of C-UV 9400E is plotted in Fig. 4d, and the mechanical property parameters of C-UV 9400E were obtained as follows: density ρs=1100 kg/m3, Young’s modulus Es=2400 MPa, Poisson’s ratio ν=0.45, yield strength σy=22.7 MPa, and ultimate stress σy=43.6 MPa.

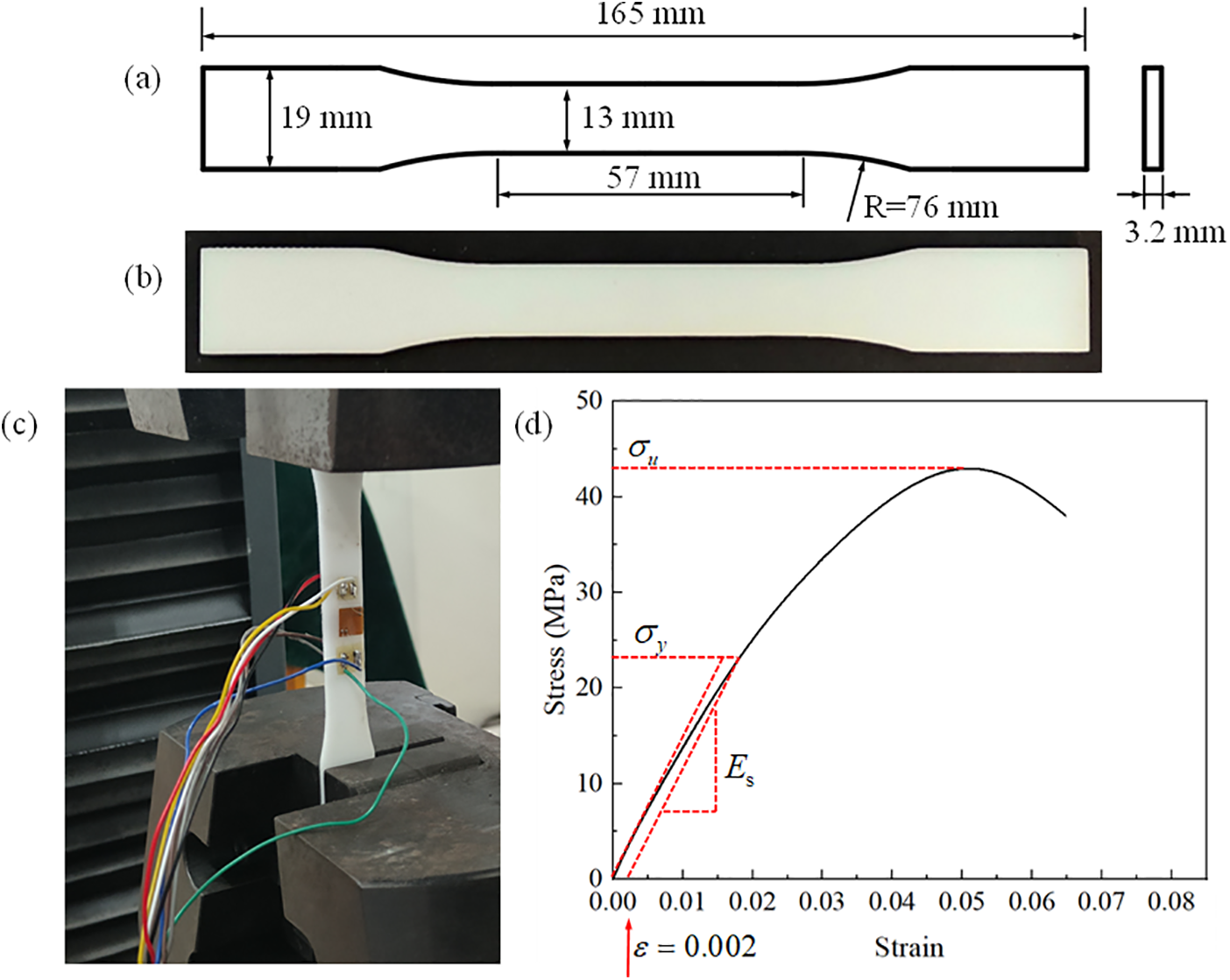
Figure 4: (a) Geometric dimensions of dog-bone shaped, (b) standard tensile specimens, (c) perform tensile test setup for standard tensile specimens, and (d) stress-strain curve of C-UV 9400E

Fig. 5a indicates that the ROH specimens consist of 6 × 5 cell elements arranged along the x × y direction. Table 1 provides the detailed geometrical parameters of these ROH specimens. The overall dimensions of the ROH specimens are 92 mm × 76 mm × 25 mm. The experimental setup adopted in this study is shown in Fig. 5b. A quasi-static compression experiment was conducted on the ROH specimen on a universal testing machine. The ROH specimen was placed at the center of the bottom plate of the testing machine. During the experiment, the upper plate remained stationary while the lower plate slowly rose at a speed of 2 mm/min until the sample was completely crushed. A total of three ROH samples were subjected to the same experiment to avoid any chance of results.

Figure 5: (a) Specimens of C-UV 9400E material fabricated by 3D printing and (b) in-plane quasi-static compressive test setup for ROH

3.3 Validation of Finite Element Modeling Method

The quasi-static compression experiment is adopted to compare the numerical results and validate the accuracy of the finite element method. The potential for excessively long computational times is used when using a low loading rate in Abaqus/Explicit. Hence, the loading mode in the finite element simulation was set to dynamic explicit, with a loading speed of 1 m/s to simulate the quasi-static compression process [4]. Fig. 6 depicts a comparative analysis of the result from quasi-static compression experiments and finite element simulations conducted on ROH. Fig. 6 indicates that the stress-strain curves from the experiments and simulations are relatively consistent, particularly between strains of 0.25 and 0.5, where the stress-strain curves from simulations closely match those from experiments. Fig. 7 shows that at a strain of 0.18, ROH undergoes uniform deformation, contracting towards the center. At a strain of 0.36, slight protrusions appear on the upper and lower parts of ROH in different directions, with a diagonal shear band forming in the middle. At a strain of 0.54, the diagonal shear band widens, leaving only the diagonals of the rectangle relatively intact. At a strain of 0.72, all cells collapse, and the honeycomb achieves densification to a large extent. During the compression process, it can be observed that the ROH contracts inward, exhibiting a pronounced negative Poisson’s ratio effect. Upon examining the deformation modes of both the experimental sample and the model, it can be found that their deformation patterns are virtually indistinguishable under the same strain. Upon comparison, it can be concluded that there is consistency between the experimental and simulated results, affirming the reliability of the finite element simulation method in studying the energy absorption characteristics of the re-entrant octagon honeycomb model. Based on the finite element simulation results, various gradient ROH impact performance and energy absorption mechanisms will be further explored.

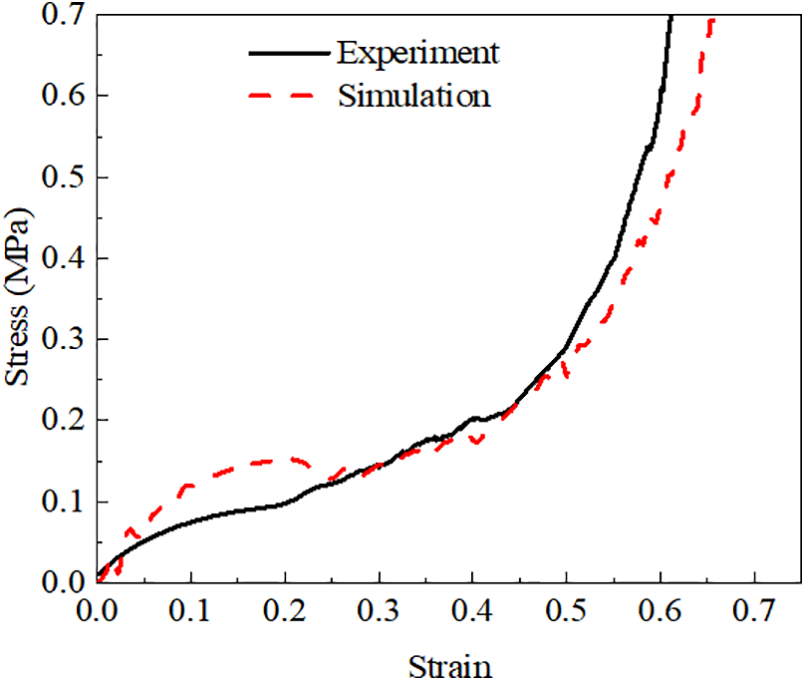
Figure 6: Comparison of experimental and simulation results

Figure 7: Comparison of deformation modes between experiments and simulations

4  Results and Discussion

4.1 Gradient Design along the Direction of Impact

Based on Xiao et al.’s study [30], when subjected to medium to high-speed impacts (greater than 20 m/s), honeycombs undergo densification strains initially near the impact end, followed by layer-by-layer deformation downward. In this section, under an impact velocity of 20 m/s, a gradient design (Fig. 8) of cell wall thickness is applied to ROH in the impact direction (i.e., the y-direction). This is done to achieve a deformation pattern similar to that of low-speed impacts (5 m/s) and then to compare the energy absorption performance of the honeycomb with the same relative density before and after the gradient design. ROH-2 with varying cell wall thickness in the y-direction was designed, as depicted in Fig. 8. In contrast, ROH-1 features a uniform wall thickness of 0.274 mm to maintain consistent relative density.

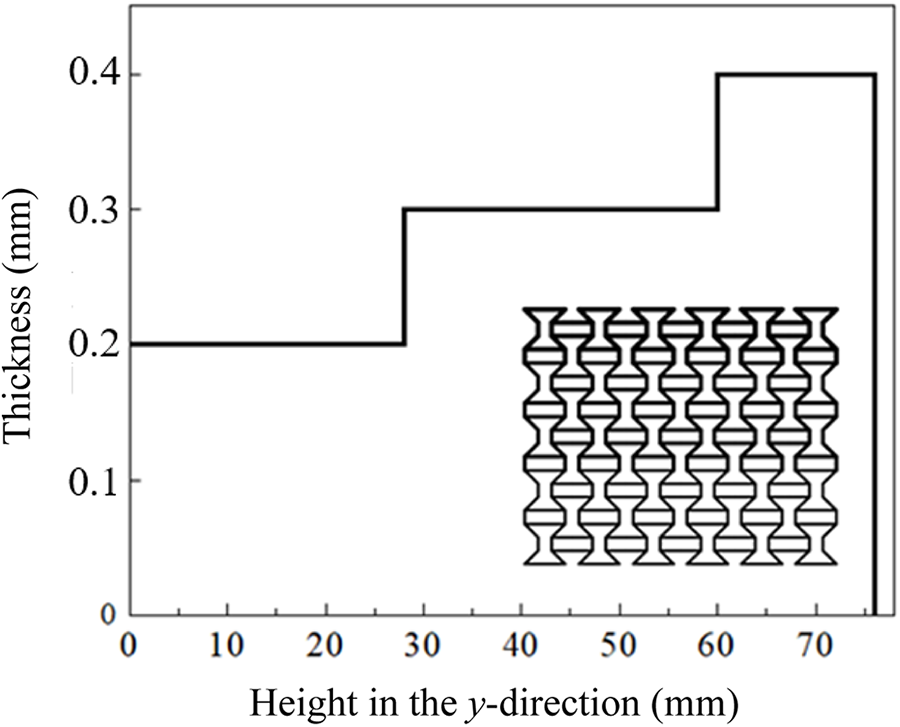
Figure 8: Cell wall thickness of ROH-2

Fig. 9a depicts the deformation pattern of the uniform wall thickness ROH-1 under an impact speed of 5 m/s. Fig. 9b illustrates the deformation pattern of the uniform wall thickness ROH-1 under an impact speed of 20 m/s. Fig. 9c shows the deformation pattern of ROH-2 that underwent gradient design along the impact direction under an impact speed of 20 m/s. Fig. 9 indicates that at a strain of 0.27, the deformation mode exhibited by ROH-2 under an impact velocity of 20 m/s is consistent with the deformation mode displayed by ROH-1 when subjected to an impact velocity of 5 m/s. Both exhibit overall contraction towards the center, with bending deformation occurring at both the impact and support ends, forming an ‘X-shaped’ shear band. In addition, ROH-1 under 20 m/s impact velocity undergoes deformation primarily near the impact zone, with no significant changes observed elsewhere.

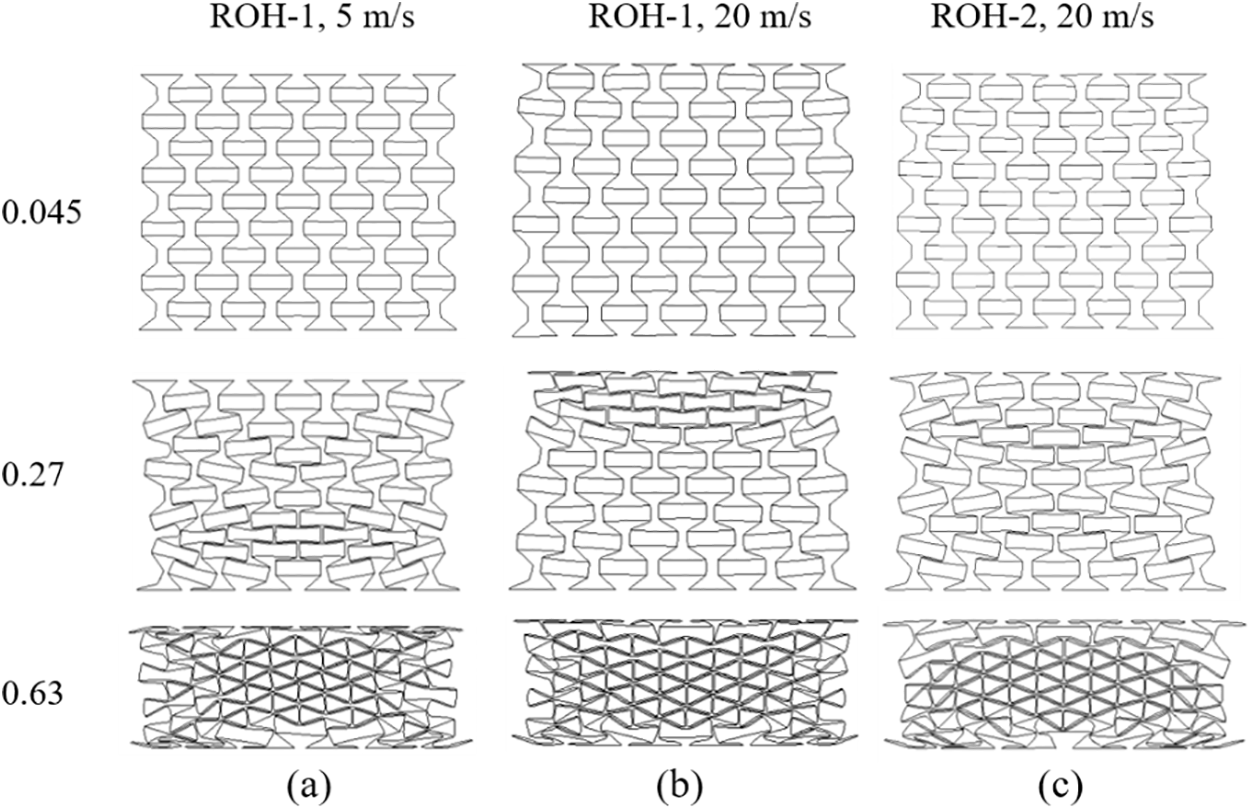
Figure 9: Deformation patterns before and after gradient design along the impact direction

Fig. 10 presents the stress-strain curves of the ROH-1 and ROH-2. It exhibits that, in the early stages of 20 m/s impact, the peak stress of ROH-2 is significantly higher than that of ROH-1. This is attributed to the larger wall thickness near the impact end of ROH-2. When strain varies from 0.1 to 0.5, the stress-strain curves of ROH-1 and ROH-2 fluctuate at the same horizontal level. When the strain exceeds 0.6, ROH-2 exhibits an increase in stress, entering the densification phase earlier. Considering the deformation mode, this can be due to the initial failure occurring at the region with a minimum wall thickness of 0.2 in ROH-2 while ROH-1 is still in the plateau stage. After a strain of 0.7, the stress of ROH-1 also begins to increase significantly, reaching densification. The plateau stresses for ROH-1 and ROH-2 are 0.345 and 0.352 MPa, respectively.

Figure 10: Stress-strain curves of ROH-1 and ROH-2 at an impact speed of 20 m/s

The comparison of the energy absorption efficiency between ROH-1 and ROH-2 shows similarities, while ROH-2 exhibits slightly higher absorption energy than ROH-1, as shown in Fig. 11. However, its inflection point of ROH-2 occurs earlier than that of ROH-1, attributed to ROH-2 entering the densification stage earlier. Fig. 12 shows that when the strain is less than 0.1, the absorption efficiency of ROH-1 is significantly higher than that of ROH-2. However, once the honeycomb enters the plateau phase, the energy absorption efficiency of ROH-2 is superior to that of ROH-1. However, once the strain surpasses 0.6, the energy absorption efficiency of ROH-2 experiences a noticeable decline, whereas for ROH-1, this decrease occurs notably after 0.7.

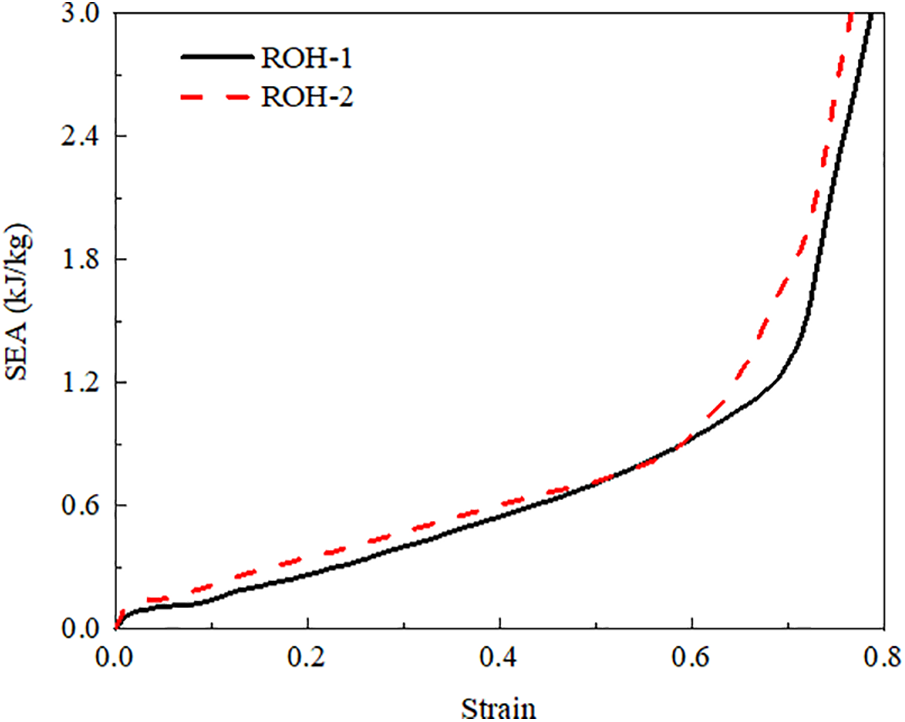
Figure 11: SEA of ROH-1 and ROH-2 under 20 m/s impact

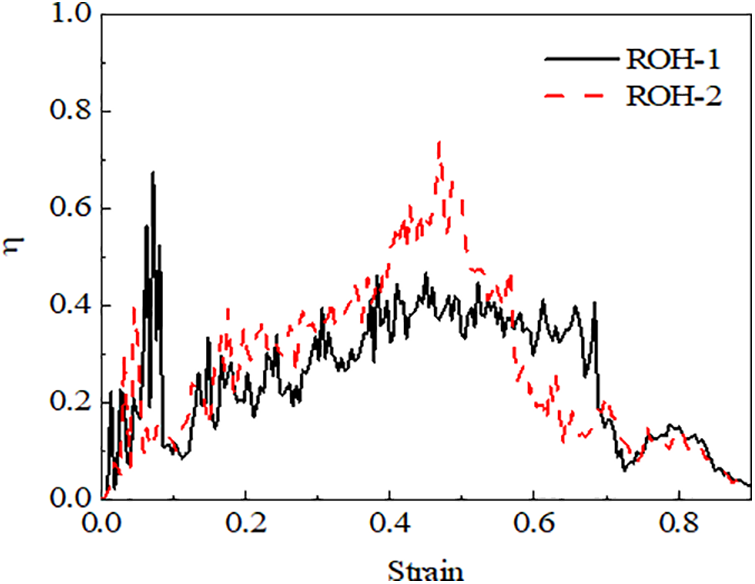
Figure 12: Energy absorption efficiency of ROH-1 and ROH-2 under 20 m/s impact

4.2 Gradient Design along the Direction Perpendicular to the Impact

This section proposes five gradient ROHs based on the wall thickness variation perpendicular to the impact direction. Fig. 13 shows the wall thickness distribution, where the same color represents the same wall thickness. The specific parameters of wall thickness are listed in Table 2.

Figure 13: The geometric configurations of ROH-6

Fig. 14 indicates that the dynamic performance of ROH follows a pattern similar to that of traditional re-entrant honeycomb [30]. Initially, upon impact, ROH remains in the elastic phase where stress and strain exhibit a linear relationship. Stress sharply rises with strain until reaching a peak stress. Following the peak stress, the honeycomb enters a plateau phase where stress fluctuates slightly with increasing strain. As the strain approaches around 0.6, the honeycomb transitions into a densification phase, marked by a significant increase in stress. Fig. 15 demonstrates that the energy absorption efficiency of each gradient is similar.

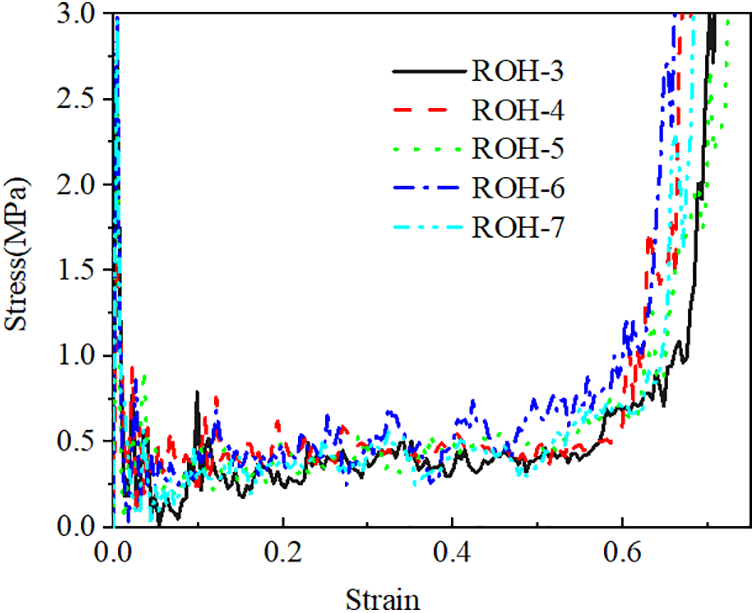
Figure 14: Stress-strain curves of each gradient at an impact speed of 20 m/s

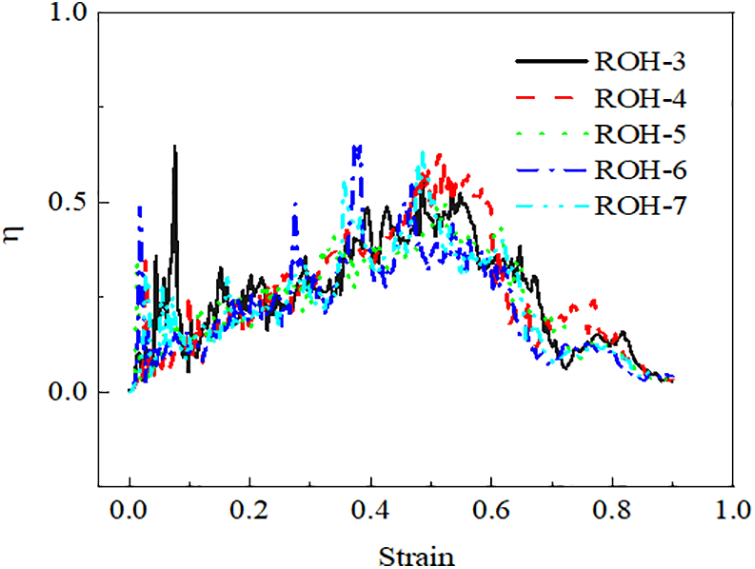
Figure 15: Energy absorption efficiency curves of each gradient at an impact speed of 20 m/s

Fig. 16 shows the plateau stresses of different gradient ROH at various velocities. As the velocity increases, the plateau stresses of all graded honeycombs become larger. ROH-6 exhibits the highest plateau stress at the same velocity, while ROH-3 has the smallest. At an impact velocity of 20 m/s, the plateau stress of ROH-6 is 50% higher than that of ROH-3, indicating that the gradient design perpendicular to the impact direction positively impacts the honeycomb’s energy absorption.

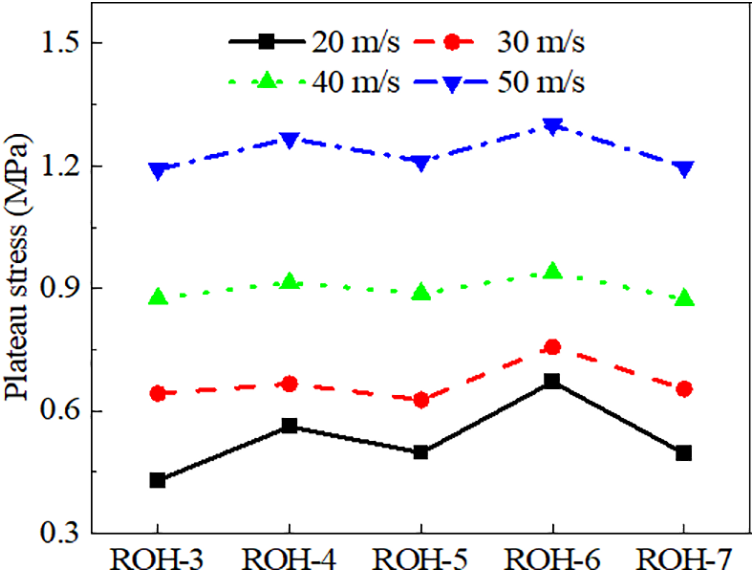
Figure 16: Plateau stress of each gradient at different speeds

Considering the specific energy absorption in Fig. 17, higher velocities result in greater specific energy absorption, and at each velocity, ROH-6 shows the highest specific energy absorption. This indicates that ROH with larger gradients perform better in energy absorption under medium to low-speed impacts (20–50 m/s).

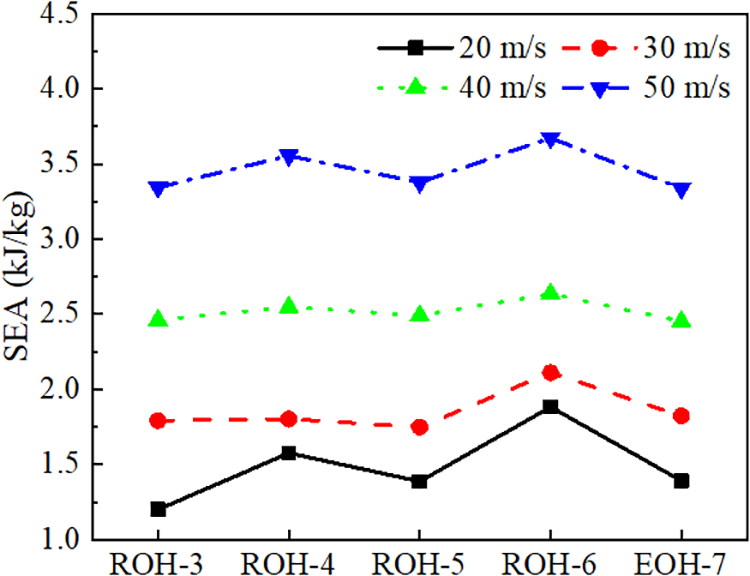
Figure 17: SEA of each gradient at different speeds

Mechanism analysis revealed that the reinforcement of the honeycomb structure is attributed to the special relationship between its graded variable relative density and graded variable compressive strength [31]. In short, by dividing a honeycomb with gradient wall thickness into different zones and calculating the compressive strength of each zone separately, the overall compressive strength can be obtained, similar to the behavior of parallel springs. For ROH, the linear relationship between the wall thickness and relative density in each zone, combined with the nonlinear relationship between the wall thickness and compressive strength, contributes to enhancing the honeycomb’s energy absorption performance. In addition, as the difference in wall thickness between zones increases, the enhancement effect becomes more significant.

When the internal wall thickness is smaller than the external wall thickness, the outer cells collapse inward, exhibiting uneven lateral deformation. This, coupled with the strength difference, leads to unstable deformation. In contrast, when the internal wall thickness is greater than the external wall thickness, the honeycomb can deform more stably along the impact direction without easily tilting to one side, resulting in smaller lateral displacement of the cells. In addition, the stress-strain curves in Fig. 14 show that the ROH with graded design enters the densification stage earlier, resembling the “shortest plank” effect, where the actual densification strain of the entire ROH is determined by the densification strain of the zone with the smallest wall thickness.

5  Conclusion

Based on the mechanical performance and energy absorption characteristics of a traditional re-entrant honeycomb, a novel re-entrant octagon honeycomb with a negative Poisson’s ratio is proposed, and its validity is confirmed through experimental validation of finite element methods. The mechanical properties and energy absorption characteristics of gradient-designed ROH along the impact and perpendicular directions under various deformation modes and impact velocities are investigated through simulation analysis. The following conclusions are drawn:

(1) Implementing a gradient design to maintain a similar deformation mode for ROH at 20 m/s as it experiences at 5 m/s does not significantly impact its energy absorption performance. However, the ROH with gradient design exhibits a notable increase in initial peak stress upon impact, and it enters the densification phase earlier.

(2) A gradient design perpendicular to the impact direction enhances the energy absorption performance of ROH to a certain extent. In addition, ROH, with a more pronounced increase in wall thickness from the inside to the outside, exhibits higher plateau stress and specific energy absorption. As the impact velocity increases, both the plateau stress (σm) and specific energy absorption (SEA) show an increasing trend, consistent with the dynamic performance pattern of traditional honeycombs.

Acknowledgement: The authors are thankful to the anonymous editors and reviewers for improving this article.

Funding Statement: This work is supported by the National Natural Science Foundation of China (No. 11902232).

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design:Y.Y.L., Y.J.L., S.L.Y. and P.W.; data collection:Y.Y.L. and Y.J.L.; analysis and interpretation of results: Y.Y.L., S.L.Y. and P.W.; draft manuscript preparation: Y.Y.L., S.L.Y. and P.W. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Tomizuka M, Vos R, Barrett R. Pressure adaptive honeycomb: a new adaptive structure for aerospace applications. Sens Smart Struct Tech Civil, Mech, Aerosp Syst. 2010;2010:721–32. [Google Scholar]

2. Zhu G, Li S, Sun G, Li G, Li Q. On design of graded honeycomb filler and tubal wall thickness for multiple load cases. Thin-Walled Struct. 2016;109:377–89. doi:10.1016/j.tws.2016.09.017. [Google Scholar] [CrossRef]

3. Wu J, Zhang Y, Zhang F, Hou Y, Yan X. A bionic tree-liked fractal structure as energy absorber under axial loading. Eng Struct. 2021;245:112914. doi:10.1016/j.engstruct.2021.112914. [Google Scholar] [CrossRef]

4. Zhao R, Yuan B, Zhou D, Li Z, Zhao M, Tao Y. On the out of plane crashworthiness of incorporating hierarchy and gradient into hexagonal honeycomb. Mech Adv Mater Struct. 2023:1–15. doi:10.1080/15376494.2023.2222315. [Google Scholar] [CrossRef]

5. Qin Q, Xia Y, Li J, Chen S, Zhang W, Li K, et al. On dynamic crushing behavior of honeycomb-like hierarchical structures with perforated walls: experimental and numerical investigations. Int J Impact Eng. 2020;145:103674. doi:10.1016/j.ijimpeng.2020.103674. [Google Scholar] [CrossRef]

6. Menon HG, Dutta S, Krishnan A, M. P. H, Shankar B. Proposed auxetic cluster designs for lightweight structural beams with improved load bearing capacity. Eng Struct. 2022;260(4):114241. doi:10.1016/j.engstruct.2022.114241. [Google Scholar] [CrossRef]

7. Zhou Y, Li Y, Jiang D, Chen Y, Xie Y, Jia L. In-plane impact behavior of 3D-printed auxetic stainless honeycombs. Eng Struct. 2022;266(9):114656. doi:10.1016/j.engstruct.2022.114656. [Google Scholar] [CrossRef]

8. Gao Z, Li H, Zhao J, Guan J, Wang Q. Analyses of dynamic characteristics of functionally graded porous (FGP) sandwich plates with viscoelastic materials-filled square-celled core. Eng Struct. 2021;248(13):113242. doi:10.1016/j.engstruct.2021.113242. [Google Scholar] [CrossRef]

9. Hu L, Cai D, Wu G, He X, Yu T. Influence of internal pressure on the out-of-plane dynamic behavior of circular-celled honeycombs. Int J Impact Eng. 2017;104:64–74. doi:10.1016/j.ijimpeng.2017.02.004. doi:10.1016/j.ijimpeng.2017.02.004. [Google Scholar] [CrossRef]

10. Wei K, Chen H, Pei Y, Fang D. Planar lattices with tailorable coefficient of thermal expansion and high stiffness based on dual-material triangle unit. J Mech Phys Solids. 2016;86:173–91. doi:10.1016/j.jmps.2015.10.004. [Google Scholar] [CrossRef]

11. Ou Y, Yan S, Wen P. In-plane impact dynamics analysis of re-entrant honeycomb with variable cross-section. Comput Model Eng Sci. 2021;127(1):209–22. doi:10.32604/cmes.2021.014828. [Google Scholar] [CrossRef]

12. Tatlıer MS, Öztürk M, Baran T. Linear and nonlinear in-plane behaviour of a modified re-entrant core cell. Eng Struct. 2021;234:111984. doi:10.1016/j.engstruct.2021.111984. [Google Scholar] [CrossRef]

13. Li G, Chen Y, Wei G. Continuous fiber reinforced meta-composites with tailorable Poisson’s ratio and effective elastic modulus: design and experiment. Compos Struct. 2024;329:117768. doi:10.1016/j.compstruct.2023.117768. [Google Scholar] [CrossRef]

14. Shen J, Xiao J. Mechanics properties of negative Poission’s ratio honeycomb structures with variable arc angle curved concave sides. Chin Mech Eng. 2019;30(17):2135–41(In Chinese). [Google Scholar]

15. Liu H, Liu J, Zhang D. In-plane impact performance of diabolo honeycomb structure with negative Poisson’s ratio. J Vib Shock. 2022;41(17):262–7. [Google Scholar]

16. Bohara RP, Linforth S, Nguyen T, Ghazlan A, Ngo T. Dual-mechanism auxetic-core protective sandwich structure under blast loading. Compos Struct. 2022;299(2):116088. doi:10.1016/j.compstruct.2022.116088. [Google Scholar] [CrossRef]

17. Liu T, Xiao Z, Huang J, Liu W. Impact resistance of new cross negative Poisson’s ratio honeycomb structure. J Vib Shock. 2023;42(11):183–92. [Google Scholar]

18. Huang Z, Lan L, Sun J. Stablishing method of constitutive relation of star-shaped honeycomb structure tittle. Chin J Appl Mech. 2022;39(5):922–31 (In Chinese). [Google Scholar]

19. Liu X, Li S, Yang J. Damping performance of a new chiral negative Poisson’s ratio structure. Acta Materiae Compositae Sinica. 2024;41(1):477–84. [Google Scholar]

20. Bohara RP, Linforth S, Ghazlan A, Nguyen T, Remennikov A, Ngo T. Performance of an auxetic honeycomb-core sandwich panel under close-in and far-field detonations of high explosive. Compos Struct. 2022;280(11):114907. doi:10.1016/j.compstruct.2021.114907. [Google Scholar] [CrossRef]

21. Zhang Y, Kong D, Liu S. Experimental study of forced convection heat transfer of graded metal honeycomb fabricated by additive manufacturing. Int Commun Heat Mass Transfer. 2018;98(3):67–73. doi:10.1016/j.icheatmasstransfer.2018.08.004. [Google Scholar] [CrossRef]

22. Baroutaji A, Arjunan A, Stanford M, Robinson J, Olabi AG. Deformation and energy absorption of additively manufactured functionally graded thickness thin-walled circular tubes under lateral crushing. Eng Struct. 2021;226:111324. doi:10.1016/j.engstruct.2020.111324. [Google Scholar] [CrossRef]

23. Zhang X, Yan S, Ou Y, Wen P. Gradient design and dynamic impact response of concave honeycomb structures with negative Poisson’s ratio. J Vib Shock. 2023;42(3):193–8. [Google Scholar]

24. Tao Y, Duan S, Wen W, Pei Y, Fang D. Enhanced out-of-plane crushing strength and energy absorption of in-plane graded honeycombs. Compos Pt B-Eng. 2017;118(10):33–40. doi:10.1016/j.compositesb.2017.03.002. [Google Scholar] [CrossRef]

25. Yuan M, Xu FX, Gong MY. In-plane impact performance of honeycomb material with gradient thickness and negative Poisson’s ratio. J Plast Eng. 2021;28(2):192–9. [Google Scholar]

26. Wu Y, Sun L, Yang P, Fang J, Li W. Energy absorption of additively manufactured functionally bi-graded thickness honeycombs subjected to axial loads. Thin-Walled Struct. 2021;164(6):107810. doi:10.1016/j.tws.2021.107810. [Google Scholar] [CrossRef]

27. Tao Y, Li W, Cheng T, Wang Z, Chen L, Pei Y, et al. Out-of-plane dynamic crushing behavior of joint-based hierarchical honeycombs. J Sandw Struct Mater. 2021;23(7):2832–55. doi:10.1177/1099636220909783. [Google Scholar] [CrossRef]

28. Zhang X, Zhang H, Wen Z. Experimental and numerical studies on the crush resistance of aluminum honeycombs with various cell configurations. Int J Impact Eng. 2014;66(3):48–59. doi:10.1016/j.ijimpeng.2013.12.009. [Google Scholar] [CrossRef]

29. ASTM D638-22. Standard test method for tensile properties of plastics. West Conshohocken, PA, USA: ASTM International; 2022. [Google Scholar]

30. Xiao D, Kang X, Li Y, Wu W, Lu J, Zhao G, et al. Insight into the negative Poisson’s ratio effect of metallic auxetic reentranthoneycomb under dynamic compression. Mater Sci Eng A. 2019;763(382):138151. doi:10.1016/j.msea.2019.138151. [Google Scholar] [CrossRef]

31. Li Z, Jiang Y, Wang T, Wang L, Zhuang W, Liu D. In-plane crushing behaviors of piecewise linear graded honeycombs. Compos Struct. 2019;207(2):425–37. doi:10.1016/j.compstruct.2018.09.036. [Google Scholar] [CrossRef]