Integrating Neighborhood Geographic Distribution and Social Structure Influence for Social Media User Geolocation

1  Introduction

Man is a natural social animal [1]. In the era of Internet advancement, social media have emerged as dynamic and thriving platforms for social engagement. These platforms provide individuals with a convenient, real-time, and expansive means of communication, leading to a growing inclination towards information acquisition and social interactions on social media [2]. As of January 2024, the monthly active users of popular social media platforms such as Twitter/X1, Instagram2, and Facebook3 have surpassed 7.5 billion4. The openness and interactivity of social media, coupled with the ever-increasing number of users, have resulted in a wealth of diverse information within online social media, such as personal interests, consumption habits, etc. Among them, the geographic locations of social media users serve as a bridge between the virtual and physical worlds, which can be applied to various location-based real-world applications [3–6]. By leveraging user location data, relevant organizations can gain more accurate insights into population distribution and activities, facilitating timely alerts and the implementation of corresponding rescue and protection measures [7,8]. Additionally, it enables the delivery of localized content to users, enhancing their quality of life [9]. However, challenges arise in directly accessing users’ residential location information due to factors such as personal privacy protection and platform policies [10,11]. Consequently, the task of leveraging publicly available social relationship data to infer users’ residential locations becomes particularly crucial.

Previous methods based on social relationships geolocate users under the assumption that users tend to engage in social interactions with other users in close proximity, allowing for the inference of user locations based on the distribution of neighbors’ locations [12–16]. However, the high ratio of location-proximate social relationships is required to achieve accurate geolocation accuracy, as demonstrated in previous studies, which does not align with the characteristics observed in real-world datasets. Similarity breeds connection [17]. In real-world social interactions, individuals tend to engage in frequent social connections with others who share similar interests, rather than location. This implies that users who have social relationships often exhibit high similarity in terms of their interests. For instance, we may interact with individuals who share our admiration for a particular celebrity, mentioning or liking their tweets. For user geolocation, relationships based on location proximity are crucial, but other multi-type relationships serve as structure noise which impacts geolocation accuracy [18]. We analyzed the location homophily of user social relationships in multiple social media datasets [19–21], as shown in Table 1. In online social media, relationships driven by location proximity constitute a relatively small proportion of the overall social relationships. Therefore, it is necessary to design appropriate metrics to distinguish location-driven social relationships from other categories, filter out location-independent ones, and thereby increase the proportion of location-driven relationships, which is more conducive to user geolocation.

Several studies [16,22] have attempted to determine location-homophilic social relationships using structure characteristic. Research [22] proposes the social closeness metric to measure the number of common neighbors between two users with a social relationship. It demonstrates that when the proportion of common first-order neighbors between two users exceeds 50%, the probability of them being within 10 km of each other is 83%. When the number of mutual friends decreases to 10%, the probability of the two users being within 10 km drops drastically to 2.4%. Based on this funding, research [16] filters out social relationships with social closeness below a certain threshold. However, as shown in Fig. 1, on a dataset from real social media, using the social closeness makes it difficult to discern whether users’ social relationships are location proximity. Figs. 1a and 1b show the distribution of social closeness in location-homophilic social relationships and location-heterophilic social relationships, respectively. It is obvious that the distribution of social closeness in these two types of relationships is similar, and both are predominantly concentrated in the lower interval (≤0.1). Therefore, it is crucial to establish a metric that can confirm location-homophilic social relationships.

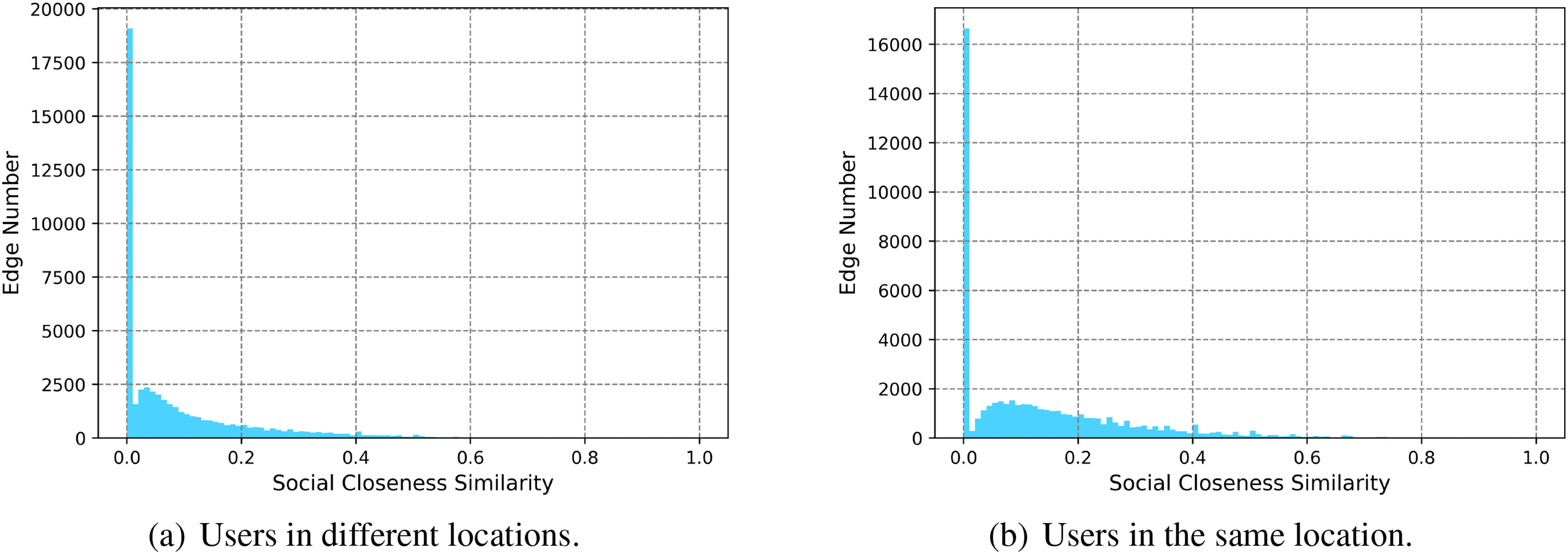
Figure 1: Distribution of social closeness across different relations. The horizontal axis represents the level of social closeness, while the vertical axis represents the number of edges. Each bar represents the number of edges at the corresponding level of social closeness

Therefore, we focus on designing an appropriate metric of discerning location-driven relationships and better utilizing the location homophily in social networks. In this paper, we propose a social media user geolocation method integrating neighborhood geographic distribution and social structure influence (NGSI). In detail, to better distinguish between location homophilic and heterophilic relationships, we design a novel metric called k-order neighborhood geographical distribution similarity (k-NGD). We discretize the continuous latitude and longitude information and assign a discrete location label to each user. Then, we compute the distribution of discrete locations for each user’s k-order neighborhood. The distribution of k-NGD is significantly different between location homophilic and heterophilic relationships. Our proposed NGSI utilizes this finding to identify and filter out heterophilic location relationships. To better leverage the filtered social network structure, we use personalized PageRank (PPR) [23] to calculate the strength of social structure influence between users. Based on this strength, a graph neural network-based (GNN-based) model is designed to performs a weighted aggregation of neighboring nodes to geolocate users.

The main contributions of this paper are as follows:

•   A novel method to evaluate the homophily of relationships based on the k-order neighborhood geographical distribution similarity of users is proposed. The k-NGD of friends exhibits significant differences between homophilic and heterophilic relationships, enabling us to identify and filter out heterophilic relationships. This method enhances the location homophily of social networks.

•   A GNN-based method utilizing social network structure influence for inferring user locations is designed. By using PPR, we obtain the structure influence between users, allowing for weighted aggregation of neighboring users. This approach enhances the exploration and utilization of location influence within the social structure, thereby improving user localization performance.

•   Series of experiments on real-world social media dataset to evaluate the effectiveness of proposed method are conducted. Compared to 7 existing social relationship-based user geolocation methods, our proposed approach outperforms others in terms of geolocation accuracy.

The remaining sections of this paper are organized as follows: In Section 2, we provide an overview of literature relevant to our study. In Section 3, we present the preliminaries required for understanding the content of this paper. Our proposed method is thoroughly described in Section 4. In Section 5, we analyze the performance of user localization in social media. Finally, we conclude the paper with a summary of our work and provide future directions for further research in Section 6.

2  Related Works

In this section, we provide a review of previous methods for social media user geolocation based on social relationships and introduce the graph deep learning methods utilized by geolocation methods.

2.1 User Geolocation Based on Social Relationships

Social relationship is the prevalent data in social media, and users tend to engage in social behavior based on certain similarities. Location similarity is one of the reasons for user interaction. Therefore, based on social relationships, it is possible to infer user location by utilizing known locations of friends. Existing approaches for geolocating users based on social relationships can be broadly classified into two categories: (1) constructing probabilistic models between social proximity and geographic distance to leverage neighbor distances and friend probabilities for location inference; (2) propagating information through edges within social network to incorporate high-order information.

For the first category of methods, Backstorm et al. [14] propose FindMe which utilizes the distances between users with known locations and their friends to construct a distance-friend probability model, establishing an association between distance magnitude and the likelihood of becoming friends. FindMe takes the locations of friends as candidate locations. The location which maximizes the probability of becoming friends with other neighbors is selected as the user’s location. Based on the research by Backstrom et al. [14], McGee et al. [24] further discriminate geographically close social relationships by utilizing a decision tree, which establishes connections between various properties of social relationships (such as direction, categories, etc.) and location proximity. The Spot-Tightness [22] analyzes the relation between distance and social closeness to construct a probability model. Building on the geolcoation from FindMe, Spot-Tightness incorporate social closeness as another factor in calculating probabilities. On the basis of Spot-Tightness, Spot-Energy [22] leverages social coefficient to further consider the structural information of user neighborhoods. In these methods, they rely primarily on the spatial distribution of the user’s first-order neighborhood, which is susceptible to the impact of sparse first-order location information.

The approach based information propagation within social networks has evolved beyond the confines of first-order friendships. Jurgens [15] propose the Spatial Label Propagation (SLP) algorithm, which treats a user’s latitude and longitude as user labels and uses the geometric median of propagated locations from neighbors as the user’s location. Through multiple rounds of propagation, higher-order information can be utilized, which can tackle the issue of sparse location information of first-order neighbors. Compton et al. [25] extend the SLP algorithm by introducing the frequency of social relationships as weights to infer user locations through weighted user location information. The Sequence Spatial Label Propagation (SSLP) [16] further considers the impact of location outliers in a user’s neighborhood on the accuracy of location inference. Therefore, SSLP filters out neighbor nodes with few common neighbors in the first order, which reduces the time required for propagation, and improves the accuracy of user geolocation. Rahimi et al. [26] propose a method based on Graph Convolutional Networks (GCN) [27] module to propagate and aggregate neighbor features. They apply adjacency matrix of social network as input features, and establish the correlation between aggregated features and location labels. By leveraging high-order social relationships, these methods enable a more comprehensive understanding of the spatial information within the network and enhances the geolocation accuracy.

Existing works have paid limited attention to non-location-proximate social relationships in user social networks. Among them, SSLP [16] utilizes user social closeness to discover and filter non-location-proximate social relationships. However, the distinction between location-homogeneous social relationships and non-homogeneous social relationships in the distribution of social closeness is not clear. In addition, previous methods based on information propagation ignore user social graph structural characteristics in user geolocation. To tackle above limitations, we propose the k-order neighborhood geographical distribution, which discerns and filters heterophilic social relationships by comparing the geographical distribution similarity of user neighborhoods. Additionally, based on the filtered social network, we calculate the structural influence between users and introduce structural influence-weighted aggregation of user neighborhood features to more accurately geolocates users.

2.2 Graph Deep Learning Method

Social network can be viewed as a natural graph structure, where users are nodes and social relationships between them are edges. As such, existing social relationship-based user geolocation algorithms are closely related to graph algorithms. This subsection will introduce commonly used graph algorithms in user geolocation.

Label Propagation (LP) algorithm [28] leverages label information of a network as node features to iteratively propagate labels among nodes based on local similarity and connectivity relationships, achieving label prediction for unlabeled nodes. DeepWalk [29] is a graph embedding method based on random walks. It generates node sequences by performing random walks on graphs, which are then used as input for word2vec [30] learning. The learned low-dimensional embedding capture adjacency relation features of nodes. Building upon DeepWalk, node2vec [31] introduces a biased random walk graph embedding algorithm. It incorporates a bias towards selecting the next node during the generation of node sequences. Recently, the rapid development of deep learning has greatly promoted the effective representation of graph data by graph neural networks, leading to significant advancements and improvements in graph-based tasks [32]. Among them, Graph Convolutional Networks (GCNs) [27] utilize the adjacency matrix to capture node relationships, propagating and aggregating features based relationships through multiple layers. Graph Attention Networks (GAT) [33] use attention mechanisms [34] to compute aggregation weights based on similarity, considering varying neighbor influences. In order to better scale GNN models to large graphs, GraphSAINT [35] introduces a GNN paradigm based on sampling subgraphs, decoupling sampling from GNN to facilitate the extension of various GNN models.

3  Preliminaries

In this section, we provide definitions for the terminologies used throughout the paper and introduce the concept of user geolocation based on social relationships.

Definition 1 (User Social Network). The user social network, denoted as G=(V,E), is constructed based on the social relationships between users. V represents the set of users, and E denotes the collection of social relationships among users, with E⊆V×V. The user set V can be divided into V=Vu∩Vl, where Vu represents the set of users without location labels, and correspondingly, Vl represents the set of users with known locations.

Definition 2 (Geographical Homophilic Edge). For eij∈E, nodes vi and vj belong to the same location, that is, li=lj.

Definition 3 (Geographical Heterophilic Edge). For eij∈E, nodes vi and vj do not belong to the same location, that is, li≠lj.

Definition 4 (Global Location Homophily). Global Location Homophily is the ratio of the number of geographical homophilic edges to the total number of edges in the graph, denoted as Eq. (1).

h=|{(vi,vj):(vi,vj)∈E∧li=lj}||E|.(1)

Definition 5 (k-order neighborhood). The k-order neighborhood of a user in a social network refers to the set of nodes that can be reached within k hops from the user. Specifically, the k-order neighborhood of user v is denoted as Nk(v).

User Geolocation Based on Social Networks. Given a social network G=(V,E) constructed from user online social relationships, along with a subset of labeled users Vl and their corresponding location information, we leverage the social relationships between unlabeled users Vu and labeled users Vl in the social network to infer user locations.

We summarize the notations used in this paper as shown in Table 2.

4  Proposed Method

To better explore and utilize the location homophilic relationships in user social networks, this paper proposes a joint approach that combines neighborhood geographical distribution and social structural influence for social media user geolocation. It consists of two parts: location homophilic relationship distinguish based on k-order neighborhood geographical distribution similarity and user location inference based on the strength of social structural influence.

For the first part, we first construct the geographical distribution characteristics of user k-order neighborhood. Then we compute the similarity of geographical distribution characteristics between two users with social relationships in their k-order neighborhood, and filter out social relationships with low similarity to reduce location-heterophilic social relationships in the social network.

For the second part, we incorporate multi-order neighborhood information of users for aggregation, further leveraging the social network structure. To avoid over-smoothing of node features caused by aggregating too much neighborhood information, we introduce personalized PageRank [23] to learn the network structural influence between users in multi-order neighborhoods, and perform a weighted aggregation of user information accordingly. Finally, user location inference is performed based on the aggregated features.

4.1 Location Homophilic Relationship Discerning Based on k-NGD

Existing methods for evaluating location homophily between two users in a social network often rely on the number of common neighbors to assess [16,22]. As shown in Fig. 1, this approach may not clearly reflect the correlation between the number of common friends and location homophily in social networks with low location homophily. As a result, filtering location-heterophilic social relationships based on social closeness alone makes it challenging for location inference algorithms to achieve satisfactory results. Therefore, we distinguish the location homophily strength of social relationships from the perspective of the geographical distribution of user neighborhoods, as Fig. 2.

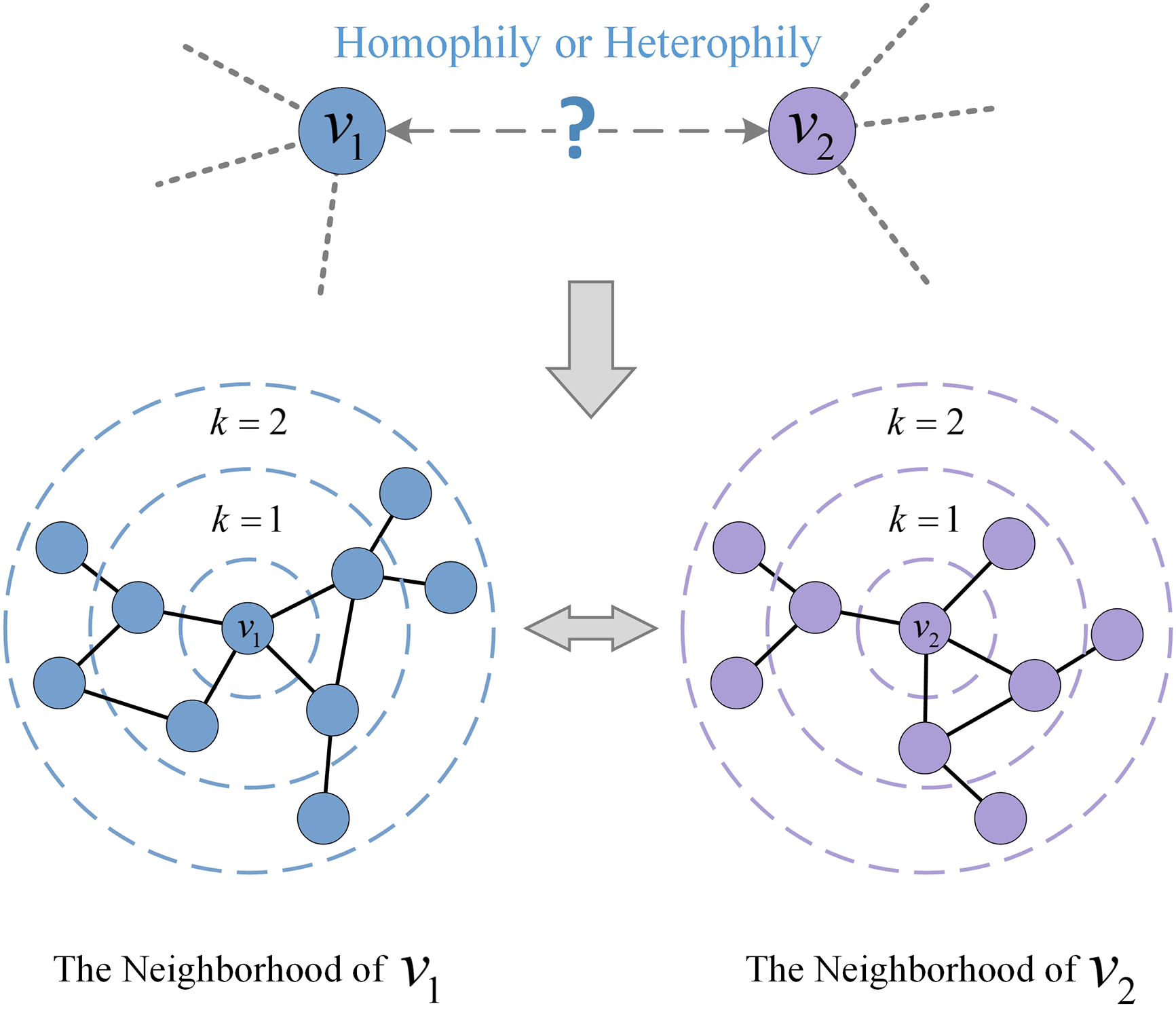
Figure 2: Illustration of homophily strength between nodes v1 and v2. Here, we use the 2-order neighborhood of the two nodes as an example

Firstly, we extract the neighboring nodes within k-order neighborhood of user v. For the nodes with known locations among them, we map their geographical location labels to the corresponding dimensions, constructing the k-order neighborhood geographical distribution feature, denoted as dvk. We calculate k-order neighborhood geographical distribution as Eq. (2).

dvk=∑u∈Nk(v)yu,(2)

where yu denotes the position label vector for user u, with only one dimension corresponding to the geographical label being 1 and the others being 0. Then, to eliminate the dimensional differences between features and improve model performance, we normalize the geographical distribution features of user neighborhoods. We adopt the Z-score normalization to process the geographical distribution features, as Eq. (3).

dvk~=norm(dvk)=[(dv1−μ(dvk))σ(dvk),(dv2−μ(dvk))σ(dvk),(dv|L|−μ(dvk))σ(dvk)],(3)

where μ(dvk) represents the mean value of each dimension in the distribution vector dvk, and σ(dvk) denotes the variance of each dimension.

Next, for two users vi and vj in the social network, we calculate the similarity score of their neighborhood geographical distribution using cosine similarity. The formula is as follows:

skij={dvik⋅dvjk|dvik||dvjk|,⟨vi,vj⟩∈E0,⟨vi,vj⟩∉E.(4)

In Eq. (4), dvi and dvj represent the neighborhood geographical distributions of nodes vi and vj respectively. When there is a social relationship between two nodes, the distribution similarity is calculated based on the similarity of their neighborhood geographical distributions. For users without social relationships, their similarity is directly set to 0. As geographical proximity is one factor driving users to build social relationships, the similarity of neighborhood location distributions between two users with the same location should be significantly higher than that between users with different locations. This idea was further validated in our subsequent experiments. Subsequently, we set a similarity threshold thet to filter out social relationships with similarity scores below this threshold, which are highly likely to be heterophilic relationships. Meanwhile, for nodes with low degrees, in order to prevent their social relationships from becoming excessively sparse during filtering location-heterophilic social relationships and to avoid the emergence of isolated nodes (nodes without any social relationships), we impose restrictions on the node degrees of the social relationships being filtered, which is shown as following:

deg(vi)>tdeg ∧ deg(vj)>tdeg,(5)

where deg() represents the degree of node. The restriction requires that only social relationships with node degrees greater than the threshold tdeg can be filtered. For nodes with very low degrees, we retain all their social relationships to prevent the social connections of these nodes from becoming excessively sparse and affecting the geolocation results.

4.2 User Geolocation Based on Social Structure Influence

In user location inference, using only the first-order neighborhood of users to infer their locations may encounter issues of sparse neighboring users and missing location information. Therefore, effectively utilizing higher-order neighborhood information of users is a primary focus of our study. GNN methods such as GCN [27], when incorporating higher-order information, may suffer from the problem of over-smoothing with excessive stacking of layers. This leads to increased similarity in node representations, making it more challenging to distinguish node location in the network. In this section, we propose a user geolocation method based on the strength of social structure influence. By leveraging structural influence to assign varying weights to neighboring nodes, weighted aggregation of neighbors’ features can effectively mitigate the over-smoothing issue.

Personalized PageRank can assess the influence of an individual user on other users within a social network by leveraging its connectivity. We calculate the positional impact between users based on social network characteristics using the filtered user social network, starting from an individual user, as follows:

A~=Normalize(A),(6)

πi=(1−β)A~πi+βIi,(7)

where A~ denotes the normalized adjacency matrix of the social network and A~∈R|V|×|V|. πi represents the stationary distribution resulting from a random walk starting at node vi, πi∈R1×|V|, which captures the user’s network structural influence on other user nodes in the network. During each propagating iteration, there is a probability of β to transition back to the starting node and restart, thereby continually enhancing the influence of neighboring users. With a probability of 1−β, the walk continues, allowing for the calculation of the influence strength between higher-order neighborhoods. For the influence among all users in social network, the global structure impact weight matrix Π is obtained by aggregating according to the Eq. (7), as shown in Eq. (8).

Π=β(I−(1−β)A~)−1.(8)

Based on the global influence matrix Π, we weight and fuse the features from multiple levels of neighbors to obtain the representation of user nodes.

H0=σ(XW+b),(9)

H=ΠH0=β(I−(1−β)A~)−1H0,(10)

where the initial feature matrix of the nodes is denoted by X. Firstly, the node features undergo a non-linear transformation to obtain the matrix H0. Then, based on the weighted aggregation using the social network structural weight matrix, the final node features H are obtained.

The global structure influence matrix among users is constructed based on their social relationships and through random walks with certain probabilities. During the random walk process, on one hand, PPR has a probability of stopping and returning to the starting node, resulting in higher weights for the low-order neighboring nodes in the influence matrix. On the other hand, when PPR continues to walk towards neighbors, the structural information such as the number of paths between two nodes contributes to varying influence weights for higher-order nodes. Therefore, based on these two factors, the PPR-based GNN exhibits significant variations in the aggregation weights of different nodes when aggregating higher-order neighborhoods. This approach not only facilitates better learning of structural information in social networks but also effectively alleviates the over-smoothing issue.

Due to the high computational complexity of computing the inverse matrix in PPR, we propose a model based on the insights from research [36]. The model formulated in Eq. (4) is shown to be equivalent to the PPR-based GNN when stacked with an infinite number of layers.

H0=XWθ+b,(11)

H(k+1)=(1−β)A~H(k)+βH0,(12)

where k denotes the propagating layers. Assuming that we use K layers, H(K) represents the final node embeddings. Finally, we utilize the node embeddings H(K) to infer user locations, as Eq. (13).

Y^=softmax(H(K)W(K)+b(K)),(13)

where W(K) is learnable parameters and b(K) denotes bias vector. This equation maps node representations to corresponding geographical locations, and each dimension of Y^ represents the probability of a user being located at the corresponding location. The location of user v is determined as follows:

Lv=maxj(y^vj).(14)

Based aforementioned methods, we summarize the overall algorithm proposed as Algorithm 1.

5  Experiments

In this section, we evaluate the proposed method on real-world dataset from various aspects.

5.1 Experiment Settings

5.1.1 Dataset Analysis

In our experiments, we use the Brightkite dataset provided by SNAP, which includes the initial social network of users and their check-in records. In this paper, our primary objective is to infer the user’s primary residence address. Therefore, we first need to determine the user’s primary residence address. We perform clustering on the check-in coordinates of users using the Density-Based Spatial Clustering of Applications with Noise algorithm (DBSCAN) [37], and determine the center location of the largest cluster as the user’s primary residence. We then use reverse geocoding to convert the user’s coordinates into “Country-State-City” format. Due to the concentration of users primarily in the United States region, we select 30,127 users located in the United States and divide them into a training set and a test set with an 8:2 ratio for geolocation experiments. We summarize the information of the dataset in Table 3. Based on the users’ primary residence locations, we plot the geographic distribution map of the users, as shown in Fig. 3.

Figure 3: Geographic distribution map of the users

5.1.2 Baselines

To comprehensively evaluate our proposed method, we compare it with two existing classes of social relationship-based user geolocation methods.

•   FindMe [14] employs the fitting distance-friend probability model and selects the friend location that maximizes the friend probability as the user’s location.

•   Friendly [24] classifies social relationships and improves the fitting formula based on the FindMe.

•   Spot-Tightness [22] constructs a probabilistic model between social intimacy and distance, estimating the user’s location based on the social intimacy estimation between the target and the neighbors.

•   Spot-Energy [22] uses the energy and social coefficient between users as measures of neighbors’ locations, selecting the neighbor with the maximum value of the joint indicators as the target user’s location.

•   SLP [15] utilizes the known latitude and longitude of users as node labels, propagates through the social network, and determines the user’s location by calculating the geometric median of neighboring locations.

•   Deepwalk-MLP [29] employs deepwalk to learn node representations of the user social network, followed by Multi-Layer Perception (MLP) for node geolocation.

•   SSLP [16] builds upon SLP by incorporating a filtering mechanism based on social intimacy scores to select neighboring users.

•   GCN-LP [26] utilizes the user adjacency matrix as the input to highway-GCN for user classification and positioning.

5.1.3 Evaluation Metrics

During the user location inference experiments, we defined two categories of labels, namely state and city. The inferred location of a user corresponds to the latitude and longitude of the city-level city. The inference error of a user is measured as the distance between the true latitude and longitude of the user and the inferred latitude and longitude, denoted as (ED)(v), with units in kilometers. The calculation of (ED)(v) is defined by Eq. (15).

ED(v)=haversine(coor(Lc(v)),coor(v)),(15)

where haversine means haversine distance and coor represents the latitude and longitude of a user or the city center.

To comprehensively assess the geolocation performance of methods, we utilize five commonly used metrics in existing research: state-level accuracy, metropolitan-level accuracy (accuracy within 161 kilometers), mean distance error, median distance error, and coverage rate. Equations for calculating the above metrics are as Eqs. (16)–(20).

Acc@State: The accuracy of user location classification at the state level.

Acc@State=|{v|Ls′(v)=Ls(v)∧v∈Vu}||Vu|.(16)

Acc@161: The accuracy of user localization within a 161-kilometer radius.

Acc@161=|{v|ED(v)≤161∧v∈Vu}||V^u|(17)

MedianED: The median error distance between inferred locations and true locations for users with unknown locations.

MedianED=median({ED(v)|v∈V^u}).(18)

MeanED: The mean error distance between inferred locations and true locations for users with unknown locations.

MeanED=∑v∈V^uED(v)|V^u|.(19)

Coverage: The ratio between the number of locatable users and the total number of users with unknown locations.

Coverage=|V^u||Vu|.(20)

In Eqs. (16)–(20), V^u represents the number of locatable users using the geolocating method. Here, Acc@State represents the geolocation accuracy of the method at the state level. According to international urban planning, the range of metropolitan areas is usually within 100 miles (161 km), and Acc@161 evaluates the geolocation accuracy of the model at the metropolitan level [38]. Acc@State and Acc@161 evaluate the accuracy of methods at different granularities. MeanED measures the overall geolocation error distances of methods, while MedianED represents the median value among all error distances. MeanED and MedianED together depict the distribution of user geolocation error distances. Coverage refers to the evaluation of the method’s ability to geolocate the range of users, that is, the proportion of users that can be geolocated.

5.1.4 Parameter Settings

We utilize DeepWalk [29] to obtain node embeddings as initial features X in the user social network. The parameters for DeepWalk were set as follows: embedding dimension of 256, walk length of 40, and window size of 8. We found that setting thet to 0.6 achieved optimal results, while Dropout rate was set to 0.4. In the graph neural network, we set K to 3 and β to 0.2. The learning rate is set to 0.01, and the L2 regularization weight is set to 0.005.

5.2 Analysis of k-NGD on Homophilic and Heterophilic Relationships

The metric proposed by existing methods have very similar distributions on location homophily and heterophily relationships, making them difficult to distinguish (as shown in Fig. 1). To verify the differential distribution of k-order neighborhood geographic similarity proposed in this paper on two types of social relationships, we conducted an analysis of the neighborhood geographic similarity between two users with social relationships. We categorize social relationships into two types: location homophily edges and location heterophily edges, and compare the distribution characteristics of k-NGD on these two types of social relationships. Based on the labeled data in the Brightkite dataset, we plotted the following distribution figures as Figs. 4 and 5.

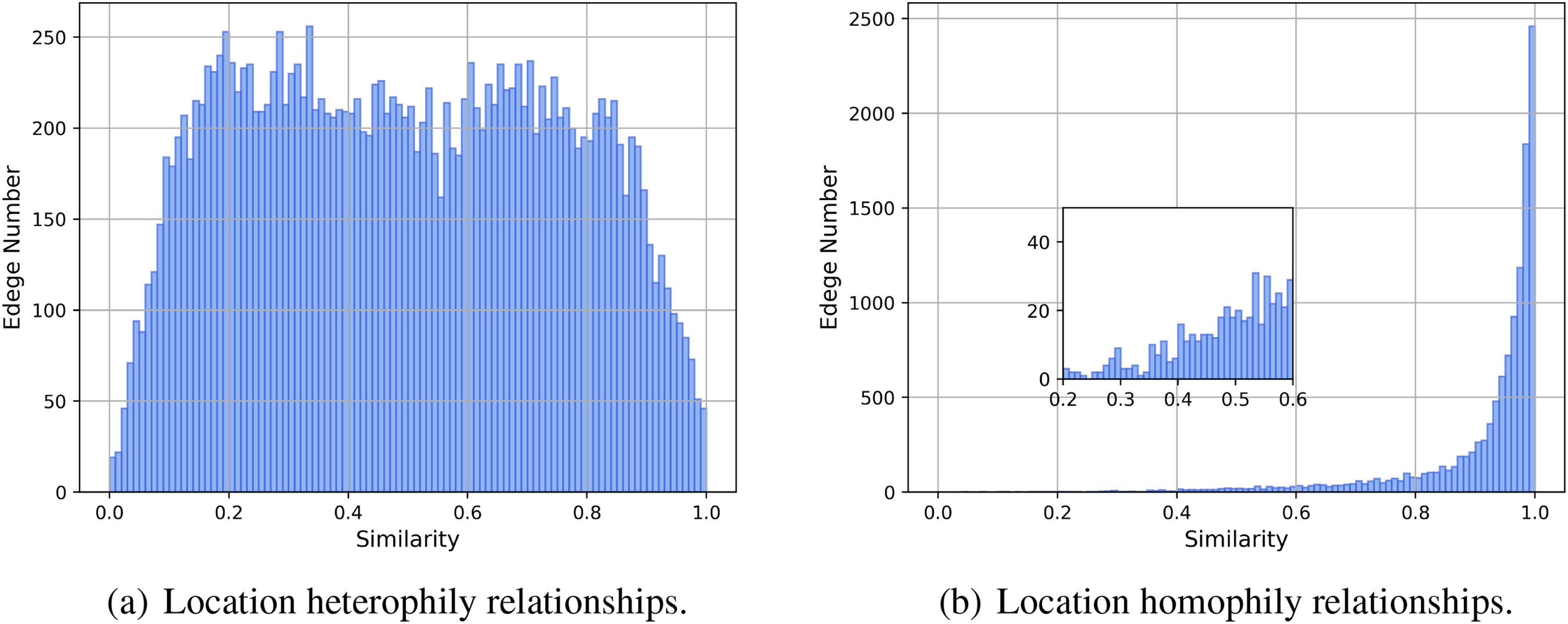
Figure 4: Distribution of NGD similarity for two types of social relationships at the state level

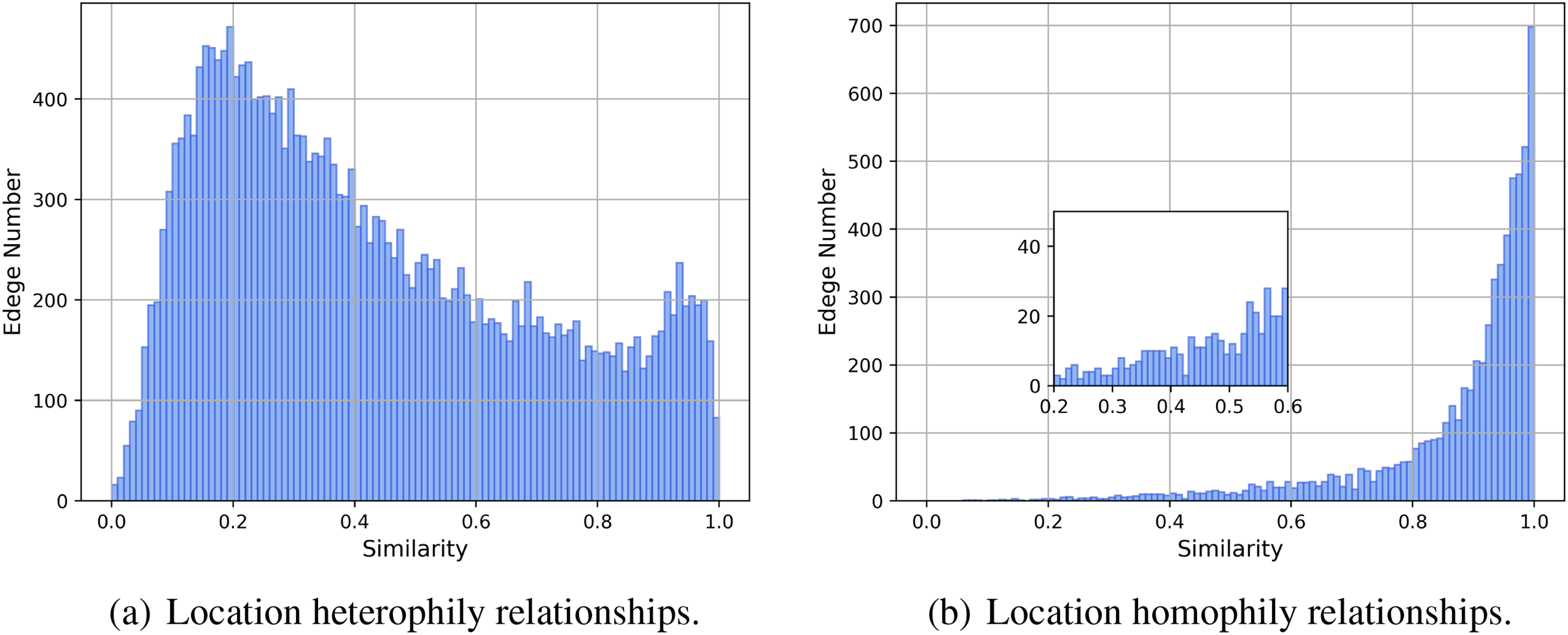
Figure 5: Distribution of NGD similarity for two types of social relationships at the city level

In Fig. 4, the 2-NGD similarity scores for heterophily edges exhibit a relatively evenly distributed concentration between 0.1 and 0.8, followed by a rapid decline in the range of 0.8 to 1.0. Conversely, the 2-NGD similarity scores for homophily edges are highly concentrated in the range above 0.9, displaying a distinctly different distribution from that of heterophily edges. At the city level as Fig. 5, the differences in similarity are more pronounced. The 2-NGD similarity scores for heterophily edges exhibit a high concentration around 0.2, with a significant decrease in the number of heterophily edges as the similarity score increases. In contrast, the number of homophily edges shows a sharp increase after 0.8. Therefore, we can effectively distinguish the homophily of user locations and efficiently filter heterophily edges by utilizing the similarity of neighborhood geographical distributions between two users. NGSI allows us to increase the proportion of homophily social relationships within the social network.

5.3 Geolocation Performance of the Proposed Method

From Table 4, it can be observed that NGSI achieves a geolocation accuracy of 68.98% at the provincial level, which represents an improvement of 4.8% and 7.3% compared to existing methods. Compared to eight existing social relationship-based user positioning methods, NGSI exhibits significant performance enhancements. The proposed approach not only enables the positioning of all users with social relationships but also achieves a higher Acc@161 by 4.84% compared to the state-of-the-art (SOTA). Additionally, it reduces the average distance error by over 100 km and decreases the median error distance by 24.4%.

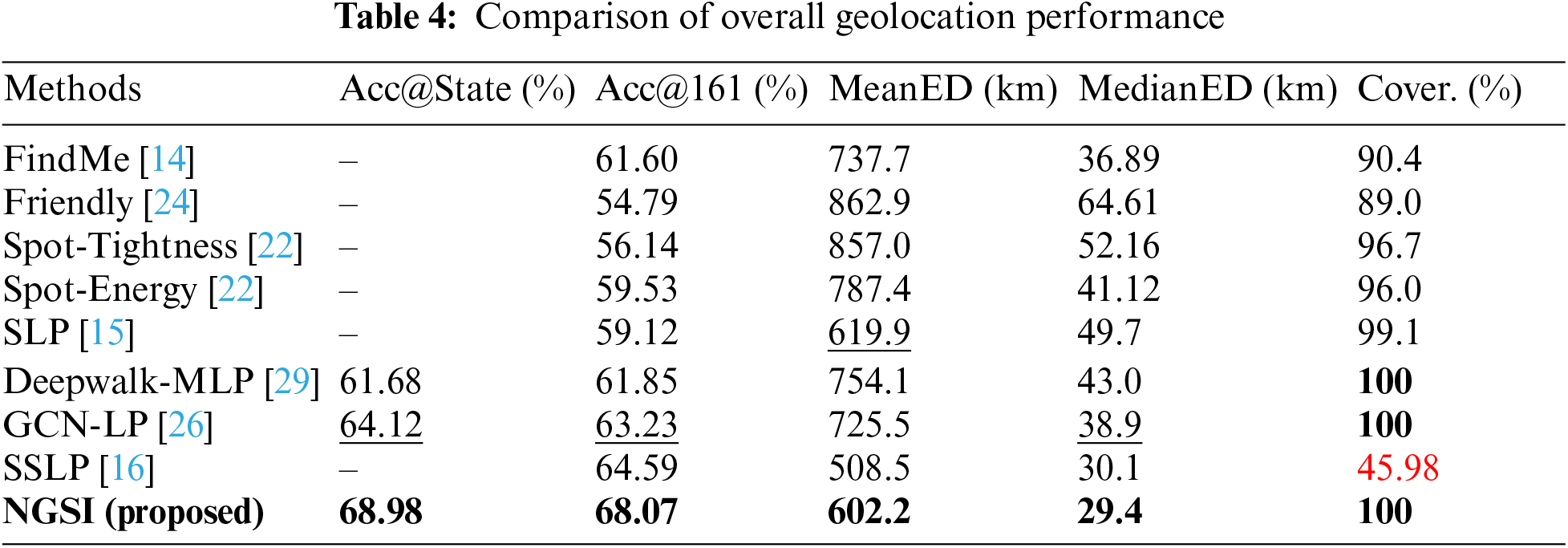
In the first category of relationship-based user geolocation methods, FindMe [14] exhibits the highest geolocation accuracy, but with lower coverage. Spot-Energy [22] demonstrates better overall geolocation performance, while Friendly [24] scores lower across all metrics. Both FindMe and Friendly geolocate users based on their first-order neighbors. When the location information of these first-order neighbors is unknown, the user cannot be geolocated, leading to low coverage. Friendly introduces local social relationship discrimination based on FindMe. But due to the dataset using in experiments containing only one type of undirected social relationship, the lack of social relationship properties such as relationship types and directions results in poor geolocation capability. Based on Spot-Tightness, Spot-Energy introduces the social coefficient of user neighborhoods, enhancing user geolocation performance. However, as Spot-Energy still relies on the distance-friend probability model, constrained by the representational capacity of the basic model, its geolocation performance remains significantly lower compared to NGSI.

Compared to the first category, the second category of methods based on information propagation exhibits significant improvements in inferring user locations. The SLP [15] algorithm achieves an average error distance that is only surpassed by the proposed method in this paper. Its smaller error distance is attributed to the fact that user location inference is obtained through the geometric mean of neighboring user locations, where the geometric mean represents the geometric center closest to each neighbor’s location, resulting in smaller inference distance errors. Although SSLP [16] achieves relatively high accuracy in location inference on this dataset, it can only infer the location of less than 50% of all users. As shown in Fig. 1, our previous analysis reveals that social closeness of users is concentrated within 0.1 and the ability to distinguish between homophilic and heterophilic locations is not strong. This results in the overall poorer performance of SSLP in location inference.

After transforming the user localization problem into a node classification problem (GCN-LP [26], Deepwalk-MLP [29], and the proposed NGSI in our paper), not only can multiple levels of localization be achieved for nodes, but also the localization performance is superior. Here, we primarily compare localization algorithms at the state level with those commonly used within a 161 km range. Deepwalk-MLP only uses node embeddings obtained from deepwalk to infer user locations, while GCN-LP and NGSI utilize the mapping between social structure relationships and location to continuously learn parameters, resulting in significantly better localization performance than Deepwalk-MLP. NGSI not only utilizes information from users with known locations to filter out a large number of heterophilic location relationships, thereby improving the homophily of the social network’s location, but also uses the influence strength of user network structure to weight the aggregation of neighborhood features, resulting in a significant improvement in user geolocation performance.

Compared to the second category of information propagation-based methods, the first category of methods that geolocation based on neighboring users’ locations generally exhibit lower coverage and lower accuracy than the second category. This is because in social networks, the first-order neighbors of users are often unlabeled nodes, making it impossible to infer the location of users in such cases, leading to a lower user coverage. Meanwhile, methods based on information diffusion can more comprehensively consider the information propagation process in the network, effectively utilizing multi-order information and network structure in social networks to achieve better geolocation results.

5.4 Analysis of thet on Geolocation Performance

In this section, we analyze the impact of the threshold value thet on the filtered number of social relationships, the proportion of location heterophilic relationships, the change in global location homophily ratio, and the accuracy of user location inference.

First, we calculate the 2-NGD to measure the geographical distribution similarity between users. We filter the social relationships that are less than the threshold thet and analyze the filtered number of social relationships and the proportion of heterophilic relationships. As shown in Fig. 6, we have chosen two partitioning methods (state-level, city-level) and selected eight intervals between 0.1 and 0.8. As the thet threshold increases, the number of filtered edges rises from 396 to 17,027. When the threshold exceeds 0.5, the number of edges filtered based on city-level labels reaches 15.86% to 21.65% of the total edges. At this stage, the overall proportion of filtered social relationships with heterophilic locations decreases, but it still remains above 90%. In the city-level, when thet is set to 0.8, out of the 22,849 filtered edges, the proportion of social relationships with heterophilic locations remains high at 94%. Despite filtering out a large number of heterophilic social relationships, the homophilic social relationships are still retained.

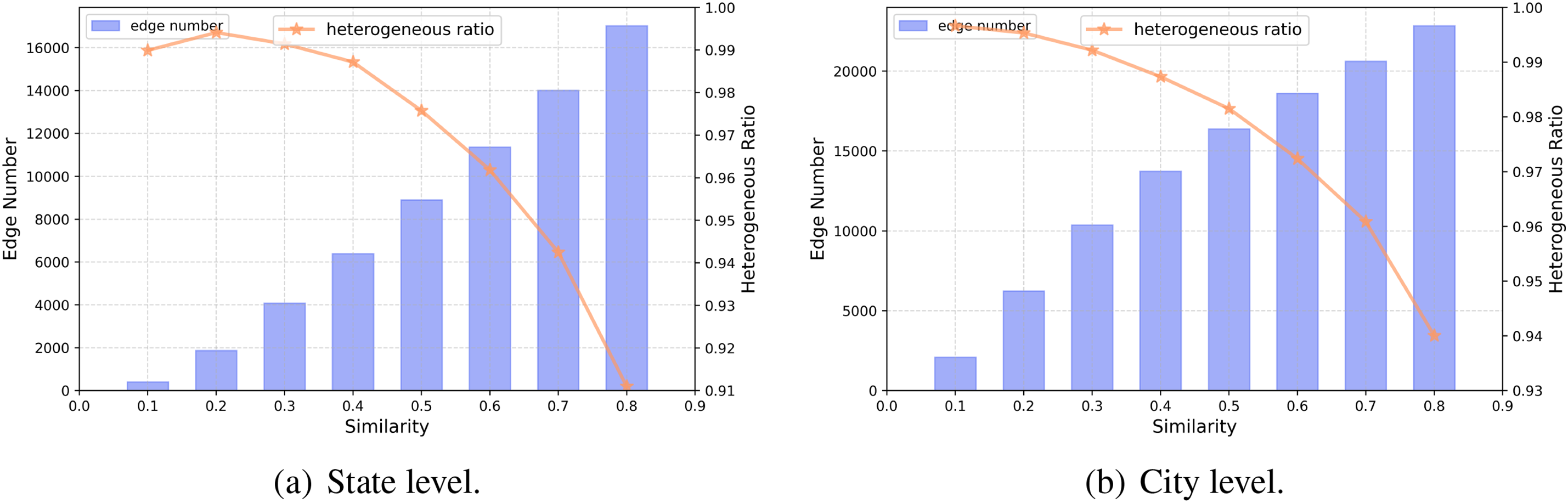
Figure 6: Relationship between threshold thet and filtered edges. The blue bars represent the number of filtered edges, while the orange stars (⋆) indicate the proportion of heterophily edges among the filtered edges

When setting different thet thresholds, we have removed a large number of user social relationships. Next, we will mainly analyze the impact of thet on the global location homophily ratio of user social networks and its influence on the accuracy of location inference. Fig. 7 illustrates the positioning results at two level granularity when thet is set from 0 to 0.8. We conducted five experiments under different thet settings and obtained the distribution of positioning accuracy as shown in Fig. 7. The global position homophily ratio consistently increases with the rise of thet. Meanwhile, the user’s geolocating accuracy initially increases, reaching its peak at thet=0.6, and then starts to decline. Thus, with appropriate filtering of social relationships, the position homophily of the social network increases, making the proximity between users and their neighbors more evident and beneficial for user location inference. However, as thet increases, excessive removal of social relationships leads to an overly sparse social network, causing a decrease in positioning accuracy. For instance, when filtering social relationships based on city-level tags, approximately 22% of social relationships can be filtered. Setting an appropriate thet and filtering the location heterophilic social relationships in the social network based on k-NGD enhances the positioning performance.

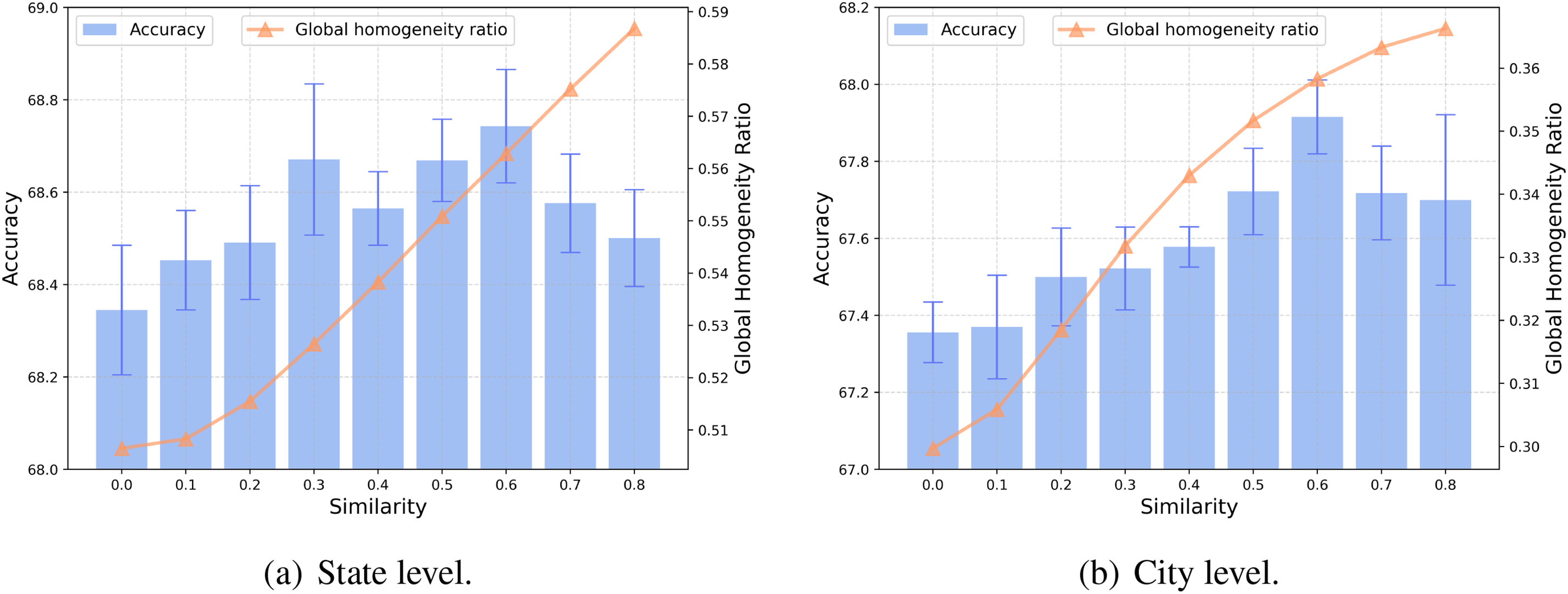
Figure 7: Accuracy and global homophily proportion at different levels. The blue bars represent the geolocation accuracy (Acc@161), while the orange triangle (▴) indicate the global homophily proportion of all edges

6  Conclusion

In this paper, we propose a social media user positioning method based on uniting neighbor geographical distribution and social structure influence, called NGSI. NGSI first utilizes the similarity of users’ neighborhood geographical distributions to filter out location-heterophily social relationships, thereby enhancing the overall geographical homophily of the social network. Furthermore, it further leverages the structural information of user social networks to calculate the strength of influence between users and selectively aggregates neighboring node features. The experimental results demonstrate that our proposed NGSI not only provides multi-granularity user positioning but also significantly outperforms existing methods for user geolocation based on social relationships. Moreover, we conduct a comprehensive analysis of neighborhood geographical distribution similarity and found significant differences in the distribution between location-homophilic and location-heterophilic social relationships. We observed that over 90% of the filtered social relationships based on 2-NGD are location-heterophilic relationships.

In future work, we aim to further integrate the multiple types of user attributes in social media and explore differentiate algorithms. This will enable more accurate filtering of location-heterophilic social relationships, thereby enhancing user positioning performance.

Acknowledgement: Authors are grateful to the valuable feedback and patient efforts of reviews and editors.

Funding Statement: This work was supported by the National Key R&D Program of China (No. 2022YFB3102904), and the National Natural Science Foundation of China (Nos. 62172435, U23A20305), and Key Research and Development Project of Henan Province (No. 221111321200).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Meng Zhang; data collection: Ningbo Huang; analysis and interpretation of results: Meng Zhang; draft manuscript preparation: Meng Zhang, Xiangyang Luo. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: https://snap.stanford.edu/data/.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

1https://www.x.com

2www.instagram.com

3www.facebook.com

4https://www.statista.com/statistics/272014/global-social-networks-ranked-by-number-of-users/

References

1. Aristotle. Politics. Available from: https://www.goodreads.com/quotes/183896-man-is-by-nature-a-social-animal-an-individual-who. [Accessed 2023]. [Google Scholar]

2. Ren R, Su L, Meng X, Wang J, Zhao M. A large-scale group decision making model based on trust relationship and social network updating. Comput Model Eng Sci. 2024;138(1):429–58. doi:10.32604/cmes.2023.027310 [Google Scholar] [CrossRef]

3. Shang L, Zhang Y, Youn C, Wang D. SAT-Geo: a social sensing based content-only approach to geolocating abnormal traffic events using syntax-based probabilistic learning. Inf Process Manag. 2022;59(2):102807. doi:10.1016/j.ipm.2021.102807. [Google Scholar] [CrossRef]

4. Anjum U, Zadorozhny V, Krishnamurthy P. Localization of unidentified events with raw microblogging data. Online Soc Netw Media. 2022;29:100209. doi:10.1016/j.osnem.2022.100209. [Google Scholar] [CrossRef]

5. Zhan XX, Zhang K, Ge L, Huang J, Zhang Z, Wei L, et al. Exploring the effect of social media and spatial characteristics during the COVID-19 pandemic in China. IEEE Trans Netw Sci Eng. 2023;10(1):553–64. doi:10.1109/TNSE.2022.3217419. [Google Scholar] [CrossRef]

6. Pellicani A, Pio G, Redavid D, Ceci M. SAIRUS: spatially-aware identification of risky users in social networks. Inf Fusion. 2023;92:435–49. doi:10.1016/j.inffus.2022.11.029. [Google Scholar] [CrossRef]

7. Kumar A, Singh JP. Deep neural networks for location reference identification from bilingual disaster-related tweets. IEEE Trans Comput Soc Syst. 2024;11:880–91. doi:10.1109/TCSS.2022.3213702. [Google Scholar] [CrossRef]

8. Lam NSN, Meyer M, Reams M, Yang S, Lee K, Zou L, et al. Improving social media use for disaster resilience: challenges and strategies. Int J Digit Earth. 2023;16(1):3023–44. doi:10.1080/17538947.2023.2239768. [Google Scholar] [CrossRef]

9. Ma Y, Cui N, Jiang ZZ, Yuan Y, Wang G. Group homophily based facility location selection in geo-social networks. World Wide Web. 2023;26(1):33–53. doi:10.1007/s11280-022-01008-3. [Google Scholar] [CrossRef]

10. Saravanan PS, Ramani S, Reddy VR, Farhaoui Y. A novel approach of privacy protection of mobile users while using location-based services applications. Ad Hoc Netw. 2023;149:103253. doi:10.1016/j.adhoc.2023.103253. [Google Scholar] [CrossRef]

11. Tong W, Tong Y, Xia C, Hua J, Li Q, Zhong S. Understanding location privacy of the point-of-interest aggregate data via practical attacks and defenses. IEEE Trans Dependable Secure Comput. 2023;20(3):2433–49. doi:10.1109/TDSC.2022.3184279. [Google Scholar] [CrossRef]

12. Ren K, Zhang S, Lin H. Where are you settling down: geo-locating twitter users based on tweets and social networks. In: Information retrieval technology. Berlin, Heidelberg: Springer; 2012. vol. 7675. [Google Scholar]

13. Davis Jr. CA, Pappa GL, de Oliveira DRR, de L, Arcanjo F. Inferring the location of twitter messages based on user relationships. Trans GIS. 2011;15(6):735–51. doi:10.1111/tgis.2011.15.issue-6. [Google Scholar] [CrossRef]

14. Backstrom L, Sun E, Marlow C. Find me if you can: improving geographical prediction with social and spatial proximity. In: Proceedings of the 19th International Conference on World Wide Web; 2010 Apr 26–30; Raleigh, North Carolina, USA. p. 4–5. [Google Scholar]

15. Jurgens D. That’s what friends are for: inferring location in online social media platforms based on social relationships. In: Proceedings of the Seventh International Conference on Weblogs and Social Media; 2013 Jul 8–11; Cambridge, Massachusetts, USA. vol. 7, no. 1, p. 273–82. [Google Scholar]

16. Haldar NAH, Reynolds M, Shao Q, Paris C, Li J, Chen Y. Activity location inference of users based on social relationship. World Wide Web. 2021;24(4):1165–83. doi:10.1007/s11280-021-00899-y. [Google Scholar] [CrossRef]

17. McPherson M, Smith-Lovin L, Cook JM. Birds of a feather: homophily in social networks. Annu Rev Sociol. 2001;27(1):415–44. doi:10.1146/soc.2001.27.issue-1. [Google Scholar] [CrossRef]

18. Ju W, Yi S, Wang Y, Xiao Z, Mao Z, Li H, et al. A survey of graph neural networks in real world: imbalance, noise, privacy and OOD challenges. 2024. doi:10.48550/arXiv.2403.04468. [Google Scholar] [CrossRef]

19. Eisenstein J, O’Connor B, Smith NA, Xing EP. A latent variable model for geographic lexical variation. In: Proceedings of the 2010 Conference on Empirical Methods in Natural Language Processing; 2010 Oct 9–11; MIT Stata Center, Massachusetts, USA. p. 1277–87. [Google Scholar]

20. Cho E, Myers SA, Leskovec J. Friendship and mobility: user movement in location-based social networks. In: Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; 2011 Aug. 21–24; San Diego, CA, USA. [Google Scholar]

21. Roller S, Speriosu M, Rallapalli S, Wing B, Baldridge J. Supervised text-based geolocation using language models on an adaptive grid. In: Proceedings of the 2012 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning; 2012 Jul 12–14; Jeju Island, Korea. p. 1500–10. [Google Scholar]

22. Kong L, Liu Z, Huang Y. SPOT: locating social media users based on social network context. Proc VLDB Endow. 2014;7(13):1681–4. doi:10.14778/2733004.2733060. [Google Scholar] [CrossRef]

23. Page L, Brin S, Motwani R, Winograd T. The pagerank citation ranking: bringing order to the web (Technical Report). Stanford InfoLab; 1998. [Google Scholar]

24. McGee J, Caverlee J, Cheng Z. Location prediction in social media based on tie strength. In: 22nd ACM International Conference on Information and Knowledge Management; 2013 Oct 27–Nov 1; San Francisco, CA, USA. p. 459–68. [Google Scholar]

25. Compton R, Jurgens D, Allen D. Geotagging one hundred million Twitter accounts with total variation minimization. In: 2014 IEEE International Conference on Big Data (Big Data); 2014 Oct 27–30; Washington DC, USA. p. 393–401. [Google Scholar]

26. Rahimi A, Cohn T, Baldwin T. Semi-supervised user geolocation via graph convolutional networks. In: Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics; 2018 Jul 15–20; Melbourne, Australia. p. 2009–19. [Google Scholar]

27. Kipf TN, Welling M. Semi-supervised classification with graph convolutional networks. In: 5th International Conference on Learning Representations; 2017 Apr 24–26; ICLR 2017, Toulon, France. [Google Scholar]

28. Kothari R, Jain V. Learning from labeled and unlabeled data. In: Proceedings of the 2002 International Joint Conference on Neural Networks (Cat. No. 02CH37290); 2002; Honolulu, HI, USA. p. 2803–8. [Google Scholar]

29. Perozzi B, Al-Rfou R, Skiena S. DeepWalk: online learning of social representations. In: The 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; 2014 Aug 24–27; New York, NY. ACM; p. 701–10. [Google Scholar]

30. Mikolov T, Chen K, Corrado G, Dean J. Efficient estimation of word representations in vector space. In: Bengio, Y, LeCun Y. 1st International Conference on Learning Representations; 2013 May 2–4; Scottsdale, Arizona, USA. [Google Scholar]

31. Grover A, Leskovec J. node2vec: Scalable feature learning for networks. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; 2016; New York, NY, USA: Association for Computing Machinery. p. 855–64. [Google Scholar]

32. Ju W, Fang Z, Gu Y, Liu Z, Long Q, Qiao Z, et al. A comprehensive survey on deep graph representation learning. Neural Netw. 2024;173:106207. doi:10.1016/j.neunet.2024.106207. [Google Scholar] [PubMed] [CrossRef]

33. Velickovic P, Cucurull G, Casanova A, Romero A, Lio’ P, Bengio Y. Graph attention networks. In: 6th International Conference on Learning Representations; 2018 Apr 30–May 3; Vancouver, BC, Canada. [Google Scholar]

34. Bahdanau D, Cho K, Bengio Y. Neural machine translation by jointly learning to align and translate. In: Bengio, Y, LeCun Y. 3rd International Conference on Learning Representations; 2015 May 7–9; San Diego, CA, USA. [Google Scholar]

35. Zeng H, Zhou H, Srivastava A, Kannan R, Prasanna VK. Graphsaint: graph sampling based inductive learning method. In: 8th International Conference on Learning Representations;2020 Apr 26–30; Addis Ababa, Ethiopia. [Google Scholar]

36. Klicpera J, Bojchevski A, Günnemann S. Predict then propagate: graph neural networks meet personalized PageRank. In: 7th International Conference on Learning Representations; 2019 May 6–9; New Orleans, LA, USA. [Google Scholar]

37. Ester M, Kriegel HP, Sander J, Xu X. A density-based algorithm for discovering clusters in large spatial databases with noise. In: Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96); 1996; Portland, Oregon, USA. [Google Scholar]

38. Han B, Cook P, Baldwin T. Geolocation prediction in social media data by finding location indicative words. In: Proceedings of COLING 2012 Dec 8–15; Mumbai, India. p. 1045–62. [Google Scholar]