 Open Access
Open Access
ARTICLE
Research on Alliance Decision of Dual-Channel Remanufacturing Supply Chain Considering Bidirectional Free-Riding and Cost-Sharing
School of Business, Qingdao University, Qingdao, China
* Corresponding Author: Yeming Dai. Email:
(This article belongs to the Special Issue: Data-Driven Robust Group Decision-Making Optimization and Application)
Computer Modeling in Engineering & Sciences 2024, 140(3), 2913-2956. https://doi.org/10.32604/cmes.2024.049214
Received 30 December 2023; Accepted 17 April 2024; Issue published 08 July 2024
Abstract
This study delves into the formation dynamics of alliances within a closed-loop supply chain (CLSC) that encompasses a manufacturer, a retailer, and an e-commerce platform. It leverages Stackelberg game for this exploration, contrasting the equilibrium outcomes of a non-alliance model with those of three differentiated alliance models. The non-alliance model acts as a crucial benchmark, enabling the evaluation of the motivations for various supply chain entities to engage in alliance formations. Our analysis is centered on identifying the most effective alliance strategies and establishing a coordination within these partnerships. We thoroughly investigate the consequences of diverse alliance behaviors, bidirectional free-riding and cost-sharing, and the resultant effects on the optimal decision-making among supply chain actors. The findings underscore several pivotal insights: (1) The behavior of alliances within the supply chain exerts variable impacts on the optimal pricing and demand of its members. In comparison to the non-alliance (D) model, the manufacturer-retailer (MR) and manufacturer-e-commerce platform (ME) alliances significantly lower both offline and online resale prices for new and remanufactured goods. This adjustment leads to an enhanced demand for products via the MR alliance’s offline outlets and the ME alliance’s online platforms, thereby augmenting the profits for those within the alliance. Conversely, retailer-e-commerce platform (ER) alliance tends to increase the optimal retail price and demand across both online and offline channels. Under specific conditions, alliance behavior can also increase the profits of non-alliance members, and the profits derived through alliance channels also exceed those from non-alliance channels. (2) The prevalence of bidirectional free-riding behavior largely remains constant across different alliance configurations. Across these models, bidirectional free-riding typically elevates the equilibrium prices in offline channel while negatively affecting the equilibrium prices in other channel. (3) The effect of cost-sharing shows relative uniformity across the various alliance models. Across all configurations, cost-sharing tends to reduce the manufacturer’s profits. Nonetheless, alliances initiated by the manufacturer can counteract these negative impacts, providing a strategic pathway to bolster CLSC profitability.Keywords
The meteoric surge in Internet utilization has markedly propelled the expansion of e-commerce, engendering significant transformations in consumer behavior. This upswing in online shopping frequency has culminated in a substantial elevation in online sales volumes. By the year 2022, the magnitude of China’s online retail market had ascended to an impressive 13.79 trillion yuan. Concurrently, traditional supply chains are undergoing adaptive changes to cater to the digital era’s requisites by integrating online channels and reconfiguring their sales frameworks [1]. Forefront industry players like Apple, Nike, Dell, and HP have embraced these shifts through the implementation of dual-channel supply chain strategies. Amid growing environmental concerns and the scarcity of resources, there is an intensified concentration on sustainable manufacturing and supply chain management. This scenario has precipitated collaborative efforts between corporations and governmental entities aimed at augmenting remanufacturing efficacy, curtailing resource consumption, and bolstering market competitiveness. Several manufacturers, including Epson, HP, Huawei, and Xiaomi, have acknowledged the multifaceted economic, environmental, and social merits of remanufacturing, integrating it within their production operations to establish a closed-loop supply chain framework [2,3]. Consequently, the notion of a dual-channel closed-loop supply chain has ascended as a focal point of interest within the ambit of current supply chain management scholarship [4]. Nevertheless, as remanufacturing gains increased visibility across diverse sectors, the task of identifying the most advantageous sales strategy for both new and remanufactured products emerges as a formidable challenge for manufacturers [5]. The juxtaposition of selling remanufactured alongside new products may cast a pall over brand perception. A case in point is HP, which encountered a consumer trust debacle when its channel dealers inadvertently marketed refurbished machines as brand new. Additionally, legal barriers, exemplified by the Sale of Goods Act in the UK, may impede the sale of remanufactured goods by retailers. In consideration of these obstacles, manufacturers commonly elect to market new and remanufactured products through segregated channels, striving to adeptly regulate the remanufactured products market while safeguarding their brand’s esteem.
In recent years, the intensification of competition across various channels has compelled supply chain participants, including manufacturers, retailers, and e-commerce platforms, to escalate their sales strategies in an effort to captivate consumers and augment product sales. This heightened emphasis on sales has produced dual marginal effects, simultaneously presenting opportunities and challenges [5]. To thrive within this competitive milieu, supply chain entities are progressively gravitating towards strategic alliances, consolidating crucial resources to boost both individual and collective profitability. Manufacturers are increasingly partnering with retailers to counteract the adverse repercussions of dual marginal effects while maximizing benefits throughout the supply chain. An illustrative case is the collaboration between Xiaomi and Youmi Korea, which is strategized to broaden Xiaomi’s footprint in South Korea’s mobile phone market. Furthermore, manufacturers are seeking alliances with e-commerce platforms to fortify their market standing. The partnership between Gree Group and JD.com is tailored towards fostering a short-circuit economy and securing exclusive distribution for a variety of product lines. In addition, world-renowned entities such as Disney and eBay have joined forces to inaugurate a co-branded shopping portal that specializes in merchandising products linked to both brands. Retailers and platforms acting as conduits for manufacturers are equally acknowledging the merits of strategic partnerships. A prominent alliance between JD.com and Five Star Electric, a foremost Chinese retailer, merges their efforts to engineer innovative online-offline cross-channel experiences, setting a precedent for the future of integrated retail. These instances underscore the burgeoning inclination towards mutual alliances among businesses, elucidating their substantial advantages. Consequently, it is becoming imperative for companies to delve into exhaustive research on the motives and strategic choices underpinning such alliances, to foster auspicious development opportunities and maintain a competitive edge in the dynamic marketplace [6].
On the other hand, manufacturers’ implementation of a dual-channel strategy instigates a competitive interplay between online and offline consumer demands, with both channels being intricately linked. This approach allows consumers to alternate between these channels for their purchases, taking advantage of the unique conveniences each channel offers. However, this very versatility also leads to the emergence of free-riding behavior [7]. Particularly prevalent in markets for experiential products like jewelry, high-tech electronics, fashion apparel, art, and perfume, free-riding emerges due to the difficulty in assessing these products’ quality and value without firsthand experience, compounded by often incomplete online descriptions. Research suggests that a notable proportion of consumers (55%) visit physical stores to inspect and experience products in person before purchasing them online, thus contributing to free-riding in the online channel [8]. Conversely, some shoppers utilize online resources to research products, consult with virtual assistants, compare information efficiently and inexpensively. They then leverage this information to make informed purchases at brick-and-mortar stores, resulting in free-rider behavior in offline channels. In today’s dual-channel supply chains, free-riding is not a one-way street but a bidirectional phenomenon [9]. Manufacturers who sell their products through both offline retailers and online e-commerce platforms (ECPs) can face a phenomenon known as two-way free-riding. When dual-channel supply chain considers alliance behavior, it can alter the supply chain’s structure and consequently impact the outcomes of such free-riding. To investigate whether enterprises adopting a dual-channel structure engage in alliance behavior and whether this behavior affects the utility derived from free-riding, this study explores the potential changes in utility associated with free-riding behavior under alliance conditions.
To study the incentive mechanism of an alliance and its impact on the whole supply chain and members’ profits, we set up four-game models. These models include three alliance-based models and one non-alliance-based model. The non-alliance model can be used as a benchmark to assess the motivation of a company to establish an alliance and the resulting consequences. On this basis, the optimal alliance model’s determination is discussed from each member’s perspective. Then, we analyze the impact of these different alliance models on supply chain operational performance. Finally, we study whether bidirectional free-riding and cost-sharing have the same effect under other alliance models.
On the flip side, the adoption of a dual-channel strategy by manufacturers prompts a competitive interaction between online and offline consumer demands, with the two channels being closely interlinked. This strategy affords consumers the flexibility to switch between channels for their purchases, capitalizing on the distinct advantages each channel provides. Nonetheless, this very adaptability also gives rise to free-riding behavior [7]. Particularly prevalent in markets for experiential products such as jewelry, high-tech electronics, fashion apparel, art, and perfume, free-riding emerges from the challenge of evaluating these products’ quality and value without direct experience, further exacerbated by the often incomplete online descriptions. Studies indicate that a significant fraction of consumers (55%) visit physical stores to examine and experience products firsthand before making their purchases online, thus contributing to free-riding on the online channel [8]. On the contrary, some shoppers exploit online resources to research products, engage with virtual assistants, and compare information efficiently and cost-effectively. They then use this insight to execute informed purchases at brick-and-mortar stores, leading to free-rider behavior in offline channels. In the current landscape of dual-channel supply chains, free-riding is a reciprocal phenomenon [9]. Manufacturers distributing their products through both offline retailers and online e-commerce platforms (ECPs) may encounter what is known as two-way free-riding. When considering alliance behavior within a dual-channel supply chain, it has the potential to reshape the structure of the supply chain and thus influence the dynamics of free-riding.
To delve into whether companies with a dual-channel setup partake in alliance behavior and how this behavior impacts the benefits derived from free-riding, this study probes into the possible shifts in utility linked to free-riding behavior under the auspices of alliances. In examining the incentive mechanism of an alliance and its influence on the entire supply chain and the profits of its members, we construct four game models. These models comprise three alliance-based frameworks and one non-alliance-based framework. The non-alliance model serves as a comparative standard to evaluate a company’s incentive to forge an alliance and the ensuing effects. Building on this, the determination of the optimal alliance model is deliberated from the standpoint of each member. Subsequently, we scrutinize the effects of these diverse alliance frameworks on the operational performance of the supply chain. Lastly, we explore whether bidirectional free-riding and cost-sharing exhibit consistent impacts across different alliance models.
Our investigation has unearthed several intriguing outcomes. (1) The behavior of alliances within the supply chain has different effects on the optimal pricing and demand of the alliance members, which in turn increases the profits of the alliance members. In contrast, ER alliances tend to reduce optimal retail prices and demand in both online and offline channels. (2) The impact of free-riding on the decision-making processes of each member remains unaffected by the behavior of the alliance. (3) While cost-sharing practices can impair the manufacturer’s profits, alliance strategies initiated by manufacturers can effectively counteract such adverse effects. Hence, adopting suitable alliance behaviors proves advantageous for manufacturers.
To encapsulate, this study contributes to the existing body of knowledge in several pivotal ways: First and foremost, to our knowledge, this represents the first effort to scrutinize alliance strategies within a dual-channel closed-loop supply chain incorporating an e-commerce platform. In this setup, manufacturers adeptly allocate new and remanufactured products across retailers and e-commerce platforms, aiming to safeguard their brand image and prevent sales chaos. This exploration, therefore, sheds light on innovative operational and managerial strategies for industry practitioners. Secondly, our analysis distinctively explores the motivations behind alliance formation from the perspective of each supply chain entity, identifying the most favorable strategy and achieving balance within alliances. This perspective distinguishes our investigation from previous works, which predominantly concentrated on centralized and decentralized decision-making processes [6,7]. Thirdly, the phenomenon of bidirectional free-riding has been underexplored in existing research. Our study is among the pioneers to comprehensively assess this phenomenon within the context of alliance mechanisms. Through the formulation of four models, we examine the dual impacts of bidirectional free-riding on the equilibrium decision-making of supply chain members, uncovering that free-riding consistently escalates the optimal price within its channel, independent of alliance behavior. Lastly, considering the direct involvement of manufacturers in product sales, our research delves into scenarios where manufacturers share a part of the sales cost with retailers and e-commerce platforms. This is the inaugural study to evaluate how such cost-sharing influences the profits of supply chain participants under various alliance behaviors within a dual-channel, closed-loop supply chain setting. The findings illustrate that although cost-sharing by manufacturers adversely affects their profits, alliances initiated by manufacturers can substantially alleviate these negative impacts.
The remainder of this paper is structured as follows: Section 2 offers an exhaustive review of pertinent literature. Section 3 outlines the research queries this paper aims to tackle. Section 4 elaborates on the developed game models and delves into the analysis of equilibrium outcomes. Section 5 engages in a comparative analysis of the results derived from each model. Lastly, Section 6 encapsulates the conclusions and suggests avenues for future inquiry.
This paper intersects three pivotal research domains: dual-channel supply chain dynamics, the behavior of member alliances, and the phenomenon of free-riding. In this chapter, we will retrospect the concerned document.
As the digital economy progresses, the attention of scholars towards dual-channel supply chains has grown significantly. This paper delves into the pricing strategies within these supply chains, underlining major advancements in this area. Pathak et al. [10] were at the forefront of researching dual-channel supply chains by formulating an optimal pricing and profit model and examining the impact of cooperative advertising and delivery times on these decisions, within a manufacturer-centric framework. Furthermore, Sun et al. [11] and Liu et al. [12] investigated the effects of free-riding behavior on optimal pricing and profits in a dual-channel supply chain that involves retailers and suppliers, considering both decentralized and centralized pricing structures. Suvadarshini et al. [13] analyzed a closed-loop supply chain that includes original equipment manufacturer (OEM), retailers, and third-party suppliers, with a focus on the efficacy of multi-channel recall systems. They assessed three return channel frameworks, taking into account aspects like competition, collection efficiency, individual rationality, and information asymmetry. Wang et al. [14] introduced a game theory model to solve a vital dilemma for supply chain participants: choosing between the agent model and the traditional resale model for platforms, and deciding whether manufacturers should outsource recycling operations or manage them in-house. Matsui [15] explored which agency sales or wholesale contracts offered by e-commerce platforms competing suppliers with typical dual-channel supply chains should be adopted. Zhong et al. [16] proposed a programmed two-channel supply chain model to explore the value added by blockchain adoption by manufacturing companies. Xu et al. [17] applied leader-follower game theory and mean-variance theory to craft optimization models for comprehensive closed-loop supply chains, focusing on manufacturers who distribute through brick-and-mortar stores. Yu et al. [18] explored the selection of collection channels in a closed-loop supply chain including manufacturers, e-commerce platforms, and third-party recyclers. Gong et al. [19] examined a closed-loop dual-channel supply chain where manufacturers participate in direct online sales and wholesale to retailers, with the latter managing reverse channel recycling. They utilized a Stackelberg game to study how free-riding and reverse revenue-sharing ratios affect the pricing strategies and service decisions of offline retailers. Sana [20] looked into an imperfect production system, taking into account the cost implications of greenhouse gases to determine the optimal reserve selling prices, sales team efforts, and production scales. In another study, Sana [21] scrutinized a dual-channel inventory model with uncertain market power for a specific product. Farouk et al. [22] focused on pricing and remanufacturing decisions in dual-channel reverse supply chains, aiming to maximize profits in both centralized and decentralized structures and developed three mathematical models for this comparative analysis.
However, these studies have not tackled the scenario where manufacturers distribute both new and remanufactured products through offline retailers and online e-commerce platforms, a gap this paper seeks to address. This approach marks a novel contribution to the field, broadening the comprehension of dual-channel supply chain strategies amidst the evolving digital marketplace.
2.2 Alliance Behavior of Supply Chain Members
Current investigations into alliances among supply chain members remain somewhat underexplored, presenting numerous perspectives awaiting full examination. Scholars to date have predominantly honed in on the dynamics of decentralized vs. centralized decision-making concerning pricing. For example, Sun et al. [11] and Liu et al. [12] scrutinized the impact of these decision-making frameworks on optimal pricing strategies and financial outcomes for supply chain participants. Likewise, Farouk et al. [22] probed into the complexities of pricing and remanufacturing decisions within dual-channel reverse supply chains, emphasizing remanufacturing and maintenance operations. Their goal was to maximize profits through the establishment and comparative analysis of both centralized and decentralized supply chain models, utilizing three distinct mathematical approaches. Moving away from conventional decision-making paradigms, recent inquiries have started to appreciate the prospects of forming partial alliances within supply chains. Notably, in the context of single-channel supply chains, specific research [23,24] has introduced models for decentralized and collaborative alliances, with an intent to examine their influence on the decision-making of supply chain entities. In the domain of closed-loop supply chains, Zheng et al. [25] investigated recycling collaboration through two models: the recycling alliance and the cost-sharing model, devising analytical tools to assess the viability and efficiency of cooperative recycling agreements between manufacturers and retailers. However, a significant oversight in these studies is the underestimation of e-commerce platforms’ role, a key element in contemporary supply chains, especially in online sales. This oversight has sparked interest in the emerging area of dual-channel supply chains, where online platforms are essential, leading to studies on alliance behavior among supply chain members. Zheng et al. [26] studied a third-order closed-loop supply chain consisting of a manufacturer, a distributor and a retailer. They derive equilibrium solutions under centralized, decentralized and different partial alliance models, and conduct a comparative analysis of equilibrium under each model to provide decision support for business managers. Ma et al. [27] investigated interactions among the different parties in a three-echelon closed-loop supply chain consisting of a single manufacturer, a single retailer and two recyclers and focus on how cooperative strategies affect closed-loop supply chain decision-making. Wang et al. [28] embarked on a foundational exploration of the incentives behind alliance formation among manufacturers, retailers, and e-commerce platforms in a dual-channel setup. Yet, they did not extend their analysis to include recycling and remanufacturing within the supply chain. A review of the literature indicates a predominant focus on decentralized and centralized decision-making, with scant attention to local alliances, particularly in dual-channel closed-loop supply chains that feature e-commerce platforms. This paper, therefore, seeks to address this gap by exploring the strategic repercussions of choosing between alliance and non-alliance routes on cooperation within dual-channel closed-loop supply chains. The aim is to deduce the optimal alliance strategy, thereby offering fresh perspectives to the supply chain management discourse.
Telser first introduced the concept of the free-riding problem [29], highlighting how it can undermine retailers’ motivation to provide informational services. This issue arises when one party benefits from efforts such as sales promotion without bearing the associated costs. A considerable amount of research has been directed towards examining unidirectional free-riding behavior [30–32], revealing both its positive and negative impacts. Sun et al. [33] studied a two-channel supply chain consisting of a piggybacking brick-and-mortar retailer, a manufacturer, and a manufacturer-owned e-commerce platform store, where piggybacking behaviors may arise between retailer e-commerce platforms. Xu et al. [34] developed a two-channel supply chain model and investigated the impact of consumer drain hitchhiking behavior on the optimal level of sales effort, optimal pricing decision and profit of each member of cross-channel return product suppliers under decentralized and centralized decision making. Zhou et al. [35] considered a two-echelon supply chain, where a manufacturer sells products through its own online channel and a traditional retailer. It was investigated how free-riding affects the pricing/service strategies and profits of the two members when the dual channel uses differential pricing and non-differential pricing scenarios, respectively. Liang et al. [36] argued that a certain level of service free-riding could actually contribute to the environmental sustainability of dual-channel supply chains. On the other hand, Yan et al. [37] found that free-riding could lead to extra profits for supply chain members. Ke et al. [38] constructed a model to explore free-riding scenarios involving a manufacturer and two retailers, as well as among the retailers themselves, concluding that free-riding tends to dampen corporate enthusiasm and reduce profits. Liu et al. [39] developed a differential game model for two competing firms, considering both immediate and future corporate perspectives. Their analysis revealed that in scenarios where the cross-innovation investment demand sensitivity coefficient between two firms is low, companies with a short-term focus can achieve higher profits than those looking ahead. However, the focus of recent research has shifted towards the effects of bidirectional free-riding on supply chain decision-making. While the majority of studies on bidirectional free-riding have concentrated on the interaction between online and offline channels [40], some researchers have ventured into examining reciprocal free-riding between retailers and e-commerce platforms. For instance, Yan et al. [37] investigated such dynamics within a dual-channel supply chain, uncovering that bidirectional free-riding can indeed generate additional profits for members, particularly in contexts involving online finance. Nevertheless, the exploration of bidirectional free-riding behavior within the realm of channel alliances remains sparse. In a dual-channel supply chain characterized by various alliance behaviors, the nature and consequences of free-riding are markedly different. Importantly, it is critical to understand that within the alliance framework, supply chain members not only enjoy the benefits of free-riding but also participate in the distribution of sales-related costs. The unique cost-sharing strategies adopted by alliance partners [35,40,41] can significantly influence the profitability of supply chain entities, as the costs associated with product sales shift according to the specific alliance behavior.
The pertinent body of literature to our study prominently features discussions on cost-sharing contracts. Zhou et al. [35] scrutinized the pricing strategies of manufacturers and introduced a service cost-sharing agreement to boost supply chain efficacy. Li et al. [40] delved into a decentralized green product supply chain consisting of a manufacturer and a retailer, each tasked with deciding the green level of the product and the marketing efforts, respectively. They examined two kinds of contracts: contract design (CD) and contract marketing (CM), with CD including three strategic models: price-only (PO), cost-sharing (CS), and revenue-sharing (RS). In the CS model, retailers contribute to the manufacturer’s green investment costs. Xu et al. [41] explored contract arrangements between manufacturers and dealers, using a Stackelberg differential game model to craft long-term agreements. They offered two cost-sharing contracts aimed at enhancing the products’ low-carbon reputation: a one-way Cost Sharing Contract (OWC) and a two-way Cost Sharing Contract (TWC), where OWC involves manufacturer support to dealers, and TWC sees both manufacturers and dealers sharing costs related to low-carbon product promotion and emission reductions. Ma et al. [42] assessed the effects of information asymmetry, noting that both cost-sharing and benefit-sharing could bolster the conservation efforts of third-party logistics service providers (TPLSPs), facilitating Pareto improvements across supply chain members. Adhikari et al. [43] proposed a model for developing green clothing supply chains in emerging markets through green cost-sharing and profit-sharing agreements, where cost-sharing means the retailer covers a predetermined part of the green expenses with the manufacturer’s greening entity. They also looked into how fairness concerns among supply chain partners influence greening and pricing strategies. The approaches to cost-sharing in these studies show considerable variation.
In essence, the majority of dual-channel supply chain research has been directed at decentralized and centralized decision-making frameworks. Nonetheless, there exists a significant void in literature addressing the intricacies of partial alliances among members, especially within dual-channel closed-loop supply chains that include e-commerce platforms. While decentralized decision-making often neglects alliance behaviors, and centralized decision-making strives for maximizing collective benefits, the concept of partial alliances suggests individual members may seek collaboration. This gap highlights a lack of understanding in alliance-based decision-making involving e-commerce platforms within dual-channel closed-loop supply chains, a niche this paper aims to fill. Moreover, existing analyses on bidirectional free-riding and cost-sharing have not thoroughly investigated how free-riding uniformly affects pricing across different alliance behaviors, nor have they fully assessed the impact of cost-sharing on member profits across diverse alliance strategies. The potential modification of such effects by alliance behaviors also remains untouched. Thus, this study intends to explore the implications of alliance behavior on equilibrium decisions and profits within dual-channel closed-loop supply chains, examining the influence of cost-sharing and bidirectional free-riding on supply chain member decisions and profitability under varied alliance strategies. This inquiry seeks to bridge a crucial gap in the literature, offering unique contributions to the discourse on supply chain management.
This study delves into the dynamics of a dual-channel closed-loop supply chain, which includes a manufacturer, a retailer, and an e-commerce platform. Within this supply chain framework, the manufacturer undertakes the recycling of old products and the production of remanufactured products at a predetermined recycling price
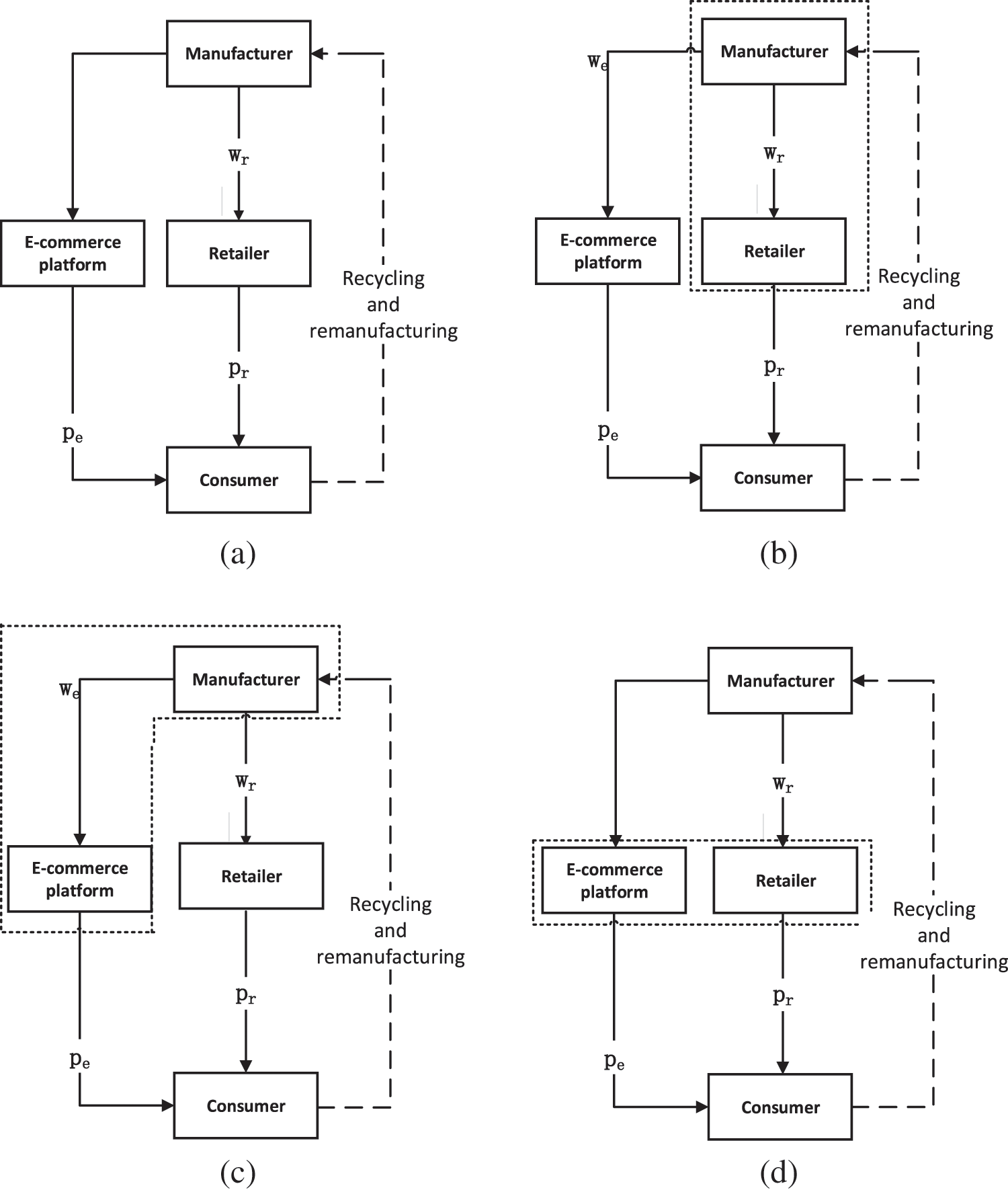
Figure 1: Different sales models in dual-channel closed-loop supply chain: (a) non-alliance model; (b) manufacturer-retailer alliance; (c) manufacturer-e-commerce platform alliance; (d) e-commerce platform-retailer alliance
The dynamics of cross-channel transactions significantly influence the demand in both online and offline channels under a bidirectional free-riding scenario. Drawing on the work of Zhou et al. [35], Yan et al. [37], and Shekarian et al. [44], we establish the demand capabilities for offline and online channels as chases:
This study assumes that the total initial market demand is standardized at 1, distinguishing the primary demand for offline channels as

The main objective of this paper is to explore the comparative advantages of different alliance configurations within a dual-channel closed-loop supply chain. This research delineates four possible alliance frameworks (comprising one non-alliance model and three alliance-based models), as illustrated in Fig. 1.
This section delves into four scenarios: the model D and three alliance configurations (models MR, ER, and ME). The model D establishes the baseline for comparative evaluation against the alliance scenarios. The analysis then proceeds to dissect the optimal/equilibrium outcomes and advantages derived from each configuration. Through backward induction, we ascertain the concavity of the profit functions with respect to the decision variables, enabling a comprehensive and solid analysis. The proofs supporting these conclusions are detailed in the Appendix.
In the model D, the manufacturer, taking the lead, sets the wholesale prices
Theorem 1. In model D, the equilibrium solutions of new and remanufactured commodities are, respectively
According to Theorem 1, the corresponding optimal demand and profit in model D are, respectively
Among them,
Building on these foundations, we explore the impact of the free-riding coefficient on key decisions within the supply chain and establish Property 1. Furthermore, we examine how the cost-sharing coefficient influences the profitability of supply chain members in model D, leading to Property 2.
Property 1 elucidates the relationship between the free-riding coefficient and decision-making in the model D:
(1)
The optimal wholesale and retail prices in the offline/online channels are found to have a positive/negative correlation with the offline channel’s free-riding parameter
Free-riding dynamics compel consumers to alternate between channels for purchases, prompting both online and offline channels to adjust sales efforts and pricing strategies to boost demand and minimize the risk of free-riding, thereby enhancing profits.
Property 2 (1) The manufacturer’s share
Property 2 indicates that in the model D, the profits for the manufacturer and retailer are inversely or directly related to the proportion of sales costs the manufacturer shares with the retailer; similarly, the profits for the manufacturer and e-commerce platform are inversely or directly related to the manufacturer’s contribution to the e-commerce platform’s sales costs. It is observed that without an alliance, the manufacturer’s participation in sharing sales costs with the retailer and e-commerce platform can boost the profits of these entities but may adversely affect the manufacturer’s profit margins.
4.2 Manufacturer-Retailer Alliance Model (Model MR)
In the model MR, the manufacturer and retailer form an alliance, positioning themselves as the primary decision-makers. They jointly determine the wholesale price
Through the application of backward induction, we derive Theorem 2 for the model MR, which outlines the equilibrium solutions for new and remanufactured products as follows:
According to Theorem 2, the corresponding optimal demand and profit under MR model are, respectively
Building on these outcomes, Property 3 is deduced by examining the impact of the free-riding coefficient on the primary decisions of supply chain participants. Further, Property 4 is identified by analyzing the influence of the cost-sharing coefficient on the optimal profits within the model MR.
Property 3 The affection of the free-riding coefficient on the optimal determination of supply chain participators in the model MR is as follows:
(1)
Property 3 explores how the free-riding coefficient affects decision-making within the model MR: It highlights that in the model MR, the optimal retail prices and demand in offline retail channels positively correlate with the offline channel’s free-ride coefficient but negatively with the online channel’s free-ride coefficient. Conversely, the optimal wholesale price, retail price, and demand in online retail channels negatively correlate with the offline channel’s free-ride coefficient but positively with the online channel’s free-ride coefficient.
Similar to the model D, free-riding behavior in the model MR encourages consumers to alternate between online and offline channels for their purchases. This shift increases demand in both channels. To capitalize on this increased demand stemming from the alliance, both channels refine their sales and pricing strategies to prevent consumers from free-riding on the opposite channel, ultimately aiming to maximize profits.
Property 4 The manufacturer’s share
Property 4 elucidates that the MR Alliance/e-commerce platform’s profitability exhibits either a passive or positive correlation with the manufacturer’s allocation, the e-commerce platform’s sales expenses within the MR framework. This dynamic stems from the manufacturer-retailer alliance’s role in reducing the burden of sales cost-sharing between them, while simultaneously, the redistribution of sales costs between the manufacturer and the e-commerce platform diminishes the MR alliance’s profitability. Conversely, this reallocation augments the e-commerce platform’s profitability due to the shared sales costs.
4.3 Manufacturer-EC Platform Alliance Model (Model ME)
In the context of the model ME, the manufacturer forms a partnership with an e-commerce platform, jointly taking the lead to set the introductory price for new products,
We apply the backward induction method to solve the equilibrium of the above model, and obtain theorem three as follows:
Theorem 3 In the model ME, the equilibrium solution of new commodities and remanufactured commodities is, respectively
According to Theorem 3, the corresponding optimal demand and profit under model ME are, respectively.
Building on these foundations, we explore the impact of the free-riding coefficient on key decisions within the supply chain and establish Property 5. Furthermore, we examine how the cost-sharing coefficient influences the profitability of supply chain members in model ER leading to Property 6.
Property 5 The affection of the free-riding coefficient on optimal policy-making of supply chain participators in the model ME is as follows:
(1)
Property 5 reveals that within the model ME, the optimal wholesale price, retail price, and demand in offline retail channels exhibit a positive association with the free-riding coefficient of offline channels, yet bear a negative relationship with that of online channels. Inversely, the demand and retail price in online channels are adversely influenced by the free-riding coefficient of offline channels but benefit from a positive correlation with that of online channels.
Drawing parallels with model D, the phenomenon of free-riding in the model ME incites consumers to alternate between online and offline channels for their purchases, thereby elevating demand across both mediums. This situation compels both online and offline channels to intensify their sales efforts, recalibrate pricing strategies to fend off free-riding by consumers from the competing channel, with the ultimate goal of maximizing their respective benefits.
Property 6 The manufacturer’s share
Property 6 delineates the dynamics within the model ME, highlighting that the manufacturer/retailer’s benefit exhibits a negative/positive correlation with the cost-sharing ratio from the manufacturer to the retailer. Furthermore, it is noteworthy that the profitability derived from the ME alliance remains unaffected by the manufacturer’s contribution rate to the e-commerce platform. This phenomenon emerges because the ME Alliance effectively obviates the need for manufacturers to engage in cost-sharing with e-commerce platforms, thereby safeguarding the manufacturers’ interests from potential harm.
4.4 Retailer-E-Commerce Platform Alliance Model (Model ER)
In the context of the model ER, depicted in Fig. 1c, the retailer and the e-commerce platform form an alliance, assuming the role of primary decision-makers. They set forth the retail prices
Theorem 4 within the model ER explicates that the manufacturer’s equilibrium retail price for remanufactured goods, alongside the retailer’s optimal/equilibrium retail price for new items and the e-commerce platform’s optimal sale price for remanufactured goods, are delineated as follows:
According to Theorem 4, the corresponding optimal demand and profit under the model ER are, respectively.
Property 7 The effect of the free-riding coefficient on the best decision-making of supply chain participators of different channels in the model ER is as chases:
(1)
Property 7 elucidates that in the model ER, the optimal inside price and resale price for the offline retail channel positively align with the free-riding coefficient of the offline channel, yet inversely with the free-riding coefficient of the online channel. Conversely, the optimal retail price within the offline channel and the optimal inside price for the online channel exhibit a negative correlation with the offline channel’s free-riding coefficient, but a positive one with the online channel’s free-riding coefficient.
Despite the distinct characteristics of online and offline channels within the model ER, the impact of free-riding behavior on the optimal decisions of channel members remains unchanged. Consequently, within the ER alliance, both channels are impelled to intensify sales efforts and implement price adjustments to mitigate the risk of being exploited by the counterpart channel, with the overarching aim of profit maximization.
Property 6 The manufacturer’s share
Property 6 elucidates that within the model ER, the profitability of the ER alliance is positively influenced by the manufacturer’s cost-sharing ratio with the retailer. Conversely, it is negatively influenced by the manufacturer’s cost-communion ratio with the e-commerce platform. Moreover, the manufacturer’s benefit exhibits a passive correlation with the cost-communion scale towards the retailer and the cost-sharing ratio towards the e-commerce platform. This dynamic suggests that while the ER alliance’s profitability benefits from the manufacturer’s cost-sharing practices with the retailer and e-commerce platform, these cost-sharing arrangements detract from the manufacturer’s own benefits due to the reduction in sales cost.
This section conducts a comprehensive comparative analysis of the optimal equilibrium solutions derived from the four models discussed: MR, ER, ME, and the benchmark model D, the proofs supporting these conclusions are detailed in the Appendix. The ensuing analysis presents the following insights:
Proposition 1 The equilibrium retail prices of new and remanufactured commodities meet the following conclusions:
(1) When
(2) When
Proposition 1 elucidates that under specific conditions related to the level of free-riding, the cost of manufacturing new products, and the cost of recycling waste products, the retail prices set within the MR and ME models are discernibly lower than those observed in the model D. Within the model ER, the strategic alliance formed between the retailer and the platform serves to diminish channel competition and mitigate conflict, thereby facilitating a cooperative approach to pricing. As a direct consequence, this alliance strategically increases retail price. Similarly, in the MR and ME models, retail prices are adjusted downward compared to the model D. This reduction can be attributed to the alliances formed between the manufacturer and either the e-commerce platform or retailer, which effectively counteract the detrimental impacts of double margins within their respective sales channels, thereby significantly stimulating market demand through lower retail prices. Additionally, the presence of horizontal competition compels retailers (or platforms) to increase their pricing further.
Proposition 2 The equilibrium sale by bulk prices of new and remanufactured commodities meets the following conditions:
(1)
Proposition 2 posits that within the model ME, the behavior of alliances exerts no discernible impact on the bulk sales price of new commodities as established in model D. Likewise, alliances within the model MR do not affect the bulk sales prices of remanufactured commodities within the samodel ME. This observation implies that an alliance between the manufacturer and an e-commerce platform does not influence the bulk sale price of new commodities in the offline channel. Similarly, an alliance between the manufacturer and a retailer does not alter the internal pricing strategies for remanufactured commodities on the online e-commerce platform. Essentially, the establishment of an alliance with one channel does not interfere with the pricing mechanisms within the other. Furthermore, partnerships within the model ER do not alter the pricing structure for either new or remanufactured products, indicating that enhanced control over end sales through these partnerships does not modify the internal pricing dynamics of the products.
Proposition 3 The equilibrium demand for new and remanufactured commodities meets the following cases:
(1)
Proposition 3 reveals that alliances in the model MR serve to mitigate the exacerbation of offline product demand attributed to the double marginalization effect inherent in new product transactions. Conversely, alliance behavior within the model ME is found to increase online product demand. This variation in demand is attributable to the pricing strategies employed by the MR and ME alliances. Specifically, the MR alliance’s approach to reducing the retail price of new goods results in an increased inclination among customers to purchase these goods through offline channels. Concurrently, the ME alliance’s strategy of lowering the retail price of remanufactured goods encourages a greater number of customers to engage in purchasing through online channels.
Proposition 4 The equilibrium profit of new and recycled products meets the following conditions:
(1)
Proposition 4 delineates that the collaborative behaviors of the MR and ME alliances enhance the overall benefits to the entire supply chain. Drawing from the insights of Propositions 1, 2, and 3, it becomes clear that such cooperative endeavors among supply chain partners serve to diminish the optimal retail prices while bolstering the demand for new products distributed offline via the model MR. Concurrently, the alliance reduces the retail price of remanufactured commodities available online through the model ME, which in turn, escalates their demand. In essence, the synergistic collaboration among retailers, e-commerce platforms, and manufacturers amplifies the market presence of their respective channels, culminating in elevated profits for all involved entities.
Proposition 5 Profits of non-alliance members in alliance models and profits of members in model D satisfy the following conditions:
(1) When
(2) When
Proposition 5 highlights that even for entities outside of the alliance, the collaborative behavior can lead to a profit increase under specific conditions related to the expenditure on new products and the costs associated with remanufactured items. This revelation underscores the potential benefits of aligning with alliance strategies now, as such collaborative efforts are instrumental in mitigating the adverse effects of double marginalization on the system.
Proposition 6 Alliance models profit meets the following conditions:
(1) When
(2) When
Proposition 6 shows that when conditions
In this section, we perform numerical simulations to test the comparative results of equilibrium decision prices, equilibrium demands, and profits for the models in Section 5.
6.1 Impact of Parameters on the Optimal/Equilibrium Prices and Demands in Game Models
Building upon the previous setup, it can be concluded that
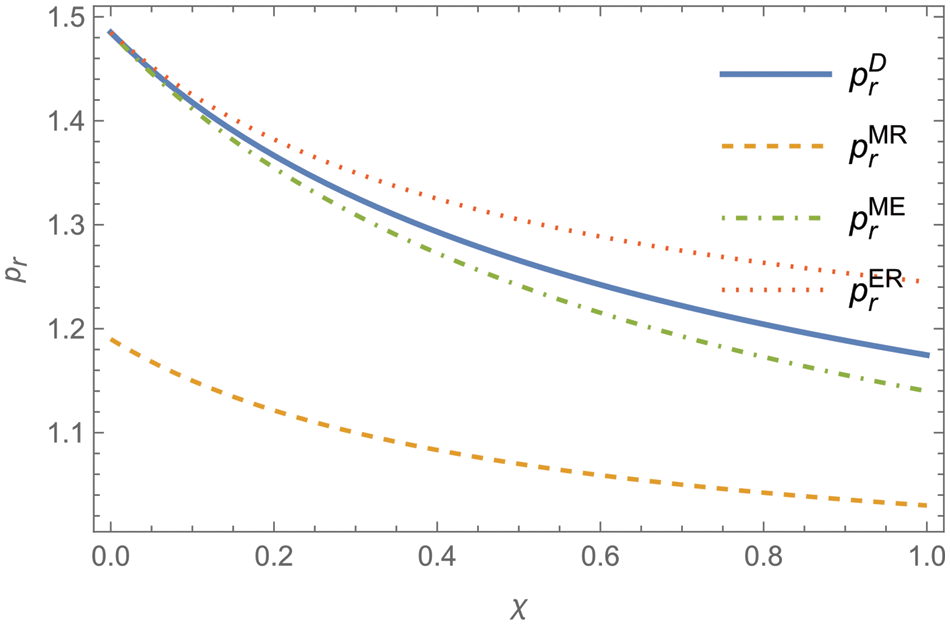
Figure 2: Variation of the equilibrium price of a new product with
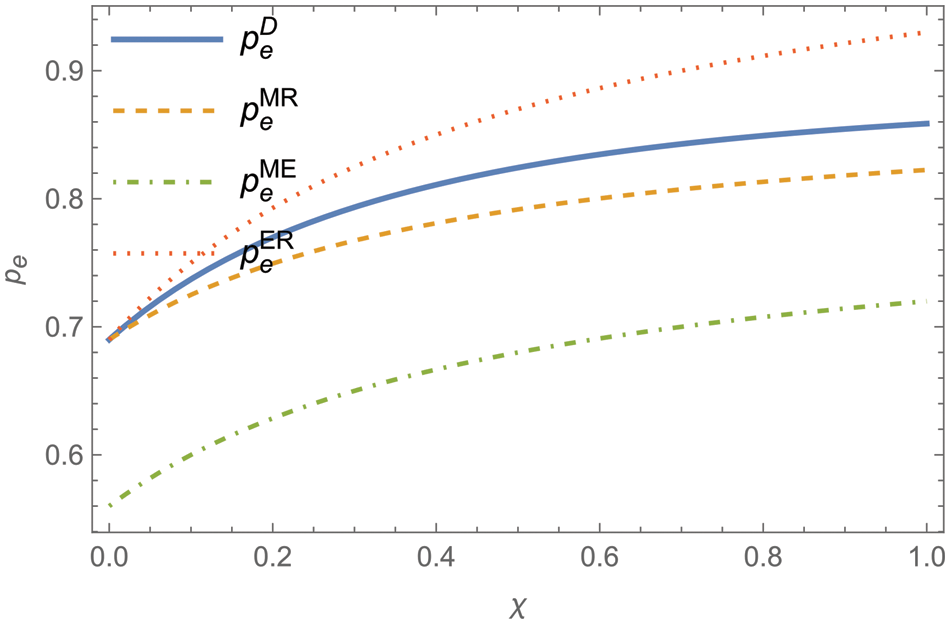
Figure 3: Variation of the equilibrium price of a remanufactured product with
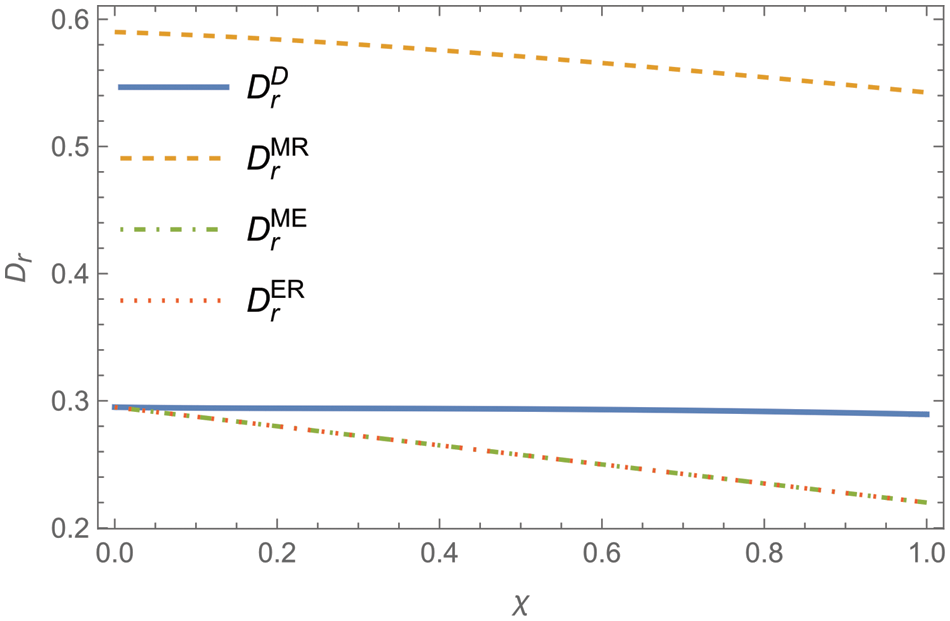
Figure 4: Variation of the equilibrium price of the offline channel with

Figure 5: Variation of the equilibrium price of the online channel with
6.2 Impact of Parameters on the Profits in Game Models
Let

Figure 6: The profits of MR alliance and model D members with

Figure 7: The profits of ME alliance and model D members with
Let

Figure 8: Variation of e-commerce platform’s profit with

Figure 9: Variation of retailer’s profit with
Let
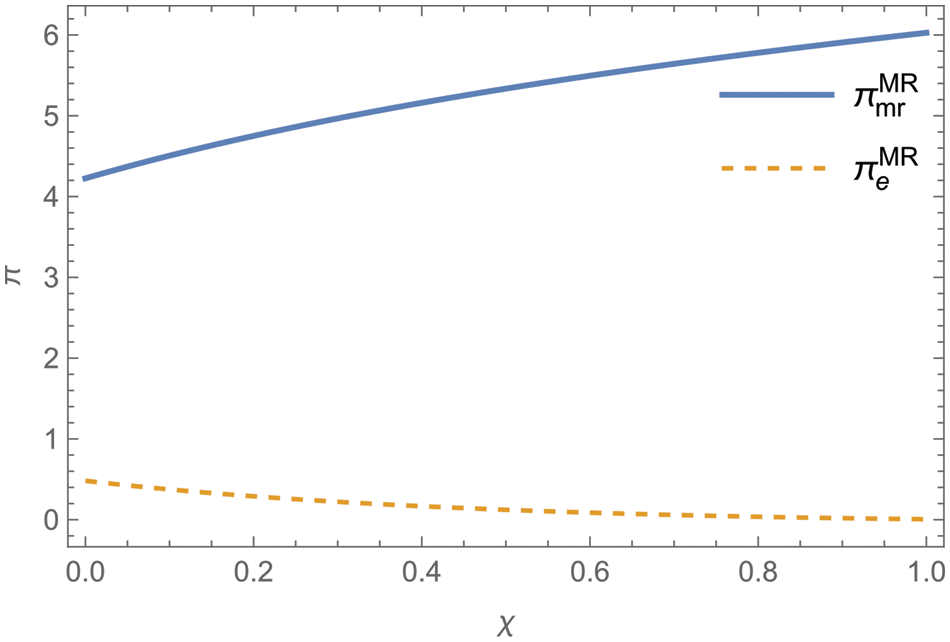
Figure 10: The variation of profits for MR alliance and e-commerce platform with

Figure 11: The variation of profits for MR alliance and e-commerce platform with
7 Conclusions and Implications
(1) The MR and ME alliances, prominently featuring the manufacturer as the central entity, play an indispensable role in counteracting the detrimental effects of double marginalization encountered during product exchanges. Compared to the baseline model D, these collaborative efforts lead to a marked reduction in both offline and online resale prices for new and remanufactured products, respectively. The pivotal influence of MR and ME alliances on the pricing strategy for these products results in an unprecedented surge in demand across both offline and online channels, thereby substantially elevating the profits of alliance participants. This phenomenon accentuates the vital contribution of alliance behavior within the supply chain to the enhancement of member profitability. Within the context of model D, it is observed that the profits accrued by members of the MR and ME alliances notably exceed those of their non-alliance counterparts. Notwithstanding, the advantages of engaging in alliance behavior extend beyond the immediate circle of participating members; under certain conditions, even entities outside the alliance framework may witness a favorable uptick in their interests as a consequence of the collective action. Nevertheless, it is critical to recognize that the repercussions of alliance behavior on supply chain profitability may vary in reality. For example, the collaboration between JD and Five Star Electric manifested in an overall profit increase. Conversely, JD.com's alliance with X5 Retail Group in 2015 was discontinued after merely six months, underscoring the notion that alliance outcomes are not uniformly beneficial and necessitate meticulous strategic consideration.
(2) The utility derived from free-riding remains unaffected by variations in alliance behavior. Within the alliance initiatives spearheaded by the manufacturer, the optimal internal and retail pricing in offline/online channels exhibit a positive/negative correlation with the free-riding behavior specific to the offline channel. In contrast, a significant correlation is observed between the free-riding behavior of the online channel and the maximal internal and retail prices. This indicates that disparate alliance practices among supply chain participants do not impinge on the utility associated with free-riding.
(3) While the cost-sharing initiatives undertaken by the manufacturer towards the retailer and the e-commerce platform may impinge upon the manufacturer’s profit margins, these measures invariably benefit both the retailer and the e-commerce platform. Conversely, the collaborative behavior involving the retailer, the e-commerce platform, and the manufacturer possesses the capability to mitigate the adverse effects of cost-sharing on the manufacturer’s profitability. In essence, the dynamics of alliance behavior possess the potential to modify the implications of cost-sharing activities.
Our study offers valuable managerial insights. Firstly, alliances can greatly affect a company’s performance and pricing strategies. In certain situations, managers have the chance to craft mutually advantageous strategies that boost profitability. Yet, it is important to acknowledge that alliances between two supply chain members do not always lead to positive overall profit outcomes. For example, collaborations between retailers and e-commerce platforms might sometimes reduce profits, particularly when consumer buying intent is strong, as illustrated by JD.com's brief partnership with X5 Retail Group in 2015. Managers need a deep understanding of the benefits and risks associated with any potential alliance. Although alliances with manufacturers may not always enhance total supply chain profits, they can increase overall supply chain efficiency, especially when consumer demand is average. Secondly, the phenomenon of bidirectional free-riding and the alliance behaviors of supply chain members are critical. Our research interestingly reveals that the utility of free-riding is not affected by alliance behaviors. Channels draw in consumers through their sales efforts and gain from free-riding within their realms. This insight is invaluable for practitioners and policymakers. Offline retailers and online e-commerce platforms should embrace free-riding; it can help boost profits despite the risk of potentially lower demand. As a strategy, downstream dealers should offset this negative effect by boosting sales efforts. Thirdly, the shared behavior of sales costs by involved manufacturers can benefit retailers and e-commerce platforms but may disadvantage manufacturers. Nevertheless, an alliance can lessen the adverse effect of cost-sharing on manufacturers’ profits. Thus, members of a dual-channel supply chain should actively form alliances and apply cost-sharing behavior judiciously. These conclusions provide essential advice for business practitioners and offer significant policy implications, advocating for a strategic stance on alliance formation and cost management in the changing landscape of dual-channel supply chains.
7.3 Limitations and Future Research
Despite the valuable conclusions reached in this paper, it identifies several areas for further exploration. The analysis presently assumes that new and remanufactured products are of uniform quality, neglecting the potential for quality variance. In reality, differences between new and remanufactured products can affect consumer perceptions and, subsequently, their buying decisions. Future research could examine the effect of these quality perception differences on supply chain decision-making, especially in the context of alliances among supply chain members. Additionally, this study is based on a supply chain model with a single retailer, which simplifies the complex dynamics of real-world markets. A more nuanced scenario involving competition among several retailers could shed light on how competitive pressures affect the balance of alliances, offering richer insights into supply chain strategies and dynamics. Furthermore, this paper explores the role of free-riding within various alliance behaviors. Future investigations could focus on how e-commerce platforms might leverage the free selling efforts of retailers, and vice versa, to enhance their understanding of the interactions between different supply chain actors and the impact on their profitability. This includes analyzing strategic measures by e-commerce platforms to benefit from retailers’ marketing and promotional efforts and the consequent effects on the profitability of all involved parties.
In summary, while this study provides important insights, the suggested directions for future research underscore the continuous evolution and complexity of dual-channel supply chains. These avenues present opportunities for further academic study and practical implementation, enriching the field’s understanding of these intricate systems.
Acknowledgement: The authors would like to express their gratitude to the editor and the anonymous reviewers for handling and reviewing our paper.
Funding Statement: This work was supported by the Humanities and Social Science Fund of Ministry of Education of China (No. 20YJA630009) and Shandong Natural Science Foundation of China (No. ZR2022MG002).
Author Contributions: Lina Dong: Conceptualization, Methodology, Formal analysis, Investigation, Writing–original draft. Yeming Dai: Validation, Writing–review & editing.
Availability of Data and Materials: Not applicable.
Conflicts of Interest: The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
1. Ha AY, Tong S, Wang Y. Channel structures of online retail platforms. Manuf Serv Oper Manage. 2022;24(3):1547–61. doi:10.1287/msom.2021.1011 [Google Scholar] [CrossRef]
2. Esenduran G, Kemahlıoğlu-Ziya E, Swaminathan JM. Impact of take-back regulation on the remanufacturing industry. Prod Oper Manage. 2017;26(5):924–44. doi:10.1111/poms.12673. [Google Scholar] [CrossRef]
3. Abbey JD, Geismar HN, Souza GC. Improving remanufacturing core recovery and profitability through seeding. Prod Oper Manage. 2019;28(3):610–27. doi:10.1111/poms.12937. [Google Scholar] [CrossRef]
4. Timoumi A, Singh N, Kumar S. Is your retailer a friend or foe: when should the manufacturer allow its retailer to refurbish? Prod Oper Manage. 2021;30(9):2814–39. doi:10.1111/poms.13548. [Google Scholar] [CrossRef]
5. Shen B, Dong C, Minner S. Combating copycats in the supply chain with permissioned blockchain technology. Prod Oper Manage. 2022;31(1):138–54. doi:10.1111/poms.13456. [Google Scholar] [CrossRef]
6. Ma M, Meng W, Huang B, Li Y. Optimal wholesale price and technological innovation under dual credit policy on carbon emission reduction in a supply chain. Front Environ Sci. 2023;11:1129547. doi:10.3389/fenvs.2023.1129547. [Google Scholar] [CrossRef]
7. Lu Q, Liu N. Effects of e-commerce channel entry in a two-echelon supply chain: a comparative analysis of single-and dual-channel distribution systems. Int J Prod Econ. 2015;165:100–11. doi:10.1016/j.ijpe.2015.03.001. [Google Scholar] [CrossRef]
8. Tian C, Xiao T, Shang J. Channel differentiation strategy in a dual-channel supply chain considering free riding behavior. Eur J Oper Res. 2022;301(2):473–85. doi:10.1016/j.ejor.2021.10.034. [Google Scholar] [CrossRef]
9. Yan L, Hong P, Wu Z. Dynamic pricing and emission reduction efforts in a dual-channel green supply chain under bidirectional free riding. J Clean Prod. 2024;438:140713. doi:10.1016/j.jclepro.2024.140713. [Google Scholar] [CrossRef]
10. Pathak U, Kant R, Shankar R. Price and profit decisions in manufacturer-led dual-channel supply chain configurations. Int J Ind Eng Comput. 2020;11(3):377–400. [Google Scholar]
11. Sun L, Cao X, Alharthi M, Zhang J, Taghizadeh-Hesary F, Mohsin M. Carbon emission transfer strategies in supply chain with lag time of emission reduction technologies and low-carbon preference of consumers. J Clean Prod. 2020;264:121664. doi:10.1016/j.jclepro.2020.121664. [Google Scholar] [CrossRef]
12. Liu C, Dan B, Zhang X, Zhang H. Composite contracts for dual-channel supply chain coordination with the existence of service free riding. J Theor Appl Electron Commer Res. 2022;17(2):789–808. doi:10.3390/jtaer17020041. [Google Scholar] [CrossRef]
13. Suvadarshini P, Biswas I, Srivastava SK. Impact of reverse channel competition, individual rationality, and information asymmetry on multi-channel closed-loop supply chain design. Int J Prod Econ. 2023;259:108818. doi:10.1016/j.ijpe.2023.108818. [Google Scholar] [CrossRef]
14. Wang YY, Chen YL, Cheng W, Wang JC, Tao F. Equilibrium analysis of transaction modes and recycling channels in a closed-loop supply chain with an online platform. Comput Ind Eng. 2023;177:109090. doi:10.1016/j.cie.2023.109090. [Google Scholar] [CrossRef]
15. Matsui K. Should competing suppliers with dual-channel supply chains adopt agency selling in an e-commerce platform? Eur J Oper Res. 2024;312(2):587–604. doi:10.1016/j.ejor.2023.06.030. [Google Scholar] [CrossRef]
16. Zhong Y, Yang T, Yu H, Zhong S, Xie W. Impacts of blockchain technology with government subsidies on a dual-channel supply chain for tracing product information. Transp Res Part E: Logist Transp Rev. 2023;171:103032. doi:10.1016/j.tre.2023.103032. [Google Scholar] [CrossRef]
17. Xu J, Bai Q, Li Z, Zhao L. Maximizing the profit of omnichannel closed-loop supply chains with mean-variance criteria. Comput Electr Eng. 2024;113:109030. doi:10.1016/j.compeleceng.2023.109030. [Google Scholar] [CrossRef]
18. Yu Y, Yang H, Zhen Z. Collection cooperation breakdown and repair in a closed-loop supply chain during supply disruption and price shock. Comput Ind Eng. 2023;183:109495. doi:10.1016/j.cie.2023.109495. [Google Scholar] [CrossRef]
19. Gong D, Gao H, Ren L, Yan X. Consumers’ free riding: pricing and retailer service decisions in a closed-loop supply chain. Comput Ind Eng. 2023;181:109285. doi:10.1016/j.cie.2023.109285. [Google Scholar] [CrossRef]
20. Sana SS. The effects of green house gas costs on optimal pricing and production lot size in an imperfect production system. RAIRO-Oper Res. 2023;57(4):2209–30. doi:10.1051/ro/2023115. [Google Scholar] [CrossRef]
21. Sana SS. Sale through dual channel retailing system—A mathematical approach. Sustain Anal Model. 2022;2:100008. [Google Scholar]
22. Farouk HA, Sadok T, Nidhal R. Pricing and remanufacturing decisions in a dual channel reverse supply chain: study of three configurations with after sales services. IFAC-PapersOnLine. 2022;55(10):1758–63. doi:10.1016/j.ifacol.2022.09.652. [Google Scholar] [CrossRef]
23. Zheng XX, Li DF, Liu Z, Jia F, Lev B. Willingness-to-cede behavior in sustainable supply chain coordination. Int J Prod Econ. 2021;240:108207. doi:10.1016/j.ijpe.2021.108207. [Google Scholar] [CrossRef]
24. Liu Z, Zheng XX, Li DF, Liao CN, Sheu JB. A novel cooperative game-based method to coordinate a sustainable supply chain under psychological uncertainty in fairness concerns. Transp Res Part E: Logist Transp Rev. 2021;147:102237. doi:10.1016/j.tre.2021.102237. [Google Scholar] [CrossRef]
25. Zheng B, Wen K, Jin L, Hong X. Alliance or cost-sharing? Recycling cooperation mode selection in a closed-loop supply chain. Sustain Prod Consum. 2022;32:942–55. doi:10.1016/j.spc.2022.06.001. [Google Scholar] [CrossRef]
26. Zheng XX, Liu Z, Li KW, Huang J, Chen J. Cooperative game approaches to coordinating a three-echelon closed-loop supply chain with fairness concerns. Int J Prod Econ. 2019;212:92–110. doi:10.1016/j.ijpe.2019.01.011. [Google Scholar] [CrossRef]
27. Ma ZZ, Zhang N, Dai Y, Hu S. Managing channel profits of different cooperative models in closed-loop supply chains. Omega. 2016;59:251–62. doi:10.1016/j.omega.2015.06.013. [Google Scholar] [CrossRef]
28. Wang TY, Chen ZS, He P, Govindan K, Skibniewski MJ. Alliance strategy in an online retailing supply chain: motivation, choice, and equilibrium. Omega. 2023;115:102791. doi:10.1016/j.omega.2022.102791. [Google Scholar] [CrossRef]
29. Telser LG. Why should manufacturers want fair trade? J Law Econ. 1960;3:86–105. doi:10.1086/466564. [Google Scholar] [CrossRef]
30. Xing D, Liu T. Sales effort free riding and coordination with price match and channel rebate. Eur J Oper Res. 2012;219(2):264–71. doi:10.1016/j.ejor.2011.11.029. [Google Scholar] [CrossRef]
31. Guo J, Zhou Y, Li B. The optimal pricing and service strategies of a dual-channel retailer under free riding. J Ind Manage Optim. 2022;18(3):2049. doi:10.3934/jimo.2021056. [Google Scholar] [CrossRef]
32. Pi Z, Fang W, Perera SC, Zhang B. Enhancing the online buyer perception of consumer experience products in a dual-channel supply chain: a new role of free-riding. Int J Prod Econ. 2022;253:108600. doi:10.1016/j.ijpe.2022.108600. [Google Scholar] [CrossRef]
33. Sun S, Liu T. Pricing and sales-effort coordination facing free riding behaviors between a brick-and-mortar retailer and a platform store owned by the manufacturer. Transp Res Part E: Logist Transp Rev. 2023;179:103285. doi:10.1016/j.tre.2023.103285. [Google Scholar] [CrossRef]
34. Xu S, Tang H, Lin Z, Lu J. Pricing and sales-effort analysis of dual-channel supply chain with channel preference, cross-channel return and free riding behavior based on revenue-sharing contract. Int J Prod Econ. 2022;249:108506. doi:10.1016/j.ijpe.2022.108506. [Google Scholar] [CrossRef]
35. Zhou YW, Guo J, Zhou W. Pricing/service strategies for a dual-channel supply chain with free riding and service-cost sharing. Int J Prod Econ. 2018;196:198–210. doi:10.1016/j.ijpe.2017.11.014. [Google Scholar] [CrossRef]
36. Liang Y, Sun X. Product green degree, service free-riding, strategic price difference in a dual-channel supply chain based on dynamic game. Optimization. 2022;71(3):633–74. doi:10.1080/02331934.2020.1812064. [Google Scholar] [CrossRef]
37. Yan N, Zhang Y, Xu X, Gao Y. Online finance with dual channels and bidirectional free-riding effect. Int J Prod Econ. 2021;231:107834. doi:10.1016/j.ijpe.2020.107834. [Google Scholar] [CrossRef]
38. Ke H, Jiang Y. Equilibrium analysis of marketing strategies in supply chain with marketing efforts induced demand considering free riding. Soft Comput. 2021;25(3):2103–14. doi:10.1007/s00500-020-05281-0. [Google Scholar] [CrossRef]
39. Liu G, Cao H, Zhu G. Competitive pricing and innovation investment strategies of green products considering firms’ farsightedness and myopia. Int Trans Oper Res. 2021;28(2):839–71. doi:10.1111/itor.v28.2. [Google Scholar] [CrossRef]
40. Li G, Wu H, Sethi SP, Zhang X. Contracting green product supply chains considering marketing efforts in the circular economy era. Int J Prod Econ. 2021;234:108041. doi:10.1016/j.ijpe.2021.108041. [Google Scholar] [CrossRef]
41. Xu C, Jing Y, Shen B, Zhou Y, Zhao QQ. Cost-sharing contract design between manufacturer and dealership considering the customer low-carbon preferences. Expert Syst Appl. 2023;213:118877. doi:10.1016/j.eswa.2022.118877. [Google Scholar] [CrossRef]
42. Ma X, Wang S, Islam SMN, Liu X. Coordinating a three-echelon fresh agricultural products supply chain considering freshness-keeping effort with asymmetric information. Appl Math Model. 2019;67:337–56. doi:10.1016/j.apm.2018.10.028. [Google Scholar] [CrossRef]
43. Adhikari A, Bisi A. Collaboration, bargaining, and fairness concern for a green apparel supply chain: an emerging economy perspective. Transp Res Part E: Logist Transp Rev. 2020;135:101863. doi:10.1016/j.tre.2020.101863. [Google Scholar] [CrossRef]
44. Shekarian E, Marandi A, Majava J. Dual-channel remanufacturing closed-loop supply chains under carbon footprint and collection competition. Sustain Prod Consump. 2021;28:1050–75. doi:10.1016/j.spc.2021.06.028. [Google Scholar] [CrossRef]
Theorem 1 proof
In model D, manufacturer is the leader, retailer and e-commerce platform are the followers, the inverse induction method is used to solve the problem as follows: The offline channel demand function
Find the second partial derivative
It is known by first-order optimality condition
The online channel demand function
Find the second partial derivative
It is obtained by the first-order optimality condition
Simultaneous
Plug
Finding the Hessian matrix of manufacturer’s profit function with respect to
The first-order and second-order principal subexpressions
According to the first-order optimality condition
Combining
And then substitute
Then the optimal demand is
Finally, we get
Property 1 proof
In the framework of model D, we derive the partial derivatives to elucidate how the retail pricing of new products varies in response to the free ride coefficients of both offline and online channels, noted as
Property 2 proof
Since
Theorem 2 proof
Model MR is a Stackelberg game model with MR alliance as the dominant leader and retailer as the follower. Backward induction method is adopted to solve the following problems: First of all, the demand function of online channel is substituted into the e-commerce platform profit function
And take the second partial derivative
According the first-order optimality condition
Second, substitute
The first-order principal subexpression
The first-order optimality condition
Combining
Substituting
In this case, we have
Property 3 proof
This integration yields the partial derivatives of the retail price of new products in relation to the free ride coefficients of offline and online channels as
Property 4 proof
For MR alliance profit with respect to the cost-sharing ratio of the manufacturer to the e-commerce platform, the first-order partial derivation is obtained as
Theorem 3 proof
The model ME is a Stackelberg game model with ME alliance as the dominant player and e-commerce platform as the follower. The solution is as follows by backward induction method: First, the demand function of offline channels and online channels is substituted into the retailer profit function
Take the second partial derivative with respect to
It is obtained by first-order optimality condition
Secondly, the demand function of offline and online channels is substituted into the profit function of ME alliance to obtain
The second partial derivative of the ME alliance profit function with respect to
take the second derivative of ME alliance profit function with respect to
is obtained from the first-order optimality condition
Substituting
Finally, the optimal demand
In this case, the profit is
Property 5 proof
The free ride coefficient of the retail price of new products with respect to offline and online channels can be obtained by obtaining the partial derivative respectively
Property 6 proof
Since
Theorem 4 proof
Employing the backward induction method, we aim to delineate the optimal strategy, beginning with the manufacturer’s decision to maximize profit. This involves incorporating the offline channel’s demand function, denoted as
Following this integration, the second derivatives of the ER alliance’s profit function with respect to are evaluated, resulting in
By solving
By combining above two formulas, we get
Substituting
Solving
Combining
Substitute
Then substitute the price equilibrium solution into the demand function to get
Solving the optimal profit function gives
Property 7 proof
For new products, these derivatives are recorded as
Property 8 proof
The first partial derivative of the profit of each member of the supply chain to the cost-sharing coefficient of manufacturer to retailer and e-commerce platform can be obtained:
Proposition 1 proof
(1) Given model D online channel demand equilibrium solution is
On account of
while
while
Comparing the equilibrium price of new products between model ER and model D, we know that when condition
then it is satisfied
(2) The online channel demand of model D is known as
Comparing model D and model MR, the equilibrium solution of remanufactured products can be found
It is also known that online channel demand equilibrium solution in model MR is
Comparing the equilibrium price of the remanufactured product of the model ER and the model D, we can see that when condition
Proposition 2 proof
(1) The optimal solution of the manufacturer’s wholesale price to the retailer in model D is
we know
(2) In model D, the optimal solution of the wholesale price of the e-commerce platform by the manufacturer is
we know
Proposition 3 proof
The optimal demand for known retailers and e-commerce platforms is
(1) Because
(2) Because
Also because
Proposition 4 proof
(1) In the known model D, the optimal demand of offline channels
because
(2) The optimal demand for channels on the middle line of model D is known as
because
Proposition 5 proof
(1)
When
(2)
When
Proposition 6 proof
(1)
When
When
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools