 Open Access
Open Access
REVIEW
Applications of Soft Computing Methods in Backbreak Assessment in Surface Mines: A Comprehensive Review
1 Department of Mining Engineering, Faculty of Engineering, Malayer University, Malayer, 9586365719, Iran
2 Institute of Innovation, Science and Sustainability, Federation University Australia, Ballarat, VIC 3350, Australia
3Marane Olia Ornamental Stone Mine, Sanandaj, 6614344588, Iran
4 Computational Mechanics Laboratory, School of Pedagogical and Technological Education, Athens, 15122, Greece
5 School of Civil and Environmental Engineering, University of Technology Sydney, Sydney, NSW 2007, Australia
* Corresponding Authors: Mojtaba Yari. Email: ; Danial Jahed Armaghani. Email:
Computer Modeling in Engineering & Sciences 2024, 140(3), 2207-2238. https://doi.org/10.32604/cmes.2024.048071
Received 27 November 2023; Accepted 17 May 2024; Issue published 08 July 2024
Abstract
Geo-engineering problems are known for their complexity and high uncertainty levels, requiring precise definitions, past experiences, logical reasoning, mathematical analysis, and practical insight to address them effectively. Soft Computing (SC) methods have gained popularity in engineering disciplines such as mining and civil engineering due to computer hardware and machine learning advancements. Unlike traditional hard computing approaches, SC models use soft values and fuzzy sets to navigate uncertain environments. This study focuses on the application of SC methods to predict backbreak, a common issue in blasting operations within mining and civil projects. Backbreak, which refers to the unintended fracturing of rock beyond the desired blast perimeter, can significantly impact project timelines and costs. This study aims to explore how SC methods can be effectively employed to anticipate and mitigate the undesirable consequences of blasting operations, specifically focusing on backbreak prediction. The research explores the complexities of backbreak prediction and highlights the potential benefits of utilizing SC methods to address this challenging issue in geo-engineering projects.Keywords
Nomenclature
| ANN | Artificial neural network |
| ABC | Artificial bee colony |
| ACO | Ant colony optimization |
| MADM | Multi-attribute decision-making |
| HHO | Harris hawks optimizer |
| ANFIS | Adaptive network-based fuzzy inference system |
| GA | Genetic algorithm |
| PSO | Particle swarm optimization |
| RF | Random forest |
| SVM | Support vector machine |
Engineering problems are experience-based issues in which a lack of data, information, and inaccurate understanding leads to various uncertainties. Data limitation and fundamental uncertainty of natural rock in geomechanics and mining engineering cause inadequate information for evaluating all aspects of problems. In 1978, Holling presented a comprehensive classification of adaptive assessments and how to deal with them [1]. Fig. 1 shows the main parts of this classification model.
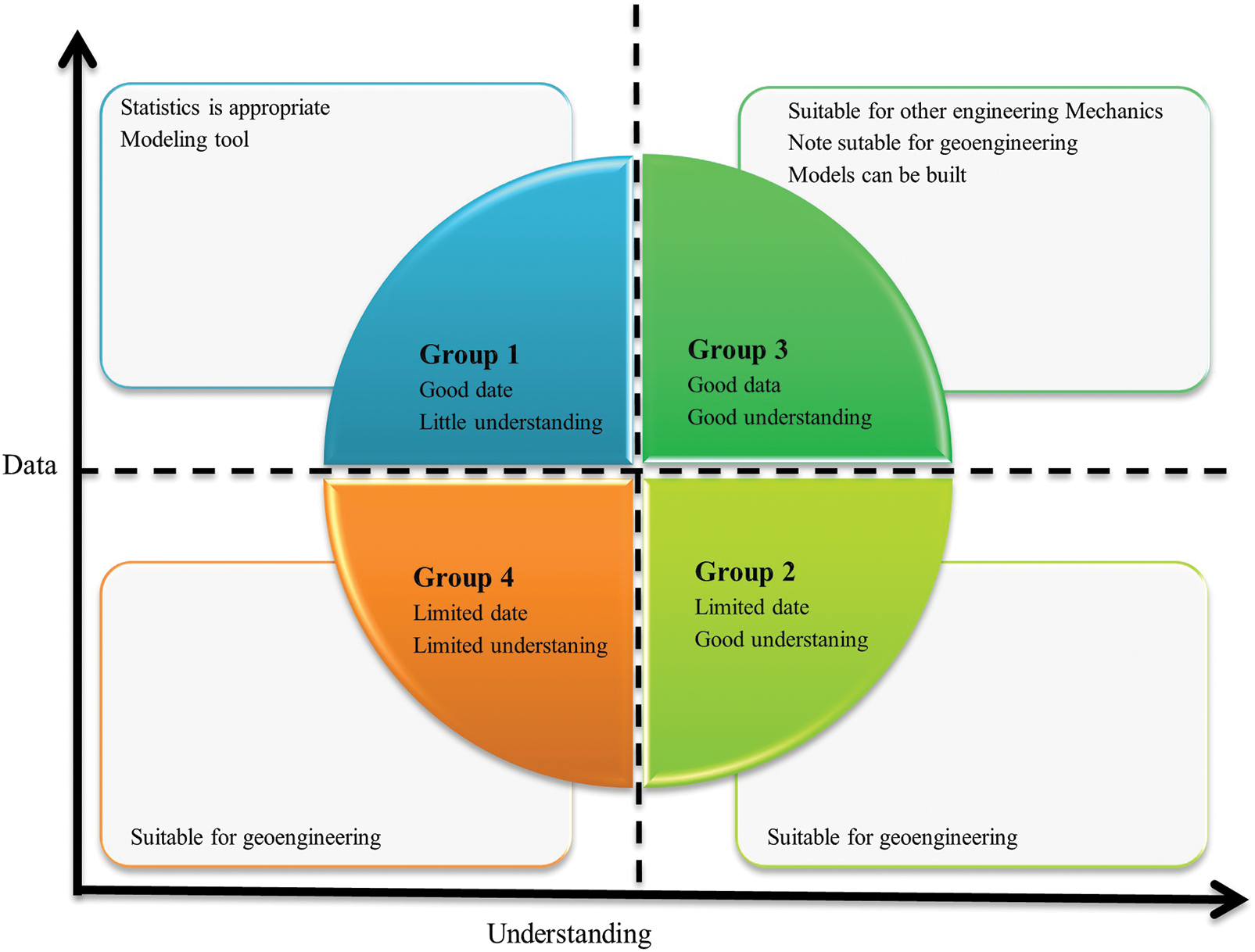
Figure 1: Modified Holling’s classification for engineering assessment and management problems
Based on this classification, assessment approaches are divided into four main types. Group 1 includes problems with sufficient data and inadequate understanding. Group 2 entails problems with insufficient data and acceptable understanding. Problems with satisfactory data and understanding are involved in Group 3. In Group 4, there is neither sufficient data nor adequate understanding. Table 1 indicates a comparative summary of the model.
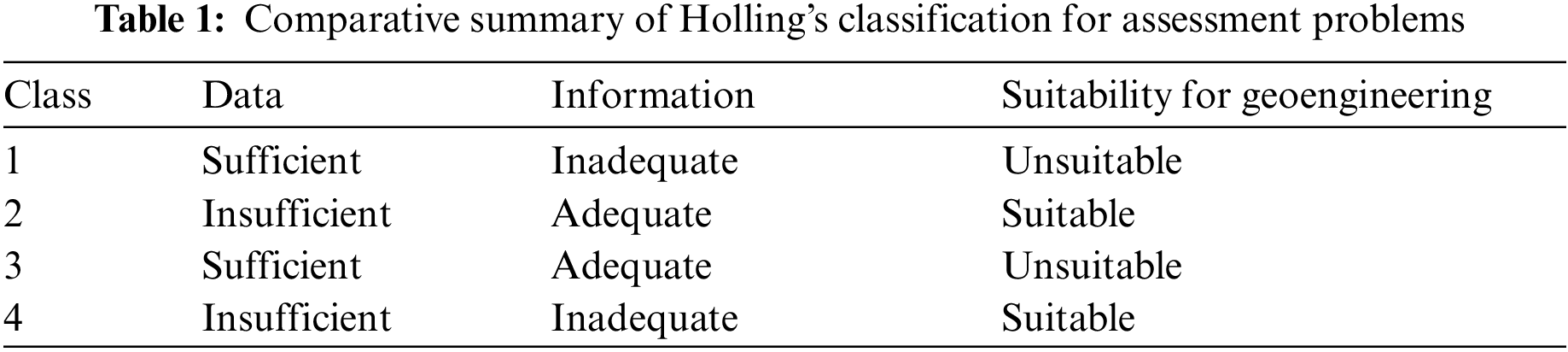
Table 1 indicates that the main part of geoengineering problems is involved in Groups 2 and 4 based on the Holling classification [2].
Based on typical restrictions of convenient analytical methods in geoengineering problems [2,3] and inappropriate results of numerical modeling [3,4], Soft Computing (SC) methods are more beneficial for this field of engineering in classes 2 and 4. Artificial Intelligence (AI) driven performance models provide data-driven insights that are impossible with traditional simulation techniques [5,6]. The results obtained from different studies have confirmed a substantial need to develop and propose intelligent systems with more input parameters to offer more accurate outputs [7].
The more acceptable definition of SC is a series of novel methods developed to solve problems in an uncertain environment with inexact factors [8]. These methods implement intelligent procedures to solve ambiguous problems or make a decision about them [9].
One of the fundamental elements of human civilization is the mining operation, which is classified as the most primitive activity of humankind [10–12]. As one of the main parts of the world’s economy, the mining industry significantly impacts other industries directly and indirectly. Simultaneously, the rapid development of such activities considerably affects the environment, namely the rock and soil medium [13,14]. Mining activities are intensely affected by state-of-the-art technologies such as high-tech computing methods, enhanced facilities, and equipment [11,12]. A severe challenge in this engineering field is the lack of precise data and accurate information for making certain decisions. The primary sources of ambiguities for decision-making in mining engineering include [15]:
1. Product markets uncertainties;
2. Field-related uncertainties include geology, macro-structures, geotechnical features, etc.;
3. Insufficient precision in qualitative terms and sentences;
4. High impacts of individual decisions;
5. Ambiguous interactions between affecting parameters;
6. Unexpected behavior of rock (as the primary material in mining operations) in different situations.
Blasting operation is one of the critical activities in hard rock mining, which influences all downstream activities such as loading, hauling, and mineral processing [16–18]. In both primary and secondary rock breakage operations, the main goal of blasting is to provide the desirable size of fragments (as input of crushers) and minimize unwanted impacts of the blasting operation. Fig. 2 describes the influence of fragmentation degree on undesirable consequences of blasting operation [19,20].
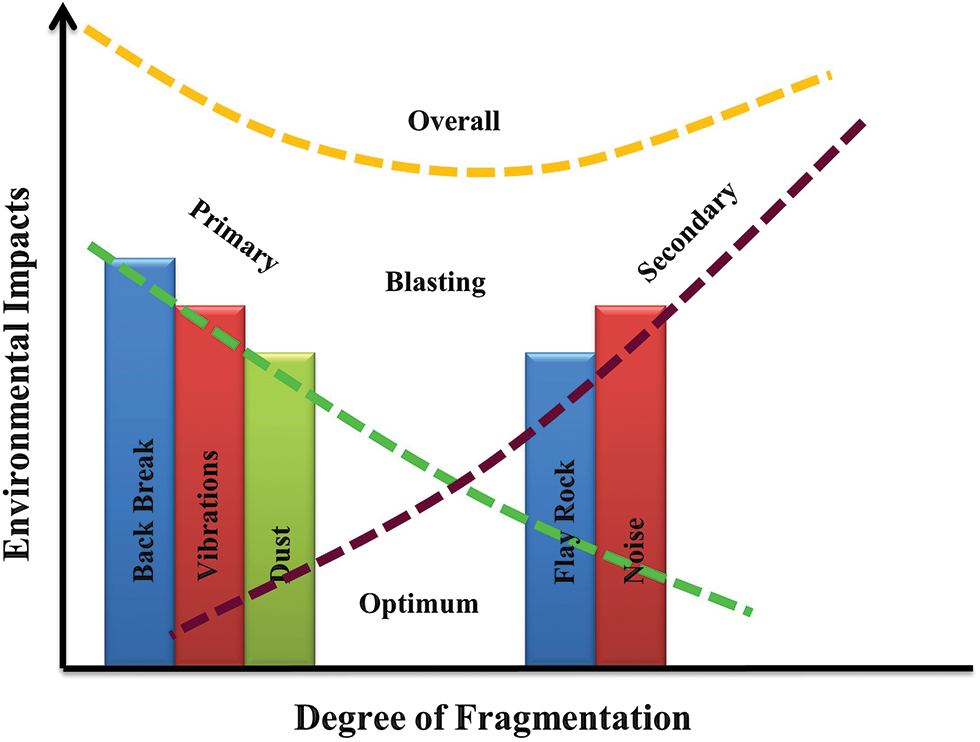
Figure 2: Impact of fragmentation degree on undesirable consequences of primary and secondary blasting operation
Flyrock, backbreak, ground vibration, and air overpressure are significant consequences of blasting operations that dramatically impact mining activities technically and economically [21,22]. In contrast, these effects considerably alter the circumambient environment [22,23]. Figs. 3 and 4 show the desirable and undesirable consequences of a blasting operation. A blasting operation must lead to appropriate fragmentation and minimum undesirable impacts [24].

Figure 3: Wanted and unwanted consequences of blasting operation
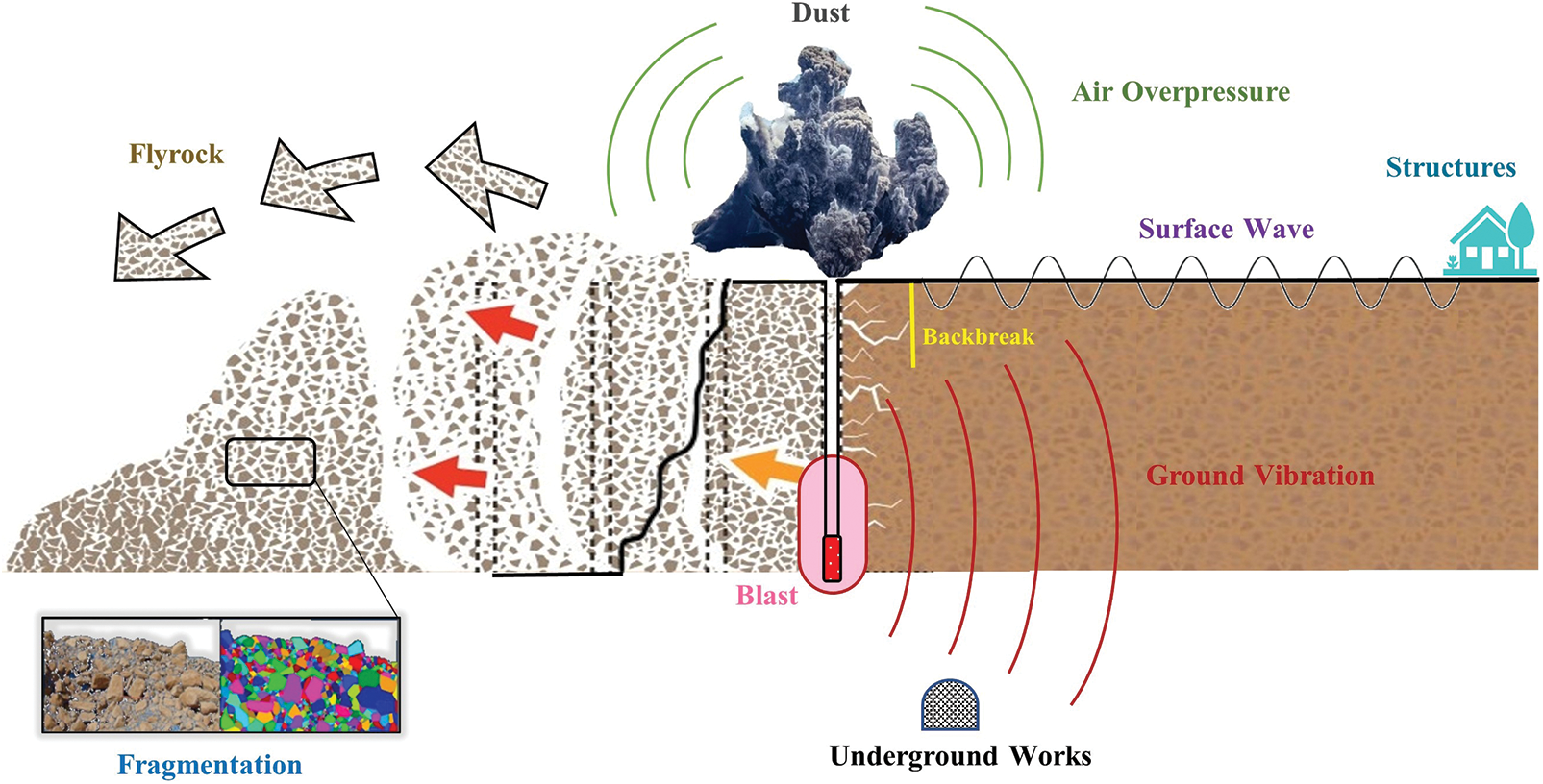
Figure 4: Schematic effects of blasting operation
One of the most significant unwanted results of blasting operation is backbreak. Based on the diversity and complexity of affecting factors and their inherent uncertainties, the exact estimation and evaluation of blasting outcomes are one of the most complicated problems in mining and civil engineering [25,26].
This study is a comprehensive attempt to investigate the applications of soft computing methods in predicting the backbreak phenomenon. The backbreak is explored in Section 2, considering definition, affecting factors, significance, methodology, and others. In Section 3, previously implemented soft computing methods for this purpose are discussed, and finally, Section 4 covers all the research performed regarding predicting backbreak using soft computing models in detail.
2 Backbreak in Opencast Mining
Backbreak stands as a crucial undesired outcome in open-pit mining endeavors. Backbreak is more appropriately described as the distance of fracturing behind the final line of blast holes [27]. Its occurrence is vital for assessing inefficient explosive usage in open-pit mining. Backbreak refers to events close to the source, encompassing areas of crushing, compressive failure, and tensile failure right around the blast holes [28]. It tends to emerge near existing fissures and fractures caused by the blasts.
All impacting factors on the back break occurrence can be divided into three main types [29]:
1. Blasting pattern design;
2. The main properties of implemented explosives;
3. The natural structure of rock mass.
Many researchers have categorized the first and second groups of affecting factors as controllable parameters of blasting operation [30,31]. The third group was defined as uncontrollable parameters [32,33]. Uncontrollable factors are natural and cannot be changed while blasting patterns change the controllable factors [34,35]. The influencing parameters of backbreak are mentioned in other research without classification, including stiffness ratio, burden, stemming, geological structures, and others [36,37].
Backbreak, as an undesirable phenomenon, impacts mining operations in all aspects of the economy, technical and safety [38,39]. From an economic point of view, higher loading and hauling costs, decreased drilling efficiency, and increased blasting operation costs are the most critical outcomes of backbreak in the literature [34,40–42]. The instability of the mine’s new walls after blasting, increasing water inflows due to cracked rock, and uneven burden for subsequent blasts indicate this phenomenon’s negative technical issues [43,44]. For the safety aspect of the blasting operation, the rock dropping, falling down the trucks or other moving vehicles, and intensive dilution have been mentioned as the negative results of the backbreak [45,46]. Additionally, Bauer emphasized that uncontrolled backbreak can reduce the overall pit slope angle, increasing the stripping ratio [47].
Considering limited independent variables, various simplified empirical methods are presented for assessing blasting consequences such as flyrock, backbreak, air overpressure, and others. The generalized assumptions and limited involving factors lead to inefficient results of empirical methods. Other statistical and probabilistic-based models implemented for the assessment of backbreak have no acceptable accuracy considering statistical indices. Considering the disadvantages of previous methods, SC models present more efficient performance for backbreak prediction and are more applicable to this kind of problem.
SC comprises methods that provide acceptable estimated solutions for complicated problems by implementing approximate computations. These methods, as computational intelligence, are usable for solving time-consuming or unsolvable problems using conventional methods. As one of the main branches of mathematics and computer science, SC models started in the 1990s. Soft computing is frequently implemented in real-world problems such as engineering, commercial, and industrial environments. Due to inherent uncertainties, SC has played a significant role in geoengineering fields in recent years. The main branches of soft computing employed to investigate the backbreak phenomenon are briefly explained. Fig. 5 indicates the main categories of soft computing models.
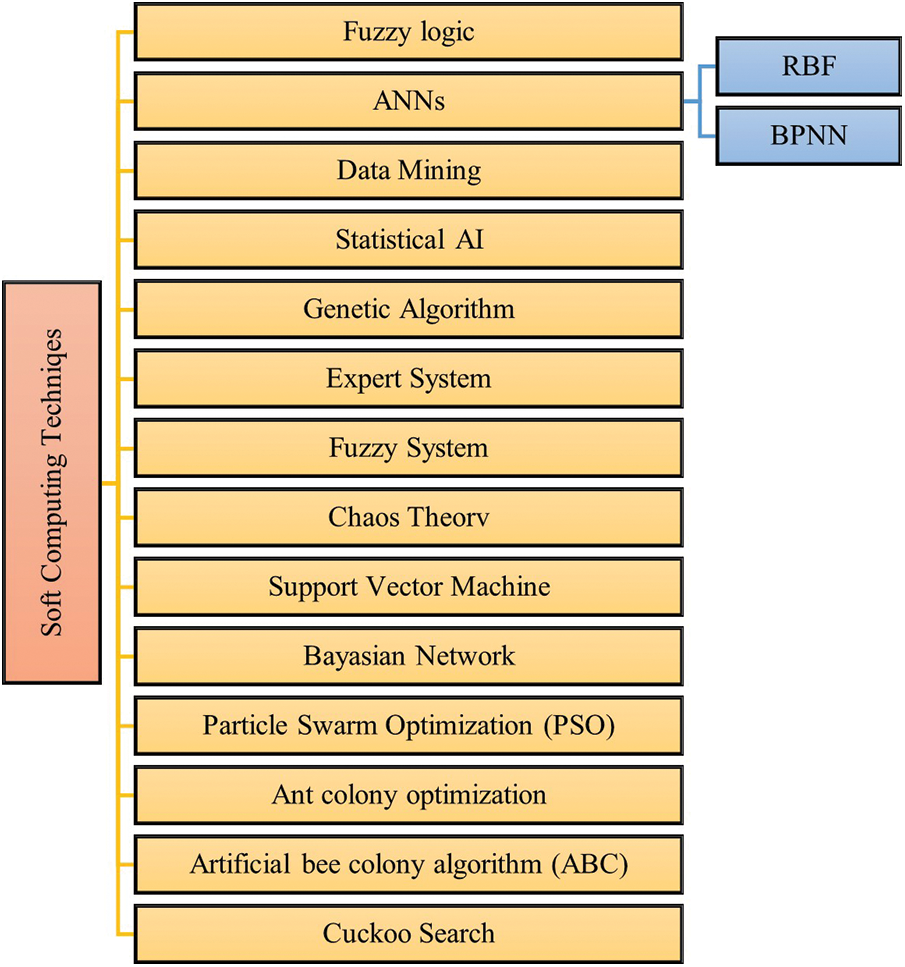
Figure 5: Main categories of soft computing
ANN plays a dominant role in solving complicated problems in the engineering field. The fundamentals of this method are based on the procedure by which the human brain makes the proper decisions. The core trend of ANN is utilizing an old, verified dataset to estimate future behaviors of the system. As the previous dataset trains the system, new inputs are applicable for predicting output values [48–51]. The structures and functions of data possessed in ANN are approximately similar to those of the human brain. The human brain uses complicated connected networks that analyze diverse tasks to provide daily responsibilities. By processing interactions of units called Neurons, the brain forms recognizing patterns, remembers processes, and analyses different information [52]. The essential elements of ANN include neurons, transfer functions, network architecture, and learning law [53]. To analyze a new dataset, ANN requires training existing data by implementing pattern recognition methods [54]. The structure of ANN is presented in Fig. 6.
Figure 6: Structure of ANN
There are various models for training datasets in ANN, such as Back Propagation Neural Network (BPNN) and Radial Bases Function (RBF). BPNN is generally utilized to achieve an acceptable prediction in diverse geoengineering fields. The main architecture of this model consists of one or more nonlinear hidden layers and a linear output layer [55]. Table 2 indicates that four different transfer functions are implemented in BPNN [56]. Mentioned networks indicate nonlinear and/or linear correlation of input(s) and output(s). The BPNN training phase can utilize diverse learning models such as Newton and gradient descent [57,58]. Also, there is a simple image representation strategy of numerical simulations in which the input and output data are all illustrated by images. The obtained results are usable by human resources and computers [59].
RBF is one of the main branches of ANN and is categorized as a multilayer feed-forward back-propagation model. In this method, each neuron has a radial function in a hidden layer, such as a Gaussian kernel as a triggering function [60]. The assigned weight vector by neurons defines the position of the kernel function in the hidden layer. During the training process, the widths of the kernel and the situation should be learned. The fundamental RBF model utilizes two basic training steps [61,62]: Step 1. Training the widths and kernel function situation to implement an unverified clustering model. Step 2. Training to compute the connection weights of the hidden and output layers using a verified least mean square algorithm.
3.2 Artificial Bee Colony Algorithm
In 2005, Karaboga presented a novel model for solving complicated engineering problems called the ABC algorithm [63]. This method simulates exploring the performance of honeybees. In nature, honeybees in a colony are divided into three main types: scouts, onlookers, and employed bees [64]. In the first step, scout bees start to find appropriate food. During the food exploration phase, onlooker bees constantly regard various bees. In a place called the dancing area, the evaluation of food source quality is done by scout bees. As founding, a food source with acceptable quality waggle dance performs by employed bees. The bees’ colony chooses the most appropriate food source considering all the mentioned systems. The optimized solution can be achieved by exploring possible solutions using the ABC model. However, the ability, flexibility, and accuracy of the ANN models modified with the ABC algorithm are much higher than statistical models [65]. Fig. 7 illustrates the structure of the ABC algorithm.
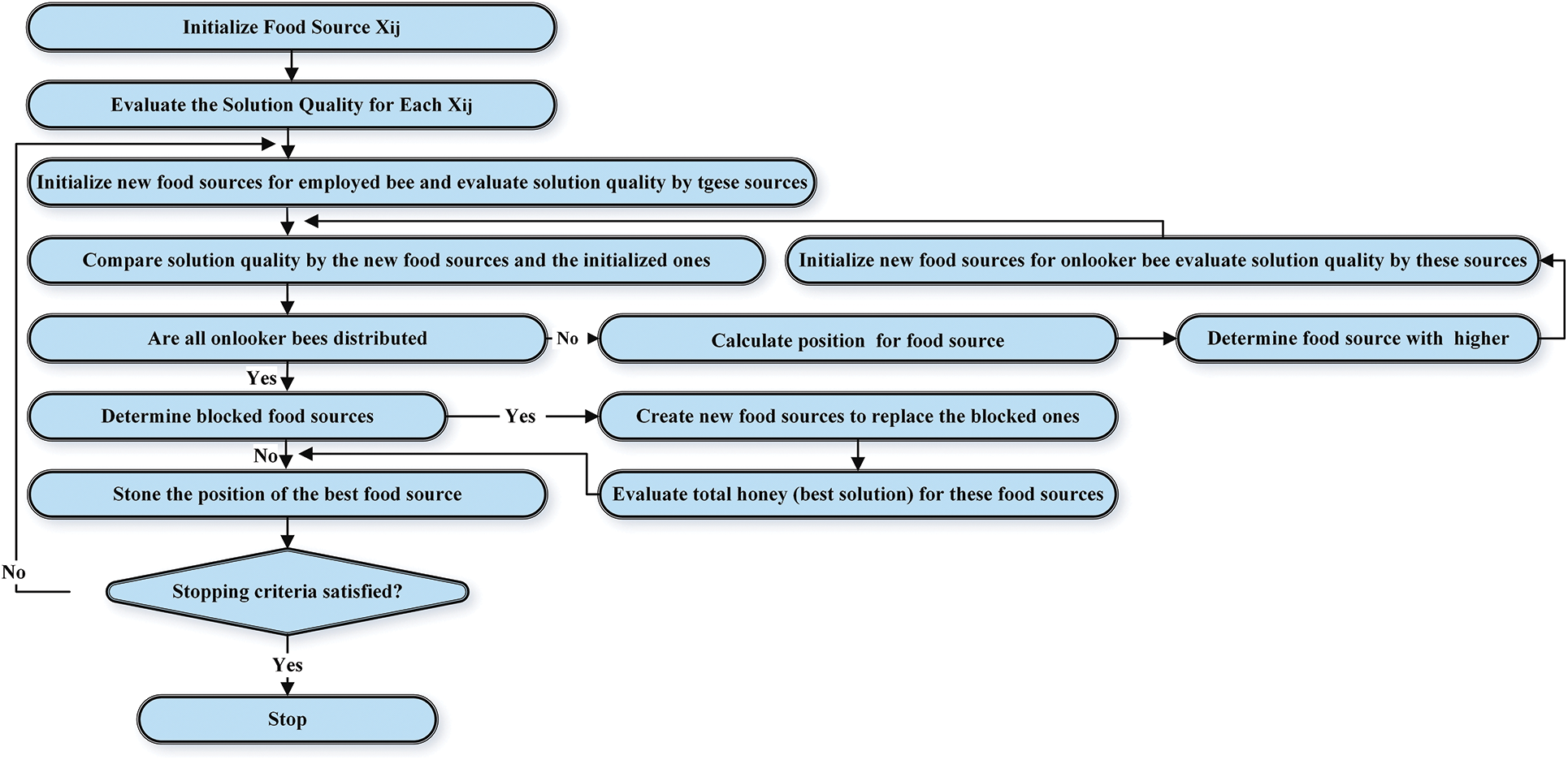
Figure 7: Structure of ABC algorithm
The ACO model was presented by Marco Dorigo in 1992 [66]. This method is one of the population-based models of optimization, which is simulated based on ants’ natural behaviors to find optimal solutions for complex problems. This method implements a means called artificial ants to explore solutions [67]. The problem should be converted to a weighted graph model to obtain an optimized path to achieve an optimized solution utilizing ACO [68]. The simulated artificial ants move on graph paths to explore the routes continuously. The optimization procedure utilizes a stochastic process influenced by a pheromone model in the operation running period [69]. This method plays a significant role in solving optimization problems [70]. Fig. 8 shows the ACO model.
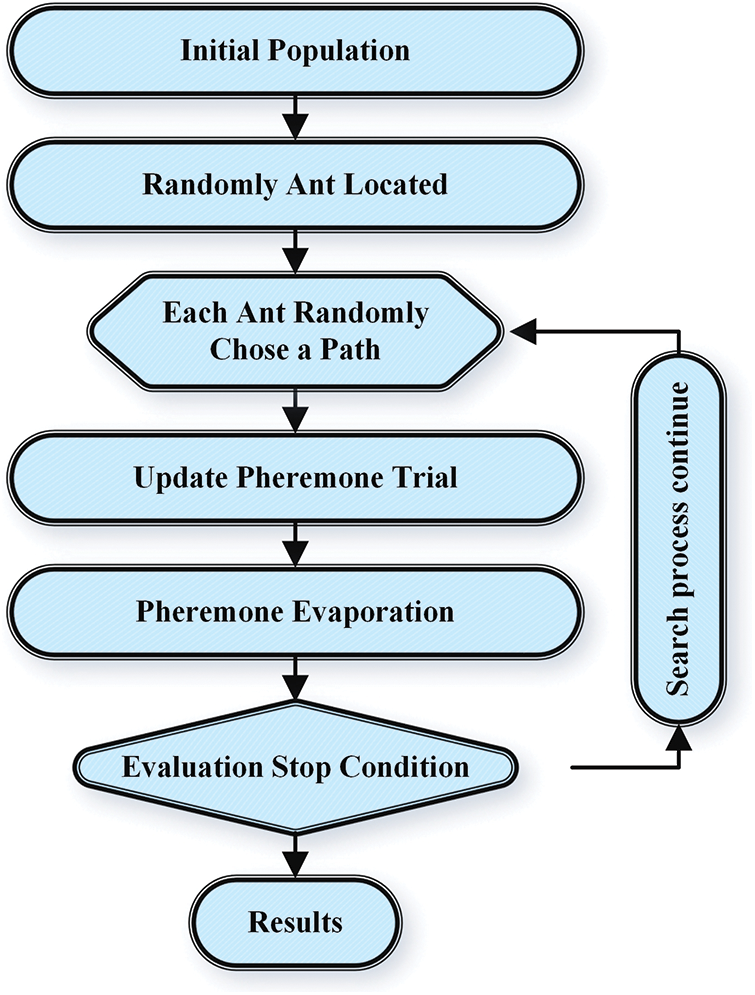
Figure 8: Flowchart of ACO model
3.4 Multi-Attribute Decision-Making Method
MADM models were developed to be implemented in assessing, ranking, and selecting the most proper solution between all existing alternatives [71]. In MADM problems, several alternatives should be ranked based on positive and negative attributes [72]. In the first stage, the weights of attributes are determined mainly using experts’ ideas. In the second stage, decision matrices are defined and after normalizing and weighting operation, based on selected MADM models such as Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), VIekriterijumsko KOmpromisno Rangiranje (VIKOR), Taxonomy, Analytic Hierarchy Process (AHP), and others for the decision-making problem, the following steps are passed to achieve the desired ranking or prioritizing [73]. In recent years, MADM methods have played a significant role in decision-making problems related to geoengineering fields [74].
HHO was developed as an innovative metaheuristic model based on the hunting manner of Harris hawks in wildlife entitled Surprise Pounce [75]. This method is implemented in engineering complex optimization problems [76,77]. Fig. 9 depicts the operation diagram for HHO. Based on this model, several hawks cooperatively pounce to hunt prey from diverse directions to surprise it. Harris Hawks can perform diverse hunting patterns considering the dynamic escaping paradigm of the prey [78]. This model simulates the dynamic paradigms and manners for providing the optimized solution.
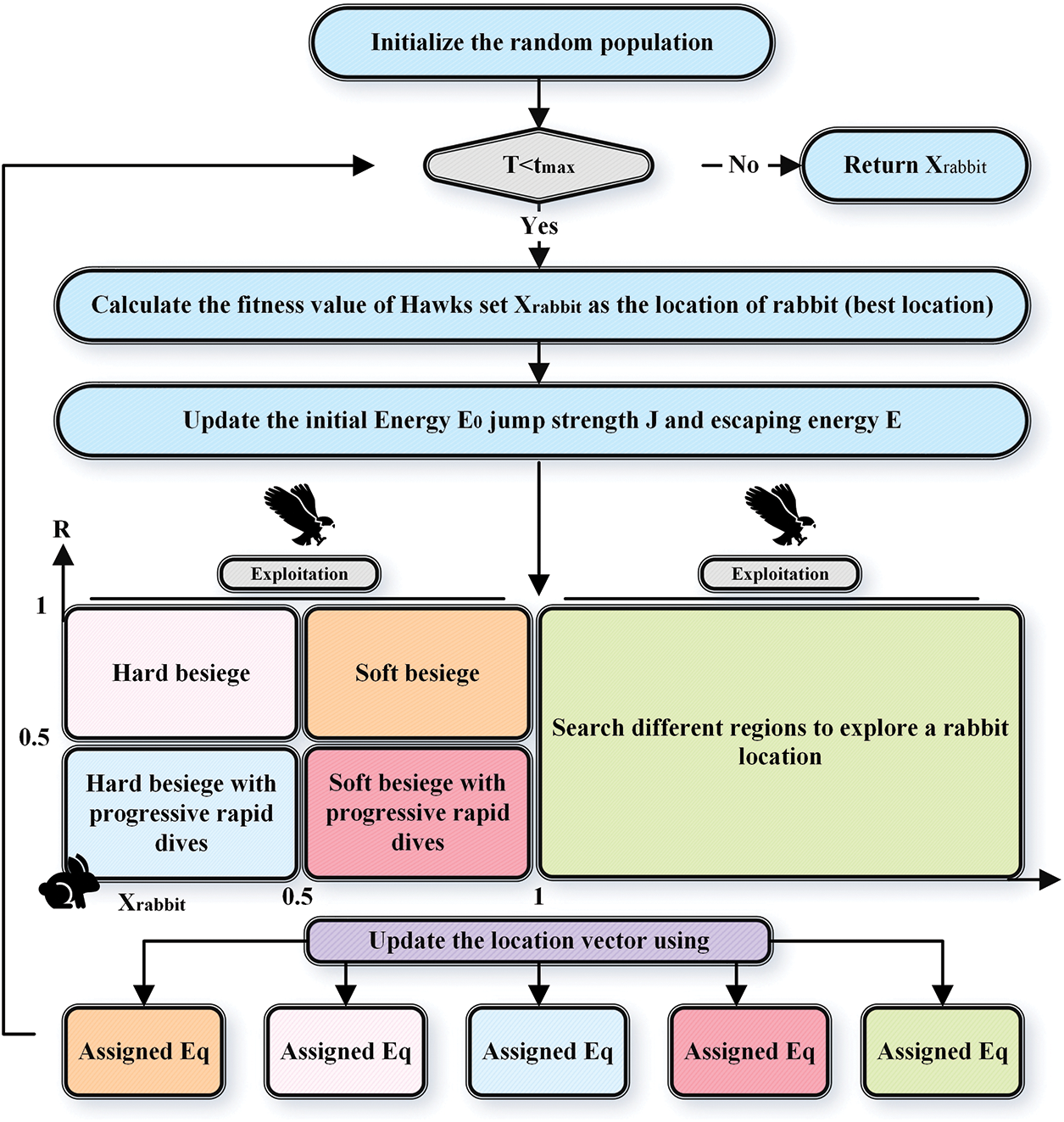
Figure 9: Operation diagram for HHO
3.6 Adaptive Network-Based Fuzzy Inference System
This method was innovated in the 1990s by combining neural networks and fuzzy logic [79]. The primary basis of ANFIS has been constructed on the Takagi–Sugeno fuzzy inference system [80,81]. The core structure of ANFIS is shaped by considering a set of fuzzy IF-THEN rules that can be trained for forecasting nonlinear functions [82], and the performance of this model mainly depends on its parameter values [83]. The architecture of ANFIS consists of two main parts of premise and consequence in five separated layers [84,85]:
Layer 1: fuzzification layer: Involve input values–defining membership function;
Layer 2: rule layer: generating the firing strengths for the rules;
Layer 3: normalization layer: normalizing the computed firing strengths;
Layer 4: defuzzification layer;
Layer 5: final output.
Fig. 10 illustrates the structure of ANFIS.
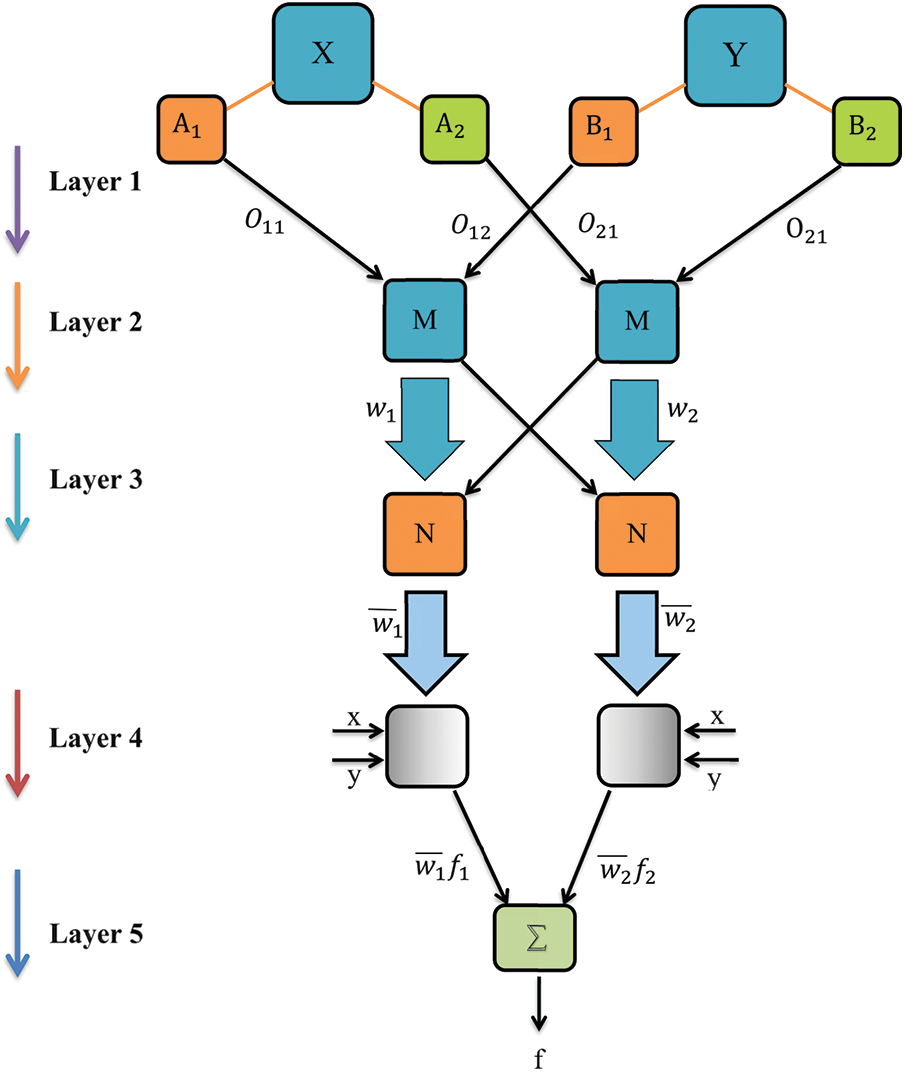
Figure 10: Structure of ANFIS
Fuzzy logic is one of the most applicable branches of soft computing, and it considers systems with inherent inexactness [86]. Zadeh [8], in 1965, presented this method. During the following decades, fuzzy logic is combined with other MADM models. For instance, fuzzy hierarchy evaluation is a synthetic risk evaluation method based on AHP and fuzzy comprehensive evaluation [87,88]. In fuzzy set theories, the values are defined using a membership function based on linguistic values. Since linguistic values are not computable inherently, the next step involves determining them by fuzzy numbers for being computable [89]. The most significant advantage of fuzzy systems is providing an acceptable description for complicated and nonlinear multivariable problems in geoengineering fields [90]. This model is utilized for solving problems by covering three main steps [91]:
Step 1. Fuzzification: Fuzzifier plans crisp data into fuzzy data or fuzzy membership functions such as trapezium, triangle, bell, Gaussian, and sigmoid;
Step 2. IF-THEN rules: Providing fuzzy outputs by a combination of membership functions and switch rules;
Step 3. Defuzzification: Converting fuzzy outputs to crisp ones utilizing defuzzifiers like Center of Gravity (CoG) and Middle of Maxima (MoM).
The Block diagram of fuzzy systems is indicated in Fig. 11.
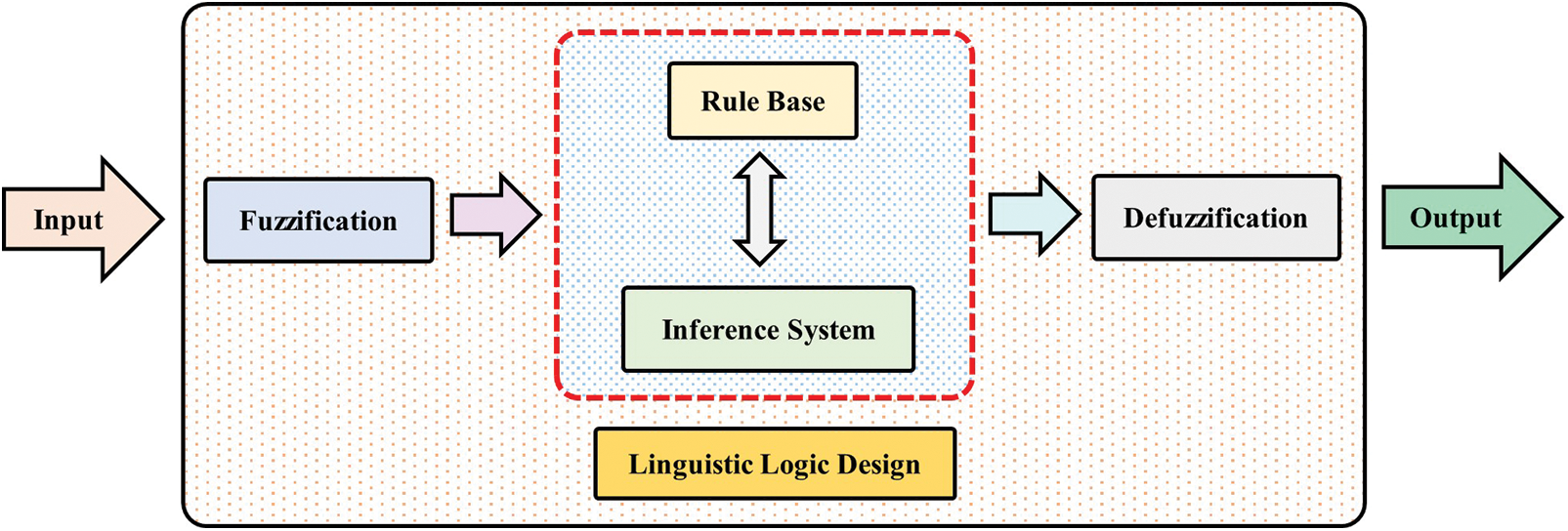
Figure 11: Block diagram of the fuzzy logic system
For the first time, Holland proposed this model [92]. GA is a population-based model whose instruction is based on Darwin’s concept of evolution for solving complex problems using genetic patterns [93]. The fundamental elements of this model are the transition of stronger features to the child by parents during the regeneration process and the elimination of weaker properties. In any irritations, the stronger features are transmitted to the next generation. As mentioned, GA is an adjustable computing model that implements genetic biological rules. In engineering branches, GA is implemented to solve optimization problems comprehensively [94–96]. Selection, crossover, and mutation are the three main steps of GA for achieving a complete optimized solution [93]. The flowchart of the GA method is illustrated in Fig. 12.
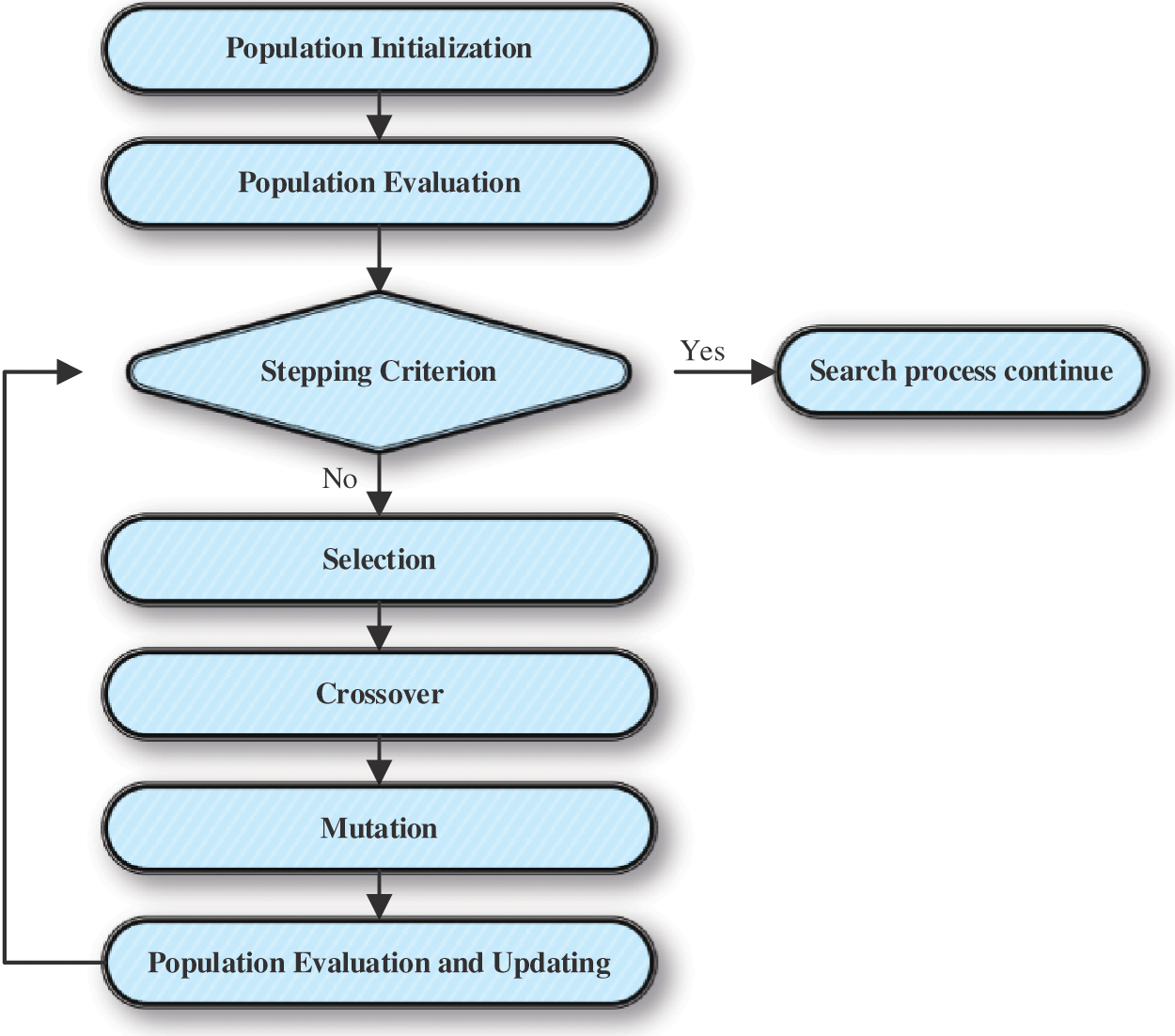
Figure 12: Flowchart of GA method
3.9 Particle Swarm Optimization
PSO is one of the optimization methods based on the repetitive improvement of a candidate solution considering assigned quality values [97]. Based on computational equations of position and velocity of particles in the search space, PSO considers a population of candidate solutions to solve unconstrained optimization problems [98]. This model is presented based on the behavior of bird or fish swarms. The achievements of PSO are confirmed in various engineering fields, and this stems from its simplicity and exploration efficiency [99]. Fig. 13 shows the structure of the PSO algorithm.
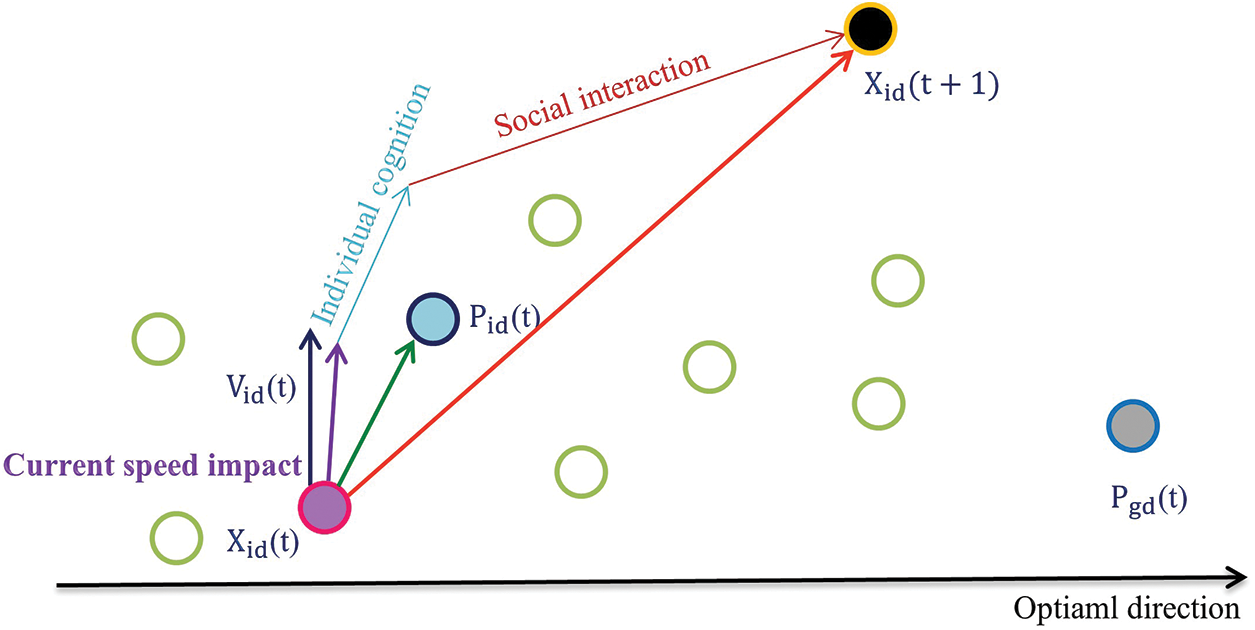
Figure 13: Structure of the PSO algorithm
A decision tree, as one of the applicable classification and regression methods, is based on bagging and selecting random variables [100]. In the RF model, the development attitude of trees is similar to the CART (classification and regression trees) method, which is partitioned recursively. The distribution and size of the experiential values in the training samples regulate the selection of the splitting variables in recursive partitioning and the exact position of the split point, so the result is not stable [101]. RF structure is a combination of diverse regression trees rather than a single tree, which solves the instability problem of CART [102,103]. Fig. 14 presents the architecture of RF.
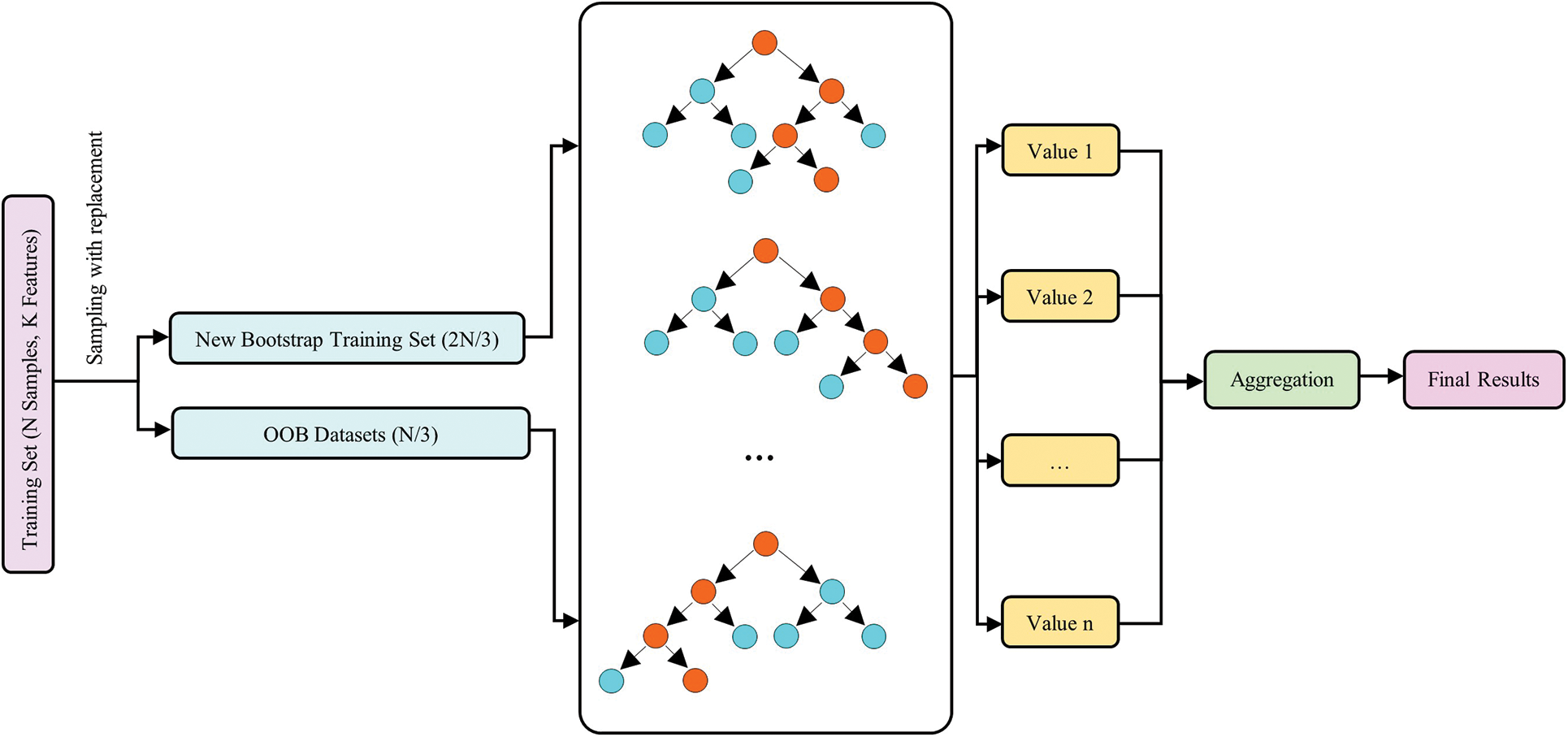
Figure 14: The architecture of the RF algorithm
Boser et al. [104] presented SVM in 1992 as a discriminative classifier, well-defined by a hyperplane (an extrication boundary line). SVM is a branch of kernel models based only on the data over dot-products [105,106]. It was defined by Nobel in 2006 as a method for maximizing a mathematical function regarding an input dataset [107]. The central concept of SVM is the placement of the hyperplane in a situation with the largest minimum distance from the learning dataset. SVM can simulate complicated nonlinear decision boundaries, which can be implemented comprehensively in engineering fields [19].
4 Soft Computing Applications in Backbreak Assessment
As mentioned before, because of inherent uncertainty, geoengineering fields utilize different SC models widely. One of their most beneficial applications in mining engineering returns to the prediction and assessment of blasting environmental issues [81]. Backbreak, as an undesirable phenomenon, has negative technical and economic influences on blasting operations, and various researchers especially consider it.
Monjezi et al. [108] presented in 2008 a new ANN model for assessing the impacts of blasting pattern factors on backbreak phenomena in the Gol-E-Gohar iron mine in Iran. The main structure of the presented model included a four-layer ANN, which is employed to provide a near-optimum blasting pattern with a decreased backbreak value [109]. As a result of this model, the backbreak was reduced from 20 to 4 m.
Monjezi et al. [110] utilized the fuzzy set theory in 2010 for forecasting backbreak. They showed a coefficient of correlation (R2) and the root means square error (RMSE) of 95.43% and 0.44%, respectively. Also, based on applied sensitivity analysis, stemming length, hole depth, burden, and hole spacing were determined as the most impactful factors in backbreak. The case study of this research was the Gol-E-Gohar iron mine, which researchers acclaimed backbreak had significant reduction using this model that resulted in a more efficient blasting operation.
A comparison study was investigated by Esmaeili et al. [111] in 2014, and it utilized multiple regression (MR), ANN, and ANFIS methods to forecast backbreak using 42 blasting datasets. R2 for ANFIS, ANN, and MR was reported as 0.96, 0.92, and 0.76 with RMSE values of 0.6, 0.88, and 1.35, respectively. They concluded that ANFIS was more effective than ANN and MR in predicting backbreak [111]. Fig. 15 illustrates a contrast between the anticipated and actual instances of backbreak, as projected by the provided ANN model.
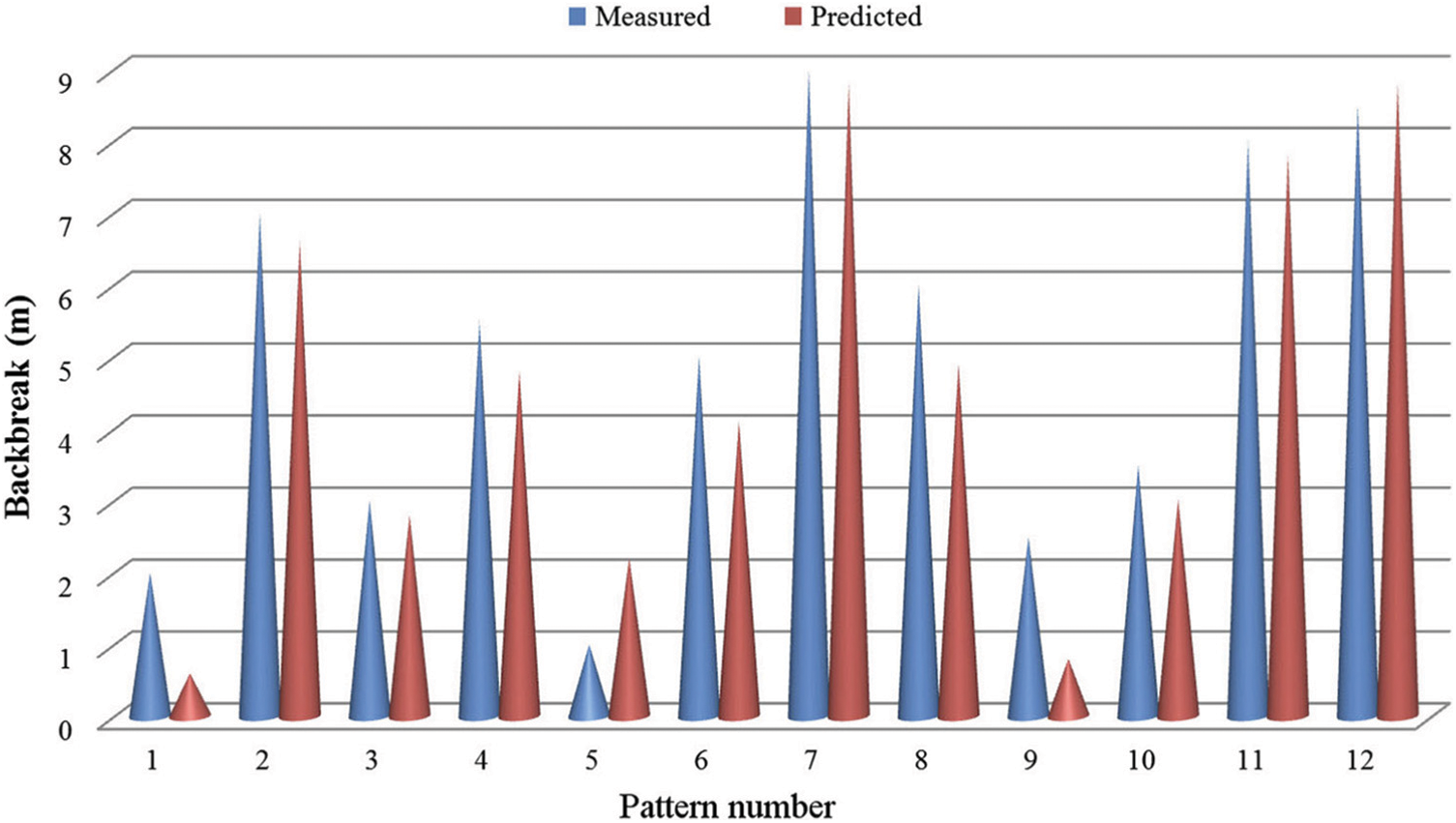
Figure 15: Comparison of measured and predicted backbreak by presented ANN model by Esmaeili et al. [111]
In 2012, Bazzazi et al. [112] developed a new prediction method of backbreak using ANFIS. For this purpose, they gathered 42 blasting datasets, including spacing to burden ratio, stiffness ratio, hole diameter (inch), stemming length (m), specific charge (kg/m3), rock density (t/m3), UCS (Mpa), number of rows, charge last row (kg), charge last row per total charge ratio. The RMSE, variance account for (VAF), and R2 of the presented ANFIS model are 0.6, 0.94, and 0.95, respectively, indicating the model’s acceptable performance [112].
Another comparative study was conducted by Sayadi et al. in 2013 on the performance of diverse ANN methods for estimating fragmentation and backbreak simultaneously in Tehran Cement Company limestone mines in Iran [56]. Two BPNN and Radial Basis Function Neural Network (RBFNN) models were implemented in this regard, and calculated R2 and RMSE of 90.2 and 0.3052 for BPNN and 51.5 and 0.3108 for RBFNN showed that the BPNN model is more efficient for backbreak prediction. The sensitivity analysis results indicated that stemming is a more influencing factor in the back break. Generalizing and transforming independent variables to the dependent ones, calculating mathematical and logical functions, parallel computations, nonlinearity processing, dealing with imprecise or fuzzy data, function approximation, and paradigm detection were mentioned as the core advantages of the ANN for predicting backbreak.
Kamran, in 2021, utilized a state-of-the-art Catboost-based T-distributed Stochastic Neighbor Embedding model to forecast backbreak in the Dewan Cement Limestone quarry. This integrated model’s creation involves 12 factors affecting backbreak due to blasting. These factors encompass parameters such as burden, spacing, hole depth, hole inclination, proportions of high explosive and Ammonium Nitrate/Fuel Oil (ANFO), stemming, powder factor, delay timing per row, hole-to-hole delay, number of rows, and count of exposed faces. This model’s efficacy is evidenced by a testing data R2 value of 97.26 and an RMSE value of 0.282 [113].
In 2015, Saghatforoush et al. investigated a new ANN model for predicting backbreak based on 97 blasting datasets of the Delkan iron mine in Iran, considering burden, spacing, hole length, stemming, and powder factor as input parameters of the ANN model. Statistical results of this research show R2 of 0.832 and RMSE of 0.063 for testing datasets. In addition, as a novel metaheuristic calculation method, ACO is proposed in this research to optimize the influential factors of backbreak. They concluded that utilizing optimized values of blasting patterns by ACO reduces the backbreak by around 58% [114]. Fig. 16 presents the evaluation of their ACO algorithm.
Figure 16: Evaluation of the presented ACO algorithm by Kiani et al. [115]
Kiani et al. [115] and Ghasemi et al. [116] implemented two models of regression tree (RT) and ANFIS for backbreak assessment in the Sungun Copper Mine (SCM), Iran. The recorded 175 datasets of blasting events in SCM, including burden, spacing, stemming length, powder factor, and geometric stiffness ratio, were the primary input factors of their model. They also mentioned that the ANFIS model presents more efficient results for backbreak prediction than RT [116].
Mohammadnejad et al. [117] employed SVM in 2013 to predict backbreak. Simple and multivariate regressions were also utilized to determine the factors most influencing backbreak occurrence. Exploring regression methods showed that the powder factor is not an impressing parameter for backbreak estimation and, therefore, is eliminated from the input factors of the SVM model. Statistical outputs proved that SVM should be considered an almost accurate back break prediction with an R2 equal to 0.94.
A novel neuro-genetic model was proposed by Monjezi et al. in 2012 for backbreak prediction in the Sungun copper mine in Iran. In this model, ANN parameters were optimized by implementing the GA technique. Several elements, including the number of neurons in the concealed layer, the learning rate, and the momentum, are employed components in the models. As a result, compared to conventional methods, the presented model indicates more reliable statistical outputs. In addition, based on the applied sensitivity analysis of this research, stemming and charge per delay are more crucial indices in backbreak assessment [118]. The architecture of the presented optimum model is shown in Fig. 17.
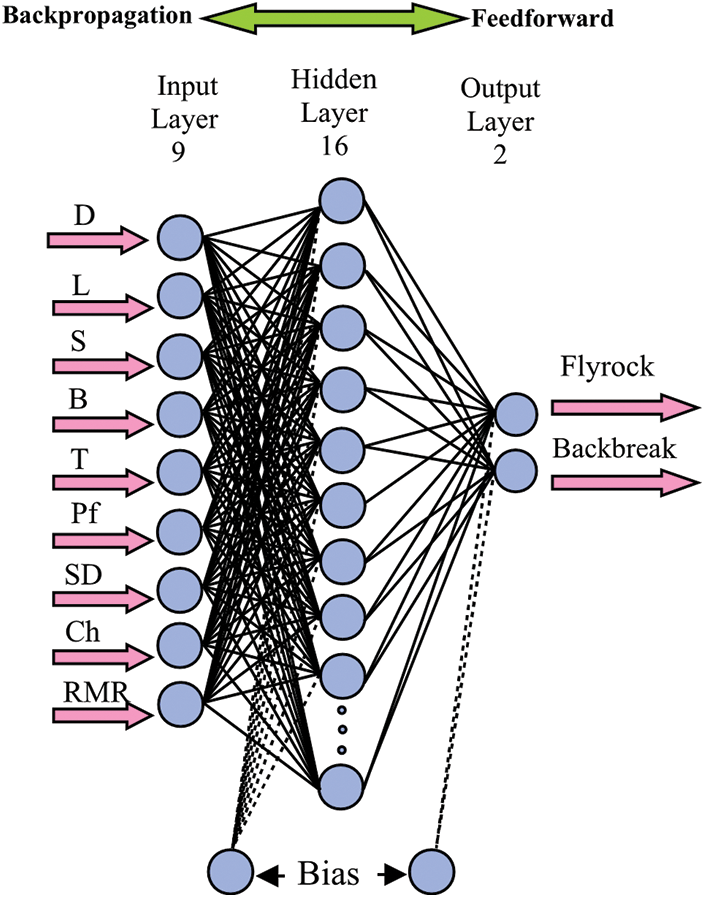
Figure 17: The architecture of the presented optimum neuro-genetic model for predicting backbreak in open pit blasting by Monjezi et al. [118]
In 2021, Zhou et al. investigated novel hybrid techniques for estimating backbreak in SCM. They combined the RF method with optimization models of HHO and the Sine Cosine Algorithm (SCA) for this purpose. They indicated that the SCA-RF model performs more appropriately in predicting backbreak by R2 of 0.9829 and RMSE of 0.0996 for the test dataset [78]. The main structure of implemented SCA in this model is shown in Fig. 18.
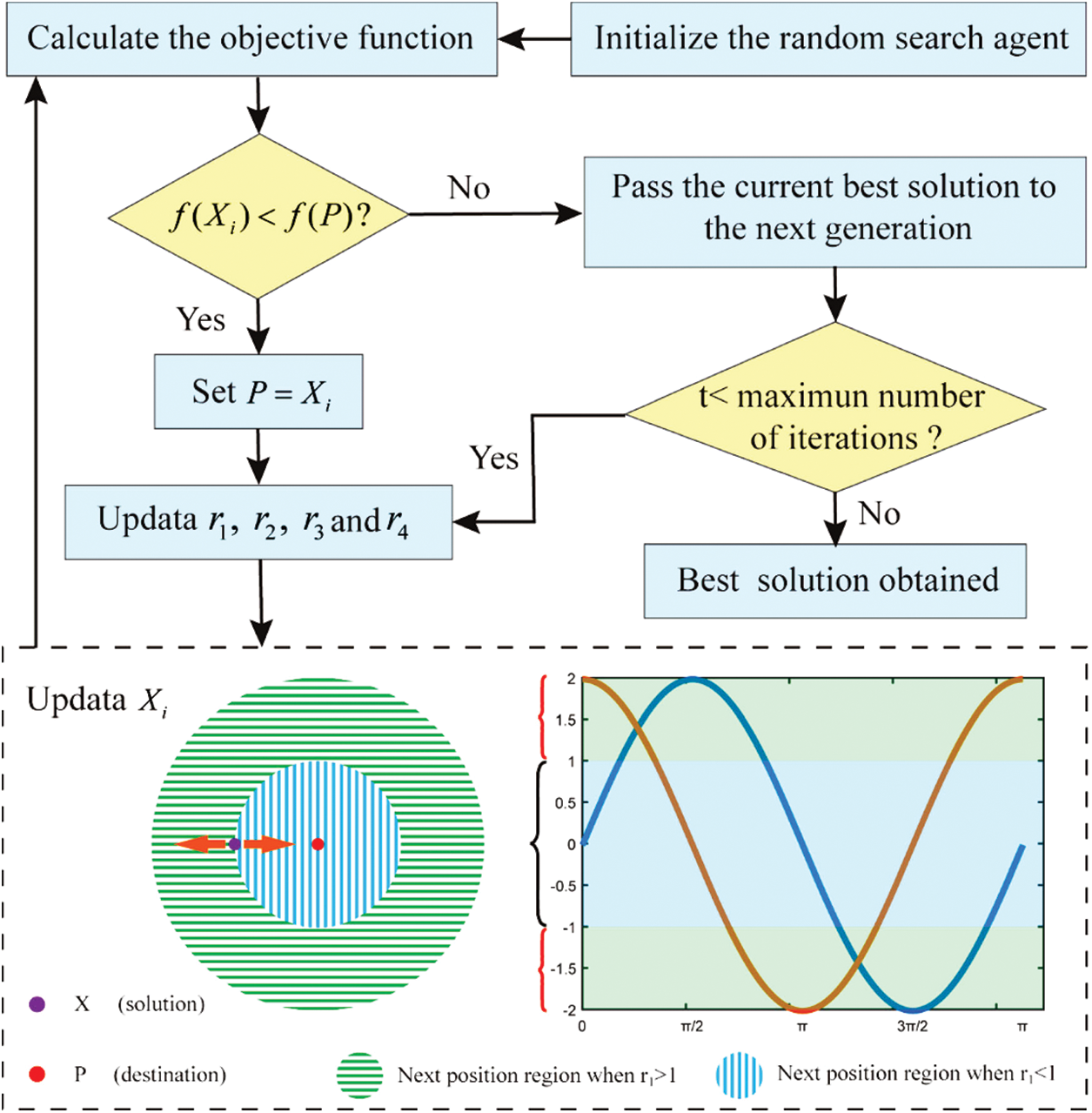
Figure 18: The structure of the implemented SCA backbreak prediction model developed by Zhou et al. [78]
The ANN model was used as a prediction model for backbreak by Monjezi et al. in 2014 for the Sangan iron mine in Iran. They acclaimed that the input rock properties are the most influencing parameter in backbreak distance. They compared the statistical results of ANN to the conventional regression model and proved that ANN with R2 of 0.868 and RMSE of 0.495 is a more proper method for this aim [119].
Backbreak estimation using the Stochastic Modeling Approach (SMA) was applied by Sari et al. in 2013. For this purpose, blasting controllable factors such as burden, spacing, stemming length, powder factor, and geometric stiffness ratio were determined for 175 blasting datasets of SCM. In this study, the Monte Carlo (MC) technique was implemented for backbreak simulation. R2 of 98.1 and RMSE of 0.31 were reported as statistical results of the presented model [120].
In 2012, Monjezi et al. presented an ANN estimating a model of backbreak for the Chadormalu iron mine in Iran using an optimum network structure of 10-7-7-1 for layers and neurons. The performance of the approved ANN model by R2 of 90.02 was much better than the conventional regression model with R2 of 68.10. Sensitivity analysis of this research determined burden as the most effective controllable parameter in backbreak [121].
Hasanipanah et al. proposed an evaluation model of backbreak using fuzzy systems. Their model was constructed based on updated Rock Engineering Systems (RES). The final forecasting model benefited from GA and the imperialist competitive algorithm (ICA). Researchers demonstrated that ICA and GA prediction models with R2 of 0.963 and 0.934 are efficient backbreak estimation models [122].
A novel hybrid technique based on Optimized SVM in combination with the Random Forest method was utilized by Yu et al. in 2021 for estimating backbreak. In this model, while evolutionary random forest determined input factors, the whale optimization algorithm (WOA) and moth-flame optimization (MFO), which are optimized SVM models, were applied as the main elements of the model structure. The scholars compared the statistical results of SVM, SVM-MFO, and SVM-WOA together and concluded that SVM-MFO performs better for backbreak prediction [29]. Fig. 19 shows the flowchart of their model.
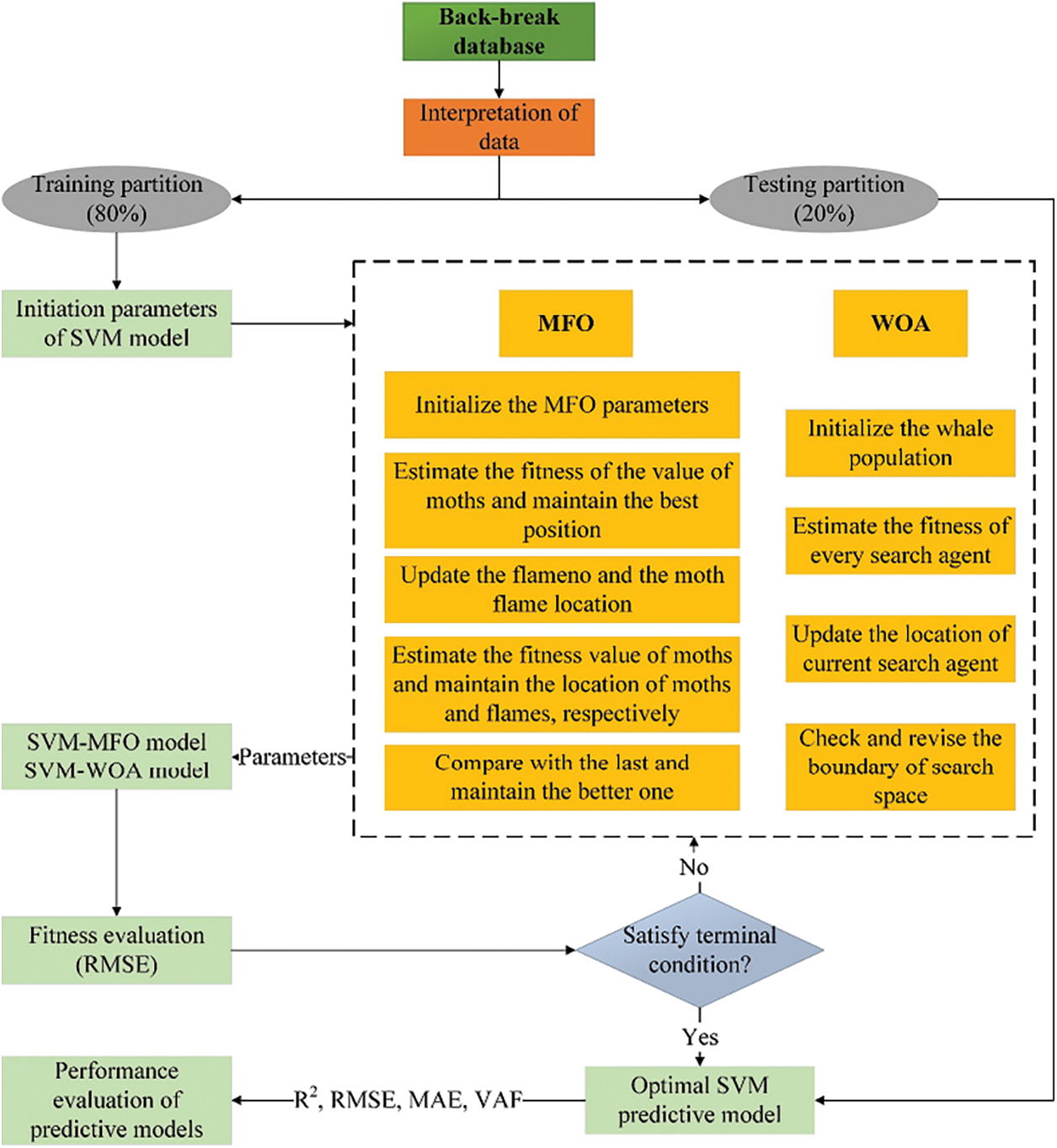
Figure 19: The optimized support vector machines, in conjunction with evolutionary random forest for the anticipation of back-break occurrences [29]
In 2021, Sharma et al. applied two multivariate regression analysis (MVRA) and genetic programming (GP) models for the same purpose. Calculated R2 and RSME of 0.8167 and 0.98 for GP and 0.6305 and 1.95 for MVRA showed that GP is more beneficial for backbreak prediction. Based on the sensitivity analysis, stemming length and powder factor are the most critical factors for backbreak [38].
A new backbreak prediction model for the Anguran mine in Iran was introduced based on ANN and ABC by Ebrahimi et al. in 2015. Burden, spacing, stemming length, hole length, and powder were considered input factors for the proposed model. The R2 value of this model was 0.77 [123].
Muhammad et al. used ANN to forecast backbreaks in the Dewan Cement limestone quarry, considering 12 controllable factors for blasting in 40 datasets. The most efficient ANN with a 12-2-1 network structure has been selected for this aim. The R2 value of 0.97 was calculated using this model to test the dataset. Sensitivity analysis indicated that backbreak reduction strongly depends on powder factor, blast hole inclination, and burden values [124].
Khandelwal et al. proposed a backbreak prediction model for SCM, implementing an SVM model. Their results were compared to those of MVRA to assess the performance of SVM. Achieved R2 of 0.987 and 0.89 for SVM and MVRA showed that SVM provides a more reliable model for predicting backbreak [125].
In 2015, Shirani Faradonbeh et al. utilized GP and nonlinear multiple regression (NLMR) techniques for the same purpose using 175 recorded blasting datasets in SCM. Their results showed that GP gave better statistical assessment indices value [126]. The tree structure of the best GP model to predict Backbreak is presented in Fig. 20.
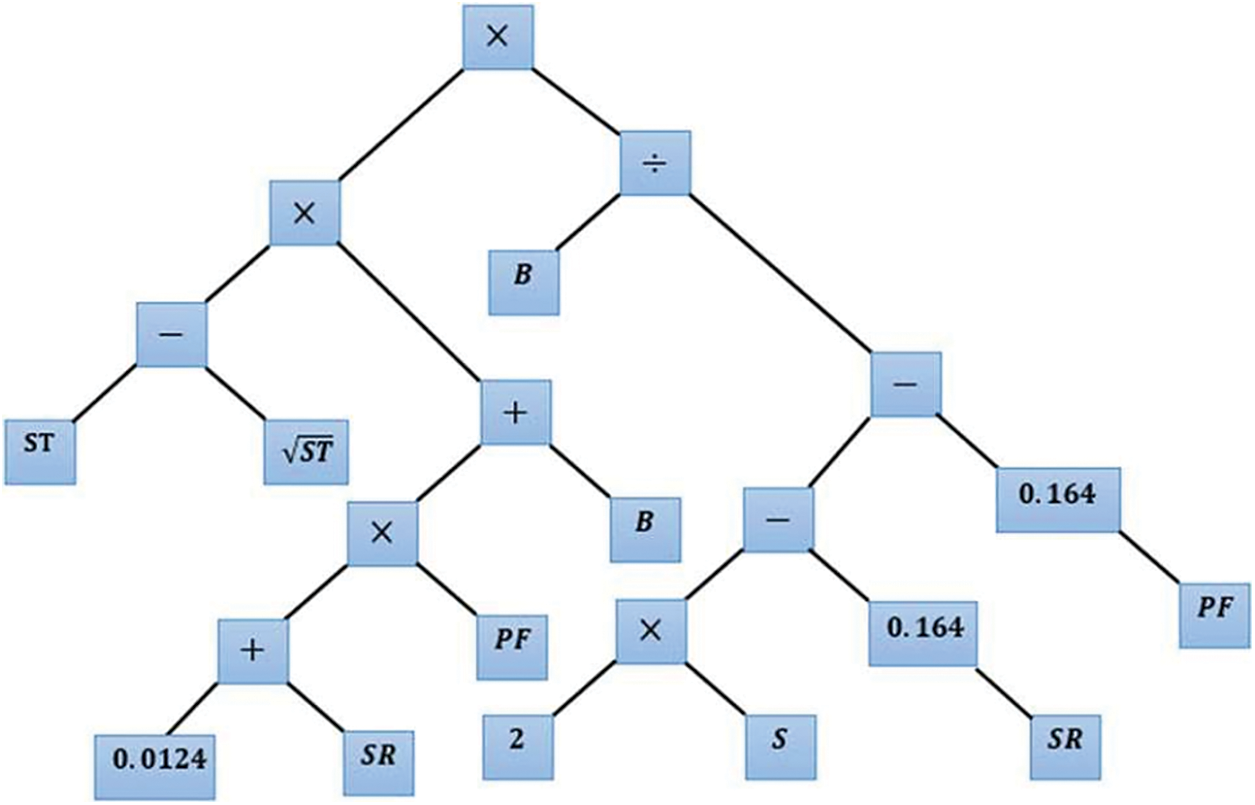
Figure 20: The tree structure of the best GP model to predict Backbreak by Shirani Faradonbeh et al.
Hasanipanah et al. formulated an alternative hybrid AI approach to forecast backbreak incidents by merging PSO and ANFIS [127]. They collected 80 sets of blasting data from the Shur River dam region in Iran, encompassing influential factors like burden, spacing, stemming, and powder factor. This model yielded an R2 value of 0.922. In 2022, Dai et al. introduced an innovative hybrid metaheuristic for predicting blasting-induced backbreak [99]. Their study combined RF and PSO to operate on the SCM blasting dataset. The findings demonstrated that a specific PSO-RF model pattern with an RMSE of 0.0811 and 0.1686 and R2 values of 0.9990 and 0.9961 for training and testing datasets displayed improved statistical performance. A visual representation of the proposed PSO-RF model is depicted in Fig. 21.
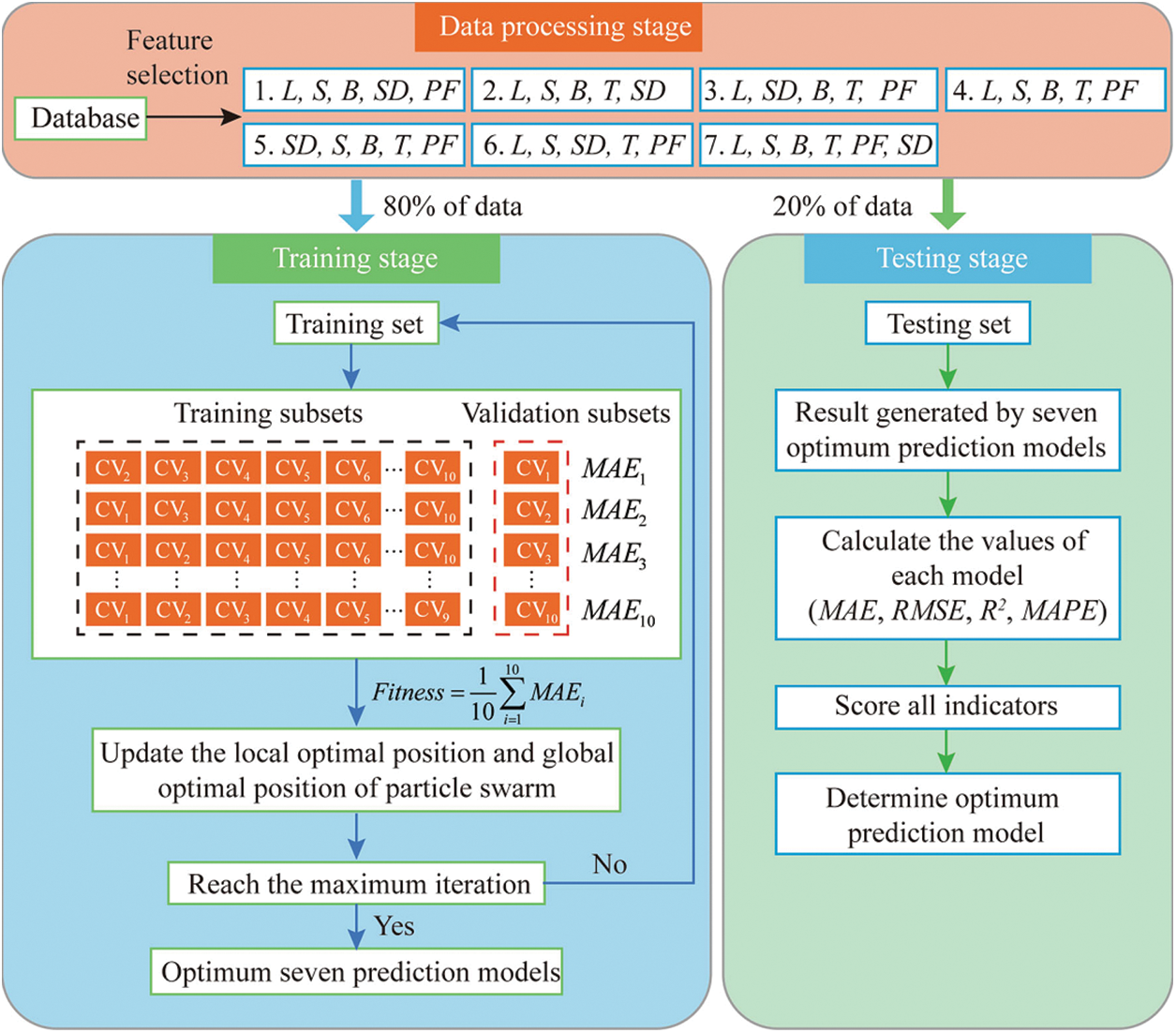
Figure 21: Flowchart of the proposed PSO-RF model by Breiman et al. [100]
The summary of all conducted research in the field of backbreak prediction is listed in Table 3. Fig. 22 indicates the statistical comparison of all implemented SC methods about R2 and RMSE indices.
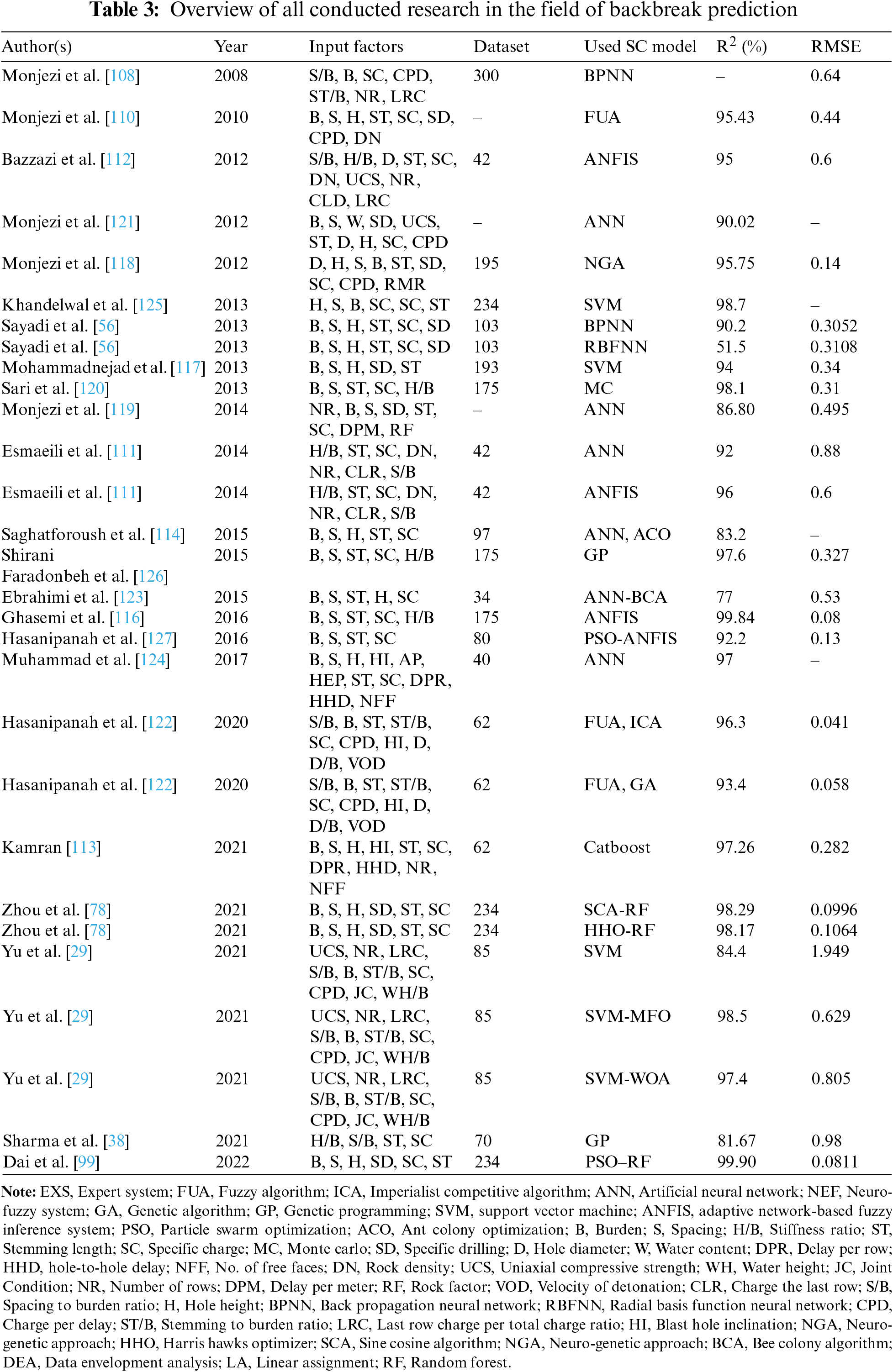
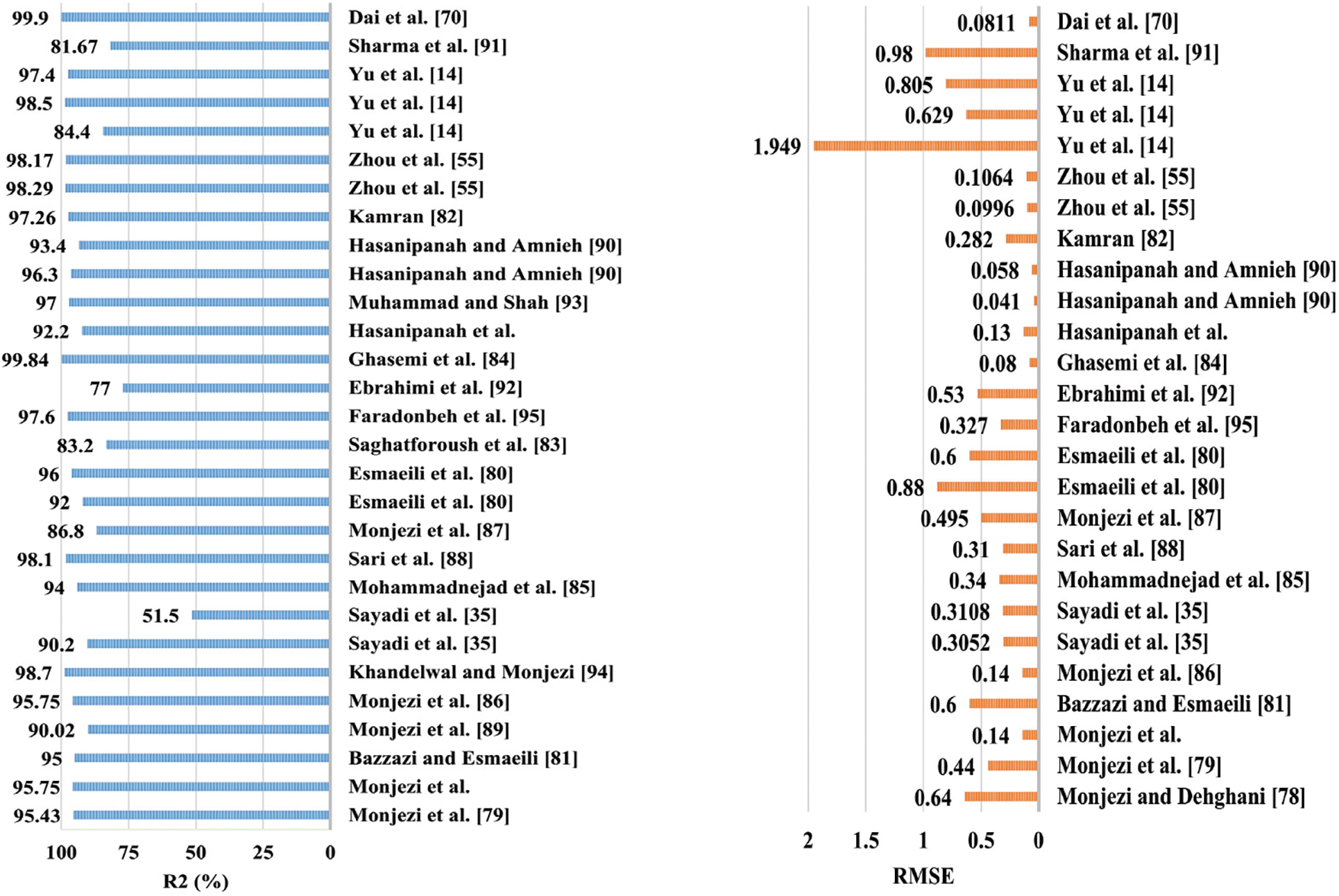
Figure 22: Statistical comparison of implemented SC methods for backbreak prediction regarding R2 and RMSE indices
Progress in backbreak forecasting using ten well-developed Machine Learning (ML) methods was obtained and will continue given the correct paths and conditions. Blasting databases that different scholars have used range from 34–300 samples, depending on their case studies. In a highly complicated environment like mine quarries where high-performance levels are in demand, future studies should consider datasets with more samples to achieve more precise results. A big database probably has a higher coefficient of determination (R²) and RMSE.
The implemented techniques were mainly studied comparatively; one primary ML technique is compared to another(s). Hybrid/ensemble ML methods are the most used ML techniques, followed by ANN, ANFIS, and SVM.
Table 3 indicates that several controllable parameters are considered. The top three parameters are burden (B), spacing (S), and hole height (H), while at the bottom of the input parameters are number of rows (NR) and joint condition (JC). Controllable factors such as blast geometry have a higher impact on the prediction models’ performance than uncontrollable parameters like geological conditions. In contrast, more valuable predictions will be achievable through the bigger participation of uncontrollable factors and considering the complexities of the mining environment.
R² and RMSE are the two main statistical performance indices employed to assess the models. Based on computed performance indices, the results confirm that hybrid/ensemble models yield higher performance degrees than the other techniques, offering higher R2 with lower RMSE values. Although. ANN-based models have been used during the last decade to evaluate and predict the backbreak, generally showing lower amounts for R2 and RMSE indices. Although some techniques like RBFNN offer a lower amount of R2, they can decrease the errors as they yield an acceptable RMSE.
5 Machine Learning Limitations
ML techniques have revolutionized various fields, but they grapple with challenges and constraints. The need for suitable modeling and project design must clarify the obtained benefit and the implemented methodologies, the availability of the needed human capital, and data privacy, which are some challenges [128]. The availability of valuable data is one of the main strains in the mining industry. Valuable data means gathering data to model the different phenomena and human annotations, enabling the application of learning methods to these data [129,130]. Despite the chosen method for acquiring information (continuous or discrete data), determining the practical conditions that optimize the efficiency of a system is hard to achieve as the available data are biased only by the operators’ best evaluation [131].
Although model interpretability remains an issue, especially in complex models such as deep neural networks [132], the inability to explain the decision is mentioned in the literature [133,134]. Data quality and bias can lead to skewed outcomes [135]. Scalability poses problems as ML algorithms demand substantial computational resources for large datasets. Overfitting and generalization errors persist, necessitating regularization techniques [136], despite the proposed models showing a higher prediction performance [137]. The lack of labeled data for certain domains hinders ML’s potential [138]. Adversarial attacks highlight vulnerabilities [139]. ML’s ‘black-box’ nature can lead to ethical concerns and regulatory challenges. This happens when an algorithm and its output are too complicated in a way that humans cannot explain or understand them [129]. Balancing predictive power and fairness adds another layer of complexity [101]. Addressing these challenges is crucial to harness ML’s potential while ensuring responsible and equitable applications.
The creative implementation of various learning paradigms and the incorporation of phenomenological models into the data analysis process will help increase the efficiency of the learning process. Developing functional models demands a phenomenological perception of the modeled processes. Hence, the main challenge for generating these models is the effective cooperation between specialists in machine learning and professionals who understand the different processes to be modeled. Theory and tribal knowledge can influence modeling assumptions, objective function, and optimization paradigm selection.
Theory-guided machine learning (TGML) represents a compelling approach that merges the power of data-driven machine learning techniques with established scientific theories. These scientific models are not only a precious source of knowledge but also construct the essence of simulations. Traditional ML often focuses on extracting patterns solely from data, lacking a clear understanding of underlying mechanisms. TGML, on the other hand, incorporates domain-specific knowledge and scientific principles into the learning process. TGML first relies on integrating real and virtual data and, secondly, on the underlying physical laws governing the domain. TGML can enhance models’ interpretability, generalizability, and robustness by integrating existing theories, physical laws, or causal relationships. This approach aids in capturing patterns within the data and ensures that these patterns align with known scientific truths. In contrast, incorporating domain expertise can help guide feature selection, model architecture, and hyperparameter tuning.
However, it is essential to balance exploiting theoretical knowledge and adapting to the nuances of the data. Successful implementation requires collaboration between domain experts and machine learning practitioners. Although TGML offers promising avenues for improving model performance and interpretability, challenges include the integration of complex theories, handling inconsistencies between data and theory, and accommodating cases where theories are incomplete or evolving. As research progresses, finding innovative ways to harmonize data-driven learning with established theories will likely remain a focal point, enabling more accurate and insightful models across diverse domains. TGML can be utilized by future research to address environmental issues, rendering the suggested solutions more generalized and practical for real-world applications.
The following conclusion remarks can be driven from this research:
1. This study presents a state-of-the-art review of SC methods and their application in backbreak assessment and prediction, one of the most significant aspects of blasting engineering. All main branches of SC, including fuzzy logic, ANFIS, GA, expert systems, ANN, PSO, ABC, and ACO, are considered for this purpose in various research.
2. Various investigations consider diverse impacting factors on the backbreak phenomenon. Most of those factors are controllable parameters of blasting patterns, including burden, spacing, hole diameter, powder factor, and others.
3. This research covers all studies that used each SC method in backbreak prediction. A review of previous studies showed that several scholars have extensively utilized ANN methods for estimating backbreak. As a result, hybrid techniques with ANN, PSO, and SVM yield more appropriate precision for estimating backbreak than their base methods.
4. TGML integrates data-driven techniques with scientific theories, enhancing model interpretability and generalizability by aligning patterns with known truths and finding applications in blasting environmental issues. However, demanding a balance between theory and data adaptation necessitates collaboration between domain experts and ML practitioners, while challenges involve complex theory integration, data-theory inconsistencies, and evolving theories.
Acknowledgement: None.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: Conceptualization, M.Y., M.K., P.A., P.G.A., E.I.K., D.J.A. Methodology, M.Y., M.K., P.A., P.G.A., E.I.K., D.J.A. Formal analysis, M.Y., M.K., P.A., P.G.A., E.I.K., D.J.A. Investigation, M.Y., D.J.A. data curation, M.Y. Writing—original draft preparation, M.Y., M.K., P.A. P.G.A., E.I.K. D.J.A. Writing—review and editing, M.Y., M.K., P.A., P.G.A., E.I.K., D.J.A. Supervision, M.K., P.G.A., D.J.A. All authors have read and agreed to the published version of the manuscript.
Availability of Data and Materials: The data will be available upon a reasonable request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Holling CS. Adaptive environmental assessment and management. New York, USA: John Wiley & Sons; 1978. [Google Scholar]
2. Starfield AM, Cundall P. Towards a methodology for rock mechanics modelling. In: International journal of rock mechanics and mining sciences & geomechanics abstracts. Amsterdam, Netherlands: Elsevier; 1988. [Google Scholar]
3. Feng XT, Katsuyama K, Wang YJ, Lin YM. A new direction-intelligent rock mechanics and rock engineering. Int J Rock Mech Min Geomech Abstr. 1997;34(1):135–41. doi:10.1016/S1365-1609(97)80039-1. [Google Scholar] [CrossRef]
4. Xue X, Xiao M. Deformation evaluation on surrounding rocks of underground caverns based on PSO-LSSVM. Tunn Undergr Space Technol. 2017;69:171–81. doi:10.1016/j.tust.2017.06.019. [Google Scholar] [CrossRef]
5. Liu L, Song Z, Li X. Artificial intelligence in tunnel construction: a comprehensive review of hotspots and frontier topics. Geohazard Mech. 2023;2:1–12. [Google Scholar]
6. Armaghani DJ, Hajihassani M, Mohamad ET, Marto A, Noorani S. Blasting-induced flyrock and ground vibration prediction through an expert artificial neural network based on particle swarm optimization. Arab J Geosci. 2014;7:5383–96. doi:10.1007/s12517-013-1174-0. [Google Scholar] [CrossRef]
7. Zhou J, Asteris PG, Armaghani DJ, Pham BT. Prediction of ground vibration induced by blasting operations through the use of the Bayesian network and random forest models. Soil Dyn Earthq Eng. 2020;139:106390. doi:10.1016/j.soildyn.2020.106390. [Google Scholar] [CrossRef]
8. Zadeh LA. Soft computing and fuzzy logic. Fuzzy sets, fuzzy logic, and fuzzy systems: selected papers by Lotfi a Zadeh. Binghmpton, New York, USA: World Scientific; 1996. p. 796–804. [Google Scholar]
9. Urošević K, Zakonović J, Ignjatović J, Gaćina R. Different aspects of soft computing methods application for blasting in mining. Podzemni Rad, 2019;2019(35):65–71. [Google Scholar]
10. Hartman HL, Mutmansky JM. Introductory mining engineering. Hoboken, New Jersey, USA: John Wiley & Sons; 2002. [Google Scholar]
11. Yari M, Bagherpour R, Jamali S, Shamsi R. Development of a novel flyrock distance prediction model using BPNN for providing blasting operation safety. Neural Comput Appl. 2016;27(3):699–706. doi:10.1007/s00521-015-1889-9. [Google Scholar] [CrossRef]
12. Yari M, Monjezi M, Bagherpour R. Selecting the most suitable blasting pattern using AHP-TOPSIS method: sungun copper mine. J Min Sci. 2013;49(6):967–75. doi:10.1134/S1062739149060178. [Google Scholar] [CrossRef]
13. Wen M, Wu W, Li L, Tian Y, El Naggar MH, Mei G, et al. Fractional derivative modelling for rheological characteristics of multilayered saturated porous rock with interfacial thermal contact resistance. Int J Numer Anal Methods Geomech. 2023;47(12):2256–82. doi:10.1002/nag.v47.12. [Google Scholar] [CrossRef]
14. Yarahmadi R, Bagherpour R, Kakaie R, Mirzaie NH, Yari M. Development of 2D computer program to determine geometry of rock mass blocks. Int J Min Sci Technol. 2014;24(2):191–4. doi:10.1016/j.ijmst.2014.01.008. [Google Scholar] [CrossRef]
15. Jang H, Topal E. A review of soft computing technology applications in several mining problems. Appl Soft Comput. 2014;22:638–51. doi:10.1016/j.asoc.2014.05.019. [Google Scholar] [CrossRef]
16. Giraudi A, Cardu M, Kecojevic V. An assessment of blasting vibrations: a case study on quarry operation. Am J Environ Sci. 2009;5(4):468–74. doi:10.3844/ajessp.2009.468.474. [Google Scholar] [CrossRef]
17. Mohamad ET, Armaghani DJ, Hajihassani M, Faizi K, Marto A. A simulation approach to predict blasting-induced flyrock and size of thrown rocks. Electron J Geotech Eng. 2013;18(B):365–74. [Google Scholar]
18. Raina AK, Bhatawdekar RM. Blast-induced flyrock: risk evaluation and management. In: Risk, reliability and sustainable remediation in the field of civil and environmental engineering. Amsterdam, Netherlands: Elsevier; 2022. p. 209–47. [Google Scholar]
19. Yari M, He B, Armaghani DJ, Abbasi P, Mohamad ET. A novel ensemble machine learning model to predict mine blasting-induced rock fragmentation. Bull Eng Geol Environ. 2023;82(5):187. doi:10.1007/s10064-023-03138-y. [Google Scholar] [CrossRef]
20. Murlidhar BR, Kumar D, Jahed Armaghani D, Mohamad ET, Roy B, Pham BT. A novel intelligent ELM-BBO technique for predicting distance of mine blasting-induced flyrock. Nat Resour Res. 2020;29(6):4103–20. doi:10.1007/s11053-020-09676-6. [Google Scholar] [CrossRef]
21. Singh T, Singh V. An intelligent approach to prediction and control ground vibration in mines. Geotech Geol Eng. 2005;23(3):249–62. doi:10.1007/s10706-004-7068-x. [Google Scholar] [CrossRef]
22. Yari M, Armaghani DJ, Maraveas C, Ejlali AN, Mohamad ET, Asteris PG. Several tree-based solutions for predicting flyrock distance due to mine blasting. Appl Sci. 2023;13(3):1345. doi:10.3390/app13031345. [Google Scholar] [CrossRef]
23. Nguyen H, Bui XN, Asteris PG, Hieu-Tran Q, Armaghani DJ, Monjezi M, et al. A comparative study of different artificial intelligence techniques in predicting blast-induced air over-pressure. Appl Metaheuristic Comput. 2020;1(2):187–202. [Google Scholar]
24. Kuzu C, Ergin H. An assessment of environmental impacts of quarry-blasting operation: a case study in Istanbul, Turkey. Environ Geol. 2005;48(2):211–7. doi:10.1007/s00254-005-1291-5. [Google Scholar] [CrossRef]
25. Bhatawdekar RM, Kumar R, Sabri Sabri MM, Roy B, Mohamad ET, Kumar D, et al. Estimating flyrock distance induced due to mine blasting by extreme learning machine coupled with an equilibrium optimizer. Sustainability. 2023;15(4):3265. doi:10.3390/su15043265. [Google Scholar] [CrossRef]
26. Nikafshan Rad H, Bakhshayeshi I, Wan Jusoh WA, Tahir M, Foong LK. Prediction of flyrock in mine blasting: a new computational intelligence approach. Nat Resour Res. 2020;29(2):609–23. doi:10.1007/s11053-019-09464-x. [Google Scholar] [CrossRef]
27. Carlos LJ, Emilio LJ, Francisco JAC. Drilling and blasting of rocks; 2017. doi:10.1201/9781315141435. [Google Scholar] [CrossRef]
28. Mohanty B. Production blasts in open pit mines and their effect on slope stability; 1977. Available from: https://www.taylorfrancis.com/chapters/edit/10.1201/9781003079286-20/production-blasts-open-pit-mines-effect-slope-stability-mohanty-chung. [Accessed 2022]. [Google Scholar]
29. Yu Q, Monjezi M, Mohammed AS, Dehghani H, Armaghani DJ, Ulrikh DV. Optimized support vector machines combined with evolutionary random forest for prediction of back-break caused by blasting operation. Sustainability. 2021;13(22):12797. doi:10.3390/su132212797. [Google Scholar] [CrossRef]
30. Agrawal H, Mishra A. Modified scaled distance regression analysis approach for prediction of blast-induced ground vibration in multi-hole blasting. J Rock Mech Geotech Eng. 2019;11(1):202–7. doi:10.1016/j.jrmge.2018.07.004. [Google Scholar] [CrossRef]
31. Armaghani DJ, Koopialipoor M, Bahri M, Hasanipanah M, Tahir M. A SVR-GWO technique to minimize flyrock distance resulting from blasting. Bull Eng Geol Environ. 2020;79(8):4369–85. doi:10.1007/s10064-020-01834-7. [Google Scholar] [CrossRef]
32. Bhandari S. Engineering rock blasting operations; 1997. Available from: Engineering rock blasting operations : Bhandari, Sushil : Free Download, Borrow, and Streaming : Internet Archive. [Accessed 2023]. [Google Scholar]
33. Jayasinghe B, Zhao Z, Chee AGT, Zhou H, Gui Y. Attenuation of rock blasting induced ground vibration in rock-soil interface. J Rock Mech Geotech Eng. 2019;11(4):770–8. doi:10.1016/j.jrmge.2018.12.009. [Google Scholar] [CrossRef]
34. Konya CJ, Walter EJ. Rock blasting and overbreak control. USA: Federal Highway Administration; 1991. [Google Scholar]
35. Yari M, Monjezi M, Bagherpour R. A novel investigation in blasting operation management using decision making methods. Rudarsko-Geološko-Naftni Zbornik. 2014;29(1):69–79. [Google Scholar]
36. Gates WC, Ortiz LT, Florez RM. Analysis of rockfall and blasting backbreak problems, US 550, Molas Pass, CO. In: The 40th U.S. Sym Rock Mechanics (USRMS2005; Anchorage, Alaska. [Google Scholar]
37. Kumar R, Choudhury D, Bhargava K. Determination of blast-induced ground vibration equations for rocks using mechanical and geological properties. J Rock Mech Geotech Eng. 2016;8(3):341–9. doi:10.1016/j.jrmge.2015.10.009. [Google Scholar] [CrossRef]
38. Sharma M, Agrawal H, Choudhary B. Multivariate regression and genetic programming for prediction of backbreak in open-pit blasting. Neural Comput Appl. 2022;34(3):1–12. doi:10.1007/s00521-021-06553-y. [Google Scholar] [CrossRef]
39. Yari M, Bagherpour R, Almasi N. An approach to the evaluation and classification of dimensional stone quarries with an emphasis on safety parameters. Rudarsko-Geološko-Naftni zbornik. 2016;31(3):15–26. doi:10.17794/rgn.2016.3.2. [Google Scholar] [CrossRef]
40. Bakhshandeh Amnieh H, Aref Mand E, Porghasemi Saghand M. Controlling backbreak and improving technical and economic parameters in Mishdovan Iron Ore Mine. J Miner Resour Eng. 2022;7(1):99–111. [Google Scholar]
41. Li C, Zhou J, Khandelwal M, Zhang X, Monjezi M, Qiu Y. Six novel hybrid extreme learning machine-swarm intelligence optimization (ELM-SIO) models for predicting backbreak in open-pit blasting. Natural Res Res. 2022;31(5):3017–39. doi:10.1007/s11053-022-10082-3. [Google Scholar] [CrossRef]
42. Scoble M, Lizotte Y, Paventi M, Mohanty B. Measurement of blast damage. Min Eng. 1997;49(6):103–8. [Google Scholar]
43. Alejano L, Pons B, Bastante F, Alonso E, Stockhausen H. Slope geometry design as a means for controlling rockfalls in quarries. Int J Rock Mech Min Sci. 2007;44(6):903–21. doi:10.1016/j.ijrmms.2007.02.001. [Google Scholar] [CrossRef]
44. Wyllie DC, Mah C. Rock slope engineering. London, UK: CRC Press; 2004. [Google Scholar]
45. Yari M, Bagherpour R. Investigating an innovative model for dimensional sedimentary rocks characterization using acoustic frequencies analysis during drilling. Rudarsko-Geološko-Naftni zbornik. 2018;33(2):17–25. doi:10.17794/rgn.2018.2.2. [Google Scholar] [CrossRef]
46. Yari M, Monjezi M, Bagherpour R, Sayadi A, editors. Blasting operation management using mathematical methods. In: Engineering geology for society and territory-volume 1: climate change and engineering geology. Switzerland: Springer; 2015. [Google Scholar]
47. Bauer A. Wall control blasting in open pits. In: Proc of the 14th Canadian Rock Mechanics Sym, 1982; Vancouver, British Columbia, Canada. [Google Scholar]
48. Monjezi M, Ghafurikalajahi M, Bahrami A. Prediction of blast-induced ground vibration using artificial neural networks. Tunn Undergr Space Technol. 2011;26(1):46–50. doi:10.1016/j.tust.2010.05.002. [Google Scholar] [CrossRef]
49. Mohamad ET, Hajihassani M, Armaghani DJ, Marto A. Simulation of blasting-induced air overpressure by means of artificial neural networks. Int Rev Model Simul. 2012;5(6):2501–6. [Google Scholar]
50. Mohamad ET, Armaghani DJ, Noorani SA, Saad R, Alvi S, Abad N. Prediction of flyrock in boulder blasting using artificial neural network. Electron J Geotech Eng. 2012;17:2585–95. [Google Scholar]
51. Mohamad ET, Noorani SA, Armaghani DJ, Saad R. Simulation of blasting induced ground vibration by using artificial neural network. Electron J Geotech Eng. 2012;17:2571–84. [Google Scholar]
52. Kubat M. Neural networks and fuzzy systems: a dynamical systems approach to machine intelligence by Kosko B, Prentice Hall, NJ; 1992. [Google Scholar]
53. Simpson P. Artificial neural system-foundation, paradigm, application and implementation. New York: Pergamon Press; 1990. [Google Scholar]
54. Hosseini S, Monjezi M, Bakhtavar E, Mousavi A. Prediction of dust emission due to open pit mine blasting using a hybrid artificial neural network. Nat Resour Res. 2021;30(6):4773–88. doi:10.1007/s11053-021-09930-5. [Google Scholar] [CrossRef]
55. Shang Y, Nguyen H, Bui XN, Tran QH, Moayedi H. A novel artificial intelligence approach to predict blast-induced ground vibration in open-pit mines based on the firefly algorithm and artificial neural network. Nat Resour Res. 2020;29(2):723–37. doi:10.1007/s11053-019-09503-7. [Google Scholar] [CrossRef]
56. Sayadi A, Monjezi M, Talebi N, Khandelwal M. A comparative study on the application of various artificial neural networks to simultaneous prediction of rock fragmentation and backbreak. J Rock Mech Geotech Eng. 2013;5(4):318–24. doi:10.1016/j.jrmge.2013.05.007. [Google Scholar] [CrossRef]
57. Demuth H, Beale M, Hagan M. Neural network toolbox user’s guide. Natick, MA, USA: The Math Work, Inc., 1994. [Google Scholar]
58. Benardos A, Kaliampakos D. Modelling TBM performance with artificial neural networks. Tunn Undergr Space Technol. 2004;19(6):597–605. doi:10.1016/j.tust.2004.02.128. [Google Scholar] [CrossRef]
59. Zhang Y, Gao Z, Wang X, Liu Q. Image representations of numerical simulations for training neural networks. Comput Model Eng Sci. 2023;134(2):821–33. [Google Scholar]
60. Lawal AI, Kwon S. Application of artificial intelligence to rock mechanics: an overview. J Rock Mech Geotech Eng. 2021;13(1):248–66. doi:10.1016/j.jrmge.2020.05.010. [Google Scholar] [CrossRef]
61. Hwang JN. Neural networks: a comprehensive foundation-Simon Haylun. New York: Macmillan and IEEE Computer Society; 1994. [Google Scholar]
62. Jain AK, Mao J, Mohiuddin KM. Artificial neural networks: a tutorial. Computer. 1996;29(3):31–44. doi:10.1109/2.485891. [Google Scholar] [CrossRef]
63. Karaboga D. An idea based on honey bee swarm for numerical optimization. Technical Report-TR06, Erciyes University; 2005. [Google Scholar]
64. Kisi O, Ozkan C, Akay B. Modeling discharge-sediment relationship using neural networks with artificial bee colony algorithm. J Hydrol. 2012;428:94–103. [Google Scholar]
65. Asteris PG, Nikoo M. Artificial bee colony-based neural network for the prediction of the fundamental period of infilled frame structures. Neural Comput Appl. 2019;31(9):4837–47. doi:10.1007/s00521-018-03965-1. [Google Scholar] [CrossRef]
66. Dorigo M, Stützle T. Ant colony optimization. In: The MIT Press; 2005. [Google Scholar]
67. Jean-Baptiste W. Nanocomputers and swarm intelligence. NY: Wiley-Blackwell; 2008. [Google Scholar]
68. Colorni A, Maniezzo V. Distributed optimization by ant colonies. In: Proceedings of ECAL91-European Conference on Artificial Life, 1991; Paris, France. [Google Scholar]
69. Dorigo M. Luca Maria Gambardella: ant colony system: a cooperative learning. IEEE Trans Evol Comput. 1997;1:53–66. doi:10.1109/4235.585892. [Google Scholar] [CrossRef]
70. Monmarché N, Guinand F, Siarry P. Artificial ants. Hoboken, USA: Wiley-iste Hoboken; 2010. [Google Scholar]
71. Hwang CL, Masud ASM. Multiple objective decision making—methods and applications: a state-of-the-art survey. New York, USA: Springer Science & Business Media; 2012. [Google Scholar]
72. Yari M, Bagherpour R, Jamali S, Asadi F. Selection of most proper blasting pattern in mines using linear assignment method: sungun copper mine. Arch Min Sci. 2015;60(1):375–86. [Google Scholar]
73. Hasanipanah M, Bagheri Golzar S, Abbasi Larki I, Yazdanpanah Maryaki M, Ghahremanians T. Estimation of blast-induced ground vibration through a soft computing framework. Eng Comput. 2017;33(1):951–59. [Google Scholar]
74. Yari M, Monjezi M, Bagherpour R, Jamali S. Developing a mathematical assessment model for blasting patterns management: sungun copper mine. J Cent South Univ. 2014;21(11):4344–51. doi:10.1007/s11771-014-2434-1. [Google Scholar] [CrossRef]
75. Heidari AA, Mirjalili S, Faris H, Aljarah I, Mafarja M, Chen H. Harris hawks optimization: algorithm and applications. Future Gener Comput Syst. 2019;97:849–72. doi:10.1016/j.future.2019.02.028. [Google Scholar] [CrossRef]
76. Du P, Wang J, Hao Y, Niu T, Yang W. A novel hybrid model based on multi-objective Harris hawks optimization algorithm for daily PM2.5 and PM10 forecasting. Appl Soft Comput. 2020;96:106620. doi:10.1016/j.asoc.2020.106620. [Google Scholar] [CrossRef]
77. Hussain K, Neggaz N, Zhu W, Houssein EH. An efficient hybrid sine-cosine Harris hawks optimization for low and high-dimensional feature selection. Expert Syst Appl. 2021;176:114778. doi:10.1016/j.eswa.2021.114778. [Google Scholar] [CrossRef]
78. Zhou J, Dai Y, Khandelwal M, Monjezi M, Yu Z, Qiu Y. Performance of hybrid SCA-RF and HHO-RF models for predicting backbreak in open-pit mine blasting operations. Nat Resour Res. 2021;30(6):4753–71. doi:10.1007/s11053-021-09929-y. [Google Scholar] [CrossRef]
79. Jang JSR. Fuzzy modeling using generalized neural networks and kalman filter algorithm. Anaheim, California, USA: AAAI; 1991. [Google Scholar]
80. Jang JS. ANFIS: adaptive-network-based fuzzy inference system. IEEE Trans Syst, Man, Cybern. 1993;23(3):665–85. doi:10.1109/21.256541. [Google Scholar] [CrossRef]
81. Ooriad FA, Yari M, Bagherpour R, Khoshouei M. The development of a novel model for mining method selection in a fuzzy environment; case study: Tazareh Coal Mine, Semnan Province, Iran. Rudarsko-Geološko-Naftni Zbornik. 2018;33(1):45–53. [Google Scholar]
82. Abraham A. Adaptation of fuzzy inference system using neural learning. In: Fuzzy systems engineering. Heidelberg, Germany: Springer; 2005. p. 53–83. [Google Scholar]
83. Parsajoo M, Armaghani DJ, Asteris PG. A precise neuro-fuzzy model enhanced by artificial bee colony techniques for assessment of rock brittleness index. Neural Comput Appl. 2022;34:1–19. [Google Scholar]
84. Jang JSR, Sun CT, Mizutani E. Neuro-fuzzy and soft computing–a computational approach to learning and machine intelligence [Book Review]. IEEE Trans Autom Control. 1997;42(10):1482–4. doi:10.1109/TAC.1997.633847. [Google Scholar] [CrossRef]
85. Tahmasebi P, Hezarkhani A. A hybrid neural networks-fuzzy logic-genetic algorithm for grade estimation. Comput Geosci. 2012;42(1):18–27. doi:10.1016/j.cageo.2012.02.004. [Google Scholar] [PubMed] [CrossRef]
86. Gupta P, Kulkarni N. An introduction of soft computing approach over hard computing. Int J Latest Trends Eng Technol. 2013;3(1):254–8. [Google Scholar]
87. Deng X, Wang R, Xu T. Risk assessment of tunnel portals in the construction stage based on fuzzy analytic hierarchy process. Arch Civil Eng. 2018;64(4/I):69–87. doi:10.2478/ace-2018-0045. [Google Scholar] [CrossRef]
88. Yari M, Bagherpour R, Khoshouei M, Pedram H. Investigating a comprehensive model for evaluating occupational and environmental risks of dimensional stone mining. Rudarsko-Geološko-Naftni Zbornik. 2020;35(1):101–9. doi:10.17794/rgn.2020.1.8. [Google Scholar] [CrossRef]
89. Chou SY, Chang YH. A decision support system for supplier selection based on a strategy-aligned fuzzy SMART approach. Expert Syst Appl. 2008;34(4):2241–53. doi:10.1016/j.eswa.2007.03.001. [Google Scholar] [CrossRef]
90. Mishra D, Basu A. Estimation of uniaxial compressive strength of rock materials by index tests using regression analysis and fuzzy inference system. Eng Geol. 2013;160:54–68. doi:10.1016/j.enggeo.2013.04.004. [Google Scholar] [CrossRef]
91. Bai Y, Wang D. Fundamentals of fuzzy logic control—fuzzy sets, fuzzy rules and defuzzifications. In: Advanced fuzzy logic technologies in industrial applications. London: Springer; 2006. p. 17–36. [Google Scholar]
92. Holland J. Adaptation in natural and artificial systems. Ann Arbor: University of Michigan Press; 1975. [Google Scholar]
93. Coley DA. An introduction to genetic algorithms for scientists and engineers. Singapore: World Scientific Publishing Company; 1999. [Google Scholar]
94. Alipour A, Khodaiari AA, Jafari A, Tavakkoli-Moghaddam R. Production scheduling of open-pit mines using genetic algorithm: a case study. Int J Manag Sci Eng Manag. 2020;15(3):176–83. [Google Scholar]
95. Hou J, Li G, Wang H, Hu N. Genetic algorithm to simultaneously optimise stope sequencing and equipment dispatching in underground short-term mine planning under time uncertainty. Int J Mini, Reclamat Environ. 2020;34(5):307–25. doi:10.1080/17480930.2019.1584952. [Google Scholar] [CrossRef]
96. Fathollahzadeh K, Asad MWA, Mardaneh E, Cigla M. Review of solution methodologies for open pit mine production scheduling problem. Int J Min, Reclamat Environ. 2021;35(8):564–99. doi:10.1080/17480930.2021.1888395. [Google Scholar] [CrossRef]
97. Bonyadi MR, Michalewicz Z. Particle swarm optimization for single objective continuous space problems: a review. Evol Comput. 2017;25(1):1–54. doi:10.1162/EVCO_r_00180. [Google Scholar] [PubMed] [CrossRef]
98. Eberhart R, Kennedy J. A new optimizer using particle swarm theory. In: MHS’95 Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan1995; IEEE. [Google Scholar]
99. Dai Y, Khandelwal M, Qiu Y, Zhou J, Monjezi M, Yang P. A hybrid metaheuristic approach using random forest and particle swarm optimization to study and evaluate backbreak in open-pit blasting. Neural Comput Appl. 2022:1–16. doi:10.1007/s00521-021-06776-z. [Google Scholar] [CrossRef]
100. Breiman L. Random forests. Mach Learn. 2001;45(1):5–32. doi:10.1023/A:1010933404324. [Google Scholar] [CrossRef]
101. Nabavi Z, Mirzehi M, Dehghani H, Ashtari P. A hybrid model for back-break prediction using XGBoost machine learning and metaheuristic algorithms in Chadormalu iron mine. J Min Environ. 2023;14(2):689–712. [Google Scholar]
102. Zhang H, Zhou J, Jahed Armaghani D, Tahir M, Pham BT, Huynh VV. A combination of feature selection and random forest techniques to solve a problem related to blast-induced ground vibration. Appl Sci. 2020;10(3):869. doi:10.3390/app10030869. [Google Scholar] [CrossRef]
103. Zhou J, Li E, Wei H, Li C, Qiao Q, Armaghani DJ. Random forests and cubist algorithms for predicting shear strengths of rockfill materials. Appl Sci. 2019;9(8):1621. doi:10.3390/app9081621. [Google Scholar] [CrossRef]
104. Boser BE, Guyon IM, Vapnik VN. A training algorithm for optimal margin classifiers. In: COLT '92: Proceedings of the Fifth Annual Workshop on Computational Learning Theory, 1992. p. 144–52. [Google Scholar]
105. Kivinen J, Smola AJ, Williamson RC. Online learning with kernels. IEEE Trans Signal Process. 2004;52(8):2165–76. doi:10.1109/TSP.2004.830991. [Google Scholar] [CrossRef]
106. Shawe-Taylor J, Williams CK, Cristianini N, Kandola J. On the eigenspectrum of the gram matrix and the generalization error of kernel-PCA. IEEE Trans Inform Theory. 2005;51(7):2510–22. doi:10.1109/TIT.2005.850052. [Google Scholar] [CrossRef]
107. Noble WS. What is a support vector machine? Nat biotechnol. 2006;24(12):1565–7. doi:10.1038/nbt1206-1565. [Google Scholar] [PubMed] [CrossRef]
108. Monjezi M, Dehghani H. Evaluation of effect of blasting pattern parameters on back break using neural networks. Int J Rock Mech Min Sci. 2008;45(8):1446–53. doi:10.1016/j.ijrmms.2008.02.007. [Google Scholar] [CrossRef]
109. Yari M, Bagherpour R, Jamali S. Development of an evaluation system for blasting patterns to provide efficient production. J Intell Manuf. 2017;28(4):975–84. doi:10.1007/s10845-015-1036-6. [Google Scholar] [CrossRef]
110. Monjezi M, Rezaei M, Yazdian A. Prediction of backbreak in open-pit blasting using fuzzy set theory. Expert Syst Appl. 2010;37(3):2637–43. doi:10.1016/j.eswa.2009.08.014. [Google Scholar] [CrossRef]
111. Esmaeili M, Osanloo M, Rashidinejad F, Aghajani Bazzazi A, Taji M. Multiple regression, ANN and ANFIS models for prediction of backbreak in the open pit blasting. Eng Comput. 2014;30(4):549–58. doi:10.1007/s00366-012-0298-2. [Google Scholar] [CrossRef]
112. Bazzazi AA, Esmaeili M. Prediction of backbreak in open pit blasting by adaptive neuro-fuzzy inference system. Arch Min Sci. 2012;57(4):1–11. [Google Scholar]
113. Kamran M. A state of the art catboost-based T-distributed stochastic neighbor embedding technique to predict backbreak at dewan cement limestone quarry. J Min Environ. 2021;12(3):679–91. [Google Scholar]
114. Saghatforoush A, Monjezi M, Shirani Faradonbeh R, Jahed Armaghani D. Combination of neural network and ant colony optimization algorithms for prediction and optimization of flyrock and back-break induced by blasting. Eng Comput. 2016;32(2):255–66. doi:10.1007/s00366-015-0415-0. [Google Scholar] [CrossRef]
115. Kiani M, Hosseini SH, Taji M, Gholinejad M. Risk assessment of blasting operations in open pit mines using FAHP method. Environ Earth Sci. 2019;13(3):76–86. [Google Scholar]
116. Ghasemi E, Amnieh HB, Bagherpour R. Assessment of backbreak due to blasting operation in open pit mines: a case study. Environ Earth Sci. 2016;75(7):1–11. doi:10.1007/s12665-016-5354-6. [Google Scholar] [CrossRef]
117. Mohammadnejad M, Gholami R, Sereshki F, Jamshidi A. A new methodology to predict backbreak in blasting operation. Int J Rock Mech Min Sci. 2013;60(2):75–81. doi:10.1016/j.ijrmms.2012.12.019. [Google Scholar] [CrossRef]
118. Monjezi M, Amini Khoshalan H, Yazdian Varjani A. Prediction of flyrock and backbreak in open pit blasting operation: a neuro-genetic approach. Arab J Geosci. 2012;5(3):441–8. doi:10.1007/s12517-010-0185-3. [Google Scholar] [CrossRef]
119. Monjezi M, Hashemi Rizi S, Majd VJ, Khandelwal M. Artificial neural network as a tool for backbreak prediction. Geotech Geol Eng. 2014;32(1):21–30. doi:10.1007/s10706-013-9686-7. [Google Scholar] [CrossRef]
120. Sari M, Ghasemi E, Ataei M. Stochastic modeling approach for the evaluation of backbreak due to blasting operations in open pit mines. Rock Mech Rock Eng. 2014;47(2):771–83. doi:10.1007/s00603-013-0438-z. [Google Scholar] [CrossRef]
121. Monjezi M, Ahmadi Z, Varjani AY, Khandelwal M. Backbreak prediction in the Chadormalu iron mine using artificial neural network. Neural Comput Appl. 2013;23(3–4):1101–7. doi:10.1007/s00521-012-1038-7. [Google Scholar] [CrossRef]
122. Hasanipanah M, Bakhshandeh Amnieh H. Developing a new uncertain rule-based fuzzy approach for evaluating the blast-induced backbreak. Eng Comput. 2021;37(3):1879–93. doi:10.1007/s00366-019-00919-6. [Google Scholar] [CrossRef]
123. Ebrahimi E, Monjezi M, Khalesi MR, Armaghani DJ. Prediction and optimization of back-break and rock fragmentation using an artificial neural network and a bee colony algorithm. Bull Eng Geol Environ. 2016;75(1):27–36. doi:10.1007/s10064-015-0720-2. [Google Scholar] [CrossRef]
124. Muhammad K, Shah A. Minimising backbreak at the Dewan Cement limestone quarry using an artificial neural network. Arch Min Sci. 2017;62(4):795–806. doi:10.1515/amsc-2017-0055. [Google Scholar] [CrossRef]
125. Khandelwal M, Monjezi M. Prediction of backbreak in open-pit blasting operations using the machine learning method. Rock Mech Rock Eng. 2013;46(2):389–96. doi:10.1007/s00603-012-0269-3. [Google Scholar] [CrossRef]
126. Shirani Faradonbeh R, Monjezi M, Jahed Armaghani D. Genetic programing and non-linear multiple regression techniques to predict backbreak in blasting operation. Eng comput. 2016;32(1):123–33. doi:10.1007/s00366-015-0404-3. [Google Scholar] [CrossRef]
127. Hasanipanah M, Shahnazar A, Arab H, Golzar SB, Amiri M. Developing a new hybrid-AI model to predict blast-induced backbreak. Eng Comput. 2017;33(3):349–59. doi:10.1007/s00366-016-0477-7. [Google Scholar] [CrossRef]
128. Ruiz del Solar J. Big Data en minería. Santiago, Chile: Beauchef Minería, Universidad de Chile; 2020. [Google Scholar]
129. Estay H, Lois-Morales P, Montes-Atenas G, Ruiz del Solar J. On the challenges of applying machine learning in mineral processing and extractive metallurgy. Minerals. 2023;13(6):788. doi:10.3390/min13060788. [Google Scholar] [CrossRef]
130. Bui XN, Nguyen H, Le HA, Bui HB, Do NH. Prediction of blast-induced air over-pressure in open-pit mine: assessment of different artificial intelligence techniques. Nat Resour Res. 2020;29(2):571–91. doi:10.1007/s11053-019-09461-0. [Google Scholar] [CrossRef]
131. Bishop CM. Pattern recognition and machine learning. In: Bishop CM, Information science and statistics. Springer; 2016. [Google Scholar]
132. Chen ZS, Galatzer-Levy IR, Bigio B, Nasca C, Zhang Y. Modern views of machine learning for precision psychiatry. Patterns. 2022;3(11):3263–81. [Google Scholar]
133. Asteris PG, Koopialipoor M, Armaghani DJ, Kotsonis EA, Lourenço PB. Prediction of cement-based mortars compressive strength using machine learning techniques. Neural Comput Appl. 2021;33(19):13089–121. doi:10.1007/s00521-021-06004-8. [Google Scholar] [CrossRef]
134. Sirjani AK, Sereshki F, Ataei M, Hosseini MA. Prediction of backbreak in the blasting operations using artificial neural network (ANN) model and statistical models (case study: gol-e-Gohar iron ore mine No. 1). Arch Min Sci. 2022;21:107–21. [Google Scholar]
135. Obermeyer Z, Emanuel EJ. Predicting the future—big data, machine learning, and clinical medicine. N Engl J Med. 2016;375(13):1216–9. doi:10.1056/NEJMp1606181. [Google Scholar] [PubMed] [CrossRef]
136. Zhang Y, Yang Q. A survey on multi-task learning. IEEE Trans Knowl Data Eng. 2021;34(12):5586–609. doi:10.1109/TKDE.2021.3070203. [Google Scholar] [CrossRef]
137. Armaghani DJ, Asteris PG. A comparative study of ANN and ANFIS models for the prediction of cement-based mortar materials compressive strength. Neural Comput Appl. 2021;33(9):4501–32. doi:10.1007/s00521-020-05244-4. [Google Scholar] [CrossRef]
138. Raghu M, Gilmer J, Yosinski J, Sohl-Dickstein J. SVCCA: singular vector canonical correlation analysis for deep learning dynamics and interpretability. Adv Neural Inform Process Syst. 2017;30:6078–87. [Google Scholar]
139. Goodfellow IJ, Shlens J, Szegedy C. Explaining and harnessing adversarial examples. arXiv preprint arXiv:14126572. 2014. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools