Calculation of Mass Concrete Temperature and Creep Stress under the Influence of Local Air Heat Transfer

1  Introduction

Currently, the global annual volume of poured concrete exceeds 200,000 tons [1]. Various factors contribute to the susceptibility of mass concrete to cracking during construction, which directly reduces the bearing capacity, durability, and waterproofing of structures. Generally, the factors influencing concrete crack formation can be categorized into two groups: internal and external. Regarding internal factors, temperature stress is the primary cause of crack formation. The temperature difference between the interior and exterior of the concrete generates tensile stress. Cracks form when this stress exceeds the tensile strength [2].

Cement hydration leads to an increase in the internal temperature of concrete. At present, cement hydration is mainly described from two perspectives: mesoscopic and macroscopic. From a mesoscopic viewpoint, the widely accepted model to describe cement hydration is the Arrhenius hydration model, which is based on chemical reaction kinetics and strictly compliant with the laws of thermodynamics. The model has been extensively validated through numerous experiments [3–5]. Numerous scholars have developed concrete calculation models incorporating hydration heat and validated them with measured data. Jrg et al. introduced the concept of mesoscale in the study of concrete material properties [6]. On the mesoscale, the hydration can be described by the thermodynamic theory of non-inert porous media [7]. This theory posits that concrete, being a porous material, consists of both reactive and inert particles. As water permeates and reacts with the reactive particles, solid product particles are generated, resulting in changes in the porous medium’s volume. The hydration reaction rate is determined by the concentration of solid mass products and fluid mass on the surface of the unreacted solid core. Establishing the physical correlation between the degree of hydration reaction, the elastic modulus of concrete, and Poisson’s ratio enables the development of a chemical–mechanical model to describe concrete hydration at an early stage [8]. Numerous scholars have explored this method and ultimately formed the aging model of concrete maturity [9] and the solidification aging model [10]. Concrete is a three-phase heterogeneous composite material composed of mortar, aggregate, and an interfacial transition zone [11]. Zheng et al. [12] considered concrete as a heterogeneous material with an uneven distribution of temperature and hydration degree. By integrating 2D and 3D aggregate models with hydration reaction chemical models, they accurately simulated the distribution characteristics of the temperature field and hydration degree of early-age concrete. Furthermore, they evaluated the effects of aggregate gradation, boundary conditions, aggregate shape, and precooling measures on the concrete hydration reaction process. Du et al. [13] employed an interfacial numerical model to simulate the chloride diffusion process in concrete. The results showed that the effects of aggregate shape and distribution on chloride diffusion are negligible, while the total content of the interfacial transition zone significantly influenced chloride diffusion. Wei et al. proposed a concrete–water–thermal–chemical coupling model capable of simulating the moisture transport, heat transfer, and hydration reaction process of freshly poured concrete [14,15]. Freitas et al. [16] employed a mixed finite element model to simulate the hydration reaction process of cement, with concrete temperature and hydration degree as two field variables. They derived the Galerkin finite element scheme for concrete temperature-chemical coupling. These studies are of great significance in elucidating the temperature rise mechanism of early-age concrete and the hydration exothermic process.

Regarding macroscopic characteristics, Luther et al. [17] examined the temperature variations in 30 mass concrete structures across North America, including dams, raft foundations, bridge pier foundations, reservoir foundations, and caissons. These case studies clarified the concrete mix ratio (including slag-containing cement) and the temperature variation caused by the ratio. Liu et al. [18] employed a support vector machine model to predict the temperature field formed by the hydration exothermic action of mass concrete. They established correlations between the post-pouring temperature of pile foundations and various influencing factors, enabling short-term temperature predictions. Additionally, they conducted a comparative study using the Back propagation model. Sargam et al. [19] used the self-programmed program ConcreteWorks to predict the thermodynamic parameters of concrete. First, thermostatic and semi-adiabatic tests were used to determine the thermodynamic parameters of the mixture (e.g., cementation performance and mix ratio). Then the parameters were used as inputs to predict the temperature variation law, maturity, and compressive strength of concrete. Finally, these predictions were compared with the real-time monitoring results of the bridge foundation. Zhao et al. [20] conducted numerical tests on hydration heat parameters and found that increasing the thermal conductivity of concrete and reducing the specific heat and temperature rise coefficient could reduce the maximum temperature of concrete. However, other thermal parameters showed no significant effect on the maximum temperature. Ouyang et al. [21] established a distributed temperature monitoring sensing system of mass concrete using an optical backscattering reflectometer, an optical fiber cable, and other equipment, and used an inversion algorithm to determine the thermodynamic parameters of concrete. This approach effectively enhanced temperature and crack control efficiency during concrete construction, enabling intelligent temperature control of mass concrete.

The deformation of concrete increases with time under continuous external forces, a phenomenon known as concrete creep. Concrete creep has been studied for over 100 years. In 1905, Woolson discovered that concrete in steel tubes exhibited flow characteristics under high stress. American society for testing materials considers that concrete creep is related to concrete plasticity. Moreover, Neville et al. [22] investigated the creep and creep recovery of concrete through experiments. Davis conducted a systematic study of creep. Through continuous exploration in recent years, engineers have gained a profound understanding of concrete creep.

The creep of concrete is affected by both internal and external factors. Generally, the main laws are as follows: The greater the stress, the greater the concrete creep. The earlier the load-holding age, the greater the creep. The greater the curing temperature and humidity, the smaller the creep. Once the specimen is subjected to loads, the higher the ambient temperature and the lower the humidity, the greater the creep. The greater the cement dosage, the greater the creep. The smaller the water-to-cement ratio, the smaller the creep. Regarding the effect of aggregate, the higher the material quality, gradation, and elastic modulus, the smaller the creep. In addition, cement type, water-reducing agent, and air-entraining agent also affect creep [23–25]. The effect of temperature on concrete creep is complex. Generally, with the increase in temperature, the elastic modulus of concrete decreases, and the creep rate increases. However, at the early age of the concrete, higher temperatures can increase the cement hydration reaction rate, accelerate the concrete hardening, and decrease the creep deformation. Furthermore, the continuous action of thermal stress caused by temperature differences also affects concrete creep. Khan’s test showed that during the curing period, the creep of concrete at 40°C was greater than that at room temperature (20°C) in the early stage of the curing period, but this trend reversed at the end of the curing period [26]. Regarding the effect of concrete shape, creep is related to the effective thickness, volume-to-surface ratio, and average thickness. The creep coefficient (the ratio of creep to elastic deformation) of concrete gradually decreases with an increase in the volume-to-surface ratio.

The creep behavior of concrete under constant load can be described using various mathematical functions, including logarithmic, power, hyperbolic, exponential, polynomial exponential, and power exponential functions. Polynomial exponential functions and power exponential functions proposed by Zhu Bofang are commonly used in China. The calculation theory of creep mainly involves methods for calculating creep under variable stress, including the effective modulus method, aging theory, elastic creep theory, elastic aging theory, and residual flow theory. American Certification Institute, International Federation for Structural Concrete and various Chinese scholars have proposed calculation formulas for creep function, such as American Concrete Institute 209 (ACI209), Euro-International Committee for Concrete-International Federation for Prestressing (CEB-FIP), B3 model, and GL2000 model. Briffaut et al. [27,28] studied the mechanical properties of early-age mass concrete through a thermal cycling test under active constraints and established a coupling model of concrete creep and damage. Furthermore, concrete also exhibits stress relaxation characteristics, in which stress decays as concrete strain continues to increase. This phenomenon is typically described by the relaxation coefficient, which is the ratio of stress to the initial elastic stress at any given time. The factors causing relaxation are similar to those causing creep, but relaxation develops more rapidly than creep. Generally, the relaxation coefficient can be calculated from creep test data [29,30].

In previous construction simulation studies, the heat exchange between the environment and the concrete was simulated by assigning corresponding boundary conditions to the concrete. This simulation method can generally meet the requirements of engineering calculations. However, for tube-shaped concrete structures, where airflow typically has a single inlet and outlet, internal temperatures can significantly increase owing to the influence of hydration heat. The use of temperature curves and thermal boundaries may not adequately reflect the impact of local temperature changes, leading to certain deviations in calculation results. Heat release from concrete hydration directly increases local air temperature and enhances the convection of hot and cold air. However, airflow promotes the dissipation of heat from the concrete surface, and changes in the concrete temperature field can lead to alterations in the stress field. Considering the above, it is essential to develop a method for solving the temperature field of air–concrete coupled heat transfer. This method should be able to calculate the temperature field of concrete during the construction period of tube-shaped structures.

Numerous scholars have investigated the mechanical properties of early-age concrete. One study [31], utilizing experimental data, outlined the evolutionary patterns of concrete creep in this context. Briffaut et al. [28] analyzed the early-age behavior of massive concrete structures and investigated the effects of thermal boundary conditions and thermal property evolutions on temperature and stress fields. Lackner et al. developed a chemoplastic material model for simulating early-age cracking in concrete structures, considering the constitutive law and numerical analyses [32]. Stefan et al. [33] predicted the elastic properties of cement pastes at early ages, which is crucial for elucidating the mechanical behavior of early-age concrete. Many scholars have investigated fluid–structure coupled heat transfer. Mardmomen et al. predicted the amplitude and time of peak temperatures of early concrete at different locations [34]. Chen et al. proposed an on-site method to obtain the concrete adiabatic temperature rise (ATR) by simply using the measured temperature at the center of the cube [35]. Smolana et al. compared and analyze the calculated results of different prediction models with the actual results [36]. Lim et al. conducted experimental and simulation studies on the viscoelastic mechanical characteristics of early concrete [37]. In structural–air heat transfer research, Agnoletto et al. [38] focused on special the components of building envelopes, including double-pane windows, open cavities with air circulation, and opaque walls with insulation. These components differ from standard components in terms of their design features and heat transfer mechanisms. Numerical simulation showed that double-pane windows provided improved insulation compared with single-pane windows, while open cavities facilitated convective and radiative heat exchange processes, enhancing energy efficiency. The insulated opaque wall reduced heat loss, thereby improving thermal performance. These special components exhibit unique characteristics that differentiate them from standard building elements and contribute to their efficiency in utilizing solar energy for heating purposes. One study [39] analyzed the transient heat conduction behavior of a microcantilever under various heating methods. The study explored the temperature response and heat transfer dynamics between the microcantilever and its surrounding air environment, considering conditions such as steady heating, pulse heating, sinusoidal heating, and repeated pulses with a duty cycle. Key aspects covered included simulation under temperature fields, analysis of heat diffusion, evaluation of thermal conductance and heat flows, determination of time constants, and discussion on effective heat transfer coefficients.

The innovation of the present paper lies in conducting a fluid-structure coupled heat transfer analysis on concrete components during the construction phase and in calculating the variation of the structural stress field based on the computed temperature field and concrete casting time. Moreover, the evolution of tensile stress in concrete is thoroughly analyzed. This paper first analyzes the pouring temperature simulation of the air–concrete coupled heat transfer involved in the construction simulation. Then, it validates the solution method for the temperature field model of air–concrete coupled heat transfer. Finally, using a ship lock head structure as a case study, the paper analyzes the impact of airflow in the corridor on concrete temperature and creep stress. Moreover, the time-varying characteristics of temperature creep stress during construction are summarized.

2  The Temperature Field Solution Method of Concrete

2.1 Air–Concrete Conjugate Heat Transfer Theory

The conjugate heat transfer theory first emerged in simulation research on electronic components, wings, engines, and other heat dissipation components [40]. Owing to the large volume of hydraulic structures, heat exchange with air primarily occurs through natural convection heat dissipation after concrete pouring. For laminar fluid, the momentum equation is expressed as follows [41]:

ddt∫VρvdV+∫Sρv⊗(v−vm)⋅ndS=−∫V∇pdV+∫Sτ⋅ndS+∫VfdV(1)

Here, V denotes the volume of air, S denotes the surface area of air, n is the normal direction outside the surface, p denotes pressure v denotes fluid velocity, vm denotes the velocity of the moving mesh, f denotes the volume force, and τ denotes the viscous shear stress.

The incompressible fluid continuity equation is expressed as follows:

∇⋅v=0(2)

The energy equation of non-isothermal fluid is expressed as follows [42]:

ddt∫VρCpθdV+∫SρCpθ(v−vm)⋅ndS=∫VrdV−∫Sq⋅ndS(3)

where Cp is the specific heat at constant pressure, θ is the fluid temperature, q is the heat flux, and r is the external heat input per unit volume.

Eqs. (1)–(3) constitute the Navier-Stoke equations. Calculating the Reynolds number of airflow inside the corridor structure is necessary. The Reynolds number is calculated as follows:

Re=ρvdμ=vdν(4)

where μ is the dynamic viscosity coefficient, Pa⋅s; ν is the kinematic viscosity coefficient, m2⋅s; v denotes fluid velocity, m/s; ρ denotes fluid density, kg/m3; and d is the hydraulic radius, m. d=A/χ, and χ is the wetted perimeter. For the ship lock corridor structure, d=3×3.5/[(3+3.5)×2]=0.08076m. For air at room temperature, ρ=1.165kg/m3, and ν=1.57×10−5m2⋅s. The surface air velocity is within 4 m/s. For calculations with surface air velocity of 1 m/s and 4 m/s, Re will be much greater than 2300, and the airflow in the corridor is assumed to be turbulent owing to the presence of disturbance.

The Spalart–Allmaras (SA) model is a prominent turbulence model [43] that effectively simulates the fluid characteristics of air. The governing equation is as follows:

ddt∫Vρv~dV+∫Sρv~(v−vm)⋅ndS=∫Vρcb1S~v~dV−∫Vρcw1fw(v~d)2dV+∫Vρ(1+cb2)σ∇{(v+v~)∇v~}dV−∫Vρcb2σ(v+v~)∇⋅∇v~dV(5)

The damping functions and model coefficients used in the above two equations are defined as follows: fw=g(1+cw36g6+cw36)16, where fw is an empirical function of r; g=r+cw2(r6−r), where g is an intermediate variable; and r is an intermediate variable. S~=S+v~κ2d2fv2, where d is the normal distance from the wall, and S~ is an intermediate variable. fv1=χ3χ3+cv13, where fv1 is empirical functions in the turbulence model. fv2=1−χ1+χfv1, where fv2 is an empirical function in the turbulence model. χ=v~v, v=μρ, and ρ is density. μ is the molecular dynamic viscosity, and v is the molecular kinematic viscosity. χ is an intermediate variable. r=v~S~κ2d2, S=2RijRij, and S the magnitude of the vorticity. κ is Karman constant. v~ is the working variable of the turbulence model. Rij=12(∂ui∂xj−∂uj∂xi), where Rij is the strain-rate tensor. xi and xj are Cartesian coordinates, and the effective turbulent viscosity is defined as vt=v~fv1. The SA model coefficients are shown in Table 1.

The pressure of air on concrete can be ignored, and the heat transfer of concrete is described by (6) [33]

∂T∂t=λρc(∂2T∂x2+∂2T∂y2+∂2T∂z2)+∂Q∂t(6)

where λ denotes the heat conductivity coefficient of concrete, c is the thermal capacity of concrete, ρ is the density of concrete, and Q is the total concrete hydration heat.

The total hydration heat Q(τ) of concrete is related to the adiabatic temperature rise as follows [38]:

Q(τ)=ρcθ(1−e−aτb)(7)

where θ is the adiabatic temperature rise of concrete, °C; ρ is the density of concrete; c is the specific heat of concrete; and a and b are test parameters. τ represents the age of concrete. Constants a and b serve as fitting parameters for the adiabatic temperature rise curve derived from experiments.

Heat transfer from a solid to its internal fluid can occur through conjugate heat transfer, while the dissipation of heat from the fluid to the external surface of the solid can occur through convective heat dissipation, as follows:

q=h(ts−tf)(8)

where q is the heat exchanged between the solid surface and the fluid surface per unit area. ts and tf denote the temperatures of the solid surface and the adjacent fluid, respectively. h is the surface convective heat transfer coefficient.

2.2 Coupled Solution

Coupled equations are incorporated to ensure that variables such as heat flow and temperature at the interface between the fluid and solid are balanced. This paper employs the SIMULIA Co-Simulation Engine build file to define coupling and rendezvous schemes for conjugate heat transfer and enables fluid-to-solid heat dissipation simulations by specifying fields exchanged across a co-simulation interface. The build file is established through the following steps:

1) The element surface heat flux and node heat flux transferred from fluid to solid or solid to fluid on the co-simulation interface are expressed as in Appendix 1.

2) The data types of incoming and outgoing fluids or solids on the interface are clarified, and the transmission fields from fluid to solid and solid to fluid are defined.

3) An iterative coupling scheme is defined. The exchange order and frequency between co-simulation analyses are determined. The coupling algorithm and the size of the coupling step are selected.

This approach enables the completion of air–concrete conjugate heat transfer calculations in the corridor through the transmission of fluid–solid boundary data, representing an indirect method for fluid–structure coupling calculation. Through conjugate heat transfer calculations, the air temperature and the velocity and pressure distribution in the corridor can be obtained. These parameters can be mapped to the corresponding structure boundary to enable air–concrete coupled heat transfer analysis.

3  Solution Method of Elastic Creep Stress

The elastic creep stress theory can describe the constitutive relationship of concrete [38]. The strain increment of concrete at time Δt is as follows:

{Δεn}={Δεne}+{Δεnc}+{ΔεnT}(9)

where {Δεne} is the elastic strain increment, {Δεnc} is the creep strain increment, and {ΔεnT} is the temperature strain increment.

According to reference [44], the sum of elastic strain increment and creep strain increment can be expressed as

{Δεne}+{Δεnc}={ηn}+1+C(tn,τn¯)E(τn¯)[Q]{Δσn}(10)

where {ηn}=∑s=1m[1−exp(−rsΔτn)]{ωsn}, and {ωsn} are state variables that change with time:

{{ωsn}={ωs,n−1}exp(−rsΔτn−1)+[Q]{Δσn−1}Ψs(τn−1¯)exp(−0.5rs Δτn−1){ωs1}={Δσ0}Ψs(τ0¯)(11)

C(t,τ)=Ψs[1−e−r(t−τ)](12)

The temperature strain increment is expressed as

{ΔεnT}=[αΔT,αΔT,αΔT,0,0,0]T(13)

In summary, the concrete stress–strain constitutive relationship can be obtained [46]

{Δσn}=E(τn¯)1+E(τn¯)C(tn,τn¯)[Q]−1({Δεn}−{ηn}−{Δεne}+{Δεnc})(14)

The temperature of concrete hydration heat was calculated using the HETVAL subroutine in ABAQUS software. The HETVAL subroutine is written in FORTRAN language, and its interface is depicted in Appendix 2.

Where, TEMP represents the unit temperature; STATEV represents the state variable, which is used to store the current pouring time of concrete; and DTIME represents the time increment.

The elastic creep stress of concrete is calculated using the UMAT subroutine. This subroutine is written in FORTRAN language, and its interface is provided in Appendix 3. Among its components, DDSDDE represents the stiffness matrix, utilized for writing the concrete viscoelasticity matrix; STATEV represents a state variable and is used in the formulation of Eq. (12); STRESS denotes stress; PROPS denotes input parameters; and DTIME indicates the time increment.

The sequential coupling method is employed to solve the concrete stress field. The basic idea of the method is to first use the HETVAL subroutine to solve the temperature field of the structure. Subsequently, the temperature field is imported, and finally, the UMAT subroutine is utilized to solve the stress field.

ABAQUS offers a convenient interface for importing temperature fields in stress analysis. Generally, the .odb file containing temperature calculation results can be directly imported. However, the result file generated by the conjugate heat transfer solution (the ABAQUS .odb file) cannot be directly imported into subsequent structural temperature stress calculations. Node temperatures at each time step can be assigned, and the .inp file can be constructed using Python. The specific implementation method is as follows:

1.    The temperature field result is derived. The writeFieldReport command of ABAQUS is used to export the concrete temperature field in batches by time step. The node number and node temperature are formed.

2.    The temperature stress solution file, which imports node temperatures, is constructed. Each analysis step of the .inp file is created using the write command in Python. The construction of each analysis step is outlined in Appendix 4, with the core process involving the cyclic assignment of temperatures to each node using the *Temperature keyword.

Through the above method, the temperature value can be assigned to all nodes in the model at each time step. Subsequently, the variation of temperature strain at each position can be obtained according to temperature changes. Finally, the temperature creep stress value can be calculated according to Eq. (14).

4  Method Validation

References [47] and [48] have conducted detailed experimental research on the temperature field of concrete, and the calculation method in this paper was verified based on the experimental results. The size of the concrete test block is 1 m × 1 m × 1 m, the temperature conductivity coefficient is 0.00328m2/h, the thermal conductivity coefficient is 7.921kJ/∘C⋅m⋅h, and the adiabatic temperature rise is θ(τ)=26.5(1−e−0.7751τ1.6). The concrete is positioned on supports 0.4 m above the ground. Its front and back surfaces have bamboo glue formwork of 1.2 and 1.5 cm thickness, respectively, with a thermal conductivity of 0.837kJ/∘C⋅m⋅h. The top surface is covered with thermal insulation quilt, which has a thermal conductivity of 0.1549kJ/∘C⋅m⋅h. The left, right, and bottom surfaces are covered with 1 cm steel templates, with a thermal conductivity of 163.29kJ/∘C⋅m⋅h. Fig. 1 depicts the air–concrete heat transfer experiment diagram. (a) illustrates the overall model, with the air area forming a rectangular space. The model is shown in Fig. 1. The air inlet velocity boundary is set at 2 m/s, with the inlet temperature boundary matching the ambient temperature shown in Fig. 1c. The outlet boundary condition is set at 0 Pa. (b) presents the concrete model. A1–A6 and E1 denote the test monitoring points, where A1–A6 represent positions 3, 6, 9, 13, 20 and 30 cm away from the center of the front surface, respectively, while E1 marks the center of the concrete. The calculated temperature values at each position are used to verify the method.

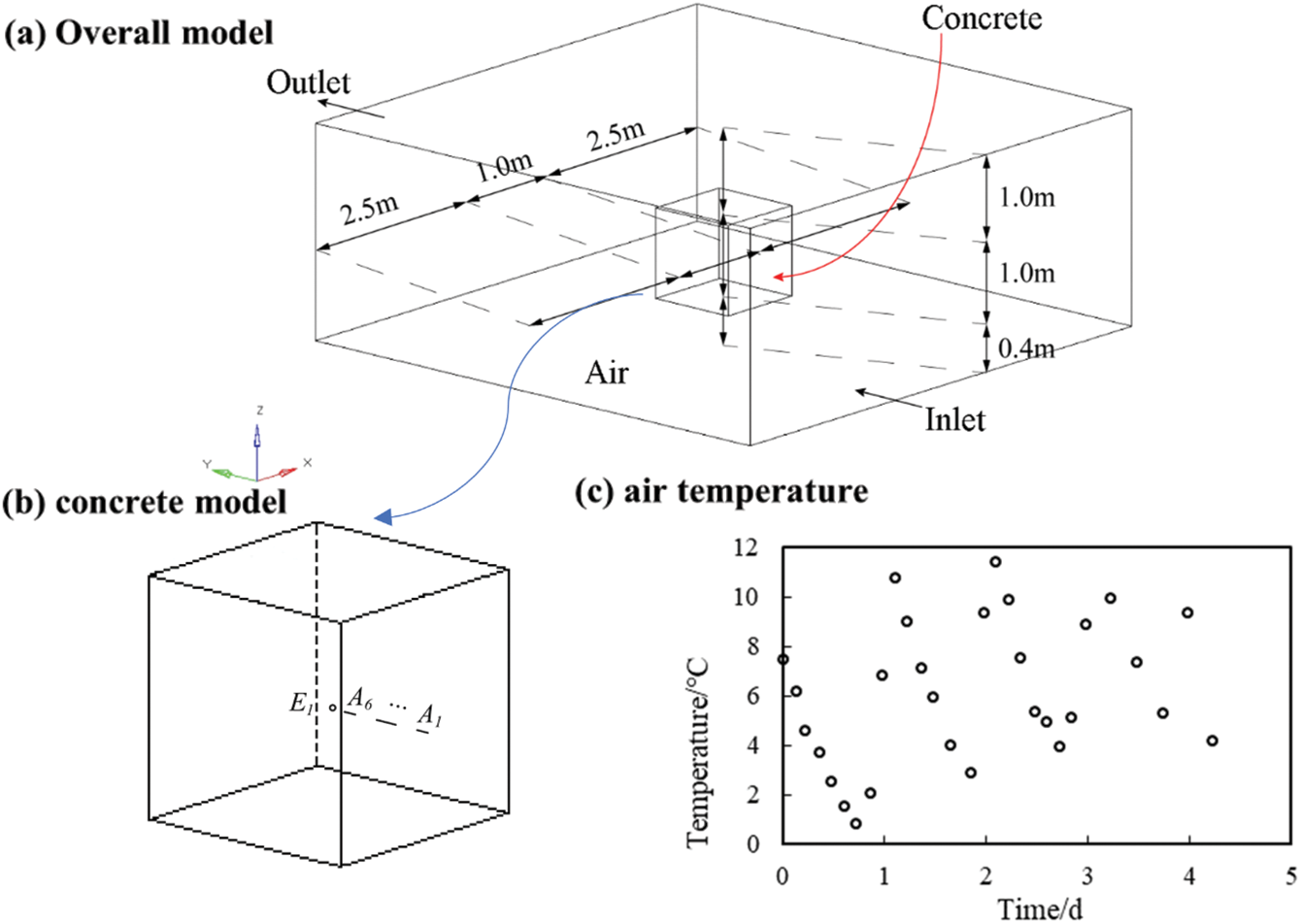
Figure 1: Air–concrete heat transfer experiment diagram

Fig. 2 displays the cloud map depicting concrete temperature (°C), air temperature (°C), air velocity (m/s), and air pressure (Pa) on day 1.75 after the concrete reaches its highest temperature. The highest temperature of the concrete reaches 20.37°C at the center, while the lowest temperature is 6.25°C at the corners of the windward side. Additionally, the surface center temperature varies from 14.45°C to 16.79°C. The air temperature cloud map indicates that the air temperature on the windward side of the concrete is significantly lower than that on the leeward side and the bottom surface. Fig. 3 compares the experimental and simulated temperature values of test points A1–A6 and E1 in the sample. The test results agree well with the model analysis results. The temperature both inside and outside the concrete gradually increases, with the temperature difference between the inside and outside of the concrete reaching its maximum on day 1.75.

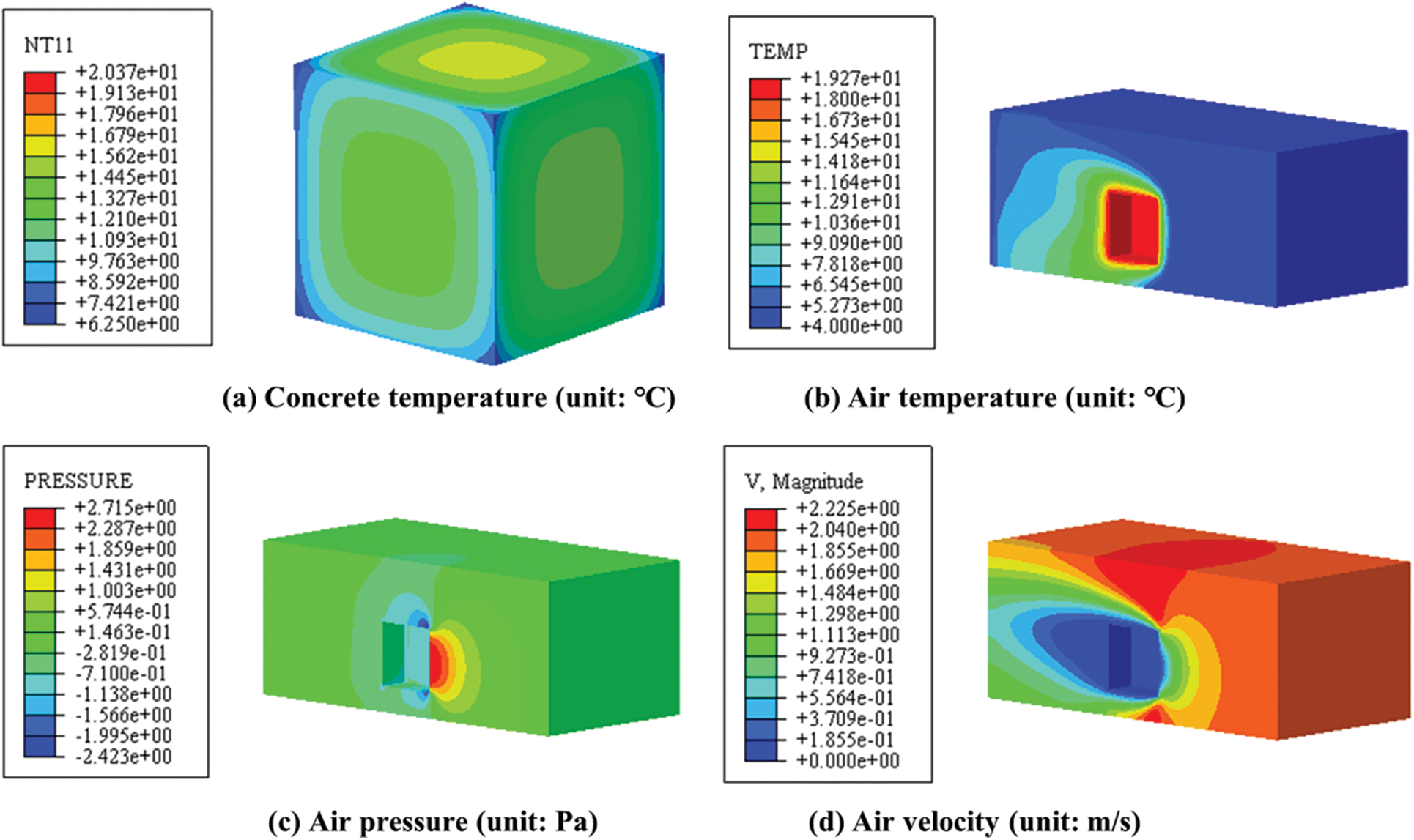
Figure 2: Calculation results for day 1.75

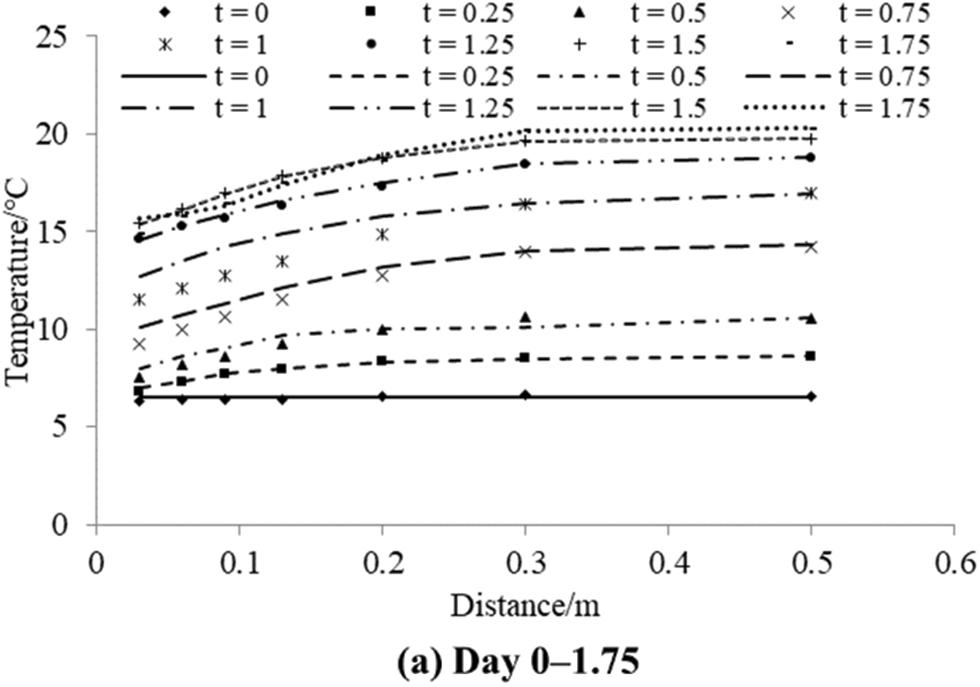
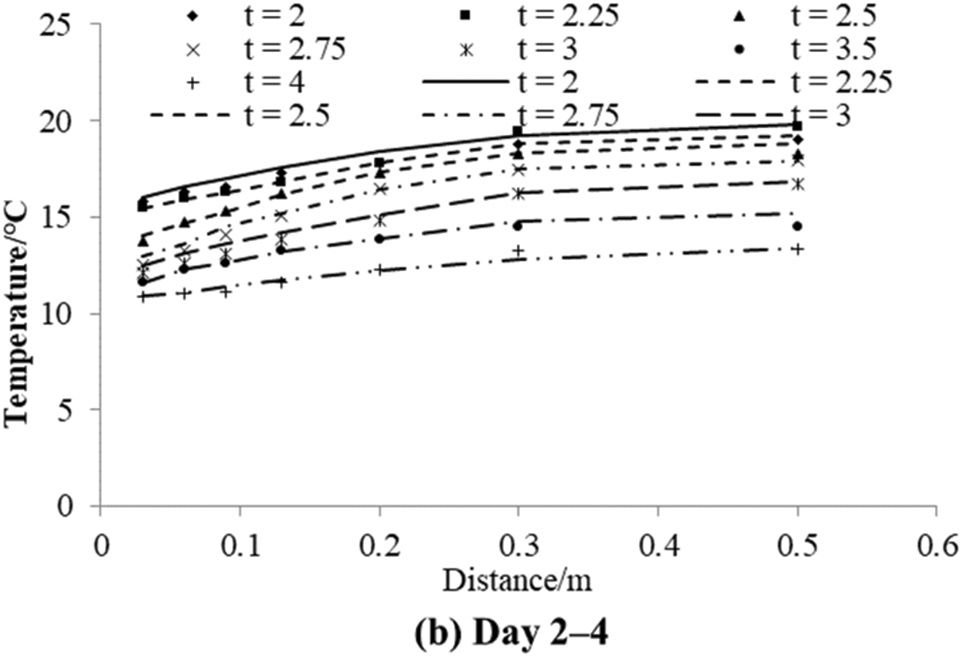
Figure 3: Comparisons between the measured and simulated temperature values at the measuring points in the sample (The points represent the test results, and the lines represent the calculation results. Unit: °C)

5  Example

5.1 Basic Information and Calculation Parameters

The ship lock head is depicted in Fig. 4. The formwork was removed 7 d after the bottom plate was poured. Following a 35-day interval, the first layer of soil was backfilled, and the left and right corridors were poured after an additional 100 d. The wooden formwork was removed after the corridor had been poured for 7 d, and subsequent construction commenced after a 42-day interval. This paper primarily focuses on analyzing the air heat transfer process within the corridor.

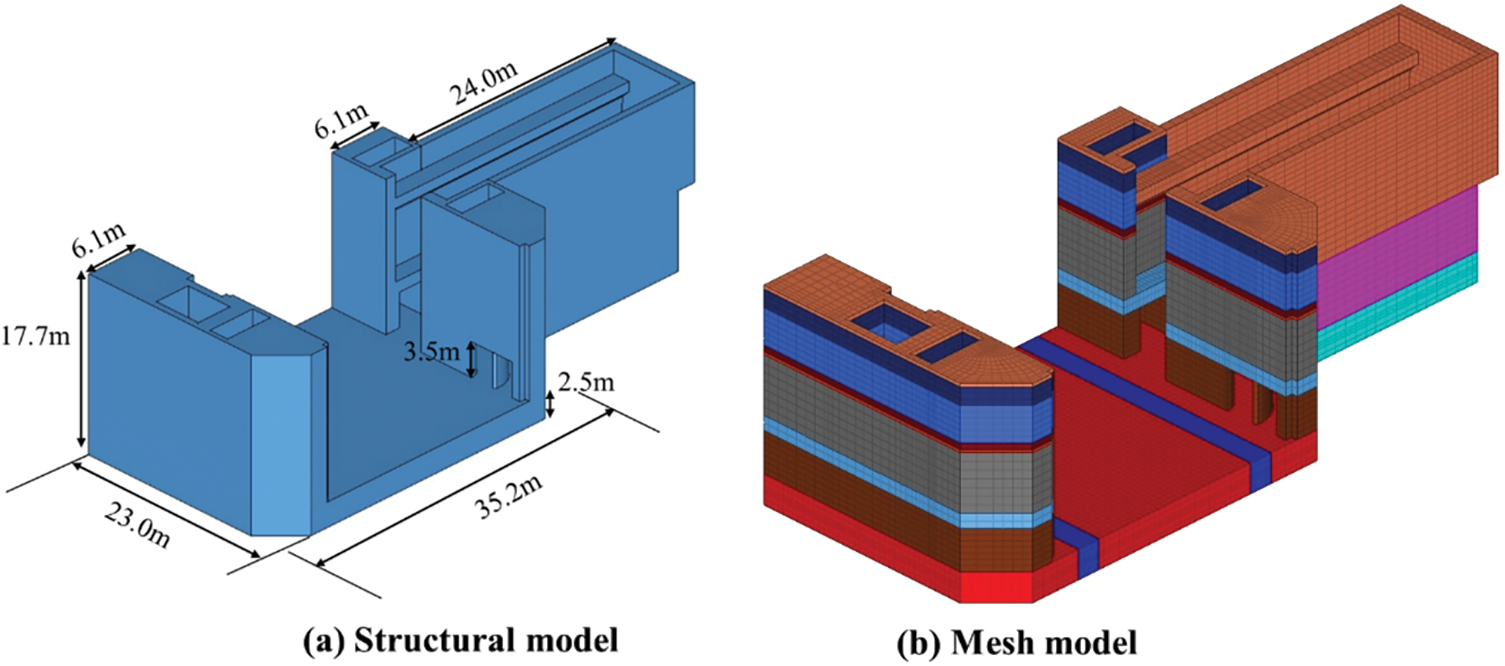
Figure 4: Ship lock head and grid model

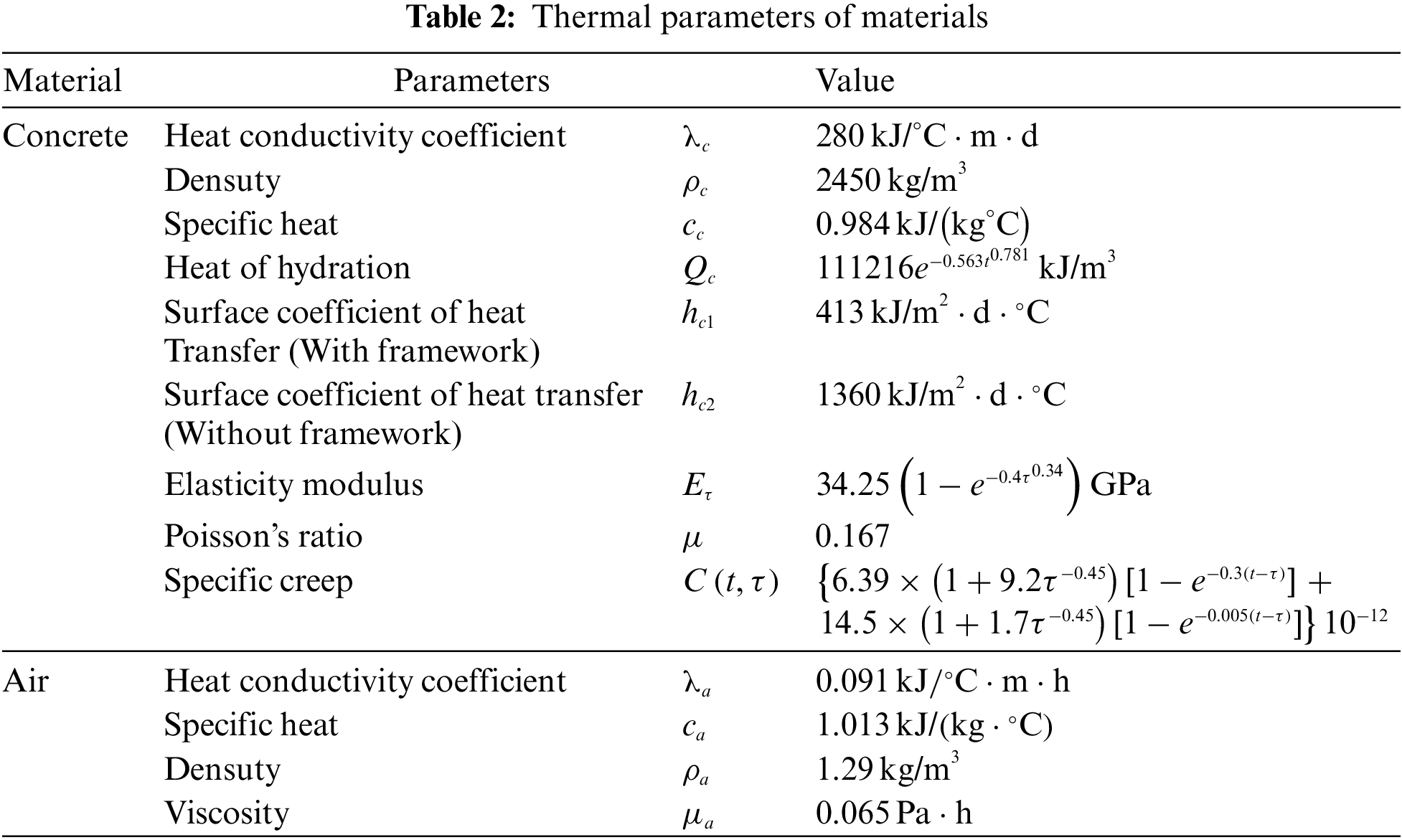
Fig. 5 illustrates the air area of the corridor. The coupled heat transfer process between air and concrete in the ship lock corridor has not been considered in previous studies. The conjugate heat transfer process of air and concrete under different flow rates was simulated to complete the air–concrete coupled heat transfer analysis in the ship lock corridor. The influence of corridor wind speed on concrete pouring was also explored. Table 2 presents the thermal parameters of concrete, air, and the mechanical parameters of concrete. Reference [49] pointed out that the surface wind speed in the middle region varied within the range of 1.6–3.4 m/s. In the present study, three working conditions of 1, 4 m/s, and no wind were considered.

Figure 5: Air area in corridor

5.2 Influence of Air Flow in Corridor on Temperature and Stress of Ship Lock

5.2.1 Traditional Calculation Method

The traditional calculation method involves directly assigning heat dissipation boundary conditions around the concrete. In this case study, the concrete has a heat dissipation coefficient of 413 kJ/m2⋅d⋅ ∘C before formwork removal, and it increases to 1360 kJ/m2⋅d⋅ ∘C after formwork removal. The formwork was removed after 7 d of casting in the canal. The Fig. 6 depicts a contour map of temperature distribution in a horizontal section of the lock chamber approach channel. According to the graph, the maximum temperatures in the channel at 25 h, 5 d, 15 d, and 42 d are 57.19°C, 46.47°C, 24.2°C, and 20.13°C, respectively.

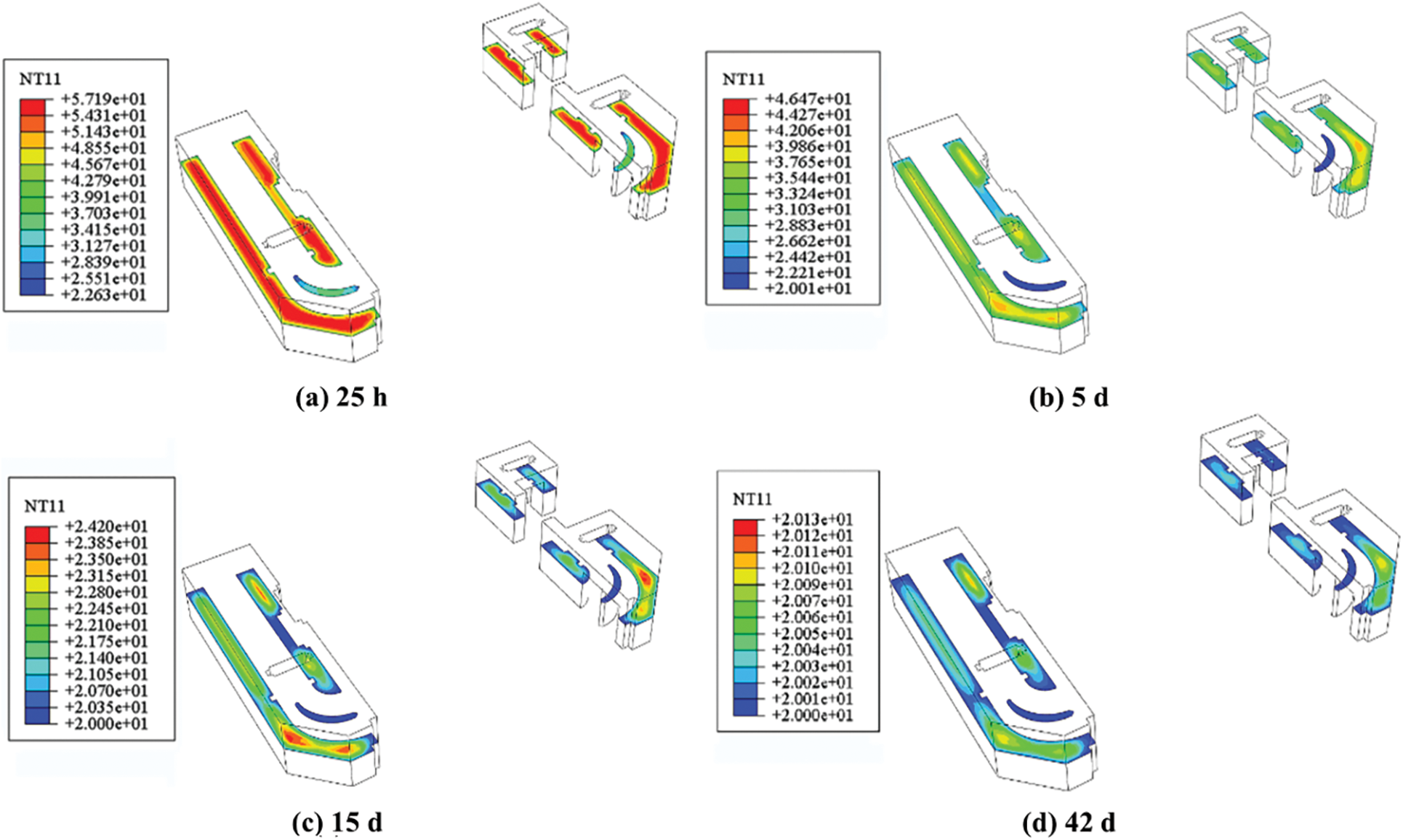
Figure 6: Horizontal profile temperature cloud diagram of ship lock corridor (unit: °C)

Fig. 7 shows the tensile stress cloud diagram of ship lock corridor. The maximum tensile stress is predominantly distributed at the chamfer location where the approach channel contacts the bottom plate. Compared with the windless condition, there is a noticeable reduction in the maximum tensile stress at each time point. At 25 h, 5 d, 15 d, and 42 d, the maximum tensile stresses in the approach channel are 0.448, 0.189, 0.981 and 1.166 MPa, respectively.

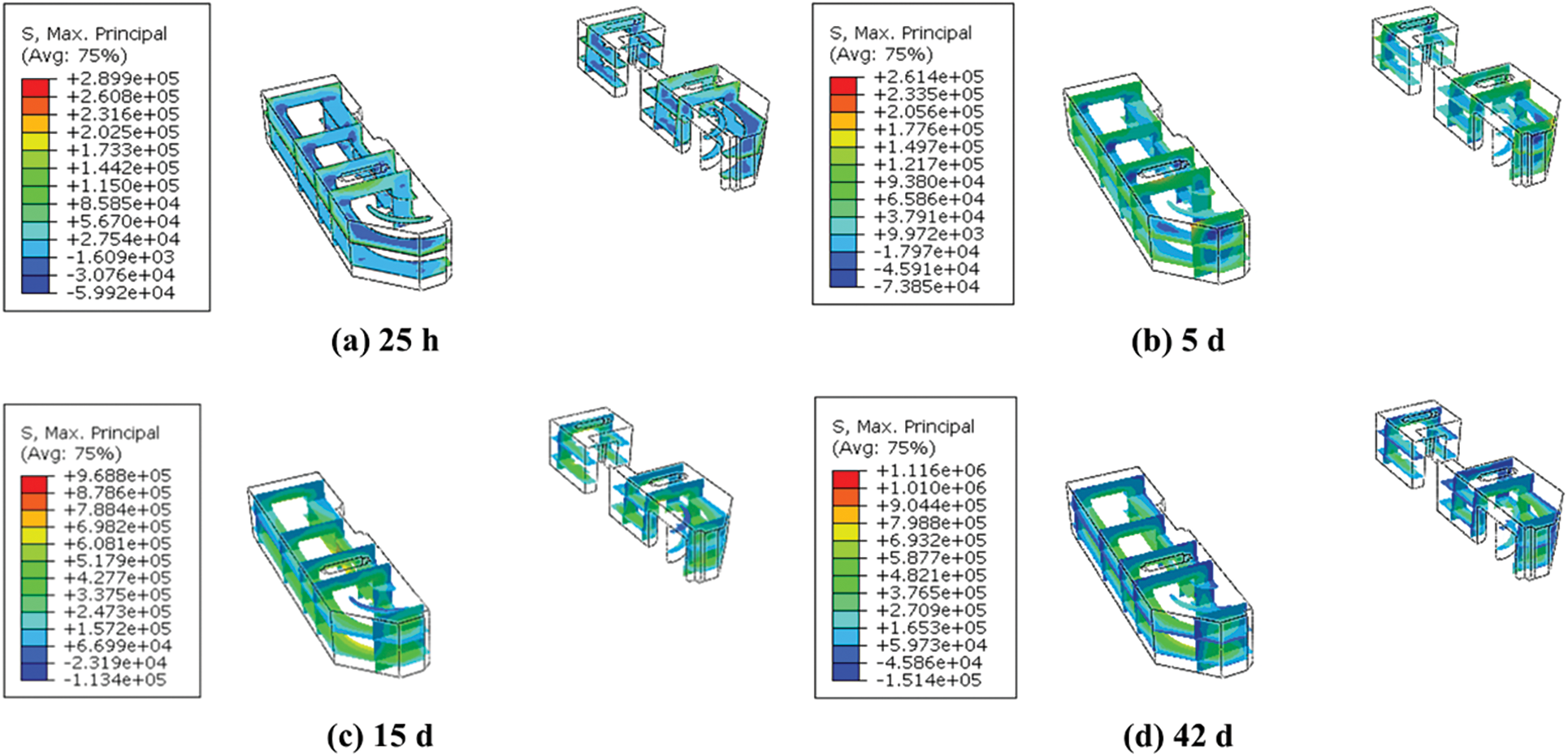
Figure 7: Tensile stress cloud diagram of ship lock corridor (unit: Pa)

5.2.2 Wind Speed of 1 m/s

Fig. 8 shows the temperature distribution cloud map of the ship lock corridor and the horizontal profile of the air at an inlet velocity of 1 m/s. Fig. 9 shows the temperature distribution cloud map of the ship lock corridor profile along the river at an inlet velocity of 1 m/s. The airflow promotes heat dissipation on the inner surface of the corridor. The maximum temperature of the corridor and air are 57.08°C and 52.3°C, respectively, at 25 h; 47.16°C and 38.61°C, respectively, at 5 d; 26.99°C and 24.71°C, respectively, at 15 d; and 20.15°C and 20.13°C, respectively, at 42 d. Compared with the case in which the airflow is not considered, the temperatures of the inner surface and the center of the corridor drop more significantly. Compared with the no-wind condition, the maximum temperature of the corridor at 25 h, 5 d, 15 d, and 42 d decreases by 1.47°C, 7.96°C, 12.66°C, and 5.80°C, respectively, while the maximum air temperature drop was 5.51°C, 16.51°C, 14.55°C, and 6.79°C, respectively.

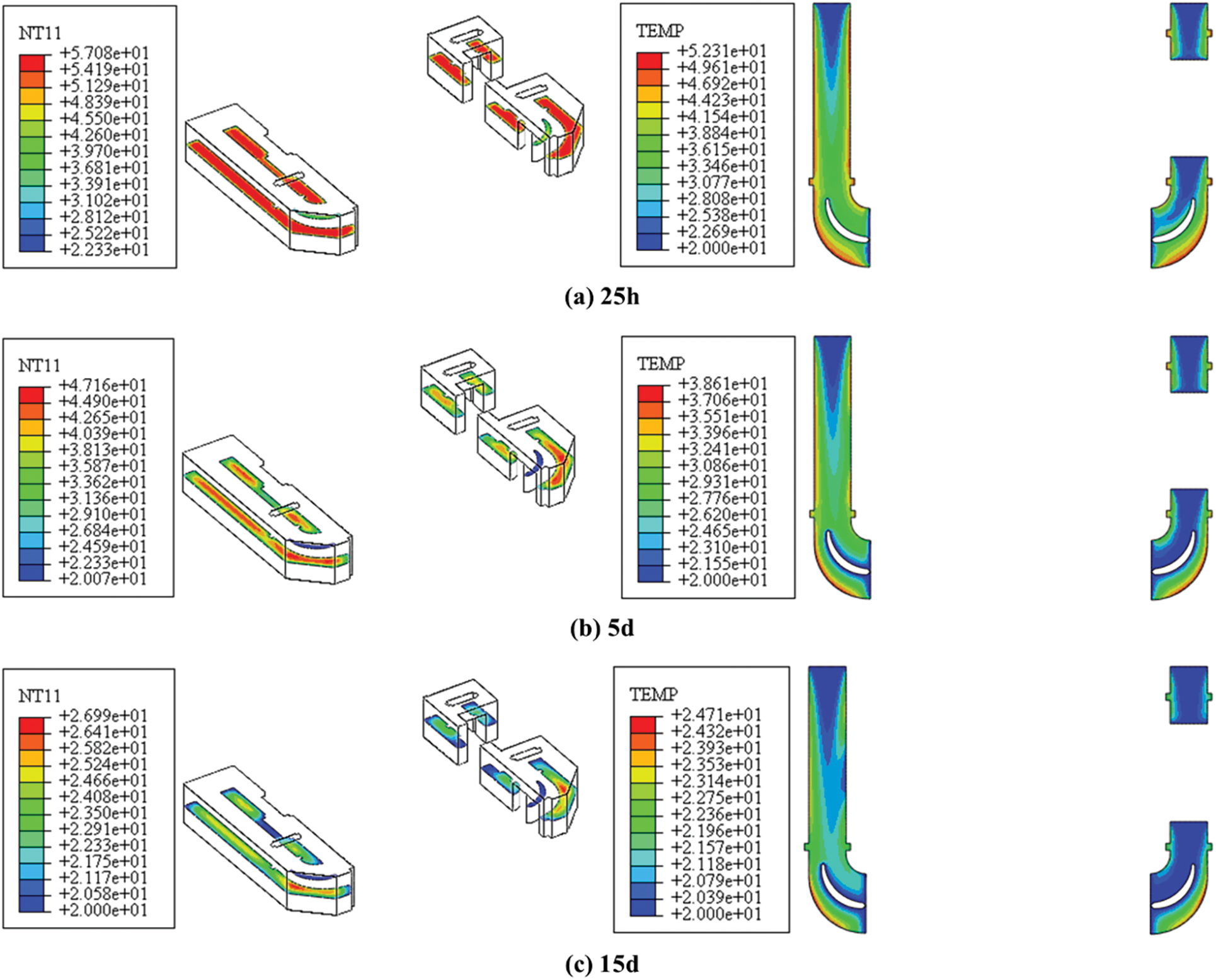
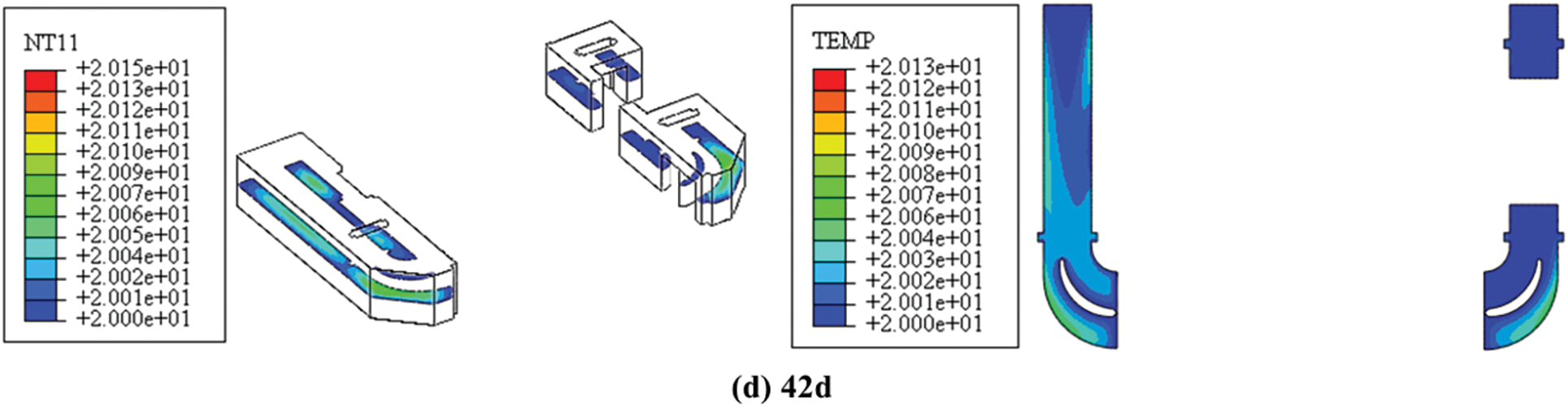
Figure 8: Temperature distribution cloud diagrams of the ship lock corridor and air along the horizontal profile (unit: °C)

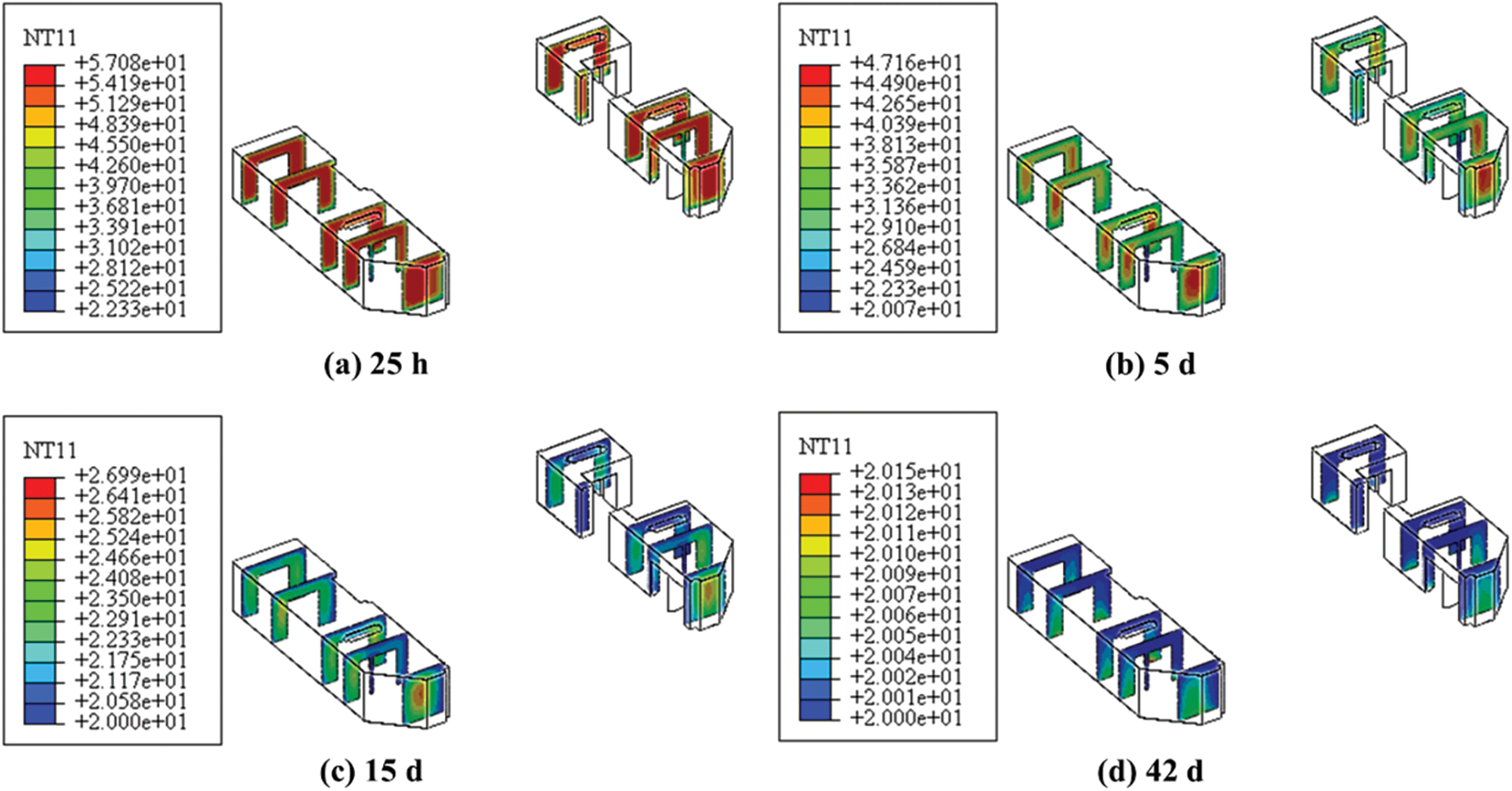
Figure 9: Cloud diagrams of temperature distribution along the river profile of the ship lock corridor (unit: °C)

Figs. 10 and 11 present cloud maps of the air velocity and pressure distributions at the inlet velocity of 1 m/s, respectively. Owing to the corridor’s structural design, the fluid bifurcates at the outlet section, with one branch experiencing significantly higher flow velocity than the other. The fluid pressure uniformly increases from the outlet toward the inlet. The velocity field exhibits minimal changes throughout the calculation period, while the pressure at each position gradually decreases over time. The maximum pressure recorded is 43.52 Pa at 25 h, 42.32 Pa at 5 d, 41.50 Pa at 15 d, and 41.34 Pa at 42 d, respectively. The maximum flow velocity at each moment is ~2.18 m/s.

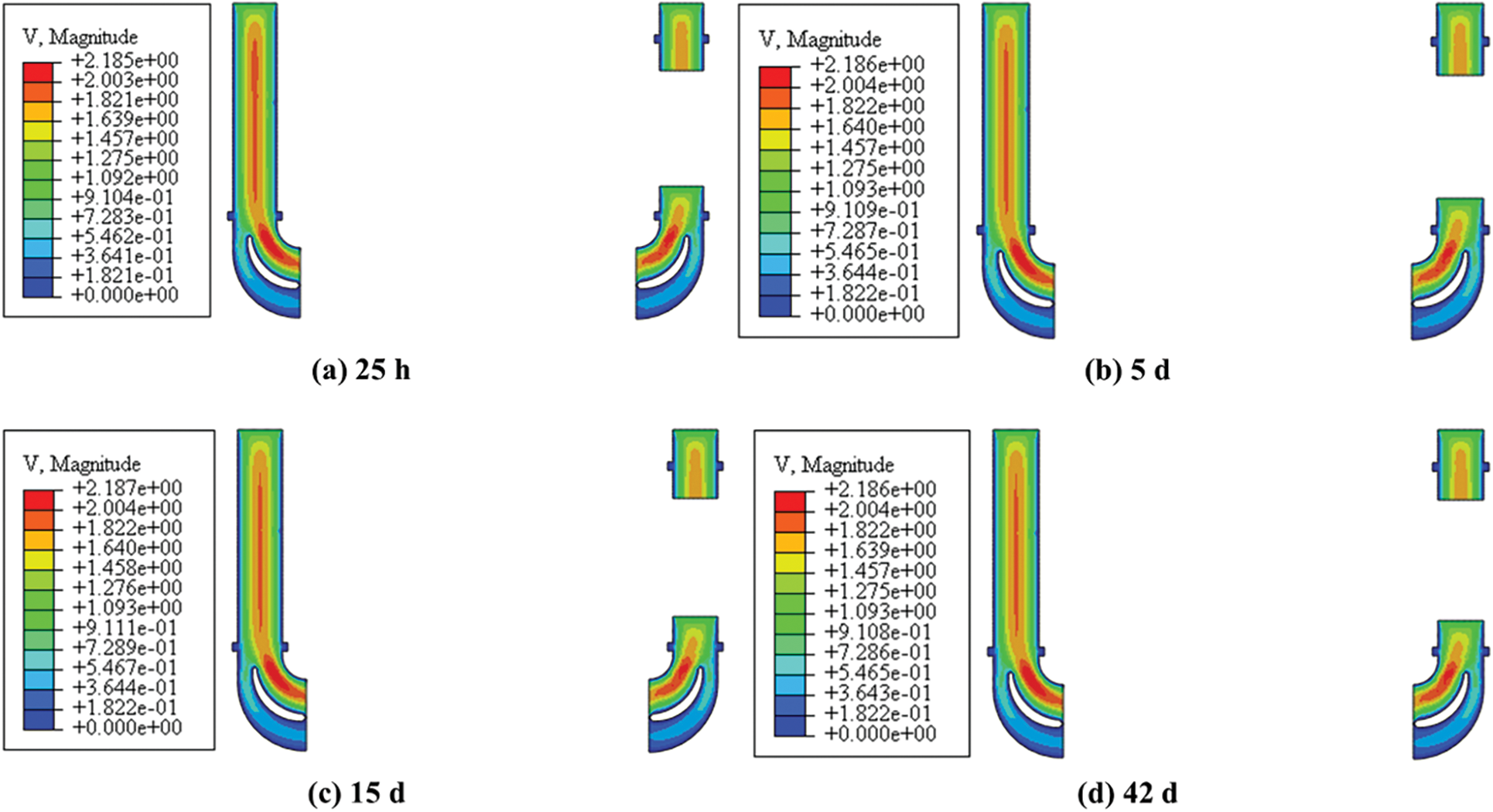
Figure 10: Air velocity cloud diagram (unit: m/s)

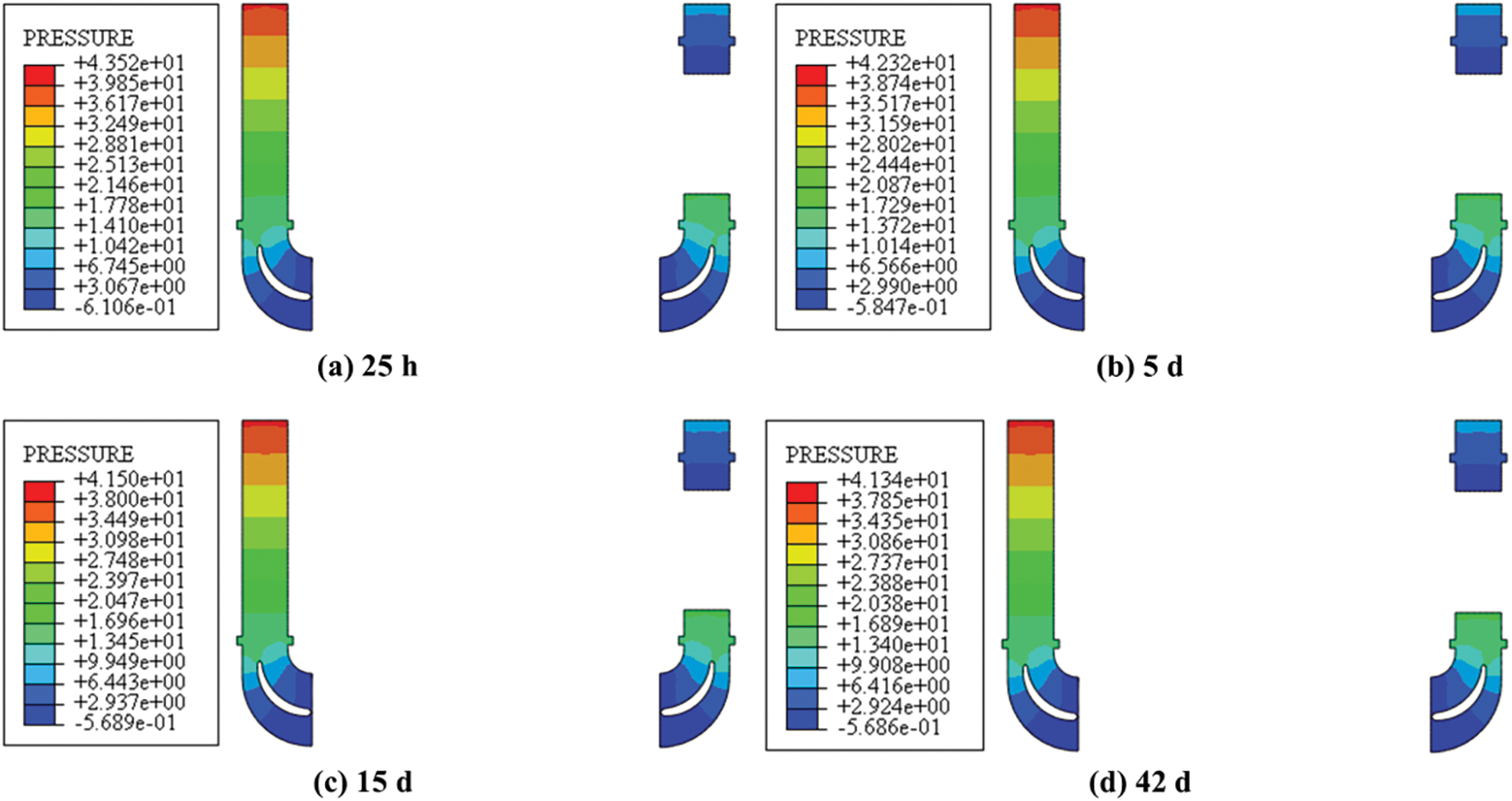
Figure 11: Air pressure cloud diagram (unit: Pa)

Fig. 12 shows a cloud diagram of the distribution of tensile stress in the ship lock corridor under an inlet velocity of 1 m/s. The highest tensile stress is primarily concentrated in the center of the corridor and at the chamfer position where it contacts the bottom plate. Compared with the no-wind condition, the maximum tensile stress at each moment is reduced. The maximum tensile stresses in the corridor at 25 h, 5 d, 15 d, and 42 d are 0.448, 0.189, 0.981 and 1.166 MPa, respectively.

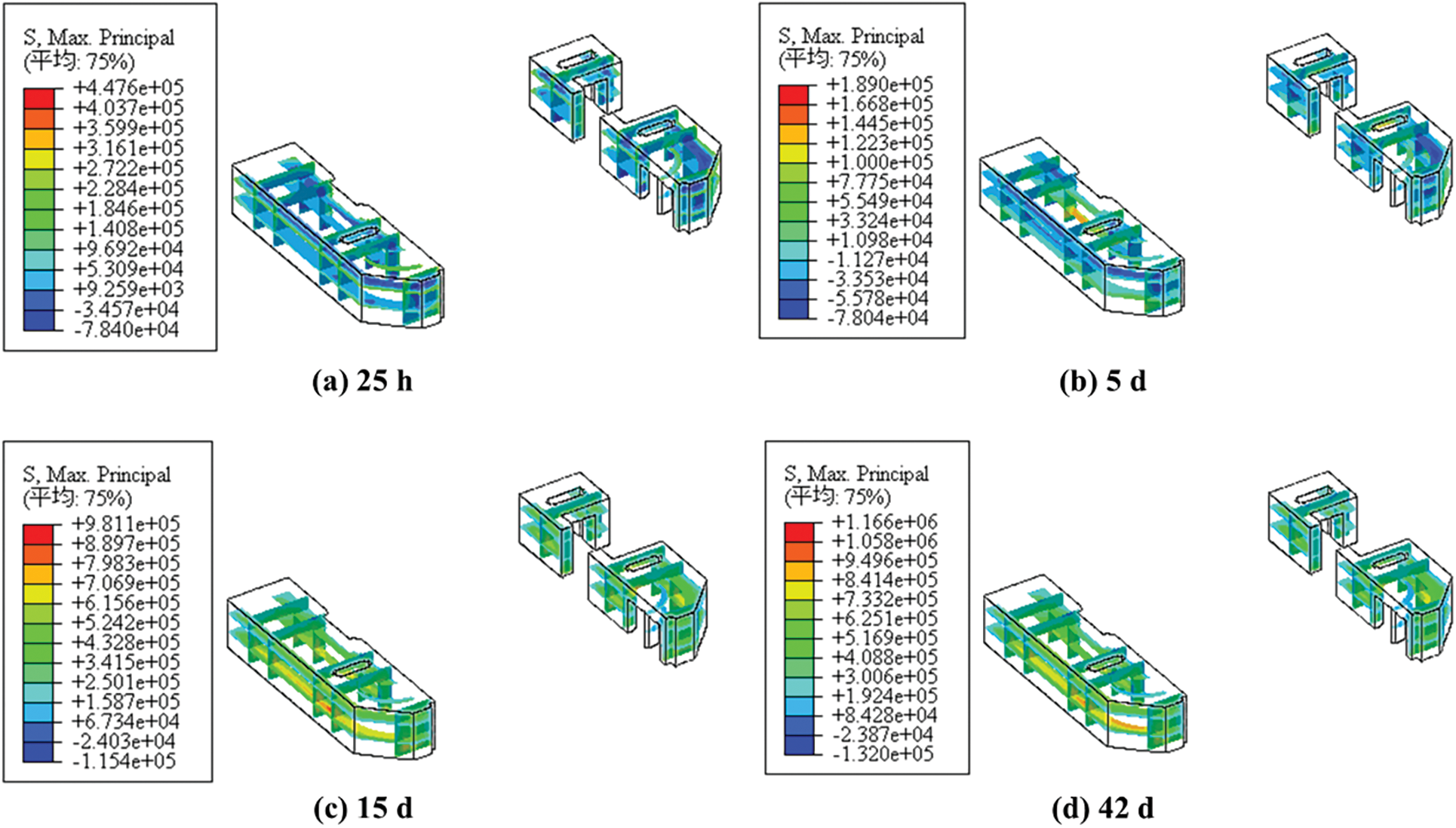
Figure 12: Tensile stress cloud diagram of ship lock corridor (unit: Pa)

5.2.3 Wind Speed of 4 m/s

Compared with the wind speed of 1 m/s, the wind speed of 4 m/s accelerates the heat dissipation in the corridor. The maximum temperatures of the corridor and air are 56.94°C and 44.06°C, respectively, at 25 h; 43.31°C and 29.17°C, respectively, at 5 d; 23.90°C and 21.43°C, respectively, at 15 d; and 20.06°C and 20.03°C, respectively, at 42 d. Moreover, the maximum temperature in the center of the corridor is lower than that at the wind speed of 1 m/s. The maximum temperature of the corridor at 25 h, 5 d, 15 d, and 42 d decreases by 0.14°C, 3.85°C, 3.09°C, and 0.09°C, respectively, while the maximum air temperature drops by 8.24°C, 9.44°C, 5.56°C, and 0.03°C, respectively.

The variation in air velocity and pressure follows a similar pattern to that at 1 m/s. The fluid’s velocity is significantly higher in one branch than in the other branch, and pressure uniformly increases from outlet to inlet, albeit with numerical increments. The maximum pressures are 221.1 Pa at 25 h, 218.1 Pa at 5 d, 216.9 Pa at 15 d, and 216.8 Pa at 42 d. Compared with the case at 1 m/s, the air pressure increases by ~175 Pa. Changes in flow velocity at each moment are not pronounced, and the maximum flow velocity is ~10.06 m/s.

As in the case of 1 m/s, the maximum tensile stress is concentrated in the center of the corridor and at the chamfer position. Compared with the 1 m/s wind speed scenario, the maximum tensile stress significantly decreases at each moment in the later stages of pouring. At 25 h, 5 d, 15 d, and 42 d, the maximum tensile stress in the corridor is 0.449, 0.228, 0.920 and 1.016 MPa, respectively.

Fig. 13 depicts the variations in temperature and tensile stress at the center of the corridor over time. Under no-wind conditions, the temperature of the chamfer position decreases slowly after an initial rise, reaching 20°C by the end of the calculation period. With the increase in wind speed, the peak temperature at this position gradually decreases. At a wind speed of 1 m/s, it drops to 20.62°C in 25 days; at a wind speed of 4 m/s, it takes 15 days to drop to 20°C. Under the three working conditions, the stress at the chamfer position changes from compressive to tensile. The maximum tensile stress gradually rises to 0.92 MPa under no-wind conditions, 0.48 MPa at 1 m/s, and 0.21 MPa at 4 m/s.

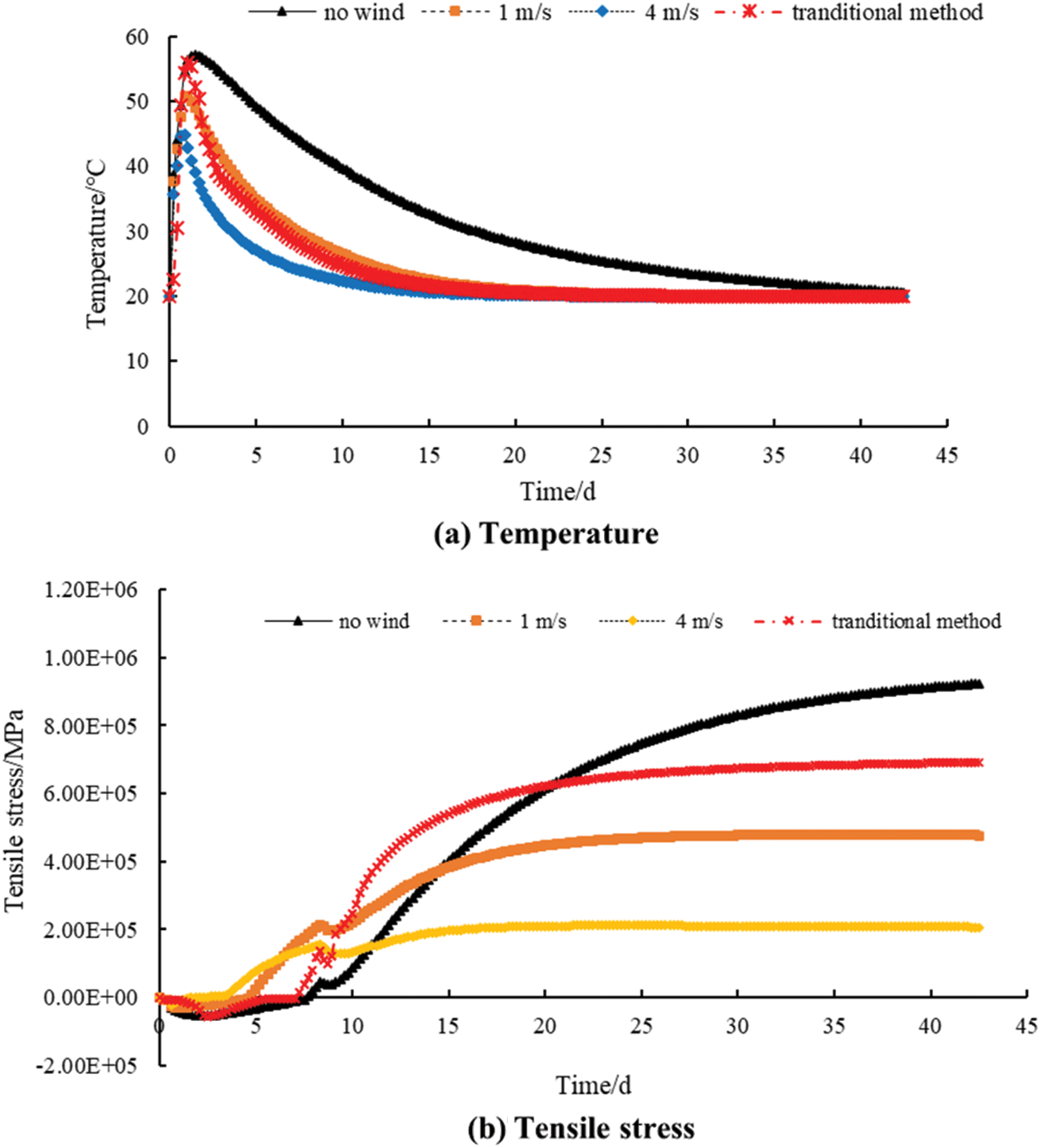
Figure 13: Variations in the temperature and tensile stress of the corridor chamfer over time

The results of the conventional method are similar to those obtained at a wind speed of 1 m/s. However, the peak temperature reached is higher (57.19°C), with a faster temperature reduction process compared with the 1 m/s wind speed scenario. The corresponding tensile stress at the bottom plate position is also greater, with a maximum tensile stress of 0.69 MPa. This is attributable to the greater temperature reduction rate in the traditional method, which results in larger temperature-induced strains and consequently higher tensile stresses.

Table 3 presents the maximum temperature and maximum tensile stress at each moment under the three working conditions. As wind speed increases, the maximum temperatures of both the corridor and air decrease, and the maximum tensile stress of the corridor also decreases at the end of the considered period The most significant impacts are observed in the rate of temperature decline and the maximum tensile stress at the chamfer position. Some necessary ventilation measures should be taken during corridor pouring to effectively reduce the tensile stress at the corridor chamfer. The calculation results show that ventilation at a speed of 4 m/s can reduce the tensile stress at the chamfer by ~0.716 MPa.

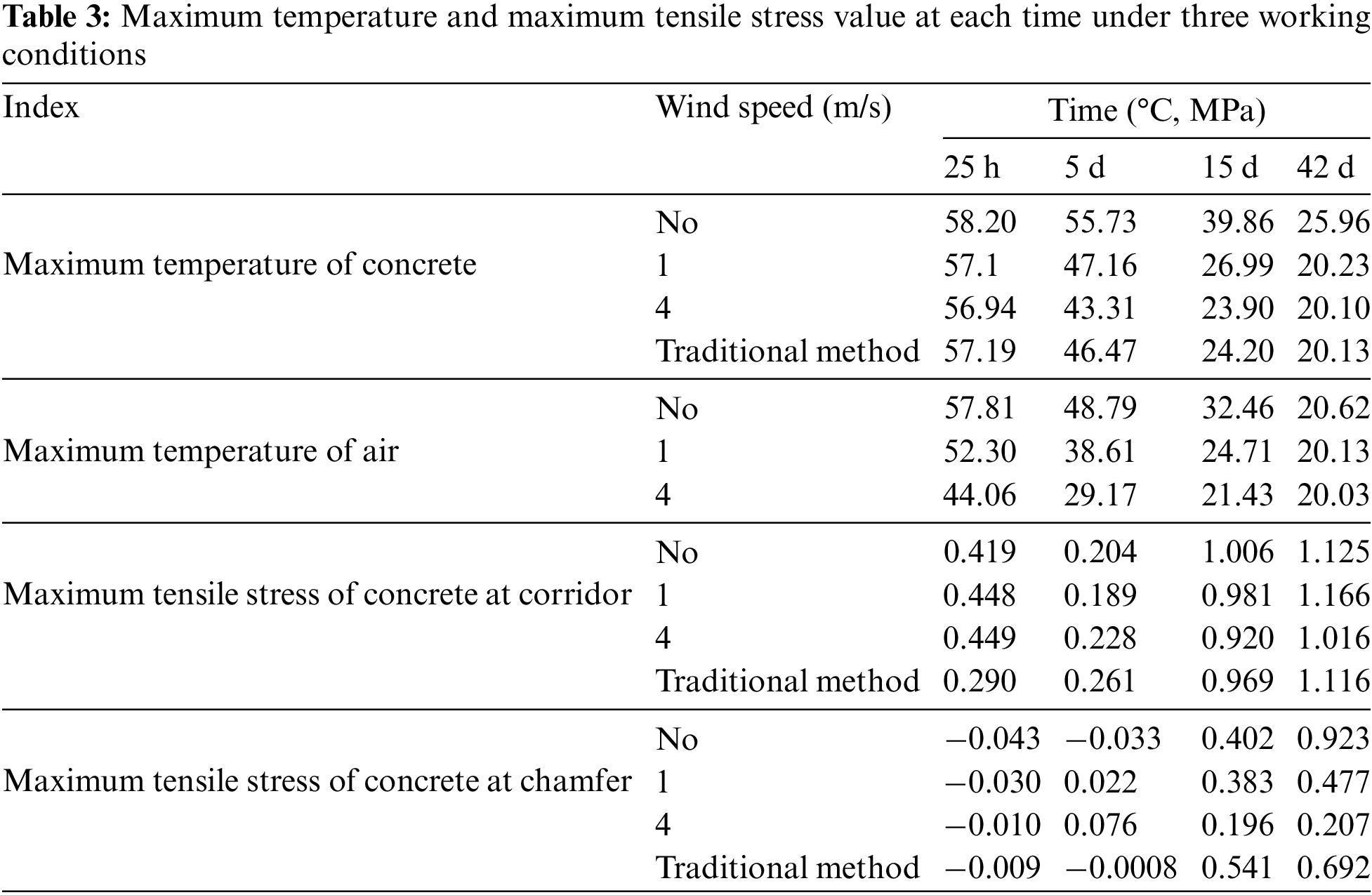
The traditional calculation method yields temperature peak values that are closer to those at a wind speed of 1 m/s, although stress values at various locations differ. This difference is mainly due to the different ways in which boundary conditions are handled, neglecting the variation in air temperature. Consequently, greater heat dissipation occurs, resulting in faster temperature reduction.

6  Conclusion

Large-scale hydraulic structures often form closed air areas, resulting in temperature variations between the interior and exterior environments. In this paper, fluid–solid conjugate heat transfer theory is applied to resolve temperature fields during the construction period of hydraulic structures, and the local air temperature and structural temperature are accurately determined. The temperature creep stress of concrete is further calculated according to the calculated temperature. The influence of air velocity on structural temperature and creep stress is explored, and the limitation of previous calculations is addressed through the incorporation of local air temperature variations. This approach is applied to accurately model the evolution of the corridor temperature field during the corridor construction phase. The airflow within the corridor affects both its temperature and stress. In scenarios where the wind speed flow is not considered, the internal air acts as a thermal insulation layer, which is not conducive to the heat dissipation of the concrete. As wind speed increases, the effect of airflow on concrete heat dissipation gradually increases. The maximum temperature at the concrete center is 58.20°C in the absence of wind within the corridor, while it drops slightly to 57.1°C at 1 m/s and further to 56.94°C at 4 m/s. The tensile stress at each position gradually decreases with the increase in wind speed. The decrease in the maximum tensile stress at surface position is less pronounced than the decrease at the chamfer position. Compared with the no-wind condition, the 4 m/s wind speed scenario yields a ~0.7 MPa reduction in the maximum tensile stress of the corridor concrete chamfer. The results of the traditional calculation method are similar to those obtained under a wind speed of 1 m/s, but the traditional method yields greater tensile stress values for the corridor chamfer.

Acknowledgement: None.

Funding Statement: This work was supported by Construction Simulation and Support Optimization of Hydraulic Tunnel Based on Bonded Block-Synthetic Rock Mass Method and Hubei Province Postdoctoral Innovative Practice Position.

Author Contributions: Study conception and design: H.Z., C.S.; data collection: H.Z.; analysis and interpretation of results: X.C., Z. S.; draft manuscript preparation: H.Z. and W.Z. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data and materials are available upon request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Crow JM. The concrete conundrum. Chem World. 2008;5(3):62–6. doi:10.1201/b12851-5. [Google Scholar] [CrossRef]

2. Chen G, Jiang W, Liu W. A review of recent advances in controlling temperature cracks in mass concrete construction. J Nat Disasters. 2016;25(3):159–65. doi:10.21595/vp.2021.21995. [Google Scholar] [CrossRef]

3. Enzo M, Eduardus A, Antonio C. A numerical recipe for modelling hydration and heat flow in hardening concrete. Cem Concr Compos. 2013;40:48–58. doi:10.1016/j.cemconcomp.2013.04.004. [Google Scholar] [CrossRef]

4. Do T, Hoang T, Thanh B. Evaluation of heat of hydration, temperature evolution and thermal cracking risk in high-strength concrete at early ages. Case Stud Therm Eng. 2020;21:100658. doi:10.1016/j.csite.2020.100658. [Google Scholar] [CrossRef]

5. Han S. Assessment of curing schemes for effectively controlling thermal behavior of mass concrete foundation at early ages. Constr Build Mater. 2020;230:117004. doi:10.1016/j.conbuildmat.2019.117004. [Google Scholar] [CrossRef]

6. Jrg F, Unger Stefan. Multiscale modeling of concrete. Arch Comput Methods Eng. 2011;18(3):341–93. doi:10.1007/s11831-011-9063-8. [Google Scholar] [CrossRef]

7. Coussy O. Mechanics of porous continua. New York, USA: Wiley; 1995. [Google Scholar]

8. Shu X, Jiang Y, Zhao Y, Xu Z, Shen M, Zhong X. Superimposed hydration exothermic model of cement slurry considering different reaction rates of various active substances. Constr Build Mater. 2023;372:130783. doi:10.1016/j.conbuildmat.2023.130783. [Google Scholar] [CrossRef]

9. Eymard R, Gallouët T, Ghilani M. Error estimates for the approximate solutions of a nonlinear hyperbolic equation given by finite volume schemes. IMA J Numer Anal. 1998;18(4):563–94. doi:10.1093/IMANUM/18.4.563. [Google Scholar] [CrossRef]

10. Zdeněk P, Bazant PS. Solidification theory for aging creep. Cem Concr Res. 1988;18(6):923–32. doi:10.1016/0008-8846(88)90028-2. [Google Scholar] [CrossRef]

11. Zhou X, Hao H. Mesoscale modelling of concrete tensile failure mechanism at high strain rates. Comput Struct. 2008;86(21–22):2013–26. doi:10.1016/j.compstruc.2008.04.013. [Google Scholar] [CrossRef]

12. Zheng Z, Wei X. Mesoscopic models and numerical simulations of the temperature field and hydration degree in early-age concrete. Constr Build Mater. 2021;266:121001. doi:10.1016/j.conbuildmat.2020.121001. [Google Scholar] [CrossRef]

13. Du X, Liu J, Ma G. A meso-scale numerical method for the simulation of chloride diffusivity in concrete. Finite Elem Anal Des. 2014;85(4):87–100. doi:10.1016/j.finel.2014.03.002. [Google Scholar] [CrossRef]

14. Zhou W, Qi T, Liu X, Feng C, Yang S. A hygro-thermo-chemical analysis of concrete at an early age and beyond under dry-wet conditions based on a fixed model. Int J Heat Mass Transf. 2017;115:488–99. doi:10.1016/j.ijheatmasstransfer.2017.08.014. [Google Scholar] [CrossRef]

15. Zhou W, Qi T, Liu X. A meso-scale analysis of the hygro-thermo-chemical characteristics of early-age concrete. Int J Heat Mass Transf. 2019;129:690–706. doi:10.1016/j.ijheatmasstransfer.2018.10.001. [Google Scholar] [CrossRef]

16. Freitas J, Cuong P, Rui F. Modelling of cement hydration in concrete structures with hybrid finite elements. Finite Elem Anal Des. 2013;77:16–30. doi:10.1016/j.finel.2013.07.008. [Google Scholar] [CrossRef]

17. Luther M, Bohme P, Wilson W. Case studies—North American mass-concrete projects featuring ASTM C989 slag cement. Int Concrete Abstracts Portal. 2009;263:13–30. [Google Scholar]

18. Liu D, Zhang W, Tang Y. Prediction of hydration heat of mass concrete based on the SVR model. IEEE Access. 2021;9:62935–45. doi:10.1109/ACCESS.2021.3075212. [Google Scholar] [CrossRef]

19. Sargam Y, Faytarouni M, Riding K. Predicting thermal performance of a mass concrete foundation–a field monitoring case study. Case Stud Constr Mater. 2019;11:e00289. doi:10.1016/j.cscm.2019.e00289. [Google Scholar] [CrossRef]

20. Zhao Y, Li G, Fan C. Effect of thermal parameters on hydration heat temperature and thermal stress of mass concrete. Adv Mater Sci Eng. 2021;2021:1–16. doi:10.1155/2021/5541181. [Google Scholar] [CrossRef]

21. Ouyang J, Chen X, Huangfu Z. Application of distributed temperature sensing for cracking control of mass concrete. Constr Build Mater. 2019;197:778–91. doi:10.1016/j.conbuildmat.2018.11.221. [Google Scholar] [CrossRef]

22. Neville A, Dilger W, Brooks J. Creep of plain and structural concrete. London and New York: Construction Press; 1983. [Google Scholar]

23. Flg A, Jsg A, Lcp A. Shrinkage and creep in structural concrete with recycled brick aggregates. Constr Build Mater. 2019;228:116750. doi:10.1016/j.conbuildmat.2019.116750. [Google Scholar] [CrossRef]

24. Zdenek P, Bazant SB. Creep and shrinkage prediction model for analysis and design of concrete structures-model B3. Mater Struct. 1995;180(28):357–65. doi:10.14359/51687453. [Google Scholar] [CrossRef]

25. Freudenthal A, Rol F. Creep and creep recovery of concrete under high compressive stress. Mater Sci. 1958;54(6):1111–42. doi:10.1617/s11527-019-1384-3. [Google Scholar] [CrossRef]

26. Khan I, Xu T, Castel A. Risk of early age cracking in geopolymer concrete due to restrained shrinkage. Constr Build Mater. 2019;229:116840. doi:10.1016/j.conbuildmat.2019.116840. [Google Scholar] [CrossRef]

27. Briffaut M, Benboudjema F, Torrenti J. A thermal active restrained shrinkage ring test to study the early age concrete behavior of massive structures. Cem Concr Res. 2011;41(1):56–63. doi:10.1016/j.cemconres.2010.09.006. [Google Scholar] [CrossRef]

28. Briffaut M, Benboudjema F, Torrenti J. Numerical analysis of the thermal active restrained shrinkage ring test to study the early age behavior of massive concrete structures. Eng Struct. 2011;33(4):1390–401. doi:10.1016/j.engstruct.2010.12.044. [Google Scholar] [CrossRef]

29. Henkensiefken R, Bentz D, Nantung T. Volume change and cracking in internally cured mixtures made with saturated lightweight aggregate under sealed and unsealed conditions. Cem Concr Compos. 2009;31(7):427–37. doi:10.1016/j.cemconcomp.2009.04.003. [Google Scholar] [CrossRef]

30. Zhang J, Hou D, Gao Y. Calculation of shrinkage stress in early-age concrete pavements. I: calculation of shrinkage strain. J Transp Eng. 2013;139(10):961–70. doi:10.1061/(ASCE)TE.1943-5436.0000582. [Google Scholar] [CrossRef]

31. Matthieu B, Farid B, Jean-Michel T, Nahas G. Concrete early age basic creep: experiments and test of rheological modelling approaches. Constr Build Mater. 2012;36:373–80. doi:10.1016/j.conbuildmat.2012.04.101. [Google Scholar] [CrossRef]

32. Lackner R, Mang HA. Chemoplastic material model for the simulation of early-age cracking: from the constitutive law to numerical analyses of massive concrete structures. Cem Concr Compos. 2004;26:551–62. doi:10.1016/S0958-9465(03)00071-4. [Google Scholar] [CrossRef]

33. Stefan L, Benboudjema F, Torrenti JM, Bissonnette B. Prediction of elastic properties of cement pastes at early ages. Comput Mater Sci. 2010;47(3):775–84. doi:10.1016/j.commatsci.2009.11.003. [Google Scholar] [CrossRef]

34. Mardmomen S, Chen H. Prediction of the early age thermal behavior of mass concrete containing SCMs using ANSYS. J Therm Anal Calorim. 2023;148:7899–7917. doi:10.1007/s10973-023-12243-9. [Google Scholar] [CrossRef]

35. Chen H, Mardmomen S, Leon G. On-site measurement of heat of hydration of delivered mass concrete. Constr Build Mater. 2020;269:121246. doi:10.1016/j.conbuildmat.2020.121246. [Google Scholar] [CrossRef]

36. Smolana A, Klemczak B, Azenha M, Schlicke D. Early age cracking risk in a massive concrete foundation slab: comparison of analytical and numerical prediction models with on-site measurements. Constr Build Mater. 2021;301:124135. doi:10.1016/j.conbuildmat.2021.124135. [Google Scholar] [CrossRef]

37. Lim S, Yang S. Laboratory evaluation of tensile creep behavior of concrete at early ages. Appl Sci-Basel. 2024;14(3):1275. doi:10.3390/app14031275. [Google Scholar] [CrossRef]

38. Agnoletto L, Cortella G, Marco M. Finite element thermal analysis of special building components. Energy Build. 1995;22(2):115–23. doi:10.4103/0970-9290.100422. [Google Scholar] [PubMed] [CrossRef]

39. Joon KK, King WP. Thermal conduction between a heated microcantilever and a surrounding air environment. Appl Therm Eng. 2009;29(8):1631–41. doi:10.1016/j.applthermaleng.2008.07.019. [Google Scholar] [CrossRef]

40. Eveloy V, Rodgers P. Prediction of electronic component-board transient conjugate heat transfer. IEEE Trans Compon Packag Technol. 2005;28(4):817–29. doi:10.1109/TCAPT.2005.848586. [Google Scholar] [CrossRef]

41. Albets-Chico X, Pérez-Segarra CD. Analysis of wall-function approaches using two-equation turbulence models. Int J Heat Mass Transf. 2008;51:4940–57. doi:10.1016/j.ijheatmasstransfer.2008.03.002. [Google Scholar] [CrossRef]

42. Launder BE, Spalding DB. The numerical computation of turbulent flows. Comput Methods Appl Mech Eng. 1974;3(2):269–89. doi:10.1016/0045-7825(74)90029-2. [Google Scholar] [CrossRef]

43. Li QB, Liang GH, Hu Y. Numerical analysis on temperature rise of a concrete arch dam after sealing based on measured data. Math Probl Eng. 2014;2014:602818. doi:10.1155/2014/602818. [Google Scholar] [CrossRef]

44. Zhu BF. Temperature stress and temperature control of mass concrete. Beijing: China Water & Power Press; 2012. [Google Scholar]

45. Xu C, Su C. Development of an effective method for calculations related to creep. Arab J Sci Eng. 2018;43(4):1561–71. doi:10.1007/s13369-017-2657-1. [Google Scholar] [CrossRef]

46. Su C, Bai J. Structural optimization of ship lock heads during construction period considering concrete creep. Math Probl Eng. 2020;2020:1–17. doi:10.1155/2020/5495202. [Google Scholar] [CrossRef]

47. Sheng Q, Erzhao L, Guangpu H. A new method to obtain surface heat dissipation coefficient based on measured concrete temperature gradient. J Hydraul Eng. 2015;46(10):1240–6. doi:10.1016/j.conbuildmat.2021.124167. [Google Scholar] [CrossRef]

48. Erzhao L. Research on hydraulic concrete temperature-moisture-stress multi-physics coupling callulation considering damage (Ph.D. Thesis). Hohai University: China; 2016. [Google Scholar]

49. Yang Q, Li M, Zu Z, Ma Z. Has the stilling of the surface wind speed ended in China? Sci China Earth Sci. 2021;64(7):1036–49. doi:10.1007/s11430-020-9738-4. [Google Scholar] [CrossRef]