Evolutionary Safe Padé Approximation Scheme for Dynamical Study of Nonlinear Cervical Human Papilloma Virus Infection Model

1  Introduction

The root cause of cervical cancer is the irregular growth of cells in the cervix and its nearby organs. No apparent symptoms appear in the early stages of cervical cancer. Over time, the disease develops aggressively, manifesting with clear symptoms such as irregular vaginal bleeding. Cervical cancer can affect women in their teenage years, but precancerous changes can be identified in their 20 and 30 s. Cases of cervical cancer among women aged 50–60 years are clearly detectable [1,2]. Generally, around 80% of cervical cancer cases are diagnosed in their early stages of development. Every year, around 500,000 positive cases are identified worldwide, with 200,000 resulting in fatalities due to the disease.

Cervical cancer progresses slowly, emphasizing the importance of early detection for successful treatment and prevention. The human body divides its cells to replace damaged or dead ones, which occurs more quickly in children than adults. Different types of cancer are caused by unchecked cell development, which affects the original site of the cancer before it can spread. The cervix, the lower part of the uterus attached to the top of the vagina, is where cervical cancer usually begins. Due to its slow growth and potential for early intervention, this disease ranks second among malignancies affecting women worldwide.

The mortality rate from cervical cancer in Pakistan is higher compared to that in several Western countries. Cervical carcinoma ranks as the fourth most prevalent cancer among Pakistani women. Inherited instances of cervical cancer can result from the transmission of disease-carrying fluids from a mother to her child during childbirth. Having multiple sexual partners can increase the risk of cervical cancer in affected women. Human Papillomavirus (HPV) infection, a sexually transmitted infection (STI), is responsible for almost all forms of cervical cancer. Many individuals remain unaware of their HPV infection. The hazardous HPV strains, HPV-16 and HPV-18, are responsible for over 70% of confirmed cancer cases. The early detection of such HPV types through the Papanicolaou or Pap smear test helps in effective treatments through vaccination administration [3–5] and adopting precautionary measures [6–8]. According to epidemiological research on this illness, more than 40 different forms of HPV affect a person’s cervix, anus, vulva, inner vaginal walls, rectum, and outer skin in the pubic region in both genders. Among several types of HPV, only a few types are due to cervical cancer [9–12]. High-risk HPV types cause warts on genital parts or skin, leading to penile and cervical cancers in men. In 2006, the United States’ federal agency of Food and Drug Administration (FDA) introduced a vaccine for protection against HPV-16 and HPV-18. Over 530,000 new cervical cancer cases are reported annually, with 275,000 women dying annually. In advanced nations, the fatality rate is over 80%. Scotland’s disease induction rate was 70.6% between 1997 and 2001. In the UK, 1,000 women die each year from 2,800 known positive cases. In Canada, 1,300 women received the diagnosis in 2008, with 380 dying. Up to twenty million people in America are infected with HPV.

Radecki et al. [13] and Winer et al. [14] have advocated for the use of HPV vaccines to reduce psychological barriers in diagnostic Pap tests. Friedman’s study found that HPV infection is mainly transmitted through mutual sex and is responsible for cervical cancer and other cell irregularities in American females. Raley et al. [15] also observed cervical neoplasia and genital warts caused by HPV infection. The American College of Obstetricians and Gynecologists (ACOG) conducted a survey to explore HPV vaccine preparation methodologies. Clifford et al.’s study found that HPV vaccines were 100% effective in reducing genital warts and HPV risks [16–18]. Chao et al.’s study found HPV as the highest source of cervical cancer. Licht et al.’s research analyzed the hazards linked to HPV vaccine administration among girls studying in public universities [19–23].

A helpful method for examining disease dynamics in living species, particularly humans, is mathematical modeling. Recently, numerous Cervical Cancer Epidemic (CCE) models have been put forth and examined [24]. During the analysis of suggested models, it was observed that, for specific values of model parameters, the conventional explicit finite difference techniques for initial value problems result in non-physical chaos under varying complexities [25]. Because of their unstable behavior, many traditional methods lose their dependability. In this case, fresh, dependable, and structure-preserving techniques are needed. Researchers are adopting the evolutionary computational [26–30] paradigm as one of the expanding contemporary problem-solving approaches for medical predictions [31,32] and solving highly nonlinear physical phenomena modeled by initial and boundary value ordinary differential equations and partial differential equations with applications in applied sciences and epidemiology [33–35].

This study designs an evolutionary computational framework for safe (non-singular) Padé approximation to model the CCE nonlinear system as an optimization problem, incorporating an efficient global search mechanism through a genetic algorithm with multi-parent crossover (GA-MPC) [36]. The proposed computational framework is named the evolutionary safe Padé approximation (ESPA) scheme, an improved version of the original Evolutionary Padé Approximation (EPA) scheme proposed by Ali et al. [37–39]. Analysis of the CCE model using our proposed ESPA scheme enables the prediction of elimination and perseverance states. The scheme is designed to preserve vital structural properties of dynamical systems.

The prominent features of the ESPA scheme include:

  (i)  Non-singular Padé approximation-based modeling of the governing equations of the CCE model for constructing the objective function.

 (ii)  Transformation of initial conditions on state variables into problem constraints.

(iii)  Construction of an unconstrained minimization problem by implementing penalty functions that control the solution’s feasibility.

(iv)  Implementation of GA-MPC for solving the formulated unconstrained optimization problem.

 (v)  Use of optimized coefficients found by the best performer algorithm to present closed-form solutions of the model.

2  Deterministic Cervical Cancer Model

This section introduces the dynamics of cervical cancer disease caused by infection with the human papillomavirus. The variables S(t), IH(t), Iu(t) and Ic(t) are the number of susceptible, HPV-infected, HPV infectious but not yet infected by CCE, and HPV infectious affected by CCE disease females, respectively. The compartmental order of the CCE model is exhibited in Fig. 1.

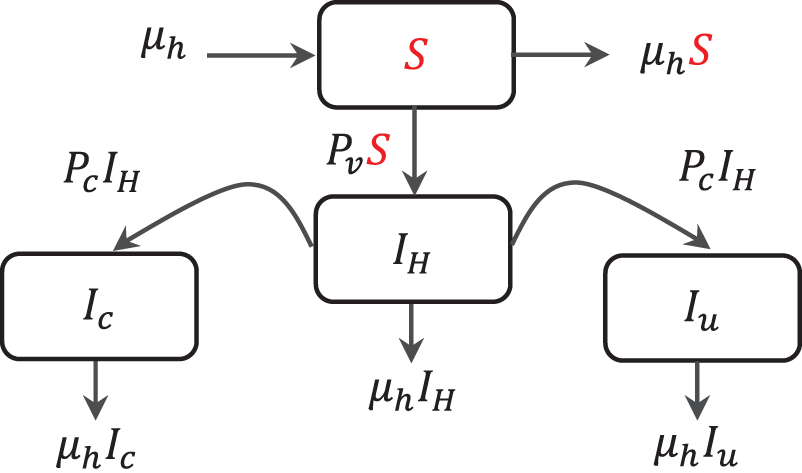
Figure 1: The compartmental structure of CCE model

where β is the human birth rate, μh is the death rate of the human population, Np is the size of the entire women population, Pv is the women’s probability of catching HPV infection, and Pc is the women’s probability of contracting cervical cancer. All variables are normalized by the total population to achieve the normalized model with Np=1. The block diagram (Fig. 1) shows that due to the non-coupling effect, one of the state variables Iu and Ic can be eliminated.

The following reduced model is achieved:

dSdt=β−PvSIH−μpS(1)

dIHdt=PvSIH−PcIH−μhIH(2)

dIcdt=PcIH−μhIc(3)

S(0)=S0;IH(0)=IH(0),Ic(0)=Ic(0)

The total population is considered constant.

S+IH+Ic+Iu=Np(4)

The necessary physical properties of the model [40] are as follows:

Theorem 1: The systems (1)–(3) subjected to Eq. (4) are bounded and positively invariant feasible regions defined by: {(S,IH,Ic):S+IH+Ic≤1,S≥0,IH≥0,Ic≥0}.

Theorem 2: The basic reproductive number of the CCE model is R0=PvPc+μh.

Theorem 3: The system has a unique disease-free equilibrium point (1,0,0) and a unique disease-persistent equilibrium point (1R0,μhPv(R0−1),PcPv(R0−1)) according as R0<1 or R0>1.

3  ESPA Scheme for the CCE Model

This section is dedicated to the architecture of the ESPA scheme for solving the dynamical CCE model. It sequences the approximation of the state variables by Padé rational functions, the conversion of governing equations to residual functions, and the handling of initial conditions, along with the physical properties of the CCE model as problem constraints, to formulate an unconstrained optimization problem. The optimization task is performed by implementing a global optimization algorithm called the genetic algorithm with multi-parent crossover (GA-MPC). The global optimum solution of the resulting unconstrained optimization problem is analogous to the solution of the underlying nonlinear CCE model.

3.1 Approximation by Safe Padé Rational Functions

State variables S, IH and Ic are approximated by following Padé rational functions of variable t∈[0,∞) with order (M,N) [41,42]:

S(t)≈𝓅S(t)=∑j=0MaSjtj1+∑j=1NbSjtj

Ic(t)≈𝓅Ic(t)=∑j=0MaIcjtj1+∑j=1NbIcjtj.

IH(t)≈𝓅IH(t)=∑j=0MaIHjtj1+∑j=1NbIHjtj

The set of safety conditions is:

{∑j=1NbSjtj≠−1,∑j=1NbIHjtj≠−1,∑j=1NbIcjtj≠−1}(5)

where aij, and bij are real numbers for all j∈W and i∈{S,IH,Ic}. The derivative of 𝓅i(t) with respect to t is again a safe Padé rational function expressed as follows:

𝓅i′(t)={∑j=1Mjaijtj−1−(∑j=1Njbijtj−1)𝓅i(t)}1+(∑j=1Nbijtj)

The Padé approximants satisfy the following natural properties [37–39]:

𝓅i(0)=ai0∀i∈{S,IH,Ic},limt→∞𝓅i(t)={0ifM<NaiMbiNifM=N∞ifM>N(6)

The properties of non-singular Padé approximants provide valuable guidelines for choosing the orders of approximants so that the physical conditions of the model are preserved.

3.2 Formation of Residual Functions

For some positive integer λ, a monotone strictly increasing finite sequence {t0,t1,t2,t3,…,tλ} is considered a subset of the domain [0,∞) of t and Δr=tr+1−tr, for r=0,1,2,…,λ. The proposed scheme does not require a uniform value for each Δr and thus is independent of any step length. Denoting the corresponding approximate solutions and their derivatives by 𝓅ir,𝓅ir′ at tr and substituting in the system (1) to (3), a system of nonlinear equations at point tr is obtained as follows:

𝓅Sr′−μp+Pv𝓅Sr𝓅IHr+μp𝓅Sr=0(7)

𝓅IHr′−𝓅Sr𝓅IHr+Pc𝓅IHr+μh𝓅IHr=0(8)

𝓅Icr′−Pc𝓅Icr+μh𝓅Icr=0(9)

For r=0,1,2,3,…,λ, residual functions involving unknown coefficients of Padé approximants are ψ1r, ψ2r and ψ3r that are defined by:

ψ1r=𝓅Sr′−μp+Pv𝓅Sr𝓅IHr+μp𝓅Sr(10)

ψ2r=𝓅IHr′−𝓅Sr𝓅IHr+Pc𝓅IHr+μh𝓅IHr(11)

ψ3r=𝓅Icr′−Pc𝓅Icr+μh𝓅Icr(12)

The initial conditions are transformed into the following constraints:

𝓅S0−S(t0)=0,𝓅IH0−IH(t0)=0,𝓅Ic0−Ic(t0)=0(13)

3.3 Formation of Unconstrained Minimization Problem Using Penalty Function Approach

The Padé approximation-based mathematical modeling of the underlying problem aims to find optimized values of D=3(N+M+2) unknown coefficients so that the absolute residuals at each discrete step are minimized by meeting all the problem constraints. Let us represent the D-dimensional vector of unknown coefficients by x=(aS,bS,aIH,bIH,aIc,bIc)∈RD obtained by concatenating the vectors aS,bS,aIH,bIH,aIc and bIc horizontally, where

aIu=(aIc0,aIc1,…,aIcN)∈RM+1;bIc=(bIc1,bIc2,…,bIcN)∈RN

aIH=(aIH0,aIH1,…,aIHN)∈RM+1;bIH=(bIH1,bIH2,…,bIHN)∈RN

aS=(aS0,aS1,…,aSN)∈RM+1;bS=(bS1,bS2,…,bSN)∈RN

Employing these notations and the Padé approximation functions 𝓅i(t) all residuals (Eqs. (10) to (12)) and the constraint functions (Eq. (13)) become real-valued functions of a D-dimensional unknown vector x. Using a penalty function approach, the following unconstrained minimization problem is constructed.

Minimizeψ(x)=13∑j=13ψj(x)+∑i=14Li×Pi(x)(14)

Each ψj(x),1≤j≤3, is the mean squared residual of a governing equation defined by:

ψj(x)=1(λ+1)∑r=0λ[ψjr(x)]2,∀j=1,2,3(15)

where L1,L2,L3 and L4 are large positive real numbers, and the constraints in Eqs. (5) and (13) are handled by the penalty functions P1(x) and P2(x) defined as follows:

P1(x)=13{(𝓅S0−S(t0))2+(𝓅IH0−IH(t0))2+(𝓅Iu0−Iu(t0))2}(16)

P2(x)=max{0,δ−|∑j=1Nbvjtj+1|:v=S,IH,Ic}(17)

where δ (a positive real number) acts as the singularity tolerance parameter. The larger value of δ well ensures the non-singularity of each approximant. The respective penalty functions for handling the positivity and feasibility of solutions are:

P3(x)=max{0,−𝓅S,−𝓅IH,−𝓅Ic}

P4(x)=max{0,𝓅S+𝓅IH+𝓅Ic−1}

3.4 Optimizer: Genetic Algorithm with Multi-Parent Crossover

The constructed objective function ψ(x) is highly nonlinear in the unknown coefficients and can contain multiple local minima. Additionally, the complexity of the optimization process increases as the order (M,N) of Padé approximation is increased. Therefore, the use of a reliable and efficient optimization algorithm is necessary. This study uses the GA-MPC algorithm [36], proving its tremendous success in real-world practical optimization problems [43].

Step 1. Generate an initial population {xj=(x1j,x2j,…,xDj):1≤j≤PS} of size PS∈N in the considered search range.

Step 2. Save the best m,1≤m≤PS, individuals (solutions) in the archive pool (Parch).

Step 3. Construct the selection pool (Pselect), of size 3×PS, by picking best solution from Tc (2 or 3) random solutions using the tournament selection technique.

Step 4. Generate three off-springs (new trial solutions) from each of PS/3 triplets of distinct parent solutions randomly selected from Pselect. Let a triplet from Pselect be xk1,xk2 and xk3 ordered as f(xk1)≤f(xk2)≤f(xk3). Then, new off-spring solutions o1,o2,o3 are computed as:

o1=xk1+β×(xk2−xk3)(18)

o2=xk2+β×(xk3−xk1)(19)

o3=xk3+β×(xk1−xk2)(20)

where β is the crossover rate and is selected randomly from normal distribution N(μ,σ) with mean μ and standard deviation σ.

Step 5. Apply diversity step on each newly generated solution with a pre-defined diversity probability (pd) as given below:

For each j=1,2,3,…,PS generate a random number r∈(0,1) for each dimension i=1,2,3,…,D choose a random solution xarch∈Parch and update off-spring as:

oij=xiarchifr<pd(21)

Step 6. Evaluate all off-springs and merge them with Parch to get m+PS solutions. Sort and choose the PS best solutions to get a new population for iteration.

Step 7. Remove duplicates, if any. Store the best solution.

Step 8. Check termination conditions.

4  Results and Discussion

The objective function of the cervical cancer model, associated with the ESPA scheme and CCE model parameters described in Table 1, is solved. The optimization results are analyzed through various performance measures to validate the stability and efficiency of the proposed ESPA scheme for the cervical cancer model. These performance measures include the goodness of the optimal value of the objective function ψ, the consistency of the optimizer in finding near-optimal solutions, and the complexity analysis of the optimizer for solving the cervical cancer model. For this purpose, the empirical data from 20 independent runs of GA-MPC on the formulated optimization problem were recorded and analyzed case-wise.

4.1 Optimization Results

The CCE nonlinear model, defined by Eqs. (1)–(3), is solved using the proposed ESPA scheme, and its performance is analyzed in this subsection. The model follows the specified initial conditions:

S(0)=0.65,IH(0)=0.25,Iu(0)=0.15,Ic(0)=0.1

The approximate solutions obtained through the ESPA scheme for the CCE nonlinear model at the Disease-Free Equilibrium (DFE) and Endemic Equilibrium (EE) are introduced in closed-form expressions with optimized coefficients. The results from 20 independent runs of the GA-MPC algorithm are also analyzed through merit indices of statistical analysis to evaluate the performance accurately. The designed global optimization problems for the CCE nonlinear model, based on (4, 4), (5, 5), and (6, 6) orders of Padé approximants, are solved by the GA-MPC algorithm as per the procedural steps given in Subsection 3.4.

Fig. 2 exhibits the final best minimized and the mean values of ψ over 20 independent runs, considering parameter settings at DFE and EE points. The components of Fig. 3 show the convergence curves of the best run and iterative means of all 20 optimization runs for the DFE point.

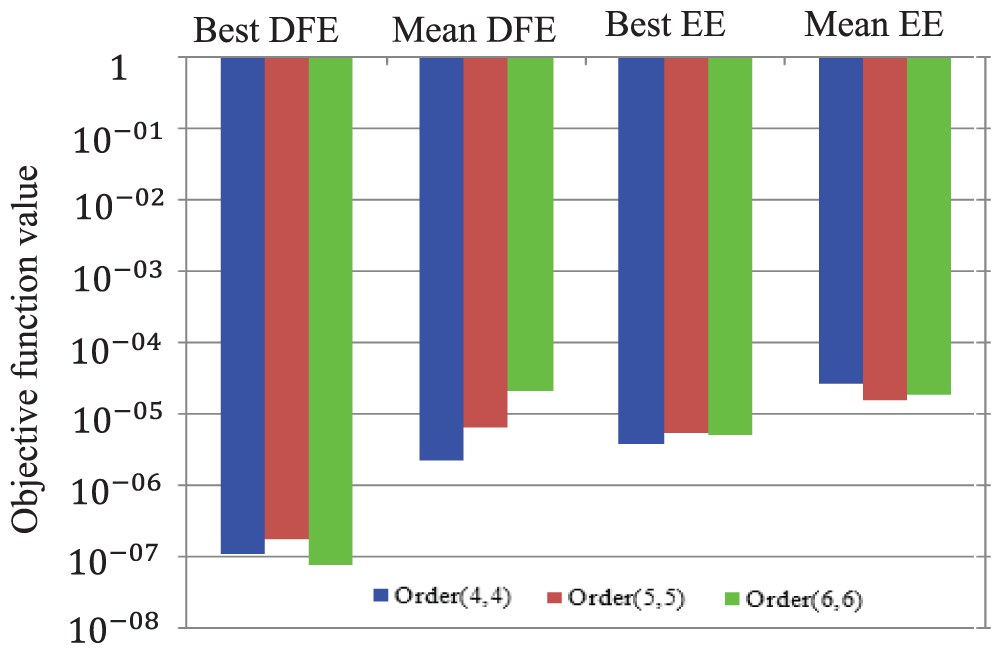
Figure 2: Best and mean minimum values of

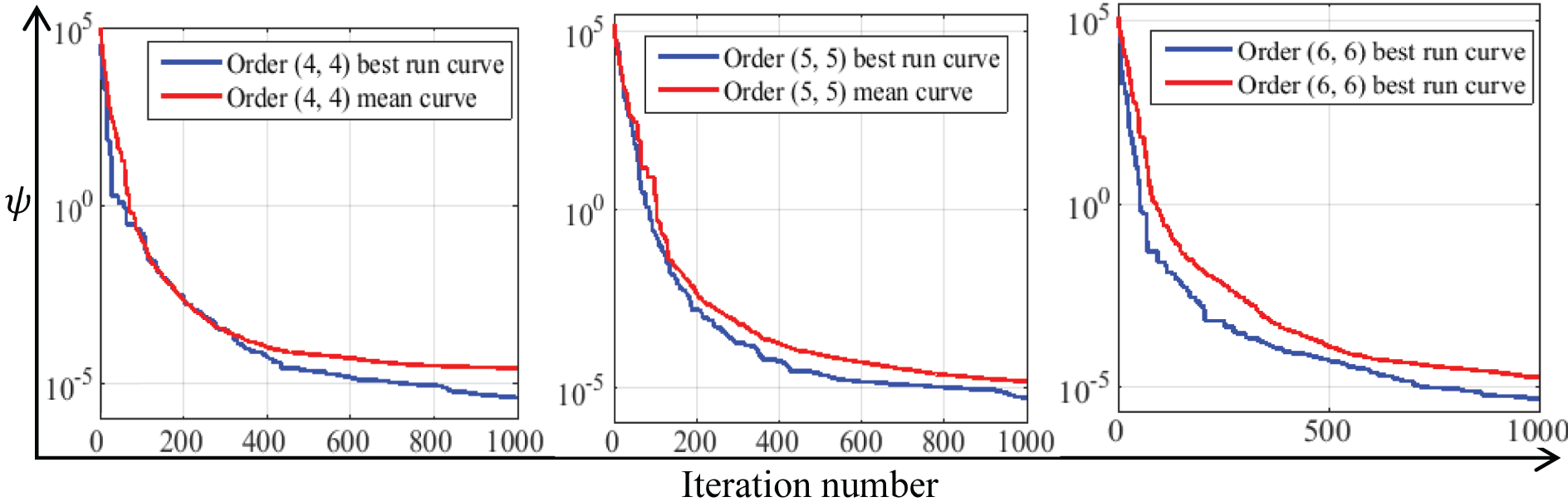
Figure 3: The best and mean convergence curves of optimization results at DFE

Fig. 3 presents the convergence curves of the simulation run about the best optimum value and the mean of all optimization runs at the DFE point.

Fig. 3 indicates that for the DFE point, the final best values of the objective function ψ with orders (4, 4), (5, 5), and (6, 6) of approximants remain lower than 10–05 whereas the mean of all final values of the objective function ψ remains slightly higher but very close to 10–05 for all considered cases.

Similarly, for the EE point, Fig. 4 shows that the final best values of the objective function ψ with orders (4, 4), (5, 5), and (6, 6) of approximants lie well below the value of 10–05 whereas the mean values for orders (4, 4) and (5, 5) are less than 10–05. The mean value for the order (6, 6) is slightly higher but in close vicinity to 10–05. Such closeness in the best and mean values of the objective function leads to small standard deviations, indicating that the optimizer is numerically consistent in optimizing the objective function associated with the CCE model.

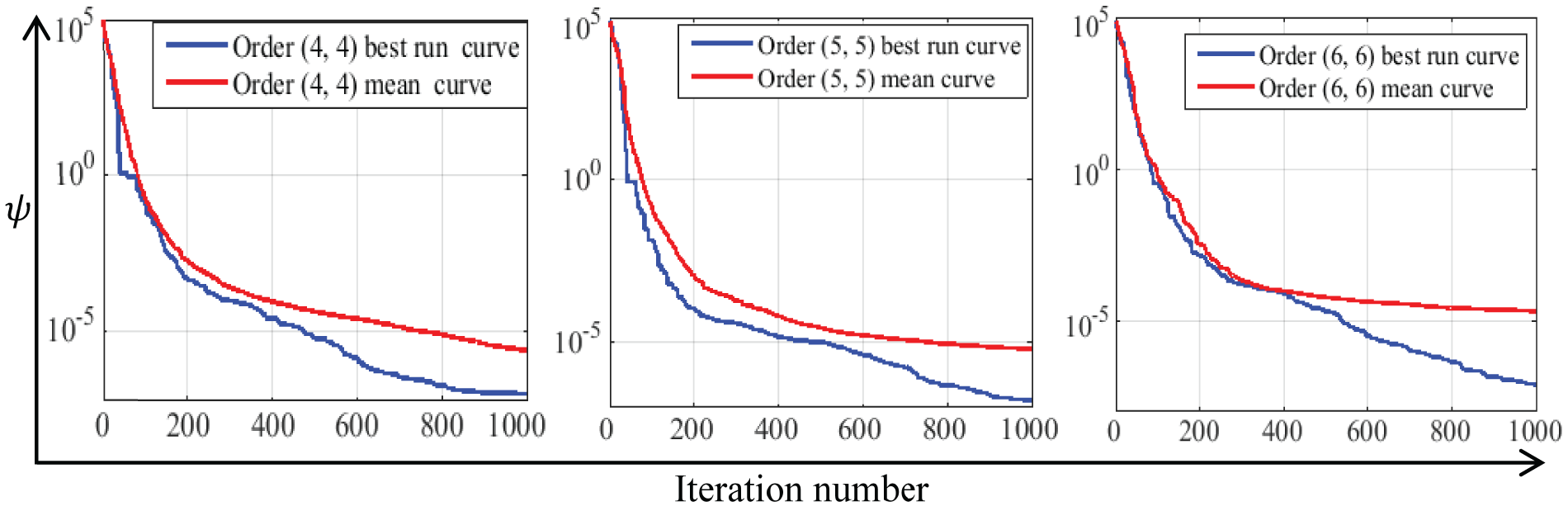
Figure 4: The best and mean convergence curves of optimization results at EE

A detailed analysis of the results obtained by the ESPA scheme is now presented. The performance of GA-MPC is compared against two state-of-the-art algorithms: Differential Evolution (DE) [27] and Particle Swarm Optimization (PSO) [26], to assess its efficacy within the ESPA scheme. This evaluation benchmarks the relative efficiency of GA-MPC across various scenarios of different Padé approximants for both points of equilibrium. All competing algorithms are allotted a population size of 50 and an equal number (1000) of iterations for uniformity. This extended statistical analysis assumes Padé approximant orders of 4, 5, 6, 8, and 10 for disease-free and endemic equilibria, yielding ten subproblems in the ESPA framework. The following normalized objective function value is used at each iteration for clarity:

ψ^k=Tmax×ψk∑k=1Tmaxψk

For one hundred mutually independent runs, the minimization of normalized functions ψ^ is carried out using three competing algorithms: GA-MPC, DE, and PSO. Each algorithm’s final values for each subproblem are noted, and Table 2 displays the best mean and standard deviation (Std) valuesThe best values found by GA-MPC, which are more accurate than those found by DE and PSO, fall within the interval [3.5E-10, 7.4E-09] for all subproblems at the DFE point. Furthermore, the GA-MPC’s mean values, which vary from 5.0E-09 to 2.3E-08, are still superior to DE and PSO’s best results. The uniform performance of the suggested approach for all orders of Padé approximants is demonstrated by low standard deviations. The best values for the EE point that GA-MPC has discovered are approximately 1.1E-09 for both higher and lower orders of Padé approximants. Conversely, higher orders of approximants have a detrimental impact on DE and PSO values. Typically, the GA-MPC algorithm yields more precise results than the DE and PSO algorithms.

4.2 Convergence Analysis

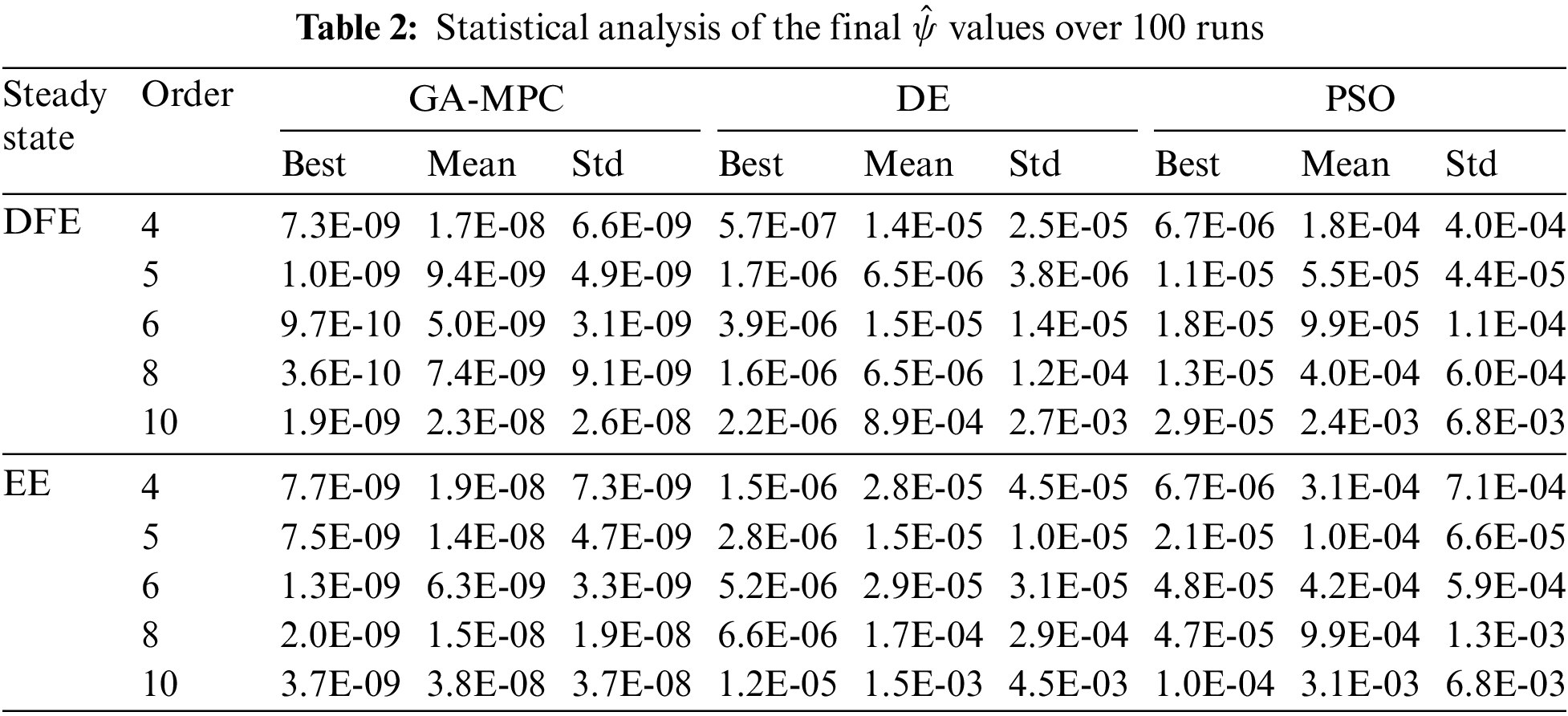
The closed-form approximate solutions with optimized coefficients for the CCE model at the DFE point are given below in Eqs. (22) to (30). The convergence curves presented in Figs. 5–7describe that the curves of susceptible S(t), HPV-infected IH and HPV infectious Ic converge towards the disease-free equilibrium point (1,0,0). The values of model parameters are set so that the primary reproductive number is maintained as R0<1 point. The convergence speed of state variables with (4, 4), (5, 5), and (6, 6) orders of approximations can be matched via Figs. 5–7.

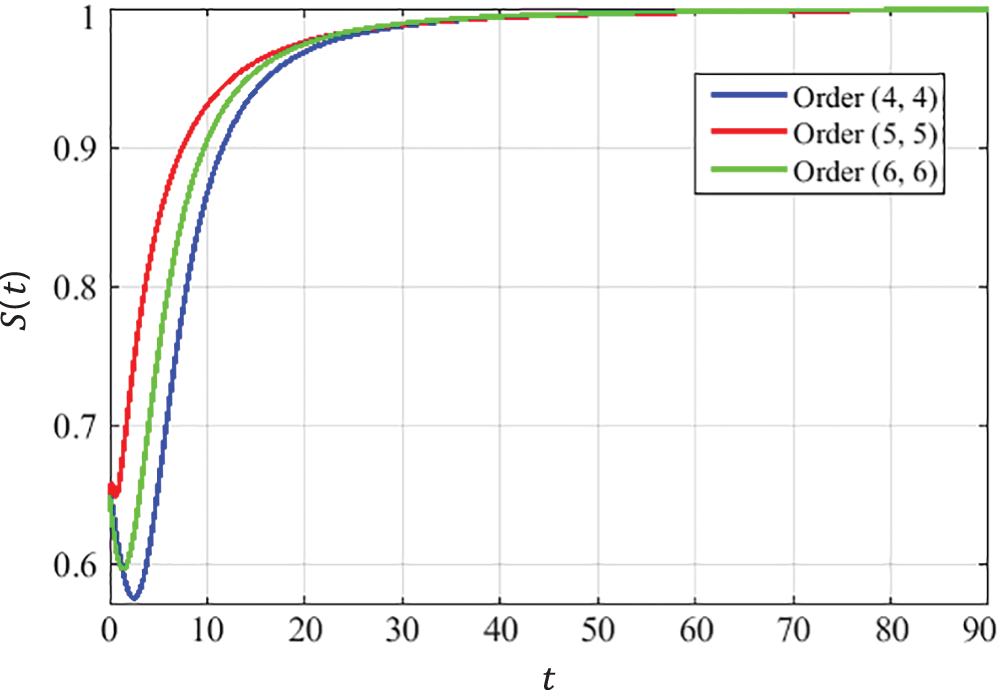
Figure 5: Behavior of susceptible population at DFE

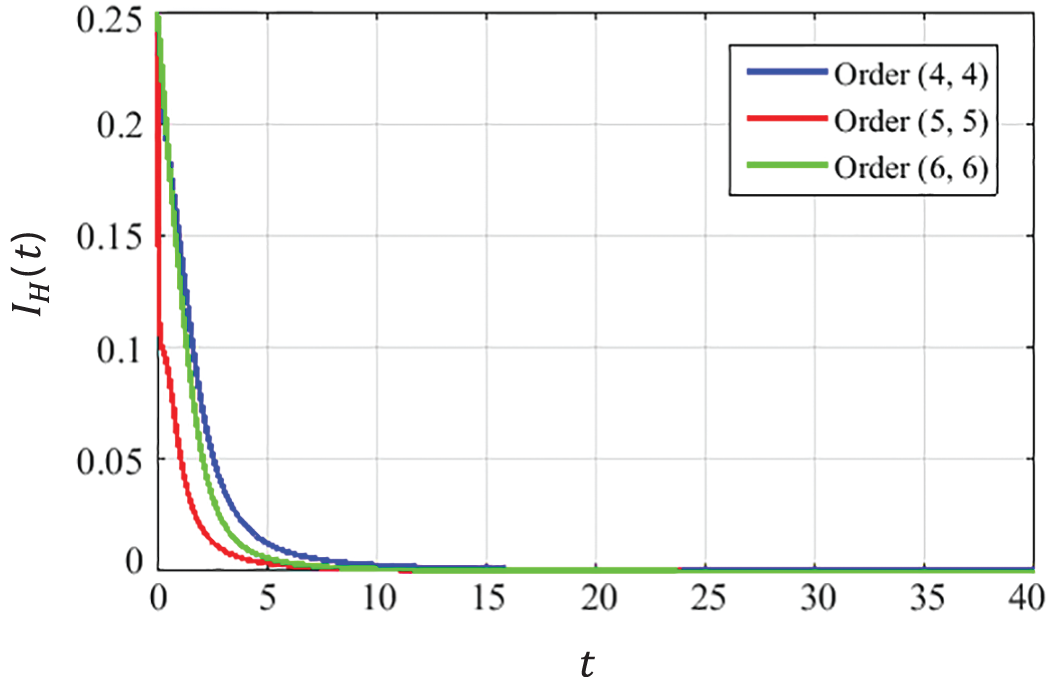
Figure 6: Dynamics of HPV infected population at DFE

Figure 7: Dynamics of HPV infectious population at DFE

S(t)(4,4)_DFE=0.65+0.401t−53.63t2+12.49t3−2.46t41+0.63t−81.84t2+12.63t3−2.46t4(22)

IH(t)(4,4)_DFE=0.25+51.00t+24.59t2+0.20t3+1.20×10−04t41+204.45t+293.69t2−113.90t3+121.70t4(23)

Ic(t)(4,4)_DFE=0.1+144.80t+318.96t2−1.54t3+7.36×10−05t41+1446.26t+1006.61t2−131.08t3+29.40t4(24)

S(t)(5,5)_DFE=0.65+89.97t+42.66t2+227.47t3+113.80t4+12.68t51+138.54t+40.14t2+434.56t3+112.78t4+12.68t5(25)

IH(t)(5,5)_DFE=aS0+57.46t+558.66t2+831.86t3−5.42t4+0.02t51+230.21t+8624.20t2−996.65t3+9817.35t4+8225.81t5(26)

Ic(t)(5,5)_DFE=aS0+66.56t+73.62t2+701.91t3−3.54t4+4.56×10−04t51+664.38t+777.47t2+4632.15t3−226.96t4+77.13t5(27)

S(t)(6,6)_DFE=0.65+63.60t−175.94t2+2735.40t3+1038.47t4+42.25t5+107.34t61+97.94t−245.44t2+4080.91t3+2274.90t4+36.21t5+107.34t6(28)

IH(t)(6,6)_DFE=0.25+21.13t+21.54t2+183.96t3+36.05t4+1.02×10−01t5+1.41×10−04t61+84.82t+130.97t2+683.90t3+1115.62t4−650.61t5+572.4t6(29)

Ic(t)(6,6)_DFE=0.1+38.31t+120.19t2+494.70t3+732.95t4−3.55t5+5.12×10−04t61+381.87t+1386.30t2+1522.54t3+4797.92t4−811.89t5+138.40t6(30)

Using the limiting property of Padé approximation described in Eq. (6), it is observed that the solutions of the CCE model found by the ESPA scheme converge to the DFE point for all considered orders of approximants, i.e., N=4,5,6.

limt→∞S(t)(N,N)_DFE={aS4bS4=−2.46211−2.46214≈1ifN=4aS5bS5=12.6803612.680451≈1ifN=5aS6bS6=107.3400107.3401≈1ifN=6

limt→∞IH(t)(N,N)_DFE≈{aIH4bIH4=1.20×10−04121.70≈0ifN=4aIH5bIH5=0.024637538225.8088≈0ifN=5aIH6bIH6=1.41×10−04572.4≈0ifN=6

limt→∞Ic(t)(N,N)_DFE≈{aIc4bIc4=7.36×10−0529.40≈0ifN=4aIc5bIc5=4.56×10−0477.133309≈0ifN=5aIc6bIc6=5.12×10−04138.40≈0ifN=6

The closed-form approximate solutions with optimized coefficients for the CCE model at the EE point are given below in Eqs. (31) to (39).

The convergence curves presented in Figs. 8–10 describe that the curves of susceptible S(t), HPV-infected IH and HPV infectious Ic converge towards the disease-free equilibrium point. Moreover, the convergence of state variables to the exact EE point can be noticed from the Figs. 9–11. The values of model parameters are set so that the basic reproductive number is maintained as R0>1 EE point. The convergence speed of state variables can be matched from the Figs. 9–11.

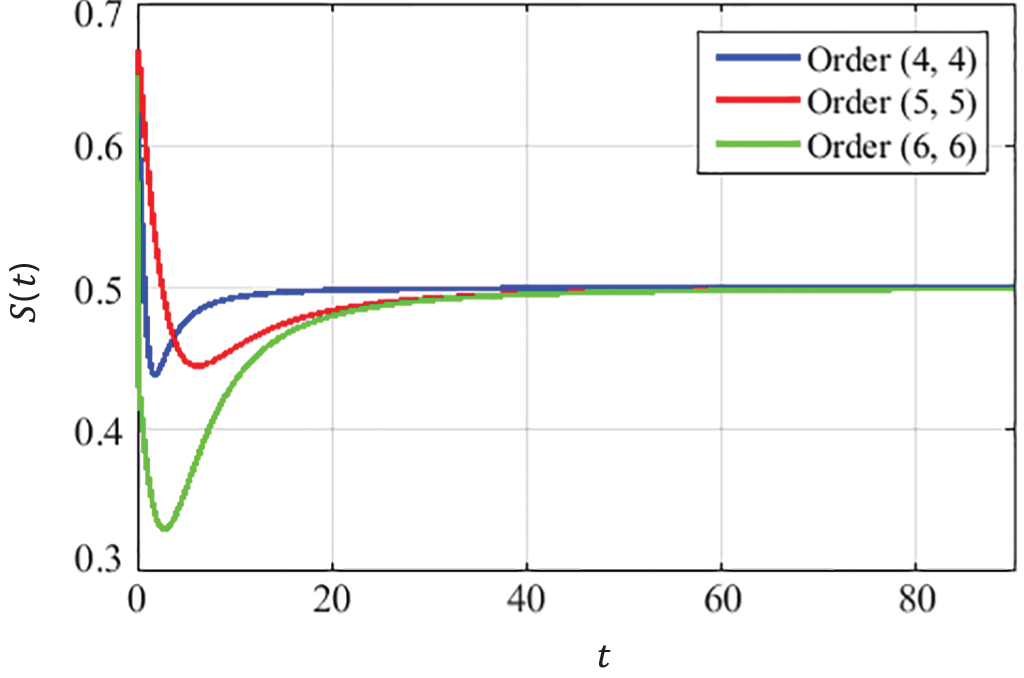
Figure 8: Dynamics of the susceptible population at EE

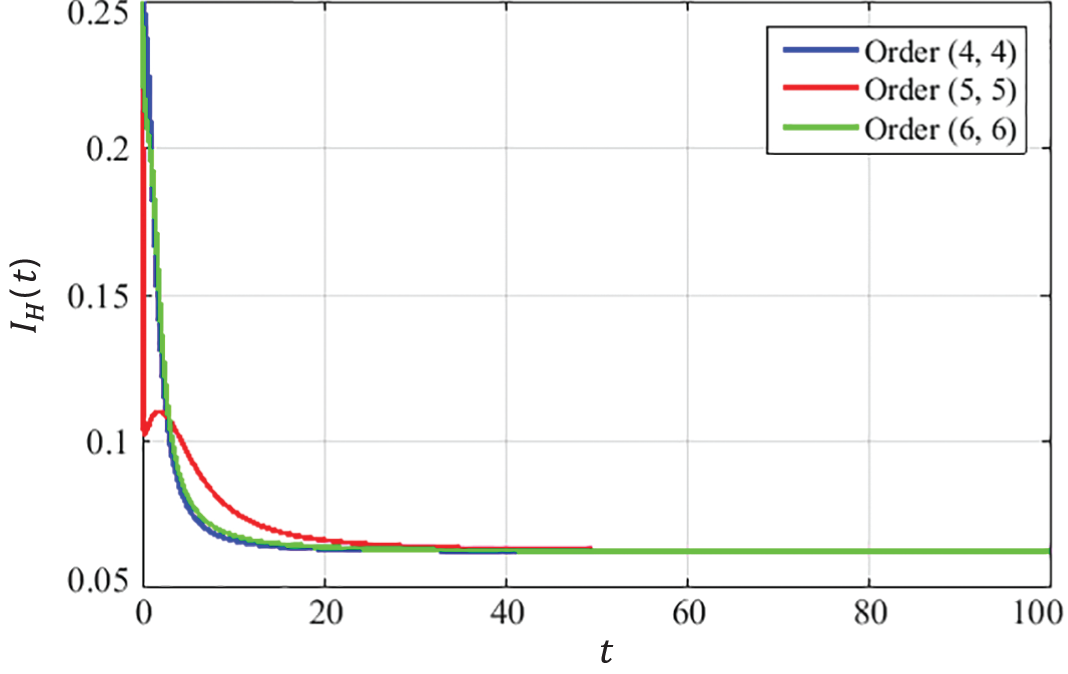
Figure 9: Dynamics of HPV infected population at EE

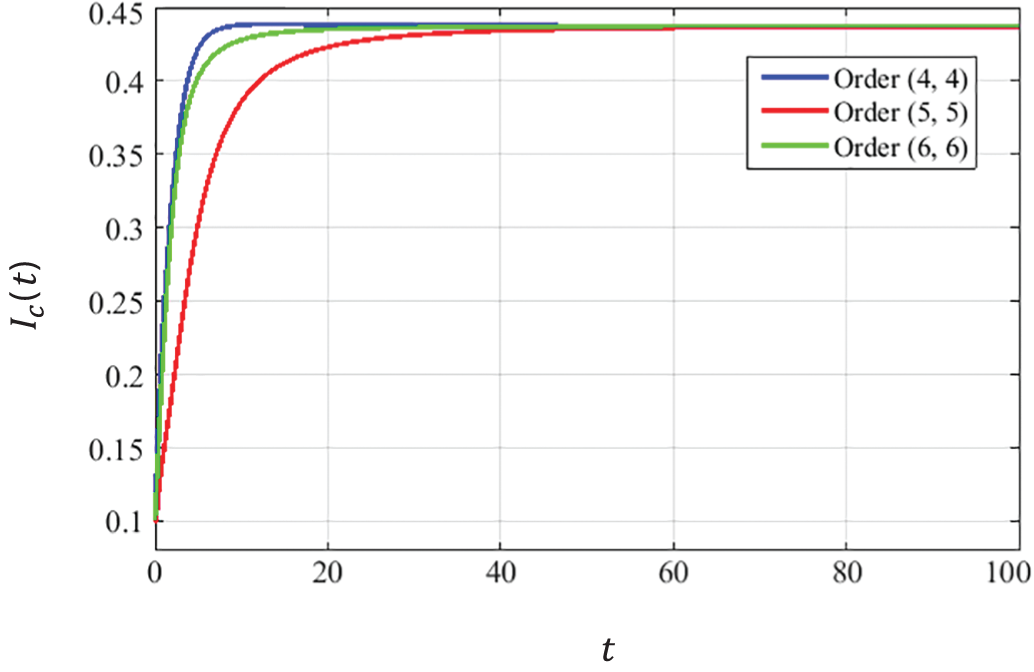
Figure 10: Dynamics of HPV infectious population at EE

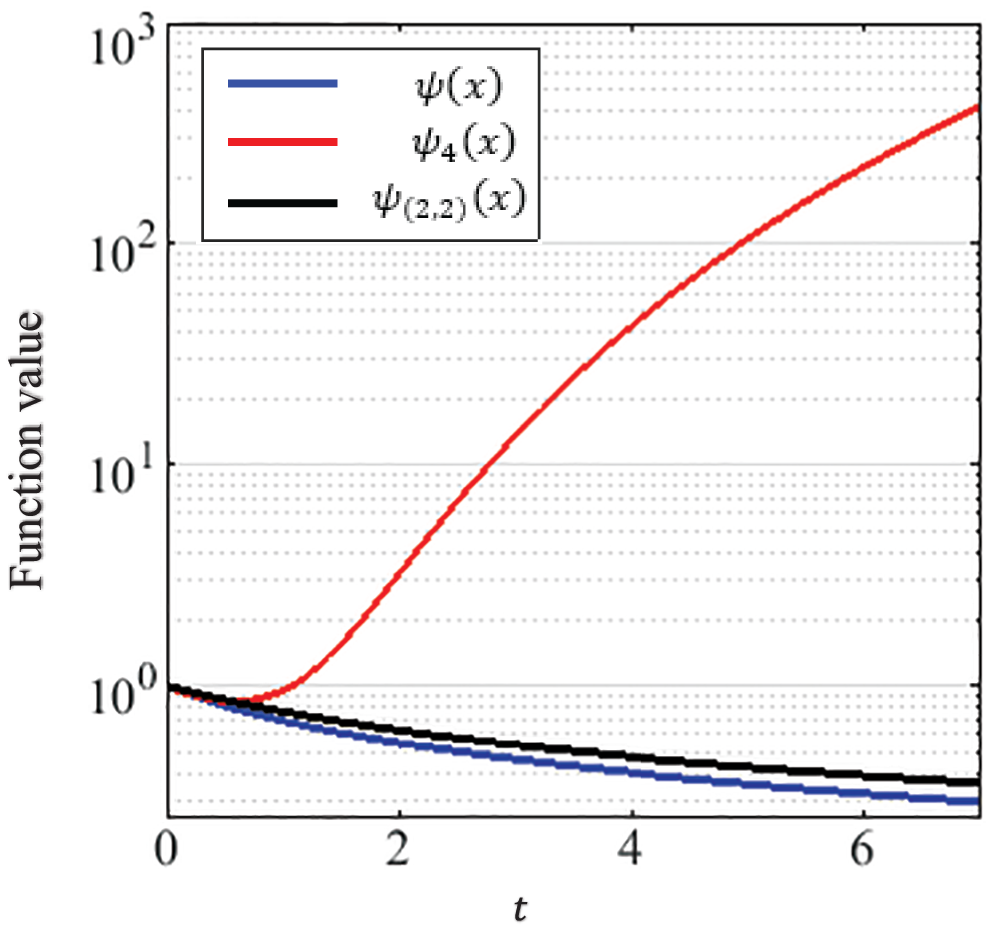
Figure 11: Convergence curves of approximations in comparison with exact function

S(t)(4,4)_EE=aS0+66.88t−4.72t2+8.40t3+12.21t41+103.24t+32.39t2+16.62t3+24.42t4(31)

IH(t)(4,4)_EE=aS0+37.18t+39.66t2+2.01t3+4.84t41+148.49t+161.14t2+34.89t3+77.41t4(32)

Ic(t)(4,4)_EE=aS0+52.48t+142.49t2−15.85t3+13.60t41+523.11t+278.79t2−35.97t3+31.08t4(33)

S(t)(5,5)_EE=aS0+0.09t+947.78t2+29.11t3+11.03t4+5.10t51+0.56t+1391.32t2+255.98t3+21.18t4+10.20t5(34)

IH(t)(5,5)_EE=aS0+3.13t+341.20t2+182.52t3+3.90t4+3.44t51+12.23t+3560.91t2+1259.34t3+74.47t4+55.09t5(35)

Ic(t)(5,5)_EE=aS0+24.95t+16.95t3+408.81t3+35.67t4+54.991t51+247.80t+315.34t2+2906.23t3+72.73t4+125.68t5(36)

S(t)(6,6)_EE=aS0−7.58t+592.08t2+622.51t3+111.78t4+15.91t5+10.78t61−11.32t+1322.83t2+1596.22t3+640.71t4+29.75t5+21.56t6(37)

IH(t)(6,6)_EE=aS0+5.93t+241.62t2−106.68t3+61.20t4+3.67t5+4.65t61++23.45t+1093.23t2−283.67t3+105.27t4+64.49t5+74.46t6(38)

Ic(t)(6,6)_EE=aS0+13.80t+45.53t2+68.10t3+75.55t4+29.47t5+40.54t61+129.27t+307.38t2+219.63t3+406.58t4+65.95t5+92.67t6(39)

The convergence is obtained for solutions at EE point (S∗,IH∗,Ic∗)≈(0.5,0.062501,0.4375) as below:

limt→∞S(t)(N,N)_EE={aS4bS4=12.2078225824.41560563≈S∗ifN=4aS5bS5=5.10032032510.20021098≈S∗ifN=5aS6bS6=10.7803873421.56079381≈S∗ifN=6

limt→∞IH(t)(N,N)_EE≈{aIH4bIH4=4.83794091477.40595419≈IH∗ifN=4aIH5bIH5=3.44435273855.08996583≈IH∗ifN=5aIH6bIH6=4.6536492274.4554758≈IH∗ifN=6

limt→∞Ic(t)(N,N)_EE≈{aIc4bIc4=13.5975758831.08020521≈Ic∗ifN=4aIc5bIc5=54.98562991125.6762732≈Ic∗ifN=5aIc6bIc6=40.5413109692.66618772≈Ic∗ifN=6

4.3 Positivity Analysis

The proposed ESPA scheme incorporates a positivity condition within the definition of the penalty function. However, a formal proof is presented as follows.

Suppose that GA-MPC returns an optimal solution x∗ with ψ(x∗)=ω upon termination. Since in all of the results, ω is non-negative, it proceed as follows:

Consider at any iteration k, the best solution be x(k) defined by:

x(k)=arg(min1≤i≤PSψ(xi))

where

ψ(x(k))=13∑j=13ψj(x(k))+∑i=14Li×Pi(x(k))

With the following inductions:

P1(x(k))=13{(𝓅S0−S(t0))2+(𝓅IH0−IH(t0))2+(𝓅Iu0−Iu(t0))2}≥0

P2(x(k))=max{0,δ−|∑j=1Nbvjtj+1|:v=S,IH,Ic}

P3(x(k))=max{0,−𝓅S,−𝓅IH,−𝓅Ic}

P4(x(k))=max{0,𝓅S+𝓅IH+𝓅Ic−1}

The positivity of solutions is ensured through the penalty function P3(x(k)). This study supposes that P3(x(k))>0 and P3(x(k))=−𝓅S that means 𝓅S is negative. Then, x∗ is optimal solution satisfies the following condition:

ψ(x∗)≤ψ(x(k))∀k

⇒ω≤13∑j=13ψj(x(k))+L3×P3(x(k))

⇒ω≤13∑j=13ψj(x(k))−L3×𝓅S(x(k))

Embedding the non-negativity of each ψj(x(k)) at each iteration in the above inequality, then:

ω−13∑j=13ψj(x(k))≤−L3×𝓅S(x(k))

𝓅S(x(k))≥1L3(13∑j=13ψj(x(k))−ω)

𝓅S(x(k))≥limL3→∞1L3(13∑j=13ψj(x(k))−ω)=0

⇒𝓅S(x(k))≥0∀k

This proves the positivity of 𝓅S for large values of penalty factor L3. On similar lines, it can also establish the positivity of 𝓅IH and 𝓅Ic. Consequently, it is concluded that the EPA scheme finds positive solutions with sufficiently large choices of penalty factors.

5  Validating ESPA Scheme

The section explains the rationale behind introducing the ESPA scheme to solve the CCE model. It justifies the utilization of MPC-GA in the ESPA framework and why non-singular Padé rational functions are preferred over alternative techniques for approximating CCE physical profiles. In addition, it emphasizes the significant advantages of the ESPA scheme over conventional semi-analytical and finite difference approaches.

5.1 Opting Safe Padé Approximations

Padé rational functions have several advantages over other approximation functions, especially the polynomials of finite degrees. Some points are listed below:

•   The primary benefit of using safe Padé approximations is that it yields a rational approximation of the solution free of singularities.

•   The unbounded Taylor series solutions that are produced by semi-analytical techniques such as the homotopy analysis method (HAM) and optimized homotopy analysis method (OHAM) limit their applicability to CCE models having steady-state conditions. On the other hand, Padé rational functions with few optimal coefficients can converge to steady states. Subsections 4.2 and 4.3 detail how this part of the underlying problem is theoretically established.

•   Selecting Padé approximation over methods with truncated Taylor series because the truncated series can diverge from the exact solution. On the other hand, low order Padé functions approximate higher-degree truncated Taylor series. Yamada et al. [45] highlighted this behavior using a counter-example. The example presents a test function ψ(t) with t=−1 as a discontinuity, truncated Taylor’s series of order four ψ4(t) at t=0 and Padé approximation ψ(2,2)(t) of ψ4(t) is described as follows:

ψ(t)=log⁡(1+t)t

ψ4(t)=1−12t+12t2−14t3+15t4

ψ(2,2)(t)=1+(7/8)t+(1/30)t21+(6/5)t+(3/10)t2

Fig. 11 shows the graphs of ψ(t), ψ4(t), and ψ(2,2)(t). The truncated approximation ψ4(t) agrees with ψ(t) until t<1 and then deviates from the actual function when t>1. The Padé rational approximation ψ(2,2)(t) high precession, on the other hand, approximates the actual function well beyond t=1. This specific example encourages using Padé approximations over other approximation functions to maintain approximation accuracy over a larger radius.

•   Safe Padé rational functions also have advantages such as better convergence, safeguarding of analytic properties, effective approximation using fewer terms, and operative management of sharp gradients. These traits augment the applicability and flexibility of safe Padé approximations across a broad range of complex problems.

5.2 Advantages of ESPA Scheme

The ESPA scheme has some advantages over existing methods for the following reasons:

•   The primary advantage of the ESPA scheme over existing methods for CCE-type models is its analytical properties in dealing with steady-state situations.

•   Equations of the CCE model immediately lead to the analytical determination of steady states, which are obtained automatically by the ESPA scheme through the optimization process. On the other hand, classical approaches, such as the Euler’s method, 4th Order Runge Kutta method (RK4), shooting method, and other numerical schemes, begin with CCE initial conditions and largely depend on discretization step lengths. They do not have the theoretical information about the steady states of the CCE model and so can diverge for larger step lengths. The ESPA system, on the other hand, is not dependent on discretization steps and provides convergence to accurate steady states by utilizing theoretical information. These facts make the EPA program a better option than traditional techniques.

•   The ESPA framework runs without the need for linearization of nonlinear terms within the model, avoiding linearization errors. Therefore, the ESPA technique is preferable over linearization-dependent methods.

•   The ESPA scheme combines mathematical techniques with artificial intelligence, complementing artificial intelligence approaches in dealing with epidemiological models, particularly artificial neural networks (ANNs). Unlike ANNs, which face issues such as overfitting and interpreting opaque predictions due to their reliance on training data, the ESPA approach is a direct solver unaffected by such data dependencies.

ESPA shows remarkable performance in the present CCE model and is expected to be a suitable alternative for similar models of fractional order [46–48] as well as integer [49–52] orders in epidemiology and image processing [53]. Despite its remarkable performance on the underlying model, it is important to highlight that each approach has limits in real-world applications when comparing alternative ways alongside the ESPA scheme. This emphasizes the need for more numerical techniques. Like other methods, when applying ESPA to a problem of a different character, careful thought is essential, especially when working with many governing equations.

6  Conclusions and Article Novelty

This study proposes an evolutionary computational paradigm for computing the closed-form approximate solution of the HPV cervical cancer model. The proposed scheme employs an optimized non-singular Padé approximation to analyze the extinction and prevalence of HPV infection in the human population. The computed equilibrium points are analytically and numerically verified. From the results obtained in the last section, it can be concluded that:

  i)  The proposed ESPA scheme is independent of discretization step length. Due to non-zero singularity tolerance, the solution for one assumed step length is valid for several other choices.

 ii)  Once the optimized values of unknown coefficients are computed, the ESPA scheme converges to steady states unconditionally.

iii)  A new concept of handling the positivity and boundedness of the model through a penalty function has been proposed and implemented successfully.

iv)  This study also provides a new idea of combining non-singular analytical rational functions and a powerful evolutionary computing technique for finding closed-form solutions of the CCE model.

This study opens several research directions in epidemiology and soft computing. For example, Padé approximants of orders (4, 4), (5, 5), and (6, 6) were used, giving rise to 27-, 33-, and 39-dimensional optimization problems, respectively, to be solved by the GA-MPC algorithm. The extended statistical analysis showed that the scalability of GA-MPC enables the ESPA scheme to find accurate solutions with even higher orders of Padé approximants. For future studies, the proposed scheme can be extended to investigate the optimal order of approximations for the epidemic model. Another dimension is to explore the computational excellence of global search optimization algorithms in solving high-dimensional optimization problems formulated for epidemiological models. The next direction is to extend the ESPA scheme to fractional, stochastic, delayed, and fuzzy epidemiological models. Finally, the proposed paradigm can be applied to boundary value problems, especially fluid dynamics models involving infinite boundary conditions.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: A. Ciancio, J. Ali; data collection: K. A. Khan, N. Raza; analysis and interpretation of results: H. M. Baskonus, M. Luqman; draft manuscript preparation: Z. U. Khan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data that support the findings of this study are included within the article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Hammer, A., Rositch, A., Qeadan, F., Gravitt, P. E., Blaakaer, J. (2016). Age-specific prevalence of HPV16/18 genotypes in cervical cancer: A systematic review and meta-analysis. International Journal of Cancer, 138(2), 2795–2803. [Google Scholar] [PubMed]

2. Wentzensen, N., Arbyn, M., Berkhof, J., Bower, M., Canfell, K. et al. (2017). How HPV knowledge is changing screening practice. International Journal of Cancer, 140(1), 2192–2200. [Google Scholar] [PubMed]

3. Lee, P. W., Kwan, T. T. C., Tam, K. F., Chan, K. K. L., Young, P. M. C. et al. (2007). Beliefs about cervical cancer and human papillomavirus and acceptability of HPV vaccination among Chinese women in Hong Kong. Preventive Medicine Journal, 45(1), 130–134. [Google Scholar]

4. Godfrey, J., Harper, M. D. (2007). Discusses the HPV vaccine and prevention of cervical cancer. Journal of Women’s Health, 16(10), 139–1401. [Google Scholar]

5. Gillison, M. L., Chaturvedi, A. K., Lowy, D. R. (2008). HPV prophylactic vaccines and the potential prevention of noncervical cancers in both men and women. European Journal of Cancer Supplements, 13(10), 3036–3046. [Google Scholar]

6. Herbert, J., Janis, C. (2008). Reducing patient risk for human papillomavirus infection and cervical cancer. Journal of American Osteopathic Association, 108(2), 65–70. [Google Scholar]

7. Muller, H., Bauch, C. (2010). When do sexual partnerships need to be accounted for in transmission models of human papillomavirus. International Journal of Environmental Research and Public Health, 1(2), 635– 650. [Google Scholar]

8. Chaturvedi, A. K., Engels, E. A., Pfeiffer, R. M., Hernandez, B. Y., Xiao, W. et al. (2011). Human papillomavirus and rising or pharyngeal cancer incidence in the United States. Journal of Clinical Oncology, 29(32), 4294–4301. https://doi.org/10.1200/JCO.2011.36.4596. [Google Scholar] [PubMed] [CrossRef]

9. Abodayeh, K., Raza, A., Arif, M. S., Rafiq, M., Bibi, M. et al. (2020). Stochastic numerical analysis for impact of heavy alcohol consumption on transmission dynamics of gonorrhoea epidemic. Computers, Materials & Continua, 62(3), 1125–1142. https://doi.org/10.32604/cmc.2020.08885 [Google Scholar] [CrossRef]

10. Giuliano, A. R., Nyitray, A. G., Kreimer, A. R., Campbell, C. M. P., Goodman, M. T. et al. (2015). EUROGIN 2014 roadmap: Differences in human papillomavirus infection natural history transmission and human papillomavirus-related cancer incidence by gender and anatomic site of infection. International Journal of Cancer, 136(2), 2752–2760. [Google Scholar] [PubMed]

11. Saslow, D., Solomon, D., Lawson, H. W., Killackey, M. D. M., Kulasingam, S. L. et al. (2012). American society for colposcopy and cervical pathology, and American society for clinical pathology screening guidelines for the prevention and early detection of cervical cancer. American Journal of Clinical Pathology, 137(2), 516–542. [Google Scholar] [PubMed]

12. Mesher, D., Cuschieri, K., Hibbitts, S., Jamison, J., Sargent, A. et al. (2015). Type-specific HPV prevalence in invasive cervical cancer in the UK prior to national HPV immunization programme baseline for monitoring the effects of immunisation. Journal of Clinical Pathology, 68(2), 135–140. https://doi.org/10.1136/jclinpath-2014-202681. [Google Scholar] [PubMed] [CrossRef]

13. Radecki, C., Pearson, H. C., Breltkopf, M. D. (2005). Poor knowledge regarding the pap test among low-income women undergoing routine screening. Perspectives on Sexual and Reproductive Health, 35(22), 78–84. [Google Scholar]

14. Winer, R., Hughes, J., Feng, Q. (2006). Condom use and the risk of genital human papillomavirus infection in young women. New England Journal of Medicine, 354(26), 45–54. [Google Scholar]

15. Raley, J. C., Followwill, K. A., Zimet, G. D., Ault, K. A. (2004). Gynecologists attitudes regarding human papilloma virus vaccination: A survey of fellows of the American college of obstetricians and gynecologists. Infectious Diseases in Obstetrics and Gynecology, 1(12), 127–133. [Google Scholar]

16. Pham, T. H., Nguyen, T. H., Herrero, R. (2003). Human papillomavirus infection among women in south and north Vietnam. International Journal of Cancer, 104(2), 213–220. https://doi.org/10.1002/ijc.v104:2 [Google Scholar] [CrossRef]

17. McCaffrey, K., Forrest, S., Waller, J., Desai, M., Szarwski, A. et al. (2003). Attitudes towards HPV testing: A qualitative study of beliefs among Indian, Pakistani, African, Caribean and white British women in the UK. British Journal of Cancer, 88(1), 42–46. https://doi.org/10.1038/sj.bjc.6600686. [Google Scholar] [PubMed] [CrossRef]

18. Clifford, G. M., Smith, J. S., Plummer, M., Munoz, N., Franceschi, S. et al. (2003). Human papillomavirus types in invasive cervical cancer worldwide: A meta-analysis. British Journal of Cancer, 88(2), 63–73. [Google Scholar] [PubMed]

19. Collins, S., Mazloomzadeh, S., Winter, H. (2002). High incidence of cervical human papillomavirus infection in women during their first sexual relationship. British Journal of Obstetrics and Gynaecology, 109(1), 96–98. https://doi.org/10.1111/bjo.2002.109.issue-1 [Google Scholar] [CrossRef]

20. Mandelblatt, J. S., Lawrence, W. F., Womack, S. M., Jacobson, D. J., Hwang, T. Y. et al. (2002). Benefits and costs of using HPV testing to screen for cervical cancer. Journal of American Medical Association, 287(23), 72–81. [Google Scholar]

21. Hausen, H. Z. (2000). Papillomaviruses causing cancer evasion from host-cell control in early events in carcinogenesis. Journal of National Cancer Institute, 96(1), 690–698. [Google Scholar]

22. Bierman, G. Y. H., Beardsley, L., Chang, C. J., Burk, R. D. (1998). Natural history of cervical-vaginal papillomavirus infection in young women. The New England Journal of Medicine, 338(1), 423–428. [Google Scholar] [PubMed]

23. Walboomers, J. M., Jacobs, M. V., Manos, M. M., Bosch, F. X., Kummer, J. A. et al. (1999). Human papillomavirus is a necessary cause of invasive cervical cancer worldwide. The Journal of Pathology, 189(1), 12–19. https://doi.org/10.1002/(ISSN)1096-9896 [Google Scholar] [CrossRef]

24. Raza, A., Arif, M. S., Rafiq, M. (2019). A reliable numerical analysis for stochastic gonorrhea epidemic model with treatment effect. International Journal of Biomathematics, 12(5), 445–465. [Google Scholar]

25. Rafiq, M., Ali, J., Riaz, M. B., Awrejcewicz, J. (2022). Numerical analysis of a bi-modal COVID-19 sitr model. Alexandria Engineering Journal, 61, 227–235. https://doi.org/10.1016/j.aej.2021.04.102 [Google Scholar] [CrossRef]

26. Kennedy, J., Eberhart, R. (1995). Particle swarm optimization. IEEE International Conference on Neural Networks, pp. 1942–1948. Perth, WA, Austrailia. [Google Scholar]

27. Storn, R., Price, K. (1997). Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 11, 341–359. https://doi.org/10.1023/A:1008202821328 [Google Scholar] [CrossRef]

28. Ali, J., Saeed, M., Tabassam, M. F., Iqbal, S. (2019). Controlled showering optimization algorithm: An intelligent tool for decision making in global optimization. Computational and Mathematical Organization Theory, 25, 132–164. https://doi.org/10.1007/s10588-019-09293-6 [Google Scholar] [CrossRef]

29. Karaboga, D., Basturk, B. (2007). A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. Journal of Global Optimization, 39, 459–471. https://doi.org/10.1007/s10898-007-9149-x [Google Scholar] [CrossRef]

30. Rao, R. V., Savsani, V. J., Vakharia, D. P. (2011). Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems. Computer-Aided Design, 43(3), 303–315. https://doi.org/10.1016/j.cad.2010.12.015 [Google Scholar] [CrossRef]

31. Bangyal, W. H., Ahmad, J., Abbas, Q. (2013). Analysis of learning rate using CPN algorithm for hand written character recognition application. IACSIT International Journal of Engineering and Technology, 5(2), 87–190. [Google Scholar]

32. Ashraf, A., Zhao, Q., Bangyal, W. H., Iqbal, M. (2023). Analysis of brain imaging data for the detection of early age autism spectrum disorder using transfer learning approaches for internet of things. IEEE Transactions on Consumer Electronics, 70(1), 4478–4489. https://doi.org/10.1109/TCE.2023.3328479 [Google Scholar] [CrossRef]

33. Ali, J., Saeed, M., Rafiq, M., Iqbal, S. (2018). Numerical treatment of nonlinear model of virus propagation in computer networks: An innovative evolutionary Padé approximation scheme. Advances in Differential Equations, 2018(1), 1–18. [Google Scholar]

34. Nisar, K. S., Ali, J., Mahmood, M. K., Ahmad, D., Ali, S. et al. (2021). Hybrid evolutionary Padé approximation approach for numerical treatment of nonlinear partial differential equations. Alexandria Engineering Journal, 60(5), 4411–4421. https://doi.org/10.1016/j.aej.2021.03.030 [Google Scholar] [CrossRef]

35. Raja, M. A. Z., Shoaib, M., Tabassum, R., Khan, M., Jagannatha, C. G. et al. (2022). A stochastic intelligent approach for entropy optimized mixed convective second-order slip flow over a movable surface. Archive of Applied Mechanics, 92, 2435–2454. https://doi.org/10.1007/s00419-022-02187-1 [Google Scholar] [CrossRef]

36. Eiben, A. E., Rau, P. E., Ruttkay, Z. S. (1994). Genetic algorithms with multi-parent recombination. Proceedings of the Parallel Problem Solving from Nature—PPSN III, pp. 78–87. Jerusalem, Israel. [Google Scholar]

37. Ali, J., Riaz, M. B., Atangana, A., Saeed, M. (2021). Evolutionary modelling of dengue fever with incubation period of virus, mathematical modelling and soft computing in epidemiology, pp. 1–18. Boca Raton, Florida, USA: CRC Press, Taylor & FrancisGroup. [Google Scholar]

38. Ali, J., Raza, A., Ahmed, N., Ahmadian, A., Rafiq, M. et al. (2021). Evolutionary optimized Padé approximation scheme for analysis of COVID-19 model with crowding effect. Operations Research Perspectives, 8, 100201. [Google Scholar]

39. Basendwah, G. A., Raza, N., Ali, J. (2023). Evolutionary Padé approximation for heat and mass transfer analysis of Falkner-Skan flow of a bio-convective casson fluid. Mathematics, 11(7), 1–25. [Google Scholar]

40. Raza, A., Rafiq, M., Alrowaili, D., Ahmed, N., Khan, I. et al. (2022). Design of computer methods for the solution of cervical cancer epidemic model. Computers, Materials & Continua, 70(1), 1649–1666. https://doi.org/10.32604/cmc.2022.019148 [Google Scholar] [CrossRef]

41. Padè, H. E. (1892). Sur la representation approchèe d’une fonction par des fractions rationnelles. Annales Scientifiques De l’École Normale Supérieure, 9, 1–93. [Google Scholar]

42. Baker, G. A. (1975). Essentials of Padé approximants. New York, USA: Academic Press. [Google Scholar]

43. Elsayed, S. M., Sarker, R. A., Essam, D. L. (2011). GA with a new multi-parent crossover for solving IEEE-CEC2011 competition problems. IEEE Congress of Evolutionary Computation (CEC), pp. 1034–1040. New Orleans, LA, USA. [Google Scholar]

44. Akgul, A., Ahmed, N., Raza, A., Iqbal, Z., Rafiq, M. et al. (2021). A fractal fractional model for cervical cancer due to human papillomavirus infection. Fractals, 29(5), 2140015. https://doi.org/10.1142/S0218348X21400156 [Google Scholar] [CrossRef]

45. Yamada, M. H. S., Ikeda, K. S. (2014). A numerical test of Padé approximation for some functions with singularity. International Journal of Computational Mathematics, 2014, 587430. [Google Scholar]

46. Jafari, H., Goswami, P., Dubey, R. S., Sharma, S., Chaudhary, A. (2023). Fractional SIZR model of Zombie infection. International Journal of Mathematics and Computer in Engineering, 1(1), 91–104. https://doi.org/10.2478/ijmce-2023-0007 [Google Scholar] [CrossRef]

47. Dubey, R. S., Goswami, P., Baskonus, H. M., Gomati, T. (2023). On the existence and uniqueness analysis of fractional blood glucose-insulin minimal model. International Journal of Modeling, Simulation, and Scientific Computing, 14(3), 2350008. https://doi.org/10.1142/S1793962323500083 [Google Scholar] [CrossRef]

48. Singh, R., Mishra, J., Gupta, V. K. (2023). Dynamical analysis of a tumor growth model under the effect of fractal fractional Caputo-Fabrizio derivative. International Journal of Mathematics and Computer in Engineering, 1(1), 115–126. https://doi.org/10.2478/ijmce-2023-0009 [Google Scholar] [CrossRef]

49. Kavya, K. N., Veeresha, P., Baskonus, H. M., Alsulami, M. (2024). Mathematical modeling to investigate the influence of vaccination and booster doses on the spread of Omicron. Communications in Nonlinear Science and Numerical Simulation, 130, 1–15. [Google Scholar]

50. Sabir, Z., Umar, M. (2023). Levenberg-Marquardt backpropagation neural network procedures for the consumption of hard water-based kidney function. International Journal of Mathematics and Computer in Engineering, 1(1), 127–138. https://doi.org/10.2478/ijmce-2023-0010 [Google Scholar] [CrossRef]

51. Umar, M., Sabir, Z., Raja, M. A. Z., Baskonus, H. M., Ali, M. R. et al. (2023). Heuristic computing with sequential quadratic programming for solving a nonlinear hepatitis B virus model. Mathematics and Computers in Simulation, 212, 234–248. https://doi.org/10.1016/j.matcom.2023.04.034 [Google Scholar] [CrossRef]

52. İlhan, Ö., Şahin, G. (2024). A numerical approach for an epidemic SIR model via Morgan-Voyce series. International Journal of Mathematics and Computer in Engineering, 2(1), 125–140. https://doi.org/10.2478/ijmce-2024-0010 [Google Scholar] [CrossRef]

53. Nambiar, V. B., Ramamurthy, B., Veeresha, P. (2024). Gender determination from periocular images using deep learning based efficient net architecture. International Journal of Mathematics and Computer in Engineering, 2(1), 59–70. https://doi.org/10.2478/ijmce-2024-0005 [Google Scholar] [CrossRef]