Efficient Penetration Testing Path Planning Based on Reinforcement Learning with Episodic Memory

Nomenclature

1  Introduction

Organized hacking attacks have been commonplace in recent years, and the cyber security threat situation is serious. Traditional defenses, such as firewalls, have limited protective effects from the point of view of defenders. Active defense technologies, such as data encryption and vulnerability assessment, have further improved the defense strategy of the system with the development of artificial intelligence and data analysis technology. Active defense technologies can prevent threats and disrupt intrusions in advance, which makes up for the shortcomings of traditional defenses.

Intelligent penetration testing (PT) has become an essential tool for network vulnerability assessment. It simulates the attack patterns and means of hackers and is able to discover the penetration paths of network systems. In the contrast with traditional manual testing, intelligent penetration testing can reduce the reliance on experts and improve penetration efficiency.

The key to intelligent penetration testing is automatically discovering penetration paths and providing testers with an execution plan. It is acknowledged as penetration testing path planning as well. A penetration path, also known as an attack path, is a sequence of actions taken in the target network to reach the target host. The study of methods of the improvement of the efficiency and effectiveness of penetration testing path planning is of great significance to promote the development of intelligent penetration testing.

Currently, reinforcement learning (RL) has achieved better-than-human performance in game fields, which inspires research in intelligent penetration testing. Researchers have attempted to apply RL in penetration testing path planning [1–3]. In these studies, RL-based approaches learn better planning strategies in less time and with less effort among existing intelligent methods.

Nevertheless, the application of reinforcement learning to intelligent penetration suffers from convergence difficulties. Unlike the game domain, reinforcement learning has a high-dimensional discrete action space. And the action space grows exponentially with the host counts [2]. The ability of reinforcement learning algorithms to handle complex environments is limited by the challenge of exploring large action spaces. This leads to difficulties in learning stable penetration strategies with existing solutions.

To address the challenge of exploring large-scale action spaces in PT scenarios, this paper proposes an episodic memory-guided Deep Q-network method (EMG-DQN) to discover the optimal penetration path efficiently. Firstly, the PT framework is transformed into an RL task. Subsequently, the episodic memory reading-writing mechanism is introduced to guide the agent’s exploration based on the Deep Q-Network (DQN) framework. Finally, extensive experiments are conducted in different scaled scenarios to verify the performance and scalability of the proposed algorithm.

The main contributions of this paper are as follows:

(1) This paper constructs a non-parametric episodic memory module for the storage of successful strategies. By reading the episodic memory, high-return penetration actions can be quickly targeted during penetration. The use of the episodic memory module resulted in the reduction of the size of action space exploration.

(2) An episodic memory-based exploration strategy is designed in this paper. The approach combines the episodic memory mechanism with ε-greedy policy to balance exploration and exploitation. The proposed strategy improves the convergence speed while ensuring the learning effect.

(3) In this paper, experiments are performed in different scaled scenarios to verify the effectiveness and scalability of the proposed scheme. The results of the comparison experiments show that EMG-DQN enjoys the state-of-the-art convergence performance and stable penetration performance.

This paper is organized as follows. Section 2 is the introduction to the related work around intelligent penetration testing. Section 3 is the presentation of the preliminary knowledge of reinforcement learning techniques. Section 4 is a presentation of the proposed method framework and design details. In Section 5, the effectiveness of the algorithm is verified by comparative and extended experiments.

2  Related Work

Work related to the field of intelligent penetration testing is presented in this section presents. Intelligent penetration testing, as an important active network defense technique, is widely used to assess the vulnerability of systems. The existing research is divided into two categories in this section: classical intelligent planning-based approaches, and reinforcement learning-based approaches.

2.1 Classical Intelligent Planning

The classical intelligent planning approach transforms the Penetration Testing (PT) problem into a planning domain description. Then, feasible penetration paths are discovered with the help of intelligent planning models.

Planning diagram techniques are capable to describe the attack process and assess security risks from the perspective of the attacker. Garrett et al. [4] modeled penetration testing as planning graph to find all attack paths. The proposed method was highly interpretable and time-consuming.

Sarraute et al. [5] applied a hierarchical task network to address the algorithm’s scalability. They divided the extensive network into several smaller networks in accordance with the network structure. Hu et al. [6] used a hierarchical clustering algorithm to decompose the network, on the basis of which they used an optimized genetic algorithm to discover the penetration paths in large-scale scenarios. However, experts are required to design the appropriate subtasks by the specific decomposition scheme. This is unrealistic in the face of dynamic and complex network scenarios.

Combinatorial optimization algorithms have also been widely used in the field of penetration testing path planning. Hu et al. [7] proposed the APU-D* method on the basis of heuristic search, introducing the action success rate to describe the degree of uncertainty in penetration testing scenarios to enhance the algorithm’s applicability in penetration testing scenarios. Chen [8] optimized the situational prediction model by applying simulated annealing (SA) algorithm and hybrid hierarchical genetic algorithm (HHGA). Gao et al. [9] added a replanning mechanism to the combinatorial optimization algorithm to quickly adjust the attack path when the host node changes.

The focus of the above research is the complete information condition. In the actual PT, obtaining the entire network topology, host configuration, and other scenario information in advance is difficult. Thus, the classic planning model is disabled to meet the demand [10].

2.2 Penetration Testing Path Planning Based on Reinforcement Learning

Reinforcement learning is the accumulation of experience by exploring the environment to learn optimal action strategies. The penetration testing process requires constant state observation of the environment to make dynamic decisions, which is similar to the learning mechanism of real-time strategy games. Recently, reinforcement learning (RL) has been applied to the modeling of the PT process and the learning of the optimal penetration paths.

Solutions based on traditional reinforcement learning have been applied to small-scale scenarios. Zhao et al. [1] proposed a RL-based penetration path recommendation model. To address the current lack of simulation environments for training PT agents, Schwartz et al. [2] modeled penetration testing as a Markov Decision Process (MDP) and designed a Network Attack Simulator (NAS) for the establishment of simulation scenarios. Ghanem et al. [3] designed an expert verification session to monitor the output penetration path of the planning system, which improves the success rate of planning.

To extend reinforcement learning algorithms in more complex scenarios, quite a few studies have used model-based optimization methods. Bland et al. [11] used formalism to model specific cyberattack patterns (cross-site scripting and spear-phishing). Erdodi et al. [12] modeled several specific penetration scenario structures to reduce the space of exploration and sampling, simplifying the learning problem. Pozdniakov et al. [13] pre-collected experts’ behavior samples. The agent imitates the trajectory of the expert through pre-training, which improves the training efficiency. Ghanem et al. [14] decomposed the target network previously based on expert experience. It reduces the difficulty of planning. The model-based approach can reduce the training difficulty by pre-training and modeling the agent with partial scene knowledge in advance. However, there is a risk in this optimization approach: the learning effect is very unstable when the agent is encountered with a previous scenario that has not been experienced before. Moreover, it is a challenge to ensure that the modeling is reliable.

In order to improve the adaptability of algorithms applied to the field of intelligent penetration, many studies have improved reinforcement learning. Nguyen et al. [15] proposed an algorithm with double agent architecture, where two agents are responsible for network topology discovery and vulnerability exploitation, but the learning is unstable. Zhou et al. [16] pruned the action space by decoupling the attack vectors and accelerated the convergence by combining mechanisms such as competing networks and noisy networks. In addition, Tran et al. [17] presented a deep hierarchical reinforcement learning architecture, which uses an algebraic approach to decompose the discrete action space of the penetration test simulator. These studies improved the agents’ planning efficiency to some extent.

In spite of this, the PT problem has a high-dimensional discrete action space. The action space grows exponentially with the scale of the scenario. It results in high convergence difficulty and long planning time for the RL algorithm, which has been a long-term challenge.

3  Preliminaries

Reinforcement learning (RL) learns the best strategy through the interaction between the agent and the environment. It discovers the action sequences that lead to the greatest cumulative reward.

RL is usually modeled as a Markov decision process (MDP), it is inscribed by the tuple <S, A, R, T, γ>. S denotes the finite set of states. A denotes the set of executable actions. The reward function R is used to evaluate the quality of the actions and is defined as: S×A→R. The state transition function T is unknown to the agent and represents the probability of transferring to the next state after executing action a in state s. γ∈[0, 1] is the discount factor used to determine the long-term reward. It is not necessary for RL to follow the dataset. The agent finds a mapping from states to actions by trying actions and observing their effects on the environment. The mapping relationship is called a policy π.

a=π(s)(1)

The agent interacts with the environment in the period of RL training process. The agent selects an action from action set A according to the learned policy at each step. As feedback, the environment returns a reward r(s,a) to the agent and transfers to the next state in accordance with transition probability p(s′|s,a). The goal of RL is the finding of the optimal strategy π∗ for the maximization of long-term cumulative rewards.

The long-term cumulative reward Rt at time step t and the optimal policy π∗ are shown in Eqs. (2) and (3).

Rt=∑k=0Kγkrk+1(2)

π∗=argmaxπ E[Rt|π](3)

where Rt is also known as the expected discounted reward. K is the number of steps taken to reach the target state from the current state. The policy π∗ gives the maximum expected reward for all states.

The action-value function Qπ(s,a) is used to denote the expected reward that is obtained by taking an action a from state s under policy π. Subsequently, the optimal action value function Q∗(s,a) is the maximum of all action values.

Q∗(s,a)=maxπQπ(s,a)=maxπE[Rt|st=s,at=a,π](4)

For the next state s′, when the corresponding optimal action-value function Q∗(s′,a′) is known, the current optimal policy is to choose an action a′ to maximize the objective function r+γQ∗(s′,a′).

Q∗(s,a)=Es′∼ε[r+γmaxa′Q∗(s′,a′)|s,a](5)

The RL algorithm can solve the optimal action-value function by the iterative update of the Bellman equation. However, it is not easy to implement it in practical applications.

The Deep Q-Network (DQN) method is based on value functions. It combines the advantages of neural networks and Q-learning, which has made good progress in previous studies. The action-value function is estimated by using a neural network with weight θ as a function approximator, which is called a Q network. DQN employs two neural networks. The online network continuously updates parameters calculating the estimated Q, while the target network updates with a particular frequency to calculate target Q. As a result, DQN reduces the correlation between the two Q values and improves the stability of learning.

4  Method

4.1 Overall Framework

To construct an episodic memory mechanism for directional exploration in the early stage of training, the EMG-DQN method proposed in this paper is designed. The overall framework of the algorithm is shown in Fig. 1. The critical components of EMG-DQN include the episodic memory module and the exploring strategy.

Figure 1: Overall framework of EMG-DQN

The episodic memory module stores and plays back advantageous action sequences. It allows the agent to make efficient use of the experience gained during penetration. The exploration strategy uses the exploration factor to dynamically adjust the proportion of episodic memory playback in accordance with the training stage. It preserves the agent’s independent exploration ability while rapidly accumulating high-quality action sequences in the early stage.

Before starting a new penetration path planning task, the agent initializes the configuration and formalizes the penetration task as an action selection process of RL. At each penetration action decision cycle, the agent receives the current observations of the target network and stores them in the experience pool. The neural network takes samples from the experience pool and updates the parameters at regular intervals. When the target host is reached, the scenario memory module reads the action trajectory from the experience pool for updating. The agent outputs the choice of action on the basis of the exploration strategy. After multiple rounds of training, the EMG-DQN converges. At this point, the agent is able to choose the optimal penetration strategy in the face of any state inputs.

4.2 PT Execution Module

PT execution module comprises of a RL agent and a scenario. RL agent is the individual who performs the attack action. The role of PT execution module is the formalization of the input information of the PT task into MDP tuples. After formalization, RL agent can continuously acquire information about the environment by interacting with the scenario, which is the basis of policy learning.

4.2.1 State Space

The state space helps the agent to express the available scenario information. A state is defined as the set of information that is currently being observed by the intrusion agent about the network. The finite state set S contains all information of compromised hosts of the target network.

The state vector is created by One-Hot encoding. As shown in Fig. 2, for a state s, it consists of host identification, service information and control information, denoted as s={Host ID,Service,Control}.

Figure 2: State vector

The Host ID is the host identification. It is uniquely determined by the subnet and host location {subnet,host}. Service is the running service information, for each available Service∈{absent,exist,uncertain}. Control reflects the damage to each host after the attack, expressed as Control={Compromised,Reachable,Discovered,Value,Access,OS}, provide feedback to the agent on the action effect. Where Value and Access are represented by numeric parameters reflecting the asset value and access of the host (1 for user and 2 for root access). The rest of the Control field is represented by the Boolean parameter {True,False}. Compromised indicates whether the host is successfully exploited. Reachable demonstrates whether a connection exists to the compromised host. Discovered indicates whether the host is probed, and OS indicates the operating system of the host’s running. Therefore, the state space is a possible combination of service and control information for each host in the network. It grows exponentially with the number of hosts and services found.

4.2.2 Action Set

The action space stores the actions that an attacker may take. It is beneficial for the agent to exploit the vulnerability present in the scenario. Executable action set A={a1,a2,a3,…,an} indicates the action space that the agent can select to control hosts on the target network. Each action vector a=<m,o> represents the execution of action of host m, including scan action, exploit action, and privilege action.

The action vector is also formalized with the help of One-Hot encoding. At each time step t, the agent in state st can select action at∈{Scan,Exploit,Privilege}. Scan defines the scanning actions that can be performed, including subnet scan, service scan, system scan and process scan, which are denoted as Scan={ServiceScan,OSScan,SubnetScan,ProcessScan}. Exploit defines the vulnerability exploitation actions. This paper assumes that there is a corresponding vulnerability exploitation action for each service running on the host. Privilege defines executable actions that can be used to elevate the user privilege to root privilege using processes that exist on the host.

An example composition of Exploit action vector, Exploit: {target, os, service, cost, prob, access}, the target host, the execution conditions, and the permissions upon successful execution were defined, as illustrated in Fig. 3. Here, based on the vulnerability rank in Metasploit and core impact, the attack success rate prob is quantified. The cost of the Exploit action is set based on Common Vulnerability Scoring System (CVSS), which is calculated as cost=sigmoid(STreat⋅SYear). Where STreat is the vulnerability threat level, this paper used the CVSS base score as the value of STreat. SYear took 20, 40 or 60 depending on the disclosure year of the vulnerability, with the earlier the year the lower the score.

Figure 3: Action vector

4.2.3 Reward Function

The reward function R defines the penetration agent optimization goal. r(s,a) defines the immediate reward obtained by performing the action a in state s.

The design of reward function refers to the work done by Chen et al. [18]. When the agent takes action at in state s and moves to the next state s′, the reward is determined by the Value of the state vector and the cost of the action vector, as shown in Eq. (6).

r(s,at)=value(s′,m)−cost(at)(6)

where value(s′,m) denotes the Value of the updated compromised host m in state s′. r(s,at) denotes the immediate reward.

In this paper, we first set a larger Value for the target sensitive host and 0 for the remaining non-target hosts. If state s′ does not produce a new compromised host compared to the previous state, then the immediate reward of the transition process is negative. Thus, the value of reward is the cost of performing action at. The reward for the transition process is the value of the new compromised host minus the cost of performing the action at if new compromised hosts appear in state s′ after the action is performed.

4.3 Episodic Memory Module

EMG-DQN leverages the successful strategies accumulated during penetration to enhance the exploration efficiency through episodic memory reading and writing. The episodic memory mechanism follows the idea of instance-based learning by creating a non-parametric dictionary structure to store the experienced good experiences. This allows a quick selection of successful policies when encountering experienced states [19]. In this paper, we set the target state at the end of the training episode: to obtain the root privileges of all sensitive hosts. Therefore, the penetration agent’s episodic memory refers to the agent’s observation received and the action taken in a specific state of an episode.

In particular, the EMG-DQN stores the state observations, actions, and corresponding rewards for each step of a given episode in the episodic memory table HE. Each key-value pair in the HE represents the maximum cumulative reward obtained after the action a is performed in state s. Thus, key records the experienced state-action pairs (s,a). The episodic memory writing process is formalized as follows:

HE(st,at)={max(HE(st,at),R(st,at))if(st,at)∈HER(st,at) otherwise (7)

where HE(st,at) is the maximum cumulative reward corresponding to (st,at) of the records in the table, and R(st,at) indicates the cumulative reward corresponding to the current episode.

After the algorithm starts training, the episodic memory table is updated via a backward replay process at the end of each episode. New state-action pairs, which have not been recorded, are written directly into the table. For state-action couples that have already been registered in the table, it is written to the episodic memory table if the cumulative reward value for the current episode is more excellent. Otherwise, it remains the same. The forgetting strategy mimics human experts’ characteristics. It replaces the least recently retrieved key-value pair to keep the table fixed in size.

In the decision-making process of the penetration agent, the episodic memory needs to be read to evaluate the value of performing each attack action in the current state st. When the agent receives state observations from the environment, the storage cost is reduced by projecting observations onto a low-dimensional vector by means of function φ. Function φ selects the random projection method. According to Johnson–Lindenstrauss Lemma, the random projection matrix maintains the original state distance proximity relationship and does not put affect the state similarity judgment. The reading process of episodic memory is formalized as follows:

ae(st,HE)=arg⁡maxaHE(st,a)(8)

where ae represents the action selected by reading the episodic memory. According to the records of the episodic memory, the agent selects the action with the largest key value HE(st,at) to execute in the current state.

4.4 Exploration Strategy Based on Episodic Memory

The majority of the existing algorithms use the ε-greedy policy to balance exploration and exploitation, which is shown in Eq. (9).

πε(s)={random(A),ς≤εarg⁡maxaQ(s,a),ς>ε(9)

where ε is the exploration factor. Based on the ε-greedy policy, the agent selects random action with probability of ε and selects action with maximum Q values with probability of 1 − ε.

In the absence of episodic memory guidance, the agent treats all attack actions equally in exploring the penetration path and repeatedly tries the entire action space to find an advantageous attack sequence, which has the problem of over-exploration. There are many low-quality penetration paths by observing the action execution traces of each episode reveals, where low-reward attack actions with similar effects are attempted multiple times on the same host or subnet.

The episodic memory table stores the historical optimal policy for a particular state experienced and contains the best penetration path learned so far. It is similar to the local knowledge of the network scenario developed by human experts during penetration testing. Therefore, the exploration strategy based on episodic memory is designed to improve the relevance of exploration. The utilization of episodic memory can rapidly accumulate high-quality penetration paths and accelerate algorithm convergence.

In the early stage of training, more use of episodic memory to guide exploration can improve the efficiency of the training when the neural network is still unstable. However, the generalization performance using neural network decisions is better in the late training period. Therefore, the strategy allocates a certain probability based on the ε-greedy policy to explore with episodic memory. It can effectively use the successful experience to accelerate learning and ensure the agent’s exploration ability to avoid one-sided exploitation. Specifically, the exploration strategy divides the training process into an exploration phase and an exploitation phase. In the exploration phase, the exploration factor ε is calculated as follows:

ε=1−steps_doneExploration_Steps∗(1−FINAL_epsilon)(10)

where the length of exploration stage is noted as Exploration_Steps. As the number of training steps increases, the ε value gradually decay from the initial value to FINAL_epsilon.

Based on the ε-greedy policy, the agent divides ε3 of the probability of the neural network decision to select the action using episodic memory. When the number of training steps exceeds Exploration_Steps, the exploration phase ends, and ε takes the value of FINAL_epsilon. Afterwards the agent mainly relies on the neural network decision. It retains a very small probability of randomly selecting an action or reading the episodic memory to select an action. The strategy is formalized as follows:

π(s)={πR→a∼random(A),ς≤επE→ae(s,HE),ε<ς≤ε(4−ε)3πQ→arg⁡maxaQ(s,a),ς>ε(4−ε)3(11)

where the selection of the action by reading the episodic memory module is denoted as πE, the policy for selecting the random action is denoted as πR, and selecting the action generated by the neural network is denoted as πQ. When selecting an attack action under state s, the corresponding strategy is selected accordance with the generated random number ς ∈ (0, 1).

As shown in Fig. 4, the agent selects the action for execution under policy πR with the probability of ε, selects the action under policy πE with the probability of ε(1−ε)3, and selects the action under policy πQ with the remaining probability. Following such a design, the agent first constructs the episodic memory table by exploring in the early training. Then the agent mainly uses the episodic memory module to guide the exploration, while exploring the action space with the probability of ε. As the number of training steps grows, the probability of using the episodic memory module decay linearly with ε. By the late stage of training, the neural network is stabilized, and the agent basically relies on the neural network for decision making.

Figure 4: Schematic diagram of exploration strategy

4.5 Training Process

Before training, the agent creates state and executable action sets for the target network scenario in accordance with the configuration. The EMG-DQN algorithm starts training:

(1)   Initialize the neural network parameters, the replay experience M, and the episodic memory table HE.

(2)   The training episode starts; the agent receives the initial state observation of the target network.

(3)   The agent selects action at according to Eq. (11) at each time step t.

(4)   Execute action at in the target network. The corresponding reward rt and the new state st+1 are gained.

(5)   Store the tuple (st,at,rt,st+1,done) in the replay experience M.

(6)   Training Q network with randomly selected batch size samples from the replay experience M and updating the target network parameters θ′ with a certain frequency.

(7)   Loop steps (3), (4), (5), and (6) until the root access to all sensitive hosts is obtained.

(8)   Calculate the discount reward corresponding to each state-action pair (st,at) and update HE(st,at) according to Eq. (7).

(9)   Reset the scenario. Go back to step (2) to start a new episode.

After the algorithm converges, the trained neural network policy can output the action sequence with the maximum reward for the input states.

5  Experiment

The experiments are divided into two parts: the comparative experiment is designed to compare the training performance of the EMG-DQN with other methods in benchmark scenarios, and the second part is to test the scalability of EMG-DQN in large-scale penetration testing scenarios.

5.1 Experiment Scenarios and Setup

The experimental network scenarios are constructed with the help of the Network Attack Simulator (NASim) [2]. NASim is an open-source research platform that provides a variety of abstract network scenarios for the testing of penetration agents using RL algorithms. It gives a scenario generator. This allows agents to be quickly tested on network scenarios of different sizes.

The structure of the benchmark scenario used for the experiments is shown in Fig. 5. The target intranet contains four subnets: DMZ (Demilitarized Zone), Office Zone, Core Management Zone, and Core Subnet. The DMZ is connected to the Office Zone and the Core Management Zone, respectively, and the Core Subnet is merely accessible through the Core Management Zone. Initially, only the DMZ can be accessed by an external network attacker whose goal is to compromise two sensitive hosts located in the Core Management Zone and the Core Subnet. To gain access, the attacker would need to compromise a host in the DMZ as a springboard to attack a sensitive host in the Core Management Zone.

Figure 5: Benchmark scenario topology

Various scale scenarios were designed based on the structure of the benchmark scenario in the comparison experiments. There are two sensitive hosts, and the value is 40. To match real-life applications more closely, scenario 2 adds a honeypot host with the value set to a negative value [20]. The agent must learn to bypass the honeypot host to find the optimal penetration path. The number of hosts, vulnerability, and complexity of the network structure gradually increase from scenario 1 to 3. Larger-scale and more complex scenarios were designed in the second part of the experiment in this paper. Specific scenario information is shown in Table 1.

The hardware configuration for the experiment includes an Intel i7-6700 CPU, 3.40 GHz Intel core, 64 G of RAM, and the operating system Windows 10. All algorithm programs in the experiments were written in python and executed in a single thread. Adam was chosen as the neural network optimizer with a learning rate of 0.0001. The meanings of the crucial hyperparameters are given in Table 2. The values of the hyperparameters are mainly referred to the domain literature and experimental validation.

The hyperparameter settings are kept consistent for the same scenario. They were adjusted appropriately according to the problem size of different scenarios. The hyperparameter settings for different scenarios are shown in Table 3.

5.2 Evaluation Metrics

In this paper, the proposed method is compared with three solutions: DQN, Double_DQN (DDQN) [21], and Hierarchy DQN (HA-DQN) [17].

DQN and DDQN are selected as the baseline algorithm to experiment with. Because DQN, as a mature deep reinforcement learning technique, has been widely applied in previous work [22]. DDQN algorithm improves the DQN parameter updating part to effectively solve the value overestimation problem. HA-DQN is a recently proposed solution on the basis of DQN. HA-DQN decomposes action space by hierarchical reinforcement learning to reduce the difficulty of exploration. According to the experiments done by Yang et al. [23], HA-DQN showed faster convergence with more stable performance among several advanced solutions.

The experiments analyze the methods’ performance by the results of the following three metrics:

•   Reward: The total rewards earned in the round were calculated as an evaluation metric at the end of each training episode. In the field of reinforcement learning, each episode’s reward could reflect the learning effect and convergence speed visually. Thus, reward can be used to evaluate the overall penetration performance.

•   Step: Step indicates the number of lengths of training track in each episode. It reflects the number of required actions to generate the penetration path to the target host. Likewise, it demonstrates the quality of the penetration path.

•   Runtime: Runtime represents the time cost required to train the same number of episodes, which visually reflects the training efficiency of the algorithm.

5.3 Results and Discussion

The first part of the experiments are to compare the algorithm of this paper with DQN, DDQN, and HA-DQN. The experimental procedure keeps the scenario and hyperparameter settings the same. The effectiveness of EMG-DQN is verified by the comparison of the experimental results of each algorithm and metric of the three scenarios.

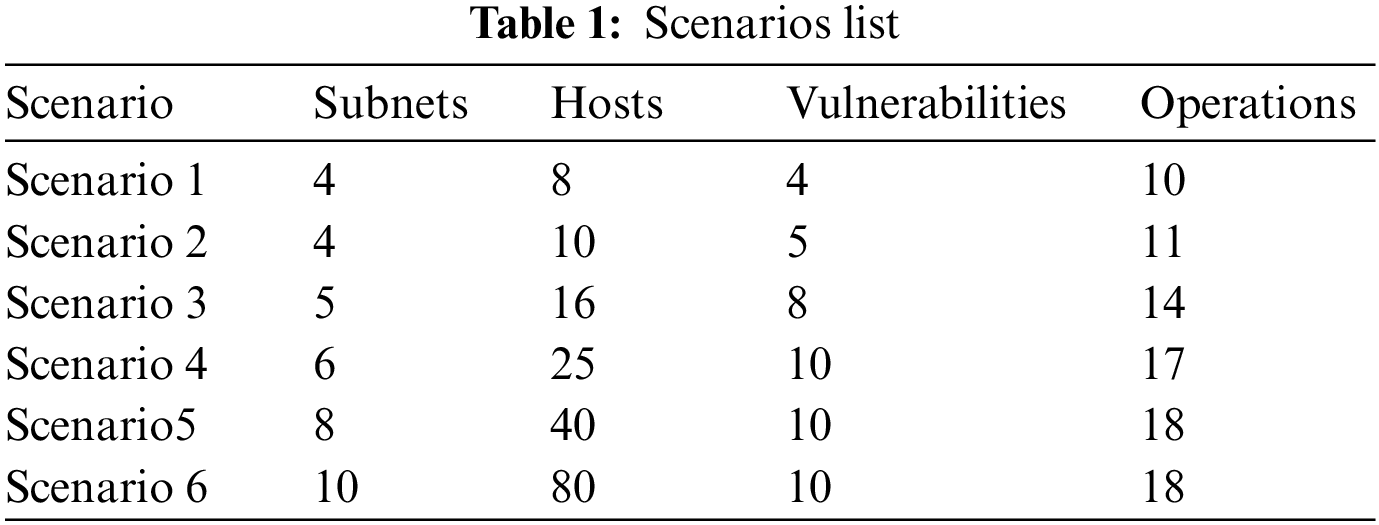
As shown in Figs. 6a–6c, all four solutions are able to learn the best attack policy in the small-scale scenario. However, the EMG-DQN requires the fewest episodes for converge. It has less fluctuation than other methods as well. In Fig. 6d, the runtime of EMG-DQN is significantly less than that of DQN and DDQN algorithms. It indicates that the proposed algorithm improves the learning efficiency of the agent. Although EMG-DQN takes more time than HA-DQN when the episodic memory table is not well constructed, HA-DQN grows significantly faster than this algorithm in terms of runtime as the number of episodes increases. According to Fig. 7, EMG-DQN learns the optimal penetration path within 100 episodes, and the learned strategies are more stable with less fluctuation of steps.

Figure 6: Comparison of reward and runtime in scenario 1

Figure 7: Comparison of step in scenario 1

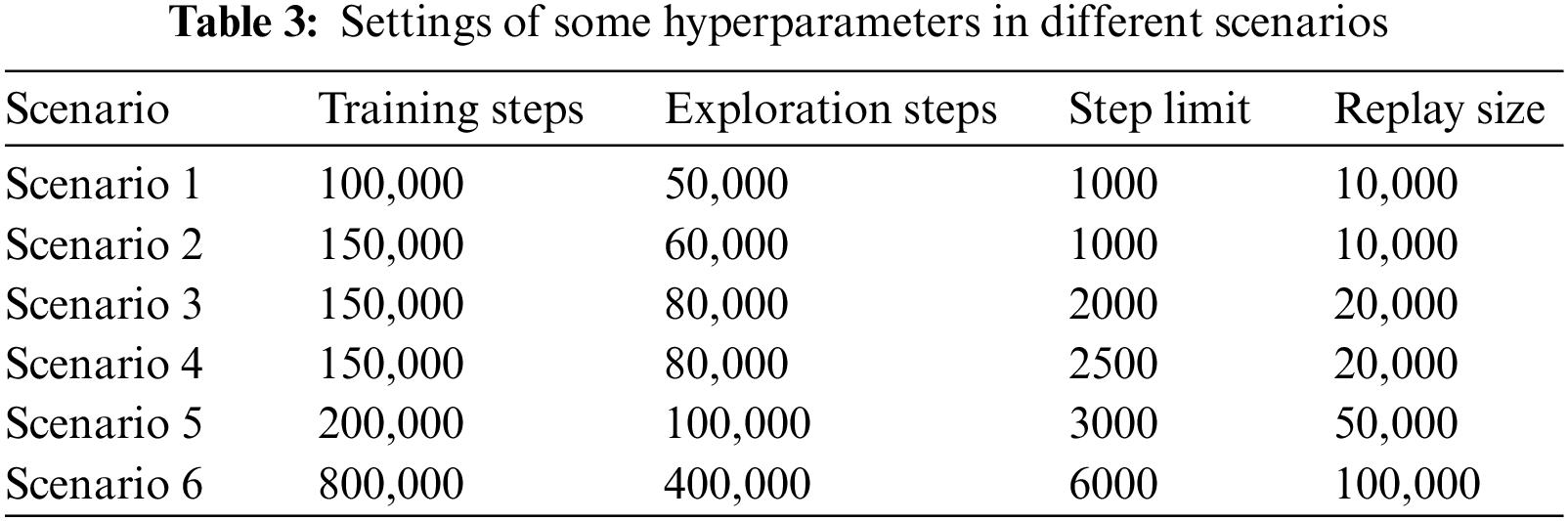
In scenario 2, a honeypot was added, and results were shown in Figs. 8 and 9. According to Figs. 8a–8c, compared to DQN and DDQN, EMG-DQN can converge in fewer episodes and exhibits better penetration performance. Although HA-DQN used fewer episodes for approximate convergence in the honeypot scenario, the fluctuation of reward before convergence was much greater. The running time of EMG-DQN was much lower as shown in Fig. 8d. In comparison with DQN and DDQN, EMG-DQN reduces the running time by 57.9% when training 800 episodes. Compared to the HA-DQN algorithm, the EMG-DQN also has an advantage in running time with a reduction of 29.2%. According to Fig. 9, EMG-DQN showed more stable penetration performance. Because training steps per episode quickly dropped to less than 50 in the early exploration phase. Moreover, the policy after the convergence of EMG-DQN showed better stability.

Figure 8: Comparison of rewards and runtime in scenario 2

Figure 9: Comparison of step in scenario 2

Fig. 10 demonstrates the results of Scenario 3. The inability of DQN and DDQN to converge on the current problem size can be seen intuitively from Fig. 10a. According to Figs. 10b and 10d, EMG-DQN and HA-DQN can find the optimal penetration path within a finite number of episodes. Although HA-DQN converges faster, EMG-DQN performs better stability after convergence. The reason is that HA-DQN uses an algebraic approach to reduce the action space before training. Therefore, the convergence performance is more prominent at the beginning. However, as the experience is accumulated, EMG-DQN uses episodic memory to guide exploration, making the learning performance more stable and efficient. As shown in Fig. 10c, as the number of episodes accumulates, the advantages of stability and efficiency of EMG-DQN emerge frequently with the accumulation of the number of episodes.

Figure 10: Results in scenario 3

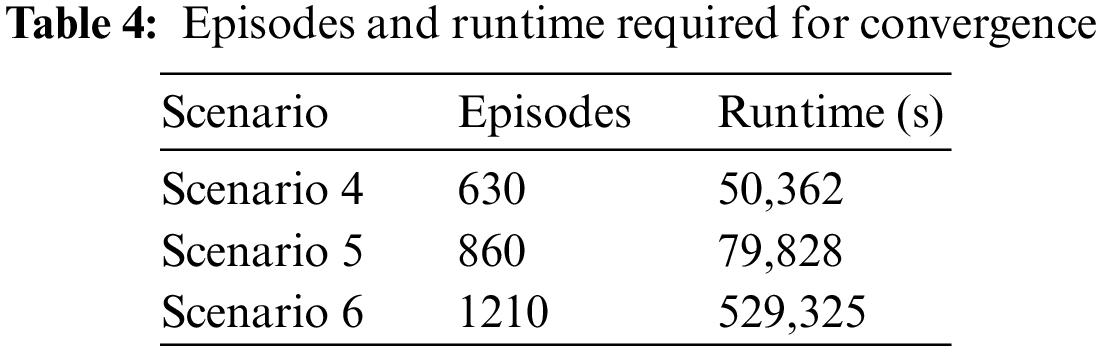
The second part is the extended experiments under large-scale scenarios 4, 5, and 6. Results are shown in Fig. 11. The EMG-DQN algorithm still has stable performance in large-scale scenarios with 25, 40 and 80 hosts. It is capable to converge within limited episodes. As the network size increases, the algorithm also requires more training episodes for convergence, with scenario 4 approximately converging at 630 episodes, scenario 5 at 860 episodes and scenario 6 at 1210 episodes. As shown in Table 4, the EMG-DQN can still learn the best penetration path in a limited time in large-scale scenarios.

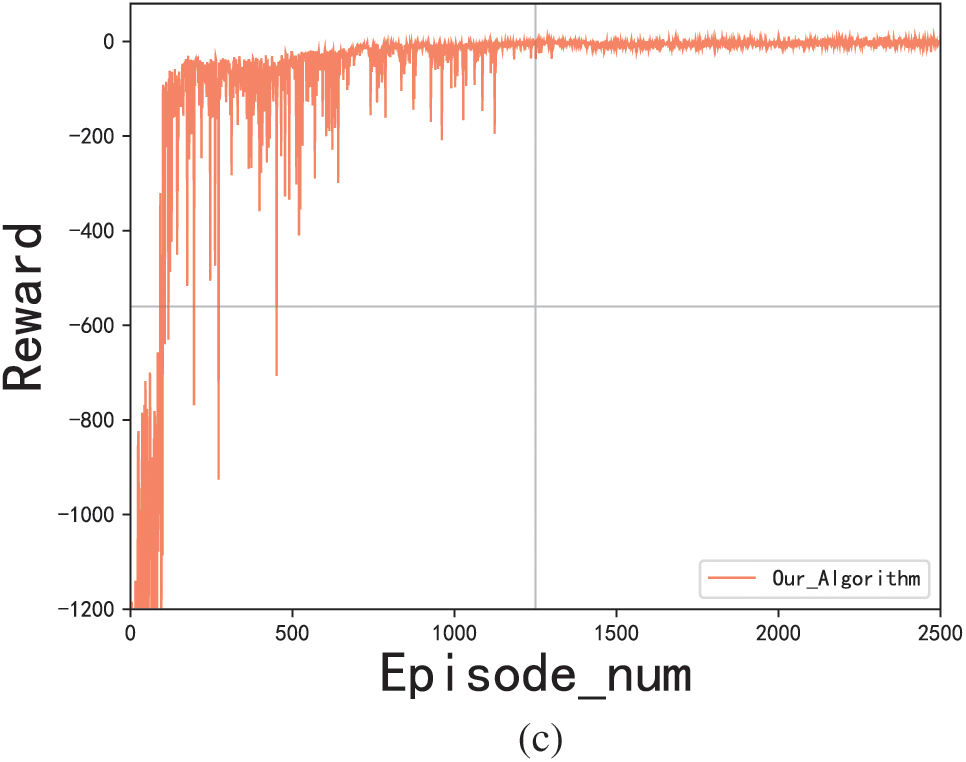
Figure 11: Results for scenario 4, scenario 5 and scenario 6

From the above experimental results, the EMG-DQN proposed in this paper shows superior penetration performance among the four solutions.

(1) EMG-DQN has faster and more stable convergence performance.

EMG-DQN is more efficient in learning infiltration strategies. The main reason is that the approach uses external memory to empower the agent to employ experience effectively. Once the agent has mastered some of the network information through trial and error, it can produce better choices on the basis of previous action sequences. While other schemes focus more on modeling the penetration testing process, exploring the high-dimensional discrete action space of the scenario relies mainly on trial and error. This makes it difficult to ensure the exploration efficiency in the face of complex scenarios.

According to the experimental results, DQN and DDQN methods are prone to convergence failure in the face of large complex scenarios. HA-DQN, as one of the most advanced schemes, reduces the difficulty of exploring the network by decomposing the action space. Such an approach achieves good convergence performance in the early stage of training. However, with the accumulation of experience, the memory-based exploration in this paper is more stable. The training efficiency is higher, and the learned penetration strategies are more stable. According to the experimental results, the time overhead of EMG-DQN is reduced by more than 20% in contrast with HA-DQN.

(2) EMG-DQN can be extended to larger penetration testing scenarios.

The scalability of EMG-DQN is verified by experimental results. In large-scale scenarios, EMG-DQN is able to learn the best planning strategy in a limited time. Although the action space size increases with the number of hosts, the optimal attack sequence is determined and occupies merely a small fraction of the action space. EMG-DQN with episodic memory module can quickly target critical attack actions during the exploration phase to overcome the challenges of large action spaces.

6  Conclusion and Future Work

From the attacker’s perspective of the analysis of the network vulnerability, penetration test path planning enjoys important research value in the field of network security. Since only some information is acknowledged in the real test and will be affected by the scenario events, the whole process has great uncertainty. The EMG-DQN method on episodic memory reinforcement learning was put forward for penetration path planning under uncertain scenarios in this paper based on the objective characteristics of penetration testing and the efficiency requirements.

The majority of the existing research improves the adaptability and feasibility of planning by continuously improving the fit of the model to the realistic penetration rules. Nevertheless, this also makes the model complexity greatly increased and the computational efficiency difficult to meet the demands. Unlike the previous research directions, EMG-DQN uses episodic memory to guide the exploration of penetration test paths and improve training efficiency. In the comparison with existing methods, EMG-DQN shows faster and more stable convergence performance and shorter running time under different scale scenarios.

The improved method in this paper features concise and practical. EMG-DQN incorporates the successful strategy of episodic memory module to guide exploration based on the deep Q-network framework. In accordance with the new exploration strategy, the constructed episodic memory module can effectively improve the quality and efficiency of exploration paths in the early stage of training. After training, the neural network can be applied for attack planning by an attacker in either state.

The introduction to situational memory also enables more possibilities for future work. First, the episodic memory module is an external memory component that can be combined with any reinforcement learning paradigm without adding additional parameters. In addition, it is the first time that historical successful strategies have been preserved through the use of external memory. The episodic memory module provides for the preservation of cross-task strategies. The focus of future work could be the transformation of cross-task strategies in conjunction with transfer learning methods, which is beneficial to shorten the cycle of penetration test path planning.

Acknowledgement: The first author acknowledges the support provided by Information Engineering University. The authors are grateful for the constructive comments by anonymous reviewers and journal editors.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Ziqiao Zhou, Tianyang Zhou, Jinghao Xu; data collection: Jinghao Xu; analysis and interpretation of results: Ziqiao Zhou, Tianyang Zhou, Junhu Zhu; draft manuscript preparation: Ziqiao Zhou, Jinghao Xu, Junhu Zhu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data supporting the conclusions of this article are included within the article. The data used and analyzed during the study are available from the corresponding author on reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Zhao, H. N., Jiao, J. (2022). Recommendation model of penetration path based on reinforcement learning. Journal of Computer Applications, 42(6), 1689–1694. [Google Scholar]

2. Schwartz, J., Kurniawati, H. (2019). Autonomous penetration testing using reinforcement learning. arXiv:1905.05965. [Google Scholar]

3. Ghanem, M. C., Chen, T. M. (2020). Reinforcement learning for efficient network penetration testing. Information, 11(1), 6–28. [Google Scholar]

4. Garrett, C. R., Lozano-Pérez, T., Kaelbling, L. P. (2018). FFRob: Leveraging symbolic planning for efficient task and motion planning. The International Journal of Robotics Research, 37(1), 104–136. https://doi.org/10.1177/0278364917739114 [Google Scholar] [CrossRef]

5. Sarraute, C., Buffet, O., Hoffmann, J. (2012). POMDPs make better hackers: Accounting for uncertainty in penetration testing. Proceedings of the 26th Conference on Artificial Intelligence, pp. 1816–1824. Toronto, Canada. [Google Scholar]

6. Hu, T. R., Gao, W. L., Zhou, T. Y., Zang, Y. C. (2021). Bi-population genetic algorithm-based attack path discovery research in large-scale networks. Proceedings of the 4th World Conference on Computing and Communication Technologies, pp. 32–38. Chengdu, China. [Google Scholar]

7. Hu, T. R., Zhou, T. Y., Zang, Y. C., Wang, Q. X., Li, H. (2020). APU-D* lite: Attack planning under uncertainty based on D* lite. Computers, Materials & Continua, 65(2), 1795–1807. https://doi.org/10.32604/cmc.2020.011071 [Google Scholar] [CrossRef]

8. Chen, Z. (2022). Research on internet security situation awareness prediction technology based on improved RBF neural network algorithm. Journal of Computational and Cognitive Engineering, 1(3), 103–108. https://doi.org/10.47852/bonviewJCCE149145205514 [Google Scholar] [CrossRef]

9. Gao, W. L., Zhou, T. Y., Zhu, J. H., Zhao, Z. H. (2022). Network attack path discovery method based on bidirectional Ant colony algorithm. Computer Science, 49(6A), 516–522. [Google Scholar]

10. Zang, Y. C., Zhou, T. Y., Zhu, J. H., Wang, Q. X. (2020). Domain-independent intelligent planning technology and its application to automated penetration testing oriented attack path discovery. Journal of Electronics & Information Technology, 42(9), 2095–2107. [Google Scholar]

11. Bland, J. A., Petty, M. D., Whitaker, T. S., Maxwell, K. P., Cantrell, W. A. (2020). Machine learning cyberattack and defense strategies. Computers & Security, 92, 101738. https://doi.org/10.1016/j.cose.2020.101738 [Google Scholar] [CrossRef]

12. Erdodi, L., Sommervoll, A. A., Zennaro, F. M. (2021). Simulating SQL injection vulnerability exploitation using Q-learning reinforcement learning agents. Journal of Information Security and Applications, 61, 102903. https://doi.org/10.1016/j.jisa.2021.102903 [Google Scholar] [CrossRef]

13. Pozdniakov, K., Alonso, E., Stankovic, V., Tam, K., Jones, K. (2020). Smart security audit: Reinforcement learning with a deep neural network approximator. Proceedings of International Conference on Cyber Situational Awareness, Data Analytics and Assessment, pp. 1–8. Dublin, Ireland. [Google Scholar]

14. Ghanem, M. C., Chen, T. M., Nepomuceno, E. G. (2022). Hierarchical reinforcement learning for efficient and effective automated penetration testing of large networks. Journal of Intelligent Information Systems, 60(2), 281–303. https://doi.org/10.1007/s10844-022-00738-0 [Google Scholar] [CrossRef]

15. Nguyen, H. V., Teerakanok, S., Inomata, A. (2021). The proposal of double agent architecture using actor-critic algorithm for penetration testing. Proceedings of the 7th International Conference on Information Systems Security and Privacy, pp. 440–449. Vienna, Austria. [Google Scholar]

16. Zhou, S. C., Liu, J. J., Hou, D. D., Zhong, X. F., Zhang, Y. (2021). Intelligent penetration testing path discovery based on deep reinforcement learning. Computer Science, 48(7), 40–46. [Google Scholar]

17. Tran, K., Standen, M., Kim, J., Bowman, D., Richer, T. (2022). Cascaded reinforcement learning agents for large action spaces in autonomous penetration testing. Applied Sciences, 12(21), 11265. https://doi.org/10.3390/app122111265 [Google Scholar] [CrossRef]

18. Chen, J. Y., Hu, S. L., Xing, C. Y., Zhang, G. M. (2022). Deception defense method against intelligent penetration attack. Journal on Communications, 43(10), 106–120. [Google Scholar]

19. Zhu, G. X., Lin, Z. C., Yang, G. W., Zhang, C. J. (2020). Episodic reinforcement learning with associative memory. Proceedings of Eighth International Conference on Learning Representations, pp. 1–15. Addis Ababa, Ethiopia. [Google Scholar]

20. Kamel, N. E., Eddabbah, M., Lmoumen, Y., Touahni, R. (2020). A smart agent design for cyber security based on honeypot and machine learning. Security and Communication Networks, 2020, 8865474. https://doi.org/10.1155/2020/8865474 [Google Scholar] [CrossRef]

21. Zhang, Y., Liu, J. J., Zhou, S. C., Hou, D. D., Zhong, X. F. et al. (2022). Improved deep recurrent Q-network of POMDPs for automated penetration testing. Applied Sciences, 12(20), 10339. https://doi.org/10.3390/app122010339 [Google Scholar] [CrossRef]

22. Hasselt, H. V., Guez, A., Silver, D. (2016). Deep reinforcement learning with double Q-learning. Proceedings of the AAAI Conference on Artificial Intelligence, pp. 2094–2100. Palo Alto, USA. [Google Scholar]

23. Yang, Y., Liu, X. (2022). Behaviour-diverse automatic penetration testing: A curiosity-driven multi-objective deep reinforcement learning approach. arXiv:2202.10630. [Google Scholar]