Predicting the Mechanical Behavior of a Bioinspired Nanocomposite through Machine Learning

1  Introduction

Composite materials are comprised of multiple constituent materials with significant differences in their physical, chemical, and mechanical properties. Composite materials can be designed with specific geometrical, structural, mechanical, and chemical properties depending on the requirement. These materials’ applications include manufacturing, construction, and biomedical fields [1–4]. The attainment of both strength and toughness is a significant challenge for most structural materials. However, these properties are usually exclusive [5]. Nature is replete with examples of tough, strong, lightweight, and multifunctional structures that can be an inspiration for better-performing materials, such as nacre and bone [6]. Nacre, as a biological material, consists of 95 wt% aragonite and 5 wt% organic materials. The hard mineral tablets contribute to its structural rigidity, while the soft organic interface facilitates damage mitigation and energy dissipation [7–9]. The structure of the nacre represents a remarkable example of high-performance bioinspired material design.

To investigate nacre’s toughening mechanisms and to provide design rules, Dastjerdi et al. [10] conducted interfacial fracture tests on different nacre samples. They observed that surfaces with higher roughness and a more resilient organic material tend to exhibit greater interfacial toughness. The outstanding mechanical properties of the nacre are attributed to its hierarchical structure and precisely designed organic-inorganic interface [11,12]. Liu et al. [13] investigated the fracture mechanism and interfacial strength of the ‘brick-mortar’ structure in nacre. Through the micro-sized cantilever beam and bend samples, they confirmed that crack deflection towards the interface between aragonite plays a significant role in achieving high overall toughness. Dutta et al. [14] established an analytical model to show that the synthetic staggered architecture materials improved stiffness, load-transfer capability, and toughness. A study by Abid et al. [15] suggested an important guideline for the design of nacre-like materials is to minimize microstructural randomness to achieve the optimal combinations of properties. Ghazlan et al. [16] presented a novel model of a nacre-mimetic composite structure. Their findings reveal the significance of tablet size and the number of laminates while indicating the minimal impact of tablet overlapping on the composite’s properties. Barthelat’s model [17] demonstrates that the staggered microstructure is advantageous only under specific conditions: when the tablets are at least five times stronger than the interfaces, and when high-volume concentrations of tablets are used. Carefully designed interfaces in bioinspired staggered composites can counteract the adverse effects of microstructural randomness inherent in current fabrication methods [18]. Those findings show that the extensibility or ductility of the interfaces, and the staggered microstructure play an important role on the toughening mechanism at the macroscale. The study of Greco et al. [19] explored platelet volume, aspect ratio, and shear modulus effects on the microscopic and the macroscopic instabilities, and found that critical stretch ratios and mode shapes are influenced by microscopic geometry and material composition.

There have been many examples of replicating nacre’s structure and properties in synthetic materials. Compared with standard brittle glass, using a laser engraving technique to implement the weak interface into glass could significantly enhance its deformability and render it up to 200 times tougher [20]. By controlling the interface bonding, regulating the interface load transfer, and understanding the failure models of hierarchical structure bulk materials, it is possible to optimize the combination of strength and energy absorption, thereby meeting diverse application requirements [21]. Cui et al. [22] found that the elastic modulus of the nacre-like composites increases with the rising tablet waviness. Moreover, they identified a critical angle for the interlocking structure, at which both high strength and toughness can be achieved. Jiao et al. [23] employed a bidirectional freeze-casting method to manufacture multiscale micro/nano-architectures featuring three hierarchy levels in the composite. Their study confirms the efficacy of nacre-inspired designs in enhancing fracture toughness in carbon systems. Flores-Johnson et al. [24] studied an aluminum alloy-based composite with layer waviness and cohesive interface. This lightweight and impact-resistant material exhibited superior ballistic performance compared to plates made of continuous layers. The improvement was credited to the increased plastic deformation area resulting from the arrangement of tablets. Begley et al. [25] described a micromechanical analysis detailing the uniaxial response of composites. These composites are comprised of elastic platelets joined together by thin elastic-perfectly plastic layers (mortar), aiming to reconcile conflicting mechanical behaviors and refine material response optimization. de Maio et al. [26] introduced a nacre-like microstructure to explore the wave propagation properties of lightweight bioinspired composite materials. Among various toughening mechanisms, it has been reported that roughly one-third of the overall toughness is based on the crack path’s highly meandering nature through the composite’s staggered architecture [14].

Machine Learning (ML) techniques are suitable for addressing research questions in many domains, such as mathematics [27], chemical [28], and material science [29]. Materials development has always been driven by human needs and desires. Traditionally, advanced materials are found by empirical or experimental approaches. With big data generated by modern experimental and computational techniques, data-driven or machine learning methods have become new paradigms for the discovery, analysis, and design of materials [30,31]. Machine Learning demonstrates outstanding efficiency in large-scale explorations in materials science. Flah et al. [32] had put forward an inspection model using deep learning techniques to identify defects within typically hard-to-reach sections of concrete structures. Lu et al. [33] built a deep learning model to predict elastoplastic properties of metals and alloys from instrumented indentation. Xiao et al. used deep learning models to predict the trabecular bone’s microarchitecture [34] and the mechanical behavior [35] based on Dual-energy X-ray absorptiometry (DXA) images. Zhu et al. [36] introduced a machine learning approach aimed at identifying geometric patterns within magnetoelectric multi-phase composites that exhibit optimal magnetoelectric coupling properties.

The combination of finite element modeling (FEM) and artificial neural networks is a popular computational framework [37–41]. Finite element models are used in many engineering applications including the modeling of composites. However, there are inherent limitations associated with these models including the trade-off between fidelity and cost, difficulties with inverse modeling, and optimization of multi-dimensional problems. Using machine learning techniques for generating optimal designs or predicting accurate results with extensive training data can significantly reduce computational costs compared to exhaustive methods [42]. The latest advancements in machine learning have, therefore, increased the expectation of the development of composite materials. Discovering new materials with excellent performance is a hot topic in materials science. In this study, we combine machine learning with finite element simulation to build the connection between material interface and bulk material properties. Our machine learning model is focused on using interface properties to predict the bioinspired nanocomposite’s bulk mechanical behavior. Our study shows the potential to use machine learning to accelerate material design and analysis. The machine learning model can be trusted as a surrogate model for the FEM with the computation time being greatly reduced by several orders of magnitude.

2  Computational Model Development

2.1 Geometry Model

The structure of this bioinspired nanocomposite material usually exhibits a polygonal structure, such as a bone extrafibrillar matrix or a single layer of nacre structure. To simulate the behavior of such materials, we use finite element analysis (FEA) to investigate their material behavior. The process started with the generation of 144 points randomly placed in a square plane and partitioned to the Voronoi diagram (Fig. 1a). To obtain an optimal partition, we use the Centroidal Voronoi Tessellation (CVT) which corresponds to the optimal distribution of the Voronoi diagram [43]. To determine the CVT, we employ the Lloyd algorithm, which is a Voronoi iteration method. The algorithm repeatedly finds the centroid of each polygon and repartitions the plane until each point coincides with the centroid of its corresponding polygon. Through this iteration process, the diagram approaches an optimal solution. After 30 iterations, we obtain the centroidal Voronoi diagram (Fig. 1b).

Figure 1: Centroidal Voronoi tessellation process: (a) Iteration 1, (b) Iteration 30

Next, we use a Python script to implement the iterated Voronoi diagram in the Abaqus simulation software. The resulting model is visualized in Fig. 2, and its dimensions are specified as Lx×Ly×Lz=8400 nm×8400 nm×500 nm.

Figure 2: A 2D solid model: (a) structure model, (b) meshed model

After meshing the whole model, we insert a 3D cohesive element layer to represent the interface between grains (Fig. 3). This layer represents the bonding layer between the grains and provides insight into the strength and behavior of the material when subjected to mechanical loading. In this simulation, a linear displacement boundary condition is applied. The bottom edge of this model is fixed. The displacement rate applied on the top edge is 10−6m/s. This allows us to study the material’s response to a controlled overall deformation.

Figure 3: The 3D cohesive element layer

2.2 Material Properties

In this finite element model, we specify the density of the hard grain material to be 3000 kg/m^{3}, and its Young’s modulus as 100 GPa. The Poisson’s ratio is set to 0.28. To describe the interface deformation behavior between grains, we use a bilinear cohesive zone model to mimic interface behaviors. The interface has a very low volume percentage, but its property has the ability to determine the bulk material response [44]. The interfacial zone model is widely used to study composite material failure processes [45–48], such as material interface modeling [49,50], nacre-like composites [51–53], and bone and bone-inspired materials [54–57]. In this study, a bilinear traction-separation law is applied at the interface surface in normal and tangential directions. We can separately control the traction-separation relationship at the surface normal and tangential direction. For simplicity, the same cohesive zone parameters are used for surface normal and tangential direction in this study. The bilinear cohesive zone model describing the relationship between traction and separation at the interface is shown in Fig. 4. Where σ is cohesive strength, δc is critical initial separation and δf is final failure separation, respectively. This model enables us to study the behavior of the material under mechanical loading conditions, providing a more complete understanding of the material’s properties.

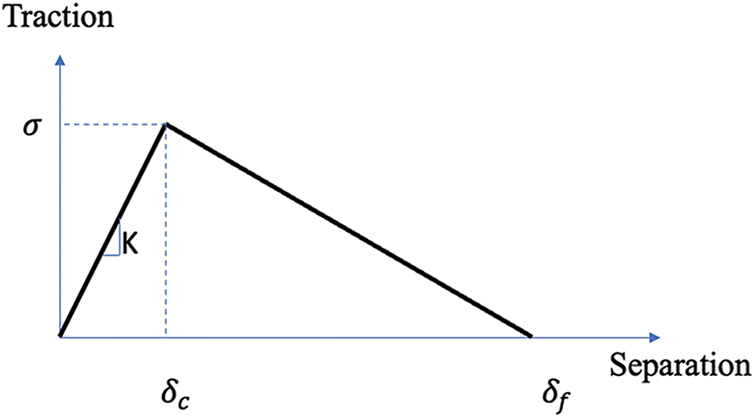
Figure 4: Bilinear cohesive zone model

2.3 Machine Learning Dataset

To create a large and diverse dataset for training our machine learning model, we first established a range and step size for each interface property parameter. The ranges of the interface parameters were obtained from the literature [58–60].To determine the range, we estimate the interface parameters from previous studies, such as organic matrix in nacre and bone structure. For organic interface in nacre, the strength is ~40 MPa [58]. For organic matrix in other model the strength is ~200 MPa [59]. For the fracture energy of organic adhesive, it was reported to be in the range of 0.18–0.27 J/m2 [60]. Based on these reported values, we may expand the range to cover more potential interface properties. The chosen interface property values were presented in Table 1.

In these ranges, we use a brute force generator to generate all possible interface models. Then we randomly select 5400 unique interface models and subjected them to finite element analysis to obtain the strain-stress curves. The stress-strain curve was then used to calculate the material’s stiffness, strength, and toughness. After conducting the analyses, we performed data cleaning to ensure the dataset was accurate and reliable. The data-cleaning operation is based on analyzing the stress-strain curve. Some simulations were terminated due to computer power limitations for multiple tasks or server restart. We checked each stress-strain curve and removed the abnormal data. The final dataset was split into three sets: training, validation, and testing, as detailed in Table 2. The training set was used to train the model, the validation set was used to fine-tune the model’s parameters, and the testing set was used to evaluate the model’s performance on unseen data.

2.4 Input and Output Data Generation via FEM in Machine Learning Model

Here we use one example to illustrate how the datasets are generated through finite element simulation. The stress distribution showed in Fig. 5 and the stress-strain curve showed in Fig. 6b is based on the interface properties σ=75 MPa,δc=2.5 nm,δf=15 nm as shown in Fig. 6a. The stress distribution and crack propagation in the nanocomposite was observed in Fig. 5. In Fig. 5a, stress distribution was largely homogeneous at the initial loading stage. And Fig. 5b shows the crack propagation path in the specimen. The interface properties and the bulk stress-strain curve of the nanocomposite are shown in Fig. 6.

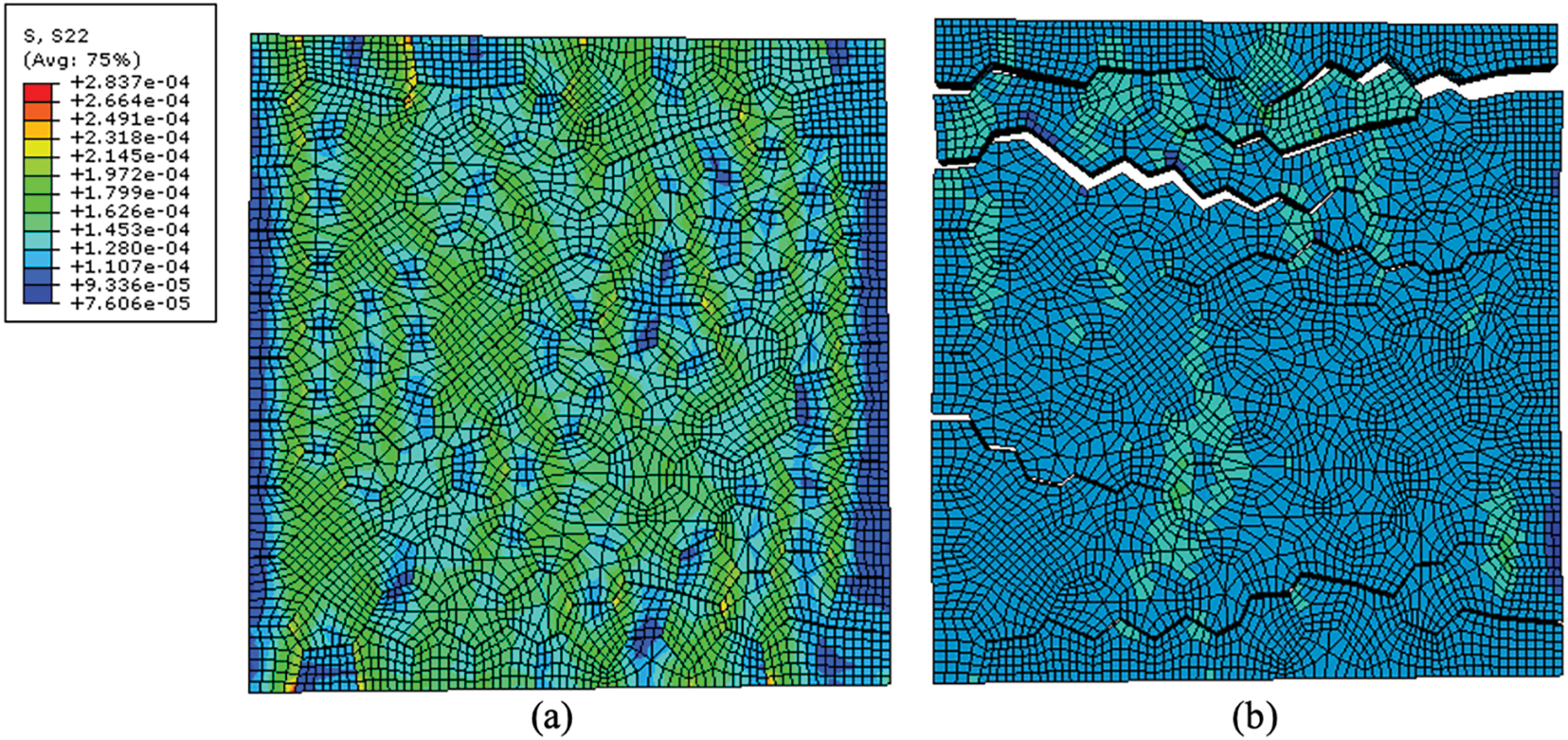
Figure 5: Snapshots of stress distribution (σ22) and crack propagation in bioinspired nanocomposite: (a) ε=0.013, (b) ε=0.043

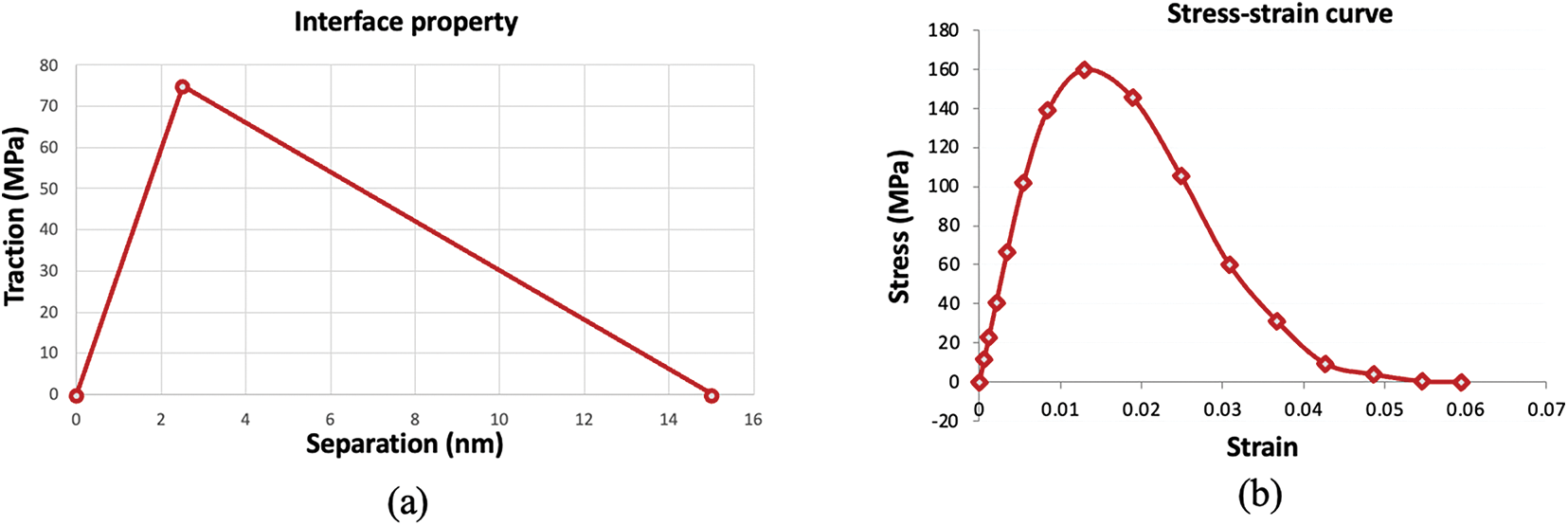
Figure 6: Interface property and the bulk composite response: (a) interface property, (b) bulk stress-strain curve

In recent years, machine learning has been very popular and has become an important component in numerous industries and research fields. The reason for its success relies on its ability to handle high-dimensional and complex data and make highly accurate predictions. With its remarkable performance, machine learning has opened new possibilities and opportunities for various applications, such as natural language processing, computer vision, and material science. In this research, we build a machine learning model to predict composites’ stiffness, strength, and toughness with the input of interface property. Fig. 7 shows the process of building the machine learning model. Python script files were generated with varying interface properties.

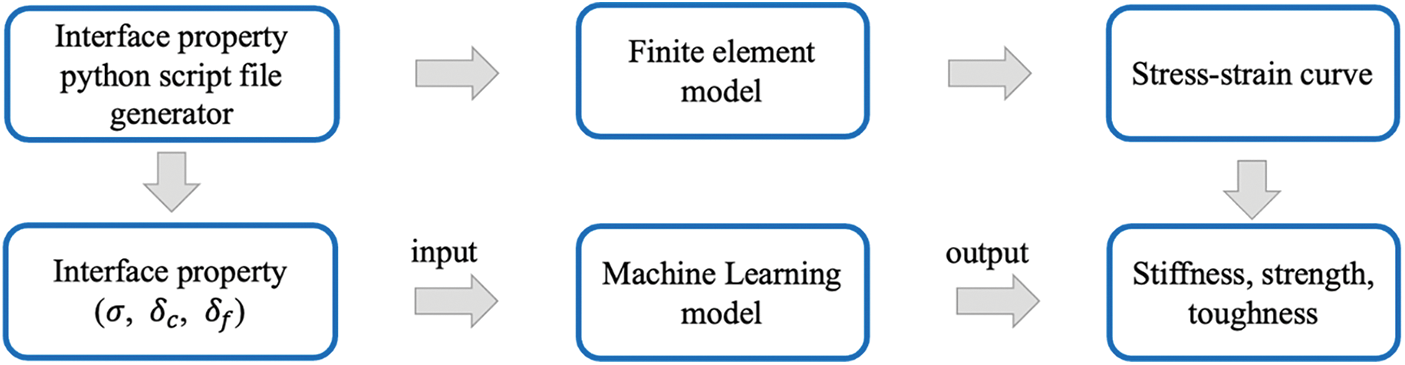
Figure 7: Flowchart of machine learning process

By running these files through finite element model analysis, we can obtain strain-stress curves, which can be used to calculate stiffness, strength, and toughness. We have trained a machine learning model to predict the stiffness, strength, and toughness of the bulk composite based on their interface properties. After comparing architectures ranging from 1 to 9 layers and neuron counts from 5 to 25, it was determined that the three-layer architecture with 15 neurons in the neural network model is optimal. The machine learning model we used is a three-layer fully connected neural network, with each layer containing 15 neurons (Fig. 8). The model uses the interface properties as inputs and produces predictions for the material’s bulk mechanical properties as outputs. This structure allows for effective processing of the interface properties as input and accurate prediction of the composite’s bulk stiffness, strength, and toughness as output.

Figure 8: Three-layer fully connected neural network model

3  Results

The machine learning model was trained and tested using interface property as the input and bulk stiffness, strength, and toughness as the output. The performance of the model was evaluated by comparing the predicted values with the actual values, shown in Figs. 9–11. The results showed that the machine learning model demonstrated a high level of accuracy in predicting the three bulk mechanical properties. The coefficient of determination (R-squared) values for stiffness, strength, and toughness predictions were 0.998, 0.996, and 0.989, respectively.

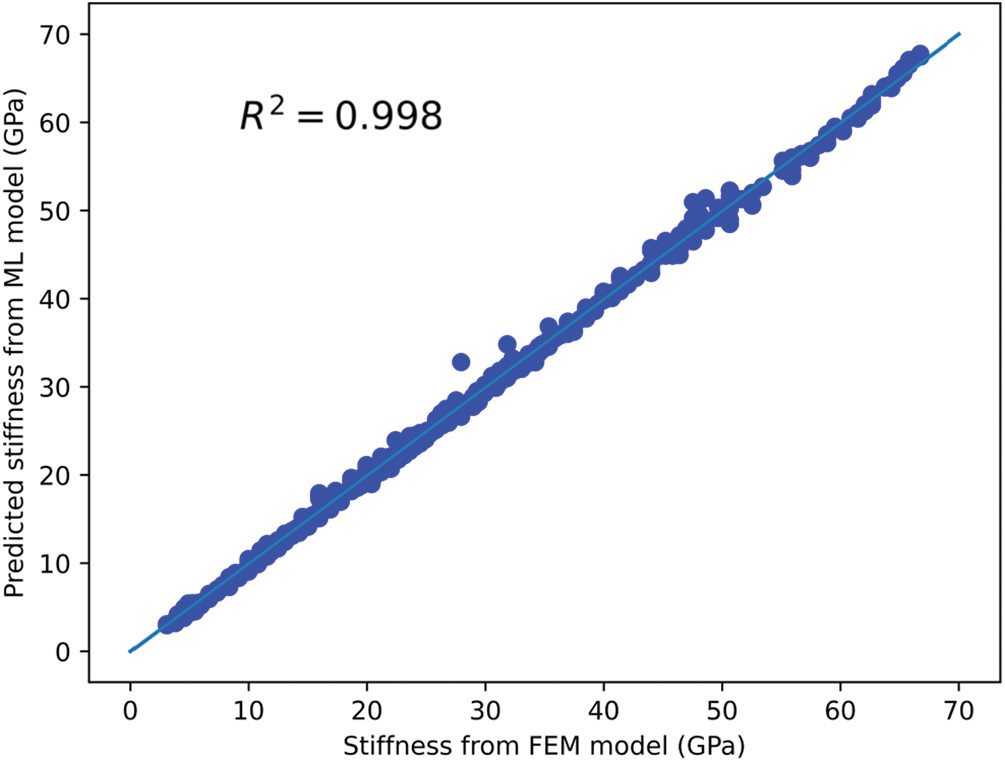
Figure 9: Predicted stiffness from ML model vs. FEM model

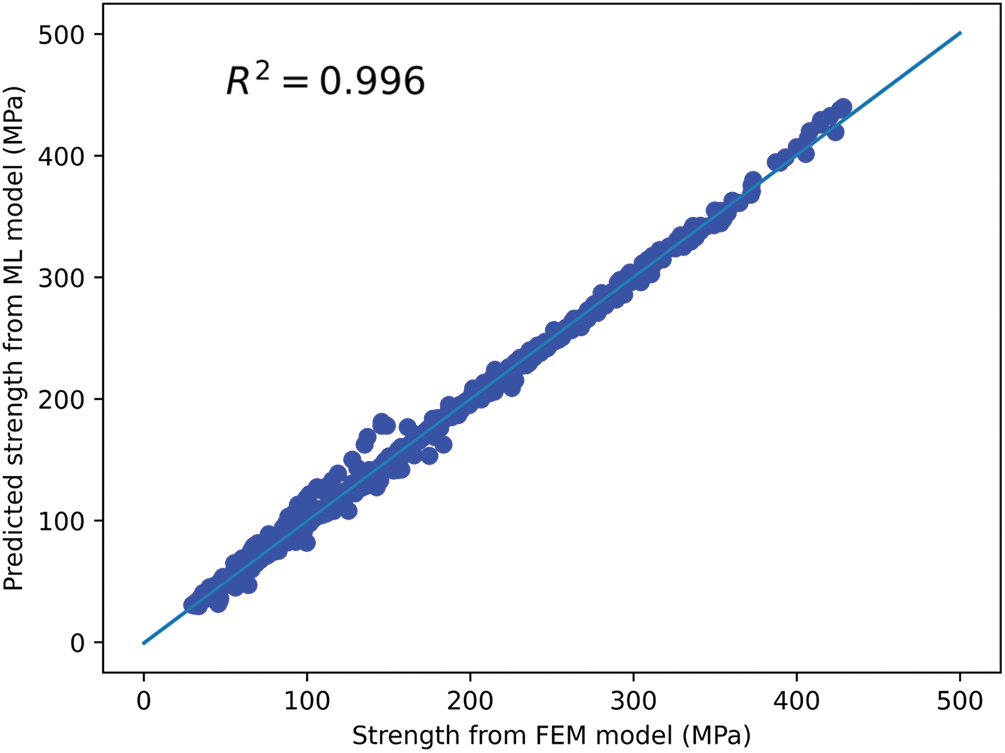
Figure 10: Predicted strength from ML model vs. FEM model

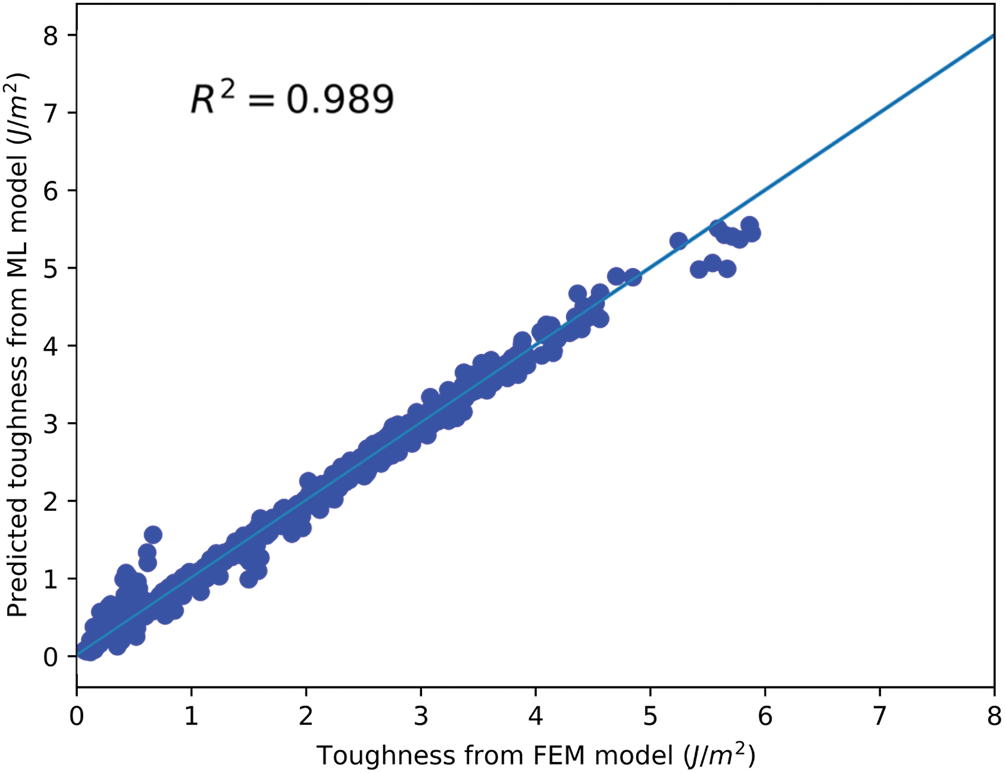
Figure 11: Predicted toughness from ML model vs. FEM model

These results suggest that the machine learning model can be a useful tool for predicting the bulk mechanical properties of nanocomposite materials with high accuracy. Machine learning models have the advantage of being faster compared to traditional finite element models. Within the same computing environment, the finite element model can take around two hundred seconds to generate the result, whereas the machine learning model can accomplish the task in just two dozen milliseconds.

We investigated the relationship between the interface property and composite bulk properties using a fixed geometry. To further understand the impact of different geometry variations on our results, we generated and analyzed 12 different models with distinct geometry. The results are shown in Fig. 12, which presents the 12 different geometries we used in our study. This allowed us to examine the influence of geometry on the mechanical properties of the composite material.

Figure 12: Geometrical model with different polygonal shape

The strain-stress curve of 12 different models with geometry variation is presented in Fig. 13. The strain-stress curves of these models are very similar, the geometry effect is minimized to study the mechanical behavior of the composite. The composites’ properties, including stiffness, strength, and toughness of each model, are shown in Fig. 14. The mean, standard deviation, and coefficient of variation of stiffness, strength, and toughness for all 12 models are presented in Table 3. The coefficient of variation for stiffness, strength, and toughness are found to be 0%, 1%, and 3%, respectively. These results indicate that the interface properties have a dominant effect on the composite material properties.

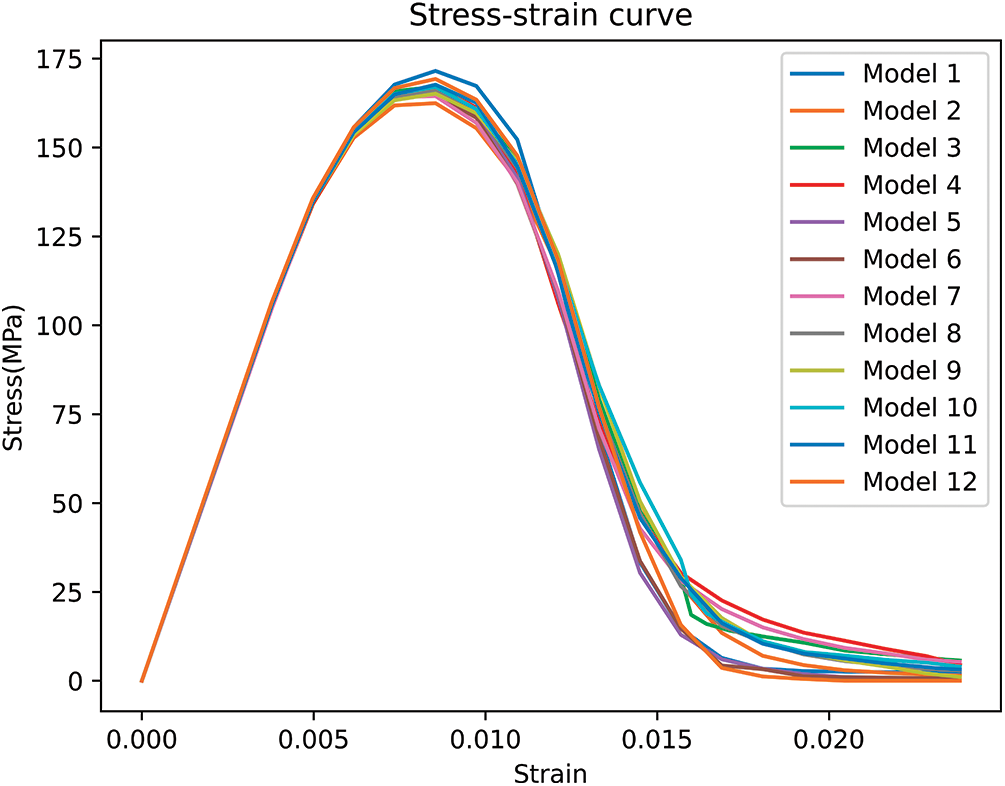
Figure 13: Stress-strain curves of 12 models

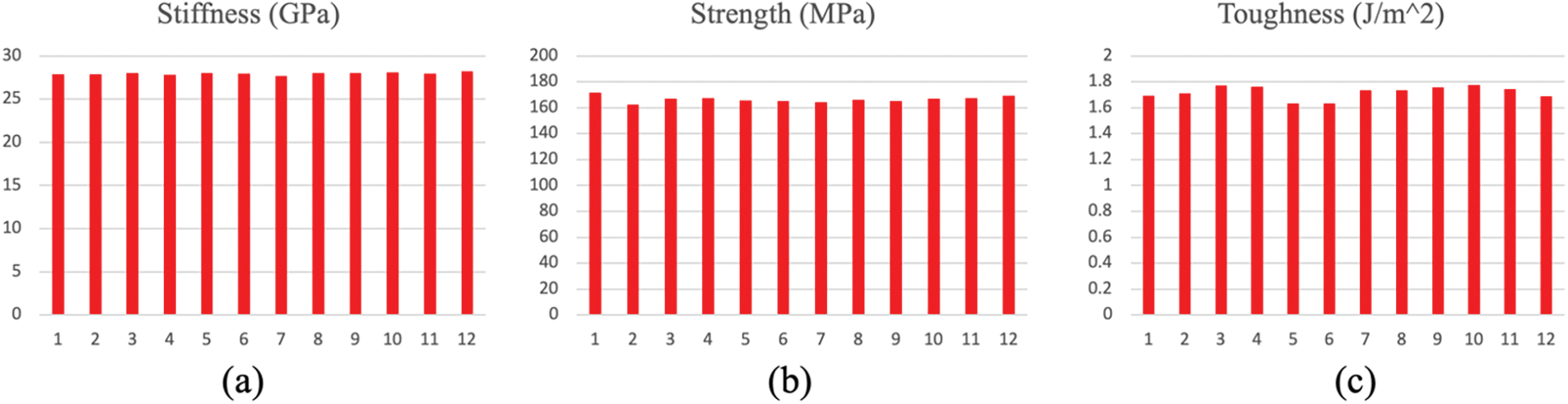
Figure 14: Bulk material properties for 12 models: (a) stiffness, (b) strength, (c) toughness

4  Conclusion

In this paper, a machine learning model was utilized to predict the material response based on the interface properties. The results of this study demonstrate the efficiency and high accuracy of the machine learning model. The machine learning model was trained on a comprehensive dataset of material response and interface properties, allowing it to make accurate predictions. The performance of the machine learning model was evaluated by comparing the predicted values with actual values, and the results showed a high level of accuracy in predicting the material response.

Machine learning models have the advantage of being faster compared with traditional finite element models. The successful application of machine learning in the material property prediction process has the potential to significantly improve the accuracy and efficiency of the material design process. The current study has certain limitations: (1) the total dataset is limited; (2) a bilinear law is used with a very limited number of interface parameters; (3) a single-layer model is used which is not able to simulate interlayer sliding in a multiple-layer 3D nacre model. The current study provides an efficient approach and simulation tool, which opens a door for more advanced studies of material property prediction and bioinspired material design. To design material interface with desired bulk material property is an inverse material design problem and finite element itself cannot achieve this goal. The application of machine learning to material property prediction holds immense promise for enhancing the efficiency and precision of material design. By using machine learning, we could delve deeper into understanding material behaviors and expedite the development of novel materials tailored to specific applications.

Acknowledgement: Valuable discussions with Dr. Mohammad Maghsoudi-Ganjeh and Dr. Liqiang Lin at Mechanical Engineering of UTSA are gratefully acknowledged.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: X.Z.; data collection: X.Y.; analysis and interpretation of results: X.Y., X.Z., W.G., X.W.; draft manuscript preparation: X.Y., X.Z. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Grossman M, Bouville F, Masania K, Studart AR. Quantifying the role of mineral bridges on the fracture resistance of nacre-like composites. Proc Natl Acad Sci U S A. 2018;115(50):12698–703. doi:10.1073/pnas.180509411. [Google Scholar] [CrossRef]

2. Ingrole A, Aguirre TG, Fuller L, Donahue SW. Bioinspired energy absorbing material designs using additive manufacturing. J Mech Behav Biomed Mater. 2021;119:104518. doi:10.1016/j.jmbbm.2021.104518. [Google Scholar] [PubMed] [CrossRef]

3. Bouville F. Strong and tough nacre-like aluminas: process-structure–performance relationships and position within the nacre-inspired composite landscape. J Mater Res. 2020;35(8):1076–94. doi:10.1557/jmr.2019.418. [Google Scholar] [CrossRef]

4. Tan G, Yu Q, Liu Z, Wang X, Zhang M, Liu Y, et al. Compression fatigue properties and damage mechanisms of a bioinspired nacre-like ceramic-polymer composite. Scr Mater. 2021;203:114089. doi:10.1016/j.scriptamat.2021.114089. [Google Scholar] [CrossRef]

5. Ritchie RO. The conflicts between strength and toughness. Nat Mater. 2011;10(11):817–22. doi:10.1038/nmat3115. [Google Scholar] [PubMed] [CrossRef]

6. Amorim L, Santos A, Nunes JP, Viana JC. Bioinspired approaches for toughening of fibre reinforced polymer composites. Mater Design. 2021;199:109336. doi:10.1016/j.matdes.2020.109336. [Google Scholar] [CrossRef]

7. Huang W, Restrepo D, Jung JY, Su FY, Liu Z, Ritchie RO, et al. Multiscale toughening mechanisms in biological materials and bioinspired designs. Adv Mater. 2019;31(43):e1901561. doi:10.1002/adma.201901561. [Google Scholar] [PubMed] [CrossRef]

8. Kakisawa H, Sumitomo T. The toughening mechanism of nacre and structural materials inspired by nacre. Sci Technol Adv Mater. 2011;12(6):064710. doi:10.1088/1468-6996/12/6/064710. [Google Scholar] [PubMed] [CrossRef]

9. Sun J, Bhushan B. Hierarchical structure and mechanical properties of nacre: a review. RSC Adv. 2012;2(20):7617–32. doi:10.1039/c2ra20218b. [Google Scholar] [CrossRef]

10. Khayer Dastjerdi A, Rabiei R, Barthelat F. The weak interfaces within tough natural composites: experiments on three types of nacre. J Mech Behav Biomed Mater. 2013;19:50–60. doi:10.1016/j.jmbbm.2012.09.004. [Google Scholar] [PubMed] [CrossRef]

11. Wang J, Cheng Q, Tang Z. Layered nanocomposites inspired by the structure and mechanical properties of nacre. Chem Soc Rev. 2012;41(3):1111–29. doi:10.1039/c1cs15106a. [Google Scholar] [PubMed] [CrossRef]

12. Greco F, Leonetti L, Pranno A, Rudykh S. Mechanical behavior of bio-inspired nacre-like composites: a hybrid multiscale modeling approach. Compos Struct. 2020;233:111625. doi:10.1016/j.compstruct.2019.111625. [Google Scholar] [CrossRef]

13. Liu J, Xu Y, Yang H, Liu Y, Yarlagadda PK, Yan C. Investigation of failure mechanisms of nacre at macro and nano scales. J Mech Behav Biomed Mater. 2020;112:104018. doi:10.1016/j.jmbbm.2020.104018. [Google Scholar] [PubMed] [CrossRef]

14. Dutta A, Tekalur SA. Crack tortuousity in the nacreous layer—Topological dependence and biomimetic design guideline. Int J Solids Struct. 2014;51(2):325–35. doi:10.1016/j.ijsolstr.2013.10.006. [Google Scholar] [CrossRef]

15. Abid N, Pro JW, Barthelat F. Fracture mechanics of nacre-like materials using discrete-element models: effects of microstructure, interfaces and randomness. J Mech Phys Solids. 2019;124:350–65. doi:10.1016/j.jmps.2018.10.012. [Google Scholar] [CrossRef]

16. Ghazlan A, Ngo TD, Tran P. Three-dimensional Voronoi model of a nacre-mimetic composite structure under impulsive loading. Compos Struct. 2016;153:278–96. doi:10.1016/j.compstruct.2016.06.020. [Google Scholar] [CrossRef]

17. Barthelat F. Designing nacre-like materials for simultaneous stiffness, strength and toughness: optimum materials, composition, microstructure and size. J Mech Phys Solids. 2014;73:22–37. doi:10.1016/j.jmps.2014.08.008. [Google Scholar] [CrossRef]

18. Abid N, Mirkhalaf M, Barthelat F. Discrete-element modeling of nacre-like materials: effects of random microstructures on strain localization and mechanical performance. J Mech Phys Solids. 2018;112:385–402. doi:10.1016/j.jmps.2017.11.003. [Google Scholar] [CrossRef]

19. Greco F, Leonetti L, de Maio U, Rudykh S, Pranno A. Macro- and micro-instabilities in incompressible bioinspired composite materials with nacre-like microstructure. Compos Struct. 2021;269:114004. doi:10.1016/j.compstruct.2021.114004. [Google Scholar] [CrossRef]

20. Mirkhalaf M, Dastjerdi AK, Barthelat F. Overcoming the brittleness of glass through bio-inspiration and micro-architecture. Nat Commun. 2014;5:3166. doi:10.1038/ncomms4166. [Google Scholar] [PubMed] [CrossRef]

21. Jia H, Li Y, Luan Y, Zheng Y, Yang J, Wang L, et al. Bioinspired nacre-like GO-based bulk with easy scale-up process and outstanding mechanical properties. Compos Part A: Appl Sci Manuf. 2020;132:105829. doi:10.1016/j.compositesa.2020.105829. [Google Scholar] [CrossRef]

22. Cui S, Lu Z, Yang Z. Effect of interlocking structure on mechanical properties of bio-inspired nacreous composites. Compos Struct. 2019;226:111260. doi:10.1016/j.compstruct.2019.111260. [Google Scholar] [CrossRef]

23. Jiao D, Zhang J, Liu YY, Liu XG, Zhang Q, Tang SF, et al. Hierarchical toughening of bioinspired nacre-like hybrid carbon composite. Carbon. 2021;171:409–16. doi:10.1016/j.carbon.2020.09.041. [Google Scholar] [CrossRef]

24. Flores-Johnson EA, Shen L, Guiamatsia I, Nguyen GD. Numerical investigation of the impact behaviour of bioinspired nacre-like aluminium composite plates. Compos Sci Technol. 2014;96:13–22. doi:10.1016/j.compscitech.2014.03.001. [Google Scholar] [CrossRef]

25. Begley MR, Philips NR, Compton BG, Wilbrink DV, Ritchie RO, Utz M. Micromechanical models to guide the development of synthetic ‘brick and mortar’ composites. J Mech Phys Solids. 2012;60(8):1545–60. doi:10.1016/j.jmps.2012.03.002. [Google Scholar] [CrossRef]

26. de Maio U, Greco F, Luciano R, Sgambitterra G, Pranno A. Microstructural design for elastic wave attenuation in 3D printed nacre-like bioinspired metamaterials lightened with hollow platelets. Mech Res Commun. 2023;128:104045. doi:10.1016/j.mechrescom.2023.104045. [Google Scholar] [CrossRef]

27. Davies A, Velickovic P, Buesing L, Blackwell S, Zheng D, Tomasev N, et al. Advancing mathematics by guiding human intuition with AI. Nature. 2021;600(7887):70–4. doi:10.1038/s41586-021-04086-x. [Google Scholar] [PubMed] [CrossRef]

28. Butler KT, Davies DW, Cartwright H, Isayev O, Walsh A. Machine learning for molecular and materials science. Nature. 2018;559(7715):547–55. doi:10.1038/s41586-018-0337-2. [Google Scholar] [PubMed] [CrossRef]

29. Das M, Sahu S, Parhi DR. Composite materials and their damage detection using AI techniques for aerospace application: a brief review. Mater Today Proc. 2021;44:955–60. doi:10.1016/j.matpr.2020.11.005. [Google Scholar] [CrossRef]

30. Liu WK, Li S, Park HS. Eighty years of the finite element method: bbirth, evolution, and future. Arch Comput Methods Eng. 2022;29(6):4431–53. doi:10.1007/s11831-022-09740-9. [Google Scholar] [CrossRef]

31. Jin H, Zhang E, Espinosa HD. Recent advances and applications of machine learning in experimental solid mechanics: a review. Appl Mech Rev. 2023;75(6):061001. 10.1115/1.4062966. [Google Scholar] [CrossRef]

32. Flah M, Suleiman AR, Nehdi ML. Classification and quantification of cracks in concrete structures using deep learning image-based techniques. Cem Concr Compos. 2020;114:103781. doi:10.1016/j.cemconcomp.2020.103781. [Google Scholar] [CrossRef]

33. Lu L, Dao M, Kumar P, Ramamurty U, Karniadakis GE, Suresh S. Extraction of mechanical properties of materials through deep learning from instrumented indentation. Proc Natl Acad Sci U S A. 2020;117(13):7052–62. doi:10.1073/pnas.1922210117. [Google Scholar] [PubMed] [CrossRef]

34. Xiao P, Zhang T, Dong XN, Han Y, Huang Y, Wang X. Prediction of trabecular bone architectural features by deep learning models using simulated DXA images. Bone Rep. 2020;13:100295. doi:10.1016/j.bonr.2020.100295. [Google Scholar] [PubMed] [CrossRef]

35. Xiao P, Zhang T, Haque E, Wahlen T, Dong XN, Huang Y, et al. Prediction of elastic behavior of human trabecular bone using a DXA image-based deep learning model. JOM. 2021;73(8):2366–76. doi:10.1007/s11837-021-04704-z. [Google Scholar] [CrossRef]

36. Zhu W, Yang C, Huang B, Guo Y, Xie L, Zhang Y, et al. Predicting and optimizing coupling effect in magnetoelectric multi-phase composites based on machine learning algorithm. Compos Struct. 2021;271:114175. doi:10.1016/j.compstruct.2021.114175. [Google Scholar] [CrossRef]

37. Baltic S, Asadzadeh MZ, Hammer P, Magnien J, Gänser HP, Antretter T, et al. Machine learning assisted calibration of a ductile fracture locus model. Mater Design. 2021;203:109604. doi:10.1016/j.matdes.2021.109604. [Google Scholar] [CrossRef]

38. Liu Y, Esan OC, Pan Z, An L. Machine learning for advanced energy materials. Energy AI. 2021;3:100049. doi:10.1016/j.egyai.2021.100049. [Google Scholar] [CrossRef]

39. Morsali S, Qian D, Minary-Jolandan M. Designing bioinspired brick-and-mortar composites using machine learning and statistical learning. Commun Mater. 2020;1(1):12. doi:10.1038/s43246-020-0012-7. [Google Scholar] [CrossRef]

40. Vinuesa R, Brunton SL. Enhancing computational fluid dynamics with machine learning. Nat Comput Sci. 2022;2(6):358–66. doi:10.1038/s43588-022-00264-7. [Google Scholar] [PubMed] [CrossRef]

41. Su M, Peng H, Yuan M, Li S. Identification of the interfacial cohesive law parameters of FRP strips externally bonded to concrete using machine learning techniques. Eng Fract Mech. 2021;247:107643. doi:10.1016/j.engfracmech.2021.107643. [Google Scholar] [CrossRef]

42. Gu GX, Chen CT, Buehler MJ. De novo composite design based on machine learning algorithm. Extreme Mech Lett. 2018;18:19–28. doi:10.1016/j.eml.2017.10.001. [Google Scholar] [CrossRef]

43. Du Q, Faber V, Gunzburger M. Centroidal Voronoi tessellations: applications and algorithms. SIAM Rev. 1999;41(4):637–76. doi:10.1137/s0036144599352836. [Google Scholar] [CrossRef]

44. Lin L, Wang X, Zeng X. Computational modeling of interfacial behaviors in nanocomposite materials. Int J Solids Struct. 2017;115–116:43–52. doi:10.1016/j.ijsolstr.2017.02.029. [Google Scholar] [PubMed] [CrossRef]

45. Lin L, Wang X, Zeng X. An improved interfacial bonding model for material interface modeling. Eng Fract Mech. 2017;169:276–91. doi:10.1016/j.engfracmech.2016.10.015. [Google Scholar] [PubMed] [CrossRef]

46. Lin L, Zeng X. Computational modeling and simulation of spall fracture in polycrystalline solids by an atomistic-based interfacial zone model. Eng Fract Mech. 2015;142:50–63. doi:10.1016/j.engfracmech.2015.05.039. [Google Scholar] [PubMed] [CrossRef]

47. Arablouei A, Kodur V. Cohesive zone model properties for evaluating delamination of spray-applied fire-resistive materials from steel structures. Eng Fract Mech. 2015;143:138–57. doi:10.1016/j.engfracmech.2015.06.037. [Google Scholar] [CrossRef]

48. Feraren P, Jensen HM. Cohesive zone modelling of interface fracture near flaws in adhesive joints. Eng Fract Mech. 2004;71(15):2125–42. doi:10.1016/j.engfracmech.2003.12.003. [Google Scholar] [CrossRef]

49. Lin L, Wang X, Zeng X. Computational modeling of interfacial behaviors in nanocomposite materials. Int. J Solids Struct. 2017;115:43–52. doi:10.1016/j.ijsolstr.2017.02.029. [Google Scholar] [PubMed] [CrossRef]

50. Lin L, Wang X, Zeng X. The role of cohesive zone properties on intergranular to transgranular fracture transition in polycrystalline solids. Int J Damage Mech. 2017;26(3):379–94. doi:10.1177/1056789515618732. [Google Scholar] [CrossRef]

51. Maghsoudi-Ganjeh M, Lin L, Yang X, Zeng X. Computational modeling and simulation of bioinspired nacre-like composites. J Mater Res. 2021;36(13):2651–61. doi:10.1557/s43578-021-00124-6. [Google Scholar] [CrossRef]

52. Maghsoudi-Ganjeh M, Lin L, Wang X, Zeng X. Bioinspired design of hybrid composite materials. Int J Smart Nano Mater. 2019;10(1):90–105. doi:10.1080/19475411.2018.1541145. [Google Scholar] [CrossRef]

53. Yan Y, Nakatani A. Stability controlled crack initiation in nacre-like composite materials. J Mech Phys Solids. 2019;125:591–612. doi:10.1016/j.jmps.2019.01.003. [Google Scholar] [CrossRef]

54. Yang X, Maghsoudi-Ganjeh M, Zeng X. Computational investigation of the mechanical behavior of a bone-inspired nanocomposite material. J Compos Sci. 2023;7(8):341. 10.3390/jcs7080341. [Google Scholar] [CrossRef]

55. Maghsoudi-Ganjeh M, Lin L, Wang X, Zeng X. Computational investigation of ultrastructural behavior of bone using a cohesive finite element approach. Biomech Model Mechanobiol. 2019;18(2):463–78. doi:10.1007/s10237-018-1096-6. [Google Scholar] [PubMed] [CrossRef]

56. Ural A, Vashishth D. Cohesive finite element modeling of age-related toughness loss in human cortical bone. J Biomech. 2006;39(16):2974–82. doi:10.1016/j.jbiomech.2005.10.018. [Google Scholar] [PubMed] [CrossRef]

57. Cox BN, Yang Q. Cohesive zone models of localization and fracture in bone. Eng Fract Mech. 2007;74(7):1079–92. doi:10.1016/j.engfracmech.2006.12.024. [Google Scholar] [CrossRef]

58. Lin AY, Meyers MA. Interfacial shear strength in abalone nacre. J Mech Behav Biomed Mater. 2009;2(6):607–12. doi:10.1016/j.jmbbm.2009.04.003. [Google Scholar] [PubMed] [CrossRef]

59. Askarinejad S, Rahbar N. Toughening mechanisms in bioinspired multilayered materials. J R Soc Interface. 2015;12(102):20140855. doi:10.1098/rsif.2014.0855. [Google Scholar] [PubMed] [CrossRef]

60. Hang F, Gupta HS, Barber AH. Nanointerfacial strength between non-collagenous protein and collagen fibrils in antler bone. J R Soc Interface. 2014;11(92):20130993. doi:10.1098/rsif.2013.0993. [Google Scholar] [PubMed] [CrossRef]