Generalized nth-Order Perturbation Method Based on Loop Subdivision Surface Boundary Element Method for Three-Dimensional Broadband Structural Acoustic Uncertainty Analysis

1  Introduction

In many engineering problems [1–5], there is an increasing focus on the consideration of uncertainty. The problem of uncertainty in stochastic data occurs frequently in engineering practice, especially when some parameters are derived from field measurements or laboratories, and the modeled engineering system’s final stochastic response is influenced by the statistical estimates of these parameters. To ascertain how input probabilistic properties affect an engineering system’s final stochastic response, several uncertainty analysis techniques have been proposed, such as stochastic spectral methods [6,7], Monte Carlo simulations (MCs) [8–11], and perturbation techniques [12–16]. Among all the stochastic approaches, MCs is the most straightforward and comprehensive probabilistic technique and is widely employed across diverse academic fields [17]. Although MCs is computationally expensive, it remains the most reliable and stable simulation technique compared to other probabilistic methods, which is often used as a reference solution [18,19]. The generalized nth-order perturbation method’s primary goal is to remove the restriction on the input second probability moments to be less than 0.15. The generalized nth-order perturbation method realizes Taylor expansions of arbitrary order by utilizing the parameters of perturbation and the computed partial derivatives of the increasing order around their expectation [20,21]. In computational mechanics, evaluating the accuracy of dependable issues has long been an unsolved issue, Kamiński [22] has obtained satisfactory accuracy by applying the nth-order perturbation technique with exact problems. Moreover, the perturbation technique is widely used in finite element method (FEM), boundary element method (BEM), and finite difference method (FDM) [23–26].

Hughes et al. [27] proposed isogeometric analysis (IGA), which is a novel spline theory-based numerical computation technique. IGA makes acoustic boundary element simulation calculations more convenient, accurate, and high precision. The method can directly analyze the CAD model without additional meshing, which reduces the discretization error of the model and also speeds up the calculation [28–30]. It uses non-uniform rational b-splines (NURBS) [31–33] and t-splines [34,35] instead of conventional finite elements. Without altering the geometry, we can increase the simulation’s accuracy by applying h- and refinements. To facilitate more versatile geometric representations in design, IGA has integrated t-splines, which feature t-joints and enable local refinement into the analysis [36–38]. Surface subdivision is a potent surface design technique, with a straightforward refinement procedure, which can effectively produce smooth surfaces from any original mesh. Catmull et al. [39] first proposed a mode of subdivision surfaces in 1978, which is a quadrilateral split to generate a cubic B-spline surface, and Loop [40] first proposed a basic triangle-based subdivision mode in 1987, which did a generalization of the box spline. Subdivided surfaces are compatible with NURBS as a standard for CAD systems and enable refinement of B-spline methods. Subdivision techniques are now widely used in modeling applications [41–45].

The boundary element method is extremely attractive when waves propagate in an infinite domain [46–50]. BEM is an important numerical method in acoustics [51–54], and is also widely used in other scientific and engineering fields. It is popular in the analysis of external acoustic fields due to its advantages, such as reduced dimensional computation and high analytical accuracy, and the boundary element method requires only a discrete boundary and, at the same time completely satisfies the radiation conditions at the infinity. Combined with the well-known Burton-Miller method [55,56], the capability of acoustic boundary elements is further improved and the problem of non-uniqueness of solutions is avoided successfully when using BEM to analyze the external sound field problem. However, the conventional BEM cannot be used in large-scale problems because the coefficient matrices formed are dense matrices with high memory requirements. Fortunately, the boundary element coefficient matrix, although dense, has the property of chunked low rank, and a series of fast methods using low-rank decompositions have been proposed, including fast multipole method [57,58], adaptive cross approximation [59,60], and other fast methods [61,62], which have successfully reduced computation and memory usage, and made it possible for boundary element method to serve complex engineering problems.

In recent years, more scholars have investigated the application of isogeometric boundary elements in some practical acoustic engineering problems. Venås et al. [63] investigated the approximation of isogeometric boundary elements for the 3D acoustic scattering problem and built a BeTSSi submarine model by combining parametric surfaces with NURBS. Chen et al. [64] simulated acoustic wave propagation in a semi-infinite space by combining the Catmull-Clark subdivision surface method in 3D computer graphics with isogeometric boundary elements. Wu et al. [65] developed an isogeometric indirect boundary element based on NURBS to analyze 3D acoustic problems and combined polynomials splines over hierarchical T-meshes with indirect boundary element for the first time. The isogeometric boundary element method (IGABEM) has also been widely used in the analysis of problems in potential [66–70], elastodynamics [71–75] and acoustic structural optimization [76–79]. A very important index of the acoustic boundary element is that it has frequency dependence, the response of the whole system is frequency-dependent, and in the real environment, the excitation load is broad frequency, not single frequency. Therefore, in this paper, we consider the stochastic analysis of the acoustic boundary element with the frequency change and use the generalized nth-order perturbation method based on the isogeometric boundary element method for uncertainty analysis.

The rest of the paper is structured as follows. Section 2 introduces the theoretical aspects of the generalized nth-order perturbation method. Section 3 presents the subdivision rules and computation of loop subdivision surfaces and proposes IGABEM for the propagation of sound waves in an infinite domain. Section 4 compares the computational results of the proposed algorithm with those under MCs through two numerical examples to confirm the accuracy and effectiveness of the proposed algorithm. Finally, in Section 5, we summarize the conclusions of this work and look forward to future work.

2  Theoretical Aspects of the Generalized nth-Order Perturbation Method

In a general stochasticity analysis, a group of random fields m(x) associated with space coordinates and their probability density functions (PDF) ρ(m) are introduced, the first two probability moments of this random field can be described as

E(m(x))=∫−∞+∞m(x)ρ(m)dm,(1)

and,

Cov(m(xr),m(xs))=∫−∞+∞∫−∞+∞(m(xr)−m0(xr))(m(xs)−m0(xs))ρ(m)dm,(2)

where m0(xr) and m0(xs) denote the first probability moments of the different variables, respectively. And Cov(m(xr),m(xs)) denotes the covariance between m0(xr) and m0(xs).

The stochastic perturbation method’s fundamental concept is to use the small parameter ε to extend all of the state functions and input variables of a given problem across its spatially expected Taylor series. For a single random variable, this state function f(m) can be expressed as

f(m)=f(0)(m)+∑n=1∞1n!εnf(n)(m)[Δm]n≅f(0)(m)+εf(1)(m)Δm+⋯+1n!εnf(n)(m)[Δm]n,(3)

where f(n)(m) is the nth partial derivative of f(m) concerns an individual random variable m, which is expressed in this way:

f(n)(m)=∂nf(m)∂mn.(4)

Next, replace m in Eq. (1) with f(m) in Eq. (3), the expectation value of the state function f(m) can be acquired by combining the Taylor series expansion:

E(f(m),m)=∫−∞+∞f(m)ρ(m)dm=∫−∞+∞[f(0)(m)+∑n=1∞1n!εnf(n)(m)[Δm]n]ρ(m)dm.(5)

The perturbation parameter ε influences the Taylor series expansion’s convergence. This power expansion is only applicable if the series converges and the state function is analytic in ε. Consequently, any criterion for convergence should take the perturbation parameter’s size into account. In many calculations, the perturbation parameter ε is set to 1. However, in this work, it is treated as a parametric variable for uncertainty analysis.

Considering the various probability distributions, one can note the essential difference between the symmetric and asymmetric distribution functions, where the symmetric distribution function ignores the odd-order terms in the Taylor expansion, and Eq. (5) can be written as

E(f(m),m)=f(0)(m)+∫−∞+∞[∑n=12A1!ε2nf(2n)(m)[Δm]2n]ρ(m)dm.(6)

The asymmetric probability density function can be described as

E(f(m),m)=f(0)(m)+∫−∞+∞[∑n=1N1[n]!εnf(n)(m)[Δm]n]ρ(m)dm.(7)

In both situations, the quantities of natural numbers A and N must ensure that the additional probability moments have a satisfactory approximation accuracy. The following statistical error measures for variance and expectation can be introduced. For the expectations:

|E(fN1(m))−E(f¯(m))|≤ε1.(8)

For the variance:

|V(fN2(m))−V(f¯(m))|≤ε2.(9)

The positive numbers ε1 and ε2 denote the permissible error in determining the expectation and variance, and the natural numbers N1 and N2 denote the order of the perturbation, the larger the value, the more the condition of satisfactory accuracy is fulfilled. E[f¯(m)] denotes the expected value obtained from Monte Carlo simulations. The precise answers to the two aforementioned equations can be found in statistical approximations [80], such as

E(f¯(m))=limA→∞1A∑i=1Af¯i(m),(10)

together with

V(f¯(m))=limA→∞1A−1∑i=1A[f¯i(m)−E(f¯(m))2],(11)

where A is a very large number denoting the total number of randomized trials used to compute the estimate of the random function f(m).

Assuming that the PDF is a symmetric distribution function, the state function f(m) can be extended to second-order deviation to its mean, denoted as

E(f(m),m) =∫−∞+∞f(m)ρ(m)dm ≅∫−∞+∞[f(0)(m)+εf(1)(m)Δm+12ε2f(2)(m)(Δm)2]ρ(m)dm =f(0)(m)+12ε2f(2)(m)μ2(m),(12)

where μ2(m) denotes the PDF and the associated second-order central probability distance.

If greater accuracy is employed, higher-order expansion terms are required, and the expansion for an eighth-order perturbation can be described as

E(f(m),m)=f(0)(m)+12ε2f(2)(m)μ2(b)+14!ε4f(4)(m)μ4(m)+16!ε6f(6)(m)μ6(m)+18!ε8f(8)(m)μ8(m),(13)

where μb(m) indicates the moments of variable m up to order bth in probability. The state function f(m) variance is expressed as

V(f(m))=∫−∞+∞[f(m)−E(f(m))]2ρ(m)dm.(14)

The sixth-order expression for the variance of the state function f(m) is as follows, based on similar considerations:

V(f(m))≅ε2[f(1)(m)]2μ2(m)+[14[f(2)(m)]2+23![f(1)(m)][f(3)(m))]ε4μ4(m) +[[13!]2[f(3)(m)]2+14![f(2)(m)][f(4)]+25![f(1)(m)][f(5)(m)]]ε6μ6(m).(15)

In this paper, we also consider the nth-order central probability moments of the widely used Gaussian distribution, denoted as

μ2n+1(m)=0,μ2n(m)=1×3×5×⋯×[2n−1]σ2n(m).(16)

The method can also be applied to approximate formulas for expectation and variance with multiple variables. The nth-order derivative values of the response’s variance and expectation as determined by Eqs. (5) and (14).

3  Isogeometric Boundary Element Method with Loop Subdivision Surface for 3D Problems

For frequency-domain acoustic problems, the system response has a certain frequency dependence. In the real environment, the excitation load is a broadband excitation, which is a range rather than a definite value. Therefore, in this paper, the nth-order perturbation method based on isogeometric boundary elements is used to analyze the wideband structural acoustics with uncertainty.

3.1 Loop Subdivision Surface

Subdivided surfaces are based on an initial control mesh and certain subdivision rules, and can be constructed from an initial control mesh of any topology. This avoids the geometric errors introduced by the traditional parametric surface modeling of cutting and splicing when constructing complex free-surface models, and subdivided surfaces are favored because of their greater flexibility. The loop subdivision provides more smooth and continuous surfaces with good adaptability to complex shapes, while the meshfree approach [81,82] applies to arbitrary shapes and topologies, and can handle a variety of complex geometries and irregular meshes, the combination of which enables better handling of complex geometries and improves the accuracy of the computational results. We plan to further explore this approach in the future.

3.1.1 Loop Subdivision Rules

For the initial control mesh, some subdivision rules are used to insert new vertices into the mesh, and then a new mesh is obtained by connecting the new vertices to the old vertices according to some topological rules. The subdivision rules are applied repeatedly, and in the limit, the mesh eventually converges to a smooth surface. In practice, the mesh is subdivided to the extent that the surface is considered smooth and is no longer subdivided. While the Loop subdivision [40] is an approximate subdivision method, it is the first proposed subdivision method based on the triangle mesh, which is a generalization of the box spline. By inserting new vertices on the edges of the triangle mesh and connecting them two by two, the triangle can be divided into four smaller triangles, and with each subdivision, the number of triangles will be increased to a fourth of the initial amount.

The amount of edges that are directly related to a vertex is known as its valence. Vertices are further categorized into regular vertex and extraordinary vertex. In triangular mesh, regular points are internal vertices with a valence of 6 or boundary points with a valence of 4. Other points are extraordinary points. In a quadrilateral mesh, a regular point is an interior vertex of value 4 or a boundary point of value 3, and the other points are extraordinary. The Loop subdivision algorithm is categorized into geometric and topological rules. The geometric rule is to add a new vertex E point on each edge and generate V points from the original vertices as shown in Fig. 1a. The topology rule connects the new vertices and edges obtained from each subdivision to obtain a new topology and control mesh, as illustrated in Fig. 1b. The geometric rules for Loop subdivision to calculate new vertices are as follows:

pE=18(p2+p3)+38(p0+p1),(17)

pV=(1−nβn)p′+βn∑i=0n−1pi,(18)

where p′ is the old vertex corresponding to pV and n is the valence of the neighborhood of vertex p′. And,

βn={316n=31n[58−(38+14cos⁡2πn)2]n>3.(19)

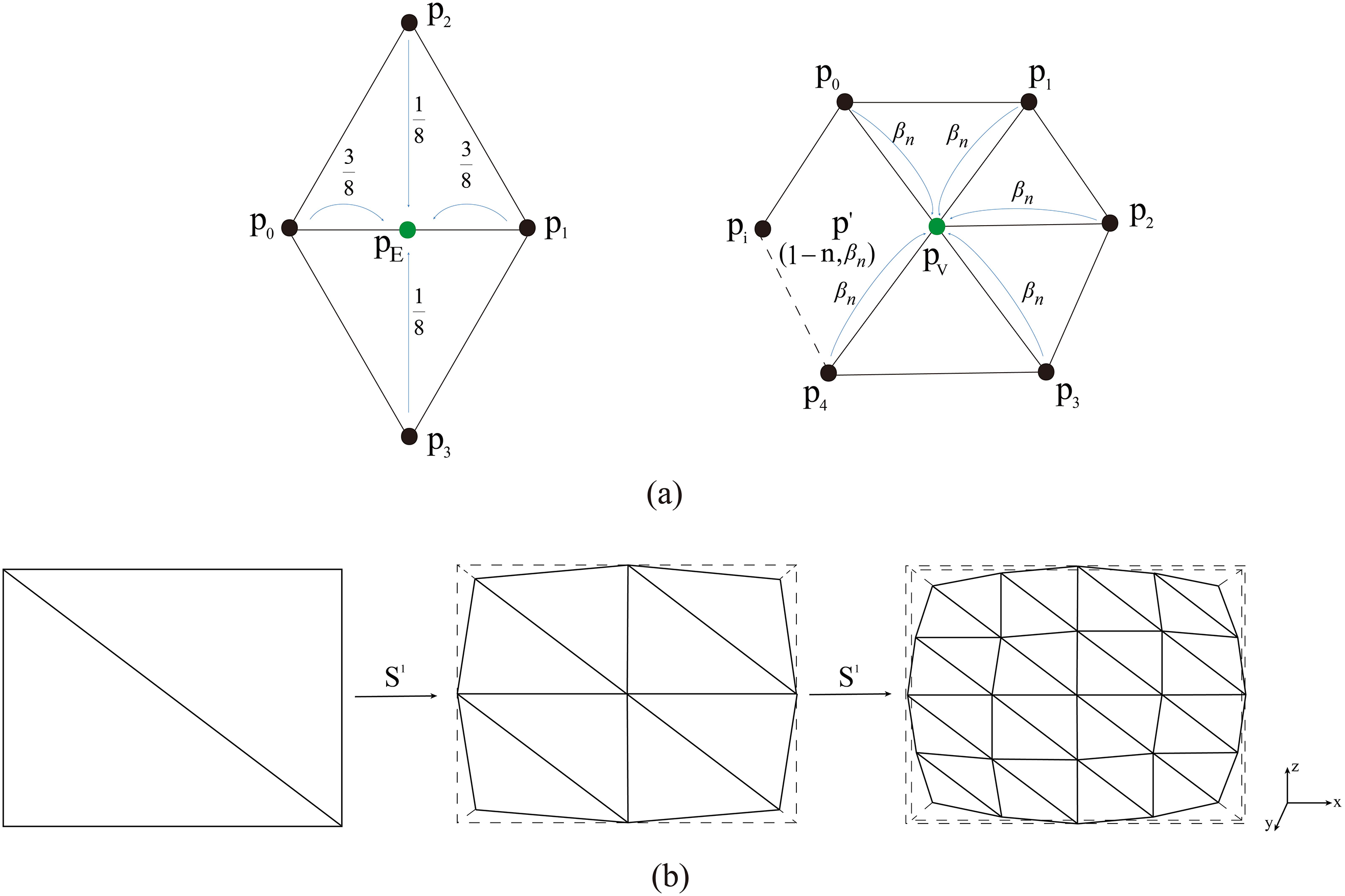
Figure 1: (a) Loop subdivision surface calculation template; (b) Loop subdivision topology rules

From Eq. (18), the point V can be obtained by weighted summation of the original vertex and the vertices in its neighborhood.

3.1.2 Calculation of Loop Subdivision Surfaces

A triangular patch is a regular cell if its three control points have valence 6 and none of its two-ring neighborhood vertices are border vertices. A quadratic box spline with 12 basis functions Ni and 12 control vertices xi can be precisely represented by

x(β1,β2)=∑i=112Ni(β1,β2)xi,(20)

where (β1,β2) is the coordinate of the center of gravity of the unit triangle.

A triangular patch that has at least one control point with the valence is 6, or one of its bicyclic neighborhood vertices is a border vertex, otherwise, it is an irregular cell, and a quadratic box spline cannot represent the resulting surface patch. Three regular sub-patches and one irregular sub-patch are created for every subdivision of an irregular patch. The limit surfaces produced by the Loop subdivision method can be C2-continuous at regular elements and C1-continuous at singular elements. For evaluating irregular patches, we need to repetitively subdivide their irregular sub-patch grids until the appropriate parameter values are contained within regular patches.

3.2 IGABEM for Acoustic Problems

The Kirchhoff-Helmholtz conventional boundary integral equation (CBIE) can be written as

C(x)ψ(x)+∫Γ∂G(x,y)∂n(y)ψ(y)dΓ(y)=∫ΓG(x,y)q(y)dΓ(y)+ψinc(x),(21)

where point x is called the field point and point y is called the source point. The geometric features at the point x determine the coefficient C(x). If point x is smooth, C(x)=1/2. ψinc denotes incident sound pressure and q(y)=∂ψ(y)∂n(y) denotes sound flux.

Consider that Eq. (21) will have spurious frequencies when solving the external sound field problem, thus leading to a non-unique solution. We use the Burton-Miller method to resolve the unique solution of the exterior acoustic problem, and the new boundary integral equation is obtained by taking a partial derivation of the conventional boundary integral equation concerning the direction of the exterior normal of the source point, described as follows:

C(x)q(x)+∫Γ[∂2G(x,y)∂n(y)n(x)ψ(y)−∂G(x,y)∂n(x)q(y)]dΓ(y)=∂ψinc(x)∂n(x),(22)

Because of the presence of super-singular integrals in Eq. (22), the equation is known as the Hyper-singular boundary integral equation. The existence of singular integrals makes it difficult to obtain an exact solution to the above equations when we solve them directly by Gaussian integration. These singular integrals require special treatment, and the singular phase elimination technique is usually accustomed to solving the singular integrals exactly [83].

The kernel function of each order for the 3D acoustic problem is:

G(x,y)=eikr4πr,∂G(x,y)∂n(y)=F(x,y)=−eikr4πr2(1−ikr)∂r∂n(y),∂G(x,y)∂n(x)=K(x,y)=−eikr4πr2(1−ikr)∂r∂n(x),∂2G(x,y)∂n(y)n(x)=H(x,y)=eikr4πr3[(3−3ikr−k2r2)∂r∂n(y)∂r∂n(x)+(1−ikr)ni(x)ni(y)],(23)

where r=|x−y| is the Euclidean distance between the field and source points, k is the wave number and i denotes the imaginary part.

Combining Eqs. (21) and (22), the Burton-Miller formula can be as follows:

(ψ(x)+αq(x))C(x)+∫Γ[F(x,y)∂n(y)ψ(y)−G(x,y)q(y)]dΓ(y)+α∫Γ[H(x,y)ψ(y)−K(x,y)q(y)]dΓ(y)=ψ~inc(x),(24)

where

ψ~inc(x)=ψinc(x)+αψinc(x)∂n(x),(25)

where α is the coupling coefficient, α=i/k when the wave number k>1; when k≤1, α=i.

In order to overcome the problem of low computational accuracy in the calculation of the traditional approximate geometric model of the Lagrangian function with physical field interpolation, in this research, the geometric model is built by using the loop subdivision surface, and the boundaries in the discretization Eq. (24) are formed into some elements as described below:

Γ=∑e=1NelΓe.(26)

where Nel is the total number of elements and e is the element index.

In fact, by fitting all levels of subdivision meshes, we can obtain the same surface model, which is consistent with the limits of the subdivision surface. Consequently, we do not need to perform the numerical computation of the limit subdivision mesh level in the numerical computational analysis; instead, we only need to select the suitable level of subdivision meshes. The field points have local coordinates x(β1,β2) within the reference element, and the sound pressure and its normal derivative are discretized using the subdivided basis functions Bκ(β1,β2):

ψ(0)(x(β1,β2))=∑κ=1nfBκ(β1,β2)ψκ(0),q(0)(x(β1,β2))=∑κ=1nfBκ(β1,β2)qκ(0),(27)

where ψκ(0) and qκ(0) denote the characteristics of acoustic pressure’s derivative and flux related to the κth coordinate points in the subdivision patch, respectively; nf is the number of collocation points.

By substituting Eq. (27) into Eq. (24), the nth-order derivative discretization equation for isogeometric boundary elements can be derived as follows:

C(x(β^1,β^2))∑κ=0nfBκ(β^1,β^2)(ψκ(0)+αqκ(0))=ψ~inc(0)(x(β^1,β^2))+∑e=1Ne∑κ=0nf∫ΓeG(0)Bκ(β1,β2)dΓ(y)qκ(0)−∑e=1Ne∑κ=0nf∫ΓeF(0)(x(β^1,β^2),y(β1,β2))Bκ(β1,β2)dΓ(y)ψκ(0)+α∑e=1Ne∑κ=0nf∫ΓeK(0)(x(β^1,β^2),y(β1,β2))Bκ(β1,β2)dΓ(y)qκ(0)−α∑e=1Ne∑κ=0nf∫ΓeH(0)(x(β^1,β^2),y(β1,β2))Bκ(β1,β2)dΓ(y)ψκ(0),(28)

where κ=0,1,…,nf, Ne is the amount of NURBS elements.

In order to create a system of equations using the boundary element approach, the same amount of boundary integral equations must be created as the amount of control points. By the resolution of this system of equations, we can derive unknown nodal solutions. Here, we use a configuration scheme to produce a system of equations. Given an element Γe, through its patch, we define the set Ce∈[xe(0,0),xe(1,0),xe(0,1)] of configuration points in this element, then the global set of configuration points is denoted as

C=∑e=1NelCe.(29)

The amount of configuration points is the same as the number of vertices, but the control vertices and configuration points do not overlap. Then, interpolation operations are performed in the elements of the corresponding regular patches or irregular parameters to acquire the coordinates of the configuration points. Finally, the equations of all configuration points are collected and represented in matrix form, the system of linear algebraic equations that follows:

F¯(0)ψ(0)=G¯(0)q(0)+ψ~inc(0).(30)

Then, the field vector ψ(0) can be obtained by Eq. (30).

3.3 Generalized nth-Order Perturbation

In this paper, the wave number k is set as a random input variable, and all state functions and variables associated with this random input variable k are extended using a Taylor series expansion about the point k0 and as the expectation of k. Then these state functions using the Δk=k−k0 expansion can be expressed as

{p(k)=p(k0)+εp(1)(k0)Δk+12ε2p(2)(k0)[Δk]2+⋯+1n!εnp(n)(k0)[Δk]n,G(k)=G(k0)+εG(1)(k0)Δk+12ε2G(2)(k0)[Δk]2+⋯+1n!εnG(n)(k0)[Δk]n,F(k)=F(k0)+εF(1)(k0)Δk+12ε2F(2)(k0)[Δk]2+⋯+1n!εnF(n)(k0)[Δk]n,K(k)=K(k0)+εK(1)(k0)Δk+12ε2K(2)(k0)[Δk]2+⋯+1n!εnK(n)(k0)[Δk]n,H(k)=H(k0)+εH(1)(k0)Δk+12ε2H(2)(k0)[Δk]2+⋯+1n!εnH(n)(k0)[Δk]n.(31)

Then, the different order expansions of the boundary integral equation of Eq. (24) are denoted as

• The zeroth-order equation is given by

(ψ(x;k0)+αq(x;k0))C(x)=∫Γ[G(x,y;k0)q(y;k0)−F(x,y;k0)ψ(y;k0)]dΓ(y)+α∫Γ[K(x,y;k0)q(y;k0)−H(x,y;k0)ψ(y;k0)]dΓ(y)+ψ~inc(x;k0),(32)

• The nth-order equation is defined by

C(x)[ψ(n)(x;k0)+αq(n)(x;k0)]=ψ~inc(n)(x;k0)+∑t=0n(nt)∫Γ[G(t)(x,y;k0)q(n−t)(y;k0)−F(t)(x,y;k0)ψ(n−t)(y;k0)]dΓ(y)+α∑t=0n(nt)∫Γ[K(t)(x,y;k0)q(n−t)(y;k0)−H(t)(x,y;k0)ψ(n−t)(y;k0)]dΓ(y).(33)

In order to obtain a direct expression for the derivative of the kernel function at tth-order in Eq. (24), it is necessary to analyze the derivative of the Hankel function. Then the derivative of the kernel function at tth-order in Eq. (24) is denoted as

G(t)(x,y;k0)=(ir)teik0r4πr,F(t)(x,y)=it4π[(t−1)rt−2+ik0rt−1]eik0r∂r∂n(y),K(t)(x,y)=it4π[(t−1)rt−2+ik0rt−1]eik0r∂r∂n(x),H(t)(x,y)=ijrt−3eikr4π{[(t−1)(t−3)+(2t−3)ikr−k2r2]∂r∂n(y)∂r∂n(x)−[(t−1)+ikr]ni(x)ni(y)}.(34)

3.3.1 Discrete Boundary Integral Equations

The sound pressure and sound pressure flux at the boundary of Eq. (24) are interpolated using the subdivision surface basis functions in the following way, applying the idea of IGA.

ψ(n)(x(β1,β2);k0)=∑κ=1nfBκ(β1,β2)ψκ(n)(k0),q(n)(x(β1,β2);k0)=∑κ=1nfBκ(β1,β2)qκ(n)(k0),(35)

where ψκ(n)(k0) and qκ(n)(k0) represent derived factors of the acoustic pressure and flux connected to the κth regulatory point in the patch of a subdivision element, respectively; nf is the number of collocation points.

Substituting Eq. (35) into Eq. (33), the nth-order derivative discretization formula for the boundary integral equation can be described as

C(x(β^1,β^2))∑κ=0nfBκ(β^1,β^2)(ψκ(n)+αqκ(n))=∑t=0n(nt)∑e=1Ne∑κ=0nf∫ΓeG(t)Bκ(β1,β2)dΓ(y)qκ(n−t)− ∑t=0n(nt)∑e=1Ne∑κ=0nf∫ΓeF(t)(x(β^1,β^2),y(β1,β2);k0)Bκ(β1,β2)dΓ(y)ψκ(n−t)(k0)+α∑t=0n(nt)∑e=1Ne∑κ=0nf∫ΓeK(t)(x(β^1,β^2),y(β1,β2);k0)Bκ(β1,β2)dΓ(y)qκ(n−t)(k0)−α∑t=0n(nt)∑e=1Ne∑κ=0nf∫ΓeH(j)(x(β^1,β^2),y(β1,β2);k0)Bκ(β1,β2)dΓ(y)pκ(n−j)(k0)+ψ~inc(n)(x(β^1,β^2);k0),(36)

where κ=0,1,…,nf; Ne is the number of NURBS elements.

Due to the presence of control points, the construction of the system of equations using the boundary element method requires the construction of boundary integral equations equal to the number of control points, and then by resolving this system of equations, the results of the unestablished nodes can be obtained. In this background, this paper constructs a set of configuration points, given an element Γe, we define a set Ce∈[xe(0,0),xe(1,0),xe(0,1)] of configuration points in this element, then the global set of configuration points can be represented as

C=∑e=1NelCe.(37)

The coordinates of the configuration points can be ascertained by performing interpolation operations on the relevant elements with regular or irregular patches. Then the discretization of the boundary integral equation with nth-orderr derivatives yields a system of linear algebraic equations by deriving the equation for each configuration point, expressed as a parallel matrix:

• The zeroth-order linear system of equation is given by

F¯(0)ψ(0)=G¯(0)q(0)+ψ~inc(0);(38)

• The first-order linear system of equation is defined by

F¯(0)ψ(1)=G¯(0)q(1)+G¯(1)q(0)−F¯(1)ψ(0)+ψ~inc(1);(39)

• The nth-order linear system of equation is expressed as

∑t=0n(nt)[{F}¯(t)ψ(n−t)−{G}¯(t)q(n−t)]=ψ~inc(n).(40)

With the boundary conditions applied and terms rearranged, the equation system can be written as follows:

Cx=D.(41)

where matrix C=F¯(0) is a non-symmetric dense matrix, x=ψ(n) is a boundary-related unknown parameter, and D is a known vector that consider the incident wave and is derived using the matrix-vector multiplication operation as follows:

D={G¯(0)q(0)+ψ~inc(0)n=0∑t=0n(nt)G¯(t)q(n−t)−∑t=1n(nt)F¯(t)ψ(n−t)+ψ~inc(n)n>0.(42)

The consequence of field vector ψ(0) can be acquired by Eq. (38) for n=0. Next, the first derivative value of the field concerning the random variable can be determined by using ψ(0) for n=1 in Eq. (39). Similarly, the field’s derivative of any order can be acquired. Finally, the expected value and variance can be obtained by substituting the nth-order derivative values into Eqs. (5) and (14).

4  Numerical Examples

In this section, we investigate the precision and effectiveness of the proposed algorithm through two numerical examples. The code was written in Fortran 90 programming language and run on a personal PC side computer with a processor of i7-8700 CPU and this research compared the expected value and standard deviation with the results of Monte Carlo simulations.

4.1 Spherical Model

The first numerical example is the spherical model, as seen in Fig. 2, with a sphere of radius r = 5 centered at (0, 0), which consists of 864 constant elements and is amplified by the amplitude ψ0 = 1, and the plane incident wave ψinc=ψ0eikrcosθ propagating along the x-positive axis. It simulates the scattered waves and confirms the suggested algorithmic approach’s efficacy.

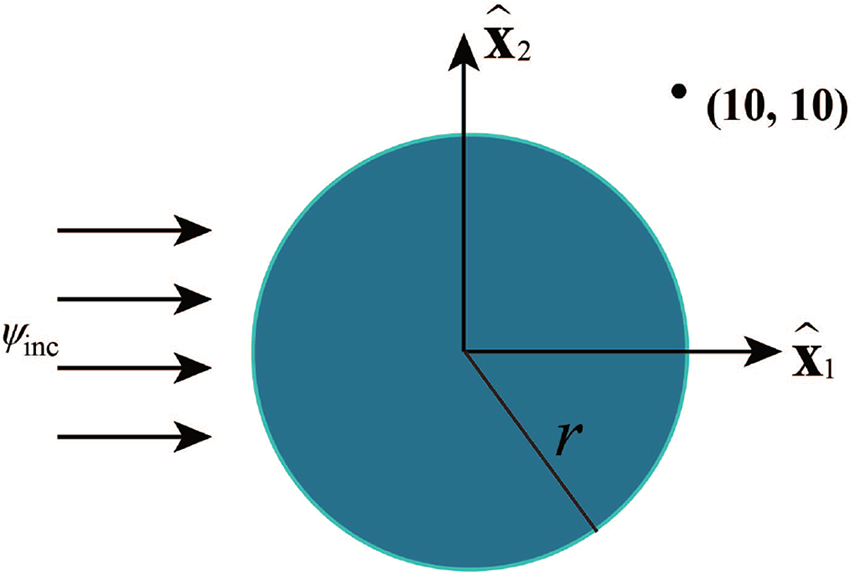
Figure 2: Illustration of the scattering process of an infinite sphere model

In this research, the numerical and analytical solutions for the real, imaginary and amplitude parts of the acoustics pressure located at the test points (10, 10, 10 m) at a range of frequencies are analyzed and are displayed in Fig. 3. For numerical computations, we employed two distinct forms of boundary integral equations: the conventional boundary integral equation provided by Eq. (21), and the combined Burton-Miller boundary integral equation (BM) provided by Eq. (24). As observed in Fig. 3, the numerical results based on CBIE exhibit a little deviation from the analytical solution at some frequencies, whereas the numerical results based on BM show a greater agreement with the analytical solution at all frequencies. The frequencies that do not match accurately are called fictitious feature frequencies, which is a problem encountered in analyzing external sound problems and is not an inherent property of the arithmetic model. We can see that the results match well using these two types of numerical calculation methods, which verifies the precision and effectiveness of the IGABEM algorithm proposed in this paper.

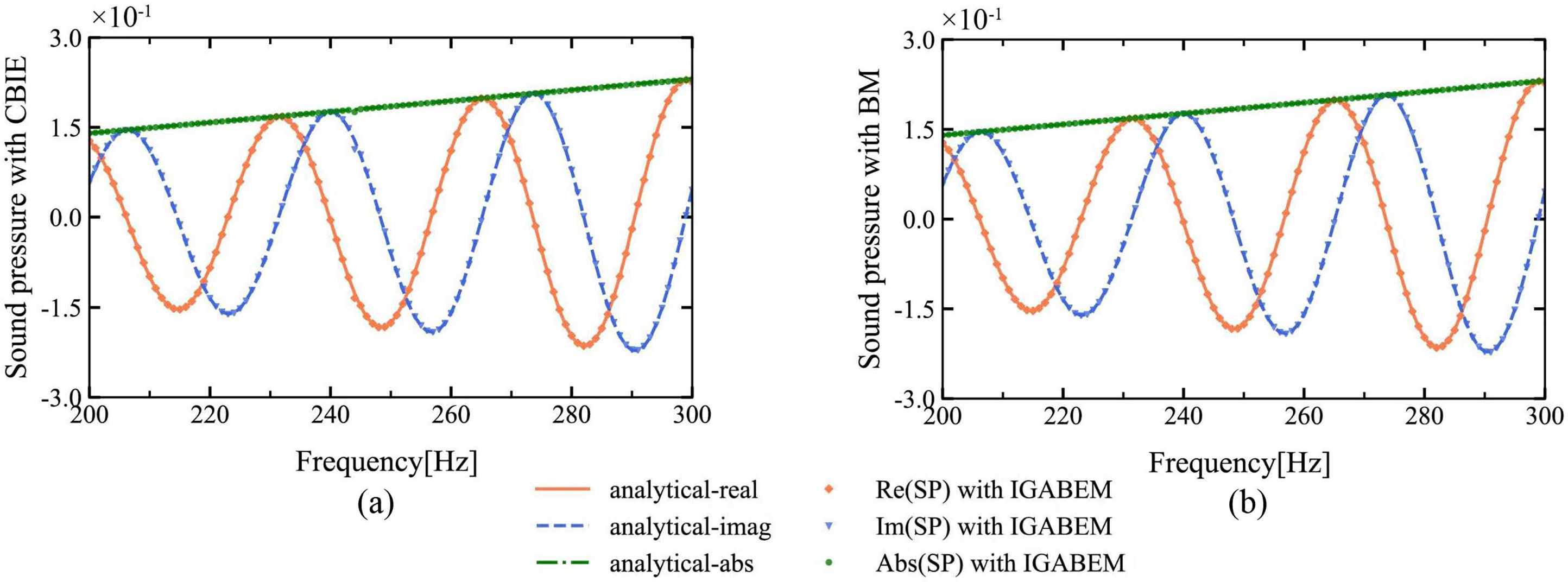
Figure 3: (a) Sound pressure with CBIE; (b) Sound pressure with BM

To directly confirm if the algorithm is accurate, we investigated the amplitude, real and imaginary distributions of the sound pressure on the limiting smooth surface of the sphere model at incident frequencies of 100, 200, and 300 Hz, as shown in Fig. 4. From the figure, it can be noticed that the amplitude part, real part, and imaginary part of the acoustics pressure also show good symmetry, and the higher the incident frequency of the incident wave, the more complex the distribution of the field function and the larger the amplitude of the sound pressure, which depicts that the sound pressure increases as the frequency increases. In conclusion, the results confirm the precision of the proposed algorithm.

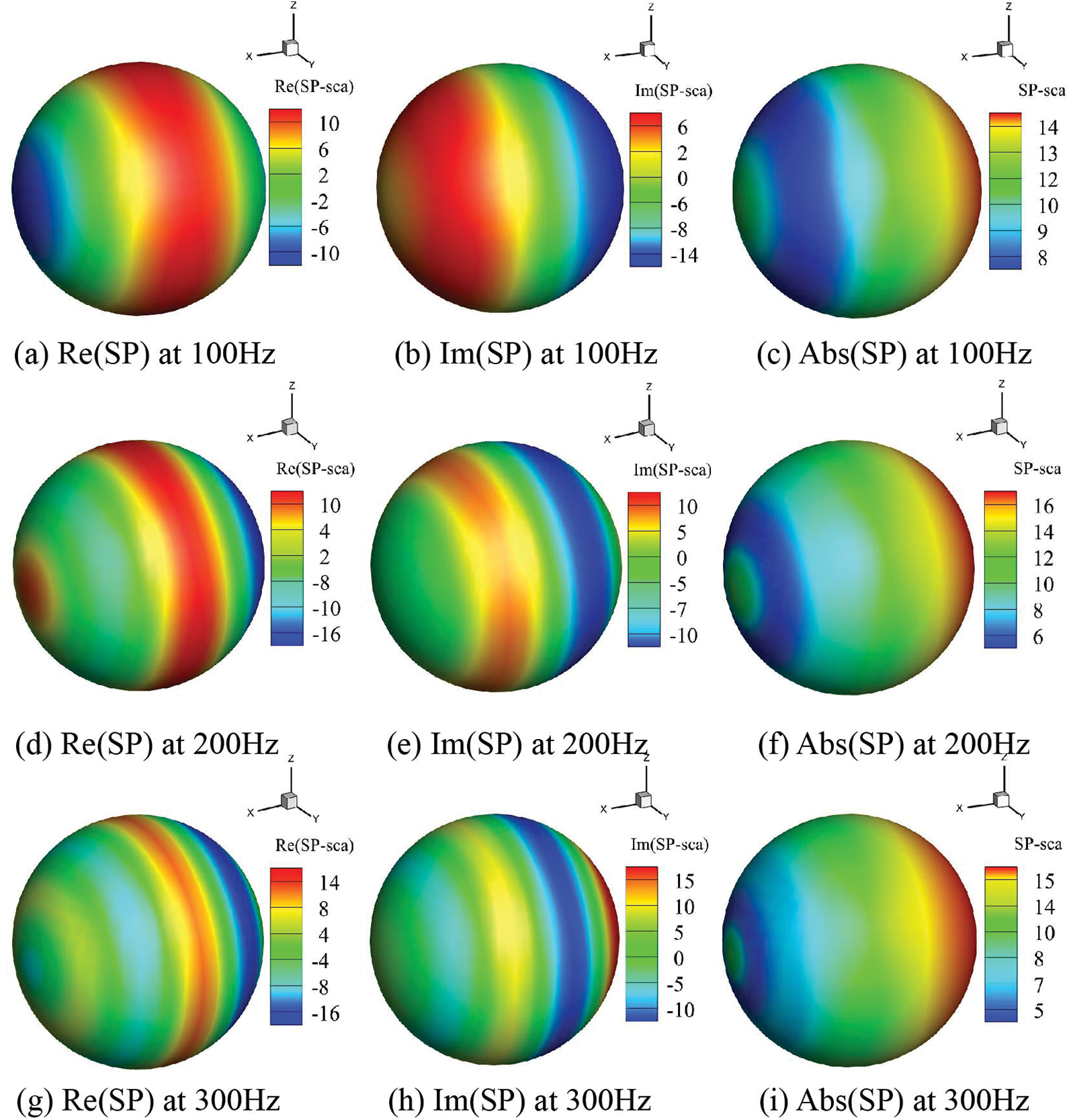
Figure 4: Sound pressure distribution on smooth surfaces in the limit of spherical models

Next, we analyze the uncertainty of the limit smooth sphere model using the generalized nth-order perturbation method. The incident frequency is defined as a random variable with a mean value μ of 1 satisfying a Gaussian distribution. Then two specific values are assigned to the coefficient of variation γ, namely 0.05 and 0.11, and the range of the associated perturbation parameter ε is taken as [0.8,1.2], the expectation and standard deviation of the 2nd, 4th, 6th, 8th, and 10th orders are investigated for different perturbation parameters ε, as depicted in Fig. 5. From the figure, it can be found that as the perturbation parameter ε increases, the expectation value and standard deviation increase, and the higher the derivative order, the more accurate the expectation value and standard deviation of the field function are, especially for larger γ. Meanwhile, when γ is larger, the advantage of higher order is more obvious.

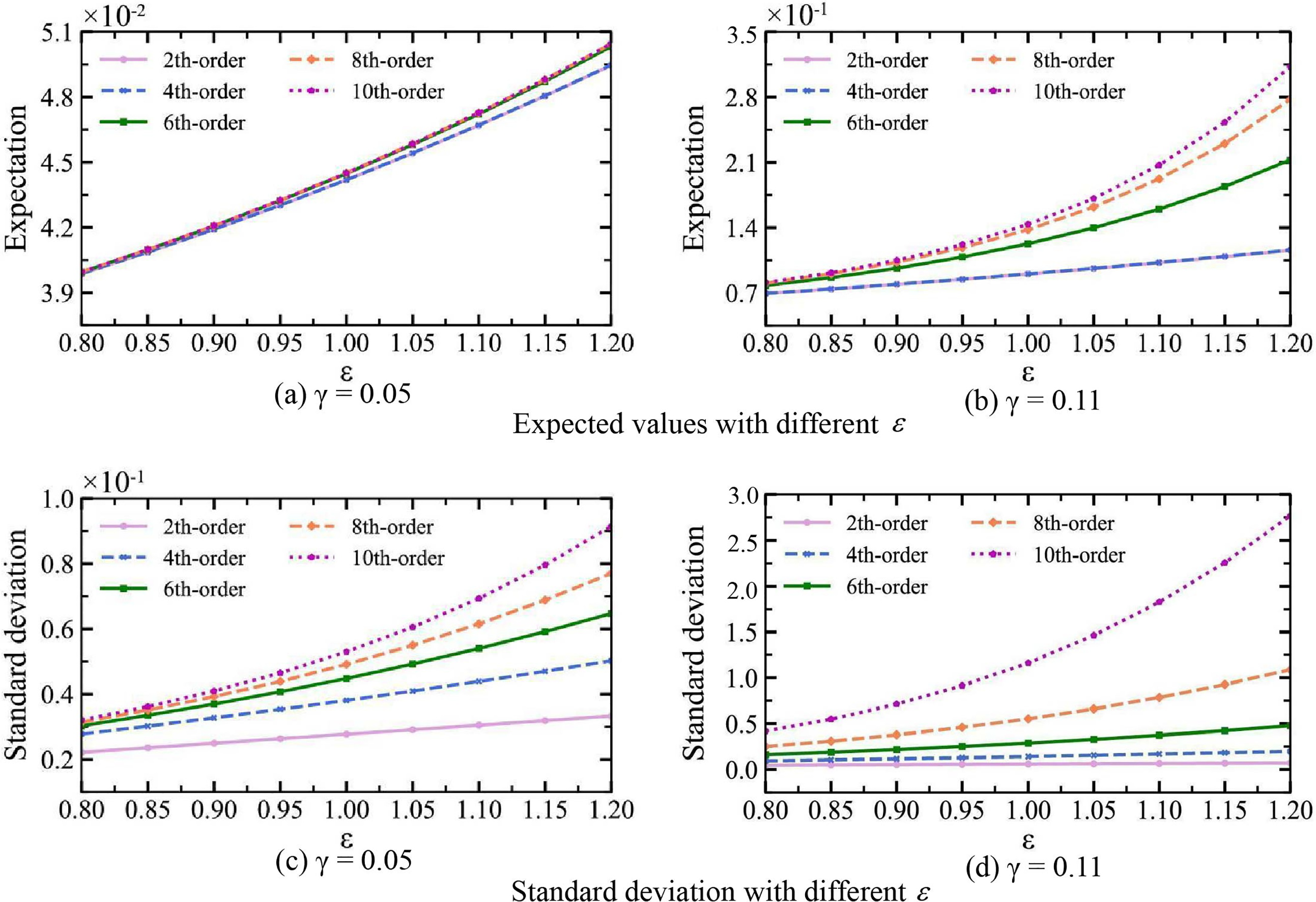
Figure 5: Expected values used 2nd, 4th, 6th, 8th, 10th orders for (a) γ = 0.05 and (b) γ = 0.11 with different ε; Standard deviation for (c) γ = 0.05 and (d) γ = 0.11 with different ε

To analyze the generalized nth-order perturbation method’s accuracy and efficacy in more detail, we investigated the expectation of the sphere model’s field function at the point (10, 10, 10) for different order expansion terms when the relevant perturbation parameter ε is 1, the mean value of the Gaussian distribution function is situated to μ = 1, and the range of intervals of the standard deviation is established as follows: σ∈[0.05,0.15], we compared it with the results under the Monte Carlo simulations, as shown in Fig. 6. MCs is a statistical method based on random sampling, in this paper, we used 500 sample points generated by a random number generator as a control group of MCs and the simulation results obtained from all the samples were statistically analyzed including the calculation of the mean and the variance in order to obtain an approximate solution to the problem. From the figure, it can be observed that as the expansion order increases, the expectation of the field function obtained by the perturbation method is closer to the value under MCs. It is evident that γ influences the perturbation method’s computational convergence, the larger the value of γ is, the smaller the convergence is. The results validate the accuracy and effectiveness of the proposed algorithm.

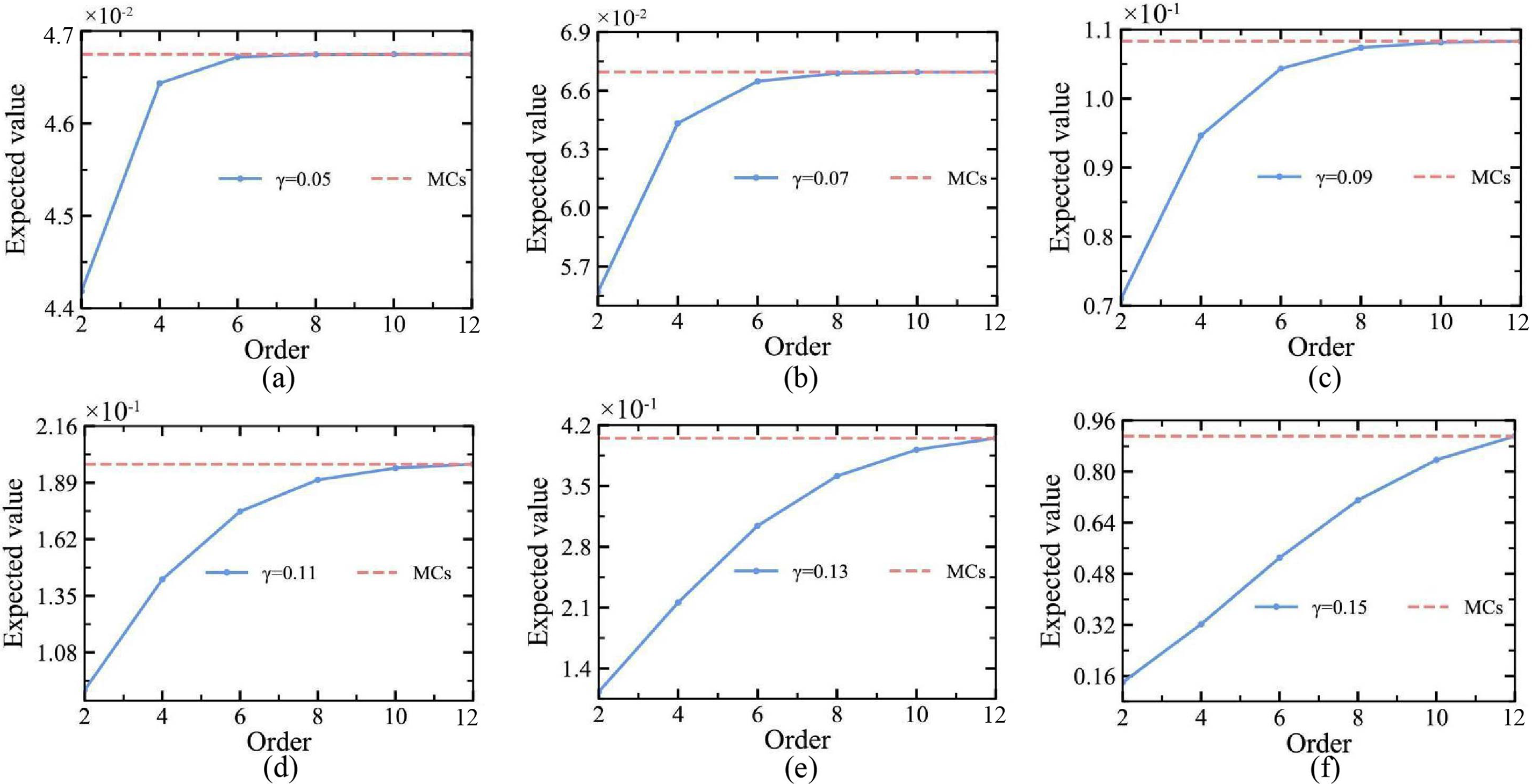
Figure 6: Expexted value results for different variation coefficients: (a) γ = 0.05; (b) γ = 0.07; (c) γ = 0.09; (d) γ = 0.11; (e) γ = 0.13; (f) γ = 0.15

4.2 Manta Ray Model

The second numerical example model is a manta ray model with limiting smoothness. We consider a manta ray model with Neumann boundary conditions and analyze it under the action of plane waves. The amplitude of the plane wave is ψ0 = 1 and is represented by ψinc=ψ0eikrcosθ, where the plane wave propagates along the positive x-axis in the positive direction. The isogeometric model of this manta ray consists of 11480 triangular elements, and its 3D solid model is shown in Fig. 7 below.

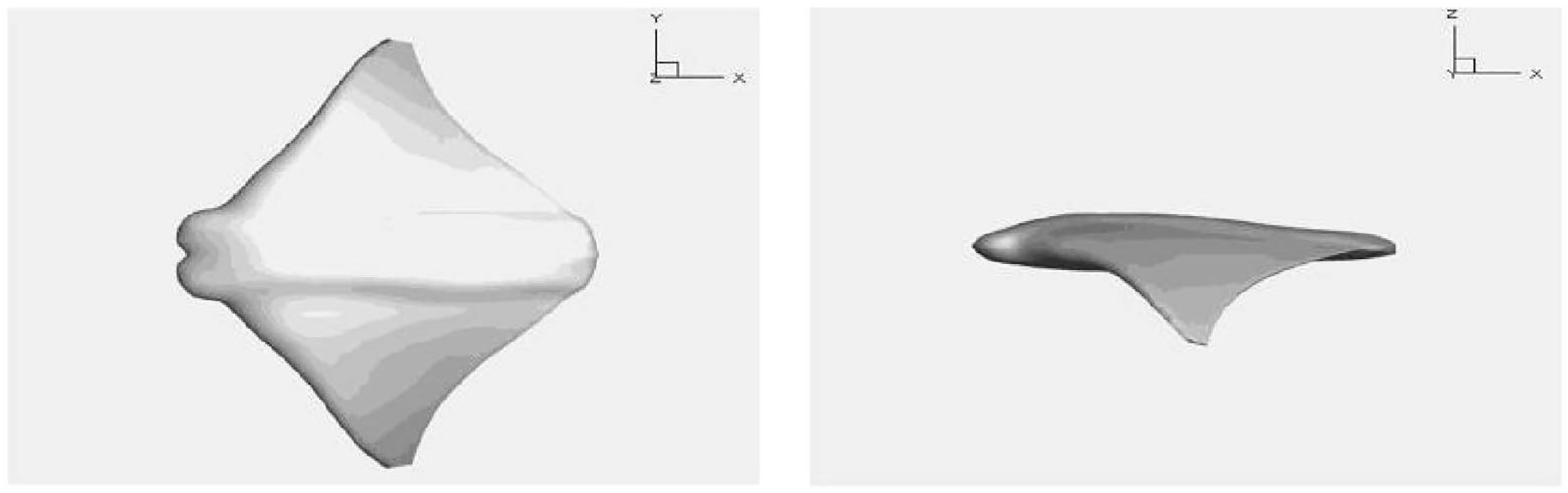
Figure 7: 3D solid modeling of the manta ray

We use the generalized nth-order perturbation method to analyze the uncertainty of the manta ray model by setting the incident frequency of the incident wave as a random variable satisfying a Gaussian distribution, with its mean μ and associated perturbation parameter ε set to 1, Fig. 8 shows the 2nd, 4th, 6th, 8th, and 10th order expectation and standard deviations computed by the perturbation method at different coefficients of variation γ, contrasted with the results of the Monte Carlo simulation. It can be noticed from the figure that as the order increases, the results acquired using the perturbation method get closer to the results under MCs, indicating that compared to lower-order procedures, higher-order methods yield more accurate results. In addition, when the coefficient of variation is [0.05,0.21], the expected value obtained using the 10th-order perturbation method is very consistent with the results under MCs. It is worth noting that the convergence of the perturbation method weakens as the coefficient of variation γ increases, which is due to the limitation of the Taylor expansion. This further validates the efficiency and accuracy of the proposed generalized nth-order perturbation method.

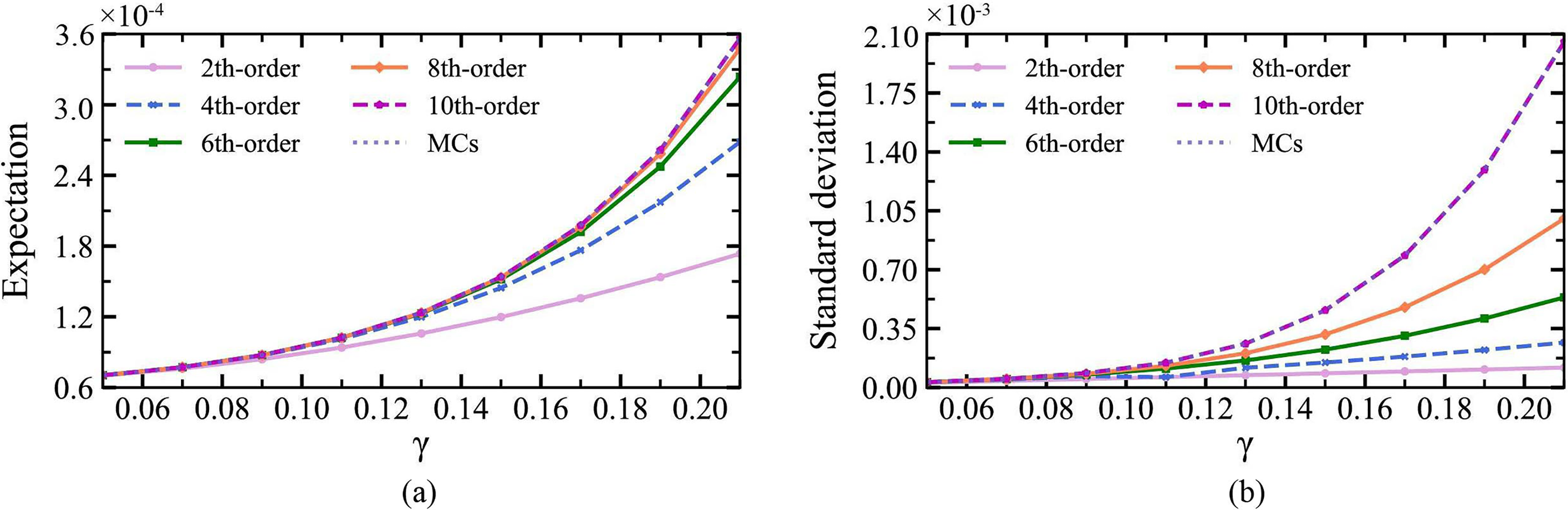
Figure 8: Expectation and standard deviation under different coefficients of variation under the perturbation method vs. results under MCs

To more naturally confirm that the method is exact, we investigated the distribution of the derivatives of the field function on the limit smooth surface of the manta ray model and analyzed the cloud distribution of the 1st–3rd order derivatives of the model’s field function when the incident frequency of incident wave at 200 Hz, as shown in Fig. 9. By analyzing the cloud graphs, we can evaluate the accuracy of the algorithm in calculating the derivatives of the field function. It can be noticed in Fig. 9 that the derivatives of the field function of the manta ray model are smooth and continuous, and the higher the derivative order, the greater the rate of change of the real and imaginary derivatives of the manta ray model field function at the same frequency. Meanwhile, the field function’s derivatives distribution shows excellent symmetry, which becomes more complicated with the increase of the derivative order. The research results confirm the correctness and effectiveness of the proposed algorithm.

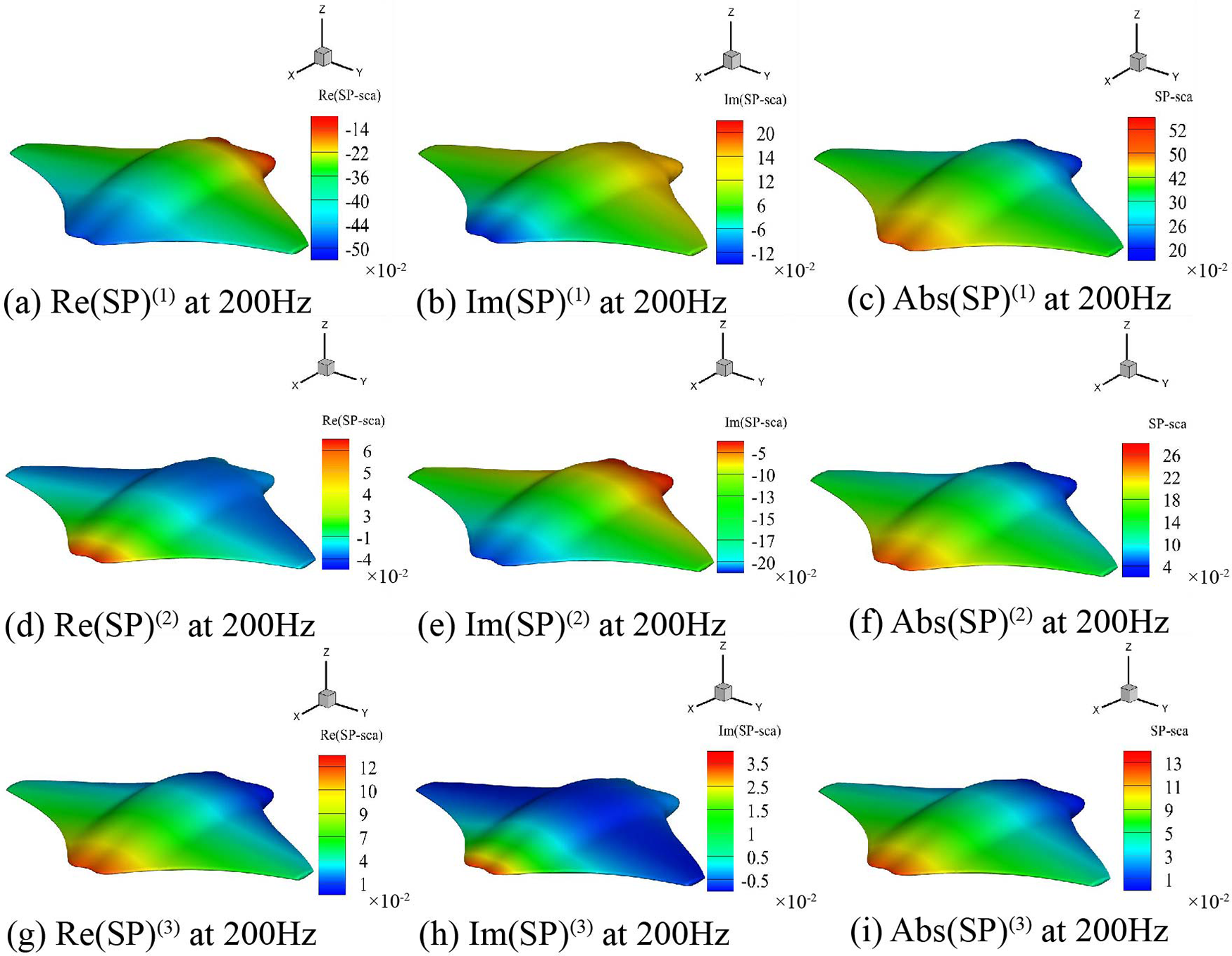
Figure 9: The 1st–3rd order derivatives of the field function of the manta ray model at an incident frequency of 200 Hz

In order to verify the reliability and applicability of the generalized nth-order perturbation method, we have conducted a study to compare the real part 1st–6th derivatives of the field function computed by the direct uncertainty analysis method (DSM) for the frequency range [200,300] with the results under the FDM, as shown in Fig. 10. In the FDM, we set different step sizes Δx of 10−1, 10−3, and 10−5. The finite difference method is a numerical computation method used to calculate the derivative of a function, which is based on the definition of the derivative and approximates the value of the derivative by computing the difference of the function at discrete points, as defined below:

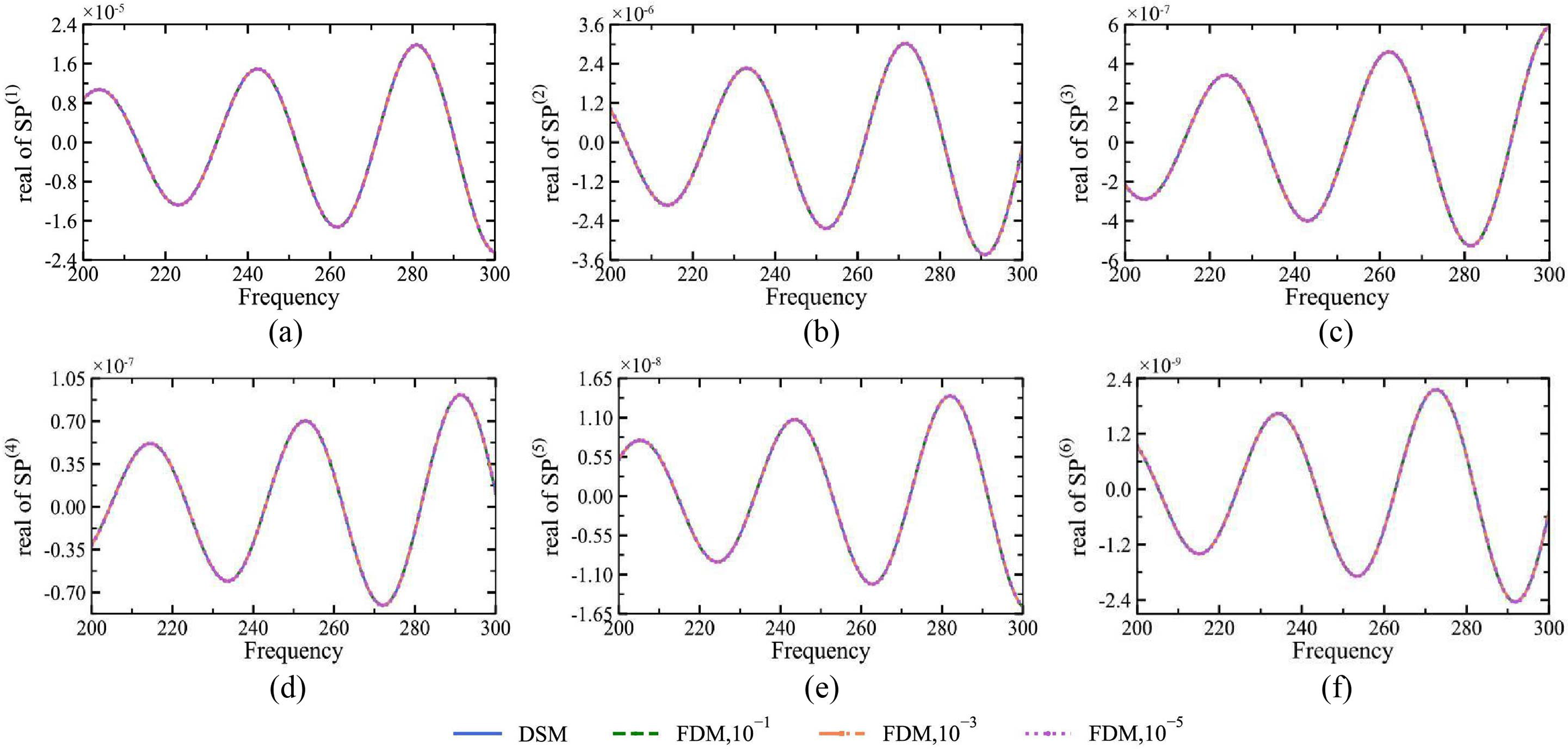
Figure 10: The 1st–6th order derivatives of the real part of the field function of the manta ray model at different frequencies

s′(x)=s(x+Δx)−s(x)Δx,(43)

where Δx indicates a small perturbation related to x.

From Fig. 10, it can be found that the results under DSM and FDM have similar numerical trend and change rule in the same position, and the value of the field function’s derivative reduces with the increase of the order under a certain frequency. Besides, the result of the derivative under DSM is very close to the result of FDM, meanwhile, these two methods remain stable throughout the whole computational region without any anomaly or divergence, which indicates that these two methods are consistent and accurate in the calculation of the derivatives. In summary, the reliability and validity of the proposed algorithm is further confirmed by comparing the derivatives of the real part of the field function computed by DSM and FDM.

To further analyze the precision of DSM and FDM, this paper compares the field function derivative error values εerr calculated by the two methods at different frequencies, with Δx set to 10−1, 10−3 and 10−5, as shown in Table 1. From the table, it is evident that the error value εerr decreases if the frequency increases. Moreover, the relative error value εerr has been kept in a small range for the field function of the manta ray model at different derivatives, and the results of the study confirm the accuracy of the proposed algorithm.

5  Conclusion

In this work, a generalized nth-order perturbation technique based on the isogeometric boundary element method is suggested for the study of uncertainty analysis of three-dimensional acoustic scattering problems. Due to the difficulty of surface slicing and splicing in the NURBS modeling process, this paper adopted the Loop subdivision surface to construct the geometric model and used the same spline function to discretize the boundary integral equations formed by the Helmholtz equations, which greatly overcomes the discontinuities and low-accuracy problems of the traditional Lagrangian function approximation of the geometric model and the interpolation of the physical field calculations. Meanwhile, we introduced the theoretical basis of the perturbation method in detail, set the incident frequency of the incident wave as the random variable that satisfies the Gaussian distribution when performing the uncertainty analysis of the three-dimensional acoustic scattering problem, and verified the precision and efficiency of the algorithm by comparing and analyzing the computed results with those under MCs through two numerical examples. In this paper, we combined IGABEM with the generalized nth-order perturbation method to consider higher-order perturbation effects by generalizing the boundary integral equation to the nth-order, and subsequently, the response of the scatterer to the incident wave is evaluated and analyzed quantitatively based on the acoustic field distribution at the surface of the scatterer obtained by the solution. Current methods have limitations in dealing with input random variables with large variability. The generalized nth-order perturbation method approximates the problem by truncating the level expansion, however, the computational complexity increases as the order increases, which makes it hard to effectively capture the statistical properties of the response function. Although expanding the Taylor expansion of the expansion term can boost computational precision, achieving this also raises computational costs. The perturbation method uses perturbation parameter expansion and approximation of the analytical solution to solve differential equations, but for highly nonlinear problems, the perturbation parameter expansion may no longer be valid, which leads to a decrease in the accuracy of the approximate solution. However, the homotopy perturbation method can handle nonlinear problems and complex boundary conditions more flexibly with higher accuracy and lower computational cost. Therefore, in future research, we can adopt the homotopy perturbation method to study complex large-scale problems and we will focus on developing an uncertainty analysis method that can effectively handle large coefficients of variation to solve this problem.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: This paper was sponsored by the Graduate Student Research and Innovation Fund of Xinyang Normal University under No. 2024KYJJ012.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Ruijin Huo, Xiaohui Yuan; data collection: Ruijin Huo; analysis and interpretation of results: Ruijin Huo, Qiangxiang Pei, Xiaohui Yuan; draft manuscript preparation: Ruijin Huo, Yanming Xu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: None.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Chen, L., Lian, H., Xu, Y., Li, S., Liu, Z. et al. (2023). Generalized isogeometric boundary element method for uncertainty analysis of time-harmonic wave propagation in infinite domains. Applied Mathematical Modelling, 114, 360–378. https://doi.org/10.1016/j.apm.2022.09.030 [Google Scholar] [CrossRef]

2. Lian, H., Chen, L., Lin, X., Zhao, W., Bordas, S. P. A. et al. (2022). Noise pollution reduction through a novel optimization procedure in passive control methods. Computer Modeling in Engineering & Sciences, 131(1), 1–18. http://dx.doi.org/10.32604/cmes.2022.019705 [Google Scholar] [CrossRef]

3. Riaz, M., Hashmi, M. R., Pamucar, D., Chu, Y. (2021). Spherical linear diophantine fuzzy sets with modeling uncertainties in MCDM. Computer Modeling in Engineering & Sciences, 126(3), 1125–1164. https://doi.org/10.32604/cmes.2021.013699 [Google Scholar] [CrossRef]

4. Cao, G., Yu, B., Chen, L., Yao, W. (2023). Isogeometric dual reciprocity BEM for solving non-fourier transient heat transfer problems in FGMs with uncertainty analysis. International Journal of Heat and Mass Transfer, 203, 123783. https://doi.org/10.1016/j.ijheatmasstransfer.2022.123783 [Google Scholar] [CrossRef]

5. Ryba, T., Rucki, M., Siemiatkowski, Z., Bzinkowski, D., Solecki, M. (2022). Design and calibration of the system supervising belt tension and wear in an industrial feeder. Facta Universitatis, Series: Mechanical Engineering, 20(1), 167–176. https://doi.org/10.22190/FUME201004026R [Google Scholar] [CrossRef]

6. Le Maître, O., Knio, O. M. (2010). Spectral methods for uncertainty quantification: with applications to computational fluid dynamics. New York: Springer Science & Business Media. [Google Scholar]

7. Abdulle, A., Pavliotis, G. A., Vaes, U. (2016). Spectral methods for multiscale stochastic differential equations. SIAM/ASA Journal on Uncertainty Quantification, 5, 720–761. [Google Scholar]

8. Shen, X., Du, C., Jiang, S., Zhang, P., Chen, L. (2024). Multivariate uncertainty analysis of fracture problems through model order reduction accelerated sbfem. Applied Mathematical Modelling, 125, 218–240. https://doi.org/10.1016/j.apm.2023.08.040 [Google Scholar] [CrossRef]

9. Shen, X., Du, C., Jiang, S., Sun, L., Chen, L. (2023). Enhancing deep neural networks for multivariate uncertainty analysis of cracked structures by POD-RBF. Theoretical and Applied Fracture Mechanics, 125, 103925. https://doi.org/10.1016/j.tafmec.2023.103925 [Google Scholar] [CrossRef]

10. Binder, K. (2022). Monte carlo simulations in statistical physics. In: Statistical and nonlinear physics, pp. 85–97. New York, NY: Springer. [Google Scholar]

11. Xu, Y., Li, H., Chen, L., Zhao, J., Zhang, X. (2022). Monte carlo based isogeometric stochastic finite element method for uncertainty quantization in vibration analysis of piezoelectric materials. Mathematics, 10(11), 1840. https://doi.org/10.3390/math10111840 [Google Scholar] [CrossRef]

12. Lagerstrom, P. A., Casten, R. (1972). Basic concepts underlying singular perturbation techniques. SIAM Review, 14(1), 63–120. https://doi.org/10.1137/1014002 [Google Scholar] [CrossRef]

13. Kokotović, P. V. (1984). Applications of singular perturbation techniques to control problems. SIAM Review, 26(4), 501–550. https://doi.org/10.1137/1026104 [Google Scholar] [CrossRef]

14. Kamiński, M. (2002). Stochastic perturbation approach to engineering structure vibrations by the finite difference method. Journal of Sound and Vibration, 251, 651–670. https://doi.org/10.1006/jsvi.2001.3850 [Google Scholar] [CrossRef]

15. Kamiński, M. (2006). On generalized stochastic perturbation-based finite elements. Communications in Numerical Methods in Engineering, 22(1), 23–31. https://doi.org/10.1002/cnm.v22:1 [Google Scholar] [CrossRef]

16. Chen, L., Cheng, R., Li, S., Lian, H., Zheng, C. et al. (2022). A sample-efficient deep learning method for multivariate uncertainty qualification of acoustic-vibration interaction problems. Computer Methods in Applied Mechanics and Engineering, 393, 114784. https://doi.org/10.1016/j.cma.2022.114784 [Google Scholar] [CrossRef]

17. Liu, K., Li, P., Wang, Z. (2021). Statistical modeling of random hail impact. Extreme Mechanics Letters, 48, 101374. https://doi.org/10.1016/j.eml.2021.101374 [Google Scholar] [CrossRef]

18. Chen, L., Lian, H., Natarajan, S., Zhao, W., Chen, X. et al. (2022). Multi-frequency acoustic topology optimization of sound-absorption materials with isogeometric boundary element methods accelerated by frequency-decoupling and model order reduction techniques. Computer Methods in Applied Mechanics and Engineering, 395, 114997. https://doi.org/10.1016/j.cma.2022.114997 [Google Scholar] [CrossRef]

19. Couto, P. R. G., Damasceno, J. C., Oliveira, S. D., Chan, W. (2013). Monte carlo simulations applied to uncertainty in measurement. Theory and Applications of Monte Carlo Simulations, 2, 27–51. [Google Scholar]

20. Kamiński, M. (2007). Application of the generalized perturbation-based stochastic boundary element method to the elastostatics. Engineering Analysis with Boundary Elements, 31(6), 514–527. https://doi.org/10.1016/j.enganabound.2006.10.005 [Google Scholar] [CrossRef]

21. Ding, C., Cui, X., Deokar, R. R., Li, G., Cai, Y. et al. (2018). Modeling and simulation of steady heat transfer analysis with material uncertainty: Generalized n th order perturbation isogeometric stochastic method. Numerical Heat Transfer, Part A: Applications, 74(9), 1565–1582. https://doi.org/10.1080/10407782.2018.1538296 [Google Scholar] [CrossRef]

22. Kamiński, M. (2010). Generalized stochastic perturbation technique in engineering computations. Mathematical and Computer Modelling, 51(3–4), 272–285. [Google Scholar]

23. Zhang, N., Yao, L., Jiang, G. (2020). A coupled finite element-least squares point interpolation/boundary element method for structure-acoustic system with stochastic perturbation method. Engineering Analysis with Boundary Elements, 119, 83–94. https://doi.org/10.1016/j.enganabound.2020.07.010 [Google Scholar] [CrossRef]

24. Hu, X., Cui, X., Feng, H., Li, G. (2016). Stochastic analysis using the generalized perturbation stable node-based smoothed finite element method. Engineering Analysis with Boundary Elements, 70, 40–55. https://doi.org/10.1016/j.enganabound.2016.06.002 [Google Scholar] [CrossRef]

25. Long, X., Jiang, C., Yang, C., Han, X., Gao, W. et al. (2016). A stochastic scaled boundary finite element method. Computer Methods in Applied Mechanics and Engineering, 308, 23–46. https://doi.org/10.1016/j.cma.2016.04.037 [Google Scholar] [CrossRef]

26. Liu, Z., Bian, P. L., Qu, Y., Huang, W., Chen, L. et al. (2024). A galerkin approach for analysing coupling effects in the piezoelectric semiconducting beams. European Journal of Mechanics–A/Solids, 103, 105145. https://doi.org/10.1016/j.euromechsol.2023.105145 [Google Scholar] [CrossRef]

27. Hughes, T. J., Cottrell, J. A., Bazilevs, Y. (2005). Isogeometric analysis: Cad, finite elements, nurbs, exact geometry and mesh refinement. Computer Methods in Applied Mechanics and Engineering, 194(39–41), 4135–4195. [Google Scholar]

28. Xue, Y., Jin, G., Ye, T., Shi, K., Zhong, S. et al. (2020). Isogeometric analysis for geometric modelling and acoustic attenuation performances of reactive mufflers. Computers & Mathematics with Applications, 79(12), 3447–3461. https://doi.org/10.1016/j.camwa.2020.02.004 [Google Scholar] [CrossRef]

29. Chen, L., Lu, C., Zhao, W., Chen, H., Zheng, C. (2020). Subdivision surfaces-boundary element accelerated by fast multipole for the structural acoustic problem. Journal of Theoretical and Computational Acoustics, 28(2), 2050011. https://doi.org/10.1142/S2591728520500115 [Google Scholar] [CrossRef]

30. Qu, Y., Pan, E., Zhu, F., Jin, F., Roy, A. K. (2023). Modeling thermoelectric effects in piezoelectric semiconductors: New fully coupled mechanisms for mechanically manipulated heat flux and refrigeration. International Journal of Engineering Science, 182, 103775. https://doi.org/10.1016/j.ijengsci.2022.103775 [Google Scholar] [CrossRef]

31. Audoux, Y., Montemurro, M., Pailhes, J. (2018). A surrogate model based on non-uniform rational b-splines hypersurfaces. Procedia CIRP, 70, 463–468. https://doi.org/10.1016/j.procir.2018.03.234 [Google Scholar] [CrossRef]

32. Simpson, R. N., Liu, Z., Vazquez, R., Evans, J. A. (2018). An isogeometric boundary element method for electromagnetic scattering with compatible b-spline discretizations. Journal of Computational Physics, 362, 264–289. https://doi.org/10.1016/j.jcp.2018.01.025 [Google Scholar] [CrossRef]

33. Rahmouni, F., Elajrami, M., Madani, K., Campilho, R. (2022). Isogeometric analysis based on non-uniform rational b-splines technology of stress and failure strength in inter-ply hybrid laminated composite. Journal of Composite Materials, 56(18), 2921–2932. https://doi.org/10.1177/00219983221105313 [Google Scholar] [CrossRef]

34. Bazilevs, Y., Calo, V. M., Cottrell, J. A., Evans, J. A., Hughes, T. J. R. et al. (2010). Isogeometric analysis using t-splines. Computer Methods in Applied Mechanics and Engineering, 199(5–8), 229–263. [Google Scholar]

35. Uhm, T. K., Youn, S. K. (2009). T-spline finite element method for the analysis of shell structures. International Journal for Numerical Methods in Engineering, 80(4), 507–536. https://doi.org/10.1002/nme.v80:4 [Google Scholar] [CrossRef]

36. Ginnis, A. I., Kostas, K. V., Politis, C. G., Kaklis, P. D., Belibassakis, K. A. et al. (2014). Isogeometric boundary-element analysis for the wave-resistance problem using t-splines. Computer Methods in Applied Mechanics and Engineering, 279, 425–439. https://doi.org/10.1016/j.cma.2014.07.001 [Google Scholar] [CrossRef]

37. Yang, J., Zhao, G., Wang, W., Du, X., Guo, M. et al. (2022). Surface blending using t-splines in semi-nurbs form. Computer Aided Design, 146, 103210. https://doi.org/10.1016/j.cad.2022.103210 [Google Scholar] [CrossRef]

38. Qu, Y., Zhu, F., Pan, E., Jin, F., Hirakata, H. (2023). Analysis of wave-particle drag effect in flexoelectric semiconductor plates via mindlin method. Applied Mathematical Modelling, 118, 541–555. https://doi.org/10.1016/j.apm.2023.01.040 [Google Scholar] [CrossRef]

39. Catmull, E. E., Clark, J. (1978). Recursively generated b-spline surfaces on arbitrary topological meshes. In: Seminal graphics: Pioneering efforts that shaped the field. New York, USA: Association for Computing Machinery. [Google Scholar]

40. Loop, C. T. (1987). Smooth subdivision surfaces based on triangles (Master’s Thesis). University of Utah, Department of Mathematics. [Google Scholar]

41. Green, S., Turkiyyah, G., Storti, D. (2002). Subdivision-based multilevel methods for large scale engineering simulation of thin shells. Proceedings of the Seventh ACM Symposium on Solid Modeling and Applications, Saarbrucken, Germany. [Google Scholar]

42. Cohen, E., Lyche, T., Riesenfeld, R. (1980). Discrete b-splines and subdivision techniques in computer-aided geometric design and computer graphics. Computer Graphics and Image Processing, 14(2), 87–111. https://doi.org/10.1016/0146-664X(80)90040-4 [Google Scholar] [CrossRef]

43. Lu, C., Chen, L., Luo, J., Chen, H. (2023). Acoustic shape optimization based on isogeometric boundary element method with subdivision surfaces. Engineering Analysis with Boundary Elements, 146, 951–965. https://doi.org/10.1016/j.enganabound.2022.11.010 [Google Scholar] [CrossRef]

44. Chen, L., Lu, C., Lian, H., Liu, Z., Zhao, W. et al. (2020). Acoustic topology optimization of sound absorbing materials directly from subdivision surfaces with isogeometric boundary element methods. Computer Methods in Applied Mechanics and Engineering, 362, 112806. https://doi.org/10.1016/j.cma.2019.112806 [Google Scholar] [CrossRef]

45. Qu, Y. L., Guo, Z. W., Zhang, G. Y., Gao, X. L., Jin, F. (2022). A new model for circular cylindrical kirchhoff-love shells incorporating microstructure and flexoelectric effects. Journal of Applied Mechanics, 89(12), 121010. https://doi.org/10.1115/1.4055658 [Google Scholar] [CrossRef]

46. Cerrato, A., Rodríguez-Tembleque, L., González, J. A., Aliabadi, M. F. (2017). A coupled finite and boundary spectral element method for linear water-wave propagation problems. Applied Mathematical Modelling, 48, 1–20. https://doi.org/10.1016/j.apm.2017.03.061 [Google Scholar] [CrossRef]

47. Sumbatyan, M., Martynova, T., Musatova, N. (2021). Boundary element methods in diffraction of a point-source acoustic wave by a rigid infinite wedge. Engineering Analysis with Boundary Elements, 125, 157–167. https://doi.org/10.1016/j.enganabound.2021.01.017 [Google Scholar] [CrossRef]

48. Tadeu, A. J., António, J. M., Kausel, E. (2002). 3D scattering of waves by a cylindrical irregular cavity of infinite length in a homogeneous elastic medium. Computer Methods in Applied Mechanics and Engineering, 191(27–28), 3015–3033. [Google Scholar]

49. Schanz, M. (2001). Application of 3D time domain boundary element formulation to wave propagation in poroelastic solids. Engineering Analysis with Boundary Elements, 24(4/5), 363–376. [Google Scholar]

50. Chen, L., Wang, Z., Lian, H., Ma, Y., Meng, Z. et al. (2024). Reduced order isogeometric boundary element methods for cad-integrated shape optimization in electromagnetic scattering. Computer Methods in Applied Mechanics and Engineering, 419, 116654. https://doi.org/10.1016/j.cma.2023.116654 [Google Scholar] [CrossRef]

51. Liu, Y. (2019). On the bem for acoustic wave problems. Engineering Analysis with Boundary Elements, 107, 53–62. https://doi.org/10.1016/j.enganabound.2019.07.002 [Google Scholar] [CrossRef]

52. Ji, Z. L., Ma, Q., Zhang, Z. H. (1994). Application of the boundary element method to predicting acoustic performance of expansion chamber mufflers with mean flow. Journal of Sound and Vibration, 173(1), 57–71. https://doi.org/10.1006/jsvi.1994.1217 [Google Scholar] [CrossRef]

53. Jiang, F., Zhao, W., Chen, L., Zheng, C., Chen, H. (2021). Combined shape and topology optimization for sound barrier by using the isogeometric boundary element method. Engineering Analysis with Boundary Elements, 124, 124–136. https://doi.org/10.1016/j.enganabound.2020.12.009 [Google Scholar] [CrossRef]

54. Zhang, S., Yu, B., Chen, L. (2024). Non-iterative reconstruction of time-domain sound pressure and rapid prediction of large-scale sound field based on IG-DRBEM and POD-RBF. Journal of Sound and Vibration, 573, 118226. https://doi.org/10.1016/j.jsv.2023.118226 [Google Scholar] [CrossRef]

55. Fu, Z. J., Chen, W., Gu, Y. (2014). Burton–miller-type singular boundary method for acoustic radiation and scattering. Journal of Sound and Vibration, 333(16), 3776–3793. https://doi.org/10.1016/j.jsv.2014.04.025 [Google Scholar] [CrossRef]

56. Chen, L., Li, H., Guo, Y., Chen, P., Atroshchenko, E. et al. (2023). Uncertainty quantification of mechanical property of piezoelectric materials based on isogeometric stochastic fem with generalized nth-order perturbation. Engineering with Computers, 83, 1–21. [Google Scholar]

57. Schanz, M. (2018). Fast multipole method for poroelastodynamics. Engineering Analysis with Boundary Elements, 89, 50–59. https://doi.org/10.1016/j.enganabound.2018.01.014 [Google Scholar] [CrossRef]

58. Abduljabbar, M., Farhan, M. A., Al Harthi, N., Chen, R., Yokota, R. et al. (2019). Extreme scale fmm-accelerated boundary integral equation solver for wave scattering. SIAM Journal on Scientific Computing, 41(3), C245–C268. [Google Scholar]

59. Zhao, K., Vouvakis, M. N., Lee, J. F. (2005). The adaptive cross approximation algorithm for accelerated method of moments computations of emc problems. IEEE Transactions on Electromagnetic Compatibility, 47(4), 763–773. https://doi.org/10.1109/TEMC.2005.857898 [Google Scholar] [CrossRef]

60. Kurz, S., Rain, O., Rjasanow, S. (2002). The adaptive cross-approximation technique for the 3D boundary-element method. IEEE Transactions on Magnetics, 38(2), 421–424. https://doi.org/10.1109/20.996112 [Google Scholar] [CrossRef]

61. Marussig, B., Zechner, J., Beer, G., Fries, T. P. (2015). Fast isogeometric boundary element method based on independent field approximation. Computer Methods in Applied Mechanics and Engineering, 284, 458–488. https://doi.org/10.1016/j.cma.2014.09.035 [Google Scholar] [CrossRef]

62. Zhou, W., Liu, B., Wang, Q., Cheng, Y., Ma, G. et al. (2017). Nurbs-enhanced boundary element method based on independent geometry and field approximation for 2D potential problems. Engineering Analysis with Boundary Elements, 83, 158–166. https://doi.org/10.1016/j.enganabound.2017.07.013 [Google Scholar] [CrossRef]

63. Venås, J. V., Kvamsdal, T. (2020). Isogeometric boundary element method for acoustic scattering by a submarine. Computer Methods in Applied Mechanics and Engineering, 359, 112670. https://doi.org/10.1016/j.cma.2019.112670 [Google Scholar] [CrossRef]

64. Chen, L., Zhang, Y., Lian, H., Atroshchenko, E., Ding, C. et al. (2020). Seamless integration of computer-aided geometric modeling and acoustic simulation: Isogeometric boundary element methods based on catmull-clark subdivision surfaces. Advances in Engineering Software, 149, 102879. https://doi.org/10.1016/j.advengsoft.2020.102879 [Google Scholar] [CrossRef]

65. Wu, Y., Dong, C., Yang, H. (2020). Isogeometric indirect boundary element method for solving the 3D acoustic problems. Journal of Computational and Applied Mathematics, 363, 273–299. https://doi.org/10.1016/j.cam.2019.06.013 [Google Scholar] [CrossRef]

66. Takahashi, T., Matsumoto, T. (2012). An application of fast multipole method to isogeometric boundary element method for laplace equation in two dimensions. Engineering Analysis with Boundary Elements, 36(12), 1766–1775. https://doi.org/10.1016/j.enganabound.2012.06.004 [Google Scholar] [CrossRef]

67. Gong, Y., Dong, C. (2017). An isogeometric boundary element method using adaptive integral method for 3D potential problems. Journal of Computational and Applied Mathematics, 319, 141–158. https://doi.org/10.1016/j.cam.2016.12.038 [Google Scholar] [CrossRef]

68. Chen, L., Li, K., Peng, X., Lian, H., Lin, X. et al. (2021). Isogeometric boundary element analysis for 2D transient heat conduction problem with radial integration method. Computer Modeling in Engineering & Sciences, 126(1), 107–119. https://doi.org/10.32604/cmes.2021.012821 [Google Scholar] [CrossRef]

69. Li, H., Chen, L., Zhi, G., Meng, L., Lian, H. et al. (2024). A direct FE2 method for concurrent multilevel modeling of piezoelectric materials and structures. Computer Methods in Applied Mechanics and Engineering, 420, 116696. https://doi.org/10.1016/j.cma.2023.116696 [Google Scholar] [CrossRef]

70. Qu, Y., Jin, F., Yang, J. (2022). Buckling of a reissner–mindlin plate of piezoelectric semiconductors. Meccanica, 57(11), 2797–2807. https://doi.org/10.1007/s11012-022-01598-2 [Google Scholar] [CrossRef]

71. Taus, M., Rodin, G. J., Hughes, T. J., Scott, M. A. (2019). Isogeometric boundary element methods and patch tests for linear elastic problems: Formulation, numerical integration, and applications. Computer Methods in Applied Mechanics and Engineering, 357, 112591. https://doi.org/10.1016/j.cma.2019.112591 [Google Scholar] [CrossRef]

72. Chen, H., Yu, B., Liu, Z., Zhou, H. (2023). A non-iterative methodology to reconstruct boundary shapes and conditions in isotropic linear elasticity based on the BEM. Engineering Analysis with Boundary Elements, 153, 12–24. https://doi.org/10.1016/j.enganabound.2023.05.019 [Google Scholar] [CrossRef]

73. Ghosh, N., Mukherjee, S. (1987). A new boundary element method formulation for three dimensional problems in linear elasticity. Acta Mechanica, 67(1–4), 107–119. [Google Scholar]

74. Lian, H., Kerfriden, P., Bordas, S. (2016). Implementation of regularized isogeometric boundary element methods for gradient-based shape optimization in two-dimensional linear elasticity. International Journal for Numerical Methods in Engineering, 106(12), 972–1017. https://doi.org/10.1002/nme.v106.12 [Google Scholar] [CrossRef]

75. Yu, B., Cao, G., Ren, S., Gong, Y., Dong, C. (2022). An isogeometric boundary element method for transient heat transfer problems in inhomogeneous materials and the non-iterative inversion of loads. Applied Thermal Engineering, 212, 118600. https://doi.org/10.1016/j.applthermaleng.2022.118600 [Google Scholar] [CrossRef]

76. Chen, L., Lian, H., Liu, Z., Chen, H. B., Atroshchenko, E. et al. (2019). Structural shape optimization of three dimensional acoustic problems with isogeometric boundary element methods. Computer Methods in Applied Mechanics and Engineering, 355, 926–951. https://doi.org/10.1016/j.cma.2019.06.012 [Google Scholar] [CrossRef]

77. Chen, L., Zhao, J., Lian, H., Yu, B., Atroshchenko, E. et al. (2023). A bem broadband topology optimization strategy based on taylor expansion and soar method-application to 2D acoustic scattering problems. International Journal for Numerical Methods in Engineering, 124(23), 5151–5182. https://doi.org/10.1002/nme.v124.23 [Google Scholar] [CrossRef]

78. Chen, L., Liu, C., Zhao, W., Liu, L. (2018). An isogeometric approach of two dimensional acoustic design sensitivity analysis and topology optimization analysis for absorbing material distribution. Computer Methods in Applied Mechanics and Engineering, 336, 507–532. https://doi.org/10.1016/j.cma.2018.03.025 [Google Scholar] [CrossRef]

79. Chen, L., Lian, H., Liu, Z., Gong, Y., Zheng, C. et al. (2022). Bi-material topology optimization for fully coupled structural-acoustic systems with isogeometric FEM-BEM. Engineering Analysis with Boundary Elements, 135, 182–195. https://doi.org/10.1016/j.enganabound.2021.11.005 [Google Scholar] [CrossRef]

80. Bendat, J. S., Piersol, A. G. (1987). Random data: Analysis and measurement procedures. https://books.google.fr/books?id=qYSViFRNMlwC (accessed on 27/10/2023). [Google Scholar]

81. Cheng, S., Wang, F., Li, P. -W., Qu, W. (2022). Singular boundary method for 2D and 3D acoustic design sensitivity analysisimage 1. Computers & Mathematics with Applications, 119, 371–386. https://doi.org/10.1016/j.camwa.2022.06.009 [Google Scholar] [CrossRef]

82. Liu, H., Wang, F. (2024). A novel semi-analytical meshless method for the thickness optimization of porous material distributed on sound barriers. Applied Mathematics Letters, 147, 108844. https://doi.org/10.1016/j.aml.2023.108844 [Google Scholar] [CrossRef]

83. Han, Z., Pan, W., Cheng, C., Hu, Z., Niu, Z. (2022). A semi-analytical treatment for nearly singular integrals arising in the isogeometric boundary element method-based solutions of 3D potential problems. Computer Methods in Applied Mechanics and Engineering, 398, 115179. https://doi.org/10.1016/j.cma.2022.115179 [Google Scholar] [CrossRef]