 Open Access
Open Access
ARTICLE
Dynamic Characteristics of Functionally Graded Timoshenko Beams by Improved Differential Quadrature Method
1 School of Architecture and Civil Engineering, Anhui Polytechnic University, Wuhu, 241000, China
2 College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing, 210098, China
* Corresponding Author: Liaojun Zhang. Email:
(This article belongs to the Special Issue: Recent Advances in Computational Methods for Performance Assessment of Engineering Structures and Materials against Dynamic Loadings)
Computer Modeling in Engineering & Sciences 2024, 140(2), 1647-1668. https://doi.org/10.32604/cmes.2024.049124
Received 28 December 2023; Accepted 06 March 2024; Issue published 20 May 2024
Abstract
This study proposes an effective method to enhance the accuracy of the Differential Quadrature Method (DQM) for calculating the dynamic characteristics of functionally graded beams by improving the form of discrete node distribution. Firstly, based on the first-order shear deformation theory, the governing equation of free vibration of a functionally graded beam is transformed into the eigenvalue problem of ordinary differential equations with respect to beam axial displacement, transverse displacement, and cross-sectional rotation angle by considering the effects of shear deformation and rotational inertia of the beam cross-section. Then, ignoring the shear deformation of the beam section and only considering the effect of the rotational inertia of the section, the governing equation of the beam is transformed into the eigenvalue problem of ordinary differential equations with respect to beam transverse displacement. Based on the differential quadrature method theory, the eigenvalue problem of ordinary differential equations is transformed into the eigenvalue problem of standard generalized algebraic equations. Finally, the first several natural frequencies of the beam can be calculated. The feasibility and accuracy of the improved DQM are verified using the finite element method (FEM) and combined with the results of relevant literature.Keywords
Functionally graded materials (FGMs) are a new kind of material whose physical properties gradually change in one or more directions. This continuity of material properties overcomes many shortcomings of bonded materials. After several years of development, the application of functionally graded materials has expanded from the initial aeronautical field to the engineering field, such as nuclear power engineering, civil engineering, and others. The dynamic characteristics of functionally graded beams have always concerned scholars. Generally, establishing physical models that accurately reflect the laws of mechanics and the solution of corresponding mathematical equations are two critical steps in analyzing engineering structures. Due to the nonlinearity of the material properties of functionally graded beams, it is difficult to obtain analytical solutions for the dynamic governing equations of such structures. Therefore, numerical methods have become commonly used for solving mathematical equations.
Many studies have been devoted to the dynamic characteristics of functionally graded beams. Kirlangic et al. [1] studied the dynamic characteristics of composite and functionally graded beams using the Ritz and Newmark average acceleration methods. Shang Hsu [2] presented a free vibration analysis of Timoshenko beam models using enriched finite element approaches. A two-node element was suggested by Moallemi-Oreh et al. [3] to analyze the stability and free vibration of Timoshenko beams. Tests showed high accuracy of the element in analyzing beams’ stability and finding its critical load and free vibration analysis. Xu et al. [4] performed the free vibration analysis of Timoshenko beams with various combinations of boundary conditions by using the discrete singular convolution (DSC). For the free vibration of functionally graded beams whose physical properties changed along the axis due to the elastic modulus, shear modulus, and density of axially functionally graded materials changing continuously along the axis, the study of the free vibration of beams was complicated [5–7]. For the free vibration and stability of functionally graded beams with material properties varying along the thickness direction, Sankar [8] assumed that Young’s modulus of the beam varied exponentially through the thickness. An elasticity solution was obtained for a functionally graded beam under transverse loads. Pu et al. [9] investigated the bending characteristics of functionally graded sandwich beams using an improved Fourier method under classical and non-classical boundary conditions. By comparing the results with other numerical methods, it was verified that the formula had high convergence speed and accuracy, but the derivation of the formula was complex. Stojanovic et al. [10] investigated the stability of uniform motion of multiple oscillators along a shear deformation beam on a viscoelastic foundation. The fully stable region is determined and discussed according to the change in the number of oscillators. Stojanovic et al. [11] studied the effects of the parameters of the laminate, the damping coefficient, and the spectral density on the random stability of the composite laminate. Qian et al. [12] studied the static deformations free and forced vibrations of FGMs cantilever beam by the Meshless Local Petrov-Galerkin (MLPG) method. Xiang et al. [13] investigated the free and forced vibration of a laminated functionally graded beam of variable thickness within the framework of Timoshenko beam theory. Gao et al. [14–16] used the two-step perturbation method to solve the nonlinear vibration governing equation, and the free vibration problem of beams with different functionally graded distributions is studied. Stojanovic et al. [17] investigated the coupled vibration and stability of multiple rectangular plates; the analytical solutions for the natural frequencies and critical buckling loads of the plates were obtained. Zheng et al. [18] proposed a general two-dimensional solution for cantilever FGMs beams under the Airy stress function. Huang et al. [19,20] developed methods to solve the natural frequency and vibration modal functions of functionally graded beams using the differential quadrature method. Choe et al. [21,22] studied the free vibration characteristics of functionally graded beams with arbitrary boundary conditions using numerical and semi-analytical methods.
Based on the literature review, there have been many studies on the vibration characteristics of beams with different gradient distributions, and numerous numerical calculation methods have also been proposed. However, they all suffer from the disadvantages of complex calculation processes and difficult programming solutions. The differential quadrature method (DQM) is a widely employed numerical technique for analyzing nonlinear structures owing to its straightforward solution process, uncomplicated programming, and superior computational efficiency. The precision of the calculation results of the method mainly depends on the discrete form of the nodes. This study modifies the discrete form of the conventional differential quadrature method. A discrete form of distribution of points in a proportional series is proposed, and the step size of nodes is adjusted by changing the common ratio to control the precision of numerical calculation. Thus, the dynamic characteristics of FGMs beams along the thickness direction are investigated using the improved DQM. Firstly, based on the first-order shear deformation theory, the governing equation of transverse free vibration of a Timoshenko beam is transformed into the eigenvalue problem of ordinary differential equations. Then, the differential quadrature method is applied to transform the eigenvalue problem of the derived differential equation into the eigenvalue problem of standard generalized algebraic equations. Finally, the first several natural frequencies of transverse free vibration of the FGMs beam can be calculated by the QR method at one time. The method is verified by literature comparison and the mature numerical calculation method, which showed the applicability and high efficiency of the proposed method for solving variable differential equations.
2 Theoretical Formulations and Calculation Method
2.1 Beam Theory of Considering the Effects of Shear Deformation and Rotational Inertia of the Cross-Section
Consider a Timoshenko beam made of ceramic-metal materials in this section. The beam’s length was denoted as L, width as b, and height as h, with a rectangular coordinate system o(x,y,z) assumed such that the x-axis was considered the neutral axis of a Timoshenko beam, the positive z-axis was directed upward and perpendicular to the x-axis, and the origin was located at the centroid of the rectangular section as shown in Fig. 1.
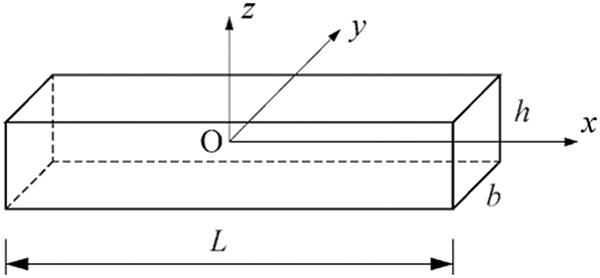
Figure 1: Schematic diagram of a beam with a gradient along the thickness direction
It was proposed that the parameters of the functionally graded materials adopt the linear mixing rate model. Hence, the elastic modulus E(z) and density ρ(z) were assumed to follow power-law functions in the thickness as Eq. (1).
{E(z)=Em+(Ec−Em)(12−zh)pρ(z)=ρm+(ρc−ρm)(12−zh)p(1)
where Ec and Em are the elastic modulus of ceramic and metal materials, respectively; ρc and ρm are the density of ceramic and metal materials, respectively; p is the volume fraction index of materials; ν is the Poisson’s ratios of ceramics and metals. Free vibration characteristics of functionally gradient beams based on first-order shear theory, the axial u and transverse displacements w at any point of a beam could be expressed as Eq. (2).
u(x,z,t)=u0(x,t)−zφ(x,t),w(x,z,t)=w0(x,t)(2)
The geometric equation is Eq. (3).
{εx(x,z,t)=du0dx−zdφdxγxz(x,z,t)=dw0dx−φ(3)
where u0 and w0 are the axial and transverse displacement at any beam point, respectively; φ is the cross-section angle; εx and γxz are the linear strains and shear strains at any point on the cross-section, respectively. Based on the basic theory of Timoshenko beams, the normal stress σx and shear stress τxz on the cross-section could be expressed as Eq. (4).
{σx=E(z)εx=E(z)(du0dx−zdφdx)τxz=G(z)γxzκ=E(z)2(1+ν)κ(dw0dx−φ)(4)
where E(z) and G(z) are the elastic modulus and shear elastic modulus of the materials, respectively; ν is the Poisson’s ratio, κ=6/5 is the correction factor of a Timoshenko rectangular cross-section beam. Based on Eq. (4), the expressions of bending moment M, axial force FN, and shear force Q in any section of the beam were stated as:
M =∫AσxxzdA=∫AE(z)z(∂u0(x,t)∂x−z∂φ(x,t)∂x)dA =∂u0(x,t)∂x∫AE(z)zdA−∂φ(x,t)∂x∫AE(z)z2dA=D1∂u0(x,t)∂x−D2∂φ(x,t)∂x(5a)
FN =∫AσxxdA=∫AE(z)(∂u0(x,t)∂x−z∂φ(x,t)∂x)dA =∂u0(x,t)∂x∫AE(z)dA−∂φ(x,t)∂x∫AE(z)zdA=D0∂u0(x,t)∂x−D1∂φ(x,t)∂x(5b)
Q =∫AτxzdA=∫AG(z)γxzκdA=∫AE(z)2(1+ν)κ(∂w0(x,t)∂x−φ(x,t))dA =(∂w0(x,t)∂x−φ(x,t))∫AE(z)2(1+ν)κdA=Dxz(∂w0(x,t)∂x−φ(x,t))(5c)
where
D0=∫AE(z)dA=∫AEm[1+(EcEm−1)(12−zh)p]dA=Embh(1+Er−1p+1)=Embhϕ0(6a)
D1=∫AE(z)zdA=∫AEm[1+(EcEm−1)(12−zh)p]zdA=Embh2−(Er−1)p2(p+1)(p+2)=Embh2ϕ1(6b)
D2 =∫AE(z)z2dA=∫AEm[1+(EcEm−1)(12−zh)p]z2dA=Embh312[1+3(Er−1)(p2+p+2)(p+1)(p+2)(p+3)] =Embh312ϕ2(6c)
where
Er=EcEm,ϕ0=1+Er−1p+1,ϕ1=(Er−1)−p2(p+1)(p+2),ϕ2=1+3(Er−1)(p2+p+2)(p+1)(p+2)(p+3)
As the beam was bent within the plane of its longitudinal symmetry, the equilibrium equations in the x and z directions were considered as follows:
{∂σx∂x+∂τxz∂z=ρ(z)∂2u∂t2∂σz∂z+∂τxz∂x=ρ(z)∂2w∂t2(7)
Then, Eq. (7) is integrated to derive Eq. (8).
{∫A(∂σx∂x+∂τxz∂z)dA=∫Aρ(z)∂2u∂t2dA∫A(∂σx∂x+∂τxz∂z)zdA=∫Azρ(z)∂2u∂t2dA∫A(∂σz∂z+∂τxz∂x)dA=∫Aρ(z)∂2w∂t2dA(8)
Substituting Eq. (2) into Eq. (8) yields the following:
{∫A(∂σx∂x+∂τxz∂z)dA=∫Aρ(z)(∂2u0∂t2−z∂2φ∂t2)dA=I0∂2u0∂t2−I1∂2φ∂t2∫A(∂σx∂x+∂τxz∂z)zdA=∫Azρ(z)(∂2u0∂t2−z∂2φ∂t2)dA=I1∂2u0∂t2−I2∂2φ∂t2∫A(∂σz∂z+∂τxz∂x)dA=∫Aρ(z)∂2w0∂t2dA=I0∂2w0∂t2(9)
where
I0=∫Aρ(z)dA=∫Aρm[1+(ρcρm−1)(12−zh)p]dA=ρmbh(1+ρr−1p+1)=ρmbh¯ϕ0(10a)
I1=∫Aρ(z)zdA=∫Aρm[1+(ρcρm−1)(12−zh)p]zdA=ρmbh2−(ρr−1)p2(p+1)(p+2)=ρmbh2¯ϕ1(10b)
I2 =∫Aρ(z)z2dA=∫Aρm[1+(ρcρm−1)(12−zh)p]z2dA=ρmbh312[1+3(ρr−1)(p2+p+2)(p+1)(p+2)(p+3)] =ρmbh312¯ϕ2(10c)
where
ρr=ρcρm,¯ϕ0=1+ρr−1p+1,¯ϕ1=−(ρr−1)p2(p+1)(p+2),¯ϕ2=1+3(ρr−1)(p2+p+2)(p+1)(p+2)(p+3)
Further derivation of Eq. (9) gave
∂FN∂x=I0∂2u0∂t2−I1∂2φ∂t2(11a)
∂M∂x−Q=I1∂2u0∂t2−I2∂2φ∂t2(11b)
∂Q∂x−q=I0∂2w0∂t2(11c)
Substituting Eq. (5) into Eq. (11), the equilibrium differential equation for free vibration is derived, considering the shear deformation and rotational inertia of the beam section.
{D0∂2u0(x,t)∂x2−D1∂2φ(x,t)∂x2=I0∂2u0∂t2−I1∂2φ∂t2D1∂2u0(x,t)∂x2−D2∂2φ(x,t)∂x2−Dxz(∂w0(x,t)∂x−φ(x,t))=I1∂2u0∂t2−I2∂2φ∂t2Dxz(∂2w0(x,t)∂x2−∂φ(x,t)∂x)=q+I0∂2w0∂t2(12)
Considering the free vibration of a beam, then the axial displacement u0, transverse displacement w0, and cross-section angle φ can be expressed as Eq. (13).
(u0(x,t),w0(x,t),φ(x,t))=(ˆu(x),ˆw(x),ˆφ(x))cosωt(13)
where ω is the circular frequency of a beam, ˆu(x),ˆw(x),ˆφ(x) are the vibration modal functions. Substitute Eqs. (1), (2), (4), and (13) into Eq. (12). Dimensionless transformation (ξ,ˆU,ˆW)=(x,ˆu,ˆw)/L, the equilibrium differential equation of a Timoshenko beam with FGMs was obtained as Eq. (14).
{ˆU ″(ξ)−a1ˆW ′(ξ)+a1ˆφ(ξ)−a2λˆu(ξ)−a3λˆφ(ξ)=0ˆφ ″(ξ)+a4ˆW ′(ξ)−a4ˆφ(ξ)−a5λˆu(ξ)−a6λˆφ(ξ)=0ˆW ″(ξ)−ˆφ ′(ξ)+α7λˆw(ξ)=0(14)
where
a1=6cϕ2κδ(1+ν),a2=δ2[cϕ2ϕ1(¯ϕ2−ϕ2¯ϕ1ϕ1)−¯ϕ112ϕ1],a3=δ3[cϕ2ϕ1(ϕ2¯ϕ2ϕ1−¯ϕ312)+¯ϕ12ϕ1]
a4=6cϕ1κδ2(1+ν),a5=cδ(¯ϕ2−ϕ2¯ϕ1ϕ1),a6=cδ2(ϕ2¯ϕ2ϕ1−¯ϕ312),a7=κ(1+ν)¯ϕ1δ26ϕ1
where c=1ϕ3−12ϕ22/ϕ1 is the coefficient related to the gradient change law of material properties; δ=h/L is the height-span ratio of a rectangular cross-section beam; λ=ρmAL4ω2EmI is the dimensionless frequency of a beam. The six dimensionless coefficients were as follows:
ϕ1=1+αp+1,ϕ2=−αp2(p+1)(p+2),ϕ3=1+3α(p2+p+2)(p+1)(p+2)(p+3)
¯ϕ1=1+βp+1,¯ϕ2=−βp2(p+1)(p+2),¯ϕ3=1+3β(p2+p+2)(p+1)(p+2)(p+3)
where K=Ec/Em, α=K−1, ¯K=ρc/ρm, β=¯K−1.
The boundary condition of simply supported (S-S) beams:
ˆU(0)=0,ˆW(0)=0,ˆφ ′(0)=0(15a)
ˆU(1)=0,ˆW(1)=0,ˆφ ′(1)=0(15b)
The boundary condition of clamped-clamped (C-C) beams:
ˆU(0)=0,ˆW(0)=0,ˆφ(0)=0(15c)
ˆU(1)=0,ˆW(1)=0,ˆφ(1)=0(15d)
The boundary condition of free-free (F-F) beams:
ˆU ′(0)=0,ˆW ′(0)−ˆφ(0)=0,ˆφ ′(0)=0(15e)
ˆU ′(1)=0,ˆW ′(1)−ˆφ(1)=0,ˆφ ′(1)=0(15f)
The boundary condition of clamped-free (C-F) beams:
ˆU(0)=0,ˆW(0)=0,ˆφ(0)=0(15g)
ˆU ′(1)=0,ˆW ′(1)−ˆφ(1)=0,ˆφ ′(1)=0(15h)
2.2 Beam Theory of Ignoring the Shear Deformation of the Beam Section and Only Considering the Effect of the Rotational Inertia of the Cross-Section
If the shear deformation was neglected and only the case of rotational inertia of the beam section was considered, the axial displacement u0, transverse displacement w0, and section turning angle φ needed to be decoupled in the derivation of the equation. Firstly, the ∂u0(x,t)∂x is solved from Eq. (5b),
∂u0(x,t)∂x=1D0[FN+D1∂φ(x,t)∂x](16)
Substituting Eq. (16) into Eq. (5a), it is obtained
M=(D21D0−D2)∂φ(x,t)∂x+D1D0FN(17)
Similarly, according to Eq. (11a)
∂2u0∂t2=1I0∂FN∂x+I1I0∂2φ∂t2=I1I0∂2φ∂t2(18)
By substituting Eq. (18) into Eq. (11b), it is obtained
∂M∂x−Q=I1I0∂FN∂x+(I21I0−I2)∂2φ∂t2(19)
Suppose q = 0. In this study, the pure bending deformation of a beam was investigated, as well as the symmetric distribution of the material properties, so that FN = 0, associating Eqs. (11c) and (19), it was obtained
∂Q∂x=I0∂2w0∂t2(20a)
∂M∂x−Q=(I21I0−I2)∂2φ∂t2(20b)
Substituting Eqs. (17) and (5c) into Eqs. (20), the derivative was simplified to obtain
∂2∂x2[(D21D0−D2)∂φ∂x]−I0∂2w0∂t2−(I21I0−I2)∂3φ∂x∂t2=0(21)
If the shear deformation is not considered, it can be obtained by substituting γxz=0, φ=∂w0∂x into Eq. (21).
∂2∂x2[(D21D0−D2)∂2w0∂x2]−I0∂2w0∂t2−(I21I0−I2)∂4w0∂x2∂t2=0(22)
Supposing ξ=x/L, w0(x,t)=ˆw(x)cosωt, then Eq. (22) is transformed into
(D21D0−D2)d4ˆw(ξ)dξ4+ω2I0L4ˆw(ξ)+ω2L2(I21I0−I2)d2ˆw(ξ)dξ2=0(23)
Substituting Eqs. (6) and (10) into Eq. (23) and Ω2=ω2ρmAL4EmI, it is obtained
d4ˆw(ξ)dξ4+Ω2¯ϕ0ϕ012ϕ21−ϕ0ϕ2ˆw(ξ)+Ω2δ2ϕ0(12¯ϕ21−¯ϕ0¯ϕ2)12¯ϕ0(12ϕ21−ϕ0ϕ2)d2ˆw(ξ)dξ2=0(24)
Thus, the natural frequency calculation of the functional gradient beam was transformed into the problem of solving Eqs. (16) and (24) under boundary conditions Eq. (10).
This study applies the improved differential quadrature method to calculate the free vibration natural frequencies of functionally graded beams. The accuracy of the differential quadrature method depends on the discrete node step size and the weight coefficient matrix A(r), which is influenced by the distribution of nodes and the number of nodes. The normalized beam length interval [0,1] was divided into N discrete elements, resulting in a total of N+1, discrete nodes, denoted by ξj(0≤j≤N), assuming ξ0=0, ξN=1. The sudden change in the beam’s stiffness near the ends of the supports, or the influence of the end boundary conditions, made the vicinity of the beam’s end the most sensitive region for displacement and internal force changes. Therefore, arranging more fine-grained, non-uniform nodes in the two end regions of the beam improved the calculation accuracy. This study adopts a distribution of discrete nodes in a discrete form of geometric sequence nodes as described in Eq. (25), i.e.,
{ξi=a+b−a2(qn/21−1)(qi1−1),(q1≥1.0,i=0,1,2,⋯,n2)ξi=b−b−a2(qn/22−1)(qn−i2−1),(q2=1q1,i=n2,n2+1,…,n)(25)
The nodes are distributed from the end of the beam to the center in a series of equal ratios with the common ratio q, which can control the numerical calculation accuracy and numerical dissipation by adjusting the common ratio to modify the step size of the nodes for a certain number of discrete n.
The function ˆU(ξ), ˆW(ξ) and ˆφ(ξ) are described using the Lagrange interpolation function as Eq. (26).
{ˆU(ξ)=N∑j=0lj(ξ)ˆU(ξj)ˆW(ξ)=N∑j=0lj(ξ)ˆW(ξj)ˆφ(ξ)=N∑j=0lj(ξ)ˆφ(ξj)(26)
where lj(ξ) is Lagrange polynomial, and it is stated as Eq. (27).
lj(ξ)=N∏k=0k≠jξ−ξkξj−ξk(27)
From Eq. (26), the first derivative of the function ˆU(ξ), ˆW(ξ) and ˆφ(ξ) is obtained, the function and its derivatives at each node were represented by a weighted linear sum of the values of discrete N+1 node functions.
{ˆU ′(ξi)=N∑j=0l ′j(ξi)ˆU(ξj)ˆW ′(ξi)=N∑j=0l ′j(ξi)ˆW(ξj)ˆφ ′(ξi)=N∑j=0l ′j(ξ)ˆφ(ξj)(28)
Eq. (28) is rewritten in vector form as follows:
{ˆU ′=A(1)ijˆUˆW ′=A(1)ijˆWˆφ ′=A(1)ijˆφ(29)
where the weight coefficient matrix A(1)ij is expressed as follows:
A(1)ij=(A(1)ij)(N+1)×(N+1)(30)
where A(1)ij is expressed as Eq. (31).
A(1)ij=l ′j(ξi)={N∏k=0k≠i,j(ξi−ξk)/N∏k=0k≠i,j(ξj−ξk)(i≠j)N∑k=0k≠i1(ξi−ξk)(i=j)(31)
In Eq. (29), the column vectors ˆU ′, ˆU, ˆW ′, ˆW, ˆφ ′ and ˆφ are as follows:
{ˆU ′=(ˆU ′(ξ0),ˆU ′(ξ1),⋯,ˆU ′(ξN))T,ˆU=(ˆU(ξ0),ˆU(ξ1),⋯,ˆU(ξN))TˆW ′=(ˆW ′(ξ0),ˆW ′(ξ1),⋯,ˆW ′(ξN))T,ˆW=(ˆW(ξ0),ˆW(ξ1),⋯,ˆW(ξN))Tˆφ ′=(ˆφ ′(ξ0),ˆφ ′(ξ1),⋯,ˆφ ′(ξN))T,ˆφ=(ˆφ(ξ0),ˆφ(ξ1),⋯,ˆφ(ξN))T(32)
Similarly, from Eq. (29), it can be inferred that Eq. (33).
{ˆU ″=A(2)ijˆUˆW ″=A(2)ijˆWˆφ ″=A(2)ijˆφ(33)
The column vectors ˆU ″, ˆW ″ and ˆφ ″ are as follows:
{ˆU ″=(ˆU ″(ξ0),ˆU ″(ξ1),⋯,ˆU ″(ξN))TˆW ″=(ˆW ″(ξ0),ˆW ″(ξ1),⋯,ˆW ″(ξN))Tˆφ ″=(ˆφ ″(ξ0),ˆφ ″(ξ1),⋯,ˆφ ″(ξN))T(34)
where the relationship between weight coefficient matrices A(2)ij and A(1)ij is Eq. (35).
A(2)ij=A(1)ijA(1)ij(35)
The boundary conditions of beams were discussed by taking C-C beams as an example. Substituting Eqs. (29) and (33) into Eqs. (15c) and (15d), it can be obtained Eq. (36).
[I]Il=0ˆU=0,[I]Il=0ˆW=0,[I]Il=0ˆφ=0(36a)
[I]Il=1ˆU=0,[I]Il=1ˆW=0,[I]Il=1ˆφ=0(36b)
where Il is the elements of Il-th row with 0 and n, [⋯]Il is a matrix, I is the identity matrix of order (n+1)×(n+1). Substituting Eqs. (29) and (33) into Eq. (16), the equation of motion of a FGMs beam is obtained as Eq.(37).
[A(2)ij−a1A(1)ija1I0a4A(1)ijA(2)ij−a4I0A(2)ij−A(1)ij](ˆUˆWˆφ)−λ[a2I0a3Ia5I0a6I0−α7I0](ˆUˆWˆφ)=(000)(37)
Simultaneous Eqs. (36) and (37) that was the Il-th row constant coefficient followed by replacing the first row and last row of the corresponding matrix of Eq. (37). Thus, based on the above formula, a general program was written in FORTRAN language to solve the natural frequency of the FGMs beams along the thickness direction.
3 Numerical Examples and Discussion
Functionally graded materials are composed of metal material aluminum and ceramic material Al2O3, the material parameters of the FGMs in Eq. (1) are listed in Table 1.
Take the number of discrete units of beam length as N = 20, solving Eq. (24) by DQM. Tables 2–5 show the dimensionless natural frequency Ω1 of FGMs beams with different boundary conditions, and material gradient parameter p are calculated by DQM.
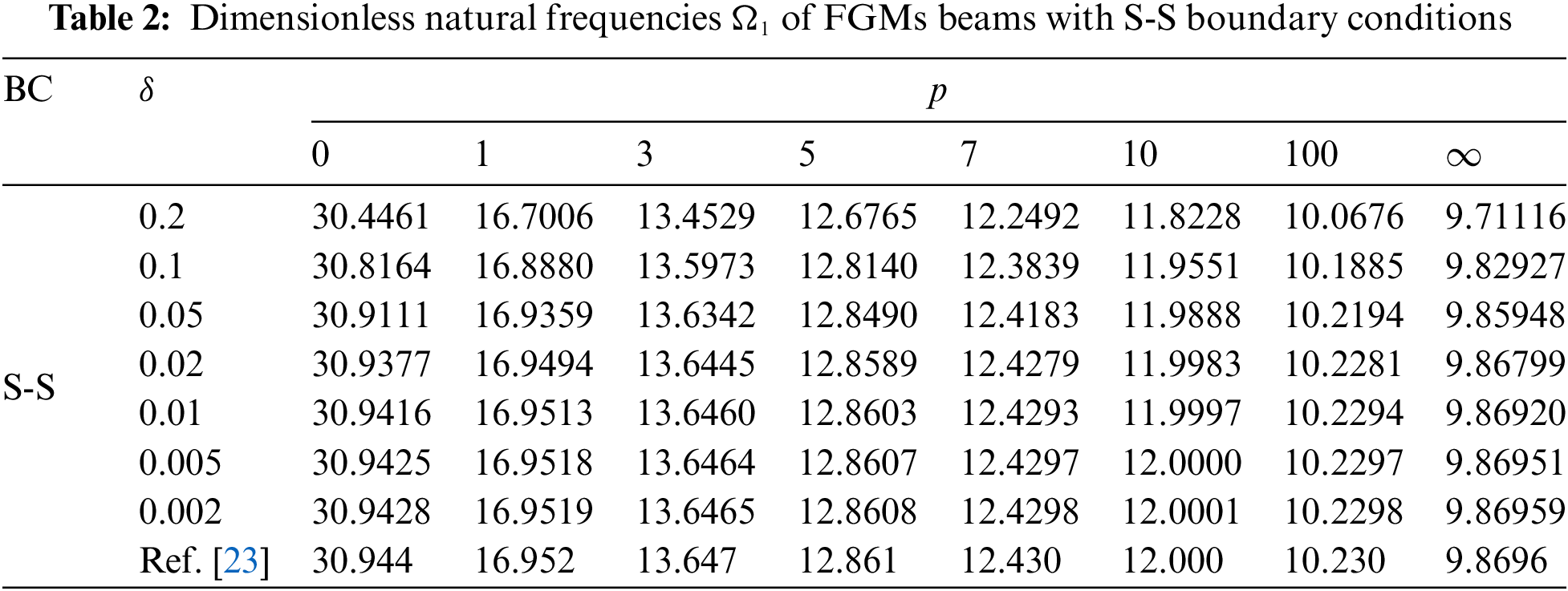
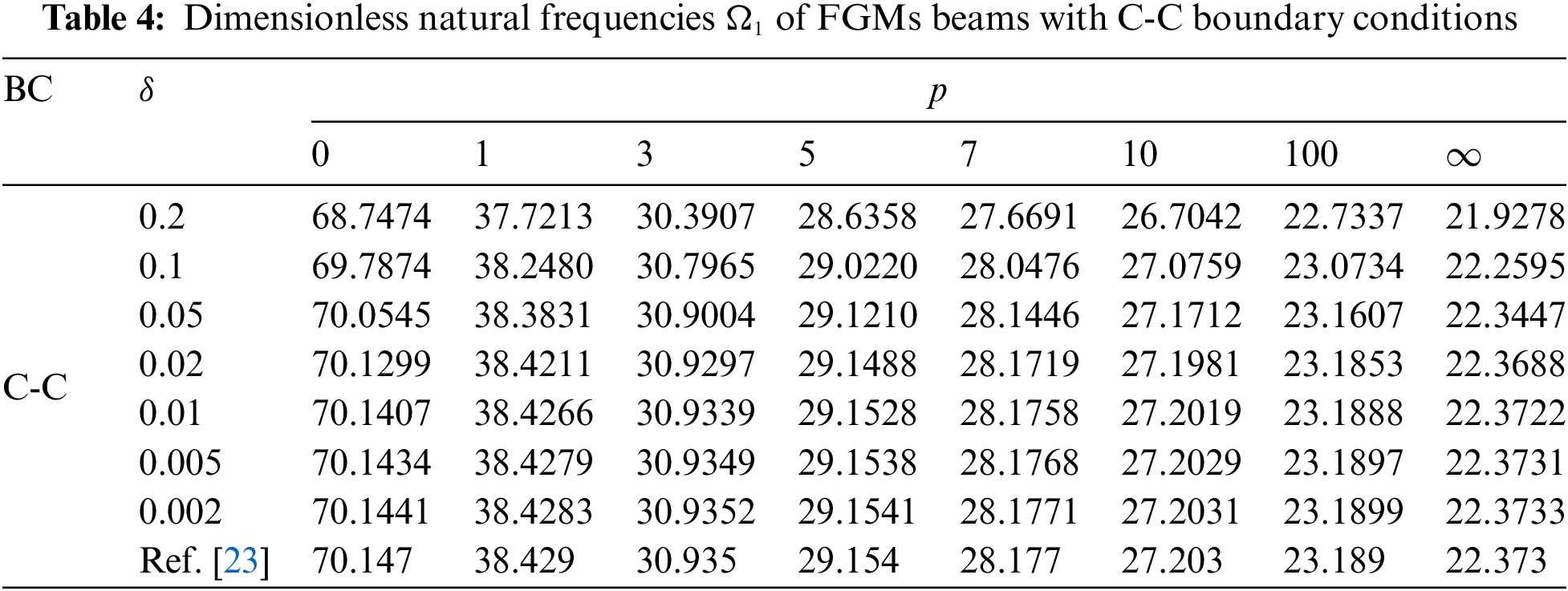
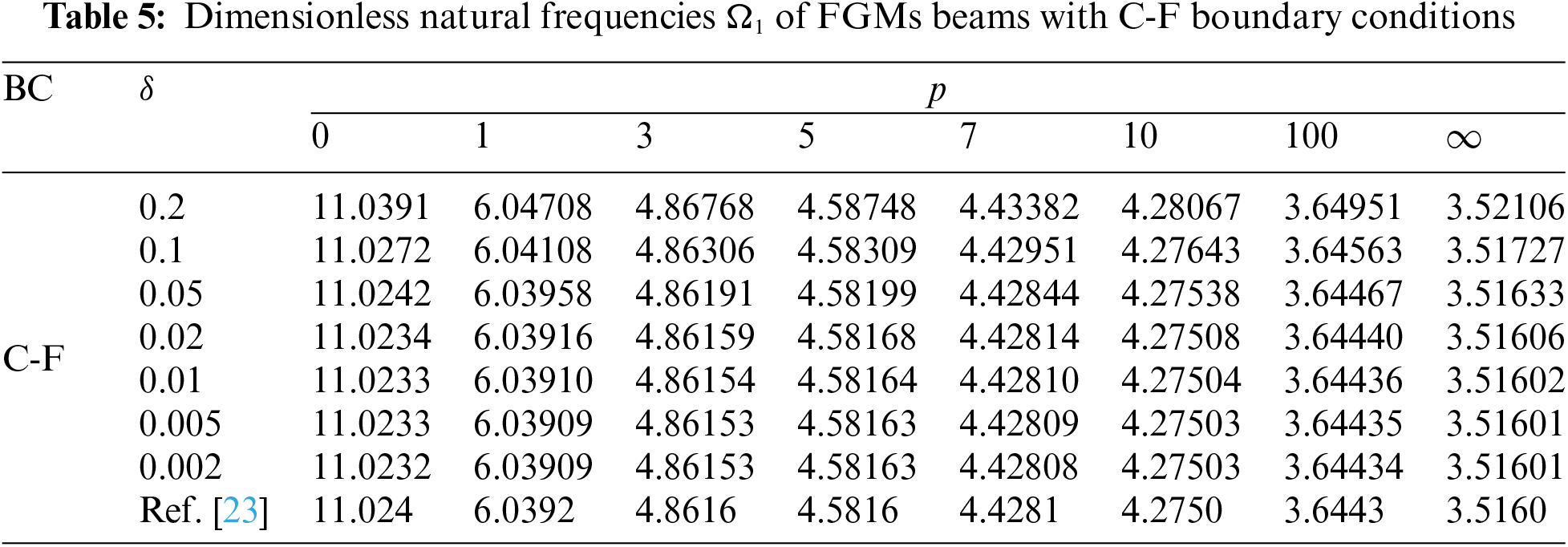
Tables 2–5 demonstrate that the results are consistent with the solution presented in reference [23], showing that as the height-span ratio h/L decreases, the section inertia of the beam has minimal impact on the natural frequency of slender beams. However, this effect is not negligible for short, thick beams.
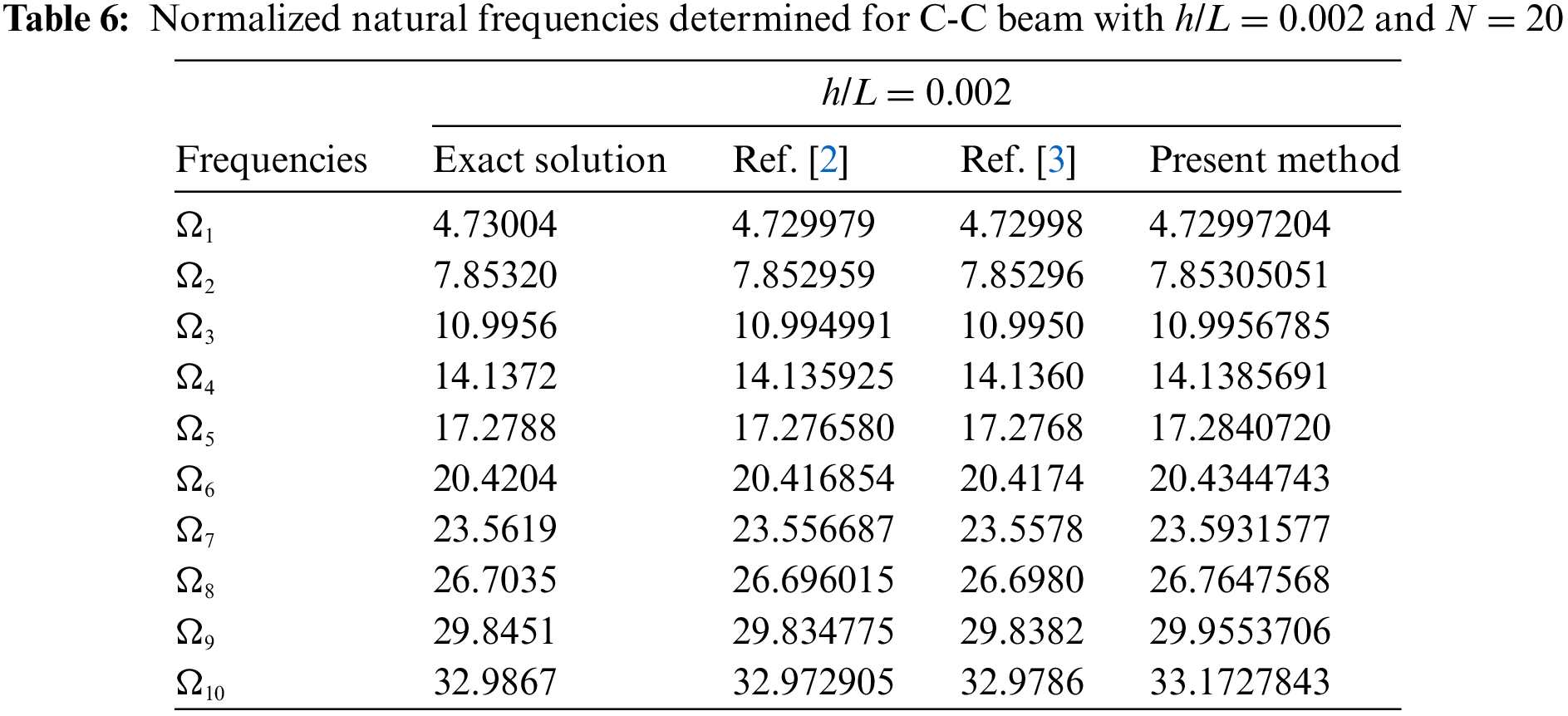
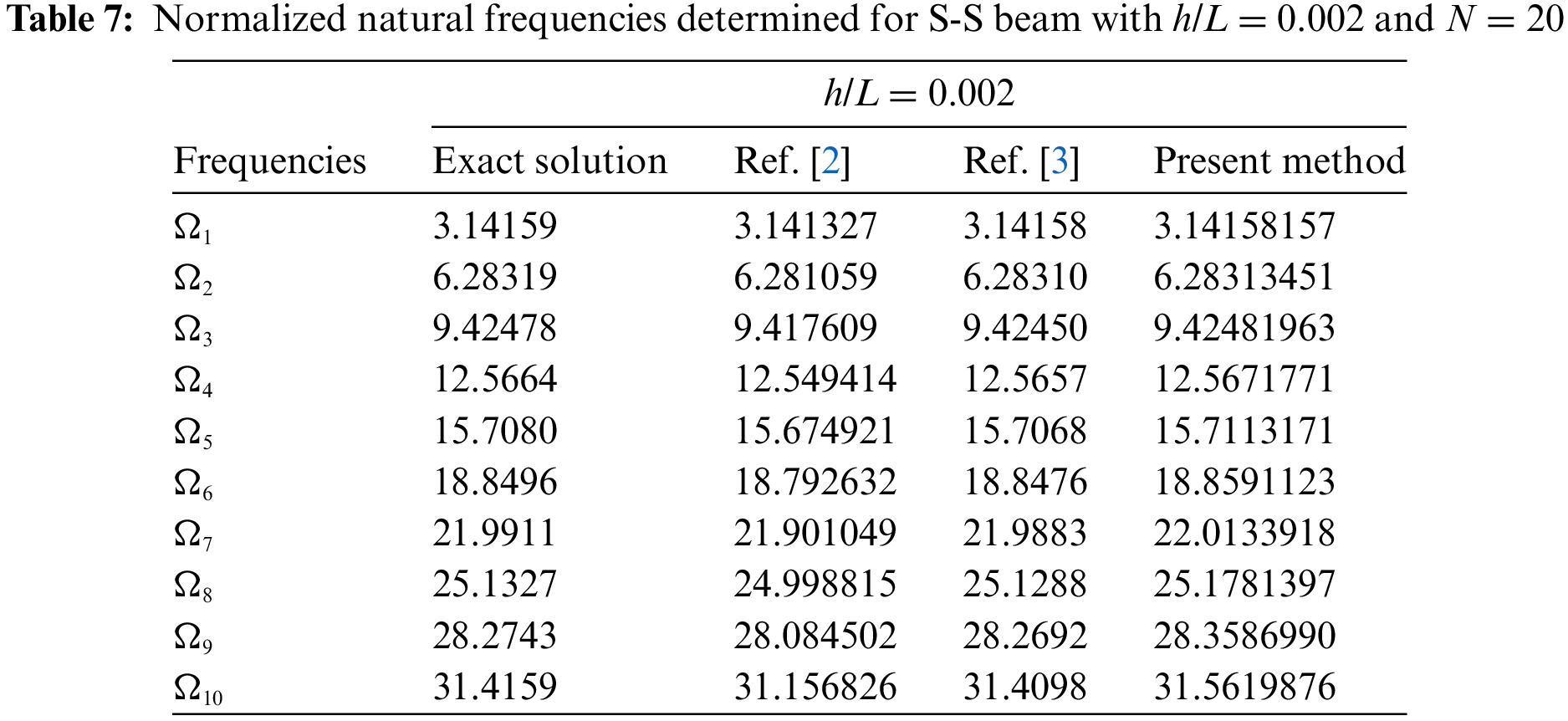
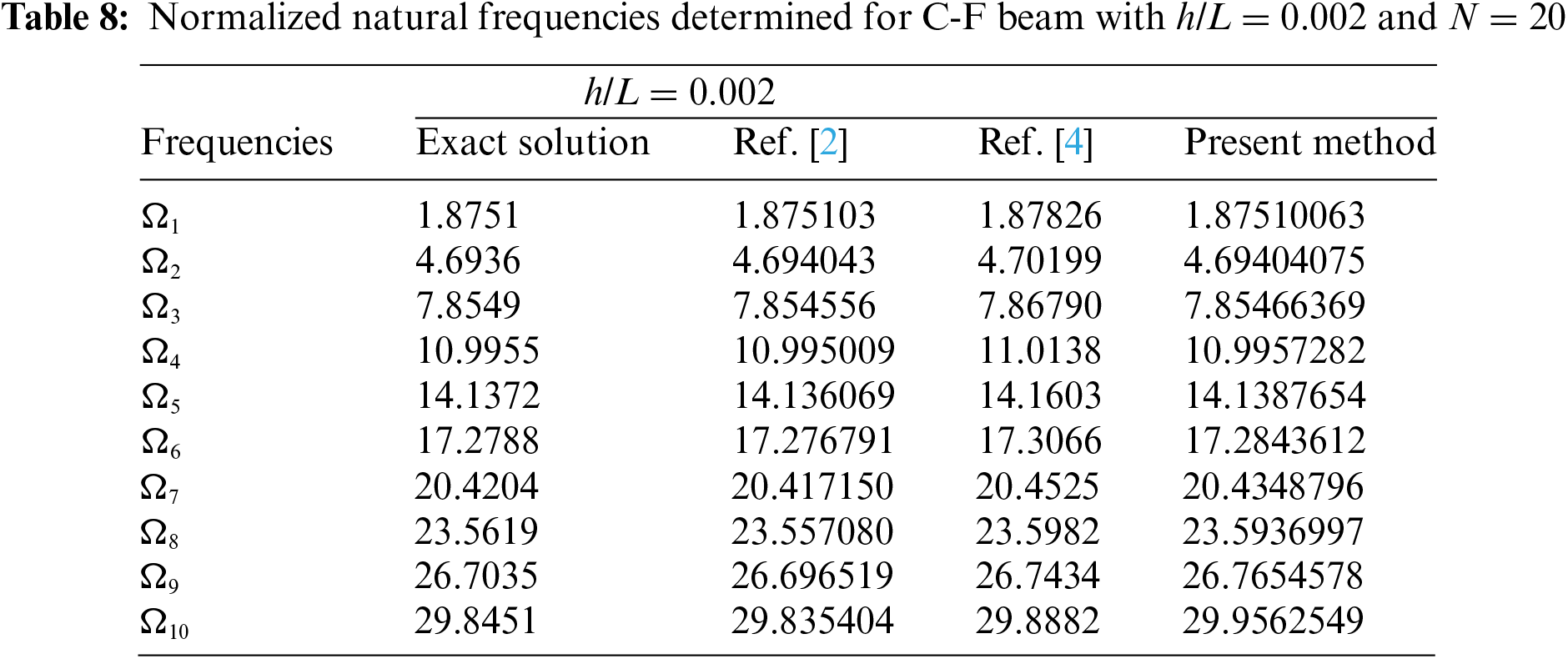
To verify the feasibility and accuracy of calculating the natural frequencies of FGMs beams using DQM, assume p = 0, thereby simplifying an FGMs beam into a uniform ceramic beam. Tables 6–8 display the first ten natural frequencies for C-C, S-S, and C-F beams when the height-span ratio is h/L = 0.002 (with the number of discrete elements of the beam N = 20). As seen from Tables 6–8, numerical results show excellent consistency with those reported in references [2,3] and exact solutions, indicating that DQM is accurate for calculating the natural frequencies of beams made of isotropic homogeneous materials. Here, the natural frequencies of beams in Tables 6–8 and the dimensionless natural frequencies of beams in references [2,3] are defined as per Eq. (38).
Ω=4√λ¯ϕ1ϕ3=4√ω2AL4ρmEmI4√¯ϕ1ϕ3(38)
Assuming p = 0, Fig. 2 illustrates the curve of the first 15 natural frequencies of Timoshenko beams with varying height-to-span ratios h/L. As observed in Fig. 2: (a–d), for smaller values of h/L, i.e., h/L = 0.002 and 0.005, the relationship between non-dimensional frequency parameters and frequency orders is almost linear. This relationship becomes nonlinear with the increase in height-to-span ratios.
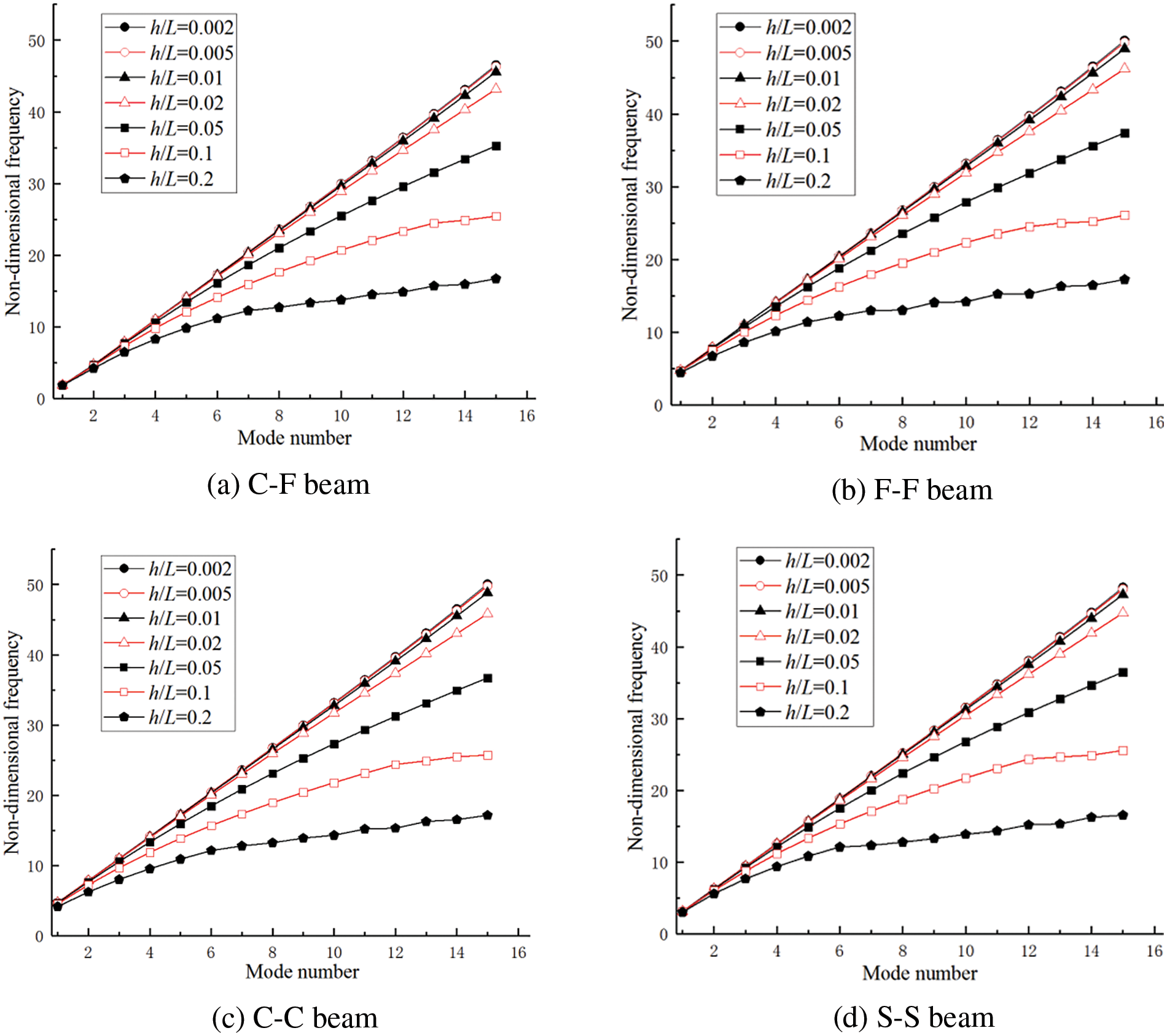
Figure 2: Non-dimensional frequency parameters Ω of the beam for different boundary conditions
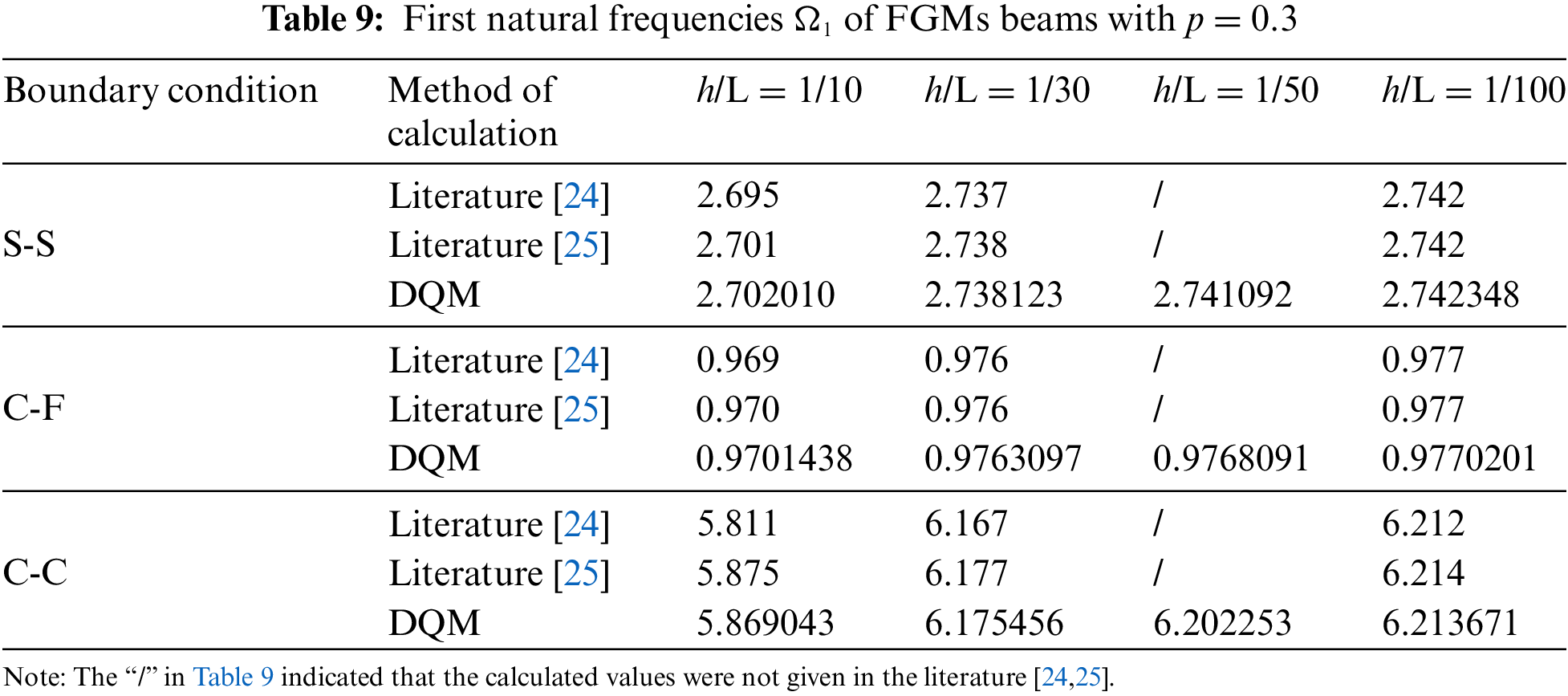
Assuming p = 0.3, the first natural frequencies of FGMs beams were calculated using DQM. The results, listed in Table 9, show excellent consistency with those reported in references [24,25], proving that DQM is effective and accurate for calculating the natural frequencies of FGMs beams. The natural frequencies of beams in Table 9 and the dimensionless natural frequencies of beams in references [24,25] are defined as per Eq. (39).
Ω=√λ¯ϕ112ϕ1=√ω2AL4ρmEmI√¯ϕ112ϕ1(39)
Based on first-order shear deformation theory, the governing Eq. (37) of a FGMs Timoshenko beam was calculated by DQM. The first natural frequency curve of the beam under different boundary conditions with material parameter p was obtained as shown in Figs. 3–5 (0.0001 ≤ p ≤ 10000).
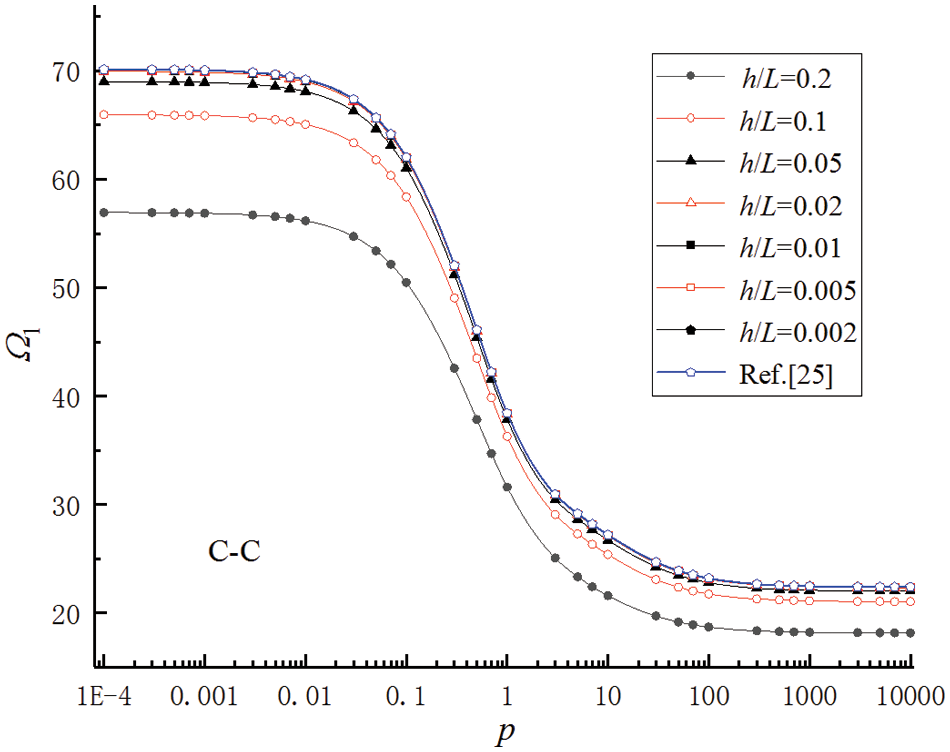
Figure 3: Relationships between the first natural frequencies Ω1 and material parameter p for FGMs beams with boundary condition C-C
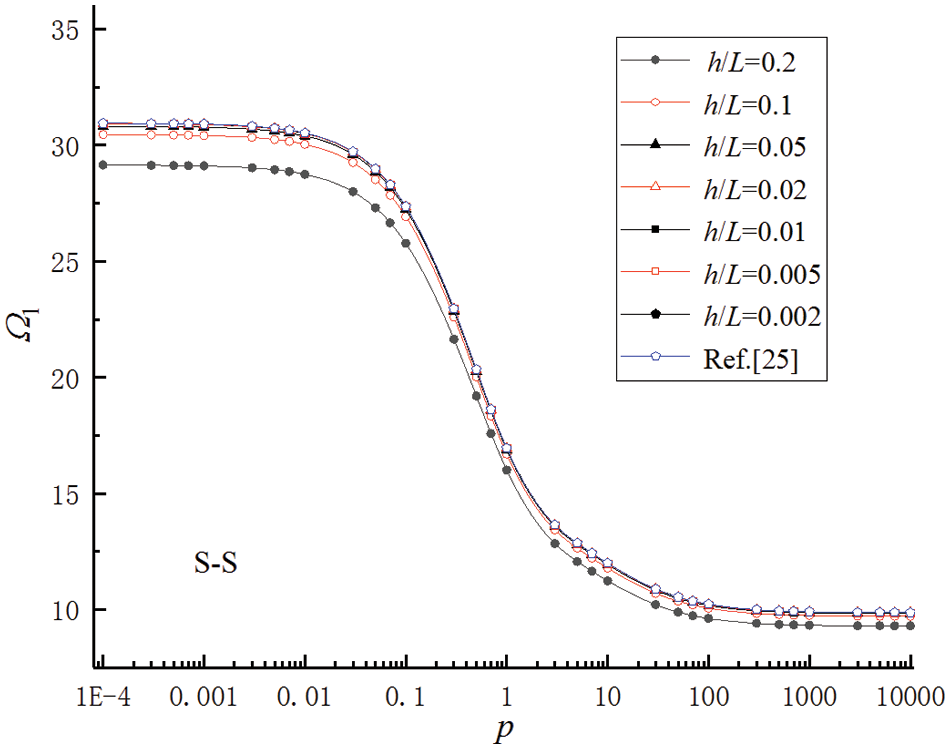
Figure 4: Relationships between the first natural frequencies Ω1 and material parameter p for FGMs beams with boundary condition S-S
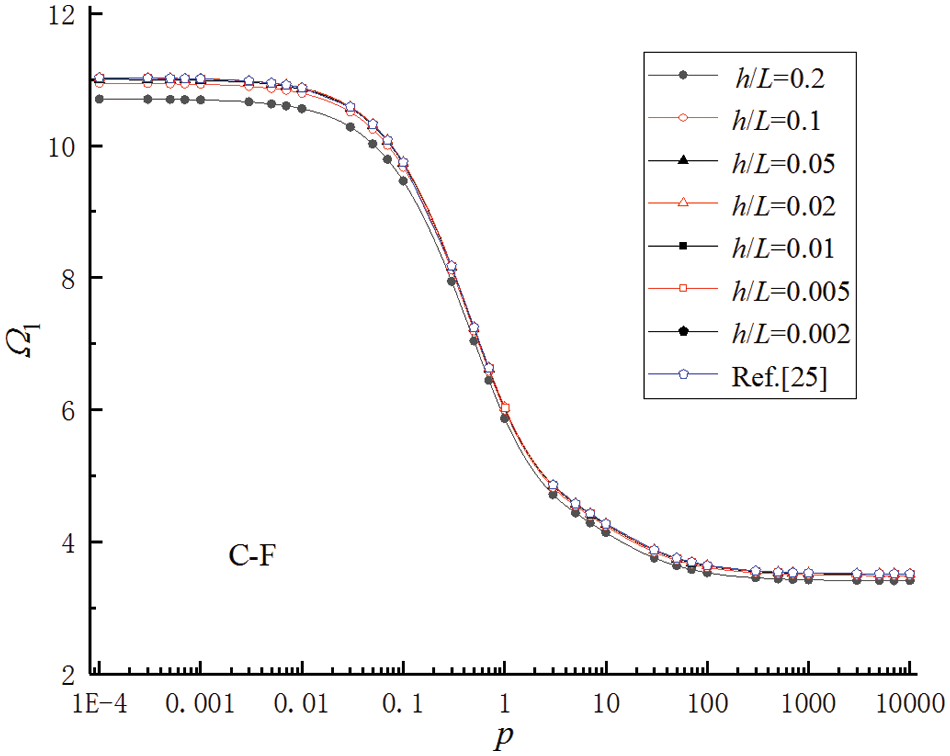
Figure 5: Relationships between the first natural frequencies Ω1 and material parameter p for FGMs beams with boundary condition C-F
The variation in the gradient parameter primarily corresponds to alterations in physical properties such as material stiffness and density, which directly impact the frequency characteristics of its compositional structure. The gradient parameter ranged from 0.1 to 10, and the stiffness and density of the FGMs beams exhibited significant variations. Therefore, any changes in the gradient parameter substantially impact the first-order natural frequency of the FGMs beams.
The calculation results showed that the Timoshenko beams approached the Euler-Bernoulli beams [26] with a decrease in the height-to-span ratios; the first natural frequencies of the beams increased gradually. For smaller values of h/L, i.e., h/L = 0.002 and 0.005, the first natural frequencies of the Timoshenko beams calculated by DQM were very close to the results in the reference. When p = 0.0001, it was very close to the first natural frequencies of the Euler-Bernoulli beams made of pure ceramic uniform materials. However, when p = 10000, it was very close to the beams made of pure metal uniform materials. These calculation results proved that DQM was effective and accurate in calculating the natural frequencies of FGMs beams along the thickness direction. The natural frequencies of beams in Figs. 3–5 and the dimensionless natural frequencies of beams were defined as Eq. (40).
Ω=√λ=√ρmAL4ω2EmI(40)
The improved DQM in this article can also provide the vibration mode functions corresponding to all frequencies simultaneously. When the height-to-span ratio h/L = 0.002 and the gradient parameter p = 2, the first three mode functions of the FGMs beam under the C-C, S-S, and C-F boundary conditions are shown in Figs. 6–8.
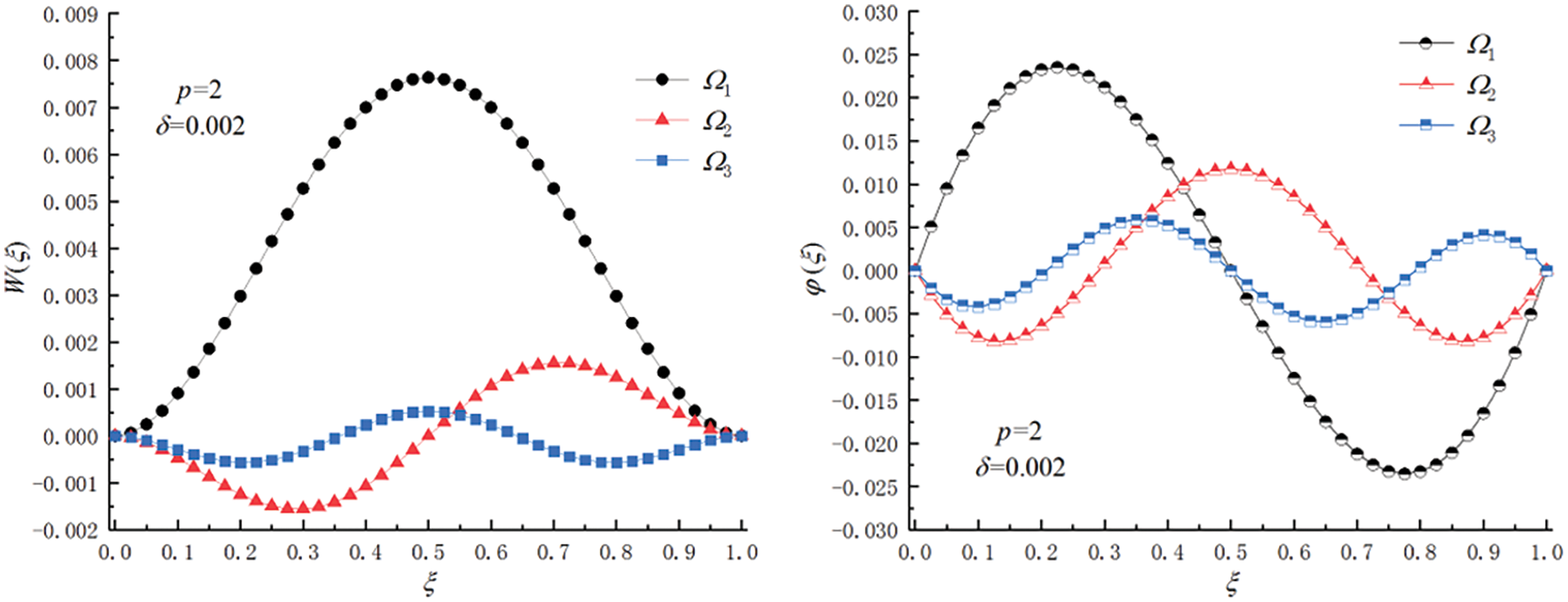
Figure 6: First three orders of modal functions of the beam under C-C boundary condition
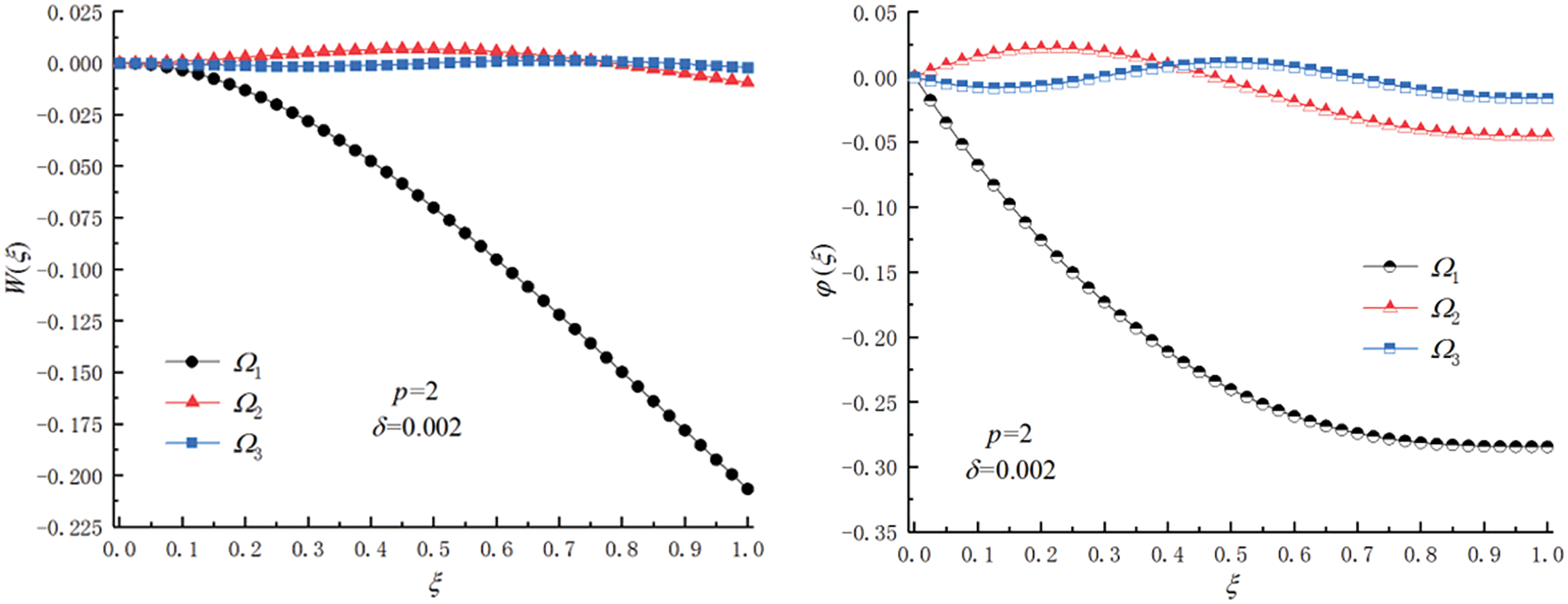
Figure 7: First three orders of modal functions of the beam under C-F boundary condition
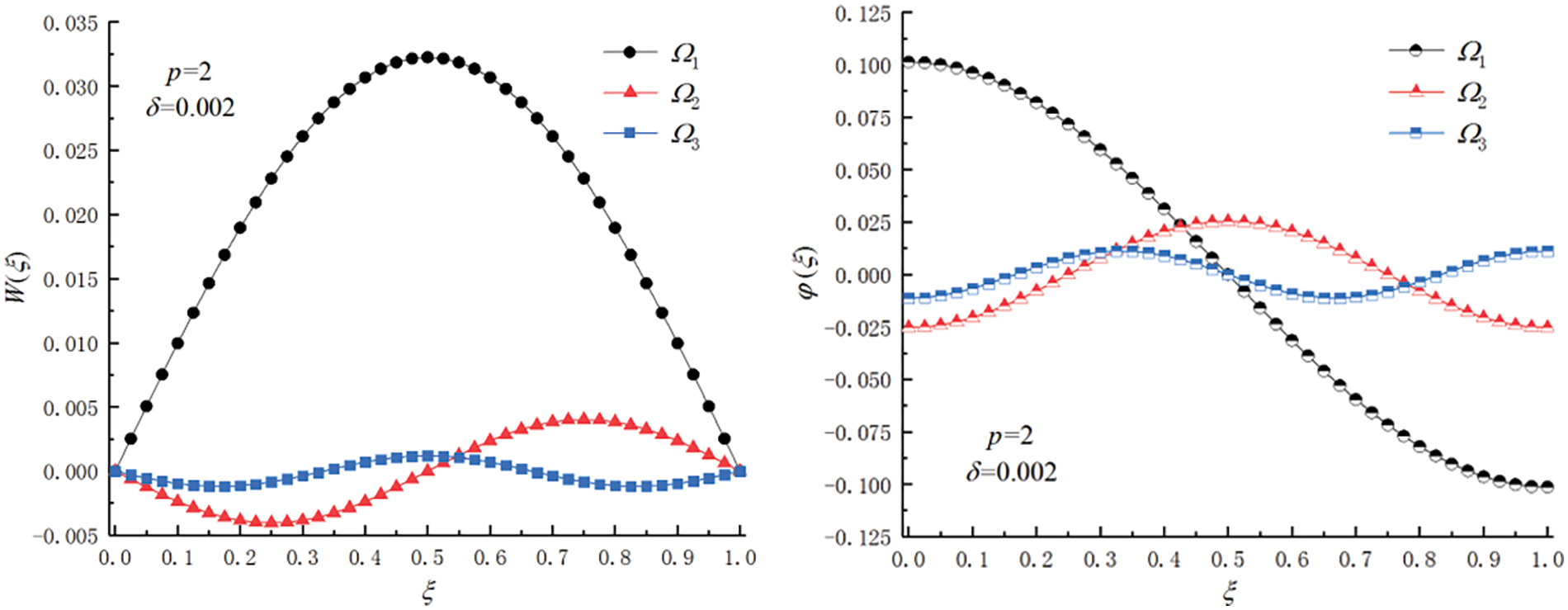
Figure 8: First three orders of modal functions of the beam under S-S boundary condition
We also used the finite element method (FEM) based on the ABAQUS software to solve the free vibration of the FGMs Timoshenko beams. Based on the geometric parameters used in the DQM, the length, width, and height of the model of the rectangular cross-sectional beam were 4000 × 200 × 200 mm. Due to the nonlinear characteristics of the beam material, a 3D entity model for the FGMs Timoshenko beam was established by the Matlab program, which was written to define the unit material properties that vary with coordinates. Then, various boundary conditions for frequency analysis and other processes were defined. The eigenfrequency in the ABAQUS software was employed to calculate the first-order frequencies of the FGMs beam. Fig. 9 shows the FEM results of the first natural frequency of an FGMs C-C beam. In the simulation procedure, the material properties are shown in Table 1. The calculated results are listed in Tables 10–12.
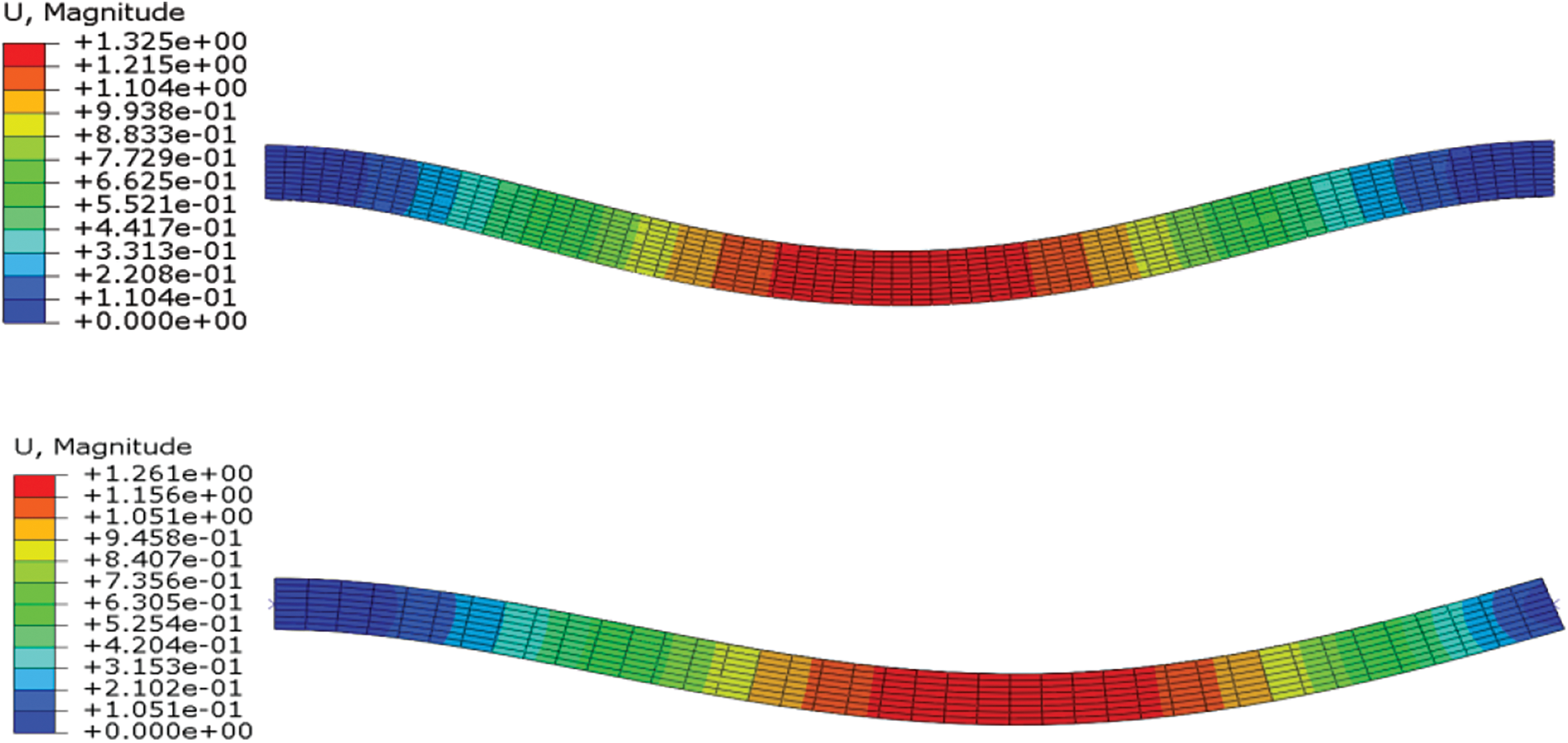

Figure 9: First natural frequency of the FGMs Timoshenko beams with different boundary conditions by the FEM
Tables 10–12 show that the first natural frequency has errors or even distortions with EFM when the boundary conditions are fixed support and simple support with a length-to-height ratio of 0.2. However, under other length-to-height ratios and boundary conditions, the results of EFM are closer to those of DQM and literature results, especially when the length-to-height ratio is relatively large, showing excellent consistency with the results in the literature [23] and those of DQM. This further indicates that the applicability of the Differential Quadrature Method for calculating the natural frequencies of FGMs beams is better than that of the Finite Element Method for short, thick beams.
This study investigates the dynamic natural characteristics of FGMs Timoshenko beams using the improved Differential Quadrature Method. Firstly, based on the first-order shear deformation theory, the governing equation of transverse free vibration of an FGMs beam is transformed into the eigenvalue problem of ordinary differential equations. Finally, the QR method can calculate the first several natural frequencies of transverse free vibration of an FGMs beam. In conjunction with the results reported in related literature, the Finite Element Method was introduced to verify the feasibility and accuracy of the developed Differential Quadrature Method. The main conclusions are as follows:
(1) The natural frequencies of the FGMs Timoshenko beams were calculated using improved DQM and EFM. The numerical results showed excellent consistency with those obtained in the reference. The applicability and high efficiency of the proposed method for calculating the natural frequencies of FGMs Timoshenko beams were proved.
(2) The shear deformation and rotational inertia of the FGMs beams’ cross-section influence the natural frequency. For smaller values of h/L, i.e., h/L = 0.002 and 0.005, the relations between the non-dimensional frequency parameter and frequency order were almost linear. The relations became nonlinear with the increase of height-to-span ratios, and the first natural frequency of the beam increases with a decreasing height-span ratio.
(3) The effects of shear deformation and rotational inertia on the natural frequencies of the FGMs beams cannot be neglected when the beams have relatively large height-span ratios (such as h/L=0.2 and h/L=0.1).
Acknowledgement: I express my gratitude to Anhui Polytechnic University and Hohai University for administrative and technical support.
Funding Statement: Anhui Provincial Natural Science Foundation (2308085QD124), Anhui Province University Natural Science Research Project (Grant No. 2023AH050918). The University Outstanding Youth Talent Support Program of Anhui Province.
Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Xiaojun Huang, Liaojun Zhang; data collection: Hanbo Cui; analysis and interpretation of results: Hanbo Cui; draft manuscript preparation: Hanbo Cui, Gaoxin Hu. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Kirlangic, O., Akbas, S. D. (2021). Dynamic responses of functionally graded and layered composite beams. Smart Structures and Systems, 27(1), 115–122. [Google Scholar]
2. Shang Hsu, Y. (2016). Enriched finite element methods for Timoshenko beam free vibration analysis. Applied Mathematical Modelling, 40(15), 7012–7033. [Google Scholar]
3. Moallemi-Oreh, A., Karkon, M. (2013). Finite element formulation for stability and free vibration analysis of timoshenko beam. Advances in Acoustics and Vibration, 2(1), 1–7. [Google Scholar]
4. Xu, S., Wang, X. (2011). Free vibration analyses of Timoshenko beams with free edges by using the discrete singular convolution. Advances in Engineering Software, 42(6), 797–806. [Google Scholar]
5. Sorrentino, S., Fasana, A., Marchesiello, S. (2007). Analysis of non-homogeneous Timoshenko beams with generalized damping distributions. Journal of Sound and Vibration, 304(3–5), 779–792. [Google Scholar]
6. Rajasekaran, S., Norouzzadeh Tochaei, E. (2014). Free vibration analysis of axially functionally graded tapered Timoshenko beams using differential transformation element method and differential quadrature element method of lowest-orde. Meccanica, 49(3), 995–1009. [Google Scholar]
7. Shahba, A., Attarnejad, R., Tavanaie Marvi, M., Hajilar, S. (2011). Free vibration and stability analysis of axially functionally graded tapered Timoshenko beams with classical and non-classical boundary conditions. Composites Part B: Engineering, 42(4), 801–808. https://doi.org/10.1016/j.compositesb.2011.01.017 [Google Scholar] [CrossRef]
8. Sankar, B. V. (2001). An elasticity solution for functionally graded beams. Composites Science & Technology, 61(5), 689–696. https://doi.org/10.1016/S0266-3538(01)00007-0 [Google Scholar] [CrossRef]
9. Pu, Y., Jia, S., Luo, Y., Shi, S. (2023). Bending analysis of functionally graded sandwich beams with general boundary conditions using a modified Fourier series method. Archive of Applied Mechanics, 93(2), 3741–3760. [Google Scholar]
10. Stojanovic, V., Petkovic, M. D., Deng, J. (2019). Stability and vibrations of an overcritical speed moving multiple discrete oscillators along an infinite continuous structure. European Journal of Mechanics-A/Solids, 75(1), 367–380. [Google Scholar]
11. Stojanovic, V., Petkovic, M. D., Deng, J. (2019). Stability of parametric vibrations of an isolated symmetric cross-ply laminated plate. Composites Part B: Engineering, 167, 631–642. https://doi.org/10.1016/j.compositesb.2019.02.041 [Google Scholar] [CrossRef]
12. Qian, L. F., Ching, H. K. (2004). Static and dynamic analysis of 2D functionally graded elasticity by using meshless local Petrov-Galerkin method. Journal of the Chinese Institute of Engineers, 27(4), 491–503. https://doi.org/10.1080/02533839.2004.9670899 [Google Scholar] [CrossRef]
13. Xiang, H. J., Yang, J. (2008). Free and forced vibration of a laminated FGM Timoshenko beam of variable thickness under heat conduction. Composites Part B: Engineering, 39(2), 292–303. https://doi.org/10.1016/j.compositesb.2007.01.005 [Google Scholar] [CrossRef]
14. Gao, Y., Xiao, W. S., Zhu, H. (2019). Nonlinear vibration analysis of different types of functionally graded beams using nonlocal strain gradient theory and a two-step perturbation method. European Physical Journal Plus, 134(1), 1–24. [Google Scholar]
15. Gao, Y., Xiao, W. S., Zhu, H. (2019). Nonlinear vibration of functionally graded nano-tubes using nonlocal strain gradient theory and a two-steps perturbation method. Structural Engineering & Mechanics, 69(2), 205–219. [Google Scholar]
16. Gao, Y., Xiao, W. S., Zhu, H. (2020). Snap-buckling of functionally graded multilayer graphene platelet-reinforced composite curved nanobeams with geometrical imperfection. European Journal of Mechanics-A/Solids, 82(5), 103993–103993. [Google Scholar]
17. Stojanovic, V., Kozic, P., Ristic, M. (2015). Vibrations and stability analysis of multiple rectangular plates coupled with elastic layers based on different plate theories. International Journal of Mechanical Sciences, 92(1), 233–244. [Google Scholar]
18. Zheng, Z., Tao, Y. (2007). Analytical solution of a cantilever functionally graded beam. Composites Science and Technology, 67(3–4), 481–488. [Google Scholar]
19. Huang, X., Zhang, L., Ge, R., Cui, H., Xu, Z. (2022). Investigation of the free vibrations of radial functionally graded circular cylindrical beams based on differential quadrature method. Computer Modeling in Engineering & Sciences, 132(3), 23–41. https://doi.org/10.32604/cmes.2022.019765 [Google Scholar] [CrossRef]
20. Huang, X., Zhang, L., Ge, R., Cui, H. (2023). Investigation of the free vibrations of bi-directional functionally graded material beams using differential quadrature method. Journal of Vibration and Control, 1(3), 95–104. [Google Scholar]
21. Choe, H. U., Zhang, J. B., Kim, W., Rim, H., Kim, H. (2023). Free vibration analysis of functionally graded straight-curved-straight beam with general boundary conditions. Journal of Vibration Engineering & Technologies, 5(4), 112–131. [Google Scholar]
22. Patil, M. A., Kadoli, R. (2023). Analytical solution for free vibration of symmetric Terfenol-D layered functionally graded beam with different boundary conditions. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 45(7), 357–328. [Google Scholar]
23. ShiRong, L., Ping, L., Similar transformation between static and dynamic solutions of functionally graded beams and homogeneous beams. Mechanics in Engineering, 32(2), 45–49. [Google Scholar]
24. Sina, S. A., Navazi, H. M., Haddadpour, H. (2009). An analytical method for free vibration analysis of functionally graded beams. Materials and Design, 30(3), 741–747. https://doi.org/10.1016/j.matdes.2008.05.015 [Google Scholar] [CrossRef]
25. Imek, M. (2010). Fundamental frequency analysis of functionally graded beams by using different higher-order beam theories. Nuclear Engineering and Design, 240(4), 697–705. https://doi.org/10.1016/j.nucengdes.2009.12.013 [Google Scholar] [CrossRef]
26. Li, S. R., Cao, D. F., Wan, Z. Q. (2013). Bending solutions of FGM Timoshenko beams from those of the homogenous Euler-Bernoulli beams. Applied Mathematical Modelling, 37(10–11), 7077–7085. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF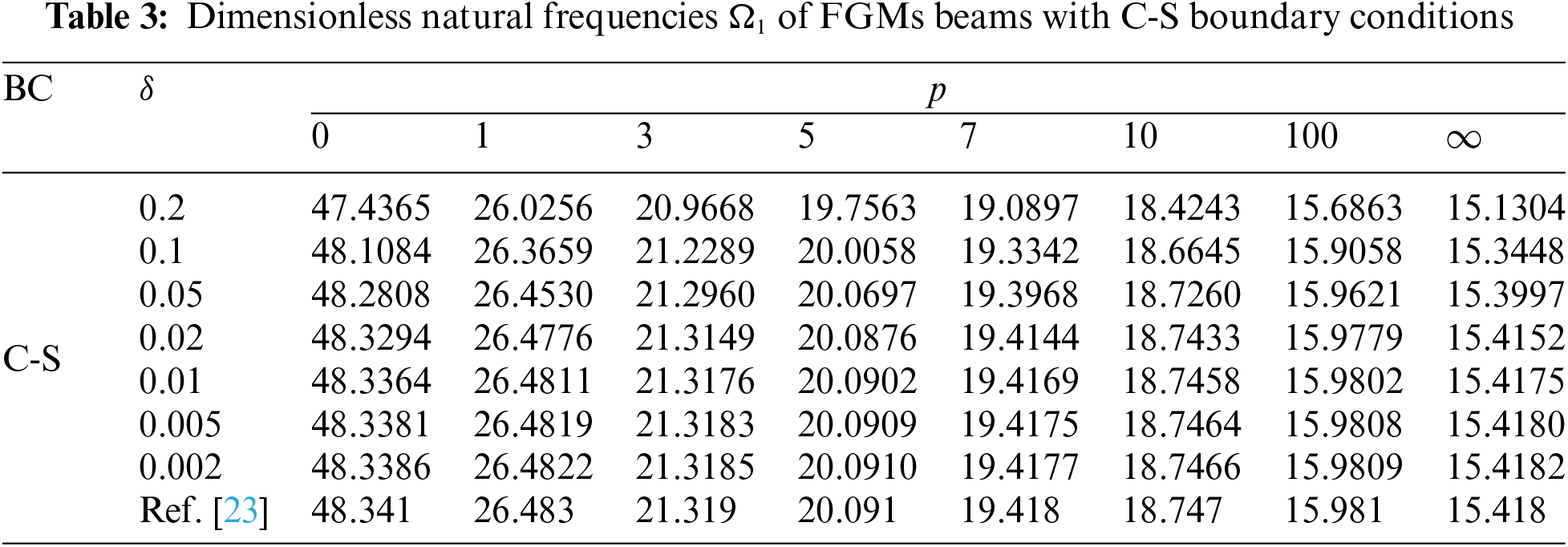
 Downloads
Downloads
 Citation Tools
Citation Tools
