 Open Access
Open Access
ARTICLE
Enhancing Renewable Energy Integration: A Gaussian-Bare-Bones Levy Cheetah Optimization Approach to Optimal Power Flow in Electrical Networks
1 Department of Electrical Engineering, College of Engineering, Majmaah University, Al-Majmaah, 11952, Saudi Arabia
2 Electrical and Computer Engineering Department, Oakland University, Rochester, MI, 48309, USA
3 Institute of Earth and Space Science, King Abdulaziz City for Science and Technology (KACST), Riyadh, 11442, Saudi Arabia
4 Computer Science and Systems Engineering, Institute Polytechnique de Paris, Palaiseau Cedex, France
* Corresponding Author: Ali S. Alghamdi. Email:
Computer Modeling in Engineering & Sciences 2024, 140(2), 1339-1370. https://doi.org/10.32604/cmes.2024.048839
Received 20 December 2023; Accepted 07 March 2024; Issue published 20 May 2024
Abstract
In the contemporary era, the global expansion of electrical grids is propelled by various renewable energy sources (RESs). Efficient integration of stochastic RESs and optimal power flow (OPF) management are critical for network optimization. This study introduces an innovative solution, the Gaussian Bare-Bones Levy Cheetah Optimizer (GBBLCO), addressing OPF challenges in power generation systems with stochastic RESs. The primary objective is to minimize the total operating costs of RESs, considering four functions: overall operating costs, voltage deviation management, emissions reduction, voltage stability index (VSI) and power loss mitigation. Additionally, a carbon tax is included in the objective function to reduce carbon emissions. Thorough scrutiny, using modified IEEE 30-bus and IEEE 118-bus systems, validates GBBLCO’s superior performance in achieving optimal solutions. Simulation results demonstrate GBBLCO’s efficacy in six optimization scenarios: total cost with valve point effects, total cost with emission and carbon tax, total cost with prohibited operating zones, active power loss optimization, voltage deviation optimization and enhancing voltage stability index (VSI). GBBLCO outperforms conventional techniques in each scenario, showcasing rapid convergence and superior solution quality. Notably, GBBLCO navigates complexities introduced by valve point effects, adapts to environmental constraints, optimizes costs while considering prohibited operating zones, minimizes active power losses, and optimizes voltage deviation by enhancing the voltage stability index (VSI) effectively. This research significantly contributes to advancing OPF, emphasizing GBBLCO’s improved global search capabilities and ability to address challenges related to local minima. GBBLCO emerges as a versatile and robust optimization tool for diverse challenges in power systems, offering a promising solution for the evolving needs of renewable energy-integrated power grids.Keywords
The escalating global demand for energy, driven by industrialization and population growth, has necessitated a transition towards sustainable energy practices. This transition is further fueled by the deregulation of electricity markets and a growing imperative to curtail greenhouse gas emissions. Renewable energy sources (RESs) have emerged as a pivotal solution, offering cleaner alternatives to traditional fossil fuels. Over recent decades, technological advancements have significantly reduced the installation costs associated with RESs, making them economically viable and environmentally sustainable [1].
In this context, wind turbine (WT) generators and photovoltaic (PV) generators stand out as key contributors to the renewable energy landscape. Projections suggest that the output power from these sources will soon become more cost-effective than that obtained from fossil fuels, marking a paradigm shift in power generation economics [1].
The challenge of Optimal Power Flow (OPF) is crucial for ensuring the economic efficiency and stable functioning of power systems. Initially conceptualized in 1962, OPF involves adjusting control variables in a large-scale, nonlinear, and nonconvex static problem [2]. With conventional OPF tailored for fossil fuel-based stations, the surge in renewable energy adoption has led to a dynamic landscape of optimization techniques [3,4], mainly favoring metaheuristic population-based methods.
A notable advancement is the Developed Grey Wolf Optimizer (DGWO) [5], refining Grey Wolf Optimization (GWO) to mitigate stagnation at local optima. Verified on the IEEE 30-bus test system, DGWO demonstrates superior performance in tackling the OPF problem when juxtaposed with other metaheuristic techniques. Ullah et al. [6] introduced Phasor Particle Swarm Optimization (PPSO) and Gravitational Search Algorithm (GSA) (PPSOGSA), a hybrid solution for OPF in wind and solar energy systems, presenting a comprehensive approach to overcome challenges associated with renewable energy integration. Elattar [7] integrated stochastic wind energy into the OPF problem, employing Modified Moth Swarm Optimization (MMSO) to enhance efficiency. The Modified Bacteria Foraging Algorithm (MBFA) has been introduced in [8], focusing on minimizing operational costs, reducing losses, and improving voltage security. Man-Im et al. [9] further developed Particle Swarm Optimization (PSO) to tackle multi-objective Optimal Power Flow (OPF) issues in wind energy systems. Salkuti [10] has proposed Glowworm Swarm Optimization (GSO) for a multi-objective OPF problem in a wind energy-integrated system. The landscape includes hybrid approaches like the optimization algorithms reported in [11], proving effective against other algorithms. Kathiravan et al. [12] employed the Flower Pollination Algorithm (FPA) for OPF in wind, thermal, and solar energy systems. Modified Artificial Bee Colony (MABC) has been introduced in [13] with a fuzzy-based approach for discrete OPF problems. Hybrid PSO-GWO [14] exceled in OPF problem-solving. Duman et al. [15] used Differential Evolutionary PSO (DEPSO) for OPF with controllable wind turbine and photovoltaic systems.
The array of approaches includes Multi-Objective Electromagnetism-Like Algorithm (MOELA) [16], Adaptive Gaussian TLBO (AGTLBO) [17], Chaotic Invasive Weed Optimization Algorithms (CIWOs) [18], and various iterations of multi-objective evolutionary algorithms [19]. MOALA [20], TLBO enhanced with Lévy mutation (LTLBO) [21], Constrained Multi-Objective Population External Optimization Algorithm (CMOPEO) [22], Slime Mould Algorithm (SMA) [23], Hybrid Optimizer via Genetic Algorithm and Teaching-Learning-Based Optimization (G-TLBO) [24], Hybrid Modified Imperialist Competitive Algorithm and Sequential Quadratic Programming Algorithm (HMICA-SQP) [25], BAT search algorithm [26], Developed Turbulent Flow of a Water-Based Optimizer (TFWO) [27], Multi-Objective Mayfly Algorithm (MOMA) [28], Bird Swarm Algorithm (BSA) [29], and Hybrid Differential Evolution and Symbiotic Organisms Search (DE-SOS) [30] contribute to the evolving toolkit for OPF challenges.
Furthermore, a hybrid multi-objective evolutionary algorithm has been proposed for solving constrained mixed-integer multi-objective Optimal Power Flow (OPF) in this article. The algorithm addresses the challenges of integrating Renewable Energy Sources (RESs) into power systems by considering both continuous and discrete decision variables [31]. Insights into the utilization and effectiveness of the whale migration algorithm (WMO) in optimizing power flow have been provided, contributing to the broader understanding of optimization techniques in power systems [32]. An extensive study utilizing beetle swarm optimization (BSO) to optimize single and multiple objectives in various OPF problems has been conducted, providing insights into its performance in addressing different power flow optimization scenarios [33]. The study has addressed the OPF of hybrid wind/solar/thermal energy integrated power systems, introducing a novel and efficient search optimization algorithm (modified turbulent flow of water-based optimization) for achieving optimal solutions. Simulations and comparisons have demonstrated the algorithm’s effectiveness in OPF while considering economic and environmental factors [34]. A multi-dimensional energy management approach utilizing an OPF model has been presented, incorporating an improved quasi-reflection jellyfish optimization (QRJFO) to OPF in complex energy systems. Simulation results have demonstrated the effectiveness of the algorithm in achieving optimal energy management and enhancing system performance [35]. A two-archive Harris hawks optimization (HHO) has been presented for efficiently solving many-objective OPF problems. The research has showcased the algorithm’s effectiveness in handling complex OPF challenges with many objectives through simulations and comparisons [36]. The study has introduced a multi-objective solution for OPF utilizing the Twin-Delayed Deep Deterministic (TD3) reinforcement learning algorithm. The research has demonstrated the capabilities of the TD3 method through simulations and comparative analyses [37]. A distributed approach for solving the AC–DC multi-objective OPF has been presented [38]. An improved cross-entropy method for solving OPF has been introduced to enhance convergence and solution quality in optimizing power systems [39]. The complexities of multi-objective optimization in power systems have been addressed, offering a distributed solution approach. Simulations and results have highlighted the effectiveness of the proposed method in achieving OPF in AC–DC systems [38]. The application of chaos-based chaotic invasive weed optimization (CIWO) techniques for solving environmental OPF problems in power systems has been explored [40]. Addressing the challenges of hybrid renewable energy systems, Monte Carlo simulation combined with a clustering technique has been utilized to solve probabilistic OPF, considering uncertainties in RESs and enhancing the accuracy of OPF [41]. An enhanced version of NSGA-III (Non-Dominated Sorting Genetic Algorithm III) integrating an eliminating strategy and dynamic constraint relaxation mechanism for solving many-objective OPF has been introduced [42]. A giant trevally optimization (GTO) has been introduced to handle probabilistic OPF in power systems with renewable energy uncertainty [43]. An improved MOEA/D algorithm has been proposed to enhance the efficiency and effectiveness of solving multi-objective optimization challenges in OPF [44]. The integration of advanced incremental PSO (AIPSO) in OPF for enhanced energy efficiency in modern power systems has been explored [45]. The Gaussian bare-bones Levy circulatory system-based optimization (GBLCSBO) has been introduced for OPF, particularly in the presence of RESs, focusing on enhancing power flow solutions in the context of RESs integration [46]. The application of the Harris hawks optimization (HHO) in addressing single-objective OPF has been explored [47]. The Grey Wolf Optimizer (GWO) has been employed to address single-objective functions in OPF, demonstrating its applicability and efficiency through simulations and comparisons [48]. A multi-objective OPF approach incorporating an emission index using the firefly algorithm (FA) has been introduced [49]. The multi-objective OPF of power systems has been addressed, employing an enhanced remora optimization (IRO) to tackle the complex challenges of OPF while considering multiple objectives [50].
In summary, the dynamic landscape of optimization techniques showcases innovative solutions and hybrid approaches, emphasizing the collective effort to address the evolving dynamics of power system optimization.
In our paper, we address the inherent weaknesses of metaheuristic population-based techniques in solving optimization problems, especially concerning renewable energy integration in power systems. These weaknesses include premature convergence, limited exploration capabilities, scalability issues with larger and more complex search spaces, and sensitivity to parameter settings requiring extensive tuning efforts. Additionally, challenges such as handling constraints effectively, lack of adaptability to evolving problem characteristics, and difficulty in maintaining solution diversity are highlighted. By recognizing these limitations, we introduce the Gaussian Bare-Bones Levy Cheetah Optimizer (GBBLCO) as a significant advancement in the field of OPF optimization. The motivation behind GBBLCO arises from a meticulous analysis of existing techniques and an understanding of the specific challenges posed by renewable energy integration, particularly in solar and wind power systems. Through a comprehensive examination of weaknesses associated with metaheuristic population-based techniques, we aim to fortify the foundations of GBBLCO. By leveraging principles from the Bare-Bones Cheetah Optimizer (CO) and integrating Gaussian and Levy flight enhancements, GBBLCO addresses the identified limitations of existing algorithms, enriching solution diversity and mitigating the risk of converging to local optima. Our comparative evaluation demonstrates GBBLCO’s superior performance, substantiating its efficacy in delivering optimal OPF solutions for power systems with renewable energy sources. Furthermore, our analysis delves into the unique challenges posed by solar and wind power systems, elucidating how GBBLCO is uniquely suited to solve them through its adaptive search strategies and robust optimization framework. Overall, our contributions establish GBBLCO as a pioneering solution poised to advance the state-of-the-art in OPF optimization, particularly in the context of modern power systems integrating renewable energy.
Furthermore, the introduction of GBBLCO is grounded in a comparative framework, where benchmark algorithms, including CO [51], Moth-Flame Optimization (MFO) [52], Elephant Herding Optimization (EHO) [53], Whale Optimization Algorithm (WOA) [54], and Bare-Bones PSO (BBPSO) [55], are assessed. This comparative evaluation serves to empirically demonstrate the superior performance of GBBLCO, substantiating its efficacy in delivering optimal OPF solutions for power systems with renewable energy sources.
The subsequent sections of the paper provide detailed insights into the OPF problem formulation, wind-solar power models, the original CO algorithm, and the proposed GBBLCO method. Additionally, the experimental study settings, benchmarks, and standards are comprehensively detailed. Finally, the conclusion section summarizes key findings and suggests avenues for future research.
2 Formulation of OPF Including Wind-Solar Energy Systems
The OPF problem assumes a central role in optimizing control parameters for economic and stable power system operation. This study is dedicated to integrating wind and solar energy into the classical OPF framework, seeking to minimize total operating costs, encompassing the fuel expenses of conventional thermal generators.
2.1 Objective Function and Variables
The overarching objective function Z denoted as f(X,Y), governs the optimization landscape of the OPF problem. This function encapsulates a comprehensive representation of the interplay between the decision variables X and Y, intricately woven into the fabric of the power system’s operational dynamics. The selection of these variables is pivotal in shaping the efficacy and efficiency of the optimization process. As we delve into the subsequent sections, a nuanced exploration of the multifaceted components constituting the objective function and the associated variables will be undertaken. This comprehensive analysis aims to shed light on the intricate optimization mechanisms deployed to enhance the economic and stable operation of power systems.
The overarching objective function, denoted as Z, is expressed as:
Z=f(X,Y)(1)
This function represents a comprehensive interplay between decision variables X and Y, governing the optimization landscape intricately woven into the power system’s operational dynamics. The objective is to optimize the system for economic and stable operation, and the specific definition of Z involves the active power of the slack generator (Pslack), voltage values of PQ buses (VL), reactive powers of wind power, thermal generating units, and the solar system (QWind,QSolar, and QThermal), as well as the apparent power of transmission lines (SL). Independent variables Y include the active powers of solar (PV) systems and thermal generating units (PPVS and PTh), the voltage values of all generator buses (VG), and the active power of wind farms (PWS). The formulation also considers the number of wind farms, thermal generating units, solar energy systems, transmission lines, and PQ buses (NW, NTHG, NPV, NTL, and NPQ).
2.2.1 Fuel Cost Modeling for Thermal Generating Units
In the context of the fuel cost model for thermal generating (TH) units, the classical fuel cost function is mathematically expressed as follows:
F(PTh)=∑NTHGi=1aiP2Th,i+biPTh,i+ci(2)
Here, PTh represents the total active power output of thermal generating units, NTHG is the total number of thermal generating units, and ai, bi, ci are coefficients associated with each unit. The function captures the relationship between the total active power output and the corresponding fuel cost, incorporating quadratic and linear terms along with constant coefficients for each unit. This model is fundamental for assessing the economic aspects of thermal generating units in the power system.
Moreover, when considering the valve point effect, the term |pi×sin(ri×[PminTh,i−PTh,i])| can be seamlessly integrated into the equation. Here, pi represents the valve point coefficient, ri is the valve point parameter, and PminTh,i denotes the minimum power output of the i-th thermal generating unit. This additional term captures the impact of valve point effects on the fuel cost, offering a more nuanced understanding of the economic dynamics in the context of thermal power generation.
2.2.2 Modeling Emissions from Thermal Generating Units
In the scope of this investigation, the total emission value is expressed by the following equation:
E(PTh)=∑NTHGi=1(σi+βiPThi+τiP2Thi)×0.01+ωie(μiPThi)(3)
Here, the terms σi, βi, τi, ωi, and μi correspond to the emission coefficients, each contributing to the comprehensive emission model. This refined formulation provides a thorough insight into the environmental impact associated with the operation of thermal generating units.
2.2.3 Modeling Prohibited Operating Zones in Thermal Generating Units
In this subsection, we delve into the intricacies of prohibited operating zones (POZs) concerning the optimal operation of thermal generating units. The concept involves defining and quantifying limits to ensure the efficient and reliable functioning of these units. A thermal generating unit with prohibited operating zones (POZs) is identified as:
Ui=∑Miy=1[PTh−(πy,i−πy−1,i)].(πy,i−πy−1,i)(4)
The parameter Mi signifies the total number of POZs, while πy−1,i and πy,i represent the lower and upper bounds of the yth POZ for the ith generator. Understanding and managing these prohibited operating zones are crucial for achieving optimal performance and stability in power systems with thermal generating units.
2.2.4 Cost Modeling for Wind and PV Energy Systems
The cost model for wind energy is represented through its direct cost coefficient, denoted as θWS,i:
CWS,i=θWS,iPWS,i(5)
Similarly, the direct cost model for the photovoltaic power system is expressed by the corresponding direct cost coefficient, θPVS,i, as follows:
CPVS,i=θPVS,iPPVS,i(6)
2.2.5 Cost Models Accounting for Uncertainty in Wind and PV Energy Systems
To capture the inherent uncertainties in renewable energy sources (RESs), the following models are employed.
• For wind power systems:
CUWS,i=δUWS,iPWS,i−ϵUWS,iPWSrated,i(7)
where δUWS,i,ϵUWS,i are overestimation and underestimation cost coefficients. PWS,i, PWSrated,i are rated and available powers of the ith wind power system.
• For PV energy systems:
CUPVS,i=δUPVS,iPPVS,i−ϵUPVS,iPPVSrated,i(8)
where
δUPVS,i, ϵUPVS,i are overestimation and underestimation cost coefficients.
PPVS,i, PPVSrated,i are rated and available powers of the ith PV energy system.
The objective function of the active power losses can be formulated as follows:
ZLoss=∑NTLs=1Ks(αi−αj)(9)
where Ks represents the conductance of the sth transmission line between buses i and j. αi−αj is the difference in voltage angles of buses i and j.
2.2.7 Voltage Deviation (V.D.)
The voltage deviation value in the proposed OPF problem is calculated as follows:
ZV.D.=∑Nbusi=1|Vi−1|(10)
2.2.8 Voltage Stability Index (VSI)
The integration of renewable energy sources (RESs) into electrical grids has emerged as a pivotal strategy in addressing energy sustainability and environmental concerns. Among RESs, wind power generation has witnessed significant growth and adoption worldwide due to its abundant resource availability and technological advancements. However, the inherent variability and unpredictability of wind power pose challenges to the stability and reliability of electrical grids.
The VSI formulation and the objective function in OPF have been calculated as follows [27,56,57]:
Lj=1−∑Ngi=1(−[YLL]−1[YLG])ViVj∠(θij+δi−δj)(11)
VSI=Min(Lj):j=1,2,…,Nbus(12)
where YLLYLG indicate sub-matrices of Y-Bus matrix. δi and δj represent the voltage phase angles of the buses i and j, respectively.
Equality constraints include active and reactive powers, voltage magnitudes, and angle differences.
Inequality constraints encompass both maximum and minimum bounds on active and reactive power values, as well as voltage magnitudes.
2.4 Fitness Function for SCOPF
The fitness function for the Security Constrained OPF (SCOPF) problem incorporates penalty coefficients:
SCOPF=Z(.)+Penalty_terms(13)
Here Z(.) is the considered objective function(s), and Penalty_terms corresponds to the penalty terms of the constraints. This comprehensive formulation and optimization approach contributes to advancing OPF methodologies, particularly in the context of integrating RESs into modern power systems.
In our study, we aim to tackle various objectives in electrical grid optimization, such as reducing operational costs, managing voltage fluctuations, and minimizing pollutants and power losses. To balance these competing goals, we employ a weighted sum approach for multi-objective optimization. These weightings, crucial for the algorithm’s performance, have been extensively researched and validated in prior studies. In our research, we maintain consistency with these established weightings for fair comparison with previous results. Through careful consideration and experimental validation, our study demonstrates the effectiveness of our approach in achieving a well-balanced and efficient optimization of the electrical grid.
3 Wind-PV Uncertainty and Power Models
Within the realm of power models and wind-PV uncertainty, the representation of wind speed distribution utilizes the Weibull probability density function (PDF). This mathematical expression is defined as:
f(vw;ξ,ψ)=ξψ(vwψ)ξ−1e−(vw/ψ)ξ(14)
incorporates parameters vw, ξ and ψ denoting the wind speed, shape and scale factors, respectively. This Weibull PDF serves as a fundamental tool for characterizing the probability distribution of wind speeds. The subsequent analysis and utilization of this distribution contribute to a comprehensive understanding of the stochastic nature inherent in wind power systems.
Fig. 1 displays the outcomes of the Weibull fitting concerning wind frequency distributions derived through an 8000-iteration Monte Carlo simulation [3,58]. The wind power system’s power output is determined as follows:
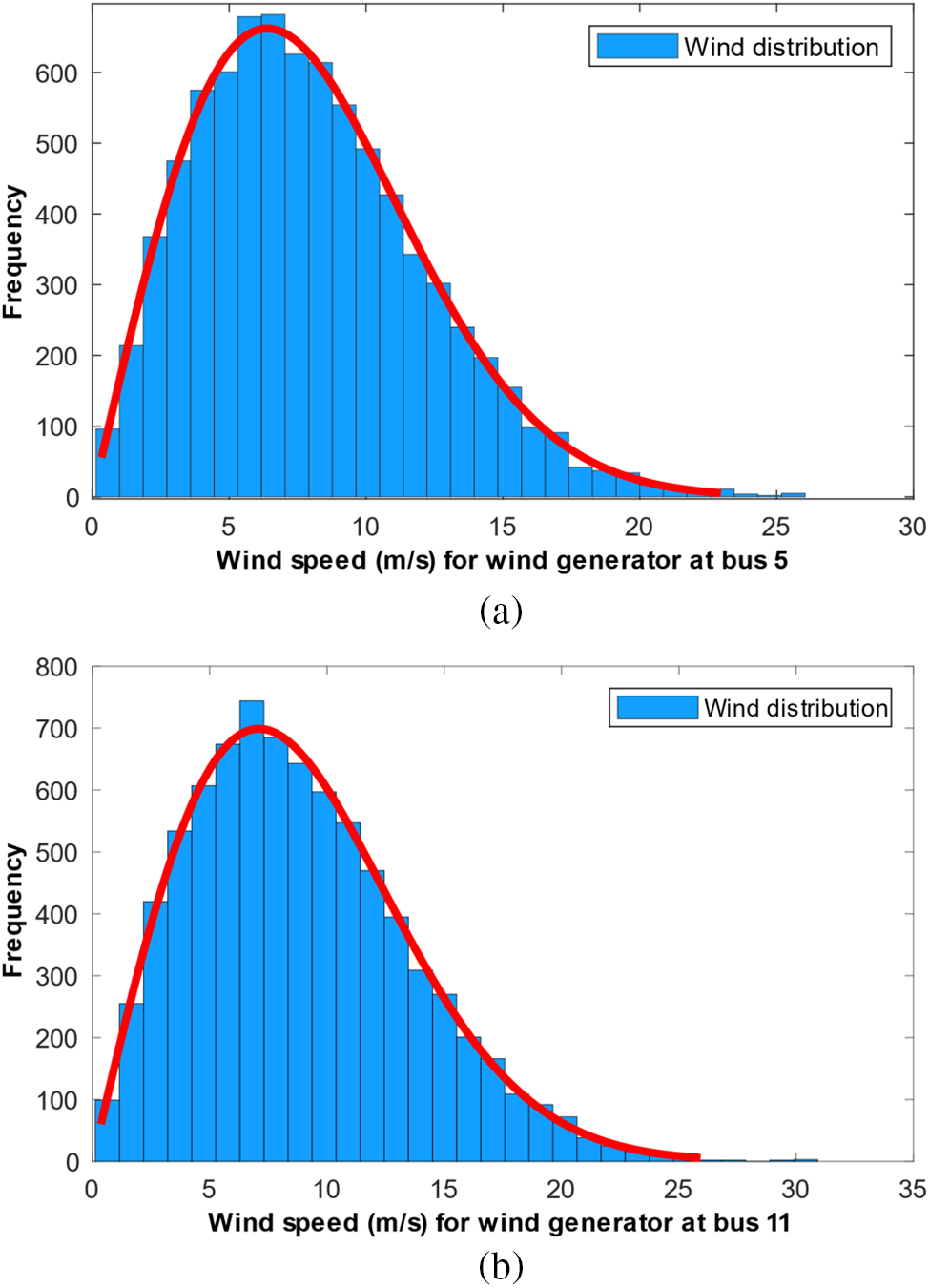
Figure 1: Weibull fitting of WPG’s distributions at bus 5 (a), and bus 11 (b)
Pwind={0vw<vwinpwr(vw−vwinvwr−vwin)3vwin≤vw<vwrpwrvwr≤vw<vwout0vw≥vwout(15)
where pwr, vwout, vwin, and vwr are, respectively, the rated power, cut-out, cut-in, and rated wind speeds.
Table 1 provides a detailed overview of the parameters associated with the probability density function (PDF) for both wind and photovoltaic (PV) energy systems. This tabulated information encompasses critical elements that characterize the probabilistic behavior of these energy sources, contributing essential insights for system analysis and optimization. For each turbine, the chosen wind speeds and rated power values are vwin=3 m/s, vwr=16 m/s, vwout=25 m/s, and 3 MW, respectively [3,58].

The power output of the PV energy systems, which is contingent on solar irradiation, is modeled using the Lognormal PDF. The mathematical representation and output power of the solar system are expressed as follows:
f(x;ζ,Ω)=1xΩ√2πe−(ln(x)−ζ)2/(2Ω2)(16)
PPV=Gpv×eGpvstdZ+Ppvrate(17)
Gpvstd, Gpv, and Ppvrate are the standard solar irradiance, probability value, and rated power of the solar system, respectively. The Lognormal PDF parameters are denoted by Ω and ζ for standard deviation and mean, respectively. The solar irradiance, represented by x, serves as the focus of this study. Z stands as the random variable in this context.
Fig. 2 presents lognormal Probability Density Functions (PDFs) for solar irradiance and photovoltaic (PV) power generation at bus 13. Fig. 2a displays the PDF of solar irradiance, offering insights into the likelihood of different irradiance levels at the specific location. Fig. 2b illustrates the PDF for PV power generation, providing a graphical representation of the probability distribution associated with varying levels of PV output. These distributions are essential for understanding the intermittent nature of solar energy and optimizing power systems with renewable sources, aiding in decision-making for efficient energy management.
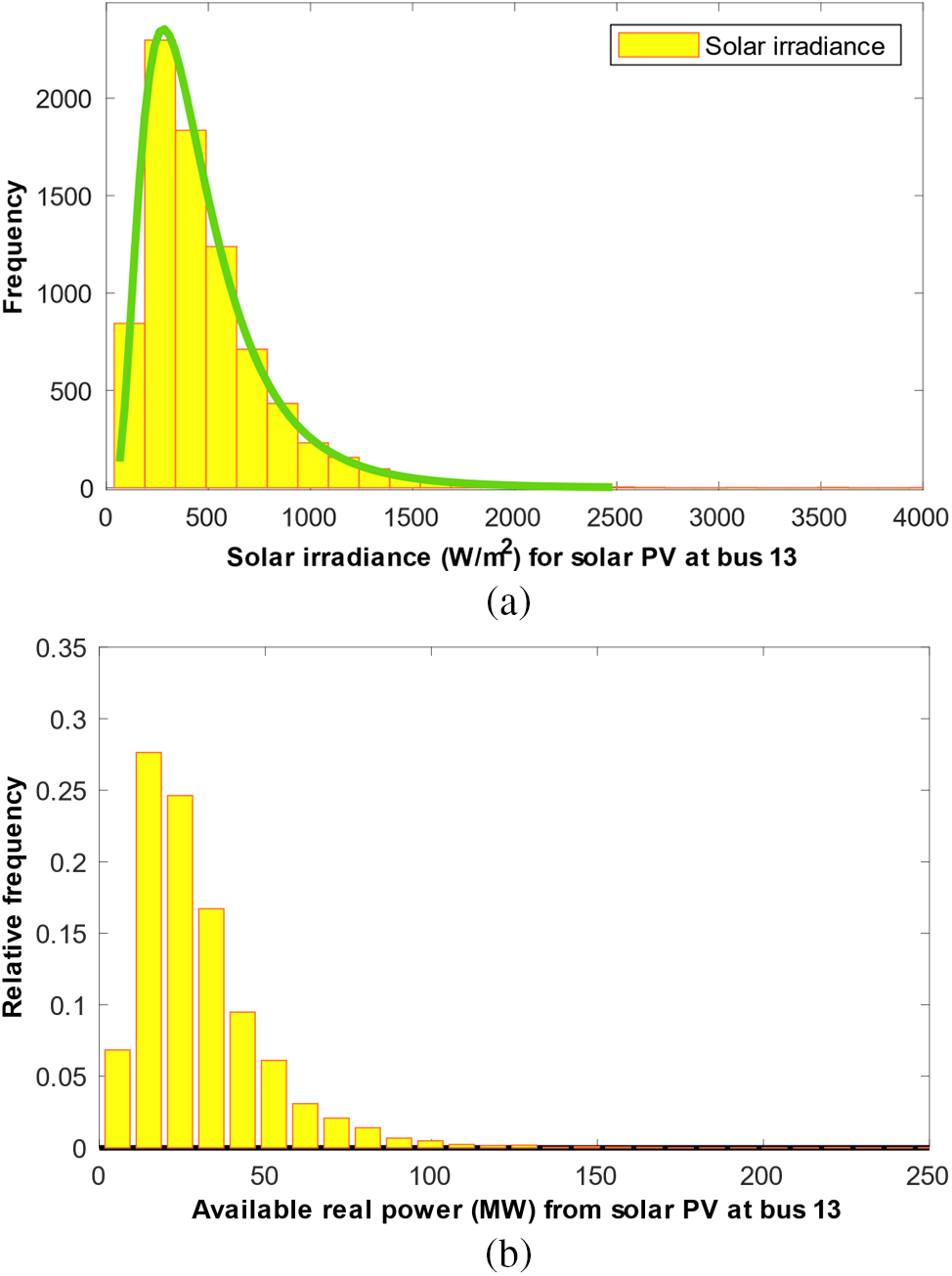
Figure 2: The lognormal PDF of solar irradiance (a), and PV power generation (b) at bus 13
The Cheetah Optimizer (CO) algorithm employs intelligent hunting strategies throughout its iterative hunting periods. The primary phases of CO are outlined as follows [51]:
Cheetahs adopt two distinct methods to locate prey during the hunting process. First, they may scan the environment while stationary or actively patrol the area. The choice between these modes depends on factors such as prey density, environmental coverage, and the cheetahs’ conditions. Mathematically, the cheetah’s position Xti,j in arrangement j is updated using a random search equation:
Xt+1i,j=Xti,j+ˆr−1i,j.αti,j(18)
In the given context, t signifies the ongoing hunting period, while T denotes the maximum duration allocated for hunting. The terms ˆr−1i,j and αti,j stand for the randomization parameter and step length, respectively. The randomization component adheres to a normal distribution, and the adjustment of αti,j is contingent on the spatial separation between cheetahs.
When prey is within sight during the search mode, cheetahs may choose to remain stationary and wait for the prey to approach. This strategy aims to prevent the prey from escaping due to the cheetah’s movement:
Xt+1i,j=Xti,j(19)
This approach enhances hunting success and avoids premature convergence by not simultaneously changing all cheetahs in each group.
In the assault phase, cheetahs harness their speed and agility to chase down prey. The recalibrated position of a cheetah in attack mode hinges on the current location of the prey:
Xt+1i,j=XtB,j+ˇri,j.βti,j(20)
In this context, XtB,j denotes the present location of the prey in arrangement j. The factors ˇri,j and βti,j come into play as the turning and interaction elements, respectively. The turning factor βti,j embodies the interplay among cheetahs, while ˇri,j injects randomness, simulating the abrupt turns characteristic of the capturing mode.
In this visual representation, the Cheetah Optimizer (CO) algorithm mimics the hunting strategies of cheetahs during the optimization process, as shown in Fig. 3. The figure depicts three key phases. The first cheetah (X1) is engaged in the search strategy. It actively patrols the environment, scanning for prey. Arrows illustrate its adaptability, choosing between active patrolling and standing depending on the prey’s condition. The second cheetah (X2) adopts the sit-and-wait strategy. Positioned strategically, it lies in wait for the prey (green star, XB). This strategy enhances the likelihood of capturing the prey without alerting it. The third cheetah (X3) transitions into the attack strategy. It uses speed and flexibility to pursue the prey (XB). Arrows show the rapid pursuit, and adjustments in direction are made to intercept the prey and block its escape route. Fig. 3 encapsulates the dynamic and adaptive nature of the CO algorithm, mirroring the versatile hunting behaviors of cheetahs. The strategies seamlessly transition in a continuous loop, optimizing the search for the best solution.

Figure 3: Cheetah hunting strategies
For the complete set of assumptions and the detailed CO algorithm, refer to the pseudo code provided in Algorithm 1.

4.5 Gaussian Bare-Bones Levy Cheetah Optimizer (GBBLCO)
The GBBLCO algorithm introduces enhancements inspired by both Bare-Bones Particle Swarm Optimization (BBPSO) and Levy flights, creating a dynamic and versatile optimization approach [41].
Originating from Particle Swarm Optimization (PSO), BBPSO refines the convergence behavior by eliminating the velocity term. The position update is governed by the following equation [59,60]:
Xt+1j=Xtj+N(μ,σ)⋅rand j(0,1)⋅Pbestt+Gbestt2(21)
where N(μ,σ) represents a Gaussian distribution with mean μ and standard deviation σ, and rand j(0,1) is a random value within [0,1] for the j-th dimension.
Incorporating the Levy-flight characteristics, the algorithm introduces a new Levy-flight CO (LCO) mechanism. This is achieved by randomization via Levy flights with a randomization parameter C, utilizing the following equation:
Xt+1j=Xtj+α.Levy(22)
The Levy is defined as [44]:
Levy=1(rand1/β)⋅rand j(0,1)(23)
where β=1.5 and α=0.001.
4.5.3 Mathematical Model of GBBLCO
Expanding on the search strategies observed in BBPSO, GBBLCO integrates Gaussian sampling as a refined exploration and exploitation technique. The novel search, sit-and-wait, and bare-bones attack strategies are outlined as follows:
• New Search Strategy:
Xt+1i,j=Xti,j+ri,j∗αti,j+αsign[rand−12]⊕Levy(24)
• New Sit-and-Wait Strategy:
Xt+1i,j={XtB,j+αsign[rand−12]⊕Levy,rand≥0.99Xti,jotherwise.(25)
• New Bare-Bones Attack Strategy:
Xt+1i,j={N(Xti,j+Xtk,j2,|Xti,j−Xtk,j|)+αsign[rand−12]⊕Levy,rand>0.85N(Xti,j+XtB,j2,|Xti,j−XtB,j|)+αsign[rand−12]⊕Levy,rand<0.15XtB,j+ri,j∗βti,j+αsign[rand−12]⊕Levy,otherwise.(26)
The proposed GBBLCO integrates several enhancements that could potentially address the local minima issues encountered by the original CO in optimizing power flow problems:
1. Enhanced Exploration: GBBLCO introduces Gaussian sampling as part of its search strategy, allowing for a more robust exploration of the search space. This enhanced exploration capability can help the algorithm escape local minima traps by enabling it to explore a wider range of solutions.
2. Diverse Search Strategies: GBBLCO incorporates multiple search strategies, including a new sit-and-wait strategy and a bare-bones attack strategy. By diversifying its search approach, GBBLCO can effectively explore different regions of the solution space, reducing the likelihood of getting stuck in local minima.
3. Levy Flights: By incorporating Levy flights into its mechanism, GBBLCO introduces a level of randomness that can facilitate escape from local optima. Levy flights enable the algorithm to make large jumps in the search space, potentially helping it overcome local minima by exploring new regions more efficiently.
4. Adaptive Parameter Tuning: GBBLCO adjusts its parameters dynamically during the optimization process, allowing it to adapt to changes in the landscape of the solution space. This adaptability can help the algorithm navigate around local minima by adjusting its search behavior accordingly.
Overall, the combination of enhanced exploration, diverse search strategies, incorporation of Levy flights, and adaptive parameter tuning in GBBLCO provides a more robust framework for tackling local minima issues compared to the original CO algorithm.
The flowchart depicted in Fig. 4 delineates the key stages and processes of the proposed algorithm, the Gaussian Bare-Bones Levy Cheetah Optimizer (GBBLCO). By incorporating enhancements from the Bare-Bones Cheetah Optimizer (CO) and integrating Gaussian and Levy flight strategies, GBBLCO emerges as a robust and adaptive algorithmic framework. The flowchart visually guides through the algorithmic steps, showcasing the innovative features that collectively contribute to GBBLCO’s efficacy in addressing optimal power flow challenges in electrical networks with renewable energy sources.
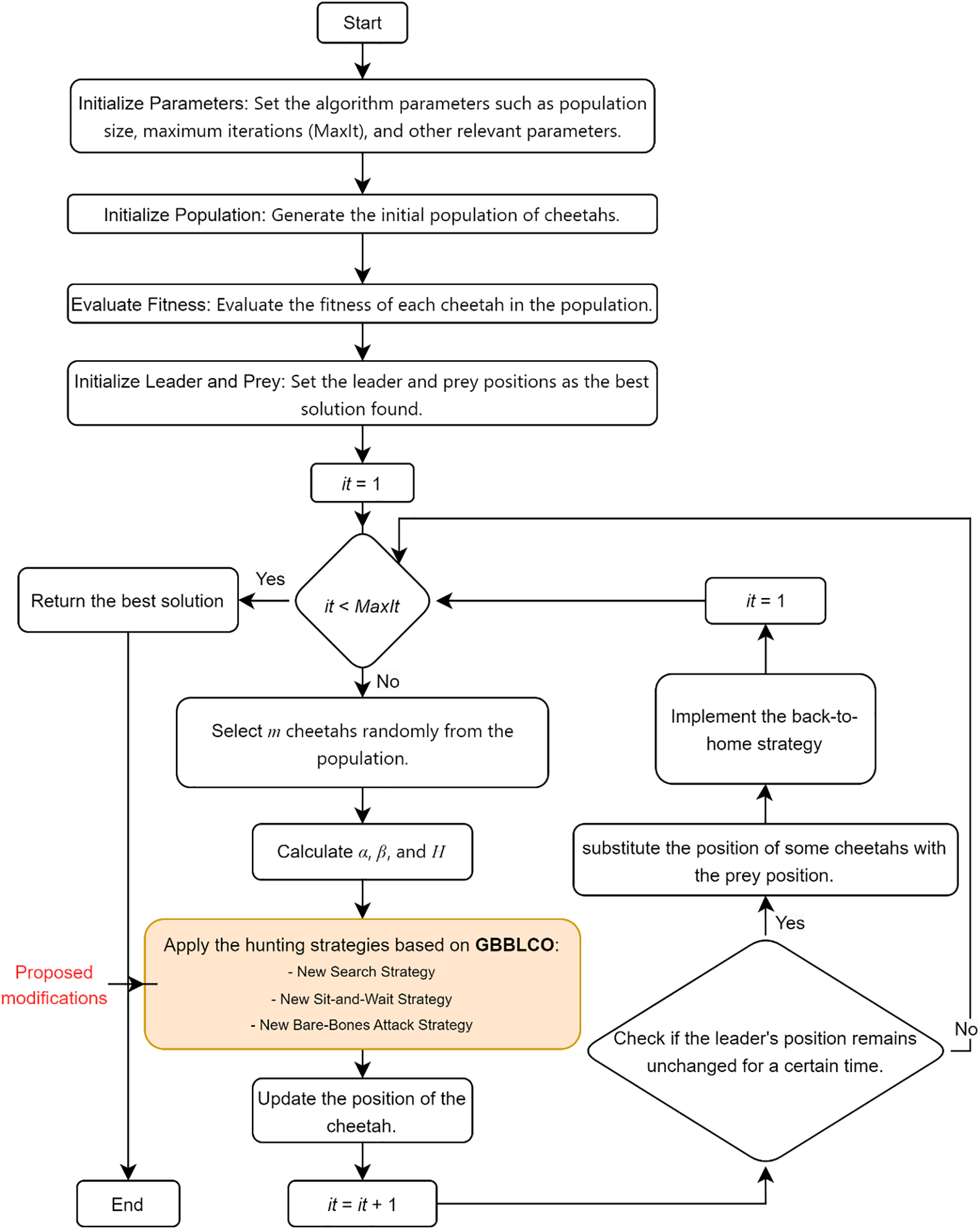
Figure 4: Flowchart of the proposed GBBLCO algorithm
5 Simulation Results: Comprehensive Analysis of Diverse OPF Scenarios
5.1 Experimental Setup and System Characteristics
The basic CO, MFO, EHO, WOA, BBPSO, and GBBLCO methods were studied on the IEEE 30-bus test system, as demonstrated in Fig. 5, to solve OPF problem involving wind and solar energy systems. The test system comprises 30 buses and 41 branches, with three thermal generating units located at buses 1, 2, and 8. Additionally, there is one swing generator at bus 1, two wind generators at buses 5 and 11, and a solar energy system at bus 13. The system also includes four transformers at branches 11, 12, 15, and 36, as well as two shunt capacitor banks at buses 10 and 24. A total of 11 control variables are employed, covering thermal, wind, and solar generating systems, along with the voltages of generator buses. The system’s total active and reactive loads are 283.4 MW and 126.2 MVAR, respectively. The PQ bus voltage limits are set within the range of [0.95–1.05] per unit. These characteristics, as detailed in the reference [61], form the basis for the experimental setup and evaluation of the proposed optimization algorithm.
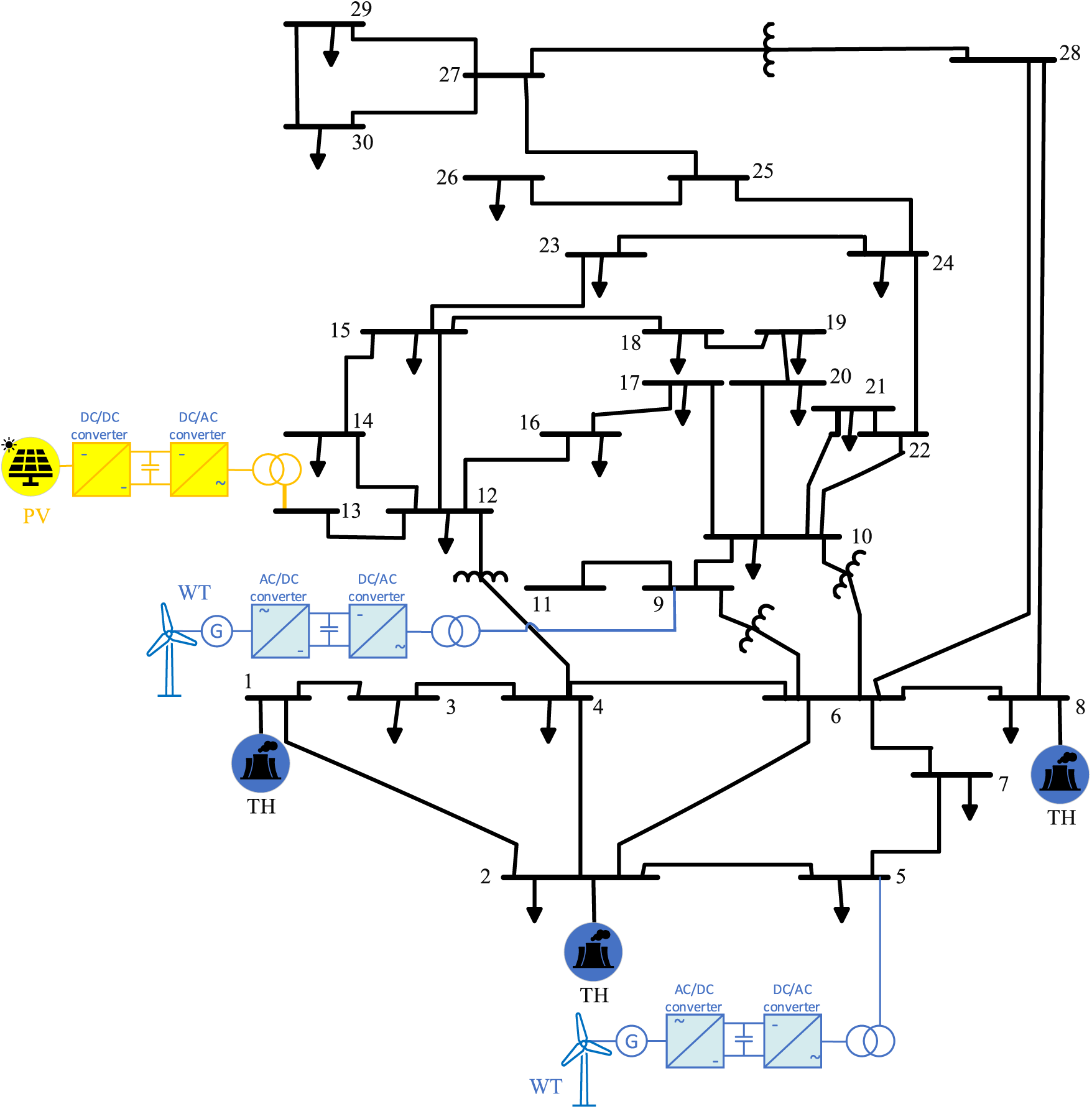
Figure 5: The IEEE 30-bus test system
Also, the control parameters of the optimization algorithms have been taken from references and given in Table 2. The system parameters of the IEEE 30-bus test system were taken from references [3,15], and shown in Table 3.
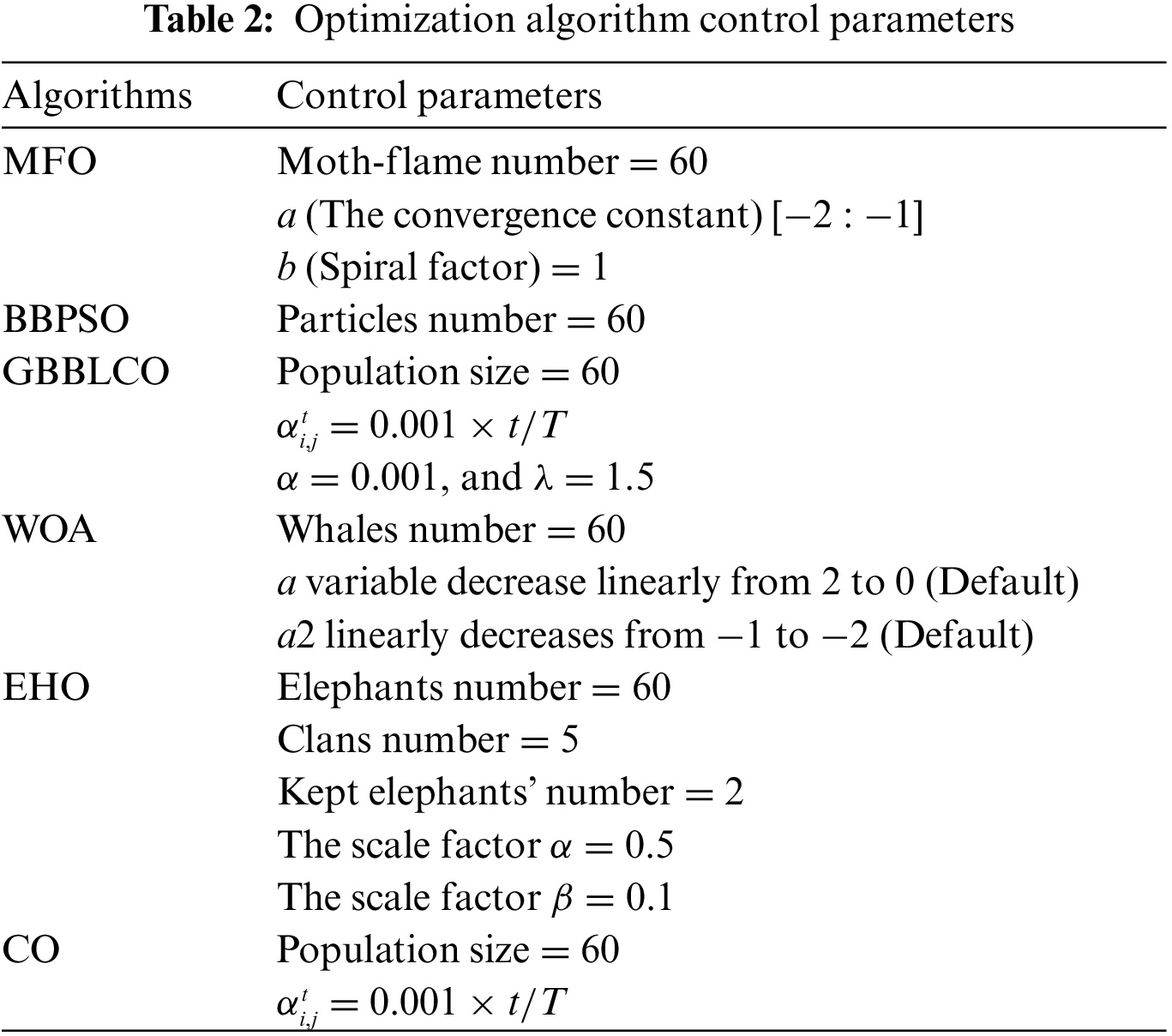

The load flow equations of the OPF problem, wind, incorporating thermal, and solar generating systems, were computed using MATPOWER [62,63]. To ensure statistical robustness, each optimization algorithm was executed 30 times across all test cases of the proposed OPF problem. The simulation studies adhered to the test cases outlined in the subsequent sections.
5.2 Exploring Diverse OPF Scenarios: A Comprehensive Analysis
In the subsequent section, we present the simulation results of various scenarios to assess the performance and robustness of the proposed OPF formulations. Each scenario represents a distinct configuration aimed at addressing specific challenges in power system optimization. The diverse cases encompass considerations such as valve point effects for thermal units, emissions and taxes, quadratic cost functions with POZs, active power losses, voltage stability index (VSI), and voltage deviations. The following analysis provides valuable insights into the effectiveness of the developed OPF formulations across a spectrum of real-world conditions.
This study examines six cases addressing different challenges in OPF. These cases involve integrating cost functions, considering emissions and taxes, exploring quadratic cost functions with POZs, and incorporating considerations for active power loss and voltage deviation. Detailed descriptions of each case are provided in the subsequent sections.
5.2.1 Multi-Objective Optimization for Total Cost Minimization with Valve Point Considerations (Case 1)
In this context, the objective is to minimize the total cost by utilizing a quadratic cost function with VPE for thermal generators and incorporating a cost model for wind and photovoltaic (PV) energy systems. The aim is to optimize the scheduled output powers from various energy sources within the modified power system, striving for the lowest basic power cost.
Table 4 provides a comprehensive summary of optimization outcomes, featuring the best, worst (Max), average (Mean), and standard deviation (Std.) values from 30 independent runs. The comparison includes EHO, TEO, MFO, PSO, and CSBO algorithms, along with the proposed GBBLCO method. The results of Case 1 underscore the remarkable effectiveness of GBBLCO. GBBLCO surpasses conventional optimization techniques such as CO, MFO, EHO, WOA, and BBPSO in OPF, showcasing rapid convergence and superior solution quality. Among the various algorithms employed, GBBLCO achieves an outstanding total power cost minimization of 781.9005 $/h.
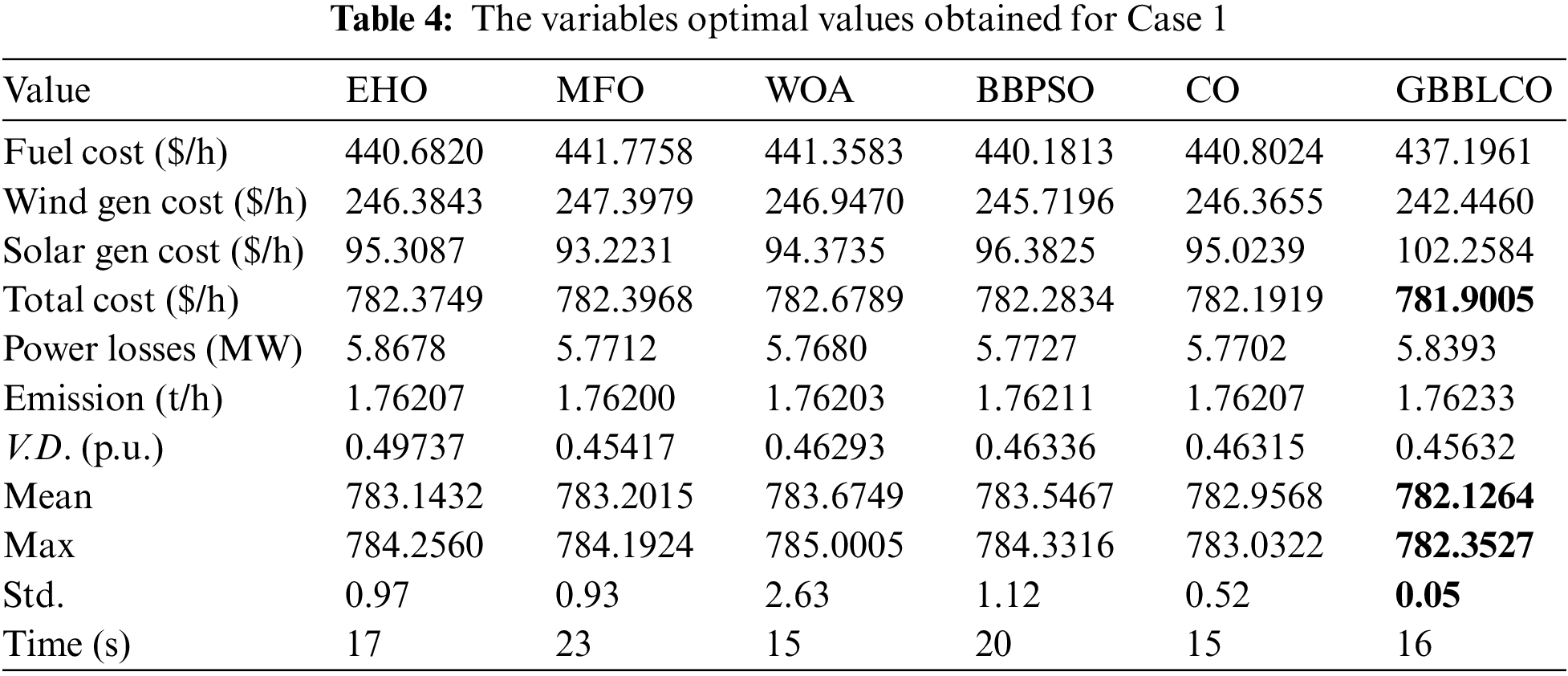
Fig. 6 visually illustrates the convergence patterns of various OPF optimization techniques, emphasizing the distinct performance of GBBLCO in achieving optimal solutions.
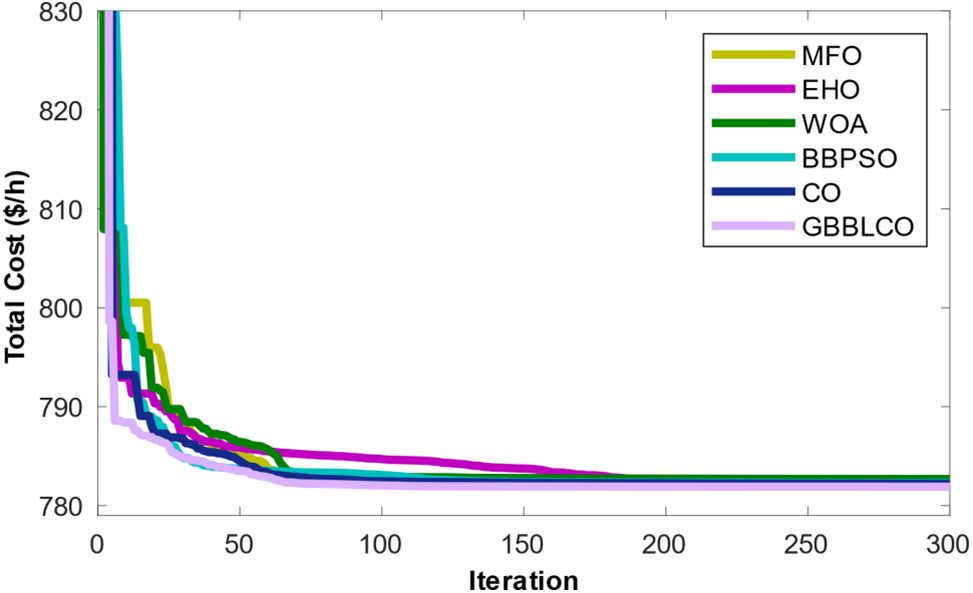
Figure 6: Convergences of the optimization techniques for Case 1
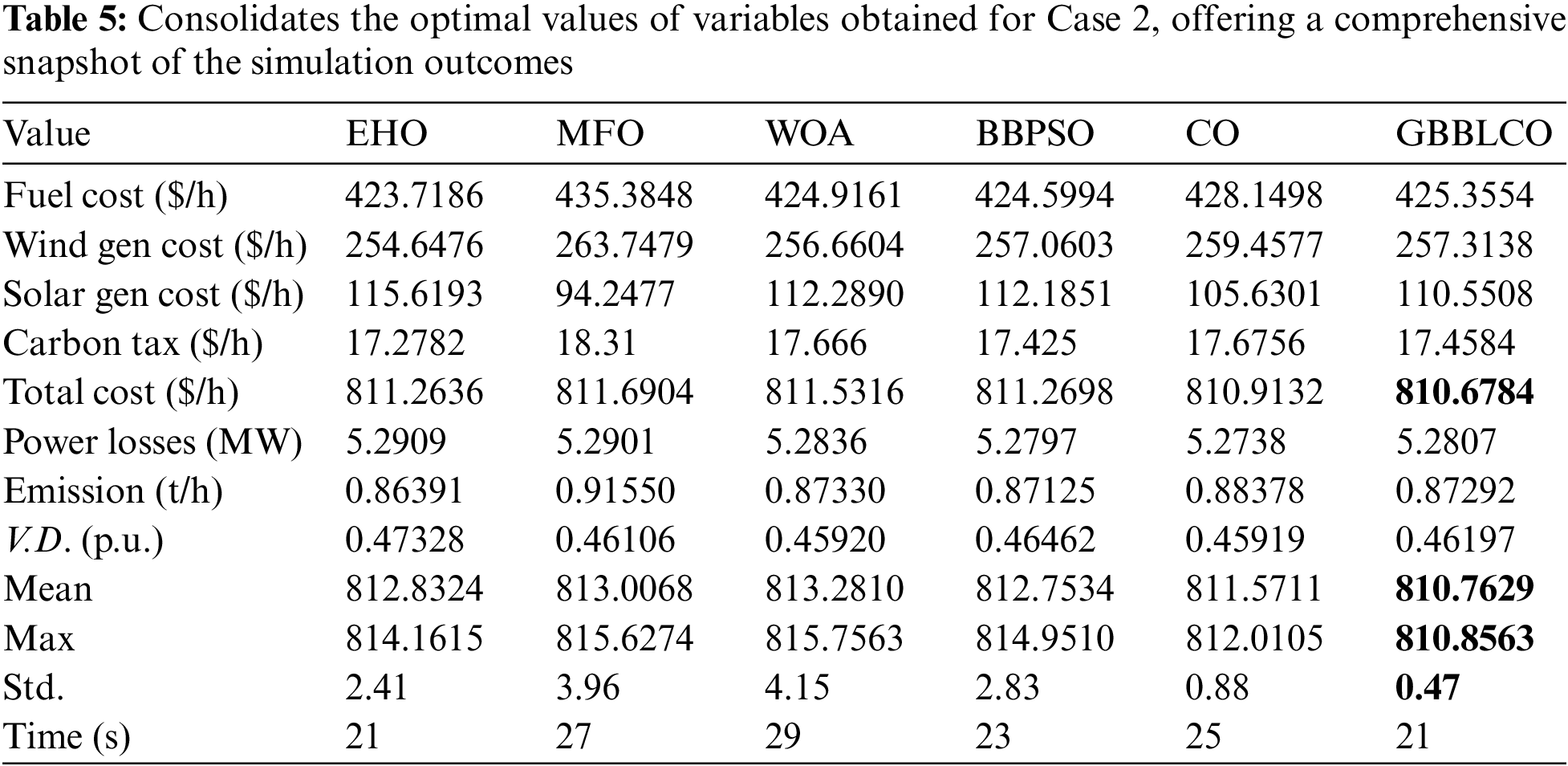
5.2.2 Strategic Optimization: Minimizing Comprehensive Costs through Emission-Aware Decisions and Carbon Tax Integration (Case 2)
In this distinct case, the primary objective is to optimize the total power cost while addressing environmental concerns by incorporating a fixed carbon tax (Carbon_tax) on thermal power generators, acknowledging their CO2 emissions. The prescribed Carbon_tax is established at 20 ($/ton) [58]. Through this simulation, the study explores how the enforced carbon tax influences the power grid, promoting increased integration of wind and solar energy sources.
Fig. 7 illustrates the distinct convergence patterns exhibited by various optimization algorithms, offering a visual representation of their performance. A detailed comparative analysis of overall cost, control variables, reactive powers, and additional parameters is meticulously presented in Table 5. Significantly, GBBLCO showcases notable efficacy by achieving a minimal total power cost of 810.6784 $/h. This highlights the clear superiority of GBBLCO over conventional CO and other applied techniques, not only in terms of cost minimization but also in the convergence of solutions.
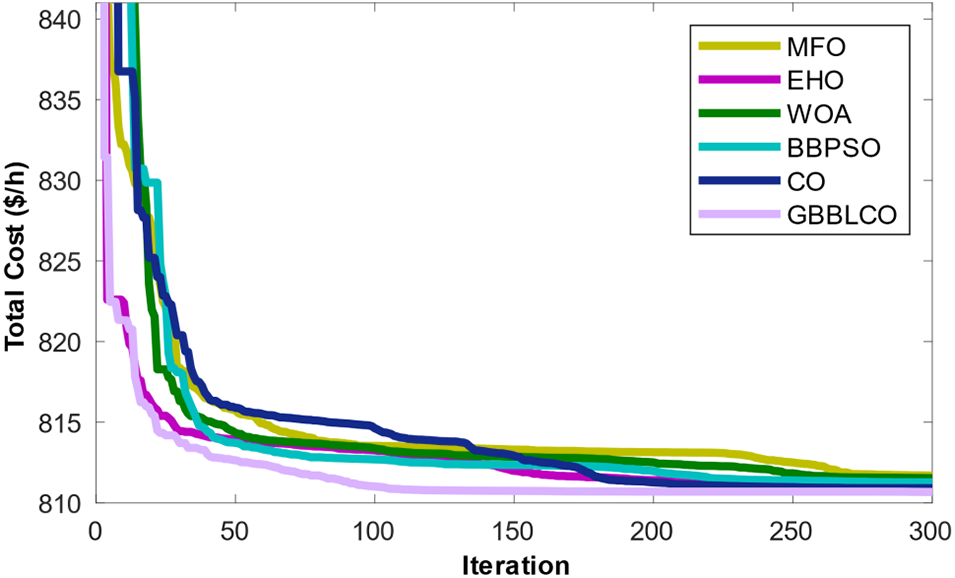
Figure 7: Convergences of the optimization techniques for Case 2
5.2.3 Maximizing Efficiency through Prohibited Operating Zones Integration (Case 3)
This case delves into the intricacies of optimizing total costs while factoring in POZs alongside the financial models for both wind and PV energy systems, aligning with the specified objective function in Eq. (10). As with the previous cases, the comparative analysis of GBBLCO, CO, MFO, EHO, WOA, and BBPSO algorithms’ convergence is visually depicted in Fig. 8. Meanwhile, Table 6 meticulously outlines the optimal results pertaining to reactive powers, control variables, overall cost, and additional parameters.
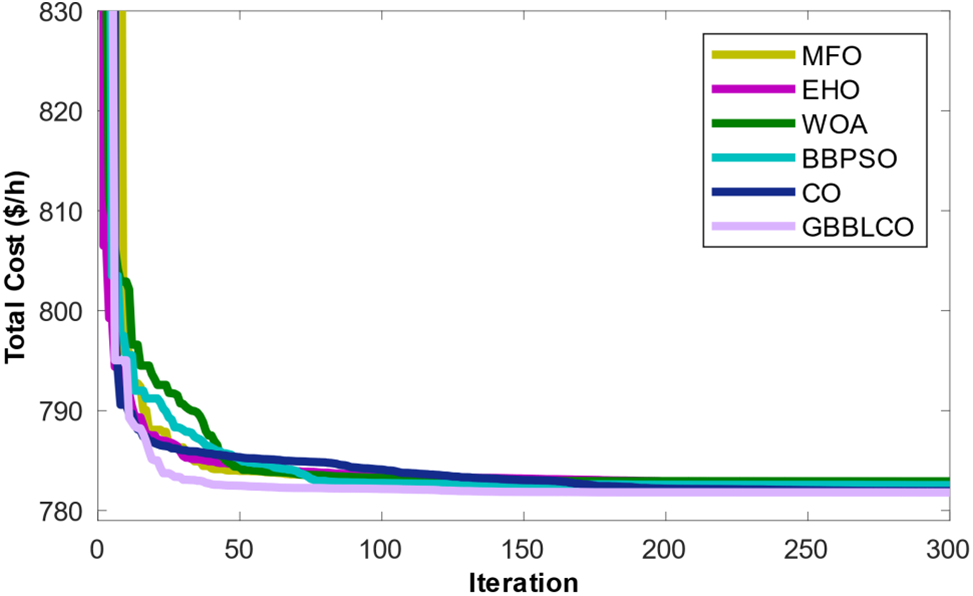
Figure 8: Convergences of the optimization techniques for Case 3
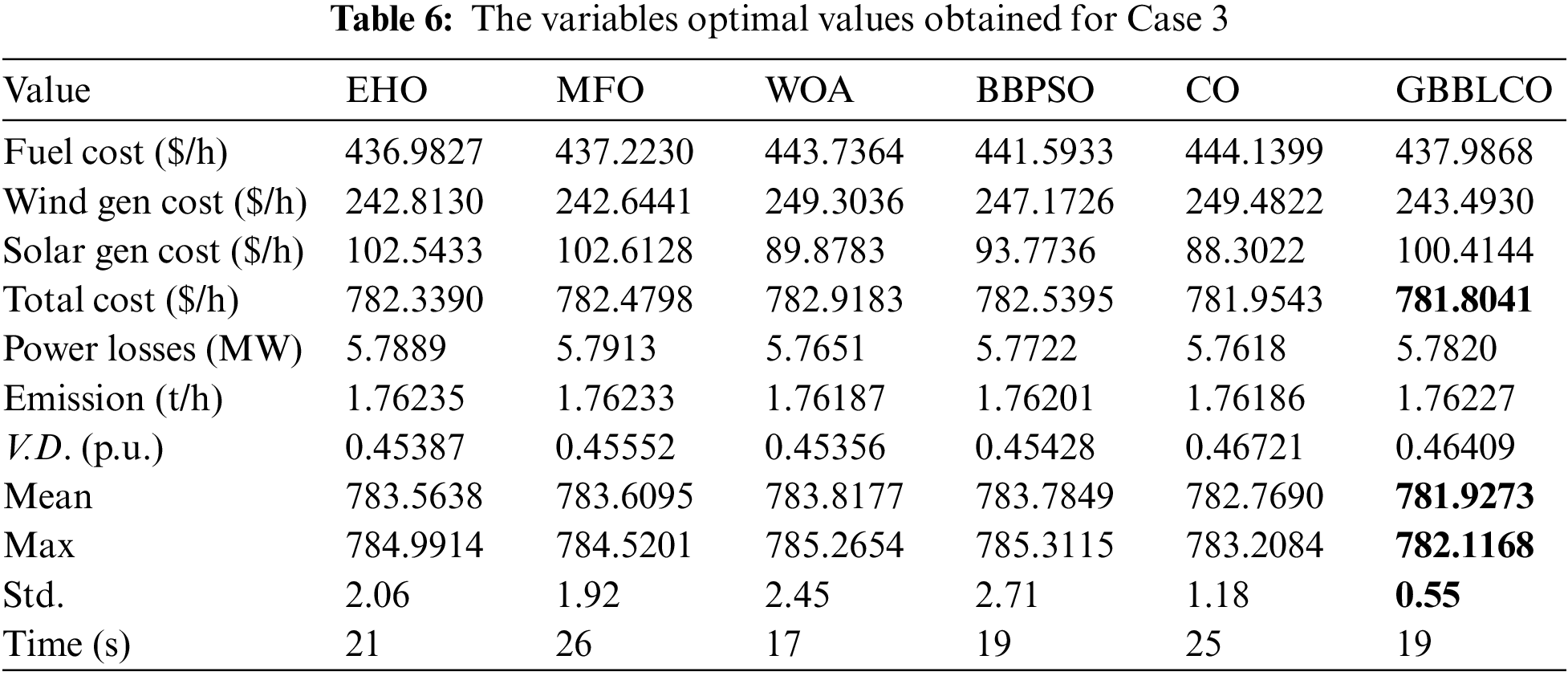
The simulation outcomes for Case 3 reveal that the proposed GBBLCO algorithm yields a noteworthy total power cost of 781.8041 $/h, surpassing the results obtained from conventional CO and other benchmark methods. This underscores GBBLCO’s efficacy in achieving superior optimization outcomes. The integration of POZ considerations, along with wind and PV energy system cost models, further exemplifies the adaptability and robust performance of GBBLCO. These results contribute to a broader understanding of the algorithm’s applicability in diverse optimization scenarios, positioning it as a promising candidate for addressing complex power system challenges.
5.2.4 Enhancing System Efficiency through Active Power Loss Minimization (Case 4)
This case focuses on optimizing active power loss within the IEEE 30-bus test system, which has been augmented with the integration of wind and PV energy sources. The goal is to enhance system efficiency by minimizing active power loss through the application of various optimization algorithms. Table 7 provides a comprehensive overview of the simulation results for Case 4, elucidating the optimal values achieved by each algorithm. Additionally, Fig. 9 visually compares the convergence patterns of GBBLCO against conventional CO, MFO, EHO, WOA, and BBPSO algorithms.
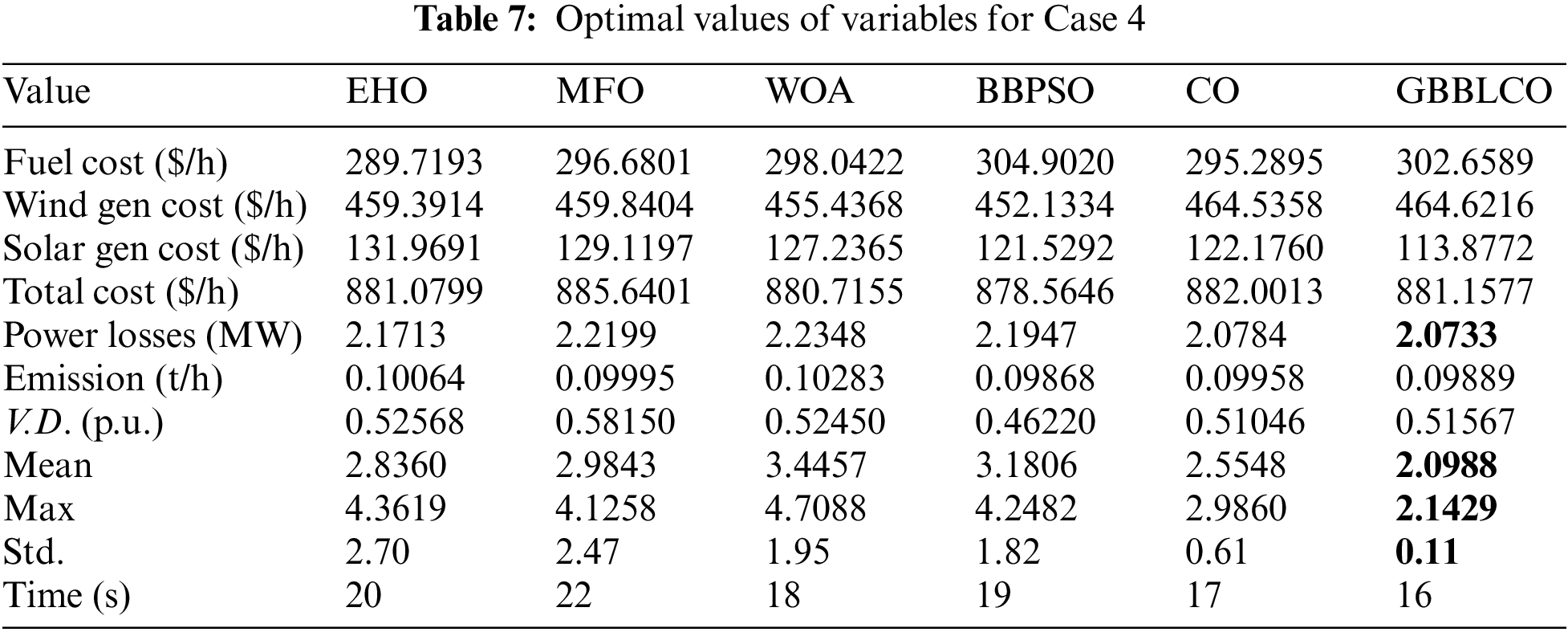
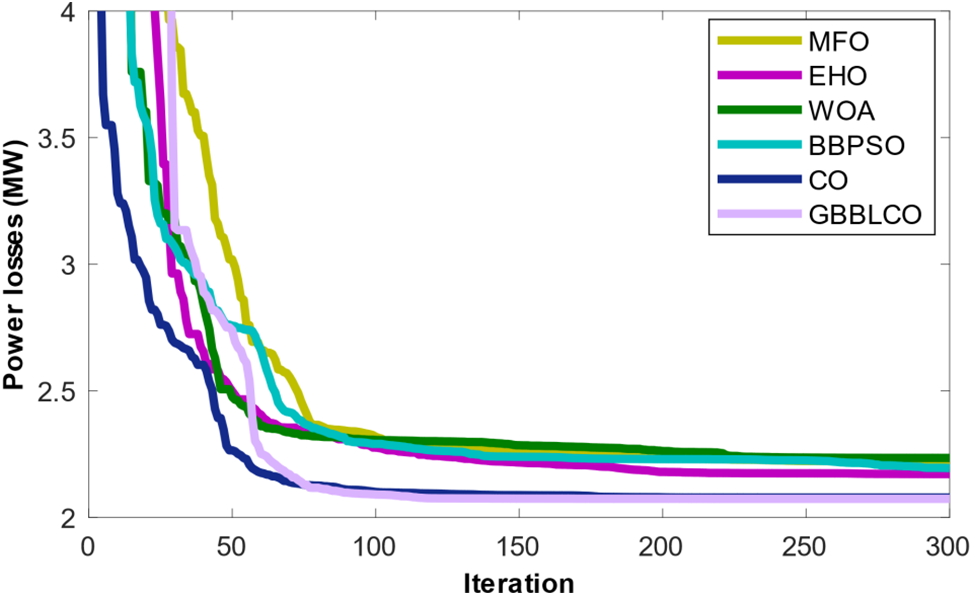
Figure 9: Convergences of the optimization techniques for Case 4
The simulation outcomes reveal that the GBBLCO algorithm attains a commendable active power loss value of 2.0733 MW, outperforming the results obtained from other algorithms. This underscores GBBLCO’s efficacy in minimizing active power loss, thereby contributing to the improved efficiency of the modified IEEE 30-bus test system. The convergence comparison presented in Fig. 9 further accentuates the algorithm’s ability to reach optimal solutions efficiently. These results position GBBLCO as a promising tool for addressing active power loss optimization challenges within power systems augmented with renewable energy sources.
5.2.5 Enhancing Voltage Deviation through Deviation Optimization (Case 5)
Case 5 focuses on optimizing the voltage deviation (V.D.) within the IEEE 30-bus test system, while considering wind and PV energy systems to enhance voltage stability. The primary goal is to minimize voltage deviation, ensuring improved stability through the application of diverse optimization algorithms. The results, detailed in Table 8, portray the achievements of the MFO, EHO, WOA, BBPSO, CO, and GBBLCO algorithms in the context of voltage deviation minimization. Table 8 reflects the superior performance of the GBBLCO algorithm, yielding a voltage deviation of 0.37576, significantly inferior to the obtained results from alternative algorithms. This underscores the effectiveness of GBBLCO in mitigating voltage deviation and reinforcing the stability of the IEEE 30-bus test system. Fig. 10 visually represents the convergence trends, emphasizing the efficient convergence of GBBLCO toward optimal solutions.
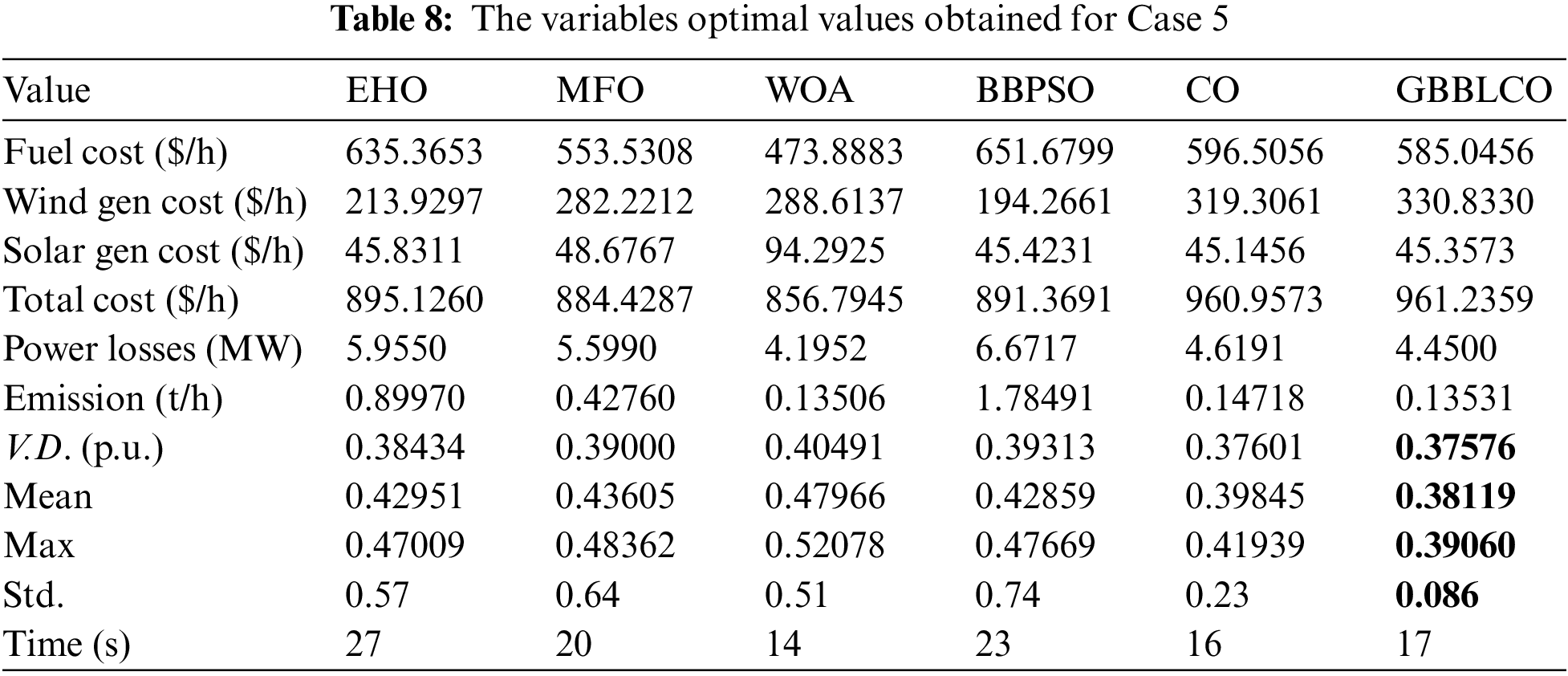
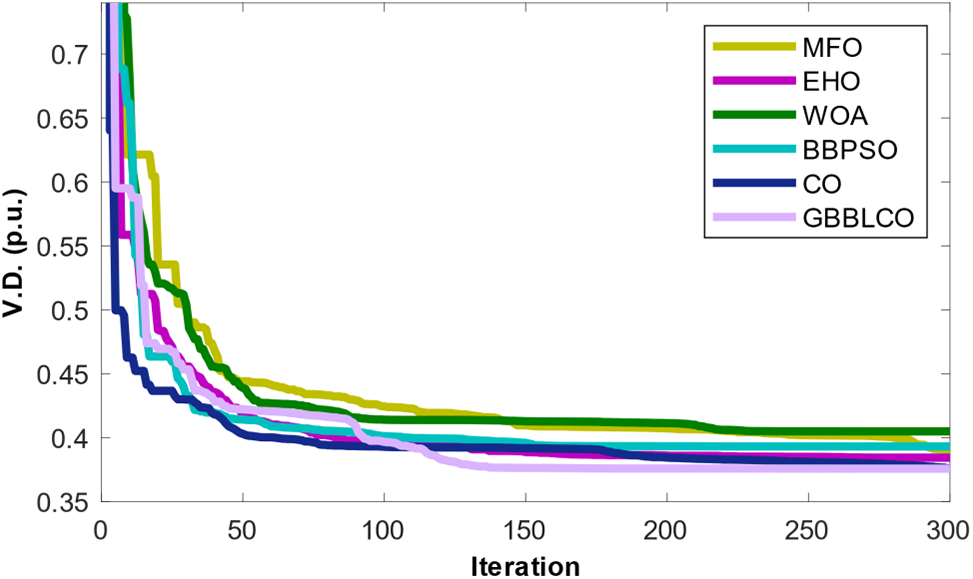
Figure 10: Convergences of the optimization techniques for Case 5
In summary, the GBBLCO algorithm is a robust solution for addressing voltage deviation optimization challenges in power systems enriched with RESs.
5.2.6 Enhancing Voltage Stability Index (VSI) (Case 6)
Focuses on optimizing the enhancing voltage stability index (VSI) within the IEEE 30-bus test system, while considering wind and PV energy systems to enhance voltage stability by Enhancing voltage stability index. The primary goal is to minimize VSI, ensuring improved stability through the application of diverse optimization algorithms. The results, detailed in Table 9, portray the achievements of the MFO, EHO, WOA, BBPSO, CO, and GBBLCO algorithms in the context of voltage deviation minimization. Table 9 reflects the superior performance of the GBBLCO algorithm, yielding a voltage deviation of 0.1007, significantly inferior to the obtained results from alternative algorithms. This underscores the effectiveness of GBBLCO in mitigating voltage deviation and reinforcing the stability of the IEEE 30-bus test system. Fig. 11 visually represents the convergence trends, emphasizing the efficient convergence of GBBLCO toward optimal solutions.
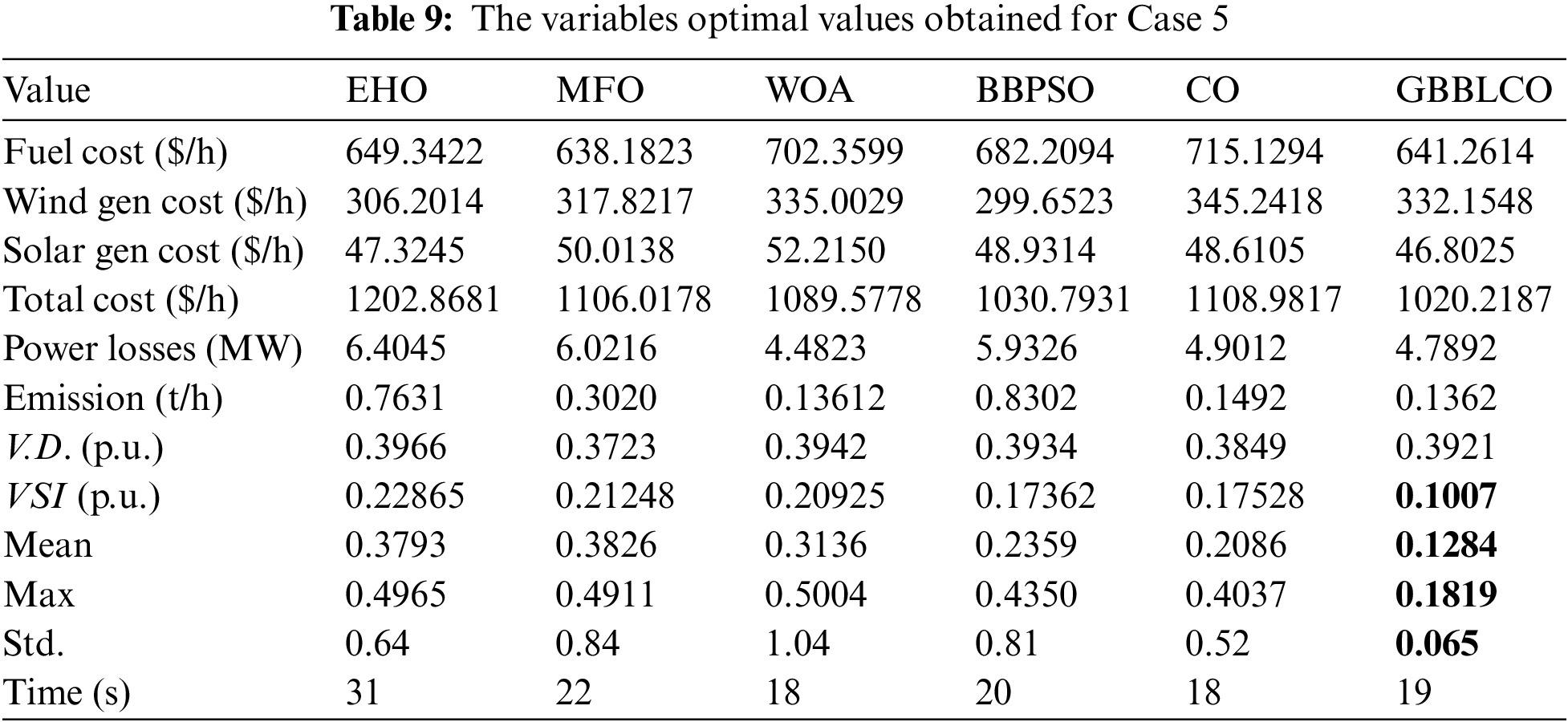
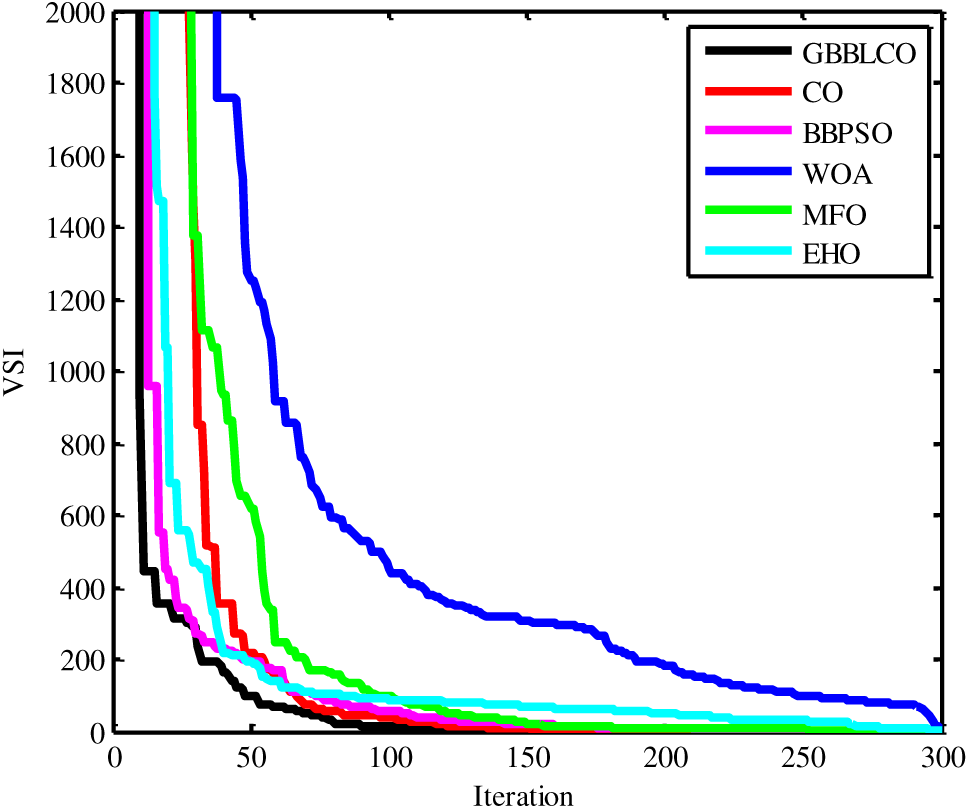
Figure 11: Convergences of the optimization techniques for Case 6
In summary, the GBBLCO algorithm is a robust solution on optimizing the enhancing voltage stability index (VSI) in power systems enriched with RESs.
5.3 Discussion: Harnessing Optimality across Multiple Power System Scenarios
The comprehensive simulation study encompassing Cases 1 to 5 illuminates the efficacy of the GBBLCO algorithm in enhancing the performance of power systems enriched by renewable energy sources. The obtained results unveil noteworthy advancements in various optimization scenarios, each shedding light on specific aspects of power system functionality.
5.3.1 Case 1: Total Cost Optimization with Valve Point Effects
In Case 1, GBBLCO remarkably outperforms conventional optimization techniques, showcasing both rapid convergence and superior solution quality. The algorithm achieves a minimal total power cost of 781.9005 $/h, underscoring its prowess in navigating the complexities introduced by VPE in thermal units and wind-PV energy systems.
5.3.2 Case 2: Total Cost Optimization with Emission and Carbon Tax
The application of a fixed carbon tax in Case 2 highlights GBBLCO’s adaptability to environmental constraints. With a minimum total power cost of 810.6784 $/h, GBBLCO surpasses other optimization methods, attesting to its adeptness in balancing economic objectives with emission reduction targets.
5.3.3 Case 3: Total Cost Optimization Considering Prohibited Operating Zones (POZs)
GBBLCO extends its dominance in Case 3, optimizing the total cost while navigating prohibited operating zones. With a total power cost of 781.8041 $/h, GBBLCO outshines competing algorithms, showcasing its efficiency in managing operational constraints alongside the cost models of RESs.
5.3.4 Case 4: Optimization of Active Power Loss
In Case 4, targeting the active power loss of the modified IEEE 30-bus test system, GBBLCO demonstrates superior performance with a minimized loss of 2.0733 MW. This underscores the algorithm’s ability to enhance grid efficiency by mitigating active power losses more effectively than other algorithms.
5.3.5 Case 5: Optimization of Voltage Deviation
GBBLCO continues its streak of success in Case 5, optimizing voltage deviation to a remarkable low of 0.37576. The results showcase GBBLCO’s aptitude in fortifying voltage stability within power systems augmented by wind and PV energy sources, surpassing the performance of alternative algorithms.
5.3.6 Case 6: Optimization of Voltage Stability Index (VSI)
GBBLCO continues its streak of success in Case 6, optimizing voltage deviation to a remarkable low of 0.1007. The results showcase GBBLCO’s aptitude in fortifying voltage stability index within power systems augmented by wind and PV energy sources, surpassing the performance of alternative algorithms.
The efficacy of the proposed GBBLCO is assessed in addressing extensive power systems within the realm of electrical engineering. The electrical network under examination encompasses 9 transformers, 54 power generators, 12 capacitors, 2 reactors, and 186 branches [64]. A total of 129 manipulated parameters are taken into account, encompassing 54 active power outputs of generators, 12 reactive power injection configurations for shunt capacitors, bus voltages, and 9 transformer tap configurations. Voltage restrictions for all buses are sustained within the range of 0.94 to 1.06 per unit. Transformer tap configurations are scrutinized within the interval of 0.90 to 1.10 per unit, and shunt capacitors contribute reactive power ranging from 0 to 30 MVAR [15].
Scenario 1: The quadratic objective function for traditional power generators in OPF, excluding solar and wind energy resources.
In Table 10, the efficacy of GBBLCO is contrasted with results from different algorithms investigated in the electrical engineering domain. An extensive literature review encompasses diverse methods employed for addressing large-scale OPF issues. The comparative examination in these tables highlights the excellence of GBBLCO in comparison to alternative optimization approaches for attaining optimal OPF solutions. The simulation findings demonstrate a significant decrease in cost, with GBBLCO accomplishing a minimum cost of $129,540.7925 per hour, outperforming the results generated by alternative algorithms.
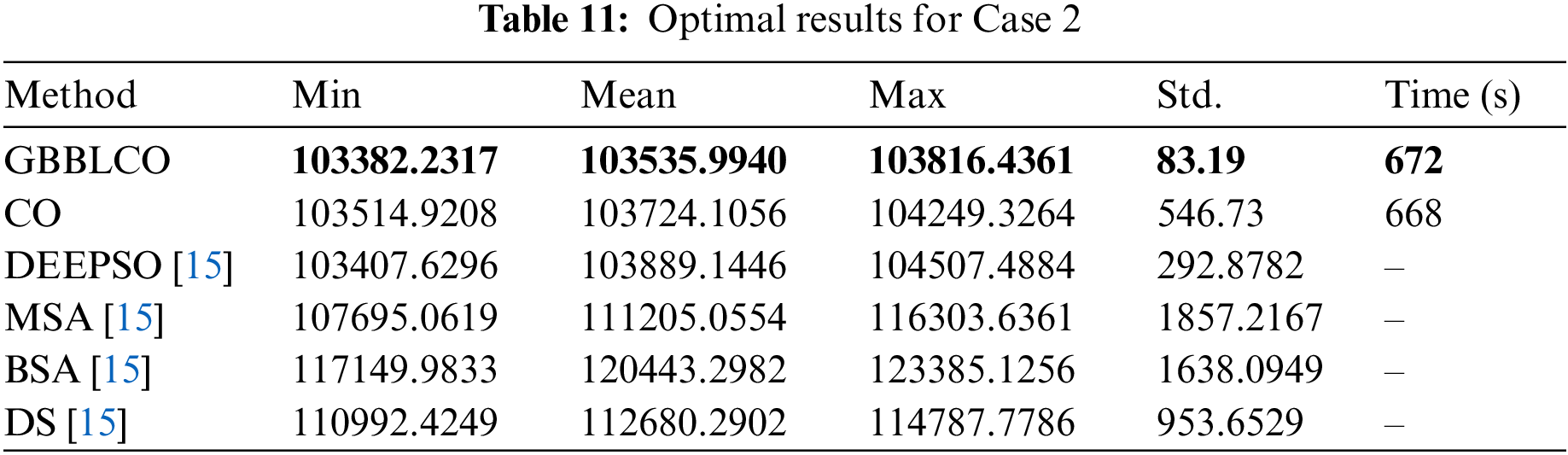
Scenario 2: OPF integrating a quadratic cost function for traditional generators and the assimilation of solar and wind energy resources.
Addressing the challenge of OPF involves crafting a quadratic cost function for conventional generators, considering their operational expenses. Moreover, the incorporation of solar and wind energy sources in this context adds intricacies due to their intermittent behavior and variable outputs. The primary objective is to enhance the optimization of power flow within the system, accounting for the distinctive features and cost implications associated with both traditional and renewable energy sources.
This system closely resembles the prior case study, integrating renewable energy sources at diverse buses. Wind energy sources are strategically positioned at buses 18, 32, 36, 55, 104, and 110, while solar energy generation units are situated at buses 6, 15, and 34, respectively.
The optimized solution for this scenario, achieved through GBBLCO, is outlined in Table 11, featuring a comparative analysis with the outcomes of the algorithms CO and the solutions derived from reference [15]. These findings compellingly indicate that GBBLCO stands out as a highly proficient algorithm for optimizing and effectively distributing loads in extensive and practical power systems.
5.5 Conclusion: Unleashing the Potential of GBBLCO
The simulation results collectively endorse GBBLCO as a versatile and robust optimization tool for diverse challenges in power systems. Its adaptability to valve point effects, emission considerations, operational constraints, power loss reduction, and voltage stability optimization underscores its potential as a comprehensive solution for modern power system management. GBBLCO’s ability to swiftly converge to optimal solutions while maintaining solution quality positions it as a promising algorithm for addressing the evolving needs of renewable energy-integrated power systems.
In conclusion, this study undertakes a systematic exploration of the Gaussian Bare-Bones Levy Cheetah Optimizer (GBBLCO) and its transformative impact on power system optimization. From the abstract’s promise of innovation to the detailed analysis presented in the introduction, methodology, and simulation results, GBBLCO emerges as a potent tool for navigating the complexities of contemporary power systems. Cases 1 to 5 serve as microcosms of real-world challenges, highlighting GBBLCO’s effectiveness in addressing diverse optimization objectives. The algorithm’s ability to handle valve point effects, emission constraints, prohibited operating zones, active power losses, and voltage stability positions it as a comprehensive solution for the intricate demands of renewable energy-integrated power systems. Simulation results not only validate the algorithm’s capabilities but also accentuate its superiority over conventional optimization techniques. The rapid convergence, high solution quality, and adept handling of multidimensional optimization landscapes underscore GBBLCO’s potential to redefine the standards of efficiency and sustainability in power system operations. In this reflective conclusion, the spotlight remains on GBBLCO as a harbinger of positive change. Its adaptability and efficiency present a promising trajectory toward optimal power systems that seamlessly integrate renewable energy sources. As the scientific community charts the course for sustainable energy futures, GBBLCO stands out as a catalyst for transformative solutions in power system optimization.
Acknowledgement: The author extends the appreciation to the Deanship of Postgraduate Studies and Scientific Research at Majmaah University for funding this research work through the Project (ICR-2024-1002).
Funding Statement: This research is supported by the Deanship of Postgraduate Studies and Scientific Research at Majmaah University in Saudi Arabia under Project Number (ICR-2024-1002).
Author Contributions: Conceptualization, A.S.A. and M.A.Z.; methodology, A.S.A. and M.A.Z.; validation, A.S.A. and M.A.Z.; formal analysis, A.S.A. and M.A.Z.; investigation, A.S.A. and M.A.Z.; resources, A.S.A. and M.A.Z.; data curation, A.S.A. and M.A.Z.; writing—original draft preparation, A.S.A., M.A.Z., and S.A.; writing—review and editing, A.S.A., M.A.Z., and S.A.; visualization, A.S.A. and M.A.Z.; supervision, A.S.A. and M.A.Z.; project administration, A.S.A. and M.A.Z. All authors have read and agreed to the published version of the manuscript.
Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article by the authors on request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Hassan, M. H., Elsayed, S. K., Kamel, S., Rahmann, C., Taha, I. B. (2022). Developing chaotic Bonobo optimizer for optimal power flow analysis considering stochastic renewable energy resources. International Journal of Energy Research, 46(8), 11291–11325. https://doi.org/10.1002/er.v46.8 [Google Scholar] [CrossRef]
2. Farhat, M., Kamel, S., Atallah, A. M., Hassan, M. H., Agwa, A. M. (2022). ESMA-OPF: Enhanced slime mould algorithm for solving optimal power flow problem. Sustainability, 14(4), 2305. https://doi.org/10.3390/su14042305 [Google Scholar] [CrossRef]
3. Guvenc, U., Duman, S., Kahraman, H. T., Aras, S., Kati, M. (2021). Fitness–distance balance based adaptive guided differential evolution algorithm for security-constrained optimal power flow problem incorporating renewable energy sources. Applied Soft Computing, 108, 107421. https://doi.org/10.1016/j.asoc.2021.107421 [Google Scholar] [CrossRef]
4. Duman, S., Kahraman, H. T., Kati, M. (2023). Economical operation of modern power grids incorporating uncertainties of renewable energy sources and load demand using the adaptive fitness-distance balance-based stochastic fractal search algorithm. Engineering Applications of Artificial Intelligence, 117, 105501. https://doi.org/10.1016/j.engappai.2022.105501 [Google Scholar] [CrossRef]
5. Abdo, M., Kamel, S., Ebeed, M., Yu, J., Jurado, F. (2018). Solving non-smooth optimal power flow problems using a developed grey wolf optimizer. Energies, 11(7), 1692. https://doi.org/10.3390/en11071692 [Google Scholar] [CrossRef]
6. Ullah, Z., Wang, S., Radosavljević, J., Lai, J. (2019). A solution to the optimal power flow problem considering WT and PV generation. IEEE Access, 7, 46763–46772. https://doi.org/10.1109/Access.6287639 [Google Scholar] [CrossRef]
7. Elattar, E. E. (2019). Optimal power flow of a power system incorporating stochastic wind power based on modified moth swarm algorithm. IEEE Access, 7, 89581–89593. https://doi.org/10.1109/Access.6287639 [Google Scholar] [CrossRef]
8. Panda, A., Tripathy, M., Barisal, A. K., Prakash, T. (2017). A modified bacteria foraging based optimal power flow framework for hydro-thermal-wind generation system in the presence of STATCOM. Energy, 124, 720–740. https://doi.org/10.1016/j.energy.2017.02.090 [Google Scholar] [CrossRef]
9. Man-Im, A., Ongsakul, W., Singh, J. G., Madhu, M. N. (2019). Multi-objective optimal power flow considering wind power cost functions using enhanced PSO with chaotic mutation and stochastic weights. Electrical Engineering, 101(3), 699–718. https://doi.org/10.1007/s00202-019-00815-8 [Google Scholar] [CrossRef]
10. Salkuti, S. R. (2019). Optimal power flow using multi-objective glowworm swarm optimization algorithm in a wind energy integrated power system. International Journal of Green Energy, 16(15), 1547–1561. https://doi.org/10.1080/15435075.2019.1677234 [Google Scholar] [CrossRef]
11. Duman, S., Li, J., Wu, L., Guvenc, U. (2020). Optimal power flow with stochastic wind power and FACTS devices: A modified hybrid PSOGSA with chaotic maps approach. Neural Computing and Applications, 32(12), 8463–8492. https://doi.org/10.1007/s00521-019-04338-y [Google Scholar] [CrossRef]
12. Kathiravan, R., Kumudini Devi, R. P. (2017). Optimal power flow model incorporating wind, solar, and bundled solar-thermal power in the restructured Indian power system. International Journal of Green Energy, 14(11), 934–950. https://doi.org/10.1080/15435075.2017.1339045 [Google Scholar] [CrossRef]
13. Khorsandi, A., Hosseinian, S. H., Ghazanfari, A. (2013). Modified artificial bee colony algorithm based on fuzzy multi-objective technique for optimal power flow problem. Electric Power Systems Research, 95, 206–213. https://doi.org/10.1016/j.epsr.2012.09.002 [Google Scholar] [CrossRef]
14. Riaz, M., Hanif, A., Hussain, S. J., Memon, M. I., Ali, M. U. et al. (2021). An optimization-based strategy for solving optimal power flow problems in a power system integrated with stochastic solar and wind power energy. Applied Sciences, 11(15), 6883. https://doi.org/10.3390/app11156883 [Google Scholar] [CrossRef]
15. Duman, S., Rivera, S., Li, J., Wu, L. (2020). Optimal power flow of power systems with controllable wind-photovoltaic energy systems via differential evolutionary particle swarm optimization. International Transactions on Electrical Energy Systems, 30(4), e12270. https://doi.org/10.1002/2050-7038.12270 [Google Scholar] [CrossRef]
16. Jeddi, B., Einaddin, A. H., Kazemzadeh, R. (2016). Optimal power flow problem considering the cost, loss, and emission by multi-objective electromagnetism-like algorithm. 2016 6th Conference on Thermal Power Plants (CTPP), Tehran, Iran, IEEE. https://doi.org/10.1109/ctpp.2016.7482931 [Google Scholar] [CrossRef]
17. Alanazi, A., Alanazi, M., Memon, Z. A., Mosavi, A. (2022). Determining optimal power flow solutions using new adaptive gaussian TLBO method. Applied Sciences, 12(16), 7959. https://doi.org/10.3390/app12167959 [Google Scholar] [CrossRef]
18. Ghasemi, M., Ghavidel, S., Akbari, E., Vahed, A. A. (2014). Solving non-linear, non-smooth and non-convex optimal power flow problems using chaotic invasive weed optimization algorithms based on chaos. Energy, 73, 340–353. https://doi.org/10.1016/j.energy.2014.06.026 [Google Scholar] [CrossRef]
19. Biswas, P. P., Suganthan, P. N., Qu, B. Y., Amaratunga, G. A. J. (2018). Multiobjective economic-environmental power dispatch with stochastic wind-solar-small hydro power. Energy, 150, 1039–1057. https://doi.org/10.1016/j.energy.2018.03.002 [Google Scholar] [CrossRef]
20. Herbadji, O., Slimani, L., Bouktir, T. (2019). Optimal power flow with four conflicting objective functions using multiobjective ant lion algorithm: A case study of the algerian electrical network. Iranian Journal of Electrical and Electronic Engineering, 15(1), 94–113. https://doi.org/10.22068/IJEEE.15.1.94 [Google Scholar] [CrossRef]
21. Ghasemi, M., Ghavidel, S., Gitizadeh, M., Akbari, E. (2015). An improved teaching-learning-based optimization algorithm using Lévy mutation strategy for non-smooth optimal power flow. International Journal of Electrical Power & Energy Systems, 65, 375–384. https://doi.org/10.1016/j.ijepes.2014.10.027 [Google Scholar] [CrossRef]
22. Chen, M. R., Zeng, G. Q., Lu, K. D. (2019). Constrained multi-objective population extremal optimization based economic-emission dispatch incorporating renewable energy resources. Renewable Energy, 143, 277–294. https://doi.org/10.1016/j.renene.2019.05.024 [Google Scholar] [CrossRef]
23. Mouassa, S., Althobaiti, A., Jurado, F., Ghoneim, S. S. M. (2022). Novel design of slim mould optimizer for the solution of optimal power flow problems incorporating intermittent sources: A case study of algerian electricity grid. IEEE Access, 10, 22646–22661. https://doi.org/10.1109/ACCESS.2022.3152557 [Google Scholar] [CrossRef]
24. Güçyetmez, M., Çam, E. (2016). A new hybrid algorithm with genetic-teaching learning optimization (G-TLBO) technique for optimizing of power flow in wind-thermal power systems. Electrical Engineering, 98(2), 145–157. https://doi.org/10.1007/s00202-015-0357-y [Google Scholar] [CrossRef]
25. Hmida, J. Ben, Chambers, T., Lee, J. (2019). Solving constrained optimal power flow with renewables using hybrid modified imperialist competitive algorithm and sequential quadratic programming. Electric Power Systems Research, 177, 105989. https://doi.org/10.1016/j.epsr.2019.105989 [Google Scholar] [CrossRef]
26. Venkateswara Rao, B., Nagesh Kumar, G. V. (2015). Optimal power flow by BAT search algorithm for generation reallocation with unified power flow controller. International Journal of Electrical Power & Energy Systems, 68, 81–88. https://doi.org/10.1016/j.ijepes.2014.12.057 [Google Scholar] [CrossRef]
27. Sarhan, S., El-Sehiemy, R., Abaza, A., Gafar, M. (2022). Turbulent flow of water-based optimization for solving multi-objective technical and economic aspects of optimal power flow problems. Mathematics, 10(12), 2106. https://doi.org/10.3390/math10122106 [Google Scholar] [CrossRef]
28. Kyomugisha, R., Muriithi, C. M., Nyakoe, G. N. (2022). Performance of various voltage stability indices in a stochastic multiobjective optimal power flow using mayfly algorithm. Journal of Electrical and Computer Engineering, 2022, 7456333. https://doi.org/10.1155/2022/7456333 [Google Scholar] [CrossRef]
29. Ahmad, M., Javaid, N., Niaz, I. A., Almogren, A., Radwan, A. (2021). A bio-inspired heuristic algorithm for solving optimal power flow problem in hybrid power system. IEEE Access, 9, 159809–159826. https://doi.org/10.1109/ACCESS.2021.3131161 [Google Scholar] [CrossRef]
30. Chang, Y. C., Lee, T. Y., Chen, C. L., Jan, R. M. (2014). Optimal power flow of a wind-thermal generation system. International Journal of Electrical Power & Energy Systems, 55, 312–320. https://doi.org/10.1016/j.ijepes.2013.09.028 [Google Scholar] [CrossRef]
31. Ali, A., Abbas, G., Keerio, M. U., Koondhar, M. A., Chandni, K. et al. (2023). Solution of constrained mixed-integer multi-objective optimal power flow problem considering the hybrid multi-objective evolutionary algorithm. IET Generation, Transmission & Distribution, 17(1), 66–90. https://doi.org/10.1049/gtd2.v17.1 [Google Scholar] [CrossRef]
32. Ghasemi, M., Rahimnejad, A., Hemmati, R., Akbari, E., Gadsden, S. A. (2021). Wild geese algorithm: A novel algorithm for large scale optimization based on the natural life and death of wild geese. Array, 11, 100074. https://doi.org/10.1016/j.array.2021.100074 [Google Scholar] [CrossRef]
33. Sriram, K., Mangaiyarkarasi, S. P., Sakthivel, S., Jebaraj, L. (2023). An extensive study using the beetle swarm method to optimize single and multiple objectives of various optimal power flow problems. International Transactions on Electrical Energy Systems, 2023, 5779700 [Google Scholar]
34. Alghamdi, A. S. (2023). Optimal power flow of hybrid wind/solar/thermal energy integrated power systems considering costs and emissions via a novel and efficient search optimization algorithm. Applied Sciences, 13(8), 4760. https://doi.org/10.3390/app13084760 [Google Scholar] [CrossRef]
35. Shaheen, A. M., Elsayed, A. M., El-Sehiemy, R. A., Ghoneim, S. S. M., Alharthi, M. M. et al. (2023). Multi-dimensional energy management based on an optimal power flow model using an improved quasi-reflection jellyfish optimization algorithm. Engineering Optimization, 55(6), 907–929. https://doi.org/10.1080/0305215X.2022.2051021 [Google Scholar] [CrossRef]
36. Khunkitti, S., Premrudeepreechacharn, S., Siritaratiwat, A. (2023). A two-archive harris hawk optimization for solving many-objective optimal power flow problems. IEEE Access, 11, 134557–134574. https://doi.org/10.1109/ACCESS.2023.3337535 [Google Scholar] [CrossRef]
37. Sun, B., Song, M., Li, A., Zou, N., Pan, P. et al. (2023). Multi-objective solution of optimal power flow based on TD3 deep reinforcement learning algorithm. Sustainable Energy, Grids and Networks, 34, 101054. https://doi.org/10.1016/j.segan.2023.101054 [Google Scholar] [CrossRef]
38. Moghadam, A. S., Suratgar, A. A., Hesamzadeh, M. R., Nikravesh, S. K. Y. (2023). A distributed approach for solving AC–DC multi-objective OPF problem. International Journal of Electrical Power & Energy Systems, 153, 109284. https://doi.org/10.1016/j.ijepes.2023.109284 [Google Scholar] [CrossRef]
39. Su, H., Niu, Q., Yang, Z. (2023). Optimal power flow using improved cross-entropy method. Energies, 16(14), 5466. https://doi.org/10.3390/en16145466 [Google Scholar] [CrossRef]
40. Ghasemi, M., Ghavidel, S., Aghaei, J., Gitizadeh, M., Falah, H. (2014). Application of chaos-based chaotic invasive weed optimization techniques for environmental OPF problems in the power system. Chaos, Solitons and Fractals, 69. https://doi.org/10.1016/j.chaos.2014.10.007 [Google Scholar] [CrossRef]
41. Hashish, M. S., Hasanien, H. M., Ji, H., Alkuhayli, A., Alharbi, M. et al. (2023). Monte carlo simulation and a clustering technique for solving the probabilistic optimal power flow problem for hybrid renewable energy systems. Sustainability, 15(1), 783. https://doi.org/10.3390/su15010783 [Google Scholar] [CrossRef]
42. Zhang, J., Cai, J., Zhang, H., Chen, T. (2023). NSGA-III integrating eliminating strategy and dynamic constraint relaxation mechanism to solve many-objective optimal power flow problem. Applied Soft Computing, 146, 110612. https://doi.org/10.1016/j.asoc.2023.110612 [Google Scholar] [CrossRef]
43. Hashish, M. S., Hasanien, H. M., Ullah, Z., Alkuhayli, A., Badr, A. O. (2023). Giant trevally optimization approach for probabilistic optimal power flow of power systems including renewable energy systems uncertainty. Sustainability, 15(18), 13283. https://doi.org/10.3390/su151813283 [Google Scholar] [CrossRef]
44. Wu, Z., Liu, H., Zhao, J., Li, Z. (2023). An improved MOEA/D algorithm for the solution of the multi-objective optimal power flow problem. Processes, 11(2), 337. https://doi.org/10.3390/pr11020337 [Google Scholar] [CrossRef]
45. Nappu, M. B., Arief, A., Ajami, W. A. (2023). Energy efficiency in modern power systems utilizing advanced incremental particle swarm optimization–based OPF. Energies, 16(4), 1706. https://doi.org/10.3390/en16041706 [Google Scholar] [CrossRef]
46. Ghasemi, M., Trojovský, P., Trojovská, E., Zare, M. (2023). Gaussian bare-bones Levy circulatory system-based optimization for power flow in the presence of renewable units. Engineering Science and Technology, an International Journal, 47, 101551. https://doi.org/10.1016/j.jestch.2023.101551 [Google Scholar] [CrossRef]
47. Al-Kaabi, M., Dumbrava, V., Eremia, M. (2023a). Application of harris hawks optimization in single objective optimal power flow. 15th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), pp. 1–6. Bucharest, Romania [Google Scholar]
48. Al-Kaabi, M., Dumbrava, V., Eremia, M. (2023b). Grey wolf optimizer for solving single objective functions optimal power flow. 13th International Symposium on Advanced Topics in Electrical Engineering (ATEE), pp. 1–5. Bucharest, Romania [Google Scholar]
49. Mezhoud, N. (2023). Multi-objective optimal power flow and emission index based firefly algorithm. Periodica Polytechnica Electrical Engineering and Computer Science, 67(2), 172–180. https://doi.org/10.3311/PPee.20922 [Google Scholar] [CrossRef]
50. Long, H., Chen, Z., Huang, H., Yu, L., Li, Z. et al. (2023). Research on multi-objective optimization power flow of power system based on improved remora optimization algorithm. Engineering Letters, 31(3), 1191–1207 [Google Scholar]
51. Akbari, M. A., Zare, M., Azizipanah-Abarghooee, R., Mirjalili, S., Deriche, M. (2022). The cheetah optimizer: A nature-inspired metaheuristic algorithm for large-scale optimization problems. Scientific Reports, 12(1), 1–20 [Google Scholar]
52. Mirjalili, S. (2015). Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowledge-Based Systems, 89, 228–249. https://doi.org/10.1016/j.knosys.2015.07.006 [Google Scholar] [CrossRef]
53. Wang, G. G., Deb, S., Coelho, L., dos, S. (2015). Elephant herding optimization. 3rd International Symposium on Computational and Business Intelligence (ISCBI), pp. 1–5. Bali, Indonesia [Google Scholar]
54. Mirjalili, S., Lewis, A. (2016). The whale optimization algorithm. Advances in Engineering Software, 95, 51–67. https://doi.org/10.1016/j.advengsoft.2016.01.008 [Google Scholar] [CrossRef]
55. Kennedy, J. (2003). Bare bones particle swarms. Proceedings of the 2003 IEEE Swarm Intelligence Symposium, pp. 80–87. Indianapolis, IN, USA. https://doi.org/10.1109/SIS.2003.1202251 [Google Scholar] [CrossRef]
56. Ghasemi, M., Zare, M., Mohammadi, S. K., Mirjalili, S. (2024). Applications of whale migration algorithm in optimal power flow problems of power systems. In: Handbook of whale optimization algorithm, pp. 347–364. Academic Press. [Google Scholar]
57. Ghasemi, M., Ghavidel, S., Rahmani, S., Roosta, A., Falah, H. (2014). A novel hybrid algorithm of imperialist competitive algorithm and teaching learning algorithm for optimal power flow problem with non-smooth cost functions. Engineering Applications of Artificial Intelligence, 29. https://doi.org/10.1016/j.engappai.2013.11.003 [Google Scholar] [CrossRef]
58. Biswas, P. P., Suganthan, P. N., Amaratunga, G. A. J. (2017). Optimal power flow solutions incorporating stochastic wind and solar power. Energy Conversion and Management, 148, 1194–1207. https://doi.org/10.1016/j.enconman.2017.06.071 [Google Scholar] [CrossRef]
59. Clerc, M., Kennedy, J. (2002). The particle swarm-explosion, stability, and convergence in a multidimensional complex space. IEEE Transactions on Evolutionary Computation, 6(1), 58–73. https://doi.org/10.1109/4235.985692 [Google Scholar] [CrossRef]
60. Van den Bergh, F., Engelbrecht, A. P. (2006). A study of particle swarm optimization particle trajectories. Information Sciences, 176(8), 937–971. https://doi.org/10.1016/j.ins.2005.02.003 [Google Scholar] [CrossRef]
61. Zimmerman, R. D., Murillo-Sanchez, C. E., Gan, D. (1997). MATPOWER. User’s Manual. Power Systems Engineering Research Center (PSERC) [Google Scholar]
62. Mohamed, A. A. A., Mohamed, Y. S., El-Gaafary, A. A. M., Hemeida, A. M. (2017). Optimal power flow using moth swarm algorithm. Electric Power Systems Research, 142, 190–206. https://doi.org/10.1016/j.epsr.2016.09.025 [Google Scholar] [CrossRef]
63. Zimmerman, R. D., Murillo-Sanchez, C. E., Thomas, R. J. (2011). MATPOWER: Steady-state operations, planning, and analysis tools for power systems research and education. IEEE Transactions on Power Systems, 26(1), 12–19. https://doi.org/10.1109/TPWRS.2010.2051168 [Google Scholar] [CrossRef]
64. Meng, A., Zeng, C., Wang, P., Chen, D., Zhou, T. et al. (2021). A high-performance crisscross search based grey wolf optimizer for solving optimal power flow problem. Energy, 225, 120211. https://doi.org/10.1016/j.energy.2021.120211 [Google Scholar] [CrossRef]
65. Zahedibialvaei, A., Trojovský, P., Hesari-Shermeh, M., Matoušová, I., Trojovská, E. et al. (2023). An enhanced turbulent flow of water-based optimization for optimal power flow of power system integrated wind turbine and solar photovoltaic generators. Scientific Reports, 13(1), 14635. https://doi.org/10.1038/s41598-023-41749-3 [Google Scholar] [PubMed] [CrossRef]
66. Hassan, M. H., Kamel, S., Selim, A., Khurshaid, T., Domínguez-García, J. L. (2021). A modified Rao-2 algorithm for optimal power flow incorporating renewable energy sources. Mathematics, 9(13), 1532. https://doi.org/10.3390/math9131532 [Google Scholar] [CrossRef]
67. El-Fergany, A. A., Hasanien, H. M. (2015). Single and multi-objective optimal power flow using grey wolf optimizer and differential evolution algorithms. Electric Power Components and Systems, 43(13), 1548–1559. https://doi.org/10.1080/15325008.2015.1041625 [Google Scholar] [CrossRef]
68. Nadimi-Shahraki, M. H., Taghian, S., Mirjalili, S., Abualigah, L., Abd Elaziz, M. et al. (2021). EWOA-OPF: Effective whale optimization algorithm to solve optimal power flow problem. Electronics, 10(23), 2975. https://doi.org/10.3390/electronics10232975 [Google Scholar] [CrossRef]
69. Bouchekara, H. R. E. H., Chaib, A. E., Abido, M. A., El-Sehiemy, R. A. (2016). Optimal power flow using an improved colliding bodies optimization algorithm. Applied Soft Computing, 42, 119–131. https://doi.org/10.1016/j.asoc.2016.01.041 [Google Scholar] [CrossRef]
70. Bai, W., Eke, I., Lee, K. Y. (2017). An improved artificial bee colony optimization algorithm based on orthogonal learning for optimal power flow problem. Control Engineering Practice, 61, 163–172. https://doi.org/10.1016/j.conengprac.2017.02.010 [Google Scholar] [CrossRef]
71. Shaheen, A. M., El-Sehiemy, R. A., Elattar, E. E., Abd-Elrazek, A. S. (2021). A modified crow search optimizer for solving non-linear OPF problem with emissions. IEEE Access, 9, 43107–43120. https://doi.org/10.1109/ACCESS.2021.3060710 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF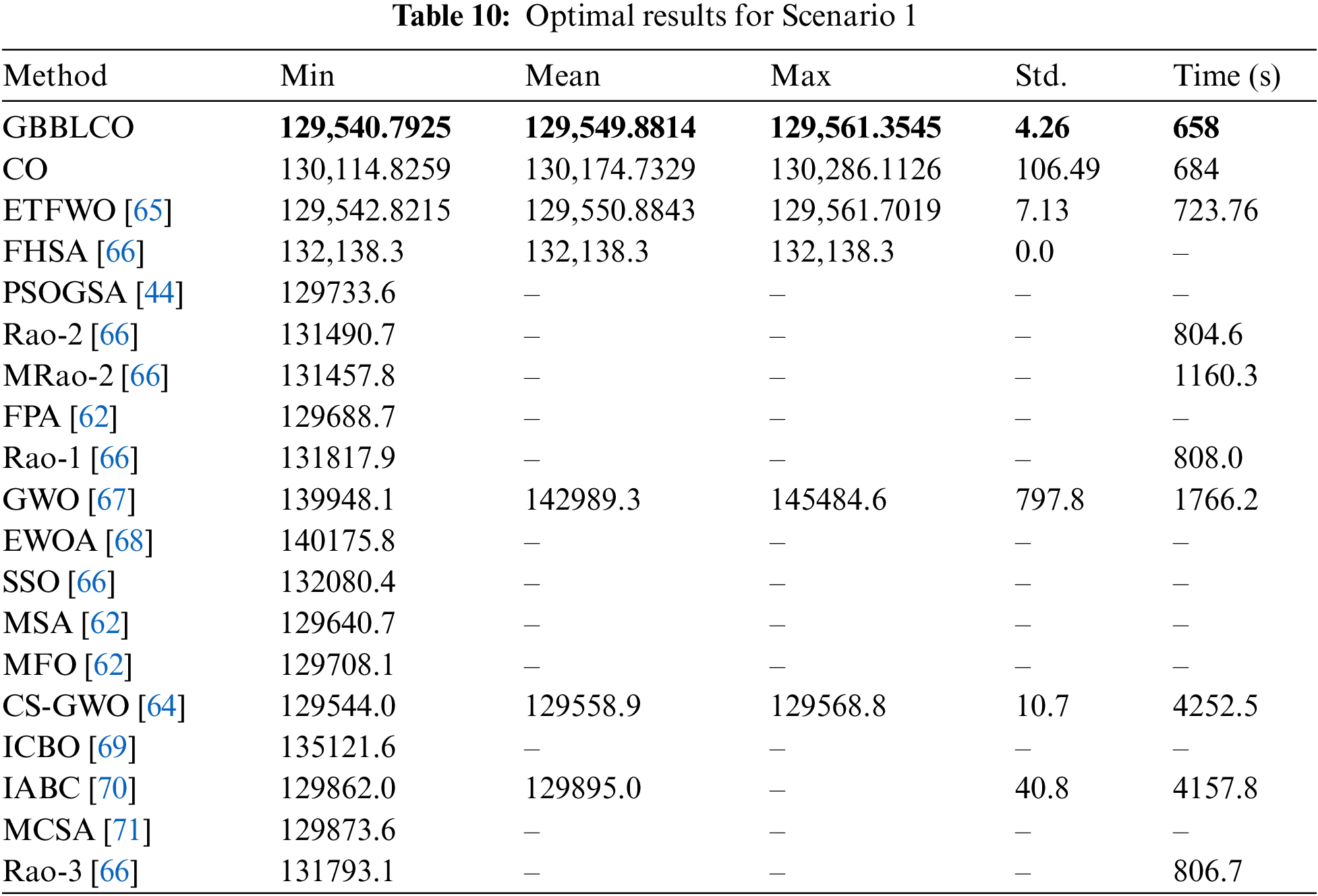
 Downloads
Downloads
 Citation Tools
Citation Tools
