A Distributionally Robust Optimization Scheduling Model for Regional Integrated Energy Systems Considering Hot Dry Rock Co-Generation

1  Introduction

Actively building a new energy-based power system is the first task to achieve the “double carbon” goal [1]. Hot dry rock (HDR) has broad development potential and prospects, due to its abundant reserves, wide distribution, green and low-carbon, and is expected to become a new direction for energy structure transformation [2,3].

High-quality HDR technology has many advantages, including that HDR resources are not affected by the external environment and climate and have abundant reserves, with the advantages of high annual utilization hours, clean and stable [4]. Thermal power generation in China represents a proportion of the country’s total power generation [5], which has led to an increase in the proportion of installed new energy capacity [6]. Also, conflicts between heat supply and power generation in thermal power plants have become more prominent, and the relationship between the interests of power auxiliary services has become more complex. The HDR-enhanced geothermal system (HDR-EGS) with HDR as the root can reasonably solve the problem of heat and power contradiction. It is conducive to promoting the market-oriented reform of auxiliary services. Furthermore, it has become a research hotspot in the field of renewable energy. In addition, HDR-EGS has a similar function to combined heat and power (CHP) and also has combined heat and power capability. Therefore, the application prospects in EGS are very promising [7,8]. For this reason, some scholars have conducted related studies on HDR-EGS. In [9], a specific study on the geothermal power generation performance of the Kalina Cycle and Organic Rankine Cycle was carried out. In [10], the power generation model was further optimized and an enhanced geothermal power generation system was constructed using carbon dioxide as the work material, thus reducing the carbon emissions in the system. In [11,12], the power generation system was designed according to an actual HDR scenario, and the development cost was also measured. In [13], a micro-energy network planning model for combined wind power (WP) and HDR thermoelectric power supply was constructed.

Regional integrated energy systems (RIES) can effectively improve energy utilization efficiency and indirectly promote renewable energy consumption through joint scheduling, coordination and optimization of multiple energy sources. In [14], a power-to-gas (P2G) device was introduced in a RIES to consume surplus WP and reduce wind abandonment. In [15], a joint economic scheduling model with P2G and low-temperature waste heat generators was established. The simulation analysis verified the effectiveness of the scheduling model in promoting WP consumption and improving system operation efficiency. Reference [16] promoted WP consumption and reduced the operating cost of RIES through the integrated demand response (DR) of the ground source heat pump (GSHP) and electric heat. However, the probability of extreme WP output scenarios is ignored, which brings severe challenges to the consumption of RIES WP. In [17], aiming at the problem of uncertainty in the system, a day-ahead-real-time two-stage coordinated robust optimal scheduling model is constructed. Robust optimization considers the worst-case scenario to solve the optimal result, and the probability of the worst-case scenario occurring in practice is extremely small, which leads to overly conservative results of robust optimization. To solve the above problem, some scholars have proposed to optimize the uncertainty problem by using a distributionally robust optimization (DRO) method. In [18], a RIES DRO-constrained day-ahead optimal scheduling model was developed for the WP output uncertainty problem. The negative effect of extreme WP output on system WP consumption is eliminated. Reference [19] introduced electric vehicles and GSHP in RIES to promote the consumption of WP. Reference [20] proposed an assessment method of WP consumption capacity and verified the effectiveness of the assessment method through simulation. Reference [21] proposed a generalized energy storage system storage and discharge optimal scheduling, which improves the consumption capacity of renewable energy. In [22,23], the effectiveness of flexible resources in facilitating the consumption of new energy is investigated. The results showed that if the utilization of flexible resources is maximized in the RIES, there will be a significant improvement in the new energy consumption as well as maintaining the economical and stable operation of the system. In [24], a flexible adjustment of the CHP thermoelectric ratio by adding a supplementary combustion device was proposed to reduce the operating cost of the system, and the WP consumption capacity was also improved. However, the existing research on HDR power generation mainly focuses on power generation system modeling, power generation performance analysis, and cost estimation. There is still a gap in the research on HDR-EGS access to RIES and collaborative optimal scheduling to promote renewable energy consumption indirectly.

Considering the shortages mentioned above, this paper proposes a DRO scheduling model for RIES considering HDR co-generation. HDR-EGS is connected to RIES for scheduling, and DRO is used to optimize the WP uncertainty problem.

The rest of the paper is organized as follows: Section 2 presents the detailed model including all components of HDR-EGS. Section 3 presents the RIES-optimized scheduling model including HDR-EGS. Section 4 presents the DRO and solution methods. Section 5 presents the simulation results of the case study. Section 6 concludes the paper.

2  HDR-EGS Combined Heat and Power Model

The HDR-EGS architecture is shown in Fig. 1, with the direction of the red arrow in the figure showing the flow of geothermal energy. The architecture consists of a geothermal power generation device, a high-temperature heating device with a heat storage system, a medium-temperature heating device, a splitter, a mixer, a recirculating pump, a producing well, and a reinjection well.

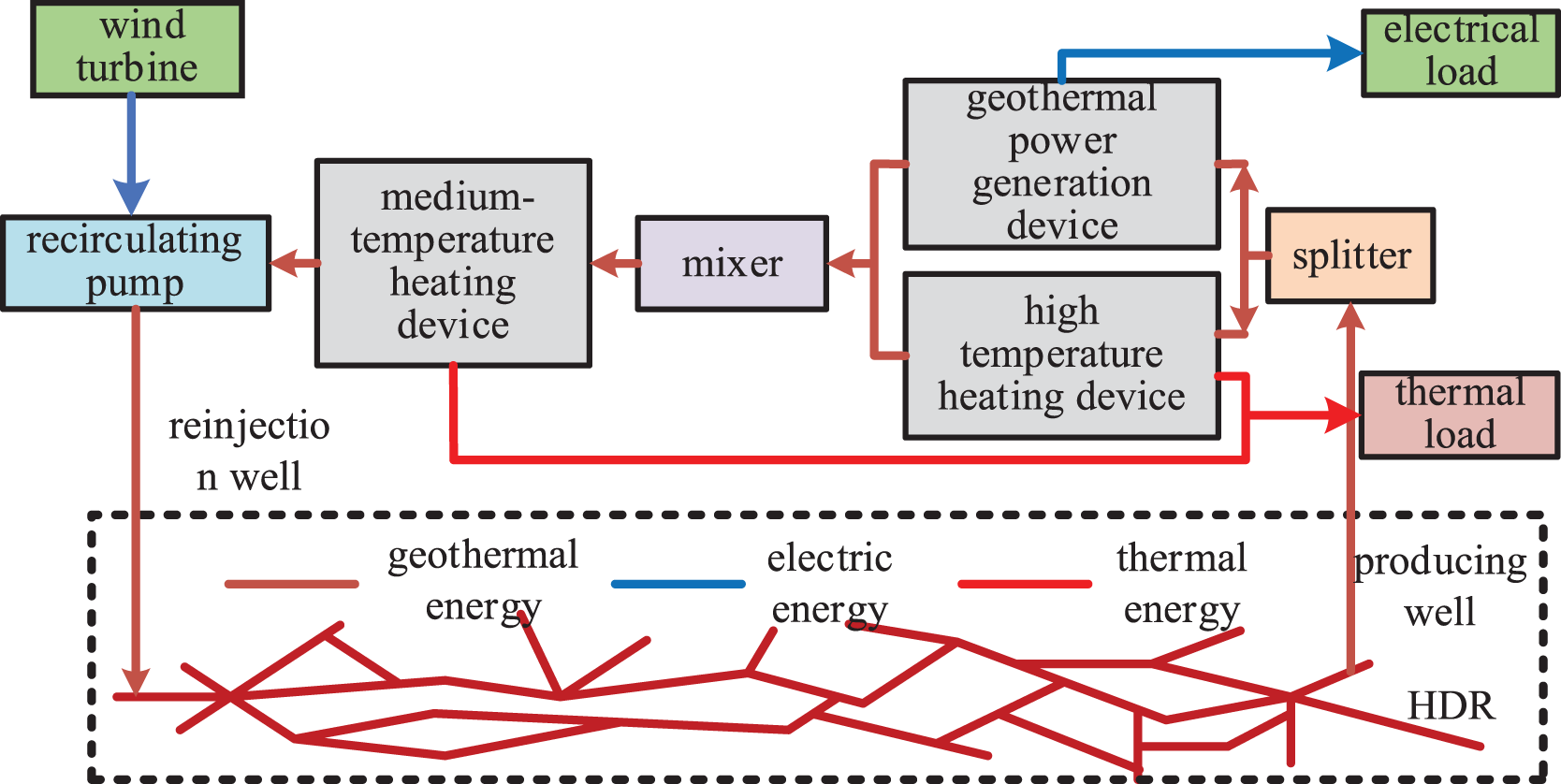
Figure 1: HDR-EGS architecture

2.1 Splitter and Mixer Model

As shown in Fig. 1, after extracting the geothermal mass from the production wells, it is flexibly distributed between the power generation device and the high-temperature heating device using a splitter. The splitter model relationship is as follows:

{qH(t)/qE(t)=A(t)/B(t)0≤A(t)≤1,A(t)+B(t)=1(1)

where A(t) is the energy factor used for power generation at time t, B(t) is the energy factor used for heating at time t, qH(t) and qE(t) is the mass flow rate used for high-temperature heating device and geothermal power generation device at time t, respectively.

The waste heat temperature after the high-temperature heating device and the waste heat temperature after the geothermal power generation device are mixed through the mixer to provide the heat temperature for the medium-temperature heating device. The mixer energy model relationship is expressed as follows:

qE(t)THW(t)+qH(t)TEW(t)=(qE(t)+qH(t))TMW(t)(2)

where THW(t) is the temperature of the residual heat of the geothermal mass after passing through the high-temperature heating device at time t, TEW(t) is the residual heat temperature of the geothermal mass after it has passed through the geothermal power plant at time t, TMW(t) is the heat temperature at the heat exchanger of the medium-temperature heating device at time t.

2.2 Geothermal Power Plant Model

With constant values of temperature, pressure and mass flow rate of the geothermal mass in the HDR heat extraction cycle; the system output can be adjusted to track the maximum power generation efficiency condition by adjusting the mass flow rate in the low-temperature power generation cycle. Assuming that the rated operating point of the geothermal power plant is always at the operating condition of maximum power generation efficiency; then, TEW(t) and ηE(t) can be considered as constants in tracking the maximum efficiency of power generation of the geothermal power plant ηEmax. The output power PHDR(t) of the geothermal power generation system model is as expressed follows:

PHDR(t)=A(t)ηEmaxqHDRcHDR(THDR−TEW)(3)

where qHDR is the mass flow of the geothermal mass, cHDR is the specific heat capacity of the geothermal mass, THDR and is the temperature of the high-temperature geothermal mass. For a short period, since the temperature of the production well remains essentially constant, THDR can be considered a constant.

2.3 Heat Supply Device Model

The high-temperature heating plant is composed of two parts: the heat storage system and the high-temperature heat exchanger. If the high-grade heat energy provided by the high-temperature heat exchanger is recorded by TH, the model relationship is expressed as follows:

qHO(t)cHO(TH−TO)=qE(t)cHDR(THDR−THW(t))(4)

where qHO(t) is the mass flow of the thermal fluid at the time t.cHO and TO are the specific heat capacity of the thermal fluid and the initial temperature, respectively. The thermal power QHI(t) acquired by the high-temperature heating device and the thermal power QHO(t) output is modeled as in Eq. (5). When the initial temperature of the heat transfer oil, the production well temperature, and the heating temperature are determined.

{QHI(t)=B(t)qHDRcHDRTHDR−B(t)THW(t)qHDRcHDRQHO(t)=qHO(t)cHO(TH−TO)=ηHEQHI(t)(5)

where ηHE indicates the heat transfer efficiency of the high-temperature heat exchanger.

The heat storage and exothermic process of the high-temperature heat storage system are realized through heat transfer between heat-conducting oil and a high-temperature heat network, which consists of a heat exchange system, electric heating device, and high-temperature heat storage tank. The model of a high-temperature heat storage system is described as follows:

SH(t+1)=(1−βH)SH(t)+(uQHSc(t)−vQHSdc(t)+βEQPHEQ(t))Δt(6)

where SH(t) is the high-temperature heat storage capacity of the heat storage system at time t, PHEQ(t) is the electric power of the electric heating device at time t, QHSc(t)/QHSdc(t) is the heat storage/exhaust power of the heat storage system at time t, βH and βEQ are the loss coefficient and electric heating coefficient, respectively. To ensure that the heat storage and exhaust processes are not carried out simultaneously, u and v are set as 0–1 variable. Δt is the device scheduling time.

{u+v≤1u,v∈{0,1}(7)

Since the model of the medium-temperature heating device is similar to that of the high-temperature heating device, it will not be repeated.

3  RIES Optimization Model with HDR-EGS

3.1 RIES Model

In China, Qinghai Province is relatively cold in winter and rich in geothermal and wind energy. There are favorable conditions for the development of HDR, GSHP, and CHP. In this paper, an area in Qinghai province is taken as an example for winter heating, and its structure diagram is shown in Fig. 2. It mainly contains HDR-EGS, CHP, wind turbine (WT), photovoltaic (PV), battery, and GSHP. The CH4 is converted into electricity by CHP and supplied to the district grid, and the district grid can interact with the main grid. The thermal load is provided by HDR-EGS, CHP, and GSHP through the district heat network. The electrical load is provided by HDR-EGS, CHP, WT, PV, battery, and main grid through the regional grid.

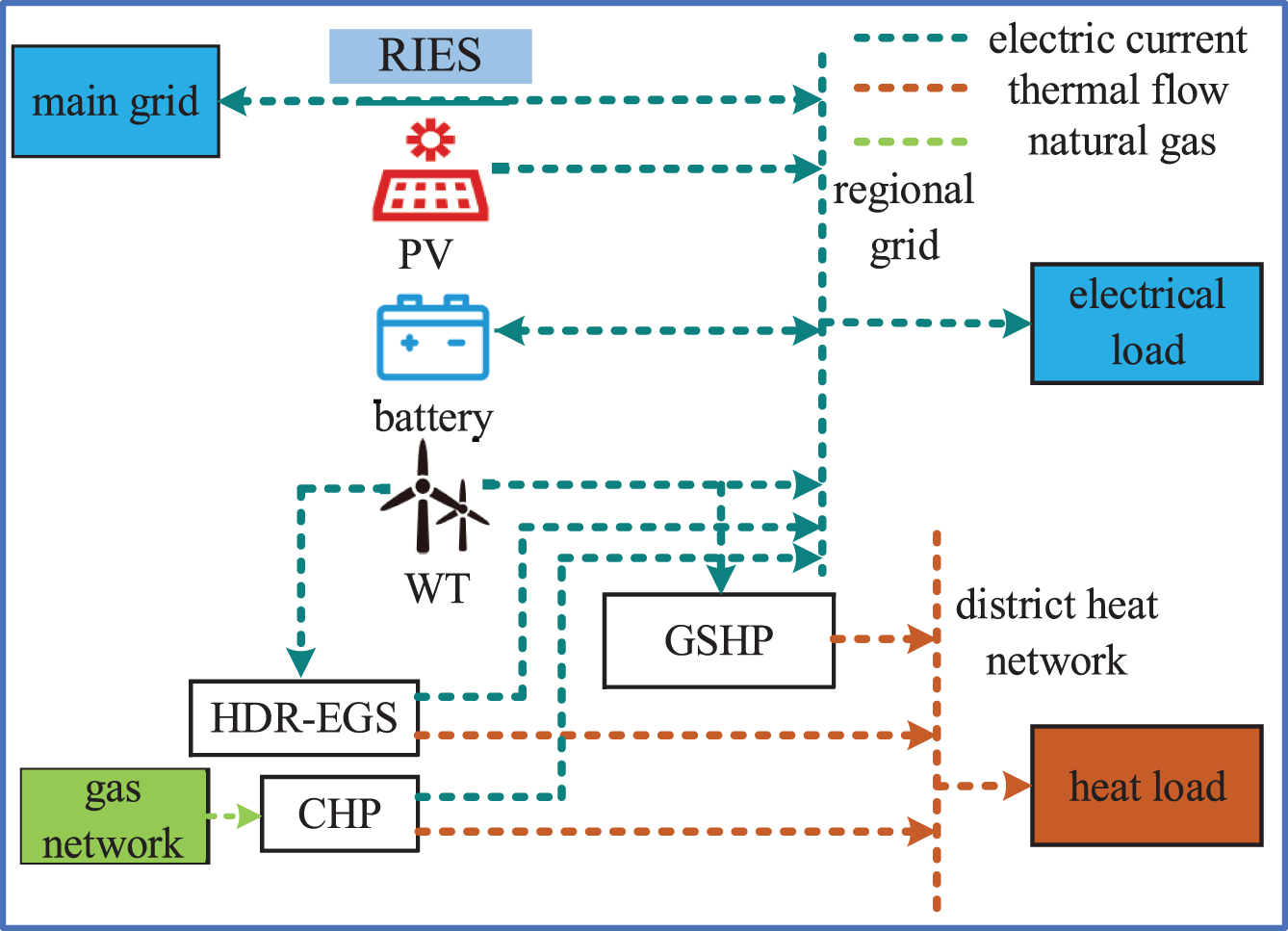
Figure 2: Structure diagram of the regionally integrated energy system

3.2 Objective Function

In this paper, the optimization objective is to minimize the total cost of RIES in a scheduling cycle. The total cost mainly includes the cost of power purchase and sale, fuel, maintenance, environmental, and wind abandonment penalty cost. The objective function can be expressed as follows:

minCST=∑t=1T(CFB(t)+COM(t)+CBS(t)+CEN(t)+CWP(t))(8)

where T is the scheduling time and equal 24 h, CST is the system’s total operating cost during the scheduling period. CFB(t), COM(t), CEN(t) and CWP(t) are the fuel cost, maintenance cost, environmental cost, and wind abandonment penalty cost of the RIES respectively at time t, CBS(t) is the cost of power purchase and sale between the system and the main grid at time t and can be calculated as follows:

CFB(t)=PCHP(t)DCH4ΔT/βCHPLCH4(9)

COM(t)=∑i=1NPi(t)Di+∑j=1MPj(t)Dj+|PES(t)|DES(10)

CBS(t)=Drb(t)max{PBS(t),0}+Drs(t)max{−PBS(t),0}(11)

CEN(t)=∑r=1L{αr[Er(P i(t))+Er(Pbuy(t))]}(12)

CWP(t)=Pwd(t)Dw(13)

where PCHP(t) is the power generated by the CHP at the time t, βCHP is the efficiency of the CHP, DCH4 is the price of CH4, LCH4 is the low calorific value of CH4, Pi(t), Pj(t), PES(t), Di, Dj, DES are the electric power and device maintenance cost of I controllable device, j renewable energy generating units and energy storage device at time t, respectively. N is the type of controllable device, M is the type of renewable energy generating device, PBS(t) is the power purchased/sold at time t. A positive value indicates that the system buys electricity from it and a negative value sells electricity to it. Drb(t) and Drs(t) are the power purchase/sale price at t time, Er(Pi(t)) is the emission of the r kind pollutant from the controllable device at time t, Er(Pbuy(t)) is the purchased power at t time r kind pollutant emission, αr is the device treatment cost of the r kind pollutant, L is the pollutant type, Pwd(t) and Dw are the power and the penalty cost per device of wind abandoned by the system at t time, respectively.

3.3 Binding Conditions

Price-based demand response (PBDR) is mainly used for the resources whose residential electricity load is not schedulable. The mathematical model of the elasticity of the user’s electrical load demand can be expressed as follows [16]:

Nt1,t2=ΔPt1P0,t1D0,t2ΔDt2{Nt1,t2≥0,t1≠t2Nt1,t2≤0,t1=t2(14)

where P0,t1 and D0,t2 are respectively the electric load at moment t1 and the electricity price at moment t2 before PBDR is taken. ΔPt1 and ΔDt2 are the change of electric load at moment t1 and the change of electricity price at moment t2 after adopting PBDR, whe t1=t2. Nt1,t2 is the self-elastic coefficient, which is denoted as Nii for the convenience of symbolic distinction, when t1≠t2, Nt1,t2 is the mutual elasticity coefficient, which is denoted as Nij.

After the DR, the change of electrical load is expressed as follows:

[ΔP1/P0,1ΔP2/P0,2⋮ΔP24/P0,24]=[N1,1⋯N1,24N2,1⋯N2,24⋮⋯⋮N24,1⋯N24,24][ΔD1/D0,1ΔD2/D0,2⋮ΔD24/D0,24](15)

The current load at any time is:

Pde(t)=P0,t(1+ΔPt/P0,t)(16)

where Pde(t) is the electrical load after the DR at the t time. The price DR mechanism of gas load can be similar to that of electricity load DR mechanism, which will not be discussed here.

CHP, WT, PV, grid power purchase and sale, energy storage, HDR-EGS electrical output, and customer DR after the electrical load, GSHP, and back injection pump consumption electrical load together constitute the power balance constraint. CHP, HDR-EGS high and medium temperature heating system, GSHP heat output, and customer thermal load together constitute a thermal energy balance constraint. The CHP, the gas purchased from the grid, and the gas load after customer DR together constitute the gas power balance constraint. The power balance of electricity, heat, and gas is shown in the following equation:

{Pde(t)+PHP(t)+PP(t)=PCHP(t)+PWT(t)+PPV(t)+PBS(t)+PES(t)+PHDR(t)PCHP,H(t)+QHO(t)+QMO(t)+PHP,H(t)=PH(t)PG,de(t)=PG,BS(t)−PG,CHP(t)(17)

where PHP(t) is the electrical power input to the GSHP at t time, PHDR(t) and PP(t) is the electrical power of the HDR-EGS and the electrical power of the reinjection pump at t time, respectively, PCHP(t), PWT(t) and PPV(t) are the power generated by the CHP, WT and PV at t time, respectively, PCHP,H(t) is the heating power of CHP at t time, QHO(t) and QMO(t) is the heating power provided to the load by the high and medium temperature heating side at t time, PHP,H(t) is the heating power of GSHP at t time, PH(t) is the RIES thermal load at t time, PG,de(t) is the gas load after the DR at t time, PG,BS(t) is the purchased gas power at t time, PG,CHP(t) is the gas consumption power of CHP at t time.

Taking the prediction error of WP as a random variable and assuming that all WP prediction errors obey normal distribution, the distribution robust chance constraint of its prediction error can be expressed as follows [25]:

Pr∼PWT{PWT(t)−PWTf(t)−ξWT(t)≤0}≥1−β,∀PWT∈PWT(18)

where PWTf(t) is the WP forecast value, ξWT(t) is the WP forecast error, PWT is the WP forecast error distribution, PWT is the set of its forecast error distribution.

RIES is an integrated system consisting of several devices working together, and the device output is limited by the upper and lower limits of the device’s output as well as by climbing constraints as follows:

{Pimin≤Pi(t)≤Pimax−βidown Δt≤Pi(t)−Pi(t−1)≤βiup Δt(19)

where Pimax, Pimin, βiup , βidown  are the maximum and minimum values of the controllable device output and its climbing power, respectively.

The power purchased and sold is constrained by the maximum values PBSmax(t) and minimum values PBSmin(t) of its power output as follows:

PBSmin(t)≤PBS(t)≤PBSmax(t)(20)

The gas network purchase of gas power is also bounded by maximum values PG,BSmax(t) and minimum values PG,BSmin(t) of its output as follows:

PG,BSmin(t)≤PG,BS(t)≤PG,BSmax(t)(21)

The constraints of the energy storage device are as follows:

{PESmin≤PES(t)≤PESmaxSmin≤S(t)≤SmaxEES(0)=EES(T)(22)

where PESmax, PESmin are the maximum and minimum values of the power output, with positive value meaning power output and negative value meaning power input, S(t), Smax and Smin are the energy storage state and its charge state maximum and minimum values at t time, respectively.

4  Model-Solving Methods

4.1 RIES Distribution Robust Scheduling Model Solving

The distributionally robust chance-constrained optimization form of the RIES scheduling model is shown in Eq. (23), which indicates that even in the worst-case scenario, the constraint still has a probability of occurring of not less than 1 − β [26–28].

{minx∈Xh(x)s.t.Pr∼P{H(x,ξ)≤0}≥1−β,∀P∈P(23)

where h(x) is the objective function, H(x,ξ) is a constraint containing random variables, x is the decision variable vector, ξ is an uncertain variable, X is the feasible region of the decision variable, P is the ξ probability distribution function, P is an uncertain set of probability distribution functions.

If KL divergence measures the distance between the distribution function P and the reference distribution P0, its distance DKL(P||P0) is defined as:

DKL(P||P0)=∫f(ξ)ln⁡f(ξ)f0(ξ)dξ(24)

where f(ξ) and f0(ξ) is the density function under P and P0, respectively. In addition, based on the fact that the distance between P and P0 cannot be exceeded η, the uncertainty set of the distribution function is constructed as follows:

P={P|DKL(P||P0)≤η}(25)

As the distribution function of an uncertain variable in Eq. (23) is unknown, it is difficult to deal with it directly. However, reference [25] shows that Eq. (23) can be converted into a chance-constrained programming problem model with the following known distributions:

{minx∈Xh(x)s.t.Pr∼P0{H(x,ξ)≤0}≥1−β__(26)

where

β__=supw>0e−η(w+1)β−1w(27)

This expression indicates that constraint conditions have a probability of occurrence of not less than 1 − β__ in the case of ξ reference distribution P0, but because this expression is a non-convex optimization problem, it still cannot be solved. After applying Bernstein approximation to treat equivalence, the distribution robust optimal chance constraint of prediction error in the model can be transformed into.

PWT−PWTf−μWT+−2σWT2ln⁡β__≤0(28)

where μWT and σWT2 are the expectation and variance of the reference distribution of WP prediction error, respectively.

4.2 Piecewise Linearization Method

In the above HDR-EGS co-generation model, the product B(t)THW(t) of two decision variables exists in Eq. (5), resulting in nonlinear problems in the model. Therefore, piecewise linearization is needed to transform the nonlinear programming problem into a mixed integer linear programming problem, and then a solver is used to solve it.

First, the minimum value of THW(t) is defined as THWmin, the number of segments is K, THW(t) is divided into 2K−1 segments, ΔT is the temperature difference, then:

T⋅HW(t)=THWmin+∑k=1K2k−1uktΔT(29)

where T⋅HW(t) represents the discrete value after piecewise linearization THW(t). To indicate whether the current segment is included in T⋅HW(t) at time t, set ukt to the variable 0–1. Then B(t)THW(t) can be rewritten as:

B(t)THW(t)≈B(t)THWmin+∑k=1K2k−1vktΔT(30)

where vkt=B(t)ukt. In this case, Eq. (30) is a linear equation, and to ensure the constraint equivalence after variable replacement, it is necessary to supplement the constraint Eqs. (31) and (32).

Bmin≤vkt≤Bmaxukt(31)

Bmin≤Bt−vkt≤Bmax(1−ukt)(32)

So far, the DRO model of RIES can be solved in MATLAB directly by using a CPLEX solver.

5  Analysis of Examples

5.1 Scheduling Results and Analysis

To verify the effectiveness of HDR-EGS and the integrated DR of electricity and gas in improving the RIES’s WP absorption capacity and reducing the RIES’s operating cost; the results of RIES scheduling are compared and analyzed in four different situations, among which case 4 is the optimal scheduling method proposed in this paper. The settings for each situation are shown in Table 1. The example parameters are described in [13,16].

The scheduling results of scenario 1 are shown in Fig. 3, from which CHP, WP, PV, battery, and the purchased and sold power between the main network share the electrical load in the RIES, and CHP bears the thermal load in the RIES. In this case, the CHP is restricted by the “fixing power by heat” operation mode, and the change of thermal load will always drive the power output, and the CHP cannot participate in the power supply adjustment independently, resulting in serious wind abandonment of the system and high scheduling cost. During the hours of 01:00–05:00 and 23:00–24:00, the power purchased and sold reaches the upper limit, and the remaining WP is forced to be abandoned.

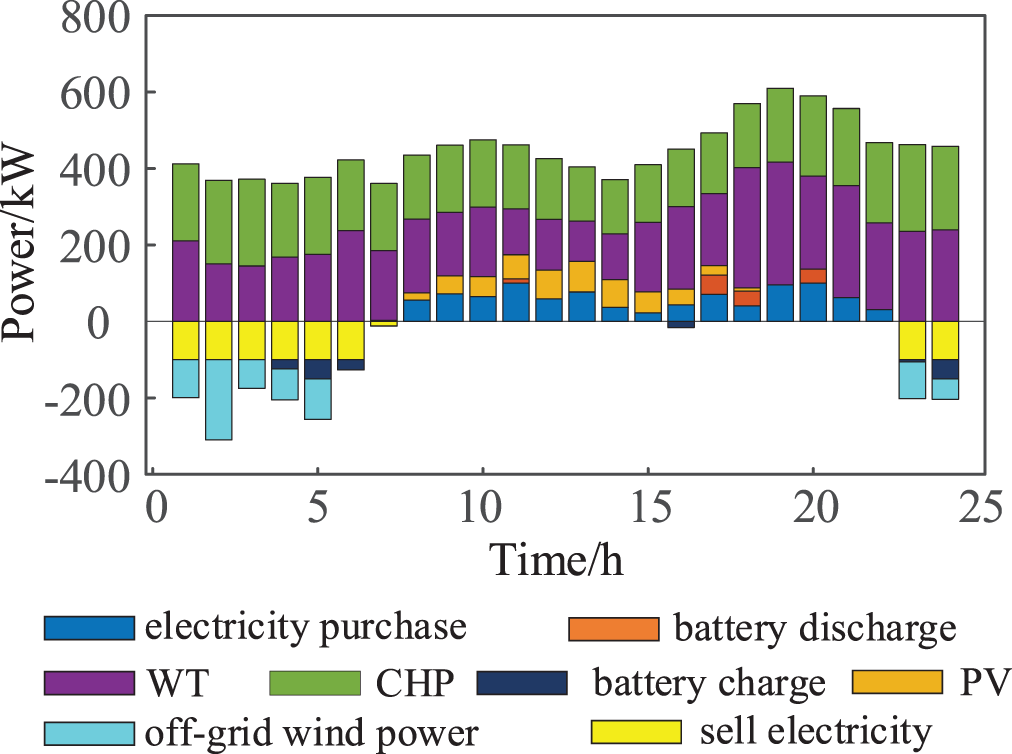
Figure 3: Scheduling results for scenario 1

The scheduling results of scenario 2 are shown in Fig. 4. During the hours of 01:00–06:00 and 23:00 to 24:00, the heating cost of the GSHP is relatively low, and it is preferentially invoked together with the CHP for heating. Compared with scenario 1, scenario 2 after adding the GSHP consumes WP, but at this time, the power is purchased and sold and the power of the GSHP reaches the upper limit. A small amount of WP is still being abandoned. In 07:00–16:00, and 17:00–22:00, the device power generation cost of CHP is lower than the cost of the RIES purchase/sale price. Affected by the operation mode of “fixing electricity by heat”, the thermal load is preferentially provided by CHP, and the GSHP is shut down.

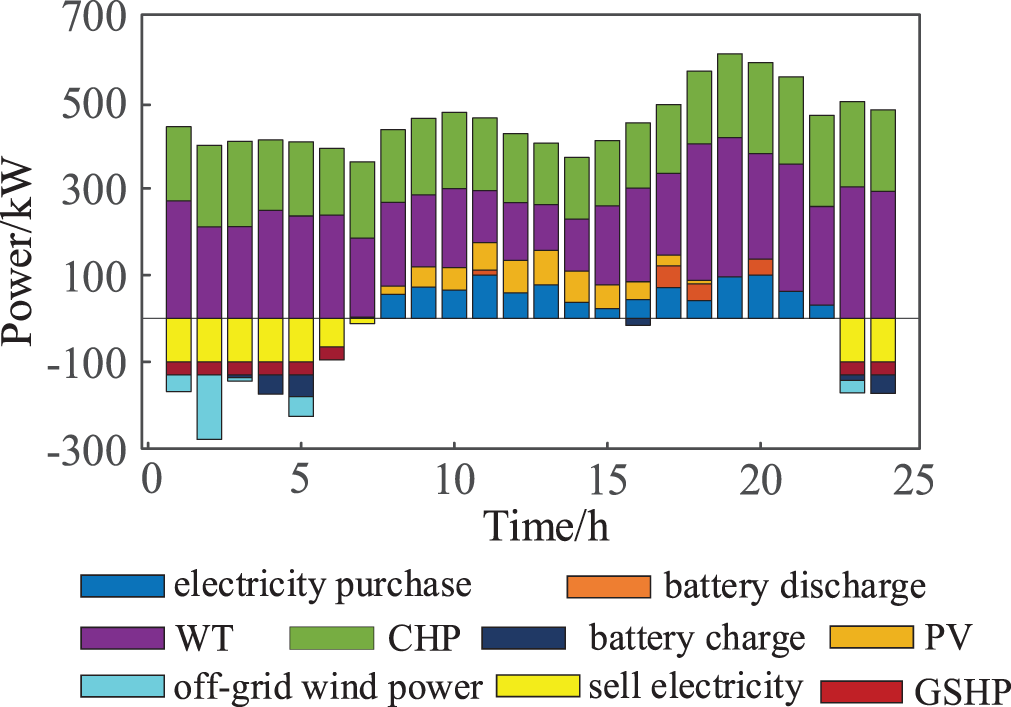
Figure 4: Scheduling results in scenario 2

The scheduling results of scenario 3 are shown in Fig. 5. As shown in Fig. 5, HDR-EGS needs to consume part of the electric load to ensure the complete operation of the entire enhanced geothermal system and build a WP-dry hot rock enhanced geothermal system to achieve the purpose of WP consumption. The GSHP is shut down during the whole operation, which is because HDR-EGS has high power generation and heating efficiency, and the system preferentially calls HDR-EGS for scheduling. The comparison of scenario 2 and scenario 3 scheduling results shows that HDR-EGS plays a more obvious role than GSHP in heating effect and WP consumption.

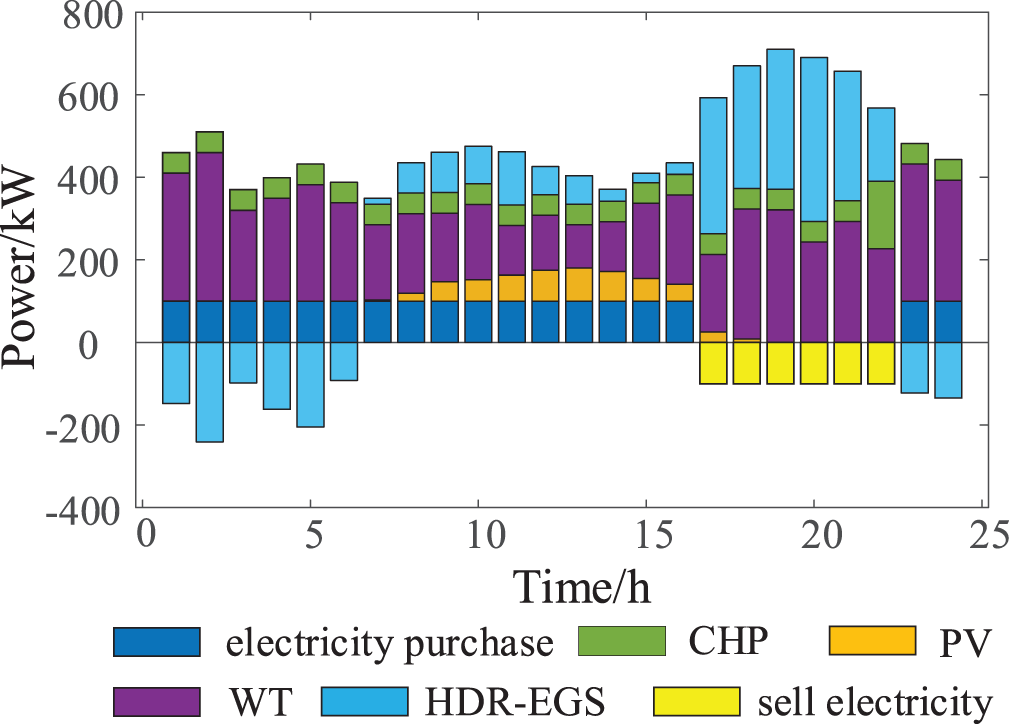
Figure 5: Scheduling results of scenario 3

Fig. 6 shows the load variation curve after considering the power-gas DR, and the scheduling results of scenario 4 are shown in Fig. 7. As shown in Fig. 7, the system carries out power-gas load transfer under the guidance of time-sharing pricing. Although scenario 3 has realized the full absorption of WP, theoretically it is conducive to improving the system’s WP absorption capacity as the power-gas power increases during the off-peak period after the DR. At the same time, with the reduction of power-gas power during peak hours, the system cost is reduced, thus improving the economy of system operation. Compared with case 3, case 4 has more advantages in terms of economy. Fig. 8 shows the time of use (TOU) electricity price and gas price.

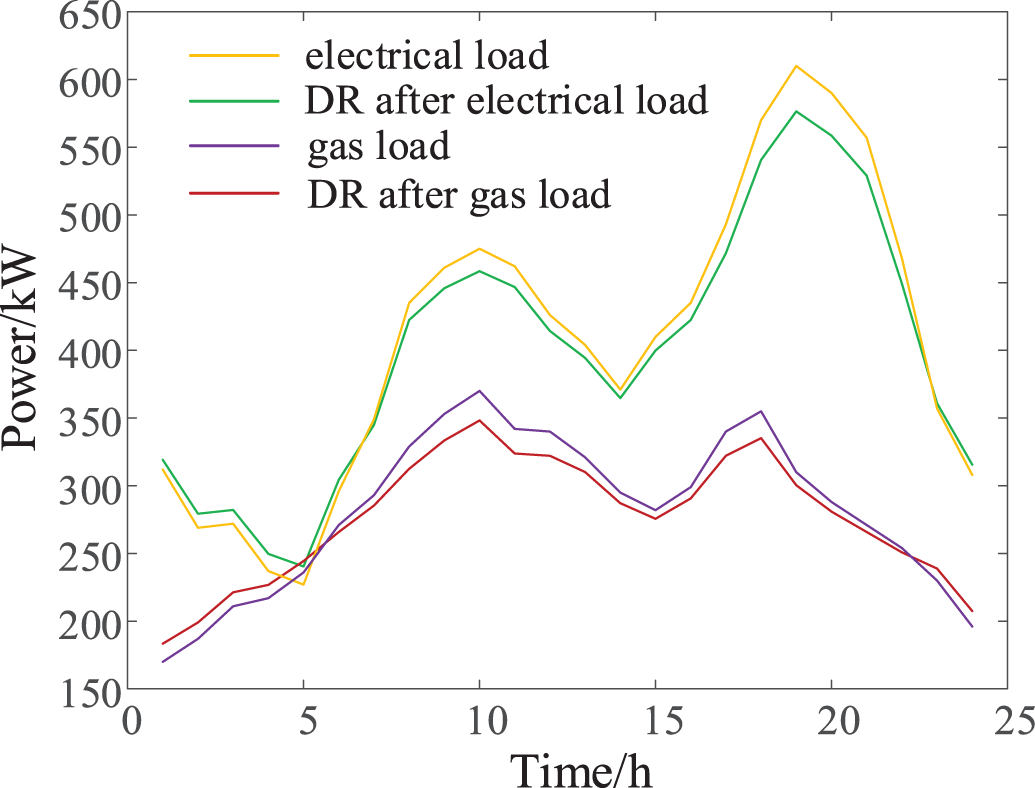
Figure 6: Load change curve

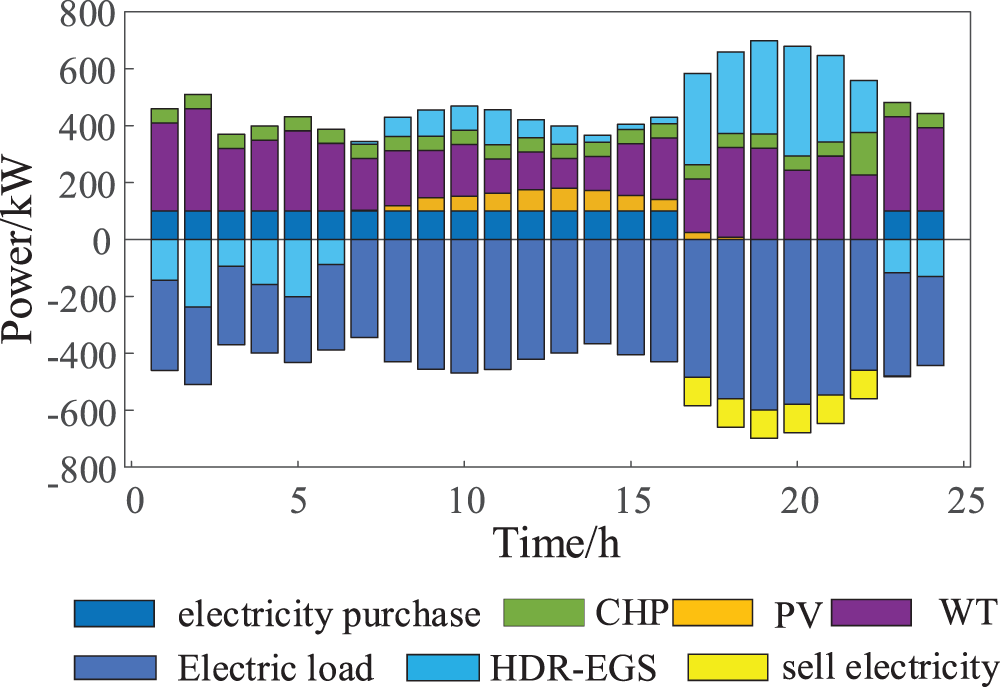
Figure 7: Scheduling results for scenario 4

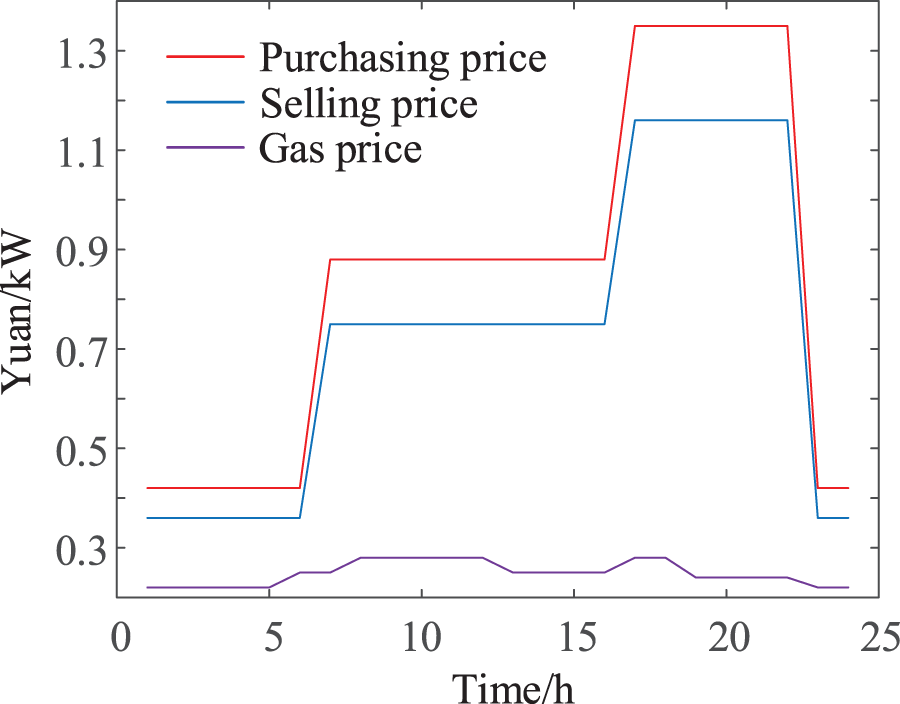
Figure 8: TOU electricity price and gas price

The operation data of each unit of the system is shown in Table 2. The parameters of the energy storage battery are shown in Table 3. The operation parameters of HDR-EGS are shown in Table 4.

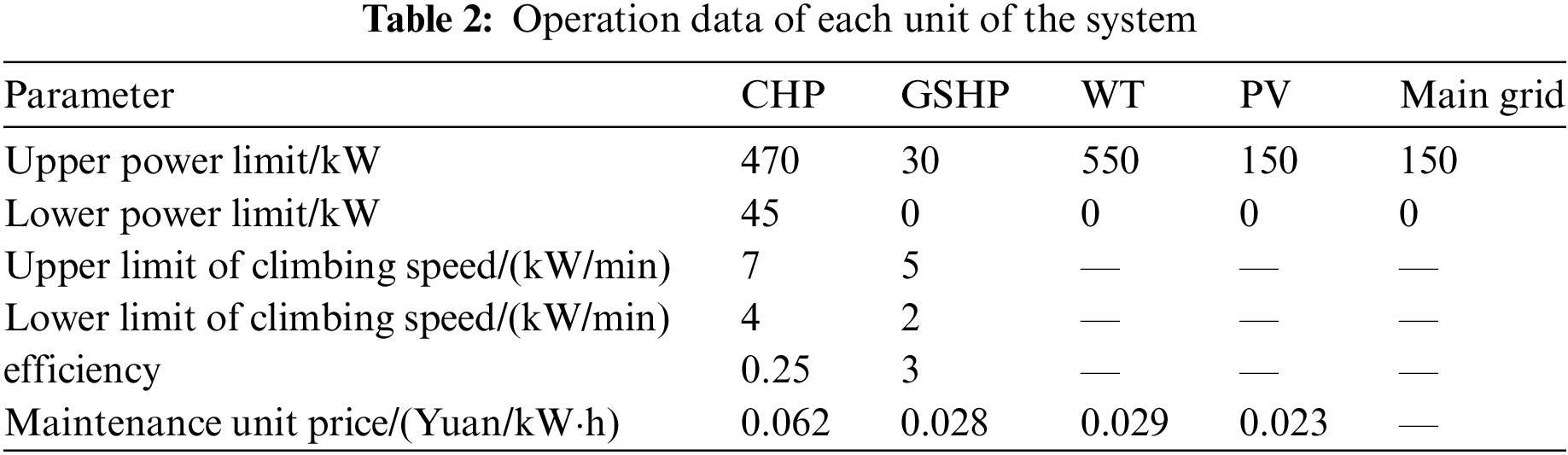
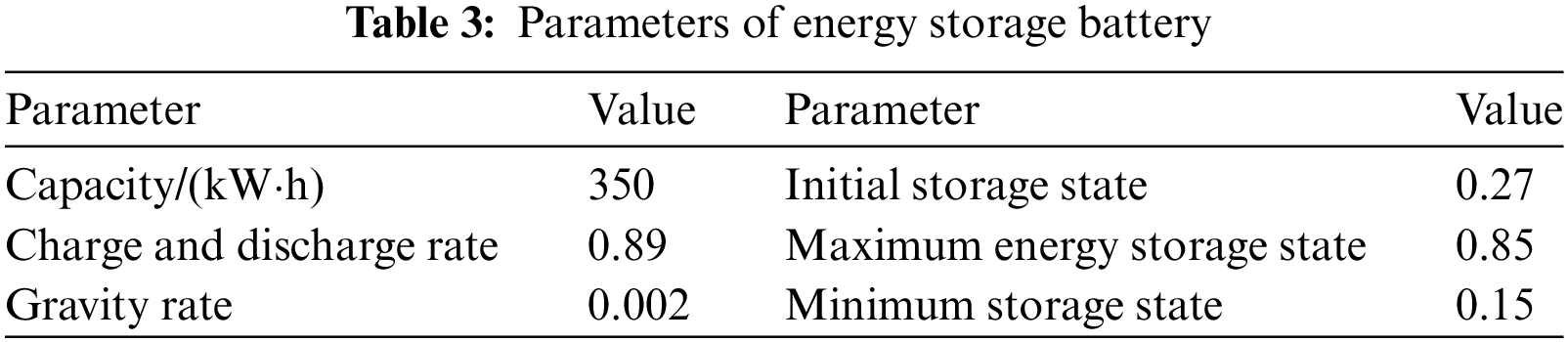
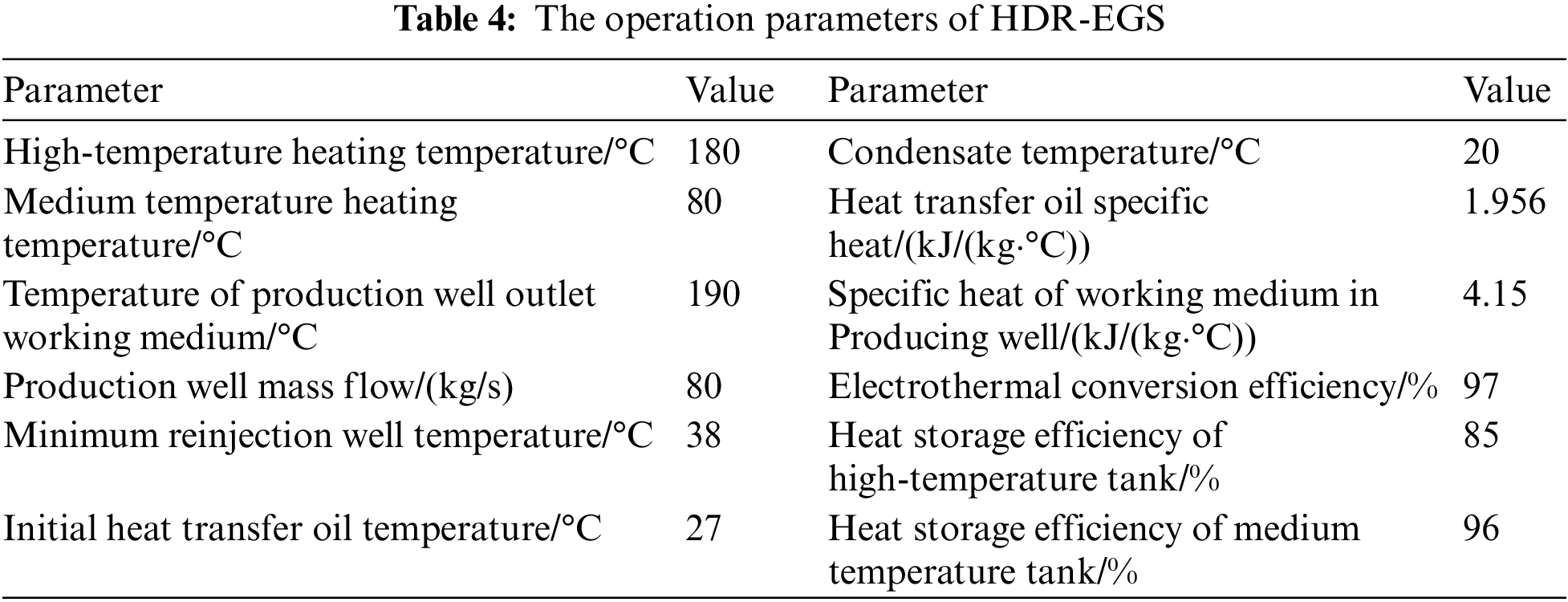
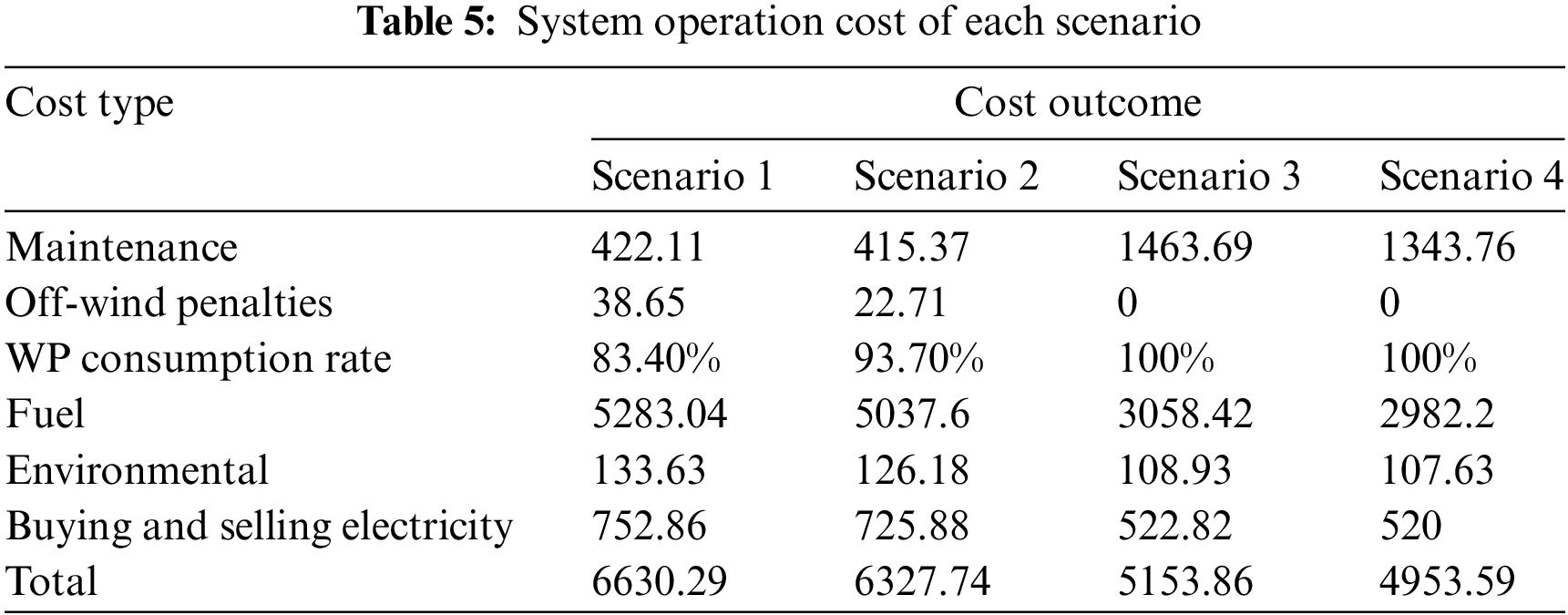
Table 5 shows the operating costs of RIES under different operating conditions in winter. According to Table 5, the scheduling result of scenario 4 is reasonable. Compared with scenarios 1, 2 and 3, the total dispatching cost is reduced by 1676.7, 1374.15 and 200.27 yuan, respectively, which has good economic benefits. The penalty cost and environmental cost of wind curtailment are 100% and 19.46% lower than scenario 1, respectively. The results show that the model has an obvious effect of energy saving and emission reduction while improving the WP absorption capacity of the system.

5.2 B Comparative Analysis of Wind Power Consumption

The WP consumption results of the four scenarios are shown in Fig. 9. Compared with scenario 1 and scenario 2, the WP consumption capacity of RIES is improved after the addition of GSHP at 01:00–06:00 and 22:00–24:00 when WP is in high frequency. The GSHP can convert the electrical load generated by the WT into thermal load. At this time, the thermal load in the RIES is shared by the CHP and the GSHP, which reduces the CHP heating power in the RIES. Limited by the operation mode of “fixing power by heat”, the CHP power supply is correspondingly reduced, thus increasing the WP consumption in the RIES. Compared with scenario 2 and scenario 3, RIES realized full absorption of WP after adding HDR-EGS. During HDR-EGS operation, the reinjection pump consumes a portion of the electrical load to ensure the complete operation of the entire enhanced geothermal system, providing both electrical and thermal load to the RIES. Through the introduction of HDR-EGS at the source side to construct a WP-dry hot rock enhanced geothermal system to optimize the heat source and power supply structure, the thermal load in the RIES is shared by CHP, GSHP, and HDR-EGS, which reduces the CHP heating and power supply power, improves the WP grid space in the RIES, and realizes the full absorption of WP. Scenario 4 considers the power-gas DR. With the increase of power-gas power in the low period after the DR, it is theoretically conducive to the consumption of WP. However, scenario 3 has achieved full consumption, so the graph trend of scenario 4 is consistent with that of scenario 3.

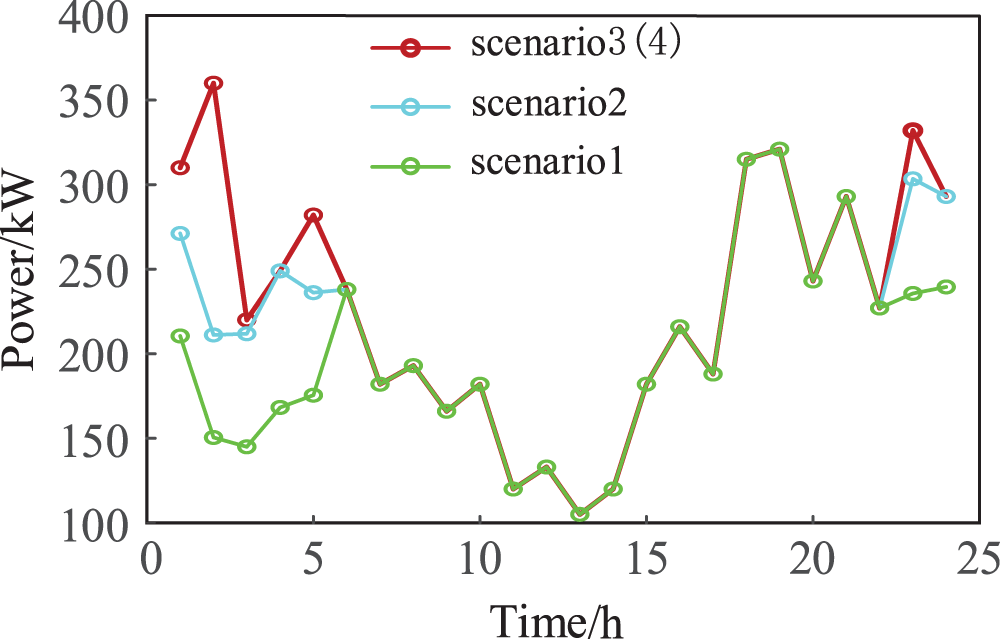
Figure 9: WP consumption comparison chart

5.3 Comparison of Different Stochastic Optimal Scheduling Models

This paper discusses the influence of three stochastic optimization models on the scheduling results: the DRO model, the chance-constrained programming model, and the robust optimization model. In the optimization of DRO, β = 0.05 and η = 0.05 were used as the relevant parameter values. The chance-constrained optimization uses β__ = 0.05 as the relevant parameter value. In the robust optimization model, the variable value is within the interval of [μ−4σ,μ+4σ] and the probability is 99.99%.

The cost results of the three models are shown in Table 6. As can be seen from Table 6, the more conservative the method, the higher the operating cost. The optimization model proposed in this paper is more robust than the chance-constrained optimization model. Although the robustness is poor compared with the robust optimization model, the optimization results have a better economy. The results show that the optimization model achieves a good balance between robustness and economy.

5.4 Influence Analysis of Parameter Setting in Distribution Robust Optimal

The decision maker’s risk preference in the distribution robust optimal depends mainly on two parameters: the confidence level 1−β and the upper limit of the distance between P and P0 in the uncertain set η. In this paper, the above two values are changed to analyze and compare the total cost calculation results of the distribution robust optimal. The calculation results under different parameters are shown in Fig. 10.

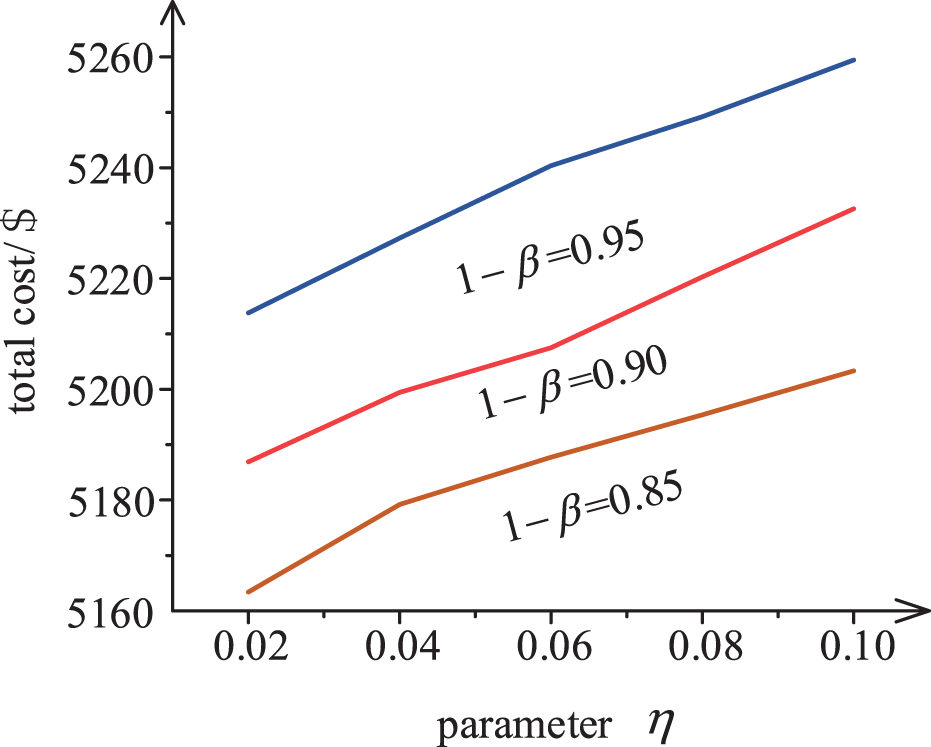
Figure 10: Scheduling results under different parameters

As can be seen from Fig. 10, when the confidence level 1−β is constant, the total cost of the RIES in one day increases with the increase of the distance to the upper limit parameter η, when the upper distance parameter η is constant, the total cost increases with increasing confidence level 1−β. The scheduling cost in the system depends on the degree of risk preference of the decision-maker. The lower the preference degree, the more the adjustment reserve demand of the dry hot rock is used to balance the output prediction error of the WT, and the scheduling cost will increase.

6  Conclusion

This paper presents a DRO scheduling model for a RIES considering HDR co-generation. The simulation was performed on a real RIES in Qinghai province, and the following conclusions were drawn:

(1) In terms of new energy utilization, the proposed scheduling method can solve the wind abandonment problem caused by CHP’s heat-determined power operation mode, and improve the system’s WP consumption capacity.

(2) From the economic point of view, the proposed scheduling method reduces the total cost by 27.52%, which effectively reduces the total cost of system operation during the scheduling cycle. From the environmental point of view, the environmental cost decreases by 19.46%, indicating that the proposed scheduling method has a more obvious effect on energy saving and emission reduction.

(3) The proposed DRO scheduling model has better robustness than the chance-constrained planning model. It is more economical than the robust optimization model. It can better balance the robustness and economy of scheduling results.

Acknowledgement: The authors present their appreciation to King Saud University for funding this research.

Funding Statement: The authors present their appreciation to King Saud University for funding this research through the Researchers Supporting Program Number (RSPD2024R704), King Saud University, Riyadh, Saudi Arabia.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: H Q, M M; data collection: H Q, M S, A A, A I, M M; analysis and interpretation of results: H Q, M S, A A, A I, M M; draft manuscript preparation: H Q, M S, A A, A I, M M. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data supporting reported results are available in the manuscript.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Sugito Y, Vazquez-Corral J, Canham T, Bertalmío M. Image quality evaluation in professional HDR/WCG production questions the need for HDR metrics. IEEE Trans Image Process. 2022;31:5163–77. doi:10.1109/TIP.2022.3190706. [Google Scholar] [PubMed] [CrossRef]

2. Dong J, Wang H, Yang J, Gao L, Wang K, Zhou X. Low carbon economic dispatch of integrated energy system considering power supply reliability and integrated demand response. Comp Model Eng Sci. 2022;132(1):319–40. doi:10.32604/cmes.2022.020394. [Google Scholar] [CrossRef]

3. Zhou B, Xu D, Li C. Optimal scheduling of biogas-solar–wind renewable portfolio for multicarrier energy supplies. IEEE Trans Power Syst. 2018;33(6):6229–39. [Google Scholar]

4. Aliyu MD, Archer RA. A thermo-hydro-mechanical model of a hot dry rock geothermal reservoir. Renew Energy. 2021;176:475–93. [Google Scholar]

5. Niu Y, Wu J, Liu W, Guo W, Lau RW. HDR-GAN: HDR image reconstruction from multi-exposed LDR images with large motions. IEEE Trans Image Process. 2021;30:3885–96. [Google Scholar] [PubMed]

6. Huang W, Cen J, Chen J. Heat extraction from hot dry rock by super-long gravity heat pipe: a field test. Energy. 2022;247:123492. [Google Scholar]

7. Wu X, Huang Z, Dai X, Song H, Zhang S. Thermo-coupled FSI analysis of LN2 jet impinging on the hot dry rock. Appl Therm Eng. 2020;165:114621. [Google Scholar]

8. Prananto LA, Zaini IN, Mahendranata BI. Use of the Kalina cycle as a bottoming cycle in a geothermal power plant: a case study of the Wayang Windu geothermal power plant. Appl Therm Eng. 2018;132:686–96. [Google Scholar]

9. Yue C, Han D, Pu W, He W. Comparative analysis of a bottoming transcritical ORC and a Kalina Cycle for engine exhaust heat recovery. Energy Conv Manag. 2015;89:764–74. [Google Scholar]

10. Zhang F, Xu R, Jiang P. Energy flow analysis of carbon dioxide capture and geothermal power generation. Nat Gas Ind. 2022;42(4):130–8. [Google Scholar]

11. Yan XX, Liu YG, Wang GL. Optimal injection rate of water in the guide basin hot dry rock mining project. Energy Explor Exploit. 2019;37(2):721–35. [Google Scholar]

12. Zhang YJ, Li ZW, Guo LL. Electricity generation from enhanced geothermal systems by oilfield produced water circulating through reservoir stimulated by staged fracturing technology for horizontal wells: a case study in Xujiaweizi Area in Daqing Oilfield, China. Energy. 2014;78:788–805. [Google Scholar]

13. Bagherian MA, Mehranzamir K. A comprehensive review on renewable energy integration for combined heat and power production. Energy Conv Manag. 2020;224:113454. [Google Scholar]

14. Lin S, Song W, Feng Z, Zhao Y, Zhang Y. Energy management strategy and capacity optimization for CCHP system integrated with electric-thermal hybrid energy storage system. Int J Energy Res. 2020;44(2):1125–39. [Google Scholar]

15. Wei Z, Huang Y, Gao H, Shui Y. Joint economic scheduling of power-to-gas and thermoelectric decoupling CHP in regional energy internet. Power Syst Technol. 2018;42(11):3512–20. [Google Scholar]

16. Chen H, Gao L, Zhang Y, Zhao C. Optimal scheduling strategy of a regional integrated energy system considering renewable energy uncertainty and heat network transmission characteristics. Energy Rep. 2022;8:7691–7703. [Google Scholar]

17. Liu D, Shang C, Cheng H. A two-stage robust optimization for coordinated planning of generation and energy storage systems. In: IEEE Conference on Energy Internet and Energy System Integration (EI22017; Beijing, China; p. 1–5. [Google Scholar]

18. Tian G, Sun ZQ. Chance constrained distributionally robust optimal HVAC scheduling for commercial building demand response. In: IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT2022; New Orleans, LA, USA; p. 1–5. [Google Scholar]

19. Yang CI, Jiang T, Zhong W. Economic scheduling approach of RIES for electric vehicle and heat pump to promote wind power accommodation. Electr Power Autom Equip. 2021;41(2):1–7. [Google Scholar]

20. Tan H, Ren Z, Yan W. A wind power accommodation capability assessment method for multi-energy microgrids. IEEE Trans Sustain Energy. 2021;12(4):2482–92. [Google Scholar]

21. Zhang Z, Song M, Liu H, Wang C, Li L, Liu W. Review of typical energy storage resources from the perspective of generalized energy storage system. In: IEEE 5th International Electrical and Energy Conference (CIEEC2022; Nanjing, China; p. 4733. [Google Scholar]

22. Abada A, St-Hilaire M, Shi W. Auction-based scheduling of excess energy consumption to enhance grid upward flexibility. IEEE Access. 2022;10:5944–56. [Google Scholar]

23. Yang L, Cai Y, Qiao Y, Yan N, Ma S. Research on optimal allocation method of energy storage considering supply and demand flexibility and new energy consumption. In: IEEE 4th Conference on Energy Internet and Energy System Integration (EI22020; Wuhan, China; p. 4368–73. [Google Scholar]

24. Wang H, Gu C, Zhang X, Li F. Optimal CHP planning in integrated energy systems considering network charges. IEEE Syst J. 2020;14:2684–93. [Google Scholar]

25. Mohamed MA, Jin T, Su W. An effective stochastic framework for smart coordinated operation of wind park and energy storage unit. Appl Energy. 2020;272:115228. [Google Scholar]

26. Tan H, Yan W, Ren Z, Wang Q, Mohamed MA. Distributionally robust operation for integrated rural energy systems with broiler houses. Energy. 2022;254:124398. [Google Scholar]

27. Tan H, Li Z, Wang Q, Mohamed MA. A novel forecast scenario-based robust energy management method for integrated rural energy systems with greenhouses. Appl Energy. 2023;330:120343. [Google Scholar]

28. Tan H, Yan W, Ren Z, Wang Q, Mohamed MA. A robust dispatch model for integrated electricity and heat networks considering price-based integrated demand response. Energy. 2022;239:121875. [Google Scholar]