 Open Access
Open Access
ARTICLE
Numerical Treatments for Crossover Cancer Model of Hybrid Variable-Order Fractional Derivatives
1 Mathematics Department, Faculty of Science, Cairo University, Giza, 12613, Egypt
2 Mathematics Department, Faculty of Education, Sana’a University, Sana’a, 1247, Yemen
3 Mathematics Department, Faculty of Science, Helwan University, Cairo, 11795, Egypt
4 Department of Mathematics, College of Science, University of Bisha, Al Namas, 67398-5644, Saudi Arabia
* Corresponding Author: Seham Al-Mekhlafi. Email:
(This article belongs to the Special Issue: Mathematical Aspects of Computational Biology and Bioinformatics-II)
Computer Modeling in Engineering & Sciences 2024, 140(2), 1619-1645. https://doi.org/10.32604/cmes.2024.047896
Received 21 November 2023; Accepted 26 February 2024; Issue published 20 May 2024
Abstract
In this paper, two crossover hybrid variable-order derivatives of the cancer model are developed. Grünwald-Letnikov approximation is used to approximate the hybrid fractional and variable-order fractional operators. The existence, uniqueness, and stability of the proposed model are discussed. Adams Bashfourth’s fifth-step method with a hybrid variable-order fractional operator is developed to study the proposed models. Comparative studies with generalized fifth-order Runge-Kutta method are given. Numerical examples and comparative studies to verify the applicability of the used methods and to demonstrate the simplicity of these approximations are presented. We have showcased the efficiency of the proposed method and garnered robust empirical support for our theoretical findings.Keywords
One of the most dreaded and feared diseases is cancer. According to statistics, there are 1300 cancer-related fatalities every day in India. The incidence of cancer has been rising steadily over the past few decades. Several numerical models were created in the meantime to describe how cancer sickness spreads, for instance [1]. To better understand the characteristics of the disease cancer models have been created [2–4].
The biological phenomena procedures that are best described by fractional differential equations have been simulated using fractional calculus. Common integer-order derivative mathematical systems, such as nonlinear models, frequently fail. Fractional calculus has grown in importance during the past several years in fields like electrical engineering, chemistry, economics, control theory, mechanics, and image and signal processing. Fractional order calculus is as old as classical calculus, however, it has only been recently used in mathematics [5,6]. A hybrid fractional operator is built in [7]. Compared to Caputo’s fractional derivative operator, this new operator is more general. It is a linear combination of the Riemann Liouville integral and Caputo fractional derivative. The generalized fractional mathematical models are supposed to be helpful for modeling purposes in epidemiology. Its key benefits are that it captures factuality, captures memory effects, is multistage, and offers superior data fitting [8]. When compared to integer-order models, which either overlook or make it difficult to account for the systems’ memory and hereditary properties, fractional epidemic models provide a powerful tool for doing so. Additionally, the fractional version offers one more degree of freedom than the integer model when it comes to data fitting. A fractional order system provides several advantages, such as the most accurate data fitting, having its memory, and its ability to choose the fractional ordered value that will most accurately characterize a model in the real world. Due to hereditary characteristics, the fractional derivatives models are additionally strengthened and therefore better suited for illustrating a real-life phenomenon [9]. It is more efficient than the standard arrangement and provides advantages for crossover behavior. In [10–12] and the references therein, various mathematical models with intriguing findings are proposed.
Additionally, it can be used to investigate complex phenomena, such as disease models in [13–15]. The hybrid fractional operator, which can be defined as a linear combination of the Riemann-Liouville fractional integral and the Caputo fractional derivative, is one of the most efficient and dependable operators. This operator is more general than the Caputo fractional operator, as shown in [7]. Such fractional-order differential equations are challenging to solve analytically. Therefore, it is crucial to create numerical methods for approximating the solutions to these models.
Some real-world problems have complicated behaviors, so in the last years, piecewise calculus has been developed to more accurately depict these issues [16–19]. Applications in several real-life problems display crossover behavior. Lately, the idea of crossover phases, both differential and integral operators, has been created and applied to many difficult real-world scenarios, like that of chaos and many epidemiologic concerns. The theory seems to perform well when predicting scenarios involving crossover behaviors; for more details see [20].
The cancer models’ fractional-order derivatives are examined in [21]. We are attempting to alter the hyperchaotic cancer model in this scenario using the concept of a piecewise differential model, where its initial portion is dependable on an integer, the second portion is a hybrid order of fractions, while the last part is a hybrid fractional of variable order to identify some hidden insights of the model which will be very helpful both from biological and mathematical perspectives. Therefore, the main aim of this study is to develop two crossover hybrid variable-order derivatives of the cancer model. Moreover, Adams Bashfourth’s fifth-step method with a hybrid variable-order fractional operator (CPC-AB5SM) will be developed to study the proposed models. Comparative studies with the generalized fifth-order Runge-Kutta method (GRK5M) will be given. Grünwald-Letnikov approximation is used to approximate the hybrid variable-order fractional operator. We will discuss the existence, uniqueness, and stability of the proposed model. Numerical examples and comparative studies to verify the applicability of the used methods and to demonstrate the simplicity of these approximations will be presented.
The basic structure of the paper is the following: “Basic Notations” introduces key concepts of hybrid fractional-order derivatives. The two types of crossover cancer models are given. Additionally, the proposed models’ existence, uniqueness, and stability analysis are presented in “The Cancer Mathematical Model”. The proposed models are solved numerically through the creation of schemes in the “Numerical Method” and the stability of these schemes is shown. The article discusses the approximation of solutions for the proposed system using CPC-AB5SM and GRK5M in “Numerical Simulations” along with a discussion. “Conclusions” presents the conclusions at the end of the paper.
Definition 2.1. The Caputo proportional constant (CPC) fractional hybrid operator is defined as [7,8]:
CPC0Dαty(t)=1Γ(1−α)(∫t0(t−s)−α(y(s)K1(α)+y′(s)K0(α))ds)=K1(α)RL0I1−αty(t)+K0(α)C0Dαty(t),(1)
where, K0(α)=αQ(1−α), K1(α)=(1−α)Qα, Q is constant, 0<α≤1.
Definition 2.2. The variable order fractional CPC integration is stated as follows [7,8]:
CPC0Iα(t)t=1K0(α(t))[∫t0exp(K1(α(t))K0(α(t))(t−s)) RL0D1−α(t)ty(s)ds].(2)
The generalized mean value theorem being applied, we drive [7]:
y(t)=y(t1)+1K0(α(t))[∫tt1exp(K1(α(t))K0(α(t))(t−s)) RL0D1−α(t)ty(s)ds].(3)
2.1 Types of Crossover Derivatives
In this part, we propose two types of crossover derivatives. Let y∈[0,T] be a differentiable function, the types of crossover differential equations are given as follows:
Type 1: The classical, fractional order, and variable order piecewise derivatives are stated as follows:
f(t,y(t))={y′(t),0≤t≤t1, CPCDαy(t),t1<t≤t2, CPCDα(t)y(t),t2<t≤T.(4)
Type 2: The variable order, integer order, and fractional order piecewise derivatives are stated as follows:
f(t,y(t))={ CPCDα(t)y(t),0≤t≤t1,y′(t),t1<t≤t2, CPCDαy(t),t2<t≤T.(5)
3 The Cancer Mathematical Model
Cancer models are developed to help better understand the traits of the illness, for further details, [2]. In [21], the fractional-order derivatives of the cancer models are investigated. Conventional derivatives are unable to simulate the sudden shifts that result in multibehavior. In light of this, some academics have lately noted that the aforementioned process can be modeled by differential equations utilizing piecewise equations. Recent publications in this field that we think are important include [22].
We will introduce two types for the crossover cancer mathematical model:
Type 1: Consider x,y,z are differentiable and defined in Table 1. The first type of crossover cancer model is given as follows:

dx(t)dt=x(t)(1−x(t))−C1x(t)y(t)−C2x(t)z(t),dy(t)dt=C3y(t)(1−y(t))−C4x(t)y(t),dz(t)dt=C5x(t)z(t)x(t)+C6−C7x(t)z(t)−C8z(t),}0≤t≤t1,(6)
where, x(0)=x0, y(0)=y0, z(0)=z0.
CPC0Dαtx(t)=x(t)(1−x(t))−C1x(t)y(t)−C2x(t)z(t), CPC0Dαty(t)=C3y(t)(1−y(t))−C4x(t)y(t), CPC0Dαtz(t)=C5x(t)z(t)x(t)+C6−C7x(t)z(t)−C8z(t),}t1<t≤t2,(7)
where, x(t1)=x1, y(t1)=y1, z(t1)=z1.
CPC0Dα(t)tx(t)=x(t)(1−x(t))−C1x(t)y(t)−C2x(t)z(t), CPC0Dα(t)ty(t)=C3y(t)(1−y(t))−C4x(t)y(t), CPC0Dα(t)tz(t)=C5x(t)z(t)x(t)+C6−C7x(t)z(t)−C8z(t),}t2<t≤T.(8)
where, x(t2)=x2, y(t2)=y2, z(t2)=z2.
Such that, C1,C2,C3,C4,C5,C6,C7 and C8 are constants.
The definition of all variables within the system in Table 1 and the details of the parameters for the cancer model, see [23]. Here dx(t)dt,dy(t)dt and dx(t)dt are the integer order for 0≤t≤t1, CPCt1Dαt2 is the fractional CPC derivative of order 0<α≤1 for t1<t≤t2 and CPCt2Dα(t)T is the variable order fractional of CPC derivative for t2<t≤T.
Type 2: Consider x,y,z are differentiable, then the second type of crossover cancer model given as follows:
CPC0Dα(t)tx(t)=x(t)(1−x(t))−C1x(t)y(t)−C2x(t)z(t), CPC0Dα(t)ty(t)=C3y(t)(1−y(t))−C4x(t)y(t), CPC0Dα(t)tz(t)=C5x(t)z(t)x(t)+C6−C7x(t)z(t)−C8z(t),}0≤t≤t1,(9)
where, x(t0)=x0, y(t0)=y0, z(t0)=z0.
dx(t)dt=x(t)(1−x(t))−C1x(t)y(t)−C2x(t)z(t),dy(t)dt=C3y(t)(1−y(t))−C4x(t)y(t),dz(t)dt=C5x(t)z(t)x(t)+C6−C7x(t)z(t)−C8z(t),}t1<t≤t2,(10)
where, x(t1)=x1, y(t1)=y1, z(t1)=z1.
CPC0Dαtx(t)=x(t)(1−x(t))−C1x(t)y(t)−C2x(t)z(t), CPC0Dαty(t)=C3y(t)(1−y(t))−C4x(t)y(t), CPC0Dαtz(t)=C5x(t)z(t)x(t)+C6−C7x(t)z(t)−C8z(t),}t2<t≤T.(11)
where, x(t2)=x2, y(t2)=y2, z(t2)=z2.
Such that, C1,C2,C3,C4,C5,C6,C7 and C8 are constants. The variable fractional order of CPC derivative for 0≤t≤t1, the integer derivative for t1<t≤t2 and fractional CPC derivative for t2<t≤T given as (1).
To study the existence of the solution for the model (7), we will use the fixed-point theorem [24]. First, convert (7) into an integral formula as shown below:
x(t)−x(0)= CPC0Iαt(x(t)(1−x(t))−C1x(t)y(t)−C2x(t)z(t)),y(t)−y(0)= CPC0Iαt(C3y(t)(1−y(t))−C4x(t)y(t)),z(t)−z(0)= CPC0Iαt(C5x(t)z(t)x(t)+C6−C7x(t)z(t)−C8z(t)).(12)
Using the fractional integral of order α provided by (3), we obtain
x(t)=x(0)+1K0(α(t))[∫t0exp(K1(α(t))K0(α(t))(t−s))RL0D1−α(t)t(x(s)(1−x(s))−C1x(s)y(s)−C2x(s)z(s))ds],y(t)=y(0)+1K0(α(t))[∫t0exp(K1(α(t))K0(α(t))(t−s))RL0D1−α(t)t(C3y(s)(1−y(s))−C4x(s)y(s))ds],z(t)=z(0)+1K0(α(t))[∫t0exp(K1(α(t))K0(α(t))(t−s))RL0D1−α(t)t(C5x(s)z(s)x(s)+C6−C7x(s)z(s)−C8z(s))ds].(13)
Among our definitions of kernels are
τ(t,x(t))=exp(K1(α(t))K0(α(t))(t−s)) RL0D1−α(t)t(x(t)(1−x(t))−C1x(t)y(t)−C2x(t)z(t)),ν(t,y(t))=exp(K1(α(t))K0(α(t))(t−s)) RL0D1−α(t)t(C3(−y+1)y)−C4xy),ϕ(t,z(t))=exp(K1(α(t))K0(α(t))(t−s)) RL0D1−α(t)t(C5x(t)z(t)x(t)+C6−C7x(t)z(t)−C8z(t)).(14)
Theorem 3.1. The Lipschitz condition can be satisfied by the kernels τ,ν, and ϕ.
Proof. For each proposed kernel, we show this condition. Let x and X be two functions for kernel 1, y and Y for kernel 2, and z and Z for kernel 3. Next, we consider the following:
||τ(t,x(t))−τ(t,X(t))||=exp(K1(α(t))K0(α(t))(t−s)) RL0D1−α(t)t||(x(t)−X(t))[1−(x(t)−X(t))]−C1(x(t)−X(t))y(t)−C2(x(t)−X(t))z(t)||,||ν(t,y(t))−ν(t,Y(t))||=exp(K1(α(t))K0(α(t))(t−s)) RL0D1−α(t)t(C3||(y(t)−Y(t))[1−(y(t)−Y(t))]−Dx(t)(y(t)−Y(t))||),||ϕ(t,z(t))−ϕ(t,Z(t))||=exp(K1(α(t))K0(α(t))(t−s)) RL0D1−α(t)t(C5||x(t)(z(t)−Z(t))x(t)+C6−C7x(t)(z(t)−Z(t))−C8(z(t)−Z(t))||).(15)
Cauchy’s inequality gives us the following:
||τ(t,x(t))−τ(t,X(t))||≤exp(K1(α(t))K0(α(t))(t−s)) RL0D1−α(t)t||(x(t)−X(t))[1−(x(t)−X(t))]−C1(x(t)−X(t))y(t)−C2(x(t)−X(t))z(t)||,||ν(t,y(t))−ν(t,Y(t))||≤exp(K1(α(t))K0(α(t))(t−s)) RL0D1−α(t)t(C3||(y(t)−Y(t))[1−(y(t)−Y(t))]−C4x(t)(y(t)−Y(t))||),||ϕ(t,z(t))−ϕ(t,Z(t))||≤exp(K1(α(t))K0(α(t))(t−s)) RL0D1−α(t)t(C5||x(t)(z(t)−Z(t))x(t)+C6−C7x(t)(z(t)−Z(t))−C8(z(t)−Z(t))||).(16)
Given the recursive formula below, we obtain
x(t)=1K0(α(t))[∫t0τ(s,xn−1(s))ds],y(t)=1K0(α(t))[∫t0ν(s,yn−1(s))ds],z(t)=1K0(α(t))[∫t0ϕ(s,zn−1(s))ds].(17)
When we apply the norm and the triangle inequality to the difference between both successive terms, we obtain
||Yn(t)||=||xn(t)−Xn−1(t)||≤1K0(α(t))‖∫t0(τ(s,xn−1(s))−τ(s,xn−2(s))ds‖,||Φn(t)||=||yn(t)−Yn−1(t)||≤1K0(α(t))‖∫t0(ν(s,xn−1(s))−ν(s,xn−2(s))ds‖,||Ψn(t)||=||zn(t)−Zn−1(t)||≤1K0(α(t))‖∫t0(ϕ(s,xn−1(s))−ϕ(s,xn−2(s))ds‖,(18)
such that,
xn(t)=∞∑m=0Ym(t);yn(t)=∞∑m=0Φm(t);zn(t)=∞∑m=0Ψm(t).(19)
The Lipschitz condition is satisfied by the kernels τ,ν, and ϕ, hence we obtain
||Yn(t)||=||xn(t)−Xn−1(t)||≤1K0(α(t))[Δ1∫t0||xn−1(t)−Xn−2(t)||ds],||Φn(t)||=||yn(t)−Yn−1(t)||≤1K0(α(t))[Δ2∫t0||yn−1(t)−Yn−2(t)||ds],||Ψn(t)||=||zn(t)−Zn−1(t)||≤1K0(α(t))[Δ3∫t0||zn−1(t)−Zn−2(t)||ds],(20)
where, K0(α(t))=α(t)Q(1−α(t)), and Q,Δ1,Δ2,Δ3 are constants. This concludes Theorem 3.1 Proof. ■
Theorem 3.2. Kernels τ, ν and ϕ satisfed Lipsctize condition by considering (20) is bounded.
Proof. The Lipschitz condition is satisfied by the kernels τ,ν, and ϕ when (20) is bounded, as we showed. With the use of the recursive method and the results from (20), we can derive the relationship shown below:
||Yn(t)||≤||x(0)||+{1K0(α(t))Δ1t}n,||Φn(t)||≤||y(0)||+{1K0(α(t))Δ2t}n,||Ψn(t)||≤||z(0)||+{1K0(α(t))Δ3t}n.(21)
As a result, Eq. (21) is smooth and exists. However, to demonstrate that the aforementioned functions represent a system of solutions, we suppose
x(t)=xn(t)−Θ1(n);y(t)=yn(t)−Θ2(n);z(t)=zn(t)−Θ2(n),(22)
where the reminder terms for the series solution are Θ1(n),Θ2(n) and Θ3(n). Thus,
||x(t)−Xn(t)||=1K0(α(t))∫t0τ(s,x−Θ1(n)),||y(t)−Yn(t)||=1K0(α(t))∫t0ν(s,y−Θ2(n))ds‖,||z(t)−Zn(t)||=1K0(α(t))∫t0ϕ(s,z−Θ3(n))ds‖.(23)
Using the Lipschitz condition and the norm on both sides, we obtain
‖x(t)−x(0)−1K0(α(t))∫t0(τ(s,x(s))ds‖≤‖Θ1(n)‖+1K0(α(t))Δ1t‖Θ1(n)‖,‖y(t)−y(0)−1K0(α(t))∫t0(ν(s,y(s))ds‖≤≤‖Θ2(n)‖+1K0(α(t))Δ2t‖Θ2(n)‖,‖z(t)−z(0)−1K0(α(t))∫t0(τ(s,z(s))ds‖≤‖Θ3(n)‖+1K0(α(t))Δ3t‖Θ3(n)‖.(24)
The result of taking the limit n→∞ is
x(t)=x(0)+1K0(α(t))∫t0(τ(s,x(s))ds,y(t)=y(0)+1K0(α(t))∫t0(ν(s,y(s))ds,z(t)=z(0)+1K0(α(t))∫t0(ϕ(s,z(s))ds.(25)
■
Theorem 3.3. The system described in (7) has a unique solution.
Proof. To show that, let us obtain other solutions, such as x(t), y(t), and z(t).
x(t)−X(t)=1K0(α(t))∫t0(τ(s,x(s))−τ(s,X(s))ds,y(t)−Y(t)=1K0(α(t))∫t0(ν(s,y(s))−ν(s,Y(s))ds,z(t)−Z(t)=1K0(α(t))∫t0(ϕ(s,z(s))−ϕ(s,Z(s))ds.(26)
When we apply the norm on the two sides, the result is
‖x(t)−X(t)‖=1K0(α(t))∫t0‖(τ(s,x(s))−τ(s,X(s))‖ds,‖y(t)−Y(t)‖=1K0(α(t))∫t0‖(ν(s,y(s))−ν(s,Y(s))‖ds,‖z(t)−Z(t)‖=1K0(α(t))∫t0‖(ϕ(s,z(s))−ϕ(s,Z(s))‖ds.(27)
Given the Lipschitz condition and the knowledge that a solution is bounded, we obtain
‖x(t)−X(t)‖≤{1K0(α(t))Δ1W1t}n,‖y(t)−Y(t)‖≤{1K0(α(t))Δ2W2t}n,‖z(t)−Z(t)‖≤{1K0(α(t))Δ2W3t}n.(28)
Since this holds for all n, x(t)=X(t);y(t)=Y(t);z(t)=Z(t). As a result, it proves the uniqueness of the proposed solution. ■
3.2 Existence and Uniqueness of the Solution Piecewisely
We validate the linear growth and Lipschitz condition characteristics to achieve this. Additionally, consider B to be a Banach space with the norm ||ψ||∞=supt∈Dψ|ψ(t)|. ∀t∈(0,t1), we assume that there are four positive constants such that ||X||∞<A1, ||Y||∞<A2 and ||Z||∞<A3.
dxdt=g1(x,y,z,t),dydt=g2(x,y,z,t),dzdt=g3(x,y,z,t),(29)
When the right-hand side of the equations in the (6) system is represented by gρ(x,y,z,t),ρ=1,2,3. First, we make sure that
|gρ(x,t)|2<kρ(|xρ|2+1),|gρ(x1,t)−|gρ(x2,t)|2<ˉkρ|x1−x2|2.(30)
To show the existence and uniqueness piecewise. We assume a function g1(x,y,z,t)
|g1(x,y,z,t)|2=|x(t)(1−x(t))−C1x(t)y(t)−C2x(t)z(t)|≤4(|x|2−|x2|2−C1|x|2|y|2−C2|x|2|z|2),≤4(|x2|−|x4|−C1|x2|||y2||∞−C2|x2|||z2||∞),≤4(1−|x2|−C1||y2||∞−C2||z2||∞)|x2|,≤4(−C1||y2||∞−c2||z2||∞)(1+1C1||y2||∞+C2||z2||∞|x2|)|x2|.(31)
Continuing the same technique g2(x,y,z,t)
|g2(x,y,z,t)|2=|C3y(t)−y2(t)−C4x(t)y(t)|≤5C3|y|2−|y2|2−C4|x|2|y|2,≤5C3|y2|−|y4|−C4|x2||y2|,≤5C3|y2|−|y4|−C4||x2||∞|y2|,≤5(C3−|y2|−C4||x2||∞)|y2|,≤5(C3−C4||x2||∞)(1+1C3−C4||x2|||y2|)|y2|.(32)
In the case of the function g3(x,y,z,t)
|g3(x,y,z,t)|2=C5|xzx+C6−C7xz−C8z|2≤4(C5|xzx+C6|2−C7|x|2|z|2−C8|z|2),≤4(C5||x2||∞||(x+C6)2||∞|z2|−C7||x2||∞|z2|−C8|z2|),≤4(C5||x2||∞||(x+C6)2||∞−C7||x2||∞−C8)|z2|,≤4(C5||x2||∞||(x+C6)2||∞−C7||x2||∞−C8)|z2|,≤−4H(−C5||x2||∞H||(x+C6)2||∞+C7C8||x2||∞+1)|z2|.(33)
To find the equilibrium points of system (6), we write
dxdt=dydt=dzdt=0.
Also, when C1=1, C2=2.5, C3=0.6, C4=1.5, C5=4.5, C6=1, C7=0.2, C8=0.5, Therefore, the system (6) has five steady states:
E1=(18.867497,0,−7.1469988),E2=(18.867497,46.1687425,−25.6144958),E3=(0.132503,0,0.3469988),E4=(0.132503,−0.6687425,0.6144958),E5=(0,1,0).(34)
At the equilibrium point E1=(18.867497,0,−7.1469988), the Jacobian matrix of system (6) is given by
J(E1)=[−18.8675−18.8675−47.16870−27.701201.34790−0.0000],(35)
which has the eigenvalues
[λ1λ2λ3]=[−27.7012−14.4752−4.3923],(36)
here λ1,λ2,λ3 are real numbers of the same sign. Therefore the equilibrium point E1 is a stable node point.
In a similar way, at the equilibrium point E2=(18.867497,46.1687425,−25.6144958), the Jacobian matrix of system is
J(E2)=[−18.8675−18.8675−47.1687−69.2531−83.103704.83090−0.0000],(37)
which has the eigenvalues
[λ1λ2λ3]=[−98.9616+0.0000i−1.5048−13.7509i−1.5048+13.7509i],(38)
therefore the equilibrium point E2 is stable node point.
Using a similar calculation E3=(0.132503,0,0.3469988), the Jacobian matrix of system is
J(E3)=[−0.1325−0.1325−0.331300.401201.14810−0.0000],(39)
which has the eigenvalues
[λ1λ2λ3]=[0.4012+0.0000i−0.0663−0.6131i−0.0663+0.6131i],(40)
here λ1 is positive real number. Therefore the equilibrium point E3 is saddle point, and so it is unstable.
At E4=(0.132503,−0.6687425,0.6144958), the Jacobian matrix of system is
J(E4)=[−0.1325−0.1325−0.33131.00311.203702.03310−0.0000],(41)
which has the eigenvalues
[λ1λ2λ3]=[1.1323+0.0000i−0.0305−0.8456i−0.0305+0.8456i],(42)
here λ1 is positive real number. Therefore the equilibrium point E4 is saddle-focus point, and so it is unstable.
At E5=(0,1,0), the Jacobian matrix of system is
J(E5)=[000−1.5000−0.6000000−0.5000],(43)
which has the eigenvalues
[λ1λ2λ3]=[−0.6000−0.50000],(44)
therefore the equilibrium point E5 is stable node point.
Let us consider the following hybrid variable-order fractional differential equation:
CPC0Dα(t)tY(t)=f(t,Y(t)),0<α(t)≤1,Y(0)=Y0,0<t≤T.(45)
Let f(tn,Yn)=fn, using the fifth order Adams-Bashfourth method (AB5M) [25], we can descretize the Eq. (45) as follows:
K1(α(tn))hα(tn)−1Yn+5+K1(α(tn))hα(tn)−1n+5∑i=1wiYn+5−i+K0(α(tn))hα(tn)Yn+5−K0(α(tn))hα(tn)n+5∑i=1μiYn+5−i−K0(α(tn))hα(tn)qn+5Y0=1901720fn+4+251720fn−1274720fn+1+2616720fn+2−2774720fn+3,(46)
where, w0=1,wi=(1−α(t)i)wi−1,μ1=α(t), μi=(−1)i−1(α(t)i),qi=iα(t)Γ(1−α(t)) and i=1,2,...n+1.
Yn+5=(1901720fn+4−2774720fn+3+2616720fn+2−1274720fn+1+251720fn−K1(α(tn))hα(t)−1n+5∑i=1wiYn+5−i+K0(α(t))hα(tn)n+5∑i=1μiYn+5−i+K0(α(tn))hα(tn)qn+5Y0)/(K1(α(tn))hα(tn)−1+K0(α(tn))hα(tn)).(47)
To determine the first four points we use the first, second, third, and fourth Adams-Bashfourth method. We can get CPC-AB1SM as follows:
Yn+1=(12f(tn,Yn)−K1(α(tn))hα(tn)−1n+1∑i=1wiYn+1−i+K0(α(tn))hα(tn)n+1∑i=1μiYn+1−i+K0(α(tn))hα(tn)qn+1Y0)/(K1(α(tn))hα(tn)−1+K0(α(tn))hα(tn)).(48)
We can get CPC-AB2SM as follows:
Yn+2=(12fn+32fn+1−K1(α(tn))hα(tn)−1n+2∑i=1wiYn+2−i+K0(α(tn))hα(tn)n+2∑i=1μiYn+2−i+K0(α(tn))hα(tn)qn+2Y0)/(K1(α(tn))hα(tn)−1+K0(α(tn))hα(tn)),(49)
Also, we can get CPC-AB3SM as follows:
Yn+3=(512fn−1612fn+1+2312fn+2−K1(α(tn))hα(tn)−1n+3∑i=1wiYn+3−i+K0(α(tn))hα(tn)n+3∑i=1μiYn+3−i+K0(α(tn))hα(tn)qn+3Y0)/(K1(α(tn))h)α(tn)−1+K0(α(tn))hα(tn)),(50)
Moreover, we can get CPC-AB4SM as follows:
Yn+4=(−5924f(n+2+5524fn+3−K1(α(tn))hα(tn)−1n+4∑i=1wiYn+4−i+K0(α(tn))hα(tn)n+4∑i=1μiYn+4−i+K0(α(tn))hα(tn)qn+4Y0)/(K1(α(tn))hα(tn)−1+K0(α(tn))hα(tn)).(51)
Now, from (48)–(51), we will obtain four points y(1),y(2),y(3), and y(4). We use these points and (47) to solve (45).
In the following, we investigate the stability of the proposed method. Consider the test problem of linear variable-order fractional differential equation. From (46), we can write the explicit solution for (45) as follows:
Yn+5=1(K1(α(tn))hα(tn)−1+K0(α(tn))hα(tn))(251720fn−1274720fn+1+2616720fn+2−2774720fn+3+1901720fn+4−K1(α(tn))hα(tn)−1n+5∑i=1wiYn+5−i+K0(α(tn))(h)α(tn)n+5∑i=1μiYn+5−i+K0(α(t))hα(tn)qn+5Y0),(52)
since (K1(α(tn))hα(tn)−1+K0(α(tn))(h)α(tn))>1, then we have: yn+5<yn+4<⋯<y1<y0. This means that the proposed scheme is stable.
Consider the variable-order fractional equation in Caputo sense given as [26]
C0Dα(t)ty=f(t,y),0<α(t)≤1,Y(0)=Y0,0<t≤T.(53)
where y(0)=y0. The approximate solution is given as follows:
Y(tn+1)=Y(tn)+190(7K1+32K3+12K4+32K5+7K6),(54)
such that,
K1=κf(tn,Yn),K2=κf(tn+12κ,Yn+12K1),K3=κf(tn+14κ,Yn+18K2+18K1),K4=κf(tn+12κ,Yn+K3−12K2),K5=κf(tn+34κ,Yn+916K4+316K1),K6=κf(tn+κ,Yn+87K5−127K4+127K3+27K2−37K1),
where, κ=hα(tn)Γ(α(tn)+1).
To investigate the stability of the proposed method, consider the test problem of linear variable-order fractional differential equation:
CPC0Dα(t)tY(t)=vY(t),t∈(0,T],α(t)∈(0,1],v<0,y(0)=y0.(55)
The solution is asymptotically stable if v is positive and increasing. GRK5M is applied to (55) as follows [27]:
Y(tj+1)=Y(tj)+190[26κvY(tj)−8.208κ2v2Y(tj)+19.6875κ3v3Y(tj)−68.501κ4v4Y(tj)−2.562κ5v5Y(tj)]+O(h5), j=1,2,3,...,n−1,(56)
Y(tj+1)=Y(tj)+κvY(tj)90[26−8.208κv+19.6875κ2v2−68.501κ3v3−2.562κ4v4]+O(h5), j=1,2,3,...,n−1,(57)
where,K1=κvY(tj),
K3=+98κvY(tj)+18κ2v2Y(tj)+116κ3v3Y(tj),
K4=κvY(tj)−58κ2v2Y(tj)−18κ3v3Y(tj)+116κ4v4Y(tj),
K6=κvY(tj)+2.1904κ2v2Y(tj)+3κ3v3Y(tj)−9.893κ4v4Y(tj)−0.366κ5v5Y(tj),
κ=hα(tj)Γ(α(tj)+1).
Now, in (57) put
A=(26−8.208κv+19.6875κ2v2−68.501κ3v3−2.562κ4v4).
Then we have
Y(tj+1)=Y(tj)+vAhα(tj)90Γ(α(tj)+1)Y(tj)+O(h5) j=1,2,3,...,n−1,(58)
Y(tj+1)=(1+vAhα(tj)90Γ(α(tj)+1))Y(tj)=((1+vAhα(tj)90Γ(α(tj)+1))jY(t0)).(59)
Therefore the stability condition as follows:
|(1+vAhα(tj)90Γ(α(tj)+1))|≤1.
To get the numerical solutions, the parameters for the piecewise cancer models (6)–(8) and (9)–(11) are: C1=1, C2=2.5, C3=0.6, C4=1.5, C5=4.5, C6=1, C7=0.2, C8=0.5 [23]. The initial conditions are given as: x(0)=0.1,y(0)=0.1,z(0)=0.1 [21]. We take the step size h=0.01 to evaluate the approximations and assume that t1=100, t2=200, T=300. The numerical simulations of the piecewise models (6)–(8) and (9)–(11) are given in Figs. 1–13. We noted that in the model (6)–(8) the crossover behavior can be observed near the values of t1=100,t2=200. After these points the behavior changes according to the model used. In the model (9)–(11), the crossover behavior can be observed near the values of t1=100,t2=200. Before these points dynamics show the behavior changes according to the model used. Hence, this crossover behavior can be observed due to piecewise fractional and variable order derivatives.
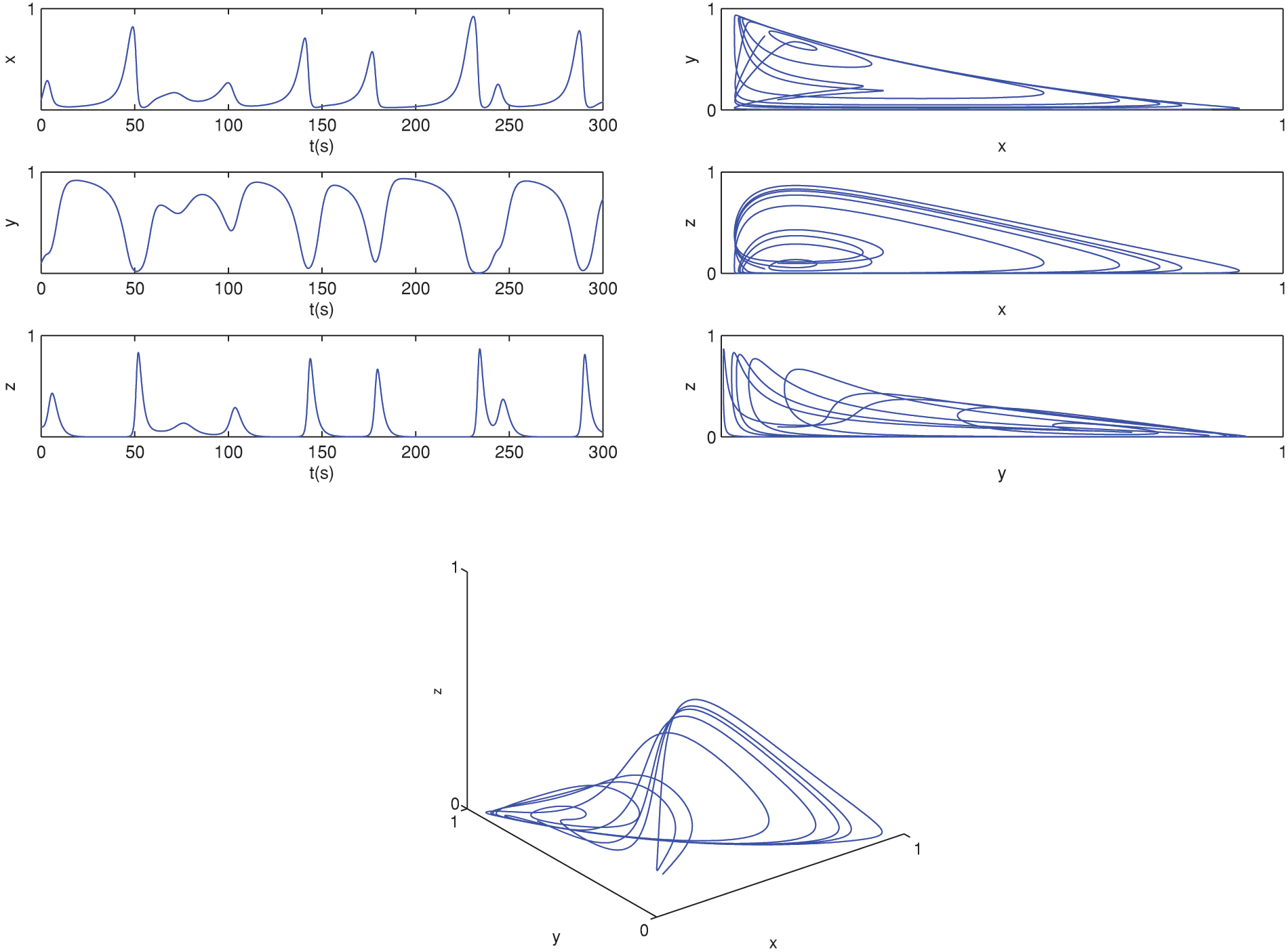
Figure 1: The behavior of the solution at classical derivative

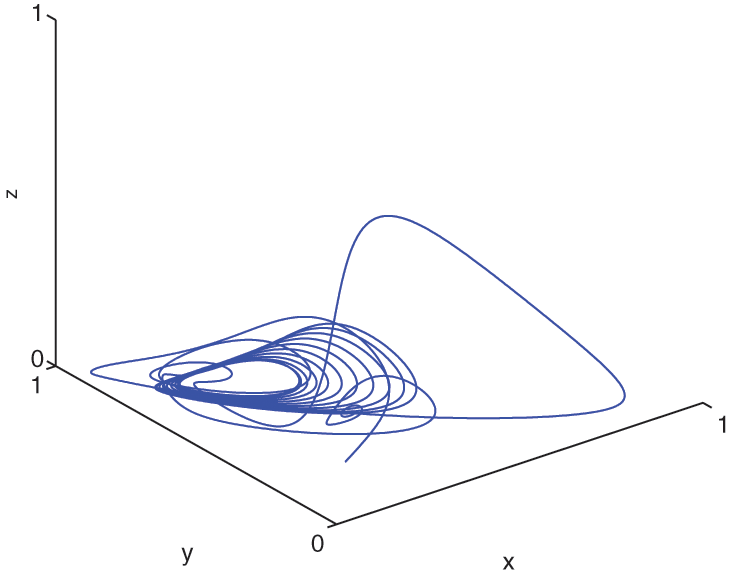
Figure 2: The behavior of the solutions for (6)–(8) at α=0.85 and α(t)=0.999−0.001cos(t/10) by CPC-AB5SM
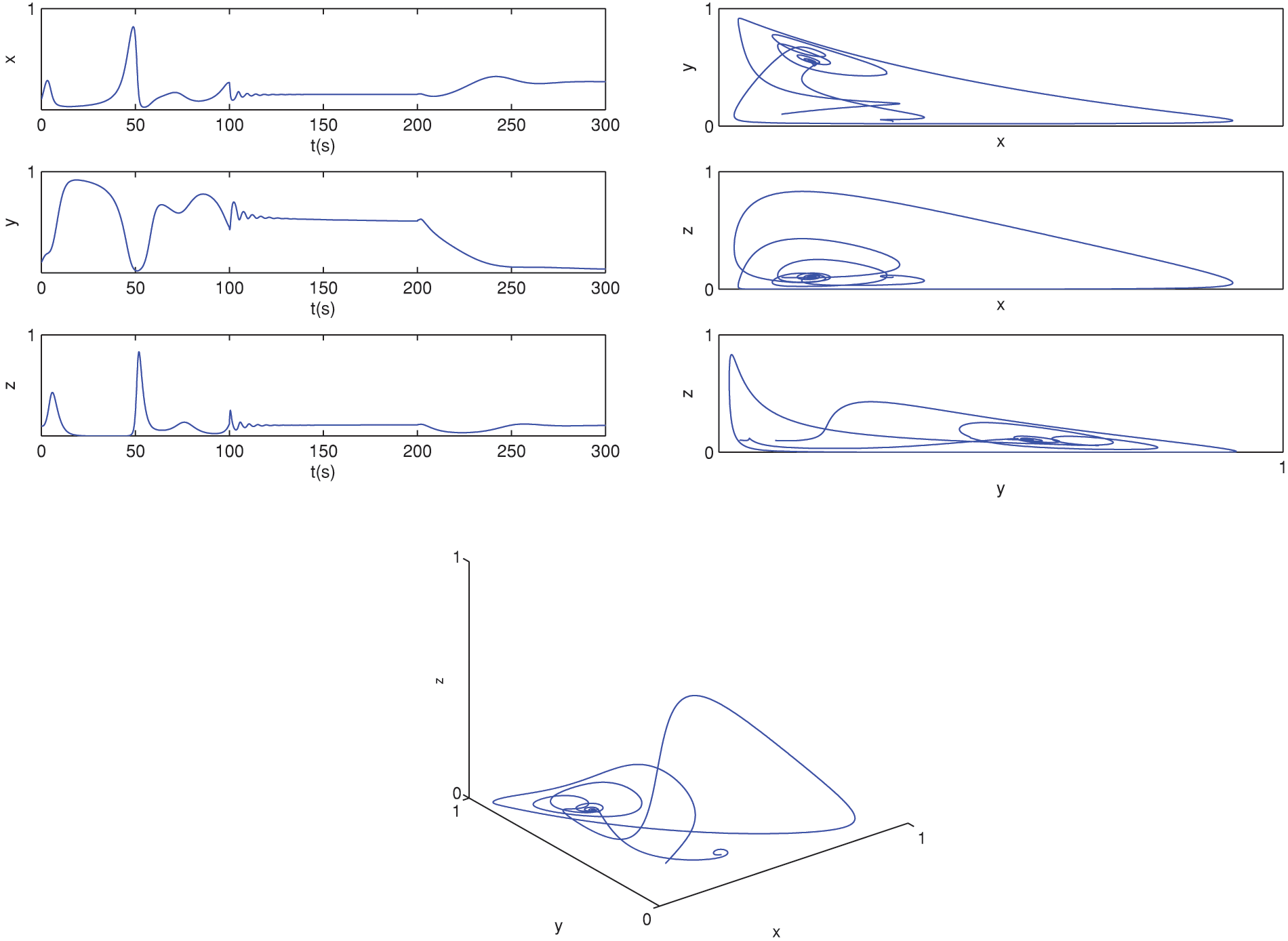
Figure 3: The behavior of the solutions for (6)–(8) at α=0.78 and α(t)=0.999−0.001cos(t/10) by CPC-AB5SM
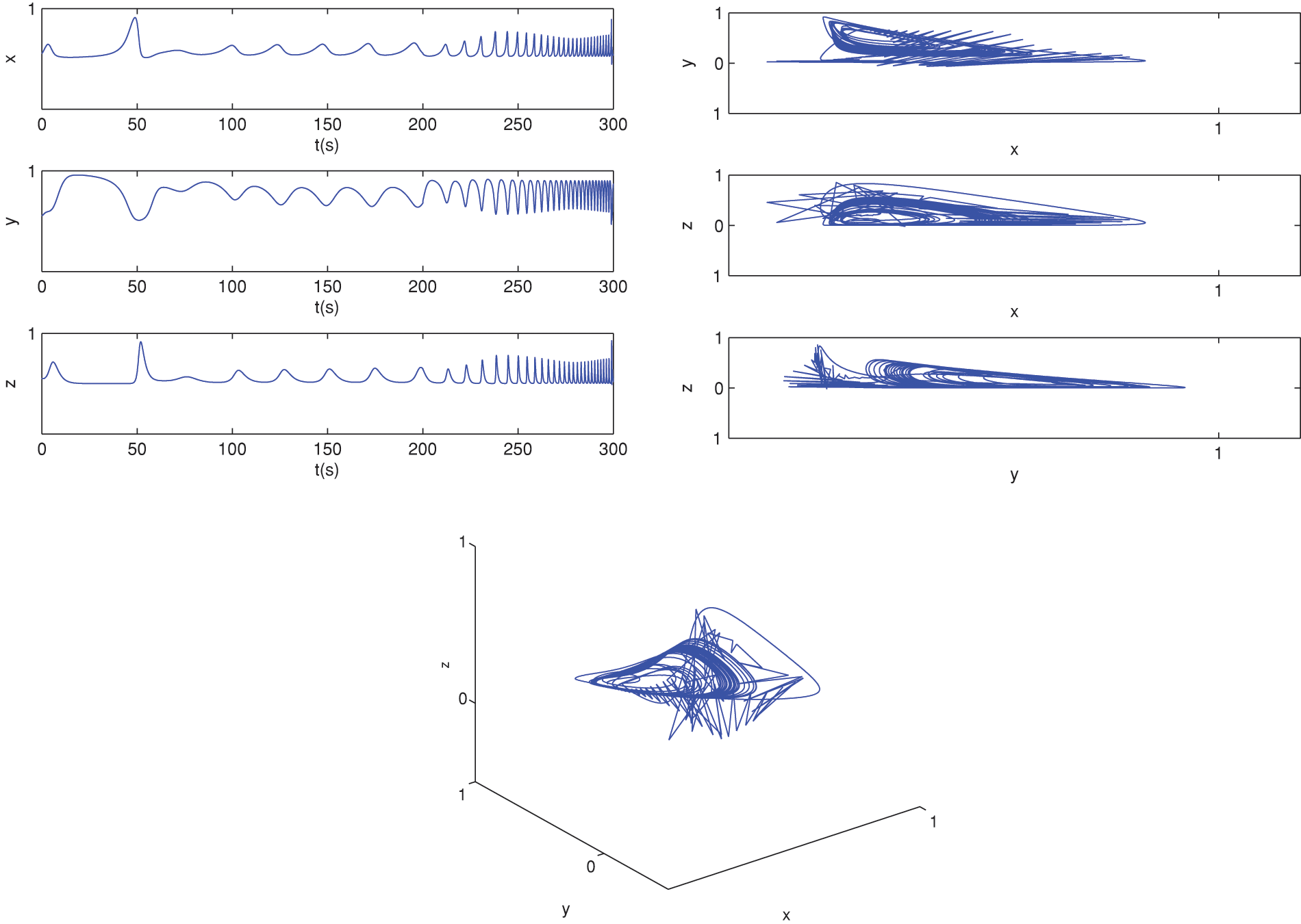
Figure 4: The behavior of the solutions for (6)–(8) at α=0.9 and α(t)=0.9−0.002t by CPC-AB5SM

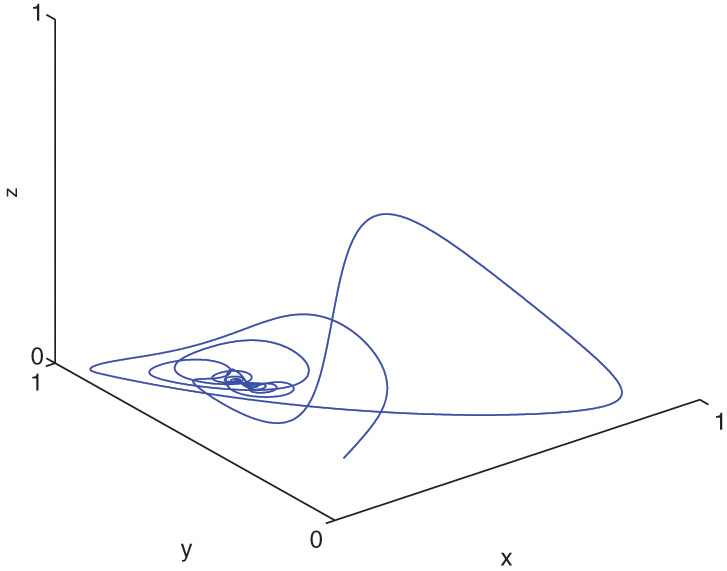
Figure 5: The behavior of the solutions for (6)–(8) at α=0.78 and α(t)=0.9−0.002t by CPC-AB5SM
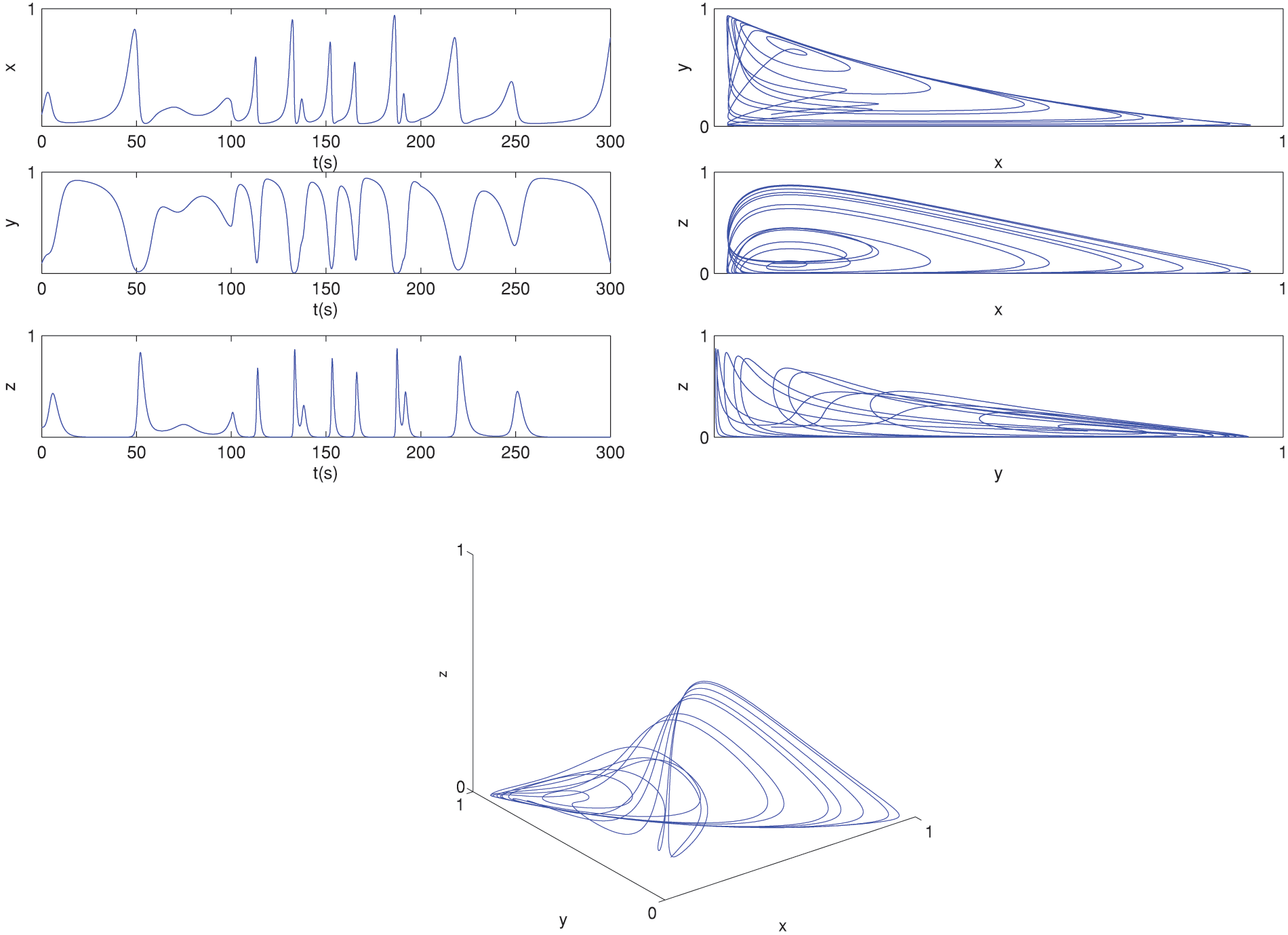
Figure 6: The behavior of the solutions for (6)–(8) at α=0.8 and α(t)=0.999−0.001cos(t/10) by GRK5M
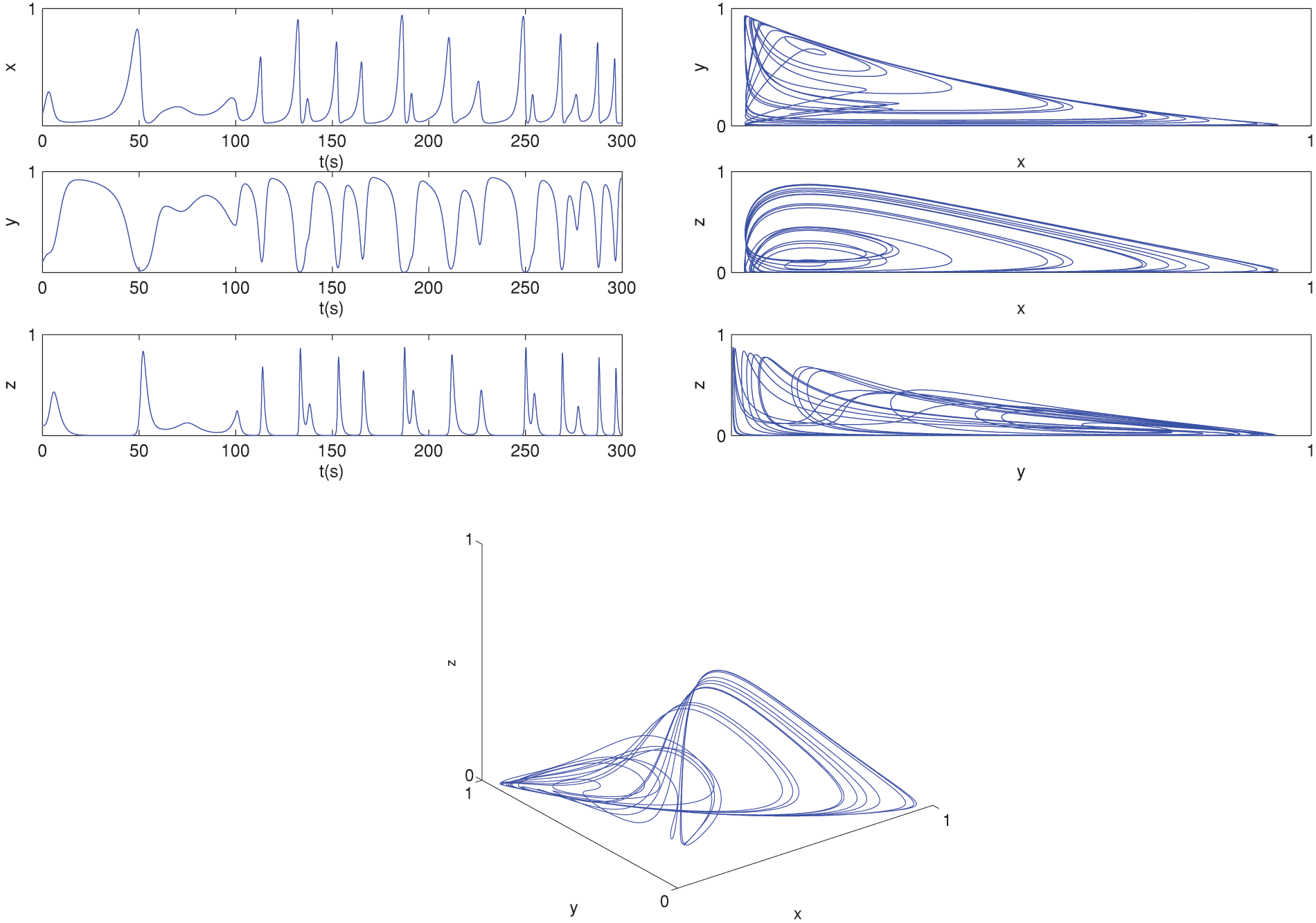
Figure 7: The behavior of the solutions for (6)–(8) at α=0.8 and α(t)=0.9−0.002t by GRK5M

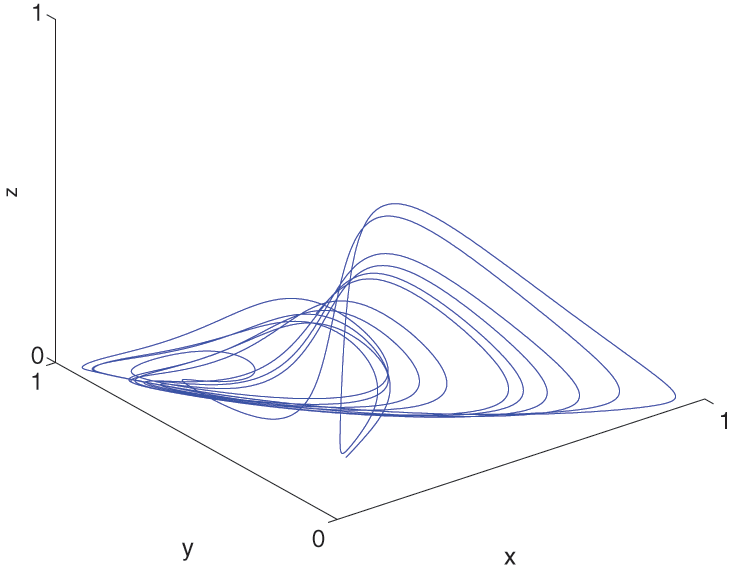
Figure 8: The behavior of the solutions for (9)–(11) at α=0.9 and α(t)=0.999−0.001cos(t/10) by CPC-AB5SM
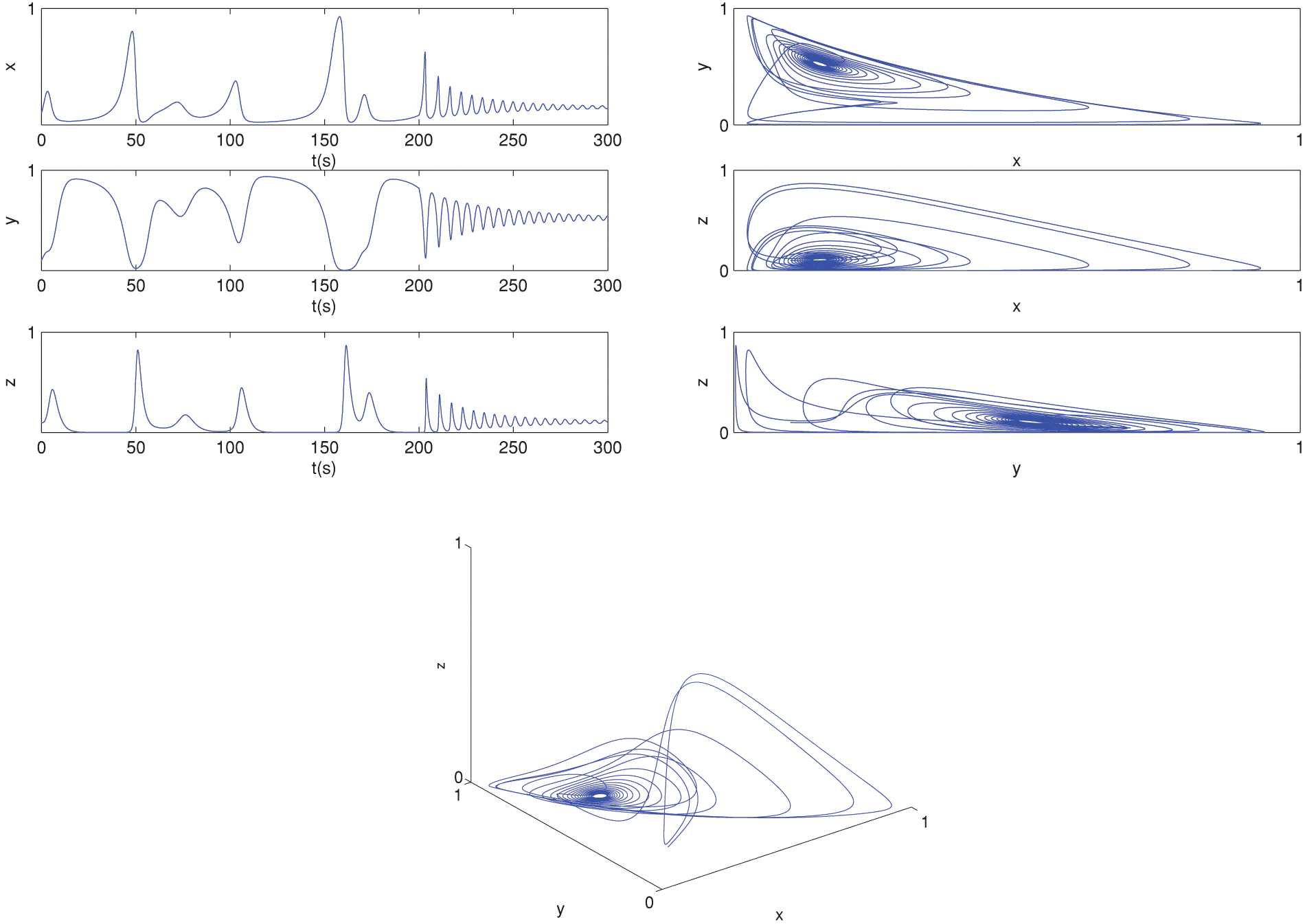
Figure 9: The behavior of the solutions for (9)–(11) at α=0.8 and α(t)=0.999−0.001cos(t/10) by CPC-AB5SM
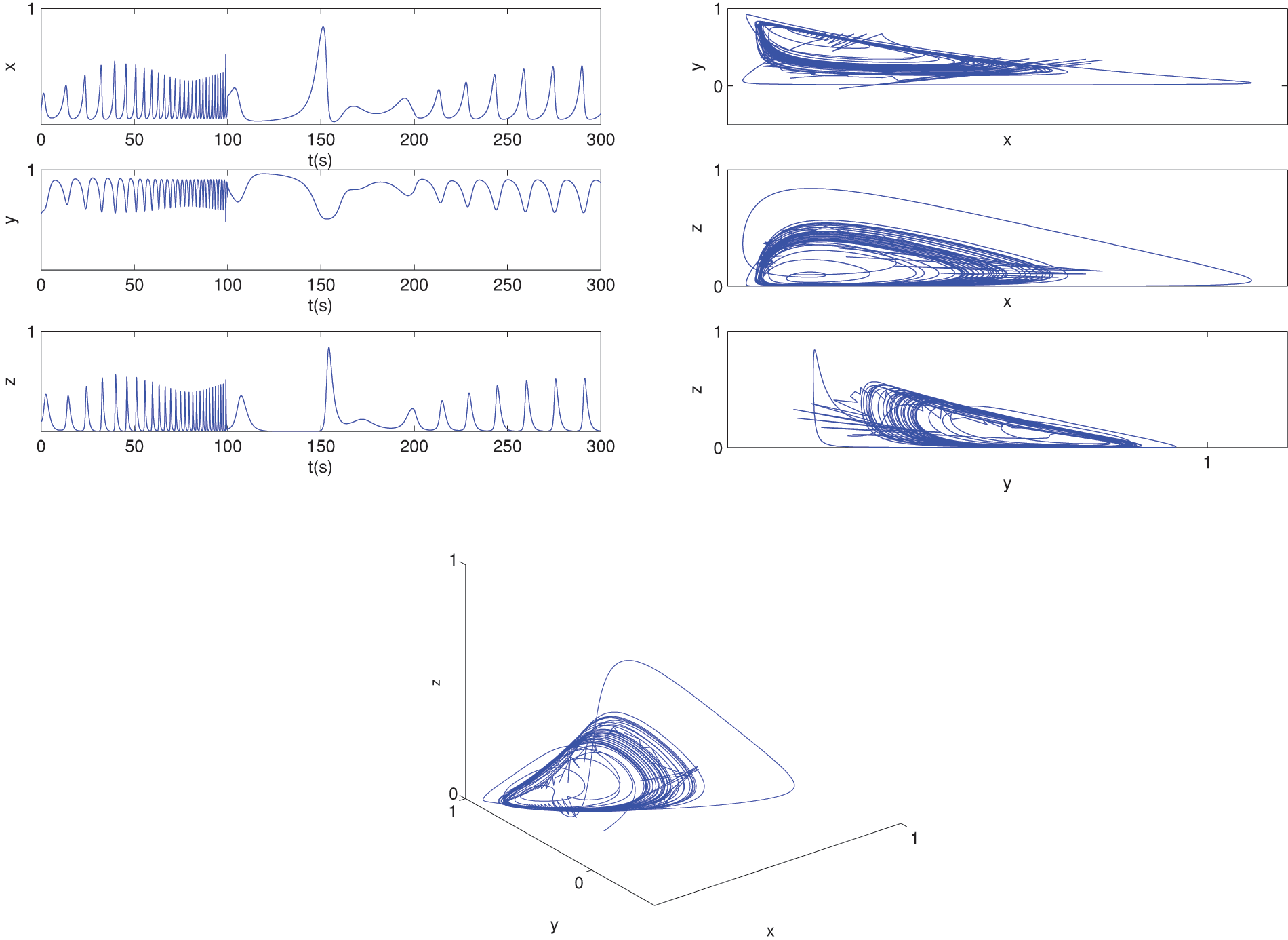
Figure 10: The behavior of the solutions for (9)–(11) at α=0.9 and α(t)=0.9−0.002t by CPC-AB5SM

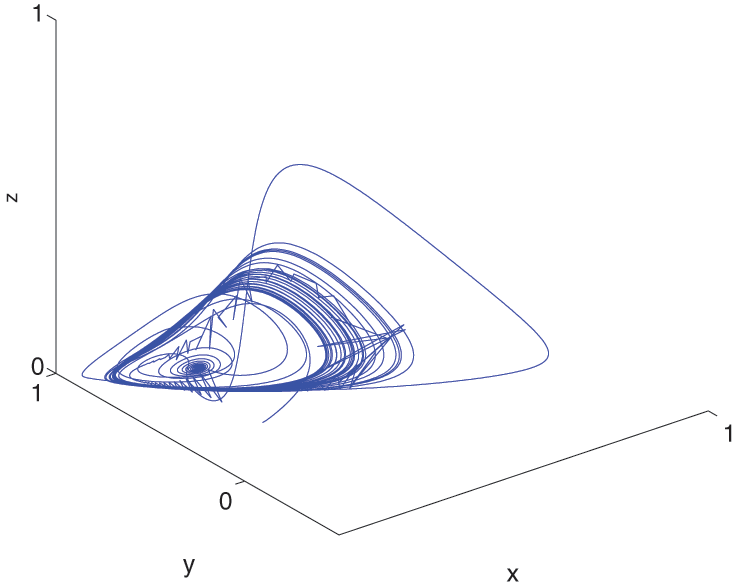
Figure 11: The behavior of the solutions for (9)–(11) at α=0.8 and α(t)=0.9−0.002t by CPC-AB5SM

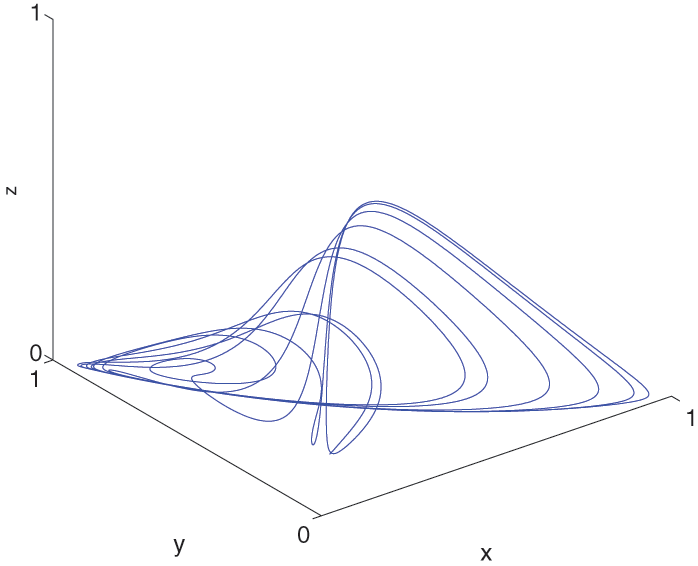
Figure 12: The behavior of the solutions for (9)–(11) at α=0.9 and α(t)=0.999−0.001cos(t/10) by GRK5M
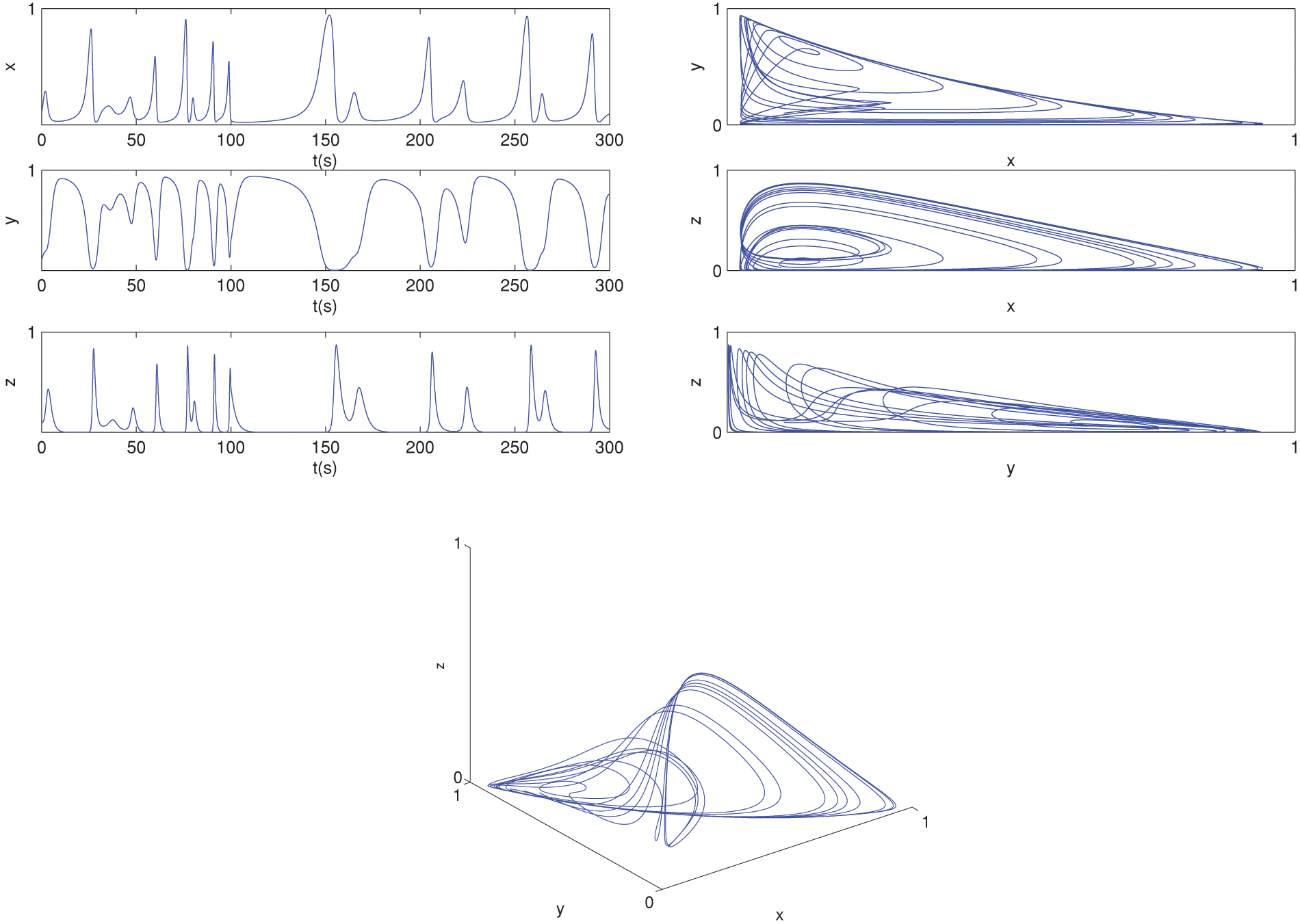
Figure 13: The behavior of the solutions for (9)–(11) at α=0.9 and α(t)=0.9−0.002t by GRK5M
Figs. 1–3 show the behavior of the piecewise model solutions (6)–(8) using CPC-AB5SM (47) with different values of α and α(t)=0.999−0.001cos(t/10). Fig. 1 shows the approximate solutions of the proposed model at α=1,α(t)=1. We noted that the behavior of the solution is the same in the previous studies such as [21,24]. Fig. 2 illustrates the solutions obtained at α=0.85, and Fig. 3 illustrates the solutions obtained at α=0.78. From Figs. 2 and 3, we notice that, after t1=100,t2=200, the behavior differs from the classical solution (Fig. 1) that was found in previous works [21,24].
The behavior of the solutions of the piecewise cancer model Eqs. (6)–(8) using CPC-AB5SM (47) with various values of α and α(t)=0.9−0.002t is shown in Figs. 4 and 5. Fig. 4 shows the approximate solutions at α=0.9 and α(t)=0.9−0.002t. We noted that the crossover behavior can be observed especially after t2=200, in general is different than the behavior in the previous studies. Fig. 5 shows the approximate solutions at α=0.78 and α(t)=0.9−0.002t. We noted that after time t=100 and t=200, there is a similar decaying oscillation in the time evolution ofx,y, and z, though with different amplitudes and different periods of oscillation. Moreover, when we compare the obtained solution in Figs. 3 and 5, we noted that the spatial evolution plots x−y,x−z, and y−z in these figures show similar, but when we plotted these variables with time, the difference between the behavior of the solution in the two figures appears after t=200; before that, they are almost identical because the derivatives have the same values of the order and after this period, the derivatives have different values of the order α(t).
Also, Fig. 6 shows the behavior of piecewise model for (6)–(8) using GRK5M (54) at α=0.8 and α(t)=0.999−0.001cos(t/10). The numerical simulations of the piecewise cancer model are given in Fig. 7. This figure shows the behavior of solutions of piecewise cancer model Eqs. (6)–(8) using the GRK5M, given in (54) at α=0.8 and α(t)=0.9−0.002t, where in this case, we put K0(α)=1andK1(α)=0 then we have the Caputo derivative and we used GRK5M to approximate the derivative.
Figs. 8 and 9 show the behavior of (9) and (10) using CPC-AB5SM (47) and different values of α and α(t)=0.999−0.001cos(t/10). Fig. 8 shows the approximate solutions at α=0.9. Fig. 9 shows the approximate solutions at α=0.8. Figs. 10 and 11 show the behavior of (9)–(11) using CPC-AB5SM (47) at different of α and α(t)=0.9−0.002t. Fig. 10 shows the approximate solutions at α=0.9 and Fig. 11 shows the approximate solutions at α=0.8. These two figures show strong oscillations in the first period up to t=100 this is due to the variable order model (a linear function varying with time).
Fig. 12 shows the behavior of (9) and (10) using the GRK5M (54) at α=0.9 and α(t)=0.999−0.001cos(t/10). Fig. 13 shows the behavior of (9) and (10) using the GRK5M (54) at α=0.9 and α(t)=0.9−0.002t. Table 2 provides a comparison between the CPU time for the proposed methods. We noted that the GRK5M is faster than CPC-AB5SM. In general, we developed a new method CPC-AB5SM to solve the proposed models this method is accurate where the order of accuracy is 5 and it presented as the first time to solve the cancer model. The disadvantage of this method it is multi-step so it is difficult to code. Moreover, we compare our results with GRK5M also an accurate method of order 5. The advantage of this method it is a step and easy to code. Also from the graphical results, we found that by comparing the results in Figs. 8, 10, 12 and 13 using two different methods, We found that the behavior of the GRK5M is more like the classical solution, while the behavior of the CPC-AB5SM is very different from the classical solution. Logically, we will obtain different behaviors in each period, and this is actually what our study obtained, so our proposed method will be more useful in solving such models than GRK5M.

In this manuscript, two new hybrid variable-order fractional piecewise cancer models have been formulated. A detailed analysis of hybrid variable-order fractional piecewise cancer models is given, where the existence, uniqueness, and stability of the proposed model are established. Caputo proportional constant Adams-Bashfourth fifth step method is constructed with the discretization of the CPC operator to solve the variable-order and fractional order models. The proposed piecewise models are numerically studied using CPC-AB5SM and GRK5M. New behaviors were presented by numerical simulations for the proposed models. Through a series of numerical tests, we have showcased the efficiency of the proposed method and garnered robust empirical support for our theoretical findings. From the obtained simulation, the proposed method is better than the GRK5M in solving such models. We conclude from the results that the piecewise mathematical model representation of cancer in this study has exposed a property that has never been considered or observed in earlier studies using mathematical models based on classical, different fractional derivatives and variable order fractional derivatives. This approach of piecewise mathematical model representation of different real-world dynamic systems is an eye-opener for researchers as the approach has the potential to uncover hidden properties in the dynamics of a system. In the future, the present study can be extended to optimal control problems. In the future, we will extend this study to more complex dynamical systems.
Acknowledgement: The authors wish to express sincere appreciation to the reviewers for their valuable comments, which significantly improved this paper.
Funding Statement: This study did not receive any funding in any form.
Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Nasser Sweilam, Seham M. Al-Mekhlafi; data collection: Aya Ahmed, Seham M. Al-Mekhlafi; analysis and interpretation of results: Nasser Sweilam, Seham M. Al-Mekhlafi; draft manuscript preparation: Aya Ahmed, Emad Abo-Eldahab, Ahoud Alsheri, Seham M. Al-Mekhlafi. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are available from the first and corresponding authors upon reasonable request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Kuznetsov, V. A., Knott, GD. (2001). Modeling tumor regrowth and immunotherapy. Mathematical and Computer Modelling, 33(12–13), 1275–1287. [Google Scholar]
2. de Pillis, L. G., Radunskaya, A. (2003). The dynamics of an optimally controlled tumor model: A case study. Mathematical and Computer Modelling, 37(11), 1221–1244. https://doi.org/10.1016/S0895-7177(03)00133-X [Google Scholar] [CrossRef]
3. Jahanshahi, H., Shanazari, K., Mesrizadeh, M., Soradi-Zeid, S. (2020). Numerical analysis of galerkin meshless method for parabolic equations of tumor angiogenesis problem. The European Physical Journal Plus, 135(11), 1–23. [Google Scholar]
4. Attia, R. A. M., Tian, J., Lu, D., Aguilar, J. F. G. (2022). Unstable novel and accurate soliton wave solutions of the nonlinear biological population model. Arab Journal of Basic and Applied Sciences, 29(1), 19–25. https://doi.org/10.1080/25765299.2021.2024652 [Google Scholar] [CrossRef]
5. Syam, M. I., Al-Refai, M., Fractional differential equations with Atangana-Baleanu fractional derivative: Analysis and applications. Chaos, Solitons & Fractals, 2, 100013. https://doi.org/10.1016/j.csfx.2019.100013 [Google Scholar] [CrossRef]
6. Sweilam, N. H., AL-Mekhlafi, S. M., Baleanu, D. (2021). A hybrid stochastic fractional order coronavirus (2019-nCov) mathematical model. Chaos, Solitons & Fractals, 145, 110762. https://doi.org/10.1016/j.chaos.2021.110762 [Google Scholar] [PubMed] [CrossRef]
7. Sweilam, N. H., Al-Ajami, T. M. (2015). Legendre spectral-collocation method for solving some types of fractional optimal control problems. Journal of Advanced Research, 6(3), 393–403. https://doi.org/10.1016/j.jare.2014.05.004 [Google Scholar] [PubMed] [CrossRef]
8. Baleanu, D., Fernandez, A., Akg, A. (2020). On a fractional operator combining proportional and classical differ-integrals. Mathematics, 8(3),360. https://doi.org/10.3390/math8030360 [Google Scholar] [CrossRef]
9. Kumar, S., Chauhan, R. P., Momani, S., Hadid, S. (2020). Numerical investigations on COVID-19 model through singular and nonsingular fractional operators. Numerical Methods for Partial Differential Equations, 1–27. https://doi.org/10.1002/num.22707 [Google Scholar] [CrossRef]
10. Safare, K. M., Betageri, V. S., Prakasha, D. G., Veeresha, P., Kumar, S. (2020). A mathematical analysis of ongoing outbreak COVID-19 in India through nonsingular derivative. Numerical Methods for Partial Differential Equations, 37(2), 1282–1298. [Google Scholar]
11. Khan, M. A., Atangana, A., Alzahrani, E., Fatmawati (2020). The dynamics of COVID-19 with quarantined and isolation. Advances in Difference Equations, 2020, 425. https://doi.org/10.1186/s13662-020-02882-9 [Google Scholar] [PubMed] [CrossRef]
12. Hajipour, M., Jajarmi, A., Baleanu, D. (2018). An efficient nonstandard finite difference scheme for a class of fractional chaotic systems. Journal of Computational and Nonlinear Dynamics, 13(2), 021013.https://doi.org/10.1115/1.4038444 [Google Scholar] [CrossRef]
13. Lin, W. (2007). Global existence theory and chaos control of fractional differential equations. Journal of Mathematical Analysis and Applications, 332(1), 709–726. https://doi.org/10.1016/j.jmaa.2006.10.040 [Google Scholar] [CrossRef]
14. Sweilam, N. H., Al-Mekhlafi, S. M., Albalawi, A. O. (2020). Optimal control for a fractional order malaria transmission dynamics mathematical model. Alexandria Engineering Journal, 59(3), 1677–1692. https://doi.org/10.1016/j.aej.2020.04.020 [Google Scholar] [CrossRef]
15. Omame, A., Abbas, M., Onyenegech, C. P. (2022). Backward bifurcation and optimal control in a co-infection model for SARS-CoV-2 and ZIKV. Results in Physics, 37, 105481.https://doi.org/10.1016/j.rinp.2022.105481 [Google Scholar] [PubMed] [CrossRef]
16. Shah, K., Abdeljawad, T., Ali, A. (2022). Mathematical analysis of the Cauchy type dynamical system under piecewise equations with Caputo fractional derivative. Chaos, Solitons and Fractals, 161(3), 112356. [Google Scholar]
17. Shah, K., Abdeljawad, T., Alrabaiah, H. (2022). On coupled system of drug therapy via piecewise equations. Fractals, 30(8), 114. [Google Scholar]
18. Shah, K., Abdeljawad, T. (2022). Study of a mathematical model of COVID-19 outbreak using some advanced analysis. Waves in Random and Complex Media. https://doi.org/10.1080/17455030.2022.2149890 [Google Scholar] [CrossRef]
19. Shah, K., Abdeljawad, T., Abdalla, B. (2023). Study of fractional order dynamical system of viral infection disease under piecewise derivative. Computer Modeling in Engineering & Sciences, 136(1), 921–941. https://doi.org/10.32604/cmes.2023.025769 [Google Scholar] [CrossRef]
20. Atangana, A., Araz, S. (2021). New concept in calculus: Piecewise differential and integral operators. Chaos, Solitons & Fractals, 145(2), 110638. https://doi.org/10.1016/j.chaos.2020.110638 [Google Scholar] [CrossRef]
21. N’Doye, I., Voos, H., Darouach, M. (2014). Chaos in a fractional-order cancer system. European Control Conference, pp. 171–176. Strasbourg, France. [Google Scholar]
22. Ma, C. Y., Shiri, B., Wu, G. C., Baleanu, D. (2020). New fractional signal smoothing equations with short memory and variable order. Optik, 218. 164507. https://doi.org/10.1016/j.ijleo.2020 [Google Scholar] [CrossRef]
23. Itik, M., Banks, S. P. (2010). Chaos in a three-dimensional cancer model. International Journal of Bifurcation and Chaos, 20(1), 71–79. https://doi.org/10.1142/S0218127410025417 [Google Scholar] [CrossRef]
24. Gómez-Aguilar, J. F., López-López, M. G., Alvarado-Martínez, V. M., Baleanu, D., Khan, H. (2017). Chaos in a cancer model via fractional derivatives with exponential decay and mittag-leffler law. Entropy, 19(12), 681.https://doi.org/10.3390/e19120681 [Google Scholar] [CrossRef]
25. Peinadoa, J., Ibáñez, J., Arias, E., Hernández, V. (2010). Adams-bashforth and adams-moulton methods for solving differential riccati equations. Computers and Mathematics with Applications, 60(11), 3032–3045.https://doi.org/10.1016/j.camwa.2010.10.002 [Google Scholar] [CrossRef]
26. Milici, C., Machado, J. T., Draganescu, G. (2019). Application of the Euler and Runge-kutta generalized methods for FDE and symbolic packages in the analysis of some fractional attractors. International Journal of Nonlinear Sciences and Numerical Simulation, 21(2). https://doi.org/10.1515/ijnsns-2018-0248 [Google Scholar] [CrossRef]
27. Sweilam, N., Al-Mekhlafi, S. M., Shatta, S. A., Baleanu, D. (2022). Numerical treatments for the optimal control of two types variable-order COVID-19 model. Results in Physics, 42, 105964. https://doi.org/10.1016/j.rinp.2022.105964 [Google Scholar] [PubMed] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
