Improving Channel Estimation in a NOMA Modulation Environment Based on Ensemble Learning

1  Introduction

The environment of mobile radio communication has rapidly evolved across generations, ushering in improved services and elevated data rates [1,2]. The advent of the Fifth Generation (5G) signifies a paradigm shift, promising ultra-high-speed mobile connectivity exceeding 10 Gbit/s [3,4]. In this transformative era, the 3rd Generation Partnership Project (3GPP) has introduced Non-Orthogonal Multiple Access (NOMA) as a pivotal access method for future mobile generations [5].

1.1 NOMA System

NOMA, a revolutionary technique enabling simultaneous connections of numerous users over shared spectral resources, has garnered significant attention. This achievement is realized by intelligently programming users across various power levels, strategically coupling user arrangements in both the downlink NOMA cell [6,7]. The NOMA system utilizes Successive Interference Cancellation (SIC) to unravel the complexities of multi-user recognition and interpretation, enabling User Equipment (UE) to discern and process signals from different users [8,9].

Researchers have explored avenues to enhance NOMA scalability, categorizing phone handlers into distinct groups and evaluating throughput data and Signal to Interference Noise Ratio (SINR) [10]. Studies emphasizing the advantages of NOMA over Orthogonal Multiple Access (OMA) underscore its relevance and adaptability within existing structures, including its integration into Long Term Evolution Advanced (LTE-A) [11–15]. Furthermore, NOMA extends beyond LTE-A, with its inclusion in the Advanced Television Systems Group’s upcoming digital television standard (ATSC) 3.0 [16]. NOMA is versatile as it employs layered multiplexing and Orthogonal Frequency Division Multiple Access (OFDMA), allowing optimization of frequency and time resources, enriching the two-dimensional time and frequency plane [17].

In wireless communication, various methods enable device access to networks, such as Code Division Multiple Access (CDMA), OFDMA, and Spatial Division Multiple Access (SDMA). NOMA simplifies the design of communication devices, reduces interference, and maximizes system data handling capacity in a unique way compared to traditional methods. It challenges conventional ideas about signal organization, paving the way for creative device connectivity [17].

1.2 Channel Estimation in 5G: Importance and Challenges

In the context of NOMA and 5G, channel estimation (CE) plays a pivotal role in ensuring efficient and reliable communication. The challenges arise from the unique characteristics of NOMA and the demands of 5G networks. Addressing these challenges is crucial for enhancing system performance. NOMA introduces complexities by allowing multiple users to share the same time and frequency resources. Precise channel estimation becomes essential to decode signals accurately and distinguish between users, especially when they experience distinct channel conditions. The challenge lies in mitigating inter-user interference and optimizing resource allocation.

In the domain of 5G, where high data rates, low latency, and massive device connectivity are paramount, accurate channel estimation is imperative. Dynamic channel conditions, varying signal paths, and the need for efficient spectrum utilization necessitate advanced channel estimation techniques. The motivation for exploring channel estimation in 5G and NOMA is rooted in the quest for optimizing spectral efficiency, minimizing interference, and ensuring the seamless coexistence of diverse devices in a shared communication environment.

This paper delves into the NOMA access system, exploring channel estimation within the realm of 5G mobile networks. As we envision the future of radio access for 5G, this study focuses on refining channel estimation methods, a critical facet of evolving wireless technologies. The study scrutinizes traditional and intelligent channel estimation techniques, aiming to introduce a novel approach based on Stacked Generalization Ensemble Learning, reducing pilot insertion, and augmenting throughput. The subsequent sections unfold a comprehensive narrative, starting with a discussion on NOMA fundamentals and multiple access in Section 2, followed by an exploration of related works in Section 3. Section 4 introduces the proposed channel estimation technique, while Section 5 delineates the system model. Various channel estimation techniques are dissected in Section 6, leading to the unveiling of the Stacked Generalization for Channel Estimation (SGCE) system model in Section 7. Finally, Section 8 presents and discusses experimentation results, shedding light on the efficacy of the proposed approach.

2  Related Works

NOMA has attracted the interest of the whole of wireless communication as a vital component of next-generation communication systems. NOMA techniques, as opposed to OMA approaches, allow users to submit data at the same time and frequency, improving spectral efficiency. Power allocation, SIC and channel estimation NOMA-assisted communication systems.

We grouped studies on channel estimation enhancement in the NOMA paradigm into two groups during our bibliographic search: Classic methods based on traditional forecasting and estimation techniques represent the first category of approaches [18–21]. The second approach is focused with intelligent procedures based on various artificial intelligence techniques; Indeed, it is within this second group of theories and techniques that complex computer programs, which can simulate human intelligence aspects (reasoning, learning, etc.); are developed to contribute to the improvement of predicting propagation channel coefficients process.

This section will examine several recent works that have been classified as belonging to the first group: In [18], the Least Square (LS) estimation approach is used to enhance channel estimate accuracy, while the Bit Error Rate (BER) is utilized to improve wireless communication performance. The BER for many classic receivers is compared in this study. Furthermore, Mean Square Error (MSE) analysis for channel estimation is performed for several types of receivers. According to the results, the Minimum Mean Square Error (MMSE) receiver outperforms the LS receiver in terms of BER. To address the performance damage produced by Delay Spread Disparities (DSDs) in cell-free huge Orthogonal Frequency Division Multiple (OFDM) systems, the authors propose an optimization strategy that optimizes the downlink sum rate in [19]. They adapt the totality degree maximization issue addicted to an iterative second-order cone program design form to attain convex estimate. They suggest a downlink CE technique using both the channel state data reference signal and the demodulation reference signal, while accounting for the effect of DSDs on the accuracy of cell-free massive OFDM CE. Reference [20] looks at the BER performance of downlink NOMA networks using binary phase-shift keying modulation. To depict the network conduct with variety and array improvements, the asymptotic BER expression in a high signal-to-noise ratio (SNR) area is generated. In the case of incomplete SIC, the maximum constraint for BER is determined, and at high SNR levels, the BER exposes an error floor, leading to a zero-diversity benefit. A fair range of power allocation coefficients is then determined in order to offer an acceptable BER performance for each user. Reference [21] offers a loss probability-based quality assisted spectrum allocation (QASA) approach for spectrum sensing in dynamic channel settings, as well as a dynamic threshold modeling method. The fading models of Rayleigh and Rician are explored, and the Lagrange mathematical notion is applied to compute bit error and decrease distortion. In terms of throughput, the proposed method surpasses the standard approach of Simultaneous wireless transmission and power transfer (SWIPT). The authors of [22] address a two-user downlink multiple-input multiple-output non-orthogonal multiple access (MIMO-NOMA) system with inadequate CEs and MMSE detection. The authors compute approximated user capacities and construct a closed-form power allocation system to maximize the minimum of them by accounting for both mistakes in CE and MMSE detection. Solving two quadratic equations is required to implement their suggested power distribution strategy. The performance of BS-NOMA (BeamSpace NOMA) utilizing an approximated BS channel is examined by authors in [23]. The BS channel is estimated using the orthogonal matching pursuit method, which makes use of a compressive sensing tool, a pilot-based CE technique, a small number of samples, and a little pilot overhead. To support more users than the planned number of chains on the BS channel, NOMA is integrated with the BS-MIMO technology. To improve BS-NOMA performance and prevent inter-beam interference, maximum ratio transmission (MRT), zero-forcing (ZF) precoders and MMSE are implemented. According to the findings of this study, the spectrum and energy efficiency performance of BS-NOMA is superior to that of BS-MIMO under the same Beamspace CE.

Following our research, traditional methods were unable to produce very satisfactory results in the context of CE, throughput enhancement, and quality improvement. Parallel to this, we examine in the literature attempts to improve interpolation quality and transfer function approximation using basic artificial neural networks. In [24], an innovative uplink Long Term Evolution Advanced (LTE-A) channel estimation method using alternate pilot transmission and neural networks is presented, yielding significant enhancements in accuracy and throughput compared to Single Carrier Frequency Division Multiple Access (SC-FDMA) systems. In [25], a semi-blind channel estimation technique for LTE-A uplink utilizes hybrid artificial neural networks, achieving faster convergence and improved efficiency by integrating fuzzy rules for parameter initialization. This method addresses bitrate loss in pilot-based estimation, reducing complexity relative to MMSE estimators. In [26], a Neuro-symbolic Learning System is introduced for LTE-A uplink channel estimation, integrating neural network modules to improve performance by acquiring and revising empirical knowledge, effectively integrating theoretical and experiential insights. The authors in [27] observed that current channel estimation techniques have been ineffective in addressing the issues of Inter-Symbol Interference (ISI) and the resulting errors in the decision-making process at the receiver in MIMO-OFDM networks. To tackle this problem, they employed the Elman Recurrent Neural network (E-RNN) algorithm, which considers reliability and scalability, to estimate the channel in MIMO-OFDM. The findings indicated that several benefits were observed, including a decrease in the Peak-to-Average Power Ratio (PAPR), a reduction in the BER, an increase in capacity and an improvement in MSE performance. The proposed approach in [28] involved implementing an OFDM system using Artificial Neural Network (ANN) and M-ary Quadrature Amplitude Modulation (M-QAM) technique. It incorporated the Backpropagation (BP) algorithm over Additive White Gaussian Noise (AWGN) channels to effectively reduce ISI in OFDM systems. Results obtained demonstrated that the ANN equalizer successfully reduces ISI, resulting in an acceptable BER and improved MSE performance compared to the conventional OFDM system. With the intention of reducing the effective BER, the authors in [29] presented a CE technique based on Extreme Learning Machine (ELM) for a two-user NOMA downlink system. To illustrate the L2-norm ELM algorithm’s efficacy, its performance was compared to that of alternative algorithms. The outcomes demonstrated that better spectral efficiency and energy efficiency values were obtained by the suggested L2-norm ELM algorithm. This shows that, in terms of reaching a higher sum capacity, NOMA schemes based on ELM and L2-norm ELM fared better than other existing algorithms. The authors of [30] stated that while Reconfigurable Intelligent Surface (RIS) is a newly developed transmission technique for use in wireless communications, the channel estimate of RIS-assisted communication systems is severely hampered. An overview of the issue of channel estimation in RIS-assisted systems is presented, along with a discussion of recent advancements in the field.

Authors in [31] proposed a spatial modulation-aided indoor visible light communication system with user mobility and random receiver orientation. Two ANNs have been suggested to predict channel state information (CSI). The authors employ estimated CSI at pilot instances derived via LS or MMSE estimation to predict CSI at intermediate sites. The numerical findings reveal that the suggested ANNs outperform a benchmark spline interpolation-based technique in terms of bit error rate. Furthermore, the second ANN proposed is demonstrated to function well in a high mobility situation. Several users arrive at multiple access points at different times in a cell-free massive MIMO system, but differing delays in an OFDM system might be similar to DSDs. It is worth noting that these networks with well-studied design can serve as an effective approximator. Other research projects have used more advanced intelligence methods, from which we will mention [32–36]. The authors provide the most current Deep Learning-aided NOMA system research activities in [32]. They also work with Deep Learning applications in other wireless technologies. The authors of [33] describe a combined CE and signal detection system based on deep learning for multi-user OFDM-NOMA schemes across Rayleigh channels that fade. They assume that the receivers lack CSI, hence they employ two forms of pilot insertions (i.e., block type and comb type). Based on the pilot responses and data signal, the proposed Downlink based detector (DLD) recognizes symbols at all users with no further procedures (e.g., CE, interference canceler, etc.). They evaluate the error performance of the proposed DLD and compare it to the benchmark for different fading channel state information. The author of [34] proposes a Deep Learning-based NOMA receiver that decodes messages for users in a single pass without explicitly calculating channels. The proposed system is taught offline using modeling data based on channel features and then used in the live implementation stage to retrieve the broadcast symbols instantly. The suggested technique outperforms traditional pilot-based CE methods because it is more resistant to changes in the number of pilot symbols. In [35], the authors suggest a new deep learning-based MIMO-NOMA receiver. They feed the testing data into the trained neural network in exchange for correctly decoded signals after training the deep neural network (DNN) by minimizing the cost function. Numerous numerical findings show that the proposed receiver outperforms the standard SIC receiver in terms of resilience and performance under defective CSI. In prior work, we used Deep Learning to estimate LTE-A uplink channel [36]. This study outlines experiments conducted with Deep Learning and traditional Neural Networks. The simulation results revealed that Deep Learning outperformed the traditional technique in terms of BER and process speed. We demonstrated that Deep Learning outperforms MMSE estimators of minimal complexity. There have been numerous studies on intelligent methods for improving CE quality, and it is noteworthy that different axes can be considered to achieve this goal. In this work, we are interested in the interpolation portion for better approximation of the channel transfer function, so we will first list the interpolation techniques used before proposing our approach. As such, we will now present the problem theoretically: we will begin with a description of the CE technique.

3  Channel Estimation

To investigate CE in a NOMA context (Fig. 1), we must first understand the NOMA function principle. Assume there are two users who communicate with the base station. From the base station we can have a different gain channel for each user in the downlink.

y1=h1px1+w1(1)

y2=h2px2+w2(2)

where xi and yi are respectively the sent signal and the received signal for User i.

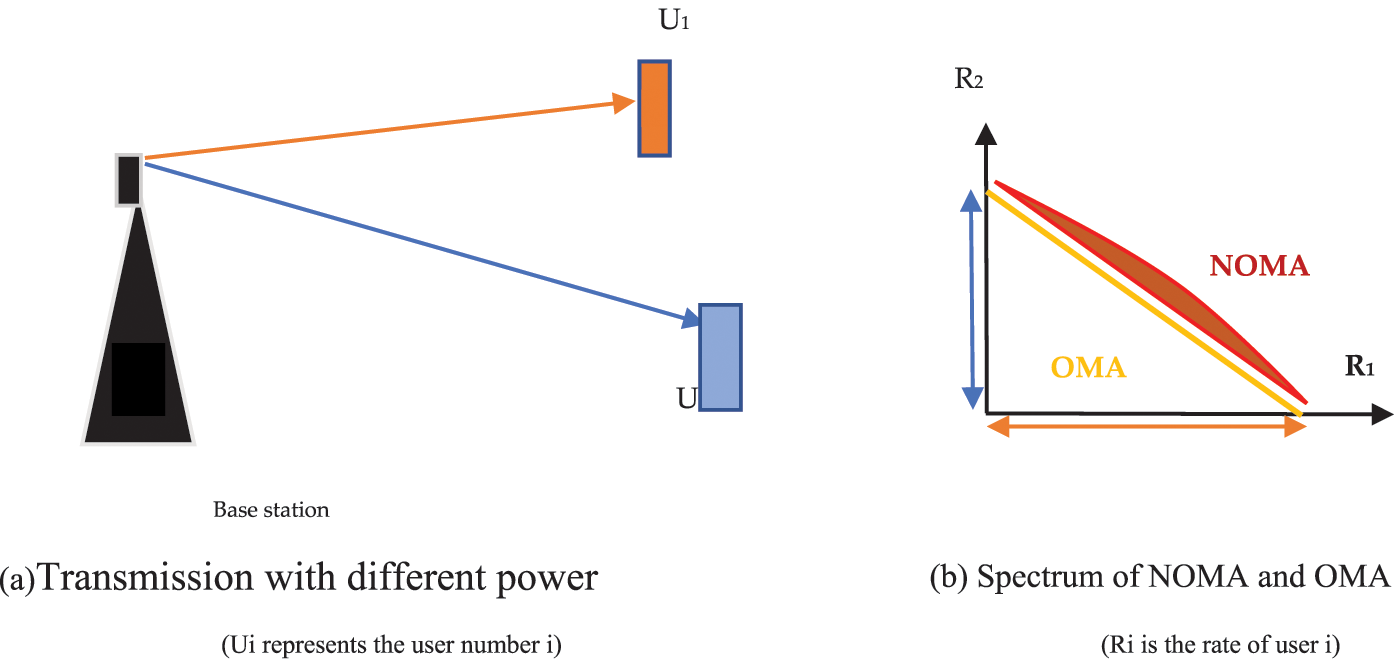
Figure 1: Description of NOMA and OMA

|h1|>|h2|, where hi is the channel gain for User i, wi is the noise for channel i, and p is the power of the signal transmitted from base station (BS) to the user.

In OMA mode (in this case TDMA: Time Division Multiple Access), time is shared between users 1 and 2, and the reception of the two signals y1 and y2 cannot occur at the same time. In contrast to an OMA system, the BS can be sent at the same time for both users. We have:

p=p1+p2(3)

The message send will be:

y2=h2(p1x1+p2x2)+w2(4)

y2=h2p2x1+h2p1x1+w2(5)

Or p1≪p2, so this term h2p1x1 will look like noise, and the noise will be more important. With the same method we calculate y1:

y1=h1p1x1+h1p2x2+w1(6)

The term h1p2x1 cannot be treated as a noise, it had to be detected and decoded. To cancel this term, we had to add the SIC term h1p2x^1:

y1=h1p1x1+h1p2x2+w1−h1p2x^1(7)

The terms in NOMA look like the terms in OMA when SIC is completed.

4  System Model

This work analyzes a downlink multi-user NOMA system N mobile receiver communicating with one base station (Fig. 2).

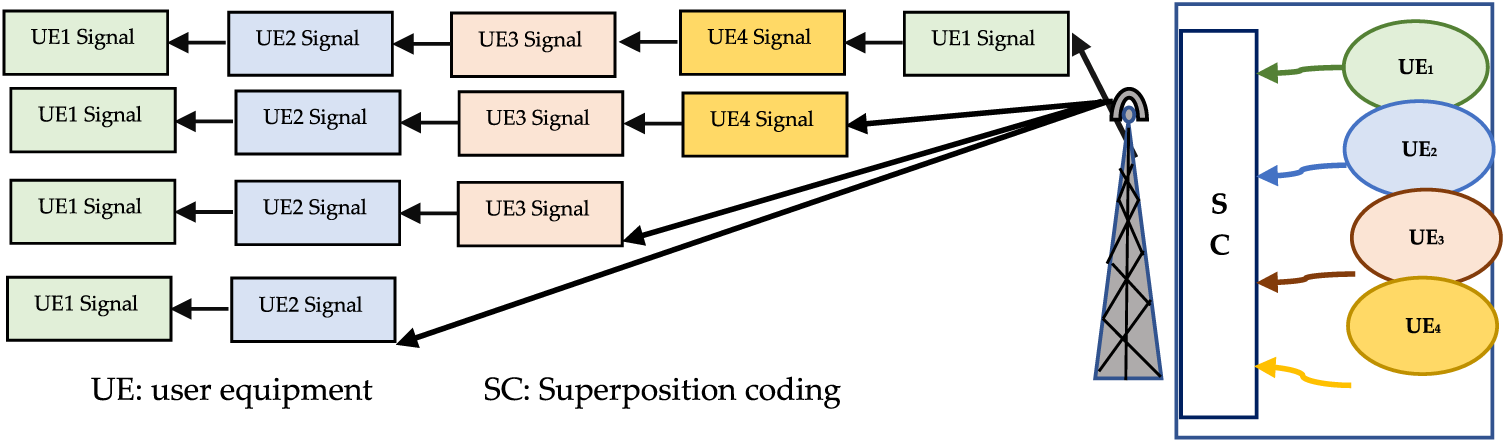
Figure 2: System model of multiuser NOMA

Each node is equipped with a single antenna. On the transmitter side, standard OFDM-NOMA is used. Pilot symbols are used to ensure that OFDM-NOMA provides CE and signal detection.

Table 1 represents mathematical Equations for the transmitted signal and Table 2 describes the mathematical equations for the received signal. To accomplish NOMA, superposition coding (SC) is implemented from BS in the context of user base-band modulated signals. N user’s SC symbol is specified as Eq. (8). Then IDFT (Inverse Discrete Fourier Transform) is used to convert SC symbols from serial to parallel. Eq. (9) sets out the OFDM-NOMA symbol, where χ(k) is a symbol in the kth OFDM subcarrier. Then, in order to evade inter-carrier interference (ICI) among OFDM subcarriers, a cyclic prefix (CP) is a guard interval and has been added to the transmitted signal (Eq. (10)). The aim for adding CP to this signal is to evade ICI between OFDM sub-carriers. The OFDM symbol is expressed after CP as Eq. (11), where Ncp represents the CP length. CP added OFDM signal is transformed to serial then transmitted through a Rayleigh channel that fades. Eq. (12) depicts the signal received by users. Pilot signals, which are well-known symbols, are placed on OFDM sub-carriers to provide information for the channel replies. We may undertake a semi-blind joint CE and signal identification based on these pilot answers.

5  Description of Some Previous Methods

The following research aims to enhance multi-user OFDM-NOMA’s BER performance by using a strength interpolation method based on stacked generalization ensemble learning interpolation. This enhancement should be visible with a decrease in the number of pilot symbols inserted, regardless of the manner of pilot model implantation chosen.

In fact, we insert two most common pilot forms used in the literature (i.e., Block and comb type pilot insertion) to evaluate the model we propose. It should be highlighted that these two sorts of combinations are the fundamental models. Other pilot insertion types exist, but they are just mixtures of the two primary models. It should be noted that the IEEE 802.11g standard uses a comb-type pilot device for CE.

5.1 Least Square Estimator

When we apply the least square estimator, the estimation of all vector’s elements is given by LS^:

LS^=YX_−1=H+WX_−1(21)

X, Y and H are respectively the diffused signal, the received signal and the channel transfer function. W is the noise.

Least square estimator is perceptible to noise, i.e., more channels contain noise, the more it gives negative estimation results.

5.2 Minimum Mean Square Estimator (MMSE)

This technique is based on the MMSE’s criterion and considers canal correlation. As a result, it is more accurate than the first technique. Yet, the MMSE technique has two drawbacks: (1) it is complex to implement as it sequentially uses two independent filters and (2) it calculates the canal’s length based on special canal properties (Doppler frequency, maximum length of sub-canals). It is obvious that MMSE estimator’s performance is far higher than LS estimator, particularly when the signal-to-noise ratio is weak. MMSE method seeks for minimizing cost function (i.e., the Mean Square Error of H−M_Yvector).

Where M is the matrix with Coefficients optimized as:

FMMSE=E{‖H−M_Y‖F2}(22)

CE is obtained by:

MMSE^=M_optY(23)

H^MMSE=R_H(R_H+(X_HX_)−1σ2I_)−1H^LS(24)

The MMSE technique complexity is far greater than traditional techniques of lesser squares. This is due to multiplication and matrix inversion operations.

However, MMSE estimator is just inconvenient because it is less sensitive to noise than LS (i.e., it is based on average quadratical error, and noise Gaussian is near zero). In addition, MMSE estimator may also be useful in the case of interpolation; particularly when pilot symbols are unevenly dispersed in the track.

5.3 Method Based on Artificial Neural Network

Since a decade, there have been numerous attempts to improve CE with intelligent methods. We have previously investigated the contribution of neural networks as an approximator, which has yielded satisfactory results in terms of lowering bit error rates. We used a neuronal network with a radial base function as well as a perceptron multilayer [36]. Given what has come before, the optimization criteria can be summarized in four points:

- Reduce the debit loss caused by the insertion of pilot symbols and achieve the lowest feasible ratio of the number of pilot symbols inserted to the number of symbols constituting the frame.

- Achieve a good performance on a variable channel in a short period of time.

- Ensure adequate algorithmic complexity.

- Create an algorithm with fast convergence.

The technique proposed reduces the frequency of insertion of pilot symbols while also interpolating the coefficients of the transmission channel of all data grilles emitted by a small number of added pilots.

Among the features of neural networks that can contribute to the subject of interpolation is their ability to perform sparse approximation. This expression reflects two different characteristics: The first is that neural networks are universal approximators. The second is that with the minimum of causes, they can give successful results. For the case of the artificial neural network, the number of weights increases linearly with the required precision, whereas in the other techniques it is an exponential increase. In comparison with linear interpolation, for example, we can only modify the coefficients of the combination, whereas in the case of a neural network, we adjust the coefficients and the functions themselves. The neural network needs each time input and output variables, extracted from a learning base to start a “black box” modeling. It seeks the regression function of the quantity to model. This is where the parsimonious character of the neural network and its advantage over a linear regression come in. Therefore, for the same number of parameters, neural networks will give better accuracy than other techniques. In general, a neural network therefore makes it possible to make better use of the available measurements.

During the learning phase, the neural network will have as input the received pilot symbols inserted into a data grid which is represented by a matrix of 12 rows and 14 columns while the desired response will be the transmitted pilot symbols inserted into the grid received after traversing the channel. The neural network will thus learn to interpolate the elements of the matrix from the pilot symbols.

The mission of the neural network is to learn first, then it is called upon to interpolate to construct the states of variation of the transfer function of the transmission channel from the samples of the pilot symbols received. The learning work is done for each channel profile. Several parameters were taken into consideration during the learning of the network, we quote the topologies chosen for the neural network, the type of modulation, the number of sub-carriers, the number of inputs/outputs of the network.

Among the characteristics of neural networks, their ability to approximate and interpolate nonlinear functions. The learning parameters and the choice of the network topology are among the basic factors for the success of the neural network mission. In previous works [36] and [25], we had introduced ANN and we have presented many improvements for CE. Furthermore, some authors used ensemble learning and deep learning applied to NOMA systems such as the authors of [37] used Ensemble Learning for energy efficiency in Full-duplex Cognitive Radio NOMA (FD CR-NOMA) Systems and the authors of [38] and [39] used Deep Reinforcement Learning for respectively allocation for MIMO-NOMA vehicular edge computing and allocation scheme for MIMO-NOMA and D2D Vehicular Edge Computing Decentralized Power.

6  Proposed Ensemble Model: Stacked Generalization for CE (SGCE)

The benchmark model employed in our study, referred to as Stacked Generalization for Channel Estimation (SGCE), is deeply rooted in the principles of ensemble learning. The adoption of SGCE is substantiated by its demonstrated effectiveness in addressing the intricate challenges associated with channel estimation tasks within mobile radio communication systems. SGCE leverages a sophisticated ensemble of machine learning models, including Random Forest (RF), Gradient Boosting (GB), Light Gradient Boosting Machine (LGBM), Support Vector Regression (SVR), Extremely Randomized Trees (ERT), and Extreme Gradient Boosting (EGB), to optimize channel coefficient predictions.

The architectural elements of SGCE encompass five base learners, each contributing unique strengths to the ensemble: RF, GBM, LGBM, SVR, and ERT. These diverse elements work collaboratively to capture intricate patterns within the channel data, facilitating a robust and accurate estimation of channel coefficients.

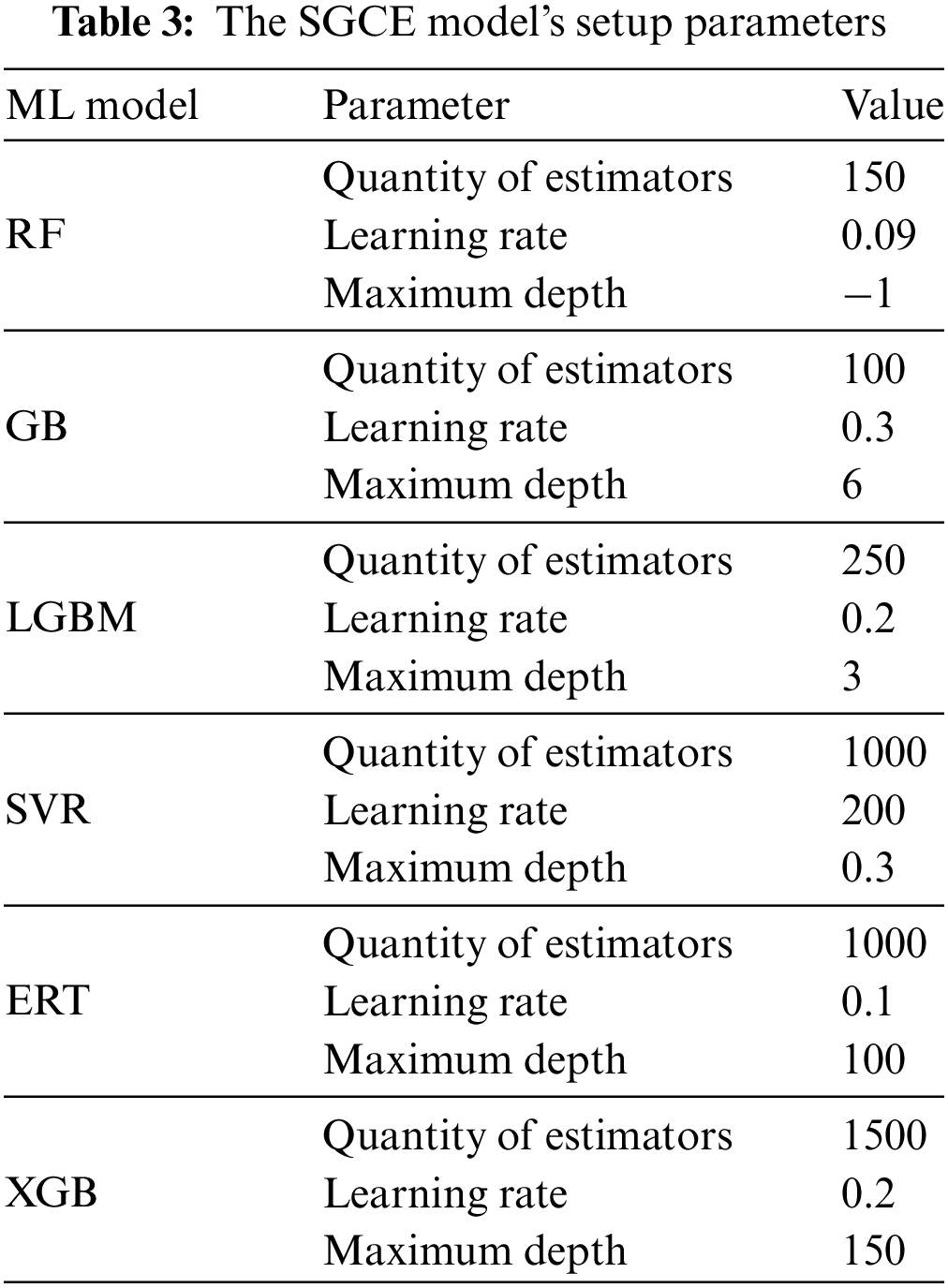
Our meticulous selection of specific model parameters for SGCE is grounded in a rigorous tuning process aimed at maximizing the model’s performance. Parameters such as the quantity of estimators, learning rate, and maximum depth have been carefully calibrated to enable the model to generalize effectively across diverse channel conditions. The tuning process ensures that SGCE adapts optimally to varying channel characteristics, contributing to its efficacy in channel estimation tasks. SGCE operates on the foundational principles of supervised learning, aligning with the overarching principles of ensemble learning. This methodology guides the model in learning from the training data, iteratively optimizing predictions from the base learners through a meta-learning step involving Extreme Gradient Boosting. These principles enable SGCE to adapt dynamically to changing channel conditions and enhance its accuracy in channel coefficient predictions.

In this work, we use supervised CE approaches, which involve the insertion of pilot symbols with a harmonious rhythm and a suitable design. Pilots carry no data and have values known to both the emitter and the receiver. The employment of pilot symbols in the output grille instead of data symbols gives the benefit of precise CE while adding connection loss. The SGCE model improves CE performance outcomes by reducing pilot insertion. SGCE is a machine learning model (Fig. 3) that incorporates five machine learning models: RF, GB, LGBM, SVR, and XGB.

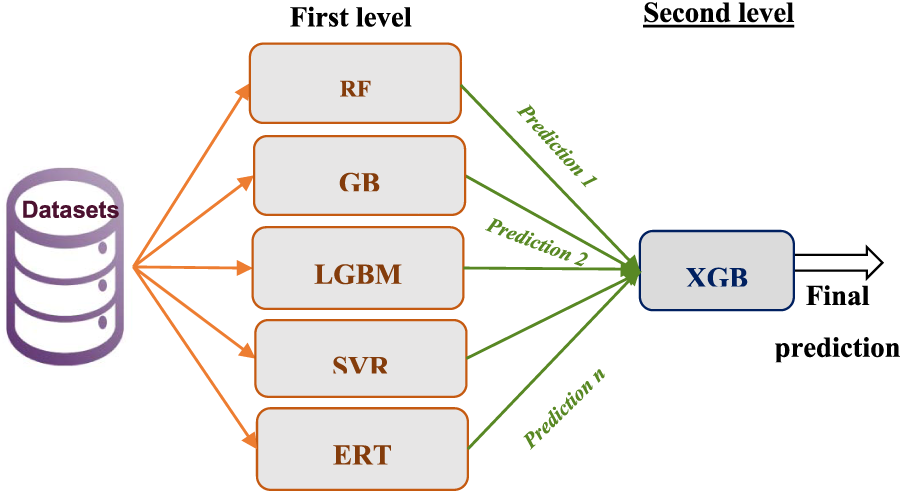
Figure 3: SGCE architecture

Stacking, referred to as ensemble learning, is a method for combining several machine learning algorithms. The stacking is composed of two levels: a basic learner makes up the first level, and a meta-learner makes up the second. The main goal of stacked generalization is to enhance estimated performance across each learner in the set and to merge prediction values from the base learners. Channel coefficients were approximated using the stacking method. Six distinct learners, RF, GB, LGBM, SVR, ERT and XGB. To guarantee channel coefficient predictions using an XGB model, the stacked model creates meta-data from these first five models. Then, modeling effectiveness is checked using the leave-one-out approach.

6.1 Base Learners

In the foundational layer of our Stacked Generalization for SGCE model, we deploy a diverse set of base learners, each bringing unique strengths to the ensemble. These base learners are essential components that contribute to the accuracy and effectiveness of the channel coefficient predictions. Let’s explore each base learner in detail:

- Random Forest: This method is effective and extremely accurate since it makes use of a vast number of decision trees. RF is an ensemble method based on decision trees. It is composed of several trees. Tree votes are the classifications offered by each tree in the forest. The final forecast is determined by combining all vote trees and choosing the one with the most votes.

- Gradient Boosting Machine is a machine learning technique used for classification and regression issues. An ensemble of weak prediction models, many of which are decision trees, are returned as a prediction model. The strategy that results when a decision tree is the weak learner is called gradient-boosted trees; it generally beats random forest. A gradient-boosted trees model is developed in the same stage-wise manner as previous boosting methods, but it generalizes the other approaches by enabling optimization of an arbitrary differentiable loss function.

- Light Gradient Boosting Machine is a high-performance gradient boosting framework based on the decision tree technique that may be used for ranking, classification, and a variety of other machine learning applications.

- Support Vector Regression is a supervised learning approach for predicting discrete values. Support Vector Regression operates on the same principles as Support Vector Machines (SVMs). SVR’s primary concept is to identify the optimum fit line. The best fit line in SVR is the hyperplane with the greatest number of points.

- Extremely randomized tree, commonly known as Extra Trees, is an ensemble machine learning technique based on decision trees. Extra Trees generate a huge number of extremely randomized decision trees out of a training sample.

In this study, the rationale for selecting the following models is for the following reasons:

- RF was chosen for its effectiveness and high accuracy. Its ability to utilize a vast number of decision trees and provide a robust ensemble makes it suitable for capturing complex relationships within channel data. However, one limitation of Random Forest is its potential for overfitting, especially in situations with noisy data or when the number of features is very high.

- GB, particularly gradient-boosted trees, excels in returning an ensemble of weak prediction models. By leveraging decision trees, GB complements RF and often outperforms it, making it a valuable addition to the ensemble. Nevertheless, gradient boosting methods like GB can be sensitive to outliers, impacting their performance, and may require careful tuning to prevent overfitting.

- LGBM is a high-performance gradient boosting framework based on decision trees. Its efficiency in handling large datasets and diverse machine learning tasks adds versatility to the ensemble, contributing to improved CE. However, a potential limitation of LGBM is its sensitivity to imbalanced datasets, which may affect its ability to generalize well across different classes.

- SVR, operating on the principles of SVMs, is chosen for its effectiveness in predicting discrete values. The optimization of the best-fit line by SVR aligns with the goals of precise CE in the SGCE framework. One limitation of SVR is its sensitivity to the choice of kernel function, and selecting an inappropriate kernel can lead to suboptimal performance.

- XGB, representing Extreme Gradient Boosting, serves as the meta-learner in the ensemble. Its tree ensemble method, where trees are gradually added, allows for minimizing errors of the forerunners, providing a powerful mechanism for combining predictions from the base learners. Yet, Extreme Gradient Boosting may be computationally expensive and memory-intensive, limiting its application in resource-constrained environments.

6.2 Meta Learner

XGboost represents Extreme Gradient Boosting by the acronym. It is Gradient Boosting-based with some modifications. It is a tree ensemble method in which the trees are gradually added, and each tree learns from its forerunners. The main objective of XGboost is to minimize the errors of the forerunners. Table 3 lists the precise parameter parameters for several machine learning techniques. XGBoost was specifically chosen as the meta-learner in the SGCE ensemble due to its unique characteristics that complement the base learners. The decision to employ XGBoost is underpinned for many considerations, such as:

- XGBoost operates as a tree ensemble method, where decision trees are incrementally added, allowing each tree to learn from its predecessors. This staged learning process enables XGBoost to minimize errors from the previous models, enhancing the overall predictive performance.

- XGBoost lies in its capability to effectively handle complex relationships within the data, providing a robust mechanism for capturing intricate patterns that may be missed by individual base learners.

- As the meta-learner, XGBoost consolidates predictions from the base learners, synthesizing their diverse outputs into a more refined and accurate estimation of channel coefficients. Its ability to weigh the contributions of each base learner allows for an adaptive and optimized combination of their strengths.

In summary, XGBoost serves as a critical component in the SGCE ensemble by acting as the meta-learner that refines and consolidates predictions from the base learners. Its unique attributes contribute to the overall efficacy of the ensemble, ensuring a comprehensive and accurate CE approach in the context of 5G mobile networks.

The choice of the leave-one-out approach for checking modeling effectiveness in our SGCE ensemble was a deliberate decision aimed at enhancing the robustness of our model evaluation process. This approach involves training the model on a subset of the dataset, leaving out a single data point for validation, and iteratively repeating this process for each data point. Our selection of the leave-one-out approach is rooted in its several advantages, such:

- Maximization of data utilization: By systematically excluding one data point at a time for validation, we ensure that each data point is utilized for both training and validation. This maximization of data usage contributes to a more comprehensive evaluation of the model’s performance.

- Reduction of overfitting concerns: Leave-one-out cross-validation provides a stringent test of the model’s generalization capabilities. It helps mitigate concerns related to overfitting by evaluating how well the model performs on unseen data points, thereby providing a more reliable estimation of its real-world effectiveness.

- Robustness to dataset variability: The leave-one-out approach is particularly robust in scenarios where the dataset exhibits variability or when dealing with limited data. It allows the model to be evaluated across a range of scenarios, making the assessment more resilient to variations in the dataset.

- Statistical Rigor: Leave-one-out cross-validation is often considered statistically rigorous, providing a more accurate estimate of the model’s performance metrics by leveraging the entire dataset iteratively.

In this work, the leave-one-out approach was chosen to strengthen the model evaluation process by maximizing data utilization, reducing overfitting concerns, ensuring robustness to dataset variability, and maintaining statistical rigor in assessing the SGCE ensemble’s effectiveness in CE for 5G mobile networks.

7  Experimentations

We selected Matlab since its toolboxes for system design provide many critical possibilities. To make comparisons between current and prior work, we used the same simulation parameters that we had previously used in previous work [36,25] (Table 4).

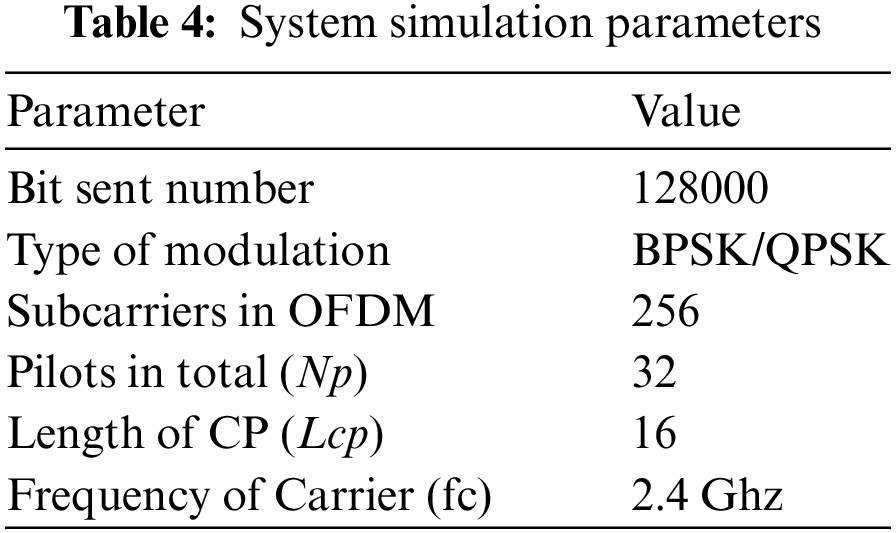
A collection of channel models that can serve as the air interface may be found in the literature. These channels are necessary for transmission and radio reception simulations, testing, and verifications between base and mobile stations. We ran simulations using the channel model called multipath fading propagation conditions [36]. We carry out the simulation of the SGCE ensemble model by comparing the results with those of the radial basis function neural networks (FBR) and perceptron multilayer neural networks (MLP) from one side and a comparison with cubic spline interpolation and MMSE estimator from the other side. The results are shown in Figs. 4 and 5. The simulation parameters are identical to those described in Table 4.

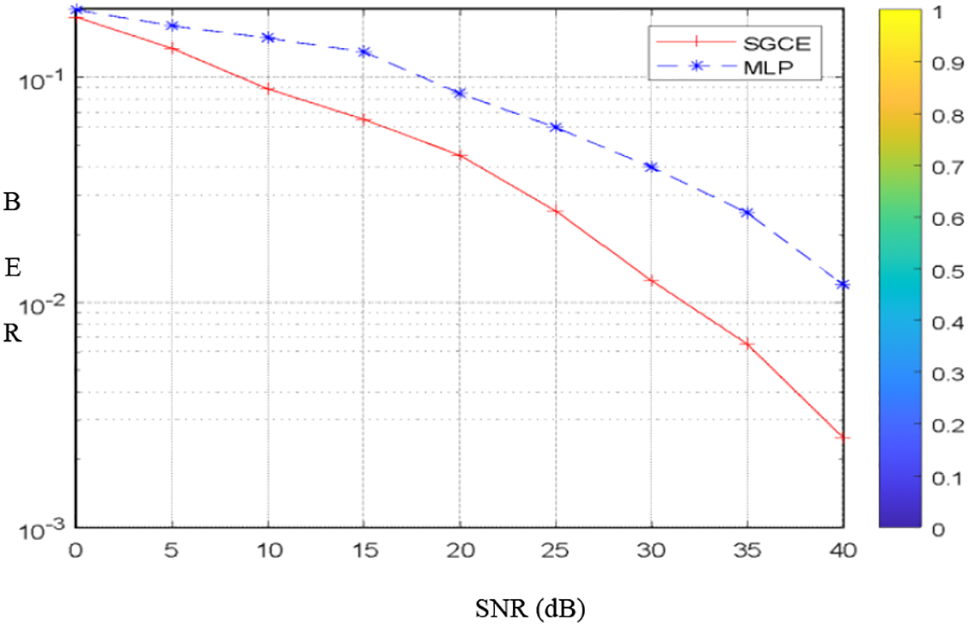
Figure 4: Performance of SGCE compared with MLP

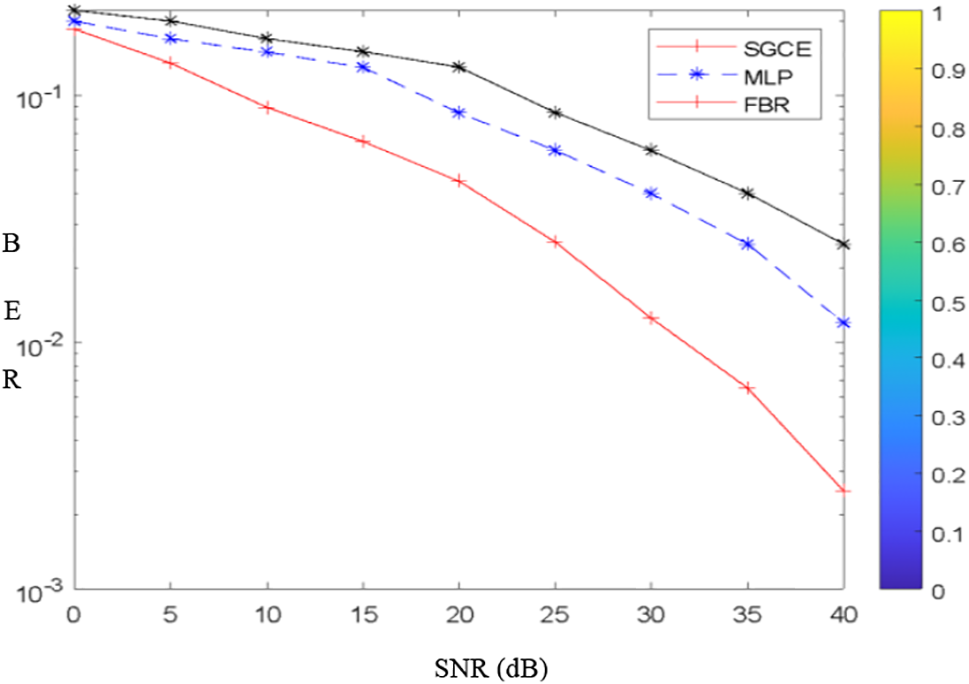
Figure 5: Performance of SGCE compared with FBR and MLP

We notice that the performances of the SGCE ensemble model are better than those of FBR and MLP. In the second experimentation, the results show that the SCGE estimator exceeded the cubic spline interpolator in these simulation conditions (Fig. 6), and is approximately near the MMSE receiver (Fig. 7).

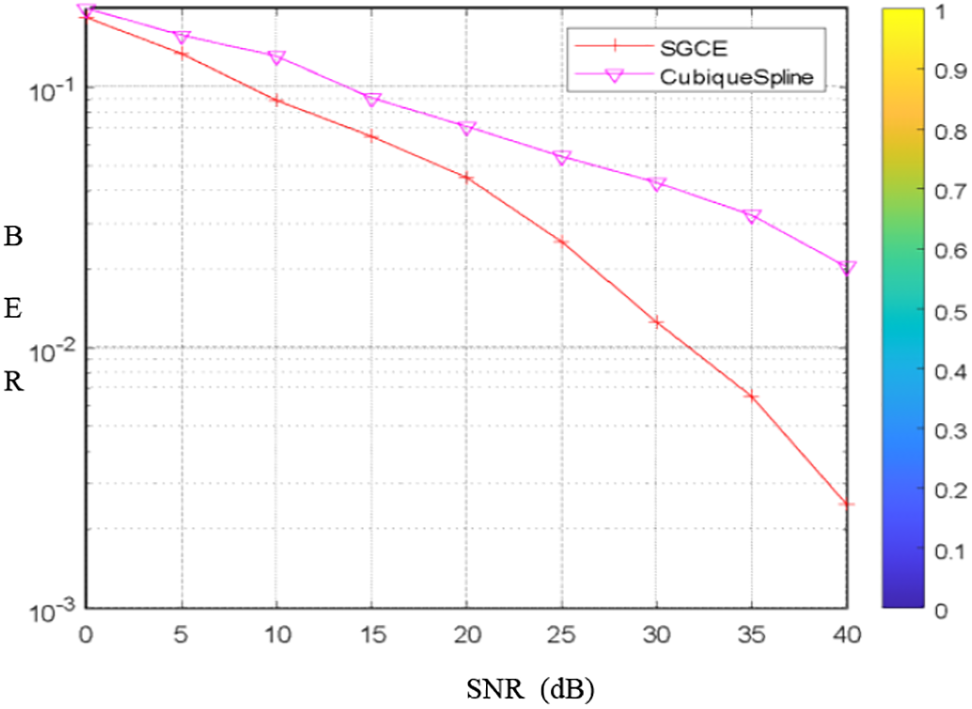
Figure 6: Performance of SGCE compared with Cubic spline interpolator

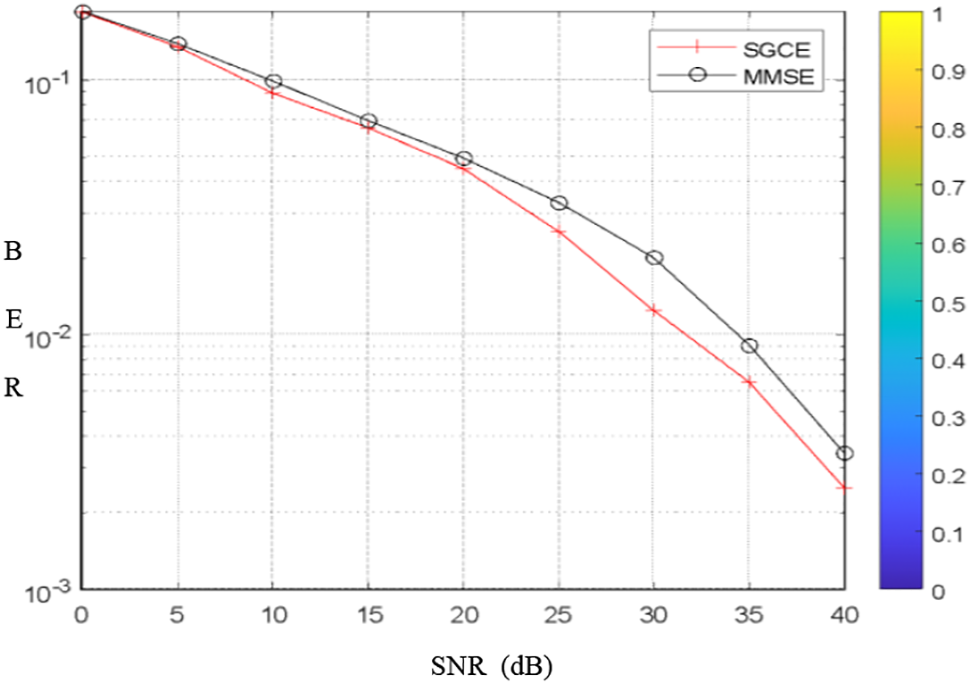
Figure 7: Performance of SGCE compared with MMSE

Fig. 8 shows that the SCGE estimator (and MMSE) produced results that were very close to those of the ideal estimator.

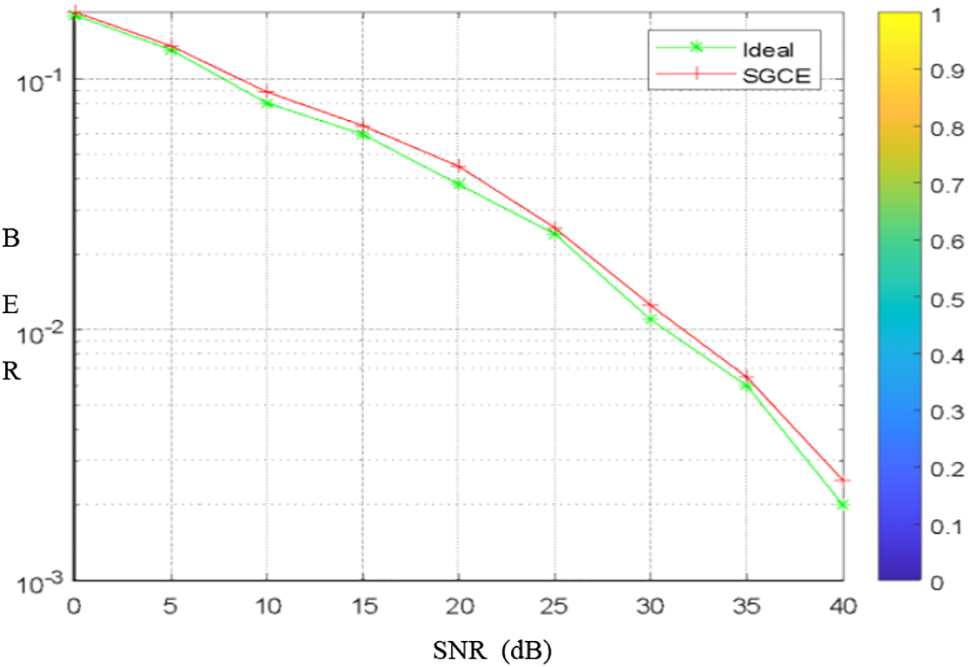
Figure 8: Performance of SGCE compared with Ideal estimator

On the other hand, by applying SGCE, an SNR gain between 1 and 3 dB for a fixed BER will be obtained. Fig. 9 shows that for a fixed SNR, the SINR of the SGCE ensemble model offers a gain greater than FBR by about 2 dB and greater than MLP by about 3 dB. From Fig. 9, we can also note that, for a fixed SNR, the throughput of this new ensemble model is about 0.5 Bits/s/Hz either side of the other two methods.

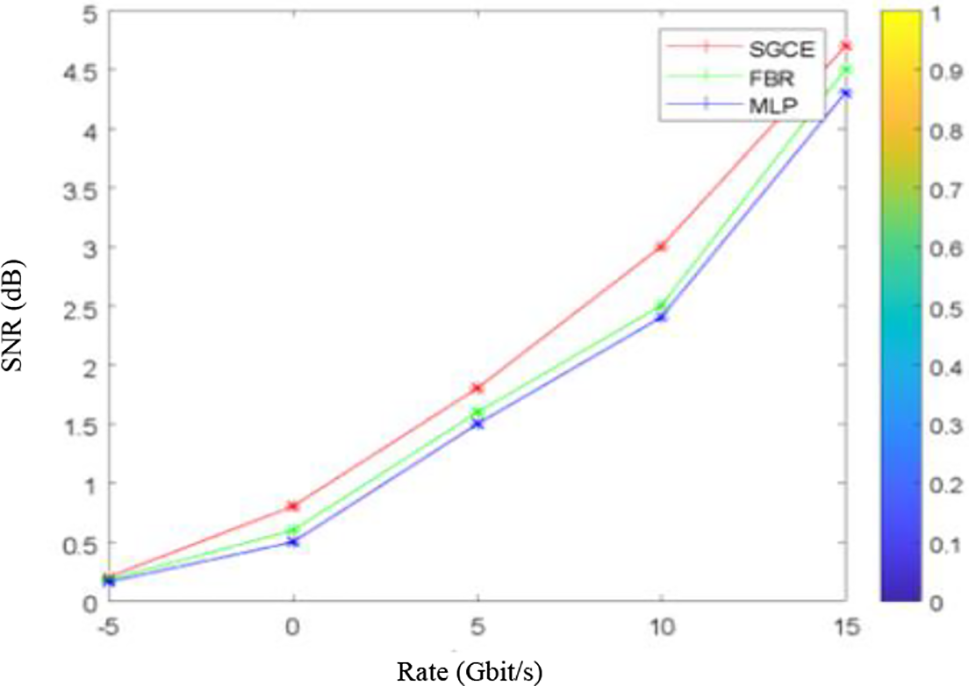
Figure 9: Gain offered by SGCE, FBR and MLP

The enhanced accuracy of the estimated channel at each symbol can be attributed to the implementation of SGCE ensemble model. To evaluate the performance of our proposed SGCE model, we compared it with the base models used in the study, considering various metrics such as accuracy, precision, and recall. In a binary classifier, the output is generated with two class values, typically denoted as “positive” and “negative,” based on the given input data. To assess the performance of the model, a test dataset containing the observed labels for all data instances is utilized. By comparing the observed labels with the expected labels after classification, the model’s performance can be determined.

While it is rare to achieve a flawless binary classifier that is effective across various contexts, the predicted labels should ideally match the observed labels. The confusion matrix, consisting of three components of binary classification, is constructed to analyze the outcomes. A binary classifier predicts whether data instances in a test dataset are positively or negatively correlated, resulting in four possible outcomes: true positive, true negative, false positive, and false negative.

Accuracy, a metric used to assess the performance of a learner, represents the percentage of correct predictions made by the model. It is calculated by dividing the total number of correct predictions by the total number of forecasts. By employing these evaluation measures and analyzing the confusion matrix, we can effectively evaluate the performance of the SGCE model and understand its accuracy in predicting channel states.

The confusion matrix is built from the five binary models. Each binary model predicts whether all of the data instances in a test dataset are positively or negatively correlated. This categorization produces four outcomes: true positive, true negative, false positive, and false negative:

Accuracy=TN+TPTN+FP+FN+TP(25)

Precision is known as positive predictive value, is the ratio of relevant to retrieve instances:

Precision=TPFP+TP(26)

Recall, known as sensitivity, is a subset of the recovered relevant occurrences:

Recall=TPFN+TP(27)

The F1-score is a statistical metric that assembles rate performance, accuracy, and recall. The Formula One score is:

F1−score=precision∗recallprecision+recall(28)

The SGCE is based on RF, GB, LGBM, SVR and ERT to ensure channel coefficient predictions using an XGB.

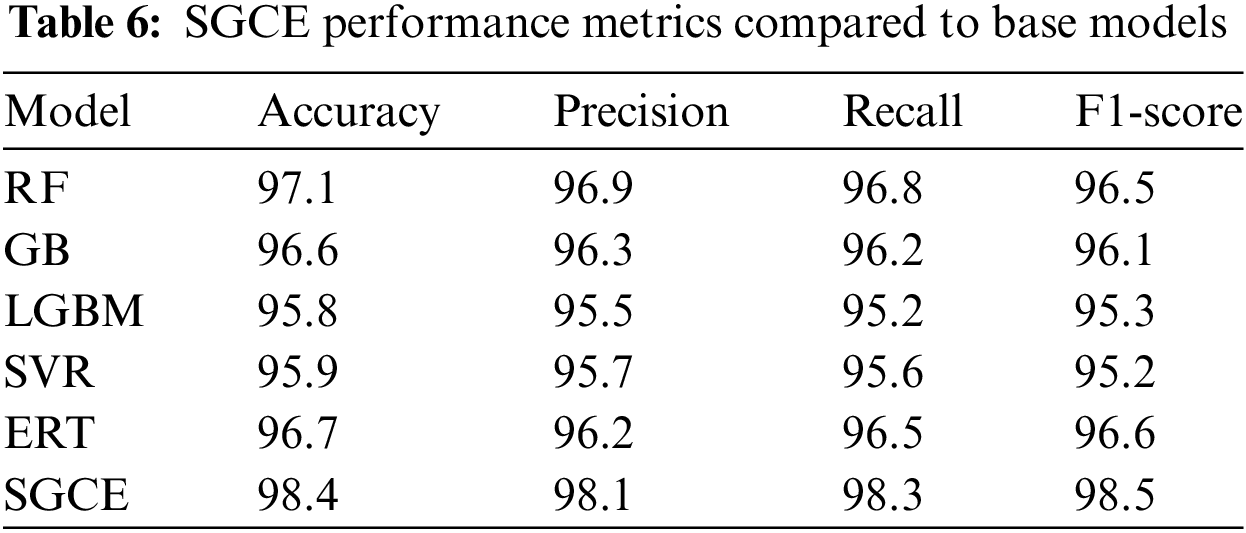
It is clear (Tables 5 and 6) that SGCE correctly predicts channel coefficients with an accuracy average of 98.4% and a precision average of 98.1%. In addition, SGCE had the highest F1-score of 98.5%.

We have to mention that quantifying the computational complexity of machine learning models, including SGCE, is challenging and often depends on various factors, including dataset size, feature dimensionality, and model hyperparameters. However, we can provide a general comparison based on certain characteristics: LS has relatively low computational complexity and is efficient for small to moderately sized datasets. LS is suitable for real-time applications due to its simplicity and quick training. MMSE Method involves matrix inversions and multiplications, making it computationally more demanding than Least Squares, and may exhibit higher complexity, especially with larger datasets, and might not be as suitable for real-time applications. Simple ANN method has typically moderate to high complexity, depending on the network architecture. It can be resource-intensive, especially with deep architectures or large datasets. Inference time might vary based on model size and complexity. Concerning the SGCE method which involves an ensemble of machine learning models, including Random Forest, Gradient Boosting, and others. The ensemble introduces additional complexity compared to individual models. The meta-learning step, particularly using XGB as a meta-learner, may increase computational demands. However, the efficiency of ensemble methods in aggregating predictions can provide a balance between accuracy and complexity.

We acknowledge certain limitations inherent in the SGCE approach. One notable consideration is the dependency on the quality and representativeness of the training dataset. The effectiveness of SGCE is contingent on the diversity and sufficiency of the data it learns from, and suboptimal datasets may impact its performance. Additionally, the computational demands associated with ensemble methods, especially with the integration of multiple machine learning algorithms, may pose challenges in real-time applications, warranting careful consideration in resource-constrained environments. We recognize these limitations and emphasize the ongoing nature of research in addressing and mitigating these challenges to enhance the applicability and versatility of the SGCE model.

8  Conclusion

In this study, we presented a novel approach for CE in mobile radio communication systems using the SGCE model. In these systems, the air interface between the base station and the mobile device is a complex multipath channel, where the receiver collects multiple copies of the original signal through various pathways, affected by reflections, attenuations, and other environmental factors.

Traditional CE methods have shown limitations in accurately estimating channel coefficients, prompting the need for smarter approaches that leverage advancements in artificial intelligence algorithms. Our proposed SGCE model addresses this challenge by combining six machine learning algorithms, namely RF, GB, LGBM, SVR, ERT, and XGB. By utilizing the stacking technique, the SGCE model leverages the strengths of these base learners and the meta-learner (XGB) to optimize channel coefficient predictions. We validate the modeling performance using the leave-one-out technique, ensuring robustness and accuracy. Our experimental results demonstrate the effectiveness of the SGCE model in improving CE performance.

The use of the SGCE model offers several advantages, including enhanced accuracy in estimating channel coefficients, reduced pilot insertion requirements, and improved overall performance compared to other methods such as radial basis function neural networks (FBR) and perceptron multilayer neural networks (MLP). The SGCE model outperforms these approaches and even approaches the performance of ideal estimators in certain simulation conditions.

The results obtained from our evaluations and comparisons highlight the superior performance of the SGCE model, with an average accuracy of 98.4%, precision of 98.1%, and an impressive F1-score of 98.5%. These metrics demonstrate the effectiveness and reliability of the SGCE model in accurately predicting channel states.

In conclusion, our proposed SGCE model provides a promising solution for CE in mobile radio communication systems. By leveraging the power of ensemble learning and machine learning algorithms, we have achieved significant improvements in CE accuracy. The SGCE model holds great potential for enhancing the performance and reliability of next-generation wireless networks, paving the way for improved communication quality and system efficiency.

Future research can investigate the potential of deep learning algorithms, such as convolutional neural networks (CNNs) or recurrent neural networks (RNNs), in enhancing CE performance. These advanced models have shown promising results in various fields and could potentially offer improvements in estimating channel coefficients. Incorporating adaptive learning mechanisms into the SGCE model can enhance its adaptability to varying channel conditions. By dynamically adjusting the model’s parameters or updating the ensemble of base learners based on real-time feedback, the SGCE model can better adapt to changing channel characteristics and improve estimation accuracy. Finally, it is crucial to validate the performance of the SGCE model in real-world scenarios with other diverse environments, interference, and noise conditions. Conducting field trials or simulations using real-world channel data will provide valuable insights into the model’s robustness and applicability in practical wireless communication systems. By pursuing these future works, researchers can further advance the field of CE and contribute to the development of more accurate and reliable wireless communication systems. Furthermore, to address the complexity challenges and advance CE, future research should optimize the computational demands of the SGCE model. Exploring techniques like model quantization and leveraging hardware accelerators such as GPUs can enhance efficiency. Researchers can also explore hybrid approaches that combine machine learning with domain-specific knowledge for streamlined models. By tackling computational challenges and seeking innovative solutions, future research can integrate advanced CE models like SGCE into practical wireless systems effectively.

Acknowledgement: The authors extend their appreciations to the Deanship of Scientific Research, Princess Nourah bint Abdulrahman University, through the Program of Research Project Funding After Publication, grant No (43-PRFA-P-58), for funding this research work.

Funding Statement: This research project was funded by the Deanship of Scientific Research, Princess Nourah bint Abdulrahman University, through the Program of Research Project Funding After Publication, grant No (43-PRFA-P-58).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: L. Jamel, L. K. Smirani; data collection: L. Jamel, L. K. Smirani, L. Almuqren; analysis and interpretation of results: L. Jamel, L. K. Smirani, L. Almuqren; draft manuscript preparation: L. Jamel, L. K. Smirani, L. Almuqren. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data supporting the conclusions of this article are available upon request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Series, M. (2017). Minimum requirements related to technical performance for IMT-2020 radio interface(s). Report ITU-R M.2410-0. International Telecommunication Union. [Google Scholar]

2. Salari, A., Shirvanimoghaddam, M., Shahab, M. B., Arablouei, R., Johnson, S. (2022). Design and analysis of clustering-based joint channel estimation and signal detection for NOMA. arXiv preprint arXiv:2201.06245. [Google Scholar]

3. Mahmood, N. H., Böcker, S., Munari, A., Clazzer, F., Moerman, I. et al. (2020). White paper on critical and massive machine type communication towards 6G. arXiv preprint arXiv:2004.14146. [Google Scholar]

4. Shahab, M. B., Abbas, R., Shirvanimoghaddam, M., Johnson, S. J. (2020). Grant-free non-orthogonal multiple access for IoT: A survey. IEEE Communications Surveys & Tutorials, 22(3), 1805–1838. https://doi.org/10.1109/COMST.2020.2996032 [Google Scholar] [CrossRef]

5. Ghanami, F., Hodtani, G. A., Vucetic, B., Shirvanimoghaddam, M. (2020). Performance analysis and optimization of NOMA with HARQ for short packet communications in massive IoT. IEEE Internet of Things Journal, 8(6), 4736–4748. https://doi.org/10.1109/JIOT.2020.3028434 [Google Scholar] [CrossRef]

6. Aldababsa, M., Toka, M., Gökçeli, S., Kurt, G. K., Kucur, O. (2018). A tutorial on nonorthogonal multiple access for 5G and beyond. Wireless Communications and Mobile Computing, 2018, 9713450. https://doi.org/10.1155/2018/9713450 [Google Scholar] [CrossRef]

7. Ma, Z., Bao, J. (2019). Sparse code multiple access (SCMA). In: Vaezi, M., Ding, Z., Poor, H. (edsMultiple access techniques for 5G wireless networks and beyond, Springer, Cham, pp. 369–416. [Google Scholar]

8. Çatak, E., Tekce, F., Dizdar, O., Durak-Ata, L. (2019). Multi-user shared access in massive machine-type communication systems via superimposed waveforms. Physical Communication, 37, 100896. https://doi.org/10.1016/j.phycom.2019.100896 [Google Scholar] [CrossRef]

9. Wu, Z., Lu, K., Jiang, C., Shao, X. (2018). Comprehensive study and comparison on 5G NOMA schemes. IEEE Access, 6, 18511–18519. https://doi.org/10.1109/ACCESS.2018.2817221 [Google Scholar] [CrossRef]

10. Chen, Z., Sohrabi, F., Yu, W. (2018). Sparse activity detection for massive connectivity. IEEE Transactions on Signal Processing, 66(7), 1890–1904. https://doi.org/10.1109/TSP.2018.2795540 [Google Scholar] [CrossRef]

11. Gurbilek, G., Koca, M., Coleri, S. (2023). Blind channel estimation for DCO-OFDM based vehicular visible light communication. Physical Communication, 56, 101942. https://doi.org/10.1016/j.phycom.2022.101942 [Google Scholar] [CrossRef]

12. Jiang, S., Yuan, X., Wang, X., Xu, C., Yu, W. (2020). Joint user identification, channel estimation, and signal detection for grant-free NOMA. IEEE Transactions on Wireless Communications, 19(10), 6960–6976. https://doi.org/10.1109/TWC.2020.3007545 [Google Scholar] [CrossRef]

13. Liu, L., Yu, W. (2018). Massive connectivity with massive MIMO—Part II: Achievable rate characterization. IEEE Transactions on Signal Processing, 66(11), 2947–2959. https://doi.org/10.1109/TSP.2018.2818070 [Google Scholar] [CrossRef]

14. Zhang, Y., Guo, Q., Wang, Z., Xi, J., Wu, N. (2018). Block sparse Bayesian learning based joint user activity detection and channel estimation for grant-free NOMA systems. IEEE Transactions on Vehicular Technology, 67(10), 9631–9640. https://doi.org/10.1109/TVT.2018.2859806 [Google Scholar] [CrossRef]

15. Salari, A., Shirvanimoghaddam, M., Shahab, M. B., Arablouei, R., Johnson, S. et al. (2020). Clustering-based joint channel estimation and signal detection for grant-free NOMA. 2020 IEEE Globecom Workshops (GC Wkshps), Taipei, Taiwan, pp. 1–6. IEEE. [Google Scholar]

16. Rossi, R. J. (2018). Mathematical statistics: an introduction to likelihood based inference. John Wiley & Sons, Inc., USA. [Google Scholar]

17. Murphy, K. P. (2012). Machine learning: a probabilistic perspective. MIT Press, USA. [Google Scholar]

18. Gaikwad, V., Naik, A. (2022). Comparison of BER performance and MSE-based channel estimation for MIMO system. Proceedings of Third Doctoral Symposium on Computational Intelligence, pp. 603–614. Singapore, Springer Nature. [Google Scholar]

19. Guo, Y., Fan, Z., Lu, A., Wang, P., Liu, D. et al. (2022). Downlink transmission and channel estimation for cell-free massive MIMO-OFDM with DSDs. EURASIP Journal on Advances in Signal Processing, 2022, 17. https://doi.org/10.1186/s13634-022-00847-6 [Google Scholar] [CrossRef]

20. Aldababsa, M., Göztepe, C., Kurt, G. K., Kucur, O. (2020). Bit error rate for NOMA network. IEEE Communications Letters, 24(6), 1188–1191. https://doi.org/10.1109/LCOMM.2020.2981024 [Google Scholar] [CrossRef]

21. Varma, D. P., Annapurna, K. (2022). Quality assisted spectrum allocation in cognitive NOMA networks. IoT and Analytics for Sensor Networks: Proceedings of ICWSNUCA 2021, pp. 371–380. Singapore, Springer. [Google Scholar]

22. Wang, C. L., Ding, Y. C., Wang, Y. C., Xiao, P. (2022). A low-complexity power allocation scheme for MIMO-NOMA systems with imperfect channel estimation. 2022 IEEE 33rd Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), pp. 234–239. Kyoto, Japan, IEEE. [Google Scholar]

23. Mengistu, F. G., Mihrete, F. B. (2022). Performance analysis of BS-NOMA for mmWave communication using lens antenna array. Cogent Engineering, 9(1), 2110206. https://doi.org/10.1080/23311916.2022.2110206 [Google Scholar] [CrossRef]

24. Smirani, L., Bouallegue, R. (2015). An uplink LTE-A channel estimation method based On connexionist system. Energy and Manufacturing Engineering (ICAEME’2015), Dubai, UAE. [Google Scholar]

25. Smirani, L., Boulahia, J., Bouallegue, R. (2017). A semi blind channel estimation method based on hybrid neural networks for uplink LTE-A. International Journal of Wireless & Mobile Networks, 8(3), 71–82. https://doi.org/10.5121/ijwmn.2016.8305 [Google Scholar] [CrossRef]

26. Smirani, L. K., Boulahia, J. A. (2015). A neuro symbolic learning method for uplink LTE—Channel estimation. XIII International Conference on Materials and Chemical Engineering, Djeddah, KSA. [Google Scholar]

27. Nandi, S., Nandi, A., Pathak, N. N. (2022). Channel estimation of massive MIMO-OFDM system using Elman recurrent neural network. Arabian Journal for Science and Engineering, 47(8), 9755–9765. https://doi.org/10.1007/s13369-021-06366-0 [Google Scholar] [CrossRef]

28. Kumar, M. S. P., Kanojia, K. (2022). Channel estimation and BER reduction using artificial neural network. International Journal of Scientific Research & Engineering Trends, 8(2), 964–967. [Google Scholar]

29. Sarkar, M., Sahoo, S., Nanda, S. (2022). Channel estimation of non-orthogonal multiple access systems based on L2-norm extreme learning machine. Signal, Image and Video Processing, 16(4), 921–929. https://doi.org/10.1007/s11760-021-02036-8 [Google Scholar] [CrossRef]

30. Danufane, F., Mursia, P., Liu, J. (2021). Channel estimation in RIS-aided networks. In: Enabling 6G mobile networks, pp. 203–220. Cham: Springer International Publishing. https://doi.org/10.1007/978-3-030-74648-3_6 [Google Scholar] [CrossRef]

31. Palitharathna, K. W., Suraweera, H. A., Godaliyadda, R. I., Herath, V. R., Thompson, J. S. (2022). Neural network-based channel estimation and detection in spatial modulation VLC systems. IEEE Communications Letters, 26(7), 1598–1602. https://doi.org/10.1109/LCOMM.2022.3166221 [Google Scholar] [CrossRef]

32. Andiappan, V., Ponnusamy, V. (2022). Deep learning enhanced NOMA system: A survey on future scope and challenges. Wireless Personal Communications, 123, 839–877. https://doi.org/10.1007/s11277-021-09160-1 [Google Scholar] [CrossRef]

33. Emir, A., Kara, F., Kaya, H., Li, X. (2021). Deep learning-based flexible joint channel estimation and signal detection of multi-user OFDM-NOMA. Physical Communication, 48, 101443. https://doi.org/10.1016/j.phycom.2021.101443 [Google Scholar] [CrossRef]

34. Thompson, J. (2019). Deep learning for signal detection in non-orthogonal multiple access wireless systems. 2019 UK/China Emerging Technologies (UCET), pp. 1–4. Glasgow, UK, IEEE. https://doi.org/10.1109/UCET.2019.8881888 [Google Scholar] [CrossRef]

35. Huang, J., Tang, Z. (2021). Deep learning based MIMO-NOMA receiver research. 2021 IEEE 4th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), vol. 4, pp. 1365–1368. Chongqing, China, IEEE. https://doi.org/10.1109/IMCEC51613.2021.9482346 [Google Scholar] [CrossRef]

36. Smirani, L. (2020). Contribution of deep learning algorithm to improve channel estimation performance. Open Access Library Journal, 7(3), 1–16. https://doi.org/10.4236/oalib.1106150 [Google Scholar] [CrossRef]

37. Garcia, C. E., Camana, M. R., Koo, I. (2022). Ensemble learning aided QPSO-based framework for secrecy energy efficiency in FD CR-NOMA systems. IEEE Transactions on Green Communications and Networking, 7(2), 649–667. https://doi.org/10.1109/TGCN.2022.3219111 [Google Scholar] [CrossRef]

38. Zhu, H., Wu, Q., Wu, X. J., Fan, Q., Fan, P. et al. (2021). Decentralized power allocation for MIMO-NOMA vehicular edge computing based on deep reinforcement learning. IEEE Internet of Things Journal, 9(14), 12770–12782. https://doi.org/10.1109/JIOT.2021.3138434 [Google Scholar] [CrossRef]

39. Long, D., Wu, Q., Fan, Q., Fan, P., Li, Z. et al. (2023). A power allocation scheme for MIMO-NOMA and D2D vehicular edge computing based on decentralized DRL. Sensors, 23(7), 3449. https://doi.org/10.3390/s23073449 [Google Scholar] [PubMed] [CrossRef]