A Privacy Preservation Method for Attributed Social Network Based on Negative Representation of Information

1  Introduction

The social network comprises a set of nodes associated with edges, where the node represents the user of social platforms like Facebook, Twitter, and WeChat, and the edge indicates a social interaction between the users connected by it [1]. Due to their enormous impact on understanding the formation of human social relations, behavior characteristics, and the law of information dissemination, social networks have drawn wide attention in recent years [2]. However, owing to privacy concerns, many users are unwilling to provide their personal information to build social networks. To alleviate the privacy concern of users, many privacy-preserving methods have been developed to prevent the attacker from recognizing a specific user from a social network, such as disturbing the edges in social networks, restricting queries in social networks, and so on [3–7].

Although existing methods have achieved a promising performance in preserving the privacy of social networks, they mainly spotlight the topology structure of social networks. A node in a social network, namely a social software user, usually owns various attributes, such as sex, age, and career, which are important for analyzing social networks, but also increase the risk of privacy disclosure, given that the attacker can recognize a specific user from a social network by using these attributes [8]. Fig. 1 gives an illustrative example, where the original attribute social network is shown in Fig. 1a, and the social network that has been preserved by a privacy-preserving method specifically tailored to the topology of the social networks [9] is shown in Fig. 1b. In Fig. 1, there are only four nodes that represent girls including nodes 1, 5, 7, and 8. Among these nodes, only node 7 owns three friends. Therefore, if the attacker knows that Alice is a girl, and she has three friends, then the attacker can uniquely recognize that node 7 in Fig. 1b is Alice. Therefore, the node attributes deserve more attention when it comes to preserving the privacy of social networks.

Figure 1: An example of attribute social network. (a) The attribute social network. (b) The anonymous attribute social network

Recently, there have been a few works on preserving the privacy of attributed social networks. For example, in [10], an early fusion-based method was developed to publish attribute networks by Wang et al., in which the structure of network and node characteristics are merged with a private probability model to construct anonymous networks that satisfy differential privacy. Moreover, Ren et al. [11] employed k-anonymity and expanded on it proposing a personalized (α,β,l,k)-anonymity model of social networks, so that the multiple attacks can be resisted, including d-neighborhood attacks of graphs, background knowledge attacks, and homogeneity attacks. Meanwhile, a variety of vertex-sensitive properties can be obtained. However, the majority of these methods treat attributes as labels for nodes. That is to say, the attributes concerned by these methods are discrete. In a social network, the nodes not only have many discrete attributes but also own various real-value attributes, such as height, weight, and salary. Consequently, the preserving-privacy methods of social attribute networks should also pay attention to real-value attributes.

The negative representation of information is a branch of the artificial immune system [12], which has been employed to collect and hide sensitive information and formed two new branches called negative survey (collect sensitive information) [13] and negative database (hide sensitive information) [14,15].

As one of the branches of negative representation of information, the negative survey was first developed by Esponda et al. [13,16] to collect sensitive information through questionnaires. To give a simple example, in the traditional survey(positive survey), the respondent may be requested to answer the following questionnaire question, which involves personally sensitive information.

Q1: In the past semester, how many of the courses did you fail?

A. 0B. 1∼3C. 4∼6D. 7∼9E. More than 10

In the positive survey, based on the respondent’s actual situation he/she needs to make a choice directly from all options, whereas in the negative survey, the respondent needs to make a different choice from the positive survey based on the following question:

Q2: In the past semester, the number of courses you failed is NOT?

A. 0B. 1∼3C. 4∼6D. 7∼9E. More than 10

A respondent who should choose B (called positive category) in Q1, when answering Q2, that is, namely in the negative survey, he/she is required to make a random choice from A, C, D, and E (called negative category) and feedback to the investigator. Following the collection of the negative categories from all respondents, the investigator estimates the distribution of positive categories from the distribution of negative categories by using the reconstruction approaches of the negative survey, such as NStoPS-I [17] and NStoPS-LP [18]. During above the process, given that the investigator cannot get the specific positive category of any respondent, the private information of the respondents can be preserved by the negative survey. Although the negative survey has been utilized in social networks to preserve their topological privacy [19], where the negative survey is used to alter the relationship between different nodes, privacy preservation is limited when there are a few nodes in social networks.

The negative database conceals sensitive information using a complementary set rather than the original dataset, and it has been shown that it is NP-hard to retrieve the original string from the negative database [15,20]. Table 1 gives an illustrative example of the negative database. In Table 1, the original information is listed in the column of database (DB) (called a hidden record), which contains only one record with three bits, namely ‘001’. The complementary information for the original data is given in the column of U−DB. Here, U={0,1}3 represents the universal set of all the binary strings. From Table 1, it can be found that the number of complementary information in U−DB is much larger than in DB, which usually consumes too much memory. To remedy this problem, the wildcard ‘*’, which can represent ‘0’ or ‘1’, is introduced into the negative database so that the complementary set of original information can be compressed, and finally, the negative database is obtained. The column of negative database (NDB) in Table 1 displays a negative database of the hidden record. For each record in the NDB, the bit represented by ‘*’ is called an unspecified bit, while the bit represented by ‘0’ or ‘1’ is called a specified bit.

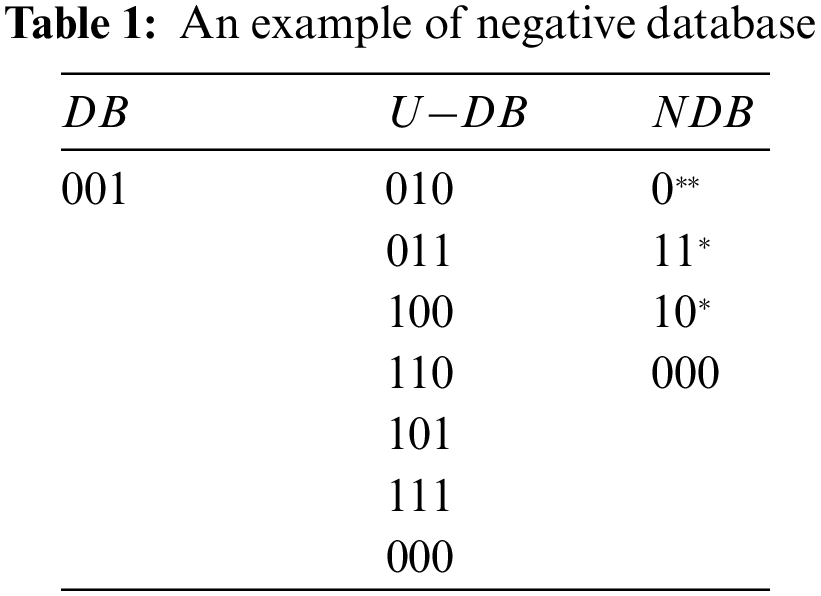
Since the negative database supports directly estimating Hamming and Euclidean distance between the hidden information, it is suitable to preserve the privacy of attributes in social networks. Therefore, the distance between different node attributes is seminal to analyzing social networks.

In this paper, a negative representation information-based method, called AttNetNRI, is developed to preserve the privacy of attributed social networks, where the negative survey is used to disturb the topology structure, while the negative database is designed to hide the attributes of nodes. The contributions of this paper are summarized as follows:

1.    Based on the negative information representation, a privacy-preserving method called AttNetNRI is proposed to preserve both the topology and node attribute privacy of the social network. Different from existing methods tailored for the attributed social network, the AttNetNRI can preserve the privacy of social networks with real-value node attributes. Moreover, compared to the existing negative information representation-based method, the AttNetNRI can still provide sufficient privacy preservation even though there are a few nodes in social networks.

2.    With the aim of verifying the effectiveness of AttNetNRI in preserving privacy in social networks, comprehensive theoretical analysis and experiments are conducted. The theoretical analyzing results demonstrate that the AttNetNRI can resist friendship, subgraph, and attribute attacks, while the experimental results indicate that compared to three privacy-preserving algorithms targeted at social attributed networks, the AttNetNRI can achieve better utility when providing the same level of privacy preservation.

The remainder of this paper is organized as follows. In Section 2, the existing privacy-preserving methods tailored for attribute networks are reviewed, and the negative representation of information is briefly introduced. Sections 3 and 4 provide the details of the developed AttNetNRI as well as the privacy analysis. In Section 5, the performance of the developed AttNetNRI is confirmed. In the end, Section 6 concludes this paper.

2  Related Work

2.1 Privacy-Preserving Methods for Attribute Networks

To resist various types of attacks in the social attribute network, some methods have been proposed. To name a few, in [21], Zhou et al. introduced the generalization method for discrete attributes to satisfy the k-anonymity aiming to anonymize social networks and proposed a coding technique for neighborhood subgraphs to deal with neighborhood attacks, which generates anonymized social networks that can still provide highly accurate answers to aggregated network queries. Moreover, Sun et al. [22] defined a new anonymity concept, called k-number of mutual friends (NMF) anonymity which aims to ensure that at any time there are k−1 pairs of friends sharing the same number of mutual friends in the attribution graph, and proposed two effective anonymization methods to satisfy the k-NMF anonymity with the preservation of utility.

In addition, differential privacy techniques are also commonly used to preserve sensitive information in social attribute networks [23]. To address the issues of poor data availability due to overprotection and the attacker obtaining the target user’s data indirectly by capturing the information of the neighbors of the target user, Zhou et al. [24] proposed a structure-attribute model to meet the requirements of differential privacy regarding the data publishing in social networks, where uncertainty graphs are introduced to maximize the maintenance of the community structure. Meanwhile, some studies are concerned about the privacy of high-dimensional data. Such as in [25], an algorithm based on local difference private high-dimensional data publishing (LoPub) was designed by Ren et al., which decreases the dimensionality and sparsity of the original dataset by partitioning the original dataset into multiple compact clusters based on the distribution and correlation information of the original dataset. In [26], Zhang et al. presented a fine-grained tailored differential privacy data publishing strategy for social networks, namely APDP, where a novel mechanism is designed to define the level of privacy protection for each user depending on the attribute values. Furthermore, to obtain a good trade-off concerning privacy and accuracy, Macwan et al. [27] developed a new differentially private recommendation algorithm that maintains the privacy of friend links and attribute values, which is primarily based on the inclusion of calibration noise in the appropriate matrix representation of the social network.

In addition to the above methods, clustering-based privacy-preserving methods for discrete attributes have been proposed to preserve attribute networks. In [28], a technique based on greedy clustering was presented by Su et al., which groups nodes according to the distance of the nodes in the attribute network and the properties of discrete attribute values.

Although there are a few works aimed at preserving the privacy of attribute networks, these works mainly focus on discrete attributes. When dealing with the widespread real-valued attributes in social networks, the performance of existing work will considerately deteriorate.

2.2 Negative Representation of Information

2.2.1 Negative Survey

The negative survey has been employed in various scenarios to accomplish the collection of sensitive information. To name a few, Xie et al. [29] proposed a method called Gaussian Negative Survey for spatial data collection. Luo et al. [30] developed a negative evaluation model to gather the rating information of goods. To preserve the privacy of users’ location information when they move, Jiang et al. [31] proposed a negative survey-based location information collection method to find the population gathering places. In addition, Jiang et al. [32] designed a real-value negative survey model to obtain data on users’ electricity consumption.

In addition to the structured data, a new method called NetNS, which is based on negative surveys, was created recently to preserve the topological privacy of social networks without node attributes [33]. In NetNS, the social network (called positive social network) is first divided into several subnetworks (called positive subnetworks) with M nodes. After that, the NetNS generates the corresponding negative subnetwork using the specific Gaussian negative survey model for each positive subnetwork. Here, the negative subnetwork indicates the network with the same node set but a different node relationship with the corresponding positive subnetwork. Subsequently, the NetNS substitutes the generated negative subnetwork for each positive subnetwork within the positive social network and finally obtains the negative social network as the output. Although the existing negative survey-based method has achieved promising performance in preserving the topology privacy of social networks, it is not very effective at striking a compromise between privacy and the utility of social networks. Even in cases when there are few nodes in the network, it is unable to maintain social network anonymity. Furthermore, the NetNS does not take into account how node properties affect social network privacy.

2.2.2 Negative Database

The negative database owns several fine properties. Firstly, it can preserve the privacy of the hidden record. It has been proved that it is NP-hard to retrieve the original string from the negative database [12]. Therefore, when the original information is long enough, the converting process is computationally infeasible. Based on the privacy-preserving property, Dasgupta et al. [34] developed a negative authentication system that utilizes the negative database to preserve the privacy of passwords. Moreover, in [15], the negative database was employed to preserve the privacy of personal information when the monitoring agency is tracking the procurement information of the target. Secondly, there is a one-to-many relationship between the hidden record and the negative database. In other words, for a hidden record, various negative databases can be generated. By utilizing this property, Zhao et al. [35] presented a dynamic password authentication scheme based on a negative database, which can resist the replay attack, guessing attack, and exhaustive attack. Thirdly, the negative database supports the similarity estimation between the hidden record and plaintext record. That is to say, for a record hidden in the negative database, its similarity with the other record (not hidden in the negative database) can be estimated directly from the corresponding negative database. Therefore, Liu et al. [36] developed a privacy-preserving clustering algorithm, where the cluster data are converted to the negative database to preserve their privacy. Furthermore, in [37], Zhao et al. presented the negative iris recognition method, which stores the iris data as a negative database so that the privacy of iris data can be preserved while implementing iris verification.

From the above analysis, it can be found that the negative database is suitable to preserve the node attributes, given that it has been proved to be NP-hard to recover the original data by negative database inverse, which can preserve the privacy of node attributes while allowing estimation of similarity between hidden information on the negative database directly. However, for an attribute with a small value range, directly converting its value to the negative database cannot guarantee the hardness of reversing the generated negative database. Moreover, estimating the similarity between two hidden records deserves further research.

2.3 Motivation

From the above analysis, it can be found that both topology structure and node attribute are important for the privacy-preserving of social networks. Although various methods have been suggested to preserve the privacy of attribute networks, these works mainly focus on discrete attributes. When dealing with the widespread real-valued attributes in social networks, the performance of existing work will considerately deteriorate. Although the negative information representation is suitable for preserving the privacy of attribute networks, existing models of negative information representation own some deficiencies, such as the limited ability to balance privacy and utility when preserving the privacy of topology structure, and limited privacy preservation when the node attributes own small value range.

To alleviate the above questions, a method based on negative representation information, called AttNetNRI, is proposed to preserve the social networks with real-value attributes in this paper, whereas an improved negative survey-based method is intended to disturb the topology structure of social networks, while a negative database based method is suggested to hide the real-value attributes. The details of the AttNetNRI will be given in the next section.

3  The Developed AttNetNRI

The process of developing AttNetNRI preserving the privacy of social attribute networks can be divided into two parts, including the disturbing of topology structure and the hiding of node attributes. In this section, we first elaborate on the steps of the AttNetNRI to disturb the topology structure. Then, we give the details of hiding the real value in the negative database. Finally, we deduce how to estimate the Euclidean distance between the hidden attributes from the negative database.

3.1 Steps of Disturbing Topology Structure

As analyzed in Section 2, the existing negative survey-based method only disturbs the edges in the social networks. Furthermore, the nodes in the networks do not change before and after disturbance, which leads to several deficiencies. To alleviate these problems, the developed AttNetNRI adds several noise nodes to the social attribute networks at the beginning of disturbing topology structure. For a social network, noise nodes refer to the nodes that do not exist but are added to the original social networks to disturb the topology structure of social networks. To add noise nodes, the following three points need to be considered:

1.    How to determine the relationship between the noise nodes and the other nodes?

2.    How to determine the attributes of the noise nodes?

3.    How to determine the number of noise nodes added to the social network?

For the first question, the noise nodes directly participate in the division of social networks. The relationship between it and the other nodes is determined by the steps of disturbing the structure of the subnetwork, where the connection between each pair of nodes in the subnetwork is randomly disturbed by the method based on developed in [33]. Here, it is worth mentioning that if there are isolated nodes, namely the nodes without any edge connected to them, in the disturbed network, the AttNetNRI will disturb the subnetwork again. The reasons for doing this are twofold. On the one hand, if the noise nodes have too many edges connected to the other nodes, it will affect the utility of the whole network. On the other hand, if the noise nodes only own a few connections with the other nodes, the networks outputted by the AttNetNRI might contain isolated nodes, which is impractical in the social network.

For the second question, the AttNetNRI randomly selects a neighbor node of the noise node and then assigns the attribute of the neighbor node to the noise node. It is because if the attributes of noise nodes are selected from the nodes belonging to the same community, the impact on community structure will be significantly reduced. However, in application, the community structure of social networks is usually unknown. Although we can employ community detection algorithms to obtain a community structure, different algorithms usually yield different results, and this process is time-consuming. In the real world, friends usually have similar interests and hobbies, and taking the attributes of neighbor nodes as that of noise nodes can reduce the effect of noise nodes on community structure. Therefore, the AttNetNRI directly selects the attributes of neighboring nodes to assign to the noise nodes. Here, the neighbor nodes of noise nodes are determined from the disturbed subnetwork.

As for the last question, the AttNetNRI adds ⌈NM⌉∗M−N+a∗M noise nodes to the social networks, where N represents the size of networks, M represents the number of nodes in the subnetworks that can be turned according to the demand of privacy preservation, and a≥0 is a parameter for controlling the level of noise nodes, which is also determined by the demand of privacy preservation. By doing so, the ability of privacy preservation can be enhanced, given that the noise nodes can mislead the attacker and decrease the probability of the attacker recognizing a specific user from a social network. In particular, when there are a few nodes in the social networks, the AttNetNRI can provide sufficient privacy preservation by increasing the parameter a. Furthermore, the parameter M in the AttNetNRI can be set greater than N2, which enhances the capability of the algorithm to compromise privacy preservation and utility.

When adding noise nodes to the social network, the connectivity of the network needs to be ensured, given that the isolated noises are easily filtered out and therefore meaningless. Consequently, the first consideration when adding noise nodes is how to determine the relationship between the noise nodes and the other nodes. Since the purpose is to preserve the privacy of attribute social networks, the noise nodes should also have attributes. However, if the attributes of noise nodes are randomly generated, the utility of social networks will be significantly reduced. Therefore, the second consideration of adding noise nodes is determining the attribute of noise nodes so that the utility of social networks can be ensured. As for the last consideration, the developed AttNetNRI divides the network into several subnetworks, and the privacy-preserving ability will be affected when the nodes in the network cannot be evenly partitioned into different subnetworks. Therefore, when adding noise nodes, we not only need to consider the demand for privacy preservation but also ensure that there are the same number of nodes in each subnetwork. The above three considerations have also been widely taken into account in [38].

Based on the answer to the above three questions, the steps of disturbing the topology structure of the social network are outlined in Algorithm 1. A social network G(V,E,A) that needs to be disturbed (Here, V is the set containing all the nodes in the network, E is the set containing all the connections between different nodes in the network, and A is the set containing the different attributes of each node in the network), the size of a subnetwork M, a parameter a that is used to control the level of noise nodes, and the variance of the Gaussian distribution σ as the inputs to Algorithm 1. The disturbed social network G′(V′,E′,A′), namely the negative social network, as the output of Algorithm 1. In Algorithm 1, the AttNetNRI first initializes G′(V′,E′,A′) (Line 1), i.e., assigns V, E, and A to V′, E′, and A′ separately, and then adds the noisy nodes Noisy_nodes to network G′ (Lines 2–3). Next, the AttNetNRI calculates a series of probability P=(p1,p2,...,pM∗(M−1)/2) according to parameter M and σ, where pi represents the probability that there are i pairs of nodes in the generated negative subnetwork having different relationship from those in the corresponding positive subnetwork. The pi can be calculated as follows:

pi=12πσexp−(i−1)22σ2∑j=1M∗(M−1)/212πσexp−(j−1)22σ2.(1)

After that, the AttNetNRI generates negative subnetworks to disrupt the topology structure of the social network (Lines 6–23). Specifically, M nodes are first randomly selected from G′ as the positive subnetwork (Line 6), and set as visited (Line 7). Then, several pairs of nodes are randomly selected from the subnetwork according to P, and the relationship between them is flipped (Lines 8–17). Specifically, the AttNetNRI will eliminate any edges present in the subnetwork if there are any between the chosen pair of nodes. If there is no edge between them, the AttNetNRI will add an edge to the subnetwork. The flipping steps will be repeated until the generated negative subnetwork is a connected graph. Next, the AttNetNRI assigns the attributes to the noise nodes (Lines 19–23), where the attribute of a noise node is set to the same as one of its neighbor nodes. The AttNetNRI will repeat the above steps until all nodes are visited.

Although the negative survey has been used to preserve the topology structure of social networks, there are two differences between the AttNetNRI and the existing method. Firstly, the existing method primarily concentrates on the private social network topology structure, while the AttNetNRI can preserve not only topology but also node attributes. Secondly, when the network contains fewer nodes, the effectiveness of existing methods to reconcile privacy concerns with the utility of social networks is constrained. By contrast, given that the AttNetNRI adds several noise nodes to networks, the AttNetNRI can always provide a better ability to balance privacy and utility no matter the size of the social network.

3.2 Steps of Hiding Node Attributes

Although directly concatenating all attributes of a node and converting the attribute string to a negative database can hide the information of attributes, it is a trivial task to recover the attribute value from the negative database when the range of attribute value is small. For a negative database with m bits in each record, the hidden record can be obtained after 2m attempts. We have tried to recover the hidden string from a negative database with different m on a computer with a 2.10 GHz CPU, and the results are given in Fig. 2. From Fig. 2, it can be found that when m<30, a computer with regular configuration can recover the attribute within 0.35 s. Therefore, it is necessary to ensure the length of the node attribute string before converting it to the negative database. However, directly copying the attribute string to multiple samples is useless, given that the attacker can significantly reduce the number of attempts by keeping the values of bit in the attribute string the same as that in each sample. For this purpose, a dedicated strategy is proposed to expand the attribute string. For each node v, the AttNetNRI randomly selects one of its neighbor nodes and then concatenates the attribute strings of the node v and the selected neighbor node. The reason for this is that the neighbor nodes usually have similar attributes, and concatenating them can not only expand the attribute string but also keep the community structure of the social network. If the length of the attribute string is still not enough after concatenating, the AttNetNRI expands the concatenated string to multiple samples. To diversify the samples, the AttNetNRI adds Gaussian noise to each attribute for every sample.

Figure 2: The time changes with the size of the attribute string m

After expanding the node attribute string, the AttNetNRI converts it to the negative database to hide the attribute information. Recently, Zhao et al. [39] designed a new negative database generation method called QK-hidden algorithm (QK-NDBs for short), which can control not only the probability of generating different types of records but also the probability of flipping each bit of a record, so that the QK-NDBs can provide more flexibility to balance the estimation accuracy and privacy level of hidden information. Therefore, the AttNetNRI employs the QK-NDBs to convert the expanded attribute string to the negative database. To better understand the steps of hiding the node attributes, here we briefly introduce the steps of QK-NDBs, of which pseudo codes are given in Algorithm 1. In Algorithm 1, s is the original string with m bits, and L is the maximum length of the attributes. To illustrate with a simple example, if the original string s contains three attributes, of which binary strings have three, four, and five bits separately, then for this string s, m=3+4+5=12 and L=max{3,4,5}=5. The size of NDBs is controlled by the parameter r, and K is the number of different types of records contained in the negative database. Here, different types of records refer to the records which have different numbers of specified bits that differ in the original string. The probability of adding a record with i specified bits to the negative database is pi, while qi indicates the probability of inversing the ith bit of an attribute when generating records in the NDB. The QK-NDBs starts with the initialization, where the negative database NDBs is set as an empty set (Line 1), and the size of NDBs is calculated by using the parameter r (Line 2). Then, the QK-NDBs repeatedly generates the record v and adds v to NDBs until its size reach Nsize (Lines 3–16). More specifically, the QK-NDBs first determines the type of the record, namely the number of specified bits in the record that are different from the original string, according to the probability P′=(p1′,p2′,...,pK−1′) (Lines 5–12). Then, the QK-NDBs randomly selects i bits from the record according to the probability Q=(q1,...,qL) and sets them as the values that are different from s (Line 13). After that, the QK-NDBs randomly selects K−i bits from the rest m−i bits and sets them as the values same as that in the string s (Line 14). At this moment, a record v is completely generated and the QK-NDBs adds it to the negative database NDBs (Line 15).

On the whole, the steps of hiding the node attributes are summarized in Algorithm 3. For each node, v in the social network, the AttNetNRI first expands the attribute string of v until its size is greater than MinSize (Lines 3–11). To be specific, a neighbor node of v is randomly selected (Line 3), and then the attribute strings of the neighbor node and v are concatenated. Here, the sequence of them is randomly assigned by the algorithm. Then, the value of each attribute in the concatenated attribute string is disturbed by Gaussian noise (Line 8) and appended to the string s (Line 9). The steps of disturbing and appending are repeated until the size of s is greater than MinSize. After obtaining the expanded attribute string, the AttNetNRI employs the QK-NDBs algorithm, namely Algorithm 2, to generate the negative database for the expanded attribute string (Line 12). Finally, the AttNetNRI updates the attribute of node v with the NDBs, to preserve the privacy of its attributes (Line 13).

An example of the steps of Algorithm 3 is given in Fig. 3, where the attribute social network with six nodes obtained by steps of disturbing topology structure of AttNetNRI is plotted in Fig. 3a. Here, each node has four attributes. For node 5, according to the steps of Algorithm 3, its neighboring node namely node 4 is first randomly selected, and then the attribute strings of nodes 4 and 5 are randomly concatenated by aligning as Att, which is plotted in Fig. 3b. Then, the value of each attribute in the Att is disturbed by Gaussian noise, which is randomly determined by the algorithm. Next, expand the value of each attribute in the set s by the same factor so that each attribute value has the length of 10 when converted to binary, and overwrite the original value in s with the expanded value. The steps of disturbing and appending are repeated until the size of s is greater than the threshold MinSize. Fig. 3c gives the size of s is greater than MinSize after the above steps are repeated i times, at which point the resulting set s is the final attribute string. After obtaining the expanded attribute string, the QK-NDBs is employed to generate the negative database for the expanded attribute string s. Next, AttNetNRI updates the attribute of node 5 with the NDB5. Repeat the above steps in Algorithm 3 until all the node attributes in the attribute social network are hidden by the negative database. Finally, the disturbed social network with hidden attributes G′ is the output of AttNetNRI, which is plotted in Fig. 3d.

Figure 3: An illustrative example of Algorithm 3. (a) The attribute social network. (b) The process of expanding the attributes for the first time in Algorithm 3. (c) The process of expanding the attributes for the last time in Algorithm 3. (d) The social network with hidden attributes

3.3 Euclidean Distance Estimation for Negative Databases

The reason for using Euclidean distance is that it is a widely used similarity metric for real-value attributes [40]. Of course, many other metrics can be exploited to provide a measure of the similarity of the attributes of different nodes. These distance estimations are similar to the estimation of the Euclidean distance, which is easy to deduce from the derivation of Euclidean distance estimation. When calculating the Euclidean distance between attributes of different nodes, the value of each attribute is required. However, in the AttNetNRI, the node attributes are hidden in the negative database, which makes the values of attributes unavailable. Therefore, how to estimate the Euclidean distance between two hidden attributes is key to the AttNetNRI. Here, it is worth mentioning that in [39], Zhao et al. suggested a method to estimate the Euclidean distance from the negative database, but it cannot be used by the AttNetNRI. It is because the method proposed in [39] is designed for estimating the Euclidean distance between the NDB and a binary string, but the AttNetNRI converts all node attributes to negative database.

From the steps shown in Algorithm 2, it can be found that the probability that each record in the QK-NDBs is different from the hidden string s in a certain binary bit is able to be calculated by the Eq. (2).

Pdiff[i]=Ndiff[i]Ndiff[i]+Nsame[i],(2)

where Ndiff[i] and Nsame[i] are the total number of records contained in the negative database where ith bit is different from or the same as the corresponding bit of the hidden string s, respectively.

Specifically, based on the characteristics of the QK-NDBs, when generating the record of the ith type, it is necessary to select i fetching inverse bits, so the total number of records for which the ith bit of the attribute is different from the corresponding bit of the hidden string s can be calculated by the following equation:

Ndiff[i]=∑j=1Km∗r∗pj∗j∗qi,(3)

Similarly, since the probability of selecting a positive bit is random, the probability of taking a positive bit for the ith bit of the attribute is 1/L. When generating the record of the ith type, K−i inverse bits need to be selected, so the total number of records where the ith bit of the attribute is the same as the corresponding bit of the hidden string s is calculated as follows:

Nsame[i]=∑j=1Km∗r∗pj∗(K−j)∗L−1,(4)

Substitute Eqs. (3) and (4) in Eq. (2), the value of Pdiff[i] can be calculated as follows:

Pdiff[i]=∑j=1Kj∗pj∗qi∑j=1Kj∗pj∗qi+∑j=1Kpj∗(K−j)∗L−1,(5)

If the jth bit of the hidden string s is at the ith bit of one attribute, then the probability that the value of the jth bit of s is ‘1’ can be estimated by the following equation:

P(sj=‘1′)=(Pdiff[i])n0∗(Psame[i])n1(Pdiff[i])n0∗(Psame[i])n1+(Pdiff[i])n1∗(Psame[i])n0(6)

where n0 and n1 are the number of ‘0’ s or ‘1’ s at the ith bit of all the records in NDBs, and Psame[i] = 1-Pdiff[i]. Based on this, the probability Qsd that the decimal value of the hidden string s is sd can be calculated as follows:

Qsd=∏i=1mP(si=sid)(7)

where m is the length of the hidden string s, and sid is the value of i-bit in the binary representation of si. Furthermore, the Euclidean distance between two hidden strings x and y from NDBx and NDBy can be estimated as follows:

E(x,y)=∑i=02m−1∑j=02m−1(i−j)2∗Qix∗Qjy(8)

where Qix is the probability that the value of the hidden string x after converting it to decimal is i, similarly, Qjy is the probability that the value of the hidden string y after converting it to decimal is j. It can be found that the length of the hidden string x and y is m, in which case the possible decimal values of x and y are 0, 1, 2,..., 2m-1.

In general, nodes of social networks may contain multiple attributes, i.e., the attributes of a node are an n-dimensional vector. Suppose that X and Y are two n-dimensional attribute vectors, and the binary length of each dimensional attribute is m1, m2,..., mn, respectively. Then, the Euclidean distance between vectors X and Y can be estimated as follows:

E(X,Y)=∑k=1n∑i=02mk−1∑j=02mk−1(i−j)2∗Qixk∗Qjyk(9)

4  Privacy Analysis of the AttNetNRI

In this paper, the attack model is assumed as follows. The attacker has several background knowledge about a user and then tries to identify the user from the social networks. Here, three different kinds of attack methods including friendship attack, subgraph attack, and attribute attack are considered, where the attacker owns different background knowledge.

4.1 Friendship Attack

In the friendship attack, the background knowledge known by the attacker is the degree of the target user and one of his/her friends in the social network. Fig. 4a gives an illustrative example of friendship attack. If the attacker knows that the degrees of the target user Alice is three and her friend Bob only owns one friend, then the attacker can uniquely identify that node 5 in Fig. 4a is Alice.

Figure 4: The illustrative example of three kinds of attacks. (a) Friendship attack. (b) Subgraph attack. (c) Attribute attack

The network outputted by the AttNetNRI can defend against the friendship attack, given that the AttNetNRI disturbs the topology structure of social networks which probably changes the degree of the nodes in the social network, which prevents the attacker from uniquely identifying the target node from the network based on the degree of the target node and its friends. To further analyze the probability of the AttNetNRI successfully defending the friendship attack, the probability that the AttNetNRI does not change the degree of two given nodes n1 and n2 is calculated as follows. Here, the connection between nodes n1 and n2 is represented by an edge. In the AttNetNRI, ⌈NM⌉∗M−N+a∗M noise nodes are first added to the network, and then the network is divided into several subnetworks. Therefore, the probability of nodes n1 and n2 are divided into the same subnetwork, namely Psame, and the calculations can be made according to the following formula:

Psame=M−1(⌈NM⌉+a)∗M−1,(10)

After obtaining all subnetworks, the AttNetNRI disturbs the structure of each subnetwork. If nodes n1 and n2 are divided into different subnetworks, then the probability that the degree of nodes n1 and n2 do not change, namely Punchangeddiff, can be calculated as follows:

Punchangeddiff=[∑i=1(M−1)∗(M−2)/2pi∗((M−1)∗(M−2)/2i)(M∗(M−1)/2i)]2,(11)

where pi is the probability that the AttNetNRI flips the relationship between i pairs of nodes in the positive subnetwork. If nodes n1 and n2 are divided into the same subnetwork, then the probability that nodes n1 and n2 do not change in degree, namely Punchangedsame, can be calculated as follows:

Punchangedsame=∑i=1(M−2)∗(M−3)/2pi∗((M−2)∗(M−3)/2i)(M∗(M−1)/2i).(12)

Accordingly, the probability that the AttNetNRI does not change the degree of two given nodes n1 and n2, namely the probability that the attacker successfully executes friendship attack can be calculated according to Eq. (13).

pfriend=psame∗Punchangedsame+(1−psame)∗Punchangeddiff.(13)

Fig. 5 displays the probability that an attacker conducts a successful friendship attack under different parameters M. In Fig. 5, the pfriend is below 0.02 when M>15, which implies that the attacker can only successfully execute friendship attack with a relatively low probability. That is to say, the network outputted by the AttNetNRI can defend the friendship attack.

Figure 5: The probability of an attacker successfully conducting a friend attack on a negative social network under different M (N = 1000, σ = 1, a = 100)

4.2 Subgraph Attack

Different from the friendship attack, the subgraph attack supposes that the attacker has knowledge of the subgraph including the target user and its neighborhood structure. As shown in Fig. 4b, if the attacker obtains a subgraph about the relationship of Alice that is plotted at the bottom of Fig. 4b, then Alice can be recognized by the attacker as node 5, even though the personal information of each node is hidden.

Since the AttNetNRI disturbs the structure of the network, the network outputted by the AttNetNRI can also resist the subgraph attack. To further analyze the probability of the AttNetNRI successfully defending the subgraph, here we suppose that the number of nodes in the subgraph known by the attacker is V. In the AttNetNRI, each node in the network is randomly segmented into several subnetworks, and there are ∑i=1C1i!∑k=0i(−1)k(ik)(i−k)n different divisions of the subgraph known by the attacker. Here, C=⌈N/M⌉+a is the number of subnetworks included in the network. For simplification, in this paper, we assume that these V nodes are evenly divided into each subnetwork, and thus there are v=VC nodes of subgraph known by the attacker in each subnetwork. According to the steps of AttNetNRI flipping the relationship between the nodes in each subnetwork, the probability that the AttNetNRI does not change the relationship between v nodes of subgraph included in one subnetwork, namely Punchangedone, can be calculated by the following equation:

Punchangedone=∑i=1(M−v)∗(M−v−1)/2pi∗((M−v)∗(M−v−1)/2i)(M∗(M−1)/2i).(14)

Since the AttNetNRI independently disturbs the structure of each subnetwork, the probability of AttNetNRI not changing the structure of the subgraph known by the attacker, namely Psubgraph, can be calculated as follows:

Psubgraph=∏i=1CPunchangedone.(15)

The curve of Psubgraph changing with parameter M is plotted in Fig. 6, where the probability of AttNetNRI not changing the structure of subgraph known by the attacker is less than 4.5∗10−18 when M<83. That is to say, it is a tiny probability event for the attacker to successfully execute a subgraph attack when M<83. Consequently, the network outputted by the AttNetNRI can defend the subgraph attack.

Figure 6: The effect of different M on the probability of an attacker successfully conducting a subgraph attack on a social network disturbed by AttNetNRI (N = 1000, σ = 1, a = 100, V = 30)

4.3 Attribute Attack

For the attribute attack, it allows the attacker not only to own the structure of a subgraph but also the attributes of the nodes in the social networks. Take the social network displayed in Fig. 4c as an illustrative example. If the attacker only knows a subgraph of Alice shown at the bottom of Fig. 4c, the attacker cannot uniquely determine Alice from the network, given that there are two subnetworks, namely {1,2,3} and {1,5,6}, own the same structure of the subgraph. However, with the help of node attributes, the attacker can directly confirm that node 5 represents Alice. For the networks outputted by the AttNetNRI, the attacker cannot know the value of node attributes, given that the node attributes are hidden in the negative database, and recovering the original string from a negative database is an NP-hard problem. To show the difficulty of an attacker recovering the attribute value from the negative database more intuitively, here we display how the number of attempts changes with the size of the attribute string in Fig. 7. Due to dramatic growth, Fig. 7 shows the logarithmic value of attempts under different sizes of the attribute string. In Fig. 7, it can be found that with the growth of attribute string size, the number of attempts required by the attacker to recover the attribute string from the negative database exponentially increases. Furthermore, even if the attacker recovers the attribute string from the negative database, he/she still cannot identify the specific value of the attributes of the node according to the attribute string. It is because the attribute string contains the attribute of two nodes with a random order, and the value of each attribute is disturbed by Gaussian noise. Therefore, the AttNetNRI can effectively preserve the privacy of topology and node attributes in the attribute social networks even though the attacker has knowledge of the structure of a subgraph and the values of the node attributes.

Figure 7: The number of attempts changes with the size of the attribute string m

5  Experimental Studies

5.1 Compared Algorithms and Data Sets

5.1.1 Compared Algorithms

In this paper, the proposed method AttNetNRI is compared with three privacy-preserving methods that are specifically tailored for attributed social networks, including KDLD [8], ACA [41] and CANA for short [42]. To be specific, to preserve the privacy of social networks, the KDLD combines k-degree anonymity with l-diversity, where for each node, there are at least k-1 other nodes sharing the same degree, and the number of nodes with the same degree having different attribute labels is l. To prevent the attacker from using node attributes to identify specific nodes, the ACA generalizes the node attributes so that for each pair of nodes, where at least k-1 pairs of nodes owing the same attributes. For the CANA, it uses a node addition strategy as well as an attributes generalization strategy to disturb the attribute social networks, which reduces the number of modified edges while ensuring the social network satisfies k-couplet anonymity.

5.1.2 Tested Data Sets

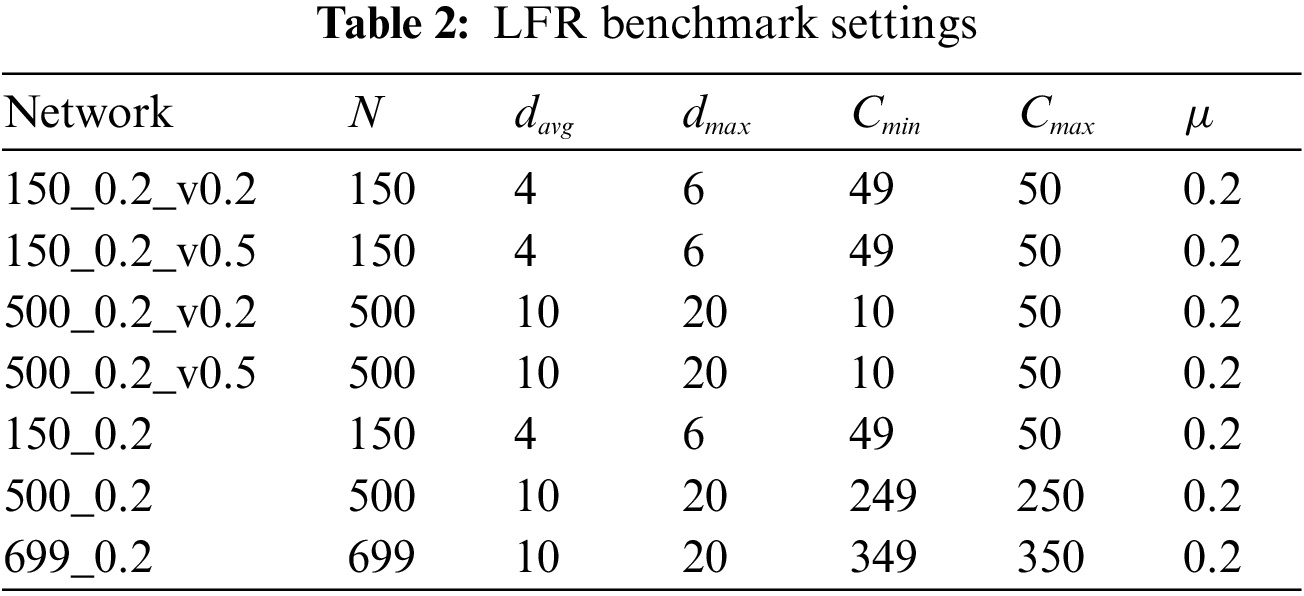
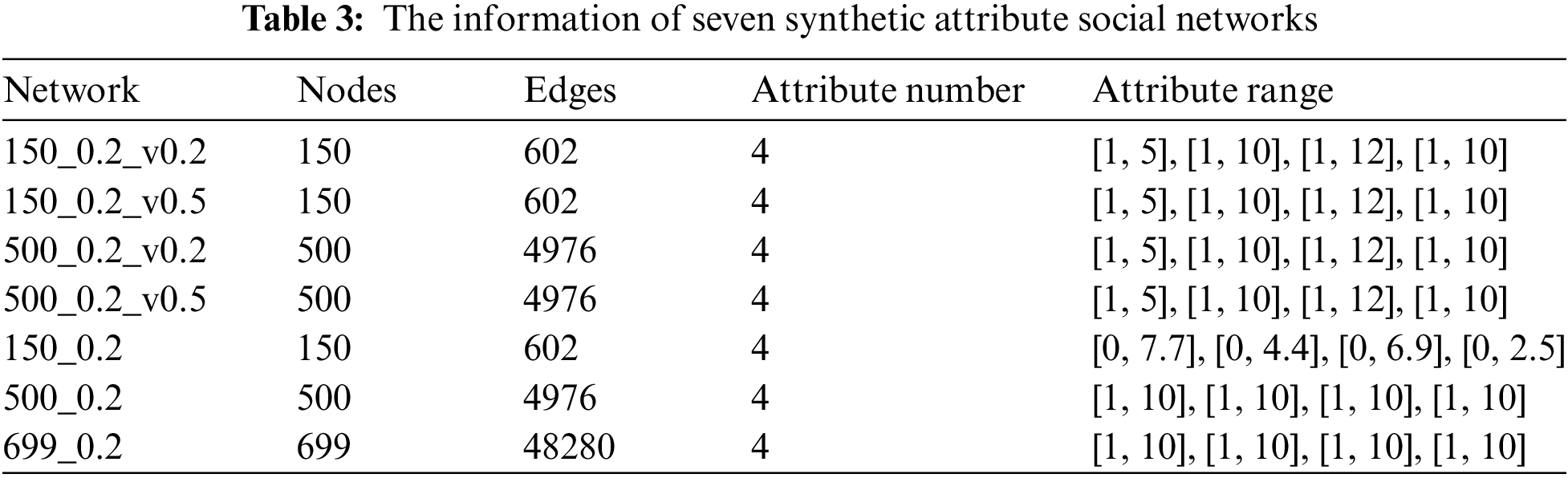
The performance of the developed AttNetNRI is verified in this paper using two groups of attribute social networks. The topology structures of them are all generated by using the LFR benchmark, which is developed by Lancichinetti et al. [43] and called after the authors with parameters including N (the number of nodes), davg (the average degree of the nodes), dmax (the maximum degree of the nodes), Cmin (the minimum of the community size), Cmax (the maximum of the community size) and μ (the mixing parameter). Here, the higher the value of μ is, the more ambiguous the structure of the network is. For the first group of social networks, their node attributes are generated by the LFR-EA method, based on the LFR benchmark, designed by Elhadi et al. [44] and also called after the authors, where the fluctuation of node attributes among one community is controlled by a parameter v. A large value of v indicates a higher fluctuation in the attributes. The second group of social networks directly uses real-world numerical datasets as their node attributes, where the nodes in the same community are assigned the attribute values belonging to the same cluster of real-world numerical datasets so that the node attributes within a community are similar to each other.

In the experiments, seven networks without node attributes are first generated by using the LFR benchmark, of which parameters are given in Table 2. For the first four networks, four types of attributes are generated by using the LFR-EA, where the attribute ranges are set as [1,5], [1,10], [1,12] and [1,10], and the fluctuating parameter v are set as 0.2, 0.5, 0.2, and 0.5 separately. For the rest two networks, the iris [45] and breast cancer datasets [46] are employed to generate their node attributes, where each record owns four numerical attributes and with classification results. Then, each community of networks is randomly assigned a cluster of the dataset. Finally, each node randomly selects a record from the assigned cluster as its attribute. The details of these seven different networks are summarized in Table 3.

5.2 Privacy and Utility Metrics

5.2.1 Privacy Metric

The information entropy is an indicator to evaluate the complexity and diversity of a system, which can be calculated as follows:

Privacy=−∑i=1Npi∗log2pi,(16)

where N is the number items in the system, and pi is the proportion of the i-item appearing in the system. The larger the value of entropy is, the more complex a system is.

In attribute social networks, two different types of information need to be preserved, namely structure information and attribute information. To this end, two types of information entropy are employed as privacy metrics in this paper. The first privacy metric is the structure information entropy, which calculates the entropy of node degree in a disturbed network to estimate the ability to preserve the privacy of structure information [47]. Regarding the structure information entropy, N represents the highest degree of nodes in social networks, and pi represents the percentage of nodes having degree i. The second metric is attribute information entropy, where the entropy of node attributes is taken into account to evaluate the privacy level of attributes [48]. In the other world, for the attribute information entropy, N represents the number of different node attribute values in attribute social networks, and pi is the probability of the value i appearing in the node attributes. It is significant to highlight that, in this paper, the attributes of the datasets used for the experiments are continuous, so it is necessary to discretize the continuous attributes to calculate the attribute information entropy. Here, the equal-width method is used for discretization, where the width of each attribute that is processed by different methods is 2.

5.2.2 Utility Metric

In this paper, the utility of a network is estimated from four aspects. The first metric is the number of triangles in the network [49], which indicates the extent of close ties and information flow in the network. The second metric is the clustering coefficient, which quantifies the extent to which nodes within the network are clustered [50]. The third metric is the cosine similarity between the shortest path of each pair of nodes in the original and disturbed networks, which assesses how each pair of nodes in the network has changed in relationship [51]. The fourth metric is the normalized mutual information [52], which estimates the similarity between the community detection results on the original and perturbed networks. The NMI can be calculated as follows:

NMI(A,B)=−2∑i=1MA∑j=1MBMi,jlog(Mi,jnMi.M.j)∑i=1MAMi.log(Mi.n)+∑j=1MBM.jlog(M.jn),(17)

where n is the size of the network, A and B are the result of community detection in original and disturbed networks, respectively, and M is the confusion matrix whose element Mi,j denotes the number of nodes belonging to the community i in partition A that are also belonging to the community j in partition B. MA(MB) is the number of communities in the partition A(B), and Mi.(M.j) is the total of M in row i(column j). In the experiments, the dual-population-based multi-objective evolutionary algorithm (DP-MOEA) [53] is used to detect communities from the attribute social networks.

5.3 Performance Analysis

5.3.1 Normalized Mutual Information

Fig. 8 plots the values of NMI of different algorithms for disturbed social networks, where a higher value of NMI signifies a better utility of the social network. From Fig. 8, it can be observed that the social networks disturbed by the AttNetNRI own the best overall utility, given that on all seven networks, the performance of the AttNetNRI consistently ranked in the top two. In contrast, the ACA and CANA are always worse than AttNetNRI. Although the KDLD performs slightly better than the AttNetNRI when the Privacy is relatively lower, its performance considerably deteriorates as the Privacy increases. The performance of KDLD is worse than that of AttNetNRI when the Privacy is higher than 4.98 on the networks of 150_0.2_v0.2 and 150_0.2_v0.5, 6.13 on the networks of 500_0.2_v0.2 and 500_0.2_v0.5, 4.99 on the networks of 150_0.2, and 6.45 on the networks of 500_0.2. Therefore, the AttNetNRI can better preserve the community structure of attribute social networks than the three comparison algorithms, especially when the Privacy is high.

Figure 8: The comparisons of NMI between AttNetNRI and three compared algorithms under different Privacy. (a) 150_0.2_v0.2. (b) 150_0.2_v0.5. (c) 500_0.2_v0.2. (d) 500_0.2_v0.5. (e) 150_0.2. (f) 500_0.2. (g) 699_0.2

5.3.2 Clustering Coefficient

The absolute value of the difference in clustering coefficient between the original social networks and attribute social networks disturbed by four algorithms(CC for short) is plotted in Fig. 9. The smaller the value of the CC is, the higher the utility the network has. Note that, to show the performance differences between different algorithms, the values of CC greater than 0.05 are directly set as 0.05. In Fig. 9, the value of CC on networks disturbed by the CANA is always greater than 0.05 on most attribute social networks. On the network with 150 nodes, the KDLD reaches competitive performance when the Privacy is relatively small, its performance considerately deteriorates with the increase of Privacy. Moreover, the performance of KDLD is far greater than 0.05 on the social network with 500 nodes when the Privacy is relatively small. Although the networks obtained by the ACA have a competitive on CC, they are still greater than that of the AttNetNRI. In comparison, the values of CC on networks disturbed by the AttNetNRI are always less than 0.05 on all networks. Consequently, the attribute social networks disturbed by the AttNetNRI own better utility than that of the other algorithms.

Figure 9: The comparisons of CC between AttNetNRI and three compared algorithms under different Privacy. (a) 150_0.2_v0.2. (b) 150_0.2_v0.5. (c) 500_0.2_v0.2. (d) 500_0.2_v0.5. (e) 150_0.2. (f) 500_0.2. (g) 699_0.2

5.3.3 Number of Triangles

Fig. 10 displays the trade-off between the Privacy and the absolute value of the difference in clustering coefficient between the original social networks and attribute social networks disturbed by different algorithms (NoT for short). It can be found from Fig. 10 that the networks disturbed by the AttNetNRI have better utility than that of the other three algorithms. Further, the superiority of the AttNetNRI is more obvious on the networks with more nodes. On the networks with 150 nodes, the AttNetNRI achieves a competitive performance when the Privacy is less than 4.99, and the best performance on most of the remaining cases. Although on the network 150_0.2_v0.2, the values of NoT of the AttNetNRI are greater than that of the ACA, their values are very close together. On the networks with 500 nodes, the AttNetNRI exhibits the best performance in most cases of Privacy. Although on the network 500_0.2_v0.2, when the Privacy is greater than 6.13, the AttNetNRI does not achieve the best performance, its performance is still similar to the best results. Accordingly, the AttNetNRI can receive social networks with better utility than the three other compared algorithms in terms of the NoT.

Figure 10: The comparisons of NoT between AttNetNRI and three compared algorithms under different Privacy. (a) 150_0.2_v0.2. (b) 150_0.2_v0.5. (c) 500_0.2_v0.2. (d) 500_0.2_v0.5. (e) 150_0.2. (f) 500_0.2. (g) 699_0.2

5.3.4 The Cosine Similarity of Shortest Path between Different Nodes

The cosine similarity between the shortest path of each pair of nodes in the original and disturbed networks (PLS for short) under different Privacy is given in Fig. 11. It can be noticed that the cosine similarity achieved by the AttNetNRI is the highest in most cases, and in those cases where the performance is not the best, the utility of networks disturbed by the AttNetNRI is close to the best one. For the CANA, the similarity achieved by it is less than that of the AttNetNRI in most cases. As for the KDLD and ACA, although they achieve better cosine similarity than the AttNetNRI in a few cases, their performance fluctuates greatly as the changes of Privacy. In contrast, the cosine similarity achieved by the AttNetNRI is always greater than 0.94. Therefore, the values of PLS in networks after being anonymized by the AttNetNRI is the most similar to the original networks among the networks disturbed by all four algorithms.

Figure 11: The comparisons of PLS between AttNetNRI and three compared algorithms under different Privacy. (a) 150_0.2_v0.2. (b) 150_0.2_v0.5. (c) 500_0.2_v0.2. (d) 500_0.2_v0.5. (e) 150_0.2. (f) 500_0.2. (g) 699_0.2

To summarize, from Figs. 8–11, the following three observations can be obtained. First, among the algorithms employed for comparison the developed AttNetNRI owns an overall best performance. Second, the AttNetNRI is more suitable for social networks with more nodes. Third, the superiority of AttNetNRI is more obvious when the privacy level is high. The reasons for the better performance of the AttNetNRI can be attributed to the following two points. On the one hand, the developed AttNetNRI modifies the topology structure is by affecting only the relationships between nodes within the same subnetwork, and the relationship between the nodes belonging to different subnetworks is unaltered, which reduces the effect on the network structure. In contrast, the compared algorithms randomly change the relationship between different nodes across the entire network, which might potentially destroy the relationships between nodes and result in low utility. On the other hand, when preserving the privacy of node attributes, the AttNetNRI only adds Gaussian noise to the attributes and then hides them in the negative database, which has little impact on the node attributes. In comparison, the other algorithms generalize node attributes to satisfy certain data publishing models, which makes the attributes of different nodes tend to be the same, and thereby decreases the utility of social networks.

5.3.5 The Comparison of Performance Stability of Different Algorithms

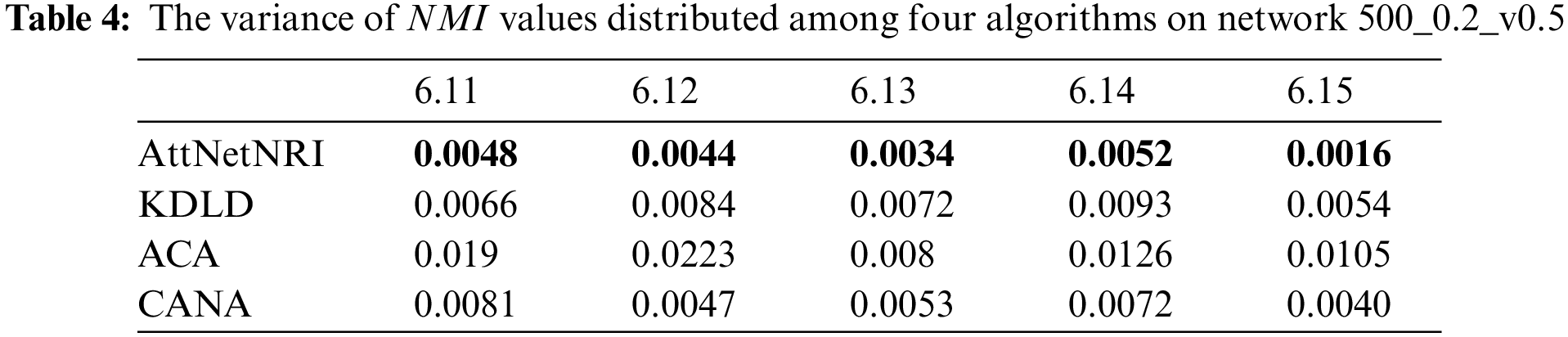
To confirm the stability of the performance between the proposed AttNetNRI and the other three comparison algorithms, the variance of NMI values distributed among four algorithms on network 500_0.2_v0.5 is calculated and displayed in Table 4. From Table 4, it can be found that the developed AttNetNRI owns the minimum variance on the network 500_0.2_v0.5, which indicates that the performance of the AttNetNRI is more stable than the other three comparison algorithms. As a result, the proposed AttNetNRI has superior stability over compared algorithms in addition to achieving improved utility.

5.4 Effectiveness of Topology Disturbing and Attribute Hiding

To verify the effectiveness of two parts of the developed AttNetNRI, two variants of AttNetNRI are developed, which are called AttNetNRI_PBCN and AttNetNRI_KAB. The AttNetNRI_PBCN is generated by replacing the topology disturbing part with PBCN [49], which is a privacy-preserving method for the topology structure, and randomly alters the relations between nodes in the social network to satisfy the differential privacy. The AttNetNRI_KAB replaces the attribute hiding part of the AttNetNRI with the KAB [54], which is a privacy-preserving method for node attributes, and clusters the data into k groups based on the clustering method and uses the black hole algorithm to find the optimal solution and then preserves the privacy by generalizing the attribute.

Table 5 lists the values of Privacy and NMI for the social networks disturbed by the AttNetNRI and its two variants under different parameter settings. Note that the values in Table 5 is the minimum and maximum values that the Privacy or NMI can reach. Here, the maximum and minimum values are used because the Privacy obtained by adjusting the parameters of different methods cannot achieve the same continuous value, and it is not possible to measure the effectiveness of the methods with the same Privacy. From Table 5, the following two observations can be obtained. First, both of topology disturbing and attribute hiding parts can improve the ability of privacy-preserving of the AttNetNRI while ensuring the utility of networks disturbed by the AttNetNRI. In Table 5, the AttNetNRI achieves the best NMI and Privcay on the first group of attribute social networks. Although the AttNetNRI_PBCN has the same Privcay as that of AttNetNRI, its NMI is worse than AttNetNRI on the four networks. In addition, as for the second group of social networks, compared to AttNetNRI_PBCN with the same value of NMI, AttNetNRI can achieve better utility of networks. Compared to AttNetNRI_KAB, AttNetNRI only obtains slightly lower NMI values, but the Privacy obtained by AttNetNRI is much higher than AttNetNRI_KAB.

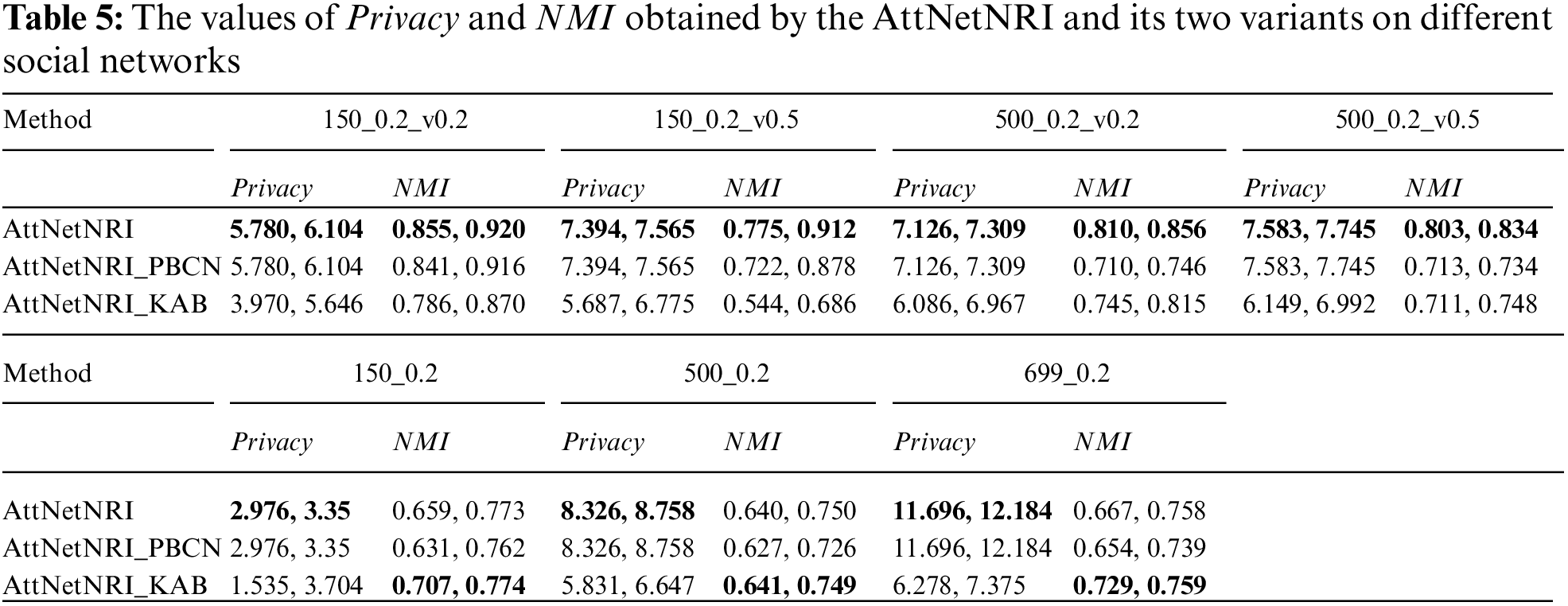
Second, compared to the topology distributing part, the attribute hiding part plays a more important role in the performance of AttNetNRI. In Table 5, the variant with other topology distributing methods, namely AttNetNRI_PBCN, achieves better Privacy than the variant having other attribute hiding methods, namely AttNetNRI_KAB, on the first group of attribute social networks, and better NMI on two networks. Conversely, the AttNetNRI_KAB only exhibits better NMI on the network 500_0.2_v0.2. Although the value of NMI obtained by AttNetNRI_PBCN on the second group of attribute social networks is lower than that of AttNetNRI_KAB, the difference is not significant. However, the value of Privacy obtained by AttNetNRI_KAB is much smaller than that of AttNetNRI_PBCN. Thus, the attribute-hiding part is more effective than the topology-distributing part.

6  Conclusion and Future Work

In this paper, we have proposed a privacy-preserving method for attributed social networks based on the negative representation of information, called AttNetNRI, in which a negative survey-based method is designed to disturb the topological structure to preserve the privacy of the topology structure, and a negative database method is suggested to hide the node attributes to preserve the privacy of them. The simulation experimental results indicate that both topology disturbing and attribute hiding parts are effective and can help the AttNetNRI to achieve an overall better performance than the other three algorithms tailored for attributed social networks.

There is also some work about the AttNetNRI that needs to be further studied. First, the social networks outputted by the AttNetNRI can only support the Euclidean distance estimation between different node attributes. However, there are many other distance metrics. In the future, it is interesting to develop an attribute hiding method that supports various distance metrics. Second, different people usually have different demands for privacy level. Therefore, the personalized privacy preservation method for attributed social networks deserves further study.

Acknowledgement: The authors thank Haiping Ma (Institutes of Physical Science and Information Technology, Anhui University, China) for their valuable help in providing the code of DP-MOEA. Moreover, The authors thank the anonymous reviewers and journal editors. Your constructive comments have improved the quality of this paper.

Funding Statement: This study is partly supported by the National Natural Science Foundation of China (Nos. 62006001, 62372001), and the Natural Science Foundation of Chongqing City (Grant No. CSTC2021JCYJ-MSXMX0002).

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Hao Jiang and Xingyi Zhang; data collection: Yuerong Liao; analysis and interpretation of results: Hao Jiang, Yuerong Liao, and Dongdong Zhao; draft manuscript preparation: Hao Jiang and Wenjian Luo. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets used in this paper are available from the first author on reasonable request. Additionally, the code of this paper is also available upon request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Can, U., Alatas, B. (2019). A new direction in social network analysis: Online social network analysis problems and applications. Physica A: Statistical Mechanics and its Applications, 535, 122372. [Google Scholar]

2. Tabassum, S., Pereira, F. S., Fernandes, S., Gama, J. (2018). Social network analysis: An overview. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 8(5), e1256. [Google Scholar]

3. Ahmed, F., Liu, A. X., Jin, R. (2019). Publishing social network graph eigenspectrum with privacy guarantees. IEEE Transactions on Network Science and Engineering, 7(2), 892–906. [Google Scholar]

4. Gao, W., Zhou, J., Lin, Y., Wei, J. (2023). Compressed sensing-based privacy preserving in labeled dynamic social networks. IEEE Systems Journal, 17(2), 2201–2212. [Google Scholar]

5. Wang, Y., Yang, L., Chen, X., Zhang, X., He, Z. (2018). Enhancing social network privacy with accumulated non-zero prior knowledge. Information Sciences, 445, 6–21. [Google Scholar]

6. Zuo, X., Li, L., Luo, S., Peng, H., Yang, Y. et al. (2020). Privacy-preserving verifiable graph intersection scheme with cryptographic accumulators in social networks. IEEE Internet of Things Journal, 8(6), 4590–4603. [Google Scholar]

7. Li, Y., Purcell, M., Rakotoarivelo, T., Smith, D., Ranbaduge, T. et al. (2023). Private graph data release: A survey. ACM Computing Surveys, 55(11), 1–39. [Google Scholar]

8. Yuan, M., Chen, L., Yu, P. S., Yu, T. (2013). Protecting sensitive labels in social network data anonymization. IEEE Transactions on Knowledge and Data Engineering, 25(3), 633–647. [Google Scholar]

9. Liu, K., Terzi, E. (2008). Towards identity anonymization on graphs. Proceedings of the ACM SIGMOD International Conference on Management of Data, pp. 93–106. [Google Scholar]

10. Wang, Y., Yang, J., Zhan, J. (2021). Differentially private attributed network releasing based on early fusion. Security and Communication Networks, 2021, 1–13. [Google Scholar]

11. Ren, X., Jiang, D. (2022). A personalized (α,β,l,k)-anonymity model of social network for protecting privacy. Wireless Communications and Mobile Computing, 2022, 7187528. [Google Scholar]

12. Luo, W., Liu, R., Jiang, H., Zhao, D., Wu, L. (2018). Three branches of negative representation of information: A survey. IEEE Transactions on Emerging Topics in Computational Intelligence, 2(6), 411–425. [Google Scholar]

13. Esponda, F., Guerrero, V. M. (2009). Surveys with negative questions for sensitive items. Statistics & Probability Letters, 79(24), 2456–2461. [Google Scholar]

14. Esponda, F., Forrest, S., Helman, P. (2004). Enhancing privacy through negative representations of data. Technical Report. Department of Computer Science, University of New Mexico, Albuquerque. [Google Scholar]

15. Esponda, F., Ackley, E. S., Helman, P., Jia, H., Forrest, S. (2007). Protecting data privacy through hard-to-reverse negative databases. International Journal of Information Security, 6(6), 403–415. [Google Scholar]

16. Esponda, F. (2006). Negative surveys. arXiv preprint arXiv:math/0608176. [Google Scholar]

17. Bao, Y., Luo, W., Zhang, X. (2013). Estimating positive surveys from negative surveys. Statistics & Probability Letters, 83(2), 551–558. [Google Scholar]

18. Jiang, H., Luo, W., Ni, L., Hua, B. (2017). On the reconstruction method for negative surveys with application to education surveys. IEEE Transactions on Emerging Topics in Computational Intelligence, 1(4), 259–269. [Google Scholar]

19. Jiang, H., Liao, Y., Yu, Q. (2022). A negative survey based method for preserving topology privacy in social networks. Proceedings of the 2022 4th International Conference on Data Intelligence and Security (ICDIS), IEEE. [Google Scholar]

20. Esponda, F., Forrest, S., Helman, P. (2009). Negative representations of information. International Journal of Information Security, 8(5), 331–345. [Google Scholar]

21. Zhou, B., Pei, J. (2008). Preserving privacy in social networks against neighborhood attacks. Proceedings of the 2008 IEEE 24th International Conference on Data Engineering, IEEE. [Google Scholar]

22. Sun, C., Philip, S. Y., Kong, X., Fu, Y. (2013). Privacy preserving social network publication against mutual friend attacks. Proceedings of the 2013 IEEE 13th International Conference on Data Mining Workshops, IEEE. [Google Scholar]

23. Jian, X., Wang, Y., Chen, L. (2023). Publishing graphs under node differential privacy. IEEE Transactions on Knowledge and Data Engineering, 35(4), 4164–4177. [Google Scholar]

24. Zhou, N., Long, S., Liu, H., Liu, H. (2022). Structure-attribute social network graph data publishing satisfying differential privacy. Symmetry, 14(12), 2531. [Google Scholar]

25. Ren, X., Yu, C. M., Yu, W., Yang, S., Yang, X. et al. (2018). Lopub: High-dimensional crowdsourced data publication with local differential privacy. IEEE Transactions on Information Forensics and Security, 13(9), 2151–2166. [Google Scholar]

26. Zhang, M., Zhou, J., Zhang, G., Cui, L., Gao, T. et al. (2023). Apdp: Attribute-based personalized differential privacy data publishing scheme for social networks. IEEE Transactions on Network Science and Engineering, 10(2), 922–933. [Google Scholar]

27. Macwan, K., Imine, A., Rusinowitch, M. (2022). Differentially private friends recommendation. Proceedings of the International Symposium on Foundations and Practice of Security, Springer. [Google Scholar]

28. Su, J., Cao, Y., Chen, Y., Liu, Y., Song, J. (2021). Privacy protection of medical data in social network. BMC Medical Informatics and Decision Making, 21, 1–14. [Google Scholar]

29. Xie, H., Kulik, L., Tanin, E. (2011). Privacy-aware collection of aggregate spatial data. Data & Knowledge Engineering, 70(6), 576–595. [Google Scholar]

30. Luo, W., Jiang, H., Zhao, D. (2017). Rating credits of online merchants using negative ranks. IEEE Transactions on Emerging Topics in Computational Intelligence, 1(5), 354–365. [Google Scholar]

31. Jiang, H., Luo, W., Zhao, D. (2017). A novel negative location collection method for finding aggregated locations. IEEE Transactions on Intelligent Transportation Systems, 19(6), 1741–1753. [Google Scholar]

32. Jiang, H., Luo, W., Zhang, Z. (2019). A privacy-preserving aggregation scheme based on immunological negative surveys for smart meters. Applied Soft Computing, 85, 105821. [Google Scholar]

33. Jiang, H., Liao, Y., Zhao, D., Li, Y., Mu, K. et al. (2023). A negative survey based privacy preservation method for topology of social networks. Applied Soft Computing, 146, 110641. [Google Scholar]

34. Dasgupta, D., Nag, A. K., Ferebee, D., Saha, S. K., Subedi, K. P. et al. (2019). Design and implementation of negative authentication system. International Journal of Information Security, 18, 23–48. [Google Scholar]

35. Zhao, D., Luo, W. (2013). A study of the private set intersection protocol based on negative databases. Procedding of the 2013 IEEE 11th International Conference on Dependable, Autonomic and Secure Computing, pp. 58–64. Chengdu, China. [Google Scholar]

36. Liu, R., Luo, W., Yue, L. (2013). Classifying and clustering in negative databases. Frontiers of Computer Science, 7, 864–874. [Google Scholar]

37. Zhao, D., Luo, W., Liu, R., Yue, L. (2015). Negative iris recognition. IEEE Transactions on Dependable and Secure Computing, 15(1), 112–125. [Google Scholar]

38. Zhao, X., Xia, F., Yuan, G., Zhang, S., Chen, S. et al. (2023). Differentially private social graph publishing with nearest neighbor structure preservation. IEEE Access, 11, 75859–75874. [Google Scholar]

39. Zhao, D., Hu, X., Xiong, S., Tian, J., Xiang, J. et al. (2019). A fine-grained privacy-preserving k-means clustering algorithm upon negative databases. Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (IEEE SSCI 2019), IEEE. [Google Scholar]

40. Yu, B., Zheng, Z., Dai, J. (2023). K-DGHC: A hierarchical clustering method based on k-dominance granularity. Information Sciences, 632, 232–251. [Google Scholar]

41. Yin, D., Shen, Y., Liu, C. (2017). Attribute couplet attacks and privacy preservation in social networks. IEEE Access, 5, 25295–25305. [Google Scholar]

42. Kiranmayi, M., Maheswari, N., Sivagami, M. (2019). Preservation of attribute couplet attack by node addition in social networks. Proceedings of the 2019 3rd International Conference on Computing and Communications Technologies (ICCCT), IEEE. [Google Scholar]

43. Lancichinetti, A., Fortunato, S., Radicchi, F. (2008). Benchmark graphs for testing community detection algorithms. Phsical Review E, 78, 046110. [Google Scholar]

44. Elhadi, H., Agam, G. (2013). Structure and attributes community detection: Comparative analysis of composite, ensemble and selection methods. Proceedings of the 7th Workshop on Social Network Mining and Analysis, pp. 1–7. [Google Scholar]

45. Fisher, R. A. (1988). Iris. UCI Machine Learning Repository. https://doi.org/10.24432/C56C76 [Google Scholar] [CrossRef]

46. Wolberg, W. (1992). Breast cancer wisconsin. UCI Machine Learning Repository. https://doi.org/10.24432/C5HP4Z [Google Scholar] [CrossRef]

47. Wu, Z., Hu, J., Pan, T., Chao, S., Jun, Y. (2019). Privacy preserving algorithms of uncertain graphs in social networks. Journal of Software, 30(4), 1106–1120. [Google Scholar]

48. Majeed, A., Lee, S. (2020). Attribute susceptibility and entropy based data anonymization to improve users community privacy and utility in publishing data. Applied Intelligence, 50(8), 2555–2574. [Google Scholar]

49. Huang, H., Zhang, D., Xiao, F., Wang, K., Gu, J. et al. (2020). Privacy-preserving approach pbcn in social network with differential privacy. IEEE Transactions on Network and Service Management, 17(2), 931–945. [Google Scholar]

50. Suri, S., Vassilvitskii, S. (2011). Counting triangles and the curse of the last reducer. Proceedings of the 20th International Conference on World Wide Web, Hyderabad, India. [Google Scholar]

51. Zhang, H., Lin, L., Xu, L., Wang, X. (2021). Graph partition based privacy-preserving scheme in social networks. Journal of Network and Computer Applications, 195, 103214. [Google Scholar]

52. Danon, L., Diaz-Guilera, A., Duch, J., Arenas, A. (2005). Comparing community structure identification. Journal of Statistical Mechanics: Theory and Experiment, 2005(9), P09008. [Google Scholar]

53. Ma, H., Liu, Z., Zhang, X., Zhang, L., Jiang, H. (2021). Balancing topology structure and node attribute in evolutionary multi-objective community detection for attributed networks. Knowledge-Based Systems, 227, 107169. [Google Scholar]

54. Kacha, L., Zitouni, A., Djoudi, M. (2022). Kab: A new k-anonymity approach based on black hole algorithm. Journal of King Saud University-Computer and Information Sciences, 34(7), 4075–4088. [Google Scholar]