 Open Access
Open Access
ARTICLE
Random Forest-Based Fatigue Reliability-Based Design Optimization for Aeroengine Structures
1 School of Energy and Power Engineering, Beihang University, Beijing, 100191, China
2 Department of Mechanical Engineering, The Hong Kong Polytechnic University, Kowloon, Hong Kong, 999077, China
3 Research Institute of Aero-Engine, Beihang University, Beijing, 100191, China
* Corresponding Author: Lu-Kai Song. Email:
(This article belongs to the Special Issue: Computer-Aided Uncertainty Modeling and Reliability Evaluation for Complex Engineering Structures)
Computer Modeling in Engineering & Sciences 2024, 140(1), 665-684. https://doi.org/10.32604/cmes.2024.048445
Received 08 December 2023; Accepted 23 February 2024; Issue published 16 April 2024
Abstract
Fatigue reliability-based design optimization of aeroengine structures involves multiple repeated calculations of reliability degree and large-scale calls of implicit high-nonlinearity limit state function, leading to the traditional direct Monte Claro and surrogate methods prone to unacceptable computing efficiency and accuracy. In this case, by fusing the random subspace strategy and weight allocation technology into bagging ensemble theory, a random forest (RF) model is presented to enhance the computing efficiency of reliability degree; moreover, by embedding the RF model into multilevel optimization model, an efficient RF-assisted fatigue reliability-based design optimization framework is developed. Regarding the low-cycle fatigue reliability-based design optimization of aeroengine turbine disc as a case, the effectiveness of the presented framework is validated. The reliability-based design optimization results exhibit that the proposed framework holds high computing accuracy and computing efficiency. The current efforts shed a light on the theory/method development of reliability-based design optimization of complex engineering structures.Keywords
Nomenclature
| MCS | Monte Carlo simulation |
| RF | Random forest |
| RF-I | RF with random subspace strategy |
| RF-II | RF with random subspace strategy and weight allocation technology |
| QP | Quadratic polynomial |
| SVR | Support vector regression |
| ANN | Artificial neural network |
| ω | rotational speed |
| T | temperature |
| E | elastic modulus |
| ρ | material density |
| λ | thermal conductivity coefficient |
| α | coefficient of thermal expansion |
| b | fatigue strength index |
| c | fatigue ductility index |
| σf′ | fatigue strength coefficient |
| ɛf′ | fatigue ductility coefficient |
| σmax | maximum stress |
| Δɛt | strain range |
| σm | mean stress |
Aeroengine structures like turbine discs usually operate in harsh multi-physics environments for long amounts of time and must fulfill a number of strict requirements like long service life and high fatigue reliability [1–3]. At present, the anti-fatigue design of modern high-reliability structures has become a barrier in the aeroengine industry that needs to be addressed. For instance, under the ground-air-ground operating cycles, the turbine disc is prone to incur low-cycle fatigue damage in the complex thermal-structure coupling environment, which seriously affects the service life and structural reliability of aeroengine turbine [4–6].
Currently, extensive efforts have been carried out to boost the resist fatigue performance of aeroengine structures [7–10], including fatigue reliability modeling under random loads [11–15], probabilistic fatigue life evaluation considering material variability [16–19], constitutive response-based fatigue failure accounting for model uncertainties [20–24], stochastic randomness-based fatigue failure evaluation [25–27], and so forth. During the above investigations, the disperse characteristics of fatigue life were sufficiently studied, laying the groundwork for fatigue reliability degree assessment. However, few works simultaneously consider the multiple uncertainties like load fluctuations [28–31], material variabilities [32–35] and model uncertainties [36–39], which disrupts the correlations between multisource uncertainties and therefore causes significant computational discrepancies in fatigue reliability assessment [40–42]. To consider multisource uncertainties in anti-fatigue design, various probabilistic analysis techniques are widely applied. For instance, Nguyen et al. [43] determined the Monte Carlo based-failure probability of planar steel frames considering the uncertainties of materials and cross-section parameters. Zhu et al. [44] proposed a first order reliability method-based hybrid intelligent approach to solving high-dimensional engineering problems. Bouledroua et al. [45] employed the second-order reliability method to assess the reliability degree of corroded pipelines.
Apart from the consideration of multiple uncertain factors, the modeling methods and/or solving algorithms are other key problems for performing reliability-based design optimization. Up to now, plenty of progress in this field has been succeed [46–49]. For example, Karar et al. [50] presented a sensitivity/elasticity factor-driven reliability modeling technique for robust design optimization. Hao et al. [51] proposed a sequential single-loop optimization and confidence analysis method for reliability-based design optimization, and its computing efficiency and accuracy were validated to be improved significantly. To simultaneously deal with the probabilistic, uncertain-but-bounded, and fuzzy parameters, Meng et al. [52] proposed a unified high-performance computation method for the reliable optimization of complicated structures. Meng et al. [53] developed a decoupling-assisted evolutionary/metaheuristic algorithm for expensive optimal problems, and its superior performance was demonstrated over other comparative algorithms. In these researches, the reliability-based design optimization problems of general engineering structures were adequately studied, and correspondingly established a solid foundation for more complex engineering structures like aeroengine structures.
For the reliability-based design optimization of aerospace structures, the mapping relationships between structural responses and random variables always show complex high-nonlinearity traits, leading to the traditional Monte Carlo methods or moment-based methods incur the issues of insufficient computing efficiency or computing accuracy. As one valuable computing method, surrogate modeling methods have emerged and attracted much attention in reliability design fields [54–57]. In the surrogate modeling method, the tremendous computing tasks of real limit state functions can be avoided by establishing a surrogate mathematical model, which is conducive to alleviating the computing burdens and improving the computing efficiency [58–60]. For instance, Meng et al. [61] proposed an enhanced collaborative optimization method based on the adaptive surrogate model for the design of high-dimensional nonlinearity systems. Wang et al. [62] built an extremum Kriging surrogate for dynamic probabilistic analysis of complex structures. Nannapaneni et al. [63] presented a probability-space surrogate for uncertain multidisciplinary design optimization. Gu et al. [64] embedded the random forest models into the framework of the evolutionary algorithm as surrogates to improve the approximation accuracy of discrete optimization problems. Unfortunately, although conventional surrogate models like response surface models and Kriging models have proven their accuracy and efficiency in general engineering optimization problems, for the fatigue reliability-based design optimization of aeroengine structures, multiple repeated calculations of reliability degree are always involved in each optimization cycle, and the large-scale calls of implicit limit state function are further nested in each calculation of reliability degree, these traditional surrogate modeling method still faces with insufficient generalization performance issues when evaluating the reliability degree in optimization cycles. By constructing multiple base decision trees as one random forest regressor, the random forest ensemble models are developed to perform the regression and classification problems efficiently. Given the benefits of assembling multiple models in terms of computing accuracy and efficiency, the random forest is chosen to analyze the fatigue reliability degree during the design optimization of aeroengine structures in this study.
In this paper, to perform high-accuracy and high-efficiency fatigue reliability-based design optimization of aeroengine structures, by fusing the random subspace strategy and weight allocation technology into bagging ensemble theory [65,66], an assigning weight technique-based random forest (RF) surrogate model is first presented, and the RF-assisted fatigue reliability-based design optimization framework is further developed by embedding the RF model into the multilevel optimization model [67,68]. The presented framework is verified by the low-cycle fatigue reliability-based design optimization of aeroengine turbine disc considering the multisource uncertainties. In what follows, Section 2 investigates random forest modeling with basic thought and mathematical modeling. Section 3 establishes the RF-based framework for fatigue reliability-based design optimization. Section 4 validates the effectiveness of the presented framework by considering aeroengine turbine disc as a case. Section 5 summarizes some conclusions.
Due to the reliability degree, regression always involves the complex computations of high-nonlinearity and high-complexity, and establishing one individual model is frequently insufficient to achieve satisfactory regression accuracy in the fatigue reliability-based design optimization of aeroengine structures. In this case, by integrating several individual basis models into the integrated framework, ensemble models like random forests have emerged and are widely applied in probabilistic analysis [69], classification [70] and regression [71], etc. However, because only the mean values of each individual decision tree are examined, generalization accuracy issues concerns may arise when utilizing typical random forests in complex regression tasks.
In this case, by merging random subspace strategy and weight allocation technology, an assigning weight technique-based RF approach is presented to map the input variables to output response accurately. The basic thought of the presented method is: firstly, multiple sets (D1, D2, …, DM) of independent sample subsets are established using bootstrap sampling techniques; then, regarding the random subspace strategy-based parallel bagging framework, the basic architecture of RF is established; moreover, instead of simply averaging of all decision trees, the weight allocation technology is employed to assign different weights for each decision tree, the RF model is accurately mathematical modeled, to enhance the generalization accuracy and regression performance. The schematic diagram of the presented assigning weight technique-based RF model is illustrated in Fig. 1.

Figure 1: Basic thought of the proposed RF model
Considering the extracted sample D = {xij, yij( xij)}, the sample space R is decomposed to M sub sample spaces R1, R2, …, RM by random subspace strategy, the basis decision tree f(x) is termed as
During the training process of the above decision trees, it is necessary to consider how to select and measure segmentation features and points. To find the best segmentation variables and points, the quality of segmentation features and points are measured by the weighted sum of impure degrees G (xi, vij) of each sub node, i.e.,
where xi indicates the segmentation feature of a node; vij the segmentation value for segmentation features; nleft, nright the sample number in the left sub node, and the right sub node, respectively; Ns and the current node; Xleft, Xright the training samples in the left, right sub node, respectively; H(X) the node impure function, which is calculated by the Mean Square Error (MSE), i.e.,
where Xs represents the samples in the current node;
By substituting the Eq. (3) into the Eq. (2), the weighted sum of impure degrees G for any segmentation point can be rewritten as
Regarding the dividing method, assuming the nl example (xi, yi) falls into the l-th leaf node (with indices from a set Dl, i.e., i ∈ Dl), the corresponding output z is acquired as
Furthermore, assuming the RF consists of T trained trees, by averaging the predicted values zt across all of the decision trees, the output zRF is acquired as
By assigning the weight wt to the t-th decision trees with the weight allocation technology, the weighted average of the tree results is gained as
where w = (w1, …, wT) indicates the weight vector, z = (z1, …, zT)T the output vector corresponding to example x. The node impure function H(Xs) is rewritten as
By calculating the mean values of the output results in each decision tree, the distributed output response of the j-th stage i-th level sub-model is acquired and the nonlinear mapping between the random input variables and the j-th stage i-th level response can be realized as
where θt indicates the independent random variables; y(xij, θt) is the output response of the decision tree based on xij and θt.
3 RF-Assisted Fatigue Reliability-Based Design Optimization Theory
For fatigue reliability-based design optimization problems of aeroengine structures, each optimization cycle involves multiple repeated calculations of reliability degree, and each calculation of reliability degree also contains large-scale calls of implicit high-nonlinearity limit state function, resulting in expensive computing cost and unsatisfactory optimization accuracy when using the direct Monte Claro Simulation and traditional surrogate methods [72]. In this study, by introducing the proposed RF model into the design optimization theory, an efficient RF-assisted fatigue reliability-based design optimization framework for aeroengine structures is established, i.e., (1) by imposing the boundary conditions into finite element simulation, the deterministic fatigue evaluation of aeroengine structure is performed; (2) a small batch of input samples are extracted, and be imposed into the deterministic simulation to generate the training samples; (3) by applying the developed bagging architecture and training algorithm, the RF models are established for replacing the complex reliability calculations; (4) by regarding the high-sensitivity parameters as the design variables, the RF-surrogate reliability degree as constraint, fatigue life as optimal objective, the fatigue reliability optimization model is established; (5) after several repeated optimization cycles in solving the fatigue reliability-based design optimization model, the best design variables for aeroengine structures are obtained. The basic modeling process is summarized as follows.
By employing the presented random forest modeling method, the constitutive responses like mean stress and strain range of aeroengine structures can be mapped by
where
For the widespread low-cycle fatigue problems in aeroengine structures, fatigue life is usually evaluated using the improved Manson-Coffin model [54], i.e.,
where σm indicates the mean stress; NL the low-cycle fatigue life; E indicates Young’s modulus; σ′f the fatigue strength coefficient; ε′f the fatigue ductility coefficient; b the fatigue strength index; c the fatigue ductility index. Regarding n0 as the actual number of operating cycles, the fatigue damage D is termed as
By regarding the a as the damage strength coefficient (usually set as 1 in aeroengine engineering) [72], the limit state function Z of the aeroengine structure can be termed as
According to the Monte Carlo simulation thought [73], the fatigue reliability degree is
By setting the high-sensitivity variables including operating loads xL, material parameters xM and life model parameters xP as the design variables, fatigue life Nf as optimization objective, reliability degree R and other boundaries as constraints, the reliability optimization model is established by
Therefore, by fusing the presented random forest model into the reliability optimization model, the large-scale of the real high-nonlinearity reliability degree calculations can be avoided effectively, which is conducive to reducing huge computational tasks and enhancing the optimal accuracy for the fatigue reliability-based design optimization of aeroengine structures. The RF-based fatigue reliability optimization workflow is constructed in Fig. 2.

Figure 2: Workflow of RF-assisted fatigue reliability-based design optimization
4 Fatigue Reliability-Based Design Optimization for Aeroengine Turbine Disc
During the operation of aircraft engines, the high-pressure turbine disc is subjected to complex environmental loads such as high-temperature, high-pressure and high-speed, resulting in uneven temperature gradients, large stress loads, and low cycle fatigue damage. To achieve the fatigue reliability-based design optimization and improve the fatigue reliability performance of aeroengine turbine disc, the presented RF method is employed, where the RF-I represents the RF method with random subspace strategy, and RF-II presents the RF method with random subspace strategy and weight allocation technology. The sketch of aeroengine turbine disc is shown in Fig. 3.

Figure 3: Schematic diagram of an aeroengine turbine disc
In view of the multisource uncertain factors co-determine the fatigue life of the turbine disc, we select the physical uncertain parameters as random variables [72–74], whose distribution traits are shown in Table 1. The dependency between elastic modulus E, thermal conductivity λ, thermal expansion α and temperature are described in Table 2. Moreover, the model uncertain parameters are also chosen as random variables, its distribution traits are shown in Table 3. Based on the radial loading criterion and temperature continuity distribution law, the steady-state thermal analysis is performed and the temperature distribution is obtained, as shown in Fig. 4a [75,76]. Moreover, by transmitting the obtained temperature loads to the structural field, the deterministic thermal-structure coupling analysis is accomplished, and the equivalent stress & strain distributions are derived in Figs. 4b and 4c. As shown in Figs. 4b and 4c [75,76], the maximum stress σmax and strain range Δɛt appear at the center of the disc. In this study, the mean stress σm = (σmax + σmin)/2 and the strain range ∆ɛt = ɛmax − ɛmin at the risk section of the turbine disc are considered as the first layer output responses [75]. It should be highlighted that it takes 23.71 s to carry out one-time thermal-structural analysis, which also shows that the large-scale finite element simulations for reliability degree calculations are unbearable in engineering. Based on the constitutive responses at dangerous sites and the model parameters in Table 3, the low-cycle fatigue life of the turbine disc is acquired as 11592 cycles.
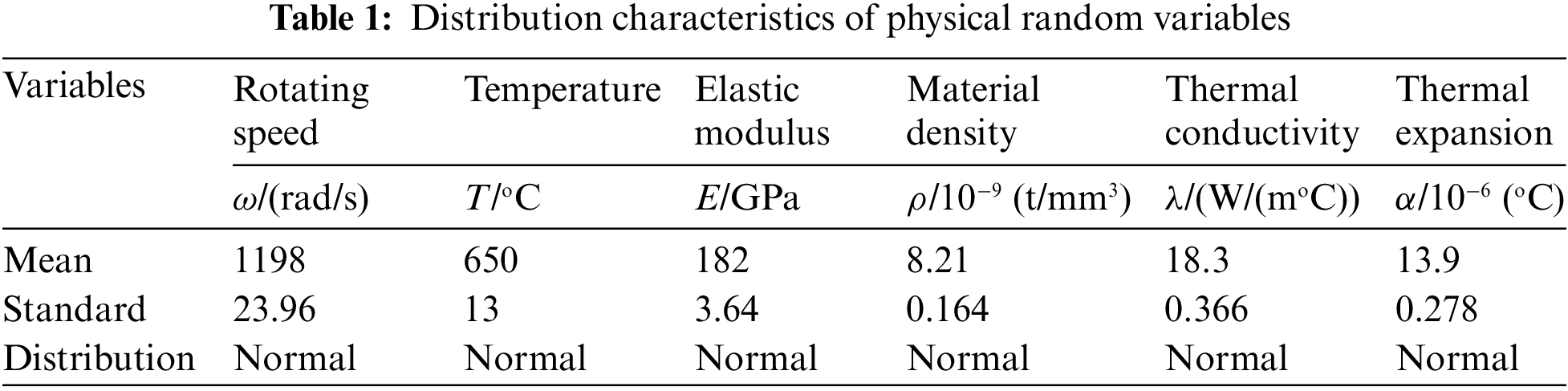

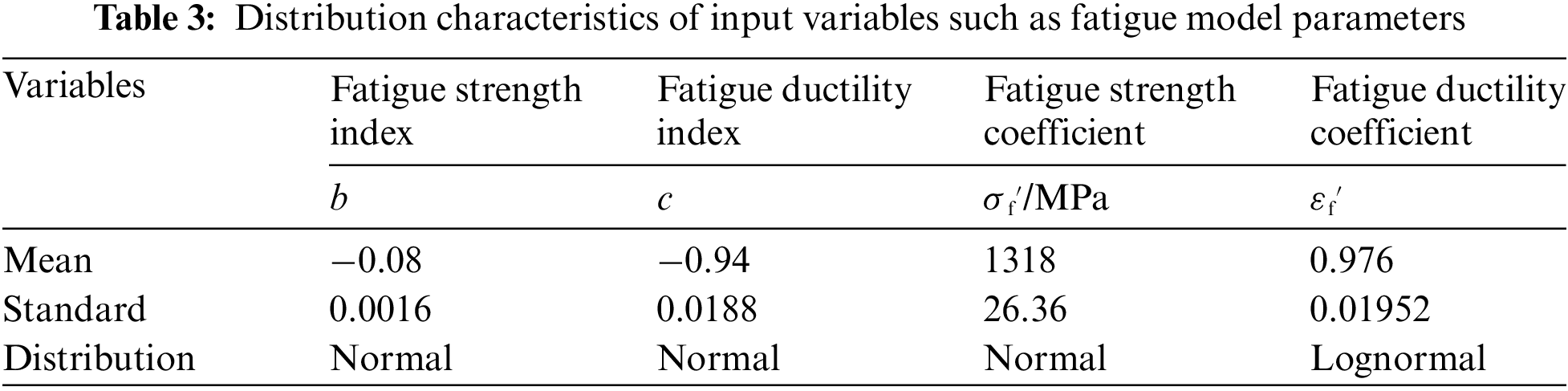

Figure 4: Response distributions after thermal-structural coupling
4.2 Reliability Optimization Modeling
To reduce the dimensionality of design variables and downsize the computing scale of fatigue reliability-based design optimization, high sensitivity parameters (ω, T, E, ρ, σf′, b) [34] are chosen as the design variables x, their range of variations are shown in Table 4. Based on the proposed RF-assisted fatigue reliability-based design optimization theory, a multilevel optimization model is established, i.e., by considering high sensitivity parameters xʹ = (ω, T, E, ρ) as design variables, the constitutive responses (i.e., σm and Δɛt) as objectives, and the value span of xʹ as constrain conditions, the first layer optimization model is established; moreover, by regarding the high sensitivity parameter xʺ = (σm, Δɛt, σf′, b) as design variable, the fatigue life Nf as objective, and the fatigue reliability and value span as the constrained conditions, the second layer reliability optimization model is established. The built optimal model is shown in Eq. (16).
4.3 Distributed Response Simulation
Based on the linkage sampling technique [37] and the probability distribution in Tables 1 and 2, 100 sets of input variables and stress/strain outputs are obtained. Herein, by taking 75% of 100 sets of data as training data and the remaining as testing data, the RF model is established, its nonlinear response surfaces are drawn. From the Figs. 5 and 6, even for the mapping of the constitutive responses, the response surfaces also show a highly nonlinear degree. By extracting 10 000 groups of input variables, the corresponding stress/strain constitutive responses are obtained by running the built RF model 10 000 times. As shown in Figs. 7 and 8, the mean stress & strain range both roughly follow normal distributions of mean values (389.93 MPa, 4.406 × 10−3 m/m) and standard deviations (7.7 MPa, 1.103 × 10−4 m/m), respectively.

Figure 5: Stress response surface

Figure 6: Strain response surface

Figure 7: Probabilistic distribution of mean stress

Figure 8: Probabilistic distribution of strain range
4.4 Fatigue Reliability Simulation
According to the stress/strain responses obtained in Section 4.3 and the fatigue model variables shown in Table 3, 100 sets of input variables and fatigue lives are obtained to build the RF-II model, their nonlinear mapping surface between high sensitivity input variables and fatigue life is drawn. From the Fig. 9, it can be observed that the fatigue lives exhibit a high degree of nonlinearity. Based on the built RF model, the probabilistic distribution characteristics of fatigue life at the dangerous site of the turbine disc are obtained. It can be found in Fig. 10 that the fatigue life roughly follows the lognormal distribution. Moreover, the correlation relationships between high-sensitivity variables (i.e., rotor speed, gas temperature, elastic modulus) and fatigue life are depicted in Fig. 11. To explore the effect of different application cycles n on fatigue damage, the fatigue damages under different application cycles n are analyzed, its distribution traits under various application cycles n are acquired. As shown in Figs. 12a and 12b, we find that the larger the number of application cycles n, the greater the cumulative damage of the turbine disc. Based on the built RF and reliability degree model, the fatigue reliability degree is acquired, as shown in Fig. 12c.

Figure 9: Fatigue life response surface

Figure 10: Probabilistic distribution of fatigue life

Figure 11: Scatter diagram between input variables and output response
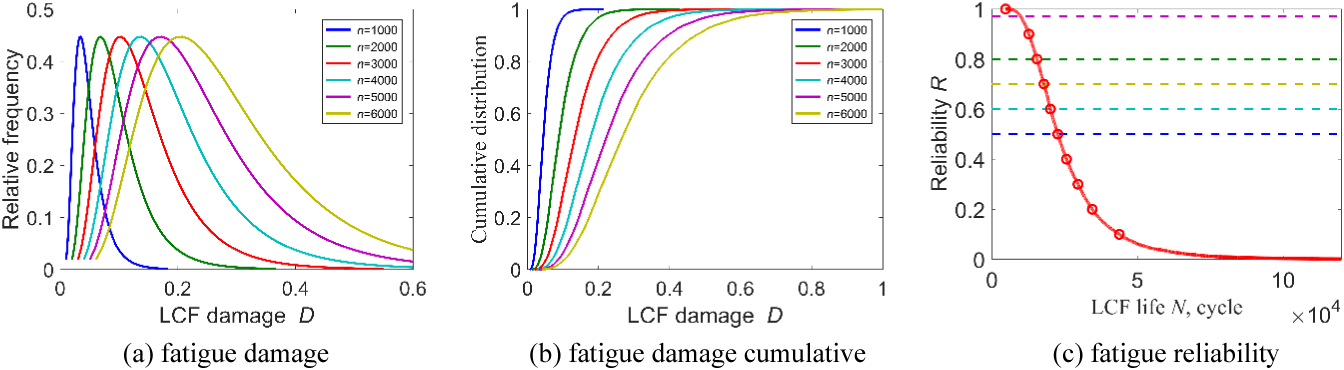
Figure 12: Cumulative damage and reliability degree of turbine disc
4.5 Fatigue Reliability-Based Design Optimization
Based on the built reliability-based design optimization model, the fatigue reliability-based design optimization of the turbine disc is completed by using the presented RF methods (i.e., RF-I, RF-II). The probabilistic distributions of maximum stress, strain range and fatigue life before and after optimized by RF-I, RF-II are revealed. In Figs. 13–15, the green curve represents the fitted probabilistic density curves and cumulative distribution curves of responses before optimization, whereas the red curve and blue curve reflect the fitted probabilistic density curves and cumulative distribution curves of responses after optimization. To validate the computing ability of the proposed method, its optimization results are compared with four state-of-the-art methods, as illustrated in Table 5. It should be noted that 10 000 simulations of surrogate models were conducted to calculate the reliability degree in the optimization cycle.

Figure 13: Probabilistic distribution of fatigue life after optimization

Figure 14: Probabilistic histogram of output responses
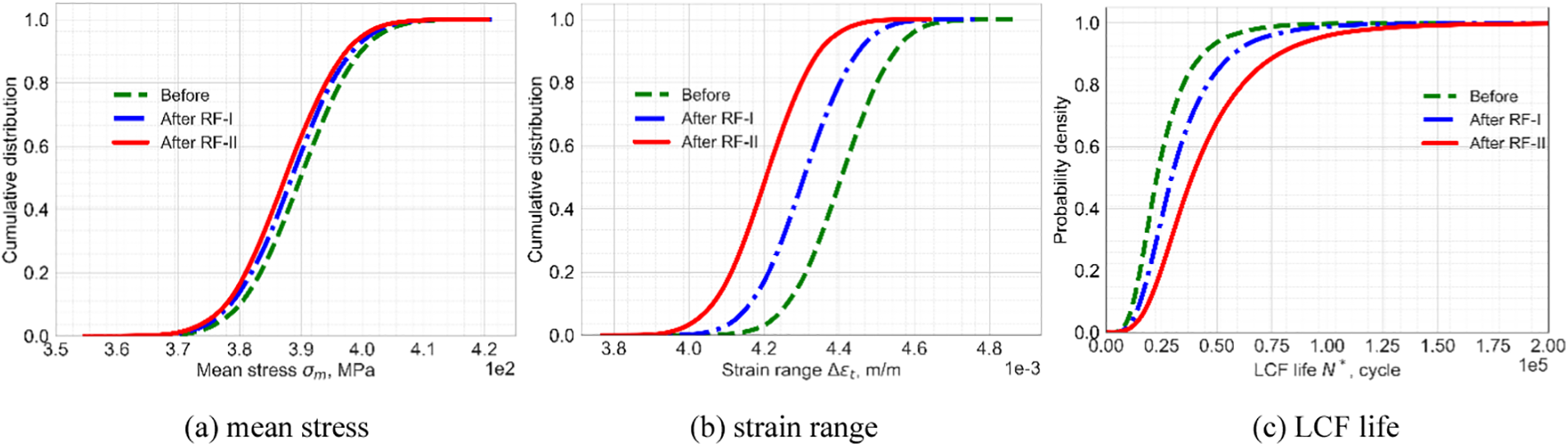
Figure 15: Comparison of cumulative distribution optimized by different models
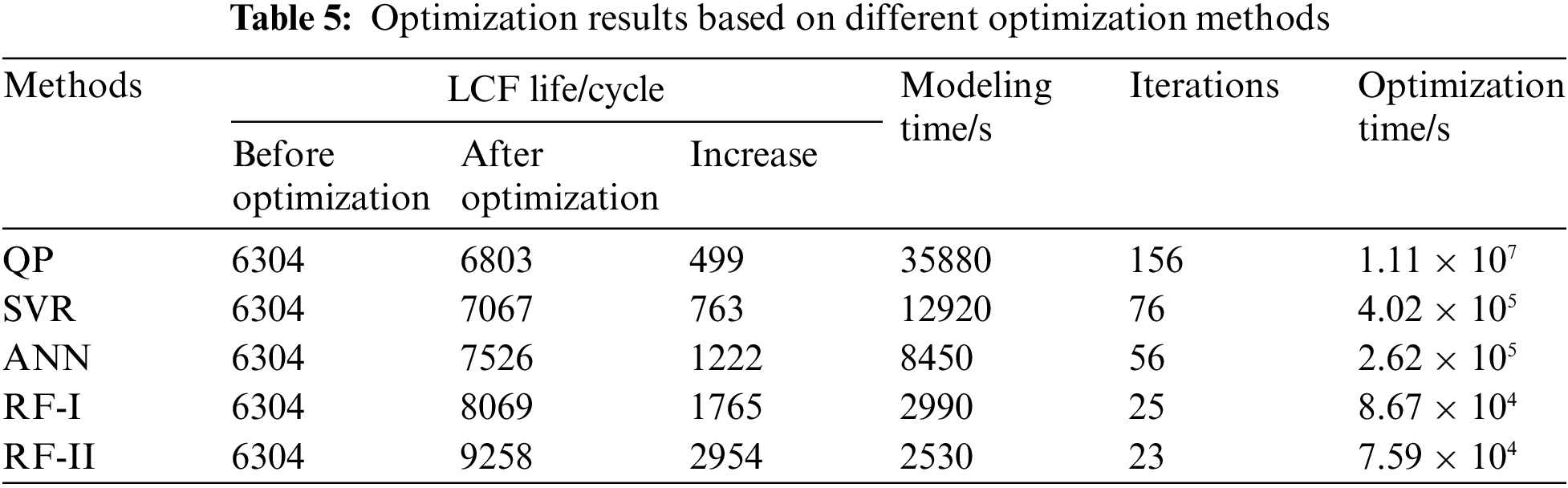
From Figs. 14 and 15, we find that regardless of before and after optimization, the stress and strain roughly obey the normal distribution and the fatigue lives roughly obey the lognormal distribution; the stress and strain optimized by RF-II are smaller than that of RF-I, while the life response optimized by RF-II is greater than that of RF-I. From Table 5, the RF-I method can prolong the fatigue life, which reaches 1765 cycles, and the RF-I method prolongs the fatigue life by 2954 cycles. Therefore, RF-II holds better optimization effects than RF-I. The main factors are (i) instead of merely averaging all decision trees, the weight allocation technology is employed to assign different weights for each decision tree, which contributes to enhancing the model regressing ability; (ii) the random subspace strategy in RF model increases the diversity and difference of decision trees, which can elevate the generalization ability of the surrogate model.
As shown in the iteration times and optimization time in Table 5, the modeling time of the RF method is shorter than that of the QP, SVR and ANN methods, and the RF-II method requires the least number of iterations and optimization time, followed by the RF-I method. The main reasons are (i) the RF method and parallel processing technique enable the model regression calculations to be simultaneously carried out, largely elevating the optimizing speed; (ii) embedding the RF model into a multilevel optimization model realizes the distributed parallel computing, which is conducive to simplifying the computing tasks and improving computing efficiency.
Therefore, the presented RF-II method can greatly reduce optimal iterations and save computational time while keeping the solving accuracy in fatigue reliability-based design optimization problems for aeroengine structures.
To perform high-efficiency and high-accuracy fatigue reliability-based design optimization for aeroengine structures, a random forest (RF) surrogate model is first presented by fusing the random subspace strategy and weight allocation technology into bagging ensemble theory; by embedding the RF surrogate into the multilevel optimal model, the RF-based fatigue reliability optimization framework is further developed. The presented framework is verified by the low-cycle fatigue reliability-based design optimization of aeroengine turbine disc considering the multisource uncertainties. Some conclusions are summarized as follows:
(1) From the fatigue reliability-based design optimization of turbine disc, the presented RF model is validated to be efficiently converged to the accurate reliability results, which can greatly accelerate the solving process in optimal models.
(2) Through the method comparisons, it has been confirmed that the RF-based reliability optimization framework that has been created has the computational benefits of high accuracy and high efficiency when it comes to designing aeroengine structures.
(3) The current work offers a brand-new RF-assisted fatigue reliability-based design optimization framework for aeroengine structures and thereby promoting the development of modeling and methodology for fatigue optimization design of aeroengine structures.
The work in this study proposed a feasible and effective method for fatigue reliability-based design optimization of aeroengine structures (i.e., Random Forest (RF) method). However, this method still has limitations regarding accuracy deviating from actual engineering. This deviation is mainly attributed to the incomplete factors considered in this study. According to current research, to further apply the proposed method framework in the future, the following issues need to be addressed:
(1) In the current reliability design of aeroengine structures, further improvement is needed to determine the random variable coefficients of model uncertainty and material randomness parameters.
(2) More sensitivity parameters that have a significant impact on the fatigue life should be further considered, the more accurate fatigue reliability optimization design should be performed.
(3) More accurate fatigue mechanics, such as creep-fatigue, and high-low cycle composite fatigue, etc., should be considered to improve the engineering application value of aerospace structures.
Acknowledgement: The authors express their appreciation to the National Natural Science Foundation of China. The authors also express gratitude for the support of the Hong Kong Polytechnic University and Beihang University.
Funding Statement: This work was supported by the National Natural Science Foundation of China under Grant (Number: 52105136), the Hong Kong Scholar program under Grant (Number: XJ2022013) China Postdoctoral Science Foundation under Grant (Number: 2021M690290), and Academic Excellence Foundation of BUAA under Grant (Number: BY2004103). The authors would like to thank them.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Lu-Kai Song; data collection: Xue-Qin Li; analysis and interpretation of results: Lu-Kai Song; draft manuscript preparation: Xue-Qin Li. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study will be made available on request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Wang, R. Z., Gu, H. H., Zhu, S. P., Li, K. S., Wang, J. et al. (2022). A data-driven roadmap for creep-fatigue reliability assessment and its implementation in low-pressure turbine disk at elevated temperatures. Reliability Engineering & System Safety, 225, 108523. [Google Scholar]
2. Zhu, S. P., Liu, Q., Lei, Q., Wang, Q. (2018). Probabilistic fatigue life prediction and reliability assessment of a high pressure turbine disc considering load variations. International Journal of Damage Mechanics, 27, 1569–1588. [Google Scholar]
3. Yu, P. C., Hou, L., Jiang, K., Jiang, Z. H., Tao, X. J. (2023). Dynamic modeling and nonlinear analysis for lateral-torsional coupling vibration in an unbalanced rotor system. Applied Mathematical Modelling, 126, 439–456. [Google Scholar]
4. Zhu, S. P., Huang, H. Z., Smith, R., Ontiveros, V., He, L. P. et al. (2016). Bayesian framework for probabilistic low cycle fatigue life prediction and uncertainty modeling of aircraft turbine disk alloys. Probabilistic Engineering Mechanics, 34, 114–122. [Google Scholar]
5. Zhu, S. P., Huang, H. Z., Ontiveros, V., He, L. P., Modarres, M. (2012). Probabilistic low cycle fatigue life prediction using an energy-based damage parameter and accounting for model uncertainty. International Journal of Damage Mechanics, 21(8), 1128–1153. [Google Scholar]
6. Zhu, S. P., Yue, P., Yu, Z. Y., Wang, Q. Y. (2017). A combined high and low cycle fatigue model for life prediction of turbine blades. Materials, 10(7), 698. https://doi.org/10.3390/ma10070698 [Google Scholar] [PubMed] [CrossRef]
7. Meng, D. B., Yang, S. Q., Zhang, Y., Zhu, S. P. (2019). Structural reliability analysis and uncertainties-based collaborative design and optimization of turbine blades using surrogate model. Fatigue and Fracture of Engineering Materials and Structures, 42(6), 1219–1227. [Google Scholar]
8. Heng, F., Gao, J. X., Xu, R. X., Yang, H. J., Cheng, Q. et al. (2023). Multiaxial fatigue life prediction for various metallic materials based on the hybrid CNN-LSTM neural network. Fatigue & Fracture of Engineering Materials & Structures, 46(5), 1647–2027. [Google Scholar]
9. Bouchenot, T., Patel, K., Gordon, A. P., Shinde, S. (2021). Microstructurally-informed life prediction modeling of combined high-cycle fatigue and creep in a Ni-base superalloy. International Journal of Fatigue, 152, 106444. [Google Scholar]
10. Banerjee, A., Sahu, J. K., Paulose, N., Fernando, C. D., Ghosh, R. N. (2016). Micromechanism of cyclic plastic deformation of alloy IN 718 at 600°C. Fatigue & Fracture of Engineering Materials & Structures, 39(7), 877–885. [Google Scholar]
11. Zhu, S. P., Huang, H. Z., Peng, W. W., Wang, H. K., Mahadevan, S. (2016). Probabilistic physics of failure-based framework for fatigue life prediction of aircraft gas turbine discs under uncertainty. Reliability Engineering & System Safety, 146, 1–12. [Google Scholar]
12. Niu, X. P., Wang, R. Z., Liao, D., Zhu, S. P., Zhang, X. C. et al. (2021). Probabilistic modeling of uncertainties in fatigue reliability analysis of turbine bladed disks. International Journal of Fatigue, 142, 105912. [Google Scholar]
13. Liu, G. S., Liu, H. J., Zhu, C. C., Mao, T. Y., Hu, G. (2021). Design optimization of a wind turbine gear transmission based on fatigue reliability sensitivity. Frontiers of Mechanical Engineering, 16(1), 61–79. [Google Scholar]
14. Song, L. K., Bai, G. C., Li, X. Q., Wen, J. (2021). A unified fatigue reliability-based design optimization framework for aircraft turbine disk. International Journal of Fatigue, 152, 106422. [Google Scholar]
15. Zhang, H., Song, L. K., Bai, G. C., Li, X. Q. (2022). Active extremum Kriging-based multi-level linkage reliability analysis and its application in aeroengine mechanism systems. Aerospace Science and Technology, 131, 107968. [Google Scholar]
16. Zhang, T. Y., Wang, X. W., Xia, X. X., Jiang, Y., Zhang, X. C. et al. (2023). A robust life prediction model for a range of materials under creep-fatigue interaction loading conditions. International Journal of Fatigue, 176, 107904. [Google Scholar]
17. Shi, T., Sun, J. Y., Li, J. H., Qian, G. A., Hong, Y. S. (2023). Machine learning based very-high-cycle fatigue life prediction of AlSi10Mg alloy fabricated by selective laser melting. International Journal of Fatigue, 171, 107585. [Google Scholar]
18. Li, X. Q., Song, L. K., Bai, G. C. (2022). Failure correlation evaluation for complex structural systems with cascaded synchronous regression. Engineering Failure Analysis, 141, 106687. [Google Scholar]
19. Deng, K., Song, L. K., Bai, G. C., Li, X. Q. (2022). Improved Kriging-based hierarchical collaborative approach for multi-failure dependent reliability assessment. International Journal of Fatigue, 160, 106842. [Google Scholar]
20. Zhang, T. Y., Wang, X. W., Ji, Y. N., Zhang, W., Hassan, T. et al. (2020). P92 steel creep-fatigue interaction responses under hybrid stress-strain controlled loading and a life prediction model. International Journal of Fatigue, 140, 105837. [Google Scholar]
21. Xu, L., Wang, R. Z., Wang, J., He, L., Itoh, T. et al. (2022). On multiaxial creep-fatigue considering the non-proportional loading effect: Constitutive modeling, deformation mechanism, and life prediction. International Journal of Plasticity, 155, 103337. [Google Scholar]
22. Bartosak, M. (2021). Constitutive modelling for isothermal low-cycle fatigue and fatigue-creep of a martensitic steel. Mechanics of Materials, 162, 104032. [Google Scholar]
23. Yang, S. Y., Meng, D. B., Wang, H. T., Chen, Z. P., Xu, B. (2023). A comparative study for adaptive surrogate-model-based reliability evaluation method of automobile components. International Journal of Structural Integrity, 14(3), 498–519. [Google Scholar]
24. Meng, D. B., Yang, S. Y., He, C., Wang, H. T., Lv, Z. Y. et al. (2022). Multidisciplinary design optimization of engineering systems under uncertainty: A review. International Journal of Structural Integrity, 13(4), 565–593. [Google Scholar]
25. Kaleva, O., Orelma, H. (2021). Modeling stress history as a stochastic process. International Journal of Fatigue, 143, 105996. [Google Scholar]
26. Frondelius, T., Kaarakka, T., Kouhia, R., Mäkinen, J., Orelma, H. et al. (2021). Stochastic continuum approach to high-cycle fatigue: Modelling stress history as a stochastic process. European Journal of Mechanics A-Solids, 92, 104454. [Google Scholar]
27. Rosa, U. L., de Lima, A. M. G., Gonçalves, L. K. S., Belonsi, M. H. (2022). A robust-based fatigue optimization method for systems subject to uncertainty. Journal of Mechanical Science and Technology, 36(9), 4571–4581. [Google Scholar]
28. Yue, P., Ma, J., Zhou, C. H., Zu, J. W., Shi, B. Q. (2021). Dynamic fatigue reliability analysis of turbine blades under combined high and low cycle loadings. International Journal of Damage Mechanics, 30(6), 825–844. [Google Scholar]
29. Yue, P., Ma, J., Zhou, C. H., Jiang, H., Wriggers, P. (2020). A fatigue damage accumulation model for reliability analysis of engine components under combined cycle loadings. Fatigue & Fracture of Engineering Materials & Structures, 43(8), 1880–1892. [Google Scholar]
30. Salvinder, S., Shahrum, A. (2019). Durability analysis using Markov chain modeling under random loading for automobile crankshaft. International Journal of Structural Integrity, 10(4), 454–868. [Google Scholar]
31. Reza, M. N., Shahrum, A., Salvinder, K. S. (2019). Reliability-based fatigue life of vehicle spring under random loading. International Journal of Structural Integrity, 10(5), 737–748. [Google Scholar]
32. Hu, D. Y., Ma, Q. H., Shang, L. H. (2017). Probabilistic framework for multiaxial LCF assessment under material variability. International Journal of Fatigue, 103, 371–385. [Google Scholar]
33. Vojdani, A., Farrahi, G. H., Mehmanparast, A., Wang, B. (2019). Probabilistic assessment of creep-fatigue crack propagation in austenitic stainless steel cracked plates. Engineering Fracture Mechanics, 200, 50–63. [Google Scholar]
34. Li, X. Q., Song, L. K., Choy, Y. S., Bai, G. C. (2023). Multivariate ensembles-based hierarchical linkage strategy for system reliability evaluation of aeroengine cooling blades. Aerospace Science and Technology, 138, 108325. [Google Scholar]
35. Wang, Y. W., Song, L. K., Li, X. Q., Bai, G. C. (2023). Probabilistic fatigue estimation framework for aeroengine bladed discs with multiple fuzziness modeling. Journal of Materials Research and Technology, 24, 2812–2827. [Google Scholar]
36. Zhang, H., Song, L. K., Bai, G. C. (2022). Moving-zone renewal strategy combining adaptive Kriging and truncated importance sampling for rare event analysis. Structural and Multidisciplinary Optimization, 65(10), 285. [Google Scholar]
37. Li, X. Q., Song, L. K., Choy, Y. S., Bai, G. C. (2023). Fatigue reliability analysis of aeroengine blade-disc systems using physics-informed ensemble learning. Philosophical Transactions of the Royal Society A-Mathematical Physical and Engineering Sciences, 381(2260), 20220384. [Google Scholar]
38. Gu, H. H., Wang, R. Z., Zhu, S. P., Wang, X. W., Wang, D. M. et al. (2022). Machine learning assisted probabilistic creep-fatigue damage assessment. International Journal of Fatigue, 156, 106677. [Google Scholar]
39. Li, X. Q., Song, L. K., Bai, G. C. (2022). Recent advances in reliability analysis of aeroengine rotor system: A review. International Journal of Structural Integrity, 13(1), 1–29. [Google Scholar]
40. Cheng, L. Y., Wang, R. Z., Wang, J., Zhu, S. P., Zhao, P. C. et al. (2021). Cycle-dependent creep-fatigue deformation and life predictions in a nickel-based superalloy at elevated temperature. International Journal of Mechanical Sciences, 206, 106628. [Google Scholar]
41. Li, X. Q., Bai, G. C., Song, L. K., Wen, J. (2021). Fatigue reliability estimation framework for turbine rotor using multi-agent collaborative modeling. Structures, 29, 1967–1978. [Google Scholar]
42. Karimi, M. S., Salehi, S., Raisee, M., Hendrick, P., Nourbakhsh, A. (2019). Probabilistic CFD computations of gas turbine vane under uncertain operational conditions. Applied Thermal Engineering, 148, 754–767. [Google Scholar]
43. Nguyen, H. D., Shin, M., Torbol, M. (2020). Reliability assessment of a planar steel frame subjected to earthquakes in case of an implicit limit-state function. Journal of Building Engineering, 32, 101782. [Google Scholar]
44. Zhu, S. P., Keshtegar, B., Ben Seghier, M. E. A., Zio, E., Taylan, O. (2022). Hybrid and enhanced PSO: Novel first order reliability method-based hybrid intelligent approaches. Computer Methods in Applied Mechanics and Engineering, 393, 114730. [Google Scholar]
45. Bouledroua, O., Zelmati, D., Hassani, M. (2019). Inspections, statistical and reliability assessment study of corroded pipeline. Engineering Failure Analysis, 100, 1–10. [Google Scholar]
46. Yang, M. D., Zhang, D. Q., Jiang, C., Wang, F., Han, X. (2024). A new solution framework for time-dependent reliability-based design optimization. Computer Methods in Applied Mechanics and Engineering, 418(A), 116475. [Google Scholar]
47. Zhang, D. Q., Zhang, J. K., Yang, M. D., Wang, R., Wu, Z. P. (2022). An enhanced finite step length method for structural reliability analysis and reliability-based design optimization. Structural and Multidisciplinary Optimization, 65(8), 231. [Google Scholar]
48. Yang, M. D., Zhang, D. Q., Wang, F., Han, X. (2022). Efficient local adaptive Kriging approximation method with single-loop strategy for reliability-based design optimization. Computer Methods in Applied Mechanics and Engineering, 390, 114462. [Google Scholar]
49. Zhang, D., Zhou, P., Jiang, C., Yang, M. D., Han, X. et al. (2021). A stochastic process discretization method combing active learning Kriging model for efficient time-variant reliability analysis. Computer Methods in Applied Mechanics and Engineering, 384, 113990. [Google Scholar]
50. Karar, N., Felkaoui, A., Djeddou, F. (2020). Reliability based robust design optimization based on sensitivity and elasticity factors analysis. Journal of Materials and Engineering Structures, 7(1), 97–111. [Google Scholar]
51. Hao, P., Yang, H., Yang, H., Zhang, Y., Wang, Y. T. et al. (2022). A sequential single-loop reliability optimization and confidence analysis method. Computer Methods in Applied Mechanics and Engineering, 399, 115400. [Google Scholar]
52. Meng, Z., Li, C. Q., Hao, P. (2023). Unified reliability-based design optimization with probabilistic, uncertain-but-bounded and fuzzy variables. Computer Methods in Applied Mechanics and Engineering, 407, 115925. [Google Scholar]
53. Meng, Z., Yıldız, A. R., Mirjalili, S. (2022). Efficient decoupling-assisted evolutionary/metaheuristic framework for expensive reliability-based design optimization problems. Expert Systems with Applications, 205, 117640. [Google Scholar]
54. Li, X. Q., Song, L. K., Bai, G. C. (2022). Deep learning regression-based stratified probabilistic combined cycle fatigue damage evaluation for turbine bladed disks. International Journal of Fatigue, 159, 106812. [Google Scholar]
55. Li, X. Q., Song, L. K., Bai, G. C. (2023). Vectorial surrogate modeling approach for multi-failure correlated probabilistic evaluation of turbine rotor. Engineering with Computers, 39(3), 1885–1904. [Google Scholar]
56. Meng, D. B., Yang, S. Y., de Jesus, A. M. P., Zhu, S. P. (2023). A novel Kriging-model-assisted reliability-based multidisciplinary design optimization strategy and its application in the offshore wind turbine tower. Renewable Energy, 203, 407–420. [Google Scholar]
57. Wang, D., Zhang, D., Meng, Y., Yang, M. D., Meng, C. Z. et al. (2023). AK-HRn: An efficient adaptive Kriging-based n-hypersphere rings method for structural reliability analysis. Computer Methods in Applied Mechanics and Engineering, 414, 116146. [Google Scholar]
58. Meng, D. B., Yang, S. Y., de Jesus, A. M. P., Fazeres-Ferradosa, T., Zhu, S. P. (2023). A novel hybrid adaptive Kriging and water cycle algorithm for reliability-based design and optimization strategy: Application in offshore wind turbine monopole. Computer Methods in Applied Mechanics and Engineering, 412, 116083. [Google Scholar]
59. Yang, S. Y., Meng, D. B., Wang, H. T., Yang, C. (2024). A novel learning function for adaptive surrogate-model-based reliability evaluation. Philosophical Transactions of the Royal Society A-Mathematical Physical and Engineering Sciences, 382, 20220395. [Google Scholar]
60. Zhang, H., Song, L. K., Bai, G. C. (2023). Active Kriging-based adaptive importance sampling for reliability and sensitivity analyses of stator blade regulator. Computer Modeling in Engineering & Sciences, 134(3), 1871–1897. https://doi.org/10.32604/cmes.2022.021880 [Google Scholar] [PubMed] [CrossRef]
61. Meng, D. B., Li, Y., He, C., Guo, J. B., Lv, Z. Y. et al. (2021). Multidisciplinary design for structural integrity using a collaborative optimization method based on adaptive surrogate modelling. Materials & Design, 206, 109789. [Google Scholar]
62. Wang, Y. Z., Zheng, X. Y., Lu, C., Zhu, S. P. (2020). Structural dynamic probabilistic evaluation using a surrogate model and genetic algorithm. Proceedings of the Institution of Civil Engineers-Maritime Engineering, 173(1), 13–27. [Google Scholar]
63. Nannapaneni, S., Mahadevan, S. (2020). Probability-space surrogate modeling for fast multidisciplinary optimization under uncertainty. Reliability Engineering & System Safety, 198, 106896. [Google Scholar]
64. Gu, Q. H., Wang, Q., Xiong, N. N., Jiang, S., Chen, L. (2021). Surrogate-assisted evolutionary algorithm for expensive constrained multi-objective discrete optimization problems. Complex & Intelligent Systems, 8(4), 2699–2718. [Google Scholar]
65. Harrison, J. W., Lucius, M. A., Farrell, J. L., Eichler, L. W., Relyea, R. A. (2021). Prediction of stream nitrogen and phosphorus concentrations from high-frequency sensors using Random Forests Regression. Science of the Total Environment, 763, 143005. [Google Scholar] [PubMed]
66. Zahura, F. T., Goodall, J. L. (2022). Predicting combined tidal and pluvial flood inundation using a machine learning surrogate model. Journal of Hydrology-Regional Studies, 41, 101087. [Google Scholar]
67. Biggs, M., Hariss, R., Perakis, G. (2022). Constrained optimization of objective functions determined from random forests. Production and Operations Management, 32(2), 397–415. [Google Scholar]
68. Kallus, N., Mao, X. J. (2022). Stochastic optimization forests. Management Science, 69(4), 1975–1994. [Google Scholar]
69. Salazar, F., Hariri-Ardebili, M. A. (2022). Coupling machine learning and stochastic finite element to evaluate heterogeneous concrete infrastructure. Engineering Structures, 260, 114190. [Google Scholar]
70. Rhodes, J. S., Cutler, A., Moon, K. R. (2023). Geometry- and accuracy-preserving random forest proximities. IEEE Transactions on Pattern Analysis and Machine Intelligence, 45(9), 10947–10959. [Google Scholar] [PubMed]
71. Sage, A. J., Genschel, U., Nettleton, D. (2023). A residual-based approach for robust random forest regression. Statistics and Its Interface, 14(4), 389–402. [Google Scholar]
72. Song, L. K., Bai, G. C., Li, X. Q. (2021). A novel metamodeling approach for probabilistic LCF estimation of turbine disk. Engineering Failure Analysis, 120, 105074. [Google Scholar]
73. Gao, H. F., Zio, E., Wang, A. E., Bai, G. C., Fei, C. W. (2020). Probabilistic-based combined high and low cycle fatigue assessment for turbine blades using a substructure-based kriging surrogate model. Aerospace Science and Technology, 104, 105957. [Google Scholar]
74. Song, L. K., Bai, G. C., Fei, C. W. (2019). Probabilistic LCF life assessment for turbine discs with DC strategy-based wavelet neural network regression. International Journal of Fatigue, 119, 204–219. [Google Scholar]
75. Gao, H. F., Zio, E., Guo, J. J., Bai, G. C., Fei, C. W. (2020). Dynamic probabilistic-based LCF damage assessment of turbine blades regarding time-varying multi-physical field loads. Engineering Failure Analysis, 108, 104193. [Google Scholar]
76. Academic committee of the superalloys (2012). China superalloys handbook. Beijing: China Zhijian Publishing House & Standards Press of China. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools