Perception Enhanced Deep Deterministic Policy Gradient for Autonomous Driving in Complex Scenarios

1  Introduction

The rapid application of autonomous driving technology has introduced significant challenges to achieving safe and efficient driving in complex scenarios. Among various urban traffic scenarios, roundabouts have garnered particular attention due to their unique structure and function. The inherent randomness of vehicle entries and exits, the potential for traffic gridlock, and the complexities of environmental perception make roundabouts a core challenge and a focal point of research in autonomous driving. In recent years, many researchers have dedicated their efforts to these issues [1–5]. These studies not only underscore the importance of roundabout scenarios in autonomous driving but also emphasize the pressing need to ensure safety and efficiency in such environments.

Despite extensive research on autonomous driving in roundabout scenarios, some key issues remain challenging. Existing studies in this domain could be summarized as environmental perception, decision-making, and path planning. For example, Belz et al. [6] proposed three distinct behavioral categories for vehicles at roundabouts: taking priority, yielding priority, and yielding at roundabout locations. Abbasi et al. [7] employed eye-tracking to investigate how drivers perceive behavior within roundabouts. Perez et al. [8] introduced the concept of lateral control in roundabouts, addressing lane-keeping issues with a focus on entrances and exits. Cao et al. [9] proposed an adaptive decision-making model based on optimized embedded reinforcement learning. Huang et al. [10] employed the Deep Deterministic Policy Gradient algorithm in a driving simulator to learn optimal driving behaviors for continuous actions, demonstrating its efficacy in scenarios like forward driving and stopping. Wei et al. [11] used a residual structure and a Transformer structure in the network structure of the generator in the adversarial network, which improved the accuracy of snow removal tasks and the safety of autonomous vehicles (AVs). These studies have made significant efforts for autonomous driving in roundabouts. However, existing studies often impose specific requirements on traffic scenarios, such as necessitating all vehicles to be interconnected or assuming single-laned roundabouts. In the real world, traffic at roundabouts on actual roads is more intricate. Variables like varying penetration rates, which is the ratio of AVs, make vehicle coordination challenging, and incorrect driving strategies can easily lead to traffic gridlock within roundabouts. Additionally, dynamic path optimization in roundabout scenarios remains a crucial challenge.

To address these issues and consider the characteristics of roundabout traffic, we propose an enhanced Perception Enhanced Deep Deterministic Policy Gradient (PE-DDPG) model to enable autonomous driving in complex roundabout scenarios. The approach ensures that vehicles can adapt to various traffic patterns and different penetration rates, thus enhancing driving efficiency, safety, and stability in complex scenarios. The main innovations of this work could be summarized as follows:

1)   To tackle the issue of traffic gridlock that roundabouts are prone to, we introduce a multi-lane dynamic path optimization mechanism within the roundabout to effectively mitigate the issue of traffic gridlock and enhance traffic flow efficiency.

2)   We Propose a Perception Enhanced Deep Deterministic Policy Gradient for Adaptive Autonomous Driving (PE-DDPG) in roundabouts. The model integrates an enhanced variational autoencoder with a spatial attention mechanism to capture and parse key features in complex traffic scenarios. Then, the model employs the Deep Deterministic Policy Gradient (DDPG) to learn and generate driving control decisions for complex roundabout scenarios.

3)   Extensive autonomous driving experiments in roundabout traffic scenarios were constructed with a joint simulation platform integrating CARLA and SUMO, and results show that the proposed PE-DDPG model outperforms the state-of-the-art models significantly.

The structure of this work is as follows: Section 2 reviews related works. Section 3 provides a detailed description and problem modeling of the issue. Section 4 describes the proposed model, including the modules of enhanced perception feature extraction, adaptive mechanisms, and the integration of the Variational Autoencoder (VAE) with the Deep Deterministic Policy Gradient for enhanced perception. Section 5 elaborates on the experimental details, analyzes the results, and discusses briefly. Finally, conclusions are presented in Section 6.

2  Related Works

In recent years, rapid growth of related studies has been carried out, and significant progress has been made for autonomous driving in various scenarios. However, in the case of complex roundabout scenes, There remain critical challenges.

2.1 Autonomous Driving Technology in Roundabouts

Roundabouts, as core components of urban transportation infrastructure, play a vital role in traffic flow and safety. Elvik [12] demonstrated that roundabouts can effectively reduce the probability of severe traffic accidents. However, the road structure and traffic flow within such scenarios are exceptionally intricate, posing significant challenges for AVs in terms of scene comprehension and intelligent control decision-making. For scenarios with complex and diverse state spaces, Deep Reinforcement Learning (DRL) emerges as the preferred method to address decision-making in roundabout autonomous driving. Academic endeavors have been made to explore autonomous driving methods tailored for roundabout scenarios. For instance, García et al. [13] proposed a method based on the Q-learning algorithm to train autonomous vehicle agents to navigate appropriately within roundabouts. Wang et al. [14] introduced a driving strategy based on the Soft Actor-Critic (SAC) algorithm to ensure safety while minimizing costs. Zhang et al. [15] employed optimization-embedded reinforcement learning (OERL) to achieve adaptive decision-making at roundabout intersections. However, many existing studies often assume relatively simplistic dynamic traffic flows within the scene [16].

In complex traffic flow scenarios, especially when considering varying penetration rates of AVs, there remains a research gap in navigating roundabouts safely, swiftly, and stably. Furthermore, research efforts have also been directed toward understanding and navigating single-lane roundabouts. Rodrigues et al. [17] developed an adaptive tactical behavior planner (ATBP) for autonomous vehicles to navigate non-signalized roundabouts, combining naturalistic behavior planning and tactical decision-making. This approach focuses on human-like motion behaviors in simpler environments. However, these studies tend to overlook the complexities of multi-lane roundabouts, where traffic patterns are more dynamic and unpredictable. The assumption of uniform and predictable traffic in single-lane studies simplifies the real-world challenges posed by multi-lane roundabouts. This work aims to bridge this research gap by developing a robust and adaptable DRL framework, specifically designed for the nuanced and complex nature of multi-lane roundabouts, incorporating comprehensive considerations for safety, efficiency, and stability under diverse traffic conditions.

2.2 Perception Enhancement Methods for AVs

To improve the perception capabilities of AVs, Singh et al. [18] proposed a parameterized two-layer optimization method to calculate optimal behavioral decisions and downstream trajectories jointly. Compared with other existing methods, the method performs well regarding collision rate in relatively simple scenarios. From a visual perspective, the VAE has begun to be applied in the field of autonomous driving, which handles high-dimensional and complex data representation, especially in visual perception and decision-making. This kind of method has shown great potential and attracted widespread attention. For example, Azizpour et al. [19] proposed a method to integrate semantic segmentation and VAE methods with a camera-based end-to-end controller. Plobe and da Lio [20] implemented a semi-supervised VAE, whose architecture best approximates two related neurocognitive theories, providing deeper visual perception for autonomous driving. In addition, to improve the interpretability of autonomous driving systems, Abukmeil et al. [21] proposed a VAE-based explainable semantic segmentation (ESS) model that uses multi-scale second-order derivatives between the latent space and the encoder layer to capture the curvature of neuron responses. These methods provide sufficient interpretability and reliability for autonomous driving systems in relatively simple scenarios. However, building an efficient representation mechanism and making vehicular driving safer and more stable in complex scenarios such as roundabouts remains a critical challenge.

3  Problem Description and Definition

Modern transportation systems pay special attention to roundabouts due to their unique structure and function. Roundabouts are designed to improve traffic flow, reduce accidents, and enhance driving safety. However, with increasing traffic and rapid urbanization, roundabouts face challenges like congestion, gridlocks, and collisions [22].

As illustrated in Fig. 1, this work focuses on the scenario of a traffic roundabout. Here, a vehicle enters at entrance A aiming for exit E. The multi-lane nature of roundabouts means the vehicle’s path can vary. Throughout its journey, actions like lane changing and overtaking are common. Vehicles must dynamically decide their route and control strategy as they drive.

Figure 1: Traffic scenario in roundabouts

Definition 1. Environmental Information: A roundabout R_A consists of entries R_E, exits R_X, lane number L, driving intentions I, and vehicles including autonomous Vehicle AV and non-autonomous Vehicle nAV vehicles. Then, the roundabout R_A with environmental information could be formally represented as:

R_A={R_E, R_X, I, AV, nAV, L}.(1)

Definition 2. Vehicular State Information: For a vehicle Q, state information includes visual data P, speed S_p, throttle and brake T, steering angle ϕ, road center deviation D, and waypoint O. Then, the vehicular state information of Q could be represented as:

Q={P, S_p, T, ϕ, D, O}.(2)

Definition 3. Driving Control Sequence: A control sequence C for vehicle Q in roundabout R_A includes operational parameters like throttle and brake T and steering angle ϕ. Then, the driving control sequence for Q in roundabout R could be formally represented as:

C={T, ϕ}.(3)

Definition 4. Markov Decision Process (MDP): The problem of intelligent driving control in roundabouts is modeled as an MDP, defined as a tuple (S,A,T,R), S is the set of states, A is the set of actions, T is the transition function denoting the probability of moving, and R is the reward function. The objective in an MDP is to find an optimal policy π∗ that maximizes the expected cumulative reward as:

π∗=arg⁡maxπE[∑t=0∞γtR(st,at)],(4)

where γ is the discount factor.

This formulation clearly states the MDP components and the optimization objective, integrating it seamlessly into the context of intelligent driving control in roundabouts.

4  Methodology

Considering the challenges of understanding the environment in roundabouts, we propose a PE-DDPG for Adaptive Autonomous Driving. As shown in Fig. 2, the framework of PE-DDPG mainly comprises a Perception Enhanced Feature Extraction module and an intelligent driving decision module. The feature extraction module is primarily used to efficiently extract critical features from raw images, while the intelligent decision module is designed to generate safe driving control strategies specific to roundabouts and implement complex control behaviors.

Figure 2: The framework of PE-DDPG for autonomous driving

In the model, the feature extraction module integrates an Enhanced Variational Autoencoder (E-VAE) with attention to improving the understanding capacity of environment information, and the intelligent driving decision module introduces a DDPG to construct a policy learning agent. The agent is employed to act with the environment and learn the driving control decisions such as “lane change”, “accelerate” or “decelerate”. In this model, we have specifically incorporated the concept of ‘lane change’ into the vehicle’s actions within roundabouts. This integration is crucial for addressing the prevalent issue of gridlocks in roundabouts. To further facilitate this, our method has been adapted to more strongly encourage lane-changing behaviors. By doing so, the model not only learns to optimize for speed and safety but also becomes adept at recognizing and reacting to potential deadlock situations commonly encountered in roundabouts. The enhanced focus on lane changing as a strategic maneuver significantly contributes to alleviating traffic congestion and improving overall traffic flow efficiency, thereby resolving the problem of roundabout gridlocks.

4.1 Perception Enhanced Feature Extraction Module

The Perception Enhanced Feature Extraction module integrates an E-VAE with spatial attention mechanisms to improve the perception ability in complex scenarios. As shown in Fig. 3, the E-VAE focuses on significant regions of images and captures information more precisely related to the specific task.

Figure 3: The perception enhanced feature extraction module

Due to every pixel in image data is associated with its surrounding pixels, a spatial attention mechanism is employed to assign a weight to each pixel and emphasize areas of greater importance for the current task. For a given input image x, a weight matrix A is first computed through the spatial attention network, given by the formula:

A=Softmax(Wsx+bs),(5)

where Ws and bs are the parameters of the spatial attention network. Here, s in Ws and bs denotes ‘spatial’, indicating that these parameters are specifically for the spatial aspect of the attention mechanism. Ws represents the weights and bs represents the bias in the spatial attention network. Considering the encoder part of the traditional VAE, we get:

qφ(z|x)=N(z;μ(x),σ2(x)I),(6)

where μ and σ are the encoder outputs and are influenced by the weighted input x′. Here, μ(x) is the mean and σ2(x) is the variance of the latent variable distribution for the weighted input. The latent variable z represents the encoded information in a compact form. N stands for the normal (Gaussian) distribution, which is used to model the distribution of the latent variables. I is the identity matrix, which is used here to represent the independence of the latent variables in the distribution. Then, the weighted input x′ is computed from the attention weights and the original input image:

x'=A⊙x.(7)

Thus, the representation of the weighted input could be rewritten as:

qφ(z|x')=N(z;μ(x')​,σ2(x')I).(8)

In this model, E-VAE maps the input image to a latent space and ensures that the representation in this space emphasizes the critical parts of the image. In the same way, a similar attention mechanism can be employed to reconstruct the input image during the decoding phase.

Building upon the previously described features of the E-VAE with spatial attention, we delve deeper into its practical implications in complex traffic environments. The spatial attention mechanism plays a pivotal role in enhancing the model’s performance under such conditions. It allows the E-VAE to selectively focus on crucial aspects within the visual field, such as identifying vehicles and pedestrians in dense and dynamic traffic scenarios. This ability is particularly beneficial in environments with high variability and unpredictability, like crowded urban intersections or roundabouts.

The integration of E-VAE with spatial attention not only refines the accuracy of feature extraction but also bolsters the model’s capacity to distinguish subtle but essential differences in the visual data. For instance, the model becomes more adept at quickly recognizing and reacting to sudden pedestrian movements, thereby elevating the safety and reliability of the autonomous driving system.

Thus, the module integrates VAE with a spatial attention mechanism to capture and distinguish subtle scene differences from imperfect data. In particular, the module could be employed to capture image features of complex roundabouts, avoiding the randomness, ambiguity, and uncertainty of scene information collection. This module provides data support for the intelligent driving decision module in the PE-DDPG framework.

4.2 The PE-DDPG for Intelligent Driving Decision

To generate reasonable driving control decisions in complex roundabout scenarios, we constructed a decision module with the DDPG, which merges deep learning with policy gradient methods and aims to achieve optimal performance in complex environments.

After the model leverages the E-VAE to capture critical features from driving scenario image data, the decision-making is modeled based on the MDP, and every action is contingent upon the current state with the objective being to maximize the expected long-term return.

Mathematically, the objective function of the reinforcement learning agent could be represented as:

J(π)=Est,atπ[∑t=0∞γtr(st,at)],(9)

where γ is the discount factor, determining the present value of future rewards; r(st,at) is the immediate reward obtained when action at is executed in state st.

As an intelligent driving model, PE-DDPG combines the control strategy based on the DDPG with VAE and the spatial attention mechanism. It aims to determine appropriate driving behaviors by real-time monitoring of various state components of the driving scene, such as road conditions, traffic flow, and driving environment. PE-DDPG takes suitable actions based on the current state and continuously improves its driving decision-making capability by learning and optimizing policies.

Specifically, the operational procedure of PE-DDPG is illustrated in the pseudocode shown in Table 1. In the model, to ensure that the system can be explored broadly in its initial stages, PE-DDPG employs the Ornstein-Uhlenbeck process to introduce noise. Moreover, PE-DDPG utilizes an experience replay mechanism to ensure learning stability, allowing the agent to draw lessons from historical interactions. Based on this, we designed a reward function to address the roundabout deadlock issue and optimize vehicle traffic efficiency.

4.3 The Perception Enhanced Reward Function

Within the deep learning framework of autonomous driving systems, the design of the reward function is crucial, as it directly dictates the vehicle’s driving behavior. We proposed a perception-enhanced reward function that integrates all three aspects to ensure that AVs exhibit efficient, safe, and stable driving behaviors in complex traffic environments. This function holistically considers three key metrics: the vehicle’s efficiency, safety, and stability.

Given the vehicle state Q and vehicle action C, the reward function R(Q,C) represents the immediate reward obtained when action C is executed in state Q. We then set the reward function based on the three criteria to evaluate the vehicle’s driving performance in roundabouts.

R(Q,C)=we×E(Q,C)+ws×S(Q,C)+wc×C(Q,C),(10)

where S(Q,C) is the safety assessment when action C is taken in state Q, E(Q,C) is the efficiency assessment when action C is taken in state Q, and C(Q,C) is the stability assessment when action C is taken in state Q. ws, we, wc are the corresponding weights.

Efficiency is a key performance metric for evaluating autonomous driving performance. Aittoniemi [23] found a consistent speed can significantly enhance the overall efficiency of traffic flow. Therefore, the proposed model considers the relationship between the vehicle’s current speed and its speed from the previous timestep. Then, we set the efficiency evaluation rules as follows:

E(Q,C)={1CurrentSpeed≥LaststepSpeed2CurrentSpeed≥2×LaststepSpeed−30CurrentSpeed<LaststepSpeed.(11)

Furthermore, safety is the core objective of autonomous driving. As pointed out by Elsagheer Mohamed et al. [24], maintaining an appropriate safety distance from other vehicles and obstacles is vital to avoiding collisions. Therefore, the reward function is computed based on the distance between the vehicle and the obstacle ahead. We have defined a minimum safety distance, denoted as MinsafetyDis1/4 and rewards or penalties are given based on the distance between the vehicle and the obstacle. Specifically, we constructed the safety evaluation rules as follows:

S(Q,C)={1Distance≥MinsafetyDis2Distance≥2×MinsafetyDis−30Distance<MinsafetyDis.(12)

Lastly, it is noteworthy that stability is also a significant evaluation metric. As described by Zeng et al. [25], abrupt acceleration and deceleration behaviors significantly impact passenger comfort. To encourage smooth driving behaviors, we have incorporated calculations for the vehicle’s abrupt acceleration and deceleration behaviors in PE-DDPG, and then we employed them as indicators of stability. The reward function is primarily defined based on an object’s jerk, which is the rate of change of acceleration.

Specifically, it is defined based on the absolute value of the time derivative of the object’s acceleration a(t). This reward function aims to penalize situations with a significant change in the object’s acceleration. In autonomous driving, significant changes in acceleration can lead to passenger discomfort or potentially unsafe driving behaviors. Thus, we construct the stability evaluation rules as follows:

C(Q,C)=−|d dta(t)|Maxa,(13)

where a(t) is the instantaneous acceleration, and Maxa represents the maximum possible value of jerk, used for normalization to ensure the reward value remains within a reasonable range. The value of the reward function approaches −1 as the jerk nears its maximum value and approaches 0 as the jerk nears 0. It implies that when there’s a significant change in the object’s acceleration, the reward will be a considerable negative value, thereby encouraging the algorithm to minimize changes in acceleration.

To ensure that the reward function could balance the three defined metrics, we referred to the method proposed by Muzahid et al. [26] and assigned appropriate weights to each metric. We could set varying weights depending on the specific requirements of different vehicles. In this work, we use the following parameter settings as an example for the research: the weight for the efficiency reward is 0.4; the weight for the safety reward is 0.4, and the weight for the stability reward is 0.2.

5  Experiments and Results Analysis

5.1 Driving Scenario and Parameter Settings

This work employs the joint simulation technology of the Carla simulator [27] and the SUMO simulation platform [28] to provide a simulation environment of complex traffic roundabout scenarios, and the joint simulation platform shows an evident advantage of reproducing the diversity and complexity of roundabout traffic. In this work, the primary task is to enable vehicles’ autonomous driving and achieve a balance of efficiency, safety, and stability. Therefore, the selected scenario simulates the roundabout traffic in the core urban area, featuring multi-lanes with a width of 3.5 meters, numerous intersection entry points, and a central circular traffic flow with a diameter of about 50 meters.

In the model training phase, we focused on the driving characteristics of AVs amidst varying numbers of nAVs. We have incorporated the inherent unpredictability of nAVs, reflecting real-world human driving behaviors such as sudden maneuvers and inconsistent speed patterns, to enhance the realism of our simulations. By adjusting the number of nAVs in the simulation, we extensively trained the vehicles in traffic flows ranging from sparse to dense, as shown in Fig. 4a. The purpose of this setup is to allow the PE-DDPG to achieve optimal adaptability in diverse traffic environments, thereby enhancing its robustness and adaptability in real-world scenarios.

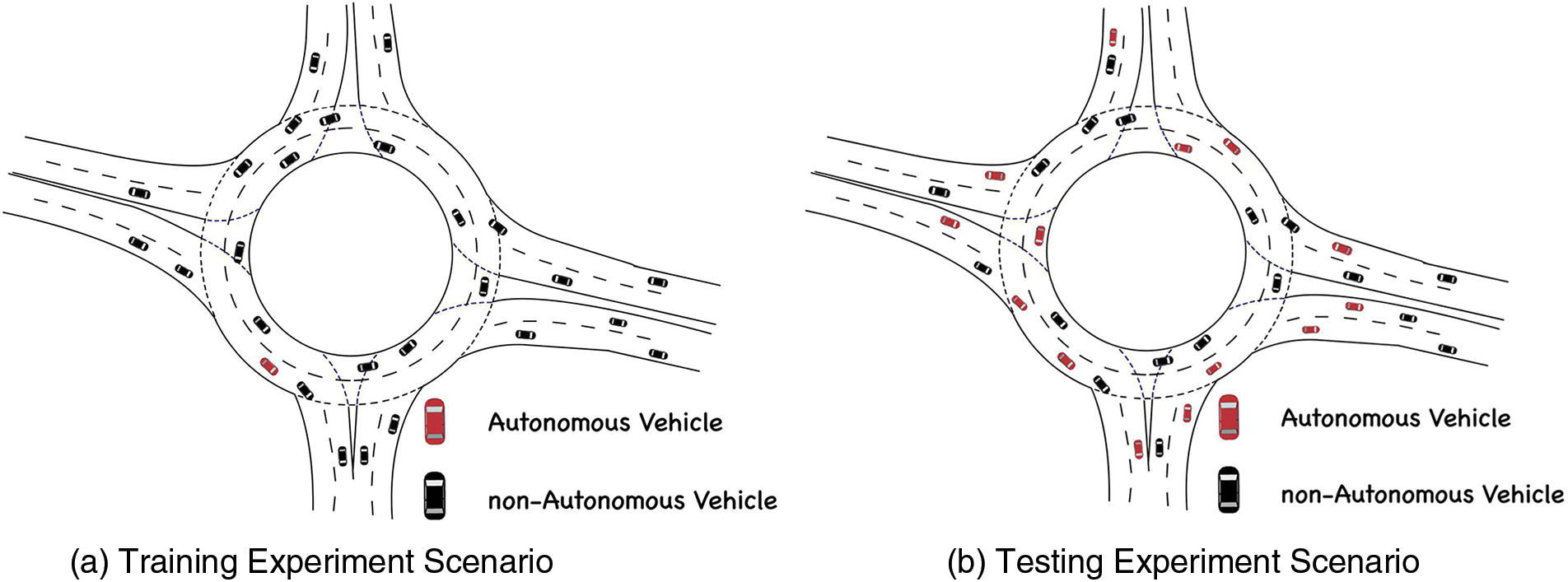
Figure 4: Schematic diagram of the autonomous driving scenario

In the model validation phase, as shown in Fig. 4b, with a constant traffic flow density, we conducted validation experiments targeting different AVs penetration rates. Specifically, the AVs penetration rates are set to 30%, 50%, and 70%. This represents that, among all traffic participants, the corresponding proportion of vehicles is controlled by the AVs, while the rest are simulated nAVs. This validation aims to deeply assess the differences in system performance under different AVs penetration rates and the interactive dynamics between it and the nAVs.

In addition to the aforementioned validation experiments, we have implemented an innovative solution to address potential traffic gridlocks within roundabouts, a common challenge in such scenarios. Our approach is centered around a dynamic path optimization mechanism specifically designed for multi-lane roundabouts. In instances where a traffic deadlock is detected in one lane, our system promptly activates a lane-changing protocol, enabling AVs to switch to less congested lanes. This mechanism not only allows for immediate alleviation of unexpected gridlocks but also ensures smoother traffic flow throughout the roundabout. This dynamic adaptability, tested under various traffic densities and AV penetration rates, showcases the robustness of our model in effectively managing real-world traffic complexities.

The experimental setup for our system primarily revolves around parameters such as discount rates and learning rates for both the critic and actor components. These were adapted from Liang et al. [29–31] who provided foundational parameter configurations. The specific parameters employed in our experiments are outlined in Table 2.

5.2 Evaluation Metrics

The comprehensiveness of evaluating autonomous driving strategy and their responsiveness in traffic environments is crucial. For this reason, we selected a series to explore the performance of the model in training and actual driving scenes. The evaluation indicators used in this work and their importance are described below.

Firstly, we considered the reward comparison figure of the training process. In the context of reinforcement learning, the reward function R(s,a) provides continuous feedback to the model in its learning process. Here, s represents the state, and a denotes the action taken. The visualization of cumulative rewards, which is calculated as ∑tR(st,at), can reveal the learning trend of the algorithm and provide insights into its convergence pattern.

To evaluate the precision of model control, we defined the “Error of Position” to assess the matching accuracy between the planned path and the actual navigational trajectory.

Ep=|pexpected−pactual|,(14)

where pexpected and pactual represent the expected and actual positions. Furthermore, to assess the vehicle’s traffic efficiency, we quantified the relative speed with the vehicle ahead, vrelative, specifically calculated as:

vrelative=vego−vfront,(15)

where vego is the speed of the AV, and vfront is the speed of the vehicle in front. To further evaluate driving quality and stability, we also examined the vehicle’s acceleration, aego. By directly collecting and monitoring the changes in aego across different scenarios, we can assess its driving stability.

Meanwhile, we further considered the vehicle’s Jerk data, which is the time derivative of acceleration, specifically defined as:

J=d3Pactualdt3,(16)

by integrating and analyzing the Jerk patterns, which, as the time derivative of acceleration, provides us with deeper insights into driving stability and smoothness.

In summary, these evaluation metrics offer a comprehensive perspective on the performance of autonomous driving in various driving scenarios, enabling us to assess and analyze it from multiple dimensions thoroughly.

5.3 Methods Studied

Recently, several models have been developed to tackle the inherent challenges in autonomous driving. To thoroughly understand the efficacy of the PE-DDPG model, a comparative study was undertaken against the state-of-the-art models.

1)   DDPG (Deep Deterministic Policy Gradient) [32]: DDPG is an model based on the actor-critic architecture.

2)   TD3 (Twin Delayed Deep Deterministic Policy Gradient) [33]: TD3 is an improved version of DDPG, and it introduces two Q-functions and policy delay updates to enhance the algorithm’s stability.

3)   DQN (Deep Q-Network) [34]: DQN combines Q-learning with deep neural networks.

4)   Quantile Regression DQN (QR-DQN) [35]: PG-DQN is an advanced deep reinforcement learning algorithm that enhances the standard DQN framework by incorporating a preference-learning mechanism.

5)   Perference-guided DQN (PG-DQN) [36]: QR-DQN is a deep reinforcement learning algorithm that extends the traditional DQN by estimating the distribution of action values using quantile regression.

6)   Traditional ACC (Adaptive Cruise Control) [37]: This is a rule-based adaptive cruise control method that mainly adjusts its speed by continuously monitoring the speed of the vehicle ahead and the distance to it, aiming to maintain a safe distance.

7)   Ballistic [38]: It is a physics-based prediction model that primarily predicts future positions based on the vehicle’s current speed and acceleration.

8)   SL2015 [39]: This is a model based on safety logic that considers various traffic situations and driver behaviors.

These models are compared with the evaluation metrics delineated in the “Evaluation Metrics” section to ascertain a performance benchmark for the proposed PE-DDPG model.

5.4 Performance Comparison

To comprehensively analyze the processing performance of the model, this work conducts systematic comparisons and analyses from aspects such as model training convergence capability comparison, comprehensive performance comparison, and traffic efficiency comparison.

5.4.1 Models’ Convergence Capability

To evaluate the actual convergence capability of the model during training, we set the reward functions of all benchmark models to be the same as that in this work and analyzed the changes in reward values during their training process [40]. To ensure the robustness and reproducibility of our results, we conducted experiments with different initial conditions by setting the random seeds to 1, 2, and 3, respectively. This approach allowed us to assess the impact of varying initializations on the training dynamics and model performance. The experimental results are shown in Fig. 5.

Figure 5: Reward progression graph for convergence comparison

Analysis of the experimental outcomes reveals a distinct advantage for the PE-DDPG model in terms of reward optimization. The model’s final convergence registers an average reward value of around −5, which is a notable improvement over the best comparative model’s average reward, which stabilizes near −10. Not only does PE-DDPG exhibit a more favorable reward profile, but it also demonstrates a more rapid and stable convergence, achieving a consistent performance after 300 episodes. In contrast, while the other models exhibit a similar timeline for initial convergence, their performance is characterized by significant volatility, with noticeable fluctuations persisting beyond the 300-episode mark. This evidence suggests that PE-DDPG not only learns more efficiently but also achieves a level of strategic stability that outperforms the alternatives in dynamic and uncertain scenarios.

5.4.2 Comprehensive Performance

To evaluate the comprehensive performance of the PE-DDPG, this work compares the model’s overall performance using indicators such as Error of Position, Velocity Delta, Velocity Acceleration, jerk, and other indicators to show the key performance indicators in the model testing phase. The experimental results are shown in Fig. 6.

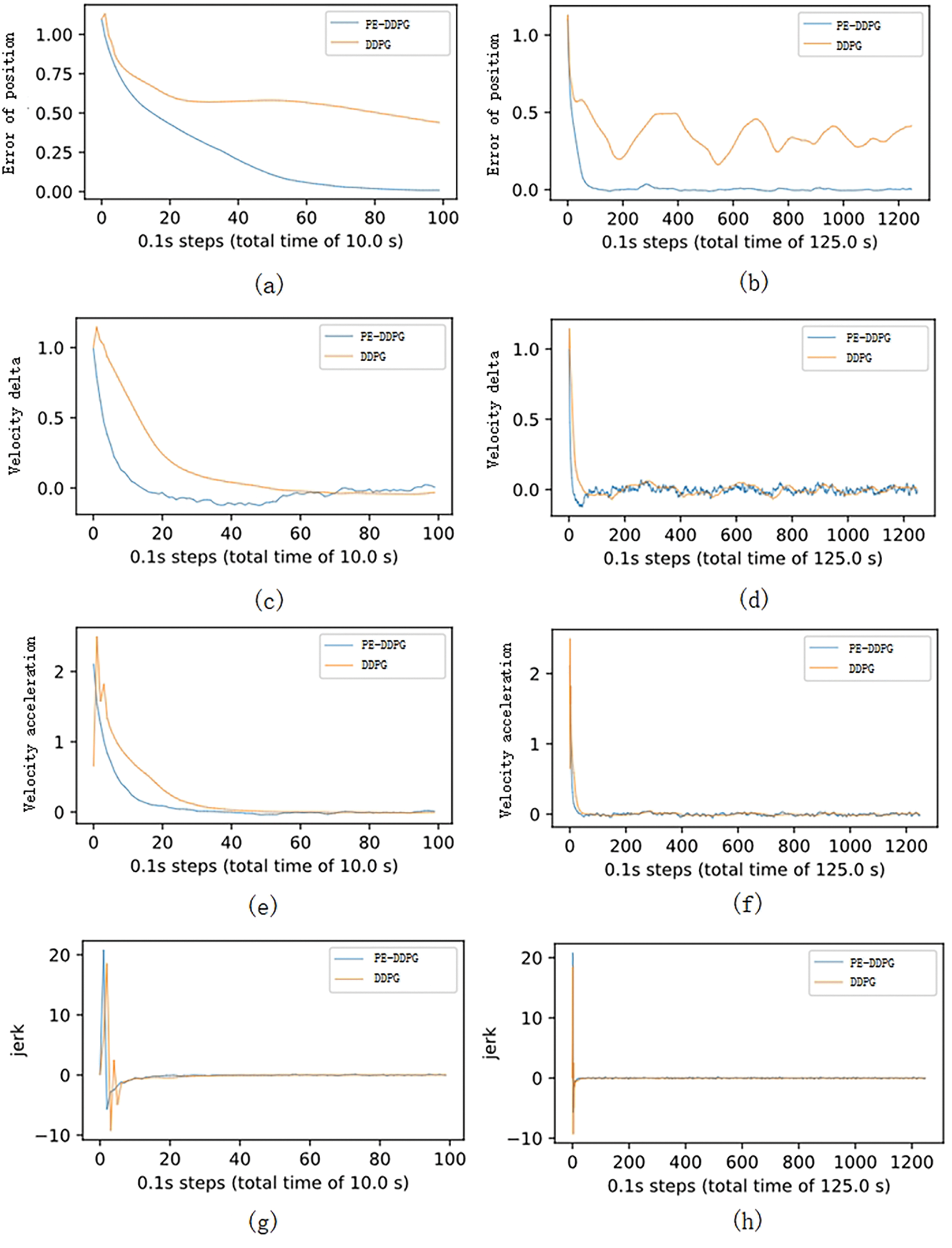
Figure 6: Performance comparison between PE-DDPG and DDPG

PE-DDPG demonstrates quantifiable advancements over DDPG in several performance metrics, as evidenced by our latest experimental analysis. In the ‘error of position’, PE-DDPG exhibits a more rapid decline to a lower error rate, settling at about 0.1, compared to DDPG’s consistently higher error level at about 0.2–0.5 and floating up or down. This represents PE-DDPG getting status information capability improvement, indicating more precise positional tracking.

When comparing the ‘velocity delta’, the curve of PE-DDPG approaches the minimum faster than DDPG. Specifically, PE-DDPG has a convergence speed of 40 steps compared to DDPG in this regard, which means it has a more consistent speed distribution and improvement in maintaining the target speed. For “velocity acceleration”, although there is not much difference in convergence values between PE-DDPG and DDPG, the convergence speed is 20 steps faster.

Lastly, the ‘jerk’ metric, which assesses the smoothness of the driving experience, shows PE-DDPG achieving a lower peak jerk value by suitable reward jerk function, and faster stabilization, reflecting PE-DDPG’s smoother driving pattern. This is critical for passenger comfort and aligns with safety standards, where PE-DDPG’s performance underscores its capability to deliver a smoother ride with controlled accelerations and decelerations.

Collectively, these results highlight PE-DDPG’s capacity to not only understand complex driving environments but also to execute control decisions that enhance the autonomous driving experience, substantiating its real-world applicability.

5.4.3 Traffic Efficiency

To assess the traffic efficiency of the proposed PE-DDPG model, we analyzed the average speed of traffic flow. This analysis was conducted at varying penetration rates of AVs. We then compared the PE-DDPG model against both traditional reinforcement learning and non-reinforcement learning algorithms were compared, such as DQN, DDPG, ACC, PR-DQN, Ballistic, and others. Specifically, we selected different traffic flow densities, about 100, 200, and 300 vehicles/steps_per_episode, and considered different AV penetration rates: 30%, 50%, and 70%. The specific results are shown in Table 3.

The data showcased in Table 3 provides a clear quantifiable comparison of autonomous driving algorithms under varying autonomous vehicle (AV) penetration rates with a dense traffic flow of 300 vehicles per episode. PE-DDPG outperforms other algorithms across all penetration rates, achieving an average traffic flow speed of 18.36 km/h at 30% penetration, which is an improvement of approximately 10.9% over DDPG and 4.1% over TD3 at the same rate. At a 50% penetration rate, PE-DDPG maintains its lead with an average speed of 19.08 km/h, marking an 8.2% increase compared to DDPG and a 6% increase over TD3. This trend continues at a 70% penetration rate, where PE-DDPG achieves the highest average speed of 19.80 km/h, 10% higher than DDPG and 5.8% more than TD3.

The results also indicate a general trend that most methods experience an increase in average speed with higher AV penetration rates. For instance, DDPG’s average speed elevates from 16.56 to 18.00 km/h, and TD3 from 17.64 to 18.72 km/h as the penetration rates rise from 30% to 70%. This pattern underscores the potential benefits of higher AV penetration in traffic flow, suggesting that an increase in AV presence may contribute to improved overall traffic speed. To illustrate this more vividly, we have visualized the average speed of all autonomous driving algorithms at a 70% penetration rate for traffic flow densities of 100 vehicles/steps_per_episode, 200 vehicles/steps_per_episode, and 300 vehicles/steps_per_episode. As shown in Fig. 7, the average speed of all methods decreases with the increase in traffic flow density. However, under any level of traffic flow density, PE-DDPG outperforms all other methods with its more exceptional performance.

Figure 7: The performance comparison of PE-DDPG with different densities

In summary, the experimental results indicated that PE-DDPG not only excels in single-vehicle navigation tasks but also significantly enhances the speed and efficiency of traffic flow in complex traffic scenarios compared to other autonomous driving algorithms. This offers a promising direction for future autonomous driving research, especially in high-penetration environments of autonomous vehicles.

5.5 Discussion

In this work, Perception Enhanced Deep Deterministic Policy Gradient shows superior performance for Autonomous Driving in Complex Scenarios. It is primarily due to the Enhanced VAE’s incorporation of spatial attention mechanisms, which significantly improves its feature extraction efficiency. Compared with directly using raw sensor data, the Enhanced VAE effectively reduces the dimensionality of high-dimensional visual information while retaining key features, providing a compact and informative input for the reinforcement learning algorithm.

Further, the Intelligent Driving Decision Module offers a precise and smooth policy update method for continuous action spaces, ensuring that vehicles can make continuous and accurate decisions in complex environments. Combining the features extracted by the Enhanced VAE with the vehicle’s dynamic information, this approach can comprehensively comprehend the environment and make more appropriate driving decisions. In summary, PE-DDPG shows evident advantages in feature extraction and policy optimization, and it could be employed to provide an efficient, robust method for autonomous driving in complex scenarios.

In contrast to traditional autonomous driving methods that rely on static, rule-based approaches and often struggle in dynamic, interaction-rich scenarios like multi-lane roundabouts, PE-DDPG offers a significant improvement with its adaptive and responsive strategy. Unlike conventional methods which fail to adjust to the complexities of real-world driving conditions, thereby limiting their effectiveness, PE-DDPG, with its integration of spatial attention and deep reinforcement learning, robustly navigates complex traffic scenarios. Additionally, its scalability to varied road networks and potential for integration with other autonomous vehicle systems showcase the model’s versatility. This adaptability extends from urban streets to highways, accommodating various traffic patterns and densities, and paves the way for collaborative traffic management and enhanced transportation systems through coordinated decision-making. Overall, PE-DDPG excels in feature extraction and policy optimization, marking a considerable advancement in autonomous driving technologies and providing an efficient, robust solution for the intricacies of autonomous driving in complex and diverse environments.

6  Conclusion

In this work, We proposed PE-DDPG to improve the capability of autonomous vehicles in complex traffic scenarios of roundabouts, which comprises a Perception Enhanced Feature Extraction Module and an Intelligent Driving Decision Module with a novel reward function. The experimental results show that PE-DDPG balances efficiency, safety, and stability and outperforms the state-of-the-art models in complex traffic scenarios of roundabouts.

In future work, we aim to enhance our model’s scalability to various road networks and its integration with other autonomous vehicle systems. While the current focus is on single roundabout scenarios, future developments will involve adapting the model for a broader range of traffic environments, including multi-lane intersections and complex urban settings. Conducting extensive real-world tests is also crucial for validating the model’s robustness and reliability in diverse and unpredictable conditions. This will not only assess the model’s performance in real-life scenarios but also explore its potential in collaborative autonomous driving systems, paving the way for more comprehensive and adaptable autonomous driving solutions.

Acknowledgement: We thank Rong Xiong (Fujian University of Technology) and Jiemao Zeng (Fujian University of Technology) helped to check the writing and provide some research suggestions.

Funding Statement: This work was supported in part by the projects of the National Natural Science Foundation of China (62376059, 41971340), Fujian Provincial Department of Science and Technology (2023XQ008, 2023I0024, 2021Y4019), Fujian Provincial Department of Finance (GY-Z230007, GY-Z23012), and Fujian Key Laboratory of Automotive Electronics and Electric Drive (KF-19-22001).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Lyuchao Liao, Hankun Xiao, Youpeng He; analysis and interpretation of results: Lyuchao Liao, Hankun Xiao, Zhenhua Gan, Jiajun Wang; draft manuscript preparation: Hankun Xiao, Pengqi Xing, Jiajun Wang, Youpeng He. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data utilized in this study is fully documented within the paper. Should there be any inquiries, please feel free to contact the authors.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Liu, D., Zhao, J., Xi, A., Wang, C., Huang, X. et al. (2020). Data augmentation technology driven by image style transfer in self-driving car based on end-to-end learning. Computer Modeling in Engineering & Sciences, 122(2), 593–617. https://doi.org/10.32604/cmes.2020.08641 [Google Scholar] [CrossRef]

2. Wang, X., Zhang, S., Peng, H. (2022). Comprehensive safety evaluation of highly automated vehicles at the roundabout scenario. IEEE Transactions on Intelligent Transportation Systems, 23(11), 20873–20888. [Google Scholar]

3. Zyner, A., Worrall, S., Nebot, E. M. (2019). Acfr five roundabouts dataset: Naturalistic driving at unsignalized intersections. IEEE Intelligent Transportation Systems Magazine, 11(4), 8–18. [Google Scholar]

4. Kim, H., Choi, Y. (2021). Self-driving algorithm and location estimation method for small environmental monitoring robot in underground mines. Computer Modeling in Engineering & Sciences, 127(3), 943–964. https://doi.org/10.32604/cmes.2021.015300 [Google Scholar] [CrossRef]

5. Liao, L., Chen, B., Zou, F., Eben Li, S., Liu, J. et al. (2020). Hierarchical quantitative analysis to evaluate unsafe driving behaviour from massive trajectory data. IET Intelligent Transport Systems, 14(8), 849–856. [Google Scholar]

6. Belz, N. P., Aultman-Hall, L., Gårder, P. E., Lee, B. H. (2014). Event-based framework for noncompliant driver behavior at single-lane roundabouts. Transportation Research Record, 2402(1), 38–46. [Google Scholar]

7. Abbasi, J. A., Mullins, D., Ringelstein, N., Reilhac, P., Jones, E. et al. (2021). An analysis of driver gaze behaviour at roundabouts. IEEE Transactions on Intelligent Transportation Systems, 23(7), 8715–8724. [Google Scholar]

8. Pérez, J., Godoy, J., Villagrá, J., Onieva, E. (2013). Trajectory generator for autonomous vehicles in urban environments. 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, IEEE. [Google Scholar]

9. Cao, Z., Xu, S., Peng, H., Yang, D., Zidek, R. (2021). Confidence-aware reinforcement learning for self-driving cars. IEEE Transactions on Intelligent Transportation Systems, 23(7), 7419–7430. [Google Scholar]

10. Huang, W., Braghin, F., Arrigoni, S. (2019). Autonomous vehicle driving via deep deterministic policy gradient. International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, vol. 59216. Hilton Anaheim, Anaheim, CA, USA, American Society of Mechanical Engineers. [Google Scholar]

11. Wei, B., Wang, D., Wang, Z., Zhang, L. (2023). Single image desnow based on vision transformer and conditional generative adversarial network for internet of vehicles. Computer Modeling in Engineering & Sciences, 137(2), 1975–1988. https://doi.org/10.32604/cmes.2023.027727 [Google Scholar] [CrossRef]

12. Elvik, R. (2003). Effects on road safety of converting intersections to roundabouts: Review of evidence from non-us studies. Transportation Research Record, 1847(1), 1–10. [Google Scholar]

13. García Cuenca, L., Puertas, E., Fernandez Andrés, J., Aliane, N. (2019). Autonomous driving in roundabout maneuvers using reinforcement learning with q-learning. Electronics, 8(12), 1536. [Google Scholar]

14. Wang, Z., Liu, X., Wu, Z. (2023). Design of unsignalized roundabouts driving policy of autonomous vehicles using deep reinforcement learning. World Electric Vehicle Journal, 14(2), 52. [Google Scholar]

15. Zhang, Y., Gao, B., Guo, L., Guo, H., Chen, H. (2020). Adaptive decision-making for automated vehicles under roundabout scenarios using optimization embedded reinforcement learning. IEEE Transactions on Neural Networks and Learning Systems, 32(12), 5526–5538. [Google Scholar]

16. Liao, L., Hu, Z., Zheng, Y., Bi, S., Zou, F. et al. (2022). An improved dynamic chebyshev graph convolution network for traffic flow prediction with spatial-temporal attention. Applied Intelligence, 52(14), 16104–16116. [Google Scholar]

17. Rodrigues, M., McGordon, A., Gest, G., Marco, J. (2018). Autonomous navigation in interaction-based environmentsaa case of non-signalized roundabouts. IEEE Transactions on Intelligent Vehicles, 3(4), 425–438. [Google Scholar]

18. Singh, A. K., Shrestha, J., Albarella, N. (2023). Bi-level optimization augmented with conditional variational autoencoder for autonomous driving in dense traffic. 2023 IEEE 19th International Conference on Automation Science and Engineering (CASE), Auckland, New Zealand, IEEE. [Google Scholar]

19. Azizpour, M., da Roza, F., Bajcinca, N. (2020). End-to-end autonomous driving controller using semantic segmentation and variational autoencoder. 2020 7th International Conference on Control, Decision and Information Technologies (CoDIT), pp. 1075–1080. Prague, Czech Republic, IEEE. [Google Scholar]

20. Plebe, A., Da Lio, M. (2019). Variational autoencoder inspired by brain's convergence—divergence zones for autonomous driving application. Image Analysis and Processing—ICIAP 2019: 20th International Conference, pp. 367–377. Trento, Italy, Springer. [Google Scholar]

21. Abukmeil, M., Genovese, A., Piuri, V., Rundo, F., Scotti, F. (2021). Towards explainable semantic segmentation for autonomous driving systems by multi-scale variational attention. 2021 IEEE International Conference on Autonomous Systems (ICAS), Montréal, Québec, Canada, IEEE. [Google Scholar]

22. Liao, L., Lin, Y., Li, W., Zou, F., Luo, L. (2023). Traj2traj: A road network constrained spatiotemporal interpolation model for traffic trajectory restoration. Transactions in GIS, 27(4), 1021–1042. [Google Scholar]

23. Aittoniemi, E. (2022). Evidence on impacts of automated vehicles on traffic flow efficiency and emissions: Systematic review. IET Intelligent Transport Systems, 16(10), 1306–1327. [Google Scholar]

24. Elsagheer Mohamed, S. A., Alshalfan, K. A., Al-Hagery, M. A., Ben Othman, M. T. (2022). Safe driving distance and speed for collision avoidance in connected vehicles. Sensors, 22(18), 7051. [Google Scholar] [PubMed]

25. Zeng, X., Cui, H., Song, D., Yang, N., Liu, T. et al. (2018). Jerk analysis of a power-split hybrid electric vehicle based on a data-driven vehicle dynamics model. Energies, 11(6), 1537. [Google Scholar]

26. Muzahid, A. J. M., Kamarulzaman, S. F., Rahman, M. A., Alenezi, A. H. (2022). Deep reinforcement learning-based driving strategy for avoidance of chain collisions and its safety efficiency analysis in autonomous vehicles. IEEE Access, 10, 43303–43319. [Google Scholar]

27. Dosovitskiy, A., Ros, G., Codevilla, F., Lopez, A., Koltun, V. (2017). CARLA: An open urban driving simulator. Conference on Robot Learning, Mountain View, California, USA. [Google Scholar]

28. Behrisch, M., Bieker, L., Erdmann, J., Krajzewicz, D. (2011). SUMO simulation of urban mobility: An overview. Proceedings of SIMUL 2011, The Third International Conference on Advances in System Simulation, Barcelona, Spain, ThinkMind. [Google Scholar]

29. Liang, Y., Guo, C., Ding, Z., Hua, H. (2020). Agent-based modeling in electricity market using deep deterministic policy gradient algorithm. IEEE Transactions on Power Systems, 35(6), 4180–4192. [Google Scholar]

30. Huang, Z., Zhang, J., Tian, R., Zhang, Y. (2019). End-to-end autonomous driving decision based on deep reinforcement learning. 2019 5th International Conference on Control, Automation and Robotics (ICCAR), Beijing, China, IEEE. [Google Scholar]

31. Chang, C. C., Tsai, J., Lin, J. H., Ooi, Y. M. (2021). Autonomous driving control using the DDPG and RDPG algorithms. Applied Sciences, 11(22), 10659. [Google Scholar]

32. Hou, Y., Liu, L., Wei, Q., Xu, X., Chen, C. (2017). A novel DDPG method with prioritized experience replay. 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, IEEE. [Google Scholar]

33. Ye, Y., Qiu, D., Wang, H., Tang, Y., Strbac, G. (2021). Real-time autonomous residential demand response management based on twin delayed deep deterministic policy gradient learning. Energies, 14(3), 531. [Google Scholar]

34. Sallab, A. E., Abdou, M., Perot, E., Yogamani, S. (2017). Deep reinforcement learning framework for autonomous driving. arXiv preprint arXiv:1704.02532. [Google Scholar]

35. Dabney, W., Rowland, M., Bellemare, M., Munos, R. (2018). Distributional reinforcement learning with quantile regression. Proceedings of the AAAI Conference on Artificial Intelligence, vol. 32. Hilton New Orleans Riverside, New Orleans, USA. [Google Scholar]

36. Huang, W., Zhang, C., Wu, J., He, X., Zhang, J. et al. (2023). Sampling efficient deep reinforcement learning through preference-guided stochastic exploration. IEEE Transactions on Neural Networks and Learning Systems, pp. 1–12. IEEE. [Google Scholar]

37. Shladover, S. E., Su, D., Lu, X. Y. (2012). Impacts of cooperative adaptive cruise control on freeway traffic flow. Transportation Research Record, 2324(1), 63–70. [Google Scholar]

38. Rahman, A., Guo, J., Datta, S., Lundstrom, M. S. (2003). Theory of ballistic nanotransistors. IEEE Transactions on Electron Devices, 50(9), 1853–1864. [Google Scholar]

39. Alekszejenkó, L., Dobrowiecki, T. P. (2019). SUMO based platform for cooperative intelligent automotive agents. International Conference on Simulation of Urban Mobility, Berlin-Adlershof, Germany. [Google Scholar]

40. Kargar, E., Kyrki, V. (2022). Vision transformer for learning driving policies in complex and dynamic environments. 2022 IEEE Intelligent Vehicles Symposium (IV), Aachen, Germany. [Google Scholar]