 Open Access
Open Access
ARTICLE
Conditional Generative Adversarial Network Enabled Localized Stress Recovery of Periodic Composites
1 Transportation and Municipal Engineering Institute, Powerchina Huadong Engineering Corporation, Hangzhou, 310014, China
2 College of Civil Engineering and Architecture, Zhejiang University, Hangzhou, 310058, China
3 Anhui Transport Consulting & Design Institute Co., Ltd., Hefei, 230088, China
4 Center for Balance Architecture, Zhejiang University, Hangzhou, 310058, China
* Corresponding Authors: Guannan Wang. Email: ; He Zhang. Email:
(This article belongs to the Special Issue: Machine Learning Based Computational Mechanics)
Computer Modeling in Engineering & Sciences 2024, 140(1), 957-974. https://doi.org/10.32604/cmes.2024.047327
Received 02 November 2023; Accepted 30 January 2024; Issue published 16 April 2024
Abstract
Structural damage in heterogeneous materials typically originates from microstructures where stress concentration occurs. Therefore, evaluating the magnitude and location of localized stress distributions within microstructures under external loading is crucial. Repeating unit cells (RUCs) are commonly used to represent microstructural details and homogenize the effective response of composites. This work develops a machine learning-based micromechanics tool to accurately predict the stress distributions of extracted RUCs. The locally exact homogenization theory efficiently generates the microstructural stresses of RUCs with a wide range of parameters, including volume fraction, fiber/matrix property ratio, fiber shapes, and loading direction. Subsequently, the conditional generative adversarial network (cGAN) is employed and constructed as a surrogate model to establish the statistical correlation between these parameters and the corresponding localized stresses. The stresses predicted by cGAN are validated against the remaining true data not used for training, showing good agreement. This work demonstrates that the cGAN-based micromechanics tool effectively captures the local responses of composite RUCs. It can be used for predicting potential crack initiations starting from microstructures and evaluating the effective behavior of periodic composites.Graphic Abstract
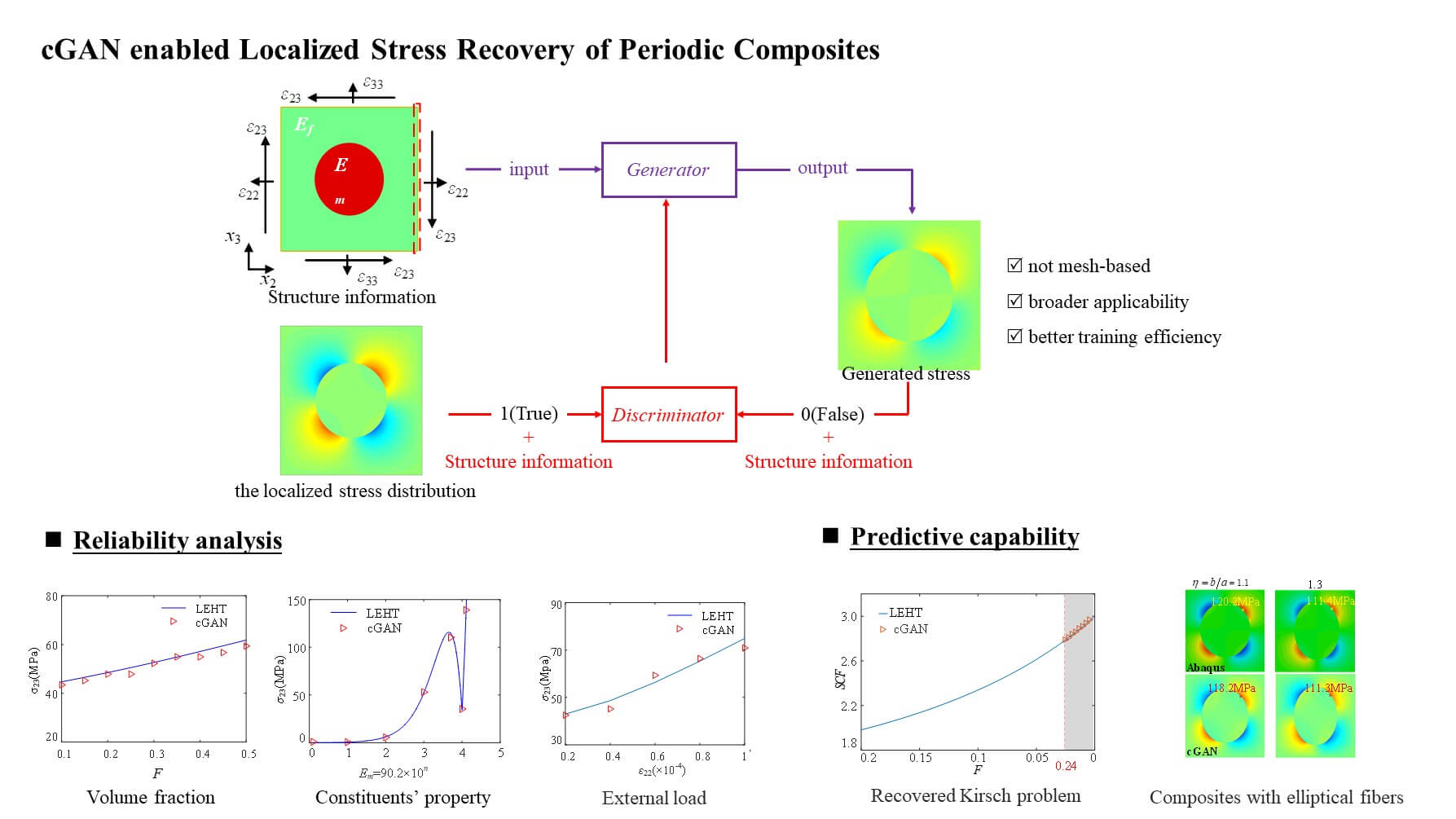
Keywords
Composite materials are extensively applied in advanced technological development and engineering applications [1]. With the long-term service of composite structures, cracks or damage are inevitably initiated from microstructures and propagate across scales, becoming detrimental to structural safety [2,3]. Accurate prediction of localized responses of composites is thus critical in estimating possible stress concentrations and crack initiations from microstructures. Additionally, capturing localized stresses is beneficial for evaluating the effective properties of composites. Based on these reasons, it is critical to develop advanced micromechanics tools to evaluate the effective and localized mechanical behavior of composites, circumventing laborious and costly experimental testing.
Micromechanics of heterogeneous media can generally be classified into two categories: one is based on microstructural detail-free analytical models. Nevertheless, the other is obtained through semi-analytical or numerical solving of internal microstructures. The former category includes several classical models, such as the rules of the mixture, the Mori-Tanaka model, and the self-consistent scheme. Most of these models, although based on simplified assumptions, can generally predict the homogenized moduli of composite materials [4,5]. However, with the long-term service of composites and due to the existence of heterogeneity, stress concentrations usually appear at the fiber/matrix interface even under external loading of small magnitudes, which could lead to interfacial cracks and be detrimental to structural integrity. Thus, local stress recovery within microstructures would benefit real-time health monitoring of composite materials and structures. However, the aforementioned analytical micromechanics models cannot fulfill the task of accurately recovering stress and deformation within microstructures.
To overcome the shortcomings of detail-free micromechanics, more sophisticated numerical or semi-analytical models are proposed by solving internal elastic partial differential equations (PDEs) and Navier’s equations in terms of displacement components, either exactly or in an approximate fashion. Readers are referred to the articles by Pindera et al. [6] for more detailed explanations. With the advancement of commercial packages, numerical (mostly finite element-based) techniques are the most dominant method in the mechanics and engineering community [7,8]. This includes FE-based or FV-based computational methods, which adopt mesh discretization to approach the real solution of elastic PDEs and thus may demand large-scale mesh refinement for complex microstructures. In the meantime, several other techniques are developed with their respective advantages [9–13]. However, numerical methods typically require mesh refinement and pre- and post-processing, incurring significant computational costs and potentially introducing errors due to meshing.
Almost all micromechanics-based multiscale models involved in material design are bottom-up, one-way homogenization; less attention is paid to the “top-down” localization/dehomogenization employed to indicate stress concentrations or crack initiation within microstructures. Efficient scale bridging and communication are critical for understanding the microstructure-property relationship. It is obvious that the aforementioned classical micromechanics models cannot easily fulfill the task of localization. Physics-based micromechanics models are the most dominant tools in recovering localized microstructural responses by solving the governing partial differential equations and imposing interfacial and boundary conditions. However, the computational cost is fairly high due to large-scale space discretization and pre- and post-processing. Despite progress in the micromechanics literature, the search for an ideal micromechanics tool continues.
With the development of machine learning (ML) and deep learning (DL) technologies, more attention is paid to employing ML-/DL-based analytical/numerical methods in the evaluation of composites [14–16]. Several papers in the literature have reported similar studies on the localization of heterogeneous materials. For instance, a regression model is employed to recover microscale elastic strains in three-dimensional voxel-based microstructures [17]. An artificial neural network (ANN) is utilized for predicting stress concentration factors and tensile strength of unidirectional fiber composites, considering fracture propagation and sequence [18]. However, a regression model like ANN is more suitable for regression tasks and not well-suited for data generation and dealing with big data. With the advancement of computer technology, convolutional neural network (CNN)-based convolution operations have been increasingly applied due to their ability to efficiently process large amounts of data [19]. The application of CNN-based technology to the computational solid mechanics area is still in the early stages of research [20,21]. For example, cGAN is implemented to achieve predictions from hierarchical composite microstructure geometry to stress and strain fields according to boundary conditions [22]. Local stress fields are predicted in fiber-reinforced composites using a CNN-based U-Net architecture [23]. Trent et al. enabled finite element analysis from the perspective of image processing [24]. The prediction of failure patterns based on microstructural geometry is achieved using a framework consisting of two stacked U-Net generators, considering the carbon-fiber reinforced plastics’s (CFRP) nonlinear stress distribution as an intermediate stage [25]. However, in the aforementioned work, the computational accuracy of the proposed data-driven method for composite materials has not been thoroughly evaluated under the influence of microstructural parameters.
In summary, the methods for solving local stress fields in composite materials primarily include analytical solutions and mesh-based approaches. Analytical methods struggle to account for local stress fields and micro-damages that may occur in composite materials during long-term service. Additionally, these solutions are not readily suitable for materials with complex geometries or conditions. Conversely, mesh-based numerical approaches necessitate large-scale mesh refinement for complex microstructures, thereby consuming significant computational resources. All the above solutions based on physical models demand a high level of accuracy regarding the microstructural model and material parameters. For instance, they must consider the interface between fibers and matrix, as well as the degradation of the material’s performance over time. This paper proposes a cGAN-based micromechanics model for recovering localized responses of microstructures. As a data-driven approach, it eliminates the need for extensive mesh refinement, thus avoiding computational inefficiency in mesh-based methods and potentially unreasonable interface modeling. It also offers broader applicability compared to analytical solutions. The cGAN-based micromechanics model, in contrast with other CNN-based generative approaches such as U-nets, comprises a pair of networks: a generator and a discriminator. The generator builds a spatial relationship between the stress nephograms and material information of composite materials using convolution and deconvolution operations. The discriminator, trained in an adversarial manner with the generator, enhances the training efficiency of the generator [26]. A large-scale data database is established through the locally exact homogenization theory, efficiently generating localized stresses for composites with a wide range of constituent property ratios and volume fractions. Utilizing the proposed cGAN-based micromechanics method, the convergence and accuracy of the proposed framework are tested, generating accurate results against the proposed locally exact homogenization theory (LEHT) and finite element (FE) simulations. The reliability of the data-driven method for composite materials is analyzed, considering the effect of microstructural parameters such as volume fractions, external loads, and elastic moduli of matrix and fiber. The classical Kirsch problem is also recovered, demonstrating that the proposed method can successfully capture the micromechanical behavior of composite material, even beyond the bounds of the training dataset. Furthermore, this framework predicts the magnitude and locations of stress concentrations within the composites’ RUCs. More importantly, the model is extended for predicting composites with elliptical fibers, where the corresponding advantages and shortcomings are discussed. The cGAN-based micromechanics tool is anticipated to be beneficial in the evaluation and design of heterogeneous media.
The remainder of this presentation is organized as follows: Section 2 introduces the proposed cGAN-based localized stress recovery methodology for periodic composites, including the cGAN framework and database establishment using LEHT. Section 3 validates the accuracy of the proposed method with statistical analysis and analyzes the influence of different fiber volume fractions, external loads, and material properties on the method’s accuracy. Section 4 summarizes the obtained conclusions and explores the potential of the method by generating stress fields for composites with irregular fibers.
In this section, the framework of the cGAN-based localized stress recovery methodology for periodic composites is introduced, encompassing the sample design, training strategy, and network architecture. This methodology is applicable to both measured and simulated data. The LEHT is employed to compute stress response data as ground truth in this work. Therefore, LEHT will be revisited in the second part of this section.
2.1 cGAN Enabled Micromechanics Framework
In the cGAN-based localized stress recovery method, the stress nephogram of a composite system is generated via image processing. The samples fed to the cGAN should contain both structural information and stress response information. Considering the composite material system with continuous reinforcements characterized by repeating material microstructure with two-dimensional (2D) periodicity, the samples for repeating unit cells (RUCs) are designed as shown in Fig. 1. The input sample (Fig. 1a1) includes the structural information of the composite material system, such as the elastic modulus of fiber (Ef) and matrix (Em), the applied displacement loading, and fiber volume fraction. The fiber and matrix are illustrated in different colors, with the corresponding RGB value denoting the values of their elastic moduli (Ef and Em). The applied displacement condition is presented as the boundary line of the RUC, with the value of displacements in three directions denoted by values in different color channels. Taking the right boundary, for instance,
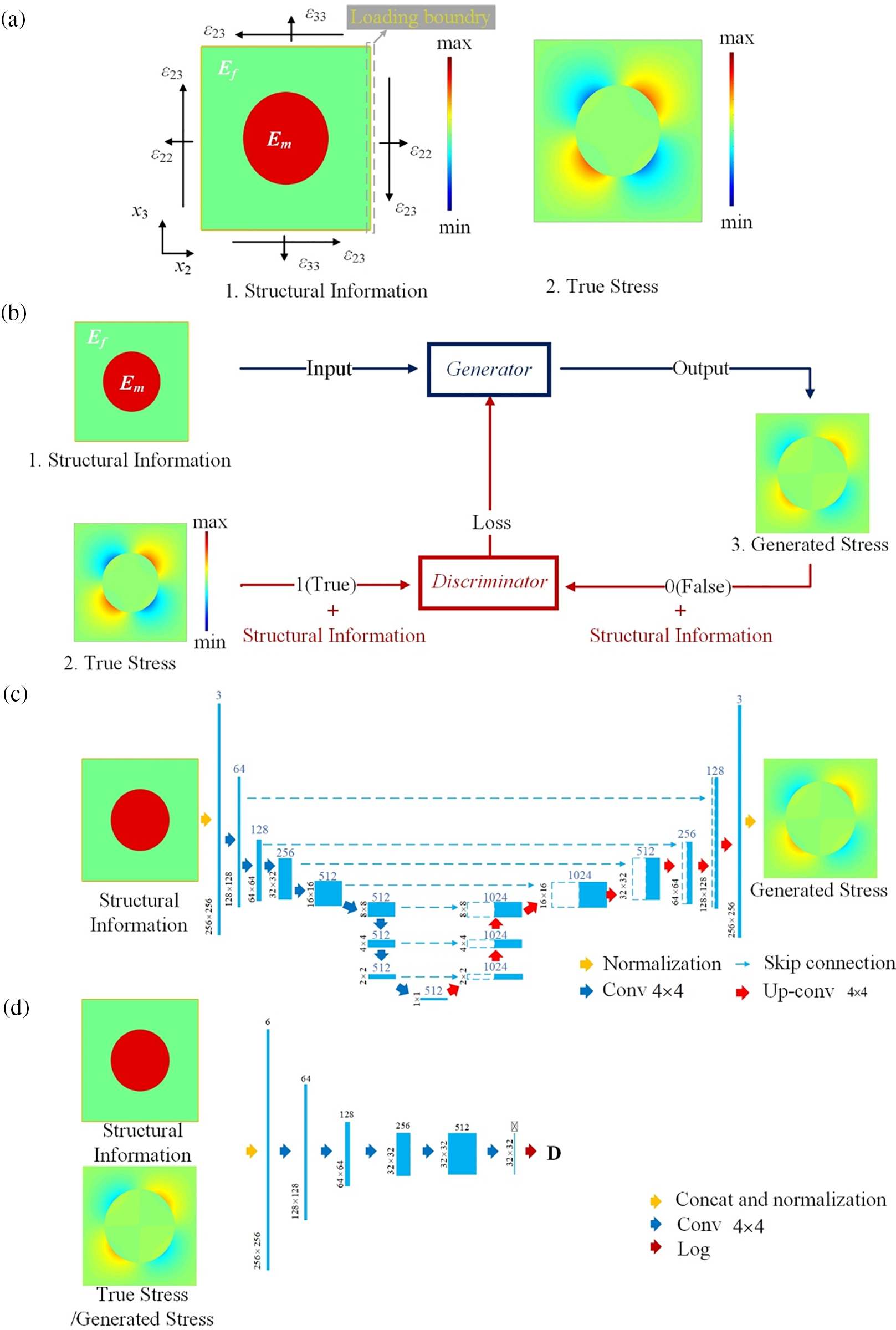
Figure 1: Framework of cGAN-based enabled localized stress recovery method: (a) Sample design; (b) Training procedure of cGAN; (c) Architecture of U-net used in generator; (d) Architecture of CNN used discriminator
The basic idea of the cGAN-based localized stress recovery method is to consider the stress nephogram simulation of composite materials as a type of generative task, recently successfully addressed by cGAN in various applications [27–30]. cGAN, a machine learning technique, is inspired by a two-player minimax game and trains a pair of networks in an adversarial manner, namely a generator and a discriminator. The entire training procedure of the present task is diagrammed in Fig. 1b. The generator synthesizes the stress nephogram of composite materials according to the input structural information (designed based on the spatial distribution of the composite material) through convolution and deconvolution processes. Meanwhile, the discriminator is trained to differentiate between the ground truth and the generated nephogram according to the paired structural information.
During the training process of cGAN, the discriminator aids the generator in creating more realistic stress nephograms. The nephograms generated by the generator are also used as error samples for the discriminator to improve its accuracy. In this adversarial manner, the generator and discriminator compete against each other and develop together. Ultimately, the optimized generator will be capable of generating stress nephograms fitting the distribution of samples in the database. In order to address this issue, a value function is proposed to train the generator and discriminator together:
In the training process, the discriminator is optimized by maximizing V(D, G), expressed as
cGAN is constructed based on Convolutional Neural Networks (CNN). Regarding the generator (Fig. 1c), an encoder-decoder network (U-net) is utilized to realize the convolution calculation and the deconvolution processes [31]. The sample for structural information (425 × 425) is normalized into regular data (256 × 256) before being substituted into the generator network. The normalized picture is then processed by eight convolutional operations using a 4 × 4 kernel and finally downsampled into a 512 × 1 latent vector. The layer numbers and the size of the kernel are adjusted accordingly. The process is then reversed by the decoder network (Fig. 1c, right). With a series of deconvolutional operations, the reduced vector representation is upsampled and resized into the inferred stress response nephogram. As for the discriminator D, it is designed as a “patchGAN” classifier architecture with five convolutional layers (Fig. 1d). The input to the discriminator is a concatenation of structural response information with the structural stress response or the ground-truth response. After the combined input data passes through a series of convolutional layers and a fully connected layer, a probability that the input comes from the ground truth will be produced. The micromechanics tool for generating the input construction for the cGAN-based prediction is now presented.
2.2 Locally-Exact Homogenization Theory Revisited
LEHT is a semi-analytical micromechanics tool developed by Drago et al. [32] and Wang et al. [33,34] based on the Trefftz concept. LEHT offers advantages over other numerical techniques in that it obtains the internal analytical solution directly by solving Navier’s equations a priori, with an explicit Fourier series expansion representation. The use of series expansion also facilitates the imposition of interfacial (dis)continuity conditions term-by-term, taking advantage of the function’s orthogonality. To ensure convergence, the remaining unknown coefficients are obtained through a weak-form balanced variational principle.
The technique has been validated against finite element (FE) and finite-volume (FV) simulations, consistently showing good agreement in the literature [35,36]. The Trefftz method is employed in the current study to generate a collection for input dataset construction to train the cGAN-based micromechanics tool. The LEHT theory is briefly revisited here to illustrate the basic idea and key steps in generating localized stress fields. For more detailed derivation, readers may refer to Drago et al. [32] and Wang et al. [33–35].
It should be noted that the stress/displacement within each RUC comprises global homogenized and local fluctuating components: the former represents the effective loading imposed on the composites, while the latter is generated due to the existence of heterogeneity. For instance, the displacement component
where x and y denote the global and local coordinate parameters, respectively;
where superscript k denotes the fiber (
The solution of Eq. (2) is obtained through assuming the series expansion:
where
The eigenvalues
where
from which the matrix coefficients can be expressed in terms of fiber coefficients. In addition, the remaining to-be-determined fiber coefficients are obtained through the weak-form periodic variational principle that was proposed by Drago and Pindera [32]:
where
It should also be noted that the periodic boundary conditions are imposed in a weak-form sense, ensuring the numerical stability of the stress recovery. Subsequently, the system of equations for unknown fiber coefficients is established, leading to the solutions for fiber and then matrix coefficients. The local analytical solutions for displacements and stresses are then obtained. It is demonstrated that quick convergence is guaranteed, requiring only about 12 harmonics to generate accurate local stress distributions for the input dataset of the cGAN construction. Moreover, the corresponding program is encapsulated into a black box with input and output construction, facilitating parametric investigation by tailoring input parameters, as well as the current cGAN training procedure.
As the fiber volume fraction F, external load
3.1 Database and Training Process
In order to validate the cGAN-driven homogenization technique in simulating the localized mechanical behavior of composites, a database is established for composites with hypothetical material constituents under certain loading conditions, with physical parameters listed in Table 1. In this study, 2100 pairs of samples are generated using the encapsulated LEHT through random generation of microstructural parameter magnitudes. The database is then divided into training data (2000) and test data (100), with the former used for training the cGAN homogenization model. The generated stress nephograms are compared against the latter for validation.

The cGAN model is trained for 800 epochs, as shown in Fig. 2. The loss function of cGAN includes both the generator’s and the discriminator’s loss. Unlike other neural networks such as CNNs, ANNs, and Recurrent Neural Networks (RNNs), where a lower loss value indicates better network performance, the evaluation of GAN training effectiveness is not solely based on the magnitude of the loss value. Instead, the stability of the loss value is considered. During cGAN training, the generator and discriminator engage in an adversarial competition, with the generator aiming to generate samples resembling real samples and the discriminator aiming to accurately distinguish between real and generated samples. As a result, the loss values of the generator and discriminator oscillate during training. The stability of these loss values, rather than a focus on achieving a value close to zero, is crucial in cGAN training. As depicted in Fig. 2, the loss values of both the generator and discriminator in the constructed cGAN stabilize, indicating that the generator has successfully learned to generate realistic samples and the discriminator has effectively learned to distinguish between real and generated samples. This stability reflects the training effectiveness of the constructed cGAN model. For further details on the effect of different convolutional kernels and the number of convolutional layers in G on the optimization speed and stability of cGAN, readers can refer to the work by Ref. [3].
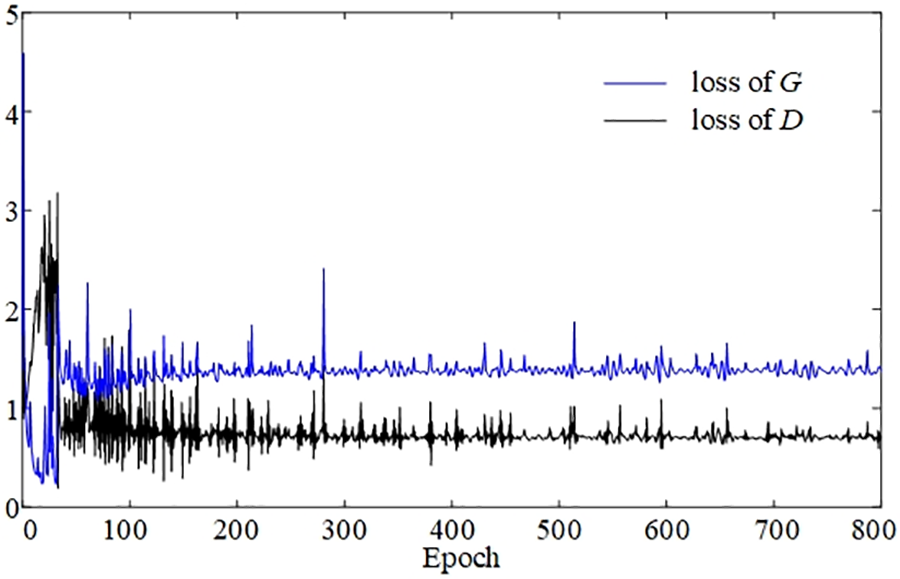
Figure 2: The training process of the constructed cGAN
3.2 Effect of Volume Fraction and Fiber Shape
The influence of fiber volume fraction (F) on the localized stress distribution is investigated through the proposed cGAN-based micromechanics tool. The transverse shear stress σ23 is predicted herein for the assumed material system with Ef =

Figure 3: Comparison of transverse shear stress distribution σ23 between the analytical solution and the cGAN generation with different fiber volume fractions F
In order to test the cGAN-based micromechanics in tackling demanding simulations and investigate the RUC with minimal boundary effect, the Kirsch problem is employed. The Kirsch problem describes the stress concentrations in an infinite plate with a circular hole of finite dimension located at the center of the plate. A stress concentration factor (SCF), which is defined as the ratio of local stress at the top and bottom interface of the hole against the macroscopic loading q,

Figure 4: Kirsch problem simulated by cGAN-based micromechanics: (a) Kirsch problem diagram; (b) Relationship between the stress concentration factor SCF and volume fraction P; (c) Specific examples of generated images by cGAN
3.3 Effect of the Constituent’s Properties
In this subsection, the influence of the elastic properties of fiber and matrix on the localized stress distributions of periodic composite materials is investigated through the proposed method. The effect of the constituents’ properties is achieved by fixing the matrix with Young’s modulus (

Figure 5: Comparison of transverse normal stress distribution σ23 between the LEHT and the cGAN generation with different Ef and Em
Additionally, the aforementioned demonstration is further validated by fixing the fiber’s properties and varying the matrix’s moduli. The effect of the constituents’ properties is achieved by fixing the fiber with Young’s modulus
3.4 The Influence of External Load
The influence of macroscopic loading on the localized stress distributions is investigated in this subsection. The shear stress distribution (
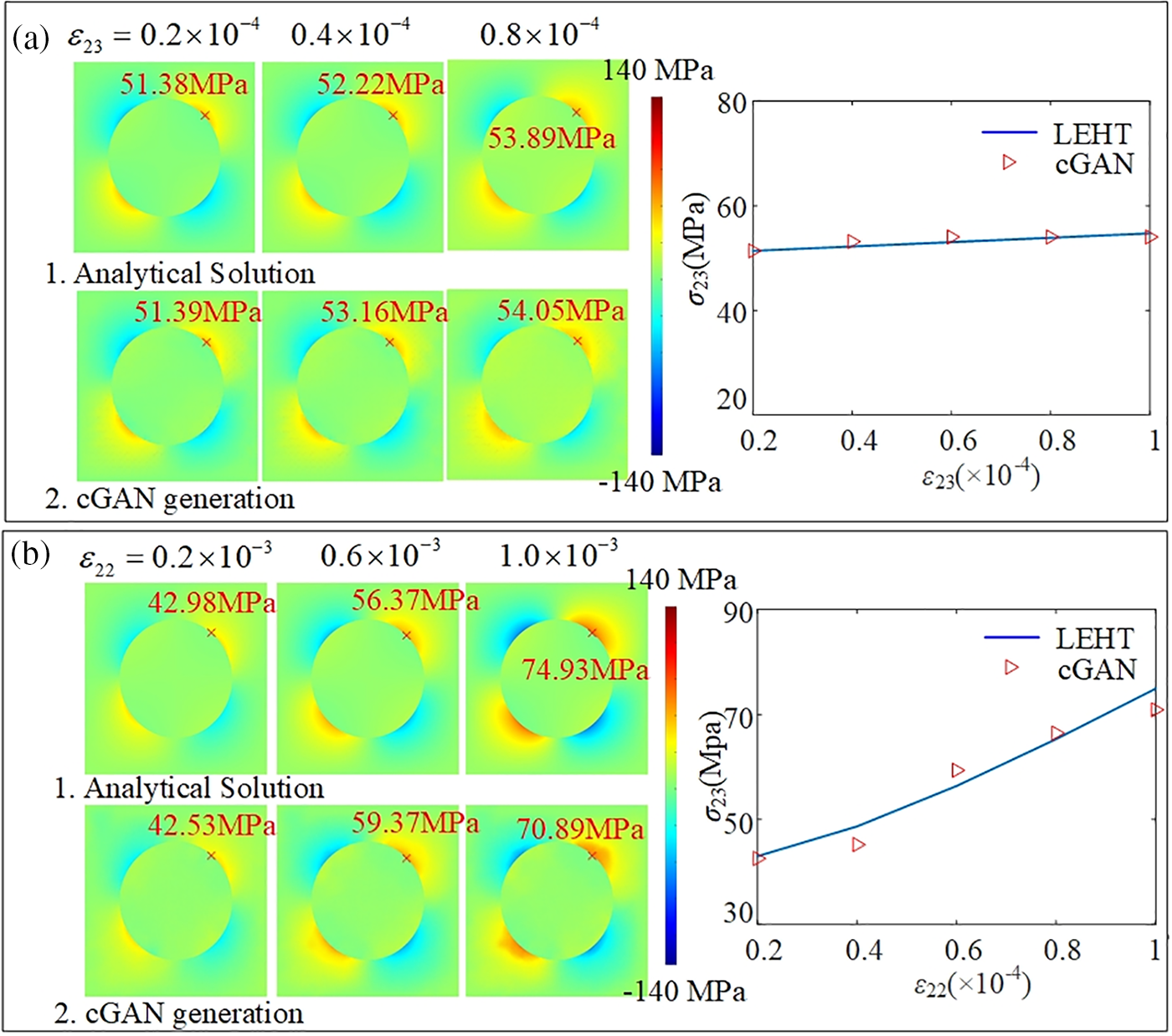
Figure 6: Comparison of transverse normal stress distribution σ23 between the analytical solution and the cGAN generation with different applied displacement conditions ε22 and ε23
Finally, statistical analysis based on quantitative evaluation in terms of the structural similarity index measure (SSIM) and peak signal-to-noise ratio (PSNR) is conducted on the quality of stress field generation using cGAN based on the validation set (100 samples), as depicted in Fig. 7.

Figure 7: Statistic result of the cGAN-generated stress fields
SSIM is used to evaluate the structural similarity between the original and generated images, which integrates luminance l, contrast c, and structure s. SSIM considers not only the value of individual pixels but also the structural arrangement of these pixels. For the reconstructed response x and real response y, the SSIM is:
where μx and μy represent the mean of the generated and original stress; σx and σy are the standard deviations; σxy is the covariance of the two stresses. Three positive constants, C1, C2, and C3, are used to avoid a null denominator. The positive value of SSIM ranges from 0 to 1. The higher the value, the more accurate the reconstructed response.
PSNR is utilized to evaluate the noise suppression performance in generation, defined as a dimensionless metric.
where K and I are the matrix representations of generated and original stresses; m and n denote the numbers of rows and columns of pixels in the image; MAXI represents the maximum pixel value of the image sample with original stress. A large PSNR value indicates a good match between the generated and original responses.
The results demonstrate impressive overall image quality in the generated stress fields, with most images exhibiting a PSNR surpassing 30, indicating excellent performance in capturing stress concentrations. However, it is noted that the SSIM of the generated stress fields tends to concentrate around 0.6, suggesting moderate quality in regions with lower stress magnitudes. Nevertheless, given the inherent importance of stress responses at maximum stress locations in material stress concentration problems, the data-driven micromechanics model showcases promising potential in addressing these critical aspects.
Moreover, a comprehensive comparison of generation efficiency is undertaken. The results show that the cGAN-based stress nephogram generation achieves an impressive speed of 0.15 s per image, significantly outperforming the LEHT method, which requires 2.6 s per image [35], and the ABAQUS-based simulations, with a considerably longer processing time of 30 s. Therefore, the data-driven approach for stress nephogram generation delivers not only remarkable quality but also fulfills real-time computational requirements with outstanding efficiency. All simulations in this study were conducted using an NVIDIA GeForce RTX 2080Ti GPU (32 GB RAM) in a workstation equipped with 16 Intel Core i9-9900K CPUs.
3.6 Stress Generation with Irregular Fiber
The limit of cGAN-based micromechanics is also preliminarily explored. Irregular fiber geometry, commonly observed in composites due to factors such as accidental manufacturing and deliberate inclusion, poses challenges in accurately predicting corresponding stress distributions. Thus, the cGAN-based micromechanics tool is employed to explore the capability of generating stress fields for composites with elliptical fibers. The specialty of the simulation lies in the fact that the training dataset is generated through LEHT for composites with circular fibers. In contrast, the final predicted results for elliptical-fiber composites are generated by cGAN after the adversarial network through repeating convolution and deconvolution operations. An aspect ratio of the elliptical fiber is defined as


Figure 8: Extension of the proposed model in generating localized stresses for composites with elliptical fibers, validated by the ABAQUS simulations
4 Conclusions and Perspectives
Bridging effective and localized responses of composites is an important issue in evaluating the mechanical behavior of composites [20,21]. Classical and numerical homogenization tools have been proposed in past decades to fulfill this task. This study develops the cGAN-based framework to recover the localized response within repeating microstructures, accurately capturing the stress-concentration phenomenon and predicting possible microstructural crack initiation, which is difficult to observe at the structural level. Through the learning and training of dataset collection, the proposed tool is capable of generating localized stress distributions for periodic composites with a wide range of candidate parameters, including fiber/hole volume fraction, fiber/matrix property ratio, external loading, and irregular (elliptical) fiber shape. Utilizing deep learning to simulate the stress field in composite materials allows for a breakthrough from the assumptions imposed by physical equations. As the depth of the network and the quantity of training samples increase, the ability to approximate actual stress distributions becomes increasingly accurate. The performance of the proposed method is evaluated by checking SSIM and PSNR. A direct comparison of the local field prediction against LEHT simulation demonstrates good correlations between the physical computations and data prediction. It should be noted that the proposed data-driven approach is not limited to simulated data but can also be extended to experimental data. When experimental data is utilized during the training process, the relationship between the information on composite materials in experiments and the local stress nephograms can be built by the trained model. The errors introduced by assumed parameters in physical modeling methods can also be avoided in this way (e.g., the interfacial stiffness used for considering the interface relationship between the matrix and fibers). The corresponding research is ongoing and will be presented in the future. The present method may also be extended with random fiber distributions and multiphysics modeling capability, which will be presented in the near future.
Acknowledgement: None.
Funding Statement: The authors acknowledge the support from the National Key R&D Program of China under Grant (Grant No. 2020YFA0711700), the National Natural Science Foundation of China (Grant Nos. 52122801, 11925206, 51978609, U22A20254, and U23A20659). G.W. is supported by the National Natural Science Foundation of China (Nos. 12002303, 12192210 and 12192214).
Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Guannan Wang, Chengkan Xu, He Zhang; data collection: Chengkan Xu, Guannan Wang, Xiaofei Wang; analysis and interpretation of results: Chengkan Xu; draft manuscript preparation: Chengkan Xu, Guannan Wang; investigation: Chengkan Xu, Guannan Wang, Yixuan Li, Xiaofei Wang; funding acquisition: Guannan Wang, He Zhang, Xiaofei Wang; supervision: Guannan Wang, He Zhang. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data for this article can be requested via Email.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Lee, M. W. (2020). Prospects and future directions of self-healing fiber-reinforced composite materials. Polymers, 12(2), 379 [Google Scholar] [PubMed]
2. Zhang, H., Xu, C. K., Zhou, Y. H., Shu, J. P., Huang, K. X. (2023). Hybrid phase-field modeling of mesoscopic failure in concrete combined with Fourier-Voronoi stochastic aggregate distribution modelling approach. Construction & Building Materials, 394, 132106. [Google Scholar]
3. Zhang, H., Xu, C. K., Jiang, J. J. (2023). A data driven based response reconstruction method of plate structure with conditional generative adversarial network. Sensors, 23(15), 6750 [Google Scholar] [PubMed]
4. Adhikari, B., Singh, B. N. (2022). A Coupled Mori-Tanaka model and FEM RVE approach for the geometrical nonlinear dynamic response of the FG-CNTRC plate based on a novel shear strain function using isogeometric finite element procedure. Composite Structures, 280, 114947. [Google Scholar]
5. Mercier, S., Molinari, A. (2009). Homogenization of elastic-viscoplastic heterogeneous materials: Self-consistent and Mori-Tanaka schemes. International Journal of Plasticity, 25(6), 1024–1048. [Google Scholar]
6. Pindera, M., Khatam, H., Drago, A. S., Bansal, Y. (2009). Micromechanics of spatially uniform heterogeneous media: A critical review and emerging approaches. Composites Part B: Engineering, 40(5), 349–378. [Google Scholar]
7. Yang, Z. Z., Yu, C. H., Buehler, M. J. (2021). Deep learning model to predict complex stress and strain fields in hierarchical composites. Science Advances, 7(15). [Google Scholar]
8. Bensoussan, A., Lions, J. L., Papanicolaou, G. (2011). Asymptotic analysis for periodic structures. Rhode Island: American Mathematical Society. [Google Scholar]
9. He, Z. (2022). Finite volume based asymptotic homogenization of viscoelastic unidirectional composites. Composite Structures, 291, 115601. [Google Scholar]
10. He, Z., Pindera, M. J. (2020). Locally exact asymptotic homogenization of periodic materials under anti-plane shear loading. European Journal of Mechanics-A/Solids, 81, 103992. [Google Scholar]
11. Yin, S., He, Z., Pindera, M. J. (2021). A new hybrid homogenization theory for periodic composites with random fiber distributions. Composite Structures, 269, 113997. [Google Scholar]
12. Yang, Z. Q., Rao, Y. P., Sun, Y., Cui, J. Z., Xiang, M. Z. (2023). A second-order strain gradient fracture model for the brittle materials with micro-cracks by a multiscale asymptotic homogenization. Computational Mechanics, 71, 1093–1118. [Google Scholar]
13. Yang, Z. Q., Ming, L., Sun, Y., Liu, Y. Z., Sun, W. (2022). A multiscale reduced homogenization approach for nonlinear viscoelastic problems of periodic heterogeneous materials. Composite Structures, 2022, 114864. [Google Scholar]
14. Chen, Q., Tu, W., Ma, M. (2020). Deep learning in heterogeneous materials: Targeting the thermo-mechanical response of unidirectional composites. Journal of Applied Physics, 127(17). [Google Scholar]
15. Jiang, J., Zhao, J., Pang, S., Meraghni, F., Siadat, A. et al. (2022). Physics-informed deep neural network enabled discovery of size-dependent deformation mechanisms in nanostructures. International Journal of Solids and Structures, 236, 111320. [Google Scholar]
16. Jiang, J., Wu, J., Chen, Q., Chatzigeorgiou, G., Meraghni, F. (2023). Physically informed deep homogenization neural network for unidirectional multiphase/multi-inclusion thermoconductive composites. Computer Methods in Applied Mechanics and Engineering, 409, 115972. [Google Scholar]
17. Liu, R., Yabansu, Y. C., Agrawal, A., Kalidindi, S. R., Choudhary, A. N. (2015). Machine learning approaches for elastic localization linkages in high-contrast composite materials. Integrating Materials and Manufacturing Innovation, 4, 192–208 [Google Scholar] [PubMed]
18. Choi, J. H., Na, W. J., Yu, W. R. (2023). Machine learning-assisted modelling of stress concentration factor of unidirectional fiber composites for predicting their tensile strength. Modelling and Simulation in Materials Science and Engineering, 31(2). [Google Scholar]
19. Cecen, A., Dai, H., Yabansu, Y. C., Kalidindi, S. R., Song, L. (2018). Material structure property linkages using three-dimensional convolutional neural networks. Acta Materialia, 146, 76–84. [Google Scholar]
20. Herriott, C., Spear, A. D. (2020). Predicting microstructure-dependent mechanical properties in additively manufactured metals with machine-and deep-learning methods. Computational Materials Science, 175, 109599. [Google Scholar]
21. Vlassis, N. N., Ma, R., Sun, W. (2020). Geometric deep learning for computational mechanics Part I: Anisotropic hyperelasticity. Computer Methods in Applied Mechanics and Engineering, 371, 113299. [Google Scholar]
22. Yang, Z. Q., Sun, Y., Liu, Y. Z. (2021). Prediction on nonlinear mechanical performance of random particulate composites by a statistical second-order reduced multiscale approach. Acta Mechanica Sinica, 37, 570–588. [Google Scholar]
23. Bhaduri, A., Gupta, A., Graham, B. L. (2022). Stress field prediction in fiber-reinforced composite materials using a deep learning approach. Composites Part B, 238, 109879. [Google Scholar]
24. Trent, S., Renno, J., Sassi, S., Mohamed, M. S. (2023). Using image processing techniques in computational mechanics. Computers & Mathematics with Applications, 136, 1–24. [Google Scholar]
25. Sepasdar, R., Karpatne, A., Shakiba, M. (2022). A data-driven approach to full-field nonlinear stress distribution and failure pattern prediction in composites using deep learning. Computer Methods in Applied Mechanics and Engineering, 397, 115126. [Google Scholar]
26. Mirza, M., Osindero, S. (2014). Conditional generative adversarial nets. https://arxiv.org/abs/1411.1784 [Google Scholar]
27. Loey, M., Manogaran, G., Khalifa, N. E. M. (2020). A deep transfer learning model with classical data augmentation and cGAN to detect COVID-19 from chest CT radiography digital images. Neural Computing & Applications, 1–13. [Google Scholar]
28. Schawinski, K., Zhang, C., Zhang, H. (2017). Generative adversarial networks recover features in astrophysical images of galaxies beyond the deconvolution limit. Monthly Notices of the Royal Astronomical Society, 467, 110–114. [Google Scholar]
29. Xue, F., Lu, W., Chen, K. (2018). Automatic generation of semantically rich as-built building information models using 2D images: A derivative-free optimization approach: Automatic generation of semantically rich as-built building information models using 2D images. Computer-Aided Civil and Infrastructure Engineering, 33, 926–942. [Google Scholar]
30. Yu, Y., Hur, T., Jung, J. (2019). Deep learning for determining a near-optimal topological design without any iteration. Structural and Multidisciplinary Optimization, 59, 787–799. [Google Scholar]
31. Ronneberger, O., Fischer, P., Brox, T. (2015). U-Net: Convolutional networks for biomedical image segmentation. In: Medical image computing and computer-assisted intervention 2015, pp. 234–241. Champ: Springer International Publishing. [Google Scholar]
32. Drago, A. S., Pindera, M. J. (2008). A locally exact homogenization theory for periodic microstructures with isotropic phases. Journal of Applied Mechanics, 75(5), 0510101–05101014. [Google Scholar]
33. Wang, G., Pindera, M. J. (2016). Locally exact homogenization of unidirectional composites with cylindrically orthotropic fibers. Journal of Applied Mechanics, 83(7), 071010. [Google Scholar]
34. Wang, G., Pindera, M. J. (2016). On boundary condition implementation via variational principles in elasticity-based homogenization. Journal of Applied Mechanics, 83(10), 101008. [Google Scholar]
35. Wang, G., Pindera, M. J. (2016). Locally-exact homogenization theory for transversely isotropic unidirectional composites. Mechanics Research Communications, 78, 2–14. [Google Scholar]
36. Yang, Z., Yabansu, Y. C., Al, B. R., Liao, W. K., Choudhary, A. N. et al. (2018). Deep learning approaches for mining structure-property linkages in high contrast composites from simulation datasets. Computational Materials Science, 151, 278–287. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools