Unsteady MHD Casson Nanofluid Flow Past an Exponentially Accelerated Vertical Plate: An Analytical Strategy

Nomenclature

1  Introduction

Heat transfer is the process by which thermal energy is exchanged between different systems, objects or regions, owing to temperature differences. It is fundamental to optimize efficiency and safety across a wide range of applications. The importance of heat transfer in biological tissues has contributed to the development of advanced medical technologies and treatment methods. In a series of studies, various authors [1–4] have investigated the heat transfer properties under different conditions. In recent years, there has been growing interest in utilizing ultrasonic vibrations as a means to enhance the heat transfer of systems working with nanofluids and to prevent the sedimentation of nanoparticles. Recent research by Delouei et al. [5] focused on an active approach to enhance heat transfer in indirect heaters at city gate stations. It employs experimental modeling to explore and improve the heat transfer process in these facilities, likely for more efficient natural gas processing and distribution. Adesanya et al. [6] focused on scrutinizing entropy generation within the flow and heat transfer of an electrically conductive couple stress fluid film along an inclined heated plate.

Nanofluids exhibit distinctive characteristics compared to traditional heat transfer fluids. Their high thermal conductivity, enhanced convective heat transfer and unique flow behavior make them particularly appealing for thermal management and energy efficiency improvement. The introduction of these nanofluids can be attributed to Choi et al. [7]. Numerous academic papers have focused on augmenting the thermal conductivity of base fluids by incorporating various types of nanoparticles. Hamad et al. [8] focused on the utilization of nanofluids in biomedical applications. Sandeep et al. [9] studied the flow of nanofluid in a magnetic field. According to their findings, the temperature field was strengthened by the magnetic parameter and volume percentage of the nanoparticles. Research on the movement of a Copper oxide (CuO) nanofluid exposed to a magnetic field was conducted by Sheikholeslami et al. [10]. They examined the nanofluid heat transfer properties and found that increasing the magnetic parameter value improved heat transmission. A study was conducted by Sridevi et al. [11] on magnetohydrodynamic (MHD) -water mixed nanofluid along with an unsteady stream and thermal transmission. Dogonchi et al. [12] examined the natural convective course of a ferric-oxide (hematite) water nanomaterial in a circular region within two trilateral spaces. This study focused on the impacts of radiation and heat source/sink factors on the flow behavior in the presence of magnetic field.

Mohan et al. [13] studied the effects of heat emission and chemical reactions in the presence of a permeable medium on the unstable MHD buoyancy-driven flow of a comprehensive Casson fluid along a vertical plate. They explored the applications of titanium dioxide nanoparticles in various industries such as toothpaste, medications, coatings, dietary supplements, sanitary products and textiles. Arif et al. [14] studied the numerical aspects of an unsteady MHD Maxwell nanofluid flow on a heated stretching sheet. Their findings are significant for industrial applications, such as polymer processing, power generation, compression, lubrication systems, food manufacturing and air conditioning. Fatima et al. [15] conducted a computational analysis on heat and mass transfer in magnetized Darcy-Forchheimer hybrid nanofluid flow, considering porous medium and slip effects. The significant outcomes of the study have practical implications in areas such as heat combustion, cooling chambers, space technology, the ceramics industry, paint, conductive coatings and biosensors.

A suspension of nanoparticles in a Casson fluid is referred to as a Casson nanofluid. Non-Newtonian fluids, known as Casson fluids, have a nonlinear viscosity relationship and yield stress. Such fluids can display improved thermal and flow characteristics relative to the basic fluid when nanoparticles are introduced, thus creating a nanofluid. Owing to their high thermal conductivity, nanoparticles in the Casson nanofluid can increase heat transfer capabilities, resulting in better convective heat transfer. Overall, compared with standard fluids, Casson nanofluids have the potential to offer improved heat transfer performance, which makes them appealing for a variety of technical and industrial applications that demand effective heat transfer and flow properties. Casson fluid models are applied in surveys of blood movement, viscoelastic performance of tissues and modelling of various biogenetic fluids. Understanding the rheological properties of blood is crucial in areas such as cardiovascular disease research, medical device design and drug delivery systems.

A study was conducted by Nadeem et al. [16] on the MHD movement of a Casson fluid across an accelerated shrinking sheet using the Adomian Decomposition Method. In their investigation, Dharmaiah et al. [17] employed nanofluid and perturbation method to solve nonlinear ordinary differential equations (ODEs). By using these methods, researchers were able to analyze the behavior of the nanofluid system under study. Rajesh et al. [18] conducted a numerical study using the Crank-Nicolson technique to analyze the heat transfer in the flow of a hybrid nanofluid (Ag-CuO/water) passing a cylinder that is moving and oscillating. Jawad et al. [19] explored the 2D MHD stagnation point flow of a hybrid nanofluid over a stretching/shrinking sheet using the Homotopy Analysis Method. The nanofluid that they have used consists of alumina and copper nanoparticles in a water base, demonstrates improved thermal characteristics in contrast to typical fluids and has numerous biomedical and engineering applications. The Lattice Boltzmann method is a viable approach for simulating unsteady flow. Afra et al. [20] have examined the integration of the Lattice Spring Method (LSM) with the Immersed Boundary-Lattice Boltzmann Method (IB-LBM) to study the interaction between fluids and elastic bodies in dynamic situations. They specifically explored the influence of the presence of a slender filament on the hydrodynamic forces acting on two consecutive cylinders. Using Laplace transform technique, references [21–24] examined the impacts of MHD over an inclined plate.

Sharma et al. [25] investigated the influence of radiation absorption on the thermophysical properties of nanofluids consisting of and titanium oxide (TiO2) in water using the Laplace transform technique. The drug delivery system greatly benefits from the anticancer properties of nanoparticles given by Rathore et al. [26]. Hussanan et al. [27] have created precise solutions for the MHD flow of nanofluids consisting of water passing an infinitely accelerating vertical plate within a porous medium. Their findings indicated that -water nanofluids exhibit superior heat transfer performance compared to -water and -water nanofluids. Vemula et al. [28] conducted an analytical study focusing on the flow and heat transfer characteristics of nanofluids near an infinitely vertical plate that was exponentially accelerating. The investigation considered several factors, including the presence of a magnetic field, thermal radiation, variable plate temperature and the use of nanofluids containing various nanoparticles such as aluminum oxide, copper, titanium oxide and silver, with nanoparticle volume fractions below 0.04. Rao et al. [29] examined the unsteady MHD free-convection flow of a Casson fluid past an infinitely tall vertical porous plate that was exponentially accelerated. Their study also considered the impact of radiation absorption and heat generation/absorption and employed the Laplace transform technique for analysis. Asjad et al. [30] conducted research where they investigated how the utilization of water-based drilling clay nanoparticles could improve heat transfer properties in the case of fractional Maxwell fluid flow over an infinite flat surface using Laplace transform technique.

Medical applications of an infinite vertical plate along with heat transfer have garnered significant interest in the literature, namely, hyperthermia treatment, cryosurgery and thermotherapy. Elangovan et al. [31] developed a theoretical solution for -- nanofluid MHD flow and investigated its possible biological uses. The distribution of medicine has been shown to be useful in increasing temperatures, which suggests its possible use in the field of cancer treatment. In a theoretical and numerical investigation, Zaman et al. [32] investigated irregular pulsing blood movement via blood vessels (arteries) with both blockage and aneurysm. The study considered the manifestation of nanoparticles (, and ) in blood movement. Arpitha et al. [33] conducted a study to analyze the thermal transfer characteristics of Casson fluid movement over an rising and compressing medium. The study incorporated SWCNT, , and nanoparticles suspended in water. The findings of this research contribute to a better understanding of various applications, such as body fluid streams in compressing tubes, biological Enhanced Oil Recovery (EOR) and gas-containing geological formations. A study on the nonlinear development of a magnetized Casson nanofluid flowing on a flat surface without an end was conducted by Waqas et al. [34] by considering as the base fluid and , , and as the nanoparticles. Kot et al. [35] research focused on a hybrid nanofluid consisting of gold and Titanium Oxide nanoparticles in blood, commonly employed for medical purposes like cancer treatment. Their study involved the development of a mathematical model that accounted for the heat transfer and its solution using Laplace and finite Hankel transforms. The most common photocatalyst is titanium dioxide (). Owing to its photocatalytic properties, which enable targeted drug delivery, it has the potential to eradicate cancer tumors [36,37].

1.1 Novelty

The previously mentioned studies served as creative sparks in the present study. This subsection explains the importance of the heat transfer characteristics of Casson nanofluids. Owing to the inspiring engineering applications of Fig. 1 and the present study, we focus on the transfer of heat and thermal radiation in an MHD flow involving a non-Newtonian Casson nanofluid and over an unbounded, vertically advancing porous surface with exponential acceleration, along with rotating effects. Based on the authors understanding and information, the current study is deemed original and has not been previously investigated, as evidenced by a thorough examination of previously published research. The novel objectives of this study are summarized as follows:

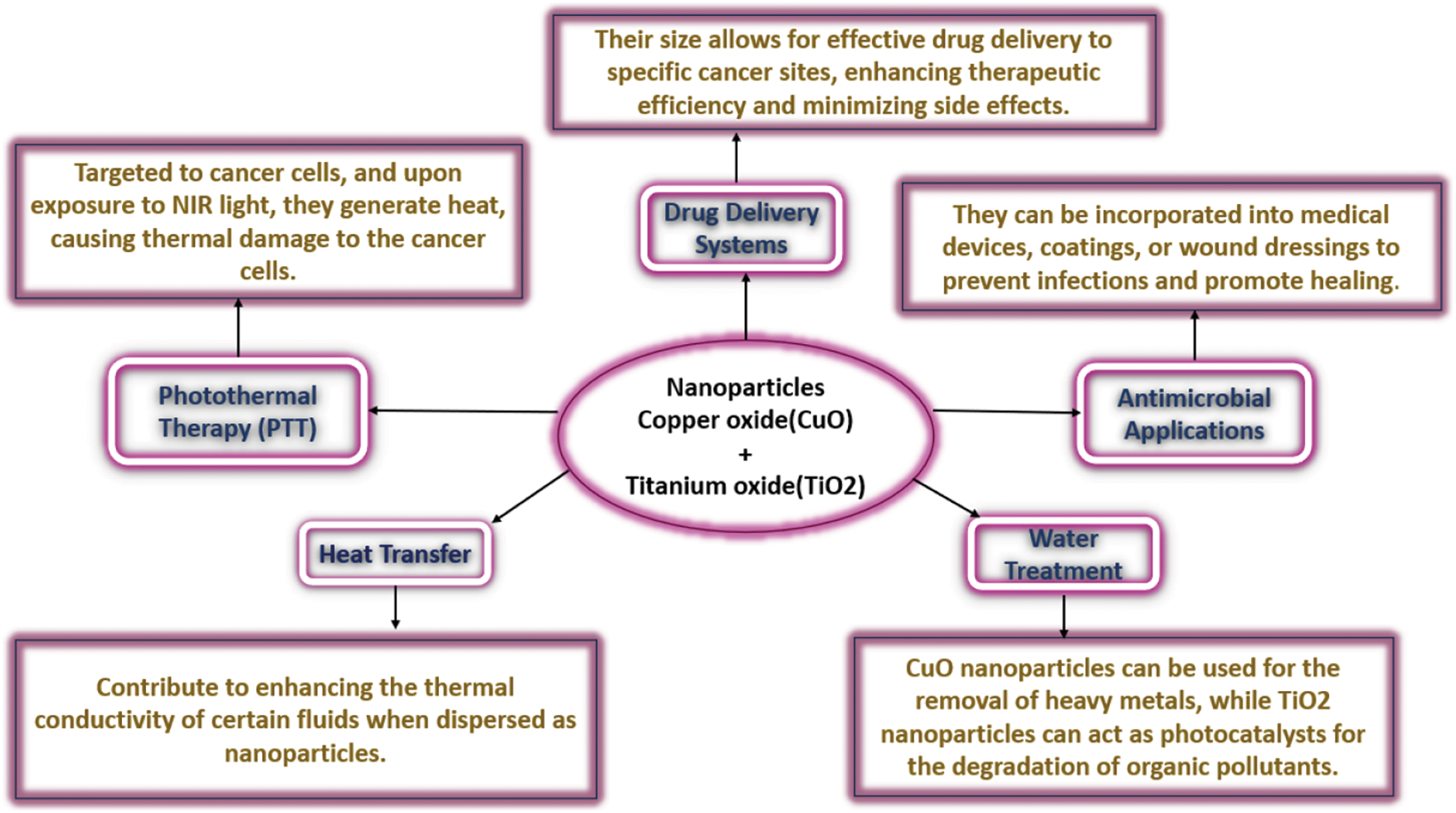
Figure 1: Some applications of + nanoparticles

•   The heat source/sink was incorporated into the heat transfer analysis to evaluate its significance in the heat transfer mechanism.

•   The heat transfer rate varies with changes in the volume percentage of solid particles and energy parameters.

•   This study provides an accurate analytical solutions that are not commonly found in existing literature.

•   Nanoparticles contribute to applications in cancer treatment when subjected to heat, making them useful in drug delivery systems.

2  Mathematical Formulation

We consider a situation in which the radiative, time-varying magnetohydrodynamic flow of an electrically conductive Casson nanofluid (specifically nanoparticles suspended in water ) flows over an infinitely extending vertical porous surface that is exponentially accelerating. This scenario was analyzed with rotating effects. Here -axis represents the upward direction along the surface, the -axis is perpendicular to the surface, and the y-axis be perpendicular to both the -planes. In this setup, we examined a scenario in which both the solid plate and fluid were subjected to the rotation of a rigid body. This rotation occurs uniformly with an angular velocity around the -axis. At the starting point, that is, when = 0, both the surface and neighboring fluid are in a restful state with a consistent temperature and concentration , which are representative of the surrounding free-stream conditions and are located some distance away from the outer layer.

After the moment(time) 0, the plate begins to accelerate along the -center (axis) direction owing to the influence of the gravitational field. This acceleration is proportional and can be described by the velocity equation, , where represents the characteristic velocity. The rotation around the direction introduces a lateral force to the movement, resulting in lateral speed slopes (referred to as perpendicular flow), effectively making the movement 2-dimensional. Here, the fluid movement is influenced by a consistent and uniform magnetic field () aligned in the direction. It is assumed that the impact of the magnetic field induced by fluid motion is negligible compared to the externally applied magnetic field. The nanofluid consisted of a combination of and nanoparticles suspended in water . Fig. 2 illustrates the physical flow of this problem. The thermophysical characteristics of this nanofluid are presented in Table 1.

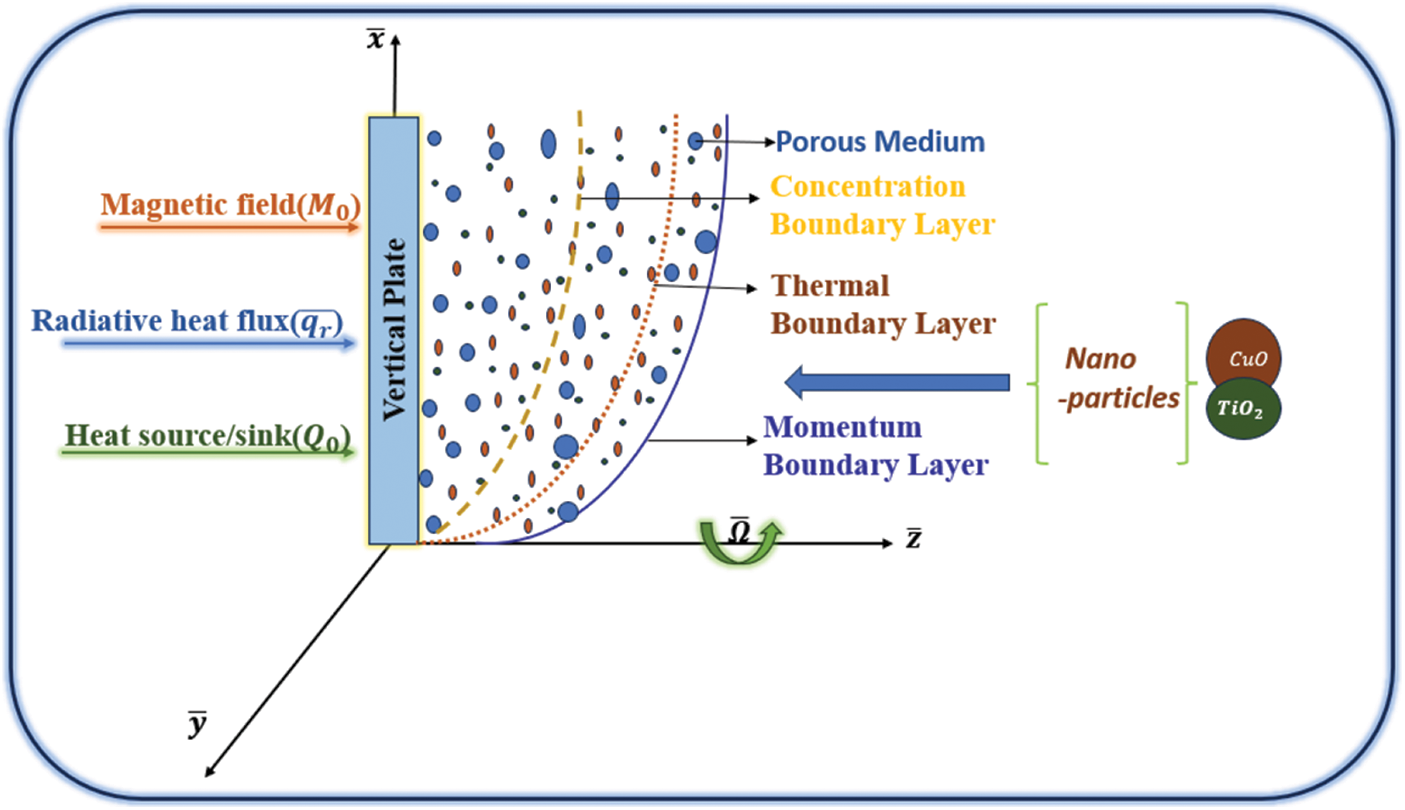
Figure 2: Physical model of the problem

The equations of momentum, energy and concentration are derived as follows [38–40]:

(1)

(2)

(3)

(4)

With the appropriate boundary constraints:

(5)

Azzam [43] noted that self-absorption occurs alongside emission in the occasion of an perceptually thick fluid, and the intake coefficient is often wavelength-dependent and considerable [44]. Therefore, the Rosseland [45] approximation for the radiative flow path, is adequate.

(6)

Because the temperature changes during the flow are thought to be relatively minor, can be represented as a straight line of temperature. To achieve this, higher-order terms were omitted in favor of an enlarged Taylor series characterizing .

(7)

Therefore, it is obtained as

(8)

Eqs. (7) and (8) in Eq. (3) are used to get

(9)

2.1 Thermophysics of Nanofluids

As previously noted, despite being a topic of innumerable literary works, classical models are still useful for determining thermophysical qualities. However, this is uncertain in the case of nanofluids. The outcomes of the tests enable us to choose the optimal model for a certain attribute. The nanofluid is described as follows:

(10)

The thermal capacity of a nanofluid is (Khanafer et al. [46]) in their study:

(11)

The thermal conductivity of the nanofluid for spherical nanoparticles are (Maxwell’s model [47]) model as follows:

(12)

(13)

The dynamic viscosity of the nanofluid is provided by the Brinkman’s model [48],

(14)

is solid volume fraction, is nanosolid particles, and is base fluid.

The introduction of non-dimensional quantities is

(15)

Using the above Eq. (15) in Eqs. (1) to (4), we have

(16)

(17)

(18)

(19)

(20)

The values of

(21)

(22)

(23)

(24)

(25)

(26)

(27)

Non-dimensional version of the constraints are

(28)

Using the replacement H = u + iv, Eqs. (16) and (17) can be written as

(29)

(30)

(31)

The initial and boundary constraints on non-dimension are

(32)

3  Analytical (Exact) Solution

This term specifies the physical factors that have been shown. The equations governed by the flow in non-dimensional form, listed from Eqs. (29) to (31), solved with associated initial condition, along with the conditions defined at boundaries Eq. (32), by the usual Laplace transform technique and the resultant solutions are derived in form of exponential function.

(33)

(34)

(35)

For inverse Laplace transformations of Eqs. (33) to (35), we get

(36)

(37)

(38)

(39)

(40)

(41)

(42)

(43)

(44)

(45)

(46)

(47)

(48)

(49)

(50)

(51)

The Appendix A contains sources for the expressions.

3.1 Engineering Interest in Quantities

The data of the Nusselt number(Heat transfer), the Sherwood number(Mass transfer) and the skin friction are calculated from the non-dimensional form as a result,

3.2 Nusselt Number

From the fluid temperature, heat flow rate can be computed from the non-dimensional form

(52)

3.3 Sherwood Number

From the concentration profile, mass flow rate can be computed from the non-dimensional form

(53)

3.4 Skin Friction

From the fluid velocity, friction flow rate can be computed from the non-dimensional form

(54)

The Appendix A contains sources for the expressions.

4  Results and Discussion

The process is governed by certain non-dimensional factors, which include the Hartmann number (M), permeability parameter (), rotation parameter (), heat source/sink parameter (), Casson fluid parameter (), acceleration parameter (), thermal Grashof number (), mass Grashof number (), solid volume fraction (), chemical reaction parameter (), Schmidt number () and time (). These parameters play a crucial role in determining the flow behavior and characteristics. For theortical results we used = 0.71, = 0.6, = 2, = 5, N = 1, = 1.5, = 1, M = 1, = 1, = 1, = 0.5, = 0.5, = 0.01 and = 1.5. These values were considered consistent throughout the study, except for the different values in the relevant figures and tables.

4.1 Behavior of Velocity Distribution

4.1.1 Effects of Thermal Grash of Number ()

Fig. 3a illustrates the unique effects of thermal Grashof number . It is observed that the aforesaid fluid speeds(velocities) ( and ) of the nanofluids increase as increases. The thermal Grashof number signifies the balance between the buoyancy force owing to temperature variations and the opposing force of the fluid thickness. This dimensionless factor, known as the Grashof number, connects the heat and mass transfer in natural convection when a solid surface is immersed in a fluid, driven by temperature changes. Consequently, the thermal buoyancy force tends to speed both the primary and secondary velocities of the fluid in the boundary layer region in both cases. Consequently, the resulting speed and width of the velocity layer increase with large values of for both scenarios. Additionally, the growing thermal buoyancy force, which is associated with temperature differences, makes gravity more influential. Exponential acceleration enhances convective effects in the flow, contributing to an increase in the velocity profile.

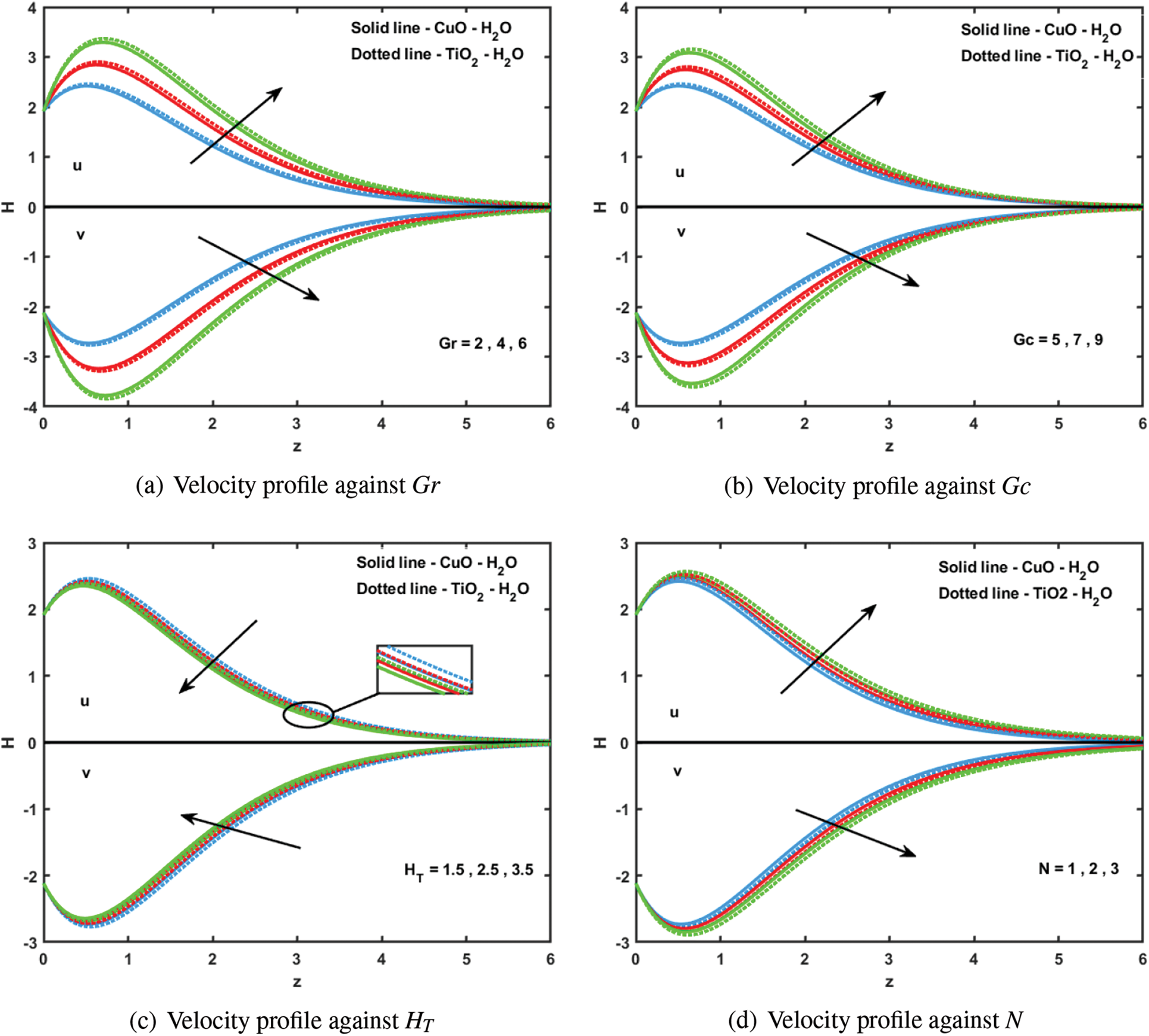
Figure 3: Velocity profile for various (a) (b) (c) and (d) N

4.1.2 Effects of Mass Grash of Number ()

When increases, an increasing trend is observed, as reflected in Fig. 3b. The fraction of buoyant energy to drag energy was determined by the mass Grashof number. With an increase in the species buoyancy force, the fluid velocity profiles ( and ) of the nanofluids also increase and become more pronounced. Consequently, the breadth of the momentum boundary layer increased as increased. As increased, the species buoyancy force became more prominent, leading to a notable increase in the velocity of the nanofluid. This heightened species buoyancy force imparts a distinctive quality to the velocity distribution with the fluid achieving a notable maximum velocity within the medium. In essence, an increase in enhances the influence of species buoyancy, thereby influencing the velocity profile of the nanofluid.

4.1.3 Effects of Heat Source/Sink Parameter ()

Fig. 3c clearly illustrates how affects primary and secondary velocity profiles of nanofluids. As increased, a decreasing trend in the velocities was observed. The presence of a heat source/sink results in the formation of heat from the surface, thereby reducing thermal conditions in the flow field. Hence, the existence of was observed to have a beneficial effect in reducing the velocity profiles.

4.1.4 Effects of Thermal Radiation Parameter (N)

Fig. 3d depicts the relationship between N and the primary and secondary velocities. An escalation in N implies the emission of thermal energy from the flow region. With elevation in the velocity profiles, there is an increased level of fluid motion and interaction within the flow region. It is evident that an increase in N leads to a significant increase in both the velocities. This outcome can be clarified by evidence that N diminishes the thermal buoyancy force, leading to a thinner thermal boundary layer. As the radiation parameter increases, signifying a heightened release of thermal energy, this extra heat has the potential to augment the overall kinetic energy of fluid particles. Simultaneously, as the velocity profiles increased, this indicated an enhanced pace of fluid motion and interaction within the flow region.

4.1.5 Effects of the Hartmann Number (M)

Fig. 4a shows the effect of M on the primary () and secondary () velocity profiles of the nanofluids. Both and decreased near the plate and this trend continued across the fluid. The presence of magnetic effects leads to an unexpected reduction in the velocity near the surface, affecting the velocity distribution at all points. In addition, the magnetic field exerted a retarding effect on the entire velocity field. This phenomenon arises from the introduction of a transverse magnetic field perpendicular to the flow direction, which generates a Lorentz force. The Lorentz force acts as a drag opposing the flow across the entire fluid region. Consequently, applying a magnetic field to a permeable material results in a decrease in the overall speed dispersion and width of the velocity layers.

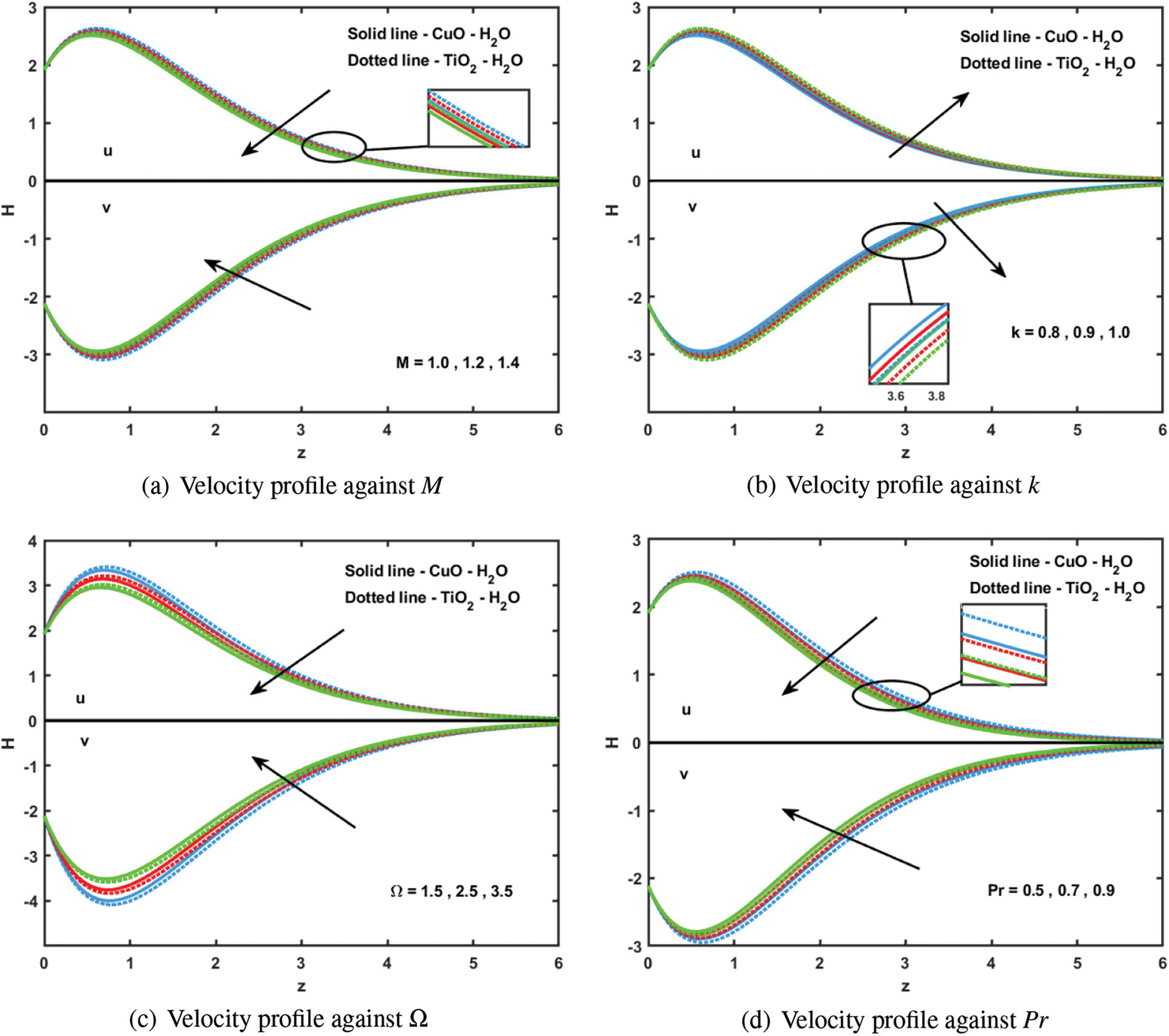
Figure 4: Velocity profile for various (a) M (b) (c) and (d)

4.1.6 Effects of Permeability Parameter ()

Fig. 4b shows the effect of on the velocity ( and ) components of the nanofluids. As increases within the nanofluid medium, both the primary velocity component () and magnitude of the secondary velocity component () also increase. When greater values of were present, the final velocity and density of the boundary momentum gradient were enhanced. On the other hand, lower values of permeability lead to lower nanofluid velocities within the flow medium containing a mixture of nano-liquids. Therefore, it was observed that an increase in the permeability parameter enhanced the overall velocity profile throughout the fluid section. This behavior is indicative of the influence of permeability on fluid speed and momentum boundary layer thickness.

4.1.7 Effects of Rotation Parameter ()

Fig. 4c shows how influences the primary and secondary velocity profiles of and nanofluids when the plate is accelerated. As the rotation parameter increases, the primary velocity decreases, and the secondary velocity component decreases across the entire fluid domain. This suggests that in the case of and nanofluids with ramped temperature, rotation tends to scale down the primary velocity within the surface layer. Despite the known impact of rotating effects on the secondary fluid velocity owing to its suppression of the primary fluid velocity, these accelerating effects are primarily noticeable near the plate surface. However, at a distance from the surface, the rotation had the same effect on the secondary fluid velocity. This is attributed to the dominance of the Coriolis force within the fluid medium along the rotating path.

4.1.8 Effects of the Prandtl Number ()

In Fig. 4d, a higher of and nanofluids is often related to a thicker thermal boundary layer compared to the momentum boundary layer. As the increases, the primary velocity decreases, also the secondary velocity component decreases across the entire fluid domain.As the plate accelerates, the thicker thermal gradient zone can result in a more efficient thermal transfer between and nanofluids and the plate. A higher Prandtl number indicates an increased impact of viscosity on fluid flow dynamics. Viscosity hinders the movement of fluid layers, resulting in a decline in velocity.

4.1.9 Effects of Acceleration Parameter ()

Fig. 5a shows the significance of on the primary() and secondary() velocities of and nanofluids. There is a positive correlation between and both velocities, indicating an increasing trend in the velocities as the acceleration parameter increases. An elevated acceleration parameter implies the application of a more significant force to propel the fluid along its flow path. This force results in the acceleration of fluid particles, leading to an increase in their velocity profile. Essentially, the fluid underwent a more substantial push in the direction of acceleration.

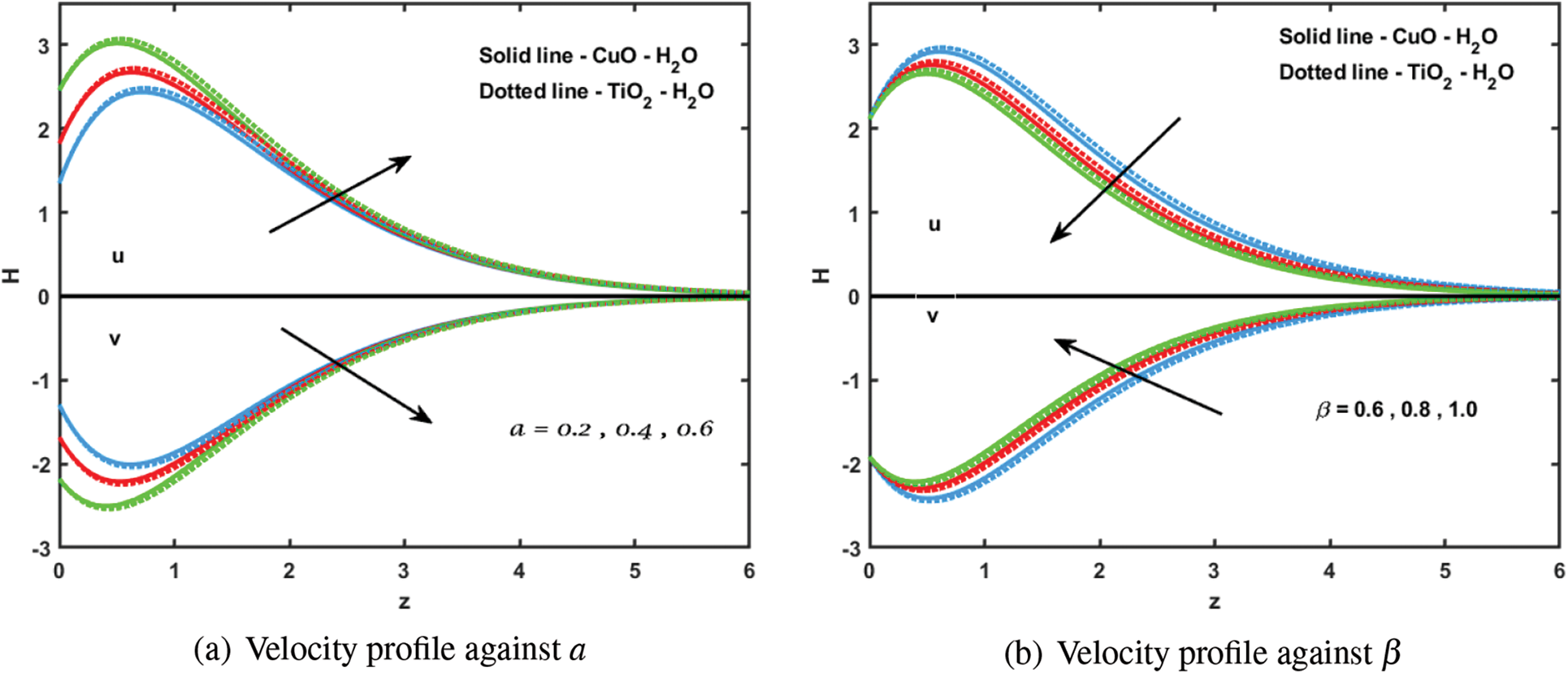
Figure 5: Velocity profile for various (a) and (b)

4.1.10 Effects of the Casson Fluid Parameter ()

Fig. 5b shows the impact of on the primary() and secondary() velocities of and nanofluids. Both velocities were shown to decrease as the value of increased. Furthermore, it is shown that has little effect on the and nanofluids as they travel away from the boundary. In the case of a high Casson parameter value, the nanofluid behavior simulates that of a Newtonian fluid with lower velocities compared to non-Newtonian fluids. Higher values of imply that the fluid requires greater force or stress to initiate and sustain the flow. This increased resistance to flow hinders the fluid from responding easily to applied forces or pressure gradients, leading to a reduction in the velocity profiles.

4.2 Behaviour of Temperature() Distribution

In Figs. 6a–6d, the flow domain is marked by a smooth temperature gradient() and nanofluids. Fig. 6a shows the impact of the heat source/sink parameter() on the temperature() profile. It is observed that the temperature() decreases as increases. denotes the degree of heat generation or absorption within the system. With an increase in , the energy equilibrium of the system is affected. In a system experiencing an increase in , the temperature typically decreases, primarily because of an elevated rate of heat extraction in the presence of a heat sink. In Fig. 6b, it can be observed that an increase in N prompts an increase in temperature(). The thermal radiation parameter(N) indicates the efficiency of the radiative heat transfer in the system. This improved radiative heat transfer contributed to an increase in the overall thermal energy of the system. The absorbed radiation added to the internal energy of the system, resulting in an elevated temperature(). Furthermore, in Fig. 6c, an increase in indicates a fluid with low thermal diffusivity, an outcome with a slight temperature decrease at all points. Higher values of indicate a slower response of the fluid to temperature change. The resulting thicker boundary layers and reduced heat transfer coefficients associated with a higher contribute to a slower heat transfer process, leading to a decrease in the temperature() profile. Additionally, Fig. 6d demonstrates that with the passage of time, the plate temperature() increases, as the boundary condition dictates that the plate temperature equals time(). The increase in the temperature() profile with time() is due to the accumulation of thermal energy within the system and variations in time-dependent boundary conditions.

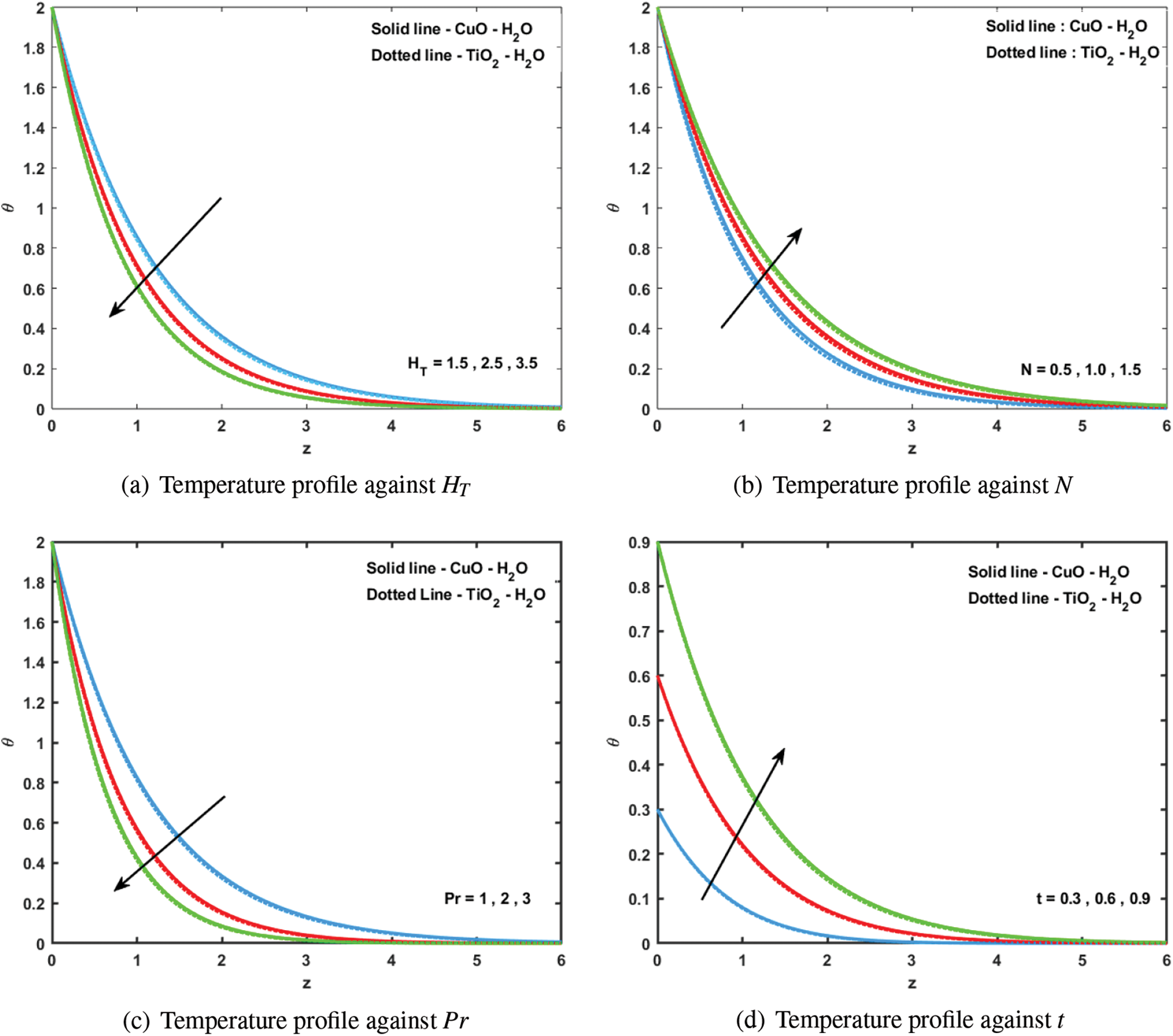
Figure 6: Temperature profile for various (a) (b) N (c) and (d)

4.3 Behaviour of Concentration(C) Distribution

Figs. 7a and 7b show the range of changes in the concentration(C) that occur throughout the flow domain. Fig. 7a shows that an upgrade in the chemical reaction parameter causes rapid shrinkage in the concentration(C) profile. This is explained by the certainty that an increased number of dispersed particle elements pass through , resulting in a reduction in C. Destructive chemical reactions significantly reduce the width of the concentrated surface layer. Chemical reaction parameters have the potential to shift the stability of the chemical system. An increase in this parameter tends to drive the system towards a state in which the concentration of specific species is minimized, leading to a swift reduction in the concentration profile. In Fig. 7b, it can be observed that the concentration level drops everywhere in the flow zone, where higher values of , which indicate heavier species with lower diffusivity, are present. Elevated Schmidt numbers result in diminished mass transfer coefficients, indicating a less efficient transport of species through the fluid. This reduced efficiency contributed to a slower mass transfer process, leading to a rapid contraction of the concentration profile.

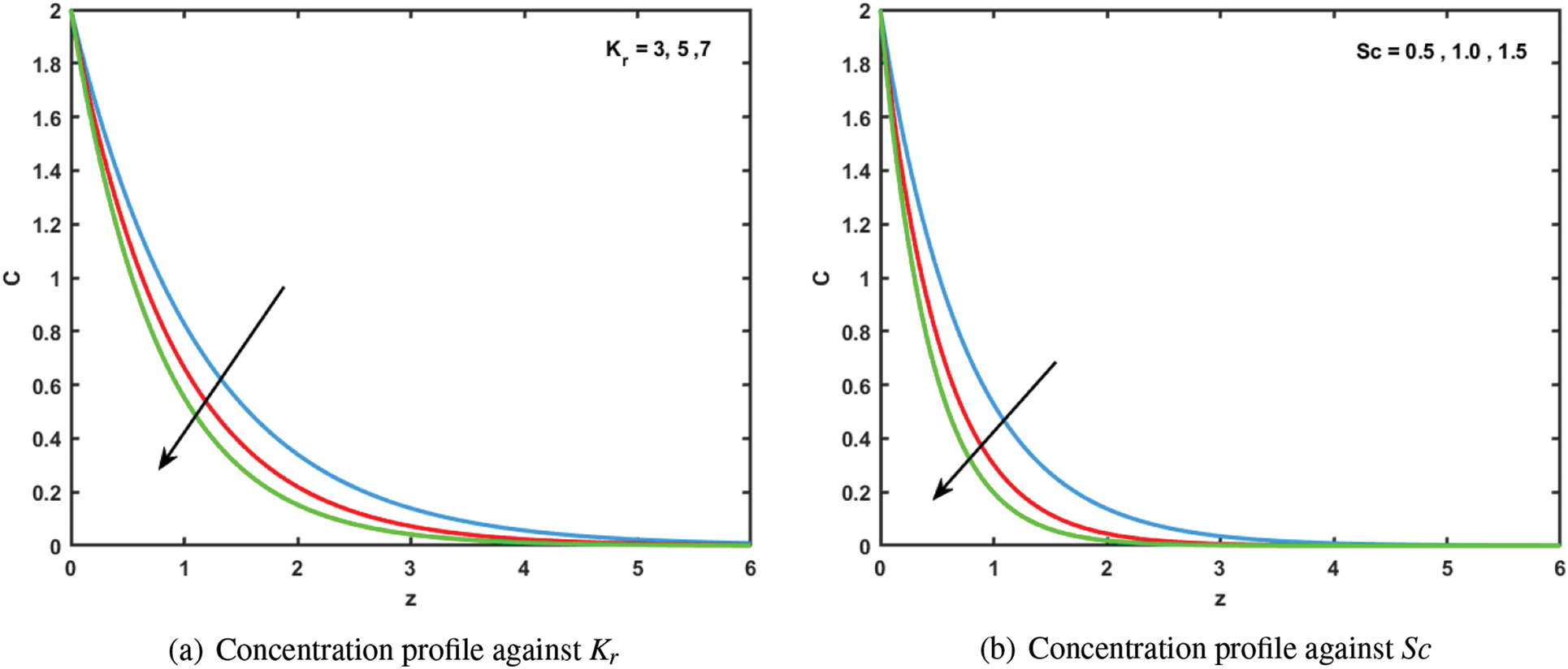
Figure 7: Concentration profile for various (a) and (b)

4.4 Investigation on the Nusselt(Nu) and Sherwood(Sh) Numbers

Figs. 8a–8d show the variation in the changes in and numbers that occur throughout the flow domain. Fig. 8a shows that an upgrade in the Prandtl number causes a rapid increase in profile. In a time-dependent scenario, an increase in the Prandtl number enhanced the transient heat transfer efficiency. The fluid provides a quicker response to temperature changes, facilitated by improved thermal diffusivity, leading to a more rapid transmission of heat and consequently, a swift increase in the Nusselt number. In Fig. 8b, there is a sudden increase in with increasing values of . A higher heat source/sink parameter can enhance the fluid motion and promote convective heat transfer. When combined with the radiative heat exchange facilitated by a higher thermal radiation parameter, the overall heat transfer efficiency increased, leading to an increase in the Nusselt number. In Fig. 8c, it can be observed that the heat transfer decreases everywhere in the flow zone where higher thermal radiation parameter(N). With an increase in the thermal radiation parameter, the system became less responsive to changes in the heat source/sink parameter. This is due to the fact that radiative heat transfer is less affected by local thermal conditions and is more efficient in evenly redistributing thermal energy across the entire flow zone. As shown in Fig. 8d, and increase with an increase in the Sherwood number(), which represents the rate of solutal concentration at the wall surface. This suggests that greater chemical reaction rates in heavier species are associated with a rising rate of medium concentrations at the surface. likely influences the rate of chemical reactions within the system. If the Sherwood number() increases with time, this implies that the chemical reactions are becoming more prominent and efficient.

Figure 8: Heat transfer for (a) and (b) N (c) and Mass transfer for (d) &

4.5 Analysis on Heat Transfer

Figs. 9a–9c show the heat transfer changes between the solid volume fraction() and certain energy parameters. As shown in Fig. 9a, the heat transfer increases with increasing values of . The increase in heat transfer with higher values of the heat source/sink parameter is due to the enhanced convective heat transfer resulting from the injection or extraction of heat. This leads to improved thermal mixing, steeper temperature gradients and an overall increase in the heat transfer efficiency. Fig. 9b demonstrates that as the effect of N increases, there is a drop in heat transfer. An increase in N, as observed in with the solid volume fraction(), is linked to the dominance of radiative heat transfer over convective heat transfer. These effects include reduced convective efficiency, thermal stratification, decreased temperature gradients and weakened thermal boundary layers. Finally, Fig. 9c displays higher values of the Prandtl number and it can be observed that the heat transfer increases everywhere. The increase in heat transfer with higher values of the Prandtl number, as reflected in the Nusselt number with the solid volume fraction, is rooted in the dominance of thermal diffusivity. This dominance leads to improved thermal conduction, steeper temperature gradients, enhanced convective heat transfer and stronger fluid motion, collectively contributing to higher heat transfer efficiency.

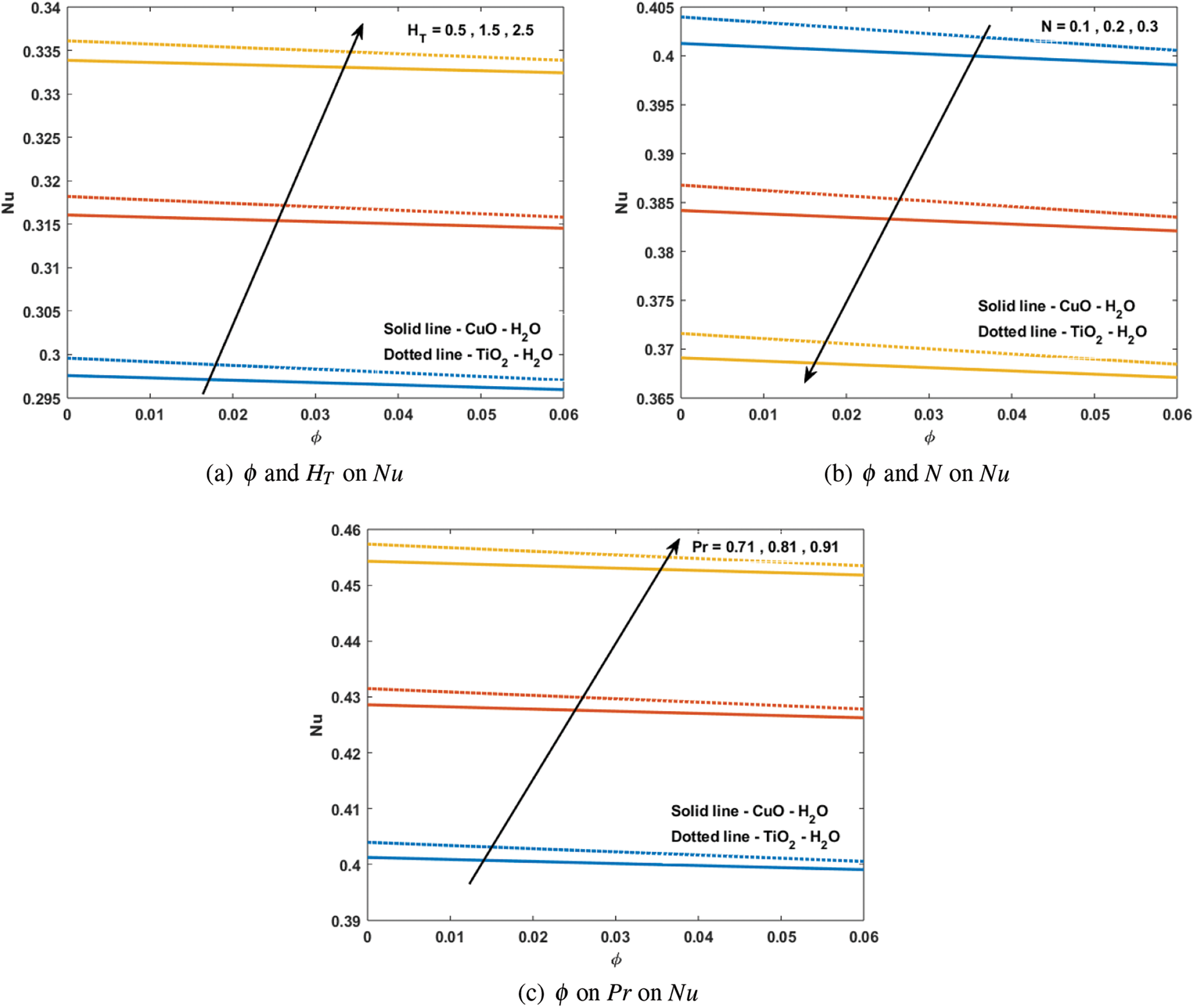
Figure 9: Heat transfer against (a) and (b) N and (c)

Table 2 lists the variations in the Nusselt number(heat transfer) for and resulting from the distinct values of the key variables. This specifically highlights how the thermal radiation parameter, heat source/sink parameter, Prandtl number and time influence the temperature slope. Generally, higher values of Prandtl number, heat source/sink parameter and time lead to a larger Nusselt number. Conversely, the thermal radiation parameter had a dissimilar result for the Nusselt number across all thermal scenarios. This trend indicates that an increase in the Prandtl number, heat source/sink parameter and time results in an increased Nusselt number, whereas a decrease in the thermal radiation parameter is associated with the same outcome. This suggests that nanofluids with lower radiative properties and higher thermal diffusivity promote a higher rate of thermal diffusion in the outer flow. Table 3 displays the alterations in Sherwood number across the dissimilarity values of the main variables. In all situations, it can be noted that the Sherwood number (Mass transfer) value rises with rising Schmidt number, chemical reaction parameter and time.

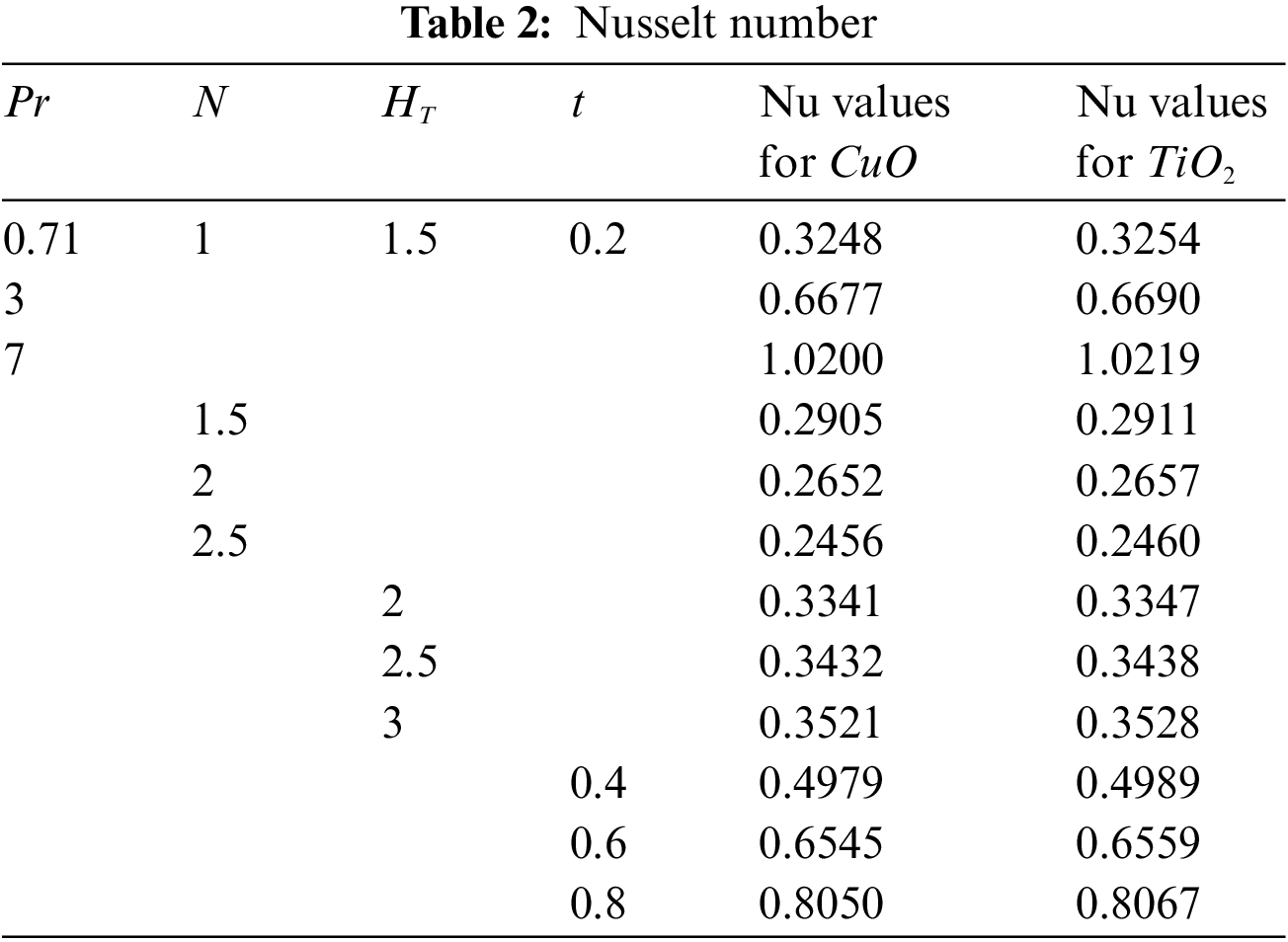
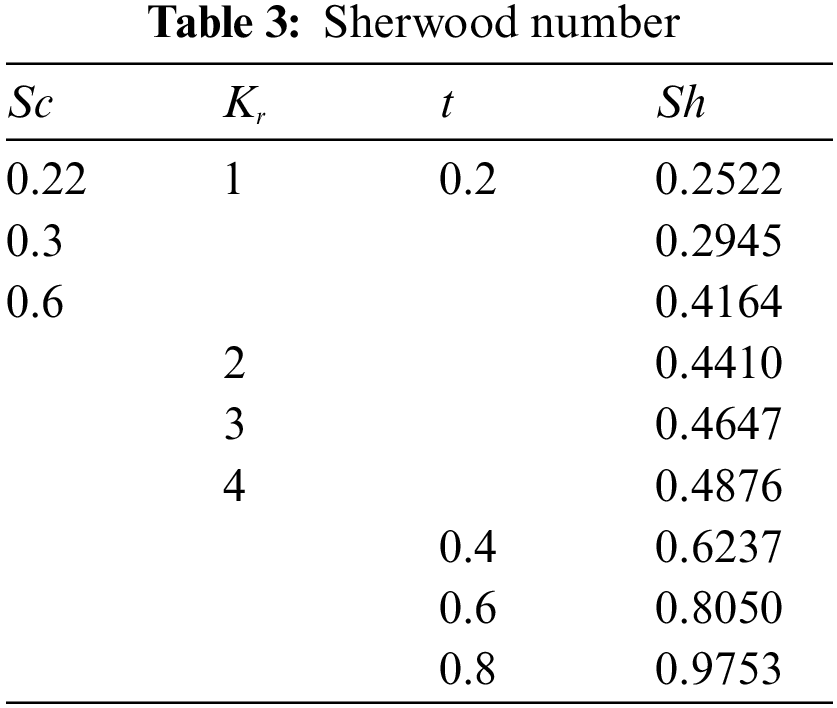
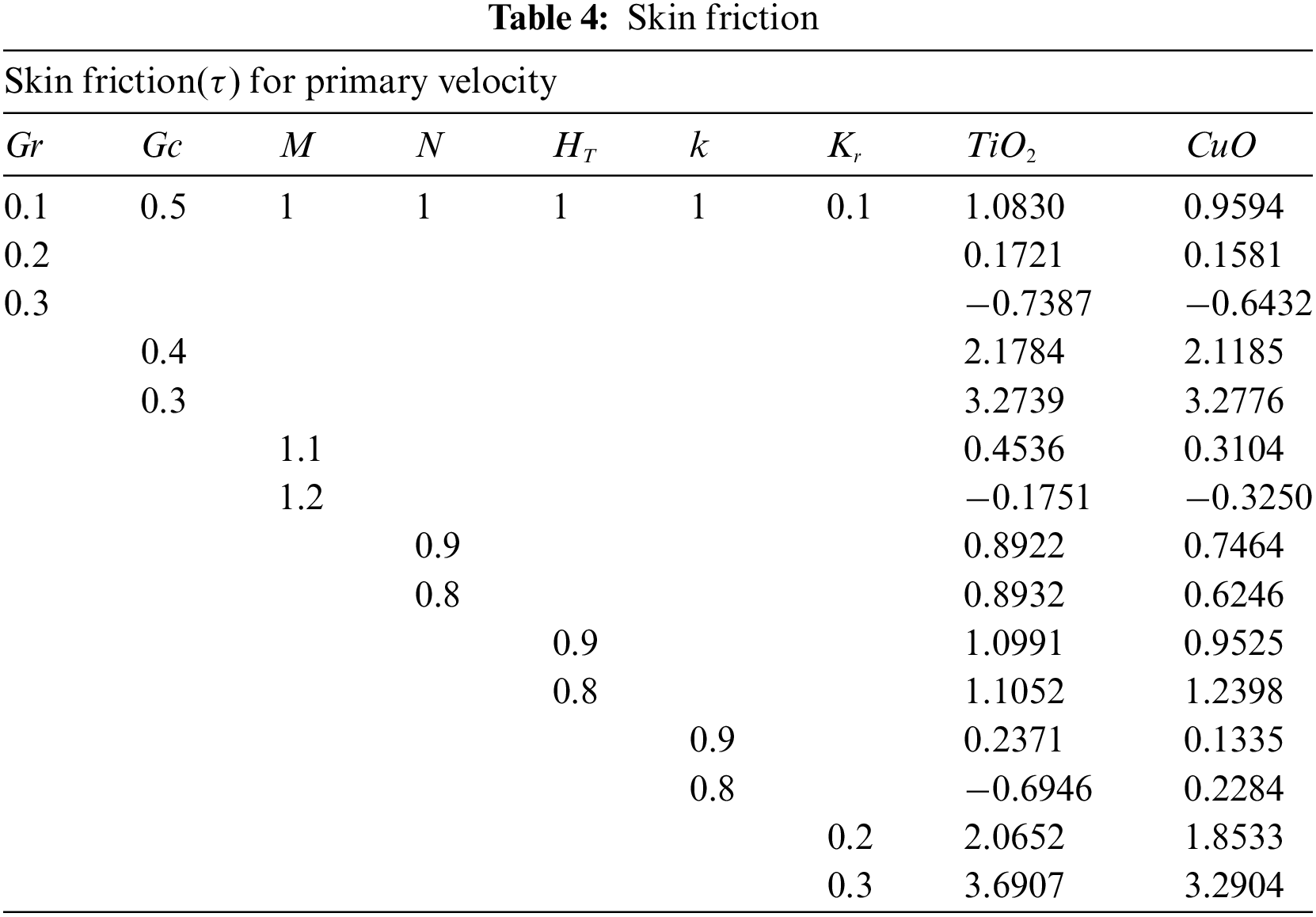
Table 4 highlights the changes in the primary flow velocity of and nanofluid for various parameters with = 0.71, = 0.6, = 0.01, = 0.1, = 0.5, = 0.1, = 0.3. A higher thermal Grashof number often results in enhanced thermal(heat) transfer rates owing to the increased convective thermal exchange. This can lead to a more efficient transfer of heat between the plate and fluid, causing the fluid to move more effectively and reduce the velocity gradient. Depending on the concentration and nature of the nanoparticles, the fluid behavior can change. If the nanofluid viscosity decreases significantly owing to the presence of nanoparticles, this could contribute to an increase in the velocity gradient. The nanofluids used are highly conductive and their behavior within a magnetic field can be influenced by electromagnetic forces. These forces might interact with the magnetic field to further suppress the fluid motion and velocity gradients. With increasing radiative heat transfer, convective heat transfer may become relatively less significant. Convective heat transfer is often associated with fluid motion and velocity gradients. If convective heat transfer decreases owing to increased radiation, it can result in less efficient mixing and subsequently, a steeper velocity gradient. In cases with reduced heat source/sink effects, the convective heat transfer might become less significant. Convective heat transfer is often associated with the fluid motion. A decrease in convective heat transfer owing to weaker heat generation or absorption could lead to less efficient heat transport and a steeper velocity gradient. A decrease in permeability might lead to a more pronounced interaction between the nanofluid and porous structure. This interaction can introduce additional resistance and drag on the fluid flow, resulting in a reduced overall fluid velocity and consequently, a lower velocity gradient. Chemical reactions can influence the turbulence and flow instability. As the chemical reaction parameter decreases, the turbulence levels might be reduced, resulting in smoother fluid motion and lower velocity gradients.

5  Code Validation

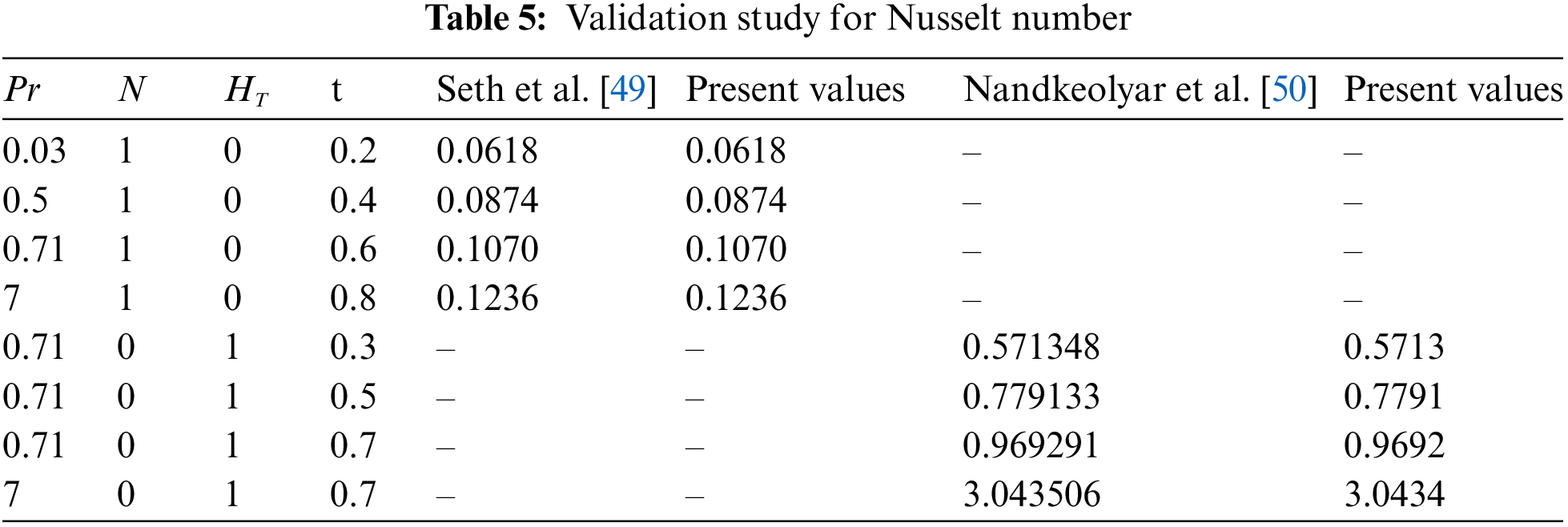
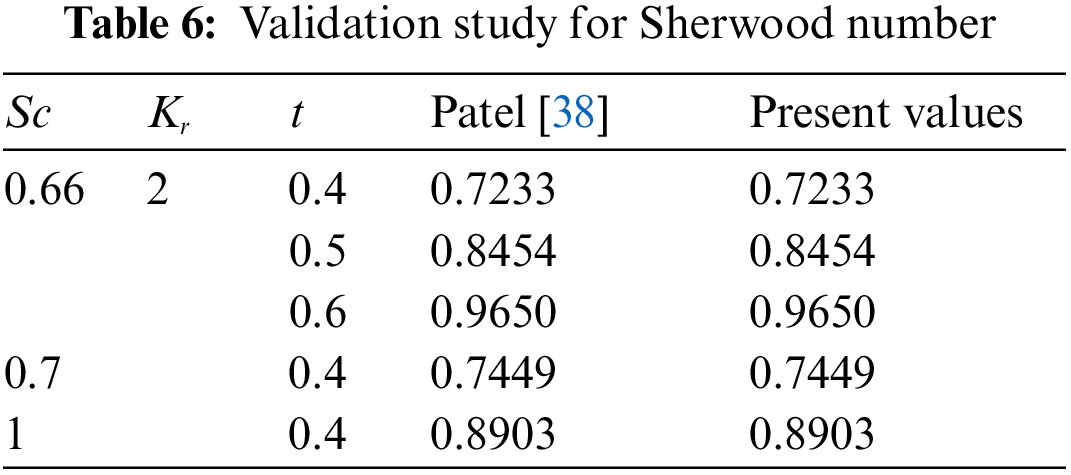
The precision of the computational techniques was simulated using MATLAB software employing Laplace transformation methodology. Using the MATLAB code, the Nusselt and Sherwood numbers were computed and are presented in Tables 5 and 6 for various values of relevant parameters, including the thermal radiation parameter, heat source/sink parameter, chemical reaction parameter and Schmidt number. Similarly, applying the same procedure to previous studies by setting = 0 (Seth et al. [49]), setting N = 0 (Nandkeolyar et al. [50]), and (Patel [38]), the results obtained are consistent with the aforementioned description and are illustrated in Tables 5 and 6, respectively, encompassing a range of significant parameter values. These congruent outcomes were observed across all three cases, indicating the accuracy and reliability of the coding approach.

6  Conclusion

This investigation focuses on the analysis of unsteady radiative (MHD) movement involving an incompressible, thick and electrically conductive nanofluid, and with non-Newtonian behavior following the Casson model. The fluid behavior above a porous vertical surface undergoing rapid exponential acceleration that was influenced by a rotating frame was examined analytically using the Laplace transform technique. The study led to the following conclusions:

•   The velocity profiles experience a decline owing to the upsurge implication of the rotation effects, Hartmann number, heat source/sink parameter, Prandtl number and Casson fluid parameter.

•   Raising the thermal radiation and time results in an elevation of the temperature profiles, whereas the opposite trend is observed in the temperature profiles for increasing the heat source/sink parameter and the Prandtl number.

•   The temperature of the Casson nanofluid was partially greater than that of the Casson nanofluid .

•   The concentration decreases as the Schmidt number and chemical reaction parameter increase.

•   The Nusselt number increases with an increase in the heat source/sink parameter and decreases with an increase in the thermal radiation parameter.

•   Elevated Schmidt numbers and chemical reaction parameters result in an increase in the Sherwood number.

•   The influence of thermal radiation, heat source/sink, Prandtl number and solid volume fraction plays a vital role in the evolution of heat transfer.

•   The Nusselt and Sherwood number in the current study closely matched the findings of previously published studies.

•   The current issue has broader applications in the fields of thermal medicine and cancer treatment.

Acknowledgement: The authors are greatly obliged and thankful to the reviewers for their valuable suggestions, which helped to improve the manuscript.

Funding Statement: The authors would like to thank Vellore Institute of Technology (VIT), for financial support.

Author Contributions: Study conception and design: T. Aghalya, R. Tamizharasi; analysis and interpretation of results: T. Aghalya, R. Tamizharasi; draft manuscript preparation: T. Aghalya. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Satya Narayana, P. V., Venkateswarlu, B., Venkataramana, S. (2015). Thermal radiation and heat source effects on a MHD nanofluid past a vertical plate in a rotating system with porous medium. Heat Transfer-Asian Research, 44(1), 1–19. [Google Scholar]

2. Saqib, M., Ali, F., Khan, I., Sheikh, N. A. (2018). Heat and mass transfer phenomena in the flow of casson fluid over an infinite oscillating plate in the presence of first-order chemical reaction and slip effect. Neural Computing and Applications, 30, 2159–2172. [Google Scholar]

3. Veera Krishna, M. (2020). Heat transport on steady MHD flow of copper and alumina nanofluids past a stretching porous surface. Heat Transfer, 49(3), 1374–1385. [Google Scholar]

4. Hayat, T., Nadeem, S. (2017). Heat transfer enhancement with Ag-CuO/water hybrid nanofluid. Results in Physics, 7, 2317–2324. [Google Scholar]

5. Delouei, A. A., Naeimi, H., Sajjadi, H., Atashafrooz, M., Imanparast, M. et al. (2024). An active approach to heat transfer enhancement in indirect heaters of city gate stations: An experimental modeling. Applied Thermal Engineering, 237, 121795. [Google Scholar]

6. Adesanya, S. O., Dairo, O. F., Yusuf, T. A., Onanaye, A. S., Arekete, S. A. (2020). Thermodynamics analysis for a heated gravity-driven hydromagnetic couple stress film with viscous dissipation effects. Physica A: Statistical Mechanics and its Applications, 540, 123150. [Google Scholar]

7. Choi, S. U. S., Eastman, J. A. (1995). Enhancing thermal conductivity of fluids with nanoparticles, pp. 99–105. No. ANL/MSD/CP-84938; CONF-951135-29). Argonne: Argonne National Lab. [Google Scholar]

8. Hamad, E. M., Khaffaf, A., Yasin, O., Abu El-Rub, Z., Al-Gharabli, S. et al. (2021). Review of nanofluids and their biomedical applications. Journal of Nanofluids, 10(4), 463–477. [Google Scholar]

9. Sandeep, N., Reddy, M. G. (2017). Heat transfer of nonlinear radiative magnetohydrodynamic Cu-water nanofluid flow over two different geometries. Journal of Molecular Liquids, 225, 87–94. [Google Scholar]

10. Sheikholeslami, M., Bandpy, M. G., Ellahi, R., Zeeshan, A. (2014). Simulation of MHD CuO-water nanofluid flow and convective heat transfer considering Lorentz forces. Journal of Magnetism and Magnetic Materials, 369, 69–80. [Google Scholar]

11. Sridevi, C., Sailakumari, A. (2023). Unsteady magnetohydrodynamic (MHD) Cu-Al2O3/water hybrid nanofluid flow and heat transfer from an exponentially accelerated plate. Journal of Nanofluids, 12, 832–841. [Google Scholar]

12. Dogonchi, A. S., Asghar, Z., Waqas, M. (2020). CVFEM simulation for Fe3O4-H2O nanofluid in an annulus between two triangular enclosures subjected to magnetic field and thermal radiation. International Communication in Heat and Mass Transfer, 112, 104449. [Google Scholar]

13. Mohan, S. R., Reddy, G. V., Varma, S. V. K., Krishna, S. B. (2017). Thermal radiation and chemical reaction effects on unsteady MHD free convection flow of a viscous dissipative casson fluid past an exponentially infinite vertical plate through porous medium with TGHS. i-Manager’s Journal on Mathematics, 6(2), 17–27. [Google Scholar]

14. Arif, M. S., Jhangir, M., Nawaz, Y., Abbas, I., Abodayeh, K. et al. (2022). Numerical study for magnetohydrodynamic (MHD) unsteady maxwell nanofluid flow impinging on heated stretching sheet. Computer Modeling in Engineering & Sciences, 133(2), 303–325. https://doi.org/10.32604/cmes.2022.020979 [Google Scholar] [CrossRef]

15. Fatima, N., Kousar, N., Rehman, K. U., Shatanawi, W. (2023). Computational analysis of heat and mass transfer in magnetized darcy-forchheimer hybrid nanofluid flow with porous medium and slip effects. Computer Modeling in Engineering & Sciences, 137(3), 2311–2330. https://doi.org/10.32604/cmes.2023.026994 [Google Scholar] [CrossRef]

16. Nadeem, S., Haq, R. U., Lee, C. (2012). MHD flow of a Casson fluid over an exponentially shrinking sheet. Scientia Iranica, 19(6), 1550–1553. [Google Scholar]

17. Dharmaiah, G., Baby Rani, C. H., Vedavathi, N., Balamurugan, K. S. (2020). Hall and ion slip effects on Ag-water based MHD nanofluid flow over a semi-infinite vertical plate embedded in a porous medium. Frontiers in Heat and Mass Transfer (FHMT), 14. [Google Scholar]

18. Rajesh, V., Chamkha, A., Kavitha, M. (2020). Numerical investigation of Ag-CuO/water hybrid nanofluid flow past a moving oscillating cylinder with heat transfer. Mathematical Methods in the Applied Sciences, 1–16. [Google Scholar]

19. Jawad, M., Khan, Z., Bonyah, E., Jan, R. (2022). Analysis of hybrid nanofluid stagnation point flow over a stretching surface with melting heat transfer. Mathematical Problems in Engineering, 2022, 1–12. [Google Scholar]

20. Afra, B., Karimnejad, S., Delouei, A. A., Tarokh, A. (2022). Flow control of two tandem cylinders by a highly flexible filament: Lattice spring IB-LBM. Ocean Engineering, 250, 111025. [Google Scholar]

21. Ali, F., Khan, I., Samiulhaq, I., Shafie, S. (2013). Conjugate effects of heat and mass transfer on MHD free convection flow over an inclined plate embedded in a porous medium. PLoS One, 8(6), e65223. [Google Scholar] [PubMed]

22. Pattnaik, J. R., Dash, G. C., Singh, S. (2017). Radiation and mass transfer efects on MHD fow through porous medium past an exponentially accelerated inclined plate with variable temperature. Ain Shams Engineering Journal, 8(1), 67–75. [Google Scholar]

23. Krishna, M. V., Ahamad, N. A., Chamkha, A. J. (2020). Hall and ion slip effects on unsteady MHD free convective rotating flow through a saturated porous medium over an exponential accelerated plate. Alexandria Engineering Journal, 59(2), 565–577. [Google Scholar]

24. Krishna, M. V. (2020). Hall and ion slip impacts on unsteady MHD free convective rotating flow of Jeffreys fluid with ramped wall temperature. International Communications in Heat and Mass Transfer, 119, 104927. [Google Scholar]

25. Sharma, R. P., Mishra, S. R., Panda, G. K. (2023). Radiation absorption impact on the thermophysical properties of Cu- and TiO2-water nanofluids: Laplace transform technique. International Journal of Modern Physics B, 2450238. [Google Scholar]

26. Rathore, N., Sandeep, N. (2022). Darcy-Forchheimer and Ohmic heating effects on GO-TiO2 suspended cross nanofluid flow through stenosis artery. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 236(20), 10470–10485. [Google Scholar]

27. Hussanan, A., Khan, I., Hashim, H., Mohamed, M. K. A., Ishak, N. et al. (2016). Unsteady MHD flow of some nanofluids past an accelerated vertical plate embedded in a porous medium. Jurnal Teknologi, 78(2), 121–126. [Google Scholar]

28. Vemula, R., Debnath, L., Chakrala, S. (2017). Unsteady MHD free convection flow of nanofluid past an accelerated vertical plate with variable temperature and thermal radiation. International Journal of Applied and Computational Mathematics, 3(2), 1271–1287. [Google Scholar]

29. Rao, S. R., Vidyasagar, G., Deekshitulu, G. V. S. R. (2021). Unsteady MHD free convection Casson fluid flow past an exponentially accelerated infinite vertical porous plate through porous medium in the presence of radiation absorption with heat generation/absorption. Materials Today: Proceedings, 42, 1608–1616. [Google Scholar]

30. Asjad, M. I., Ali, R., Iqbal, A., Muhammad, T., Chu, Y. M. (2021). Application of water based drilling clay-nanoparticles in heat transfer of fractional Maxwell fluid over an infinite flat surface. Scientific Reports, 11(1), 18833. [Google Scholar] [PubMed]

31. Elangovan, K., Subbarao, K., Gangadhar, K. (2022). An analytical solution for radioactive MHD flow TiO2-Fe3O4/H2O nanofluid and its biological applications. International Journal of Ambient Energy, 4(1), 7576–7587. [Google Scholar]

32. Zaman, A., Ali, N., Kousar, N. (2018). Nanoparticles (Cu, TiO2, Al2O3) analysis on unsteady blood flow through an artery with a combination of stenosis and aneurysm. Computers & Mathematics with Applications, 76(9), 2179–2191. [Google Scholar]

33. Arpitha, R., Kumar, N. N., Srikanth, D. (2023). Bioconvective squeezing flow of chemically reacting casson nanofluid between two parallel plates. Iranian Journal of Science and Technology, Transactions of Mechanical Engineering, 47, 1615–1632. [Google Scholar]

34. Waqas, H., Fida, M., Liu, D., Manzoor, U., Muhammad, T. (2022). Numerical simulation of entropy generation for nanofluid with the consequences of thermal radiation and Cattaneo-Christov heat flux model. International Communications in Heat and Mass Transfer, 137, 106293. [Google Scholar]

35. Kot, M. E., Elmaboud, Y. A. (2021). Hybrid nanofluid flows through a vertical diseased coronary artery with heat transfer. Journal of Mechanics in Medicine and Biology, 21(2), 2150012. [Google Scholar]

36. Reddy, P. S., Chamkha, A. (2017). Heat and mass transfer analysis in natural convection flow of nanofluid over a vertical cone with chemical reaction. International Journal of Numerical Methods for Heat and Fluid Flow, 27(1), 2–22. [Google Scholar]

37. Rana, P., Al-Kouz, W., Mahanthesh, B., Mackolil, J. (2021). Heat transfer of TiO2-EG nanoliquid with active and passive control of nanoparticles subject to nonlinear Boussinesq approximation. International Communications in Heat and Mass Transfer, 126, 105443. [Google Scholar]

38. Patel, H. R. (2019). Effects of heat generation, thermal radiation, and hall current on MHD Casson fluid flow past an oscillating plate in porous medium. Multiphase Science and Technology, 31(1), 87–107. [Google Scholar]

39. Kataria, H. R., Patel, H. R. (2019). Effects of chemical reaction and heat generation/absorption on magnetohydrodynamic (MHD) Casson fluid flow over an exponentially accelerated vertical plate embedded in porous medium with ramped wall temperature and ramped surface concentration. Propulsion and Power Research, 8(1), 35–46. [Google Scholar]

40. Kataria, H. R., Mittal, A. S. (2017). Velocity, mass and temperature analysis of gravity-driven convection nanofluid flow past an oscillating vertical plate in the presence of magnetic field in a porous medium. Applied Thermal Engineering, 110, 864–874. [Google Scholar]

41. Ashlin, T. S., Mahanthesh, B. (2019). Exact solution of non-coaxial rotating and non-linear convective flow of Cu-Al2O3-H2O hybrid nanofluids over an infinite vertical plate subjected to heat source and radiative heat. Journal of Nanofluids, 8(4), 781–794. [Google Scholar]

42. Krishna, M. V., Ahammad, N. A., Chamkha, A. J. (2021). Radiative MHD flow of Casson hybrid nanofluid over an infinite exponentially accelerated vertical porous surface. Case Studies in Thermal Engineering, 27, 101229. [Google Scholar]

43. Azzam, G. E. (2002). Radiation effects on the MHD mixed free-forced convective flow past a semi-infinite moving vertical plate for high temperature differences. Physica Scripta, 66(1), 71. [Google Scholar]

44. Bestman, A. R. (1985). Free convection heat transfer to steady radiating non?Newtonian MHD flow past a vertical porous plate. International Journal for Numerical Methods in Engineering, 21(5), 899–908. [Google Scholar]

45. Rosseland, S. (1931). Auf atomtheoretischer grundlage. Berlin: Springer-Verlag. [Google Scholar]

46. Khanafer, K., Vafai, K., Lightstone, M. (2003). Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. International Journal of Heat and Mass Transfer, 46(19), 3639–3653. [Google Scholar]

47. Maxwell, J. C. (1873). A treatise on electricity and magnetism. England: Clarendon Press. [Google Scholar]

48. Brinkman, H. C. (1952). The viscosity of concentrated suspensions and solutions. The Journal of Chemical Physics, 20(4), 571. [Google Scholar]

49. Seth, G. S., Ansari, M. S., Nandkeolyar, R. (2011). MHD natural convection flow with radiative heat transfer past an impulsively moving plate with ramped wall temperature. Heat and Mass Transfer, 47, 551–561. [Google Scholar]

50. Nandkeolyar, R., Das, M., Sibanda, P. (2013). Exact solutions of unsteady MHD free convection in a heat absorbing fluid flow past a flat plate with ramped wall temperature. Boundary Value Problems, 2013(247), 1–16. [Google Scholar]

Appendix A