A Simplified Method for the Stress Analysis of Underground Transfer Structures Crossing Multiple Subway Tunnels

1  Introduction

Given the ongoing evolution of urban construction, the practice of conducting tunnel construction in proximity to existing pile foundations and pile foundation construction near operational tunnels has become commonplace. Scholars worldwide have extensively investigated the reciprocal influence between tunnels and pile foundations [1–3]. The examination of tunnel excavation effects on nearby existing pile foundations primarily employs methods such as theoretical analysis, analysis of on-site monitoring data [4], finite element method (FEM) calculations, and physical model testing [5–9]. The theoretical analysis method predominantly employs a two-stage analysis approach. In the initial stage, column hole expansion theory, ball hole expansion theory [6], and plane hole contraction theory [9,10] were employed to deduce the displacement field of the surrounding soil resulting from tunnel excavation. In the subsequent stage, the pile foundation was treated as Winkler elastic foundation beam [11], Pasternak elastic foundation beam [12], and Kerr elastic foundation beam [9], applying the displacement field obtained in the first stage to the elastic foundation beam enables the determination of the impact of tunnel excavation on nearby existing pile foundations. In the case of U-shaped tunnels, the conformal mapping method can project them onto the unit circle, and then an analytical solution for the impact of U-shaped tunnel excavation on adjacent pile foundations can be derived by integrating the complex function method and load transfer method [13]. The analytical equation for the failure surface of the upper pile foundation’s end-bearing layer resulting from tunnel excavation can be derived using the variational principle [14]. Given the convenience and cost-effectiveness of the finite element method, numerous studies on the impacts of tunnel excavation on nearby existing pile foundations were conducted through this method [15,16]. This encompassed an exploration of various aspects, mainly including the influence of diverse geometric parameters [17], the impact of different construction parameters [18,19], the distinct effects of tunnel excavation on individual pile and group piles [20,21], and the varied effects of the construction sequence of double-track tunnels on pile foundations [22,23].

Extensive research has been conducted on the influence of tunnel excavation on nearby existing pile foundations, yet there is a paucity of studies addressing the impact of pile foundation construction on adjacent existing tunnels. Wang et al. [24] introduced an analytical solution for the longitudinal settlement of tunnels resulting from the axial loading of single pile or pile groups. This was based on the extended shear displacement method and the dual parameter elastic foundation beam model, subsequently validated through finite element numerical calculations. Lueprasert et al. [25] explored the impact of axial loading on nearby existing tunnels through finite element numerical calculation methods. Liu et al. [26] employed the tunnel project of Wuxi Metro Line 2 in China as the background. They utilized finite element numerical calculation methods and integrated on-site measured data to elucidate the impact mechanism of static pile pressing on the existing subway tunnel structure. Gao et al. [27] analyzed the impact of a pile foundation construction method combining Benoto bored pile and conventional circulating mud construction technology on adjacent tunnels. They employed on-site monitoring methods, with the Nanjing subway tunnel serving as the study background.

The use of a one-column-one pile foundation finds diverse applications in engineering. However, in certain cases, the design specifications may necessitate the installation of long pile foundations directly above shallow-buried tunnels. During practical construction, it becomes necessary for the pile foundation to traverse the tunnel’s upper portion and reach the rock layer beneath, a practice that is evidently impractical. Addressing the challenge of transferring comparable column loads to deep soil without causing a substantial impact on nearby tunnels is a pressing concern in engineering. Grounded in the first phase project of the Hangzhou Convention and Exhibition Center, this paper introduces an underground transfer structure spanning multiple subway tunnels. Employing theoretical analysis methods, we established a simplified mechanical model for the transfer structure that can concurrently account for soil stratification, pile foundation behavior, and plate action. The finite difference method and Newton-Simpson method were employed to solve the established mechanical model, elucidating the mechanical mechanism of the transfer structure. The key innovations are as follows: ① Proposal of an underground transfer structure spanning multiple subway tunnels, facilitating the transfer of loads from upper structural columns to the pile foundation beneath the beams through the transfer structure, thus transmitting to the deep soil and ensuring minimal impact on adjacent tunnels. ② Provision of a simplified analysis method for the force mechanism of the transfer structure by integrating theoretical analysis methods. The established simplified analysis method in this paper is applicable for stress analysis of transfer structures, considering soil stratification, pile foundation behavior, and plate action simultaneously. ③ The practical application of transfer structures and the corresponding simplified analysis methods in engineering has substantiated the effectiveness of these simplified structures and analysis approaches.

2  Proposal of Transfer Structure

2.1 Project Introduction and Difficulties

The upper main structure of the first phase project of the Hangzhou Convention and Exhibition Center comprises a steel structure, wherein the central corridor aligns closely with the longitudinal direction of the tunnel. The central corridor directly overlies the tunnel, with the parallel sections spanning nearly 600 m. As illustrated in Fig. 1, the steel structure column of the central corridor descends directly above the tunnel structure. Considering the shallow buried depth of the tunnel at 14.4 m, employing a one-column-one pile foundation in a pile length of 75 m. Consequently, it is unfeasible to conduct pile foundation construction directly beneath the column, impeding the direct transmission of the upper load carried by the column into the foundation.

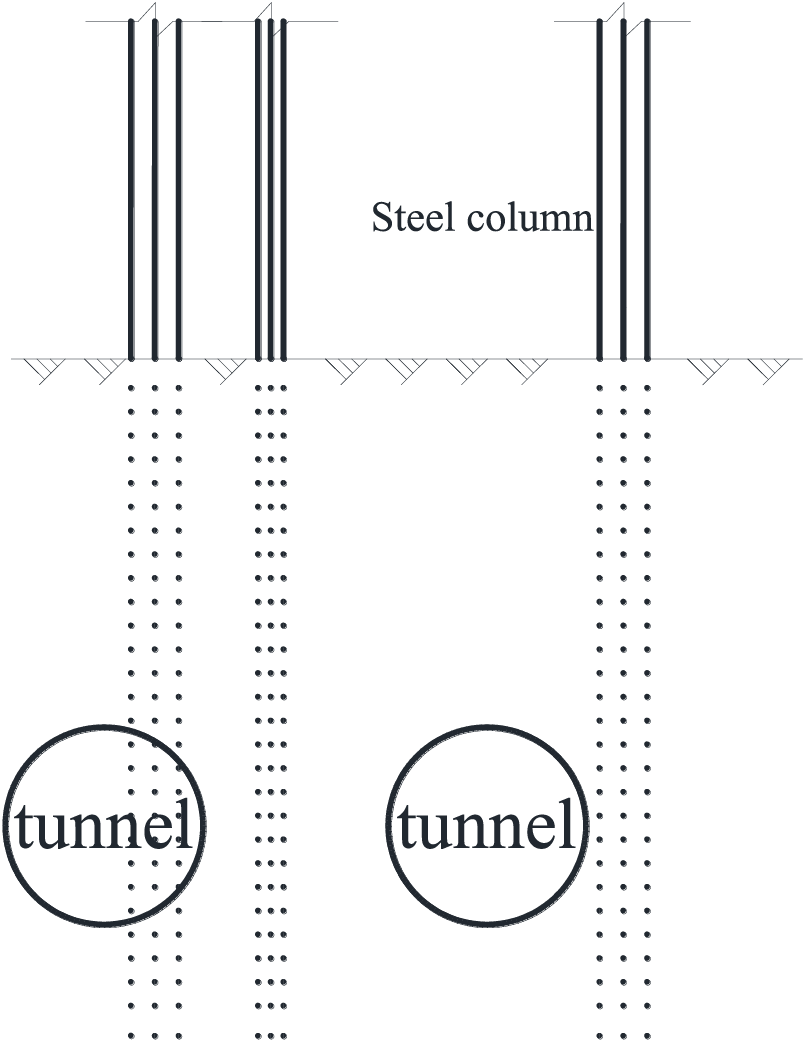
Figure 1: The relative position relationship between steel structure columns and tunnels

2.2 Proposal of Transfer Structure

To seamlessly transfer the load of the steel structure column within the central corridor to the foundation, mitigating any substantial impact on adjacent tunnels, an underground transfer structure spanning multiple subway tunnels was suggested, as depicted in Fig. 2. This approach ensures that the load carried by the upper structural columns is effectively transferred to the pile foundation beneath the beams through the transfer structure, subsequently reaching to the deep soil and minimizing any adverse effects on nearby tunnels.

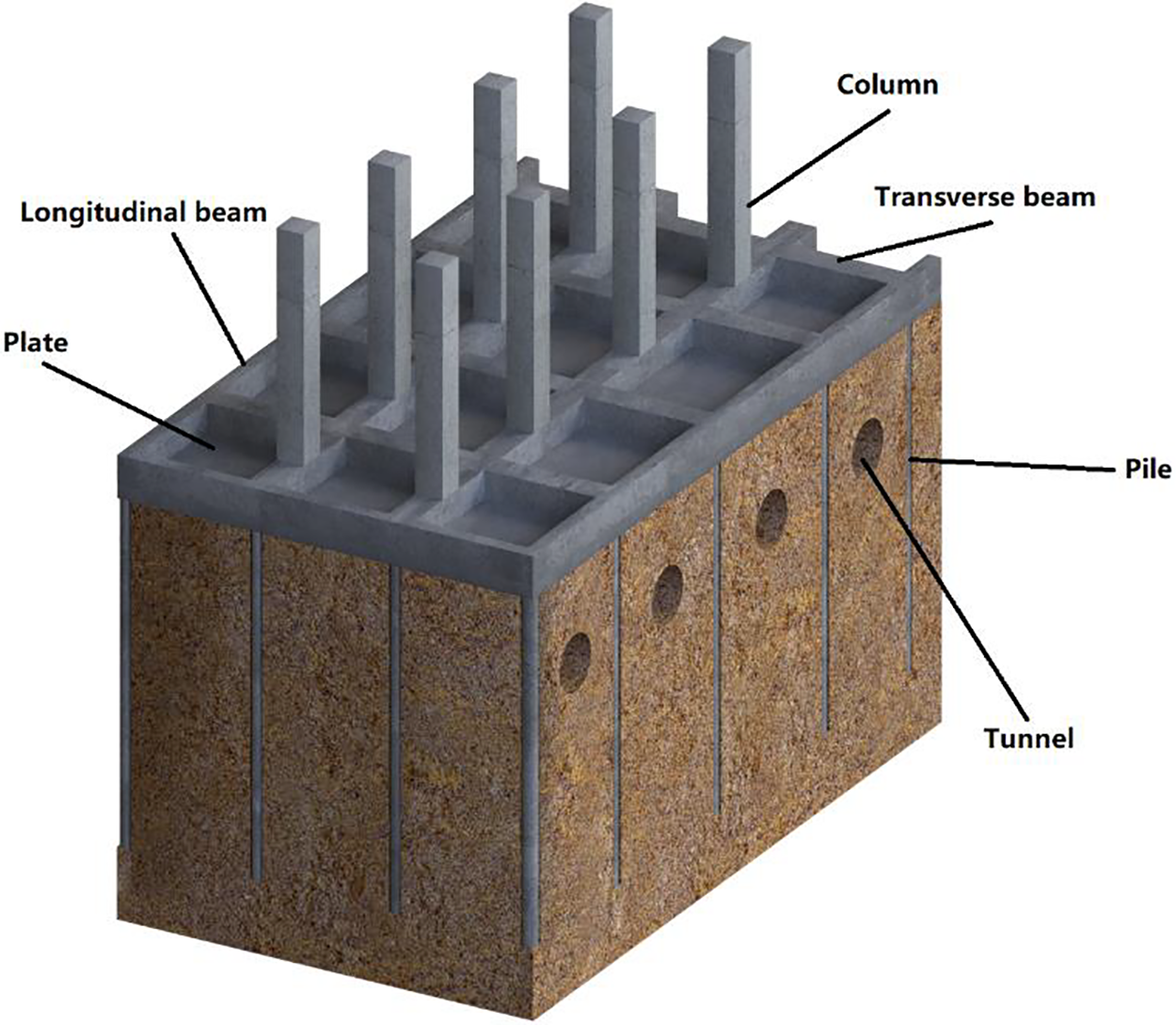
Figure 2: Transfer structure 3D diagram

3  Simplified Mechanical Model of Transfer Structure

3.1 Clarification of the Transmission System

As illustrated in Fig. 3, the transfer sequence of the transfer structure for the distributed load and self-weight of the bearing plate unfolds as follows: a portion of the load is conveyed to the longitudinal and transverse beams through the bearing plate, while another portion is transferred to the soil beneath the plate. Both the longitudinal and transverse beams bear not only the load transmitted by the bearing plate but also the vertical load transmitted from the upper structural column. Consequently, the load carried by these beams is distributed, with a segment transmitted to the soil under the beam and another segment directed to the pile foundation.

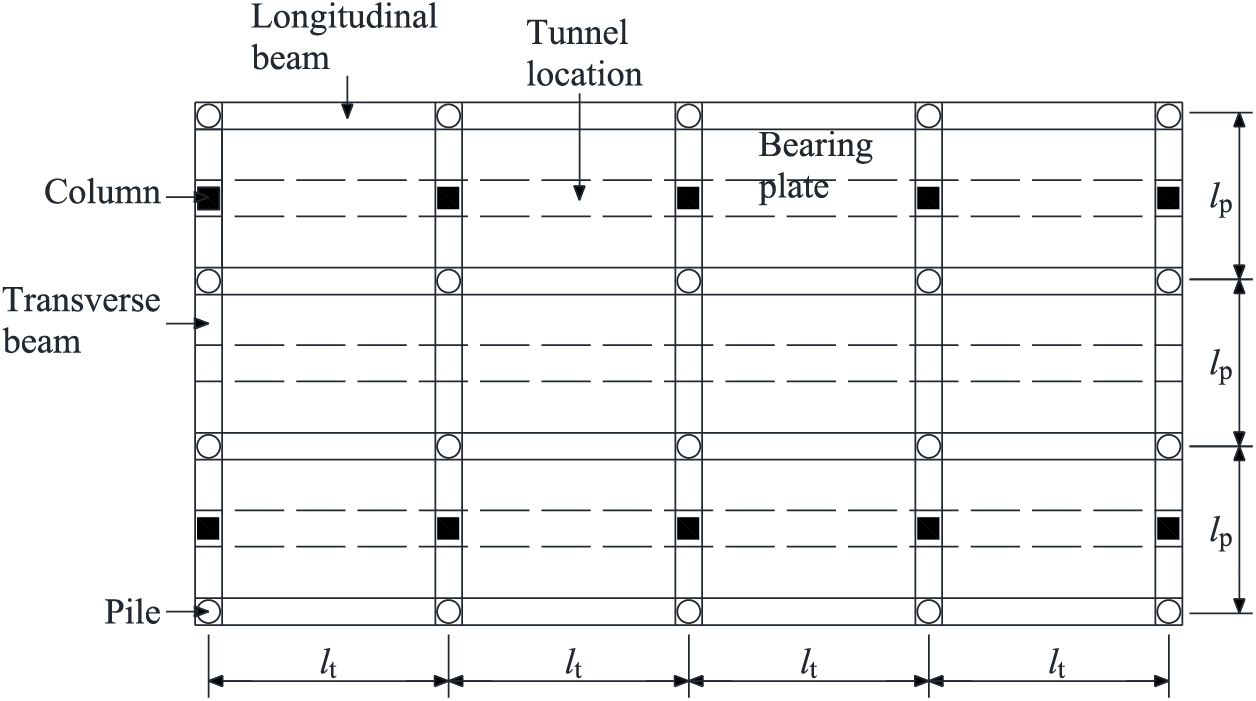
Figure 3: Transfer structure 3D diagram transfer structure plan diagram

3.2 Establishment of Mechanical Model

Given that both the distributed load carried by the bearing plate and the vertical load transmitted by the upper structural column primarily pass through the pile foundation via longitudinal and transverse beams, these beams were selected as the focal analysis components. This led to a simplified mechanical model for the transverse beams, depicted in Fig. 4a, and a simplified mechanical model for the longitudinal beams, illustrated in Fig. 4b.

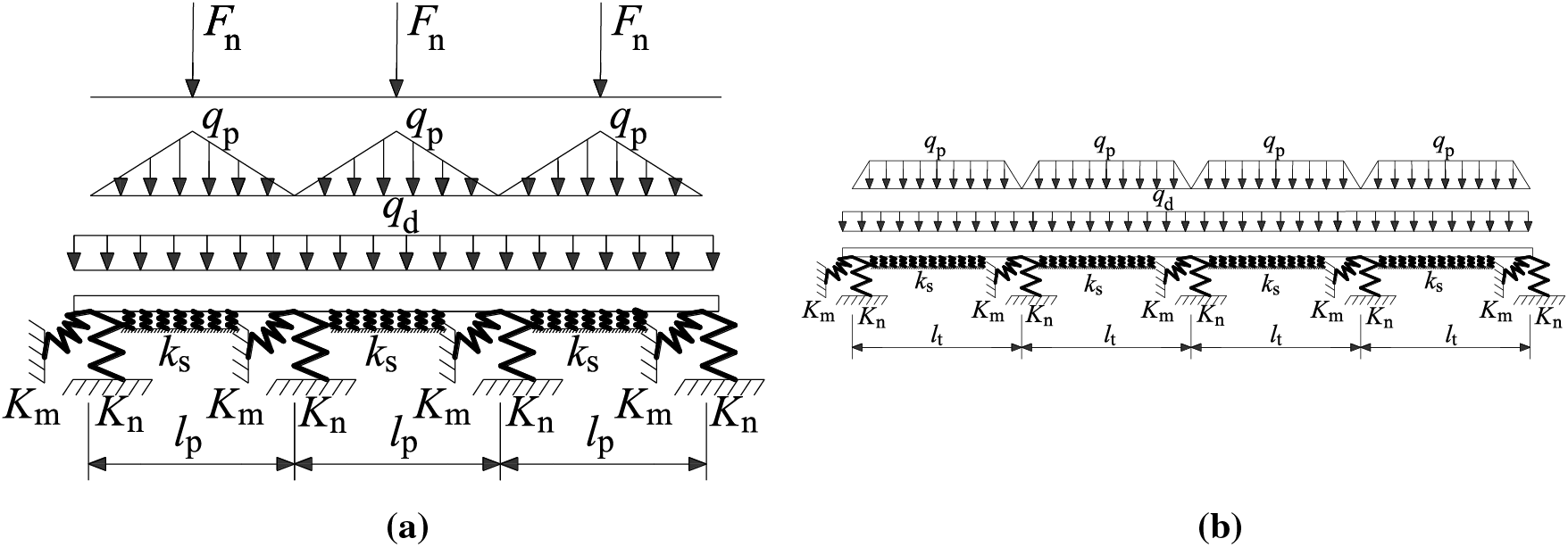
Figure 4: Simplified mechanical model: (a) Transverse beams; (b) Longitudinal beams

As illustrated in Fig. 4a, the upper load supported by the transverse beams encompasses three components: ① The vertical load transmitted by the upper structural column, denoted as Fn; ② the summation of the self-weight and the distributed load on the plate, minus the residual load borne by the soil beneath the plate—commonly simplified for practical engineering calculations as a triangular distributed load with a maximum value of qp; ③ the self-weight distribution load of the transverse beams, represented as qd. The upper load supported by the transverse beam is divided, with a portion transmitted to the soil beneath the beam and the remainder directed to the pile foundation. To streamline the analysis, accounting for the intricate interaction between the beam, soil, and the pile-soil system directly would result in an excessively complex solution model. Therefore, a simplified approach is proposed, wherein the pile foundation is replaced by springs featuring bending stiffness Km and axial stiffness Kn. Similarly, the soil beneath the beam is approximated by a distributed spring with axial stiffness ks.

As depicted in Fig. 4b, the upper load supported by the longitudinal beams comprises two components: ① the summation of the plate’s self-weight and the distributed load on the plate, minus the residual load borne by the soil beneath the plate—typically simplified for practical engineering calculations as a trapezoidal distributed load with a maximum value of qp; ② the self-weight distribution load of the longitudinal beam. Analogous to the transverse beams, longitudinal beams transmit a portion of the upper load they bear to the soil beneath the beam and the remaining portion to the pile foundation. To streamline the analysis, it is proposed to substitute the pile foundation with springs featuring bending stiffness Km and axial stiffness Kn, while the soil under the beam is approximated by distributed springs with axial stiffness ks.

3.3 Stress Analysis of Bearing Plate

Assuming that the load on the upper section of the bearing plate is uniformly distributed, and likewise, the self-weight is uniformly distributed, the bottom reaction force provided by the soil is also uniformly distributed. The uniformly distributed surface load, denoted as pptl, is carried by the bearing plate.

pptl=ppe+ppg−pps(1)

where ppe represents the surface load carried by the plate; ppg denotes the self-weight surface load of the plate.

ppg=ρpgtp(2)

where ρp and tp stand for the density and thickness of the plate, respectively, g representing the acceleration due to gravity. pps denotes the uniformly distributed surface load corresponding to the reaction force supplied by the soil at the bottom of the plate.

Pps=ksabs(wpd−wpc)+(wpd−wpc)2(3)

where wpc and wpd represent the void and the average deflection at the bottom of the plate. As shown in Eq. (3), it is apparent that when the void amount wpc at the plate’s bottom exceeds the average deflection wpd, the corresponding uniformly distributed surface load pps of the soil at the plate’s bottom is zero—a scenario consistent with practical expectations.

Upon determining the uniformly distributed surface load, pptl, borne by the bearing plate as per Eq. (1), the load is then transferred to the longitudinal and transverse beams following the bidirectional plate configuration depicted in Fig. 5. By intersecting the four corners of the grid plate diagonally at a 45° with the centerline parallel to the longitudinal beams, each grid plate is divided into two trapezoidal plates and two triangular plates. The load on each small plate is conveyed to its supporting beam. Beyond the to the weight of the beam and other directly borne loads, the supporting longitudinal beam in the long direction carries the trapezoidal load, while the supporting transverse beam in the short direction bears the triangular load. The maximum values corresponding to trapezoidal and triangular loads are determined.

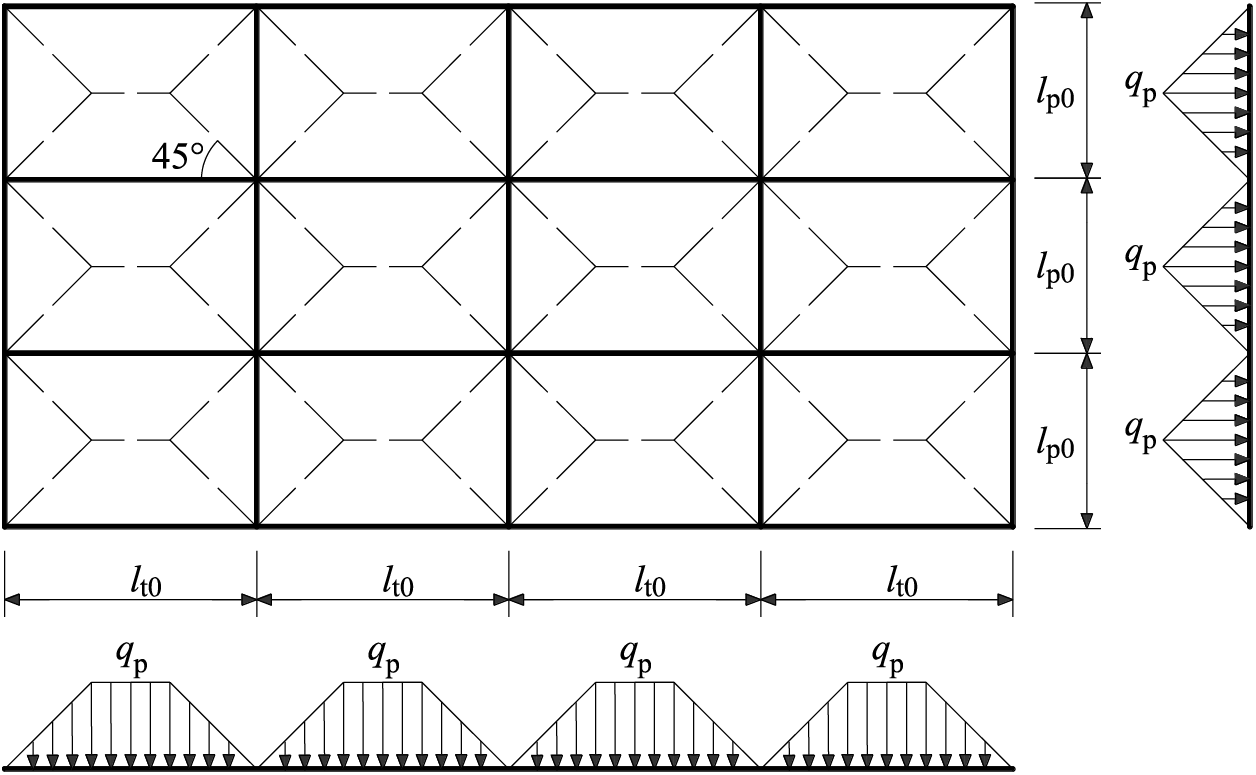
Figure 5: Load bearing plate stress model

qp=pptllp02(4)

In Fig. 4, lp0 and lt0 represent the calculated spans for short and long spans, respectively.

3.4 Calculation of Axial Stiffness ks of Soil Spring Considering Soil Stratification

The pivotal step in determining soil reaction force at the plate’s bottom involves the calculation of the axial stiffness, ks, of the soil spring. The physical interpretation of the axial stiffness, ks, for a soil spring is the pressure corresponding to the vertical deflection per unit area. In practical engineering, where the soil is layered, the finite compression layer model [28] proves valuable as it accounts for soil stratification. This model enables the characterization of the relationship between surface settlement and surface pressure, thereby allowing the derivation of the axial stiffness, ks, for the soil spring. Consequently, an effort was made to derive an expression for the axial stiffness, ks, of the soil spring, considering soil stratification through the finite compression layer model.

According to the finite compression layer model, the calculation formula for the settlement s of the finite compression layer foundation is [28]

s=∑j=1mσ¯zjhjEsj(5)

where the parameters Esj, hj and σ¯zj represent the compressive modulus, thickness, and average additional stress of the jth soil layer, respectively. In the case of layered foundations, the additional stress, σ¯zj, can be determined through the transfer matrix method [29,30]. However, due to the method’s complexity, and to enhance its practical applicability in engineering, the Boussinesq solution for the elastic half-space problem was adopted. Specifically, if a pressure, p, acts on a square unit area of the soil at the plate’s bottom, the resulting additional stress at the center of the jth soil layer directly beneath the square is given by [29,30]

σ¯zjc=2pπ [ arctanm′n1+m′2+n2+m′⋅n1+m′2+n2(1m′2+n2+11+n2) ](6a)

Eq. (6a) is equivalent to

σ¯zjc=ζ(Zj)p(6b)

In Eq. (6a), m'=lb, n=2zjb, l and b are the length and width of the square, both valued 1.0 m, zj is the vertical distance between the pressure p action position and the middle position of the jth soil layer, which can be expressed as

zj=(∑k=1jhk)−hj2(7)

Let,

ζ(zj)=2π[ arctanm′n1+m′2+n2+m′⋅n1+m′2+n2(1m′2+n2+11+n2) ](8)

Similarly, the additional stress caused by the pressure p in the middle of the jth soil layer directly below the square corner is [29,30]

σ¯zjp=ζ′(zj)p(9)

where

ζ′(zj)=12π [ arctanm′n′1+m′2+n′2+m′⋅n′1+m′2+n′2(1m′2+n′2+11+n′2) ](10)

n′=zjb(11)

Substituting Eq. (6b) into Eq. (5) to obtain the settlement of the foundation directly below the center of the square:

sc=p∑j=1mζ(zj)hjEsj(12)

Substituting Eq. (9) into Eq. (5) to obtain the settlement of the foundation directly below the square corner point as

sp=p∑j=1mζ′(zj)hjEsj(13)

After obtaining the settlement of the foundation directly below the center and corner of the square, the overall settlement of the foundation is approximately calculated according to the following equation:

s=4sp+sc5=p∑j=1m(4ζ′(zj)+ζ(zj)5hjEsj)(14)

The axial stiffness ks of soil spring can be seen as the ratio of pressure p to settlement s, hence

ks=ps=1∑j=1m(4ζ′(zj)+ζ(zj)5hjEsj)(15)

3.5 Calculation of Axial Stiffness Kn of Pile Foundation Considering Soil Stratification

The axial stiffness, Kn, of a pile foundation is defined as the ratio of the axial force at the pile top to the settlement at the pile top. Currently, common methods for calculating single pile settlement mainly include load transfer method [30], shear displacement method [31], elastic theory method [32], boundary element method [33], finite element method, etc. [34]. The load transfer method is widely employed in engineering due to its ability to account for soil stratification, requiring fewer parameters for solving, and eliminating the need for extensive numerical calculations. To maintain simplicity in calculations, the pile-soil interaction model depicted in Fig. 6 simulates the interaction using a series of springs, where u(z) and hi represent the soil spring stiffness and soil layer thickness for the ith soil layer, and Kb is the pile end spring stiffness. If the pile’s circumference is Cp, the modulus is Ep, and the cross-sectional area is Ap, then the differential equation governing the pile body is

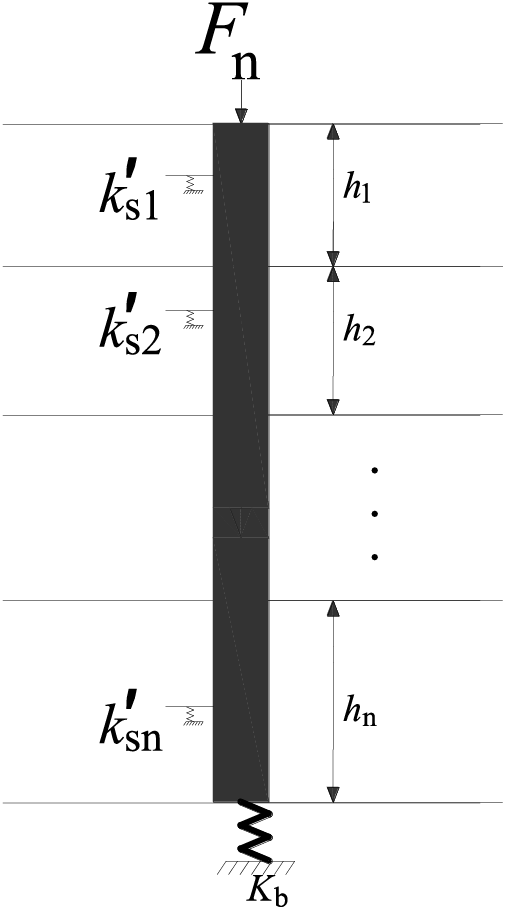
Figure 6: Pile soil vertical interaction model

EPAPd2u(z)d2z=ks′CPu(z)(16)

where the symbol u(z) represents the variation in pile displacement with depth z, while ks' denotes the vertical stiffness of soil spring, typically varying across different soil layers. By performing segmented integration on Eq. (16) based on soil stratification and considering the boundary conditions at the pile bottom, along with the deformation coordination conditions at the soil stratification position of the pile body, the axial stiffness of the pile top can be readily obtained [35]

Kn=EPAPλ1tanh⁡(λ1h1+α1)(17)

where

λi=ksi′⋅CPEPAP,i=1,2,3,⋯,n

αn=artanhKbEPAPλn

αj=artanh(λj+1λjtanh⁡(λj+1hj+1+αj+1))j=n−1,n−2,n−3,⋯,1

3.6 Calculation of Bending Stiffness Km of Pile Foundation Considering Soil Stratification

The stress analysis methods for horizontally loaded piles can be broadly categorized into four groups: elastic analysis method [36], foundation reaction method [37], p-y curve method [38], and numerical analysis method [39]. In the engineering field, the m method in the foundation reaction method [40] is frequently employed. To maintain tractability, the m method is utilized for determining the bending stiffness, Km, of pile foundations. As illustrated in Fig. 7, the horizontally loaded foundation pile, subjected to a bending moment M0 at its top, undergoes bending deformation with depth y(z) under external forces. Treating the pile foundation as a beam, and the horizontal interaction between the pile and soil is simulated through horizontal springs. In elastic foundation, the beam differential equation corresponding to the pile is

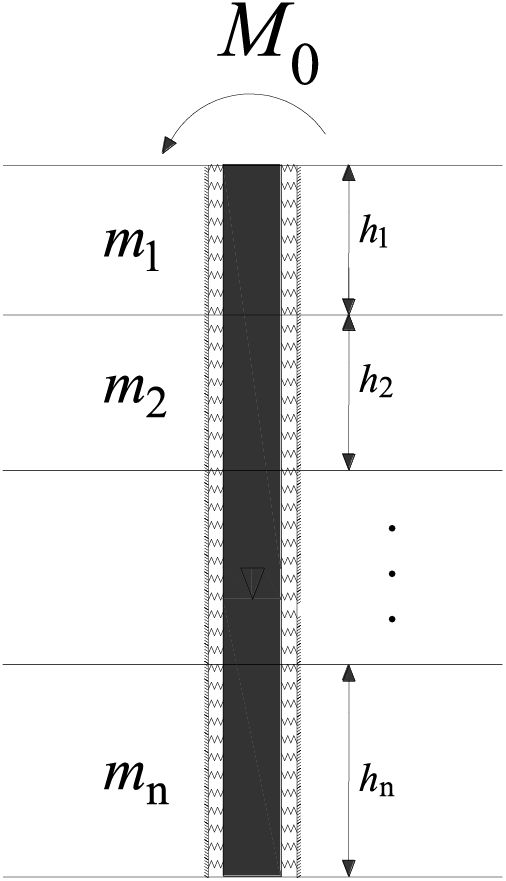
Figure 7: Pile soil lateral interaction model

EPIPd4y(z)dz4+BPmzy(z)=0(18)

where EPIP is the bending stiffness of the pile; y(z) means the variation of horizontal displacement of the pile body with depth z; BP denotes the width of the pile, for circular piles, when the diameter D < 1 m, BP=0.9(1.5D+0.5), when D > 1 m, BP=0.9(1.0D+1.0), for square piles, when the pile width b ≤ 1 m, BP=1.5b+0.5, when the pile width b > 1 m, BP=1.0b+1.0; m represents the coefficient that characterize the variation of the horizontal resistance coefficient of the foundation with depth, which is generally different for different soil layers.

After solving Eq. (18) based on boundary conditions, the rotation angle of the pile at the pile top position can be obtained

φ0=φ(z)|z=0=dy(z)dz|z=0(19)

The boundary conditions primarily encompass those at the bottom and top of the pile, along with the coordination conditions at the soil stratification location. Assuming the bottom of the pile as a fixed end, the deflection deformation y and rotation angle Km are both zero, satisfying the conditions

y(z)|z=lp′=0(20a)

φ′(z)|z=lp′=dy(z)dz|z=lp′=0(20b)

M(z)|z=0=−EPIPd2y(z)dz2|z=0=M0(21a)

FV(z)|z=0=−EPIPd3y(z)dz3|z=0=0(21b)

At the interface between the i-th and i+1-th soil layers, the conditions of identical bending deformation, rotation angle, bending moment, and shear force are satisfied. Once the rotation angle φ0 at the pile’s top is determined, the bending stiffness, Km, of the pile foundation can be calculated using the following formula:

Km=M0φ0(22)

4  Solution of Simplified Mechanical Model for Transfer Structures

Upon elucidating the interaction among piles, plates, and soil, the next step involves resolving the transverse and longitudinal multi-span beam systems depicted in Fig. 3. Presently, complex beam systems are typically addressed using methods such as finite element method [41] and finite difference method [42] are mainly used to solve. Opting for the finite difference method due to its programming convenience, this method is employed to solve the beam system illustrated in Fig. 3.

4.1 Center Difference Method

The fundamental concept of the finite difference method involves substituting differential equations and boundary conditions with difference equations. This transformation turns the solution of differential equations into the solution of linear equations, significantly mitigating the complexity of the problem-solving process. In the case of the equationy=f(x), the central difference’s core equation is

(dydx)|x=xi+xi+12=f(xi+1)−f(xi)xi+1−xi(23)

4.2 Finite Difference Basic Equation

The differential equation governing deflection in the Winkler elastic foundation beam model [11] is

EbIbd4w(x)dx4=q(x)−bbksw(x)(24)

where the bending stiffness of the beam is denoted as EbIb; w(x) represents the deflection of the beam, with positive values indicating downwards deflection; ks is the vertical soil foundation coefficient; bb signifies the width of the beam cross-section; q(x) is the top line load acting downward. The associated parameters, including the rotation angle (positive for clockwise rotation), bending moment (positive for tension on the lower side), and shear force (positive for the moment generated on adjacent sections in a clockwise direction) of the beam, are given, respectively.

φ(x)=dw(x)dx(25)

M(x)=−EbIbd2w(x)dx2=−EbIbdφ(x)dx(26)

Fv(x)=−EbIbd3w(x)dx3=dM(x)dx(27)

Write Eqs. (24)–(27) as matrix expressions

(dw(x)dxdφ(x)dxdM(x)dxdFv(x)dx)=(010000−1EbIb000010000)(w(x)φ(x)M(x)Fv(x))+(000bbksw(x)−q(x))(28)

Partition the foundation beam into n segments, not necessarily equal in length, with node numbers 1,2,3... and n+1. The two ends of the i-th beam segment are designated as i and i+1. In practical segmentation, nodes are established at points of abrupt changes in local load, such as the three key points of triangular load and the four key points of trapezoidal load, as well as the concentrated load and various support types. Denoting the length of the i-th beam segment as Li, the segment must satisfy the differential equation presented in Eq. (28) at its center. Considering the central difference equation, the i-th beam segment adheres to the following linear equation system:

(−1Li−12000−1Li12EIi/2000−1Li−12−bbi/2ks200−1Li)(wiφiMiFvi)+(1Li−120001Li12EIi/20001Li−12−bbi/2ks2001Li)(wi+1φi+1Mi+1Fvi+1)=(000−qi/2)(29)

where EIi/2 is the bending stiffness at the midpoint of the i-th beam segment; qi/2 is the distributed load value at the midpoint of the i-th beam segment; bbi/2 is the width at the midpoint of the i-th beam segment.

4.3 Compatibility Condition

To address the beam system with multiple transverse and longitudinal spans depicted in Fig. 3, it is essential not only to adhere to the fundamental linear equation system Eq. (29) but also to meet the compatibility conditions at the points of concentrated force application and at the intersection nodes of longitudinal and transverse beams.

For nodes subjected to concentrated forces, it is possible to establish one node on each side of the given node. The left beam segment of the node can be computed as the left node, and the right beam segment as the right node. However, the left and right nodes must adhere to compatibility conditions, ensuring uniform deflection s, identical rotation angle, consistent bending moment, and equilibrium between shear force and concentrated force on both sides. In other words, both sides must satisfy

(1000010000100001)(wlφlMlFvl)+(−10000−10000−10000−1)(wrφrMrFvr)=(000Fn)(30)

where Fn represents the concentrated force, with a positive orientation vertically downwards. The physical quantity with the superscript l denotes the physical quantity corresponding to the left node, while the physical quantity with the superscript r indicates the physical quantity corresponding to the right node.

At the intersection nodes of the longitudinal and transverse beams, illustrated in Fig. 8, three primary types of nodes exist: L-shaped nodes (01, 01), T-shaped nodes (01, 02), and cross-shaped nodes (02, 02). Each node type corresponds to distinct compatibility conditions.

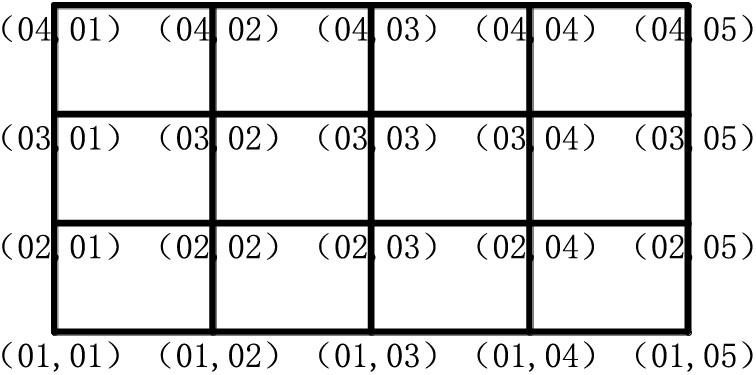
Figure 8: Intersection nodes of longitudinal and transverse beams

The L-shaped node represented by nodes (01, 01) can be deconstructed into an upper node and a right node, both exhibiting the identical deflection. The reaction force of the rotating spring support at the right node is equilibrated with the bending moment of the right node. Similarly, the reaction force of the rotating spring support at the upper node is counterbalanced by the bending moment of the upper node. Additionally, the reaction force of the vertical spring support is harmonized with the shear force and vertical concentrated force of the upper right two nodes. This configuration ensures

(10000Km100000Kn00−1)(wrφrMrFvr)+(−100000000Km10000−1)(wtφtMtFvt)=(000Fn)(31a)

where the physical quantity denoted by a superscript t corresponds to the upper node. Similarly, the L-shaped nodes depicted in nodes (01, 05) adhere to

(10000Km100000Kn00−1)(wtφtMtFvt)+(−100000000Km−100001)(wlφlMlFvl)=(000Fn)(31b)

Node (04, 01) satisfies

(10000Km−100000Kn001)(wbφbMbFvb)+(−100000000Km10000−1)(wrφrMrFvr)=(000Fn)(31c)

where the physical quantity represented by a superscript b corresponds to the lower node. Node (04, 05) adheres to

(10000Km−100000Kn001)(wlφlMlFvl)+(−100000000Km−100001)(wbφbMbFvb)=(000Fn)(31d)

For the T-shaped nodes represented in nodes (01, 02), they can be deconstructed into right, upper, and left nodes. The deflection among these three nodes is identical. The rotation angles of the right and left nodes are equal, and the bending moment of the spring support at the right and left nodes is counterbalanced by the bending moment at these respective nodes. Moreover, the reaction force of the rotating spring support at the upper nodes is equilibrated with the bending moment at the upper nodes. The reaction force of the vertical spring support is also harmonized with the shear force and the vertical concentrated force Fn at the three nodes. This configuration ensures

(1000000001000Km100000Kn00−1)(wrφrMrFvr)+(−10001000000000000Km10000−1)(wtφtMtFvt)+(0000−10000−10000−1000000001)(wlφlMlFvl)=(00000Fn)(32a)

Similarly, the T-shaped nodes shown in nodes (02, 01) satisfy

(1000000001000Km−100000Kn001)(wbφbMbFvb)+(−10001000000000000Km10000−1)(wrφrMrFvr)+(0000−10000−10000100000000−1)(wtφtMtFvt)=(00000Fn)(32b)

the T-shaped nodes shown in nodes (02, 05) satisfy

(1000000001000Km100000Kn00−1)(wtφtMtFvt)+(−10001000000000000Km−100001)(wlφlMlFvl)+(0000−10000−10000−1000000001)(wbφbMbFvb)=(00000Fn)(32c)

(1000000001000Km−100000Kn001)(wlφlMlFvl)+(−10001000000000000Km−100001)(wbφbMbFvb)+(0000−10000−10000100000000−1)(wrφrMrFvr)=(00000Fn)(32d)

The cross shaped nodes illustrated in nodes (02, 02) can be deconstructed into upper, left, lower, and right nodes, adhering to the requirements of four nodes with identical deflection, upper and lower nodes sharing the same rotation angle, and the left and right nodes also possessing identical rotation angles. The reaction force of the rotating spring support at the upper and lower nodes is counterbalanced by the bending moment of the upper and lower nodes, while the reaction force of the rotating spring support at the left and right nodes is harmonized with the bending moment of the left and right nodes. The reaction force of the vertical spring support is equilibrated with the shear force at all four nodes and the vertical concentrated force Fn, thus satisfying

(100000000000010000000Km100000Kn00−1)(wtφtMtFvt)+(−1000100000000000010000000Km−100001)(wlφlMlFvl)+(0000−100010000−100000000−1000000001)(wbφbMbFvb)+(00000000−100000000−10000000010000−1)(wrφrMrFvr)=(0000000Fn)(33)

4.4 Calculation and Processing of Distributed Load on Beams

In principle, upon the completion of the beam system discretization, a comprehensive linear equation system is formulated by amalgamating Eq. (29) with compatibility conditions Eqs. (30)–(33). The resolution of this linear equation system yields the deflection, rotation angle, bending moment, and shear force at each node, facilitating the determination of internal forces and deformations in the foundation beam corresponding to the transfer structure. However, before undertaking the solution process, it is imperative to ascertain the distributed load on the beam, encompassing the beams’ self-weight and the line load transmitted from the bearing plate to the longitudinal and transverse beams. Calculating the self-weight of the beam is straightforward, with the primary focus directed toward elucidating the line load transmitted by the bearing plate to the longitudinal and transverse beams.

Substitute Eqs. (2) and (3) into Eq. (1) to derive the line load transmitted from the bearing plate to the longitudinal and transverse beams.

qp=(ppe+ρpgtp−ksabs(wpd−wpc)+(wpd−wpc)2)lp02(34)

Considering the specific transfer structure within a particular stratum, known quantities include the surface load ppe, plate density ρp, gravity acceleration g, plate thickness tp, axial stiffness of soil spring ks, plate bottom clearance wpc, and calculated span lp0 of beam short span that the plate surface bears are all known quantities. The average deflection wpd at the bottom of the plate is associated with the deflection of the adjacent beams. To simplify calculations, it is assumed that the average deflection wpd at the bottom of the plate equals the average value of the center deflection of the adjacent four beams wbm1 wbm2 wbm3 wbm4, satisfying

wpd=14(wbm1+wbm2+wbm3+wbm4)(35)

By substituting Eq. (35) into Eq. (34), we can establish the relationship between the line load transmitted by the bearing plate to the longitudinal and transverse beams and the deflection at the center of the beam

qp=(ppe+ρpgtp−ksabs(14(wbm1+wbm2+wbm3+wbm4)−wpc)+(14(wbm1+wbm2+wbm3+wbm4)−wpc)2)lp02(36)

By synthesizing Eqs. (29)–(33), and (36), a nonlinear equation system is derived for the deflection, rotation angle, bending moment, shear force, and line load transmitted from the bearing plate to the longitudinal and transverse beams. The Newton Simpson iteration method [41] can be applied to solve this equation, facilitating the solution for the internal forces and deformations of the foundation beams corresponding to the transfer structure.

4.5 Solving Process

In summary, the process for establishing and solving solution the transformational structural mechanics model is depicted in Fig. 9. Initially, the geometric and physical-mechanical parameters of the piles, longitudinal beams, transverse beams, and plates are determined for both the original and transfer structure. The formation parameters encompass the thickness of soil layers, the compression modulus for each layer of soil, the coefficient of horizontal resistance varying with depth, the vertical stiffness for each soil layer, and the spring stiffness of the pile end soil. The pile parameters mainly include diameter, length, elastic modulus, and pile end soil stiffness. The parameters of longitudinal and transverse beams comprise length, width, height, density, elastic modulus, and the concentrated force transmitted by the structural column to the beam. The plate parameters include uniformly distributed external load on the plate surface, density, thickness, and the void at the bottom of the plate. Subsequently, based on the geological parameters, Eq. (15) is employed to determine the axial stiffness ks of the soil spring, accounting for soil stratification. Utilizing the geological and pile foundation parameters, Eqs. (17) and (22) are applied to obtain the axial stiffness Kn and flexural stiffness Km of the pile foundation, considering soil stratification. The longitudinal and transverse beam system is discretized, and Eq. (29) is established for each beam segment element. Compatibility Eqs. (30) to (33) is formulated based on the compatibility conditions at points of concentrated force action and the intersection nodes of longitudinal and transverse beams. Eq. (36) is derived from the coordination equation. Finally, the difference equation, compatibility equation, and beam-plate coordination equation are combined to form a nonlinear equation system. This system incorporates unknown variables such as deflection, rotation angle, bending moment, shear force, and line load transmitted from the bearing plate to the longitudinal and transverse beams. The Newton-Simpson iteration method is then applied to solve the nonlinear equation system, enabling the determination of the internal force and deformation of the foundation beam and achieving the solution for the transformational structural mechanics model.

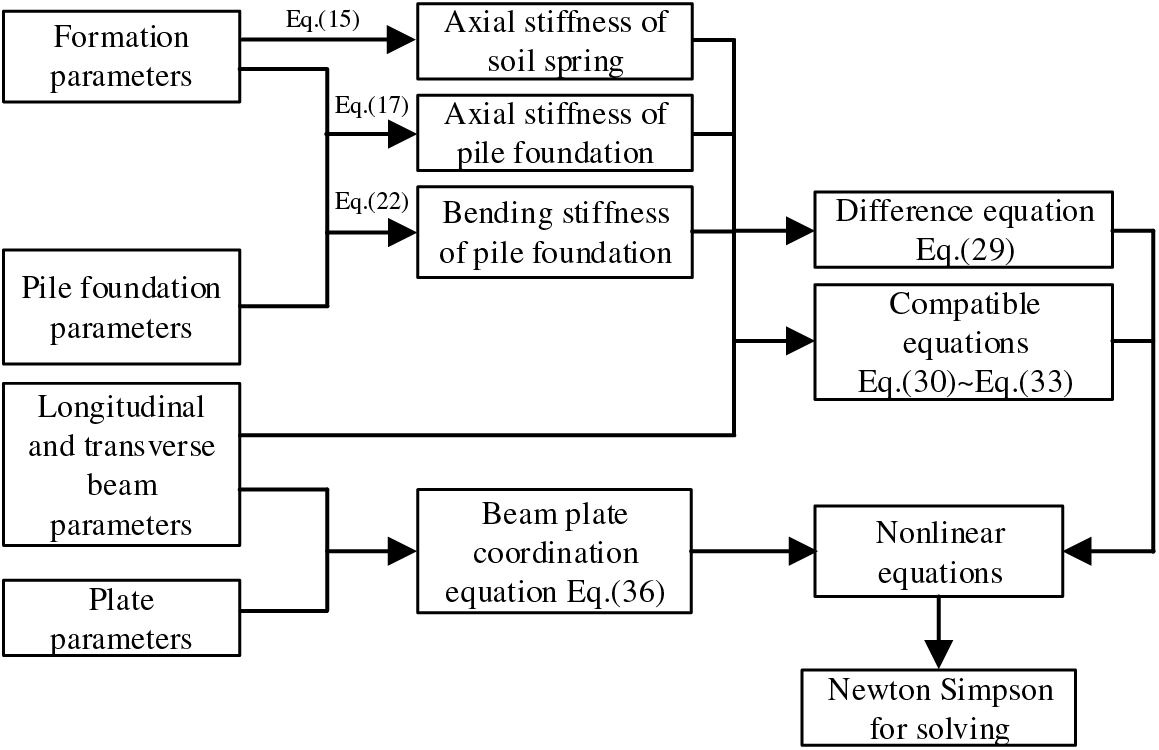
Figure 9: Mechanical model establishment and solution process

5  Application of Simplified Mechanical Model for Transfer Structure

5.1 Model Parameters

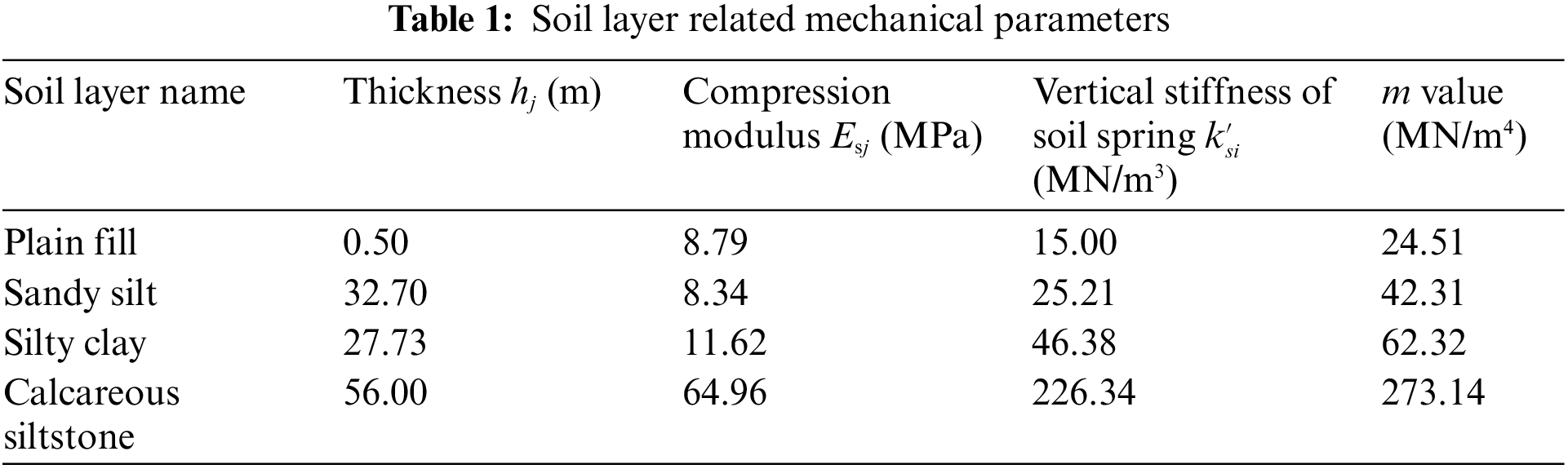
To facilitate the seamless transfer of the load from the central corridor steel structure column to the foundation while minimizing impact on the adjacent tunnel, a transfer structure, illustrated in Fig. 2, was implemented during the initial phase of the Hangzhou Convention and Exhibition Center project. Table 1 presents the pertinent parameters of the strata within which the transfer structure is situated.

The transfer structure is horizontally segmented into 2 spans along the tunnel and vertically into 5 spans for analysis. The transverse beams boast a 16 m span and a cross-sectional profile of 1800 mm × 2000 mm, while the longitudinal beams feature a 9 m span and a cross-sectional specification of 600 mm × 1200 mm, accompanied by a plate thickness of 250 mm. Pile foundations are strategically positioned at the intersection points of longitudinal and transverse beams, each with a 0.9 m diameter. The piles on the sides extend to a length of 75 m, while those in the middle row are 78 m long. The concrete used for beams and plates is of C40 grade with elastic modulus of 3.25 × 104 MPa, and for piles, C45 grade concrete is employed, also with elastic modulus of 3.25 × 104 MPa. The soil stiffness at the pile end is considered as 210.00 MN/m, and the concrete density is set at 2500 kg/m3. The plate’s bottom clearance is assumed to be 0.00 mm, and a uniformly distributed external load of 2.50 kPa is applied to the board surface. The location and magnitude of concentrated loads on the beams are outlined in Table 2.

5.2 Transfer Structure Stress

Combining the model parameters and the solution process illustrated in Fig. 9 facilitates the derivation of the internal force diagrams and deformation diagrams for the transfer structure, as depicted in Fig. 10. To validate the proposed simplified analysis method, we present corresponding results obtained through finite element analysis in Fig. 10. A clear comparison between the two methods reveals that the simplified calculation approach in this paper exhibits high accuracy and is practical for engineering calculations. The figure illustrates a maximum deflection of approximately 2.5 mm and a maximum bending moment of 7800 kN/min the middle span of the transverse beam. These extremities align closely with the positions of concentrated loads application. To optimize material strength and ensure even distribution of the bending moment along the beam length, it is advisable to consider a moderate increase in pile length at the mid-span beam position. Meanwhile, the longitudinal beam in the middle span exhibits a maximum deflection of about 2.75 mm and a maximum bending moment of 1300 kN/min. The distribution of bending moments along the beam length is notably more uniform than in the transverse beams. When designing the transfer structure, factors such as pile length, pile section size, and beam section size should be carefully considered to achieve an even distribution of bending moments. Prioritizing adjustments to the pile length is recommended for achieving uniform bending moment distribution, taking into account the practicalities of the construction process.

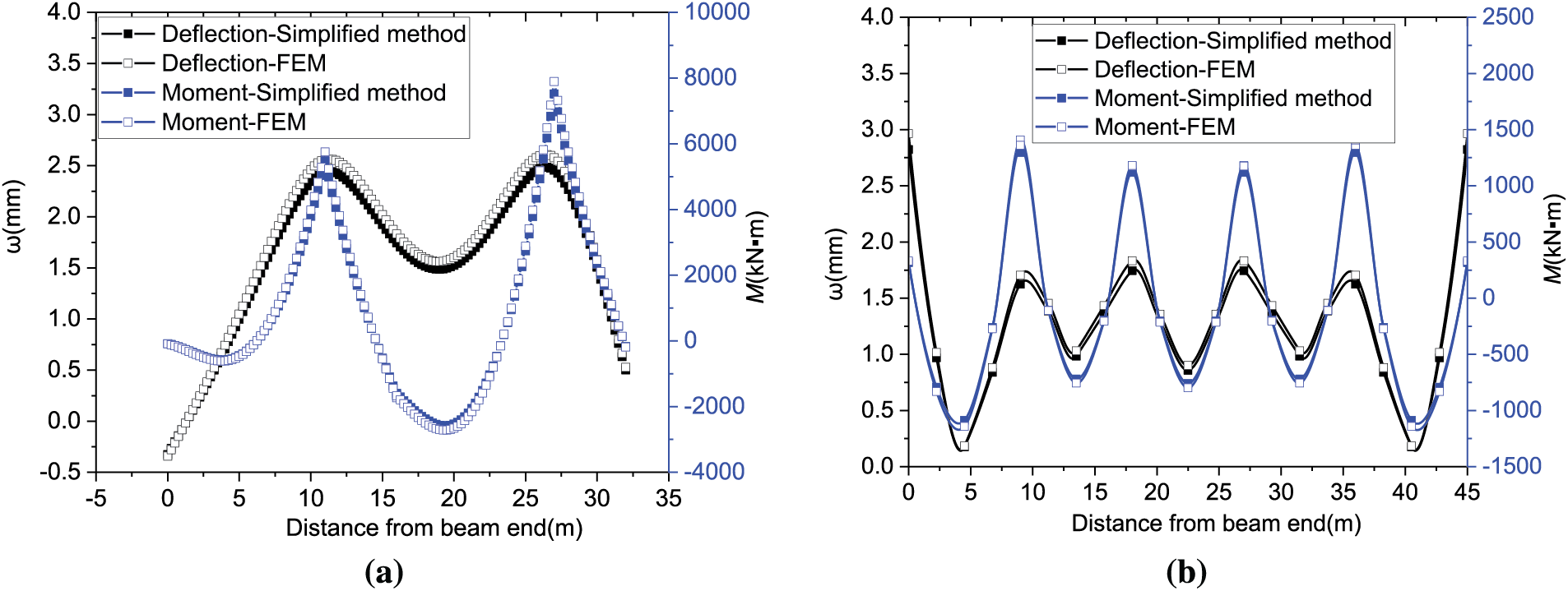
Figure 10: Transfer structure calculation results: (a) Mid span-transverse beam; (b) Mid span longitudinal beam

5.3 Discussion

Section 3.2 of this paper establishes a simplified analysis method for the transfer structure, treating the beam system of longitudinal and transverse beams as a Winkler elastic foundation beam. In Figs. 4a and 4b, the pivotal aspects of Winkler elastic foundation beams involve determining the axial stiffness (ks) of the soil spring, the axial stiffness Kn of the pile foundation, and the bending stiffness Km of the pile foundation. Eq. (15) highlights the influence of soil layering and the compressive modulus of each layer on the axial stiffness of the soil spring, significantly impacting the elastic foundation beam’s solution results. Similarly, Eqs. (17) and (18) demonstrate that soil layering, mechanical properties of each soil layer, and pile foundation characteristics affect the axial and bending stiffness of pile foundations, consequently influencing the solution results of elastic foundation beams. In summary, soil stratification affects Winkler elastic foundation beams through the collective impact of soil spring axial stiffness, pile foundation axial stiffness, and pile foundation bending stiffness. Simultaneously, pile foundation characteristics affect Winkler elastic foundation beams through the combined influence of pile foundation axial stiffness and bending stiffness. Considering that the simplified analysis method in this paper is grounded in the Winkler elastic foundation beam model, its applicability should align with the scope of this model. Thus, it is primarily suited for relatively weak soil layers and not suitable for rock foundations.

The derivation process of the simplified analysis method for the transfer structure reveals that this paper approximates pile-soil interaction, beam-soil interaction, and plate-soil interaction in a linear fashion. It is evident that the derived simplified analysis method is not suitable for scenarios involving substantial deformations, such as considerable relative displacement at the pile-soil interface or extensive bending deformation of the beam. Additionally, in practical engineering applications, issues like pile foundation failure or uneven settlement may arise. To address pile foundation failure, one can simply assign zero values to the corresponding axial stiffness and bending stiffness of the pile foundation. As for uneven settlement problems of pile foundations, the simplified analysis method presented in this paper remains applicable as long as there is no significant deformation.

The transmission of load from the upper structure is channeled through columns to the longitudinal and transverse beams. Interactions occur between the longitudinal and transverse beams and the underlying soil, as well as between these beams and pile foundations. This sequential process effectively conveys the upper load to the soil and piles beneath the beams. As the soil beneath the beams bears the load, stress is disseminated to the deeper layers. Similarly, when the pile foundation assumes the load, it distributes it to the surrounding soil and the deeper layers through both the pile side and pile end. Clearly, this load transfer process imposes stringent demands on the connection nodes of longitudinal and transverse beams, as well as on the construction quality of piles. Any failure in nodes or pile foundations can alter the course of load transfer. Therefore, during the actual construction, it is imperative to rigorously ensure the quality of both node and pile foundation construction.

Given the intricate nature of soil behavior, the variability in soil properties, and the ultimate transfer of upper loads to the soil by the transfer structure, the param defining the interaction between soil and the conversion structure become pivotal in stress analysis. For enhanced safety in actual engineering design, it is advisable to prudently diminish the values of param such as Esj, ksi′, and m during design analysis, for instance, by employing a reduction factor of 0.9.

6  Conclusion

To address the engineering challenge of accommodating pile foundations traversing through tunnels, a subterranean transfer structure spanning multiple subway tunnels is proposed. This study offers a streamlined analysis approach to elucidate the force mechanism within the transfer structure by amalgamating various theoretical analysis methods. The primary conclusions are as follows:

(1) The vertical load imposed on the upper structural columns is transmitted through the transfer structure to the pile foundation beneath the beams, subsequently transferring to the deep soil. This process ensures minimal impact on adjacent tunnels.

(2) The simplified analysis method established in this study facilitates stress analysis of transfer structures, concurrently considering soil stratification, pile foundation behavior, and plate action.

(3) When designing the transfer structure, careful consideration of pile length, pile section size, and beam section size is essential to accommodate the characteristics of the upper load, ensuring an even distribution of the beam bending moment.

The paper introduces an innovative underground transfer structure spanning multiple subway tunnels and employs theoretical analysis methods to elucidate its stress mechanism However, practical engineering often seeks to minimize engineering costs while maintaining safety. The optimization of the design for underground transfer structures with numerous variables to reduce engineering costs represents a valuable avenue for future research. Intelligent optimization methods are recommended for achieving optimal designs in the future transfer structure projects.

Acknowledgement: This work was supported by the Construction and Scientific Research Project of the Zhejiang Provincial Department of Housing and Urban-Rural Development; the Scientific Research Project of China Construction 4th Engineering Bureau; and the Natural Science Foundation of Hubei Province. The financial support is greatly appreciated.

Funding Statement: This work was supported by the Construction and Scientific Research Project of the Zhejiang Provincial Department of Housing and Urban-Rural Development (No. 2021K126, Granted by M.J., Long, URL: https://jst.zj.gov.cn/); the Scientific Research Project of China Construction 4th Engineering Bureau (No. CSCEC4B-2022-KTA-10, Granted by Z.C., Bai, URL: https://4bur.cscec.com/); the Scientific Research Project of China Construction 4th Engineering Bureau (No. CSCEC4B-2023-KTA-10, Granted by D.J., Geng, URL: https://4bur.cscec.com/); the Natural Science Foundation of Hubei Province (No. 2022CFD055, Granted by N., Dai, URL: https://kjt.hubei.gov.cn/); and the National Key Research and Development Program of China under Grant No. 2022YFC3803002.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: D.J., Geng, M.J., Long; data collection: D.J., Geng, Z.C., Bai; analysis and interpretation of results: S., Yan, N., Dai; draft manuscript preparation: S., Yan, D.J., Geng. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data, models, or code that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Fang, X. Q., Zhang, T. F., Li, B. L., Yuan, R. J. (2020). Elastic-slip interface effect on dynamic stress around twin tunnels in soil medium subjected to blast waves. Computers and Geotechnics, 119, 103301. [Google Scholar]

2. Li, B. L., Fang, X. Q., Zhang, T. F., Yang, S. P. (2020). Elastic-slip interface effect on dynamic response of underwater convey tunnel in saturated poroelastic soil subjected to plane waves. Tunnelling and Underground Space Technology, 103, 103468. [Google Scholar]

3. Fang, X. Q., Ma, H. W., Zhu, C. S., Ding, Q. L., Zhu, Z. G. et al. (2023). Imperfect interface model and dynamic interaction mechanism around tunnels under seismic waves: A review. Tunnelling and Underground Space Technology, 137, 105120. [Google Scholar]

4. Dias, T. G. S., Bezuijen, A. (2015). Data analysis of pile tunnel interaction. Journal of Geotechnical and Geoenvironmental Engineering, 141(12), 04015051. [Google Scholar]

5. He, S. Y., Lai, J. X., Li, Y., Wang, K., Wang, L. X. et al. (2022). Pile group response induced by adjacent shield tunnelling in clay: Scale model test and numerical simulation. Tunnelling and Underground Space Technology, 120, 104039. [Google Scholar]

6. Yoo, C., Abbas, Q. (2021). Interaction between two-arch tunnel and pile supported bridge-An experimental investigation. Tunnelling and Underground Space Technology, 112, 103869. [Google Scholar]

7. Soomro, M. A., Mangi, N., Xiong, H., Kumar, M., Mangnejo, D. A. (2020). Centrifuge and numerical modelling of stress transfer mechanisms and settlement of pile group due to twin stacked tunnelling with different construction sequences. Computers and Geotechnics, 121, 103449. [Google Scholar]

8. Marshall, A. M., Haji, T. (2015). An analytical study of tunnel-pile interaction. Tunnelling and Underground Space Technology, 45, 43–51. [Google Scholar]

9. Zhang, Z. G., Zhang, C. P., Jiang, K. M., Wang, Z. W., Jiang, Y. J. et al. (2019). Analytical prediction for tunnel-soil-pile interaction mechanics based on Kerr foundation model. KSCE Journal of Civil Engineering, 23, 2756–2771. [Google Scholar]

10. Basile, F. (2014). Effects of tunnelling on pile foundations. Soils and Foundations, 54(3), 280–295. [Google Scholar]

11. Franza, A., Marshall, A. M., Haji, T., Abdelatif, A. O., Carbonari, S. et al. (2017). A simplified elastic analysis of tunnel-piled structure interaction. Tunnelling and Underground Space Technology, 61, 104–121. [Google Scholar]

12. Zhang, Z. G., Huang, M. S., Xu, C., Jiang, Y. J., Wang, W. D. (2018). Simplified solution for tunnel-soil-pile interaction in Pasternak’s foundation model. Tunnelling and Underground Space Technology, 78, 146–158. [Google Scholar]

13. Liu, B., Yu, Z. W., Yao, B., Han, Y. H., Liu, H. et al. (2021). Responses of the ground and adjacent pile to excavation of U-shaped tunnel. Computers and Geotechnics, 130, 103919. [Google Scholar]

14. Huang, F., Wang, Z. Q., Zhang, M., Li, S. Y. (2022). Failure mechanism of the bearing stratum at the end of a pile induced by shield tunnel excavation beneath a piled building. KSCE Journal of Civil Engineering, 26(2), 942–954. [Google Scholar]

15. Soomro, M. A., Ng, C. W. W., Liu, K., Memon, N. A. (2017). Pile responses to side-by-side twin tunnelling in stiff clay: Effects of different tunnel depths relative to pile. Computers and Geotechnics, 84, 101–116. [Google Scholar]

16. Khabbaz, H., Gibson, R., Fatahi, B. (2019). Effect of constructing twin tunnels under a building supported by pile foundations in the Sydney central business district. Underground Space, 4(4), 261–276. [Google Scholar]

17. Soomro, M. A., Hong, Y., Ng, C. W. W., Lu, H., Peng, S. Y. (2015). Load transfer mechanism in pile group due to single tunnel advancement in stiff clay. Tunnelling and Underground Space Technology, 45, 63–72. [Google Scholar]

18. Jeon, Y. J., Jeon, S. C., Jeon, S. J., Lee, C. J. (2020). Study on the behaviour of pre-existing single piles to adjacent shield tunnelling by considering the changes in the tunnel face pressures and the locations of the pile tips. Geomechanics and Engineering, 21(2), 187. [Google Scholar]

19. Li, Y. Q., Zhang, W. G. (2020). Investigation on passive pile responses subject to adjacent tunnelling in anisotropic clay. Computers and Geotechnics, 127, 103782. [Google Scholar]

20. Lee, C. J. (2012). Three-dimensional numerical analyses of the response of a single pile and pile groups to tunnelling in weak weathered rock. Tunnelling and Underground Space Technology, 32, 132–142. [Google Scholar]

21. Liu, C., Zhang, Z. X., Regueiro, R. A. (2014). Pile and pile group response to tunnelling using a large diameter slurry shield-Case study in Shanghai. Computers and Geotechnics, 59, 21–43. [Google Scholar]

22. Huang, K., Sun, Y. W., Huang, X. Q., Li, Y. J., Jiang, M. et al. (2021). Effects of different construction sequences on ground surface settlement and displacement of single long pile due to twin paralleled shield tunneling. Advances in Civil Engineering, 2021, 1–14. [Google Scholar]

23. Soomro, M. A., Kumar, M., Xiong, H., Mangnejo, D. A., Mangi, N. (2020). Investigation of effects of different construction sequences on settlement and load transfer mechanism of single pile due to twin stacked tunnelling. Tunnelling and Underground Space Technology, 96, 103171. [Google Scholar]

24. Wang, Y. X., Liu, J., Guo, P. P., Zhang, W., Lin, H. et al. (2021). Simplified analytical solutions for tunnel settlement induced by axially loading single pile and pile group. Journal of Engineering Mechanics, 147(12), 04021116. [Google Scholar]

25. Lueprasert, P., Jongpradist, P., Jongpradist, P., Suwansawat, S. (2017). Numerical investigation of tunnel deformation due to adjacent loaded pile and pile-soil-tunnel interaction. Tunnelling and Underground Space Technology, 70, 166–181. [Google Scholar]

26. Liu, X. Z., Sang, Y. L., Zhao, F., Shi, G., Heng, Y. (2019). Evaluation of effects of static pile driving on existing metro tunnel structure. Journal of Performance of Constructed Facilities, 33(4), 04019045. [Google Scholar]

27. Gao, G. Y., Zhuang, Y., Wang, K. Y., Chen, L. (2019). Influence of Benoto bored pile construction on nearby existing tunnel: A case study. Soils and Foundations, 59(2), 544–555. [Google Scholar]

28. Ai, Z., Cai, J. B. (2017). A BEM for interaction between layered foundations and an elastic thin plate. Journal of Hunan University (Natural Sciences), 44(3), 120–125. [Google Scholar]

29. You, L. Y., Yan, K. Z., Shi, T. W., Man, J. H., Liu, N. Y. (2019). Analytical solution for the effect of anisotropic layers/interlayers on an elastic multi-layered medium subjected to moving load. International Journal of Solids and Structures, 172, 10–20. [Google Scholar]

30. Ravera, E., Sutman, M., Laloui, L. (2020). Load transfer method for energy piles in a group with pile-soil–slab-pile interaction. Journal of Geotechnical and Geoenvironmental Engineering, 146(6), 04020042. [Google Scholar]

31. Zhang, Y. P., Wu, W. B., Jiang, G. S., Wen, M. J., Wang, K. H. et al. (2021). A new approach for estimating the vertical elastic settlement of a single pile based on the fictitious soil pile model. Computers and Geotechnics, 134, 104100. [Google Scholar]

32. Bokov, I. A., Fedorovskii, V. G. (2021). Taking into account the soil depth inhomogeneity in calculation of the piles settlement. Soil Mechanics Foundation Engineering, 58(4), 267–272. [Google Scholar]

33. Luamba, E. S., de Paiva, J. B. (2022). Static analysis of axially loaded piles in multilayered soils using a BEM/FEM formulation. Engineering Analysis with Boundary Elements, 135, 63–72. [Google Scholar]

34. Lu, Q. S., Ai, Z. Y., Jiang, M. J., Liu, W. J. (2021). Time effect of vertically loaded pile groups partially embedded in multilayered cross-anisotropic fractional viscoelastic saturated soils. Engineering Analysis with Boundary Elements, 133, 19–29. [Google Scholar]

35. Wang, T., Lu, S. Q., Chen, J. X., Shen, Y. Y. (2015). Analytical solution on the load-settlement of single pile using the multi-linear load transfer method. Journal of Shenyang Jianzhu University (Natural Science), 31(3), 442–448 (In Chinese). [Google Scholar]

36. Zhu, M. X., Zhang, Y. B., Gong, W. M., Wang, L., Dai, G. L. (2017). Generalized solutions for axially and laterally loaded piles in multilayered soil deposits with transfer matrix method. International Journal of Geomechanics, 17(4), 04016104. [Google Scholar]

37. Chiou, J. S., You, J. Q. (2020). Theoretical solutions of laterally loaded fixed-head piles in elastoplastic soil considering pile-head flexural yielding. Canadian Geotechnical Journal, 57(5), 650–660. [Google Scholar]

38. Rathod, D., Muthukkumaran, K., Sitharam, T. G. (2018). Effect of slope on p-y curves for laterally loaded piles in soft clay. Geotechnical and Geological Engineering, 36, 1509–1524. [Google Scholar]

39. Taborda, D. M. G., Zdravkovic, L., Potts, D. M., Burd, H. J., Byrne, B. W. et al. (2020). Finite-element modelling of laterally loaded piles in a dense marine sand at Dunkirk. Géotechnique, 70(11), 1014–1029. [Google Scholar]

40. Dong, M. M., Wang, L. Q., Ge, Y. F., Wang, C. (2017). Mechanical characteristics of anti-sliding pile considering comprehensive foundation coefficient of sliding bed on composite inclined rock mass. Rock and Soil Mechanics, 38(10), 3000–3008. [Google Scholar]

41. Geng, D. J., Dai, N., Guo, P. J., Zhou, S. H., Di, H. G. (2021). Implicit numerical integration of highly nonlinear plasticity models. Computers and Geotechnics, 132, 103961. [Google Scholar]

42. Loghman, E., Kamali, A., Bakhtiari-Nejad, F., Abbaszadeh, M. (2021). Nonlinear free and forced vibrations of fractional modeled viscoelastic FGM micro-beam. Applied Mathematical Modelling, 92, 297–314. [Google Scholar]