Investigation of Projectile Impact Behaviors of Graphene Aerogel Using Molecular Dynamics Simulations

1  Introduction

Graphene is a two-dimensional material with numerous outstanding properties, such as a large surface area [1], excellent thermal [2], and electrical conductivity [3], and a high elastic modulus [4]. These characteristics show great potential in engineering applications. In order to enhance material properties, extensive investigations have converted two-dimensional graphene materials into three-dimensional structures, creating novel materials through delicate designs. Notably, Gao et al. [5] pioneered the use of freeze-drying techniques in 2013 to fabricate graphene aerogel (GA). This unprecedentedly lightweight solid material has garnered considerable attention from the scientific community. For example, compared to other lightweight 3D graphene networks [6,7], GA possesses significant potential in nanoparticle capture owing to its much lower density. However, observing GA’s mechanical response to high-velocity impacts by nanoparticles presents considerable difficulties, thereby imposing challenges in conducting comprehensive investigations into GA’s projectile impact behaviors.

The synthesis of GA, along with its chemical and conductive characteristics, has been extensively explored in previous studies [8–11]. Results show that three-dimensional GA can fully exploit graphene’s inherent properties compared to two-dimensional materials due to π-π stacking interactions within graphene layers. For example, in energy storage applications, GA has been widely used in electrode fabrication due to properties such as high surface area, high porosity, high specific capacitance, and high cyclic stability [12–14]. Furthermore, GA exhibits considerable adsorption capabilities, making it suitable for adsorbing spilled oil and other organic pollutants in environmental conservation applications [15]. Although there has been much research on GA, its mechanical properties have rarely been studied in detail [16].

Molecular dynamics (MD) simulation provides a novel approach for in-depth investigations of the mechanical properties and behaviors of two-dimensional materials. Recently, there has been an increase in research focused on using MD simulations to analyze GA. Qin et al. [17] employed MD simulations to study the 3D GA system, emphasizing the investigation of its mechanical characteristics, including tensile strength, compression strength, buckling modulus, and Young’s modulus. The findings demonstrate that GA exhibits superior mechanical properties compared to most polymeric cellular materials. Patil et al. [18] conducted a study on the fracture behaviors of GAs subjected to tensile loading with pre-existing cracks. The investigation focused on the impact of aspect ratio on fracture strength and toughness. The findings revealed a decrease in fracture strength with increasing aspect ratio, while the fracture toughness remained constant across all densities. Moreover, Patil et al. [19] also employed the reverse-ballistic method to investigate GA’s shock wave propagation behaviors. The research findings show a direct proportionality between the shock and particle velocities, while the slope of the Shock-Hugoniot curve exhibits a discernible correlation with GA density. Specifically, as GA density increases, the slope of the Shock-Hugoniot curve also increases. Despite these noteworthy contributions, the mechanical performance of GA under projectile impact loadings has not been reported.

In this work, MD simulation is performed to investigate the mechanical performance of GA subjected to nano-projectile impacts. The remainder of this article is organized such that Section 2 presents the construction of the GA model with various densities and the MD simulation details. Section 3 briefly introduces the penetration equations for low-density materials. Section 4 thoroughly investigates the mechanical performances of GA under projectile impacts, revealing the energy absorption mechanism and capacity of GAs. Finally, Section 5 concludes the paper with some remarks.

2  Method and Materials

In this study, molecular dynamics simulations were performed using the large-scale atomic/molecular massively parallel simulator (LAMMPS) [20]. The OVITO software [21] was utilized to visualize the simulation results and obtain snapshots during the simulations.

2.1 Interatomic Potentials

In molecular dynamics simulations, selecting a reasonable interatomic potential function that accurately replicates the system’s mechanical performance is paramount. This work employed the adaptive intermolecular reactive empirical bond order (AIREBO) potential [22,23] to describe the interatomic interactions between carbon atoms of graphene sheets. This potential is a well-established force field extensively utilized in MD simulations. It has been validated as reliable for simulating the mechanical performances of graphene materials, as observed in many experimental studies [24,25].

In the modeling process, the total potential energy of the system is given by:

E=EC−C+EC−inclusion+Einclusion−inclusion(1)

The first term, EC−C, is the interatomic potential of carbons, which is defined as follows:

EC−C=12∑i∑i≠j[EijREBO+EijLJ+∑k≠i,j∑l≠i,j,kEkijlTORSION](2)

where EijREBO is the REBO term in AIREBO potential, which denotes the short-range interactions that govern the potential energy of C-C covalent bonds; EijLJ is the LJ term that characterizes the intermolecular interactions within the system; EkijlTORTION is the TORTION term which represents the TORSION term that relies on the dihedral angles.

Furthermore, this study adopted the pairwise interaction potential EC−inclusion to describe the interactions between carbon atoms and inclusion particles and the pairwise interaction potential Einclusion−inclusion to describe the interactions between two inclusion particles. The 12−6 Lennard-Jones potential was adopted for EC−inclusion and Einclusion−inclusion:

EC−inclusion=Einclusion−inclusion=∑i∑j≠i4εij[(σijrij)12−(σijrij)6](3)

where εij represents the depth of the potential well, σij is the zero potential distance; rij denotes the interparticle distance. Note that the GA system with different densities can be obtained by changing the values of σij in Einclusion−inclusion. In this study, parameters εij = 0.65 eV and σij = 10–14 Å were adopted. This results in GAs with a density range of 275–546 kg/m3. Moreover, the cutoff distance for the LJ term in AIREBO potential was modified in this study. Specifically, the cutoff distance is rd1 = 1.7 Å in the modeling process and rd2 = 10.2 Å in the impact simulations.

2.2 Modeling Process

The all-atom GA models with different densities were constructed to investigate the mechanical response under projectile impact loadings. The GA models consist of 750 randomly distributed graphene sheets and 750 inclusion particles within the simulation box, as shown in Fig. 1a. The initial density of the model is 3.9 kg/m3, closely resembling air density. Inclusions were introduced to control the porous microstructure, mimicking the effects of water clusters in the laboratory synthesis of GA using the freeze-casting method [26]. Periodic boundary conditions were applied in all three directions of the simulation box during the construction of the MD model.

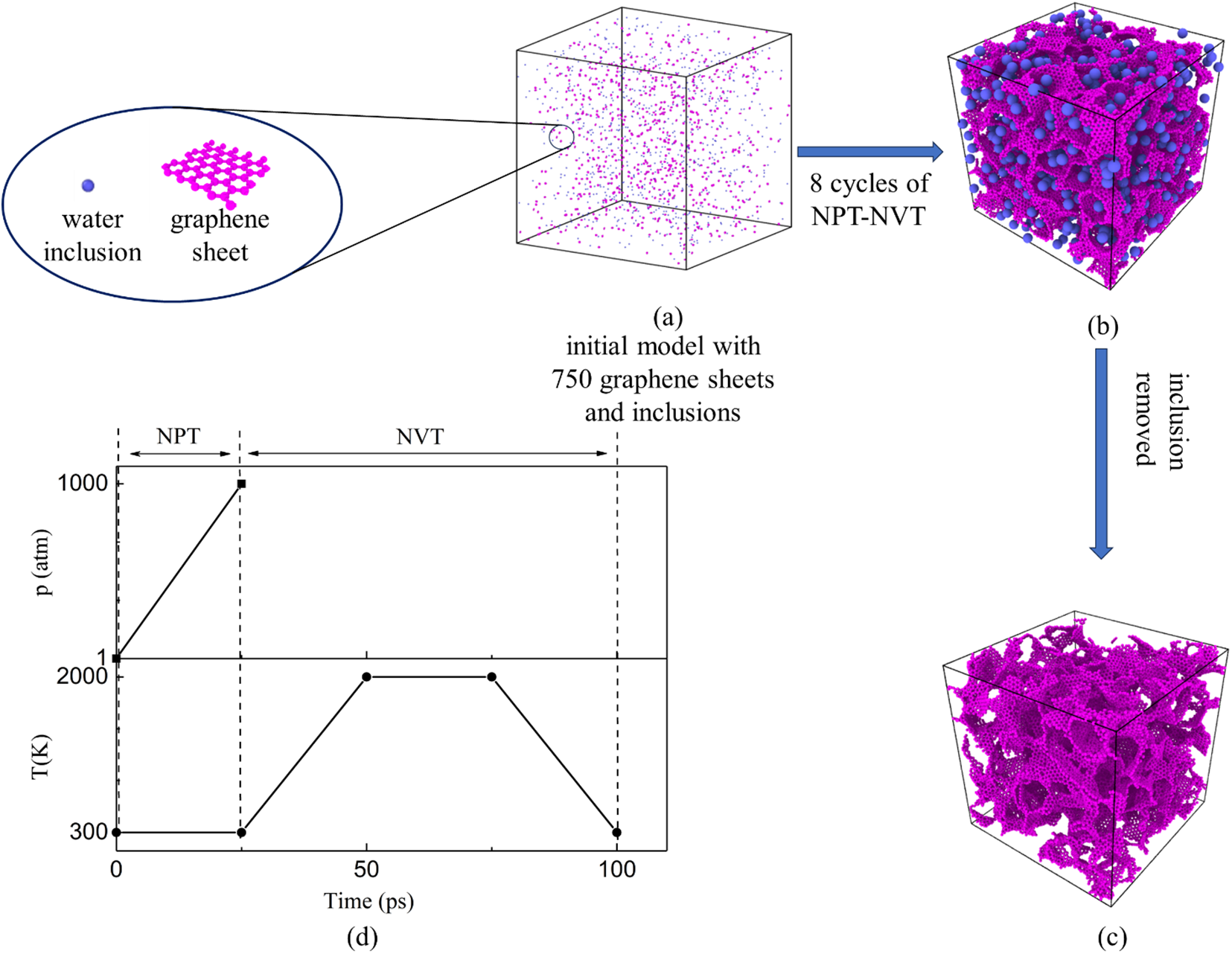
Figure 1: Schematic representation of the all-atom model creation process: (a) initial model in which water inclusions and graphene sheets are randomly distributed; (b) equilibrated graphene-inclusion structure after eight cycles of NPT-NVT; (c) GA model with a density of 546 kg/m3 after removing the water inclusions; (d) Pressure p, temperature T as a function of simulation time during the modeling process

According to the GA modeling procedures reported in previous work [17–19], the model was first equilibrated under the NPT ensemble (constant number of atoms N, pressure P, and temperature T), with a constant temperature of 300 K and pressure of 1 atm. Thereafter, a program consisting of multiple pretreatment cycles was implemented to achieve a stable GA model, as illustrated in Fig. 1d. Each cycle comprised four steps: (i) first increasing the pressure of the system from 1 to 1000 atm at a constant temperature of 300 K under the NPT ensemble; (ii) then increasing the system’s temperature from 300 to 2000 K; (iii) maintaining a constant temperature of 2000 K; (iv) reducing the temperature back to 300 K. The last three steps were carried out under the NVT ensemble (constant number of atoms N, volume V, and temperature T). Stable GA models with different densities were successfully obtained by repeating this cycle eight times, with each step lasting for a simulation time of 25 ps.

2.3 Simulation Details

In this study, nanoscale diamond projectiles were used to impact the GA with different densities. The 12–6 Lennard-Jones potential was selected to represent the interaction between the projectile and the graphene sheets, with the parameters εij = 0.035 eV and σij = 3.46 Å [27]. The simulations were conducted in the NVE ensemble (constant number of atoms N, volume V, and energy E), and the projectile was initially positioned 2 nm away from the upper surface of the GA model. The model dimensions are given in Table 1. The impact region was defined as a cylindrical area with a radius of R = L/2 Å, while the boundary region remained fixed during impact, as shown in Fig. 2. The diamond projectile was used with a diameter of D = 2.6 nm and an initial velocity varying from 1–7 km/s.

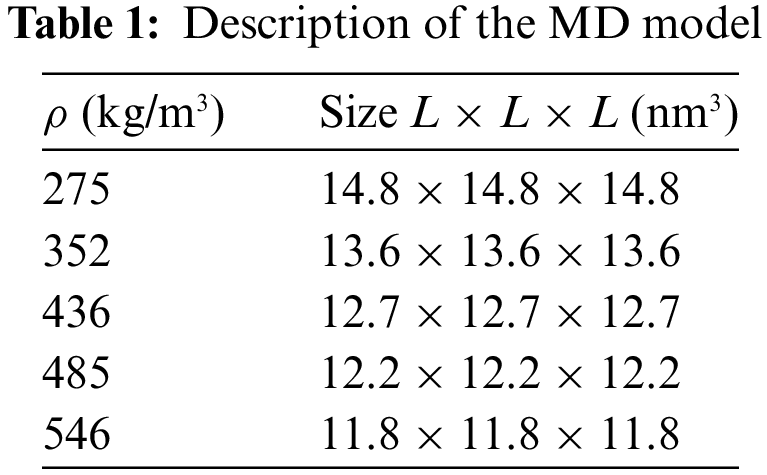
Figure 2: (a) Schematic representation of the initial state of the MD model; (b) Top view of the GA model

3  Penetration Equation of Low-Density Material

When the projectile penetrates a low-density target material, it overcomes both static and dynamic resistance. According to works [28,29], the rigid body penetration process can be described by the following equation:

mpdV(t)dt=−Skρt−ΓSρtV2(t)(4)

where mp is the mass of the projectile; V(t) is the velocity of the projectile at time t during penetration; ρt is the density of GA; Γ is the drag coefficient; S is the cross-sectional area of the projectile that remains constant. Besides, the scaling factor k is introduced to quantify the relationship between the crushing strength σc and the GA density, namely:

σc=kρt(5)

Eq. (4) can be equivalently expressed by dividing its sides by the cross-sectional area S as follows:

43ρPrdV(t)dt=[−k−ΓV(t)2]ρt(6)

where r represents the radius of the projectile; ρp denotes the density of the projectile. By applying the chain rule of differentiation and subsequently integrating both sides of Eq. (6), the following expression can be obtained:

∫0h3ρp⋅4rdz=−1ρt∫V00V(t)k+ΓV(t)2dV(t)(7)

After a simple algebraic operation, it finally yields:

h2r=ρpρt13Γln⁡(1+ΓkV02)(8)

4  Results and Discussion

4.1 Mechanical Response under Projectile Impact

Fig. 3 depicts the Mises stress distributions of the penetration process with three different GA densities, namely ρ = 275, 436, and 546 kg/m3. The initial impact velocity of the projectile is 10 km/s. Due to the intrinsic porous structure of GA, the impact of a projectile affects only a localized region of the GA structure, as observed in Fig. 3. Notably, the impact-induced penetration of the projectile leads to the collapse of the pore structure, and the graphene sheet undergoes stretching, subsequently leading to the rupture of covalent bonds. This contributes to GA’s energy absorption efficiency and its resistance to projectile impact compared to other porous materials, such as silica aerogel and aluminum foam. Moreover, the observed penetration patterns exhibit substantial differences for the three distinct densities under the same impact velocity, thus demonstrating the pivotal influence of GA density on the impact response.

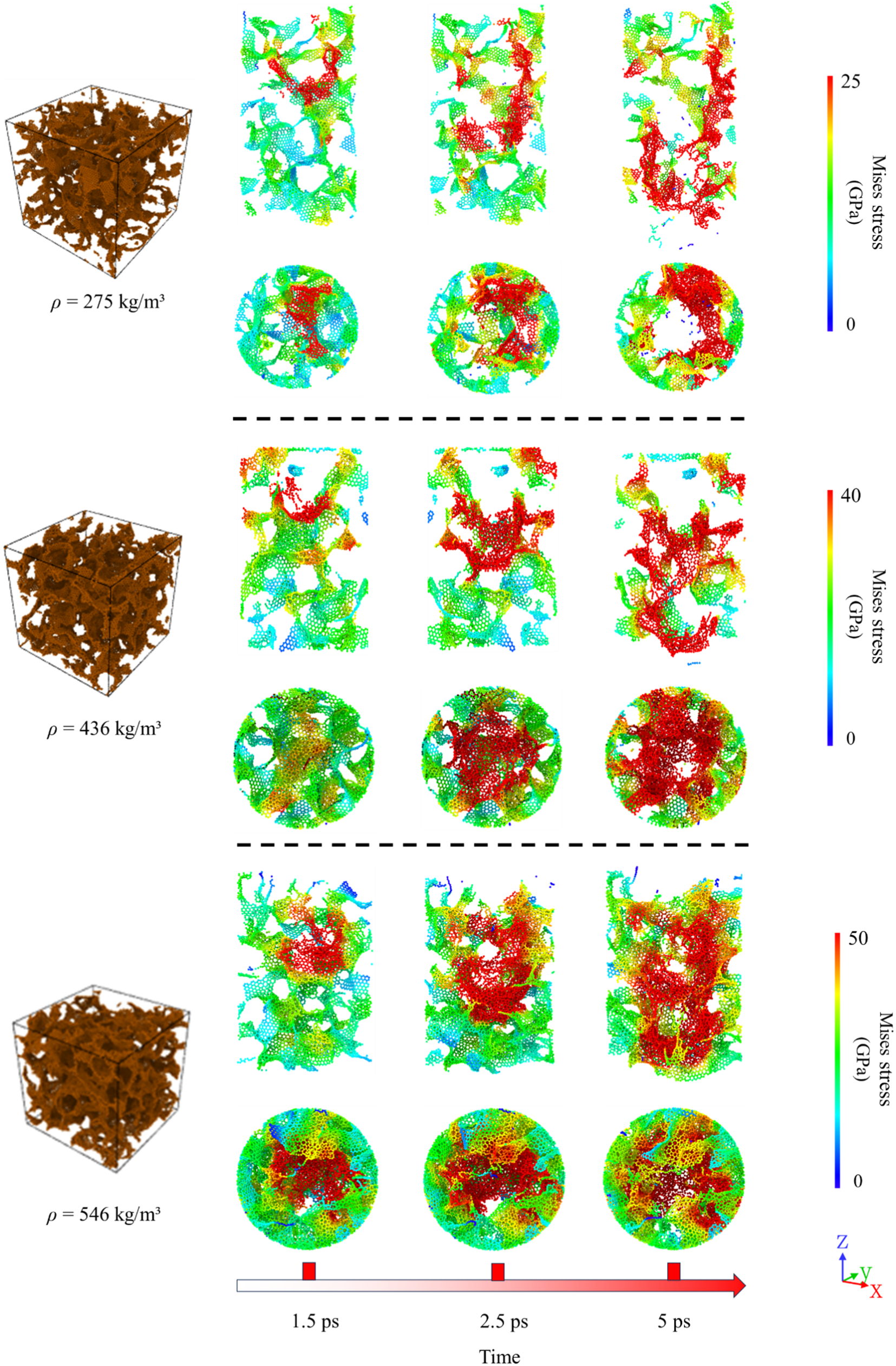
Figure 3: Schematic representation of the GA models to highlight the mises stress of each atom during impact simulation at the impact velocity of 10 km/s

For GA with low density, the large pores allow for greater motion flexibility of graphene sheets during projectile impact, which in turn leads to significant irreversible deformation of GA. In contrast, high-density GA exhibits smaller pore sizes, leading to reduced flexibility and rotational movement of graphene sheets.

The variations of different energy components, namely EREBO, ELJ, and ETORSION, are illustrated in Fig. 4. It is observed that the EREBO potential term, characterizing the alteration of the C-C covalent bond energy, experiences the most substantial fluctuation during the projectile impact process. In contrast, the contribution of the Lennard-Jones potential is minimal. Further assessment of the LJ potential’s impact is achieved by comparing the residual projectile velocity curves with and without LJ interatomic interactions, as shown in Fig. 5. Notably, the LJ potential energy has a minimal influence on the residual projectile velocity, suggesting that the interfacial interactions between GA sheets have negligible effects in halting the projectile impact.

Figure 4: (a) Penetration depth vs. time curves for different GA densities; (b–d) the variations of ΔEREBO, ΔELJ, and ΔETORSION vs. time for each GA with different densities (The initial velocity of the projectile is 10 km/s)

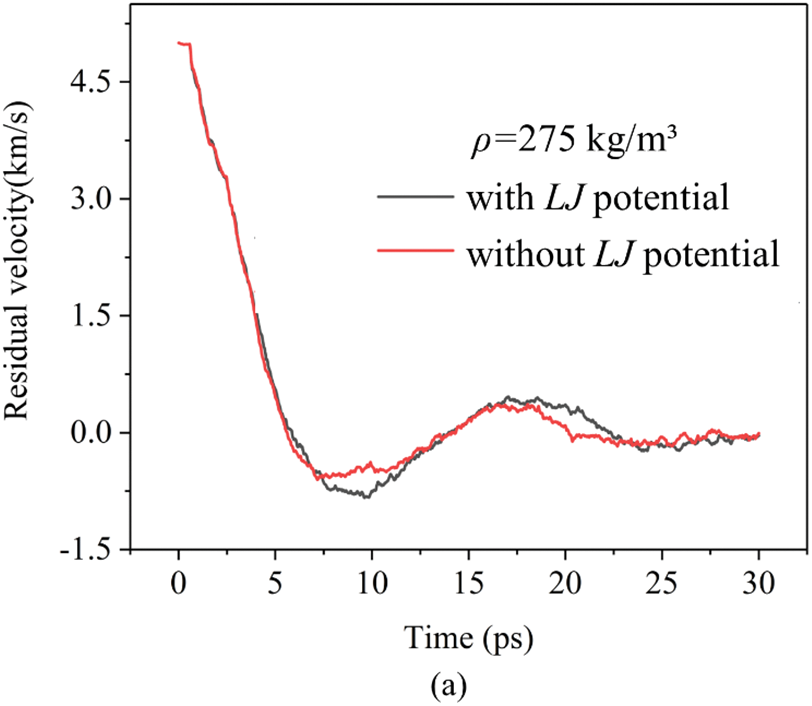
Figure 5: Comparison of residual projectile velocity with and without LJ interatomic interactions with different GA densities: (a) 275 kg/m3; (b) 436 kg/m3; (c) 564 kg/m3 (The initial velocity of the projectile is 5 km/s)

The normalized penetration depth h/2r vs. V0 curves are depicted in Fig. 6, wherein the analytical curves are fitted using Eq. (8). It is observed that the normalized penetration depth diminishes with an increase in GA density at a constant impact velocity. This observation signifies that GAs with higher density exhibit superior projectile capture capabilities compared to those with lower density. Furthermore, the simulation data presented in Fig. 6 enable the determination of the crushing strength of GA with different densities. Herein, a fitting relationship between the crushing strength σc and the normalized GA density ρ/ρs (ρs is the density of graphene) is obtained, as demonstrated in Fig. 7. It is seen that the strength increases nonlinearly with an increase in GA density.

Figure 6: The normalized penetration depth vs. impact velocity curves

Figure 7: Crushing strength vs. the normalized density curve

4.2 Effect of Temperature on Projectile Impact

For many applications, such as in aerospace engineering, structural materials may encounter extensive temperature variations. As a novel material with potential applications in aerospace engineering, the influence of temperature on projectile impact is a key concern. In order to address this issue, the impact simulation is performed at varying temperatures employing two different GA densities, namely 436 and 546 kg/m3. The initial velocity of the projectile was set at 6 km/s, aligning with observations from laboratory experiments.

The research conducted by Burchell et al. [30] focused on examining the particle-capturing capabilities of silica aerogel at temperatures ranging from 175 to 763 K. The findings indicate that the penetration depth of silica aerogel remains unaffected when the temperature is below 400K, as illustrated in Fig. 8b. However, beyond this critical temperature, there is a significant decline in penetration depth. When the temperature reaches 763 K, the penetration depth reduces by about 30% compared to GA. In contrast, results show that ambient temperature has minimal impact on the penetration depth of GA at different densities, as illustrated in Fig. 8a. This demonstrates GA’s thermal stability and mechanical reliability in terms of impact loadings across a wide range of temperatures.

Figure 8: Normalized penetration depth vs. temperature for: (a) GA; (b) silica aerogel

4.3 Energy Absorption for Projectile Impact

4.3.1 Kinetic Energy of GA

Fig. 9 shows the variations in the total kinetic energy of GA with different densities. During the penetration process, the carbon-carbon covalent bonds undergo elongation and rupture. Observations indicate that GA with higher density exhibits a pronounced advantage in terms of kinetic energy absorption, attributable to the greater number of covalent bonds involved in breaking within the impacted region. Notably, all three density curves exhibit non-smooth behavior, characterized by multiple peaks occurring at different intervals. Prior to the peak, the carbon-carbon covalent bonds within the impacted region mainly undergo extension. Thus, the kinetic energy of the projectile converts to the strain energy of GA. As the penetration continues, numerous covalent bonds break, leading to the conversion of strain energy into the kinetic energy of GA. Since GA is a highly porous structure, this process repeats until full penetration, giving rise to the formation of multiple peaks in the kinetic energy curves.

Figure 9: Variation of total kinetic energy of GA vs. normalized penetration depth for different densities. (The initial velocity of the projectile is 12 km/s)

4.3.2 Energy Absorption Density

Previous studies have demonstrated the potential of carbon-based nanomaterials as highly promising candidates for structural energy absorption owing to their excellent mechanical properties [31]. In this work, the energy absorption density (EAD) parameter was studied to gain a better understanding of GA’s energy absorption performance. EAD represents the kinetic energy absorbed per unit volume of GA, defined as follows:

EAD=ΔEkπr2L(9)

where ΔEk represents the kinetic energy dissipation of the projectile. In this section, the projectiles are launched at a velocity ranging from 12 to 20 km/s, resulting in the initial kinetic energy of the projectiles from 2.31 × 10−15 to 6.42 × 10−15 J.

As depicted in Fig. 10, the EAD value exhibits a positive correlation with both the impact velocity and GA density. During complete penetration, irreversible deformation occurs within GA, accompanied by the conversion of energy from the projectile to GA. At higher impact velocities, the fracture of carbon covalent bonds in the impact region becomes more pronounced, resulting in a higher capacity for kinetic energy absorption and consequently leading to a larger EAD value compared to that observed under lower impact velocities. Additionally, the EAD value increases with increasing GA density, which is explainable by the fact that GA with higher density possesses a greater density of covalent bonds in the impact region, facilitating more covalent bond breakages and thus absorbing more kinetic energy from the projectile.

Figure 10: A fitting surface of EAD as a function of GA density and impact velocity (GA density varies from 275 to 546 kg/m3, and impact velocity varies from 12 to 15 km/s)

4.3.3 Energy Absorption Efficiency

In this subsection, the concept of energy absorption efficiency (EAE) was introduced to further evaluate the energy absorption capacity of GA during projectile impact. The EAE parameter η is defined as follows:

η=ΔEkE0(10)

where E0 is the initial kinetic energy of the projectile. According to the energy conservation principle, the dissipated kinetic energy of the projectile is transformed into the kinetic energy (ΔEkinetic) and the potential energy (ΔEpotential) of GA as follows:

ΔEk=ΔEpotential+ΔEkinetic(11)

The energy absorption efficiency is illustrated in Fig. 11 with varying initial velocities of the projectile. It is observed that η experiences a decrease as the impact velocity increases in Region I. However, once the projectile velocity surpasses 24 km/s, the value of η remains relatively unchanged in Region II. This phenomenon is attributable to the fact that as the initial impact velocity rises, both E0 and ΔEk concurrently increase. Nevertheless, the increase in E0 surpasses that of ΔEk. In accordance with Eq. (10), this results in a decline in EAE, as depicted in Region I. When the initial velocity of the projectile surpasses the critical threshold of 24 km/s, the higher impact velocity leads to a larger impact region. Consequently, a greater number of covalent bonds break compared to those at lower impact velocities, thereby inducing a significant increase in ΔEk and leading to a relatively stable value of η in Region II instead of its anticipated decline in Region I.

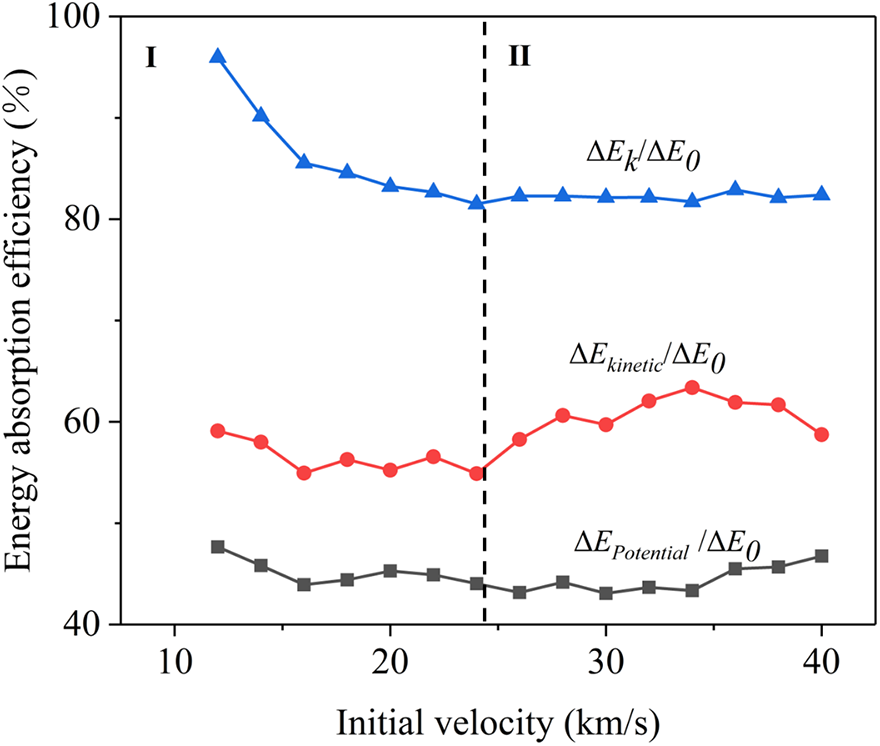
Figure 11: Energy absorption efficiency under different impact velocities (from 12 to 40 km/s) for GA density 546 kg/m3

5  Conclusions

In this study, MD simulation is used to investigate the mechanical performance of graphene aerogel subjected to nano-projectile impacts. A full-atomic GA model with different densities is first developed, followed by MD simulations to thoroughly investigate the mechanical responses and energy absorption mechanisms under impact loadings. The results show that the porous structure and density are key factors determining the mechanical response of GA. Specifically, the impact-induced penetration of the projectile leads to the collapse of the pore structure, causing stretching and subsequent rupture of covalent bonds in the graphene sheet. Therefore, the REBO term in the AIREBO potential contributes to the main part of the energy absorption during all the impact simulations, while the contribution of the LJ and TORSION terms is minimal.

Moreover, the influence of temperature on GA has been investigated and determined to be insignificant, thereby highlighting the mechanical stability of GA over a wide range of temperatures. Besides, the EAD and EAE parameters are adopted to assess the energy absorption capacity of GA during projectile penetration. Results show that at higher initial projectile velocities, a larger number of covalent bonds involved in the impact process contribute to energy absorption, which results in a relatively stable and higher energy absorption efficiency. The research findings of this work demonstrate the significant potential of GA for energy absorption applications.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions, which greatly improved the presentation of this paper.

Funding Statement: This work was supported by the National Natural Science Foundation of China (No. 12102256).

Author Contributions: Xinyu Zhang: Writing—original draft, Software, Visualization, Data curation. Wenjie Xia: Methodology, Writing—review & editing. Yang Wang: Methodology, Writing—review & editing. Liang Wang: Conceptualization, Methodology, Formal analysis, Supervision, Writing—review & editing, Project administration, Funding acquisition. Xiaofeng Liu: Methodology, Writing—review & editing.

Availability of Data and Materials: All materials and data used in this review are readily accessible to interested readers.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Kamedulski, P., Skorupska, M., Binkowski, P., Arendarska, W., Ilnicka, A. et al. (2021). High surface area micro-mesoporous graphene for electrochemical applications. Scientific Reports, 11(1), 22054. [Google Scholar] [PubMed]

2. Wang, J., Mu, X., Wang, L., Sun, M. (2019). Properties and applications of new superlattice: Twisted bilayer graphene. Materials Today Physics, 9, 100099. [Google Scholar]

3. Cao, M., Xiong, D. B., Yang, L., Li, S., Xie, Y. et al. (2019). Ultrahigh electrical conductivity of graphene embedded in metals. Advanced Functional Materials, 29(17), 1806792. [Google Scholar]

4. Luo, B., Wu, L., Li, D., Zhang, Z., Yu, X. et al. (2022). Novel atomic-scale graphene metamaterials with broadband electromagnetic wave absorption and ultra-high elastic modulus. Carbon, 196, 146–153. [Google Scholar]

5. Sun, H., Xu, Z., Gao, C. (2013). Multifunctional, ultra-flyweight, synergistically assembled carbon aerogels. Advanced Materials, 25(18), 2554–2560. [Google Scholar] [PubMed]

6. Zhang, S., Wang, F., Huang, P. (2021). Enhanced hall-petch strengthening in graphene/Cu nanocomposites. Journal of Materials Science & Technology, 87, 176–183. [Google Scholar]

7. Wu, Y. C., Shao, J. L., Mei, Y., Mu, X., Chen, P. (2023). Spall characteristics of three-dimensional graphene networks with embedded copper: A molecular dynamics study. Mechanics of Materials, 186, 104803. [Google Scholar]

8. Chen, C., Yang, Q. H., Yang, Y., Lv, W., Wen, Y. et al. (2009). Self-assembled free-standing graphite oxide membrane. Advanced Materials, 21(29), 3007–3011. [Google Scholar]

9. Chen, H., Müller, M. B., Gilmore, K. J., Wallace, G. G., Li, D. (2008). Mechanically strong, electrically conductive, and biocompatible graphene paper. Advanced Materials, 20(18), 3557–3561. [Google Scholar]

10. Cheng, Z., Wang, R., Wang, Y., Cao, Y., Shen, Y. et al. (2023). Recent advances in graphene aerogels as absorption-dominated electromagnetic interference shielding materials. Carbon, 205, 112–137. [Google Scholar]

11. Qi, P., Zhu, H., Borodich, F., Peng, Q. (2023). A review of the mechanical properties of Graphene Aerogel materials: Experimental measurements and computer simulations. Materials, 16(5), 1800. [Google Scholar] [PubMed]

12. Tan, C., Cao, J., Khattak, A. M., Cai, F., Jiang, B. et al. (2014). High-performance tin oxide-nitrogen doped graphene aerogel hybrids as anode materials for lithium-ion batteries. Journal of Power Sources, 270, 28–33. [Google Scholar]

13. Wang, R., Xu, C., Sun, J., Gao, L. (2014). Three-dimensional Fe2O3 nanocubes/nitrogen-doped graphene aerogels: Nucleation mechanism and lithium storage properties. Scientific Reports, 4(1), 7171. [Google Scholar] [PubMed]

14. Zhang, X., Sui, Z., Xu, B., Yue, S., Luo, Y. et al. (2011). Mechanically strong and highly conductive graphene aerogel and its use as electrodes for electrochemical power sources. Journal of Materials Chemistry, 21(18), 6494–6497. [Google Scholar]

15. Hong, J. Y., Sohn, E. H., Park, S., Park, H. S. (2015). Highly-efficient and recyclable oil absorbing performance of functionalized graphene aerogel. Chemical Engineering Journal, 269, 229–235. [Google Scholar]

16. Xu, Z., Zhang, Y., Li, P., Gao, C. (2012). Strong, conductive, lightweight, neat graphene aerogel fibers with aligned pores. ACS Nano, 6(8), 7103–7113. [Google Scholar] [PubMed]

17. Qin, Z., Jung, G. S., Kang, M. J., Buehler, M. J. (2017). The mechanics and design of a lightweight three-dimensional graphene assembly. Science Advances, 3(1), e1601536. [Google Scholar] [PubMed]

18. Patil, S. P., Shendye, P., Markert, B. (2020). Molecular investigation of mechanical properties and fracture behavior of graphene aerogel. The Journal of Physical Chemistry B, 124(28), 6132–6139. [Google Scholar] [PubMed]

19. Patil, S. P., Kulkarni, A., Markert, B. (2021). Shockwave response of graphene aerogels: An all-atom simulation study. Computational Materials Science, 189, 110252. [Google Scholar]

20. Plimpton, S. (1995). Fast parallel algorithms for short-range molecular dynamics. Journal of Computational Physics, 117(1), 1–19. [Google Scholar]

21. Stukowski, A. (2009). Visualization and analysis of atomistic simulation data with OVITO-the open visualization tool. Modelling and Simulation in Materials Science and Engineering, 18(1), 015012. [Google Scholar]

22. Brenner, D. W., Shenderova, O. A., Harrison, J. A., Stuart, S. J., Ni, B. et al. (2002). A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons. Journal of Physics: Condensed Matter, 14(4), 783. [Google Scholar]

23. Stuart, S. J., Tutein, A. B., Harrison, J. A. (2000). A reactive potential for hydrocarbons with intermolecular interactions. The Journal of Chemical Physics, 112(14), 6472–6486. [Google Scholar]

24. Qin, Z., Taylor, M., Hwang, M., Bertoldi, K., Buehler, M. J. (2014). Effect of wrinkles on the surface area of graphene: Toward the design of nanoelectronics. Nano Letters, 14(11), 6520–6525. [Google Scholar] [PubMed]

25. Wei, Y., Wu, J., Yin, H., Shi, X., Yang, R. et al. (2012). The nature of strength enhancement and weakening by pentagon-heptagon defects in graphene. Nature Materials, 11(9), 759–763. [Google Scholar] [PubMed]

26. Xie, X., Zhou, Y., Bi, H., Yin, K., Wan, S. et al. (2013). Large-range control of the microstructures and properties of three-dimensional porous graphene. Scientific Reports, 3(1), 2117. [Google Scholar] [PubMed]

27. Ruiz, L., Xia, W., Meng, Z., Keten, S. (2015). A coarse-grained model for the mechanical behavior of multi-layer graphene. Carbon, 82, 103–115. [Google Scholar]

28. Anderson Jr, C. E. (2017). Analytical models for penetration mechanics: A review. International Journal of Impact Engineering, 108, 3–26. [Google Scholar]

29. Kadono, T. (1999). Hypervelocity impact into low density material and cometary outburst. Planetary and Space Science, 47(3–4), 305–318. [Google Scholar]

30. Burchell, M. J., Fairey, S. A., Foster, N. J., Cole, M. J. (2009). Hypervelocity capture of particles in aerogel: Dependence on aerogel properties. Planetary and Space Science, 57(1), 58–70. [Google Scholar]

31. Chen, H., Zhang, L., Becton, M., Nie, H., Chen, J. et al. (2015). Molecular dynamics study of a CNT-buckyball-enabled energy absorption system. Physical Chemistry Chemical Physics, 17(26), 17311–17321. [Google Scholar] [PubMed]