A Robust Framework for Multimodal Sentiment Analysis with Noisy Labels Generated from Distributed Data Annotation

1  Introduction

Sentiment analysis detects people’s attitudes, emotions, moods, and other subjective information [1–3] which can benefit many applications, such as emotional care service, mental health test and depression detection. The advent of distributed data collection and annotation has ushered in a new era, enabling the acquisition of extensive multimodal sentiment datasets from diverse sources such as search engines, video media, and social platforms like WeChat, Twitter, and Weibo [4]. This abundance of data sources has greatly accelerated progress in the field of multimodal sentiment analysis. Regrettably, the inherent differences in annotators’ proficiency levels have led to the introduction of a significant number of noisy labels [5–7]. Recent unimodal research reveals that deep neural networks (DNNs) will overfit to noisy labels leading to a poor performance [8]. So, it is a challenging problem for multimodal sentiment analysis with noisy labels.

To address this challenging problem, numerous unimodal methods are proposed to explore the robust training of DNNS in the presence of noisy labels, such as sample selection methods [9–12] which adopt a clean sample selection strategy to identify and discard noisy data before DNN training, and label correction methods which attempt to find correct labels for noisy data [13–16]. Although these noisy label learning methods reach promising performance with unimodal data, they cannot simultaneously tackle multimodal scenarios, such as multimedia data.

Moreover, existing multimodal sentiment analysis methods are not explicitly tailored to address noisy labels, potentially leading to overfitting the noisy data [17,18]. We conducted an empirical study on an existing multimodal sentiment analysis method tensor fusion network (TFN) [19] trained with noisy labels. Fig. 1 illustrates the accuracy of TFN on different training epochs. We can observe that the accuracy on the training dataset has been increasing, but the accuracy on the validation dataset is declining which shows the DNNs tend to memorize the noisy labels rapidly, leading to a deterioration in performance. Hence, it is valuable and significant to explore how to train a robust multimodal sentiment analysis model with noisy labels, but as far as we know, there has been little related literature in this direction over the past years.

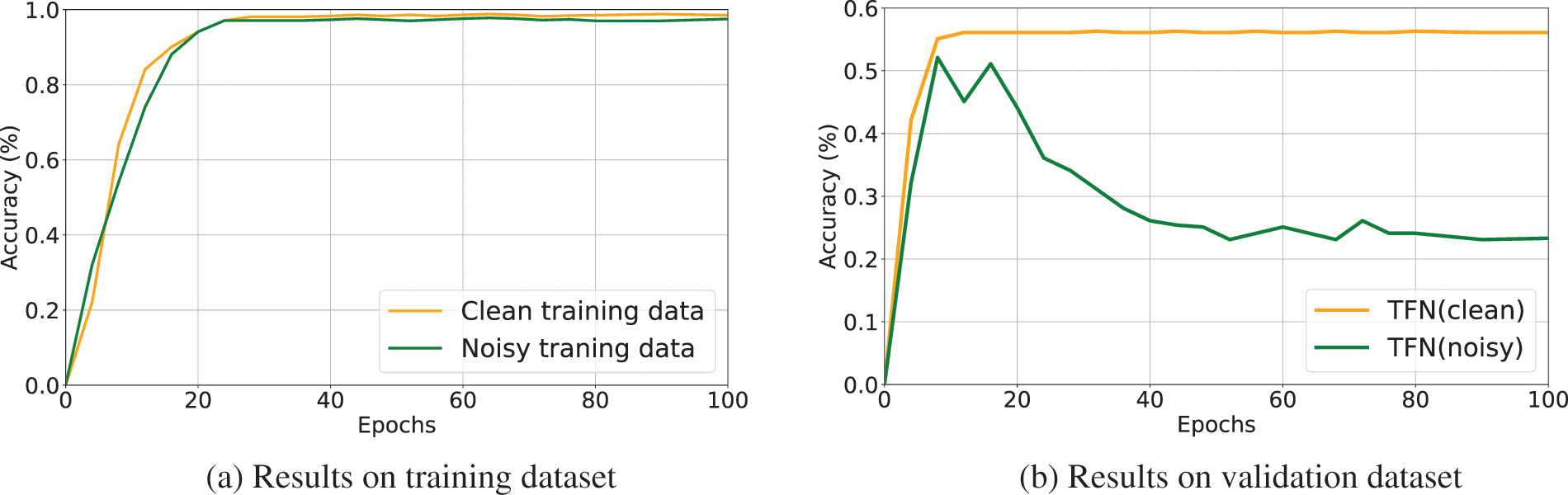
Figure 1: We train an existing multimodal sentiment analysis model TFN on the Yelp-5 dataset with clean labels and 80% symmetric noisy labels (introduced in Section 4.1). The accuracy on different epochs is shown in the figures: (a) accuracy for the clean and noisy training dataset; (b) accuracy for the clean validation dataset

In fact, given a multimodal dataset with noisy labels, to design a noise-tolerant label multimodal sentiment analysis method, two sub-tasks should be carefully considered, i.e., how to correct the noisy labels? and how to conduct multimodal sentiment analysis?

In this paper, we introduce the Multimodal Robust Meta Learning (MRML) framework designed to enhance multimodal sentiment analysis by mitigating the effects of noisy labels across different modalities while concurrently establishing correlations between them. The framework optimizes the whole procedure of label correction and network training through a three-stage process. In the first stage, we propose a two-layer fusion net to correlate the different modalities deeply. Inspired by the attention mechanism [20], we first use feature fusion where we calculate the weight for each modality feature and then average them. Second, instead of simply concatenating the two feature vectors, we use modality early fusion where we apply two linear layers to calculate the attention weights for each modality feature. Compared with the unimodal feature, the multimodal fused feature has complementary information for label correction and network training.

In the second stage, we present a multiple meta-learner strategy to automatically correct the noisy labels iteratively by using the multimodal fused feature. Similar to the recent noisy label learning work called Co-teaching [10], we use two meta-learners and exploit the different information from multiple models during the label correction procedure to increase the quality of the generated correct label and prevent the model from overfitting to noisy labels. After label correction, we train the learner with the corrected labels generated by the meta-learner. In the third stage, we update the meta-learner by minimizing the loss of clean validation data. Such a three-stage optimization process is expected to train a faithful meta label corrector and a robust learner by leveraging the clean validation data.

The main contributions of our paper are as follows:

•   We propose a robust multimodal sentiment analysis framework with noisy labels that can robustly train the network with multimodal noisy labels.

•   We introduce a two-layer fusion network that effectively integrates information from diverse modalities. This integration enhances the quality of extracted multimodal data features, thereby contributing to improved label correction and network training outcomes.

•   A novel multiple meta-learner strategy is proposed to robustly map noisy labels to the corrected ones by using the different information from multiple meta-learners.

•   We implement experiments on three popular multimodal sentiment analysis datasets with varying noise levels and types to demonstrate the robust performance of our method.

The organization of the forthcoming sections of this paper is as follows: Section 2 outlines the standard unimodal meta label correction network, while Section 3 delves into the comprehensive implementation details of MRML. In Section 4, we provide an account of the outcomes attained from our experimental evaluation. The examination of relevant research is presented in Section 5, with the final summary and conclusions offered in Section 6.

2  Preliminaries

In this section, we briefly summarize the typical unimodal meta label correction net [16,21]. For an unimodal sentiment analysis task, (x, y) is the input and the corresponding label. Given a noisy training dataset D={(xi,yi),1≤i≤N}, where xi is the i-th sample and yi is the original (potentially noisy) label. Let Dv={(xiv,yiv),1≤i≤M} be the clean validation dataset where M≪N. We denote the meta-learner (label corrector) which generates corrected labels as y¯i=gϕ(h(xi),yi), where h(xi) is a feature representation of input xi and y¯i is the corrected (pseudo) label outputted by the meta-learner, yi denotes the original label and ϕ denotes the meta-learner parameters.

Meanwhile, we denote the learner (classifier) as y^i=fθ(xi), where y^i is the predicted value, θ denotes the parameters of learner. The training objective (goal of learner) is to get a minimal loss on the training dataset D as

θ∗(ϕ)=arg⁡minθ⁡∑i=1Nℒ(y^i,y¯i)(1)

where ℒ(y^i,y¯i) denotes the training loss function to measure the difference between corrected label y¯i and predicted value y^i.

For given a ϕ, we can get the optimal θ∗(ϕ) through Eq. (1). So there is a functional relationship between θ and ϕ, we denote the relationship as θ=θ∗(ϕ). To this end, the meta-training objective (objective of meta-learner) is to get a minimal loss on the validation dataset Dv as

ϕ∗=arg⁡minϕ⁡∑i=1Mℒv(yiv,fθ∗(ϕ)(xiv))(2)

where the ℒv denotes the meta-training loss on clean validation dataset.

Bi-Level Optimization. There is a dependence between learner θ and meta-learner ϕ. So it requires updating the optimal θ∗ whenever ϕ updates which has been defined as a bi-level optimization procedure. Recently, Ren et al. [22] proposed a one-step stochastic gradient descent (SGD) method to approximate the optimal θ∗ for ϕ updating once. Specifically, at the t-th iteration, method updates θ as

θt+1′=θt−η∇θℒ(gϕt(xi,yi),fθt(xi))(3)

where η is the step size for θ. Then it uses gradient descent to update ϕ as

ϕt+1=ϕt−η∇ϕℒv(yiv,fθt+1′(xiv))(4)

where η is the step size for ϕ. Then it uses ϕt+1 to update θ as

θt+1=θt−η∇θℒ(gϕt+1(xi,yi),fθt(xi))(5)

where θt+1 is a better parameter than θt+1′.

Finally, the method uses Eqs. (3)–(5) to optimize θ and ϕ until convergence.

Analysis. The effectiveness of employing an uncontaminated validation dataset to steer model training in the presence of noisy labels is evident. The bi-level optimization approach is well-suited for implementing this strategy, enabling the framework to be trained seamlessly from start to finish.

However, the aforementioned description shows the current two shortcomings of the existing unimodal meta label correction net. First, the current framework can only handle unimodal data and is not suitable for multimodal application scenarios. Another, due to the inherent uncertainty and inconsistency introduced by the noisy data, the predictions of the single meta-learner can fluctuate greatly during training with noisy labels which will further degrade the correctness of the corrected label y¯ [23].

3  MRML Implementation

Fig. 2 shows our novel Multimodal Robust Meta Learning (MRML) framework for multimodal sentiment analysis with noisy labels where we treat the whole procedure of label correction and network training as a three-stage optimization process, i.e., Multimodal Data Fusion, Label Correction and Learner Training, Meta-Learner Optimization. The corresponding pseudo-code is provided in Algorithm 1.

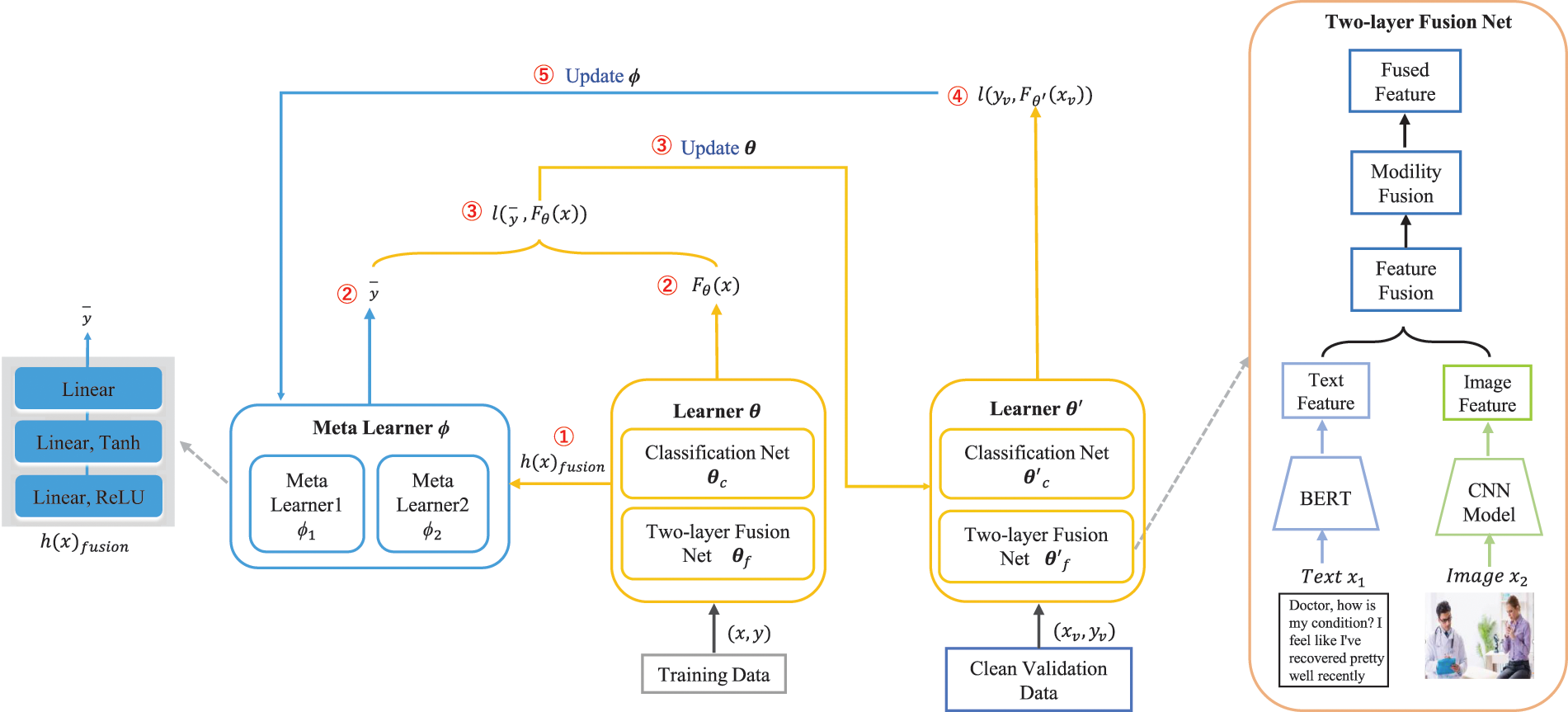
Figure 2: Overview of MRML architecture and computation flow. Here is the model’s operational flow: (1) Noisy training data input: it inputs the noisy training data into the learner and then obtains the logits and fused features from the learner. (2) Label correction: subsequently, the fused feature is fed into the meta-learner, which generates corrected labels. (3) Training loss computation: the next step involves the calculation of the training loss by using the logits and corrected labels to update the learner. (4) Validation loss computation: the updated learner then receives clean validation data and calculates the validation loss. (5) Meta-learner parameter update: finally, the gradient of the meta-learner’s parameters is calculated through the validation loss to update the meta-learner

3.1 Notations

This section provides several notation definitions for clarity. Given a K-category multimodal training dataset with noisy labels as D={xi,yi}i=1N where xi={(xij,yi)j=1m} is the i-th data, xij is the j-th modality from the i-th data and yi is the original label (potentially noisy). In this paper, we treat text and image as two modalities and each modality contains a single sample. Similarly, given a K-category multimodal clean validation datasets Dv={xiv,yiv}i=1n where xiv={(xivj,yiv)jv=1M} is the j-th data where M≪N, xivj is the j-th modelity from the i-th data and yiv is the clean label.

3.2 Overview

For a clear understanding, we first briefly introduce MRML architecture and the three-stage optimization process. Three models are involved in the framework, one learner and two meta-learners. The learner is defined as

y^i=Fθ(xi)θ=(θc,θf)(6)

where θ is the parameters of learner, in which θc and θf denote the parameters of classification net and two-layer fusion net, respectively. And the two meta-learners are defined as

y¯i=Gϕ(h(xi))ϕ=(ϕ1,ϕ2)(7)

where h(xi) is the fused feature of input xi, ϕ is the meta-learner parameters and y¯i denotes the corrected label.

The three-stage workflows of MRML are:

Stage 1: Multimodal Data Fusion. The primary objective of this stage is to construct the input for Stage 2, facilitating label correction and learner training. For this purpose, we introduce a two-layer fusion network that individually represents text and image data, followed by the amalgamation of these features.

Stage 2: Label Correction and Learner Training. In this stage, we propose a multiple meta-learner strategy to generate corrected labels by using the fused feature h(xi). Then, we compute the training loss with the logits of learner fθ(xi) and the corrected label y¯i to update learner θ to θ'.

Stage 3: Meta-Learner Optimization. This stage uses a clean validation dataset Dv for meta-learner optimization. Specifically, we input the multimodal validation data to the updated main learners θ' and compute the validation loss, then compute the gradient of the validation loss of the parameters to meta learner to update the meta learner.

3.3 A Two-Layer Fusion Net

As shown in the right part of the Fig. 2, the two-layer fusion net θf is the main component of learner θ and it will correlate each multimodal data as the input for Stage 2 that could augment the label correction with more information through the fused feature. The quality of the fused feature extracted by the two-layer fusion net is crucial for the label correction, where the fused feature generates the corrected label. First, we use BERT [24] and ResNet [25] to represent text and image data as follows:

Text representation. We use the mean pooling to all tokens’ hidden states from the BERT to represent text data as h(xitext)=Bert(xitext).

Image representation. Image representation is based on ResNet model. We use the final output vector of the ResNet after the global pooling layer. The output size of the last convolutional layer in ResNet is 14 × 14 × dr, where 14 × 14 denotes 196 block regions Ii,j(i,j=1,2…,14) in an image. Each regional feature representation can be defined as Vi,j=ResNet(Ii,j). The extracted features of block regions Vi,ji,j=114 are arranged into an image block embedding sequence b1=V1,1Wr,...,b196=V14,14Wr, where Vi,j∈R1×dr and Wr∈Rdr×dBERT to match the embedding size of BERT, and dr = 2048 when working with ResNet-50.

h(xiimage)=∑i,j=1nrVi,jnr(8)

where nr is the number of regions and is 196 in this paper. Hence, each modality’s representation feature can be defined as

H(xi)=(h(xitext),h(xiimage))(9)

After representing two modalities, we use two fusion strategies namely feature fusion and modality fusion to combine the features h(xitext) and h(xiimage).

(1) Feature fusion. Inspired by attention mechanism in multimodal tasks [20,26], feature fusion aims to utilize multimodal information to refine representation features of all modalities h(xitext),h(xiimage). The key is to calculate the weight for each h(xij)j. The weighted average then becomes the new representation h(xij) of modality j. For the j-th modality, we calculate two weights Wff' from the different modalities j'. The final reconstruction weight is the average of the weights wjj1.

wjj′=W2⋅tanh(W1⋅[h(xij);h(xij′)]+b1)+b2(10)

wjj′=softmax(wjj′)(11)

wj=∑j′∈{image,text}wjj′2(12)

h(xij)=wjh(xij)(13)

where j,j′∈ {image,text} denotes modalities; wjj′ is the weight for the modality j under the guidance of modality j′; wj is the final reconstruction weight for the modality j; W1, W2 are weight matrices and b1, b2 are biases. After feature fusion, h(xij) is now considered feature vectors of each modality and ready to serve as inputs of the next layer.

(2) Modality early fusion. Motivated by the work of [27], we perform modality early fusion instead of simply concatenating the different modalities’ feature vectors. We implement two linear layers to calculate the attention weights for each modality feature h(xij).

w^j=W2′⋅tanh(W1′⋅h(xij)+b1′)+b2′(14)

w^j=softmax(w^j)(15)

h′(xij)=tanh(W3′⋅h(xij)+b3′)(16)

h(xi)fusion=∑j′∈{text,image}w^jh′(xij)(17)

where j denotes the modalities, w^j is the weight for the modality j; W1′, W2′, W3′ are weight matrices and b1′, b2′, b3′ are biases and h(xi)fusion is the fused feature.

3.4 Multiple Meta-Learner Strategy

Multi-network strategies and ensemble learning have been shown their efficient for numerous different deep learning problems [10,28,29]. The main goal is to enhance the performance of the DNNs against noise. Hence, we add a second meta-learner to increase the quality of label correction which can be defined as

Gϕ=(gϕ1,gϕ2)(18)

y¯i=gϕ1(h(xi)fusion)+gϕ2(h(xi)fusion)2(19)

where y¯i is the corrected label.

The utilization of a multiple meta-learner strategy offers two significant viewpoints [30]. The initial aspect of introducing a second meta-learner is aimed at enhancing label correction, leading to more accurate labels. This corrective measure mitigates the potential of overfitting by refining labels not solely reliant on a single model. The second perspective involves enhancing the learner’s knowledge through additional information derived from these improved labels. On the contrary, a good learner will generate a high-quality fused feature which is crucial for the meta-learner to correct the noisy label. We demonstrate these two perspectives in the ablation study. The meta-learner and learner will help each other to learn with noisy labels.

3.5 Bi-Level Optimization

As mentioned in Section 2, the bi-level optimization in MRML can be defined as

minϕE(xv,yv)∈Dv ℒ(yv,Fθϕ*(xv))s.t.θϕ*=argminθE(x,y)∈D ℒ(G(h(x)fusion),Fθ(x))(20)

where ℒ is the loss function for classification, i.e., cross-entropy, and h(x)fusion is the fused feature.

One-step SGD method for bi-level optimization. Outside of meta label correction research, various other studies [31–33] also have used a similar bi-level problem. Instead of updating the optimal θ∗ for each ϕ, a one-step SGD optimization method has been employed to update the θ and approximate the optimal learner for a given φ

θϕ*≈θ′(ϕ)=θ−η∇θℒD(G(h(x)fusion),Fθ(x))(21)

where η is the learning rate of the learner. Since the loss of meta-learner can be defined as ℒDv(Fθ(x),y), the bi-level optimization problem with one-step SGD now becomes

min⁡ℒD(θ−η∇θℒD(G(h(x)fusion),Fθ(x)))(22)

4  Experiments

In this section, we describe the extensive experiments performed to evaluate the effectiveness of MRML and compare it with the baselines under different noisy types and ratios.

4.1 Datasets and Noise Settings

Datasets. In a manner that does not compromise the breadth of applicability, we assess the performance of MRML using three extensively employed datasets for multiple sentiment analysis, as detailed in Table 1. We briefly introduce them as follows:

•   Yelp-5, a dataset of online reviews scraped from Yelp.com in the food and restaurants category [34]. Altogether, the dataset comprises over 44,000 reviews paired with corresponding images. Each individual review is associated with a single image.

•   Twitter-15, a dataset consists of image-text reviews, where each multimodal sample contains text, a corresponding image, and an emotion target [35]. It contains 3179 training samples, 1122 testing samples and 1037 development samples.

•   Multi-ZOL, a dataset of online reviews about shopping, economy, society, people’s livelihood, news, etc. [36]. The dataset encompasses 5288 multimodal reviews, with each of these reviews containing both textual content and a set of images.

Noise settings. Following the related work [13], as shown in Fig. 3, we corrupt the label of training data with two settings:

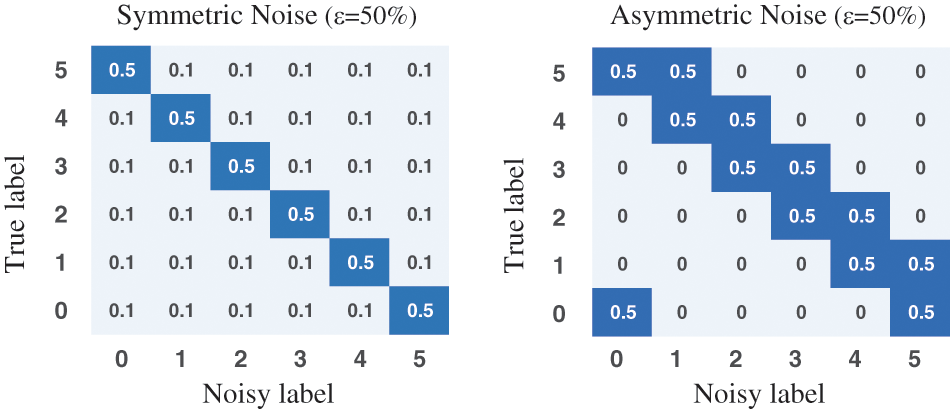
Figure 3: Examples of the noise transition matrix for symmetric and asymmetric noise (taking 6 classes and noise ratio p = 50% as an example)

•   Symmetric noise: At noise ratio is p, a clean sample’s label is corrupted to other labels with probability pn−1 and is kept in original label with probability 1−p, where n is the number of classes.

•   Asymmetric noise: At noise ratio is p, a clean sample’s label is corrupted to one of the other n−1 labels with probability p and is kept in original label with probability 1−p, where n is the number of classes.

4.2 Baselines and Experiment Details

Baselines. Since it is rarely touched on previous methods about multimodal sentiment analysis with noisy labels, we evaluate our method against the following baseline methods in multimodal sentiment analysis:

•   MIMN, the multi-interactive memory network incorporates a pair of interactive memory networks. These networks are designed to oversee both textual and visual information, guided by the provided aspect [36].

•   VistaNet, a framework that harnesses both textual and visual elements, utilizing visual cues to align and highlight essential sentences within a document through the application of attention mechanisms [34].

•   HFIR, a hybrid fusion method based on the information relevance (HFIR) for multimodal sentiment analysis [27].

•   ITIN, a novel Image-Text Interaction Network to explore the intricate relationship between affective image regions and textual content for multimodal sentiment analysis [37].

Data preparation. Since our method needs additional clean validation data, we follow related work [13,22] to randomly select 100 samples per class from the training dataset before adding noise as clean validation data.

Model preparation. (1) For data representation, we use BERT (the mean pooling to all tokens’ hidden states) and ResNet-50 (the final output vector after the global pooling layer) to represent text and image data, respectively. (2) For two meta-learners, as shown in Fig. 2, we use the same 3-layer fully connected networks with dimensions of (768,128), (128,128), (128,label_numbers) initialized with different parameters for label correction. And we apply the linear activation function ReLU and the nonlinear activation function Tanh to enhance the model learning ability and use a classification layer to output corrected label distribution. (3) For the classification net in the learner, we use a simple 4-layer fully connected network for classification given as Table 2.

Training details. (1) In early training epochs, the meta-learner has a poor ability to correct labels resulting in producing more error labels. We began to correct labels at a later 5 epochs as an initial warm-up. (2) In all conducted experiments, we utilize the ADAM optimizer [38] to train our approach. We set a maximum of 100 epochs for each dataset, initializing the learning rate to 0.0001. Additionally, we follow a consistent practice of saving testing results when the best outcomes are achieved on the development set across all methods. Our experimentation was carried out using Python 3.8 and PyTorch 1.8, executed on an RTX 3090Ti GPU. The reported results are averaged over five separate runs.

4.3 Comparison with the Baselines

We perform multimodal sentiment analysis across three distinct datasets to assess both MRML and the baseline methods. The accuracy results of our experiments are presented in Tables 3–5 for the respective datasets. Our method MRML achieves the best performance on all test cases. For example, MRML outperforms HFIR by up to 24.1%, 31.4% and 23.9% on Yelp-5, Twitter-15 and Multi-ZOL datasets, respectively. It shows that our MRML is more robust to noisy labels and could provide guidance for future multimodal sentiment analysis with noisy labels.

One similar trend that can be derived in the three tables is that the performance of all baselines degrades as the noise ratio goes up which confirms the noisy labels remarkably influence the performance of existing multimodal sentiment analysis methods. On the contrary, our method has no such issues. MRML achieves 30.8% on the Multi-ZOL dataset under 80% symmetric noise, which is significantly higher than that obtained by VistaNet (8.3%), MIMN (19.6%) and HFIR (6.9%), ITIN (21.46%). Especially, the degrading speed for VistaNet is even faster (from 45.5% to 6.9% with 20%-symmetric to 80%-symmetric). This is because VistaNet has no specified mechanism for dealing with noisy labels. On the other hand, we can observe that MIMN and ITIN have certain noise-tolerant abilities. For example, on the Multi-ZOL dataset with 80%-symmetric noise, MIMN achieves 19.6% which is obviously higher than 8.3% of VistaNet and 6.9% of HFIR. Similarly, ITIN outperforms VistaNet, MIMN and HFIR by up to 12.6%, 1.5% and 10.7% on Twitter-15 dataset with 80%-symmetric noise, respectively. The main reason behind this may be that they use a multiple model strategy (i.e., MIMN uses two memory networks for text and image data and ITIN a novel image-text interaction network) like our MRML, thus indicating the superiority of our multiple meta-learner strategy.

Observing the data presented in Table 5, it is evident that the performance of all methods is comparatively lower on the Multi-ZOL dataset in comparison to the other two datasets, particularly in instances of elevated noise ratios. This phenomenon highlights the influence of class count on the ability to counteract interference caused by noisy labels. Notably, the robust fitting capabilities of DNNs can lead to a higher susceptibility to overfitting in more challenging tasks, particularly those involving a larger number of classes and the presence of noisy labels.

4.4 Ablation Study

MRML introduces two main components which are the two-layer fusion net and a second meta-learner. Therefore, it is necessary to conduct further experiments for an in-depth analysis of the contributions of each component.

(1) Two-Layer Fusion Net. We implement MRML with one, multiple modalities and a concat fusion strategy.

•   Text. Text vectors after the mean pooling to all tokens’ hidden states of BERT are inputs of the classification net and meta-learner.

•   Image. Image vectors after the pooling layer of ResNet are inputs of the classification net and meta-learner.

•   Concat. Previous research concats multimodal feature vectors. We implement this concatenation strategy to fuse multimodal data [39].

(2) Multiple Meta-Learner Strategy. We conduct experiments by using a single meta-learner for label correction and others remain the same.

Tables 6 and 7 show the results in terms of classification accuracy on Yelp-5 and Multi-ZOL datasets. In general, we can see that both components provide an improvement over other methods. Moreover, the collaborative integration of the two components within MRML results in a more effective synergy, leading to enhanced classification accuracy through their combined efforts. The most significant improvements are gained on Multi-ZOL under 20%-symmetric noise with up to 13.5% increase in accuracy.

Another, the feature based only on the image modality does not perform well, while text performs much better, demonstrating the important role of text modality. Compared with the concat fusion strategy, our proposed two-layer fusion net further improves the classification performance, revealing that our fusion net leverages features of two modalities in a more effective way.

Fig. 4 shows the results in terms of label correction accuracy on Yelp-5 dataset. Similar to the above classification results, the two meta-learners with the fused feature generated by our two-layer fusion net achieve the best label correction performance, indicating that the high quality of multimodal features and a second meta-learner are beneficial for label correction. Based on this insight, it is reasonable to anticipate that the introduction of a third network could potentially lead to additional performance enhancements. However, since the huge computation for bi-level optimization, we only consider the addition of more models when the computation resources are sufficient.

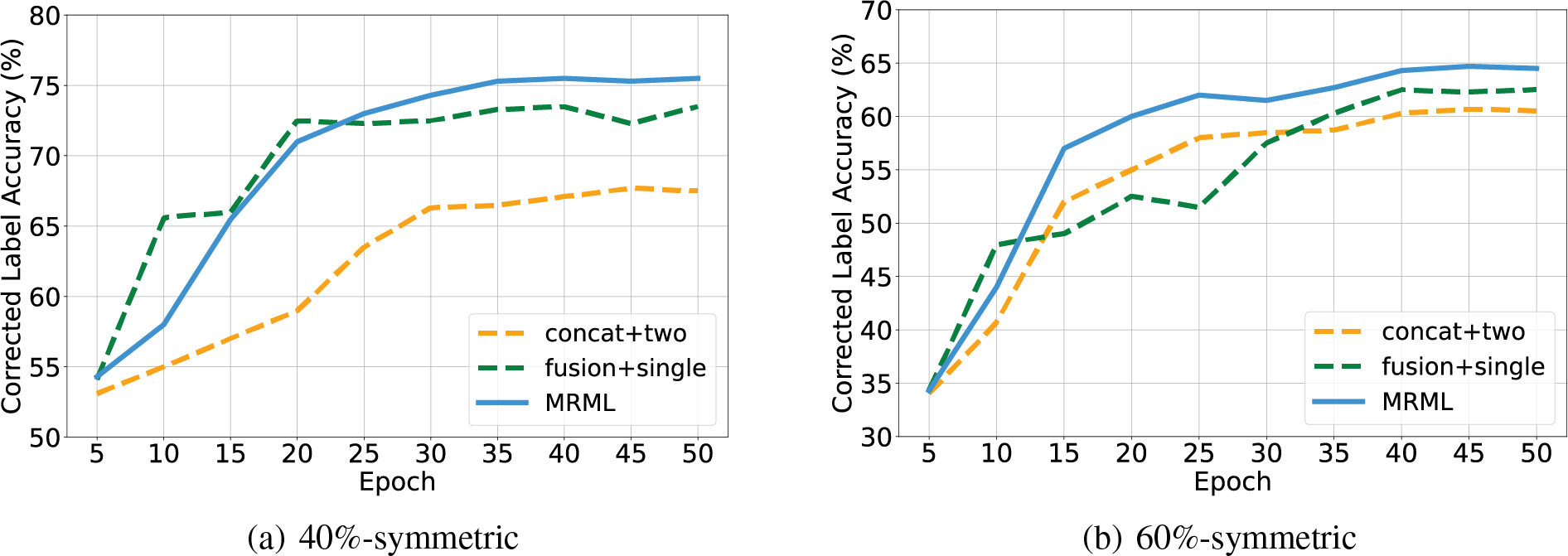
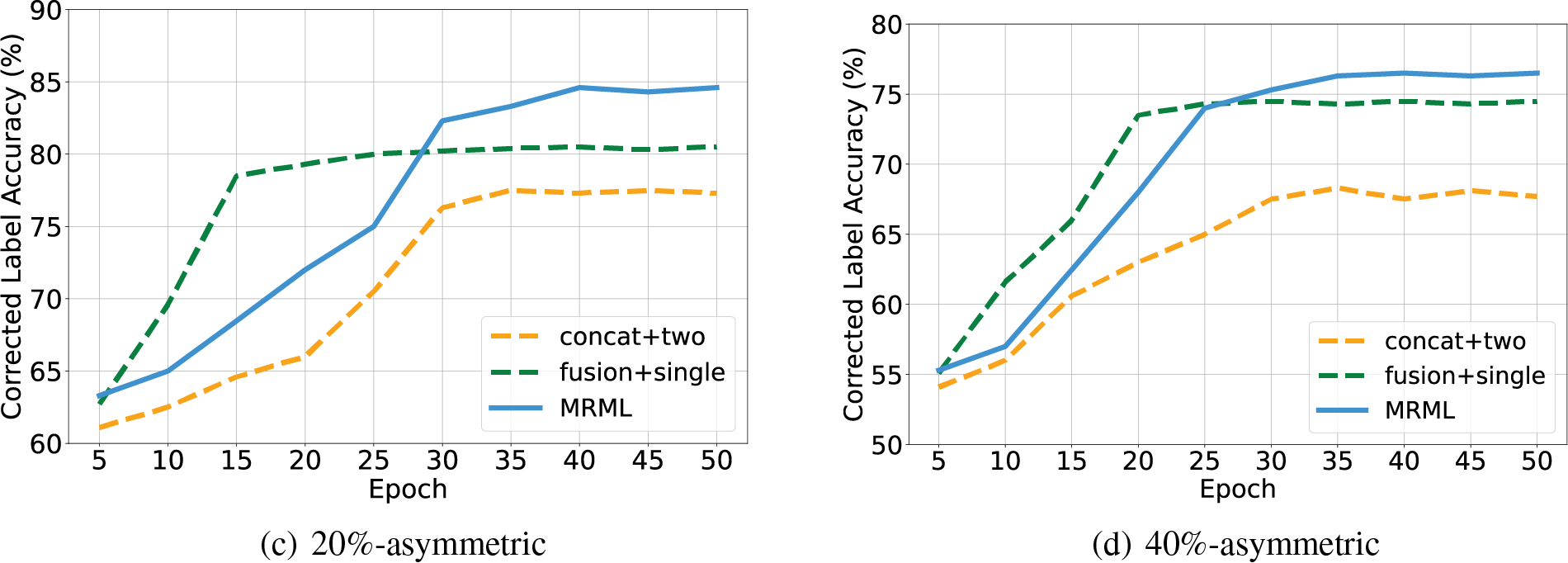
Figure 4: The corrected label accuracy of ablation study on Yelp-5 dataset with different noise types and noise ratios. “concat + two” denotes “concat + two meta-learners” and “fusion + single” denotes “two-layer fusion net + single meta-learner”. (a) The accuracy of corrected label on 40%-symmetric noise. (b) The accuracy of corrected label on 60%-symmetric. (c) The accuracy of corrected label on 20%-asymmetric. (d) The accuracy of corrected label on 40%-asymmetric

5  Related Work

In this section, we describe the related works about unimodal learning with noisy labels methods and multimodal sentiment analysis methods.

5.1 Learning with Noisy Labels

Few methods have been revealed by far on how to effectively conduct multimodal sentiment analysis with noisy labels. However, many unimodal methods with noisy labels have been proposed which can be divided into three parts.

Sample selection. Sample selection methods focus on using a data selection method to identify and discard noisy samples before training the model. Confident learning [11] calculated the confidence value of data and discarded the noisy data from the training dataset. Co-teaching [10] simultaneously trained two networks, and each model chooses the data with less loss to each other. Elkan [40] estimated the noisy data through positive-unlabeled learning. SELF [41] proposed a noisy data filtering method through model ensemble learning which utilizes the model’s predictions in different epochs to remove the noisy samples. AUM [9] identified the noisy data by measuring the mean difference between the logits of the sample’s assigned class. These methods have a common shortcoming in that a large amount of data would be discarded which reduces the robustness of the model when the noise ratio is high.

Sample reweighting. Many existing methods aim to reweight the noisy data. Ren et al. [22] used a meta-reweighting method to assign small weights to the noisy data which could reduce the model’s negative impact. Wang et al. [42] reweighted the model’s noisy data through a weighting scheme. Shu et al. [43] also used a meta-reweight framework with a clean validation dataset and learned a loss-weighting function. All of these methods need a clean validation dataset to reweight noisy data. Xue et al. [44] estimated the noisy probability of data by using a probabilistic local outlier factor. Jiang et al. [12] proposed a model named MentorNet which leverages lesson plans by learning samples that are likely to be correct and dynamically learns data-driven lessons through StudentNet. Harutyunyan et al. [45] reduced the memorization of noisy labels through the mutual information between weights and updated the weights of data based on the gradients of the last layers. These sample reweighting methods always assign small weights to noisy data which would cause a waste of data information and degenerate the robustness of the model.

Sample relabeling. The sample relabeling methods aim to correct the noisy labels which could leverage all the training data. Mixup [46] corrects the noisy labels by using data augmentation techniques. Hendrycks et al. [13] estimated the label corruption matrix, and then trained the network leveraging this corruption matrix. Mixmatch [47] used data augmentation and a single model’s prediction to relabel data. DivideMix [48] first identified the noisy training data through the Mixture of Gaussians. Then it utilizes two networks based on the co-teaching mechanism to correct noisy labels. Finally, it used the Mixmatch strategy [47] to train the two networks. Recently, many methods based on meta-learning [16,21,32,49,50] have been proposed. They adopt the meta-process as label correction, which aims to generate corrected labels for noisy data. All these methods use a clean validation dataset to guide the network training with noisy labels.

5.2 Multimodal Sentiment Analysis

Given the widespread use of diverse user-generated content, such as text, images, and speech, sentiment analysis has expanded beyond just text-based analysis. The field of multimodal sentiment analysis is dynamic, involving the automated extraction of people’s sentiments from various forms of communication channels.

Multimodal data often comprises both text and image information, which can synergistically enhance and complement each other. Early research primarily focused on feature-based approaches. For instance, Borth et al. [51] introduced textual features derived from English grammar, spelling, and style scores, alongside visual features obtained through the extraction of adjective-noun pairs from images. More recently, the advancement of deep learning has led to the emergence of numerous neural network-based techniques for multimodal sentiment analysis. An example is the work by Yu et al. [52], where they pre-trained models for text and images to individually capture their respective feature representations. These features were subsequently combined and used to train a logistic regression model. Some work [53,54] concatenated features from different multimodal data and input it into the model. Another, some works applied late−fusion methods that combine the predicting values from the individual unimodal models through a learning model [55,56] or an ensemble strategy like voting scheme [57–59]. In Salur et al. [60], a soft voting-based ensemble model was proposed that takes advantage of the effective performance of different classifiers on different modalities. However, these methods ignore the connection between modalities. In response to these challenges, numerous researchers have employed LSTM cells and gating mechanisms to capture interaction dynamics within multimodal data [61–64]. Han et al. [65] employed a gated control mechanism within the Transformer architecture to further enhance the ultimate output. Zadeh et al. [66] introduced a multiview gated memory unit to capture and forecast cross-modality interactions. Zhu et al. [37] presented a novel Image-Text Interaction Network (ITIN) for exploring the intricate connection between emotional image regions and textual content. While these techniques significantly enhance performance, their intricate architectures and substantial computational demands impede model interpretability. To address these limitations, our paper introduces an innovative fusion approach based on lightweight attention mechanisms.

6  Conclusion

This paper offers a concise examination of the challenge of multiple sentiment analysis involving noisy labels. Recent advancements in unimodal meta label correction have showcased promising potential in mitigating the impact of noisy labels. Building upon this foundation, we introduce a novel approach named Multimodal Robust Meta Learning (MRML) framework for multimodal sentiment analysis. This framework aims to counteract the influence of noisy labels in multimodal scenarios and simultaneously establish correlations across distinct modalities. Our MRML framework encompasses a three-stage optimization process.

In the initial stage, we propose a two-layer fusion network to merge multimodal features. The subsequent stage involves a multiple meta-learner strategy, responsible for generating corrected labels and training the learner using these improved labels. In the final stage, we leverage a clean validation dataset to fine-tune the meta-learner. Through comprehensive experiments across three widely-utilized datasets, we validate the efficacy of MRML. Looking ahead, our future endeavors are centered around enhancing the MRML framework and extending its application to diverse domains.

Acknowledgement: Thanks to the three anonymous reviewers and the journal editors for their invaluable contributions to the improvement of the logical organization and content quality of this paper.

Funding Statement: This research was partially supported by STI 2030-Major Projects 2021ZD0200400, National Natural Science Foundation of China (62276233 and 62072405) and Key Research Project of Zhejiang Province (2023C01048).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Kai Jiang, Bin Cao, Jing Fan; data collection: Kai Jiang; analysis and interpretation of results: Kai Jiang, Bin Cao, Jing Fan; draft manuscript preparation: Kai Jiang, Bin Cao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data used in this article are freely available in the mentioned references.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Wang, X., He, J., Jin, Z., Yang, M., Wang, Y. et al. (2021). M2Lens: Visualizing and explaining multimodal models for sentiment analysis. IEEE Transactions on Visualization and Computer Graphics, 28(1), 802–812. [Google Scholar] [PubMed]

2. Wankhade, M., Rao, A. C. S., Kulkarni, C. (2022). A survey on sentiment analysis methods, applications, and challenges. Artificial Intelligence Review, 55(7), 5731–5780. [Google Scholar]

3. Tomihira, T., Otsuka, A., Yamashita, A., Satoh, T. (2020). Multilingual emoji prediction using BERT for sentiment analysis. International Journal of Web Information Systems, 16(3), 265–280. [Google Scholar]

4. Atzori, L., Iera, A., Morabito, G. (2010). The Internet of Things: A survey. Computer Networks, 54(15), 2787–2805. [Google Scholar]

5. Sukhbaatar, S., Fergus, R. (2014). Learning from noisy labels with deep neural networks. arXiv preprint arXiv:1406.2080. [Google Scholar]

6. Yan, Y., Rosales, R., Fung, G., Subramanian, R., Dy, J. (2014). Learning from multiple annotators with varying expertise. Machine Learning, 95, 291–327. [Google Scholar]

7. Yu, X., Liu, T., Gong, M., Tao, D. (2018). Learning with biased complementary labels. Proceedings of the European Conference on Computer Vision (ECCV), pp. 68–83. Munich, Germany. [Google Scholar]

8. Zhang, C., Bengio, S., Hardt, M., Recht, B., Vinyals, O. (2021). Understanding deep learning (still) requires rethinking generalization. Communications of the ACM, 64(3), 107–115. [Google Scholar]

9. Pleiss, G., Zhang, T., Elenberg, E., Weinberger, K. Q. (2020). Identifying mislabeled data using the area under the margin ranking. Advances in Neural Information Processing Systems, 33, 17044–17056. [Google Scholar]

10. Han, B., Yao, Q., Yu, X., Niu, G., Xu, M. et al. (2018). Co-teaching: Robust training of deep neural networks with extremely noisy labels. Advances in Neural Information Processing Systems, 31, 8536–8546. [Google Scholar]

11. Northcutt, C., Jiang, L., Chuang, I. (2021). Confident learning: Estimating uncertainty in dataset labels. Journal of Artificial Intelligence Research, 70, 1373–1411. [Google Scholar]

12. Jiang, L., Zhou, Z., Leung, T., Li, L. J., Fei-Fei, L. (2018). MentorNet: Learning data-driven curriculum for very deep neural networks on corrupted labels. International Conference on Machine Learning, vol. 80, pp. 2304–2313. [Google Scholar]

13. Hendrycks, D., Mazeika, M., Wilson, D., Gimpel, K. (2018). Using trusted data to train deep networks on labels corrupted by severe noise. Advances in Neural Information Processing Systems, 31, 10477–10486. [Google Scholar]

14. Patrini, G., Rozza, A., Menon, A., Nock, R., Qu, L. (2016). Making neural networks robust to label noise: A loss correction approach. Stat, 1050, 13. [Google Scholar]

15. Xia, X., Liu, T., Wang, N., Han, B., Gong, C. et al. (2019). Are anchor points really indispensable in label-noise learning? Advances in Neural Information Processing Systems, 32, 6835–6846. [Google Scholar]

16. Zheng, G., Awadallah, A. H., Dumais, S. (2021). Meta label correction for noisy label learning. Proceedings of the AAAI Conference on Artificial Intelligence, vol. 35, no. 12, pp. 11053–11061. [Google Scholar]

17. Hu, P., Peng, X., Zhu, H., Zhen, L., Lin, J. (2021). Learning cross-modal retrieval with noisy labels. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 5403–5413. Kuala Lumpur, Malaysia. [Google Scholar]

18. Yang, E., Yao, D., Liu, T., Deng, C. (2022). Mutual quantization for cross-modal search with noisy labels. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 7551–7560. New Orleans, Louisiana, USA. [Google Scholar]

19. Zadeh, A., Chen, M., Poria, S., Cambria, E., Morency, L. P. (2017). Tensor fusion network for multimodal sentiment analysis. Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, pp. 1103–1114. Copenhagen, Denmark. [Google Scholar]

20. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L. et al. (2017). Attention is all you need. Advances in Neural Information Processing Systems, 30, 6000–6010. [Google Scholar]

21. Algan, G., Ulusoy, I. (2022). MetaLabelNet: Learning to generate soft-labels from noisy-labels. IEEE Transactions on Image Processing, 31, 4352–4362. [Google Scholar] [PubMed]

22. Ren, M., Zeng, W., Yang, B., Urtasun, R. (2018). Learning to reweight examples for robust deep learning. International Conference on Machine Learning, vol. 80, pp. 4334–4343. [Google Scholar]

23. Mallem, S., Hasnat, A., Nakib, A. (2023). Efficient meta label correction based on meta learning and bi-level optimization. Engineering Applications of Artificial Intelligence, 117, 105517. [Google Scholar]

24. Kenton, J. D. M. W. C., Toutanova, L. K. (2019). BERT: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805v2. [Google Scholar]

25. He, K., Zhang, X., Ren, S., Sun, J. (2016). Deep residual learning for image recognition. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 770–778. Las Vegas, Nevada, USA. [Google Scholar]

26. Gao, H., Huang, J., Tao, Y., Hussain, W., Huang, Y. (2022). The joint method of triple attention and novel loss function for entity relation extraction in small data-driven computational social systems. IEEE Transactions on Computational Social Systems, 9(6), 1725–1735. [Google Scholar]

27. Gu, Y., Yang, K., Fu, S., Chen, S., Li, X. et al. (2018). Hybrid attention based multimodal network for spoken language classification. Proceedings of the Conference. Association for Computational Linguistics. Meeting, vol. 2018. Melbourne, Australia. [Google Scholar]

28. Renuka Devi, D., Sasikala, S. (2021). Ensemble incremental deep multiple layer perceptron model–sentiment analysis application. International Journal of Web Information Systems, 17(6), 714–727. [Google Scholar]

29. Sagi, O., Rokach, L. (2018). Ensemble learning: A survey. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 8(4), e1249. [Google Scholar]

30. Gao, H., Wang, X., Wei, W., Al-Dulaimi, A., Xu, Y. (2023). Com-DDPG: Task offloading based on multiagent reinforcement learning for information-communication-enhanced mobile edge computing in the internet of vehicles. IEEE Transactions on Vehicular Technology, 1–14. [Google Scholar]

31. Liu, H., Simonyan, K., Yang, Y. (2018). DARTS: Differentiable architecture search. arXiv preprint arXiv:1806.09055. [Google Scholar]

32. Finn, C., Abbeel, P., Levine, S. (2017). Model-agnostic meta-learning for fast adaptation of deep networks. International Conference on Machine Learning, 70, 1126–1135. [Google Scholar]

33. Nichol, A., Achiam, J., Schulman, J. (2018). On first-order meta-learning algorithms. arXiv preprint arXiv:1803.02999. [Google Scholar]

34. Truong, Q. T., Lauw, H. W. (2019). VistaNet: Visual aspect attention network for multimodal sentiment analysis. Proceedings of the AAAI Conference on Artificial Intelligence, vol. 33, no. 1, pp. 305–312. [Google Scholar]

35. Zhang, Q., Fu, J., Liu, X., Huang, X. (2018). Adaptive co-attention network for named entity recognition in tweets. Proceedings of the AAAI Conference on Artificial Intelligence, vol. 32, no. 1, pp. 5674–5681. [Google Scholar]

36. Xu, N., Mao, W., Chen, G. (2019). Multi-interactive memory network for aspect based multimodal sentiment analysis. Proceedings of the AAAI Conference on Artificial Intelligence, vol. 33, no. 1, pp. 371–378. [Google Scholar]

37. Zhu, T., Li, L., Yang, J., Zhao, S., Liu, H. et al. (2022). Multimodal sentiment analysis with image-text interaction network. IEEE Transactions on Multimedia, 25, 3375–3385. [Google Scholar]

38. Kingma, D. P., Ba, J. (2014). Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980. [Google Scholar]

39. Schifanella, R., De Juan, P., Tetreault, J., Cao, L. (2016). Detecting sarcasm in multimodal social platforms. Proceedings of the 24th ACM International Conference on Multimedia, pp. 1136–1145. Amsterdam, The Netherlands. [Google Scholar]

40. Elkan, C., Noto, K. (2008). Learning classifiers from only positive and unlabeled data. Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 213–220. Las Vegas, Nevada, USA. [Google Scholar]

41. Nguyen, D. T., Mummadi, C. K., Ngo, T. P. N., Nguyen, T. H. P., Beggel, L. et al. (2019). Self: Learning to filter noisy labels with self-ensembling. arXiv preprint arXiv:1910.01842. [Google Scholar]

42. Wang, Y., Liu, W., Ma, X., Bailey, J., Zha, H. et al. (2018). Iterative learning with open-set noisy labels. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 8688–8696. Salt Lake City, Utah, USA. [Google Scholar]

43. Shu, J., Xie, Q., Yi, L., Zhao, Q., Zhou, S. et al. (2019). Meta-Weight-Net: Learning an explicit mapping for sample weighting. Advances in Neural Information Processing Systems, 32, 1917–1928. [Google Scholar]

44. Xue, C., Dou, Q., Shi, X., Chen, H., Heng, P. A. (2019). Robust learning at noisy labeled medical images: Applied to skin lesion classification. 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), pp. 1280–1283. Venice, Italy. [Google Scholar]

45. Harutyunyan, H., Reing, K., Ver Steeg, G., Galstyan, A. (2020). Improving generalization by controlling label-noise information in neural network weights. International Conference on Machine Learning, 119, 4071–4081. [Google Scholar]

46. Zhang, H., Cisse, M., Dauphin, Y. N., Lopez-Paz, D. (2017). mixup: Beyond empirical risk minimization. arXiv preprint arXiv:1710.09412. [Google Scholar]

47. Berthelot, D., Carlini, N., Goodfellow, I., Papernot, N., Oliver, A. et al. (2019). MixMatch: A holistic approach to semi-supervised learning. Advances in Neural Information Processing Systems, 32, 1050–1060. [Google Scholar]

48. Li, J., Socher, R., Hoi, S. C. (2020). Dividemix: Learning with noisy labels as semi-supervised learning. arXiv preprint arXiv:2002.07394. [Google Scholar]

49. Wu, Y., Shu, J., Xie, Q., Zhao, Q., Meng, D. (2021). Learning to purify noisy labels via meta soft label corrector. Proceedings of the AAAI Conference on Artificial Intelligence, vol. 35, no. 12, pp. 10388–10396. [Google Scholar]

50. Wang, Z., Hu, G., Hu, Q. (2020). Training noise-robust deep neural networks via meta-learning. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 4524–4533. Seattle, USA. [Google Scholar]

51. Borth, D., Ji, R., Chen, T., Breuel, T., Chang, S. F. (2013). Large-scale visual sentiment ontology and detectors using adjective noun pairs. Proceedings of the 21st ACM International Conference on Multimedia, pp. 223–232. Barcelona, Spain. [Google Scholar]

52. Yu, Y., Lin, H., Meng, J., Zhao, Z. (2016). Visual and textual sentiment analysis of a microblog using deep convolutional neural networks. Algorithms, 9(2), 41. [Google Scholar]

53. Lazaridou, A., The Pham, N., Baroni, M. (2015). Combining language and vision with a multimodal skip-gram model. Proceedings of the 2015 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, pp. 153–163. Denver, CO, USA. [Google Scholar]

54. Ngiam, J., Khosla, A., Kim, M., Nam, J., Lee, H. et al. (2011). Multimodal deep learning. Proceedings of the 28th International Conference on Machine Learning (ICML-11), pp. 689–696. Bellevue, WA, USA. [Google Scholar]

55. Glodek, M., Tschechne, S., Layher, G., Schels, M., Borsch, T. et al. (2011). Multiple classifier systems for the classification of audio-visual emotional states. Affective Computing and Intelligent Interaction: Fourth International Conference, pp. 359–368. Memphis, TN, USA. [Google Scholar]

56. Ramirez, G. A., Baltrušaitis, T., Morency, L. P. (2011). Modeling latent discriminative dynamic of multi-dimensional affective signals. Affective Computing and Intelligent Interaction: Fourth International Conference, pp. 396–406. Memphis, TN, USA. [Google Scholar]

57. Ghorbanali, A., Sohrabi, M. K. (2023). Capsule network-based deep ensemble transfer learning for multimodal sentiment analysis. Expert Systems with Applications, 239, 122454. [Google Scholar]

58. Nojavanasghari, B., Gopinath, D., Koushik, J., Baltrušaitis, T., Morency, L. P. (2016). Deep multimodal fusion for persuasiveness prediction. Proceedings of the 18th ACM International Conference on Multimodal Interaction, pp. 284–288. Tokyo, Japan. [Google Scholar]

59. Ghorbanali, A., Sohrabi, M. K., Yaghmaee, F. (2022). Ensemble transfer learning-based multimodal sentiment analysis using weighted convolutional neural networks. Information Processing & Management, 59(3), 102929. [Google Scholar]

60. Salur, M. U., Aydın, İ. (2022). A soft voting ensemble learning-based approach for multimodal sentiment analysis. Neural Computing and Applications, 34(21), 18391–18406. [Google Scholar]

61. Huddar, M. G., Sannakki, S. S., Rajpurohit, V. S. (2021). Attention-based multimodal contextual fusion for sentiment and emotion classification using bidirectional LSTM. Multimedia Tools and Applications, 80, 13059–13076. [Google Scholar]

62. Chen, M., Wang, S., Liang, P. P., Baltrušaitis, T., Zadeh, A. et al. (2017). Multimodal sentiment analysis with word-level fusion and reinforcement learning. Proceedings of the 19th ACM International Conference on Multimodal Interaction, pp. 163–171. Glasgow, Scotland. [Google Scholar]

63. Rajagopalan, S. S., Morency, L. P., Baltrusaitis, T., Goecke, R. (2016). Extending long short-term memory for multi-view structured learning. Computer Vision–ECCV 2016: 14th European Conference, pp. 338–353. Amsterdam, The Netherlands. [Google Scholar]

64. Mai, S., Xing, S., Hu, H. (2021). Analyzing multimodal sentiment via acoustic-and visual-lstm with channel-aware temporal convolution network. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 29, 1424–1437. [Google Scholar]

65. Han, W., Chen, H., Gelbukh, A., Zadeh, A., Morency, L. P. et al. (2021). Bi-bimodal modality fusion for correlation-controlled multimodal sentiment analysis. Proceedings of the 2021 International Conference on Multimodal Interaction, pp. 6–15. Montreal, Quebec, Canada. [Google Scholar]

66. Zadeh, A., Liang, P. P., Mazumder, N., Poria, S., Cambria, E. et al. (2018). Memory fusion network for multi-view sequential learning. Proceedings of the AAAI Conference on Artificial Intelligence, vol. 32, no. 1, pp. 5634–5641. [Google Scholar]