A Sharding Scheme Based on Graph Partitioning Algorithm for Public Blockchain

1  Introduction

Blockchain, which serves as the underlying technology for Bitcoin [1], integrates a variety of computer technologies, including cryptography, distributed consensus mechanisms, smart contracts, distributed data storage, and peer-to-peer networking, to establish a novel distributed application paradigm [2]. Blockchain has attracted much attention for its technical advantages, such as decentralization, tamper-resistant data, collaborative operations, and anonymous privacy protection. As a transformative technology, blockchain, which offers a strong driving force for the development of the digital economy, has found widespread application across domains including finance, supply chain management, digital copyright protection, the Internet of Things, intelligent manufacturing, digital asset trading, and other sectors [3,4].

Although blockchain technology has become an important engine for upgrading traditional industries, it still suffers from some technical bottlenecks [5,6], notably highlighted in terms of transaction capacity and scalability. For example, the transaction capacity of Bitcoin is only 7 transactions per second, and that of Ethereum is only a dozen transactions per second, which is far below the capacity requirements of applications such as high-frequency transactions. As a result, the existing blockchain systems are not adequate for most industrial applications due to the low transaction capacity. Performance bottleneck has become the main challenge of blockchain that seriously hinders the process of its large-scale application.

To improve blockchain’s transaction capacity and scalability, researchers put forth some on-chain scaling technologies, including Lightning Network [7], directed acyclic graph (DAG) technology [8], state channels [9], and sharding mechanisms [10]. Lightning Network is an off-chain scaling technology that processes transactions off-chain and subsequently verifies transaction results on-chain. Directed acyclic graph technology is an architecture scaling technology for blockchain that mainly improves blockchain state storage. State channels develop new off-chain channels to process most transactions. In comparison, sharding exhibits significant potential as an on-chain scalability technique that aims to enhance transaction parallel processing capabilities and ultimately improve the overall performance of the blockchain network. Sharding involves dividing the blockchain network into multiple sub-networks. Transactions within the network are allocated to process in different shards subsets of blockchain nodes. With multiple shards operating in parallel to execute and validate transactions, the blockchain system’s transaction capacity can be significantly enhanced.

Although sharding has substantially boosted the blockchain’s performance, it still faces the following challenges. Firstly, a great quantity of asynchronous cross-shard transactions contribute to increased communication costs for blockchain. As shown in Fig. 1, the survey shows that as the number of shards increases, cross-shard transactions account for over 95% of the total transaction volume in existing blockchain sharding systems. Due to the more complex transaction logic, cross-shard transactions will add extra transaction load to the blockchain system and the difficulty of ensuring the final atomicity of the transaction. Secondly, the workload imbalance among shards reduces transaction efficiency for the blockchain. The sharding with too much workload will cause transaction congestion and delay transaction confirmation. However, the sharding with too little workload will waste resources such as computing power and bandwidth.

Figure 1: Cross-shard tx ratio vs. number of shards

This paper will deeply analyze the reasons that lead to the issues related to excessive cross-shard transactions and imbalanced shard load within existing sharding frameworks. Taking the cross-shard transaction ratio and workload balance into account as crucial considerations, we aim to transform the challenges into a graph partitioning problem and present a graph-based public blockchain sharding scheme that efficiently balances transaction distribution. The proposed allocation strategy in the scheme converts continually acquired transaction information into a graph structure to optimize performance by graph partitioning. By reducing cross-shard transactions and balancing the workload between shards, the scheme reduces latency for transaction confirmation and boosts the blockchain system’s transaction processing capabilities.

In the simulation experiments, we replayed over 250,000 actual Ethereum transactions to perform the proposed blockchain sharding scheme. The experiment results demonstrate that the system effectively reduces cross-shard transaction counts to varying degrees for different numbers of shards while maintaining a balanced workload distribution. Notably, the system achieved a threefold increase in throughput compared to hash-based methods [10,11]. It is shown that the proposed scheme is able to decrease the cross-shard transaction ratio to a range of 35%–56% in a blockchain with no more than 25-shard, which is well below that of the hash-based random partitioning scheme [10,11], and the Monoxide scheme [12].

The primary contributions of this paper can be outlined as follows:

(1) A graph-based public blockchain sharding scheme that efficiently and evenly distributes transactions is proposed based on an improved LDG algorithm that can handle public blockchain transaction data that obeys power law distribution. We formalize the cross-shard transactions and shard load problems in the existing shards and transform the problems into graph partitioning problems starting from transaction allocation methods. The transaction relationship and frequency among accounts can be easily shown in the graph in this way.

(2) The scheme reduces transaction confirmation latencies and improves blockchain system performance by reducing cross-shard transactions and balancing workloads between shards. The allocation strategy transforms continuously acquired transaction information into the structure of a graph. It optimizes the transaction capacity through graph partitioning and balances the cross-shard transaction ratios and workload. Moreover, the scheme also achieves intra-shard transaction load balancing by employing a shard load threshold.

(3) By setting up a dedicated primary shard for blockchain sharding work, the sharding efficiency and security are improved. Compared with traditional fixed-random shards, ordinary shards’ burden of processing transactions is significantly reduced.

(4) We used more than 250,000 real Ethereum transaction data to simulate experiments in reality and implemented the blockchain sharding system. The experiment results show a significant improvement in the performance of the system. The scheme outperforms other baselines in terms of transaction capacity, cross-shard transaction ratio, and transaction confirmation latency.

The rest of the paper is organized as follows. Section 2 focuses on the preparatory and related work for blockchain sharding. We describe the model of the implemented blockchain partitioning system and outline the process of transaction allocation in Section 3. Section 4 specifically analyzes the transaction sharding problem and details the process of transaction allocation. The dataset, the setup, and the results of the experiments are shown in Section 5. Finally, Section 6 summarizes the paper.

2  Preparatory and Related Work

2.1 Blockchain and Blockchain Sharding

As a promising decentralized technology derived from cryptocurrencies such as Bitcoin and Ethereum [13], blockchain has great potential in many scenarios, for example, the infrastructures and applications, including the Internet of Things [14] and digital health [15–17]. Regrettably, current blockchain systems experience limited transaction processing capabilities and significant delays. Therefore, it seriously hinders the widespread application of blockchain in many scenarios with high transaction throughput and real-time transaction processing.

Researchers have proposed various different blockchain sharding schemes with the aim of enhancing the transaction performance and scalability of conventional blockchain systems. Existing sharding schemes can be divided into star architecture and parallel architecture according to network architecture.

Parallel architecture: Kokoris-Kogias et al. [11] proposed a stateful sharding protocol named OmniLedger to counter DoS attacks [18] and improve transaction capacity by a ByzCoinX consensus algorithm under the UTXO (Unspent Transaction Output) transaction model. However, the overhead of the sharding reconfiguration of it [19] is too high. OmniLedger proposed the Atomix protocol to process cross-shard transactions. By partial reconfiguration, Zamani et al. [20] proposed RapidChain to reduce the overhead of sharding and its impact on blockchain performance. Sonnino [21] proposed a sharding mechanism called Chainspace, with a special distributed atomic commit prototype that supports smart contracts. Alternatively, a client-driven BFT-based sharding mechanism was proposed in Chainspace. Wang et al. [12] proposed a more cutting-edge blockchain sharding technique, Monoxide, based on the account/balance model in 2019. Although Monoxide can improve system throughput, it inevitably leads to too many cross-shard transactions.

Star architecture: Luu et al. [10] presented the Elastico algorithm, which introduces the sharding approach of database scaling [22–24] into the blockchain. It is considered the first sharding scheme for the public blockchain. In the scheme, random functions are employed in the process of sharding configuration and sharding reconfiguration to enhance the balance of transaction sharding. But it reduces the security of the blockchain system. Tao et al. [25] proposed a dynamic sharding system based on smart contracts. This scheme utilizes inter-sharding merging algorithms with incentives for merging small shards dynamically to improve system throughput. Huang et al. [26] proposed an online stochastic exploration algorithm, MVCom, to optimize the design of sharding reconfiguration for the Elastico protocol. It selects the most valuable part of the committee for each round of several blockchain shards by designing a distributed algorithm [27]. The mechanism can find a balance between the transaction capacity of the partitioned blockchain and the transaction waiting latency within the partition. Serving as the core of the architecture, the Beacon chain is responsible for connecting the main chain as well as managing the individual shards in the designed architecture of Ethereum 2.0 [28].

2.2 Transaction Model and Existing Transaction Allocation Strategies

Currently, there are two main transaction models to organize transactions in the blockchain system: the UTXO model [1] and the account model [2]. The UTXO model [1] employed in Bitcoin, Elastico, OmniLedger, and RapidChain can be simply understood as a collection that has not yet been spent. In this model, each transaction spends the outputs of previous transactions and generates new outputs that transactions may consume in the future. All unspent transactions are kept in each fully synchronized node. In the account-based blockchain model [2], which utilizes Ethereum, each account records the user’s own balance like the bank accounts. Each transaction involves only one sender account and one receiver account, unlike the UTXO model [1], where a transaction may involve multiple inputs and outputs. The account model [2] is often considered more versatile than UTXO [1] because it can easily support smart contracts [29]. Moreover, the account model [2] can be extended to use for more complex scenarios and applications beyond cryptocurrencies. For this reason, the proposed scheme is built on top of the account model [2].

So, how do you assign transactions to different shards in a blockchain sharding system? There are two ways. Firstly, transactions are independently placed in different shards based on their transaction ID in the UTXO model. Secondly, transactions are assigned to different shards based on their sending account in the account model. In both, transactions originating from the same sender’s account are assigned to the same shard. These two allocation methods of transactions cause not only too many cross-shard transactions but also too many accounts in some shards with a high workload. Therefore, a reasonable transaction allocation method needs to be designed to achieve a good blockchain sharding.

2.3 Performance Evaluation Indicators of Blockchain Sharding System

Performance evaluation indicators of blockchain sharding systems mainly include transaction capacity, transaction confirmation latency, security, etc.

Transaction Capacity: Transaction capacity is the transaction number a system can process per unit of time, which describes the processing power and efficiency of the system. For blockchain, including the sharded system, transaction capacity refers to the total transaction number that can be processed by the entire network. TPS, which denotes the transaction number that can be executed per second, is usually employed to evaluate the transaction capacity of a blockchain. Ideally, TPS should scale linearly with the number of shards in a blockchain sharding scheme. Limited to factors such as the system’s network latency, storage capacity, and computational power, TPS may decrease compared to the ideal one in some blockchain sharding systems.

Transaction Confirmation Latency: Transaction confirmation latency is the duration between the moment a transaction is submitted and the moment it is confirmed on the blockchain. A lower transaction confirmation latency means that the blockchain system has a high ability for transactions to process with a fast response speed. It is helpful to provide a real-time response as well as a better user experience. However, current blockchain sharding systems suffer from high latency. As a result, the systems do not meet the requirements of high-frequency trading processing in terms of transaction confirmation latency. There is a significant gap in transaction confirmation latency for different types of transactions, which will affect the user experience. Therefore, a low transaction confirmation latency is an essential requirement for a blockchain sharding system.

Security: Security refers to the ability of a system to prevent malicious behaviour and protect the integrity of data. The blockchain sharding system needs to have an effective security mechanism. It should include strong encryption algorithms, authentication mechanisms, and authority control to ensure secure communication and interaction among each shard without attacks such as double-spending. However, current blockchain sharding systems have some loopholes caused by sharding. It is worth noting that sharding should not introduce new security issues to the blockchain system.

2.4 Cross-Shard Transaction Processing and Sharding Load Imbalance

In blockchain sharding systems, cross-shard transaction processing and sharding load imbalance are two unavoidable challenges. They are considered as two factors that impair the performance of existing blockchain sharding systems.

Cross-shard transactions: In cases where a transaction spans multiple shards, cross-shard transaction processing becomes a complex issue. Cross-shard transactions generally add extra time and network overhead compared to intra-shard transactions. In reality, the majority of the currently existing blockchain sharding system has the problem of too many cross-shard transactions. Many scholars have done research on how to deal with cross-shard transactions. OmniLedger [11] proposes the Atomix protocol to process cross-shard transactions, which adopts a client-driven two-phase commit mechanism to ensure the atomicity of cross-shard transactions. The relay transaction mechanism is employed to achieve the ultimate atomicity of cross-shard transactions in Monoxide [12]. Hong et al. [30] proposed a hierarchical sharding blockchain system, Pyramid, which employs bridge shards as bridges between shards and store blocks for multiple other shards. In the scheme, cross-shard transactions are handled by bridge-shard nodes that serve both shards. In the sharding architecture, BrokerChain [31], the system allows some ordinary users to act as “intermediary accounts” by voluntarily mortgaging certain assets. Intermediary accounts are stored in two or more shards to participate in the coordination of several cross-shard transactions.

Shard load imbalance: In the blockchain shard system, different shards may carry different shard loads due to some unreasonable distribution method. In this way, some shards are overloaded, while other shards are relatively light. As a result, unbalanced performance and waste of resources may occur. Because once an account is assigned to a shard, all its transactions will be assigned to it. The issue of shard load imbalance in the account model is more prominent than in the UTXO model. It is necessary to design a distribution algorithm for the account model that can balance the workload.

The methods to overcome the problem of shard load imbalance include dynamic sharding, load balancing algorithms, cross-shard transaction compression, and so on. The dynamic sharding method automatically adjusts the number and size of shards to balance the load based on the real-time shard load situation. By monitoring the load on the system and dynamically reallocating transactions to different shards based on demand, the method achieves a more balanced load distribution. Among them, scheme [32] proposed a load balancing mechanism combining transaction load prediction and account relocation algorithms. Scheme [33] presented a load-balancing framework in which objects (e.g., accounts) are frequently reallocated to shards. Load balancing algorithms can evenly distribute transactions to different shards. For example, polling, random selection, or load-based allocation algorithms are used to balance the transaction load. Cross-shard transaction compression is to reduce the size and complexity of transactions to mitigate the problem of shard load imbalance. By analyzing the above methods, we find that the shard load imbalance can be mitigated by reducing the transactions’ size and adjusting the shards’ size.

3  System Overview

In this section, we briefly describe the model of the implemented blockchain sharding system and outline the process of transaction allocation.

In order to avoid the two problems of too many cross-shard transactions and unbalanced shard load, a graph-based sharding system model for public blockchains is proposed in this section. By the method of graph division, this sharding achieves efficient and balanced blockchain sharding.

The proposed sharding system for blockchain aims to reduce the excessive cross-shard transactions and improve the load balancing of shards. Similar to the existing sharding systems, the system divides the entire blockchain network into multiple independent shards, which contain a portion of nodes and transaction data. Each shard can run independently and process its own transactions without waiting for confirmation from the whole network. Although the shards are independent, the system still allows cross-shard transactions for global interoperability. Once each shard processes its own transaction, the consensus node verifies and packages the transactions within the shard with the PBFT (Practical Byzantine Fault Tolerance) consensus algorithm. Finally, the block is generated and uploaded to the chain by cryptographic algorithms.

The new node of this system will establish a unique on-chain node identity by solving the PoW-based (Proof of Work) puzzle. It not only ensures the system’s security but also effectively defends against Sybil attacks. Sharded consensus nodes are randomly selected based on VRF (Verifiable Random Functions) to prevent nodes from doing evil.

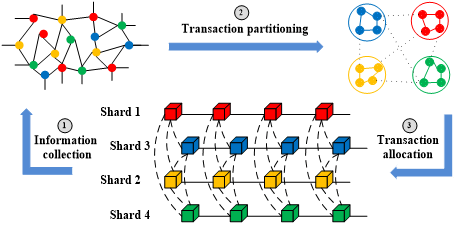
The model of the sharding system is shown in Fig. 2. The dotted lines in the figure indicate cross-shard transactions. The system involves two types of shards: a primary shard and several common shards. The primary shard is responsible for sharding tasks. The common shards are utilized to process transaction tasks. There are three main steps at the system’s every epoch: the first one is the preparation work for information collection, the second one is the partitioning work for transaction partitioning algorithm, and the last one is the allocation work for transaction allocation. While performing the sharding task, the primary shard constructs a transaction graph by continuously collecting account and transaction information and the pending transactions in the transaction pool. By a graph partitioning algorithm, the transaction graph is decomposed to find a number of non-overlapping subgraphs, which will be taken as a shard for the next epoch. Finally, the corresponding transactions are allocated to the specified shard according to the division rules of the primary shard. Therefore, the generated subgraph transactions are as balanced as possible, and the transactions between individual subgraphs are minimized.

Figure 2: System model

These three tasks will be performed at each epoch to keep the system at optimal performance. At the same time, regular re-sharding will prevent the evil nodes from doing further evil and ensure the security of the system.

4  Transaction Allocation

The transaction allocation aims to reduce cross-chain transactions and balances the transaction load in different shards. In this section, we will specifically introduce the process of transaction allocation, which has three phases: information collection, transaction partitioning algorithm, and transaction allocation.

4.1 Information Collection

In order to achieve better sharding results at a later stage, the primary shard creates a transaction graph G(V,E) by monitoring the account and transaction information of all common shards and the pending transactions in the transaction pool, where the vertex V in the graph denotes an account, the edge E denotes the existence of a transaction between two accounts, and the number of edges existing between two accounts denotes the number of transactions between accounts. The neighbours of an account v are denoted as N(v).

Since this information changes over time, the information collection effort is dynamic. Through the collection of these accounts and transaction information, on the one hand, it is helpful for subsequent transaction partitioning algorithms to compute more efficient transaction partitioning results. On the other hand, it increases the effectiveness and reliability of the system.

4.2 Transaction Partitioning Algorithm

In a complex blockchain network, we transform the shard problem into a graph partitioning problem. Graph partitioning refers to the division of nodes in a graph into several disjoint subsets to operate in a distributed system. The optimization objectives of graph partitioning encompass two main aspects: load balancing and minimum cut. Both objectives are designed to enhance the performance of computation within a distributed system. Load balancing aims to distribute workloads evenly among multiple computers within a distributed system so that no computers would be overloaded, thus avoiding congestion. The minimum cut, on the other hand, is to decrease the communication cost between computers. Optimizing both objectives simultaneously is currently known to be an NP-hard problem. However, our optimization goals for sharding also include load balancing and minimizing cross-shard transactions. Therefore, we transform the sharding problem into a graph partitioning problem.

An improved LDG (Linear Deterministic Greedy) algorithm is utilized in the graph partitioning algorithm. The original LDG algorithm divides the set of points in the graph into parts. It is often used in VLSI (large-scale integrated circuit) design, parallel computing, industrial network optimization design, image segmentation, and other fields. Each point in the graph, along with its associated data, is stored within a partitioned subgraph. The edge between the two vertices may turn into edge cuts when two vertices are separated into different subgraphs. The size of the edge cut set directly influences the communication cost of the distributed algorithm. The algorithm only stores part of the graph and divides the continuous input data in real-time, so it has extremely high efficiency in larger-scale graph partitions. Although the Original LDG algorithm achieves intra-shard vertex load balancing and minimum cut, it does not take intra-shard edge load balancing into account for public blockchain transaction data that obeys a power-law distribution. For this reason, we improve the algorithm according to the actual situation of blockchain sharding, set the shard load threshold, and finally realize the load balancing of intra-shard transactions (i.e., edges).

In the system, the primary shard analyzes the transaction graphs using a modified LDG algorithm. Several mutually disjoint transaction subgraphs are found, such that the generated transaction subgraphs are as balanced as possible and the transactions between individual subgraphs are minimized. These subgraphs will be used as candidates for common shards in the next epoch.

The improved LDG algorithm takes the transaction graph G(V,E) and the maximum number of iterations t as input. The shard mapping is the output. Next, we elaborate on the algorithm in detail.

(1) Initialize: assign an initial value to each account based on the shard ID where each account is currently located. It is stored in the shard map. ID is used to identify different shards.

(2) Execute the Partitioning Algorithm: the primary shard iterate through each account in the transaction graph and each account’s neighbours. Then, the objective function f(v,i) is called, and it computes the function value of account v assigned to the shard i where the neighbor is located. Here, the objective function f(v,i) represents the optimization score of account v in shard i. Finally, each account selects the shard where the neighbor node with the largest function value is located as the target shard, joins the shard, and updates the shard mapping. If more than one shard with the largest objective function value exists, the shard where the neighbor node with the largest function value is located is randomly selected as the target shard. The objective function f(v,i) is defined as follows:

f(v,i)=|Ei∩E(v)|g(i),

g(i)=1−|Ei|C,

C=β*|E|S,β≥1.

The formula v denotes the account being partitioned. E(v) denotes the set of edges of the account with its neighbours. i is the identifier of the shard i. Ei denotes the set of edges of the shard i, including edges within the shard and edges across the shard. The execution algorithm computes an objective function f(v,i) for account v in each neighbouring shard. The function consists of two parts. One part, |Ei∩E(v)|, indicates the number of edges between account v and its neighbors in shard i. The larger the value of this part, the fewer cuts are generated by dividing v into shard i, i.e., the fewer cross-shard transactions. The second component, g(i), represents the number of transactions that the current shard i can accommodate in a balanced state, and also serves as a constraint on the shard transaction load. The larger the value of g(i), the greater the number of transactions that shard i can accommodate, and the smaller the load on shard i. Shards with a larger number of edges will accommodate fewer transactions and suffer greater penalties. C denotes the maximum transaction capacity of each shard load. β is an adjustable parameter set by the user. E represents the number of transactions in all the shards. S denotes the number of shards. Account v is assigned to the shard with the largest objective function value. The algorithm achieves both optimized load balancing and measurement of cross-shard transactions.

The specific execution of the algorithm is shown in Algorithm 1.

(3) Iteratively update the mapping and repeat the previous step until the maximum number of iterations. After each update iteration, the accounts of the same mapping are divided into the same shard so that a set of shards is obtained.

(4) Output Partitioning Result: output the final segmentation result to get the segmentation result of the transaction graph.

Next, the primary shard reaches a consensus on the shard result via PBFT. It broadcasts the shard result to all common shards.

4.3 Transaction Allocation

When both the information collection work and the transaction partitioning algorithm are finished, the primary shard broadcasts the shard results to the common shard, which validates its results. After successful validation, the accounts and their transactions are purposefully transferred to the specific shard, and the updated state is synchronized. The completion of the transaction allocation work represents the end of this epoch. The updated shard will start in a new epoch.

The scheme maps a complex blockchain transaction network into a transaction graph firstly, and then analyzes the transaction graphs using a modified LDG algorithm. By analyzing the transaction relationship and transaction number of each account in the graph, multiple disjoint transaction subgraphs are identified using Algorithm 1, in which step 5 is employed to minimize across subgraph transactions, step 6 is employed to balance transaction load among subgraphs. Finally, shards are formed with these transaction subgraphs.

5  Evaluation

This section describes the dataset, setup, and experiment results.

5.1 Dataset

We use the full node of Ethereum to obtain data on the blockchain and download its transaction history. 250000 transaction records are extracted along with their transaction accounts and employed for experimental replay to evaluate the scheme’s performance.

5.2 Setup

A go-based simulator experiment is implemented to evaluate the effectiveness of the scheme. The simulator runs periodically like the existing sharding blockchain. We set an epoch of 100 s and generate a block every 5 s. Each block contains up to 2000 transactions, in which the rate of transactions sent to the system within 25 shards defaults to 2000 TPS.

The following metrics are utilized to evaluate the performance of the scheme:

(1) Transaction capacity. In the experiments, average transaction capacity is adopted to evaluate the scheme. The average transaction capacity for a particular epoch can be defined as:

tpsi=niti,

where ni represents the total number of transactions processed in epoch i, ti represents the time which is used to process transactions in epoch i. Therefore, the average transaction capacity over all epochs can be defined as:

tps=NT,

where N denotes the total number of transactions processed in all epochs, i.e., N=∑i=1kni. T denotes the time used to process transactions in all epochs, i.e., =∑i=1kti.

(2) Transaction confirmation latency. It can be defined as:

Latencyj=ntimej−ctimej,

where ntimej denotes the confirmation on-chain time of transaction j and ctimej denotes the submission time of transaction j. The average transaction confirmation latency in epoch i can be defined as:

avgLatencyi=∑j=1mLatencyjm.

The average transaction recognition latency over all epochs can be defined as:

avgLatency=∑i=1kavgLatencyik.

(3) Cross-shard transaction rate. It refers to the ratio of cross-shard transactions in all transactions in the blockchain, which can be defined as:

ctxRatio=ctxalltx,

where ctx denotes the number of cross-shard transactions, and alltx represents the number of all transactions in the blockchain.

Baseline. We will compare it with the following two state-of-the-art methods. The first one, the hash-based random partitioning method [10,11], is a traditional blockchain sharding method. Transactions in this method are assigned to a given shard based on the hash of the account address. However, the cross-shard transactions and shard load balancing are not considered. The second one, Monoxide [12], also is a classic blockchain shard method. The method dramatically improves performance by introducing the concepts of asynchronous consensus groups and relay transactions.

We also verify the impact of the following parameters on the system performance. The first one is the number of shards. We perform the blockchain system from 2 to 25 shards, respectively. As the number of shards increases, the transaction capacity, latency, shard load, and cross-shard transactions will be affected. The second one is the sharding load capacity. We evaluate the impact on the system when β is 1, 1.5, and 2, respectively, where β≥1. In which β=1 indicates that the system is in a state of balanced shard load capacity, β=1.5 demonstrates that the shard load capacity is 1.5 times the balanced state, and β=2 shows that the shard load capacity is two times the balanced state.

5.3 Experiment Results

(1) Transaction Capacity

In the experiments, we evaluate the average transaction capacity to describe the overall situation of the system. The effect of the number of shards on the throughput is shown in Fig. 3. It can be observed that the average transaction capacity linearly increases as well as the increase of shards in the scheme. It is also clear that the average transaction capacity of the Monoxide scheme [12] is lower than that of the proposed one. Moreover, the transaction capacity of the proposed scheme is three times higher than that of the hash-based scheme [10,11] when the shards are 25. The experiment results show that the presented scheme is desirable and effective.

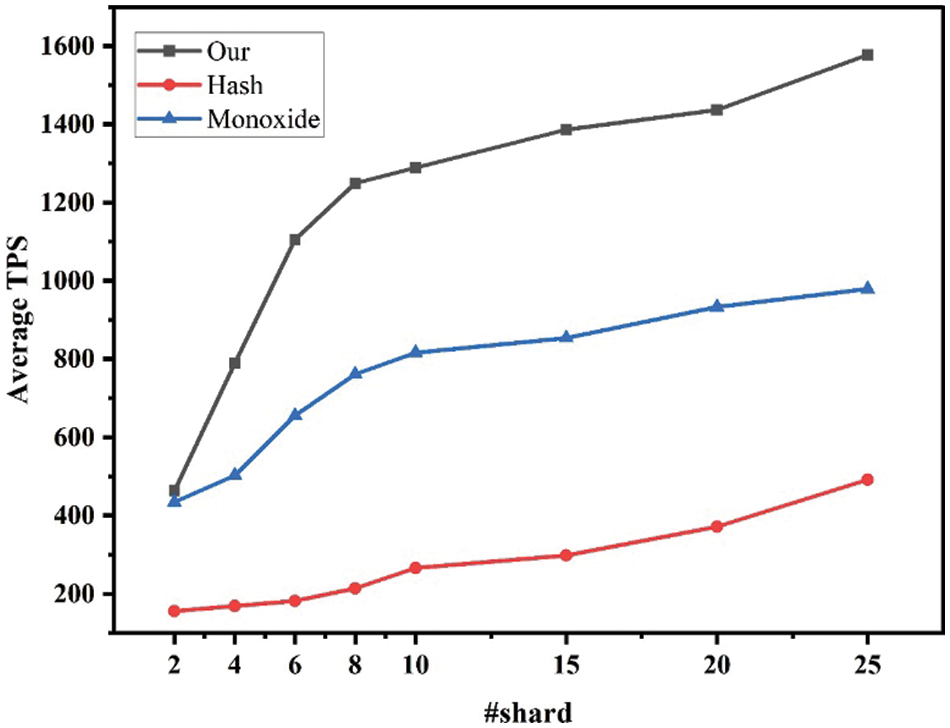
Figure 3: Average TPS vs. number of shards

The effect of different shard load capacities on transaction capacity is shown in Fig. 4. When β=1, i.e., the shard load capacity is balanced, the transaction capacity is always higher than that of cases when β=1.5 and β=2. It is indicated that the transaction capacity is optimal when the shard load capacity is balanced. The system transaction capacity decreases when β=1.5 or β=2. This is due to partial redundancy in the capacity and unbalanced transactions among the shards.

Figure 4: Average TPS vs. number of shards

(2) Transaction Confirmation Latency

As shown in Fig. 5, the average transaction confirmation latency of the proposed scheme remains consistently low as the number of shards increases. Compared with the other two baselines, the average transaction confirmation latency of the proposed method is 2 and 1 lower when the number of system shards is 25, respectively. The average transaction confirmation latency is as low as about 6 s. The latency of the hash-based random partitioning method and Monoxide is consistently higher due to the load imbalance among shards and more cross-shard transactions. It is shown that the proposed scheme is more reasonable and feasible.

Figure 5: Average latency vs. number of shards

The effect of different shard load capacity parameters on transaction confirmation latency is shown in Fig. 6. It can be observed that the system has the lowest transaction confirmation latency when β=1, i.e., when the shard load capacity is balanced. When β=1.5 or β=2, the transaction confirmation latency of the system is always higher than that of the balanced state when β=1. This phenomenon occurs because as the shard load capacity increases, there is an imbalance in load between the shards, thus not guaranteeing fast transaction confirmation. The transaction confirmation latency is thus reduced when the shard load capacity is balanced.

Figure 6: Average latency vs. number of shards

(3) Cross-Shard Transaction Ratio

Fig. 7 describes the relationship between the number of shards and the cross-shard transaction rate. It can be seen that the cross-shard transaction rate gradually increases as the number of shards increases. This is due to the fact that a more significant number of shards generates more cross-shard transactions. Conversely, the fewer the number of shards, the fewer the number of cross-shard transactions generated. The proposed scheme has a cross-shard transaction rate of around 30%–50%, which is lower than the other two schemes [10,12]. Furthermore, the other two shard methods have a cross-shard transaction rate of 95% when the shards are 25. Intuitively, the reason for this phenomenon is that they do not take the problems of load unbalancing by excessive cross-shard transactions into account.

Figure 7: Cross-shard tx ratio vs. number of shards

The effect of different shard load capacity parameters on cross-shard transactions is shown in Fig. 8. We can find that the higher the shard load capacity, the higher the cross-shard transaction rate. When the shard load capacity is balanced, i.e., β=1, the cross-shard transaction rate is the lowest. However, when the shard load capacity exceeds the equilibrium state, i.e., β>1, some shards have redundancy, and some shards are oversaturated. It ultimately leads to load imbalance among the shards. In fact, a higher load on some shards will result in an increased demand for cross-shard transactions. Thus, the frequency of cross-shard transactions increases as the degree of load imbalance increases.

Figure 8: Cross-shard tx ratio vs. number of shards

6  Conclusion

The paper reveals that too many cross-shard transactions and the unbalanced load of shards are some of the factors affecting the performance of the system. To distribute transactions efficiently and evenly, we propose a graph-based public blockchain sharding scheme based on an improved LDG algorithm. The scheme reduces cross-shard transactions and balances the workload among shards by graph partitioning, which can reduce the transaction confirmation delay and improve the throughput of the blockchain system. Furthermore, the effectiveness of the scheme is demonstrated through simulation. Notably, our scheme outperforms other baselines regarding throughput, cross-shard transaction ratio, and transaction confirmation delay. This work assumes historical transactions as future transactions, so we consider the prediction of future transactions as the future work.

Acknowledgement: This paper’s logical organization and content quality have been enhanced, so the authors thank anonymous reviewers and journal editors for assistance.

Funding Statement: This work was supported by Shandong Provincial Key Research and Development Program of China (2021CXGC010107, 2020CXGC010107), the Shandong Provincial Natural Science Foundation of China (ZR2020KF035), the New 20 Project of Higher Education of Jinan, China (202228017).

Author Contributions: Study conception and design: S. Xu, and Z. Wang; analysis and interpretation of results: S. Xu, Z. Wang, L. Wang, and M. Mihaljević; draft manuscript preparation: Z. Wang, S. Zhang, Wei Shao, and Q. Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The experimental dataset is derived from Ethereum historical transaction data which are available at https://xblock.pro/#/.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Nakamoto, S., Bitcoin, A. (2008). A peer-to-peer electronic cash system. Bitcoin, 4(2), 15. https://bitcoin.org/bitcoin.pdf (accessed on 01/01/2023). [Google Scholar]

2. Wood, G. (2014). Ethereum: A secure decentralised generalised transaction ledger. Ethereum Project Yellow Paper, 151, 1–32. [Google Scholar]

3. Javaid, M., Haleem, A., Singh, R. P., Khan, S., Suman, R. (2021). Blockchain technology applications for Industry 4.0: A literature-based review. Blockchain: Research and Applications, 2(4), 100027. [Google Scholar]

4. Pan, Q., Wu, J., Bashir, A. K., Li, J., Vashisht, S. et al. (2022). Blockchain and ai enabled configurable reflection resource allocation for IRS-aided coexisting drone-terrestrial networks. IEEE Wireless Communications, 29(6), 46–54. [Google Scholar]

5. Zheng, Z., Xie, S., Dai, H. N., Chen, X., Wang, H. (2018). Blockchain challenges and opportunities: A survey. International Journal of Web and Grid Services, 14(4), 352–375. [Google Scholar]

6. Han, X., Yuan, Y., Wang, F. (2019). Blockchain security: Research status and prospects. Journal of Automation, 45(1), 206–225. [Google Scholar]

7. Poon, J., Dryja, T. (2016). The bitcoin lightning network: Scalable off-chain instant payments. https://static1.squarespace.com/static/6148a75532281820459770d1/t/61af971f7ee2b432f1733aee/1638897446181/lightning-network-paper.pdf (accessed on 01/01/2023). [Google Scholar]

8. Pervez, H., Muneeb, M., Irfan, M. U., Haq, I. U. (2018). A comparative analysis of DAG-based blockchain architectures. 2018 12th International Conference on Open Source Systems and Technologies (ICOSST), pp. 27–34. Lahore, Pakistan. [Google Scholar]

9. Dziembowski, S., Faust, S., Hostáková, K. (2018). General state channel networks. Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, pp. 949–966. Toronto, Canada. [Google Scholar]

10. Luu, L., Narayanan, V., Zheng, C., Baweja, K., Gilbert, S. et al. (2016). A secure sharding protocol for open blockchains. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, pp. 17–30. Xi’an, China. [Google Scholar]

11. Kokoris-Kogias, E., Jovanovic, P., Gasser, L., Gailly, N., Syta, E. et al. (2018). Omniledger: A secure, scale-out, decentralized ledger via sharding. 2018 IEEE Symposium on Security and Privacy (SP), pp. 583–598. San Francisco, CA, USA. [Google Scholar]

12. Wang, J., Wang, H. (2019). Monoxide: Scale out blockchains with asynchronous consensus zones. 16th USENIX Symposium on Networked Systems Design and Implementation (NSDI 19), pp. 95–112. Boston, USA. [Google Scholar]

13. Swan, M. (2015). Blockchain: Blueprint for a new economy. O’Reilly Media, Inc. [Google Scholar]

14. Novo, O. (2018). Blockchain meets IoT: An architecture for scalable access management in IoT. IEEE Internet of Things Journal, 5(2), 1184–1195. [Google Scholar]

15. Gupta, B. B., Li, K. C., Leung, V. C., Psannis, K. E., Yamaguchi, S. (2021). Blockchain-assisted secure fine-grained searchable encryption for a cloud-based healthcare cyber-physical system. IEEE/CAA Journal of Automatica Sinica, 8(12), 1877–1890. [Google Scholar]

16. Nguyen, G. N., Le Viet, N. H., Elhoseny, M., Shankar, K., Gupta, B. B. et al. (2021). Secure blockchain enabled cyber-physical systems in healthcare using deep belief network with ResNet model. Journal of Parallel and Distributed Computing, 153, 150–160. [Google Scholar]

17. Raj, A., Prakash, S. (2022). A privacy-preserving authentic healthcare monitoring system using blockchain. International Journal of Software Science and Computational Intelligence (IJSSCI), 14(1), 1–23. [Google Scholar]

18. Saad, M., Cook, V., Nguyen, L., Thai, M. T., Mohaisen, A. (2019). Partitioning attacks on bitcoin: Colliding space, time, and logic. 2019 IEEE 39th International Conference on Distributed Computing Systems (ICDCS), pp. 1175–1187. Dallas, Texas, USA. [Google Scholar]

19. Syta, E., Jovanovic, P., Kogias, E. K., Gailly, N., Gasser, L. et al. (2017). Scalable bias-resistant distributed randomness. 2017 IEEE Symposium on Security and Privacy (SP), pp. 444–460. San Jose, CA, USA. [Google Scholar]

20. Zamani, M., Movahedi, M., Raykova, M. (2018). Rapidchain: Scaling blockchain via full sharding. Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, pp. 931–948. Toronto, Canada. [Google Scholar]

21. Sonnino, A. (2018). Chainspace: A sharded smart contract platform. Network and Distributed System Security Symposium 2018 (NDSS 2018), San Diego, USA. [Google Scholar]

22. Corbett, J. C., Dean, J., Epstein, M., Fikes, A., Frost, C. et al. (2013). Spanner: Google’s globally distributed database. ACM Transactions on Computer Systems (TOCS), 31(3), 1–22. [Google Scholar]

23. Glendenning, L., Beschastnikh, I., Krishnamurthy, A., Anderson, T. (2011). Scalable consistency in Scatter. Proceedings of the Twenty-Third ACM Symposium on Operating Systems Principles, pp. 15–28. Cascais, Portugal. [Google Scholar]

24. Danezis, G., Meiklejohn, S. (2015). Centrally banked cryptocurrencies. arXiv preprint arXiv:1505.06895. [Google Scholar]

25. Tao, Y., Li, B., Jiang, J., Ng, H. C., Wang, C. et al. (2020). On sharding open blockchains with smart contracts. 2020 IEEE 36th International Conference on Data Engineering (ICDE), pp. 1357–1368. Dallas, Texas, USA. [Google Scholar]

26. Huang, H., Huang, Z., Peng, X., Zheng, Z., Guo, S. (2021). MVCom: Scheduling most valuable committees for the large-scale sharded blockchain. 2021 IEEE 41st International Conference on Distributed Computing Systems (ICDCS), pp. 629–639. Washington DC, USA. [Google Scholar]

27. Fréville, A. (2004). The multidimensional 0-1 knapsack problem: An overview. European Journal of Operational Research, 155(1), 1–21. [Google Scholar]

28. Ethereum 2.0 Spec, Ethereum 2.0 phase 0-the beacon chain. https://github.com/ethereum/consensus-specs/blob/dev/specs/phase0/beacon-chain.md (accessed on 01/01/2023). [Google Scholar]

29. Buterin, V. (2014). A next-generation smart contract and decentralized application platform. White Paper, 3(37). [Google Scholar]

30. Hong, Z., Guo, S., Li, P., Chen, W. (2021). Pyramid: A layered sharding blockchain system. IEEE INFOCOM 2021-IEEE Conference on Computer Communications, pp. 1–10. [Google Scholar]

31. Huang, H., Peng, X., Zhan, J., Zhang, S., Lin, Y. et al. (2022). BrokerChain: A cross-shard blockchain protocol for account/balance-based state sharding. IEEE INFOCOM 2022-IEEE Conference on Computer Communications, pp. 1968–1977. Beijing, China. [Google Scholar]

32. Woo, S., Song, J., Kim, S., Kim, Y., Park, S. (2020). GARET: Improving throughput using gas consumption-aware relocation in Ethereum sharding environments. Cluster Computing, 23, 2235–2247. [Google Scholar]

33. Król, M., Ascigil, O., Rene, S., Sonnino, A., Al-Bassam, M. et al. (2021). Shard scheduler: Object placement and migration in sharded account-based blockchains. Proceedings of the 3rd ACM Conference on Advances in Financial Technologies, pp. 43–56. [Google Scholar]