KSKV: Key-Strategy for Key-Value Data Collection with Local Differential Privacy

1  Introduction

Enterprises frequently collect data for analysis with the aim of enhancing the quality of their services. However, such data often contain sensitive information, necessitating robust privacy protection measures. Differential Privacy (DP) [1] has become the de facto standard for privacy preservation, ensuring the security of data irrespective of an adversary's background knowledge or computational power. In environments lacking a trusted aggregator, the Local Differential Privacy (LDP) offers robust privacy assurances during the data collection phase. Under LDP, users independently apply a privacy-preserving mechanism to their data before transmission to the aggregator. Notably, several leading enterprises, including Google [2], Apple [3], and Microsoft [4], have implemented LDP.

Initial research in LDP primarily addressed basic statistical data types, focusing on frequency estimation of discrete variables and mean estimation of continuous variables. Further studies extended the paradigm to more sophisticated structured data, including set values [5–7] and graph data [8,9]. Despite this progress, investigations into key-value data queries remain relatively sparse [10–12]. Key-value data, prevalent in practice, necessitates simultaneous analysis of key frequencies and the means of values associated with each key. The accuracy of multidimensional data collection under LDP is particularly challenging due to the constraints of the privacy budget. Moreover, traditional LDP algorithms can significantly distort the intrinsic associations among multidimensional data. The significance of key-value data in big data analytics cannot be overstated, and the correlation between keys and their associated values is typically strong. Thus, the collection of key-value data within the stringent privacy budget constraints of LDP presents a substantial and noteworthy challenge. For example, as illustrated in Table 1, to accurately determine a movie’s rating, a sufficient number of reviews, or the frequency of keys, is first required. Subsequently, the mean of these key values represents the movie's rating. Accurate key frequencies not only enable more precise value calculations (since the value under each key is derived from the sum of all values divided by the key’s frequency) but also facilitate a more accurate ranking of keys.

Motivations. Effective management of key-value collections critically relies on two principal factors: the frequency of keys and the mean of the values associated with each key. The primary challenge lies in maximizing the utility of key-value data within the LDP framework, while maintaining robust privacy guarantees. In LDP models, the privacy budget parameter, denoted as ε, is pivotal, serving as a quantitative measure of privacy protection. Given the dual nature of key-value pairs, the privacy budget is judiciously allocated to protect the confidentiality of both the keys and their corresponding values, without compromising their intrinsic correlation. Ye et al. [10] originally proposed a method that equally divided the privacy budget between keys and values; however, this approach did not result in an optimized budget allocation within the LDP paradigm. Later, Gu et al. [12] introduced a unified privacy budget allocation strategy, employing a shared privacy budget for keys and values. Nevertheless, in the context of key-value data, an inaccurate selection of keys can render the associated values meaningless. As such, this paper advocates for a Joint Privacy Budget mechanism, oriented towards enhancing the accuracy of keys. This method not only substantiates the precision of key identification but also improves value computation by: (1) satisfying key frequency estimation requirements, and (2) enabling more accurate mean estimation due to the enhanced accuracy of frequency estimation.

Contribution. This paper aims to address the existing challenges by introducing innovative mechanisms that prioritize key strategies, aimed at increasing the utility of key-value data collection in both interactive and non-interactive environments. For non-interactive frameworks, we propose the Key-Strategy Unary Encoding (KS-UE), strategically allocating a predominant portion of the privacy budget to key frequencies to enhance utility. In interactive environments, we employ the Key-Strategy Generalized Randomized Response (KS-GRR), which uses a group-and-iteration approach across various tasks to yield superior estimation results. Furthermore, the paper thoroughly examines the flexibility of these strategies in situations where users hold either single or multiple key-value pairs.

The salient contributions of this work can be summarized as follows:

•   Acknowledging the paramountcy of accurate keys in key-value collection, we advance the key-strategy mechanisms KS-UE for non-interactive frameworks and KS-GRR for interactive frameworks within the confines of LDP.

•   By leveraging KS-UE and KS-GRR, we formulate algorithms tailored for contexts wherein users hold either singular or multiple key-value pairs, enhancing the adaptability of our approach.

•   We provide rigorous theoretical substantiation for the minimal variance of KS-UE. Additionally, empirical evaluations corroborate that strategies KS-UE and KS-GRR can ascertain more precise frequent keys while maintaining the integrity of mean accuracy.

Roadmap. Section 2 will elaborate on related works. Subsequently, Section 3 will provide background information and the theoretical foundation for our study. In Section 4, we introduce our key-strategy algorithms for single and multiple key-value pairs within the framework of Local Differential Privacy. Section 5 will present the experimental results, while Section 6 will conclude the paper.

2  Related Work

Local Differential Privacy is a potent technique employed to safeguard sensitive user data during the data collection process. The fundamental mechanism of LDP yields a probability distribution as output rather than revealing authentic statistical information. Randomized Response (RR), first introduced in the 1960s, is recognized as a precursor to LDP methods [13] and was later formalized as a local privacy model by Dwork [14,15]. Subsequent research has led to the development of methodologies such as RAPPOR [2], Optimal-RR (O-RR), Optimal-RAPPOR (O-RAPPOR) [16], Sampled Histogram (SH) [17], Optimal Unary Encoding (OUE), and Optimal Local Hashing (OLH) [18] for singleton frequency estimation. Additional studies [4,19] have focused on mean estimation with numerical attributes. More complex data structures such as set values [5,6], marginal release [20,21], numerical values [19,22], graph data [8,9,23,24], spatiotemporal data [1,25], time-series [26], distribution estimation [27], range queries [28], and machine learning [29,30] have been examined. Further, strategies to counteract attacks have been proposed [31–33]. Nevertheless, only a limited number of studies [10–12,34] have concentrated on key-value data queries.

Ye et al. [10] were the first to formalize two tasks in key-value data collection under LDP: estimating the frequencies of keys and the mean of values under each key. They proposed PrivKV for non-interactive frameworks and later introduced optimized versions, PrivKVM and PrivKVM+, for interactive frameworks. Ye et al. further improved PrivKVM+ in [34]. Sun et al. [11] offered another approach within the PrivKV framework, but they did not analyze the impact of the correlation between perturbations on the tighter budget composition. Gu et al. [12] addressed this issue by proposing an optimized budget allocation and an advanced 'padding-and-sampling' mechanism. They used budget allocation to optimize privacy parameters for better estimation results. In this paper, we propose a more effective scheme, termed key-strategy frameworks, for key-value data collection under LDP.

3  Preliminaries

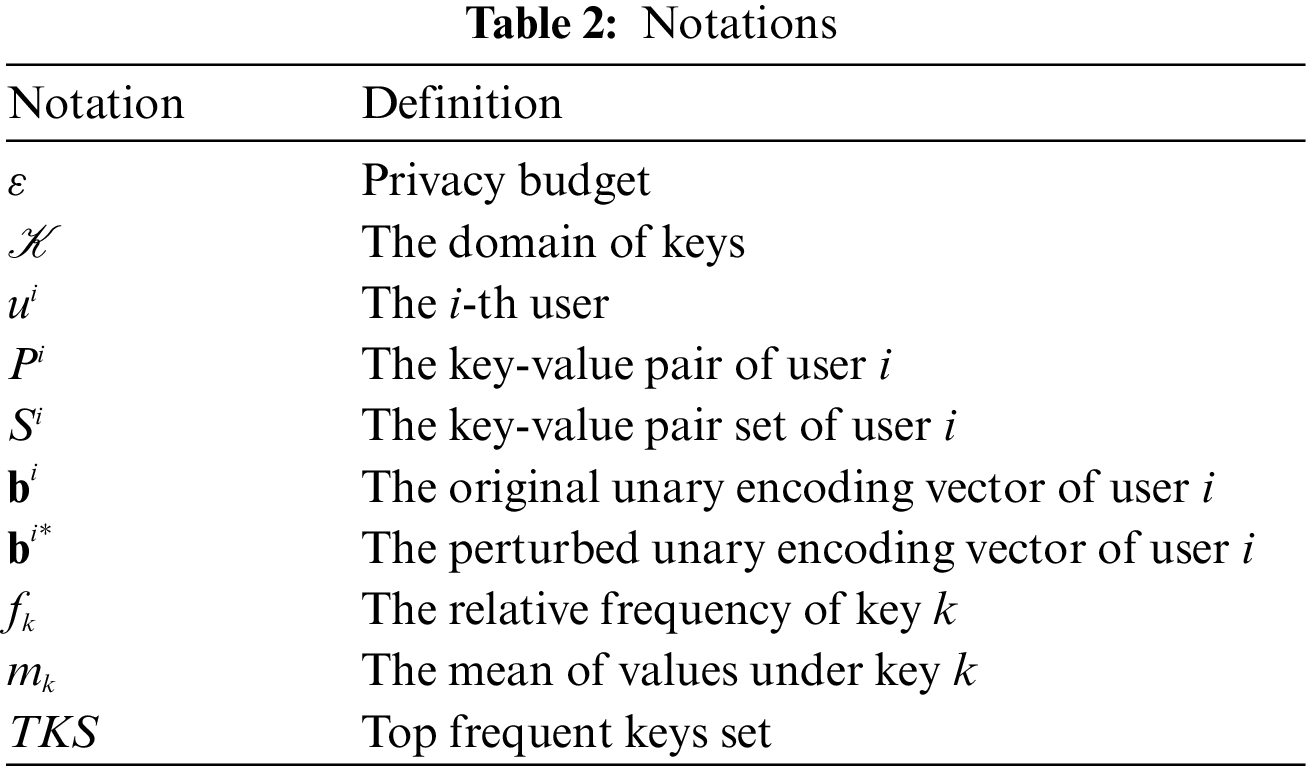
In this section, we initially delineate the problem, followed by an introduction to the concept of LDP. The notations used in this paper are summarized in Table 2.

3.1 Problem Definition and Challenge

Key-Value Data Collection. The issue of key-value data collection under LDP was first put forth by [10]. Assume there are n users (denoted as ui∈𝒰 where i=1,2,...,n). Each user ui possesses either a single or a set of key-value data. The key-value pair is denoted as Pi:=<ki,vi> (where k∈K and v∈V), forming a domain P. The domain size of the key is |K|=d and the domain of the value v is within the range of [−1, 1]. The objective of the aggregator is to estimate the statistical data of the users, specifically, the frequency of keys and the mean of values under each key.

•   Frequency Estimation: The purpose of this task is to estimate the frequency of each key k, defined as: fk^=|{Pi|∃k∈Pi}n

•   Mean Estimation: The goal of this task is to estimate the mean of values associated with each key k, defined as: mk^=∑i=1,k∈Pinvin⋅fk^

In practical application scenarios, most users possess multiple values Pi:={<ki1,vi1>,<ki12,vi2>,...,<kil,vil>}. The existence of multiple key-value pairs implies an added dimension to key-value data, symbolizing a synthesis of set-value and key-value data. The aggregator also estiamte the statistical data fk^ and mk^. This amalgamation is also one of the potential developmental trajectories in LDP.

3.2 Local Differential Privacy

LDP is a localized model of DP intended for data collection without a trustworthy aggregator [5,18,35,36]. An LDP algorithm, denoted as Ψ, ensures that the probability of one value being transmitted to the aggregator closely approximates the probability of any other values being sent. The notion of ε-LDP is defined as follows.

Definition 3.1(ε-local differential privacy.). A randomized mechanism Ψ with domain Dom(Ψ) and range Ran(Ψ) is ε-local differential private if for any input items v,v ′∈Dom(Ψ), and any output s∈Ran(Ψ), the following inequality holds:

Pr[Ψ(v)=s]Pr[Ψ(v ′)=s]≤eε(1)

The privacy budget, ε, can be adjusted to strike a balance between data availability and privacy intensity. LDP can offer a stronger level of privacy protection than a centralized framework as each user reports only the perturbed data.

3.3 Mechanism under LDP

We assume the size of domain 𝒟 is d, each user has one item of 𝒟.

Randomized Response(RR)/Generalized Randomized Response(GRR). The perturbation function of GRR [18] is

Pr[Ψ(v)=s]={eεeε+d−1,ifs=v1eε+d−1,ifs≠v

where RR is the special situation d=2.

Unary Encoding (UE). [18] Each user transforms her item into a vector of length d, where only the mapped position is 1, and all others are 0s. Subsequently, each bit is independently perturbed through the function

Pr[Ψ(v∗[j])=1]={p,ifv[j]=1q,ifv[j]=0

where p+q need not be equal to 1.

When p=12 and q=1eε+1, the variance of frequency is minimized; therefore, under these conditions, it is termed as Optimized Unary Encoding (OUE).

Optimal Local Hashing (OLH). [18] The OLH protocol was developed to ameliorate the challenges posed by attributes with extensive categories. Initially, the client-side algorithm transforms the user’s actual value v to a diminished hash value domain g utilizing a precise hash function. Subsequent to this transformation, the algorithm applies a randomized response to the hash value within this condensed domain. The parameter g represents a balanced compromise between the information loss occurring during the hashing and the subsequent randomization step; the balance is deemed optimal when g=eε+1. The temporal complexity of this algorithm is characterized as O(log⁡n), while the spatial complexity is quantified as O(nlog⁡|D|).

3.4 Padding-and-Sampling Protocol

Originally utilized for itemset data [6], the ‘padding-and-sampling’ protocol was first adopted for key-value data in [12]. In this setup, each user samples a single key-value pair from their set. A crucial parameter, denoted as l, ensures a consistent sampling rate while l dummy key-value pairs are generated. A key-value pair from the user's set Si is selected randomly with a probability of |Si|max{|Si|,l}, and a dummy key-value pair is chosen with the remaining probability.

3.5 Competitor

PrivKV. Ye et al. [10] proposed PrivKV and improved version PrivKVM and PrivKVM+ on key-value data collection under LDP first time. The primary process comprises: (a) encoding the key-value pair to a position of a vector, leaving all other positions as <0,0>; (b) the key is perturbed first at each vector position, followed by the value perturbation, with the privacy budget split equally between them.

PCKV-UE and PCKV-GRR. Gu et al. [12] proposed PCKV-UE and PCKV-GRR, leveraging the privacy budget in a more efficient manner. They employed a joint perturbation strategy, rather than dividing the privacy budget evenly. The value's perturbation is contingent upon the key's perturbation, which optimizes the privacy budget composition. Both methods, theoretically and experimentally, outperform those proposed by Ye et al. Thus, we have excluded the PrivKV series from our experiment. The variances of keys and means in PCKV-UE are as follows:

Var(fk^)=8(eε+1)(eε−1)2n+fknVar[mk^]≤8(eε+1)2n(eε+3)(eε−1)2nk2+2(eε+1)2(eε+3)(eε−1)nk

It is noteworthy that both theoretically and experimentally, Gu et al. have demonstrated that PCKV-UE and PCKV-GRR are superior to the series of PrivKV algorithms under equivalent conditions. Even after the conditions in [34] were collectively altered, PCKV-UE and PCKV-GRR still showcased excellent performance. Therefore, this paper solely compares PCKV-UE and PCKV-GRR.

For multiple key-value. In [12], when PCKV-UE and PCKV-GRR address multiple key-value pairs, they pre-set an average length l, yielding favorable results for datasets conforming to this specified length, while performance deteriorates for those that do not align with the set length. In contrast, PrivKV [10], when dealing with multiple key-value pairs, directly employs a “padding-and-sampling” approach to simplify multidimensional data into unidimensional data. Given that PCKV-UE and PCKV-GRR outperform PrivKV significantly, this paper solely compares the superior PCKV-UE and PCKV-GRR algorithms.

4  Key-Strategy and Mechanisms

Our mechanisms aim to gather the frequencies of keys and the mean of values under each key. If most keys have low frequencies, the mean values corresponding to these keys are largely irrelevant. Hence, if the domain is large, it becomes essential to reduce the domain in order to find top frequent keys. In this section, we introduce two key-strategy mechanisms for a singleton key-value pair under LDP: key-strategy unary encoding (KS-UE) in non-interactive frameworks and key-strategy generalized randomized response (KS-GRR) in interactive frameworks. When each user possesses multiple key-value pairs, padding-sampling is utilized to convert them into a singleton key-value pair. Subsequently, each user can implement the aforementioned two mechanisms.

4.1 KS-UE for Singleton Pair in Non-Interactive Frameworks

In non-interactive frameworks, users transmit their perturbed data to the aggregator using a one-way communication model. Here, the unary encoding (UE) mechanism comes into play, encoding each pair into a bit vector with only the bit corresponding to the key set to a value, and all others to zero. Building upon previous algorithms, KS-UE skews the privacy budget in favor of key frequencies to improve utility. The KS-UE methodology unfolds in three distinct phases: Discretization, Encoding and Perturbation, and Decoding, as delineated in Algorithm 2.

Discretization. To alleviate communication and time complexity, the initial step discretizes the value of the key-value pair from float type to binary {1,−1} using formula (2). Consequently, the domain for all key-value pairs becomes {<1,1>,<1,−1>,<0,0>}. In an attempt to further reduce communication costs, we simplify them to three single values {1,−1,0}. If a value is zero, the key is also set to zero; otherwise, the key is set to one.

v∗={1w.p.1+v2−1w.p.1−v2(2)

Encoding and Perturbation. The first operation here is to employ UE to create a bit vector b of size d. The position in b corresponding to the key is v∗, and all other positions are set to zero. Subsequently, each bit of the vector undergoes perturbation in accordance with formula (3) (b[j]=0) and formula (4) (b[j]≠0).

b∗[j]={1w.p.0.5a−1w.p.0.5a0w.p.1−a(3)

b∗[j]={b[j]w.p.p−b[j]w.p.1−2p0w.p.p,(4)

where p=eε+12(eε+2) and a=2eε+2 (13<p<12and0<a<12). Finally, b* is sent to the aggregator. According to the above perturbation strategy, the disturbed vector b* can be obtained in client-side and sent to the aggregator.

Decoding. The aggregator collects b* from each user. Then, the aggregator need to calculate three statistic results nk−1, nk1 and sumk. The aggregator collects b* from each user. Then, the aggregator computes three statistical results: nk−1, nk1 and sumk.

{nk−1:=Count(b[kindex]=−1)nk1:=Count(b[kindex]=1)sumk:=nk1−nk−1,

where nk−1 and nk1 represent the count of 1 and −1 under key k respectively, and sumk indicates the summation of values under key k. Finally, the aggregator can estimate fk^ and mk^=sumk/fk^.

fk^=(nk−1+nk1)/n−a1−p−a(5)

Having estimated the frequency of key k, the mean value under key k, mk^ can be estimated.

mk^=nk1−nk−1(3p−1)fk^n.(6)

4.2 KS-GRR for Singleton Pair in Interactive Frameworks

Within interactive frameworks, users are systematically assembled into random group, and the entirety of the privacy budget is meticulously allocated to facilitate involvement in two distinct tasks for each assembly, as depicted in Fig. 1: (1) the estimation of the most prevalent keys within key-value pairs; (2) the computation of the frequencies of the aforementioned prevalent keys, as well as the mean of the values corresponding to these keys. Then, the aggregator is enabled to process and extrapolate the preliminary results from the initial group, subsequently deriving the conclusive frequencies of the superior keys and the corresponding mean values from the subsequent group. The KS-GRR model employs a sophisticated grouping methodology, aiming to optimize the efficacy of the data collection process, thereby contributing to enhanced accuracy and utility in the realization of key-value collection goals.

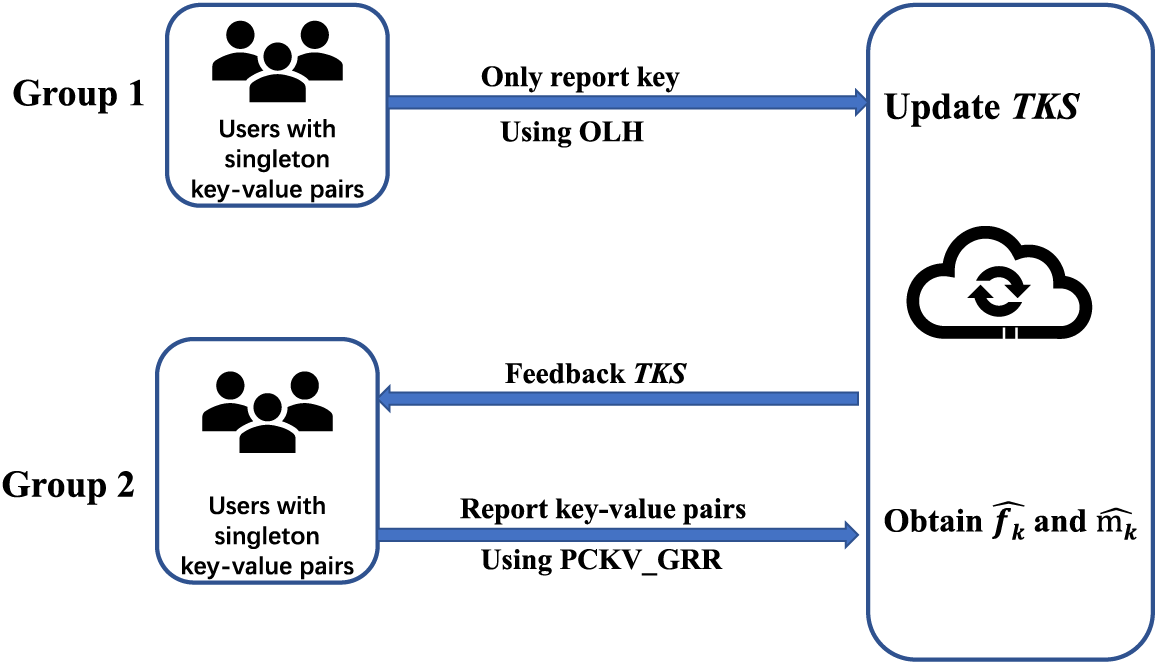
Figure 1: Illustration of KS-GRR for singleton key-value pair

Top frequent keys. In the context of top frequent keys, the value in key-value pairs is deemed irrelevant, as the focus here is solely on estimating the frequencies of keys. Thus, this stage transforms the collection of key-value pairs into a singleton keys collection under LDP, directly utilizing the OLH algorithm. To obtain the top-t frequent keys, the top frequent-2t keys should be identified and used as a candidate set TKS in this task.

Frequency and mean. The aggregator transmits the top-2t candidate keys set TKS to the remaining users for final estimation. If the key is within TKS, each user retains their key-value pair; otherwise, a dummy key-value pair <⊥,±1> is used to replace the original key-value pair. Since the potential number of keys is currently 2t+1, we set TKS∩{⊥} as 𝒦 ′. Subsequently, discretizes the value of the key-value pair from float type to binary {1,−1} using formula (2). Then, each user with value <ki,vi> is perturbed using formula (7) and sent to the aggregator. The aggregator can estimate f^ of the top-t frequent keys and m^ under these keys through computation.

<ki∗,vi∗> ={<ki,vi>w.p.eεeε+4t+1<ki,−vi>w.p.1eε+4t+1<α,1>(α∈𝒦 ′\ki)w.p.1eε+4t+1<α,−1>(α∈𝒦 ′\ki)w.p.1eε+4t+1(7)

4.3 KS-UE and KS-GRR for Multiple Key-Value Pairs

The scenario of multiple key-value pairs indicates that each user possesses a set of such pairs. In order to accommodate this situation, we employ an advanced protocol known as ‘padding-and-sampling’ as described in Gu et al. [12], specifically designed to enhance the performance of key-value data analysis.

The ‘padding-and-sampling’ protocol necessitates a global parameter l to ensure uniform sampling rate across all users. Consequently, l dummy key-value pairs are introduced into the key-value pairs domain. When |Si|<l, the user ui incorporates dummy key-value pairs DS to achieve a total of |Si∪DS|=l. However, the parameter l within the ‘padding-and-sampling’ protocol can lead to biased estimations. The bias escalates with an increase in l, conversely the variance diminishes. Then, user ui randomly selects one key-value pair to participate in the KS-UE or KS-GRR algorithms.

KS-UE for multiple key-value pairs. In order to allow for a comparison with PCKV-UE, KS-UE employs the same ‘padding-and-sampling' protocol as PCKV-UE. Consequently, following the ‘padding-and-sampling' protocol, each user will have a singleton key-value pair. The KS-UE algorithm (discussed in Section 4.1) is utilized to ascertain the frequencies of the top-t frequent keys and the mean under these keys.

KS-GRR for multiple key-value pairs. The process of KS-GRR is recalibrated for the case of multiple key-value pairs, as depicted in Fig. 2. Given the tripartite tasks involved in KS-GRR, the users are accordingly segmented into three groups, each group catering to a specific task.

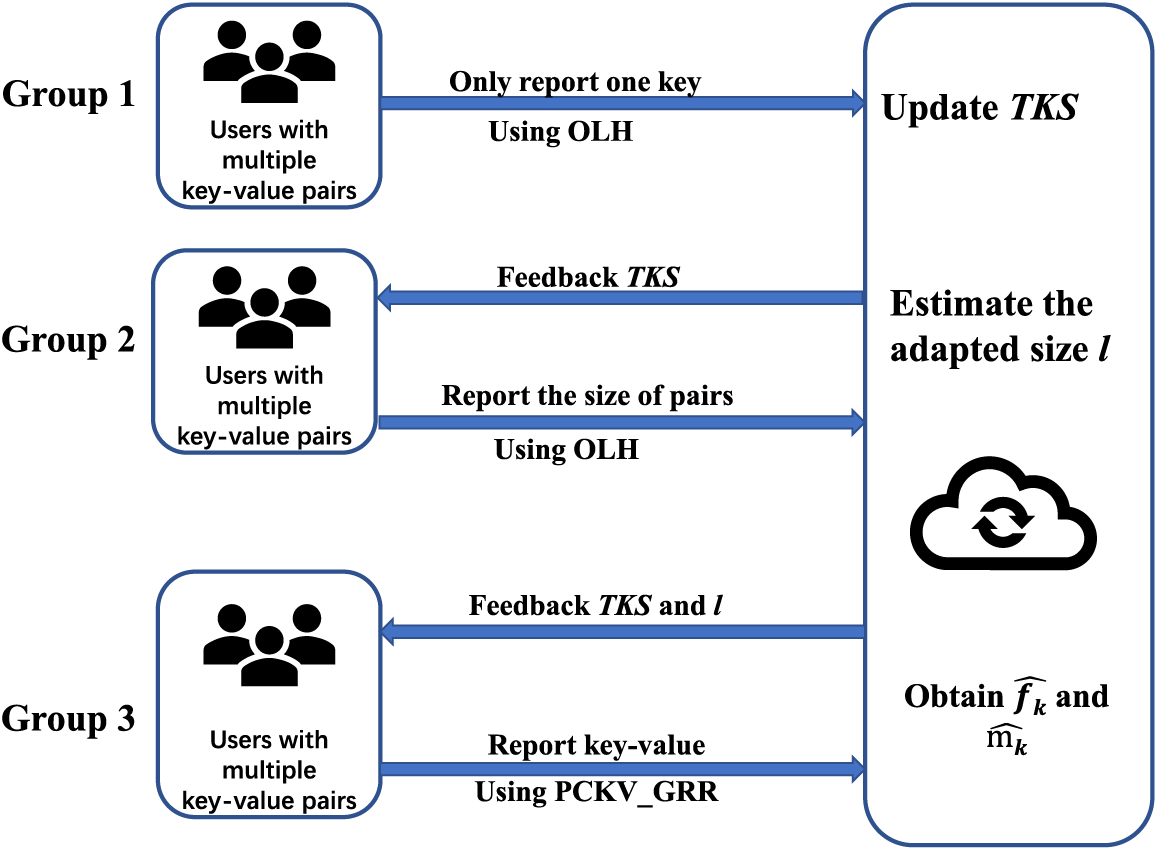
Figure 2: Illustration of KS-GRR for multiple key-value pairs

•   Task 1: Users in this group bypass the ‘padding-and-sampling' protocol and opt to randomly select one of their keys to be transmitted to the aggregator via the OLH algorithm. This technique does not ascertain the frequencies of the keys; however, it reliably preserves the ordinal information of the keys. Notably, the estimations remain stable and unaffected by variations in the value of l.

•   Task 2: For the users engaged in this task, the aggregator provides feedback on the top keys set TKS. This task requires a limited number of users to identify an appropriate l. Moreover, the data essential for this task pertains to the size of each user's set, not the key-value pair. Initially, every user generates her new key-value pairs set, ensuring that the keys belong to TKS. Subsequently, each user submits the size of the private set, and the aggregator identifies the smallest l such that ∑ls=1lΦOLH(ls)∑ls=1allΦOLH(ls)>0.9.

•   Task 3: For the users participating in this task, the aggregator provides feedback on the top keys set TKS as well as the adjusted l. Users maintain key-value pairs if the keys are found in TKS, and subsequently implement the ‘padding-and-sampling’ protocol with the l determined in task 2. This facilitates the estimation of the frequencies of top frequent keys and the mean under these keys.

4.4 Privacy and Analysis

In this section, we will initially provide evidence to confirm that KS-UE satisfies ε-LDP. Subsequently, we will conduct an analysis on the estimation error of KS-UE. The error yielded by KS-UE is demonstrably less than that produced by preceding algorithms.

Theorem 4.1. KS-UE satisfies ε-LDP.

Proof. Let 𝒮 be a key-value pair set, and each key-value pair <k,v> ∈𝒮 has domain k∈𝒦 and v∈{1,−1}. For any two key-value pairs Pi= <ki,vi> and Pj= <kj,vj> (Pi,Pj∈𝒮) has the maximum different probability of outputting a same vector when ki≠kj.

Prupper=Pr(b∗[i]=vi,b∗[j]=0|b[i]=vi,b[j]=0)=p(1−a)

Prlower=Pr(b∗[i]=vi,b∗[j]=0|b[i]=0,b[j]=±vi)=12ap=Pr(b∗[i]=vi,b∗[j]=0|b[i]=−vi,b[j]=±vi)=(1−2p)p

Then, Pi and Pj are indistinguishable at most through KS-UE:

Pr(y|Pi)Pr(y|Pj)≤PrupperPrlower=eε

Theorem 4.2. (Estimation Error Analysis). The expectation and variances of fk^ and mk^ are as following:

E(fk^)=fk(8)

Var(fk^)=8eε(eε−1)2n+(eε−3)fk(eε−1)n(9)

E[mk^]≈∑nvkink[1+8eεn(eε−1)2nk2−4(eε−1)nk](10)

Var[mk^]≤8(eε+2)n(eε−1)2nk2+2(eε+2)(eε−1)nk(11)

Proof. For formula (8). For convenience, let nk denotes the real count of key k and nk∗=nk1+nk−1, then nk^=nk∗−na1−a−p. We first prove the unbiasedness.

E(nk^)=E(nk1)+E(nk1)−na1−a−p=(pnk+(n−nk)12a)+((1−2p)nk+(n−nk)12a)−na1−a−p=nk(p−12a+1−2p−12a)1−a−p=nk

Therefore, the relative frequency E(fk^)=Emk^n=fk.

For formula (9). Next, we calculate the variance of fk^:

Var(nk^)=∑nk(1−p)p+∑n−nk(1−a)a=nk(p−p2)+(n−nk)(a−a2)=n2eε(eε+2)2+nk((eε−1)(eε−3)4(eε+2)2)

∴Var(fk^)=Var(nk^)n2(1−a−p)2=nk(p−p2)+(n−nk)(a−a2)n2(1−a−p)2=4(eε+2)2n2(eε−1)2[n2eε(eε+2)2+nk((eε−1)(eε−3)4(eε+2)2)]=8eε(eε−1)2n+(eε−3)fk(eε−1)n

For formulas (10) and (11). We calculate the expectation and variance of mean estimation. From the multivariate Taylor Expansions of functions of random variables, the expectation of quotient of two random variables X and Y can be approximated by

E[XY]≈E[X]E[Y]−CovX,YE[Y]2+E[X]E[Y]3⋅Var[Y]Var[XY]≈Var[X]E[Y]2−2E[X]CovX,YE[Y]3+E[X]2E[Y]4Var[Y](12)

For convenience, we denote Xk=nk1−nk−1, Yk=nk1+nk−1+na, then

mk^=XY⋅1−a−p3p−1,E[Xk]=(3p−1)∑nvi,E[Yk]=(1−p−a)nk

The variances are

Var[Xk]=na+nk(1−p−a)−(3p−1)2∑nvi2=2(eε+2)n+eε−12(eε+2)nk−(eε−1)24(eε+2)2∑nvi2Var[Yk]=nk[(1−p)p−(1−a)a]+na(1−a)=(eε−1)(eε−3)4(eε+2)2nk+2eε(eε+2)2nCovX,Y=Cov[nk1−nk−1,nk1+nk−1]=E[(nk1−nk−1)(nk1+nk−1)]−E[nk1−nk−1]⋅E[nk1+nk−1]=E[nk1−nk−1]−[E[nk1]2−E[nk−1]2]=Var[nk1]−Var[nk−1]=p⋅E(X)

E[X], E[Y], Var[Y] and CovX,Y are computed by their exact values.

∴E[mk^]=(1−p−a)E[XY](3p−1)≈(1−p−a)(3p−1)[1−pE[Y]+Var[Y]E[y]2]⋅E[X]E[Y]=∑nvkink[1+8eεn(eε−1)2nk2−4(eε−1)nk]

∴Var[mk^]=8(eε+2)n(eε−1)2nk2+2(eε+2)(eε−1)nk+[8eεn(eε−1)2nk4−(eε+5)(eε−1)nk3−1nk2](∑nvi2)

The proof is completed.

5  Experimental Evaluation

In this section, we set up experiments on real datasets to validate our analysis with different approaches.

5.1 Experimental Setup

Datasets. We ran experiments on the following datasets:

•   E-Commerce (Ecommerce rating dataset)1: This dataset contains the merchant transactions of 23,486 users with 1,206 keys. Each user has only one key-value pair. This dataset is used in both singleton and multiple scenarios.

•   Clothing (Clothing fit and rating dataset)2: This dataset contains the merchant transactions of 47,959 users with 5,850 keys. Each user has multiple key-value pair. For singleton key-value pair collection, we treat each key-value pair as a individual record. Thus, clothing-singleton dataset has 82,789 records with 5,850 keys.

Metrics. This study aimed to find the frequent itemsets together with their frequencies, which requires different metrics to evaluate their utilities. We adopted the normalized cumulative rank (NCR) [6,18] and squared error (SE) to assess the frequent itemsets and frequencies, respectively.

1). Normalized Cumulative Rank (NCR). The quality function with the most t keys ranked is as follows: Score(kj)=t−j+1 for j-th highest-ranked key, and all other non-top keys have scores 0. To normalize this into a value between 0 and 1, we divide the sum of scores by the maximum possible score (i.e., t(t+1)2). Thus, a higher score indicates better identification.

2). Squared Error (Var). We measured the estimation accuracy for both frequency and mean by using averaged Mean Squared Error. That is

MSEfreq=1|𝒳|∑k∈𝒳(fk^−fk)2,MSEmean=1|𝒳|∑k∈𝒳(mk^−mk)2

where fk and mk are the real set of frequency and mean of key k. Note that we account only for top-t frequent keys that are successfully identified by the algorithm, i.e., 𝒳 is the intersection of the real top-t keys set and the estimated top-t keys set. Thus, lower variance means more accurate estimation.

Parameter settings. In KS-GRR for multiple pairs, we use 40% of all users to find top-2t frequent keys TFK, 10% to report the size of their key-value pairs whose keys are in TFK, and 50% to obtain final results.

Selected approaches. We compare our KS-UE and KS-GRR with the following approaches. The approaches used in the evaluation are as follows:

(i) PCKV-UE [12]. PVKV-UE is the state-of-the-art approach for key-value pairs collection.

(ii) PVKV-GRR [12]. PCKV-GRR can obtain benifit from ‘padding-and-sampling’ than PCKV-UE, but only performs well when |𝒦| is small.

(iii) KS-Adap. KS-Adap is a manifestation for multiple key-value pairs of KS-GRR. We use 40% of all users to find top-2t frequent keys TFK, 10% to report the size of their key-value pairs whose keys are in TFK, and 50% to obtain final results for multiple pairs.

For KS-UE, PCKV-UE and PCKV-GRR, we set l = 2 for multiple key-value pairs. For KS-GRR, two groups of users are equally divided for singleton pair.

All experiments were conducted on an Intel Core(TM) i7-6700 3.40 GHz PC with 16 GB RAM. The results are averaged over 10 runs.

Singleton key-value pair. Figs. 3–5depict the metric evaluation on the E-Commerce and Clothing singleton key-value pair datasets.

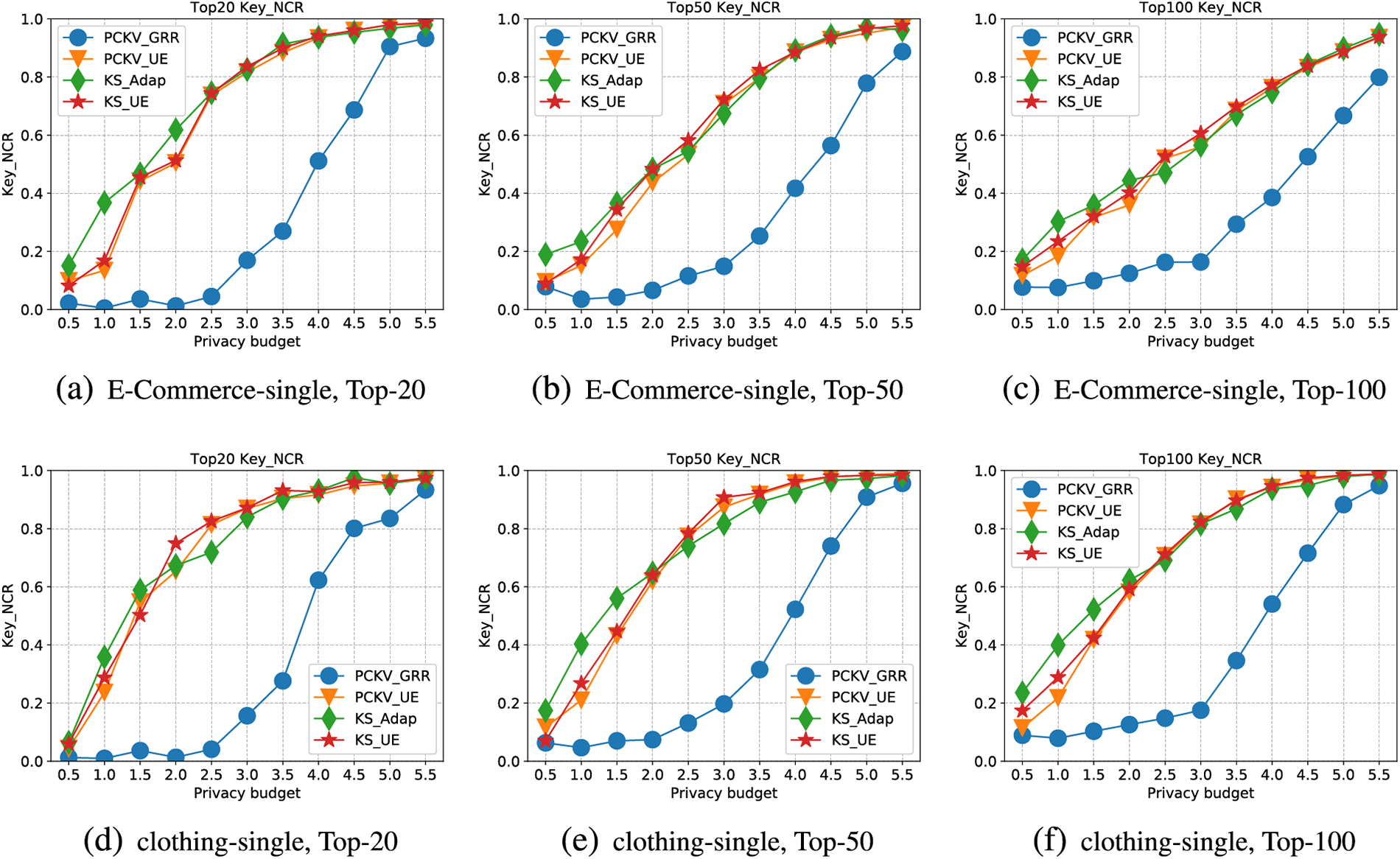
Figure 3: NCR for single dataset

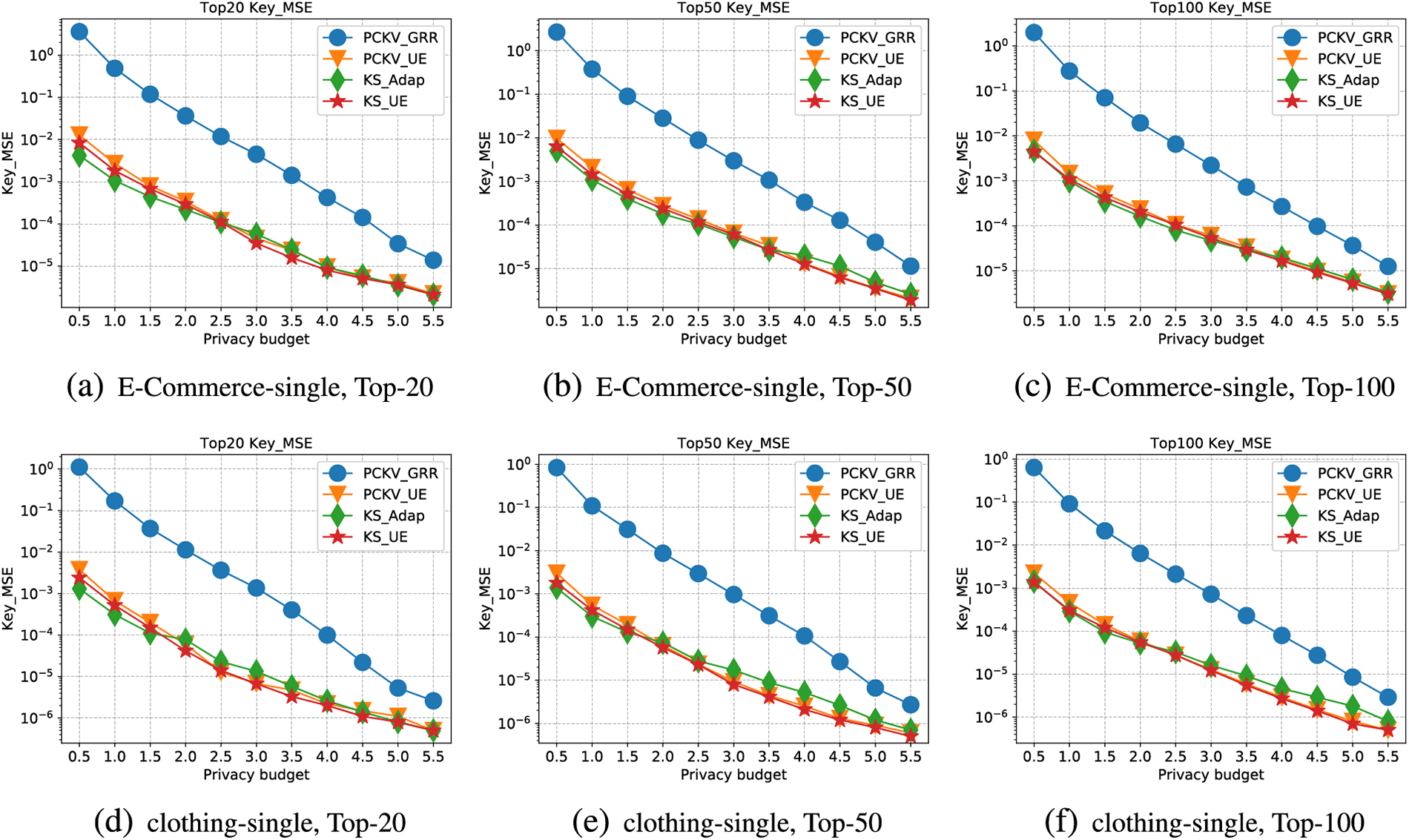
Figure 4: Key-MSE for single dataset

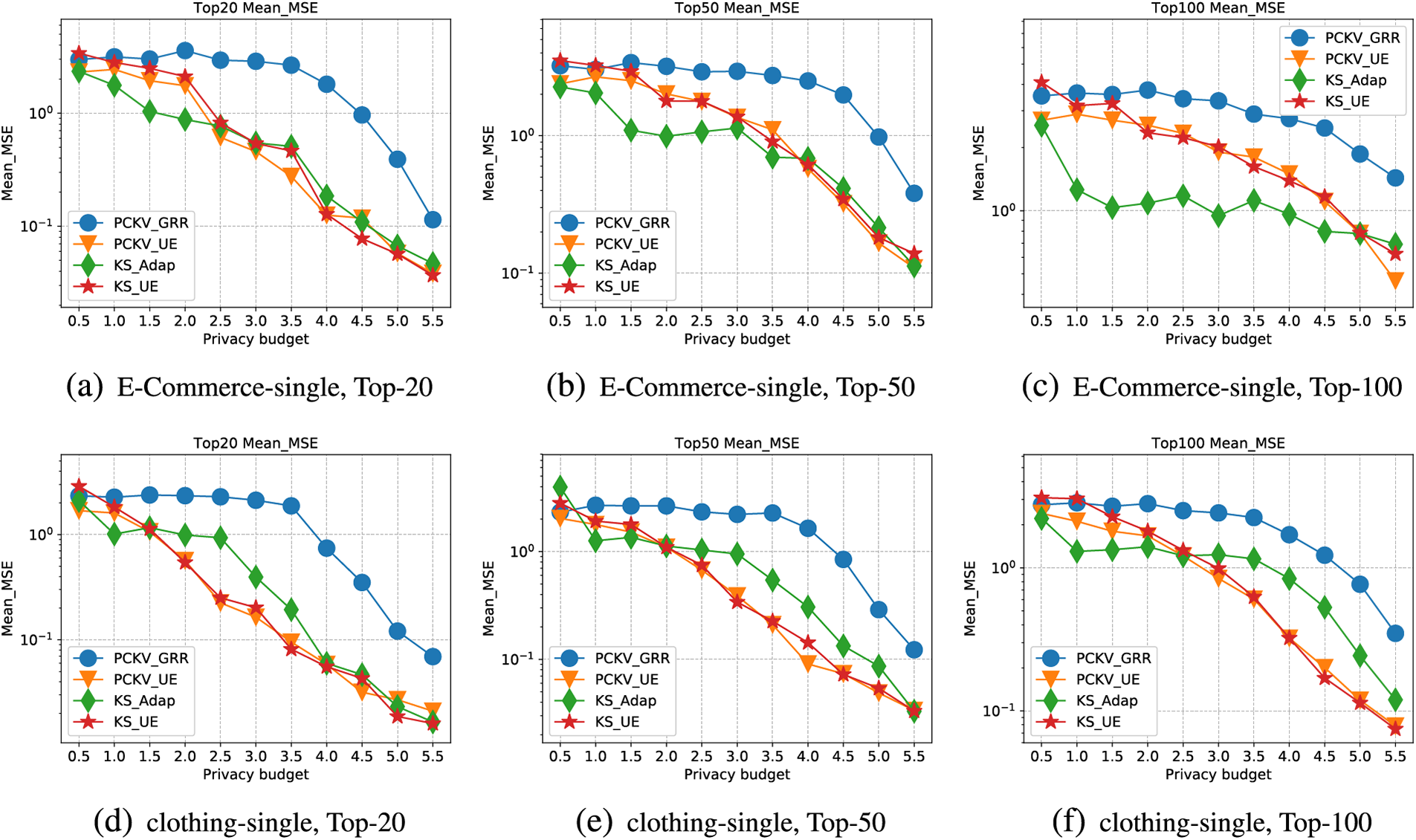
Figure 5: Mean-MSE for single dataset

Firstly, Fig. 3 presents the trendlines of NCR for keys with an increasing privacy budget (ε) when selecting the top 20, 50, and 100 values. As per the NCR definition, higher trendlines correlate with more accurate identification. Our analysis revealed that KS-UE consistently outperforms PCKV-UE. Similarly, KS-GRR notably surpasses PCKV-GRR, exhibiting the best performance at smaller values of ε. Therefore, both KS-UE and KS-GRR demonstrate robust performance in terms of the NCR of f^.

Secondly, Fig. 4 illustrates the trendlines of MSE for keys with an incrementing privacy budget (ε), selecting the top 20, 50, and 100 values. As per the MSE definition, lower trendlines are indicative of higher accuracy. It is observed that KS-UE continuously outstrips PCKV-UE. Moreover, KS-GRR considerably outperforms PCKV-GRR. Consequently, KS-UE and KS-GRR display robust performance regarding the MSE of f^.

Lastly, Fig. 5 demonstrates the trendlines of MSE for the mean values with an increasing privacy budget (ε), while selecting the top 20, 50, and 100 values. The trendlines of KS-UE and PCKV-UE closely intersect. Although KS-UE matches the utility of PCKV-UE, the allocated budget for the value is smaller and a higher NCR implies more identified keys. Therefore, KS-UE exhibits exceptional performance. For ε>3, the variance of KS-GRR is lower than that of PCKV-GRR. Moreover, for ε≥6, KS-GRR even surpasses both PCKV-UE and KS-UE. When combined with the NCR and MSE of f^, the m^ of KS-GRR demonstrates an improvement over PCKV-GRR, though it does not exhibit a significant advantage over PCKV-UE. On the whole, KS-UE and KS-GRR exhibit effectiveness and efficiency, which is consistent with our theoretical results.

Multiple key-value pairs. Figs. 6–8 present the metric evaluation for the E-Commerce and Clothing datasets featuring multiple key-value pairs.

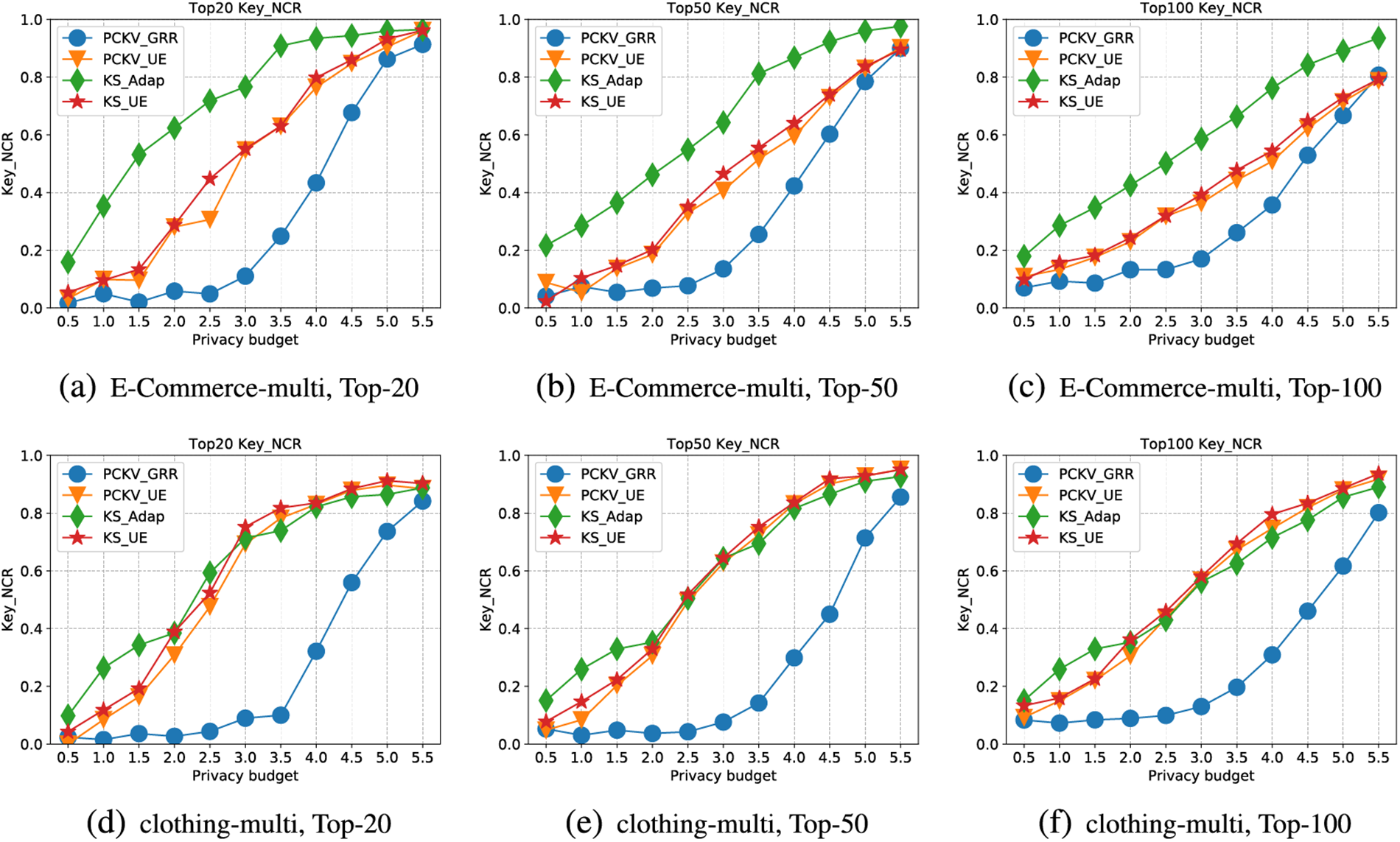
Figure 6: NCR for multiple dataset

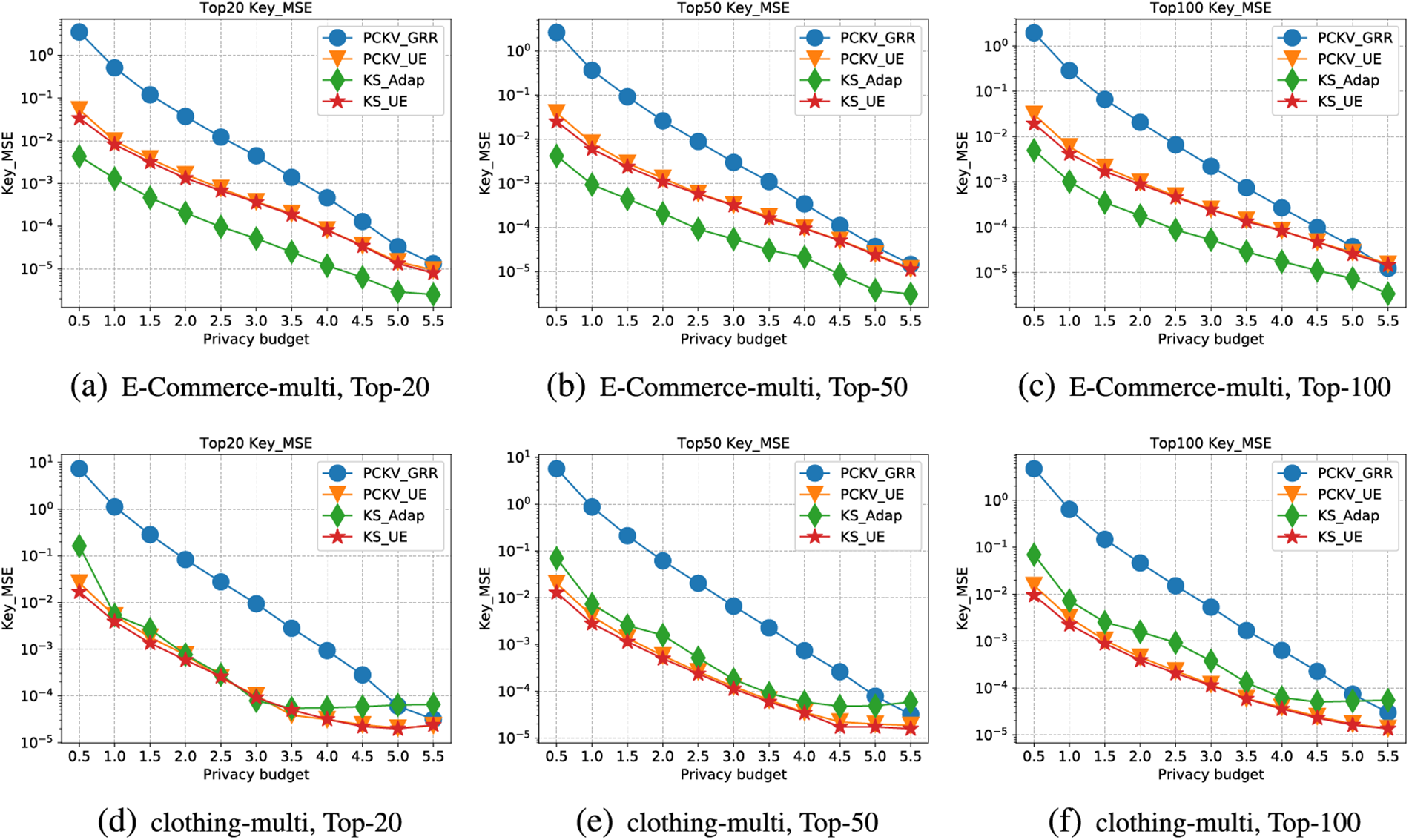
Figure 7: Key-MSE for multiple dataset

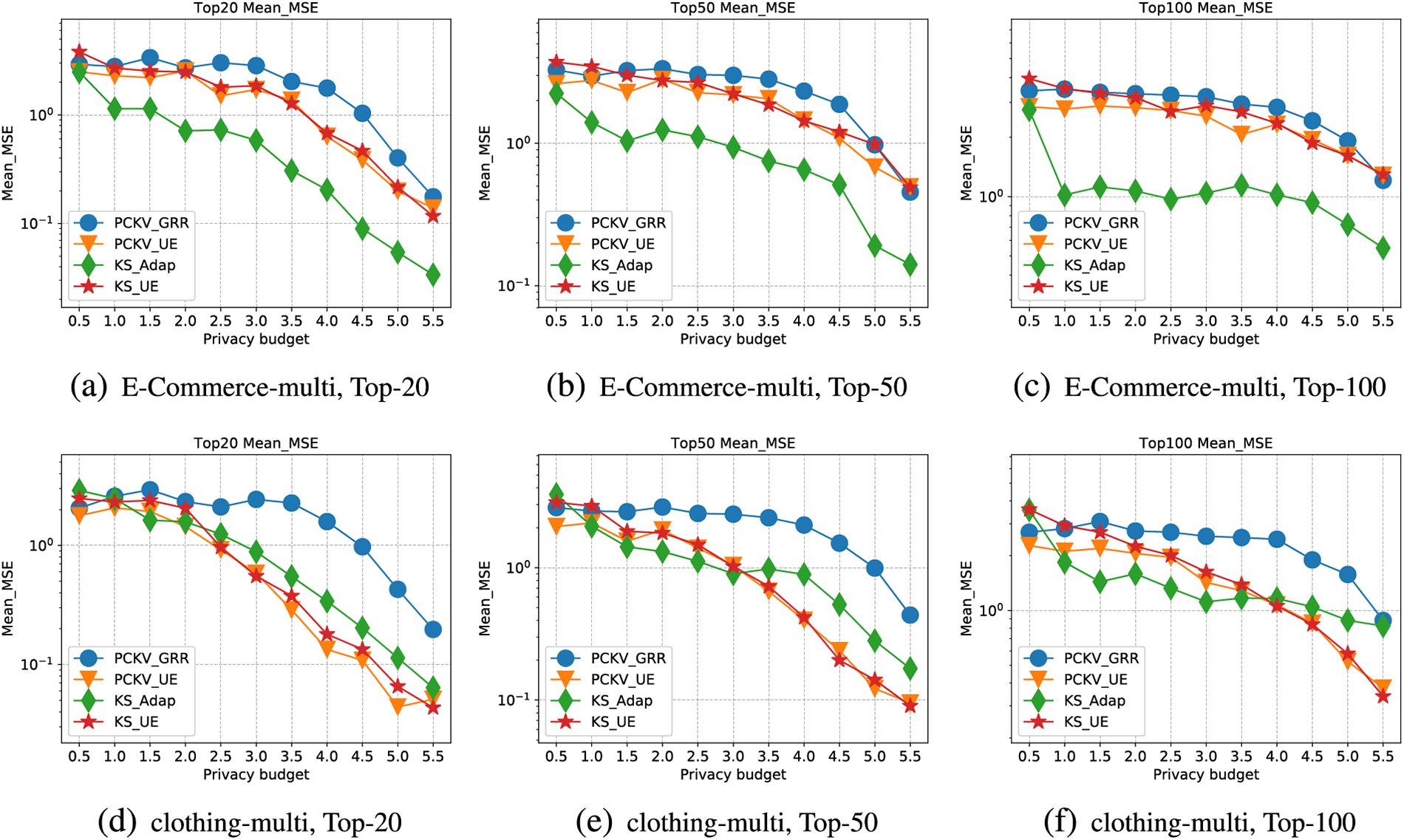
Figure 8: Mean-MSE for multiple dataset

Firstly, Fig. 6 depicts the trendlines for the NCR of keys, corresponding to the increasing privacy budget (ε), for the top 20, 50, and 100 selected values. By definition, a higher trendline suggests more accurate identification. KS-UE consistently outperforms PCKV-UE, and KS-GRR significantly surpasses PCKV-GRR. In particular, KS-GRR exhibits the best performance across all ε values for the E-Commerce-multiple dataset, and performs optimally under smaller privacy budgets for the clothing-multiple dataset. Hence, both KS-UE and KS-GRR demonstrate excellent performance in terms of the NCR of f^.

Secondly, Fig. 7 illustrates the MSE trendlines for keys, with respect to the incrementing privacy budget (ε), for the top 20, 50, and 100 selected values. In line with the definition of MSE, lower trendlines equate to more accurate identification. Here, KS-UE consistently surpasses PCKV-UE, and KS-GRR considerably outperforms PCKV-GRR, even showing the best performance for large privacy budgets on the E-Commerce-multiple dataset. Thus, both KS-UE and KS-GRR excel in relation to the MSE of f^.

Lastly, Fig. 8 presents the MSE trendlines for the mean values with increasing ε, for the top 20, 50, and 100 selected values. The trendlines of KS-UE and PCKV-UE closely intertwine. Although KS-UE attains equivalent utility with PCKV-UE, the budget allocation for value is smaller and a higher NCR implies more identified keys, signifying excellent performance by KS-UE. KS-GRR generally performs optimally for small ε values. For large ε values, KS-GRR exhibits the best performance for E-Commerce-multiple and is relatively efficient in the clothing-multiple dataset. Combined with the NCR and MSE of f^, the m^ of KS-GRR demonstrates improvement over PCKV-GRR, although it does not hold a significant advantage over PCKV-UE. Overall, KS-UE and KS-GRR both exhibit effectiveness and efficiency, which aligns with our theoretical findings.

Analysis. The experimental outcomes reveal that the KS-UE and KS-GRR algorithms predominantly surpass other algorithms in most situations. The advantages of KS-UE have already been discerned in the error analysis in Section 4.4; its Mean Squared Error (MSE) is lower than prior algorithms, thus reflecting more superior results in the experiments. KS-GRR, by adopting a key-priority strategy, ensures the accuracy in collecting keys and the validity of the values under such keys, once accurate keys have been obtained by collecting the frequency of keys.

6  Conclusions

In this research, we explore methods for key-value data collection under the constraint of local differential privacy to obtain key frequencies and corresponding mean values. We design two innovative strategies, namely, Key Strategy KS-UE and KS-GRR, applicable in interactive and non-interactive frameworks, respectively. Since mean estimation is intrinsically dependent on key frequencies, precise key collection is vitally important not only for estimating key frequencies but also for deriving accurate mean values. KS-UE is specifically designed to tilt the privacy budget towards the key, thereby enhancing the estimation of keys, while KS-GRR implements a group-and-interactive strategy to identify the top frequent keys, subsequently enabling accurate frequency and mean estimation. Empirical validation supports our theoretical analysis, demonstrating the effectiveness of both KS-UE and KS-GRR. In terms of future work, we aim to enhance the efficiency of the candidate domain and reduce both communication and time complexity. These refinements will potentially allow for the broader implementation of these methodologies in practical applications, thereby contributing significantly to the field of privacy protection.

Acknowledgement: This papers logical organisation and content quality have been enhanced, so the authors thank anonymous reviewers and journal editors for assistance.

Funding Statement: This work is supported by a grant from the National Key R&D Program of China.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Dan Zhao, Chuanwen Lu; data collection: Dan Zhao, Yang Liu; analysis and interpretation of results: Dan Zhao, Yang You; draft manuscript preparation: Dan Zhao, Chuanwen Luo, Ting Chen,Yang Liu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data is from https://www.kaggle.com/nicapotato/womens-ecommerce-clothing-reviews and https://www.kaggle.com/rmisra/clothing-fit-dataset-for-size-recommendation.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

1https://www.kaggle.com/nicapotato/womens-ecommerce-clothing-reviews

2https://www.kaggle.com/rmisra/clothing-fit-dataset-for-size-recommendation

References

1. Chen, R., Li, H., Qin, A., Kasiviswanathan, S. P., Jin, H. (2016). Private spatial data aggregation in the local setting. 2016 IEEE 32nd International Conference on Data Engineering (ICDE), pp. 289–300. Helsinki, Finland. [Google Scholar]

2. Erlingsson, Ú., Pihur, V., Korolova, A. (2014). RAPPOR: Randomized aggregatable privacy-preserving ordinal response. Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security, pp. 1054–1067. Scottsdale, Arizona, USA. [Google Scholar]

3. Tang, J., Korolova, A., Bai, X., Wang, X., Wang, X. (2017). Privacy loss in apple’s implementation of differential privacy on macos 10.12. arXiv preprint arXiv:1709.02753. [Google Scholar]

4. Ding, B., Kulkarni, J., Yekhanin, S. (2017). Collecting telemetry data privately. Proceedings of the 31stInternational Conference on Neural Information Processing Systems (NIPS), pp. 3571–3580. Long Beach, CA, USA. [Google Scholar]

5. Qin, Z., Yang, Y., Yu, T., Khalil, I., Xiao, X. et al. (2016). Heavy hitter estimation over set-valued data with local differential privacy. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, pp. 192–203. Vienna, Austria. [Google Scholar]

6. Wang, T., Li, N., Jha, S. (2018). Locally differentially private frequent itemset mining. 2018 IEEE Symposium on Security and Privacy (SP), pp. 127–143. San Francisco, CA, USA. [Google Scholar]

7. Zhao, D., Zhao, S., Chen, H., Liu, R., Li, C. et al. (2023). Hadamard encoding based frequent itemset mining under local differential privacy constraints. Journal of Computer Science and Technology, 38(6), 1403–1422. [Google Scholar]

8. Qin, Z., Yu, T., Yang, Y., Khalil, I., Xiao, X. et al. (2017). Generating synthetic decentralized social graphs with local differential privacy. Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, pp. 425–438. Dallas, USA. [Google Scholar]

9. Liu, Y., Zhao, S., Liu, Y., Zhao, D., Chen, H. et al. (2022). Collecting triangle counts with edge relationship local differential privacy. 2022 IEEE 38th International Conference on Data Engineering (ICDE), pp. 2008–2020. Kuala Lumpur, Malaysia. [Google Scholar]

10. Ye, Q., Hu, H., Meng, X., Zheng, H. (2019). PrivKV: Key-value data collection with local differential privacy. 2019 IEEE Symposium on Security and Privacy (SP), pp. 317–331. San Francisco, CA, USA. [Google Scholar]

11. Sun, L., Zhao, J., Ye, X., Feng, S., Wang, T. et al. (2019). Conditional analysis for key-value data with local differential privacy. arXiv preprint arXiv:1907.05014. [Google Scholar]

12. Gu, X., Li, M., Cheng, Y., Xiong, L., Cao, Y. (2020). PCKV: Locally differentially private correlated key-value data collection with optimized utility. 29th USENIX Security Symposium (USENIX Security 20), pp. 967–984. Berkeley, CA, USA. [Google Scholar]

13. Warner, S. L. (1965). Randomized response: A survey technique for eliminating evasive answer bias. Journal of the American Statistical Association, 60(309), 63–69. [Google Scholar] [PubMed]

14. Dwork, C. (2008). Differential privacy: A survey of results. International Conference on Theory and Applications of Models of Computation, pp. 1–19. Xi’an, China. [Google Scholar]

15. Dwork, C., Roth, A. (2014). The algorithmic foundations of differential privacy. Foundations and Trends® in Theoretical Computer Science, 9(3–4), 211–407. [Google Scholar]

16. Kairouz, P., Bonawitz, K., Ramage, D. (2016). Discrete distribution estimation under local privacy. arXiv preprint arXiv:1602.07387. [Google Scholar]

17. Bassily, R., Smith, A. (2015). Local, private, efficient protocols for succinct histograms. Proceedings of the Forty-Seventh Annual ACM Symposium on Theory of Computing, pp. 127–135. Portland, OR, USA. [Google Scholar]

18. Wang, T., Blocki, J., Li, N., Jha, S. (2017). Locally differentially private protocols for frequency estimation. Proceedings of the 26th USENIX Security Symposium, pp. 729–745. Vancouver, BC, Canada. [Google Scholar]

19. Wang, N., Xiao, X., Yang, Y., Zhao, J., Hui, S. C. et al. (2019). Collecting and analyzing multidimensional data with local differential privacy. 2019 IEEE 35th International Conference on Data Engineering (ICDE), pp. 638–649. Macau, China. [Google Scholar]

20. Kulkarni, T., Cormode, G., Srivastava, D. (2017). Marginal release under local differential privacy. arXiv preprint arXiv:1711.02952. [Google Scholar]

21. Zhang, Z., Wang, T., Li, N., He, S., Chen, J. (2018). CALM: Consistent adaptive local marginal for marginal release under local differential privacy. Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, pp. 212–229. Copenhagen, Denmark. [Google Scholar]

22. Nguyên, T. T., Xiao, X., Yang, Y., Hui, S. C., Shin, H. et al. (2016). Collecting and analyzing data from smart device users with local differential privacy. arXiv preprint arXiv:1606.05053. [Google Scholar]

23. Ye, Q., Hu, H., Au, M. H., Meng, X., Xiao, X. (2020). Towards locally differentially private generic graph metric estimation. 2020 IEEE 36th International Conference on Data Engineering (ICDE), pp. 1922–1925. Dallas, TX, USA. [Google Scholar]

24. Ye, Q., Hu, H., Au, M., Meng, X., Xiao, X. (2020). LF-GDPR: Graph metric estimation with local differential privacy. IEEE Transactions on Knowledge and Data Engineering (TKDE), 10, 4905–4920. [Google Scholar]

25. Cao, Y., Xiao, Y., Xiong, L., Bai, L. (2019). PriSTE: From location privacy to spatiotemporal event privacy. 2019 IEEE 35th International Conference on Data Engineering (ICDE), pp. 1606–1609. Macau, China. [Google Scholar]

26. Ye, Q., Hu, H., Li, N., Meng, X., Zheng, H. et al. (2021). Beyond value perturbation: Local differential privacy in the temporal setting. IEEE INFOCOM 2021–IEEE Conference on Computer Communications, pp. 1–10. Vancouver, BC, Canada. [Google Scholar]

27. Li, Z., Wang, T., Lopuhaä-Zwakenberg, M., Li, N., Škoric, B. (2020). Estimating numerical distributions under local differential privacy. Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data, pp. 621–635. Portland, Oregon, USA. [Google Scholar]

28. Kulkarni, T. (2019). Answering range queries under local differential privacy. Proceedings of the 2019 International Conference on Management of Data, pp. 1832–1834. Amsterdam, Netherlands. [Google Scholar]

29. Arachchige, P. C. M., Bertok, P., Khalil, I., Liu, D., Camtepe, S. et al. (2019). Local differential privacy for deep learning. IEEE Internet of Things Journal, 7(7), 5827–5842. [Google Scholar]

30. Liu, R., Wu, F., Wu, C., Wang, Y., Cao, Y. et al. (2022). PrivateRec: Differentially private training and serving for federated news recommendation. arXiv preprint arXiv:2204.08146. [Google Scholar]

31. Chai, Y., Du, L., Qiu, J., Yin, L., Tian, Z. (2022). Dynamic prototype network based on sample adaptation for few-shot malware detection. IEEE Transactions on Knowledge and Data Engineering, 35(5), 4754–4766. [Google Scholar]

32. Qiu, J., Tian, Z., Du, C., Zuo, Q., Su, S. et al. (2020). A survey on access control in the age of internet of things. IEEE Internet of Things Journal, 7(6), 4682–4696. [Google Scholar]

33. Tian, Z., Luo, C., Qiu, J., Du, X., Guizani, M. (2019). A distributed deep learning system for web attack detection on edge devices. IEEE Transactions on Industrial Informatics, 16(3), 1963–1971. [Google Scholar]

34. Ye, Q., Hu, H., Meng, X., Zheng, H., Huang, K. et al. (2023). PrivKVM*: Revisiting key-value statistics estimation with local differential privacy. IEEE Transactions on Dependable and Secure Computing, 1, 17–35. [Google Scholar]

35. Bassily, R., Nissim, K., Stemmer, U., Thakurta, A. G. (2017). Practical locally private heavy hitters. Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS), pp. 2288–2296. Long Beach, CA, USA. [Google Scholar]

36. Bun, M., Nelson, J., Stemmer, U. (2018). Heavy hitters and the structure of local privacy. Proceedings of the 35th ACM SIGMOD-SIGACT-SIGAI Symposium on Principles of Database Systems, pp. 435–447. New York, USA. [Google Scholar]