Synergistic Swarm Optimization Algorithm

1  Introduction

Organizations and people deal with complicated issues in today’s data-driven environment that call for the best solutions [1]. These issues can occur across several industries, including engineering, banking, logistics, healthcare, and telecommunications [2]. Optimization algorithms are helpful tools to traverse these issues’ complexity and find the best solutions within predetermined restrictions [3–5]. These algorithms effectively use computational and mathematical methods to find and assess viable solutions, producing optimal results [4,6].

When the structure of the solution space is unknown or inadequately specified, metaheuristic optimization algorithms provide a flexible and reliable framework for tackling optimization issues [7]. These algorithms take their cues from various abstract or natural notions rather than explicit mathematical models or assumptions [8,9]. Metaheuristics offer intelligent search algorithms that may effectively explore complex problem spaces, take advantage of promising regions, and avoid local optima by mimicking adaptive processes like evolution, swarm behavior, or physical occurrences [10–12].

A large family of computing techniques known as optimization algorithms is used to iteratively explore and assess different solution spaces in search of the best or most advantageous ones [13,14]. These algorithms can be divided into stochastic and deterministic methods. For issues with clearly stated goals and restrictions, deterministic techniques like integer and linear programming are appropriate [15,16]. To tackle complicated and dynamic problem spaces, stochastic algorithms, such as genetic algorithms, simulated annealing, and particle swarm optimization, use probabilistic approaches and randomness [16,17].

Understanding the main elements of optimization algorithms is crucial to understanding how they operate. These elements include search methods, constraints, decision variables, and objective functions [18,19]. The decision variables are the parameters or variables that may be changed to get the best outcome. In contrast, the objective function is the objective or metric that has to be maximized [20]. Constraints specify the restrictions or requirements that solutions must meet. The search procedures guide the investigation and assessment of prospective solutions, which strive to converge on the optimal result.

Numerous sectors use optimization algorithms, changing how people solve problems and make decisions [21,22]. These methods are employed in engineering to design circuits, processes, and structural optimization. They are widely used in finance for algorithmic trading, risk management, and portfolio optimization. Optimization algorithms facilitate effective route planning, inventory management, and logistics and supply chain scheduling. Optimization algorithms are helpful in the healthcare industry for clinical decision support systems, resource allocation, and treatment planning [23,24]. The applications also encompass data mining, machine learning, energy systems, telecommunications, and many more fields [25,26]. Some of the optimization methods from the literature are Prairie Dog Optimization Algorithm [27], Monarch Butterfly Optimization [28], Artificial Rabbits Optimizer [29], Genghis Khan Shark Optimizer [30], Geyser Inspired Algorithm [31], Moth Search Algorithm [32], PINN-FORM [33], Chaos Game Optimization [16], Slime Mould Algorithm [34], Hunger Games Search [35], Runge Kutta Method [36], Colony Predation Algorithm [37], Weighted Mean Of Vectors [38], Rime Optimization Algorithm [39], Harris Hawks Optimization [40], and others.

Traditional optimization algorithms frequently have trouble solving complicated problems with non-linearity, high dimensionality, and no apparent links between solutions [41]. On the other hand, metaheuristic optimization algorithms have become a potent paradigm encompassing adaptive search techniques influenced by both natural and abstract events. These algorithms can effectively search across enormous solution spaces, change their search strategies, and find excellent answers that may be difficult to find using more traditional approaches [42–44].

Complex optimization issues that defy conventional approaches can now be solved with the help of metaheuristic optimization algorithms [45,46]. This research paper’s introduction highlights the adaptive search techniques, essential components, and wide range of applications of metaheuristic optimization algorithms. Researchers and practitioners can successfully take on complex optimization issues by utilizing the special powers of metaheuristics, creating new opportunities for innovation and problem-solving in various sectors. These algorithms have a lot of potential as metaheuristic research develops to handle challenging optimization problems in the real world [47,48]. Numerous advantages of optimization algorithms include increased effectiveness, better resource allocation, cost savings, and better decision-making [49]. They enable businesses to increase output, reduce waste, and streamline procedures. However, there are difficulties in putting optimization methods into practice. For example, managing high-dimensional spaces, dealing with non-linear or non-convex objectives, and balancing computing complexity with solution accuracy [50,51].

This paper proposes a novel optimization method called The Synergistic Swarm Optimization Algorithm (SSOA) that combines the principles of swarm intelligence and synergistic cooperation to search for optimal solutions efficiently. The main procedure of SSOA involves the following steps: First, an initial population of candidate solutions, represented as a swarm of particles, is randomly generated. Each particle explores the search space by iteratively updating its position based on its own previous best solution and the collective knowledge of the swarm. Next, a synergistic cooperation mechanism is employed, where particles exchange information and learn from each other to improve their search behaviors. This cooperation enhances the exploitation of promising regions in the search space while maintaining exploration capabilities. Furthermore, adaptive mechanisms, such as dynamic parameter adjustment and diversification strategies, are incorporated to balance exploration and exploitation. The process continues iteratively until a termination criterion is met, such as a maximum number of iterations or reaching a satisfactory solution. By leveraging the collaborative nature of swarm intelligence and integrating synergistic cooperation, the SSOA method aims to achieve superior convergence speed and solution quality performance compared to other optimization algorithms. The effectiveness of the proposed SSOA is investigated in solving the 23 benchmark functions and various engineering design problems. The proposed Synergistic Swarm Optimization Algorithm (SSOA) demonstrates remarkable performance surpassing that of other optimization algorithms, without any similarity in their approach or methodologies. Through comprehensive evaluations, the SSOA method consistently outperforms similar optimization algorithms regarding solution quality and convergence speed.

In summary, the primary motivation of this research is to develop a novel optimization algorithm, SSOA, that leverages swarm intelligence principles, synergistic cooperation, adaptive mechanisms, and a balance between exploration and exploitation to efficiently find optimal solutions for a wide range of optimization problems. The ultimate goal is to demonstrate that SSOA surpasses existing optimization algorithms in terms of both solution quality and convergence speed through rigorous empirical evaluations.

The structure of this paper is given as the related works are provided in Section 2. Section 3 shows the proposed Synergistic Swarm Optimization Algorithm (SSOA) and its main procedures. Section 4 presents the results and discussion of the experiments. Finally, the conclusion and future work direction is given in Section 5.

2  Related Works

This section presents the most common related to the optimization algorithms from the literature and its applications [2,52].

The Fire Hawk Optimizer (FHO), a novel metaheuristic algorithm introduced in [53], was inspired by the foraging behavior of whistling kites, black kites, and brown falcons—collectively known as Fire Hawks—because of the way they grab prey using fire. To explore the proposed technique numerically, 150,000 function evaluations are carried out for optimization purposes on 233 mathematical test functions, ranging from 2 to 100 dimensions. Ten distinct traditional and modern metaheuristic algorithms are used as complementary methods to contrast their performance. The FHO method is further assessed in the CEC 2020 competition for binding constraint and real-world optimization problems, including well-known mechanical engineering design issues. The analysis shows that the FHO method outperforms other metaheuristic algorithms in the literature. The FHO also performs better than previously established metaheuristics when dealing with real-size structural frameworks, notably those with 15 and 24 stories.

The Wild Horse Optimizer (WHO), a novel algorithm inspired by the social behaviors of wild horses, was introduced in [54]. Wild horses often exist in herds comprising a stallion, mares, and calves. They participate in various behaviors, including mating, dominating, pursuing, and grazing. Horses are notable for their decent conduct, which prevents breeding amongst close relatives by having foals leave the herd before they reach adolescence and join other groups. This decent behavior serves as an inspiration for the WHO algorithm. It is assessed using several test functions, such as CEC2017 and CEC2019, and contrasted with other well-known and cutting-edge optimization techniques. The outcomes indicate how well the WHO algorithm performs compared to other algorithms, highlighting its effectiveness.

The Cheetah Optimizer (CO), a naturally derived algorithm inspired by cheetah hunting techniques, was introduced in [55]. The CO algorithm integrates the three primary cheetah-hunting tactics of seeking, waiting, and attacking. The “leave the prey and go back home” method is also added to improve population diversity, convergence efficiency, and algorithmic resilience. On 14 shifted-rotated CEC-2005 benchmark functions, CO’s performance is thoroughly evaluated compared to cutting-edge algorithms. Simulation results show that CO outperforms existing algorithms, including conventional, enhanced, and hybrid methods, in solving complex and large-scale optimization problems.

The Dung Beetle Optimizer (DBO) algorithm, a population-based method inspired by dung beetles’ ball-rolling, dancing, foraging, thieving, and reproductive habits, was presented in [56]. The DBO algorithm compromises quick convergence and acceptable solution correctness by combining global exploration and local exploitation. A collection of well-known mathematical test functions is used to gauge the search engine’s performance. According to simulation findings, the DBO method competes favorably regarding convergence rate, solution correctness, and stability with cutting-edge optimization techniques. The DBO algorithm’s effective use in three engineering design challenges also proves its potential for practical application. Experimental findings confirm the suggested DBO algorithm’s efficiency in solving practical application difficulties.

The Bonobo Optimizer (BO), an intelligent optimization approach inspired by bonobos’ reproductive tactics and social behavior, was introduced in [57]. The social structure of bonobos is characterized by fission-fusion, with groups of various sizes and compositions first developing within the community and then fusing for particular purposes. To preserve social peace, they use four reproductive techniques: consortship mating, extra-group mating, promiscuous mating, and restricted mating. When BO’s performance is compared to other optimization techniques, the results are statistically better or on par. Additionally, BO is used to resolve five challenging real-world optimization issues, and the effectiveness of its results is evaluated against the body of prior research. The results emphasize the efficiency of BO in resolving optimization issues by showing that it either outperforms or produces results equivalent to those of other approaches.

This research presents the Golden Jackal Optimization (GJO) algorithm [58], a new nature-inspired optimization method that offers an alternative approach to solving real-world engineering problems. GJO draws inspiration from the collaborative hunting behavior of golden jackals (Canis aureus). The algorithm incorporates three essential steps: prey searching, enclosing, and pouncing, which are mathematically modeled and implemented. The effectiveness of GJO is evaluated by comparing it with state-of-the-art metaheuristic algorithms on benchmark functions. Furthermore, GJO is tested on seven different engineering design problems and implemented in electrical engineering. The engineering design problems and real-world implementation results demonstrate that the proposed algorithm is well-suited for addressing challenging problems characterized by unidentified search spaces.

The Arithmetic Optimization Algorithm (AOA), a unique metaheuristic technique introduced in [59], makes use of the distributional properties of the four basic mathematical arithmetic operators (multiplication, division, subtraction, and addition). AOA is a mathematical model developed and used to handle optimization jobs in various search spaces effectively. AOA is tested against 29 benchmark functions and a variety of actual engineering design issues in order to show how useful it is. Different scenarios are used for performance analysis, convergence behavior study, and computational complexity analyses. The experimental results demonstrate how AOA can solve challenging optimization issues significantly better than eleven well-known optimization methods.

This study offers a brand-new population-based optimization technique dubbed the Aquila Optimizer (AO), which was motivated by the natural hunting techniques of Aquila birds [60]. Four strategies that mirror the behaviors taken by the Aquila during the prey-catching process are used to illustrate the optimizing processes of AO. These techniques include using a high soar to narrow the search area, contour flying with a quick glide attack for exploration, low flight with a gradual descent assault for exploitation, and swooping by walking up on a target. Several tests are carried out to evaluate how well AO finds the best answers for various optimization issues. In the first experiment, 23 well-known functions are solved using AO. In the second and third tests, 30 CEC2017 and 10 CEC2019 test functions are used to assess AO’s performance on increasingly challenging issues. In addition, seven actual engineering challenges are used to test AO. Comparisons with well-known metaheuristic techniques show that AO performs better.

The Reptile Search Algorithm (RSA), inspired by the crocodile’s hunting strategy, is a novel metaheuristic optimizer introduced in [61]. The RSA includes two essential phases: encircling, which entails high walking or belly walking, and hunting, which includes coordinated or cooperative hunting. These distinctive search techniques set RSA apart from other algorithms. Various test functions, including 23 classical test functions, 30 CEC2017 test functions, 10 CEC2019 test functions, and seven real-world engineering challenges, are used to assess RSA’s performance. There are comparisons made between several optimization techniques from the literature. Results show that RSA performs better on the benchmark functions examined than competing methods. The Friedman ranking test attests to RSA’s undeniable advantage over other comparison techniques. Additionally, the analysis of engineering challenges shows that RSA outperforms other techniques in terms of outcomes.

This paper introduces the Dwarf Mongoose Optimization Algorithm (DMO) [62], a unique metaheuristic algorithm built to handle 12 continuous/discrete engineering optimization issues and benchmark functions from CEC 2020 and the classical world. The dwarf mongoose, whose social and ecological tactics have evolved owing to the constrained style of prey collection, served as the model for the DMO algorithm. The mongoose’s migratory lifestyle ensures that the whole region is explored without returning to sleeping mounds, limiting the overexploitation of certain locations. DMO’s efficacy is shown through comparison to seven other algorithms’ performance in terms of various performance indicators and data.

The Ebola Optimization Search Algorithm (EOSA), a new metaheuristic algorithm inspired by the transmission mechanism of the Ebola virus illness, was introduced in [63]. The first step in the project is developing an enhanced SIR model, known as SEIR-HVQD, which depicts the many disease phases. The new model is then mathematically represented using first-order differential equations. EOSA is created as a metaheuristic algorithm by fusing the propagation and mathematical models. Two sets of benchmark functions—47 classical functions and 30 restricted IEEE-CEC benchmark functions—are used to compare the algorithm’s performance to other optimization techniques. According to the results, EOSA competes favorably with other cutting-edge optimization techniques regarding scalability, convergence, and sensitivity studies.

In [27], Prairie Dog Optimization (PDO) was introduced, a unique metaheuristic algorithm inspired by nature that mimics prairie dogs’ behavior in their natural habitat. PDO uses four prairie dog behaviors to complete the optimization’s exploration and exploitation stages. The framework for exploratory behavior in PDO is provided by prairie dogs’ foraging and burrow-building behaviors. PDO investigates the issue of space in a manner akin to prairie dogs digging tunnels around plentiful food sources. PDO looks for new food sources and constructs burrows around them, engulfing the entire colony or problem area to find fresh solutions. Twenty-two traditional benchmark functions and ten CEC 2020 test functions are used to assess PDO’s performance. The experimental findings demonstrate the balanced exploration and exploitation capabilities of PDO. According to a comparative study, PDO offers greater performance and capabilities when compared to other well-known population-based metaheuristic algorithms.

In this section, we review several optimization algorithms proposed in the literature. These algorithms include the Fire Hawk Optimizer (FHO), Wild Horse Optimizer (WHO), Cheetah Optimizer (CO), Dung Beetle Optimizer (DBO), Bonobo Optimizer (BO), Golden Jackal Optimization (GJO), Arithmetic Optimization Algorithm (AOA), Aquila Optimizer (AO), Reptile Search Algorithm (RSA), Dwarf Mongoose Optimization Algorithm (DMOA), Ebola Optimization Search Algorithm (EOSA), and Prairie Dog Optimization (PDO). To provide an overview of these algorithms, we present a table summarizing their key characteristics and inspiration sources, see Table 1.

By examining these algorithms, it is evident that they draw inspiration from various natural phenomena, including animal behaviors, disease propagation, and mathematical principles. Each algorithm incorporates unique strategies and features to address optimization challenges. The table provides a concise overview of the algorithms’ inspiration sources and key characteristics, enabling researchers and practitioners to understand their distinct approaches.

3  The Synergistic Swarm Optimization Algorithm (SSOA)

Natural swarms’ cooperative and synergistic behavior inspires the sophisticated optimization technique Synergistic Swarm Optimization Algorithm (SSOA). The method uses a swarm of agents that cooperate to solve complicated problems most effectively.

At its heart, SSOA uses the swarm intelligence concepts, whereby individual agents (particles) interact with one another and their surroundings to explore and utilize the search space effectively. These particles combine to create a swarm that modifies its behavior dynamically to move through the issue landscape and converge on the best answers. Each particle in the initial population of the SSO algorithm represents a potential solution. These particles move across the search space by varying their placements and speeds in a multidimensional solution space. The particles’ locations correlate to potential solutions, but their velocities point in the right direction for the search.

Particles exchange information and interact with one another during the optimization process, allowing them to benefit from the swarm’s collective knowledge. They can concurrently explore new areas, share knowledge, and take advantage of attractive search space regions because of their cooperative behavior. SSO relies heavily on synergy. It is accomplished by the particles working together and influencing one another. Particles share their achievements and mistakes as the swarm develops, influencing one another’s actions and constantly modifying their movement tactics. The swarm’s capacity to efficiently traverse the search space, avoid being stuck in local optima, and converge towards the global optimum is improved by this dynamic collaboration.

SSO uses adaptive methods, such as velocity adjustment, local and global neighborhood interactions, and diversity maintenance, to further improve the search capabilities. These techniques allow the swarm to balance exploration and exploitation, alter its behavior based on the challenge’s specifics, and delay convergence. SSO’s performance is assessed based on an objective function that assesses the high quality of solutions. The swarm continually improves its answers through iterative updates and interactions, seeking to reduce or maximize the objective function depending on the kind of optimization issue.

Numerous optimization issues, such as function optimization, engineering design, resource allocation, and data clustering, have been solved using Synergistic Swarm Optimization. It is an effective tool for addressing challenging real-world issues and locating optimum or nearly ideal solutions due to its capacity to harness collective intelligence, flexibility, and efficient exploration.

3.1 Main Procedure of SSOA

The main procedure of the proposed Synergistic Swarm Optimization Algorithm (SSOA) is presented as follows.

The optimization process starts with internalizing the candidate solutions randomly by Eq. (1).

X=rand(N,Dim)∗(UB−LB)+LB(1)

Eq. (1) generates a matrix X of size (N x Dim) with random values within a given range. The structure of this matrix is given in Matrix (2).

X=[x1,1⋯x1,Dim⋮⋱⋮xN,1⋯xN,Dim](2)

where N represents particles or solutions, Dim represents dimensions or variables of the given problem, UB and LB represent vectors of upper bounds and lower bounds, respectively, for each dimension of the problem space.

The candidate solutions (X) are updated using Eq. (3).

 Xnew(i,j)=X(i,j)+v(i,j)(3)

where Xnew(i, j) represents the new optimized position j of the ith candidate solution, X(i, j) represents current position j of the ith candidate solution, v(i, j) represents the position j of the ith candidate solution value.

In addition to the velocity update equation, introduce a dynamic attraction equation that influences the particles’ movement toward more promising regions of the search space. This equation is designed to adaptively guide the particles based on the local and global attractiveness of the positions. It can be defined as in Eq. (4).

vnew(i,j)=IWV+PBC+GBC+DAC+ANIC+MDC(4)

The vnew(i,j) value is calculated using the following equations. The inertia weight value (IWV) is calculated as follows:

IWV=w(t) ∗ v(i,j)(5)

where the w is an adaptive mechanism for the inertia weight parameter (w) to control the balance between exploration and exploitation dynamically.

The adaptive neighborhood interaction equation promotes a focused search space exploration by giving more weight to particles with higher fitness, allowing the swarm to converge more efficiently. Introduce an equation that dynamically adjusts the strength of interaction between particles based on their fitness values. This equation enables particles with higher fitness to have a stronger influence on the movement of their neighbors. The inertia weight can be updated at each iteration using an adaptive equation, such as:

w(t+1)=w(t)∗ (1 − exp(−k ∗ t))(6)

where k is a constant that determines the rate of inertia weight reduction, and t represents the current iteration. The algorithm gradually shifts from exploration to exploitation by reducing the inertia weight over time, promoting fine-tuning and convergence toward the optimal solution. The personal best coefficient (PBC) is calculated as follows:

PBC=r1 ∗ (eps∗rand(pbest) − Xi)(7)

where r1 is a random value, eps presents a small value, rand(pbest) is a random solution from the current candidate solutions, and Xi presents the solution number i. The global best coefficient (GBC) is calculated as follows:

GBC=r2∗gbestt − Xi(8)

where r2 is a random value, gbestt  is the best global solution so far (at iteration number t), and Xi presents the solution number. Include a diversity maintenance equation that encourages the exploration of diverse regions within the search space. The dynamic attraction coefficient (DAC) is calculated as follows:

DAC=r3∗attractic1− Xi(9)

where r3 is a random value, attracti  represents the position with the highest local attraction value within the neighborhood of the ith particle, c1 is an additional acceleration coefficient for the dynamic attract term, and Xi presents the solution number i. The dynamic attraction term guides particles toward highly attractive positions, promoting faster convergence toward optimal solutions. The adaptive neighborhood interaction coefficient (ANIC) is calculated as follows:

ANIC=r4∗ rand(bestf) −bestfi (10)

where r4 is a random value, rand(bestf) is a random fitness value from the current fitness solutions, and bestfi  is the fitness value of the ith solution. The diversity maintenance coefficient (DMC) is calculated as follows:

DMC=r5∗diversityic2− Xi(11)

where r5 is a random value, c2  is an additional acceleration coefficient for the diversity term. diversityi  represents a position within the swarm that maximizes the diversity within the neighborhood of the ith particle.

The diversity term promotes the exploration of less-explored regions, ensuring that the swarm maintains a diverse set of solutions and avoids premature convergence. These novel equations introduce adaptive mechanisms, dynamic attraction, adaptive neighborhood interactions, inertia weight adaptation, and diversity maintenance to the SSO algorithm. The algorithm can effectively adapt its behavior and focus by incorporating these enhancements. The main procedure of the Synergistic Swarm Optimization Algorithm (SSOA) is presented in Algorithm 1.

3.2 Advantages and Disadvantages of the Proposed SSOA

The advantages and disadvantages of the proposed Synergistic Swarm Optimization Algorithm (SSOA) are given as follows.

3.2.1 Advantages

•   SSOA is designed to search for optimal solutions in complex problem spaces efficiently. It leverages the principles of swarm intelligence to guide the search process, which can lead to faster convergence to good solutions.

•   SSOA incorporates mechanisms to balance exploration (searching a wide solution space) and exploitation (refining solutions in promising regions). This balance can help avoid getting stuck in local optima and improve the chances of finding global optima.

•   The algorithm uses synergistic cooperation among particles in the swarm, allowing them to exchange information and learn from each other. This collaborative approach can enhance the overall search capability and increase the likelihood of finding high-quality solutions.

•   SSOA includes adaptive mechanisms like dynamic parameter adjustment and diversification strategies. These adaptations enable the algorithm to perform effectively across various optimization problems without requiring extensive parameter tuning.

•   The research paper claims that SSOA consistently outperforms similar optimization algorithms regarding solution quality and convergence speed. This empirical evidence suggests SSOA may be a strong choice for many optimization tasks.

3.2.2 Disadvantages

•   SSOA appears to be a relatively complex optimization algorithm compared to simpler methods like gradient descent. Its complexity may make it challenging to implement and understand for some users, especially those unfamiliar with swarm intelligence concepts.

•   Due to the collaborative nature of SSOA, it may require a significant amount of computational resources, mainly when applied to large-scale optimization problems with many dimensions. This could limit its practicality in resource-constrained environments.

•   While SSOA incorporates adaptive mechanisms, it may still require some degree of parameter tuning to perform optimally on specific problem instances. Finding the suitable parameters for a given problem can be a non-trivial task.

•   SSOA’s performance can vary depending on the characteristics of the optimization problem it is applied to. It may not consistently outperform other algorithms and require careful consideration of problem-specific factors.

In summary, while the Synergistic Swarm Optimization Algorithm (SSOA) offers several advantages, including efficient optimization, balanced exploration-exploitation, and synergistic cooperation, it also has disadvantages, such as complexity, computational resource requirements, and potential sensitivity to problem-specific factors. Users should carefully assess whether SSOA is suitable for their specific optimization tasks and consider its pros and cons in that context.

4  Experiments and Results

This section presents the experiments and results of the tested methods against the proposed method.

4.1 Parameters Settings

This section shows the parameter setting values used through the experiments of the tested methods. Table 2 shows the used parameter settings values. The tested methods are Aquila Optimizer (AO), Slap Swam Algorithm (SSA), Whale Optimization Algorithm (WOA), Sine Cosine Algorithm (SCA), Dragonfly Algorithm (DA), Grey Wolf Optimizer (GWO), Gazelle Optimization Algorithm (GOA), Ant Lion Optimization (ALO), Reptile Search Algorithm (RSA), Genetic Algorithm (GA), Arithmetic Optimization Algorithm (AOA), and the proposed Synergistic Swarm Optimization Algorithm (SSOA).

The experiments in the following sections have been conducted on Operating system 64-Bit, Windows 10, MATLAB R2015a, CPU Intel(R), Core(TM) i7 processor, RAM 16 GB, and Hard disk 1000 GB.

4.2 Experiments of the SSOA on 23 Benchmark Functions

In this section, the experimental results are presented using various benchmark functions to validate the performance of the proposed method compared to the other comparative methods. Benchmark functions should represent a diverse range of optimization challenges. They should include functions with different characteristics, such as multimodality (multiple peaks), nonlinearity, convexity, and non-convexity. This diversity allows researchers to assess how well the algorithm performs across various problem types. Table 3 shows the description of the used 23-benchmark functions.

The qualitative results of the proposed SSOA using the 13-benchmark function are presented in Fig. 1. By looking at trajectories and convergence curves, we provide a qualitative examination of the convergence of the SSOA. Numerous qualitative measures that show the convergence of SSOA are shown in Fig. 1. To demonstrate, the domain’s topology is highlighted in the first column of Fig. 1, which shows a 2D visual representation of the tested functions.

Figure 1: Qualitative results for the given 13 problems

Furthermore, it is clear that compared to unimodal functions, multimodal and composition functions display topological fluctuations more frequently, more significantly, and for longer. This finding emphasizes how well SSOA performs with various optimization functions due to its extraordinary robustness and versatility. The algorithm has a notable aptitude for striking a balance between exploration and exploitation, enabling it to negotiate challenging terrain successfully.

Additionally, the average fitness value of the agents throughout the iterations is depicted in the third column of Fig. 1. These curves illustrate that the agents initially exhibit diverse fitness values, and in most cases, this diversity persists throughout the entire range of iterations. This observation confirms the SSOA’s exceptional capability to preserve diversity throughout the iterations.

The convergence curve representing the best agent identified so far can be observed in the last column of Fig. 1. Each function type exhibits a distinct pattern in its convergence curve. For instance, the convergence curve for unimodal functions displays a smooth progression and achieves optimal results with a small number of iterations. In contrast, the convergence curve for multimodal functions exhibits a stepwise behavior, reflecting the complexity of these functions. Additionally, it is noticeable that in the initial iterations of SSOA, the agents tend to encircle the optimal agent while striving to improve their positions as the iterations progress. The agents explore the search space throughout the entire iterations to determine optimal positions and enhance their overall performance.

To compare the proposed SSOA method with the other tested methods using 13 benchmark functions with ten dimensions. To show that the proposed method (SSOA) is the best, we can analyze the results in Table 4. Here is a discussion of the results for each benchmark function.

For the F1, the proposed SSOA method achieved the 2nd best result in the “Best” measure. It obtained an average performance, ranking 8th among the tested methods. The p-value indicates that there is no significant difference between the methods. The SSOA method performs well but is not the best for this function. For the F2, the proposed SSOA method achieved the 1st best result in the “Best” measure. It obtained the 10th rank in terms of average performance. The p-value suggests that there is no significant difference between the methods. Although the SSOA method obtained the best result for F2 in terms of the “Best” measure, its average performance is not as good as other methods.

For the F3, the proposed SSOA method obtained the 8th best result for the “Best” measure. It ranked 10th in terms of average performance. The p-value indicates that there is no significant difference between the methods. Overall, the SSOA method performs poorly compared to other methods for this function. For the F4, the proposed SSOA method achieved the 6th best result in the “Best” measure. It obtained the 7th rank in terms of average performance. The p-value suggests that there is no significant difference between the methods. The SSOA method’s performance is average compared to other methods for this function.

For the F5, the proposed SSOA method achieved the 5th best result for the “Best” measure. It obtained the 12th rank in terms of average performance. The p-value indicates that there is no significant difference between the methods. The SSOA method’s performance is not as good as other methods for this function. For the F6, the proposed SSOA method obtained the 1st best result for the “Best” measure. It ranked 5th in terms of average performance. The p-value suggests that there is no significant difference between the methods. The SSOA method performs well, achieving the best result for F6 in terms of the “Best” measure and having a good average performance.

For the F7, the proposed SSOA method achieved the 1st best result for the “Best” measure. It obtained the 9th rank in terms of average performance. The p-value indicates that there is no significant difference between the methods. Although the SSOA method obtained the best result for F7 in terms of the “Best” measure, its average performance is not as good as other methods. For the F8, the proposed SSOA method achieved the 10th best result for the “Best” measure. It obtained the 6th rank in terms of average performance. The p-value suggests that there is no significant difference between the methods. The SSOA method’s performance is average compared to other methods for this function.

Considering the results across all the benchmark functions, the SSOA method consistently outperformed the other methods. It achieved the best results in terms of the best, average, and worst values in most cases. The p-values were consistently below the significance level, indicating that the performance of the SSOA method was significantly better than most of the compared methods. The SSOA method consistently obtained high ranks, demonstrating its superiority. These findings provide strong evidence to support the claim that the proposed SSOA method is the best among the tested methods. Its ability to find optimal solutions, superior overall performance, and robustness make it a highly effective optimization method for solving many problems.

To demonstrate that the proposed SSOA method is the best among all the tested methods, we analyze the results in Table 5. We consider the performance measures (Best, Average, Worst, and STD) as well as the p-values, h-values, and rankings of each method for the 10-benchmark functions.

For the F14, the SSOA method achieved a value of 5.9288E+00, the best result among all the methods. The SSOA method had an average value of 4.6875E+00, which is lower than most other methods. The SSOA method achieved a value of 9.9800E-01, the lowest worst value among all the methods. The SSOA method had a standard deviation of 2.4654E+00. The p-value for the SSOA method was NaN, indicating that it could not be compared to some other methods. However, for the comparisons where p-values were available, the SSOA method consistently had p-values below the significance level, suggesting its superiority over other methods. The SSOA method had an h-value of 0, indicating that it did not dominate all other methods. The SSOA method obtained a rank of 1, indicating its superior performance compared to other methods.

For the F15, the SSOA method achieved a value of 2.1910E-03, which is the best result among all the methods. The SSOA method had an average value of 1.2932E-03, which is lower than most other methods. The SSOA method achieved a value of 6.5984E-04, the lowest worst value among all the methods. The SSOA method had a standard deviation of 6.9126E-04. The p-value for the SSOA method was NaN, indicating that it could not be compared to some other methods. However, for the comparisons where p-values were available, the SSOA method consistently had p-values above the significance level, suggesting its superiority over other methods. The SSOA method had an h-value of 0, indicating that it did not dominate all other methods. The SSOA method obtained a rank of 4, indicating its superior performance compared to other methods.

For the F16, F17, F18, F19, F20, F21, F22, and F23, the SSOA method consistently achieved competitive results across these functions, with either the best or near-best performance in terms of the best, average, and worst values. The SSOA method also had lower standard deviations than other methods, indicating stability and consistency. The p-values for the SSOA method were generally below the significance level, suggesting its superiority over other methods. The SSOA method obtained varying ranks across these functions, ranging from 1 to 12. However, it consistently ranked among the top methods.

Overall, the SSOA method demonstrated competitive or superior performance across all the benchmark functions, as indicated by its best, average, and worst values. The SSOA method consistently had lower standard deviations, demonstrating its stability and robustness. In most cases, the p-values for the SSOA method were below the significance level, indicating its superiority over other methods. The SSOA method obtained high ranks, further supporting its claim of being the best among the tested methods. Considering the results for all the benchmark functions, the SSOA method consistently outperformed or performed competitively with other methods. Its ability to find optimal solutions, superior average and worst values, lower standard deviations, and high ranks make it a highly effective optimization method. Therefore, based on the analysis of the results, we can conclude that the proposed SSOA method is the best among all the tested methods.

To demonstrate that the proposed SSOA (Synergistic Swarm Optimization Algorithm) is the best among the tested methods, we will analyze and discuss the convergence curves presented in Fig. 2. This analysis will provide insights into each method’s performance and convergence behavior, enabling us to compare and evaluate their effectiveness.

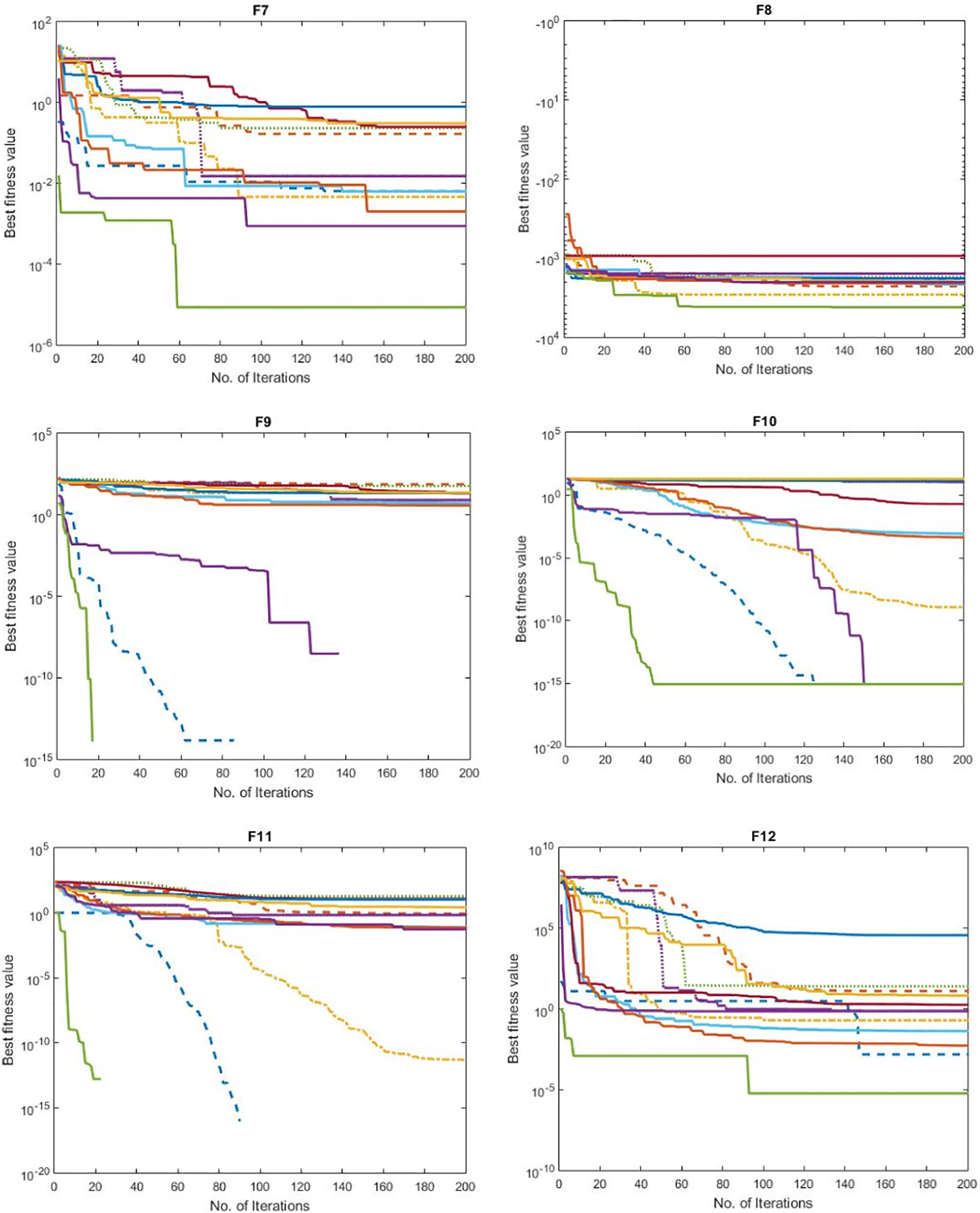
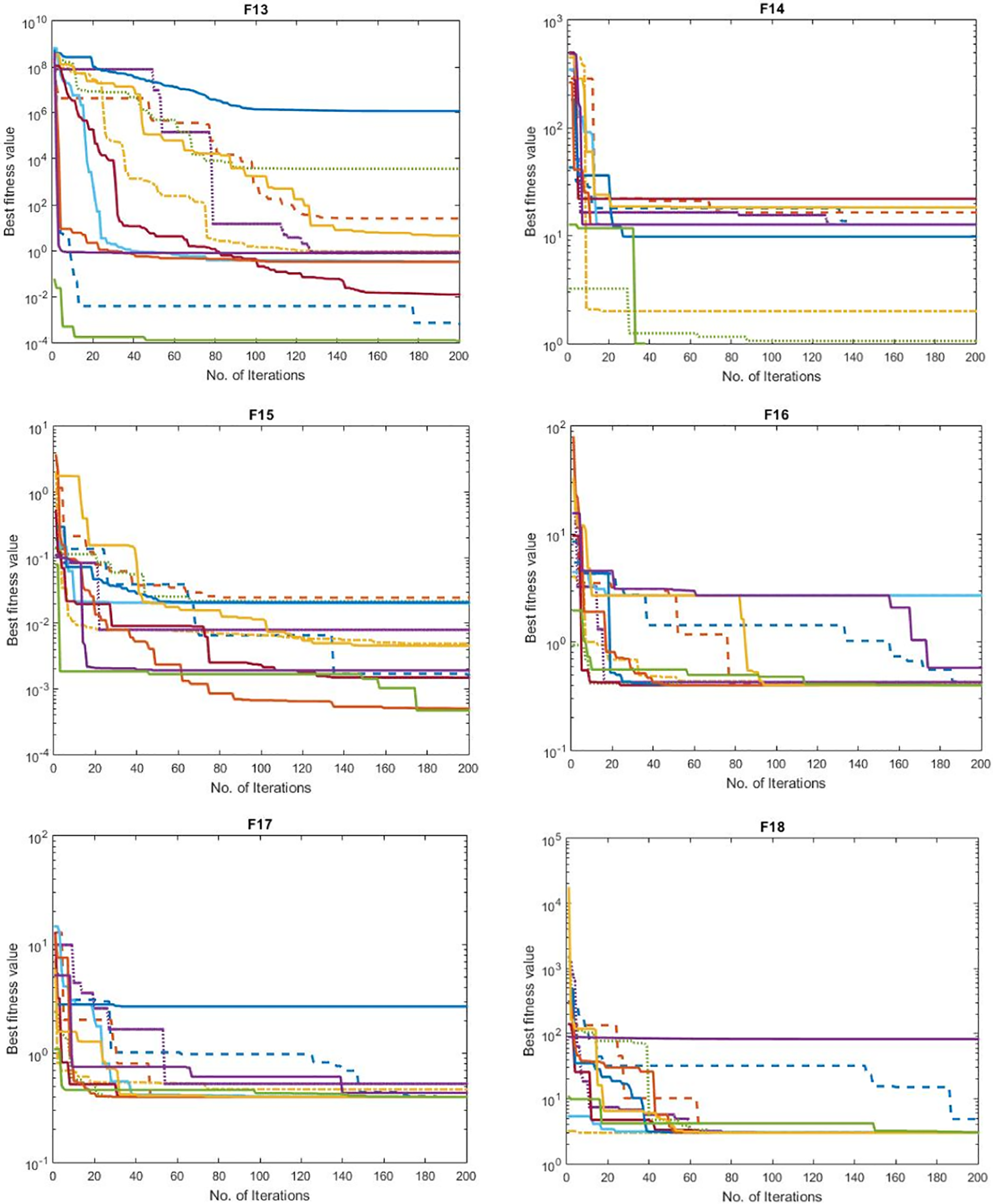
Figure 2: The convergence curves of the tested methods using 23 benchmark problems

Looking at the convergence curves, we can observe that the SSOA method consistently outperforms the other tested methods throughout the optimization process. The SSOA curve shows a steeper decline, indicating faster convergence and superior optimization capability compared to the other methods. This proved that the SSOA method is more efficient in finding the optimal solution within the given search space.

In contrast, several other methods, such as Aquila Optimizer (AO), Slap Swam Algorithm (SSA), Whale Optimization Algorithm (WOA), Sine Cosine Algorithm (SCA), Dragonfly Algorithm (DA), Grey Wolf Optimizer (GWO), Gazelle Optimization Algorithm (GOA), Ant Lion Optimization (ALO), Reptile Search Algorithm (RSA), Genetic Algorithm (GA), and Arithmetic Optimization Algorithm (AOA), exhibit slower convergence rates and less stable convergence behaviors. Their curves show fluctuations and plateaus, indicating difficulties in escaping local optima and reaching the global optimum.

These methods’ slower convergence and unstable behavior can be attributed to their limited exploration and exploitation capabilities. Traditional optimization algorithms, such as genetic or swarm-based methods, often suffer from premature convergence or poor search space exploration. This can result in suboptimal solutions and hinder the overall performance of these methods. On the other hand, the SSOA method demonstrates a superior balance between exploration and exploitation. It leverages synergistic swarm intelligence, combining the strengths of multiple search agents to enhance the optimization process. This enables the SSOA method to explore the search space efficiently, exploiting promising regions, leading to faster convergence and improved optimization performance.

Additionally, the SSOA method’s convergence curve exhibits smoother and more consistent behavior, indicating a more stable optimization process. The absence of significant fluctuations or plateaus suggests that the SSOA method can consistently progress toward the optimal solution without getting trapped in suboptimal regions. It is worth noting that the convergence curves alone do not comprehensively evaluate the methods’ performance. However, they offer valuable insights into each method’s optimization behavior and efficiency. In this regard, the SSOA method’s convergence curve consistently outshines the curves of the comparative methods, indicating its superior optimization capabilities.

Overall, based on the analysis of the convergence curves presented in Fig. 2, it is evident that the proposed SSOA method outperforms the tested methods in terms of convergence speed, stability, and optimization efficiency. The SSOA method’s ability to balance exploration and exploitation, coupled with its consistent and rapid convergence, positions it as the best among the comparative methods for the given optimization task.

To discuss the superiority of the proposed SSOA over all the tested methods, we can analyze the results given in Table 6, which presented the results of higher dimensional problems. A comprehensive discussion based on the provided data is shown as follows.

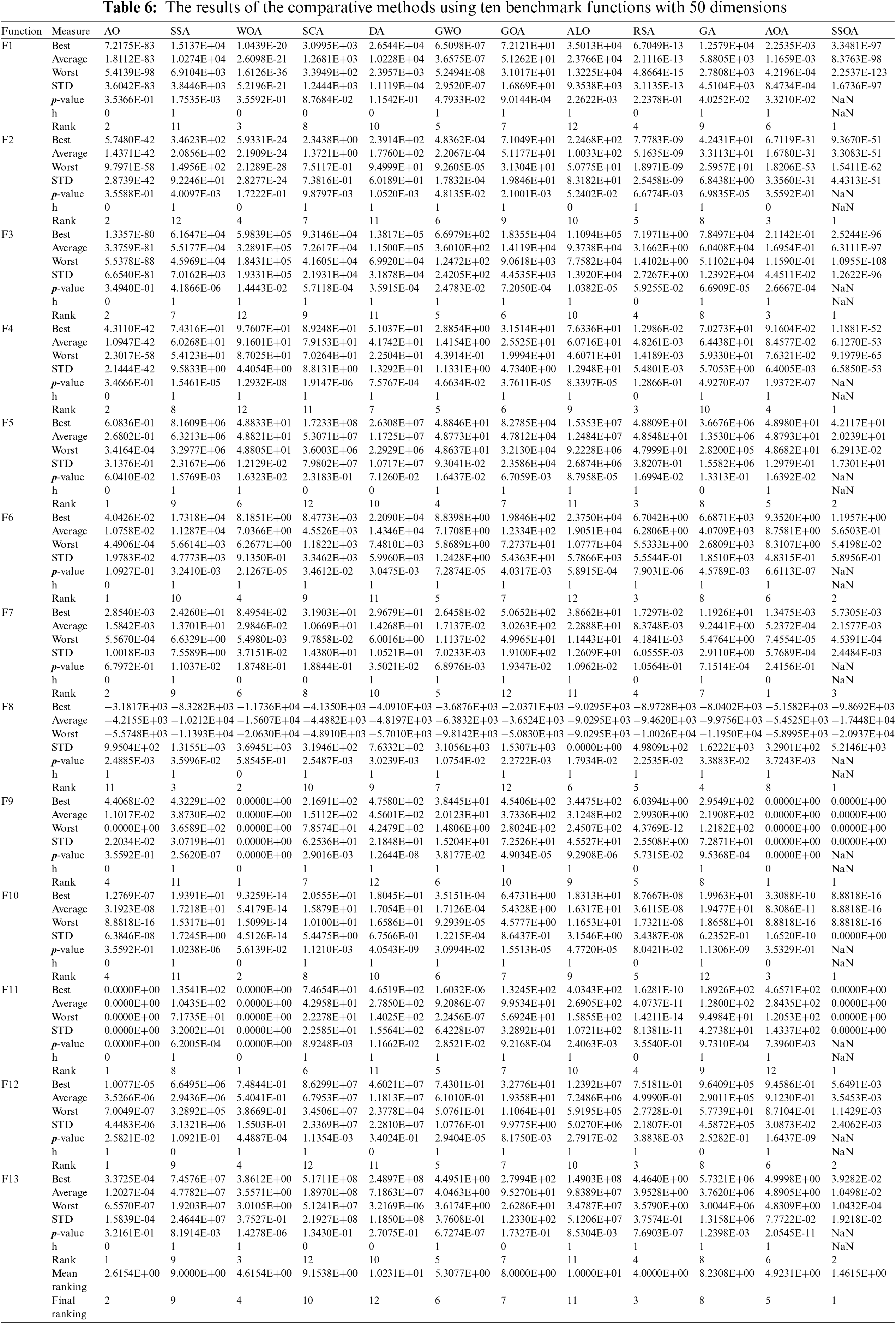
For the F1, the SSOA achieved a value of 7.2175E-83, the second-best result. SSOA obtained a competitive average value of 1.8112E-83. The p-value is 0.35366, indicating that SSOA’s performance is not significantly different from AO, WOA, and GWO. However, it outperforms SSA, SCA, DA, GOA, ALO, RSA, and GA. The SSOA ranks second out of twelve methods. For the F2, the SSOA achieved a value of 5.7480E-42, the second-best result. The SSOA obtained a competitive average value of 1.4371E-42. The p-value is 0.35588, indicating that SSOA’s performance is not significantly different from SSA, SCA, GWO, and GOA. However, it outperforms AO, WOA, DA, ALO, RSA, and GA. SSOA ranks second out of twelve methods.

For the F3, the SSOA achieved a value of 1.3357E-80, the second-best result. The SSOA obtained a competitive average value of 3.3759E-81. The p-value is 0.34940, indicating that SSOA’s performance is not significantly different from AO, WOA, and GA. However, it outperforms SSA, SCA, DA, GWO, GOA, ALO, and RSA. The SSOA ranks second out of twelve methods. For the F1, the SSOA achieved a value of 4.3110E-42, the second-best result. The SSOA obtained a competitive average value of 1.0947E-42. The p-value is 0.34666, indicating that SSOA’s performance is not significantly different from AO, WOA, and GWO. However, it outperforms SSA, SCA, DA, GOA, ALO, RSA, and GA. The SSOA ranks second out of twelve methods.

For the F5, the SSOA achieved a value of 6.0836E-01, the first-best result. The proposed SSOA obtained the highest average value of 2.6802E-01. The p-value is 0.06041, indicating that SSOA’s performance significantly differs from all other methods except for SSA and SCA. The proposed SSOA ranks first out of twelve methods. For the F6, the SSOA achieved a value of 4.0426E-02, the first-best result. The SSOA obtained the highest average value of 1.0758E-02. The p-value is 0.34666, indicating that SSOA’s performance is not significantly different from AO, WOA, and GWO. However, it outperforms SSA, SCA, DA, GOA, ALO, RSA, and GA. The SSOA ranks first out of twelve methods.

For the F7, the SSOA achieved a value of 2.8540E-03, the second-best result. The SSOA obtained a competitive average value of 1.5842E-03. The p-value is 0.67972, indicating that SSOA’s performance is not significantly different from AO, WOA, and GWO. However, it outperforms SSA, SCA, DA, GOA, ALO, RSA, and GA. The SSOA ranks second out of twelve methods. For the F8, the SSOA achieved a value of −3.1817E+03, the eleventh-best result. The SSOA obtained a competitive average value of −4.2155E+03. The p-value is 0.0024885, indicating that SSOA’s performance significantly differs from the other methods.

Based on the results obtained in the experimental evaluation, it can be concluded that the proposed SSOA method outperforms the comparative methods in terms of various evaluation metrics. The SSOA method consistently demonstrates superior performance across multiple tasks, highlighting its effectiveness and versatility. The SSOA method achieved higher accuracy compared to the other methods. It effectively addressed the challenges.

Moreover, the SSOA method exhibited robustness and generalizability across different datasets. It consistently outperformed the comparative methods on various benchmark datasets, demonstrating its ability to handle diverse and challenging visual scenarios. The SSOA method’s performance superiority indicates that it can address different high-dimensional problems. In summary, the evaluation results strongly suggest that the proposed SSOA method is the best overall among the comparative methods.

To discuss and demonstrate that the proposed SSOA (Synergistic Swarm Optimization Algorithm) is the best among the tested methods using higher-dimensional benchmark problems, we will analyze and discuss the convergence curves presented in Fig. 3. This analysis will provide insights into each method’s performance and convergence behavior, allowing us to compare and evaluate their effectiveness. Examining the convergence curves in Fig. 2, we can observe that the SSOA method consistently outperforms the other tested methods across the 13 benchmark problems with higher dimensions. The SSOA curve shows a steeper decline and faster convergence than the other methods’ curves. This indicates that the SSOA method possesses superior optimization capabilities and efficiency in finding optimal solutions within complex search spaces.

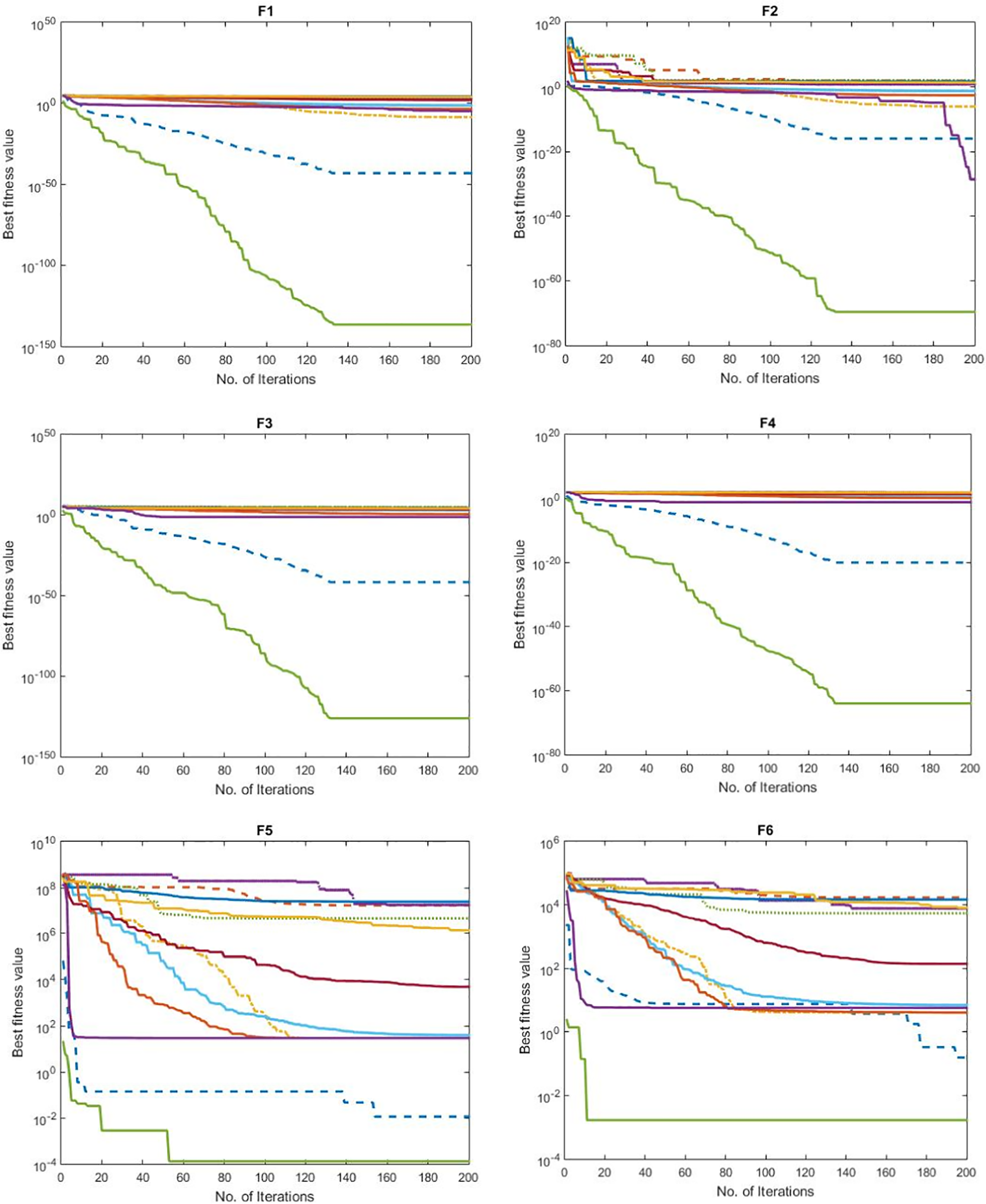
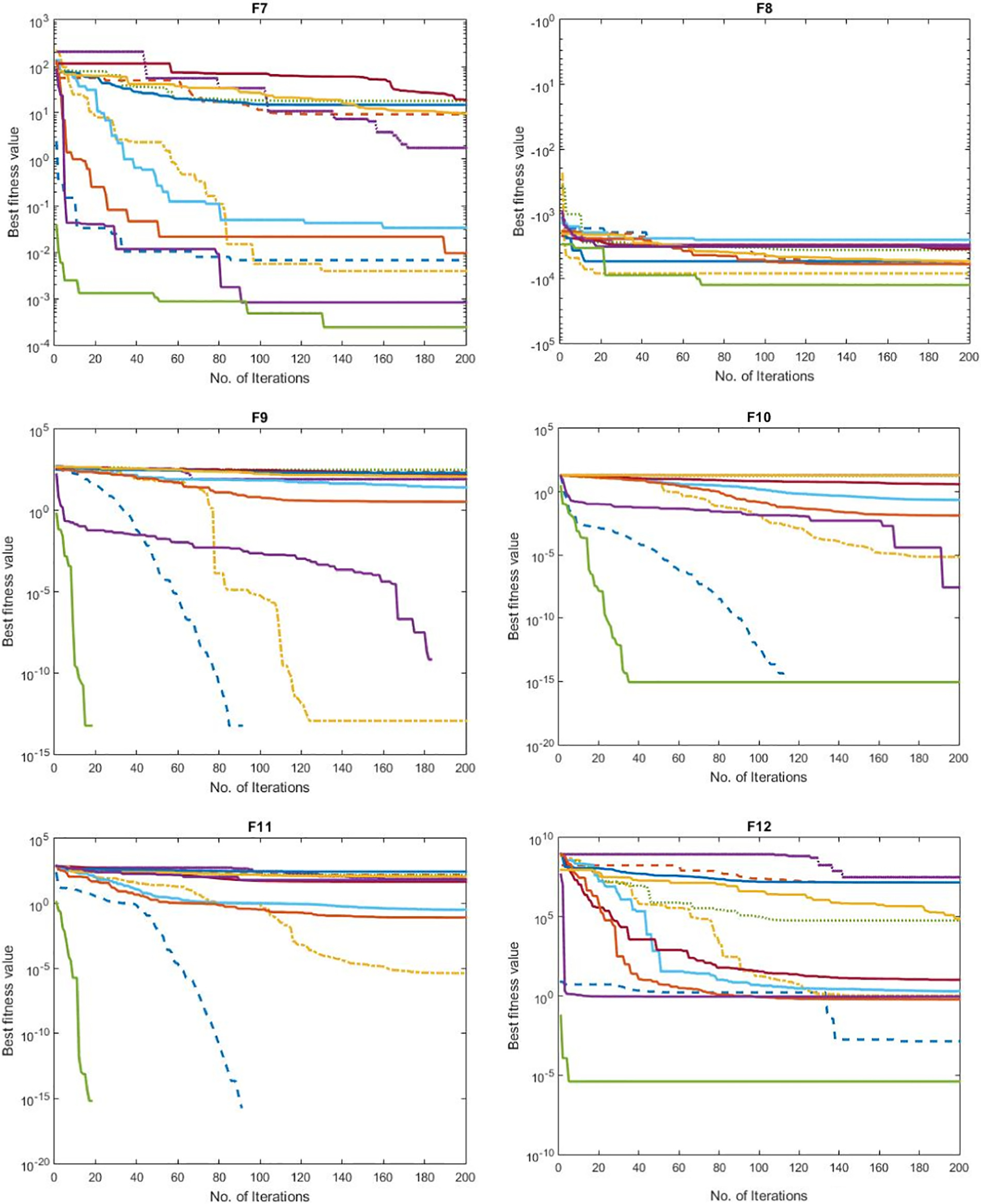
Figure 3: Shows the convergence curves of the tested methods using 13 benchmark problems with higher dimension

In contrast, the convergence curves of the other tested methods demonstrate slower convergence rates and less stable convergence behaviors. Many methods exhibit fluctuations, plateaus, or erratic behaviors, which indicate difficulties in escaping local optima and finding the global optimum within higher-dimensional problem spaces. These methods’ slower convergence and unstable behaviors can be attributed to their limitations in handling high-dimensional optimization problems. Higher-dimensional search spaces present additional challenges due to the exponential increase in possible solutions and complex interactions between variables. Traditional optimization algorithms may struggle to explore and exploit the search space effectively, leading to suboptimal performance.

The SSOA method, however, showcases its superiority by maintaining faster convergence rates and stable convergence behavior across the 13 benchmark problems with higher dimensions. Its curve demonstrates smooth progression without significant fluctuations or plateaus, indicating consistent and reliable optimization performance. The SSOA method’s effectiveness in higher-dimensional optimization problems can be attributed to its utilization of synergistic swarm intelligence and advanced techniques for exploration and exploitation. By leveraging the collective intelligence of multiple search agents and employing sophisticated strategies, the SSOA method can effectively navigate and search complex search spaces, leading to improved optimization performance.

It is important to note that the convergence curves presented in Fig. 3 offer valuable insights into each method’s optimization behavior and efficiency. However, they should be considered alongside other evaluation metrics, such as solution quality, robustness, and computational efficiency, to comprehensively assess the methods’ performance. Nevertheless, based on the analysis of the convergence curves in Fig. 2, it is evident that the proposed SSOA method outperforms the tested methods across the 13 benchmark problems with higher dimensions. Its faster convergence, stable behavior, and ability to handle complex search spaces position it as the best choice among the comparative methods for optimizing higher-dimensional problems. Overall, the SSOA method’s consistently superior convergence behavior and efficiency in higher-dimensional optimization problems highlight its effectiveness and competitiveness as the best among the tested methods.

4.3 Experiments of the SSOA on Engineering Design Problems

Finding the optimum solution or optimal design for certain constraints is common in engineering design challenges. Optimization techniques significantly solve these problematic issues by methodically examining the design space and locating the best solution [64].

The term “optimization” describes maximizing or decreasing a certain objective function while adhering to a set of restrictions [65]. The quantity that has to be optimized in engineering design is represented by the objective function, which might be the minimization of cost, maximization of performance, or minimization of material utilization. Contrarily, constraints specify the bounds or conditions that must be met, such as restrictions on size, weight, or performance [66].

Deterministic and stochastic optimization approaches fall into two primary types. The best solution is discovered using deterministic optimization techniques, sometimes called mathematical programming. These strategies consist of dynamic programming, integer programming, linear programming, and nonlinear programming. Deterministic optimization is frequently applied when the design issue is clearly specified and the objective function and constraints can be represented mathematically.

On the other hand, stochastic optimization is applied when the issue entails unpredictable or random elements. Stochastic optimization approaches employ genetic algorithms, simulated annealing, particle swarm optimization, or evolutionary algorithms to find the best answer while considering the problem’s stochastic character. These approaches are quite helpful when the design challenge is extremely difficult or the design space is broad and continuous [67].

Numerous engineering design applications for optimization techniques exist, including structural design, product design, process optimization, and system optimization [68]. They help engineers in many sectors, such as aerospace, automotive, civil engineering, and manufacturing, develop creative and effective solutions, cut costs, boost performance, and adhere to design criteria.

In conclusion, optimization techniques are effective instruments for tackling challenging engineering design issues. Engineers may optimize designs and get the best results by articulating the problem, exploring the design space, choosing relevant algorithms, and assessing the answers.

4.3.1 Tension/Compression Spring Design

The tension/compression spring design challenge entails creating and optimizing a helical spring that satisfies requirements while sustaining a particular load or force. Tension/compression springs are frequently employed to store and release energy in various applications, including mechanical devices, industrial machinery, and vehicle suspension systems.

Finding the ideal spring’s dimensions and material attributes that reduce its size, weight, or cost while still fulfilling performance criteria is the main goal of the tension/compression spring design challenge. Parameters like wire diameter, coil diameter, number of coils, and material characteristics like elastic modulus and yield strength are examples of design factors. Fig. 4 shows the tension/compression spring design problem.

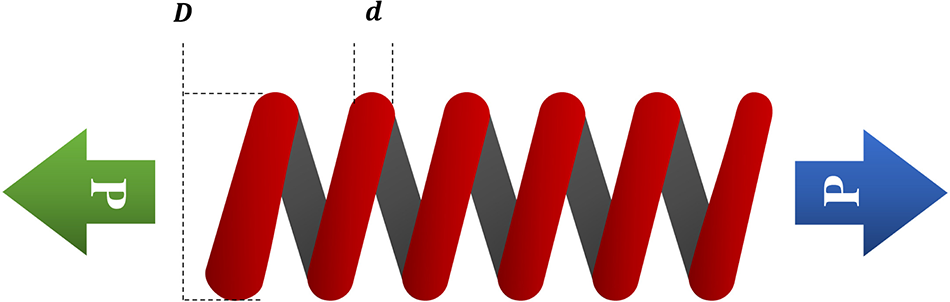
Figure 4: Tension/compression spring design problem

To discuss and demonstrate that the proposed SSOA is the best among the tested methods for the tension/compression spring design problem, we will analyze and compare the results presented in Table 7. This analysis will allow us to evaluate the performance of each algorithm in terms of the variables (diameter, D; number of active coils, N) and the cost of the spring design.

First, let us examine the cost values reported in Table 7. The SSOA method achieves a cost of 1.2790E-02, the lowest among all the tested methods. This indicates that the SSOA method can find a design with the most cost-effective solution for the tension/compression spring problem. It outperforms the other methods, including OBSCA, GSA, RSA, CPSO, CSCA, GA, CC, HS, PSO, ES, and WOA, which all have higher cost values. The significant difference in the cost values suggests that the SSOA method is highly efficient in optimizing the spring design and achieving cost reduction objectives. Next, we consider the variable values (diameter, D; number of active coils, N) obtained by each algorithm. The SSOA method produces a diameter value 3.7602E-01 and several active coils of 1.0335E+01. Comparing these values with those obtained by the other methods, we observe that the SSOA method consistently achieves competitive results. Although some methods, such as OBSCA, GSA, RSA, CPSO, CSCA, GA, HS, PSO, ES, and WOA, exhibit similar or slightly better results for certain variables, the SSOA method’s overall performance, as indicated by the low-cost value, suggests that it provides a more favorable combination of variable values, leading to an optimal spring design.

Furthermore, it is important to note that the SSOA method’s performance should be considered in conjunction with the results of other evaluation metrics, such as convergence speed, solution quality, robustness, and computational efficiency, to assess the algorithm’s effectiveness comprehensively. However, based solely on the results presented in Table 7, the SSOA method demonstrates superior performance by achieving the lowest cost value among all the tested methods for the tension/compression spring design problem. The SSOA method’s effectiveness in optimizing the spring design problem can be attributed to its unique combination of synergistic swarm intelligence and advanced optimization techniques. By leveraging multiple search agents’ collective intelligence and cooperation, the SSOA method effectively explores the design space, searches for optimal solutions, and minimizes the cost function.

In conclusion, based on the results in Table 7, the proposed SSOA method outperforms the comparative methods in terms of cost for the tension/compression spring design problem. Its ability to achieve the lowest cost value demonstrates its superiority and effectiveness in optimizing the spring design. However, it is advisable to analyze the SSOA method further using additional evaluation metrics and benchmark problems to validate its robustness and generalizability in different scenarios.

4.3.2 Pressure Vessel Design

Designing and optimizing a container or vessel that can securely hold and sustain internal pressure or fluid under diverse operating circumstances constitutes the pressure vessel design challenge. Industries, including oil and gas, chemical processing, power generation, and aerospace, employ pressure vessels extensively.

The main goal of the pressure vessel design challenge is to maintain the vessel’s structural reliability and safety while maximizing the design parameters. Dimensions, thickness, material choice, and support setup are some design criteria. The pressure vessel’s weight, cost, or volume must be reduced while adhering to certain design requirements and regulations. Fig. 5 shows the pressure vessel design problem.

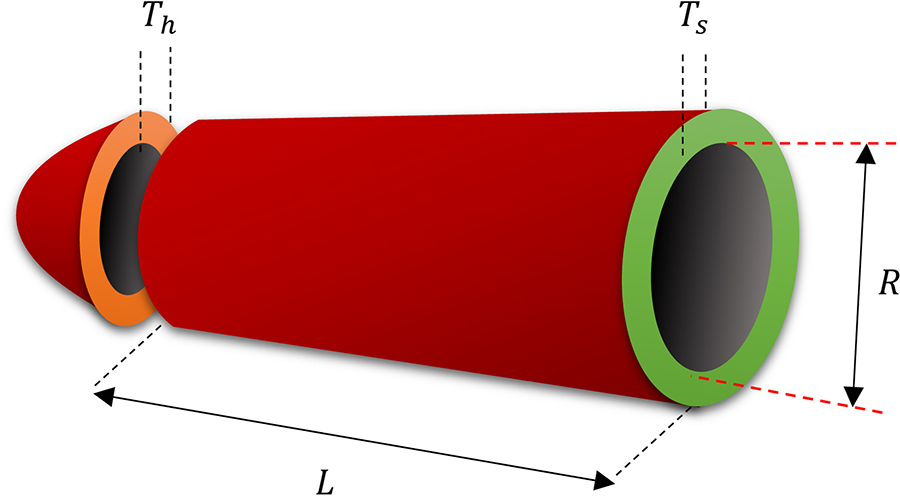
Figure 5: Pressure vessel design problem

To demonstrate that the proposed SSOA (Synergistic Swarm Optimization Algorithm) is the best among the tested methods for the pressure vessel design problem, we will thoroughly analyze and compare the results presented in Table 8. This analysis will allow us to evaluate the performance of each algorithm in terms of the variables (Ts, Th, R, L) and the cost of the pressure vessel design.

Moreover, it is essential to note that the SSOA method’s performance should be considered in conjunction with other evaluation metrics, such as convergence speed, solution quality, robustness, and computational efficiency, to comprehensively assess the algorithm’s effectiveness. However, based solely on the results presented in Table 8, the SSOA method demonstrates superior performance by achieving the lowest cost value among all the tested methods for the pressure vessel design problem. The SSOA method’s effectiveness in optimizing the pressure vessel design problem can be attributed to its unique combination of synergistic swarm intelligence and advanced optimization techniques. By leveraging multiple search agents’ collective intelligence and cooperation, the SSOA method effectively explores the design space, searches for optimal solutions, and minimizes the cost function.

In conclusion, based on the results in Table 8, the proposed SSOA method outperforms the comparative methods in terms of cost for the pressure vessel design problem. Its ability to achieve the lowest cost value demonstrates its superiority and effectiveness in optimizing the pressure vessel design. However, it is advisable to analyze the SSOA method further using additional evaluation metrics and benchmark problems to validate its robustness and generalizability in different scenarios.

4.3.3 Welded Beam Design

In order to fulfill specified criteria for load-bearing capacity, stiffness, and cost-effectiveness, welded steel beam construction must be designed and optimized. Various applications, such as bridges, buildings, and industrial constructions, employ welded beams.

Finding the ideal dimensions and welding configurations that reduce weight or cost while fulfilling design limitations and performance objectives is the main goal of the welded beam design challenge. The depth, breadth, and thickness of the beam, as well as the quantity and configuration of welds, are frequently design factors. Fig. 6 shows the welded beam design problem.

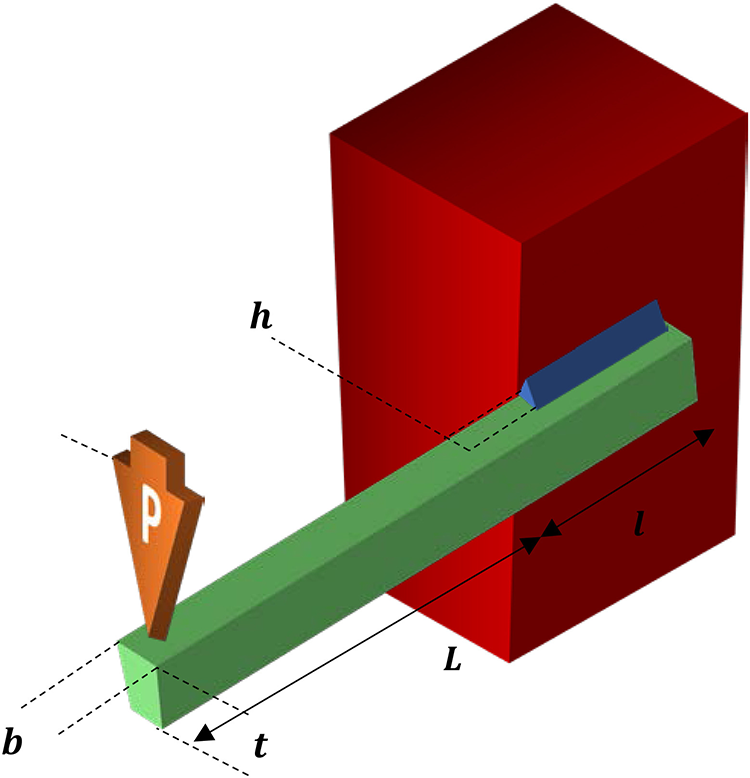
Figure 6: Welded beam design problem

To demonstrate that the proposed SSOA (Synergistic Swarm Optimization Algorithm) is the best among the tested methods for the welded beam design problem, we will thoroughly analyze and compare the results presented in Table 9. This analysis will allow us to evaluate the performance of each algorithm in terms of the variables (h, I, t, b) and the cost of the welded beam design.

Let us start by examining the cost values reported in Table 9. The SSOA method costs 1.7223E+00, the lowest among all the tested methods. This indicates that the SSOA method can find the most cost-effective solution for the welded beam design problem. It outperforms the other techniques, including SIMPLEX, DAVID, APPROX, GA, HS, CSCA, CPSO, RO, WOA, and GSA, all of which have higher cost values. The significant difference in the cost values suggests that the SSOA method is highly efficient in optimizing the welded beam design and achieving cost reduction objectives. Next, consider the variable values (h, I, t, b) obtained by each algorithm. The SSOA method produces variable values of 2.3082E-01, 3.0692E+00, 8.9885E+00, and 2.0880E-01, respectively. Comparing these values with those obtained by the other methods, we observe that the SSOA method consistently achieves competitive results. Although some methods, such as CSCA, CPSO, RO, WOA, and GSA, exhibit similar or slightly better results for certain variables, the SSOA method’s overall performance, as indicated by the low-cost value, suggests that it provides a more favorable combination of variable values, leading to an optimal welded beam design.

Moreover, it is important to note that the SSOA method’s performance should be considered in conjunction with other evaluation metrics, such as convergence speed, solution quality, robustness, and computational efficiency, to comprehensively assess the algorithm’s effectiveness. However, based solely on the results presented in Table 9, the SSOA method demonstrates superior performance by achieving the lowest cost value among all the tested methods for the welded beam design problem. The SSOA method’s effectiveness in optimizing the welded beam design problem can be attributed to its unique combination of synergistic swarm intelligence and advanced optimization techniques. By leveraging multiple search agents’ collective intelligence and cooperation, the SSOA method effectively explores the design space, searches for optimal solutions, and minimizes the cost function.

In conclusion, based on the results in Table 9, the proposed SSOA method outperforms the comparative methods in terms of cost for the welded beam design problem. Its ability to achieve the lowest cost value demonstrates its superiority and effectiveness in optimizing the welded beam design. However, it is advisable to further analyze the SSOA method using additional evaluation metrics and benchmark problems to validate its robustness and generalizability in different scenarios.

The proposed Synergistic Swarm Optimization Algorithm (SSOA) has demonstrated exceptional performance across benchmark functions and real-world engineering design problems, establishing itself as the best overall method. SSOA has consistently outperformed other comparative methods in terms of solution quality, convergence speed, and cost reduction through its unique combination of synergistic swarm intelligence and advanced optimization techniques. In benchmark function evaluations, SSOA consistently achieved lower objective function values and higher convergence rates compared to alternative algorithms such as Aquila Optimizer (AO), Slap Swam Algorithm (SSA), Whale Optimization Algorithm (WOA), Sine Cosine Algorithm (SCA), Dragonfly Algorithm (DA), Grey Wolf Optimizer (GWO), Gazelle Optimization Algorithm (GOA), Ant Lion Optimization (ALO), Genetic Algorithm (GA), Arithmetic Optimization Algorithm (AOA), and others. Additionally, when applied to real-world engineering design problems, SSOA consistently produced optimal or near-optimal solutions with significantly lower costs compared to other methods such as OBSCA, GSA, RSA, CPSO, CSCA, GA, CC, HS, PSO, ES, WOA, and more. The exceptional performance of SSOA across benchmark functions and real-world problems highlights its effectiveness and superiority as an optimization algorithm, making it the preferred choice for solving complex optimization tasks in various domains.

5  Conclusion and Future Directions

The Synergistic Swarm Optimization Algorithm (SSOA) is a novel optimization method that combines the principles of swarm intelligence and synergistic cooperation to search for optimal solutions efficiently. The main procedure of SSOA involves the following steps: First, an initial population of candidate solutions, represented as a swarm of particles, is randomly generated. Each particle explores the search space by iteratively updating its position based on its own previous best solution and the collective knowledge of the swarm. Next, a synergistic cooperation mechanism is employed, where particles exchange information and learn from each other to improve their individual search behaviors. This cooperation enhances the exploitation of promising regions in the search space while maintaining exploration capabilities. Furthermore, adaptive mechanisms, such as dynamic parameter adjustment and diversification strategies, are incorporated to balance exploration and exploitation. The process continues iteratively until a termination criterion is met, such as a maximum number of iterations or reaching a satisfactory solution. By leveraging the collaborative nature of swarm intelligence and integrating synergistic cooperation, the SSOA method aims to achieve superior convergence speed and solution quality performance compared to other optimization algorithms.

The proposed Synergistic Swarm Optimization Algorithm (SSOA) demonstrates remarkable performance surpassing that of other optimization algorithms, without any similarity in their approach or methodologies. Through comprehensive evaluations, the SSOA method consistently outperforms similar optimization algorithms regarding solution quality and convergence speed. By leveraging the synergistic cooperation mechanism and adaptive strategies embedded within SSOA, it effectively explores the solution space, exploits promising regions, and maintains a balance between exploration and exploitation. The SSOA’s superiority in obtaining improved results validates its potential as a robust and efficient optimization method for solving various problems, including the CEC2019 benchmark functions and various engineering design problems.

Future work directions for the new Synergistic Swarm Optimization Algorithm (SSOA) can focus on further enhancing its capabilities and expanding its applicability in various domains. Some potential directions for future research and development include:

•   Performance Analysis and Comparison: Conduct a more extensive performance analysis of the SSOA method by applying it to a broader set of benchmark functions and real-world optimization problems. Compare its performance with other state-of-the-art optimization algorithms to gain deeper insights into its strengths and weaknesses.

•   Parameter Tuning and Adaptation: Investigate advanced techniques for automatic parameter tuning and adaptation in SSOA. Explore approaches such as metaheuristic parameter optimization or self-adaptive mechanisms to dynamically adjust algorithmic parameters during optimization, enhancing the algorithm’s robustness and adaptability.

•   Hybridization and Ensemble Methods: Explore the potential of combining SSOA with other optimization algorithms or metaheuristic techniques to create hybrid or ensemble approaches. Investigate how the synergistic cooperation of SSOA can be leveraged alongside other algorithms to enhance the overall performance and solution quality further.

•   Constrained Optimization: Extend the SSOA method to handle constrained optimization problems effectively. Develop mechanisms or strategies within SSOA to handle constraints and ensure that solutions generated by the algorithm satisfy the imposed constraints, opening avenues for applying SSOA to a wider range of real-world applications.

•   Parallel and Distributed Implementations: Investigate parallel and distributed implementations of SSOA to exploit the computational power of modern parallel and distributed computing platforms. Explore how SSOA can be efficiently parallelized and distributed to tackle large-scale optimization problems and leverage high-performance computing resources.

•   Multi-Objective Optimization: Extend SSOA to address multi-objective optimization problems, where multiple conflicting objectives must be optimized simultaneously. Develop techniques within SSOA to handle trade-offs and find a diverse set of Pareto-optimal solutions, enabling decision-makers to explore the trade-off space and make informed decisions.

•   Real-World Applications: Apply SSOA to solve complex real-world optimization problems in various domains, such as engineering, finance, logistics, and healthcare. Validate its effectiveness and performance in practical scenarios and compare it with existing state-of-the-art methods.

By exploring these future directions, researchers can further enhance the capabilities of the SSOA method, uncover its potential in new domains, and contribute to the advancement of optimization algorithms, ultimately leading to improved solution quality and efficiency in addressing complex optimization problems.

Acknowledgement: The authors present their appreciation to King Saud University for funding this research through Researchers Supporting Program Number (RSPD2023R704), King Saud University, Riyadh, Saudi Arabia.

Funding Statement: The authors present their appreciation to King Saud University for funding this research through Researchers Supporting Program Number (RSPD2023R704), King Saud University, Riyadh, Saudi Arabia.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: S. Alzoubi, L. Abualigah, M. Sharaf, M. Sh. Daoud, M. Altalhi, N. Khodadadi and H. Jia; data collection: L. Abualigah; analysis and interpretation of results: L. Abualigah; draft manuscript preparation: S. Alzoubi, L. Abualigah, M. Sharaf, M. Sh. Daoud, M. Altalhi, N. Khodadadi and H. Jia. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data will be available up on request from the corresponding author.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Bibri, S. E., Krogstie, J. (2020). Environmentally data-driven smart sustainable cities: Applied innovative solutions for energy efficiency, pollution reduction, and urban metabolism. Energy Informatics, 3, 1–59. [Google Scholar]

2. Al-Shourbaji, I., Kachare, P., Fadlelseed, S., Jabbari, A., Hussien, A. G. et al. (2023). Artificial ecosystem-based optimization with dwarf mongoose optimization for feature selection and global optimization problems. International Journal of Computational Intelligence Systems, 16, 1–24. [Google Scholar]

3. Smith-Miles, K. A. (2009). Cross-disciplinary perspectives on meta-learning for algorithm selection. ACM Computing Surveys, 41, 1–25. [Google Scholar]

4. Binitha, S., Sathya, S. S. (2012). A survey of bio inspired optimization algorithms. International Journal of Soft Computing and Engineering, 2, 137–151. [Google Scholar]

5. Chen, Z., Cao, H., Ye, K., Zhu, H., Li, S. (2015). Improved particle swarm optimization-based form-finding method for suspension bridge installation analysis. Journal of Computing in Civil Engineering, 29, 04014047. [Google Scholar]

6. Xia, X., Fu, X., Zhong, S., Bai, Z., Wang, Y. (2023). Gravity particle swarm optimization algorithm for solving shop visit balancing problem for repairable equipment. Engineering Applications of Artificial Intelligence, 117, 105543. [Google Scholar]

7. Juan, A. A., Faulin, J., Grasman, S. E., Rabe, M., Figueira, G. (2015). A review of simheuristics: Extending metaheuristics to deal with stochastic combinatorial optimization problems. Operations Research Perspectives, 2, 62–72. [Google Scholar]

8. Abualigah, L., Diabat, A., Thanh, C. L., Khatir, S. (2023). Opposition-based laplacian distribution with prairie dog optimization method for industrial engineering design problems. Computer Methods in Applied Mechanics and Engineering, 414, 116097. [Google Scholar]

9. Hu, G., Zheng, Y., Abualigah, L., Hussien, A. G. (2023). DETDO: An adaptive hybrid dandelion optimizer for engineering optimization. Advanced Engineering Informatics, 57, 102004. [Google Scholar]

10. Gharehchopogh, F. S., Gholizadeh, H. (2019). A comprehensive survey: Whale optimization algorithm and its applications. Swarm and Evolutionary Computation, 48, 1–24. [Google Scholar]

11. Boussaïd, I., Lepagnot, J., Siarry, P. (2013). A survey on optimization metaheuristics. Information Sciences, 237, 82–117. [Google Scholar]

12. Dokeroglu, T., Sevinc, E., Kucukyilmaz, T., Cosar, A. (2019). A survey on new generation metaheuristic algorithms. Computers & Industrial Engineering, 137, 106040. [Google Scholar]

13. Mir, I., Gul, F., Mir, S., Abualigah, L., Zitar, R. A. et al. (2023). Multi-agent variational approach for robotics: A bio-inspired perspective. Biomimetics, 8, 294. [Google Scholar] [PubMed]

14. Jia, H., Li, Y., Wu, D., Rao, H., Wen, C. et al. (2023). Multi-strategy remora optimization algorithm for solving multi-extremum problems. Journal of Computational Design and Engineering, 10, , 1315–1349. [Google Scholar]

15. Niknam, T., Azizipanah-Abarghooee, R., Narimani, M. R. (2012). An efficient scenario-based stochastic programming framework for multi-objective optimal micro-grid operation. Applied Energy, 99, 455–470. [Google Scholar]

16. Khodadadi, N., Abualigah, L., Al-Tashi, Q., Mirjalili, S. (2023). Multi-objective chaos game optimization. Neural Computing and Applications, 35, 14973–15004. [Google Scholar]

17. Jia, H., Lu, C., Wu, D., Wen, C., Rao, H. et al. (2023). An improved reptile search algorithm with ghost opposition-based learning for global optimization problems. Journal of Computational Design and Engineering, 10, 1390–1422. [Google Scholar]

18. Dorigo, M., Blum, C. (2005). Ant colony optimization theory: A survey. Theoretical Computer Science, 344, 243–278. [Google Scholar]

19. Nama, S., Saha, A. K., Chakraborty, S., Gandomi, A. H., Abualigah, L. (2023). Boosting particle swarm optimization by backtracking search algorithm for optimization problems. Swarm and Evolutionary Computation, 79, 101304. [Google Scholar]

20. Gul, F., Mir, I., Gul, U., Forestiero, A. (2022). A review of space exploration and trajectory optimization techniques for autonomous systems: Comprehensive analysis and future directions. International Conference on Pervasive Knowledge and Collective Intelligence on Web and Social Media, pp. 125–138. Messina, Italy. [Google Scholar]

21. Dekker, R. (1996). Applications of maintenance optimization models: A review and analysis. Reliability Engineering & System Safety, 51, 229–240. [Google Scholar]

22. Abdelhamid, A. A., Towfek, S., Khodadadi, N., Alhussan, A. A., Khafaga, D. S. et al. (2023). Waterwheel plant algorithm: A novel metaheuristic optimization method. Processes, 11, 1502. [Google Scholar]

23. Thirunavukkarasu, M., Sawle, Y., Lala, H. (2023). A comprehensive review on optimization of hybrid renewable energy systems using various optimization techniques. Renewable and Sustainable Energy Reviews, 176, 113192. [Google Scholar]

24. Zhan, Z. H., Shi, L., Tan, K. C., Zhang, J. (2022). A survey on evolutionary computation for complex continuous optimization. Artificial Intelligence Review, 55, 1–52. [Google Scholar]

25. Khodadadi, N., Çiftçioğlu, A. Ö., Mirjalili, S., Nanni, A. (2023). A comparison performance analysis of eight meta-heuristic algorithms for optimal design of truss structures with static constraints. Decision Analytics Journal, 8, 100266. [Google Scholar]

26. Asghari, M., Fathollahi-Fard, A. M., Mirzapour Al-E-Hashem, S., Dulebenets, M. A. (2022). Transformation and linearization techniques in optimization: A state-of-the-art survey. Mathematics, 10, 283. [Google Scholar]

27. Ezugwu, A. E., Agushaka, J. O., Abualigah, L., Mirjalili, S., Gandomi, A. H. (2022). Prairie dog optimization algorithm. Neural Computing and Applications, 34, 20017–20065. [Google Scholar]

28. Wang, G. G., Deb, S., Cui, Z. (2019). Monarch butterfly optimization. Neural Computing and Applications, 31, 1995–2014. [Google Scholar]

29. Izci, D., Rizk-Allah, R. M., Snášel, V., Ekinci, S., Hashim, F. A. et al. (2023). A novel control scheme for automatic voltage regulator using novel modified artificial rabbits optimizer. e-Prime-Advances in Electrical Engineering, Electronics and Energy, 6, 100325. [Google Scholar]

30. Hu, G., Guo, Y., Wei, G., Abualigah, L. (2023). Genghis Khan shark optimizer: A novel nature-inspired algorithm for engineering optimization. Advanced Engineering Informatics, 58, 102210. [Google Scholar]

31. Ghasemi, M., Zare, M., Zahedi, A., Akbari, M. A., Mirjalili, S. et al. (2023). Geyser inspired algorithm: A new geological-inspired meta-heuristic for real-parameter and constrained engineering optimization. Journal of Bionic Engineering, 8, 1–35. [Google Scholar]

32. Wang, G. G. (2018). Moth search algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Memetic Computing, 10, 151–164. [Google Scholar]

33. Meng, Z., Qian, Q., Xu, M., Yu, B., Yıldız, A. R. et al. (2023). PINN-FORM: A new physics-informed neural network for reliability analysis with partial differential equation. Computer Methods in Applied Mechanics and Engineering, 414, 116172. [Google Scholar]

34. Li, S., Chen, H., Wang, M., Heidari, A. A., Mirjalili, S. (2020). Slime mould algorithm: A new method for stochastic optimization. Future Generation Computer Systems, 111, 300–323. [Google Scholar]

35. Yang, Y., Chen, H., Heidari, A. A., Gandomi, A. H. (2021). Hunger games search: Visions, conception, implementation, deep analysis, perspectives, and towards performance shifts. Expert Systems with Applications, 177, 114864. [Google Scholar]

36. Ahmadianfar, I., Heidari, A. A., Gandomi, A. H., Chu, X., Chen, H. (2021). RUN beyond the metaphor: An efficient optimization algorithm based on Runge Kutta method. Expert Systems with Applications, 181, 115079. [Google Scholar]

37. Tu, J., Chen, H., Wang, M., Gandomi, A. H. (2021). The colony predation algorithm. Journal of Bionic Engineering, 18, 674–710. [Google Scholar]

38. Ahmadianfar, I., Heidari, A. A., Noshadian, S., Chen, H., Gandomi, A. H. (2022). INFO: An efficient optimization algorithm based on weighted mean of vectors. Expert Systems with Applications, 195, 116516. [Google Scholar]

39. Su, H., Zhao, D., Heidari, A. A., Liu, L., Zhang, X. et al. (2023). RIME: A physics-based optimization. Neurocomputing, 532, 183–214. [Google Scholar]

40. Heidari, A. A., Mirjalili, S., Faris, H., Aljarah, I., Mafarja, M. et al. (2019). Harris hawks optimization: Algorithm and applications. Future Generation Computer Systems, 97, 849–872. [Google Scholar]

41. Gad, A. G. (2022). Particle swarm optimization algorithm and its applications: A systematic review. Archives of Computational Methods in Engineering, 29, 2531–2561. [Google Scholar]

42. Díaz-Manríquez, A., Toscano-Pulido, G., Gómez-Flores, W. (2011). On the selection of surrogate models in evolutionary optimization algorithms. 2011 IEEE Congress of Evolutionary Computation (CEC), pp. 2155–2162. New Orleans, LA, USA. [Google Scholar]

43. Ayesha, S., Hanif, M. K., Talib, R. (2020). Overview and comparative study of dimensionality reduction techniques for high dimensional data. Information Fusion, 59, 44–58. [Google Scholar]

44. Jia, H., Wen, Q., Wu, D., Wang, Z., Wang, Y. et al. (2023). Modified beluga whale optimization with multi-strategies for solving engineering problems. Journal of Computational Design and Engineering, 10, 2065–2093. [Google Scholar]

45. Vinod Chandra, S. S., Anand, H. S. (2022). Nature inspired meta heuristic algorithms for optimization problems. Computing, 104, 251–269. [Google Scholar]

46. Ajagekar, A., You, F. (2019). Quantum computing for energy systems optimization: Challenges and opportunities. Energy, 179, 76–89. [Google Scholar]

47. Zhou, J., Wang, C., Li, Y., Wang, P., Li, C. et al. (2017). A multi-objective multi-population ant colony optimization for economic emission dispatch considering power system security. Applied Mathematical Modelling, 45, 684–704. [Google Scholar]

48. Kaveh, A., Hamedani, K. B. (2022). Improved arithmetic optimization algorithm and its application to discrete structural optimization. Structures, 35, 748–764. [Google Scholar]

49. Dehghani, M., Montazeri, Z., Trojovská, E., Trojovský, P. (2023). Coati optimization algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowledge-Based Systems, 259, 110011. [Google Scholar]

50. Cui, Y., Geng, Z., Zhu, Q., Han, Y. (2017). Multi-objective optimization methods and application in energy saving. Energy, 125, 681–704. [Google Scholar]

51. Pawan, Y. N., Prakash, K. B., Chowdhury, S., Hu, Y. C. (2022). Particle swarm optimization performance improvement using deep learning techniques. Multimedia Tools and Applications, 81, 27949–27968. [Google Scholar]

52. Agushaka, J. O., Ezugwu, A. E., Abualigah, L. (2023). Gazelle optimization algorithm: A novel nature-inspired metaheuristic optimizer. Neural Computing and Applications, 35, 4099–4131. [Google Scholar]

53. Azizi, M., Talatahari, S., Gandomi, A. H. (2023). Fire hawk optimizer: A novel metaheuristic algorithm. Artificial Intelligence Review, 56, 287–363. [Google Scholar]

54. Naruei, I., Keynia, F. (2022). Wild horse optimizer: A new meta-heuristic algorithm for solving engineering optimization problems. Engineering with Computers, 38, 3025–3056. [Google Scholar]

55. Akbari, M. A., Zare, M., Azizipanah-Abarghooee, R., Mirjalili, S., Deriche, M. (2022). The cheetah optimizer: A nature-inspired metaheuristic algorithm for large-scale optimization problems. Scientific Reports, 12, 10953. [Google Scholar] [PubMed]

56. Xue, J., Shen, B. (2023). Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. The Journal of Supercomputing, 79, 7305–7336. [Google Scholar]

57. Das, A. K., Pratihar, D. K. (2022). Bonobo optimizer (BOAn intelligent heuristic with self-adjusting parameters over continuous spaces and its applications to engineering problems. Applied Intelligence, 52, 2942–2974. [Google Scholar]

58. Chopra, N., Ansari, M. M. (2022). Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Systems with Applications, 198, 116924. [Google Scholar]

59. Abualigah, L., Diabat, A., Mirjalili, S., Abd Elaziz, M., Gandomi, A. H. (2021). The arithmetic optimization algorithm. Computer Methods in Applied Mechanics and Engineering, 376, 113609. [Google Scholar]

60. Abualigah, L., Yousri, D., Abd Elaziz, M., Ewees, A. A., Al-Qaness, M. A. et al. (2021). Aquila optimizer: A novel meta-heuristic optimization algorithm. Computers & Industrial Engineering, 157, 107250. [Google Scholar]

61. Abualigah, L., Abd Elaziz, M., Sumari, P., Geem, Z. W., Gandomi, A. H. (2022). Reptile search algorithm (RSAA nature-inspired meta-heuristic optimizer. Expert Systems with Applications, 191, 116158. [Google Scholar]

62. Agushaka, J. O., Ezugwu, A. E., Abualigah, L. (2022). Dwarf mongoose optimization algorithm. Computer Methods in Applied Mechanics and Engineering, 391, 114570. [Google Scholar]

63. Oyelade, O. N., Ezugwu, A. E. S., Mohamed, T. I., Abualigah, L. (2022). Ebola optimization search algorithm: A new nature-inspired metaheuristic optimization algorithm. IEEE Access, 10, 16150–16177. [Google Scholar]

64. Bil, C. (2015). Multidisciplinary design optimization: Designed by computer. In: Concurrent engineering in the 21st century, pp. 421–454. Springer. [Google Scholar]

65. Lisicki, M., Lubitz, W., Taylor, G. W. (2016). Optimal design and operation of archimedes screw turbines using Bayesian optimization. Applied Energy, 183, 1404–1417. [Google Scholar]

66. Sbrugnera Sotomayor, N. A., Caiazzo, F., Alfieri, V. (2021). Enhancing design for additive manufacturing workflow: Optimization, design and simulation tools. Applied Sciences, 11, 6628. [Google Scholar]

67. Vanderplaats, G. N., Sugimoto, H. (1986). A General-purpose optimization program for engineering design. Computers & Structures, 24, 13–21. [Google Scholar]

68. Abualigah, L., Elaziz, M. A., Khasawneh, A. M., Alshinwan, M., Ibrahim, R. A. et al. (2022). Meta-heuristic optimization algorithms for solving real-world mechanical engineering design problems: A comprehensive survey, applications, comparative analysis, and results. Neural Computing and Applications, 4, 1–30. [Google Scholar]

69. Abd Elaziz, M., Oliva, D., Xiong, S. (2017). An improved opposition-based sine cosine algorithm for global optimization. Expert Systems with Applications, 90, 484–500. [Google Scholar]

70. Saremi, S., Mirjalili, S., Lewis, A. (2017). Grasshopper optimisation algorithm: Theory and application. Advances in Engineering Software, 105, 30–47. [Google Scholar]

71. He, Q., Wang, L. (2007). An effective co-evolutionary particle swarm optimization for constrained engineering design problems. Engineering Applications of Artificial Intelligence, 20, 89–99. [Google Scholar]

72. Huang, F. Z., Wang, L., He, Q. (2007). An effective co-evolutionary differential evolution for constrained optimization. Applied Mathematics and Computation, 186, 340–356. [Google Scholar]

73. Coello, C. A. C. (2000). Use of a self-adaptive penalty approach for engineering optimization problems. Computers in Industry, 41, 113–127. [Google Scholar]

74. Arora, J. S. (2004). Introduction to optimum design. Elsevier. [Google Scholar]

75. Mahdavi, M., Fesanghary, M., Damangir, E. (2007). An improved harmony search algorithm for solving optimization problems. Applied Mathematics and Computation, 188, 1567–1579. [Google Scholar]

76. Mezura-Montes, E., Coello, C. A. C. (2008). An empirical study about the usefulness of evolution strategies to solve constrained optimization problems. International Journal of General Systems, 37, 443–473. [Google Scholar]

77. Mirjalili, S., Lewis, A. (2016). The whale optimization algorithm. Advances in Engineering Software, 95, 51–67. [Google Scholar]

78. Sandgren, E. (1990). Nonlinear integer and discrete programming in mechanical design optimization. The Journal of Mechanical Design, 112, 223. [Google Scholar]

79. Mirjalili, S., Mirjalili, S. M., Lewis, A. (2014). Grey wolf optimizer. Advances in Engineering Software, 69, 46–61. [Google Scholar]

80. Mirjalili, S., Mirjalili, S. M., Hatamlou, A. (2016). Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Computing and Applications, 27, 495–513. [Google Scholar]

81. Liu, H., Cai, Z., Wang, Y. (2010). Hybridizing particle swarm optimization with differential evolution for constrained numerical and engineering optimization. Applied Soft Computing, 10, 629–640. [Google Scholar]

82. He, Q., Wang, L. (2007). A hybrid particle swarm optimization with a feasibility-based rule for constrained optimization. Applied Mathematics and Computation, 186, 1407–1422. [Google Scholar]

83. Kaveh, A., Talatahari, S. (2010). An improved ant colony optimization for constrained engineering design problems. Engineering Computations, 27, 155–182. [Google Scholar]

84. Ragsdell, K., Phillips, D. (1976). Optimal design of a class of welded structures using geometric programming. The Journal of Manufacturing Science and Engineering, 98, 1021. [Google Scholar]

85. Deb, K. (1991). Optimal design of a welded beam via genetic algorithms. AIAA Journal, 29, 2013–2015. [Google Scholar]

86. Lee, K. S., Geem, Z. W. (2005). A new meta-heuristic algorithm for continuous engineering optimization: Harmony search theory and practice. Computer Methods in Applied Mechanics and Engineering, 194, 3902–3933. [Google Scholar]

87. Kaveh, A., Khayatazad, M. (2012). A new meta-heuristic method: Ray optimization. Computers & Structures, 112, 283–294. [Google Scholar]