An Optimization Approach of IoD Deployment for Optimal Coverage Based on Radio Frequency Model

1  Introduction

Intelligent Transportation Systems (ITS) have gradually emerged as a leading technology for exploiting smart devices to improve transportation systems. It is proposed as a solution endowed with cutting-edge technological devices and has become an indispensable part of smart cities. Many applications, such as control analysis, sensing, communication technology, and post-disaster relief missions, have been enabled to improve mobility, efficiency, and security [1–4]. In such applications, the information is processed and shared to minimize environmental impact, address congestion, and enhance traffic management [5,6]. This technological development aims to improve smart cities’ infrastructure and distribute facilities and services that simplify human life. Furthermore, the overall transportation system automation cannot be achieved through vehicles automating only. Indeed, other components of the end-to-end transportation system and road also need to be automated using Unmanned Aerial Vehicles (UAVs), such as rescue teams, field support team, road surveys, and traffic police.

The coverage of interest region is becoming a hot research field due to the emergence of several coverage applications such as search and rescue in disaster application, environmental sensing, and traffic management [7].

Coverage problems with ground vehicles have been examined extensively in the literature [8,9]. However, harsh terrains can significantly limit the maneuverability of mobile ground vehicles. Several challenges have been faced due to the rapid growth of mobile-connected devices. One of the main challenges faced is the network coverage and capacity. Therefore, it is necessary to utilize smart object to enhance coverage.

The rapidly growing popularity of UAVs due to their unique features such as agility, mobility, flexibility, and quick deployment, offers salient attributes to today’s fixed infrastructure, including instant, flexible deployment and an extra degree of freedom for controlled mobility [10]. The UAV is already used in several applications, such as transportation systems in an accident scene reporting [11]. Moreover, a swarm of UAVs, or internet of drones (IoD), can navigate in remote, rough areas, which is difficult to access by humans [12,13]. Moreover, various UAVs are available for different applications, including fixed-wing and multi-rotor crafts, which are equipped with enhanced computational power and energy efficiency.

IoD can operate in an effective operation mode in which UAVs in IoD are highly coordinated to accomplish common missions. Additionally, IoD can accept many potential use cases in wireless networks. For instance, wireless capacity and coverage at hot spots or temporary events, such as outdoor events, can be enhanced by deploying IoD aerial base stations. Moreover, they can support disaster relief activities in public safety scenarios and enable communications when traditional terrestrial networks are damaged [14]. The IoD can be utilized in data-gathering applications by moving throughout the area, helping obtain objects’ locations, and supporting topological information in real-time. Furthermore, in the context of disaster applications, the formation of the IoD can leverage image capture and analysis capabilities to accurately represent affected areas. This enables the efficient rescue of both humans and animals, providing crucial assistance during critical situations [15].

IoD is widely used in environmental monitoring for various fields, such as search and rescue and surveillance operations. Drones are equipped with cameras and sensors, which make them the best choice for such applications. An example of collaboration of UAVs swarm deployment for traffic monitoring in a smart city is illustrated in Fig. 1.

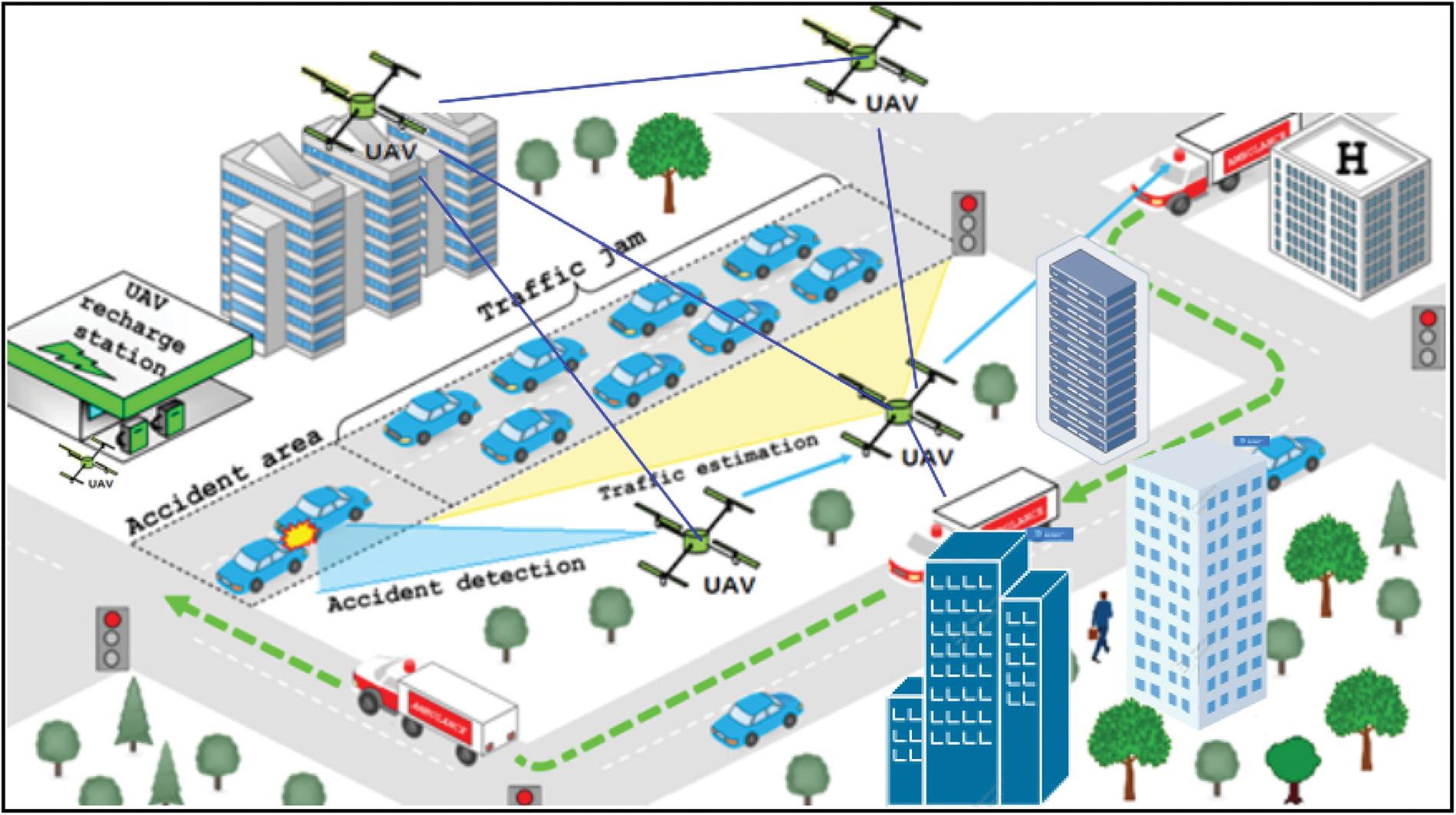
Figure 1: Collaboration of UAVs deployment for traffic monitoring of a smart city

Numerous approaches have been proposed to study IoD deployment for coverage problems. However, such deployment poses a daunting challenge. The Interference occurring between nodes within a network can significantly impact its performance that leads to corruption, data loss, and re-transmissions, resulting in increased latency. Another challenge is the deployment altitude. Although deploying an IoD at a high altitude offers improved LOS conditions, it also results in an increased distance between the IoD network and ground vehicles, leading to higher path loss.

To cope with the above challenges, we propose a multi-objective three dimension IoD deployment approach to optimally deploy IoD network into the most appropriate location such that the coverage of the target area is maximized. More importantly, the proposed algorithm analyzes the problem of signal interference and coverage quality simultaneously, and the drone’s signal interference is reduced while coverage quality is enhanced as much as possible. The goal is to minimize the impact of interference, support communication, and maximize the coverage. To achieve this goal, we apply the improved version of particle swarm optimization (IPSO).

The contribution of this work is a developing of a multi-objective 3D IoD deployment algorithm. This algorithm aims to achieve an optimal deployment of IoD by taking into account the 3D distribution of users on the ground. The primary objectives of the algorithm are to maximize the coverage area and minimize interference. To achieve this, the algorithm considers the specifications of the radio frequency model. Specifically, it takes into account the LOS and NLOS down-link coverage probability of drones in ground communication. By considering these factors, the algorithm can determine the most suitable deployment strategy for the IoD network. By optimizing the deployment based on user distribution and considering the RF model, the algorithm ensures that the coverage area is maximized, allowing for efficient communication and connectivity. Moreover, by minimizing interference, the algorithm enhances the overall performance and reliability of the IoD network.

It is important to consider the potential interference that can arise as the number of UAVs increases. As the number of UAVs, operating in close proximity to each other increases, the likelihood of interference between them also increases, which has a negative impact on the quality of coverage provided by the UAV network.

To tackle this issue, the proposed approach aim to maximize the coverage of the target region while minimizing the number of UAVs required. By achieving maximum coverage with the fewest possible UAVs, the interference between them can be minimized, that helps mitigate the degradation of coverage occurred due to interference.

The rest of this paper is organized as follows: Section 2 presents the state of the art. In Section 3, the Radio Frequency Propagation Model description is illustrated. Section 4 explains the Optimization Approach for Optimal Coverage. In Section 5, the simulation results and the corresponding analysis are discussed. Section 6 provides a discussion paragraph. Finally, the conclusions are drawn in Section 7.

2  State of the Art

Recently, several works have investigated the integration of UAVs and ground networks, i.e., UAV-assisted, to enhance the ground network performance, such as coverage of the target area which has been studied extensively in the literature, especially for circular sensing patterns of the agents [16]. In most of these approaches, areas of interest are partitioned based on a Voronoi or similar partitioning [17–20], use game theory, model predictive control, and distributed optimization [21,22]. Furthermore, area monitoring is studied in several works by Mobile Aerial Agents (MAAs) equipped with cameras [23]. In such pioneering research efforts, maximum allowable height by the MAAs is not allowed, and overlapping of their covered areas is considered an advantage as opposed to the same area viewed by a single camera.

The optimal placement of drones is investigated in different works in the literature [24–26]. The work in [26] applied multiple UAVs to detect dynamic objects on the ground. The aim was to obtain the optimal placement of UAVs that achieve the objective with minimum required UAVs. In [24], the placement problem of mobile and static drones is investigated by deriving a mathematical model for optimal drone placement formulation. Finally, the authors in [25] considered the optimal placement of drones. They assumed that sufficient drones are available to cover a set of mobile targets.

However, the previous studies did not considered the maximum coverage of application area for the drones.

In [27], the optimal location of drones deployed as base stations was presented in the area with different target densities. The aim was to obtain the minimum number of drones and their optimal 3D placement to serve all users. Further, in [28], the optimal locations for static drones were presented. The aim was to maximize the coverage of a target area. The optimal placement problem was solved for both uniformly and clustered targets. In [29], the area coverage problem was addressed by deploying a swarm of drones equipped with a directional antenna, i.e., a download-facing camera. All users in the sensing range were covered by deploying drones. To do so, the target area was partitioned using a partitioning algorithm, and the drone’s altitude was restricted by a new gradient based on control law. As a result, the local optimal configuration was achieved for the whole network, and the optimal coverage was achieved by controlling the drone altitude. However, these requirements increased the computational time and complexity.

Moreover, the work in [30] studied a similar problem and considered different criteria, such as customer satisfaction, number of UAVs, and total distance the drones navigated simultaneously. However, these works did not consider the optimal placement of drones.

Due to difficulties of deploying ground BSs in harsh and remote environments, the UAV-assisted has the potential to revolutionize many fields by providing connectivity and communication for ground users. In this case, UAV acts as wireless BS or RSU, especially when the capacity of terrestrial infrastructure is not sufficient. Therefore, to extend the coverage in such environments, UAVs-assisted can be utilized for this purpose.

The authors in [31] proposed a deployment strategy to provide better coverage for the ground users, where the UAVs acted as wireless base stations. The download coverage probability was defined as a function of the antenna gain and the UAV’s height. The objective was to calculate the 3D positions of UAVs that maximize the lifetime of drones, and achieve the maximum coverage for the whole region. However, the drone’s height should be defined based on the coverage requirement and the beamwidth of a directional antenna.

In [32], a UAV placement strategy was formulated as a maximization optimization problem. More specifically, throughput and coverage were optimized where the UAV’s memory constraint was considered. That is, the optimal location of the drone was achieved, and the optimal caching strategy was solved.

In [33], a Particles Swarm Optimization (PSO) was implemented to obtain the optimal placement of UAVs where the objective was to maximize the coverage area while the capacity of UAV was considered in the scope of public safety and disaster.

Furthermore, the researchers in [34] proposed an optimization approach to cover all targets on the ground while minimizing the dissatisfaction data rate between end devices and their communication services using the available number of UAVs.

The work in [35] proposed a coverage path planning algorithm to fully cover a region of interest with minimum energy consumption. The problem was formulated as an optimization problem and solved using exact and approximate solutions. The work considered single and multiple UAVs. The optimal allocation of the sub-region was assigned to appropriate UAVs so that the energy consumption was minimized. The proposed approach also considered a number of turns in the optimization to reduce energy consumption, reducing the required number of drones to cover the area of interest.

In [36], the optimal UAVs flight path was obtained using multi-objective bio-inspired algorithms. In addition, different objectives were included, such as sensing ability, energy consumption, flight time, and associated risk. Moreover, the authors in [37] proposed using the available UAVs to obtain their optimal heights in a 3D environment. More specifically, the objectives to be optimized were the quality of Service (QoS), energy consumption, and target coverage. The connectivity of UAVs was maintained using a grid-based connectivity network. Additionally, the drones’ altitudes were optimized for generating a near-optimal height to cover the target devices and achieve minimum energy consumption of transmitted data and QoS. In urban terrain, the communication and movement of the vehicles are constrained by buildings and infrastructures [38].

The use of drones as flying RSUs can greatly enhance VANET connectivity, as they have the ability to fly at high altitudes beyond terrestrial infrastructures. This allows UAVs to move with less interference from terrestrial constraints, resulting in fewer obstacles affecting its transmission. In [39], the UAVs were deployed to detect the incidents on the urban road. Moreover, UAVs’ deployment aimed to provide vehicle emergency guidance. Besides, a hybrid of drone and ad-hoc networks was designed to reduce the end-to-end delay among cars [40].

In [41], a novel IoD collaborative communication approach has been proposed to improve the communication of the VANET network. The UAVs are optimally deployed to maximize the coverage area and enhance the quality of the received signal. Although the proposed approach achieves an optimal value of coverage area, the simulation is conducted in a flat area, and the impact of high-level terrain is neglected. Then, this work was extended in [42] by proposing a 3D simulation model for the IoD network in the air and the VANET network in the ground to improve the communication of the VANET network. The UAVs are optimally deployed to maximize the coverage area and enhance the quality of the received signal. Furthermore, the Digital elevation model was applied to extract the terrain elevation, and then the impact of high-level terrain was considered. The proposed approach achieved an optimal coverage area value reflecting more realistic results. The work in [43] proposed a UAV-assisted VANET for safety application in Intelligent Transportation Systems (ITS). The challenge to traditional VANET was highlighted. A highway scenario was considered in the simulation. A vehicle’s velocity, density, and road length were analyzed in a highway.

The impacts of a minimum number of drones on coverage quality were studied in [44], where the drones were deployed using a proposed greedy algorithm. In [45], a decentralized deployment approach of UAV-BSs was proposed based on Voronoi partitioning. According to the neighboring UAV-BSs and the measured information about the users, each UAV-BS is able to determine its movement that quickly achieved the local optimum of user coverage. To maximize the number of covered users, an efficient 3D placement method for drone-BS using the minimum required transmit power was proposed in [46]. However, the optimal drone deployment in these works was achieved by only considering signal coverage.

For further optimizing the deployment, the connectivity of the drones’ network has been considered to make deployment more reasonable. In [47], the drone allocation problem was solved to boost capacity and improve coverage by formulating a neural-based cost function approach. Further, the coverage was improved, and network capacity was increased in some recent algorithms [48–50]. However, the interference effects among drones were not considered.

Although the surveyed algorithms have achieved the deployment of a drone to a certain extent, they rarely consider signal interference and coverage at the same time.

Our proposed mechanism aims to design an IoD-assisted to boost ground communication performances. The aim is to maximize the coverage of a target area and reduce the interference between adjacent UAVs as much as possible at the same time. To achieve these objectives, an optimization approach, IPSO, is implemented to dispatch the interconnected IoD network into the optimal location so that the coverage of the target area is maximized and the the interference between neighboring drones is minimized.

3  Radio Frequency Propagation Model

Two propagation links can be defined for UAV-to-ground communication. The first propagation link includes LOS and NLOS, while the second link has no LOS, but the ground nodes can be covered by diffraction and reflection from the main signal. As shown in Fig. 2, the transmitted signal by UAV is propagated in the space till hitting the urban area, where the signal suffers from scattering and shadowing problems due to buildings and other distributing things in the region. Therefore, the UAV-to-ground link suffers from loss. The Doppler shift effect that results from the mobility of UAVs is assumed to be perfectly adjusted.

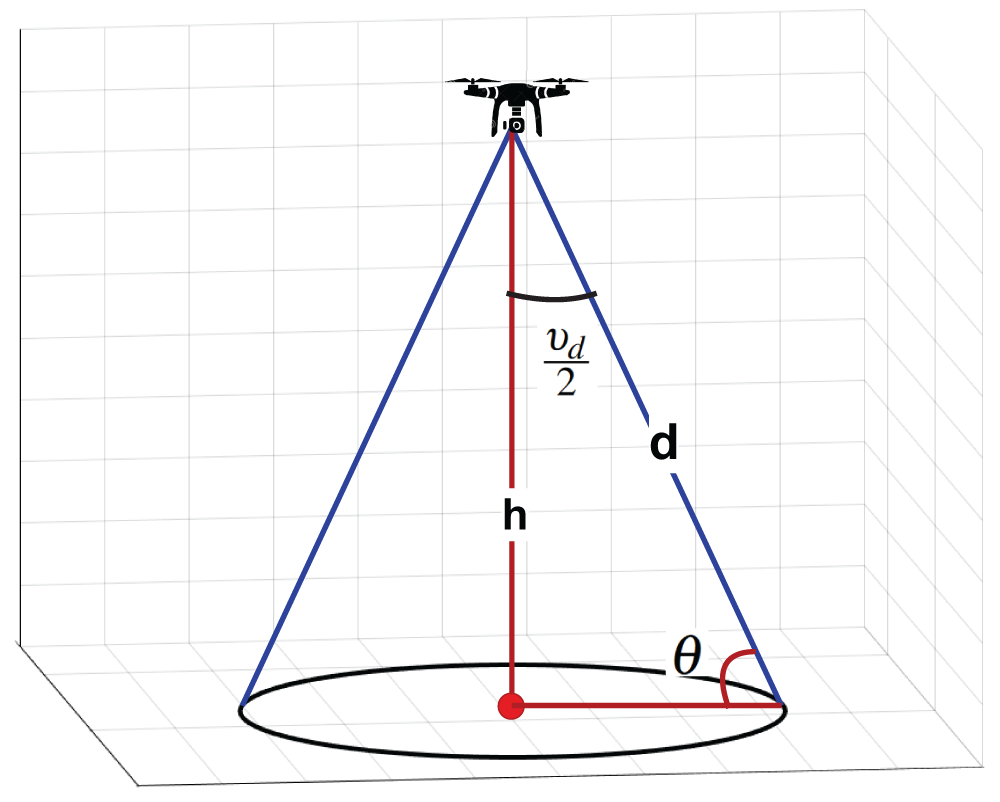
Figure 2: Deployment of UAV at h altitude

Notably, UAVs in the target area share comparable attributes such as identical transmission power and are strategically positioned. Each UAV has a directional antenna equipped for sensing tasks, with a fixed beam angle υd measured in degrees.

The gain can be calculated as in [51] as follows:

Gain={29000υd2−υd2≤ϕ≤υd2,1sin2(3π2(N0))otherwise(1)

where 29000υd2 is the main lobe gain of directional antenna, 1sin2(3π2(N0)) is the side lobe gain, ϕ is the sector angle, and N0 represents the number of antennas equipped in a drone. The scattering and shadowing effect in NLOS is higher than that in LOS. The received signal power at any user u from drone k can be defined based on [52] as follows:

Pu,k={Ptx+G0−PLdB−ζ1,LOS link,Ptx+G0−PLdB−ζ2,NLOS link,(2)

PLk=(4πfcdkv)α,(3)

σLOS=α1e−α2θk,σNLOS=β1e−β2θk,(4)

PLOS=α(180πθk)γ,(5)

PNLOS=1−PLOS.(6)

4  Optimization Approach for Optimal Coverage

This section explains our optimization based on the coverage probability function. We also describe how to solve the deployment problem with less power and interference requirements to achieve maximum coverage. Each UAV movement in IoD aims to maximize the overall coverage of a target area. Specifically, each UAV updates its location by exploring the space each iteration. The optimal value can represent the total coverage of the target region.

4.1 Coverage and Interference Model

The coverage model is responsible for finding the coverage ratio of drones in the target area. The model is also responsible for reflecting the interference effect among UAVs and considers it to optimize IoD deployment. It has to be stressed that the interference can be reduced by increasing the distance between drones. In general, signal interference is unavoidable due to the limited distance and frequency channels. Hence, to optimize IoD deployment, the drone signal interference needs to be considered.

Let the projection points of all drones denoted by Pr, and locations of all users in the target area, denoted by Loc be represented as follows:

Pr=(pr1,pr2,pr3,…,prn).Loc=(Loc1,Loc2,…,Locm).(7)

Then, the collection of all users within a coverage radius (CR) of drone i is represented as

S(Loc)=Loc|D(Loc,Pri)<=CR,(8)

where CR is the coverage radius of dronei, and D(Loc,Pri) is the distance between Loc and projection point Pri.

The coverage and interference model can be defined as follows: Let Pm be the minimum received power which can be defined as

Pm=10log(βN+βI).(9)

which is a function of signal to interference and noise ratio (β), noise power (N), and the mean interference (I) from the closest drones.

The mean interference effects can be obtained based on [31] by Eq. (10).

f(UAVi,UAVj)=Ptx(1sin(3π2(N0)))(10−μLOS10∗PLOSm+10−μNLOS10∗PNLOSm)x(4πfcdkv)−n0,(10)

The total interference in drone i from other drones can be computed as in Eq. (11).

ΓTotal=∑j∈[1,IoD],j≠if(UAVi,UAVj)(11)

The coverage probability can be evaluated by Eq. (12).

Pcov=PLOSkQ(pm+PL−ptx−G0−μLOSσLOS)+PNLOSkQ(pm+PL−ptx−G0−μNLOSσNLOS),(12)

From Eq. (12), the coverage probability changes directly as the drone altitude changes due to changing the elevation angle, which in turn changes PLOS, PNLOS, sensing radius, and distance. It is worth mentioning that flying at high altitudes increases LOS conditions and path loss. Moreover, the interference increases as drones fly close to each other. Therefore, the transmission power should be adjusted to achieve the best coverage and less interference.

Based on the coverage probability function, the coverage value of each block (b) can be defined by the following formula:

Covb,IoD=(1−∏k∈IoD(1−Pcov(b,k)))(13)

Then the overall coverage over the whole region is determined using

TCovIoD=(∑b∈[1:m](Covb,IoD))(14)

The proposed approach aims to maximize the coverage of a target region by an interconnected IoD network and minimize the interference between adjacent UAVs simultaneously.

In coverage problems, obtaining the best location for the IoD network by trying all possibilities consumes many resources and time because the coverage problem is an NP-hard problem and cannot be solved in a reasonable time. To deal with such problem, a sophisticated solution is provided using a meta-heuristic approach where the iterative manner is used to search for the optimal solution. Among population-based algorithms, an improved version of PSO implemented in [13] is utilized to efficiently dispatch the IoD network into the best location to maximize a target region’s coverage.

4.2 Problem Formulation

In IoD deployment, the interference increases when the number of deployed drones increases, resulting in bad quality of communication. On the other hand, deploying a few drones cannot satisfy the coverage demand. So, obtaining the optimal deployment of IoD can be achieved by maximizing the overall coverage.

The problem can be formulated as a maximized multi-objective optimization problem as follows:

Γoptimal=max∑b∈[1:m](Covb,IoD),(15)

Subject to

Pr∈R2,(16)

HD(Pri,Prj)>IRi≠j,(17)

where IR is interference range, R2 is coverage area, and HD is the horizontal distance between projection of UAVi and UAVj. The constraint in Eq. (16) ensures the projection of all UAVs are inside the coverage area defined by R2. The constraint in Eq. (17) prevents the interference between UAVi and UAVj.

4.3 IPSO for Optimal Coverage

This section describes optimizing the IoD deployment and the optimization approach used. In this work, we implement IPSO, developed in [41], which represents an enhanced version of standard PSO in which the rapidity and optimality of the PSO are improved, which lead to avoiding trapping in local optima and obtaining the global optima in a more accurate and faster way. The objective function evaluates the generated solution based on the coverage probability function. The optimal value can represent the overall coverage of the target region.

The proposed optimization approach for optimal coverage using IPSO is explained in Algorithm 1. It starts with the initial part that is responsible for initializing RF as well as IPSO parameters. The initial locations of IoD are also generated in this part. Next, the algorithm receives environment constraints, i.e., boundary, cell size (block size), and RF parameters, and returns the optimal coverage. Then, the algorithm procedure starts by updating IPSO parameters, and the locations of IoD are evolved with iterations and then evaluated using the objective function that returns the coverage for all populations. Afterwards, the best coverage is stored, and the IoD locations are updated.

The objective function, Obj_Fun, is used to evaluate the coverage. The function takes the current positions of the UAVs and the radio frequency model, RF model, as inputs and returns the corresponding coverage value (Coveragei) which represents the normalized coverage value of the region using the set of UAVs based on a given RF parameters. The objective function can be summarized as follow: it recessives the current location of IoD nodes and RF model specifications as input. then, the overall interference is obtained using Eqs. (10) and (11), respectively. Afterward, the coverage probability is determined by Eq. (12). The coverage of each block, b, is then calculated by Eq. (13). Finally, the overall coverage of the area is obtained by Eq. (14).

5  Simulation Results and Discussion

This section will explain the effectiveness of the proposed optimization approach according to optimal coverage. The network is first described, then the results of performance metrics are explained. The simulation is repeated 100 times, and the normalized coverage and other parameters are calculated. Without loss of generality and to simplify the analysis of coverage performance, the coverage is normalized to unity. The simulation is conducted in Matlab on PC with a Core i7 CPU, 2.5 GHz, and 3 GB Ram.

5.1 Simulation Parameters Settings

The simulation parameters used throughout this work are abstracted in Table 1. The geographical range is 10000 m × 10000 m. Ten UAVs are randomly distributed in a square region as initial locations. The area is divided into 100 × 100 cells to find the covered cells by each UAV at any time. We assumed that information about the region was known in advance. The communication network parameters are illustrated in Table 1. These specifications listed in Table 1, and other needed setting based on the following researches [31,53–55].

5.2 Optimal Coverage

In this work, the simulation of the coverage problem is demonstrated over a target region without failure and with no obstacles between drones. Then, the effectiveness of the drones cooperative network using our proposed optimization approach is investigated.

We demonstrate the normalized coverage with respect to iterations using varying numbers of drones, ranging from 2 to 10 UAVs. These drones are randomly distributed at a fixed altitude. The transmission power for the drone is set to 30 dBm. Results of normalized coverage with respect to a number of iterations are illustrated in Fig. 3.

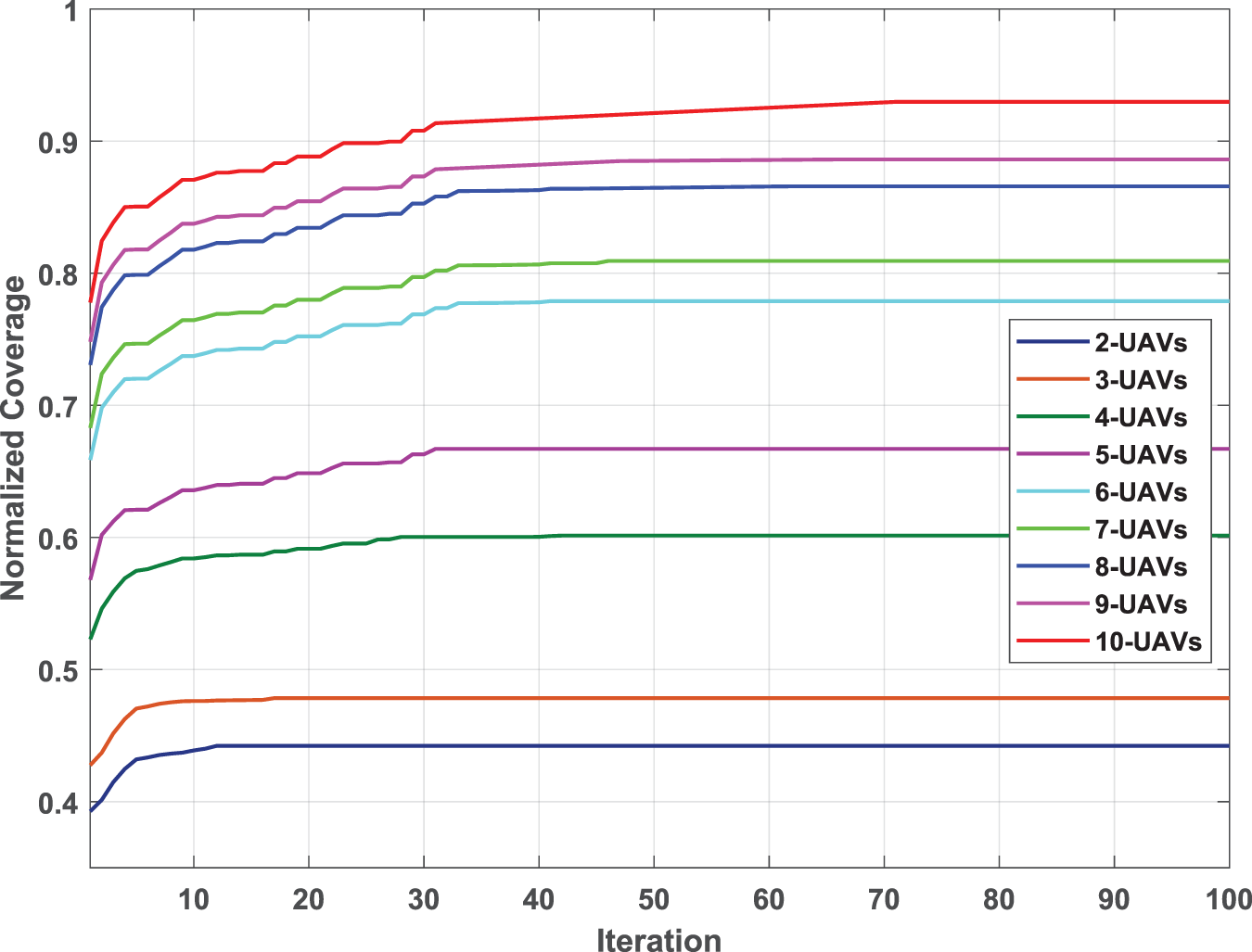
Figure 3: The average normalized coverage with respect to iteration for different IoD sizes

It can be noticed that the coverage region increases as the number of UAVs increases with the same transmission power, demonstrating the impact of UAVs on optimal coverage. However, the interference and overlap region might increase as the number of UAVs increases. To cope with such a problem, we minimize the interference problem by maintaining a sufficient safety distance between drones equal to or greater than the sum of their sensing radius. In Fig. 3, the coverage is enhanced with iteration until it reaches the maximum coverage at the end of iteration for all UAVs.

The Fig. 3 also shows that the needed iterations to reach the steady state for 2-UAVs is less than that in 3-UAVs and other scenarios, while the coverage in the 10-UAVs scenario is the highest compared with other scenarios.

5.3 Impact of Transmission Power on Optimal Coverage

To further investigate the proposed optimization approach’s performance, we study the effectiveness of power transmission on optimal coverage. Fig. 4 exhibits the normalized coverage vs. iterations with different transmission power (20, 30, 35, and 40 dBm). As such, the impact of power transmission on coverage is examined, where coverage is observed to improve continuously with increased transmission power as expected.

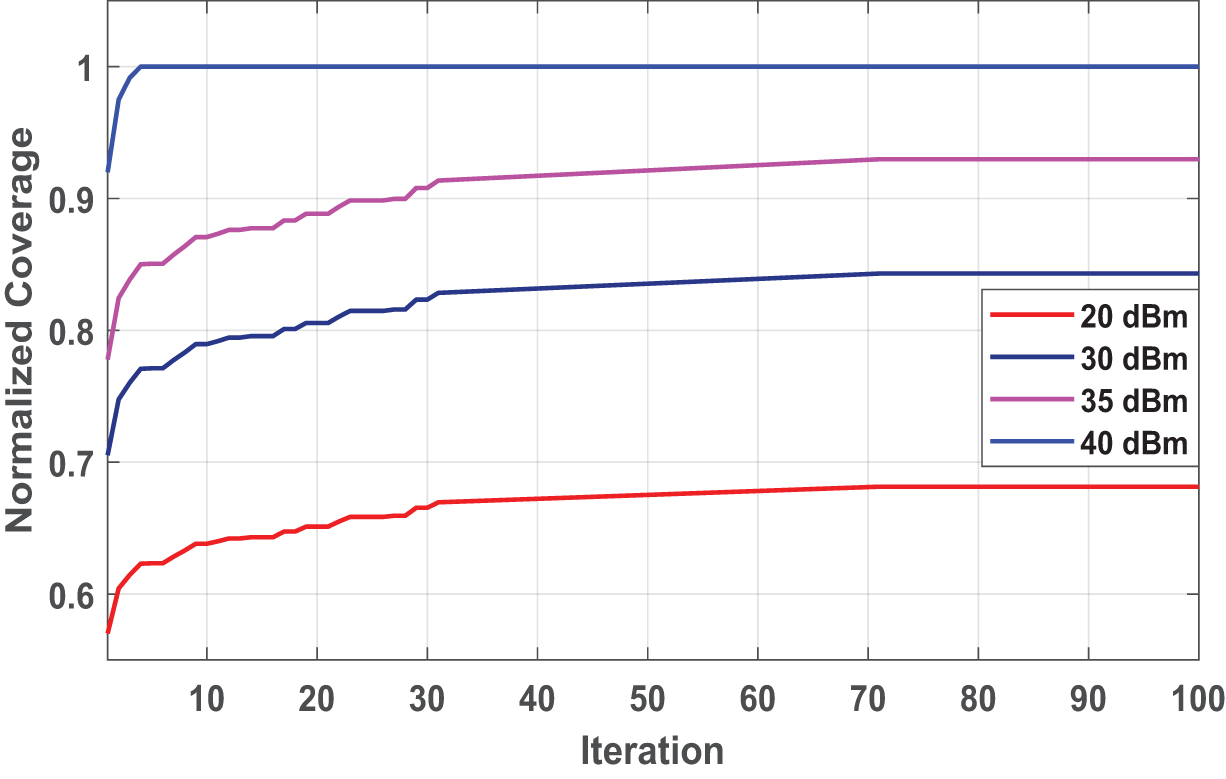
Figure 4: The average normalized coverage with respect to iteration for different transmission power

It is clear from the figure that the higher the transmitting power, the wider the range, which leads to covering a larger number of users and improving overall coverage. The coverage starts with a small value and continues to increase until it reaches a steady state, which represents the maximum coverage. It is important to stress that increasing the transmission power also increases the interference between adjacent UAVs. Therefore, the UAVs must maintain a sufficient distance from each other.

5.4 Comparison with Other Approach

We compare our optimization approach against non game-based CVACA presented in [56] and game-based approach [21]. We select the method illustrated in [56] and [21] due to their simplicity and ease of implementation compared with other approaches discussed in the literature. Also, the proposed approach and the these approaches depend on the download-facing camera, i.e., directional antenna, to achieve the required coverage. Moreover, the UAV’s angle sector and altitude are the variables that can be adjusted to achieve optimal coverage. Table 2 illustrates the parameters setting for compassion.

The maximum normalized coverage with respect to number of iterations is the main performance metric utilized in the comparison for 100 iterations. UAVs are randomly distributed in multilevel networks. Each UAV tries to adjust its location to maximize the overall coverage and minimize interference between adjacent drones. The normalized coverage is enhanced with iteration till it reaches the maximum coverage at the end of iterations for all UAVs. We record the maximum coverage for all approaches, and the results are shown in Figs. 5 and 6.

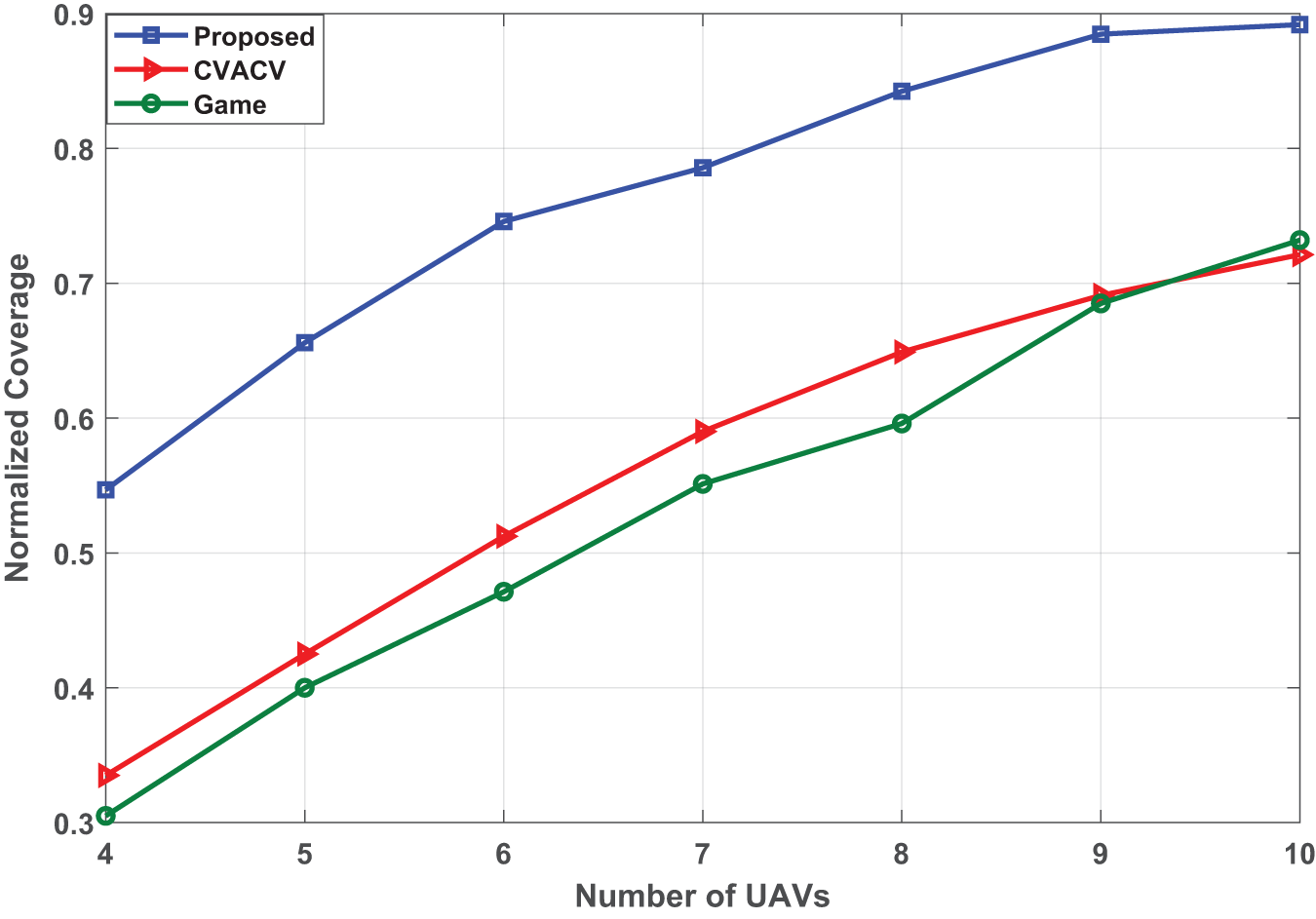
Figure 5: The average normalized coverage with respect to number of UAVs for the proposed approach and both CVACA and game approaches

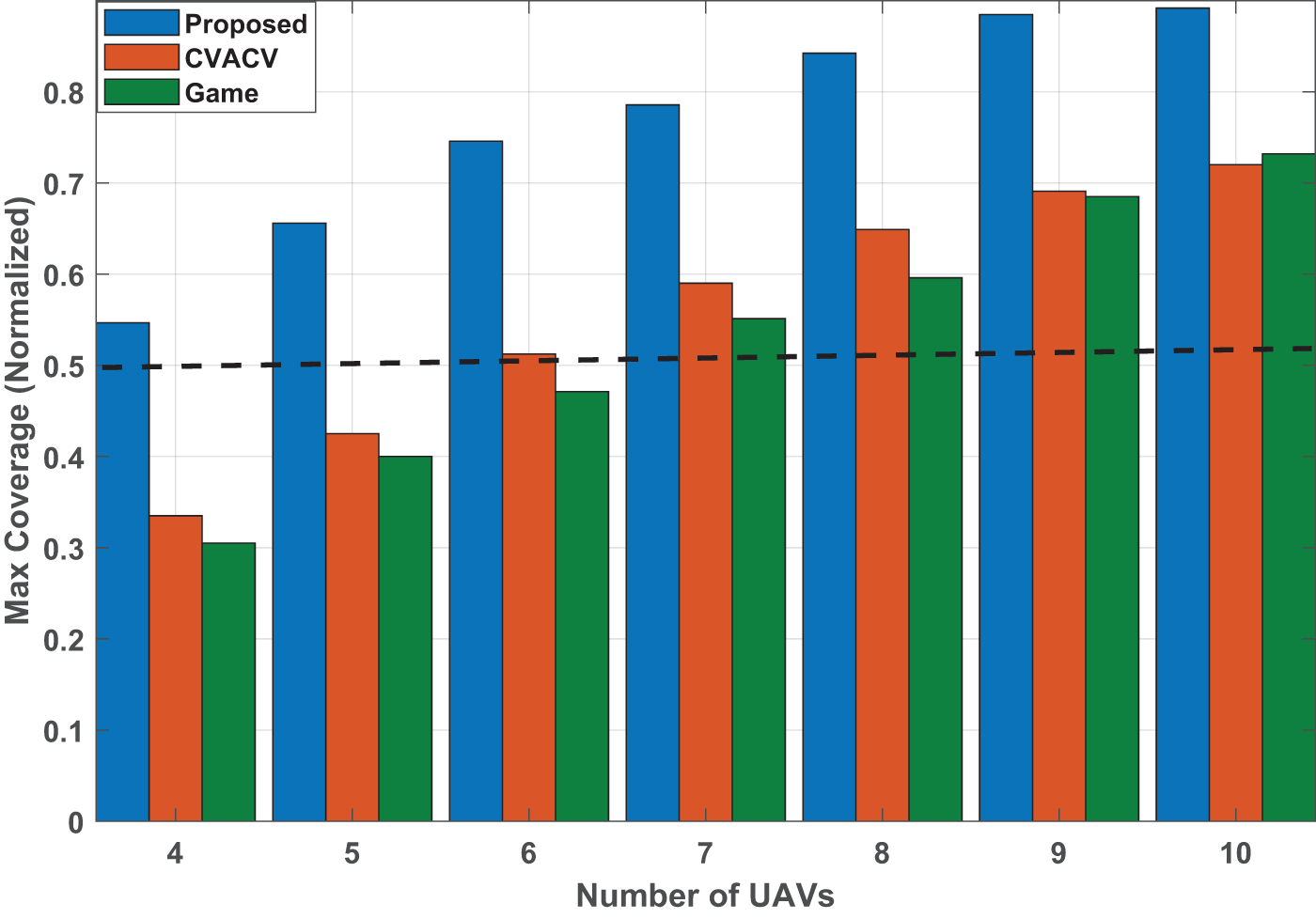
Figure 6: The maximum average normalized coverage with respect to number of UAVs for proposed and both CVACA and game approaches

As illustrated in Fig. 5, the optimal coverage increases as the number of UAVs increases. The optimal coverage is low at the beginning when the available UAVs are 4 UAVs, and it is improved as IoD size increases. This advantage tends to grow at a higher rate in our proposed approach than that in CVACA and game approach. The normalized coverage observed in Fig. 6 for the CVACA and game approaches is in [0.33 0.72], and [0.301 0.73] for 4-UAVs and 10 UAVs, respectively. For 4-UAVs and 5-UAVs, the maximum coverage cannot reach an acceptable value, which is less than 0.5, where the communication model cannot achieve the communication demand. For other scenarios [6, 7, 8, 9, 10] UAVs, the normalized coverage is greater than 0.5, which can be considered acceptable in some practical scenarios. However, our proposed optimization approach achieves normalized coverage greater than acceptable coverage for all UAV scenarios.

To further investigate the effectiveness of the proposed approach, we study the normalized coverage and the needed iterations to achieve the optimal coverage with respect number of UAVs that achieve the acceptable coverage, and the result is exhibited in Fig. 7.

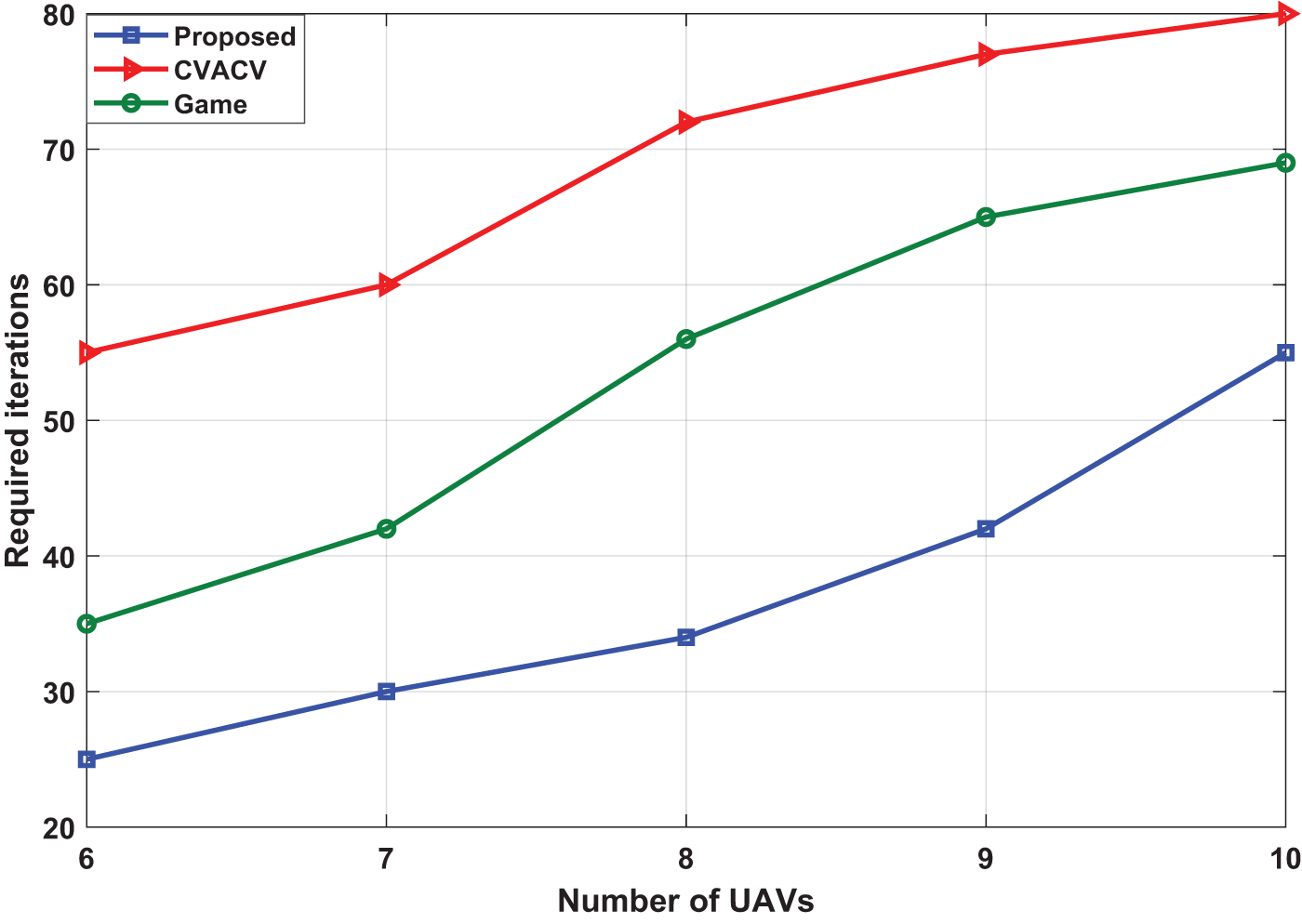
Figure 7: Required iterations to reach the optimal coverage for the proposed approach and both CVACA and game approaches

The number of iterations required to achieve optimal coverage depends on various factors, such as the size of the area being covered, algorithm being employed, etc. The process of optimizing coverage involves iteratively adjusting the deployment of IoD until the desired level of coverage is achieved. Each iteration involves collecting data on the current level of coverage, analyzing the data to identify areas of low coverage, and making adjustments to improve coverage. The number of iterations is a metrics that can be used to evaluate the algorithm. The needed number of iterations for the proposed approach and both CVACA and game to reach the optimal coverage is illustrated in Fig. 7. The figure shows that our proposed approach provides fewer iterations to achieve optimal coverage.

5.5 Effect of Noise on RF Model Performance

To assess the robustness of the proposed RF model, we have considered two distinct ranges of noise: range1 spanning from −120 to −90 dBm, and range2 spanning from −90 to −70 dBm for different numbers of UAVs. Results are illustrated in Figs. 8 and 9 for range1 and range2, respectively. The figures show the normalized coverage with respect to the number of UAVs for different noise power in both controlled and uncontrolled environments. It can be observed that the RF model demonstrates higher resilience in the presence of noise within range1. Noise levels within this range do not significantly impact the performance of the RF model, and the normalized coverage remains nearly unchanged in controlled and uncontrolled environment. However, as noise levels increase to range2, i.e., ranging from −90 to −70 dBm, the performance of the RF model is noticeably affected, resulting in a degradation of the normalized coverage. These results suggest that noise falling within this range has a significant influence on the RF model’s performance.

Figure 8: Normalized coverage with respect to number of UAVs for different nois power in range −120 to −90 dBm

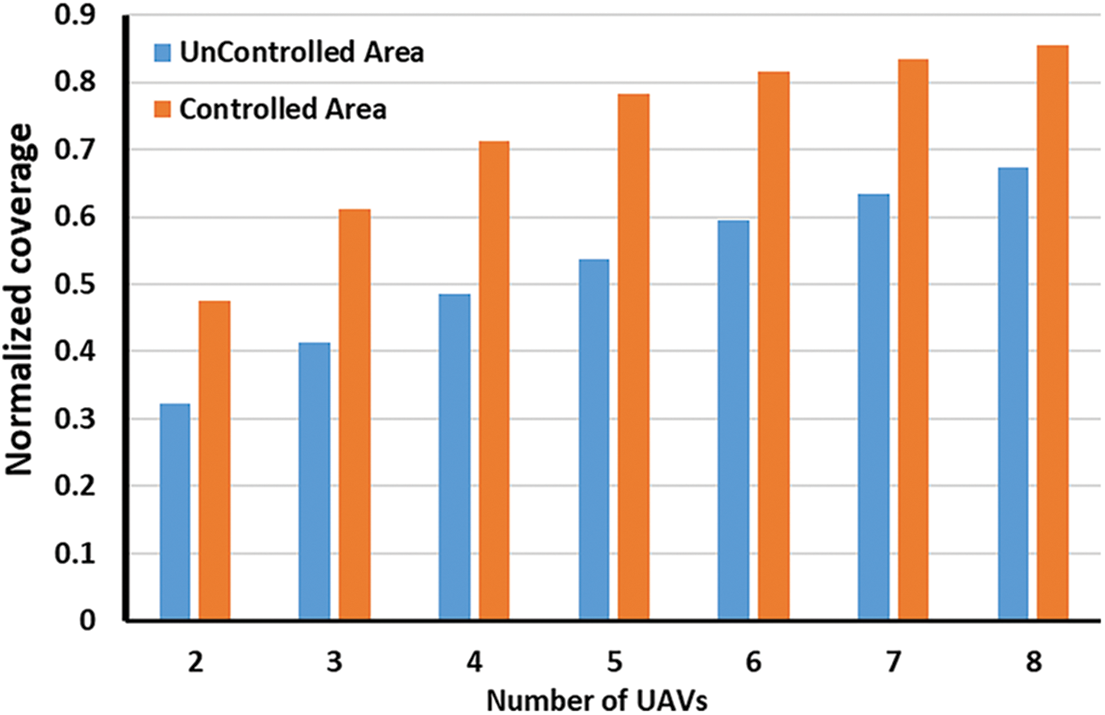
Figure 9: Normalized coverage with respect to number of UAVs for different nois power in range −90 to −70 dBm

6  Discussion and Remark

This part discuss the advantages of our proposed approach on other approaches. The proposed optimization approach based on IPSO outperforms both game and non-game approaches for area maximization due to its ability to efficiently and effectively explore the search space. The reason behind that is the IPSO used in the proposed approach effectively combines the advantages of swarm intelligence and optimization techniques to efficiently explore the search space and find optimal solutions. Compared with game approach, IPSO focuses on finding the best possible solution without the complexities introduced by strategic interactions among multiple players. While game-theoretic approaches may capture the dynamics of competition or cooperation, they can be computationally intensive and may not guarantee the globally optimal solution. The CVACA tries to use the maximum sensing radius for each UAV while avoiding the overlapping problem with the neighboring UAVs. Consequently, in smaller networks, this objective can be achieved quickly. However, as the number of UAVs increases, the overlapping region also expands proportionally, resulting in a greater number of required iterations to achieve optimal coverage without any overlap.

7  Conclusion

In this paper, we developed an efficient autonomous decision-making approach based on an optimization strategy. The proposed approach could efficiently dispatch the IoD network to the most appropriate location to maximize overall coverage and minimize interference between drones. All specifications of the RF model were considered for LOS and NLOS down-link coverage probability of drones regarding ground communication. Furthermore, the proposed approach’s mathematical formulation model and simulation experiment were presented. The simulation results showed that the proposed approach provided a fast convergence and maximum coverage based on the RF model and altitude value using minimum power transmission. Finally, we compared our approach against CVACA and game-based approaches, and the results showed that our proposed approach provided higher coverage, could deploy the IoD into the most appropriate location, and showed faster convergence as it needed fewer iterations to reach the optimal coverage.

As a future work, we plan to extend this work by studying the effect of different antenna configurations on area coverage. Furthermore, some factors like weather conditions, regulatory constraints, and hardware limitations will be considered to study their inference on the proposed cooperative approach. Also, we plan to study the energy consumption metric of the UAV assisted network using this optimization approach.

Acknowledgement: Authors at KFUPM would like to acknowledge the support received under University Funded Grant # INML2300. The author at Hasselt University acknowledges the support received from Special Research Fund (BOF) under Grant # BOF23KV17.

Funding Statement: This research was funded by Project Number INML2104 under the Interdisciplinary Center of Smart Mobility and Logistics at King Fahd University of Petroleum and Minerals. This study also was supported by the Special Research Fund BOF23KV17.

Author Contributions: The authors confirm contribution to the paper as follows: (1) Derive the RF model: Tarek Sheltami, Gamil Ahmed; (2) Formulate the deployment problem, Design of objective and constraints: Tarek Sheltami, Gamil Ahmed; (3) Implementing of IPSO for IoD deployment: Gamil Ahmed (4) Analysis and interpretation of results: Tarek Sheltami, Gamil Ahmed, and Ansar Yasar; (5) Draft manuscript preparation: Tarek Sheltami, Gamil Ahmed. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors did not use any data or materials.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Liu, Y., Xie, J., Xing, C., Xie, S. (2022). Access control and deployment design for multi-uav assisted wireless networks. IEEE Wireless Communications Letters, 11(11), 2380–2384. [Google Scholar]

2. Huang, H., Savkin, A. V., Ni, W. (2021). Navigation of a UAV team for collaborative eavesdropping on multiple ground transmitters. IEEE Transactions on Vehicular Technology, 70(10), 10450–10460. [Google Scholar]

3. Panahi, F. H., Panahi, F. H. (2023). Reliable and energy-efficient UAV communications: A cost-aware perspective. IEEE Transactions on Mobile Computing, (1), 1–12. [Google Scholar]

4. Ye, Z., Wang, K., Chen, Y., Jiang, X., Song, G. (2022). Multi-UAV navigation for partially observable communication coverage by graph reinforcement learning. IEEE Transactions on Mobile Computing, 22(7), 4056–4069. [Google Scholar]

5. Narang, N. K. (2023). Mentor’s musings on the role of standards in improving the privacy, trust and reputation management in Internet of Vehicles (IoV). IEEE Internet of Things Magazine, 6(2), 18–23. [Google Scholar]

6. Sheikh, M. S., Peng, Y. (2022). A comprehensive review on traffic control modeling for obtaining sustainable objectives in a freeway traffic environment. Journal of Advanced Transportation, 2022, 1–22. [Google Scholar]

7. Liu, X., Li, Z., Zhao, N., Meng, W., Gui, G. et al. (2018). Transceiver design and multihop D2D for UAV IoT coverage in disasters. IEEE Internet of Things Journal, 6(2), 1803–1815. [Google Scholar]

8. Abubakar, A. I., Mollel, M. S., Onireti, O., Ozturk, M., Ahmad, I. et al. (2023). Coverage and throughput analysis of an energy efficient uav base station positioning scheme. Computer Networks, 232, 109854. [Google Scholar]

9. Abd El-Malek, A. H., Aboulhassan, M. A., Salhab, A. M., Zummo, S. A. (2023). Performance analysis and optimization of UAV-assisted networks: Single UAV with multiple antennas versus multiple uavs with single antenna. IEEE Systems Journal, 17, 3468–3479. [Google Scholar]

10. El-Ferik, S. (2020). Biologically based control of a fleet of unmanned aerial vehicles facing multiple threats. IEEE Access, 8, 107146–107160. [Google Scholar]

11. Liu, Y., Bai, B., Zhang, C. (2017). UAV image mosaic for road traffic accident scene. 2017 32nd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Hefei, China, IEEE. [Google Scholar]

12. Boccadoro, P., Striccoli, D., Grieco, L. A. (2021). An extensive survey on the internet of drones. Ad Hoc Networks, 122, 102600. [Google Scholar]

13. Ahmed, G., Sheltami, T., Mahmoud, A., Yasar, A. (2020). Iod swarms collision avoidance via improved particle swarm optimization. Transportation Research Part A: Policy and Practice, 142, 260–278. [Google Scholar]

14. Ahmed, G., Sheltami, T., Deriche, M., Yasar, A. (2021). An energy efficient iod static and dynamic collision avoidance approach based on gradient optimization. Ad Hoc Networks, 118, 102519. [Google Scholar]

15. Micheletto, M., Petrucci, V., Santos, R., Orozco, J., Mosse, D. et al. (2018). Flying real-time network to coordinate disaster relief activities in urban areas. Sensors, 18(5), 1662. [Google Scholar]

16. Cortes, J., Martinez, S., Bullo, F. (2005). Spatially-distributed coverage optimization and control with limited-range interactions. ESAIM: Control, Optimisation and Calculus of Variations, 11(4), 691–719. [Google Scholar]

17. Cortes, J., Martinez, S., Karatas, T., Bullo, F. (2004). Coverage control for mobile sensing networks. IEEE Transactions on Robotics and Automation, 20(2), 243–255. [Google Scholar]

18. Stergiopoulos, Y., Tzes, A. (2010). Convex voronoi-inspired space partitioning for heterogeneous networks: A coverage-oriented approach. IET Control Theory & Applications, 4(12), 2802–2812. [Google Scholar]

19. Arslan, O., Koditschek, D. E. (2016). Voronoi-based coverage control of heterogeneous disk-shaped robots. 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, IEEE. [Google Scholar]

20. Das, S., Ahuja, N. (1990). Active stereo based surface reconstruction. Proceedings. 5th IEEE International Symposium on Intelligent Control 1990, Philadelphia, PA, USA, IEEE. [Google Scholar]

21. Nemer, I. A., Sheltami, T. R., Mahmoud, A. S. (2020). A game theoretic approach of deployment a multiple UAVs for optimal coverage. Transportation Research Part A: Policy and Practice, 140, 215–230. [Google Scholar]

22. Nguyen, M. T., Maniu, C. S. (2016). Voronoi based decentralized coverage problem: From optimal control to model predictive control. 2016 24th Mediterranean Conference on Control and Automation (MED), Athens, Greece, IEEE. [Google Scholar]

23. Schwager, M., Julian, B. J., Angermann, M., Rus, D. (2011). Eyes in the sky: Decentralized control for the deployment of robotic camera networks. Proceedings of the IEEE, 99(9), 1541–1561. [Google Scholar]

24. Zorbas, D., Pugliese, L. D. P., Razafindralambo, T., Guerriero, F. (2016). Optimal drone placement and cost-efficient target coverage. Journal of Network and Computer Applications, 75, 16–31. [Google Scholar]

25. Zorbas, D., Razafindralambo, T., Guerriero, F. (2013). Energy efficient mobile target tracking using flying drones. Procedia Computer Science, 19, 80–87. [Google Scholar]

26. Pugliese, L. D. P., Guerriero, F., Zorbas, D., Razafindralambo, T. (2016). Modelling the mobile target covering problem using flying drones. Optimization Letters, 10(5), 1021–1052. [Google Scholar]

27. Kalantari, E., Yanikomeroglu, H., Yongacoglu, A. (2016). On the number and 3D placement of drone base stations in wireless cellular networks. 2016 IEEE 84th Vehicular Technology Conference (VTC-Fall), Montreal, QC, Canada, IEEE. [Google Scholar]

28. Tuba, E., Capor-Hrosik, R., Alihodzic, A., Tuba, M. (2017). Drone placement for optimal coverage by brain storm optimization algorithm. International Conference on Hybrid Intelligent Systems, Delhi, India, Springer. [Google Scholar]

29. Sharma, V., Choudhary, G., Ko, Y., You, I. (2018). Behavior and vulnerability assessment of drones-enabled Industrial Internet of Things (IIoT). IEEE Access, 6, 43368–43383. [Google Scholar]

30. Guerriero, F., Surace, R., Loscri, V., Natalizio, E. (2014). A multi-objective approach for unmanned aerial vehicle routing problem with soft time windows constraints. Applied Mathematical Modelling, 38(3), 839–852. [Google Scholar]

31. Mozaffari, M., Saad, W., Bennis, M., Debbah, M. (2016). Efficient deployment of multiple unmanned aerial vehicles for optimal wireless coverage. IEEE Communications Letters, 20(8), 1647–1650. [Google Scholar]

32. Jiang, B., Yang, J., Xu, H., Song, H., Zheng, G. (2018). Multimedia data throughput maximization in Internet-of-Things system based on optimization of cache-enabled UAV. IEEE Internet of Things Journal, 6(2), 3525–3532. [Google Scholar]

33. He, X., Yu, W., Xu, H., Lin, J., Yang, X. et al. (2018). Towards 3D deployment of UAV base stations in uneven terrain. 2018 27th International Conference on Computer Communication and Networks (ICCCN), Hangzhou, China. [Google Scholar]

34. Sabino, S., Grilo, A. (2018). Topology control of unmanned aerial vehicle (UAV) mesh networks: A multi-objective evolutionary algorithm approach. 4th ACM Workshop, New York, NY, USA. [Google Scholar]

35. Ahmed, G., Sheltami, T., Mahmoud, A., Yasar, A. (2023). Energy-efficient uavs coverage path planning approach. Computer Modeling in Engineering & Sciences, 136(3), 3239–3263. https://doi.org/10.32604/cmes.2023.022860 [Google Scholar] [CrossRef]

36. Yang, Q., Yoo, S. J. (2018). Optimal uav path planning: Sensing data acquisition over iot sensor networks using multi-objective bio-inspired algorithms. IEEE Access, 6, 13671–13684. [Google Scholar]

37. Gupta, M., Varma, S. (2021). Optimal placement of UAVs of an aerial mesh network in an emergency situation. Journal of Ambient Intelligence and Humanized Computing, 12(1), 343–358. [Google Scholar]

38. Sommer, C., Eckhoff, D., German, R., Dressler, F. (2011). A computationally inexpensive empirical model of IEEE 802.11 p radio shadowing in urban environments. 2011 Eighth International Conference on Wireless On-Demand Network Systems and Services, Bardonecchia, Italy. [Google Scholar]

39. Oubbati, O. S., Lakas, A., Lorenz, P., Atiquzzaman, M., Jamalipour, A. (2019). Leveraging communicating uavs for emergency vehicle guidance in urban areas. IEEE Transactions on Emerging Topics in Computing, 7, 1. [Google Scholar]

40. Wang, X., Fu, L., Zhang, Y., Gan, X., Wang, X. (2016). VDNet: An infrastructure-less UAV-assisted sparse VANET system with vehicle location prediction. Wireless Communications and Mobile Computing, 16(17), 2991–3003. [Google Scholar]

41. Ahmed, G. A., Sheltami, T. R., Mahmoud, A. S., Imran, M., Shoaib, M. (2021). A novel collaborative IoD-assisted VANET approach for coverage area maximization. IEEE Access, 9, 61211–61223. [Google Scholar]

42. Ahmed, G., Sheltami, T., Mahmoud, A., Yasar, A. (2023). 3D simulation model for IoD-to-vehicles communication in IoD-assisted VANET. Frontiers in Built Environment, 9, 1–18. [Google Scholar]

43. Raza, A., Bukhari, S. H. R., Aadil, F., Iqbal, Z. (2021). An UAV-assisted vanet architecture for intelligent transportation system in smart cities. International Journal of Distributed Sensor Networks, 17(7), 15501477211031750. [Google Scholar]

44. Huang, H., Savkin, A. V., Ding, M., Kaafar, M. A. (2019). Optimized deployment of drone base station to improve user experience in cellular networks. Journal of Network and Computer Applications, 144, 49–58. [Google Scholar]

45. Savkin, A. V., Huang, H. (2018). Deployment of unmanned aerial vehicle base stations for optimal quality of coverage. IEEE Wireless Communications Letters, 8(1), 321–324. [Google Scholar]

46. Alzenad, M., El-Keyi, A., Lagum, F., Yanikomeroglu, H. (2017). 3-D placement of an unmanned aerial vehicle base station (UAV-BS) for energy-efficient maximal coverage. IEEE Wireless Communications Letters, 6(4), 434–437. [Google Scholar]

47. Sharma, V., Bennis, M., Kumar, R. (2016). UAV-assisted heterogeneous networks for capacity enhancement. IEEE Communications Letters, 20(6), 1207–1210. [Google Scholar]

48. Huang, H., Savkin, A. V. (2018). An algorithm of efficient proactive placement of autonomous drones for maximum coverage in cellular networks. IEEE Wireless Communications Letters, 7(6), 994–997. [Google Scholar]

49. Pathania, A., Venkatramani, V., Shafique, M., Mitra, T., Henkel, J. (2016). Optimal greedy algorithm for many-core scheduling. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 36(6), 1054–1058. [Google Scholar]

50. Zhang, H., Feng, T., Yang, G. H., Liang, H. (2014). Distributed cooperative optimal control for multiagent systems on directed graphs: An inverse optimal approach. IEEE Transactions on Cybernetics, 45(7), 1315–1326. [Google Scholar] [PubMed]

51. Venugopal, K., Valenti, M. C., Heath, R. W. (2016). Device-to-device millimeter wave communications: Interference, coverage, rate, and finite topologies. IEEE Transactions on Wireless Communications, 15(9), 6175–6188. [Google Scholar]

52. Al-Hourani, A., Kandeepan, S., Jamalipour, A. (2014). Modeling air-to-ground path loss for low altitude platforms in urban environments. 2014 IEEE Global Communications Conference, Austin, TX, USA, IEEE. [Google Scholar]

53. Ruan, L., Chen, J., Guo, Q., Jiang, H., Zhang, Y. et al. (2018). A coalition formation game approach for efficient cooperative multi-UAV deployment. Applied Sciences, 8(12), 2427. [Google Scholar]

54. Salah, K. (2013). A queueing model to achieve proper elasticity for cloud cluster jobs. 2013 IEEE Sixth International Conference on Cloud Computing, Santa Clara, CA, USA, IEEE. [Google Scholar]

55. El Kafhali, S., Salah, K. (2017). Efficient and dynamic scaling of fog nodes for IoT devices. The Journal of Supercomputing, 73, 5261–5284. [Google Scholar]

56. Papatheodorou, S., Tzes, A., Stergiopoulos, Y. (2017). Collaborative visual area coverage. Robotics and Autonomous Systems, 92, 126–138. [Google Scholar]