 Open Access
Open Access
ARTICLE
Blockchain-Based Certificateless Bidirectional Authenticated Searchable Encryption Scheme in Cloud Email System
1 College of Mathematics and Statistics, Northwest Normal University, Lanzhou, 730070, China
2 College of Computer Science and Engineering, Northwest Normal University, Lanzhou, 730070, China
* Corresponding Author: Xiaoni Du. Email:
(This article belongs to the Special Issue: The Bottleneck of Blockchain Techniques: Scalability, Security and Privacy Protection)
Computer Modeling in Engineering & Sciences 2024, 139(3), 3287-3310. https://doi.org/10.32604/cmes.2023.043589
Received 06 July 2023; Accepted 23 October 2023; Issue published 11 March 2024
Abstract
Traditional email systems can only achieve one-way communication, which means only the receiver is allowed to search for emails on the email server. In this paper, we propose a blockchain-based certificateless bidirectional authenticated searchable encryption model for a cloud email system named certificateless authenticated bidirectional searchable encryption (CL-BSE) by combining the storage function of cloud server with the communication function of email server. In the new model, not only can the data receiver search for the relevant content by generating its own trapdoor, but the data owner also can retrieve the content in the same way. Meanwhile, there are dual authentication functions in our model. First, during encryption, the data owner uses the private key to authenticate their identity, ensuring that only legal owner can generate the keyword ciphertext. Second, the blockchain verifies the data owner’s identity by the received ciphertext, allowing only authorized members to store their data in the server and avoiding unnecessary storage space consumption. We obtain a formal definition of CL-BSE and formulate a specific scheme from the new system model. Then the security of the scheme is analyzed based on the formalized security model. The results demonstrate that the scheme achieves multi-keyword ciphertext indistinguishability and multi-keyword trapdoor privacy against any adversary simultaneously. In addition, performance evaluation shows that the new scheme has higher computational and communication efficiency by comparing it with some existing ones.Keywords
Email systems have become an essential component of modern communication tools and revolutionized the way we conduct business, education, and personal communication, facilitating effective and efficient communication. However, the widespread usage of email has raised significant concerns regarding email security. Searchable encryption [1], as a promising security solution, has been successfully applied in many fields, including email systems. It can not only provide users with convenient search and data management methods while preserving data privacy and security but also enrich the overall user experience while safeguarding email confidentiality. That is, searchable encryption technology has become an indispensable security protection measure within email systems.
Public key Encryption with Keyword Search (PEKS) is a form of searchable encryption within the asymmetric category proposed by Boneh et al. [2] which optimises the security and privacy of email and improves users’ experience and the system performance. Since then, several PEKS schemes with varying functionality have been proposed including secure channel-free PEKS [3] and certificateless PEKS [4,5]. Although these schemes offer numerous keyword search methods suitable for encrypted email systems, there are still some security issues to be concerned with, specifically the Keyword Guessing Attack (KGA) [6]. In fact, the limited keyword space and low entropy render most PEKS schemes vulnerable to both online and offline KGA.
To defend against KGA, Huang et al. [7] introduced the Public Key Authenticated Encryption with Keyword Search (PAEKS) as a new variant of PEKS in 2017 and proved that the proposed PAEKS scheme achieved Ciphertext Indistinguishability (CI)-secure and Trapdoor Privacy (TP)-secure. Considering against chosen multi-keyword attacks and multi-keyword guessing attacks, Qin et al. [8] presented a new security model as Multi-Ciphertext Indistinguishability (MCI) in 2020 and Pan et al. formalized Multi-Trapdoor Privacy (MTP) in [9], which are the enhancement of CI-secure and TP-secure, respectively.
It is obvious that all PEKS/PAEKS systems cannot avoid the inherent burden of certificate management and key escrow issues due to their reliance on public key infrastructure cryptosystem or identity-based cryptosystem. A common approach to overcome these problems is to incorporate the PEKS/PAEKS system in certificateless public key cryptography (CL-PKC) [10]. As a result, Peng et al. [5] proposed the first certificateless PEKS scheme and He et al. [11] developed the first certificateless PAEKS scheme. However, the CL-PKC scheme still suffers from two types of attackers. The distributed nature of blockchain makes it impossible to tamper the data stored on the chain, which solves the trust problem and guarantees data security. Therefore, in CL-PKC, in order to avoid forgery attacks launched by attackers using public parameters, part of the user’s private key is created by a blockchain smart contract [12].
All of the above improvements to PEKS/PAEKS including the enhancement of security and the introduction of certificateless cryptosystem have significantly optimized their application for protecting the data security and privacy, enhancing user experience and improving system performance. Moreover, Zhang et al. [13] highlighted a crucial aspect of encrypted email systems: users must not only search for encrypted emails received from others but also retrieve encrypted emails sent to others, and they developed a new cryptographic approach named Public-key Encryption with Bidirectional Keyword Search (PEBKS). Inspired by the above ideas, it is imperative to develop a certificateless authenticated bidirectional searchable encryption scheme with a designated server test that can achieve both MCI and MTP security.
The following is a list of the main contributions of this paper:
• Considering the actual application scenario of cloud email system that the data owner also needs to retrieve emails with target keywords. We apply the bidirectional searchable functionality to CL-PAEKS cryptosystem by introducing a trapdoor generation algorithm for the data owner, put forward a cryptographic concept named CL-BSE. This allows the data owner not only to encrypt and send an email to the cloud email server, but also to generate its own trapdoor for specified keyword and retrieve the corresponding email.
• On the one side, the scheme in this paper achieves bidirectional searchable functionality, on the other side, it establishes dual authentication functions. In the process of generating the ciphertext with the keyword, the data owner not only uses the public key of the data receiver, but also uses his own private key. Similarly, the data receiver uses both his own private key and the public key of the data owner to generate the corresponding trapdoor, which authenticates the identity of the data owner. Meanwhile, the blockchain can also verify the legitimacy of the ciphertexts, which effectively saves the storage space. Furthermore, the scheme satisfies designated server test which makes secure channel free.
• We formalize the definition of the new cryptographic concept CL-BSE, then give a concrete construction of the scheme under the bilinear pairing. Meanwhile, we formally define the security model of CL-BSE scheme and show that in the random oracle model, it is able to achieve both MCI and MTP security levels against inside KGA under the CBDH hardness assumption. Through the experimental comparison, our scheme has more advantages and higher efficiency in computation and communication costs.
The rest of this paper is arranged as follows. The next section presents some basic symbols and notations, including bilinear pairing and hardness assumption. Section 3 illustrates the framework of our scheme including the system model in 3.1, the formalized definition in 3.2 and the formalized security model in 3.3. Section 4 is the concrete construction of our CL-BSE scheme and Section 5 guarantees the security of the new scheme. In Section 6, we analyze the performance by comparing it with existing works. Eventually, we draw a conclusion of the paper in Section 7.
Boneh et al. [2] presented the first PEKS scheme in 2014, which effectively solved the distribution and management of the secret-key in the symmetric searchable encryption (SSE) cryptosystem [14–16]. However, Baek et al. [3] pointed out that the trapdoor transmission channel must be secure in [2], and then proposed a secure channel free PEKS (SCF-PEKS) scheme by giving the server a public/private key pair so that only the designated server could execute the test algorithm. Rhee et al. in [17] improved the trapdoor security of [3] and then constructed a new SCF-PEKS scheme called dPEKS under the new security model. Nevertheless, Byun et al. [6] claimed that both PEKS and SCF-PEKS schemes were vulnerable to (offline) KGA and a variety of improved PEKS and SCF-PEKS schemes [18–20] were proposed to overcome the series security threats in the years including [17]. Unfortunately, it turns out that none of them can really resist the offline KGA [21]. What’s worse is that Yau et al. [22] pointed out that these existing PEKS schemes suffered from another generic attack called online KGA or inside KGA in 2013.
In order to defend against both online KGA and offline KGA, Huang et al. [7] introduced a new primitive of PAEKS and proposed the first PAEKS scheme in 2017. The essence of PAEKS is to insert the data owner’s public/private key pair into PEKS so that it can authenticate the keyword while encrypting it. Meanwhile, they defined the security as TP and CI for trapdoor and ciphertext, respectively. After that, Noroozi et al. [23] pointed out some weaknesses of the previous security in terms of multi-user settings. In 2020, Qin et al. [8] found that the CI & TP security in [7] does not protect the information whether two different files extract identical keywords or the same file contains how many identical keywords so they improved the security model as MCI, and they proposed a PAEKS scheme satisfying MCI instead of MTP. In 2021, Pan et al. claimed that their new scheme in [9] achieved both MCI and MTP secure until Cheng et al. [24] presented an effective attack method on MTP. In addition to the security efforts, contributions to the functionality of PEKS/PAEKS have also been made. Fuhr et al. [25] and Hofheinz et al. [26] inserted the ciphertext decryptable function on PEKS schemes in different types of models. Zhang et al. [13] observed that in practical application, a data owner also needed to retrieve encrypted files containing specified keywords, then proposed a cryptographic system Public-key Encryption with Bidirectional Keyword Search (PEBKS) and constructed a concrete scheme.
All of the above schemes, including PEKS, PAEKS and PEBKS are identity-based cryptosystem with key escrow and certificate management issues. Peng et al. [5] constructed the first PEKS under CL-PKC named CLPEKS. In 2018, Ma et al. [4] proposed an improved CLPEKS scheme and it was improved again in the literature [27], which was been pointed out cannot achieve both MCI and MTP secure and was subsequently improved by Yang et al. [28]. But, the cryptanalysis in [29] demonstrates that these CLPEKS frameworks also suffer from the security vulnerability caused by the keyword guessing attack and in order to remedy these security weakness and provide resistance against both inside and outside keyword guessing attacks, they propose a new CLEKS scheme by embedding the owner’s private key into the calculation of keyword ciphertexts, which actually is CL-PAEKS. Later, combining [4], He et al. [11] proposed a CL-PAEKS scheme, and Shiraly et al. [30] constructed a pairing-free CL-PAEKS. However, their security and functionality still need to be improved and promoted.
The symbols and notations used in this paper are presented in the Table 1.

Bilinear pairing [31] is an important tool in the construction of many pairing based cryptographic schemes, including our CL-BSE scheme, and we usually construct it using the Weil pairing and the Tate pairing [31–33].
Definition 2.1 (Bilinear Pairing). Let
Bilinearity: For any
Non-Degeneracy: There exists a
Computability: For any
Definition 2.2 (The CBDH Assumption [31]). The Computational Bilinear Diffie-Hellman (CBDH) problem states that given
where the probability is taken over the random choices of
There are three principal works in this section. First, we illustrate the system model of our protocol in this paper based on [13], and then formalise the definition of our CL-BSE scheme. Finally, we define the security model based on [8,9].
As shown in Fig. 1, the system model of our protocol includes the following five parties: cloud email server (CS), smart contract-based key generation center (SC-KGC), blockchain (BC), data owner (DO) and data receiver (DR). They are interacting as follows:

Figure 1: System model
• SC-KGC: Deployed on the blockchain, the smart contract key generation center is a combination of a smart contract and a conventional key generation center. It is responsible for producing and storing the public parameters on the blockchain, generating and distributing partial private keys and the master key to the corresponding parties.
• Blockchain: To avoid the system public parameters being tampered with, blockchain stores and then transmits them to all clients. The blockchain is also responsible for verifying the validity of the ciphertext, and then transferring the verified ciphertext to the cloud server.
• Cloud Email Server: The cloud email server plays an “honest but curious” role in the system model, i.e., it stores the real data, retrieves keyword sets by rules and returns the corresponding results correctly. Meanwhile, it may launch keyword guessing attacks on a set of received search tokens. Furthermore, it also performs the test algorithm and then sends the search results to the data receiver.
• Data Owner: The data owner is a client who wants to store the encrypted data files with keyword indexes in the email server while sending it to the data receiver through the cloud email server, so that he/she can retrieve it by generating a trapdoor using his/her own private key.
• Data Receiver: The data receiver is one who receives emails from the cloud email server by sending a trapdoor for the keywords he/she interested in using his/her own private key.
We have formalized the architecture of our certificateless bidirectional authenticated searchable encryption (CL-BSE) scheme for the cloud email system.
Definition 3.1. The CL-BSE scheme consists essentially of nine PPT algorithms: Setup, Extract-PPK, Set-secret-value, Set-private-key, Set-public-key, CL-BSE, Trapdoor-DR, Trapdoor-DO and Test. They are described below:
• Setup (
• Extract-PPK (
• Set-secret-value (
• Set-private-key (
• Set-public-key (
• CL-BSE (
• Trapdoor-DR (
• Trapdoor-DO (
• Test (
Correctness. The correctness of our CL-BSE scheme is defined as follows. For any legally registered clients
As with other certificateless cryptosystems [5,10,28,34,35], the CL-BSE scheme considers two types of adversary with different privileges: Type-I adversary
• Type-I adversary
• Type-II adversary
Now, the above queries are listed as follows, which are actually interactions between an adversary
– Extract-PPK query. When
– Extract-secret-value query. When
– Request-public-key query. When
– Replace-public-key query.
– Ciphertext query. When
– Data receiver trapdoor query. When
– Data owner trapdoor query. When
In order to capture chosen multi-keyword attacks and multi-keyword guessing attacks, the security model of our CL-BSE scheme are defined as MCI [8] and MTP [9], which are the enhancement of CI-secure and TP-secure [7], respectively. Their formal definitions are described by the following games, which are interactions between an challenger
Game 1: The MCI Security against Adversary
• Setup. Given security parameter
• Phase 1.
• Challenge. After
• Phase 2. As in Phase 1,
• Guess. Finally,
The following probability equation defines
Game 2: The MCI Security against Adversary
• Setup. Given security parameter
• Phase 1. As in Game 1,
• Challenge. When
• Phase 2. This phase is the same as Game 1,
• Guess. Finally,
The advantage of
Definition 3.2 (MCI security). The CL-BSE scheme is said MCI security if for any PPT adversary
Game 3: The MTP Security against Adversary
• Setup. The setup algorithm is the same as Game 1,
• Phase 1. Same as process Phase 1 in Game 1.
• Challenge. When
• Phase 2. Same as process Phase 2 in Game 1.
• Guess. Finally,
The advantage of
Game 4: The MTP Security against Adversary
• Setup. The setup algorithm is the same as Game 2, the challenger
• Phase 1. Same as process Phase 1 in Game 2.
• Challenge. After
• Phase 2. Same as process Phase 2 in Game 2.
• Guess. Finally,
The advantage of
Definition 3.3 (MTP security). The CL-BSE scheme is said MTP security for both data receiver trapdoor and data owner trapdoor, if for any PPT adversary
In this section, we give a concrete construction as the formal definition of the CL-BSE scheme in Section 3.2 with a designated server, it consists of nine PPT algorithms in five phases: System initialization, Key generation, Keyword encryption, Trapdoor generation and Test.
Phase A. System Initialization.
• Setup (
(1) Select a cyclic additive group
(2) Pick a random number
(3) Define six different cryptographic hash functions
(4) Broadcast the public parameters
Phase B. Key Generation.
• Extract-PPK (
(1) For CS, SC-KGC selects
(2) For
Set-secret-value (
Set-private-key (
Set-public-key (
Phase C. Keywords Encryption.
• CL-BSE (
(1) Compute
(2) Compute
(3) Select
(4) Compute
(5) Upload the ciphertext
Upon receiving
If and only if the owner is a legal member of the system, the blockchain then stores the verified ciphertexts to the cloud server, which can effectively save storage space.
Phase D. Trapdoor Generation.
Both DR and DO can generate their own trapdoor in the following ways:
• Trapdoor-DR (
(1) Recall
(2) Select a random number
(3) Output
• Trapdoor-DO (
Phase E. Test Process.
• Test (
holds. Output “
Actually, from the verification equation it can be seen that since
Correctness.
(1)
(2)
and
The verification process described above demonstrates the correctness of the data owner’s trapdoor and ciphertext test, the verification with respect to the data receiver’s trapdoor is similar and we omit it.
Based on the formal definition of security models in Section 3.3 and the CBDH hardness assumption in Section 2.3, we give the security proof of our scheme in this section.
Theorem 5.1 (MCI security). In the random oracle model, our CL-BSE scheme achieves semantically MCI security against outside chosen multi-keyword attacks under the CBDH hardness assumption.
The proof of Theorem 5.1 can be achieved by the following two lemmas.
Lemma 5.1. In the random oracle model, for any PPT adversary
if
Proof. Give a bilinear pair
• Setup. For a given security parameter
• Phase 1.
–
–
–
–
–
–
– Extract-PPK query.
– Request-public-key query.
– Replace-public-key query. When
– Extract-private-key query. When the identity
– Ciphertext query. Upon
Otherwise
– Trapdoor query. No matter the trapdoor is queried to be generated by the data receiver or the data owner.
Finally, it outputs
• Challenge. After
• >Phase 2. As in Phase 1,
• Guess. Finally,
Now, suppose
Since
and
we have
Lemma 5.2. In the random oracle model, for any PPT adversary
if
Proof. Similar with Lemma 5.1, given an instance of the CBDH assumption
• Setup.
• Phase 1.
– Hash queries.
– Request-public-key query.
– Extract-private-key query. When the identity
– Ciphertext query. Upon
where
– Trapdoor query. No matter
where
• Challenge. After
• Phase 2. This phase is same as Game 2,
• Guess. Finally,
Now, suppose
Since
and
we have
Theorem 5.2 MTP security. In the random oracle model, our CL-BSE scheme achieves semantically MTP security against inside multi-keywords guessing attacks under the CBDH hardness assumption.
The proof of Theorem 5.2 can be achieved by the following two lemmas:
Lemma 5.3. In the random oracle model, for any PPT adversary
if
Proof. The interaction process in the proof is basically the same as Lemma 5.1 except the Challenge phase and the Guess phase. They are
• Challenge.
• Guess. Finally,
The analysis process of the advantages
Lemma 5.4. In the random oracle model, for any PPT adversary
if
Proof. The interaction process in the proof is basically the same as Lemma 5.2 except the Challenge phase and the Guess phase. They are
• Challenge.
Guess. Finally,
The analysis process of the advantages
In this section, we analyze the performance of our scheme by comparing it with some existing schemes in [4,5,28–30,36,37].
First, we give some basic operations used in the scheme and the executing times of a single operation in Table 2. These times of operations are averaged over 1000 runs on a personal computer (Lenovo with Windows 10 operating system, Intel (R) Core (TM) i7 −7700 CPU @ 3.60 GHz and 8 GB RAM memory) using the Pairing-Based Cryptography (PBC) library [38] in Ubuntu10.

Figs. 2–5 and Table 3 describe the computation overhead of different algorithms in each scheme. Specifically, the computational overhead in the ciphertext generation (Fig. 3) of our scheme is slightly higher than [30,36]. In trapdoor generation process (Fig. 4), the computational overhead of the scheme is higher than [4,5,30] since the enhanced trapdoor privacy and authentication functionality. In test process (Fig. 5), its computational overhead is slightly higher than in [29,30] because our scheme is server-designated, that is, the public/private key pairs of the server are involved in the operation. However, in terms of total time, the time overhead of our new scheme is only slightly higher than [30]. It has some advantages when DO (or DU) retrieves emails and is more in line with practical application scenarios.

Figure 2: Computation overhead in each phase

Figure 3: Running time of encryption
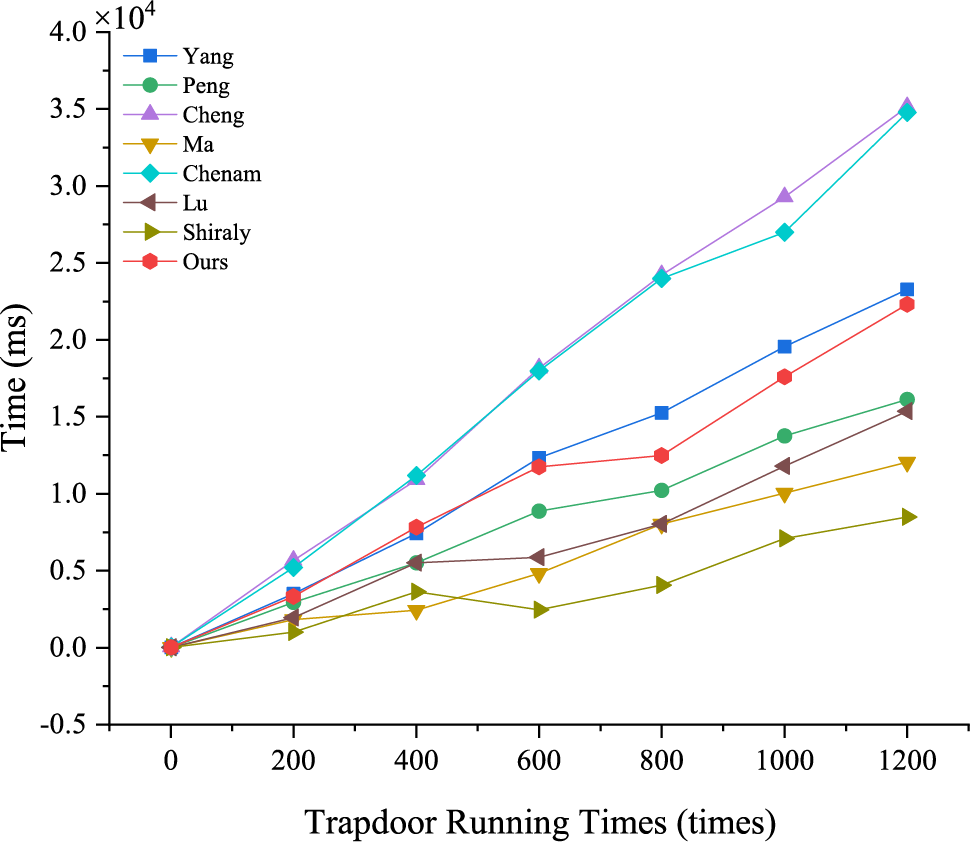
Figure 4: Running time of trapdoor

Figure 5: Running time of test

Subsequently, we make a comparison in terms of communication costs, including the size of public key |PK|, ciphertext |CT| and trapdoor |TD|, which are presented in Table 4. In the table, the notations

Finally, we present some additional performance comparisons in the Table 5. In the table, SCF denotes designated server test, AUT denotes authenticated function, BSE denotes bidirectional searchable encryption and ASSUM denotes the difficulty assumption of the scheme security depends on. Finally, we find that our scheme is a certificateless authenticated bidirectional searchable encryption scheme with a designated server test that achieves both MCI and MTP security under the CBDH hardness assumption.

Based on the certificateless public key authenticated encryption with keyword search (CL-PAEKS) cryptosystem and the bidirectional searchable functionality, this paper proposed a new cryptographic approach named blockchain-based certificateless authenticated bidirectional searchable encryption (CL-BSE). To some extent, it can be regarded as avoiding the key escrow and certificate management problem in the PEBKS scheme, and can also be considered as appending distinctive features which allow a data owner to retrieve the keyword ciphertext from server in the CL-PAEKS cryptosystem. Taking the cloud email system as the actual application scenario, we build a concrete construction of the CL-BSE scheme. The security analysis of the scheme indicates that it can achieve both MCI-secure and MTP-secure against IKGA under the CBDH hardness assumption.
Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.
Funding Statement: This work was supported by the National Natural Science Foundation of China (Nos. 62172337, 62241207) and Key Project of Gansu Natural Science Foundation (No. 23JRRA685).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Y. Sun, X. Du; data collection: Y. Sun; analysis and interpretation of results: Y. Sun, X. Du, X. Yang; draft manuscript preparation: Y. Sun, S. Niu. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Song, D., Wagner, D., Perrig, A. (2000). Practical techniques for searching on encrypted data. IEEE Symposium on Security and Privacy, pp. 44–55. Berkeley, USA. [Google Scholar]
2. Boneh, D., di Crescenzo, G., Ostrovsky, R., Persiano, G. (2004). Public key encryption with keyword search. International Conference on the Theory and Applications of Cryptographic Techniquespp, pp. 506–522. Interlaken, Switzerland. [Google Scholar]
3. Baek, J., Safavi-Naini, R., Susilo, W. (2008). Public key encryption with keyword search revisited. International Conference on Computational Science and its Applications, pp. 1249–1259. Perugia, Italy. [Google Scholar]
4. Ma, M., He, D., Kumar, N., Choo, K. K. R., Chen, J. (2018). Certificateless searchable public key encryption scheme for industrial Internet of Things. IEEE Transactions on Industrial Informatics, 14(2), 759–767. [Google Scholar]
5. Peng, Y., Cui, J., Peng, C., Ying, Z. (2014). Certificateless public key encryption with keyword search. China Communications, 11(11), 100–113. [Google Scholar]
6. Byun, J. W., Rhee, H. S., Park, H., Lee, D. H. (2006). Off-line keyword guessing attacks on recent keyword search schemes over encrypted data. Third VLDB Workshop on Secure Data Management, pp. 75–83. Seoul, Korea. [Google Scholar]
7. Huang, Q., Li, H. (2017). An efficient public-key searchable encryption scheme secure against inside keyword guessing attacks. Information Sciences, 403(C), 1–14. [Google Scholar]
8. Qin, B., Chen, Y., Huang, Q., Liu, X., Zheng, D. (2020). Public-key authenticated encryption with keyword search revisited: Security model and constructions. Information Sciences, 516, 515–528. [Google Scholar]
9. Pan, X., Li, F. (2021). Public-key authenticated encryption with keyword search achieving both multi-ciphertext and multi-trapdoor indistinguishability. Journal of Systems Architecture, 115(C), 102075. [Google Scholar]
10. Al-Riyami, S. S., Paterson, K. G. (2003). Certificateless public key cryptography. 9th International Conference on the Theory and Application of Cryptology and Information Security, pp. 452–473. Taipei, Taiwan. [Google Scholar]
11. He, D., Ma, M., Zeadally, S., Kumar, N., Liang, K. (2018). Certificateless public key authenticated encryption with keyword search for industrial internet of things. IEEE Transactions on Industrial Informatics, 14(8), 3618–3627. [Google Scholar]
12. Yang, X., Wen, H., Liu, L., Ren, N., Wang, C. (2023). Blockchain-enhanced certificateless signature scheme in the standard model. Mathematical Biosciences and Engineering, 20(7), 12718–12730. [Google Scholar] [PubMed]
13. Zhang, W., Qin, B., Dong, X., Tian, A. (2021). Public-key encryption with bidirectional keyword search and its application to encrypted emails. Computer Standards & Interfaces, 78, 103542. [Google Scholar]
14. Curtmola, R., Garay, J., Kamara, S., Ostrovsky, R. (2011). Searchable symmetric encryption: Improved definitions and efficient constructions. Journal of Computer Security, 19(5), 895–934. [Google Scholar]
15. Kamara, S., Papamanthou, C. (2013). Parallel and dynamic searchable symmetric encryption. International Conference on Financial Cryptography and Data Security, pp. 258–274. Okinawa, Japan. [Google Scholar]
16. Li, J., Huang, Y., Wei, Y., Lv, S., Liu, Z. et al. (2021). Searchable symmetric encryption with forward search privacy. IEEE Transactions on Dependable and Secure Computing, 18(1), 460–474. [Google Scholar]
17. Rhee, H. S., Park, J. H., Susilo, W., Lee, D. H. (2010). Trapdoor security in a searchable public-key encryption scheme with a designated tester. Journal of Systems and Software, 83(5), 763–771. [Google Scholar]
18. Chen, R., Mu, Y., Yang, G., Guo, F., Huang, X. et al. (2016). Server-aided public key encryption with keyword search. IEEE Transactions on Information Forensics and Security, 11(12), 2833–2842. [Google Scholar]
19. Hu, C., Liu, P. (2012). An enhanced searchable public key encryption scheme with a designated tester and its extensions. Journal of Computers, 7(3), 716–723. [Google Scholar]
20. Tang, Q., Chen, L. (2010). Public-key encryption with registered keyword search. Proceedings of the 6th European Workshop on Public Key Infrastructures, Services and Applications, pp. 163–178. Pisa, Italy. [Google Scholar]
21. Wu, T. Y., Chen, C. M., Wang, K. H., Pan, J. S., Zheng, W. et al. (2018). Security analysis of Rhee et al.’s public encryption with keyword search schemes: A review. Journal of Network Intelligence, 3(1), 16–25. [Google Scholar]
22. Yau, W. C., Phan, R. C. W., Heng, S. H., Goi, B. M. (2013). Keyword guessing attacks on secure searchable public key encryption schemes with a designated tester. International Journal of Computer Mathematics, 90(12), 2581–2587. [Google Scholar]
23. Noroozi, M., Eslami, Z. (2019). Public key authenticated encryption with keyword search: Revisited. IET Information Security, 13(4), 336–342. [Google Scholar]
24. Cheng, L. X., Meng, F. (2021). Security analysis of Pan et al.’s “Public-key authenticated encryption with keyword search achieving both multi-ciphertext and multi-trapdoor indistinguishability”. Journal of Systems Architecture, 119, 102248. [Google Scholar]
25. Fuhr, T., Paillier, P. (2007). Decryptable searchable encryption. Proceedings of the First International Conference on Provable Security, pp. 228–236. Wollongong, Australia. [Google Scholar]
26. Hofheinz, D., Weinreb, E. (2008). Searchable encryption with decryption in the standard model. Cryptology ePrint Archive. [Google Scholar]
27. Wu, T. Y., Chen, C. M., Wang, K. H., Wu, J. M. T. (2019). Security analysis and enhancement of a certificateless searchable public key encryption scheme for IIoT environments. IEEE Access, 7, 49232–49239. [Google Scholar]
28. Yang, G., Guo, J., Han, L., Liu, X., Tian, C. (2022). An improved secure certificateless public-key searchable encryption scheme with multi-trapdoor privacy. Peer-to-Peer Networking and Applications, 15(1), 503–515. [Google Scholar]
29. Lu, Y., Li, J. (2019). Constructing certificateless encryption with keyword search against outside and inside keyword guessing attacks. China Communications, 16(7), 156–173. [Google Scholar]
30. Shiraly, D., Pakniat, N., Noroozi, M., Eslami, Z. (2022). Pairing-free certificateless authenticated encryption with keyword search. Journal of Systems Architecture, 124, 102390. [Google Scholar]
31. Boneh, D., Franklin, M. (2003). Identity-based encryption from the weil pairing. SIAM Journal on Computing, 32(3), 586–615. [Google Scholar]
32. Barreto, P. S. L. M., Kim, H. Y., Lynn, B., Scott, M. (2002). Efficient algorithm for pairing-based cryptosystems. 22nd Annual International Cryptology Conference Santa Barbara, pp. 354–369. California, USA. [Google Scholar]
33. Joux, A. (2002). The weil and tate pairing as building blocks for public key cryptosystems. 5th International Algorithmic Number Theory Symposium, pp. 20–32. Sydney, Australia. [Google Scholar]
34. Han, M., Xu, P., Xu, L., Xu, C. (2022). TCA-PEKS: Trusted certificateless authentication public-key encryption with keyword search scheme in cloud storage. Peer-to-Peer Network Appliction, 16(1), 156–169. [Google Scholar]
35. Uwizeye, E., Wang, J., Cheng, Z., Li, F. (2019). Certificateless public key encryption with conjunctive keyword search and its application to cloud-based reliable smart grid system. Annals of Telecommunications, 74(7), 435–449. [Google Scholar]
36. Chenam, V. B., Ali, S. T. (2022). A designated cloud server-based multi-user certificateless public key authenticated encryption with conjunctive keyword search against IKGA. Computer Standards & Interfaces, 81(C), 103603. [Google Scholar]
37. Cheng, L. X., Meng, F. (2023). Certificateless public key authenticated searchable encryption with enhanced security model in IIoT applications. IEEE Internet of Things Journal, 10(2), 1391–1400. [Google Scholar]
38. PBC Library: The pair-based cryptography library. http://crypto.stanford.edu/pbc/ (accessed on 06/01/2023). [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools