 Open Access
Open Access
ARTICLE
Predicting the International Roughness Index of JPCP and CRCP Rigid Pavement: A Random Forest (RF) Model Hybridized with Modified Beetle Antennae Search (MBAS) for Higher Accuracy
1 College of Civil and Environmental Engineering, Hunan University of Science and Engineering, Yongzhou, 425006, China
2 School of Mines, China University of Mining and Technology, Xuzhou, 221116, China
3 School of Civil Engineering, Guangzhou University, Guangzhou, 510006, China
* Corresponding Author: Jiandong Huang. Email:
(This article belongs to the Special Issue: Meta-heuristic Algorithms in Materials Science and Engineering)
Computer Modeling in Engineering & Sciences 2024, 139(2), 1557-1582. https://doi.org/10.32604/cmes.2023.046025
Received 15 September 2023; Accepted 30 October 2023; Issue published 29 January 2024
Abstract
To improve the prediction accuracy of the International Roughness Index (IRI) of Jointed Plain Concrete Pavements (JPCP) and Continuously Reinforced Concrete Pavements (CRCP), a machine learning approach is developed in this study for the modelling, combining an improved Beetle Antennae Search (MBAS) algorithm and Random Forest (RF) model. The 10-fold cross-validation was applied to verify the reliability and accuracy of the model proposed in this study. The importance scores of all input variables on the IRI of JPCP and CRCP were analysed as well. The results by the comparative analysis showed the prediction accuracy of the IRI of the newly developed MBAS and RF hybrid machine learning model (RF-MBAS) in this study is higher, indicated by the RMSE and R values of 0.2732 and 0.9476 for the JPCP as well as the RMSE and R values of 0.1863 and 0.9182 for the CRCP. The accuracy of this obtained result far exceeds that of the IRI prediction model used in the traditional Mechanistic-Empirical Pavement Design Guide (MEPDG), indicating the great potential of this developed model. The importance analysis showed that the IRI of JPCP and CRCP was proportional to the corresponding input variables in this study, including the total joint faulting cumulated per KM (TFAULT), percent subgrade material passing the 0.075-mm Sieve (P200) and pavement surface area with flexible and rigid patching (all Severities) (PATCH) which scored higher.Graphic Abstract
Keywords
Abbreviation
| IRI | International Roughness Index |
| JPCP | Jointed Plain Concrete Pavements |
| CRCP | Continuously Reinforced Concrete Pavements |
| MBAS | Improved Beetle Antennae Search Algorithm |
| RF | Random Forest |
| RF-MBAS | MBAS and RF Hybrid Machine Learning Model |
| MEPDG | Mechanistic-Empirical Pavement Design Guide |
| TFAULT | Total Joint Faulting Cumulated per KM |
| P200 | Percent Subgrade Material Passing the 0.075-mm Sieve |
| PATCH | Pavement Surface Area with Flexible and Rigid Patching (all Severities) |
| LTPP | Long-term Pavement Performance |
| IRII | Initial International Roughness Index |
| AGE | Pavement Age in Years |
| TC | Percentage of Slabs with Transverse Cracking (All Severities) |
| SPALL | Percentage of Joints Spalled |
| FI | Freezing Index |
| PUNCH | All Severities of Punchouts Number Per Mile |
In recent years, with the development of road transportation, the total amount of road freight is also growing, and the phenomenon of overload of large trucks is common [1,2]. Cement pavement refers to pavement composed of cement concrete panels or base, also known as rigid pavement, which is widely used in heavy traffic because of its advantages of large stiffness, strong bearing capacity, good stability, good durability, high compressive strength, and tensile strength [3–5]. JPCP is a pavement consisting of a concrete surface layer and a base or substratum, with reinforced concrete pavement only in the joint zone and local areas, also known as white pavement [6,7], and JPCP has the advantages of low initial cost and low maintenance cost compared with other cement pavement, so it is widely used [8]. CRCP is a pavement form that controls cracks caused by longitudinal shrinkage of concrete pavement by placing sufficient continuous reinforcement in the longitudinal direction [9–11], and also a kind of high-performance cement pavement that can effectively overcome the diseases caused by the weak links such as transverse shrinkage joints in the joint concrete pavement [12].
The smoothness of the pavement is the main factor in the vehicle running environment and is one of the important indexes of pavement performance [13], the road is not flat will increase the vehicle vibration and resistance in the process of moving, which affects the service life of the dynamic vehicle system and transmission system [14]. The research shows that the smoothness of the pavement, especially the initial smoothness of the pavement, seriously influences the service life of the road surface [15]. Therefore, it is of great practical significance to study the roughness of road surfaces [16]. The MEPDG, developed by the American Association of State Highway and Transportation Officials and the National Cooperative Highway Research Program, is one of the most commonly used models for predicting pavement performance [17–20], which adopts to evaluate the smoothness of the pavement [21]. However, with the development of the times, researchers have found that the accuracy of MEDPG in predicting pavement performance has certain limitations [22,23]. Hence, it is extremely important to develop a more accurate model for predicting pavement performance [24–26].
In recent years, machine learning has been applied in various fields (including slope stability classification, compressive strength prediction, rock joint shear strength prediction, and loading-bearing capacity of structures) because of its excellent performance. Also, proposed soft computing approaches, such as tree-based intelligent techniques, regression models, and nonlinear models were applied [27–32]. Researchers have also introduced it into the research of pavement performance direction and achieved remarkable results [33,34]. Yan et al. proposed a hybrid machine learning model of Particle Swarm Optimization and Support Vector Machine to establish the evaluation model of the performance of asphalt pavement, with Pavement Condition Index, Pavement Structure Strength Index, Skidding Resistance Index and IRI as evaluation indexes. The PCI prediction model based on machine learning was established by using SSI, SRI, and IRI. The results showed that the model can evaluate the performance of asphalt pavement simply and efficiently [35]. Wang et al. researched a fuzzy regression method to predict the IRI and compared the results of MEPDG, conventional grey model, and fuzzy grey model with the actual long-term pavement performance (LTPP) data. The results showed that the fuzzy regression model based on the grey theory has a better prediction effect on the IRI [36]. Kaloop et al. improved the results of optimal pruning extreme learning machine by combining optimal pruning extreme learning machine and wavelet analysis [37]. Li et al. studied the sensitivity of different variables to the creep of concrete based on the existing data and the SVM model re-selected the indicators based on the results, and re-trained the SVM model based on the newly selected parameters, verifying that the parameters with low sensitivity and strongly correlated parameters have a positive impact on improving the robustness of the model [38]. Zounemat-Kermani et al. proposed to use new machine learning models to simulate the degradation of concrete caused by environmental factors used machine learning models to analyze the sensitivity of parameters causing concrete corrosion and confirmed the effectiveness of machine learning in performance prediction and sensitivity analysis [39]. However, currently, much research on machine learning in the direction of the smoothness pavement was based on single machine learning models [33,40,41], which had low prediction accuracy and did not involve the important analysis of variables.
To improve the prediction accuracy on the smoothness of JPCP and CRCP and explore the influence of input indexes on output index, this study proposed the smoothness prediction model of JPCP and CRCP based on RF-MBAS and the main contents of the study are as follows. Firstly, dataset used to evaluate JPCP and CRCP are selected based on LTPP, and the feasibility of indicators and dataset selection was verified through statistical analysis and correlation analysis. Then, based on hyperparameter tuning [42], the accuracy of the models are proved by the analysis of the consistency between the predicted value and the actual value. Finally, the sensitivity of all input indexes and human intervention indexes to the IRI of the two types of pavement are creatively analyzed. The research process is shown in Fig. 1.
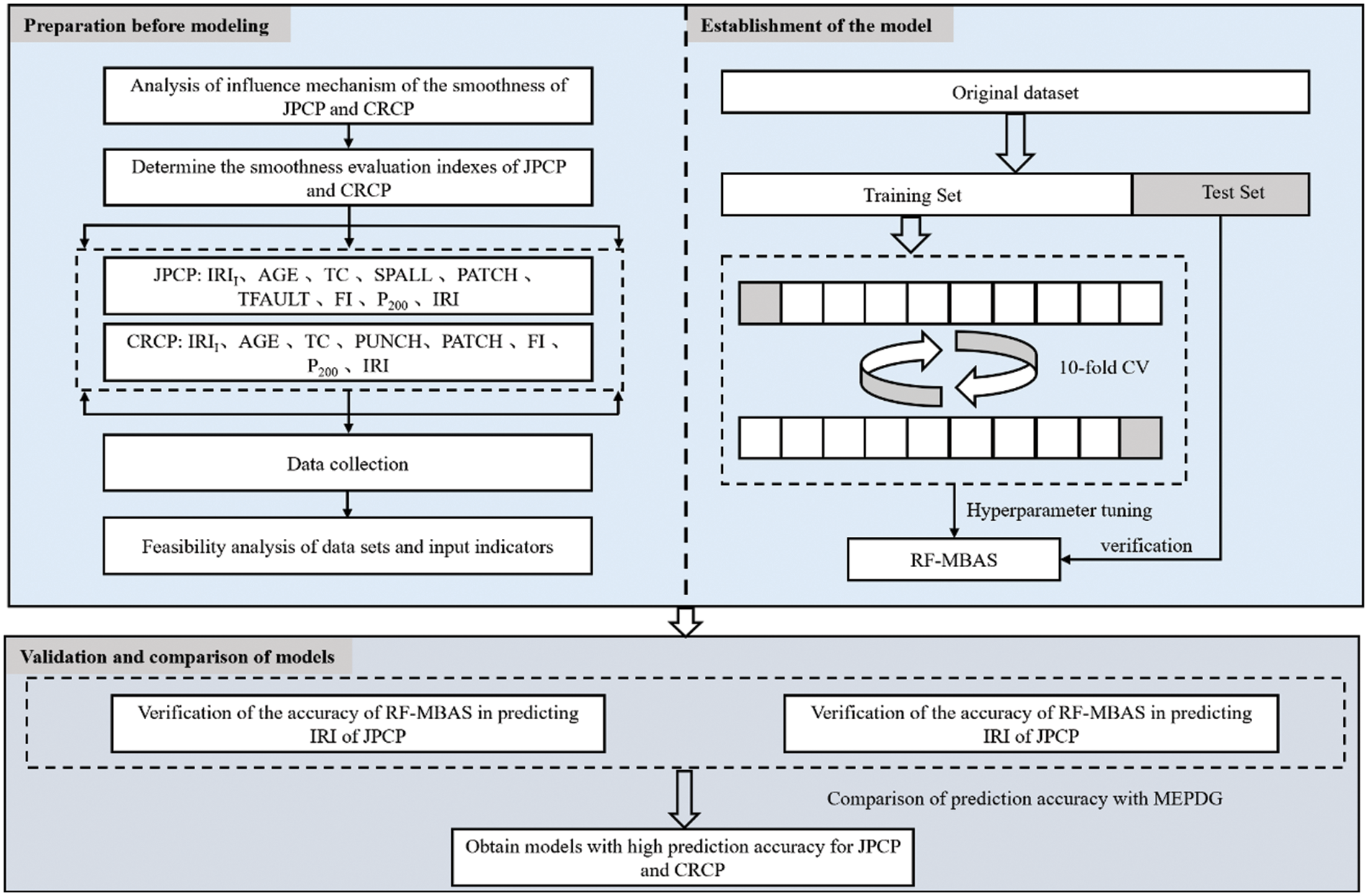
Figure 1: Flow chart of the study
In order to solve the problem of low prediction accuracy and efficiency of traditional evaluation methods on the smoothness of JPCP and CRCP, this study proposed RF-MBAS. The prediction accuracy of RF-MBAS needs to be evaluated by the hyperparameter tuning effect of MBAS on RF and the prediction accuracy of the RF-MBAS on the IRI of JPCP and CRCP. Further analysis of the importance of the indicators to the IRI of the JPCP and CRCP is necessary to assess the extent to which they affect the smoothness on the two types of pavement. Hence, the specific research objectives are summarized as follows:
• Evaluate the hyperparameter tuning effect of MBAS on FA that predicts the IRI of JPCP and CRCP.
• Compare and analyze the accuracy of RF-MBAS and MEPDG in predicting the IRI of JPCP and CRCP.
• Analyze the importance score of input indicators on IRI of JPCP and CRCP, and provide feasible suggestions for civil engineers to build and maintain JPCP and CRCP.
2.1 Description of the Dataset
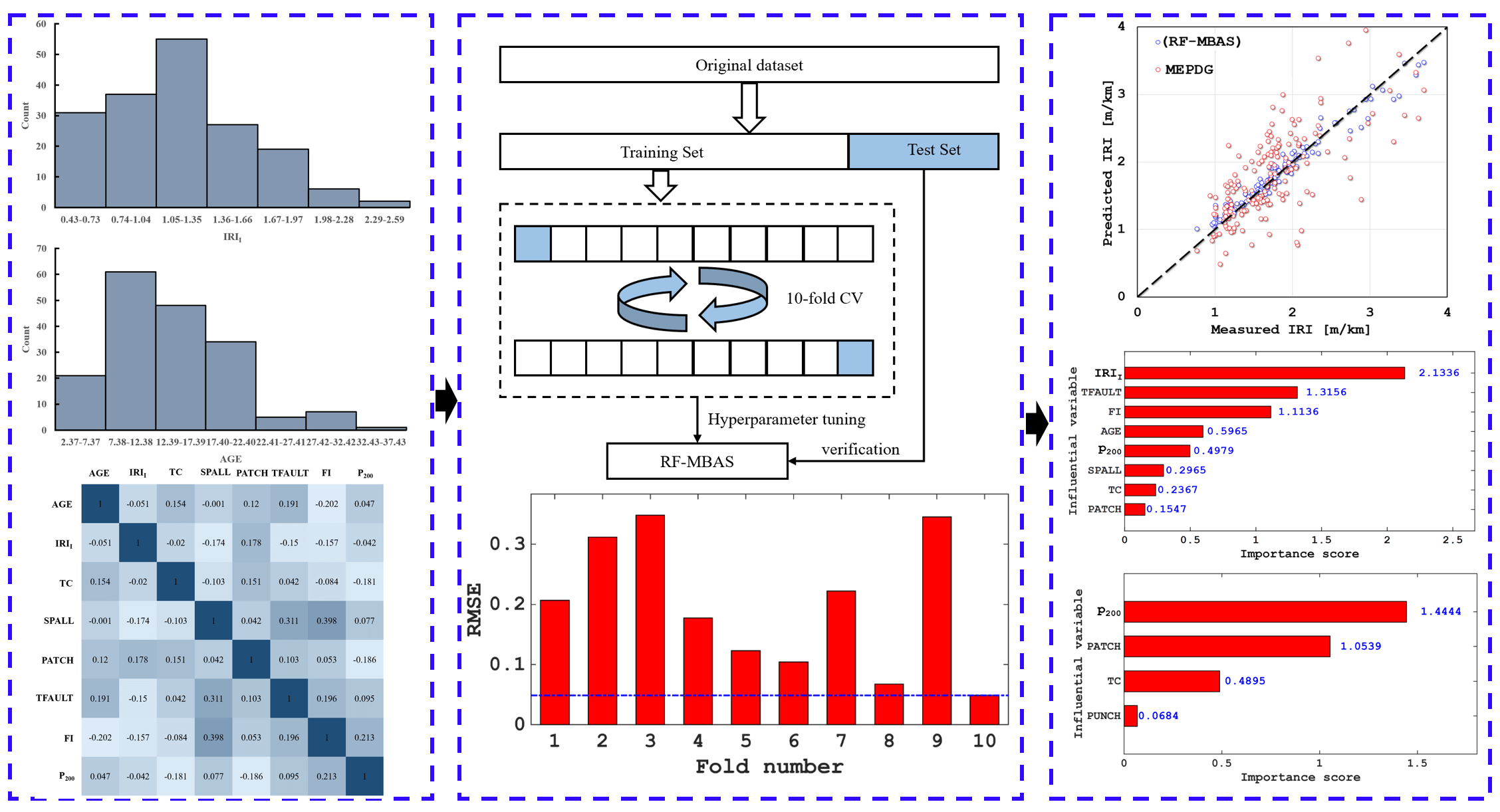
A reliable database is a basis to verify the accuracy of the prediction of IRI for JPCP and CRCP. The data of the database established in this study came from the LTPP database, which is a large and reliable database of different pavement structures in the United States, Canada, and other regions. LTPP includes the data on the performance of pavement related to summary, structural, climatic, traffic, and road performance modules. Considering the influence mechanism of JPCP and CRCP comprehensively, including pavement disease, traffic load, pavement structure, and field condition, and considering the IRI evaluation index of JPCP and CRCP by MEPDG to ensure the reliability of model comparison results, this study finally selected initial smoothness measured as IRI (IRII), pavement age in years (AGE), percentage of slabs with transverse cracking (all severities) (TC), percentage of joints spalled (SPALL), PATCH, TFAULT, freezing index (FI), P200 as input variables to predict the IRI of JPCP, and IRII, AGE, TC, PATCH, all severities of Punchouts number per mile (PUNCH), FI, and P200 as input variables to predict the IRI of JPCP and CRCP (as shown in Appendix A). The rationality of data distribution is the basis to evaluate the accuracy of the prediction model, this study analyzed the mathematical statistical and frequency histograms of the variables of JPCP and CRCP, and the results are shown in Table 1 and Fig. 2. Fig. 2 mainly depicts the data coverage and distribution of the variables, as can be seen, the frequency distribution histogram of IRII and AGE in input variables of JPCP show the single-peak pattern, and the frequency distribution of P200 is relatively stable. In short, the data distribution of each input variable have the wide and reasonable coverage. Hence, the frequency distribution histogram of IRI in the corresponding database is the single-peak type. The frequency distribution histograms of IRII, AGE, and P200 in the input variables of CRCP are single-peak type, and the final data distribution frequency histogram of IRI also shows the single-peak pattern.
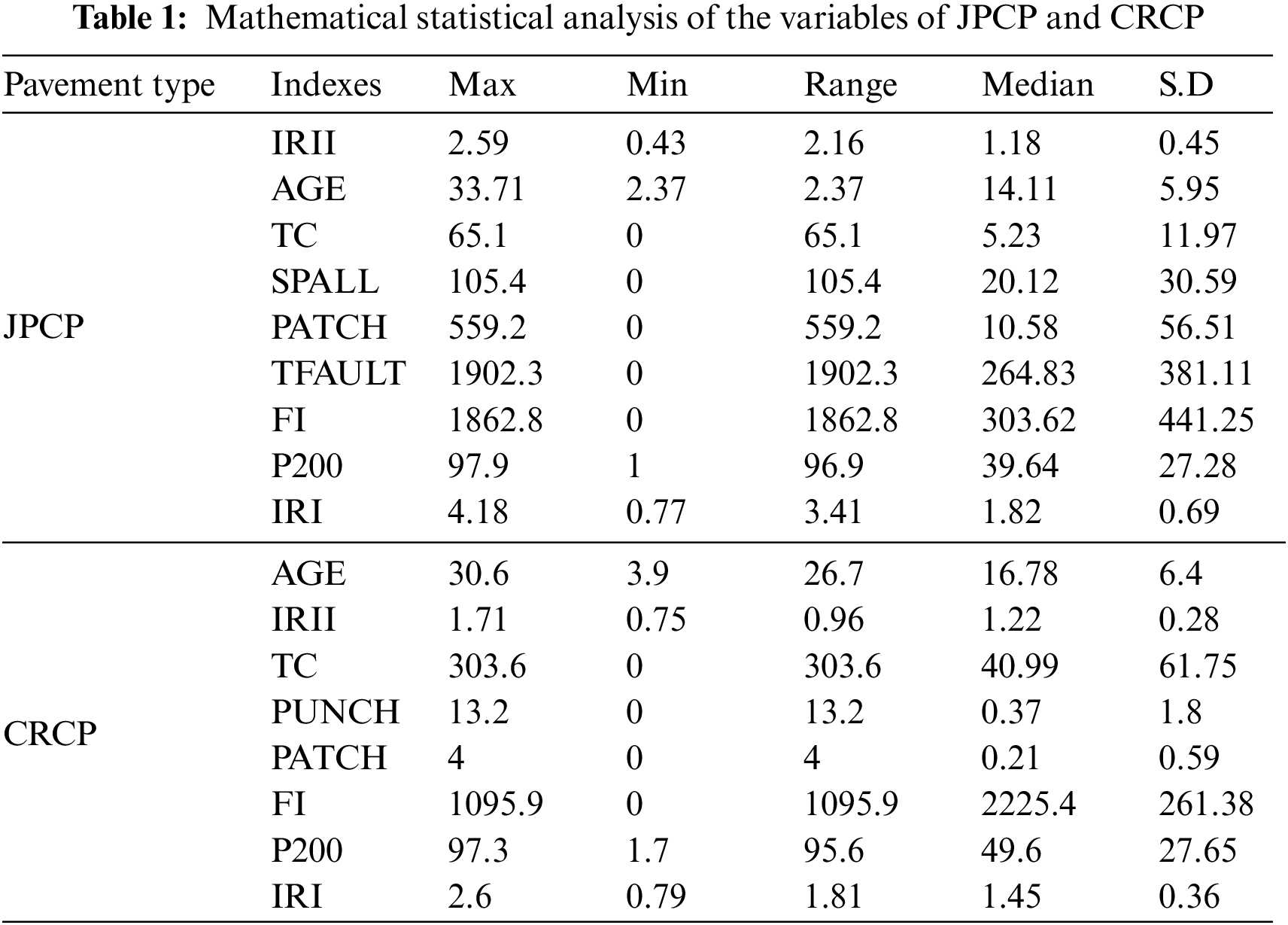
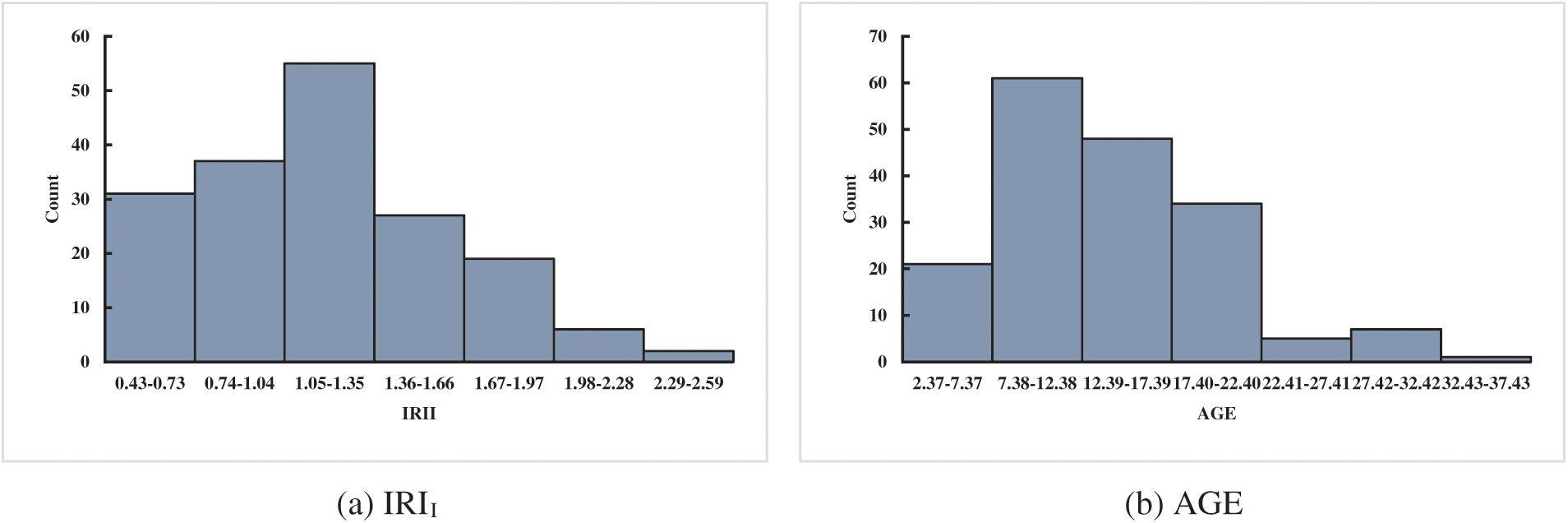
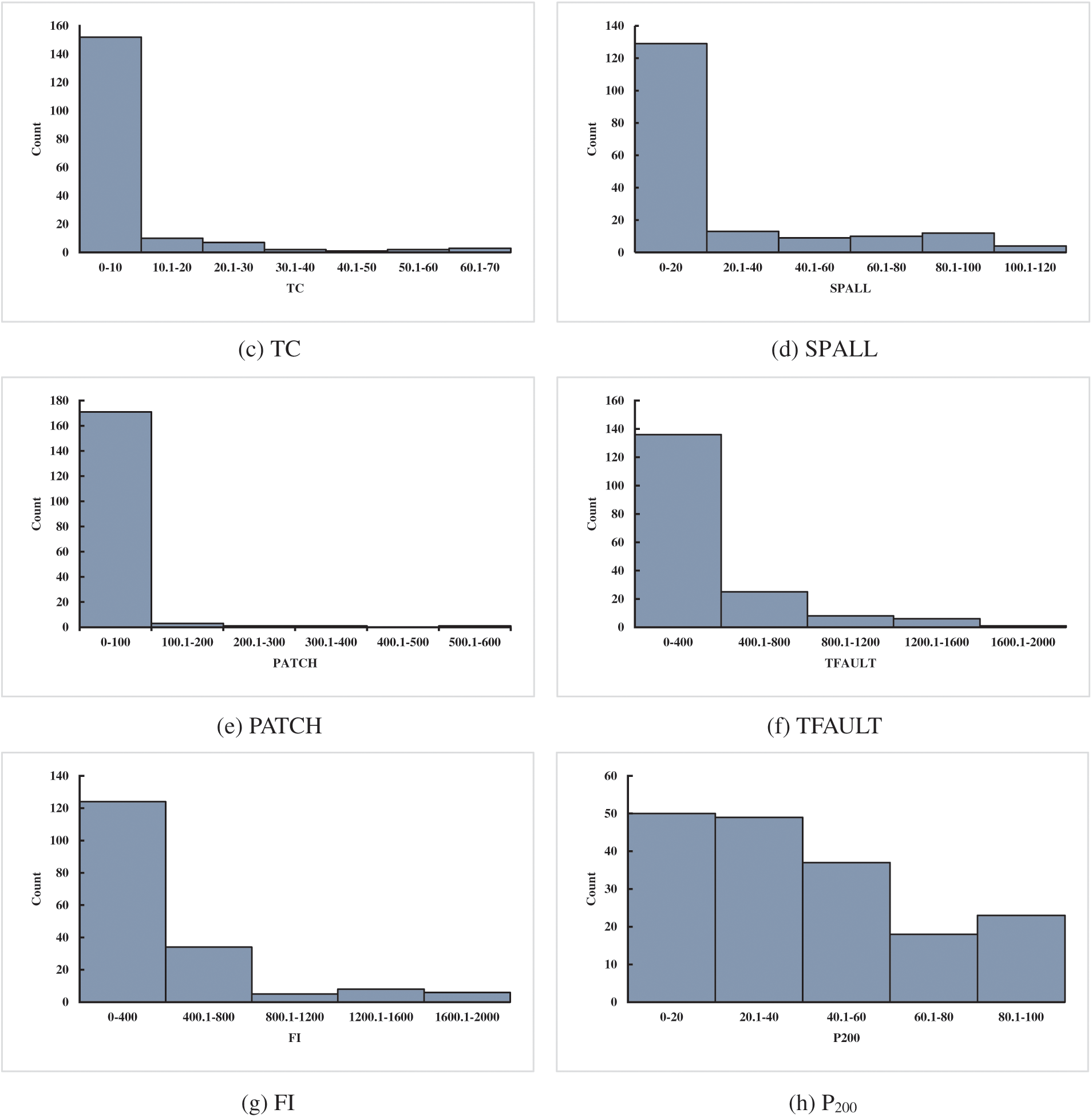
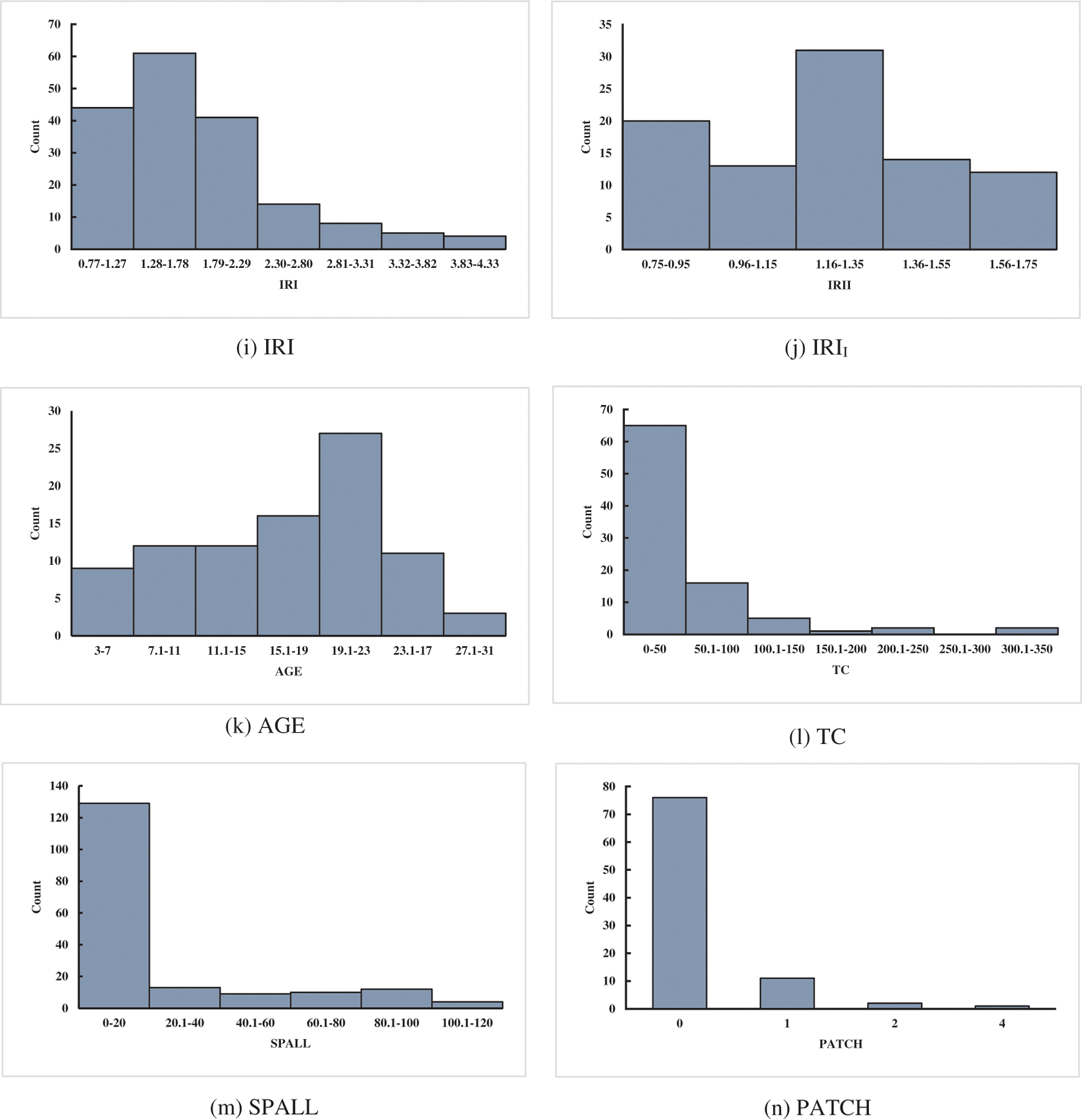
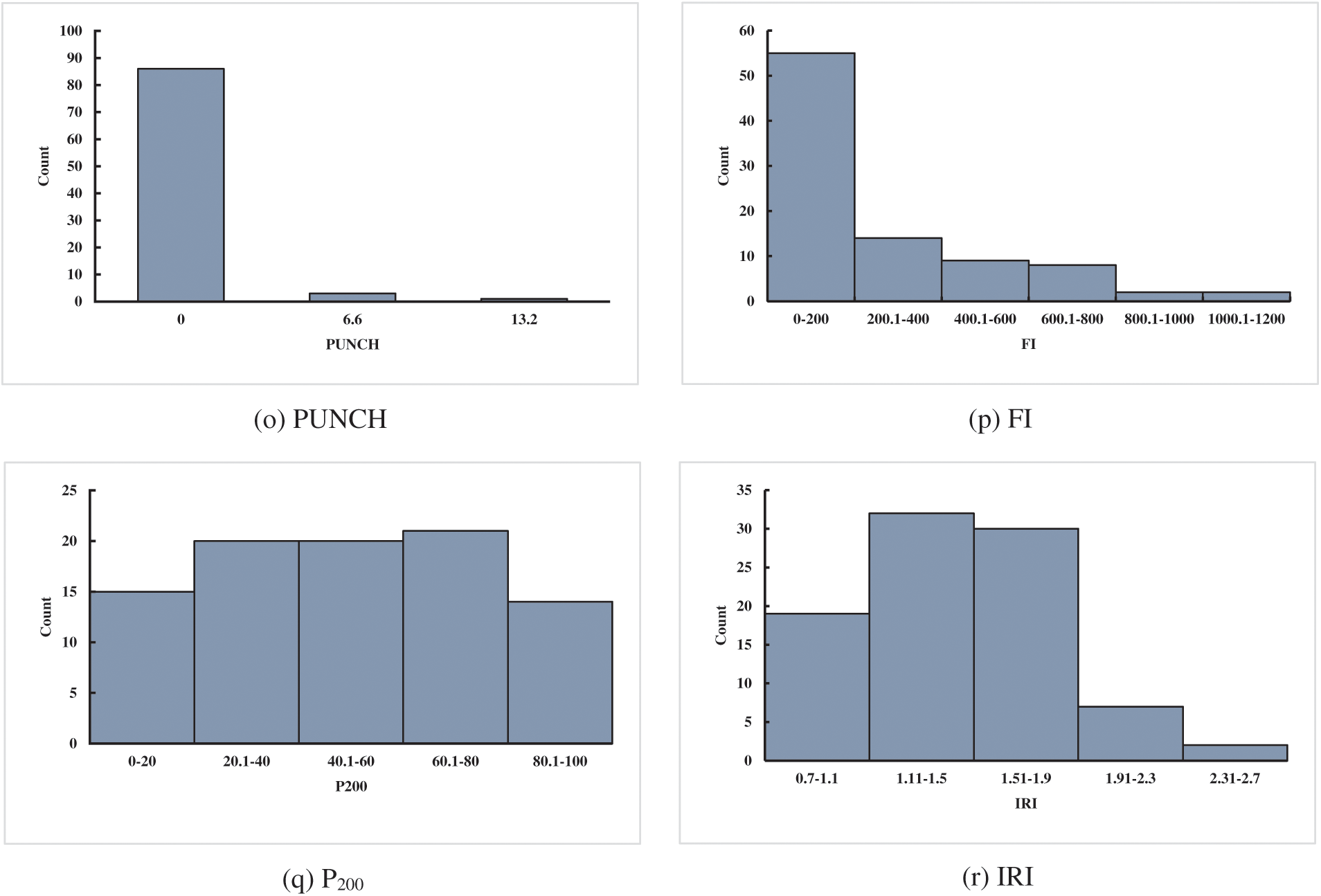
Figure 2: Frequency distribution histogram of the variables of JPCP and CRCP (JPCP: a–i, CRCP: j–r)
The analysis of two or more variables that are correlated is called correlation analysis [43,44]. Correlation analysis can measure the degree of closeness between two factors [42,45,46], and the existence of certain connections or probability between elements is the basis for correlation analysis of elements [47]. The correlation analysis results between the input variables of JPCP and CRCP are shown in Fig. 3. It is obvious that the correlation values on the diagonal line from the bottom left to the top right of JPCP and CRCP are all 1, indicating that the correlation coefficients between the same variables are 1, while the correlation coefficients at other positions except the diagonal are all less than 0.5, manifesting that the correlation coefficients between different variables are all less than 0.5. The above analysis results show that there is a certain correlation between the input variables used to predict the IRI of JPCP and CRCP in this study, and the correlation between the variables is low, thus the prediction effect of the model will not be affected by the multicollinearity between the input variables [48–50].
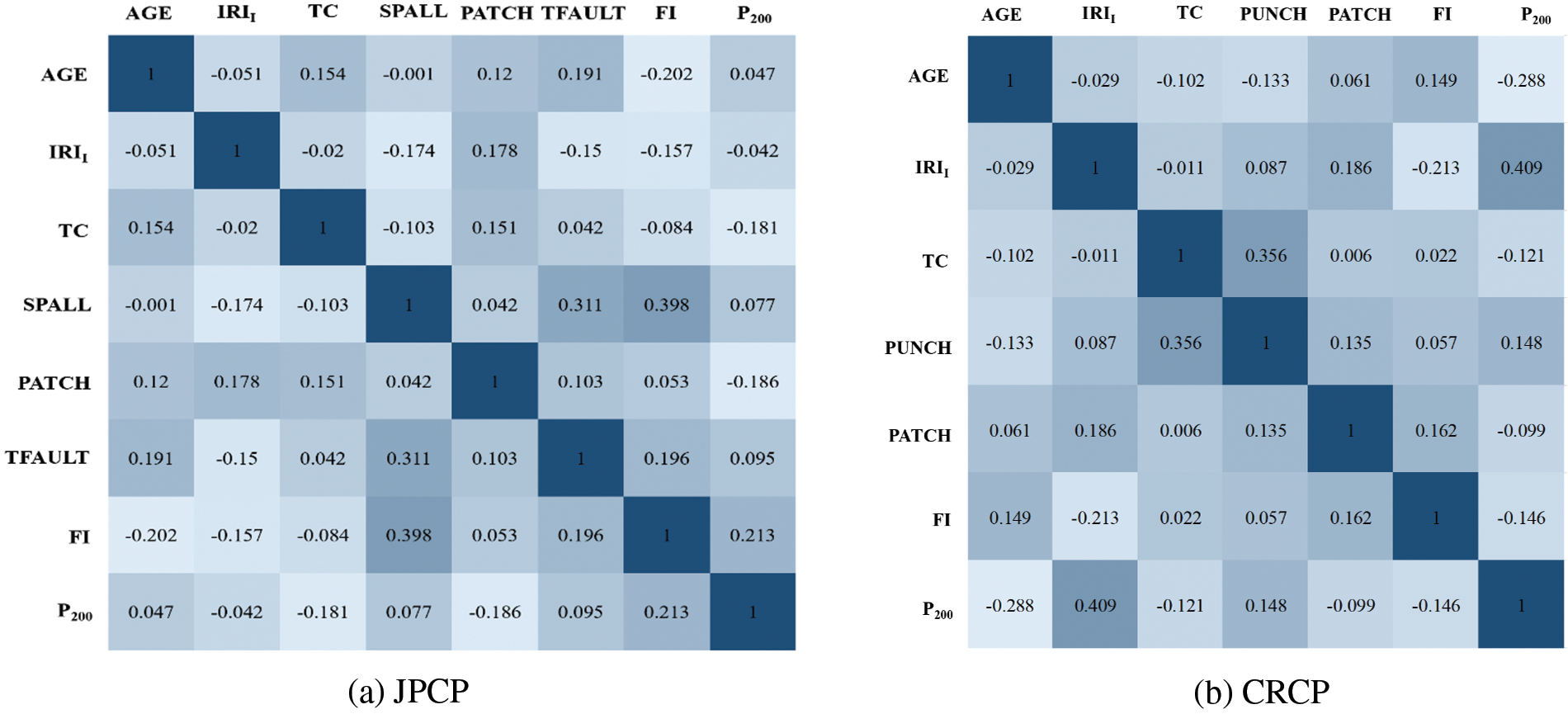
Figure 3: Correlation analysis of input variables
2.3.1 Mechanistic-Empirical Pavement Design Guide (MEPDG)
MEPDG was first proposed by the American Association of State Highway and Transportation Officials and the U.S [51]. National Highway Research Program, Since then, researchers have carried out more in-depth studies on MEPDG and made corresponding updates and improvements. Currently, MEDPG has been widely used in the United States and also attracted the attention of transportation experts worldwide [52]. The subject of MEDPG involves a wide range of research directions. At present, the research mainly focuses on the four directions of structure, material, model, and mechanical analysis [53].
2.3.2 Improved Beetle Antennae Search (MBAS)
(1) Basic BAS
BAS algorithm is a meta-heuristic algorithm proposed by researchers inspired by the foraging behavior of beetles [54,55]. The beetles swing their scent-picking whiskers to get the location of the food, choose the direction of their next flight based on the concentration of food odor received by their left and right whiskers, and keep updating their position until they find food [56]. In the BAS algorithm, the objective function to be optimized is regarded as food, and the variables in the objective function are regarded as the position of the beetle [57,58]. The flow chart of BAS is performed in Fig. 4.
(2) Improvement of BAS
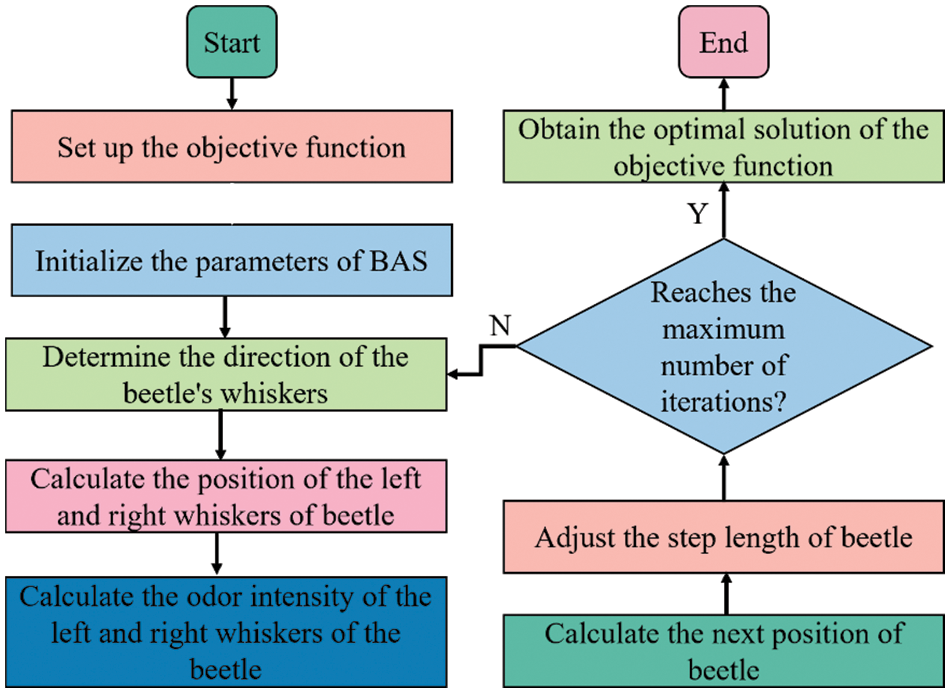
Figure 4: Flow chart of BAS
BAS has been widely used to solve practical problems in engineering due to its good optimization ability [59]. However, the BAS algorithm has some shortcomings such as the limited ability of the individual to search for optimal value, and the individual cannot make full use of the obtained optimal value information [60]. The optimization of BAS relies too much on parameter setting, which is related to the convergence and solution accuracy of the algorithm [20,61]. However, there are few types of research on the improvement of the BAS algorithm. This study proposed the MBAS based on Levy flight and self-inertial weight optimization. Levy flight was used to update the position of individual beetle in the process of beetle position update, to expand the search capability, which jump out of the local optimal solution. The formula for increasing beetle step size is as follows:
In the formula, x is a random parameter, and
In the formula,
In this study, the adaptive weight method with exponential change was used to ensure the search range. With the increment of the number of iterations, the weight decreases exponentially, which greatly increases the local optimization capability of the algorithm. The adaptive weight monotone decreasing equation is:
In the formula,
In the formula,
RF is a common classification machine learning method combining Bagging ensemble learning and based on multiple decision trees [62,63]. Firstly, RF needs to learn the sub-model of the trained weak classifier, then combine the weak classifier according to the results, and finally get the final result of the model according to the voting result of the subset or average value [64]. The steps of RF are shown in Fig. 5.
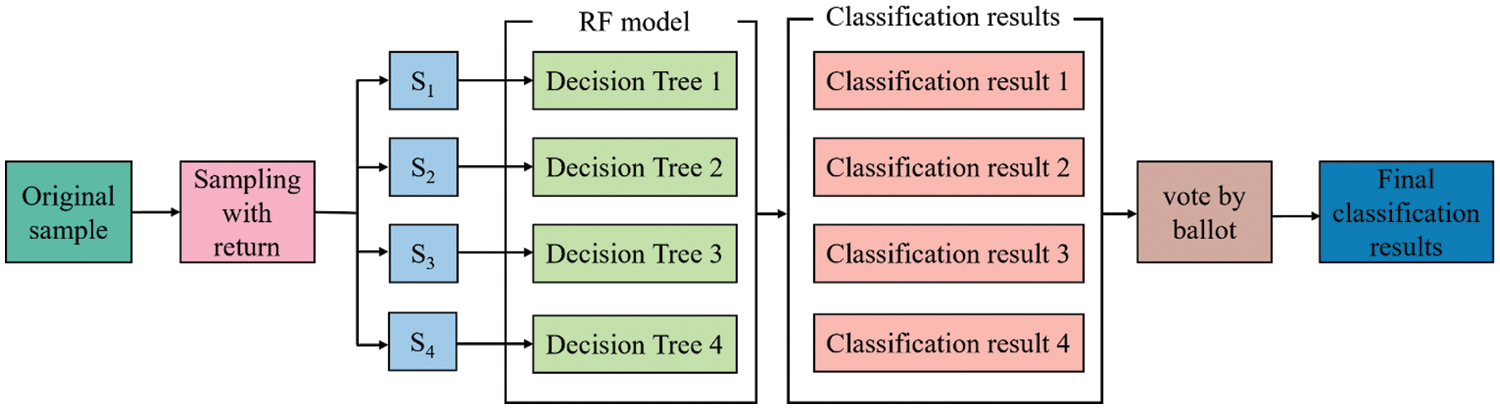
Figure 5: The framework flow chart of the RF
In this study, root mean square error (RMSE) was used to measure the results of hyperparameter tuning [65]. RMSE is calculated as follows:
where
In the process of training, the model often matches the training data well but fails to predict the data outside the training set, which is called overfitting [66–69]. Therefore, it is necessary to verify the effect on the hyperparameter tuning of the model. According to previous studies, this study chose 10-fold cross-validation to verify and further optimize the effect of MBAS on RF. The diagram of 10-fold cross-validation is shown in Fig. 6, the original data used for validation was divided into 10 groups, and each group of data in 10 groups was taken as the validation set in turn, and the remaining 9 groups were taken as the training set, and obtained 10 models [70]. As can be seen from Fig. 7, the RMSE values of the IRI prediction models of the two kinds of pavement with MBAS hyperparameter optimization are all low at each cross-validationthe, which proves the effectiveness of hyperparameter tuning, and the minimum RSME value of JPCP is obtained at the 7th iteration, the minimum RSME value of CRCP is obtained at the 10th iteration, which reflects at the 7th iteration and 10th iteration models with the most accuracy.
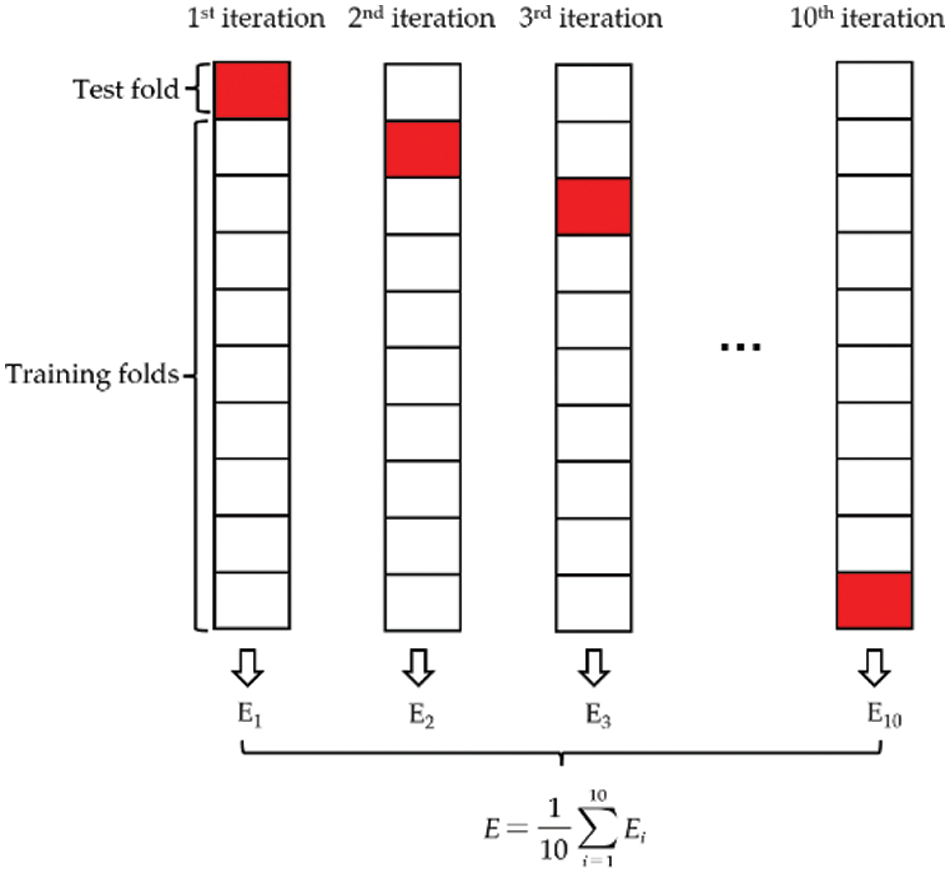
Figure 6: 10-fold cross-validation method process
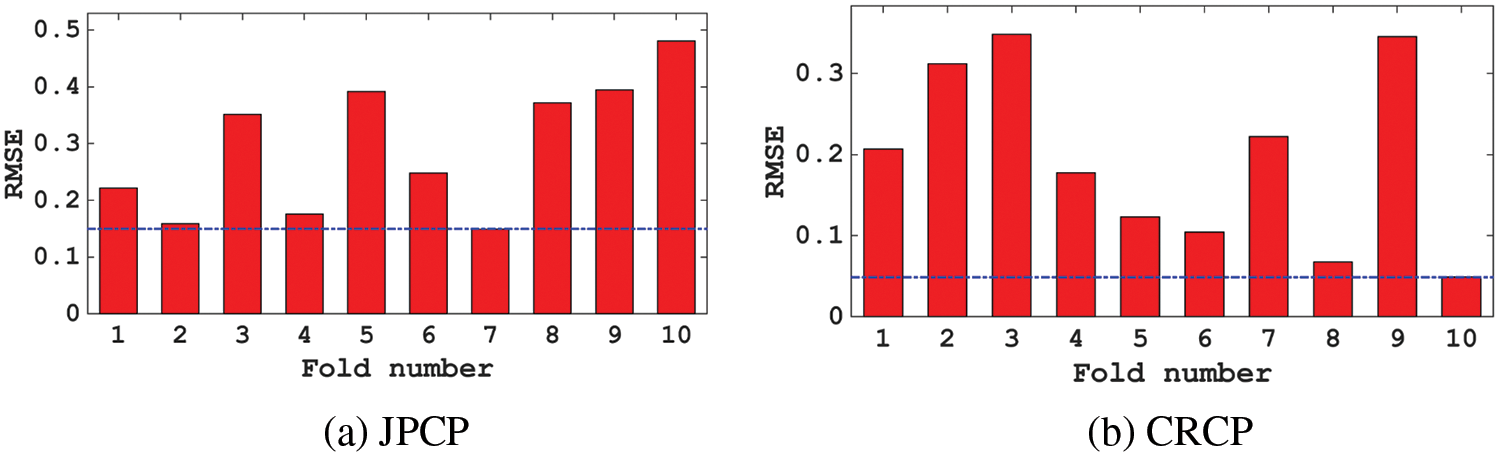
Figure 7: RMSE results of the hyperparameter tuning
To verify the accuracy of the prediction on IRI of JPCP and CRCP by the newly developed RF-MBAS, we analyzed the fitting effect between the predicted and actual values and the result are shown in Fig. 8. We can clearly see that the consistency between the predicted values and the actual values of the test set of JPCP and CRCP is high, only a few points with large errors exist, but these points do not affect the prediction effect of the model on the whole. The test set of JPCP had a high R-value (0.9476) and low RSME-value (0.2732), and the test set of CRCP also had a high R-value (0.9182) and low RSME-value (0.1863). Also, from the above calculation, it can be obtained the MAE values of 0.2358 and 0.1657 for the IRI prediction of the JPCP and CRCP, respectively. The above results proved that RF-MBAS has high prediction accuracy on the IRI of JPCP and CRCP.
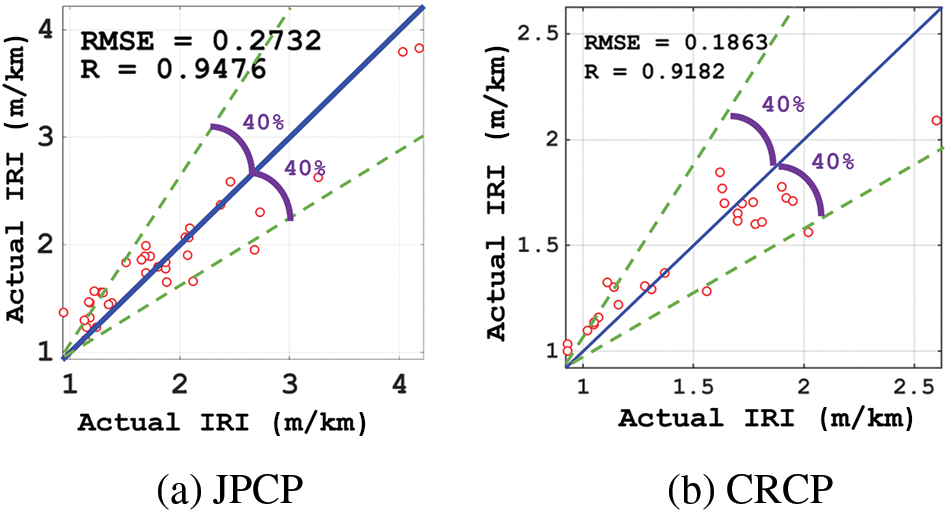
Figure 8: Actual measured vs. predicted measured values of the IRI
To more intuitively prove that the prediction accuracy of RF-MBAS is significantly improved compared with that of MEPDG, this study analyzed the predicted values and actual values on the IRI of JPCP and CRCP by RF-MBAS and MEPDG, respectively, and the comparison results are shown in Fig. 9. It can be clearly seen from Fig. 9 that the fitting effect of RF-MBAS on the predicted values and actual values on the IRI of the two kinds of road pavement is better than that of the traditional MEPDG, which proves once again that the RF-MBAS developed in this study has better prediction effect.
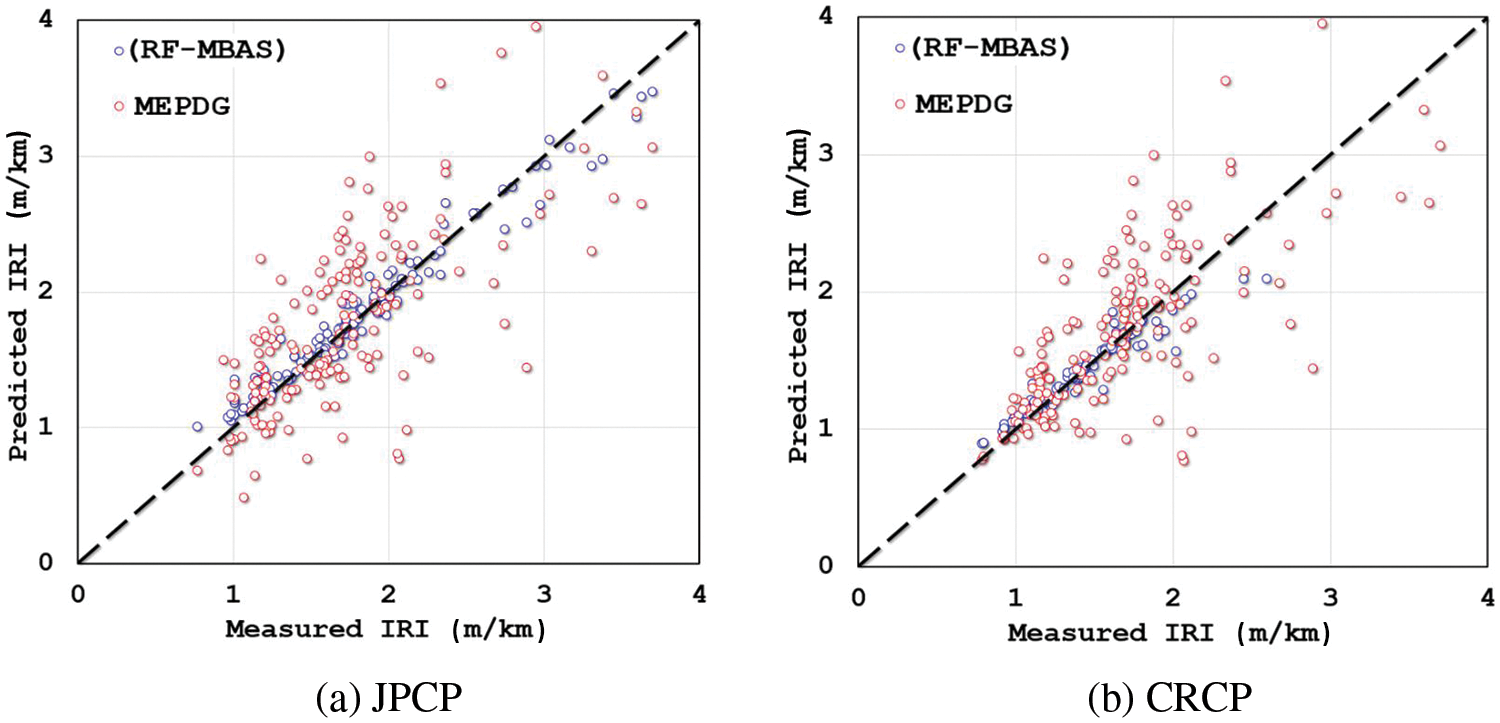
Figure 9: Comparison of the actual value and predicted value of IRI of RF-MBAS and MEPDG
Fig. 10 shows the analysis results of importance scores of input variables on the IRI of JPCP and CRCP. The importance scores of the eight input variables for the IRI of JPCP decrease in order of IRII, TFAULT, FI, AGE, P200, SPALL, TC, and PATCH, and for the IRI of CRCP decreases in the order of IRII, FI, P200, AGE, TC, PATCH and PUNCH.
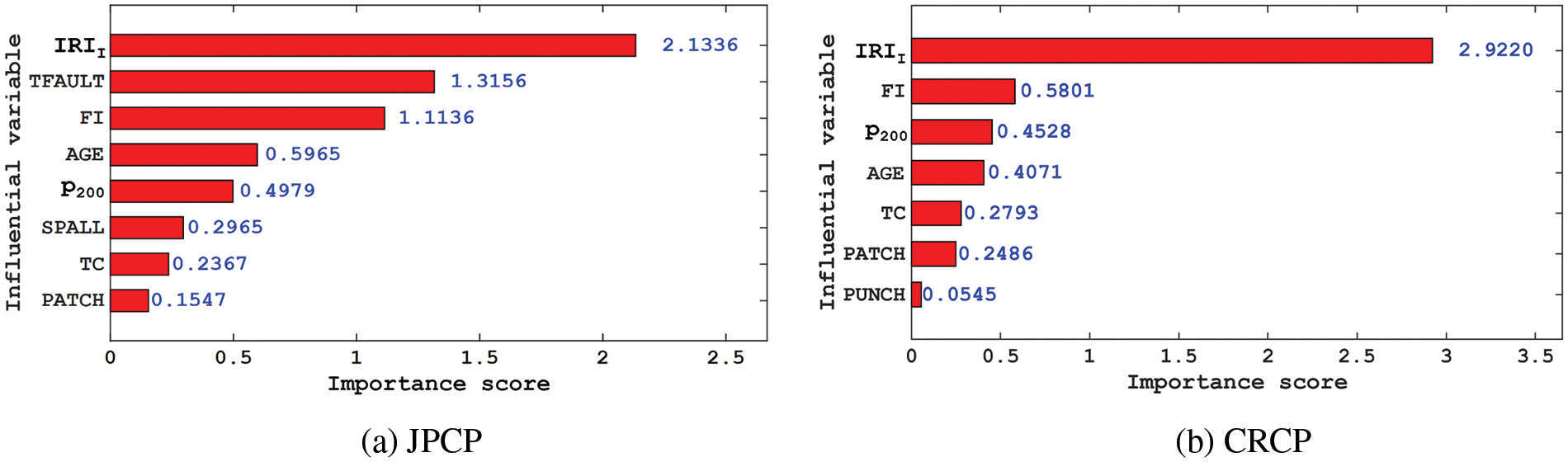
Figure 10: The importance score of the input variable
Through further analysis of the input variables of JPCP and CRCP, it can be found that IRII, FI, and AGE cannot be manually interfered with, so engineers cannot increase IRI by changing the above variables when designing and maintaining JPCP and CRCP. It is important to analyze the importance of the variables that can be manipulated for engineers to enhance the IRI during design and maintenance. In the input variables of JPCP and CRCP, the importance score of the variables that can be manipulated is shown in Fig. 11. It can be seen that the input variables of JPCP that can be manually intervened are TFAULT, P200, PATCH, TC, and SPALL, respectively, and their importance scores to IRI are 2.0089, 0.9715, 0.4523, 0.4439, and 0.3122, respectively. The importance score of TFAULT and P200 to the IRI of JPCP is high, that is, engineers can focus on the fineness of TFAULT and P200 to increase the IRI when designing and maintaining JPCP. The variables of CRCP that can be interfered with are P200, PATCH, TC, and PUNCH, respectively, among which P200 and PATCH have relatively high importance scores to the IRI, with 1.4444 and 1.0539, indicating that the IRI of CRCP shows higher sensitivity to P200 and PATCH.
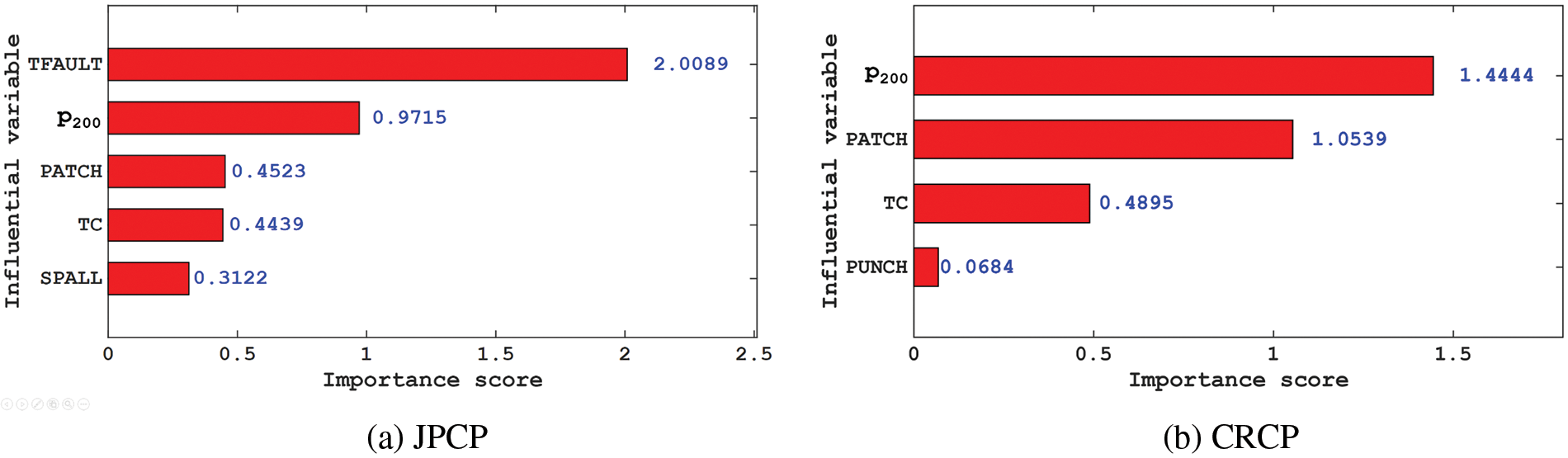
Figure 11: The importance score of the input variable that can be artificially interfered with
To overcome the weakness of the prediction models in the previous MEPDG, this study developed RF-MBAS to predict the IRI of JPCP and CRCP and compared the prediction effect of RF-MBAS and MEPDG. The 10-fold cross-validation was applied to verify the reliability and accuracy of the model. In addition, this study creatively proposes to analyze the importance score of all input variables that can be interfered with by humans. After the above research, the following conclusions are drawn:
(1) To achieve the two goals of jumping out of the optimal local solution and improving the convergence accuracy, levy flight, and adaptive weight methods were used to improve the basic BAS algorithm. From the relationship between the number of iterations and RSME values, the RSME values converge rapidly and drop to a lower value with the increase of iterations proving MBAS shows a good efficiency on the hyperparameter tuning of RF. The proposed evolved RF-MBAS model was an important innovation point of this study to characterize and predict pavement IRI.
(2) The predicted values predicted by RF-MBAS have high consistency with the actual values for IRI of JPCP and CRCP. This study compared the prediction effects of MEPDG and RF-MBAS, and the results further proved that the RF-MBAS has better prediction effects on the IRI of JPCP and CRCP, and the machine learning model shows great superiority in predicting IRI compared to the traditional MEPDG.
(3) The importance of the input variables of IRI used to evaluate JPCP and CRCP is ranked from highest to lowest as IRII, TFAULT, FI, AGE, P200, SPALL, TC, PATCH and IRII, FI, P200, AGE, TC, PATCH, PUNCH, the higher scores of JPCP were TFAULT and P200 (2.0089 and 0.9715) and the highest scores of CRCP were P200 and PATCH (1.4444 and 1.0539), respectively. The IRI of JPCP and CRCP was proportional to the corresponding input variables in this study, including TFAULT, P200, PATCH which scored higher.
The RF-MBAS model developed in this study has satisfactory accuracy in the evaluation of the IRI of JPCP and CRCP. However, the optimization of JPCP and CRCP involves multiple conflicting goals such as usage performance and economic performance. Hence, in the future, researchers need to develop multi-objective optimization models that can simultaneously optimize multiple conflicting objectives of JPCP and CRCP.
Acknowledgement: This research was supported by the Fundamental Research Funds for the Central Universities. The writers are grateful for this support.
Funding Statement: This research was supported by the Fundamental Research Funds for the Central Universities (Grant No. 2021QN1006), Natural Science Foundation of Hunan (Grant No. 2023JJ50418), and Hunan Provincial Transportation Technology Project (Grant No. 202109). The writers are grateful for this support.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Jiandong Huang, Mengmeng Zhou; data collection: Jiandong Huang, Qiang Wang; analysis and interpretation of results: Jiandong Huang, Mengmeng Zhou, Qiang Wang; draft manuscript preparation: Jiandong Huang, Mengmeng Zhou. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data supporting this study’s findings are available on request from the corresponding author, upon reasonable request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Cao, X., Zhou, B., Tang, Q., Li, J., Shi, D. (2018). Urban wasteful transport and its estimation methods. Sustainability, 10, 4562. [Google Scholar]
2. Habib, Y., Xia, E., Hashmi, S. H., Ahmed, Z. (2021). The nexus between road transport intensity and road-related Co2 emissions in G20 countries: An advanced panel estimation. Environmental Science and Pollution Research, 28, 58405–58425. [Google Scholar] [PubMed]
3. Bardel, T., Kadzielawski, G. (2019). Effectiveness of cement in stabilizing subgrade of pavement as based on static plate load tests. Cement Wapno Beton, 24, 116–125. [Google Scholar]
4. Khan, S., Nagabhushana, M. N., Hossain, K., Tiwari, D., Guruvittal, U. K. et al. (2022). Performance evaluation of fly ash-based inverted pavement system. Journal of Transportation Engineering, Part B:Pavements, 148, 4022028. [Google Scholar]
5. Asteris, P. G., Lourenco, P. B., Roussis, P. C., Adami, C. E., Armaghani, D. J. et al. (2022). Revealing the nature of metakaolin-based concrete materials using artificial intelligence techniques. Construction and Building Materials, 322, 126500. [Google Scholar]
6. Hsieh, Y. A., Yang, Z., Tsai, Y. C. J. (2021). Convolutional neural network for automated classification of jointed plain concrete pavement conditions. Computer-Aided Civil and Infrastructure Engineering, 36,1382–1397. [Google Scholar]
7. Hu, C., Sun, Z., Wang, L. (2013). Characteristics of jointed plain concrete pavement (JPCP) built-in temperature in different climate conditions. 8th International Conference on Road and Airfield Pavement Technology (ICPT), pp. 960–967. Taipei, Taiwan. [Google Scholar]
8. Shan, J., Guo, Z. (2011). Study on joint deflection of existing joint plain concrete pavement upon adoption of hot mixture asphalt overlay. 8th International Conference on Fracture and Strength of Solids (FEOFS), pp. 253–258. Kuala Lumpur, Malaysia. [Google Scholar]
9. Chen, X., Huang, X., Tong, J. (2011). In study on deformation and stress of crcp under concentrated vertical load with hollow foundation. 1st International Conference on Civil Engineering, Architecture and Building Materials (CEABM 2011), pp. 3415–3420. Haikou, China. [Google Scholar]
10. Choi, J. H., Chen, H. L. (2015). Design of gfrp reinforced crcp and its behavior sensitivity to material property variations. Construction and Building Materials, 79, 420–432. [Google Scholar]
11. Choi, P. (2015). Spalling related to coefficient of thermal expansion (CoTE) of continuously reinforced concrete pavement in texas. KSCE Journal of Civil Engineering, 19, 1747–1756. [Google Scholar]
12. de Salles, L. S., Khazanovich, L., Balbo, J. T. (2020). Structural analysis of transverse cracks in short continuously reinforced concrete pavements. International Journal of Pavement Engineering, 21, 1853–1863. [Google Scholar]
13. Huang, J., Li, X., Kumar, G. S., Deng, Y., Gong, M. et al. (2021). Rheological properties of bituminous binder modified with recycled waste toner. Journal of Cleaner Production, 317, 128415. [Google Scholar]
14. Babu, A., Baumgartner, S. V., Krieger, G. (2022). Approaches for road surface roughness estimation using airborne polarimetric sar. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 15, 3444–3462. [Google Scholar]
15. Daraghmi, Y. A., Wu, T. H., Ik, T. U. (2022). Crowdsourcing-based road surface evaluation and indexing. IEEE Transactions on Intelligent Transportation Systems, 23, 4164–4175. [Google Scholar]
16. Kanafi, M. M., Tuononen, A. J. (2017). Top topography surface roughness power spectrum for pavement friction evaluation. Tribology International, 107, 240–249. [Google Scholar]
17. Al-Qaili, A. H., Al-Solieman, H. (2021). Enhancing mepdg distress models prediction for Saudi Arabia by local calibration. Road Materials and Pavement Design, 23, 1681–1693. [Google Scholar]
18. Gungor, O. E., Al-Qadi, I. L., Gamez, A., Hernandez, J. A. (2017). Development of adjustment factors for mepdg pavement responses utilizing finite-element analysis. Journal of Transportation, Engineering Part A:Systems, 143, 4017022. [Google Scholar]
19. Huang, J., Zhang, J., Li, X., Qiao, Y., Zhang, R. et al. (2022). Investigating the effects of ensemble and weight optimization approaches on neural networks’ performance to estimate the dynamic modulus of asphalt concrete. Road Materials and Pavement Design, 24, 1939–1959. [Google Scholar]
20. Huang, J., Zhou, M., Sabri, M. M. S., Yuan, H. (2022). A novel neural computing model applied to estimate the dynamic modulus (DM) of asphalt mixtures by the improved beetle antennae search. Sustainability, 14, 5938. [Google Scholar]
21. Hall, K. D., Xiao, D. X., Pohl, E. A., Wang, K. C. P., (2012). Reliability-based mechanistic-empirical pavement design with statistical methods. Transportation Research Record, 2305, 121–130. [Google Scholar]
22. Moharekpour, M., Liu, P., Schmidt, J., Oeser, M., Jing, R. (2022). Evaluation of design procedure and performance of continuously reinforced concrete pavement according to aashto design methods. Materials, 15, 2252. [Google Scholar] [PubMed]
23. Shakhan, M. R., Topal, A., Sengoz, B. (2021). Data collection for implementation of the mechanistic-empirical pavement design guide (MEPDG) in Izmir, Turkey. Teknik Dergi, 32, 11361–11380. [Google Scholar]
24. Huang, J., Suhatril, M., Baharom, S., Alaskar, A., Assilzadeh, H. (2020). Influence of porosity and cement grade on concrete mechanical properties. Advances in Concrete Construction, 10, 393–402. [Google Scholar]
25. Huang, J., Leandri, P., Cuciniello, G., Losa, M. (2022). Mix design and laboratory characterisation of rubberised mixture used as damping layer in pavements. International Journal of Pavement Engineering, 23, 2746–2760. [Google Scholar]
26. Huang, J., Losa, M., Leandri, P., Kumar, S. G., Zhang, J. et al. (2021). Potential anti-vibration pavements with damping layer: Finite element (Fe) modeling, validation, and parametrical studies. Construction and Building Materials, 281, 122550. [Google Scholar]
27. Asteris, P. G., Rizal, F. I. M., Koopialipoor, M., Roussis, P. C., Ferentinou, M. et al. (2022). Slope stability classification under seismic conditions using several tree-based intelligent techniques. Applied Sciences, 12, 1753. [Google Scholar]
28. Ali, R., Muayad, M., Mohammed, A. S., Asteris, P. G. (2022). Analysis and prediction of the effect of nanosilica on the compressive strength of concrete with different mix proportions and specimen sizes using various numerical approaches. Structural Concrete, 24, 4161–4184. [Google Scholar]
29. Mahmood, W., Mohammed, A. S., Asteris, P. G., Ahmed, H. (2022). Soft computing technics to predict the early-age compressive strength of flowable ordinary portland cement. Soft Computing, 27, 3133–3150. [Google Scholar]
30. Fattahi, H., Hasanipanah, M. (2021). An indirect measurement of rock tensile strength through optimized relevance vector regression models, a case study. Environmental Earth Sciences, 80, 748. [Google Scholar]
31. Hasanipanah, M., Meng, D., Keshtegar, B., Nguyen-Thoi, T., Duc-Kien, T. (2021). Nonlinear models based on enhanced kriging interpolation for prediction of rock joint shear strength. Neural Computing & Applications, 33, 4205–4215. [Google Scholar]
32. Tien-Thinh, L. (2020). Surrogate neural network model for prediction of load-bearing capacity of cfss members considering loading eccentricity. Applied Sciences, 10, 3452. [Google Scholar]
33. Asteris Panagiotis, G., Armaghani Danial, J., Hatzigeorgiou George, D., Karayannis Chris, G., Pilakoutas, K. (2019). Predicting the shear strength of reinforced concrete beams using artificial neural networks. Computers and Concrete, 24, 469–488. [Google Scholar]
34. Huang, J., Duan, T., Sun, Y., Wang, L., Lei, Y. (2020). Finite element (FE) modeling of indirect tension to cylindrical (IT-CY) specimen test for damping asphalt mixtures (DAMs). Advances in Civil Engineering, 2020, 1–11. [Google Scholar]
35. Yan, K. Z., Zhang, Z. (2011). Research in analysis of asphalt pavement performance evaluation based on pso-svm. International Conference on Civil Engineering and Transportation (ICCET 2011), pp. 203–207. Jinan, China. [Google Scholar]
36. Wang, K. C. P., Li, Q. (2011). Pavement smoothness prediction based on fuzzy and gray theories. Computer-Aided Civil and Infrastructure Engineering, 26, 69–76. [Google Scholar]
37. Kaloop, M. R., El-Badawy, S. M., Ahn, J., Sim, H. B., Hu, J. W. et al. (2022). A hybrid wavelet-optimally-pruned extreme learning machine model for the estimation of international roughness index of rigid pavements. International Journal of Pavement Engineering, 23, 862–876. [Google Scholar]
38. Li, K., Long, Y. P., Wang, H., Wang, Y. F. (2021). Modeling and sensitivity analysis of concrete creep with machine learning methods. Journal of Materials in Civil Engineering, 33, 4021206. [Google Scholar]
39. Zounemat-Kermani, M., Alizamir, M., Yaseen, Z. M., Hinkelmann, R. (2021). Concrete corrosion in wastewater systems: Prediction and sensitivity analysis using advanced extreme learning machine. Frontiers of Structural and Civil Engineering, 15, 444–460. [Google Scholar]
40. Momeni, E., Armaghani, D. J., Hajihassani, M., Amin, M. F. M. (2015). Prediction of uniaxial compressive strength of rock samples using hybrid particle swarm optimization-based artificial neural networks. Measurement, 60, 50–63. [Google Scholar]
41. Mahdiyar, A., Hasanipanah, M., Armaghani, D. J., Gordan, B., Abdullah, A. et al. (2017). A monte carlo technique in safety assessment of slope under seismic condition. Engineering with Computers, 33, 807–817. [Google Scholar]
42. Sari, P. A., Suhatril, M., Osman, N., Mu’azu, M. A., Dehghani, H. et al. (2019). An intelligent based-model role to simulate the factor of safe slope by support vector regression. Engineering with Computers, 35, 1521–1531. [Google Scholar]
43. Asteris, P. G., Roussis, P. C., Douvika, M. G. (2017). Feed-forward neural network prediction of the mechanical properties of sandcrete materials. Sensors, 17, 1344. [Google Scholar] [PubMed]
44. Huang, J., Zhou, M., Zhang, J., Ren, J., Vatin, N. I. et al. (2022). Development of a new stacking model to evaluate the strength parameters of concrete samples in laboratory. Iranian Journal of Science and Technology, Transactions of Civil Engineering, 46, 4355–4370. [Google Scholar]
45. Safa, M., Sari, P. A., Shariati, M., Suhatril, M., Trung, N. T. et al. (2020). Development of neuro-fuzzy and neuro-bee predictive models for prediction of the safety factor of eco-protection slopes. Physica A: Statistical Mechanics and its Applications, 550, 124046. [Google Scholar]
46. Zeng, F., Nait Amar, M., Mohammed, A. S., Motahari, M. R., Hasanipanah, M. (2021). Improving the performance of lssvm model in predicting the safety factor for circular failure slope through optimization algorithms. Engineering with Computers, 38, 1755–1766. [Google Scholar]
47. Huang, J., Zhang, J., Gao, Y. (2022). Evaluating the clogging behavior of pervious concrete (PC) using the machine learning techniques. Computer Modeling in Engineering & Sciences, 130(2), 805–821. https://doi.org/10.32604/cmes.2022.017792 [Google Scholar] [CrossRef]
48. Shan, F., He, X., Armaghani, D. J., Zhang, P., Sheng, D. (2022). Success and challenges in predicting tbm penetration rate using recurrent neural networks. Tunnelling and Underground Space Technology, 130, 104728. [Google Scholar]
49. He, B., Armaghani, D. J., Lai, S. H. (2023). Assessment of tunnel blasting-induced overbreak: A novel metaheuristic-based random forest approach. Tunnelling and Underground Space Technology, 133, 104979. [Google Scholar]
50. Indraratna, B., Armaghani, D. J., Correia, A. G., Hunt, H., Ngo, T. (2023). Prediction of resilient modulus of ballast under cyclic loading using machine learning techniques. Transportation Geotechnics, 38, 100895. [Google Scholar]
51. Al Fuhaid, A. F., Arifuzzaman, M., Gul, M. A. (2022). Application of mechanistic empirical pavement design guide software in Saudi Arabia. Applied Sciences, 12, 8165. [Google Scholar]
52. Li, H., Khazanovich, L. (2021). PittRigid ME: Simplified mechanistic-empirical design tool for pennsylvania rigid pavements design and analysis. Journal of Transportation Engineering, Part B: Pavements, 147, 4021052. [Google Scholar]
53. Mu, F., Vandenbossche, J. M., Gatti, K. A., Sherwood, J. A. (2012). An evaluation of JPCP faulting and transverse cracking models of the mechanistic-empirical pavement design guide. Road Materials and Pavement Design, 13, 128–141. [Google Scholar]
54. Fan, M., Zhao, H., Wen, J., Yu, L., Xia, H. (2023). A novel calibration method for kinematic parameter errors of industrial robot based on levenberg-marquard and beetle antennae search algorithm. Measurement Science and Technology, 34, 105024. [Google Scholar]
55. Fei, S. W., Liu, Y. Z. (2022). Fault diagnosis method of bearing utilizing GLCM and MBASA-based KELM. Scientific Reports, 12, 17368. [Google Scholar] [PubMed]
56. Khan, A. T., Cao, X., Li, Z., Li, S. (2021). Enhanced beetle antennae search with zeroing neural network for online solution of constrained optimization. Neurocomputing, 447, 294–306. [Google Scholar]
57. Kou, B., Ren, D., Guo, S. (2022). Geometric parameter identification of medical robot based on improved beetle antennae search algorithm. Bioengineering, 9, 58. [Google Scholar] [PubMed]
58. Liao, L., Zhang, F. (2020). Ieee comp, S.O.C. in beetle antennae search algorithm for community detection in complex network. 16th International Conference on Computational Intelligence and Security (CIS), pp. 253–258. Nanning, China. [Google Scholar]
59. Wu, Q., Lin, H., Jin, Y., Chen, Z., Li, S. et al. (2020). A new fallback beetle antennae search algorithm for path planning of mobile robots with collision-free capability. Soft Computing, 24, 2369–2380. [Google Scholar]
60. Wang, Q., Zhou, M., Sabri, M. M. S., Huang, J. (2022). A comparative study of AI-based international roughness index (IRI) prediction models for jointed plain concrete pavement (JPCP). Materials, 15, 5605. [Google Scholar] [PubMed]
61. Wang, Q. A., Zhang, J., Huang, J. (2021). Simulation of the compressive strength of cemented tailing backfill through the use of firefly algorithm and random forest model. Shock and Vibration, 2021, 1–8. [Google Scholar]
62. Abellan-Garcia, J., Sebastian Guzman-Guzman, J., (2021). Random forest-based optimization of uhpfrc under ductility requirements for seismic retrofitting applications. Construction and Building Materials, 285, 122869. [Google Scholar]
63. Sun, Y., Cheng, H., Zhang, S., Mohan, M. K., Ye, G. et al. (2023). Prediction & optimization of alkali-activated concrete based on the random forest machine learning algorithm. Construction and Building Materials, 385, 131519. [Google Scholar]
64. Gong, H., Sun, Y., Shu, X., Huang, B. (2018). Use of random forests regression for predicting IRI of asphalt pavements. Construction and Building Materials, 189, 890–897. [Google Scholar]
65. Huang, J., Xue, J. (2022). Optimization of SVR functions for flyrock evaluation in mine blasting operations. Environmental Earth Sciences, 81, 434. [Google Scholar]
66. Armaghani, D. J., Mirzaei, F., Shariati, M., Trung, N. T., Shariati, M. et al. (2020). Hybrid ANN-based techniques in predicting cohesion of sandy-soil combined with fiber. Geomechanics and Engineering, 20, 191–205. [Google Scholar]
67. Parsajoo, M., Armaghani, D. J., Mohammed, A. S., Khari, M., Jahandari, S. (2021). Tensile strength prediction of rock material using non-destructive tests: A comparative intelligent study. Transportation Geotechnics, 31, 100652. [Google Scholar]
68. Ghanizadeh, A. R., Delaram, A., Fakharian, P., Armaghani, D. J. (2022). Developing predictive models of collapse settlement and coefficient of stress release of sandy-gravel soil via evolutionary polynomial regression. Applied Sciences, 12, 9986. [Google Scholar]
69. Li, D., Liu, Z., Xiao, P., Zhou, J., Armaghani, D. J. (2022). Intelligent rockburst prediction model with sample category balance using feedforward neural network and Bayesian optimization. Underground Space, 7, 833–846. [Google Scholar]
70. Huang, J., Zhou, M., Zhang, J., Ren, J., Vatin, N. I. et al. (2022). The use of GA and PSO in evaluating the shear strength of steel fiber reinforced concrete beams. KSCE Journal of Civil Engineering, 26, 3918–3931. [Google Scholar]
Appendix A: Input and Output Variables Employed in the Study
(a) JPCP
(b) CRCP
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools