 Open Access
Open Access
ARTICLE
A Reverse Path Planning Approach for Enhanced Performance of Multi-Degree-of-Freedom Industrial Manipulators
1 Key Laboratory of Light Field Manipulation and System Integration Applications in Fujian Province, School of Physics and Information Engineering, Minnan Normal University, Zhangzhou, 363000, China
2 Department of Electrical and Computer Engineering, University of Nevada, Las Vegas, 89154, USA
3 College of Material Engineering, Fujian Agriculture and Forestry University, Fuzhou, 350000, China
* Corresponding Author: Hui Wang. Email:
Computer Modeling in Engineering & Sciences 2024, 139(2), 1357-1379. https://doi.org/10.32604/cmes.2023.045990
Received 14 September 2023; Accepted 17 November 2023; Issue published 29 January 2024
Abstract
In the domain of autonomous industrial manipulators, precise positioning and appropriate posture selection in path planning are pivotal for tasks involving obstacle avoidance, such as handling, heat sealing, and stacking. While Multi-Degree-of-Freedom (MDOF) manipulators offer kinematic redundancy, aiding in the derivation of optimal inverse kinematic solutions to meet position and posture requisites, their path planning entails intricate multi-objective optimization, encompassing path, posture, and joint motion optimization. Achieving satisfactory results in practical scenarios remains challenging. In response, this study introduces a novel Reverse Path Planning (RPP) methodology tailored for industrial manipulators. The approach commences by conceptualizing the manipulator’s end-effector as an agent within a reinforcement learning (RL) framework, wherein the state space, action set, and reward function are precisely defined to expedite the search for an initial collision-free path. To enhance convergence speed, the Q-learning algorithm in RL is augmented with Dyna-Q. Additionally, we formulate the cylindrical bounding box of the manipulator based on its Denavit-Hartenberg (DH) parameters and propose a swift collision detection technique. Furthermore, the motion performance of the end-effector is refined through a bidirectional search, and joint weighting coefficients are introduced to mitigate motion in high-power joints. The efficacy of the proposed RPP methodology is rigorously examined through extensive simulations conducted on a six-degree-of-freedom (6-DOF) manipulator encountering two distinct obstacle configurations and target positions. Experimental results substantiate that the RPP method adeptly orchestrates the computation of the shortest collision-free path while adhering to specific posture constraints at the target point. Moreover, it minimizes both posture angle deviations and joint motion, showcasing its prowess in enhancing the operational performance of MDOF industrial manipulators.Graphic Abstract
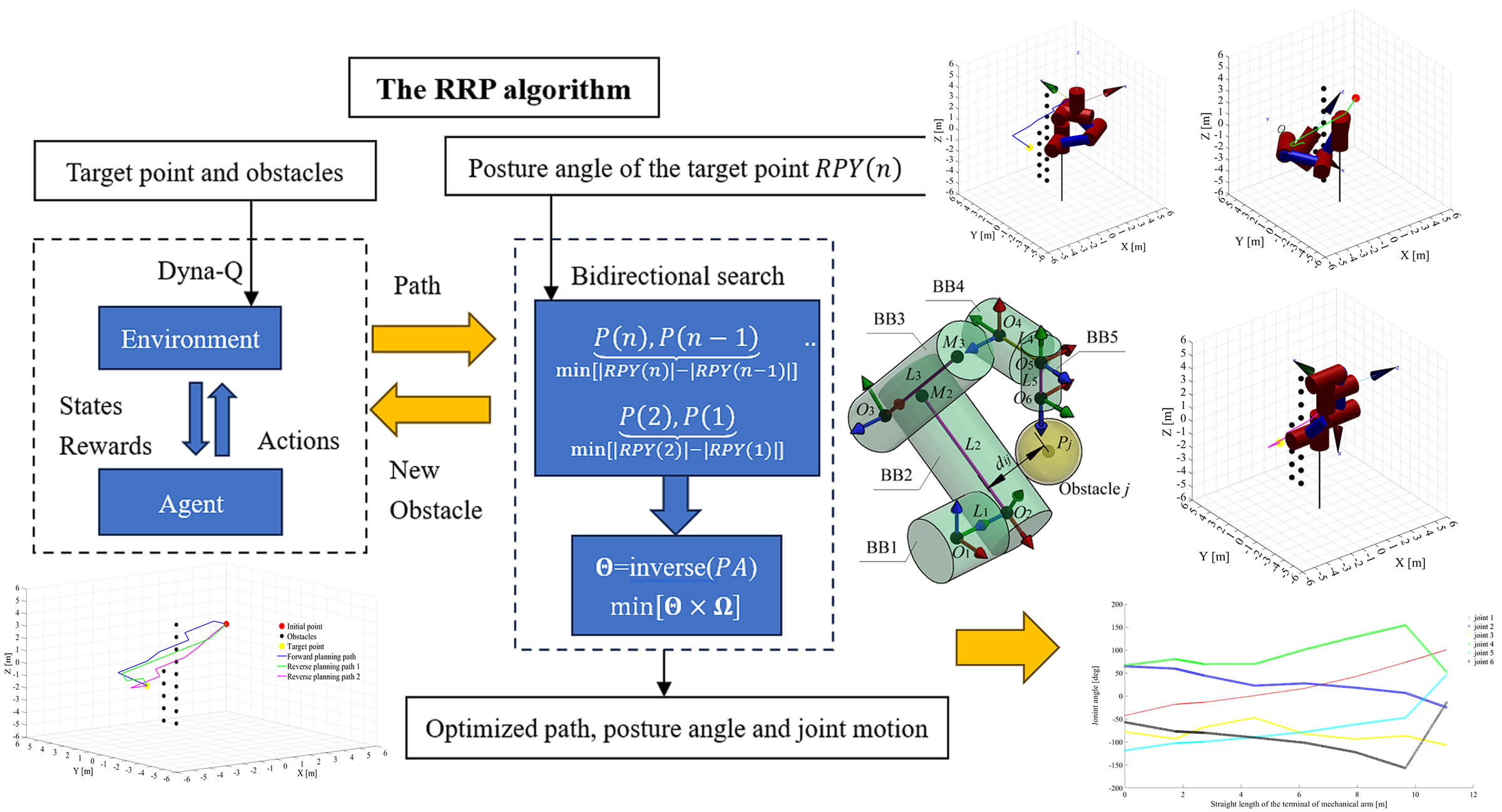
Keywords
The implementation of autonomous path planning for industrial manipulators empowers them to assume the responsibilities traditionally carried out by humans in executing intricate tasks within challenging environments characterized by elevated temperatures, heightened pressures, radiation exposure, and limited oxygen availability [1]. The essence of path planning problems lies in finding a collision-free path from a starting point to a target point within a limited workspace while satisfying kinematic constraints. This path should also optimize for minimal workspace utilization and energy consumption. The level of sophistication in this design directly affects the operational efficiency and accuracy of the robot [2].
Due to the considerable number of degrees of freedom and geometric intricacies inherent in manipulators, the process of path planning cannot be likened to the straightforward movement of a point within three-dimensional space. In practice, researchers frequently employ bounding volume technology to streamline the representation of the manipulator’s shape [3]. Subsequently, they address the determination of configurations within both the manipulator’s Cartesian workspace and its joint configuration space, accounting for various constraints including obstacle avoidance, posture restrictions, and joint limitations. Therefore, path planning for manipulators is a multi-objective optimization problem under these constraints.
The planned path information does not involve variables such as velocity and acceleration. Instead, it is based on a purely geometric motion path composed of a series of discrete via nodes. These nodes can be solved in either the joint configuration space or the Cartesian workspace of the manipulator [4,5]. When planning obstacle avoidance paths in the joint configuration space, the joint configurations serve as the via nodes. The planned path is described as a series of ordered discrete configurations, starting from the initial configuration and leading to the target configuration. By substituting these configurations into forward kinematics calculations, the corresponding end-effector paths can be derived. Alternatively, when planning paths in the workspace, the position and posture of the end-effector are used as the via nodes. The planned obstacle avoidance path is described as an ordered sequence of three-dimensional discrete coordinate points, originating from the initial end-effector position and extending to the target position. In order to calculate the joint configurations through inverse kinematics, these discrete points must also include posture information. Regardless of whether the obstacle avoidance paths are planned in the joint configuration space or the Cartesian workspace, it is essential to minimize the path length, avoid obstacles, ensure smooth motion of the end-effector, and consider joint limits and singularity [6]. To tackle these challenges, researchers have proposed classical themes and algorithms that address these concerns.
In situations where the path planner benefits from precise environmental data, collision-free path planning has been extensively utilized, with several classical theories and algorithms proposed. The graph-based Dijkstra algorithm has proven to be a highly effective solution for determining the most efficient path between two points [7]. However, it is essential to note that this algorithm may need to be better suited for searching for the shortest paths in extensive maps due to its computational demands and associated limitations. As an enhancement, the A* algorithm, another approach for finding the shortest path in a static environment, builds upon the Dijkstra algorithm [8]. The improved A* algorithm enhances the success rate of robot path planning and optimizes the efficiency of the robot’s path [9,10]. These algorithms are commonly employed by mobile robots for obstacle avoidance and shortest-path calculations in two-dimensional Euclidean spaces [11].
When a multi-degree-of-freedom (MDOF) manipulator is tasked with obstacle avoidance in high-dimensional or non-Euclidean spaces, several related studies have been undertaken. Khatib’s artificial potential field algorithm [12] is a classic method for planning obstacle avoidance paths in configuration space. This approach guides the manipulator along a collision-free trajectory by incorporating attractive or repulsive fields around designated target and obstacle locations. However, as the degree of freedom of the robotic arm increases, the configuration space obstacle of the artificial potential field algorithm exhibits exponential growth, making the calculation process cumbersome and costly [13]. Moreover, this algorithm relies on gradient descent for the optimal solution, and the manipulator is susceptible to local optima during motion, necessitating the introduction of appropriate random disturbances to escape local minima [14]. Sampling-based path planning algorithms such as the probabilistic road map (PRM) proposed by Kavraki et al. [15] and the rapidly exploring random tree (RRT) proposed by Lavalle [16] are popular options. These two algorithms, which offer probability completeness, enable random exploration during the sampling process and provide advantages regarding path search speed and success rates. However, they do not guarantee the optimal path. Building upon these foundations, introducing the RRT* algorithm [17] ensures asymptotically optimal planned paths, mitigating the shortcomings of PRM and RRT algorithms.
In further research, many scholars have sought to enhance adaptability and global optimization by leveraging the strengths of different algorithms, employing a multi-algorithm fusion approach to address complex manipulator path planning problems [18,19]. More recently, techniques such as particle swarm optimization [20], ant colony algorithms [21], and reinforcement learning [22,23] have been employed for collision avoidance in industrial robots. Compared to traditional algorithms, these heuristic intelligent algorithms are less prone to getting trapped in local optima in multi-extremum problems, making the planned path for the manipulator’s obstacle avoidance shorter and smoother.
The algorithms mentioned above are primarily employed for path planning in the joint space of manipulators. While they can determine the shortest path in joint space, they lack direct control over the real-time trajectory and posture of the end-effector. This study focuses on efficient path planning in the workspace to address the end-effector’s position and posture in Cartesian space. In this study, the path planning for multi-degree-of-freedom (MDOF) manipulators is divided into two phases. The first phase involves utilizing a planning algorithm to compute collision-free discrete points for the end-effector, ensuring the resulting path is globally optimized and the shortest. The second phase entails assigning appropriate posture angles for each discrete point on the collision-free path and employing inverse kinematics to calculate the corresponding joint angles. Planning efficiency is impacted by three challenges: planning algorithm design, posture angle configuration, and collision detection.
Planning algorithm design: Compared to traditional path planning methods, our preference leans towards selecting intelligent algorithms with trial-and-error characteristics and completeness to search for discrete path points. Among the various intelligent algorithms available, reinforcement learning (RL) holds two significant advantages. Firstly, using Hindsight Experience Replay (HER) assists the RL algorithm in handling sparse rewards during path planning, thus facilitating rapid algorithm convergence. Secondly, the agent’s state and action sets are flexible and intuitive, enabling the derivation of a globally optimized policy for constructing obstacle avoidance paths [24]. Throughout the iteration process, the RL algorithm not only identifies the best match between states and actions from existing experience pools but also expands the experience pool through random exploration. Consequently, the RL algorithm showcases the advantages of completeness and global optimality, making it highly suitable for path planning.
Posture Angle Configuration: After performing calculations within the workspace, the planned path is represented in Cartesian space, while the specific joint configuration of the manipulator remains undetermined. Consequently, it is not feasible to ascertain the joint configuration via inverse kinematics or to precompute whether the end-effector will experience unnecessary twists along the path. Therefore, it becomes essential to establish the posture angles for each discrete point along the obstacle avoidance path to capture a comprehensive path description. Given the segmentation of the path planning process into two phases within this study, iterative computations are performed between these phases, resulting in a substantial computational overhead. To accelerate convergence, this study dispenses with the constraint condition concerning the initial posture, which has no discernible impact on the operational performance of the manipulator. Instead, it devises a highly adaptable approach for configuring the posture angles at each discrete point along the obstacle avoidance path from the target position to the initial position to ensure a multiplicity of solutions for inverse kinematics, thereby enabling the manipulator to navigate around obstacles effectively.
Collision Detection: After configuring the posture angles for each discrete point along the obstacle avoidance path, it is necessary to transform the position and posture information of these points into joint angles for the manipulator using inverse kinematics. Subsequently, the process involves utilizing bounding volume technology for collision detection. However, this step comes with a notably high time complexity, given the need for checking potential collisions at each step. Hence, there is a crucial need to design a swift collision detection technique to expedite the speed of these repetitive calculations.
This paper introduces a novel path planning approach termed Reverse Path Planning (RPP) to address the abovementioned challenges. Compared to the traditional path planning techniques, RPP eliminates the constraint of the initial posture, which does not affect the performance of the robotic arm. Hence, RPP uses the position and posture of the end-effector at the target point as the initial conditions and plans an obstacle avoidance path in reverse from the target point to the initial point. Simultaneously, this algorithm tackles the issues of end-effector posture continuity and joint configuration optimization during the end-effector’s motion along this path. The main contributions of this study are as follows:
1) Path Planning through Reinforcement Learning: The paper employs a reverse planning strategy, starting from the target point and working back to the initial point, to determine the optimal path using reinforcement learning. To enhance path efficiency, a discrete action set comprising 26 distinct actions is defined to explore the most efficient route. Additionally, the Dyna-Q method is employed to enhance the conventional Q-learning algorithm and streamline the path search process.
2) Collision Detection: Leveraging the DH parameter characteristics of the manipulator, a rapid collision detection method is established. This method involves modeling cylindrical bounding boxes (CBBs) and measuring linear distances between the CBB centerlines and the geometric centers of obstacles.
3) Bidirectional Search and Motion Planning: Considering the end-effector posture at the target point, the posture angles of all nodes along the path are calculated in reverse. A bidirectional search approach is introduced to ensure minimal posture angle increments between adjacent nodes. The positions and posture angles of path nodes in Cartesian space are mapped to joint space. Collision-free inverse solutions are then identified, and weighting coefficients are designed to minimize rotation angles of high-power joints.
These contributions collectively advance the field of manipulator path planning by addressing key challenges and presenting innovative methodologies for optimizing trajectory planning, collision detection, posture smoothness, and joint motion planning.
The remaining parts of this paper are organized as follows. Section 2 presents the manipulator’s specific tasks and provides the manipulator’s DH parameters and 3D model. In Section 3, this paper introduces the basic framework of the RPP algorithm. Section 3 also provides a detailed discussion on obstacle avoidance path planning, collision detection technology, and the optimization of the end-effector’s posture and joint motion in the RPP algorithm. A six-degree-of-freedom (DOF) manipulator is simulated to validate the effectiveness of the proposed algorithms in Section 4. Finally, Section 5 presents the conclusions of this paper.
Attention is directed towards the prevailing scenario in automated operations for 6-DOF industrial manipulators, such as handling, heat sealing, and stacking. These specific manipulators must autonomously determine collision-free paths within determined environments and execute tasks at target points with designated posture. The formulated path planning for these manipulators must adhere to the following stipulations:
1. The precision position and its posture angle (PA) of the target point is imperative for the manipulators to effectively accomplish tasks like gripping, thermal sealing, and stacking post reaching the assigned target position.
2. The collision-free path is established through a succession of linked straight-line segments, connecting ordered nodes. Minimizing postures between adjacent nodes is essential to ensure the smooth motion of the end-effector.
3. Try to shorten the collision-free path and reduce the joint travel as much as possible to improve the working efficiency of the manipulator and save energy consumption;
In this paper, the description of the end-effector’s PA is facilitated using Cartesian coordinates and Roll-Pitch-Yaw (RPY) angles. On the collision-free path, the depiction of the position and orientation of the
The incorporation of Denavit-Hartenberg (DH) parameters for the robot and the associated joint limits as indicated in Table 1, underpins this research. The corresponding three-dimensional model of the manipulator corresponding to Table 1 is visually illustrated in Fig. 1, where the red, green, and blue arrows distinctly denote the X, Y, and Z axes of the coordinate system belonging to each link.
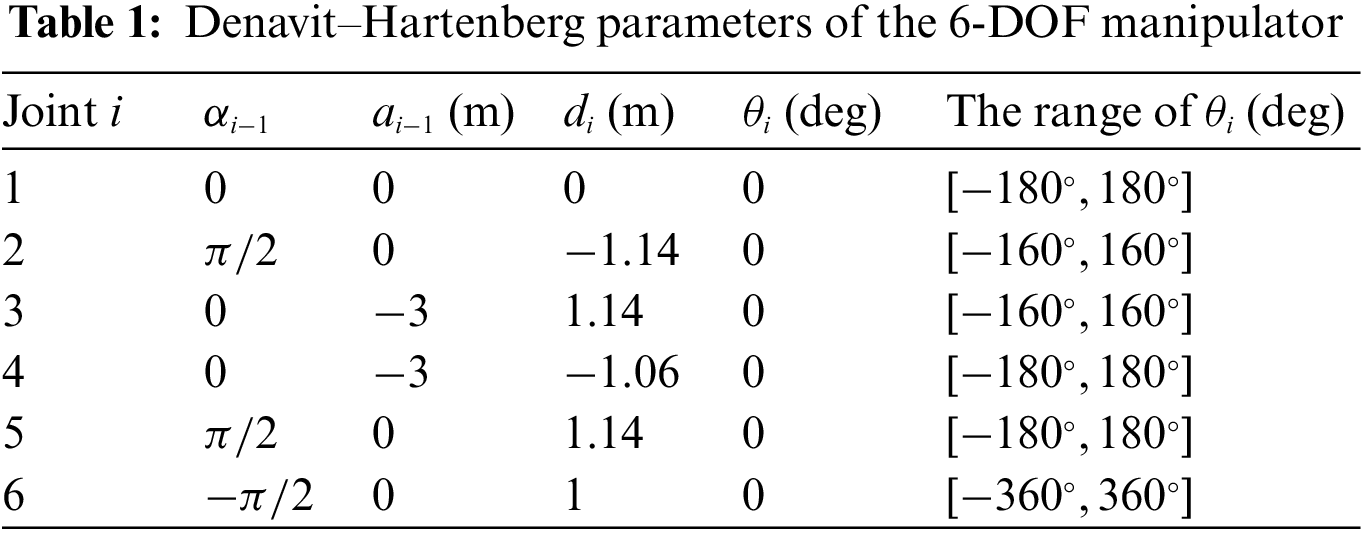
Figure 1: Manipulator structure and link coordinate systems
Considering the problem statement in Section 2, where the manipulator needs to meet a specific posture at the target position, this study is dedicated to the pursuit of reverse path planning within Cartesian space. The succession of positions and associated posture angles (PA values) derived through the path planning process necessitates conversion into the manipulator’s joint space via inverse kinematics. Subsequently, collision-free joint motions, characterized by minimal posture alteration and adherence to joint constraints, are chosen. Fig. 2 provides a visual representation of the foundational framework of the Reverse Path Planning (RPP) algorithm, with the ensuing steps delineated as follows:
1. In the first phase of RPP computation, this study employs the Dyna-Q algorithm from reinforcement learning to obtain a collision-free path composed of points for the manipulator’s end-effector. This path traverses from the target point to the starting point. The connection of these points with ordered straight-line segments culminates in the initial establishment of a collision-free path.
2. During the second phase of RPP computation, a bidirectional search algorithm is deployed in the opposite direction of the established collision-free path, utilizing the RPY posture angles of the target point. This process aims to determine the posture angles of all nodes while ensuring minimal posture increments between adjacent nodes.
3. The linear segment paths between adjacent nodes undergo discretization, resulting in a series of sub-paths. The complete PA information for these discrete path nodes comprises the positional value obtained in Step 1 for each node, along with the corresponding posture angle value from Step 2. These PA values are then applied in inverse kinematics to calculate all potential manipulator poses at each node while assessing whether any poses lead to collisions between the manipulator and obstacles. Nodes, where collisions are inevitable in all computed poses, are identified as new obstacles. In such a situation, the RPP algorithm reverts to Phase 1 to recommence the search for an obstacle-free path. Otherwise, RRP proceeds to select and optimize joint configurations from these inverse kinematic solutions.
4. The first phase of RPP is once again utilized to chart a new path from the target point to the starting point. This freshly computed path is optimized in terms of end-effector posture and joint configurations. Should the manipulator still confront unavoidable collisions, Steps 1 to 4 are reiterated.
5. In scenarios where all sub-paths from Step 3 exhibit no collisions with obstacles, an approach employing weighting coefficients is implemented. This methodology aids in the selection of joint configurations with minimal joint motion.
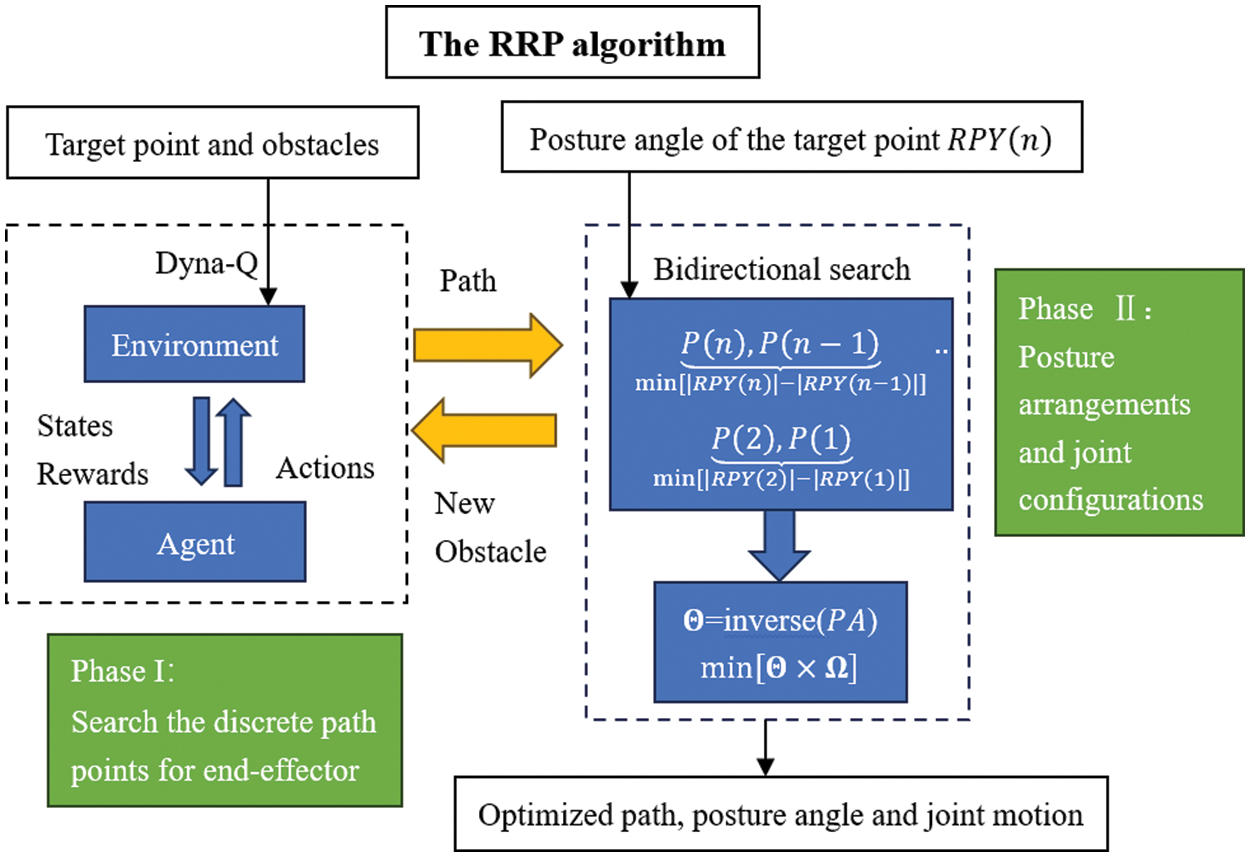
Figure 2: The framework of reverse path planning algorithm
3.2 Path Planning for Manipulator’s End-Effector
In the pursuit of attaining optimal collision-free paths, this study introduces reinforcement learning as the designated methodology, designating the manipulator’s end-effector as the intelligent agent. In tandem with this, the research acknowledges the uncertainties inherent in the environment and, as such, adopts a model-free exploration approach. This signifies that the intelligent agent engages directly with the environment, consistently acquiring real-time experiential data. This data forms the basis for learning and optimizing its collision-free path. Q-learning [25] stands out as an effective model-free strategy whose stability has been validated in both deterministic and non-deterministic Markov processes. Its learning rule is as follows:
where α ∈ [0,1] represents the learning rate, γ ∈ (0, 1) is the discount factor, A is the set of actions, and r denotes the reward function. From Eq. (2), it is evident that estimating the action-value function
Indeed, the collision-free path is segmented into discrete nodes, systematically positioned between the initial point and the target point. Subsequently, each sub-path undergoes further discretization into a finite number of shorter line sub-paths. Through the utilization of the reinforcement learning agent tasked with locating these ordered nodes, the collision-free trajectory for the manipulator’s end-effector is derived. Consequently, the study defines the set of reachable node coordinates in the manipulator’s end-effector workspace as agent’s state space
where
When
3.2.2 Action Modeling and Selection
The collision-free path is constituted by a series of discrete nodes. In cases where the distance between adjacent nodes is determined by a random integer, it may result in an expansive defined action space, potentially leading to the issue of dimensionality curse. To address this issue and to facilitate a rapid validation of the proposed RPP algorithm, the study establishes the following provisions: 1. Coordinate values of the initial point, target point, intermediate nodes, and geometric centers of obstacles are all integers. 2. When the agent moves along any of the X, Y, or Z directions, the absolute value of the step increment is 1 unit length. Considering all the possible movement directions of the manipulator’s end-effector within the workspace, this study defines a discrete action set containing 26 actions:
where
3.2.3 Action Selection Strategy
The agent employs a greedy strategy to select an action
where
The reward function employed in this study encompasses four key components. Firstly, achieving the goal point is prioritized, with successful attainment yielding the highest reward of 200. Additionally, the proximity of the agent to the goal point is considered, where a decrease in the Euclidean distance between the current node and the target results in a reward increase of 1, indicating closer proximity. The occurrence of a collision and the breach of the reachable workspace are also factored into the reward function. This comprehensive approach to defining rewards ensures a balanced consideration of critical aspects in the path planning process, promoting effective and collision-free trajectory generation for the manipulator’s end-effector. Conversely, a reward decrease of 1 occurs if the distance increases. If the manipulator’s end-effector collides with obstacles or goes beyond the reachable workspace, the reward is assigned a negative value. The analytical description of the reward above function is as follows:
where
In this study, the workspace of the manipulator’s end-effector is designated as the state space, effectively discretizing and determining the environment for path planning. To expedite the learning process of reinforcement learning (RL), this study enhances the standard Q-learning framework by introducing a Dyna-Q framework. This modification involves the creation of an environment model that stores past experiences, facilitating more efficient and effective learning in the path planning process. The virtual samples generated by this model can serve as learning samples for the iterative update of Q-values [27,28], thus accelerating algorithm convergence within a finite number of iterations. As depicted in Fig. 3, under the Dyna-Q framework, during the manipulator’s end-effector seeking its target position, each interaction with the actual environment yields direct real experience

Figure 3: The framework of Dyna-Q
3.3 Collision Detection and Multi-Objective Optimization in Reverse Path Planning
Bounding volume technology stands as a classic technique in manipulator collision detection. This technology encompasses well-known approaches such as Aligned Axis Bounding Box (AABB), Oriented Bounding Box (OBB), and Discrete Orientation Polytope (DOP) [29], all of which contribute to reducing computational demands. This paper introduces a novel approach using DH parameters of the robot to model cylindrical bounding volumes, facilitating accelerated collision detection.
Suppose the coordinates of the joint origins of manipulator links
1. When
2. When
After obtaining the centerlines for all cylindrical bounding blocks of the individual links, the overall cylindrical envelope of the manipulator can be defined by taking a radius slightly larger than the radial dimension

Figure 4: The cylinder bounding box of robot
Subsequently, this study employs sphere-bound volumes to simplify obstacles. The
Here, the symbol
During autonomous path planning of a six-axis manipulator, the RPP algorithm derives the manipulator’s various joint angles
3.3.2 End-Effector’s Posture Optimization
The collision-free paths obtained via reinforcement learning algorithms offer an initial outline of the manipulator end-effector’s coordinate trajectory, but do not precisely define its specific posture. In subsequent research, this study endeavors to refine the Reverse Path Planning (RPP) algorithm, specifically targeting the enhancement of end-effector posture smoothness and minimizing joint movement. This refinement aims to optimize the manipulator’s autonomous obstacle avoidance process, ensuring a seamless and efficient operational workflow.
As outlined in the problem description in Section 2, the posture angles
The values of
The combinations of orientations’ increments in the X, Y, and Z directions are arranged using
Based on the description mentioned above, if
3.3.3 Joint Motion Optimization
The steps mentioned above have guided the manipulator’s end-effector in achieving a collision-free path while ensuring smooth posture angles at the path nodes. These obtained path points’ positional and PA values can be used to deduce the manipulator’s various joint angles. The manipulator’s kinematic inverse solutions must adhere to Pieper criteria [30]. On this basis, according to reference [31], a 6R-type manipulator with a given posture can obtain eight kinematic inverse solutions. Among these solutions, the study first eliminates those that violate joint limits, are singular, or collide with obstacles. Subsequently, considering the rated power of each joint in the manipulator from the remaining solutions, the study designs weighting coefficients
Assuming at Node
where
In the RPP algorithm, the optimization processes for the manipulator’s end-effector orientation and joint motion are transformed into a graphical representation, as depicted in Fig. 5. The pseudocode summarizing this process is provided in Algorithm 1. In Algorithm 1,


Figure 5: Schematic diagram of posture and joint motion optimization in the RPP method
The D-H parameters used by the six-DOF manipulator arm are shown in Table 1. The other simulation parameters are as follows:
The weighting coefficients:
All computations in this paper have been performed on a 2.5 GHz. Intel Core (TM) i5-7300HQ processor with 16 GB of RAM.
4.2 The Iterative Process of RL
The number of nodes of all the episodes in the first learning process of the RPP algorithm are shown in Fig. 6. At the beginning of the iteration, to update Q-values more frequently, Dyn-Q searches more nodes than Q-learning. Since the 700-th episode, the number of nodes obtained by Dyn-Q began to decrease gradually. After the 4000-th episode, the algorithm converges basically, and the number of path nodes is also within the range of 8–10 stably. In Fig. 6, it is evident that the iteration curve of Dyn-Q significantly outperforms that of Q-learning. Notably, the iteration time required for Q-learning is 1853 s, whereas the iteration time for Dyn-Q stands at a notably lower 1531 s. This iterative computation process serves as compelling evidence that Dyn-Q exhibits a swifter convergence rate compared to Q-learning. Consequently, this accelerated convergence ensures that the Reverse Path Planning (RPP) algorithm can expeditiously generate an initial collision-free path, contributing to enhanced efficiency in path planning.

Figure 6: Learning process of Q learning and Dyn-Q
For comparison, the forward planning (FP) method [32] without additional bidirectional search and weighting coefficients is used to obtain the collision-free path. The blue line in Fig. 7a shows the result. All the nodes’ coordinates and posture angles are arranged in Table 2.

Figure 7: The path of the end-effector of the manipulator in different situations
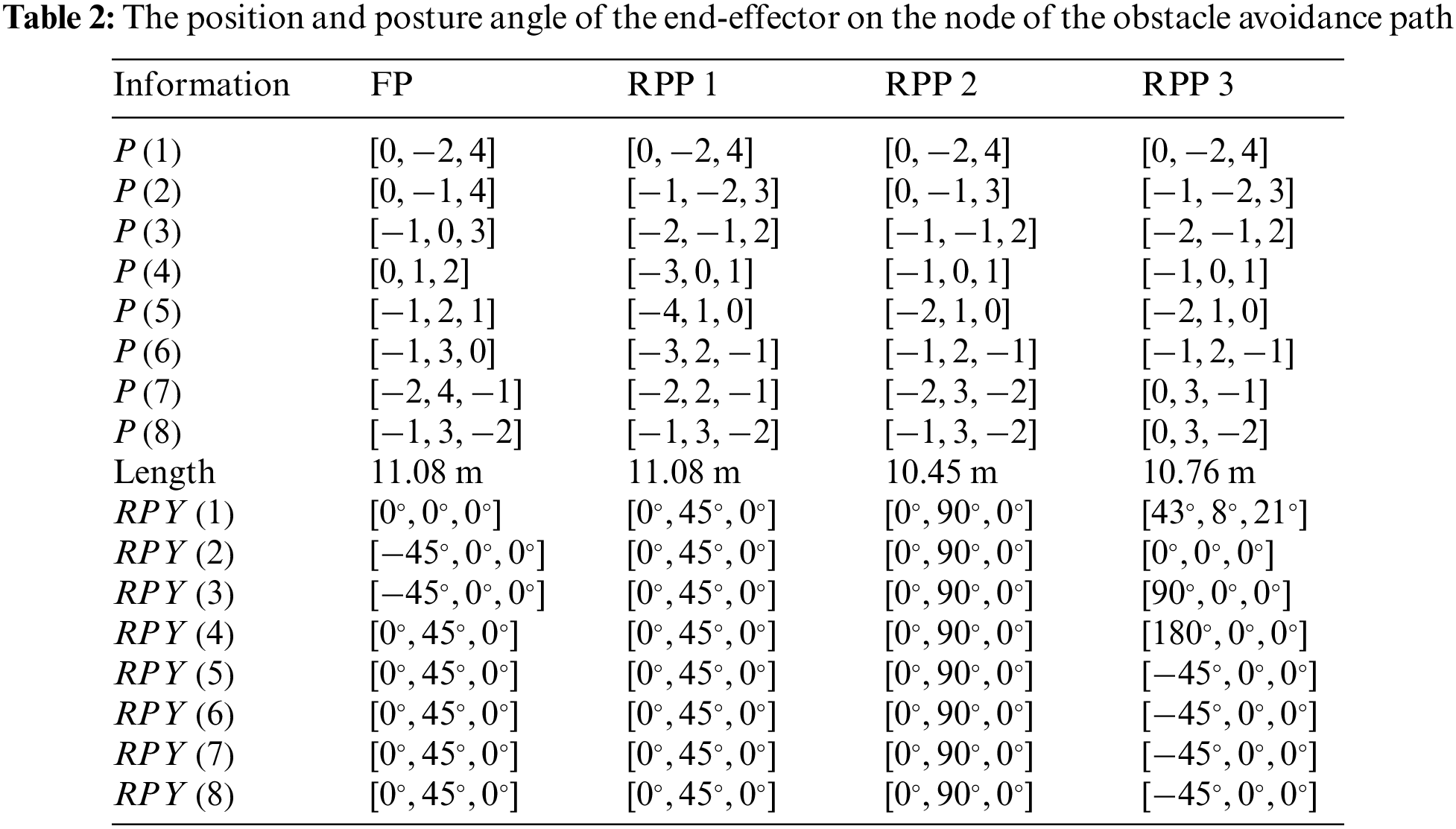
The collision-free of the manipulator in Fig. 7a includes 8 nodes and 7 linear segment sub-paths. The closer a node is to the target point, the shorter the distance between it and the target point. For example, the distances between nodes 1, 2, and 3 and the target point are 7.874 m, 7.28 m, and 5.83 m, respectively. The effectiveness of the reward function defined in Eq. (7) is clearly demonstrated in its capacity to discern the optimal action for each state. This ensures a gradual approach of the manipulator towards the target point, ultimately resulting in the determination of the shortest path. However, owing to the inherent nature of forward planning, wherein calculations proceed from the starting point to the target point, there arises a limitation. Specifically, the manipulator’s end-effector encounters difficulty in achieving effective control precisely at the target point. Regrettably, this circumstance does not align with the specific task requirements detailed in Section 2. Furthermore, the last 8 data in the first column of Table 2 indicate that the posture of the end-effector fluctuates to a certain extent between adjacent nodes, with a posture angle variation of

Figure 8: The results of the joint angles in different situation
To verify the effectiveness of the proposed RPP algorithm, tests were carried out in a scenario in which the posture angle of the target point is the same as the FP method. The green line in Fig. 7a represents the path obtained using the RPP algorithm. Due to the re-planning of the terminal posture Angle, the green line does not coincide with the blue line. The calculations reveal that both the RPP and FP paths share an identical total length, measuring precisely 11.08 m. This observation underscores that the node coordinates for both RPP and FP exhibit a congruent distribution pattern, progressively converging towards the target point. Furthermore, the last eight data points in the second column of Table 2 show that due to the addition of the bidirectional search method, the posture angle of the manipulator’s end-effector is always maintained at
To further test the RPP algorithm, the obstacle and target positions were kept unchanged, and the posture angle of the target point was set to
The above three experiments demonstrate that for a manipulator with a known target point position and posture, the proposed RPP algorithm while ensuring a collision-free path, exhibits three significant advantages: 1. Ensuring the shortest straight-line path length; 2. Smooth the end-effector’s posture; 3. Reduce the motion of high-power joints.
In order to validate the RPP algorithm proposed in this paper more generally, the positions of the target point and obstacles are changed, and the posture angle of the target point is also randomly set to
The collision-free path obtained by the RPP algorithm is shown in cyan in Fig. 7b, with the coordinates of path nodes and posture angles compiled in the fourth column of Table 2. Upon comparison, the total length of this collision-free path is approximately the same as the three paths in Fig. 7a, and the change rule of node coordinates aligns with the previous three cases. The joint motion for collision-free of the manipulator is shown in Fig. 8d. The angle variation range of joint 1 to joint 6 is
In the conclusive phase, Matlab’s Robotics Toolbox was employed to visually represent the collision-free motion of the 6-degree-of-freedom (6-DOF) manipulator across the four experiments, as indicated in Fig. 9. All the figures labeled (a) in Fig. 9 depict the manipulator’s initial pose, while those labeled (b) and (c) represent the manipulator’s poses at intermediate nodes, and (d) show the manipulator’s target pose. Throughout the process, the end-effector strictly follows the obstacle avoidance path shown in Fig. 7, successfully avoiding obstacles and safely reaching the target point. In Figs. 9b to 9d, while the manipulator is engaged in obstacle avoidance, the end-effector undergoes minimal changes in posture, and it arrives at the target location in the specified posture.

Figure 9: The action of the 6-DOF manipulator in different situations
The sequential execution times for the three RPP experiments mentioned above were 1840, 1810, and 4426 s, respectively. Notably, Experiment 3 exhibited the longest computation time, while the computation times for the first two experiments were relatively close. Further investigation revealed that Experiment 3 involved three alternations between two complete phases of the RPP algorithm, whereas the first two experiments included only one alternation between two complete phases. This observation suggests that while RPP can identify the shortest path within the first phase, it cannot guarantee the acquisition of suitable posture angles and feasible kinematic solutions in the second phase. Consequently, the computational complexity of the RPP algorithm is predominantly determined by the second phase. In Experiment 3, the cramped space between obstacles and the manipulator compelled the RPP algorithm to explore all conceivable postures during the initial two complete iterations. However, none of these attempts proved successful in avoiding collisions with obstacles. Consequently, in cases where, during the second phase of RPP computation, all posture angles configured by the algorithm lead to collisions between the manipulator and obstacles, the RPP algorithm fails to converge. Furthermore, when the target point falls outside the reachable workspace of the manipulator, the RPP algorithm also fails to converge.
This paper addresses the intricate task of collision-free path planning for industrial manipulators, which encompasses the optimization of path, end-effector posture, and joint motion. To account for real-world scenarios, the study introduces the Reverse Path Planning (RPP) algorithm, which effectively devises collision-free paths originating from the target point and extending back to the initial point. By leveraging reinforcement learning, a sequence of nodes is obtained and subsequently connected to establish a collision-free trajectory. To enhance path search efficiency, the Q-learning approach is augmented as Dyn-Q. Additionally, collision detection leverages the Denavit-Hartenberg (DH) parameters of the manipulator, ultimately yielding a collision-free path through reverse planning. Furthermore, in the process of planning end-effector posture and joint motion, the utilization of bidirectional search and weighted coefficient methods proves instrumental in achieving significant improvements in the smoothness of both end-effector posture and joint movements. The most significant contribution of this study is the realization of multi-objective optimization in the path planning process, particularly for MDOF manipulators that demand precise posture adjustments at the target position.
It is essential to acknowledge that, to mitigate computational complexity in this study, we designated node coordinates, target point coordinates, and obstacle center coordinates as integers. In practical engineering scenarios, there exists the potential to refine measurement units and augment positioning precision following specific application requirements. Additionally, polynomial or B-spline fitting techniques can be employed to further smooth the obstacle avoidance paths. We hope to implement these in future work.
Acknowledgement: The authors wish to express their appreciation to the reviewers for their valuable suggestions that enhanced the paper’s quality. We also sincerely appreciate the editors for their patience, supportive reminders, and dedicated efforts in editing the manuscript. We extend heartfelt thanks to all the authors for contributing to this paper.
Funding Statement: This research work is supported by the National Natural Science Foundation of China under Grant No. 62001199; Fujian Province Nature Science Foundation under Grant No. 2023J01925.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Zhiwei Lin; data collection: Zhiwei Lin, Jianmei Jiang; analysis and interpretation of results: Zhiwei Lin, Hui Wang, Tianding Chen; manuscript writing: Zhiwei Lin, Hui Wang, Tianding Chen. manuscript review and editing: Yingtao Jiang, Yingpin Chen. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The manuscript included all required data and implementing information.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Nagatani, K., Fujino, Y. (2019). Research and development on robotic technologies for infrastructure maintenance. Journal of Robotics and Mechatronics, 31(6), 744–751. [Google Scholar]
2. Fang, H. C., Ong, S. K., Nee, A. Y. C. (2016). Robot path planning optimization for welding complex joints. The International Journal of Advanced Manufacturing Technology, 90(9), 3829–3839. [Google Scholar]
3. Lu, Y. A., Tang, K., Wang, C. Y. (2021). Collision-free and smooth joint motion planning for six-axis industrial robots by redundancy optimization. Robotics and Computer-Integrated Manufacturing, 68, 91–107. [Google Scholar]
4. Wei, Y. Z., Gu, K. F., Cui, X. J., Hao, C. Z., Wang, H. G. et al. (2016). Strategies for feet massage robot to position the pelma acupoints with model predictive and real-time optimization. International Journal of Control, 14(2), 628–636. [Google Scholar]
5. Li, Y., Liu, K. P. (2019). Two-degree-of-freedom manipulator path planning based on zeroing neural network. 2019 IEEE 7th International Conference on Computer Science Communication and Network Security, pp. 1–8. Dalian, China. [Google Scholar]
6. Secil, S., Ozkan, M. (2023). A collision-free path planning method for industrial robot manipulators considering safe human-robot interaction. Intelligent Service Robotics, 16(3), 323–359. [Google Scholar]
7. Dijkstra, E. W. (1959). A note on two problems in connexion with graphs. Numerische Mathematik, 1, 269–271. [Google Scholar]
8. Hart, P. E., Nilsson, N. J., Raphael, B. (1968). A formal basis for the heuristic determination of minimum cost paths. IEEE Transactions on Systems Science and Cybernetics, 4(2), 100–107. [Google Scholar]
9. Fu, B., Chen, L., Zhou, Y. T., Zheng, D., Wei, Z. Q. et al. (2018). An improved A* algorithm for the industrial robot path planning with high success rate and short length. Robotics and Autonomous Systems, 106, 26–37. [Google Scholar]
10. Persson, S. M., Sharf, I. (2014). Sampling-based A* algorithm for robot path-planning. The International Journal of Robot Res, 33(13), 1683–1708. [Google Scholar]
11. Macenski, S., Moore, T., Lu, D. V., Merzlyakov, A., Ferguson, M. (2023). From the desks of ROS maintainers: A survey of modern & capable mobile robotics algorithms in the robot operating system 2. Robotics and Autonomous Systems, 168, 1–12. [Google Scholar]
12. Khatib, O. (1986). Real-time obstacle avoidance for manipulators and mobile robots. The International Journal of Robotics Research, 5(1), 90–98. [Google Scholar]
13. Wang, W. R., Zhu, M. C., Wang, X. M., He, S., He, J. P. et al. (2018). An improved artificial potential field method of trajectory planning and obstacle avoidance for redundant manipulators. International Journal of Advanced Robotic Systems, 15(5), 1–13. [Google Scholar]
14. Xu, T. Y., Zhou, H. B., Tan, S. X., Li, Z. Q., Ju, X. (2021). Mechanical arm obstacle avoidance path planning based on improved artificial potential field method. Industrial Robot, 49(2), 271–279. [Google Scholar]
15. Kavraki, L. E., Svestka, P., Latombe, J. C., Overmars, M. H. (1996). Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Transactions on Robotics and Automation, 12(4), 566–580. [Google Scholar]
16. Lavalle, S. M. (1998). Rapidly-exporing random trees: A new tool for path planning. In: Algorithmic and computational robotics new direction, pp. 293–308. USA: Tech Science Press. [Google Scholar]
17. Gao, Q. Y., Yuan, Q. N., Sun, Y., Xu, L. Y. (2023). Path planning algorithm of robot arm based on improved RRT* and BP neural network algorithm. Journal of King Saud University—Computer and Information Sciences, 35(8), 1–14. [Google Scholar]
18. Qureshi, A. H., Ayaz, Y. (2016). Potential functions based sampling heuristic for optimal path planning. Autonomous Robots, 6, 1079–1093. [Google Scholar]
19. Kumar, A., Raj, R., Kumar, A., Verma, B. (2023). Design of a novel mixed interval type-2 fuzzy logic controller for 2-DOF robot manipulator with payload. Engineering Applications of Artificial Intelligence, 123, 1–15. [Google Scholar]
20. Izquierdo, R. C., Cukla, A. R., Lorini, F. J., Perondi, E. A. (2023). Optimal two-step collision-free trajectory planning for cylindrical robot using particle swarm optimization. Journal of Intelligent & Robotic Systems, 108(3), 1–15. [Google Scholar]
21. Wang, S. X., Wang, W. J., Cao, Y. T., Luo, Y., Wang, X. H. (2023). Obstacle avoidance path planning of 7-DOF redundant manipulator based on improved ant colony optimization. Recent Patents on Mechanical Engineering, 16(3), 177–187. [Google Scholar]
22. Zhong, J., Wang, T., Cheng, L. L. (2022). Collision-free path planning for welding manipulator via hybrid algorithm of deep reinforcement learning and inverse kinematics. Complex and Intelligent Systems, 8, 1899–1912. [Google Scholar]
23. Park, K. W., Kim, M. S., Kim, J. S., Park, J. H. (2022). Path planning for multi-arm manipulators using soft actor-critic algorithm with position prediction of moving obstacles via LSTM. Applied Sciences, 12(19), 9837–9857. [Google Scholar]
24. Yu, J. X., Arab, A., Yi, J. G., Pei, X. F., Guo, X. X. (2022). Hierarchical framework integrating rapidly-exploring random tree with deep reinforcement learning for autonomous vehicle. Applied Intelligence, 53(13), 16473–16486. [Google Scholar]
25. Watkins, C. J. C. H., Dayan, P. (1992). Technical note: Q-learning. Machine Learning, 8, 279–292. [Google Scholar]
26. Lin, Z. W., Chen, T. D., Jiang, Y. T., Wang, H., Lin, S. Q. et al. (2023). B-Spline-based curve fitting to cam pitch curve using reinforcement learning. Intelligent Automation & Soft Computing, 36(2), 2145–2164. https://doi.org/10.32604/iasc.2023.035555 [Google Scholar] [CrossRef]
27. Hwang, K. S., Jiang, W. C., Chen, Y. J. (2015). Model learning and knowledge sharing for a multiagent system with Dyna-Q learning. IEEE Transactions Cybernetics, 45(5), 964–976. [Google Scholar]
28. Hwang, K. S., Jiang, W. C., Chen, Y. J., Hwang, I. (2017). Model learning for multistep backward prediction in Dyna-Q learning. IEEE Transactions on Systems Man and Cybernetics Systems, 48(9), 1470–1481. [Google Scholar]
29. Aalhasan, A., Tang, X. Q., Song, B. (2016). Collision detection and trajectory planning for palletizing robots based OBB. Indonesian Journal of Electrical Engineering and Computer Science, 1(1), 109–118. [Google Scholar]
30. Pieper, D. L. (1968). The kinematics of manipulators under computer control (Ph.D. Thesis). University of Stanford, USA. [Google Scholar]
31. Ananthanarayanan, H., Ordóñez, R. (2015). Real-time inverse kinematics of (2n+1) DOF hyper-redundant manipulator arm via a combined numerical and analytical approach. Mechanism and Machine Theory, 91, 209–226. [Google Scholar]
32. Jia, Y. S., Li, Y. C., Xin, B., Chen, C. L. (2020). Path planning with autonomous obstacle avoidance using reinforcement learning for six-axis arms. 2020 IEEE International Conference on Networking, Sensing and Control, pp. 1–6. Nanjing, China. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools