IoT Task Offloading in Edge Computing Using Non-Cooperative Game Theory for Healthcare Systems

1  Introduction

In recent years, the convergence of Internet of Things (IoT) and edge computing has brought transformative changes across industries, notably in the healthcare sector. The widespread use of connected medical devices and the growing demand for real-time data analysis have underscored the need for innovative solutions capable of efficiently managing and processing the vast volumes of data generated by these devices [1,2]. A key strategy in addressing this challenge lies in leveraging edge computing, where data is processed in proximity to its source, reducing latency and enhancing overall system performance.

With advancements in wireless communication, the contemporary distributed network offers expanded coverage, higher capacity, and improved connectivity, facilitating the realization of IoT. IoT devices are increasingly tasked with computationally intensive and time-sensitive operations, especially with the development of sophisticated load control and real-time computing. This has given rise to the need for efficient resource management solutions, given the constraints of limited computation and storage resources on the device side [3]. While IoT devices can offload tasks to the nearest edge servers to mitigate delays and conserve energy, the burgeoning number of terminal devices in IoT has made computational tasks more challenging.

As the demand for communication and spectrum resources continues to surge, the development of resource allocation and management algorithms has become urgent. Non-Orthogonal Multiple Access (NOMA) technology presents a practical solution for efficiently using scarce spectrum resources [4,5]. However, several challenging problems persist. Jointly optimizing resource unit allocation, computing resource offloading, and task division algorithms is computationally complex due to the coupling between these entities. Moreover, striking a balance between long-term optimization goals and real-time decision-making amplifies the computational complexity of the model. The intricacies of multidimensional task allocation without future data, such as task arrival times and channel state information, add to the challenge. Additionally, the dynamic interference among devices when the same resource units are allocated to different devices creates externalities, leading to exponentially complex resource unit allocation problems.

In response to these challenges, the research explores a multi-time scale multidimensional resource allocation approach for NOMA-based Mobile Edge Computing (NOMA-MEC) in IoT. The proposed algorithm aims to minimize long-term device consumption by jointly optimizing resource unit allocation and task splitting. This approach dissects the long-term stochastic joint optimization problem into three short-term deterministic problems using the Lyapunov technique. It focuses on wireless spectrum allocation, task splitting, and task computation. To enhance efficiency and reduce complexity, IoT devices and resource units are grouped based on clustering schemes [6,7]. Wireless spectrum allocation is treated as a one-to-many matching problem, resolved on a larger time scale and executed on the base station (BS) side. The suggestion is to use group-switching matching to allocate resource units. Devices and resource units are initially categorized into several groups, with switching matching performed within each group. Task splitting and computing resource allocation are then handled on the device side in a distributed manner on a smaller time scale [8].

The research presents a novel algorithm for resource unit allocation, which optimizes energy consumption while taking into account the dynamic nature of IoT device preferences and the scarcity of spectrum resources [9].

- Task Splitting Efficiency: The study introduces a task splitting approach that improves the overall system performance by jointly optimizing work partitioning and computing resource allocation, reducing queue backlogs.

- Multi-Time Scale Solution: By addressing long-term queuing delay constraints, the research offers a multi-time scale, multidimensional resource allocation strategy for NOMA-MEC in IoT, striking a balance between complexity and network performance.

- Group-Based Approach: The proposed approach utilizes clustering schemes to group IoT terminals and resource units, reducing computational complexity and enhancing efficiency in wireless spectrum allocation.

2  Related Works

With the advent of Industry 4.0, Industrial IoT (IIoT) has become a pivotal technology, addressing various challenges in smart factories, including the management of industrial big data, equipment monitoring, and maintenance [10,11]. IIoT devices generate a substantial amount of data, and some industries require real-time data processing. Conventionally, industrial data is transferred to centralized cloud servers for processing due to their powerful computing capabilities [12]. However, the sheer number of IIoT devices can lead to network congestion, causing delays in data transmission and impacting real-time tasks. Therefore, a network infrastructure capable of real-time and efficient data processing is essential for IIoT.

Edge computing is emerging as a valuable complement to cloud computing, utilizing a distributed computing approach to alleviate network congestion and reduce transmission delays associated with cloud computing’s centralized processing [13]. By distributing computing tasks across multiple servers throughout the network, edge computing ensures a quicker response to user requests and tasks [14]. To minimize data transmission delays in long-distance communication, edge servers are strategically placed closer to the devices.

Several ongoing studies explore the application of edge computing in IIoT environments. These studies optimize time and energy costs to achieve the efficient distribution of green and energy-saving computing resources [15,16]. They addressed offloading challenges for multi-hop computing tasks in hybrid edge cloud computing environments, utilizing game theory to meet service quality requirements [17]. In [18], authors introduced an innovative approach that integrates Wireless Power Transfer (WPT) with Mobile Edge Computing (MEC) for efficient computation offloading, achieving real-time performance in large-scale networks and addressing energy and latency constraints in wireless environments. In [19], authors optimized task dependencies in IoT edge computing using a directed cyclic graph model and priority-aware scheduling, outperforming other offloading methods in terms of throughput and task satisfaction rate. In [20], authors addressed the growing need for data analysis in the context of IoT systems, where the volume of generated data poses performance challenges. It introduces the IoT-SCOM model, focusing on minimizing transmission latency in edge-cloud-hybrid systems. Experimental results show that IoT-SCOM offers improved accuracy and efficiency compared to existing methods, enhancing data-intensive service element deployment in the edge-cloud environment. Moreover, a hybrid computing architecture with intelligent resource planning is proposed to meet real-time requirements [21].

In summary, edge computing offers solutions to meet quality of service demands and reduce system overhead by deploying at the network edge, closer to field devices, and providing suitable computing resources. This research investigates computing resource allocation and task offloading in IIoT environments using edge computing and NOMA. It aims to resolve issues related to communication delay, energy consumption, and system scalability by efficiently allocating computer resources and offloading responsibilities from edge servers. The contributions of this paper are twofold.

1. Decomposition based on multi-dimensional optimization: Utilizing Lyapunov optimization, the complex, long-term stochastic multi-dimensional optimization problem is decomposed into three deterministic problems that can be solved effectively.

2. Resource Allocation Problem based on group Switching Matching: The proposed resource unit allocation algorithm, based on group switched matching, provides a more efficient, less complex, and flexible approach to handle interdependencies among IIoT devices and various resources.

The remainder of this paper is structured as follows. Our system model is introduced in the second section. The introduction of the problem model, transformation, and queuing delay limitations follows in Section 3. The proposed algorithm is further explained in Section 4. The simulation results and data analysis are presented in the fifth section. The paper is finally summarized in the sixth section.

3  System Model

This paper examines a common NOMA MEC-based IIoT example, which includes a base station, an edge server, and a significant number of IIoT devices with low energy and computing capacities. The BS is place d where the edge server is, as stated in Fig. 1, and it offers radio access and computing services for N IIoT devices. The node symbolizes the attack state, and its set is N, with the set being defined as 𝒩={1,2,…,n,…,N}. The IIoT device either partially processes its tasks or offloads them to the BS. Comparable to [22], we investigate a discrete timeslot form that splits the optimization process into T time slots, each with a duration τ, as displayed in Fig. 2. The timeslot collection is indicated by the expression 𝒯={1,…,t,…, T}. Consider a quasi-static example where the CSI varies between time slots but stays the same in one time slots. Each subsequent T′ timeslot is connected to a time epoch denoted by the symbols s∈S, S={1,2,…,S}. The definition of the s-th time epoch is 𝒯(s)={(s−1)T′+1,…, sT′,sT′+1,…,(s+1)T′}.

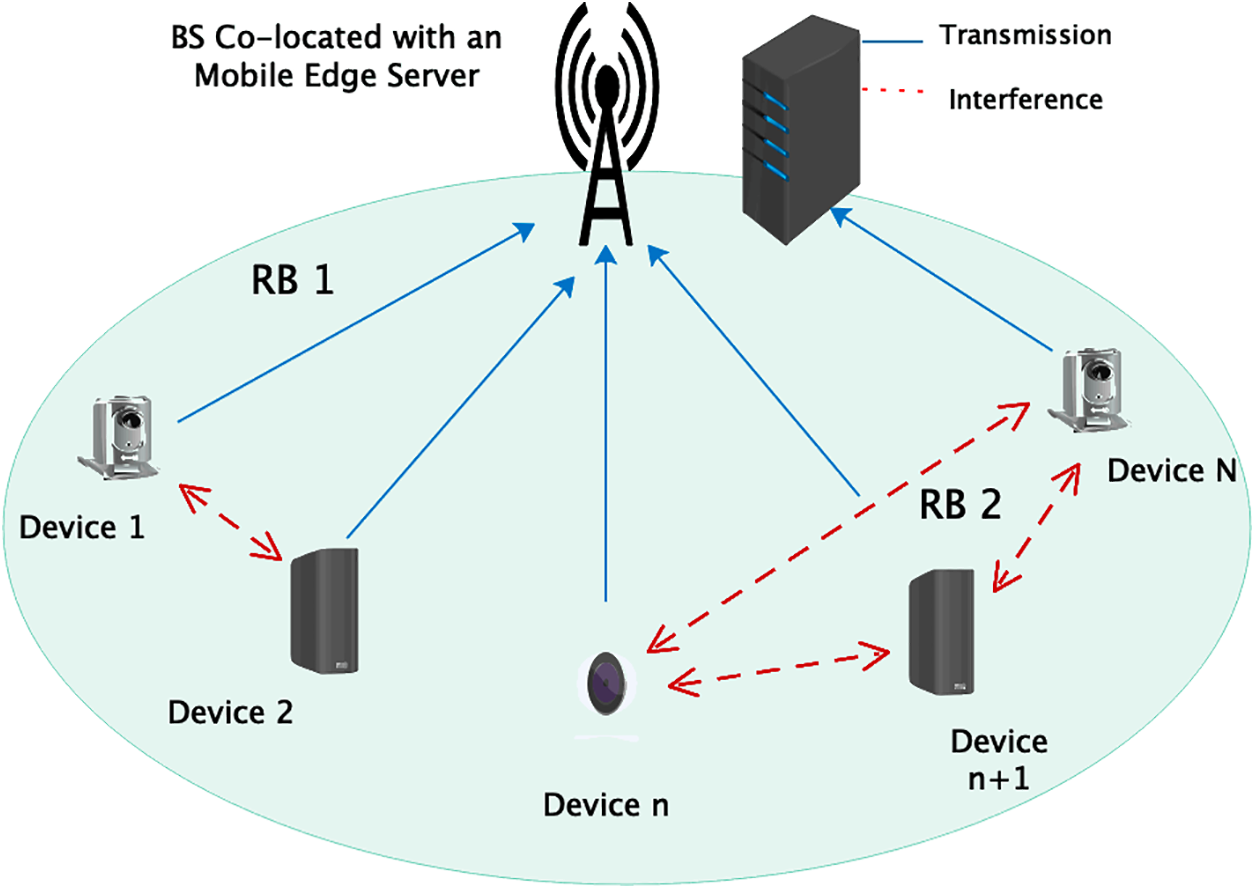
Figure 1: System model

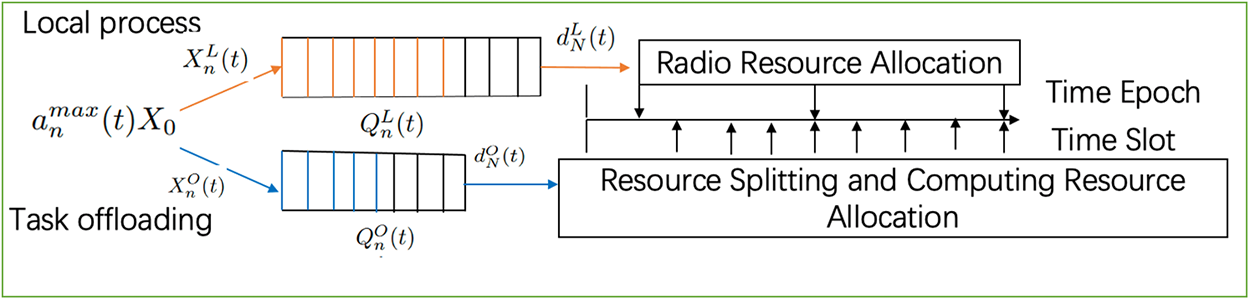
Figure 2: Discrete timeslot model

The resource is divided into M time-frequency resources units with bandwidth B and a time period of T′τ, the union of which is ℳ={1,…,m,…, M}. The multi-dimensional resource allocation and splitting problems are studied. At the start of each time interval, the infinite resource allocation scheme is optimized over a major timescale. The resource allocation scheme is represented through the binary indicator y(s)={ynm(s), n∈𝒩, m∈ℳ}, where ynm(s)=1 dicates that resource unit m is allocated to the device n in the s-th time interval, otherwise ynm(s)=0. Next, computing resource allocation and splitting are jointly optimized on a small-time scale based on resource unit allocation strategy in each timeslot.

A. Traffic Model on the Device

The notations used in the mathematical analysis is represented in Table 1 whereas description of each equation is mentioned in Table 2. The task partitioning system is used in this paper [23], and it allows for the division of each task into separate sub-tasks of size X0(bit). Assume that anmax(t) subtasks reach the device n at the t-th timeslot. The arriving job can be split into an(t) sub-tasks for local operation and anmax(t)−an(t) sub-tasks for task offloading, which are two different and parallel models. Given the foregoing, the task splitting at device n in timeslot t is defined as

{XnL(t)+XnO(t)=anmax(t)X0,XnL(t)=an(t)X0, an(t)∈{0,1,…,anmax(t)} (1)

which XnL(t) is the task length of local processing of device n at time t, and XnO(t) represents the task length when the device n performs computing offloading at time t.

QnL(t) and QnO(t) are used to store local operation and offloading resource, separately. As shown in Fig. 1, QnL(t) and QnO(t) [12] evolved into

QnL(t+1)=max{QnL(t)−dnL(t),0 }+XnL(t)(2)

QnO(t+1)=max{ QnO(t)−dnO(t)​,0  }+XnO(t) (3)

which dnL(t) and dnO(t) respectively indicate the amounts of data departure QnL(t) and QnO(t).

B. Locally Task Data Processing Scheme

The quantity of locally executed data for the t-th timeslot is defined as

dnL(t)=τfn(t)ln (4)

where fn(t) denotes the number of CPU cycles that were allocated to device N during the t-th timeslot, this is based on the 3GPP channel model. The required number of CPU cycles per bit, or computation intensity, is ln. At the t-th timeslots, the local processing computing delay and the corresponding energy consumption generated by device n are defined as

DnL(t)=min{τ, QnL(t)lnfn(t)}(5)

EnL(t)=κnfn3(t)min{τ, QnL(t)lnfn(t)}(6)

where the chip structure regulates a constant power coefficient called κn.

C.   Based on Task Offloading Scheme

Typically, BS uses successive interference cancellation (SIC) in NOMA-based systems to lessen the acquired signal’s interference. All other signals are viewed as interference, but the BS decodes signals from equipment with higher channel gains in the right order. The channel gain of the uplink from device n to resource unit m in the t-th timeslot is written as hnm(t), and the signal noise ratio (SNR) received at BS is given as follows:

SNRnm(t)=p|hnm(t)|2∑i=1,i≠nN[yim(s)p|him(t)|2]+(θ)2(7)

The transmission power is p. Intracellular interference caused by other low channel gain devices makes up the first part of the denominator, while Additive White Gaussian Noise Power makes up the second. The volume of data from a task that can be offloaded in the t-th timeslot and the transmission speed of device n using resource unit m are therefore determined below:

Rnm(t)=Blog2[1+SNRnm(t)](8)

dnO(t)=τ∑m=1M⁡ynm(s)Rnm(t)(9)

The corresponding energy consumption produced by device n in the t-th timeslot is obtained as follows:

EnO(t)=pmin{τ,QnO(t)∑m=1Mynm(s)Rnm(t)}(10)

4  Problem Definition and Formulation

In this section, the queueing delay constraint is introduced first. Next, the optimization problem of multi-dimensional resource allocation and task splitting is presented. Later on, the proposed Algorithm is addressed.

A. Queued Delay Constraint

The queueing delay constraint is controlled to assure the effectiveness and timeliness of the offloading task. Little’s Law [24] states that the queuing delay of QnL(t) and QnO(t) is calculated as

limT→∞⁡1T∑t=1T⁡QnL(t)MAnL(t)≤Dn,maxL(11)

limT→∞⁡1T∑t=1T⁡QnO(t)MAnL(t)≤Dn,maxO(12)

where MAnL(t)  and MAnL(t)  are the average data arrival rate of moving time of QnL(t) and QnO(t), respectively. Their corresponding maximum tolerated queuing delays are Dn,maxL and Dn,maxO.

B.   Problem Description

By collectively optimizing resource unit allocation, splitting, and computing task scheduling, in the case of queue delay restrictions, the goal is to decrease the overall cumulative long-term energy consumption of all devices. It is possible to express the multidimensional resource allocation and split optimization strategy as

P1: maxy,a,fE¯=1T∑t=1T∑n=1NE{EnL(t)+EnO(t)}

C1: an(t)∈{0,1,…,anmax(t)}, ∀n∈𝒩,∀t∈𝒯

C2:0≤fn(t)≤fnmax, ∀n∈𝒩,∀t∈𝒯

C3: ynm(s)∈{0,1}, ∀n∈𝒩, ∀m∈ℳ, ∀s∈𝒮

C4: ∑m=1Mynm(s)≤1,∀n∈𝒩,∀s∈𝒮

C5: ∑n=1Nynm(s)≤Nm,∀m∈ℳ,∀s∈𝒮

C6: ynm(s)SNRnm(t)≥SNRn, ∀n∈𝒩, ∀t∈𝒯

where y={y(s)}, s∈S represents the resource unit allocation vector, a={a(t)}, t∈𝒯 represents the radio resource splitting vector, and a(t)={an(t), n∈𝒩}, f={f(t)=fn(t), n∈𝒩, t∈𝒯} represents the computation resource allocation vector. C1  is rhe resource splitting constraint. The computational resource allocation restriction on the device is indicated by C2. C3−C5  denote that each device can use a maximum of one resource unit. The resource unit m can be allocated to devices up to Nm. According to C6, the resource unit allocated to device n  must make sure that the SNR obtained at BS is more than the required minimum SNRn.

C.   Transformation of the Problem

P1 is an non-deterministic polynomial (NP)-hard issue that is challenging to directly solve. By using Lyapunov optimization [25], the original long term stochastic optimization issue is split up into several deterministic subproblems in the short term. Formulas (11) and (12) can be transformed into the queue stability constraint problem for the virtual queue concept. It is possible to convert the matching virtual queues ΔnL(t) and ΔnO(t) into

ΔnL(t+1)=max{VQnL(t)+QnL(t)MAnL(t)−Dn,maxL, 0} (13)

ΔnO(t+1)=max{VQnO(t)+QnO(t)MAnO(t)−Dn,maxO, 0}(14)

When ΔnL(t) and ΔnO(t) are average rate stable, the formulas (11) and (12) will be maintained automatically. So P1 can be converted to

P2: min{y(s),a(t), f(t)}∑n=1N{Vκnfn3(t)min[τ,QnL(t)lnfn(t)]

+Vpmin[τ,QnO(t)∑m=1Mynm(s)Rnm(t)]

+QnL(t)[an(t)X0−τfn(t)ln]

+QnO(t)[(anmax(t)−an(t))X0–τ∑m=1Mynm(s)Rnm(t)]

+ΔnL(t)[QnL(t)1t[∑i=1t−1XnL(i)+an(t)X0]]

+ΔnO(t)[QnO(t)1t[∑i=1t−1XnO(i)+((anmax(t)−an(t)X0]]}(15)

s.tC1−C6

It can be concluded that P2 will be decomposed into three optimization sub-tasks, namely SP1: resource unit allocation sub-problem, SP2: task splitting sub-problem, and SP3: computing resource allocation sub-problem.

5  Resource Allocation and Task Splitting

In this section, we first introduce the three decomposed sub-schemes and their related responses and then conclude the raised scheme.

A.   Resource Unit Allocation Optimization

At the start of each interval in SP1, device n  and BS choose the resource unit allocation strategy. As hnm(t), QnO(t) and Rnm(s) vary dynamically in timeslot, their empirical averages, namely, hnm(t)¯,  QnO(t)¯ and Rnm(s)¯ are considered. So SP1 is going to be

SP1: miny(s)∑n=1N{Vpmin[τ, QnO(s)¯∑m=1Mynm(s)Rnm(t)¯]

 −QnO(t)¯τ∑m=1M⁡ynm(s)Rnm(s)¯}(16)

s.tC3−C6

A 1-to-n matching method between devices and resource unit is the default setting for SP1. The 1-to-n matching function eta that we are modeling here performs as follows:

(1)λ(n)⊂ℳ∪{∅}, and |λ(n)|∈{0,1}, ∀n∈𝒩,

(2) λ(m)⊂𝒩, and |λ(n)|≤Nm, ∀m∈ℳ,

(3) λ(n)=m ⇔n∈λ(m), ∀m∈ℳ,∀n∈𝒩.(17)

Performances 1 and 2 dealt with the constraints C4 and C5, while performance 3 suggests that if device m and resource unit m match, then resource unit m is assigned to device n, and the opposite is true. In particular, there is a strong link between the resource unit allocation index ynm(s) and λ.

{ynm(s)=1, if λ(n)=m,ynm(s)=0,otherwise(18)

The following are the utility functions for device n and resource unit m:

Un(m)=−Vpmin[τ, QnO(s)¯∑m=1Mynm(s)Rnm(s)¯]+ QnO(s)¯τynm(s)Rnm(s)¯(19)

Un(m)=∑n=1N{−Vpmin[τ, QnO(s)¯∑m=1M⁡ynm(s)Rnm(s)¯]+QnO(s)¯τynm(s)Rnm(s)¯}(20)

It is not practical to match all devices and resource unit due to the extensive IIoT networks’ high matching complexity. So, we start by dividing devices and resource unit into sets. Especially, based on the clustering strategy [26], devices and resource unit are partitioned into K sets, i.e., 𝒩={𝒩𝒢1,…,𝒩𝒢k,…, 𝒩𝒢K} and ℳ={ℳ𝒢1,…,ℳ𝒢k,…, ℳ𝒢K}, Each union has Ng=N/k devices and Mg=M/k resource unit, respectively. The devices in every union usually have regulated resource unit, i.e., MGK allocated to the NGK  for offloading. Then, switching matching is carried out in each set in a semi-distributed mode, allowing resource unit and devices to build their priorities in descending order based on their utilities. Therefore, two-end group switching matching is used to settle the resource unit assignment problem.

Definition 1. Define matches λ and two device resource unit pairs (n,m), (v,l)∈λ, namely, λ(m)=n, and λ(v)=l, ∀n≠v and n,v∈𝒩𝒢k, ∀m≠l, m,l∈ℳ𝒢k, if they meet

Un(l)≤Un(m) and Uv(n)≤Uv(l)

Um(v)≤Um(n) and Ul(n)≤Um(v)(21)

λnvml={λ(n,m), (v,l)}∪{(n,l), (v,m)} is depicted as the variables λ and λnvml≻λ swapping process.

Definition 2. when there is no exchange match, the matched λ is bilateral exchange stable. The proposed algorithm summarizes the details of resource unit allocation based on group switching matching. During initialization, devices and resource unit are divided into K unions, and each device union is assigned resource unit set, namely 𝒩𝒢k←ℳ𝒢k. Subsequently, if only all the restrictions in formula (15) are met, the devices and resource unit in the allocation group will randomly match each other. Each device and resource unit produces a preference based on the formula (20).

In the switching matching period, each device n in NGK currently matching the resource unit m  in MGK takes a program to its most desired resource unit l in MGK. For each device v in NGK that existing match l in MGK, If λnvml≻λ and satisfies all the requirements in formula (15), the old match λ is replaced with the new match  λnvml. Otherwise, λ stays the same. The stage ends until no matches are exchanged.

At the end stage, the formula (19) transforms the final λ into the resource unit allocation index y∗(s).

B.   Task Splitting and Resource Allocation Optimization

Task splitting issue with the following formula, in the t-th timeslot, SP2 distributes the task splitting decision between local operation and offloading.

SP2: minan(t)Γ(an(t))=QnL(t)am(t)X0+QnO(t)[anmax(t)−an(t)X0]

+ΔnL(t)[QnL(t)1t[∑i=1t−1XnL(i)+an(t)X0]]

+ΔnO(t)[QnO(t)1t[∑i=1t−1XnO(i)+((anmax(t)−an(t)X0]](22)

s.t C1

Computing resource allocation sub-scheme SP3 controls the number of CPU cycle frequencies each device allocates for local operation in the t-th timeslot, which is gained via the following formula:

SP3: min{f(t)}=Vκnfn3(t)min[τ,QnL(t)lnfn(t)]−QnL(t)τfn(t)ln(23)

s.tC2

Both SP2 and SP3 are convex optimization problems, and Lagrange duality decomposition is easy to resolve. Reference can be made to similar specific derivation process [27].

C.   Our Proposed Algorithm

The proposed algorithm consists of three steps, namely

Step 1: Initialize all queue backlog and resource unit allocation strategy metrics.

Step 2: The best resource unit allocation y∗(s) is achieved by each device in a partially distributed fashion according to Algorithm 1 and sends data using the allocated resource unit.

Step 3: Each device learns the ideal resource allocation and task distribution approach. The efficiency of data transmission, power usage, queue overhang, queue delay, and updates QnL(t+1), QnO(t+1),  VQnL(t+1) and VQnO(t+1) according to the formulas (2), (3), (13), and (14), are then taken into account by each device. Up until t>T, the iteration between the second and third steps continues.

6  Experiments

This part uses simulation to assess the suggested algorithm. In this study, a unitary cell with a 2000 m radius is considered. Each 100 group contains 20 devices, dividing all equipment and resource unit in the same way. Table 3 lists the exact simulation parameters.

ACRA (Access Control and Resource Allocation Algorithm): ACRA is an advanced algorithm designed for resource allocation and access control in the context of edge computing and IoT (Internet of Things). It addresses the challenge of efficiently managing resources and allocating them to IoT devices. The key features of ACRA include:

Resource Allocation: ACRA optimizes the allocation of computing and communication resources to IoT devices, ensuring efficient utilization of available resources. Access Control: It implements an access control mechanism, allowing IoT devices to submit tasks to the nearest edge server for processing. This minimizes task delays and conserves energy. Real-time Decision-Making: ACRA balances the need for long-term optimization goals with the requirement for real-time decision-making. This is crucial for ensuring that tasks are processed efficiently and in a timely manner. Multi-Time Scale Optimization: ACRA decomposes the complex, long-term stochastic optimization problem into short-term deterministic sub-problems. This approach simplifies resource allocation and improves system performance. Clustering Schemes: The algorithm employs clustering schemes to group IoT terminals and resource units, reducing computational complexity and enhancing efficiency in wireless spectrum allocation.

SMRA (Switch Matching Resource Allocation Algorithm): SMRA is another resource allocation algorithm that focuses on optimizing energy consumption within IoT networks. It is designed to allocate resources efficiently, particularly in terms of energy usage. Key characteristics of SMRA include: Energy Optimization: SMRA primarily aims to minimize energy consumption in IoT networks. It is especially well-suited for scenarios where energy efficiency is a critical consideration. Task Processing: It ensures that devices submit tasks to edge servers when they cannot be completed within the required timeframe. This reduces task delays and saves energy. Subtask Offloading: SMRA emphasizes offloading subtasks from devices to edge servers to reduce queue backlogs and enhance overall system performance.

Comparison and Evaluation: To provide a clear understanding of their respective roles and effectiveness, ACRA and SMRA should be compared based on various evaluation parameters, such as: Energy Efficiency: A comparison should be made to determine which algorithm is more effective in optimizing energy consumption. Task Processing Speed: Evaluation should assess which algorithm minimizes task delays and enhances real-time performance. Queue Backlogs: The impact of ACRA and SMRA on queue backlogs and system performance should be compared. Resource Utilization: An analysis of how efficiently these algorithms allocate and utilize computing and communication resources. Complexity: Assess the computational complexity of each algorithm, which can affect practical implementation.

We compared the two most advanced algorithms. The first is the resource unit allocation algorithm based on switch matching (SMRA) proposed in [28]. It should be noted that in the simulation, minimization of energy consumption replaces SMRA maximum of energy efficiency. The second is due to the Lyapunov optimization and pricing matching based Access control and resource allocation algorithm (ACRA) developed. The task split phase is determined randomly, and the local computing resource are set to maximum values in the SMRA and ACRA.

Figs. 3–5 show the average power consumption and the average backlog of QnL and QnO with timeslots. SMRA outperforms other algorithms in terms of energy consumption because only energy optimization is considered, but at the expense of much inferior backlog performance. Our suggested technique reduces QLM by 45.32% and 17.25% percentage compared to SMRA and ACRA because it jointly optimizes work partitioning and computing resource allocation. In addition, due to the consideration of externalities, our proposed algorithm betters than SMRA and ACRA by 27.31% and 74.12% on QnO.

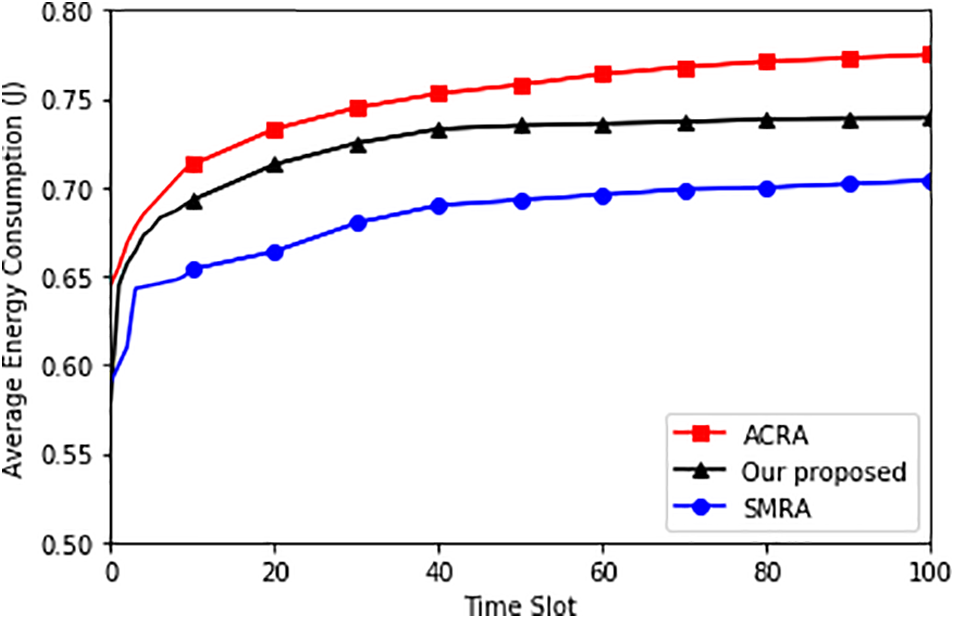
Figure 3: Average energy consumption

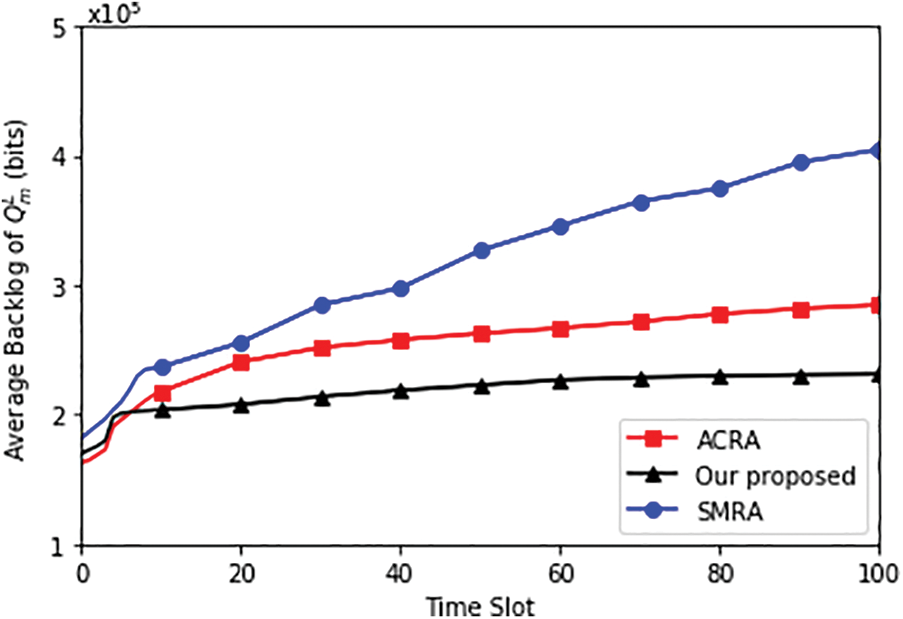
Figure 4: Average backlog of QnL

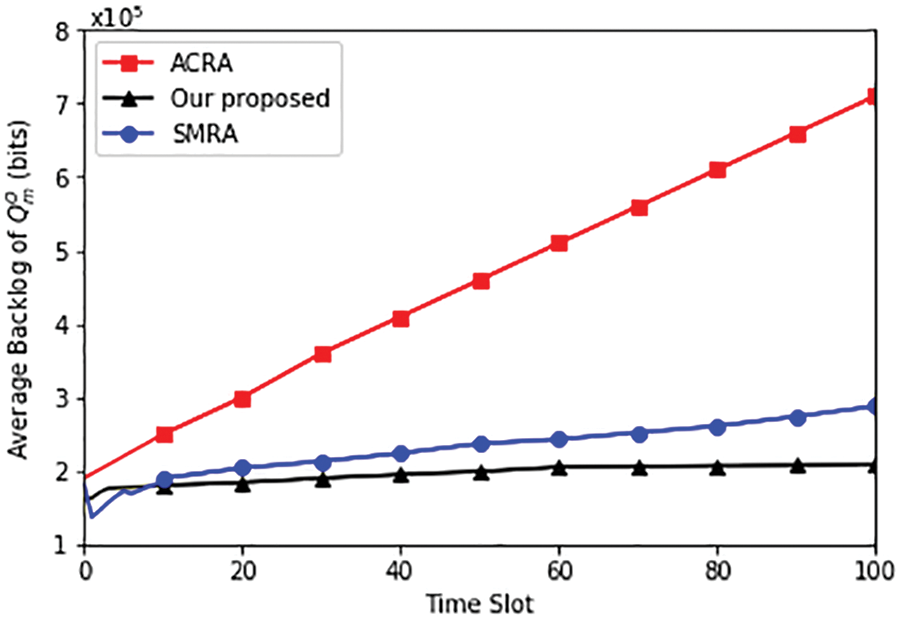
Figure 5: Average backlog of QnO

As a result, queue backlogs can be decreased by offloading more subtasks from the device to the edge server.

Fig. 6 illustrates how the number of devices in each group of Ng affects the complexity and average power consumption of our suggested approach. Define the whole number of devices to N = 200. Complexity is set as the number of iterations of the exchange demanded to fulfill the match between all resource unit and devices. When Ng is reduced from 200 to 50, the complexity of our proposed algorithm is decreased by 97.21%, whereas the energy consumption is just increased by 7.35%. We can draw the conclusion that our suggested algorithm can effectively balance complexity and network performance.

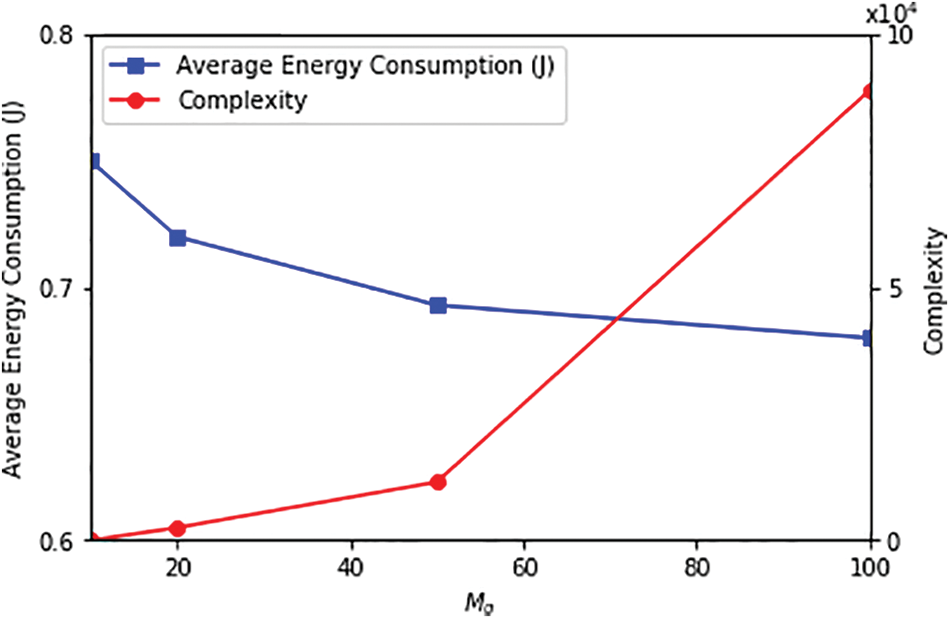
Figure 6: Impact of Ng

7  Discussion

The proposed algorithm is superior to the existing algorithms, SMRA and ACRA, based on several critical metrics:

Energy Consumption: The primary metric indicating the superiority of the proposed algorithm is energy consumption. The results show that the proposed algorithm effectively optimizes energy consumption compared to SMRA. This is a crucial metric for IoT systems where energy efficiency is paramount. The exact percentage reduction in energy consumption should be provided to quantify this improvement.

Queue Backlog: Another important metric is the queue backlog (QLM), specifically for QnL and QnO. The proposed algorithm significantly reduces QLM, as indicated by a 45.32% and 17.25% reduction compared to SMRA and ACRA. A lower queue backlog is essential for real-time and delay-sensitive applications, ensuring that tasks are processed promptly.

Complexity: The complexity of the algorithm is also a vital consideration. As demonstrated in the experiments, when the number of devices (Ng) is reduced from 200 to 50, the complexity of the proposed algorithm decreases by 97.21%. Lower complexity is desirable for practical implementation, as it reduces the computational burden and improves system efficiency.

Externalities: The proposed algorithm outperforms both SMRA and ACRA by 27.31% and 74.12% in QnO due to the consideration of externalities. Externalities are crucial in a real-world IoT environment where devices may interfere with each other. Minimizing externalities is essential for efficient resource allocation and network performance.

8  Conclusion

In conclusion, this study has introduced a comprehensive framework for optimizing resource allocation and task offloading in Industrial IoT (IIoT) environments, leveraging edge computing and Non-Orthogonal Multiple Access (NOMA). Through the use of directed cyclic graphs, priority-aware scheduling, and Markov decision processes, the proposed approach addresses the challenges of network congestion, delay sensitivity, and efficient resource management in IIoT. The results indicate that our strategy outperforms various offloading methods in terms of both throughput and task satisfaction rate. By considering deadlines, user mobility, and dynamic task dependencies, we have shown the potential for real-time, efficient, and responsive IIoT systems.

For future directions, research can explore:

1. Dynamic Network Topologies: Investigating how the proposed framework performs in scenarios with changing network topologies, which is common in IIoT environments.

2. Security and Privacy: Expanding the framework to incorporate enhanced security and privacy measures to protect sensitive IIoT data.

3. Energy-Efficient Edge Servers: Exploring methods to optimize the energy consumption of edge servers, further enhancing the sustainability of IIoT systems.

4. Scalability: Extending the framework’s scalability to accommodate a growing number of IIoT devices and applications.

5. Hybrid Approaches: Combining edge computing with other emerging technologies, such as blockchain or quantum computing, to explore synergies for IIoT applications.

Acknowledgement: Authors would like to thank the anonymous reviewers for their valuable time and feedback in reviewing the manuscript.

Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through large group research project under Grant Number RGP2/474/44.

Author Contributions: The authors confirm contribution to the paper as follows: Problem statement and proposed idea: Dinesh Mavaluru, Anil Carie Chettupally, Satish Anamalamudi; Data collection: Ahmed I. Alutaibi, Bayapa Reddy Narapureddy; Mathematical analysis and interpretation of results: Murali Krishna Enduri, Satish Anamalamudi, Ahmed I. Alutaibi; Draft manuscript preparation: Md Ezaz Ahmed, Anil Carie Chettupally, Dinesh Mavaluru. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The simulation code is not yet available to public due to extended project proposal.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Saad, W., Bennis, M., Chen, M. (2020). A vision of wireless systems: Applications, trends, technologies, and open research problems. IEEE Network, 34(3), 134–142. [Google Scholar]

2. Aljeri, N., Boukerche, A. (2022). A novel proactive controller deployment protocol for 5G-enabled software-defined vehicular networks. Computer Communications, 182, 88–97. [Google Scholar]

3. Mukherjee, M., Kumar, S., Mavromoustakis, C. X., Mastorakis, G., Matam, R. et al. (2020). Latency-driven parallel task data offloading in fog computing networks for industrial applications. IEEE Transactions on Industrial Informatics, 16(9), 6050–6058. [Google Scholar]

4. Hassan, S. R., Ahmad, I., Nebhen, J., Rehman, A. U., Shafiq, M. et al. (2022). Design of latency-aware IoT modules in heterogeneous fog-cloud computing networks. Computers, Materials & Continua, 70(3), 6057–6072. https://doi.org/10.32604/cmc.2022.020428 [Google Scholar] [CrossRef]

5. Rafique, W., Qi, L., Yaqoob, I., Imran, M., Rasool, R. U. et al. (2020). Complementing IoT services through software defined networking and edge computing: A comprehensive survey. IEEE Communications Surveys and Tutorials, 22(3), 1761–1804. [Google Scholar]

6. Adeel, I., Hyun, C., (2022). Computational analysis of metal transfer mode, dynamics, and heat transfer under different pulsating frequencies in pulsed wire-arc additive manufacturing. Journal of Computational Design and Engineering, 9(3), 1045–1063. [Google Scholar]

7. Jameel, F., Sharma, N., Khan, M. A., Khan, I., Alameis, M. M. et al. (2020). Machine learning techniques for wireless powered ambient backscatter communications: Enabling intelligent IoT networks in 6G era. Convergence of Artificial Intelligence and the Internet of Things, pp. 187–211. [Google Scholar]

8. Kiani, A., Ansari, N., (2018). Edge computing aware noma for 5G networks. IEEE Internet of Things Journal, 5(2), 1299–1306. [Google Scholar]

9. Ding, Z., Xu, J., Dobre, O. A., Poor, H. V. (2019). Joint power and time allocation for noma-mec offloading. IEEE Transactions on Vehicular Technology, 68(6), 6207–6211. [Google Scholar]

10. Liu, C. F., Bennis, M., Debbah, M., Poor, H. V. (2019). Dynamic task offloading and resource allocation for ultra-reliable low-latency edge computing. IEEE Transactions on Communications, 67(6), 4132–4150. [Google Scholar]

11. Ng, H. S. (2021). Opportunities, challenges, and solutions for Industry 4.0. In: Research anthology on cross-industry challenges of Industry 4.0. [Google Scholar]

12. Zheng, X., Li, M., Tahir, M., Chen, Y., Alam, M. (2019). Stochastic computation offloading and scheduling based on mobile edge computing. IEEE Access, 7, 72247–72256. [Google Scholar]

13. Zeng, F., Liu, L. (2021). Improving the quality of ideological and political education in colleges and universities in big data age. Journal of Physics Conference Series, 1852(3), 032034. [Google Scholar]

14. Sabireen, H., Neelenarayanan, V. (2021). A review on fog computing: Architecture, fog with IoT, algorithms and research challenges. ICT Express, 7(2), 162–176. [Google Scholar]

15. Sarker, V., Queralta, J. P., Gia, T. N., Tenhunen, H., Westerlund, T. (2019). A survey on lora for IoT: Integrating edge computing. International Workshop on Smart Living with IoT, Cloud and Edge Computing (SLICE 2019), Rome, Italy. [Google Scholar]

16. Kim, J. A., Park, D. G., Jeong, J. (2020). Design and performance evaluation of costeffective function-distributed mobility management scheme for software-defined smart factory networking. Journal of Ambient Intelligence and Humanized Computing, 11(6), 2291–2307. [Google Scholar]

17. Vu, T. T., Nguyen, D. N., Hoang, D. T., Dutkiewicz, E., Nguyena, T. V. (2021). Optimal energy efficiency with delay constraints for multilayer cooperative fog computing networks. IEEE Transactions on Communications, 69(6), 3911–3929. [Google Scholar]

18. Hong, Z., Chen, W., Huang, H., Guo, S., Zheng, Z. (2019). Multi-hop cooperative computation offloading for industrial IoT-edge-cloud computing environments. IEEE Transactions on Parallel and Distributed Systems, 30(12), 2759–2774. [Google Scholar]

19. Zhou, Z., Yu, H., Mumtaz, S., Al-Rubaye, S., Tsourdos, A. et al. (2020). Power control optimization for large-scale multi-antenna systems. IEEE Transactions on Wireless Communications, 19(11), 7339–7352. [Google Scholar]

20. Alameddine, H. A., Sharafeddine, S., Sebbah, S., Ayoubi, S., Assi, C. (2019). Dynamic task offloading and scheduling for low-latency IoT services in multi-access edge computing. IEEE Journal on Selected Areas in Communications, 37(3), 668–682. [Google Scholar]

21. Liao, H., Zhou, Z., Zhao, X., Wang, Y. (2021). Learning-based queue-aware task offloading and resource allocation for space-air ground-integrated power IoT. IEEE Internet of Things Journal, 8(7), 5250–5263. [Google Scholar]

22. Zhou, Z., Guo, Y., He, Y., Zhao, X., Bazzi, W. M. (2019). Access control and resource allocation for M2M communications in industrial automation. IEEE Transactions on Industrial Informatics, 15(5), 3093–3103. [Google Scholar]

23. Liao, H., Zhou, Z., Zhao, X., Zhang, L., Mumtaz, S. et al. (2020). Learning-based context-aware resource allocation for edge computing-empowered industrial IoT. IEEE Internet of Things Journal, 7(5), 4260–4277. [Google Scholar]

24. Zeng, M., Yadav, A., Dobre, O. A., Poor, H. V. (2019). Energy-efficient joint user-RB association and power allocation for uplink hybrid NOMA-OMA. IEEE Internet of Things Journal, 6(3), 5119–5131. [Google Scholar]

25. Zhou, Z., Ota, K., Dong, M., Xu, C. (2017). Energy-efficient matching for resource allocation in D2D enabled cellular networks. IEEE Transactions on Vehicular Technology, 66, 5256–5268. [Google Scholar]

26. Mustafa, E., Shuja, J., Bilal, K., Mustafa, S. (2023). Reinforcement learning for intelligent online computation offloading in wireless powered edge networks. Cluster Computing, 26(2), 1053–1062. [Google Scholar]

27. Maray, M., Mustafa, E., Shuja, J., Bilal, M. (2023). Dependent task offloading with deadline-aware scheduling in mobile edge networks. Internet of Things, 23, 100868. [Google Scholar]

28. Pal, S., Jhanjhi, N. Z., Abdulbaqi, A. S., Akila, D., Almazroi, A. A. et al. (2023). A hybrid edge-cloud system for networking service components optimization using the Internet of Things. Electronics, 12(3), 649. [Google Scholar]