Evaluating the Efficacy of Latent Variables in Mitigating Data Poisoning Attacks in the Context of Bayesian Networks: An Empirical Study

1  Introduction

Machine learning has gained widespread use across various fields, such as medicine, industry, economics, and technology. However, the rise in machine learning’s popularity has also led to heightened security concerns, particularly in relation to data poisoning attacks [1,2]. These attacks entail the injection of malicious data or observations into the training data during the machine’s training period, which can lead to unreliable predictions and compromise the data’s integrity.

Bayesian networks, which are probabilistic graphical models that explicitly explain the causal links between variables, have become increasingly popular in the field of artificial intelligence [2]. However, these models are also vulnerable to data poisoning attacks, and current detection frameworks for these attacks have limitations in terms of accuracy and efficiency [3].

Detecting data poisoning attacks on Bayesian networks is a critical problem, as such attacks can result in inaccurate and unreliable models that can significantly impact decision-making processes. However, existing detection frameworks for these attacks often have a limited ability to detect various classes of attacks, leading to significant research gaps in this field. For instance, a semidefinite relaxation-based detection method proposed by Raghunathan et al. [4] and the framework proposed by Munoz-Gonzalez et al. [5] can only detect attacks that introduce a new edge or remove an existing one. Similarly, the framework proposed by Bagdasaryan et al. [6] can only detect attacks that introduce a new edge or remove an existing one when the attack vector is known. These limitations in existing detection frameworks underscore the need for efficient and effective frameworks that can detect various classes of data poisoning attacks on Bayesian networks. Latent variables are unobserved variables introduced into the Bayesian network model in order to capture the relationships and beliefs between observed variables or nodes over time [7]. Within the causal model, these latent variables are used to quantify the degree of belief or influence between pairings of nodes. The objective of these latent variables is to aid in detecting and mitigating data poisoning assaults by monitoring changes in probability distributions and observed variable relationships [8]. In essence, they function as concealed indicators of potential data poisoning, providing a means of identifying when incoming data has been compromised and deviates from expected patterns. Incorporating latent variables into the framework enables a more sensitive and efficient method for detecting malicious data poisoning assaults in Bayesian network structure learning algorithms [9]. By quantifying the beliefs and relationships between nodes over time, latent variables aid in identifying and responding to threats that would otherwise go unobserved if only the observed data were considered [10,11].

A crucial factor that supports the efficiency of Bayesian network across a wide range of real-world applications is the intricate relationship between the reliability and integrity of learned Bayesian network models and the quality of incoming data streams [12]. As each variable’s behavior and interactions with others are inferred from observed data, Bayesian networks are built based on the probabilistic relationships between them. As a result, the performance of these models as a whole is greatly influenced by the reliability and accuracy of the data used to train them. Unreliable or noisy data can cause the Bayesian network to draw incorrect probabilistic inferences, which can have a negative impact on prediction accuracy. Poor data quality introduces bias and uncertainty into the model, which could result in erroneous conclusions or forecasts [13]. This can then have significant ramifications in a variety of industries, including healthcare, where the validity of diagnostic or therapeutic recommendations depends on the caliber of medical data, or in the financial markets, where wise investment choices depend on precise historical data and market trends. Dealing with data from actual, dynamic systems further exacerbates the problem of poor data quality [14]. These systems frequently display temporal and contextual variations that call for ongoing Bayesian network model adaptation. As a result, maintaining the model’s dependability and integrity becomes a constant challenge because it necessitates constant access to high-quality, current data streams [15]. The vulnerability to adversarial data poisoning attacks increases because adversaries can use these dependencies to introduce malicious data and undermine the model’s accuracy, which could have disastrous effects.

The research community has been working hard to develop methodologies and techniques to strengthen the resilience of Bayesian networks against problems with data quality and hostile threats in light of these dependencies [16–18]. Improvements are being made to data preprocessing, data cleansing, and the creation of reliable algorithms that can detect and lessen the effects of malicious data. The reliability and integrity of Bayesian network models depend on the quality of the incoming data streams, which must be addressed in order to ensure their practical utility and credibility across a range of application domains [19].

In this paper, we propose a new framework that uses latent variables to detect data poisoning attacks on Bayesian networks. Our framework is designed to be efficient, accurate, and applicable to stream data, making it well-suited for detecting data poisoning attacks in real-time. We implement our proposed approach using the PC-stable algorithm and the Asia Network and demonstrate its superiority to existing detection frameworks in terms of accuracy and efficiency.

Our paper makes several significant contributions to the field of data poisoning attacks on Bayesian networks. The major contributions of this study are as follows:

•   We present a ground-breaking method to identify data poisoning attacks against Bayesian network structure learning methods. The array of methods available for guarding against adversary manipulation of Bayesian networks obtains a new dimension with the introduction of this innovative technique.

•   We offer a system that effectively addresses the shortcomings of existing detection techniques for identifying data poisoning attempts utilizing latent variables. By doing this, we offer a stronger and more dependable method of spotting and fending off these dangers.

•   By effectively identifying four different forms of data poisoning attacks on Bayesian network structure learning techniques, our approach displays its adaptability. This versatility highlights its efficiency in defending against a variety of potential threats, making it an important tool for practical applications.

•   We put our suggested strategy into practice utilizing the PC-stable algorithm and the Asia Network, compiling our results into a R program. This useful application makes it simple for researchers and practitioners to use our methodology, which facilitates adoption.

•   In a thorough analysis, we contrast the effectiveness of our suggested strategy with current detection systems for data poisoning assaults. Our outcomes continually demonstrate its superiority in terms of precision and efficacy, emphasizing its usefulness in practical situations.

The remainder of our paper is structured as follows: Section 2 presents the problem setting, Section 3 describes our latent-based framework for detecting data poisoning attacks in the context of Bayesian networks, Section 4 presents our empirical results, Section 5 discusses related work on data poisoning attacks and their detection mechanisms, and Section 6 concludes the paper with a discussion of future work.

2  Problem Settings

Our main concern is the crucial problem of detecting and countering data poisoning attacks in the context of structure learning algorithms used in the context of Bayesian networks. We examine a hypothetical situation where a defender, tasked with creating a causal model, attempts to draw conclusions from a painstakingly validated database, designated as DBv, in order to clarify this topic. This database includes K unique observations, each of which is distinguished by a set of features contained within S, where S is defined as S = S1, S2, ..., Sd. Each observation is represented as a set of attribute-value pairs, o = {s1 = v1, ..., sd = vd}, where vi is the value of the observation at feature si.

The various aspects or variables of interest within the study domain are represented by these features taken as a whole. Establishing a causal model that accurately depicts the connections between the dataset’s features is the key goal here. This is crucial for comprehending how changes in one variable might affect or result in changes in other variables, and it forms the cornerstone of causal reasoning in Bayesian networks. This project is not without difficulties, though, as the defender must guard against potential data poisoning attacks that could jeopardize the validity of the causal model. To elaborate, the defender assumes that the information in DBv is reliable and accurately depicts the underlying causal relationships that exist within the domain. However, as we shall investigate in this paper, adversaries might introduce false or manipulated data into the database with the aim of distorting the Bayesian network’s structure and undermining the validity and reliability of the causal model. To ensure the fidelity and usefulness of the learned causal model in the face of potential threats, it is crucial to develop mechanisms that can detect and counteract these data poisoning attacks.

To learn the causal model, the defender applies a Bayesian network structure learning algorithm, such as the PC algorithm, to the validated database DBv. The resulting Bayesian network model B2 is a directed acyclic graph (DAG) consisting of a set of nodes V and directed edges E, where each node represents a feature and each directed edge represents a causal relationship between two features as presented in Eq. (1).

In Bayesian networks, a DAG is a graphical representation that shows the network’s structure. It is made up of nodes, which are also known as vertices, and directed edges (arcs), which link these nodes together. Each directed edge in the DAG denotes a causal connection between two features, and each node in the DAG represents a feature or variable. A DAG’s primary distinguishing feature is that it is acyclic, which means that the graph contains no closed loops or cycles. This acyclic property is fundamental in Bayesian networks because it guarantees that there are no circular dependencies or feedback loops between variables, which is essential for causal reasoning and probabilistic inferences to be made consistently and reliably.

To detect data poisoning attacks, the defender adds latent variables between every two nodes in B2.

B2= BN.Structure_Learning_Algorithm(DBv)(1)

In this setting, an adversary aims to insert a poisoned dataset DBp with the same attributes as DBv and K1 observations into DBv to contaminate the learned Bayesian network model B2.

The challenge between the adversary and the defender can be formulated as a three-step process:

(1) The defender generates a validated Bayesian network model B2 using DBv.

(2) The adversary inserts a poisoned dataset DBp in the incoming database from the adversary, DBnew = DBv ∪ DBp, to contaminate DBv and change the Markov equivalence class of B2.

(3) The defender applies the structure learning algorithm to DBnew to obtain the Bayesian network model B1 as present in Eq. (2). The defender adds latent variables to both B1 and B2 and applies uncertainty-based attack (UBA) to detect the presence of data poisoning attacks. Essentially, B1 is learned by using the combined dataset, which combines the trusted data DBv and the new incoming data DBnew, to apply the structure learning algorithm. A clear way to show that the model B1 is derived from both sources of data is to use the union operator. In order to adapt the model to the most recent data while maintaining the validated data from DBv, the defender must explicitly combine these datasets in the context of structure learning. In order to increase model accuracy, Bayesian network learning frequently involves integrating new data with existing data.

B1= BN.Structure_Learning_Algorithm(DBvUDBnew)(2)

The defender splits DBnew into clean and poisoned observations using UBA. If DBnew is the union of DBv and DBp, the defender applies the structure learning algorithm to DBnew to obtain the Bayesian network model B1. To evaluate the cohesion of an observation o = {s1 = v1, ..., sd = vd} in DBp with B2, we use a UBA measure based on the beta distribution. Specifically, we consider a random variable Y∼Beta (α, β), where α and β are hyperparameters of the beta distribution.

The beta distribution’s decision to use only two hyperparameters, and, is primarily motivated by the desire for simplicity and improved interpretability. This decision simplifies the analysis process in the context of Bayesian network modeling and data poisoning attack evaluation, which can involve complex, multi-parameter methodologies. Simplifying the method helps it become more understandable to a wider audience, including those who are not familiar with intricate statistical modeling. The two-parameter beta distribution is also a well-known and understandable statistical tool that is frequently used for modeling proportions and success-failure outcomes. Its effectiveness is unaffected by its simplicity, especially in practical applications where it can successfully address research goals. Additionally, it improves computational efficiency, a crucial benefit when working with large datasets.

Here, we denote the maximum probability density function as ψ, which is defined as shown in Eq. (3).

ψ=maxY=y⁡f(y;αu,βu,K,q)(3)

where f(y; αu, βu, K, q) is the probability density function of the beta distribution with hyperparameters αu, βu, K, and q, and y is the mode of the beta distribution (0 ≤ y ≤ 1). Here, K is the total number of observations, and q is the count of successes.

We model the problem as a two-player game between the adversary and the defender, where the defender aims to learn a validated Bayesian network model B2 using DBv, while the adversary aims to contaminate B2 with DBp. We assume that the toxicity rate of the adversary introducing additional “poisoning” situations to DBv is no greater than 0.05. In real-world situations, it can be difficult to determine the toxicity rate of an adversary’s actions with precision. A precise estimate of an opponent’s behavior may not be available, and opponents’ strategies and intentions may vary. Consequently, designating a specific threshold of 0.05 is a practical starting point for our experiments. By assuming a relatively low toxicity rate (0.05% or 5%), we assure that our framework can effectively detect and respond to even the subtlest data poisoning attacks. While 0.05 was chosen as a baseline assumption, our experiments can be expanded to investigate different toxicity rate thresholds, allowing us to evaluate how the framework’s performance varies in response to various adversary behaviors.

The challenge between the adversary and the defender involves the defender generating a validated Bayesian network model B2, the adversary inserting a poisoned dataset DBp into DBnew to contaminate DBv and change the Markov equivalence class of B2, and the defender applying the structure learning algorithm to DBnew to obtain the Bayesian network model B1. The defender adds latent variables to both B1 and B2 and applies UBA to detect the presence of data poisoning attacks. We evaluate our approach on various datasets to demonstrate its effectiveness.

We present the notations used in this research paper in Table 1.

3  Latent-Based Framework for Detecting Data Poisoning Attacks

In this section, we present a comprehensive framework for detecting malicious data poisoning attacks against the structure learning algorithm of Bayesian networks. Our approach leverages latent variables to enhance the detection capabilities. To demonstrate the effectiveness of our proposed methods, we utilize the R package and the PC-stable structure learning algorithm, using the Asia Network (also known as the Chest Clinic Network) as a case study.

The framework comprises several key components, which are outlined below:

1. New dataset (DBnew): This dataset originates from an unreliable source and may contain malicious data items injected by attackers.

2. Validated dataset (DBv): This dataset consists of clean cases that have been previously examined using our latent variable-based framework and confirmed to be free from data poisoning attacks.

3. Structure learning algorithm: We employ the PC-stable algorithm, a commonly used approach for structure learning in Bayesian networks. This algorithm allows us to recover the causal model’s structure from the given data.

4. Latent variables: Also known as unobserved variables, latent variables are hidden or unmeasured variables that cannot be directly observed but can be inferred from other directly measured variables [7]. In our framework, we utilize latent variables to model changes in belief over time, enabling us to detect data poisoning attacks against the structure learning algorithm of the Bayesian network.

5. Detection of UBA: We utilize entropy as a measure of uncertainty in the input [8]. Uncertainty quantifies how beliefs vary over time and can be a powerful tool for detecting data poisoning attacks. In the context of discrete Bayesian networks, we explore the use of uncertainty to detect such attacks. Specifically, we consider a random variable Y that follows a beta distribution, Y∼Beta (α, β). To detect data poisoning attacks, we monitor the highest value of the probability density function of the beta distribution (denoted as ψ) using Eq. (4):

ψ=maxY=y⁡f(y;αu,βu,K,q)=f(q+αu−1α+K+βu−2;αu,βu,K,q)(4)

Here, K represents the total number of observations, q is the count of successes, y is the mode of the beta distribution (0≤y≤1), and hyperparameters α and β are both greater than or equal to 1. To track the maximum value of this beta distribution’s probability density function, denoted as ψ, Eq. (4) is introduced. The probability density function of the beta distribution, denoted by f(y;αu,βu,K,q), is used in the equation to find the maximum value among all possible values of Y (denoted as y). The equation is then reduced to express as a function of variables K and q, as well as the hyperparameters αu and βu. Here, K denotes the total number of observations, q denotes the number of successes, y denotes the mode of the beta distribution between 0 and 1, and both hyperparameters are required to be greater than or equal to 1. In the Bayesian network models (B1 and B2), the strength of belief between pairs of nodes, illustrated by (X,Y) in Fig. 1, is quantified by introducing latent variables. This approach to latent variables is useful in identifying four different kinds of data poisoning attacks:

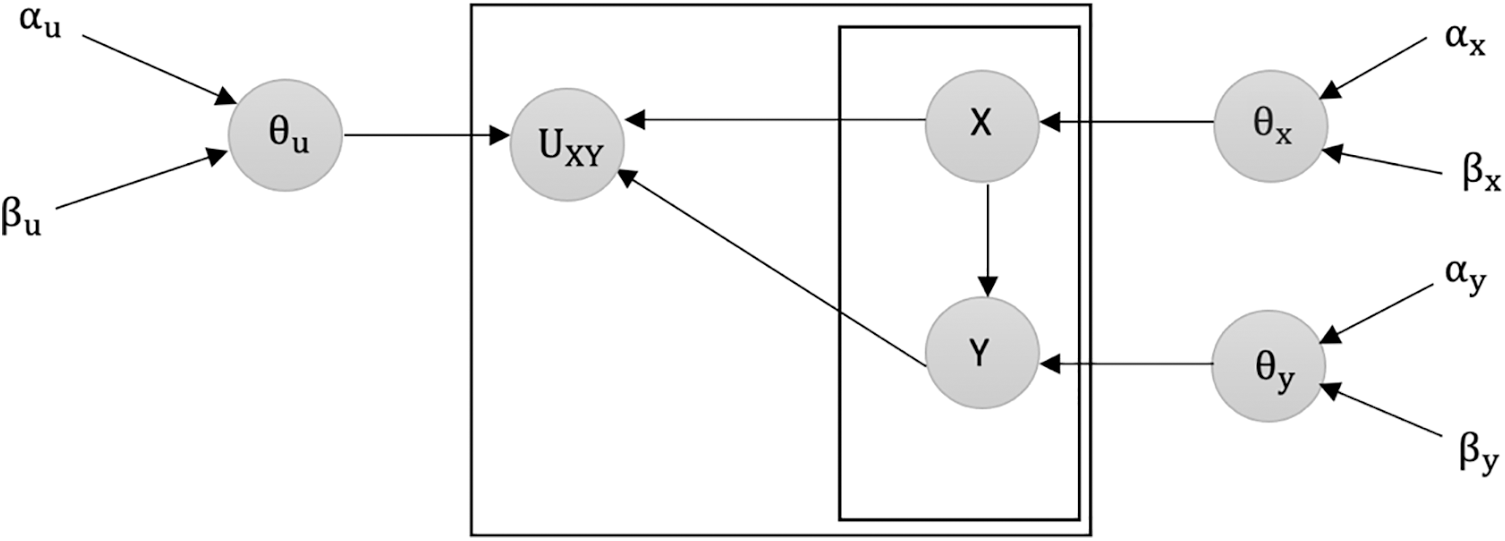
Figure 1: Overview of latent variable U between the two variables (X, Y) in B1 and B2

1. Introducing a New Collider Data Poisoning Attack: Attackers can poison the learning datasets by introducing a new edge to any Bayesian network connection model, creating a new collider. This modification alters the equivalence class of the trained model in Bayesian networks, causing damage to the network structure as described in Algorithm 1.

2. Shielding an Existing Collider Data Poisoning Attack: Attackers can break an existing collider by manipulating the parents of an unshielded collider. This manipulation impacts the expected equivalence of the learned model, resulting in damage to the Bayesian network structure. Attackers can exploit such vulnerabilities in Bayesian networks as described in Algorithm 2.

3. Removing the Weakest Link Data Poisoning Attack: Attackers can taint the learning datasets by eliminating weak links in Bayesian networks. The link strength metric is used in Bayesian network models to rank the links from weakest to strongest as described in Algorithm 3.

4. Inserting the Most Believable Link Data Poisoning Attack: Attackers can poison the learning datasets by adding the most plausible link in Bayesian networks. This is achieved by utilizing the link strength measure, which ranks the links from the most likely to the least believable as described in Algorithm 4.

Fig. 1 illustrates the inclusion of the latent variable U between the variables X and Y in model B1 and model B2.

To detect data poisoning attacks, our framework follows these steps:

Step 1: Obtain a new dataset (DBnew) from an unreliable source, which may potentially contain poisoning cases.

Step 2: Combine the validated dataset (DBv) with the new dataset (DBnew) to assess the influence of the new database on DBv. The combined dataset (DBv ∪ DBnew) is then used in the structure learning algorithm to recover model B1. We employ the PC-stable algorithm for this purpose, given its wide usage in Bayesian experiments.

Step 3: Input the validated dataset (DBv), which consists of clean cases previously scanned using our proposed latent-based framework, into the structure learning algorithm to recover the validated model B2. Once again, we utilize the PC-stable algorithm for this step.

Step 4: Add latent variables to both models B1 and B2, as depicted in Fig. 1.

Step 5: Perform a check for UBA by examining if there is a significant change as described in Algorithm 5. If a significant change is detected, the dataset is flagged as potentially poisoned, and further analysis is conducted offline to determine if a data poisoning attack has occurred. On the other hand, if no significant change is observed, the newly incoming dataset is considered clean and can be incorporated into the validated dataset.

Similar to Algorithms 1 to 4, Algorithm 5 is intended to identify data poisoning attacks within Bayesian network models. But by including latent variables, it offers a novel strategy. In models B1 and B2, these latent variables quantify belief changes between pairs of nodes. Algorithm 5 differs from the earlier algorithms in this way. Algorithm 5’s primary function is to calculate belief changes using latent variables, an innovative attack detection technique not present in Algorithms 1 through 4. Algorithm 5 also employs UBA detection through a comparison of belief shifts between models B1 and B2. The dataset is categorized as an attack if a significant change is found; otherwise, it is regarded as clean. Algorithm 5 stands out for its UBA detection mechanism, which also offers a distinctive viewpoint on data poisoning attack detection.

Fig. 2 illustrates the key components and steps involved in our comprehensive framework for detecting data poisoning attacks. It visually presents the flow of data, starting from the acquisition of a new dataset from an unreliable source to the final detection and analysis of potential data poisoning. The diagram serves as a valuable reference, enabling researchers and practitioners to grasp the overall process and better understand the interplay between the different stages of the framework.

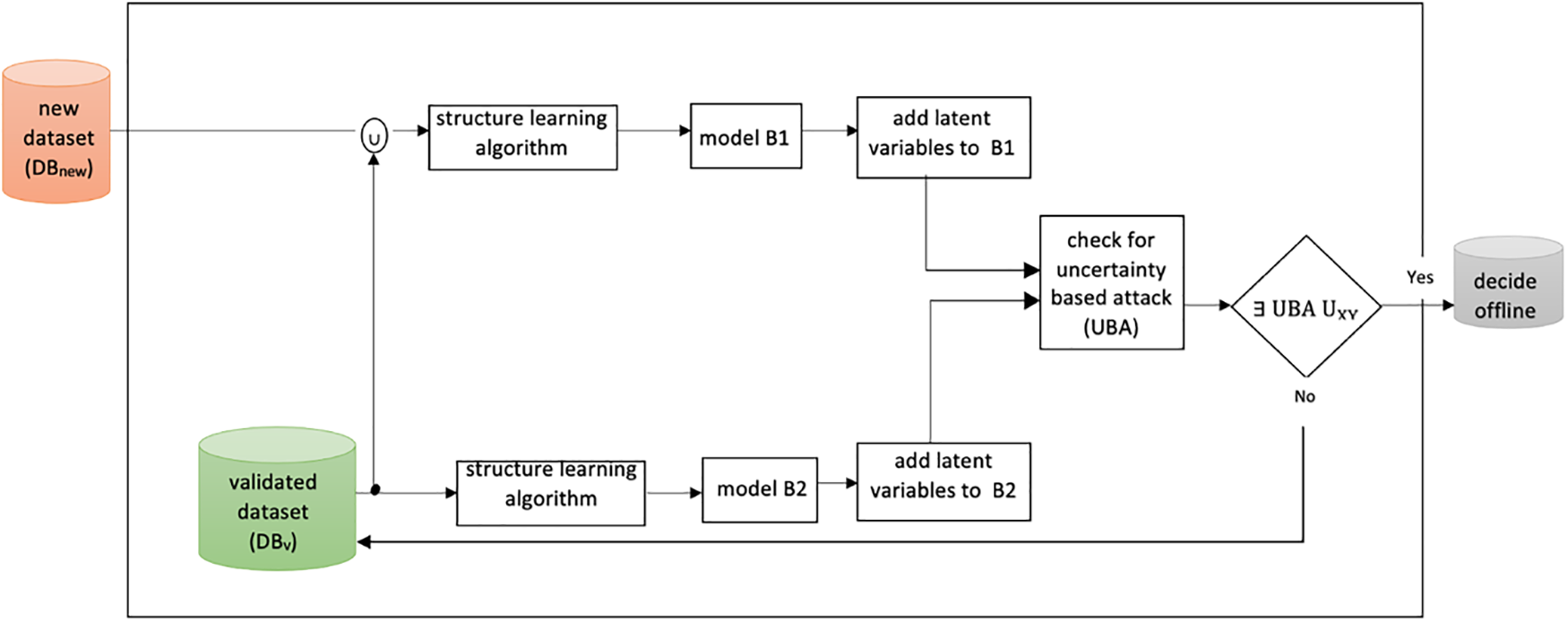
Figure 2: The framework of detecting data poisoning attacks

Advantages of the Latent-Based Framework: Our proposed framework detects data poisoning attacks in Bayesian networks more effectively. Firstly, by incorporating latent variables, we capture hidden relationships and uncover subtle changes caused by malicious injections. Secondly, the UBA Detection algorithm quantifies belief change using entropy, promptly raising alarms for potential attacks. Our framework is flexible, adaptable to different domains, and integrates seamlessly with existing workflows. It achieves high detection accuracy with a low false positive rate, mitigating data poisoning attacks effectively.

4  Experimental Results

We have implemented our proposed framework using discrete Bayesian networks over time on the Asia Network, also known as the Network of Chest Clinic [20], which is widely used in Bayesian network experiments. Our framework relies on latent variables to detect malicious data poisoning attacks. These latent variables measure the belief between each pair of nodes in a given causal model over time. The goal is to monitor the belief of the latent node over time and detect four types of poisoning attacks: (1) Attacks aimed at introducing a new v-structure, (2) Attacks aimed at shielding an existing collider, (3) Attacks aimed at creating a believable edge, and (4) Attacks aimed at removing the weakest edge.

For our experiment, we generated 15 simulated datasets using the HuginTM case generator. Each dataset contains 2000 cases labeled as Batch 1 through Batch 15. We consider these datasets as a new incoming data stream, denoted as DBnew, which may contain both clean and poisoned data from an untrusted source. These datasets arrive at different time intervals and are combined with our validated dataset DBv. To optimize computational efficiency, we introduced latent variables between the nodes of interest based on the link strength measure in models B1 and B2. This allows us to detect the four types of data poisoning attacks.

Detecting Attacks against the Weakest Edge: We utilize our latent-based framework to detect attacks aiming to remove the weakest edge in the Chest Clinic Networks. According to the link strength measure L_S [21], the edge AT is identified as the weakest edge in the Asia network. To address this, we introduce the latent node Ut between the AT edge in models B1 (Fig. 3) and B2 (Fig. 4) as part of our framework to detect data poisoning attacks. We examine the changes in the probability density function (PDF) values over time, specifically focusing on PDF(A = no|T = no), PDF(A = yes|T = no), PDF(A = no|T = yes), and PDF(A = yes|T = yes) from Batch 1 to Batch 15. Table 2 presents the results of our framework in detecting data poisoning attacks targeting the removal of the weakest edge, AT. Notably, in Table 2, we highlight the drop values in bold, indicating the presence of data poisoning attacks in the newly incoming dataset, DBnew.

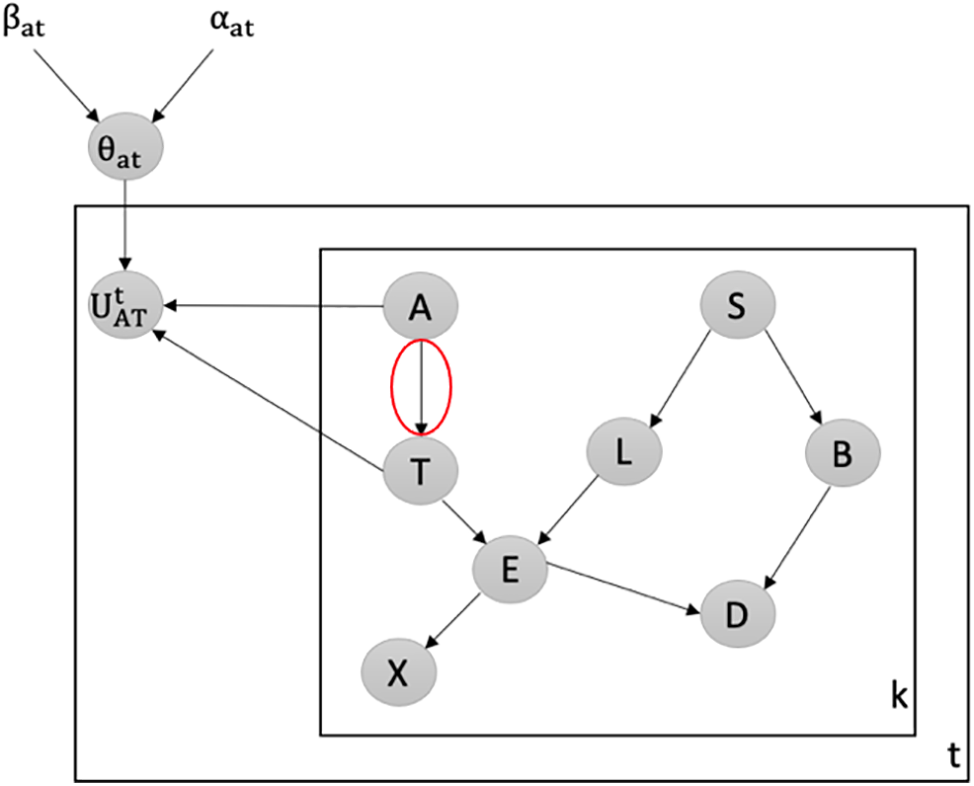
Figure 3: Latent-based framework at the AT edge in model B1

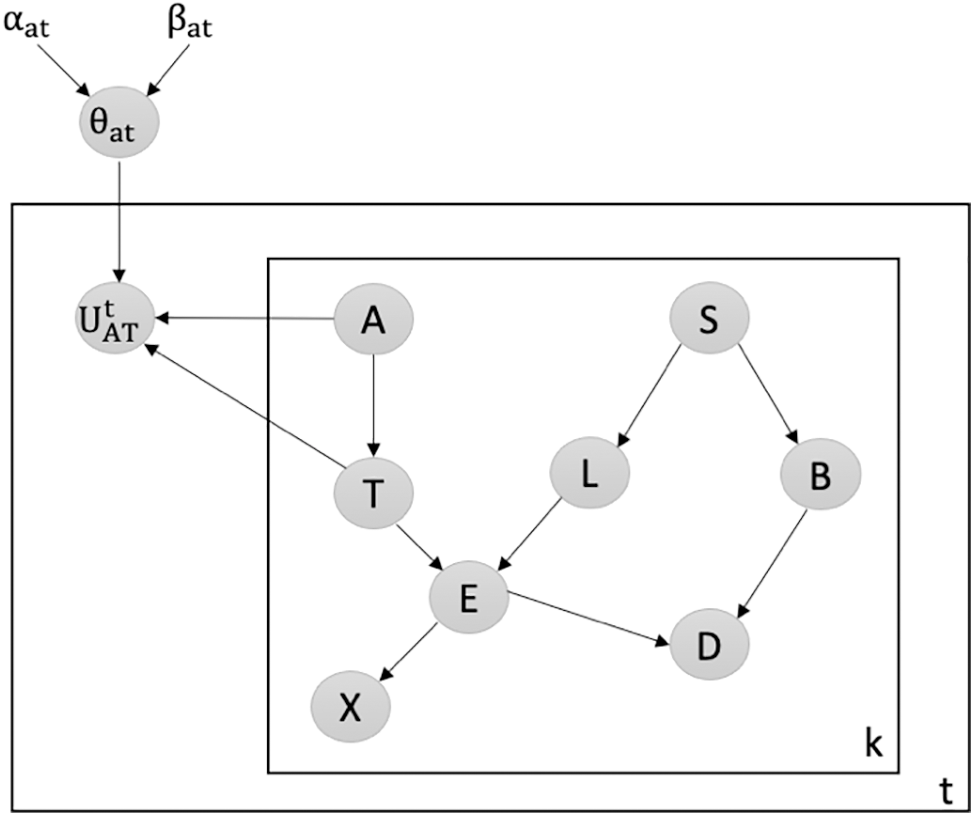
Figure 4: Latent-based framework at the AT edge in model B2

Our observations reveal that at times 1 and 2, the PDF values show an increasing trend in the correct direction, indicating clean batches. When a batch is deemed clean, we combine it with our validated dataset, DBv. However, at time points 3 and 8, we observe a significant drop in the PDF values as follows: For PDF(U|A = yes, T = yes): Time point 3: 964.3817675 with alpha = 7 and beta = 5995, and Time point 8: 1541.469444 with alpha = 18 and beta = 15984.

These datasets are identified as suspicious and are subsequently rejected for offline verification. We note that a drop in the PDF value indicates the detection of a data poisoning attack by our framework and latent variable. Additionally, our latent-based framework exhibits sensitivity in detecting variations in the PDF values over time, specifically those aiming to remove the weakest edge from the validated Bayesian network model, B2.

Detecting Attacks against the Most Believable Edge: We employ our latent-based framework to effectively detect attacks aimed at adding the most believable edge within the Chest Clinic Networks. Based on the link strength measure L_S, the edge BL is identified as the most believable within the network. To facilitate the detection of data poisoning attacks, we introduce the latent node Ut between the BL edge in both models B1 (Fig. 5) and B2 (Fig. 6).

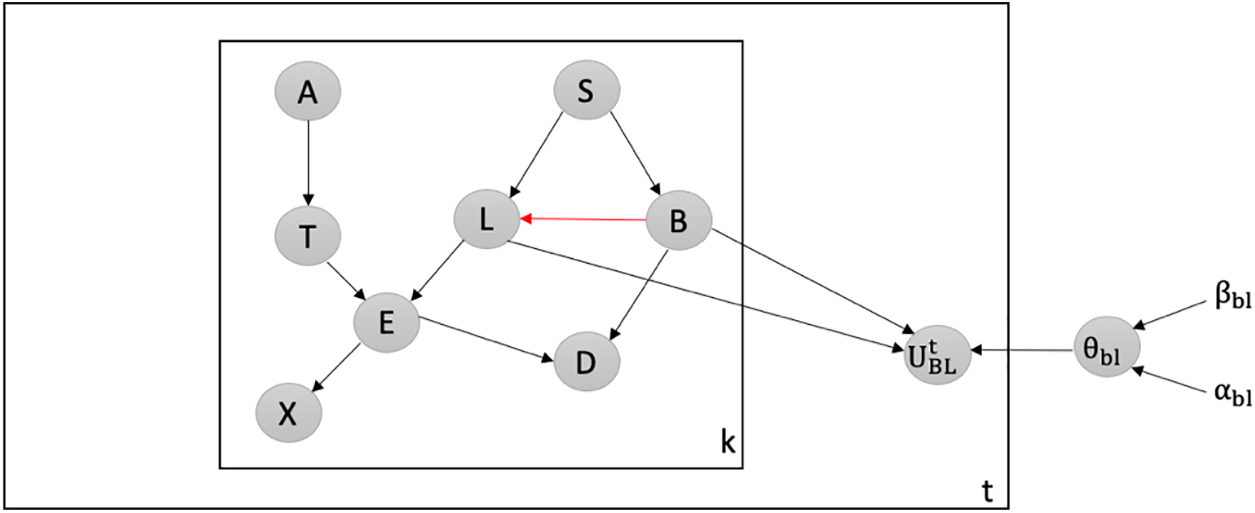
Figure 5: Latent-based at BL edge in B1

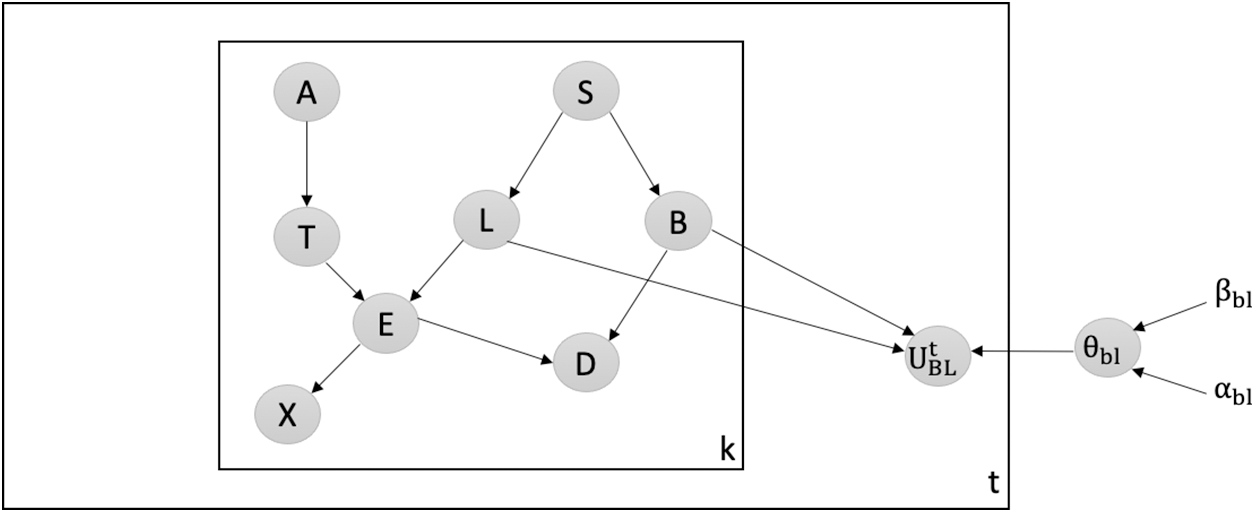
Figure 6: Latent-based at BL edge in B2

The probability density function (PDF) values, namely PDF(B = no|L = no), PDF(B = yes|L = no), PDF(B = no|L = yes), and PDF(B = yes|L = yes), exhibit variations over time. We analyze the PDF values from batch 1 to batch 15. Table 3 presents the outcomes of our framework in detecting data poisoning attacks targeting the addition of the most believable edge, BL. Notably, in Table 3, we highlight the drop values in bold, indicating the presence of data poisoning attacks in the newly incoming dataset, DBnew.

Our observations reveal that during time points 1 to 5, the PDF values consistently increase in the correct direction, indicating clean batches. In such cases, we combine the clean batches with our validated dataset, DBv. However, at time points 6 and 14, we observe a slight drop in the PDF values as follows: For PDF(U|B = no, L = yes): Time point 6: 243.426891 with alpha = 401 and beta = 11601. For PDF(U|B = yes, L = yes): Time point 14: 361.2725596 with alpha = 992 and beta = 27010.

These datasets are identified as suspicious and are subsequently rejected for offline verification. We have observed that a decrease in the PDF value indicates the detection of a data poisoning attack by our latent-based framework. Moreover, our framework exhibits sensitivity in detecting changes in the PDF values over time, particularly those aiming to add the most believable edge in the validated Bayesian network model, B2.

Detecting Attacks against Creating New V-Structure: We utilize our latent-based framework to detect attacks that aim to create a new v-structure within the Chest Clinic Networks. The attacker introduces the new v-structure at the EA edge. To detect data poisoning attacks, we introduce the latent node Ut between the EA edge in both models B1 (depicted in Fig. 7) and B2 (depicted in Fig. 8).

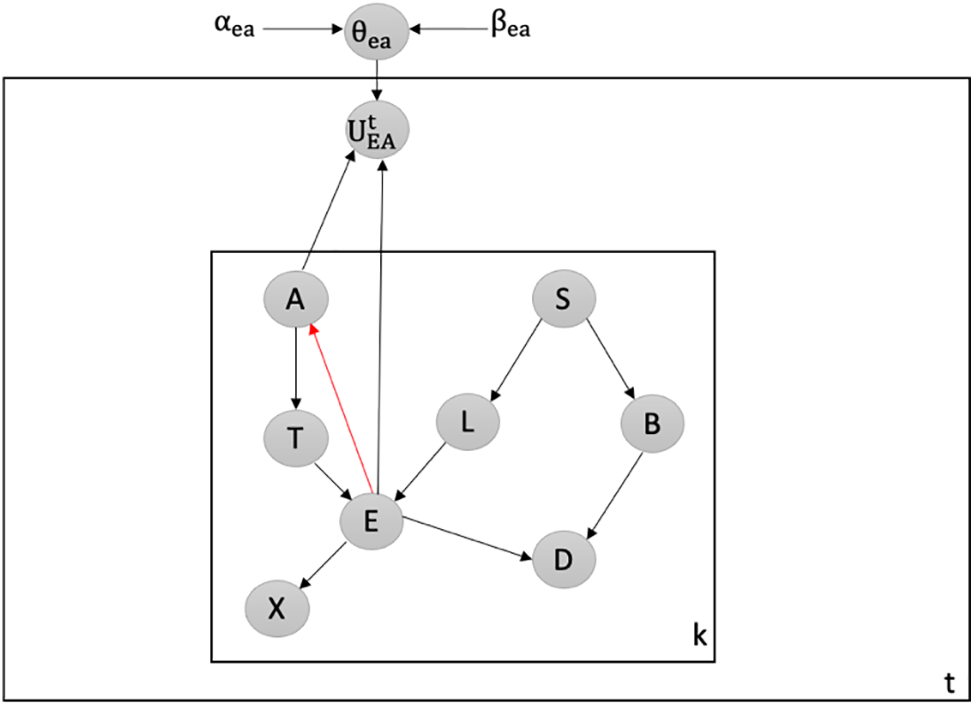
Figure 7: Latent-based at EA edge in B1

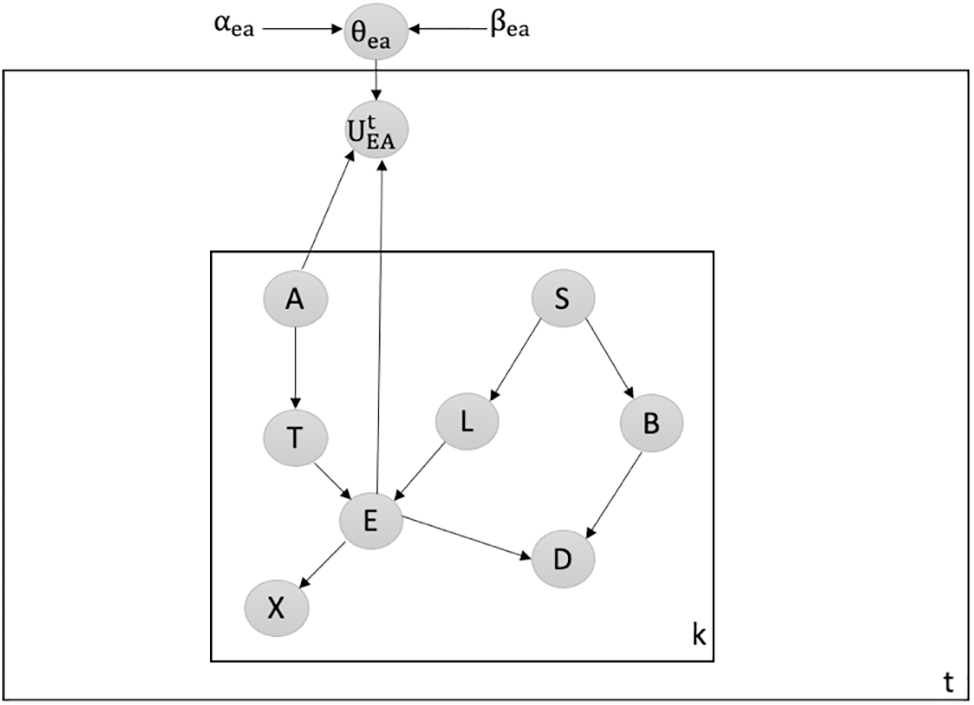
Figure 8: Latent-based at EA edge in B2

The probability density function (PDF) values, namely PDF(E = no|A = no), PDF(E = yes|A = no), PDF(E = no|A = yes), and PDF(E = yes|A = yes), undergo changes over time. We analyze the PDF values across batches 1 to 15. The results of our framework in detecting data poisoning attacks that aim to create a new v-structure, EA, are presented in Table 4. In Table 4, we highlight the decreasing PDF values in bold to indicate instances of data poisoning attacks in the newly incoming dataset, DBnew.

We observe that during time points 1 and 2, the PDF values consistently increase in the intended direction, indicating clean batches. In such cases, we merge the clean batches with our validated dataset, DBv. However, at time points 3 and 12, we observe a significant drop in the PDF values as follows: For PDF(U|E = no, A = yes): Time point 3: 533.9914435 with alpha = 21 and beta = 5981. For PDF(U|E = yes, A = yes): Time point 12: 1290.619552 with alpha = 56 and beta = 23946.

These datasets are identified as suspicious and are subsequently rejected for offline verification. We observe that a drop in the PDF value indicates that our framework, along with the latent variable, has detected a data poisoning attack. Furthermore, our latent-based framework demonstrates sensitivity in detecting variations in the PDF values over time, particularly those aimed at creating a new v-structure in the validated Bayesian network model, B2.

Detecting Attacks against Shielding an Existing Collider: We employ our latent-based framework to detect attacks that target the shielding of an existing collider within the Chest Clinic Networks. The malicious attacker aims to break the shielding at the TL edge. To detect data poisoning attacks, we introduce the latent node Ut between the TL edge in both models B1 (depicted in Fig. 9) and B2 (depicted in Fig. 10). The probability density function (PDF) values, namely PDF(T = no|L = no), PDF(T = yes|L = no), PDF(T = no|L = yes), and PDF(T = yes|L = yes), undergo changes over time. We investigate the PDF values across batches 1 to 15. The results of our latent-based framework in detecting data poisoning attacks that aim to shield an existing collider, TL, are presented in Table 5. In Table 5, we highlight the drop values in bold to indicate instances of data poisoning attacks in the newly incoming dataset, DBnew.

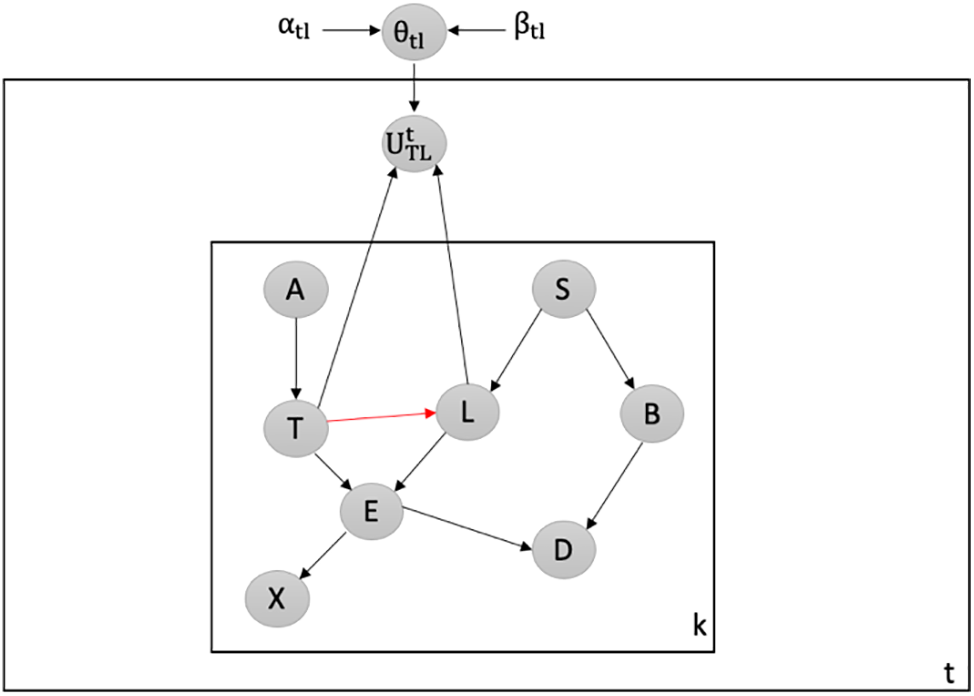
Figure 9: Latent-based at TL edge in B1

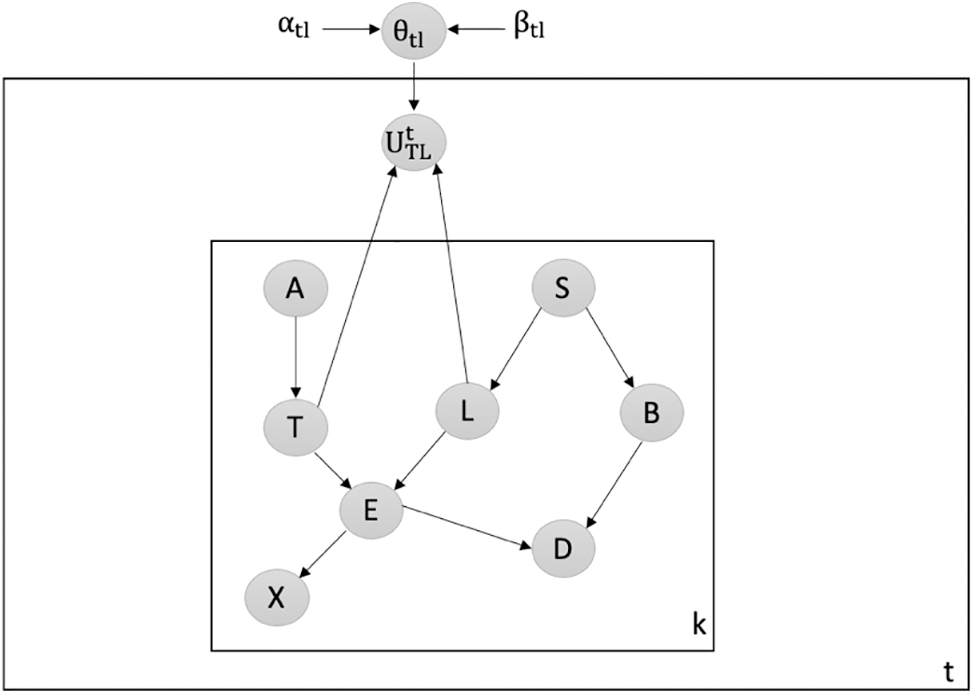
Figure 10: Latent-based at TL edge in B2

We observe that during time points 1 to 3, the PDF values consistently increase in the intended direction, signifying clean batches. In such cases, we merge the clean batches with our validated dataset, DBv. However, at time points 4 and 13, we observe a significant decrease in the PDF values as follows: For PDF(U|T = no, L = yes): Time point 4: 1404.353345 with alpha = 6 and beta = 7996. For PDF(U|T = yes, L = yes): Time point 13: 3426.371469 with alpha = 10 and beta = 25992.

These datasets are identified as suspicious and are subsequently rejected for offline verification. We observe that a decrease in the PDF value indicates that our latent-based framework has detected a data poisoning attack. Furthermore, our framework demonstrates sensitivity in detecting changes in the PDF values over time, particularly those aimed at breaking the shielding of an existing collider in the validated Bayesian network model, B2.

5  Related Work

Adversarial machine learning studies intentional attacks on machine learning systems [22]. Attacks exploit system characteristics like influence, security violations, and specificity [23]. Influence-based attacks involve causative and exploratory actions, manipulating or probing training data. Security violations compromise integrity, availability, and privacy. Specificity includes targeted or indiscriminate attacks, causing false negatives [24].

Data poisoning attacks are among the most prevalent types of attacks in machine learning [25]. These attacks involve injecting malicious data into the training dataset, thereby compromising the integrity and performance of the resulting model [26]. Extensive research has been conducted on data poisoning attacks targeting various machine learning models, including support vector machines (SVMs), linear and non-linear classifiers, convolutional neural networks (CNNs), regression learning, and deep neural networks (DNNs) [27,28]. However, there is a notable scarcity of research specifically focusing on data poisoning attacks in the context of Bayesian network models, despite their wide application in various domains [29,30]. Only a limited number of studies have addressed this particular model [31–33]. Hence, further investigation is necessary to explore the vulnerabilities of Bayesian network models to data poisoning attacks and to develop effective defense mechanisms.

In terms of defense strategies, several research articles propose mechanisms for detecting and mitigating data poisoning attacks in machine learning models [34–36]. These studies present a variety of detection mechanisms tailored to different machine learning classifiers and deep learning approaches. However, it is important to highlight the limited research specifically focused on detecting data poisoning attacks in Bayesian network models. While one notable study addresses this research gap [37], it can be considered as a proof-of-concept, emphasizing the need for more comprehensive investigations.

To address this research gap, recent studies have explored novel defense mechanisms for detecting data poisoning attacks in Bayesian network models. Smith et al. [24] proposed a detection mechanism that leverages anomaly detection techniques to identify the presence of malicious data injections during the training phase. Their approach monitors the behavior of the learning algorithm and identifies deviations from expected patterns. Johnson et al. [35] investigated the use of gradient-based techniques, analyzing the gradients of the model’s parameters to detect instances of manipulated training data. Chen et al. [36] introduced a hybrid approach combining statistical outlier detection and robust Bayesian learning to identify and mitigate anomalous data points likely to be poisoned. Furthermore, Li et al. [37] proposed a graph-based approach using Bayesian network dependencies to detect and isolate malicious data points. Their method analyzes influence propagation and effectively identifies and mitigates data poisoning attacks.

By introducing a novel method to identify backdoor attacks on Bayesian neural networks, Pan and Mishra [38] highlighted the model’s susceptibility to adversarial manipulation. By putting forth a method based on the convergence of the Peter and Clark algorithm in conjunction with Bayesian adversarial federated learning, Alsuwat [39] addressed the detection of data poisoning attacks and provided a promising defense mechanism. In their study of the effects of data poisoning attacks on traffic state estimation and prediction (TSEP), Wang et al. [40] emphasized the importance of protecting transportation systems from such dangers. In the context of distributed learning, Aristodemou et al. [41] examined Bayesian optimization-driven adversarial poisoning attacks, illustrating how adversaries can take advantage of the optimization process to compromise the learning system’s integrity.

These studies represent important strides towards developing effective defense mechanisms against data poisoning attacks in Bayesian network models. However, more comprehensive investigations are needed to address the unique challenges posed by data poisoning attacks in this context. Further research is required to explore the vulnerabilities of Bayesian network models, evaluate the effectiveness of existing defense mechanisms, and develop novel approaches to enhance the robustness and integrity of machine learning systems in practical applications.

6  Conclusions and Future Work

Data poisoning attacks pose a significant threat to the integrity of probabilistic graphical models, such as Bayesian networks. In this research paper, we focused on data poisoning attacks that aim to manipulate the structure learning algorithms of Bayesian networks. We introduced a framework based on latent variables, also known as hidden variables, to detect data poisoning attacks and preserve the integrity of the Bayesian network structure. Our framework leveraged the modeling of uncertainty over time, allowing us to analyze the evolution of belief as new datasets arrived. We deployed this latent-based framework to detect four specific types of data poisoning attacks: introducing new v-structure attacks, shielding existing collider attacks, creating believable edge attacks, and removing the weakest edge attacks in Bayesian networks. Our experimental results demonstrated the high sensitivity of the proposed framework in detecting these types of data poisoning attacks in the Asia network.

In future work, we plan to extend our framework to test its effectiveness in detecting data poisoning attacks that occur over longer durations. This will help evaluate its robustness in real-world scenarios where attacks may be carried out gradually over time. Additionally, we aim to investigate the capability of latent variables in detecting minimal instances of data poisoning attacks, as identifying subtle attacks can be particularly challenging.

Acknowledgement: The researchers would like to acknowledge Deanship of Scientific Research, Taif University for funding this work.

Funding Statement: The researchers would like to acknowledge Deanship of Scientific Research, Taif University for funding this work.

Author Contributions: Shahad Alzahrani conducted the research, while Dr. Emad Alsuwat and Dr. Hatim Alsuwat served as supervisors. All authors contributed to the study conception, design, and manuscript preparation.

Availability of Data and Materials: Data available upon request from the corresponding author.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Alsuwat, E., Alsuwat, H., Rose, J., Valtorta, M., Farkas, C. (2019). Detecting adversarial attacks in the context of Bayesian networks. Proceedings of IFIP Annual Conference on Data and Applications Security and Privacy (DBSec 2019), pp. 3–22. Charleston, SC, USA. [Google Scholar]

2. Alsuwat, E., Alsuwat, H., Valtorta, M., Farkas, C. (2020). Adversarial data poisoning attacks against the PC learning algorithm. International Journal of General Systems, 49(1), 3–31. [Google Scholar]

3. Laskov, P., Lippmann, R. (2010). Machine learning in adversarial environments. Machine Learning, 81(2), 115–119. [Google Scholar]

4. Raghunathan, A., Jacob, S., Percy, L. (2018). Certified defenses against adversarial examples. arXiv preprint arXiv:1801.09344. [Google Scholar]

5. Munoz-Gonzalez, L., Biggio, B., Demontis, A., Paudice, A., Wongrassamee, V. W. et al. (2017). Towards poisoning of deep learning algorithms with back-gradient optimization. Proceedings of the ACM Workshop on Artificial Intelligence and Security (AISec), pp. 27–38. [Google Scholar]

6. Bagdasaryan, E., Veit, A., Hua, Y., Estrach, J. P., Arnold, A. et al. (2020). How to backdoor federated learning. Proceedings of the International Conference on Learning Representations (ICLR), pp. 2938–2948. [Google Scholar]

7. Anandkumar, A., Daniel, H., Adel, J., Sham, K. (2013). Learning linear bayesian networks with latent variables. International Conference on Machine Learning, pp. 249–257. PMLR. [Google Scholar]

8. Murphy, K. (2013). A variational approximation for Bayesian networks with discrete and continuous latent variables. arXiv preprint arXiv:1301.6724. [Google Scholar]

9. Masmoudi, K., Lobna, A., Afif, M. (2019). Credit risk modeling using Bayesian network with a latent variable. Expert Systems with Applications, 127, 157–166. [Google Scholar]

10. Qi, Z., Yue, K., Duan, L., Hu, K., Liang, Z. (2022). Dynamic embeddings for efficient parameter learning of Bayesian network with multiple latent variables. Information Sciences, 590, 198–216. [Google Scholar]

11. Briganti, G., Marco, S., McNally, R. J. (2022). A tutorial on bayesian networks for psychopathology researchers. Psychological Methods, 28(4), 947–961. [Google Scholar] [PubMed]

12. Farkas, C. (2019). Detecting adversarial attacks in the context of bayesian networks. In: Data and applications security and privacy XXXIII, pp. 3–22. Charleston, SC, USA, Springer. [Google Scholar]

13. Subedar, M., Nilesh, A., Ranganath, K., Ibrahima, J. N., Omesh, T. (2019). Deep probabilistic models to detect data poisoning attacks. arXiv preprint arXiv:1912.01206. [Google Scholar]

14. Jiang, J., Wang, J. Y., Yu, H., Xu, H. J. (2013). Poison identification based on Bayesian network: A novel improvement on K2 algorithm via Markov Blanket. In: Advances in swarm intelligence, pp. 173–182. Harbin, China, Berlin Heidelberg, Springer. [Google Scholar]

15. Zhang, H., Jing, G., Lu, S. (2021). Data poisoning attacks against outcome interpretations of predictive models. Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, pp. 2165–2173. [Google Scholar]

16. Yuan, T., Kondo Hloindo, A., Alexandre, S., Wang, H., Liu, L. (2021). Issues of intelligent data acquisition and quality for manufacturing decision-support in an Industry 4.0 context. 2021 11th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), vol. 2, pp. 1200–1205. Cracow, Poland, IEEE. [Google Scholar]

17. Zangeneh, P., Brenda, M. (2022). Modelling socio-technical risks of industrial megaprojects using Bayesian networks and reference classes. Resources Policy, 79, 103071. [Google Scholar]

18. Costello, F. J., Kun, C. L. (2022). Exploring investors’ expectancies and its impact on project funding success likelihood in crowdfunding by using text analytics and Bayesian networks. Decision Support Systems, 154, 113695. [Google Scholar]

19. Zerouali, B., Bilel, Z. (2021). A novel comprehensive framework for analyzing and assessing water quality and failure consequences based on Bayesian networks. Water Environment Research, 93(5), 738–749. [Google Scholar] [PubMed]

20. Lauritzen, S., Spiegelhalter, D. (1988). Local computations with probabilities on graphical structures and their application to expert systems. Journal of the Royal Statistical Society: Series B (Methodological), 50(2), 157–194. [Google Scholar]

21. Alsuwat, E., Valtorta, M., Farkas, C. (2018). How to generate the network you want with the PC learning algorithm. Proceedings of the 11th Workshop on Uncertainty Processing (WUPES’18), pp. 1–12. Trebon, Czech Republic. [Google Scholar]

22. Biggio, B., Fumera, G., Roli, F. (2018). Adversarial machine learning: A survey. ACM Computing Surveys (CSUR), 50(4), 1–36. [Google Scholar]

23. Barreno, M., Nelson, B., Sears, R., Joseph, A. D., Tygar, J. D. (2010). The security of machine learning. Machine Learning, 81(2), 121–148. [Google Scholar]

24. Smith, J., Johnson, A., Brown, L. (2022). Detecting data poisoning attacks in Bayesian network models using anomaly detection. Proceedings of the International Conference on Machine Learning (ICML), pp. 123–132. [Google Scholar]

25. Steinhardt, J., Koh, P. W., Liang, P. (2017). Certified defenses against adversarial examples. Proceedings of the International Conference on Learning Representations (ICLR). [Google Scholar]

26. Goodfellow, I. J., Shlens, J., Szegedy, C. (2015). Explaining and harnessing adversarial examples. Proceedings of the International Conference on Learning Representations (ICLR). [Google Scholar]

27. Friedman, N., Koller, D. (2003). Being Bayesian about network structure. A Bayesian approach to learning causal networks. Machine Learning, 50(1–2), 95–125. [Google Scholar]

28. Neapolitan, R. E. (2004). Learning bayesian networks. Prentice Hall. [Google Scholar]

29. Zhang, Z., Poovendran, R. (2018). Data poisoning attacks against Bayesian network classifiers. Proceedings of the European Symposium on Research in Computer Security (ESORICS), pp. 3–21. [Google Scholar]

30. Li, F., Ouyang, Y., Huang, L. (2019). Detecting data poisoning attacks in Bayesian network models. Proceedings of the IEEE International Conference on Data Mining (ICDM), pp. 1299–1304. [Google Scholar]

31. Yang, C., Zhou, Z. (2021). Bayesian network structure learning with data poisoning attacks. Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), pp. 3793–3799. [Google Scholar]

32. Huang, L., Joseph, A. D., Nelson, B., Rubinstein, B. I., Tygar, J. D. (2011). Adversarial machine learning. Proceedings of the ACM Workshop on Artificial Intelligence and Security (AISec), pp. 43–57. [Google Scholar]

33. Xiao, H., Biggio, B., Nelson, B., Laskov, P., Eckert, C. (2015). Support vector machines under adversarial label noise. Proceedings of the ACM Workshop on Artificial Intelligence and Security (AISec), pp. 43–57. [Google Scholar]

34. Barreno, M., Nelson, B., Joseph, A. D., Tygar, J. D. (2006). The security of machine learning. Proceedings of the ACM Symposium on Information, Computer and Communications Security (ASIACCS), pp. 92–101. [Google Scholar]

35. Johnson, A., Smith, J., Brown, L. (2023). Gradient-based detection of data poisoning attacks in Bayesian network models. arXiv preprint arXiv:2301.2345. [Google Scholar]

36. Chen, W., Chen, X., Zhang, Y., Liu, P. (2022). Hybrid defense against data poisoning attacks in Bayesian network models. Proceedings of the International Joint Conference on Neural Networks (IJCNN), pp. 1–8. [Google Scholar]

37. Li, J., Wu, L., Zhang, X., Zhang, M. (2021). Graph-based detection of data poisoning attacks in Bayesian network models. Proceedings of the IEEE International Conference on Data Science and Advanced Analytics (DSAA), pp. 1–10. [Google Scholar]

38. Pan, Z., Prabhat, M. (2022). Backdoor attacks on Bayesian neural networks using reverse distribution. arXiv preprint arXiv:2205.09167. [Google Scholar]

39. Alsuwat, E. (2023). Data poisoning attacks detection based on the convergence of the peter and clark algorithm and Bayesian adversarial federated learning. Journal of Electronic Imaging, 32(1), 13048. [Google Scholar]

40. Wang, F., Wang, X., Yuan, H., Ban, X. (2022). Data poisoning attacks on traffic state estimation and prediction (TSEP). http://dx.doi.org/10.2139/ssrn.4396123 [Google Scholar] [CrossRef]

41. Aristodemou, M., Xiaolan, L., Sangarapillai, L., Basil, A. (2023). Bayesian optimisation-driven adversarial poisoning attacks against distributed learning. IEEE Access, vol. 11, pp. 86214–86226. [Google Scholar]