An Encode-and CRT-Based Scalability Scheme for Optimizing Transmission in Blockchain

1  Introduction

Since the emergence of Bitcoin, blockchain has gradually attracted people’s attention as its underlying technology, and has developed rapidly under the impetus of the digital economy. Blockchain is a P2P distributed ledger technology that connects them into a chain structure through time-series-based data blocks and cryptographic algorithms. In the blockchain network, each node maintains a global account book, which realizes the characteristics of decentralization, data traceability and immutability. This innovative technology provides a new solution to the problems of high single point failure rate, poor security, and low data transparency of centralized systems [1]. At present, blockchain is widely studied in the fields of finance [2], medical care [3], energy [4], and food traceability [5]. In the context of the Internet of Things (IoT), the innate distributed characteristics of both blockchain and IoT render them amenable to a fruitful integration, thereby proffering novel solutions for the forthcoming requirements pertaining to data sharing within the IoT landscape [6].

However, compared with centralized systems, blockchain still has some limitations in scalability. Currently, the low transmission efficiency of block networks is one of the reasons for the poor scalability of blockchain [7,8]. The transaction processing capacity of an ordinary blockchain is limited to a few transactions per second, e.g., the throughput of Bitcoin, a typical application of blockchain, is 5–7 transactions per second (TPS) [9], and the throughput of Ethereum is about 17 TPS [10]. Obviously, the current throughput of blockchain is unacceptable to cope with application scenarios such as fast payment [11].

One approach to increasing throughput is by directly augmenting the block size [12], which allows for the accommodation of more transactions. Nevertheless, at the network level, broadcasting a large block within the blockchain network consumes more bandwidth, resulting in significant communication delays that undermine the network transmission efficiency of the block. The transmission of large blocks takes longer to complete, compelling other nodes to wait for the complete block data before they can verify and confirm it. This communication delay adversely affects the throughput and overall performance of the entire blockchain network.

Furthermore, at the data storage level, blocks with substantial data volumes impose a heavier storage burden on nodes. As of May 2023, the stored data in Bitcoin has exceeded 480 GB [13], and in Ether blocks, it exceeds 630 GB [14]. These figures are continuously growing at a substantial rate. The ongoing data growth places heightened demands on the blockchain system, potentially burdening the system and negatively impacting its performance. The storage of substantial volumes of data necessitates increased hardware resources and physical space, while the processing of this data requires additional computational power and greater bandwidth capacity [15]. Consequently, delayed data synchronization between nodes, prolonged transaction confirmation times, and potential network and transaction congestion [16] may ensue.

Another avenue for increasing throughput involves techniques to reduce the block size through the utilization of transaction hashes to represent transactions within the block [17]. Nevertheless, the effectiveness of these techniques hinges on the complete synchronization of the node’s transaction pool. Based on the findings of a study [18], it is observed that there is approximately a 53% probability that a node’s transaction pool contains all the transactions from the block to be propagated, approximately 17% probability of missing one transaction, and around 9% probability of missing two transactions. When a node’s transaction pool lacks certain transactions, it must request the missing transaction data from other nodes, which results in unnecessary bandwidth consumption and diminishes the network transmission efficiency of the block. Due to the need for constant communication among nodes to obtain the missing transaction data, not only does the network transmission overhead increase, but the block propagation time is also extended.

These issues indicate that the current large block scheme and compact block scheme possess certain limitations that impact the network transmission efficiency and block bandwidth utilization. Consequently, there is a need to propose more effective methods to address these challenges and enhance the transmission efficiency and scalability of the blockchain system, ensuring efficient storage and processing of the growing data volume. In this study, we introduce ECSS, a novel blockchain data transmission and storage scheme as solutions to address scalability bottlenecks. Firstly, ECSS employs clustering to group neighboring nodes into domains, effectively diminishing the system’s network diameter and enhancement overall network efficiency. Secondly, ECSS engages in block processing, which encompasses the generation of a checksum block through RS encoding and the utilization of a compressed block protocol to condense the block’s body. This multifaceted approach significantly reduces both broadcast communication overhead and transaction request overhead. Finally, ECSS leverages the Chinese remainder theorem to map consensus-completed blocks onto multiple moduli, thus dispersing storage across nodes to achieve compression and alleviate storage burdens.

In all, the main contributions of this study are summarized as follows:

•   We propose a novel Encode-and CRT-based Scalability Scheme (ECSS) for blockchain. It can effectively improve the broadcasting efficiency of blocks and reduce the storage pressure on nodes.

•   ECSS employs an enhanced RS coding-based compact block broadcasting mechanism, which achieves both propagation reliability and significantly reduces the bandwidth consumption essential for block propagation.

•   ECSS incorporates the Chinese remainder theorem into block compression, utilizing it as a key technique. By targeting the block body for compression, the scheme effectively maps the block body to multiple moduli, and then distributes the compressed data across various nodes in a decentralized fashion. As a result, the storage cost for individual nodes is significantly reduced.

•   The results from simulation experiments show that the ECSS scheme is able to reduce the communication overhead by 72% and the total storage cost by 63.6% compared to the compact block protocol.

The rest of the paper is organized as follows. Section 2 introduces the related work. Section 3 briefly describes the background knowledge related to ECSS. Section 4 describes the design of ECSS in detail. The performance of the ECSS is analyzed and simulated in Section 5. Finally, conclusions are given in Section 6.

2  Related Work

Several researchers had addressed block propagation latency reduction to enhance the scalability of blockchain by optimizing block propagation protocols. Zhang et al. [19] introduced a novel block propagation protocol, replacing the existing store-and-forward tight block relay scheme with a pass-through compact block relay scheme. Additionally, they employed ratio-less erasure codes to improve block propagation efficiency. However, this approach demands high communication performance from nodes. Zhao et al. [20] proposed the LightBlock scheme, which uses transaction hashes to replace original transactions, thereby reducing block size during propagation. When receiving the transaction hash, nodes reconstruct the complete block by recovering the corresponding transaction from their transaction pool. Although this scheme optimizes bandwidth resources during propagation, there is no guarantee that all nodes’ transaction pools are synchronized, leading to potential bandwidth wastage when gaps exist in other nodes’ transaction pools. Ahn et al. [21] employed a packet aggregation scheme to compress network-generated traffic. This scheme utilizes XOR operation on received packets to connect blockchain traffic with the same destination. Experiments demonstrated a 23% reduction in PBFT processing time and a corresponding increase in transaction throughput. Nevertheless, implementing this scheme in real networks may be challenging since it requires nodes to have multiple network interfaces. Hao et al. [22] proposed the BlockP2P-EP broadcasting protocol, which utilizes parallel spanning tree broadcasting on a trust-enhanced blockchain topology to achieve fast data broadcasting between nodes within and between clusters. However, congestion within the cluster arises as the network size increases, leading to reduced synchronization efficiency within the cluster.

Some scholars had utilized coding schemes [23] to enhance the efficiency of network block transmission. Wang et al. [24] introduced an innovative data distribution protocol, A-C, which integrates erasure coding into a two-tier publish-subscribe mechanism based on a named data network. This approach achieves rapid data dissemination and bandwidth efficiency for blocks. Jin et al. [25] proposed a protocol utilizing erasure coding to reduce bandwidth during the transmission of lost transactions. Chawla et al. [26] presented a fountain code-based block propagation method that decentralizes block delivery through multiple nodes, effectively reducing network congestion. Cebe et al. [27] devised a network coding-based method that slices blocks, applies network coding techniques to compress their size, and subsequently combines the chunks into packets for transmission, thereby reducing transmission overhead. Choi et al. [28] implemented a new network coding approach in the context of the Practical Byzantine Fault Tolerant (PBFT) consensus protocol to enhance scalability by reducing communication overhead between nodes. Ren et al. [29] integrated regenerative coding with blockchain technology in the context of edge computing, effectively mitigating bandwidth inefficiencies and enhancing the security and reliability of data storage within edge computing environments.

Several researchers had explored compression schemes to enhance transmission efficiency. Chen et al. [30] introduced a Slicing-and Coding-based Consensus Algorithm (SCCA) based on slicing and FR codes, effectively improving communication efficiency while reducing node storage costs. Similarly, Qu et al. [31] developed a TFR code with network scalability based on FR code and implemented a slicing network storage scheme for blockchain. Mei et al. [32] proposed a block storage optimization scheme using the residue number system and the Chinese Residue Theorem to compress blocks, reducing storage on each node. However, this scheme only compresses account data and does not achieve a high compression rate for overall blocks. In contrast, Guo et al. [33] also utilized the Chinese remainder theorem for storage compression, incorporating an adaptive mechanism to compress transactions in the block. Nonetheless, when recovering the block, hundreds or thousands of transactions must be recovered first, increasing communication and computation between nodes. Spataru et al. [34] proposed a blockchain architecture with adaptive smart contract compression, adopting a hybrid compression algorithm combining Hoffman coding and LZW compression. However, their focus lies solely on reducing smart contract storage overhead, and the effect of data compression on the block as a whole may not be readily apparent.

3  Background Knowledge

3.1 Compact Block

Compact block [35] represents an optimization technique implemented in the Bitcoin network to enhance the transmission and validation speed of blocks, ultimately leading to increased throughput and improved efficiency in the Bitcoin network.

The core concept of a compact block revolves around broadcasting only essential information contained within the block, rather than the entire block data. When a miner successfully mines a block, they broadcast the block header along with a portion of the transaction data, referred to as a short transaction ID or transaction hash, to other nodes in the network. The block header includes metadata like the block version, hash of the previous block, timestamp, and other relevant details. Leveraging this information, other nodes can verify the legitimacy of the compact block without the need to receive the complete block data.

Upon verifying the compact block and confirming the missing transaction data, other nodes can request the corresponding transaction data from the miner. The miner then fulfills these requests by providing the required transaction data, enabling the verifying nodes to reconstruct the complete block. This on-demand access to transaction data significantly reduces the network transmission load and enhances the overall transmission efficiency, thereby streamlining the block propagation process.

3.2 RS Coding

RS coding, also known as Reed-Solomon coding [36], is a powerful error detection and correction coding technique that employs forward error correction. It operates within the framework of finite domains, also referred to as Galois domains, using polynomial operations to achieve error detection and correction. The versatility and efficacy of RS codes make them extensively employed in communication and storage systems. These codes play a vital role in enhancing data transmission reliability by effectively detecting and correcting errors, thereby bolstering the system’s resistance to noise and ensuring more robust and dependable data transmission and storage.

The RS code’s fundamental concept entails the selection of an appropriate generator polynomial g(x), ensuring that the code word polynomial computed for each information field is a multiple of g(x). The presence of errors in the received codeword can be ascertained by examining the remainder resulting from dividing the received codeword polynomial by the generator polynomial. Subsequently, error correction can be carried out through further calculations.

In GF(2m) domain, RS(n,k) denotes the following: m denotes that each code element consists of m binary digits; n denotes that there are a total of n code elements in a code block; k denotes that a code block has k information code elements; and t=n−k denotes that there is t checksum code elements in a code block, and also denotes the number of code elements that can be corrected.

For an information code element polynomial d(x), the RS check code element generation polynomial takes the general form of

g(x)=∏i=0n−k−1(x−aK0+i)(1)

with K0 representing the offset, typically set as either K0=0 or K0=1, and ai being an element in GF(2m). The resulting RS code can tolerate the loss or corruption of n−k coded blocks.

Using RS(8,5) as an illustration, the initial 5 information code elements undergo RS encoding to produce 8 code elements, of which 3 are check code elements within a code block. In the event that any 3 out of these 8 code elements (comprising both information code elements and check code elements) are lost or damaged, the RS decoding algorithm can recover the 3 lost or damaged code elements.

3.3 The Chinese Remainder Theorem

The Chinese Remainder Theorem (CRT) [37] is significant in number theory, with its origins in ancient Chinese mathematics. It offers an efficient solution for systems of residual numbers. According to the Chinese residue theorem, when provided with a set of moduli that are mutually prime, a numerical value can be expressed as a congruence relation among the residue classes corresponding to each modulus. By partitioning the computation task into independent subtasks based on these moduli, CRT facilitates the combination of results into raw values.

Described in mathematical language, the Chinese remainder theorem gives the solution determination conditions for the unary linear congruential equations such as:

{x≡a1(mod1)x≡a2(mod2)⋮x≡an(modn)(2)

Assuming that the integers m1,m2,…,mn are mutually prime positive integers, where M=∏i=1kmi, the system of Eq. (2) has a unique solution for any integers a1,a2,…,an and modulo M. The solution is shown in Eq. (3), and ei satisfies Eq. (4).

x≡(Mm1e1a1+Mm2e2a2+⋯+Mmkekak)(3)

Mmiei≡1(mod mi)(i=1,2,…,k)(4)

The Chinese remainder theorem, relying on modulo operations and leveraging the mutually independent nature of moduli, enables the division of the computational task into distinct independent subtasks. The results obtained from these subtasks can then be combined using CRT to yield the final result. This parallelized computation approach leads to notable enhancements in computational efficiency, substantially reducing computation time and resource consumption. Researchers have successfully applied CRT to improve throughput, facilitate multi-signature transactions, achieve distributed storage, and ensure privacy protection.

4  Design

Fig. 1 illustrates the system architecture of ECSS, which comprises three modules: system initialization, broadcasting model, and compressed storage model. In the system initialization phase, ECSS conducts node clustering to group neighboring nodes into domains, thereby reducing network topology complexity and network diameter. Moreover, routing nodes and monitoring nodes are designated within each domain to facilitate parallel broadcasting within the domain. Moving on to the broadcast model, ECSS introduces a novel approach based on the compact block protocol and RS coding. The compact block protocol effectively reduces block size, while RS coding ensures block transmission integrity and reliable data transmission. In the compressed storage model, ECSS targets the block body for compression. Utilizing the Chinese remainder theorem, the block body is mapped to multiple moduli and stored across multiple nodes, achieving efficient storage and alleviating node storage pressure.

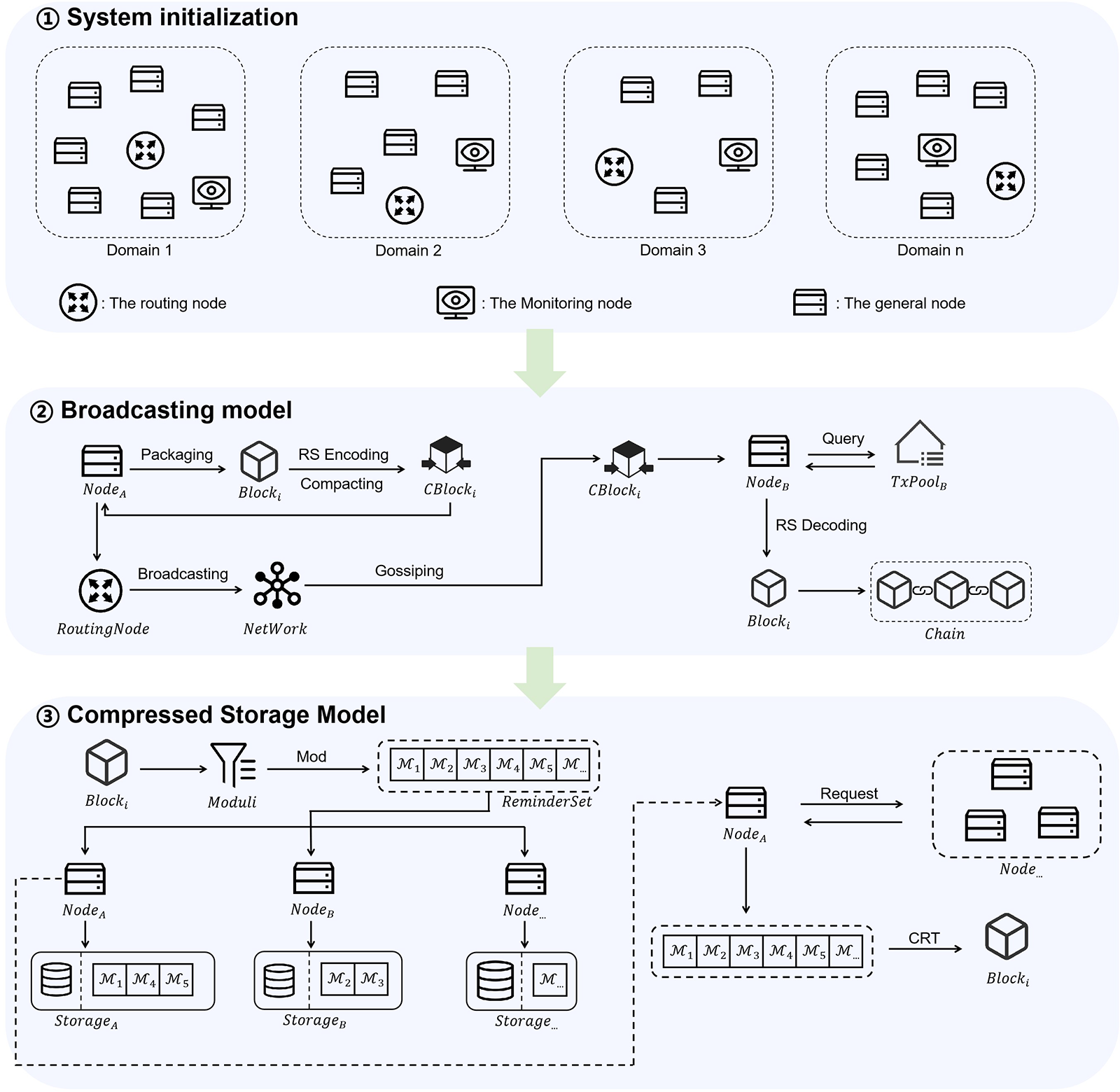
Figure 1: The framework of ECSS

In order to establish robust and secure connections between system layers, ECSS implements a comprehensive set of security measures. Firstly, it leverages asymmetric encryption to safeguard the confidentiality of transmitted data, ensuring that sensitive information remains protected. Simultaneously, digital signatures play a critical role in verifying data integrity and authenticity, mitigating the risk of tampering during transmission. Furthermore, ECSS facilitates node interactions through a peer-to-peer network model. This design ensures that only authorized nodes possess the capability to directly establish connections with one another, significantly reducing potential vulnerabilities stemming from unauthorized access. To fortify security even further, ECSS deploys access tokens and fine-grained permission settings. This strategic approach guarantees that only nodes with explicit authorization can access sensitive data, thereby restricting access to crucial information to legitimate nodes within the system. These multifaceted security measures collectively contribute to the establishment of a robust and secure interlayer connection framework, underscoring ECSS’s commitment to overall system security and integrity.

4.1 System Initialization

To optimize the network transmission efficiency of the system, the initial step involves node clustering. ECSS achieves this by grouping nodes that are closer to each other and experience minimal communication delay into the same domain, utilizing methods such as geographic information-based clustering or communication delay clustering. The clustering process divides the nodes into different domains, resulting in reduced network distance between nodes within the same domain. Consequently, the system’s network diameter is decreased, effectively shortening the longest communication path between nodes, leading to accelerated data transmission and communication.

After clustering, the system establishes multiple domains. To facilitate data broadcasting and synchronization, synchronization is essential between nodes within each domain and across different domains. To address this requirement, the paper categorizes nodes within the domain into three distinct categories: routing nodes, monitoring nodes, and general nodes.

•   Routing nodes: The routing node serves as the central hub for inter-domain data transmission, taking responsibility for storing and managing routing information from other domains. By establishing connections with other domains, routing nodes ensure seamless data exchange across domain boundaries, enabling smooth data broadcasting and delivery between different domains. When a common node sends data to the routing node of its domain, the routing node receives and assumes the responsibility of delivering the data to other domains. Simultaneously, upon receiving data from other domains, the routing node is accountable for broadcasting within its own domain and disseminating the data to ordinary nodes within that domain.

•   Monitoring nodes: The monitoring node assumes the responsibility of overseeing the behavior of the routing node and identifying any potential illegal activities. Before initiating data broadcasts to nodes within the domain or to other domains, the routing node must undergo authentication by the monitoring node. Additionally, the monitoring node functions as a backup for the routing node, storing information pertaining to the routing node and network details of other domains. In the event of a faulty or offline routing node, the monitoring node will step in as the new routing node, guaranteeing uninterrupted data transmission and inter-domain connectivity.

•   General nodes: General nodes are tasked with packing, validating, and synchronizing blocks.

To bolster transaction query efficiency and fortify the reliability of blockchain system, each domain’s routing node assumes dual roles as a full node. Upon receiving a broadcasted block, these routing nodes initially engage in comprehensive block recovery and subsequently store it locally. To address the concern of centralization, routing nodes must undergo dynamic scheduling in accordance with predefined rules, thus ensuring system decentralization and equilibrium.

4.2 Brocasting Model

In this paper, we present a novel compact block broadcast transmission extension model based on RS code. This model leverages the compact block protocol and corrective censoring code technique to effectively reduce the size of the block to be broadcast, thereby enhancing network transmission efficiency. By constructing a compact block that comprises a collection of hash values of transactions in the block body, unique identifiers for the transactions are achieved. However, it is important to note that the node’s local transaction pool may not always contain all the transactions in the compact block. As a result, in such cases, the node needs to request the missing transaction data from other nodes, leading to bandwidth wastage and a reduction in the network transmission efficiency of the block.

In order to solve this problem, reduce bandwidth waste and improve the reliability of data recovery, ECSS introduces RS codes. The checksum block constructed by RS code ensures that complete block data can be recovered even if some of the node’s transactions are missing or corrupted. RS code can be adjusted according to the node’s performance and demand to determine the size of the checksum bit, thus controlling the number of missing transactions that the system can tolerate. By using RS codes, the system is able to handle the situation of missing transactions more efficiently, reducing the requests to other nodes and improving the reliability and transmission efficiency of the system.

Before delving into the specific steps, it is essential to clarify that the RS code employed in ECSS is established within the Galois domain G(28). Moreover, represents the RS checksum bit set by the system, indicating the generation of redundant checksum blocks through RS encoding, while also denoting the number of missing transactions that a node can withstand.

4.2.1 Encoding of Blocks

First, the node packages the block to generate the block and then processes the block body. Since the information to be encoded needs to be divided into multiple information segments before RS encoding, ECSS takes a complete transaction information in a block body as an information segment. Assuming that the number of transactions in a block body is n, then the block body is divided into n information segments, and the set composed of information segments is expressed as TxSet={Tx1,Tx2,...,Txn}.

Subsequently, based on the predefined check digit v, the node performs RS encoding on the set of information segments, resulting in a set containing z=w+v encoded blocks, denoted as Eq. (5). According to the properties of RS encoding, rsSet contains TxSet as well as the set of checksums VerifySet.

reSet=RSCode(TxSet,v)={Tx1,Tx2,...,Txn,Verify1,Verify2,...,Verifyv}(5)

The node processes the original block according to the compact block protocol to generate a compacted block containing only the set of transaction hashes and generates a compact block with checksum through Eq. (6). Finally, the node sends cBlock to the routing node in its domain, which then broadcasts it.

cBlock=Compact(Block,VerifySet)(6)

4.2.2 Decoding of Blocks

Upon receiving cBlock, the node proceeds to access its local transaction pool and retrieves the corresponding transaction data based on the set of transaction hashes present in the block. If the node’s local transaction pool contains all the transactions found in the compact block, then the node can directly reconstruct the complete block.

If there are missing transactions in the local transaction pool, then the recovery step is as follows: assuming that the number of missing transactions in the node’s local transaction pool is q, then when q≤v, the node can utilize the w−q transactions owned in the passed local transaction pool and the VerifySet in cBlock for RS decoding, so as to recover the missing transactions, and finally get the complete block data.

When q>v, following the characteristics of RS encoding, the v checksums are insufficient to enable the node to recover the missing transaction data through RS decoding. In such cases, the node records the hash value of the missing transaction and subsequently requests the routing node to provide the missing transaction data. Once the missing transactions are replenished, the node can then reconstruct the complete block.

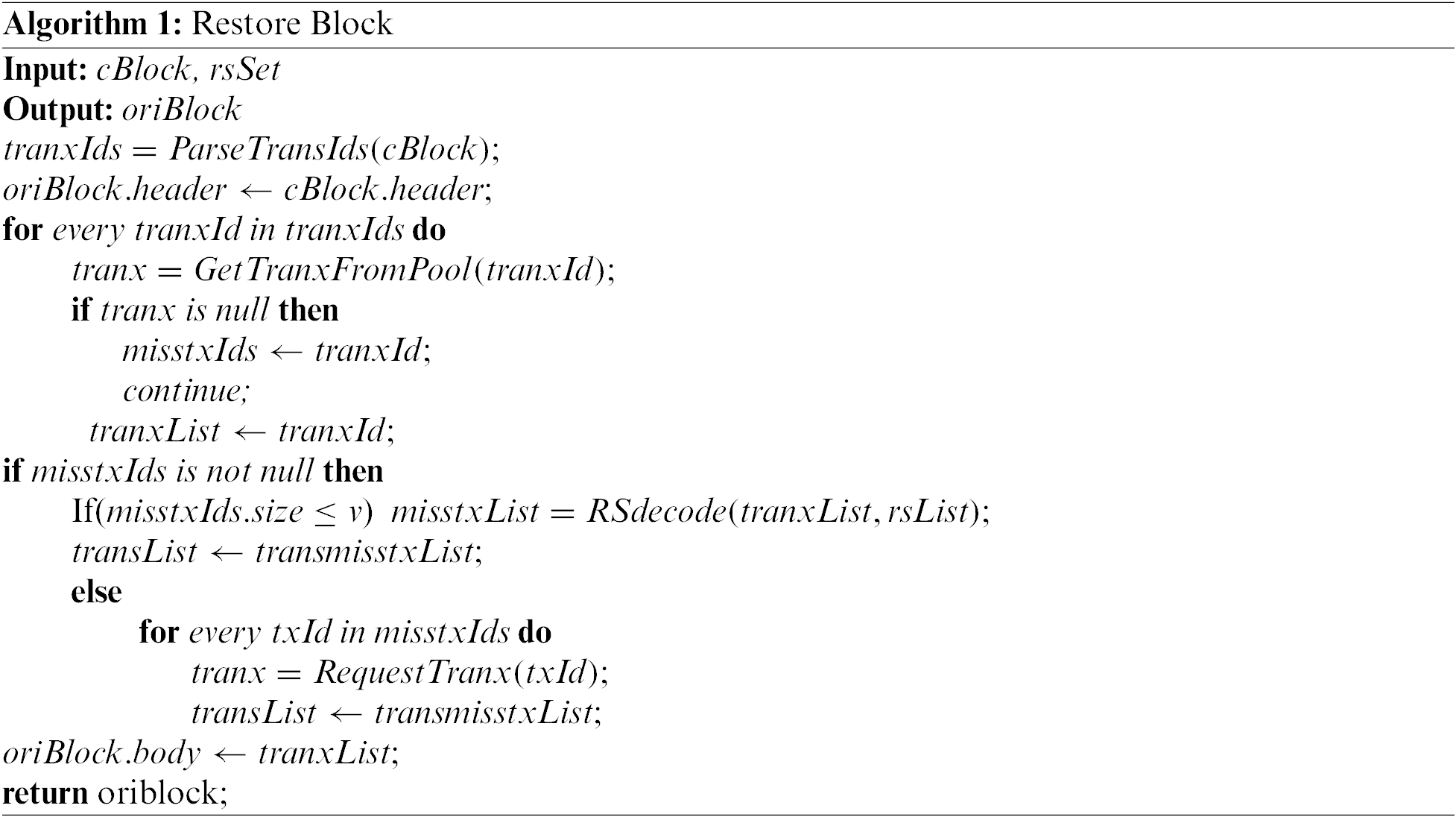
The algorithm for decoding the block is shown in Algorithm 1.

4.3 Compressed Storage Model

4.3.1 Parameter Initialization

When the system is initialized, it is necessary to preset the segmentation bit width λ and a global modulus set Φn={k1,k2,...,kn}, and the elements in Φn need to satisfy pairwise mutual prime. λ limits the size of the cut chunks, and the maximum number that can be represented by each chunk is cmax=2λ−1. The maximum number that can be expressed under the condition of Φn is ω=∏i=1nki. This paper sets the standard interval: Γ=[0,ω], so that all positive integers within the standard interval, can be uniquely represented by the elements in the Φn.

It is important to highlight that, for the Chinese remainder theorem to operate effectively, it is crucial to ensure cmax∈Γ to maintain the uniqueness of the theorem when presetting λ and Φn. Additionally, the size of the modulus set Φn needs comprehensive evaluation. If n is too small, it results in larger block mappings to each modulus, potentially increasing storage burdens on certain nodes. Conversely, an excessively large n can lead to inefficient compression and heightened bandwidth demands on nodes. To optimize system performance, the choice of λ should be made with reference to the system block size. For n, it is imperative to ensure that the product of n prime numbers is greater than cmax. After conducting experiments, ECSS prescribes nmin=λ+1. To prevent inefficient compression due to an overly large n, it’s advisable to set nmax=2nmin, so n∈[λ+1,λ+1]. System administrator should select n within the recommended range to uphold system performance standards.

4.3.2 Block Pre-Processing

In the system, blocks are usually of variable size and presented as characters. However, the Chinese remainder theorem operates solely on numerical values. Hence, to employ this theorem for compression, a digitization process is required to convert the character-based blocks into numerical form. Additionally, before compression, the blocks of varying sizes need to be sliced into appropriate chunks for further processing.

As shown in the Fig. 2, the steps are as follows:

1)   First, the data in the block body is converted to binary form, and the length of the converted data is Lb.

2)   Then, the binarized block body is split to p=⌈Lbλ⌉ chunks. For the last chunk that is less than λ bits, zeros are added after it to make the length its up to λ bits.

3)   Finally, each of the sliced binary chunks is converted to a decimal number to obtain Zp={φ1,φ2,...,φp}. Through such processing, we can convert the block into a digital form for subsequent compression using the Chinese remainder theorem.

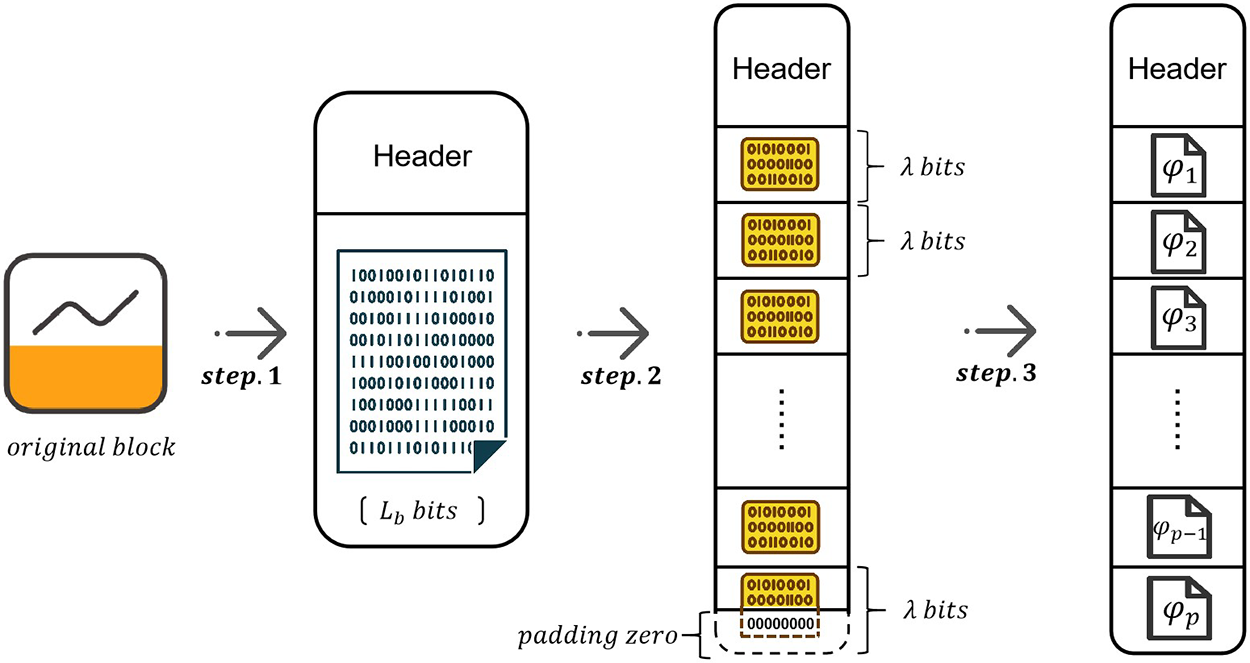
Figure 2: The detail of block pre-processing

4.3.3 Block Compression

The node uses the modulus in the Lt to calculate the remainder of the number set Zp corresponding to Zp chunks, and obtains a t×p remainder matrix M, where Mt,p is the remainder result of φp to st. The node saves the M matrix locally to complete the local compression of the blocks.

Fig. 3 represents the local compression of the three nodes against the first chunk φ1 when the global modulus set size is 8. The Node1 locally stores four moduli (k1,k3,k4,k5). It utilizes these moduli to calculate the remainder of φ1 individually, resulting in four remainders denoted as (M1,1,M1,3,M1,4,M1,5). These remainders are then saved locally, completing the local compression of the first chunk. Both Node2 and Node3 store only 2 moduli locally, so after computation they only need to store the two corresponding remainders.

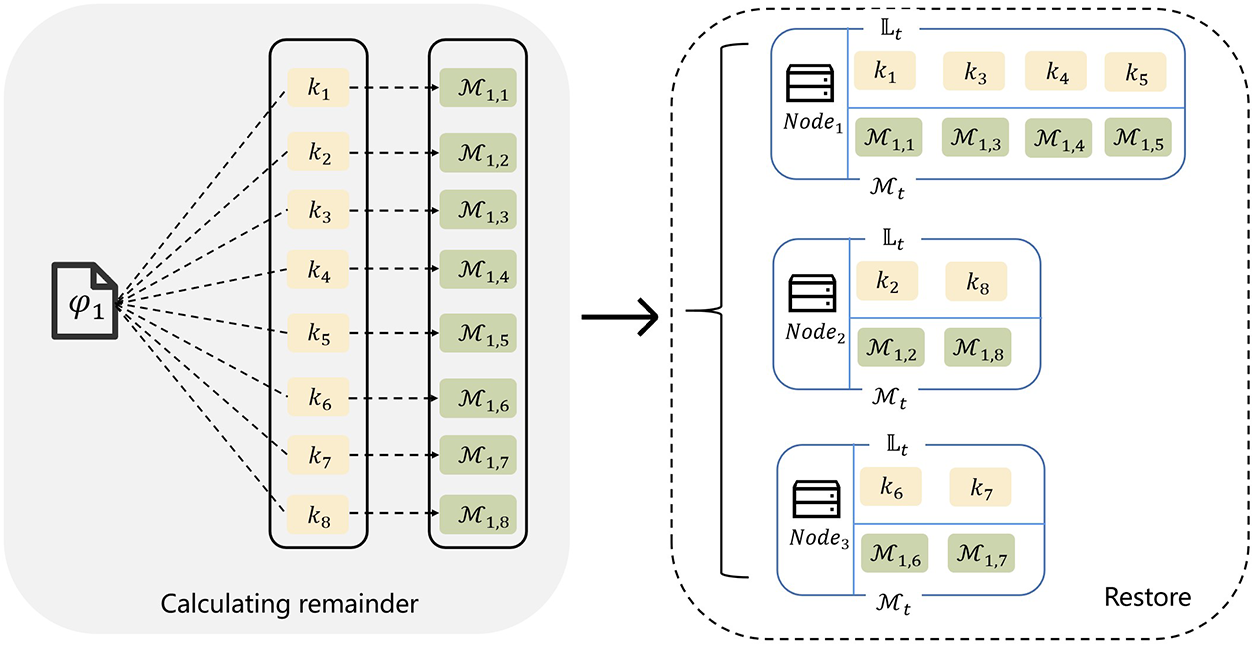
Figure 3: The detail of block compression

4.3.4 Block Restoration

When a node receives a request for block information, it follows the following steps. First, the node computes the set of local missing moduli Gj=Φn−Lt and extracts the locally stored compressed residue matrix M based on the hash value of the block. Then, the node sends a request to other nodes in the domain to obtain the missing remainder matrix G and restore the global remainder matrix D = M + G. Finally, the node restores the global remainder matrix to decimal data chunks through CRT, and then converts these chunks into binary form to restore the original block body data.

Fig. 4 shows the process of restoring blocks when the global modulus set size is 8. First, Node1 calculates the local missing modulus set G4:

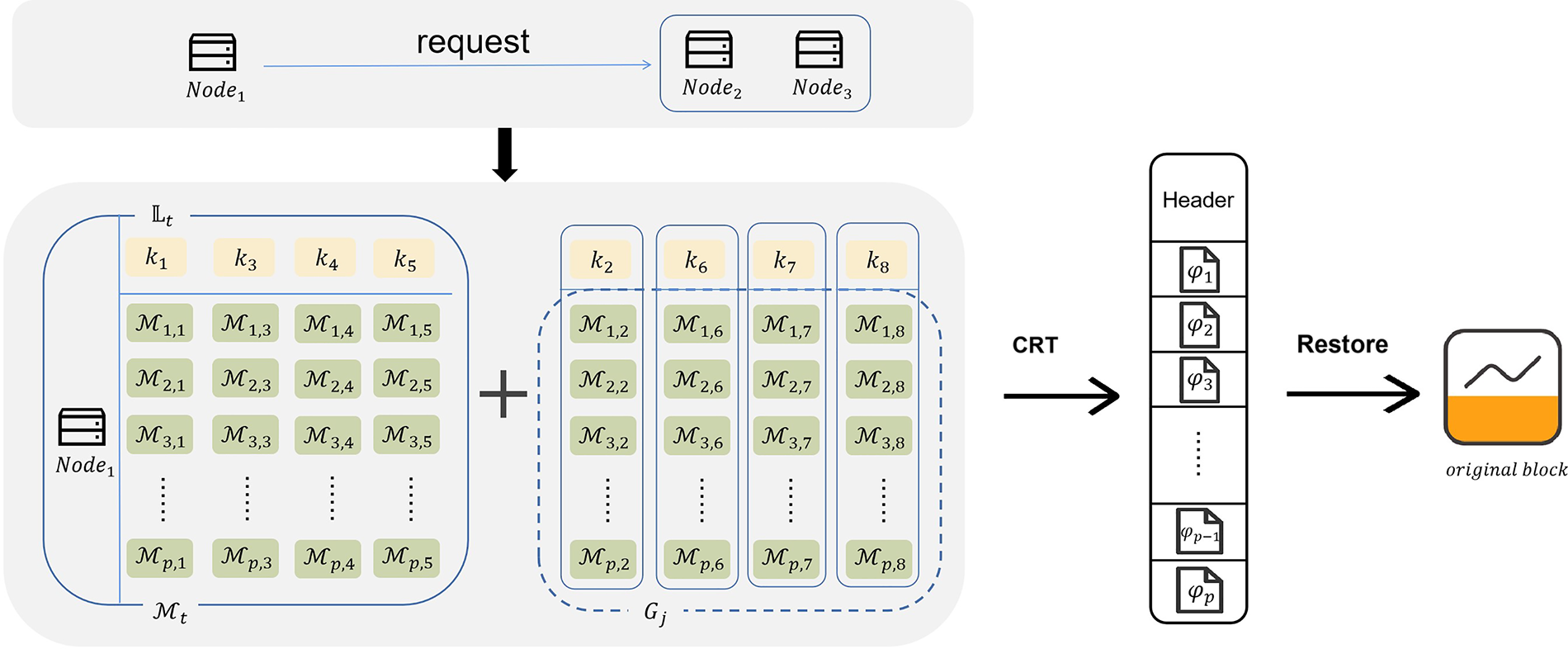
Figure 4: The detail of block restoration

G4=Φ8−L4={k2,k6,k7,k8}(7)

Since the residue matrix corresponding to {k2,k8} is kept in Node2 and the residue matrix corresponding to {k6,k7} is kept in Node3, Node1 requests from Node2 and Node3 for the missing residue matrix G:

G=ReqAbs(blockHash,G4)(8)

Based on the hash value of the block, Node1 extracts the corresponding compressed residue matrix M and recovers the global matrix D = M + G. Finally, the nodes are reduced to decimal data chunks using the Chinese remainder theorem by Eq. (9). The complete original block is obtained by converting to binary and recovering the character data.

Zp=CRT(Φn,D)(9)

5  Experiment and Results Analysis

To evaluate the performance of ECSS, we designed an experimental platform for blockchain systems using the Peersim [38] simulation platform. In our simulation network, we have employed the event-driven engine provided by Peersim, which is composed of three integral components: the underlying network protocol, the broadcast transport protocol, and the link interface. The underlying network protocol governs the communication mechanisms between nodes, while the broadcast transmission protocol dictates how blocks are disseminated, and the link interface manages the connections between nodes. For the purposes of this experiment, we have adopted the peer-to-peer (P2P) protocol as our underlying network protocol. Notably, in line with the prevalent practices in the blockchain domain, we have implemented the push-based Gossip transmission protocol for broadcasting. It is pertinent to mention that our focus lies primarily in enhancing the network and storage layers of the blockchain system, with no direct alterations to the consensus layer. As a result, the ECSS scheme holds the potential to be seamlessly integrated with various consensus algorithms. In an effort to mirror real-world network scales, we have configured our simulation to accommodate a maximum of 10,000 network nodes, a reference point drawn from the existing Ethernet infrastructure, which currently boasts 10,639 nodes [39]. We established the transaction pool of nodes using redis, and data persistence was achieved through Mysql. The experimental platform was deployed on a machine running the Win 10 operating system, equipped with an Intel(R) Core(TM) i7-8750H CPU @ 2.20 GHz and 16 GB RAM. This configuration ensured a reliable environment to conduct our performance evaluations.

In this section, we conduct a comprehensive analysis and experimental evaluation of the performance of the ECSS scheme in terms of communication overhead, network scalability, and compression rate. To ensure clarity and ease of understanding, Table 1 provides a list of symbols and their corresponding meanings used throughout the analysis and experiments.

5.1 Communication Overhead

The communication overhead of ECSS consists of two main components: the broadcasting overhead and the transaction overhead. To ensure the validity of the experimental comparison, we compare the ECSS scheme with the original block scheme, the LightBlock scheme [20], and the SCCA scheme [30]. The LightBlock scheme represents the compact block protocol type of scheme, which replaces the original transaction by a hash of the transaction, compressing the block and thus reducing the communication overhead. The SCCA scheme represents the encoding scheme, which utilizes the encoding of blocks or transactions to reduce communication overhead. ECSS combines the compact block scheme and the encoding scheme, and thus the comparison with the above two schemes illustrates the validity of the experiments.

5.1.1 Broadcasting Overhead

The block broadcasting overhead refers to the network bandwidth consumed when a block is broadcasted to all nodes. Eq. (10) presents the formula used to calculate the block size in ECSS, where VH denotes the size of the space occupied by the block header, VTXS represents the size of the set of transaction hashes contained in the block, and VRS indicates the size of the checksum resulting from the RS encoding of the block.

Sblock=VH+VTXS+VRS(10)

After initialization, the system consists of T domains, with an average of Numd¯ nodes contained in each domain. The number of neighbors of a node is denoted as Numnei. Utilizing the gossip algorithm for push-based data transmission, the block broadcasting overhead can be calculated as the Eq. (11).

Bbk=Numd¯×T×Numnei×Sblock(11)

In this experiment, we set T=5 and Numnei=20. After referring to the existing blocks, we determined the average transaction size to be 1.2 kb and the number of transactions in each block to be 2000. All the coding calculations were performed in the GF(28) Galois domain.

Fig. 5 illustrates the comparison of the broadcasting overhead across the original block scheme, the SCCA scheme and ECSS for varying network sizes. For a network scale of 10,000, the broadcasting overhead of the original block scheme and the SCCA scheme is 468,750 and 72,312 mb, whereas the ECSSv=6 with a check digit value of 6 results in a broadcasting overhead of 35,786 mb. Notably, the broadcasting overhead of ECSS accounts for a mere 49% of that observed in the SCCA scheme and a mere 7.6% of that of the original block scheme. This observation underscores the remarkable efficiency of ECSS in conserving propagation bandwidth when compared to both the original block scheme and the SCCA scheme.

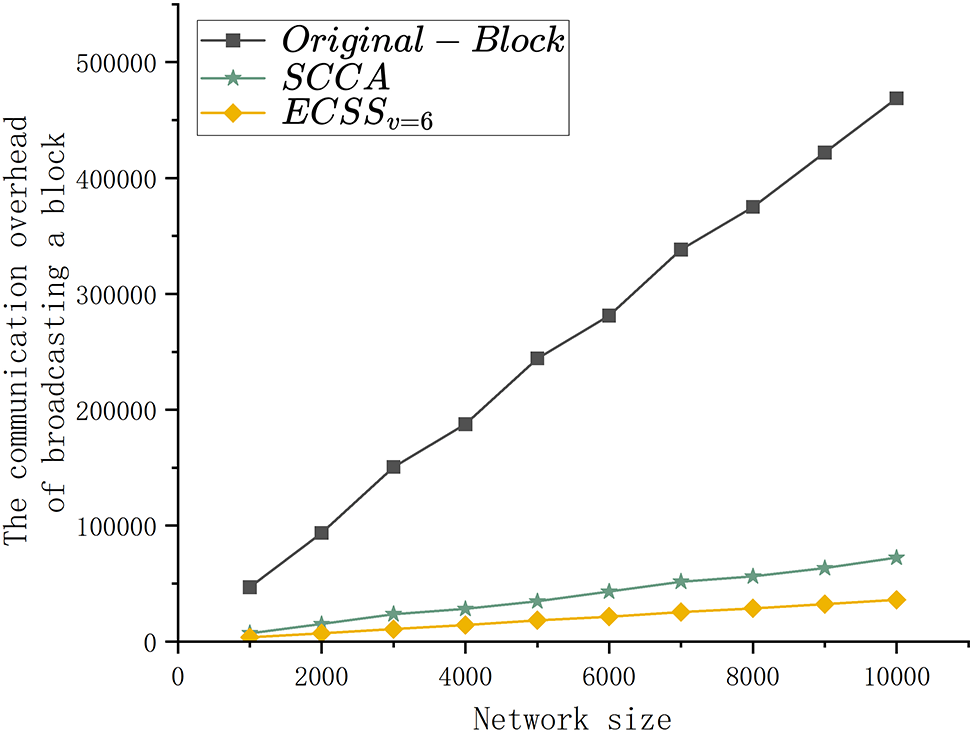
Figure 5: The broadcasting overhead comparison of original block, SCCA and ECSS

Fig. 6 shows the block broadcasting overhead of ECSS with the different check digit value compared to the LightBlock scheme. It can be observed that as the network size increases, the block broadcast overhead also increases, but the difference between the block broadcast overhead of the LightBlock scheme and ECSS is very small. When the network size is 10,000, the broadcasting overhead of the LightBlock scheme is 34,391 mb, while the broadcasting overhead for ECSSv=6 is 35,786 mb, which is only 4% more than that of the LightBlock scheme. ECSSv=2 has a broadcasting overhead of 34,855 mb, which is only 1.3% more than that of the LightBlock scheme.

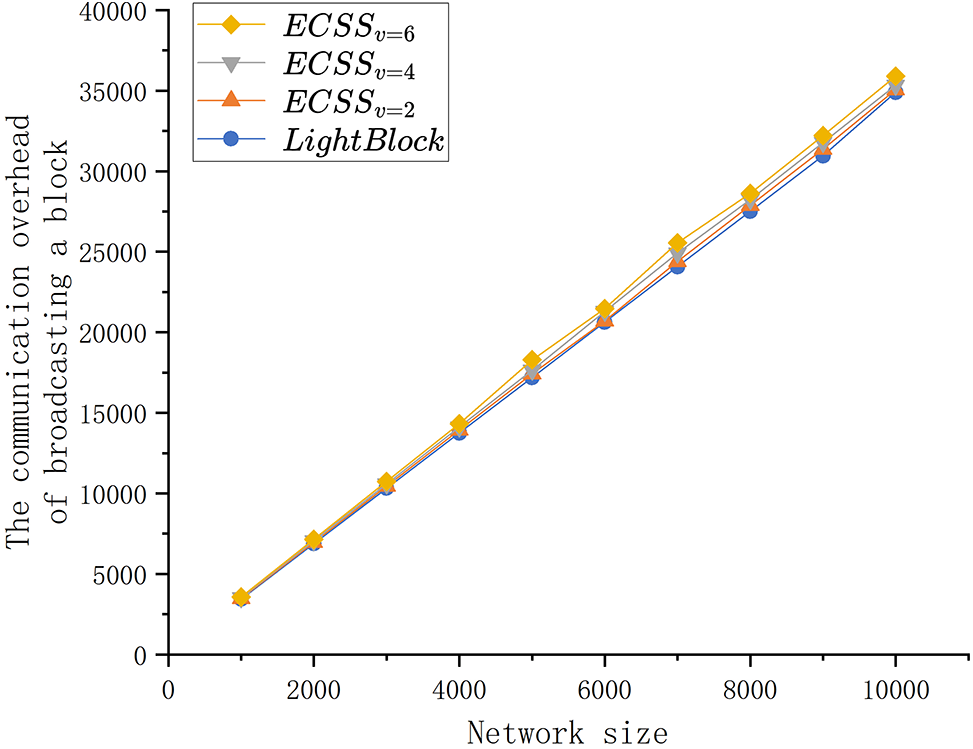
Figure 6: The broadcasting overhead comparison of LightBlock and ECSS with different check digit value

Compared to the LightBlock scheme, ECSS adds checksum blocks to the broadcasted blocks, the number of which depends on the size of the check digit value chosen by the system. According to [18], the number of missing transactions in a node’s transaction pool rarely exceeds six. Considering the current network transmission rate, it can be assumed that the block broadcasting overhead of the LightBlock scheme and the ECSS scheme is almost the same when choosing a small v.

5.1.2 Transaction Overhead

The transaction overhead refers to the communication overhead incurred by a node requesting missing transactions. Since the SCCA scheme does not involve the case of requesting missing transactions, this experiment is mainly compared with the LightBlock scheme. We designate the maximum number of missing transactions for a node as j, the check digit value as v, the probability of a node missing different numbers of transactions as pi, and the size of a transaction as Stx. When j>v, the transaction request overhead incurred by a node while requesting a missing transaction from a routing node is denoted as Eq. (12).

Btxs=∑i=1jNumd¯×T×pi×Stx(12)

Fig. 7 represents the comparison of the transaction overhead between the LightBlock scheme and ECSS. When the blockchain network size is 10,000, the transaction overhead generated under the LightBlock scheme is 17,040 kb, while the ECSSv=6 is only 4680 kb, which is a 72% reduction in overhead. In comparison, the transaction overhead of the LightBlock scheme is 3.64 times that of ECSSv=6, 2.15 times that of ECSSv=4, and 1.46 times that of ECSSv=2. As the network size increases, the transaction overhead generated also increases. However, it is evident that for the same network size, the transaction overhead of the LightBlock scheme is substantially higher compared to that of ECSS. Moreover, due to the retrieval of missing transactions, the LightBlock scheme requires establishing more connections with other nodes for communication, resulting in additional time consumption.

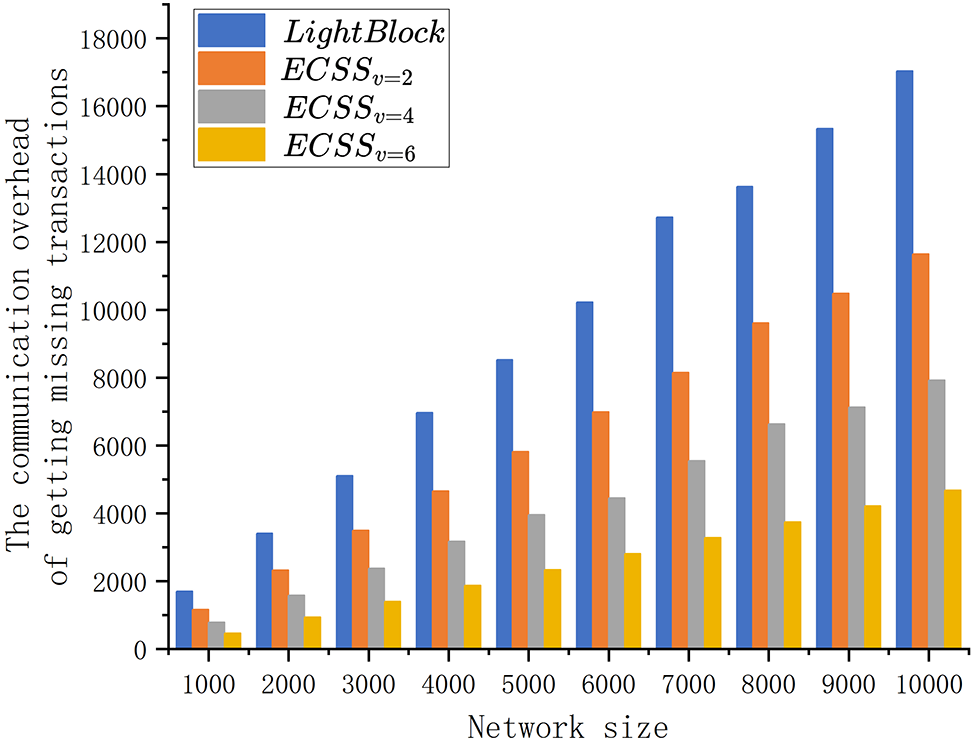
Figure 7: The broadcasting overhead comparison of LightBlock and ECSS with different check digit value

In summary, ECSS has advantages in transaction request overhead and network synchronization speed, and ECSS ensures propagation reliability and effectively reduces the bandwidth consumption required for block propagation.

5.2 Network Scalability

Network scalability refers to the performance of a blockchain system under different network sizes, and a good network scalability indicates that the system is able to withstand larger scale operations. In this experiment, we compare the network scalability by linearly increasing the network size so that the number of nodes in the blockchain network gradually increases from 1000, 2000 to 10,000, and then observe the synchronization time of the blocks.

Fig. 8 presents a comprehensive experimental comparison among the original block scheme, LightBlock scheme, SCCA scheme, and ECSS across various network sizes. When the number of nodes in the blockchain network is 10000, the original block scheme necessitates 10,523 ms for synchronization. In comparison, SCCA reduces this time to 3423 ms, LightBlock further trims it to 2760 ms, while ECSS remarkably excels with a mere 1692 ms to achieve synchronization. Remarkably, ECSS demonstrates remarkable efficiency, accounting for only 63% of the synchronization time required by the LightBlock scheme, 49.4% of the SCCA scheme, and a mere 16.1% of the original block scheme.

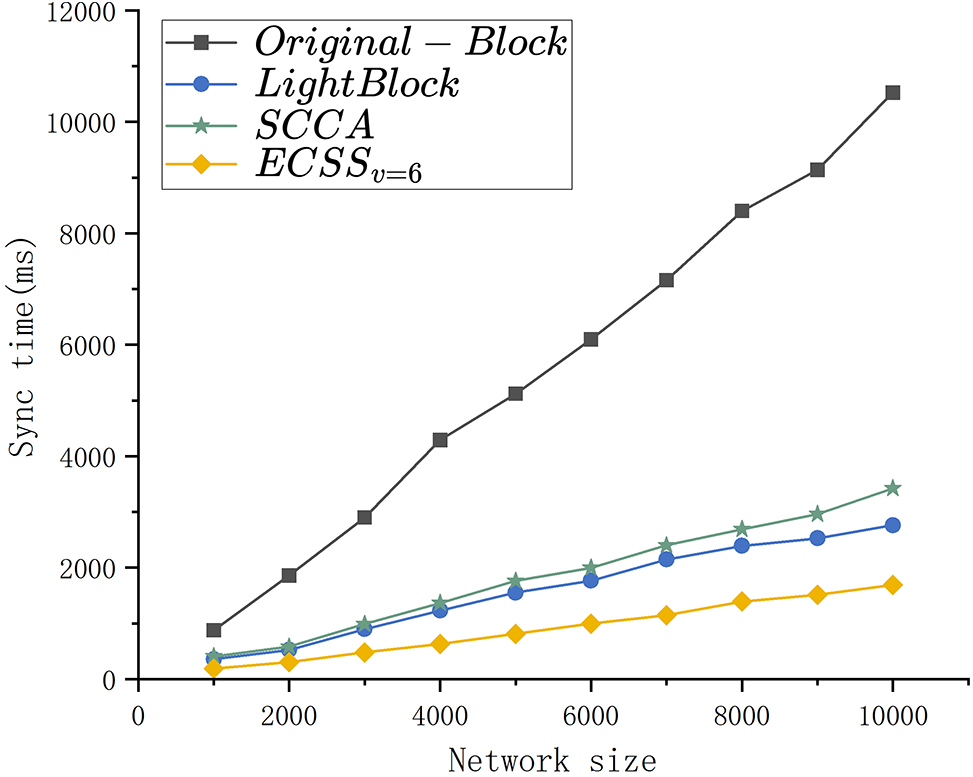
Figure 8: The sync time comparison of different schemes

Fig. 9 shows the network scalability comparison of ECSS with different check digit value. When the check digit value is 2, 4, and 6, the synchronization time of ECSS is 2375, 1967 and 1692 ms, respectively. Notably, shorter synchronization times are observed with larger checksum bit value. This phenomenon is attributed to the fact that, in comparison to ECSSv=6, ECSSv=2 requests more complete transactions from routing nodes, consequently elongating its network communication time.

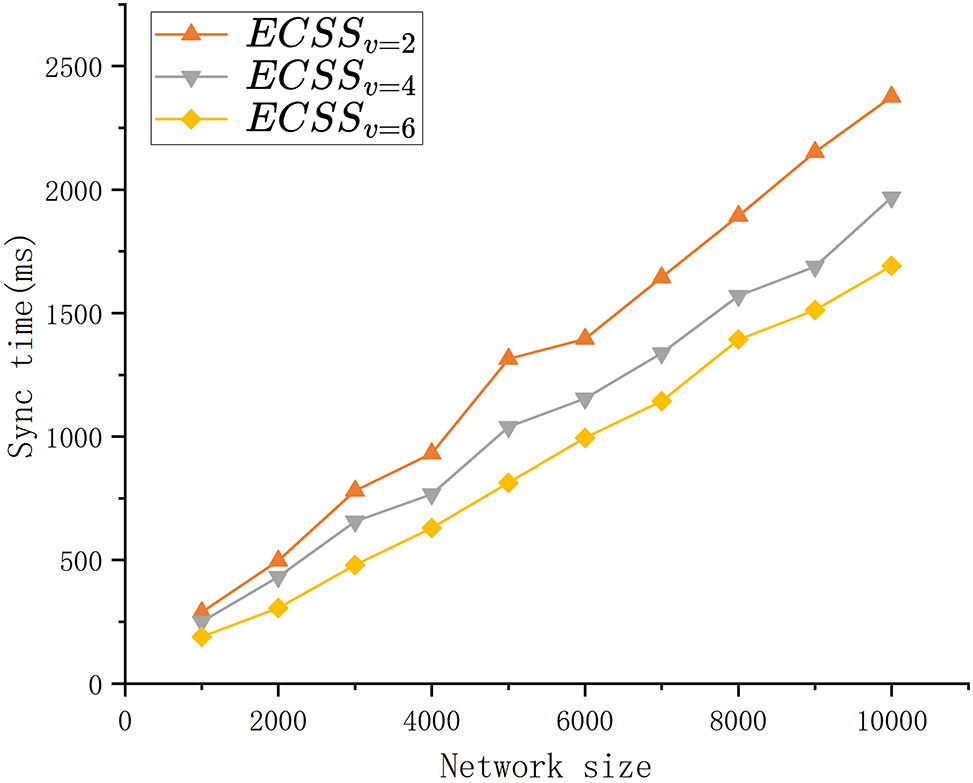
Figure 9: The sync time comparison of ECSS with different check digit value

As a result, it can be concluded that the ECSS exhibits superior network scalability and achieves faster block synchronization in large-scale networks when compared to the other schemes.

5.3 The Storage Compression Rate

5.3.1 The Storage Compression Rate of Nodes

We assume that VR is the size of a modulus, VH is the size of a block header. Lb is the length of the block body after binaryization, and λ denotes the size of the segmentation bit width. For a node with t moduli stored locally, the size of the storage space occupied after compressing a block is the Eq. (13).

VCR=Lbλ×t×VR+VH(13)

When a node stores a complete block, it can be considered as storing a global modulus set, which implies locally storing n moduli. Therefore, the original block storage size can be represented by the Eq. (14).

VOR=Lbλ×n×VR+VH(14)

We obtain that for a node with local modulus set size, the storage compression rate is

γ=1−VCRVOR=1−Lbλ×t×VR+VHLbλ×n×VR+VH(15)

Given that the size of the block header is significantly smaller than the size of the block body, we can approximate the local storage compression ratio as the Eq. (16).

γ≈1−Lbλ×t×VRLbλ×n×VR=1−tn(16)

From Eq. (16), γ is negatively correlated with t since the size of the global modulus set is fixed. When t is larger the γ is smaller, the corresponding saved modulo mapping chunks are more, the number of missing cut blocks that need to be requested from other nodes when recovering the block is less, and the communication overhead is small. On the contrary, the smaller t is, the larger γ is. At this time, the node saves fewer modulo mapping chunks, and the communication overhead used for recovering the block is also larger.

Fig. 10 illustrates the variation in the local compression ratio as nodes store different sizes of local modulus sets. For t=2, the local compression ratio of ECSSn=33 reaches 94%, while for t=10, the local compression ratio of ECSSn=33 is only 69.7%. It can be observed that the local compression ratio gradually decreases as the size of the local modulus set increases. When t=8, the local compression ratio of ECSSn=33 is 75.6%, while for ECSSn=17, the local compression ratio is 50.9%. Thus, for the same t, choosing a larger n results in a higher local compression rate. This phenomenon is attributed to the fact that a larger n implies finer-grained chunks, leading to smaller individual cut block sizes.

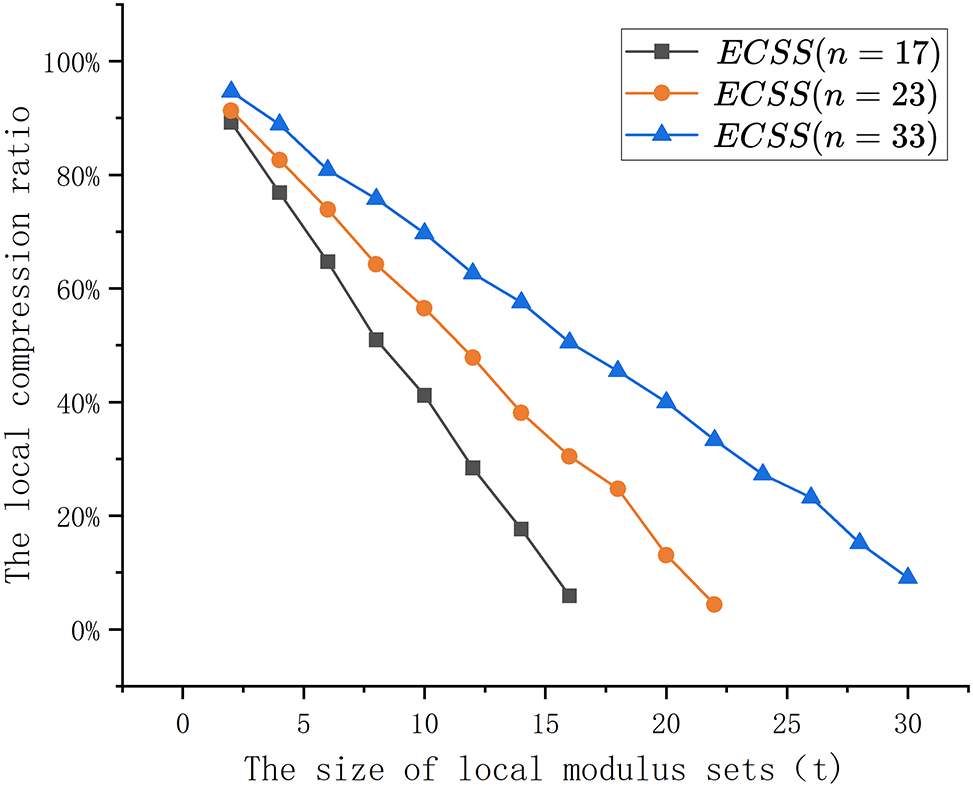
Figure 10: The local compression rate comparison of different t

In summary, the size of the local modulus set significantly influences the local compression rate, and a larger local modulus set can lead to a higher local compression rate.

5.3.2 The Storage Compression Rate of System

Suppose there are T domains in the system after initialization, Numd¯ is the average number of nodes contained in each domain, SizeB¯ is the average size of each block, and VOriB is the total size of a original block, then we can get Eq. (17).

VOriB=T×Numd¯×SizeB¯(17)

After compressing the block using the CRT, the size of the modulus set corresponding to node Ni is denoted as ti, and the total storage space occupied by the block is VCrtB. Therefore, we have Eq. (18).

VCrtB=∑i=1n(L¯bλ×ti×VR+VH)(18)

The total storage compression ratio of the system can be calculated as Eq. (19).

γ′=1−VCrtBVOriB=1−∑i=1n(L¯bλ×ti×VR+VH)T×Numd¯×SizeB¯(19)

In the experiments aimed at evaluating the total storage compression rate, we chose a block of size 622 kb as the test block and selected several widely recognized compression algorithms to compare with ECSS. For the ECSS scheme, we used specific parameters (λ=1024,n=33) in our experiments.

The experimental results are shown in Fig. 11. By observing the results, we can find that ECSS is relatively efficient in compressing and decompressing blocks. Specifically, the Lzw method exhibits the slowest block compression, taking 517 ms, while the Gzip method is the slowest in block decompression, taking 366 ms. In contrast, the ECSS compression takes 190 ms and decompression takes 141 ms, showcasing higher efficiency. Moreover, concerning the total compression rate of the blocks, the ECSS achieves 63.6%, which is 6% higher than the Zlib scheme. Hence, in comparison to other compression schemes, the ECSS not only demonstrates faster compression and decompression efficiency but also boasts a higher compression rate.

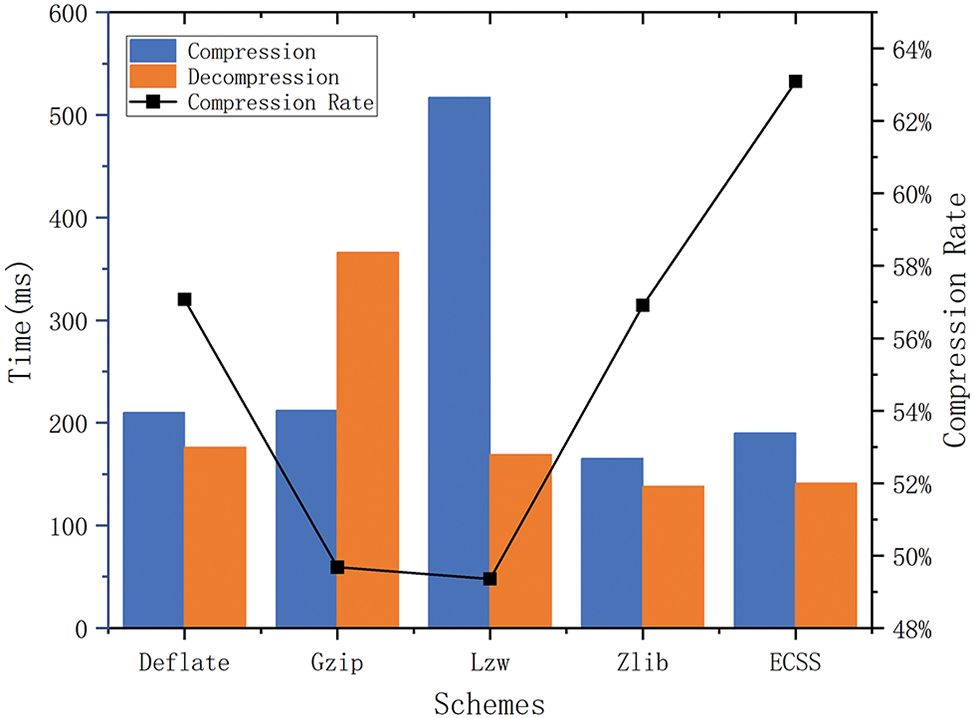
Figure 11: The system compression rate and speed of processing comparison of different schemes

6  Conclusion

In this paper, we propose an Encode-and CRT-based Scalability Scheme (ECSS) with the aim of enhancing the network transmission efficiency, communication overhead, and storage burden in existing blockchain systems. ECSS employs a proximity clustering algorithm to group nodes into neighboring domains, effectively reducing the network’s diameter and increasing the propagation rate. To minimize communication overhead during block broadcasting, an improved compact block protocol based on RS encoding is introduced, resulting in reduced block size and decreased additional communication overhead. Additionally, ECSS utilizes the Chinese remainder theorem to compress the block body and decentralize data storage, effectively reducing the storage burden on nodes. Through thorough analysis and experimental verification, we demonstrate that the ECSS scheme significantly lowers communication overhead and storage pressure while achieving better network scalability.

In our future research, we aim to delve deeper into enhancing both security and efficiency aspects. Additionally, we will closely examine related incentive mechanisms to ensure efficient resource sharing among nodes.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Study conception and design: Qianqi Sun, Fenhua Bai; Analysis and interpretation of results: Qianqi Sun, Fenhua Bai; Draft manuscript preparation: Qianqi Sun. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Available upon request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Malik, H., Anees, T., Faheem, M., Chaudhry, M. U., Ali, A. et al. (2023). Blockchain and Internet of Things in smart cities and drug supply management: Open issues, opportunities, and future directions. Internet of Things, 23, 100860. [Google Scholar]

2. Ren, Y. S., Ma, C. Q., Chen, X. Q., Lei, Y. T., Wang, Y. R. (2023). Sustainable finance and blockchain: A systematic review and research agenda. Research in International Business and Finance, 64, 101871. [Google Scholar]

3. Liu, Q., Liu, Y., Luo, M., He, D., Wang, H. et al. (2022). The security of blockchain-based medical systems: Research challenges and opportunities. IEEE Systems Journal, 16(4), 5741–5752. [Google Scholar]

4. Junaidi, N., Abdullah, M. P., Alharbi, B., Shaaban, M. (2023). Blockchain-based management of demand response in electric energy grids: A systematic review. Energy Reports, 9, 5075–5100. [Google Scholar]

5. Peng, X., Zhao, Z., Wang, X., Li, H., Xu, J. et al. (2023). A review on blockchain smart contracts in the agri-food industry: Current state, application challenges and future trends. Computers and Electronics in Agriculture, 208, 107776. [Google Scholar]

6. Wang, J., Wei, B., Zhang, J., Yu, X., Sharma, P. K. (2021). An optimized transaction verification method for trustworthy blockchain-enabled IIoT. Ad Hoc Networks, 119, 102526. [Google Scholar]

7. Akrasi-Mensah, N. K., Tchao, E. T., Sikora, A., Agbemenu, A. S., Nunoo-Mensah, H. et al. (2022). An overview of technologies for improving storage efficiency in blockchain-based IIoT applications. Electronics, 11(16), 2513. [Google Scholar]

8. Chauhan, B. K., Patel, D. B. (2022). A systematic review of blockchain technology to find current scalability issues and solutions. Proceedings of Second Doctoral Symposium on Computational Intelligence, pp. 15–29. Singapore: Springer. [Google Scholar]

9. Zaghloul, E., Li, T., Mutka, M. W., Ren, J. (2020). Bitcoin and blockchain: Security and privacy. IEEE Internet of Things Journal, 7(10), 10288–10313. [Google Scholar]

10. Li, W., He, M. (2020). Comparative analysis of bitcoin, ethereum, and libra. 2020 IEEE 11th International Conference on Software Engineering and Service Science (ICSESS), Beijing, China. [Google Scholar]

11. Khan, D., Jung, L. T., Hashmani, M. A. (2021). Systematic literature review of challenges in blockchain scalability. Applied Sciences, 11(20), 9372. [Google Scholar]

12. Alshahrani, H., Islam, N., Syed, D., Sulaiman, A., Al Reshan, M. S. et al. (2023). Sustainability in blockchain: A systematic literature review on scalability and power consumption issues. Energies, 16(3), 1510. [Google Scholar]

13. Blockchair. Bitcoin size. https://blockchair.com/bitcoin (accessed on 04/05/2023) [Google Scholar]

14. Blockchair. Ethereum size. https://blockchair.com/ethereum (accessed on 04/05/2023) [Google Scholar]

15. Zhang, J., Zhong, S., Wang, J., Yu, X., Alfarraj, O. (2021). A storage optimization scheme for blockchain transaction databases. Computer Systems Science and Engineering, 36(3), 521–535. https://doi.org/10.32604/csse.2021.014530 [Google Scholar] [CrossRef]

16. Nasir, M. H., Arshad, J., Khan, M. M., Fatima, M., Salah, K. et al. (2022). Scalable blockchains—A systematic review. Future Generation Computer Systems, 126, 136–162. [Google Scholar]

17. Zhang, G., Zhao, X., Si, Y. W. (2023). A comparative analysis on volatility and scalability properties of blockchain compression protocols. arXiv preprint arXiv:2303.17643. [Google Scholar]

18. Clifford, A., Rizun, P. R., Suisani, R., Stone, A., Tschipper, P. Towards massic on-chain scaling: Block propagation results with xthin. Part 4 of 5: Fewer bytes are required to communicate a xthin block. https://medium.com/@peter_r/towards-massive-on-chain-scaling-block-propagation-results-with-xthin-3512f3382276 (accessed on 06/06/2016). [Google Scholar]

19. Zhang, L., Wang, T., Liew, S. C. (2022). Speeding up block propagation in bitcoin network: Uncoded and coded designs. Computer Networks, 206, 108791. [Google Scholar]

20. Zhao, C., Wang, T., Zhang, S. (2021). Lightblock: Reducing bandwidth required to synchronize blocks in ethereum network. 2021 International Conference on Communications, Information System and Computer Engineering (CISCE), Beijing, China. [Google Scholar]

21. Ahn, S., Kim, T., Kwon, Y., Cho, S. (2020). Packet aggregation scheme to mitigate the network congestion in blockchain networks. 2020 International Conference on Electronics, Information, and Communication (ICEIC), Barcelona, Spain. [Google Scholar]

22. Hao, W., Zeng, J., Dai, X., Xiao, J., Hua, Q. S. et al. (2020). Towards a trust-enhanced blockchain P2P topology for enabling fast and reliable broadcast. IEEE Transactions on Network and Service Management, 17(2), 904–917. [Google Scholar]

23. Yang, C., Chin, K. W., Wang, J., Wang, X., Liu, Y. et al. (2022). Scaling blockchains with error correction codes: A survey on coded blockchains. arXiv preprint arXiv:2208.09255. [Google Scholar]

24. Wang, R., Njilla, L., Yu, S. (2023). A-C: An NDN-based blockchain network with erasure coding. 2023 International Conference on Computing, Networking and Communications (ICNC), Honolulu, HI, USA. [Google Scholar]

25. Jin, M., Chen, X., Lin, S. J. (2019). Reducing the bandwidth of block propagation in bitcoin network with erasure coding. IEEE Access, 7, 175606–175613. [Google Scholar]

26. Chawla, N., Behrens, H. W., Tapp, D., Boscovic, D., Candan, K. S. (2019). Velocity: Scalability improvements in block propagation through rateless erasure coding. 2019 IEEE International Conference on Blockchain and Cryptocurrency (ICBC), Seoul, Korea (South). [Google Scholar]

27. Cebe, M., Kaplan, B., Akkaya, K. (2018). A network coding based information spreading approach for permissioned blockchain in iot settings. Proceedings of the 15th EAI International Conference on Mobile and Ubiquitous Systems: Computing, Networking and Services, New York, NY, USA. [Google Scholar]

28. Choi, B., Sohn, J. Y., Han, D. J., Moon, J. (2019). Scalable network-coded PBFT consensus algorithm. 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France. [Google Scholar]

29. Ren, Y., Leng, Y., Cheng, Y., Wang, J. (2019). Secure data storage based on blockchain and coding in edge computing. Mathematical Biosciences and Engineering, 16(4), 1874–1892. [Google Scholar] [PubMed]

30. Chen, P., Bai, F., Shen, T., Gong, B., Zhang, L. et al. (2022). SCCA: A slicing‐and coding‐based consensus algorithm for optimizing storage in blockchain-based IoT data sharing. Peer-to-Peer Networking and Applications, 15(4), 1964–1978. [Google Scholar]

31. Qu, B., Wang, L. E., Liu, P., Shi, Z., Li, X. (2020). GCBlock: A grouping and coding based storage scheme for blockchain system. IEEE Access, 8, 48325–48336. [Google Scholar]

32. Mei, H., Gao, Z., Guo, Z., Zhao, M., Yang, J. (2019). Storage mechanism optimization in blockchain system based on residual number system. IEEE Access, 7, 114539–114546. [Google Scholar]

33. Guo, Z., Gao, Z., Liu, Q., Chakraborty, C., Hua, Q. et al. (2022). RNS-based adaptive compression scheme for the block data in the blockchain for IIoT. IEEE Transactions on Industrial Informatics, 18(12), 9239–9249. [Google Scholar]

34. Spataru, A. L., Pungila, C. P., Radovancovici, M. (2021). A high-performance native approach to adaptive blockchain smart-contract transmission and execution. Information Processing & Management, 58(4), 102561. [Google Scholar]

35. Corallo, M. (2022). Compact block relay: BIP 152. https://github.com/bitcoin/bips/wiki/Comments:BIP-0152 (accessed on 06/06/2016) [Google Scholar]

36. Wicker, S. B., Bhargava, V. K. (1999). Reed-solomon codes and their applications. John Wiley & Sons. [Google Scholar]

37. Pei, D., Salomaa, A., Ding, C. (1996). Chinese remainder theorem: Applications in computing, coding, cryptography. World Scientific. [Google Scholar]

38. Montresor, A., Jelasity, M. (2009). Peersim: A scalable P2P simulator. 2009 IEEE Ninth International Conference on Peer-to-Peer Computing, Seattle, WA, USA. [Google Scholar]

39. Etherscan. The network scale of ethereum. https://goto.etherscan.com/nodetracker (accessed on 04/05/2023) [Google Scholar]