Natural Convection and Irreversibility of Nanofluid Due to Inclined Magnetohydrodynamics (MHD) Filled in a Cavity with Y-Shape Heated Fin: FEM Computational Configuration

1  Introduction

Entropy is a fundamental property of any dynamic thermal system, serving as a quantitative representation of the disorder introduced by the irreversibility process at work during heat exchange. The second rule of thermodynamics asserts that total entropy uniformly predominates in reversible processes and rises with time in non-reversible techniques, leading to entropy measurement in thermalized systems. Bejan [1] was one of the pioneers in entropy development by inventing an approach to thermodynamic optimization. The purpose of optimizing the structure of entropy thermal hydraulic systems is to enhance their performance in several fields. Moreover, entropy analysis can improve the performance of heating equipment such as heat engines, heat pumps, coolers, cooling electronic chips, and micro-thermal channels. Parvin et al. [2] investigated the entropy irreversibility of metal nanoparticles in a water-saturated chamber. Rayleigh and Bejan numbers correlate, affecting their impact on entropy variation. Kefayati [3] employed the Lattice Boltzmann method to explore the effects of natural convection and an external magnetic source on a ferrofluid in a cavity. Nanoscale ferromagnetic cobalt particles were suspended in kerosene. There is a negative correlation between the percentage of nanoscale ferromagnetic particles in the volume and the heat transmission for a range of Ra. Rabbi et al. [4] utilized pure mixed convection magnetized investigation directed toward the cavity to investigate the impacts of two different geometric heater configurations. A single-phase model of ferrofluid was employed as a working fluid. Heaters on the bottom wall were always kept on, while those on the vertical side walls were preserved at a steady, low temperature. The top wall permanently moved at the same rate and temperature in geometric layouts. The Galerkin weighted residuals approach of finite element analysis was employed to solve the flow equations. Merji et al. [5] and Mahmoudi et al. [6] investigated the process of entropy and how it is carried out in a square cage filled with water and features the fusing of hybrid nanoparticles. They described the volume of nanoparticle fraction on the accumulative entropy procedure. Including alumina nanoparticles, Armaghani et al. [7] evaluated the entropy generation characteristics in the baffle of an L-shaped water-saturated duct, which are flow-differentiated by buoyant thermal convection. Zamily [8] assessed the various thermal features of water along with Ti O2 particles, and the randomness of entropy by determining the thermal sources at cavity boundaries. Bouchouch et al. [9] investigated nanofluid irreversibility (H2O/Al2O3) by introducing wavy input in a symmetrical enclosure. They indicated that entropy is enhanced and more massively within the system when considering the free convection environment. It has been shown that scattering solid particles increases entropy and energy transmission. Oztop et al. [10] studied natural convection inside rectangular enclosures that were only partially heated and carried nanofluids. Sheremet et al. [11] deliberately formed thermal flow by transfer of variable wall temperature due to irreversibility changes in a cavity. They revealed that significant change appears in entropy, evaluating the dominance of natural convection by improving the Rayleigh number (Ra). Siavashi et al. [12] capitalized the two-phase mixtures of H2O and Cu to quantify a free-flow entropic characteristic in a fine-furnished permeable cavity. Kashyap et al. [13] examined nanofluid two-phase (water/cu) flow along with the performance under distinct boundary conditions and the irreversibility in a porous cavity. Gibanov et al. [14] demonstrated an analysis of thermophysical characteristics arising from entropy in nanofluid generated by a lid-driven cavity. In the permeable square enclosure under magnetizing devices, Mansour et al. [15] investigated the characteristics of a hybrid nanofluid (water-Cu-Al2O3). They demonstrated that entropy rises as ϕ increases. Rahimi et al. [16] examined the thermal dimensions of the nanofluids inside the cavity with fins and approximate declines in entropy generation towards fractional volume nanoparticles.

Flow analysis is not only exciting but also thought-provoking. Further numerical and experimental research is needed across various topics, although several technology applications and scientific challenges exist. This study explores the effects of friction and heat transfer in viscous fluid flows across solid surfaces and in ducts and channels. These consequences must be factored into evaluating the fluid’s qualities. The issue can be solved in either an experimental or theoretical setting. Numerical approaches, such as finite differences, finite elements, and finite volumes, are developed for solving incompressible Newtonian flow problems. The most well-known approach is the traditional PARDISO algorithm, which first presents the idea of a stalled grid in conjunction with the pressure adjustment equation. It indicates a dearth of information in the literature on non-Newtonian fluid flows, particularly polymer melts in the molding process, evaluated in [17–20]. Khan et al. [21] examined a comprehensive study of hydromagnetic thermal flow effects over a cavity cylinder. They implemented a finite element scheme for solving the nonlinear coupled equations. Soomro et al. [22] considered a constructional design-based study to analyze the features of thermal flows in a semi-circular cavity. They concluded that as Richardson’s number increases, heat transport slows down. In addition, as the Hartmann number grows, the heat transmission rate improves. Chelia et al. [23] investigated the characteristics of natural convection with nanofluid in a cavity utilizing the famous numerical approach, the Lattice Boltzmann Method (LBM). In addition, they indicated that the heat transmission rate from a bottom-heated cavity is greater than that of a sidewall-heated cavity.

This study explains an entropy-generating process, including an angled magnetic field induction and a natural convection component. It discusses various types of irreversibility against different effective parameters that have not yet been revealed. The research’s result can be a reference for future studies.

2  Mathematical Modeling

This study considered the unit dimensions of the cavity are saturated by water and copper nanoparticles were induced. Flow domain density variations include the addition of Boussinesq approximation to the buoyancy term, containing the role of natural convection in the flow domain. The constant B0 magnetization magnitude measures the maximum change in nanoparticles’ flow in an orthogonal direction. The cavity’s top wall is considered insulated, and the fin is heated uniformly while the other walls are colder. There are no slip conditions to all boundaries. Fig. 1 shows the physical configuration.

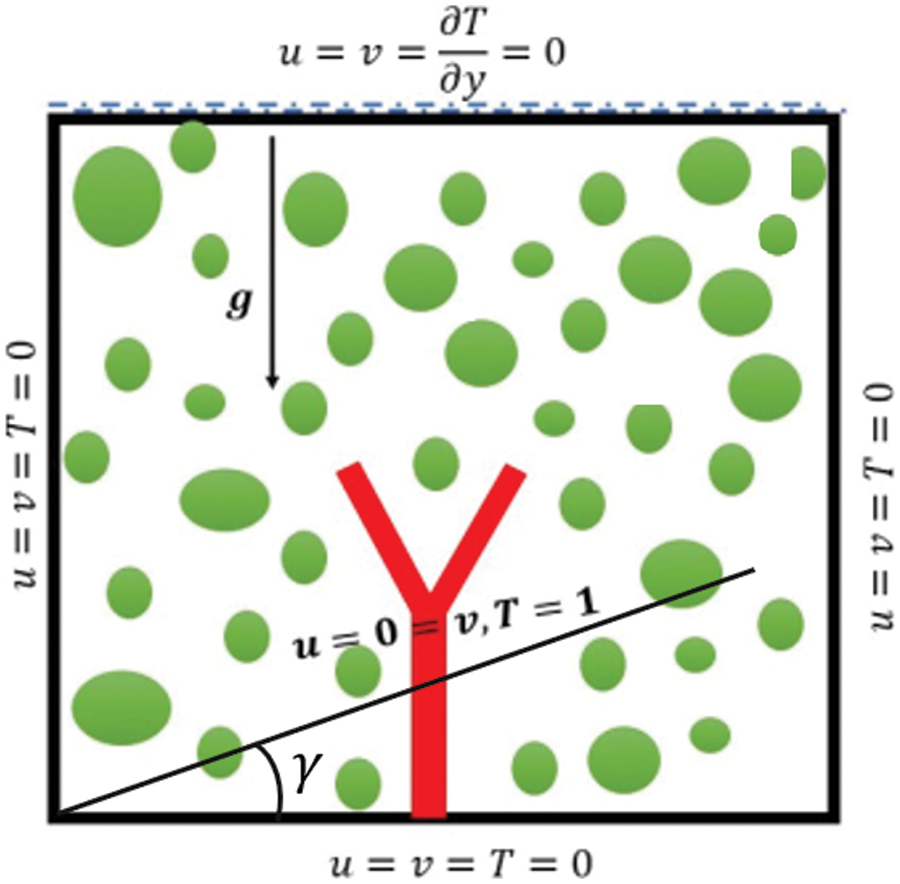
Figure 1: Physical structuring of problem

The continuity, flow velocity, and heat equation [24–26] for a copper fluid are described in a non-dimensional mathematical form as follows:

∂u∂x+∂v∂y=0,(1)

u∂u∂x+v∂u∂y+∂p∂x=μcfρcf(∂2u∂x2+∂2u∂y2)+ρfρcfσcfσfPrfHa2(vsinγcosγ−usin2γ),(2)

u∂v∂x+v∂v∂y+∂p∂y=μcfρcf(∂2v∂x2+∂2v∂y2)+(ρβ)cfρcfβfRαfPrfT+ρfρcfσffσfPrfHa2(usinγcosγ−vcos2γ),(3)

∂T∂t+u∂T∂x+v∂T∂y=αcfαf(∂2T∂x2+∂2T∂y2)(4)

The boundary conditions are given below:

•   Th = 1, at the fin.

•   (u,v) = 0, at all walls of the cavity and fin.

•   ∂T∂n = 0, at the upper wall of the cavity.

•   T=0, other walls of the cavity.

2.1 Properties of Copper Fluid

These equations are appropriate for the thermo-physical properties of the nanofluid in this study [13–15]. The physical characteristics of copper fluid are listed in Table 1.

•   Density: ρcf=(1−φ)ρf+φρs,

•   Thermal diffusivity: αcf=kff(ρCp)cf,

•   Electrical conductivity: σcf=σf[1+3(σ−1)φ(σ+2)−(σ−1)φ],σ=σsσf,

•   Specific heat: (ρCp)cf=(1−φ)(ρcp)f+φ(ρcp)s,

•   Thermal conductivity: kcfkf=ks+2kf−2φ(kf−kp)ks+2kf+φ(kf−kp),

•   Thermal expansion coefficient: (ρβ)cf=(1−φ)(ρβ)f+φ(ρβ)s,

•   Dynamic viscosity: μcfμf=1(1−φ)2.5,

•   Average Nusselt number Nuavg= −kskf∫s ∂θ∂ndS.

2.2 Entropy Generation

The term “irreversibility analysis” refers to quantifying the local entropy production resulting from the sum of the conjugated fluxes and the forces that are generated. A convective process subject to a magnetic field yields the following expression for the non-dimensional local entropy production:

Si=kcfkf[(∂T∂x)2+(∂T∂y)2]+ψ[2(∂u∂x)2+2(∂v∂y)2+(∂u∂y+∂v∂x)2]+σcfσfHa2ψ(usinγ−vcosγ)2(5)

On the right-hand side of Eq. (5) initially stands the energy entropy, then viscous entropy, and finally, magnetic entropy located at the top right side. The irreversibility ratio (ψ) of a distribution can be calculated using Eq. (6).

ψ=μcfkfTo(αfHΔT)2(6)

where To is the average temperature of the heated and cold walls.

3  Numerical Procedure

The velocity field and temperature at every location in the analyzed physical model must be known to numerically calculate the production of local entropy using Eq. (5). A numerical approach called the finite element method (FEM) is applied to compute an estimation of the solution to the model problem because analytical solutions to the coupled equations are not possible due to the nonlinearity of the governing equations. This was conducted to better understand how the model problem will be solved. In order to solve the underlying discrete nonlinear system of equations, Newton’s method was employed to linearize the system, and then the direct solver PARDISO was applied to address the linearized inner systems. The PARDISO solver has numerous benefits. LU matrix factorization is employed to achieve the needed level of convergence with a minimum number of iterations. This reduces the total number of necessary iterations. Fig. 2a depicts the computing grid.

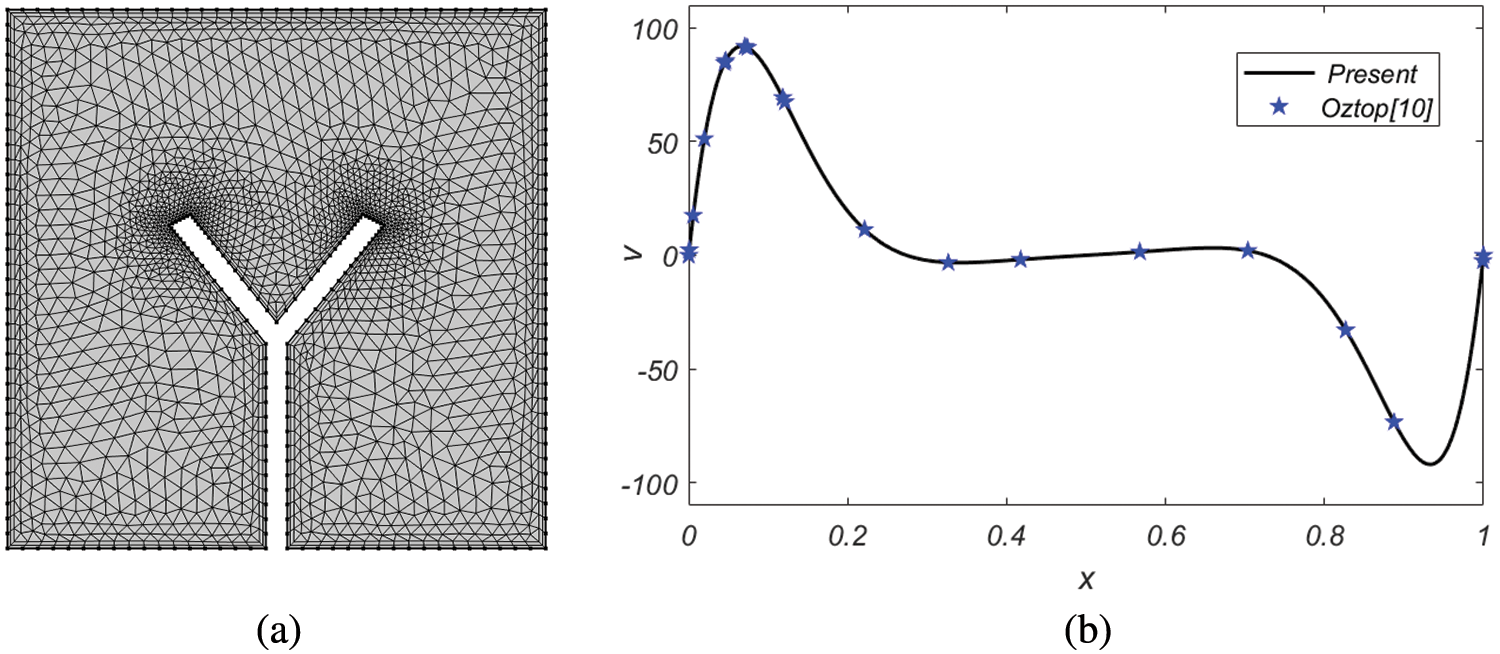
Figure 2: (a): Discretization of the computational domain (b): Comparison of the present study with Oztop [10]

Domain coarse-resolution meshing is conducted using a pressure-velocity finite element pair. Fig. 2a indicates that coarser-grained rectangular and triangular elements represent the entire computational domain. A nonlinear system is iterated until the convergence requirement is satisfied, typically defined as a residual of less than 10−6.

Fig. 2b shows vertical velocity profiles along the center of the cavity, as measured with different nanofluids. The results demonstrate good agreement with the Oztop study [10].

4  Results and Discussion

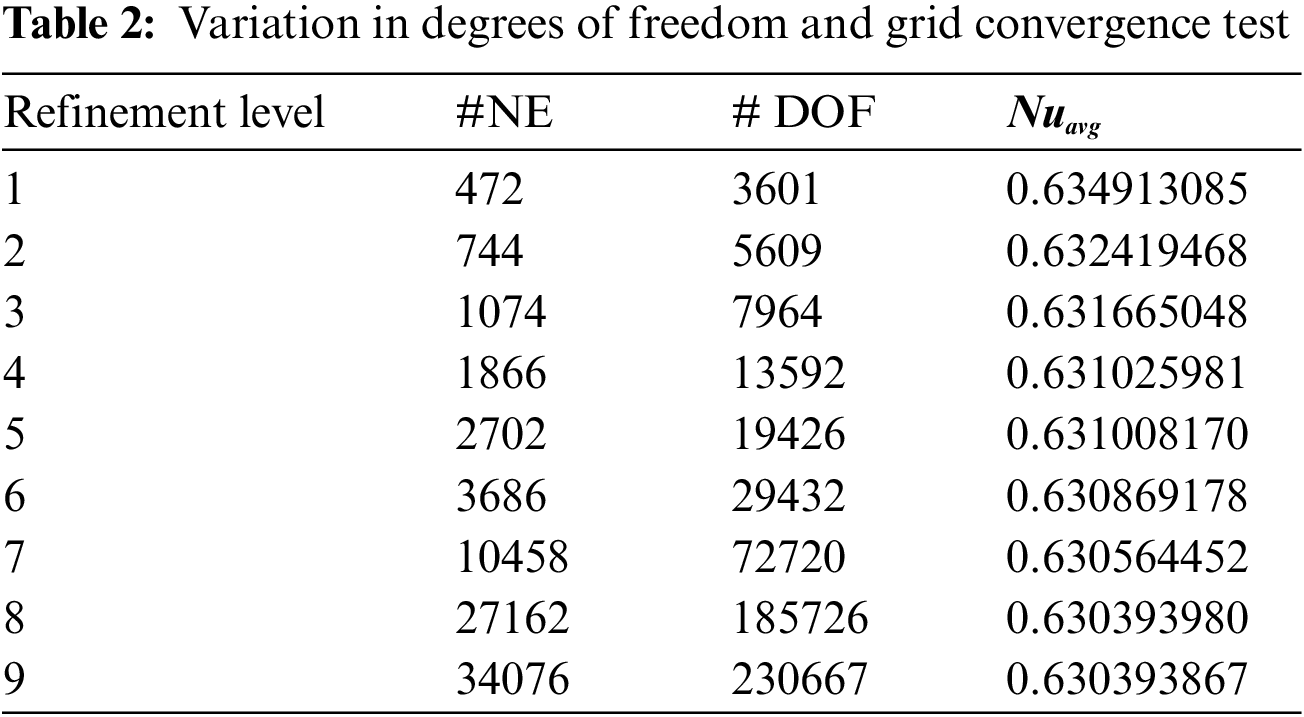
This section demonstrates how entropy quantities change in response to modifications in flow-controlling parameters. Galerkin finite element method and hybridized meshing are applied to achieve highly accurate results. Elements with triangular and rectangular shapes are employed to represent domain discretization. Table 2 lists data about the number of elements and degrees of freedom at nine levels. It shows the results of a grid independence analysis for Nuavg.

Figs. 3a–3h display streamline and isotherm patterns with varying Ha ranging from 0 to 100 and nanoparticle ϕ=0.02, Ra=1000, and Pr=6.2 as a fixed parameter. It indicates that the magnetic field at an inclination of γ=30∘ changes the pattern of the lines, and the flow field is depicted as a symmetrical collection of concentric circles. The leftmost cell rotates anticlockwise, whereas the rightmost cell rotates in the other direction. In addition, when Ha rises, the center of the interconnected cells moves upward towards the top cavity and the strength of the lines and their magnitudes decrease. The strength of the flows is diminished because the magnetic field is guiding the currents in a vertical direction. Since the magnetic field is now applied vertically, it does not affect flow along the x-axis. Figs. 3a–3h explain the change in isotherms in terms of Hartmann number by varying its magnitude (Ha). Isotherms show less relaxation at lower values of Ha, such as 0 and 40, while compression occurs as Ha increases. The upper boundary of the enclosure is insulated, and the fin is heated uniformly, while the rest of the walls are kept cold, resulting in thermal gradients.

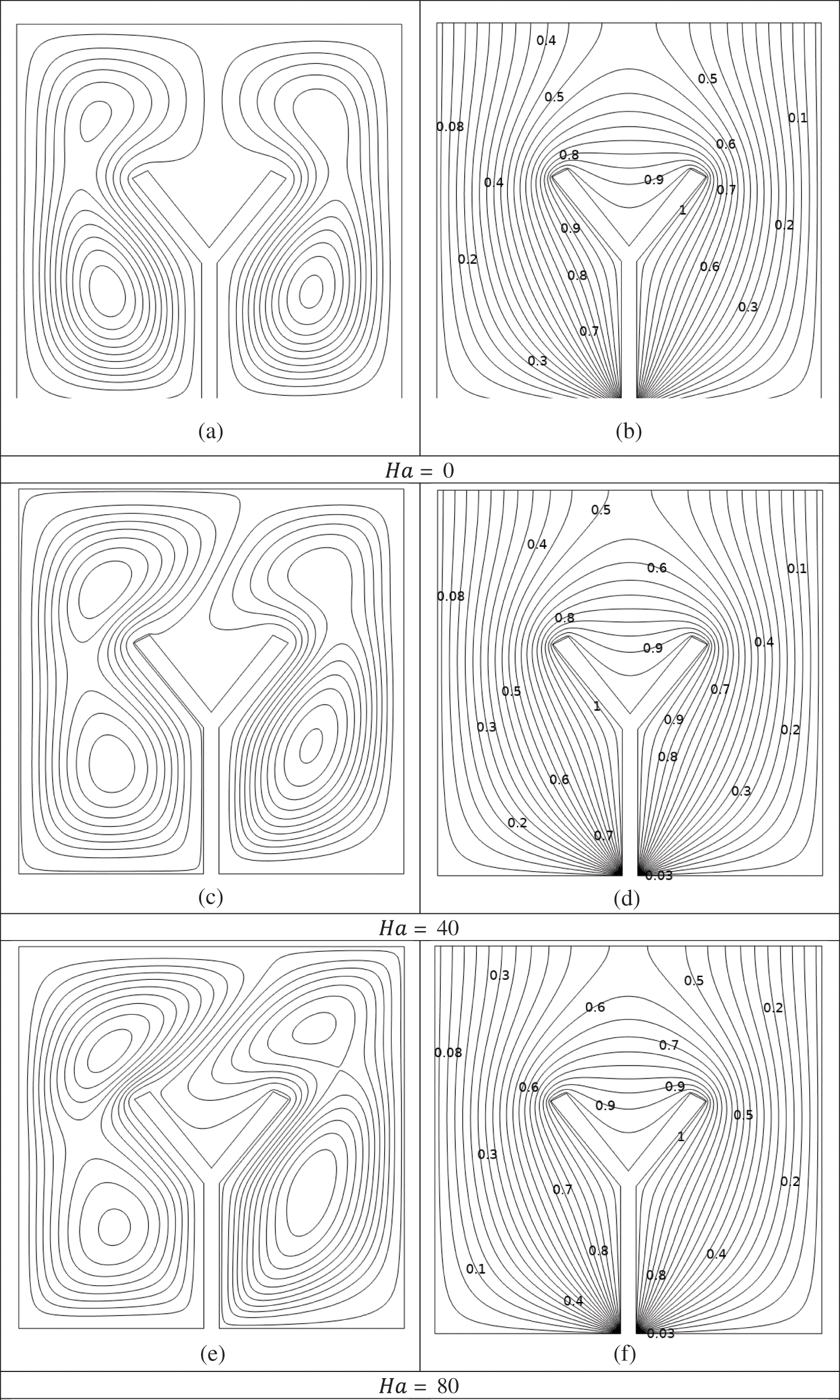
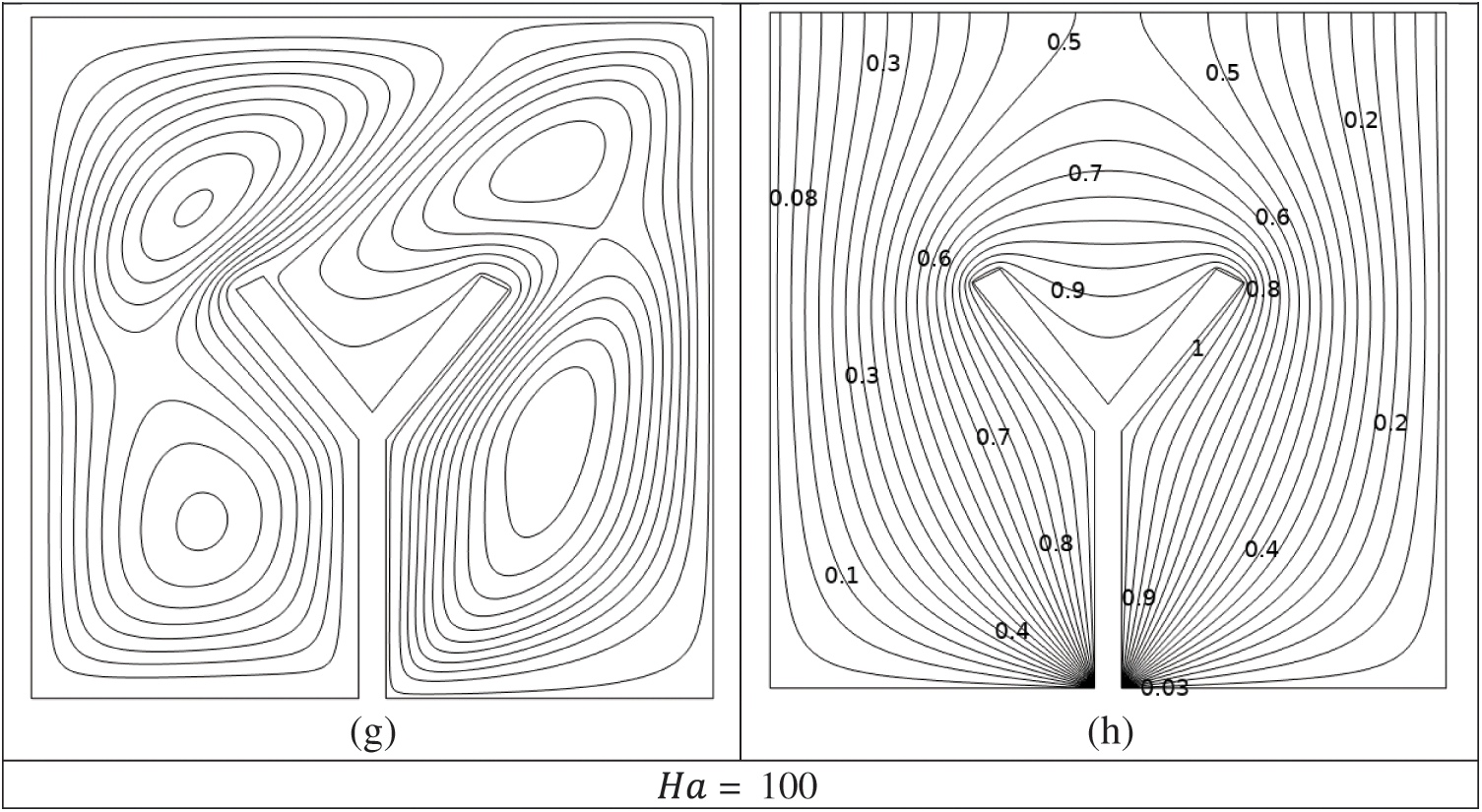
Figure 3: (a–h) Impacts of Ha on streamline (Left) and isotherm (Right)

In Figs. 4a–4f, the γ varies between 30∘,60∘,and90∘ on velocity and isotherm contours, respectively. The parameters ϕ=0.02, Ha=20, Ra=103, and Pr=6.2 are used in this study. As γ increases, so does the intensity of fluid circulation represented by streamlines, and because the γ=90∘ fluid flow is severely impeded. The mid-plane x=0.5 symmetry is achieved at γ=60∘and90∘, as well as with a growth in the shapes of cells deformed at γ=60∘and90∘. Anticlockwise movement is seen in left-hand cells, and clockwise movement is shown in right-hand cells

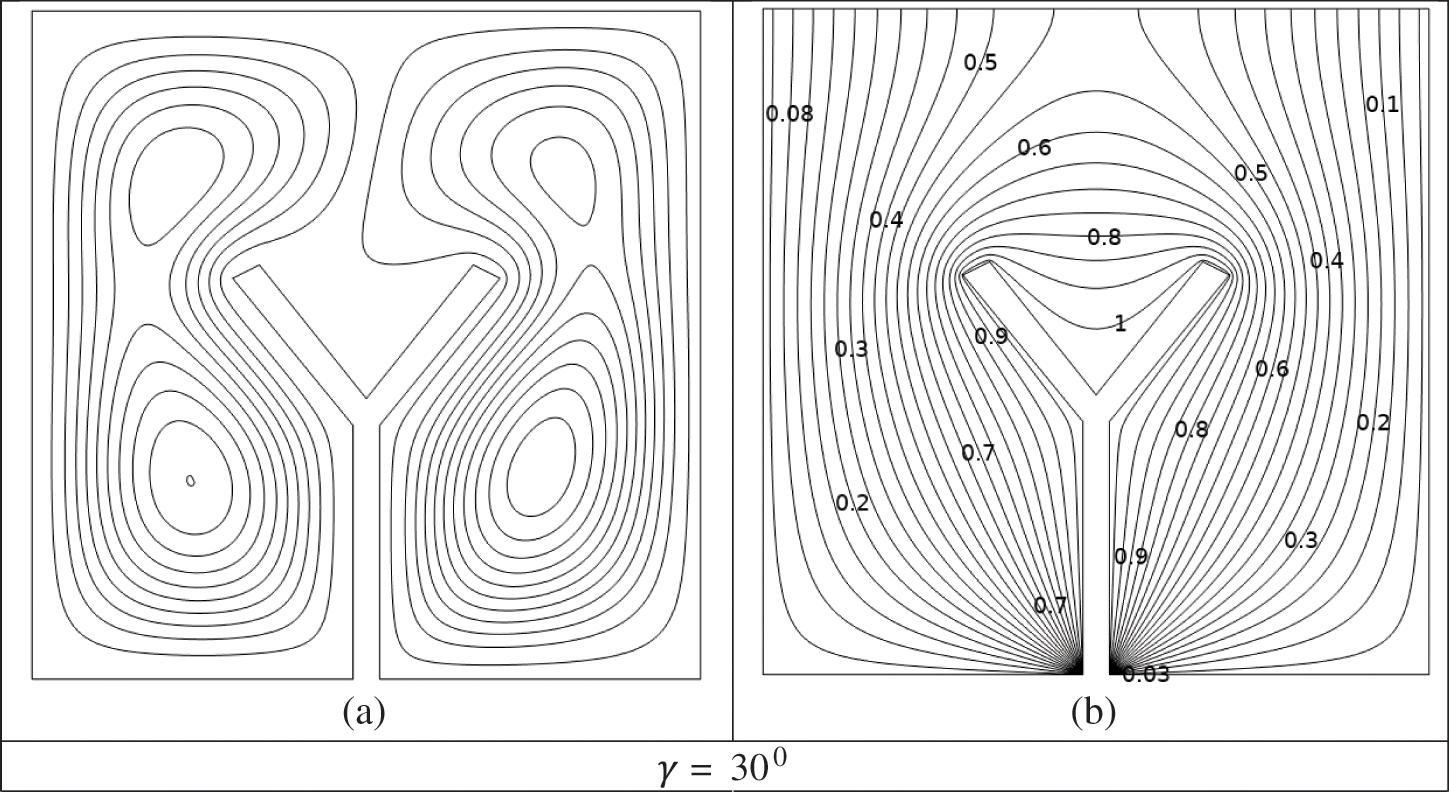
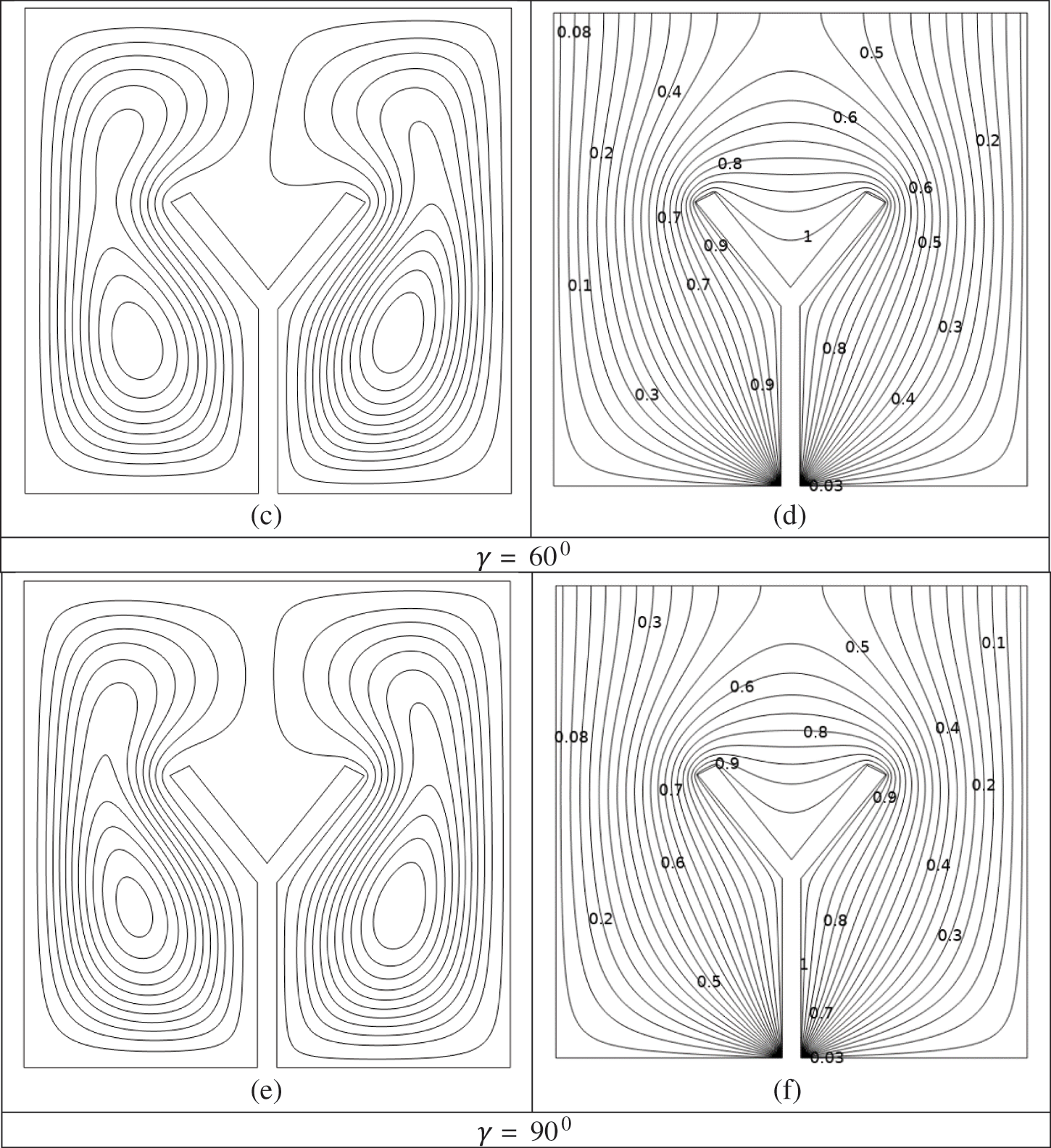
Figure 4: (a–f) Impacts of γ on streamline (Left) and isotherm (Right)

It was reported that nanoparticle volume fraction significantly impacts STherm, SVisc, and SMag along with a variety of Ha in Figs. 5a–5d. Other parameters such as Ra=1000, γ=300, and Pr=6.2 are fixed to achieve optimal change in this case. Fig. 5a demonstrates that the STherm has a uniform for Ha=0 and increases as Ha rises and ϕ decreases. By comparing the deprecating behavior of the temperature gradient to an increase in ϕ, this can be explained. Fig. 5b illustrates the behavior of entropy generation due to viscous forces against increasing values of ϕ and Ha. As the value of Ha and ϕ increase, the SVisc curves are in decrement. As (Ha) increases, viscous forces become dominant, and the reduction movement of fluid particles enriches as a result of viscous forces decaying, this occurs. (SVisc) approaches zero when Ha>0. Fig. 5c indicates that it can predict how the entropy generation process will behave when the flow field magnetic strength changes. It is shown that Smagn=0 when Ha=0. A maximum of Ha=40 is reached, then it reduces to the maximum amplitude of the curve. By controlling the ϕ, it can influence the magnitude of randomness generated by a magnetic field. The impact of ϕ and Ha diminishes. Total entropy STotal generation coefficient depends on ϕ and Ha, as shown in Fig. 5d. There is evidence that the total entropy coefficient decreases with an increase in (Ha) in the range of (0.02≤ϕ≤0.08) and (0≤Ha≤100).

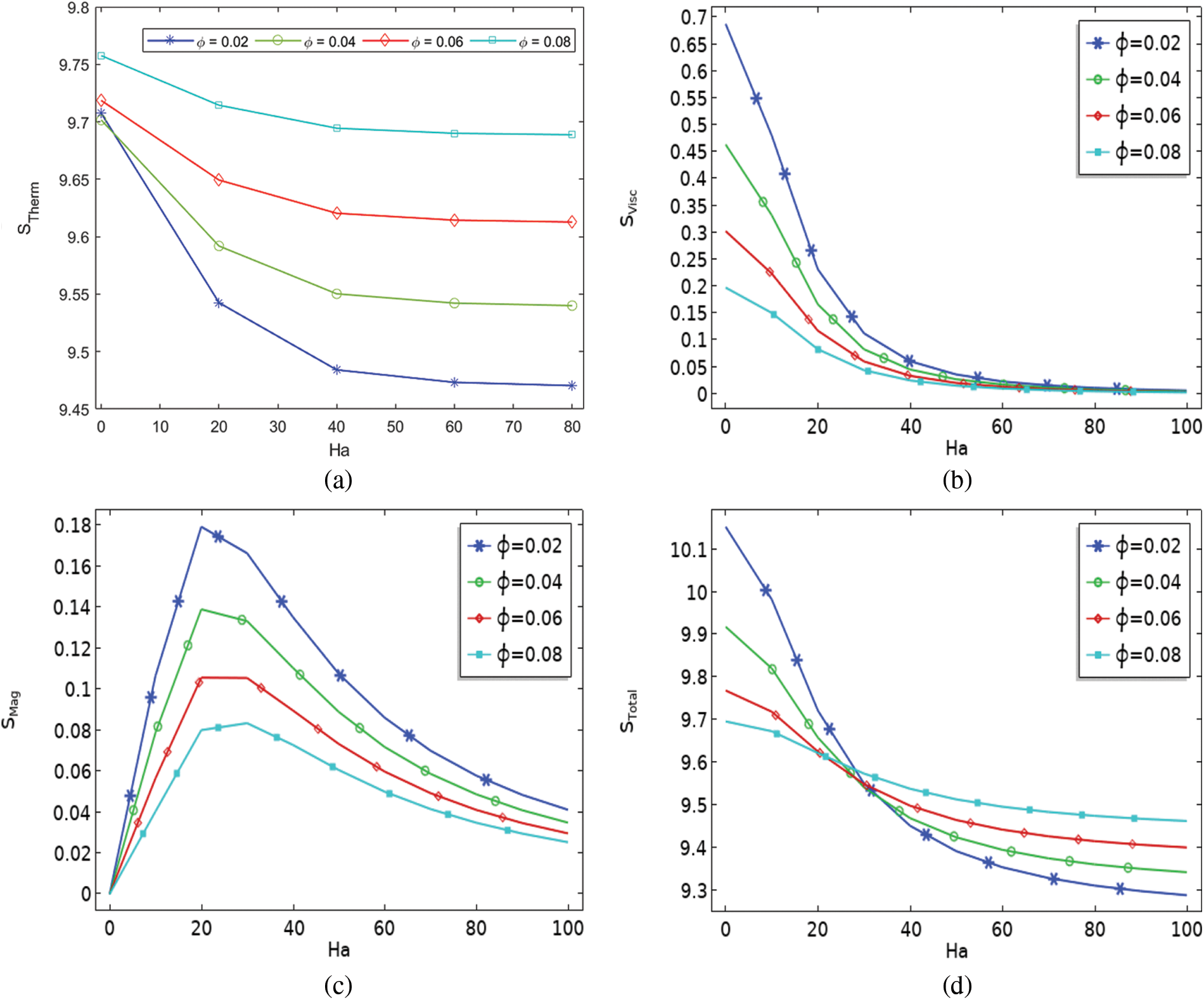
Figure 5: (a–d) Impacts of ϕ on irreversibilities against Ha

For different ϕ and Ha, the variations of the components (u and v) of the velocity vector at x=0.5 are shown in Fig. 6. When the volume fraction and Hartmann number increase, the u-component of the speed vector decreases, while velocity increases when these parameters decrease in the (0.25≤x≤0.45) low regime. When volume fractions and Hartmann numbers reduce, the v-component of velocity increases.

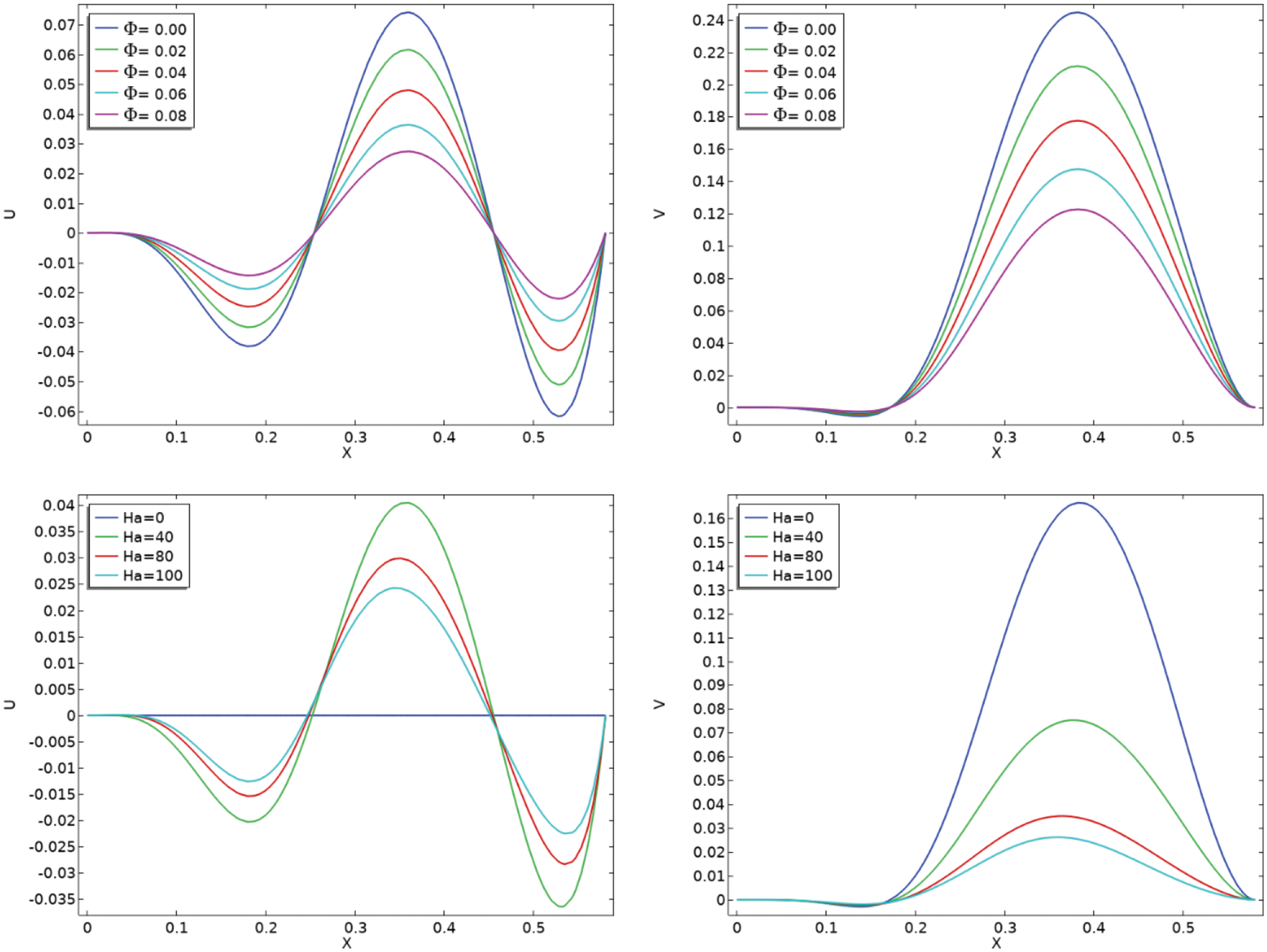
Figure 6: Velocity line graphs for different ϕ and Ha at x = 0.5(verticle)

Figs. 7a and 7b depict the effect of the magnetic fields γ and the Ha on the thermal, viscous, and magnetic irreversibilities. By fixing the Ra and the Pr to 103 and 6.2, respectively, the response of the irreversibility coefficients can be observed in a meaningful fashion. Fig. 7a illustrates the relationship between the Ha and the γ, and the resulting change in thermal entropy production. It indicates that the coefficient of thermal entropy reaches its maximum value of 8.4 along the vertical axis when Ha=0. In addition, the size of (STherm) decreases as the Ha increases from 0 to 100, but the opposite behavior is represented in the case of increasing the magnitude of the γ. An increase in the γ explains this effect by raising the temperature gradients within the enclosure through increased convection currents. Fig. 7b shows the variation in the viscous entropy coefficient as a function of γ and Ha is shown in. It indicates that when Ha increases, the (SVisc) profile drops, while the γ causes the profile to rise. The argument behind this is that an increase in γ causes a greater temperature difference between the inside and outside of the enclosure, causing thermal buoyancy forces to be formed and, ultimately, executes a convective current.

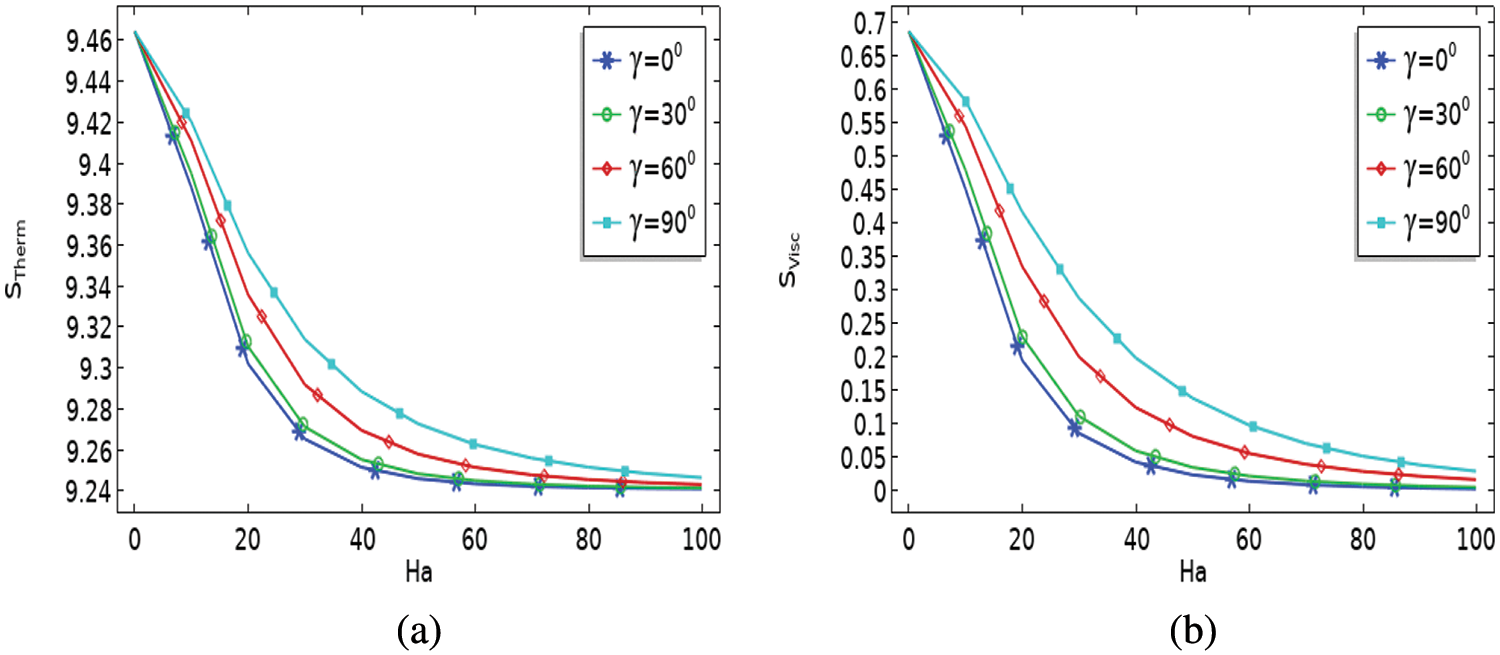
Figure 7: (a–b) Entropy variation against (γ)

Fig. 8 reveals the dependence of the heat flux coefficient on the Ha and the ϕ. It indicates that the Nuavg rises as Ha grows in magnitude, with values ϕ ranging from 0.02 to 0.08.

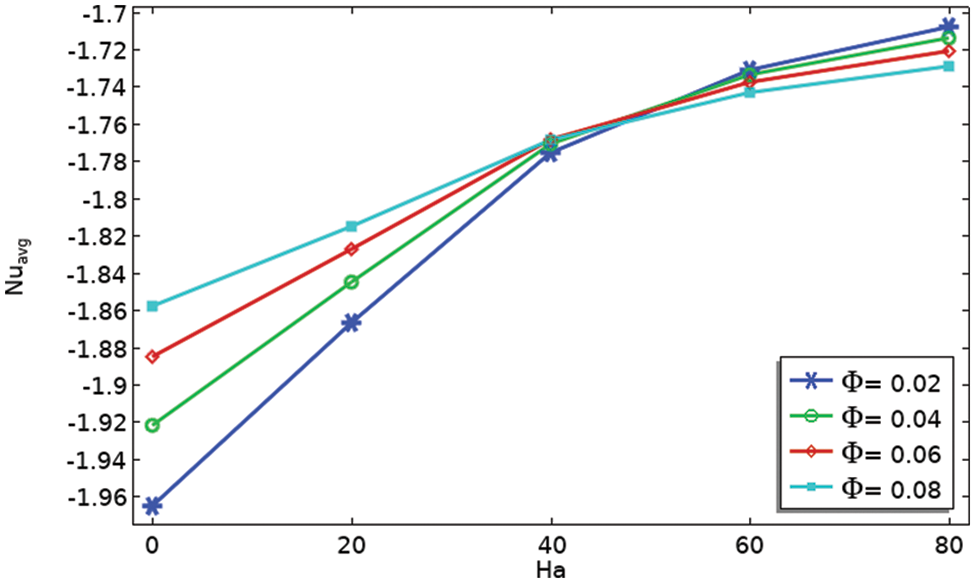
Figure 8: Impacts on Nuavg for numerous Ha

5  Conclusion

This study discusses the issue of irreversibility during the natural convective thermal flow of a Cu-H2O nanofluid inside a cavity. The effect of the magnetic field’s inclination on the irreversibility process is evaluated by applying the field at varying angles. An upward temperature gradient is created in the flow domain by heating the upper wall of the enclosure at a consistent rate while cooling the other borders. The problem considered mathematically is formulated as a connected partial differential system. Utilizing a finite element approach allows the governing equations to be solved. As a result, the current study focuses on making predictions about the elements that influence entropy measurements and disclosing any differences we find in the entropy generated within the enclosure. The most important results are listed below:

•   Because of the created temperature disparity, heat is transferred in the shape of parabolic curves and starts at the top of the enclosure.

•   For Ha=0 with ϕ = 0.02 and γ = 30o fixed, a symmetrical stream line contour is produced at the mid plane, x=0.5.

•   For Ha > 0, a diminishing trend of (STherm) with an increasing value of ϕ was observed. However, for Ha=0, a consistent magnitude of (STherm) across the range of ϕ from 0.02 to 0.08 was observed.

•   It can be observed that as ϕ shifts, the corresponding curves show fluctuations in (SVisc) going to zero.

•   It is widely accepted that the variation in magnetic entropy becomes zero at Ha=0, rises for Ha < 40, and then declines after passing this critical range.

Acknowledgement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through a small group Research Project under Grant Number RGP1/154/44.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Afraz Hussain Majeed, Sayed M Eldin; methodology: Imran Siddique, Rashid Mahmood; data collection: S. Saleem, Muhammad Jawad; analysis and interpretation of results: Rashid Mahmood Sayed M Eldin; draft manuscript preparation: Muhammad Jawad, Afraz Hussain Majeed; writing—review and editing: Imran Siddique; funding acquisition: Sayed M Eldin: supervisor: Rashid Mahmood. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data used to support the findings of this study are available from the corresponding author upon request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Bejan, A. (1980). Second law analysis in heat transfer. Energy, 5, 720–732. https://doi.org/10.1016/0360-5442(80)90091-2 [Google Scholar] [CrossRef]

2. Parvin, S., Chamkha, A. J. (2014). An analysis on free convection flow, heat transfer and entropy generation in an odd-shaped cavity filled with nanofluid. International Communications in Heat and Mass Transfer, 54, 8–17. https://doi.org/10.1016/j.icheatmasstransfer.2014.02.031 [Google Scholar] [CrossRef]

3. Kefayati, G. H. R. (2014). Natural convection of ferrofluid in a linearly heated cavity utilizing LBM. Journal of Molecular Liquids, 191, 1–9. https://doi.org/10.1016/j.molliq.2013.11.021 [Google Scholar] [CrossRef]

4. Rabbi, K. M., Saha, S., Mojumder, S., Rahman, M. M., Saidur, R. et al. (2016). Numerical investigation of pure mixed convection in a ferrofluid-filled lid-driven cavity for different heater configurations. Alexandria Engineering Journal, 55, 127–139. https://doi.org/10.1016/j.aej.2015.12.021 [Google Scholar] [CrossRef]

5. Mejri, I., Mahmoudi, A., Abbassi, M. A., Omri, A. (2014). Magnetic field effect on entropy generation in a nanofluid-filled enclosure with sinusoidal heating on both side walls. Powder Technology, 266, 340–353. https://doi.org/10.1016/j.powtec.2014.06.054 [Google Scholar] [CrossRef]

6. Mahmoudi, A., Mejri, I., Abbassi, M. A., Omri, A. (2014). Analysis of the entropy generation in a nanofluid-filled cavity in the presence of magnetic field and uniform heat generation/absorption. Journal of Molecular Liquids, 198, 63–77. https://doi.org/10.1016/j.molliq.2014.07.010 [Google Scholar] [CrossRef]

7. Armaghani, T., Kasaeipoor, A., Alavi, N., Rashidi, M. M. (2016). Numerical investigation of water-alumina nanofluid natural convection heat transfer and entropy generation in a baffled L-shaped cavity. Journal of Molecular Liquids, 223, 243–251. https://doi.org/10.1016/j.molliq.2016.07.103 [Google Scholar] [CrossRef]

8. Al-Zamily, A. M. J. (2017). Analysis of natural convection and entropy generation in a cavity filled with multi-layers of porous medium and nanofluid with a heat generation. International Journal of Heat and Mass Transfer, 106, 1218–1231. https://doi.org/10.1016/j.ijheatmasstransfer.2016.10.102 [Google Scholar] [CrossRef]

9. Bouchoucha, A. E. M., Bessaïh, R., Oztop, H. F., Al-Salem, K., Bayrak, F. (2017). Natural convection and entropy generation in a nanofluid filled cavity with thick bottom wall: Effects of non-isothermal heating. International Journal of Mechanical Sciences, 126, 95–105. https://doi.org/10.1016/j.ijmecsci.2017.03.025 [Google Scholar] [CrossRef]

10. Oztop, H. F., Abu-Nada, E. (2008). Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. International Journal of Heat and Fluid Flow, 29, 1326–1336. https://doi.org/10.1016/j.ijheatfluidflow.2008.04.009 [Google Scholar] [CrossRef]

11. Sheremet, M. A., Grosan, T., Pop, I. (2017). Natural convection and entropy generation in a square cavity with variable temperature side walls filled with a nanofluid: Buongiorno’s mathematical model. Entropy, 19, 337. https://doi.org/10.3390/e19070337 [Google Scholar] [CrossRef]

12. Siavashi, M., Yousofvand, R., Rezanejad, S. (2018). Nanofluid and porous fins effect on natural convection and entropy generation of flow inside a cavity. Advanced Powder Technology, 29, 142–156. https://doi.org/10.1016/j.apt.2017.10.021 [Google Scholar] [CrossRef]

13. Kashyap, D., Dass, A. K. (2018). Two-phase lattice Boltzmann simulation of natural convection in a Cu-water nanofluid-filled porous cavity: Effects of thermal boundary conditions on heat transfer and entropy generation. Advanced Powder Technology, 29, 2707–2724. https://doi.org/10.1016/j.apt.2018.07.020 [Google Scholar] [CrossRef]

14. Gibanov, N. S., Sheremet, M. A., Oztop, H. F., Abu-Hamdeh, N. (2018). Mixed convection with entropy generation of nanofluid in a lid-driven cavity under the effects of a heat-conducting solid wall and vertical temperature gradient. European Journal of Mechanics–B/Fluids, 70, 148–159. https://doi.org/10.1016/j.euromechflu.2018.03.002 [Google Scholar] [CrossRef]

15. Mansour, M. A., Siddiqa, S., Gorla, R. S. R., Rashad, A. M. (2018). Effects of heat source and sink on entropy generation and MHD natural convection of Al2O3-Cu/water hybrid nanofluid filled with square porous cavity. Thermal Science and Engineering Progress, 6, 57–71. https://doi.org/10.1016/j.tsep.2017.10.014 [Google Scholar] [CrossRef]

16. Rahimi, A., Sepehr, M., Lariche, M. J., Kasaeipoor, A., Malekshah, E. H. et al. (2018). Entropy generation analysis and heatline visualization of free convection in nanofluid (KKL model-based)-filled cavity including internal active fins using lattice Boltzmann method. Computers & Mathematics with Applications, 75, 1814–1830. https://doi.org/10.1016/j.camwa.2017.12.008 [Google Scholar] [CrossRef]

17. Bilal, S., Majeed, A. H., Mahmood, R., Khan, I., Seikh, A. H. (2020). Heat and mass transfer in hydromagnetic second-grade fluid past a porous inclined cylinder under the effects of thermal dissipation, diffusion and radiative heat flux. Energies, 13, 278. https://doi.org/10.3390/en13010278 [Google Scholar] [CrossRef]

18. Majeed, A. H., Bilal, S., Mahmood, R., Malik, M. Y. (2020). Heat transfer analysis of viscous fluid flow between two coaxially rotated disks embedded in permeable media by capitalizing non-Fourier heat flux model. Physica A: Statistical Mechanics and its Applications, 540, 123182. https://doi.org/10.1016/j.physa.2019.123182 [Google Scholar] [CrossRef]

19. Mahmood, R., Bilal, S., Majeed, A. H., Khan, I., Sherif, E. S. M. (2020). A comparative analysis of flow features of Newtonian and power law material: A new configuration. Journal of Materials Research and Technology, 9, 1978–1987. https://doi.org/10.1016/j.jmrt.2019.12.030 [Google Scholar] [CrossRef]

20. Bilal, S., Mahmood, R., Majeed, A. H., Khan, I., Nisar, K. S. (2020). Finite element method visualization about heat transfer analysis of Newtonian material in triangular cavity with square cylinder. Journal of Materials Research and Technology, 9, 4904–4918. https://doi.org/10.1016/j.jmrt.2020.03.010 [Google Scholar] [CrossRef]

21. Khan, Z. A., Usman, M., Khan, W. A., Hamid, M., Haq, R. U. (2022). Thermal treatment inside a partially heated triangular cavity filled with casson fluid with an inner cylindrical obstacle via FEM approach. The European Physical Journal Special Topics, 231, 2683–2694. https://doi.org/10.1140/epjs/s11734-022-00587-6 [Google Scholar] [CrossRef]

22. Soomro, F. A., Hamid, M., Hussain, S. T., Haq, R. U. (2022). Constructional design and mixed convection heat transfer inside lid-driven semicircular cavity. The European Physical Journal Plus, 137, 781. https://doi.org/10.1140/epjp/s13360-022-03009-7 [Google Scholar] [CrossRef]

23. Chelia, W., Laouer, A., Mezaache, E. H., Teggar, M., Arici, M. et al. (2023). Investigation of nanofluid natural convection inside a square cavity for two orientations using lattice boltzmann method. Journal of Nanofluids, 12, 889–903. https://doi.org/10.1166/jon.2023.1964 [Google Scholar] [CrossRef]

24. Mahmood, R., Khan, Y., Rehman, N., Majeed, A. H., Alameer, A. et al. (2022). Numerical computations of entropy generation and MHD ferrofluid filled in a closed wavy configuration: Finite element based study. Frontiers of Physics, 10, 916394. https://doi.org/10.3389/fphy.2022.916394 [Google Scholar] [CrossRef]

25. Mahmood, R., Rehman, N., Majeed, A. H., Rehman, K. U., Shatanawi, W. (2023). Numerical solution for heat transfer in a staggered enclosure with wavy insulated baffles. AIMS Mathematics, 8(4), 8332–8348. https://doi.org/10.3934/math.2023420 [Google Scholar] [CrossRef]

26. Rehman, N., Mahmood, R., Majeed, A. H., Rehman, K. U., Shatanawi, W. (2023). Finite element analysis on entropy generation in MHD Iron (III) Oxide-Water NanoFluid equipped in partially heated fillet cavity. Journal of Magnetism and Magnetic Materials, 565, 170269. https://doi.org/10.1016/j.jmmm.2022.170269 [Google Scholar] [CrossRef]