User Purchase Intention Prediction Based on Improved Deep Forest

1  Introduction

In the era of the Internet, e-commerce has been widely adopted due to its convenience and efficiency [1]. Against this backdrop, e-commerce platforms generate a wealth of user behavior data. Through the application of deep learning techniques [2] to analyze and predict these data, businesses can delve into the shopping intentions and demands of consumers, thereby offering more precise, personalized services and products. This can further increase customer satisfaction and business competitiveness. Among the numerous deep learning models, Deep Neural Networks (DNNs) have been extensively utilized due to their excellent predictive performance. However, their training process requires a large amount of hyperparameter tuning and lacks sufficient interpretability [3], undoubtedly increasing the complexity of business decision-making and understanding of user behavior patterns.

In recent years, the Deep Forest (DF) [4] model, with its efficient computational performance and good model interpretability, has attracted the attention of researchers and businesses. Compared to Deep Neural Networks, Deep Forest exhibits significant advantages in processing different scales of data and model interpretability. However, despite the application of the Deep Forest model in scenarios such as user purchase intention prediction [5,6], there is still room for improvement in its predictive performance and model generalization ability. Therefore, this paper proposes an improved Deep Forest model to further enhance the accuracy of purchase intention prediction.

The main contributions of this paper are as follows:

•   The Binary Differential Evolution algorithm is used for model selection. This provides a broader model selection space for Deep Forest, thereby accommodating complex data patterns.

•   A feature importance weighting strategy is adopted to operate on the original features in the cascading structure. This strategy exhibits efficient performance in guiding the training process of the next cascading forest, not only significantly improving the performance of the model but also ensuring its interpretability.

•   Meta-classifiers are introduced at each layer of the cascading forest. This strategy allows the model to further optimize the prediction results of the previous layer at each layer, thereby significantly enhancing the model’s predictive accuracy.

•   A deep ensemble strategy based on ensemble learning is implemented in the model to enhance its robustness and generalization capability.

The remainder of this paper is organized as follows. In Section 2, we will discuss related work. Section 3 introduces the relevant theories needed for the article. In Section 4, we present the specific design of the model. In Section 5, we present the simulation results and analysis. Finally, the conclusions and prospects of this paper are presented.

2  Related Work

In the field of e-commerce, predicting user purchase intentions is a crucial area of research. With the rapid growth and complexity of data, traditional machine learning models, such as Logistic Regression (LR) [7], are often too simplistic, have weaker generalization capabilities, and limit improvements in predictive performance. Hybrid models, which combine various models or algorithms to produce a collective prediction result, have been applied. For instance, Tang et al. [8] combined Support Vector Machine (SVM) and Firefly Algorithm (FA), while Hu et al. [9] used SVM and LR together. These combinations effectively resolved the inadequacy of a single traditional model’s fitting capabilities. However, the combining process of these hybrid models is rather rudimentary and lacks flexibility, making further optimization challenging. Consequently, ensemble learning was introduced and has been widely applied in various prediction tasks. The main models include Random Forest (RF) [10] ensemble by bagging [11] method, and models like Extreme Gradient Boosting (XGBoost, XGB) [12], Light Gradient Boosting Machine (LightGBM, LGB) [13], Adaptive Boosting (AdaBoost, AdaB) [14], CatBoost (CatB) [15] and Gradient Boosting Decision Tree (GBDT) [16] that ensemble by boosting [17] method. These models integrate multiple different machine learning algorithms, overcoming the limitations of single algorithms. They offer high prediction accuracy, fast training speed, and low memory consumption, becoming mainstream solutions for data mining tasks [18]. However, these ensemble learning methods still rely on human-defined model designs and feature selection, often requiring extensive experiments or expert knowledge to acquire the optimal model structure and parameter configuration. This limits their application in complex and large-scale problems. To overcome these limitations, the concept of Evolutionary Ensemble Learning [19] was introduced. Evolutionary Ensemble Learning incorporates evolutionary algorithms like Genetic Algorithm (GA) [20] and Differential Evolution Algorithm (DE) [21], allowing for the automation and data-driven optimization of models. Wen et al. [22] proposed an ensemble learning framework based on a voting mechanism. This framework employs the voting mechanism for classification decisions and integrates the advantages of various constraint-handling techniques. To further enhance the performance of ensemble learning, a DE variant is used as the search engine, combined with four search strategies to generate new individuals, ensuring a balance between population diversity and convergence.

Despite these models being part of shallow machine learning, they can enhance prediction accuracy but still struggle to perfectly express complex relationships within non-structured data [23]. The DF model, a combination of ensemble learning and deep learning, possesses both the high accuracy of ensemble learning and the robust expressive ability of deep learning while avoiding the drawbacks of deep neural networks. Therefore, as a deep level ensemble model, DF has gradually gained attention and shown immense potential in purchase prediction tasks. In this regard, Ge et al. [6] proposed a user purchase behavior prediction method based on DF; Fu et al. [5] introduced a multilayer heterogeneous ensemble algorithm, constructing a user purchase behavior prediction algorithm framework based on the DF model. Although they validated the effectiveness of their methods and frameworks through experiments, there is still room for further optimization.

In light of this, this paper integrates the advantages of evolutionary ensemble learning and deep forests to propose a Deep Adaptive Evolutionary Ensemble model for predicting user purchase intentions. A series of innovative research has been conducted in areas such as base model selection in deep forests, feature weight adjustment strategies, and model hierarchy optimization strategies, providing new solutions for purchase intention prediction in the e-commerce domain.

3  Theoretical Foundation

3.1 Deep Forest

The Deep Forest model consists of two parts: Multi-Grained Scanning and Cascade Forest. Multi-Grained Scanning improves the ability of deep learning to represent data effectively by applying different sampling windows. Cascade Forest, on the other hand, is inspired by the layer-by-layer processing strategy of original features in neural networks, as shown in Fig. 1. In this cascading structure, each forest attempts to further optimize data representation based on the previous forest.

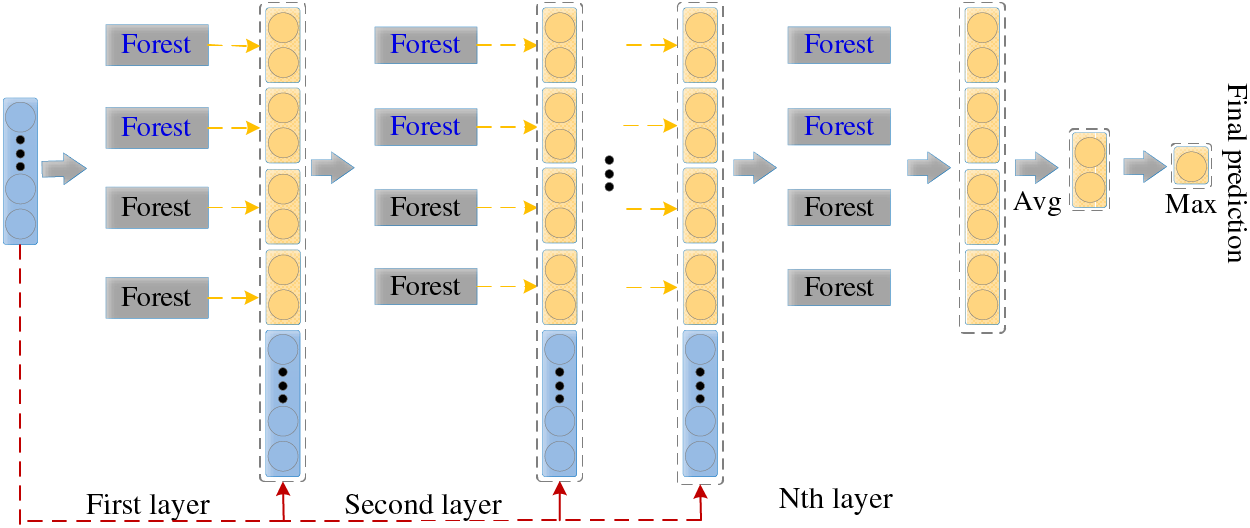
Figure 1: Cascade forest workflow

In the Cascade Forest, each level is composed of several Random Forests (blue) and Extra Trees (ET) (black), with each forest consisting of multiple decision trees. In a regular Random Forest, each decision tree, during splitting, selects the feature with the optimal Gini value from a random subset of features to split. Extra Trees differ in that when deciding how to split a node, they randomly select a subset of features from all features and then randomly select a split point (instead of finding the optimal split point) until each leaf node contains only one category or no more than 10 samples. In this way, each decision tree outputs a result in the form of a class vector. Suppose it is a binary classification problem; it generates a two-dimensional class vector. The mean of the output class vector results of all decision trees is taken as the decision result of the Random Forest. The class vector output by each forest will serve as an enhanced feature vector and, after being concatenated with the original feature vector, will serve as the input for the next level. This process is repeated until the last level of the cascade, where the mean of the outputs of the last forest is calculated, and the category corresponding to the maximum value is taken as the final prediction result.

To prevent overfitting in the deep structure, each forest’s enhanced vector is obtained through K-fold cross-validation. When the cascade extends to a new level, the performance of the entire cascade will be evaluated through the validation set. If there is no significant performance improvement, the training process will end. Therefore, the advantage of Deep Forest is that it can automatically adjust the model complexity to adapt to different scales of data sets, which is more adaptable compared to neural networks.

3.2 Differential Evolution Algorithm

The differential evolution algorithm is a population-based heuristic search algorithm that simulates the process of cooperation and competition among individuals within a population. Due to its clear algorithmic structure, few control variables, strong adaptability, and rapid convergence rate, it has been widely applied across various domains [24,25]. The main algorithmic flow is as follows:

(1) Initialization of the Population

Based on the characteristics of the target task, the problem is abstracted into a manageable search space, with the problems to be solved converted into individuals. Each individual in the initialized population is a solution within the search range. In the solution space, M individuals are randomly and uniformly generated. Each individual is composed of an n-dimensional vector as the initial population, which is denoted as:

Xi(0)=(Xi,1(0),Xi,2(0),Xi,3(0),⋯,Xi,n(0))(1)

The method of obtaining the jth dimension for the ith individual could be described as follows:

Xi,j=Lj_min+rand(0,1)(Lj_max−Lj_min) i=1,2,3,⋯,M j=1,2,3,⋯,n(2)

(2) Evolutionary Operation

1) Mutation Operation:

For each parameter vector, three distinct individuals are randomly selected from the population to generate a mutant vector. The mutation equation is shown in Eq. (3).

Vi(g)=Xr1(g)+F⋅(Xr2(g)−Xr3(g))(3)

where Xr1(g), Xr2(g), and Xr3(g) are three individuals selected from the population, selected randomly; r1, r2, and r3 are integers and r1 ≠ r2 ≠ r3; Xr2(g) − Xr3(g) is the differential vector; g represents the g-th generation; F is the scale factor used to control the magnitude of mutation.

2) Crossover Operation:

The crossover operation involves recombining the target vector Xi,j(g) and mutant vector Vi,j(g) to produce a new trial vector Ui,j(g), thus retaining the information of the original individual and adding the information of the mutant individual. The specific equation is shown in Eq. (4).

Ui,j(x)={Vi,j(g),if rand(j)<CRXi,j(g), otherwise(4)

3) Selection Operation:

The selection strategy is based on the assessment of the fitness of the trial vector and the original individual to select the strategy for the next generation. Its purpose is to select the optimal individual in the population so that the population gradually converges to the global optimal solution. The specific selection method is as follows:

Xi(g+1)={Ui(g),if f(Ui(g))>f(Xi(g))Xi(g), else(5)

where f represents the fitness function. A greedy selection strategy is adopted between Ui(g) and Xi(g), with the superior individual serving as the new individual.

4  User Purchase Intention Prediction Method Design

4.1 Model Selection of Binary Differential Evolution Algorithm

The traditional Cascade Forest model mainly uses RF and ET as base models. However, both of these models use the same ensemble method at their core, which may not fully capture all the effective information in the prediction task. The goal of the Cascade Forest is to improve final performance by integrating predictions from multiple models. However, models based on a single structure may limit the complementarity between models, thereby affecting the model’s expressive power and generalization performance. Although some research has enhanced model diversity by introducing heterogeneous models [26,27], this strategy also has its undeniable limitations. For example, without strict model selection and optimization, it might introduce models that do not perform well on specific tasks or datasets, which could weaken the overall performance of the model. To overcome these problems, this paper proposes a method for multi-model optimized cascade forest structure, using a binary differential evolution algorithm for model selection, and introduces heterogeneous models into the cascade layer.

Firstly, a population is initialized. If there are N classifiers in the target task, then a 1 * N binary sequence is initialized, where the value of each element is either 0 or 1. The coding method is shown in Fig. 2.

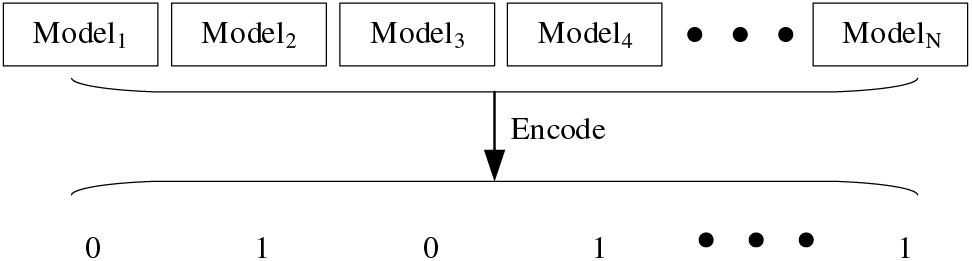
Figure 2: Binary differential evolution algorithm encoding method

Based on the number of classifiers, an appropriate population size NP is set, and the above binary encoding is repeated NP times to obtain a set containing NP binary sequences.

The fitness value for this classifier is defined as the mean of the Accuracy and Area Under the Curve (AUC) obtained after the Decision Tree classifier performs 5-fold cross-validation on the input data. Its definition is as follows:

Fitness=Accuracy5−fold(X)+AUC5−fold(X)2(6)

where X represents the subset of classifiers represented by the binary vector; Accuracy5-fold(X) and AUC5-fold(X) refer to the Accuracy and AUC values obtained by performing 5-fold cross-validation of the classifier on the training data.

After the mutation operation is performed, Eq. (7) is used to correct the mutation vector to ensure that each element is between 0 and 1. This guarantees that each element of the individual after mutation is a binary bit, ensuring the correctness of the algorithm.

Vi(g)={1,Vi(g)>10,Vi(g)<0(7)

During multiple rounds of iteration, the algorithm will perform evolutionary operations (including mutation, and crossover operations) on the individuals of each round to generate new binary sequences (new individuals). Then, based on the scoring results of the fitness function, comparisons and selections are made between the newly generated individuals and the original individuals. Finally, when the binary differential evolution algorithm reaches the preset maximum number of iterations, the optimal model combination is selected from the predefined classifier set and passed to the cascade layer for use.

4.2 Improved Cascade Forest Model

For the deep forest model, it enhances the model's prediction performance by performing layered feature extraction and combination through multi-level cascading. However, as the number of cascading layers increases, the problem of “feature degradation” starts to emerge. This is because the weight of the original features in the feature vector may gradually decrease [28], and even in subsequent cascade layers, they may be completely replaced by the feature vectors output from the first few layers. Ignoring the different contributions of each feature to the classification result and simply concatenating the original features with the output feature vectors of the cascade layer may “dilute” the information of important features with relatively less important features, which undoubtedly has a negative impact on the model performance.

In binary classification problems like purchase intention prediction, each cascade layer’s forest will produce two category probability vectors (purchase and non-purchase), the sum of the probabilities of these two vectors is 1. These probability outputs will serve as inputs for the next level, leading to an increase in data dimensions [29,30]. In addition, since the probability features newly added in each cascade layer are highly correlated with the existing features, the amount of information they add is relatively limited, leading to redundancy in the feature vector, and also increasing the computational cost of the model.

Therefore, in response to the above problems, this paper has optimized the original feature vector and the output of prediction probability in a series of ways. As shown in Fig. 3.

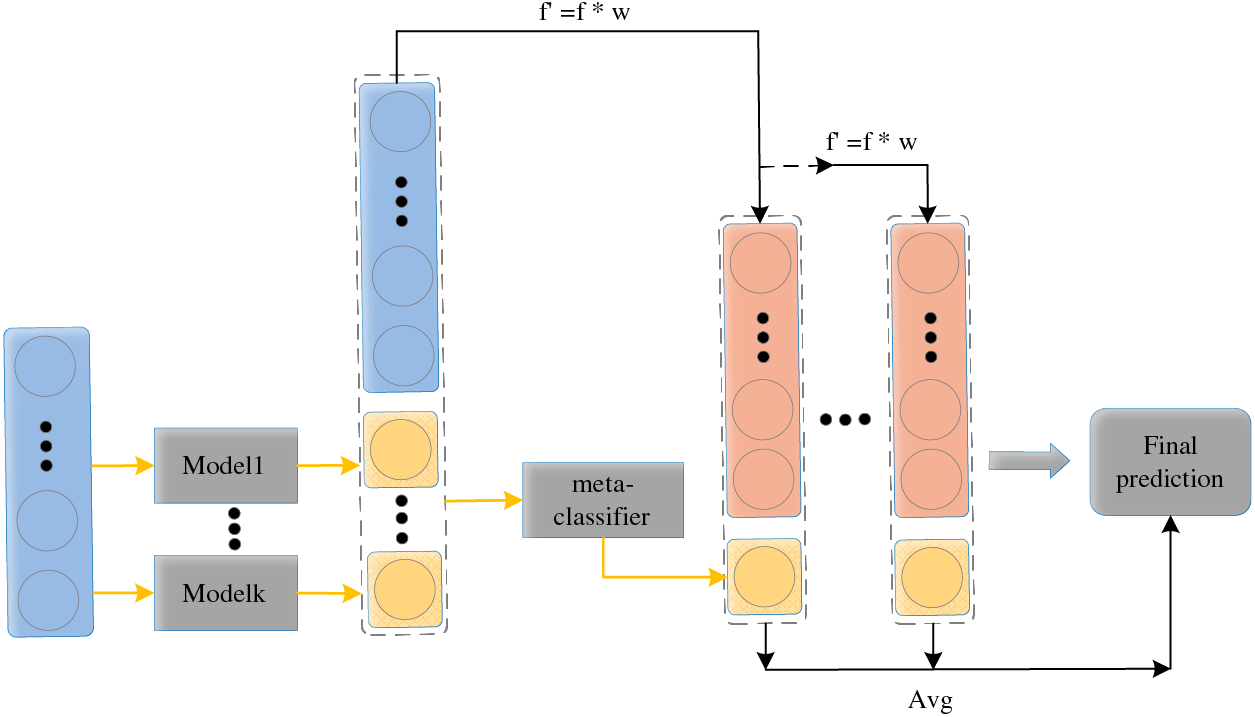
Figure 3: Improved cascade forest structure

In the processing of feature vectors, a feature weighting strategy is adopted to enhance the model’s prediction performance and interpretability. First, the importance of each feature is calculated in each ensemble-based classifier, and these importance values reflect the degree of contribution of each feature to the prediction result. Then, we calculate the average feature importance across all models, which serves as the feature weight. The corresponding equation is as follows:

wi=(Imp(M1,fi)+Imp(M2,fi)⋯+Imp(Mn,fi))n(8)

where n is the number of base classifiers, wi is the weight of feature fi, and Imp(M, f) is the importance score assigned by the model M to feature f, this process is implemented by the feature_importances_ function in the sklearn library.

Each feature fi will be adjusted according to its corresponding weight wi, as shown in Eq. (9).

fi′=fi∗wi(9)

where fi′ represents the feature value after weight adjustment, and fi represents the original feature value, i.e., the value of the feature before adjustment.

In each layer of the cascading structure, the importance of features will be reevaluated and these features will be adjusted according to this. This process allows the feature weight calculation of subsequent layers to be based on the weighted features of the previous layer, thus achieving layer-by-layer enhancement of important features. This cascaded weighting plays an important role in the cascade forest model, enhancing the model’s learning ability for important features, and allowing the model to more accurately use the information contained in these key features for prediction. In addition, reducing the model’s sensitivity to the evaluation errors of individual base classifiers significantly improves the robustness of the model.

In the aspect of processing class probability vectors, this paper only uses the positive class (label 1) probability as the enhanced feature, different from the traditional approach (i.e., considering both positive and negative class probabilities). For each cascade layer, a set of base classifiers are trained independently and generate their positive class probability predictions. Then, a meta-classifier is used to learn these positive class probabilities, understand the correlation between the prediction results of each base classifier, and output an integrated prediction probability. This prediction probability represents the cascade model’s prediction at that level and directly affects the output of the current layer. In addition, this prediction result is also introduced as a new enhanced feature into the next layer, forming a self-learning and self-optimization mechanism. In the training process, if there is no significant improvement in model performance in three consecutive cascade layers, the cascade forest process is terminated. Finally, the model's prediction result is obtained by collecting the prediction probabilities of each meta-classifier at each level and taking their average.

The improved cascade forest introduces the feature importance assessment of the base learner and dynamically adjusts the weights of the features at each level, making the model more focused on those features with higher discriminative power and reducing the noise impact of irrelevant features. At the same time, by training a group of base classifiers to output positive class probability predictions, and using a meta-classifier to learn and integrate prediction probabilities, effectively reducing feature dimensionality while incorporating information from all base classifiers. These strategies effectively integrate the predictive power of multiple algorithms, capturing the complexity of data at different levels, thereby improving the accuracy and robustness of model prediction.

4.3 Overall Structure

Following the above enhancements to the cascade structure, a Deep Adaptive Evolutionary Ensemble model was constructed for user purchase intention prediction in this paper. The architecture of this model is illustrated in Fig. 4.

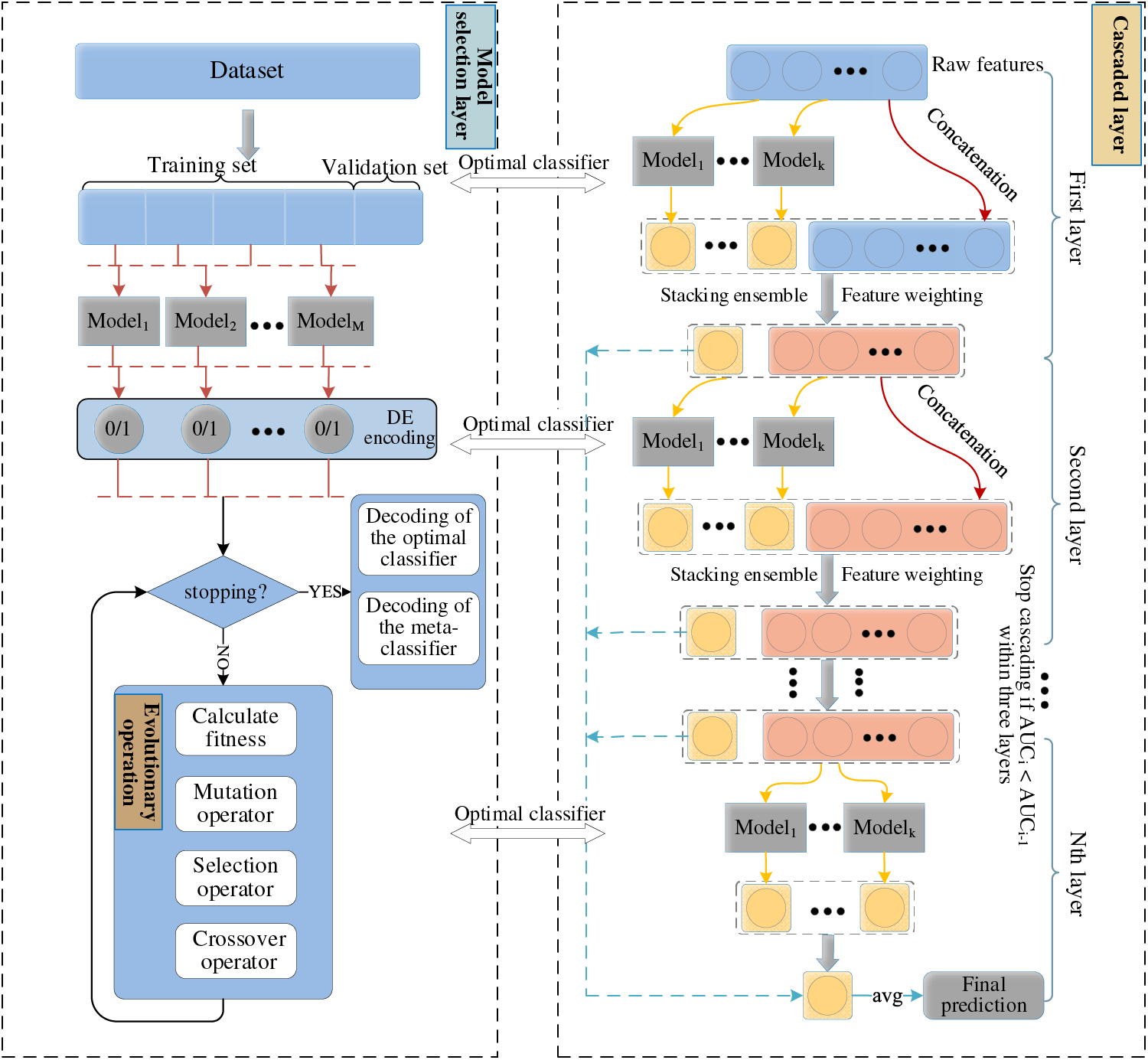
Figure 4: Framework of the deep adaptive evolutionary ensemble learning model

On a given dataset, an evolutionary ensemble learning strategy is employed in the model selection layer. This strategy optimizes the objective function to select a set of classifiers, and the results of these classifiers are then fed back into the cascade forest. In the cascade forest, if the initial input feature dimension is 400 and each cascade layer consists of four base classifiers (as determined by the model selection layer), the prediction probabilities from each base classifier are first concatenated together to form a matrix. This matrix serves as the input to the meta-classifier. The meta-classifier learns from this input data and predicts a target variable, which is then concatenated with the weighted feature vector. Therefore, at the end of the first layer, we get a feature vector of 401 dimensions. This vector serves as the input to the next layer. This process continues until the stopping condition for layer expansion is met.

During the testing phase, the cascade structure is used to make predictions on the test instances, yielding the final layer’s prediction results. The final prediction is the average of the prediction probabilities obtained by the meta-classifier at each layer. If this average value is greater than or equal to 0.5, the instance is predicted to be a positive case; otherwise, it is predicted as negative.

5  Experimental Analysis

5.1 Data Description

The experimental data used in this paper is from real online transaction data of JD.com, comprising 4 categories and a total of 6 datasets. For detailed information, please refer to Table 1.

JD Mall provided data from February 01, 2016, to April 15, 2016, including behavioral data of 105,321 users, totaling 50,601,736 records; at the same time, it also includes 558,552 review data of 24,187 products.

5.2 Evaluation Metrics

The experiment in this paper uses Accuracy, Precision, Recall, F1-score, and AUC as the performance evaluation indicators of the model. The calculation equations are shown as follows (Eqs. (10) to (14)):

precision=TPTP+FP(10)

recall=TPTP+FN(11)

F1=2×precision×recallprecision+recall(12)

AUC=∑i∈positiveClassranki−T(1+T)2(T×N)(13)

Accuracy=TP+TNTP+TN+FP+FN(14)

5.3 Experimental Environment and Parameter Settings

Table 2 lists the software and hardware environments, model methods, etc., used in the experiment.

Table 3 provides detailed records of the parameter configuration information for all models used in this paper’s experiments.

5.4 Experimental Results

5.4.1 Model Selection Results

To implement the multi-model ensemble framework, this paper selects seven traditional ensemble models: RandomForest, XGBoost, CatBoost, LightGBM, AdaBoost, GBDT, and ET. The most suitable model combination for the purchasing intention dataset is determined by using the binary differential evolution algorithm for model selection. Upon reaching the preset maximum number of iterations, the optimal model combination {XGB, ET, RF} is obtained.

As shown in Fig. 5, in the evaluation of fitness values, the LightGBM model performs the best with a fitness value of 0.8458. This is closely followed by the XGBoost and RandomForest models, with fitness values of 0.8387 and 0.8332, respectively. These results demonstrate that the LightGBM model performs best in terms of adaptability and has a high classification accuracy. However, it is worth noting that despite LightGBM having the highest fitness value, it appears relatively infrequently in the best combination during the iterative process. This could be because the parameter setting and model architecture of LightGBM did not reach the optimum during the search process of the binary differential evolution algorithm.

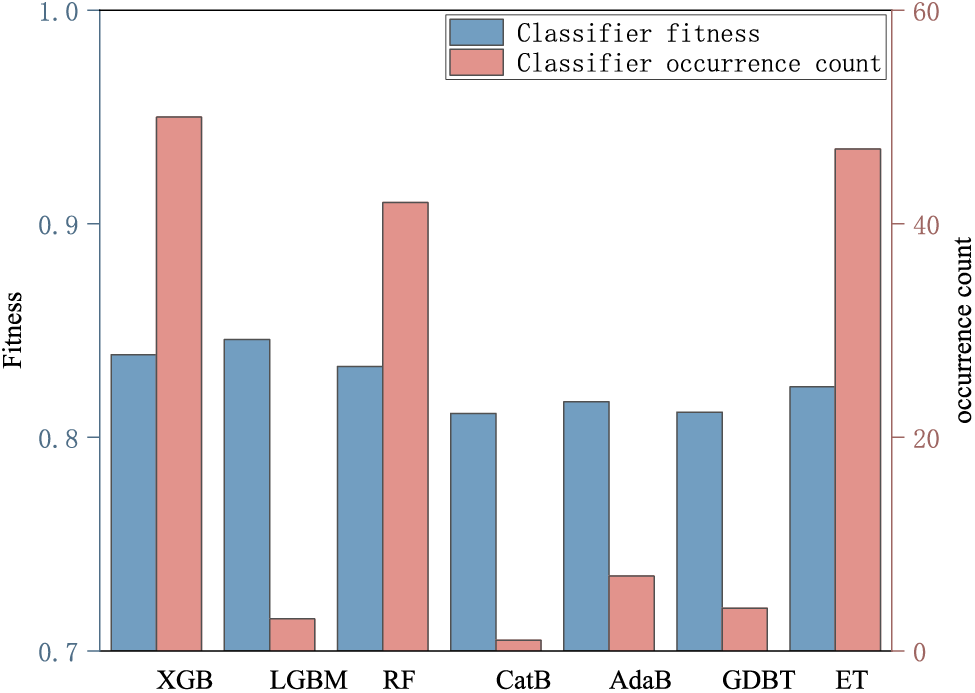
Figure 5: Fitness values and occurrences of each classifier during the model selection process

5.4.2 Comparison Experiment with Base Models

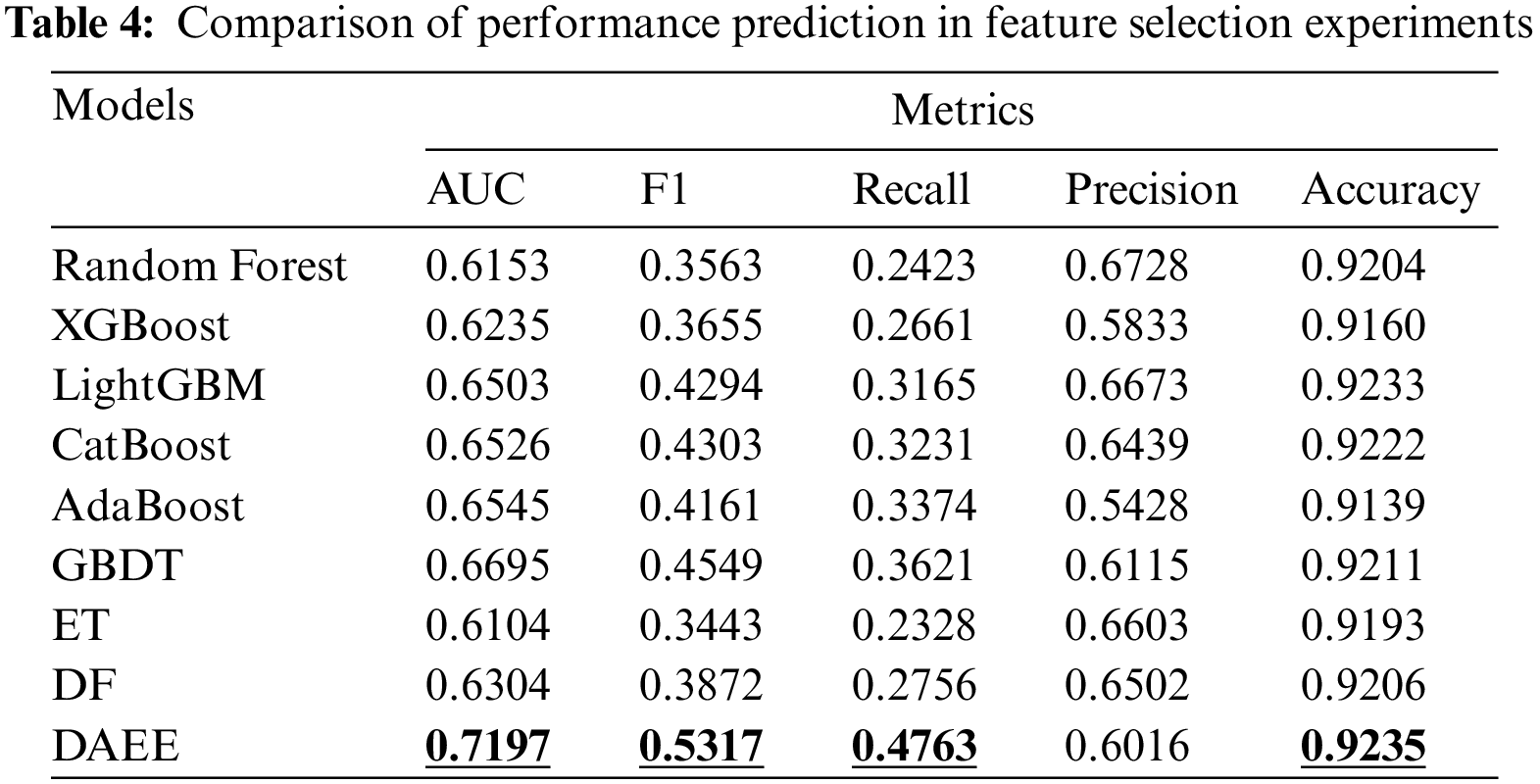
Table 4 thoroughly compares the performance of the DAEE model with the original Deep Forest model and seven traditional single ensemble models on five evaluation metrics. The experimental results indicate that, compared with these eight models, the DAEE model, as an architecture based on heterogeneous models and multi-level ensembles, has achieved significant performance improvements on all metrics except the precision indicator. Notably, the DAEE model scored 71.97% on the AUC metric, demonstrating its significant superiority in classification tasks compared to other models.

5.4.3 Comparison Experiment with Deep Models

In this experiment, several versions of deep neural networks are included: DNN_50, DNN_100, DNN_150, and DNN_200. The primary difference between these versions lies in the number of epochs for training, which are 50, 100, 150, and 200, respectively.

From the experimental results in Table 5, it can be observed that as the number of training epochs for the DNN increases, the model’s performance on the test set shows an improving trend in the initial stages. However, when the number of epochs exceeds 150, the performance of the model declines. This could be due to overfitting during the training process, which adversely impacts the performance on the test set. Moreover, as the number of epochs increases, the model’s training time also correspondingly increases.

DAEE outperforms DNN_50, DNN_100, and DNN_200 on the AUC, F1, recall, and precision metrics. Compared to DNN_150, although the DAEE model scores slightly lower on all metrics, the runtime of DNN_150 is six times that of the DAEE model. This makes the DAEE model exhibit higher feasibility in real-time or large-scale application scenarios.

5.4.4 Comparison Experiment of Different Meta-Classifiers

To validate the stability of the DAEE model in adaptively adjusting the combination of base learners, selecting meta-classifiers, and optimizing the deep forest method, the best-selected learners were compared using them as meta-classifiers in experimental tests. In Table 6, DAE_XGB, DAE_RF, and DAE_ET respectively represent scenarios where the selected learners in the selection layer were used as meta-classifiers in sequence. The results show that the difference in AUC values between the best-performing and worst-performing meta-classifiers is 0.0107. This indicates that the proposed model’s overall performance remains excellent regardless of which meta-classifier is used. It further confirms the high stability and robustness of the DAEE model when handling purchase intention prediction data.

Fig. 6 shows the performance comparison of models with three different meta-classifiers and traditional models on four indicators: AUC, F1, recall, and Accuracy. Regardless of which optimal learner is chosen as the meta-classifier, the performance of the proposed model on all indicators is significantly better than that of the single ensemble model, fully verifying the effectiveness of our proposed Deep Evolutionary Ensemble Learning model.

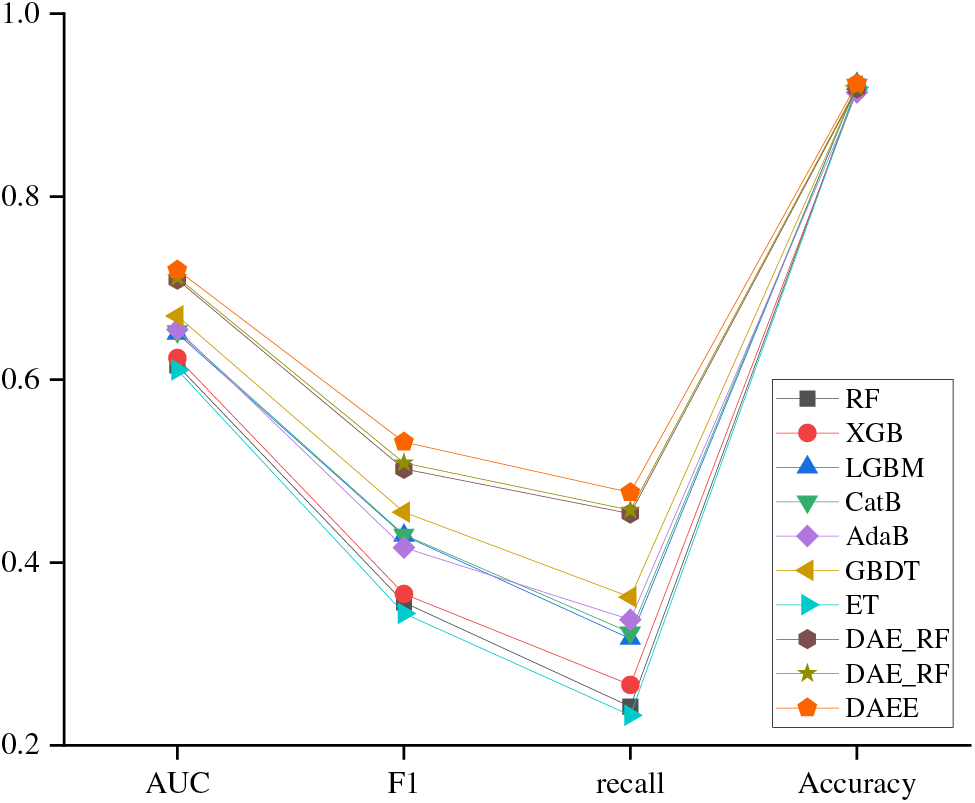
Figure 6: Performance comparison between different meta-classifiers and other models

RF and ET models, which are ensembled using Bagging, do not perform as well as models ensembled using Boosting. This might be due to the fact that the parallel sampling and resampling strategy of Bagging methods cannot effectively deal with complex and unbalanced purchase prediction problems. In contrast, models ensembled using the Boosting method can adjust sample weights based on training results [31], assigning higher weights to samples with incorrect predictions, hence performing relatively better on the indicators. It is worth noting that when RF and ET, together with the XGBoost model, which is ensembled using Boosting, are inputted into the Deep Forest as the optimal model combination, good results are achieved on all indicators. This result indicates that through model diversity, layered training, and self-enhancement mechanisms, the prediction performance of the model can be significantly improved, further demonstrating the excellent performance of the proposed model in prediction tasks.

5.4.5 Ablation Experiment

To verify the effectiveness of the DAEE model in adaptively introducing heterogeneous models, handling meta-classifier prediction probabilities, and adjusting feature weight strategies, an ablation study was conducted in this paper. The experimental configurations are as follows:

(1) Eliminating the feature importance weighting operation, denoted as w/o FI.

(2) Not using the meta-classifier prediction probability, but directly using the average of the classifier prediction values as output, labeled as w/o ML.

(3) Simultaneously ignoring feature importance and meta-classifier prediction probability, marked as w/o FI&ML.

(4) Excluding the model selection layer and only using the RF and DT models to predict within the improved cascading layer, denoted as w/o MS.

For detailed experimental results, refer to Table 7.

From Table 7, it is evident that when not using the meta-classifier prediction probability, the model’s prediction performance (measured by the AUC value) decreased by 3.55%. When relying solely on the improved cascading layer for prediction, with RF and DT acting as intra-layer classifiers, the AUC dropped by 5.04%. In scenarios without feature weighting, the model’s predictive performance declined by 6.42%, highlighting the crucial role of feature weight in model prediction. When both feature importance and meta-classifier prediction probability are disregarded, the prediction performance exhibits the most significant decline. However, thanks to the heterogeneous models integrated within the cascading layer, its performance still surpasses that of the original DF model.

5.4.6 Comparison Experiment with Other Improved Methods

There is a wealth of research on improving the cascade forest part of the Deep Forest model. References [29] and [30] optimized the enhancement vectors: the former designed a strong cascade forest model that selects class vectors generated at each level to achieve effective representation, while the latter used the mean value of the same class classification probability results output by similar forest models as input to achieve dimensionality reduction. Reference [28] introduced the AdaBoost algorithm to enhance the self-adjusting ability of the Deep Forest model and recombined it with the mean of the class distribution vectors output by each cascade layer after updating the weights of the features according to the classification error rate at each level, achieving simultaneous optimization of features and enhancement vectors. This paper introduces these three algorithms for comparison with the DF and DAEE models.

As shown in parts (a) and (b) of Fig. 7, we compare the DAEE model with the benchmark model DF21 and the models proposed in references [28,29], and [30] on the AUC and Accuracy indicators. On the AUC indicator, the performance of the DAEE model surpassed the benchmark model DF and the models in references [29] and [30], but was slightly lower than the model in reference [28]. This result indicates that the strategy of simultaneously adjusting original features and enhancement vectors can effectively improve the performance of the model. Similarly, the DAEE model also performs well on the accuracy indicator.

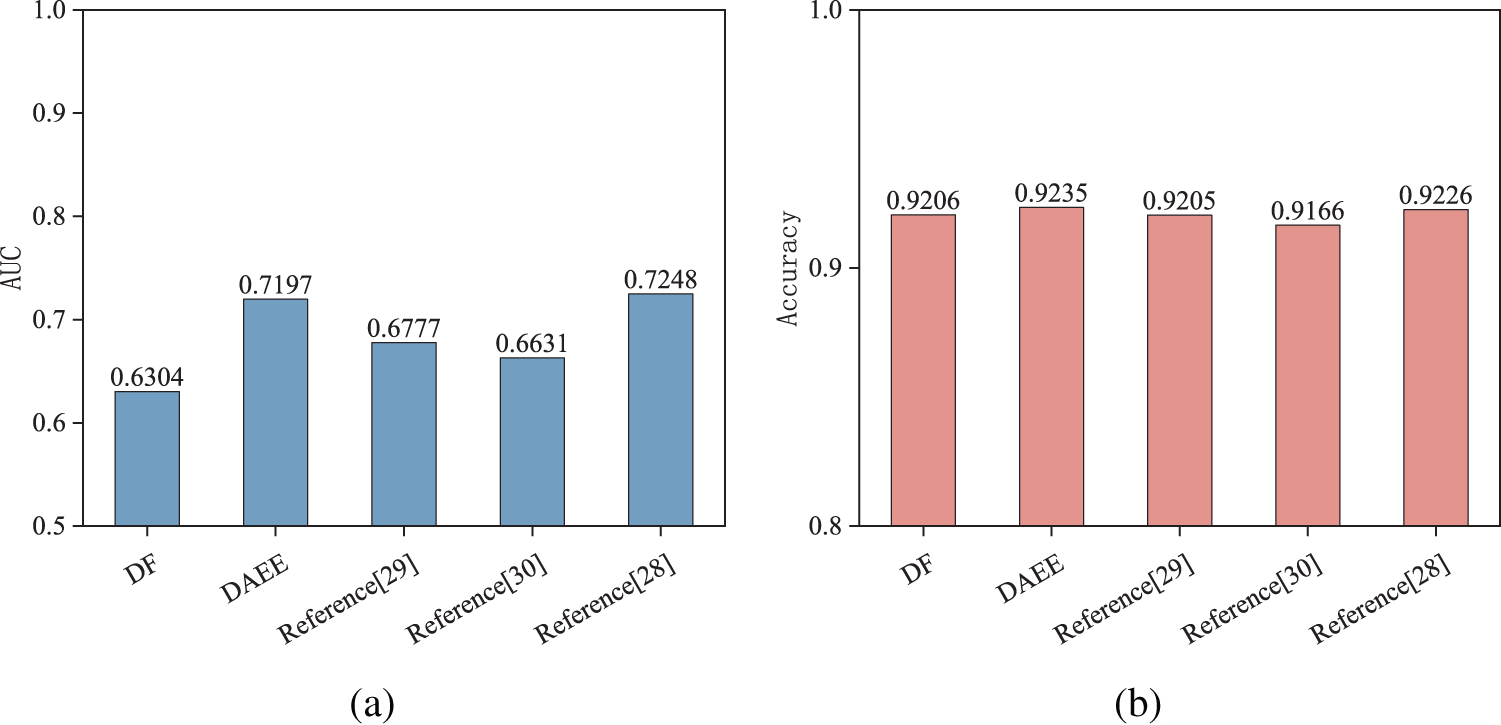
Figure 7: Comparison experiment with other improved methods. (a) AUC metrics; (b) accuracy metrics

6  Conclusion and Prospect

To address the limitations of deep neural networks in terms of data volume and hyperparameters, and to achieve adaptive optimization in the model structure, this paper introduces a Deep Adaptive Evolutionary Ensemble model applied to user purchase intention prediction. This model consists of two core components: the model selection layer and the cascading layer. In the model selection layer, a binary differential evolution algorithm is utilized to adaptively select models, and the chosen high-performing models are then integrated into the cascading forest layer-by-layer. In the cascading layer, strategies based on positive class probability enhanced features, meta-classifier prediction probability enhancement, and feature weight adjustment are applied to further optimize the original cascading structure. Experimental results show that compared to single ensemble models, this model has higher classification performance, improving the AUC value by 5.02%. In terms of training speed, this model is six times faster than deep models. Furthermore, its prediction accuracy increased by 0.9% compared to other optimization schemes. In summary, the model proposed in this paper effectively integrates the advantages of various machine learning techniques, and through ensemble-based deep integration and various optimization strategies, it significantly enhances learning efficiency and predictive performance when dealing with complex purchase prediction problems. In future work, various intelligent algorithms will be explored to validate the superiority of the proposed model.

Acknowledgement: The author thanks the School of Computer Science and Engineering of North Minzu University for providing equipment support.

Funding Statement: This paper is financially supported by Ningxia Key R&D Program (Key) Project (2023BDE02001); Ningxia Key R&D Program (Talent Introduction Special) Project (2022YCZX0013); North Minzu University 2022 School-Level Research Platform “Digital Agriculture Empowering Ningxia Rural Revitalization Innovation Team”, Project Number: 2022PT_S10; Yinchuan City School-Enterprise Joint Innovation Project (2022XQZD009); “Innovation Team for Imaging and Intelligent Information Processing” of the National Ethnic Affairs Commission.

Author Contributions: Study conception and design: Y.Z., Q.Y.; data processing: Y.Z. and L.Z.; draft manuscript preparation: Y.Z., L.Z.; correction of errors and writing instructions: Q.Y.

Availability of Data and Materials: The experimental data used in this study is actual online transaction data from JD.com, which has been anonymized for the purpose of protecting user privacy. Please visit the following link to access the data: https://www.datafountain.cn/competitions/247/datasets.

Conflicts of Interest: The authors declare they have no conflicts of interest to report regarding the present study.

References

1. Liu, X. W. (2022). Research and application of personalized recommendation in e-commerce in the era of big data. The Business Circulate, 23–25. https://doi.org/10.14097/j.cnki.5392/2022.15.014 [Google Scholar] [CrossRef]

2. Roscher, R., Bohn, B., Duarte, M. F., Garcke, J. (2020). Explainable machine learning for scientific insights and discoveries. IEEE Access, 8, 42200–42216. https://doi.org/10.1109/ACCESS.2020.2976199 [Google Scholar] [CrossRef]

3. Liu, D. C., Deng, A. D., Zhao, M., Bian, W. B., Xu, M. (2022). Fault diagnosis method of rotating machinery based on improved deep forest model. Journal of Vibration and Shock, (21), 19–27. https://doi.org/10.13465/j.cnki.jvs.2022.21.003 [Google Scholar] [CrossRef]

4. Zhou, Z. H., Feng, J. (2019). Deep forest. National Science Review, 6(1), 74–86. https://doi.org/10.1093/nsr/nwy108 [Google Scholar] [PubMed] [CrossRef]

5. Fu, H. Y., He, H. (2023). Application of deep forest in user purchase prediction. Computer Applications and Software, (1), 298–305. https://doi.org/10.2969/j.issn.1000-386x.2023.01.046 [Google Scholar] [CrossRef]

6. Ge, S. L., Ye, J., He, M. X. (2019). Prediction model of user purchase behavior based on deep forest. Computer Science, (9), 190–194. https://doi.org/10.11896/j.issn.1002-137X.2019.09.027 [Google Scholar] [CrossRef]

7. Cruz, A. G., Cadena, R. S., Faria, J. A., Oliveira, C. A., Cavalcanti, R. N. et al. (2011). Consumer acceptability and purchase intent of probiotic yoghurt with added glucose oxidase using sensometrics, artificial neural networks and logistic regression. International Journal of Dairy Technology, 64(4), 549–556. https://doi.org/10.1111/j.1471-0307.2011.00722.x [Google Scholar] [CrossRef]

8. Tang, L., Wang, A., Xu, Z., Li, J. (2017). Online-purchasing behavior forecasting with a firefly algorithm-based SVM model considering shopping cart use. Eurasia Journal of Mathematics, Science and Technology Education, 13(12), 7967–7983. https://doi.org/10.12973/ejmste/77906 [Google Scholar] [CrossRef]

9. Hu, X., Yang, Y., Zhu, S., Chen, L. (2020). Research on a hybrid prediction model for purchase behavior based on logistic regression and support vector machine. 2020 3rd International Conference on Artificial Intelligence and Big Data (ICAIBD), pp. 200–204. Chengdu, China, IEEE. https://doi.org/10.1109/ICAIBD49809.2020.9137484 [Google Scholar] [CrossRef]

10. Ghosh, S., Banerjee, C. (2020). A predictive analysis model of customer purchase behavior using modified random forest algorithm in cloud environment. 2020 IEEE 1st International Conference for Convergence in Engineering (ICCE), pp. 239–244. Kolkata, India, IEEE. https://doi.org/10.1109/ICCE50343.2020.9290700 [Google Scholar] [CrossRef]

11. Breiman, L. (1996). Bagging predictors. Machine Learning, 24, 123–140. [Google Scholar]

12. Wang, W., Xiong, W., Wang, J., Tao, L., Li, S. et al. (2023). A user purchase behavior prediction method based on XGBoost. Electronics, 12(9), 2047. https://doi.org/10.3390/electronics12092047 [Google Scholar] [CrossRef]

13. Lu, C. J., Lee, T. S., Lian, C. M. (2012). Sales forecasting for computer wholesalers: A comparison of multivariate adaptive regression splines and artificial neural networks. Decision Support Systems, 54(1), 584–596. https://doi.org/10.1016/j.dss.2012.08.006 [Google Scholar] [CrossRef]

14. Algawiaz, D., Dobbie, G., Alam, S. (2019). Predicting a user’s purchase intention using AdaBoost. 2019 IEEE 14th International Conference on Intelligent Systems and Knowledge Engineering (ISKE), pp. 324–328. Dalian, China, IEEE. https://doi.org/10.1109/ISKE47853.2019.9170316 [Google Scholar] [CrossRef]

15. Cao, W., Wang, K., Gan, H., Yang, M. (2021). User online purchase behavior prediction based on fusion model of CatBoost and Logit. Journal of Physics: Conference Series, 12011. https://doi.org/10.1088/1742-6596/2003/1/012011 [Google Scholar] [CrossRef]

16. Zhao, E., Li, Y., Zhang, J., Li, Z. (2023). Interval prediction model of deformation behavior for dam safety during long-term operation using Bootstrap-GBDT. Structural Control and Health Monitoring, 2023, 1–14. https://doi.org/10.1155/2023/6929861 [Google Scholar] [CrossRef]

17. Grabner, H., Bischof, H. (2006). On-line boosting and vision. 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'06), pp. 260–267. New York, NY, USA, IEEE. https://doi.org/10.1109/CVPR.2006.215 [Google Scholar] [CrossRef]

18. Ye, Z. Y., Feng, A. M., Gao, H. (2019). Customer purchasing power prediction of Google store based on deep LightGBM ensemble learning model. Journal of Computer Applications, 39(12), 3434–3439. https://doi.org/10.11772/j.issn.1001-9081.2019071305 [Google Scholar] [CrossRef]

19. Hu, Y., Qu, B. Y., Liang, J., Wang, J., Wang, Y. L. (2021). A survey on evolutionary ensemble learning algorithm. Chinese Journal of Intelligent Science and Technology, (1), 18–33. https://doi.org/10.11959/j.issn.2096 [Google Scholar] [CrossRef]

20. Li, X., Yu, Q., Yang, Y., Tang, C., Wang, J. (2023). An evolutionary ensemble model based on GA for epidemic transmission prediction. Journal of Intelligent & Fuzzy Systems, 44(5), 7469–7481. https://doi.org/10.3233/JIFS-222683 [Google Scholar] [CrossRef]

21. Storn, R., Price, K. (1997). Differential evolution–A simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 11, 341–359. [Google Scholar]

22. Wen, X., Wu, G., Fan, M., Wang, R., Suganthan, P. N. (2020). Voting-mechanism based ensemble constraint handling technique for real-world single-objective constrained optimization. 2020 IEEE Congress on Evolutionary Computation (CEC), pp. 1–8. Glasgow, UK, IEEE. https://doi.org/10.1109/CEC48606.2020.9185632 [Google Scholar] [CrossRef]

23. Xue, C. G., Yan, X. F. (2018). Software defect prediction based on improved deep forest algorithm. Computer Science, (8), 160–165. https://doi.org/10.11896/j.issn.1002-137X.2018.08.029 [Google Scholar] [CrossRef]

24. MA, L.S. (2022). Study on state evaluation of ship power system based on differential evolution algorithm. Ship Science and Technology, (23), 113–116. https://doi.org/10.3404/j.issn.1672-7649.2022.23.022 [Google Scholar] [CrossRef]

25. Gubin, P. Y., Oboskalov, V. P., Mahnitko, A., Gavrilovs, A. (2020). An investigation into the effectiveness of the differential evolution method for optimal generating units maintenance by EENS criteria. 2020 IEEE 61th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), pp. 1–5. Riga, Latvia, IEEE. https://doi.org/10.1109/RTUCON51174.2020.9316580 [Google Scholar] [CrossRef]

26. Wang, Y., Bi, X., Chen, W., Li, Y., Chen, Q. et al. (2019). Deep forest for radar HRRP recognition. The Journal of Engineering, 2019(21), 8018–8021. https://doi.org/10.1049/joe.2019.0723 [Google Scholar] [CrossRef]

27. Marreddy, M., Oota, S. R., Agarwal, R., Mamidi, R. (2019). Evaluating the combination of word embeddings with mixture of experts and cascading gcforest in identifying sentiment polarity. 25th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (SIGKDD-2019), Anchorage, Alaska, USA. [Google Scholar]

28. Li, Q., Li, W., Wang, J., Cheng, M. (2019). A SQL injection detection method based on adaptive deep forest. IEEE Access, 7, 145385–145394. https://doi.org/10.1109/ACCESS.2019.2944951 [Google Scholar] [CrossRef]

29. Zhou, B. W., GAO, J., Shao, X. (2021). Strong deep forest with circular scanning. Computer Engineering and Applications, (8), 160–168. https://doi.org/10.3778/j.issn.1002 [Google Scholar] [CrossRef]

30. Guo, Y. Y., Zhang, L., Xiao, C., Sun, P. W. (2019). Research on fault diagnosis of wind turbine based on improved deep forest algorithm. Renewable Energy Resources, (11), 1720–1725. https://doi.org/10.13941/j.cnki.21-1469/tk.2019.11.023 [Google Scholar] [CrossRef]

31. Li, X., Yu, Q., Tang, C., Lu, Z., Yang, Y. (2022). Application of feature selection based on multilayer GA in stock prediction. Symmetry, 14(7), 1415. https://doi.org/10.3390/sym14071415 [Google Scholar] [CrossRef]