Transformer-Aided Deep Double Dueling Spatial-Temporal Q-Network for Spatial Crowdsourcing Analysis

1  Introduction

With the development of intelligent transportation, spatial crowdsourcing attracts more and more attention. Various applications of spatial crowdsourcing appear, such as spatial crowd-sensing which may collect and analyze traffic data from edge clients (e.g., vehicles, traffic lights) to help predict and solve traffic jams. Besides, spatial crowdsourcing platforms like DiDi and Uber also utilize edge vehicles to provide intelligent services. For these spatial crowdsourcing applications, how to choose the appropriate crowdsourcing worker is an essential task. Therefore, in this paper, we study how to assign appropriate workers (i.e., spatial vehicles and drivers) for spatial delivery tasks on spatial crowdsourcing platforms by analyzing workers’ historical behavior data.

Similar to traditional crowdsourcing platforms, spatial crowdsourcing platforms comprise three components: the task/request, the worker, and the platform. However, the tasks released on spatial crowdsourcing platforms are spatial tasks with spatio-temporal attributes. Spatial delivery tasks have spatio-temporal constraints, such as start and target locations, start times, and deadlines. A spatial delivery task is completed only if the requester is picked up at the source location within the requested time and successfully delivered to the target location before the deadline. In spatial crowdsourcing platforms, the positions of workers and requesters may change dynamically, especially the spatio-temporal attributes of workers during the completion of tasks are always changing. This paper focuses on common spatial delivery tasks in daily real-time ride-hailing services, such as Uber and DiDi Chuxing.

In terms of spatial delivery task assignment on spatial crowdsourcing platforms, the key is to recommend a suitable task list to workers in a dynamic environment to maximize the benefits of workers, requesters and the platform. Traditional task assignment approaches to spatial crowdsourcing platforms mainly utilize matching approaches. However, with the explosive growth of vehicles in intelligent transportation, task allocation should take into account not only the location matching information but also the workers’ preferences. The preferences of the workers and the requestors have a greater impact on the completion of the task. This can be critical to the user experience in real applications. For instance, DiDi Chuxing needed to serve 25 million ride requests a day and have more than 21 million registered drivers (i.e., workers). Some requesters may choose a female driver for safety, while others may choose a male driver for speed. Some drivers may prefer delivery orders over downtown to get more future orders, while some drivers may prefer orders nearby to avoid traffic jams. In addition, we observed that the preferences of requesters and workers may change over time, making the presetting of preferences is impractical in real-world applications [1–3].

To deal with the complex preferences of requesters and workers, neural networks are utilized to find appropriate task assignments. Shan et al. [4] was a state-of-the-art study that proposed a deep reinforcement learning model to solve the task scheduling problem in traditional non-spatial crowdsourcing platforms. However, task assignment of spatio-temporal delivery tasks is more complex since it is closely related to the spatio-temporal attributes of requesters and workers, and the constraints of task completion are also complex. The deep Q-network in [4] cannot deal with the input types of spatio-temporal tasks and workers well, moreover, it cannot extract the interrelation between workers, tasks, and the workers/requesters’ preferences. As a result, it is impossible to recommend appropriate spatial delivery tasks to spatial crowdsourcing workers, resulting in poor revenue for the entire platform.

In order to apply reinforcement learning models to solve task assignments on spatial crowdsourcing platforms, we refine the deep Q-network model in [4] by revising the architecture of deep Q-Network, including a State Transformer to process spatio-temporal input information. We propose a Double Dueling Deep Spatial Q Network (D3SQN) based on deep reinforcement learning framework specifically for spatio-temporal crowdsourcing task scheduling. In detail, we model the interaction between the spatiotemporal crowdsourcing environment (workers and requests) and the agent (platform) as a new Markov decision process (MDP), taking into account the longitude and latitude information of the task and worker. We apply our proposed D3SQN network to estimate the reward for recommending each task to an upcoming worker. D3SQN takes into account both current and future returns in the online environment, as well as workers’ and requesters’ preferences and how these preferences interrelate with spatio-temporal properties in the task. Applying reinforcement learning models to utilize user preferences in spatial crowdsourcing platforms has not been studied in previous literature, but this information is very important as the completion degree and satisfaction of the next task in the spatio-temporal crowdsourcing scenario are strongly related to it. Our contributions can be summarized as follows:

•   As far as we know, we are the first to apply deep reinforcement learning to assign tasks in spatial crowdsourcing platforms, and our proposed D3SQN can handle both current and future rewards to achieve long-term optimal allocation. In addition, the Q-value is quantified by using the user’s historical behavior, so that the model can reflect the user’s preference adaptively.

•   In addition to using the structure of Double DQN, we also modify the loss function and include a state transformer, which further improves the overall performance.

•   We use real data sets to demonstrate the effectiveness and efficiency of our framework.

2  Related Work

In this section, most related research is discussed.

2.1 Deep Q Networks and Transformer

Deep Q Network (DQN) [5] is a combination of deep learning and reinforcement learning, that is, neural networks are used to replace the Q table in Q-learning. In addition to being widely used in reference scenarios, more and more improved models have been proposed for the defects of DQN [5]. For example, DDQN [6], a target network is added on the basis of DQN, which can reduce overestimation to some extent. D3QN uses Dueling Network [7] architecture on the basis of DDQN. It uses the network to express two estimators, namely the state value function and the action advantage function depending on the state. This factorization generalizes the learning of actions. Rainbow [8] combines 6 extended improvements to the DQN [5] algorithm, including DDQN [6], Dueling DQN [7], Prioritized Boy-Replay [9], Multi-step Learning [10], Distributional RL [11] and Noisy Net [12].

EndToEnd [4] proposed the framework of deep reinforcement learning (RL) for task scheduling, which is a key issue for the success of crowdsourcing platforms. However, the original DQN [5] model is still used in EndToEnd [4], and the original DQN [5] and its variants are not well adapted to the spatio-temporal crowdsourcing problem.

The transformer [13] has excelled in a wide variety of areas, including language modeling [14], summarization [15], question answering [16], and machine translation [17], etc. The transformer has made a significant breakthrough in reinforcement learning (RL) with the work of Parisotto et al. [18]. The GTrxl architecture proposed by this work enables it to learn dependencies beyond a fixed length without breaking the temporal coherence. This allows it to make predictions using current input trajectories plus past trajectories. Not only that, but Transformer-XL introduces a new relative location encoding scheme that not only learns longer term dependencies, but also addresses context fragmentation. However, GTrxl cannot cope well with the input in the spatio-temporal crowdsourcing environment because of the permutation invariance of the input.

2.2 Sptial Crowdsourcing

Spatio-temporal crowdsourcing is a process in which a group of crowdsourcing tasks with spatio-temporal attributes are given to a group of workers. The spatio-temporal attributes of the workers must meet the spatio-temporal constraints of the tasks before they can perform the corresponding tasks. The research on spatial crowdsourcing has been very popular in recent years. Hassan et al. [19] defined an online space task allocation framework based on the formalization of the multi-armed robber problem to solve the online space task allocation problem. Wang et al. [20] designed a new adaptive batch-based constant competitive ratio solution framework to solve the dynamic bipartite graph matching (DBGM) problem. Liu et al. [21] proposed a two-stage solution to the on-demand food delivery problem in FooDNet. Cheng et al. [22] proposed two optimization methods, task-first greed (TPG) and game theory (GT), to solve the cooperative perceptual spatial crowdsourcing (CA-SC) problem. Shan et al. [4] proposed a deep reinforcement learning (RL) task assignment framework and used DQN for task recommendation in traditional non-spatial crowdsourcing platforms. However, their model cannot work well for spatial delivery tasks directly.

In summary, none of the existing models can work well for spatial delivery task assignments. Inspired by the existing literature, we propose a variation of D3QN which applies transformer to reinforce learning to solve spatio-temporal crowdsourcing task assignment problems.

3  Problem

3.1 Problem Summary

The goal of the task scheduling system of spatio-temporal crowdsourcing is to recommend a sorted list of tasks to a coming valid worker. As the platform’s profit model is to complete tasks on commission, the system should satisfy both workers and requesters.

For each worker, as many suitable tasks as possible can be found (within the acceptable time and space of the worker). Requesters expect their tasks to be served as efficiently and comfortably as possible. That is, the task is picked up at the designated location before the expected start time of the task and the task is completed at the destination as early as possible before the specified time.

In addition, since tasks and staff change dynamically, the system should cope with dynamically changed workers’ and requesters’ sets as well as their various and changeable preferences globally in real-time.

3.2 Problem Definition

In this section, we formally define our spatio-temporal crowdsourcing task allocation problem.

In the spatio-temporal crowdsourcing platform, a worker is represented by wi, where i is the moment when the worker goes online. The coordinate of the worker at this moment is Lwi, and the worker can wait for WWi to allocate the task at most. RWi represents the maximum distance radius between the starting coordinate of the worker accepting the task and Lwi. The worker will be marked as invalid while performing the task and will be reset to valid when the task is complete.

Let T=<LSt,LDt,tSTj,tDTj>, denote the task/request that appears on the platform, the start coordinate of the task is LST, the target coordinate is LDT, the expected start time of the task is tST, and the expected arrival time is tDT. The task is completed only when the worker picks up the request on LST and successfully delivers it at a coordinate LDT.

Unlike commercial crowdsourcing, a spatio-temporal crowdsourcing task is considered successful even if the workers take the order after the estimated start time or delays the completion after the estimated completion time, as long as the worker completes the two actions of pick and deliver. However, both late pickup and late delivery will affect the quality of task completion, reducing both requesters’ satisfaction and workers’ reward. Therefore, this paper studies the case of pickup before the expected time. Therefore, the task will only be completed if the worker picks up the request on LST before tST and successfully delivers it at a coordinate LDT before tDT.

In summary, tasks that conform to the following constraints are optional tasks for wi:

•   The task is within the acceptable range of the worker, i.e., distance (LST,Lwi)<Rwi.

•   The task appears before the worker leaves, i.e., i+Wwi>=tST. Workers need to arrive at the starting point to pick up the task before the expected start time of the task, i.e., Costtime(LST,LWi)<=tST.

4  System Overview

We model the task scheduling problem in spatio-temporal crowdsourcing as a reinforcement learning problem. When a spatio-temporal crowdsourcing platform (broker) interacts with requesters and workers (environment), the requester influences the pool of available tasks in the broker by setting the start and end dates and start and end coordinates of tasks, and getting the results of the tasks after the completion of each task. The agent recommends tasks to future workers, and workers influence the agent through the completion of the tasks. Following the end-to-end MDP setting, since workers and requestors have different optimization goals, we use two Markov decision processes (MDP) to optimize workers and requestors separately, and finally combine them together for simultaneous optimization.

For a coming worker wi at timestamp i, his available tasks Ti are obtained. The features of wi and all tasks in Ti constitute the state feature fsi. With fsi, Q-Network(W) and Q-Network(R) compute the Q-values that are aggregated to determine the action ai . ai recommends a sorted list of tasks and the worker selects one accordingly. The action’ s feedback as well as corresponding reward ri are passed to the predictor for future state estimation si+1. Finally, ri , ai , si and si+1 are stored in the Memory for the Learner to train Q-Networks continuously.

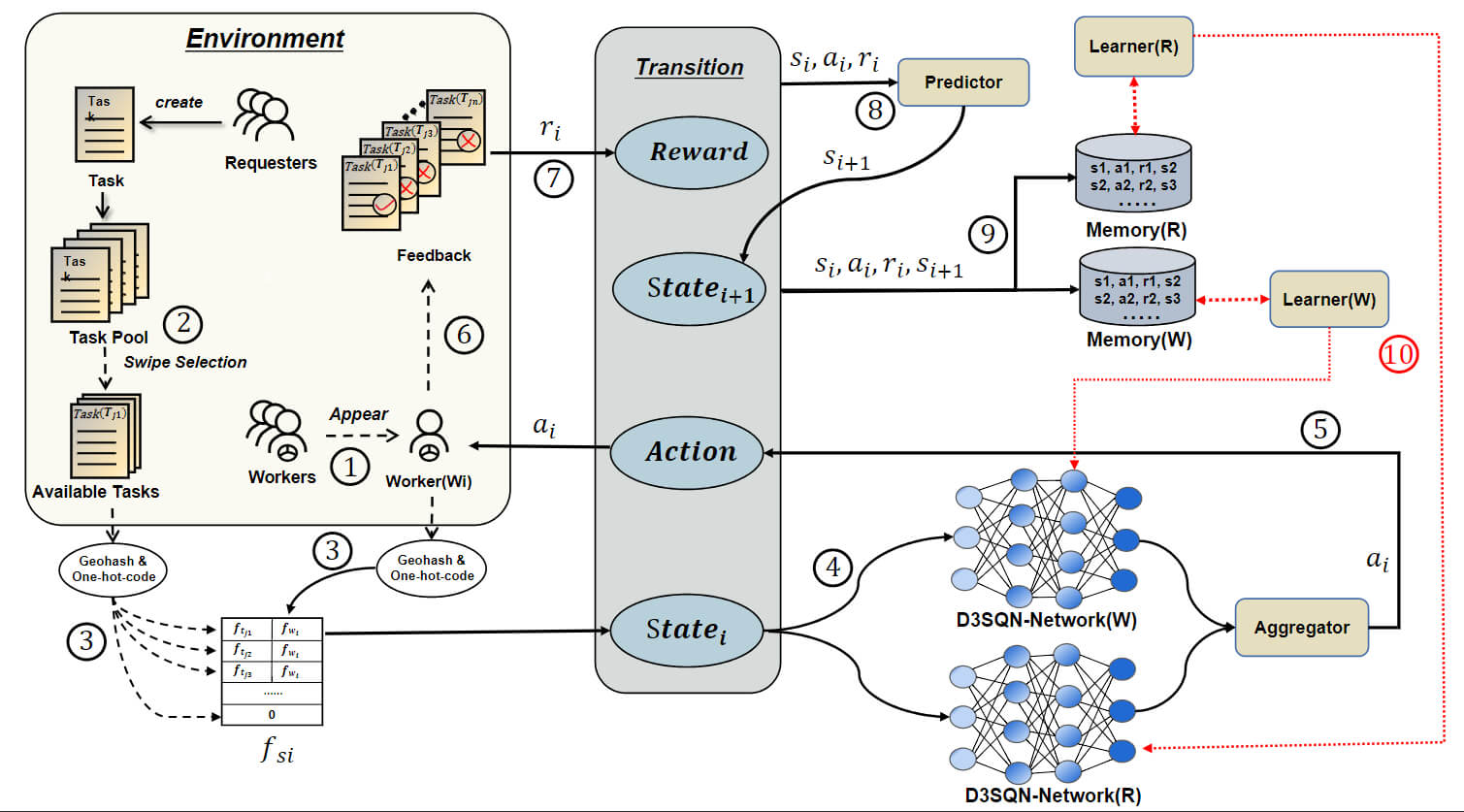
Fig. 1 illustrates the system framework of the overall process. The timestamp i requestor release tasks on the platform. At the moment, a driver wi online platform (Step 1) at the moment. We picked out a set of drivers from the task pools available task T∗, T∗ length less than or equal to maxT, these tasks are according to the above constraints (Step 2). Driver wi features and T∗ ailable in the task of location information by geohash and one-hot coding or word2vec embedding coding, generation task pool each task fTj vector feature vector and the driver’s fwi, connection alignment padding constitutes fsi, which represents the platform of state vector (Step 3). Then, we input fsi into two D3SQN-networks, namely D3SQN-Networks (W) and D3SQN-networks (R). considering the worker's benefit Qw(si,ai) and the requester’s benefit Qr(si,ai), respectively, and predict the Q-value of each possible action ai in state si where ai represents which task the user chooses. Each network outputs a vector of maxT×1, where each value represents the Q value of the corresponding task T (Step 4). According to the aggregator will two network output Qw(si,ai) and Qr(si,ai) polymerization to produce the final task list σwi={Tj1,Tj2,Tj3,…}, the aggregator performs a weighted calculation of the two network output values to balance the workers and requesters, with a default value of 0.5. Corresponding Q(si,Tj∗), ∗ in descending order aggregation scores Q(si,Tj∗) as a recommended list of tasks for the drivers (step 5). When wi sees a sorted task list, we assume that the driver follows a cascade model to view the task list and complete the first task of interest, which is the task with the largest Q-value as the driver’s ai at the moment. The feedback is the completed tasks and the unfinished tasks suggested to wi (Step 6). Then through quantitative feedback rewarded ri (Step 7). The predictor postulates that the outcome of D3SQN determines the ultimate action of the present worker. Subsequently, it constructs the following state, assuming the current sequence is chosen, by aggregating the set of available tasks for the next incoming worker and the relevant details of the next worker, culminating in the formation of the resultant future state si+1 (step 8). Then, we will be successful tuples (si,ai,ri,si+1) in the memory pool, the ai is to complete tasks, and the memory pool is used for storing training data (Step 9). Each time we store an extra tuple into the memory pool, we use learners to update the parameters of the two D3SQN Networks, obtain good estimates of Qw(si,ai) and Qr(si,ai), and derive the optimal strategy (Step 10).

Figure 1: System framework

In the next section, we will introduce the characteristics of these parts of the system in detail. The model is introduced in Section 5.

5  Feature Construction

For Task Tj=<LSTj,LDTj,tSTj,tDTj>, we use fTj=(VLSTj,VLDTj,rTj,ΔtTj,dTj,GTj) represents the eigenvector of task j. Where VLSTj and VLDTj is the GeoHash encoded one pot vector of the starting coordinate and destination coordinate, Δt is the estimated time consumed by the task, GTj is the estimated fuel cost consumed, and dTj is the distance span of the whole task. The formal expression is as follows:

VLSTj=OneHot(GeoHash(LSTj)),VLDTj=OneHot(GeoHash(LDTj)),Δt=tDTj−tSTj

dTj=distance(LSTj,LDTj),GTj=dTj∗G(1)

where G is the average fuel consumption per kilometer.

For worker wi=<Lwi,Rwi,Wwi>, we use fwi=<VLwi,hwi> to represent the feature vector of the worker that goes online on the platform at time i.

where VLwi is the one-hot vector encoded by the GeoHash of the coordinates of worker i, and hwi is the feature vector composed of the historical completed tasks of worker wi. We believe that each worker has its own task preferences, which are often reflected in his past task history. For example, some drivers prefer long journeys. The ratio of time consuming to distance length usually reflects some attributes of the task. For example, long time consuming but short distance is usually in the urban road section with heavy traffic; short time consuming but long distance is usually in the suburban road section of the city, etc. To sum up, we combine the historical task feature vector of workers with the current position vector of workers to represent the feature vector of workers, so as to better capture the preference of workers and the relationship between tasks. The formal expression is as follows:

VLwi=OneHot(GeoHash(Lwi)),hwi=((f1wi⋅γ1+f2wi)⋅γ1…+fmaxT−1wi)⋅γ1+fmaxTwi(2)

where γ1∈[0,1] is the attenuation factor. In order to capture the long-term and short-term preferences of workers, we attenuated the historical task information so that the short-term interest accounted for more and the long-term preferences of workers could also be reflected.

When the wi online platform seeks for task orders at time i, the system will select the available task list for the wi according to the constraints in Section 3.2. Then, the feature vectors of the tasks in the available list and the feature vectors of the workers are concatenated to obtain the feature representation vector fsi of the state at time i. Since the number of available tasks varies at different timestamps, we set the maximum number of available tasks maxT and use zero padding, that is, adding zero to the end of fsi, so that each fsi is denoted as: [maxT,|fTjn|+|fwi|], where Tjn⊆σ(wi), which σ(wi) is wi available task set.

6  Double Dueling Deep Spatial Q Network (D3SQN)

In this section, we introduce our proposed Q-learning-based deep reinforcement learning network model specifically for spatio-temporal crowdsourcing.

As shown in Fig. 2, based on the system state vector fsi at time i, the optimal allocation of spatiotemporal tasks is achieved through D3SQN. Specifically, this model uses the architecture of Dueling Network and two Spatial State Transformers to respectively predict the State Q-value and the dominant feature vector composed of the advantages of each action. Finally, Vsi and Va are spliced into the final action value vector VQa.

Figure 2: Double dueling deep spatial Q network (D3SQN) framework and details. (a) shows the framework of D3SQN. The network architecture is divided into two parts: the upper spatial state transformer used to predict the action advantage value Va and the lower spatial state transformer used to predict the state value Qsi. (b) shows the specific details of the encoder and decoder of the spatial state transformer

Different from the traditional DQN, the states that need to be processed by our proposed D3SQN are significantly different from the traditional DQN network under spatio-temporal crowdsourcing.

Most of the traditional DQN, including its variants, are suitable for the input of temporal or sequentially related feature vectors. For example, in a game scenario, the representation of state may be a vector matrix of continuous pictures, and the sorting of these pictures and the distribution of pixels inside the pictures are fixed. Once the distribution of these pixels changes, the prediction results of the network will be affected. However, in our spatial crowdsourcing environment, the representation of the state is the connection of a string of available lists and worker feature vectors, which is a set feature. The sorting order of these available lists will not affect the result of the final predicted action. It is difficult for traditional DQN and DQN variants to mine and learn the complex and dynamic spatio-temporal correlations in such permutation invariant inputs. Because this permutation invariant set feature is a global feature, the ability of CNN or traditional neural network architecture to extract local structural features limits the extraction ability of such global high-dimensional features. The spatial state Transformer is better able to handle high-dimensional and global information, mainly because the structure of the Transformer itself is better suited to extract this information. Therefore, this paper proposes Spatial State Transformer, a new deep reinforcement learning network model for spatial-temporal crowdsourcing. It will not affect the result of prediction even if he faces the state vector with a changed order.

We use the structure of Double DQN and Dueling Network to alleviate the overestimation problem in Q-learning. Next, we will introduce the details and functions of Dueling Network and Spatial State Transformer, respectively.

6.1 Dueling Network

When we recommend a task set to a worker, the tasks in the optional task set are all the tasks that the worker may take orders from next, and each task represents an action. When there are several actions with multiple redundant or approximately equal Q-values, the original network will prefer to choose the first task, but in fact, different actions will lead to different states, and we may not be able to jump out of the optimal action under the current state, so the structure of Dueling network is adopted. Instead of relying solely on the value of the action, the state can make a separate value prediction. The performance of the network model is better.

Using the structure of Dueling Network, the original direct predictive action value is divided into predictive state value and dominant value of each action. This effectively avoids the original over-estimation problem of Q-learning. The traditional network of DQN is approximate Q∗(s,a)=maxπQπ(s,a) by network, which represents the value function of optimal action a under strategy π and state s. The architecture of Dueling Network is to separate State from action to a certain extent, which is formalized as follows:

Q∗(s,a)=A∗(s,a)+V∗(s,a),V∗(s,a)=maxπVπ(s)=maxπQ∗(s,a),

A∗(s,a)=Q∗(s,a)−V∗(s),maxaA∗(s,a)=maxaQ∗(s,a)−V∗(s)=0(3)

As can be seen in Fig. 2a, the Dueling Network in our proposed D3SQN consists of two Spatial State Transformer, which are formalized as follows:

A∗(s,a)=SpatialStateTransformerQ(fsi),V∗(s,a)=SpatialStateTransformerAdvantage(fsi)maxaQ∗(s,a)=maxaA∗(s,a)+V∗(s)(4)

6.2 Spatial State Transformer

In this section, we introduce the spatial state Transformer: an attention-based neural network for processing state vectors under spatial crowdsourcing.

As shown in Fig. 2a, Spatial State Transformer consists of EnCoder and DeCoder, our motivation for designing the spatial state converter is that self-attention allows the extraction of key global associations in the collection data, as well as spatio-temporal information associations. This makes the spatial state converter a more effective and efficient way to encode the entire collection simultaneously. At the same time, our model needs to extract high-level feature representations in order to use the self-attention mechanism to extract associations between information, which is why our model is designed as Encoder and Decoder architecture. Encoder and Decoder are the attention-based spatial set operation modules defined by us. The main purpose of the encoder is to represent permutation invariant state inputs, encoding independently a set of tasks of available size and each element fwi. The decoder aggregates these encoding features fmsi and uses self-attention mechanism to extract associations between high-level representations. All the blocks described here are neural network blocks with their own parameters, not fixed functions.

We made improvements by referring to the structure of SetTransformer, without retaining the original pooling operation, and made improvements in EnCoder and DeCoder modules suitable for reinforcement learning, We tune the layerNorm layer after the feature input, instead of before the feature input as the Transformer usually does and replace the general residual connection with GatingLayer. In this way, the learning and training of Transformer structure in RL can be stabilized. We use this structure of SetTransformer, but do not retain the pooling operation, because the pooling operation in SetTransformer aims to extract the correlation between features from multiple dimensions. However, the state expression of spatio-temporal crowdsourcing is different from 3D data, which is three-dimensional collection data strongly correlated among multiple dimensions. The previous SetTransformer architecture is mainly aimed at such low-latitude replacement and unchanged collection data. What we need to mine is the relationship between the features of each element in each list (including task and worker address information), so it is counterproductive to try to improve the dimension to learn. We only need to use the feature expression proposed by Encoder and use Decoder to aggregate and finally get the prediction result.

In the remainder of this section, we’ll describe the details of individual modules.

DeCoder: As seen in Fig. 2b, the Decoder module is designed to extract various aspects of spatio-temporal features fmsi obtained from the Encoder through self-attention. By stacking multiple Decoders, we can extract deeper spatio-temporal interaction information from the input set. The decoder structure includes layer normalization, multi-head self-attention, and a gating layer. We also use an identity map reordering technique inspired by GTrxl [18] to facilitate policy optimization, which is used to help with policy optimization by initializing the agent in a manner that is similar to a Markov policy/value function.

Identity Map Reordering: We applied a modification called Identity Map Reordering to the Spatial Temporal Transformer, inspired by the GTrxl [18] design. This involved rearranging the order of Layer Norm and applying ReLU activation to the output of each submodule before joining with the residual connection. This reordering enables an identity mapping from the input of the Transformer at the first layer to the output at the last layer, which facilitates policy optimization in reinforcement learning. Specifically, this allows the agent to learn reactive actions first before focusing on memory-based behavior. In the spatio-temporal crowdsourcing environment, this also allows the agent to learn to select actions before using memory, even if the experience has not yet entered the memory. This modification improves the efficiency of learning and enables the agent to effectively utilize memory to improve performance.

Gated-Recurrent-Unit-Type Gating: We use an explicit initialization of the GRU gating mechanism to approach the identity map. Gated recursive unit (GRU) is a recursive network, which behaves like LSTM, but with fewer parameters. The formalization is as follows:

r=σ(Wry+Urx),z=σ(Wzy+Uzx−bg),h=tanh(Wgy+Ug(r)∗x)

GatingLayer(x,y)=(1−z)∗x+z∗h(5)

where bg is the bias in the applicable gating layer. Initially setup bg>0 can greatly improve the learning speed.

Encoder: The Decoder architecture in the Spatial State Transformer eliminates position encoding, enabling the network to extract mutual relationships between sets in the state embedding. However, using the Decoder directly can result in quadratic time complexity, which is not practical for large-scale set-structured datasets. To address this issue, we introduce trainable inducing points I into the Encoder architecture, which reduces the time complexity. An Encoder with m inducing points I is defined as follows:

G3=GatingLayer(MultiHead(I,LayerNorm(X),LayerNorm(X);w),X)∈Rnd

G2=GatingLayer(G3,rFF(LayerNorm(G3)))∈Rnd

G1=GatingLayer(MultiHead(X,LayerNorm(G2),LayerNorm(G2);w),G2)∈Rnd

Encoderm(X):=GatingLayer(G1,rFF(LayerNorm(G1)))∈Rnd(6)

Encoder first converts I through multi-head processing of input set, and then enters GRU processing through input set X, and finally generates a set containing N elements.

The Encoder's objective is to extract a high-dimensional representation of the set state while mitigating the computational complexity resulting from the set’s size. In this study, the Encoder is responsible for extracting an attention-based spatio-temporal state embedding representation, which serves as a basis for discerning the spatio-temporal relationships between Workers and Requesters. Attention is computed between sets of size m and n, with the Encoder’s time complexity being O(mn), a substantial improvement over the quadratic complexity of the Decoder. Both set operations (Encoder and Decoder) are permutation invariant.

Loss Function: we adopt a recently developed loss function, DQNReg, which is inspired by earlier researches [23–27]. The formula for DQNReg is presented below:

Yt=rt+γ∗maxaQtrag(st,a),δ=Q(st,at)−Yt,LDQNReg=k∗Q(st,at)+δ2(7)

The first term of the loss function introduces regularization by multiplying Q-values with an adjustable weighted term, which helps to alleviate overestimation of Q-values. The second term encourages Q-values to approach target Q-values. DQNReg effectively prevents overestimation by directly regularizing Q-values with a weighted term that is always active. The adjustable weighted term in the loss function is set to 0.1 in the experiment.

7  Experiment

7.1 Experimental Setup

Dataset: We conducted experiments on two real-world datasets, collected by DiDi Chuxing in Xi’an, China, the DiDi dataset released through its GAIA initiative, and the dataset from ELM released by Tianchi. Each piece of DiDi’s dataset contains drivers’ ID, task ID, timestamp, longitude and latitude. From this data, we can get information about each task and worker. For our experiment, we utilized a sample of 80,000 orders that were recorded continuously throughout October 2016 in the didi dataset [28]. We obtained the ELM dataset [29] which contains identical information and used the same methodology to acquire an equivalent amount of data. The ELM and DiDi datasets contain different numbers of workers because the average completion time per order on the ELM platform, which is a food delivery service, is much smaller than that of taxis. Therefore, the difference in the number of workers required for the same number of orders is significant. As shown in Table 1, the ELM dataset of 80,000 orders only has 857 workers, while DiDi has 15,367 workers.

Settings: Over time, we will resume the process of staff arrival, task creation, or task expiration. The collected dataset records each timestamp I at which a worker wi starts a task, and we assume that a start corresponds to a worker arrival and that the tasks completed by workers in the dataset are considered interesting. Since we do not know the available task list information that the platform assigns to the wi when it arrives, we cannot use the tasks completed by the wi in the original data set as our target for predicting success. Therefore, when wi arrives, we will use the completed orders of a worker in the real data as the workers' preference and match a target task ttargetw from the current available event pool based on this preference. Considering the interests of workers, if the recommended task is ttargetw, then the reward/label (for reinforcement/supervised learning) is 1. For the benefit of requesters, the reward/tag is the quality gain of tj. And the final reward will be the sum of the ratio of the workers and requesters, in our experiment, this ratio is split equally between the workers and requesters.

Evaluation Measures: Considering that we are recommending a task or a list of tasks, we use CR and nDCG-CR as the metrics:

CR=∑jRjnumberofcompletedtasks,nDCG−CR=∑j∑r=1Nyjrlog2(1+r)numberofcompletedtasks(8)

•   CR: Worker Completion Rate (CR). When the workeri arrives at timestamp i, the agent recommends a task. If the task is the same as the one actually selected by workeri, Rj is 1, otherwise 0.

•   nDCG-CR: Normalized Discount Cumulative Gain. Instead of one task, the agent recommends a list of tasks. nDCGCR is more suitable for evaluating the recommended list σwi={Tj1,Tj2,Tj3,…}. r is the rank position of tasks in the list, N is the number of available tasks when the workeri arrives. If the r(Tjn) is the same as the one actually selected by the workeri , yjr= 0 is 1, otherwise 0.

Competitors: We compare our method with three alternatives to reinforcement learning, namely DDQN, D3QN, and EndToEnd. All these methods are trained on real datasets, and the characteristics of workers and tasks are updated in real time. By aggregating the Q-values of the predicted tasks relative to the worker and the request, an available task is selected or the available tasks are ranked according to the aggregated Q-values. The model updates the parameters in real time after each recommendation.

•   DDQN [6]: Double DQN is the deep Learning realization of Double Q-learning, and uses Target network to reduce the overestimation problem in Q-learning. The training is based on the parameters of the current Q network, rather than the parameters of target-Q as in DQN. In this way, overestimation is reduced to a certain extent, so that the Q-value is closer to the real value.

•   D3QN [7]: Dueling Double Network, using dominance function to further solve the overestimation problem. Dueling DQN can estimate Q-value more accurately and select more appropriate actions after collecting data of only one discrete action. Double DQN, selects the target Q-value by the action of the target Q-value selection, thereby eliminating the problem of overestimating the Q-value. D3QN combines the advantages of Dueling DQN and Double DQN.

•   EndToEnd [4] proposes a DQN network model with permutation invariant input property, which is suitable for a commercial crowdsourcing environment, and depends on the previous task allocation model in the end-to-end crowdsourcing reinforcement learning framework.

7.2 Experimental Results

In this section, we depict the experimental results of D3SQN in terms of both effectiveness and efficiency.

Implementation Details: Our model consists of two D3SQNs, and after experimental evaluation, the number of neurons in each layer of D3SQN is set to 128. Moreover, for other hyper-parameters in D3SQN, we set target Q update frequency as 50, learning rate as 0.001, buffer size as 1200, discount factor Gamma as 0.35 and batch size as 128. We used PyTorch to implement the entire algorithm, and the code ran on a GeForce GTX 2080 TI GPU. We use the definition in Sections 4 and 7.1 to construct the environment, action, state, and reward necessary for reinforcement learning, and our model learns spatio-temporal crowdsourced task allocation strategies within this framework. The number of layers of our encoder layer and decoder layer is the same as that of EndToEnd [4], and the complexity of our model is on the same order of magnitude as that of endtoend in terms of neuron parameters.

Effectiveness: In Section 3, we constructed two D3SQNs, namely D3SQN(R) and D3SQN(W), for requesters and workers, respectively, and evaluated their benefits along with the aggregated balance in our experiment. We presented the CR, CR(W), CR(R), nDCG, nDCG(W), and nDCG(R) measures for each method and dataset in Fig. 3. CR(W) and CR(R) denote the proportion of maximum Q-values chosen by the two sub-networks of D3SQN that align with the final target. Similarly, nDCG(W) and nDCG(R) have the same interpretation. To account for both workers and requesters, we employed a ratio of 1:1 to aggregate the Q-values computed by the two sub-networks. This approach ensures that the workers and requesters contributions to the overall reward are equally weighted.

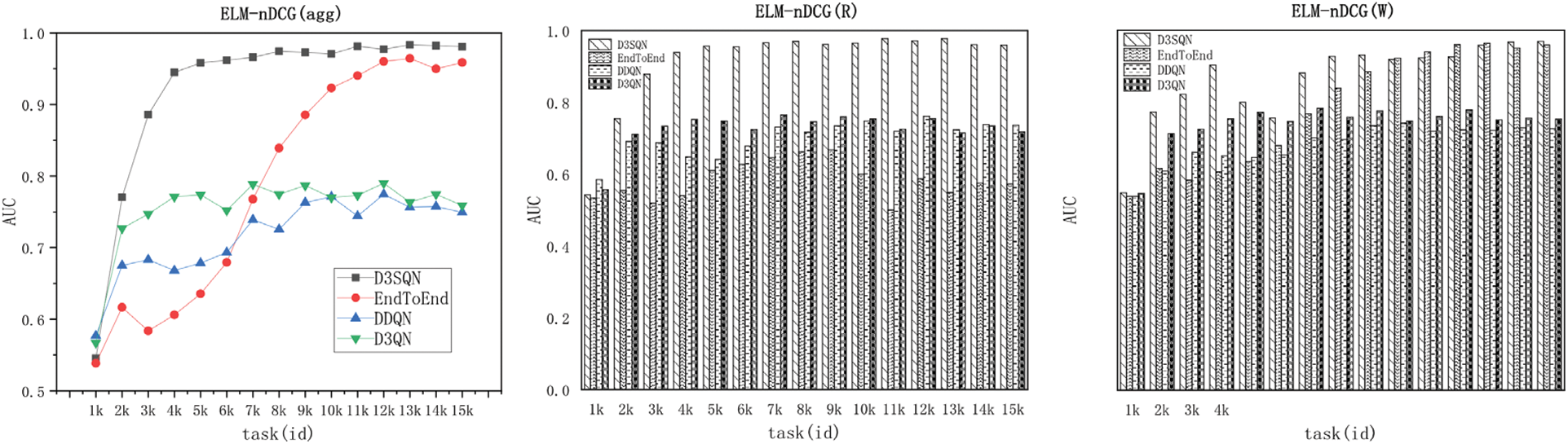
Figure 3: Benefits of workers & requesters

The results, as depicted in Fig. 3, demonstrate that D3SQN outperforms all competitors in terms of aggregated CR and aggregated nDCG-CR for both datasets. In contrast, DDQN performs poorly because it ignores the preferences of requesters and workers. Additionally, neither DDQN nor D3QN can handle permutation-invariant feature inputs, which leads to suboptimal performance.

The D3SQN algorithm demonstrates superior performance in CR(W) and nDCG-CR (W) compared to the End-to-End method due to its consideration of spatio-temporal constraints and features. Our model outperforms all other competitors in both datasets. However, in terms of CR(R) and nDCG-CR (R), our model surpasses all competitors in the ELM dataset, performs better than most competitors in the DiDi's dataset, and slightly lags behind the End-to-End method. This is attributed to our model's attention to spatio-temporal attributes, which gives more weight to workers in each task’s spatio-temporal attributes. In datasets with relatively less user data, our model prioritizes the weight associated with learning workers, resulting in the best aggregation effect. Moreover, our model exhibits exceptional efficiency, achieving the fastest convergence rate and outperforming all metrics in both datasets.

7.3 Ablation Study

In this section, we will test the effect of each Module, we will test the SetTranformer architecture, GatingLayer & Identity Map Reordering and Dueling Network architecture in D3SQN.

As shown in Fig. 4, removing each improvement from the model reduces the prediction of the model. Especially when the SetTransformer structure is removed, the prediction effect of the model decreases most obviously. This is because the SetTransformer structure learns the worker preferences of all the training samples and is not affected by the variable task order.

Figure 4: Ablation experiments with different point

However, removing the GatingLayer & Identity Map Reordering significantly decreases the performance of the model, as the absence of the identity mapping makes it harder for the transformer architecture to learn memory-based policies in complex feature representations within the RL environment. In addition, removing the Dueling structure slows down the training process since the Dueling network architecture allows for feature sharing between different actions, which accelerates the learning process.

7.4 Limitations

Our experiments still have some limitations. For instance, there are too few open source spatio-temporal crowdsourcing datasets for us to verify the generalization of our model on more datasets, which may limit the generalizability of our proposed model to other platforms. However, we believe that the data from these two platforms (DiDi and ELM) are representative of a significant portion of the spatial crowdsourcing platforms, as they are widely used in the transportation industry. Secondly, our data set comes from the desensitization data of some crowdsourcing platforms, which lack more information of users and order feedback. The influence of this part of real information on the verification of the model effect also increases the limitation of our experiment.

8  Conclusion

This study proposed a deep reinforcement learning framework network D3SQN for spatial delivery task assignment in spatial edge intelligence platforms. It considered the critical role of spatio-temporal attributes in task assignment, and the spatio-temporal preferences of workers and requesters with respect to published tasks to facilitate better task assignment. The spatial temporal transformer proposed herein can effectively extract the interchangeable spatial-temporal state vector, and excavate the complex deep relationship between spatial-temporal attributes, workers and requesters in the task. This enables D3SQN to achieve optimal assignment in dynamic spatio-temporal crowdsourcing scenarios. The experimental results show that D3SQN provides effective and efficient assignment performance.

Acknowledgement: We would like to thank Dr. Caihua Shan for sharing her code and data with us.

Funding Statement: This work was supported in part by the Pioneer and Leading Goose R&D Program of Zhejiang Province under Grant 2022C01083 (Dr. Yu Li, https://zjnsf.kjt.zj.gov.cn/), Pioneer and Leading Goose R&D Program of Zhejiang Province under Grant 2023C01217 (Dr. Yu Li, https://zjnsf.kjt.zj.gov.cn/).

Author Contributions: Study conception and design: Yu Li, Mingxiao Li; data collection: Yu Li, Mingxiao Li; analysis and interpretation of results: Yu Li, Mingxiao Li, Dongyang Ou; draft manuscript preparation: Mingxiao Li, Junjie Guo, Pangyuan Fan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Our data access link is placed in the citation, and we access the data from the link in the citation; we are not the direct data publisher.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Rani, S., Kumar, M. (2022). Ranking community detection algorithms for complex social networks using multilayer network design approach. International Journal of Web Information Systems, 18(5/6), 310–341. [Google Scholar]

2. Nafea, I. T. (2021). Simulation of crowd management using deep learning algorithm. International Journal of Web Information Systems, 17(4), 321–332. [Google Scholar]

3. Silva, L., Silva, N. F., Rosa, T. (2020). Success prediction of crowdfunding campaigns: A two-phase modeling. International Journal of Web Information Systems, 16(4), 387–412. [Google Scholar]

4. Shan, C., Mamoulis, N., Cheng, R., Li, G., Li, X. et al. (2020). An end-to-end deep RL framework for task arrangement in crowdsourcing platforms. Proceedings of the IEEE 36th International Conference on Data Engineering (ICDE), pp. 49–60. Dallas, TX, USA. [Google Scholar]

5. Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J. et al. (2015). Human-level control through deep reinforcement learning. Nature, 518(7540), 529–533. [Google Scholar] [PubMed]

6. Wang, Z., Schaul, T., Hessel, M., van Hasselt, H.,, Lanctot, M. et al. (2016). Dueling network architectures for deep reinforcement learning. Proceedings of the 33rd International Conference on Machine Learning, vol. 48, pp. 1995–2003. New York, USA. [Google Scholar]

7. van Hasselt, H., Guez, A., Silver, D. (2016). Deep reinforcement learning with double Q-learning. Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, pp. 2094–2100. Phoenix, Arizona, USA. [Google Scholar]

8. Hessel, M., Modayil, J., van Hasselt, H., Schaul, T., Ostrovski, G. et al. (2018). Rainbow: Combining improvements in deep reinforcement learning. Proceedings of AAAI'18/IAAI'18/EAAI'18, pp. 393–400. New Orleans, USA. [Google Scholar]

9. Schaul, T., Quan, J., Antonoglou, I., Silver, D. (2016). Prioritized experience replay. Proceedings of the 4th International Conference on Learning Representations, pp. 322–355. San Juan, Puerto Rico. [Google Scholar]

10. de Asis, K., Hernandez-Garcia, J., Holland, G., Sutton, R. (2018). Multi-step reinforcement learning: A unifying algorithm. AAAI, pp. 1–7. New Orleans, Louisiana, USA. [Google Scholar]

11. Bellemare, M. G., Dabney, W., Munos, R. (2017). A distributional perspective on reinforcement learning. Proceedings of the 34th International Conference on Machine Learning, pp. 449–458. Sydney, Australia. [Google Scholar]

12. Fortunato, M., Azar, M. G., Piot, B., Menick, J., Hessel, M. et al. (2018). Noisy networks for exploration. Proceedings of the 6th International Conference on Learning Representations, pp. 1–13. Vancouver, British Columbia, Canada. [Google Scholar]

13. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L. et al. (2017). Attention is all you need. Proceedings of the 31st International Conference on Neural Information Processing Systems, pp. 6000–6010. Long Beach, California, USA. [Google Scholar]

14. Dai, Z., Yang, Z., Yang, Y., Carbonell, J. G., Le, Q. V. et al. (2019). Transformer-XL: Attentive language models beyond a fixed-length context. Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pp. 2978–2988. Florence, Italy. [Google Scholar]

15. Liu, Y., Lapata, M. (2019). Text summarization with pretrained encoders. Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), pp. 3730–3740. Hong Kong, China. [Google Scholar]

16. Herrmann, J., Bierbuesse, D., Negra, R. (2018). Universal model for millimeter-wave integrated transformers. 15th International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design (SMACD), pp. 197–200. Prague, Czech Republic. [Google Scholar]

17. Yang, Z., Dai, Z., Yang, Y., Carbonell, J., Salakhutdinov, R. et al. (2019). XLNet: Generalized autoregressive pretraining for language understanding. Proceedings of the 33rd International Conference on Neural Information Processing Systems, pp. 5753–5763. New York, USA, Curran Associates Inc. [Google Scholar]

18. Parisotto, E., Song, F., Rae, J., Pascanu, R., Gulcehre, C. et al. (2020). Stabilizing transformers for reinforcement learning. Proceedings of the 37th International Conference on Machine Learning, pp. 7487–7498. [Google Scholar]

19. Hassan, U. U., Curry, E. (2014). A multi-armed bandit approach to online spatial task assignment. Proceedings of the 2014 IEEE 11th International Conference on Ubiquitous Intelligence and Computing and 2014 IEEE 11th International Conference on Autonomic and Trusted Computing and 2014 IEEE 14th International Conference on Scalable Computing and Communications and its Associated Workshops, pp. 212–219. Ayodya Resort, Bali, Indonesia. [Google Scholar]

20. Wang, Y., Tong, Y., Long, C., Xu, P., Xu, K. et al. (2019). Adaptive dynamic bipartite graph matching: A reinforcement learning approach. 2019 IEEE 35th International Conference on Data Engineering (ICDE), pp. 1478–1489. Macao, China. [Google Scholar]

21. Liu, Y., Guo, B., Chen, C., Du, H., Yu, Z. et al. (2019). FooDNet: Toward an optimized food delivery network based on spatial crowdsourcing. IEEE Transactions on Mobile Computing, 18(6), 1288–1301. [Google Scholar]

22. Cheng, P., Chen, L., Ye, J. (2019). Cooperation-aware task assignment in spatial crowdsourcing. Proceedings of the 2019 IEEE 35th International Conference on Data Engineering (ICDE), pp. 1442–1453. Macao, China. [Google Scholar]

23. Co-Reyes, J. D., Miao, Y., Peng, D., Real, E., Levine, S. et al. (2022). Evolving reinforcement learning algorithms. arXiv:2101.03958. [Google Scholar]

24. Gao, H., Liu, L., Liu, K., Yang, Y. (2022). The joint method of triple attention and novel loss function for entity relation extraction in small data-driven computational social systems. IEEE Transactions on Computational Social Systems, 9(6), 1725–1735. [Google Scholar]

25. Gao, H., Qiu, B., Barroso, R. J. D., Hussain, W., Xu, Y. et al. (2023). TSMAE: A novel anomaly detection approach for Internet of Things time series data using memory-augmented autoencoder. IEEE Transactions on Network Science and Engineering, 10(5), 2978–2990. [Google Scholar]

26. Gao, H., Dai, B., Miao, H., Yang, X., Barroso, R. J. D. et al. (2023). A novel GAPG approach to automatic property generation for formal verification: The GAN perspective. ACM Transactions on Multimedia Computing, Communications, and Applications, 19(1), 16. [Google Scholar]

27. Gao, H., Wang, X., Wei, W., Al-Dulaimi, A., Xu, Y. (2023). Com-DDPG: Task offloading based on multiagent reinforcement learning for information-communication-enhanced mobile edge computing in the internet of vehicles. IEEE Transactions on Vehicular Technology, 1–14. https://ieeexplore.ieee.org/document/10233027 (accessed on 20/10/2020) [Google Scholar]

28. GAIA (2020). https://huggingface.co/datasets/seablue/DiDi_GAIA_dataset (accessed on 20/10/2020) [Google Scholar]

29. Elmme (2022). https://tianchi.aliyun.com/competition/entrance/231777/information (accessed on 20/10/2020) [Google Scholar]