Deep Global Multiple-Scale and Local Patches Attention Dual-Branch Network for Pose-Invariant Facial Expression Recognition

1  Introduction

Facial expressions, as the most intuitive signals for conveying human inner thoughts and psychological states, have attracted considerable interest in human-computer interaction (HCI), such as driver safety [1], entertainment services [2,3], and facial expression recognition [4,5]. Over the past few years, many feasible and effective techniques have been reported for frontal or nearly frontal FER. Nevertheless, in real-life scenarios, the collected emotional images are often determined by the position of the capture device. When the head-pose turns away, the performances of the frontal parameter model cannot achieve satisfactory recognition results in non-frontal views. Psychological experiments have also shown that even with a 15° head pose change, the analysis and prediction of emotions will be affected conspicuously [4]. Consequently, there is a growing need to develop a way to improve the identification results among different observation angles effectively.

In the past few decades, some researchers attempted to crop facial images into small patches or extract critical patches from regions of interest (ROIs) to minimize the impact of pose variation and self-occlusion on expression recognition. Moore et al. [4] split facial images into 8×8 uniform sub-patches and extracted local binary patterns (LBP) to represent emotional features. Subsequently, these extracted features are integrated into a feature vector used for multi-view FER. Li et al. [5] divided facial images into five kinds of strategies, including two regular patches (6×6, 8×8) and three irregular patches (6×5, 8×5, and 8×7), to explore the effect of patch size on recognition accuracy. In addition, Hu et al. [6] developed a multi-view landmark-patches cropping model and extracted local binary pattern (LBP) for multi-view FER. Zhang et al. [7] utilized the active appearance model (AAM) to capture a group of critical patches from dissimilar observation angles and then learned a mixed model combining landmark and texture features for pose-robust expression recognition. Happy et al. [8] extracted 19 critical patches surrounding eyes, nose, and mouth regions to represent facial expressions and then extracted LBP features for pose-invariant FER. Wu et al. [9] introduced a locality-constrained linear coding-based bi-layer (LLCBL) model for multi-view FER, which first derived scale-invariant feature transform (SIFT) features from a sequence of crucial feature blocks and then trained a bag-of-feature model using locality constrained coding techniques for pose estimation and expression recognition.

As deep convolutional neural networks (DCNNs) have advanced speedily in recent years, some scholars indicated that using multi-model and multi-channel methods can effectively increase the performance of pose variation and self-occlusion FER. As illustrated in Fig. 1, in Liu et al. [10], a deep dynamic multi-branch metric network (DML-Net) is designed for pose-aware and identity-invariant FER, where branch-M1, branch-M2, and branch-M3 are developed to extract features from global, eyes and mouth regions separately. Afterward, the extracted features are merged for expression recognition. Similarly, in Fan et al. [11], facial images are divided into 3×1 local patches along with a horizontal spatial axis. Subsequently, three parallel CNNs are utilized to extract semantic features from the local patches, and then different prediction scores from each sub-CNN are integrated to improve the final recognition accuracy. Liu et al. [12] presented a multi-branch pose-aware convolution neural network (MPCNN) for pose-invariant FER, where MPCNN is composed of three sub-CNNs, learning salient features from local patches and then integrated them for FER. Zhang et al. [13] also introduced a deep dual-channel network to extract global and local facial features and employed constant loss weighting parameters to increase identification accuracy. Zheng et al. [14] inserted the adaptive dynamic weight (ADW) model into three branches to shrink salient features, enhancing multi-branch networks' representational power and lowering the overfitting probability.

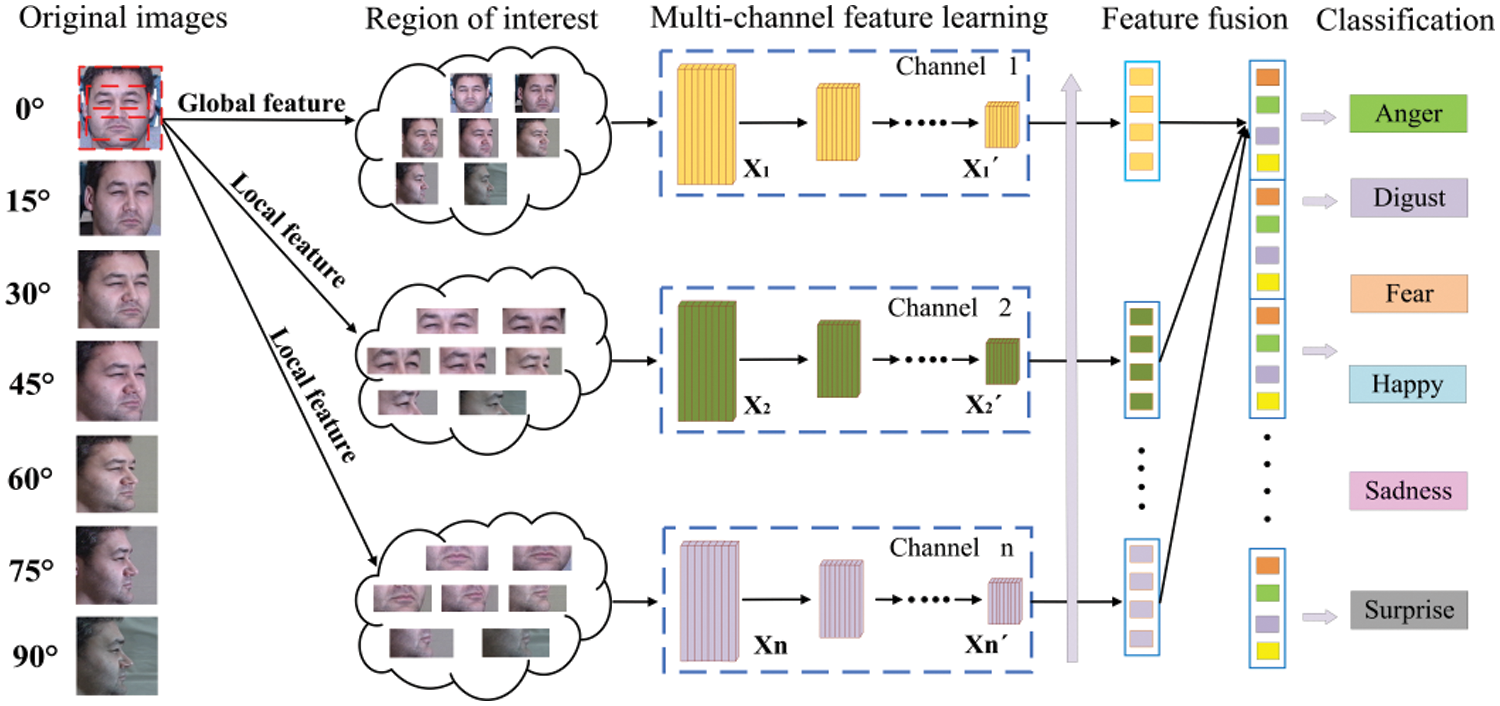
Figure 1: The structure of multi-branch networks for pose-invariant FER

Despite promising performance has been materialized in previous studies, these techniques still have some shortcomings. For instance, most traditional-based methods require manually cropped facial images before feature extraction, which usually increases the difficulty of feature extraction and limits the construction of an automatic emotion classification system. In addition, simply using local patches while ignoring global features cannot precisely and completely convey the initial meanings of emotions. The multi-branch features learning approach displays remarkable advantages in multi-view FER for deep learning-based methods. However, the deeper convolution layer is usually susceptible to pose variation and self-occluded scenarios, especially with the enlargement of the receptive field, which usually elevates the sensitivity of the deep CNN in multi-view FER. Additionally, multi-branch feature learning methods often require several pre-trained models from diverse regions of interest (ROIs). Each branch will have a corresponding loss function, increasing the computational amount and making the network structure more complex in practical applications.

Accordingly, this study proposes a deep global multiple-scale (GMS) and local patches attention (LPA) dual-branch network for pose-invariant FER. For the conventional DCNNs, the deeper convolution layer contains a larger receptive field and richer texture features, while the shallow convolution layer usually includes a narrow receptive field and richer geometry features [15]. The wider receptive field in the deeper convolution layer is susceptible to pose variation and self-occlusion, whereas incorporating shallow geometric features can effectively lower sensitivity. In such cases, deep convolutional neural networks can learn more comprehensive features. Multiple-scale feature learning is a feasible method to extract multi-level semantic information from a shallower convolutional layer, which can effectively heighten the robustness and diversity of the global receptive field. Motivated by Res2Net [16], an improved symmetrical multiple-scale is adopted to acquire global features within a basic residual unit. Meanwhile, the features extracted from local patches are crucial to cope well with the issues of pose variation and self-occlusion. Therefore, the local patches attention (LPA) model is developed to extract local salient features, reducing the influence of self-occlusion and non-frontal pose situations. Notably, the LPA model does not require pre-segmentation or pre-labeling to acquire local facial patterns, which is simpler but more efficient than early studies. The primary concepts of the GMS-LPA network are illustrated in Fig. 2. The GMS network aims to learn multiple-scale features to increase the global feature diversity in the first branch. The LPA model splits spatial features into a group of patches in the second branch, and then these sub-patches are propagated into several parallel local patch attention networks. Subsequently, a model-level feature fusion method is exploited to achieve optimal performance between GMS and LPA networks. The main contributions of this study are summarized as:

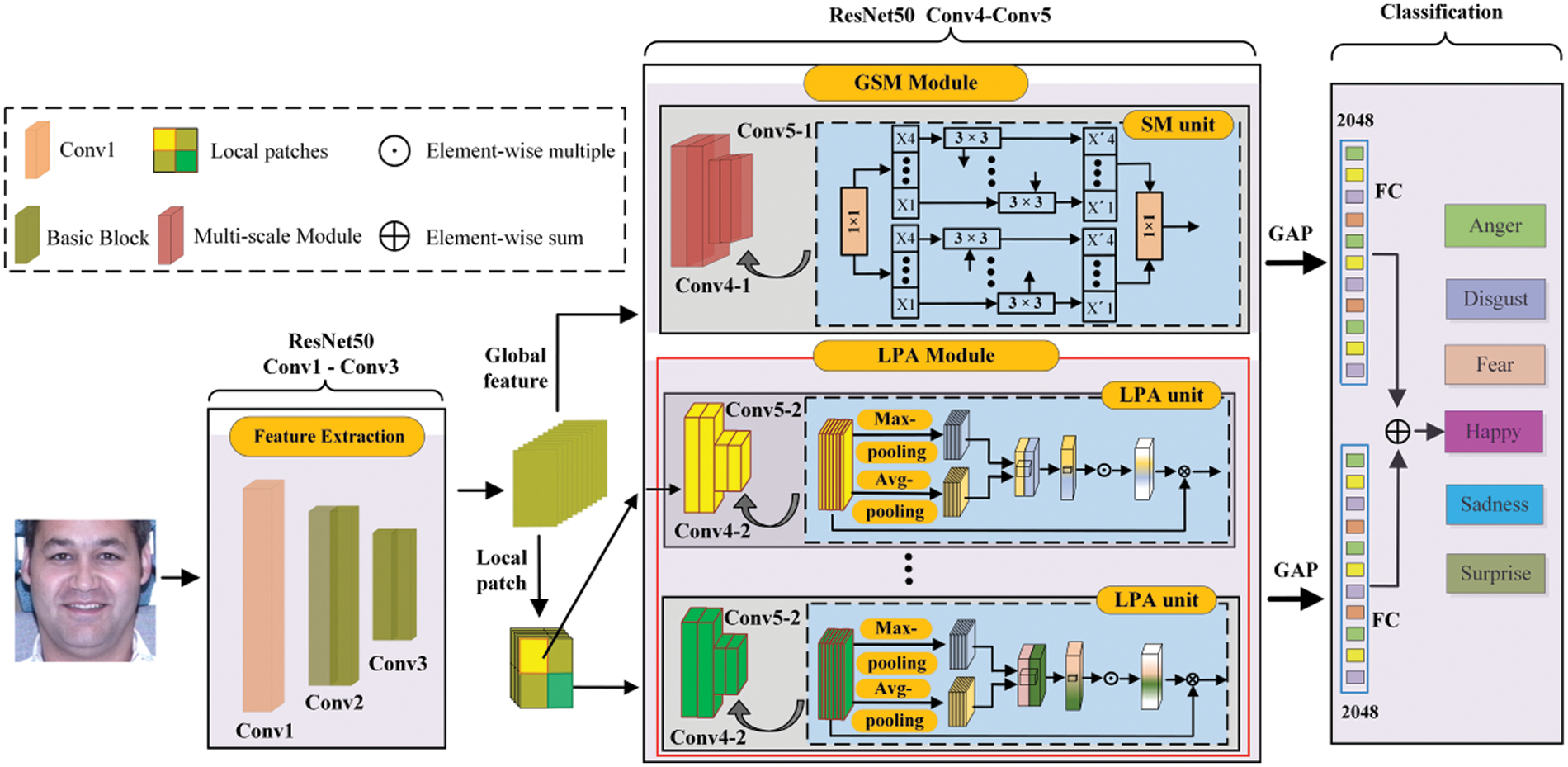
Figure 2: The structure of the GMS-LPA network. It contains four main parts, i.e., a feature extraction module, a global multiple-scale module (GMS), a local patches attention module (LPA), and a model-level fusion model. GAP presents a global average pooling operation, and FC presents a fully connected operation

1) A GMS-LPA dual-branch network is developed for pose-invariant FER, where the GMS and LPA models can extract features from global and local regions, both beneficial for pose-variant and self-occlusion FER.

2) The GMS model can extract global multiple-scale features within a basic residual unit, improving the receptive field and strengthening the characterization power of deep CNNs.

3) The LPA model is designed to extract features from local patches, forcing the network to focus on important local features and reducing the influence of pose variation and self-occlusion.

4) Experiments are conducted on the BU-3DFEP1, BU-3DFEP2, Multi-PIE, Pose-RAF-DB, and Pose-AffectNet datasets, and the recognition results indicated that the designed GMS-LPA network can effectively improve the identification accuracy in both controlled and real-world scenarios.

The rest of this paper is described as follows: Section 2 presents some relevant works on pose-invariant FER. Then, the GMS and LPA modules are explained in Section 3, and the experiment and analysis are described in Section 4. Finally, Section 5 provides the conclusions.

2  Related Work

2.1 Pose-Invariant FER with DCNNs

The deep convolutional neural network (DCNN) has emerged as a prominent direction in the field of pose-invariant FER [17–22]. For instance, Fasel [17], among the first scholars on this topic, proposed a five-layer structural framework for pose-invariant facial expression recognition. Accordingly, Zhang et al. [18] suggested eight-layer CNNs for pose robust expression recognition, where head poses associated with scale-invariant feature transform (SIFT) features are extracted separately. Afterward, the extracted features were fed into CNNs to address pose variation and self-occlusion issues. Liu et al. [19] introduced a soft threshold squeeze-and-excitation (SE) network for pose-invariant FER, where both SE and GAP operations were placed in the classic residual unit of ResNet50 to extract salient semantic information. Each observation angle can train the optimal threshold for emotion recognition as the convolutional layer increases. Shao et al. [20] designed three kinds of network frameworks (pre-trained-CNNs (ResNet101), light-CNNs, and dual-CNNs) to explore the influence of deep convolutional layers on pose-invariant expression classification tasks. The pre-trained-CNNs (ResNet101) have achieved the highest recognition accuracy in the experiment. Researchers in another study [21] designed a sixteen-layer transductive deep transfer learning network (TDTLN) to address cross-domain multi-view FER problems. The feature model in this approach can learn expression features from different views except the testing ones, and the transfer model is devised to reduce the difference between source data and target data. After fusing the higher semantic information, the TDTLN framework can achieve superior performance in cross-domain multi-view FER. Zhang et al. [22] also exhibited a deep principal component analysis network (PCANet) for pose-robust FER. This research designs the PCANet to learn mapping features between non-frontal and frontal ones and then train a unified descriptor for facial expression recognition.

2.2 Global-Local Features for FER

Integrating global-level and local-level features is an advisable choice and can further improve identification accuracy. For example, in [23], a multi-task global-local learning framework was developed for FER. This framework employed three part-based models to collect mouth, nose, and eye regions, while a global face model was designed to capture global appearance information. Subsequently, global and local models were assigned different weight values separately to improve identification accuracy. He et al. [24] proposed a global and local ensemble network for FER. The ensemble network in this study contained one local extraction model and a global information-perceiving network. The local extraction model aimed to find salient features from ROIs, and then local and global features were fused to a weight level, which can ameliorate the representation of the network. In [25], researchers developed a weakly supervised local-global feature attention network for FER. They employed an attention map generator to obtain a sequence of local attention maps and a selective feature unit to refine local features from attention maps. These selected feature maps were subsequently fused with global information for emotion classification. Li et al. [26] developed a whole-face and slide-patches attention network for FER, where the whole-face was utilized to characterize global semantic information. The slide-patch attention model focused on local salient features from different local patches, and then the extracted features were fused for expression recognition.

2.3 Attention Mechanisms for FER

The attention mechanism, as a weight adaptive allocation mode in the vision system, has been widely used in FER. Li et al. [27] presented a patch-based attention network (pACNN) for occlusion-aware expression recognition. In this study, facial images were first cropped into several ROIs in accordance with the related facial landmarks. Afterward, pACNN was utilized to weigh the importance of patches from all inputs, mitigating the impact of occlusion awareness and pose variation in expression recognition. Shao et al. [28] selected 36 feature points as anchors to generate a set of attention feature patches in the regions around the eyes, nose, and mouth. These attentive patches were subsequently utilized as a Facial Action Coding System (FACS) to present the texture features of different facial images, exhibiting conspicuous advantages in micro-expression classification tasks. Wang et al. [29] introduced a region attention network (RAN) for pose and self-occlusion robust FER. They first cropped the input facial images into several regions and then employed the RAN model to assign a weight for each local patch. Afterward, these attentive patches were aggregated into a fixed-length feature for FER. Liu et al. [30] proposed a patch attention convolutional vision transformer for self-occlusion FER. This method applied the sliding-crop model to split the deep feature maps into multiple patches, employing patch-level attention mechanisms to extract salient features from different patches. Subsequently, a vision transformer model was adopted to generate global long-range features between adjacent local patches to mitigate self-occlusion's effect on the recognition results. Similarly, Huang et al. [31] proposed a deep grid-wise attention and a visual transformer network for expression recognition, where the grid attention mechanism can extract salient features from local patches. In contrast, the visual transformer employed a set of visual tokens to connect adjacent grid patches and obtain a refined feature description to address the issues of non-frontal and self-occlusion FER in the wild.

3  Proposed Method

This section outlines the architecture of the proposed deep global multiple-scale and local patches attention (GMS-LPA) dual-branch network. Afterward, it will explain its fundamental components: the global multiple-scale (GMS) model, the local patches attention (LPA) model, and the loss function.

3.1 Network Architecture

Fig. 2 indicates that the designed GMS-LPA network consists of four components: the feature extraction module, global multiple-scale (GMS) module, local patch attention (LPA) module, and model-level feature fusion model. The feature extraction module includes one convolutional layer and four residual building units, which can extract features from the input facial images and initialize them with the same size. This study adopts ResNet50 to extract deep feature maps, and Fig. 3a exhibits a classical residual unit. These extracted features are then propagated into the GMS and LPA branch network for feature learning. In the GMS branch, a symmetrical multiple-scale module extracts global multiple-scale features. In the LPA branch, the extracted feature maps are first split into several sub-patches along the spatial axis, and then several parallel local attention networks are adopted to obtain salient feature information from local patches. Subsequently, the extracted global multiple-scale features and local patch attention features are propagated separately into GAP and FC layers. Afterward, a model-level feature fusion method is used for expression recognition.

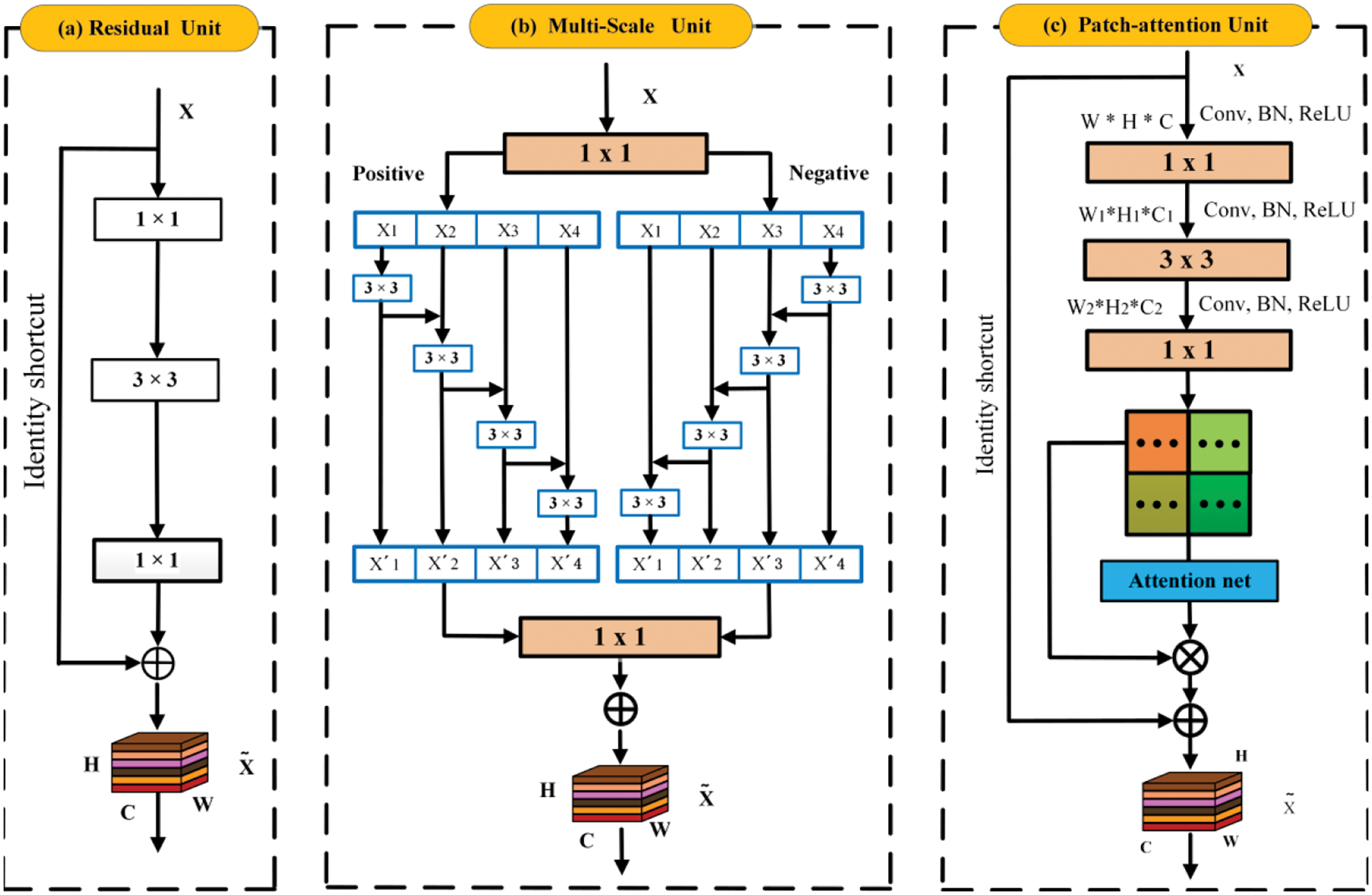
Figure 3: Three types of primary units are utilized in the GMS-LPA network, where (a) is the classic residual unit, (b) is the multiple-scale unit, and (c) is the local patches attention unit

3.2 Global Symmetrical Multiple-Scale Network

Multiple-scale feature learning is an effective way to improve the receptive fields of CNNs, which have been extensively used in object detection [32], semantic segmentation [33], face recognition [34], and expression recognition [29,30]. Most previous approaches learned multiple-scale features in a layer-by-layer manner. Based on Res2Net [16], a symmetrical multiple-scale unit was designed to extract global features within a residual unit, which can simultaneously obtain semantic information in the positive and negative directions. Fig. 3b indicates that after the feature extraction module, the extracted feature maps X were divided into n subsets along with channel axis, which can be denoted by Xi, i∈{1,2,⋅⋅⋅,s}, where each subset Xi contains the same spatial size but 1/n channels relate to the inputs X. Subsequently, the divided subset Xi was propagated into the corresponding 3×3 convolution operations, which can be represented by Vi(⋅). The middle layer in Fig. 3b illustrates the constructs of the symmetrical multiple-scale unit, representing the directions and the output of vi(⋅). As a result, the output feature map X~∈{positive,negative} can be described by the following formula:

X~ipositive={vipositive(Xi)i=1vipositive(Xi+X~i−1positive)1<i≤n(1)

X~inegative={vinegative(Xi)i=nvinegative(Xi+X~i−1negative)1≤i<n(2)

As described in Eq. (1), each 3×3 convolution operation Vi(⋅) can autonomously receive all the semantic features from the former subsets {Xj,j≤i}. Similarly, as illustrated in Eq. (2), each 3×3 convolution operation Vi(⋅) can receive all the semantic features from the latter subsets {Xj,n≥j≥i}. As a result, the output X~ipositive contains a wider receptive field than {Xk,k≤i}, while X~inegative(⋅) includes a wider receptive field than{Xk,k>i}. In order to capture more scalar semantic information, all the subsets n were concatenated from X~ipositive and X~inegative, and then passed through 1×1 the convolution layer to generate the output feature maps Output(X~ipositive) and Output(X~inegative), respectively. Afterwards, these extracted features are concatenated along the channel axis to generate the final output features, and the process can be described as:

Xi=Output(X~ipositive)+Output(X~inegative)(3)

where Xi is the output from both positive and negative directions, n is the number of subsets. A larger value of n potentially enables features to collect richer information but can boost computational overheads. This study set n to 4, making a trade-off between computation and performance.

The upper part of Fig. 2 presents the GMS module, where four symmetrical multiple-scale units are inserted into the last two convolution layers of ResNet50. Each convolution layer maintains the original spatial dimensions and channel numbers. After one operation, it can learn 2048×7×7 global feature maps in the GMS branch. Subsequently, these extracted feature maps are propagated into the global average pooling layer to generate a uniform feature vector. To further illustrate the superiority of the GMS model, visualization operations were performed on the classic ResNet50 and the improved GMS networks, as shown in Fig. 4, where the lighter colors indicate the regions of greater interest to the network. Due to the multiple-scale model considering both shallow geometric and deep semantic features, the learned features increase the diversity of the global semantic information and lessen the sensitivity of deeper convolution layers. As a result, the GMS network can obtain a larger receptive field and more accurately cover regions of interest compared with the classic ResNet50 network.

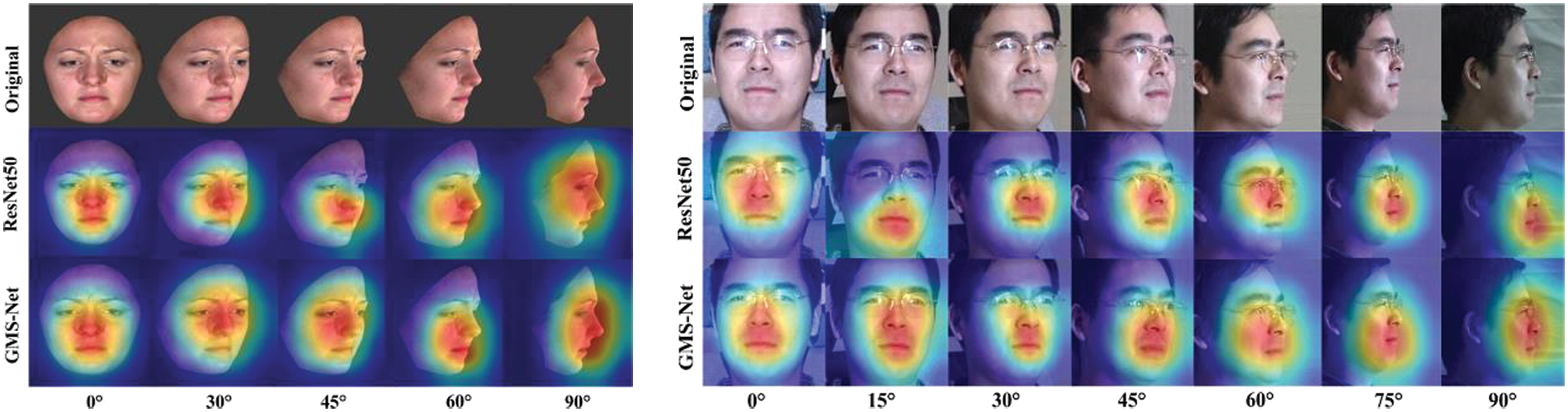
Figure 4: The visualization operations on BU-3DFEP1 and Multi-PIE datasets, where GMS is a global multiple-scale network

3.3 Local Patches Attention Network

For local patches, the mid-level feature maps are divided into several local patches and then fed into a corresponding attention mechanism for feature refinement. The mid-level feature maps P evenly split into several uniform patches Pi along with a spatial axis to explore the effect of local slice size on the recognition results, where i∈{1,2,⋅⋅⋅,m} is the number of patches. This research considers i=4 in the experiment and an ablation study in Section 4.2.2 proves that dividing facial images into four sub-patches is advantageous for expression recognition. As a result, the output feature maps Pi contain half spatial (1/2) but the same channel dimension compared to the mid-level feature maps P.

Fig. 3c shows the constructs of the patches-attention unit. After three basic convolution operations, it can obtain regional feature maps denoted by Pi∈RH×W×C. Afterward, a local patch attention model (LPA) is designed as the local attention network. In Zagoruyko et al. [35], the authors reported that pooling operation along with the channel axis can highlight informative regions, effectively filtering out noticeable texture features from deeper convolutional layers. This study also adopted a symmetrical structure to filter out salient features, where max-pooling and average-pooling operations were first utilized to extract texture information along with the channel axis and then concatenated to generate local patch feature descriptors. To further refine the salient features, a convolutional layer and sigmoid function were employed to extract spatial-level salient features. Subsequently, these refined spatial-level features and input feature maps were multiplied to obtain the attention-level feature maps. The specific structure is depicted in Fig. 5. For the pooling-level convolution layer, the filter size, stride, and padding are set to k=3, s=1, respectively, extracting features with two different manners and maintaining the spatial dimension consistency. For the spatial-level convolution layer, the filter size, stride, and padding values are set to k=3, s=2 and p=1, respectively, and the specific operation can be described as follows:

{OutputSpatial(Xi′)=σ(f([Avgpool(Xi′)⊕Maxpool(Xi′)]))OutputFeature(Xi)=OutputSpatial(Xi′)⊗Xi′(4)

where σ is the sigmoid function, f is the convolution operation, ⊗ is the element-wise multiplication operation, ⊕ is the element-wise sum operation. Notably, due to the different dimensions of the input feature maps and the spatial-level feature maps, the dimension of spatial-level feature maps is consistent with the input feature maps when performing element-wise multiplication operations. Moreover, the LPA is an exclusive and lightweight module that can be embedded into classic residual units seamlessly with negligible overheads.

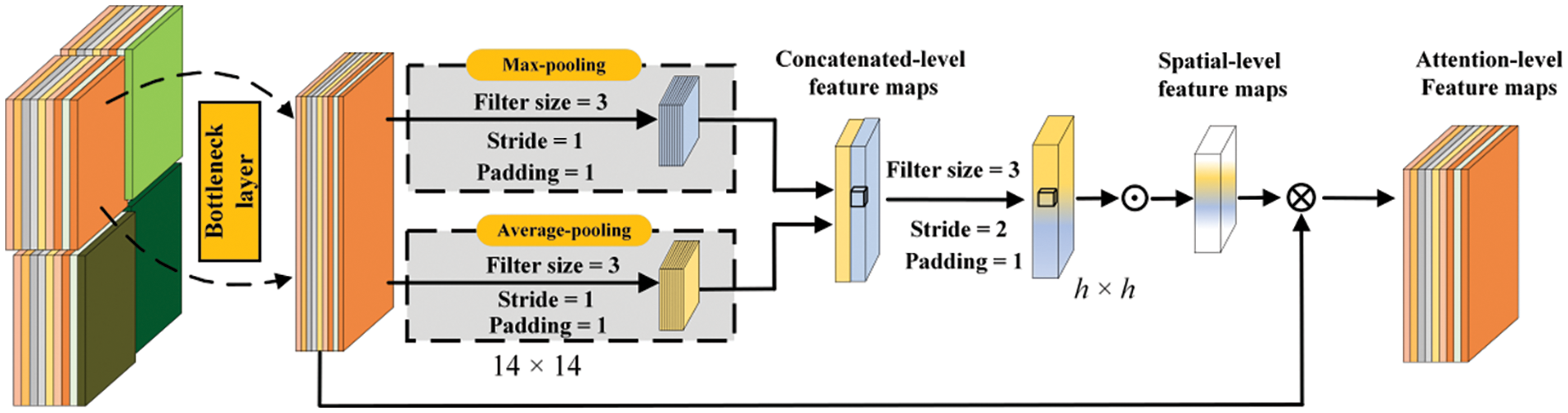
Figure 5: The structure of the local patch attention block. h is the size of feature maps after the concatenated-level convolution layer and ⊙ is a sigmoid function

The lower part of Fig. 2 depicts the LPA module, comprising four parallel attention networks; each network includes four patch-attention units. Specifically, the local patch attention module takes four identical feature maps 512×14×14 as the inputs, which are then propagated into four parallel attention networks for feature extraction. It is possible to learn four uniform local 2048×7×7 attention feature maps with the local patch attention module. The four uniform local attention feature maps are then reintegrated along with the spatial axis, and the global average pooling layer is utilized on the reintegrated feature maps 2048×14×14 to obtain a uniform feature vector with a dimension of 2048. Visualization operation (CAM) is conducted in the LPA network to demonstrate the influence of the LPA module. Fig. 6 indicates that the second and third rows represent the performance of classic ResNet50 and LPA networks under different facial views. Compared to ResNet50, the patch-attention-based CAM can guide the LPA-Net to focus on the local salient features, which are essential to improve the robustness towards non-frontal and self-occlusion facial expression conditions.

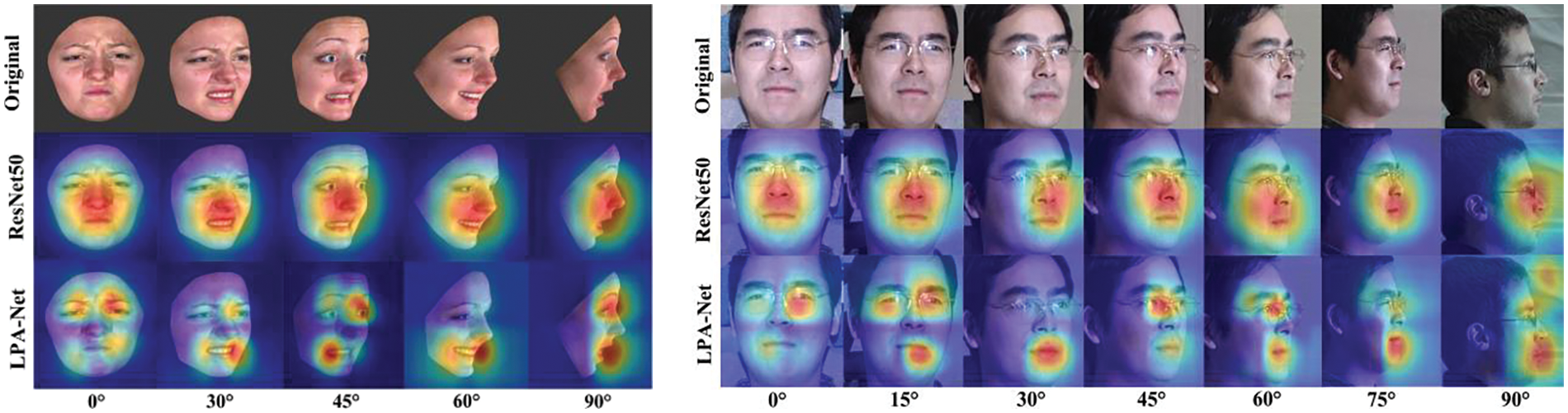
Figure 6: The visualization operation on BU-3DFE and Multi-PIE datasets, where LPA-Net is a local patch attention network

3.4 Loss Function

Model- and feature-level fusion are conventional techniques in facial expression classification tasks [36]. This research selected the model-level feature fusion strategy in the designed GMS-LPA network because GMS and LPA networks acquired feature parameters from two branches. Specifically, after the GAP operation, it can get two kinds of feature vectors with dimensions of 2048 and 2048, respectively, which can be expressed by v(ψ), where ψ∈{global,local}. The loss function in the proposed method includes two cross-entropy losses that can be described by the following formula:

Lψ=−1N∑i=0N−1log⁡eWyi(ψ)Tvi(ψ)+byi(ψ)∑j=0C−1eyi(ψ)Tvi(ψ)+byi(ψ)(5)

where N is the number of min-batch; C is expression classes. Wψ is the weight matrix, bψ is the bias; vi(ψ) is the ith sample; yi is the number of input class labels. The following formula can represent the GMS-LPA loss function:

L=αLlocal+(1−α)Lglobal(6)

where α is a hyper-parameter to balance local and global regions; α is set to 0.6, as detailed in Section 4.2.4.

4  Experimental Results

4.1 Datasets

In order to estimate the effectiveness of the designed GMS-LPA network, this study conducted experiments on four different datasets, including two controlled scenarios (BU-3DFE [37] and Multi-PIE [38]) and two real-world scenarios (Pose-RAF-DB [29] and Pose-AffectNet [29]). Figs. 7a–7d show some samples from four different datasets. Since the BU-3DFE and Multi-PIE databases do not precisely divide training and testing sets, the 5-fold cross-validation protocol is employed in these databases. In addition, to ensure the network can achieve enough training data, data augmentation operation (i.e., random rotation, flipping, shifting, and scaling) is adopted in this research, which can effectively lessen overfitting problems.

Figure 7: Some examples on BU-3DFEP1, BU-3DFEP2, Multi-PIE, Pose-RAF-DB, and Pose-AffectNet datasets

The BU-3DFE database includes 100 3D expression subjects, and each participant performs six basic expressions (anger (AN), disgust (DI), fear (FE), happiness (HA), sadness (SA), surprise (SU), and one neutral expression (neutral (NE)). The original BU-3DFE database requires rotating 3D facial images at multiple fixed observation angles to generate corresponding 2D texture images to facilitate multi-view expression recognition. Among all existing methods, two main protocols of the BU-3DFE database are widely used in pose variation and self-occlusion FER, which can be described as follows:

1) The first protocol of the BU-3DFE (BU-3DFEP1) dataset provides 100 subjects under five observation angles (0°, 30°, 45°, 60°, and 90°), and each expression includes four intensity levels. Therefore, a total of 5×4×6×100=12000 2D synthetic facial images are collected in this dataset, and the corresponding facial images with six basic emotions are depicted in Fig. 7a.

2) The second protocol of the BU-3DFE (BU-3DFEP2) dataset also provides 100 subjects and six basic expressions, but only the most vital intensity levels are selected. Compared to the BU-3DFEP1 dataset, BU-3DFEP2 pays more attention to the influence of mixed angles on recognition results; the pan observation angles are extended from −45° to +45°, and tilt observation angles are extended from −30° to +30°, respectively. As a result, a total of 7×5×6×100=21000 expression images are collected in this dataset, and the corresponding emotions with 35 head poses are illustrated in Fig. 7b.

3) The Multi-PIE dataset includes 377 subjects, each exhibiting six basic emotions (neutral (NE), disgust (DI), smile (SM), scream (SC), surprise (SU), and squint (SQ)) using seven head poses (0°, 15°, 30°, 45°, 60°, 75°, and 90°). This study adopted the same settings in literature [4,9,39,40,41], where 100 public subjects in four different sessions were collected for pose-invariant FER. Therefore, a total of 7×6×100=4200 expression images were captured in this dataset. The corresponding emotions are shown in Fig. 7c.

4) The Pose-RAF-DB and Pose-AffectNet datasets are refined from RAF-DB and AffectNet test datasets, exploring the influence of pose variation and self-occlusion on FER in real-world conditions. Specifically, images with head-pose (yaw or pitch) exceeding 45° or 30° are chosen as candidates for expression classification. It is worth indicating that the extracted emotional images contain positive and negative angles. As a result, the Pose-RAF-DB dataset comprises 12,271 facial images for training and 1,806 (1,248 (>30°) and 558 (>45°)) facial images for testing, respectively. Similarly, the Pose-AffectNet dataset consists of 283,901 facial images for training and 2,933 (1,948 (>30°) and 985 (>45°)) facial images for testing, respectively. The specific emotional images are depicted in Fig. 7d.

4.2 Ablation Analysis

This research conducted an ablation study on BU-3DFEP1 and Multi-PIE datasets to validate the effectiveness of each component in the GMS-LPA network, providing the most accurate observation angles and different experimental environments (both synthetic and real-world conditions) for multi-view expression classification tasks. In the experiments, the multiple-scale model was separately studied, local patch attention model, fusion strategy, and hyper-parameter value α, in which the two models were implemented in both the single-branch and dual-branch networks.

4.2.1 Global Multiple-Scale Model

This study first verified the validity of the global multiple-scale (GMS) module. Specifically, as illustrated in Fig. 2, multiple-scale and improved symmetrical multiple-scale units replaced the last two convolution layers for the single-branch network. The second dual-branch (SDB) was replaced with the designed symmetrical multiple-scale unit for the dual-branch network. In addition, the single-branch baseline network used ResNet50 as the basic architecture, and the dual-branch baseline network employed an improved ResNet50 as the basic architecture, in which each branch contained two identical convolution stages of ResNet50.

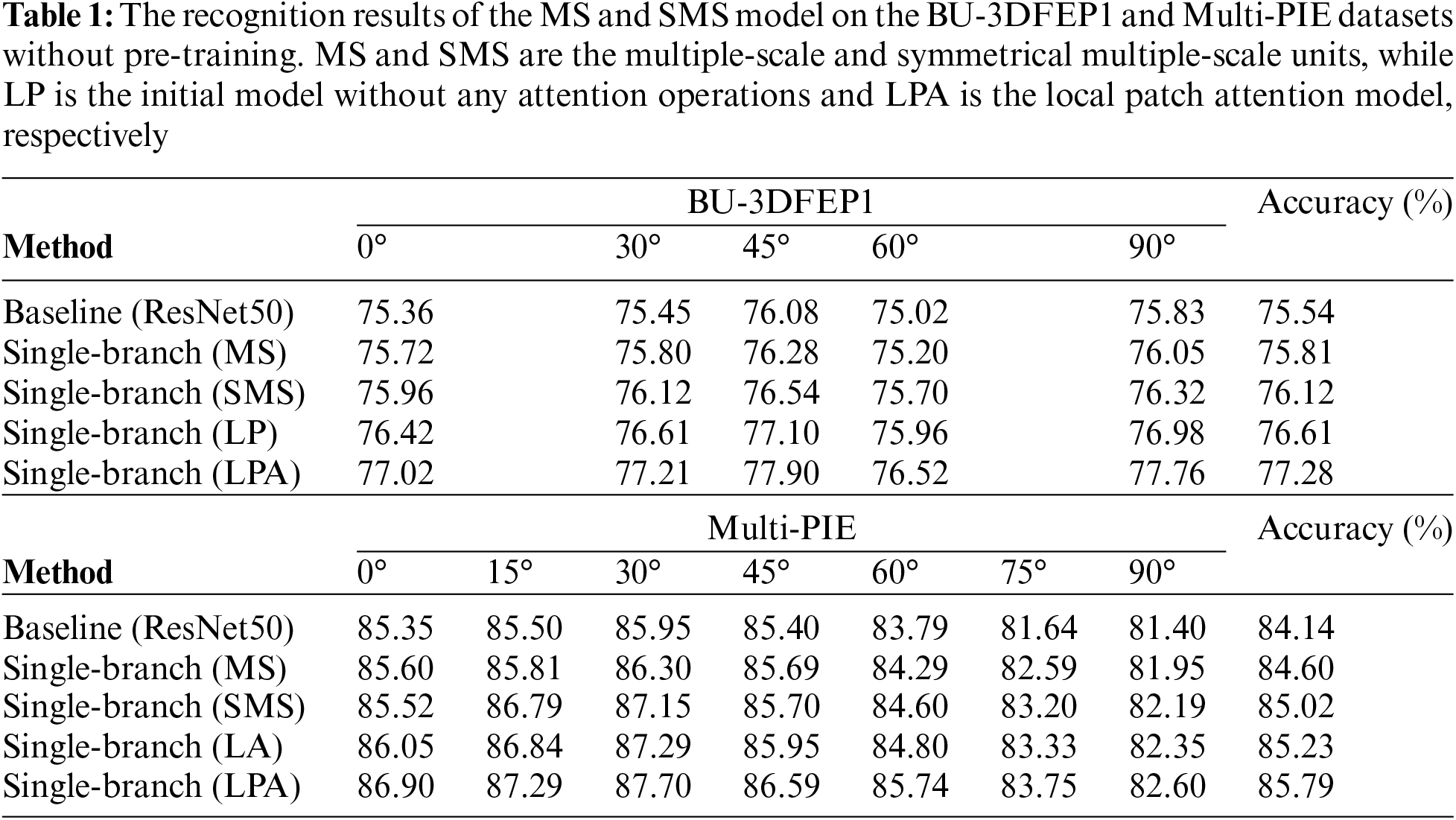
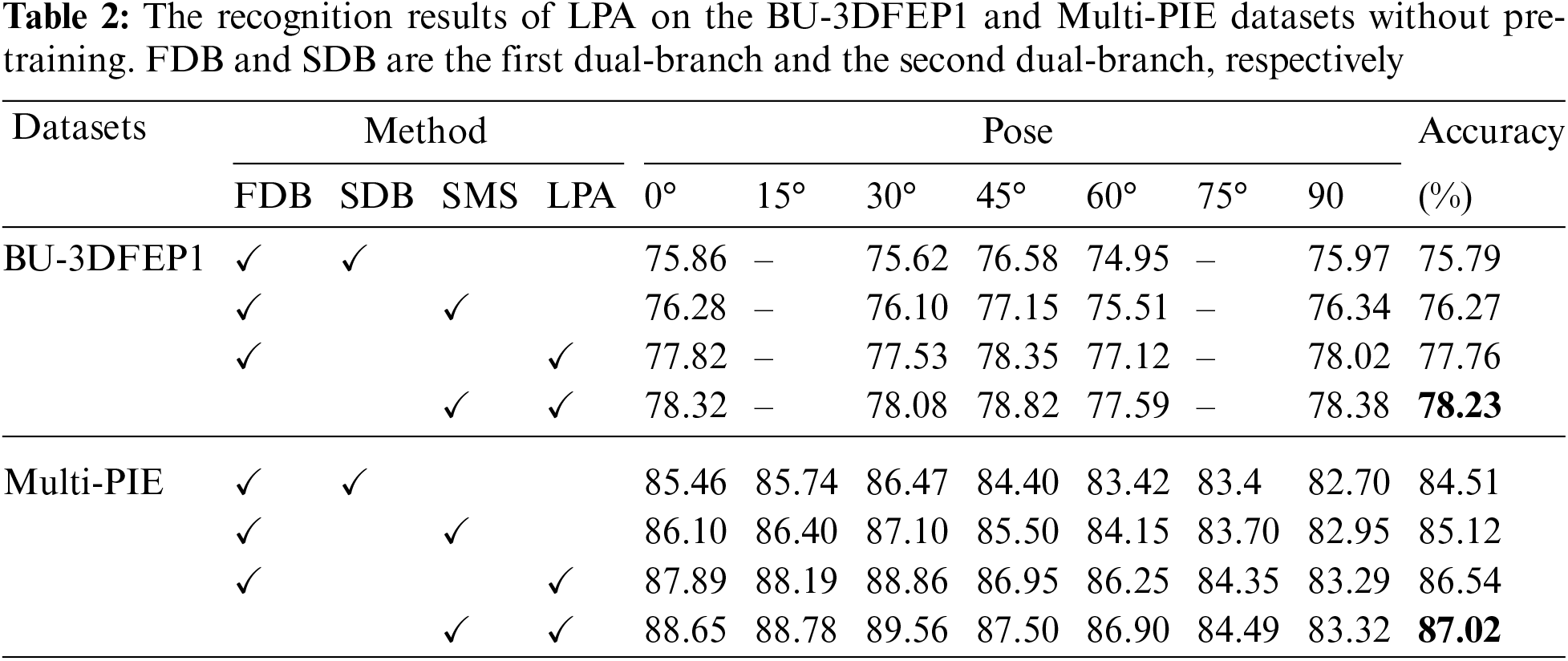
The corresponding recognition results of the multiple-scale and symmetrical multiple-scale models in single-branch and dual-branch networks are listed in Tables 1 and 2, respectively. They exhibited that the symmetrical multiple-scale network performs more than the multiple-scale network. The average recognition accuracy is used as the contrast criterion. When the symmetrical multiple-scale model is embedded into a single-branch network, the single-branch (SMS) has an average recognition result of 76.12% and 85.02% on BU-3DFEP1 and Multi-PIE database, respectively, which are 0.31% and 0.42% higher than those of the single-branch (MS) network. When the symmetrical multiple-scale model is embedded into the first dual-branch (FDB), the dual-branch (SMS) network achieves an average recognition result of 76.27% and 85.12% on BU-3DFEP1 and Multi-PIE database, which is 0.48% and 0.61% greater than dual-baseline (ResNet50), respectively. The results also show that the symmetrical multiple-scale model can further heighten the recognition accuracy when the other branch adds a local patches attention model. In addition, for the baseline network (ResNet50), the recognition accuracy of the single-branch (MS) network on BU-3DFEP1 and Multi-PIE database is improved by 0.27% and 0.46%, respectively, while the recognition accuracy of the dual-branch (SMS) is increased by 0.73% and 0.98%, respectively. The findings indicate that both multiple-scale and symmetrical multiple-scale models can enhance recognition accuracy, but the symmetrical multiple-scale model exhibits a more substantial representation capability, which is more striking in dual-branch networks. Therefore, the SMS model is chosen to extract the global semantic information in the following experiment.

4.2.2 Local Patches Attention Module

This study subsequently evaluated the effectiveness of the local patch attention (LPA) model. It used average recognition accuracy as the contrast criterion. Tables 1 and 2 demonstrate that for the single-branch network, the initial local patch (LP) model has an accuracy of 76.61% and 85.23% on BU3-DFEP1 and Multi-PIE databases, respectively. When the LP model cooperates with the local attention operation, the recognition results can be heightened to 77.28% and 85.79%, respectively, which is 1.74% and 1.65% higher than the single-branch (ResNet50) network. Similarly, when the LPA model replaces the second dual-branch (SDB) for the dual-branch network, the recognition accuracy shows an amelioration of 1.97% and 2.03% compared to the dual-branch (ResNet50) network. The result demonstrates that the LPA module can also materialize better identification results in the dual-branch network. In addition, when the GMS and LPA models are concurrently considered, the recognition accuracy forcefully improves to 78.23% and 87.02% on BU-3DFEP1 and Multi-PIE database. Due to the differentiation of feature level between the first dual-branch (FDB) and LPA module, the dual-branch network adopts the model-level loss function, and the hyper-parameter α is set to 0.6 in the experiment. The corresponding interpretations are introduced in Sections 4.2.3 and 4.2.4.

To further analyze the impact of local patches on recognition accuracy, four kinds of division strategies were selected to evaluate recognition results on the dual-branch (ResNet50) network. Table 3 lists the recognition accuracy among different observation angles, whereas Figs. 8a through Fig. 8d display the corresponding patch segmentation sizes. Table 3 indicates that division patches generally achieve better recognition accuracy than these non-division ones, and the optimal segmentation strategy is 2×2with an accuracy of 77.76% and 86.54% on BU-3DFEP1 and Multi-PIE databases, followed by 3×3 a segmentation strategy of 77.43% and 85.78% and then is 4×4 segmentation strategy with 76.91% and 85.17%, respectively. However, small patches lead to insufficient presentation ability of local features. In addition, dividing the deep feature maps into four patches highly corresponds with the distribution of biometric organs on the face, such as eyebrow corners, mouth, and lip corners, which is conducive to the expression classification in practical applications.

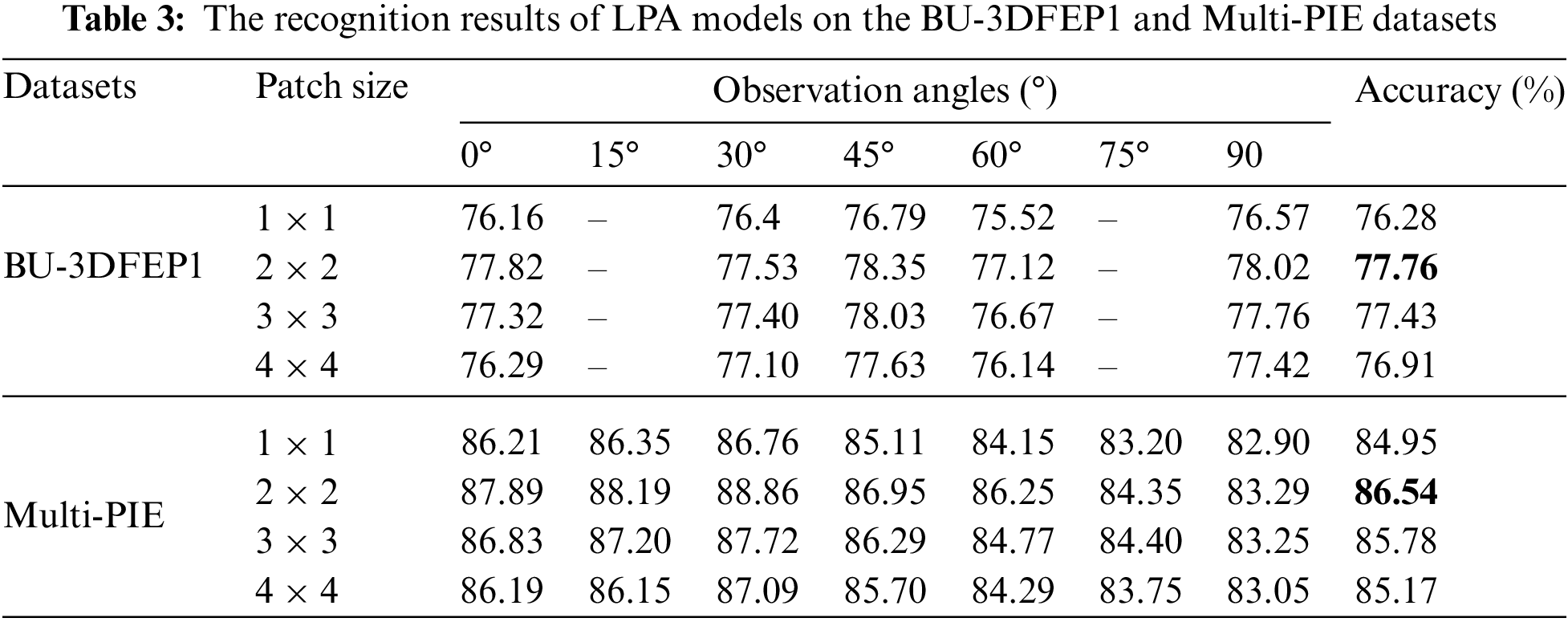
Figure 8: Four kinds of deep feature map segmentation strategy. (a) treats whole feature maps as an input feature map, which can be represented by one 1×1 vector. (b) divides the whole feature maps into four patches, which can be represented by one 2×2 vector. (c) divides the whole feature maps into nine patches, which can be depicted by one 3×3 vector. (d) divides the whole feature maps into 16 patches, which can be represented by one 4×4 vector

4.2.3 Fusion Strategy

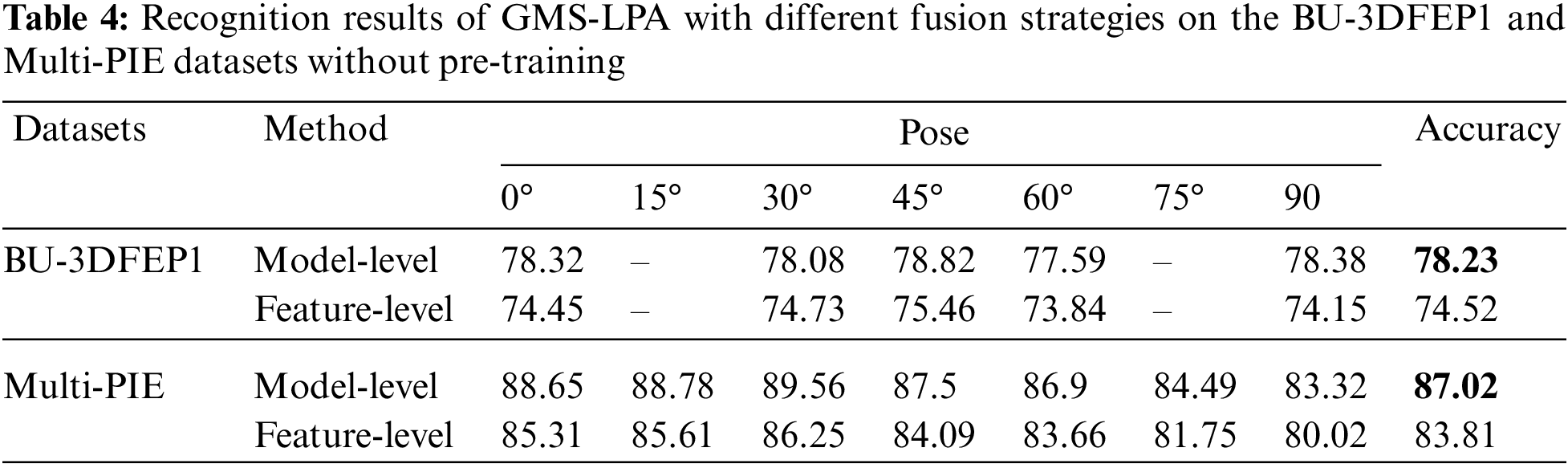
Given that the GMS and LPA models provide two types of feature vectors, this study adopted two conventional strategies, feature-level and model-level feature, to explore the influence of feature fusion strategy on recognition results. Specifically, the former extracts feature vectors from different branches and then directly fuses them to train a classifier for FER. At the same time, the latter extracts feature vectors from different branches and subsequently allocates different weight scores to each branch to achieve optimal recognition results. For a fair comparison, both methods do not require pre-training operations during the emotion classification process. The results in Table 4 indicate that the model-level fusion is superior to the feature-level fusion strategy in the proposed GMS-LPA network. When feature-level fusion strategy is utilized in the GMS-LPA network, it achieves 74.52% and 83.81% accuracy on the BU-3DFEP1 and Multi-PIE datasets. Similarly, when the model-level fusion is utilized, the recognition accuracy can be improved to 78.23% and 87.02%, respectively. Intuitively, the phenomenon can be attributed to the extracted global and local patch features, where the GMS model provides a global multiple-scale feature to represent the emotional information, and the LPA model incorporates multiple local-patch attentive feature maps to enhance network characterization ability, which contains a relatively weak complementarity in the feature-levels. As a result, the model-level feature fusion strategy is utilized in the designed GMS-LPA network.

4.2.4 Weight Value α

Moreover, to further explore the influence of α on the designed GMS-LPA network, this study adopted the enumeration method to analyze the performance of each weight value on the BU-3DFEP1 and Multi-PIE datasets and selected the optimal α value for all the experiments. The α value was equally divided into nine copies with a step size of 0.1, corresponding to the weight value of the local patch attention (LPA) module and 1−α represented the weight of the global multiple-scale (GMS) module. Fig. 9 shows the recognition accuracy of the GMS-LPA network at different weight model levels. It demonstrates that the identification accuracy increases with the parameter value α and maintains the optimal identification state when the weight value is set to 0.6. The results indicate that the LPA model performs better than GMS in the experiment, which is also consistent with the ablation studies in Tables 2 and 3, where the LPA network has better recognition results than the GMS network on BU-3DFEP1 and Multi-PIE datasets. Hence, the hyper-parameter α is set to 0.6 in the proposed GMS-LPA network.

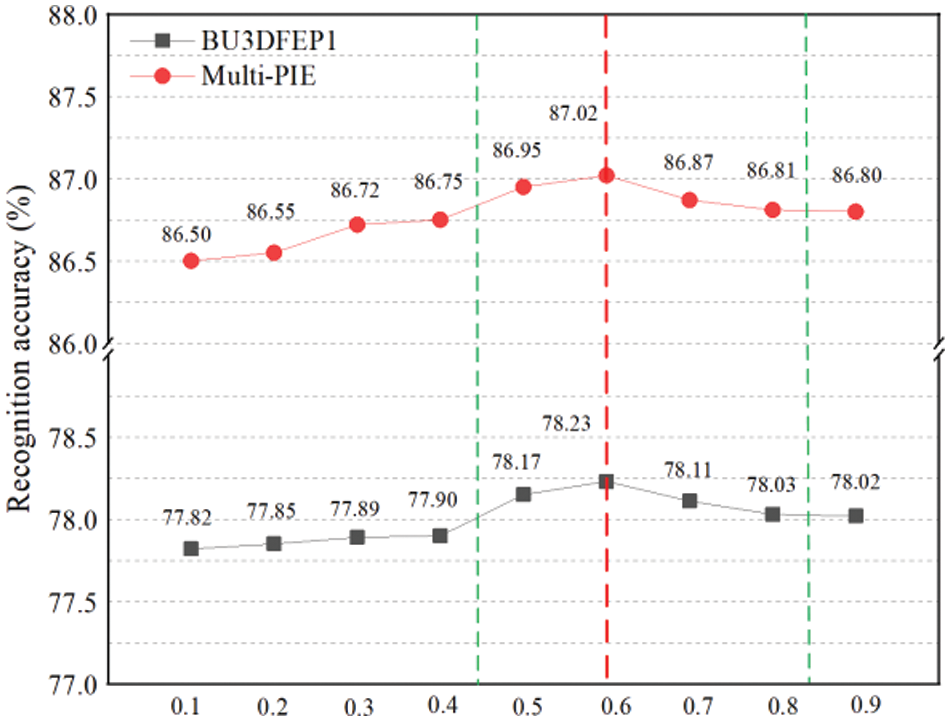
Figure 9: Recognition results of different weight values α on BU-3DFEP1 and Multi-PIE datasets

4.3 Experiment and Comparison on Different Pose-Invariant Datasets

In the subsequent experiments, the performance of the GMS-LPA network was evaluated in different pose-invariant scenarios. Specifically, experiments were conducted on three controlled datasets, BU3DFEP1, BU3DFEP2, and Multi-PIE, and two wild datasets, Pose-RAF-DB and Pose-AffectNet. Since each dataset consists of various observation angles and different emotion types, the experiment results were depicted in two ways: (I) detailing the recognition results on different datasets and (II) comparing the recognition results with manual-based and deep learning-based methods.

1) Experiment on the BU-3DFEP1 Dataset: This study initially tested the designed GMS-LPA network on the BU-3DFEP1 dataset for the controlled scenarios. The detailed recognition results are summarized in Table 5, where the bottom row presents the average identification rates among six basic facial expressions, and the right-most column lists the average identification rates of five observation angles. Table 5 indicates that the identification rate varies with the change of observation angles. The optimal view for expression recognition is 45°, with an accuracy of 78.82%, while the worst view is 60°, with an accuracy of 77.59%. The identification rates for the six basic emotions are also various, with surprise and happiness being the most prominent emotions. Their average identification rate is 87.18% and 84.36%, respectively, followed by disgust and anger, with an identification accuracy of 78.71% and 77.54%, respectively, and fear is the most challenging expression, with an identification accuracy of 67.43% in the experiment. Fig. 10a through Fig. 10f show each observation angle and confusion matrix. Fig. 10f exhibits that sadness and anger are more prone to be confused. There are 10.54% of anger expressions are misclassified as sadness, and 11.51% of sadness expressions are misclassified as anger. This is the reason why these two expressions achieve comparatively low recognition accuracy. Apart from that, all the misclassification rates of fear expression to other expressions are relatively high, making the recognition accuracy of fear expression the lowest among the six basic emotions.

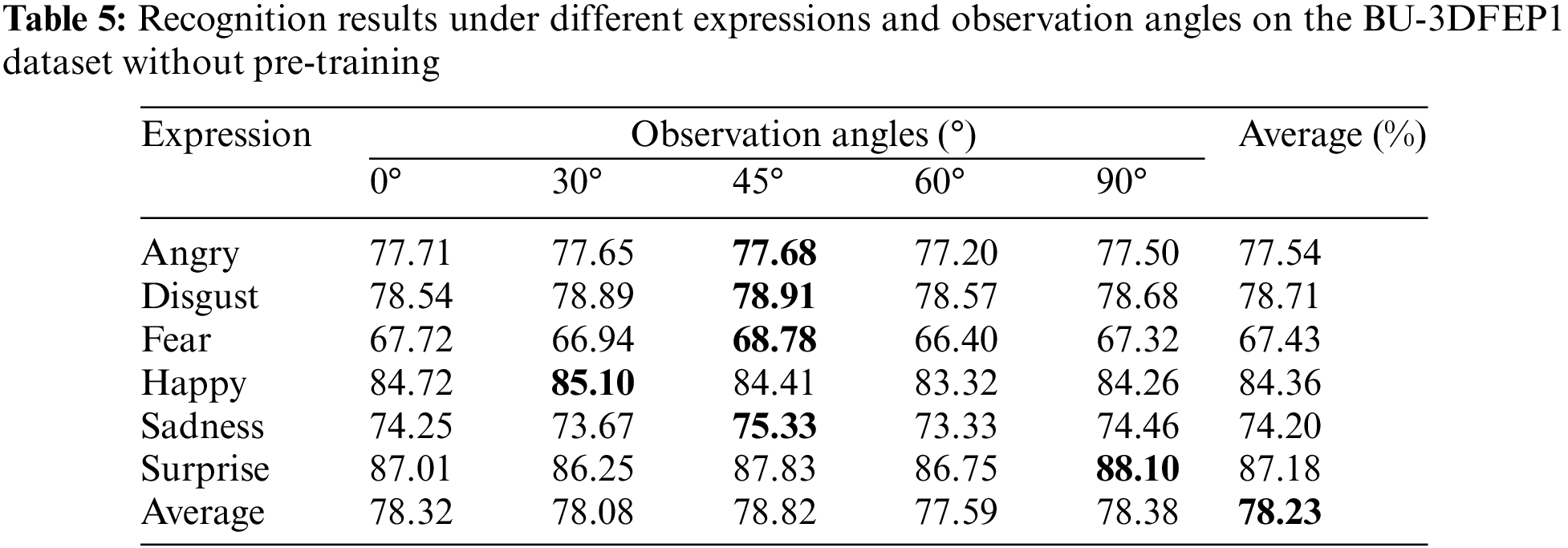
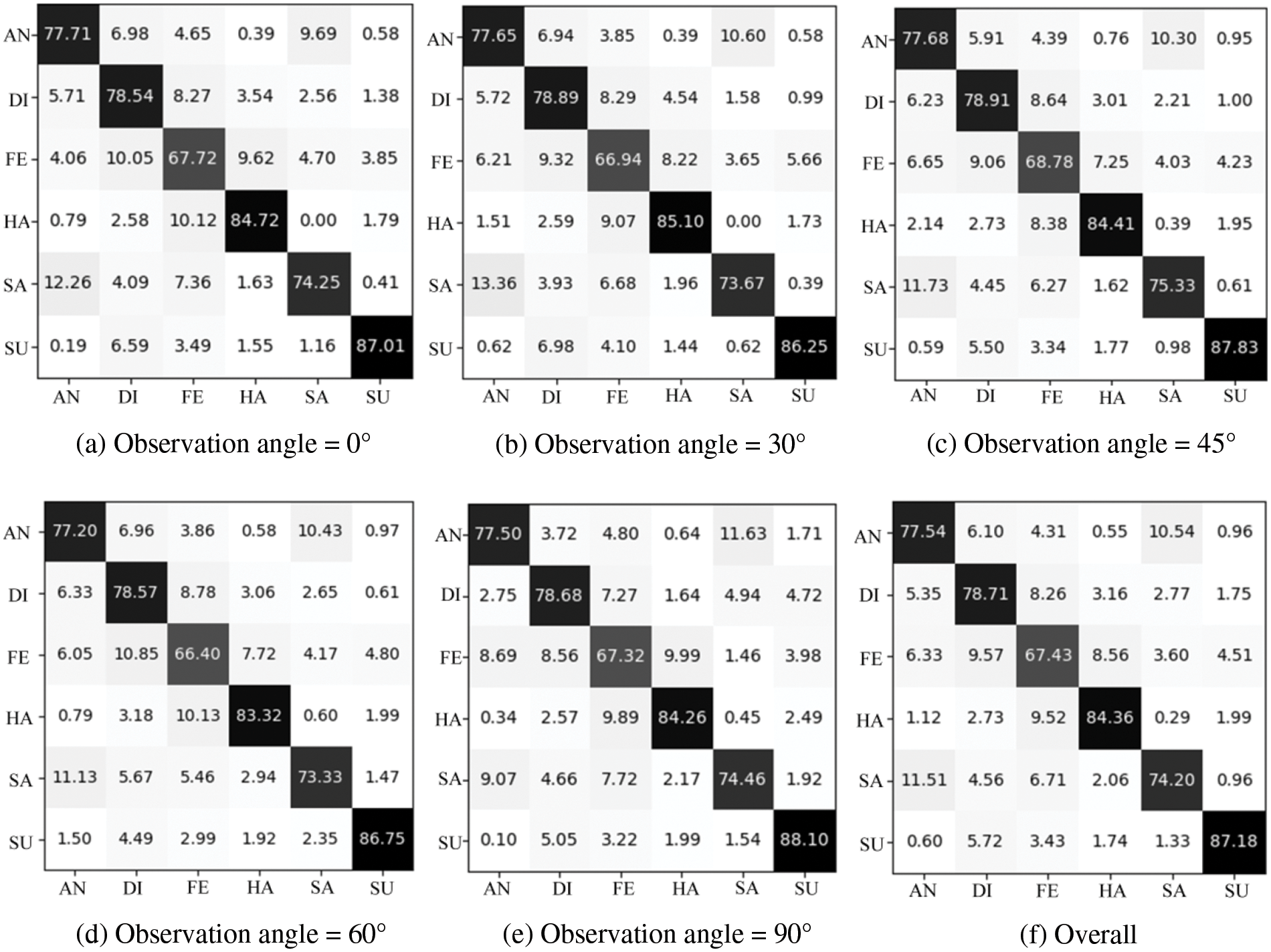
Figure 10: The confusion matrices on the BU-3DFEP1 datasets. (a–e) are five different observation angles, and (f) is the overall confusion matrix

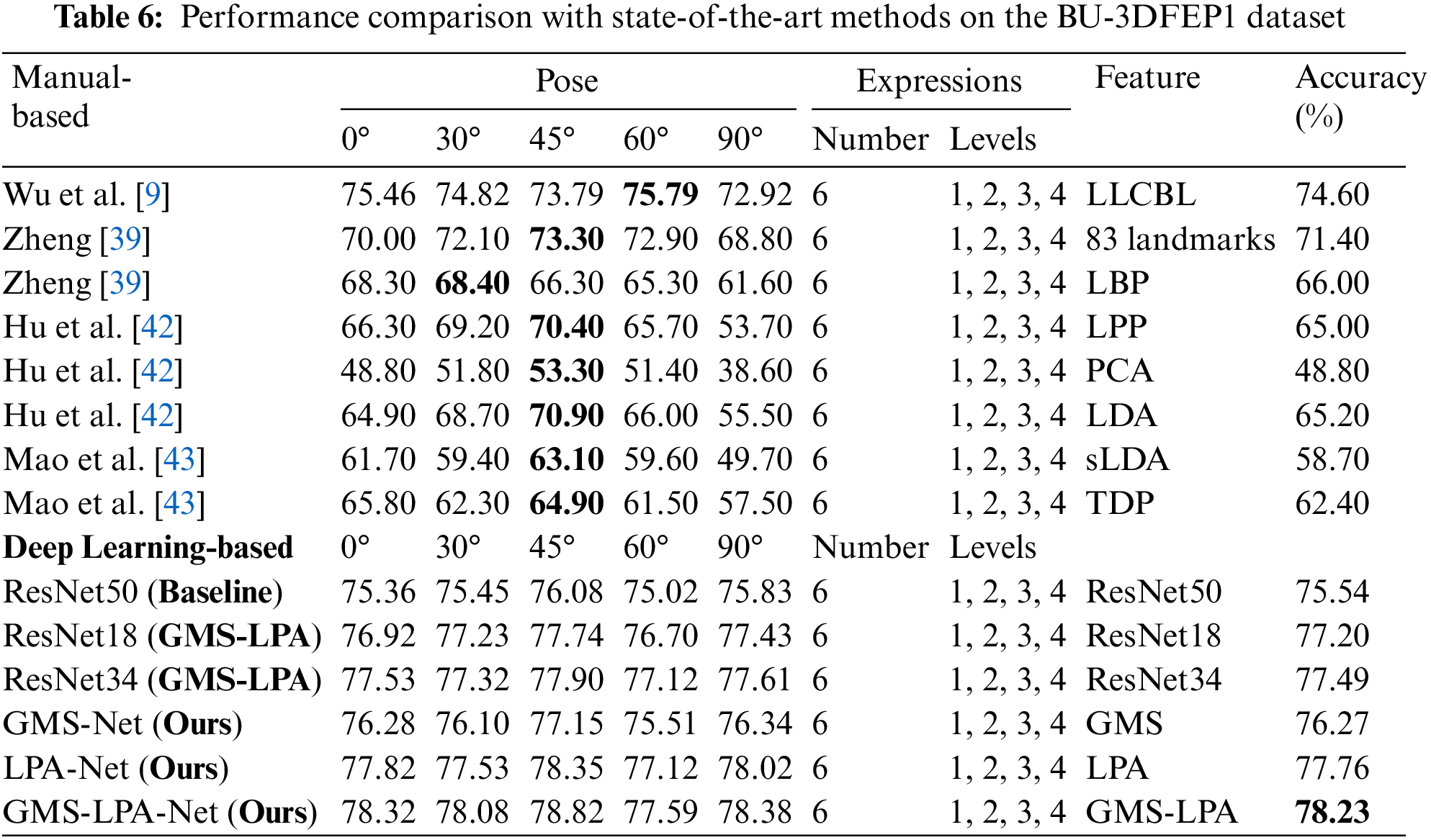
Table 6 compares the recognition results of the proposed GMS-LPA network with the achieved by several state-of-the-art techniques on the BU-3DFEP1 dataset, including several manual-based features and three classic (ResNet18, ResNet34, and ResNet50) residual neural networks. For manual-based methods, some well-established techniques were reported for pose-invariant FER, such as LLCBL [9], geometry [39], LBP [39], LPP [42], PCA [42], LDA [42], sLDA [43], and TDP [43] features. The detailed results across all views are listed in Table 6. The experimental findings demonstrate that the proposed method has an overall average recognition rate of 78.23% on the BU-3DFEP1 dataset. The result surpasses the others with a conspicuous improvement from 3.63% to 29.43% in the experiment. Specifically, although the manual-based techniques cannot perform well under 0° and 90°, the method can significantly improve the recognition accuracy by 2.86% to 29.52% and 5.46% to 39.78%, respectively. Similarly, the optimal observation angle (under 45°) increases from 5.03% to 25.52%. Furthermore, for other views, the GMS-LPA network can also obtain highly competitive results in the experiment. In terms of average recognition accuracy, the proposed method immensely outperforms these conventional features, such as landmarks, LBP, LPP, PCA, LDA, sLDA and TDP, even though the recognition results of the dual-branch (SMS) network increased by 4.87%, 10.27%, 11.27%, 27.47%, 11.07%, 17.57% and 13.87%, respectively. The improvement is triggered by deep convolutional features, which avoid manual feature extraction and provide more diverse semantic information for pose-robust expression recognition. For learning-based methods, to apply this approach to the task, this study also replaced the fourth and fifth convolutional layers with the designed GMS-LPA model in ResNet18 and ResNet34 networks. Due to the difference in the basic residual units between ResNet50 and ResNet18, the SMS operation is followed by one 3×3 convolution operation. The lower part of Table 6 lists the corresponding recognition results. The improved ResNet18 (GMS-LPA) and ResNet34 (GMS-LPA) networks also exhibit superior performance on the BU-3DFEP1 dataset, with an average recognition result of 77.20% and 77.49%, respectively. The results illustrate that the designed GMS and LPA models can effectively extract salient features from global and local facial images, which is advantageous for weakening the impact of pose variation and self-occlusion on emotional classification tasks.

2) Experiment on the BU-3DFEP2 Dataset: this research subsequently evaluated the GMS-LPA network on the BU-3DFEP2 dataset, and the recognition accuracy is displayed in Table 7. The right-most column lists the average recognition rates among seven observation angles, and the bottom row lists the average classification rates of six basic expressions. It must be noted that this dataset tends to explore the impact of mixed observation angles (both tilt and pan) on emotion classification, and only the most vital intensity levels are applied in the experiment. The results demonstrate that the best observation angle is −15°, with an identification rate of 82.52%, while the worst observation angle is 15°, with an identification rate of 82.12%, and the overall average recognition accuracy is 82.24%. For the six basic expressions, as shown in Table 7 and Fig. 11h, the average recognition results are consistent with the BU-3DFEP1 dataset, with surprise and happy expressions achieving the highest recognition rates, followed by anger and disgust. Fear remains the most challenging emotion, but the average recognition results show remarkable improvement in this dataset.

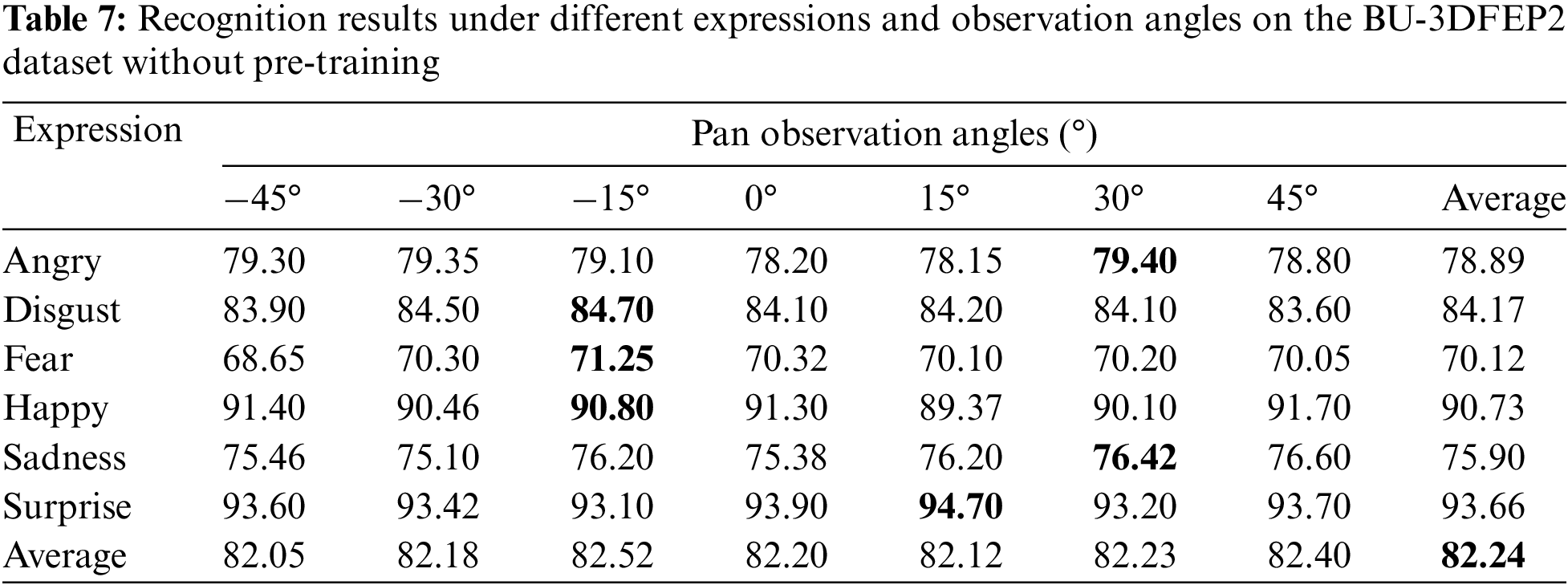
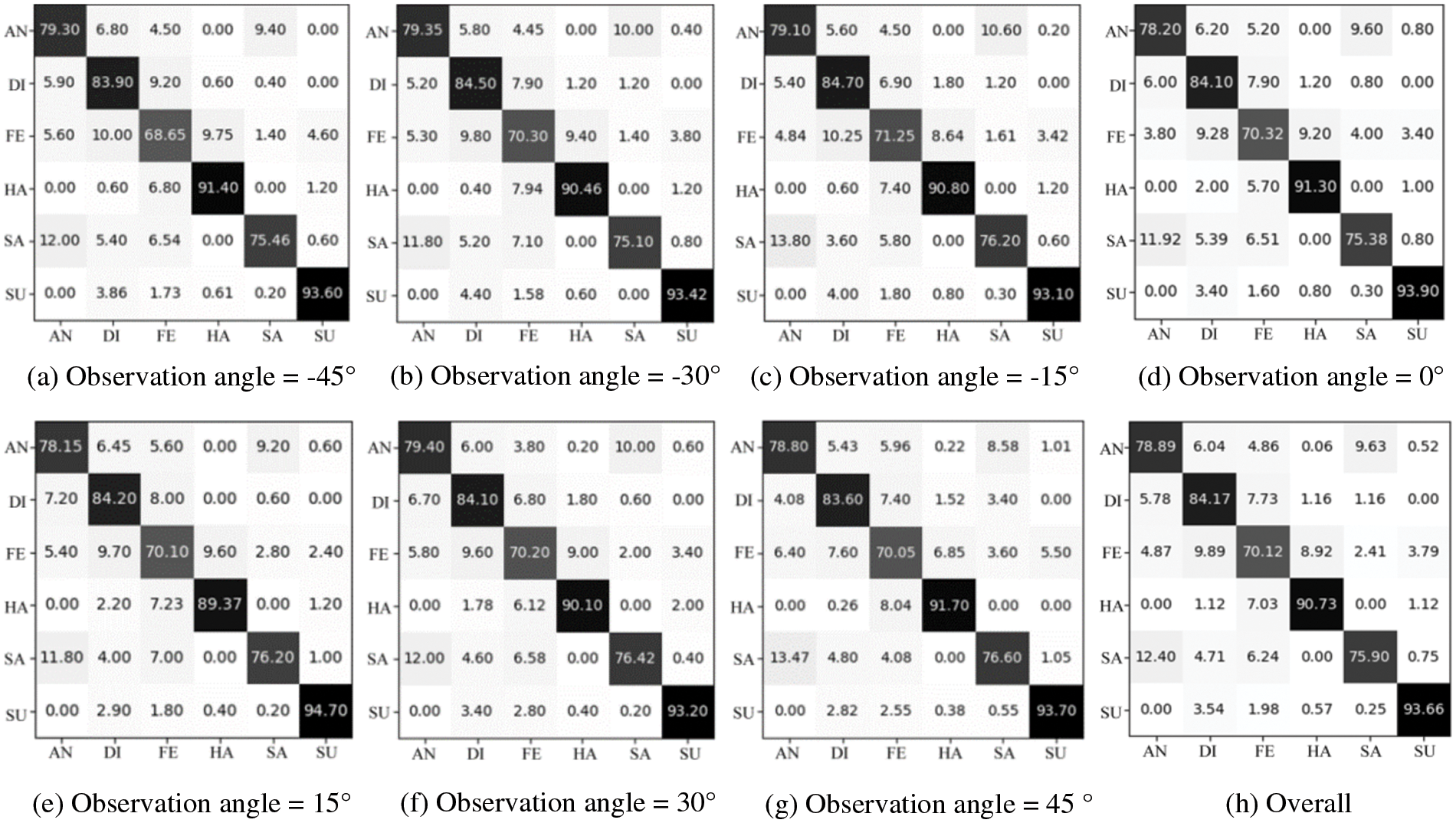
Figure 11: The confusion matrices on the BU-3DFEP2 datasets, where (a–g) denotes seven different observation angles and (h) denotes the overall confusion matrices

Subsequently, the recognition result of the proposed method is compared to nine frequently referenced techniques based on manual-based features, which can be found in [7,9,44–50] and three classic learning-based (ResNet18, ResNet34, and ResNet50) methods. Methods [7,9,44–50] train their classification models based on manual feature Landmarks (83 feature points), LLCBL, dense SIFT, LBP+HOG, and LBP+SIFT, respectively. This study adopted the improved (ResNet18 and ResNet34) networks for the deep learning-based methods to conduct facial expression classification tasks. In Jampour et al. [47], dense SIFT features are manual features that must be pre-trained and fed into the convolutional neural network for expression classification. Different from this training method, the proposed one is an end-to-end learning model that eliminates the pre-training process. The detailed identification results regarding each reported method are listed in Table 8. For the manual-based feature, although the local-patches linear coding-based BoF (LLCBL) model has actualized a high-light performance in early studies, the proposed method can further strengthen the identification accuracy in the experiment. Moreover, for the manual feature fusion deep learning-based technique, the designed GMS-LPA network performs more satisfactorily than this method [47] with a 3.60% gap. The gains can result from the original input features, where dense SIFT features cannot describe the emotional semantic information completely and precisely compared to the original facial images. For deep learning-based methods, the fourth and fifth convolutional layers of ResNet18 and ResNet34 were also replaced with the GMS-LPA model. The recognition results are listed in the lower part of Table 8, where the proposed method achieves an identification rate of 82.24% on the BU-3DFEP2 dataset. Moreover, the improved ResNet18 (GMS-LPA) and ResNet34 (GMS-LPA) networks have an identification accuracy of 81.24% and 81.90%, respectively, which is 1.51% and 2.17% higher than the baseline (ResNet50) network.

3) Experiment on the Multi-PIE Dataset: This study tested the developed GMS-LPA network on the Multi-PIE dataset. Similarly, the right-most column presents the average recognition results under seven views, while the bottom row presents the average recognition results among six basic facial expressions. Table 9 indicates that the prominent observation angle for emotion classification is 30°, with a recognition accuracy of 89.56%, while the worst is 90°, with an accuracy of 83.32%, and the overall average recognition accuracy is 87.02%. Fig. 12a through Fig. 12h present the confusion matrices of each observation angle and the overall confusion matrix of the experiment. Table 9 and Fig. 12a through Fig. 12g demonstrate that among these six basic expressions, smile, surprise, and scream expressions are more accessible to identify, while their average recognition rates are over 90%. Disgust and squint are more challenging to identify, while their average recognition rates are 76.35% and 79.41%, respectively. In addition, Fig. 12h shows that disgust and squint are more likely to be confused. There are 13.77% of disgust confused with the squint expression and 18.10% of squint confused with the disgust expression. The high misclassification rates can be attributed to the squint and disgust expressions containing similar texture features around the eyes, eyebrows, and lip corners.

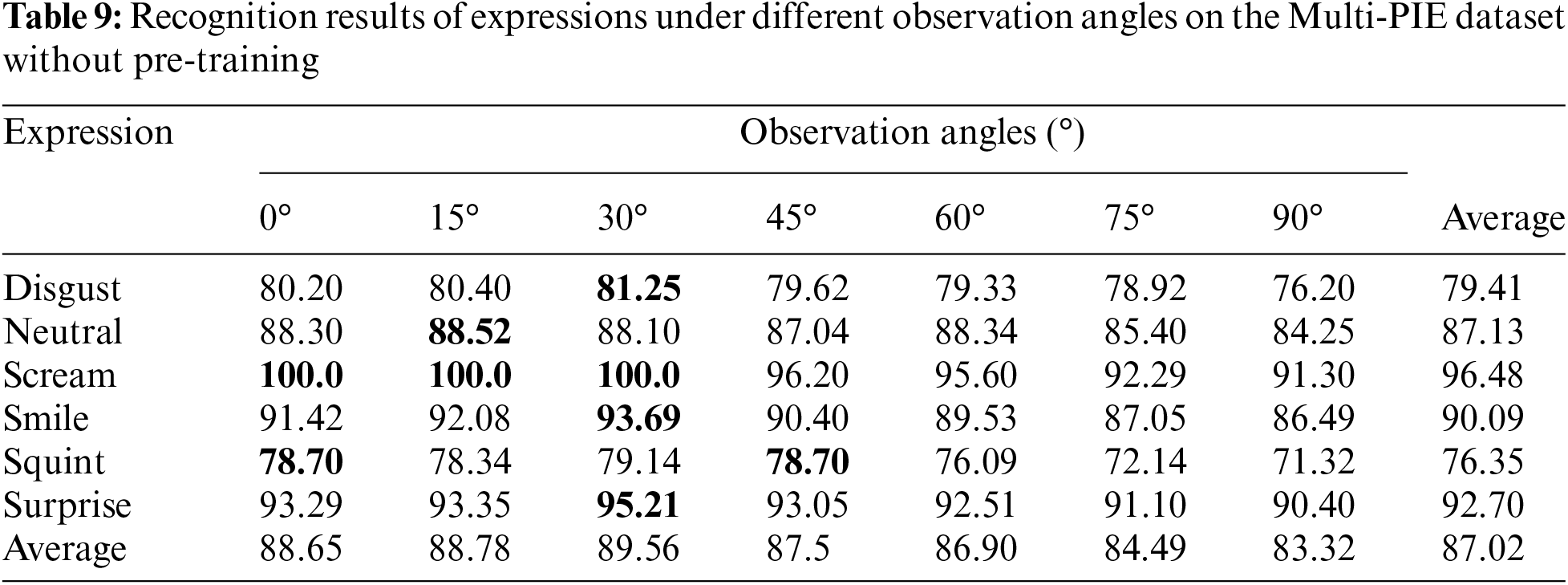
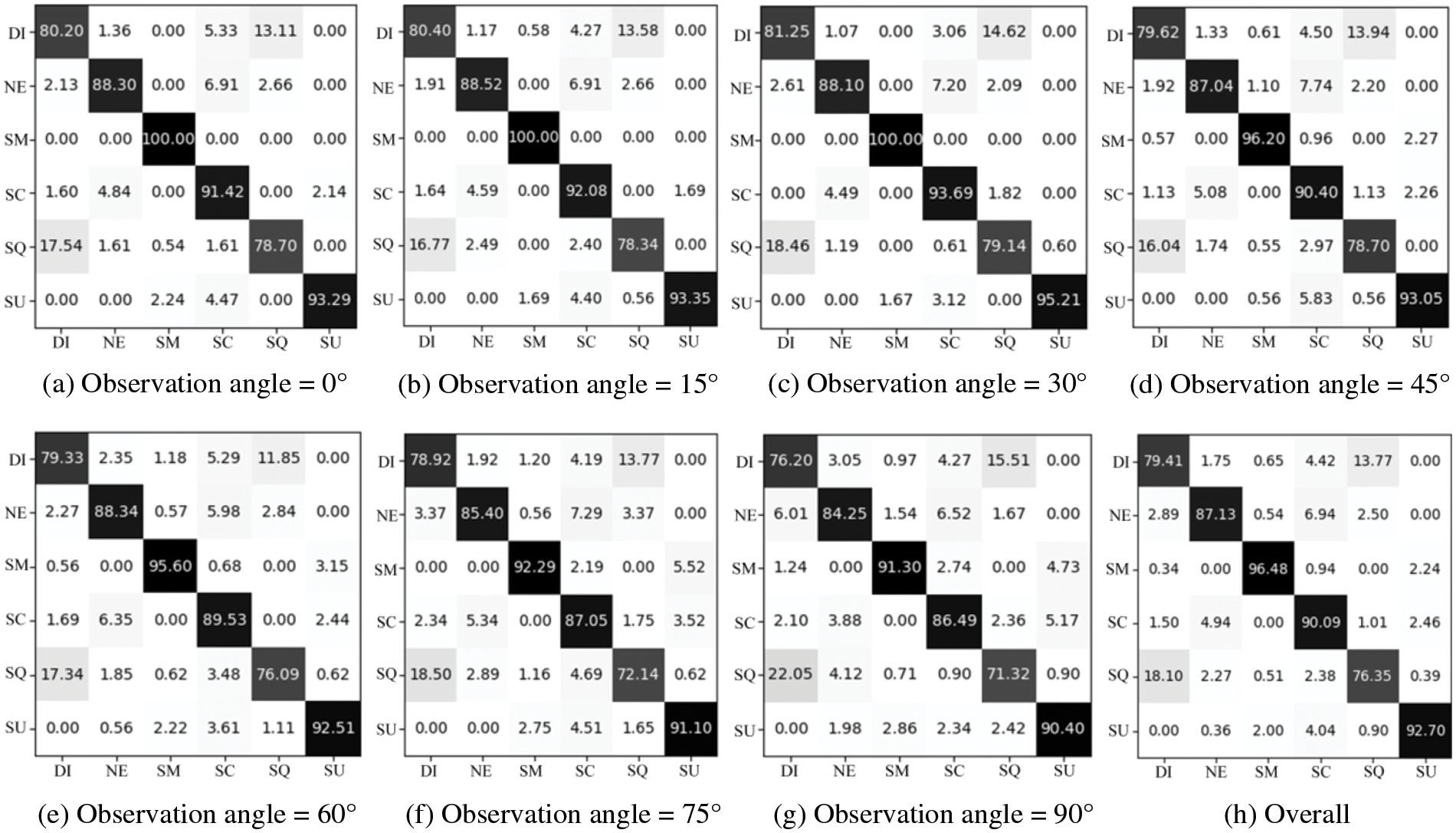
Figure 12: The confusion matrices on the Multi-PIE datasets. (a–g) are seven different observation angles, and (h) is the overall confusion matrices

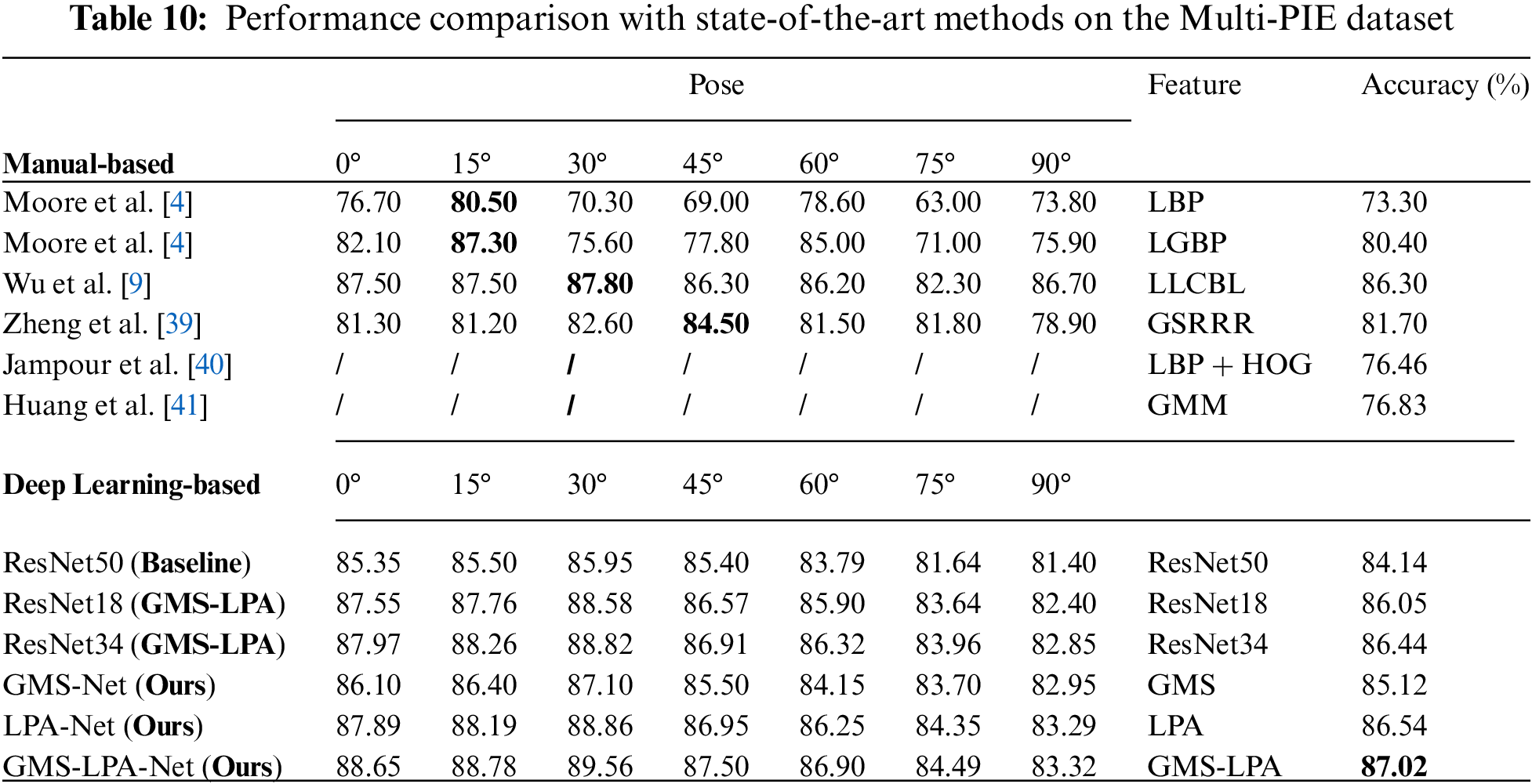
Thereafter, this study evaluates the proposed method on the Multi-PIE dataset. In the manual-based setting, the method proposed in this study was compared with several well-established techniques in pose-invariant FER, including LBP [4], LGBP [4], LLCBL [9], GSRRR [39], LBP+HOG [40] and GMM [41], and the detailed results are listed in Table 10. The method herein also outperforms most manual-based features among seven observation angles and achieves an overall average identification rate of 87.02% in the experiment. Using the average identification accuracy as the comparison criterion, the proposed GMS-LPA network has improved by 0.72%, 5.32%, and 10.19% compared to conventional manual-based features (LLCBL, GSRRR, and GMM). The method herein has a noticeable improvement for the classic features, such as LBP, LGBP, and LBP+HOG, with the recognition accuracy increasing by 13.72%, 6.62%, and 10.56%, respectively. For the deep learning-based method, this study compares the proposed method with the baseline (ResNet50), improved ResNet18 (GMS-LPA), and ResNet34 (GMS-LPA) networks. The detailed recognition results are listed in the lower part of Table 10. For the classic ResNet50 network, the proposed method exhibits a striking optimization, with an identification rate increase of 2.88% on the Multi-PIE dataset. The results illustrate that the designed GMS-LPA network is suitable for synthetic expression recognition environment and achieves excellent performance in a closely real-world scenario. For the improved networks, the designed GMS-LPA network has achieved a slight betterment for them, with an identification rate increased by 0.97% and 0.58%, respectively.

4) Experiment in the wild conditions: To further analyze the impact of pose variation and self-occlusion on FER in the wild, this study also tested the GMS-LPA network on two refined sub-datasets collected from raw RAF-DB and AffectNet datasets. As introduced in Section 4.1, the same experimental settings [19,29,51,52] are adopted, including seven basic emotions (AN, DI, FE, HA, NE, SA, and SU) and two head poses (>30° and >45°), and the last three rows of Table 11 shows the recognition results. The designed dual-branch network can still effectively increase the recognition accuracy in the wild scenes, and the GMS-LPA network has a recognition accuracy of 87.18% (>30°) and 86.65% (>45°) on the Pose-RAF-DB dataset and 60.31% (>30°) & 60.92% (>45°) on the Pose-AffectNet dataset, respectively. Fig. 13a through Fig. 12d show the corresponding confusion matrix. They indicate that the happy expression acts as the most distinguishable emotion among the four refined datasets, with a recognition accuracy of 97.50% (>30°) and 95.36% (>45°) on the Pose-FAF-DB dataset and 79.21% (>30°) and 80.87% (>45°) on the Pose-AffectNet dataset, followed by the neutral expression with an accuracy 93.38% (>30°) and 94.53% (>45°) on the Pose-FAF-DB dataset and the fear expression, with an accuracy of 67.79% (>30°) and 66.80% (>45°) on the Pose-AffectNet. The disgust expression is the most challenging emotion in the four refined datasets. It is generally confused with the happy and sad expressions on the Pose-RAF-DB dataset and more easily confused with the anger and neutral expressions in the Pose-AffectNet database, which pulls down the average recognition rate among seven basic expressions.

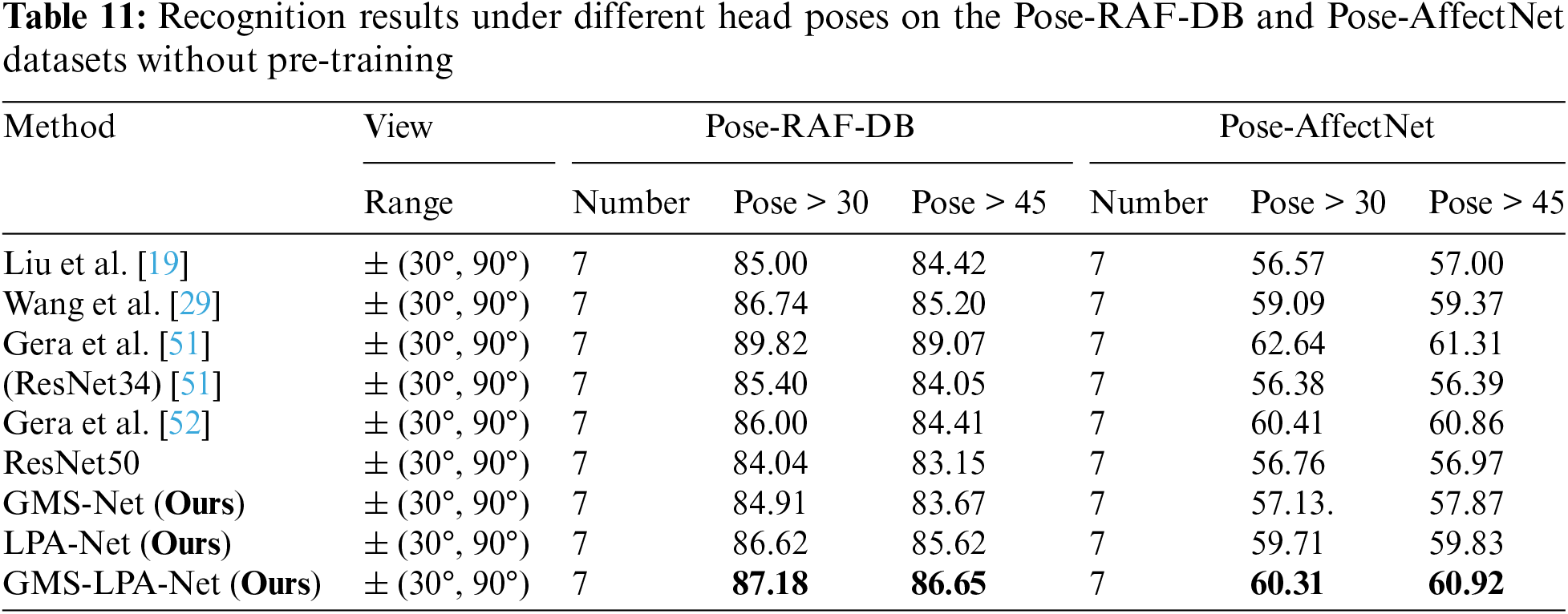
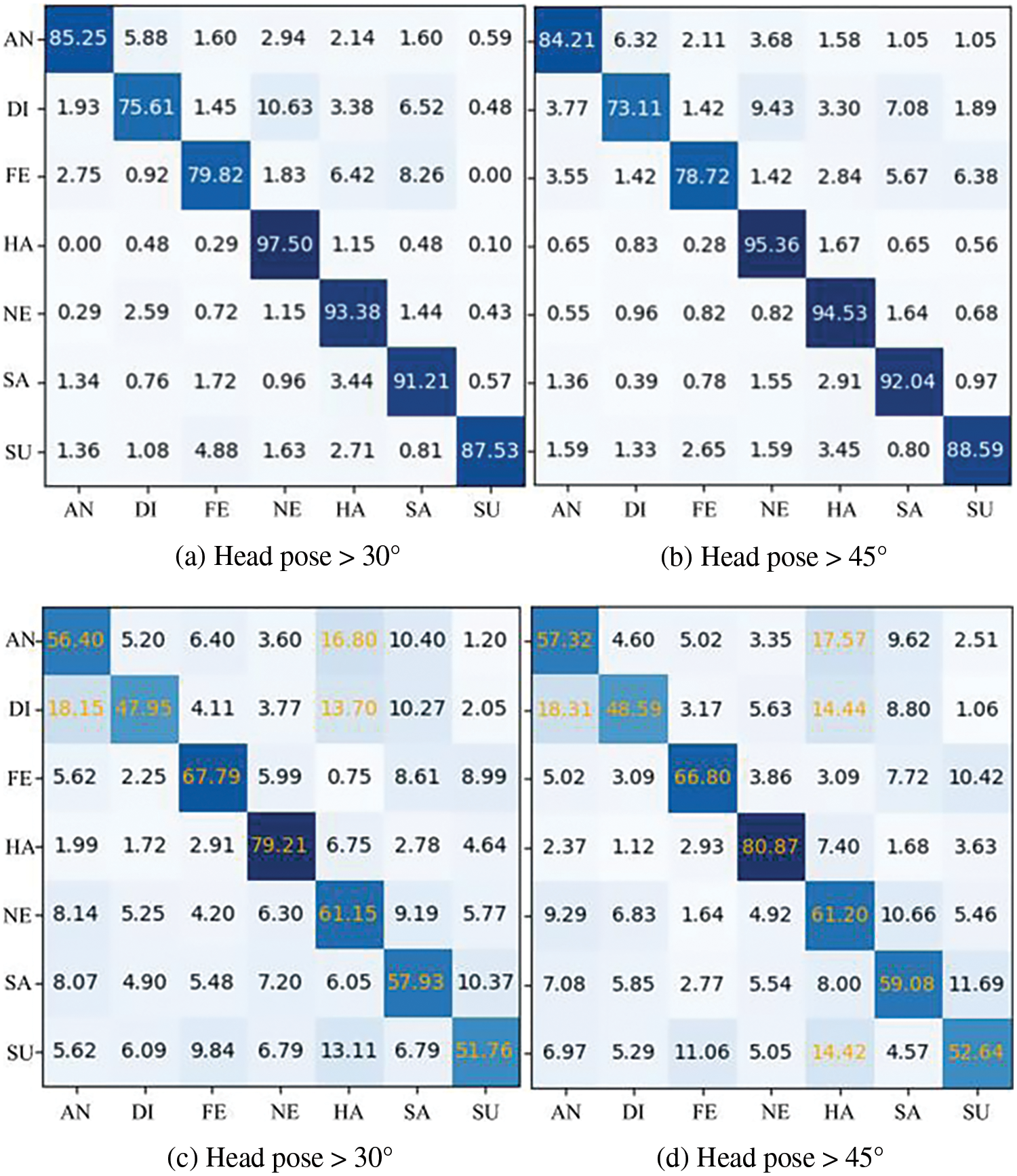
Figure 13: Confusion matrices of GMS-LPA network on Pose-RAF-DB (a–b) and Pose-AffectNet (c–d) datasets

Given that the Pose-RAF-DB and Pose-AffectNet datasets are primarily used for deep learning-based methods, this study compares comprehensively with several state-of-the-art methods proposed in recent years. Table 10 lists the corresponding recognition results. It indicates that the designed GMS-LPA network surpasses most previous works except Grea et al. [51,52]. However, the multi-task learning method described in [51,52] requires learning geometric features as auxiliary attributes to enhance network representation. In contrast, the proposed technique achieves competitive recognition accuracy by solely global-local features and does not require pre-training operations in the experiment. For the classic ResNet50, GMS-Net outperforms these recognition results with 0.87% (>30°) and 0.52% (>45°) on the Pose-RAF-DB dataset and by 0.37% (>30°) and 0.90% (>30°) on the Pose-AffectNet dataset, respectively. Meanwhile, LPA-Net further enhances the performance of the GMS model, with recognition accuracies improved by 2.58% (>30°) and 2.47% (>45°) on the Pose-RAF-DB dataset, while 2.95% (>30°) and 2.86% (>30°) on the Pose-AffectNet dataset, respectively. Fig. 14a through Fig. 14d present the corresponding visualization operations (CAM) on the Pose-RAF-DB and Pose-AffectNet datasets. They indicate that the proposed method can effectively capture salient features in a real-world environment.

Figure 14: The visualization operations on Pose-RAF-DB (a and b) and Pose-AffectNet (c and d) datasets

4.4 Cross Database & Cross-View Experiments

In order to assess the generalization ability of the GMS-LPA network, cross-database and cross-view FER experiments were conducted in this study. Specifically, the BU-3DFEP1 and Pose-AffectNet datasets were assigned as source datasets, and the Multi-PIE and Pose-RAF-DB datasets were assigned as target datasets, respectively. It is worth mentioning that the public emotions in the source and target datasets were extracted for cross-view experiments. The BU-3DFEP1 and Multi-PIE datasets include four common expressions: disgust (DI), happy (HA), surprise (SU), and neutral (NE), while the Pose-AffectNet and Pose-RAF-DB datasets consist of seven common expressions: anger (AN), disgust (DI), fear (FE), happy (HA), neutral (NE), sadness (SA), and surprise (SU). Moreover, this study selected 0° to 60° facial views in BU-3DFEP1 and Multi-PIE datasets as well as 30° and 45° in Pose-AffectNet and Pose-RAF-DB to conduct cross-view experiments. Table 12 presents the detailed experimental results, and Fig. 15 exhibits the corresponding confusion matrix under dissimilar observation angles. Table 12 indicates that GMS, LPA, and GMS-LPA networks can still effectively improve the recognition accuracy in cross-datasets and cross-view FER experiments, and the proposed method has an accuracy of 64.10%, 65.40%, 63.70%, and 62.80% in a controlled scenario, and an accuracy of 50.13% and 50.70% in real-world scenarios. Nevertheless, when examining the raw datasets, there is a significant decrease in identification rates during the experiments, especially in the BU-3DFEP1 (source) and Multi-PIE (target) datasets, with the identification error exceeding 20%. However, the decrease is relatively slight in two real-world scenarios, with an error of 10.18% and 10.22% for pose-AffectNet (>30°) and pose-AffectNet (>45°), respectively. This phenomenon can be triggered by the characteristic of raw facial images, with the BU-3DFEP1 dataset being collected in a synthesized scenario while the Multi-PIE dataset is recorded in a closely real-world environment. Fig. 15a through Fig. 15d present the cross-view confusion matrix in controlled environments. It indicates that the recognition results are roughly consistent among four common expressions. Neutral and surprise expressions are more easily identified, while disgust is relatively difficult and usually confused with neutral expressions. Similarly, Figs. 15e and 15f present the cross-view confusion matrix in real-world scenarios, where the overall FER recognition results are generally less than 60% except for happy expression, whose recognition accuracy is 87.86% (>30°) and 85.96% (>45°), respectively, followed by neutral, surprise and sadness, with the recognition rates of 57.72%, 53.46%, 50.75% and 58.59%, 53.96%, 51.20%, on the Pose-AffectNet (>30°) and Pose-AffectNet (>45°) dataset, respectively. Furthermore, the anger, disgust, and fear expressions are more easily misclassified by all expressions on these datasets, which reduces the identification accuracy.

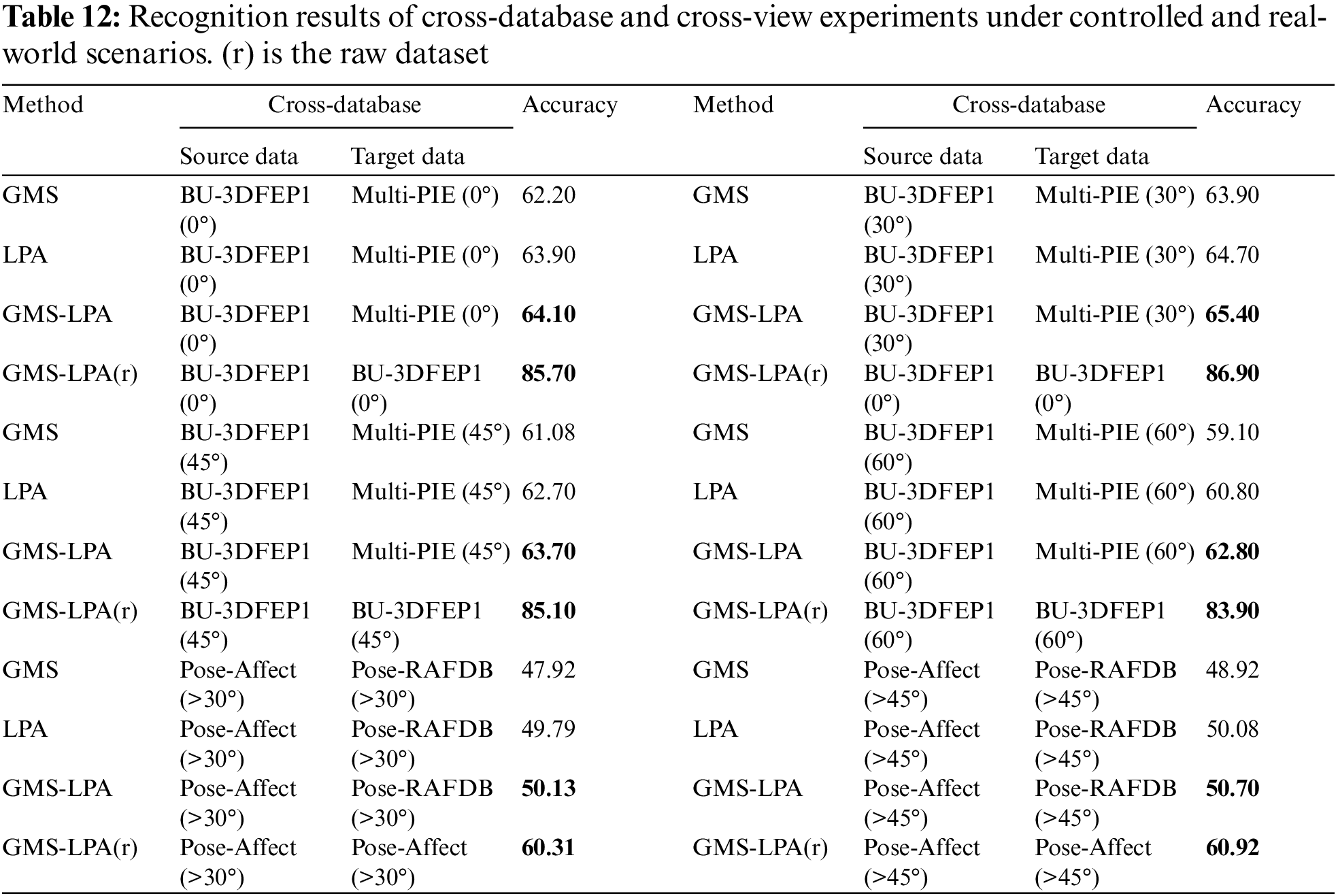
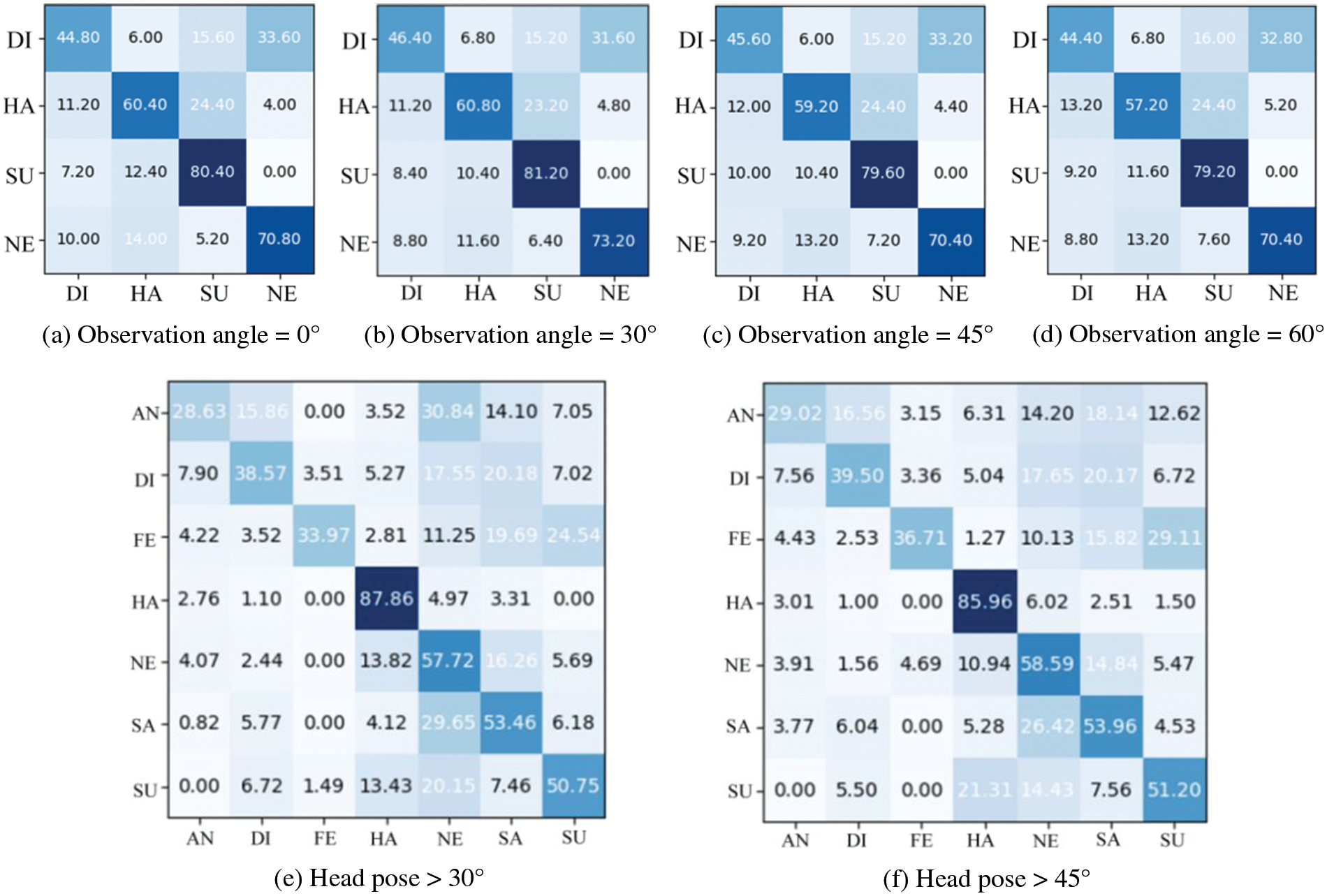
Figure 15: The confusion matrices of cross-database and cross-view FER on controlled and real-world scenarios. (a–d) are the cross-database experiments in a controlled environment, and (e–f) are the cross-database experiments in a real-world environment

4.5 Comparison with Other State-of-the-Art Methods

Finally, to comprehensively estimate the proposed algorithm, this study also summarizes some state-of-the-art methods published in recent years on the BU-3DFEP1, BU-3DFEP2, Multi-PIE, RAF-DB, and AffectNet datasets. Experiments were conducted on more complex original (RAF-DB and AffectNet) datasets to estimate the performance of the GMS-LPA network in the wild. Table 13 lists the corresponding recognition results. It indicates that Generative Adversarial Network (GAN) [10,53–56] adopted data-driven approaches to augment synthetic facial images and fed them into CNN for FER, widely used in multi-view FER. Since ST-SE [19] employed a channel-level attention model to force the network to concentrate on salient features in the current view. Feratt [57] utilized a spatial-level attention model to extract conspicuous features from different observation angles, enabling the deep convolution layer to obtain richer features to lessen the impact of pose-variant and self-occlusion on FER. In Li et al. [27] and [58], a patch-level (gACNN and PG-CNN) attentive model was added to both global and local feature maps, and these refined features were then fused to address variation and self-occlusion problems. In Zeng et al. [59], the fine-tuning method was employed to train the classification model, and the pre-trained model was then employed to initialize the LINet model to improve the identification accuracy. The recognition accuracy was separately compared between controllable and real-world scenarios to make fair comparisons.

Specifically, in a controllable setting, channel-level [19] and spatial-level [57] methods have an accuracy of 76.20% and 77.90% on the BU3DFEP1 dataset, respectively. The proposed algorithm achieves an accuracy of 78.23%, which is 2.03% and 0.33% higher than these methods, respectively. GAN [55] has an accuracy of 73.13%, and the proposed algorithm is strikingly improved, with a recognition accuracy increased by 5.10%. Furthermore, conventional CNNs (CNN and DBN) achieve recognition accuracy of 68.90% and 73.50%, respectively, and the proposed method over them with 9.33% and 4.73%, respectively. In the BU3DFEP2 dataset, channel-level (ST-SE [19]) obtains a fantastic performance by deepening the convolutional layer numbers (50 layers), while the proposed method has a comparable result merely adopting shallow global multiple-scale and local patches feature information. Meanwhile, the geometry guide generative adversarial network (GAN-GG) also performs well on the dataset, where a set of facial landmark patches expresses the input expression and pose, and then these extracted features are employed to enlarge the training set for pose-invariant FER. However, the proposed method does not have a landmark detection operation and has more satisfactory recognition results in the experiment. In the Multi-PIE dataset, the proposed method is superior to all state-of-the-art algorithms, although the encoder-decoder generative adversarial network (GAN-ED) achieves the optimal recognition results, while the proposed method is 0.33% higher than this approach. In addition, for other advanced approaches, the proposed method is superior to DBN (76.10%) and CNN (77.80%) and slightly higher than ST-SE (86.10%) and pure GAN (86.74%) in the experiment.

In a real-world setting, to comprehensively estimate the effectiveness of the proposed algorithm, this study adopted three feature fusion methods (both global and local) and two fine-tuning methods for comparison. The recognition results are exhibited in the right-most columns of Table 13. The proposed GMS-LPA method has an accuracy of 86.58% and 56.96% on the original RAF-DB and AffectNet datasets, while the highest recognition accuracy among global-level and local-level (gACNN and PG-CNN) attention algorithm is 85.07% and 55.33%, which is 1.51% and 1.63% lower than those of the proposed method. In the meantime, the fine-tuning method [59] obtains the best performance on these real-world datasets and actualizes an accuracy of 86.77% and 57.31% in the experiment, respectively. However, fine-tuning methods often require a multitude of datasets as a foundation. When only training parameter models on a single dataset, the recognition results will drop back to 85.10% and 56.51%, lower than the proposed GMS-LPA network.

4.6 Complexity Analysis

This study presents the computational requirements in this section, namely the running environment, the consuming time on the training and testing set, and the parameters of each model to demonstrate the feasibility of the proposed method. In general, deep learning-based methods often take longer to train the classification model, which is typically related to the computer equipment. This study performed the GMS-LPA network using Pytorch, a widely used deep learning framework. The experiment was conducted on a Windows 10 operator system and an NVIDIA GeForce GTX 1660 Super GPU with 6GB memory. The initial learning rate, batch size, momentum, and weight decay are set to 0.1, 128, 0.9, and 0.001, respectively. Detailed hardware, software, and version are present in Table 14.

In general, the training and testing time is regarded as one of the criteria for complexity analysis, which can correctly reflect the feasibility and effectiveness of the designed network. Hence, this study recorded the number of training and testing times for each model on pose-RAFD-DB and pose-AffectNet datasets, and the results are listed in Table 15. The latter typically requires a longer time to train the classification model than the former. This is because there are more facial images in the pose-AffectNet dataset. For the best recognition result, namely, the GMS-LPA model, it takes 55 min to train the classification model on the pose-RAFD-DB dataset and 4.6 h on the pose-AffectNet dataset. Meanwhile, in the testing stage, the time to identify the expression categories on the two datasets is 54 s and 77 s, respectively. Furthermore, this study also conducted gACNN and PG-CNN FER experiments under the running environment. The training and testing times are listed in the first and second rows of Table 15. For fairness, this research compares the proposed GMS-LPA model with gACNN. Specifically, the training time of the GMS-LPA model on each dataset is about half that of gACNN, which is 129 min and 10.2 h, respectively. Meanwhile, the testing time of the GMS-LPA model also performs conspicuous superiority, which is 8 and 5 s less than the gACNN model, respectively. Considering there are more than 1,200 facial images on the pose-RAFD-DB (>30°) dataset, the average recognition time of each image is less than 54/1200≈0.04 seconds. In addition, when the GMS-LPA is compared to the PG-CNN network, the conclusion is also correct in the experiment.

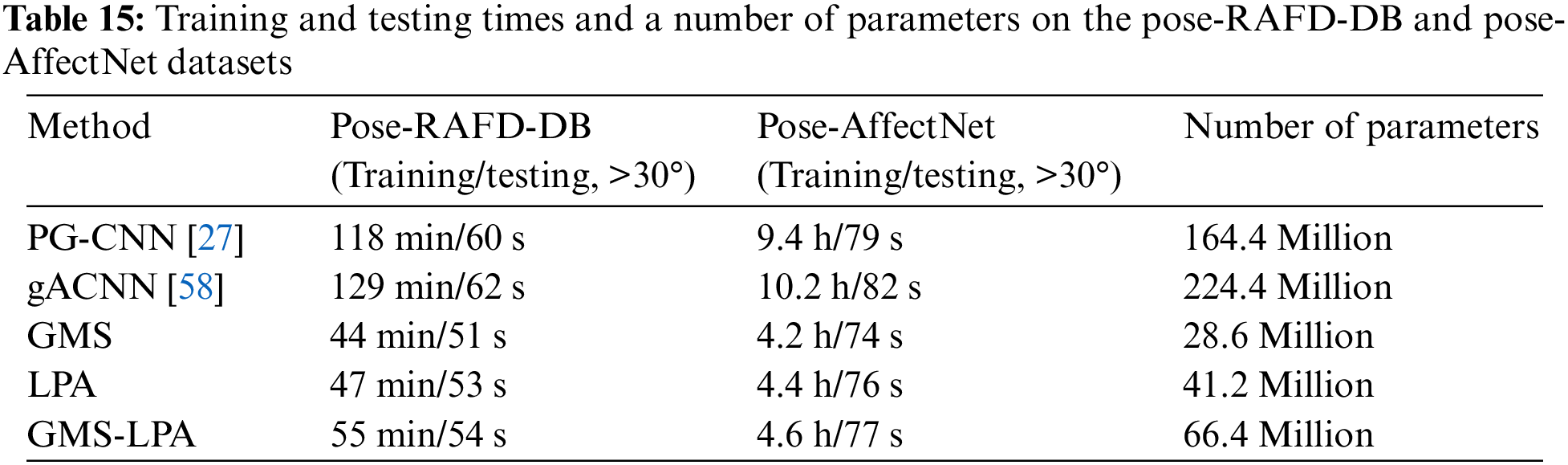
Furthermore, model parameters serve as another decisive evaluation criterion, which typically determines the number of operations in different models, training time, and generation ability. Thus, the number of each model is calculated and presented in Table 15. The designed GMS, LPA, and GMS-LPA models have 28.6, 41.2 and 66.4 million parameters, respectively. Comparing the three models, it is possible to find that the number of parameters increases with the addition of the GMS and LPA model in the dual-branch network. The number of parameters in the developed GMS-LPA model is approximately one-third that of the gACNN model, which is 224.4 million. In the meantime, the training and testing time also increases with the number of parameters in the model, but it still displays a clear advantage over gACNN and PG-CNN models. The fewer model parameters and shorter training and testing time make the proposed method to train classification models faster and easier to meet the computational requirements in practical applications.

4.7 Experiment Results and Analysis

The recognition results of GMS-LPA networks on four public pose-robust expression databases revealed that the designed dual-branch framework can obtain comparable recognition results as the state-of-the-art methods. This section selects the baseline (ResNet50) network as the contrast criterion. For the developed GMS network, the recognition accuracies improved by 0.73%, 0.68%, 0.98%, (0.87% (>30°), 0.52% (>45°)) and (0.37% (>30°), 0.90% (>45°)) on BU-3DFEP1, BU-3DFEP2, Multi-PIE, Pose-RAF-DB and Pose-AffectNet datasets, respectively. For the developed LPA network, the recognition accuracies improved by 2.22%, 1.79%, 2.40%, (2.58% (>30°), 2.47% (>45°)) and (2.95% (>30°), 2.86% (>45°)), respectively. In the meantime, the GMS-LPA network further enhances the accuracy by 2.69%, 2.51%, 2.88%, (3.14% (>30°), 3.50% (>45°)) and (3.55% (>30°), 3.95% (>45°)) in the experiment. Three essential components can explain this improvement. The first is the symmetrical multiple-scale unit, where the GMS model can fuse the global feature information with diverse receptive fields, effectively lowering the susceptibility of deeper convolution layers in pose-variant and self-occlusion scenarios. The second is the LPA model, where the LPA model divides the input feature maps into smaller patches, and then the spatial attention mechanism can guide the network to focus on local discriminative information. The third one is the model-level feature fusion strategy, which allocates different weight scores between GMS and LPA models to improve the identification results. All of them are advantageous for pose-invariant expression recognition tasks.

As for the impact of experimental environments, this study also compares the identification results of GMS, LPA, and GMS-LPA networks under controlled and real-world conditions. Fig. 16a through Fig. 16d depict the detailed results of GMS, LPA, and GMS-LPA networks, and the corresponding average experiment scores can be found in Tables 5, 7, 11, and 9, respectively. Concerning the controlled environments, the performance of GMS, LPA, and GMS-LPA networks is generally consistent, with the GMS-LPA network performing the best, followed by the LPA network and the GMS network performing the worst. The standard deviation (SD) value of 5-fold cross-validation also demonstrates that the GMS-LPA network can provide more stable recognition results than GMS and LPA networks, and this phenomenon is more pronounced in the Multi-PIE database, where the minimum SD values of GMS-LPA network is 0.18, while that of GMS and LPA network is 0.37 and 0.63, respectively. For real-world environments, the recognition results maintain the same trend as the controlled conditions, with the GMS-LPA network being the best, followed by the LPA network and then the GMS network. The results indicate that the proposed method not only ameliorates the stability performance in a controlled environment but also is more robust in the real-world scenarios.

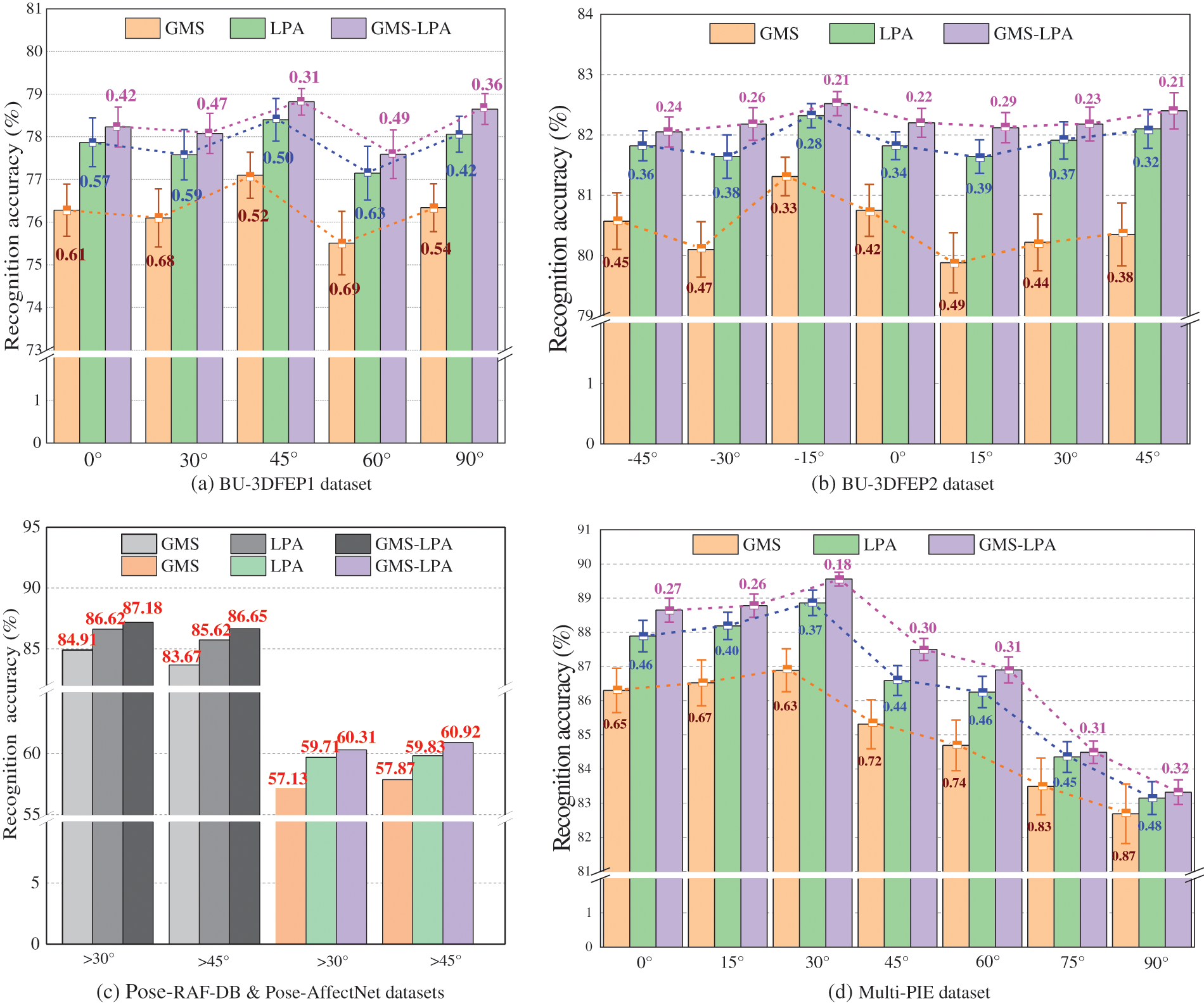
Figure 16: The recognition results of GMS, LPA, and GMS-LPA networks on controlled and real-world datasets

For the impact of expression intensity levels, as depicted in Tables 6 and 8, the BU-3DFEP2 dataset often has higher identification accuracy than the others. The result originates from the small muscle deformations of the low-intensity-level expressions and the considerable variation of facial image views. A 5-fold cross-validation was conducted on the BU-3DFEP1 dataset to examine the effect of intensity levels, and the recognition results are given in Fig. 17. Based on the recognition results, the identification accuracy increases with the strength of emotional intensity levels. As described in Section 4.1, the BU-3DFEP1 dataset contains four emotional intensities (I, II, III, and IV), and the BU-3DFEP2 dataset only has the strongest intensity level (IV) involved. In this case, the high-level facial images can provide a stronger emotional representation ability than the low-level ones. As a result, the identification accuracy of the GMS-LPA network on BU-3DFEP2 will perform more satisfactorily than the BU-3DFEP1 dataset.

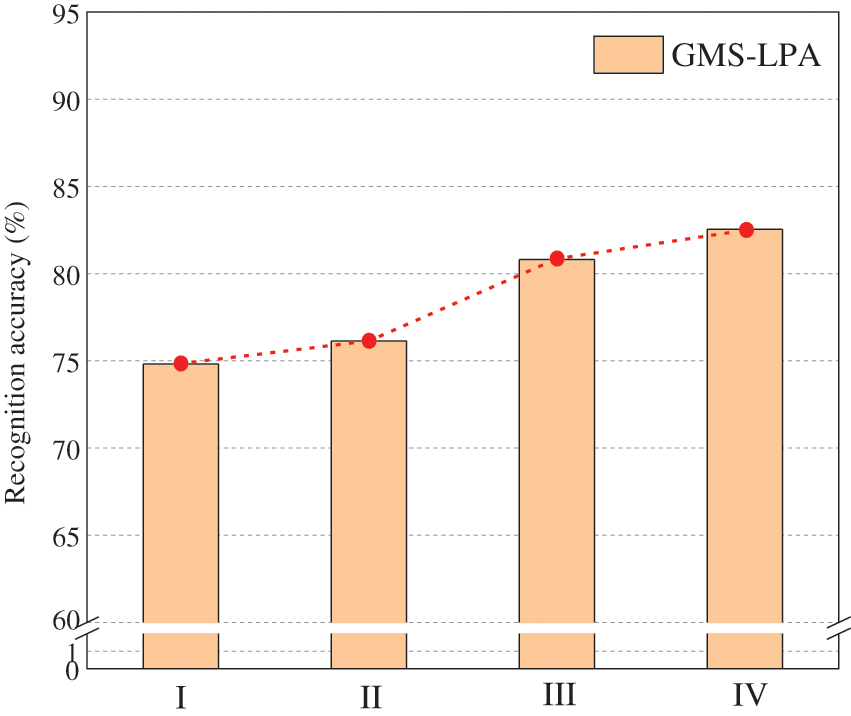
Figure 17: Influence of four expression intensity levels on the BU-3DFEP1 dataset

Confused emotional images are closely related to the facial textures among different expressions. As described in [60], 44 action units are defined in the forehead, eyes, and mouth regions to describe emotional features. When facial images contain excessively similar action units, they are prone to be confused. For example, Figs. 10f and 11h show that anger and sadness are more likely to be confused in the BU-3DFEP1 and BU-3DFEP2 datasets, which can be due to the similar muscle deformations among facial action units in these facial images. The corresponding raw facial images are depicted in Figs. 7a and 7b. On the contrary, when facial muscles deform very differently, their misclassification probability is relatively low. For instance, happy and sad expressions display opposite inner emotions, presenting a lower probability of confusion in the experiment.

For the influence of observation angles, it can see that the observation angle less than ±45° is beneficial for pose-invariant FER. The recognition results are relatively reduced when the observation angle exceeds ±45°. The reason can be ascribed to the action units on the facial images. When the observation angle is larger than ±45°, these action units (such as eyebrow corners, mouth, and lip corners) are no longer notable, decreasing recognition accuracy. Tables 5, 7, and 9 indicate that the highest recognition view is not 0° but is more prone to maintain in the near-frontal range. In practical terms, most pure frontal facial images are regarded as symmetrical features during the model training process. In other words, half or more of the frontal images can adequately characterize entire facial expression characteristics. The pure frontal facial expression images usually contain superfluous information compared to the near-frontal ones. Consequently, a micro-rotated face image can protect the semantic information of the frontal features and add some detailed side texture features, which can be conducive to emotion classification tasks in deep convolutional neural networks.

5  Conclusion

This study designs a deep global multiple-scale and local patches attention (GMS-LPA) dual-branch network for pose-invariant FER, where the GMS model can extract deep global features with multi-scalar characteristic information. In contrast, the LPA model can force the network to concentrate on local features, effectively enhancing the representation ability and reducing the sensitivity to non-frontal FER. Extensive experiments were conducted in both controlled and real-world scenarios to verify the effectiveness of the GMS-LPA network. The experiment results indicated that the developed GMS-LPA-Net has fantastic robustness towards pose-variant and self-occlusion facial expression recognition.

Acknowledgement: The authors are grateful to the National Natural Science Foundation of China, the Advantage Discipline Construction Project of Jiangsu University, and the Key Laboratory of Multi-environment Testing and Controlling.

Funding Statement: This work is supported by the National Natural Science Foundation of China (No. 31872399), Advantage Discipline Construction Project (PAPD, No. 6-2018) of Jiangsu University.

Author Contributions: The authors’ contributions to the paper are as follows: Study conception and design: Xingqiao Liu; Data collection: Xingqiao Liu, Chaoji Liu; Analysis and interpretation of results: Xingqiao Liu, Chaoji Liu, Chong Chen; Draft manuscript preparation: Xingqiao Liu, Chaoji Liu, Chong Chen; Writing-review & editing: Xingqiao Liu, Chaoji Liu, Chong Chen, Kang Zhou. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets used or analyzed during the current study are available from the corresponding author upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Ward, N. J., Finley, K., Otto, J. (2020). Traffic safety culture and prosocial driver behavior for safer vehicle-bicyclist interactions. Journal of Safety Research, 75(1), 24–31. https://doi.org/10.1016/j.jsr.2020.07.003 [Google Scholar] [PubMed] [CrossRef]

2. Gogic, I., Manhart, M., Pandzic, I. S. (2020). Fast facial expression recognition using local binary features and shallow neural networks. Visual Computer, 36(1), 97–112. https://doi.org/10.1007/s00371-018-1585-8 [Google Scholar] [CrossRef]

3. Goh, K. M., Li, L. L. (2020). Micro-expression recognition: An updated review of current trends, challenges and solutions. Visual Computer, 36(3), 445–468. https://doi.org/10.1007/s00371-018-1607-6 [Google Scholar] [CrossRef]

4. Moore, S., Bowden, R. (2011). Local binary patterns for multi-view facial expression recognition. Computer Vision and Image Understanding, 115(4), 541–558. https://doi.org/10.1016/j.cviu.2010.12.001 [Google Scholar] [CrossRef]

5. Li, X. L., Ruan, Q. Q., Jin, Y. (2015). Fully automatic 3D facial expression recognition using polytypic multi-block local binary patterns. Signal Processing, 108(2), 297–308. https://doi.org/10.1016/j.sigpro.2014.09.033 [Google Scholar] [CrossRef]

6. Hu, Y., Zeng, Z., Yin, L. (2008). Multi-view facial expression recognition. Proceeding of 8th IEEE International Conference on Automatic Face and Gesture Recognition, Amsterdam, Netherlands. [Google Scholar]

7. Zhang, W., Zhang, Y., Ma, L. (2015). Multimodal learning for facial expression recognition. Pattern Recognition, 48(10), 3191–3202. https://doi.org/10.1016/j.patcog.2015.04.012 [Google Scholar] [CrossRef]

8. Happy, S., Routray, A. (2015). Robust facial expression classification using shape and appearance features. Proceeding of the 8th International Conference on Advances in Pattern Recognition (ICAPR), pp. 1–5. Kolkata, India. [Google Scholar]

9. Wu, J., Lin, Z., Zheng, W. (2017). Locality-constrained linear coding based bi-layer model for multi-view facial expression recognition. Neurocomputing, 239(2), 143–152. https://doi.org/10.1016/j.neucom.2017.02.012 [Google Scholar] [CrossRef]

10. Liu, Y. Y., Wei, D., Fang, F. (2021). Dynamic multi-channel metric network for joint pose-aware and identity-invariant facial expression recognition. Information Sciences, 578(3), 195–213. https://doi.org/10.1016/j.ins.2021.07.034 [Google Scholar] [CrossRef]

11. Fan, Y., Lam, J., Li, V. (2018). Multi-region ensemble convolutional neural network for facial expression recognition. Proceeding of the 27th International Conference on Artificial Neural Networks (ICANN), pp. 84–94. Rhodes, Greece. https://doi.org/10.1007/978-3-030-01418-6_9 [Google Scholar] [CrossRef]

12. Liu, Y., Zeng, J., Shan, S. (2018). Multi-channel pose-aware convolution neural networks for multi-view facial expression recognition. Proceeding of the 13th IEEE International Conference on Automatic Face & Gesture Recognition, pp. 458–465. Xi’an, China. https://doi.org/10.1109/FG.2018.00074 [Google Scholar] [CrossRef]

13. Zhang, K. H., Huang, Y. Z. (2017). Facial expression recognition based on deep evolutional spatial-temporal networks. IEEE Transactions on Image Processing, 26(9), 4193–4203. https://doi.org/10.1109/TIP.2017.2689999 [Google Scholar] [PubMed] [CrossRef]

14. Zheng, H., Wang, R. (2020). Discriminative deep multi-task learning for facial expression recognition. Information Sciences, 533(2), 60–71. https://doi.org/10.1016/j.ins.2020.04.041 [Google Scholar] [CrossRef]

15. Zeiler, M. D., Fergus, R. (2014). Visualizing and understanding convolutional networks. Proceeding of the 13th European Conference on Computer Vision (ECCV), pp. 818–833. Zurich, Switzerland. https://doi.org/10.1007/978-3-319-10590-1_53 [Google Scholar] [CrossRef]

16. Gao, S. H., Cheng, M. M., Zhao, K. (2021). Res2Net: A new multi-scale backbone architecture. IEEE Transactions on Pattern Analysis and Machine Intelligence, 43(2), 652–662. https://doi.org/10.1109/TPAMI.2019.2938758 [Google Scholar] [PubMed] [CrossRef]

17. Fasel, B. (2002). Head-pose invariant facial expression recognition using convolutional neural networks. Proceeding of the 14th IEEE International Conference on Multimodal Interfaces, pp. 529–534. Pittsburgh, PA, USA. https://doi.org/10.1109/ICMI.2002.1167051 [Google Scholar] [CrossRef]

18. Zhang, T., Zheng, W., Cui, Z. (2016). A deep neural network-driven feature learning method for multi-view facial expression recognition. IEEE Transactions on Multimedia, 18(12), 2528–2553. https://doi.org/10.1109/TMM.2016.25 [Google Scholar] [CrossRef]

19. Liu, C. J., Liu, X. Q., Chen, C. (2022). Soft thresholding squeeze-and-excitation network for pose-invariant facial expression recognition. Visual Computer, 39, 2637–2652. https://doi.org/10.1007/s00371-022-02483-5 [Google Scholar] [CrossRef]

20. Shao, J., Qian, Y. (2019). Three convolutional neural network models for facial expression recognition in the wild. Neurocomputing, 355(2), 82–92. https://doi.org/10.1016/j.neucom.2019.05.005 [Google Scholar] [CrossRef]

21. Yan, K., Zheng, W., Zhang, T. (2019). Cross-domain facial expression recognition based on transductive deep transfer learning. IEEE Access, 10(7), 108906–108915. https://doi.org/10.1109/ACCESS.2019.2930359 [Google Scholar] [CrossRef]

22. Zhang, F., Yu, Y., Mao, Q. (2016). Pose-robust feature learning for facial expression recognition. Frontiers of Computer Science, 10(5), 832–844. https://doi.org/10.1007/s11704-015-5323-3 [Google Scholar] [CrossRef]

23. Yu, M. J., Zheng, H. C., Peng, Z. F. (2020). Facial expression recognition based on a multi-task global-local network. Pattern Recognition Letters, 131(2), 166–171. https://doi.org/10.1016/j.patrec.2020.01.016 [Google Scholar] [CrossRef]

24. He, Z., Meng, B., Wang, L. (2022). Global and local fusion ensemble network for facial expression recognition. Multimedia Tools and Applications, 82(4), 5473–5494. https://doi.org/10.1007/s11042-022-12321-4 [Google Scholar] [CrossRef]

25. Le, N., Nguyen, K., Nguyen, A. (2021). Global-local attention for emotion recognition. Neural Computing & Applications, 34(24), 21625–21639. https://doi.org/10.1007/s00521-021-06778-x [Google Scholar] [CrossRef]

26. Li, Y., Lu, G., Li, J. (2023). Facial expression recognition in the wild using multi-level features and attention mechanisms. IEEE Transactions on Affective Computing, 14(1), 451–462. https://doi.org/10.1109/TAFFC.2020.3031602 [Google Scholar] [CrossRef]

27. Li, Y., Zeng, J., Shan, S. (2019). Occlusion aware facial expression recognition using CNN with attention mechanism. IEEE Transactions on Image Processing, 28(5), 2439–2450. https://doi.org/10.1109/TIP.2018.2886767 [Google Scholar] [PubMed] [CrossRef]

28. Shao, W. Z., Xu, J. J., Chen, L. (2019). On potentials of regularized wasserstein generative adversarial networks for realistic hallucination of tiny faces. Neurocomputing, 364, 1–15. https://doi.org/10.1016/j.neucom.2019.07.046 [Google Scholar] [CrossRef]

29. Wang, K., Peng, X., Yang, J. (2020). Region attention networks for pose and occlusion robust facial expression recognition. IEEE Transactions on Image Processing, 29(1), 4057–4069. https://doi.org/10.1109/TIP.2019.2956 [Google Scholar] [CrossRef]

30. Liu, C., Hirota, K., Dai, Y. P. (2023). Patch attention convolutional vision transformer for facial expression recognition with occlusion. Information Sciences, 619, 781–794. https://doi.org/10.1016/j.ins.2022.11.068 [Google Scholar] [CrossRef]

31. Huang, Q., Huang, H. (2021). Facial expression recognition with grid-wise attention and visual transformer. Information Science, 580, 35–54. https://doi.org/10.1016/j.ins.2021.08.043 [Google Scholar] [CrossRef]

32. Shen, W., Zhao, K., Jiang, Y. (2017). DeepSkeleton: Learning multi-task scale-associated deep side outputs for object skeleton extraction in natural images. IEEE Transactions on Image Processing, 26(11), 5298–5311. https://doi.org/10.1109/TIP.2017.2735182 [Google Scholar] [PubMed] [CrossRef]

33. Shu, X., Yang, J., Yan, R. (2021). Expansion-squeeze-excitation fusion network for elderly activity recognition. IEEE Transactions on Circuits and Systems for Video Technology, 32(8), 5281–5292. https://doi.org/10.1109/TCSVT.2022.3142771 [Google Scholar] [CrossRef]

34. Peng, S., Huang, H. B., Chen, W. J. (2020). More trainable inception-resnet for face recognition. Neurocomputing, 411, 9–19. https://doi.org/10.1016/j.neucom.2020.05.022 [Google Scholar] [CrossRef]

35. Zagoruyko, S., Komodakis, N. (2017). Paying more attention to attention: Improving the performance of convolutional neural networks via attention transfer. https://doi.org/10.48550/arXiv.1612.03928 [Google Scholar] [CrossRef]

36. Cai, J., Meng, Z. B., Khan, A. S. (2019). Feature-level and model-level audiovisual fusion for emotion recognition in the wild. Proceeding of the 2nd IEEE International Conference on Multimedia Information Processing and Retrieval (MIPR), pp. 443–448. San Jose, CA. https://doi.org/10.1109/MIPR.2019.00089 [Google Scholar] [CrossRef]

37. Yin, L., Wei, X., Sun, Y. (2006). A 3D facial expression database for facial behavior research. Proceeding of the IEEE International Conference on Automatic Face Gesture Recognition, pp. 211–216. Southampton. https://doi.org/10.1109/FGR.2006.6 [Google Scholar] [CrossRef]

38. Gross, R., Matthews, I., Cohn, J., Kanade, T. (2010). Multi-PIE. Image and Vision Computing, 28(5), 807–813. [Google Scholar]

39. Zheng, W. (2014). Multi-view facial expression recognition based on group sparse reduced-rank regression. IEEE Transactions on Affective Computer, 5(1), 71–85. https://doi.org/10.1109/TAFFC.2014.2304712 [Google Scholar] [CrossRef]

40. Jampour, M., Lepetit, V., Mauthner, T. (2017). Pose-specific non-linear mapings in feature space towards multiview facial expression recognition. Image and Vision Computing, 58, 38–46. https://doi.org/10.1016/j.imavis.2016.05.002 [Google Scholar] [CrossRef]

41. Huang, X. H., Zhao, G. Y. (2013). Emotion recognition from facial images with arbitrary views. Proceeding of the 24th British Machine Vision Conference, Bristol, England. https://doi.org/10.5244/C.27.76 [Google Scholar] [CrossRef]

42. Hu, Y., Zeng, Z. (2008). A study of non-frontal-view facial expressions recognition. Proceeding of the 19th International Conference on Pattern Recognition (ICPR), pp. 1–4. Tampa, FL, USA. [Google Scholar]

43. Mao, Q. R., Zhang, F. F. (2019). Cascaded multi-level transformed dirichlet process for multi-pose facial expression recognition. Computer Journal, 61(11), 1605–1619. https://doi.org/10.1093/comjnl/bxy016 [Google Scholar] [CrossRef]

44. Tariq, U., Yang, J., Huang, T. (2014). Supervised super-vector encoding for facial expression recognition. Pattern Recognition Letters, 46, 89–95. https://doi.org/10.1016/j.patrec.2014.05.011 [Google Scholar] [CrossRef]

45. Tariq, U., Yang, J., Huang, T. (2012). Multi-view facial expression recognition analysis with generic sparse coding feature. Proceeding of the 12th European Conference on Computer Vision (ECCV), pp. 578–588. Florence, Italy. [Google Scholar]

46. Tang, H., Hasegawa-Johnson, M. (2010). Non-frontal view facial expression recognition based on ergodic hidden Markov model supervectors. IEEE International Conference on Multimedia and Expo (ICME), pp. 1202– 1207. Singapore. https://doi.org/10.1109/ICME.2010.5582576 [Google Scholar] [CrossRef]

47. Jampour, M., Mauthner, T., Bischof, H. (2015). Multi-view facial expressions recognition using local linear regression of sparse codes. Proceeding of the Computer Vision Winter Workshop Paul Wohlhart (CVWW), Seggau, Austria. [Google Scholar]

48. Jampour, M., Mauthner, T., Bischof, H. (2015). Pairwise linear regression: An efficient and fast multi-view facial expression recognition. Proceeding of the 11th IEEE International Conference and Workshops on Automatic Face and Gesture Recognition (IEEE FG), Ljubljana, Slovenia. [Google Scholar]

49. Rudovic, O., Pantic, M., Patras, I. (2013). Coupled gaussian processes for pose-invariant facial expression recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 35(6), 1357–1369. https://doi.org/10.1109/TPAMI.2012.233 [Google Scholar] [PubMed] [CrossRef]

50. Mao, Q. R., Rao, Q. Y., Yu, Y. (2017). Hierarchical bayesian theme models for multipose facial expression recognition. IEEE Transactions on Multimedia, 19(4), 861–873. https://doi.org/10.1109/TMM.2016.2629282 [Google Scholar] [CrossRef]

51. Gera, D., Balasubramanian, S. (2022). CERN: Compact facial expression recognition net. Pattern Recognition Letters, 155, 9–18. https://doi.org/10.1016/j.patrec.2022.01.013 [Google Scholar] [CrossRef]

52. Gera, D., Balasubramanian, S. (2021). Landmark guidance independent spatio-channel attention and complementary context information based facial expression recognition. Pattern Recognition Letters, 145, 58–66. https://doi.org/10.1016/j.patrec.2021.01.029 [Google Scholar] [CrossRef]

53. Zhang, F. F., Zhang, T., Mao, Q. (2020). Geometry guided pose invariant facial expression recognition. IEEE Transaction on Image Processing, 29, 4445–4460. https://doi.org/10.1109/TIP.2020.2972114 [Google Scholar] [PubMed] [CrossRef]

54. Zhang, F. F., Mao, Q. R., Shen, X. (2018). Spatially coherent feature learning for pose-invariant facial expression recognition. ACM Transaction on Multimedia Computing Communication and Application, 14(1). https://doi.org/10.1145/3176646 [Google Scholar] [CrossRef]

55. Lai, Y., Lai, S. (2018). Emotion-preserving representation learning via generative adversarial network for multi-view facial expression recognition. Proceedings of the 13th IEEE International Conference on Automatic Face & Gesture Recognition (FG), pp. 263–270. Xi’an, China. https://doi.org/10.1109/FG.2018.00046 [Google Scholar] [CrossRef]

56. Li, D. J., Li, Z. J., Luo, R. (2019). Multi-pose facial expression recognition based on generative adversarial network. IEEE Access, 7, 143980–143989. https://doi.org/10.1109/ACCESS.2019.2945423 [Google Scholar] [CrossRef]

57. Fernandez, P., Pena, F., Ren, T. (2019). Feratt: Facial expression recognition with attention net. Proceeding of the 32nd IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPR), pp. 837–846. Long Beach, CA. https://doi.org/10.1109/CVPRW.2019.00112 [Google Scholar] [CrossRef]

58. Li, Y., Zeng, J. B., Shan, S. G. (2018). Patch-gated CNN for occlusion-aware facial expression recognition. Proceedings of the 24th International Conference on Pattern Recognition (ICPR), pp. 2209–2214. Beijing, China. [Google Scholar]

59. Zeng, J. B., Shan, S. G., Chen, X. (2018). Facial expression recognition with inconsistently annotated datasets. Proceeding of the 15th European Conference on Computer Vision (ECCV), pp. 227–243. Munich, Germany. https://doi.org/10.1007/978-3-030-01261-8_14 [Google Scholar] [CrossRef]

60. Tian, Y., Kanade, T., Cohn, J. (2001). Recognizing action units for facial expression analysis. IEEE Transactions on Pattern analysis and Machine Intelligence, 23(2), 79–117. https://doi.org/10.1109/34.908962 [Google Scholar] [PubMed] [CrossRef]