Evolutionary Neural Architecture Search and Its Applications in Healthcare

1  Introduction

Deep learning (DL) has made remarkable strides in several areas. How to design automatic neural architecture search (NAS) methods has received substantial interest. NAS has surpassed hand-design architectures on some difficult tasks, particularly in the medical fields [1]. Medical image data account for 90% of electronic medical data. Most imaging data are standardized for communication and storage, which is crucial for rapid diagnosis and prediction of disease. Convolutional neural networks (CNNs) can be used to solve various computer vision problems, including medical image classification and segmentation. However, manually designed network architectures are overparameterized. To optimize deep CNNs for NAS, multiobjective evolutionary algorithms (MOEAs) have made important contributions to reduce the parameter amount and trade off the accuracy and the model complexity [2]. Therefore, NAS has become popular for medical image data in healthcare. Moreover, NAS can efficiently and automatically complete analytical tasks in electronic health records (EHRs), including disease prediction and classification, data enhancement, privacy protection, and clinical event prediction [3].

NAS can be used to solve the combinatorial optimization problem of hyperparameters. Traditional hyperparameter optimization mainly uses grid search and manual intervention. It has very limited flexibility [4]. NAS uses some strategies to obtain the optimal network architecture when a set of candidate neural network (NN) structures are given. As shown in Fig. 1, the fundamental concept of NAS involves exploring a search space containing various candidate NN architectures, using specific strategies to discover the most efficient network structure. Performance evaluation involves analyzing the strengths and weaknesses of an architecture, which can be quantified using various indicators, including model size and accuracy. The search space of NAS defines candidate architectures that can be searched. A good search space should not only be constrained but also possess enough flexibility [5]. In efficient neural architecture search (ENAS) [6], the first weight-sharing NAS method, the searching is based on only a very small block search space, and the whole neural architecture is constructed by stacking a few blocks. This indicates that better performance can be obtained while exploring the block-based search space [7] by simply changing the block structure, that is, changing the number and the sizes of convolutional kernels. This also enables the neural architecture to be easily transferred to other tasks. The ENAS algorithm forces all models to share the same weights, rather than training the model to converge from scratch, and the weights in previous models can be applied. Therefore, each time that you train a new model, transfer learning can be applied, and the convergence speed is much faster. AutoGAN [8] connects generative adversarial networks and NAS, using weight sharing and dynamic resetting to accomplish NAS, which is very competitive. Therefore, under various constraints, weight sharing can be used to accelerate NAS in various devices. Evolutionary algorithms (EAs) are applicable to different search spaces for NAS [9–11]. Moreover, based on changing the block structure [11] and transfer learning [12] for NAS, EAs can achieve high search efficiency at the initial stage of the search.

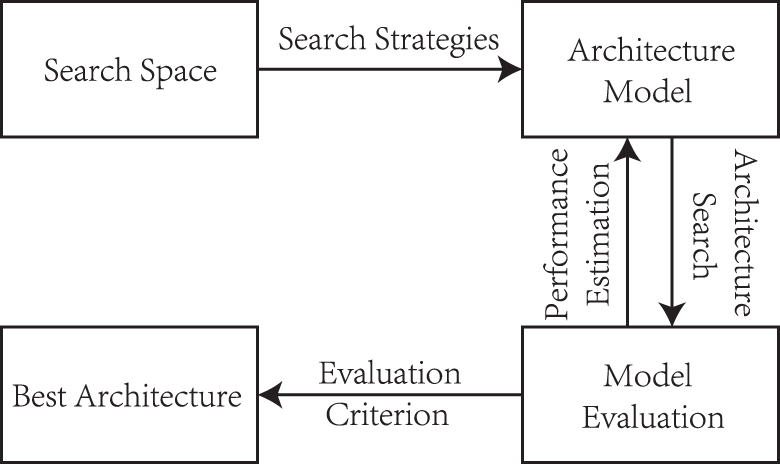
Figure 1: NAS principle

Search strategies determine the approach for searching fundamental architecture to achieve the desired search objectives and establish the configuration of network architecture. The search strategy of NAS [13] can be roughly divided into reinforcement learning (RL), gradient-based methods, and EAs, according to the optimization algorithm used. RL is regarded as a meta-controller to exploit various strategies to auto-perform NN architecture design [14]. NAS only needs to set state-action space and reward function to complete the search process. RL requires extensive interaction to explore the search space. The RL-based search method cannot flexibly optimize multiple objectives and consumes vast amounts of time and resources. The gradient-based algorithm is more effective than the RL algorithm in some aspects, but the gradient-based searching assumes the optimization problem has some particular mathematical properties, such as continuous, convex, and so on. However, the search space of NAS is discrete. Therefore, for the gradient-based methods, the key issue is to convert the discrete network space into continuous and obtain the optimal architecture from its continuous representation. The most representative approach is that of differentiable architecture search (DARTS) [15], in which the authors proposed a differential approach and used gradient descent to solve the architecture search problem. The softmax function has been used to transform the search space. This process increases the training time.

EAs is different from RL. Neuroevolution of augmenting topologies (NEAT) enables artificial evolution to replicate the formation of brain structures and connections, determine the appropriate number of connections, and eliminate ineffective ones [16]. When DL models are scaled up, the amount of parameters expands rapidly, which poses difficulties to the coding space and computing efficiency problems for the optimization strategies [11,17,18]. To enhance optimization efficiency, we concentrate on employing various neuroevolutionary strategies for NAS. Neuroevolution strategies have the advantages of parallel search and high adaptability [19,20]. Neuroevolution is the application of evolutionary ideas to the hyperparameter optimization of NNs. It uses EAs to optimize NNs, which can avoid falling into the local optimum. The work by [21] incorporated a torus walk instead of a uniform walk to improve local search capability. Neuroevolution can mimic biological evolution to evolve NNs, which can learn building blocks, block connections, and even optimization algorithms, and it has inherent parallelism and global exploration characteristics [22]. Neuroevolution approaches have achieved superior performance in medical field. Jajali et al. [23] proposed the MVO-MLP to facilitate early diagnosis of cardiovascular diseases. EvoU-Net used a genetic algorithm (GA) to search the precise and simple CNNs for MRI image segmentation [24].

MOEAs can automatically design simple and efficient network architectures [25] as well as discover and explore optimal neural architectures that meet various performance criteria effectively. The work by [9] demonstrated that large-scale evolution algorithms could achieve high accuracy from a simple initial condition in CIFAR-10 and CIFAR-100 for image classification. Since then, extensive studies have been conducted on the utilization of EAs for NAS. As shown in Fig. 2, EAs for NAS have shown a substantially growing trend from 2017 to 2021. We used the keywords “NAS+EAs,” “NAS+Health,” “NAS+EAs+health,” “NAS+multiobjective optimization,” and “NAS+large-scale multiobjective” to show the publication status of NAS-related studies in the Web of Science (WOS) database in the past five years. It was observed that few papers have focused on EAs for NAS in deep neural networks (DNN). Most of the existing NAS studies describe how to implement NAS using different search strategies [26,27], but only few studies focus on EAs for NAS. Studies related to EAs for NAS, including multiobjective and large-scale MOEAs for NAS, are currently very uncommon. Given the survey summary depicted in Fig. 2, in response to the lack of research in the aforementioned direction, we develop a research classification for NAS, as shown in Fig. 3. In this study, we analyze the advantages and disadvantages of EAs to optimize the NN architecture and provide a detailed guidance for researchers who want to use EAs to optimize the NNs. The existing large-scale multiobjective algorithms are summarized to provide a feasible method for researchers to improve the design and efficiency of NAS. Moreover, we propose large-scale multiobjective neuroevolution strategies and distributed parallel neuroevolution strategies for medical data processing that combine privacy protection with medical data security concerns.

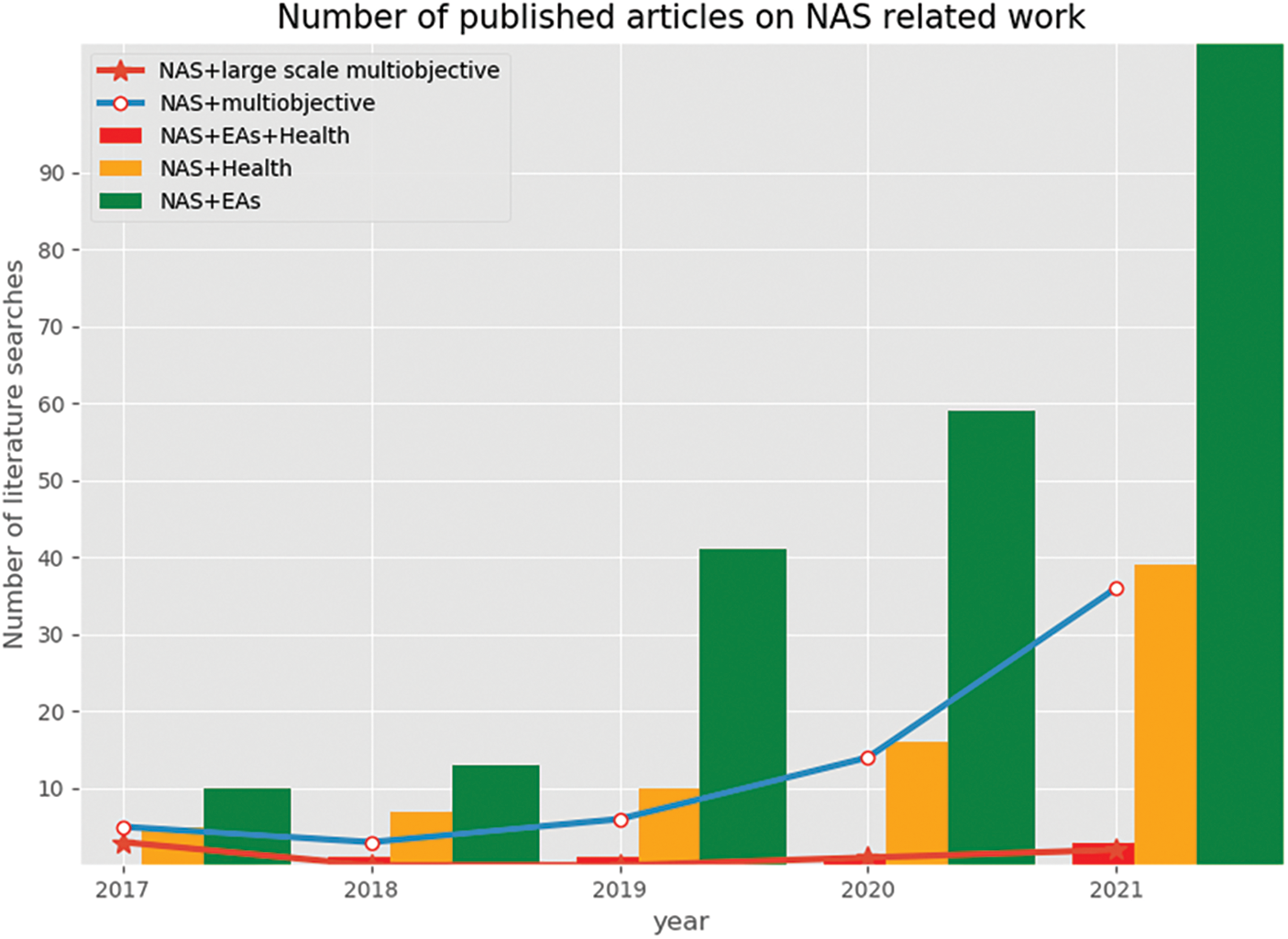
Figure 2: Number of published articles on NAS-related work

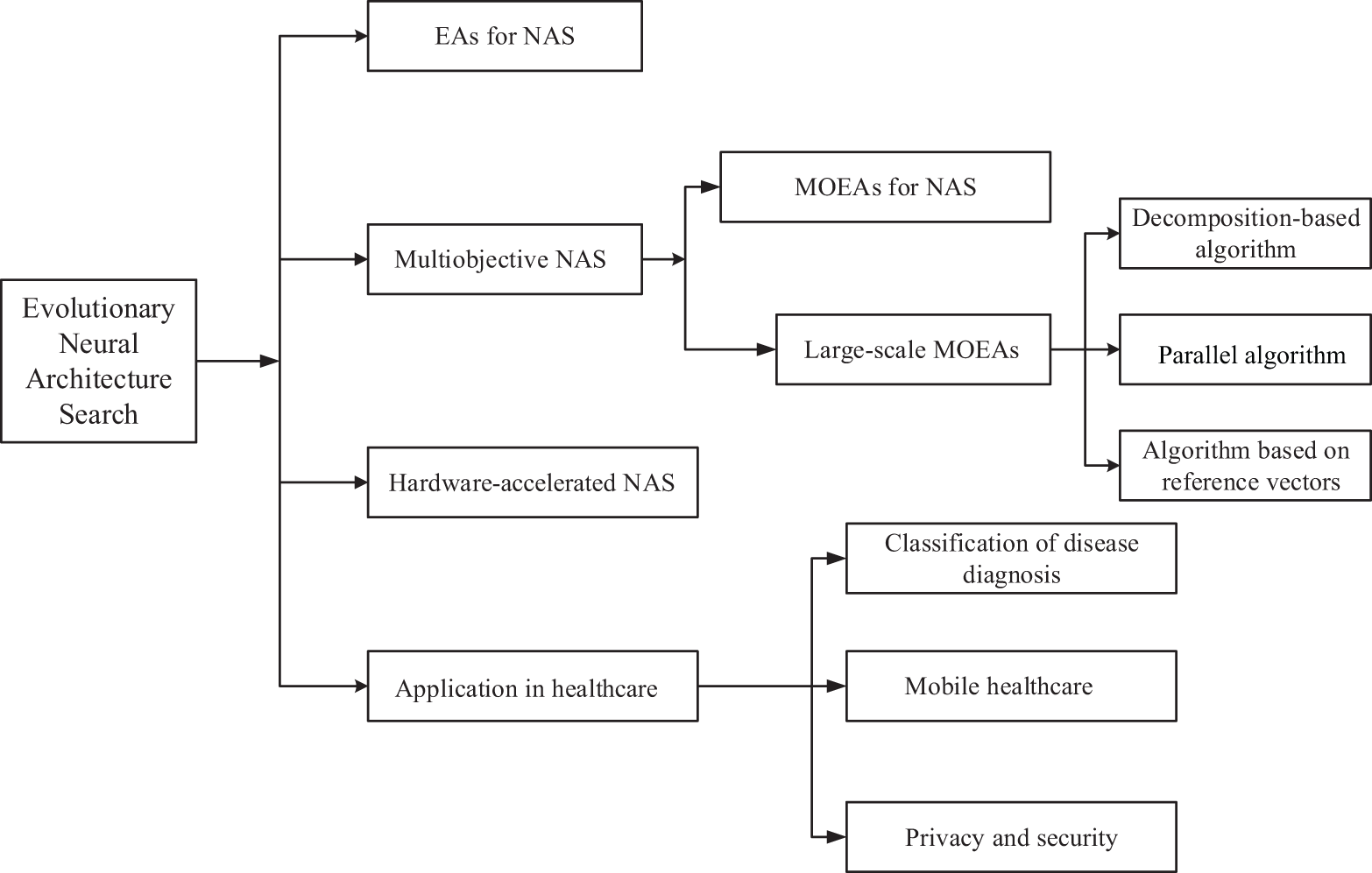
Figure 3: Evolutionary neural architecture search

The remainder of this paper can be organized as follows. Section 2 presents EAs for NAS. We explore MOEAs, large-scale multiobjective evolutionary optimization for NAS, parallel EAs for NAS or hardware accelerated NAS methods in Section 3, and these novel search methods can greatly reduce manual intervention and achieve automatic search. Section 4 discusses the healthcare application of EA-based NAS and interpretable network architecture. Section 5 proposes an interpretable evolutionary neural architecture search based on federated learning (FL-ENAS) framework applied to healthcare to address search efficiency and privacy concerns. Future direction is presented to guide readers to research the NAS via EAs in Section 6. We conclude this paper in Section 7.

2  Evolutionary Algorithms for NAS

EAs can tackle black-box functions for global optimization with population-based strategies. The evolutionary process usually includes initialization, crossover, mutation, and selection. The optimization of NN using EAs can be traced back 30 years to a technique called neuroevolution. Angeline et al. [28] proposed optimizing the structures and weights simultaneously by applying genetic strategies in 1994. In 1997, Yao et al. [29] proposed an evolutionary programming neural network (EPNet) to construct the architecture of ANNs. In addition to optimizing the neural architecture, the weights are also optimized. As these NNs are very small, they are easy to solve, but after that, the NN becomes very large in scale, which cannot be optimized directly. At the beginning of the 20th century, research on encoding ways had a breakthrough. Indirect encoding was introduced to auto-design effective topological structures in 2002 [16,30]. This neuroevolution of augmented topologies is one of the earliest and most well-known examples of using EAs for NN optimization (NEAT). Additionally, it modifies not only the weights and bias but also the structure of the whole network. The NASnet [12] model designed two different block architectures: cells of the normal and reduction types. The superiority of NASnet resided in automatically generating CNNs and applying transfer learning for large-scale image classification and objective detection. Cantu-Paz et al. [31] proved that EAs for NNs could attain the more accurate classification than hand-designed neural architectures in 2005. Since then, numerous researchers have optimized the neural architectures by changing the encoding methods; for example, the indirect encoding with innovation proposed by Stanley et al. [32]. EAs that search DNNs for image classification could obtain the optimal individual from the population by applying mutation and crossover operators [33]. A memetic algorithm (MA) could improve search efficiency. Through the implementation of a novel encoding method, study by [9] utilized an EA to search for deep neural architectures, demonstrating that EAs could achieve high-accuracy architectures from a basic starting point for CIFAR-10 and CIFAR-100 data sets. This had garnered considerable attention. Real et al. [34] proposed AmoebaNet with the aging evolution, which was a variant of the tournament selection. In the progress of evolution, the younger models that could help in exploration were preferred and compared to RL and random search, EAs were faster and could produce better architectures [35]. EAs could improve optimization efficiency by setting suitable hyperparameters, including mutation rate, population size, and selection strategy [36].

2.1 Evolutionary NAS Framework

RL was based on gradient and could be stuck in local optima [37]. However, EAs optimizing NNs has been an active research area for many years, proved as an effective technique, and continues to experience ongoing innovation [38]. EAs are very similar; they first randomly sample a population, then select parents, and generate offspring via evolutionary operators such as crossover and mutation until the final population is attained. The EAs process for NAS is shown as Algorithm 1. First, input some necessary parameters such as population size P, evolution generation number NGEN, etc. The initial population of neural network architectures is generated randomly or based on some heuristic approaches. Architecture fitness is obtained based on evaluating the objective function, such as classification accuracy or computational efficiency. Then, initialize the algorithm parameters. There are some parameter settings in the algorithm, such as mutation probability, mutation intensity, and crossover probability. Lines 4 to 8 are the main part of EAs, which is the population evolution. In each generation, there are parent selection, mutation, and crossover operations. The fitness of each new architecture is evaluated at every generation. The algorithm terminates when a stopping criterion is met, such as a satisfactory fitness level. Lastly, output the evolved final population, which is the optimal architecture. The processing diagram for EAs on NAS is similar to that of traditional EAs, but designed specifically for searching the space of NAS. Through this process, EAs can optimize architectures more efficiently than manually designing neural architectures. However, NAS using EAs may require significant computing resources due to its iterative process and the size of the architecture search space [39].

In the progress of EAs, the crossover and mutation are the most important operations for the autogeneration of new NN architectures. Crossover operation can dramatically alter the NN architecture by exchanging a fraction of architecture between a group of NN architectures. The mutation changes the NN architecture with slight possibilities. EAs can use flexible encoding for NAS. The encoding space can indicate various complex structures [40,41]. EAs can guide the exploration and determine the search direction by simple genetic operators and survival of the fittest in natural selection. EAs use the population to organize the search, which makes it possible to concurrently explore multiple regions of the solution space, so this is particularly suitable for large-scale parallelism. For the evolutionary algorithm (EA) for NAS approach, The critical factor lies in designing an effective EA and a suitable coding strategy. At its core, NAS is aimed at addressing combinatorial optimization problems. The variants of EAs can be effectively employed in addressing combinatorial problems. Therefore, in theory, all EA variants hold potential to be utilized as NAS methods. The effect of EAs on NN architecture optimization is particularly obvious [41]. For example, the multiobjective optimization algorithm NSGA-II [42] was utilized to optimize the NAS problem [43]. Based on the basic GA, each individual was stratified according to the relationship between Pareto dominance and non-dominance as well as crowding distance. MOEAs could simultaneously optimize network architecture and model accuracy for complex medical image segmentation [25]. MOEAs could automatically design simple and efficient network architectures, and the flexibility of the architecture and the convergence of the EA need to be improved. Therefore, improving EAs’ search efficiency remains the primary challenge in the EA for NAS methods. We will address this problem in Section 3.

2.2 Major EAs for NAS

In Table 1, we summarize major EAs for NAS, the representative algorithms and their main contributions, and the objective number (single or multiple) of these algorithms. We provide a guide to how the EAs can generate the best NN architecture. NAS based on GA [77,78] could use a binary string as a representation of the architecture, whereas NAS based on genetic programming (GP) [49,50] used a tree-based representation with nodes representing operations. NAS based on evolutionary programming (EP) [53] used continuous or discrete representations. NAS based on particle swarm optimization (PSO) [40,56,55] used a swarm of particles to represent neural network architectures. NAS based on ant colony optimization (ACO) [79,62] used pheromone trails to guide the search. Moreover, large-scale MOEAs could avoid overfitting on a single objective, handle a substantial amount of decision variables and constraints, and autogenerate the best NN architecture [80–82]. The most representative algorithm was the GA for NAS. GA could be employed to train CNNs. Because each parameter was considered as a chromosome element in the traditional encoding scheme, the challenge was how to map a network to a chromosome [77]. However, this coding scheme made the chromosome too large in scale, leading to problems such as genetic operator failure in the large-scale problem. An alternative would be for each convolution layer (or another layer) to be treated as an element of the chromosome. All the layer connection weights were contained in each chromosome element. This encoding scheme significantly reduced the chromosome structure, which had faster operation speed, faster convergence speed, and higher accuracy. Through crossover and mutation, good individuals were generated and selected, and bad ones were eliminated; thus, the optimal solution could be searched out through the evolution [83]. Greedy exploration based on experience and transfer learning could accelerate GA to optimize both hyperparameters and NNs. Moreover, the genes could represent any part, such as block type, loss function, or learning strategy of an NN [46]. A gene map could encode a deep convolutional neural networks (DCNN) [47]. Evolving deep convolutional neural networks (EvoCNNs) had used a flexible encoding way to optimize the DCNN and connection weight initialization values [48]. EAs used chromosome information encoded in each solution, mutation and crossover, to simulate the evolution of populations [84].

GP based on grammar-guided constraints can generate population individuals (i.e., candidate architectures) according to the defined grammar rules. Suganuma et al. [49] presented a novel method encoding the CNN architecture based on cartesian genetic programming (CGP), which utilized highly functional modules such as convolution block as their node function in CGP. The CNN architecture and connection were optimized based on CGP, and a more competitive architecture could be achieved. Improved gene expression programming optimized the NN structure, weight, and threshold. The efficiency could be improved by adjusting the fitness function and genetic operator [50]. Hybrid meta-evolutionary programming (EP) combined with ANN could develop a structured and automatic way to optimize NNs [53]. EP is often combined with other algorithms for NAS, but it has not been widely used in recent years; consequently, it needs further exploration. PSO originates from simulating the foraging behavior of the bird swarm. Its superiority is based on few adjustable parameters, simple operation, and a very fast convergence speed. It has no crossover and mutation operations, as in GAs, and it finds the global optimum by following the optimal candidates in the current search. Wang et al. [56] used PSO to optimize CNNs to automatically explore the appropriate structure, where Internet protocol (IP) address type encoding could be combined with PSO for the evolution of the DCNN. PSO could optimize the internal parameters in hidden layers [40]. In PSO, for DCNNs to perform image classification tasks, a new direct encoding scheme and the velocity operator were designed, allowing for the optimization of CNNs with fast-converging PSO [55]. PSO could be used to simplify models with maintained performance. Multiobjective NN simplification could be achieved via NN pruning and tuning; thus, a simplified NN with high accuracy could be obtained. PSO could also be combined with other algorithms to facilitate the information processing of NNs [85]. DE is a kind of heuristic and stochastic search algorithm based on individual differences. The differential mutation operator is the biggest difference between DE and other EAs. Adaptive DE combined with ANNs could be used for classification problems. Mininno et al. [86] proposed the compact differential evolution (cDE) algorithm. This method had a small hardware demand and was suitable for practical applications with large search space dimensions and limited cost. However, in a constrained environment, DE had some drawbacks, including low convergence and early convergence [87,88].

In addition to searching through a large search space of NAS efficiently, EAs-based NAS is ideal for complex tasks that require many parameters to be adjusted [75,74]. Because it can consider combinations of operations and structures that are difficult for humans. EA-based NAS has some common advantages. First, using multiple populations can improve solution diversity and efficiency [89,90]. Second, EAs-based NAS has high scalability, and can explore a large search space, which can be difficult to handle manually. Lastly, in addition to flexibility, multiobjective EAs-based NAS can be customized for specific applications to meet specific requirements. Moreover, GA-based, GP-based, and EP-based NAS exhibit parallelization [91], which means that they can simultaneously be executed on multiple CPUs or GPUs. This results in a search space exploration that is faster and more efficient. GA was one of the most effective ways to evolve deep neural networks [92,93]. Xie et al. [11] used the traditional GA to automatically generate CNNs, proposed a novel encoding scheme on behalf of the fix-length binary string, and then generated a set of random individuals to initialize the GA. Sun et al. [94] used GA to evolve the deep CNN’s neural architecture and the initial connection weight value for image classification.

However, one limitation of EA-based NAS is that it could be computationally expensive, especially for large search spaces or complex objective functions. It also has some disadvantages, such as dependence on hyperparameters and limited exploration. Population initialization is crucial to metaheuristic algorithms, such as PSO and DE, which improve diversity and convergence. Quasirandom sequences were more effective than random distributions for initializing the population [95]. Furthermore, researchers were currently focused on swarm convergence as a high-priority challenge in EAs [87]. Researchers were exploring various techniques for improving swarm convergence in EAs, such as using adaptive swarm sizes, incorporating diversity into the swarm, and applying advanced communication and coordination strategies. To solve the convergence efficiency problem, the work by [96] proposed two DE variants. The search’s efficiency could be significantly affected by the choice of EAs technique and the parameters used in the algorithm. Additionally, the fitness may not always capture all aspects of the desired performance, leading to suboptimal architectures. Multiobjective or large-scale multiobjective algorithms [73] could solve these problems. Optimizing multiple objectives simultaneously, such as accuracy and computational efficiency, can result in optimal architectures that trade off between different objectives. Researchers have proposed methods, such as surrogate models, to accelerate the search, which reduces computational costs.

Interpretability of the resulting architectures is also critical. Most of EAs for NAS can result in complex architectures that are difficult to interpret or understand, which can be a disadvantage. However, GP [84] added interpretability to NAS. GP used a tree-like structure of interconnected nodes to generate neural architectures through an evolutionary approach. The architecture could be visualized and interpreted easily, allowing researchers to identify the critical components that contribute to its performance. In addition, researchers could understand its functionality. Researchers have also simplified architectures using network pruning. To compare EA-based NAS algorithms, it is imperative to have standardized evaluation metrics and benchmarks. Evaluating EA-based NAS algorithms is another significant area of research. For image recognition tasks, several benchmark and evaluation metrics were commonly used, including CIFAR-10 and ImageNet, and floating-point operations per second (FLOPs) for computation efficiency [1,43]. The abbreviations “FLOPs” and “FLOPS” have different meanings. In this study, the complexity of neural networks is typically expressed in terms of “FLOPs”. FLOPs mean floating-point operations, understood as calculations. It can be used to measure the complexity of algorithms or models [43,74,97]. Usually, FLOPS, an acronym for Floating Point Operations Per Second, means “In computing, floating point operations per second (FLOPS, flops, or flop/s) is a measure of computer performance” or hardware speed [98,99].

Some researchers have used the integrated algorithms of tabu search, SA, GA, and back propagation (BP) to optimize the network architecture and weights, in which connections between layers were optimized to control the network size, constructing a new way to find the optimal network architecture [66,68]. In the work by [100], five metaheuristic algorithms (GA, whale optimization algorithm, multiverse optimizer, satin bower optimization, and life choice-based optimization algorithms) were used to fine-tune the hyperparameters, biases, and weights of CNN for detecting the abnormalities of breast cancer images. Although EAs have been used for NNs for many years and have solved many practical problems, these previous methods cannot fit the complicated and large-scale NAS or optimization of numerous connection weights. Improving search efficiency and trade-off the multiple requirements (objectives) of real-world applications poses a significant challenge for EAs in NAS. In Section 3, we introduce multiobjective and hardware-accelerated NAS methods to solve these problems.

3  Multiobjective NAS

With the continuous development of MOEAs, the scalability of MOEAs has attracted increasing attention. In general, the scalability of an algorithm characterizes the tendency of the algorithm’s performance (such as running time) variable based on problem size. In multiobjective optimization, the problem mainly includes two aspects: the increase in the objective function and the increase in decision variables. Therefore, multiobjective NAS mainly includes MOEAs for NAS and large-scale MOEAs for NAS. Moreover, low efficiency and search constraints can cause significant challenges in searching NNs, so new methods have emerged to overcome these difficulties. Federated learning (FL) [101], large-scale MOEAs [80], hardware-accelerated NAS methods [81,82], and fully automatic searching are some efficient methods used to address these problems. In the work of [72], multiobjective evolution was utilized for NAS in FL. Some studies had discussed the full automation to seek the best neural architecture (hyperparameters) [6,102]. Complete automation in search could be achieved through the utilization of large-scale MOEAs [19] and hardware-accelerated methods [81,82].

3.1 MOEAs for NAS

The primary goal of NAS is to maximize accuracy. Thus, researchers are always focusing on this single objective in optimization. In an actual scenario, there are other properties such as computation complexity, energy consumption, model size, and inference time. When NNs have certain requirements for robust, it should be considered in the search progress. Therefore, NAS could be considered as a multiobjective optimization problem [103]. For example, researchers might be interested in the neural architecture level and weight level [43]; in the meantime, researchers could also consider the objectives of hardware awareness and hardware diversity [104,105]. Multiobjective optimization may need to simultaneously restrict the size of the neural architecture and attain high accuracy, so light-weight NNs should be attained to solve this problem [103]. Moreover, NN model compression [106] could satisfy budget constraints. Table 1 shows some major MOEAs for NAS.

One of the challenges of multiobjective optimization is that it can be tough to discover a single solution that optimize all of the objectives, so Pareto optimality [42] could be considered. Some researchers utilize aggregation to transform multiple objectives into a single objective via weights. However, the weights are difficult to determine, and trial and error experiments are necessary. For this issue, MOEAs can generate a population of solutions by simultaneously considering multiple objectives in a self-organized manner, resulting in diversified solutions for conflicting objectives. Traditionally, there are three strategies for MOEAs: decomposition [107], Pareto dominance [42], and indicator [108,109]. One of the most popular methods is decomposition [107], where multiobjective problems are divided into a series of aggregated single-objective problems. We can also use surrogate models to optimize and improve the efficiency of NAS search. To complete various competitive tasks, Lu et al. [43] proposed two surrogate models: the architecture and weight levels. In the process of NAS, the surrogate model is efficient, which aims to simulate the original model to alleviate the high computational cost. In the work of [99], network expansion was applied to construct efficient DCNNs with high accuracy. Therefore, the DCNNs can be optimized under a small budget to reduce computation complexity and then be expanded for large-scale problems.

3.2 Large-Scale MOEAs

Large-scale MOEAs can complete automation search, which could be effective and accelerated NAS methods [110–112]. Inspired by large-scale single-objective optimization algorithms, some proven strategies are introduced into large-scale MOEAs. As in the work by [113], large-scale optimization methods have been reviewed, and the algorithms can be categorized into two types: those that decompose and those that not. Non-decomposition algorithms approach the optimization problem as a unified entity and enhance the algorithm’s performance by creating efficient operators or integrating them with other optimization techniques. Based on the EA of decomposition, the strategy of divide and conquer is used to decompose large-scale optimization problems into a set of small-scale problems. Each small-scale problem is optimized through a collaborative framework. The variable grouping methods have been proposed, including fixed grouping, random grouping [114], dynamic grouping [110], differential grouping [115], and delta grouping [116]. The existing large-scale MOEAs include these categories [117]: methods based on decision variable analysis, cooperative coevolution frameworks, and problem-based transformation. These classifications are relative, and different algorithms can be divided into different classes from various perspectives. Table 2 shows a summary of major variants of large-scale MOEAs.

NAS can be seen as a large-scale multiobjective optimization problem (LSMOP). Numerous parameters are set to optimize the accuracy and model architecture complexity [73]. Based on competitive decomposition, the multiobjective optimization method decomposes the original problem into several subproblems. This method can solve the issues of irregular Pareto front, population degeneration, etc. In the work by [111], the author regarded the NAS as an LSMOP problem with constraints in which the nondifferentiable, nonconvex, and black box nature of this problem makes EAs a promising solution. Multimodal multiobjective optimization problems (MMOPs) with a high quantity of variables cannot be handled well by EAs. A sparse Pareto optimal EA is proposed for large-scale MMOPs. MMOPs as much as 500 decision variables can be addressed by using this approach. Moreover, they have competitive performance for NAS [112]. EAs targeting at LSMOPs for NAS are effective and they can tackle issues that traditional EAs cannot solve. However, related papers about LSMOP for NAS are still in the initial stage and need further research.

3.2.1 Decomposition-Based Algorithm

Cooperative coevolutionary generalized differential evolution (CCGDE3) proposed by Antonio et al. [118] used a cooperative coevolution framework to solve LSMOP. It tested the maximum scale decision variables of 5000. Experiments showed that it could be expanded well while the amount of variables grows. However, this method has not been analyzed in more complex test sets, such as WFG or DTLZ. Since Zhang et al. [107] proposed a general evolutionary multiobjective optimization algorithm based on decomposition (MOEA/D) in 2007, decomposition-based MOEAs have attracted substantial attention from researchers [120]. Qi et al. [119] developed a parameter adaptation strategy that combined neighboring domain size selection and genetic operator selection and introduced it into MOEA/D. Antonio et al. [120] studied the effects of scalability in MOEA/D, and proposed MOEA/D2 combining MOEA and collaborative evolution techniques. Ma et al. [121] employed this decomposition strategy into the large-scale MOEA, and proposed a large-scale MOEA according to decision variables analysis, namely a multiobjective EA based on decision variables analysis (MOEA/DVA). It took into account the relevance of decision variables, as well as the impact of the decision variable on optimization objectives. For the former, this work analyzed whether any two variables were related by sampling and divided unrelated variables into different groups. With regard to the latter, this study analysed the control properties of variables through sampling. Using the analysis of the variables described above, the LSMOP was detached into several smaller sub-problems. This algorithm was tested on up to 200 decision variables. Further studies have been conducted on MOEA/DVA. Song et al. proposed a random dynamic grouping strategy called random dynamic grouping (RDG) [122], which used decision variable analysis to divide variables for cooperative evolution. To reduce the number of evaluations, RDG used a dynamic grouping strategy based on MOEA/DVA framework to determine suitable variable groups.

Based on decision variable clustering, an EA for large-scale many-objective optimization (LMEA) was proposed by Zhang et al. [123], which was according to a correlation analysis of variables and decision attributes. Different strategies were optimized separately due to the different decision variables involved in the problem. LMEA used clustering to accomplish study of decision variables’ attributes rather than sampling-based strategies. The group with the smaller clustering angle was divided into convergence variables, and the group with the larger clustering angle was divided into diversity variables. Different strategies were used to optimize convergence and diversity variables, respectively. Such issues not only had high-dimensional decision space space, but their objective space is also high dimensional. Research on this kind of problem is also worthy of further attention. The experimental results showed that these algorithms achieved good results. However, when it was difficult to discriminate between decision variables, these methods might fail. Additionally, analyzing the above-mentioned decision variables required multiple times for fitness evaluations, and the scale of the problem increased rapidly. Fitness evaluations in practical problems is often time-consuming, which limits the scalability of this kind of algorithm to some extent.

3.2.2 Parallel Algorithm

Scholars use the divide-and-conquer mechanism to decompose the decision vector into small components and solve them in parallel [130]. Cao et al. [80] proposed a distributed parallel cooperative coevolutionary MOEA (DPCCMOEA) based on message passing interface (MPI). In DPCCMOEA, the decision variables were split into multiple groups using an improved variable analysis method, and each group was optimized by a different subpopulation (species). As each species was further divided into multiple subspecies (groups), the amount was determined by the number of CPUs available, which increased parallelism and allows for adaptive achievement. Therefore, the calculation time could be considerably reduced, and the calculation efficiency was higher.

Garcia-Sanchez et al. [126] proposed a coevolution algorithm based on the island model. Multiple subpopulations (islands) were executed in parallel, and different regions in the decision variable space were explored in this model. In particular, it divided the decision variable into multiple parts and used a subpopulation to optimize each part. According to these results, overlapping schemes performed better than disjoint schemes when the number of islands increased. Using a parallel framework, Chen et al. [127] proposed separating the environment selection operator from the entire evolutionary process, thus reducing data transmission and dependency between sub-processes. A novel parallel EA (PEA) was designed based on the parallel framework. PEA convergence was achieved through independent subgroups. Moreover, an environmental selection strategy was proposed without considering convergence to improve diversity.

3.2.3 Algorithm Based on Reference Vectors

Yang et al. [131] proposed a new high-dimensional optimization framework called dynamic evolutionary constrained clustering with grouping (DECC-G), which was used for large-scale optimization problems. The key ideas behind the DECC-G framework were grouping and adaptive weighting strategies. DECC-G could effectively solve large-scale single-objective optimization problems of up to 1000 dimensions. Inspired by scholars, such as Zhang et al. [131], Zille et al. [125] and other scholars introduced the large-scale single-objective grouping strategy and adaptive weighting strategy into the large-scale MOEA and proposed a weighted optimization framework (WOF) [125]. Some scholars grouped variables together and applied weights to each group [131,132]. The framework for accelerating large-scale multiobjective optimization by problem reformulation (LSMOF) [117] also employed an adaptive weighting strategy, which transformed the decision variables optimization into the weighting variables optimization. Compared with WOF, where the search weight variable was unidirectional, the weight variable in the proposed LSMOF was bidirectional, and the search coverage was larger. Although the transformation strategy could somewhat reduce the the decision space dimensionality, the subproblems of transformation were optimized respectively, therefore the relationship between various weight variables was not taken into account. The conversion result depended significantly on the grouping technology used, which had yet to be strengthened in terms of stability and computational effectiveness [133,134].

Beume et al. [135] proposed a multiobjective selection algorithm based on dominant hypervolume, referred to as 𝒮 metric selection evolutionary multiobjective optimization algorithm (SMS-EMOA). Because SMS-EMOA directly maximized the supervolume, it had relatively limited search space while tackling small-scale multiobjective optimization problems, and the algorithm performed well. However, When there are many variables, it may be difficult to transfer the Pareto set in the decision space to the Pareto front in the objective space, resulting in complicated search guidance. Hong and other scholars proposed the double local search in MOEA, called DLS-MOEA [109], utilizing scalable indicators. DLS-MOEA used an innovative solution generator to enhance SMS-EMOA’s diversified capabilities, while inheriting SMS-EMOA’s advantages in convergence. This type of algorithm provided a clear research direction in the high-dimensional decision space involved in LSMOPs.

3.3 Hardware-Accelerated NAS Method

The NAS for DNNs and large-scale data could be treated as a large-scale optimization problem, which has high complexity and consumes lots of time. Meanwhile, EAs are population-based, which have inherent parallel properties. Accordingly, based on specific hardware platforms with numerous CPU, GPU, and FPGA resources, distributed parallel EAs can be designed. Compared to traditional NAS based on EA, the efficiency of the distributed NAS will be significantly improved [136].

In distributed parallel EAs (DPEAs) [91], several populations can be formed to explore the solution space, which can also contribute to sufficiently utilizing the computational resources. A distributed parallel MOEA, DPCCMOEA, had been proposed in [80] to tackle large-scale multiobjective problems. DPCCMOEA algorithm used an improved variable analysis method [121,137] to split the decision variables into different groups, with each group being optimized by subpopulation. In order to increase parallelism and achieve adaptive implementations of different numbers of CPUs, each population was further broken down into multiple subpopulations (groups), the number of which was determined by the number of available CPUs. Therefore, the calculation time can be greatly reduced and the calculation efficiency is higher. Based on DPCCMOEA, a distributed parallel cooperative coevolutionary multiobjective large-scale evolution algorithm (DPCCMOLSEA) was proposed [138], which modified the parallel structure to evolve each subgroup serially in each main CPU core of each subgroup. Optimization performance had improved because it was easy to reference the overall information of subgroups without having to communicate between CPU cores, and several adaptive strategies had been tried. The work of [81] proposed the distributed parallel cooperative coevolutionary multiobjective large-scale immune algorithm (DPCCMOLSIA), which solved multiobjective large-scale problems by constructing a distributed parallel framework with three layers. Therefore, the CPU core belonged to a subgroup that targeted one objective (or all objectives) and a group of variables. Similar to DPCCMOLSEA, the evolution of a subpopulation was performed in serial in a main CPU. Using the same parallel strategy, the multi-population distributed parallel cooperative coevolutionary multiobjective large-scale EA (DPCCMOLSEA-MP) [82] also constructed a distributed parallel framework with three layers. The difference was that DPCCMOLSIA is according to non-dominated sorting as in NSGA-II, while DPCCMOLSEA-MP was based on problem decomposition as in MOEA/D. In addition, further improvements were made to DPCCMOLSEA and DPCCMOLSIA [19]. One population was constructed to optimize each variable group, and all populations cooperate for better performance [139]. Then, the individuals in each population were further decomposed to realize larger-scale parallelism. For large-scale search, Li et al. [140] analyzed the disadvantages of previous NAS methods and pointed out that random search could achieve better performance than ENAS [6] and DARTS [15]. Greff et al. [141] presented the large-scale analysis of LSTM, and used the random search method to optimize the hyperparameters [142]. They put forward an effective and accurate adjustment policy. Moreover, more effective parallel structures could be devised via modification [138] or by adding parallel layers [81,82].

Via combining distributed MOEAs (DMOEAs) with the fuzzy rough NN, a multiobjective evolutionary interval type-2 fuzzy rough NN framework has been proposed to tackle the time series prediction [143] task in the work of [19], in which, the connections and weights are optimized by simultaneously considering the network simplicity and precision. In future work, DMOEAs can be applied to NAS by simultaneously encoding the network architecture and weights to generate light-weight NNs, and the back-propagation [144] can also be employed.

4  NAS for Healthcare Application

Image classification [2,10,47,48,55,145–147] and image segmentation [8,24,25,70,71,148–150] are the most widely used fields of NAS in healthcare. In the traditional working mode, doctors often use the naked eye to scan under the microscope for judgment, use the manual experience to find the lesions, and then use the high-power lens for review, diagnosis, classification, and decision, which is a complicated process. This is a huge workload and a time-consuming task. Moreover, these lesion images are very sparse, and the DL model needs to sample local medical images under conditions of high magnify to make an accurate diagnosis and classification. Therefore, the method of DL increases the calculation cost, the utilization efficiency of medical images is low, and the correlation information of diagnosis is weak. Researchers have used EAs to automatically design efficient NNs for disease diagnosis to help doctors make efficient and intelligent diagnostic decisions [2].

NAS is generally considered a single objective optimization problem aiming at finding a high-precision network architecture. Most practical problems require not only high precision but also efficient network architectures with low complexity, so as to reduce computation and memory. However, DNNs are overparameterized and inefficient in the whole learning process. A multiobjective optimization algorithm provides an effective strategy for designing network architecture automatically and efficiently. In healthcare, MOEAs can simultaneously optimize classification accuracy and improve network efficiency, which have been applied to the field of image classification. For image segmentation, MOEAs based on minimizing the segmentation error rate and model size can automatically design efficient networks to complete specific image segmentation tasks. Multiobjective optimization is helpful for completing architecture search and difficult medical tasks.

4.1 NAS for Classification of Disease Diagnosis

The purpose of traditional DL methods is to implement an automatic disease diagnosis system. Cancer cells are classified by using a preset collection of manual features obtained from histological images and trained with a classifier. The extraction of features and their classification within a uniform learning structure have been popular in medical image processing in recent years [151]. Image classification tasks are widely performed by using CNNs [100]. CNN may, however, suffer from disappearing gradients and saturation accuracy owing to a great increase in depth. NAS combined with CNN can help medical practitioners make more accurate and efficient medical diagnosis classification decisions while minimizing human intervention.

As shown in Table 3, MOEAs can combine with deep CNN for NAS to efficiently complete image segmentation and image classification in healthcare. For skin lesions, Anupama et al. [148] proposed backtracking search optimization algorithm with entropy-based thresholding (BSA-EBT) to improve image segmentation accuracy. For prostate cancer and cardiology, Calisto et al. [149] proposed a surrogate-assisted multiobjective evolutionary algorithm (SaMEA) for minimizing the architecture size and search time, aiming to complete 3D image segmentation. Baldeon et al. [71] used a multiobjective adaptive CNN (AdaResU-Net) to optimize the performance and size of the model. These two models were evaluated on two publicly available data sets: the MICCAI PROMISE12 challenge data set and the MICCAI ACDC challenge data set. Yang et al. [152] proposed continuous evolution for efficient NAS (CARS) that could offer models in the Pareto front with very high efficiency for CIFAR-10 and ILSVRC2012. Its contribution was to propose a highly efficient multiobjective NAS framework with a continuous evolution strategy, taking advantage of a mechanism with protection (pNSGA-III) [159]. For lung and colon cancer image classification, Liu et al. [2] proposed a CIT2FR-FL-NAS model, which could reduce network complexity and add interpretability. For colorectal cancer, retinal diseases, and liver tumor, Silva et al. [153] proposed multiobjective grammatical evolution algorithm, it could reduce model complexity and improve model accuracy. For thorax disease and COVID-19, Louati et al. [145,160] used GA to compress the deep CNN. He et al. [155] proposed efficient evolutionary multiobjective architecture search (EMARS) to implement COVID-19 computed tomography (CT) classification. The advanced multiobjective evolutionary NAS can not only improve model performance but also reduce network complexity in healthcare. NAS can be applied in healthcare for image classification and image segmentation. Additionally, it can efficiently process the EHR data sets. The work by [161] proposed MUltimodal Fusion Architecture SeArch (MUFASA) model that could process structured and unstructured EHR data and automatically learn the multi-modal characteristic architecture of EHR. This study allowed non-experts to develop differential privacy (DP) models that could be customized for each data profile of the EHR and to find the ability to effectively integrate clinical records, continuous data, and discrete data. This method could help doctors make the right diagnostic decisions, make personalized treatment plans, and advance health care for patients.

Therefore, the use of evolutionary NAS in healthcare applications is necessary. Firstly, healthcare datasets are often massive and complex, making them challenging to extract relevant information and insights using traditional machine learning approaches. Traditional RL for NAS cannot optimize multiple objectives flexibly and can lead to heavy computing [14]. Using gradient-based search [15] need to make the discrete network space into continuous, which add training time. Neuroevolution strategies can accelerate search efficiency, real-time processing these datasets, consequently enhancing accuracy, reducing model size and minimizing errors in healthcare [154]. Secondly, evolutionary NAS can adapt to meet the multiple requirements of a given task. Multiobjective evolutionary NAS applications in healthcare can attain high accuracy, improve model performance and reduce model size [2,71,149,153–155]. Large-scale multiobjective neuroevolution strategies [73,110–113] and distributed parallel EAs strategies [80,91,121,137,138] can accelerate the evolution process and search process of NAS. Using multiple GPUs, the training is also accelerated. In FL, multiple federated client terminals search simultaneously, which will greatly improve efficiency. NAS can process medical data and help doctors make accurate and rapid diagnostic decisions [162]. By automating the design process, NAS can help reduce the time and cost required to develop new AI solutions in healthcare, while also improving their performance and reducing the risk of human error. Moreover, NAS can automatically predict and classify diseases, so as to assist doctors to make personalized diagnoses and treatment. Medical data leakage will cause adverse effects. Due to legal and ethical requirements, the privacy protection of medical data is particularly important. In Section 5, we develop an interpretable evolutionary neural architecture search based on federated learning (FL-ENAS) framework applied to healthcare, to address search efficiency and privacy concerns.

4.2 NAS for Mobile Healthcare

Aging, the contradiction between medical supply and demand, and the medical burden are major economic and social problems facing most countries in the world. Solving this problem requires enormous healthcare costs and labor resources. The main problem with traditional hospital-centered healthcare is long waiting times, which, if not addressed effectively, can lead to delays and even life-threatening conditions. Mobile healthcare technology’s application and innovation can decrease the medical burden, shorten waiting times, facilitate patients access to medical care, and prevent diseases before their onset [163]. Mobile healthcare uses sensors and portable devices to collect clinical healthcare data, deliver healthcare information to both hospital researchers and patients, monitor vital signs, and furnish personalized diagnoses and services through telemedicine.

In mobile healthcare, activity recognition for smartphones and smartwatches has various applications for the health management of people. By sensing human activity, smartphones and smartwatches can significantly enhance human health and well-being [164]. An unhealthy diet and lack of exercise are the main causes of chronic diseases, while regular physical exercise can protect human health and reduce the risk of mortality. Overindulgence in junk food can also lead to sub-optimal health and pose significant health risks. Activity recognition via smartphones and smartwatches can supply precise, real-time insights into sedentary behavior, exercise, and eating habits to help counteract inactivity and overeating. Moreover, with the help of Medical 4.0 technology, a patient-centric paradigm has replaced doctor-centric treatment methods [165]. Wearable devices can be connected to edge computing to process large amounts of data, thus avoiding privacy risk and low computing efficiency during data transmission in mobile healthcare. To save limited resources, the Early-Exit (EEx) option was applied in multiobjective NAS to process time series data requiring real-time monitoring in wearable devices [166]. This model achieves not only high classification accuracy but also the goal of energy saving and high efficiency. It has been effectively applied in mobile data sets, diagnosis decisions of heart infarction, human activity recognition, and real-time monitoring of human health status. Human activity recognition based on wearable sensors is beneficial to human health supervision. DNN models in mobile phones and other small sensor devices can accurately identify human activity, such as going up and down stairs [167].

A multiobjective NAS strategy has been effectively used in mobile healthcare. NAS algorithms can achieve high accuracy while achieving other optimization goals, such as reducing time, minimizing parameters, and reducing model size, to effectively deploy resources within limited resources. By enhancing the performance of the model on wearable devices and reducing its size, the author proposed NAS for photoplethysmography (NAS-PPG), a lightweight NN model for heart rate monitoring [168]. In the work by [39], the authors presented a BioNetExplorer framework that enabled hardware-aware DNN and reduced search time by GAs for biosignal processing. To balance the performance and computing speed of a model, the multiobjective search algorithm NSGA-II [42] was utilized, and lightweight architecture human activity recognition using neural architecture search (HARNAS) was designed for human behavior recognition [97]. NAS used neuroevolution to search for the best architectures not only for image recognition data set (CIFAR-10) but also for PAMAP2 data sets in human activity recognition (HAR) [97]. MOEAs search can perform the constrained search process, that is, the search space’s parameters are set within the given range, and can fully use the available resources for strategic deployment. Moreover, FL combined multiobjective NAS can protect medical data security and reduce model complexity. As shown in Fig. 4, it shows the use of FL for AI terminals.

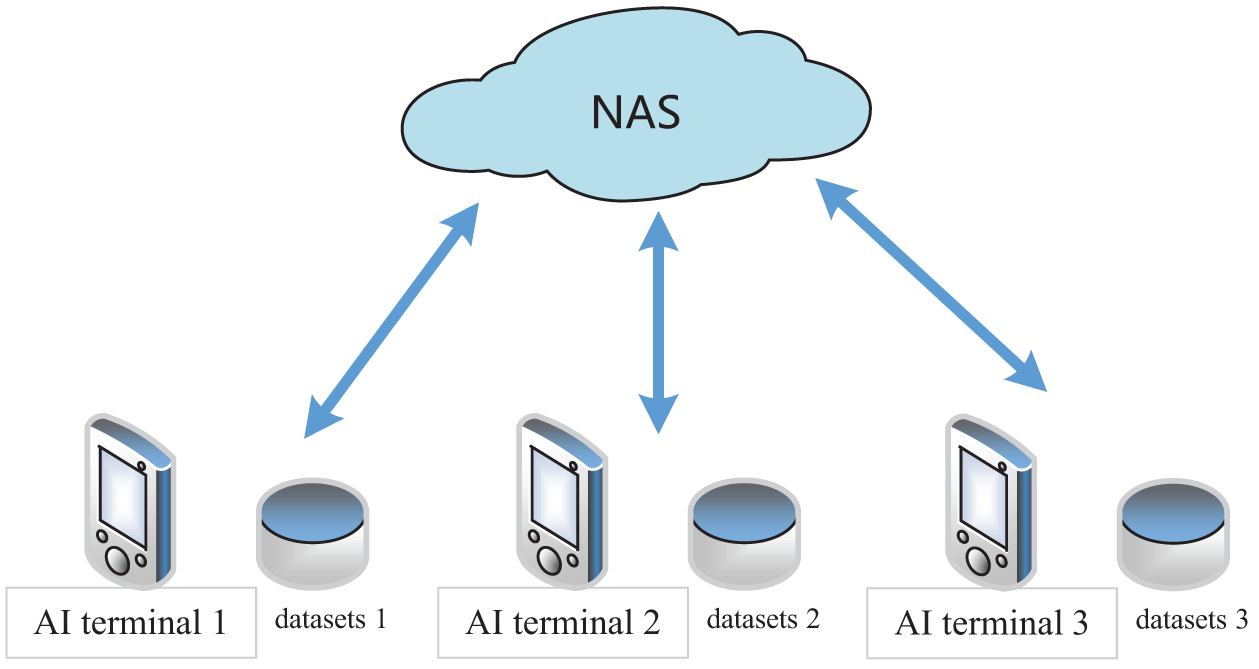
Figure 4: Federated neural architecture search for AI terminals

4.3 Interpretable Network Architecture for Healthcare

With their excellent performance (as shown in Table 3), CNNs have been successfully applied in medical image classification [169,170]. Nonetheless, one of the most significant drawbacks of deep CNNs is their lack of interpretability [171]. Zhang et al. [172] designed a loss for the feature maps, thus making the knowledge representation of the high convolutional layers clearer and easier to understand the logic of CNNs. High interpretability can break the black box bottleneck of DL and make the CNN presentation process visible [173]. The CNN model should be accurate and interpretable in medical diagnosis [174]. For example, for the diagnosis and treatment management of breast cancer, CNNs can be used to segment suspicious areas in images and provide heat maps to help pathologists make decisions [175]. Few papers have previously combined interpretability with NAS for healthcare data analysis.

Fuzzy rough neural network (FRNN) unites fuzzy set theory, rough set theory, and NNs simultaneously, so it has powerful learning and interpretability abilities. Instead of the value 0 or 1, fuzzy set theory [176] can represent every input feature as a “degree” in the range [0,1] [84]. By transforming input feature values into fuzzy domain, fuzzy set theory is an important medium between the precise computational world and the fuzzy human world. It can mimic human decision making based on “if-then”, so as to better solve real world problems. Rough set theory emphasizes the unidentifiability of knowledge in information systems, it deals with all kinds of imprecision and incomplete information, and finds hidden laws. Fuzzy rough set theory can process complex data and generate interpretable knowledge [177]. DFRNN can be built and optimized with EAs [178,179] to solve complex problems in real world, especially in medical image classification [180].

Integrating gene expression programming into FRNN can improve the effectiveness and interpretability of NNs [19]. Yeganejou et al. [181] combined CNN and explainable fuzzy logic to propose an explainable model in which CNN was employed to extract features, and fuzzy clustering is utilised to further process features. Evolution-based NAS could automatically search for the optimal network architecture and hyperparameters [182]. This could be used in FL environments [101] to achieve multiobjective optimization. CNN is an efficient DL model for medical image processing [183], and evolution-based NAS has been applied to medical image recognition. For example, neuroevolutionary algorithms are used to automatically design the DL architecture of COIVD-19 diagnostics based on X-ray images [184]. For CT and MRI image datasets, an evolutionary CNN framework with an attention mechanism is applied to 2D and 3D medical image segmentation [185]. Attention mechanisms are an effective AI techniques. For example, multiple instances of learning CNN incorporate an attention mechanism to recognize sub-slice area in medical images, so as to solve the explainable multiple abnormality classification problems [186].

Evolution-based NAS can automatically search the architecture of NNs and construct NNs models, avoiding the manual design of NNs and greatly reducing the work burden. In addition, MOEAs can optimize multiple objectives at the same time, thus taking into account multiple properties of multiobjective optimization problems (MOPs), such as network error, interpretability, etc. For FRNNs, it is helpful to comprehensively optimize and analyzed clearly MOPs. The combination of fuzzy rules and neuroevolution based on fuzzy sets can be regarded as “the combination of rules and learning”, and the multiobjective FRNNs evolution is a useful exploration of “high accuracy and interpretability” in healthcare.

5  NAS for Privacy and Security of Healthcare

Although big data in medicine can be helpful in diagnostics and therapies, the release of private information can result in social panic. Thus, medical data security and privacy have become increasingly important [187,188]. This biomedical data is highly sensitive, making it subject to strict regulations on data protection and privacy issues. On the premise of privacy protection for organizational pathological data, how to make efficient artificial intelligence classification and diagnosis decisions is a problem worthy of further exploration. Federated NAS [101] can effectively trade off privacy against model architecture choices. The traditional centralized learning process leads to the disclosure of private information. FL transmits only models, and local training of data can effectively protect data privacy. However, hundreds of millions of devices are involved in the interaction between the user client and the cloud server, which significantly increases the communication burden and cost [189]. A certain communication bottleneck exists between the local client and server; this is partly due to a great deal of parameters exchanged as well as a significant number of participating clients, and partly due to the limited broadband of networks, which has become a bottleneck in the development of FL [190]. Deploying NAS algorithms in the FL framework can simultaneously consider privacy protection and model architecture selection in the process of cancer diagnosis [2].

The deep fuzzy rough NN model was used for image classification in the FL environment. This model can add to the explanation of NAS. A deep fuzzy rough NN [2] uses NAS to solve the tuning and optimization problems in the FL environment. NAS is divided into two parts. The first part is the search part. After the local model parameters are uploaded to the cloud server, the cloud server integrates the model and returns the parameters or models. The second part is the training and inheritance part to obtain the optimal neural architecture. Federated NAS is divided into online federated NAS and offline NAS. The difference between online and offline is whether the two parts are performed separately or simultaneously [101]. Most researchers believe that NAS is a two-level optimization problem: internal and external optimization. NSGANetV2 [43] is a typical architecture for NAS optimization using a multiobjective optimization algorithm. This NAS model uses the initial weight as the initial value for the underlying optimization. The upper layer agent adopts an online learning algorithm and concentrates on the network architecture that is close to the optimal balance in the search space, which can significantly improve search efficiency.

In this paper, we propose an interpretable FL-ENAS framework that incorporates neuroevolution to address search efficiency and privacy concerns for healthcare data analysis. The algorithm flow of evolutionary NAS is shown in Fig. 5. First, define the search space, supernet, and optimization objectives, as well as set the initial number of samples, and maximum number of training epochs. The agent model is constructed. Second, starting from a model, the MOEA is used to optimize the accuracy, complexity, and other objectives, and the selected architecture is trained. The candidate architecture is evaluated while improving the prediction agent model and this process is continued until the maximum amount of iteration is achieved. Lastly, the optimal non-dominant solution set is derived from the evaluated architectures.

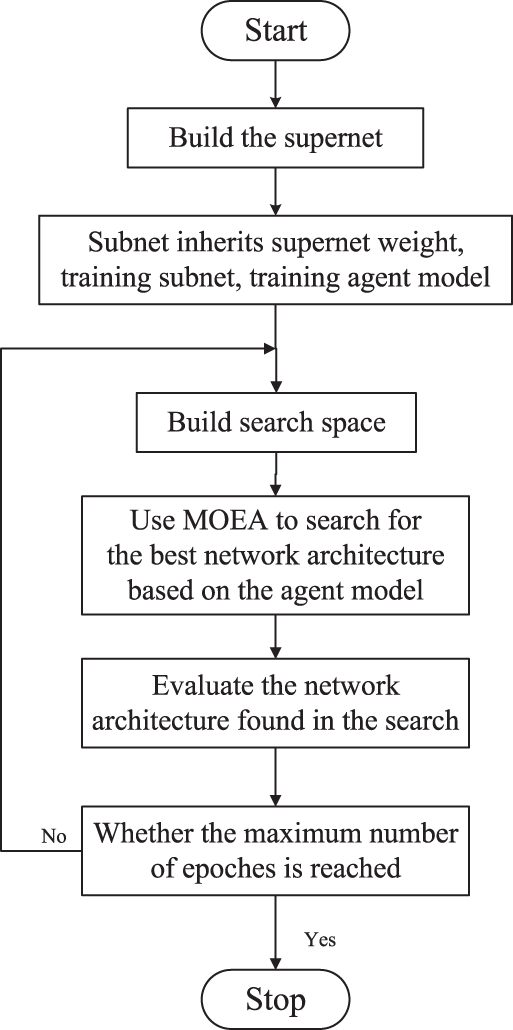
Figure 5: Evolutionary NAS algorithm flow

The search space is mainly constructed in multiple dimensions of the deep neural network; for example, with respect to deep CNN, the considered dimensions include depth (number of layers), width (number of channels), convolution kernel size, and input resolution [191]. The CNN architecture considered in this paper can be decomposed into several sequentially connected blocks. The network gradually reduces the size of the feature map and increases the amount of channels from shallow to deep. The overall algorithm flow of FL-ENAS is shown in Fig. 6. The algorithm operates as follows: (1) Federated feature engineering: including data preprocessing, indicator construction. At the same time, the deep fuzzy rough neural networks model is constructed. (2) Design a search space: search space for NAS should be designed. The search space can be defined or designed by using existing architectures to encode the set of possible architectures that the algorithm can explore. (3) Implement FL: to train a shared network model across multiple devices, we need to implement the FL framework. (4) Implement evolutionary NAS: using distributed parallel large-scale multiobjective neuroevolution strategies, we can conduct the search for the best network architecture once the FL framework is set up. (5) Evaluate the architecture: once the network architecture is optimized, it needs to be evaluated for the target task. (6) If the selected architecture does not perform well, further explore the search space and adjust evolutionary parameters. Our ultimate goal is to analyze and process healthcare data generated by users, predict or classify diseases, and effectively supervise human health in real time.

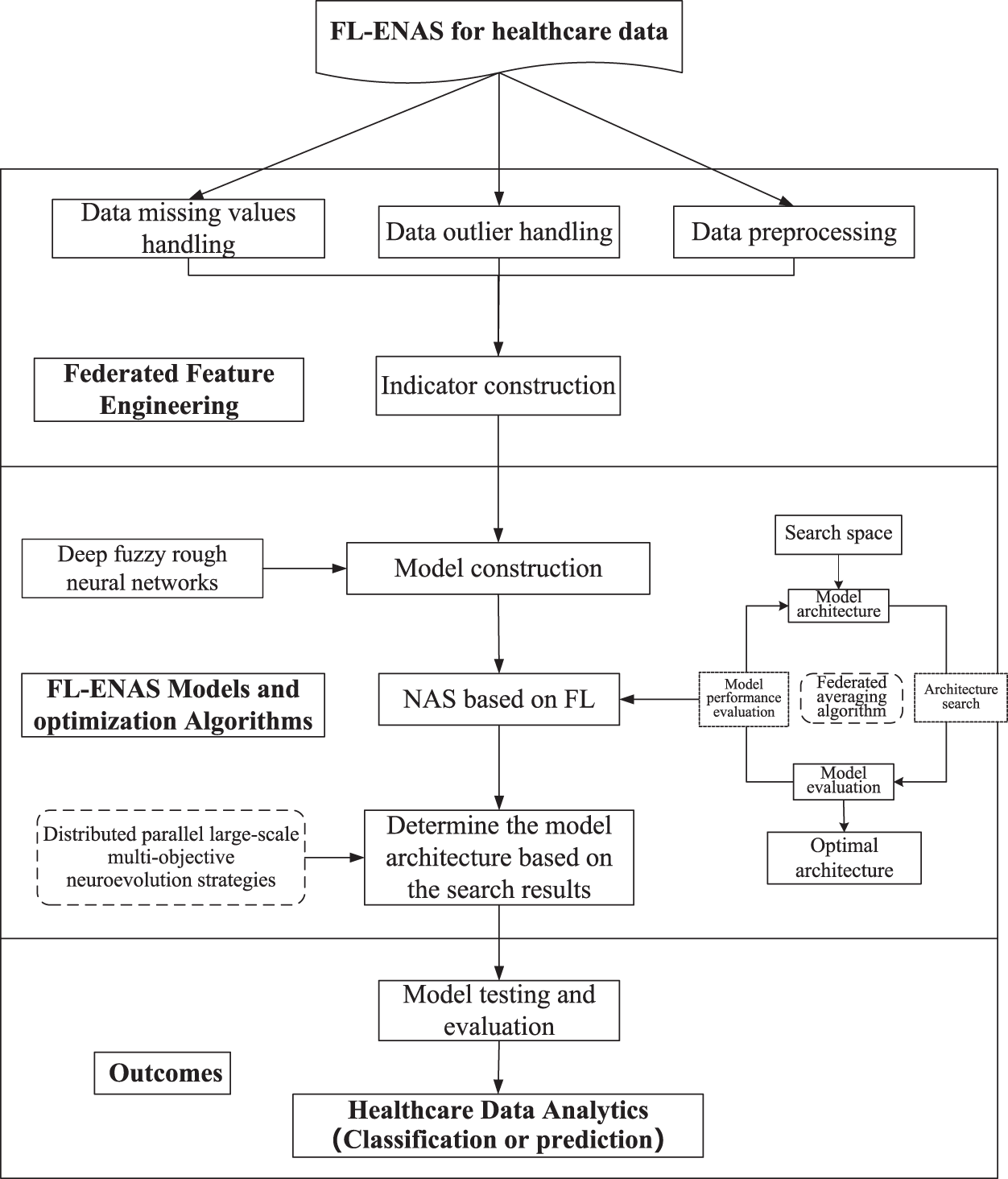
Figure 6: FL-ENAS framework

5.1 Deep Fuzzy Rough Neural Networks

Deep fuzzy rough neural networks (DFRNN) can handle the complex and uncertain data. Multiple layers of neurons form the architecture of the network, and each layer generates a set of fuzzy values based on its inputs. Using rough set theory, the most relevant features are then identified based on these fuzzy values. FRNN did not consider neuroevolution when first proposed by Sarkar et al. [192], that was, its architecture was programmed manually. Lingras [193] studied the serial combination of fuzzy rough and rough fuzzy, and explored the connection mode of fuzzy neurons and rough neurons, without involving the automatic construction of architecture. By coding the network structure and parameters, EAs were used to conduct FRNN architecture search and parameter adjustment [2]. Although network accuracy and comlexity indexes were taken into consideration, the fitness calculation was derived through a weighted sum of the two indexes. The weight was primarily determined by the experience of the researchers, which imposed subjective limitations. Studies on FRNN evolution are scarce, and do not involve MOEAs-based multiobjective evolution strategies, which need to be further explored.

In DFRCNNs, fuzzy rough set theory was incorporated into DCNNs. As shown in Fig. 7, the proposed deep fuzzy rough neural network architecture basically includes fuzzification layer, fuzzy rule layer, rough layer, defuzzification layer, and finally output classification results. As shown in Fig. 8, it shows DFRNNs with three different architectures. In the basic FRNN architecture (FRNN), each input node is assigned to a number of clusters by the fuzzification layer. Each node in the fuzzy rule layer connects to at most one cluster of each input. After the fuzzy rough membership layer, the classification is output. DFRNN1 is extended to CNN, where the inputs are images and the CNN is interpreted and constructed based on fuzzy rough theory. DFRNN2 is also a basic FRNN architecture; it includes multiple FRNN modules, and every FRNN module includes high interpretable fuzzification layer, fuzzy rule layer, fuzzy rough membership layer, defuzzification layer, etc. Multiple FRNN modules are connected deeply to handle complex inputs. To improve interpretability, fuzzy rough theory is combined with CNNs. Multiple attributes of the DNN are quantified, and multiple optimization objectives are constructed for comprehensive optimization. The optimization of the deep neuroevolution model is perceived as a large-scale multiobjective optimization problem, and a large-scale multiobjective evolution strategy is proposed. Based on the classical modules in the existing DNNs, including convolutional, fully connected, and various modules in the fuzzy rough neural network, the coding scheme is designed to flexibly generate various DNN models and construct a general deep fuzzy rough CNN architecture. Various attributes of DNNs are summarized, and multiple optimization objectives are extracted, including network performance, complexity, and interpretability, to comprehensively optimize DNNs and improve optimization performance. Next, to optimize DFRNN models in the FL-ENAS framework, we propose large-scale multiobjective neuroevolution strategies, and distributed parallel neuroevolution strategies. As shown in Fig. 9, distributed large-scale multiobjective optimization strategies is illustrated in FL-ENAS framework.

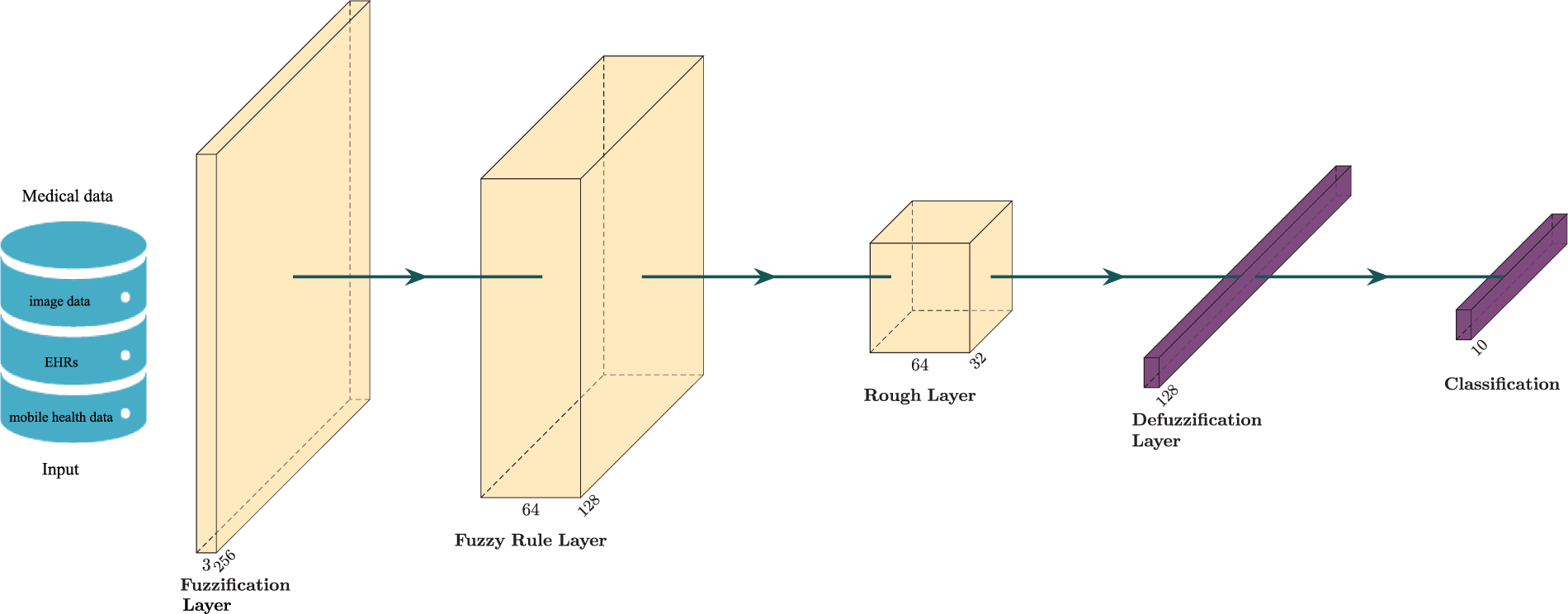
Figure 7: Deep fuzzy rough neural network architecture

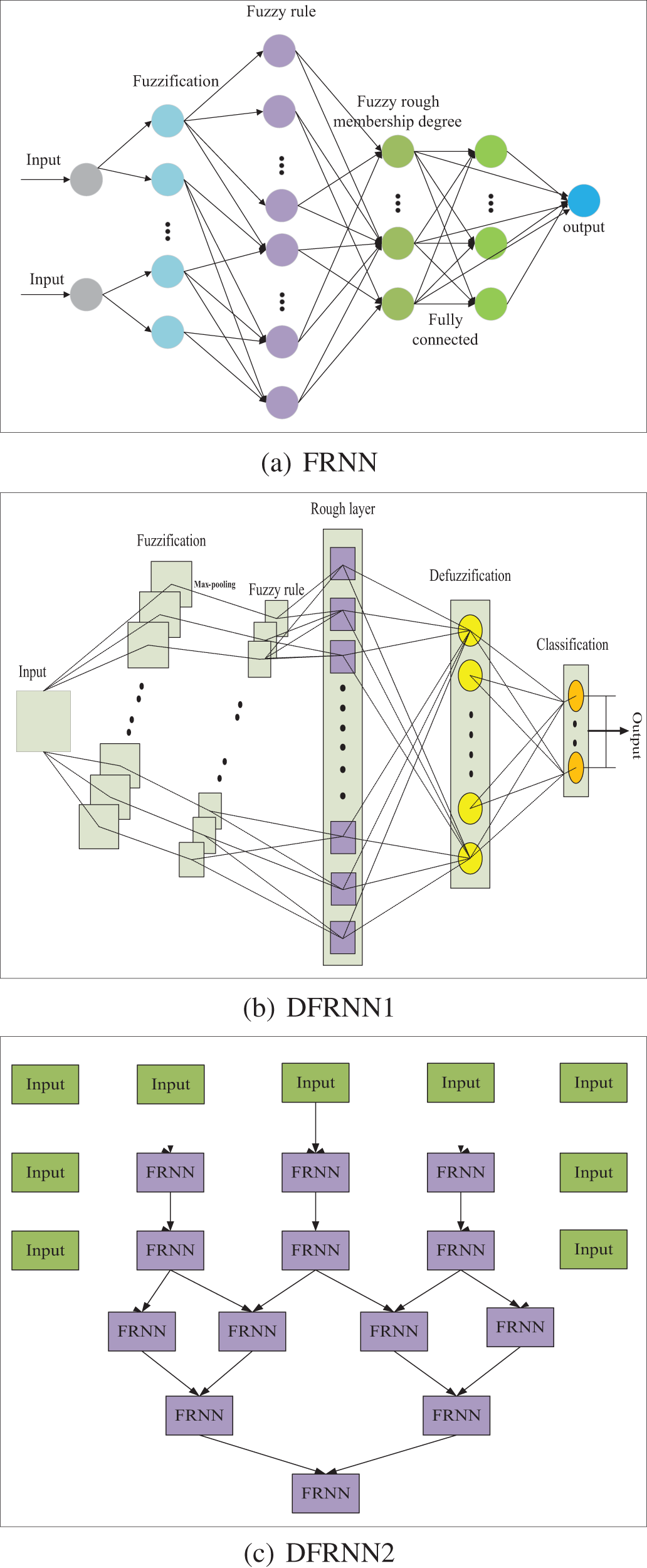
Figure 8: DFRCNN architectures

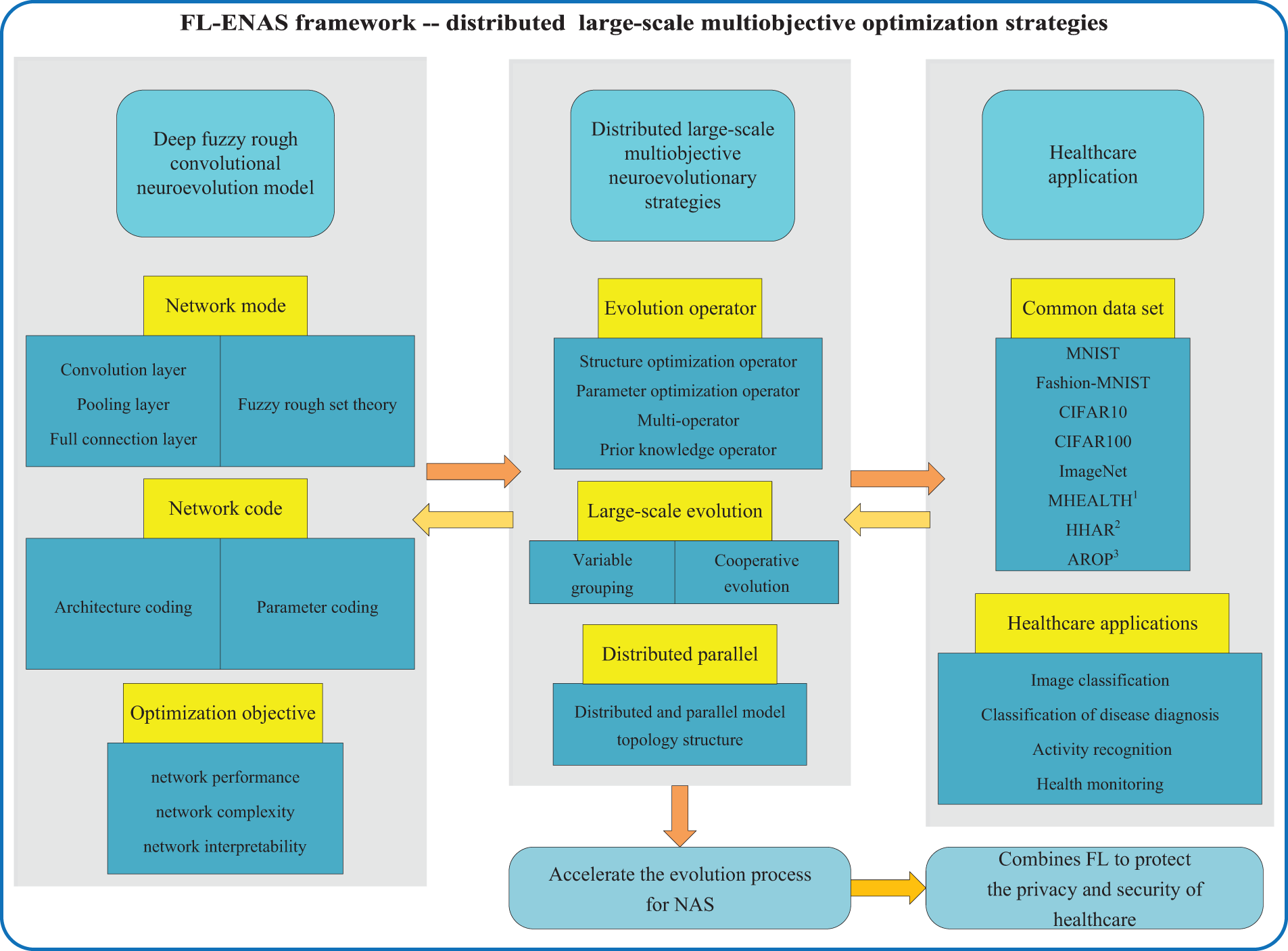
Figure 9: Distributed large-scale multiobjective optimization strategies in FL-ENAS framework

5.2 Large-Scale Multiobjective Neuroevolution Strategies

Evolution operators are crucial parts of large-scale multiobjective evolution strategies. First, the coding optimization of the model architecture needs to be addressed. The discrete evolution operator is intended to be adopted. Crossover operators may destroy useful architecture, so some neuroevolution algorithms eliminate crossover operators. To reduce significant changes in the crossing process, statistics can be conducted on the two selected paternal individuals inheriting common characteristics, and certain probabilities are given to determine whether to activate the corresponding variables for different characteristics.

Second, parameter coding optimization of the models is also important. The values of the variables used for parameter coding are continuous, and continuous evolution operators are used for optimization. Many operations of the EA are affected by random numbers, and the sequences generated by chaotic mapping have nonlinearity and unpredictability. Therefore, they are proposed to replace the traditional uniform random numbers and to improve the performance of the operator. The chaotic maps [194,195] include the following mapping: Chebyshev, Circle, Gauss, and Logistic mapping. Here, piecewise linear mapping can be summarized as follows:

ri+1={ria,ri<a,ri−a0.5−a,ri<0.5,1−a−ri0.5−a,ri<1−a1−ria,otherwise,(1)

where ri denotes the value of the input random number and ri+1 denotes the value of the random number currently obtained.

Third, multiple operators need to be considered. Different evolutionary operators have numerous advantages. The dominant operators of neuroevolution need to be tested for specific neuroevolution problems. Different operators (or operators with different parameters) influence the optimization effect differently at evolution’s different phases. Combining different operators may be useful.

Fourth, operators can use prior knowledge. The pseudo-inverse method [196], which is accurate and fast, is used to obtain the weight for learning the width output layer.

Large-scale evolution could adopt variable grouping and cooperative evolution [5]. Large-scale evolution necessitates the efficient grouping of large-scale problems. The encoding parameters and architecture variables are divided into groups. We can continue dividing if each group still has many variables. The partitioning strategies include network layer partitioning, node partitioning, module partitioning, and matrix cutting. To achieve large-scale evolution, coevolutionary methods are needed, particularly distributed parallel large-scale evolution. An NN model can be built by combining all variables into one complete solution. To reduce communication costs and information exchange frequency, the information of variables in other groups is temporarily stored in each subpopulation of a variable group. Multiple objectives are optimized simultaneously in the process of NAS. These objectives might include training accuracy, model size, and FLOPs. By doing so, we can discover a set of NN architectures that balance these objectives and achieve high performance while minimizing computational cost.

5.3 Distributed Parallel Neuroevolution Strategies

Multi-layer-distributed parallel architecture suitable for the above algorithm is proposed. Considering the characteristics of hardware architecture and the need for practical medical engineering problems, based on variable grouping, each variable component is transferred to different nodes for evolution and cooperation. If each island corresponds to multiple nodes, the master–slave model can be applied to assign the assessment of individual fitness values on the island to multiple nodes to form the island–master–slave model. To further increase parallelism and diversity, multiple populations could be used, and each population optimizes one or several objectives. In the top-level island model, a cluster of the island–island–master/slave models is formed. The NN can be loaded into multiple GPUs or CPUs for parallel evaluation, further expanding the construction of island–master/slave-master/slave models and island–island–master/slave–master/slave models to improve evaluation efficiency. Ultimately, a multi-layer distributed parallel architecture is constructed. Agent-assisted multi-terminal collaborative parallel architecture is proposed. To evaluate the network architecture, a agent model with low computational complexity is used to estimate the performance of the neural architecture. By leveraging the agent model to assist in the evaluation of network architecture, a multi-end collaborative parallel architecture is constructed to fully utilize computing resources.

Based on distributed parallel technology, parallel EAs can accelerate the evolution process for NAS and improve the efficiency of healthcare data analysis. In FL-ENAS framework, the distributed parallel neuroevolution strategy optimizes NAS process and combines FL to protect the privacy and security of healthcare. The distributed parallel neuroevolution strategy uses multiple GPUs to train simultaneously to accelerate the training process. In FL-ENAS, multiple federated clients search at the same time based on distributed parallel neuroevolution strategy for NAS, which will improve the search efficiency for healthcare data processing and analysis.

5.4 FL-ENAS Applications

Many publicly available data sets can be used, including MNIST data set, Fashion-MNIST data set, CIFAR10 data set, CIFAR100 data set, ImageNet data set, MHEALTH1, activity recognition with healthy older people using a batteryless wearable sensor data set (AROP)2 and heterogeneity activity recognition data set (HHAR)3. The proposed FL-ENAS framework can be tested, evaluated, and improved by these data sets to realize the tasks of image classification, human activity recognition, and other health-related tasks in healthcare.

This FL-ENAS framework can be applied to disease prevention and treatment. In scenarios where patient data is stored across multiple healthcare institutions or wearable devices, this framework can assist in developing a distributed healthcare data analysis and processing system. This distributed approach allows researchers and healthcare professionals to gain insights from a broader perspective while preserving data ownership and compliance with data protection regulations. Disease is predicted from these healthcare data, facilitating making corresponding countermeasures or prevention and control of disease risk. By analyzing healthcare data from a diverse set of patients, FL-ENAS can be used to identify patterns that may enable more accurate diagnosis and treatment planning. This framework can assist in providing personalized recommendations to healthcare providers, tailoring treatment plans to specific patients based on large-scale data analysis.

The crucial aspect is that this framework can be used for real-time monitoring of human health status. The multiobjective FL-ENAS framework will complete real-time healthcare data analysis tasks with low latency, as well as good accuracy, interpretability, and privacy protection. As shown in Fig. 10, health-related data can be collected from various sources such as wearable devices, smartphones, electronic health records, or medical sensors. Based on these devices, this framework automates the search for the optimal architecture for healthcare data analysis and real-time supervision of human health. It allows the model to learn from a diverse range of local data sources, leading to personalized and accurate health supervision without the need for data centralization. By continuously automating the updating of the global model using local device data, the FL-ENAS framework will allow for real-time monitoring of human health. This enables timely detection of health anomalies, such as abnormal heart rate or blood pressure, allowing for immediate intervention or alert notifications. Overall, the FL-ENAS framework provides a powerful and privacy-preserving approach for disease prevention and treatment as well as real-time human health supervision. It ensures personalized and accurate health monitoring while balancing data availability and privacy protection, allowing for the development of robust models that can contribute to the analysis and processing of healthcare data.

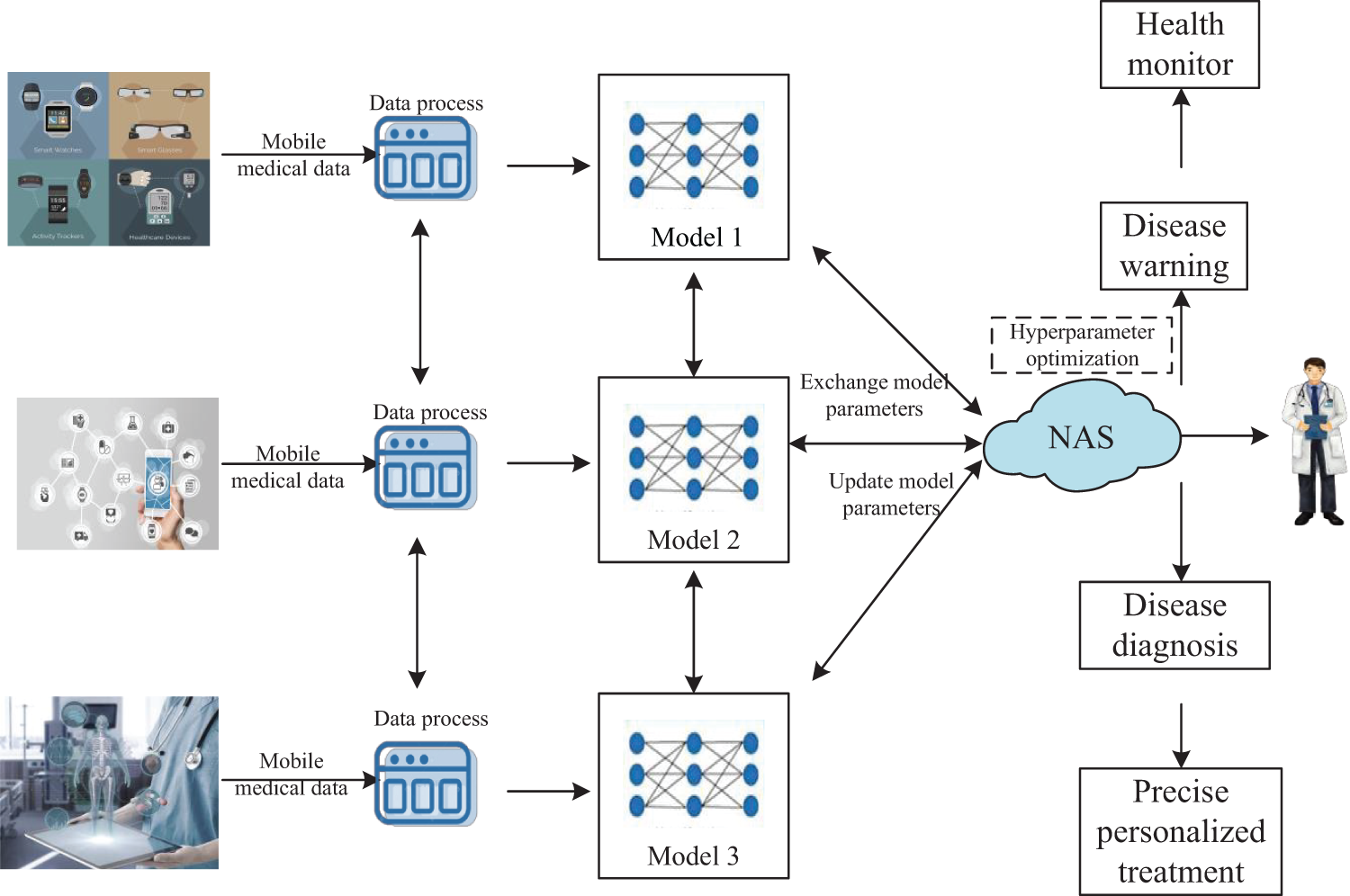
Figure 10: FL-ENAS framework application

6  Future Directions

To provide a guide for readers to do research on the NAS via EAs, corresponding future directions are presented in the following subsections.

6.1 NAS Based on Large-Scale MOEAs

Future research includes achieving NAS utilizing large-scale MOEAs. Current work is still limited in the curse of dimensionality problem, the convergence pressure problem and the problem of maintaining population diversity in the process of neuroevolution. Although there are some works to enhance MOEAs by dimensionality reduction and introducing local search operators, their performance improvement for many large-scale multiobjective problems is still very limited. One possible factor is that most of these existing large-scale MOEAs simply use the research results of large-scale single-objective optimization and many-objective optimization, while the research on the difficulties of large-scale multiobjective optimization itself is not enough. Although large-scale multiobjective optimization optimization is related to these two research directions to some extent, there are still essential differences: on the one hand, multiobjective optimization seeks the optimal solution set of a set of compromise solutions, while single-objective optimization only seeks a global optimal solution. Therefore, it is difficult to effectively solve large-scale multiobjective optimization by simply using the research results of large-scale single-objective optimization. On the other hand, in multiobjective optimization problems, the mapping between the decision vector and the objective is often very complicated, so the design method for the high-dimensional objective space may not be effective in dealing with the high-dimensional decision space. Therefore, more efficient grouping and dimensionality reduction methods need to be further studied for large-scale multiobjective NAS.

As to multiobjective search, NAS can be designed according to different tasks related to the application scenario. Medical data security in mobile healthcare requires reliable and effective execution of hardware, as well as error recovery and performance optimization in the NAS framework [197]. The architecture search for different platforms is to be proposed, which makes these tasks gradually transformed into the automatic design. MOEAs can combine FL for NAS [72]. FL can effectively help multiple institutions to use data and machine learning under the requirements of user personal data security and government regulations [189]. The key operation of FL is to implement parameter passing between the client and cloud server. In the future, NAS will focus on full automatic to seek the best neural architecture. NN can find the best network architecture via solving the multiobjective NAS optimization problem. The flexibility of the architecture and the convergence of the EA need to be improved. EAs can attain high performance to optimize and find the best NN architecture. It is a trend of NAS in the future that large-scale optimization and MOEAs [198] should be simultaneously and comprehensively considered.

6.2 Distributed Parallel Implementation Based on Hardware Characteristics

For the training of the DNNs, GPUs are usually utilized for acceleration. As to the NAS based on EAs, the promising NN architectures are searched in the defined solution space, resulting in high time consumption. Therefore, further parallelism should be considered to improve evolutionary efficiency. Owing to the inherent parallel characteristic that the NN individuals in the population of EAs can be evaluated in parallel, different individuals can be separated into different computational resources. Therefore, EAs can be implemented with distributed parallelism according to the specific hardware characteristics. The message-passing interface (MPI) can be utilized. There are communications among individuals, while the communication cost among distributed computing resources are high. Correspondingly, highly efficient communication strategies are of high research significance. As the DNNs are usually trained via GPUs, the EAs can also be paralleled based on GPUs. To further facilitate the parallelism of EAs, specific EA-based AI chips can be designed.

7  Conclusion

We study NAS in this paper and mainly focus on evolutionary computation for NAS, such as EA, GA, GP, PSO, and hybrid methods, especially multiobjective optimization for NAS. An overview of the advantages and disadvantages of using EAs to optimize NN architectures is provided for researchers. The problem of the low optimization efficiency of NAS is also studied. From the aspects of disease diagnosis, mobile healthcare, and privacy protection, the application of NAS is introduced and summarized for healthcare. Although many new neural architectures emerge, automatically searching neural architectures have continued to make significant progress in promoting efficiency. We can use multiobjective optimization to search the DNNs and automatically design lightweight NNs. MOEAs for multiobjective NAS can be explored further so that we can simultaneously attain accuracy and control the size of the neural architecture. Large-scale multiobjective search is expected to be the future research trend in the field of NAS.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China (NSFC) under Grant No. 61976242, in part by the Natural Science Fund of Hebei Province for Distinguished Young Scholars under Grant No. F2021202010, and in part by the Fundamental Scientific Research Funds for Interdisciplinary Team of Hebei University of Technology under Grant No. JBKYTD2002. This work was also funded by Science and Technology Project of Hebei Education Department under Grant No. JZX2023007. This work is also supported by 2022 Interdisciplinary Postgraduate Training Program of Hebei University of Technology under Grant No. HEBUT-Y-XKJC-2022122.

Author Contributions: The authors’ contributions to the paper are as follows: Study conception and design: Xin Liu, Jie Li; Methodology: Xin Liu, Jie Li, Jianwei Zhao; Interdisciplinary guidance: Jie Li, Rongge Yan; Original draft manuscript preparation: Xin Liu; Writing-review and editing: Jie Li, Jianwei Zhao, Bin Cao, Rongge Yan, Zhihan Lyu. All authors reviewed and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

1https://archive.ics.uci.edu/ml/datasets/MHEALTH+Dataset.

2https://archive.ics.uci.edu/ml/datasets/Activity+recognition+with+healthy+older+people+using+a+batteryless+wearable+sensor.

3https://archive.ics.uci.edu/dataset/507/wisdm+smartphone+and+smartwatch+activity+and+biometrics+dataset.

References

1. Lu, Z., Whalen, I., Dhebar, Y., Deb, K., Goodman, E. D. et al. (2021). Multiobjective evolutionary design of deep convolutional neural networks for image classification. IEEE Transactions on Evolutionary Computation, 25(2), 277–291. https://doi.org/10.1109/TEVC.2020.3024708 [Google Scholar] [CrossRef]

2. Liu, X., Zhao, J., Li, J., Cao, B., Lv, Z. (2022). Federated neural architecture search for medical data security. IEEE Transactions on Industrial Informatics, 18(8), 5628–5636. https://doi.org/10.1109/TII.2022.3144016 [Google Scholar] [CrossRef]

3. Xiao, C., Choi, E., Sun, J. (2018). Opportunities and challenges in developing deep learning models using electronic health records data: A systematic review. Journal of the American Medical Informatics Association, 25(10), 1419–1428. https://doi.org/10.1093/jamia/ocy068 [Google Scholar] [PubMed] [CrossRef]

4. Akl, A., El-Henawy, I., Salah, A., Li, K. (2019). Optimizing deep neural networks hyperparameter positions and values. Journal of Intelligent & Fuzzy Systems, 37(5), 6665–6681. https://doi.org/10.3233/JIFS-190033 [Google Scholar] [CrossRef]

5. Liu, X., Zhao, J., Li, J., Xu, D., Tian, S. et al. (2022). Large-scale multiobjective federated neuroevolution for privacy and security in the Internet of Things. IEEE Internet of Things Magazine, 5(2), 74–77. https://doi.org/10.1109/IOTM.001.2100179 [Google Scholar] [CrossRef]

6. Pham, H., Guan, M. Y., Zoph, B., Le, Q., Dean, J. (2018). Efficient neural architecture search via parameter sharing. International Conference on Machine Learning, vol. 80. San Diego. https://doi.org/10.48550/arXiv.1802.03268 [Google Scholar] [CrossRef]

7. Zhong, Z., Yan, J., Wu, W., Shao, J., Liu, C. L. (2018). Practical block-wise neural network architecture generation. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, UT, USA, IEEE. https://doi.org/10.1109/CVPR.2018.00257 [Google Scholar] [CrossRef]

8. Gong, X., Chang, S., Jiang, Y., Wang, Z. (2019). AutoGAN: Neural architecture search for generative adversarial networks. 2019 IEEE/CVF International Conference on Computer Vision (ICCV). Seoul, Korea (SouthIEEE. https://doi.org/10.1109/ICCV.2019.00332 [Google Scholar] [CrossRef]

9. Real, E., Moore, S., Selle, A., Saxena, S., Suematsu, Y. L. et al. (2017). Large-scale evolution of image classifiers. Proceedings of the 34th International Conference on Machine Learning, vol. 70, pp. 2902–2911. Sydney, NSW, Australia, ACM. https://dl.acm.org/doi/10.5555/3305890.3305981 [Google Scholar]

10. Suganuma, M., Shirakawa, S., Nagao, T. (2017). A genetic programming approach to designing convolutional neural network architectures. Proceedings of the 2017 Genetic and Evolutionary Computation Conference (GECCO’17), New York, Assoc Computing Machinery. https://doi.org/10.1145/3071178.3071229. [Google Scholar] [CrossRef]

11. Xie, L., Yuille, A. (2017). Genetic CNN. 2017 IEEE International Conference on Computer Vision (ICCV), New York, IEEE. https://doi.org/10.1109/ICCV.2017.154 [Google Scholar] [CrossRef]

12. Zoph, B., Vasudevan, V., Shlens, J., Le, Q. V. (2018). Learning transferable architectures for scalable image recognition. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New York, IEEE. https://doi.org/10.1109/CVPR.2018.00907 [Google Scholar] [CrossRef]

13. Elsken, T., Metzen, J. H., Hutter, F. (2019). Neural architecture search: A survey. Journal of Machine Learning Research, 20(1), 1997–2017. https://doi.org/10.5555/3322706.3361996 [Google Scholar] [CrossRef]

14. Chen, Y., Wang, Z., Wang, Z. J., Kang, X. (2020). Automated design of neural network architectures with reinforcement learning for detection of global manipulations. IEEE Journal of Selected Topics in Signal Processing, 14(5), 997–1011. https://doi.org/10.1109/JSTSP.2020.2998401 [Google Scholar] [CrossRef]

15. Liu, H., Simonyan, K., Yang, Y. (2019). Darts: Differentiable architecture search. ICLR 2019. New Orleans, Louisiana, USA: OpenReview.net. https://openreview.net/pdf?id=S1eYHoC5FX [Google Scholar]

16. Stanley, K. O., Miikkulainen, R. (2002). Evolving neural networks through augmenting topologies. Evolutionary computation, 10(2), 99–127. https://doi.org/10.1162/106365602320169811 [Google Scholar] [PubMed] [CrossRef]

17. Mahmoudi, M. T., Taghiyareh, F., Forouzideh, N., Lucas, C. (2013). Evolving artificial neural network structure using grammar encoding and colonial competitive algorithm. Neural Computing & Applications, 22(1), S1–S16. https://doi.org/10.1007/s00521-012-0905-6 [Google Scholar] [CrossRef]

18. de Campos, L. M. L., de Oliveira, R. C. L., Roisenberg, M. (2016). Optimization of neural networks through grammatical evolution and a genetic algorithm. Expert Systems with Applications, 56, 368–384. https://doi.org/10.1016/j.eswa.2016.03.012 [Google Scholar] [CrossRef]

19. Cao, B., Zhao, J., Lv, Z., Gu, Y., Yang, P. et al. (2020). Multiobjective evolution of fuzzy rough neural network via distributed parallelism for stock prediction. IEEE Transactions on Fuzzy Systems, 28(5), 939–952. https://doi.org/10.1109/TFUZZ.2020.2972207 [Google Scholar] [CrossRef]

20. Zhang, H., Hao, K., Gao, L., Wei, B., Tang, X. (2023). Optimizing deep neural networks through neuroevolution with stochastic gradient descent. IEEE Transactions on Cognitive and Developmental Systems, 15(1), 111–121. https://doi.org/10.1109/TCDS.2022.3146327 [Google Scholar] [CrossRef]

21. Bangyal, W. H., Ahmed, J., Rauf, H. T. (2020). A modified bat algorithm with torus walk for solving global optimisation problems. International Journal of Bio-Inspired Computation, 15(1), 1–13. https://doi.org/10.1504/IJBIC.2020.105861 [Google Scholar] [CrossRef]

22. Stanley, K. O., Clune, J., Lehman, J., Miikkulainen, R. (2019). Designing neural networks through neuroevolution. Nature Machine Intelligence, 1(1), 24–35. https://doi.org/10.1038/s42256-018-0006-z [Google Scholar] [CrossRef]

23. Jalali, S. M. J., Karimi, M., Khosravi, A., Nahavandi, S. (2019). An efficient neuroevolution approach for heart disease detection. 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), New York, IEEE. https://doi.org/10.1109/SMC.2019.8913997 [Google Scholar] [CrossRef]

24. Hassanzadeh, T., Essam, D., Sarker, R. (2020). EvoU-Net: An evolutionary deep fully convolutional neural network for medical image segmentation. Proceedings of the 35th Annual ACM Symposium on Applied Computing, pp. 181–189. Czech Technical University, Electrical network, ACM. https://doi.org/10.1145/3341105.3373856 [Google Scholar] [CrossRef]

25. Baldeon Calisto, M., Lai-Yuen, S. K. (2020). AdaEn-Net: An ensemble of adaptive 2D–3D fully convolutional networks for medical image segmentation. Neural Networks, 126, 76–94. https://doi.org/10.1016/j.neunet.2020.03.007 [Google Scholar] [PubMed] [CrossRef]

26. Baymurzina, D., Golikov, E., Burtsev, M. (2022). A review of neural architecture search. Neurocomputing, 474, 82–93. https://doi.org/10.1016/j.neucom.2021.12.014 [Google Scholar] [CrossRef]

27. Ren, P., Xiao, Y., Chang, X., Huang, P. Y., Li, Z. et al. (2021). A comprehensive survey of neural architecture search: Challenges and solutions. ACM Computing Surveys, 54(4), 1–34. https://doi.org/10.1145/3447582 [Google Scholar] [CrossRef]

28. Angeline, P. J., Saunders, G. M. (1994). An evolutionary algorithm that constructs recurrent neural networks. IEEE Transactions on Neural Networks, 5(1), 54–65. https://doi.org/10.1109/72.265960 [Google Scholar] [PubMed] [CrossRef]

29. Yao, X., Liu, Y. (1997). A new evolutionary system for evolving artificial neural networks. IEEE Transactions on Neural Networks, 8(3), 694–713. https://doi.org/10.1109/72.572107 [Google Scholar] [PubMed] [CrossRef]

30. Martinez, A. D., Del Ser, J., Villar-Rodriguez, E., Osaba, E., Poyatos, J. et al. (2021). Lights and shadows in evolutionary deep learning: Taxonomy, critical methodological analysis, cases of study, learned lessons, recommendations and challenges. Information Fusion, 67, 161–194. [Google Scholar]

31. Cantu-Paz, E., Kamath, C. (2005). An empirical comparison of combinations of evolutionary algorithms and neural networks for classification problems. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 35(5), 915–927. https://doi.org/10.1109/TSMCB.2005.847740 [Google Scholar] [PubMed] [CrossRef]

32. Stanley, K., D’Ambrosio, D., Gauci, J. (2009). A hypercube-based encoding for evolving large-scale neural networks. Artificial Life, 15(2), 185–212. https://doi.org/10.1162/artl.2009.15.2.15202 [Google Scholar] [PubMed] [CrossRef]

33. Dong, J., Zhang, L., Hou, B., Feng, L. (2020). A memetic algorithm for evolving deep convolutional neural network in image classification. 2020 IEEE Symposium Series on Computational Intelligence (SSCI), New York, IEEE. https://doi.org/10.1109/SSCI47803.2020.9308162 [Google Scholar] [CrossRef]

34. Real, E., Aggarwal, A., Huang, Y., Le, Q. V. (2019). Regularized evolution for image classifier architecture search. Thirty-Third AAAI Conference on Artificial Intelligence/Thirty-First Innovative Applications of Artificial Intelligence Conference/Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, Palo Alto, Association for the Advancement Artificial Intelligence. https://doi.org/10.48550/arXiv.1802.01548 [Google Scholar] [CrossRef]

35. Zhang, H., Jin, Y., Cheng, R., Hao, K. (2021). Efficient evolutionary search of attention convolutional networks via sampled training and node inheritance. IEEE Transactions on Evolutionary Computation, 25(2), 371–385. https://doi.org/10.1109/TEVC.2020.3040272 [Google Scholar] [CrossRef]

36. Mahdaddi, A., Meshoul, S., Belguidoum, M. (2021). EA-based hyperparameter optimization of hybrid deep learning models for effective drug-target interactions prediction. Expert Systems With Application, 185, 115525. https://doi.org/10.1016/j.eswa.2021.115525 [Google Scholar] [CrossRef]

37. Jaafra, Y., Luc Laurent, J., Deruyver, A., Saber Naceur, M. (2019). Reinforcement learning for neural architecture search: A review. Image and Vision Computing, 89, 57–66. https://doi.org/10.1016/j.imavis.2019.06.005 [Google Scholar] [CrossRef]

38. Unal, H. T., Basciftci, F. (2022). Evolutionary design of neural network architectures: A review of three decades of research. Artificial Intelligence Review, 55(3), 1723–1802. https://doi.org/10.1007/s10462-021-10049-5 [Google Scholar] [CrossRef]

39. Prabakaran, B. S., Akhtar, A., Rehman, S., Hasan, O., Shafique, M. (2021). BioNetExplorer: Architecture-space exploration of biosignal processing deep neural networks for wearables. IEEE Internet of Things Journal, 8(17), 13251–13265. https://doi.org/10.1109/JIOT.2021.3065815 [Google Scholar] [CrossRef]

40. Khalifa, M. H., Ammar, M., Ouarda, W., Alimi, A. M. (2017). Particle swarm optimization for deep learning of convolution neural network. Proceedings of 2017 Sudan Conference on Computer Science and Information Technology (SCCSIT), New York, IEEE. https://doi.org/10.1109/SCCSIT.2017.8293059 [Google Scholar] [CrossRef]

41. Vargas-Hákim, G. A., Mezura-Montes, E., Acosta-Mesa, H. G. (2022). A review on convolutional neural network encodings for neuroevolution. IEEE Transactions on Evolutionary Computation, 26(1), 12–27. https://doi.org/10.1109/TEVC.2021.3088631 [Google Scholar] [CrossRef]

42. Deb, K., Pratap, A., Agarwal, S., Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6(2), 182–197. https://doi.org/10.1109/4235.996017 [Google Scholar] [CrossRef]

43. Lu, Z., Deb, K., Goodman, E. (2020). NSGANetV2: Evolutionary multi-objective surrogate-assisted neural architecture search. 16th European Conference on Computer Vision, pp. 35–51. Glasgow, UK: Springer Science and Business Media Deutschland GmbH. https://doi.org/10.1007/978-3-030-58452-8_3 [Google Scholar] [CrossRef]

44. O’Neill, D., Xue, B., Zhang, M. (2021). Evolutionary neural architecture search for high-dimensional skip-connection structures on densenet style networks. IEEE Transactions on Evolutionary Computation, 25(6), 1118–1132. https://doi.org/10.1109/TEVC.2021.3083315 [Google Scholar] [CrossRef]

45. Ronoud, S., Asadi, S. (2019). An evolutionary deep belief network extreme learning-based for breast cancer diagnosis. Soft Computing, 23(24), 13139–13159. https://doi.org/10.1007/s00500-019-03856-0 [Google Scholar] [CrossRef]

46. Liu, P., El Basha, M. D., Li, Y., Xiao, Y., Sanelli, P. C. et al. (2019). Deep evolutionary networks with expedited genetic algorithms for medical image denoising. Medical Image Analysis, 54, 306–315. https://doi.org/10.1016/j.media.2019.03.004 [Google Scholar] [PubMed] [CrossRef]

47. Ma, B., Li, X., Xia, Y., Zhang, Y. (2020). Autonomous deep learning: A genetic DCNN designer for image classification. Neurocomputing, 379, 152–161. https://doi.org/10.1016/j.neucom.2019.10.007 [Google Scholar] [CrossRef]

48. Sun, Y., Xue, B., Zhang, M., Yen, G. G. (2020). Evolving deep convolutional neural networks for image classification. IEEE Transactions on Evolutionary Computation, 24(2), 394–407. https://doi.org/10.1109/TEVC.2019.2916183 [Google Scholar] [CrossRef]

49. Suganuma, M., Kobayashi, M., Shirakawa, S., Nagao, T. (2020). Evolution of deep convolutional neural networks using cartesian genetic programming. Evolutionary Computation, 28(1), 141–163. https://doi.org/10.1162/evco_a_00253 [Google Scholar] [PubMed] [CrossRef]

50. Wang, R., Zha, B. (2019). A research on the optimal design of BP neural network based on improved GEP. International Journal of Pattern Recognition and Artificial Intelligence, 33(3). https://doi.org/10.1142/S0218001419590079 [Google Scholar] [CrossRef]

51. Bianco, S., Buzzelli, M., Ciocca, G., Schettini, R. (2020). Neural architecture search for image saliency fusion. Information Fusion, 57, 89–101. https://doi.org/10.1016/j.inffus.2019.12.007 [Google Scholar] [CrossRef]

52. Tan, S. C., Lim, C. P. (2011). Fuzzy artmap and hybrid evolutionary programming for pattern classification. Journal of Intelligent and Fuzzy Systems, 22(2–3), 57–68. https://doi.org/10.3233/IFS-2011-0476 [Google Scholar] [CrossRef]

53. Johari, D., Rahman, T. K. A., Musirin, I., Aminudin, N. (2010). Application of meta-evolutionary programming in ANN-based lightning prediction system. International Review of Electrical Engineering, 5(4), 1824–1832. [Google Scholar]

54. Pinos, M., Mrazek, V., Sekanina, L. (2022). Evolutionary approximation and neural architecture search. Genetic Programming and Evolvable Machines, 23(3), 351–374. https://doi.org/10.1007/s10710-022-09441-z [Google Scholar] [CrossRef]

55. Fernandes Junior, F. E., Yen, G. G. (2019). Particle swarm optimization of deep neural networks architectures for image classification. Swarm and Evolutionary Computation, 49, 62–74. https://doi.org/10.1016/j.swevo.2019.05.010 [Google Scholar] [CrossRef]

56. Wang, B., Sun, Y., Xue, B., Zhang, M. (2018). Evolving deep convolutional neural networks by variable-length particle swarm optimization for image classification. 2018 IEEE Congress on Evolutionary Computation (CEC), New York, IEEE. https://doi.org/10.1109/CEC.2018.8477735 [Google Scholar] [CrossRef]

57. Tan, T. Y., Zhang, L., Lim, C. P. (2020). Adaptive melanoma diagnosis using evolving clustering, ensemble and deep neural networks. Knowledge-Based Systems, 187, 104807. https://doi.org/10.1016/j.knosys.2019.06.015 [Google Scholar] [CrossRef]

58. Balasubramanian, K., Ananthamoorthy, N. P., Ramya, K. (2022). An approach to classify white blood cells using convolutional neural network optimized by particle swarm optimization algorithm. Neural Computing & Applications, 34(18), 16089–16101. https://doi.org/10.1007/s00521-022-07279-1 [Google Scholar] [CrossRef]

59. Jiang, J., Han, F., Ling, Q., Wang, J., Li, T. et al. (2019). Efficient network architecture search via multiobjective particle swarm optimization based on decomposition. Neural Networks, 123, 305–316. https://doi.org/10.1016/j.neunet.2019.12.005 [Google Scholar] [PubMed] [CrossRef]

60. Salama, K. M., Abdelbar, A. M. (2015). Learning neural network structures with ant colony algorithms. Swarm Intelligence, 9(4), 229–265. https://doi.org/10.1007/s11721-015-0112-z [Google Scholar] [CrossRef]

61. Byla, E., Pang, W. (2020). DeepSwarm: Optimising convolutional neural networks using swarm intelligence. In: Advances in computational intelligence systems (UKCI 2019), vol. 1043. Cham: Springer International Publishing Ag. https://doi.org/10.1007/978-3-030-29933-0_10 [Google Scholar] [CrossRef]

62. Suda, E., Iba, H. (2020). Neural architecture search and weight adjustment by means of ant colony optimization. 2020 5th International Conference on Intelligent Informatics and Biomedical Sciences (ICIIBMS 2020), New York, IEEE. https://doi.org/10.1109/ICIIBMS50712.2020.9336395 [Google Scholar] [CrossRef]

63. Dahou, A., Elaziz, M. A., Zhou, J., Xiong, S. (2019). Arabic sentiment classification using convolutional neural network and differential evolution algorithm. Computational Intelligence and Neuroence, 2019, 1–16. https://doi.org/10.1155/2019/2537689 [Google Scholar] [PubMed] [CrossRef]

64. Huang, J., Xue, B., Sun, Y., Zhang, M. (2022). EDE-NAS: An eclectic differential evolution approach to single-path neural architecture search. In: Aziz, H., Correa, D., French, T. (Eds.AI 2022: Advances in artificial intelligence, vol. 13728. Cham: Springer International Publishing Ag. https://doi.org/10.1007/978-3-031-22695-3_9 [Google Scholar] [CrossRef]

65. Ghosh, A., Jana, N. D., Mallik, S., Zhao, Z. (2022). Designing optimal convolutional neural network architecture using differential evolution algorithm. Patterns, 3(9), 100567. https://doi.org/10.1016/j.patter.2022.100567 [Google Scholar] [PubMed] [CrossRef]

66. Zanchettin, C., Ludermir, T. B. (2005). Hybrid technique for artificial neural network architecture and weight optimization. In: Knowledge discovery in databases: PKDD 2005, vol. 3721, pp. 709–716. Berlin: Springer-Verlag Berlin. https://doi.org/10.1007/11564126_76 [Google Scholar] [CrossRef]

67. Termritthikun, C., Xu, L., Liu, Y., Lee, I. (2021). Neural architecture search and multi-objective evolutionary algorithms for anomaly detection. 2021 International Conference on Data Mining Workshops (ICDMW), Auckland, New Zealand, IEEE. https://doi.org/10.1109/ICDMW53433.2021.00130 [Google Scholar] [CrossRef]

68. Zanchettin, C., Ludermir, T. B., Almeida, L. M. (2011). Hybrid training method for MLP: Optimization of architecture and training. IEEE Transactions on Systems Man & Cybernetics Part B, 41(4), 1097–1109. https://doi.org/10.1109/TSMCB.2011.2107035 [Google Scholar] [PubMed] [CrossRef]

69. Schorn, C., Elsken, T., Vogel, S., Runge, A., Guntoro, A. et al. (2020). Automated design of error-resilient and hardware-efficient deep neural networks. Neural Computing and Applications, 32(24), 18327–18345. https://doi.org/10.1007/s00521-020-04969-6 [Google Scholar] [CrossRef]

70. Zhou, Y., Yen, G. G., Yi, Z. (2020). Evolutionary compression of deep neural networks for biomedical image segmentation. IEEE Transactions on Neural Networks and Learning Systems, 31(8), 2916–2929. https://doi.org/10.1109/TNNLS.2019.2933879 [Google Scholar] [PubMed] [CrossRef]

71. Baldeon-Calisto, M., Lai-Yuen, S. K. (2020). AdaResU-Net: Multiobjective adaptive convolutional neural network for medical image segmentation. Neurocomputing, 392, 325–340. https://doi.org/10.1016/j.neucom.2019.01.110 [Google Scholar] [CrossRef]

72. Zhu, H., Jin, Y. (2020). Multi-objective evolutionary federated learning. IEEE Transactions on Neural Networks and Learning Systems, 31(4), 1310–1322. https://doi.org/10.1109/TNNLS.2019.2919699 [Google Scholar] [PubMed] [CrossRef]

73. Ji, J., Zhao, J., Lin, Q., Tan, K. C. (2022). Competitive decomposition-based multiobjective architecture search for the dendritic neural model. IEEE Transactions on Cybernetics, 53(11), 6829–6842. https://doi.org/10.1109/TCYB.2022.3165374 [Google Scholar] [PubMed] [CrossRef]

74. Liu, X., Gong, X., Plaza, A., Cai, Z., Xiao, X. et al. (2022). MO-CNN: Multiobjective optimization of convolutional neural networks for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing, 60, 1–14. https://doi.org/10.1109/TGRS.2022.3220748 [Google Scholar] [CrossRef]

75. Kanwal, S., Younas, I., Bashir, M. (2021). Evolving convolutional autoencoders using multi-objective particle swarm optimization. Computers & Electrical Engineering, 91, 107108. https://doi.org/10.1016/j.compeleceng.2021.107108 [Google Scholar] [CrossRef]

76. Geraeinejad, V., Sinaei, S., Modarressi, M., Daneshtalab, M. (2021). RoCo-NAS: Robust and compact neural architecture search. 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, IEEE. https://doi.org/10.1109/IJCNN52387.2021.9534460 [Google Scholar] [CrossRef]

77. Tong, D. L., Mintram, R. (2010). Genetic Algorithm-Neural Network (GANNA study of neural network activation functions and depth of genetic algorithm search applied to feature selection. International Journal of Machine Learning and Cybernetics, 1(1–4), 75–87. https://doi.org/10.1007/s13042-010-0004-x [Google Scholar] [CrossRef]

78. Dubey, R., Agrawal, J. (2022). An improved genetic algorithm for automated convolutional neural network design. Intelligent Automation and Soft Computing, 32(2), 747–763. https://doi.org/10.32604/iasc.2022.020975 [Google Scholar] [CrossRef]

79. Dorigo, M., Caro, G. D., Gambardella, L. M. (1999). Ant algorithms for discrete optimization. Artificial Life, 5(2), 137–172. https://doi.org/10.1162/106454699568728 [Google Scholar] [PubMed] [CrossRef]

80. Cao, B., Zhao, J., Lv, Z., Liu, X. (2017). A distributed parallel cooperative coevolutionary multiobjective evolutionary algorithm for large-scale optimization. IEEE Transactions on Industrial Informatics, 13(4), 2030–2038. https://doi.org/10.1109/TII.2017.2676000 [Google Scholar] [CrossRef]

81. Cao, B., Zhao, J., Yang, P., Lv, Z., Liu, X. et al. (2018). Distributed parallel cooperative coevolutionary multi-objective large-scale immune algorithm for deployment of wireless sensor networks. Future Generation Computer Systems, 82, 256–267. https://doi.org/10.1016/j.future.2017.10.015 [Google Scholar] [CrossRef]

82. Cao, B., Zhao, J., Yang, P., Yang, P., Liu, X. et al. (2019). deployment optimization for heterogeneous wireless directional sensor networks on smart city. IEEE Transactions on Industrial Informatics, 15(3), 1798–1808. https://doi.org/10.1109/TII.2018.2884951 [Google Scholar] [CrossRef]

83. Park, K. M., Shin, D., Chi, S. D. (2019). Variable chromosome genetic algorithm for structure learning in neural networks to imitate human brain. Applied Sciences, 10(5). https://doi.org/10.3390/app9153176 [Google Scholar] [CrossRef]

84. Cao, B., Zhao, J., Liu, X., Arabas, J., Tanveer, M. et al. (2022). Multiobjective evolution of the explainable fuzzy rough neural network with gene expression programming. IEEE Transactions on Fuzzy Systems, 30(10), 4190–4200. https://doi.org/10.1109/TFUZZ.2022.3141761 [Google Scholar] [CrossRef]

85. Kentzoglanakis, K., Poole, M. (2012). A swarm intelligence framework for reconstructing gene networks: Searching for biologically plausible architectures. IEEE-ACM Transactions on Computational Biology and Bioinformatics, 9(2), 358–371. https://doi.org/10.1109/TCBB.2011.87 [Google Scholar] [PubMed] [CrossRef]

86. Mininno, E., Neri, F., Cupertino, F., Naso, D. (2011). Compact differential evolution. IEEE Transactions on Evolutionary Computation, 15(1), 32–54. https://doi.org/10.1109/TEVC.2010.2058120 [Google Scholar] [CrossRef]

87. Rauf, H. T., Gao, J., Almadhor, A., Haider, A., Zhang, Y. D. et al. (2023). Multi population-based chaotic differential evolution for multi-modal and multi-objective optimization problems. Applied Soft Computing, 132, 109909. https://doi.org/10.1016/j.asoc.2022.109909 [Google Scholar] [CrossRef]

88. Rauf, H. T., Malik, S., Shoaib, U., Irfan, M. N., Lali, M. I. (2020). Adaptive inertia weight bat algorithm with sugeno-function fuzzy search. Applied Soft Computing, 90, 106159. https://doi.org/10.1016/j.asoc.2020.106159 [Google Scholar] [CrossRef]

89. Yang, Q. T., Zhan, Z. H., Kwong, S., Zhang, J. (2022). Multiple populations for multiple objectives framework with bias sorting for many-objective optimization. IEEE Transactions on Evolutionary Computation, 27(5), 1340–1354. https://doi.org/10.1109/TEVC.2022.3212058 [Google Scholar] [CrossRef]

90. Zhou, Y., Yen, G. G., Yi, Z. (2022). Evolutionary shallowing deep neural networks at block levels. IEEE Transactions on Neural Networks and Learning Systems, 33(9), 4635–4647. https://doi.org/10.1109/TNNLS.2021.3059529 [Google Scholar] [PubMed] [CrossRef]

91. Gong, Y. J., Chen, W. N., Zhan, Z. H., Zhang, J., Li, Y. et al. (2015). Distributed evolutionary algorithms and their models: A survey of the state-of-the-art. Applied Soft Computing, 34, 286–300. https://doi.org/10.1016/j.asoc.2015.04.061 [Google Scholar] [CrossRef]

92. Bagheri-Esfeh, H., Safikhani, H., Motahar, S. (2020). Multi-objective optimization of cooling and heating loads in residential buildings integrated with phase change materials using the artificial neural network and genetic algorithm. Journal of Energy Storage, 32, 101772. [Google Scholar]

93. Ma, Y., Xie, Y. (2022). Evolutionary neural networks for deep learning: A review. International Journal of Machine Learning and Cybernetics, 13(10), 3001–3018. https://doi.org/10.1007/s13042-022-01578-8 [Google Scholar] [CrossRef]

94. Sun, Y., Xue, B., Zhang, M., Yen, G. G. (2020). Completely automated CNN architecture design based on blocks. IEEE Transactions on Neural Networks and Learning Systems, 31(4), 1242–1254. https://doi.org/10.1109/TNNLS.2019.2919608 [Google Scholar] [PubMed] [CrossRef]

95. Bangyal, W. H., Nisar, K., Ibrahim, A. A. B. A., Haque, M. R., Rodrigues, J. J. P. C. et al. (2021). Comparative analysis of low discrepancy sequence-based initialization approaches using population-based algorithms for solving the global optimization problems. Applied Sciences, 11(16), 7591. https://doi.org/10.3390/app11167591 [Google Scholar] [CrossRef]

96. Rauf, H. T., Bangyal, W. H. K., Lali, M. I. (2021). An adaptive hybrid differential evolution algorithm for continuous optimization and classification problems. Neural Computing and Applications, 33(17), 10841–10867. https://doi.org/10.1007/s00521-021-06216-y [Google Scholar] [CrossRef]

97. Wang, X., Wang, X., Lv, T., Jin, L., He, M. (2021). HARNAS: Human activity recognition based on automatic neural architecture search using evolutionary algorithms. Sensors, 21(20), 6927. https://doi.org/10.3390/s21206927 [Google Scholar] [PubMed] [CrossRef]

98. https://en.wikipedia.org/wiki/FLOPS (accessed on 07/11/2023) [Google Scholar]

99. Tan, M., Le, Q. V. (2019). EfficientNet: Rethinking model scaling for convolutional neural networks. International Conference on Machine Learning, vol. 97. San Diego, USA. https://doi.org/10.48550/arXiv.1905.11946 [Google Scholar] [CrossRef]

100. Oyelade, O. N., Ezugwu, A. E. (2022). Characterization of abnormalities in breast cancer images using nature-inspired metaheuristic optimized convolutional neural networks model. Concurrency and Computation: Practice and Experience, 34(4), e6629. https://doi.org/10.1002/cpe.6629 [Google Scholar] [CrossRef]

101. Zhu, H., Zhang, H., Jin, Y. (2021). From federated learning to federated neural architecture search: A survey. Complex & Intelligent Systems, 7(2), 639–657. https://doi.org/10.1007/s40747-020-00247-z [Google Scholar] [CrossRef]

102. Hajewski, J., Oliveira, S., Xing, X. (2022). Distributed evolution of deep autoencoders. In: Arai, K. (Ed.Intelligent computing. Cham: Springer International Publishing. https://doi.org/10.48550/arXiv.2004.07607 [Google Scholar] [CrossRef]

103. Tan, M., Chen, B., Pang, R., Vasudevan, V., Sandier, M. et al. (2019). MnasNet: Platform-aware neural architecture search for mobile. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR 2019), Los Alamitos, IEEE Computer Society. https://doi.org/10.1109/CVPR.2019.00293 [Google Scholar] [CrossRef]

104. Zhang, L. L., Yang, Y., Jiang, Y., Zhu, W., Liu, Y. (2020). Fast hardware-aware neural architecture search. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, IEEE. https://doi.org/10.1109/CVPRW50498.2020.00354 [Google Scholar] [CrossRef]

105. Jiang, Y., Wang, X., Zhu, W. (2020). Hardware-aware transformable architecture search with efficient search space. 2020 IEEE International Conference on Multimedia and Expo (ICME), London, UK, IEEE. https://doi.org/10.1109/ICME46284.2020.9102721 [Google Scholar] [CrossRef]

106. Yu, R., Li, A., Chen, C., Lai, J., Morariu, V. I. et al. (2018). NISP: Pruning networks using neuron importance score propagation. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, IEEE. https://doi.org/10.1109/CVPR.2018.00958 [Google Scholar] [CrossRef]

107. Zhang, Q., Li, H. (2007). MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Transactions on Evolutionary Computation, 11(6), 712–731. https://doi.org/10.1109/TEVC.2007.892759 [Google Scholar] [CrossRef]

108. Zitzler, E., Künzli, S. (2004). Indicator-based selection in multiobjective search. In: Yao, X., Burke, E. K., Lozano, J. A., Smith, J., Merelo-Guervós, J. J. et al. (Eds.Parallel problem solving from nature—PPSN VIII. Berlin, Heidelberg: Springer. https://link.springer.com/chapter/10.1007/978-3-540-30217-9_84 (accessed on 10/01/2020) [Google Scholar]

109. Hong, W., Tang, K., Zhou, A., Ishibuchi, H., Yao, X. (2019). A scalable indicator-based evolutionary algorithm for large-scale multiobjective optimization. IEEE Transactions on Evolutionary Computation, 23(3), 525–537. https://doi.org/10.1109/TEVC.2018.2881153 [Google Scholar] [CrossRef]

110. L, X., Y, X. (2012). Cooperatively coevolving particle swarms for large scale optimization. IEEE Transactions on Evolutionary Computation, 16(2), 210–224. https://doi.org/10.1109/TEVC.2011.2112662 [Google Scholar] [CrossRef]

111. Zhou, X., Qin, A. K., Gong, M., Tan, K. C. (2021). A survey on evolutionary construction of deep neural networks. IEEE Transactions on Evolutionary Computation, 25(5), 894–912. https://doi.org/10.1109/TEVC.2021.3079985 [Google Scholar] [CrossRef]

112. Tian, Y., Liu, R., Zhang, X., Ma, H., Tan, K. C. et al. (2021). A multipopulation evolutionary algorithm for solving large-scale multimodal multiobjective optimization problems. IEEE Transactions on Evolutionary Computation, 25(3), 405–418. https://doi.org/10.1109/TEVC.2020.3044711 [Google Scholar] [CrossRef]

113. Mahdavi, S., Shiri, M. E., Rahnamayan, S. (2015). Metaheuristics in large-scale global continues optimization: A survey. Information Sciences, 295, 407–428. https://doi.org/10.1016/j.ins.2014.10.042 [Google Scholar] [CrossRef]

114. Yang, Z., Tang, K., Yao, X. (2008). Large scale evolutionary optimization using cooperative coevolution. Information Sciences, 178(15), 2985–2999. https://doi.org/10.1016/J.INS.2008.02.017 [Google Scholar] [CrossRef]

115. Omidvar, M. N., Li, X., Mei, Y., Yao, X. (2014). Cooperative co-evolution with differential grouping for large scale optimization. IEEE Transactions on Evolutionary Computation, 18(3), 378–393. https://doi.org/10.1109/TEVC.2013.2281543 [Google Scholar] [CrossRef]

116. Omidvar, M. N., Li, X., Yao, X. (2010). Cooperative co-evolution with delta grouping for large scale non-separable function optimization. 2010 IEEE Congress on Evolutionary Computation (CEC), New York, IEEE. https://doi.org/10.1109/CEC.2010.5585979 [Google Scholar] [CrossRef]

117. He, C., Li, L., Tian, Y., Zhang, X., Cheng, R. et al. (2019). Accelerating large-scale multiobjective optimization via problem reformulation. IEEE Transactions on Evolutionary Computation, 23(6), 949–961. https://doi.org/10.1109/TEVC.2019.2896002 [Google Scholar] [CrossRef]

118. Antonio, L. M., Coello, C. A. C. (2013). Use of cooperative coevolution for solving large scale multiobjective optimization problems. 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, IEEE. https://doi.org/10.1109/CEC.2013.6557903 [Google Scholar] [CrossRef]

119. Qi, Y., Bao, L., Ma, X., Miao, Q., Li, X. (2016). Self-adaptive multi-objective evolutionary algorithm based on decomposition for large-scale problems: A case study on reservoir flood control operation. Information Sciences, 367, 529–549. https://doi.org/10.1016/j.ins.2016.06.005 [Google Scholar] [CrossRef]

120. Miguel Antonio, L., Coello Coello, C. A. (2016). Decomposition-based approach for solving large scale multi-objective problems. In: Parallel problem solving from nature—PPSN XIV, vol. 9921. Cham: Springer International Publishing Ag. https://doi.org/10.1007/978-3-319-45823-6_49 [Google Scholar] [CrossRef]

121. Ma, X., Liu, F., Qi, Y., Wang, X., Li, L. et al. (2016). A multiobjective evolutionary algorithm based on decision variable analyses for multiobjective optimization problems with large-scale variables. IEEE Transactions on Evolutionary Computation, 20(2), 275–298. https://doi.org/10.1109/TEVC.2015.2455812 [Google Scholar] [CrossRef]

122. Song, A., Yang, Q., Chen, W. N., Zhang, J. (2016). A random-based dynamic grouping strategy for large scale multi-objective optimization. 2016 IEEE Congress on Evolutionary Computation (CEC), New York, IEEE. https://doi.org/10.1109/CEC.2016.7743831 [Google Scholar] [CrossRef]

123. Zhang, X., Tian, Y., Cheng, R., Jin, Y. (2018). A decision variable clustering-based evolutionary algorithm for large-scale many-objective optimization. IEEE Transactions on Evolutionary Computation, 22(1), 97–112. https://doi.org/10.1109/TEVC.2016.2600642 [Google Scholar] [CrossRef]

124. Qian, H., Yu, Y. (2017). Solving high-dimensional multi-objective optimization problems with low effective dimensions. Thirty-First AAAI Conference on Artificial Intelligence, Palo Alto, Association for the Advancement Artificial Intelligence. https://doi.org/10.1109/10.5555/3298239.3298367 [Google Scholar] [CrossRef]

125. Zille, H., Ishibuchi, H., Mostaghim, S., Nojima, Y. (2016). Weighted optimization framework for large-scale multi-objective optimization. Proceedings of the 2016 Genetic and Evolutionary Computation Conference (Gecco’16 Companion), New York, Association for Computing Machinery. https://doi.org/10.1145/2908961.2908979 [Google Scholar] [CrossRef]

126. Garcia-Sanchez, P., Ortega, J., Gonzalez, J., Castillo, P. A., Merelo, J. J. (2016). Addressing high dimensional multi-objective optimization problems by coevolutionary islands with overlapping search spaces. In: Applications of evolutionary computation, pp. 107–117. Cham: Springer International Publishing Ag. https://doi.org/10.1007/978-3-319-31153-1_8 [Google Scholar] [CrossRef]

127. Chen, H., Zhu, X., Pedrycz, W., Yin, S., Wu, G. et al. (2018). PEA: Parallel evolutionary algorithm by separating convergence and diversity for large-scale multi-objective optimization. 2018 IEEE 38th International Conference on Distributed Computing Systems (ICDCS), New York, IEEE. https://doi.org/10.1109/ICDCS.2018.00031 [Google Scholar] [CrossRef]

128. Chen, H., Cheng, R., Wen, J., Li, H., Weng, J. (2020). Solving large-scale many-objective optimization problems by covariance matrix adaptation evolution strategy with scalable small subpopulations. Information Sciences, 509, 457–469. https://doi.org/10.1016/j.ins.2018.10.007 [Google Scholar] [CrossRef]

129. Gu, Z. M., Wang, G. G. (2020). Improving NSGA-III algorithms with information feedback models for large-scale many-objective optimization. Future Generation Computer Systems, 107, 49–69. https://doi.org/10.1016/j.future.2020.01.048 [Google Scholar] [CrossRef]

130. Tan, K., Yang, Y., Goh, C. (2006). A distributed cooperative coevolutionary algorithm for multiobjective optimization. IEEE Transactions on Evolutionary Computation, 10(5), 527–549. https://doi.org/10.1109/TEVC.2005.860762 [Google Scholar] [CrossRef]

131. Zhang, Y. H., Gong, Y. J., Gu, T. L., Yuan, H. Q., Zhang, W. et al. (2019). DECAL: Decomposition-based coevolutionary algorithm for many-objective optimization. IEEE Transactions on Cybernetics, 49(1), 27–41. https://doi.org/10.1109/TCYB.2017.2762701 [Google Scholar] [PubMed] [CrossRef]

132. Zhang, Y., Zhou, M., Jiang, Z., Liu, J. (2015). A multi-agent genetic algorithm for big optimization problems. 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, IEEE. https://doi.org/10.1109/CEC.2015.7256959 [Google Scholar] [CrossRef]

133. Maltese, J., Ombuki-Berman, B. M., Engelbrecht, A. P. (2018). A scalability study of many-objective optimization algorithms. IEEE Transactions on Evolutionary Computation, 22(1), 79–96. https://doi.org/10.1109/TEVC.2016.2639360 [Google Scholar] [CrossRef]

134. Cheng, R., Jin, Y., Olhofer, M., Sendhoff, B. (2017). Test problems for large-scale multiobjective and many-objective optimization. IEEE Transactions on Cybernetics, 47(12), 4108–4121. https://doi.org/10.1109/TCYB.2016.2600577 [Google Scholar] [PubMed] [CrossRef]

135. Beume, N., Naujoks, B., Emmerich, M. (2007). SMS-EMOA: Multiobjective selection based on dominated hypervolume. European Journal of Operational Reaearch, 181(3), 1653–1669. https://doi.org/10.1016/j.ejor.2006.08.008 [Google Scholar] [CrossRef]

136. Ye, Q., Sun, Y., Zhang, J., Lv, J. (2021). A distributed framework for EA-based NAS. IEEE Transactions on Parallel and Distributed Systems, 32(7), 1753–1764. https://doi.org/10.1109/TPDS.2020.3046774 [Google Scholar] [CrossRef]

137. Cao, B., Zhao, J., Gu, Y., Ling, Y., Ma, X. (2020). Applying graph-based differential grouping for multiobjective large-scale optimization. Swarm and Evolutionary Computation, 53, 100626. https://doi.org/10.1016/j.swevo.2019.100626 [Google Scholar] [CrossRef]

138. Cao, B., Zhao, J., Yang, P., Lv, Z., Liu, X. et al. (2018). 3-D multiobjective deployment of an industrial wireless sensor network for maritime applications utilizing a distributed parallel algorithm. IEEE Transactions on Industrial Informatics, 14(12), 5487–5495. https://doi.org/10.1109/TII.2018.2803758 [Google Scholar] [CrossRef]

139. Ma, X., Li, X., Zhang, Q., Tang, K., Liang, Z. et al. (2019). A survey on cooperative co-evolutionary algorithms. IEEE Transactions on Evolutionary Computation, 23(3), 421–441. https://doi.org/10.1109/TEVC.2018.2868770 [Google Scholar] [CrossRef]

140. Li, L., Talwalkar, A. (2020). Random search and reproducibility for neural architecture search. 35th Uncertainty in Artificial Intelligence Conference (UAI 2019), vol. 115. San Diego, AUAI. https://proceedings.mlr.press/v115/li20c.html [Google Scholar]

141. Greff, K., Srivastava, R. K., Koutník, J., Steunebrink, B. R., Schmidhuber, J. (2016). LSTM: A search space odyssey. IEEE Transactions on Neural Networks & Learning Systems, 28(10), 2222–2232. https://doi.org/10.1109/TNNLS.2016.2582924 [Google Scholar] [PubMed] [CrossRef]

142. Ergen, T., Kozat, S. S. (2018). Online training of LSTM networks in distributed systems for variable length data sequences. IEEE Transactions on Neural Networks and Learning Systems, 29(10), 5159–5165. https://doi.org/10.1109/TNNLS.2017.2770179 [Google Scholar] [PubMed] [CrossRef]

143. Han, M., Zhong, K., Qiu, T., Han, B. (2019). Interval type-2 fuzzy neural networks for chaotic time series prediction: A concise overview. IEEE Transactions on Cybernetics, 49(7), 2720–2731. https://doi.org/10.1109/TCYB.2018.2834356 [Google Scholar] [PubMed] [CrossRef]

144. Rumelhart, D. E., Hinton, G. E., Williams, R. J. (1986). Learning representations by back-propagating errors. Nature, 323, 533–536. https://doi.org/10.1038/323533a0 [Google Scholar] [CrossRef]

145. Louati, H., Louati, A., Bechikh, S., Ben Said, L. (2022). Design and compression study for convolutional neural networks based on evolutionary optimization for thoracic X-Ray image classification. In: Computational collective intelligence, vol. 13501. Cham, Springer International Publishing Ag. https://doi.org/10.1007/978-3-031-16014-1_23 [Google Scholar] [CrossRef]

146. Rawat, W., Wang, Z. (2017). Deep convolutional neural networks for image classification: A comprehensive review. Neural Computation, 29(9), 2352–2449. https://doi.org/10.1162/neco_a_00990 [Google Scholar] [PubMed] [CrossRef]

147. Oyelade, O. N., Ezugwu, A. E. (2021). A bioinspired neural architecture search based convolutional neural network for breast cancer detection using histopathology images. Scientific Reports, 11(1), 19940. https://doi.org/10.1038/s41598-021-98978-7 [Google Scholar] [PubMed] [CrossRef]

148. Anupama, C. S. S., Natrayan, L., Lydia, E. L., Sait, A. R. W., Escorcia-Gutierrez, J. et al. (2022). Deep learning with backtracking search optimization based skin lesion diagnosis model. Computers, Materials & Continua, 70(1), 1297–1313. https://doi.org/10.32604/cmc.2022.018396 [Google Scholar] [CrossRef]

149. Calisto, M. B., Lai-Yuen, S. K. (2021). EMONAS-Net: Efficient multiobjective neural architecture search using surrogate-assisted evolutionary algorithm for 3D medical image segmentation. Artificial Intelligence in Medicine, 119, 102154. https://doi.org/10.1016/j.artmed.2021.102154 [Google Scholar] [PubMed] [CrossRef]

150. Gómez-Flores, W., Hernández-López, J. (2020). Automatic adjustment of the pulse-coupled neural network hyperparameters based on differential evolution and cluster validity index for image segmentation. Applied Soft Computing, 97, 105547. https://doi.org/10.1016/j.asoc.2019.105547 [Google Scholar] [CrossRef]

151. Alabed, A., Kambhampati, C., Gordon, R. (2020). Genetic algorithms as a feature selection tool in heart failure disease. In: Intelligent computing, pp. 531–543. Cham: Springer International Publishing. https://doi.org/10.1007/978-3-030-52246-9_38 [Google Scholar] [CrossRef]

152. Yang, Z., Wang, Y., Chen, X., Shi, B., Xu, C. et al. (2020). CARS: Continuous evolution for efficient neural architecture search. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New York, IEEE. https://doi.org/10.1109/CVPR42600.2020.00190 [Google Scholar] [CrossRef]

153. Da Silva, C. A., Miranda, P. B., Cordeiro, F. R. (2021). A new grammar for creating convolutional neural networks applied to medical image classification. 2021 34th SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI), Gramado, Rio Grande do Sul, Brazil, IEEE. https://doi.org/10.1109/SIBGRAPI54419.2021.00022 [Google Scholar] [CrossRef]

154. Wen, Y. W., Peng, S. H., Ting, C. K. (2021). Two-stage evolutionary neural architecture search for transfer learning. IEEE Transactions on Evolutionary Computation, 25(5), 928–940. https://doi.org/10.1109/TEVC.2021.3097937 [Google Scholar] [CrossRef]

155. He, X., Ying, G., Zhang, J., Chu, X. (2022). Evolutionary multi-objective architecture search framework: Application to COVID-19 3D CT classification. In: Medical image computing and computer assisted intervention, vol. 13431. Cham, Springer International Publishing Ag. https://doi.org/10.1007/978-3-031-16431-6_53 [Google Scholar] [CrossRef]

156. Miahi, E., Mirroshandel, S. A., Nasr, A. (2022). Genetic neural architecture search for automatic assessment of human sperm images. Expert Systems with Applications, 188, 115937. https://doi.org/10.1016/j.eswa.2021.115937 [Google Scholar] [CrossRef]

157. Samir, A. A., Rashwan, A. R., Sallam, K. M., Chakrabortty, R. K., Ryan, M. J. et al. (2021). Evolutionary algorithm-based convolutional neural network for predicting heart diseases. Computers & Industrial Engineering, 161, 107651. https://doi.org/10.1016/j.cie.2021.107651 [Google Scholar] [CrossRef]

158. Dong, J., Hou, B., Feng, L., Tang, H., Tan, K. C. et al. (2022). A cell-based fast memetic algorithm for automated convolutional neural architecture design. IEEE Transactions on Neural Networks and Learning Systems, 1–14. https://doi.org/10.1109/TNNLS.2022.3155230 [Google Scholar] [PubMed] [CrossRef]

159. Deb, K., Jain, H. (2014). An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Transactions on Evolutionary Computation, 18(4), 577–601. https://doi.org/10.1109/TEVC.2013.2281535 [Google Scholar] [CrossRef]

160. Louati, H., Bechikh, S., Louati, A., Aldaej, A., Ben Said, L. (2022). Evolutionary optimization for CNN compression using thoracic X-Ray image classification. In: Fujita, H., Fournier-Viger, P., Ali, M., Wang, Y. (Eds.Advances and trends in artificial intelligence: theory and practices in artificial intelligence, vol. 13343. Cham: Springer International Publishing Ag. https://doi.org/10.1007/978-3-031-08530-7_10 [Google Scholar] [CrossRef]

161. Xu, Z., So, D. R., Dai, A. M. (2021). MUFASA: Multimodal fusion architecture search for electronic health records. Thirty-Fifth AAAI Conference on Artificial Intelligence, Thirty-Third Conference on Innovative Applications of Artificial Intelligence and the Eleventh Symposium on Educational Advances in Artificial Intelligence, vol. 35. Palo Alto, Association for the Advancement Artificial Intelligence. https://doi.org/10.48550/arXiv.2102.02340 [Google Scholar] [CrossRef]

162. Abd Elaziz, M., Dahou, A., Mabrouk, A., Ibrahim, R. A., Aseeri, A. O. (2023). Medical image classifications for 6G IoT-enabled smart health systems. Diagnostics, 13(5), 834. https://doi.org/10.3390/diagnostics13050834 [Google Scholar] [PubMed] [CrossRef]

163. Lee, M., Lee, H., Kim, Y., Kim, J., Cho, M. et al. (2018). Mobile app-based health promotion programs: A systematic review of the literature. International Journal of Environmental Research and Public Health, 15(12), 2838. https://doi.org/10.3390/ijerph15122838 [Google Scholar] [PubMed] [CrossRef]

164. Stisen, A., Blunck, H., Bhattacharya, S., Prentow, T. S., Kjaergaard, M. B. et al. (2015). Smart devices are different: Assessing and mitigating mobile sensing heterogeneities for activity recognition. SenSys’15: Proceedings of the 13th ACM Conference on Embedded Networked Sensor Systems, New York, Association for Computing Machinery. https://doi.org/10.1145/2809695.2809718 [Google Scholar] [CrossRef]

165. Haleem, A., Javaid, M., Pratap Singh, R., Suman, R. (2022). Medical 4.0 technologies for healthcare: Features, capabilities, and applications. Internet of Things and Cyber-Physical Systems, 2, 12–30. https://doi.org/10.1016/j.iotcps.2022.04.001 [Google Scholar] [CrossRef]

166. Odema, M., Rashid, N., Faruque, M. A. A. (2021). EExNAS: Early-exit neural architecture search solutions for low-power wearable devices. 2021 IEEE/ACM International Symposium on Low Power Electronics and Design (ISLPED). Boston, MA, USA, IEEE. https://doi.org/10.1109/ISLPED52811.2021.9502503 [Google Scholar] [CrossRef]

167. Hernandez, F., Suarez, L. F., Villamizar, J., Altuve, M. (2019). Human activity recognition on smartphones using a bidirectional lstm network. 2019 XXII Symposium on Image, Signal Processing and Artificial Vision (STSIVA), New York, IEEE. https://doi.org/10.1109/STSIVA.2019.8730249 [Google Scholar] [CrossRef]

168. Song, S. B., Nam, J. W., Kim, J. H. (2021). NAS-PPG: PPG-based heart rate estimation using neural architecture search. IEEE Sensors Journal, 21(13), 14941–14949. https://doi.org/10.1109/JSEN.2021.3073047 [Google Scholar] [CrossRef]

169. Shin, H. C., Roth, H. R., Gao, M., Lu, L., Xu, Z. et al. (2016). Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning. IEEE Transactions on Medical Imaging, 35(5), 1285–1298. https://doi.org/10.1109/TMI.2016.2528162 [Google Scholar] [PubMed] [CrossRef]

170. Zhou, T., Ye, X., Lu, H., Zheng, X., Qiu, S. et al. (2022). Dense convolutional network and its application in medical image analysis. Biomed Research International, 2022, 2384830. https://doi.org/10.1155/2022/2384830 [Google Scholar] [PubMed] [CrossRef]

171. Barredo Arrieta, A., Diaz-Rodriguez, N., Del Ser, J., Bennetot, A., Tabik, S. et al. (2020). Explainable artificial intelligence (XAIConcepts, taxonomies, opportunities and challenges toward responsible AI. Information Fusion, 58, 82–115. https://doi.org/10.1016/j.inffus.2019.12.012 [Google Scholar] [CrossRef]

172. Zhang, Q., Wu, Y. N., Zhu, S. C. (2018). Interpretable convolutional neural networks. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New York, IEEE. https://doi.org/10.1109/CVPR.2018.00920 [Google Scholar] [CrossRef]

173. Zhang, Q. S., Zhu, S. C. (2018). Visual interpretability for deep learning: A survey. Frontiers of Information Technology & Electronic Engineering, 19(1), 27–39. https://doi.org/10.1631/FITEE.1700808 [Google Scholar] [CrossRef]

174. Saeed, T., Loo, C. K., Kassim, M. S. S. (2022). Ensembles of deep learning framework for stomach abnormalities classification. Computers, Materials & Continua, 70(3), 4357–4372. https://doi.org/10.32604/cmc.2022.019076 [Google Scholar] [CrossRef]

175. Zeiser, F. A., da Costa, C. A., Ramos, G. D. O., Bohn, H. C., Santos, I. et al. (2021). DeepBatch: A hybrid deep learning model for interpretable diagnosis of breast cancer in whole-slide images. Expert Systems with Applications, 185, 115586. https://doi.org/10.1016/j.eswa.2021.115586 [Google Scholar] [CrossRef]

176. Boffa, S. (2023). Extracting concepts from fuzzy relational context families. IEEE Transactions on Fuzzy Systems, 31(4), 1202–1213. https://doi.org/10.1109/TFUZZ.2022.3197826 [Google Scholar] [CrossRef]

177. Ji, W., Pang, Y., Jia, X., Wang, Z., Hou, F. et al. (2021). Fuzzy rough sets and fuzzy rough neural networks for feature selection: A review. Wiley Interdisciplinary Reviews-Data Mining and Knowledge Discovery, 11(3), e1402. https://doi.org/10.1002/widm.1402 [Google Scholar] [CrossRef]

178. Hussain, K., Salleh, M. N. M., Cheng, S., Shi, Y. (2019). Metaheuristic research: A comprehensive survey. Artificial Intelligence Review, 52(4), 2191–2233. https://doi.org/10.1007/s10462-017-9605-z [Google Scholar] [CrossRef]

179. Del Ser, J., Osaba, E., Molina, D., Yang, X. S., Salcedo-Sanz, S. et al. (2019). Bio-inspired computation: Where we stand and what’s next. Swarm and Evolutionary Computation, 48, 220–250. https://doi.org/10.1016/j.swevo.2019.04.008 [Google Scholar] [CrossRef]

180. Affonso, C., Sassi, R. J., Barreiros, R. M. (2015). Biological image classification using rough-fuzzy artificial neural network. Expert Systems with Applications, 42(24), 9482–9488. https://doi.org/10.1016/j.eswa.2015.07.075 [Google Scholar] [CrossRef]

181. Yeganejou, M., Dick, S., Miller, J. (2020). Interpretable deep convolutional fuzzy classifier. IEEE Transactions on Fuzzy Systems, 28(7), 1407–1419. https://doi.org/10.1109/TFUZZ.2019.2946520 [Google Scholar] [CrossRef]

182. Operiano, K. R. G., Iba, H., Pora, W. (2020). Neuroevolution architecture backbone for X-ray object detection. 2020 IEEE Symposium Series on Computational Intelligence (SSCI), pp. 2296–2303. Canberra, ACT, Australia. https://doi.org/10.1109/SSCI47803.2020.9308453 [Google Scholar] [CrossRef]

183. Li, H., Chen, D., Nailon, W. H., Davies, M. E., Laurenson, D. I. (2022). Dual convolutional neural networks for breast mass segmentation and diagnosis in mammography. IEEE Transactions on Medical Imaging, 41(1), 3–13. https://doi.org/10.1109/TMI.2021.3102622 [Google Scholar] [PubMed] [CrossRef]

184. Ahmadian, S., Jalali, S. M. J., Islam, S. M. S., Khosravi, A., Fazli, E. et al. (2021). A novel deep neuroevolution-based image classification method to diagnose coronavirus disease (COVID-19). Computers in Biology and Medicine, 139, 104994. https://doi.org/10.1016/j.compbiomed.2021.104994 [Google Scholar] [PubMed] [CrossRef]

185. Hassanzadeh, T., Essam, D., Sarker, R. (2021). Evolutionary deep attention convolutional neural networks for 2D and 3D medical image segmentation. Journal of Digital Imaging, 34(6), 1387–1404. https://doi.org/10.1007/s10278-021-00526-2 [Google Scholar] [PubMed] [CrossRef]

186. Draelos, R. L., Carin, L. (2022). Explainable multiple abnormality classification of chest CT volumes. Artificial Intelligence in Medicine, 132, 102372. https://doi.org/10.1016/j.artmed.2022.102372 [Google Scholar] [PubMed] [CrossRef]

187. Akter, S., Reza, F., Ahmed, M. (2022). Convergence of Blockchain, k-medoids and homomorphic encryption for privacy preserving biomedical data classification. Internet of Things and Cyber-Physical Systems, 2, 99–110. https://doi.org/10.1016/j.iotcps.2022.05.006 [Google Scholar] [CrossRef]

188. Wang, K., Xie, S., Rodrigues, J. (2022). Medical data security of wearable tele-rehabilitation under Internet of Things. Internet of Things and Cyber-Physical Systems, 2, 1–11. https://doi.org/10.1016/j.iotcps.2022.02.001 [Google Scholar] [CrossRef]

189. Zhang, J., Ning, Z., Xue, F. (2023). A two-stage federated optimization algorithm for privacy computing in internet of things. Future Generation Computer Systems, 145, 354–366. https://doi.org/10.1016/j.future.2023.03.042 [Google Scholar] [CrossRef]

190. Zhang, K., Song, X., Zhang, C., Yu, S. (2022). Challenges and future directions of secure federated learning: A survey. Frontiers of Computer Science, 16(5), 165817. https://doi.org/10.1007/s11704-021-0598-z [Google Scholar] [PubMed] [CrossRef]

191. Lu, Z., Goodman, E., Banzhaf, W., Boddeti, V. (2020). Evolutionary multi-objective bi-level optimization for efficient deep neural network architecture design (Ph.D. Thesis). Michigan State University, USA. https://doi.org/10.5555/AAI28025436 [Google Scholar] [CrossRef]

192. Sarkar, M., Yegnanarayana, B. (1998). Fuzzy-rough neural networks for vowel classification. SMC’98 Conference Proceedings. 1998 IEEE International Conference on Systems, Man, and Cybernetics (Cat. No. 98CH36218), vol. 5, pp. 4160–4165. San Diego, CA, USA, IEEE. https://doi.org/10.1109/ICSMC.1998.727497 [Google Scholar] [CrossRef]

193. Lingras, P. (2001). Fuzzy-rough and rough-fuzzy serial combinations in neurocomputing. Neurocomputing, 36(1), 29–44. https://doi.org/10.1016/S0925-2312(00)00334-9 [Google Scholar] [CrossRef]

194. Ozer, A. B. (2010). CIDE: Chaotically initialized differential evolution. Expert Systems with Applications, 37(6), 4632–4641. https://doi.org/10.1016/j.eswa.2009.12.045 [Google Scholar] [CrossRef]

195. Sayed, G. I., Darwish, A., Hassanien, A. E. (2018). A new chaotic whale optimization algorithm for features selection. Journal of Classification, 35(2), 300–344. https://doi.org/10.1007/s00357-018-9261-2 [Google Scholar] [CrossRef]

196. Chen, C. L. P., Liu, Z. (2018). Broad learning system: An effective and efficient incremental learning system without the need for deep architecture. IEEE Transactions on Neural Networks and Learning Systems, 29(1), 10–24. https://doi.org/10.1109/TNNLS.2017.2716952 [Google Scholar] [PubMed] [CrossRef]

197. Kairouz, P., McMahan, H. B., Avent, B., Bellet, A., Bennis, M. et al. (2021). Advances and open problems in federated learning. Foundations and Trends? Machine Learning, 14(1–2), 1–210. [Google Scholar]

198. Trivedi, A., Srinivasan, D., Sanyal, K., Ghosh, A. (2017). A survey of multiobjective evolutionary algorithms based on decomposition. IEEE Transactions on Evolutionary Computation, 21(3), 440–462. https://doi.org/10.1109/TEVC.2016.2608507 [Google Scholar] [CrossRef]