 Open Access
Open Access
ARTICLE
An Effective Meshless Approach for Inverse Cauchy Problems in 2D and 3D Electroelastic Piezoelectric Structures
1 School of Automation, Qingdao University, Qingdao, 266071, China
2 School of Mathematics and Statistics, Qingdao University, Qingdao, 266071, China
3 Weifang University of Science and Technology, Weifang, 262700, China
* Corresponding Authors: Wenzhen Qu. Email: ; Guanghua Wu. Email:
(This article belongs to the Special Issue: New Trends on Meshless Method and Numerical Analysis)
Computer Modeling in Engineering & Sciences 2024, 138(3), 2955-2972. https://doi.org/10.32604/cmes.2023.031474
Received 20 June 2023; Accepted 11 August 2023; Issue published 15 December 2023
Abstract
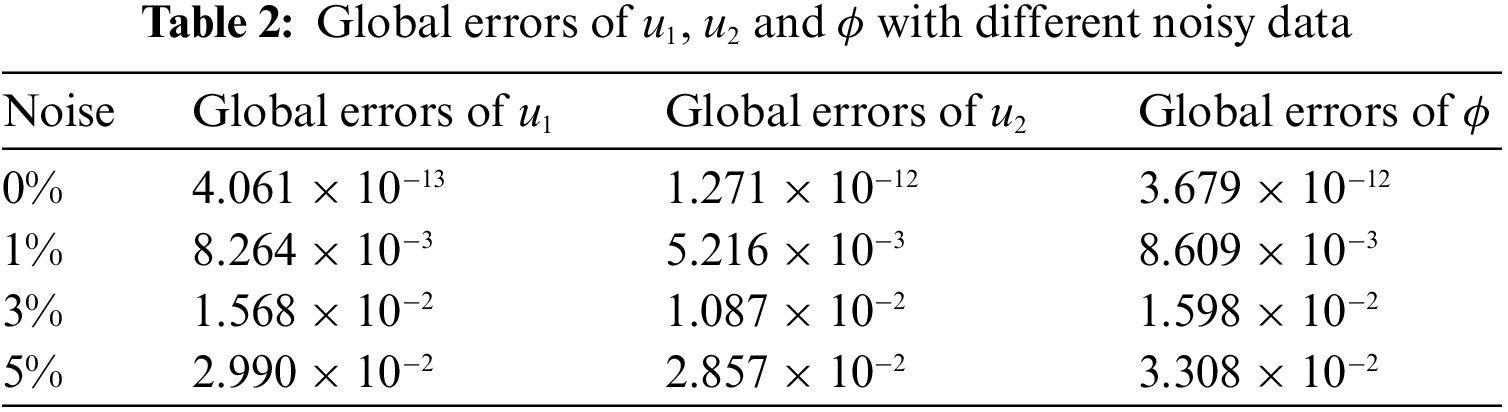
In the past decade, notable progress has been achieved in the development of the generalized finite difference method (GFDM). The underlying principle of GFDM involves dividing the domain into multiple sub-domains. Within each sub-domain, explicit formulas for the necessary partial derivatives of the partial differential equations (PDEs) can be obtained through the application of Taylor series expansion and moving-least square approximation methods. Consequently, the method generates a sparse coefficient matrix, exhibiting a banded structure, making it highly advantageous for large-scale engineering computations. In this study, we present the application of the GFDM to numerically solve inverse Cauchy problems in two- and three-dimensional piezoelectric structures. Through our preliminary numerical experiments, we demonstrate that the proposed GFDM approach shows great promise for accurately simulating coupled electroelastic equations in inverse problems, even with 3% errors added to the input data.Keywords
In modern engineering applications, advanced structures incorporating piezoelectric materials have gained widespread utilization and design. The interaction between electrical effects and mechanical deformation is one of the most appealing characteristics of piezoelectric materials. However, traditional mathematical analysis using various analytical and semi-analytical methodologies falls in addressing practical piezoelectric problems [1,2], particularly those involving complex geometry and loading conditions. Hence, the demand for accurate and efficient numerical models becomes imperative [3–7].
In the field of computational mechanics, numerical tools such as the finite difference (FDM) and finite element (FEM) methods have been widely used as the primary techniques for solving various PDEs. However, the traditional FEM and FDM models possess inherent limitations, particularly when it comes to re-meshing processes or dealing with highly distorted elements [8–12]. In the past two decades, substantial efforts have been made to develop innovative computational techniques that overcome or significantly mitigate these issues associated with the classical FEM and FDM. As a result, a multitude of meshless methods have been developed in response to this need [13–17].
During the past few years, the GFDM has emerged as an efficient meshless collocation technique for solving diverse boundary value problems. Its high accuracy and excellent computational efficiency have garnered significant attention from researchers in engineering and mathematical communities. The method’s core idea was initially proposed by Liszka et al. in the early 1980s [18] and has since been extended and refined by numerous others [19–23]. The GFDM involves dividing the entire domain into multiple sub-domains. Within each sub-domain, explicit formulas for the necessary partial derivatives of the PDEs can be obtained through the application of Taylor series expansion and moving-least square approximation methods. The concept of “local star” or “local subdomain” employed in GFDM results in a sparse coefficient matrix, making the method particularly suitable for large-scale computations.
This study represents the pioneering effort to apply GFDM to address the numerical solution of inverse electroelastic analysis concerning both 2D and 3D piezoelectric structures. Solving such problems poses a formidable challenge within the computational mechanics community. The research obstacles stem from the intricate interplay of electroelastic behaviors in piezoelectric materials, as well as the ill-conditioning problem inherent in inverse problems [24–26]. This study will present the numerical procedures of the GFDM, focusing on its application for inverse Cauchy piezoelectric problems. It will demonstrate that the proposed GFDM can achieve accurate and stable solutions for such problems.
2 Inverse Cauchy Problems in 2D and 3D Electroelastic Piezoelectric Structures
2.1 Two-Dimensional (2D) Piezoelectric Problems
Consider a 2D domain bounded by a given boundary
where
where
with
with the corresponding boundary conditions:
where
2.2 Three-Dimensional (3D) Piezoelectric Problems
Similarly, for 3D problems, the constitutive equations are as follows [29]:
where the relation
In inverse Cauchy problems, only a specific portion of the boundary, referred to as
Without loss of generality, we focus on describing the numerical implementation of the GFDM for general 3D problems in this context. However, for 2D problems, the numerical procedures can be found in [28,30]. In the GFDM approach, the first step involves scattering a cloud of points throughout the entire computational domain. Subsequently, the method establishes a series of sub-domains and applies the following procedure to match the solution within each sub-domain.
Let
where
where
where
and
Minimizing error function
where
and
To ensure the solvability of Eq. (16), a minimum of 9 points should ideally be selected within each local sub-domain. However, to mitigate potential issues arising from ill-conditioning, it is common practice to choose slightly more points within each sub-domain. By employing the moving least-squares method, the solution to Eq. (16) can be sought. References [32,33] provided valuable guidance for selecting suitable collocation points. According to Eq. (16), the vector
Let
For inverse Cauchy problems, the interpolation matrix tends to suffer from severe ill-conditioning. Traditionally, popular regularization techniques like Tikhonov or truncated singular value decomposition methods have been employed to achieve accurate and stable solutions for such problems. In line with the approach outlined in [34], we utilize the moving least-squares technique, which can be considered as a form of regularization, to alleviate the ill-posed nature of the inverse Cauchy problems. Further details can be found in [34,35] for interested readers.
Here are three examples provided to demonstrate the practicality of the current method. The first two examples are derived from a previous study reported by Cao et al. [36], while the third example is based on the work of Xia et al. [29]. The stability of the method is thoroughly examined by introducing the following noise into the input data:
where b represents the exact data, rand denotes a randomly generated number using the MATLAB function ‘2 * rand − 1’, and
where
4.1 Test Problem 1: Simple Tension of a Piezoelectric Prism
Firstly, a PZT-4 piezoelectric prism subjected to a simple tension (
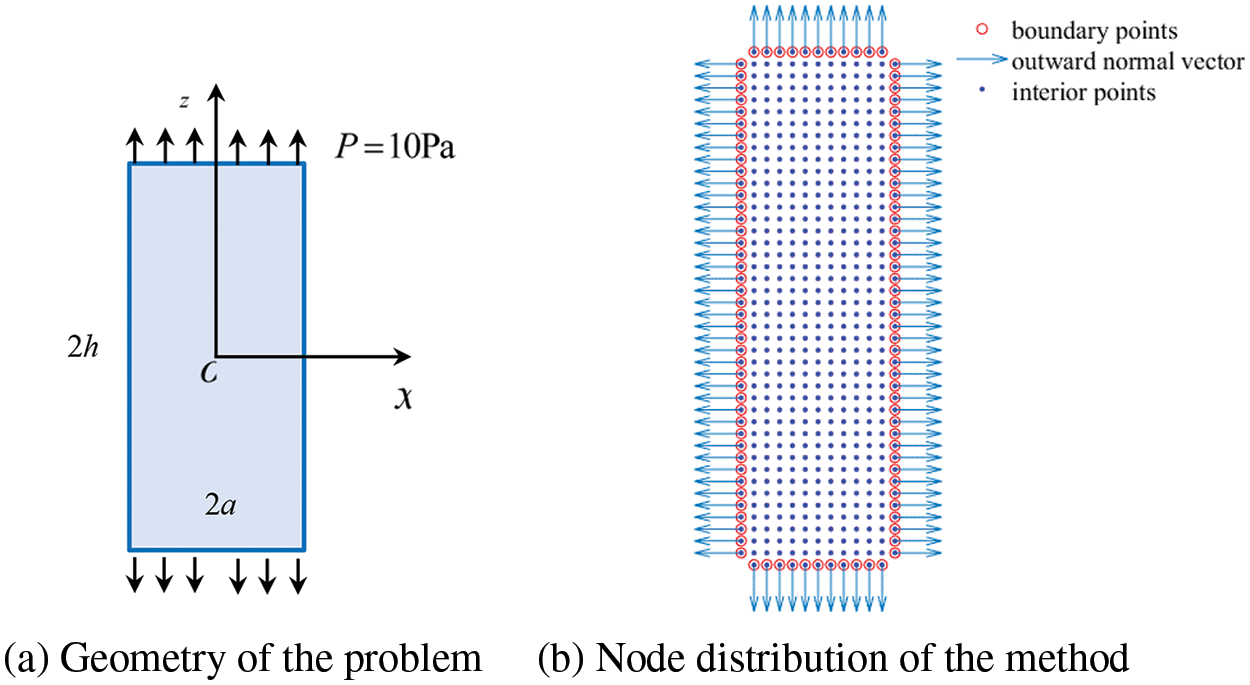
Figure 1: (a) Geometry of the problem and (b) the node distribution of method
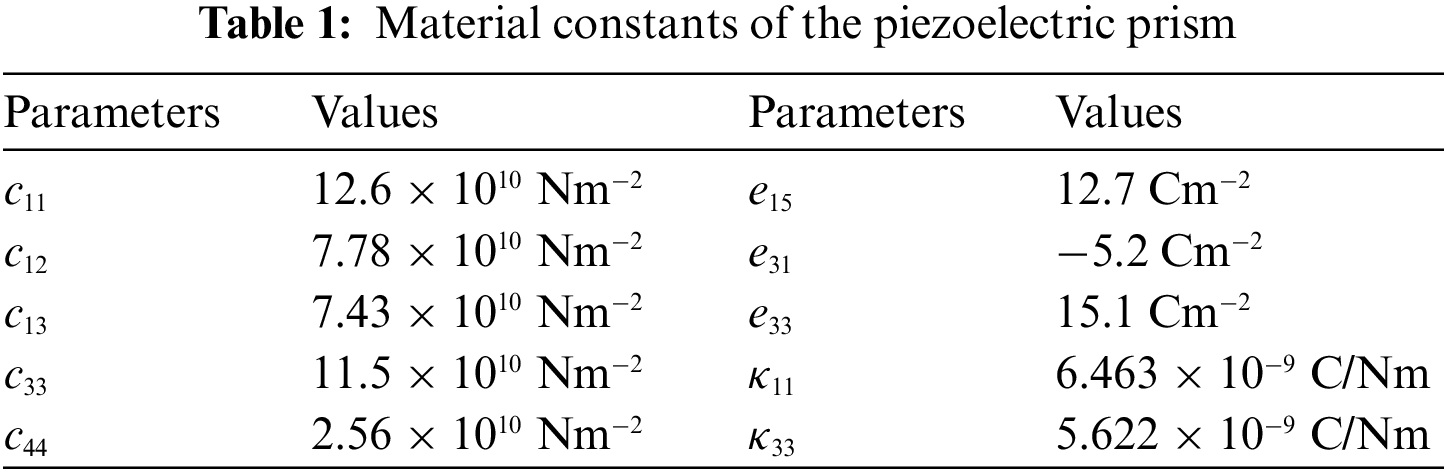
Figs. 2a–2c display contour plots showcasing the errors of the electrical potential
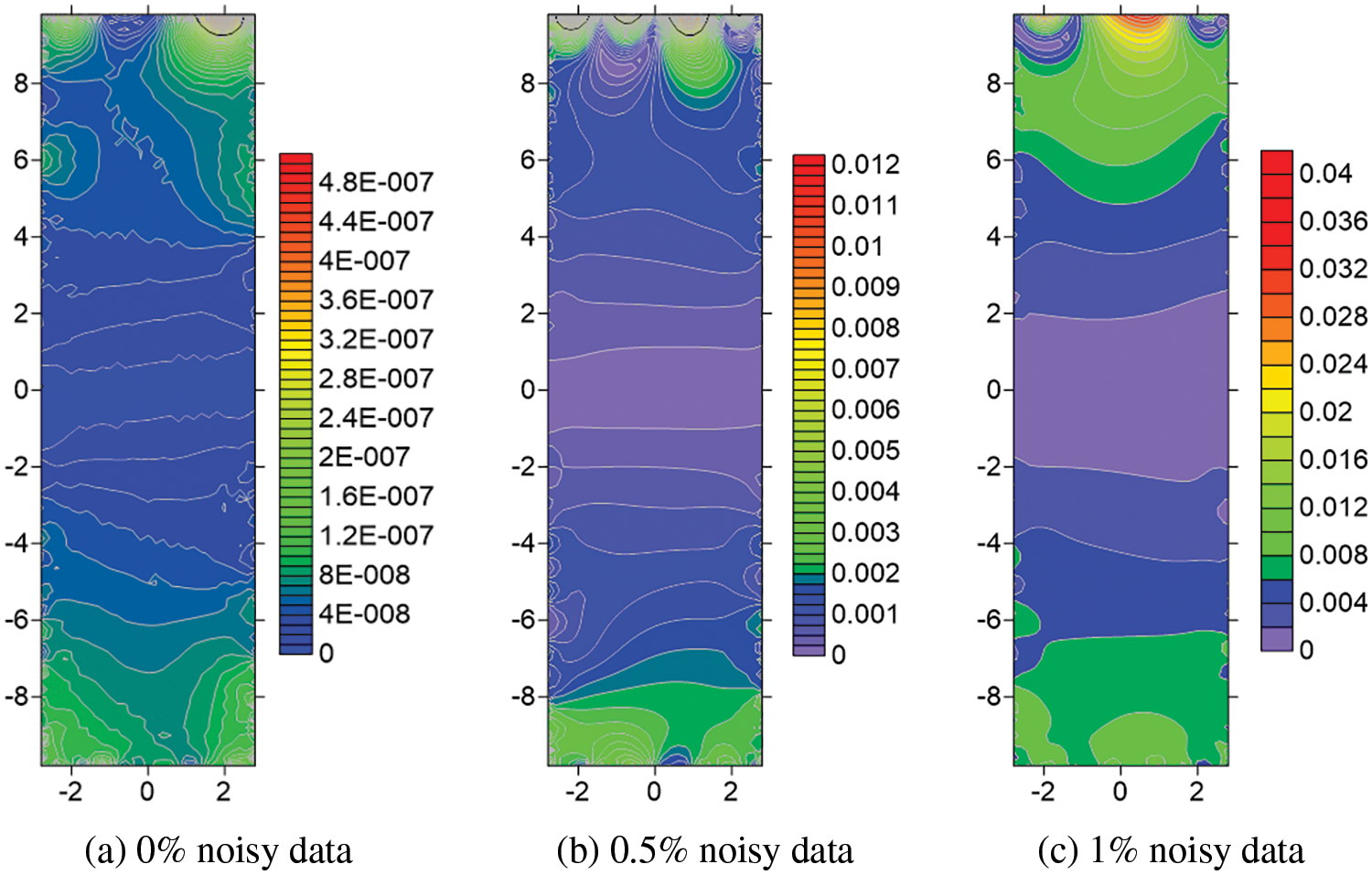
Figure 2: Contour plots of the relative errors of the calculated
Figure 3: Contour plots of the errors of the calculated
We proceed to examine the sensitivity of the method in relation to m, which denotes the number of collocation points within each local sub-domain. Fig. 4 illustrates the global errors of
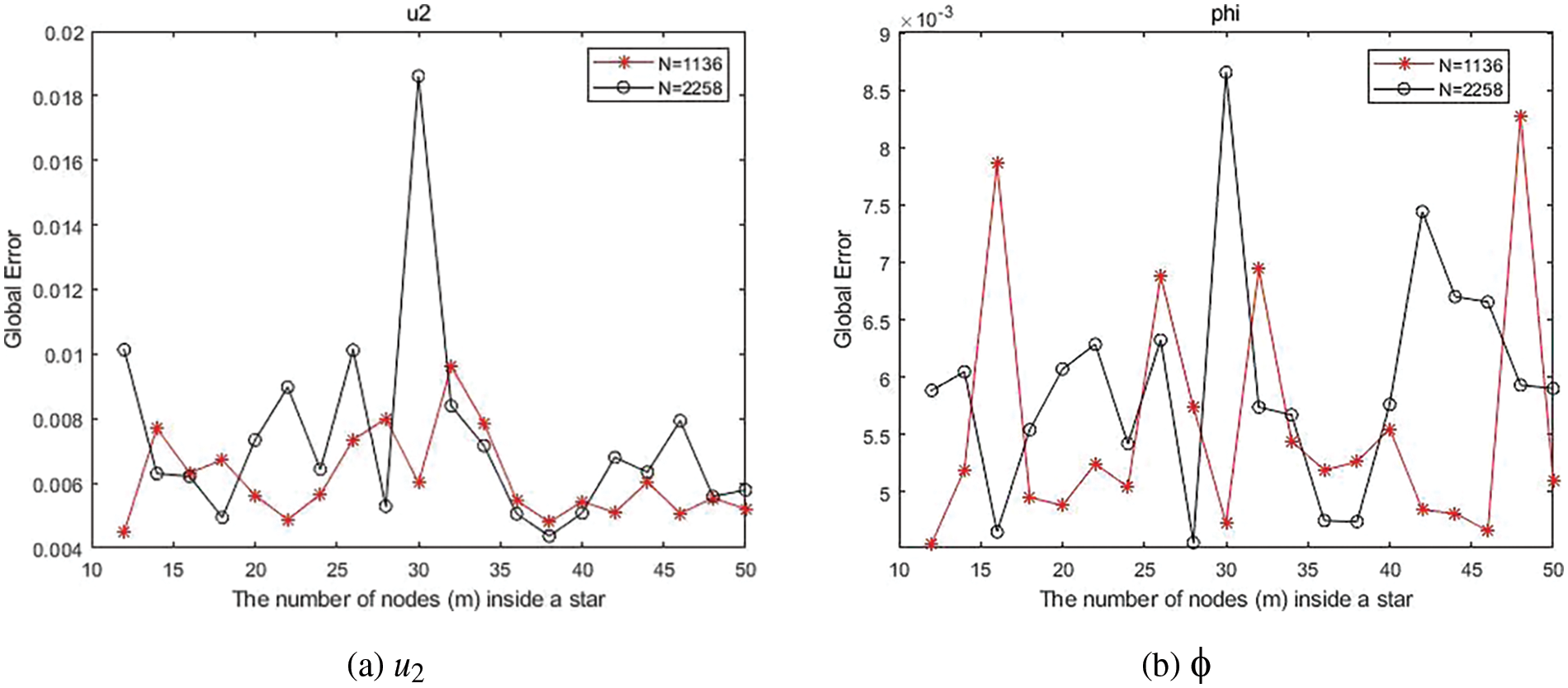
Figure 4: Errors of (a)
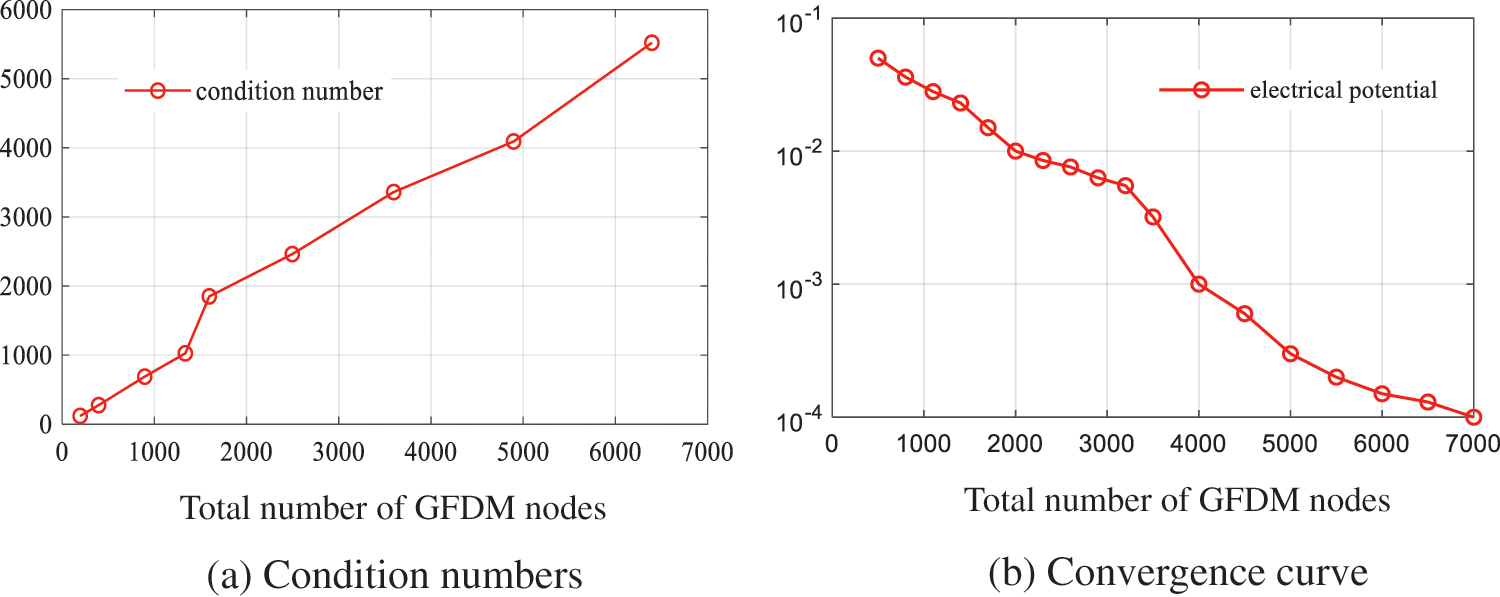
Figure 5: (a) Condition numbers of the current GFDM method and (b) the convergence curve of the electrical potential with 1% noisy data
4.2 Test Problem 2: Bending of a Piezoelectric Panel
As illustrated in Fig. 6, we examine again a piezoelectric strip composed of PZT-4 material (
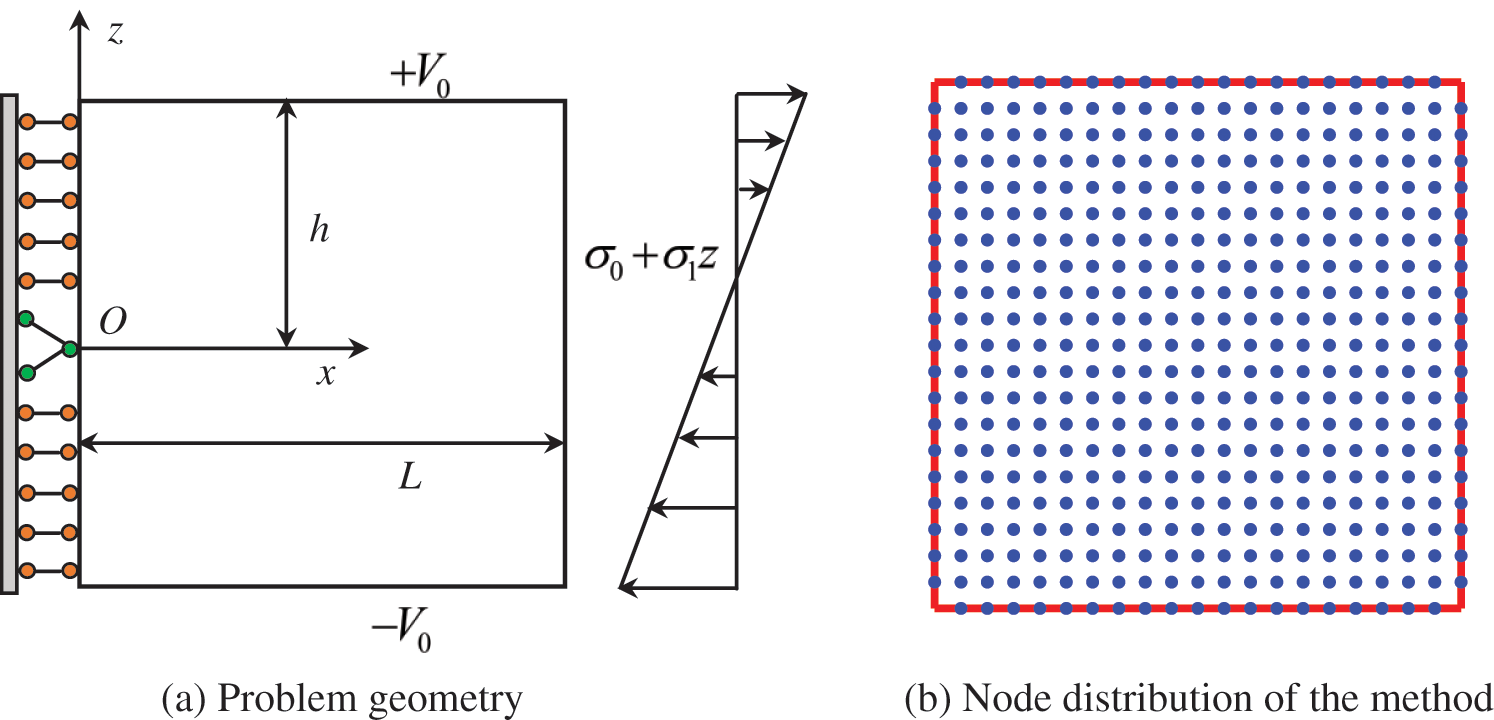
Figure 6: (a) Problem geometry and (b) node distribution of the method
Figs. 7a–7d depict the deformation of the structure with 0%, 1%, 3%, and 5% noisy data, respectively. The background red line represents the original shape. The mechanical deformation obtained throughout the entire domain aligns closely with the results reported in [28,37]. This demonstrates that the present GFDM offers an accurate and stable analysis for this example. Figs. 8a–8d display contour plots illustrating the retrieved displacement (
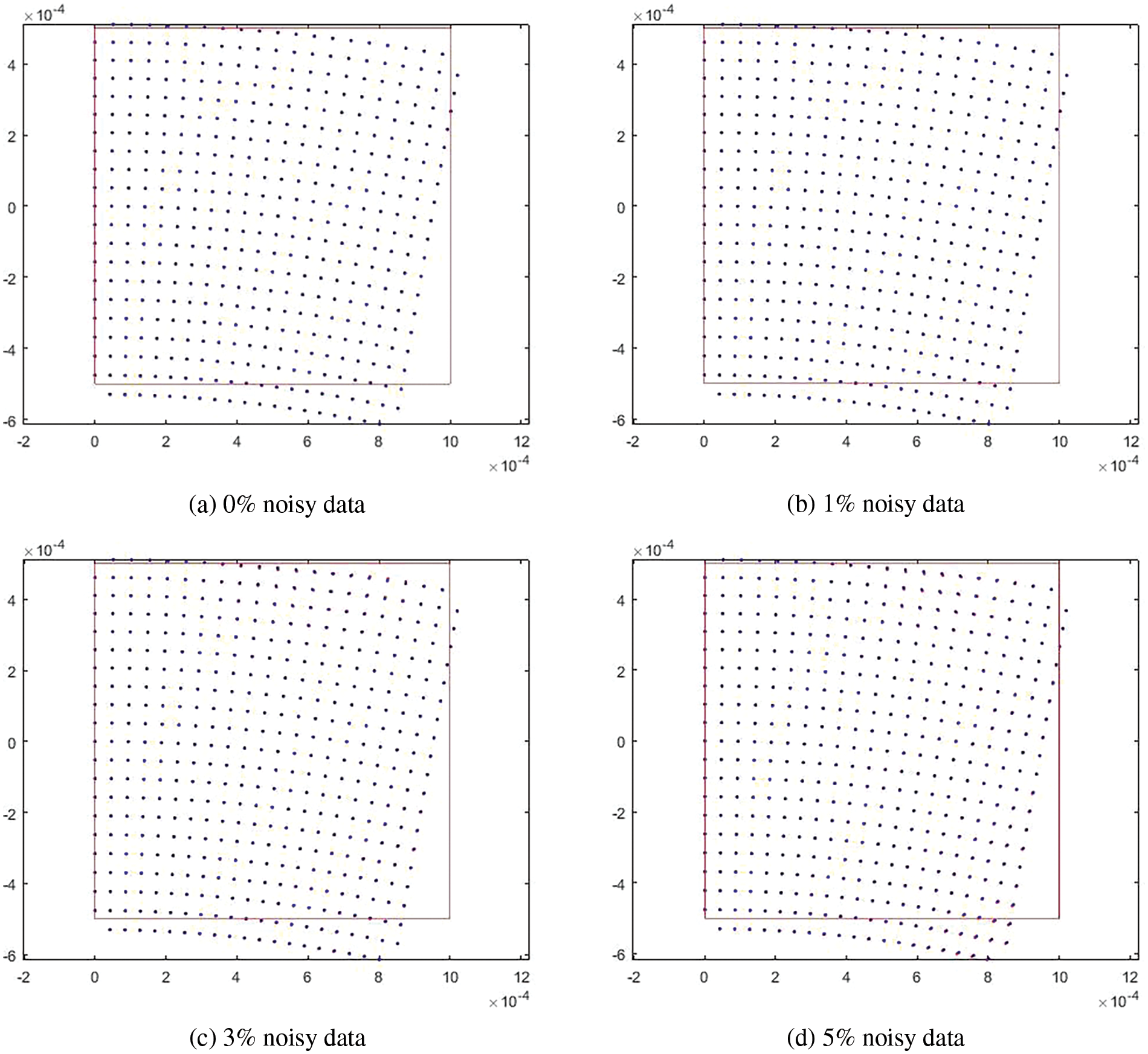
Figure 7: Mechanical deformation of the structure, with (a) 0% noisy data, (b) 1% noisy data, (c) 3% noisy data, and (d) 5% noisy data
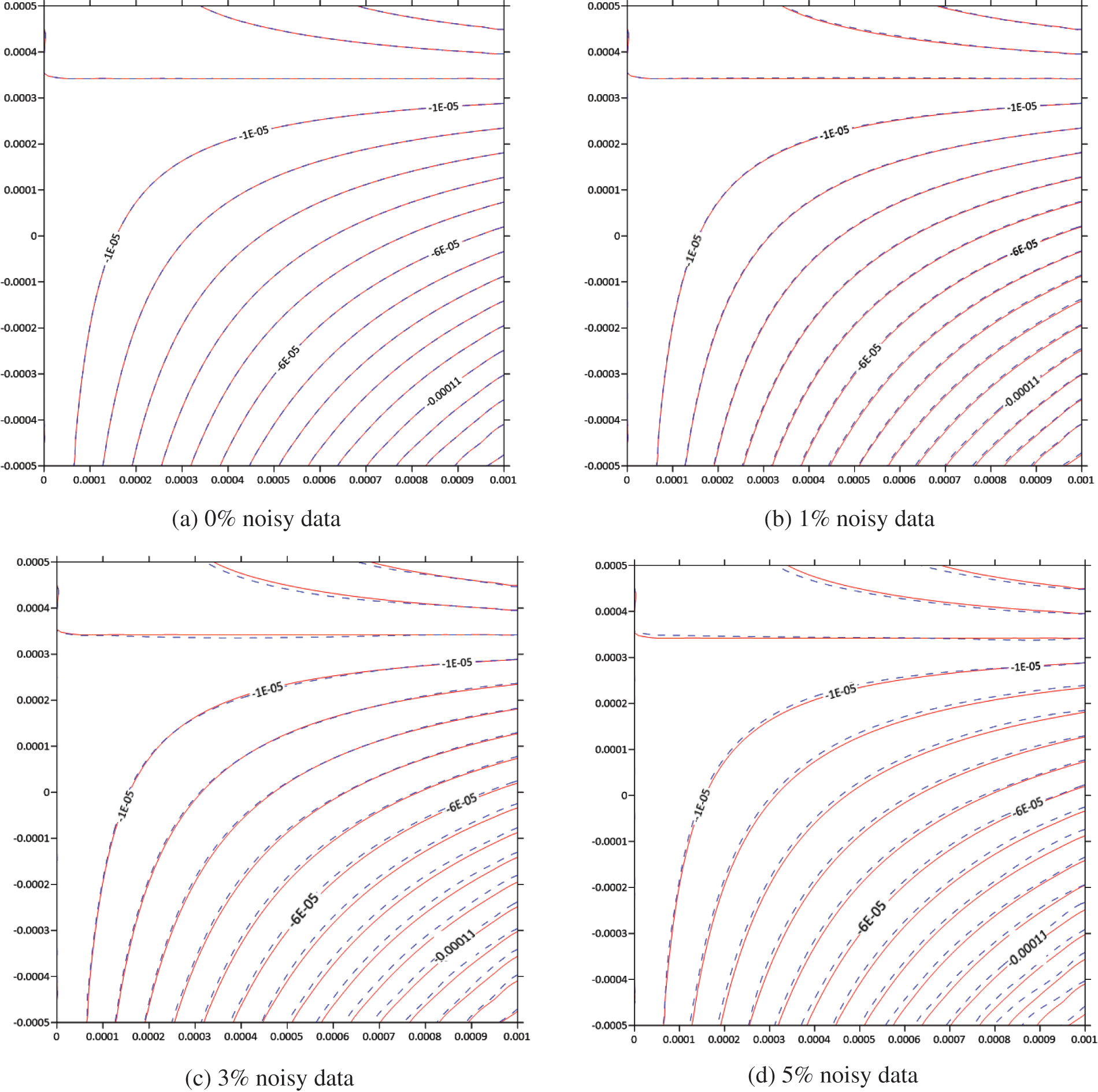
Figure 8: Contour plots of the calculated displacement
4.3 Test Problem 3: A 3D Piezoelectric Column under Uniaxial Tension
In Fig. 9, we examine the inverse electroelastic problem within a 3D cubic domain (
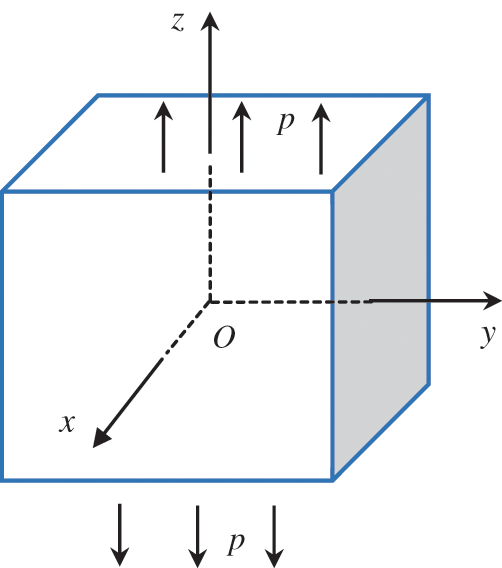
Figure 9: Geometry of the problem
Figs. 10a–10d present contour plots illustrating the retrieved displacements (
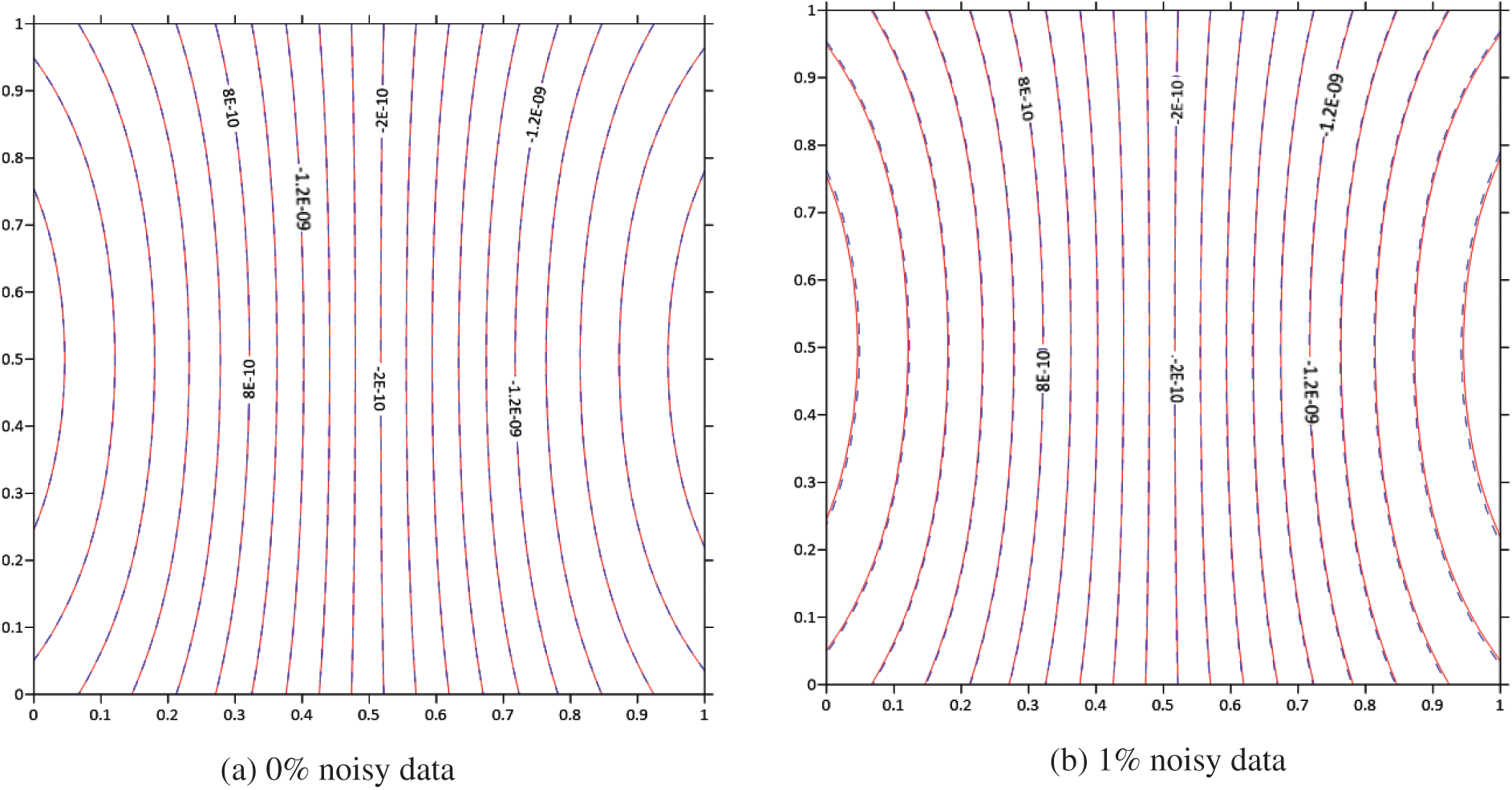
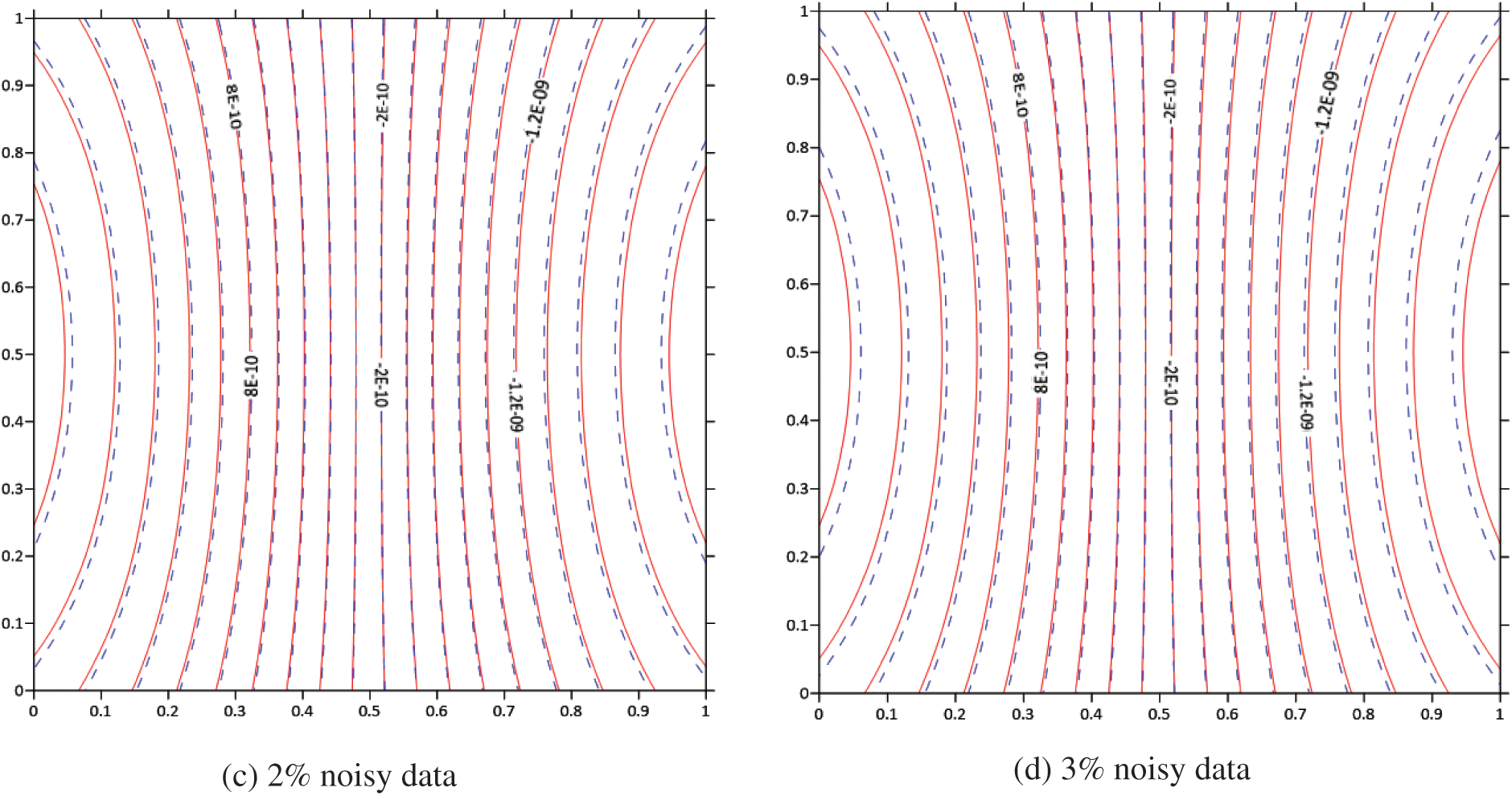
Figure 10: Contour plots of the calculated displacement
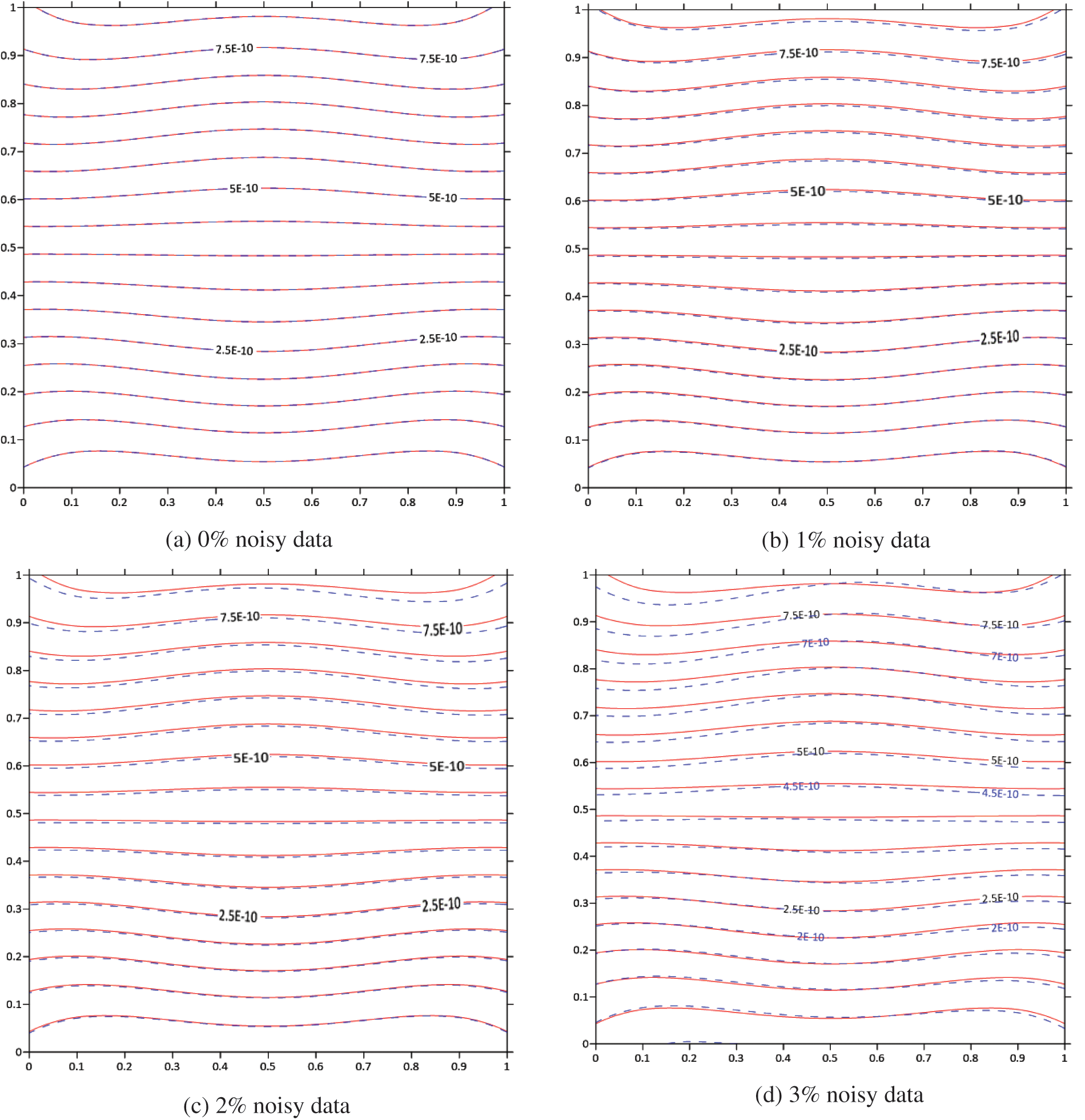
Figure 11: Contour plots of the calculated displacement
4.4 Test Problem 4: A 3D Solid with Irregular Shape
Finally, we consider a 3D solid with an irregular shape, as shown in Fig. 12. The principal dimension of the solid is 5 m in length, 1.5 m in width, and 5 m in height. A total number of 4650 irregularly distributed GFDM nodes are discretized across the entire domain, where the nodes are generated by using the popular CAE software Hypermesh. The over-specified boundary is taken to be the left-half surface of the boundary, i.e.,
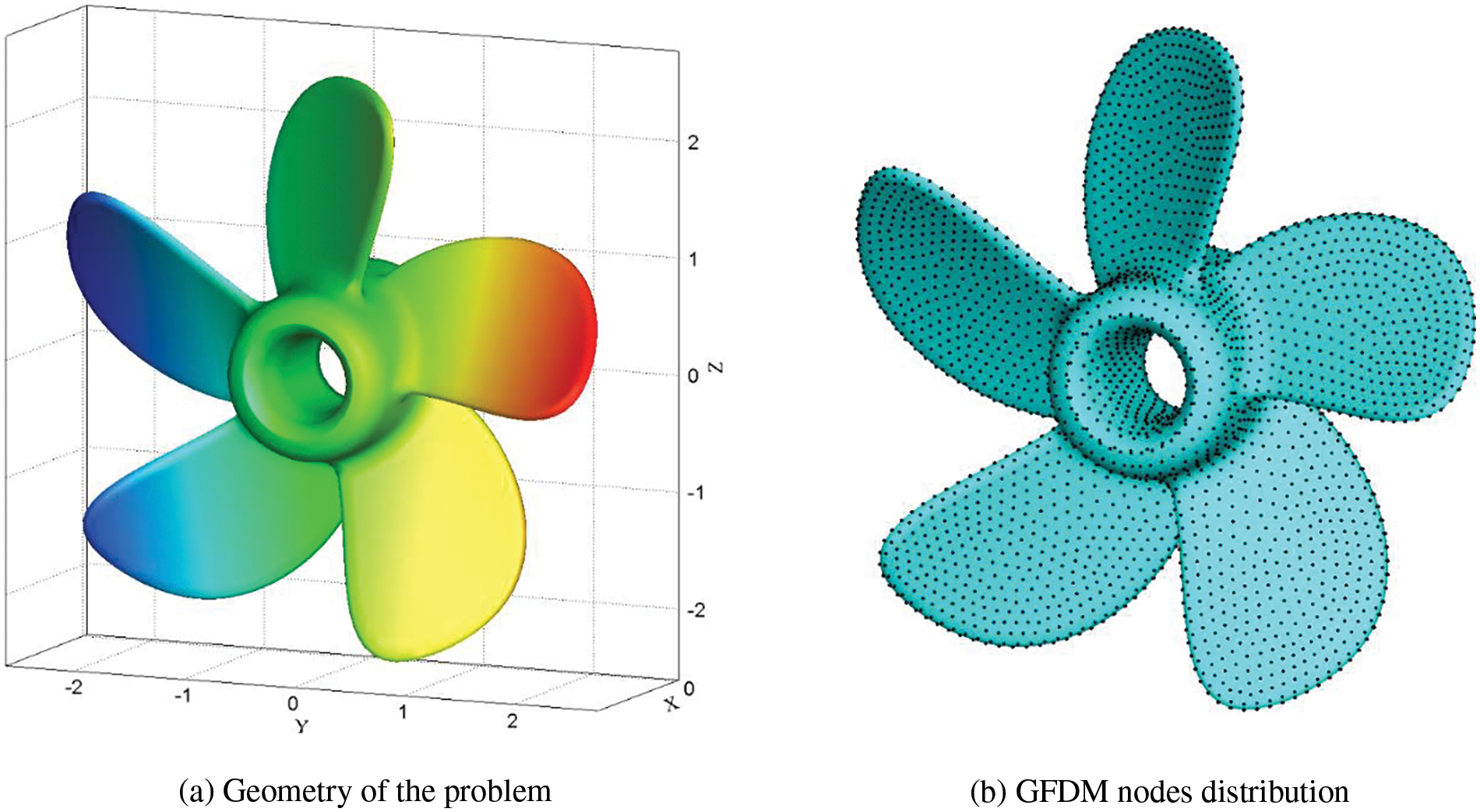
Figure 12: (a) Geometry of the problem and (b) the configuration of the GFDM nodes distribution

This study presents the first application of the GFDM for inverse electroelastic analysis in both 2D and 3D piezoelectric structures. The GFDM divides the domain into overlapping small domains and utilizes the Taylor approximation and moving least-squares tool within each local sub-domain to obtain explicit formulas for partial derivatives of PDEs. In inverse Cauchy problems, numerical procedures can become highly unstable, and even small errors in the input data can significantly reduce the overall accuracy of the results. Therefore, we tested the accuracy and stability of the current GFDM by introducing different noisy data into the input data. Our initial numerical experiments demonstrate that the proposed GFDM approach shows great promise for accurately simulating inverse electroelastic problems. Moreover, the method holds the potential for analyzing various other problems, including wave propagation, flow problems, and nonlinear problems. Work in these areas is already underway.
Acknowledgement: The authors would like to acknowledge the valuable feedback provided by the reviewers.
Funding Statement: The research presented in this paper received support from the Natural Science Foundation of Shandong Province of China (Grant No. ZR2022YQ06), the Development Plan of Youth Innovation Team in Colleges and Universities of Shandong Province (Grant No. 2022KJ140), and the Key Laboratory of Road Construction Technology and Equipment (Chang’an University, No. 300102253502).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: W.Z. Qu; analysis and interpretation of results: Z.Q. Bai, G.H. Wu; draft manuscript preparation: Z.Q. Bai, W.Z. Qu, G.H. Wu. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: No availability of data and materials.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Lin, J., Liu, C. S. (2022). Recovering temperature-dependent heat conductivity in 2D and 3D domains with homogenization functions as the bases. Engineering with Computers, 38(S3), 2349–2363. [Google Scholar]
2. Jiang, S., Gu, Y., Golub, M. V. (2022). An efficient meshless method for bimaterial interface cracks in 2D thin-layered coating structures. Applied Mathematics Letters, 131, 108080. [Google Scholar]
3. Gu, Y., Sun, L. (2021). Electroelastic analysis of two-dimensional ultrathin layered piezoelectric films by an advanced boundary element method. International Journal for Numerical Methods in Engineering, 122(11), 2653–2671. [Google Scholar]
4. Ju, B., Qu, W. (2023). Three-dimensional application of the meshless generalized finite difference method for solving the extended Fisher–Kolmogorov equation. Applied Mathematics Letters, 136, 108458. [Google Scholar]
5. Qu, W., He, H. (2022). A GFDM with supplementary nodes for thin elastic plate bending analysis under dynamic loading. Applied Mathematics Letters, 124, 107664. [Google Scholar]
6. Gu, Y., Lin, J., Fan, C. M. (2023). Electroelastic analysis of two-dimensional piezoelectric structures by the localized method of fundamental solutions. Advances in Applied Mathematics and Mechanics, 15(4), 880–900. [Google Scholar]
7. Zhao, S., Gu, Y. (2023). A localized Fourier collocation method for solving high-order partial differential equations. Applied Mathematics Letters, 141(5–6), 108615. [Google Scholar]
8. Gu, Y., Fan, C. M., Fu, Z. (2021). Localized method of fundamental solutions for three-dimensional elasticity problems: Theory. Advances in Applied Mathematics and Mechanics, 13(6), 1520–1534. [Google Scholar]
9. Han, Y., Yan, Z., Lin, J., Feng, W. (2022). A novel model and solution on the bending problem of arbitrary shaped magnetoelectroelastic plates based on the modified strain gradient theory. Journal of Intelligent Material Systems and Structures, 33(8), 1072–1086. [Google Scholar]
10. Gu, Y., Fu, Z., Golub, M. V. (2022). A localized Fourier collocation method for 2D and 3D elliptic partial differential equations: Theory and MATLAB code. International Journal of Mechanical System Dynamics, 2(4), 339–351. [Google Scholar]
11. Li, Y., Liu, C., Li, W., Chai, Y. (2023). Numerical investigation of the element-free Galerkin method (EFGM) with appropriate temporal discretization techniques for transient wave propagation problems. Applied Mathematics and Computation, 442, 127755. [Google Scholar]
12. Sun, W., Ma, H., Qu, W. (2023). A hybrid numerical method for non-linear transient heat conduction problems with temperature-dependent thermal conductivity. Applied Mathematics Letters, 124, 108868. https://doi.org/10.1016/j.aml.2023.108868 [Google Scholar] [CrossRef]
13. Qu, W., Fan, C. M., Li, X. (2020). Analysis of an augmented moving least squares approximation and the associated localized method of fundamental solutions. Computers & Mathematics with Applications, 80(1), 13–30. [Google Scholar]
14. Fu, Z., Xi, Q., Gu, Y., Li, J., Qu, W. et al. (2023). Singular boundary method: A review and computer implementation aspects. Engineering Analysis with Boundary Elements, 147(3), 231–266. [Google Scholar]
15. Li, X., Li, S. (2021). A linearized element-free Galerkin method for the complex Ginzburg-Landau equation. Computers & Mathematics with Applications, 90, 135–147. [Google Scholar]
16. Gu, Y., Fan, C. M., Xu, R. P. (2019). Localized method of fundamental solutions for large-scale modeling of two-dimensional elasticity problems. Applied Mathematics Letters, 93(7), 8–14. [Google Scholar]
17. Gu, Y., Lin, J., Wang, F. (2021). Fracture mechanics analysis of bimaterial interface cracks using an enriched method of fundamental solutions: Theory and MATLAB code. Theoretical and Applied Fracture Mechanics, 116(3), 103078. [Google Scholar]
18. Liszka, T., Orkisz, J. (1980). The finite difference method at arbitrary irregular grids and its application in applied mechanics. Computers & Structures, 11(1–2), 83–95. [Google Scholar]
19. Li, P. W., Fan, C. M. (2017). Generalized finite difference method for two-dimensional shallow water equations. Engineering Analysis with Boundary Elements, 80(8), 58–71. [Google Scholar]
20. Fan, C. M., Huang, Y. K., Li, P. W., Chiu, C. L. (2014). Application of the generlized finite-difference method to inverse biharmonic boundary-value problems. Numerical Heat Transfer, Part B: Fundamentals, 65(2), 129–154. [Google Scholar]
21. Gu, Y., Qu, W., Chen, W., Song, L., Zhang, C. (2019). The generalized finite difference method for long-time dynamic modeling of three-dimensional coupled thermoelasticity problems. Journal of Computational Physics, 384, 42–59. [Google Scholar]
22. Jiang, S., Gu, Y., Fan, C. M., Qu, W. (2021). Fracture mechanics analysis of bimaterial interface cracks using the generalized finite difference method. Theoretical and Applied Fracture Mechanics, 113, 102942. [Google Scholar]
23. Gu, Y., Sun, H. (2020). A meshless method for solving three-dimensional time fractional diffusion equation with variable-order derivatives. Applied Mathematical Modelling, 78, 539–549. [Google Scholar]
24. Hu, W., Gu, Y., Zhang, C., He, X. (2019). The generalized finite difference method for an inverse boundary value problem in three-dimensional thermo-elasticity. Advances in Engineering Software, 131(6), 1–11. [Google Scholar]
25. Gong, R., Wang, M., Huang, Q., Zhang, Y. (2023). A CCBM-based generalized GKB iterative regularization algorithm for inverse Cauchy problems. Journal of Computational and Applied Mathematics, 432(1), 115282. [Google Scholar]
26. Zhang, Y. (2022). On the acceleration of optimal regularization algorithms for linear ill-posed inverse problems. Calcolo, 60(1), 6. [Google Scholar]
27. Ding, H. J., Wang, G. Q., Chen, W. Q. (1998). A boundary integral formulation and 2D fundamental solutions for piezoelectric media. Computer Methods in Applied Mechanics and Engineering, 158(1–2), 65–80. [Google Scholar]
28. Xia, H., Gu, Y. (2021). Short communication: The generalized finite difference method for electroelastic analysis of 2D piezoelectric structures. Engineering Analysis with Boundary Elements, 124(2), 82–86. [Google Scholar]
29. Xia, H., Gu, Y. (2021). Generalized finite difference method for electroelastic analysis of three-dimensional piezoelectric structures. Applied Mathematics Letters, 117, 107084. [Google Scholar]
30. Wang, Y., Gu, Y., Fan, C. M., Chen, W., Zhang, C. (2018). Domain-decomposition generalized finite difference method for stress analysis in multi-layered elastic materials. Engineering Analysis with Boundary Elements, 94(33–40), 94–102. [Google Scholar]
31. Ureña, F., Gavete, L., García, A., Benito, J. J., Vargas, A. M. (2019). Solving second order non-linear parabolic PDEs using generalized finite difference method (GFDM). Journal of Computational and Applied Mathematics, 354(4), 221–241. [Google Scholar]
32. Benito, J. J., Ureña, F., Gavete, L. (2001). Influence of several factors in the generalized finite difference method. Applied Mathematical Modelling, 25(12), 1039–1053. [Google Scholar]
33. Wang, K., Li, L., Lan, Y., Dong, P., Xia, G. (2019). Application research of chaotic carrier frequency modulation technology in two-stage matrix converter. Mathematical Problems in Engineering, 2019, 2614327. [Google Scholar]
34. Fan, C. M., Li, P. W., Yeih, W. C. (2015). Generalized finite difference method for solving two-dimensional inverse Cauchy problems. Inverse Problems in Science and Engineering, 23, 737–759. [Google Scholar]
35. Gu, Y., Wang, L., Chen, W., Zhang, C., He, X. (2017). Application of the meshless generalized finite difference method to inverse heat source problems. International Journal of Heat and Mass Transfer, 108(3), 721–729. [Google Scholar]
36. Cao, C., Qin, Q. H., Yu, A. (2012). Hybrid fundamental-solution-based FEM for piezoelectric materials. Computational Mechanics, 50(4), 397–412. [Google Scholar]
37. Ohs, R. R., Aluru, N. R. (2001). Meshless analysis of piezoelectric devices. Computational Mechanics, 27(1), 23–36. [Google Scholar]
38. Ding, H., Liang, J. (1999). The fundamental solutions for transversely isotropic piezoelectricity and boundary element method. Computers & Structures, 71(4), 447–455. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools