A Formal Model for Analyzing Fair Exchange Protocols Based on Event Logic

1  Introduction

The rapid advancement of e-commerce technology on the Internet has brought about a pressing need to address security concerns in the realm of e-commerce. Among various security mechanisms, the fair exchange protocol holds a pivotal position in ensuring the secure operation of e-commerce applications. It finds widespread application in electronic payment systems and electronic signing [1–3], as it directly impacts the trust and security of transactions in these areas. By ensuring fair exchanges, these protocols contribute to enhancing the reliability, and efficiency of digital interactions, thereby enabling safer and more trustworthy online environments [4,5]. The fundamental principle underlying fair exchange protocols is the guarantee of fairness, which entails that no participant in the protocol should possess an undue advantage at any stage of its execution. If one party engages in dishonest behavior (such as premature termination or misconduct), the fairness of the protocol cannot be achieved. Intruders can exploit the fairness vulnerabilities to launch attacks, preventing users from obtaining their expected transaction outcomes and causing financial losses [6,7]. Consequently, the design of efficient and concise analysis methods to verify the fulfillment of expected security properties by fair exchange protocols assumes great importance.

The fair exchange protocol offers fair exchange services to untrusted parties within unreliable network environments, typically relying on a trusted third party (TTP) to mediate disputes. This protocol type typically comprises two subprotocols: the exchange subprotocol and the resolve subprotocol. The exchange subprotocol facilitates the fair exchange of information, while the resolve subprotocol manages disputes that may arise during the information exchange, necessitating TTP involvement to ensure protocol fairness. Given the involvement of a TTP, these protocols exhibit a more intricate structure, often featuring branching or composed of multiple subprotocols. Compared to general protocols, this protocol type involves a significantly higher number of messages. In scenarios where protocol participants engage in malicious actions, each participant can independently initiate or terminate the execution of subprotocols, or even simultaneously execute multiple subprotocols. Consequently, the message sequence of the entire protocol remains indeterminate until protocol execution. Furthermore, fairness, unlike security properties such as authentication and confidentiality, is less well-defined and more challenging to express and verify. Consequently, classical analysis methods are insufficient for directly analyzing fair exchange protocols.

The fair exchange protocol exhibits a distinct intruder model compared to traditional authentication protocols and key exchange protocols [8]. In traditional authentication protocols and key exchange protocols, it is generally assumed that the Dolev-Yao (DY) model [9] is a standard intruder model. In such protocols, honest participants consistently collaborate to accomplish protocol objectives, such as identity authentication or key consistency. Participants aim to cooperate to successfully complete the protocol, assuming mutual trust. However, in fair exchange protocols, participants exhibit mutual distrust and deliberately deviate from the prescribed protocol execution steps for personal benefit. Additionally, fair exchange protocols employ different communication models than traditional security protocols. Typically, the communication channel between the protocol participant and the trusted third party (TTP) in fair exchange protocols is resilient and not entirely controlled by the attacker, contrary to the assumption of complete control by the intruder over the communication channel in traditional models. Moreover, some protocol participants may choose to send false messages or prematurely terminate the protocol to further their own interests. Consequently, the primary security threats within fair exchange protocols originate from within the protocol itself, and the construction of an effective intruder model is a crucial consideration when analyzing fair exchange protocols.

Therefore, considering the existing challenges encountered in the formal analysis of fair exchange protocols, this study puts forward a formal model aimed at analyzing such protocols. The main contributions are summarized as follows:

1.    From the perspective of distinguishing between an honest participant and a malicious one, we propose a formal definition of fairness that accurately captures the inherent requirements of fair exchange protocols. By adopting this definition, we can effectively assess the fairness of protocol executions in scenarios where one participant behaves honestly while the other acts maliciously.

2.    Considering the absence of a mechanism to represent the knowledge set possessed by a participant in the fair exchange protocol, we address this limitation by introducing the time factor into predicates and proposing knowledge set axioms based on event logic. This enhanced logic enables the abstraction of participants, messages, actions, knowledge, and states involved in the protocol. By incorporating the time factor, the logic is capable of describing the state and knowledge of a participant at various time points, as well as reasoning about the knowledge possessed by a participant.

3.    Within the fair exchange protocol, various security threats are present, including eavesdropping, message interception, tampering caused by channel errors, as well as the malicious actions of participants seeking personal gains through cheating or prematurely terminating the protocol. To effectively capture these threats, this paper introduces an intruder model that translates channel errors into explicit intruder behaviors. Additionally, the protocol participants are categorized into honest participants and malicious participants, enabling a comprehensive analysis that maximizes the intruder’s capabilities and accounts for their potential impact on the protocol’s security.

4.    By analyzing a representative fair exchange protocol, this paper demonstrates the detailed steps involved in using the proposed model for protocol analysis. It provides a comprehensive overview of the protocol’s operation during an attack scenario, thoroughly elucidating the underlying cause of the attack. Furthermore, this paper presents an appropriate solution to address the identified security vulnerability.

The rest of this paper is organized as follows. In Section 2, we summarize the related work. In Section 3, the formal model of fair exchange protocol is described in detail. The case study is conducted in Section 4. The conclusions and future works are discussed in Section 5.

2  Related Work

The primary objective of fair exchange protocols is to address the challenge of achieving fair exchange. These protocols aim to facilitate the exchange of data between parties without granting any party an unfair advantage in terms of obtaining more information than the other. They ensure that both parties engage in the exchange honestly, without deception, thereby promoting fair transactions among untrusted partners. However, the design of fair exchange protocols is a complex task that is prone to errors. In order to verify whether the security properties of the protocol meet the expected requirements, formal methods are usually used to analyze it [10]. Formal analysis of security protocols is an effective approach that involves various steps, such as accurately describing the protocol’s operating environment, precisely defining the behavior of security protocol actions, explicitly specifying the security properties of the protocol, and verifying whether the protocol achieves the intended security goals. The formal analysis of security protocols can be categorized into two main approaches: model checking and theorem proving [11]. By adopting formal analysis techniques from these two perspectives, researchers endeavor to enhance the understanding, evaluation, and improvement of fair exchange protocols. These methods provide a systematic and rigorous framework for assessing the security properties of fair exchange protocols, contributing to the development of robust and reliable protocols in the field of secure data exchange.

The analysis method based on model checking [12] focuses on using state exploration to check the security properties of protocols, and determines whether the protocol satisfies the expected security properties by traversing all the states of the protocol model. This method has the advantage of high automation, does not require user participation in the verification process, and finds many new attacks of the protocol that have not been found before. Vitaly et al. [13] used the model checker Murφ to analyze the ASW protocol and finds that malicious attackers can generate inconsistent versions of the contract. Li et al. [14] proposed a formal verification method of fair exchange protocol based on alternating temporal logic. The model checker mocha is used to verify the fairness, timeliness of an electronic contract signing protocol, it is found that the protocol has fairness defects. In [15], a formal verification method of fair exchange protocol based on channel credibility was proposed, and the impact of channel errors on the fairness of the protocol was analyzed. Guo [16] proposed a modeling method of fair exchange protocols based on probabilistic timed automata, and uses prism, a probabilistic model checker, to quantitatively study the fairness of protocols. In the above research, general model checkers are used to verify the protocol model. In recent years, some special security protocol analysis tools such as ProVerif [17], SmartVerif [18], Scyther [19] and Tamarin Prover [20] have become popular, which can perform formal verification and semantic analysis for protocols. However, it is very complicated to construct the protocol model which can be handled by analysis tools, and how to describe the fairness of fair exchange protocols accurately is also a challenge.

The analysis method based on theorem proving focuses on the demonstration of protocol security properties by means of proof, which has the advantages of a simple proof process and a high level of security proof. Datta et al. [21,22] proposed Protocol Composition Logic (PCL), which uses cord calculus and trace to describe protocol operation, and then analyzes protocol security through logical axioms and modular reasoning methods, but the logic has insufficient ability to analyze fairness. Backes et al. [23] improved PCL and proposed IF assertion. PCL was first used in the formal analysis of electronic contract signing protocols, but this method can only analyze weak fairness. In view of the shortcomings of this method, Gao et al. [24] proposed the combination of PCL and Kailar logic to study the fair exchange protocol, and applied PCL to the field of e-commerce, expanding the scope of application of this theory. In view of the defect that the belief logic is difficult to analyze the fairness and timeliness of optimistic fair exchange protocols, a formal model for logic reasoning and fair exchange protocols was proposed by Chen et al. [25]. The method is characterized by defining the protocol as an evolved system that has the Kripke structure, and verifying all running states of the protocol by using the idea of model checking.

3  The New Formal Model

In this section, we present a formal model that aims to facilitate the formal analysis of fair exchange protocols. The key components of the model include a formal definition of fairness, pointing out the defects of event logic and improving it, and the proposal of an intruder model specifically designed for fair exchange protocols.

To begin with, we provide a precise and rigorous definition of fairness within the context of fair exchange protocols. By establishing this formal definition, we ensure that the inherent requirements of fairness are accurately captured and properly addressed. Subsequently, we identify and address the limitations and shortcomings of the existing event logic that hinder its effectiveness in analyzing fair exchange protocols. Through our improvements, we enhance the expressive power and analytical capabilities of the event logic, enabling it to effectively capture the intricacies of fair exchange protocols. Furthermore, we propose an intruder model tailored specifically to fair exchange protocols. This model encompasses the behaviors and actions of both honest participants and malicious entities, with the aim of maximizing the intruder’s capabilities within the protocol context. By introducing this specialized intruder model, we create a more comprehensive and realistic framework for analyzing the security aspects of fair exchange protocols.

By presenting this formal model, we lay the foundation for subsequent analysis and evaluation of fair exchange protocols. This model serves as a valuable tool to understand, evaluate, and enhance the security properties of fair exchange protocols in diverse real-world scenarios.

3.1 The Formal Definition of Fairness

The primary objective of fair exchange protocols is to ensure the fairness of information exchange in unreliable network environments. Fairness is crucial for the security of fair exchange protocols. This property ensures that all participating entities in the protocol are on an equal footing at any stage of protocol execution. After the protocol is executed, each party either obtains what they need or receives nothing, without causing any loss to any party. Therefore, fairness is a crucial property that must be satisfied by these protocols. In the context of fair exchange protocols involving two parties, denoted as P and Q, the exchanged information is represented as itemP and itemQ, respectively. Fairness, in essence, implies that upon the completion of a protocol, two parties who lack trust in each other within the unreliable network environment either receive the exchanged information correctly or do not receive it at all. Alternatively, if one party fails to receive the exchanged information correctly, it can initiate the resolve subprotocol to obtain the information again. Therefore, we define fairness with respect to the honesty of the originator and the recipient. The protocol achieves fairness only when it satisfies both originator fairness and recipient fairness.

Definition 1 (Originator Fairness) In the case where the originator is an honest participant and the recipient is a malicious participant, a fair exchange protocol satisfies originator fairness. If any run of the protocol satisfies one of the following conditions. (1) When the exchange subprotocol ends, the originator P obtains itemQ and it is verified as valid. (2) When the originator P does not obtain the itemQ at the end of the exchange subprotocol, the originator can obtain non-repudiation of recipient (NRR), and then execute the resolve subprotocol with the help of TTP and obtain the itemQ correctly. Originator fairness can be formalized as follows:

Fairenss(P)≜Honest(P)∧Dishonest(Q)[Exchange]PHas(P,itemQ,te)∧⊥itemQ∨Has(P,NRR,te)[Resolve]PHas(P,itemQ,tr)(1)

Definition 2 (Recipient Fairness) In the case where the recipient is an honest participant and the originator is a malicious participant, a fair exchange protocol satisfies recipient fairness. If any run of the protocol satisfies one of the following conditions. (1) When the exchange subprotocol ends, the recipient Q obtains itemP and it is verified as valid. (2) When the recipient Q does not obtain the itemP at the end of the exchange subprotocol, the recipient can obtain non-repudiation of originator (NRO), and then execute the resolve subprotocol with the help of TTP and obtain the itemQ correctly. Recipient fairness can be formalized as follows:

Fairenss(Q)≜Honest(Q)∧Dishonest(P)[Exchange]QHas(P,itemP,te)∧⊥itemQ∨Has(Q,NRO,te)[Resolve]QHas(Q,itemP,tr)(2)

where te and tr represent the end times of the exchange subprotocol and the resolve subprotocol, respectively.

Definition 3 (Fairness) When a fair exchange protocol satisfies both originator fairness and recipient fairness, then the protocol satisfies fairness.

Fairness(FEP)≜Fairness(P)∧Fairness(Q)(3)

3.2 The Event Logic and Its Extension

3.2.1 Brief Introduction of Event Logic and Its Defects

Event logic [26,27] is a theory proposed by our research team for formal analysis of security protocols. It proves protocol security through axioms, theorems, and inference rules, it can be used to analyze identity authentication and message confidentiality. Event logic is composed of protocol modeling language and proof system. Protocol modeling language is a tool for modeling concurrent distributed systems. It has powerful description ability, and can accurately describe the interaction behavior between participants in security protocols. The proof system of event logic is improved from first-order logic, including a series of axioms, theorems, and inference rules. The axiom system of event logic includes six core axioms, which are key axiom, causality axiom, disjoint axiom, honesty axiom, flow relation, and random number axiom [28,29]. These axioms constitute the core of logic proof system, which can be used to prove whether the authentication and confidentiality of the protocol are satisfied.

Event logic overcomes the shortcomings of PCL in the protocol analysis [30], successfully analyze the Robust Confidentiality Integrity and Authentication (RCIA) protocol [31] in the Internet of Things, Physical Unclonable Function-based (PUF-based) mutual authentication protocol [32] and wireless mesh [33] network authentication protocol, and successfully finds out the security vulnerabilities in the protocols.

Event logic offers a flexible and adaptable framework for the formal analysis of security protocols. By employing logical reasoning steps, it facilitates the assessment of whether a given protocol satisfies the desired security properties. However, when applied to the analysis of fair exchange protocols, event logic exhibits certain limitations and shortcomings that need to be addressed.

1. Event logic is primarily employed to analyze identity authentication and message confidentiality in protocols. However, it falls short in terms of its analytical capacity when it comes to assessing the fairness of fair exchange protocols. When utilizing event logic to analyze security protocols, identity authentication is examined by deducing the temporal correlation between protocol actions, while message confidentiality is assessed by verifying whether confidential messages can be obtained by unauthorized parties. Nevertheless, the formal analysis of fairness still lacks a robust axiom system and a precise formal definition of fairness has yet to be established.

2. Event logic is deficient in its ability to capture the dynamics of participants’ knowledge sets in fair exchange protocols and lacks the capacity to analyze and reason about participants’ knowledge. The concept of fairness in fair exchange protocols primarily pertains to the successful acquisition of expected information by participants and the achievement of mutually agreed termination states. Alternatively, fairness can also be defined by the absence of the expected information for bothparties. In essence, fairness revolves around the inclusion of expected messages in participants’ knowledge sets. However, event logic faces difficulties in describing participants’ knowledge and conducting reasoning about their knowledge.

3.2.2 The Extension of Event Logic

In view of the defects of event logic, this paper extends and improves this theory, including the introduction of time factor into the original predicate of event logic, so that the improved logic can express the knowledge possessed by various participants at different time points. The syntax of the improved event logic is shown in Table 1.

An action formula is used to describe that a specific action has been executed by the protocol participant. Specifically, formula Send(X,m,t) means that participant X has sent message m at time t. Similarly, some predicates (including Receive, New, Encrypt, Decrypt, Sign, Verify, Check) indicate that the corresponding action has been executed. These action formulas play a crucial role in describing fairness, because these predicates cover the actions of protocol participants during their interactions. The formula ϕ consists of the following parts. (1) Action formulas a consist of formulas ϕ. (2) If a is a formula, then the formula composed of connectives ⇁,⊃,∧,∨ is also a formula. (3) Has, ⊥m and Timer consist of formulas ϕ. Predicate formula Has(X,m,t) denotes that participant X possesses message m at time t, this formula can be used to describe the knowledge possessed by the protocol participant at different time points during protocol execution. ⊥m indicates that message m is valid at the current time. The formula Timer is used to describe the transition between the waiting and active states of a participant when triggered by sending and receiving events. Timer has three states: opening, closing, and timeout, denoted by ⨁Timer, ⨂Timer and ⨀Timer, respectively. When a participant sends one message and waits for receiving another message, the timer opens (⨁Timer). When a participant correctly receives the message, the timer closes (⨂Timer) and participant state is transferred from waiting to acting. When a participant fails to receive the message correctly within the pre-set maximum waiting time, the timer enters a timeout state (⨀Timer). At this time, the participant will terminate the protocol or request TTP to execute a conflict resolution according to the protocol definition. The occurrence of protocol events triggers changes in the state of protocol agents, which is crucial for analyzing protocol fairness. Therefore, this paper introduces timers to describe the transitions between states such as waiting, active, and terminated for protocol agents.

In a protocol, a formula can be true or false. The semantic relationship P,R,st⊨φ indicates that in the run R of the protocol P, the formula φ holds in the state S at time t. R can be a complete run in which all sessions started can be successfully completed, or it can be an incomplete run in which some participants may need to wait for messages to complete one or more sessions. Action formulas can be intuitively defined as a participant executing the corresponding actions during a protocol run. The predicate Has is used to model the knowledge set owned by a participant. As the security protocol executed, the knowledge possessed by protocol agents also increases. Therefore, in order to model the knowledge possessed by protocol agents, we introduce the predicate Has to describe it. Taking the formula Has(X,m,t) as an example, there are two cases that can make it true. One case is to directly possess the message m, which is either a free variable or the participant has the action of receiving or generating m. In another case, it is known indirectly that m can be obtained from known terms through one or more operations, including encryption and decryption based on known keys, as well as cascading or decomposing messages. The truth condition of the formula Timer can be defined based on the specific actions executed by a participant triggering a change in the current state. The semantics of various formulas are given below. For the sake of simplicity, if and only if is abbreviated to iff.

(1)   P,R,st⊨¬φ iff P,R,st⊭φ.

(2)   P,R,st⊨φ∨ψ iff P,R,st⊨φ or P,R,st⊨ψ.

(3)   P,R,st⊨φ∧ψ iff P,R,st⊨φ and P,R,st⊨ψ.

(4)   P,R,st⊨φ⊃ψ iff P,R,st⊭φ or P,R,st⊨ψ.

(5)   P,R,st⊨Send(X,m,t) iff in the run R of protocol P, participant X sent the message m at time t.

(6)   P,R,st⊨Receive(X,m,t) iff in the run R of protocol P, participant X received the message m at time t.

(7)   P,R,st⊨New(X,m,t) iff in the run R of protocol P, participant X generated the message m at time t.

(8)   P,R,st⊨Encrypt(X,m,k,t) iff in the run R of protocol P, participant X encrypted the message m with k and generated {m}k at time t.

(9)   P,R,st⊨Dncrypt(X,{m}k,k−1,t) iff in the run R of protocol P, participant X decrypted the message {m}k with k−1 and generated m at time t.

(10)   P,R,st⊨Sign(X,m,k,t) iff in the run R of protocol P, participant X signed the message m with k and generated SIGk{|m|} at time t.

(11)   P,R,st⊨Verify(X,SIGk{|m|},k−1,t) iff in the run R of protocol P, participant X verified the validity of the signature SIGk{|m|} at time t.

(12)   P,R,st⊨Check(X,m,t) iff in the run R of protocol P, participant X checked the validity of message m at time t.

(13)   P,R,st⊨Has(X,m,t) if there exists an i such that Hasi(X,m,t),where Hasi is inductively as follows:

(a)   Has0(X,m,t) iff participant X generated the message m at time t.

(b)   Has0(X,m,t) iff participant X received the message m at time t.

(c)   Hasi+1(X,m,t) iff Hasi(X,m,t).

(d)   Hasi(X,(m,m′),t) iff Hasi(X,m,t) and Hasi(X,m′,t).

(e)   Hasi(X,{m}k,t) iff Hasi(X,m,t) and Hasi(X,k,t).

(f)   Hasi(X,m,t) iff Hasi(X,{m}k,t) and Hasi(X,k,t).

P,R,st⊨⊥m iff in the run R of protocol P, the message m was valid at time t.

P,R,st⊨⨁TimerX iff in the run R of protocol P, participant X has sent messages at time t′(t′=t−1) and is waiting to receive messages.

P,R,st⊨⨂TimerX iff in the run R of protocol P, participant X has correctly received expected messages for which he is waiting at time t′(t′=t−1).

P,R,st⊨⨀TimerX iff in the run R of protocol P, participant X has not correctly received expected messages at time t within the maximum waiting time.

Axioms in event logic can be used to prove whether the authentication and confidentiality of protocols meet the requirements, but there is a lack of corresponding axioms for proving the fairness of fair exchange protocols. The fairness is mainly reflected in whether expected messages can be inferred from the knowledge set owned by protocol participants. Therefore, we propose the knowledge set axiom from the characteristics of fairness, which makes it possible to analyze and infer the knowledge owned by protocol participants.

ORIG New(X,m,t)⊃Has(X,m,t)

REC Receive(X,m,t)⊃Has(X,m,t)

TUP Has(X,m1,t1)∧Has(X,m2,t2)⊃(∃t3=max(t1,t2))∧Has(X,(m1,m2),t3)

PROJ Has(X,(m1,m2),t)⊃Has(X,m1,t)∧Has(X,m2,t)

ENC Has(X,m,t1)∧Has(X,k,t2)⊃(∃t3,t3=max(t1,t2))∧Has(X,{m}k,t3)

DEC Has(X,{m}k,t1)∧Has(X,k−1,t2)⊃(∃t3,t3=max(t1,t2))∧Has(X,m,t3)

The knowledge set axioms include the above six sub-axioms, which represent that a participant possesses a message by means of generating an original message (ORIG), receiving (REC), tuple (TUP), projection (PROJ), encryption (ENC), decryption (DEC), respectively. ORIG and REC state respectively that a participant possesses the message m at time t if he freshly generated it or if he received it. TUP indicates that if participant X possesses messages m1 and m2 at time t1 and t2, then participant X possesses a message (m1,m2) composed of messages m1 and m2 at time t3(t3=max(t1,t2)). The content described by PROJ is opposite to TUP. If participant X possesses a tuple consisting of two messages, then participant X possesses sub-messages in the tuple. ENC indicates that if participant X possesses the message m and encryption key k at time t1 and t2, respectively, then participant X possesses the encrypted message {m}k at time t3(t3=max(t1,t2)). The content described by DEC is opposite to ENC. If participant X possesses an encrypted message {m}k and a decryption key k−1 at time t1 and t2, respectively, then participant X possesses a decryption message m at time t3(t3=max(t1,t2)).

For a logical system, soundness is the most important attribute, which ensures that a formula can be proven by the formulas in the formula set and all axiomatic systems or inference rules. The following is the reliability proof of the improved event logic. The soundness proof of the improved event logic is provided below.

Theorem 1 The improved event logic is soundness, if Γ⊢Υ, then Γ⊨Υ.

Proof: To prove this theorem, it is necessary to prove that its axioms are valid. The validity of other axioms in event logic has been explained in detail in the literature. The validity of the improved knowledge set axioms is demonstrated below.

Taking the ENC as an example to prove. When P,R,st⊨Has(X,m,t1)∧Has(X,k,t2) is true, it is known from the semantics of symbol ∧ that P,R,st⊨Has(X,m,t1) and P,R,st⊨Has(X,k,t2) are true. Let’s assume that the relationship between t, t1 and t2 is t≤t1≤t2, then P,R,st2⊨Has(X,m,t2) and P,R,st2⊨Has(X,k,t2) are true,thus P,R,st2⊨Has(X,{m}k,t2) is true. The validity proof of other axioms is similar and will not be repeated here.

The following inference rule is used in the analysis of fair exchange protocols: Υ∧(Υ⊃φ)⊃φ, where γ,φ represents a formula in event logic and ⊃ means implication. The meaning of this inference rule is that if γ is known to be true and φ can be inferred from γ, then φ is true.

3.3 The Intruder Model

In fair exchange protocols, the interaction among different participants can be viewed as communication between processes operating in an asynchronous environment. These processes engage in the exchange of messages over an unreliable channel, which introduces potential vulnerabilities. The messages exchanged between participants are subject to various threats during transmission, including channel errors and active attacks orchestrated by malicious participants. Given the significance of ensuring fairness in fair exchange protocols, it is essential to establish an appropriate intruder model that takes into account the impact of both channel errors and malicious participants on the fairness of the protocol. The intruder model serves as a framework for analyzing and evaluating the security properties of the protocol. By considering the effects of channel errors and malicious participants within the intruder model, we aim to develop a comprehensive understanding of the vulnerabilities and risks inherent in fair exchange protocols.

Channel error is an important issue when analyzing fair exchange protocols. In an open network environment, messages may be lost or replayed during the transmission process due to channel errors. The quality of service provided by the channel is crucial to the protocol, so before formalizing a fair exchange protocol, first we need to give the channel assumption. Current mainstream solutions generally assume that the channel between two parties is an unreliable channel, and messages transmitted over this channel will be delayed or lost, while the channel between the participants and the TTP is a resilient channel, although messages transmitted over this type of channel will be also delayed or replayed, and can be correctly delivered to the destination receiver after a limited but unknown time.

In addition, there are malicious participants in fair exchange protocols who choose not to obey the protocol strictly for their benefit. For example, the message is delayed, so that the message cannot reach its designated receiver on time; the malicious participant conspires with the intruder to tamper or forge the sent message; the malicious participant intentionally terminates the sending message and exits the protocol, resulting in the honest participant being forced to terminate the operation of a protocol due to prolonged waiting time; the message is replayed.

Through the above analysis, we can see that channel errors and malicious participants can cause messages to be delayed and tampered with, but messages transmitted in a resilient channel will eventually reach the designated receiver, which is the essential difference between the resilient channel and the unreliable channel. Based on the above considerations, this paper views malicious behavior between protocol participants and unreliable channel errors as the result of attacks caused by standard DY intruders [25], and views malicious behavior made by protocol participants towards TTP and resilient channel errors as the result of attacks caused by weak DY intruder. The definition of a weak DY intruder is given below.

Definition 4 (Weak DY Intruder) A weak DY intruder can delay, tamper, forge, and replay messages transmitted on the channel, but cannot prevent any messages from reaching the designated recipient correctly.

In fair exchange protocol, participants can be divided into honest participants (assuming that TTP is always an honest participant) and malicious participants. Malicious participants can be regarded as weak DY intruders, which gain advantages in the exchange process by executing strategies beneficial to their interests. We consider such a two-party fair exchange protocol, which can be divided into the following three models based on whether the participant is honest or not. (1) Both parties are honest, and the intruder comes from the outside. (2) One of the participants is an honest participant and the other is a malicious participant, and the malicious participant attacks the honest participant to gain an advantage in the exchange process. (3) Both parties are malicious participants, and they deceive each other. In models (1) and (3), the capability of both parties is equal. In model (2), the honest participant always communicates with the intruder, while the malicious participant, as a weak DY intruder, controls the communication between the honest participant and the TTP. Obviously, in these three cases, model (2) has the strongest attack capability, the honest participant is in a disadvantaged position compared to the malicious participant, and the honest participant faces the greatest security threat. Therefore, we only need to prove that the fair exchange protocol is able to obtain the expected message correctly under the intruder model (2), and then the protocol satisfies fairness.

Because both channel errors and intruder behavior can result in message loss or tampering, we transform channel errors into intruder behavior, which effectively simplifies the complexity of protocol analysis. This approach provides a more comprehensive and realistic perspective on the security analysis of the protocol. By considering channel errors as part of the intruder model, we can assess the protocol’s resilience against potential attacks originating from both intruder actions and channel errors. This helps in addressing security weaknesses and enhancing the overall robustness of the protocol, and providing a more comprehensive and realistic perspective on the security analysis of the protocol.

3.4 Analysis Process

Before providing an analysis process for fair exchange protocols based on the new formal model, we first introduce the following definitions.

Definition 5 (Protocol Participant’s Strategy) A strategy indicates the actions that a protocol participant may choose to perform when sending a message, denoted by the symbol σ. The honest participant has only one optional strategy σ:=sendX,m, that is, the honest participant always obeys the protocol strictly during the communication process, and there is no fraudulent action. The malicious participant has three optional strategies, denoted as σ:=sendX,m, σ′:=sendX,m∗ and σ″:=ε, which indicates that the malicious participant sends a message according to the protocol regulations, or sends a fake message, or does not send a message.

Definition 6 (Protocol Trace) A protocol trace is the action sequence consisting of sending and receiving actions of a protocol participant.

Definition 7 (Protocol State) Protocol state is a four-tuple (X,Θ,Γ,t), which is denoted as s, the meaning of each symbol is defined as follows:

(1)   X represents the protocol identifier, including the originator, recipient and TTP.

(2)   Θ∈ {Ini, Wai, Act, Abo, Exi, Suc} is a description of the current process state, including the following five states: initialization, waiting, active, abort, and success.

(3)   Γ denotes the knowledge set that participant X possesses in the current state. The knowledge possessed by participant X at time t is represented as ΓXt=(MXt,KXt), where MXt is the set of messages generated or received by participant X at time t, and KXt is the set of keys possessed by participant X at time t.

(4)   t∈{0,1,…,n} represents the time point of current state, which consists of a set of discrete time series.

In security protocols, the knowledge and state of participants evolve over time, and this temporal evolution is crucial for analyzing the fairness of fair exchange protocols. Fairness is defined as whether the participants receive the expected messages when the protocol execution completes, which requires the participants’ knowledge to include the expected messages and the participants to be in a termination state. Therefore, in the proposed formal model of this paper, based on event logic, we introduce time factors in predicates to incorporate the temporal aspect, enabling the logic to express the knowledge and state of participants at different time points in the protocol, and facilitating the analysis of protocol fairness.

Definition 8 (State Transition) State transition is defined as a function δ:S×2E→S, where E refers to the set of events executed by a participant, and state transition refers to the transition between two states with temporal and causal relationships. When a participant executes the relevant events, it will trigger a change in its state. For ∀sXt∈S, when an event e is executed by participant X, there is a state sXt′ that the formula δ(sXt,e)=sXt′ holds, where sXt represents the state of participant X at time t.

Definition 9 (Protocol Formalization) Protocol formalization refers to the conversion of a protocol described informally into a logical formula described in a formal language. The set of these logical formulas is called a formal protocol and is denoted as P~.

Based on the above definitions, the general flow of fair exchange protocol analysis is given. For a protocol P, the process for analyzing its fairness based on the formal model is as follows:

(1)   For a protocol P, the protocol formalization includes abstracting the participants, messages and actions involved in the protocol and formally describing it with event logic. As a result, the formal description of the protocol P~ is obtained.

(2)   Listing the originator fairness and recipient fairness that the protocol needs to satisfy, and using event logic to describe it and obtain a formula set θ.

(3)   Listing all the paths composed of the optional strategies of the malicious participant, and filtering out the paths that may cause fairness defects. Starting from the initial state of the protocol, based on the axioms, theorems, and inference rules in the improved event logic, we analyze whether the honest participant satisfies fairness, that is, proving whether the formula P~⊢θ is true or not.

4  Case Study

Based on the existing research progress and the identified issues in the formal analysis of fair exchange protocols, we put forward a formal model in Section 3 of this paper for the purpose of analyzing such protocol. In order to demonstrate the practicality and effectiveness of the proposed model, we have chosen an electronic contract signing protocol as a representative example for illustration.

4.1 Protocol Description

Micali proposed an electronic contract signing protocol [34] (Micali protocol for short). The purpose of the protocol is to enable two untrusted parties to exchange digital signatures of electronic contracts in a fair way on an open network with the help of TTP. In the process of electronic contract signing, disputes between participants are inevitable. Therefore, a complete electronic contract signing protocol usually needs to be composed of an exchange subprotocol and a resolve subprotocol. The exchange subprotocol is used to deal with the signing of electronic contracts, and the resolve subprotocol is used to deal with the disputes arising from the signing of electronic contracts. The protocol description is shown in Table 2, where steps 1, 2 and 3 are exchange subprotocol and steps 4, 5 and 6 are resolve subprotocol.

{.}KX−1 represents the message signed with the private key of participant X, C denotes an electronic contract, N is a random and unpredictable message, Z={A,B,N}KTTP denotes a message generated by encrypting A, B, N with the public key of TTP. In order to guarantee the fairness of the protocol, when the exchange subprotocol ends, A gets the non-repudiation evidence of B, that is {{C,Z}KB−1,{Z}KB−1}, and B gets the non-repudiation evidence of A, that is {{C,Z}KA−1,N}. If B does not receive N correctly, then a resolve subprotocol is initiated. TTP calculates N from the message sent by B, otherwise TTP stops executing the resolve subprotocol.

4.2 Formal Analysis of the Micali Protocol

In the formal model of fair exchange protocols based on event logic, we regard the protocol as a state transition system that evolves over time. Starting from the initial states of the protocol, we analyze the impact of various events on the knowledge and states of protocol entities by combining event logic axioms and inference rules, thereby analyzing the fairness of the protocol. Therefore, when analyzing the fairness of the protocol, it is necessary to first provide the initial state of the protocol.

The initial state of the Micali protocol is defined as (X,Θ0,Γ0,t0), where:

(a)   X∈{A,B,TTP},ΘXt0=Ini,t0=0

(b)   ΓAt0={ΣAt0={A,B,TTP},MAt0={C},KAt0={KA.enc,KA.dec,KX.ver}}

(c)   ΓBt0={ΣBt0={B},MBt0={∅},KAt0={KB.enc,KB.dec,KX.ver}}

(d)   ΓTTPt0={ΣTTPt0={TTP},MTTPt0={∅},KAt0={KTTP.enc,KTTP.dec,KX.ver}}

The initial state of the Micali protocol describes the state of each participant, the message set and the key set possessed by each participant before the protocol is executed. The initial key set of a participant includes their own private key used to decrypt and sign, the public keys of all participants used to encrypt and verify the signature. The participant’s message set represents some messages that a participant already possesses before the protocol runs, because A possesses contract C, so C belongs to A’s knowledge set, and the knowledge sets of other participants are empty. Since the protocol does not start running at time t0, each participant is in an initialization state.

When the protocol starts to run, honest participants exchange messages according to the action sequence and message format specified in the protocol, while malicious participants have three different optional strategies: sending correct messages according to protocol regulations, or sending false messages, or not sending messages. The fairness of the protocol is analyzed from two aspects: the originator is a malicious participant and the recipient is a malicious participant. In the proposed intruder model, when one party is honest and the other is malicious, the malicious party has the strongest attack capability, thereby gaining an advantage in the exchange. Therefore, we consider both the malicious recipient and the malicious originator to analyze whether the fairness of the protocol is satisfied.

4.2.1 The First Attack Scheme When the Originator Is a Malicious Participant

During the execution of the fair exchange protocol, when the originator A is a malicious participant and the recipient B is an honest participant, the target of the attack launched by A is to obtain the commitment of the recipient B to the contract C. According to the Definition 5, A selects different strategies to form all possible protocol traces, which is shown in Fig. 1.

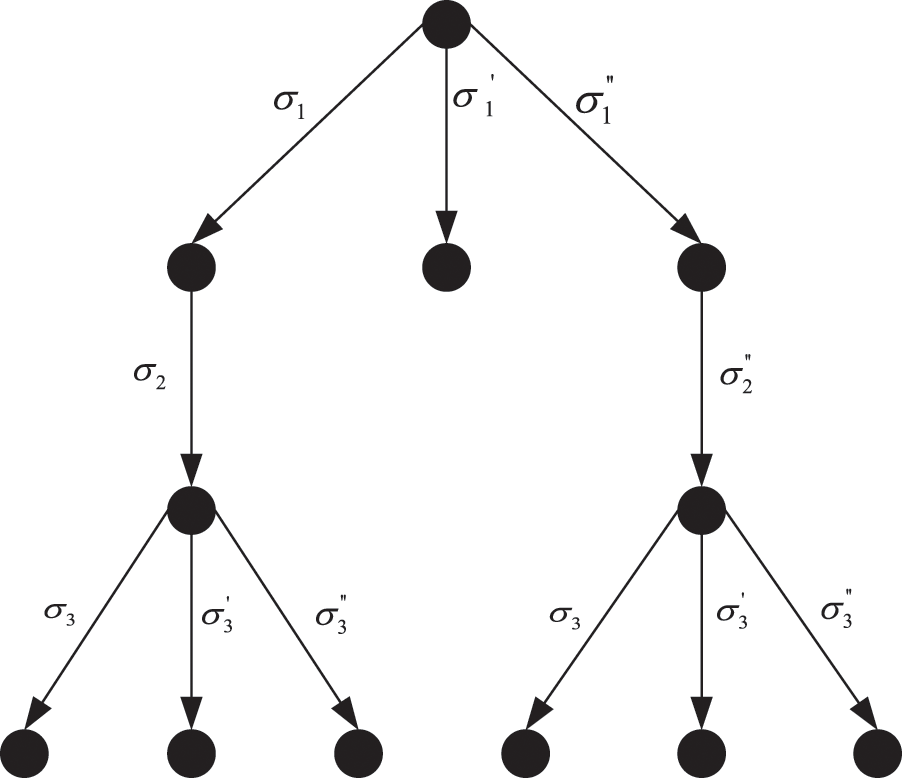
Figure 1: The protocol trace when the originator is a malicious participant

From the Fig. 1, it can be seen that when originator A is a malicious participant executing first message, there are three optional strategies σ1,σ1′,σ1″, where σ1 := sendA,{C,Z}KA−1, σ1′ := ε, σ1″ := sendA,{C,Z∗}KA−1. The meanings of the above symbols represent that A sends the message {C,Z}KA−1 correctly according to the protocol regulations, or does not send the message, or forges Z∗ and sends {C,Z∗}KA−1 to recipient B. Since the contract C is negotiated before the exchange between the two parties, and the validity of the contract C can be verified when the fair exchange protocol is executed, the malicious party can only choose to forge Z∗. When recipient B receives messages from originator A, because B is an honest participant, he will not make malicious behaviors such as sending false messages or exiting protocol in advance. Instead, B will send the signature of contract according to protocol regulations, σ2:=sendB,{C,Z}KB−1,{Z}KB−1, σ2:=sendB,{C,Z∗}KB−1,{Z∗}KB−1. When originator A performs step 3, it has three optional strategies σ3,σ3′,σ3″, where σ3:=sendA,N, σ3′:=ε, σ3″:=sendA,N∗. It represents that A sends a message N correctly, or A does not send message and exits protocol, or A sends a false message N∗. Next, we analyze whether the recipient fairness of honest participant B can be satisfied in protocol traces formed by malicious participant A choosing different strategies.

When the protocol trace is π=σ1, it means that A does not initiate the protocol, B will not execute any sending action at this time, and therefore the protocol satisfies fairness. When the protocol trace is π=σ1σ2σ3, both parties execute their own actions according to protocol regulations. At the end of the protocol, A gets the B’s commitment {{C,Z}KB−1,{Z}KB−1} to the contract, and B also gets the A’s commitment {{C,Z}KA−1,N} to the contract, and the protocol also satisfies fairness. When the protocol trace is π=σ1σ2σ3′ or π=σ1σ2σ3″, it indicates that A cheated B in step 3, and then A chose to exit the protocol or sent a fake message N∗ to B. If a response form A is not received within maximum waiting time or receiving false messages, B will choose to execute the resolve subprotocol. After receiving request messages from B, TTP decrypts Z={A,B,N}KTTP with private key KTTP−1, B can get N again with the help of TTP, and therefore the protocol still satisfies fairness.

When A chooses to cheat B in first message, that is, A chooses to execute the action σ1″:=sendA,{C,Z∗}KA−1. Then, originator A receives feedback from honest participant B, at this time, A has three alternative strategies σ3,σ3′,σ3″. Therefore, originator A has three possible protocol traces, that is, π=σ1″σ2σ3, π=σ1″σ2σ3′, π=σ1″σ2σ3″. Based on the formal model for analyzing fair exchange protocols proposed in this paper, we analyze whether the protocol satisfies sender fairness in this case. The goal to be proven is θ1, which is formalized as follows:

θ1≜Honest(B)∧DisHonet(A)[Exchange]BHas(B,{{C,Z}KA−1,N},te)∧⊥{{C,Z}KA−1,N}∨Has(B,{C,Z}KA−1,te)[Resolve]BHas(B,{{C,Z}KA−1,N},tr)(4)

Formula θ1 indicates that in the case where originator A is a malicious participant and recipient B is an honest participant, B has A’s commitment to the contract when the exchange subprotocol ends. Perhaps B receives only a part of the commitment {C,Z}KA−1 after the exchange subprotocol ends, and B receives N after executing the resolve subprotocol.

Proof: The detailed analysis process is shown below.

Table 3 shows the states of each participant in the exchange subprotocol when the originator is a malicious participant. The knowledge set and state change process of each participant are inferred using the proposed knowledge set axioms. For example, the axiom ORIG is applied in step (1), and the other steps are similar to step (1), where the symbol ∅ indicates that the message received by the protocol participant is empty, tcomA and tcomB indicate the local calculation time of A and B when processing messages (encryption, decryption and other operations), and ttrau indicates the time of message transmission in unreliable channels. According to the definition of unreliable channels [35], the transmission time of messages in this type of channel is uncertain. When a message is delayed or lost, the transmission time can be considered infinite, which makes it difficult to analyze. The intruder model proposed in this paper is used to convert the channel error into the ability of malicious participants, which simplified the analysis steps. This is also the advantage and characteristic of the formal model proposed in this paper compared with other analysis methods. From the above analysis results, it can be seen that under the premise of originator A being malicious, when the protocol trace is π=σ1″σ2σ3, even if recipient B receives false Z∗ in first message, it can correctly calculate Z by receiving N in third message, and its state is Suc. Therefore, the protocol satisfies fairness. When the protocol trace of originator A is π=σ1″σ2σ3′ or π=σ1″σ2σ3″, recipient B does not receive feedback from originator A, or cannot correctly calculate Z after receiving false N∗, and B is in the Abo state. The exchange subprotocol cannot satisfies the fairness. At this point, B chooses to execute the resolve subprotocol to restore fairness. Table 4 shows the detailed proof to analyze whether the resolve subprotocol can satisfy the fairness.

ttrar represents the time required for a message to be transmitted in resilient channel, and tB represents the maximum waiting time of recipient B. It can be seen from the above analysis that, after TTP receives the request from B, the validity of the request cannot be verified by decrypting Z∗ with the private key KTTP−1. For example, Z∗ can be randomly generated by malicious participant A and have the same length as message Z, or it can be generated in collusion with another participant A′, both of which make Decrypt(Z∗)≠(A,B,N) true. When the validity of Z∗ cannot be verified by TTP, he rejects the request of recipient B and stops executing the resolve subprotocol, and B will choose to terminate the protocol if the waiting time exceeds tB. Therefore, when the resolve subprotocol ends, recipient B does not receive a message N from originator A, and the protocol does not satisfy recipient fairness. A graphical representation of this attack using the strand space model is shown in Fig. 2.

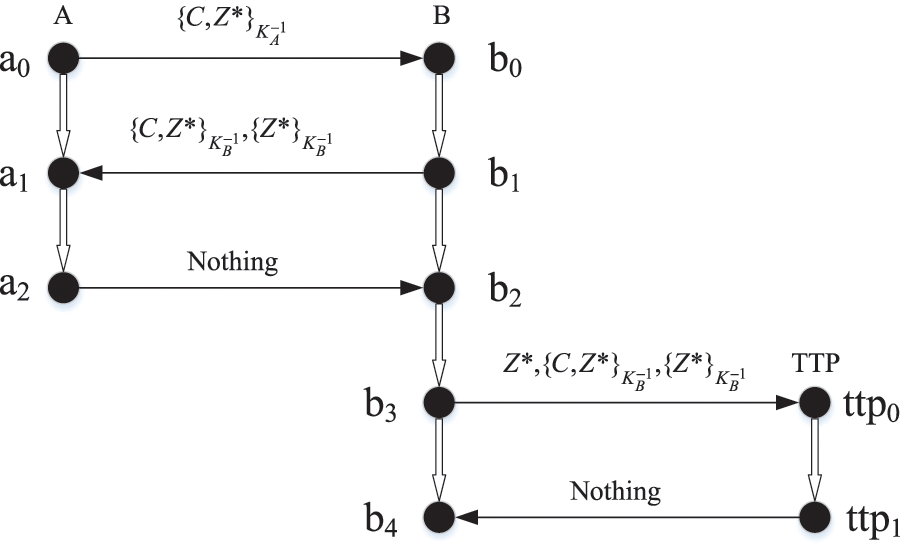
Figure 2: The attack on the Micali protocol when the originator is a malicious participant

The main reason for this attack is that in the exchange subprotocol, the participant identity is not bound to the message, and in the resolve subprotocol, TTP is unable to effectively handle disputes. To fix this vulnerability, an effective solution is to modify the messages in steps 1 and 2 to {A,B,TTP,C,Z}KA−1 and {A,B,TTP,C,Z}KB−1, respectively. Where Z={A,B,N,H(C)}KTTP indicates binding the contract with the participant identity, H(.) denotes one-way hash function. This improvement associates the contract with the identity of participants, which can prevent the contract from being tampered with and forged. In addition, the message in step 4 is modified to be {A,B,TTP,C,Z}KA−1 and {A,B,TTP,C,Z}KB−1, and B forwards messages received and sent in the exchange subprotocol to TTP, which can effectively prevent the protocol from interrupting due to the false message Z∗ not being verified by TTP. After TTP verifies the validity of the request, {A,B,TTP,C,Z}KA−1 and {A,B,TTP,C,Z}KB−1 are sent to A and B, respectively.

4.3 The Second Attack Scheme When the Recipient Is a Malicious Participant

On the other hand, assuming that the recipient is a malicious participant and the originator is an honest participant, the recipient’s goal is to get the originator’s commitment to the contract without paying their own commitment. When the recipient sends a message, there are also three optional strategies, that is, sending a message correctly, sending a false message for its own benefit, and not sending a message and terminating the protocol in advance, while the originator honestly performs the sending action according to the protocol regulations. Therefore, the protocol trace in the case where the recipient is a malicious participant is shown in Fig. 3.

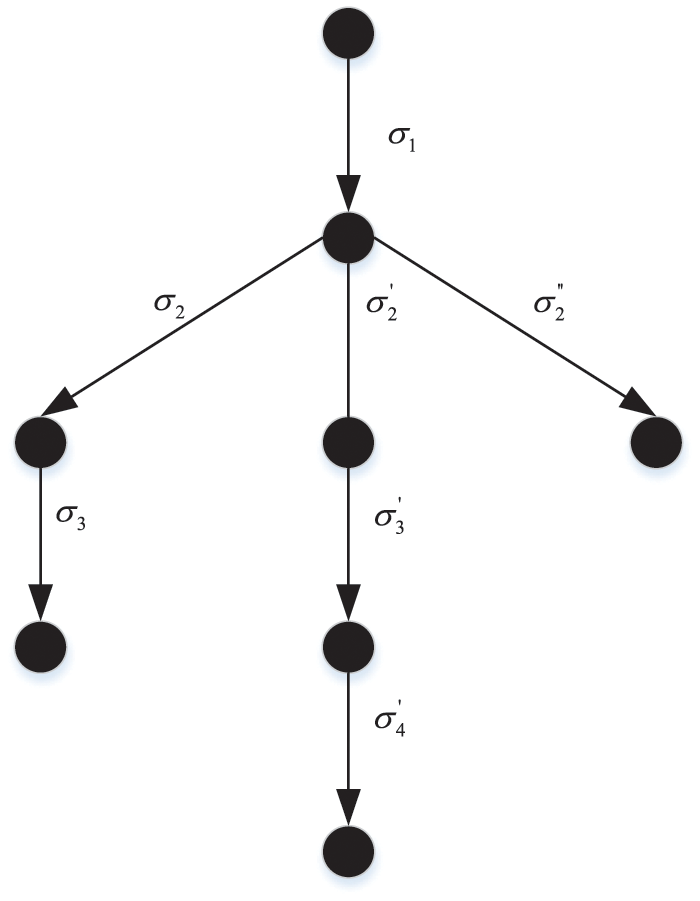
Figure 3: The protocol trace when the recipient is a malicious participant

From the protocol trace in Fig. 3, it can be seen that when malicious recipient B receives a request from originator A, there are three selectable strategies σ2σ2′σ2″, σ2:=sendB,{C,Z}KB−1,{Z}KB−1, σ2′:=ε, σ2″:=sendB,{C,Z∗}KB−1,{Z∗}KB−1, which means that B sends a message correctly accord to the protocol regulations, or does not send a message, or sends a false message. When the protocol trace is π=σ1σ2σ3, A receives the correct message {C,Z}KB−1,{Z}KB−1 from B, verifies the validity of C and Z, and executes the sending action σ3:=sendA,N. In this case, both parties obey the protocol strictly, and the protocol can satisfy fairness. When the protocol trace is σ1σ2″, after A receives B’s false message, A refuses to send message N to B and exits the fair exchange subprotocol because it cannot verify the validity of Z∗. B only receives a part of A’s commitment to contract C, and the fairness can still be satisfied. When the protocol trace is π=σ1σ2′σ3′σ4′, it means that A terminates and exits the exchange subprotocol after the waiting time exceeds tA because A has not received messages from B for a long time. At this point, B chooses to execute the resolve subprotocol in order to obtain another part of A’s commitment to contract C. Next, we analyze and infer whether the originator fairness of A can be satisfied when the protocol trace is π=σ1σ2′σ3′σ4′. That is, the goal we want to prove is θ2, which is formally expressed as:

θ2≜Honest(A)∧DisHonet(B)[Exchange]AHas(A,{{C,Z}KB−1,{Z}KB−1},te)∧⊥{{C,Z}KB−1,{Z}KB−1}(5)

The formula θ2 indicates that in the case where originator A is an honest participant and recipient B is a malicious participant, A has B’s commitment to the contract when the exchange subprotocol ends. Since this protocol does not include the resolve subprotocol initiated by A, it only considers whether A receives B’s commitment to the contract after the exchange subprotocol ends, but the malicious participant B can initiate the resolve subprotocol while executing the exchange subprotocol.

Proof: The specific proof process is as follows.

From the above analysis results in Table 5, it can be seen that when the resolve subprotocol ends, the status of malicious participant B is {N}∈ΓB∧ΘB=Suc, which means that B obtains A’s non-repudiation evidence of the contract and successfully ends the protocol. The status of honest participant A is {{C,Z}KB−1,{Z}KB−1}∉ΓB∧ΘA=Abo, which means that A has not obtained B’s non-repudiation evidence of the contract, and exits the protocol due to waiting time exceeding tA. Therefore, the protocol does not meet the originator fairness.

The attack against the protocol is described as follows: B maliciously terminates the protocol after receiving A’s request, and executes the resolve subprotocol after exceeding maximum waiting time tA. TTP verifies the validity of request from B, and then sends a message N to B. Therefore, B gets {C,Z}KA−1 and N without sending the contract signature {C,Z}KB−1,{Z}KB−1. Similarly, TTP sends a message {C,Z}KB−1,{Z}KB−1 to A, but A exits the protocol due to waiting time tA exceeding, which prevents A from receiving the message correctly. In the case that the recipient is a malicious participant and the originator is an honest participant, the recipient gets the expected contract signature but the originator does not, and the Micali protocol does not satisfy the originator fairness. The main reason for this attack is that the end time of the resolve subprotocol exceeded the waiting time tA, resulting in the termination of exchange subprotocol due to the timeout. In addition, A did not request TTP to verify the status of B. The attack scheme is shown in Fig. 4.

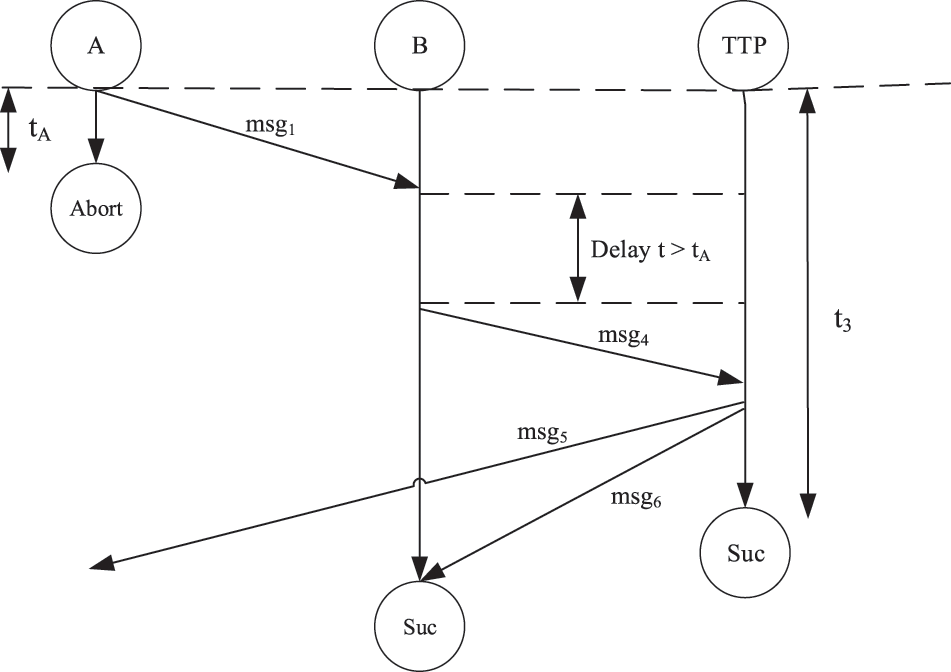
Figure 4: The Attack on the Micali protocol when the recipient is a malicious participant

In order to remedy this defect, a time parameter t4 (t4>t3) should be defined. After A sends msg1, the waiting time must be at least t4. During this period, if A does not receive the message {C,Z}KB−1,{Z}KB−1 correctly from B or TTP, then A must access TTP to obtain the termination status of the protocol. If B has executed the resolve subprotocol and the protocol status is Suc, then A will choose to continue waiting for reception or request TTP to resend {C,Z}KB−1,{Z}KB−1. If there is no relevant record (using the protocol session ID as the identifier), it indicates that B has not executed the resolve subprotocol and A terminates the protocol. Therefore, after executing the resolve subprotocol, TTP should also record and publish the termination status of the protocol, and cache {C,Z}KB−1,{Z}KB−1,N for protocol participants to query.

5  Conclusions and Future Works

In this research, we have presented a formal model for analyzing fair exchange protocols. A formal definition of fairness within the model is proposed, ensuring that the proposed notion of fairness accurately captures the essential requirements of fair exchange protocols. We have identified and improved upon the shortcomings of event logic by introducing the time factor into predicates and proposing the knowledge set axiom. As a result, the enhanced logic enables the representation of participant states and knowledge at different time points, facilitating the analysis and inference of participant knowledge. Furthermore, our model addresses the limitations of event logic by transferring channel errors to the intruder’s behaviors and categorizing protocol participants into honest and malicious entities, thus maximizing the intruder’s capabilities.

To demonstrate the efficacy of our model, we have conducted a thorough analysis of a representative fair exchange protocol. Through this example, we have outlined the step-by-step process of utilizing our formal model to analyze the protocol, uncovering fairness flaws within the protocol. Additionally, we have presented a comprehensive depiction of the protocol’s operation in the presence of an attack, offering valuable insights into the underlying causes of the attack. Finally, we have proposed corresponding solutions to address the identified vulnerabilities. Overall, our research contributes to the field of fair exchange protocols by providing a robust formal model and demonstrating its effectiveness through practical analysis and problem-solving.

Although this paper has achieved some accomplishments in the formal analysis of fair exchange protocols, there is still room for improvement and further research in several aspects. The following directions are identified for future work. Firstly, there is a need to delve into the implementation of automated reasoning techniques based on the event logic. Developing efficient algorithms and tools for automated analysis and verification can significantly enhance the practicality and applicability of the proposed model. Secondly, extending the methodology presented in this paper to multi-party fair exchange protocols is an intriguing and valuable research area. Multi-party scenarios introduce additional complexities and challenges, such as coordinating interactions among multiple participants and ensuring fairness among all involved parties. Investigating these aspects and providing solutions will contribute to a more comprehensive understanding of fair exchange protocols.

Acknowledgement: The authors would desire to express their appreciation to the editor and the three anonymous reviewers for useful guidance and helpful observations.

Funding Statement: This work was funded by the National Natural Science Foundation of China (Nos. 61562026, 61962020), Academic and Technical Leaders of Major Disciplines in Jiangxi Province (No. 20172BCB22015), Special Fund Project for Postgraduate Innovation in Jiangxi Province (No. YC2020-B1141), Jiangxi Provincial Natural Science Foundation (No. 20224ACB202006).

Author Contributions: Study conception and design: Ke Yang, Meihua Xiao; data collection: Ke Yang; analysis and interpretation of results: Ke Yang, Meihua Xiao, Zehuan Li; draft manuscript preparation: Ke Yang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Gao, Y., Wu, J. (2018). Efficient multi-party fair contract signing protocol based on blockchains. Journal of Cryptologic Research, 5(5), 556–567. https://doi.org/10.13868/j.cnki.jcr.000265 [Google Scholar] [CrossRef]

2. Lu, L., He, J., Tian, H. (2018). Fair contract signing protocols using blockchains. Journal of Cyber Security, 3(3), 1–7. https://doi.org/10.19363/j.cnki.cn10-1380/tn.2018.05.02 [Google Scholar] [CrossRef]

3. Wu, J., Gao, Y., Zhang, Z. (2018). A multi-party privacy preserving fair contract signing protocol based on blockchains. Journal of Cyber Security, 3(3), 8–16. https://doi.org/10.19363/j.cnki.cn10-1380/tn.2018.05.02 [Google Scholar] [CrossRef]

4. Guru, A., Mohanta, B. K., Mohapatra, H., Al-Turjman, F., Altrjman, C. et al. (2023). A survey on consensus protocols and attacks on blockchain technology. Applied Sciences, 13(4), 2604. https://doi.org/10.3390/app13042604 [Google Scholar] [CrossRef]

5. Hitesh, M., Subhashree, R., Subarna, P., Ranjan, K. (2020). Handling of man-in-the-middle attack in WSN through intrusion detection system. International Journal of Emerging Trends in Engineering Research, 8(5), 1503–1510. [Google Scholar]

6. Fenyvesi, É., Pintér, T. (2020). Characteristics of the hidden economy in Hungary before and after the regime change. Journal of Corporate Governance, Insurance, and Risk Management, 7(2), 1–13. https://doi.org/10.56578/jcgirm070201 [Google Scholar] [CrossRef]

7. Chawasemerwa, T., Taifa, I. W., Hartmann, D. (2018). Development of a doctor scheduling system: A constraint satisfaction and penalty minimisation scheduling model. International Journal of Research in Industrial Engineering, 7(4), 396–422. https://doi.org/10.22105/riej.2018.160257.1068 [Google Scholar] [CrossRef]

8. Gao, Y. X. (2013). Design and formal analysis of electronic commerce security protocols (Ph.D. Thesis). Southwest Jiaotong University, China. [Google Scholar]

9. Dolev, D., Yao, A. C. (1983). On the security of public key protocol. IEEE Transaction on Information Theory, 29(2), 198–208. https://doi.org/10.1109/TIT.1983.1056650 [Google Scholar] [CrossRef]

10. Wang, J., Zhan, N. J., Liu, Z. M., Feng, X. Y. (2019). Overview of formal methods. Journal of Software, 30(1), 33–61. https://doi.org/10.13328/j.cnki.jos.005652 [Google Scholar] [CrossRef]

11. Kulik, T., Dongol, B., Larsen, P. G. (2022). A survey of practical formal methods for security. Formal Aspect of Computing, 34(1), 1–39. https://doi.org/10.1145/3522582 [Google Scholar] [CrossRef]

12. Clarke, E. M., Henzinger, T. A., Veith, H., Bolem, R. (2018). Handbook of model checking. Berlin, Germany: Springer. https://link.springer.com/book/10.1007/978-3-319-10575-8 [Google Scholar]

13. Vitaly, S., Mitchell, J. C. (2000). Analysis of a fair exchange protocol. Proceedings of the Network and Distributed System Security Symposium, pp. 1–12. San Diego, California, USA. [Google Scholar]

14. Li, Q., Chen, Q. L. (2015). Formal verification of fair exchange protocols based on alternating-time temporal logic. Computer Engineering and Applications, 51(19), 32–26. [Google Scholar]

15. Yang, J. J., Shen, R. H., Chen, Q. L. (2018). Formal verification method for fair exchange protocol by channel credibility. Journal of Chinese Computer Systems, 39(2), 240–244. [Google Scholar]

16. Guo, X. (2022). Fairness analysis of extra-gain guilty of a non-repudiation protoco1. Frontiers of Information Technology & Electronic Engineering, 23(6), 893–908. https://doi.org/10.1631/FITEE.2100413 [Google Scholar] [CrossRef]

17. Blanchet, B. (2016). Modeling and verifying security protocols with the applied Pi calculus and ProVerif. Foundations and Trends in Privacy and Security, 1(1), 1–135. https://doi.org/10.1561/3300000004 [Google Scholar] [CrossRef]

18. Xiong, Y., Su, C., Huang, C. (2020). SmartVerif: Push the limit of automation capability of verifying security protocols by dynamic strategies. Proceedings of the 29th USENIX Security Symposium, pp. 253–270. Boston, MA, USA. [Google Scholar]

19. Cremers, C. (2008). The scyther tool: Verification, falsification, and analysis of security protocols. Proceedings of the 20th International Conference of Computer Aided Verification, pp. 414–418. Princeton, NJ, USA. [Google Scholar]

20. Meier, S., Schmidt, S., Cremers, C., Basin, D. (2013). The TAMARIN prover for the symbolic analysis of security protocols. Proceedings of the 25th International Conference of Computer Aided Verification, pp. 696–701. Saint Petersburg, Russia. [Google Scholar]

21. Datta, A. (2005). Security analysis of network protocols: Compositional reasoning and complexity-theoretic foundations (Ph.D. Thesis). Stanford University, USA. [Google Scholar]

22. Datta, A., Derek, A., Mitchell, J. C., Roy, A. (2007). Protocol composition logic (PCL). Electronic Notes in Theoretical Computer Science, 172(1), 311–358. https://doi.org/10.1016/j.entcs.2007.02.012 [Google Scholar] [CrossRef]

23. Backes, M., Datta, A., Derek, A., Mitchell, J. C., Turuani, M. (2006). Compositional analysis of contract-signing protocols. Theoretical Computer Science, 367(1), 33–56. https://doi.org/10.1016/j.tcs.2006.08.039 [Google Scholar] [CrossRef]

24. Gao, Y. X., Peng, D. Y., Yan, L. (2013). Analysis and improvement of a certified e-mail protocol. Journal of University of Electronic Science and Technology of China, 42(2), 300–305. https://doi.org/10.3969/j.issn.1001-0548.2013.02.023 [Google Scholar] [CrossRef]

25. Chen, M., Wu, K. G., Wu, C. F. (2011). Formal logic for fair exchange protocols. Journal of Software, 22(3), 509–521. https://doi.org/10.3724/SP.J.1001.2011.03945 [Google Scholar] [CrossRef]

26. Bickford, M., Xiao, M. H. (2009). Component specification using event classes. Proceedings of the International Symposium on Component-Based Software Engineering, pp. 140–155. Pennsylvania, USA. [Google Scholar]

27. Xiao, M. H., Bickford, M. (2009). Logic of events for proving security properties of protocols. Proceedings of the IEEE International Conference on WISM’09, pp. 122–128. Shanghai, China. [Google Scholar]

28. Xiao, M. H., Ma, C. L., Deng, C. Y. (2015). A novel approach to automatic security protocol analysis based on authentication event logic. Chinese Journal of Electronics, 24(1), 187–192. https://doi.org/10.1049/cje.2015.01.031 [Google Scholar] [CrossRef]

29. Xiao, M. H., Liu, X. Q., Li, Y. N. (2016). Security certification of three-party network protocols based on strong authentication theory. Journal of Frontiers of Computer Science and Technology, 10(12), 1701–1710. https://doi.org/10.3778/j.issn.1673-9418.1607032 [Google Scholar] [CrossRef]

30. Cremers, C. (2008). On the protocol composition logic PCL. Proceedings of the 2008 ACM Symposium on Information, Computer and Communications Security, pp. 66–76. Tokyo, Japan. [Google Scholar]

31. Zhong, X. M., Xiao, M. H., Zhang, T. (2022). Proving mutual authentication property of RCIA protocol in RFID based on logic of events. Chinese Journal of Electronics, 33(1), 79–88. [Google Scholar]

32. Song, J. W., Xiao, M. H., Zhang, T. (2021). Proving authentication property of PUF-based mutual authentication protocol based on logic of events. Soft Computing, 26(2), 841–852. https://doi.org/10.1007/s00500-021-06163-9 [Google Scholar] [CrossRef]

33. Xiao, M. H., Li, Y. N., Song, J. W. (2019). Security analysis of authentication protocol of WMN client and LTCA based on logic of events. Journal of Computer Research and Development, 56(6), 1275–1289. [Google Scholar]

34. Micali, S. (2003). Simple and fast optimistic protocols for fair electronic exchange. Proceedings of 22nd Annual Symposium on Principles of Distributed Computing, pp. 12–19. Boston, Massachusetts, USA. [Google Scholar]

35. Alotaibi, A., Aldabbas, H. (2012). A review of fair exchange protocols. International Journal of Computer Networks & Communications, 4(4), 307–319. https://doi.org/10.5121/ijcnc.2012.4420 [Google Scholar] [CrossRef]