 Open Access
Open Access
ARTICLE
An Improved JSO and Its Application in Spreader Optimization of Large Span Corridor Bridge
1 Fujian Key Laboratory of Digital Simulations for Coastal Civil Engineering, School of Architecture and Civil Engineering, Xiamen University, Xiamen, 361005, China
2 Xiamen Transportation Infrastructure Intelligent Management and Maintenance Engineering Technology Research Center, Xiamen, 361005, China
3 Fuzhou Company of China Communications Construction Co., Ltd., Fuzhou, 350005, China
* Corresponding Authors: Xinye Wu. Email: ; Yixin Hu. Email:
Computer Modeling in Engineering & Sciences 2024, 138(3), 2357-2382. https://doi.org/10.32604/cmes.2023.031118
Received 15 May 2023; Accepted 02 August 2023; Issue published 15 December 2023
Abstract
In this paper, given the shortcomings of jellyfish search algorithm with low search ability in the early stage and easy to fall into local optimal solution, this paper introduces adaptive weight function and elite strategy, improving the global search scope in the early stage and the ability to refine the local development in the later stage. In the numerical study, the benchmark problem of dimensional optimization with a 10-bar truss structure and simultaneous dimensional shape optimization with a 15-bar truss structure is adopted, and the corresponding penalty method is used for constraint treatment. The test results show that the improved jellyfish search algorithm can provide better truss sections as well as weights. Because when the steel main truss of the large-span covered bridge is lifted, the site is limited and the large lifting equipment cannot enter the site, and the original structure does not meet the problem of stress concentration and large deformation of the bolt group, so the spreader is used to lift, and the improved jellyfish search algorithm is introduced into the design optimization of the spreader. The results show that the improved jellyfish algorithm can efficiently and accurately find out the optimal shape and weight of the spreader, and through Midas Civil simulation, the spreader used can meet the requirements of weight and safety.Graphic Abstract
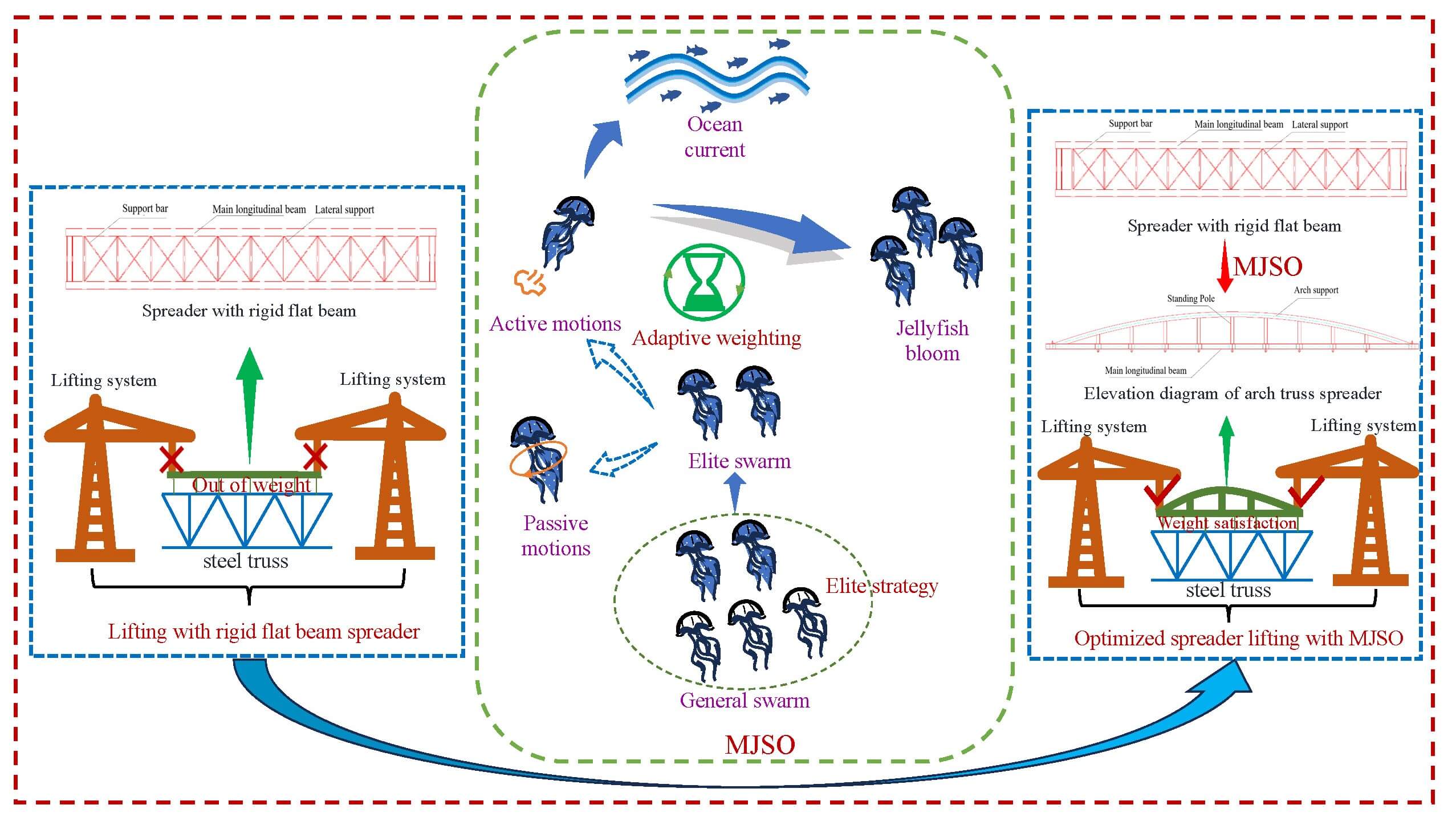
Keywords
In recent years, the emergence of various lifting equipment, construction site various installation and lifting technology is becoming more and more mature, but in the face of the problem of lifting the superstructure of the large-span covered bridge, due to the limitation of large-scale lifting equipment, coupled with the influence of the river bank, it is difficult to build a lifting structure, and can only consider the use of jacks for lifting on the original structure. At this point it is about whether the weight of the structure to be lifted can meet the lifting limits of the jack and whether the force can meet the safety requirements.
Nowadays, the continuous in-depth research of intelligent algorithms by scholars from all over the world has introduced various algorithms into the weight, shape and topology optimization of structures, and solved many engineering problems.
Shi et al. [1] proposed a new hybrid algorithm, namely the improved plant growth simulation algorithm and the genetic mixing algorithm, and the optimization efficiency and effect of PGSA-GA are better than other algorithms and methods through the case studies of typical trusses and single-layer lattice shells; Kim et al. [2] proposed an efficient two-stage optimization program based on force method to correctly identify the location and extent of multiple damage in planar and space truss structures; Viet-Hung et al. [3] developed a robust method for dimensional optimization (RBDO) of truss structures by integrating nonlinear inelastic analysis, structural reliability analysis methods, and optimization methods based on differential evolution (DE) algorithms. Azad et al. [4] solved the problem of simultaneous optimization of dimensions and geometry of dynamically excited steel truss structures. Using the well-known Big Bang-Big Crunch algorithm, the minimum weight design of steel truss is carried out under periodic and a periodic excitation; Grzywinski et al. [5] proposed a novel and effective Jaya optimization algorithm for optimization the best quality of the supporting dome structure with natural frequency constraints; Habibi et al. [6] considered the geometric nonlinearity problem using the total Lagrangian formula, and obtain a nonlinear solution by introducing and minimizing the objective function constrained by the displacement type; Artar et al. [7] studied the optimal design of steel space truss towers under seismic load by using the Jaya optimization algorithm; Kaveh et al. [8] proposed a new Gaussian diagram-based Chaotic Firefly Algorithm (CGFA) for structural optimization problems. Wong et al. [9] investigated a new meta-heuristic algorithm called symbiotic organism search (SOS) for component size optimization of relatively large steel trusses; Ha et al. [10] developed an effective method to optimize nonlinear steel frames under several load combinations, considering the panel area for the first time in the optimization design. The double-layer board is designed to prevent shear deformation of the panel area; Gholizadeh et al. [11] proposed a new and efficient meta-heuristic, the Newtonian meta-heuristic (NMA). Seismic design optimization for steel bending moment frames based on discrete properties; Es-Haghi et al. [12] proposed an asymmetric genetic algorithm (AGA) to solve the optimization problem of steel frames, and optimized a 15-layer three-layer steel flat frame through AGA, AGA can reduce the analysis time, the number of analyses and the total weight of the structure; Truong et al. [13] proposed a gradient tree boosting (GTB) algorithm for the safety assessment of steel trusses, which was first generated using advanced analysis methods to consider the geometry of the structure and the non-linearity of the material. Then, four GTB models are proposed to predict the ultimate bearing capacity and displacement of the structure for safety evaluation of strength and suitability. Zhou et al. [14] proposed a hybrid strategy based on butterfly optimization algorithm (BOA) and differential evolution algorithm (DE), and experimental tests of 8-layer shear steel frame structure in the laboratory to evaluate its performance. Numerical and experimental results show that the proposed HBODEA is more powerful in detecting the stiffness reduction of limited sensors and contamination measurement results. Bigham et al. [15] proposed an improved electrical search algorithm to solve the topology optimization problem of nonlinear single-layer domes; Gholizadeh et al. [16] used the proposed algorithm to design a 6-layer and 12-layer steel bending moment frame and evaluate it. The optimal design of seismic performance and collapse capacity used the failure index and incremental dynamic analysis, and evaluated their seismic failure cost and adjusted collapse allowance ratio; Artar et al. [17] proposed teaching-based optimization (TLBO) and biogeography-based optimization (BBO) algorithms to study the optimal discrete size design of steel truss steel bridges to minimize structural weight; Azad et al. [18] proposed a computationally efficient multi-stage guided random search algorithm for the optimization and standardization of real-size free steel double-layer grids. Carbas et al. [19] investigated the design of the optimal discrete dimensions of a steel plane truss containing the effects of seismic loads by teaching-based optimization (TLBO) and biogeography-based optimization (BBO) meta-heuristics; In order to obtain better vibration response data, based on the improved particle swarm optimization algorithm, Zhao et al. [20] proposed an optimal arrangement scheme of measurement points of long-span steel beams to improve the accuracy of the modal test results of long-span steel beams. Ojha et al. [21] adaptive search space decomposition method and a new formula based on gradient-free optimization for the anterior and post-buckling analysis of spatial truss structures. Eser et al. [22] proposed a volumetric controlled search (CCS) algorithm that is capable of handling dimensional optimization of particularly large steel frames under multi-strength and multi-displacement constraints. Sang-To et al. [23] presented a new shrimp tiger associative search algorithm (SGA) for efficient optimization of truss-based structural health monitoring (SHM). SGA can get rid of local optimization better and converge faster than the population-based algorithm. Azizi et al. [24] proposed a novel metaheuristic algorithm—Energy Valley Optimizer (EVO), and it can provide competitive and outstanding results in dealing with complex benchmarks and real-world problems. Kadkhoda et al. [25] proposed the coronavirus metamorphosis optimization algorithm (CMOA), and the CMOA is applied to three engineering problems including optimal design of a welded beam, a three-bar truss and a pressure vessel, showing its high potential in solving such practical problems and effectiveness in finding global optima.
This paper presents a modified variant of a recently introduced natural heuristic algorithm, the Jellyfish Search optimizer [26]. Two modifications are proposed in the basic JSO to form the modified variant, which is applied to the optimization of the main truss lifting spreader of the long span gallery bridge.
Jellyfish Search optimizer (JSO). The algorithm proposed by Chou et al. [26] in 2020, and the algorithm mainly simulates the characteristics of jellyfish drifting with ocean currents and the internal motion of jellyfish population, and introduces a time control mechanism. Compared with other bionic algorithms, this algorithm exhibits superior computational results.
Any meta-heuristic algorithm has two main stages: early exploration to enrich population diversity; later development, strengthen the approximation optimal solution. The JSO algorithm is also developed based on these two stages.
Before designing the algorithm, Chou et al. assumed the motion law of jellyfish as follows:
1. Jellyfish move in two ways, either with ocean currents or within populations, and the time control mechanism controls the transition between the two motions.
2. Jellyfish are more easily attracted to places with more food in the ocean.
The current contains a lot of nutrients, and jellyfish are attracted to it. The direction of the current is the convergence trend of the algorithm, which is defined as the average vector position of each jellyfish to the current best jellyfish position:
Ocean currents are calculated as follows:
So the position update formula for each jellyfish as follows:
The movement of jellyfish is mainly divided into passive movement (type A) and active movement (type B). Initially, when the jellyfish colony was first formed, most of the jellyfish only followed the movement of the population, so they showed A-type movement. Over time, jellyfish gradually exert their own initiative, so they increasingly exhibit B-type movements. Type A locomotion is the movement of a jellyfish around its own position:
where
When a certain section of the ocean current contains abundant food, jellyfish gather in groups to feed each other. When the temperature or wind changes the current, the jellyfish swarm moves towards another current, forming another jellyfish swarm. Therefore, Chou et al. introduced a time control mechanism to simulate this passive to active process. To regulate the movement of jellyfish following ocean currents and moving within the jellyfish swarm, time control mechanisms include the time control function
When
The JSO algorithm introduces a logistic chaos mapping as the initialization:
The JSO algorithm takes into account that the earth is circular, so a boundary buffering strategy is adopted:
Through the analysis process of JSO algorithm, it can be seen that the algorithm has good robustness, and the buffer strategy of the boundary avoids the situation that individuals concentrate on searching the domain boundary, thereby improving the population diversity.
3 Modified the Jellyfish Search Algorithm (MJSO)
For the JSO algorithm in the early stage, it relies on determining the position of the optimal jellyfish, and the best position of the jellyfish generated at this time is still random, and the position update of the jellyfish is determined by the direction of the ocean current, and the ocean current is determined by the average of the random position generated by the jellyfish, which is easy to cause the global search ability of the algorithm in the early stage to be relatively low, so the elite strategy is introduced. After the population is initialized, the set of best positions of jellyfish is determined, and for the previous global search stage, the average value of the best position set of jellyfish (
Eq. (16) indicates that
Elite is the set of the best individuals of a certain number of jellyfish in the population.
In addition to the above elite strategy, aiming at the shortcomings of the overall process of JSO algorithm that the search range is not large in the early stage and the development is easy to fall into local optimization in the later stage, the adaptive weight function is introduced to improve the global search ability and calculation time, and the improved jellyfish algorithm is formed.
Adaptive weight inertia weight is a very important parameter in the particle swarm, when the inertia weight is large, the algorithm search ability is strong, can search a larger area, when the inertia weight is small, the algorithm later search ability is strong, can be finely searched around the optimal solution.
Introducing the particle swarm algorithm inertia weights and modifying them accordingly to obtain the adaptive weight function
where
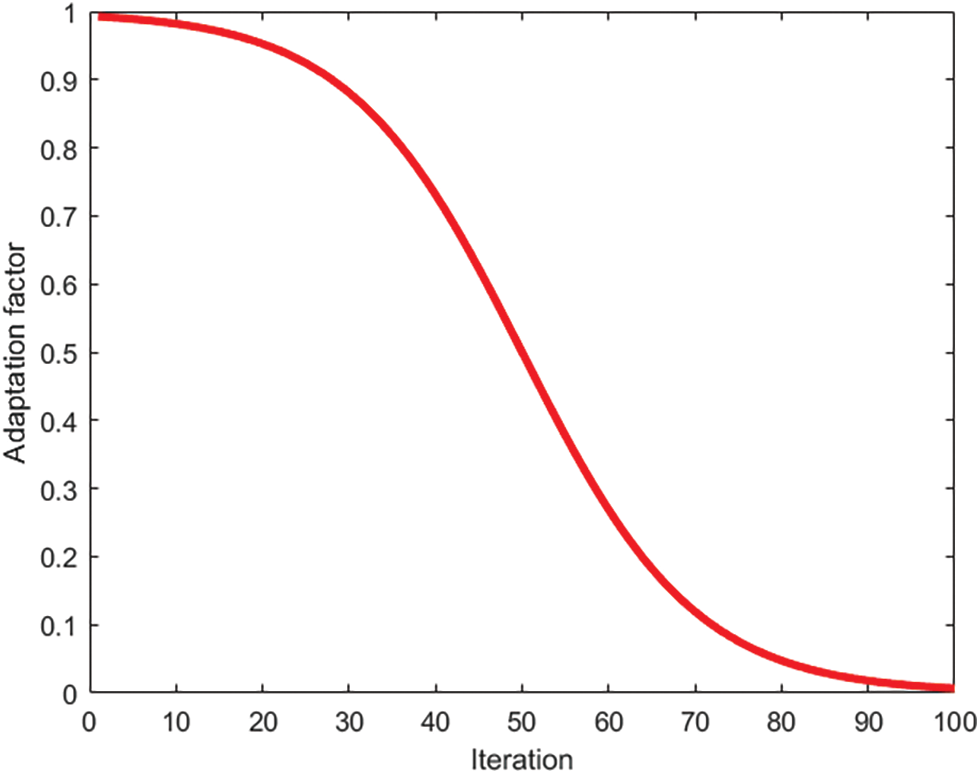
Figure 1: Adaptive function
The improved jellyfish update formula is as follows:
The early stage follows the ocean current search stage:
A-type movement development stage:
The MJSO pseudo-code is as follows:

The MJSO algorithm pseudo-code can be seen that the proposed MJSO algorithm does not contain any additional loops. Only some modifications have been made to the search formula. Therefore, the time complexity of MJSO (O = N × d × Maxit) is the same as the standard JSO algorithm.
3.3 Algorithm Performance Testing
The MJSO algorithm and JSO algorithm were compared with the JSO algorithm for benchmark function testing, and 50 functions described in Table 1 of the literature [26], including separate, non-separable, single-modal and multi-modal functions, were tested with MATLAB R2021b, and the computer processor was: AMD Ryzen7 4800H with Radeon Graphics 2.90 GHz. The initial population size is 50, the number of iterations is 10,000, and 30 cycles are performed, taking the mean, standard deviation, and average time to each optimization. Table 2 shows the calculation results.
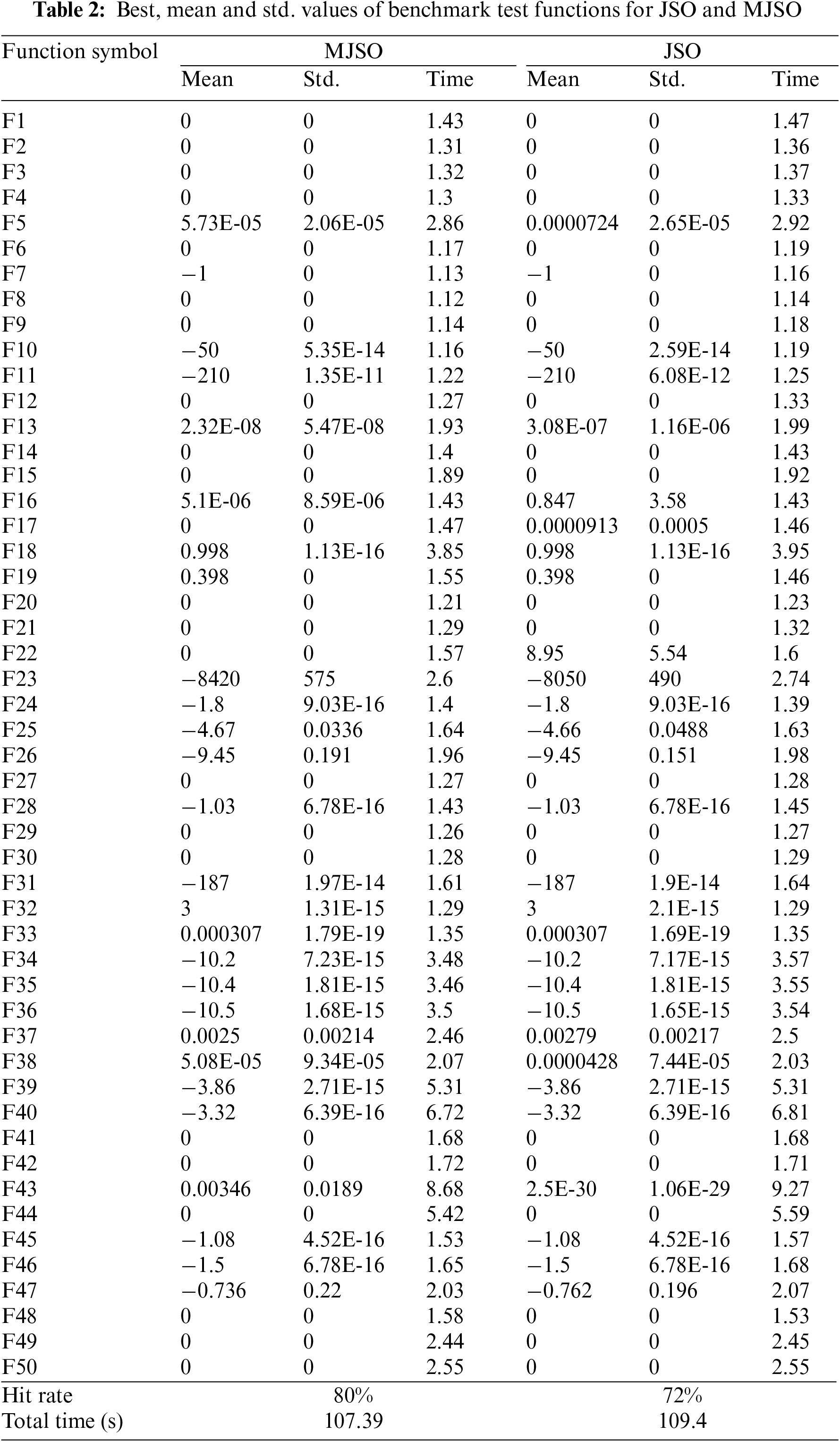
According to the optimal solution hit rate, the MJSO algorithm has a hit rate of 80% for the optimal solution calculated for 50 benchmark functions, and the JSO algorithm has a hit rate of 72%, which shows that the optimal solution optimization ability of the MJSO algorithm is better than that of the JSO algorithm. The time spent by the two algorithms is approximately the same, which also indicates that there is no increase in time complexity of the improved MJSO algorithm. The errors of both algorithms are approximately the same, and the original literature has verified that the robustness test is more stable than other metaheuristic algorithms.
It can be seen from Fig. 2 that the MJSO algorithm is optimized for unimodal separable (F3), unimodal inseparable function (F8), multimodal separable function (F23) and multimodal inseparable function (F42). The number of iterations required to converge the optimal solution is less than that of the JSO algorithm, and the overall image shows that the local search for the optimal solution of the MJSO algorithm is stronger, which can avoid falling into the local optimum.
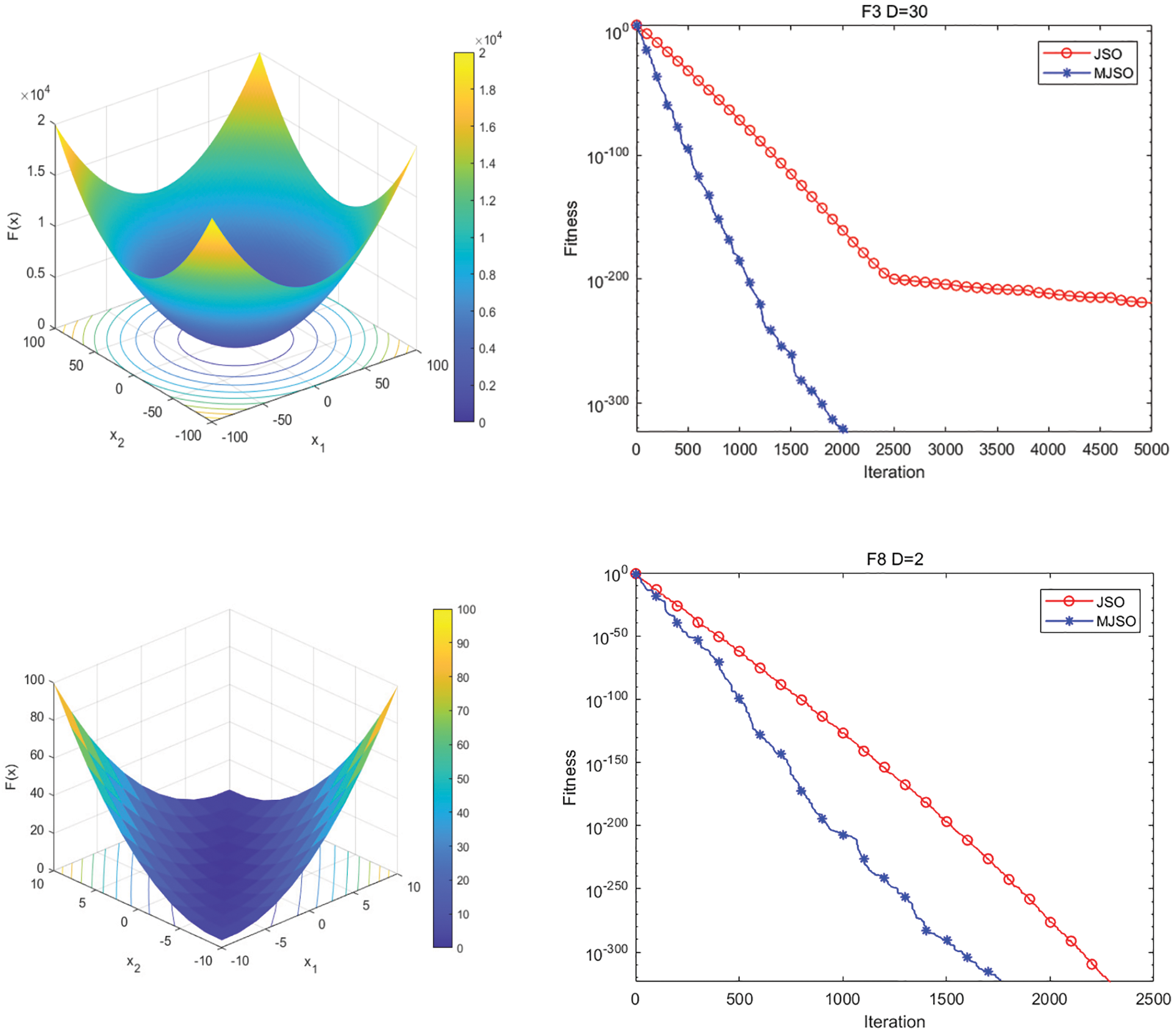
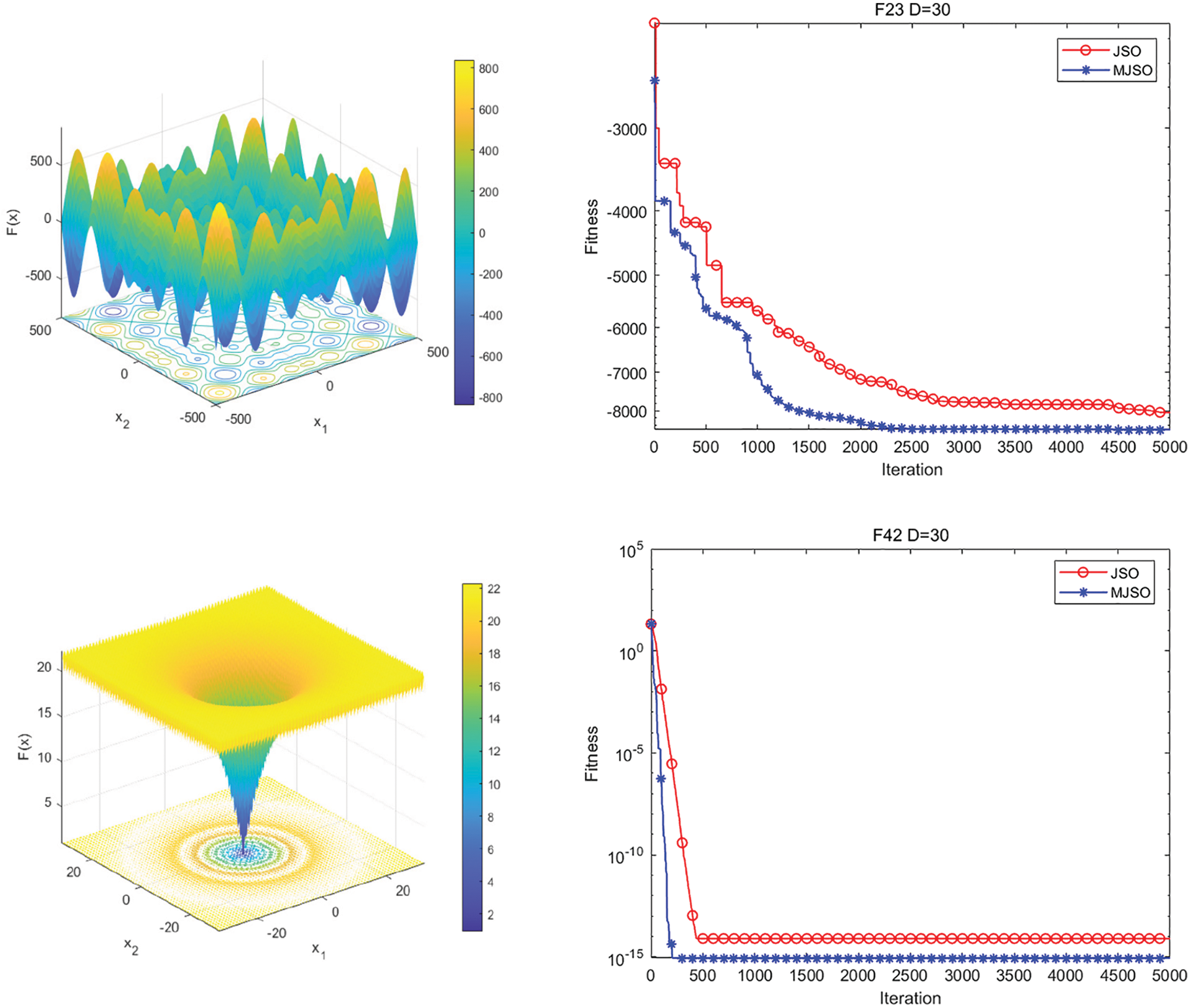
Figure 2: MJSO and JSO algorithm convergence comparison
3.3.2 10-Bar Truss Weight Optimization Test
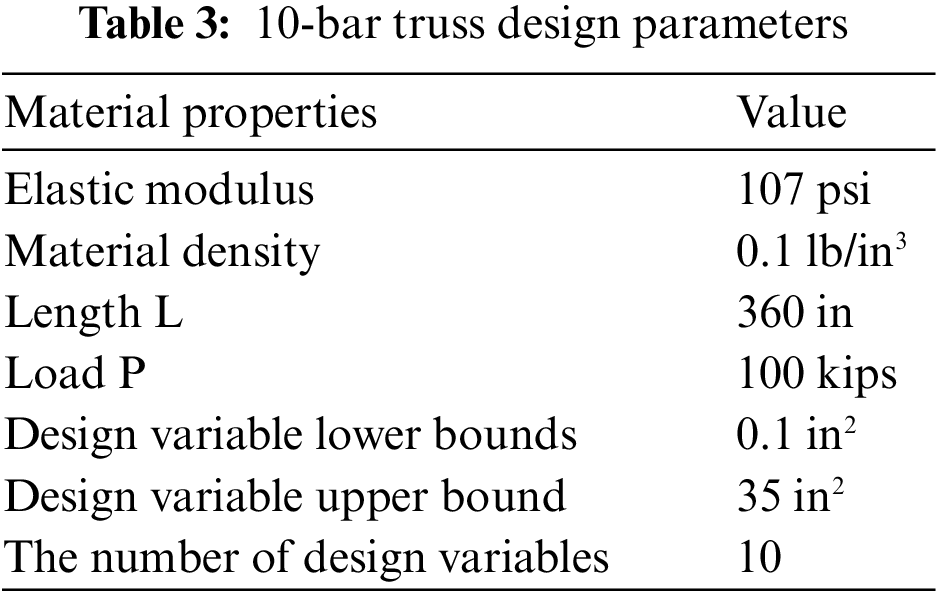
Fig. 3 shows a 10-pole planar truss structure. The design variable is the cross-sectional area of the 10 truss elements. Table 3 lists the upper and lower bounds of material properties, load conditions, and design variables. The constraint is the allowable stress and allowable displacement of the planar truss. The maximum allowable displacement of each node in the ±x and ±y directions is equal to 2 in, while the maximum allowable stress for tension and compression is 25 ksi, with the goal of minimizing the weight of the structure under the specified constraints.
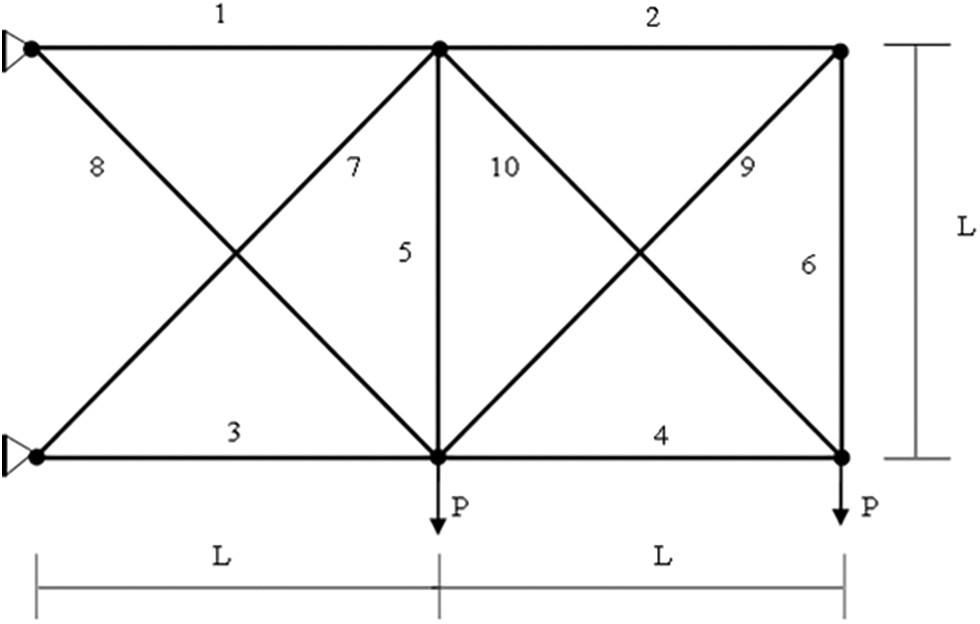
Figure 3: Diagram of a 10-bar truss
The average evolution of the objective function using 1000 iterations of the 10-bar truss with an initial population of 50 for MJSO, JSO, PSO, GWO and ACOR, respectively, as the number of iteration steps increases, is shown in Fig. 4, from which it can be seen that MJSO continuously provides better values than others, enabling it to provide a better adaptation of the results at each stage of execution.
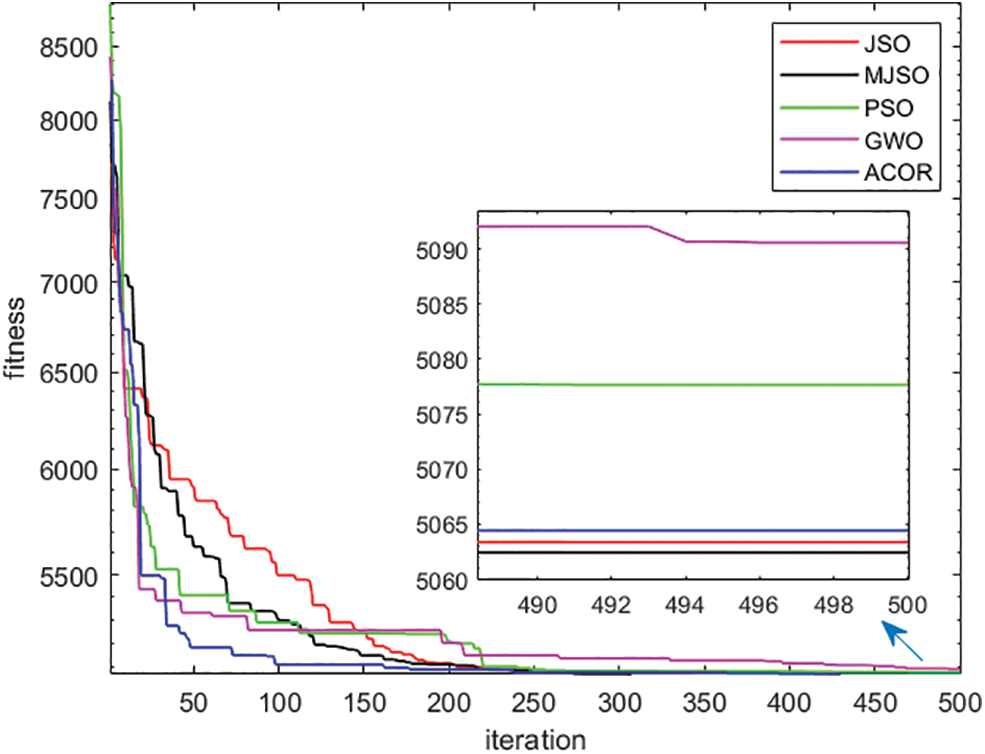
Figure 4: MJSO, JSO, PSO, GWO and ACOR the convergence process of the 10-bar truss
MJSO, JSO, PSO, GWO and ACOR algorithms were optimized for each unit section of the 10-bar truss, respectively, for 30 cycles, and the results of section optimization as well as the optimal weight optimum, average value and standard deviation after optimization are shown in Table 4.
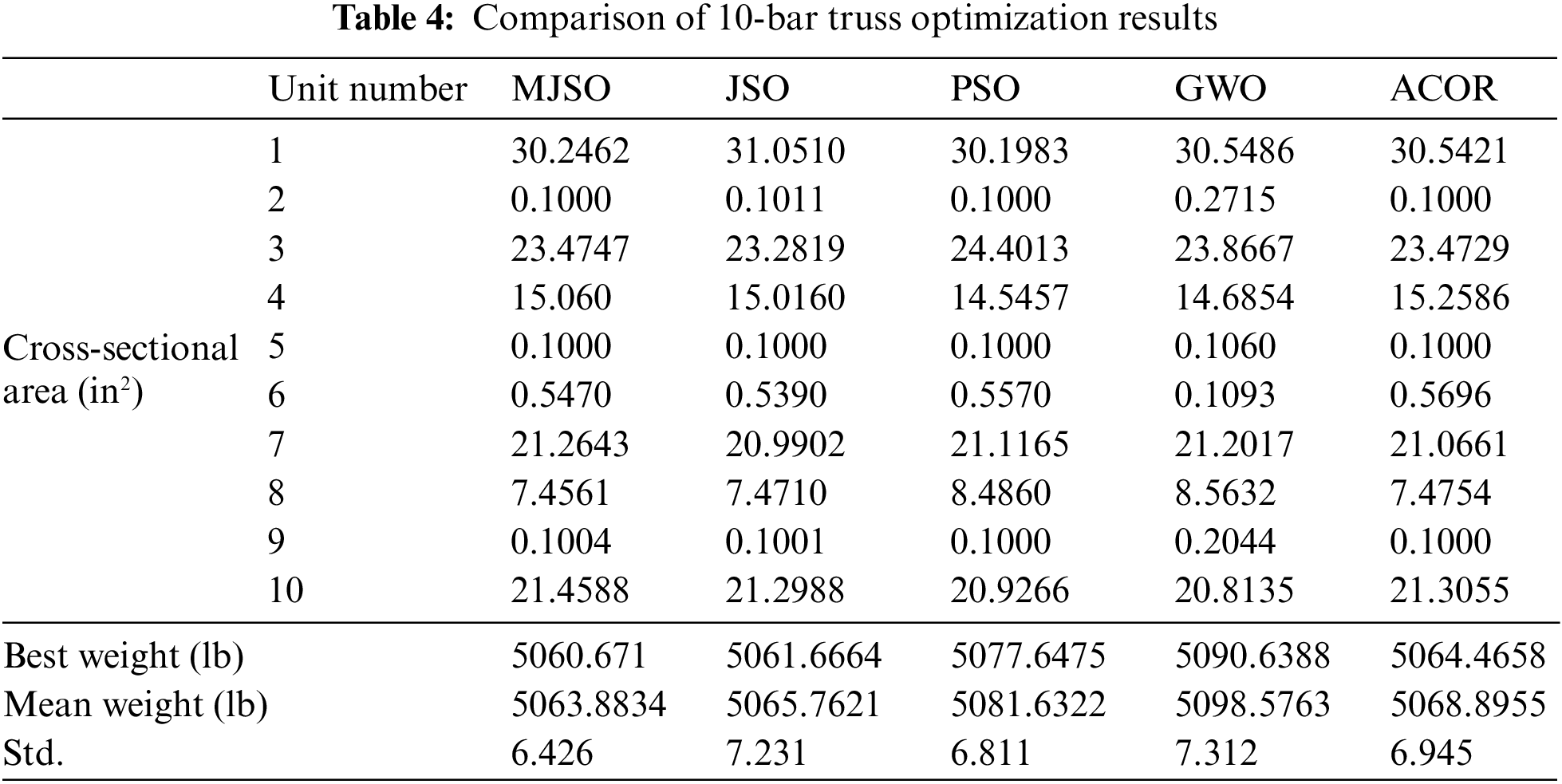
It can be seen from the above table that the optimization results of 10-bar truss lightweight are superior and more robust than those of others.
3.3.3 15-Bar Truss Weight and Shape Optimization
Fig. 5 shows the structure of a 15-bar truss. The design variables for this problem are 15 unit cross-sectional areas (A1 to A15) and 8 nodal shape variables (X5 = X6, X3 = X4, Y1, Y2, Y3, Y4, Y5, Y6). Table 5 shows the material properties, loading conditions and discrete boundaries for cross-sectional area and continuous boundaries for shape variables. The constraint is the allowable stress of the plane truss with a maximum stress constraint of ±172.3689 MPa. No displacement limit is assumed. The objective is to optimize the shape and minimize the weight of the structure under the specified constraints.
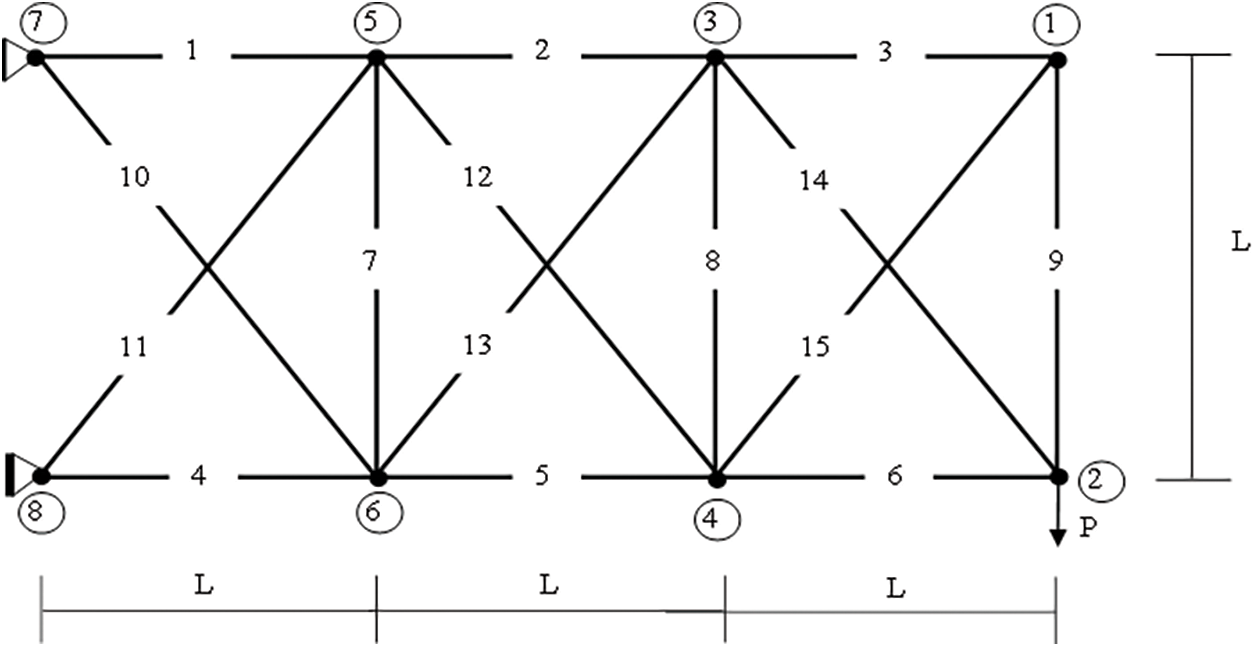
Figure 5: 15-bar truss

The convergence process of the objective function is shown in Fig. 6 as the number of iterations increases using 100 iterations of the 15-bar truss with an initial population of 50 by MJSO and JSO, respectively, from which it can be seen that the MJSO algorithm is clearly superior to the JSO algorithm in terms of search capability after the inclusion of the elite strategy in the early stage, and the entire convergence process MJSO algorithm shows superior exploration capability than the JSO algorithm.
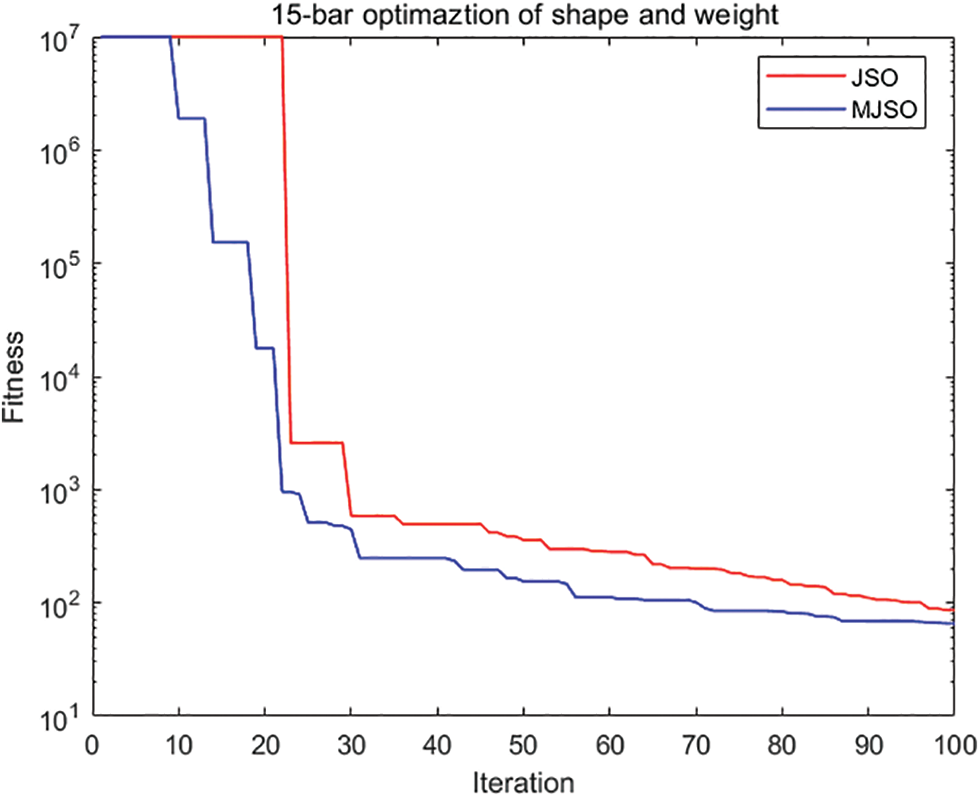
Figure 6: MJSO and JSO optimized the convergence process of 15-bar truss
Figs. 7 and 8 show the optimized structural shape of the truss after 100 iterations of the MJSO algorithm and the JSO algorithm. MJSO optimization is less than the original structure of two bars, JSO optimized only one bar.
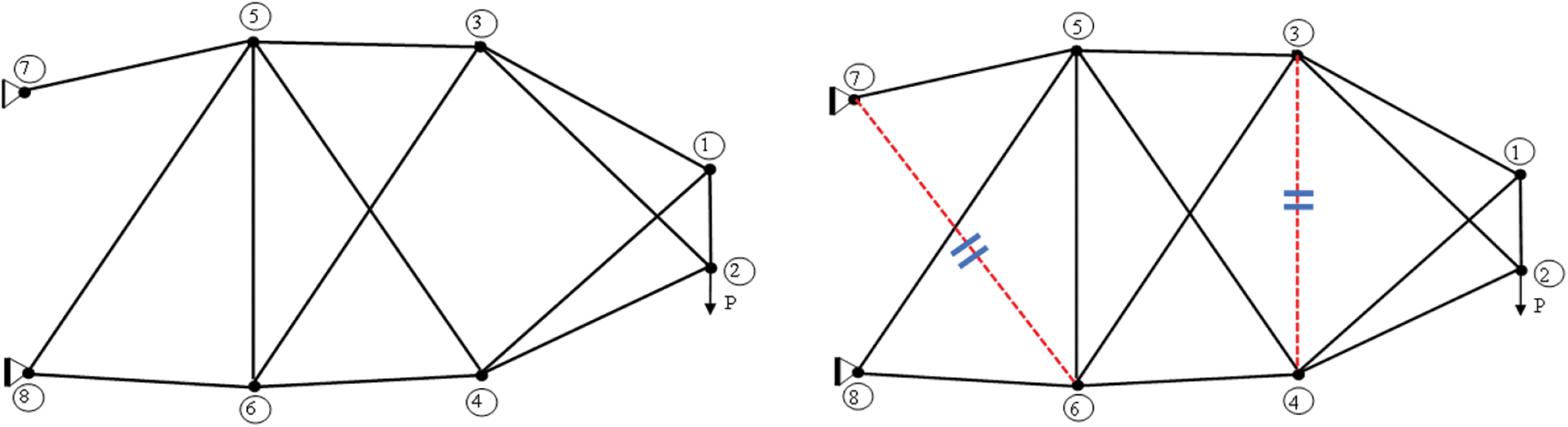
Figure 7: MJSO optimization results
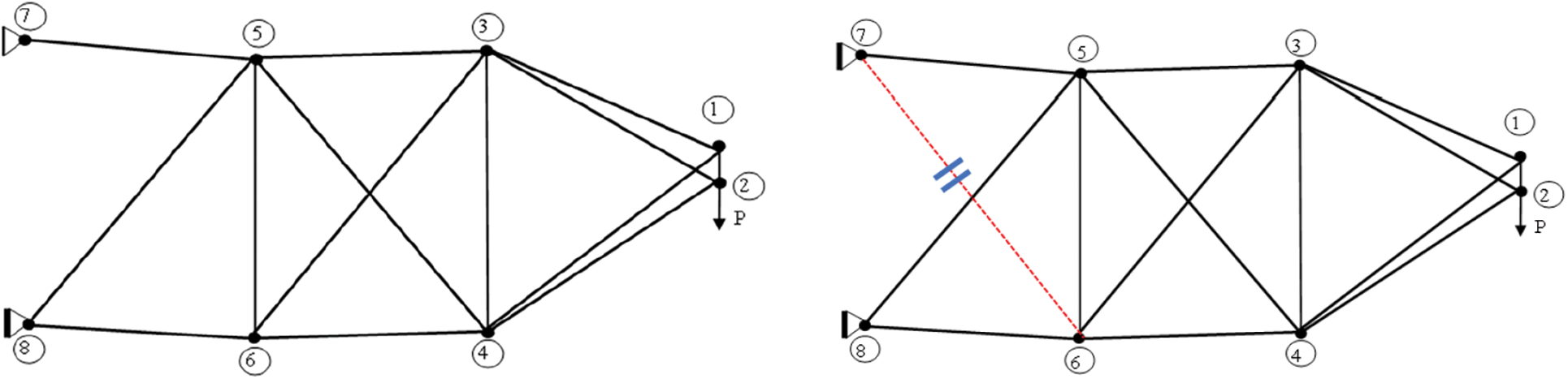
Figure 8: JSO optimization results
The MJSO and JSO algorithms were optimized for each unit section of the 15-bar truss, respectively, for 30 cycles, and the results of section optimization as well as the optimal weight optimum, average value and standard deviation after optimization are shown in Table 6.

From the above table, it can be seen that for the optimization of the 15-bar truss, the MJSO algorithm has one less string bar than the JSO algorithm when the constraints are satisfied, and the optimized weight average is 26% less than the JSO algorithm weight, which is more superior, and the overall standard deviation is smaller and more robust than the JSO algorithm.
4 Optimization of Steel Truss Lifting Spreader for Long-Span Covered Bridges
The project is a 54 m span corridor bridge with steel truss as the main structure. In the steel truss lifting stage, due to the site limitation, large lifting equipment cannot enter the site, so the project can only set up lifting brackets on the structure of Guanjiang Pavilion on both sides and use 4 lifting power of 70 tons jack to lift the steel truss.
The steel truss beam model is established according to the material and cross section provided by the design, the hoisting bracket adopts the beam unit, the steel beam adopts the truss unit, the wire rope adopts the cable unit for simulation, and the vertical rigid frame of the hoisting bracket and Guanjiang Pavilion adopts the rigid connection. Midas civil was used for the lifting analysis without considering the effect of live load.
The jack is directly connected to the upper lugs of the steel joist through the steel strand to lift the steel joist with the structure arrangement as shown in the Fig. 9.
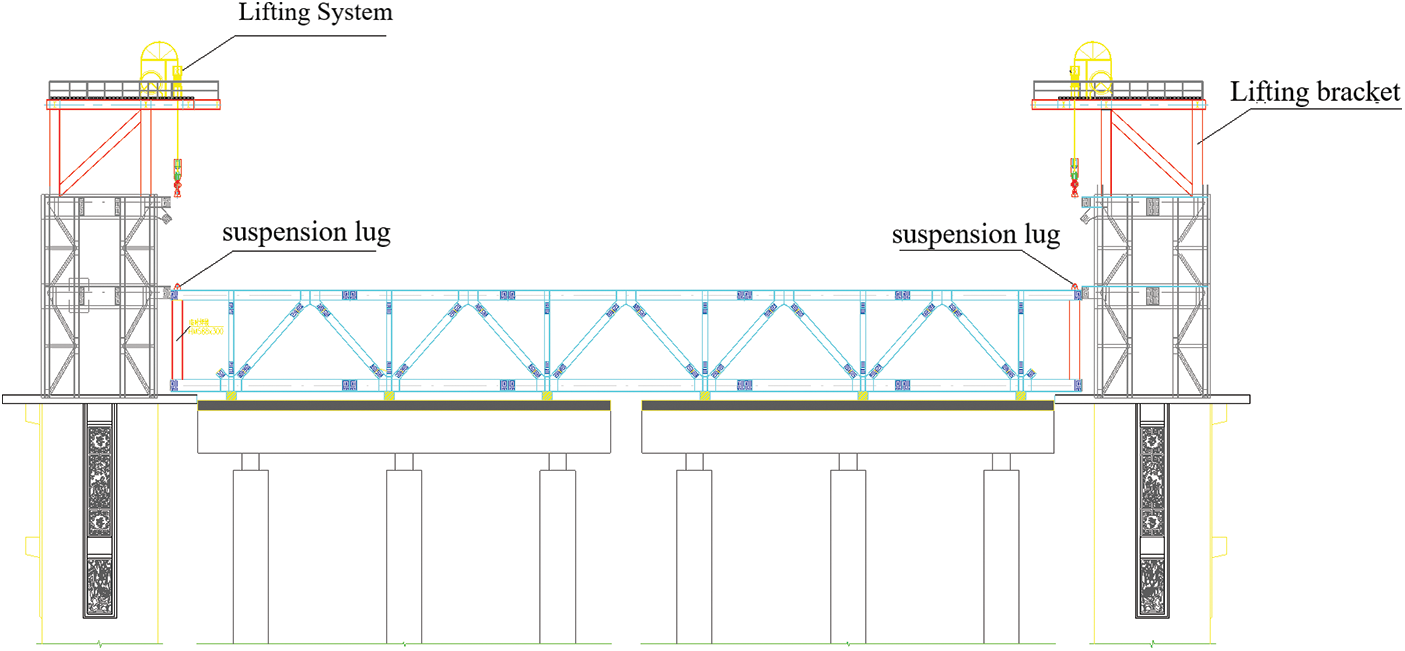
Figure 9: Lifting without spreader
The structure is simulated by Midas Civil to analyze the construction process of the steel truss as a whole. The calculation shows that the maximum stress of the steel main truss of the spreading gallery is 203 MPa < 300 MPa, which meets the structural stress limit; the maximum deflection is 37.6 mm < L/400 = 135 mm, which meets the deflection limit. The relative displacement of adjacent section beam is 33 mm > 0.75 mm, which does not satisfy the construction condition of group bolts. Therefore, the lifting method needs to be reconsidered.
4.2 Lifting with Rigid Flat Beam Spreader
For the common method of overall lifting construction, a rigid flat beam spreader is designed to meet the construction conditions of group bolts by connecting the steel strand with the rigid flat beam spreader to reduce the deformation between the beams of the steel joist. The structure is shown Fig. 10.

Figure 10: Spreader with rigid flat beam
The main longitudinal beam structure adopts square steel beam with cross-section height 1.4 m, width 0.9 m, web thickness 25 mm, top and bottom plate thickness 30 mm, cross brace structure adopts HM588 × 300 section steel, support bar structure adopts I32a.
Using Midas civil calculations, it can be obtained that the maximum stress of the steel truss is 45 Mpa, the maximum deflection is 13.5 mm, and the relative displacement of the adjacent internode beam is 0.7 mm, all of which meet the limit requirements, but the weight of the spreader itself is 120 tons, plus the weight of the steel truss 180 tons, exceeding the lifting power limit of the jack, required weight optimization of the spreader.
4.3 Optimization of Rigid Flat Stretcher Spreader Based on MJSO Algorithm
In optimizing the steel joist structure, section A with nodal vertical displacement X is set as the design variable. The maximum load is kept constant and the known permissible stresses, elastic modulus, stress parameters and permissible displacements of the nodes are the constraints in order to achieve the minimum mass of the structure.
① Design variables
A is the design variable of the structure; n is the number of section variable groups of continuous bars.
② Objective function
f (x) is the weight of the structure;
③ Constraints
K is the total number of bars; m is the total number of nodes;
④ Treatment of constrained condition
As with other direct search methods, MJSO cannot be used directly for constrained optimization problems. The penalty function method is one of the most widely used constraint processing techniques [27]. In this paper, a self-adaptive penalty function strategy is proposed to solve constrained optimization problems. Based on this method, Tao et al. [28] proposed a self-adaptive penalty function strategy for solving constrained optimization problems and the fitness function is written as Eqs. (24)–(26):
where
The MJSO algorithm is introduced according to the steel joist structure optimization model, and its optimization process is shown in Fig. 11.
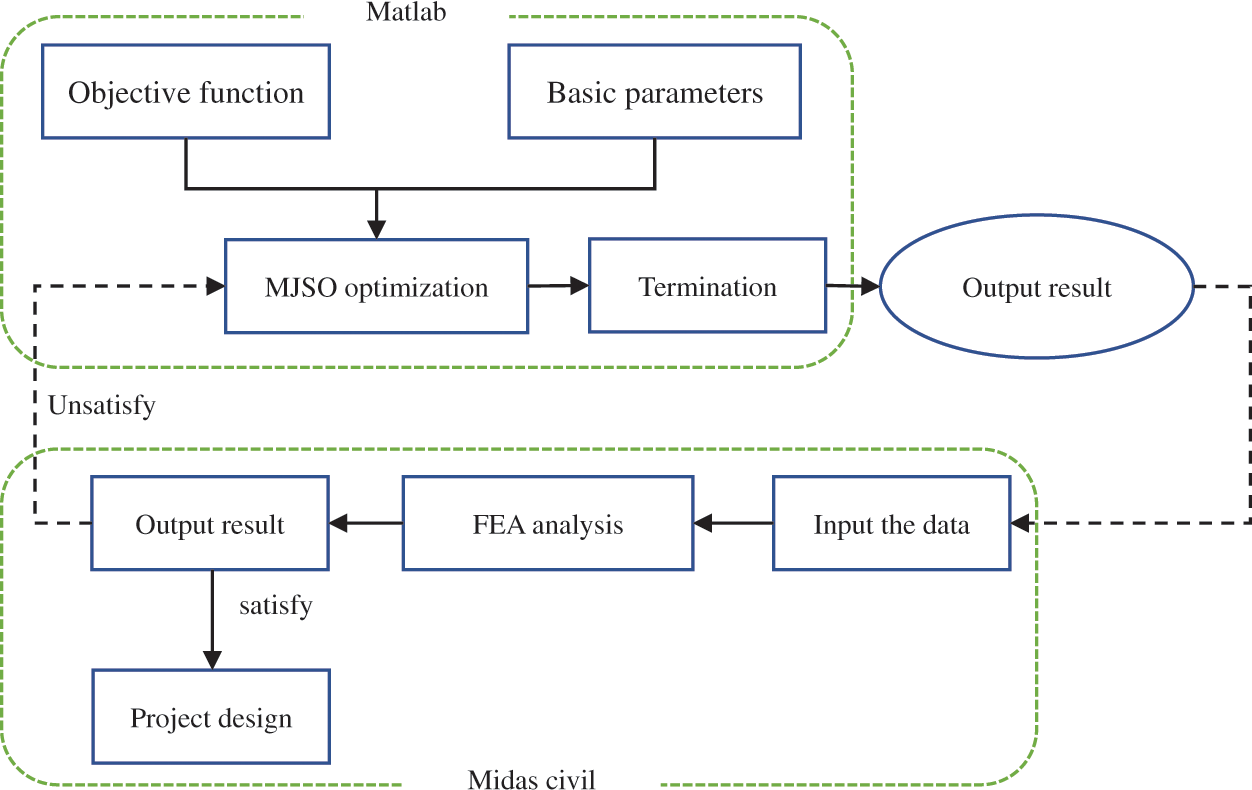
Figure 11: Flow chart of optimized steel truss by MJSO
4.3.2 Optimized Design of MJSO Algorithm Spreader
Based on the flat beam model, a truss model is established as in Fig. 12, with steel strength of Q345 steel, density of 7850 kg/m3 and modulus of elasticity of 2.06E+08 kN/m2. The cross-section size of the string bar is HM588 × 300, and the cross-section size of the middle support bar is I32a. 18 nodes and 26 units are set up, and the constraints are node 1 and node 10 are rigidly connected, while other nodes are not constrained. In this node 1, node 10 vertical applied jack maximum lifting weight of 70 tons of force P. The upper limit of stress constraint is 125768.5 kN/m2, the maximum vertical displacement is 0.135 m, the cross-sectional area optimization boundary between 0–0.121 m2, the node optimization boundary between 2–4 m. The design variables are section A1–A26, Y11 = Y18, Y12 = Y17, Y13 = Y16, Y14 = Y15, total 30 variables. The calculation was performed by MATLAB with 200 iterations and an initial population of 50, and the optimization results of MJSO and JSO are shown in the Table 7.
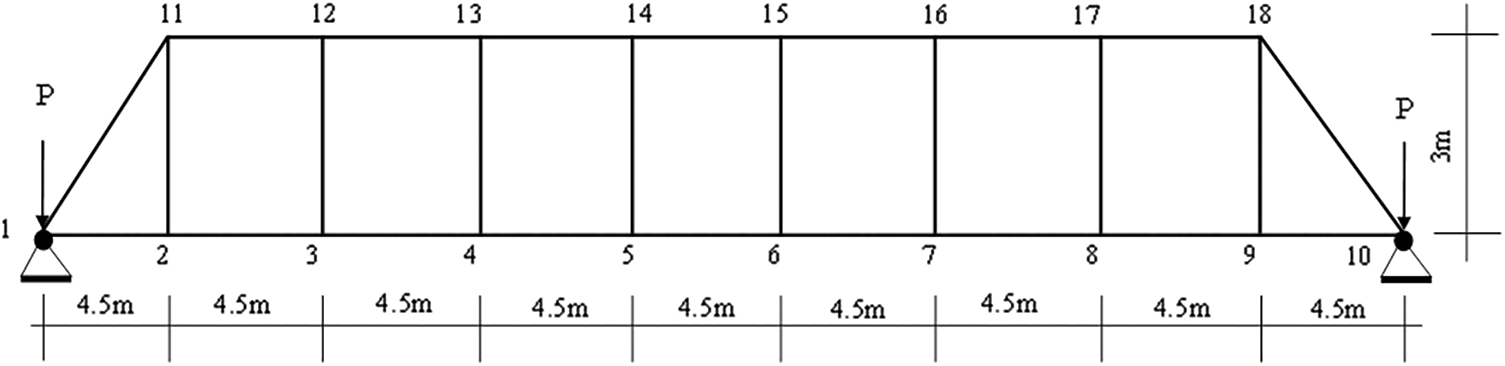
Figure 12: Spreader truss model diagram

Figs. 13 and 14 show the optimized shape of the spreader for 100 vs. 200 iterations of MJSO, respectively. As can be seen from Fig. 15, MJSO has better optimization efficiency than JSO, and as can be seen from Table 6, MSJO is 37% lighter than JSO in optimizing spreader, and MSJO has better overall performance than JSO.
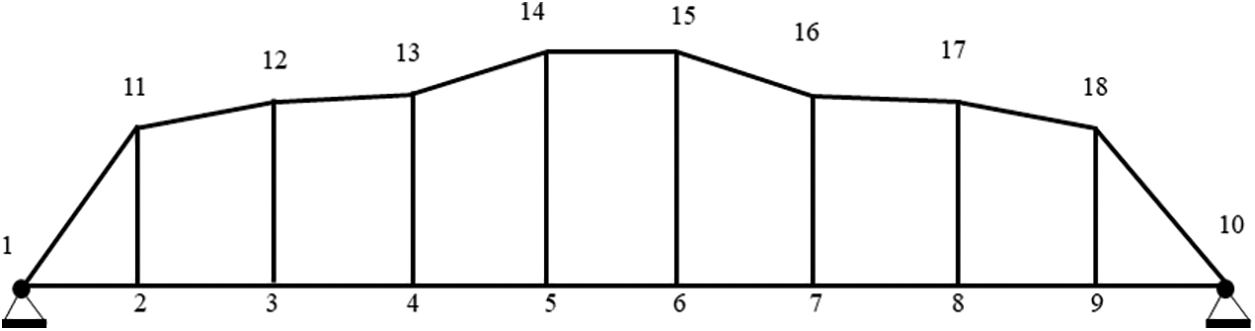
Figure 13: MJSO iteration 100th model
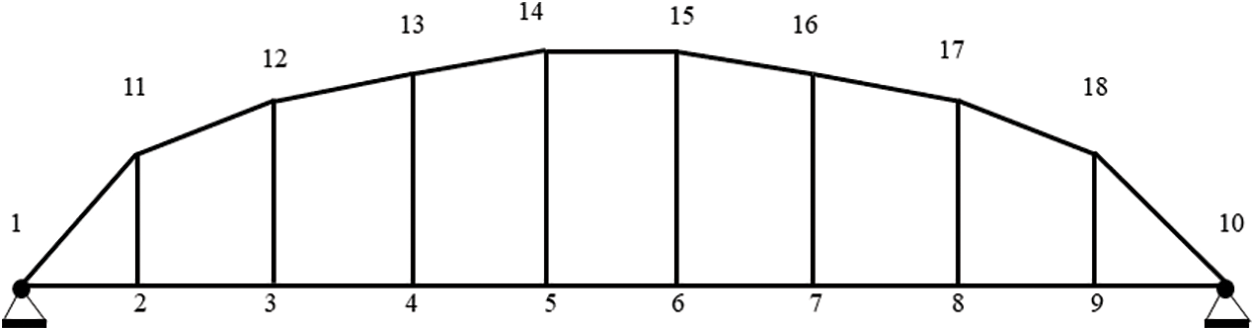
Figure 14: MJSO iteration 200th model
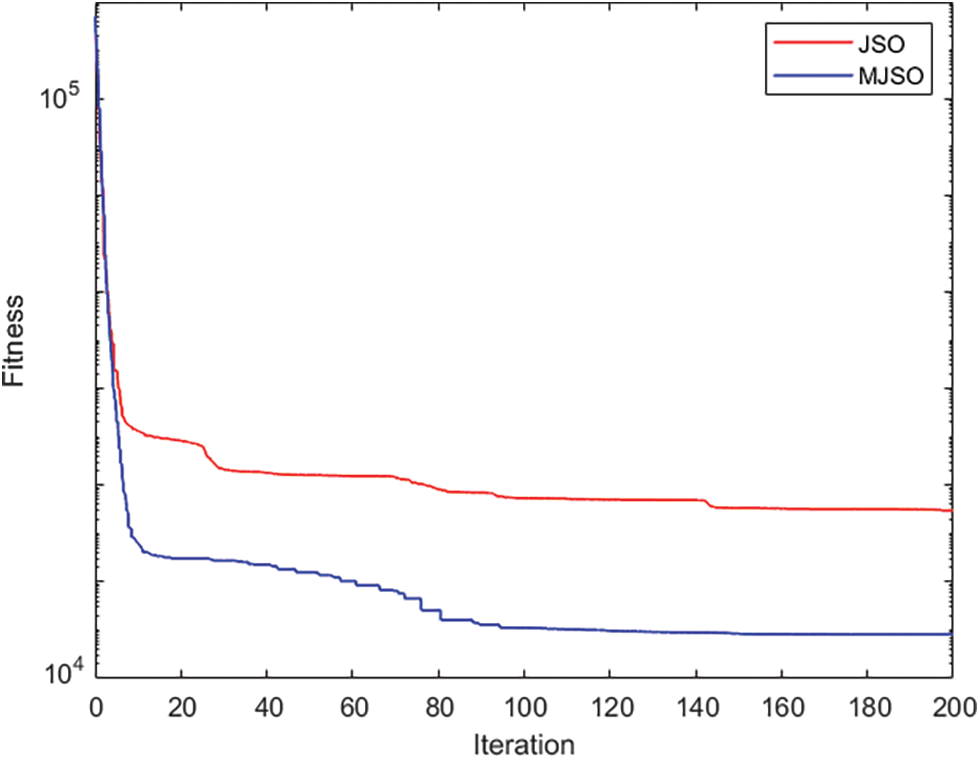
Figure 15: MJSO and JSO optimizes spreader convergence process
4.3.3 Finite Element Analysis after Optimization
Finite element analysis is performed on the optimized structure, and the model is established and calculated according to the actual situation and actual construction working conditions. The size is selected according to the optimized cross-section, and the overall shape such as arch structure is considered after optimization, i.e., the curve is selected for monolization. The two arch spreaders are connected by support bars and props are set in each span, and the overall spreader is shown in Fig. 16. In this study, Midas civil is used for lifting operation of the optimized spreader, and the force as well as deformation of the optimized spreader are analyzed.
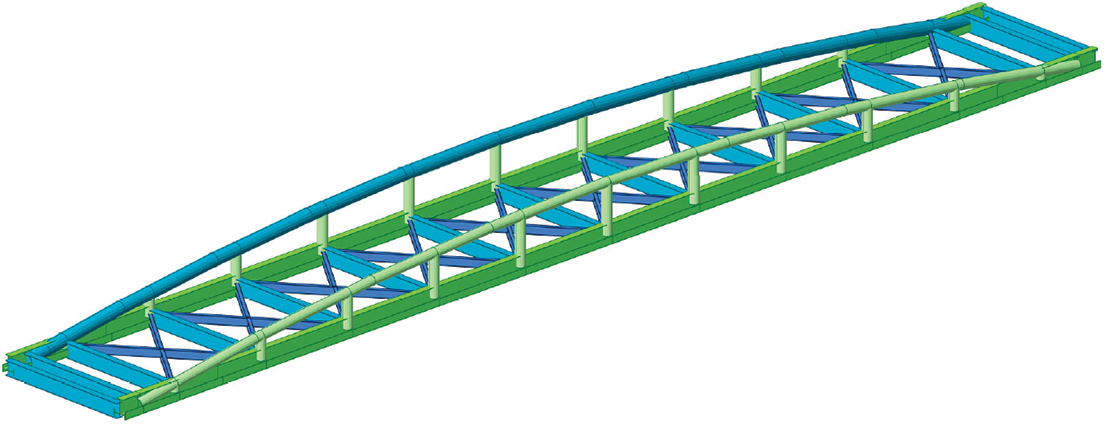
Figure 16: Schematic diagram of arch truss spreader
According to the optimization results, according to the Chinese steel design code standard for section selection, the main longitudinal beam adopts 2HM588 × 300 mm section steel, the arch support and upright bar all adopt Φ426 * 10 mm steel pipe, the support bar selects HM588 × 300 mm, the spreader elevation and plane are shown in Figs. 17 and 18.
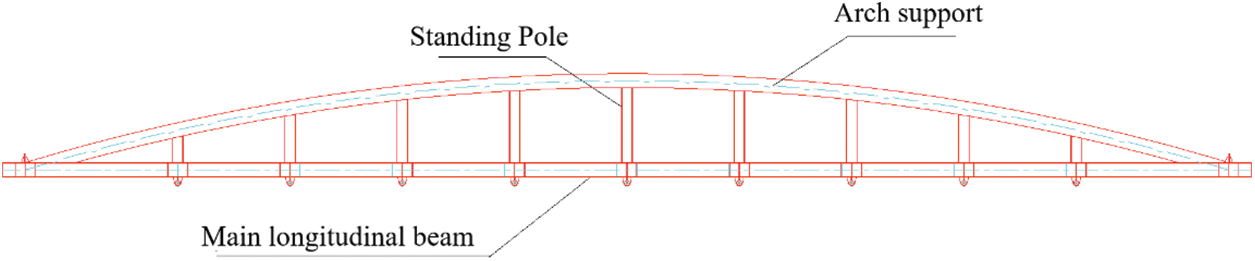
Figure 17: Elevation diagram of arch truss spreader
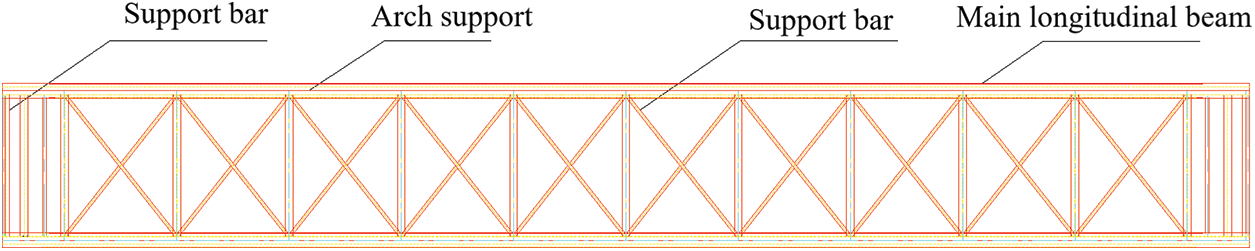
Figure 18: Schematic diagram of arch truss spreader plan
Installed under no wind or light wind condition, the load combination is as follows:
Self-weight of lifting bracket + Weight of spreader + Weight of main truss;
After software calculation, the maximum stress of all bars is 180 MPa, which is less than the strength design value [f] = 215 MPa, so it meets the requirements.
The maximum deformation under this working condition is 77.5 mm, and the deformation is as follows:
L/200 = 51910/400 = 129 mm;
which meets the requirement according to the cantilever member allowable deflection value specified in the Code for design of steel structures. The deformation difference of upper and lower chords is as follows:
74.899 − 74.775 = 0.114 mm < 0.75 mm;
which meets the requirements of group bolt construction. The spreader weighs about 50 tons, and the main truss weighs 110 tons, which is 46% lighter than the flat beam spreader and the requirement of jacking lifting limit.
To solve the truss shape and size optimization problem more effectively and efficiently, this paper proposes an improved jellyfish search algorithm (MJSO) by integrating the advantages of adaptive weight function and elite strategy through the jellyfish search algorithm. This algorithm improves the global search ability in the early stage of the algorithm by the elite strategy and the adaptive weight function and enhances the local search ability in the late stage of the algorithm by the adaptive weight function to avoid falling into the local optimum. Through testing and application, the advantages of the MJSO algorithm are as follows:
(1) In the benchmark function test, the MJSO algorithm performs better than the JSO algorithm overall for unimodal, multi-modal, separable, and non-separable functions.
(2) The MJSO algorithm is more robust than the JSO, PSO, GWO, and ACOR algorithms in terms of the effect of truss lightweight, and the optimization results are better.
(3) In the test of simultaneous optimization of truss shape and weight, the MJSO algorithm reduced two chords while JSO reduced only one chord under the constraints, and the weight of MSJO was 26% lighter than that of JSO, and the standard deviation of MJSO through 30 cycles was 1.84 smaller than that of JSO, and the robustness of MJSO is also superior. In general, MSJO is superior to JSO in optimizing the shape and weight of trusses.
(4) For the restricted construction environment of the site, the structure needs to be lifted using a spreader. Through the optimization of the lifting spreader by MJSO and JSO, the result of lightweight spreader by MJSO is better than JSO, and the problem of large lifting weight of steel joist as a whole is solved.
Since the MJSO algorithm improvement is only optimized for the passive motion in the early ocean currents and the later local search, it lacks the optimization for the active motion part, which needs to be enhanced here.
Acknowledgement: Open Access funding enabled and organized by Xiamen Transportation Infrastructure Intelligent Management and Maintenance Engineering Technology Research Center. The authors gratefully acknowledge the support.
Funding Statement: This research was funded by the National Natural Science Foundation of China (Grant No. 51305372), the Open Fund Project of the Transportation Infrastructure Intelligent Management and Maintenance Engineering Technology Center of Xiamen City (Grant No. TCIMI201803) and the Project of the 2011 Collaborative Innovation Center of Fujian Province (Grant No. 2016BJC019).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: X.W., S.F. and Y.H.; data collection: S.F., W.W., Z.L. and F.J.; analysis and interpretation of results: X.W., S.F., W.W. and Y.H.; draft manuscript preparation: S.F., X.W. and Y.H. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Shi, K., Ruan, Z., Jiang, Z., Lin, Q., Wang, L. (2018). Improved plant growth simulation and genetic hybrid algorithm (PGSA-GA) and its structural optimization. Engineering Computations, 35(1), 268–286. https://doi.org/10.1108/EC-03-2017-0113 [Google Scholar] [CrossRef]
2. Kim, N. I., Kim, Y. W., Lee, J., Kang, J. W. (2018). Two-stage optimization based on force method for damage identification of planar and space trusses. International Journal of Steel Structures, 18(1), 1–12. https://doi.org/10.1007/s13296-018-0301-x [Google Scholar] [CrossRef]
3. Viet-Hung, T., Seung-Eock, K. (2018). Reliability-based design optimization of nonlinear inelastic trusses using improved differential evolution algorithm. Advances in Engineering Software, 121(4), 59–74. https://doi.org/10.1016/j.advengsoft.2018.03.006 [Google Scholar] [CrossRef]
4. Azad S. K., Bybordiani M., Azad S. K., Jawad F. K. J. (2018). Simultaneous size and geometry optimization of steel trusses under dynamic excitations. Structural and Multidisciplinary Optimization, 58(6), 2545–2563. https://doi.org/10.1007/s00158-018-2039-7 [Google Scholar] [CrossRef]
5. Grzywinski, M., Dede, T., Ozdemir, Y. I. (2019). Optimization of the braced dome structures by using Jaya algorithm with frequency constraints. Steel and Composite Structures, 30, 47–55. https://doi.org/10.12989/scs.2019.30.1.047 [Google Scholar] [CrossRef]
6. Habibi, A., Bidmeshki, S. (2019). An optimized approach for tracing pre- and post-buckling equilibrium paths of space trusses. International Journal of Structural Stability and Dynamics, 19(4), 1950040. https://doi.org/10.1142/S0219455419500408 [Google Scholar] [CrossRef]
7. Artar, M., Daloglu, A. T. (2019). Optimum design of steel space truss towers under seismic effect using Jaya algorithm. Structural Engineering and Mechanics, 71, 1–12. https://doi.org/10.12989/sem.2019.71.1.001 [Google Scholar] [CrossRef]
8. Kaveh, A., Moghanni, R. M., Javadi, S. M. (2019). Optimum design of large steel skeletal structures using chaotic firefly optimization algorithm based on the Gaussian map. Structural and Multidisciplinary Optimization, 60(3), 879–894. https://doi.org/10.1007/s00158-019-02263-1 [Google Scholar] [CrossRef]
9. Wong, F. T., Prayogo, D., Putra, R. E., Joseph, J. (2020). Member sizing optimization of large scale steel space trusses using a symbiotic organisms search algorithm. Journal of Physics: Conference Series, 1625. https://doi.org/10.1088/1742-6596/1625/1/012019 [Google Scholar] [CrossRef]
10. Ha, M. H., Vu, Q. V., Truong, V. H. (2020). Optimization of nonlinear inelastic steel frames considering panel zones. Advances in Engineering Software, 142, 102771. https://doi.org/10.1016/j.advengsoft.2020.102771 [Google Scholar] [CrossRef]
11. Gholizadeh, S., Danesh, M., Gheyratmand, C. (2020). A new Newton metaheuristic algorithm for discrete performance-based design optimization of steel moment frames. Computers & Structures, 234. https://doi.org/10.1016/j.compstruc.2020.106250 [Google Scholar] [CrossRef]
12. Es-Haghi, M. S., Shishegaran, A., Rabczuk, T. (2020). Evaluation of a novel asymmetric genetic algorithm to optimize the structural design of 3D regular and irregular steel frames. Frontiers of Structural and Civil Engineering, 14, 1110–1130. https://doi.org/10.1007/s11709-020-0643-2 [Google Scholar] [CrossRef]
13. Truong, V. H., Vu, Q. V., Thai, H. T., Ha, M. H. (2020). A robust method for safety evaluation of steel trusses using gradient tree boosting algorithm. Advances in Engineering Software, 147(5), 102825. https://doi.org/10.1016/j.advengsoft.2020.102825 [Google Scholar] [CrossRef]
14. Zhou, H., Zhang, G., Wang, X., Ni, P., Zhang, J. (2020). A hybrid identification method on butterfly optimization and differential evolution algorithm. Smart Structures and Systems, 26, 345–360. https://doi.org/10.12989/sss.2020.26.3.345 [Google Scholar] [CrossRef]
15. Bigham, A., Gholizadeh, S. (2020). Topology optimization of nonlinear single-layer domes by an improved electro-search algorithm and its performance analysis using statistical tests. Structural and Multidisciplinary Optimization, 62(4), 1821–1848. https://doi.org/10.1007/s00158-020-02578-4 [Google Scholar] [CrossRef]
16. Gholizadeh, S., Fattahi, F. (2021). Multi-objective design optimization of steel moment frames considering seismic collapse safety. Engineering with Computers, 37(2), 1315–1328. https://doi.org/10.1007/s00366-019-00886-y [Google Scholar] [CrossRef]
17. Artar, M., Carbas, S. (2021). Discrete sizing design of steel truss bridges through teaching-learning-based and biogeography-based optimization algorithms involving dynamic constraints. Structures, 34(11), 3533–3547. https://doi.org/10.1016/j.istruc.2021.09.101 [Google Scholar] [CrossRef]
18. Azad, S. K., Aminbakhsh, S., Shaban, S. S. S. (2021). Multi-stage guided stochastic search for optimization and standardization of free-form steel double-layer grids. Structures, 34(1), 678–699. https://doi.org/10.1016/j.istruc.2021.07.068 [Google Scholar] [CrossRef]
19. Carbas, S., Artar, M. (2022). Optimum discrete design of steel planar trusses comprising earthquake load impact. In: Kim, J., Deep, K., Geem, Z., Sadollah, A., Yadav, A. (Eds.Proceedings of 7th International Conference on Harmony Search, Soft Computing and Applications, pp. 369–379. https://doi.org/10.1007/978-981-19-2948-9_36 [Google Scholar] [CrossRef]
20. Zhao, J., Wang, K., Wu, D., Huang, Q., Yu, M. (2022). Optimization strategy for modal test measurement points of large-span steel beams based on improved particle swarm optimization algorithm with random weights. Applied Sciences, 12(23), 12082. https://doi.org/10.3390/app122312082 [Google Scholar] [CrossRef]
21. Ojha, V., Panto, B., Nicosia, G. (2023). Adaptive search space decomposition method for pre- and post-buckling analyses of space truss structures. Engineering Applications of Artificial Intelligence, 117. https://doi.org/10.1016/j.engappai.2022.105593 [Google Scholar] [CrossRef]
22. Eser, H., Hasancebi, O. (2023). Capacity controlled search: A new and efficient design-driven method for discrete size optimization of steel frames. Computers & Structures, 275. https://doi.org/10.1016/j.compstruc.2022.106937 [Google Scholar] [CrossRef]
23. Sang-To, T., Le-Minh, H., Abdel Wahab, M., Thanh, C. L. (2023). A new metaheuristic algorithm: Shrimp and Goby association search algorithm and its application for damage identification in large-scale and complex structures. Advances in Engineering Software, 176(1), 103363. https://doi.org/10.1016/j.advengsoft.2022.103363 [Google Scholar] [CrossRef]
24. Azizi, M., Aickelin, U., Khorshidi, H. A., Baghalzadeh Shishehgarkhaneh, M. (2023). Energy valley optimizer: A novel metaheuristic algorithm for global and engineering optimization. Scientific Reports, 13(1), 1–23. https://doi.org/10.1038/s41598-022-27344-y [Google Scholar] [PubMed] [CrossRef]
25. Kadkhoda Mohammadi, S., Nazarpour, D., Beiraghi, M. (2023). A novel metaheuristic algorithm inspired by COVID-19 for real-parameter optimization. Neural Computing and Applications, 35(14), 10147–10196. https://doi.org/10.1007/s00521-023-08229-1 [Google Scholar] [PubMed] [CrossRef]
26. Chou, J. S., Truong, D. N. (2021). A novel metaheuristic optimizer inspired by behavior of jellyfish in ocean. Applied Mathematics and Computation, 389, 125535. https://doi.org/10.1016/j.amc.2020.125535 [Google Scholar] [CrossRef]
27. Coello, C. A. (2002). Theoretical and numerical constraint-handling techniques used with evolutionary algorithms: A survey of the state of the art. Computer Methods in Applied Mechanics and Engineering, 191(11–12), 1245–1287. https://doi.org/10.1016/S0045-7825(01)00323-1 [Google Scholar] [CrossRef]
28. Tao, R., Meng, Z., Zhou, H. (2021). A self-adaptive strategy based firefly algorithm for constrained engineering design problems. Applied Soft Computing, 107(Suppl 1), 107417. https://doi.org/10.1016/j.asoc.2021.107417 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools