 Open Access
Open Access
ARTICLE
Modified Black Widow Optimization-Based Enhanced Threshold Energy Detection Technique for Spectrum Sensing in Cognitive Radio Networks
1 School of Computing, SASTRA Deemed University, Thanjavur, 613401, India
2 School of Electrical & Electronics Engineering, SASTRA Deemed University, Thanjavur, 613401, India
* Corresponding Author: R. Saravanan. Email:
Computer Modeling in Engineering & Sciences 2024, 138(3), 2339-2356. https://doi.org/10.32604/cmes.2023.030898
Received 01 May 2023; Accepted 31 July 2023; Issue published 15 December 2023
Abstract
This study develops an Enhanced Threshold Based Energy Detection approach (ETBED) for spectrum sensing in a cognitive radio network. The threshold identification method is implemented in the received signal at the secondary user based on the square law. The proposed method is implemented with the signal transmission of multiple outputs-orthogonal frequency division multiplexing. Additionally, the proposed method is considered the dynamic detection threshold adjustments and energy identification spectrum sensing technique in cognitive radio systems. In the dynamic threshold, the signal ratio-based threshold is fixed. The threshold is computed by considering the Modified Black Widow Optimization Algorithm (MBWO). So, the proposed methodology is a combination of dynamic threshold detection and MBWO. The general threshold-based detection technique has different limitations such as the inability optimal signal threshold for determining the presence of the primary user signal. These limitations undermine the sensing accuracy of the energy identification technique. Hence, the ETBED technique is developed to enhance the energy efficiency of cognitive radio networks. The projected approach is executed and analyzed with performance and comparison analysis. The proposed method is contrasted with the conventional techniques of the Whale Optimization Algorithm (WOA) and Grey Wolf Optimization (GWO). It indicated superior results, achieving a high average throughput of 2.2 Mbps and an energy efficiency of 3.8, outperforming conventional techniques.Graphic Abstract
Keywords
Abbreviation
| ΛslcΛslc | Complete test statistics of complete signals identified based on receiver chains of the secondary user |
| ΛRΛR | Test statistics for signals identified at the receiver chain of the secondary chain |
| nn | Complete number of secondary users of receiver chains |
| rr | Count of secondary users in receiver chains |
| YR(N)YR(N) | Detected signal vector at the receiver chain of the secondary user in the spectrum sensing period |
| RR | Number of receiver chains on the secondary side |
| hoho | Hypothesis |
| λ(N)λ(N) | Detection threshold |
| Var[.]Var[.] | Variance operator |
| e[.]e[.] | Expectation operator |
| 2σ2ωR(N)2σ2ωR(N) | Noise changes of the identified signal |
| HR(N)HR(N) | Uniform gain of the channel |
| HH | Complex matrix of the channel gain |
| λDλD | Detection threshold |
| Q(.)Q(.) | Gaussian Q function |
| λfaλfa | False alarm threshold level |
| λDdtλDdt | Level of decision threshold |
| ndtndt | Count of sampling points |
| SNRAVGSNRAVG | Average SNR of every secondary user |
| Nvar×NpopNvar×Npop | Candidate widow matrix |
Radio spectrum is attractive and excessively scarce as wireless communication technology develops quickly and as novel knowledge like 5G and the Internet of Things (IoT) emerge [1]. Spectrum resources can be underutilized because of the extreme variation in complete band consumption, which is reported by the spectrum allocation and occupancy movement and ranges from 7 to 35 percent [2]. The previously present trade-off between spectrum availability in addition exponential development has been overcome via cognitive radio (CR) [3]. These radios can detect and change their locations to provide the best performance conceivable without interfering with the signals of additional licensed users [4].
A cognitive radio’s constant spectrum sensing method outcomes in low data transmission and high energy consumption, especially in areas with large population densities. Spectrum sensing takes care of the CR’s energy usage in the promising technology known as energy harvesting in CRNs [5]. Energy harvesters have the strong ability to capture and store energy from different energy sources as well as ambient energy. Continuous performance enhancement is essential for such wireless networks. These networks employ harvesters, therefore energy efficiency (EE), transmission time, sensing duration, and throughput are employed to measure their performance [6].
The concealed terminal problem, which arises when the cognitive radio is shaded, in situations of extreme multipath fading, or inside structures with significant penetration loss, while a main user (PU) is operating nearby [7], is one of the major difficulties in implementing spectrum sharing. A cognitive radio might not detect PU because of the hidden terminal issue; therefore, it might access the licensed channel and interfere with the licensed system. In cognitive radio networks [8], several cognitive users can work together to undertake spectrum sensing to solve the hidden terminal problem. It has been demonstrated that increasing the number of cooperative partners can significantly enhance the presentation of spectrum sensing. The metaheuristic technique is used to tackle the spectrum-sharing problem [9].
Here employed various previously proposed prediction methods in this study and primarily focused on a resource allocation problem in a CR network. When tackling this issue, we assumed that its size was proportionate to the number of users and spectrum channels. To decrease the magnitude of the problem, several studies showed that all users shared the same spectrum channel and that only power control was examined. However, because of user interference, the spectrum channel cannot adequately support the huge data transmission over the whole network. Other research showed that each user transmits at a constant power or data rate. However, these studies have only addressed spectrum allocation, which may lead to power waste during data transmission. As a result, it is fair to investigate the joint allocation of power and spectra to realize the full potential of a CR network.
Most optimization issues are non-convex, making it challenging to identify a single global optimal solution. Using traditional mathematical optimization procedures, it will be difficult to tackle optimization problems with a wide search space or that are more sophisticated [10]. The various metaheuristic optimization methods that are used in the research community are quite effective at resolving challenging optimization issues. Each metaheuristic optimization algorithm offers unique advantages and room for development. Some of them might converge more quickly, while others would require more time to reach the best result. Yet, there can be still a lot of room for advancement in metaheuristic techniques [11].
1.1 The Main Contribution and Organization of the Research
• This paper develops an ETBED for spectrum sensing in a cognitive radio network. The threshold detection method is implemented in the received signal at the secondary user with a basis of square law.
• The proposed method is implemented with the signal transmission of multiple outputs-orthogonal frequency division multiplexing. Additionally, the proposed method is defined as the dynamic identification threshold adjustments and energy detection spectrum sensing technique in cognitive radio systems.
• In the dynamic threshold, the signal ratio-based threshold is fixed. The threshold is computed by considering the MBWO. In the BWO, the mutation function is enhanced by considering boosting operation.
The remaining part of the paper is organized as below, Section 2 gives the related work of the spectrum sensing in CRN. The system model and proposed approach are presented in Section 3. The outcome performances are presented in Section 4. The conclusion of the portion is presented in Section 5.
In the literature section, different spectrum sensing techniques are developed by authors in a cognitive radio network. Few works are reviewed to analyze the importance of developing a spectrum sensing technique in a cognitive radio network.
A framework for distributed online execution and centralized offline training based on cooperative multi-agent reinforcement learning (MARL) has been presented by Tan et al. [12]. Use the deep recurrent Q-network (DRQN) in this situation to address the partial observability of every cognitive user’s state. The objective was to discover a collaborative method that enhances the aggregate throughput of a cognitive radio architecture in a dispersed manner without coordinating information transmission amongst cognitive users. Lastly, run thorough experiments to validate the suggested approach in diverse contexts.
Extreme learning machines (ELM) and long short-term memory (LSTM) have been combined in a hybrid manner by Mohanakurup et al. [13] to learn temporal features from spectral information and to take advantage of remaining conservational activity statistics like duty cycle, distance, and energy for the enhancement of sensing presentation. The proposed system has been examined on many platforms, including a Raspberry Pi Model B+ and the GNU-radio experimental testbed.
A unique Modified Whale Optimization Algorithm (MWOA) trained Spiking Neural Network (SNN) based spectrum sensing approach for the effective identification of spectrum gaps has been described by Eappen et al. [14]. The SNN’s weights are trained in this case using MWOA to accurately forecast the spectrum holes. Using continuous wavelet transforms, the suggested technique makes use of the underlying structural information of the object or event.
Gul [15] proposed a myopic policy for opportunistic access based on average throughput. The topic of multi-channel access in a cognitive radio network with M primary users and a multi-channel secondary user (SU) is addressed in this letter. SU chooses K channels for transmission without knowing the channel statuses or channel evolution process data. If SU detects an available channel, it delivers data over that channel at that time. Otherwise, it is not used in that slot by SU.
Gul [16] described a cognitive radio network with M primary users, M primary receivers, a secondary user with K channels, and K secondary receivers. Each primary user is allotted a channel for data transmission to a primary receiver. As data is backlogged, a secondary user is assumed. The secondary user has no direct knowledge of the statuses (good or negative) of M channels, nor the channel evolution process statistics. In each time slot, the secondary user selects K channels for transmission.
A ResNet-based multi-level transmission power recognition (MTPR) design has been described by Tan et al. [17] Also, the suggested architecture was used in two instances with various observational information. In the initial instance, the covariance matrix (CM) of the received signal, which contains extensive energy data, was employed as the comment information for the CM-MTPR technique. In another instance, the quadrature-stage and in-stage (IQ) information tested from the received signal which conserves high unique data is arranged as the observation data of the IQ-MTPR technique. This further increases the identification accuracy.
A hybrid optimization technique that combines a Shapley value and a game theoretic idea into metaheuristics was presented by Bakshi et al. [18]. The improved hybrid algorithm is derived from particle swarm optimization grey wolf optimization (PSOGWO) in this case. To improve PSOGWO, the idea of wolves’ objectivity is also included. By carefully examining coupled spectrum sharing and energy collecting in a cognitive radio network, multi-objective optimization was developed (CSSEH). By upgrading the velocity with the weights in PSOGWO, the Pareto best solutions for the multi-objective optimization issue of throughput and energy efficiency can be found.
Many spectrum resources can be licensed in addition to assigned as an outcome of the fast empowerment of wireless requests. In this scenario, in different places and moments, there happens a huge helping of the required spectrum may be unfeasible. This suggests that spectrum scarcity is brought on by spectrum management applications compared to a physical restriction on the range of frequencies that can be utilized. Hence, in this paper, an efficient spectrum sensing technique is developed and analyzed. A detailed explanation of the spectrum sensing approach is given in this portion.
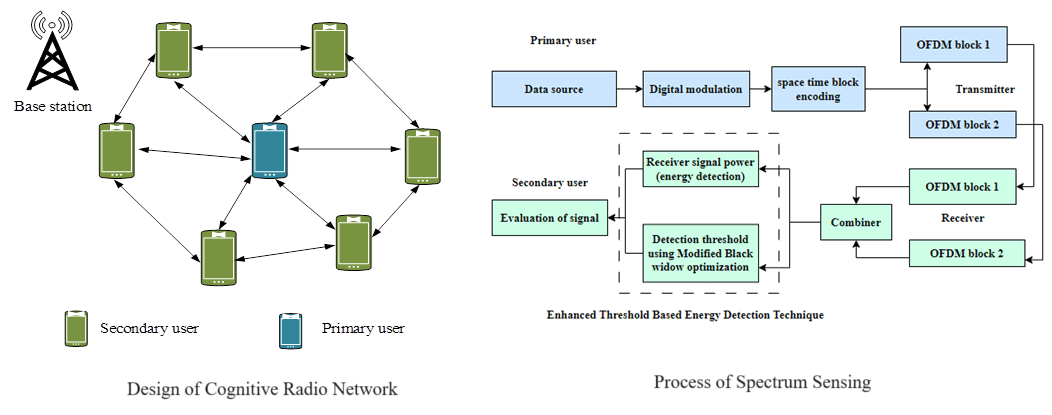
In this article, the OFDM-based CRN is considered which consists of a primary network with different orthogonal channels. The complete available frequency bandwidth is split into bandwidth spanned by an OFDM channel and orthogonal sub-channels with equivalent size. Additionally, the spectrum is considered flat. After that, this network is developed with primary and secondary users as shown in Fig. 1a. Additionally, the primary users contain primary base stations, and it is related to primary users. Similarly, the secondary user contains the secondary access points with cognitive users.
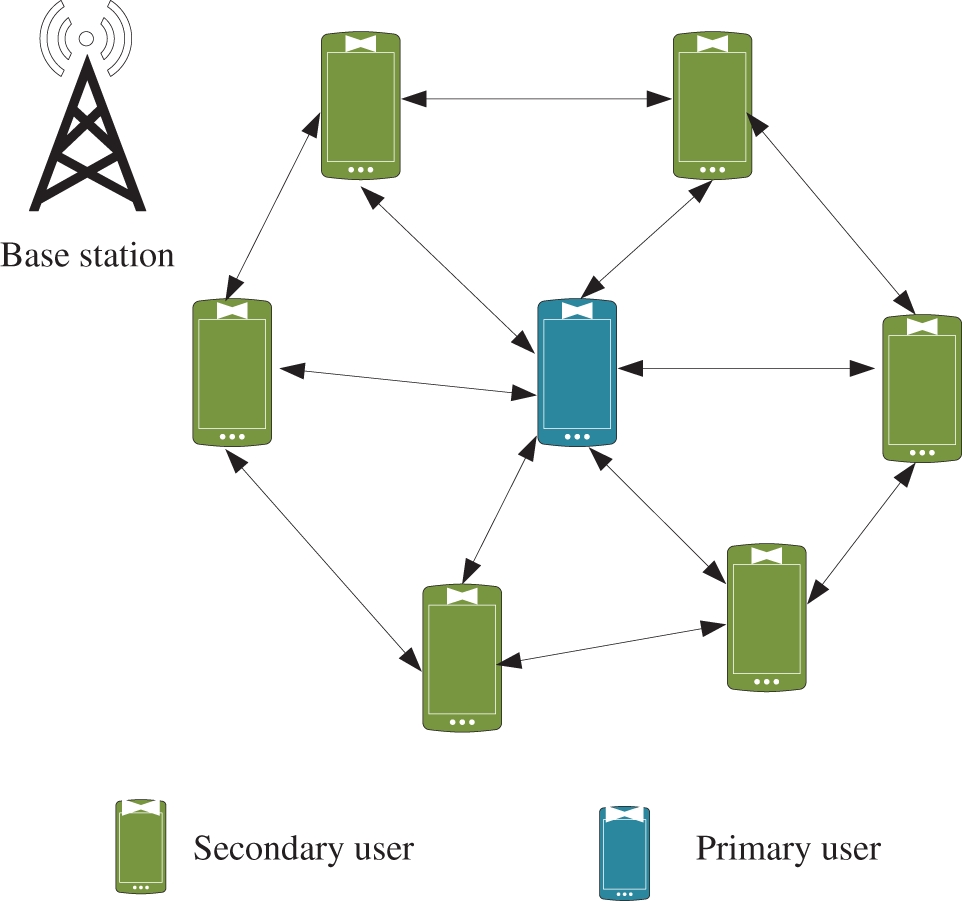
Figure 1(a): Design of cognitive radio network
In this article, cognitive users and secondary users are interchangeable. The cognitive users can be dispersed considering the transmission period of the primary base station, and complete users are in the area with physical nearness. In this study, the uplink spectrum access issues of the users in the cognitive radio network are considered based on their transmit packet to their related receivers or wireless channels. The CRN is designed for primary and secondary users. Additionally, to enable the communication process, a base station is attached to the network access. In the CRN, the spectrum allocation is a main problem which is diminished by considering the optimal spectrum allocation process. To obtain the optimal spectrum sensing and allocation process, the enhanced threshold-based energy detection technique is developed as depicted in Fig. 1b. Initially, the system model is intended for primary and secondary users with transmitter and receiver sides. On the receiver side, spectrum sensing can be achieved by applying the proposed spectrum sensing technique.
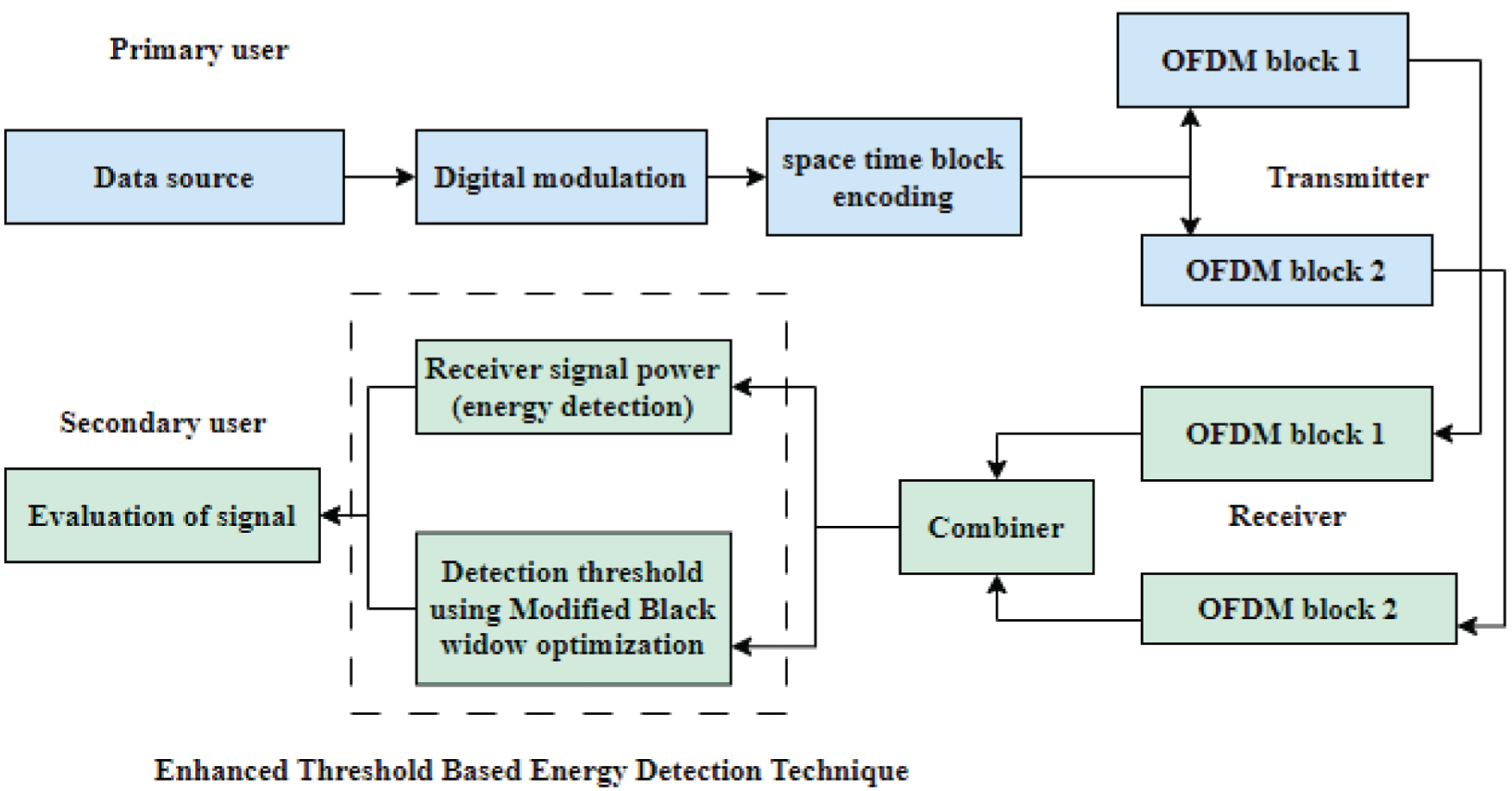
Figure 1(b): Process of spectrum sensing
The process of energy detection considering the square law combining method in CRN systems objective to exploit the spectrum sensing of the primary signal with the consideration of receiver chains of the secondary user. Based on the SLC technique [19], the signals achieved on the receiver are combined and squared to achieve the whole received signal energy defined as the test measurement. The complete statistic can be computed as follows:
Λslc=∑rR=1ΛR=∑rR=1∑nN=1|YR(N)|2Λslc=∑rR=1ΛR=∑rR=1∑nN=1|YR(N)|2(1)
Here, ΛslcΛslc is defined as the complete test statistics of complete signals identified based on receiver chains of the secondary user, ΛRΛR is defined as the test statistics for signals identified at the receiver chain of the secondary chain, nn is defined as the complete number of secondary users of receiver chains, rr is defined as the count of secondary users in receiver chains, YR(N)YR(N) is described as the detected signal vector at the receiver chain of the secondary user in the spectrum sensing period, RR is defined as the number of receiver chains on the secondary side. The opinion related to spectrum occupancy through the primary user is achieved by the contrast of the test statistic with a detection threshold. This is dynamically chosen for every sample utilized in the spectrum sensing procedure:
Λslc(N)<λ(N):ho,∀Nϵ{1,…,n}Λslc(N)<λ(N):ho,∀Nϵ{1,…,n}(2)
Λslc(N)>λ(N):h1,∀Nϵ{1,…,n}Λslc(N)>λ(N):h1,∀Nϵ{1,…,n}(3)
Here, hoho is defined as the hypothesis that describes the non-existence of the primary user signal λ(N)λ(N) is defined as the detection threshold, and h1h1 is defined as the hypothesis that describes the existence of the primary user signal. Based on the distribution of complete test statistics and adequate count of sampling points are formulated as a normal distribution,
Λslc∼𝒩(∑eR=1∑nN=1e[|YR(N)|2]∑eR=1∑nN=1Var[|YR(N)|2])(4)
Here, Var[.] is defined as the variance operator, and e[.] is defined as the expectation operator. In the spectrum sensing period N, the noise variance of the identified signal and uniform gain of the wireless station is formulated as follows:
HR(N)=H,∀R=1,…,r,∀N=1,…,n(5)
2σ2ωR(N)=2σ2ω∀R=1,…,r;∀N=1,…,n(6)
Here, 2σ2ωR(N) is defined as the noise changes of the identified signal, HR(N) is defined as the uniform gain of the channel and H is defined as the complex matrix of the channel gain of the receiver chains. Managing the spectrum sensing with the consideration of energy detection technique. In spectrum sensing, the square law technique is utilized for analysis of the demand’s information regarding the regular stage of the received power at the projections of the secondary user chains. Hence, the complete instant primary user of the signal is transmitted by means of transmission chains within the specific time which is equivalent to complete signal changes at the receiver chain of the secondary user. The complete test statistics are computed as follows:
Λslc∼{𝒩(rn(2σ2ωR),rn((2σ2ωR))2):ho𝒩(n(2σ2ω)(r+γslc),n(2σ2ω)2(r+2γslc):h1(7)
Related to the complete test statistic defined as the above equation for hypotheses and the false alarm and detection probability aimed at energy detection considering square law diversity method in CRN system is designed.
Normally, the validation of energy detection with spectrum sensing is achieved by considering two probabilities such as false alarm probability and detection probability. This probability of sensing the conveyed primary user signal at the location of the secondary user when it can be conveyed is defined as the probability of detection. The detection probability of the energy detection technique considering the square law approach in the CRN system is formulated as follows:
PD[PR(Λslc>λ)|h1]≈Q(λD−n(2σ2ω)(r+2γslc)√n(r+2γslc)(2σ2ω))≈Q(λD−rn(2σ2ω)(r+¯γslc)√rn(1+2¯γslc)(2σ2ω))(8)
≈Q(λD−rn(2σ2ωi)(1+p2rσ2ω)√1+p2rσ2ω(2σ2ω))(9)
Here, λD is defined as the detection threshold, Q(.) is defined as the Gaussian Q function and p is defined as the primary user. To achieve primary user signal identification, a huge detection probability can be attained. The huge detection probability enhances the spectrum usage and energy detection performance of the secondary user. Similarly, the false alarm probability can be described as the sensing probability of the primary user signal with the consideration of the secondary user when the primary signal cannot send. It is validated by the verification of the hypothesis. The false alarm probability is a presentation metric of energy detection considering the square law technique in CRN is formulated as follows:
Pfa[PR(Λslc>λ)|ho]≈Q(λfa−rn(2σ2ω)√rn(2σ2ω))(10)
Here, λfa is defined as the false alarm threshold level. Related to the above formulations, the false alarm probability in addition to detection probability is related to the false alarm thresholds, level of defined detection, the number of receiver chains, variance of the noise, and several sampling points. After that, the above equation defined that the identification probability will also relate to the stage of primary user transmission power.
3.3 Identification of Threshold Computation
Related to the above section, detection probabilities of false alarms are affected by the related threshold parameters. Computing the stage of detection threshold is the major behavior that affects the choice accuracy related to the presence or absence of the primary user signal. The fixed threshold identification does not consider the signal fluctuations in the frequency channel present. Moreover, the fluctuations should be considered in the wireless channel, and the techniques related to the decision threshold adjustments [20] have developed. To maximize the probability of detection, the false alarm threshold should be identified efficiently. This method is defined as a Constant false alarm rate, and it is used for the spectrum sensing approach that needs the maximal usage of the wireless channel. Related to this approach, the fixed false alarm threshold does not provide efficient false alarm detection in the CRN network. So, the dynamic decision threshold is considered. The dynamic decision threshold adaption with a probability of detection is presented as follows:
Pdtd=minλ′dtε[dp′,p′λdtd]q(λD−rndt(2σ2ω)(1+prσ2ω)√rndt(1+prσ2ω)(2σ2ω))=q(λDdtp′−rndt(2σ2ω)(1+prσ2ω)√rndt(1+prσ2ω)(2σ2ω))(11)
Pdtfa=maxλ′dtε[λdtfap′,p′λdtd]q(λ′dt−rndt(2σ2ω)√rndt(2σ2ω))=q(p′λdtfa−rndt(2σ2ω)√rndt(2σ2ω))(12)
Here, λDdt and ndt are defined as the level of decision threshold and count of sampling points utilized in the energy detection with dynamic decision threshold adjustments. Based on the above equation, the stage of the dynamic decision threshold is formulated as follows:
λDdt=[q−1(Pdtd)+√(1+prσ2ω)+√rn(1+prσ2ω]√rndt(2σ2ω)p′(13)
Additionally, the stage of the false alarm threshold is computed and presented as follows:
λfadt=[q−1(Pdtfa)+√rndt]√rndt(2σ2ωp′)(14)
The minimal count of sampling points for managing exact energy detection in the square law approach in CRN. The sampling point is formulated as follows:
ndt=[q−1(Pdtfa)−√p′2(1+2¯γslc)q−1(Pdtd)]2r[p′2¯γslc+(p′2−1)]2(15)
The correlation among detection in the case of systems operating decision threshold and energy detection and probability of false alarm is mathematically presented as follows:
Pdtd=q(q−1(Pdtfa)−√rndt(p′2¯γslc+(p′2−1))√p′2(1+2¯γslc))(16)
=q(q−1(Pdtfa)−√rndt(p′2P2rσ2ω+(p′2−1))√p′2(1+2¯γslc))(17)
=q(q−1(Pdtfa)−(p′2P√ndt2√rσ2ω+√rndt(p′2−1))√p′2(1+Prσ2ω))(18)
Normally, the threshold decision is computed by using two approaches such as fixed threshold detection and dynamic threshold detection. Based on the noise variance, the count of sampling theory, and the count of receiver chains, the fixed decision technique level is calculated based on fixed false alarm probability related to the below formulation:
λfa=[q−1(pfa)+√rn]√rn2σ2ω(19)
Based on the evaluation, the procedure of signal detection is achieved by decision threshold adjustments. The threshold adjustments also degrade the presentation of spectrum sensing in the CRN network. The threshold adjustment parameter is optimally selected by using modified black widow optimization. The detailed explanation of the proposed algorithm is explained below.
3.4 Modified Black Widow Optimization
This algorithm is initiated with the consideration of spider behaviors. Every spider is defined as a potential solution. Based on the spiders, try to generate a new solution. Here, cannibalism is achieved when the female black widow eats the male during the mating process. Based on this, an algorithm is developed and the mutation operation is enhanced by considering boosting operation. The mathematical explanation of the BWO is presented in the below sections.
Initial population: The random threshold parameters are initialized with the black widow population. To solve an optimization issue, the parameters of the issue parameters should consider, and form a specific design for the solution of the present problem [21]. The initial population of the black widows (threshold parameters) is presented as follows:
widow=[X1,X2,…,XNvar](20)
Here, 1×Nvar is defined as the solution to the problem in the array structure and Nvar is defined as a dimensional optimization issue. Every parameter [X1,X2,…,XNvar] is a floating-point count.
Fitness evaluation: Additionally, the fitness widow is achieved by considering the fitness function and widow array. The fitness function is considered the SINR ratio of the signal. The fitness function is formulated as follows:
fitness=f(widow)=f[X1,X2,…,XNvar](21)
min∂IJ∑NI=J∑MI=1δJ×δIJ×|SNRIJ−SNRAVG|(22)
Subject to:
C1:δJ=1,∀n(23)
C2:∑MJ=1∂IJ=cn,∀n(24)
C3:∑NJ=1∂IJ=1,∀m(25)
Here, C3 is defined as the selection of threshold per primary user channel, C2 is defined as the one secondary user cannot act as the threshold of multiple channels, C1 is defined as only secondary user with sufficient extra energy for sensing and data transmission is participate in threshold selection, ∂IJ is defined as a secondary user of the channel, δJ=1 is defined as a secondary user considered as residual energy for spectrum sensing with data transmission, SNRAVG is defined as the average SNR of every secondary user for every channel and SNRIJ is defined as the SNR of the secondary user. To initiate the optimization issues, a candidate widow matrix of size Nvar×Npop is created with the basis of spider population. After that, the parent pair is normally chosen to manage the procreating phase based on the mating process, and the male black widow is attack the female during the mating process or after completing the mating process.

Procreate: In the BWO [20], the pairs are dependent on each other, and they start to mate to regenerate the new creation. This algorithm is considered to reproduce the array and it is named alpha it must be generated as long as a widow array with the basis of random creation. After that, the offspring is generated by utilizing the parameters of parents and offspring which are presented as follows:
{y1=α×x1+(1−α)×x2y2=α×x2+(1−α)×x1(26)
Here, x2 and x1 are parents and y1 and y2 are offspring. This procedure is continuously achieved with Nvar/2 times and randomly selected numbers must not be duplicated, and α is considered as [0,1]. At last, the mom and children can be added to an array and arranged with the basis of fitness parameters related to cannibalism rating.
Cannibalism: BWO consists of three types of cannibalism. The first one is sexual cannibalism, that the female black widow eats her husband during mating or after mating. The second one is sibling cannibalism; the strong siblings eat the weaker siblings. The third one is that the surviving strong baby spiders eat their mother.
Boosted Mutation: In this phase, randomly choose the mute pop count of individuals from a population. The mute pop is computed based on the mutation rate [22]. The mutation parameter is important to generate efficient convergence speed. At any local operation, the mutation operation is utilized to reduce trapping conditions and enhance convergence. Three general parameters are associated with generating the mutation rules such as generation with randomly chosen individuals, generation with the present individual in the population, and generation with the optimal individual in the population. At last, the former two parameters are deterministic. After that, a new parameter like a generation with a specific individual in the population is added. The optimal mutation rule is generated with the assistance of the novel ingredient with an average of a few chosen individuals. When compared with the previous generation, the surviving individual in the generation consists of at least or better comparable fitness parameters. The mutation operation connects the direction data which achieves optimal determinism and high definite. Hence, the average mutation rule with a specified direction is formulated as follows:
vjI=yjI+f1⋅(yjavg−yj−1I)+f2⋅(yjRI1−yjRI2)(27)
Here, j>1. The optimal individual of the generation is denoted as yjavg and it is measured as:
yjavg=1s∑sk=1yjk(28)
If j=1, the general mutation rule is considered as follows:
vjI=yjRI3+fo⋅(yjRI4−yjRI5)+fo⋅(yjRI6−yjR1)(29)
Some mutual random variables selected from {0,1,…,PN} are defined with the consideration of subscripts of R. The interval range [0.5,1] is considered to fix variables like fo,f1 and f2.
Convergence: Based on the algorithm process, three terminate conditions are defined such as achieving the defined stage of accuracy, adherence of no variation in the fitness parameter of the optimal widow for different iterations, and a defined count of iterations. With the consideration of the fitness function, the algorithm is identified the best solutions. At the first iteration, the local optima solution is considered the best solution. After that, based on the fitness function, the optimal solution is selected and checked with the local optima solution which one is best, that saved as an optimal solution. Similarly, the iteration is processed until the optimal solution is obtained. Based on this modified black widow optimization algorithm can be utilized to select the optimal threshold in the threshold adjustments for achieving spectrum sensing in the CRN network.
To justify the proposed method, the performances are analyzed and presented in this section. The projected method is developed for attaining spectrum sensing in the cognitive radio network. The proposed approach is executed in the MATLAB software R2016b. The proposed method is utilized a few parameters are arranged in Table 1. This methodology is validated by considering various measures like energy efficiency, average network throughput, number of selected sensing nodes, total error probability, missed detection probability, sensing performance gain, false alarm probability, and probability of detection. The proposed method is contrasted with conventional techniques such as WOA and GWO, respectively.
The probability of detection with a spectrum sensing period is analyzed and given in Fig. 2. In the figure, the proposed methodology is consuming a high probability of detection when contrasted with the conventional techniques of GWO and WOA, respectively. In the sensing time of 0.1, the proposed method achieved 0.71 probability detection and, the GWO and WOA achieved 0.5 and 0.11. Based on this evaluation, the proposed method achieved a 25% higher probability of detection in the spectrum sensing of cognitive radio networks.
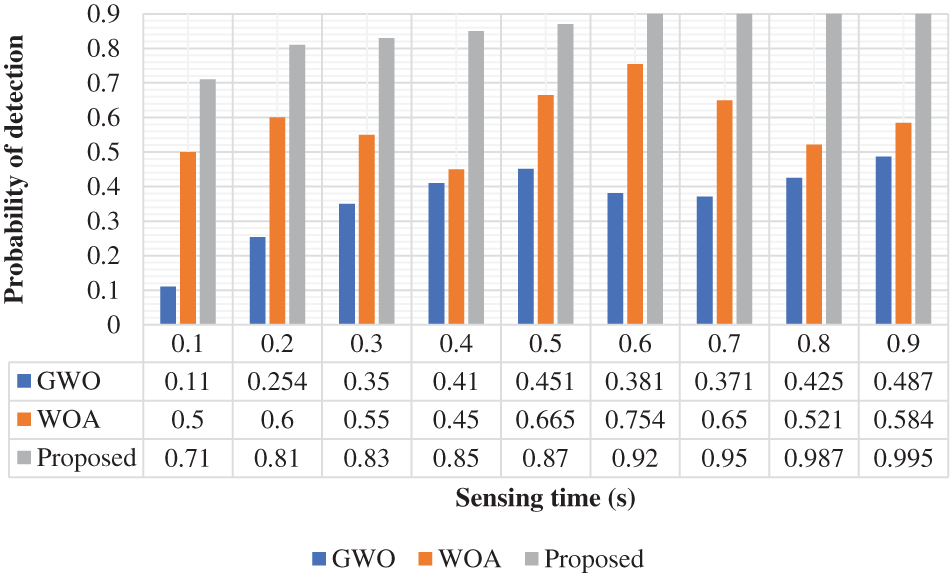
Figure 2: Probability of detection
The false alarm probability is analyzed with a few cognitive users as shown in Fig. 3. Additionally, it is compared with conventional techniques. In the 10 cognitive users, the proposed approach achieved a 0.65 false alarm probability. It is analyzed for validation purposes. This measure should be low level. In this evaluation, the proposed technique attained a low false alarm probability. This false alarm probability function is a validation measure of the spectrum sensing of cognitive radio users. The sensing performance gain is an effective measure of the computing performance of the spectrum sensing approach in cognitive users. The performance gain is validated and analyzed in Fig. 4. For the cognitive users of 10, the performance gain of the projected approach is 0.09, and WOA and GWO are achieved at 0.07 and 0.06, respectively. With this validation measure, the proposed approach achieved high-performance gain in the spectrum sensing procedure. It is computed based on below formulation:
ΔPfj=pf(j−1)−pf(j)(30)
Here, pf(j) is defined as the false alarm probability of cooperative nodes. And, it is defined as the sensing performance gain introduced by adding the jth cooperative node to the cooperative sensing node-set.
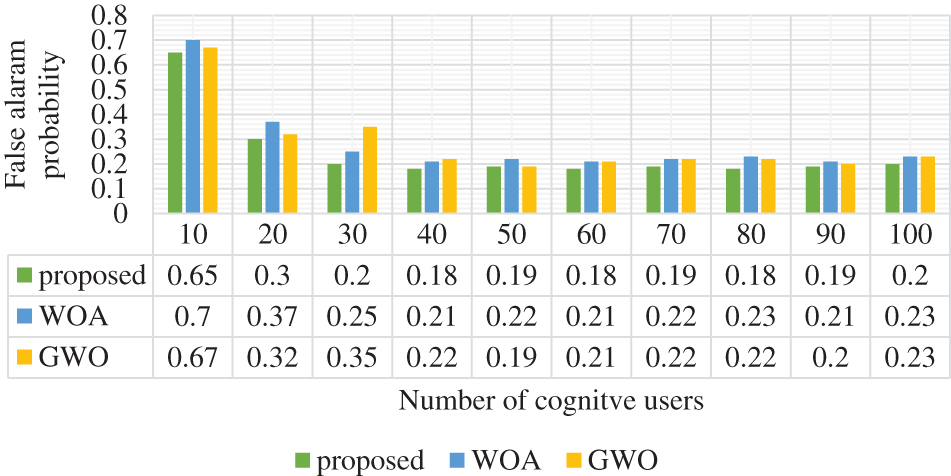
Figure 3: False alarm probability
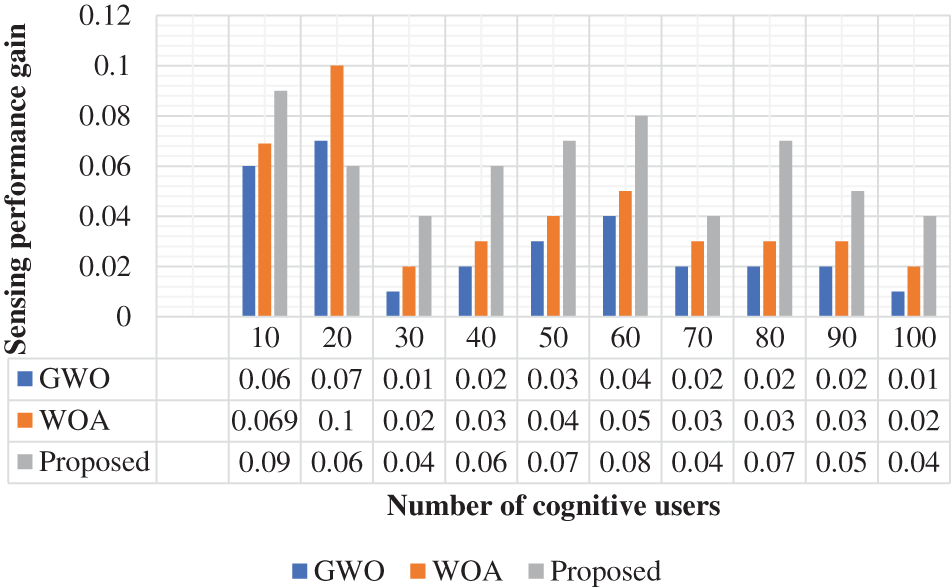
Figure 4: Sensing performance gain
The missed detection probability function is validated and analyzed in Fig. 5. The proposed approach is contrasted with the assistance of the WOA and GWO. The missed detection probability function is analyzed with different frame length variations. The frame length function is varied and missed detection probability function is evaluated. In the 10-frame length, the proposed approach achieved 0.27, WOA and GWO achieved 0.32, and 0.3 missed detection probability function. This function is formulated as the secondary user misses the primary user’s presence because of the AWGN channel model and noise. So, the missed detection probability should be present at a low level. In this validation, the missed detection probability attained a low missed detection probability function.
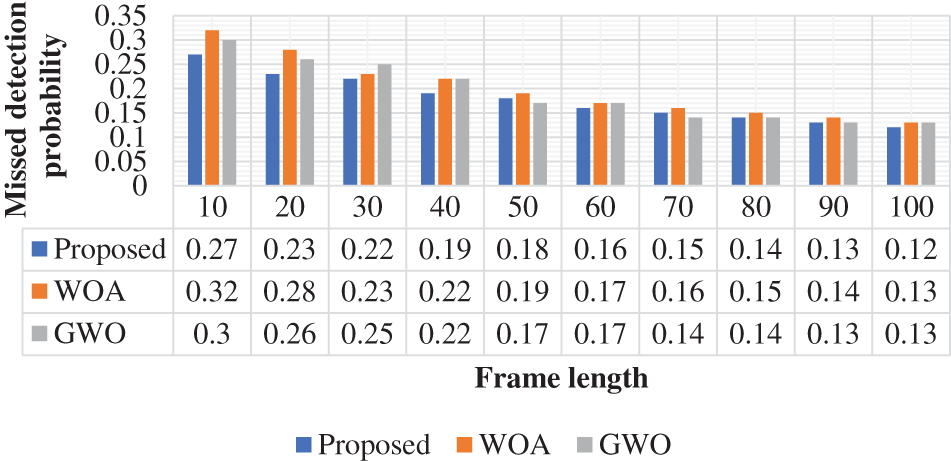
Figure 5: Missed detection probability
The total error probability function is computed and illustrated in Fig. 6. This error function is computed based on the cognitive user’s variation. In the total error probability, the proposed method attained 0.15 at 10 users. Similarly, the WOA and GWO achieved 0.16 and 0.15, respectively. From the analysis, the projected approach can be obtained with a low total error probability when contrasted with conventional approaches. Additionally, the projected approach obtained a 0.05% higher efficiency of the total error probability function. During spectrum sensing, the selected cognitive user plays a significant role because high-count users should be connected to the network to increase the efficient utilization of spectrum sensing. The selected users for spectrum sensing are analyzed and illustrated in Fig. 7. From the validation, the projected approach is obtained as 10% efficient when measured with the number of selected users in cognitive networks. When compared with the traditional approaches, the proposed methodology selected a high count of selected users. Based on this condition, the selected users are considered for spectrum allocation in the CRN network. The average network throughput is analyzed and presented in Fig. 8. The throughput should be high for the optimal spectrum allocation process in CRN. Based on the review, the proposed approach is obtained optimal throughput. The proposed approach obtained 1.2 throughputs at 10 users. Similarly, the WOA and GWO obtained 1 and 0.8 throughput, respectively.
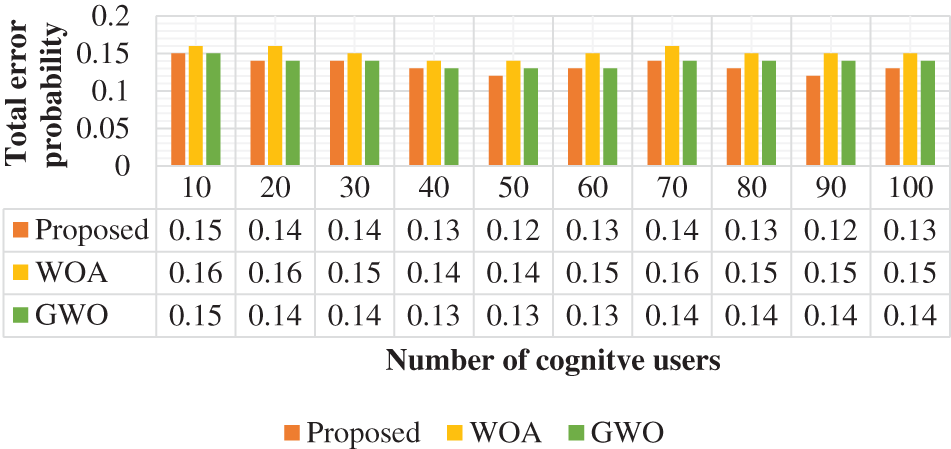
Figure 6: Total error probability
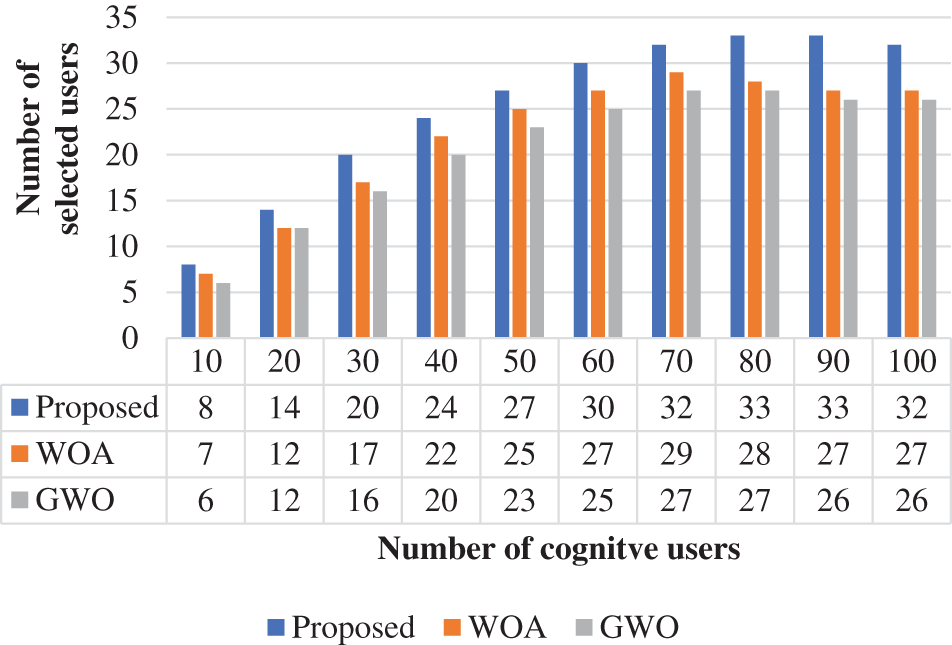
Figure 7: Number of selected users
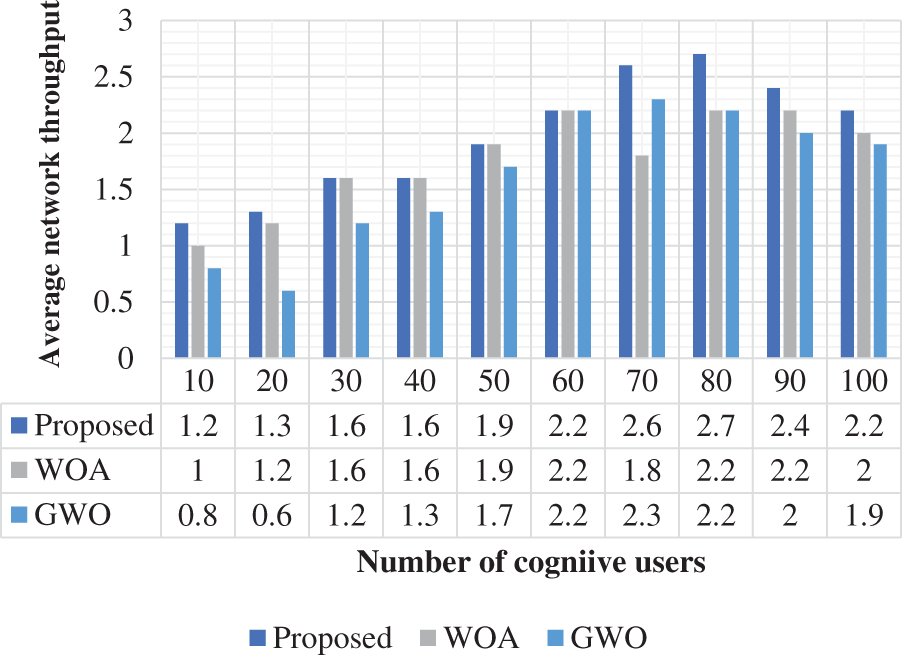
Figure 8: Average network throughput
The average network throughput is a measure to validate the proposed approach which is given in Fig. 8. The proposed method achieved a throughput of 1.2 at 10 users. The WOA and GWO achieved 1 and 0.8 throughput at 10 users. Throughput is a measure to analyze the communication process in CRN. The throughput should be present at a high level. Based on this evaluation, the proposed approach achieved 0.13% higher throughput when compared with the conventional techniques. Energy efficiency is a measure to validate the proposed approach which is given in Fig. 9. The proposed method achieved an energy efficiency of 0.7 for 10 users. The WOA and GWO achieved 0.5 and 0.5 energy efficiency at 10 users. Based on this evaluation, the proposed approach achieved 0.22% higher energy efficiency when compared with the conventional techniques.
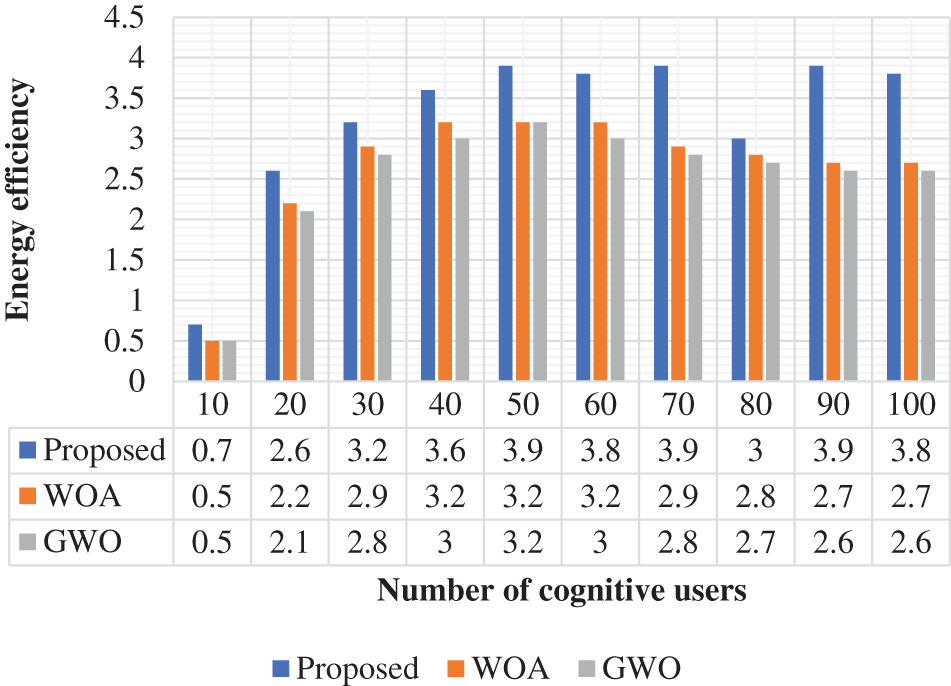
Figure 9: Energy efficiency
This paper develops the ETBED approach for spectrum sensing approach in cognitive radio networks. The threshold detection is achieved by considering the received signal with the secondary user and contains square law. This CRN has been designed with the signal transmission of multiple outputs-orthogonal frequency division multiplexing. In this proposed approach, dynamic detection threshold adjustments have been considered in spectrum sensing. The dynamic threshold parameter is tuned by considering the MBWO. In the BWO, the mutation function has been enhanced by using the boosting approach. The boosting approach has enhanced the BWO process of the system. Finally, spectrum sensing has been efficiently achieved based on the proposed approach. The proposed approach is evaluated by considering different measures such as energy efficiency, average network throughput, number of selected sensing nodes, total error probability, missed detection probability, sensing performance gain, false alarm probability, and probability of detection. The proposed method is compared to conventional techniques such as WOA and GWO, respectively. The analysis indicated that the proposed approach yields superior throughput and energy efficiency results. It performs an average throughput of 2.2 Mbps and an energy efficiency of 3.8 compared to conventional techniques. In future work, real-time analysis will be considered for evaluating the proposed approach in spectrum sensing applications.
Acknowledgement: We sincerely thank the SASTRA Deemed University for providing an excellent infrastructure to carry out the research work.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: R. Saravanan, R. Muthaiah; data collection: R. Saravanan; analysis and interpretation of results: R. Saravanan, A. Rajesh; draft manuscript preparation: R. Saravanan, R. Muthaiah, A. Rajesh. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data will be made available on request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Lin, S., Zheng, B., Chen, F., Zhang, R. (2022). Intelligent reflecting surface-aided spectrum sensing for cognitive radio. IEEE Wireless Communications Letters, 11(5), 928–932. [Google Scholar]
2. Nair, R. G., Narayanan, R. (2023). Cooperative spectrum sensing in cognitive radio networks using machine learning techniques. Applied Nanoscience, 13(3), 2353–2363. [Google Scholar]
3. Nasser, A., Hassan, H. A. H., Mansour, A., Yao, K. C., Nuaymi, L. (2022). Intelligent reflecting surfaces and spectrum sensing for cognitive radio networks. IEEE Transactions on Cognitive Communications and Networking, 8(3), 1497–1511. [Google Scholar]
4. Wu, J., Zhang, J. (2022). Quick cooperative spectrum sensing in cognitive unmanned aerial vehicles networks. Transactions on Emerging Telecommunications Technologies, 33(5), e4441. [Google Scholar]
5. Arshid, K., Jianbiao, Z., Hussain, I., Pathan, M. S., Yaqub, M. et al. (2022). Energy efficiency in cognitive radio network using cooperative spectrum sensing based on hybrid spectrum handoff. Egyptian Informatics Journal, 23(4), 77–88. [Google Scholar]
6. Banumathi, J., Sangeetha, S. K. B., Dhaya, R. (2022). Robust cooperative spectrum sensing techniques for a practical framework employing cognitive radios in 5G networks. In: Artificial intelligent techniques for wireless communication and networking, pp. 121–138. Wiley: Scrivener Publishing LLC. [Google Scholar]
7. Prasad, R. K., Jaya, T. (2023). Intelligent spectrum sharing and sensing in cognitive radio network by using AROA (adaptive rider optimization algorithm). International Journal of Computational Intelligence and Applications, 22(1), 2341007. [Google Scholar]
8. Kumar, A., Thakur, P., Pandit, S., Singh, G. (2022). HSA-SPC: Hybrid spectrum access with spectrum prediction and cooperation for performance enhancement of multiuser cognitive radio network. Computer Networks, 203, 108596. [Google Scholar]
9. Ji, C., Qi, Q. (2022). Cooperative spectrum sensing algorithm based on evolutionary game theory. IEEE Access, 10, 71557–71565. [Google Scholar]
10. Marriwala, N., Punj, H., Panda, S., Kaur, I., Rathore, D. (2022). An authentication based approach for prevention of spectrum sensing data falsification attacks in cognitive radio network. Wireless Personal Communications, 124(1), 119–145. Springer. https://doi.org/10.1007/s11277-021-09329-8 [Google Scholar] [CrossRef]
11. Xing, H., Qin, H., Luo, S., Dai, P., Xu, L. et al. (2022). Spectrum sensing in cognitive radio: A deep learning based model. Transactions on Emerging Telecommunications Technologies, 33(1), e4388. [Google Scholar]
12. Tan, X., Zhou, L., Wang, H., Sun, Y., Zhao, H. et al. (2022). Cooperative multi-agent reinforcement-learning-based distributed dynamic spectrum access in cognitive radio networks. IEEE Internet of Things Journal, 9(19), 19477–19488. [Google Scholar]
13. Mohanakurup, V., Baghela, V. S., Kumar, S., Srivastava, P. K., Doohan, N. V. et al. (2022). 5G cognitive radio networks using reliable hybrid deep learning based on spectrum sensing. Wireless Communications and Mobile Computing, 2022, 1–17. [Google Scholar]
14. Eappen, G., Shankar, T., Nilavalan, R. (2022). Cooperative relay spectrum sensing for cognitive radio network: Mutated MWOA-SNN approach. Applied Soft Computing, 114, 108072. [Google Scholar]
15. Gul, O. M. (2019). Average throughput of myopic policy for opportunistic access over block fading channels. IEEE Networking Letters, 1(1), 38–41. [Google Scholar]
16. Gul, O. M. (2021). Near-optimal opportunistic spectrum access in cognitive radio networks in the 5G and IoT Era. In: 2021 IEEE 46th Conference on Local Computer Networks (LCN), pp. 403–406. Edmonton, Alberta, Canada, IEEE. [Google Scholar]
17. Tan, Z., Wang, D., Liu, Q., Li, Z., Zhang, N. et al. (2023). Deep learning aided multi-level transmit power recognition in cognitive radio networks. IEEE Transactions on Cognitive Communications and Networking, 9, 332–344. [Google Scholar]
18. Bakshi, S., Sharma, S., Khanna, R. (2023). Shapley-value-based hybrid metaheuristic multi-objective optimization for energy efficiency in an energy-harvesting cognitive radio network. Mathematics, 11(7), 1656. [Google Scholar]
19. Lorincz, J., Ramljak, I., Begusic, D. (2021). Algorithm for evaluating energy detection spectrum sensing performance of cognitive radio MIMO-OFDM systems. Sensors, 21(20), 6881. [Google Scholar] [PubMed]
20. Ramljak, I., Begušić, D., Lorincz, J. (2022). Operational characteristics of square-law combining energy detector in MIMO-OFDM cognitive radio systems. Applied Sciences, 12(9), 4684. [Google Scholar]
21. Hayyolalam, V., Kazem, A. A. P. (2020). Black widow optimization algorithm: A novel meta-heuristic approach for solving engineering optimization problems. Engineering Applications of Artificial Intelligence, 87, 103249. [Google Scholar]
22. Hu, G., Du, B., Wang, X., Wei, G. (2022). An enhanced black widow optimization algorithm for feature selection. Knowledge-Based Systems, 235, 107638. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
