 Open Access
Open Access
ARTICLE
Prediction of Damping Capacity Demand in Seismic Base Isolators via Machine Learning
1 Department of Civil Engineering, Istanbul University–Cerrahpaşa, Istanbul, 34320, Turkey
2 Department of Informatics, Mimar Sinan Fine Arts University, Istanbul, 34427, Turkey
3 Department of Civil and Environmental Engineering, Temple University, Philadelphia, PA, 19122, USA
4 Department of Smart City, Gachon University, Seongnam, 13120, Korea
* Corresponding Authors: Gebrail Bekdaş. Email: ; Zong Woo Geem. Email:
(This article belongs to the Special Issue: Meta-heuristic Algorithms in Materials Science and Engineering)
Computer Modeling in Engineering & Sciences 2024, 138(3), 2899-2924. https://doi.org/10.32604/cmes.2023.030418
Received 04 April 2023; Accepted 26 July 2023; Issue published 15 December 2023
Abstract
Base isolators used in buildings provide both a good acceleration reduction and structural vibration control structures. The base isolators may lose their damping capacity over time due to environmental or dynamic effects. This deterioration of them requires the determination of the maintenance and repair needs and is important for the long-term isolator life. In this study, an artificial intelligence prediction model has been developed to determine the damage and maintenance-repair requirements of isolators as a result of environmental effects and dynamic factors over time. With the developed model, the required damping capacity of the isolator structure was estimated and compared with the previously placed isolator capacity, and the decrease in the damping property was tried to be determined. For this purpose, a data set was created by collecting the behavior of structures with single degrees of freedom (SDOF), different stiffness, damping ratio and natural period isolated from the foundation under far fault earthquakes. The data is divided into 5 different damping classes varying between 10% and 50%. Machine learning model was trained in damping classes with the data on the structure’s response to random seismic vibrations. As a result of the isolator behavior under randomly selected earthquakes, the recorded motion and structural acceleration of the structure against any seismic vibration were examined, and the decrease in the damping capacity was estimated on a class basis. The performance loss of the isolators, which are separated according to their damping properties, has been tried to be determined, and the reductions in the amounts to be taken into account have been determined by class. In the developed prediction model, using various supervised machine learning classification algorithms, the classification algorithm providing the highest precision for the model has been decided. When the results are examined, it has been determined that the damping of the isolator structure with the machine learning method is predicted successfully at a level exceeding 96%, and it is an effective method in deciding whether there is a decrease in the damping capacity.Keywords
Nomenclature
| AI | Artificial intelligence |
| ANN | Artificial neural networks |
| AUC | Area under the ROC curve |
| DT | Decision tree |
| FEMA | Quantification of building seismic performance factors |
| ML | Machine learning |
| MLP | Multilayer perceptron |
| MR | Magnetorheological |
| NB | Naïve bayes |
| OmniXAI | Omni explainable artificial intelligence |
| RF | Random forest |
| ROC | Receiver operating characteristic |
| SDOF | Single degrees of freedom |
| SVM | Support vector machines |
| TMDs | Tuned mass dampers |
| XAI | Explainable artificial intelligence |
| e.g., | |
| Damping coefficient | |
| Stiffness | |
| The mass of the isolator | |
| The mass of the structure | |
| The total mass of the isolated system | |
| Period | |
| Natural angular frequency | |
| Damping ratio | |
Seismic base isolators act as a vibration separator for the structure from the ground motion. The most important control element in an isolator design is the flexibility of the isolator. The structural base isolators could not only move sufficiently against major earthquakes but also prevent the structure from moving too much against minor earthquakes or aftershocks. The sufficient ductility of base isolators prevents the building structure from acting too flexible and compromising the safety of the structure under possible major earthquakes [1,2]. The flexibility of the base isolator can be determined according to the seismic zones of the structures, which is a parameter related to its damping ratio for the seismic design. It is known that increasing the damping ratio reduces the mobility requirement of the isolator [3]. An isolator placed at an optimum level requires maintenance and repair in monthly or annual periods depending on the type of isolator. Isolators can be placed indoors or outdoors. Those installed indoors need maintenance due to dust, while those installed outside need maintenance due to natural reasons such as air temperature, dust, and water. Particularly, dust accumulation in pendulum-type friction isolators causes roughness on the surface of the pendulum ball and negatively affects its movement. It is known that if the steel material used in isolators can be corroded by water, it will adversely affect the isolator. Sağıroğlu et al. stated that pendulum-type isolators used in a hospital in a city where temperatures are below 5 degrees Celsius most of the year are mounted between steel plates to prevent the possibility of cold weather conditions causing volume change and cracking of the concrete [4]. Considering the isolator effect of the air temperature, the assembly of the isolator is made from different materials. Apart from natural weather and environmental conditions, other situations require isolator maintenance. Isolator maintenance must be done after medium and major earthquakes that affect the area where the structure is located. It should not be forgotten that there may be environmental effects that may reduce the damping capacity of the system for isolators that are generally designed as vertically rigid and horizontally mobile. Natural disasters such as earthquakes can affect the isolator as well as other human-made disruptions like construction, renovation, foundation excavation, and natural gas explosion around the structure. Any accident that will cause strong vibrations is also some of the factors that affect the damping capacity of the isolator. The aforementioned conditions may cause abrasions in the mechanical parts of the isolator, isolator bed, or joints such as bolts, which require maintenance and repair [5]. Minor earthquakes may have some effect on the isolator. Although this change in damping performance is not alarming for maintenance when it is small, a 10% decrease in damping capacity is a harbinger of a loss that needs to be reviewed. The use of artificial intelligence, which is today’s technology, for the detection of such situations, is important in terms of time and cost savings, as well as isolator life and sustainability.
Machine learning, a sub-branch of artificial intelligence, is a method where a machine can be trained with the collected data and predict a new situation in the light of the trained data. Prediction model studies have been carried out with machine learning in many different areas including the hydraulic conductivity of sandy floors, liquefaction of fine-grained ground, geopolymers of construction demolition waste, cement-based materials of carbon nanotubes, post-fire compressive strength of slag-based concrete, a nominal cutting capacity of a reinforced concrete wall, slope stability, axial load-bearing capacity of concrete-filled steel pipes, shear strength of reinforced concrete beams with and without striation, construction cost, shear strength of the ground, location after blasting operations, vibrations and migration mode of reinforced concrete curtain walls, building mechanics, building materials, construction management, etc. in the field of civil engineering [6–18]. Machine learning algorithms have a wide range of applications that can be applied to classification and regression-type problems. The level of success varies depending on the type of problem and the dependency and correlation of the data inputs used. Algorithms should be compared to create the most successful model for the data. While the K-Nearest Neighbors algorithm is an advantageous choice in cases where the similarity of the data inputs is remarkable, the Naïve Bayes algorithm comes to the fore when each feature is independent of the other. The Support Vector Machine (SVM) algorithm works well when there is a clear margin of separation in the data and the features are chosen correctly. In their study using various SVM models, Zeng et al. examined the effect of choosing the correct value on the SVM precision level in estimating the peak particle velocity induced by a quarry explosion [19]. While the linear relationship between dependent and independent variables in the data facilitates the linear regression algorithm to provide high accuracy, it is possible to search for a linear combination of features that distinguish two or more classes with the linear discriminant analysis algorithm. In making a model individual machine-learning model can be created, or ensemble learning models can be used by combining more than one result. It is also common to use a combination of algorithms for various types of classification and regression. Cavaleri et al. used a successful ensemble learning technique with multiple machine learning algorithms including resultant regression algorithms like random forest, adaboost, and bagging regression for the estimation of reinforced concrete bond strength, and also took into account the effect of sub-models on the success level [20]. Barkhordari et al. produced an ensemble learning model with bagging and boosting algorithms like support vector machine, adaboost regressor, bagging regressor, and gradientboost regressor for the estimation of compressive strength of fly ash concrete, and obtained satisfactory results [21]. Another technique used outside of ensemble learning algorithms is extreme machine learning. With this method, Asteris et al. presented a model that predicts clay compressibility with less than 20% bias [22].
Machine learning is a frequently used method in the design of dampers for the vibration control of structures and the estimation of structural response. Sun et al. using structural health monitoring data for machine learning to evaluate the performance of tuned mass dampers (TMDs) related to the wind-induced oscillation of a bridge, developed a model that predicts structure acceleration based on wind characteristics and temperature [23]. Bae et al. experimentally investigated the fatigue performance of a passive metallic damper under earthquake load and observed that machine learning was successful when they compared fatigue vs. damper performance predictions of machine learning to experimental results [24]. Farrokhi et al. modeled the predictive behavior of TMDs used in a tall steel framed structure under various earthquake records using machine learning methods such as Naïve Bayes (NB), Decision Tree (DT), Support Vector Machines (SVM) and Artificial Neural Networks (ANN) and found that SVM outperforms the story drift estimation [25]. Yucel et al. proposed an artificial neural network model that predicts the optimum period and damping ratio parameters of TMDs [26]. Li et al. in the estimation of the optimum damper distribution, suggested the number of dampers, construction properties, etc. It has achieved good results with Support Vector Machine (SVM) and multilayer perceptron (MLP) machine learning methods using parameters as input [27]. Machine learning techniques have been used effectively in magnetorheological (MR) dampers as a semi-active system used in the prevention of vibrations in a wide range from vehicles to aircraft landing gear, apart from structures, as well as being used in the estimation of various damping device parameters and structural behavior [28–32]. In recent years, considering its successful applications in control devices, it has become a preferred method in the design of base isolation systems, fault detection, and structure displacement estimation. Moeindarbari et al. used artificial neural networks to estimate the failure probability of seismic base isolators and determined that the results are very close to the exact predictions [33]. Nakabayashi et al. applied the machine learning-based deep learning method, which involves image pre-processing for the detection and inspection of air bubbles that arise from concrete pouring [34]. Barakat introduced the artificial neural network model created by recording the behavior of a structure with natural rubber support and viscous fluid damping under close fault earthquakes as a tool that can be used in the isolator pre-design process [35]. Nguyen et al. have developed models for predicting the maximum lateral displacement of seismically isolated structures under earthquake load with machine learning methods such as Artificial Neural Network (ANN), Support Vector Machine (SVM), and Random Forest (RF) [36]. Instead of long trials in determining the properties of multi-stage frictional pendulums used in base isolation systems such as effective period, damping, and displacement capacity, Habib et al. developed a physics-minded neural network model to shorten the design process and observed that it had a remarkable accuracy by comparing it with a physics-knowledgeable, data-based approach [37].
When the research on damping and base isolation systems is examined, it is seen that such control devices have successful applications in determining the optimum design parameters and estimating the structural displacement levels. The development of a failure probability prediction model of isolators is important for inventing control devices. However, it is necessary to determine the performance loss of the control systems before they reach the failure stage and to make a preliminary determination of the maintenance-repair requirement to prevent their irreversible deterioration for the control systems to provide long-term benefits. Today’s technology has pioneered the development of sensors that make it possible to record the smallest displacements in the structure. Various sensors like the linear variable differential transformer (LVDT) have been able to detect improved linear displacement for dimensional measurement [38]. The ability to record the displacements in the structure in this way provided a resource for the development of motion prediction models to be produced with artificial intelligence technologies. Displacement sensors can be used in the losses that will occur in the damping capacity of the control systems as a result of various environmental and dynamic effects. With this change in position, it is possible to estimate the damping ratio required for motion with the artificial intelligence model to be developed for isolators and similar control systems. Considering the damping characteristics of the device placed in the structure before, the amount and importance of the loss in the damping ratio for the control device can be determined by comparing the isolator damping for the displacement amount obtained with the help of sensors. This study aimed to predict the decrease in the damping capacity of seismic base isolators and to determine the maintenance-repair requirement with the artificial intelligence forecasting model.
In this study, a model that helps to predict the decrease in damping performance of the isolator on a class basis and to decide whether it needs maintenance and repair due to natural or environmental effects, a model was created with the machine learning model trained by using the structural properties and the behavior of the structure. For this purpose, the behavior of structures with a single degree of freedom (SDOF) was recorded for different randomly selected stiffness, and periods under FEMA P-695 distant fault earthquakes and used in machine training [39]. Base isolators placed in different building models are divided into 5 classes with 10%, 20%, 30%, 40%, and 50% maximum damping ratio limits. Parameters such as the structural displacement, acceleration, total acceleration, and period placed in different structures under earthquakes were taken as input and the 5-class isolators class was taken as output. By using various machine learning classification algorithms, it has been tried to predict the isolator class from a new structure behavior record. The fact that the estimated class in the isolator class is higher than the placed isolator indicates that the isolator is damaged or requires maintenance and repair due to various reasons.
In this section, basic parameter equations of seismic base isolators and machine learning methods used in artificial intelligence applications are given.
2.1 Optimization of Seismic Isolator System
Seismic base isolators are control devices placed on the base of the superstructure with a weight of one solid of the structure. The total mass of a system operating as a single degree of freedom (SDOF) is calculated as in Eq. (1).
where the total mass of the isolated system is
The main parameter affecting the ductility level of isolators is the period. In an SDOF system, the structure, and the isolator act together as a single mass and have a common period, stiffness, and damping coefficient. The common period of the SDOF system is calculated as in Eq. (2), its stiffness in Eq. (3), and the damping coefficient as given in Eq. (4).
where
Machine learning is a method that includes data training, which is considered a sub-branch of artificial intelligence. The purpose of the method is to provide the estimation of the desired output of the new data, thanks to the model it creates, by training the machine with the data at hand, which reduces the human factor as much as possible. Machine learning is divided into sub-branches such as Supervised Learning, Unsupervised Learning, Reinforced Learning, and Deep Learning. Depending on the type of problem and the input and output of the data, the sub-branch of machine learning is decided in practice. Supervised machine learning is an artificial intelligence method that creates a training result prediction model with the inputs and output of data. When the output in the data set specifies a type, class, or group, classification is categorized as a problem, whereas regression specifies a numerical value [40,41]. In unsupervised machine learning, the machine is asked to make a distinction based on the input data, without the predicted desired output. Whether one part of the data is different from the other part as input is determined by the machine, and the estimation of the new data is made with the distinctive features of the data at hand. Unsupervised machine learning is divided into sub-branches such as data clustering, size reduction techniques, and association analysis [40,42]. Reinforcement learning refers to a mapping process from previous actions to increase the reward-to-benefit margin, especially used in robotic technology [40,43]. Deep learning, on the other hand, is a cutting-edge learning method in machine learning where more specific and more data is used to derive highly precise meanings [44].
2.2.1 Classification Algorithms
Classification is a machine learning method used in supervised learning when the data to be estimated indicates a group of species or class. In problems suitable for classification, algorithms such as logistic regression, support vector machine, nearest neighbor algorithm, linear discriminate analysis, Naïve Bayes, and decision tree are used. Except these, there are bagging and boosting resultant methods based on community learning. In bagging algorithms, decision trees are created by drawing random samples from the data, and a community is formed by creating a different sample sequence each time by leaving the sample back. The final estimate is made by taking the majority or average of the votes of each decision tree in the obtained community. On the other hand, boosting algorithms tried to create a whole model to make a single predictive model by combining weak classifiers and eliminating erroneous predictions. There are varieties of resultant algorithms such as Bagged Decision Tree, Random Forest, AdaBoost, Catboost, XGBoost, and Voting Ensemble. In machine learning, such classifiers make predictions by making decisions based on the models created. The increase in the diversity in the models provides more successful estimations in the case of using the resultant methods.
Logistic Regression is a classification algorithm that performs regression based on the least squares algorithm and estimates a dependent variable through an independent variable [45,46]. It makes a classification by making a probability estimation for the dependent variable according to the independent variable in the data. The argument to be used in classification is categorical. It gives more successful results when the independent variable is binary.
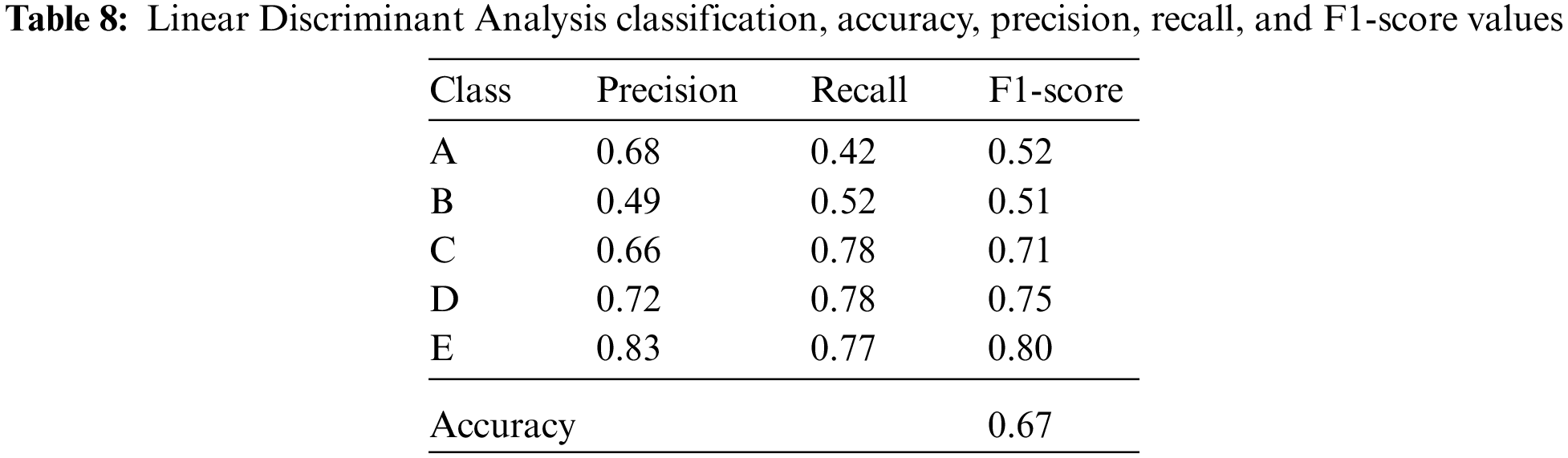
Linear Discriminant Analysis is a classification algorithm that seeks a linear combination between two or more data classes by identifying the best features that distinguish them from each other [47]. It is also known as the size reduction method. It is the search for dimensions that optimizes the distinguishing features between classes.
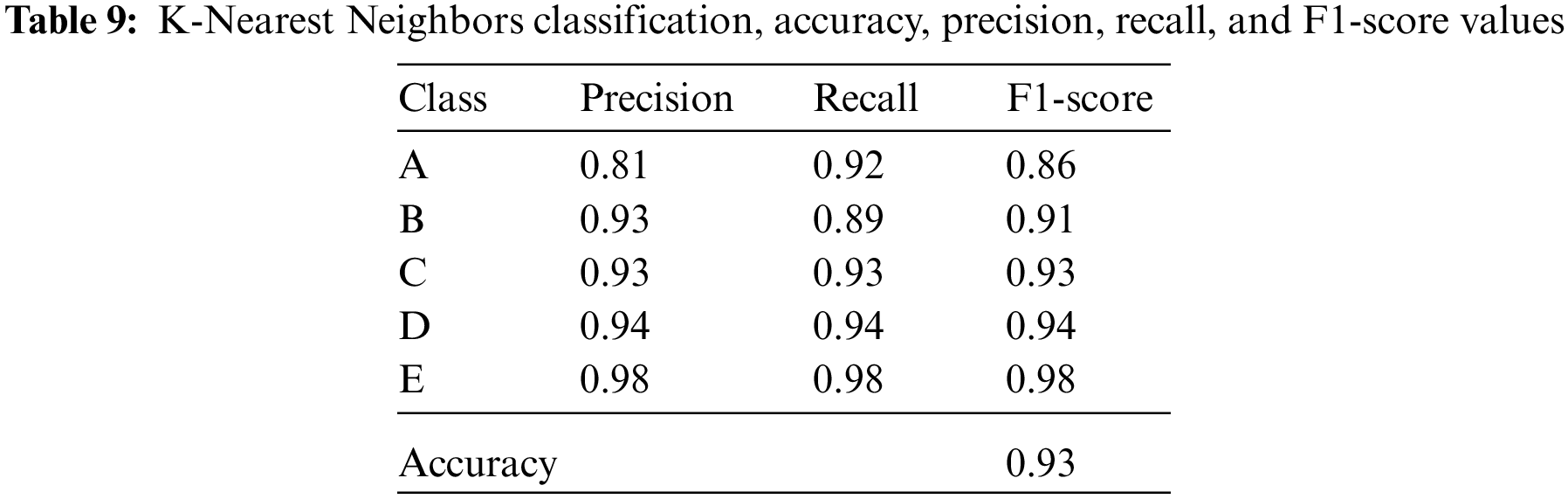
K-Nearest Neighbors perceive the data in the data set as a point and measure the distance between them and other data. It decides the class of the data based on the k value, which expresses the similarity of the closest element. Apart from categorical data classification problems, it is a machine learning algorithm suitable for numerical regression problems [48]. The distance between data points is implemented by choosing the weight vector and the number of nearest neighbors [49].
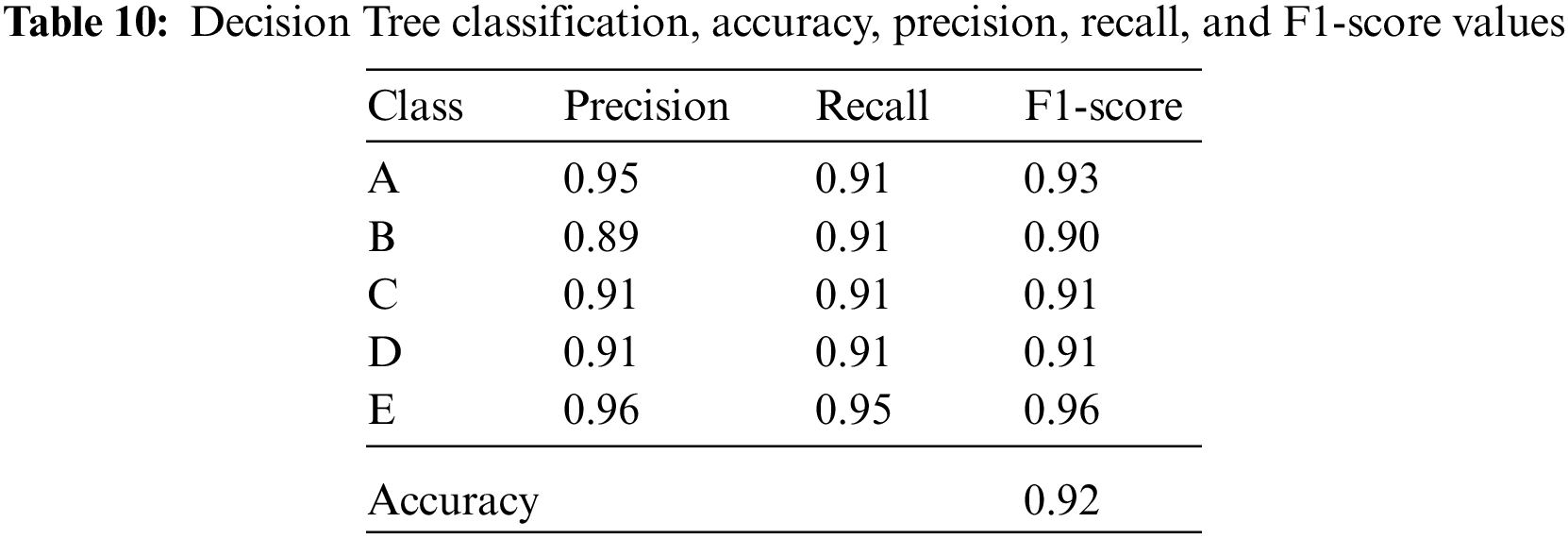
A Decision Tree is a classification algorithm whose features are represented as nodes and the test results of the trained data form the branches of the tree [50]. These nodes refer to three nodes as decision nodes, chance nodes, and end nodes [46,51]. The input data is grouped until the final class is obtained. The data grouped with the questions belonging to the if/else structure takes on a shape resembling the branches of a tree from the starting node point to the final class, and the classification process is completed.
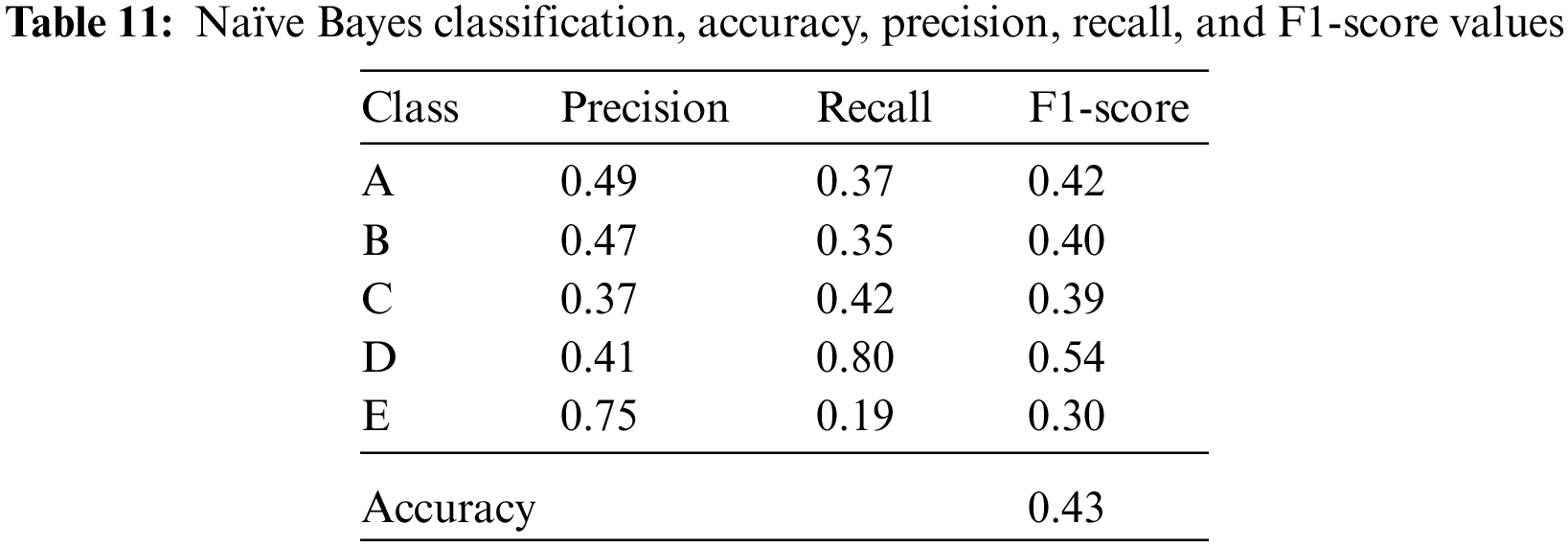
Naïve Bayes calculates the probabilities of each element in a data set, whether it is a class such as a, b, or c, and decides on the class with the highest probability. In the Naïve Bayes approach, it assumes that the feature that determines the class is not related to the existence of another feature, but that a single feature is a feature that determines the distinctive class [46,52].
The Support Vector Machine is based on the separation of non-large-scale data with the help of a line drawn to separate data belonging to different classes on a plane. This line should be as far away from the data classes as possible. The larger the margin indicating the distance to the line range of the data classes, the better the data is decomposed. It is an algorithm suitable for solving both classification and regression problems [53,54].
A Bagged Decision Tree is a machine learning algorithm trained with randomly selected decision trees from the data allocated to training, to increase the variance of the training model. First, the data is divided into subsets. Then, a decision tree is created for each separated cluster, and classification is made by taking the average of the predicted values or the most given decision.
Random Forest is a selection by taking the class that each tree knows best from the trained decision trees created for the data set, and in classification or regression problems, it makes predictions according to the most selected and averages of randomly selected trees [47]. Although it tends to fit the training data, this can be overcome by creating a forest where each decision tree is taken differently [46,55].
Among the ensemble learning algorithms, AdaBoost uses a decision tree algorithm by creating a classifier ensemble to increase the sensitivity of the ensemble. It increases the level of prediction success by giving higher weights to the misclassified tuples [47,56].
CatBoost is a resultant estimation algorithm that can use numerical or categorical data to increase the gradient using decision trees [57,58]. Even with relatively little data, it can give successful results against algorithms that require training with intensive data.
XGBoost is an improved version of the gradient boosting algorithm, which is one of the gradient boosting algorithms with high predictive power [59]. In this algorithm, weak decision trees are strengthened, penalizing complex models to avoid overfitting data.
Voting Ensemble is a machine learning algorithm that uses multiple classification algorithms and gives the most successful result among the models it creates. It is used to select the algorithm that gives the best prediction model among multiple algorithms.
In classification with machine learning classification algorithms, firstly, data attributes are introduced to the system. It is separated as test and training data in the most appropriate measures to prevent excessive learning and rote predictions of the machine. The separated data is modeled with the chosen classification algorithm and is expected to predict the values in the test data. When the obtained estimates are compared with the actual values, the success level of the estimate is obtained. An example of the flow chart created for the XGBoost algorithm, one of the classification algorithms used in the study, is shown in Fig. 1.
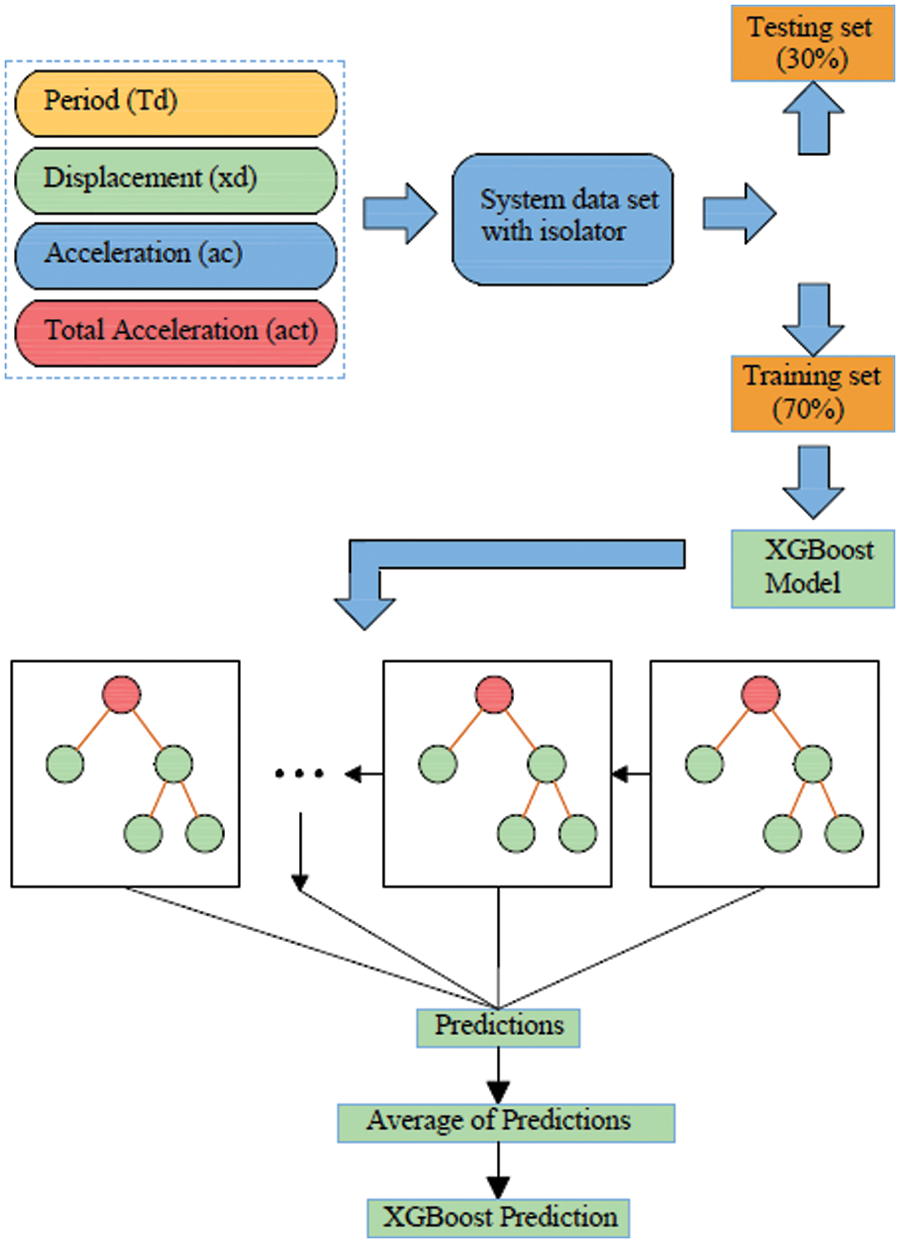
Figure 1: XGBoost flowchart example
The same algorithm may not work well for every problem. Therefore, choosing the best classifier by comparing multiple algorithms will enable machine learning to give more reliable results. With classification algorithms, data is separated; some for training and some for testing. The consistency of machine learning is determined by testing the separated data. Incorrect estimates in the test results of the trained data are recorded in a confusion matrix. When we name the predicted output as true and false, the machine predictions we may encounter from the confusion matrix. Table 1 shows the contents of a confusion matrix.
Displacement
Acceleration
Total Acceleration
Key metrics that are used to assess the performance of a classification model are Accuracy, Precision, Recall, and F1-score.
Accuracy: The accuracy is the rate of correct predictions to all predictions made by the model. The other three metrics used in the evaluation were precision, recall, and F1-scores. These were calculated for each class separately.
Precision: The precision is the ratio of true positives (TP) to the sum of true positives and false positives (FP) (i.e., total predicted positives), and as a formula, Precision = TP/(TP + FP) = TP/TPP.
Recall: The recall is the ratio of true positives to the sum of true positives and false negatives (FN) (i.e., total actual positives), and as a formula, Recall = TP/(TP + FN) = TP/TAP.
F1-score: The F1-score is calculated as 2 * (Precision * Recall)/(Precision + Recall). When the class distribution in data is uneven, F1-score acts as a better metric than Accuracy to measure model performance.
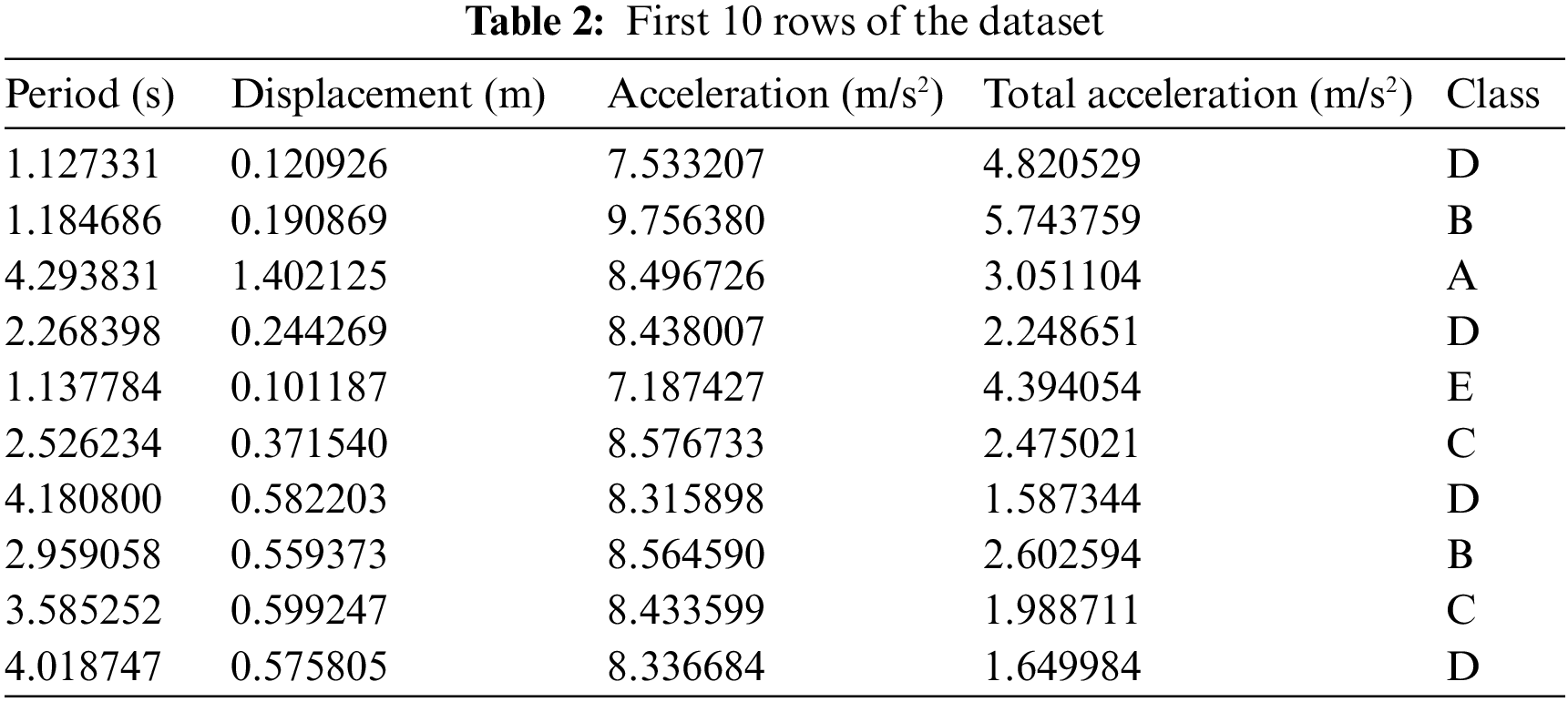
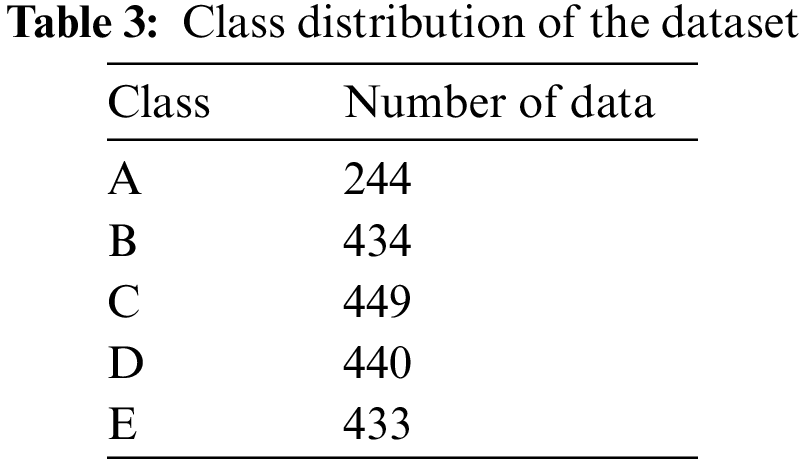
In this study, a seismic base isolator system is placed at the base of a single-degree-of-freedom (SDOF) structural model. By using a randomly selected period between 1 and 5 s and randomly selected damping ratios in the range of 10%–50%, building versions with different stiffness were created for the fixed building mass. In the earthquake simulation created by Matlab Simulink, FEMA P-695 distant fault earthquakes were selected and excited to the structure [39,61]. The top floor displacement, acceleration, and total acceleration values of the building for the record with maximum responses were recorded for the machine learning dataset. A data set of 2000 lines in total, which includes period, structure displacement, structure acceleration, and total acceleration of the structure, and output as the isolator classes for the damping used in the building, was created via dynamic analysis. The isolator classes were chosen according to the required amount of damping to obtain the displacement and acceleration demands. For that reason, these classes are matched with the maximum limits (10% to 50% with 10% intervals) of five classes named from A (the one with the lowest capacity) to E (the one with the highest capacity). The structure model with the isolator placed is shown in Fig. 2. A part of the data set containing 2000 pieces of data created for the isolator is given in Table 2. The distribution of data by classes is shown in Table 3 and data characteristics are shown in Table 4.
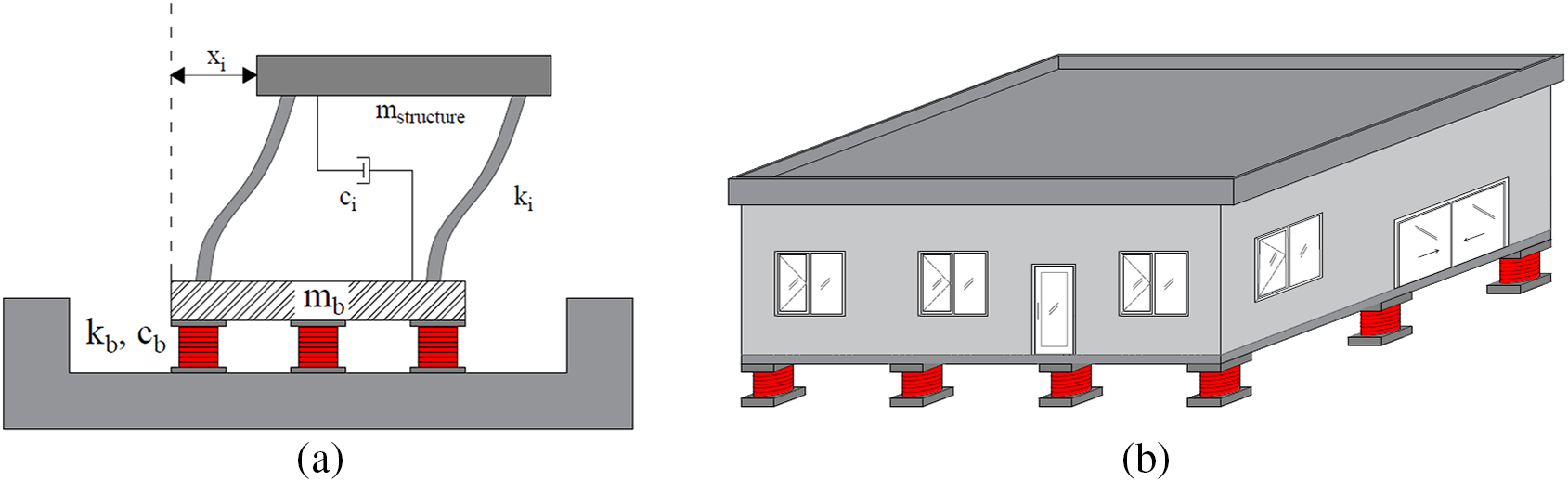
Figure 2: (a) SDOF structure model with base isolator (b) 3D view of the model
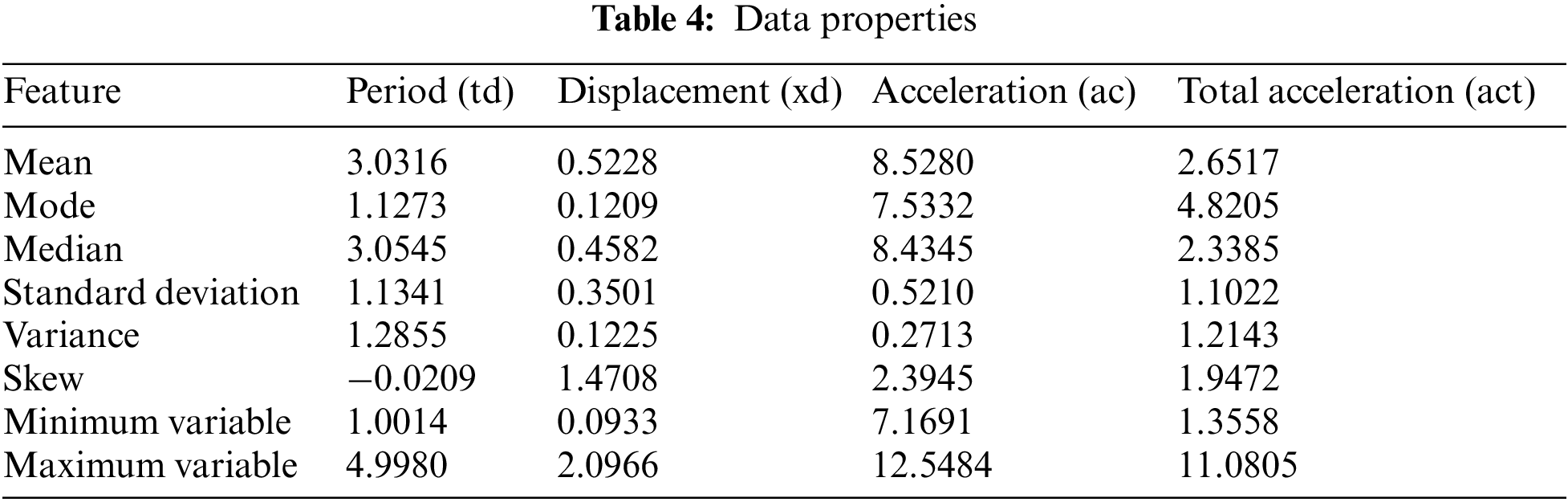
The correlation matrix values of the data set are shown in Table 5 and the correlation graph is in Fig. 3. Data histograms and scatter plots are given in Figs. 4 and 5.
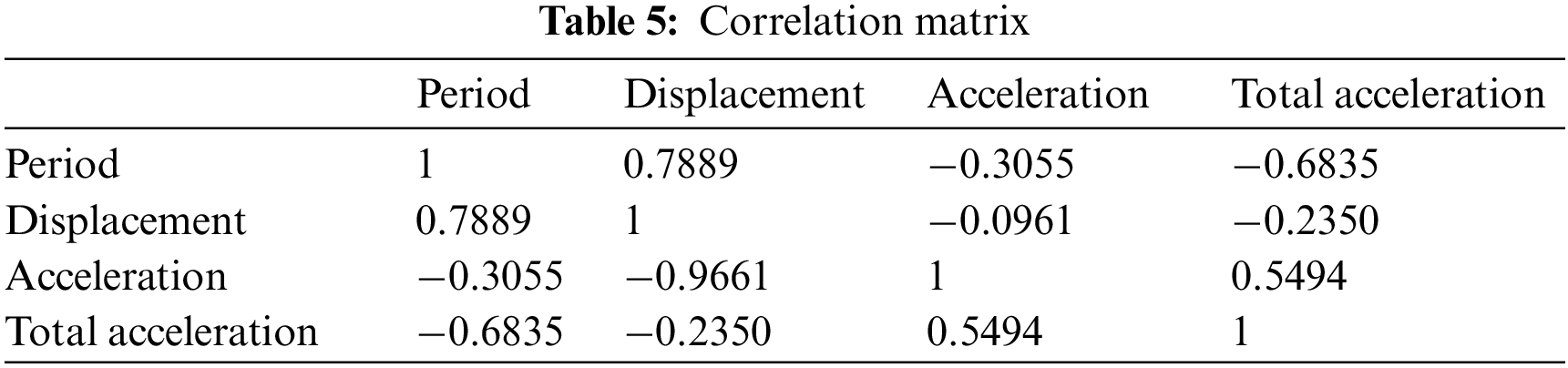
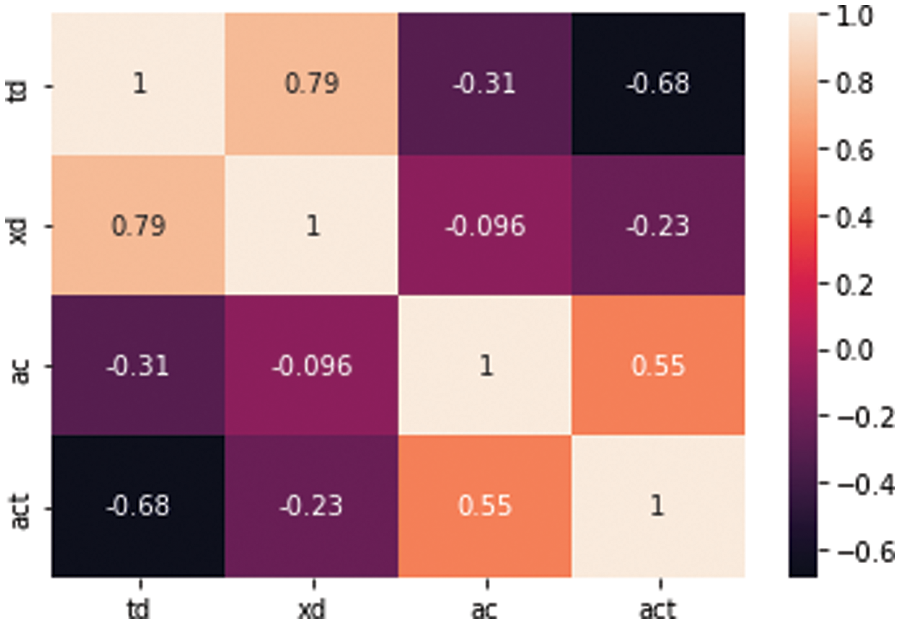
Figure 3: Correlation matrix graph
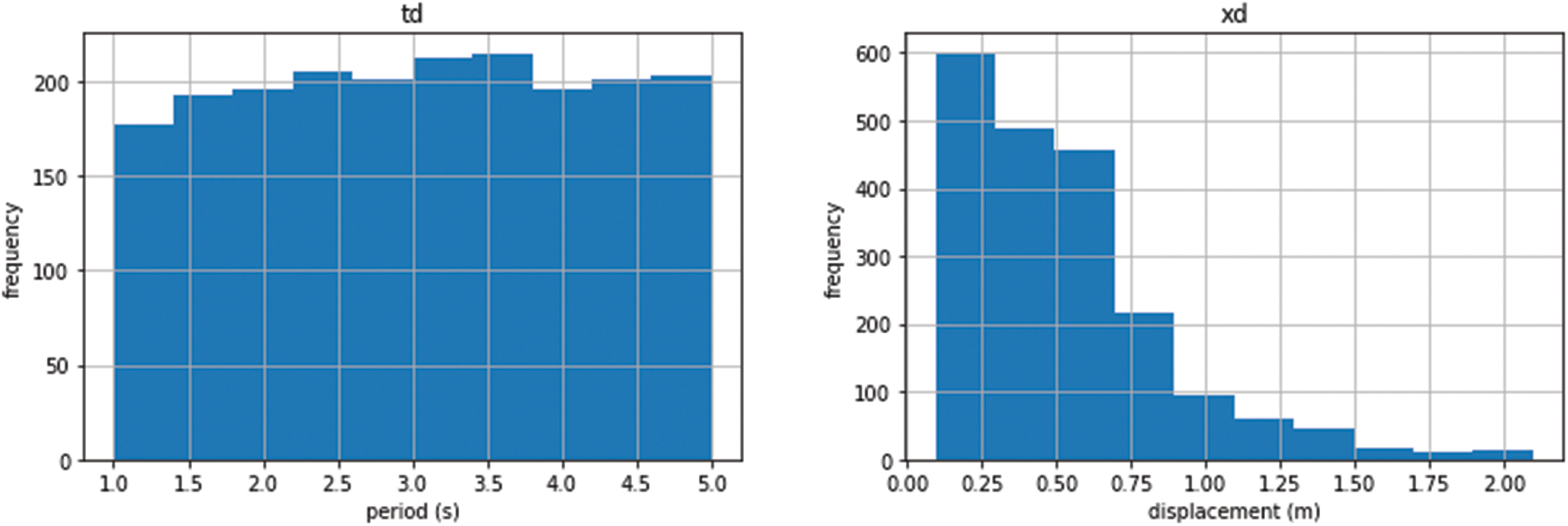
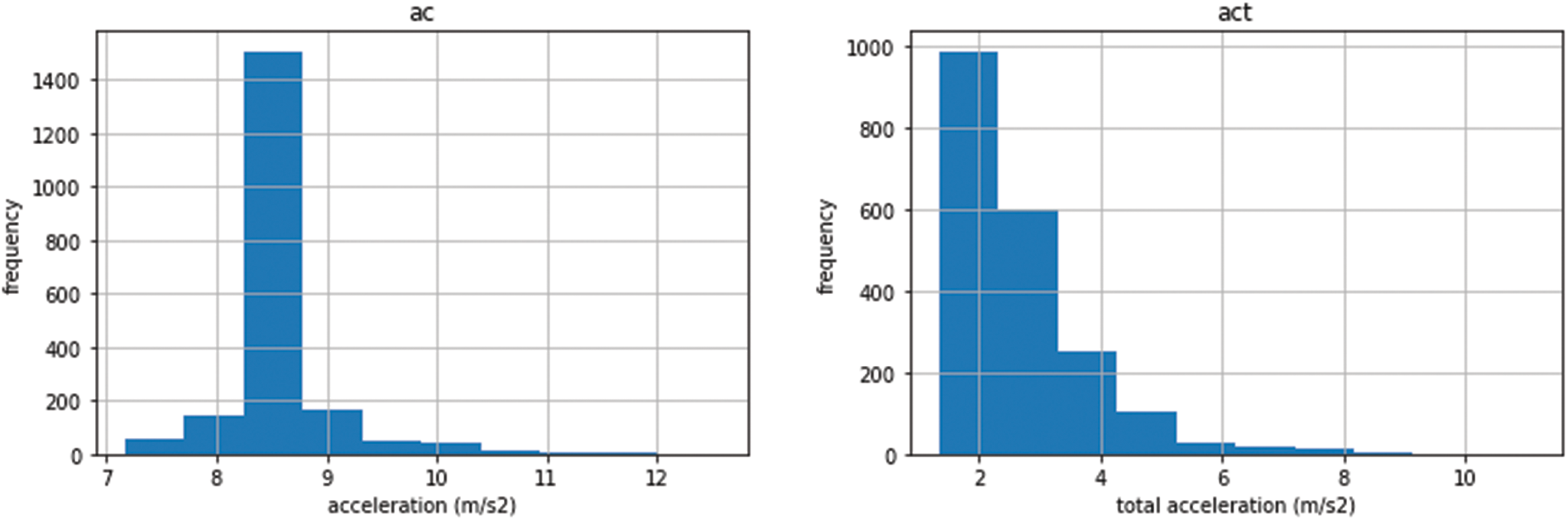
Figure 4: Dataset histogram
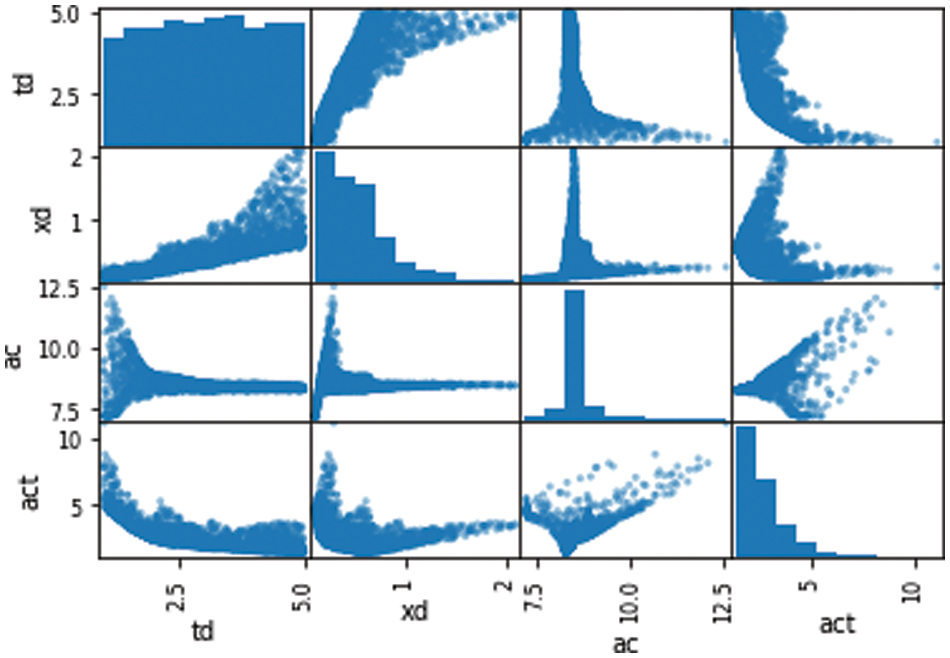
Figure 5: Dataset scatterplot
3.1 Optimization Development of the ML Model
By using the behavior of the seismic base isolator system under randomly selected distant fault earthquakes in machine learning, a prediction model was created utilizing logistic regression, support vector machine, nearest neighbor algorithm, linear discriminate analysis, Naïve Bayes, and decision tree classification algorithms of Scikit-Learn package [62]. Classification algorithms were compared to select the algorithm with the highest prediction success level among the prediction models created with the data set training. In classification, a 10-fold cross-validation technique was used. The maximum number of iterations was taken as 1000. The prediction success comparison of the algorithms is shown as a percentage in Table 6 and with box-whisker diagrams in Fig. 6. The confusion matrices obtained after training are shown in Fig. 7 for logistic regression and linear discriminant analysis, in Fig. 8 for K-nearest neighbors and decision tree, and in Fig. 9 for Naïve Bayes and support vector machine.
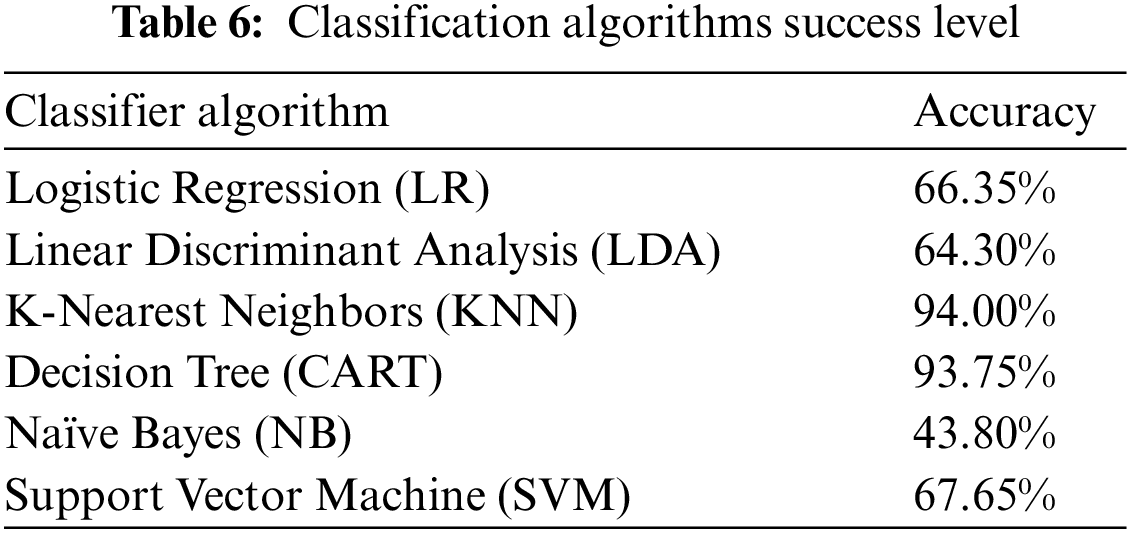
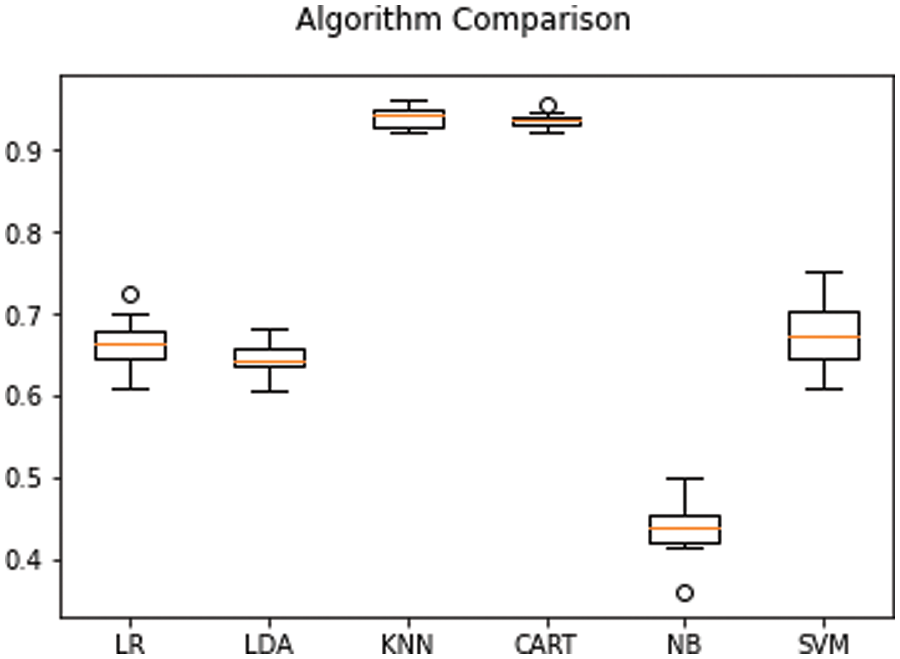
Figure 6: Classification algorithm comparison box whisker diagram
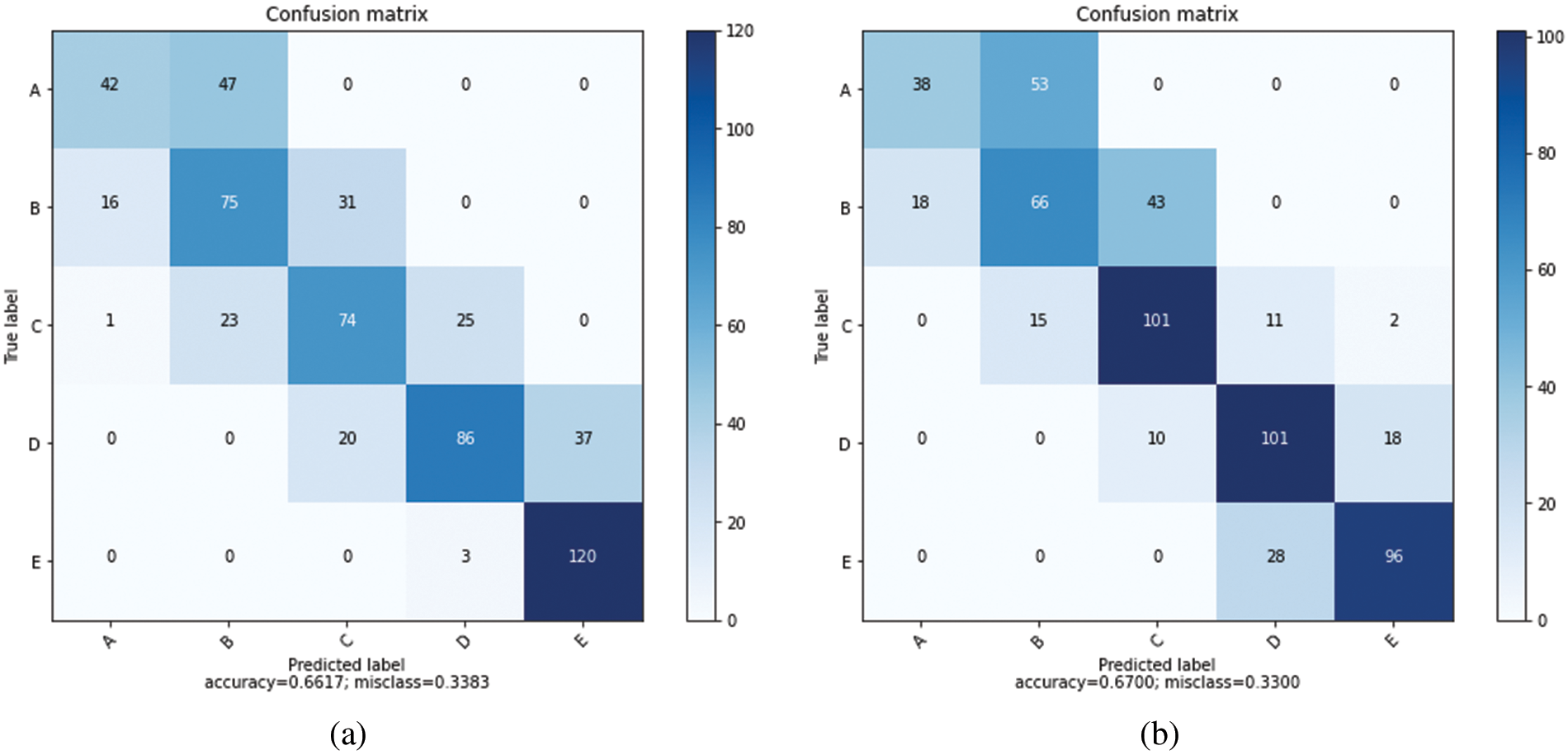
Figure 7: (a) Logistic Regression confusion matrix, (b) Linear Discriminant Analysis confusion matrix
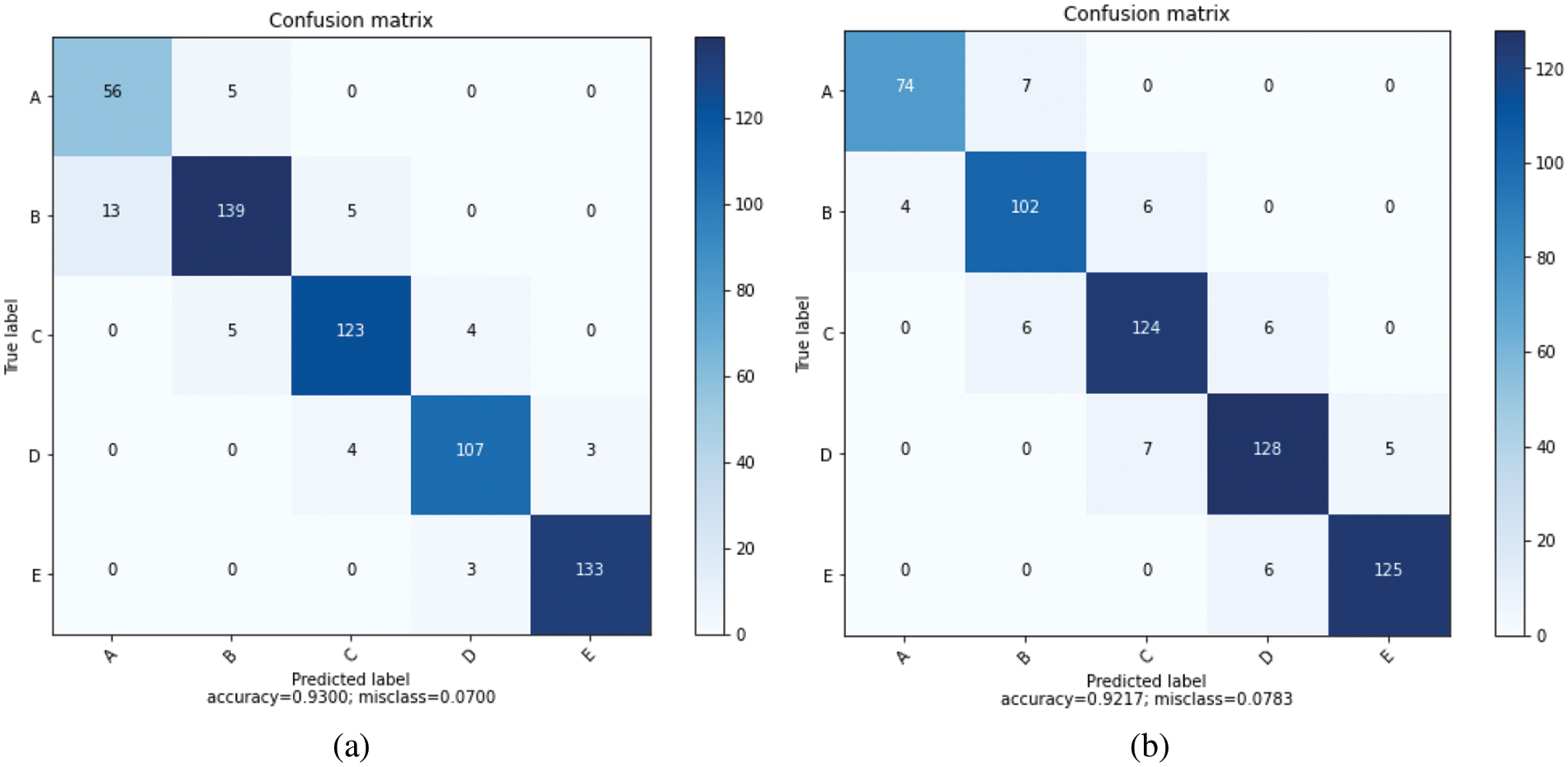
Figure 8: (a) K-Nearest Neighbors confusion matrix, (b) Decision Tree confusion matrix
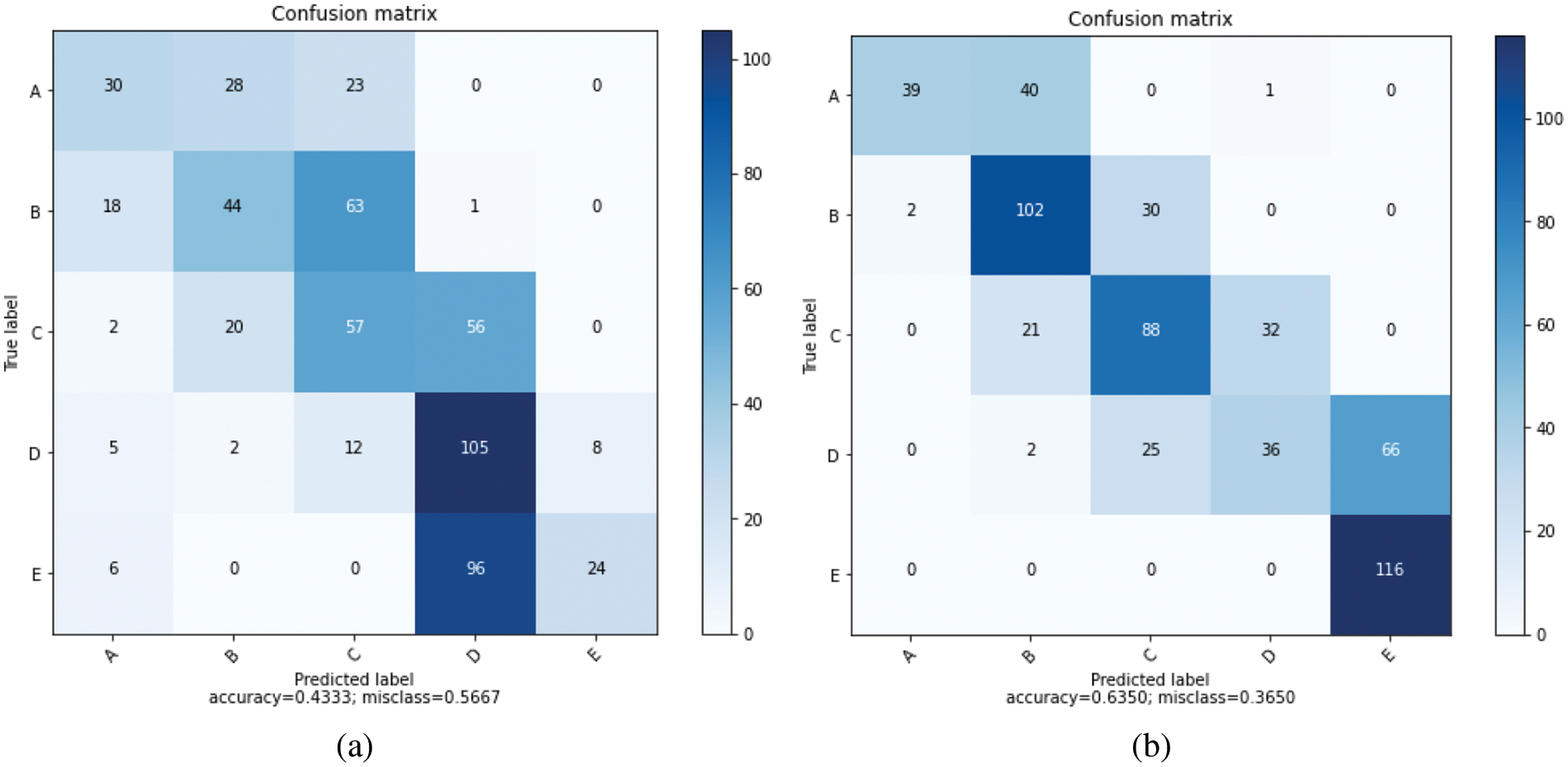
Figure 9: (a) Naïve Bayes confusion matrix, (b) Support Vector Machine confusion matrix
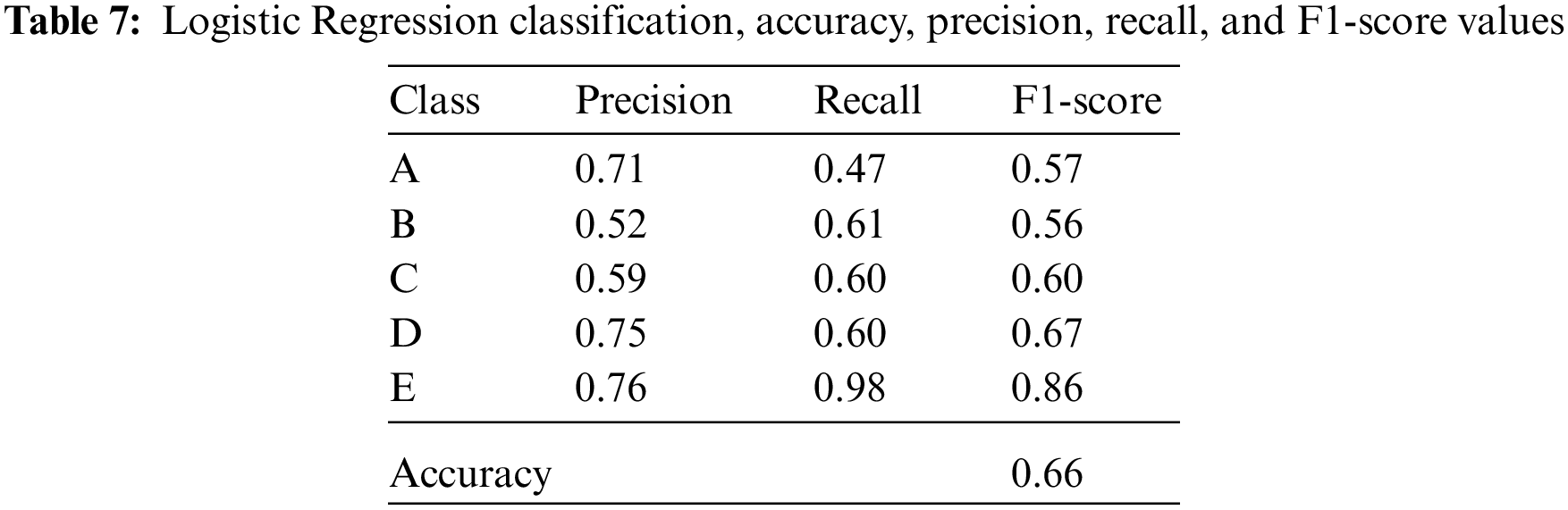
Isolator classes expressing 10%, 20%, 30%, 40%, and 50% damping ratios are divided into five classes A, B, C, D, and E, respectively. The accuracy, precision, recall, and F1-score values of the five classes for Logistic Regression, Linear Discriminant Analysis, K-Nearest Neighbors, Decision Tree, Naïve Bayes, and Support Vector Machine classification algorithms are given in Tables 7–12.
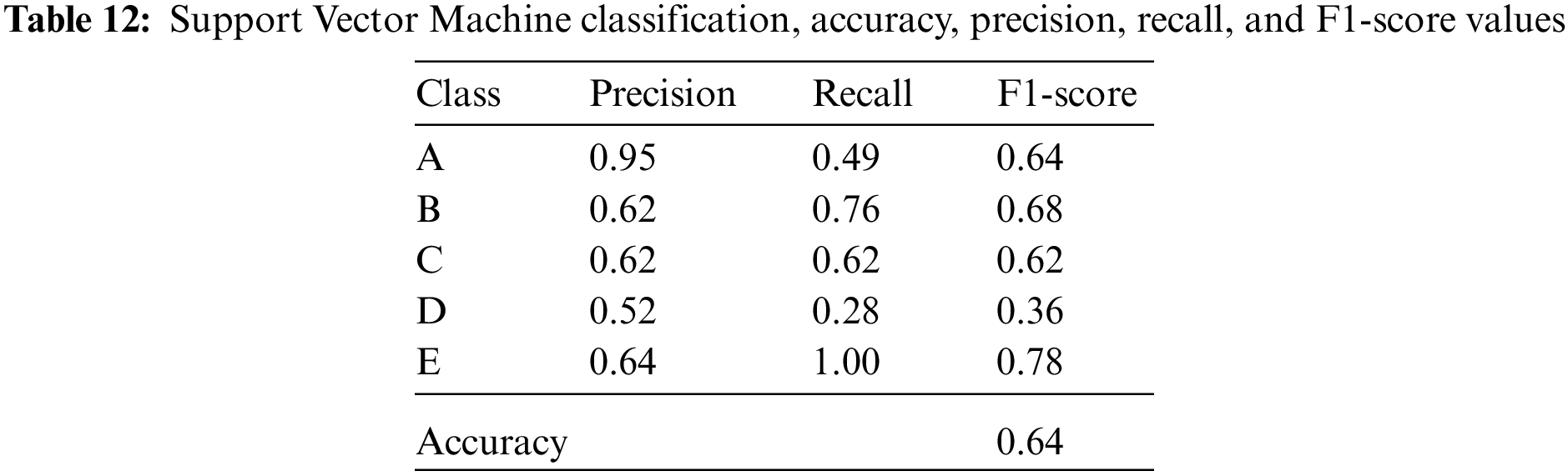
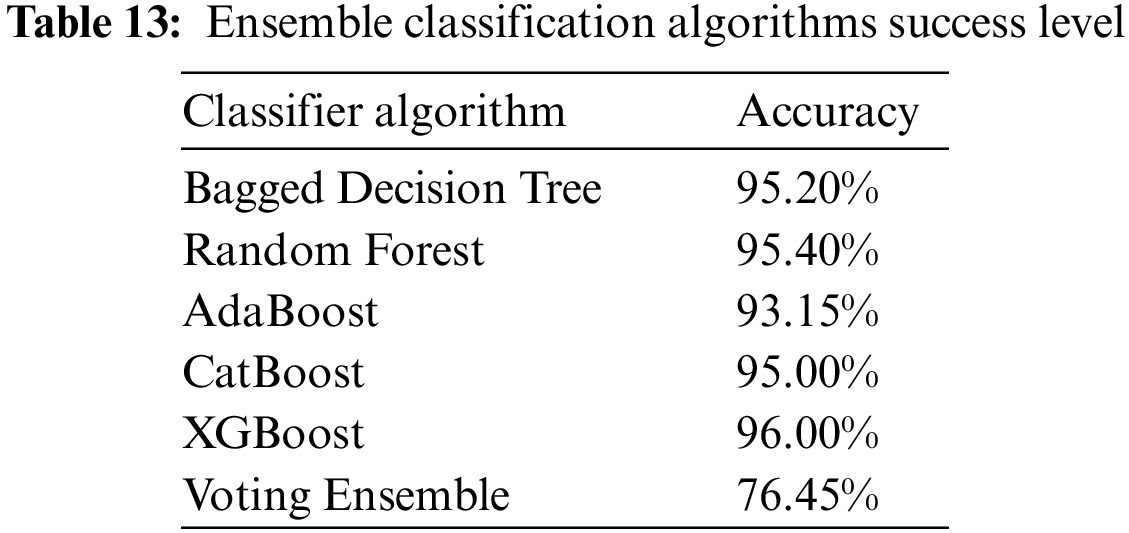
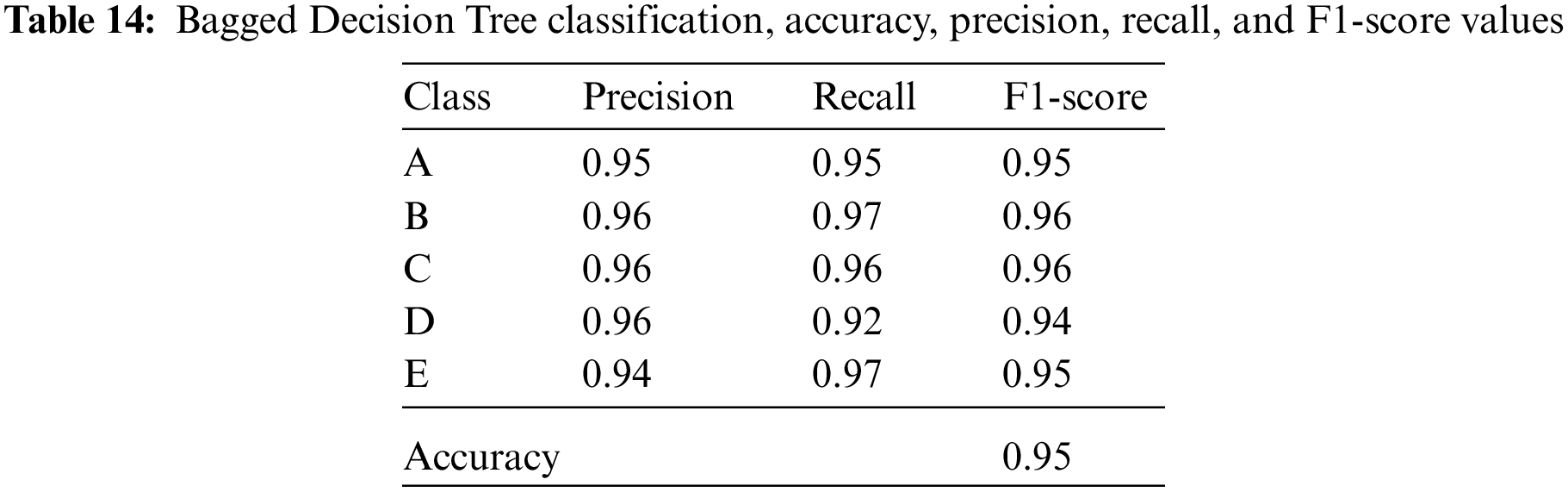
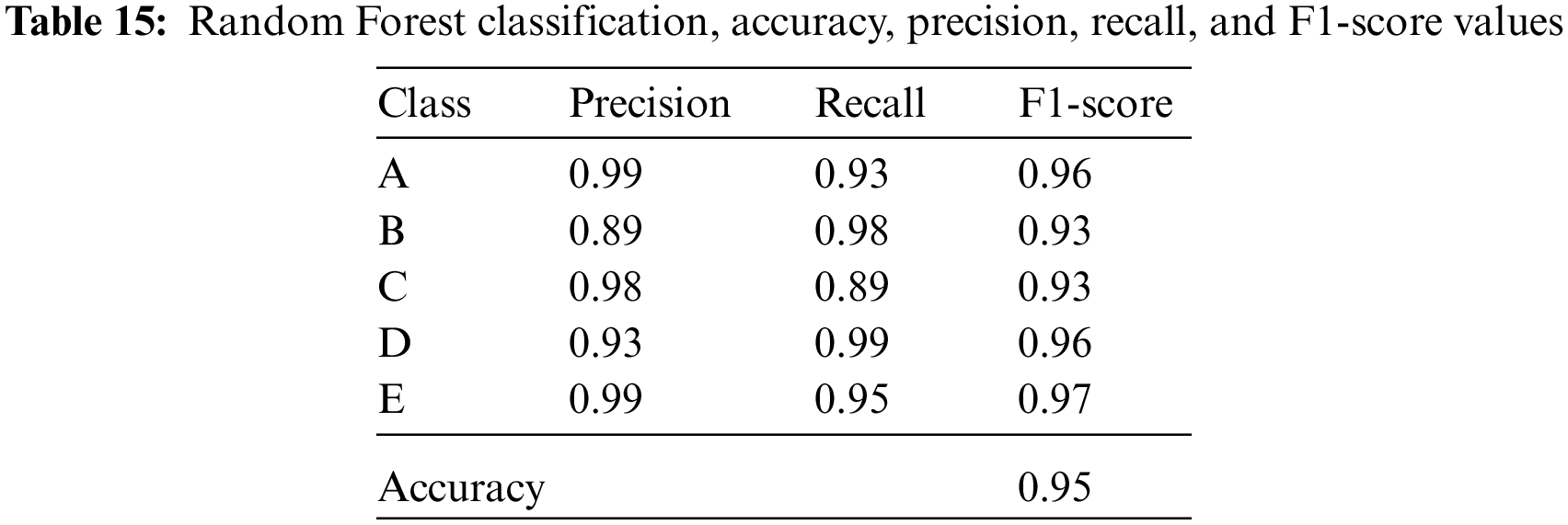
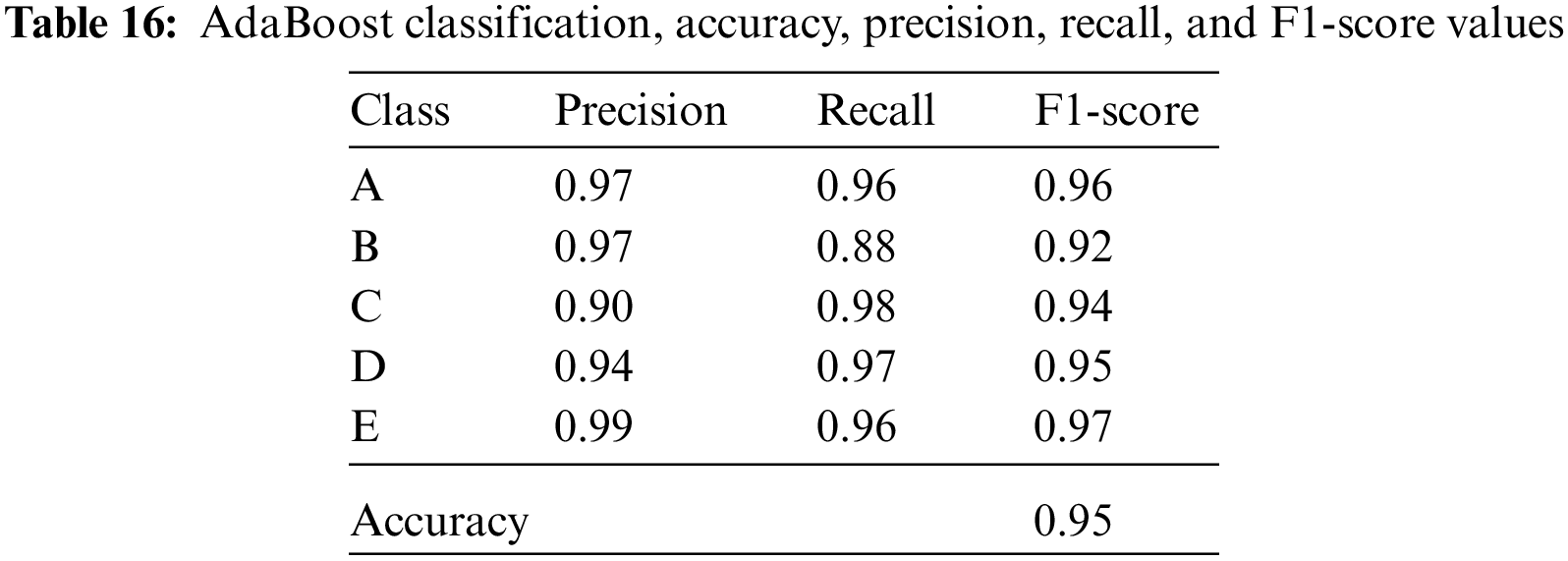
The prediction model was created with ensemble learning algorithms including machine learning resultant methods. Among the resultant methods, Bagged Decision Tree, Random Forest, AdaBoost, CatBoost, XGBoost, and Voting Ensemble algorithms were used [56–58,63,64]. 70% of the data is reserved for training and 30% for testing. The success rates obtained from the Bagging and Boosting resultant methods are given in Table 13.
Confusion matrices obtained after training with resultant algorithms Bagged Decision Tree and Random Forest in Fig. 10 for AdaBoost and CatBoost in Fig. 11 and Voting Ensemble in Fig. 12 are given.
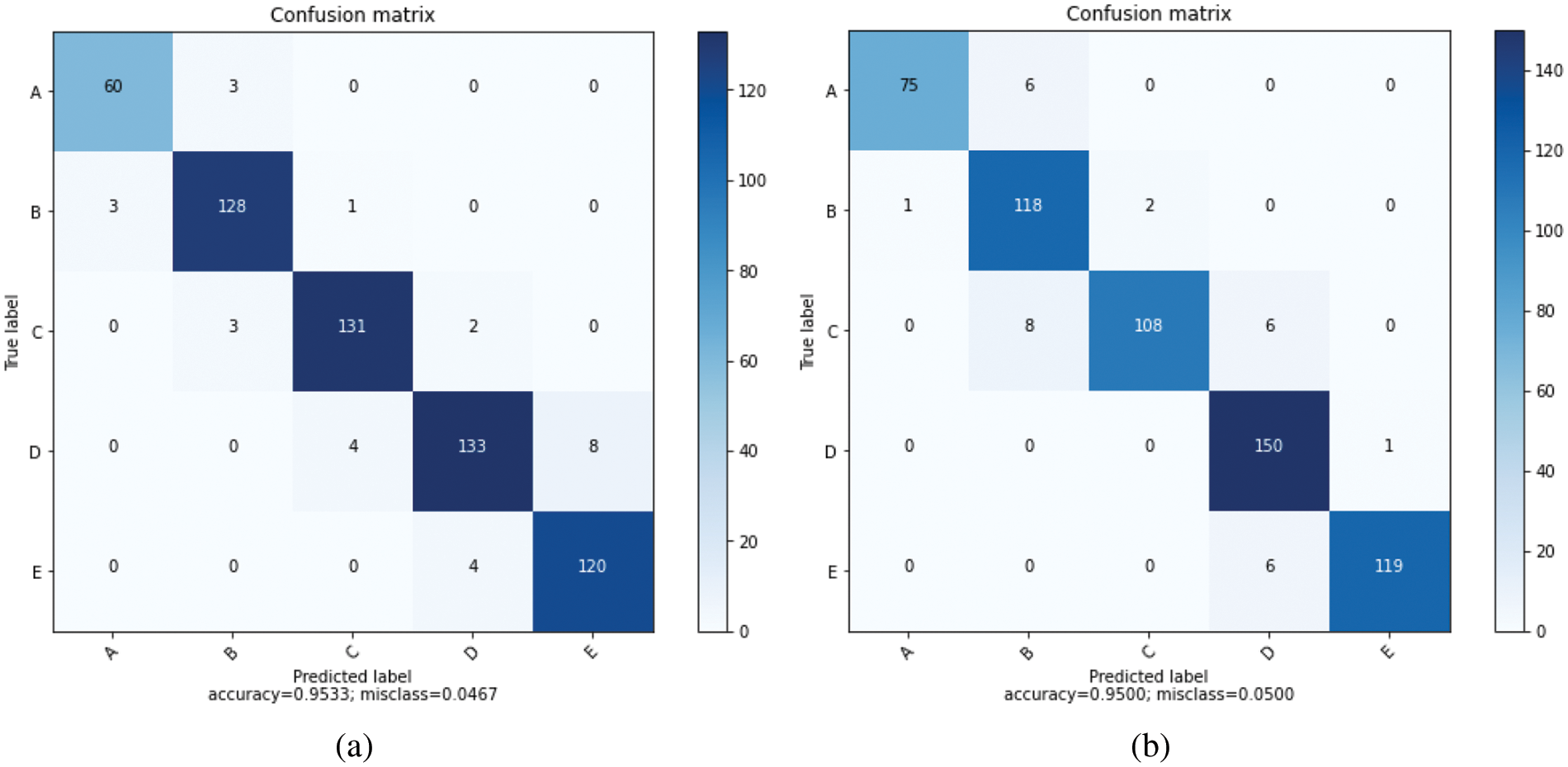
Figure 10: (a) Bagged Decision Tree confusion matrix, (b) Random Forest confusion matrix
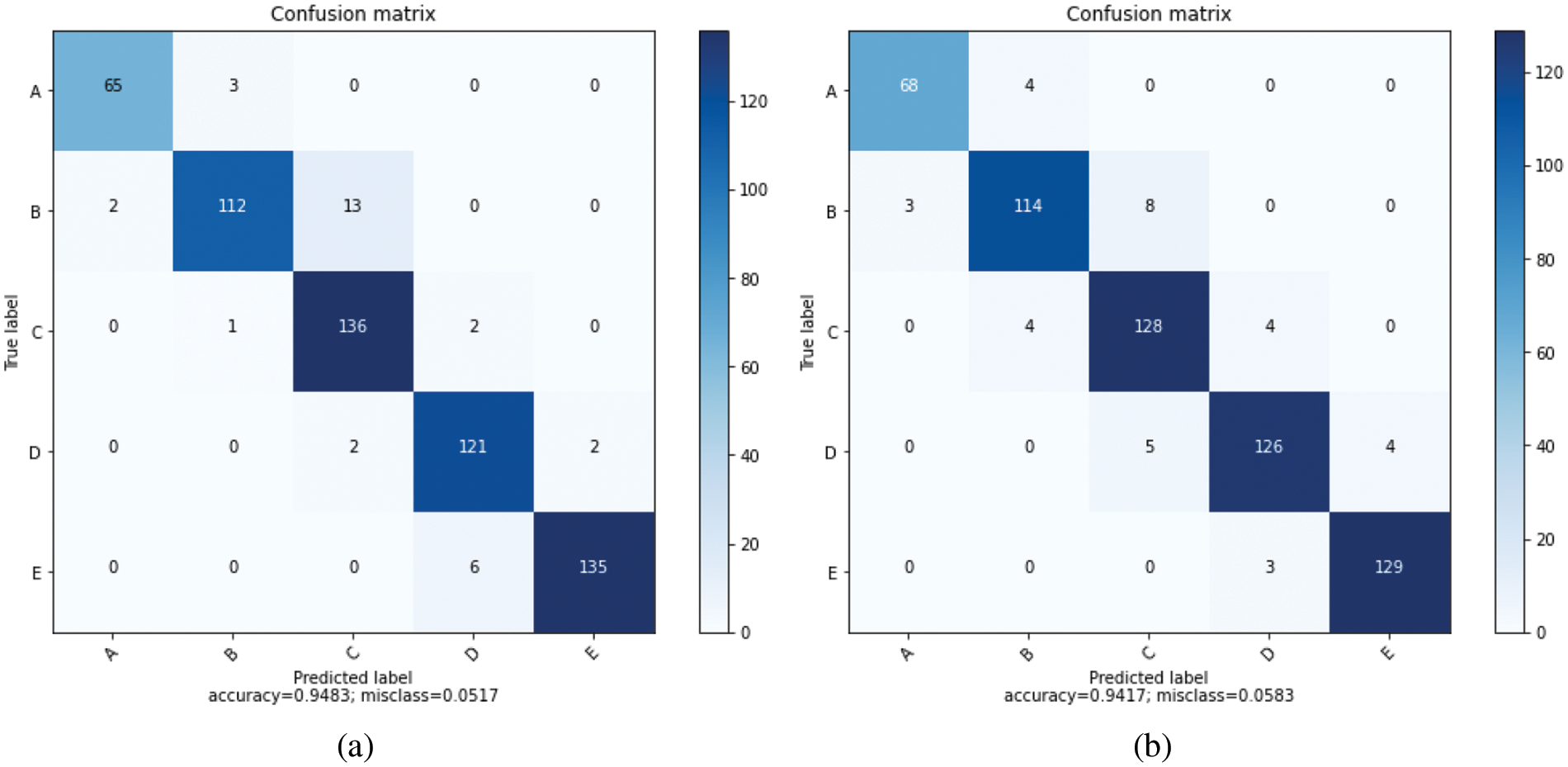
Figure 11: (a) AdaBoost confusion matrix, (b) CatBoost confusion matrix
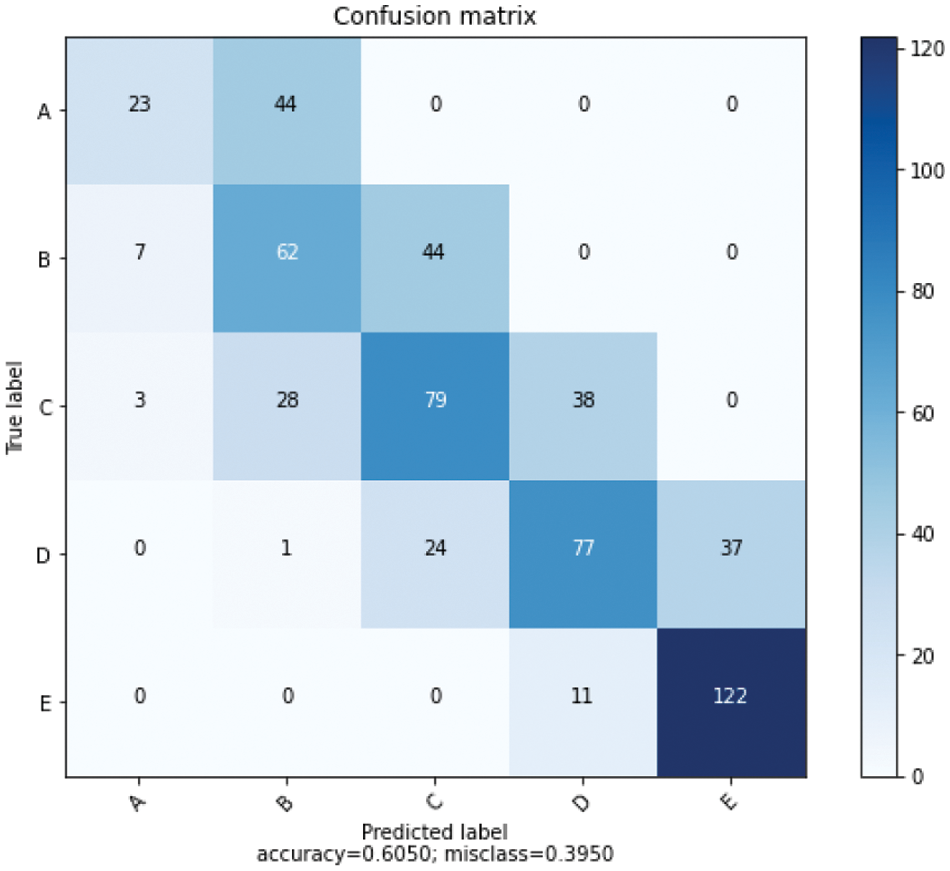
Figure 12: Voting ensemble confusion matrix
The accuracy, precision, recall, and F1-score values of the isolator damping classes are given in Tables 14–18 for the resultant classification algorithms of Bagged Decision Tree, Random Forest, AdaBoost, CatBoost, XGBoost, and Voting Ensemble, respectively.
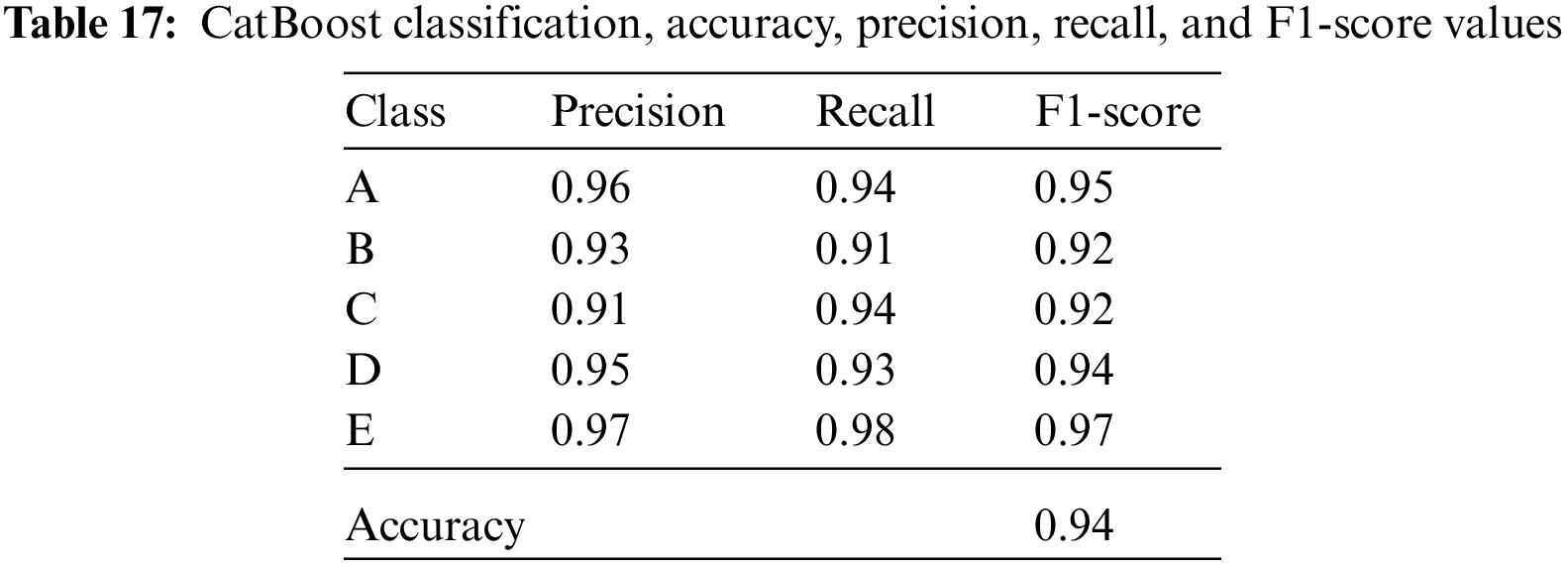
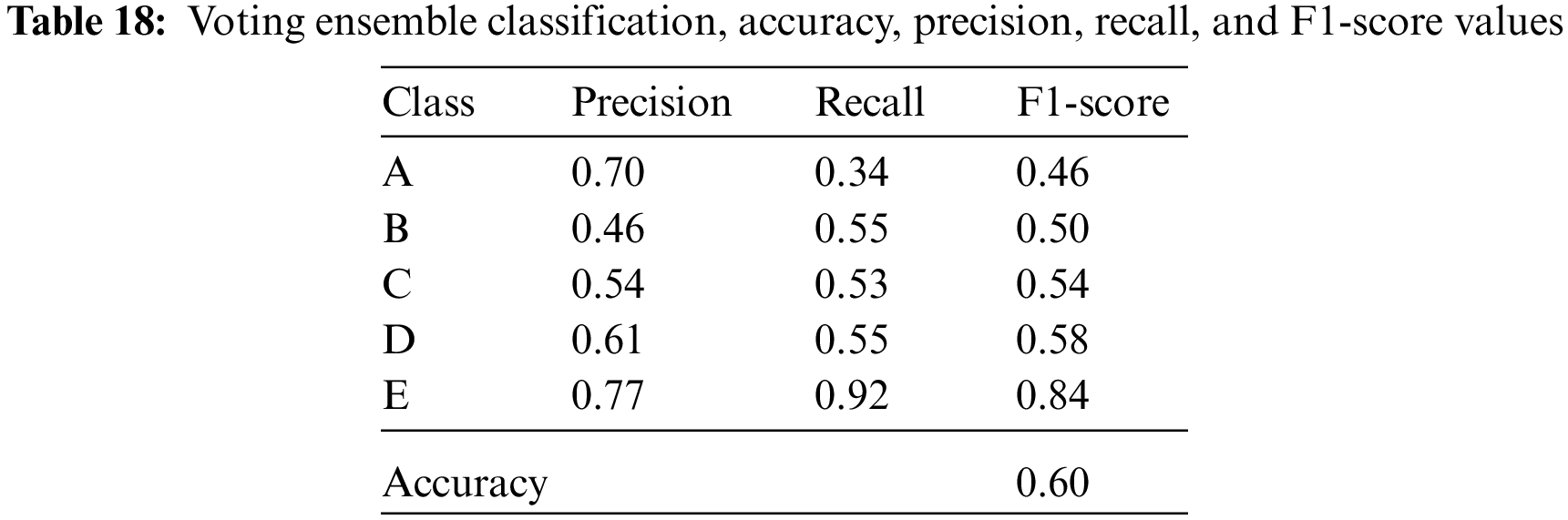
3.2 Interpretation of the ML Model
In the development process of the ML model, XGBoost is found as the most accurate method for model development, where an accuracy of 96% is achieved. Thus, we have chosen XGBoost as the algorithm for the development of the model. According to the XGBoost model, the most important feature for the classification is displacement (xd), followed by total acceleration (act), which is followed by acceleration (ac). The least important feature for the classifier was found as period (td).
In the next stage, we implemented Explainable ML methods to understand the capabilities and limitations of the model. Omni eXplainable AI (OmniXAI) is used as the Interpretable ML tool for this purpose. OmniXAI is a Python-based machine-learning library for explainable AI (XAI), giving omni-way explainable AI and interpretable machine-learning capabilities to overcome many weak points in explaining decisions made by machine-learning models in practice [59,65].
The first metric set provided by OmniXAI provides classification, accuracy, precision, recall, F1-score, and AUC values for each class. Once AUC values are checked for each class the best AUC is 0.9998 for class E and the worst AUC is 0.9978 for class B. The (1-AUC) value for all classes is < 0.005 which indicates that the model performs excellently in terms of class separation capacity. The ROC graph shown in Fig. 13 also reinforces this argument. The class with the lowest precision is A (0.9412), and the highest precision is D (0.9740), while the class with the lowest recall is C (0.9367) while the class with the highest recall is E (1.0000).
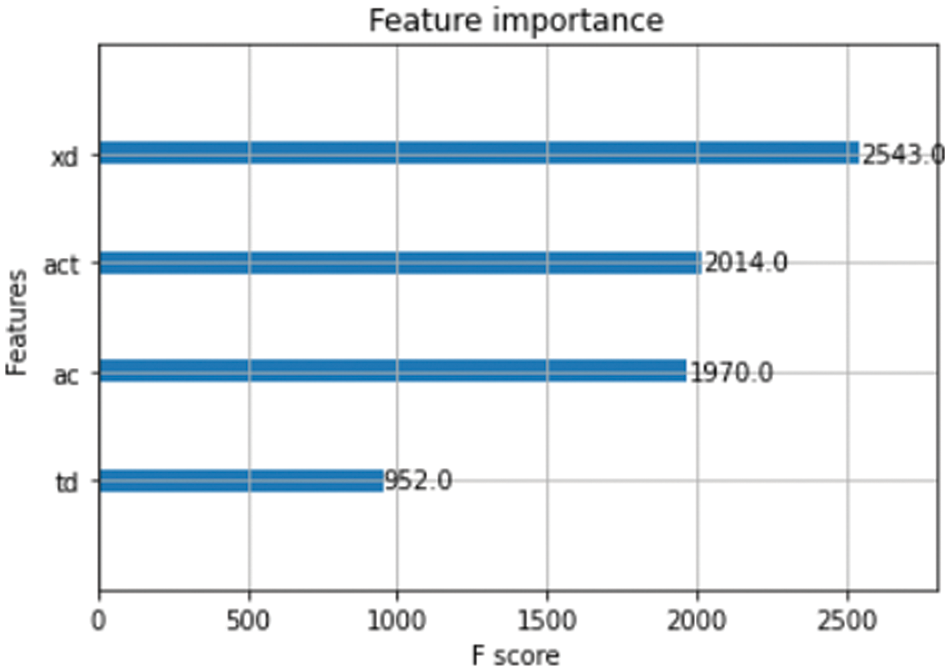
Figure 13: Feature importance
The ability of the XGBoost model to classify positive samples in the model is highest for class D and lowest considering class A, but the ability of the model to detect positive samples is highest for call E and lowest for class C. Class E is the class with the highest F1-score (i.e., the harmonic mean of the model’s precision and recall, the harmonic mean is used in F1-score instead of a simple average because it penalizes the extreme values). In a model where class accuracies are very similar, such as this one, the class with the optimal balance of recall and precision will have the highest F1-score (Fig. 14).
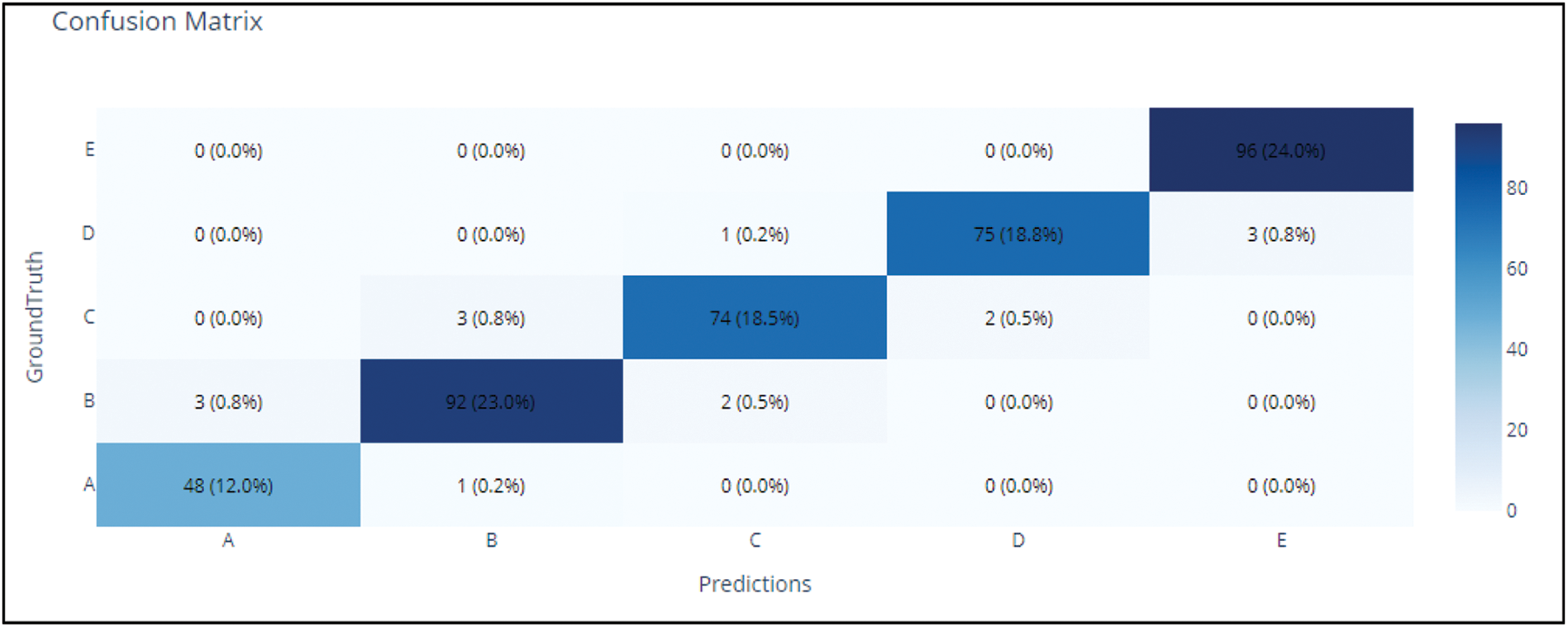
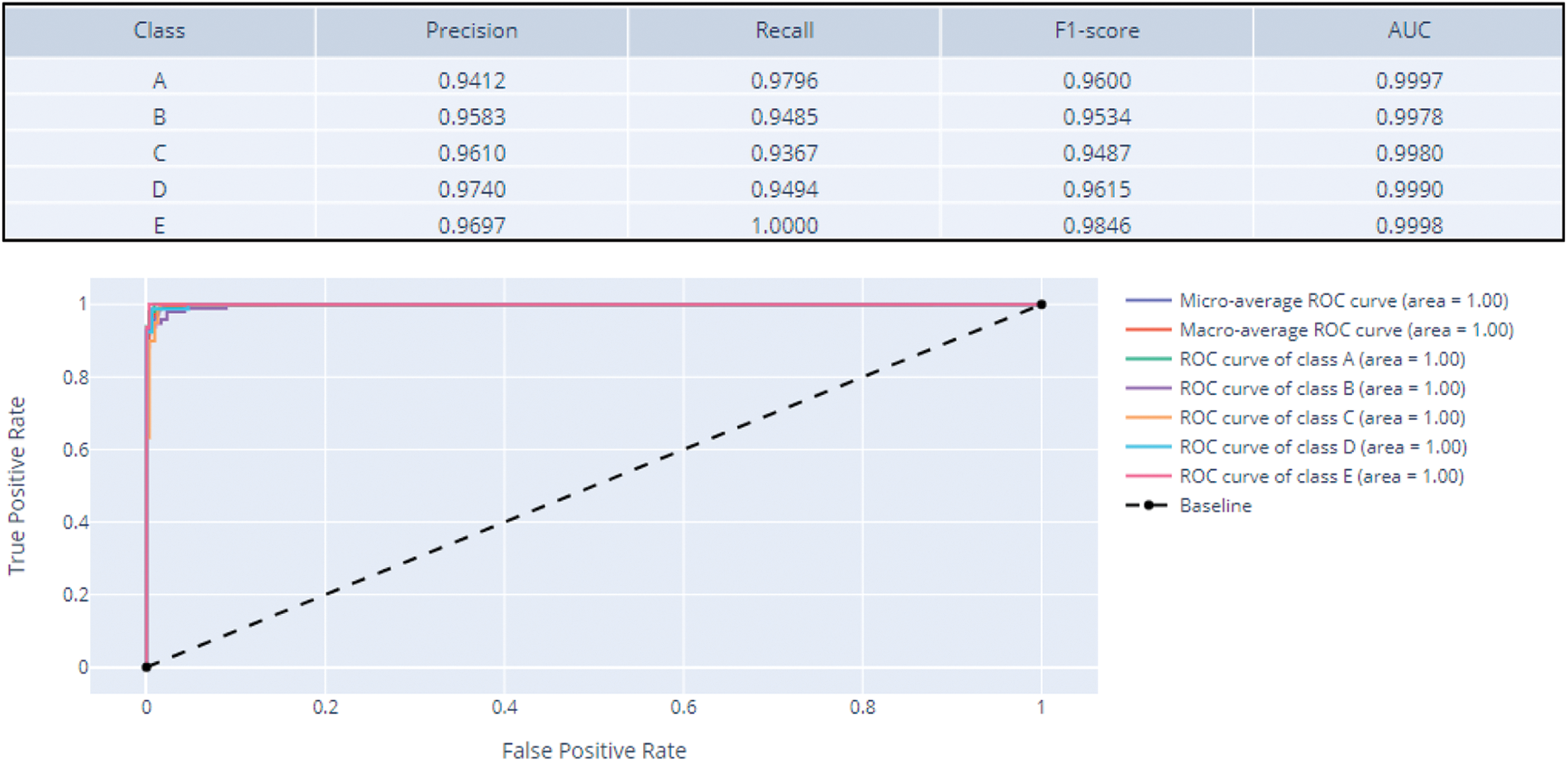
Figure 14: XGBoost confusion matrix, precision, recall, F1-score, AUC values, and ROC
In this study, the machine learning method was used to detect a decrease in the damping ratio due to natural or environmental effects of structures with base seismic isolators with different period and response demands. Machine learning is applied to isolator system behaviors with different damping classes under random earthquakes. With each new recorded behavior of the structure with the trained machine, it has been tried to estimate the reductions that may have a remarkable effect on the damping ratio and that may require maintenance and repair. Since a class-based change in the isolator damping will create a damping loss of 10%, it has been requested to estimate the extraordinary maintenance and repair requirements outside the annual maintenance periods of the isolator and to extend the life of the isolator. The accuracy level reaching 96% was achieved in the classification algorithms machine learning prediction models. In Fig. 15, the accuracy values of the algorithms are presented as a summary graphic.

Figure 15: Algorithm accuracy levels summary chart
According to the graph in Fig. 15, the lowest estimating algorithm was Naïve Bayes, while linear discriminant analysis, logistic regression, support vector machine, and voting ensemble algorithms performed poorly alongside other algorithms exceeding 90%. Looking at the correlation between data attributes, it is seen that there is a high correlation and each of the data attributes is interrelated within itself. The Naïve Bayes algorithm can give better results when the features are independent of each other. The data correlation in this study may be the reason why the Naïve Bayes algorithm is the lowest estimator in classification. When the reasons for the low success of the support vector machine algorithm are examined, it is seen that it is more unsuccessful in its estimation than other algorithms because there is no clear separation of data features. In the study, ensemble learning algorithms K-Nearest Neighbors, and Decision Tree have been quite successful. The fact that these algorithms are successful, the similarity of data attributes is at a good level, and the high correlation supports the reasons for the lower algorithm success levels. The Voting Ensemble algorithm, one of the ensemble learning algorithms, has achieved an average success rate of 76% compared to other algorithms. When the algorithms used in the study were examined, Logistic Regression, Decision Tree, and Support Vector Machine algorithms were used in coding for the Voting Ensemble algorithm. Although an algorithm like Decision Tree that provides approximately 94% accuracy has been used, the lower precision of other algorithms used has affected the success level of the Voting Ensemble algorithm.
While K-Nearest Neighbors and Decision Tree classification algorithms provide an accuracy of about 94%, a model production process that makes successful predictions at values up to 96% in an average band of 95% is provided with resultant methods. Based on this situation, it can be said that the resultant classifier methods give remarkably good results in estimating the isolator damping class consisting of 5 groups.
Control systems require a serious maintenance procedure and high costs for their longevity. It is important to add such devices to the structure to protect the health of the building and to prevent destructive vibrations such as earthquakes that negatively affect human life and threaten life. It is known that the placed devices can be affected by various environmental factors like dust, heat, and humidity, as well as by factors like small and medium earthquakes, excavation, and blasting operations. In such cases, it is important to determine the necessity of maintenance and repair of control devices like isolators. Even small changes in the friction properties of a system with isolators cause loss of performance, and maintenance-repair that is not done on time reduces the life of the device irreversibly. For the continuity of these very costly systems, it is important to determine the performance loss and maintenance requirement of such systems just before the failure occurs. In this study, an artificial intelligence model was created that predicts the change in damping capacity to determine the maintenance and repair conditions of seismic base isolators, and it is aimed to determine the decrease in damping capacity and damage. With the machine learning classification process, a model was produced that predicts the decrease in the isolator damping capacity exceeding 96%. It has been understood that the success levels of the algorithms used are related to the data correlation, and the similarity between the data attributes greatly affects the prediction success. It has been observed that Decision Tree and K-Nearest Neighbors play an important role in classification algorithms for highly correlated data. Based on this, it is seen that the data training period can be effective in creating a more successful model. Considering the result that a decrease in the damping class will require maintenance and repair, it is understood that machine learning techniques make successful predictions, and it will be beneficial to use them in the control of systems with isolators future studies, it is aimed to investigate the effects of damping system types by taking into account the prediction success of seismic isolators.
Acknowledgement: We want to thank to our universities (Istanbul University–Cerrahpaşa, Mimar Sinan Fine Arts University and Gachon University) for their support.
Funding Statement: This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (2020R1A2C1A01011131). This research was also supported by the Energy Cloud R&D Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT (2019M3F2A1073164).
Author Contributions: A.O. and Ü.I. generated the analysis codes; A.O., Ü.I., and G.B. developed the theory, background, and formulations of the problem; Verification of the results was performed by A.O. and Ü.I.; The text of the paper was written by A.O., Ü.I., G.B., and S.M.N.; The text of the paper was edited by G.B., S.K., and Z.W.G.; The figures were drawn by A.O.; G.B. and Z.W.G. supervised the research direction. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data is available on request to authors.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Sheikh, H., van Engelen, N. C., Ruparathna, R. (2022). A review of base isolation systems with adaptive characteristics. Structures, 38, 1542–1555. [Google Scholar]
2. Bao, Y., Becker, T. C. (2018). Inelastic response of base-isolated structures subjected to impact. Engineering Structures, 171, 86–93. [Google Scholar]
3. Ocak, A., Nigdeli, S. M., Bekdaş, G., Kim, S., Geem, Z. W. (2022). Optimization of seismic base isolation system using adaptive harmony search algorithm. Sustainability, 14(12), 7456. [Google Scholar]
4. Sağıroğlu, M., Maali, M., Aydın, A. C. (2018). Installation and maintenance principles of seismic isolators: Erzurum health campus. The Open Civil Engineering Journal, 12(1), 83–95. [Google Scholar]
5. GNMA (2023). Seismic Isolator Installation & Maintenance. https://www.china-gnma.com/technology/installation-maintenance.html [Google Scholar]
6. Ur Rehman, Z., Khalid, U., Ijaz, N., Mujtaba, H., Haider, A. et al. (2022). Machine learning-based intelligent modeling of hydraulic conductivity of sandy soil considering a wide range of grain sizes. Engineering Geology, 311, 106899. [Google Scholar]
7. Ozsagir, M., Erden, C., Bol, E., Sert, S., Özocak, A. (2022). Machine learning approaches for prediction of fine-grained soils liquefaction. Computers and Geotechnics, 152, 105014. [Google Scholar]
8. Shen, J., Li, Y., Lin, H., Li, H., Lv, J. et al. (2022). Prediction of compressive strength of alkali-activated construction demolition waste geopolymers using ensemble machine learning. Construction and Building Materials, 360, 129600. [Google Scholar]
9. Li, Y., Li, H., Shen, J. (2022). The study of the effect of carbon nanotubes on the compressive strength of cement-based materials based on machine learning. Construction and Building Materials, 358, 129435. [Google Scholar]
10. Toufigh, V., Palizi, S. (2022). Performance evaluation of slag-based concrete at elevated temperatures by a novel machine learning approach. Construction and Building Materials, 358, 129357. [Google Scholar]
11. Chou, J. S., Liu, C. Y., Prayogo, H., Khasani, R. R., Gho, D. et al. (2022). Predicting the nominal shear capacity of the reinforced concrete wall in a building by metaheuristics-optimized machine learning. Journal of Building Engineering, 61, 105046. [Google Scholar]
12. Zhang, W., Li, H., Han, L., Chen, L., Wang, L. (2022). Slope stability prediction using ensemble learning techniques: A case study in Yunyang County, Chongqing, China. Journal of Rock Mechanics and Geotechnical Engineering, 14, 1089–1099 [Google Scholar]
13. Bardhan, A., Biswas, R., Kardani, N., Iqbal, M., Samui, P. et al. (2022). A novel integrated approach of augmented grey wolf optimizer and ann for estimating axial load carrying-capacity of concrete-filled steel tube columns. Construction and Building Materials, 337, 127454. [Google Scholar]
14. Zhang, J., Sun, Y., Li, G., Wang, Y., Sun, J. et al. (2020). Machine-learning-assisted shear strength prediction of reinforced concrete beams with and without stirrups. Engineering with Computers, 38, 1–15. [Google Scholar]
15. Matel, E., Vahdatikhaki, F., Hosseinyalamdary, S., Evers, T., Voordijk, H. (2022). An artificial neural network approach for cost estimation of engineering services. International Journal of Construction Management, 22(7), 1274–1287. [Google Scholar]
16. Nguyen, Q. H., Ly, H. B., Ho, L. S., Al-Ansari, N., Le, H. V. et al. (2021). Influence of data splitting on the performance of machine learning models in prediction of shear strength of the soil. Mathematical Problems in Engineering, 2021, 4832864. [Google Scholar]
17. Zhou, J., Asteris, P. G., Armaghani, D. J., Pham, B. T. (2020). Prediction of ground vibration induced by blasting operations through the use of the Bayesian network and random forest models. Soil Dynamics and Earthquake Engineering, 139, 106390. [Google Scholar]
18. Mangalathu, S., Jang, H., Hwang, S. H., Jeon, J. S. (2020). Data-driven machine-learning-based seismic failure mode identification of reinforced concrete shear walls. Engineering Structures, 208, 110331. [Google Scholar]
19. Zeng, J., Roussis, P. C., Mohammed, A. S., Maraveas, C., Fatemi, S. A. et al. (2021). Prediction of peak particle velocity caused by blasting through the combinations of boosted-CHAID and SVM models with various kernels. Applied Sciences, 11(8), 3705. [Google Scholar]
20. Cavaleri, L., Barkhordari, M. S., Repapis, C. C., Armaghani, D. J., Ulrikh, D. V. et al. (2022). Convolution-based ensemble learning algorithms to estimate the bond strength of the corroded reinforced concrete. Construction and Building Materials, 359, 129504. [Google Scholar]
21. Barkhordari, M. S., Armaghani, D. J., Mohammed, A. S., Ulrikh, D. V. (2022). Data-driven compressive strength prediction of fly ash concrete using ensemble learner algorithms. Buildings, 12(2), 132. [Google Scholar]
22. Asteris, P. G., Mamou, A., Ferentinou, M., Tran, T. T., Zhou, J. (2022). Compressibility using a novel Manta ray foraging optimization-based extreme learning machine model. Transportation Geotechnics, 37, 100861. [Google Scholar]
23. Sun, Z., Feng, D. C., Mangalathu, S., Wang, W. J., Su, D. (2022). Effectiveness assessment of TMDs in bridges under strong winds incorporating machine-learning techniques. Journal of Performance of Constructed Facilities, 36(5), 04022036. [Google Scholar]
24. Bae, J., Lee, C. H., Park, M., Alemayehu, R. W., Ryu, J. et al. (2020). Modified low-cycle fatigue estimation using machine learning for radius-cut coke-shaped metallic damper subjected to cyclic loading. International Journal of Steel Structures, 20(6), 1849–1858. [Google Scholar]
25. Farrokhi, F., Rahimi, S. (2020). Supervised probabilistic failure prediction of tuned mass damper-equipped high steel frames using machine learning methods. Studia Geotechnica et Mechanica, 42(3), 179–190. [Google Scholar]
26. Yucel, M., Bekdaş, G., Nigdeli, S. M., Sevgen, S. (2019). Estimation of optimum tuned mass damper parameters via machine learning. Journal of Building Engineering, 26, 100847. [Google Scholar]
27. Li, L., Zhao, X. (2019). Application of machine learning in the optimized distribution of dampers for structural vibration control. Earthquakes and Structures, 16(6), 679–690. [Google Scholar]
28. Luong, Q. V., Jo, B. H., Hwang, J. H., Jang, D. S. (2021). A supervised neural network control for magnetorheological damper in an aircraft landing gear. Applied Sciences, 12(1), 400. [Google Scholar]
29. Bahiuddin, I., Imaduddin, F., Mazlan, S. A., Ariff, M. H., Mohmad, K. B. et al. (2021). Accurate and fast estimation for the field-dependent nonlinear damping force of meandering valve-based magnetorheological damper using extreme learning machine method. Sensors and Actuators A: Physical, 318, 112479. [Google Scholar]
30. Khalid, M., Yusof, R., Joshani, M., Selamat, H., Joshani, M. (2014). Nonlinear identification of a magneto-rheological damper based on dynamic neural networks. Computer-Aided Civil and Infrastructure Engineering, 29(3), 221–233. [Google Scholar]
31. Chong, J. W., Kim, Y., Chon, K. H. (2014). Nonlinear multiclass support vector machine–based health monitoring system for buildings employing magnetorheological dampers. Journal of Intelligent Material Systems and Structures, 25(12), 1456–1468. [Google Scholar]
32. Li, C., Liu, Q., Lan, S. (2012). Application of support vector machine-based semiactive control for seismic protection of structures with magnetorheological dampers. Mathematical Problems in Engineering, 2012, 268938. [Google Scholar]
33. Moeindarbari, H., Taghikhany, T. (2018). Seismic reliability assessment of base-isolated structures using artificial neural network: Operation failure of sensitive equipment. Earthquakes and Structures, 14(5), 425–436. [Google Scholar]
34. Nakabayash, T., Wada, K., Utsumi, Y. (2020). Automatic detection of air bubbles with deep learning. Proceedings of the 37th International Symposium on Automation and Robotics in Construction, pp. 27–28. Kitakyushu, Japan. [Google Scholar]
35. Barakat, S. (2020). Design of the base isolation system with artificial neural network models. Proceedings of 2020 the 4th International Conference on Compute and Data Analysis, pp. 79–83. Silicon Valley, CA, USA. [Google Scholar]
36. Nguyen, H. D., Dao, N. D., Shin, M. (2022). Machine learning-based prediction for the maximum displacement of seismic isolation systems. Journal of Building Engineering, 51, 104251. [Google Scholar]
37. Habib, A., Yildirim, U. (2022). Developing a physics-informed and physics-penalized neural network model for the preliminary design of multi-stage friction pendulum bearings. Engineering Applications of Artificial Intelligence, 113, 104953. [Google Scholar]
38. Tian, G. Y., Zhao, Z. X., Baines, R. W., Zhang, N. (1997). Computational algorithms for linear variable differential transformers (LVDTs). IEE Proceedings-Science, Measurement and Technology, 144(4), 189–192. [Google Scholar]
39. FEMA P-695. (2009). Quantification of building seismic performance factors. Washington DC: Federal Emergency Management Agency. [Google Scholar]
40. Abioye, S. O., Oyedele, L. O., Akanbi, L., Ajayi, A., Delgado, J. M. D. et al. (2021). Artificial intelligence in the construction industry: A review of present status, opportunities, and future challenges. Journal of Building Engineering, 44, 103299. [Google Scholar]
41. Kotsiantis, S. B., Zaharakis, I., Pintelas, P. (2007). Supervised machine learning: A review of classification techniques. Emerging Artificial Intelligence Applications in Computer Engineering, 160(1), 3–24. [Google Scholar]
42. Gentleman, R., Carey, V. J. (2008). Unsupervised machine learning. In: Bioconductor case studies, pp. 137–157. USA: Springer. [Google Scholar]
43. Sutton, R. S. (1992). Introduction: The challenge of reinforcement learning. In: Reinforcement learning, pp. 1–3. USA: Springer. [Google Scholar]
44. LeCun, Y., Bengio, Y., Hinton, G. (2015). Deep learning. Nature, 521(7553), 436–444. [Google Scholar] [PubMed]
45. Harrell, F. E. (2001). Regression modeling strategies: With applications to linear models, logistic regression, and survival analysis, vol. 608. USA: Springer. [Google Scholar]
46. Mellit, A., Kalogirou, S. (2022). Artificial intelligence techniques: Machine learning and deep learning algorithms. In: Handbook of Artificial Intelligence Techniques in Photovoltaic Systems, pp. 43–83. [Google Scholar]
47. Subasi, A. (2020). Machine learning techniques. In: Practical machine learning for data analysis using Python, pp. 91–202. UK: Academic Press. [Google Scholar]
48. Cover, T., Hart, P. (1967). Nearest neighbor pattern classification. IEEE Transactions on Information Theory, 13(1), 21–27. [Google Scholar]
49. Anava, O., Levy, K. (2016). K*-nearest neighbors: From global to local. In: Advances in neural information processing systems 29 (NIPS 2016). [Google Scholar]
50. Morales, E. F., Escalante, H. J. (2022). A brief introduction to supervised, unsupervised, and reinforcement learning. In: Biosignal processing and classification using computational learning and intelligence, pp. 111–129. UK: Academic Press. [Google Scholar]
51. Matheus, C. J., Rendell, L. A. (1989). Constructive induction on decision trees. International Joint Conference on Artificial Intelligence, 89, 645–650. [Google Scholar]
52. McCallum, A., Nigam, K. (1998). A comparison of event models for Naïve Bayes text classification. AAAI-98 Workshop on Learning for Text Categorization, 752(1), 41–48. [Google Scholar]
53. Huang, S., Cai, N., Pacheco, P. P., Narrandes, S., Wang, Y. et al. (2018). Applications of support vector machine (SVM) learning in cancer genomics. Cancer Genomics & Proteomics, 15(1), 41–51. [Google Scholar]
54. Pezoulas, V. C., Exarchos, T. P., Fotiadis, D. I. (2020). Machine learning and data analytics. In: Medical data sharing, harmonization, and analytics, pp. 227–309. [Google Scholar]
55. Müller, A. C., Guido, S. (2016). Introduction to machine learning with Python: A guide for data scientists. USA: O’Reilly Media, Inc. [Google Scholar]
56. Freund, Y., Schapire, R. E. (1997). A decision-theoretic generalization of online learning and an application to boosting. Journal of Computer and System Sciences, 55(1), 119–139. [Google Scholar]
57. Hastie, T., Tibshirani, R., Friedman, J. H., Friedman, J. H. (2009). The elements of statistical learning: Data mining, inference, and prediction, vol. 2, pp. 1–758. USA: Springer. [Google Scholar]
58. Xu, J. G., Hong, W., Zhang, J., Hou, S. T., Wu, G. (2022). Seismic performance assessment of corroded RC columns based on data-driven machine-learning approach. Engineering Structures, 255, 113936. [Google Scholar]
59. Friedman, J. H. (2001). Greedy function approximation: A gradient boosting machine. Annals of Statistics, 29(5), 1189–1232. [Google Scholar]
60. Zhou, J., Huang, S., Qiu, Y. (2022). Optimization of the random forest through the use of MVO, GWO, and MFO in evaluating the stability of underground entry-type excavations. Tunnelling and Underground Space Technology, 124, 104494. [Google Scholar]
61. MathWorks Inc. (2022). MATLAB R2022b. Natick, MA, USA. [Google Scholar]
62. Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B. et al. (2022). Scikit-learn: Machine learning in Python. https://scikit-learn.org/stable/about.html#citing-scikit-learn [Google Scholar]
63. CatBoost Developers (2022). Catboost Python package. https://pypi.org/project/catboost/ [Google Scholar]
64. XGBoost Developers (2022). XGBoost Python package. https://pypi.org/project/XGBoost/1.7.2/ [Google Scholar]
65. Yang, W., Le, H., Laud, T., Savarese, S., Hoi, S. C. H. (2022). OmniXAI: A Library for Explainable AI. https://arxiv.org/abs/2206.01612 [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools