Finite Element Simulations on Failure Behaviors of Granular Materials with Microstructures Using a Micromechanics-Based Cosserat Elastoplastic Model

1  Introduction

Granular materials are composed of solid particles and inter-particle voids, which exhibit nonlinearity, heterogeneity, and other microscopic characteristics that usually cause complex failure behavior, i.e., localized failure phenomena for granular materials [1–4]. A thorough understanding of the failure behavior of granular materials is important to improve the prediction of natural disasters such as landslides and mudslides. Discrete element models (DEMs) are physically closer to the discrete nature of granular materials [5]. In addition, the models provide convenient and accurate simulations of failure behaviors by using microscopic geometric information. However, since solid particles in practice are numerous, there are limitations of DEMs to solve engineering problems by the computational scale. Therefore, it is appropriate and feasible to use continuum modeling or multiscale modeling for mechanical behaviors of granular materials, and the development of appropriate models to characterize the mechanical behaviors is crucial within continuous medium mechanics [2,6,7].

Granular materials have been studied using the Cosserat continuum theory [8–11]. There is a degree of freedom (DOF) related to the micro-rotation of the particles, as well as characteristic lengths describing the microstructures. Therefore, the Cosserat continuum theory can provide the regularization mechanism to solve the pathological mesh dependence problem in simulation on the width of strain localization, which usually results from the loss of ellipticity of the control equations in the classical continuum theory [10]. However, these are still some problems for models based on classical or traditional Cosserat continuum theory to study mechanical behaviors of granular materials, because deformation modes for microstructures in granular materials cannot be completely predicted by these models, or effects of microscopic mechanisms such as relative sliding and rotation and particle arrangement cannot be correctly reflected on the strain localization and size effect of granular materials. Nevertheless, the importance of the deformation mode caused by the microstructures has been emphasized in previous studies [12,13]. Chang et al. [13] developed a microstructural or micromechanical-based Cosserat continuum model of granular materials, where microstructural effects and interactions are taken into account. As a result, Cosserat constitutive relationships can be obtained based on macroscopic measures that reflect discrete properties [14]. However, their work used an isotropic contact density distribution hypothesis, which describes only partial microstructural information and does not consider the arrangement of particles and their voids in the material. Many studies have developed macroscopic continuum models based on the isotropic or anisotropic contact density distribution hypothesis [4,7,15–18]. However, studies on continuum models that consider microstructures with more detailed information are still being carried out. Chang et al. [19] proposed a first gradient micromechanics-based model using Voronoi cells through two-dimensional rhombic and hexagonal packings. Chang et al. [20,21] proposed a micromechanics-based Cosserat model using a two-dimensional micro-scale lattice network to simulate the fracture of concrete. Using a micro-scale Voronoi cell model, Li et al. [22] proposed a micromechanically informed macroscopic constitutive model of the effective Cosserat continuum for granular materials. To identify elastic constants of granular materials, Zhou et al. [23] developed a micromechanical Cosserat model based on an elliptical granular assembly. Xiu et al. [24,25] used a micromechanics-based micromorph model to analyze wave propagation behaviors in granular crystals with different microstructures. However, studies based on a micromechanics-based continuum model that can be used to provide more specific information about microstructures, i.e., to comprehensively and thoroughly reveal effects of microstructural information or interactions on failures of granular materials, are still lacking.

This study uses a micromechanics-based Cosserat constitutive model, in which the macroscopic constitutive modulus tensors are obtained by microstructural information. Different microstructures of granular materials are determined by particle’s arrangements, sizes, void ratios and coordination numbers, and it can categorize microstructures into a medium dense one and two dense ones. Using this micromechanics-based Cosserat model, macroscopic constitutive modulus tensors are determined for granular materials with different microstructures. In addition, a micromechanics-based Cosserat elastoplastic model is proposed using an extended Drucker-Prager yield criterion, and this model provides the finite element formulation. Numerical simulations are performed using the User Element (UEL) interface in ABAQUS to investigate the capacity of the model and the influences of microscopic parameters on modeling of failure behaviors of granular materials with different microstructures. Mesh independence is analyzed for the presented model. The results are compared with those based on DEM to associate some macroscopic parameters with microscopic ones.

2  Basic Equations for the Cosserat Continuum Theory

According to the Cosserat continuum theory, material points are treated as infinitesimal solids with characteristic lengths. There are three translational DOFs and three rotational DOFs, namely the displacement vector u={u1u2u3}T and the rotation vector ω={ω1ω2ω3}T. Afterward, basic equations in Cosserat continuum theory are given by [26]:

1) Kinematic equations

εij=ui,j−eijkωk,κij=ωi,j(1)

where εij and κij are respectively the strain and the micro-curvature, eijk is the Levi-Civita notation, and i,j,k=1,2,3.

2) Elastic constitutive relationships

σij=Cijklεij,μij=Dijklκij(2)

where σij and μij are the stress and the couple stress, respectively, and Cijkl and Dijkl are constitutive modulus tensors expressed as follows:

Cijkl=G[(1+a)δikδjl+(1−a)δilδjk+2ν1−2νδijδkl](3)

Dijkl=2Glc(δikδjl+bδilδjk+cδijδkl)(4)

where δij is Kronecker delta, G and ν are the shear modulus and Poisson’s ratio, a, b and c are the additional Cosserat constants, and lc is a characteristic length. a is the ratio between the Cosserat shear modulus Gc and the shear modulus G: Gc=aG.

3) Balance equations and boundary conditions

{σij,i+fj=0μij,i+ejklσkl+mj=0(5)

where fj and mj are respectively the external force and couple.

{niσij=tjσ niμij=mjμ (6)

in which tjσ and mjμ are tractions of the force and the couple stress, respectively, and ni is the normal vector.

3  The Micromechanics-Based Cosserat Model for Granular Materials with Different Microstructures

3.1 Micromechanics-Based Cosserat Constitutive Relationships

The micromechanics-based Cosserat model can identify the constitutive modulus tensors in Eqs. (3) and (4) by microstructural information. And the previous studies [7,13,24] have given the micromechanics-based micromorphic constitutive relationships. The micromorphic model considers the material point (in Fig. 1) as a deformable body with additional DOFs relative to the macroscopic deformation, while the Cosserat model considers it as a rigid body with additional rotational DOFs. It is noted that the Cosserat model can be considered as a reduced micromorphic model if the relative deformation is ignored for the micromorphic model. Then, we can obtain the micromechanics-based Cosserat constitutive modulus tensors in Eqs. (3) and (4). And our previous study [18] has a similar derivation process, so it is omitted here to save space. Then, the modulus tensors are shown in Eq. (7) below:

{Cijkl=1V∑c=1nKikcuLlcLjcDijkl=1V∑c=1nKnmcremkqLlcRpcenipLjcRqc+1V∑c=1nGikcrLlcLjc(7)

where c denotes the contact in the volume element, V is the volume of volume element, Kklcu,r and Gklcr are contact stiffness parameters in a contact constitutive relation, and Rpc and Ljc are respectively the radius of the reference particle and the branch vector connecting particles’ centroids. It shows that the constitutive modulus tensors Cijkl and Dijkl are in discrete summation forms of microstructural parameters including contact stiffness parameters and internal lengths. One object in the study is to identify Cijkl and Dijkl based on two ways as follows.

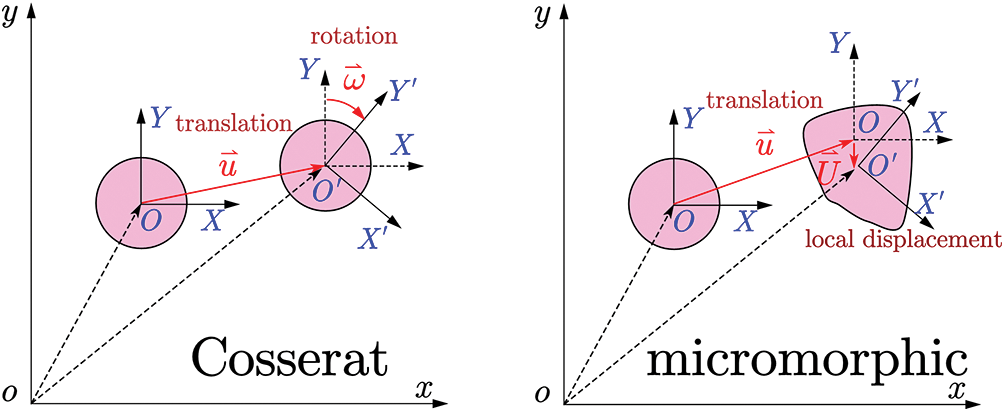
Figure 1: Diagrams of Cosserat vs. micromorphic material points

3.2 Identification of Constitutive Modulus Tensors for Granular Materials with Microstructures

(A) Isotropic directional density distribution function of contacts

There is usually a difference in contact stiffness parameters and internal lengths among contacts within a volume element. The material is assumed to be isotropic to simplify the analysis, and we consider an isotropic directional density distribution function of contacts ξ(α,β)=1/4π [13]. Thus, discrete summation forms can be used to calculate macroscopic constitutive parameters:

Cijkl=1V∑c=1nKikcuLlcLjc=l2NV∫0π∫02π(Kikcunlnj)ξsin⁡αdβdα(8)

Dijkl=1V∑c=1nKnmcremkqLlcRpcenipLjcRqc+1V∑c=1nGikcrLlcLjc=l2r2NV∫0π∫02π(Knmcremkqnlnpenipnjnq)ξsin⁡αdβdα+l2NV∫0π∫02π(Gikcrnlnj)ξsin⁡αdβdα(9)

where NV represents the contact density of the volume element, and the size of particle is assumed to be equal: Ljc=lnj and Rjc=rnj. nj is a unit vector normal to the contact plane, and the other two orthogonal unit vectors, sj and tj are on the contact plane. Then, Kijcu,r=Knninj+Kt(sisj+titj), and Gijcr=Gnninj+Gt(sisj+titj). Kn and Kt (Gn and Gt) are normal and tangential contact stiffness parameters for contact forces (moments). In this way, macroscopic constitutive parameters can be expressed in terms of microscopic constitutive parameters by solving these integrals:

{Ciiii=l2NV15(3Knu+2Ktu)Ciijj=Cijji=l2NV15(Knu−Ktu)Cijij=l2NV15(Knu+4Ktu)Cijkl=0,  otherwise(10)

{Diiii=l2r2NV15(2Ktr)+l2NV15(3Gnr+2Gtr)Diijj=Dijji=l2r2NV15(−Ktr)+l2NV15(Gnr−Gtr)Dijij=l2r2NV15(4Ktr)+l2NV15(Gnr+4Gtr)Dijkl=0, otherwise(11)

where i≠j.

(B) Specific microstructures

To include more microstructural information, we use three different three-dimensional microstructures defined by different ordered particle arrangements as shown in our previous study [24]. A microstructure cell consists of a reference particle and a first ring of neighbors at contacts. Fig. 2 shows the differences in particle arrangements, void ratios, and coordination numbers in the microstructures. Therefore, the three microstructures are classified as a medium dense one and two dense ones. It is noted that we also consider a loose microstructure by a simple cubic arrangement, however, it should not exist in reality since it shows almost no resistance to shear deformation. Therefore, the loose microstructure is not investigated in this study. For the medium dense microstructure, it appears as a hexagonal close-packed arrangement in the x-y plane, and as a cubic arrangement in x-z and y-z planes. The dense microstructure in one-sized particles is in a hexagonal close-packed arrangement. Smaller particles are used to fill voids in a simple cubic arrangement to create a dense microstructure in two-sized particles. Smaller particles with a radius (3−1)r are tangent to larger ones. It is noted that a microstructure must have a cell V as its minimum element, and then a granular assembly is made of microstructures with periodic arrangements of cells in Fig. 2. For simplicity and clarity, granular materials based on the isotropic contact density distribution are shortened to GMiso, and granular materials with medium dense and two dense microstructures are shortened to GMmedium, GMdense_onesized and GMdense_twosized, respectively. And Table 1 shows the different coordination numbers and void volume ratios of the three microstructures.

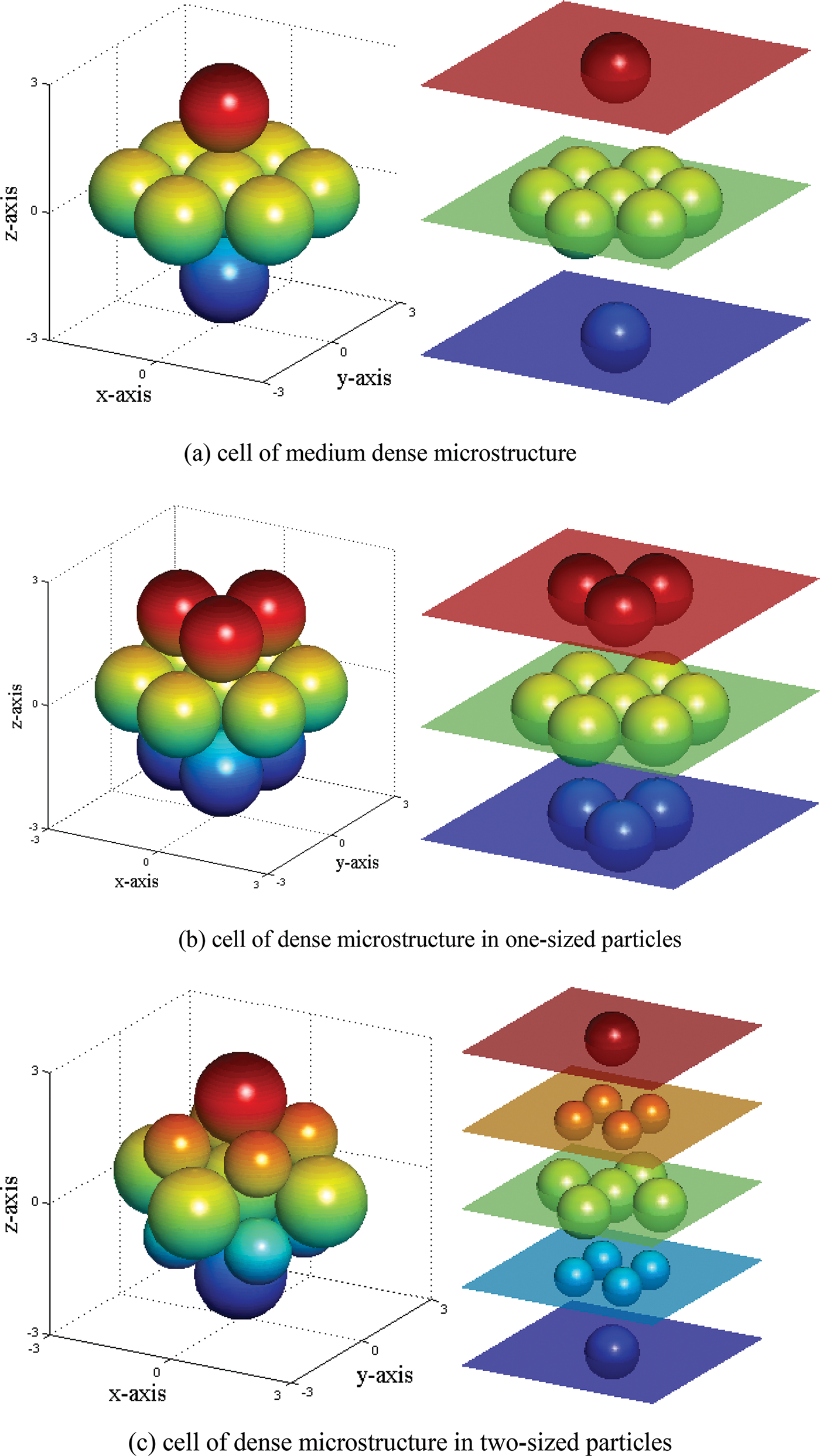
Figure 2: Schematic diagram for cells of three microstructures

Then, the constitutive modulus tensors of these granular materials with different microstructures can be obtained by directly solving the discrete summations as shown in Eq. (7). And the constitutive modulus tensors are derived and shown as follows:

(1) Medium dense microstructure

{C1111=C2222=3l24V(3Knu+Ktu), C3333=2l2VKnuC1212=C2121=3l24V(Knu+3Ktu)C3131=C3232=3l2VKtu, C1313=C2323=2l2VKtuC1122=C2211=C1221=C2112=3l24V(Knu−Ktu)Cijkl=0,otherwise(12)

{D1111=D2222=3l24V(r2Ktr+3Gnr+Gtr), D3333=2l2VGnrD2121=D1212=3l24V(3r2Ktr+Gnr+3Gtr)D1313=D2323=23D3131=23D3232=2l2V(r2Ktr+Gtr)D2211=D1122=D1221=D2112=−3l24V(r2Ktr−Gnr+Gtr)Dijkl=0,otherwise(13)

(2) Dense microstructure in one-sized particles

{C1111=4l23V(2Knu+Ktu), C2222=C3333=l22V(5Knu+3Ktu)C1212=C2121=C3131=C1313=2l23V(Knu+5Ktu), C2332=C3223=l26V(5Knu+19Ktu)C2211=C3311=C1122=C1221=C1133=C1331=C2112=C3113=2l23V(Knu−Ktu)C3232=C3322=C2323=C2233=5l26V(Knu−Ktu)Cijkl=0,otherwise(14)

{D1111=4l23V(r2Ktr+2Gnr+Gtr), D2222=D3333=l22V(3r2Ktr+5Gnr+3Gtr)D2121=D3131=D1212=D1313=2l23V(5r2Ktr+Gnr+5Gtr)D3232=D2323=l26V(19r2Ktr+5Gnr+19Gtr)D2211=D3311=D1221=D1331=D2112=D1122=D3113=D1133=−2l23V(r2Ktr−Gnr+Gtr)D3322=D2332=D3223=D2233=−5l26V(r2Ktr−Gnr+Gtr)Dijkl=0,otherwise(15)

(3) Dense microstructure in two-sized particles

{C1111=C2222=C3333=4l23V(2Knu+Ktu)C2121=C3131=C1212=C3232=C1313=C2323=2l23V(Knu+5Ktu)C2211=C3311=C1221=C1331=C2112=C1122=2l23V(Knu−Ktu)C3322=C2332=C3113=C3223=C1133=C2233=2l23V(Knu−Ktu)Cijkl=0,otherwise(16)

{D1111=D2222=D3333=4l23V(r2Ktr+2Gnr+Gtr)D2121=D3131=D1212=D3232=D1313=D2323=2l23V(5r2Ktr+Gnr+5Gtr)D2211=D3311=D1221=D1331=D2112=D1122=−2l23V(r2Ktr−Gnr+Gtr)D3322=D2332=D3113=D3223=D1133=D2233=−2l23V(r2Ktr−Gnr+Gtr)Dijkl=0,otherwise(17)

4  Yield Function and Plastic Potential Function

According to Forest et al. [27], the equivalent st31rain is defined by

ε¯=23(eijeij+lc2κijκij)(18)

where eij is the deviator of the strain εij. And the equivalent stress is defined by

σ¯=32(sijsij+lc−2μijμij)(19)

where sij is the deviatoric stress tensor.

The Cosserat continuum is used to describe plastic behavior of granular materials by using an extended Drucker-Prager yield criterion:

f=σ¯+Aϕp+Bϕ(20)

where p=13(σ1+σ2+σ3) is the first invariant of stress, Aϕ and Bϕ are material parameters in expressions of internal fiction angle ϕ and cohesion c. If the yield surfaces of the Drucker-Prager and Mohr-Coulomb criteria coincide at the inner edge of the Mohr-Coulomb surface, then material parameters can be expressed as

Aϕ=6sin⁡ϕ3+sin⁡ϕ,Bϕ=−c6cos⁡ϕ3+sin⁡ϕ(21)

Based on the piecewise linear hardening/softening assumption, the cohesion is written as follow:

c=c0+hpε¯p(22)

where c0 is the initial cohesion, hp is hardening/softening parameter, and ε¯p is the equivalent plastic strain.

The non-associated flow rule is assumed in granular materials, which implies the plastic potential function g≠f. Thus, a plastic potential function is defined by

g=σ¯+Aψp+Bψ(23)

in which

Aψ=6sin⁡ψ3+sin⁡ψ,Bψ=−c6cos⁡ψ3+sinψ(24)

where ψ is the dilatancy angle, and the dilatancy angle is smaller than the internal fiction angle ϕ.

5  Numerical Simulations

Appendix shows the finite element formulation of the micromechanics-based Cosserat elastoplastic model, and a user element program is coded using the ABAQUS UEL subroutine interface.

The numerical examples focus on the following issues: (1) the capacity of the micromechanics-based Cosserat model on modeling strain localization and softening of granular materials; (2) effects of different microstructures on failure behaviors; (3) effects of microscopic parameters including contact stiffness parameters and characteristic length on failure behaviors; (4) the mesh independence of the presented model; (5) comparisons of simulations between FEM and DEM.

5.1 Strain Localization and Strain Softening of Granular Materials with Different Microstructures

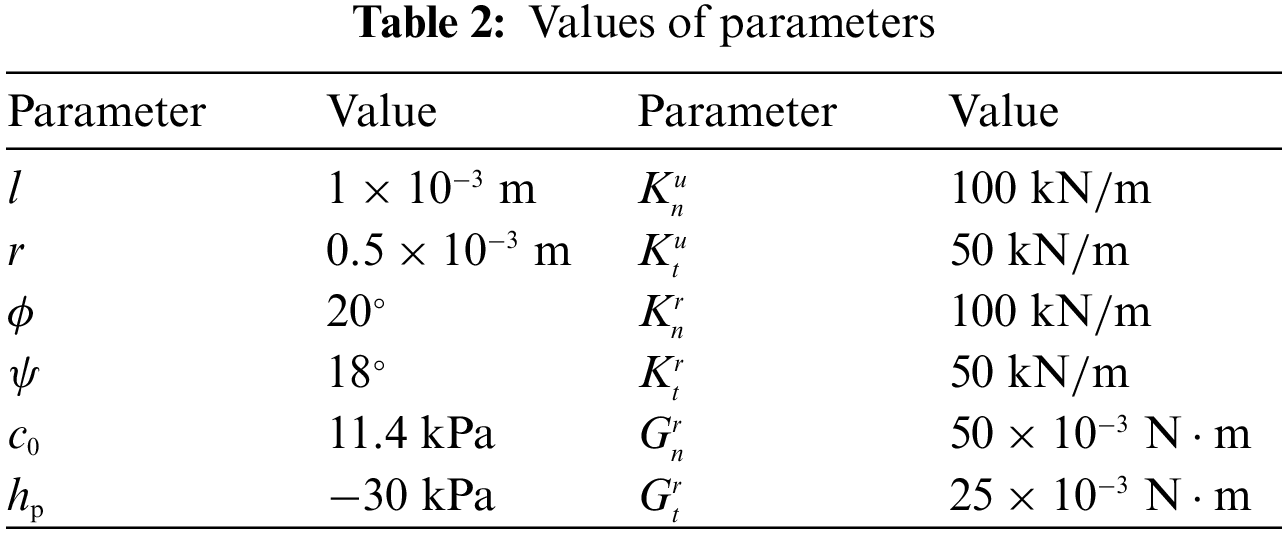
The numerical simulations concern a rectangular panel with the size of 1 m × 2 m (Fig. 3a), and an eight-node iso-parametric element with four integration points is used for the plane strain problem (Fig. 3b). The panel is subjected to compression under a displacement-controlled symmetrical load with a displacement of 0.012 m each at the top and bottom. Nodes at the top and bottom boundaries are fixed in the horizontal direction, and those on the left and right boundaries are free. The material and microstructural parameters are specified in Table 2. The characteristic length lc is considered as the internal length l. And the panel is meshed by 15 × 30 in this example.

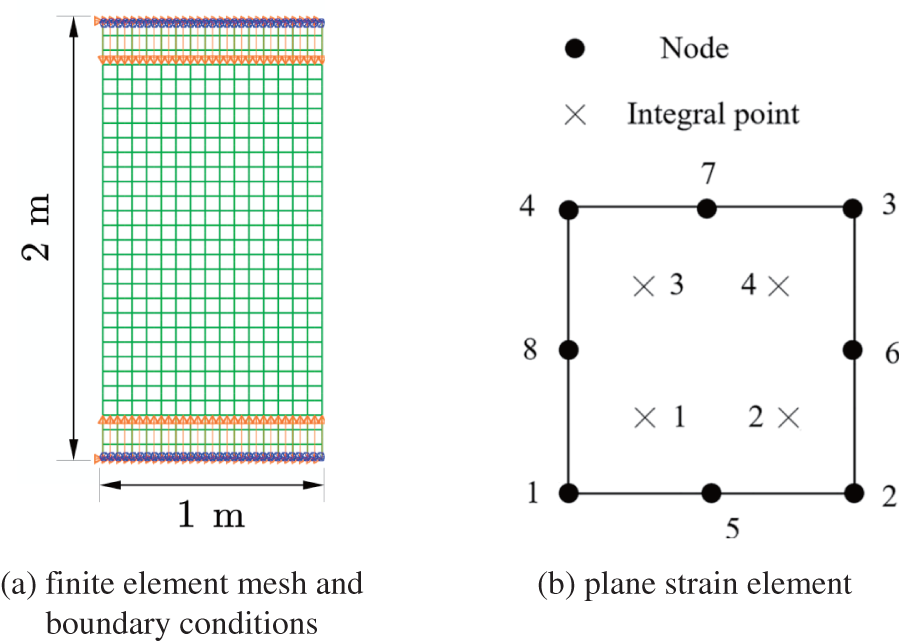
Figure 3: Finite element mesh for the panel model

First, Fig. 4 shows the load-displacement curves of granular materials with microstructures, i.e., GMmedium, GMdense_onesized, GMdense_twosized, and GMiso, simulated by the micromechanics-based Cosserat model. Meanwhile, Fig. 5 shows their corresponding equivalent plastic strain distributions. From Fig. 4, the curves are close to each other, except for that of GMiso, which shows a lower stiffness in the elastic stage and a lower degree of softening in the strain-softening stage. It can be speculated that the assumption of isotropic directional density distribution is too strong, and some microstructural information may be washed out to cause the difference in the curve of GMiso. More specifically, the curves of GMdense_onesized and GMdense_twosized are almost the same, while the curve of GMmedium has a greater stiffness at the elastic stage than those of GMdense_onesized and GMdense_twosized. However, the difference between GMmedium and GMdense_onesized or GMdense_twosized seems to be small. This is because the macroscopic equivalent elastic constants of GMmedium, GMdense_onesized and GMdense_twosized are of small difference, whose ratio is given by 1.18:1:1. Moreover, the differences between GMmedium and GMdense_onesized or GMdense_twosized at plastic stages are even smaller. It is speculated that plastic mechanical responses are controlled not only by elastic and plastic parameters, but also by the microstructural information such as coordination number and void volume ratio, which may affect the arrangement of particles at the plastic stage. Therefore, descriptions and simulations of plasticity for granular materials with different microstructures are quite complex. And our next study contributes to the development of micromechanics-based yield criterion and plastic potential function, which may contribute to the explanation of the plastic response of granular materials with different microstructures.

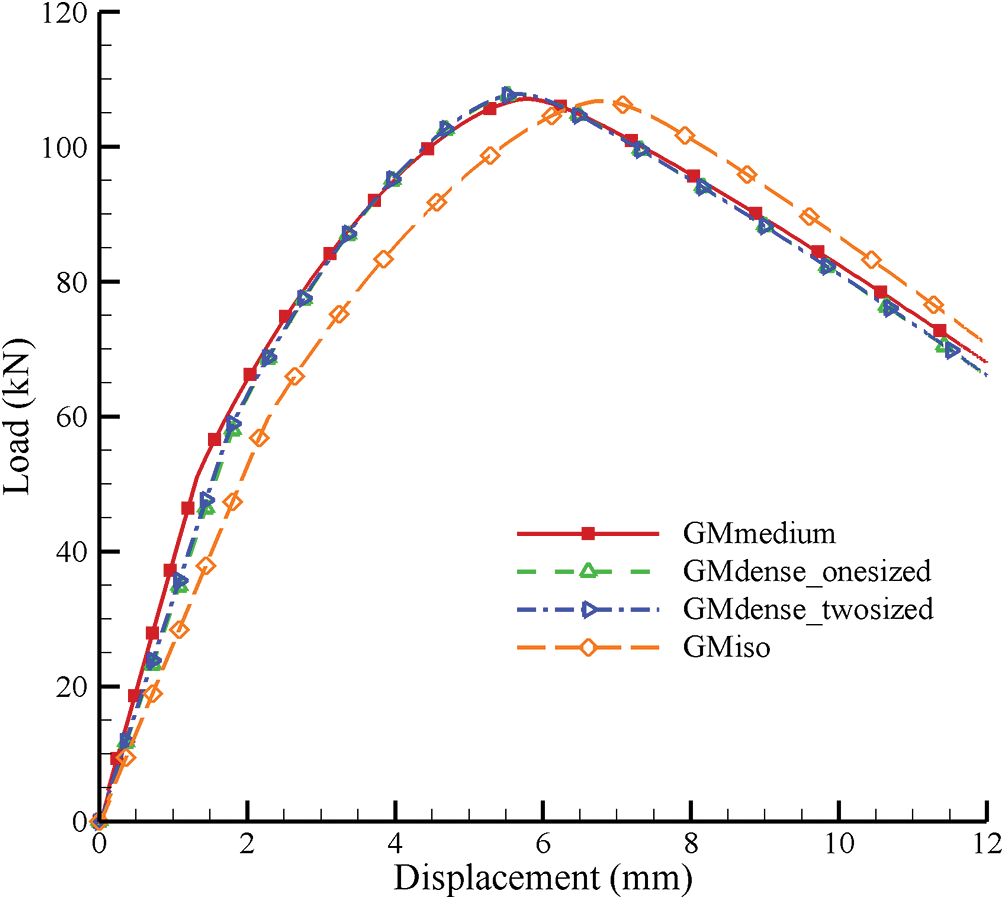
Figure 4: Load-displacement curves of GMmedium, GMdense_onesized GMdense_twosized, and GMiso simulated by micromechanics-based Cosserat model

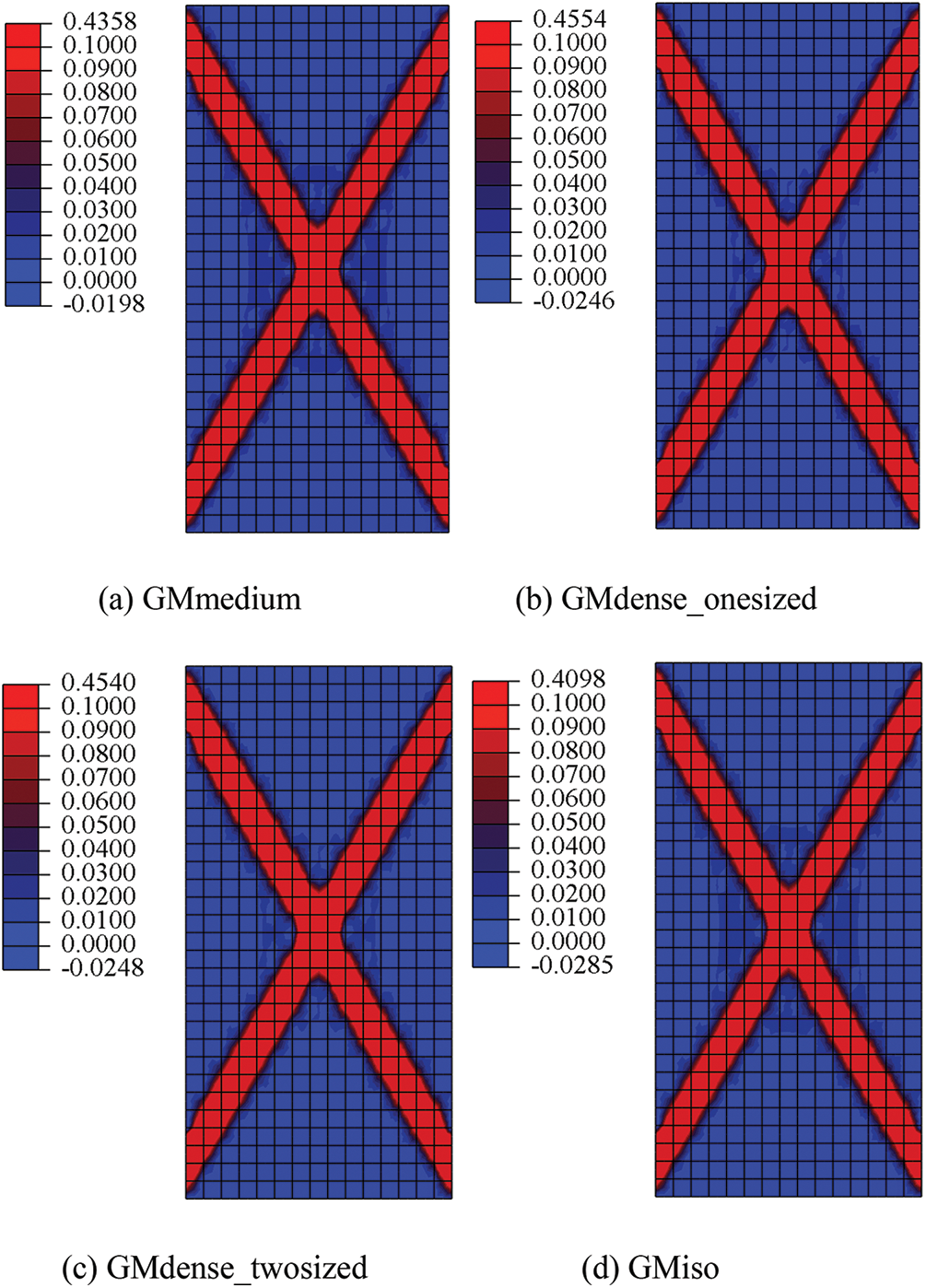
Figure 5: Equivalent plastic strain distributions of GMmedium, GMdense_onesized GMdense_twosized, and GMiso simulated by micromechanics-based Cosserat model

Furthermore, Fig. 5 shows that the strain localizations, i.e., the shear bands, have almost the same width and shape for all granular materials. And similar to the above analysis for Fig. 4, GMiso has a minimal equivalent plastic strain, and GMdense_onesized and GMdense_twosized have almost the same equivalent plastic strain. Back to Table 1, GMdense_onesized and GMdense_twosized have similar void volume ratio, and they have almost the same load-displacement relationship and equivalent plastic strain, which are different from those of GMmedium, which has a larger void volume ratio. This may reflect the influence of void volume ratio on failure behaviors of granular materials.

The Cosserat model can describe the rotational DOF for granular materials. Fig. 6 gives the rotation ω3 distributions of GMmedium, GMdense_onesized GMdense_twosized, and GMiso simulated by the micromechanics-based Cosserat model. It can be seen that the rotations show X-shaped distributions with respect to the shear bands. Similarly to the equivalent plastic strain rule, GMdense_onesized and GMdense_twosized have almost the same rotation, followed by GMmedium and finally GMiso. Therefore, we can see that in terms of simulations on strain localizations and rotations, GMiso shows a slight underestimation compared to GMmedium, GMdense_onesized and GMdense_twosized.

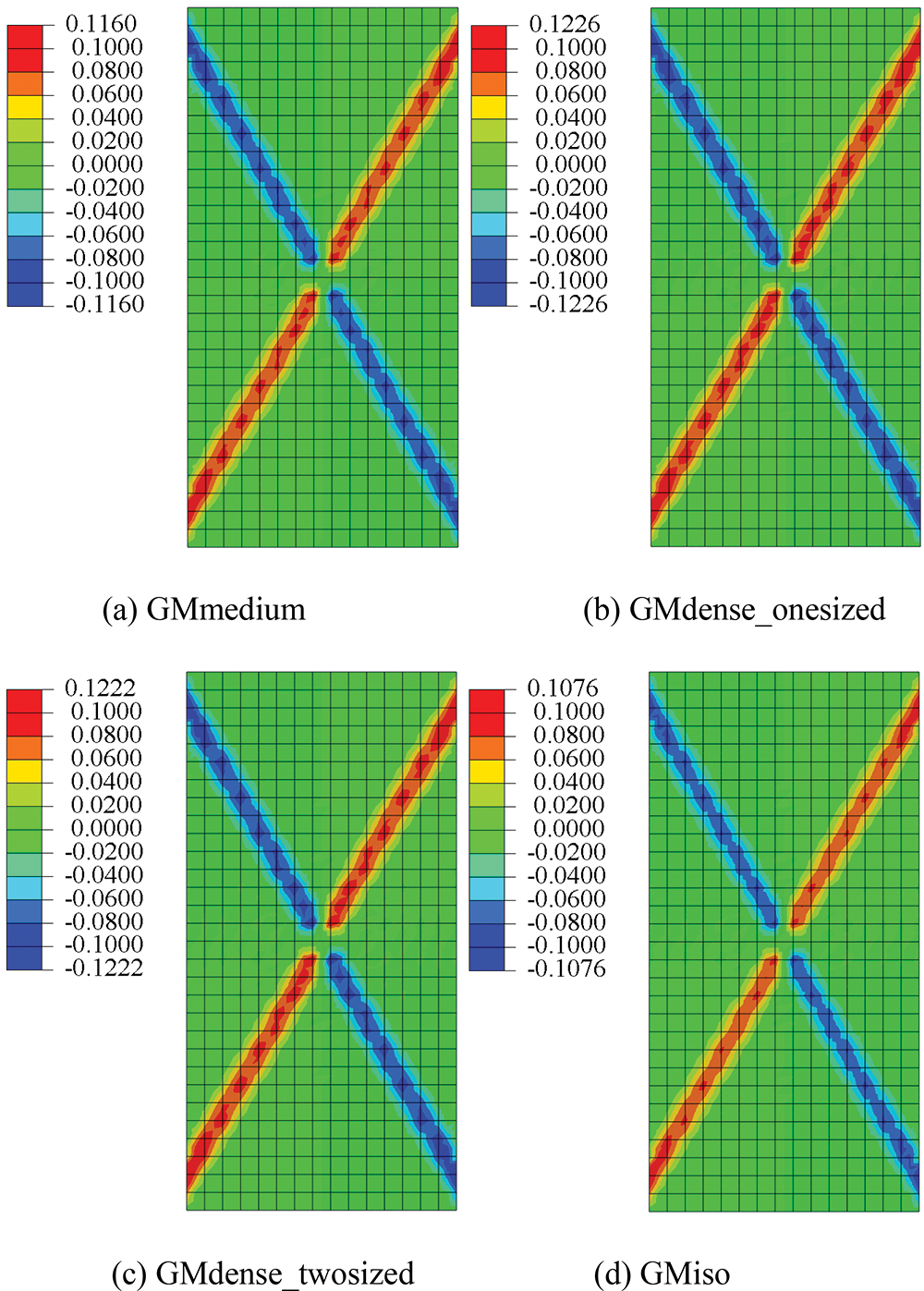
Figure 6: Rotation ω3 distributions of GMmedium, GMdense_onesized GMdense_twosized, and GMiso simulated by micromechanics-based Cosserat model

5.2 Effects of Contact Stiffness Parameters

This part investigates the effects of contact stiffness parameters on failure behaviors of granular materials with microstructures for the micromechanics-based Cosserat model. For the sake of simplicity, GM medium is used as a representative.

First, to consider the effects of microscopic parameters, we should compare failure behaviors simulated by the micromechanics-based Cosserat model to those by the classical Cosserat one without microscopic parameters. The elastic constants of the classical Cosserat model can be identified by E=37.97 MPa, Gc=11.25 MPa and ν=0.125 to match those of the micromechanics-based Cosserat one. Fig. 7 shows the load-displacement curves of GMmedium simulated by the micromechanics-based Cosserat model compared with the classical Cosserat one. In the linear elastic stage, the load-displacement curves for two Cosserat models are in good agreement. As for the plastic stage, the ultimate strength simulated by the classical Cosserat model is about 7.9% higher than that simulated by the micromechanics-based Cosserat model, and the load-displacement curve of the classical Cosserat model reaches the ultimate strength at about 5.2 mm displacement before that of the micromechanics-based Cosserat model at 5.8 mm displacement. The degree of strain softening simulated by the classical Cosserat model is slightly larger as the load increases. Therefore, the equivalent plastic strain simulated by the classical Cosserat model is correspondingly larger, as shown in Fig. 8. It is noteworthy that, unlike the classical Cosserat model, the proposed micromechanics-based Cosserat model has the ability to investigate the effects of the microstructural information on failure behaviors for granular materials with microstructures. In particular, the elastic constitutive modulus tensors of the micromechanics-based Cosserat model have eight microstructural parameters as shown in Eqs. (12)–(13), while the classical Cosserat model has three macroscopic elastic constants and one characteristic length to describe the elastic constitutive relationship. Therefore, the two models do not have mutually compatible elastic constitutive modulus tensors, much less plastic ones. Then, the mechanical response of the elastic stage may coincide between two models, as shown in Figs. 7 and 8, but the microstructural feature of the micromechanics-based Cosserat model leads to differences of simulations on plasticity and failure from the classical Cosserat one, because the micromechanics-based Cosserat model provides more influencing factors, i.e., microstructural parameters. Further discussion focuses on the analysis of how the microscopic parameters affect the failure behavior as follows.

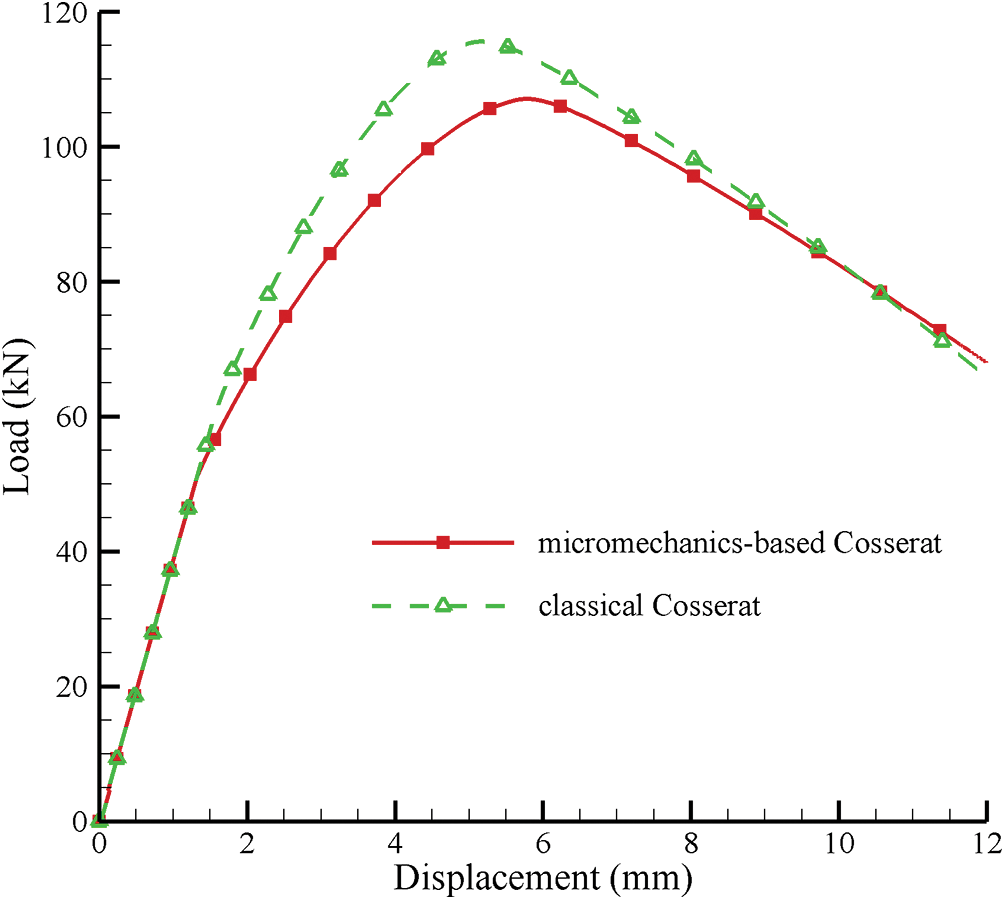
Figure 7: Load-displacement curves of GMmedium simulated by micromechanics-based Cosserat model vs. classical Cosserat model

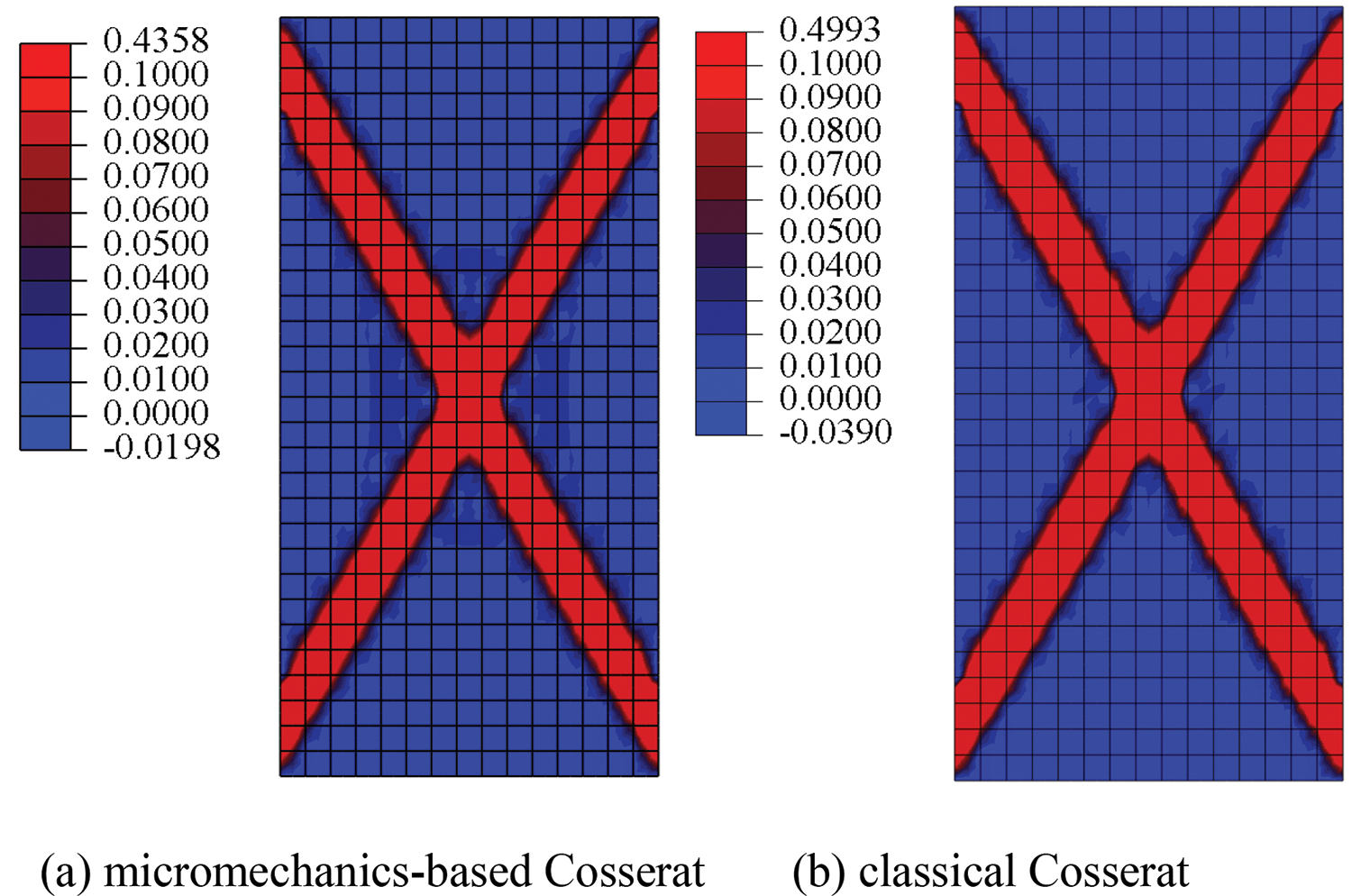
Figure 8: Equivalent plastic strain distributions of GMmedium simulated by micromechanics-based Cosserat model vs. classical Cosserat model

Then, the effect of the contact stiffness parameter related to displacement Knu (Ktu) is investigated, and Knu is respectively set to 500,200,100,50,20 kN/m. And the ratio between Ktu and Knu remains 0.5 for convenience. Fig. 9 shows the load-displacement curves of GMmedium simulated by micromechanics-based Cosserat model for situations with Knu=500,200,100, 50, 20 kN/m. It can be seen that the situation with larger Knu shows the larger stiffness at the elastic stage and the larger softening degree. And with the decrease of Knu, it gradually tends to show the strain hardening instead of the strain softening, and the strength also gradually decreases slightly. Besides, it is noted that the displacements for situations with Knu=500,200 kN/m can be loaded to 10.4 and 10.8 mm, so their equivalent plastic strains are smaller than those for the situation with Knu=100 kN/m as shown in Fig. 10. And the smaller strain softening leads to the smaller strain localization as shown in Fig. 10d, especially, the situation with Knu=20 kN/m cannot show the strain localization due to its strain hardening. Furthermore, we investigated the rotation ω3 distributions for situations with different Knu as shown in Fig. 11. It shows that the contact stiffness parameter related to displacement Knu affects the rotation ω3 distribution, that is to say, the deformation caused by the displacement can lead to the rotation of the particle in granular materials. And this rotation has a positive relationship with Knu and Ktu.

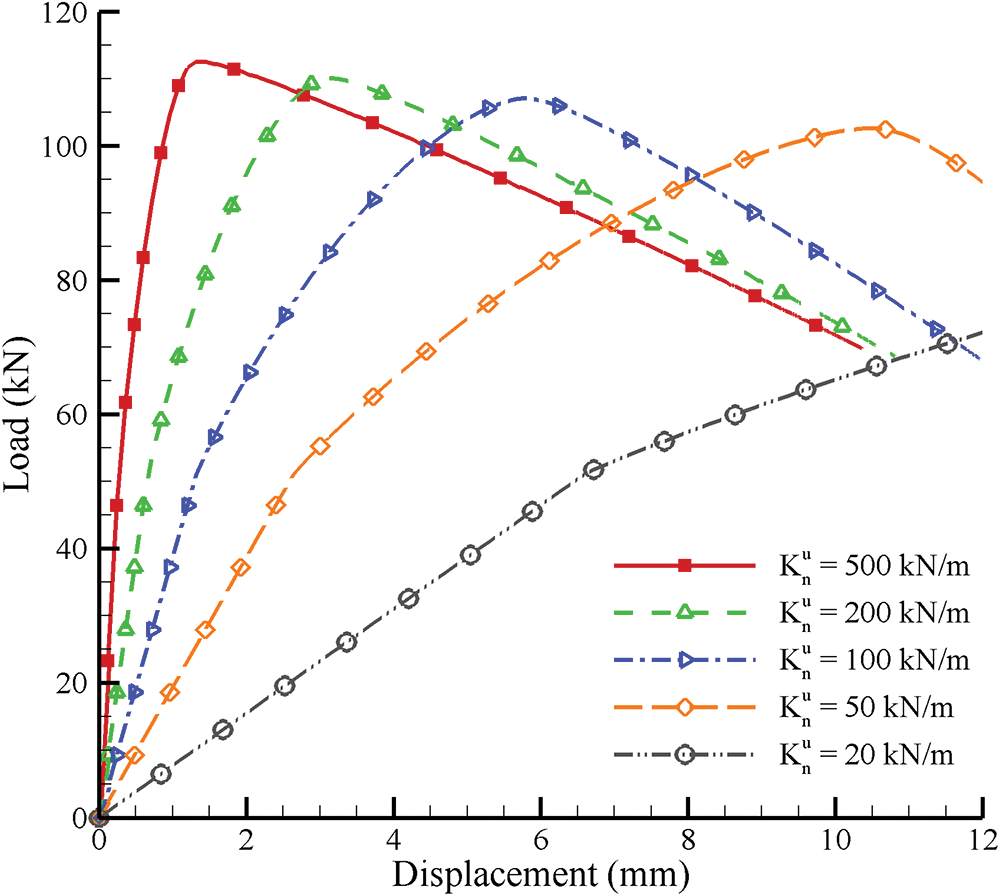
Figure 9: Load-displacement curves of GMmedium simulated by micromechanics-based Cosserat model for situations with Knu=500,200,100, 50, 20 kN/m and Ktu=0.5×Knu

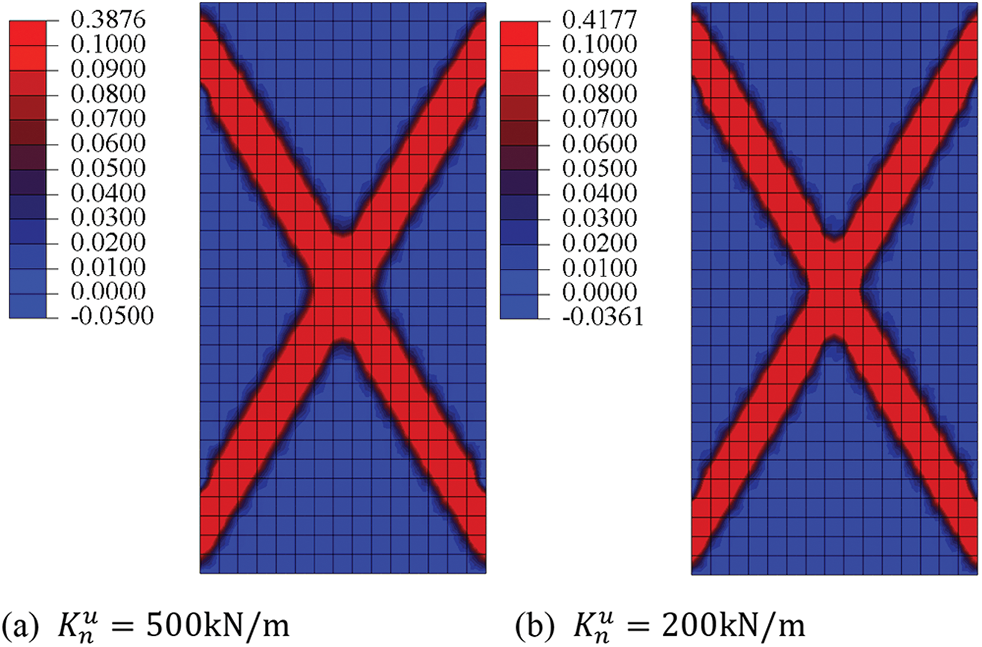
Figure 10: Equivalent plastic strain distributions of GMmedium simulated by micromechanics-based Cosserat model for situations with Knu=500,200,100, 50, 20 kN/m and Ktu=0.5×Knu

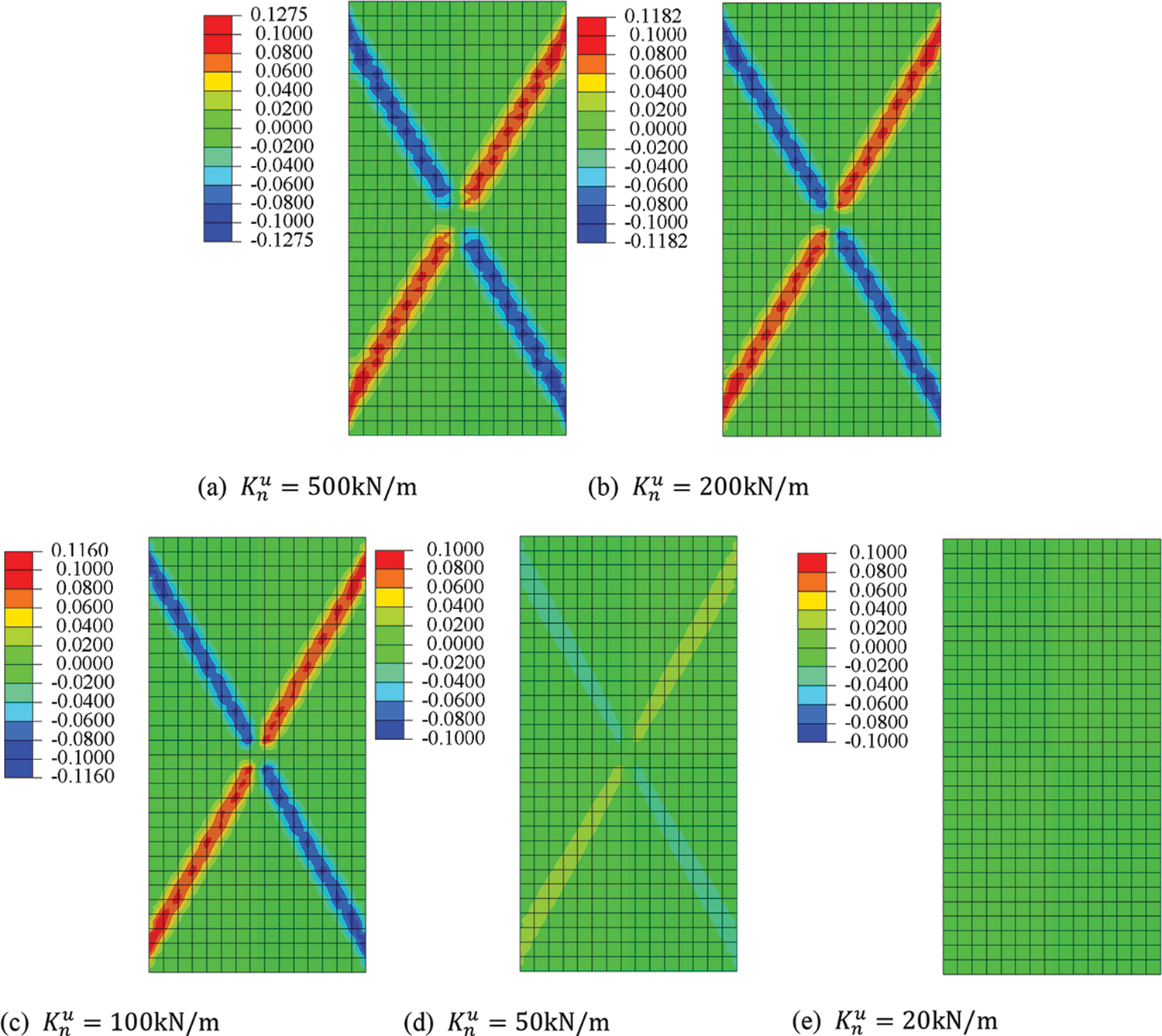
Figure 11: Rotation ω3 distributions of GMmedium simulated by micromechanics-based Cosserat model for situations with Knu=500,200,100, 50, 20 kN/m and Ktu=0.5×Knu

The effects of contact stiffness parameters related to rotation Knr (Ktr) and Gnr (Gtr) are also investigated. Knr is respectively set to 40000,5000,1000,100,10 kN/m, and Gnr is respectively set to 1000,200,50, 10×10−3N⋅m. The ratios Ktr/Knr and Gtr/Gnr remain 0.5. If Knr (Ktr) or Gnr (Gtr) is changed, the other parameters remain as those in Table 2. Figs. 12 and 13 respectively shows the load-displacement curves of GMmedium simulated by micromechanics-based Cosserat model for situations with Knr=400000, 40000, 5000,1000,100,10 kN/m and Gnr=200000,20000,1000,200,50, 10×10−3N⋅m. As we can see in Figs. 12 and 13, the load-displacement curves for all situations are coincident before reaching the ultimate strength, and the ultimate strength is slightly larger for the one with larger contact stiffness parameters related to rotation. This illustrates that the contact stiffness parameters related to rotation have little effect on the elastic and hardening stages of granular materials. As for the softening stage, the curves can converge to those with smaller values of Knr or Gnr as shown by the red solid lines. And with the increase of Knr or Gnr, the degree of softening gradually decreases, especially when Knr=400000 kN/m and Gnr=200000×10−3N⋅m, the curves cannot show the softening stages. This result is opposite to that shown in Fig. 9 where the situation with larger Knu shows higher degree of softening. Correspondingly, the rules of distributions of equivalent plastic strains and rotations for situations with different Knr or Gnr are opposite to those shown in Figs. 10 and 11, i.e., the situations with larger Knr or Gnr show lower degrees of strain localizations. For reasons of space, these figures are not shown here. Thus, it can be seen that the rotation of the particle has no effect on the elastic and hardening stages, but an obvious effect on the softening stage of granular materials. And to better show the strain localization and softening phenomena, we recommend that contact stiffness parameters related to rotation Knr and Gnr are within about 1000 kN/m and 1000×10−3N⋅m, respectively.

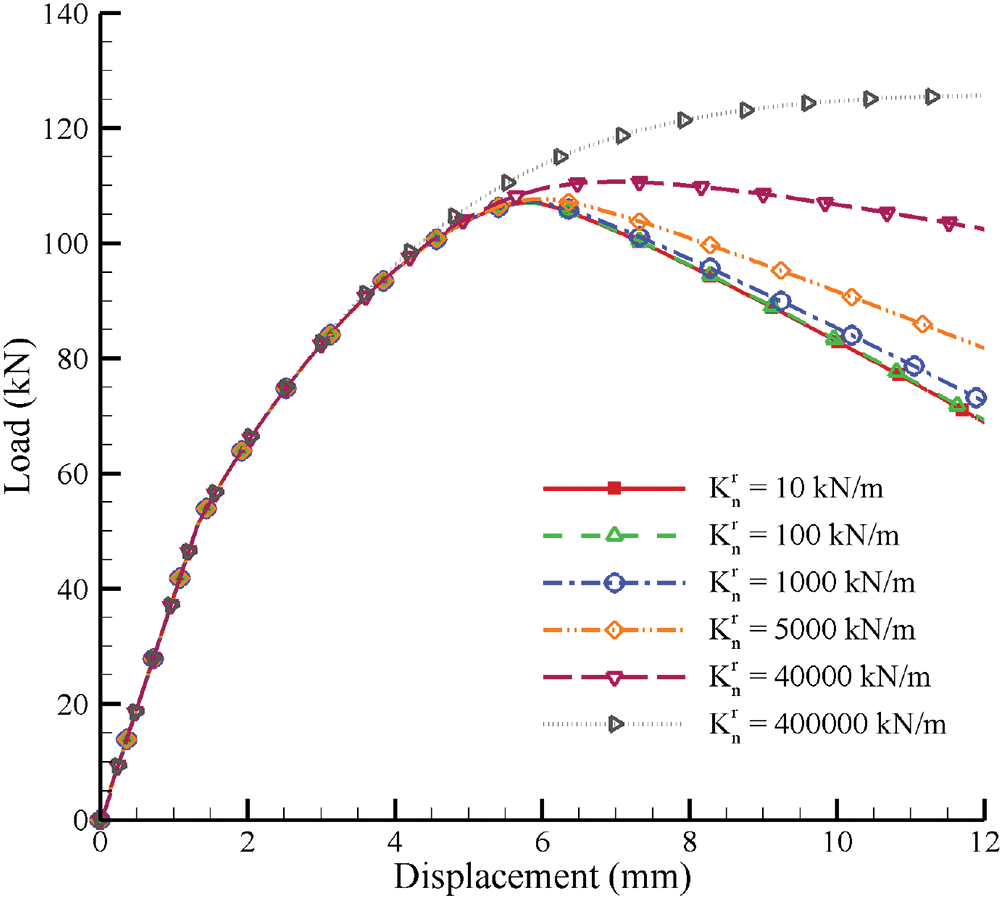
Figure 12: Load-displacement curves of GMmedium simulated by micromechanics-based Cosserat model for situations with Knr=400000, 40000, 5000,1000,100,10 kN/m and Ktr=0.5×Knr

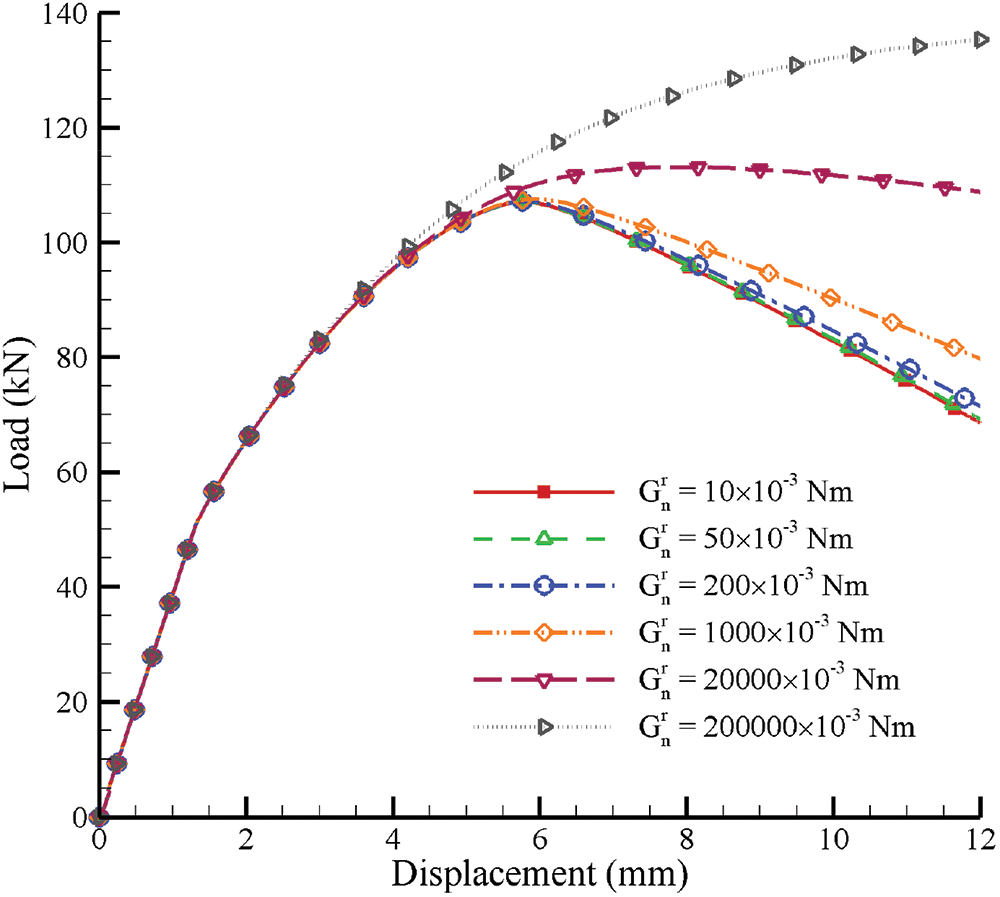
Figure 13: Load-displacement curves of GMmedium simulated by micromechanics-based Cosserat model for situations with Gnr=200000,20000,1000,200,50, 10×10−3N⋅m and Gtr=0.5×Gnr

5.3 Effect of Characteristic Length

Similarly, only GMmedium is discussed in this part. The characteristic length can reflect the size of the microstructure in granular materials, which is an important parameter in the Cosserat model and other microstructural models. Effects of the characteristic length lc are analyzed on strain localization and softening behaviors in this part.

Fig. 14 shows the load-displacement curves of GMmedium simulated by the micromechanics-based Cosserat model for situations with lc=100,10, 1, 0.1, 0.01×10−3m. And Fig. 15 shows their equivalent plastic strain distributions. As we can see, the degree of strain softening gradually increases with the decrease of lc, and it can also reach a convergence when lc decreases under 10−3m, as the blue, orange and gray lines in Fig. 14 show. A same rule is also presented that the equivalent plastic strain distribution tends to be the same and obviously X-shaped with the decrease of lc. And there cannot be an obvious X-shaped shear band for the situation when lc=100×10−3m. The situation with larger lc can represent that the microstructural scale tends to the macroscopic one, which smears out the microscopic information and causes the smaller strain softening and localization. Conversely, the situation with smaller lc emphasizes the microstructural effect on the strain softening and localization. And the microstructural effect remains at the same level when lc is smaller than 10−3m.

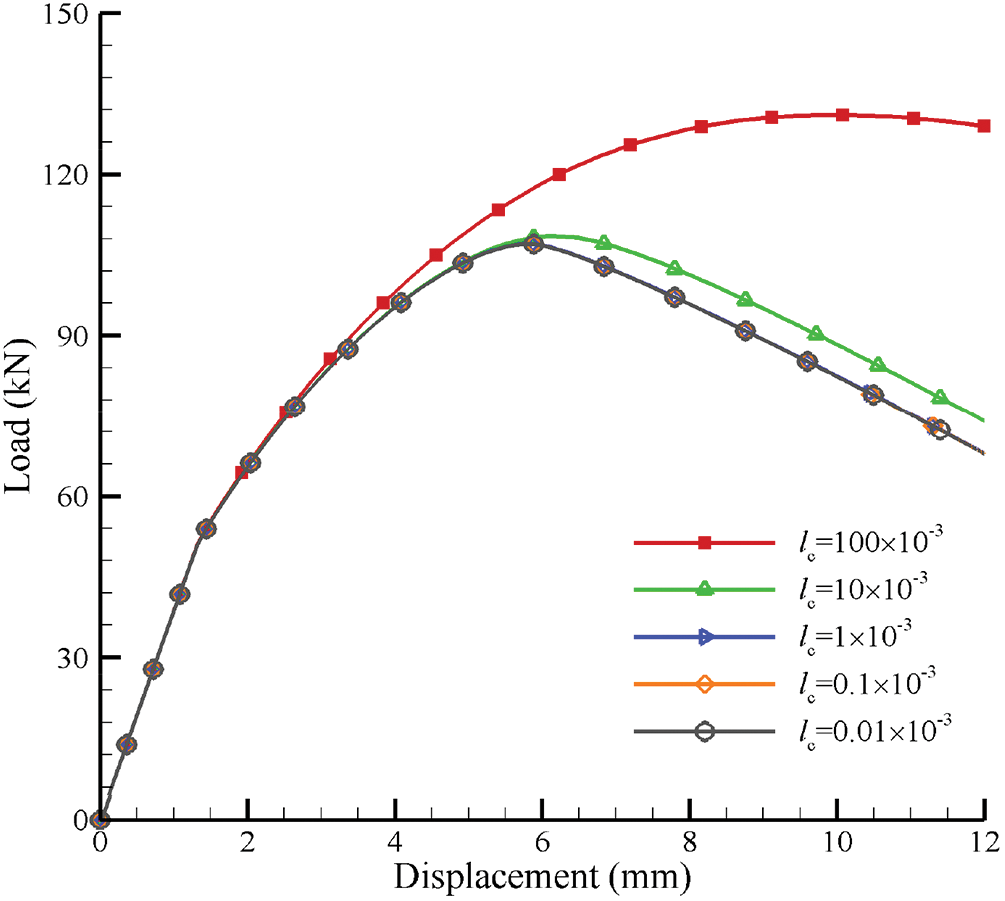
Figure 14: Load-displacement curves of GMmedium simulated by micromechanics-based Cosserat model for situations with lc=100,10, 1, 0.1, 0.01×10−3m

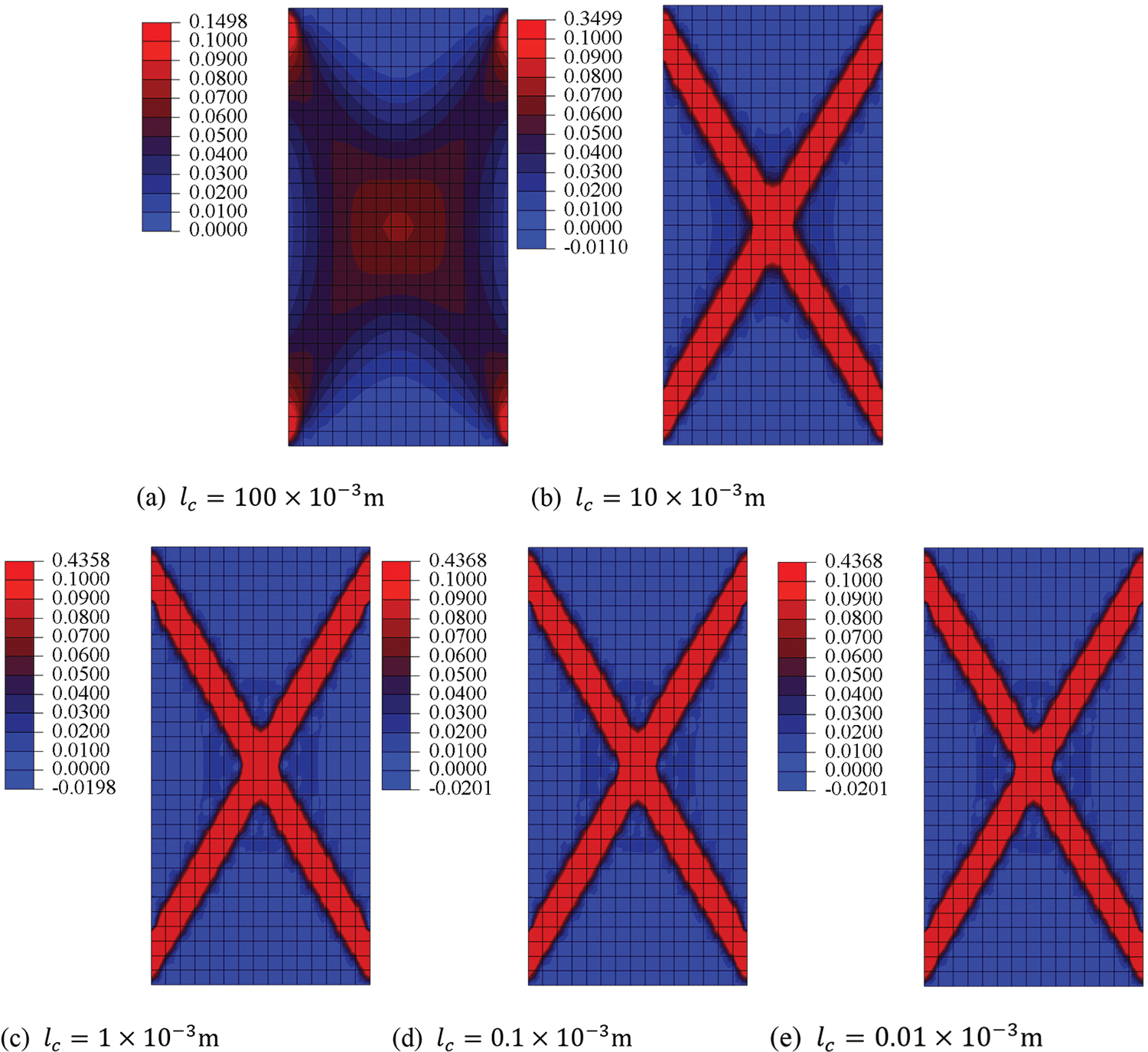
Figure 15: Equivalent plastic strain distributions of GMmedium simulated by micromechanics-based Cosserat model for situations with lc=100,10, 1, 0.1, 0.01×10−3m

It is noted that the micromechanics-based Cosserat model with infinitesimal lc cannot be reduced to the classical Cauchy one, because it still has the microstructures although lc tends to be zero. The elastic constants of the classical model are identified by E=37.97 MPa and ν=0.125 to match those of the micromechanics-based Cosserat one with infinitesimal lc. And we can compare the curves of the micromechanics-based Cosserat with small lc with the classical one, as shown in Fig. 16. The elastic stages can coincide with each other, but the hardening and softening stages have some differences. The result of the differences between two models is similar to that shown in Fig. 7, which indicates that the microstructural feature of the micromechanics-based Cosserat model cannot be eliminated just by making lc tend to zero.

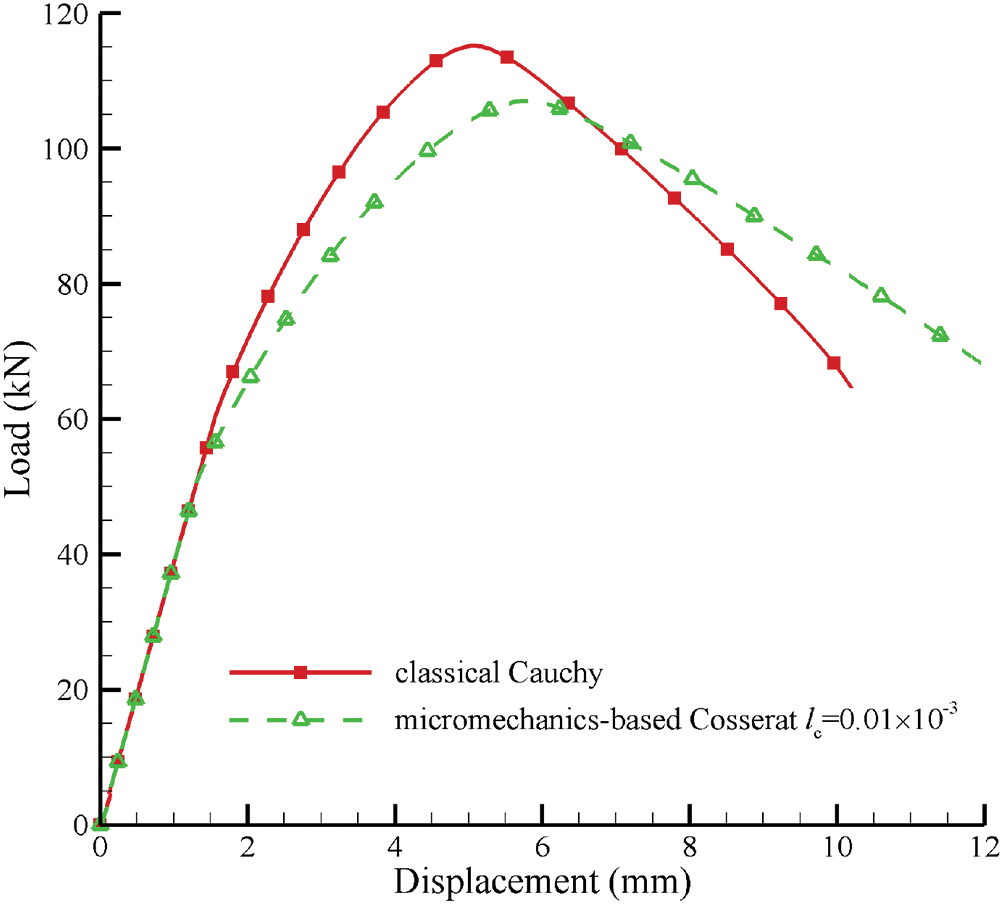
Figure 16: Load-displacement curves of GMmedium simulated by micromechanics-based Cosserat model with lc=0.01×10−3m vs. classical Cauchy model

5.4 Mesh Dependence Analysis

The Cosseat model can provide a regularization mechanism by introducing a characteristic length to reduce the pathological mesh dependence for the localization problem in the classical continuum model, and our previous study [10] has proved this Cosseat effect by comparing the computational results of the Cosseat model with the classical continuum using the Drucker-Prager yield criterion. In this part, the mesh dependence is further analyzed using the micromechanics-based Cosseat elastoplastic model for granular materials with microstructures, taking GMmedium as an example. And the parameters are also used in Table 2. Fig. 17 shows the load-displacement curves of GMmedium for situations with meshes 8×16, 10×20, 15×30 and 20×40. The situations with different meshes show the similar strength but the different degrees of strain softening, and that with the finest mesh has the largest degree of strain softening. And their equivalent plastic strain distributions are shown in Fig. 18, which shows that the shear band width depends on the mesh size, i.e., the situation with the finer mesh leads to the smaller width of shear band. However, there should be no mesh dependence according the Cosserat theory. We speculate that the reason for this mesh dependence may be the small value of the characteristic length lc=10−3m, which causes some behaviors simulated by the Cosserat model to be close to those simulated by the classical model.

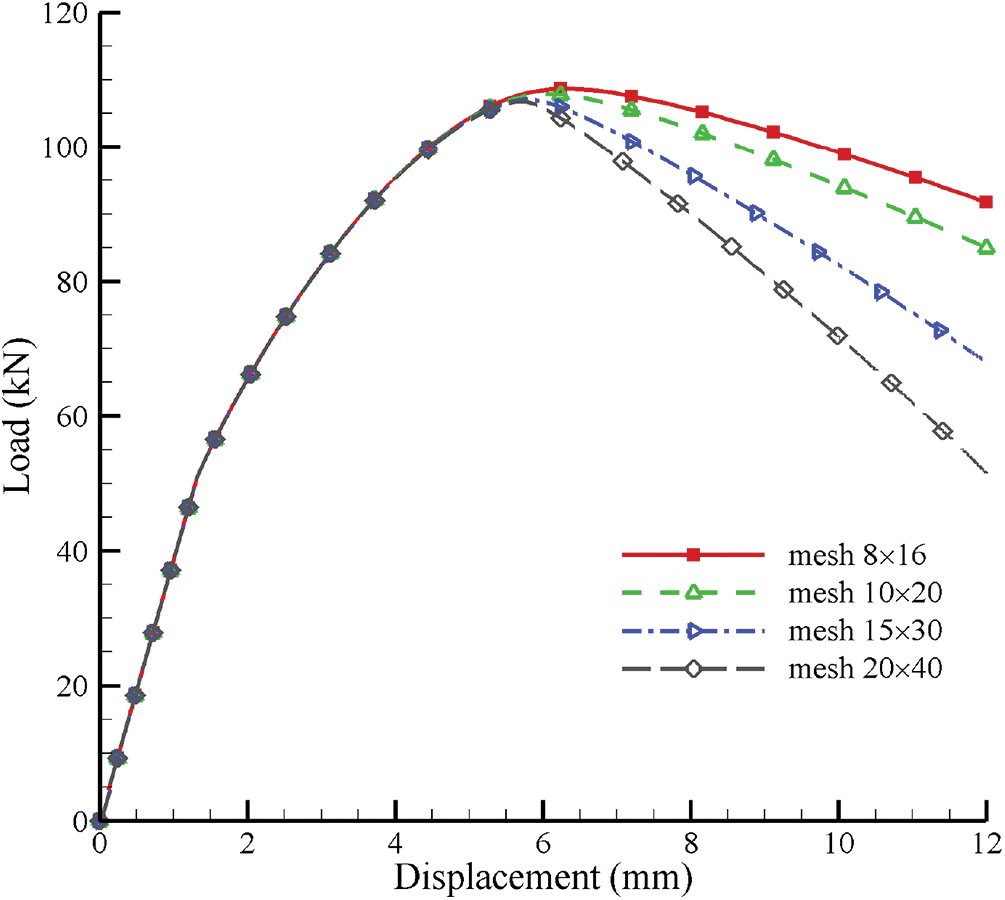
Figure 17: Load-displacement curves of GMmedium for situations with meshes 8×16,10×20,15×30and20×40

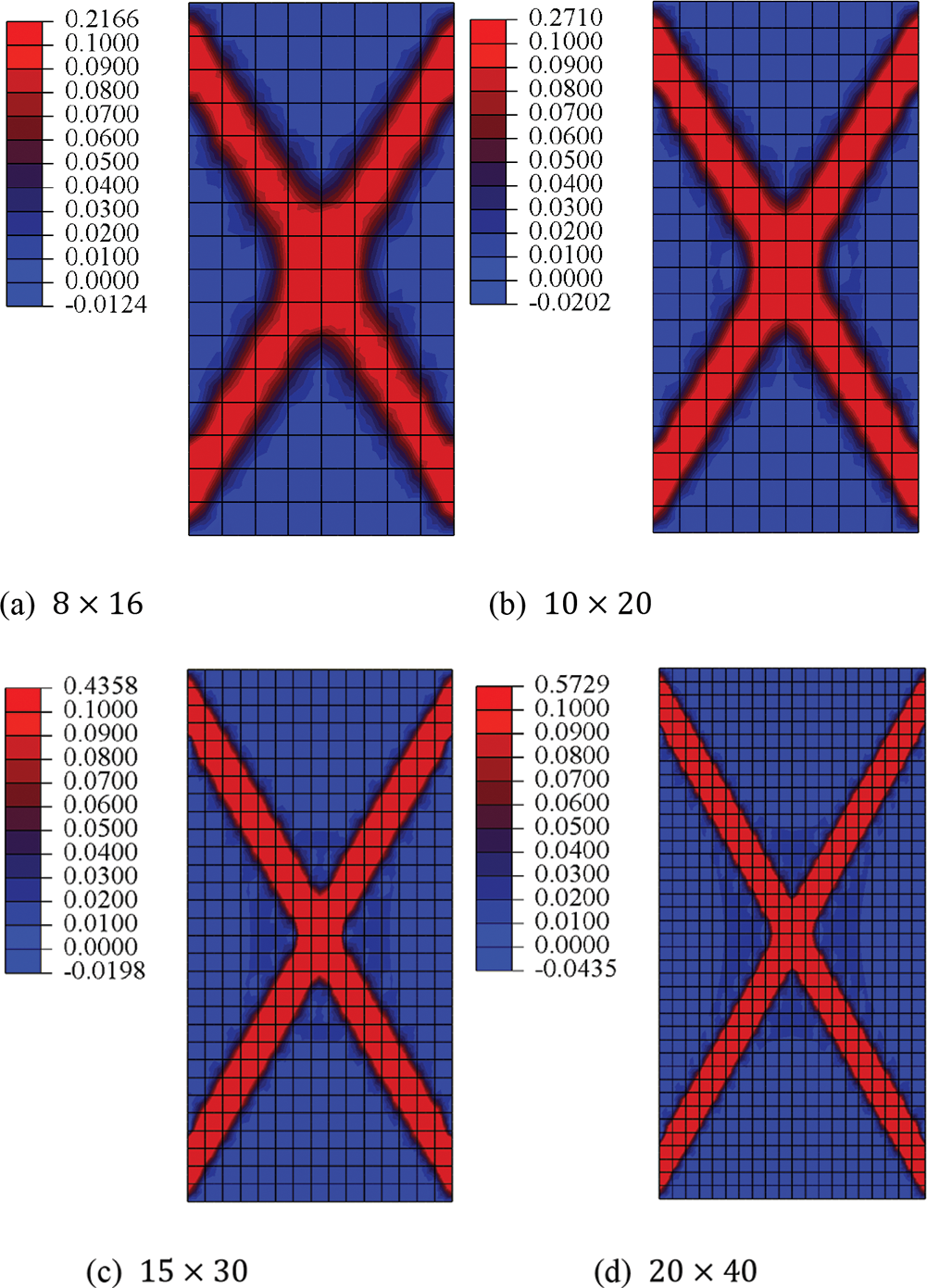
Figure 18: Equivalent plastic strain distributions of GMmedium for situations with meshes 8×16,10×20,15×30and20×40

Therefore, we further investigate the mesh dependence for situations with larger characteristic length lc=20,10×10−3m, and the load-displacement curves and their equivalent plastic strain distributions are respectively shown in Figs. 19 and 20. The load-displacement curve gradually converges to that of the 50×100 mesh with the increase of lc, as shown in Fig. 19b compared with Figs. 17 and 19a. Comparing the equivalent plastic strain distributions, the width of the shear band for the 50×100 mesh when lc=20×10−3m shown in Fig. 20e is about 1.5 times that when lc=10×10−3m. It is noted that the equivalent plastic strain distributions when lc=10×10−3m are not given due to space limitations. And comparing Fig. 20e with Fig. 20a, the width of the shear band for the 50×100 mesh is almost equal to that for the 8×16 mesh. It can indicate that the degree of the mesh dependence gradually decreases with the increase of lc. Therefore, the mesh dependence is closely related to the characteristic length lc, i.e., the larger value of lc can eliminate the mesh dependence in the Cosserat model. As for the situation where lc is larger than 20×10−3m, the strain localization is not obvious as shown in Fig. 15a. Therefore, lc=20×10−3m is an appropriate value to balance between the mesh independence and the strain localization for the simulation by the Cosserat model. And this result is the same as that in our previous study [10], which has proved the mesh independence by the classical Cosserat when lc=20×10−3m.

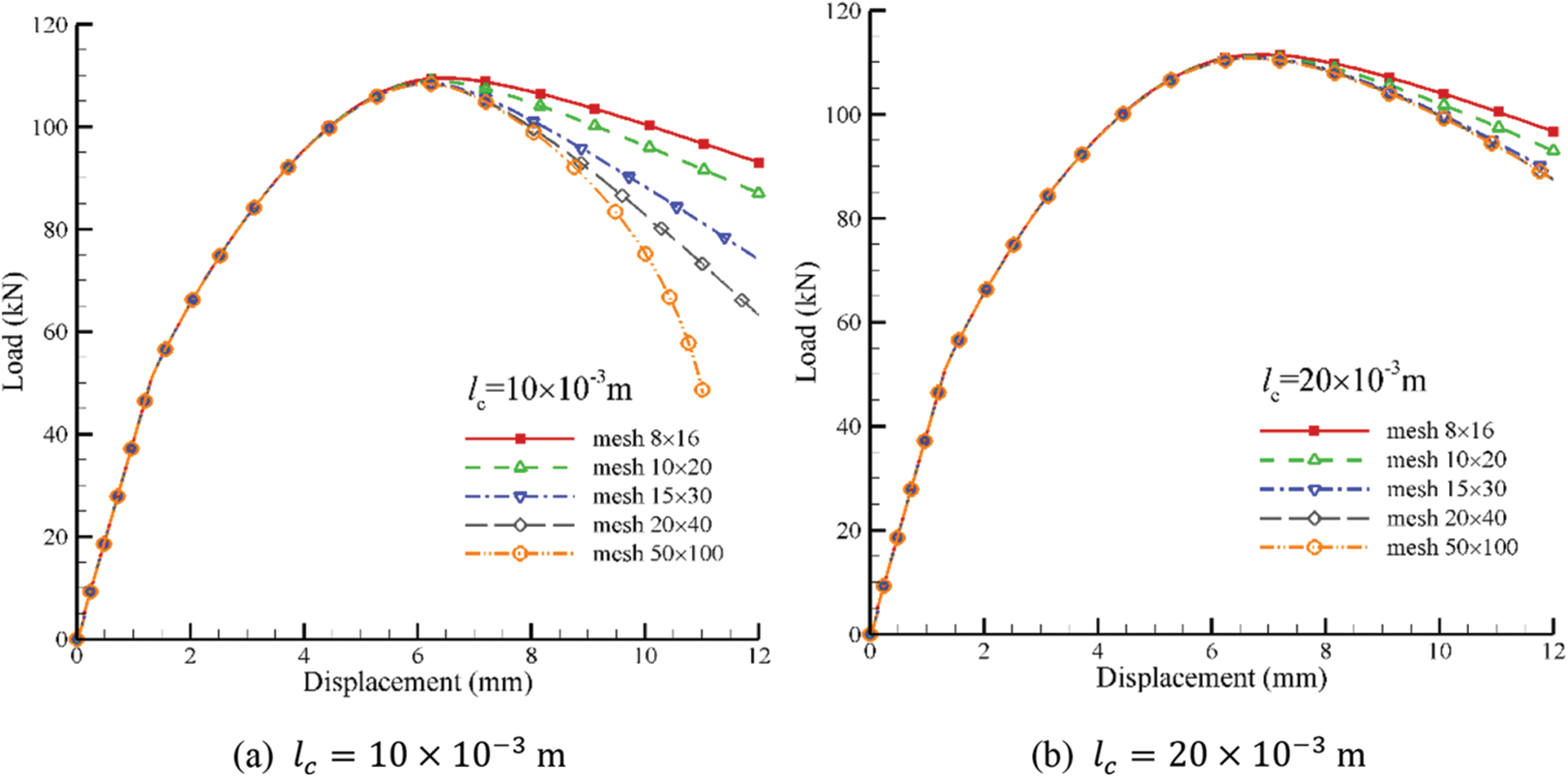
Figure 19: Load-displacement curves of GMmedium for situations with meshes 8×16,10×20,15×30and20×40and50×100whenlc=10,20×10−3m

Figure 20: Equivalent plastic strain distributions of GMmedium for situations with meshes 8×16,10×20,15×30and20×40and50×100whenlc=20×10−3m

It is noted that the non-orthogonal flow behavior [28,29] is also one of the reasons resulting in the mesh dependency problem. And the non-orthogonal flow can usually be obtained by constructing the dilatancy relation or the plastic potential function as presented in this study. Therefore, it is meaningful to reveal the law between the non-orthogonal flow and the mesh dependency. Some studies [28,29] have made significant contributions to the non-orthogonal flow behavior, which provides an important reference value. And our next study will focus on this issue.

5.5 Simulations by the Micromechanics-Based Cosserat Model vs. Discrete Element Model

The micromechanics-based Cosserat model can provide the effects of microscopic information on failures of granular materials, therefore, it is meaningful to compare simulations of failures by this model with those by the discrete element model. In this part, GMmedium is investigated. Then, there is an issue that how to compare results of simulations between FEM and DEM. Usually, in the computational homogenization method for granular materials, the integration point is considered as a representative volume element (RVE) of the particle assembly. In this study, an RVE is considered by a hexagonal close-packed particle assembly as shown in Fig. 21 to represent the average response of four integration points of No. 84 element in the FEM model, and this element is in the shear band. It is found that the 2D hexagonal close-packed particle assembly corresponds to the microstructure of the GMmedium when considering the plane strain problem. Besides, the linear rolling resistance model in DEM is used to consider the effect of particle rotation. And the microscopic parameters in DEM are the same as those in Table 2. However, there are two problems in DEM, which are the size of RVE and its confining pressure, which are not involved in FEM. Therefore, the choice of the size of RVE and its confining pressure is open for DEM. In this study, the size of RVE is 0.03 m × 0.03 m, containing 1050 particles with the radius of 0.5 mm, and the confining pressure is 900 Pa.

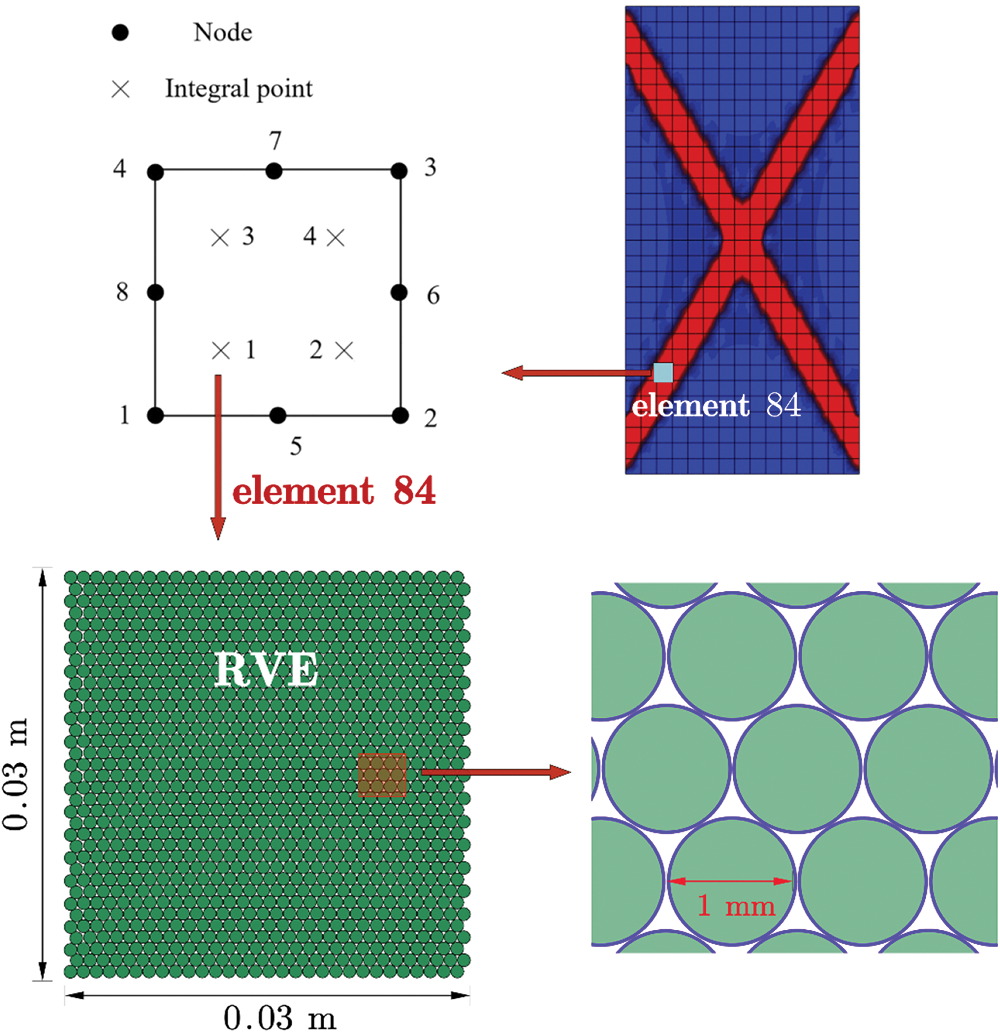
Figure 21: The hexagonal close-packed particle assembly in DEM for RVE

Fig. 22 shows the comparison of stress-strain relationships between No. 84 element in FEM and the RVE in DEM for GMmedium. It shows that the linear elastic stages are in good agreement with each other. However, the plastic stages have quite a difference. The reason for this difference is that a macroscopic Drucker-Prager yield criterion is used in the proposed Cosserat model, and c0 and hp are not associated with microscopic parameters those are used in DEM. Therefore, we can see that the after-peak stage, i.e., the softening stage, decreases continuously in FEM, but a sudden drop is presented in DEM due to the rearrangement of particles in the RVE under load. Then, we further discuss how c0 and hp affect the plastic behavior by FEM and their comparisons with those under different conditions by DEM. Fig. 23 shows the curves for FEM with different c0 and different hp and curves for DEM with different confining pressures. It shows that c0 has a positive correlation with the strength of the FEM simulation, and the confining pressure has a positive correlation with the strength of the DEM simulation, so c0 is related to the confining pressure to some extent. Besides, hp affects the softening behavior of the FEM simulation, which corresponds to the rearrangement of particles in the DEM simulation. Furthermore, we compare the stress-strain relationships of FEM with different c0 to those of DEM with different confining pressures, as shown in Fig. 24. The curve of the stress-strain relationship by FEM with c0=6.4 kPa coincides with that by DEM with 300 Pa confining pressure at the elastic and hardening stages, and the softening stage still has a large difference for these two curves. With the increases of c0 and confining pressure, the difference between FEM and DEM starts to appear at the hardening stage, where the strength by FEM simulation is lower than that by DEM simulation, and the DEM simulation shows a longer-term elastic stage, but the FEM simulation shows a more obvious hardening stage. Therefore, the FEM simulation can more accurately match the DEM one if a smaller c0 corresponds to a smaller confining pressure. In Fig. 23b, hp can increase the degree of softening in FEM simulation. Then, we further increase the value of hp on the basis of that in Fig. 24 to investigate simulations between FEM and DEM, as shown in Fig. 25. hp can help curves by FEM close to those by DEM at the softening stage, but only to a limited extent. It needs more and deeper studies on the relationship between hp and microscopic parameters.

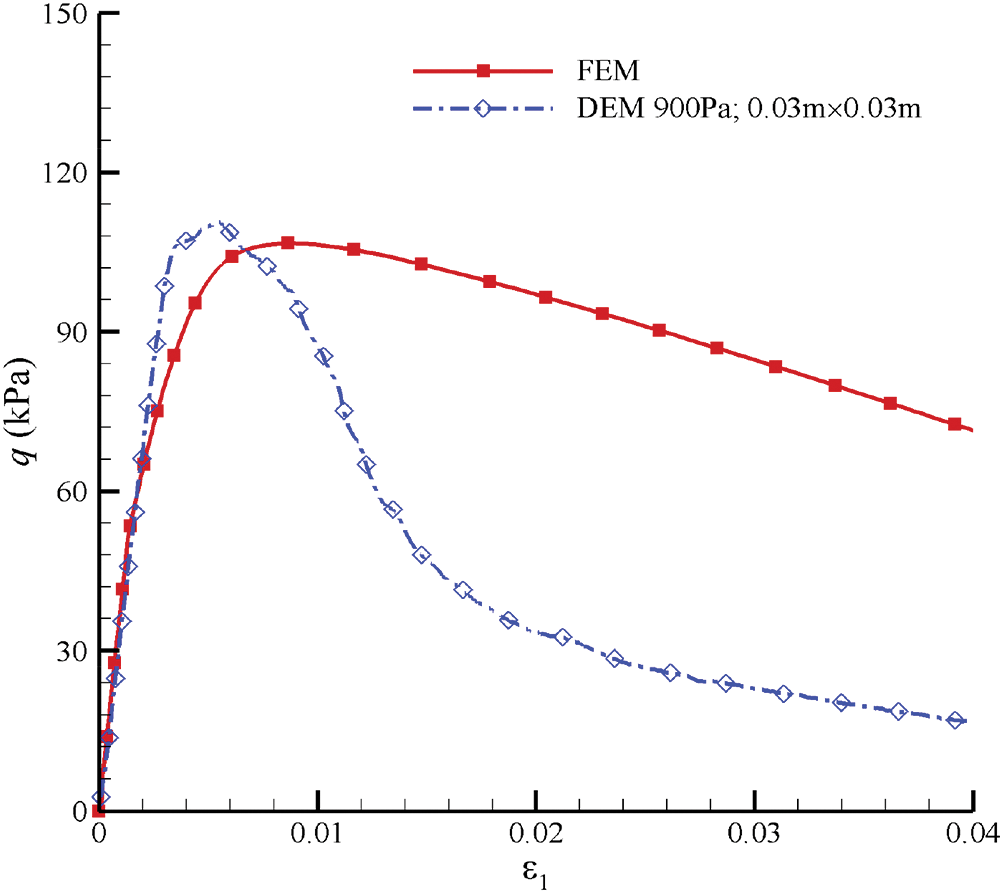
Figure 22: Curves of stress-strain relationships simulated by FEM and DEM for GMmedium

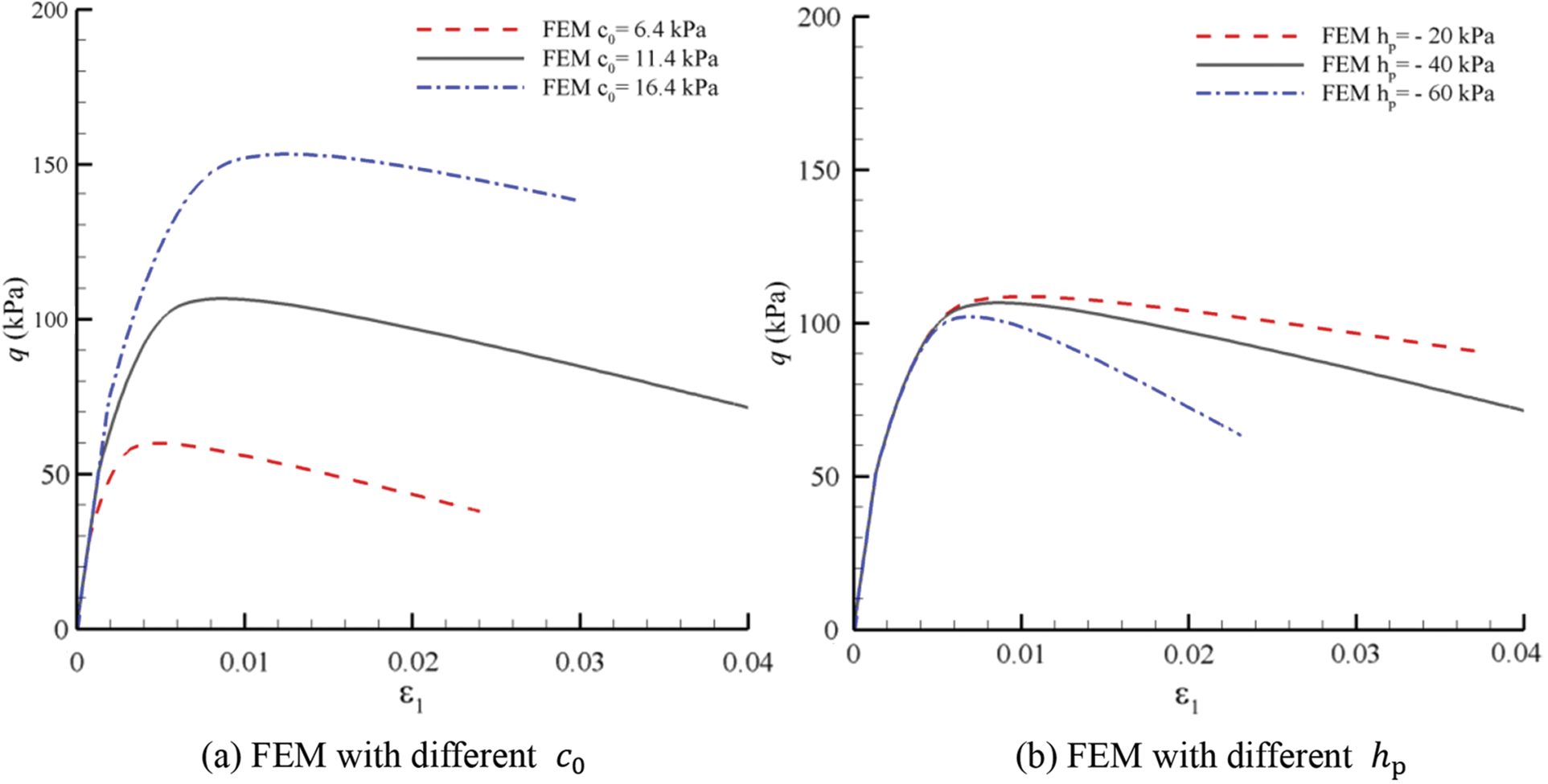
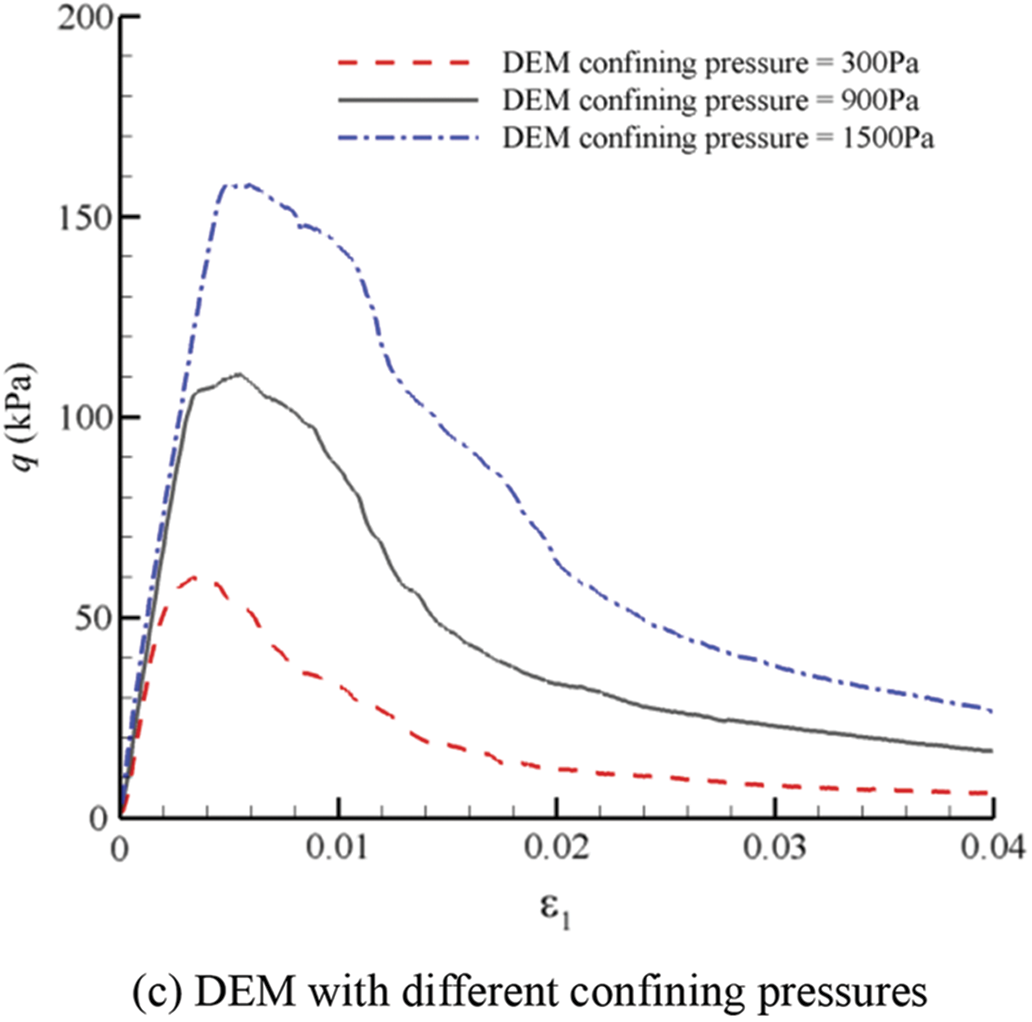
Figure 23: Curves of stress-strain relationships simulated by FEM and DEM with different conditions for GMmedium

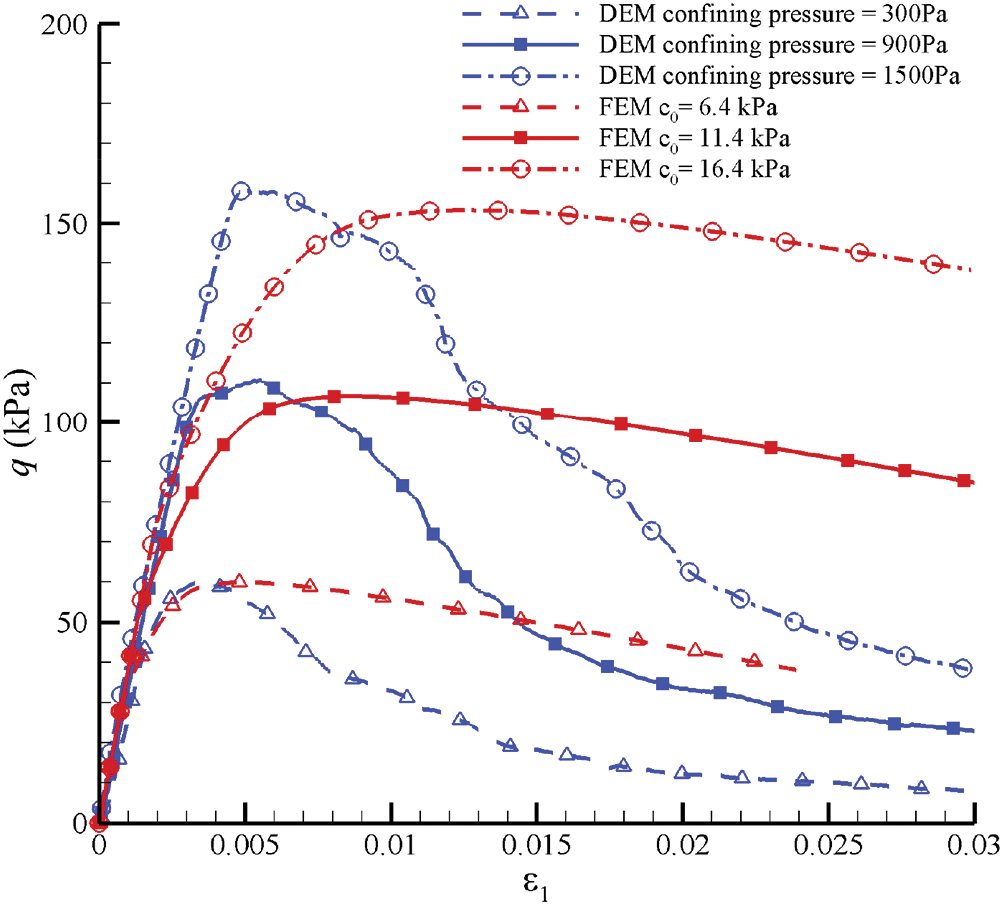
Figure 24: Curves of stress-strain relationships simulated by FEM with different c0 verse DEM with different confining pressures for GMmedium

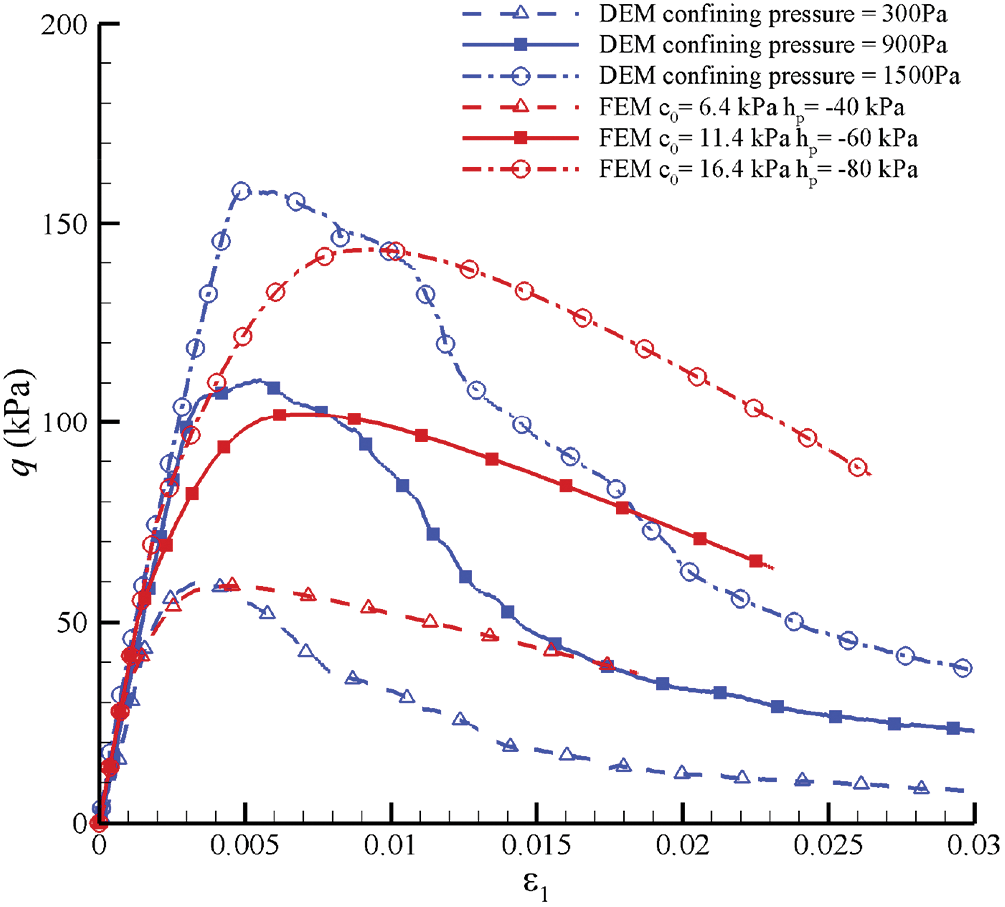
Figure 25: Curves of stress-strain relationships simulated by FEM with different c0 and different hp verse DEM with different confining pressures for GMmedium

As mentioned above, the choice of RVE’s size in DEM is open. Then, we compare the stress-strain relationships simulated by FEM with those simulated by DEM with different sizes of RVEs based on Fig. 22, as shown in Fig. 26. It can overestimate the strength and underestimate the stiffness of DEM simulation with smaller RVE’s size, because it cannot provide sufficient number of particles leading to the loss of representativeness. And it has been proved that the size of RVE must be large enough [2,30]. Meanwhile, the strength by the DEM simulation with 0.05m×0.05m RVE is about 20% lower than that by the DEM simulation with 0.03m×0.03m RVE. It is speculated that a larger RVE may smear out some microstructural information [31]. Therefore, an appropriate size of RVE is important for the DEM simulation to match the FEM one, but the size of RVE and its relationship with macroscopic information are still controversial. This study partially gives the relationships between macroscopic parameters c0 and hp and microscopic ones such as confining pressure and RVE’s size, and we hope to develop a micromechanics-based plastic model to reveal the relationships between macroscopic and microscopic information in the next study.

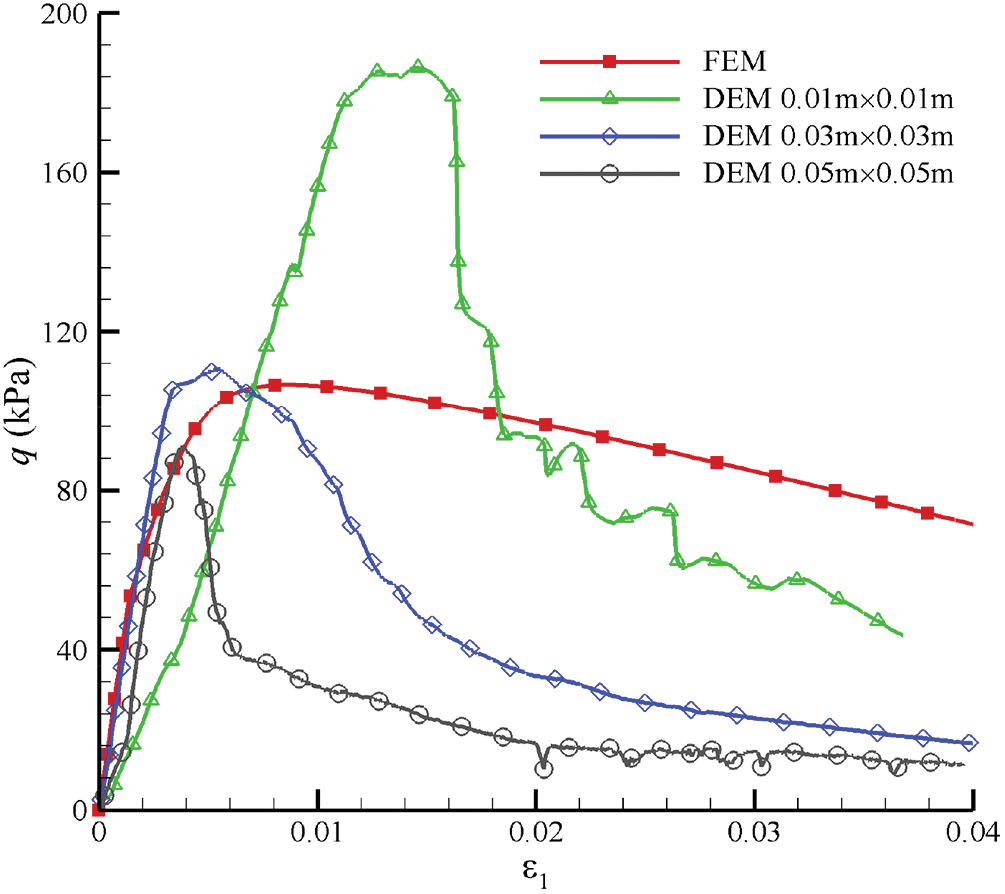
Figure 26: Curves of stress-strain relationships simulated by FEM verse DEM with different sizes of RVEs for GMmedium

To ensure the generality of the macroscopic mechanical responses, the comparative study between DEM and FEM is needed under the same microstructure of granular materials when different microscopic parameters such as the contact stiffness are arranged. Fig. 27 shows the curves of stress-strain relationships simulated by FEM and DEM for GMmedium for situations with Knu=200,100, 50 kN/m and Ktu=0.5×Knu. It is shown that the linear elastic stages can be well consistent between FEM and DEM simulations under the same Knu and Ktu, and it proves the rationality of the micromechanics-based Cosserat model at least for the elastic stage. And the difference between FEM and DEM simulations begins at the hardening stage, where the micromechanics-based yield criterion and plastic potential function need to be further developed to provide more micromechanical information on the plastic response simulated by FEM.

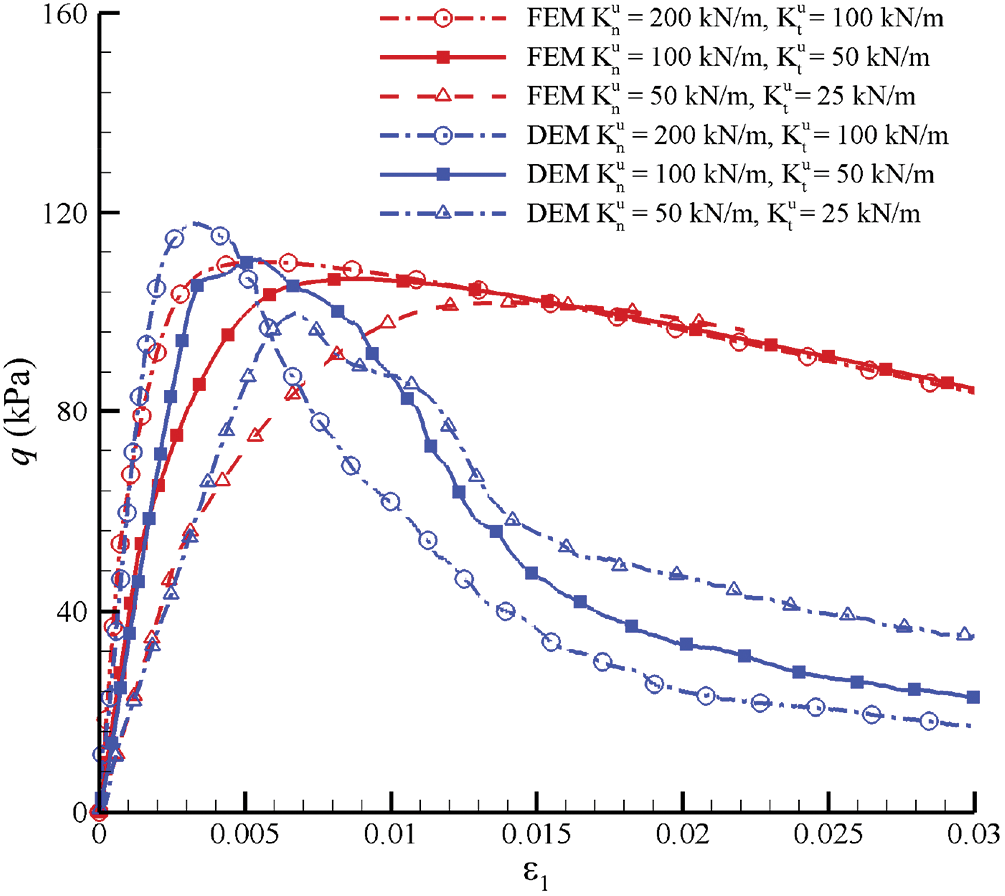
Figure 27: Curves of stress-strain relationships simulated by FEM verse DEM for GMmedium for situations with Knu=200,100, 50 kN/m and Ktu=0.5×Knu

6  Conclusions

The effects of microstructures on failure behaviors in granular materials can be analyzed by the micromechanics-based Cosserat model. First, we consider granular materials with different microstructures consisting of different particle arrangements and sizes, void ratios, and coordination numbers. Using the extended Drucker-Prager yield criterion, a Cosserat elastoplastic model is proposed for granular materials with microstructures, and a user element program coded by the ABAQUS UEL subroutine interface is implemented. Then, the presented model is used to investigate failure behaviors of different granular materials and the main conclusions are given as follows:

(1) Strain localization and softening behaviors are obtained for granular materials respectively with medium dense microstructure (GMmedium), dense microstructure in one-sized particles (GMdense_onesized) and dense microstructure in two-sized particles (GMdense_twosized), which are compared with those for granular materials based on isotropic contact density distribution (GMiso). Similar and greater degrees of strain localization and strain softening for GMdense_onesized and GMdense_twosized, followed by GMmedium, and finally, GMiso.

(2) The contact stiffness parameters related to displacement have obvious positive correlations with degrees of rotation, strain localization, and softening of the GMmedium. The contact stiffness parameters related to rotation have no effect on the elastic and hardening stages, but have an obvious effect on the softening stage of granular materials.

(3) The characteristic length has no effect on the elastic stage. After the elastic stage, the degrees of strain localization and softening are negatively related to the characteristic length when the characteristic length is greater than 10−3m. The simulated mechanical responses can be consistent for situations where the characteristic length is less than 10−3m.

(4) The mesh independence is related to the characteristic length. The mesh dependence is prominent when the characteristic length is below 10−3m. The presented model can gradually overcome the mesh dependence with the increase of the characteristic length. However, the larger characteristic length also weakens the ability to simulate strain localization and softening for the presented model. Therefore, this study proposes a characteristic length of about 20×10−3m for the mesh independence of the micromechanics-based Cosserat model.

(5) The FEM simulations for GMmedium by the micromechanics-based Cosserat model can agree well with the DEM ones in the elastic stage, but the hardening and softening stages show some differences because of the arrangements of particles in DEM due to discreteness, which is absent in FEM. Macroscopic parameters c0 and hp describing plasticity are proved to be partly related to microscopic factors such as confining pressure and RVE’s size.

Acknowledgement: The authors would like to thank Dr. Jiao Wang of Southwest Jiaotong University for suggestions on DEM simulations, and thank the editors and the anonymous referees for helpful guidance.

Funding Statement: The authors are pleased to acknowledge supports of this work by the National Natural Science Foundation of China through Contract/Grant Numbers 12002245, 12172263 and 11772237, and by Chongqing Jiaotong University through Contract/Grant Number F1220038.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Chenxi Xiu, Xihua Chu; data collection: Chenxi Xiu; analysis and interpretation of results: Chenxi Xiu, Xihua Chu; draft manuscript preparation: Chenxi Xiu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data are available from the corresponding author on reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Cambou, B., Chaze, M., Dedecker, F. (2000). Change of scale in granular materials. European Journal of Mechanics-A/Solids, 19(6), 999–1014. [Google Scholar]

2. Zhao, J. D., Guo, N. (2014). Rotational resistance and shear-induced anisotropy in granular media. Acta Mechanica Solida Sinica, 27(1), 1–14. [Google Scholar]

3. Chang, J. F., Chu, X. H., Xu, Y. J. (2017). The role of non-coaxiality in the simulation of strain localization based on classical and Cosserat continua. International Journal for Numerical and Analytical Methods in Geomechanics, 41(3), 382–399. [Google Scholar]

4. Ma, G., Regueiro, R. A., Zhou, W., Liu, J. Y. (2019). Spatiotemporal analysis of strain localization in dense granular materials. Acta Geotechnica, 14, 973–990. [Google Scholar]

5. Wang, J., Chu, X. H., Wang, J. B. (2022). The material deformation and internal structure development of granular materials under different cyclic loadings. Computer Modeling in Engineering & Sciences, 130(2), 653–670. https://doi.org/10.32604/cmes.2022.018207 [Google Scholar] [CrossRef]

6. Torquato, S., Haslach, H. (2002). Random heterogeneous materials: Microstructure and macroscopic properties. Applied Mechanics Reviews, 55(4), B62. [Google Scholar]

7. Xiu, C. X., Chu, X. H. (2020). A micromorphic elastoplastic model and finite element simulation on failure behaviors of granular materials. International Journal for Numerical and Analytical Methods in Geomechanics, 44(4), 484–515. [Google Scholar]

8. Suiker, A. S. J., Metrikine, A. V., de Borst, R. (2001). Comparison of wave propagation characteristics of the cosserat continuum model and corresponding discrete lattice models. International Journal of Solids and Structures, 38(9), 1563–1583. [Google Scholar]

9. Maugin, G. A., Metrikine, A. V. (2010). Mechanics of generalized continua: One hundred years after the Cosserats. New York, NY: Springer Science. [Google Scholar]

10. Chang, J. F., Chu, X. H., Xu, Y. J. (2014). Finite-element analysis of failure in transversely isotropic geomaterials. International Journal of Geomechanics, 15(6), 04014096. [Google Scholar]

11. Merkel, A., Luding, S. (2017). Enhanced micropolar model for wave propagation in ordered granular materials. International Journal of Solids and Structures, 106–107, 91–105. [Google Scholar]

12. Tordesillas, A., Muthuswamy, M., Walsh, S. D. C. (2008). Mesoscale measures of nonaffine deformation in dense granular assemblies. Journal of Engineering Mechanics, 134(12), 1095–1113. [Google Scholar]

13. Chang, C. S., Ma, L. (1990). Modeling of discrete granulates as micropolar continua. Journal of Engineering Mechanics, 116(12), 2703–2721. [Google Scholar]

14. Chang, C. S., Ma, L. (1992). Elastic material constants for isotropic granular solids with particle rotation. International Journal of Solids and Structures, 29(8), 1001–1018. [Google Scholar]

15. Chang, C. S., Shi, Q. S., Liao, C. L. (2003). Elastic constants for granular materials modeled as first-order strain-gradient continua. International Journal of Solids and Structures, 40(21), 5565–5582. [Google Scholar]

16. Walsh, S. D. C., Tordesillas, A. (2004). A thermomechanical approach to the development of micropolar constitutive models of granular media. Acta Mechanica, 167, 145–169. [Google Scholar]

17. Hicher, P. Y., Chang, C. S. (2006). Anisotropic nonlinear elastic model for particulate materials. Journal of Geotechnical and Geoenvironmental Engineering, 132(8), 1052–1061. [Google Scholar]

18. Xiu, C. X., Chu, X. H., Wang, J., Wu, W. P., Duan, Q. L. (2020). A Micromechanics-based micromorphic model for granular materials and prediction on dispersion behaviors. Granular Matter, 22, 74. [Google Scholar]

19. Chang, C. S., Misra, A. (1989). Theoretical and experimental study of regular packings of granules. Journal of Engineering Mechanics, 115(4), 704–720. [Google Scholar]

20. Chang, C. S., Wang, T. K., Sluys, L. J., van Mier, J. G. M. (2002). Fracture modeling using a micro-structural mechanics approach-I. Theory and formulation. Engineering Fracture Mechanics, 69(17), 1941–1958. [Google Scholar]

21. Chang, C. S., Wang, T. K., Sluys, L. J., van Mier, J. G. M. (2002). Fracture modeling using a micro-structural mechanics approach-II. Finite element analysis. Engineering Fracture Mechanics, 69(17), 1959–1976. [Google Scholar]

22. Li, X. K., Du, Y. Y., Duan, Q. L. (2013). Micromechanically informed constitutive model and anisotropic damage characterization of Cosserat continuum for granular materials. International Journal of Damage Mechanics, 22(5), 643–682. [Google Scholar]

23. Zhou, Z. H., Wang, H. N., Jiang, M. J. (2021). Elastic constants obtained analytically from microscopic features for regularly arranged elliptical particle assembly. Granular Matter, 23, 29. [Google Scholar]

24. Xiu, C. X., Chu, X. H., Wang, J. (2021). The micromorphic constitutive parameters and dispersion behaviors in different granular crystals. Powder Technology, 392, 325–343. [Google Scholar]

25. Xiu, C. X., Chu, X. H. (2022). Study on dispersion and wave velocity in 2D elliptic granular crystals by a micromechanics-based micromorphic model. Advances in Mechanical Engineering, 14(8), 1–20. [Google Scholar]

26. de Borst, R., Sluys, L. J. (1991). Localisation in a Cosserat continuum under static and dynamic loading conditions. Computer Methods in Applied Mechanics and Engineering, 90(1–3), 805–827. [Google Scholar]

27. Forest, S., Sievert, R. (2003). Elastoviscoplastic constitutive frameworks for generalized continua. Acta Mechanica, 160(1–2), 71–111. [Google Scholar]

28. Lu, D. C., Liang, J. Y., Du, X. L., Ma, C., Gao, Z. W. (2019). Fractional elastoplastic constitutive model for soils based on a novel 3D fractional plastic flow rule. Computers and Geotechnics, 105(209), 277–290. [Google Scholar]

29. Zhou, X., Lu, D. C., Du, X. L., Wang, G. S., Meng, F. P. (2019). A 3D non-orthogonal plastic damage model for concrete. Computer Methods in Applied Mechanics and Engineering, 360(3), 112716. [Google Scholar]

30. Li, X. K., Liu, Q. P., Zhang, J. B. (2010). A Micro-macro homogenization approach for discrete particle assembly-Cosserat continuum modeling of granular materials. International Journal of Solids and Structures, 47(2), 291–303. [Google Scholar]

31. Tordesillas, A., Walsh, S. D. C. (2002). Incorporating rolling resistance and contact anisotropy in micromechanical models of granular media. Powder Technology, 124(1–2), 106–111. [Google Scholar]

32. Lu, D. C., Zhang, Y. N., Zhou, X., Su, C. C., Gao, Z. W. et al. (2023). A robust stress update algorithm for elastoplastic models without analytical derivation of the consistent tangent operator and loading/unloading estimation. International Journal for Numerical and Analytical Methods in Geomechanics, 47(6), 1022–1050. [Google Scholar]

33. de Borst, R. (1993). A generalisation of J2-flow theory for polar continua. Computer Methods in Applied Mechanics and Engineering, 103(3), 347–362. [Google Scholar]

34. Li, X. K., Tang, H. X. (2005). A consistent return mapping algorithm for pressure-dependent elastoplastic Cosserat continua and modelling of strain localisation. Computers and Structures, 83(1), 1–10. [Google Scholar]

35. Chang, J. F., Li, S. F., Wang, W., Niu, Q. H. (2022). A study of non-coaxial effects on strain localization via micropolar plasticity model. Acta Geotechnica, 17, 721–739. [Google Scholar]

Appendix

A.1 Implementation of finite element method for the micromechanics-based Cosserat model in a plane strain problem

For a plane strain problem, the displacement vector in the Cosserat continuum is given by

u=(u1u2ω3)T(A1)

According to the displacement fields, the strain vector is written by

ε=(ε1ε2ε3ε12ε21κ31lcκ32lc)T(A2)

The relation between displacement components and strain components are rewritten in a matrix form by

ε=Lu(A3)

in which L is a differential operator matrix written by

L=[∂∂x1000∂∂x200000∂∂x1−1∂∂x20100lc∂∂x100lc∂∂x2](A4)

The stress vector is given by

σ=(σ1σ2σ3σ12σ21m31/lcm32/lc)T(A5)

Then, the constitutive equation is obtained by

σ=Ce(ε−εp)(A6)

where the subscript p represents plasticity, and Ce is the elastic constitutive modulus matrix written by

Ce=[C1111C1122C113300C2211C2222C223300C3311C3322C333300000D3131/lc200000D3232/lc2](A7)

The matrix form of the equilibrium equation is as follows:

LTσ+f=0(A8)

For a plane strain problem, we consider an eight-node iso-parametric element with four integration points (CPER8), and the node displacement of the element is written by

aie=(u1eu2eω3e)T(A9)

in which the superscript e represents the element. The displacement after interpolation is written by

u=Nae(A10)

where N is a 3×24 matrix expressed as the following partitioned matrix:

N3×24=[N1N2N3N4N5N6N7N8](A11)

Ni=INi,i=1∼8(A12)

where Ni is a 3×3 matrix, I is a 3×3 identity matrix, and Ni is the shape function.

When the element displacement is obtained after interpolation of node displacement, the strain vector can be obtained as follows:

ε=Lu=LNae=Bae(A13)

where B is a 7×24 strain matrix expressed as the following partitioned matrix:

B7×24=[B1B2B3B4B5B6B7B8](A14)

And the partitioned matrix Bi (i=1∼8) is a 7×3 matrix expressed as

Bi=LNi(A15)

Then, the element stress can be obtained by the constitutive equation:

σ=Ce(ε−εp)=Cepε=CepBae=Sae(A16)

where Cep is the elastoplastic modulus matrix, and S is the stress matrix expressed as the following partitioned matrix:

S7×24=[S1S2S3S4S5S6S7S8](A17)

And the partitioned matrix Si (i=1∼8) is written by

Si=CepBi(A18)

Based on the principle of virtual work, the matrix form of the incremental total potential energy for an element is obained by

δΔΠ=∫VδεTσdV−∫VδuTfdV−∫SδuTtdS=0(A19)

where f and t are respectively matrices of body force and surface traction. Thus, the FEM equation is built for an element as

Keae=Pe(A20)

where the element stiffness matrix Ke and equivalent load matrix Pe can be written by

Ke=∫VBTCepBdV,Pe=∫VNTfdV+∫SNTtdS(A21)

Finally, the FEM equation for a whole structure can be derived by Ka=P, and the process is omitted.

A.2 Stress update and consistent elastoplastic tangent modulus matrix

For a rate-independent elastoplastic constitutive model, the mathematical equations describing the stress-strain relationship are generally defined by a set of ordinary differential equations with constraints as follows:

σ˙=Ce:ε˙e=Ce:(ε˙−ε˙p)

ε˙p=λ˙gσ

q˙=λ˙h

f˙=fσ:σ˙+fq:q˙=0

λ˙≥0, f≤0, λ˙f≤0(A22)

where λ is the plastic multiplier, gσ is the plastic flow direction, q is the internal variable, is h the plastic modulus, fσ and fq are respectively derivatives of yield function with respect to stress and internal variable.

An important step in the secondary development of UEL in ABAQUS is to update the stress, also known as constitutive iteration, and then perform equilibrium iteration to achieve the purpose of numerical calculation. Scholars are engaged in the development of stress integration algorithms. For instance, Lu et al. [32] presented a robust and concise implicit stress integration algorithm of elastoplastic models without loading/unloading estimation and analytical derivation operation for the stress update, which improves the computational efficiency. Studies [10,33–35] have introduced the extended Drucker-Prager yield into the Cosserat model, and developed a consistent return mapping algorithm, where the stress update and the corresponding consistent elastoplastic tangent modulus matrix are obtained. The detailed operational process is omitted here. The final formulas of the stress update and the consistent elastoplastic tangent modulus matrix are presented as follows:

The updated stress is

σ=CαsE+(pE−KAΔλ)m(A23)

where

sE=σE−pEm

pE=13(σ1E+σ2E+σ3E)

m=(1110000 )T

Cα=(I+GΔλσ¯M)−1

M=[M100M2]

M1=[3000003000003000003/23/20003/23/2],M2=[3003]

Δλ={0 if fE≤0fEξ  if fE>0

fE=σ¯E+AϕpE+Bϕ

ξ=(G+KAψAϕ)+6hpcos⁡ϕ3+sin⁡ϕ(A24)

Here, the superscript E represents the elastic trial variables. K and G are bulk modulus and shear modulus, which can be identified by microscopic parameters.

The consistent elastoplastic tangent modulus matrix is presented here.

Cep=[Cα+G(αΔλσ¯−1ξ)Pσ(Pσ)T18σ¯2]CdP∗+( K−KAψAϕKξ)mmT−K3σ¯ξ[GAϕPσmT+Aψ2(Pσ)TCdP∗](A25)

where

P=[P100P2]

P1=[2−1−100−12−100−1−12000003000003],P2=[3003]

P∗=13P

C d = Ce − C m · (Ce shown in A7)

Cijm=K−23G, i,j=1,3; Cijm=0, i,j=4,7

α=σ¯E−GΔλσ¯E(A26)