An Evidence-Based CoCoSo Framework with Double Hierarchy Linguistic Data for Viable Selection of Hydrogen Storage Methods

1  Introduction

Developing countries like India have a high energy demand, and to strike a balance between demand and sustainability, countries globally focus on clean and sustainable energy [1]. Hydrogen is one such clean energy source that can effectively balance the demand and sustainability aspects of the nation. India made an ambitious commitment concerning mitigating carbon trace and presented an updated resolution in the nationally determined contribution (NDC) to reduce emissions by 45% within 2030 (www.bbc.com dated: 13.12.2022). India pledged to adopt 50% of non-fossil fuels for energy generation by 2030. In this line of thought, hydrogen is seen as a potential alternative for energy production.

A recent report from economic-times (www.economictimes.com dated: 13.12.2022) claimed that India is planning a massive move to green hydrogen production to reduce its dependence on fossil fuels and promote green and sustainable habits nationwide. By 2047, New Delhi (India) is estimated to produce 26 million tonnes of hydrogen capacity annually. Besides, in 2020, India launched an initiative called the National Hydrogen Mission that focuses on generating energy via hydrogen to meet the growing demand and maintain sustainability across the nation. Also, the mission aims to make India the world’s largest hydrogen hub. Accompanied by the initiative, there is also the focus on active storage of produced hydrogen to effectively meet present and future demand by supporting the economy and ecosystem.

Recently, researchers have concentrated on energy storage to meet the demand of people. Energy storage is the procedure for obtaining and preserving energy in various forms for future purposes. It is crucial because it improves energy security and helps to tame renewable energy sources’ fluctuations. A more dependable and sustainable energy system is created by enabling the integration of distributed energy resources and lowering peak demand. Considerable research is being conducted to identify more efficient means of storing renewable energy, such as solar, wind, and geothermal energy, despite the availability of various renewable energy storage methods. Naveenkumar et al. [2] highlighted the potential of phase change materials (PCMs) in various solar energy storage methods and applications due to the sporadic nature of solar radiation. Watil et al. [3] proposed a battery charge controller and energy management algorithm for a standalone wind energy conversion system, which dynamically adapts to available wind power, battery state, and DC load demand to improve the system’s efficiency and extend the battery life. Liu et al. [4] proposed an integrated framework for subsurface geothermal energy storage and carbon dioxide (CO2) sequestration and utilization, where CO2 is injected into geothermal layers for energy accumulation and then introduced into a target oil reservoir for CO2 utilization and geothermal energy storage, showing potential for large-scale geothermal energy storage and carbon neutrality.

Researchers have developed novel approaches for hydrogen storage, such as material-based storage, cryogenic tank-based storage, cylinder-based storage, chemical bond-based storage, oxidation-based storage, and so on [5]. It can be observed that these methods have trade-offs among criteria, and as a result, the selection of a viable hydrogen storage method (HSM) is crucial and complex. Researchers adopted multi-criteria decision-making (MCDM) models to support the remedy for the issue. Here, we review relevant and recent literature on HSM evaluation using decision models. Hydrogen is an interesting form of energy that can satisfy countries’ demands and promote sustainability and green practices globally. It is a clean form of energy with minimum emission of greenhouse gases and reduced harm to the ecosystem. With this view, hydrogen storage is essential for better usage and distribution. Some authors reviewed different hydrogen storage methods and concluded a promising future for hydrogen as a clean energy based on their well-planned storage. Niaz et al. [6] reviewed various hydrogen-producing and storing methods for creating a hydrogen economy, highlighting the latest advancements in hydrogen-storing materials and technologies and their classification based on storage mechanisms, advantages, and disadvantages. Pang et al. [7] discussed the importance of analyzing hydrogenation and dehydrogenation behaviors using kinetic models to understand the kinetic mechanism for hydrogen storage materials, highlighting the challenges and presenting a summary of existing models and analysis methods, introducing some recently proposed ones. Usman [8] reviewed hydrogen storage strategies and recent developments in the field, highlighting the challenges presented by hydrogen’s lightweight and gaseous nature and the advantages and disadvantages of various physical and chemical storage techniques.

From these reviews, it is clear that there is a high scope for hydrogen shortly, and countries are working on strategies and mechanisms to store hydrogen in a feasible way to serve the needs better. Owing to the diversity in the criteria/factors associated with hydrogen storage and multiple options for storing hydrogen, researchers view the problem as an MCDM problem. In this line, some extant models for selecting a suitable hydrogen storage method are presented here. Wu et al. [9] determined the performance of hydrogen storage projects from the sustainability aspect by considering interval-type 2 AHP and TOPSIS (“technique for order preference by similarity to ideal solution”) methods. Wu et al. [10] developed an intuitionistic fuzzy-based model for evaluating the investment in projects concerning photovoltaic coupled hydrogen storage by adopting mixed approaches. Yi et al. [11] adopted a cloud-based hesitant fuzzy linguistic model for determining suitable storage methods for hydrogen. Çolak et al. [12] extended the VIKOR (“VIsekriterijumska Optimizcija I Kompromisno Resenje”) method under a hesitant fuzzy context for grading storage methods for hydrogen. Karatas [13] developed an axiomatic design-based fuzzy decision model with AHP for selecting rational hydrogen storage methods. Pamucar et al. [14] extended the MAIRCA (“multi-attribute ideal real comparative analysis”) approach to neutrosophic numbers for ranking methods for hydrogen storage. Recently, Guo et al. [15] adopted fuzzy and linguistic versions for data collection along with entropy, DEMATEL (“decision-making trial and evaluation laboratory”), and PROMETHEE (“preference ranking organization method for enrichment evaluation”) approaches for evaluating the investment in hydrogen storage projects coupled with wind-photovoltaic contexts. Dhumras et al. [16] extended TOPSIS and VIKOR methods under bi-parametric picture fuzzy numbers for ranking hydrogen fuel cell schemes.

From the review provided above, there is an urge to use MCDM approaches to assess HSMs, and there is scope for proposing novel MCDM models to select methods for the storage of hydrogen appropriately. Researchers have focused on site selection for storage with MCDM [17–19], but selecting suitable methods/technology for hydrogen storage with MCDM needs exploration. This claim motivates the authors to propose a novel integrated model in the present study. Extant models put forward by researchers, indicate the following research gaps such as (i) experts cannot flexibly provide her/his opinions in the natural language form but are directed to follow pre-defined qualitative scales; (ii) experts’ reliability values are not calculated methodically, causing inaccuracies and biases in the decision process; (iii) hesitation, interrelationship of experts and variability in the distribution of preferences are not effectively captured during experts/criteria weight assessment, and (iv) ranking based on different compromise solution driven operations is not adequately explored in the extant HSM selection models.

To resolve these gaps, authors gain motivations, and some contributions are presented:

•   “Double hierarchy hesitant fuzzy linguistic term set (DHHFLTS)” is considered for rating so that experts can effectively provide her/his views in natural language form, which could be modeled as complex linguistic expressions by using the two hierarchies. The second hierarchy is the concrete supplement of the first hierarchy.

•   Criteria importance through inter-criteria correlation (CRITIC) scheme is put forward with DHHFLTS for calculating experts’ weights methodically, which would not only reduce subjectivity and biases but also capture the hesitation of experts.

•   The weighted evidence-based Bayesian method (EBM) is put forward under DHHFLTS for criteria weight calculation, which can effectively consider the hesitation of experts during choice elicitation along with variability within the distribution of preferences.

•   The three-stage rank algorithm is developed to effectively rank HSMs from different compromise strategies and comprehensively determine order based on analyzing the criteria weight component.

DHHFLTS is a powerful linguistic model that can not only express preferences flexibly but also provide ease to experts for expressing ratings in the natural form modeled as complex linguistic expressions by adopting the double hierarchy structure. Notably, the model offers maximum possible linguistic combinations (PLC) compared to other linguistic models such as the probabilistic linguistic model, 2-tuple linguistic models, hesitant fuzzy linguistic models, etc. Suppose the cardinality of the first hierarchy is q and the cardinality of the second hierarchy is r; then the PLC of DHHFLTS is q.r, which is not the case with other linguistic forms [20]. To better understand the structure of DHHFLTS, terms such as ‘not so bad’ and ‘slightly big’ cannot be modeled by earlier linguistic models. DHHFLTS offers flexibility to experts to model such natural expressions [21]. The main advantages of DHHLFTS that motivated authors to use the structure in this study are: (i) it can model natural expressions effectively; (ii) provide maximum PLC compared to other linguistic models, which could give experts ease of expression of views and choices; and (iii) allow more than one instance to capture hesitation of experts during the preference articulation process.

The rest of the article is organized as Section 2, which describes the literature studies related to DHHFLTS, CRITIC, EBM, and CoCoSo; Section 3 provides the core implementation part with a methodical description, a case example is explained in Section 4, followed by a comparative study in Section 5 and concluding remarks with future directions in Section 6.

2  Literature Review

2.1 DHHFLTS-Based MCDM Models

Rodriguez et al. [22] put forward a variant of the linguistic term set (LTS) by introducing hesitancy, which attracted many researchers to use the set for MCDM [23]. Handling complex expression was an issue, which was circumvented by Gou et al. [21] with DHHFLTS, which had two hierarchies where the second hierarchy concretely complemented the first hierarchy and attracted by the set; researchers used it for the decision process [24]. The review reveals that DHHFLTS has a wide scope from both the theoretical and application point of view. This section extends the review and briefly describes DHHLFTS models for MCDM.

Researchers have focused on aggregation operators, information measures, ranking methods, and variants of DHHFLTS for promoting the decision process. Ranking methods such as VIKOR (“Viekriterijumsko kompromisno rangiranje”) [25] and TODIM (“Interactive multi-criteria decision-making”) [26] are put forward for rational selection of an option from the set of options. Theoretical aspects such as quality function deployment [27], weighted distance measure [28], entropy measures [29], evidence measure [30], and similarity measure [31] are presented under the DHHFLTS context for setting a concrete foundation of the set for efficient applicability. Aggregation operators such as the Hamacher operator [32], hybrid operator [20], and generalized power operator [33] are proposed for rational aggregation of double hierarchy information.

Some variants of DHHFLTS are free DHHFLTS [34], probabilistic DHHFLTS [35], and interval-valued DHHFLTS [36]. Applications such as green supplier selection [37], warhead power grading [38], risk assessment [39], zero-carbon measure [40], medicine evaluation [41], sustainable supplier selection [42], and passenger evaluation [43] are explored with DHHFLTS based frameworks.

From the review above, it is clear that DHHFLTS is a flexible structure that can model natural terms as complex linguistic expressions and use two hierarchies to model. The second hierarchy is the concrete complement of the primary. Besides, flexibility is gained through possible linguistic combination, which accounts for the a×b factor, where the cardinality of the primary hierarchy is, and b is the cardinality of the second hierarchy. It is also noted that different MCDM problems adopt DHHFLTS for arriving at rational decision-making.

2.2 CRITIC, Evidence, and CoCoSo Methods

Diakoulaki et al. [44] introduced CRITIC (CRiteria Importance Through Intercriteria Correlation), a method for determining objective weights of relative importance in multi-criteria decision-making (MCDM) problems. CRITIC incorporates contrast intensity and conflict in the decision problem structure by analytically investigating the evaluation matrix to extract all relevant information from the evaluation criteria.

Voorbraak [45] discussed the computational complexity of Dempster-Shafer’s theory for handling uncertainty in expert systems and proposed the Evidence-based method. (EBM), It is a Bayesian approximation of belief functions that is computationally less involved than combining belief functions, making it a practical alternative in many applications.

The CoCoSo method, developed by Yazdani et al. [46], aims to provide a compromise solution to rank alternatives based on three levels of compromise space: sum, minimum, and maximum. This method aggregates weights of compared alternatives using the multiplication rule and weighted power of distance methods, calculates a ranking index based on the three measures, and provides the final ranking of alternatives.

Predominant authors have utilized the CRITIC, Evidence, and CoCoSo methods in recent times. Table 1 summarizes a few works which have been published using this method.

3  Methodology

The proposed integrated framework considers DHHFLTS as preference information used for modeling complex linguistic expressions to consider rating from experts in the natural language form flexibly. Experts provide her/his rating on HSMs based on the criteria. Also, experts rate the criteria used for determining the weights of criteria. Decision matrices from experts are used to calculate their relative importance by applying the procedure outlined in Section 3.2. This section also guides the formation of a criteria weight vector, which incorporates both the preference vector from experts on each criterion and the experts’ weight vector. Finally, the decision matrices from experts, along with the criteria weight vector and experts’ weight vector, are fed as input to Section 3.3 for determining the rank values of HSMs and ordering of HSMs.

CRITIC approach is extended to determine the weights of experts; a weighted evidence measure is put forward to determine the weights of criteria, and a CoCoSo-based ranking algorithm is developed for determining the rank ordering of HSMs. The stepwise procedure for these approaches is given below for clarity to readers.

3.1 Preliminaries

We provide some basics of linguistic sets for MCDM.

Definition 1 [67]: FT={sy|y=0,1,…,g} is an LTS with g+1 as the cardinality and s0 and sg are the initial and final elements. Some postulates are,

•   If d>f, then sd>sf

•   Negation of sf=sd if d+f=g.

Definition 2 [17]: FT is an LTS. Now, HFLTS is a continuous finite subset from FT that is given by,

TY={f,h(f)|f∈F}(1)

where h(f) denotes continuous terms from FT, and h(f)={syv|v=1,2,…,#h(f),y=0,1,…,g} and #h(f) is the instance number.

Definition 3 [22]: FT is an LTS. P={pxv|x=0,1,2,…,h} is another LTS. Now DHHFLTS is given by,

DT={sy<pxv>v|v=1,2,…,#dt,y=0,1,…,g,x=0,1,2,…,h}(2)

where #dt is the instance number of double hierarchy element, y, and x are the primary and secondary hierarchy subscripts.

Note 1: A special case of DHHFLTS is called the double hierarchy linguistic term set, which has one instance or, in other words, v=1.

Note 2: Let dti={sy<pxv>v|v=1,2,…,#dt,y=0,1,…,g,x=0,1,2,…,h} is called the double hierarchy hesitant fuzzy linguistic element (DHHFLE), and their collection forms the DHHFLTS. The two hierarchies are adapted from [68].

Definition 4 [22]: Two DHHFLEs are dt1 and dt2 as before. Some arithmetic operations are provided as,

dt1⨂dt2=R−1(∪γ1∈R(dt1),γ2∈R(dt2)(γ1γ2))(3)

dt1⨁dt2=R−1(∪γ1∈R(dt1),γ2∈R(dt2)(γ1+γ2−γ1γ2))(4)

τdt1=R−1(∪γ1∈R(dt1)1−(1−γ1)λ)λ≥0(5)

dt1τ=R−1(∪γ1∈R(dt1)(γ1)λ)λ≥0(6)

where R and R−1 are functions from [22].

Multiplication, addition, scalar multiplication, and power operation of DHHFLEs are shown in Eqs. (3)–(6).

Here, R(z)=x+2g4g and R−1(z)=(2z−1).(2g) is used to perform arithmetic operations in Definition 4.

3.2 Weight Calculation

Determination of weights methodically is highly substantial for rational decision-making. In general, weight is an essential component in the decision process that influences MCDM owing to the diverse nature and trade-offs among entities. Experts and criteria pose a certain level of importance represented in the decision process through weights. Also, from MCDM, it is clear that experts and criteria are crucial components, and determining their weights is crucial. Works from Kao [69] and Koksalmis et al. [70] clarified the urge for methodical determination of weights, and they claim that direct assignment of weights causes inaccuracies and biases, which affect the decision process.

Commonly, researchers determine weights through partially known information or fully unknown information. In the former context, certain information about the weights of entities must be known apriori [71], which in practical cases poses an overhead. Latter context does not require such overhead, but weights are determined from the preference set. Popular approaches in the latter context are entropy measures [72], analytical hierarchy process [73], weighted ratio analysis [74], and alike.

Step 1: Prepare q decision matrices of a×b order with an HSM rated based on b criteria by q experts.

Step 2: Determine the score measure of DHHFLEs by applying Eq. (7). q matrices of a×b are formed.

Aijl=∑v=1#dt(yijv.  xiv)(7)

where Aijl is the score value associated with HSM I based on criteria j for the data from expert l.

Step 3: Interrelationship among criteria are calculated by using Eq. (8), and intuitively, the hesitation of experts are captured.

ρuvl=∑j=1b((Aijl−Ajl¯)u.(Aijl−Ajl¯)v)(∑j=1b((Aijl−Ajl¯)u)2),(∑j=1b((Aijl−Ajl¯)v)2)(8)

where Ajl¯ is the mean of accuracy value for expert l and Ajl¯ is the mean value of the score.

Step 4: The weights of experts are calculated by using Eq. (9), and it can be seen that these values are in the 0 to 1 range and sum to unity.

ηl=σl2.∑vρuvl∑l(σl2.∑vρuvl)(9)

where ηl is the weight of expert l.

The weight vector is obtained by applying Eq. (9). Based on the information value, it can be seen that the criterion with high information gains high importance. Besides the interrelationship factor among criteria, variability in the distribution concerning criteria is observed. Hence, the combined effect of interaction and variability plays a crucial role in determining criteria weights. From Eq. (9), the weights of experts are determined that of order 1×q. Typically, any criterion with high interaction with other criteria and considerable variability in their distribution of choices gains high importance, which is mapped in the formulation presented above.

Step 5: Get opinion vectors from experts on each criterion. p vectors of 1×b are obtained. The score is determined by applying Eq. (7).

Step 6: Determine the weighted score by using Eq. (10), and a weighted score matrix of p×b is formed.

wslj=ηl.Alj(10)

where Alj is the score determined via Eq. (7).

Step 7: Normalize the weighted score and determine the net evidence by using Eqs. (11) and (12).

wslj∗=wslj∑jwslj(11)

nwsj=p−∑l=1pwslj∗(12)

where wslj∗ is the normalized weighted score, and nwsj is the net weighted score.

Step 8: Bayesian approximation is determined through Eq. (13) and a matrix of p×b order is obtained.

Blj=∑U⊆VM(V)∑Z⊆ΩM(Z).|Z|(13)

where |.| is the cardinality.

Consider n mutually exclusive assertions in the form Ω=(U1,U2,…,Un), and the basic probability assignment M(.):2Ω→[0,1] is a mapping with an empty set equal to zero a full set equal to unity. Gupta et al. [75] claimed that the evidence measure needs complete solution space to determine the solution, and embedding Bayesian approximation to the measure reduces the search space to find the feasible solution, which inspired authors to present this formulation in the present section.

Step 9: Aggregate the approximation values from Step 8 by applying Eq. (14). A vector of 1×b is obtained, and further normalized to obtain the criteria weights.

wj=∏l=1p(Blj)ηl∑j∏l=1p(Blj)ηl(14)

3.3 Ranking Algorithm with CoCoSo

This section presents a novel ranking algorithm for determining a suitable HSM from a set of HSMs. In general, ranking is a crucial phase of MCDM that supports selecting a suitable HSM and ordering HSMs. A combined compromise solution (CoCoSo) is an attractive ranking approach that performs ranking from multiple stages by determining rank values via different compromise solutions, which are combined to obtain a cumulative ranking of HSMs that supports the rational selection of a suitable HSM. Besides, the CoCoSo approach is simple and elegant with three operations, namely sum, minimum, and maximum, to determine the compromise solutions.

Driven by the features, a ranking algorithm is put forward with the CoCoSo formulation in this section. The steps for calculation are given below:

Step 1: Consider p decision matrices of a×b order from the previous section for determining rank values of HSMs. Weight vectors of criteria and experts are also considered from the previous section.

Step 2: Apply Eq. (15) to aggregate data from Step 1. p matrices of a×b are aggregated to form a single matrix of a×b.

ADTij={∏l=1pyijηl,∏l=1pxijηl}(15)

where y and x are the subscripts of primary and secondary hierarchies.

Step 3: Determine the score values by applying Eqs. (7) and (10) is applied to determine the weighted score values. A matrix of a×b order is obtained.

Step 4: Determine three-stage compromise solutions for the HSMs using Eqs. (16)–(18). Each equation yields a vector of 1×a order.

Xi=∑j=1b(wsij∑iwsij)(16)

X2=∑j=1b(wsijmini(wsij))(17)

X3=∑j=1b(wsijmaxi(wsij))(18)

where wsij is the weighted score value, min(.) and max(.) are the minimum and maximum operators.

Step 5: Combine the compromise solutions from Step 4 to obtain a net ranking vector of 1×a. Eq. (19) is applied to obtain the rank values.

NXi=X1.X2.X33+(X1+X2+X33)(19)

where NXi is the net rank value of HSM i.

The HSMs are ordered based on the NXi values, and the HSM is a high value preferred, and so on. Hence, the HSMs are arranged in descending order.

From Fig. 1, it is clear that an integrated approach for HSM selection is put forward. Preferences in natural language are modeled as DHHFLTS, allowing experts to express their opinions flexibly. Further, experts’ weights are determined via the CRITIC method, which is used along with the opinion vector from experts on criteria to determine the weights of criteria. Evidence measure is put forward for determining weights of criteria. Besides, a ranking algorithm is proposed for determining the ordering of HSMs based on the data from experts and weight vectors of experts and criteria. The model shows that three-stage rank vectors are determined, which are further combined to form the final rank ordering, which is typically a compromise solution for each HSM.

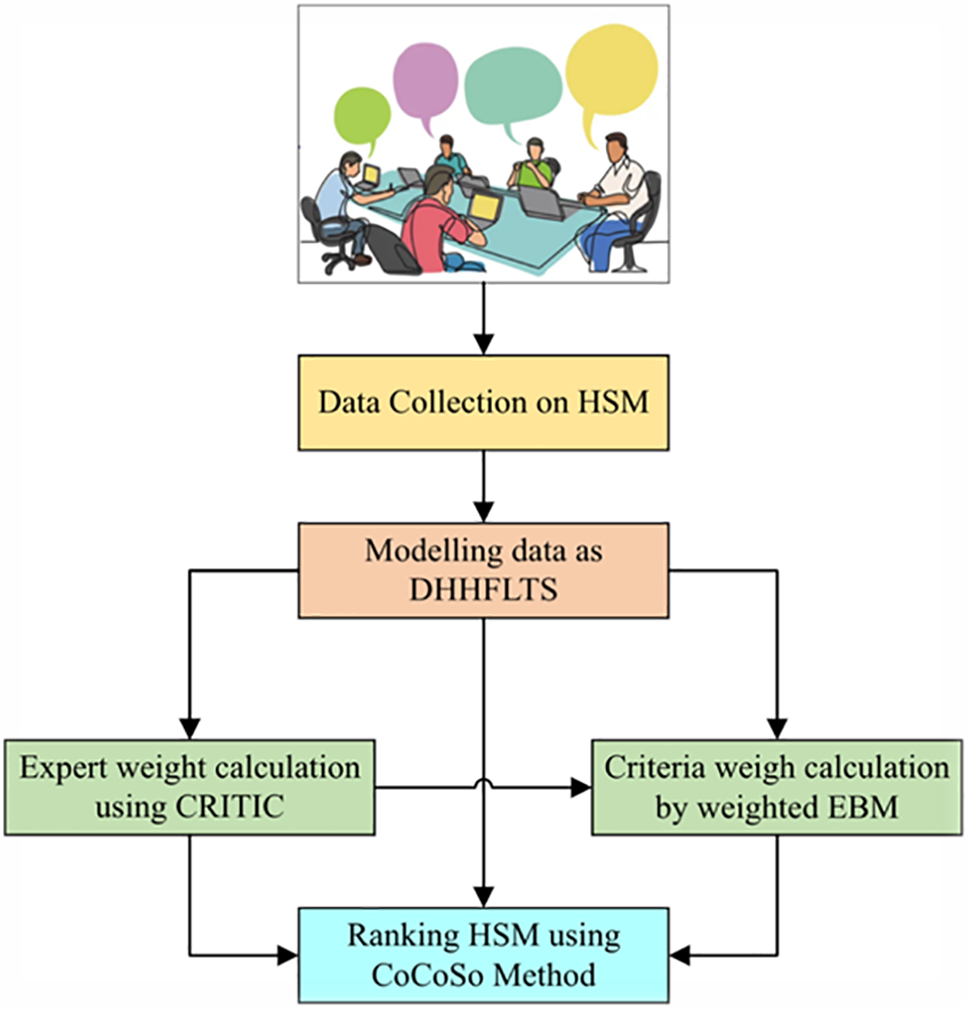
Figure 1: HSM selection model with DHHFLTS preference information

4  Case Study

This section presents an example of HSM selection to exemplify the usefulness of the proposed model. Typically, there is a high energy demand in India, and the nation needs to balance both demand and the ecosystem. For such reasons, countries globally started focusing on sustainable or renewable energy forms that emit less or zero carbon and prevent the planet from climate change and global warming [76]. Energy from hydrogen is a clean form of energy, and India has always shown keen interest in hydrogen energy adoption. As per the recent report from economictimes.indiatimes.com, India has a demand of about 9 million tonnes in 2020, which will increase to about 11 million tonnes by 2030.

Further, a report from S&P Global shows that about 26 projects in India primarily focus on meeting the energy demand and considerably reducing emissions of greenhouse gases to provide a sustainable and green ecosystem. These projects allowed India to generate close to 2,550,000 tonnes every year, so the demand and eco-friendliness aspects can be satisfied. Based on these discussions, it is clear that hydrogen as a kind of clean energy is attractive, and its use can reduce carbon trace and the ill effects of climate change [12].

Interestingly, storing hydrogen energy is crucial, and it accounts maximum for the success of hydrogen-based clean energy utilization. As a result, researchers have actively worked on mechanisms for hydrogen storage [77]. Owing to diverse methods for hydrogen storage and multiple criteria that influence the selection of a viable storage method, the problem is seen as an MCDM problem. In the present study, a panel of four experts has seven to eight years of experience in energy storage and distribution. These experts include a senior professor from the sustainable energy division, technical personnel from the energy sector, finance and audit personnel, and an industry professional from the hydrogen energy-driven sector. These experts are invited via emails and phone calls to participate in the decision process. Based on their approval, we circulated a questionnaire to these experts for data collection concerning criteria and alternatives. These experts surf the web sources for multiple storage options, and based on their expertise and voting, five HSMs are shortlisted. These candidates are rated based on 12 criteria that are from technical, socio-economic, and environmental categories. Criteria considered for rating these HSMs are storage capacity, need for R&D, geo-diversity, technical support, demographic growth, job creation, security aspect, public safety, government support, monitoring and maintenance risk, total cost, and pollution. Five alternative storage methods are salt caverns, cryogenic tanks, storage on host metals, pressure cylinders, and chemical bond-based storage:

•   Salt cavern storage is a method of storing various substances, such as natural gas, petroleum, and chemicals, in large underground caverns created in salt deposits. These caverns are created by injecting water into the salt deposit, which dissolves the salt and creates a void space. Once the cavern is formed, it can be used to store a variety of materials.

•   Cryogenic tanks are specialized containers designed to store materials at extremely low temperatures. They are used to store and transport liquefied gases such as nitrogen, oxygen, argon, and helium, as well as liquefied natural gas (LNG). Cryogenic tanks are typically made of high-strength materials such as stainless steel or aluminum and are insulated to minimize heat transfer and maintain the extremely low temperatures required for the stored materials.

•   Storage on host metals refers to a process in which hydrogen or other gases are stored on the surface of a host metal, such as palladium, titanium, or zirconium. The process involves adsorption, in which gas molecules adhere to the surface of the metal, creating a stable and reversible storage system.

•   Pressure cylinders are containers that are designed to store gases under high pressure. They are commonly used for the storage and transport of compressed gases, such as oxygen, nitrogen, argon, and carbon dioxide. Pressure cylinders are made of high-strength materials such as aluminum or steel and are designed to withstand the high pressures that are generated by the stored gases.

•   Chemical bond-based storage refers to the storage of energy using chemical bonds in molecules or compounds. This type of storage is often used for energy sources such as batteries and fuel cells. The energy is stored in the chemical bonds of the molecules, which can be released through chemical reactions when the energy is needed.

It must be noted that data is collected from experts by circulating questionnaires, and the sample questionnaire is provided in Table A1 of the Appendix section. Experts give her/his rating in the natural language form that is then modeled as DHHFLTS. Data is collected from experts on HSMs rated over criteria and on each criterion. For ease of representation, let us denote experts as EX1, EX2, EX4, and EX3. HSMs are denoted as D1, D2,…, D5 and criteria are denoted by RB1, RB2,…,RB12. The steps for ranking HSMs are given below:

Step 1: Construct three matrices of 5×12 order by considering five HSM-rated over 12 criteria by using Likert scales to form complex expressions in the natural language form. Four experts provide her/his rating information in the natural form that is modeled to DHHFLTS (refer to Table 2).

FT={sy|wheny=1−disastrous,y=2−worse,y=3−bad,y=4−dissatisfactory,y=5isnormal,y=6issatisfactoryandy=7−good,y=8−better,y=9−perfect} and P={px|whenx=1−critically,x=2−nothighly,x=3−notso,x=4−somewhat,x=5−simply,x=6−just,x=7−so,x=8−highly,x=9−considerably} are the linguistic terms for two hierarchies considered in this study. Table 2 describes the rating information from experts on HSMs based on diverse criteria. DHHFLTS is utilized for this purpose. Four experts give their rating on five HSMs based on 12 criteria.

Step 2: Determine the weights of experts by considering data from Step 1 and the procedure in Section 3.2.

Interrelationship values among criteria are calculated by using Eq. (8), and the heatmaps associated with the interactions of criteria for each expert’s preference are determined. Later, Eq. (9) is applied to determine the information vector and, finally, the weights of experts. From Eq. (8), it can be seen that four 12×12 interaction matrices are obtained that are represented as heatmaps in Figs. 2–5 for experts EX1, EX2, EX3, and EX4, respectively. The colors in each square denote the heat range, and the bar to the right denotes the correlation value among criteria. The lighter the color of the square, the higher the correlation value. Pearson correlation measure is applied to calculate the interaction among criteria. The variation vector is calculated with order 1×4, and from Eq. (9), the weights are calculated as 0.14, 0.40, 0.13, and 0.33, respectively.

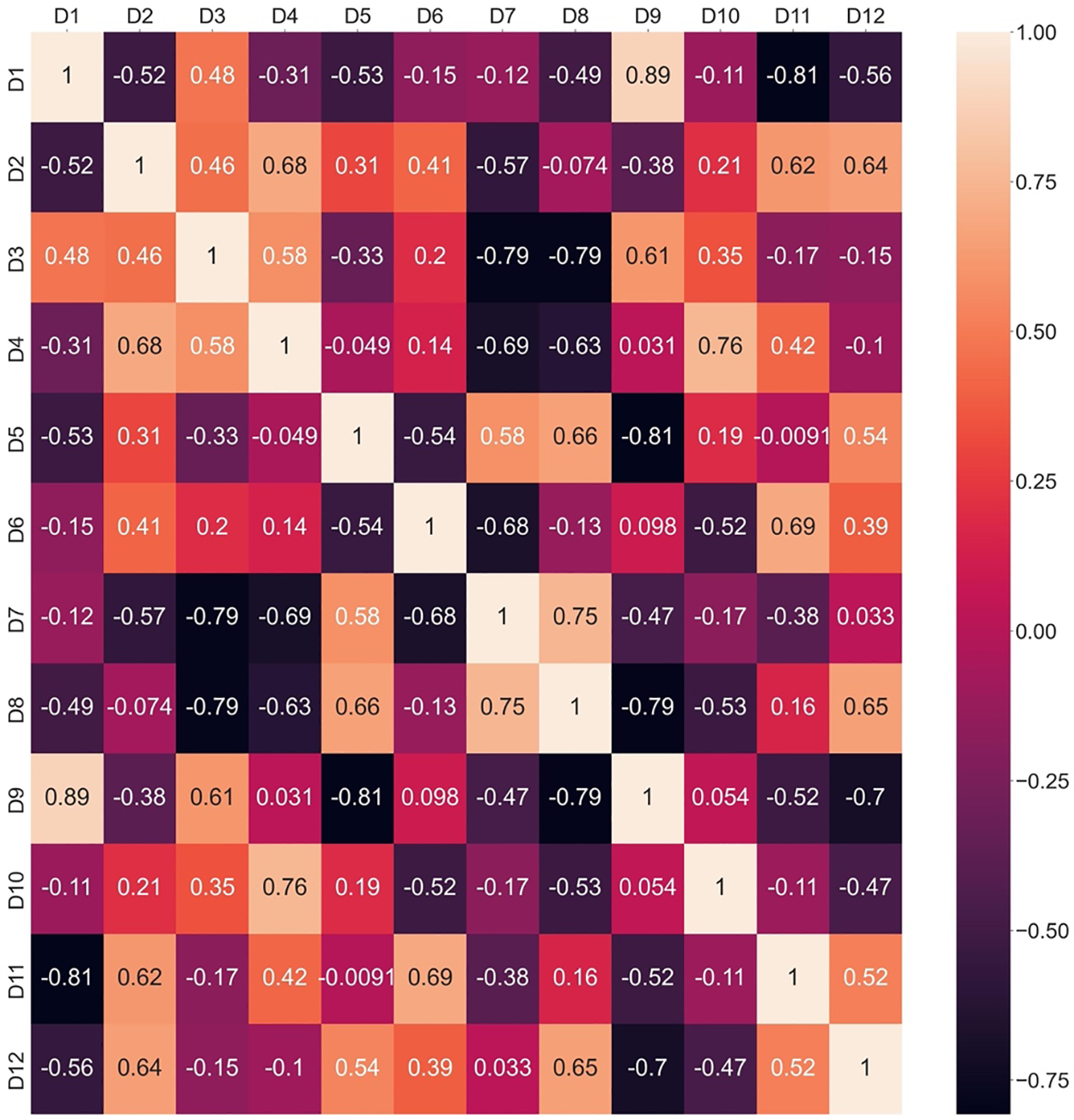
Figure 2: Interrelationship among criteria based on Pearson correlation for EX1

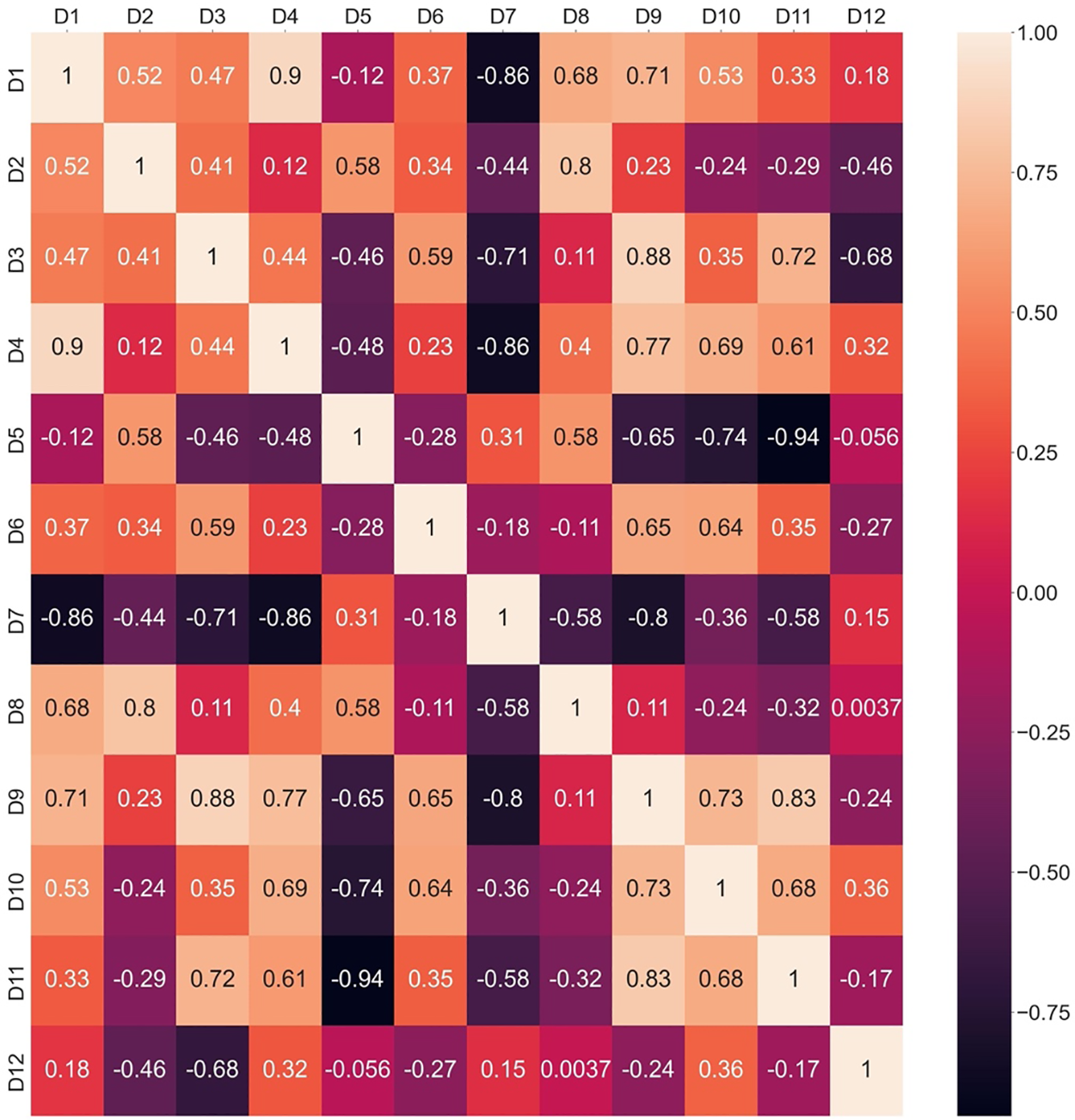
Figure 3: Interrelationship among criteria based on Pearson correlation for EX2

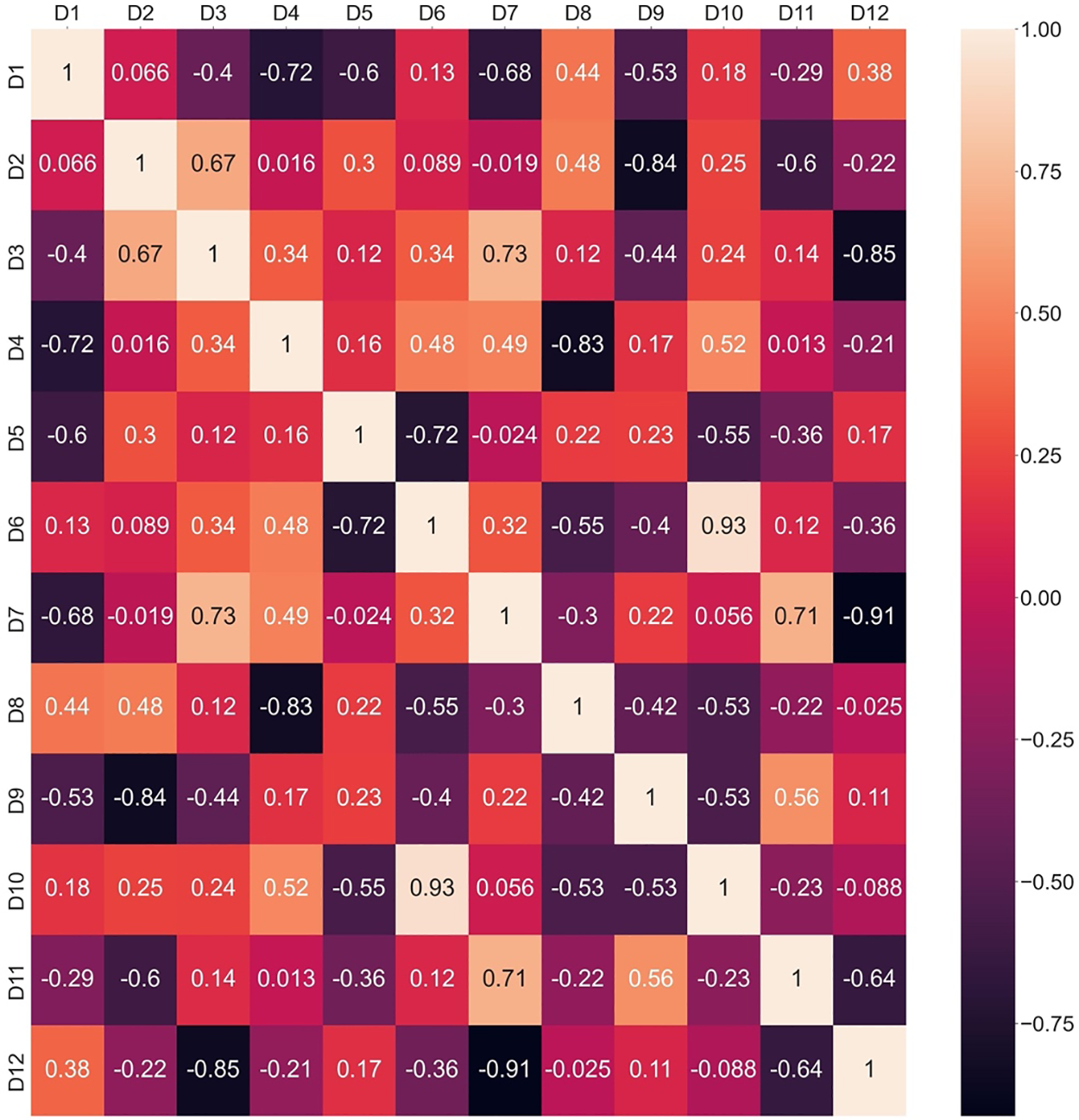
Figure 4: Interrelationship among criteria based on Pearson correlation for EX3

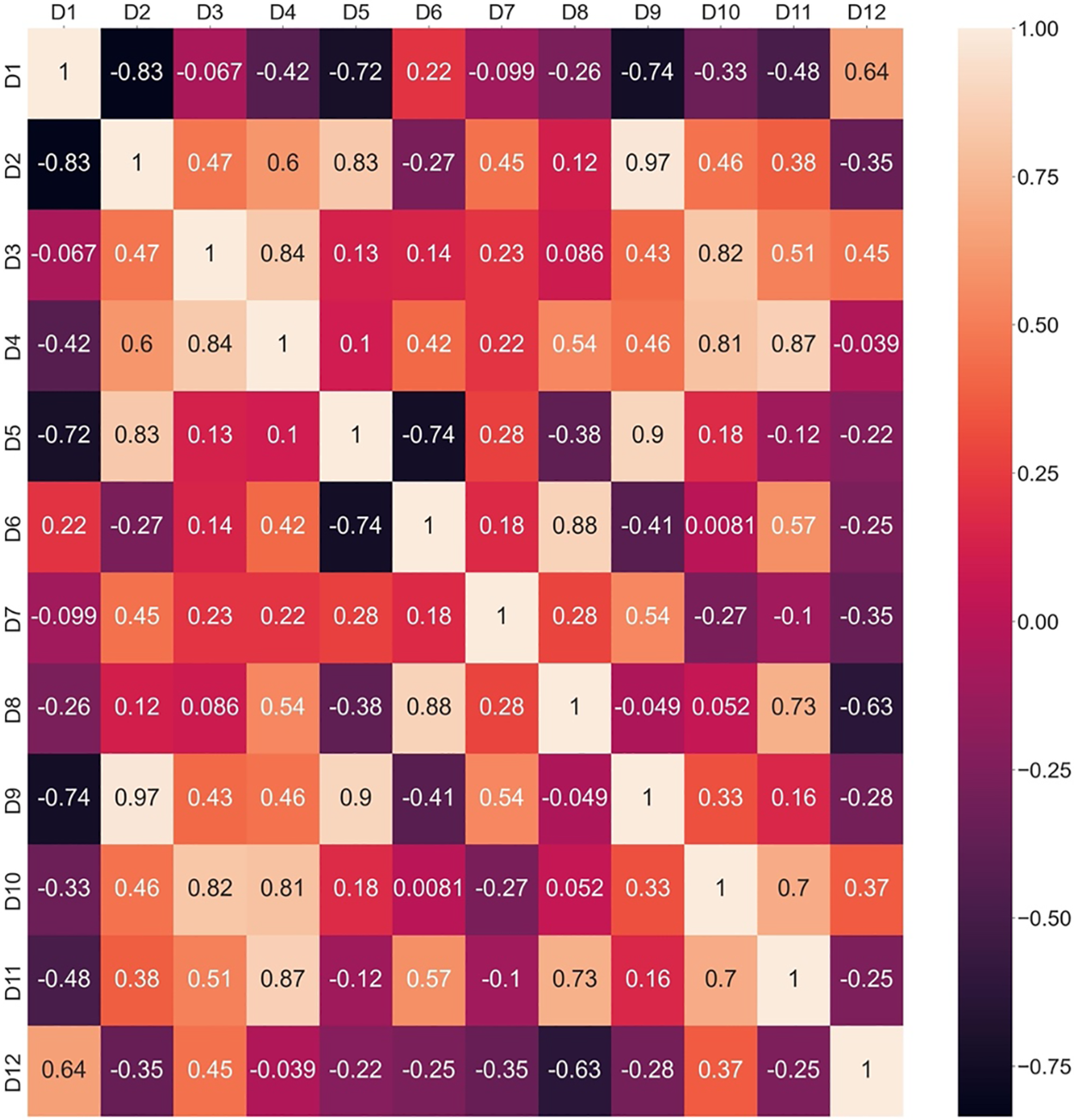
Figure 5: Interrelationship based on Pearson correlation for EX4

Step 3: Form three opinion vectors of 1×12 to determine the weights of the criteria. DHFLEs are used for rating, and the procedure in Section 3.2 is applied for weight calculation.

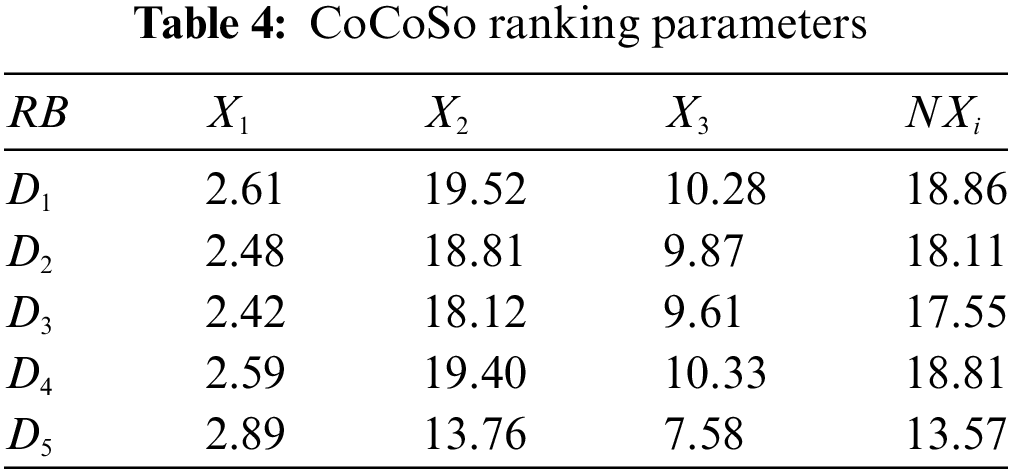
Table 3 provides the opinion vectors from experts on criteria, which are in the DHHFLTS form. Four experts give their rating on 12 criteria that are considered as input, along with experts’ weights from Step 2. By applying Eqs. (13) and (14), the weights of criteria are calculated as 0.15, 0.05, 0.15, 0.14, 0.17, 0.02, 0.07, 0.04, 0.08, 0.01, 0.11, and 0.01, respectively.

Step 4: Rank the HSMs based on the data from Step 1, weight vectors from Step 2 and Step 3, and the algorithm proposed in Section 3.3.

In Table 4, the rank values of five HSMs are presented in the last column, which can be determined based on the three-stage of compromise ranking values viz., sum, minimum, and maximum depicted as X1, X2, and X3, respectively (calculated using Eqs. (16)–(18)). Based on Table 4, it can be seen that the ordering of HSM is determined as D1≻D4≻D2≻D3≻D5, with theD1 method being the highly preferred HSM. D4 is also closely preferred for hydrogen storage.

5  Sensitivity and Comparative Investigation

This section reveals the effect of criteria weights on ranking order, and a two-way comparison with extant models is performed by considering studies from the application and methodical perspectives. Since there are 12 criteria, a1×12 weight vector is obtained. Based on the rotation of weights, 12 sets of weight vectors are obtained that are used along with the preference data for rank estimation. Each weight set will yield a rank vector of 1×5 order, and as a result, 12 such vectors are determined. It must be noted that single-bit left rotation is applied to the weight vector of 1×12, and hence, 12 new sets of 1×12 are obtained. When these sets are applied to the ranking algorithm along with the preference data, compromise rank values for each HSM are determined.

In Fig. 6, we consider 12 new weight vectors of order 1×12 order, which are obtained by rotating the weights. Rotation here refers to assigning the weight of criterion 12 to criterion 1, criterion 1 to criterion 2, criterion 2 to criterion 3, and so on. Likewise, we get 12 sets of weight vectors, which are fed as input to the ranking algorithm for determining the ordering of HSMs. In general, if there are n criteria, n sets of criteria weights can be obtained by rotation each of order 1×n. From Fig. 6, it can be inferred that the framework proposed is robust even after criteria weights are adequately altered to form new sets. Intuitively, it can be seen that though there is a change in rank values, the rank orders do not change, indicating that the framework is robust and weight alterations do not majorly affect the decision process.

Figure 6: Criteria-based sensitivity analysis

From the application point of view, extant HSM models are considered such as Wu et al. [9], Çolak et al. [12], Guo et al. [15], and Dhumraz et al. [16] for comparison with the proposed framework which is summarized in Table 5.

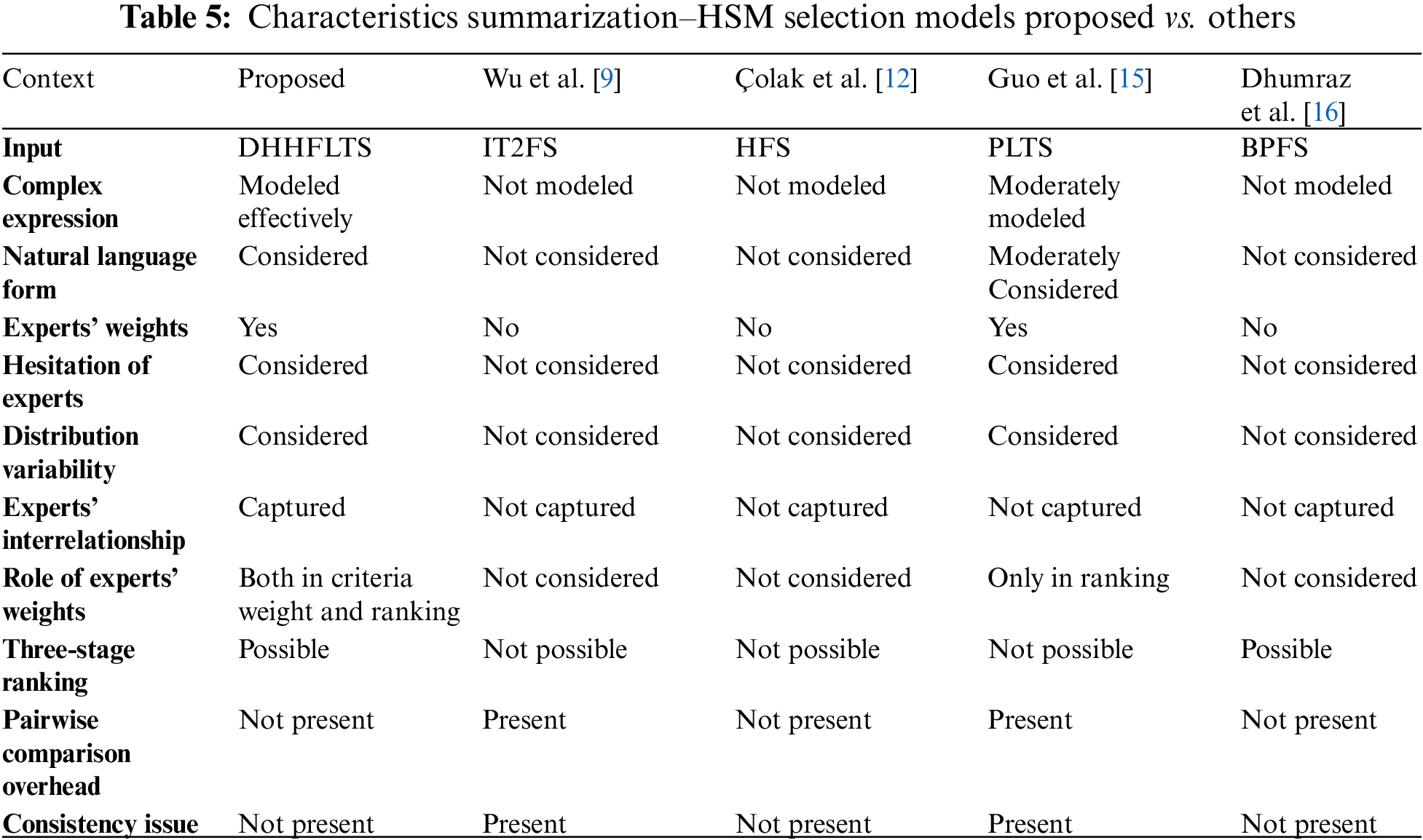
Table 5 provides a summarized view of the novelties. These novelties are explained as follows:

•   DHHLFTS is utilized for modeling uncertainty effectively by considering preferences in the natural language form and presenting complex expressions with two hierarchies where the secondary hierarchy is the concrete supplement of the primary hierarchy.

•   The weights of both experts and criteria are methodically determined with a focus on capturing the variability in the distribution of opinions and hesitation of experts.

•   Further, the interrelationship among experts is also captured during the importance assessment of experts, which needs to be improved in the extant models.

•   Additionally, unlike extant models, the importance of experts is embedded in the formulation of criteria weight assessment, which offers an intuitive advantage of the inclusion of potential information in the weight calculation.

•   Unlike some extant models, the proposed framework does not involve pairwise comparison, which reduces computational overhead and mitigates the management of consistency issues.

•   Also, unlike extant models, the proposed model allows the inclusion of experts’ weights in both ranking and criteria weight estimation, which provides a sense of rational determination of rank values as experts play a crucial role in MCDM by offering their choices on both alternatives (HSMs) and criteria.

•   Ranking of HSM is possible from three dimensions, such as the sum, minimum, and maximum operations, which yield a compromise vector of HSM that is cumulatively combined to obtain the final ordering of HSM.

Extant DHHFLTS-based models such as Teng et al. [25], Krishankumar et al. [26], Liu et al. [33], and Gou et al. [21] are compared with the proposed integrated model to understand the efficacy from the methodical perspective. Consistency measure is testified by providing the data to all these models and obtaining rank values, which are further given to Spearman correlation for determining the coefficient values. Proposed vs. other models yield values as 1.0, 0.60, 1.0, 0.50, and 0.60, respectively, and the values are depicted in Fig. 7. The decision matrices presented in Table 2 of Section 4 are considered by these models as the source of data and the criteria weights are determined from Section 4. These data are fed as input to all the models (both proposed and extant) to determine rank values, which are then given as input to Spearman correlation for determining the consistency coefficient (refer to Fig. 7).

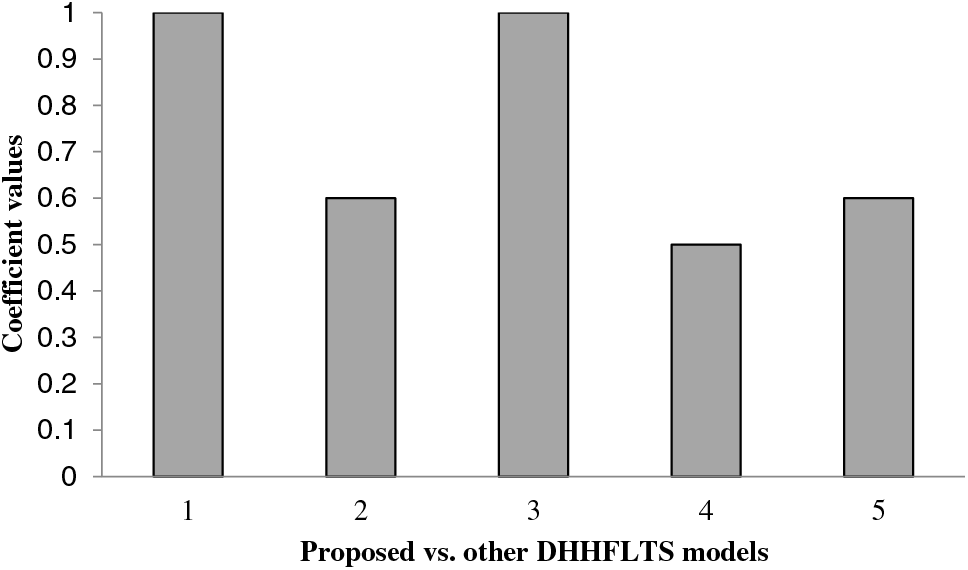
Figure 7: Proposed vs. other methods–Consistency test (in X axis 1 is Proposed vs. Proposed; 2 is Proposed vs. [24]; 3 is Proposed vs. [25]; 4 is Proposed vs. [35]; and 5 is Proposed vs. [22]) (1, 0.6, 1, 0.5, 0.6)

Data from Step 4 is fed as input to different models and the rank values are determined as D1≻D4≻D2≻D3≻D5 by applying the proposed model, D1≻D4≻D2≻D5≻D3 by applying the model in [24], D1≻D4≻D2≻D3≻D5 by applying the model in [25], D1≻D2≻D3≻D5≻D4 by applying the model in [35], and D1≻D4≻D2≻D5≻D3 by applying the model in [22].

6  Conclusion

This paper presents a new integrated model with DHHFLTS as preference information and adds value to the hydrogen storage domain. The proposed model is utilized for the rational selection of storage methods for hydrogen by presenting integrated methods with reduced human intervention. The weights of experts and criteria are determined methodically with appropriate capturing of hesitation and interrelationship among entities. Besides, the variability in the distribution of preferences by experts is also captured during the decision process.

A three-stage ranking with a compromise solution strategy is put forward that determines final ordering based on sum, minimum, and maximum utility operations. Also, unlike other models for HSM selection, the developed model can effectively consider rating in the natural language form that is modeled as complex linguistic expressions. From the theoretical sense, the model is novel and focuses on the methodical calculation of decision parameters that eventually reduces human intervention.

Apart from the theoretical strength, it can be seen that the developed model is consistent with the extant models and has a robust nature to the alteration of criteria weights. From the comprehensive sensitivity analysis of weights and Spearman correlation, the inference can be made. Some implications of the study are: (i) the developed model is a ready-to-use tool that can effectively provide decisions with mathematical support to stakeholders; (ii) the framework can consider natural language preferences and model them as DHHFLTS; (iii) the model can be used effectively, provided that experts gain some training with the framework and the DHHFLTS structure to arrive at meaningful inference; (iv) the tool can be used in a bi-directional way by both scientists who develop HSM and organization/stakeholders that plan on adopting a certain method for hydrogen storage; and (v) finally, features such as hesitation, interrelationship, and uncertainty are handled effectively by the framework.

Besides these superiorities, some limitations are: (i) unavailability of values cannot be handled by the present model, and (ii) partial information on weights cannot be modeled by the current model. As for future scope, plans are made to tackle the limitations of the present model. Also, new methods are planned with DHHFLTS for addressing HSM selection. Also, new applications in the business, sustainability, environment, and economy can experiment with the proposed model. Also, a new structure with probability variants can be experimented with, and the inclusion of recommendation and machine learning concepts is also considered.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: R. Krishankumar, S. Dhruva, K. S. Ravichandran; data collection: R. Krishankumar, S. Dhruva; analysis and interpretation of results: R. Krishankumar, S. Dhruva, K. S. Ravichandran; draft manuscript preparation: R. Krishankumar, S. Dhruva, K. S. Ravichandran, E. K. Zavadskas; supervision: K. S. Ravichandran, E. K. Zavadskas. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data and materials are provided in the manuscript itself.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Singhal, A. (2021). A sustainable growth of clean energy in India: A target 2022. Information Technology in Industry, 9(2), 1069–1076. [Google Scholar]

2. Naveenkumar, R., Ravichandran, M., Mohanavel, V., Karthick, A., Aswin, L. S. R. L. et al. (2022). Review on phase change materials for solar energy storage applications. Environmental Science and Pollution Research, 29(7), 9491–9532. [Google Scholar] [PubMed]

3. Watil, A., El Magri, A., Lajouad, R., Raihani, A., Giri, F. (2022). Multi-mode control strategy for a standalone wind energy conversion system with battery energy storage. Journal of Energy Storage, 51(4), 104481. [Google Scholar]

4. Liu, Y., Hu, T., Rui, Z., Zhang, Z., Du, K. et al. (2023). An integrated framework for geothermal energy storage with CO2 sequestration and utilization. Engineering, 133(50), 20164. [Google Scholar]

5. Züttel, A. (2004). Hydrogen storage methods. Naturwissenschaften, 91(4), 157–172. [Google Scholar]

6. Niaz, S., Manzoor, T., Pandith, A. H. (2015). Hydrogen storage: Materials, methods, and perspectives. Renewable and Sustainable Energy Reviews, 50(7), 457–469. [Google Scholar]

7. Pang, Y., Li, Q. (2016). A review of kinetic models and corresponding analysis methods for hydrogen storage materials. International Journal of Hydrogen Energy, 41(40), 18072–18087. [Google Scholar]

8. Usman, M. R. (2022). Hydrogen storage methods: Review and current status. Renewable and Sustainable Energy Reviews, 167, 112743. [Google Scholar]

9. Wu, Y., Xu, C., Zhang, B., Tao, Y., Li, X. et al. (2019). Sustainability performance assessment of wind power coupling hydrogen storage projects using a hybrid evaluation technique based on interval type-2 fuzzy set. Energy, 179(9), 1176–1190. [Google Scholar]

10. Wu, Y., Wu, C., Zhou, J., He, F., Xu, C. et al. (2020). An investment decision framework for photovoltaic power coupling hydrogen storage project based on a mixed evaluation method under intuitionistic fuzzy environment. Journal of Energy Storage, 30(19), 101601. [Google Scholar]

11. Yi, L., Li, T. (2020). Linguistic hesitant fuzzy sets and cloud model-based risk assessment of gaseous hydrogen storage in China. ICPES 2019, pp. 133–143. Singapore: Springer. [Google Scholar]

12. Çolak, M., Kaya, İ. (2020). Multi-criteria evaluation of energy storage technologies based on hesitant fuzzy information: A case study for Turkey. Journal of Energy Storage, 28(3), 101211. [Google Scholar]

13. Karatas, M. (2020). Hydrogen energy storage method selection using fuzzy axiomatic design and analytic hierarchy process. International Journal of Hydrogen Energy, 45(32), 16227–16238. [Google Scholar]

14. Pamucar, D., Deveci, M., Schitea, D., Erişkin, L., Iordache, M. et al. (2020). Developing a novel fuzzy neutrosophic number-based decision-making analysis for prioritizing energy storage technologies. International Journal of Hydrogen Energy, 45(43), 23027–23047. [Google Scholar]

15. Guo, F., Gao, J., Liu, H., He, P. (2022). A hybrid fuzzy investment assessment framework for offshore wind-photovoltaic-hydrogen storage project. Journal of Energy Storage, 45(2), 103757. [Google Scholar]

16. Dhumras, H., Bajaj, R. K. (2022). On prioritization of hydrogen fuel cell technology utilizing bi-parametric picture fuzzy information measures in VIKOR & TOPSIS decision-making approaches. International Journal of Hydrogen Energy, 27(8), 739. [Google Scholar]

17. Iordache, M., Schitea, D., Deveci, M., Akyurt, İ. Z., Iordache, I. (2019). An integrated ARAS and interval type-2 hesitant fuzzy sets method for underground site selection: Seasonal hydrogen storage in salt caverns. Journal of Petroleum Science and Engineering, 175(3), 1088–1098. [Google Scholar]

18. Wu, Y., He, F., Zhou, J., Wu, C., Liu, F. et al. (2021). Optimal site selection for distributed wind power coupled hydrogen storage project using a geographical information system based multi-criteria decision-making approach: A case in China. Journal of Cleaner Production, 299(19), 126905. [Google Scholar]

19. Kokkinos, K., Nathanail, E., Gerogiannis, V., Moustakas, K., Karayannis, V. (2022). Hydrogen storage station location selection in sustainable freight transportation via intuitionistic hesitant decision support system. Energy, 260(5), 125008. [Google Scholar]

20. Krishankumar, R., Subrajaa, L. S., Ravichandran, K. S., Kar, S., Saeid, A. B. (2019). A framework for multi-attribute group decision-making using double hierarchy hesitant fuzzy linguistic term set. International Journal of Fuzzy Systems, 21(4), 1130–1143. [Google Scholar]

21. Gou, X., Liao, H., Xu, Z., Herrera, F. (2017). Double hierarchy hesitant fuzzy linguistic term set and MULTIMOORA method: A case of study to evaluate the implementation status of haze controlling measures. Information Fusion, 38(6), 22–34. [Google Scholar]

22. Rodriguez, R. M., Martinez, L., Herrera, F. (2011). Hesitant fuzzy linguistic term sets for decision making. IEEE Transactions on Fuzzy Systems, 20(1), 109–119. [Google Scholar]

23. Liao, H., Xu, Z., Herrera-Viedma, E., Herrera, F. (2018). Hesitant fuzzy linguistic term set and its application in decision making: A state-of-the-art survey. International Journal of Fuzzy Systems, 20(7), 2084–2110. [Google Scholar]

24. Gou, X., Xu, Z. (2021). Double hierarchy linguistic term set and its extensions: The state-of-the-art survey. International Journal of Intelligent Systems, 36(2), 832–865. [Google Scholar]

25. Teng, F., Shen, M. (2023). Unbalanced double hierarchy linguistic group decision-making method based on SWARA and S-ARAS for multiple attribute group decision-making problems. Artificial Intelligence Review, 56(2), 1349–1385. [Google Scholar]

26. Krishankumar, R., Ravichandran, K. S., Kar, S., Gupta, P., Mehlawat, M. K. (2021). Double-hierarchy hesitant fuzzy linguistic term set-based decision framework for multi-attribute group decision-making. Soft Computing, 25(4), 2665–2685. [Google Scholar]

27. Wang, Z. L., Liu, H. C., Xu, J. Y., Ping, Y. J. (2021). A new method for quality function deployment using double hierarchy hesitant fuzzy linguistic term sets and axiomatic design approach. Quality Engineering, 33(3), 511–522. [Google Scholar]

28. Fu, Y., Zhang, C., Chen, Y., Gu, F., Baležentis, T. et al. (2021). Ordered weighted logarithmic averaging distance-based pattern recognition for the recommendation of traditional Chinese medicine against COVID-19 under a complex environment. Kybernetes, 51(8), 2461–2480. [Google Scholar]

29. Dai, J., Pang, J., Luo, Q., Huang, Q. (2022). Failure evaluation of electronic products based on double hierarchy hesitant fuzzy linguistic term set and K-means clustering algorithm. Symmetry, 14(12), 2555. [Google Scholar]

30. Yao, T., Wang, W., Miao, R., Dong, J., Yan, X. (2022). Damage effectiveness assessment method for anti-ship missiles based on double hierarchy linguistic term sets and evidence theory. Journal of Systems Engineering and Electronics, 33(2), 393–405. [Google Scholar]

31. Gou, X., Xu, Z., Liao, H., Herrera, F. (2018). Multiple criteria decision making based on distance and similarity measures under double hierarchy hesitant fuzzy linguistic environment. Computers & Industrial Engineering, 126(3), 516–530. [Google Scholar]

32. Li, X., Xu, Z., Wang, H. (2021). Three-way decisions are based on some Hamacher aggregation operators under a double-hierarchy linguistic environment. International Journal of Intelligent Systems, 36(12), 7731–7753. [Google Scholar]

33. Liu, Z., Zhao, X., Li, L., Wang, X., Wang, D. (2019). A novel multi-attribute decision-making method based on the double hierarchy hesitant fuzzy linguistic generalized power aggregation operator. Information, 10(11), 339. [Google Scholar]

34. Liu, P., Shen, M., Teng, F., Zhu, B., Rong, L. (2021). A multiple attribute decision-making method based on free double hierarchy hesitant fuzzy linguistic information considering the prioritized and interactive attributes. International Journal of Information Technology & Decision Making, 20(1), 225–259. [Google Scholar]

35. Gou, X., Xu, Z., Liao, H., Herrera, F. (2021). Probabilistic double hierarchy linguistic term set and its use in designing an improved VIKOR method: The application in smart healthcare. Journal of the Operational Research Society, 72(12), 2611–2630. [Google Scholar]

36. Wang, X., Gou, X., Xu, Z. (2022). A continuous interval-valued double hierarchy linguistic GLDS method and its application in performance evaluation of bus companies. Applied Intelligence, 52(4), 4511–4526. [Google Scholar]

37. Krishankumar, R., Arun, K., Kumar, A., Rani, P., Ravichandran, K. S. et al. (2021). Double-hierarchy hesitant fuzzy linguistic information-based framework for green supplier selection with partial weight information. Neural Computing and Applications, 33(21), 14837–14859. [Google Scholar]

38. Yao, T., Wang, W., Miao, R., Hu, Q., Dong, J. et al. (2022). Warhead power assessment based on double hierarchy hesitant fuzzy linguistic term sets theory and gained and lost dominance score method. Chinese Journal of Aeronautics, 35(4), 362–375. [Google Scholar]

39. Shen, M., Liu, P. (2021). Risk assessment of logistics enterprises using FMEA under free double hierarchy hesitant fuzzy linguistic environments. International Journal of Information Technology & Decision Making, 20(4), 1221–1259. [Google Scholar]

40. Krishankumar, R., Pamucar, D., Deveci, M., Ravichandran, K. S. (2021). Prioritization of zero-carbon measures for sustainable urban mobility using integrated double hierarchy decision framework and EDAS approach. Science of the Total Environment, 797(1), 149068. [Google Scholar] [PubMed]

41. Zhang, R., Gou, X., Xu, Z. (2021). A multi-attribute decision-making framework for Chinese medicine medical diagnosis with correlation measures under double hierarchy hesitant fuzzy linguistic environment. Computers & Industrial Engineering, 156(5), 107243. [Google Scholar]

42. Krishankumar, R., Pamucar, D., Pandey, A., Kar, S., Ravichandran, K. S. (2022). Double hierarchy hesitant fuzzy linguistic information based framework for personalized ranking of sustainable suppliers. Environmental Science and Pollution Research, 29(43), 1–20. [Google Scholar]

43. Li, Q., Liu, R., Zhao, J., Liu, H. C. (2022). Passenger satisfaction evaluation of public transport using alternative queuing method under hesitant linguistic environment. Journal of Intelligent Transportation Systems, 26(3), 330–342. [Google Scholar]

44. Diakoulaki, D., Mavrotas, G., Papayannakis, L. (1995). Determining objective weights in multiple criteria problems: The critic method. Computers & Operations Research, 22(7), 763–770. [Google Scholar]

45. Voorbraak, F. (1989). A computationally efficient approximation of Dempster-Shafer theory. International Journal of Man-Machine Studies, 30(5), 525–536. [Google Scholar]

46. Yazdani, M., Zarate, P., Zavadskas, E. K., Turskis, Z. (2019). A combined compromise solution (CoCoSo) method for multi-criteria decision-making problems. Management Decision, 57(9), 2501–2519. [Google Scholar]

47. Wang, S., Wei, G., Lu, J., Wu, J., Wei, C. et al. (2022). GRP and CRITIC method for probabilistic uncertain linguistic MAGDM and its application to site selection of hospital constructions. Soft Computing, 26(1), 237–251. [Google Scholar]

48. Polcyn, J. (2022). Determining value-added intellectual capital (VAIC) using the TOPSIS-CRITIC method in small and medium-sized farms in selected European countries. Sustainability, 14(6), 3672. [Google Scholar]

49. Haktanır, E., Kahraman, C. (2022). A novel picture fuzzy CRITIC & REGIME methodology: Wearable health technology application. Engineering Applications of Artificial Intelligence, 113(4), 104942. [Google Scholar]

50. Mishra, A. R., Chen, S. M., Rani, P. (2023). Multi-criteria decision-making based on novel score functions of Fermatean fuzzy numbers, the CRITIC method, and the GLDS method. Information Sciences, 623(1), 915–931. [Google Scholar]

51. Yin, J., Wang, J., Wang, C., Wang, L., Chang, Z. (2023). CRITIC-TOPSIS based evaluation of smart community governance: A case study in China. Sustainability, 15(3), 1923. https://doi.org/10.3390/su15031923 [Google Scholar] [CrossRef]

52. Pan, Y., Zhang, L., Li, Z., Ding, L. (2019). Improved fuzzy Bayesian network-based risk analysis with interval-valued fuzzy sets and D-S evidence theory. IEEE Transactions on Fuzzy Systems, 28(9), 2063–2077. [Google Scholar]

53. Zhu, C., Qin, B., Xiao, F., Cao, Z., Pandey, H. M. (2021). A fuzzy preference-based Dempster-Shafer evidence theory for decision fusion. Information Sciences, 570(1), 306–322. [Google Scholar]

54. Gao, X., Pan, L., Deng, Y. (2021). Quantum Pythagorean fuzzy evidence theory: A negation of quantum mass function view. IEEE Transactions on Fuzzy Systems, 30(5), 1313–1327. [Google Scholar]

55. Pang, J., Dai, J., Li, Y. (2022). An intelligent fault analysis and diagnosis system for electromagnet manufacturing process based on fuzzy fault tree and evidence theory. Mathematics, 10(9), 1437. [Google Scholar]

56. Denoeux, T. (2023). Reasoning with fuzzy and uncertain evidence using epistemic random fuzzy sets: General framework and practical models. Fuzzy Sets and Systems, 453(1), 1–36. [Google Scholar]

57. Wen, Z., Liao, H., Ren, R., Bai, C., Zavadskas, E. K. et al. (2019). Cold chain logistics management of medicine with an integrated multi-criteria decision-making method. International Journal of Environmental Research and Public Health, 16(23), 4843. [Google Scholar] [PubMed]

58. Banihashemi, S. A., Khalilzadeh, M., Zavadskas, E. K., Antucheviciene, J. (2021). Investigating the environmental impacts of construction projects in time-cost trade-off project scheduling problems with CoCoSo multi-criteria decision-making method. Sustainability, 13(19), 10922. [Google Scholar]

59. Mishra, A. R., Rani, P., Krishankumar, R., Zavadskas, E. K., Cavallaro, F. et al. (2021). A hesitant fuzzy combined compromise solution framework based on discrimination measures for ranking sustainable third-party reverse logistic providers. Sustainability, 13(4), 2064. [Google Scholar]

60. Qiyas, M., Naeem, M., Khan, S., Abdullah, S., Botmart, T. et al. (2022). Decision support system based on the CoCoSo method with the picture fuzzy information. Journal of Mathematics, 2022(3), 1476233. [Google Scholar]

61. Tripathi, D. K., Nigam, S. K., Rani, P., Shah, A. R. (2023). New intuitionistic fuzzy parametric divergence measures and score function-based CoCoSo method for decision-making problems. Decision Making: Applications in Management and Engineering, 61(1), 535–563. [Google Scholar]

62. Ghoushchi, S. J., Jalalat, S. M., Bonab, S. R., Ghiaci, A. M., Haseli, G. et al. (2022). Evaluation of wind turbine failure modes using the developed SWARA-CoCoSo methods based on the spherical fuzzy environment. IEEE Access, 10, 86750–86764. [Google Scholar]

63. Ghoushchi, S. J., Bonab, S. R., Ghiaci, A. M. (2023). A decision-making framework for COVID-19 infodemic management strategies evaluation in a spherical fuzzy environment. Stochastic Environmental Research and Risk Assessment, 37(4), 1635–1648. [Google Scholar]

64. Wang, H., Mahmood, T., Ullah, K. (2023). Improved CoCoSo method based on frank softmax aggregation operators for T-spherical fuzzy multiple attribute group decision-making. International Journal of Fuzzy Systems, 25(3), 1–36. [Google Scholar]

65. Zhang, H., Wei, G. (2023). Location selection of electric vehicle charging stations by using the spherical fuzzy CPT-CoCoSo and D-CRITIC method. Computational and Applied Mathematics, 42(1), 60. [Google Scholar]

66. Su, D., Zhang, L., Peng, H., Saeidi, P., Tirkolaee, E. B. (2023). Technical challenges of blockchain technology for sustainable manufacturing paradigm in Industry 4.0 era using a fuzzy decision support system. Technological Forecasting and Social Change, 188(9), 12227. [Google Scholar]

67. Herrera, F., Herrera-Viedma, E., Verdegay, J. L. (1995). A sequential selection process in group decision-making with a linguistic assessment approach. Information Sciences, 85(4), 223–239. [Google Scholar]

68. Krishankumar, R., Ravichandran, K. S., Shyam, V., Sneha, S. V., Kar, S. et al. (2020). Multi-attribute group decision-making using double hierarchy hesitant fuzzy linguistic preference information. Neural Computing and Applications, 32(17), 14031–14045. [Google Scholar]

69. Kao, C. (2010). Weight determination for consistently ranking alternatives in multiple criteria decision analysis. Applied Mathematical Modelling, 34(7), 1779–1787. [Google Scholar]

70. Koksalmis, E., Kabak, Ö. (2019). Deriving decision makers’ weights in group decision making: An overview of objective methods. Information Fusion, 49, 146–160. [Google Scholar]

71. Sivagami, R., Krishankumar, R., Sangeetha, V., Ravichandran, K. S., Kar, S. (2021). Assessment of cloud vendors using interval-valued probabilistic linguistic information and unknown weights. International Journal of Intelligent Systems, 36(8), 3813–3851. [Google Scholar]

72. Liu, P., Shen, M., Teng, F., Zhu, B., Rong, L. et al. (2021). Double hierarchy hesitant fuzzy linguistic entropy-based TODIM approach using evidential theory. Information Sciences, 547(1), 223–243. [Google Scholar]

73. Anbuudayasankar, S. P., Srikanthan, R., Karthik, M., Nair, P. R., Sivakarthik, N. et al. (2020). Cloud-based technology for small and medium scale enterprises: A decision-making paradigm using IPA, AHP and fuzzy-AHP techniques. International Journal of Integrated Supply Management, 13(4), 335–352. [Google Scholar]

74. Rani, P., Mishra, A. R., Krishankumar, R., Mardani, A., Cavallaro, F. et al. (2020). Hesitant fuzzy SWARA-complex proportional assessment approach for sustainable supplier selection (HF-SWARA-COPRAS). Symmetry, 12(7), 1152. [Google Scholar]

75. Gupta, P., Mehlawat, M. K., Grover, N. (2016). Intuitionistic fuzzy multi-attribute group decision-making with an application to plant location selection based on a new extended VIKOR method. Information Sciences, 370, 184–203. [Google Scholar]

76. Pandey, A. K., Krishankumar, R., Pamucar, D., Cavallaro, F., Mardani, A. et al. (2021). A bibliometric review on decision approaches for clean energy systems under uncertainty. Energies, 14(20), 6824. [Google Scholar]

77. Moradi, R., Groth, K. M. (2019). Hydrogen storage and delivery: Review of the state of the art technologies and risk and reliability analysis. International Journal of Hydrogen Energy, 44(23), 12254–12269. [Google Scholar]

Appendix

A sample questionarre is provided in Table A1 for clarity to readers on how data is collected.

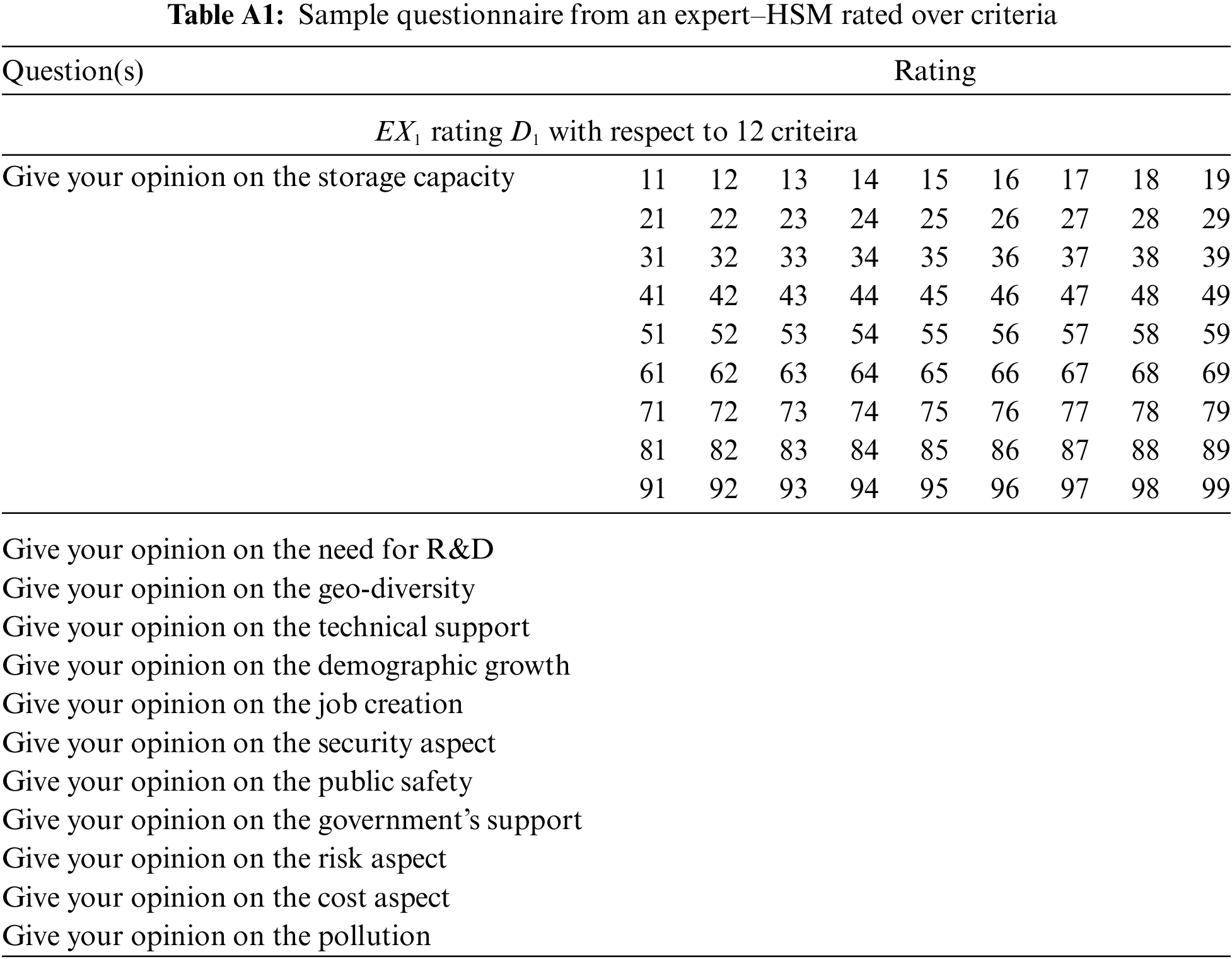
It must be noted that such a 9×9 matrix is considered for each question, and experts shade the position that reflects the double hierarchy information that she/he chooses for a particular HSM rated based on a specific criterion. FT={sy|wheny=1−disastrous,y=2−worse,y=3−bad,y=4−dissatisfactory,y=5isnormal,y=6issatisfactoryandy=7−good,y=8−better,y=9−perfect} and P={px|whenx=1−critically,x=2−nothighly,x=3−notso,x=4−somewhat,x=5−simply,x=6−just,x=7−so,x=8−highly,x=9−considerably} are the linguistic terms for two hierarchies considered in this study.

So 11 is called ‘critically disastrous,’ likewise 42 is called ‘not highly dissatisfactory,’ 35 is called ‘simply bad,’ and so on.