Attention-Based Residual Dense Shrinkage Network for ECG Denoising

1  Introduction

ECG signal plays an important role in clinical analysis, which can reflect the heart’s electrical activity. However, ECG signals received from instruments and equipment may be polluted by various noises, which will lead to the problem of abnormal detection [1]. It will significantly affect the accuracy of diagnosis and mislead the subsequent medical pathological analysis. Therefore, denoising has become the most important task in ECG processing. The typical ECG noise is baseline wander (BW) [2], muscle artifact (MA) [2], electrode motion (EM) [3], and power line interference (PLI) [3]. BW is manifested as a deviation of the ECG signal from the normal baseline position. MA generally originates from muscle contractions and tremors. EM is caused by skin impedance and skin potential changes [4]. The PLI is mainly caused by the interference of AC power in the signal acquisition process. So far, there are many methods to denoise ECG. Traditional methods mostly used filters (e.g., the low-pass filter [5], adaptive filter [6], and filter banks [7]) to achieve ECG denoising. For the adaptive filter, it can be divided into the linear filter [8–10] and the nonlinear filter [11,12]. Although they have the advantages of automatically adjusting their own parameters and fast convergence, they also have some disadvantages: The traditional linear adaptive filter may have a large mean square error and lead to performance degradation. The computational complexity of a nonlinear filters increases exponentially with the increase of filter order. To avoid these problems, time domain-based signal decomposition techniques become popular, such as wavelet transform [13] and empirical mode decomposition [14]. However, the limitation of wavelet transform method is that signal analysis can not be carried out outside the frequency domain, and the empirical mode decomposition method has subjectivity in IMF component. To solve the problems of traditional methods, researchers began to apply deep learning techniques to ECG signal denoising tasks.

Deep learning is a complex artificial intelligence technology, which can be used to extract deeper and more abstract feature information such as rules and structures from a large number of sample data. At present, the application field of deep learning has been extended to medical image segmentation [15–17], video action recognition [18], object tracking [19] and many other fields, and remarkable achievements have been made. Scholars are gradually using deep learning methods for ECG denoising. Reference [20] proposed a DNN scheme based on improved DAE, which combined the traditional wavelet-based method and the deep learning method. It can effectively remove the residual noise. In [21], a GAN-based ECG denoising method is proposed, which uses residual networks as the backbone to solve the problems of insufficient signal details in traditional denoising methods. Reference [22] proposed a periodicity ECG signal denoising scheme. It utilized the correlation between cardiac cycles to construct the CNN denoising model. Reference [23] proposed a GAN-based network to filter noisy ECG signals. Compared with traditional technologies, these schemes based on deep learning have gained a good performance on ECG denoising, but they still have the problems of incomplete retention of original waveform features and low signal-to-noise ratio. Therefore, the denoising method of ECG signal based on deep learning still has some room for improvement.

Recently, soft threshold schemes have been proven to be a powerful tool for denoising tasks [24]. It essentially filters out noise features by a set of thresholds. Soft threshold is not only widely used in traditional methods [25,26], but also is often used as the most important step in deep learn-based ECG denoising schemes [27,28]. It can reach the asymptotic approximation optimal in the sense of minimax mean square error (MSE) and tends to be a super-smooth function with certain smoothness. Therefore, it can be used to remove high-frequency components efficiently.

Attention mechanism has become an important part of deep learning to construct global dependency models [29–31]. It is often used in sequential tasks, such as machine translation [32], image generation [33], and speech enhancement [34]. It can make use of information from distant regions, and each location can combine the information of similar or related regions to ensure the regional consistency of the generated target. Therefore, self-attention can be utilized for ECG signal enhancement.

Recently, residual-dense networks [35] have achieved good results in various fields, such as image denoising [36], image blur [36], and image fog removal [36]. It is mainly the dense network inside [37] and residual learning [38] that play a key role in fully learning different hierarchical features in local and global ways, so that the network can be wider and deeper, showing strong advantages in extracting local and non-local features. Therefore, it may be helpful for the extraction of pathological signal features.

Based on the above reasons, this paper proposes an Attention-based Residual Dense Shrinkage Network (ARDSN) to effectively achieve noise reduction. The contributions of this work are summarized as follows:

1.    In this paper, to overcome the problem of incomplete signal morphology retention and low SNR after noise reduction, an ARDSN for ECG denoising is proposed.

2.    We specially designed an adaptive learning threshold shrinkage network (ALTSN) in the residual dense shrinkage attention block (RDSAB) to learn the optimal threshold of the soft threshold function, so as to better suppress the noise information. And a simulated self-attention module (SSAM) is used to further improve the signal quality and obtain a more complete noise-free signal.

3.    Experimental results and analysis illustrate its good performance in ECG denoising.

The rest of the paper is arranged as follows. The proposed ECG denoising scheme is described in Section 2. Experimental results and analysis are provided in Section 3. Finally, some conclusions are made in Section 4.

2  The Proposed Scheme

In this part, the proposed ECG denoising scheme is described in detail. Firstly, a noisy-contaminated ECG signal is input to the network, and then ARDSN is used to learn the local and non-local fine features of the ECG signal. In this way, not only rich waveform features can be learned, but also the noise waveform-related features can be eliminated adaptively.

2.1 The Framework of Proposed Scheme

As shown in Fig. 1, the ARDSN is mainly composed of three parts: shallow feature extraction network (SFEN), residual dense shrinkage attention block (RDSAB), and feature fusion representation (FFR). INoise and IDenoise represent the input (noisy signal) and output (estimated clean signal) of the network, separately. Inspired by [23], we set the convolution kernel to be 1  ×  31. Firstly, we use three 1  ×  31 Conv layers to extract the shallow ECG characteristics. Its expression is as follows:

F0=HSFEN(INoise)(1)

where INoise represents the noisy signal of network input, HSFEN (.) represents the convolution operation, and F0 represents the output of SFEN. It is used as the input of RDSAB and global feature fusion. Assuming that there are N residual dense shrinkage blocks, the Nth RDSAB can be represented as follows:

FN=HRDSAB,N(HRDSAB,i(⋯(HRDSAB,1(F0))⋯))(2)

where HRDSAB,i(.) represents the ith RDSAB, FN represents the corresponding output of the Nth RDSAB. It can be regarded as a local fine feature, and a detailed description of RDSAB can be seen in Section 2.2.

Figure 1: Framework of the proposed ECG denoising scheme, named ARDSN

In order to further improve the accumulated useful waveform feature information, we carry out FFR for the refined hierarchical features extracted by multiple RDSAB. The FFR can be represented as follows:

IFF=HFFR(F0,…,Fi,…,FN)(3)

where IFF represents the output of the FFR, and a detailed description of the FFR can be seen in Section 2.3. Finally, the residual structure is used in FFR to reconstruct the de-noised ECG signal, which is defined as:

IDenoise=INoise+IFF(4)

2.2 Residual Dense Shrinkage Attention Block (RDSAB)

This section describes the details related to the residual dense shrinkage attention block in Fig. 2. The RDSAB includes dense feature learning network (DFLN), adaptive threshold learning threshold sub-networks network (ALTSN), soft threshold activation function (STAF) and simulated self-attention module (SSAM).

Figure 2: The network structure of ith RDSAB

2.2.1 Dense Feature Learning Network (DFLN)

The DFLN is used to extract low-frequency signal features. The network structure is shown in Fig. 3. We use 1  ×  1 Conv to decrease network training parameters and improve computational efficiency. It is expressed in the ith RDSAB as follows:

Fi,DF=Hi,DFLN(Fi−1)(5)

where Fi−1 represents the output of the (i−1)th RDSAB and the input of the ith RDSAB, Hi,DFLN (.) represents the DFLN in ith RDSAB. It includes a series of convolution and ReLU [39] operations. Assuming that there are m convolution layers in DFLN, the feature map of the mth Conv layer is calculated by K0 + K  ×  (m−1), where K0 is the input channels and K represents the growth rate [37]. Fi,DF is the output of DFLN and the input for ALTSN and STAF.

Figure 3: The network structure of DFLN

2.2.2 Adaptive Learning Threshold Sub-Network (ALTSN)

Inspired by [28], we designed an ALTSN in order to learn the optimal threshold adaptively and retain a more complete waveform shape of the noiseless signal. As a part of RDSAB, ALTSN is used to learn the threshold of soft threshold activation function. In our ALTSN, two fully connected layers in [28] are replaced by convolution. Because the nonlinear cross-channel interaction realized by two fully connected layers, it may lose some useful feature information due to feature dimension reduce due to feature dimension reduction. To solve this problem, we use one-dimensional convolution. Local cross-channel information interaction is achieved without dimensionality reduction. The structure of ALTSN is shown in Fig. 4. First, the input feature Fi,DF is transformed into a one-dimensional vector μc by taking absolute value and global averaging pooling (GAP), and then μc is transmitted to the convolution layer to achieve cross-channel interaction. Then the sigmoid function is used to get λc. Finally, the threshold Fi,ALT is achieved by multiplying λc and μc. In this way, we obtain a positive and not too large soft threshold. The effectiveness of this improvement is demonstrated in Section 3.

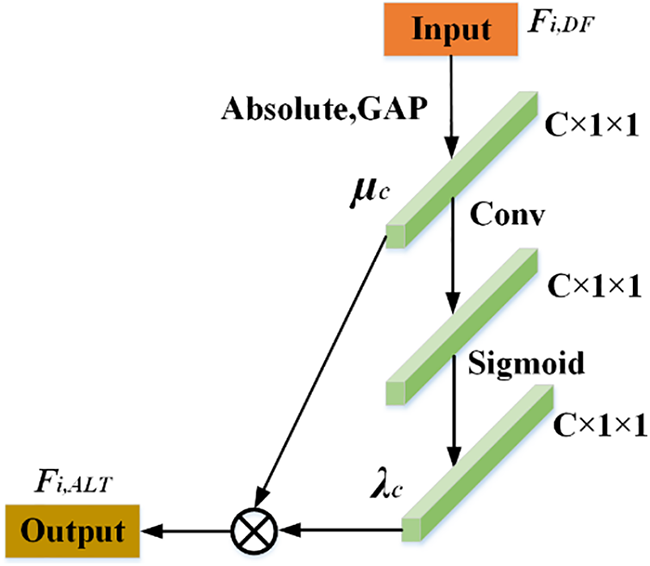
Figure 4: The network structure of ALTSN

2.2.3 Soft Threshold Activation Function(STAF)

Through the soft threshold activation function, we could apply the threshold set obtained by ALTSN to each channel of the feature map to remove the features associated with noise. The basic principle of soft threshold activation function processing is to set the coefficient less than a certain threshold value in the signal to zero, and retain the coefficient greater than the threshold value to achieve the purpose of signal denoising. The soft threshold activation function is defined as follows:

t={v−ε0v+εx>ε−ε≤x≤εx<−ε(6)

where v denotes the original characteristics, t denotes the adjusted characteristics, and ɛ denotes the threshold.

The combination of STAF and ALTSN can retain a relatively complete waveform shape. In ith RDSAB, the output features of STAF can be represented as follows:

Fi,ST=Hi,STAF(Fi,DF,Fi,ALT)(7)

where Hi,STAF (.) represents the activation function, Fi,DF represents input features of STAF, and Fi,ALT represents the threshold.

2.2.4 Simulated Self-Attention Module (SSAM)

In order to prevent some details not relevant to the task from being filtered out after the use of STAF, the ECG characteristics were further corrected with the simulated self-attention mechanism. This paper draws on the idea of self-attention mechanism [40,41] and proposes a simulated self-attention module. Since the input ECG signal is a sequential signal, by using SSAM, we could perform signal context aggregation to predict the next signal sample from the current signal. SSAM can prevent the network from mistakenly viewing the original pathological information as noise when learning noise-free waveform features. The network structure of SSAM is shown in Fig. 5. It is expressed as follows:

Fi,SSA=HSSAM(Fi,ST)(8)

where HSSAM(.) represents the simulated self-attention module, Fi,ST is the output of the STAF, and Fi,SSA represents the output features of SSAM. Local residual learning could further enhance the learning ability of the network, and its formula is as follows:

Fi=Fi,SSA+Fi−1(9)

where Fi−1 and Fi represent the input features and output features of the ith RDSAB, separately.

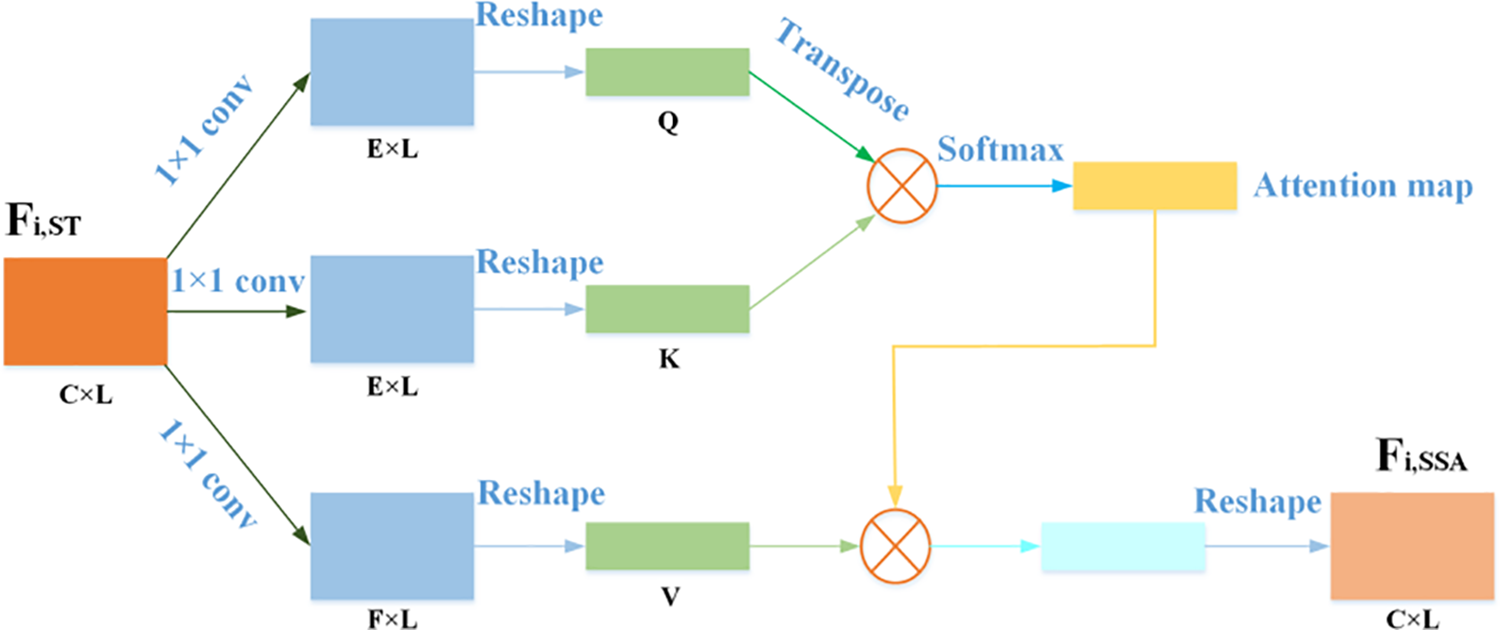
Figure 5: The network structure of SSAM

2.3 Feature Fusion Representation

FFR enhances feature representation ability in a global manner and reconstructs the de-noised ECG signal. First, concatenation and 1  ×  1 convolution operation are used to fully fuse the previously accumulated functional features, then 1  ×  31 convolution is used to further learn features, and then residual learning is used to accelerate the learning of clean signal features in a global manner to obtain the dense shrinkage feature fusion. Finally, 1  ×  31 convolution is introduced to enhance the feature representation ability. The dense shrinkage feature fusion is expressed as follows:

IDSFF=Conv1×31(Conv1×1(Concat(F1,…,FN)))+F0(10)

where Concat(.) and Conv1  ×  1(.) denotes concatenation operation and 1  ×  1 convolution operation, respectively. Conv1  ×  31(.) denotes 1  ×  31 convolution operation. IDSFF represents the output of dense shrinkage feature fusion and the input of the next convolution. Therefore, we can go further with the following operations:

IFF=Conv1×31(IDSFF)(11)

where Conv1  ×  31 represents 1  ×  31 convolution operation, the purpose of introducing convolution is to learn features again after global residual learning, so as to enhance feature representation ability, and IFF is the output of convolution operation.

3  Experiments and Analysis

3.1 Database Setup

To demonstrate the effectiveness of the proposed ECG denoising method, all experiments were performed on public reference databases: MIT-BIH Arrhythmia Database [42] and MIT-BIH Noise Stress Test Database (NSTDB) [43]. The MIT-BIH Arrhythmia database contains 48 ECG records. Each record containing two leads is approximately half an hour in length with a sampling rate of 360 Hz. Following previous works [20,22], lead II was selected. In this paper, the MIT-BIH arrhythmia database is used as a clean training distribution to train a network model. It is split into two sets: the training set and the test set. And divide the training set and test set by a ratio of three to one. NSTDB is applied to simulate real noise (BW, MA, and EM). Since the noise is a sample sequence, we can generate a noisy ECG signal by intercepting a sample from the entire noise source (the same length as the clean signal sample) and then artificially adding noise. To increase randomness, the starting point of each intercept is a random indication. Three types of noise were incorporated into the electrocardiogram (ECG) signal, resulting in the formation of three distinct datasets for the purpose of model training. In light of the learning characteristics of neural networks, the normalization method described in [22] has been employed to normalize the noisy ECG signal.

3.2 Evaluation Criteria

In the following experiments, several metrics, signal-to-noise ratio (SNR) and root mean square error (RMSE), are selected to assess the ECG denoising performance [20,44]. The higher the SNR value and the lower the RMSE value, the denoising ability of the network model is better. The SNR and RMSE are represented as follows:

SNR=10log10⁡∑n=1N(x(n))2∑n=1N(x^(n)−x(n))2(12)

RMSE=1N∑n=1N(x^(n)−x(n))2(13)

where N represents the total number of samples under evaluation, x(n) represents the original ECG signal, and x^(n) represents the desired ECG signal.

3.3 Implementation Detail

In order to ensure the generalizability of the model and find the proper hyper-parameters, the training data of the network consists of noise-free ECG signals and noisy ECG signals. During training, a sliding window technique with 50% overlap (512 samples) was used to cut the data into 1024 samples as a segment (about 3 s of ECG data). No overlap was used during the test, namely, it is continuously truncated every 1024 samples.

The proposed network uses the L1 loss function, Adam optimizer, and max-min normalization. The learning rate is empirically set as 0.00005 followed by Bengio’s work [45]. The training epoch, batch size, the number of convolutional layers in DFLN, the number of RDSAB, and the growth rate are set to 60, 1, 6, 10, and 64, respectively. The convolutional kernel size is 1  ×  31 for all networks except for ALTSN, which has a convolutional kernel size of 1  ×  1.

3.4 Experimental Results

3.4.1 The Structure Selection of ALTSN

We conducted Two groups of experiments on these two structures, that is, the two FC structures and Conv structures were embedded into ALTSN respectively to compare their performance. The first set of experiments used two FC structures as the construction structure of the ALTSN, and the second set of experiments used a Conv structure as the construction structure of the ALTSN. All other parameters being equal, the SNR of the first group was 26.30 dB, and the SNR of the second group was 27.66 dB, based on the results of our device environment run. According to the results obtained, it is proved that the improvement proposed in this work is beneficial.

3.4.2 Ablation Experiment

Table 1 shows the ablation studies of ALTSN and SSAM. The baseline was obtained without ALTSN and SSAM with poor performance (SNR = 26.44 dB). This may be caused by the difficulty of training as well as too many redundant features, and also proves that only stacking many residual dense blocks in a deep network does not lead to better performance.

ALTSN and SSAM were added to the baseline in different combinations, and a total of four sets of experiments were performed. As shown in Table 1, each structure can effectively improve the baseline performance, and the optimal performance is achieved by both ALTSN and SSAM added to the baseline. While the incorporation of ALTSN and SSAM provides a notable advantage, it should be noted that the activation function within ALTSN may result in signal smoothing and the loss of certain details.

3.4.3 Selection of the Soft Threshold Function

In order to show the effectiveness of the soft threshold function, a set of comparison experiments are designed to replace the soft threshold function in the network with the hyper shrinkage function [46], and the anti-noise performance of the two models is compared. As shown in Table 2, in the soft threshold activation function experiment, the experimental result is 27.66 dB, while the other set of experiments is 27.05 dB. The above experiments show that the soft threshold function is more advantageous than the hyper shrinkage function in the ECG denoising task. Because the deep learning model itself is a nonlinear system, and excessive introduction of nonlinear is easy to lead to excessive signal smoothing, so the nonlinear hyper shrinkage function is adopted, which decreases the model’s anti-noise performance.

3.4.4 Performance Comparison

To evaluate the effectiveness of the proposed scheme, the experimental results of the proposed scheme are compared with the existing three ECG denoising methods in [20,22,23] on different types of noise (BW, MA, and EM). The same as [20], the contaminated ECG is made from the corresponding noise-free ECG signal by adding EM, BW, and MA noise with input SNR (namely SNRin) of 0, 1.25, and 5 dB, separately. The performance comparison between the proposed method and some state-of-the-art ECG denoising methods in various sources of noise (BW, MA, and EM) and input SNR (namely SNRin = {0, 1.25, 5 dB}) are listed in Tables 3–5.

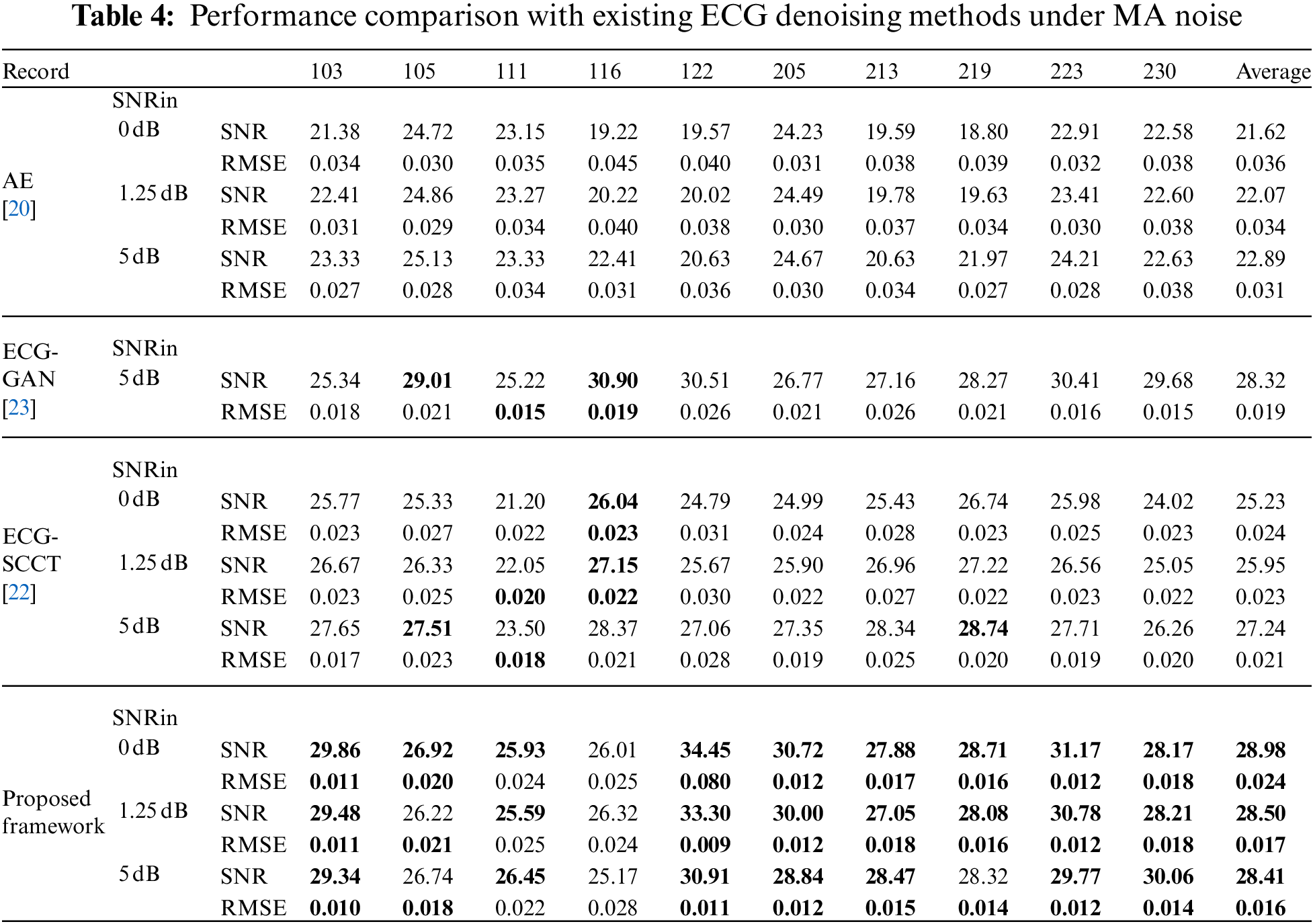
As seen from Tables 3–5, it can be found that the proposed denoising scheme significantly outperformance AE [20] in three types of noise. In addition, the proposed framework shows comparable results with ECG-GAN [23] and ECG-SCCT [22] in BW noise conditions, but it outperforms those methods in EM and MA noise conditions.

Furthermore, to illustrate the effectiveness of ECG denoising, the visualized denoising records in three types of noise (BW, MA, and EM) are shown in Fig. 6. Here, for simplicity, only the denoising effect of the proposed method at SNR 5 dB noise is shown. The result demonstrates that our proposed method could obtain a denoised ECG signal basically consistent with the noise-free ECG signal (original ECG signal). The results demonstrate that the proposed ARDSN can remarkably suppress the impact of BW, MA, and EM noise on ECG signals.

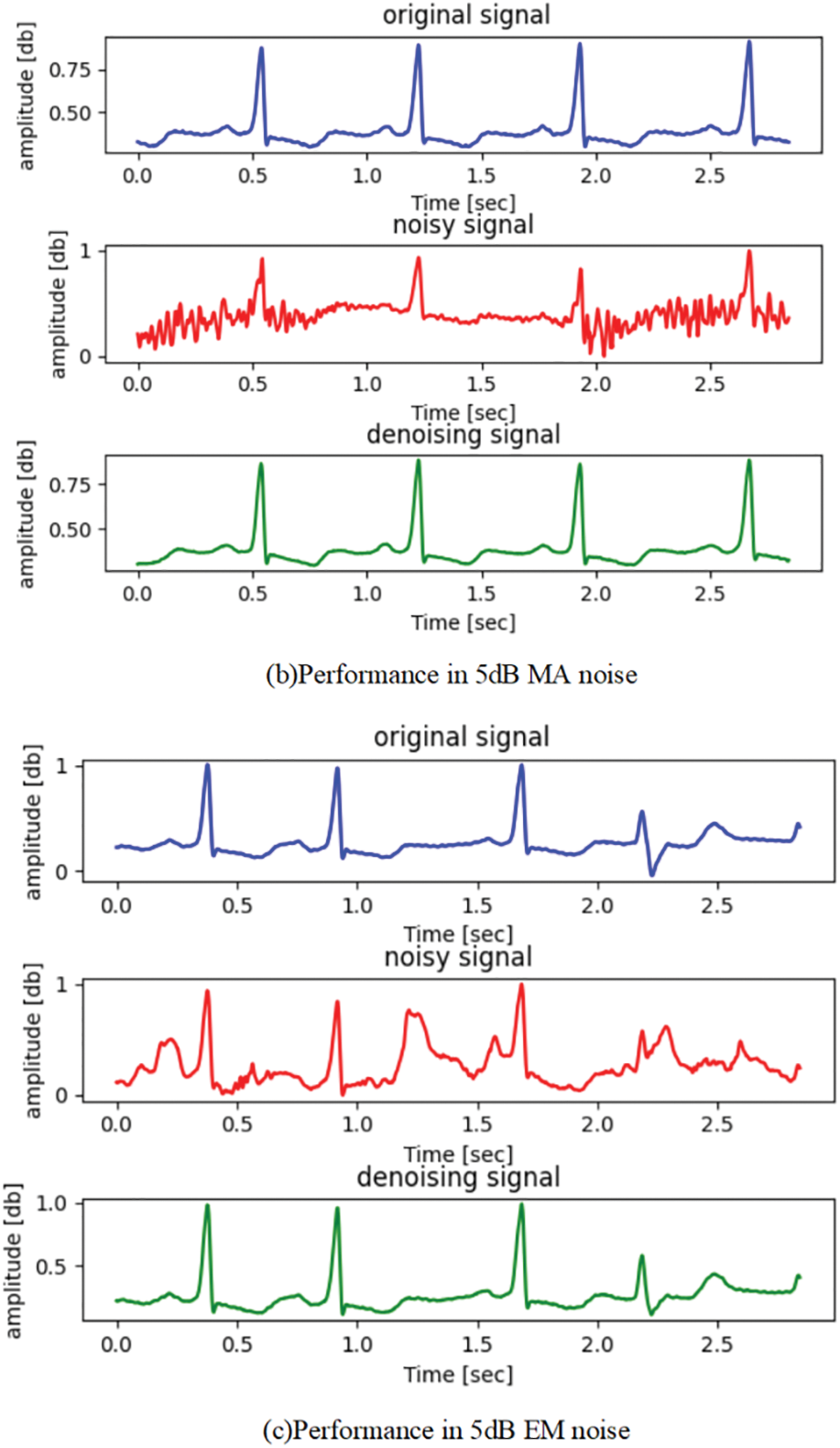
Figure 6: The denoising performance of ECG signal record 223: The blue wave line represents the original ECG signal, the red wave line represents the ECG signal, and the green wave line represents the estimated signal output by the proposed framework

4  Conclusion

In this paper, an ARDSN is proposed for ECG denoising. The designed RDSAB, as the basic block of ARDSN, learns fine features in a local form. In each RDSAB, the dense connections between each convolutional layer are used to extract rich waveform features, then ATDB is used to adaptive suppress the noise, and SSAM is used to correct the learned noise-free signal. In addition, our FFR enhances network representation in a global manner to further learn noise-free signal features. The experimental results demonstrate that the proposed ARDSN can realize fairly good ECG denoising performance. However, it is worth noting that the proposed method does have a couple of limitations that should be taken into consideration. Firstly, the utilization of a soft threshold denoising technique may result in the loss of finer details due to signal smoothing. Additionally, the convolution kernel used in the method is relatively large, resulting in a higher number of trainable parameters and increased computational complexity. Therefore, there remains a margin for refinement and amplification of this method’s efficacy.

Acknowledgement: The authors are thankful to the previous contributors of deep learning technology that used in this research.

Funding Statement: This project was supported by the National Natural Science Foundation of China under Grant 62172059 and 62072055; Hunan Provincial Natural Science Foundations of China under Grant 2022JJ50318 and 2022JJ30621; Scientific Research Fund of Hunan Provincial Education Department of China under Grant 22A0200 and 20K098.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Dengyong Zhang, Minzhi Yuan; data collection: Minzhi Yuan; analysis and interpretation of results: Dengyong Zhang, Minzhi Yuan, Feng Li; draft manuscript preparation: Minzhi Yuan, Lebing Zhang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Publicly available datasets were analyzed in this study. The ECG Dataset (MIT-BIH Arrhythmia Database) and the MIT-BIH Noise Stress Test Database (NSTDB) for this study can be found in https://www.physionet.org/content/mitdb/1.0.0/ and https://www.physionet.org/content/nstdb/1.0.0/, respectively.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Jothiramalingam, R., Jude, A., Hemanth, D. J. (2021). Review of computational techniques for the analysis of abnormal patterns of ECG signal provoked by cardiac disease. Computer Modeling in Engineering & Sciences, 128(3), 875–906. https://doi.org/10.32604/cmes.2021.016485 [Google Scholar] [CrossRef]

2. de Pinto, V. (1992). Filters for the reduction of baseline wander and muscle artifact in the ECG. Journal of Electrocardiology, 25, 40–48. https://doi.org/10.1016/0022-0736(92)90060-D [Google Scholar] [PubMed] [CrossRef]

3. Clifford, G. D., Azuaje, F., Mcsharry, P. (2006). ECG statistics, noise, artifacts, and missing data. Advanced Methods and Tools for ECG Data Analysis, 6(1), 18. [Google Scholar]

4. Rooijakkers, M. J., Song, S., Rabotti, C., Oei, S. G., Bergmans, J. W. et al. (2014). Influence of electrode placement on signal quality for ambulatory pregnancy monitoring. Computational and Mathematical Methods in Medicine, 2014. https://doi.org/10.1155/2014/960980 [Google Scholar] [PubMed] [CrossRef]

5. Slonim, T. Y., Slonim, M. A., Ovsyscher, E. A. (1993). The use of simple FIR filters for filtering of ECG signals and a new method for post-filter signal reconstruction. Proceedings of Computers in Cardiology Conference, pp. 871–873. IEEE. https://doi.org/10.1109/CIC.1993.378347 [Google Scholar] [CrossRef]

6. Thakor, N. V., Zhu, Y. S. (1991). Applications of adaptive filtering to ECG analysis: Noise cancellation and arrhythmia detection. IEEE Transactions on Biomedical Engineering, 38(8), 785–794. https://doi.org/10.1109/10.83591 [Google Scholar] [PubMed] [CrossRef]

7. Afonso, V. X., Tompkins, W. J., Nguyen, T. Q., Trautmann, S., Luo, S. (1995). Filter bank-based processing of the stress ECG. Proceedings of 17th International Conference of the Engineering in Medicine and Biology Society, vol. 2, pp. 887–888. Montreal, QC, Canada, IEEE. https://doi.org/10.1109/IEMBS.1995.579254 [Google Scholar] [CrossRef]

8. Muhsin, N. K. (2011). Noise removal of ECG signal using recursive least square algorithms. Al-Khwarizmi Engineering Journal, 7(1), 13–21. [Google Scholar]

9. Islam, M. Z., Sajjad, G. S., Rahman, M. H., Dey, A. K., Biswas, M. A. M. et al. (2012). Performance comparison of modified LMS and RLS algorithms in de-noising of ECG signals. International Journal of Engineering and Technology, 2(3), 466–468. [Google Scholar]

10. Sayadi, O., Shamsollahi, M. B. (2008). ECG denoising and compression using a modified extended Kalman filter structure. IEEE Transactions on Biomedical Engineering, 55(9), 2240–2248. https://doi.org/10.1109/TBME.2008.921150 [Google Scholar] [PubMed] [CrossRef]

11. Sameni, R., Shamsollahi, M. B., Jutten, C., Clifford, G. D. (2007). A nonlinear Bayesian filtering framework for ECG denoising. IEEE Transactions on Biomedical Engineering, 54(12), 2172–2185. https://doi.org/10.1109/TBME.2007.897817 [Google Scholar] [PubMed] [CrossRef]

12. Schreiber, T., Kaplan, D. T. (1996). Nonlinear noise reduction for electrocardiograms. Chaos, 6(1), 87–92. https://doi.org/10.1063/1.166148 [Google Scholar] [PubMed] [CrossRef]

13. Tajane, K., Pitale, R., Umale, J. (2014). Comparative analysis of mother wavelet functions with the ecg signals. Journal of Engineering Research and Applications, 4(1), 38–41. [Google Scholar]

14. Huang, N. E., Shen, Z., Long, S. R., Wu, M. C., Shih, H. H. et al. (1998). The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 454(1971), 903–995. https://doi.org/10.1098/rspa.1998.0193 [Google Scholar] [CrossRef]

15. Yu, M., Han, M., Li, X., Wei, X., Jiang, H. et al. (2022). Adaptive soft erasure with edge self-attention for weakly supervised semantic segmentation: Thyroid ultrasound image case study. Computers in Biology and Medicine, 144, 105347. https://doi.org/10.1016/j.compbiomed.2022.105347 [Google Scholar] [PubMed] [CrossRef]

16. Chen, Y., Yang, X. H., Wei, Z., Heidari, A. A., Zheng, N. et al. (2022). Generative adversarial networks in medical image augmentation: A review. Computers in Biology and Medicine, 105382. https://doi.org/10.1016/j.compbiomed.2021.105063 [Google Scholar] [PubMed] [CrossRef]

17. Chen, Y., Gan, H., Chen, H., Zeng, Y., Xu, L. et al. (2023). Accurate iris segmentation and recognition using an end-to-end unified framework based on MADNet and DSANet. Neurocomputing, 517, 264–278. https://doi.org/10.1016/j.neucom.2022.10.064 [Google Scholar] [CrossRef]

18. Zhou, S., Chen, L., Sugumaran, V. (2020). Hidden two-stream collaborative learning network for action recognition. Computers, Materials & Continua, 63(3), 1545–1561. https://doi.org/10.32604/cmc.2020.09867 [Google Scholar] [CrossRef]

19. Zhang, J., Sun, J., Wang, J., Yue, X. G. (2021). Visual object tracking based on residual network and cascaded correlation filters. Journal of Ambient Intelligence and Humanized Computing, 12, 8427–8440. https://doi.org/10.1007/s12652-020-02572-0 [Google Scholar] [CrossRef]

20. Xiong, P., Wang, H., Liu, M., Zhou, S., Hou, Z. et al. (2016). ECG signal enhancement based on improved denoising auto-encoder. Engineering Applications of Artificial Intelligence, 52, 194–202. https://doi.org/10.1016/j.engappai.2016.02.015 [Google Scholar] [CrossRef]

21. Xu, B., Liu, R., Shu, M., Shang, X., Wang, Y. (2021). An ECG denoising method based on the generative adversarial residual network. Computational and Mathematical Methods in Medicine, 2021, 1–23. https://doi.org/10.1155/2021/5527904 [Google Scholar] [CrossRef]

22. Rasti-Meymandi, A., Ghaffari, A. (2022). A deep learning-based framework for ECG signal denoising based on stacked cardiac cycle tensor. Biomedical Signal Processing and Control, 71, 103275. https://doi.org/10.1016/j.bspc.2021.103275 [Google Scholar] [CrossRef]

23. Singh, P., Pradhan, G. (2020). A new ECG denoising framework using generative adversarial network. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 18(2), 759–764. https://doi.org/10.1109/TCBB.2020.2976981 [Google Scholar] [PubMed] [CrossRef]

24. Donoho, D. L. (1995). De-noising by soft-thresholding. IEEE Transactions on Information Theory, 41(3), 613–627. https://doi.org/10.1109/18.382009 [Google Scholar] [CrossRef]

25. Samadi, S., Shamsollahi, M. B. (2014). ECG noise reduction using empirical mode decomposition based on combination of instantaneous half period and soft-thresholding. 2nd Middle East Conference on Biomedical Engineering, pp. 244–248. Doha, Qatar, IEEE. https://doi.org/10.1109/MECBME.2014.6783250 [Google Scholar] [CrossRef]

26. Cherkassky, V., Kilts, S. (2001). Comparison of wavelet thresholding methods for denoising ECG signals. Artificial Neural Networks—ICANN 2001: International Conference, Vienna, Austria, pp. 625–629. Berlin Heidelberg, Springer. [Google Scholar]

27. Isogawa, K., Ida, T., Shiodera, T., Takeguchi, T. (2017). Deep shrinkage convolutional neural network for adaptive noise reduction. IEEE Signal Processing Letters, 25(2), 224–228. https://doi.org/10.1109/LSP.2017.2782270 [Google Scholar] [CrossRef]

28. Zhao, M., Zhong, S., Fu, X., Tang, B., Pecht, M. (2019). Deep residual shrinkage networks for fault diagnosis. IEEE Transactions on Industrial Informatics, 16(7), 4681–4690. https://doi.org/10.1109/TII.2019.2943898 [Google Scholar] [CrossRef]

29. Chen, X., Mishra, N., Rohaninejad, M., Abbeel, P. (2018). Pixelsnail: An improved autoregressive generative model. International Conference on Machine Learning, pp. 864–872. PMLR. https://doi.org/10.48550/arXiv.1712.09763 [Google Scholar] [CrossRef]

30. Gregor, K., Danihelka, I., Graves, A., Rezende, D., Wierstra, D. (2015). Draw: A recurrent neural network for image generation. International Conference on Machine Learning, pp. 1462–1471. PMLR. https://doi.org/10.48550/arXiv.1502.04623 [Google Scholar] [CrossRef]

31. Zhang, Y., Zhang, X., Zhu, W. (2021). ANC: Attention network for COVID-19 explainable diagnosis based on convolutional block attention module. Computer Modeling in Engineering & Sciences, 127(3), 1037–1058. https://doi.org/10.32604/cmes.2021.015807 [Google Scholar] [CrossRef]

32. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L. et al. (2017). Attention is all you need. Advances in Neural Information Processing Systems, 30. https://doi.org/10.48550/arXiv.1706.03762 [Google Scholar] [CrossRef]

33. Zhang, H., Goodfellow, I., Metaxas, D., Odena, A. (2019). Self-attention generative adversarial networks. International Conference on Machine Learning, pp. 7354–7363. PMLR. https://doi.org/10.48550/arXiv.1805.08318 [Google Scholar] [CrossRef]

34. Zhao, Y., Wang, D., Xu, B., Zhang, T. (2020). Monaural speech dereverberation using temporal convolutional networks with self attention. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 28, 1598–1607. https://doi.org/10.1109/TASLP.2020.2995273 [Google Scholar] [PubMed] [CrossRef]

35. Zhang, Y., Tian, Y., Kong, Y., Zhong, B., Fu, Y. (2018). Residual dense network for image super-resolution. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 2472–2481. https://doi.org/10.1109/CVPR.2018.00262 [Google Scholar] [CrossRef]

36. Zhang, Y., Tian, Y., Kong, Y., Zhong, B., Fu, Y. (2020). Residual dense network for image restoration. IEEE Transactions on Pattern Analysis and Machine Intelligence, 43(7), 2480–2495. https://doi.org/10.48550/arXiv.1812.10477 [Google Scholar] [CrossRef]

37. Huang, G., Liu, Z., Van Der Maaten, L., Weinberger, K. Q. (2017). Densely connected convolutional networks. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 4700–4708. Honolulu, HI, USA. https://doi.org/10.1109/CVPR.2017.243 [Google Scholar] [CrossRef]

38. He, K., Zhang, X., Ren, S., Sun, J. (2016). Deep residual learning for image recognition. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 770–778. Las Vegas, NV, USA. https://doi.org/10.1109/CVPR.2016.90 [Google Scholar] [CrossRef]

39. Glorot, X., Bordes, A., Bengio, Y. (2011). Deep sparse rectifier neural networks. Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, pp. 315–323. [Google Scholar]

40. Pandey, A., Wang, D. (2021). Dense CNN with self-attention for time-domain speech enhancement. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 29, 1270–1279. https://doi.org/10.1109/TASLP.2021.3064421 [Google Scholar] [PubMed] [CrossRef]

41. Liu, Y., Thoshkahna, B., Milani, A., Kristjansson, T. (2020). Voice and accompaniment separation in music using self-attention convolutional neural network. https://doi.org/10.48550/arXiv.2003.08954 [Google Scholar] [CrossRef]

42. Moody, G. B., Mark, R. G. (2001). The impact of the MIT-BIH arrhythmia database. IEEE Engineering in Medicine and Biology Magazine, 20(3), 45–50. https://doi.org/10.1109/51.932724 [Google Scholar] [PubMed] [CrossRef]

43. Moody, G. B., Muldrow, W., Mark, R. G. (1984). A noise stress test for arrhythmia detectors. Computers in Cardiology, 11(3), 381–384. [Google Scholar]

44. Singh, P., Pradhan, G. (2018). Exploring the non-local similarity present in variational mode functions for effective ECG denoising. 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 861–865. Calgary, AB, Canada, IEEE. https://doi.org/10.1109/ICASSP.2018.8461768 [Google Scholar] [CrossRef]

45. Bengio, Y. (2012). Practical recommendations for gradient-based training of deep architectures. Neural Networks: Tricks of the Trade: Second Edition, 437–478. https://doi.org/10.1007/978-3-642-35289-8_26 [Google Scholar] [CrossRef]

46. Poornachandra, S., Kumaravel, N., Saravanan, T. K., Somaskandan, R. (2005). WaveShrink using modified hyper-shrinkage function. 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference, vol. 2006, pp. 30–32. Shanghai, China, IEEE. https://doi.org/10.1109/IEMBS.2005.1616334 [Google Scholar] [PubMed] [CrossRef]