New Antenna Array Beamforming Techniques Based on Hybrid Convolution/Genetic Algorithm for 5G and Beyond Communications

1  Introduction

The synthesis of antenna arrays has become an important study now, as it has many applications in the fields of communications, radar, etc. Therefore, the requirement for an array with a directive beam and reduced SLL prompted the search for promising antenna array synthesis techniques. SLL reduction or cancellation can be achieved by adjusting the amplitude and phase of excitations while keeping the spacing between the elements as in conventional arrays. They can also be accomplished by adjusting the spacing between antenna elements while keeping the excitation’s amplitude and phase. This is beneficial for avoiding interfering and undesired signals. There are two ways to improve the synthesis of antenna array patterns, the deterministic method, and the stochastic method [1]. The deterministic method is divided into analytical and semi-analytical methods. The deterministic method is characterized by the fact that the total calculation time for the synthesis process is very low, which makes it very suitable for real-time applications that distinguish it from the stochastic method. On the other hand, the stochastic method is known for its expensive calculations. However, it is more efficient and flexible than the deterministic method. In recent years, many algorithms have been developed to solve the synthesis problems of antenna arrays. A new mathematical formula of the array factor of linear antenna array was introduced in [2] to improve its performance in terms of directivity and SLL. It is based on the principle of mixing or hybridizing two different linear arrays and the resultant array is treated as a new linear array to fulfill the required purposes. The simulations revealed that the suggested formula outperformed the Chebyshev array that has the same number of antenna elements in terms of SLL, excitation coefficients, and directivity. The radiation pattern of non-uniform LAA is improved iteratively to obtain the optimum radiation pattern using a reduced number of elements and achieve SLL lower than −20dB through Genetic algorithm (GA) optimization of the elements spacing and number of elements [3]. Lower numbers of elements and iterations were used to obtain SLL lower than −20dB than other algorithms. In [4], the ant lion optimization technique (ALO) was used to synthesize the LAAs for SLL reduction, pattern nulling at specific directions, and precise beam steering by optimizing the element spacing and excitation currents. The ALO’s parameters to be defined for each problem are fewer than the other optimization algorithms. The ALO results showed its excellence in SLL reduction over other optimization techniques such as particle swarm optimization (PSO), ant colony optimization (ACO), cat swarm optimization (CSO), and biogeography-based optimization (BBO) at the expense of widening the HPBW of the synthesized array. In [5], the grey wolf optimization (GWO) algorithm was introduced for SLL reduction and minimization of the first side lobe level (FSLL) by the optimization of interelement spacing and excitations. The GWO algorithm introduced a significant reduction in the SLL of LAA compared to other state-of-the-art optimization techniques such as PSO, BBO and CSO. However, it also suffers from the increased HPBW. In [6], a new scatter-search based technique was introduced for SLL reduction and pattern nulling of LAAs. It employed a weighted cost function in finding the optimal positions of the array elements, which improved its performance compared to the non-weighted cost function-based techniques. Another SLL reduction technique based on pulse compression (PC) using a WOO filter was introduced in [7]. This method showed a significant improvement in integrated SLL (ISL) and peak SLL compared with other PC techniques. In [8], the convolution method and time scaling property are used to obtain the element's excitations to reduce the SLL of any uniform spacing LAA. The results showed that the SLL is reduced by two times or more, but the HPBW is increased. To control the SLL and address the issues with the other window functions that were unable to improve the SLL due to the high value of the dynamic range ratio (DRR) of the excitation currents, a fast iterative method based on the Fourier relationship between the array factor and the excitation currents was introduced in [9]. It applied the raised cosine window function to improve the SLL with acceptable DRR. It improved the SLL compared to the Kaiser window function but with a wider HPBW. In [10,11], two optimization-based synthesis techniques for SLL reduction of linear and circular antenna arrays were introduced. They are based on the inverse weed optimization (IWO) technique and the whale optimization algorithm (WOA). These techniques depend on the optimal selection of the excitation currents to obtain the desired radiation patterns. However, they did not provide significant reductions in the SLL. In [12], a two-stage piecewise linear frequency modulation (PWLFM) signal model was used to instead of the linear frequency modulation (LFM) signal to reduce the first side lobe level in radar systems. That is because the autocorrelation of the PWLFM signal has a low peak SLL ratio compared to the LFM signal. In addition, various types of convolution window functions were applied for more SLL reduction such as (Cauchy, Power of cosine, Papoulis, and Parzen). However, the power of the cosine window function proved its superiority in reducing the SLL. In [13], a new iterative method was developed. This algorithm relies on the iterative addition by rotation or translation of antenna array elements, then the synthesized pattern proves its approximation to the desired pattern in the sense of the Hilbert space specified standard. This iterative algorithm can also be used to synthesize several patterns, but with different excitations, for the same array shape.

Newly proposed hybrid beamforming techniques for minimizing the size of uniform planar antenna arrays (UPAA) and reducing their SLL were presented in [14]. They are based on the hybridization between the two-dimensional (2D) convolution and GA. The SLL reduction is performed by controlling both the elements’ excitations and separation. The differential evolutionary (DE) algorithm was used in [15] to introduce a new approach for reducing SLL and rejecting interference signals in concentric hexagonal antenna arrays (CHAA). In the proposed approach, the CHAA was chosen because it would offer a lower SLL compared to circular and linear antenna arrays, which is considered a drawback of the approach.

In [16], the Eisenstein fractile array was presented to use the special geometrical characteristics of fractiles that permit multiband and wideband operation and prevent the appearance of grating lobes. In order to reduce the high SLL experienced at large-scale arrays, the proposed antenna array was thinned using the GA optimization technique. This was done by identifying the optimal set of “on” and “off” antenna elements that correspond to the minimum SLL without sacrificing the directivity of the array radiation pattern.

In [17], new hybrid array beamforming techniques based on the integration between the virtual antenna array (VAA) concept, PSO technique, and hyper-beamforming were introduced for SLL reduction and thinning of elliptical cylindrical antenna arrays (ECAA) in radar systems. The VAA decomposes the ECAA into created LAA and EAA. The number of antenna elements, element spacing, and excitations of the created LAA and EAA are optimized using PSO to produce efficient patterns with low SLL. Additional SLL reductions were achieved by using hyper-beamforming. In [18], new low SLL wideband planar antenna array designs based on the space-filling curves technique were presented. These arrays’ special geometrical properties are used to provide wideband operation and prevent the emergence of grating lobes. Wideband operation, SLL reduction, and grating lobe removal are only a few of the advantages of the newly proposed array designs over their traditional periodic planar array equivalents in terms of the radiation pattern. In [19], a new structure for a 1 × 8 slotted S-band waveguide array with non-uniform offset slot locations was proposed for SLL reduction. The slots on the upper metallic wall of the waveguide are distributed following a binomial distribution. The simulations revealed that the proposed array provided significantly reduced SLL compared to the slot array with a uniform offset location. In [20], a hybrid beamforming technique based on the combination of the genetic algorithm and the Gauss elimination algorithm denoted as GA/GE has been introduced for a specific side lobe cancellation of LAAs that reduces the received interference in the appropriate directions, which improves the receiver sensitivity. However, the GA/GE did not result in a general decrease in SLL. The performance of upcoming 5G cellular networks that utilize the mm-wave spectrum could be greatly improved by employing SLL reduction, which is considered one of the most crucial array beamforming techniques. The use of effective beamforming techniques such as SLL reduction and beam steering for antenna arrays at mobile base stations has several advantages, including longer battery life, a lower probability of an outage, much higher bit rates across a larger coverage area, lower infrastructure costs, and a higher capacity for numerous simultaneous users in both licensed and unlicensed spectrums. Due to its substantial unlicensed capacity, mm-wave communication is viewed as a key player for 5G and subsequent networks. There are significant difficulties, though, such as penetration and propagation losses. Antenna array beamforming is used to solve these problems as introduced in [21,22]. In [23], a highly efficient approach to improve the performance of multi-antenna elements-based spectrum sensing (SS) techniques in cognitive radio (CR) systems using SLL reduction has been introduced. It significantly improved the probability of detection of the CR system at much lower signal-to-noise ratio and signal-to-interference ratio scenarios. Furthermore, it improved the SS capability of the CR system further than SS based on array beamforming for maximum gain realization introduced in [24] and SS without array beamforming introduced in [25].

In this paper, two highly efficient SLL reduction techniques based on the hybrid combination between the convolution algorithms (single convolution algorithm (Conv) and the double convolution algorithm (DConv)) and the GA denoted as Conv/GA and DConv/GA, respectively, are proposed. In the Conv/GA technique, the convolution between the array excitation vector of length (M) and itself is used to adjust the excitations of the array elements. However, the convolution process generates a longer excitation vector with a length of (2M−1), from which the appropriate set of (M) excitations can be selected for SLL reduction. Generally, the convolution process reduces the SLL but at the expense of widening the array HPBW. To alleviate this issue, the element spacing is optimized using the GA to optimize the array size that achieves the same HPBW as the original array. The proposed Conv/GA technique provides almost the same HPBW as the original LAA with a two-fold reduction in the SLL. While the proposed DConv/GA technique provides a relatively wider HPBW and an almost four-fold reduction in the SLL compared to the original LAA. Several simulations are performed to verify the effectiveness of the proposed techniques.

The rest of the paper is organized as follows: Section 2 presents the related work. In Section 3, the proposed Conv/GA and DConv/GA beamforming techniques are introduced. Section 4 introduces the simulation results and discussions. Finally, the conclusion is presented in Section 5.

The following is a summary of the contributions provided by this paper:

1.    The convolution approach has been employed in a unique way to synthesize LAAs using the proposed Conv/GA technique, achieving the same HPBW as the original LAA pattern while reducing the SLL by two-fold.

2.    When applying the proposed DC/GA technique to LAAs, the SLL can be reduced by a quad-fold with minimal changes in the HPBW. This is beneficial for avoiding interfering, jamming, and unwanted signals.

3.    When applying the proposed Conv/GA technique, the uniform linear antenna array (ULAA) and Chebyshev array synthesis using middle excitations provided a slightly higher SLL than the original arrays but with a much narrower HPBW. This main beam thinning effectively minimizes multipath signals and makes it suitable for positioning systems to increase location accuracy in 5G and beyond communications. Additionally, the outer antenna elements of the synthesized arrays can be turned off in order to execute array thinning. However, this array thinning causes the synthesized arrays’ SLL and HPBW to increase. Nevertheless, by adjusting the element spacing, the HPBW can be readjusted.

2  Linear Antenna Array Geometry and Genetic Algorithm

This section explains the geometrical construction of the linear antenna array (LAA) and the GA optimization technique while highlighting their key variables and parameters. Firstly, the GA is one of the most commonly used population-based metaheuristics optimization techniques that employ multiple candidate solutions during the search process. These metaheuristics preserve diversity in the population and avoid stuck solutions in the local optima. The GA is an optimization algorithm inspired by natural selection, which uses the concept of survival of the fit test [26]. New populations are produced through the frequent use of genetic operators over the existing individuals in the population. The major components of GA are the chromosome representation, selection, crossover, mutation, and computation of fitness functions. The GA procedure started by random initialization of a population (Y) of n chromosomes. Each chromosome's fitness in Y is determined. According to the fitness value, two chromosomes denoted as C1 and C2 are selected from the populationY. The crossover likelihood (Cp) single-point crossover operator is applied to C1 and C2 to generate an offspring denoted as O. A uniform mutation operator with mutation probability (Mp) is then applied to the generated offspring O to generate O′. In the new population, the new offspring O′ is put. The selection, crossover, and mutation operations in the current population will be replicated before the completion of the new population. Through the probabilities of crossover and mutation, GA dynamically alters the search process and reaches the optimal solution. The encoded genes can be changed by GA. GA can analyze multiple individuals and create multiple optimal solutions. GA, therefore, has greater potential for global search. It is likely that the offspring formed from the crossover of parent chromosomes would abolish the admirable genetic schemes, and the crossover formula R is given by [26]:

R=(G+2g)/3G(1)

where G is the cumulative number of population-specified evolutionary generations and g is the number of generations. Eq. (1) shows that R is dynamically updated and increases with an increase in the number of evolutionary generations. The resemblance between individuals is very poor in the initial stage of GA. To ensure that the new population does not ruin the excellent genetic schema of individuals, the value of R should be small. The resemblance between individuals is very high at the end of evolution and the value of R should be high.

Secondly, the geometrical structure of the LAA is described considering an LAA consisting of M identical antenna elements arranged on a Z-axis with a uniform element spacing d=λ/2 as shown in Fig. 1. The array factor 𝒜ℱ(θ) of the LAA is given by:

𝒜ℱ(θ)=∑m=1Mamejβ(m−1)dcos⁡(θ)(2)

where am is the complex excitation coefficient of the mth antenna element, β=2π/λ is the wave number, and λ is the wavelength. Let A be the vector of the M-element excitations that can be written as:

A=[a1,a2,a3,…,aM](3)

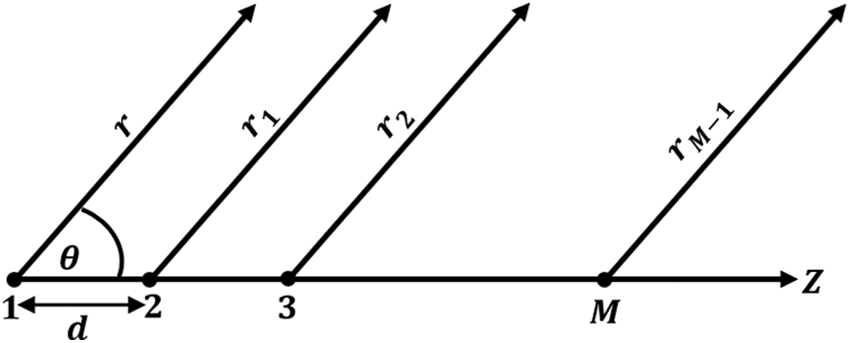
Figure 1: Structure of linear antenna array

3  Proposed Conv/GA and DConv/GA Beamforming Techniques

In this section, two proposed highly efficient SLL reduction techniques based on the hybrid combination between the convolution algorithms (single convolution algorithm (Conv) and the double convolution algorithm (DConv)) and the genetic algorithm (GA) denoted as Conv/GA and DConv/GA, respectively, are introduced. The convolution process determines the element’s excitations while the GA optimizes the element spacing.

In general, it is widely understood from Mathematical theory that the convolution of two sequences of lengths K and M yields a new sequence of length N=(K+M−1) [8]. Given two vectors A=[a1,a2,a3,…,aM] and B=[b1,b2,b3,…,bK], then the convolution of A and B (A∗B) is a vector C=[c1,c2,c3,…,cK+M−1], x=1,2,3,…,K+M−1 where cx is given by:

cx=∑u=uminumaxaubx−u+1(4)

where u ranges over all legal subscripts for au and bx−u+1, and the upper and lower limits of u are given by:

u={max(1,x−K+1)min(x,M)(5)

Accordingly, umin=min(u) and umax=max(u).

3.1 Proposed Conv/GA Technique

In this section, the proposed Conv/GA beamforming technique is introduced. It is based on calculating the convolution of the vector of excitations A by itself, which provides a new vector Ac of length N=(2M−1) that is given by:

Ac=A∗A(6)

Ac=[c1,c2,c3,…,c2M−1](7)

where cx can be calculated by (4) as follows:

c1=a1a1

c2=a1a2+a2a1

c3=a1a3+a2a2+a3a1…

cM=a1aM+a2aM−1+…+aMa1…

c2M−1=aMaM(8)

The resultant vector Ac is divided into three different sets of excitations including the odd excitations Aodd, even excitations Aeven, and middle excitations Amid of lengths M, M−1, and M, respectively. When the same element spacing of the original LAA is used, it is noticed that the odd and even excitations provide much lower SLL than that of the LAA but with much wider HPBW. While the middle excitations give the same HPBW as the original LAA with higher SLL. So, the middle excitation solution is avoided. To mitigate the problem of odd and even excitations, the GA optimization is used for beam thinning of the synthesized arrays by determining the optimum element spacing ds that minimizes the designed cost function Cf given below:

Cf={‖HPBWs−HPBW‖+1‖‖SLLs‖−‖SLL‖‖}|‖SLLs‖>‖SLL‖(9)

where HPBWs and HPBW are the half power beamwidths of the synthesized and original arrays, respectively. SLLs and SLL are the side lobe levels of the synthesized and original arrays in dB, respectively. In order to minimize the designed cost function, the first term should be as minimum as possible, while the denominator of the second term ‖‖SLLs‖−‖SLL‖‖ should be as maximum as possible under the constraint that the synthesized SLL is larger than that of the original one (‖SLLs‖>‖SLL‖). The GA optimizes the element spacing within the range 0.5λ<ds<0.9λ to avoid the appearance of grating lobes in the synthesized patterns, which are calculated by:

𝒜ℱs(θ)|odd=∑x=1MAodd(x)ejβ(x−1)dscos⁡(θ)(10)

𝒜ℱs(θ)|even=∑x=1M−1Aeven(x)ejβ(x−1)dscos⁡(θ)(11)

where 𝒜ℱs(θ)|odd and 𝒜ℱs(θ)|even are the synthesized patterns using odd excitations Cxo and even excitations Cxe, respectively that are calculated from cx given in (4) such that:

Aodd=[c1,c3,c5…,c2M−1](12)

Aeven=[c2,c4,c6,…,c2M−2](13)

3.2 Proposed DConv/GA Technique

In this section, the proposed DConv/GA beamforming technique is introduced. It is based on calculating the convolution of the two aforementioned excitation vectors Aodd and Aeven by themselves such that:

BO=Aodd∗Aodd(14)

BE=Aeven∗Aeven(15)

where

BO=[b1o,b2o,b3o,…,b(2M−1)o](16)

BE=[b1e,b2e,b3e,…,b(2M−3)e](17)

The vector BO is divided again into two sets of excitations including the odd excitations BO−odd and even excitations BO−even of lengths M and M−1, respectively as follows:

BO−odd=[b1o,b3o,…,b(2M−1)o](18)

BO−even=[b2o,b4o,…,b(2M−2)o](19)

In this case, the two synthesized patterns are calculated by:

𝒜ℱDO(θ)|odd=∑x=1MBO−odd(x)ejβ(x−1)dscos⁡(θ)(20)

𝒜ℱDO(θ)|even=∑x=1M−1BO−even(x)ejβ(x−1)dscos⁡(θ)(21)

While the vector BE is divided again into two sets of excitations including the odd excitations BE−odd and even excitations BE−even of lengths M−1 and M−2, respectively as follows:

BE−odd=[b1e,b3e,…,b(2M−3)e](22)

BE−even=[b2e,b4e,…,b(2M−4)e](23)

In this case, the two synthesized patterns are calculated by:

𝒜ℱDE(θ)|odd=∑x=1M−1BE−odd(x)ejβ(x−1)dscos⁡(θ)(24)

𝒜ℱDE(θ)|even=∑x=1M−2BE−even(x)ejβ(x−1)dscos⁡(θ)(25)

Also, to mitigate the HPBW problem, GA optimization is used for beam thinning of the synthesized arrays by determining the optimum element spacing ds that minimizes the same designed cost function Cf given by (9). In general, after elaboration, a simplified map was made to explain the proposed algorithms, as shown in Fig. 2.

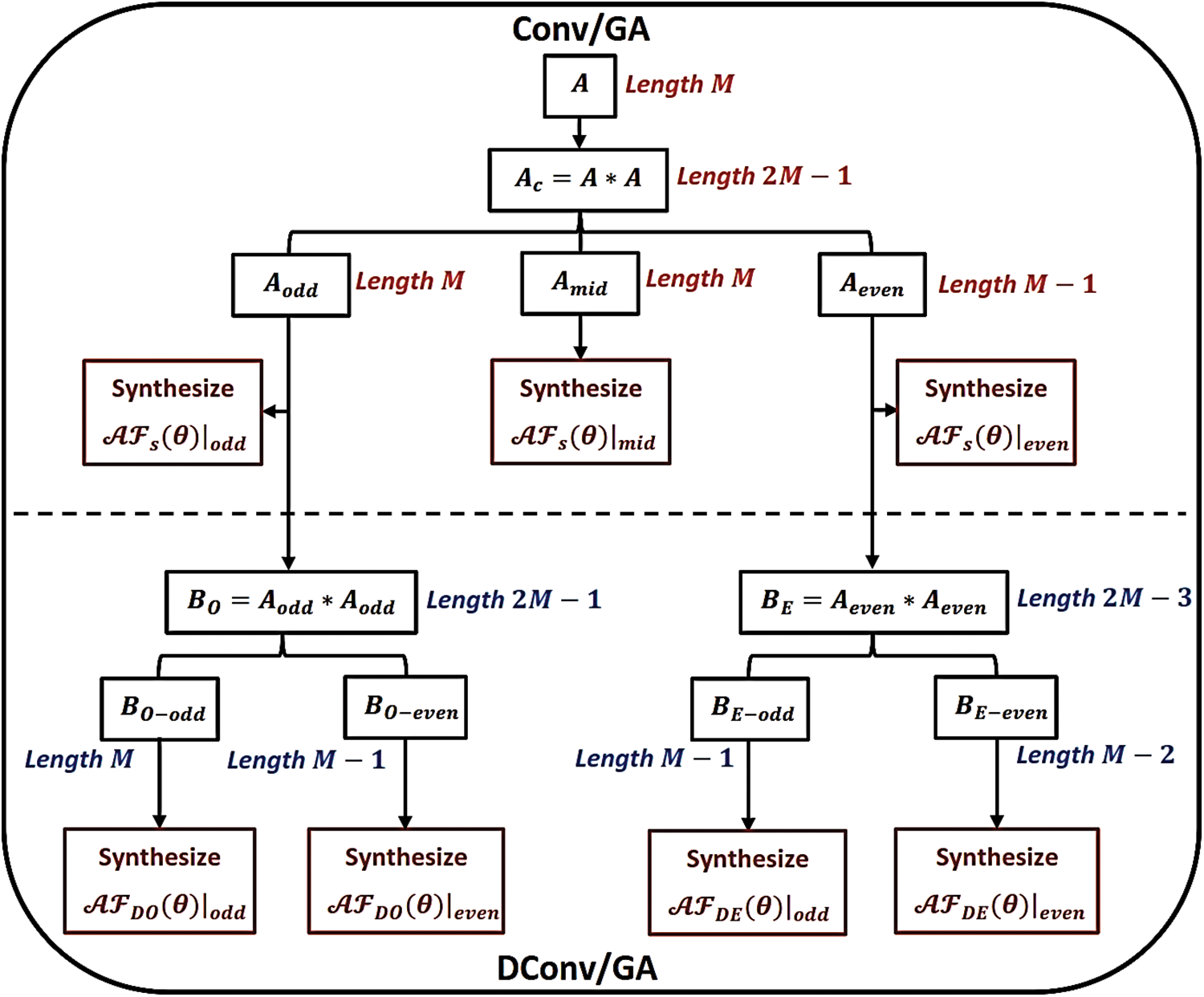
Figure 2: The flow chart that explains the proposed Conv/GA and DConv/GA algorithms

4  Simulation Results

In this section, the simulation results of the proposed Conv/GA and DConv/GA beamforming techniques are introduced for SLL reduction of non-uniform Chebyshev arrays and uniform linear antenna arrays.

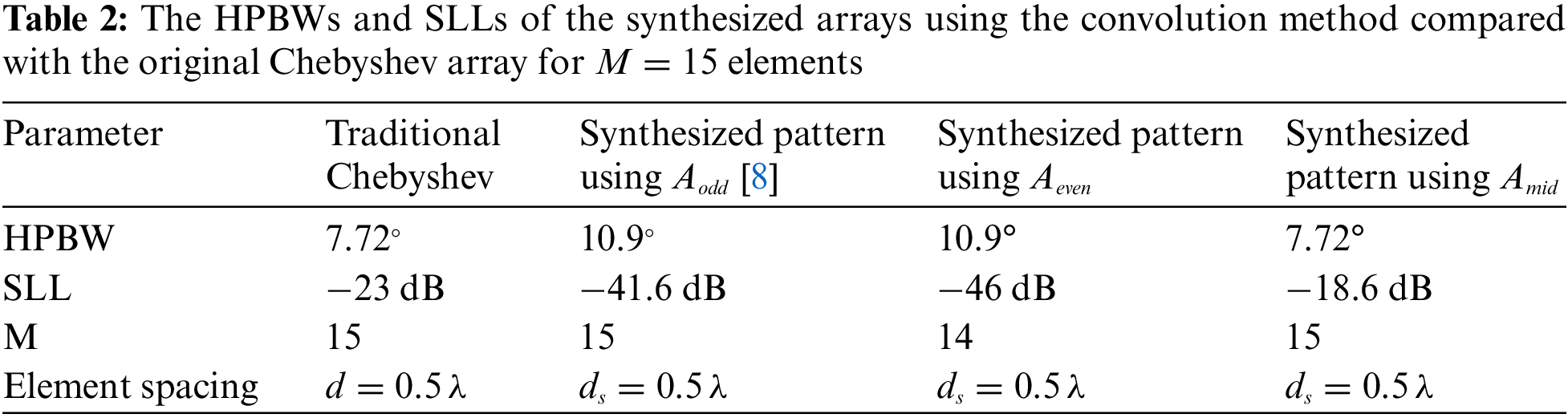
Test Case 1: SLL Reduction of Odd Chebyshev Array Using Convolution Method

Consider a broadside Chebyshev array with odd number of elements M=15 elements, d=0.5λ, and SLL=−23 dB as in [8]. By taking the convolution of the excitation coefficient vector A by itself, the resultant excitation coefficient vector Ac of length N=29 is listed in Table 1. This vector is divided into three groups including the odd excitation coefficient vector Aodd of length Nodd=15, even excitation coefficient vector Aeven of length Neven=14, and the middle excitation coefficient vector Amid of length Nmid=15. These excitation vectors are applied to the antenna elements with the same element spacing ds=d=0.5λ as the original array to generate three different array factors as shown in Fig. 3. By analyzing the results listed in Table 2, it is clear that both the odd and even excitations provide SLLs of −41.6dB and −46dB, respectively, which are much lower than the SLL=−23dB of the original Chebyshev pattern. However, their HPBWs=10.9∘ are 3.18∘ wider than that of the original pattern HPBW=7.72∘. While the middle excitations provide the same HPBW as the original pattern with an increase of 4.4dB in the SLL.

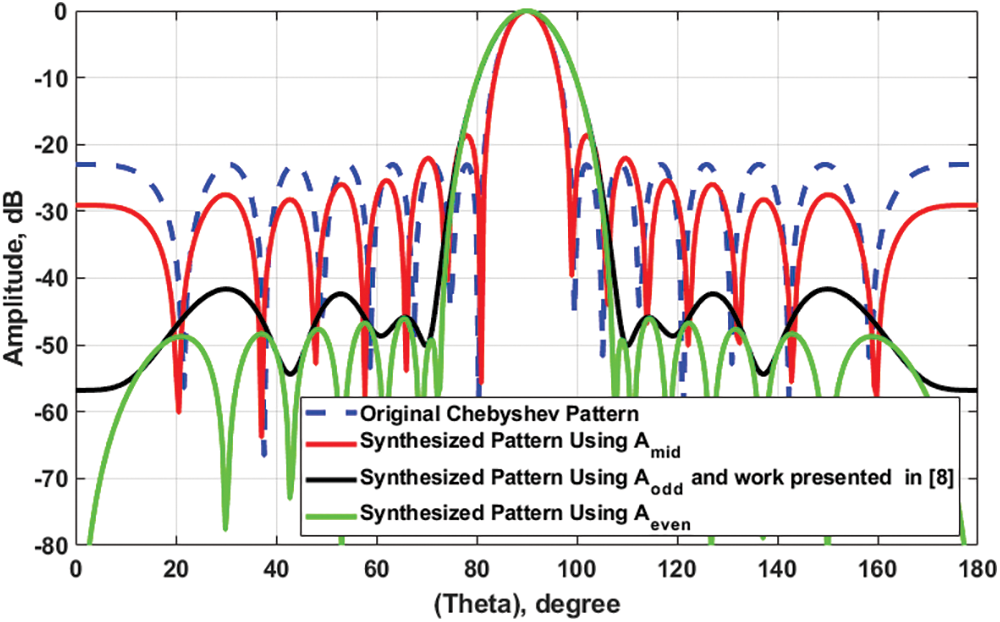
Figure 3: Synthesized array patterns using convolution method compared with the original Chebyshev pattern for M=15 elements and d=0.5λ

Test Case 2: SLL Reduction of Odd Chebyshev Array Using the Proposed Conv/GA Technique

In this case, the HPBW problem that occurred in the test case (1) is mitigated by using the proposed Conv/GA technique where the element spacing is optimized to minimize the designed cost function in Eq. (9). Fig. 4 shows the synthesized patterns using the odd, even, and middle excitation coefficients with optimized element spacing ds=0.79λ. By analyzing the results listed in Table 3, it is clear that the synthesized patterns using odd and even excitations provide the same HPBWs=7.72∘as the original pattern with SLLs of −41.6 dB and −46 dB, respectively, which are much lower than that of the original pattern SLL=−23 dB as listed in Table 3. While the synthesized pattern using middle excitations still has high SLLs=−18.6 dB but with narrowerHPBWs=4.67∘. From the simulation results, we can conclude that the synthesized array using the even excitation coefficients provides the lowest SLLs, which is exactly equal to twice the original SLL, provides the same HPBWs as the original array HPBW, and saves the number of elements by one element.

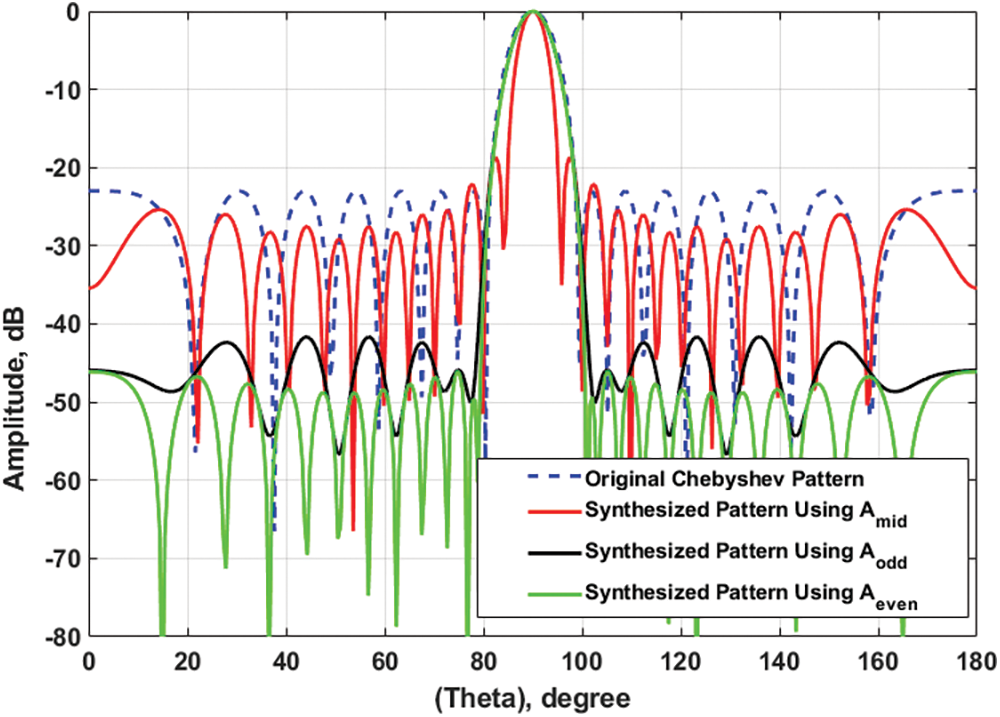
Figure 4: Synthesized array patterns using the proposed Conv/GA compared with the original Chebyshev pattern for M=15 elements and ds=0.79λ

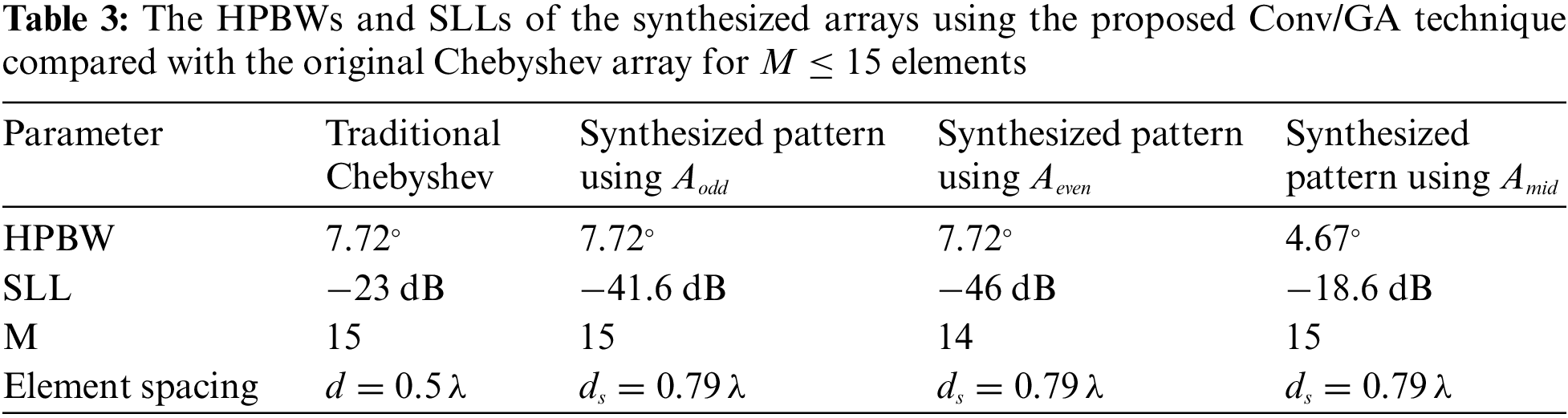
Test Case 3: SLL Reduction of Even Chebyshev Array Using Convolution Method

Consider a broadside Chebyshev array with even number of elements M=20 elements, d=0.5λ, and SLL=−23dB. By taking the convolution of the excitation coefficient vector A by itself, the resultant excitation coefficient vector Ac of length N=39 is listed in Table 4. This vector is divided into three groups including the odd excitation coefficients Aodd of length Nodd=20, even excitation coefficients Aeven of length Neven=19, and the middle excitation coefficients Amid of length Nmid=20. These new excitation vectors are used with the same element spacing ds=d=0.5λ as the original array in order to produce three different array factors as seen in Fig. 5. By analyzing the results listed in Table 5, it is clear that both the odd and even excitations provide SLLs of −47.64dB and −40dB, respectively, which are much lower than the SLL=−23dB of the original Chebyshev pattern. However, their HPBWs are 2.21∘ wider than that of the original pattern. While the middle excitations provide the same HPBW as the original pattern with an increase of 5.1dB in the SLL.

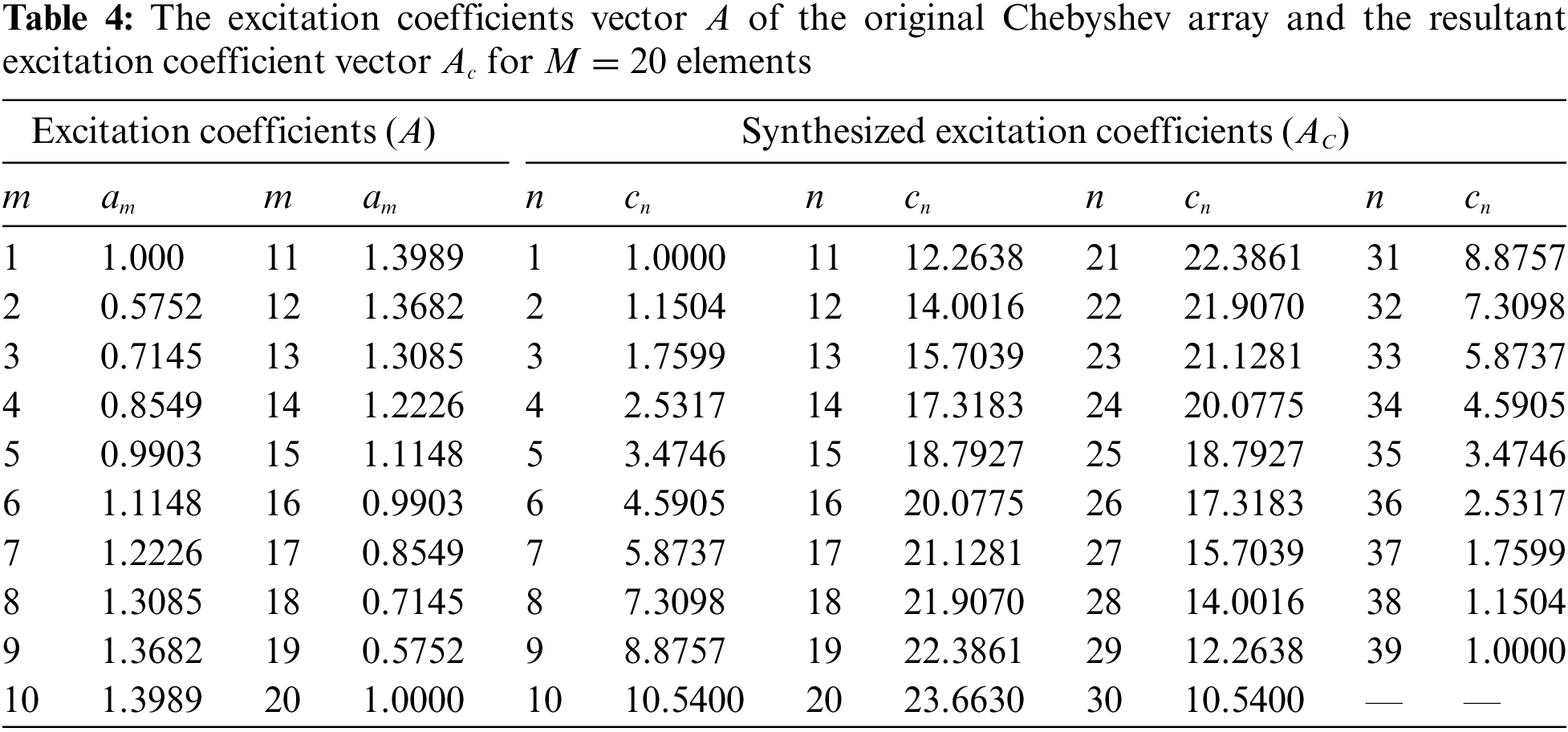
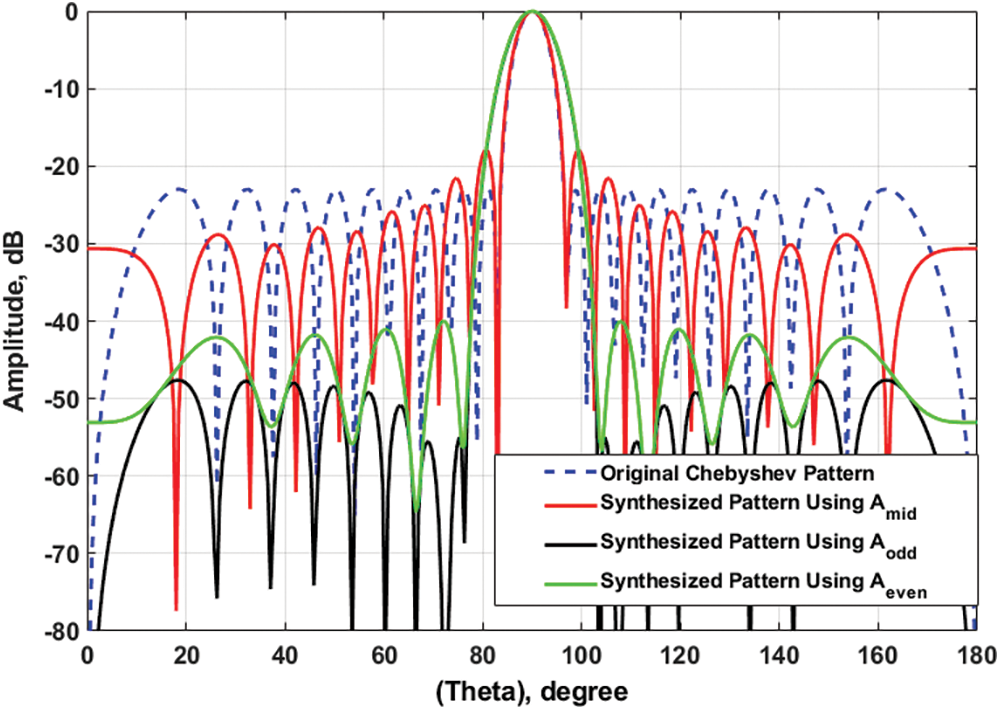
Figure 5: Synthesized array patterns using convolution method compared with the original Chebyshev pattern for M=20 elements and d=0.5λ

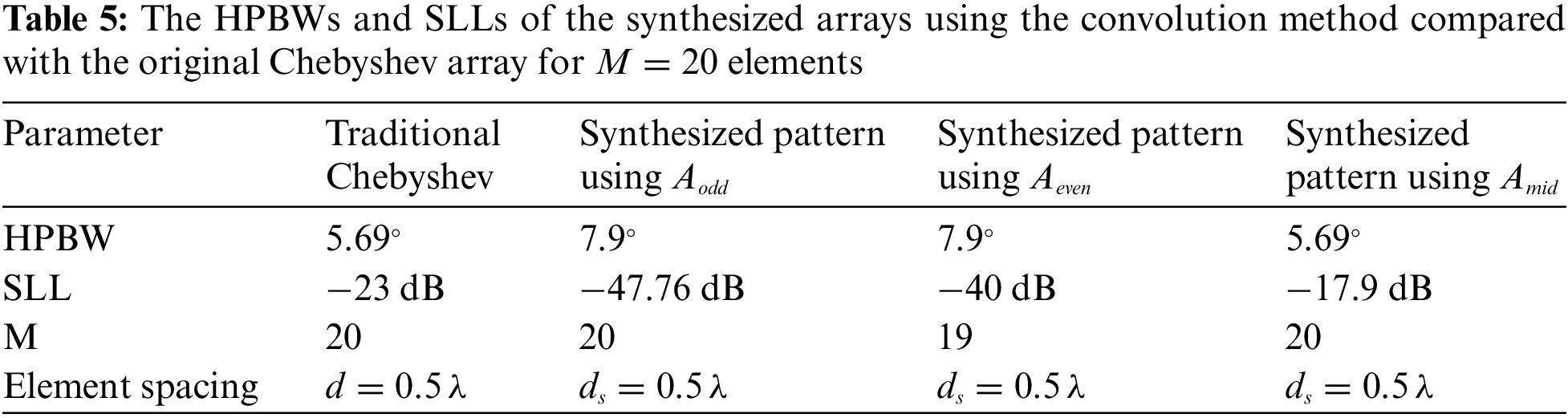
Test Case 4: SLL Reduction of Even Chebyshev Array Using the Proposed Conv/GA Technique

By applying the Conv/GA, the optimized element spacing is found to be ds=0.79λ. The synthesized array patterns using the odd, even, and middle excitation coefficients are shown in Fig. 6. It is clear that the synthesized patterns using odd and even excitations provide the same HPBWs=5.69∘ as the original pattern and provide SLLs of −47.76 dB and −40 dB, respectively that are much lower that of the original pattern SLL=−23dB as listed in Table 6. While the synthesized pattern using middle excitations still has the high SLLs=−17.8 dB but with narrower HPBWs=3.86∘. From the simulation results, we can conclude that the array synthesis using the odd excitation coefficients provides the lowest SLLs=−47.76 dB which is 2.076 times lower than that of the original array SLL. In addition, it provides the same HPBW as the original array.

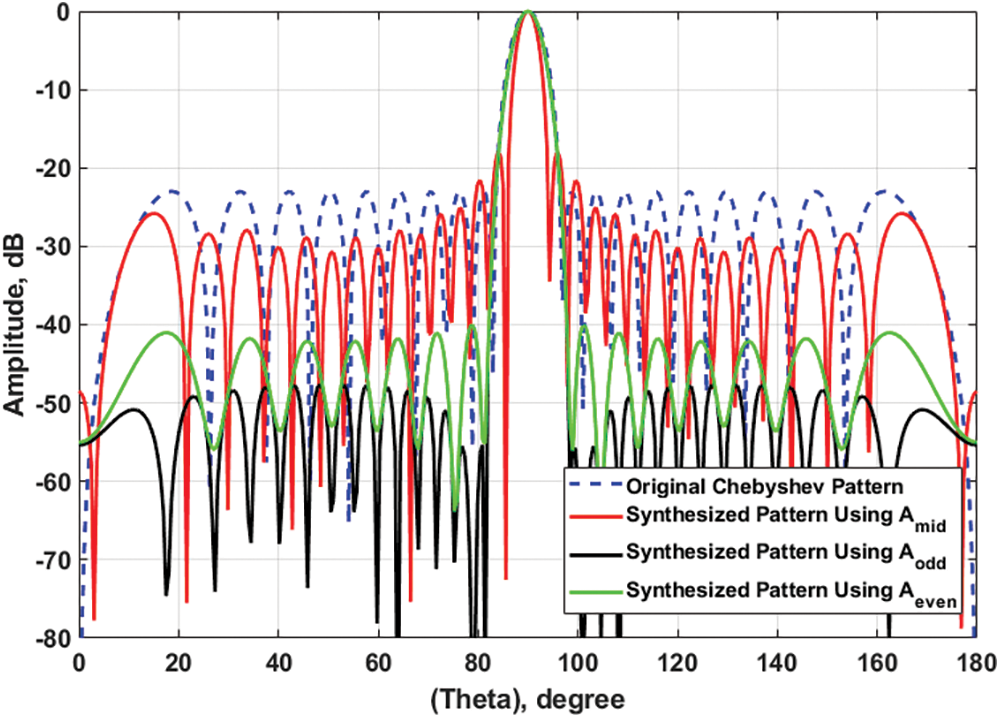
Figure 6: Synthesized array patterns using the proposed Conv/GA compared with the traditional Chebyshev pattern for M=20 elements and ds=0.79λ

Test Case 5: SLL Reduction of Chebyshev Array Using the Proposed DConv/GA Technique and BO Excitations

In this section, the proposed DConv/GA technique is applied to the odd excitation vector Aodd of length M=15. The resultant excitation vector BO of length 2M−1=29 is listed in Table 7. By applying the excitations BO−odd and BO−even of lengths M=15 and M−1=14, respectively the optimized element spacings are found to be ds=0.69λ and ds=0.69λ, respectively. The synthesized arrays patterns compared to the original Chebyshev array pattern are shown in Fig. 7. It is clear that the synthesized patterns using odd and even excitations have the same HPBWs=11.36∘ that is wider than that of the original pattern by 3.64∘. While BO−odd and BO−even excitations provide SLLs of −81.1 dB and −87.2 dB, respectively which are much lower than the original pattern SLL=−23 dB as listed in Table 8. From the simulation results, we can conclude that the array synthesis using BO−even excitation coefficients provides the lowest SLLs=−87.2 dB that is 3.791 times lower than that of the original array SLL. In addition, it saves the number of array elements by one antenna element.

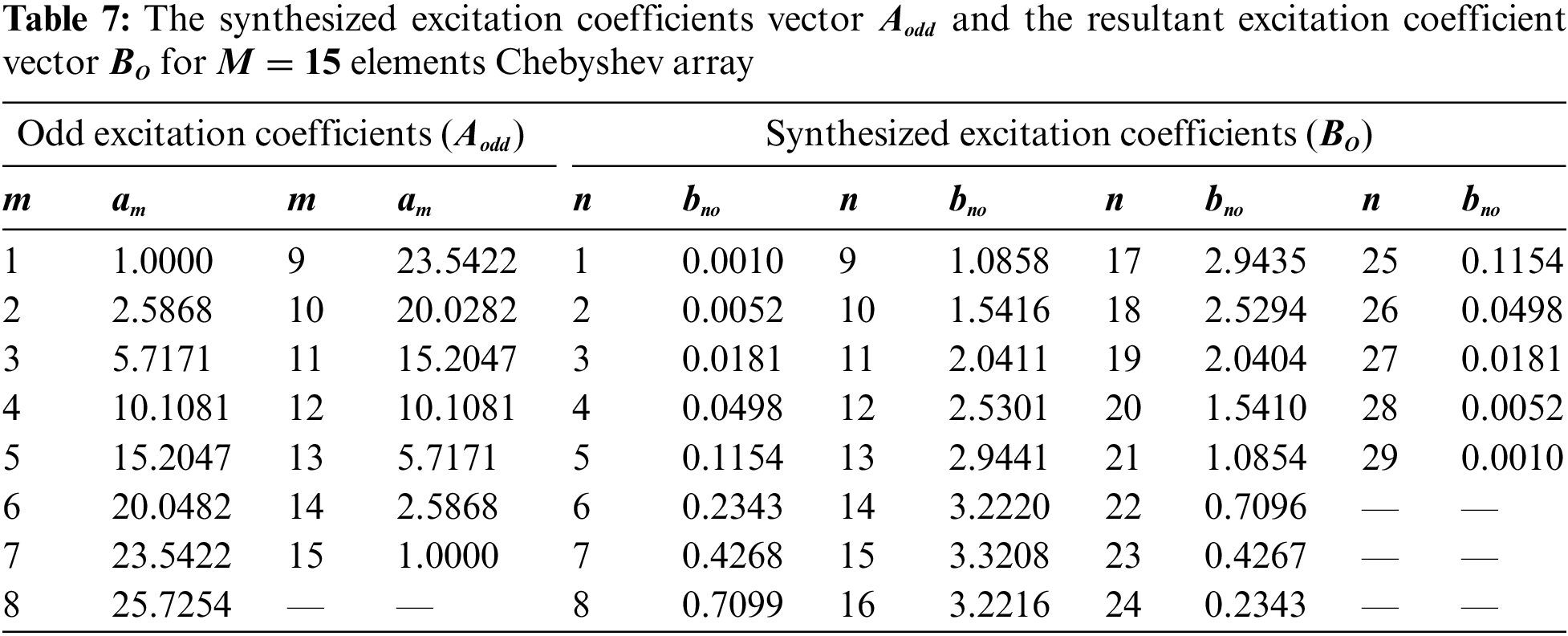
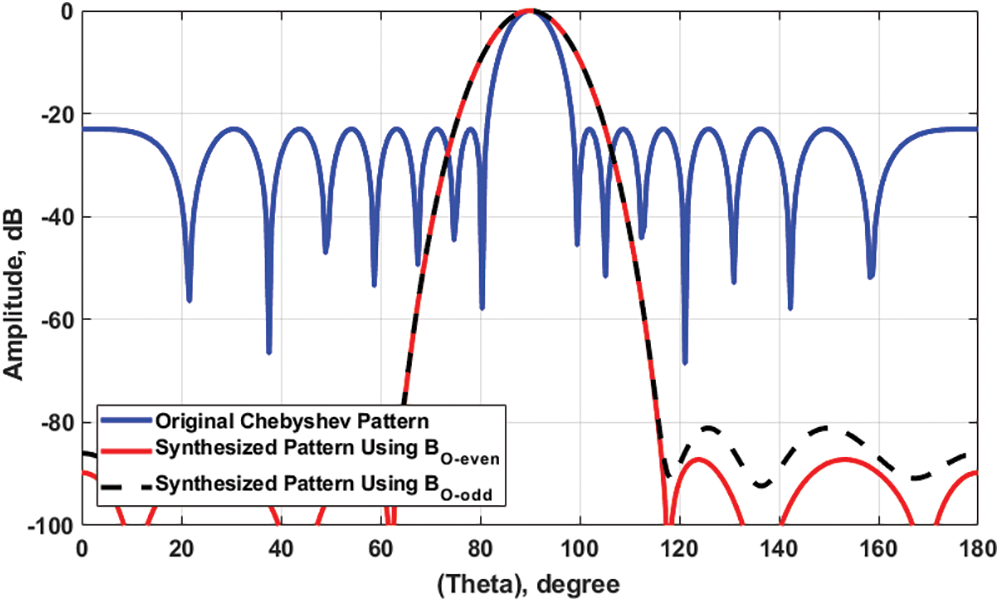
Figure 7: The synthesized arrays patterns using BO−odd and BO−even compared to the original Chebyshev array for M = 15 elements

Test Case 6: SLL Reduction of Chebyshev Array Using the Proposed DConv/GA Technique and BE Excitations

In this section, the proposed DConv/GA technique is applied to the even excitation vector Aeven of length M=14. The resultant excitation vector BE of length 2M−1=27 is listed in Table 9. By applying the excitations BE−odd and BE−even of lengths M=14 and M−1=13, respectively the optimized element spacings are found to be ds=0.69λ and ds=0.69λ, respectively. The synthesized array patterns compared to the original Chebyshev array pattern are shown in Fig. 8. It is clear that the synthesized patterns using odd and even excitations have the same HPBWs=11.36∘ that is wider than that of the original pattern by 3.64∘. While BE−odd and BE−even excitations provide SLLs of −94 dB and −89.2 dB, respectively, which are much lower than the original pattern SLL=−23 dB as listed in Table 10. From the simulation results, we can conclude that the array synthesis using BE−odd excitation coefficients provides the lowest SLLs=−94 dB that is 4.08 times lower than that of the original array SLL. In addition, it saves the number of array elements by one antenna element.

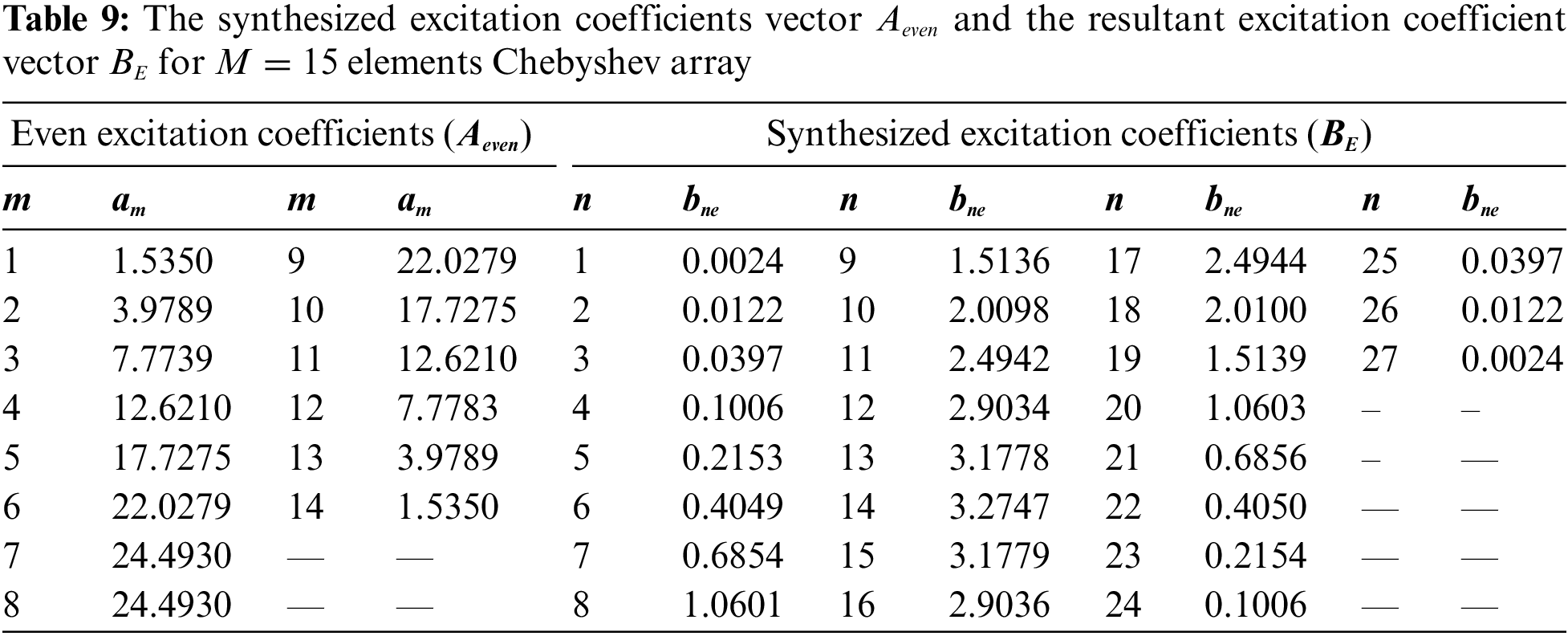
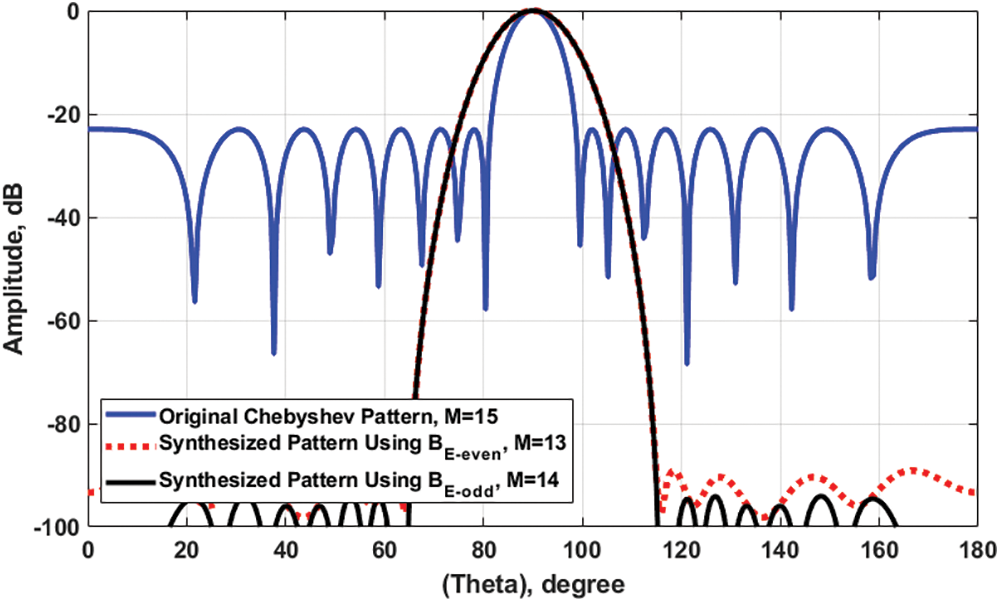
Figure 8: The synthesized arrays patterns using BE−odd and BE−even compared to the original Chebyshev array for M = 15 elements

Test Case 7: SLL Reduction of Uniform Linear Antenna Array Using the Proposed Conv/GA Technique

In this section, the proposed Conv/GA technique is used to synthesis a uniform linear antenna array (ULAA) consisting of M=10 elements with uniform element spacing d=0.5λ.

By taking the convolution of the excitation coefficient vector A by itself, the resultant excitation coefficient vector Ac of length N=19 is listed in Table 11. This vector is divided into three groups including the odd excitation coefficient vector Aodd of length Nodd=10, even excitation coefficient vector Aeven of length Neven=9, and the middle excitation coefficient vector Amid of length Nmid=9. By applying the Conv/GA, the optimized element spacing is found to be ds=0.67λ. The synthesized array patterns using the odd, even, and middle excitation coefficients are shown in Fig. 9. It is clear that the synthesized patterns using odd and even excitations provide the same HPBWs=10.44∘ as the original uniform array pattern and provide SLLs of −28.2 dB and −24 dB, respectively, that are much lower than that of the original pattern SLL=−12.97dB as listed in Table 12. Also, the synthesized pattern using middle excitations provides lower SLL than the uniform array that equals SLLs=−17.8dB with narrower HPBWs=9.4∘. It is evident that the proposed Conv/GA approach significantly reduces SLL compared to the original uniform antenna array employing the synthesized middle, even, and odd excitations. In light of the simulation results, we can conclude that the array synthesis using the odd excitation coefficients provides the lowest SLLs=−28.2 dB which is 2.174 times lower than that of the original uniform array. For more significant SLL reductions, the proposed DConv/GA technique can be utilized as in previous test cases.

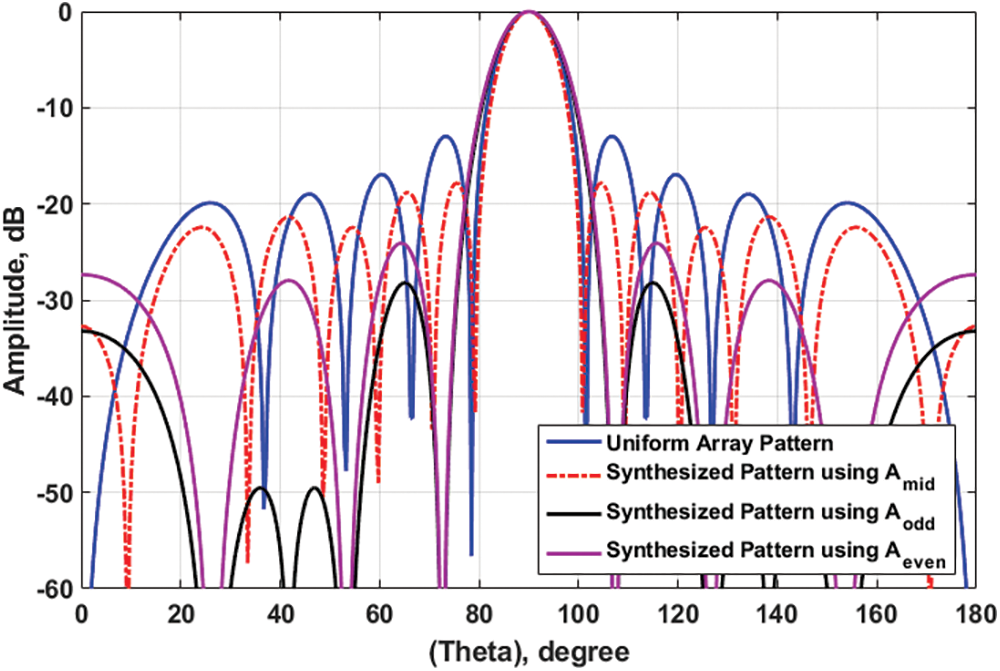
Figure 9: Synthesized array patterns using the proposed Conv/GA technique compared with the original uniform array pattern for M=10 elements and d=0.5λ

5  Conclusion

In this paper, simple and highly effective SLL reduction techniques for LAAs denoted as Conv/GA and DConv/GA are introduced. The convolution method is used to determine the element’s excitations that minimize the array SLL. GA is used to determine the optimum spacing between the elements, which guarantees the same HPBW as the original array in the case of the Conv/GA technique and guarantees the least change in HPBW in the case of the DConv/GA technique. For Chebyshev array consisting of an odd number of elements, the even excitation vector provides the lowest SLL that is two times lower than that of the original array and saves the number of elements by one element. While for LAA consisting of an even number of elements, the odd excitation vector provides the lowest SLL which is 2.076 times lower than that of the original array using the same number of elements. On the other hand, the DConv/GA provided about 4 times reduction in the SLL compared to the original array SLL with minimal changes in the HPBW of the main beam and saves one or two antenna elements according to the selected coefficients. In the case of the uniform antenna array, the proposed Conv/GA technique provides much lower SLL than the original array pattern using the synthesized middle, even, and odd excitations. It is evident that the proposed algorithms reduced the SLL by two fixed and distinct amounts for any type of linear antenna array, whether ULAA or Chebyshev array, which are two-fold, or quad-fold reduction compared to the original SLL.

Acknowledgement: The authors would like to thank the King Saud University, Saudi Arabia for supporting this work.

Funding Statement: This research is funded by Research Supporting Project Number (RSPD2023R585), King Saud University, Riyadh, Saudi Arabia.

Author Contributions: Shimaa M. Amer, Ashraf A. M. Khalaf, Amr H. Hussein, Salman A. Alqahtani, Mostafa H. Dahshan, and Hossam M. Kassem are contributed equally in study conception and design, data collection, analysis and interpretation of results, reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All the readers can contact Dr. Amr H. Hussein for any future inquiries.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding.

References

1. Buttazzoni, G., Babich, F., Vatta, F., Comisso, M. (2019). Comparison between deterministic and stochastic methods for the synthesis of aperiodic arrays. 2019 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting, pp. 51–52. Atlanta, GA, USA, IEEE. [Google Scholar]

2. Gassab, O., Azrar, A. (2016). Novel mathematical formulation of the antenna array factor for side lobe level reduction. The Applied Computational Electromagnetics Society Journal (ACES), 31(12), 1452–1462. [Google Scholar]

3. Todnatee, S., Phongcharoenpanich, C. (2016). Iterative GA optimization scheme for synthesis of radiation pattern of linear array antenna. International Journal of Antennas and Propagation, 2016, 1–8. [Google Scholar]

4. Saxena, P., Kothari, A. (2016). Ant lion optimization algorithm to control side lobe level and null depths in linear antenna arrays. AEU-International Journal of Electronics and Communications, 70(9), 1339–1349. [Google Scholar]

5. Prerna, S., Kothari, A. (2016). Optimal pattern synthesis of linear antenna array using grey wolf optimization algorithm. International Journal of Antennas and Propagation, 2016, 1–11. [Google Scholar]

6. Žarko, R., Mihić, O. (2016). Linear antenna array synthesis with minimum side lobe level and null controling. Revue Roumaine des Sciences Techniques, Série Électrotechnique et Énergétique, 61(4), 414– 417. [Google Scholar]

7. Ankur, T., Talluri Raju, S. (2017). A novel pulse compression technique for side-lobe reduction using woo filter concepts. International Conference on Communication and Signal Processing (IEEE), pp. 1086–1090. Chennai, India. [Google Scholar]

8. Alijani, M. G. H., Neshati, M., Boozari, M. (2017). Side lobe level reduction of any type of linear equally spaced array using the method of convolution. Progress in Electromagnetics Research Letters, 66, 79–84. [Google Scholar]

9. Santos, F. E. S., Azevedo, J. A. R. (2017). Adapted raised cosine window function for array factor control with dynamic range ratio limitation. 11th European Conference on Antennas and Propagation (EUCAP), pp. 2020–2024. Paris, France, IEEE. [Google Scholar]

10. Geng, S., Liu, Y., Han, L., Liang, S., Wang, A. et al. (2018). An antenna array sidelobe level reduction approach through invasive weed optimization. Hindawi International Journal of Antennas and Propagation, 2018, 1–16. [Google Scholar]

11. Zhang C., Fu X., Ligthart L. P., Peng S., Xie M. (2018). Synthesis of broadside linear aperiodic arrays with sidelobe suppression and null steering using whale optimization algorithm. IEEE Antennas and Wireless Propagation Letters, 17(2), 347–350. [Google Scholar]

12. AdithyaValli, N., Elizabath Rani, D., Kavitha, C. (2019). Convolution windows for side lobe reduction. International Journal of Innovative Technology and Exploring Engineering (IJITEE), 8(10), 3526–3529. [Google Scholar]

13. Károly, M., Kracek, J., Bilicz, S. (2020). Antenna array pattern synthesis using an iterative method. IEEE Transactions on Magnetics, 56(2), 1–4. [Google Scholar]

14. Elkhawaga, A. M., Mahmoud, N. M., Abd Elnaby, M. M., Hussein, A. H. (2022). New hybrid approaches for SLL reduction and size miniaturization of planar antenna arrays based on 2D convolution and genetic algorithm. Alexandria Engineering Journal, 61(9), 7233–7264. [Google Scholar]

15. Akhitha, K., Ram, G. (2022). Side lobe reduction and interference rejection in concentric hexagonal antenna array using differential evolutionary algorithm. 2022 IEEE Microwaves, Antennas, and Propagation Conference (MAPCON), pp. 681–685. Bangalore, India. [Google Scholar]

16. El-Khamy, S. E., El-Sayed, H. F., Eltrass, A. S. (2022). Synthesis of wideband thinned eisenstein fractile antenna arrays with adaptive beamforming capability and reduced side-lobes. IEEE Access, 10, 122486–122500. [Google Scholar]

17. Dawood, H., El-Khobby, H., Abd Elnaby, M. M., Hussein, A. (2021). Optimized VAA based synthesis of elliptical cylindrical antenna array for SLL reduction and beam thinning using minimum number of elements. IEEE Access, 9, 50949–50960. [Google Scholar]

18. El-Khamy, S., El-Sayed, H. F., Eltrass, A. (2023). New wideband antenna arrays with low sidelobe based on space filling curves. 2023 International Microwave and Antenna Symposium (IMAS), pp. 56–61. Cairo, Egypt. [Google Scholar]

19. Dipankar, S., Saha, C., Siddiqui, J. Y. (2022). Binomially distributed slotted array antenna with highly reduced sidelobe level. 2022 IEEE 19th India Council International Conference (INDICON), pp. 1–3. Kochi, India, 2022 [Google Scholar]

20. Abdelrahman, S. I., Hussein, A. H., Shaalan, A. E. A. (2021). A hybrid GA/GE beamforming technique for side lobe cancellation of linear antenna arrays. Advanced Electromagnetics, 10(2), 67–77. [Google Scholar]

21. Theodore, S. R., Sun, S., Mayzus, R., Zhao, H., Azar, Y. et al. (2013). Millimeter wave mobile communications for 5G cellular: It will work!. IEEE Access, 1, 335–349. [Google Scholar]

22. Nor, A. M., Halunga, S., Fratu, O. (2022). Survey on positioning information assisted mmWave beamforming training. Ad Hoc Networks, 135(9), 102947. https://doi.org/10.1016/j.adhoc.2022.102947 [Google Scholar] [CrossRef]

23. Hager, S. F., Nasr, M. E., Hussein, A. H. (2022). A highly efficient approach for performance enhancement of multiple antenna elements based spectrum sensing techniques using side lobe level reduction. Alexandria Engineering Journal AEJ, 61(8), 5983–5999. [Google Scholar]

24. Hussein, A., Shawky Fouda, H., Hussein Abdullah, H., Khalaf, A. A. M. (2020). A highly efficient spectrum sensing approach based on antenna arrays beamforming. IEEE Access, 8, 25184–25197. [Google Scholar]

25. Ahmed, A. K., Hussein, A. H., Khalaf, A. A. M., Hamed, H. F. A. (2019). A utilization of multiple antenna elements for matched filter based spectrum sensing performance enhancement in cognitive radio system. AEU-International Journal of Electronics and Communications, 107, 98–109. [Google Scholar]

26. Katoch, S., Chauhan, S. S., Kumar, V. (2021). A review on genetic algorithm: Past, present, and future. Multimedia Tools and Applications, 80(5), 8091–8126. [Google Scholar] [PubMed]